lOMoAR cPSD| 48541417 1. Hai tiên ß 3 2 1
" Nguyên lý t±¡ng ßi Galilei: các hißn t±ÿng c¡ hßc dißn ra nh± . Hai tiên ß 3 1
nhau trong mßi hß quy chi¿u quán tính.
" Tiên ß 1 mß rßng nguyên lý t±¡ng ßi cho mßi hißn t±ÿng v¿t lý.
" Thí nghißm Michelson-Morley (1887): o sÿ phÿ thußc cÿa v¿n
tßc ánh sáng vào tr¿ng thái chuyßn ßng cÿa ngußn nh±ng th¿t b¿i.
" Do ó ã xác nh¿n tiên ß 2. A. Einstein (1905)
" Các hißn t±ÿng v¿t lý dißn ra nh± nhau trong
mßi hß quy chi¿u quán tính.
" V¿n tßc cÿa ánh sáng trong chân không là mßt h¿ng sß (c
= 3.108 m/s), không phÿ thußc vào hß quy chi¿u và ph±¡ng truyßn. ) CuuDuongThanCong.com
https://fb.com/tailieudientucntt lOMoAR cPSD| 48541417 2a. 2 a. Thßi gian dãn ra 3 2 Thßi gian dãn ra 3 1
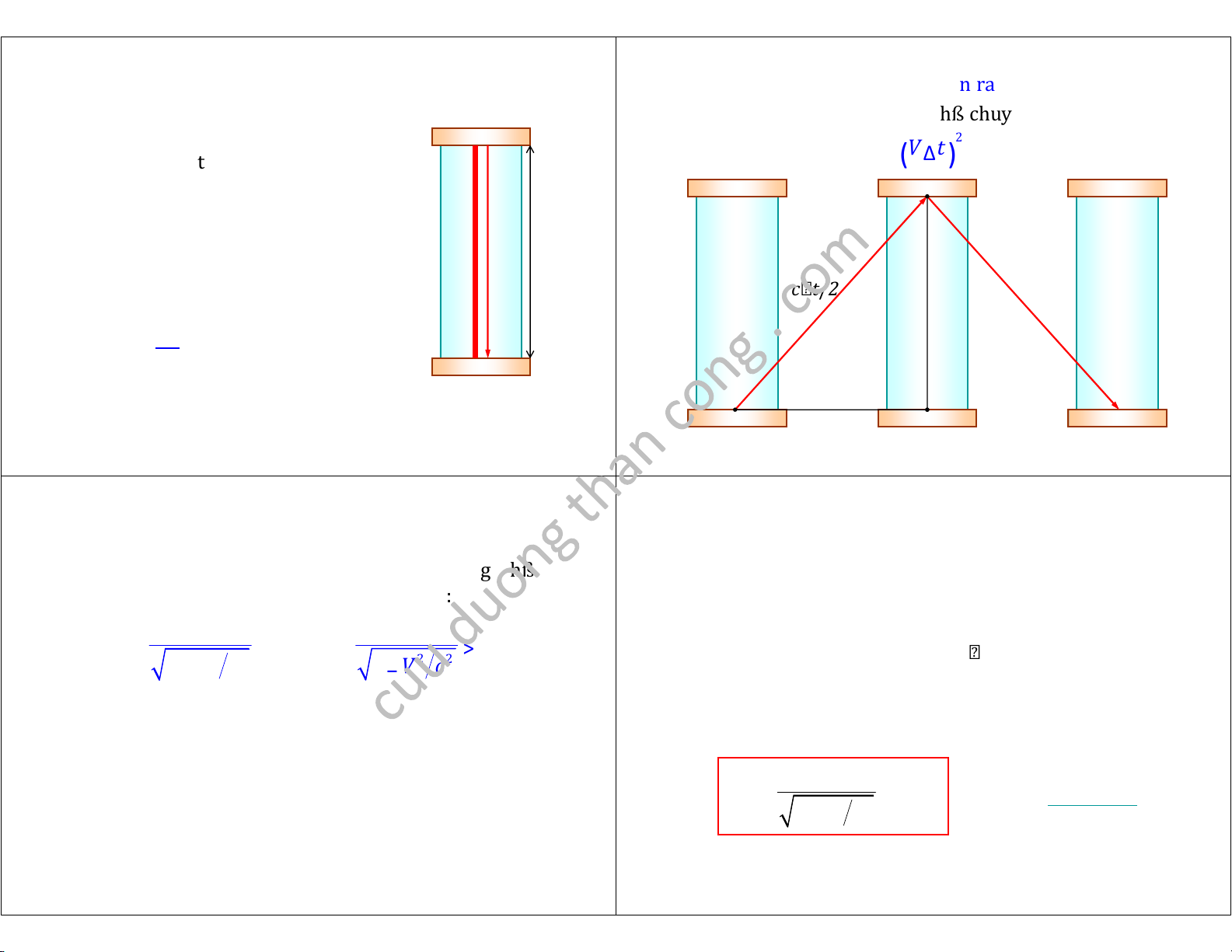
" Trong hqc nhìn th¿y ßng hß chuyßn ßng vßi
" Xét mßt ßng hß ánh sáng, v¿n tßc V : 2 2 2 c t V t t " c ∆ = ∆ + ∆
Mßt < tích t¿c= là mßt l¿n ánh ( ) ( ) ( 0 )
sáng i tÿ d±ßi lên trên và ph¿n x¿ trß vß.
" Trong hß quy chi¿u g¿n lißn vßi L ßng hß , "
c — t / 2
thßi gian cÿa mßt c — t 0 /2 2 L t ∆ 0 = c
V — t /2 2a. Thßi gian dãn ra 3 3 2a. Thßi gian dãn ra 3 4
" V¿y ßi vßi quan sát viên nhìn th¿y ßng hß
" Khi hai bi¿n cß x¿y ra t¿i cùng mßt n¡i trong
chuyßn ßng, mßt tích t¿c cÿa ßng hß là:
mßt hß quy chi¿u quán tính, t ∆ 1
" kho¿ng thßi gian giÿa chúng, o trong hqc ¿y, 0 t 1 ∆ = γ 2 2 ≡ > ±ÿc gßi là ( t ) 1 2 2
thßi gian riêng — 0 . V c 1 V c − −
" Kho¿ng thßi gian giÿa hai bi¿n cß ó, o trong t t
mßi hß quy chi¿u khác, ßu lßn h¡n thßi gian ∆ > ∆ 0 riêng: "
Theo quan sát viên nhìn th¿y ßng hß chuyßn
ßng, ßng hß có nhßp ißu dãn ra. t ∆ 0 t " t ∆ = ≡ γ ∆ 0 Minh hßa.
Mßi ßng hß khác cing v¿y. ( Theo tiên ß 1) 2 2 1 v c −
" v là v¿n tßc giÿa hai hß quy chi¿u. lOMoAR cPSD| 48541417 2a. Thßi gian dãn ra 3 5 2a. Thßi gian dãn ra 3 6
" Chuyßn Tÿ Thÿc thßi hißn ¿i.
" Tÿ Thÿc du hành ¿n mßt ngôi sao xa vßi v¿n tßc V =
" H¿t muon ÿng yên có thßi gian sßng là —t0 = 2,200 ¿s.
0,9996c. Sau 3 nm thì trß vß.
" Khi chuyßn ßng vßi v¿n tßc V = 0,9994c, thßi gian sßng cÿa muon s¿ dài ra.
" Theo ng±ßi trên Trái ¿t thì thßi gian cÿa chuy¿n du hành = 28
là: ∆t =γ∆t V c 0,9994 , 87 0 β = = 1 γ = 1−β2 =35 , 36 t t 28 ∆ = γ ∆ 0 , 87 2,200 = µ s 51µs ) = γ=1 ( )( 1 106,1n −(0,9996)2 63,
" ißu này ã ±ÿc thÿc nghißm kißm chÿng. ∆t =( 35,36)(3n) " = ã h¡n 100 nm trôi qua trên Trái ¿t! ) CuuDuongThanCong.com
https://fb.com/tailieudientucntt lOMoAR cPSD| 48541417
2b. Chißu dài co ng¿n l¿i 3 2
2 b. Chißu dài co ng¿n l¿i 3 1
" Tuy nhiên, theo Tintin thì thßi gian giÿa hai bi¿n cß là: —t = ³—t0 > —t0
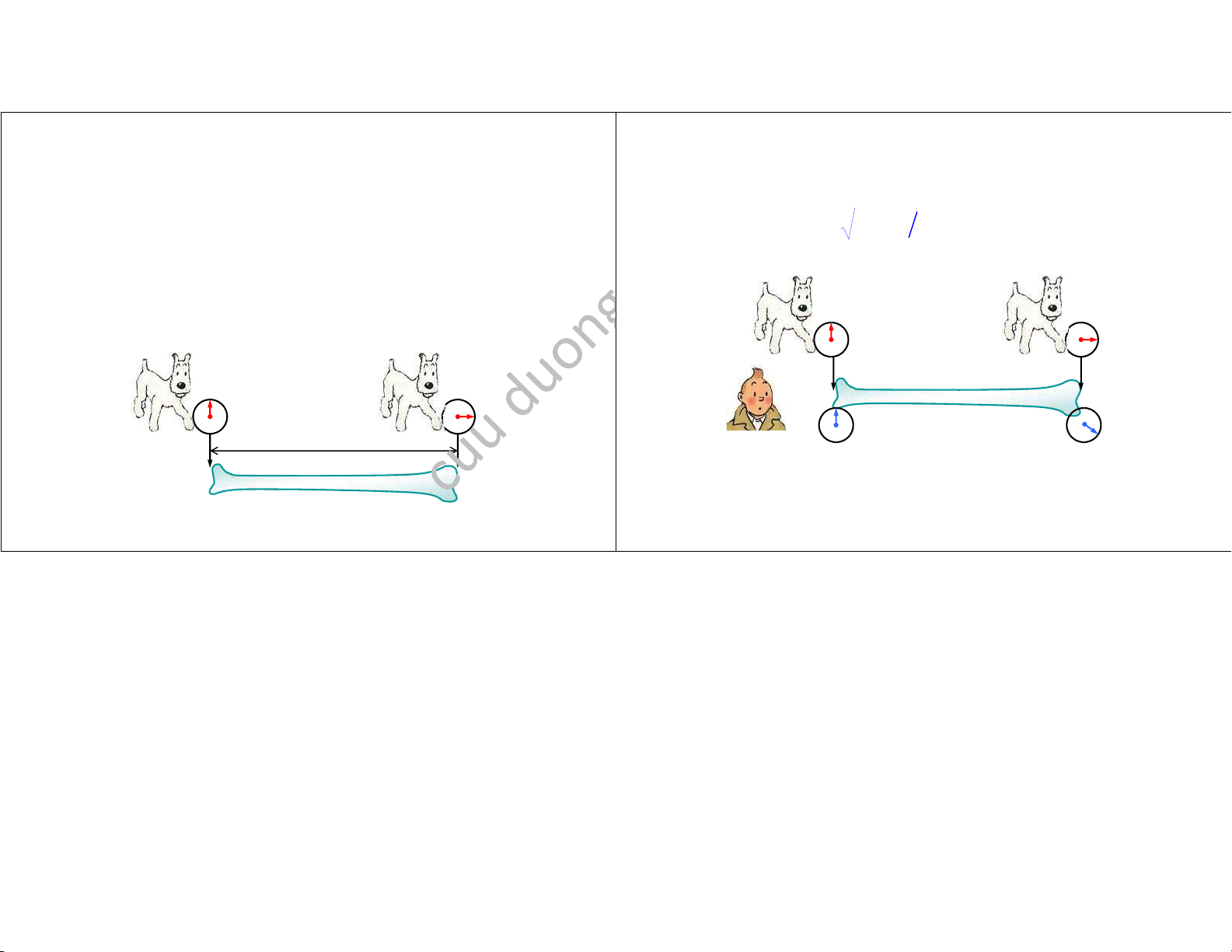
" Chó Milou ang ch¿y ch¡i vßi v¿n tßc V thì th¿y
" Do ó chißu dài khúc x±¡ng là: L 0 =
V — t > L
mßt khúc x±¡ng, và mußn o chißu dài cÿa nó. " 2 2 Suy ra: L L 1 V 0 c = − " Milou o thßi gian —
t 0 giÿa hai l¿n i qua hai
" Chißu dài v¿t chuyßn ßng co ng¿n l¿i. ¿u khúc x±¡ng.
" Và suy ra chißu dài khúc x±¡ng là: L = V — t 0 V — t 0 lOMoAR cPSD| 48541417
2 b. Chißu dài co ng¿n l¿i 3 3
2 c. Tính t±¡ng ßi cÿa sÿ ßng thßi 3 1
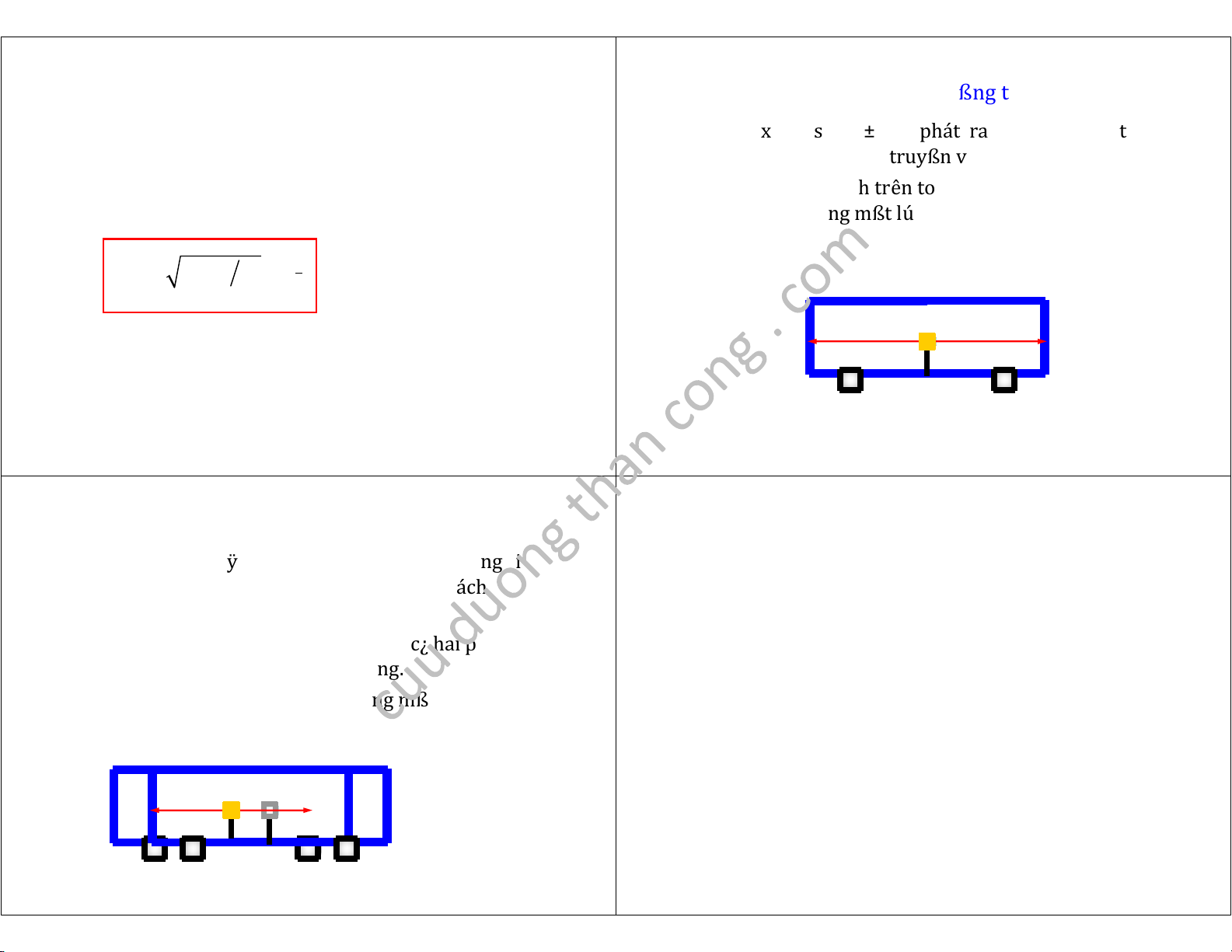
" Chißu dài cÿa mßt v¿t o trong hqc quán tính " Mßt x
ung sáng ±ÿc phát ra tÿ giÿa mßt toa
g¿n lißn vßi v¿t ±ÿc gßi là chißu dài riêng ( L 0 . )
tàu ang i vào ga, và truyßn vß hai ¿u toa.
" Chißu dài cÿa cùng v¿t ó, o trong mßi hß quy
" Theo hành khách trên toa, hai tia sáng ¿t tßi
chi¿u khác, ßu nhß h¡n chißu dài riêng: hai ¿u toa cùng mßt lúc. L 2 2 0
L L 1 v c = 0 − ≡ γ
" v là v¿n tßc giÿa hai hß quy chi¿u. 2c. T
ính t±¡ng ßi cÿa sÿ ßng thßi 3 2 Bài t¿p áp dÿng 1
" Theo ng±ßi ÿng d±ßi sân ga, tia sáng i
Mßt h¿t không bßn i vào mßt máy dò và ß l¿i
ng±ÿc chißu chuyßn ßng cÿa tàu ¿t tßi vách
mßt vßt dài 1,05 mm tr±ßc khi phân rã. V¿n tßc tr±ßc.
h¿t ßi vßi máy dò là 0,992 c .
" Vì v¿n tßc ánh sáng là không ßi vß c¿ hai phía,
Thßi gian sßng riêng cÿa h¿t là bao nhiêu?
và vì vách này ti¿n l¿i g¿p tia sáng.
" Hai bi¿n cß x¿y ra ßng thßi trong mßt hqc, l¿i
không ßng thßi trong mßt hqc khác. ) CuuDuongThanCong.com
https://fb.com/tailieudientucntt lOMoAR cPSD| 48541417 Tr¿ lßi BT 1 Bài t¿p áp dÿng 2
" Thßi gian sßng cÿa h¿t ßi vßi máy dò là:
Trong mßt ßi ng±ßi, lißu có thß du hành ¿n mßt
∆t =d V d là chißu dài cÿa vßt
thiên hà ß cách xa Trái ¿t 23.000 nm ánh 1,05×10−3m sáng hay không? ∆t = 8m s =3,53ps 0,992×3×10
" Thßi gian sßng riêng luôn luôn ng¿n h¡n và xác ßnh tÿ: ∆ ∆t t 0 = γ= 1 2 =7 , 92 γ 1−0,992 3,53ps ∆t0 = = 0,45ps 7 , 92 lOMoAR cPSD| 48541417 Tr¿ lßi BT 2 3 1 Tr¿ lßi BT 2 3 2
" Gßi V = ³c là v¿n tßc phi hành gia. " Hay: β 1−β2 =287,5
" Ánh sáng m¿t 23.000 nm ß bay ¿n thiên hà thì phi
" Gi¿i ph±¡ng trình trên ta ±ÿc:
hành gia ph¿i m¿t 23.000/³ nm, theo thßi gian " ³ = 0,998265393 trên Trái ¿t.
" Cing có thß l¿p lu¿n nh± sau.
" Gi¿ sÿ tußi thß trung bình cÿa con ng±ßi là 80 nm.
" Phi hành gia ph¿i chuyßn ßng sao cho ßi vßi ông
ta kho¿ng cách 23.000 nas (chißu dài riêng) co l¿i
" Phi hành gia mußn thÿc hißn chuy¿n bay trong 80 còn 80³ nas:
nm (thßi gian riêng). Do ó: γ= ∆t ∆t0 =(23.000n
γ= L0 L = 23.000nas 80βnas β) 80n óγβ= 23.000 80 = 287,5 óγβ= 23.000 80 = 287,5 ) CuuDuongThanCong.com
https://fb.com/tailieudientucntt lOMoAR cPSD| 48541417 3 a. Phép bi¿n ßi Galilei 3 b. Phép bi¿n ßi Lorentz
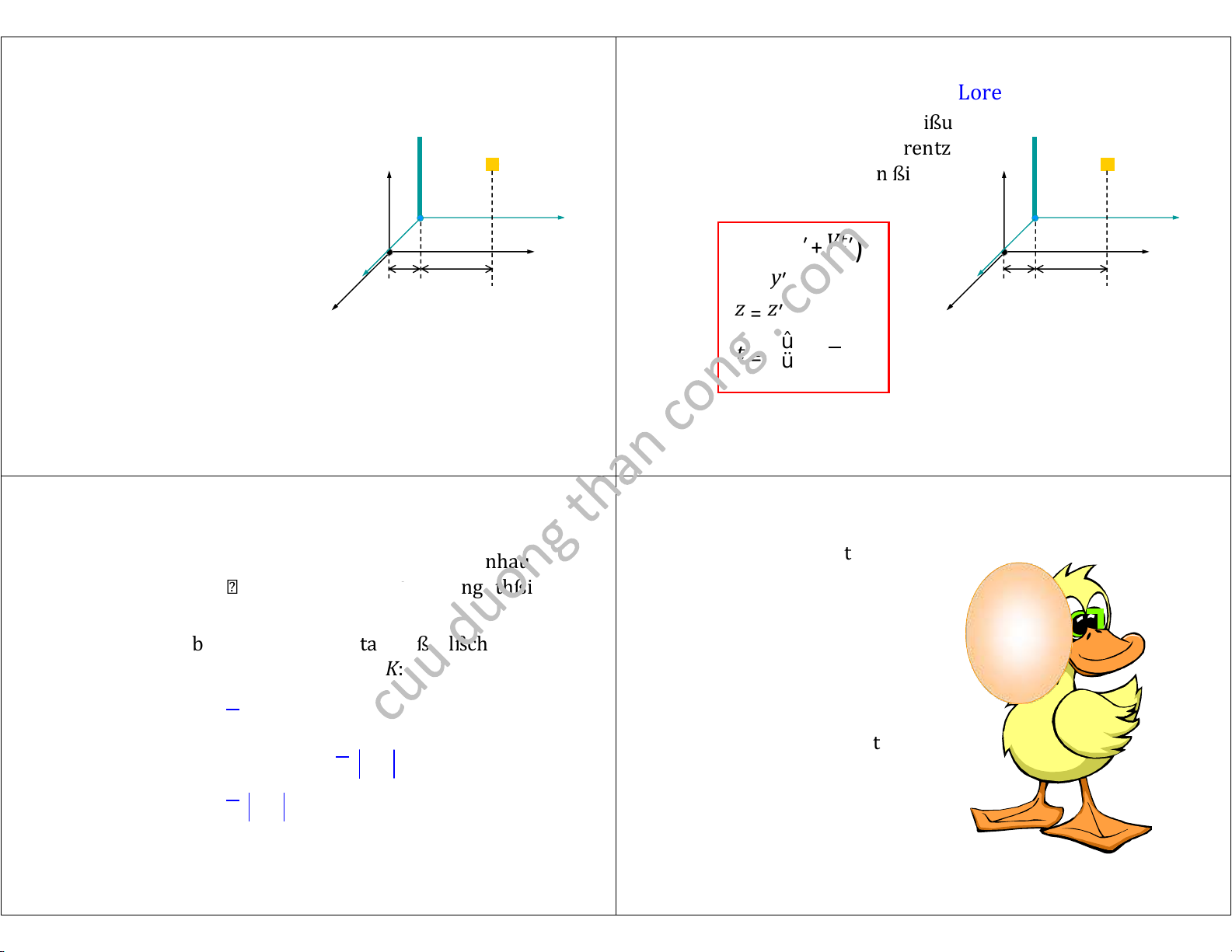
" Hqc K chuyßn ßng theo
" ß phù hÿp vßi các hißu trÿc 9
x cÿa hqc K vßi v¿ n ÿng t±¡ng ßi, Lorentz tßc V . ±a ra các phép bi¿n ßi " mßi:
Lúc K c K thì t = t = 0. " Mß 9 t bi¿n cß x¿y 9 ra trong x x = ′ Vt + ′ K có tßa ß ( γ ( )
x , y , z , t ) y " y = ′ 9
ßi vßi K s¿ 9 có 9 tßa9 ß:9 Vt x9 Vt x9 z x z = ′ x Vt = ′ + û
Khi V << c , V y þ y = t ′ t = ü ′ x γ + 2 ³ ý c ′ ÿ
³ 1, V / c 2 ³ 0 z ø z = ′ Lorentz ³ Galilei. t t = ′ 4a. 4 Quan hß nhân qu¿ 3 1 a. Quan hß nhân qu¿ 3 2 " " Ph¿i chng trong mßt
Xét hai bi¿n cß x¿y ra trong hqc K , ß cách nhau mßt hqc chuyßn ßng ßi vßi
kho¿ng — x , lßch nh au 9 mßt kho¿ng thßi gian — Trái ¿t ng±ßi ta có thß t . 9 th¿y " Tÿ 9
phép bi¿n ßi Lorentz ta có ß lßch thßi
gian giÿa hai bi¿n cß trong hqc " K :
chú vßt cß tr¿ d¿n thành
vßt con, rßi chui l¿i vào vß û V þ trÿng !? t t ∆ = ∆ ü ′ x + ∆ ′ ÿ γ 2 ý c ø V " Th¿t ra, không thß ¿o "
N¿u — t > 0 và — x < 0, và x 2 ∆ ′ t > ∆ ′ ng±ÿc thÿ tÿ cÿa các c 9 û V 9 t þ bi¿n cß trên ây, t ∆ = ∆ ü ′ x − ∆ ′ 0 γ ÿ< 2 ý c ø
" vì chúng có quan hß nhân
" Thÿ tÿ cÿa hai bi¿n cß ã bß ¿o ng±ÿc! qu¿ vßi nhau. lOMoAR cPSD| 48541417 4a. Quan hß nhân qu¿ 3 3
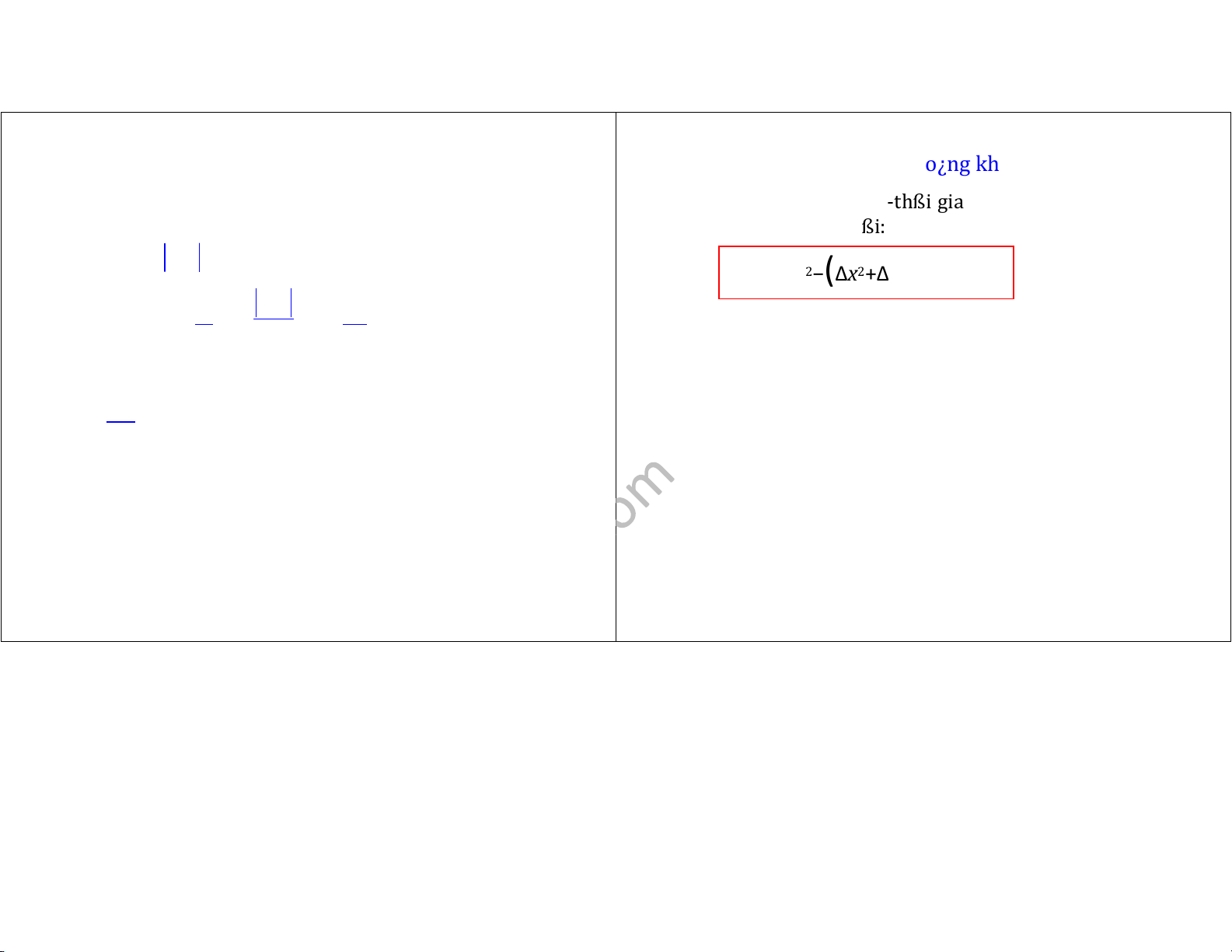
4b. Sÿ b¿t bi¿n cÿa kho¿ng không-thßi gian
" Ph¿i có thông tin ±ÿc truyßn i tÿ nguyên nhân ¿n
" Kho¿ng cách không-thßi gian —s giÿa hai bi¿n cß k¿t qu¿, ±ÿc ßnh ngh)a bßi:
" Do ó: ∆x′ =v∆t′ v: tßc ß truyßn thông tin " Tÿ phép bi¿n
∆s2 =c2∆t2−(∆x2+∆y2+∆z2 ) ßi Lorentz, ta û
V ∆ ∆x′ þø û1−Vv 2 þ ÿ có thß chÿng minh là
∆t =γ∆t′üý1− c 2
t′ ÿ =γ∆t′üý c ø
kho¿ng —s không thay ßi khi chuyßn hß quy
Vv <1 ó∆t > 0 chi¿u : c2 2 2 s s ∆ = ∆ ′
" Không thß ¿o ng±ÿc thÿ tÿ cÿa hai bi¿n cß có quan hß nhân qu¿. ) CuuDuongThanCong.com
https://fb.com/tailieudientucntt lOMoAR cPSD| 48541417
4c. Công thÿc cßng v¿n tßc mßi Bài t¿p áp dÿng 3
" Xét mßt ch¿t ißm chuyßn ßng trong hqc K9 vßi v¿n
Mßt nhà thÿc nghißm thÿc hißn mßt m¿ch ißn giúp tßc:
ông ta b¿t cùng mßt lúc hai bóng èn, bóng màu ß ß
dx′ dy′ dz′ v′x = v′y =
gßc hß quy chi¿u và bóng màu vàng ß kho¿ng cách v′z = x = 30 km.
dt′ dt′ dt′
ßi vßi quan sát viên chuyßn ßng theo trÿc x d±¡ng
" Tÿ phép bi¿n ßi Lorentz, ta tìm ±ÿc v¿n tßc cÿa ch¿t vßi v¿n tßc 0,250c: ißm ßi vßi hqc K: a)
Kho¿ng thßi gian giÿa hai bi¿n cß là bao dx v vx = = nhiêu? ′x +V 2 b)
Bóng nào ±ÿc b¿t sáng tr±ßc?
dt 1+v′xV c dy γv′
vy = = Vy c 2 t±¡ng tÿ cho v z dt 1+v′x lOMoAR cPSD| 48541417 Tr¿ lßi BT 3 3 1 Tr¿ lßi BT 3 3 2
" Theo qsv K thì K " Hay:
chuyßn ßng 9 vßi v¿n 1 tßc
V = 0,250 c theo V K9 β t ∆ 0,250 ′ x = − ∆ β = chißu âm 2 c cÿa trÿc x , 1 − β " Bi¿n ßi Lorentz cho ta: " Ta có: x x x 30 km û
∆ = vang − do = V t ′ t þ — x x = γ ü − ÿ 2 ý c ø K " 5 − Do ó: t ∆ ′ t = ′ t − ′ 2 ,58 10 s " vang do = − × Thßi gian giÿa hai bi¿n cß là: û
" Theo K thì èn vàng b¿t sáng tr±ßc mßt V V t þ ∆ t ′ t x = γ ∆ ü − 2 ∆ ′ x = γ − ∆ kh 9 o¿ng thßi gian là 25,8 ý c ∆ ÿ 2 ¿s . c ø Bài t¿p áp dÿng 4 Tr¿ lßi BT 4 3 1
Hai thiên hà A và B ang i ra xa khßi chúng ta ß
" ßi vßi thiên hà A chúng ta có v¿n tßc 3 V , do ó
hai phía ßi dißn vßi cùng v¿n tßc 0,55
thiên hà B có v¿n tßc cho bßi: c .
Tìm v¿n tßc cÿa thiên hà B ßi vßi thiên hà A. v V x v − x ′ = 2 1 v
− x V c
" V¿n tßc cÿa thiên hà B ßi vßi chúng ta: v x = 3 V V V V A K9 v9 A K9 B B K K ) CuuDuongThanCong.com
https://fb.com/tailieudientucntt lOMoAR cPSD| 48541417 Tr¿ lßi BT 4 3 2 a.
5 Khßi l±ÿng t±¡ng ßi tính " Suy ra:
" Khßi l±ÿng cÿa mßt ch¿t ißm: V
" o trong hß quy chi¿u g¿n lißn vßi ch¿t ißm V 2 c 0 , 55 − − × v ′ 0, c ó, là x =
khßi l±ÿng nghß m 2 2 = − 2 84 1 = − 0 cÿa nó. V c 1 , 0 55 + +
" o trong mßt hß quy chi¿u khác, trong ó ch¿t " ißm chuyßn ß
ng vßi v¿n tßc v , th ì lßn h¡n
Khác vßi k¿t qu¿ theo c¡ hßc cß ißn (1,10 c ) . khßi l±ÿng nghß: " Công thÿc cßng v¿n
tßc cÿa thuy¿t t±¡ng ßi
¿m b¿o r¿ng v¿n tßc tßng hÿp luôn nhß h¡n c . m 0 m m = ≡ γ 0 2 2 1 v c −
5 b. ßng l±ÿng t±¡ng ßi tính
5 c. Nng l±ÿng t±¡ng ßi tính
" ßng l±ÿng cÿa mßt ch¿t ißm trong thuy¿t " Nng l±ÿng cÿa mßt 2 t±¡ng ßi là: E mc ch¿t ißm chuyßn ßng: = p " Nng l±ÿng nghß: 2 E m c = mv m = = 0 v γ 0 0 " 2
Ph±¡ng trình ßng lÿc hßc: " ßng nng: K = ( m m c − 0 ) dp d( m γ 0 v ) F " 2 2 2 2 dt = = Hß thÿc giÿa ßng E pc m c dt l±ÿng và nng l±ÿng: = ( ) + ( 0 ) 2 2 ( 2 pc K 2Km ) 0 c = + lOMoAR cPSD| 48541417 Bài t¿p 5.1 Tr¿ lßi BT 5.1 3 1
Mßt h¿t pion (mà = 273me) ang ÿng yên phân rã "
Nng l±ÿng ±ÿc b¿o toàn trong ph¿n ÿng:
thành mßt muon (m¿ = 207me) và mßt ph¿n 2 2 2 m c K m neutrino (m K m c c = + + +
ÿ j 0) theo ph¿n ÿng: π µ µ υ υ 2 j 0 m m c K K − = + π− →µ− +υ ( π µ ) µ υ ß hÿt khßi —m Tìm (b¿ng eV): cÿa ph¿n ÿng (a)ßng nng cÿa muon. 2 K K mc 1 + µ = υ ∆ ( )
(b) ßng nng cÿa ph¿n neutrino.
" ßng l±ÿng ±ÿc b¿o toàn: 2 2 0 p p = ó p c p c ( = µ + υ µ ) ( υ ) ) CuuDuongThanCong.com
https://fb.com/tailieudientucntt lOMoAR cPSD| 48541417 Tr¿ lßi BT Tr¿ lßi BT 5.1 3 2
5.1 3 2 " Bißu dißn qua ßng "
—m = (2732207)me = 66me nng:
µ 662me2c2 = 4356mc e 2 K =
Kµ2 + 2Kµmµc2 =Kυ2 273m (2) e 273 2 " Thay K µ " mec2 = 0,511 MeV ) ÿ tÿ (1): " K¿ = 4,07 MeV K " K 2 ÿ = 29,6 MeV
µ +2Kµmµc2 =(∆mc2−K =(∆mc2)2−2K 2 µ∆mc2+Kµ ó2K ( )
µ ∆m+mµ c2 =(∆mc2)2 ∆
m2c2 Kµ= mπ