Tích phân đường | Giải tích 3 | Trường Đại học Khoa học Tự nhiên, Đại học Quốc gia Hà Nội
Bài tập cần thực hiện: Bài 1 Tính theo các đường cong kín C (có chiều ngược chiều kim đồng hồ) bao miền R bằng công thức Green với , R là hình chữ nhật có các đỉnh (0,0); (2,0); (2,3); (0,3). Ngôn ngữ sử dụng: MATLAB Yêu cầu 1: Dùng lệnh có sẵn trong thư viện, hoặc tự lập trình, vẽ trường vector của hàm vector đã cho đối với một miền đủ lớn chứa đường cong C đã cho trong đề bài. Tài liệu được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Môn: Giải tích 3 (HUS) 10 tài liệu
Trường: Trường Đại học Khoa học tự nhiên, Đại học Quốc gia Hà Nội 687 tài liệu
Tác giả:
Preview text:
Phần 2: Ngày sinh: 25/08
Bài tập cần thực hiện: Bài 1
Tính theo các đường cong kín C (có chiều ngược chiều kim
đồng hồ) bao miền R bằng công thức Green với , R là hình chữ
nhật có các đỉnh (0,0); (2,0); (2,3); (0,3).
Ngôn ngữ sử dụng: MATLAB
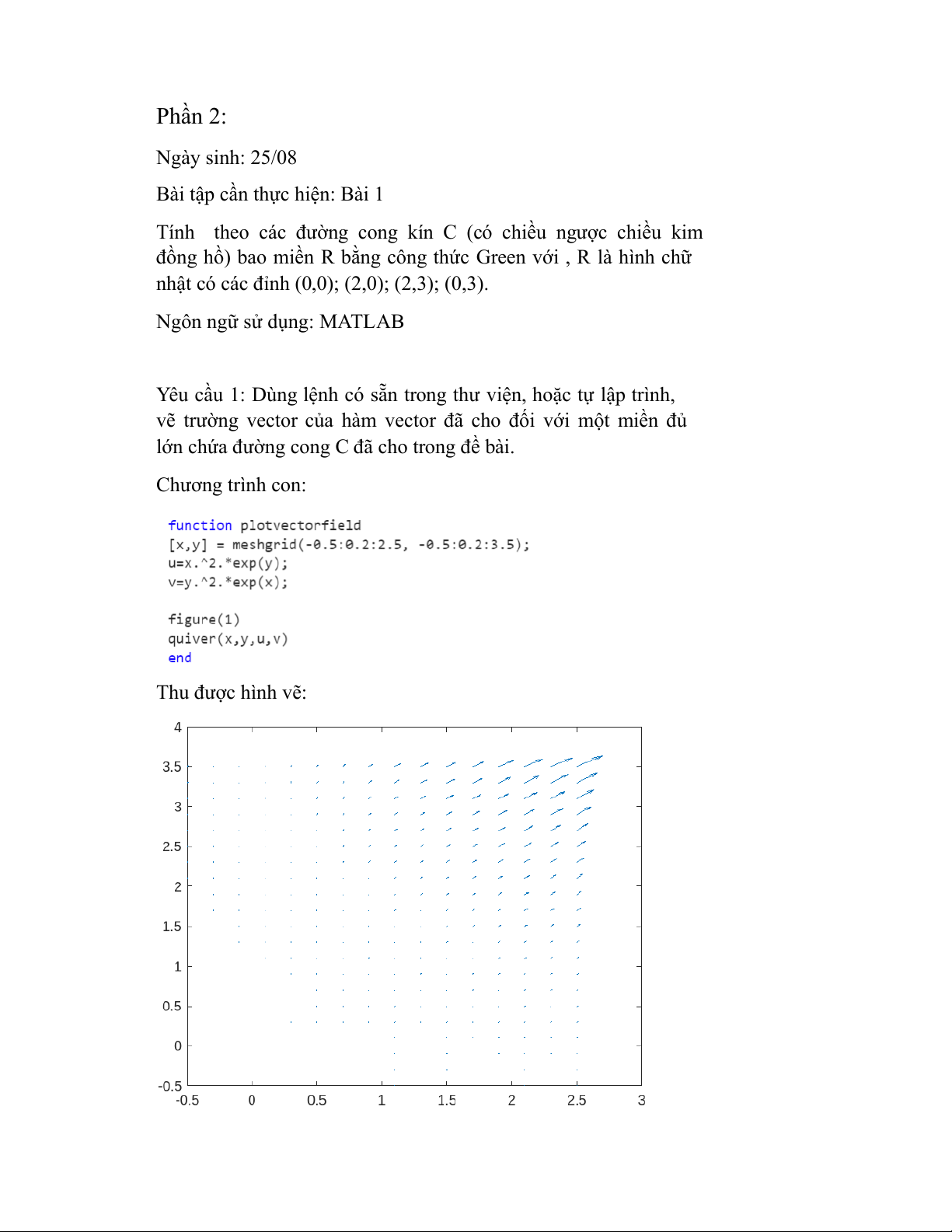
Yêu cầu 1: Dùng lệnh có sẵn trong thư viện, hoặc tự lập trình,
vẽ trường vector của hàm vector đã cho đối với một miền đủ
lớn chứa đường cong C đã cho trong đề bài. Chương trình con: Thu được hình vẽ:
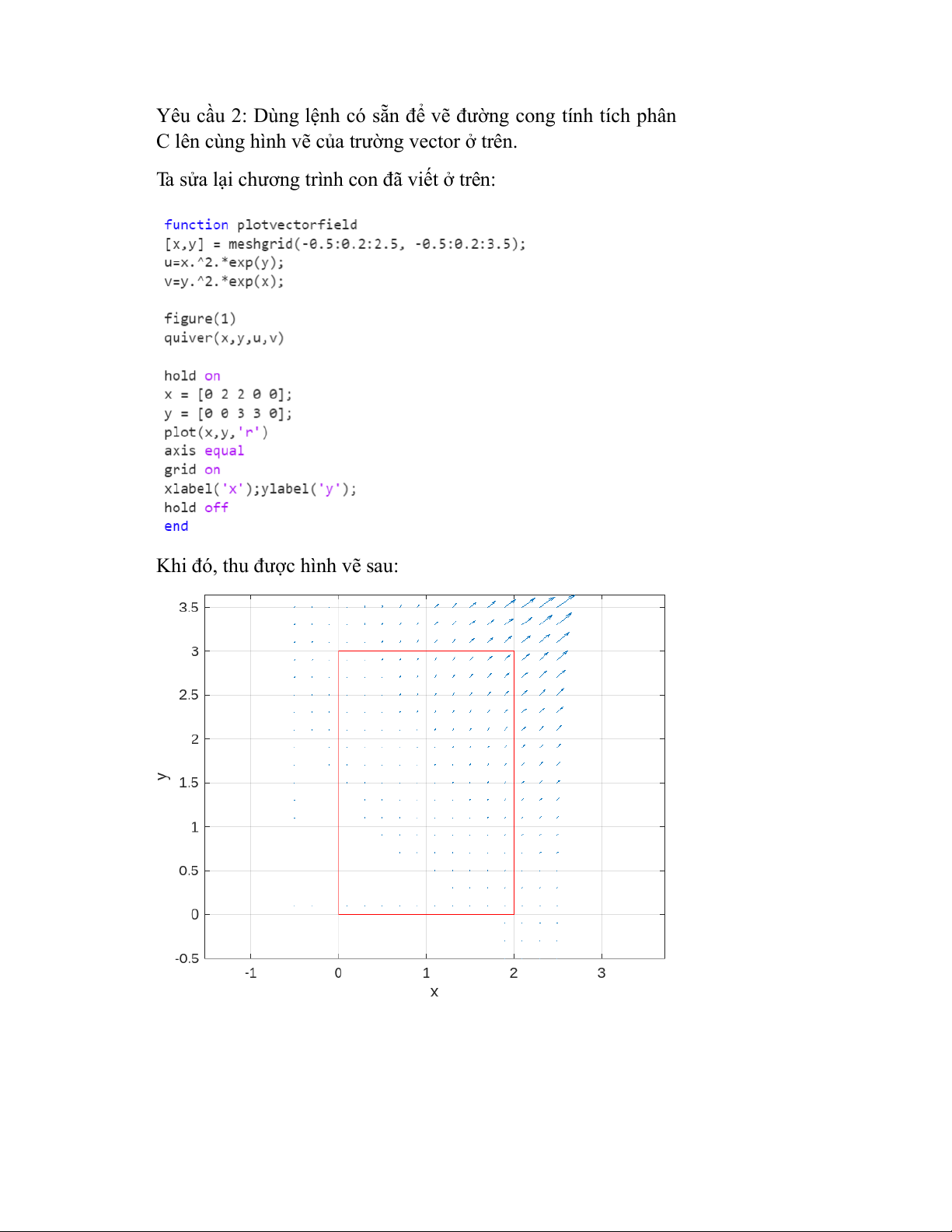
Yêu cầu 2: Dùng lệnh có sẵn để vẽ đường cong tính tích phân
C lên cùng hình vẽ của trường vector ở trên.
Ta sửa lại chương trình con đã viết ở trên:
Khi đó, thu được hình vẽ sau:
Yêu cầu 3: Dùng lệnh có sẵn trong thư viện của phần mềm tính tính phân.
Ta sử dụng công thức Green đưa tích phân đường ban đầu về tích phân 2 lớp:
Chương trình con tính tích phân:
Chạy chương trình này trong chương trình chính thu được kết quả:
So sánh với kết quả chính xác đã làm phần lý thuyết ở phần 1:
Vậy giá trị tích phân thu được bằng với kết quả đã làm phần lý thuyết ở phần 1.
Kết quả phù hợp với hình vẽ trường vector và đường C.