TRƯỜNG ĐẠI HỌC SƯ PHẠM TP.HỒ CHÍ MINH KHOA TOÁN – TIN.    ĐỀ TÀI :
“ CÁC PHÉP CHIẾU XUYÊN TÂM VÀ
CÁC PHÉP THẤU XẠ. THỂ HIỆN TRONG
MÔ HÌNH XẠ ẢNH CỦA KHÔNG GIAN AFFINE”
GVHD: PGS.TS LÊ ANH VŨ.
SVTH: NHÓM 3 – TOÁN 2A KHÓA 34.
NĂM HỌC: 2009 – 2010. Tháng 5 / 2010 1 MỞ ĐẦU:
Felix Klein là người đầu tiên đưa ra cách phân loại hình học theo nhóm các biến
đổi trong nó, dựa vào cách phân loại này thì hình học xạ ảnh là môn hình học tổng quát
nhất trong tất cả các môn hình học cao cấp và sơ cấp sử dụng công cụ tuyến tính. Số
lượng khái niệm, định lí của hình học xạ ảnh không nhiều nhưng nó đúng cho mọi hình
học khác. Hơn thế từ một số khái niệm, định lí của hình học xạ ảnh có thể suy ra được
các khái niệm, định lí của hình học sơ cấp và affine. Thế mạnh của hình học xạ ảnh là có
thể giải quyết các bài toán về tính đồng qui và thẳng hàng (đặc biệt là hình học phẳng)
một cách tổng quát. Ngoài ra ta có thể sáng tạo các bài toán sơ cấp qua nguyên lý đối
ngẫu, phương pháp đưa điểm ra vô tận.... 2 MỤC LỤC Đề tài:
Các phép chiếu xuyên tâm và các phép thấu xạ. Thể hiện trong
mô hình xạ ảnh của không gian Affine.
A. Mô hình xạ ảnh của không gian Affine. I. Xây dựng mô hình.
II. Một số thể hiện trong mô hình. B. Phép chiếu xuyên tâm. I. Định nghĩa. II. Các định lý.
III. Đối ngẫu của phép chiếu xuyên tâm.
IV. Phép chiếu xuyên tâm và đối ngẫu của nó trong P2. V. Một số ứng dụng. C. Phép thấu xạ. I. Phép thấu xạ cặp. II. Phép thấu xạ đơn.
III. Các phép thấu xạ trong không gian xạ ảnh P2 và P3 .
IV. Các phép biến đổi affine sinh ra bởi các phép thấu xạ . V. Bài tập. 3
A. MÔ HÌNH XẠ ẢNH CỦA KHÔNG GIAN AFFINE
I. XÂY DỰNG MÔ HÌNH:
Xuất phát từ không gian affine An ta đã biết cách xây dựng mô hình của không
gian xạ ảnh Pn bằng cách thêm vào An những điểm vô tận. Bây giờ ngược lại, từ không
gian xạ ảnh Pn ta hãy bỏ bớt đi một số điểm nào đó để xây dựng mô hình của không gian affine.
Ta hãy chọn trong Pn một siêu phẳng  bất kỳ và đặt
An = Pn \ là tập hợp những điểm thuộc Pn mà không thuộc . Ta sẽ chứng minh An là một không gian affine
Gọi Vn+1 là không gian vecto nền của không gian xạ ảnh Pn .
Trang bị cho Vn+1 cấu trúc affine chính tắc: n 1 + n 1 + n 1 ϕ :V V V + × → uur
(x, y) a xy := y − x Khi đó, ( n 1 + n 1 V ,V + , ) ϕ là một
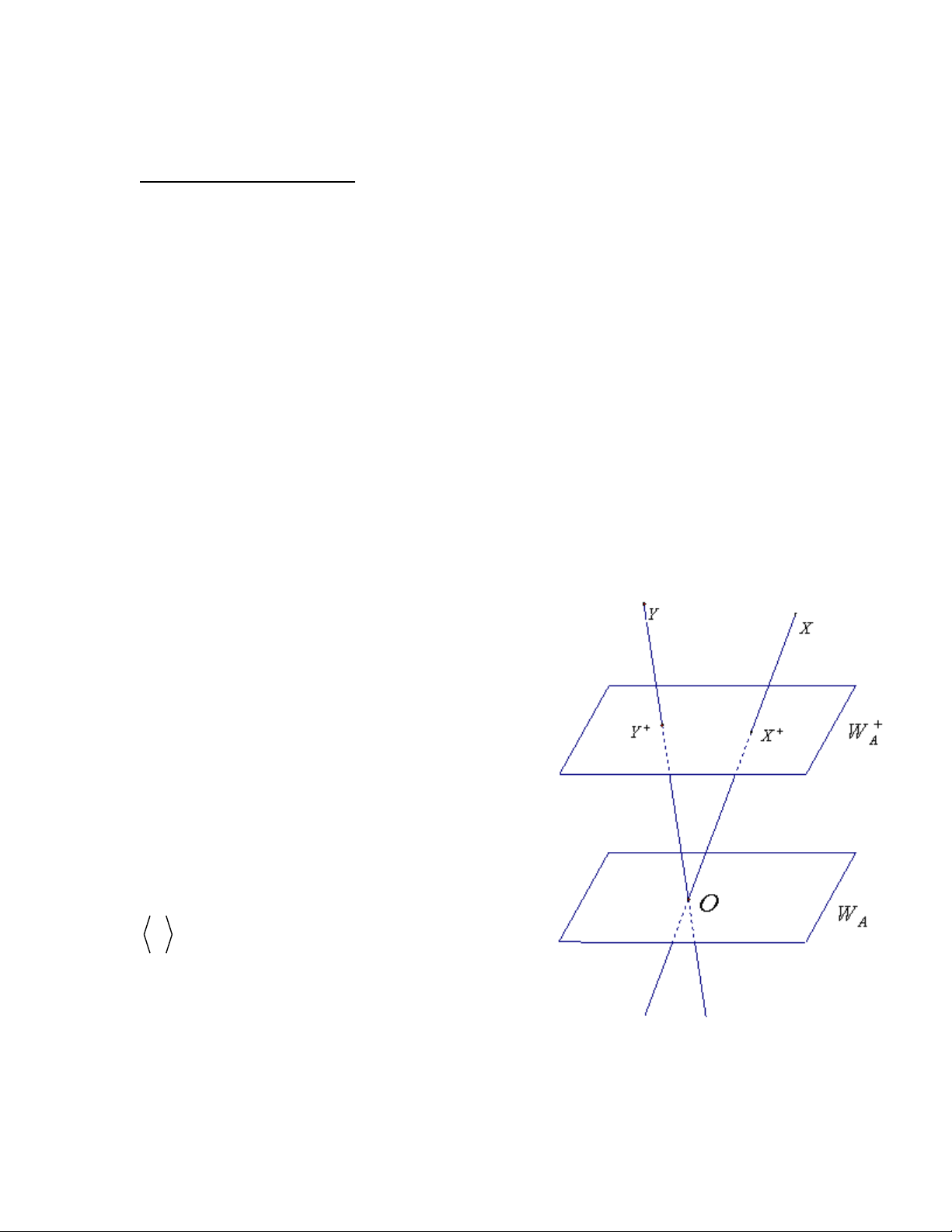
không gian affine, kí hiệu lại là n 1 V + và kí A r hiệu 1 0 n V + ∈ là điểm 1 0 n V + ∈ . A Mỗi điểm n n 1 X P [V + ∈ ] (đại diện bởi r vectơ n 1 x V + ∈
) tương ứng với một không
gian vectơ con một chiều của Vn+1 . Xét đường
thẳng affine dX qua O có không gian phương là r r
x ( không gian vectơ 1 chiều sinh bởi x ).
Đường thẳng affine này chỉ phụ thuộc điểm X
mà không phụ thuộc vectơ đại diện. 4 Cho siêu phẳng xạ ảnh °
∆ =π(W ) trong Pn[Vn+1] ( W là không gian vectơ con n
chiều trong Vn+1 ). Đặt WA là siêu phẳng affine qua O nhận W làm không gian phương. Ta trang bị cho n n
A = P [V ] \ ∆cấu trúc không gian affine liên kết với W như sau: Trong n 1
V + lấy một siêu phẳng affine W + song song (nhưng khác) với W . A A A
Khi đó, W + là một không gian affine n chiều nhận W làm không gian phương. A Lấy n X A ∈ , tức là n X P
∈ [V ] và X ∉∆ . Khi đó vectơ đại diện của r r  x ∩W ={0} r  X là x W ∉ . Suy ra  r . n 1
 x ⊕W = V +  d W + X + ∩ = Từ đó, ta có: X A
, X + là duy nhất và ánh xạ θ : n A →W +A X a X + là song ánh. An , W cùng với ánh xạ : n n f A × A W → uuur uuuuuu r
( X ,Y ) a XY := X Y + +
là một không gian affine, thật vậy: r A n X A v W X + W + ∀ ∈ ∀ ∈ ∃ ∈ θ + = 1 : , : ! ( X )
X ,( θ là song ánh). a
Mặt khác doW + là không gian affine n chiều nhận W làm không gian phương nên tồn A uuuuuu r r tại duy nhất Y + W + ∈ sao cho: + +
. Lại vì θ là song ánh nên có duy nhất a X Y v = uuur uuuuuur r n
Y ∈ A (tương ứng với Y+ qua 1 θ − ) thỏa: XY X Y + + = = v . r uuu r r Vậy n ∀ ∈ ,∀ ∈ , ! n X A v W ∃Y A ∈ : XY v = 5
uuur uur uuuuuur uuuuur uuuuuur uuur A n + + + + + + 2 : X
∀ ,Y, Z ∈ A : XY +YZ = X Y +Y Z = X Z = XY
Vậy ta đã trang bị cho n n
A = P [V ] \ ∆ cấu trúc không gian affine liên kết với W.
II. MỘT SỐ THỂ HIỆN TRONG MÔ HÌNH:
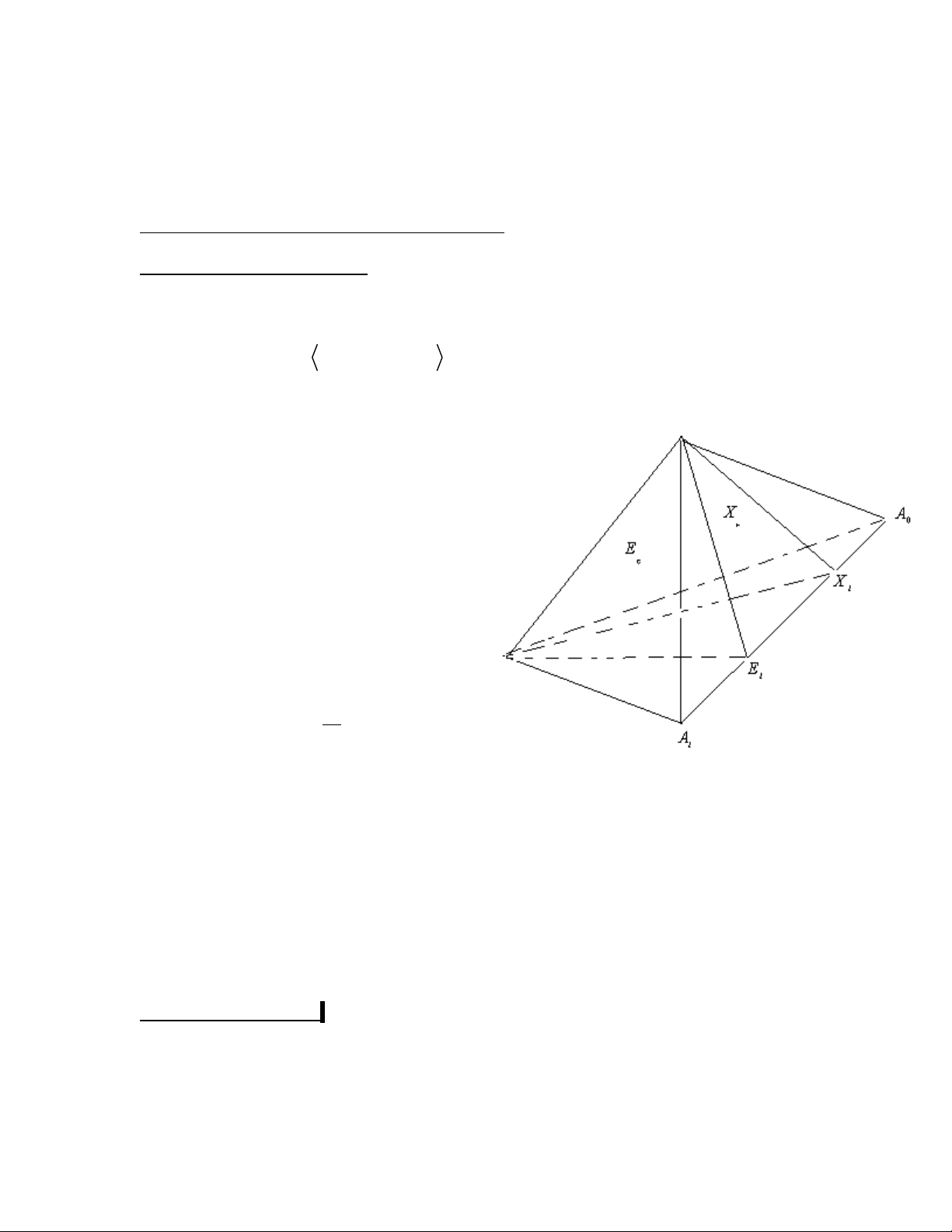
1. Tọa độ và mục tiêu affine: Xét mục tiêu xạ ảnh ( )
ℜ :{ A , A , A ,....., A , E 0 1 2 n
} của không gian xạ ảnh Pn .
Chọn siêu phẳng ∆ = A , A ,...., A 1 2 n làm siêu phẳng vô tận.
Gọi Ei là giao điểm của đường thẳng A0Ai với siêu phẳng chứa các đỉnh Ai còn lại
của mục tiêu và điểm E (i=1..n). uuuur
Đặt ei = A E (i=1..n), ta được hệ 0 i
vectơ {ei}i=1..n là các vectơ cơ sở trong không
gian vectơ Vn. Do đó ta có thể dùng bộ điểm
{A0; E1, E2,…, En} (1) làm mục tiêu affine
của không gian affine An = Pn \.
Một điểm X trong Pn có tọa độ xạ
ảnh là X(x0: x1:…: xn).(X∉ ). x Do đó x i 0 ≠ 0. Ta đặt Xi= (i=1..n). x0
Vậy tọa độ điểm X(1:X1: X2:…: Xn).
Với điểm O đã chọn (trong cách xây dựng mô hình affine ), ta có: uuur uuuur
ϕ ( OX ) = X, ϕ ( OA = A ,ϕ e = A i ∀ =1,2,...,n 0 ) 0 ( i ) i nên uuur uuuur uuuuur uuuuur
OX = OA +X A E +…+X A E 0 1. 0 1 n. 0 n uuuur uuuuur uuuuur
Suy ra A X =X A E +…+X A E 0 1. 0 1 n. 0 n
Vậy trong không gian affine, điểm X có tọa độ đối với mục tiêu (1) là X(X1, X1,…, Xn).
2.Các m_phẳng affine: 6
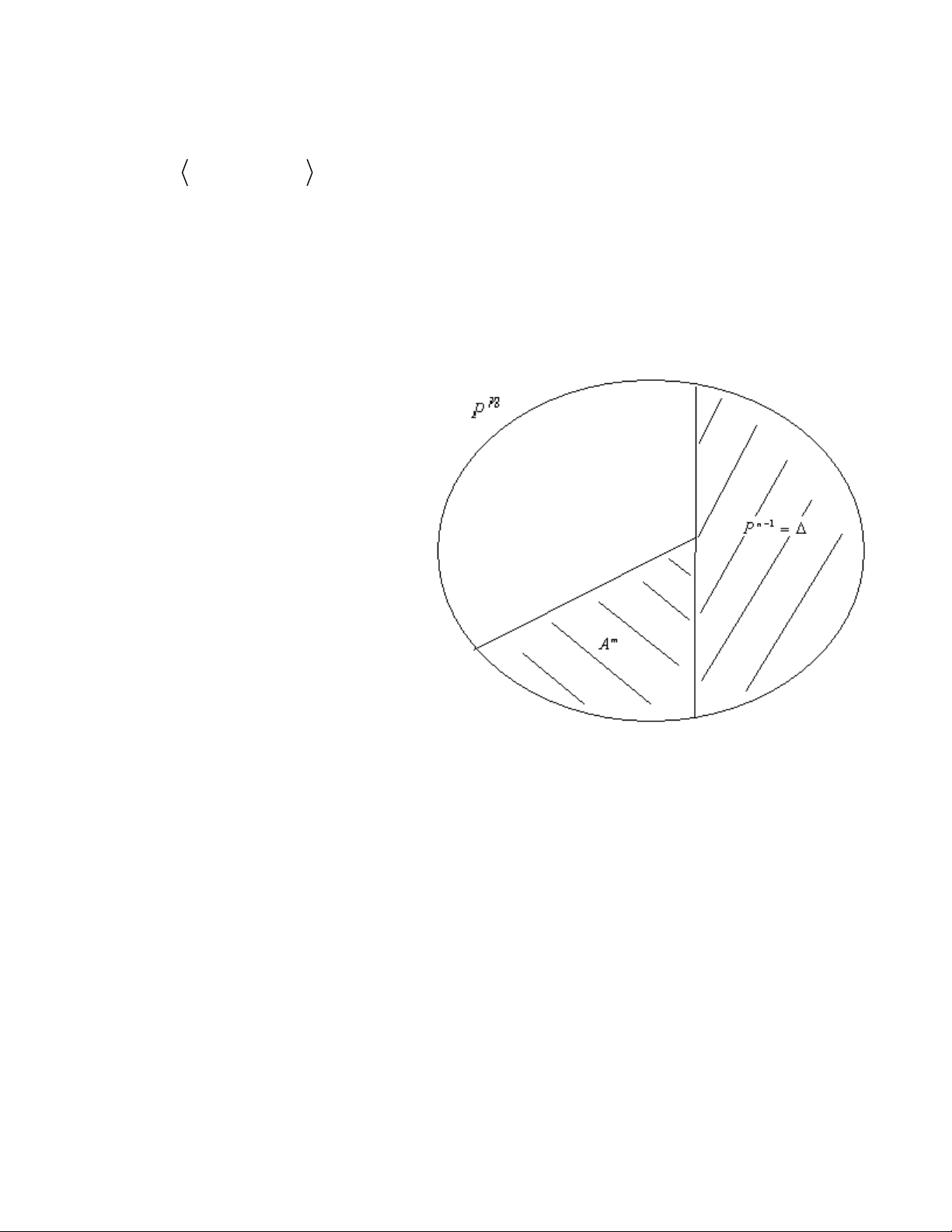
Xét một m_phẳng Pm nào đó của Pn mà không nằm trong siêu phẳng Pn-1 = ( Với
∆ = A , A ,...., A 1 2 n
) . Đối với mục tiêu xạ ảnh đã chọn,  có phương trình x0 = 0 và Pm có phương trình là: n a .x ∑
= 0 , i =1,2,..., n − m ij j j=0
Trong đó ma trận A=(a)ij có hạng rank(A) = n – m .
Gọi Am là tập hợp những điểm X
thuộc Pm mà không thuộc  tức là
Am= Pm I An và có tọa độ X(x0: x1: …: xn). Ta có: n a .x ∑
= 0 , i =1, 2,..., n −m ij j j 0 =
Do X không thuộc  nên x0 ≠ 0 nên
chia 2 vế của phương trình m_phẳng cho x0, ta được: n a .X ∑
+a = 0 , i =1, 2,..., n −m (I) ij j io j 1 =
Ta thấy ma trận hệ số của hệ phương trình này cũng có hạng là n – m.
Thật vậy, ta hãy xét hệ phương trình sau: n  a .x ∑ =0 ij j j 0 = , i 1
= , 2,..., n −m . x  =0  o Đặt 7 a a a L a  10 11 12 1n   a a L a  11 12 1n a a a L a 20 21 22 2n   a a L a  21 22 2 B = K  và n B   = 1 .   K  a a a L a     n−m,0 n−m,1 n−m,2 n−m,n a a L a  n  
 −m,1 n−m,2 n−m,  1 0 0 K 0 n   
Ta có rank(B) = n – m + 1 vì Pm không thuộc .
Nếu rank(B1) < n – m thì rank(B) < n – m +1 (vô lý) nên rank(B1) = n – m.
Vậy hệ (I) xác định phương trình của một m_phẳng affine.
3. Các phép biến đổi affine:
Trong tập hợp tất cả những phép biến đổi xạ ảnh của Pn, ta xét những phép biến
đổi xạ ảnh biến siêu phẳng Pn-1 thành chính nó. Mỗi phép biến đổi như vậy biến mỗi
điểm có tọa độ xạ ảnh (x ’ ’ ’
0: x1:…: xn) thành điểm có tọa độ xạ ảnh (x0 : x1 :…: xn ) sao cho nếu x ’ ’
0 = 0 thì x0 = 0 và nếu x0 ≠ 0 thì x0 ≠ 0. Muốn vậy phương trình của phép biến đổi
xạ ảnh cần phải có phương trình x ’
0 = x0 .Do đó phương trình của phép biến đổi xạ ảnh có dạng: n
 'x = a .x , i ∑ =1,2,...,n  i ij j j  =0  'x = x  0 0
Trong đó ma trận A của phép biến đổi xạ ảnh là một ma trận vuôn cấp n+1 không suy biến và có dạng: a a L a  10 11 1n a a L a  20 21 2n   A= L L L    a a L a  n0 1 n nn  1  0 L 0   
Khi đó phép biến đổi xạ ảnh nói trên của Pn sẽ sinh ra trên không gian affine An
một phép biến đổi affine. Thực vậy, ta hãy lấy một điểm X∈An có tọa độ xạ ảnh là (x0:
x1:…: xn), trong đó x0 ≠ 0. Qua phép biến đổi xạ ảnh nói trên điểm X biến thành điểm X’
có tọa độ xạ ảnh là (x ’ ’ ’
0 : x1 :…: xn ). Chuyển tọa độ xạ ảnh của X và của X’ sang tọa độ
affine ta có phép biến đổi là: 8 '
X = a .X + a .X +...+ a .X + a 1 11 1 12 2 1n n 10  '
X = a .X + a .X +...+ a .X + a x x ' 2 21 1 22 2 2n n 20 
(*) Với Xi= i , X’i= i (i=1..n). ...  x x 0 0  '
X = a .X + a .X + ...+ a .X + a  n 1 n 1 n2 2 nn n n0
Trong đó ma trận A’=(aij),( i,j=1..n) là ma trận vuông cấp n không suy biến nên ta
được phương trình (*) là phương trình một phép biến đổi affine. 4. Tỉ số kép:
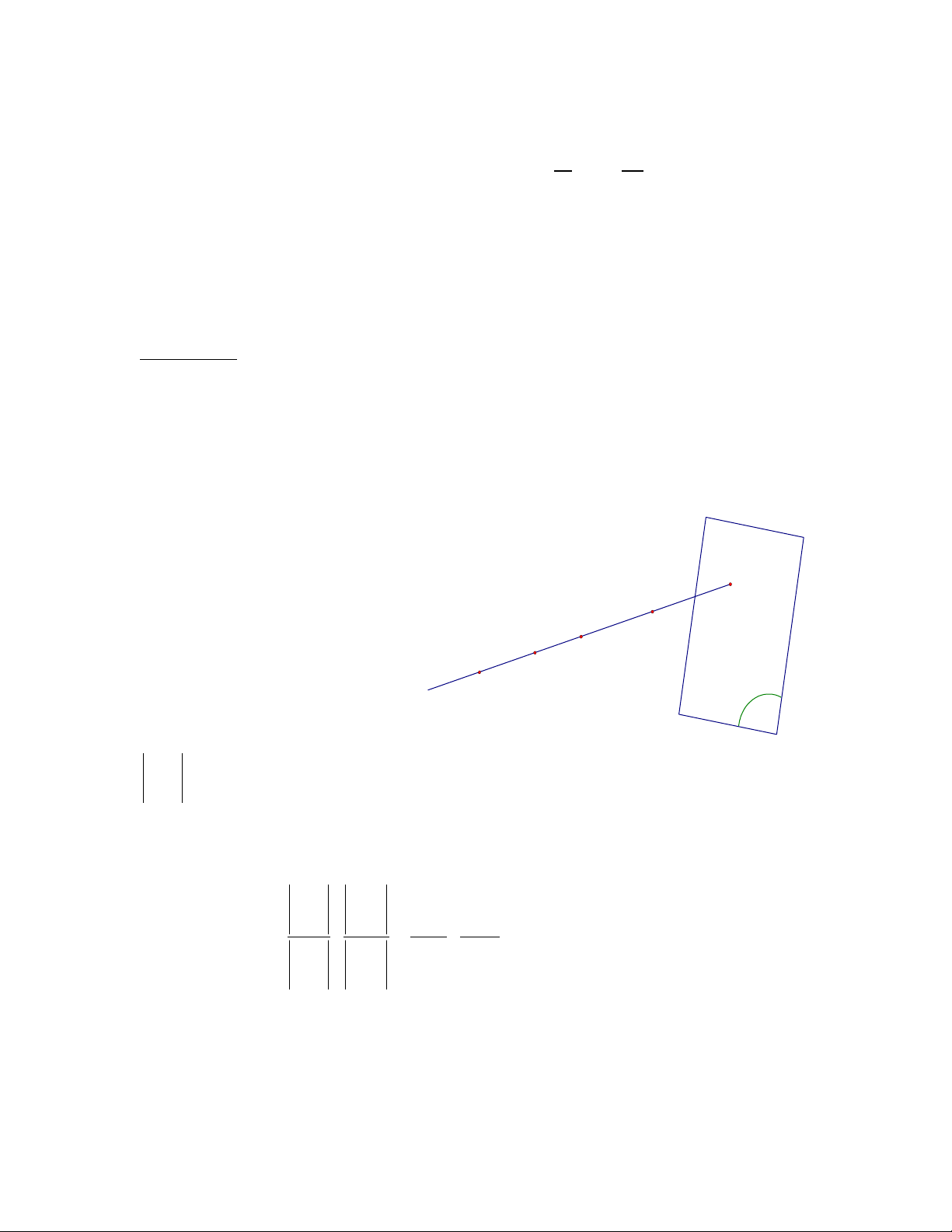
a. Giả sử A,B,C,D là bốn điểm phân biệt nằm trên một đường thẳng xạ ảnh (d) của Pn
nhưng không có điểm nào trong bốn điểm nằm trên siêu phẳng vô tận =Pn-1. Ta chọn mục tiêu xạ ảnh {E ≡ i;E}i=0..n sao cho E0
A, E1=(d) I . Khi đó các điểm B,C,D có tọa độ
biểu thị tuyến tính qua E0 và E1.
Ta có: A ≡ E0(1:0:0:…:0), E1(0:1: …:0). E1
Do đó tọa độ các điểm còn lại là: D B(1:b:0:…:0), C(1:c:0:…:0), C E0 B D(1:d:0:…:0). A (d)
Do A ≠ B nên b ≠ 0. Suy ra Pn-1 1 1 =b≠ 0. 0 b Vậy ta có 1 1 1 1 0 c 0 d c d (ABCD)= : = : . 1 1 1 1
c − b d − b b c b d
Nếu chuyển tọa độ các điểm xạ ảnh sang tọa độ affine ta có:
A(0,0,…,0), B(b,0,…,0), C(c,0,…,0), D(d,0,…,0).
Từ đó ta tính được tọa độ các vectơ sau: 9 uuur uuur uuur uuur
CA =(-c,0,…,0), CB =(b-c,0,…,0) , DA =(-d,0,…,0), DB =(b-d,0,…,0) c d Do đó (ABC)= và (ABD)= c − b d − b (ABC)
Vậy ta được (ABCD)= (ABD)
b. Nếu có một trong bốn điểm A,B,C,D là điểm vô tận, chẳng hạn là điểm D thì khi đó ta có D ≡ E1 và ta có: 1 1 1 0 0 c 0 1 c 1 c (ABCD)= : = : = . 1 1 1 0
c − b 1 c − b b c b 1 Vậy (ABCD ∞ )=(ABC).
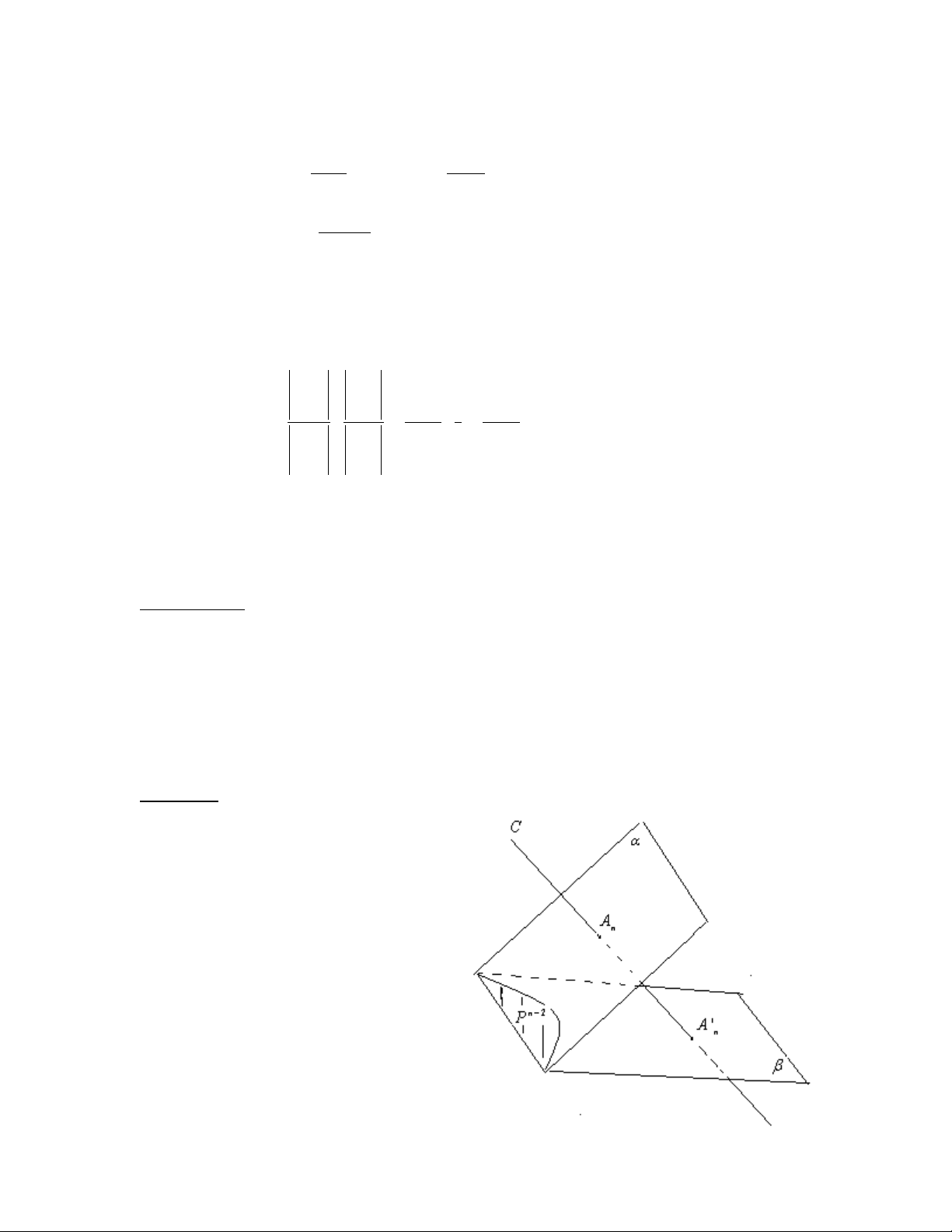
A. PHÉP CHIẾU XUYÊN TÂM I. Định nghĩa Trong không gian xạ ảnh n
P cho 2 siêu phẳng α và β và điểm n C P ∈ \ {α∪ } β Và p :α → β p X = X ∩β = X c sao cho X α ∈ thành ( ) ' c sao cho CX '
Khi đó pc được gọi là phép chiếu xuyên tâm từ α lên β với tâm C. Nhận xét:
- Phép chiếu xuyên tâm hoàn toàn
xác định bởi cặp siêu phẳng α , β và tâm chiếu C.
- Phép chiếu xuyên tâm giữ bất động
tất cả những điểm giao của hai siêu phẳng α và β. 10
II. Một số định lý 1.Định lý 1 :
Nếu coi 2 siêu phẳng α và β là 2 không gian xạ ảnh (n-1) - chiều thì phép chiếu xuyên
tâm là một đẳng cấu xạ ảnh. Chứng minh:
Gọi Wn và W 'n là 2 không gian vecto nền của α và β
Đặtδ = α ∩ β là (n-2)-phẳng
Cho {A ,..., A , A } 1 n 1 −
n hệ điểm độc lập xạ ảnh của α Trong đó: A ∈δ i ∀ =1,n −1 i A ∈α \ δ n Ta có: '
A = p (A ) n c n Hệ '
{A ,..., A , A } 1 n 1 − độc lập xạ ảnh. n Thật vậy: nếu '
{A ,..., A , A } 1 n 1 − phụ thuộc xạ ảnh n Thì ' '
A ∈δ ⇒ A ∈α (vô lý.!) ( Do A ,..., A n n 1 n 1
− độc lập xạ ảnh trong δ ) Gọi e ∀ =
i là vector đại diện của A i 1, n i '
e là vector đại diện của ' A n n
e là vector đại diện của C Ta có: '
C, A , A thẳng hàng n n Suy ra: '
e = ae + be n n Nếu: ' '
• a = 0 ⇒e = .
b e ⇒ A ≡C n n ' '
• b =0 ⇒e = .
a e ⇒ A ≡ A n n n n 11
Vậy a, b ≠ 0 chọn a=1 suy ra: '
e = e + be n n
ε = {e ,...,e ,e } 1 n 1 − n Đặt
là 2 cơ sở của Wn và W 'n '
ε ' = {e ,...,e ,e } 1 n 1 − n Do dim n =dim 'n W W
suy ra tồn tại duy nhất đẳng cấu tuyến tính ϕ: n → 'n W W sao cho ' (
ϕ e ) = e i ∀ =1, n 1 − và ( ϕ e ) = e i i n n
Ta sẽ chứng minh X ∈α có vector đại diện x thì sẽ có p (X ) = X '∈ β c vector đại
diện là ϕ(x) = x '
Lấy X ∈α có vector đại diện x . Suy ra: p (X ) = X '∈ β c Do X α
∈ ⇒x = x e + x e +....+ x e 0 0 1 0 n n ⇒ (
ϕ x) = x ϕ e + x ϕ e +....+ x ϕ e 0 ( 0 ) 1 ( 0 ) n ( n ) ' ⇒ (
ϕ x) = x e + x e +....+ x e 0 0 1 0 n n ⇒ (
ϕ x) = x e + x e +....+ x e +be 0 0 1 0 n ( n ) ⇒ (
ϕ x) = x e + x e +....+ x e + x be 0 0 1 0 n n n ⇒ (
ϕ x) = x +ce (c = x b) n Suy ra: (
ϕ x), x,e phụ thuộc tuyến tính nên ba điểm mà (
ϕ x), x,e đại diện thẳng
hàng, tức ϕ(x) đại diện cho một điểm nào đó thuộc đường thẳng CX . Mặt khác: ( ϕ ) W ∈ 'n x và CX β ∩ = X ' Dẫn đến: (
ϕ x) là vector đại diện của X’
Vậy ta đã chứng minh pc được cảm sinh từ đẳng cấu tuyến tính ϕ sao cho
X ∈α có vector đại diện x thì sẽ có p (X ) = X '∈ β c vector đại diện là
ϕ(x) = x ' . Do đó pc là một đẳng cấu xạ ảnh. 2.Định lý 2: 12
Cho 2 siêu phẳngα,α ' trong n n 1
P [V + ] thì ánh xạ xạ ảnh f :α → α ' là một phép
chiếu xuyên tâm khi và chỉ khi mọi phần tử của α ∩α ' là tự ứng. Tức là M
∀ ∈α ∩α ', f (M ) = M Chứng minh: Cách 1:
Rõ ràng phép chiếu xuyên tâm biến mọi điểm M ∈α ∩α ' thành chính nó.
Ngược lại: giả sử f :α → α ' là ánh xạ xạ ảnh mà M
∀ ∈α ∩α ', f (M ) = M Nếu:
+ α = α ' thì f = idα và f là phép chiếu xuyên tâm với tâm C ∉α + α ≠ α '
Đặt W,W’ lần lượt là không gian vector nền của α và α '
Và Z = W ∩W ' γ → n ² n 1 + Gọi: : W
W ' là đẳng cấu tuyến tính cảm sinh bởi φ với P = [ ϕ V ] lúc đó: f = ϕ ( γ ) Nhận xét: f = id ⇒ = ≠ ∩ ∩ γ ∩ λid , ∩ λ 0 |α α ' |α α ' |W W ' |W W '
( Giờ ta sẽ chứng minh với 3 điểm thẳng hàng M α ∈ \ (α∩ '
α ) , M ' = f (M ) ∈ ' α \ (α∩ ' α ) , C ( ∉α∪ ) β thì với X α ∈
và f ( X ) =X ' ∈ '
α cũng đi qua điểm C. từ đó kết luận C là tâm chiếu ). Lấy M α ∈ \ (α α
∩ ') có w∈W \ Z làm vector đại diện Suy ra: γ( )
w =w ' là vector đại diện của f (M ) =M ' α ∈ '\ (α α ∩ ')
Khi đó: W = Z ⊕ < w > , W ' = Z ⊕< w' > và {w,w’} độc lập tuyến tính.
Xét điểm C ∈ MM ' có vector đại diện ( w'− w λ ) ( ∉ W W ∪ ') . Lấy X α
∈ có vector đại diện là x
f (X ) = X '∈α ' có vector đại diện là γ (x) = x '. Ta có: 13
x = z + aw (z ∈Z)
⇒γ (x) = γ ( z) +γ ( aw)
⇒γ (x) = λz + aw'
⇒γ (x) −λx = a ( λw − w')
Điều này nói cho chúng ta biết: X, X’ đi qua C . Tức là f là phép chiếu xuyên tâm từ C lên α lên α ' . Cách 2: Gọi Pn-2 = α ∩ β.
+) Chiều thuận: f là một phép chiếu xuyên tâm thì hiền nhiên nó giữ bất động những điểm nằm trên Pn-2.
+) Chiều đảo: f là ánh xạ xạ ảnh có tính chất f(M) = M với mọi M thuộc Pn-2 cần chứng
minh f là phép chiếu xuyên tâm.
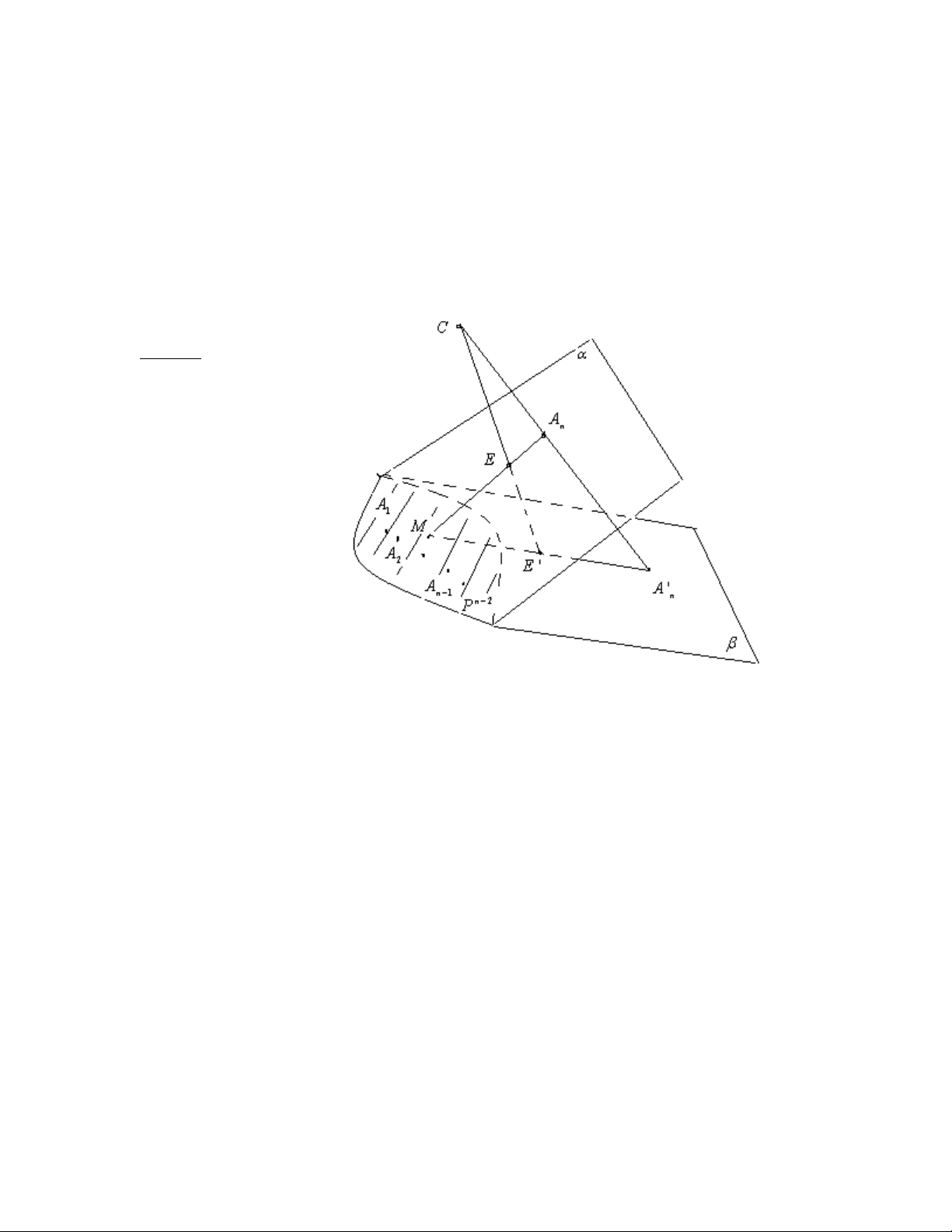
Trong α chọn một mục tiêu xạ ảnh là {A1, A2, …An-1,An, E} với A1, A2, …,An-1 thuộc
Pn-2, ta có An, E không thuộc Pn-2 , gọi A’n = f(An) và E’ = f(E).
Trên β ta có mục tiêu là {A1, A2, …An-1,A’n, E’} là ảnh của mục tiêu
{A1, A2, …An-1,An, E} qua f. Gọi M = AnE ∩ β thì M thuộc Pn-2 do f(M) = M nên
đường thẳng A’nE’ cũng qua M. Trong mặt phẳng xạ ảnh tạo bởi hai đường thẳng AnE và
A’nE’ gọi C là giao điểm của AnA’n và EE’. Gọi f ’ là phép chiếu xuyên tâm có cơ sở nền
là α và β với tâm chiếu là C. Ta có: f ’(Ai) = Ai với i = 1,2,…,n-1 do Ai với i = 1,2,…,n-1
nằm trên Pn-2 và f ’(An) = A’n và f ’(E) = E’. Do sự xác định duy nhất của phép biến đổi xạ
ảnh xác định bởi {A1, A2, …An-1,An, E} và {A1, A2, …An-1,A’n, E’} nên f ≡ f ’.
Vậy f là phép chiếu xuyên tâm. 14 3.Định lý 3: Trong n
P với cho hai siêu phẳng α vàα ' . Giả sử f :α → α ' là một ánh xạ xạ ảnh,
không phải là phép chiếu xuyên tâm. Khi đó ta có thể phân tích f thành tích của m phép
chiếu xuyên tâm với m ≤ n +1 Chứng minh:
• Xét trường hợpα ≠ α ' và trong α ∩ α ' có một p-phẳng β mà mọi điểm
β của đều tự ứng đối với f ( 0 ≤ p < n − 2) .
Vì f không phải là phép chiếu xuyên tâm nên β ≠ α ∩α ' .
Lấy một điểm A∈α nhưng A α
∉ ' , điểm I ∈β , điểm B trên đường thẳng IA mà không trùng với I, A.
Đặt A’=f(A), B’=f(B), thì A’B’ đi qua I.
Do đó AA’ và BB’ cắt nhau tại một điểm C nào đó.
Lấy một siêu phẳng α1 chứa β và A nhưng không chứa A’ thì chứa cả B. Gọi g :α ' → α 1
1 là phép chiếu xuyên tâm bởi tâm C.
Khi đó, tích g o f :α → α 1
1 là một ánh xạ xạ ảnh,
(p+1)-phẳng tổng β + A nằm trên giao α ∩α1 và mọi điểm của (p+1)-phẳng tổng
β + A đều bất động đối với g o f 1
(vì các điểm trên β đều bất động khi qua f và g1
nên β bất động qua g o f 1
và A qua f biến thành A’ mà A’ qua g1 biến thành giao điểm
của CA’ với α1 tức là điểm A vậy A bất biến qua g o f , mọi điểm thuộc β + A đều 1
biểu thị qua p+1 điểm độc lập trong β và A suy ra nó bất động ). Nếu g o f β + A ≠ α ∩α 1
không phải là phếp chiếu xuyên tâm ( tức là 1 ) thì cho g o f g :α → α 1
đóng vai trò như f ban đầu ta lại có phép chiếu xuyên tâm 2 1 2 sao 15 cho g g o o f :α →α 2 1
2 giữ bất động mọi điểm của một (p+2)- phẳng nào đó nằm trong α ∩α2 .
Tiếp tục cách làm như thế sau một số hữu hạn bước ta có thể tìm được các phép chiếu
xuyên tâm g :α ' → α , g :α → α ,...., g :α → − α 1 1 2 1 2 p p 1 p sao cho tích h = g . o ... g o o f :α → α q 1
q giữ bất động các điểm của một (n-2)-phẳng.
Do đó h là một phép chiếu xuyên tâm. Suy ra 1 − 1 f g .... g− = o o h o
q + p ≤ n + 1 q
là tích của q+1 phép chiếu xuyên tâm. Vì 2
nên q +1 ≤ n − p −1 ≤ n −1.
• Xét trường hợp α ≠ α ' và trong α ∩α ' không có điểm nào tự ứng dối
với f. Lấy một điểm C ∈α , đặt C’=f(C) rồi lấy một siêu phẳng α ' đi qua
C, không đi qua C’ mà α ' ≠ α . Gọi s :α ' → α ' là phép chiếu xuyên tâm
bởi tâm là một điểm U ∈CC ' , thì s o f :α → α ' là một ánh xạ xạ ảnh có
điểm C ∈α ∩α ' tự ứng . Áp dụng trường hợp trên suy ra là tích của một
số ≤ n −1 phép chiếu xuyên tâm. Do đó f là tích của một số n ≤ phép chiếu xuyên tâm.
• Cuối cùng xét trường hợp α = α ' . Chỉ cần lấy một phép chiếu xuyên tâm
r :α ' →α '' nào đó thì r of :α → α '' là một ánh xạ xạ ảnh rơi vào một
trong hai trường hợp trên. Suy ra f là tích của một số ≤ n +1 phép chiếu xuyên tâm.
III.Đối Ngẫu Của Phép Chiếu Xuyên Tâm:
Cũng như nhiều các khái niệm, định lý trong hình học xạ ảnh thì phép chiếu xuyên tâm
cùng với các định lý bài tập về nó thì đều có đối ngẫu. Do tính đối ngẫu cho nên ở đây 16
chúng tôi chỉ nêu khái niệm và định lý mà không chứng minh lại. Và hãy xem như là một bài tập 1 Định nghĩa: Trong không gian xạ ảnh n
P cho 2 điểm O và O’ và siêu phẳng n α ∈ P \ OO'
Gọi B là bó đường thẳng tâm O , B’ là bó đường thẳng tâm O’
Và p : B → B ' = α
theo quy tắc ∀m ∈ B biến thành p (m) m ' α sao cho
(α ∩m) O' = m'
Khi đó pα được gọi là phép chiếu xuyên siêu phẳng từ O lên O’ với cơ sở α và 2 tâm O,O’
n=2 phép chiếu xuyên siêu phẳng được gọi lại là phép chiếu xuyên trục.
2. Một số định lý:
Định lý 1: phép chiếu xuyên siêu phẳng là một ánh xạ xạ ảnh.
Định lý 2: Điều kiện cần và đủ để một ánh xạ xạ ảnh là phép chiếu xuyên siêu phẳng là
đường nối hai tâm phải tự ứng.
Định lý 3: Một ánh xạ xạ ảnh không phải là phép chiếu xuyên xạ ảnh đều có thể phân tích
thành không quá n+1 phép chiếu xuyên siêu phẳng.
3. Bài tập áp dụng.
Hãy phát biểu các bài tập ở mục 1.4 dưới dạng bài toán đối ngẫu rồi chứng minh bằng
phép chiếu xuyên siêu phẳng.
I V. Phép chiếu xuyên tâm và đối ngẫu của nó trong P 2 : 1. Định nghĩa : a) Định nghĩa 1:
Trong mặt phẳng xạ ảnh, một ánh xạ xạ ảnh giữa hai hàng điểm gọi là phép chiếu
xuyên tâm (phép phối cảnh) nếu các đường thẳng nối các điểm tương ứng luôn đi qua
một điểm C cố định, điểm C được gọi là tâm phối cảnh. 17
b) Đối ngẫu của định nghĩa 1:
Trong mặt phẳng xạ ảnh, một ánh xạ xạ ảnh giữa hai chùm đường thẳng được gọi là
phép chiếu xuyên trục (phép phối cành) nếu giao điểm của các cặp đường thẳng tương
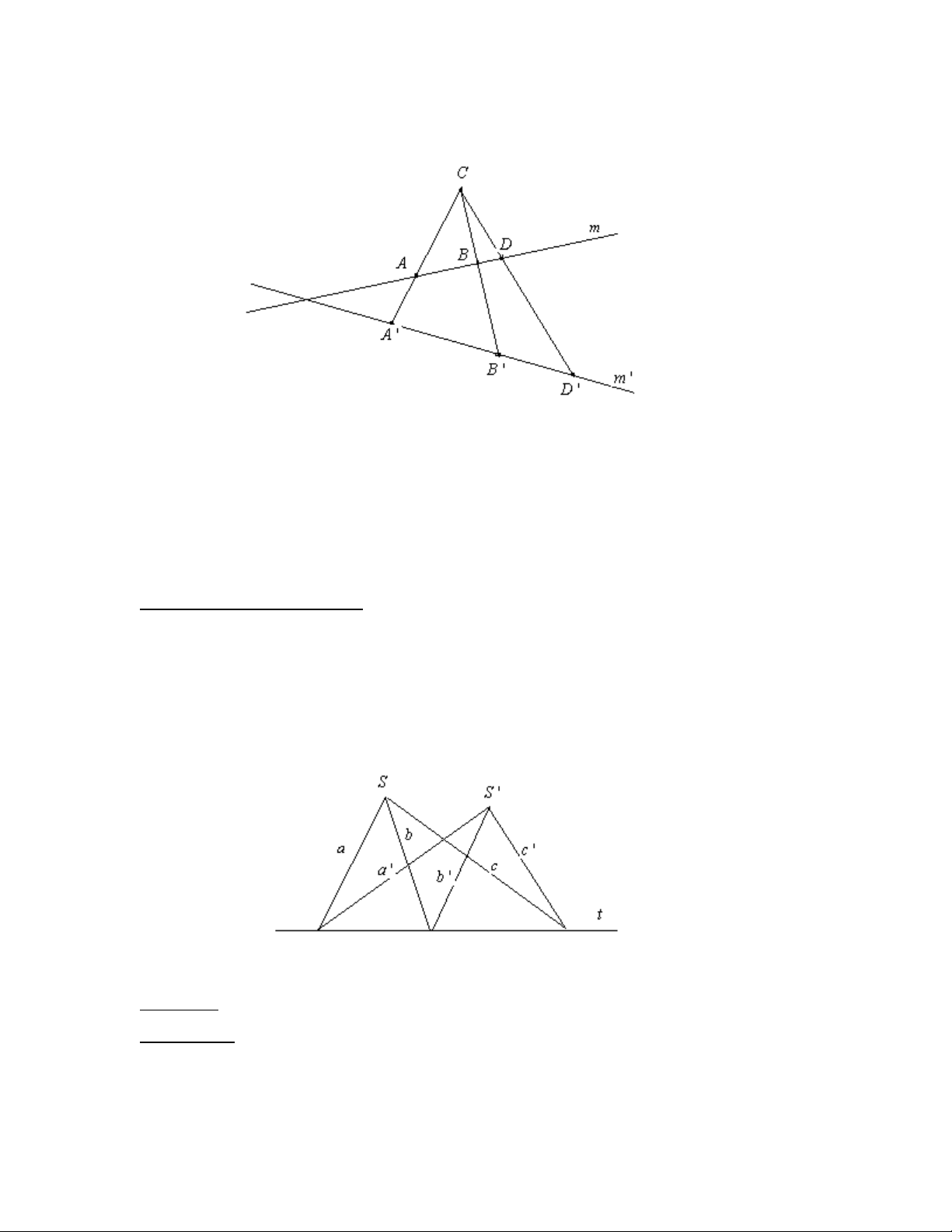
ứng luôn nằm trên một đường thẳng t cố định, đường thẳng t được gọi là trục phối cảnh. 2.Định lý: a) Định lý 1:
Điều kiện cần và đủ để một ánh xạ xạ ảnh f giữa hai hàng điểm {m} và {m’} là
phép chiếu xuyên tâm là giao điểm O của hai giá tự ứng, tức f(O) = O. 18
b) Định lý đối ngẫu của định lý 1:
Điều kiện cần và đủ để một ánh xạ xạ ảnh f giữa hai chùm đường thẳng {S} và
{S’} là phép chiếu xuyên trục là đường thẳng nối S và S’ tự ứng, tức f(SS’) = SS’. V . M ột số áp dụng:
Áp dụng 1 : Chứng minh định lý papus bằng phép chiếu xuyên tâm
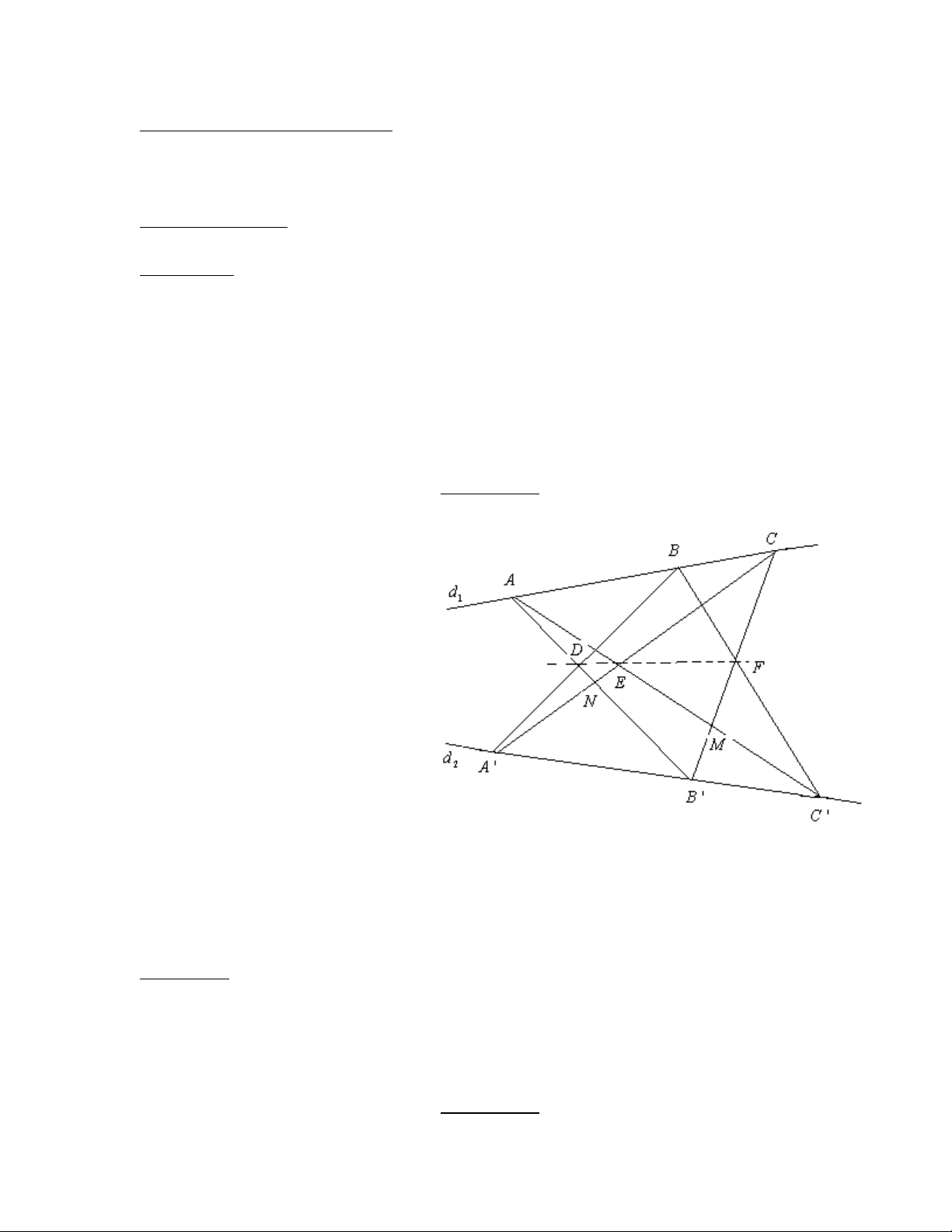
Trong mặt phẳng xạ ảnh cho 2 đường thẳng phân biệt d , d 1
2 cắt nhau tại O. Trên d1 cho 3 điểm phân biệt ,
A B,C ≠ O . Trên d2 cho 3 điểm phân biệt A’, B’, C’ khác O . Gọi D,E,F
lần lượt là giao điểm của BC’ và B’C, CA’ và AC’ , AB’ và A’B. Khi đó D,E,F thẳng hàng. Chứng minh:
Gọi M = AC '∩ B 'C và
N = AB '∩ A'C
Xét các phép chiếu xuyên tâm
h : AB ' → d1 với tâm A’ và
g : d → B 'C 1 với tâm C’
Đặt f = gh : AB ' → B 'C
f biến B’ thành B’ => f là phép
chiếu xuyên tâm từ AB’ đến B’C.
Ngoài ra, f lần lượt biến A,F,N lần lượt thành M,D,C.
Vì vậy, AM ( ≡ AC ') ,DF, NC ( ≡ A'C) đồng quy tại tâm chiếu của f.
Mà AC '∩ A'C = E suy ra D,E,F thẳng hàng.
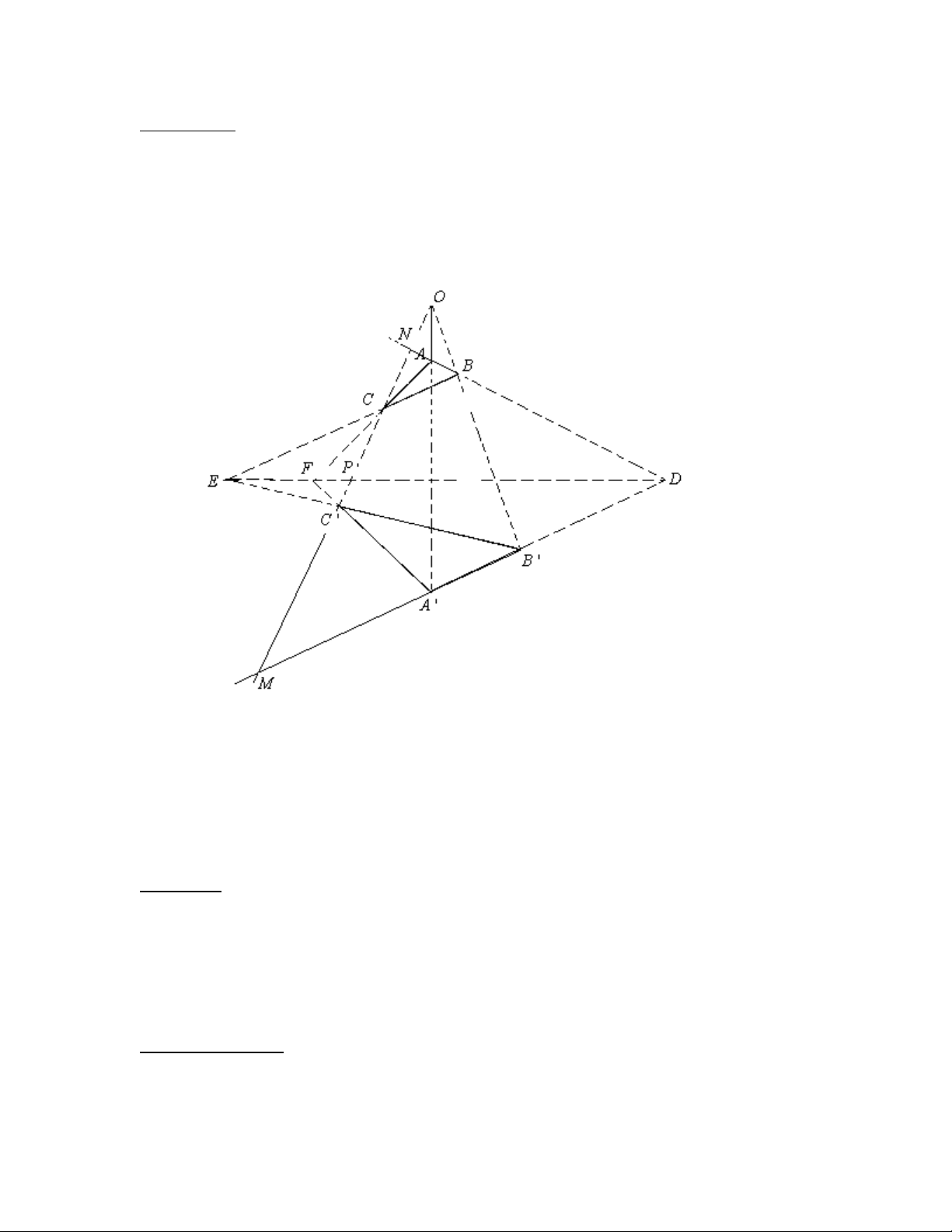
Áp dụng 2: (Chứng minh định lý Desargues thứ I )
Trong mặt phẳng xạ ảnh cho hai tam đỉnh ABC và A’B’C’.
D = AB ∩ A' B ', E = BC ∩ B 'C ', F = AC ∩ A'C '
Chứng minh D,E,F thẳng hàng khi và chỉ khi AA’,BB’,CC’ đồng quy. Chứng minh: 19 Chiều thuận:
Gọi M = CC '∩ A' B ', N = CC '∩ DF, P = CC '∩ AB .
Xét 2 phép chiếu xuyên tâm sau:
h : AB → DF với tâm C biến A,B,D,P thành F,E,D,N
g : DF → AB ' với tâm C’ biến F,E,D,N thành A’,B’,D,M Đặt f = g h
o : AB → A' B ' là phép chiếu xuyên tâm
(Do là tích của các phép chiếu xuyên tâm và f giữ bất động D = AB ∩ A' B ' )
Do đó: AA’, BB’,MP ( ≡ CC ') phải đồng quy tại tâm chiếu O của f.
Suy ra: AA’, BB’, CC’ đồng quy. Chiều đảo:
Xét hai tam đỉnh DBB’ và FCC’ có A = DB∩FC, A’ = DB’∩FC’, O = BB’∩CC’ do O,
A, A’ thẳng hàng (do AA’, BB’, CC’ đồng qui tại O ) nên áp dụng chiều thuận của định
lý Desargues thứ I thì BC, B’C’, DF đồng qui tại E, tức D, E, F thẳng hàng. Bài Tập áp dụng:
Chứng minh các bài toán sau bằng phép chiếu xuyên tâm: 20