Tiểu Luận Cuối Kỳ: Đề Số 3 Tính Toán Nhíp | Môn Thiết kế ô tô - Đại học Sư phạm Kỹ thuật Thành phố Hồ Chí Minh

lOMoAR cPSD| 58797173 lOMoAR cPSD| 58797173
ĐỀ SỐ 3: Tính toán, kiểm tra nhíp đặt dọc, dạng nhíp Công-xôn ở cầu sau một xe tải 2 cầu. Cầu
sau chủ động có tải trọng tĩnh tác dụng lên nó là G2. Hãy tính toán ứng suất xuất hiện ở nhíp
theo 3 chế độ tải trọng đặc biệt sau đây:
1. Trường hợp 1: Xi = 0, Y = 0 (Yi = 0), Zi = Zi max = Zbx 2.
2. Trường hợp 2: Xi = Xi max , Y = 0, Zi = Zbx
3. Trường hợp 3: Xi = 0, Y = Ymax = m2G2φy , Zi = Zbx lOMoAR cPSD| 58797173
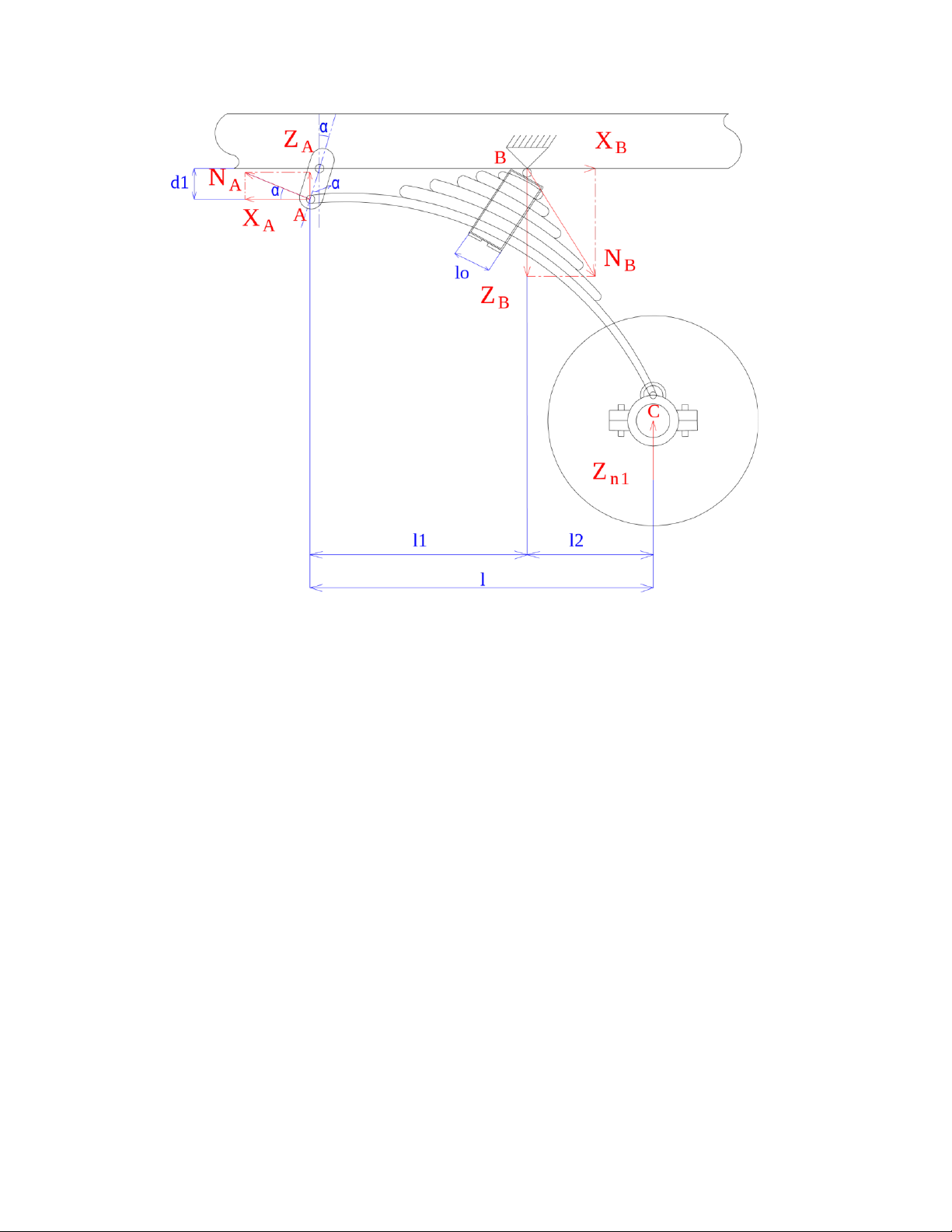
CHƯƠNG 1: CHÚ THÍCH CÁC ĐẠI LƯỢNG -
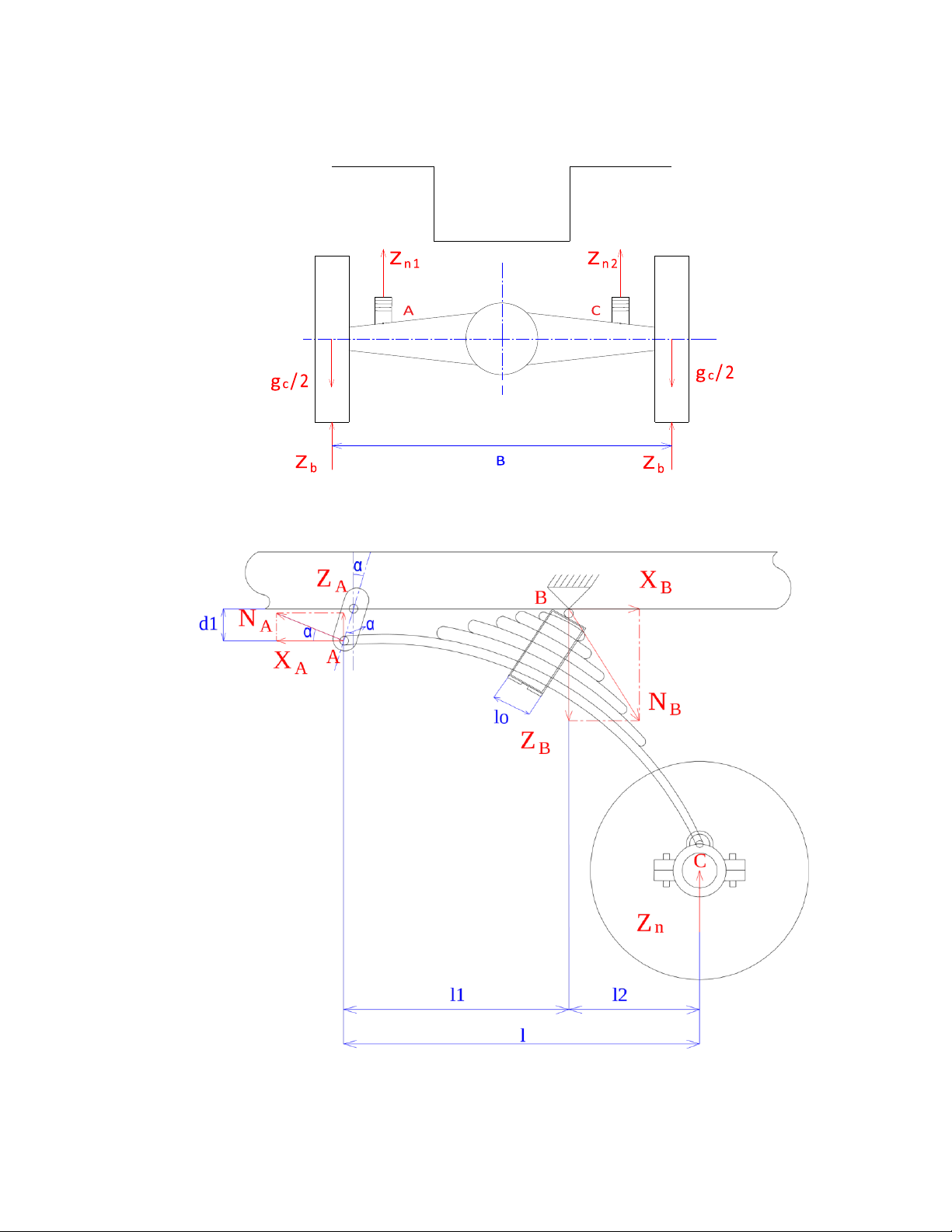
: lần lượt là các lực thành phần của theo phương ngang và phương thẳng đứng tại điểm A,B (Đơn vị: N) -
: phản lực tổng hợp tác dụng lên nhíp (Đơn vị: N) -
: lần lượt là các phản lực tiếp tuyến, ngang, pháp tuyến tại bánh xe (Đơn vị: N) -
: lực thẳng đứng tác dụng lên nhíp (Đơn vị: N) -
: trọng lượng phần không được treo (Đơn vị: N) -
: phản lực từ mặt đường tác dụng lên bánh xe (Đơn vị: N) -
: góc nghiêng của tai nhíp so với mặt phẳng đứng (Đơn vị: độ) -
: khoảng cách giữa các quai nhíp (Đơn vị: m) -
, l: lần lượt là chiều dài nửa nhíp bên trái, bên phải, chiều dài toàn bộ nhíp (Đơn vị: m) -
b: chiều rộng lá nhíp (Đơn vị: m) -
: chiều dày của lá nhíp thứ i (Đơn vị: m) -
hc: chiều dày của lá nhíp chính (Đơn vị: m) -
: ứng suất uốn (Đơn vị: N/ -
σk: ứng suất kéo (Đơn vị: N/ -
: moment chống uốn của mặt cắt ngang (Đơn vị: N.m) -
: lực thẳng đứng tác dụng lên cầu sau (Đơn vị: MN) -
Y: phản lực tổng hợp của lực ngang tác dụng lên xe (Đơn vị: kN) - : hệ số bám ngang -
: hệ số thay đổi tải trọng lên cầu sau. - : lực kéo (Đơn vị: N) - : lực phanh (Đơn vị: N) -
X: phản lực của lực kéo hoặc lực phanh trong trường hợp kéo hoặc phanh tương ứng (Đơn vị: N) -
B: chiều rộng cơ sở (Đơn vị: m) - B1:khoảng cách giữa hai nhíp. -
d1: là khoảng cách từ chốt nhíp phía trên tới chốt nhíp dưới tại A (Đơn vị: m) -
d2: là khoảng cách từ chốt nhíp dưới tại A tới mặt đường (Đơn vị: m) - d: là
khoảng cách từ chốt nhíp phía trên tới mặt đường, d=d 1+d2 (Đơn vị: m) - p: là
khoảng cách từ trọng tâm xe đến mặt phẳng tựa của nhíp. lOMoAR cPSD| 58797173
CHƯƠNG 2: TÍNH TOÁN NHÍP ĐẶT DỌC CÔNG XÔN I.
TRƯỜNG HỢP 1: Xi = 0, Y = 0 (Yi = 0), Zi = Zi max = Zbx. - Ta có: lOMoAR cPSD| 58797173
- Chiếu lên hệ quy chiếu, ta lại có: Zn = ZB – ZA, mà XA = XB = - Xét phương trình cân
bằng moment tại điểm A:
ZB . l1 + XB . d1 – Zn . l = 0 => ZB .l1= Zn . l – XB . d1
=> ZB = = (1) (do XA = XB = )
- Xét phương trình cân bằng moment tại điểm B:
Ta được: ZA . l1 + XA .d1 – Zn . l2 = 0
=> ZA . l1 + .d1 – Zn . l2 = 0 (do XA = XB = )
=> ZA Zn .l2 = 0 => ZA = = (2)
Thay biểu thức số (2) vào biểu thức số (1) ta được: ZB = =
- Xét moment uốn ứng với nửa nhíp bên trái và bên phải:
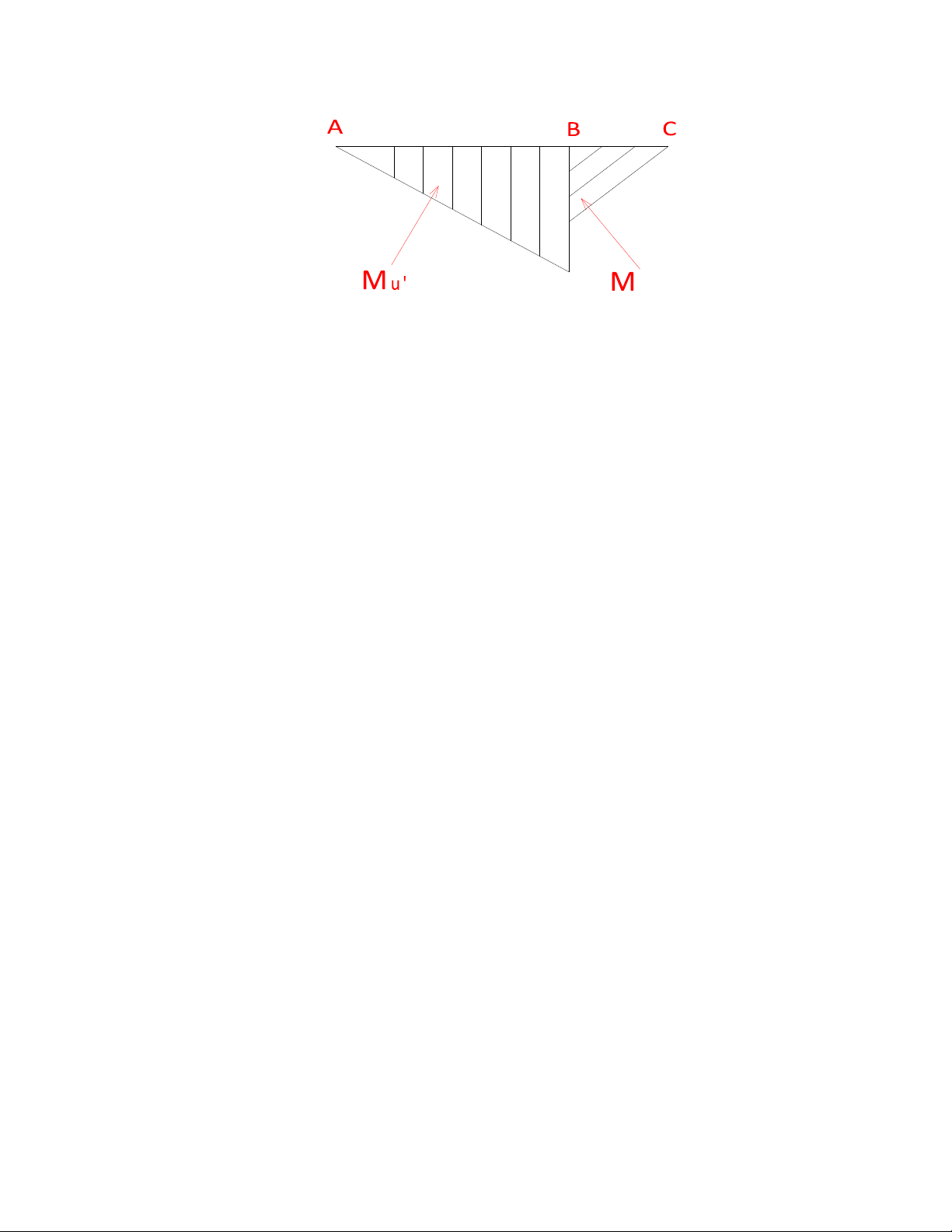
Mu’ = ZA . l1 và Mu” = Zn . l2 Mà ta có Mà
Do moment uốn Mu” lớn hơn, tính toán ứng suất tại B theo moment : MuB = Mu” = Zn . l2
=> Ứng suất uốn lá nhíp: hi b
Ta có công thức ứng suất uốn: σu = , với Wui =
=> σu = σu ], ta cần phải chọn ứng suất phù hợp để thỏa mãn điều kiện bền.
- Ngoài ra, lá nhíp chính ngoài chịu ứng suất uốn σu còn tồn tại σk σk = σk ]
Cần chọn ứng suất thỏa mãn điều kiện bền.
- Từ đó ta có biểu đồ moment: A B C lOMoAR cPSD| 58797173 M u' M u" lOMoAR cPSD| 58797173 II.
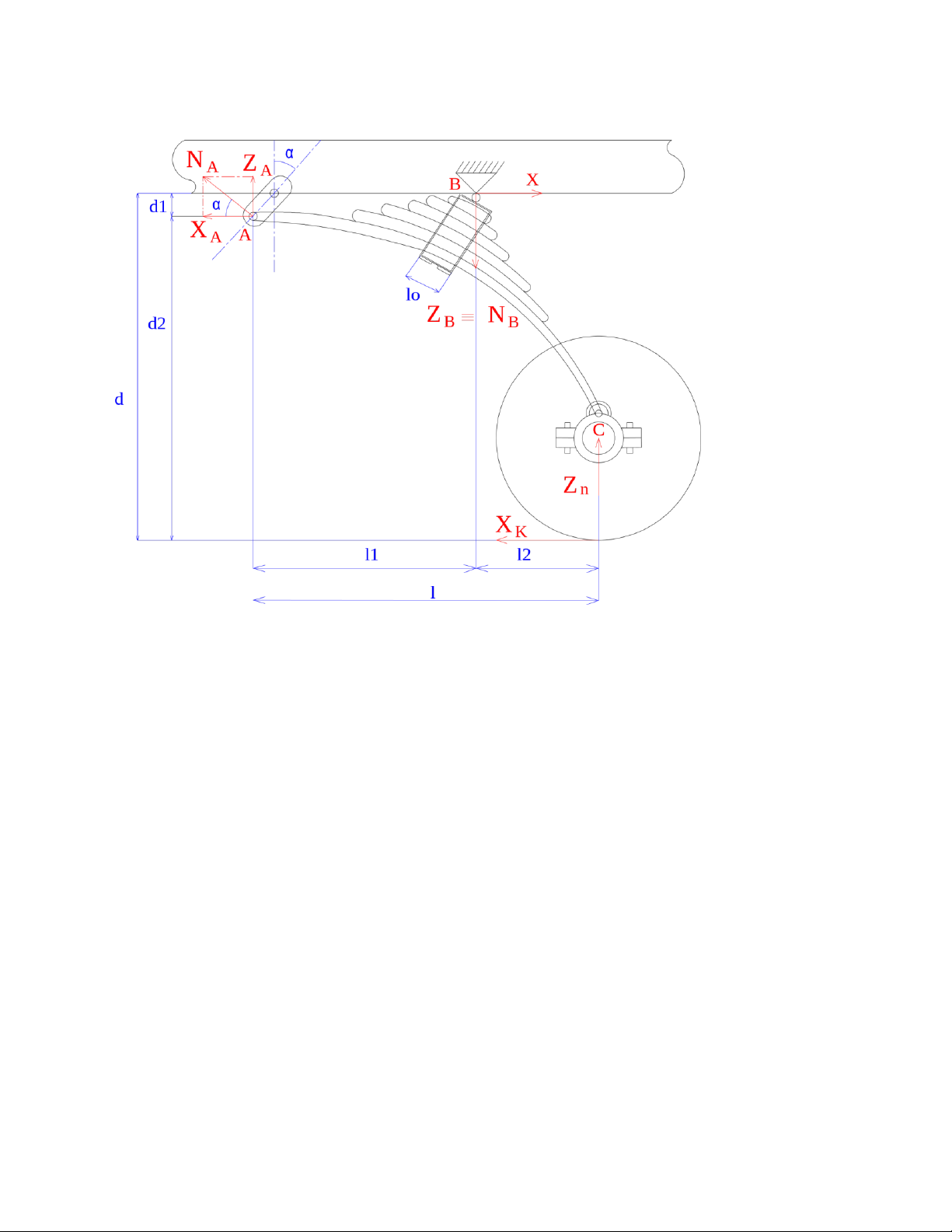
TRƯỜNG HỢP 2: Xi = Ximax ; Y = 0 ; Zi ≠ 0 - KHI TRUYỀN LỰC KÉO Khi truyền lực kéo: , -
Xét phương trình cân bằng moment tại điểm B: => ) = (2.1) -
Xét phương trình cân bằng moment tại điểm A: => => -
Thay biểu thức (2.1) vào ta được: lOMoAR cPSD| 58797173 - = = = = Mà => => -
Ứng suất chính tác dụng lên nhíp bên trái: =>
Ứng suất chính tác dụng lên nhíp bên phải: => -
gây ra ứng suất uốn phụ: -
Ứng suất uốn toàn bộ tác dụng lên nhíp:
Ứng suất uốn toàn bộ tác dụng lên nhíp bên trái: =+=
Ứng suất uốn toàn bộ tác dụng lên nhíp bên phải: = ≤ [ Do < - Ta có đồ thị moment: A B C M u' M u" lOMoAR cPSD| 58797173
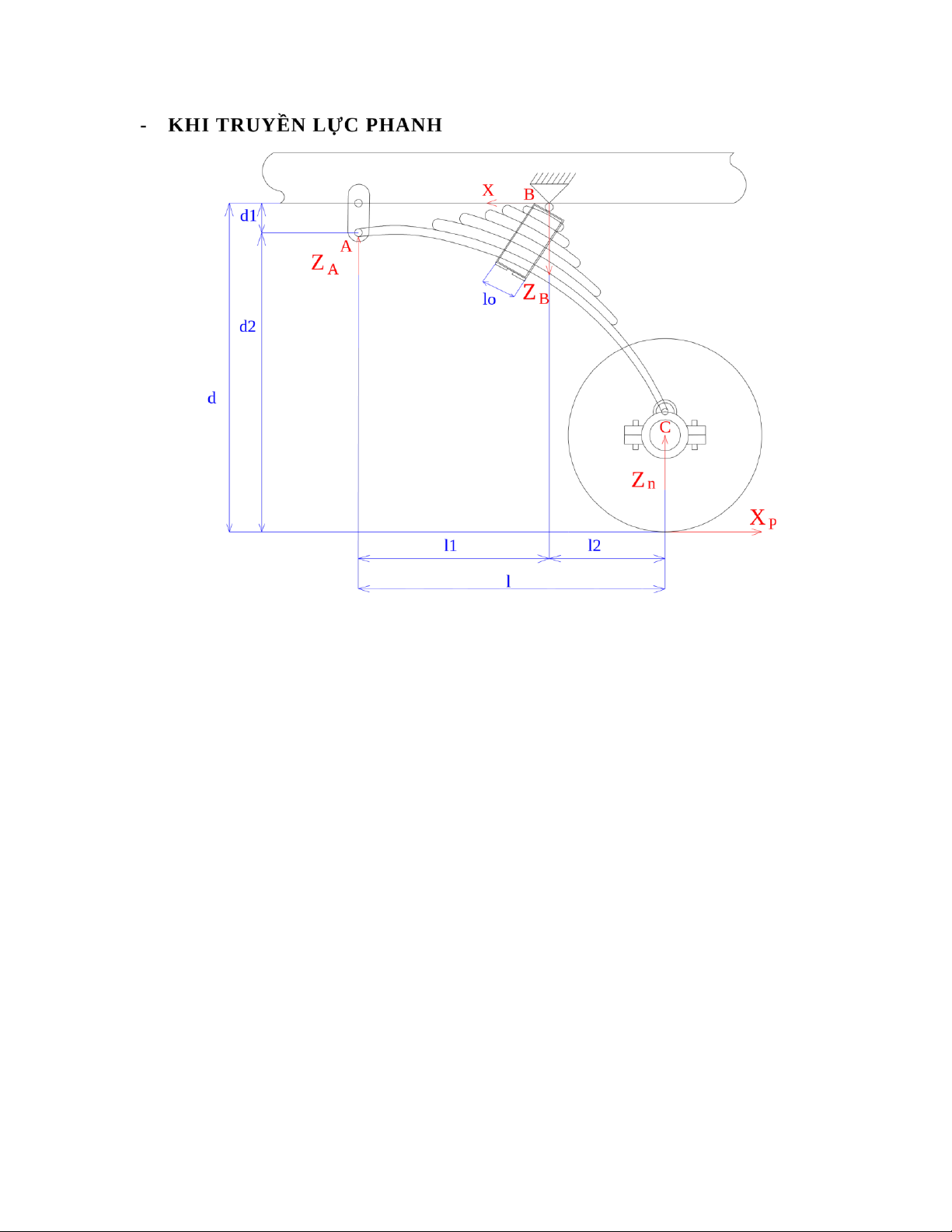
- Khi truyền lực phanh cực đại Xp = Xpmax , Y = 0, Zi = Zbx - Tai nhíp ở vị trí thẳng đứng: = 00 lúc đó ta được: XA = XB = 0 Zn = ZB – ZA X = Xp
- Xét phương trình cân bằng moment tại điểm B:
ZA.l1 – Zn.l2 – Xp.d = 0 => ZA.l1 = Zn.l2 + Xp.d => ZA =
- Xét phương trình cân bằng moment tại điểm A:
ZB.l1 – X.d1 – Zn.l – Xp.d2= 0 => ZB.l1 = Xp.d1 + Zn.l + Xp.d2 (do X = Xp) = (do d1 + d2 = d)
- Moment uốn do ZA gây ra trên nhíp bên trái có giá trị bằng: Mu’ = ZA. = Zn.l2 + Xp.d
- Moment uốn do Zn gây ra trên nhíp bên phải có giá trị bằng: Mu” = Zn.
- Do Mu’ > Mu” nên ta có biểu đồ moment như sau: lOMoAR cPSD| 58797173 u "
- Các moment này gây ra ứng suất uốn chính: Ta có: Wui = .b.
+ Ứng suất chính tác dụng lên nửa nhíp bên trái: uc’ = => uc’ =
+ Ứng suất chính tác dụng lên nửa nhíp bên phải: uc” = =
- Lực Xp gây ra ứng suất phụ: up = =
=> Ứng suất uốn toàn bộ: u uc +up
- Ứng suất uốn bên trái: u’ uc’ +up = + =
- Ứng suất uốn bên phải: u” uc” +up = + =
Dễ dàng thấy: u’ - u” = - => u’ > u”
- khi tính toán bền ta cần phải đảm u’ σu ] để thỏa mãn điều kiện bền. lOMoAR cPSD| 58797173 III.
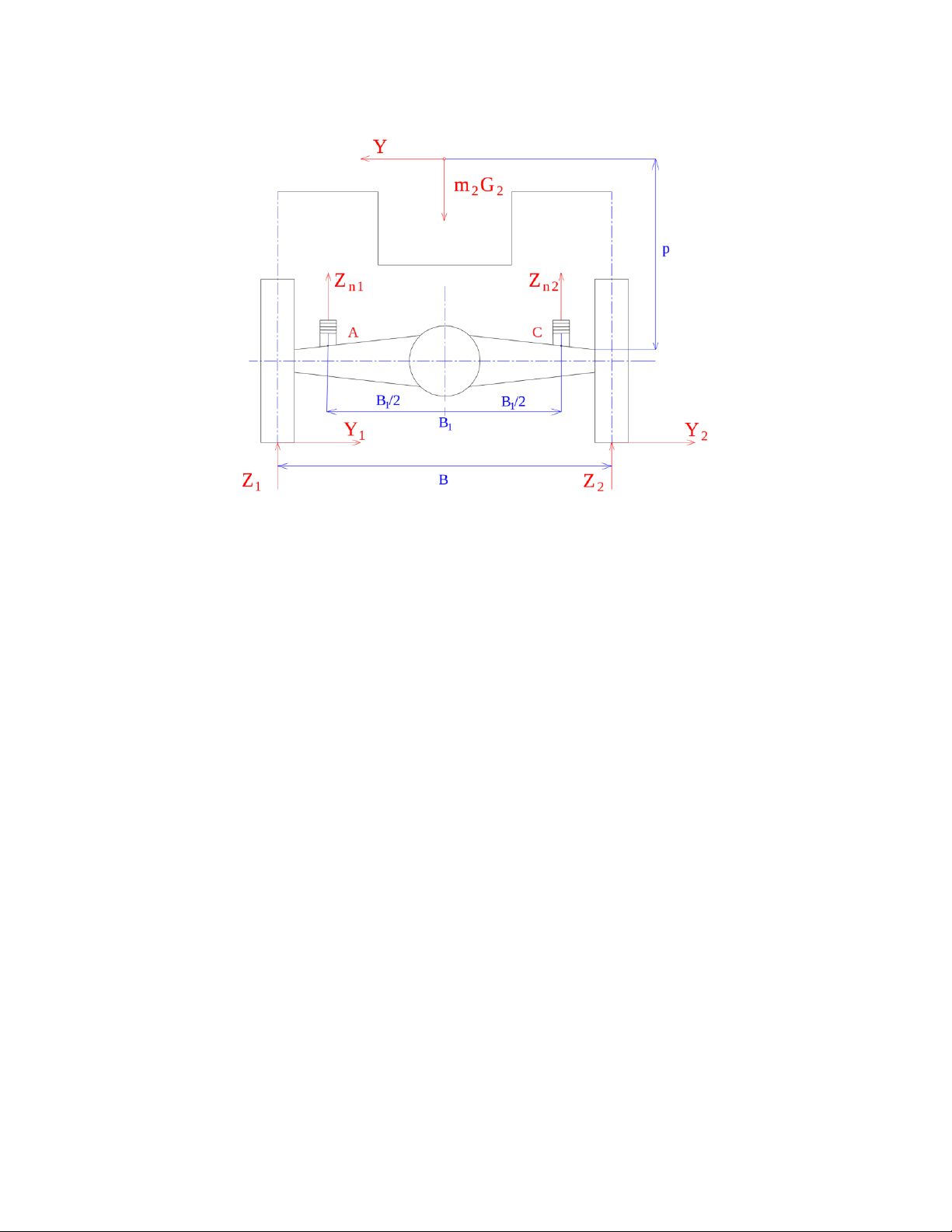
TRƯỜNG HỢP 3: Xi = 0; Y = Ymax = m2G2 y; Zi = Zbx
- Trong trường hợp xe bị trượt ngang, nhíp bị uốn, kéo và nén, tuy nhiên ứng suất nén và
kéo tương đối nhỏ nên ta bỏ qua trong lúc tính toán. Nửa nhíp bên phải sẽ chịu tổng số
2 moment uốn do Z2 và Y2 sinh ra. Nửa nhíp trái sẽ chịu hiệu số 2 momen uốn sinh ra do Z1 và Y1.
- Xét phương trình cân bằng moment tại điểm C:
Ta được: Zn1.B1 - Y.p - = 0 => Zn1.B1 = + Y.p => Zn1 = +
- Xét phương trình cân bằng moment tại điểm A:
Ta được: - Zn2.B1 - Y.p + = 0 => Zn2.B1 = - Y.p => Zn2 = - - Zn1 Zn2 = + =
=> Zn1 > Zn2 Ta cần phải tính toán nhíp theo giá trị Zn1 -
Giá trị Zn1 đạt giá trị cực đại (Zn1 = Zn1max) khi Y = Ymax = .. - Thay
giá trị Y = Ymax = .. vào biểu thức (3.1) ta được: Zn1 = + => Zn1 = .
- Khi Y = Ymax => Xe bắt đầu trượt ngang => m2 = 1 - Khi m2 = 1 thì Zn1 = .
- Tính toán ứng suất cho nhíp bên trái tương tự trường hợp 1: lOMoAR cPSD| 58797173
- Xét phương trình cân bằng moment tại điểm A:
Ta được: ZB . l1 + XB . d1 – Zn1 . l = 0 => ZB .l1= Zn1 . l – XB . d1
=> ZB = = (1) (do XA = XB = )
- Xét phương trình cân bằng moment tại điểm B:
Ta được: ZA . l1 + XA .d1 – Zn1 . l2 = 0
=> ZA . l1 + .d1 – Zn1 . l2 = 0 (do XA = XB = )
=> ZA Zn .l2 = 0 => ZA = = (2)
Thay biểu thức số (2) vào biểu thức số (1) ta được: ZB = =
- Xét moment uốn đối với Mu’ = ZA . l1 và Mu” = Zn . l2 Mà ta có Mà
- Từ đó ta có biểu đồ moment: lOMoAR cPSD| 58797173 A B C M u' M u"
Do moment uốn Mu” lớn hơn, tính toán ứng suất tại B theo moment : MuB = Mu” = Zn1 . l2
=> Ứng suất uốn lá nhíp: hi b
- Moment uốn tại B do Zn1 gây ra: = Zn1.l2 -
Ta có công thức ứng suất uốn: σu = , với Wui = => σu = σu ] Trong đó . 1 +
Ta cần phải chọn ứng suất phù hợp để thỏa mãn điều kiện bền.