Tiểu luận Dự Đoán Chiến Thắng NASCAR | Môn Thống kê ứng dụng - Đại học Bách Khoa Hà Nội

BÀI TIỂU LUẬN
HỌC PHẦN: THỐNG KÊ ỨNG DỤNG
CASE 2: PREDICTING WINNINGS FOR NASCAR DRIVERS
Giảng viên hướng dẫn: Hà Thị Thư Trang
Nhóm sinh viên thực hiện: nhóm 11 MSSV 20202976 20182027 20203068 Nguyễn Hương Giang 20203005 Phùng Kim Thu 20192305 HÀ NỘI – 07/2022 lOMoAR cPSD| 61601590 LỜI CẢM ƠN
Bản tiểu luân được hoàn thành trên cơ sở đóng góp của các thành viên ̣ với
vốn kiến thức được đúc kết ra từ quá trình học và nghiên cứu môn Thống Kê Ứng
Dụng. Đây cũng là một cơ hội thực hành khiến chúng em có thể hiểu rõ hơn về
các phân tích và kiểm định đặc trưng có liên quan, áp dụng kiến thức trên giảng
đường để làm quen và rút ra được nhưng kết luân bổ ích về những ̣ hiện tượng
trong những mối tương quan khác nhau và sự ảnh hưởng lẫn nhau giữa các nhân
tố. Chúng em xin gửi lời cảm ơn sâu sắc tới cô Hà Thị Thư Trang, Viện Kinh tế
và Quản lý, Trường Đại học Bách khoa Hà Nội đã đồng hành cùng chúng em suốt
quá trình nghiên cứu và học tâp, cảm ơn cô đã tậ n tìnḥ giảng dạy và truyền thụ
kiến thức, kinh nghiệm cũng như phong cách trình bày, để chúng em có thêm những bài học quý báu.
Do vốn kiến thức và kĩ năng còn hạn chế nên chắc hẳn bản báo cáo này
không thể tránh khỏi sai sót, chúng em rất mong nhân được sự góp ý động viên ̣
của cô để chúng em có thể hoàn thiện hơn, áp dụng tốt hơn trong các công việc sau này.
Chúng em xin chân thành cảm ơn Cô.
ĐÓNG GÓP CỦA CÁC THÀNH VIÊN
1. Thực hiện thống kê mô tả các biến: Nguyễn Thị Hương Giang
2. Phân tích các câu hỏi gợi ý trong Case Problems: Lại Thế Việt, Phạm
Văn Hoan, Đặng Ngọc Chính
3. Phần ước lượng mô hình hồi quy bội: Cả nhóm
4. Tổng kết nội dung, trình bày: Phùng Kim Thu
5. Thực hiện Slide thuyết trình: Phùng Kim Thu lOMoAR cPSD| 61601590 MỤC LỤC
I. ĐẶT VẤN ĐỀ .................................................................................................................................... 3
II. PHÂN TÍCH ..................................................................................................................................... 5
1.Thống kê mô tả các biến: .................................................................................................................. 5
1.1. Tóm tắt dữ liệu: ........................................................................................................................ 5
1.2. Bảng tần số và đồ thị của dữ liệu: ........................................................................................... 5
2. Phân tích theo các câu hỏi được gợi ý trong Case-Problems ........................................................ 9
a. Câu 1: ....................................................................................................................................... 10
b. Câu 2:............................................................................................................................................... 12
c. Câu 3: ............................................................................................................................................... 14
d. Câu 4:............................................................................................................................................... 17 lOMoAR cPSD| 61601590 I. ĐẶT VẤN ĐỀ 1. Đề bài:
Matt Kenseth đã thắng được cuộc đua Daytona 500 mùa giải 2012, cuộc đua
quan trọng nhất của mùa giải NASCAR. Chiến thắng của anh ấy không có gì ngạc
nhiên vì trong mùa giải 2011, anh ấy đứng thứ 4 trong bảng xếp hạng điểm với
2330 điểm, sau Tony Stewart (2403 điểm), Carl Edwards (2403 điểm) và Kevin
Harvick (2345 điểm). Năm 2011, anh kiếm được 6.183.580 đô la khi thắng ba Ba
Lan (tay đua nhanh nhất vòng loại), chiến thắng ba cuộc đua, về đích ở top 5 với
12times và về đích ở top 10 với 20times. Hệ thống tính điểm của NASCAR năm
2011 đã phân bổ 43 điểm cho tay đua về đích đầu tiên, 42 điểm cho tay đua về
thứ hai, và cứ thế giảm xuống 1 điểm cho tay đua về đích ở vị trí thứ 43. Ngoài
ra, bất kỳ tay đua nào dẫn đầu vòng đua nhận được 1 điểm thưởng, tay đua dẫn
đầu vòng đua nhiều nhất nhận được thêm điểm thưởng và người chiến thắng cuộc
đua được thưởng 3 điểm thưởng. Tuy nhiên, số điểm tối đa mà một tay đua có thể
kiếm được trong bất kỳ cuộc đua nào là 48. Bảng 1 hiển thị dữ liệu của mùa giải
2011 cho 35 tay đua hàng đầu (trích: trang web
NASCAR. 28 tháng 2 năm 2011) Driver Points
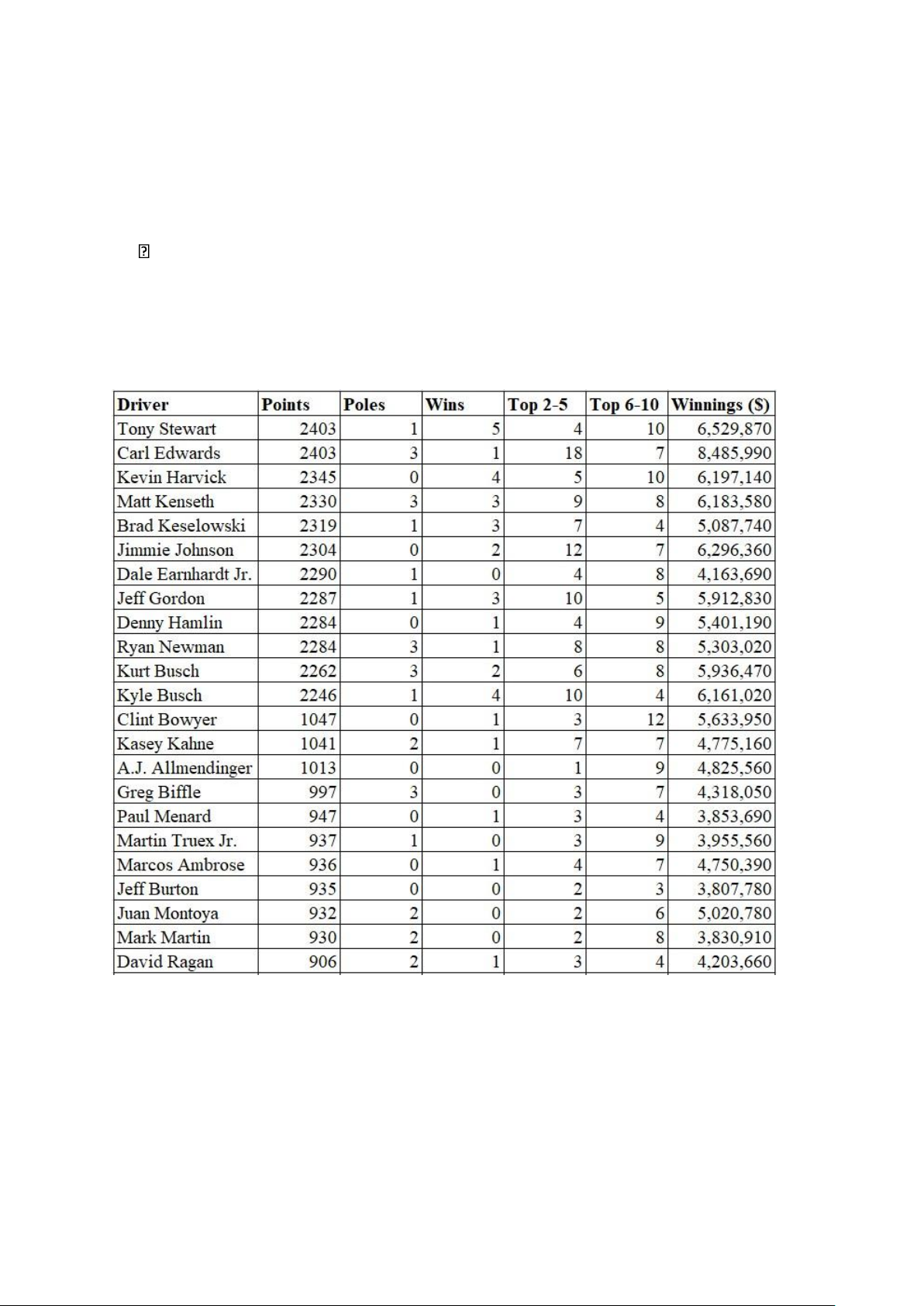
Poles Wins Top 5 Top 10 Winnings ($) Tony Stewart 2403 1 5 9 19 6,529,870 Carl Edwards 2403 3 1 19 26 8,485,990 Kevin Harvick 2345 0 4 9 19 6,197,140 Matt Kenseth 2330 3 3 12 20 6,183,580 Brad Keselowski 2319 1 3 10 14 5,087,740 Jimmie Johnson 2304 0 2 14 21 6,296,360 Dale Earnhardt Jr. 2290 1 0 4 12 4,163,690 Jeff Gordon 2287 1 3 13 18 5,912,830 Denny Hamlin 2284 0 1 5 14 5,401,190 lOMoAR cPSD| 61601590 Ryan Newman 2284 3 1 9 17 5,303,020 Kurt Busch 2262 3 2 8 16 5,936,470 Kyle Busch 2246 1 4 14 18 6,161,020 Clint Bowyer 1047 0 1 4 16 5,633,950 Kasey Kahne 1041 2 1 8 15 4,775,160 A.J. Allmendinger 1013 0 0 1 10 4,825,560 Greg Biffle 997 3 0 3 10 4,318,050 Paul Menard 947 0 1 4 8 3,853,690 Martin Truex Jr. 937 1 0 3 12 3,955,560 Marcos Ambrose 936 0 1 5 12 4,750,390 Jeff Burton 935 0 0 2 5 3,807,780 Juan Montoya 932 2 0 2 8 5,020,780 Mark Martin 930 2 0 2 10 3,830,910 David Ragan 906 2 1 4 8 4,203,660 Joey Logano 902 2 0 4 6 3,856,010 Brian Vickers 846 0 0 3 7 4,301,880 Regan Smith 820 0 1 2 5 4,579,860 Jamie McMurray 795 1 0 2 4 4,794,770 David Reutimann 757 1 0 1 3 4,374,770 Bobby Labonte 670 0 0 1 2 4,505,650 David Gilliland 572 0 0 1 2 3,878,390 Casey Mears 541 0 0 0 0 2,838,320 Dave Blaney 508 0 0 1 1 3,229,210 Andy Lally* 398 0 0 0 0 2,868,220 Robby Gordon 268 0 0 0 0 2,271,890 lOMoAR cPSD| 61601590 J.J. Yeley 192 0 0 0 0 2,559,500
Bảng 1: Dữ liệu mùa giải 2011 cho 35 tay đua hàng đầu II. PHÂN TÍCH
1. Thống kê mô tả các biến:
1.1.Tóm tắt dữ liệu:
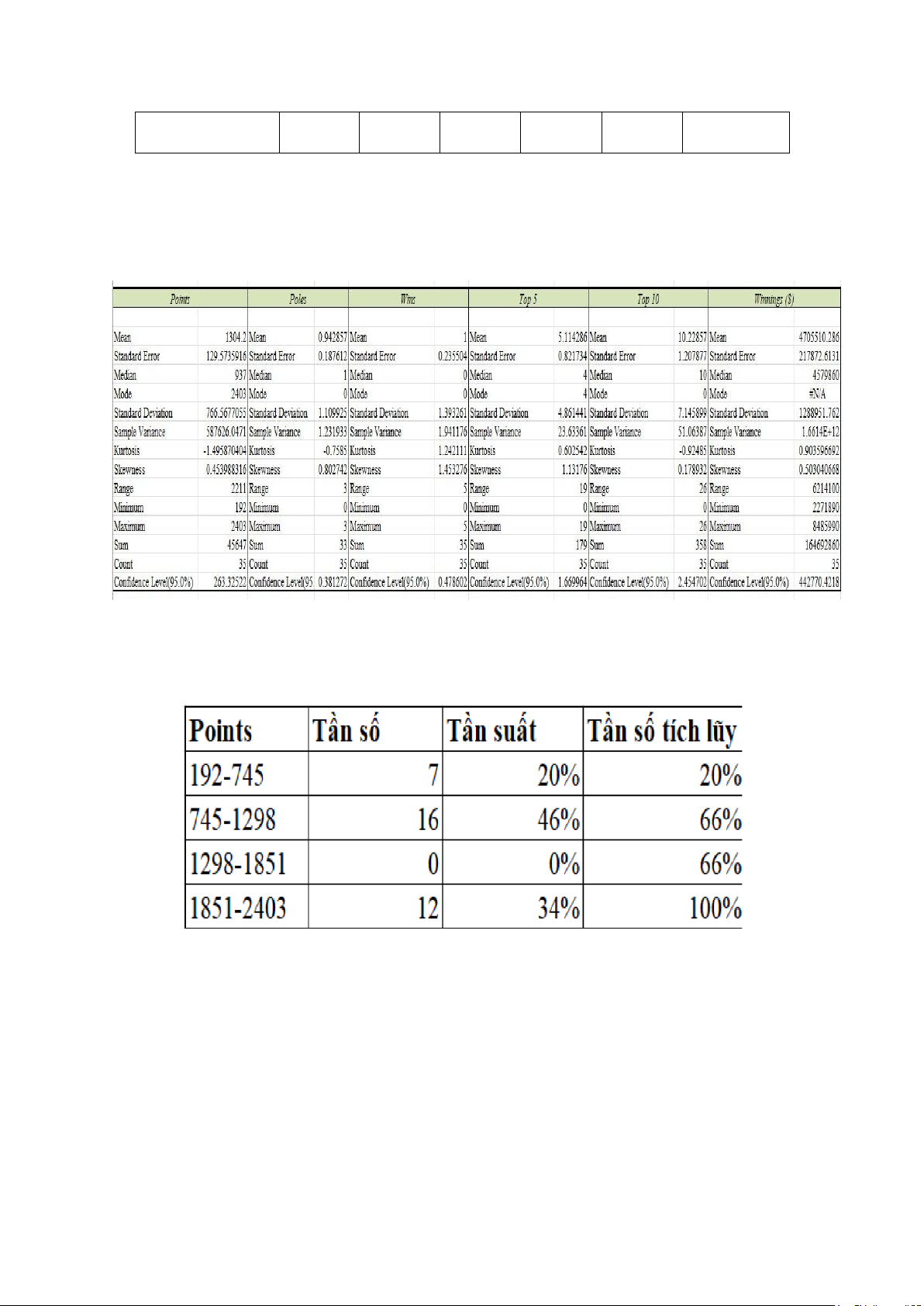
1.2. Bảng tần số và đồ thị của dữ liệu:
1.2.1. Điểm số (Points) lOMoAR cPSD| 61601590 % % % % % % % % % % % Tần số tích lũy Nhận xét:
Điểm (Points) chủ yếu tập trung trong khoảng từ 745-1298 và từ 1851-2403, khá cao.
- Giá trị trung bình: 1304,2 - Độ lệch chuẩn: 766,6
- Biến thiên từ 192 đến 2403
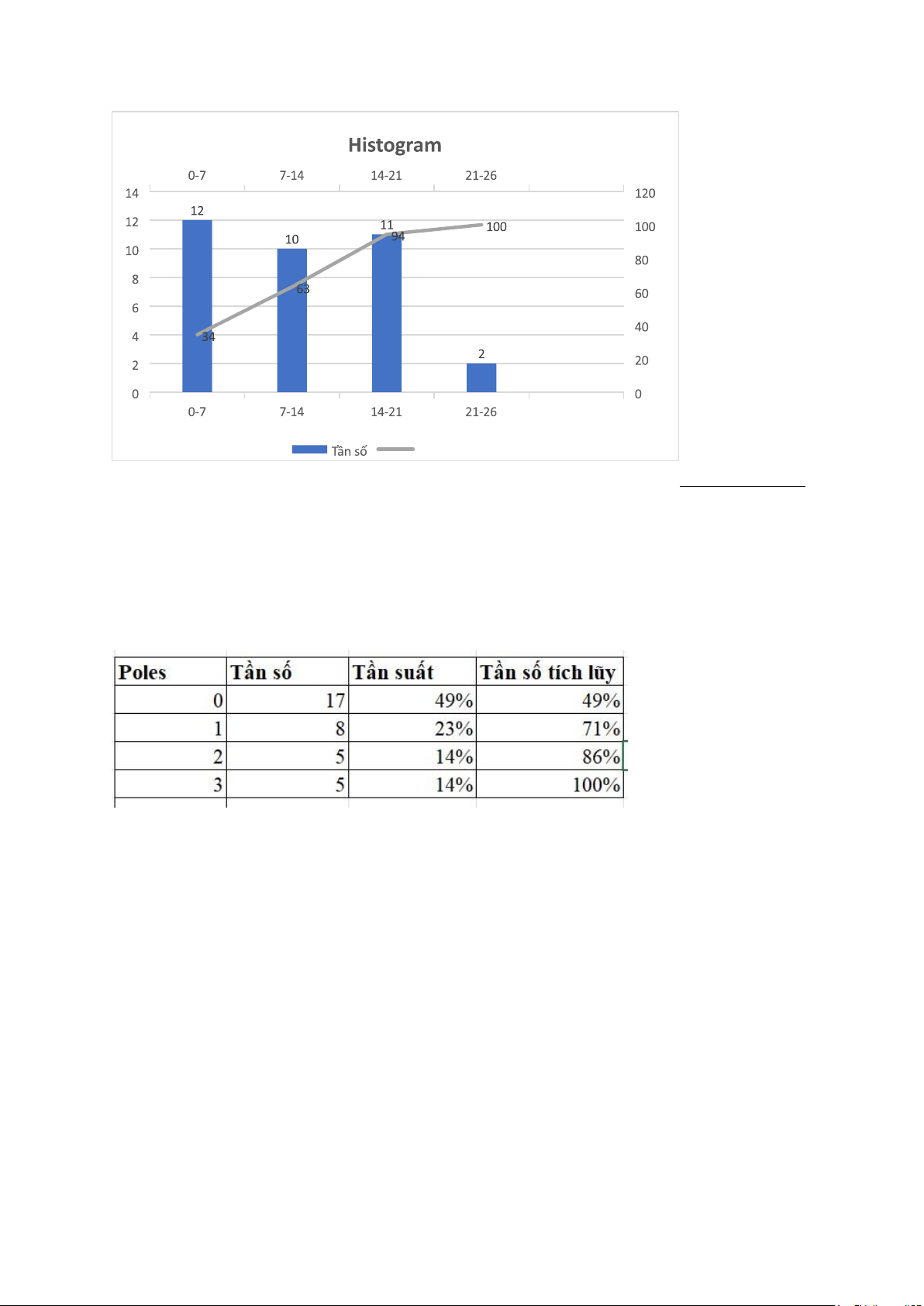
I.2.2. Số lần thắng Pole (Poles) lOMoAR cPSD| 61601590
Nhận xét: Hầu hết các tay đua đều không giành được pole, một số giành được
pole 1 lần và số ít người được 2, 3 lần pole.
- Giá trị trung bình: 0,94 - Độ lệch chuẩn: 1,1099 - Biến thiên từ 0 đến 3.
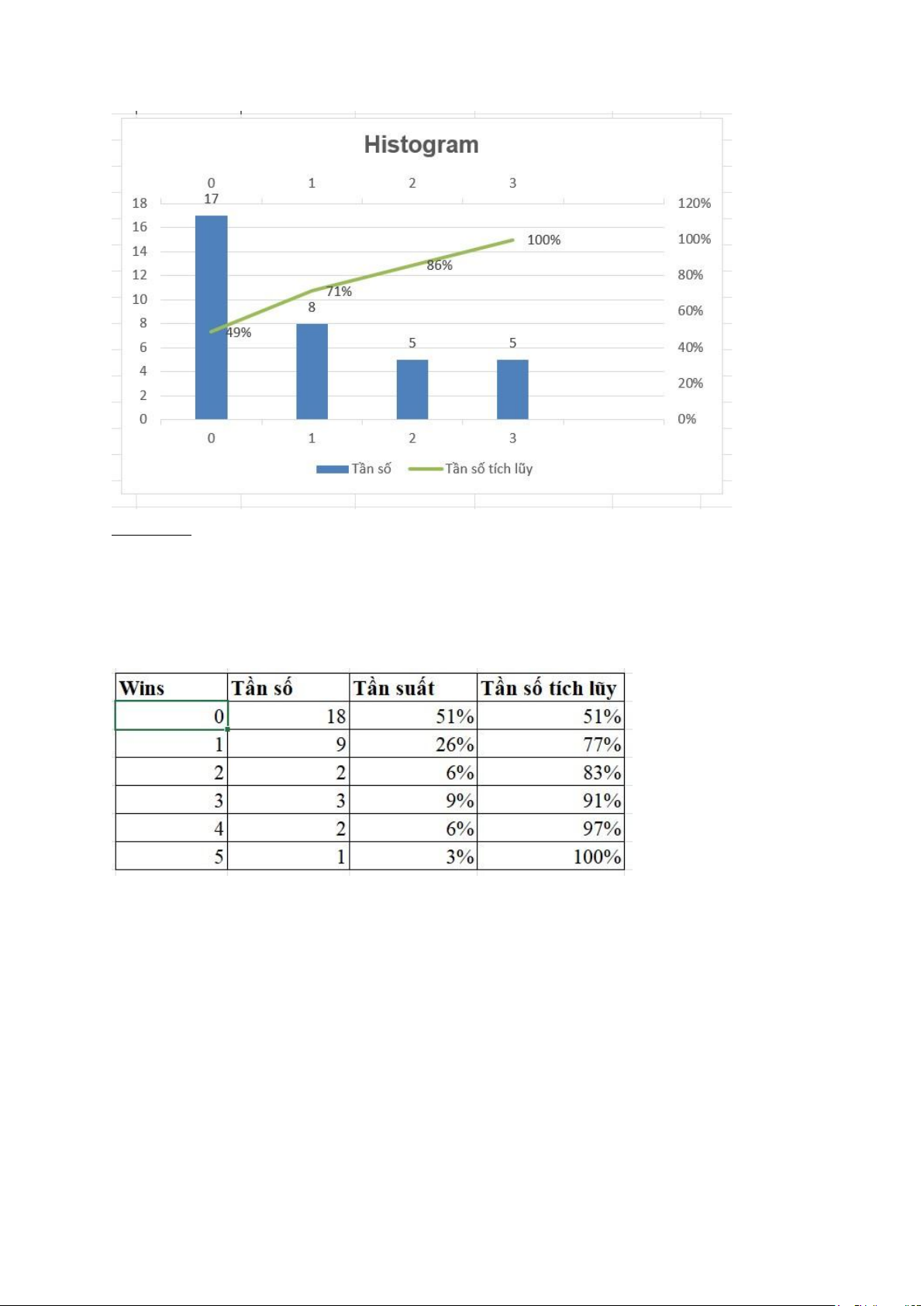
I.2.3. Số lần thắng (Wins) : lOMoAR cPSD| 61601590
Nhận xét: Hầu hết số lần thắng của các tay đua là 0. - Giá trị trung bình: 1
- Độ lệch chuẩn: 1,4 - Biến thiên từ 0 đến 5
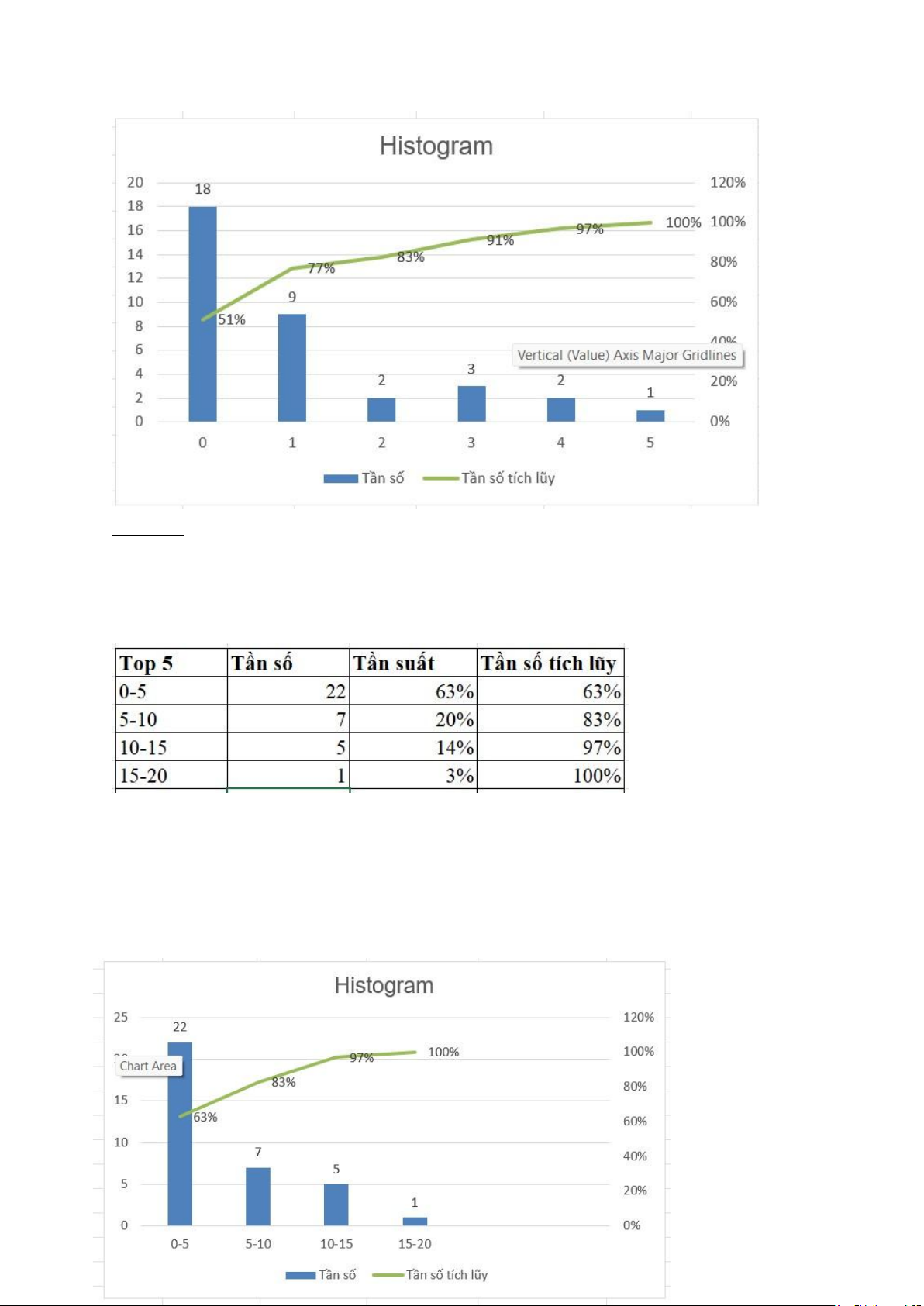
I.2.4. Số lần trong top 5 (Top 5):
Nhận xét: Phần lớn các tay đua nằm trong Top 5 từ 0-5 lần.
- Giá trị trung bình: 5,11 - Độ lệch chuẩn: 4,86
- Biến thiên từ 0 đến 20
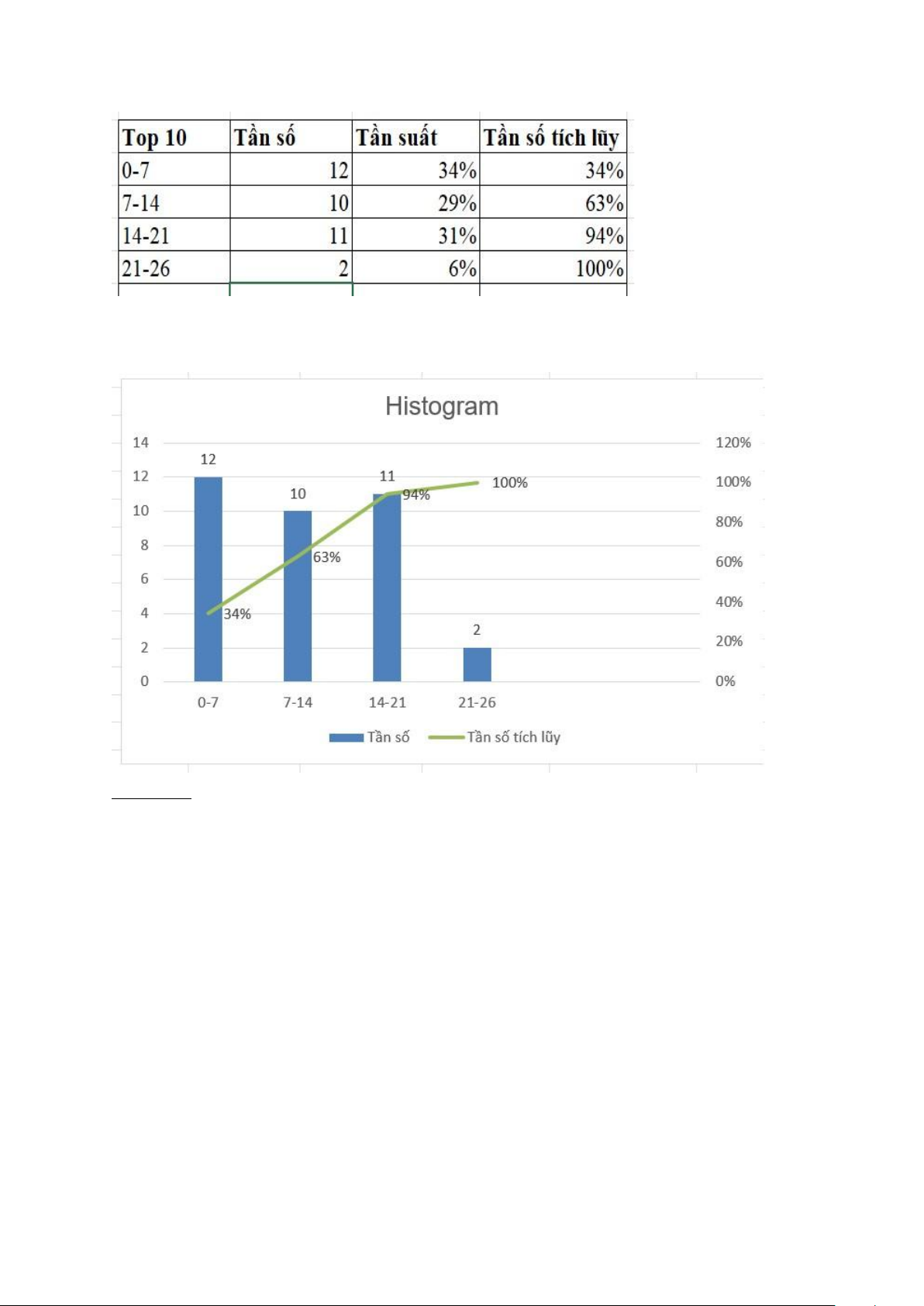
I.2.5. Số lần trong Top 10 (Top 10): 9
Downloaded by Nguyen Linh (nguyennhutgianglinh31@gmail.com) lOMoAR cPSD| 61601590
Nhận xét: Số lần đạt trong Top 10 phân bổ khá đều trong khoảng từ 0-21 lần,
riêng khoảng từ 21-26 lần đạt Top 10 chỉ có 2 người chiếm 6%. Độ tin cây được ̣
dự đoán chủ yếu là Tốt và Rất Tốt.
- Giá trị trung bình: 10,23 - Độ lệch chuẩn: 7,15
- Biến thiên từ 0 đến 26
2. Phân tích theo các câu hỏi được gợi ý trong Case-Problems Phân tích hồi quy Giả sử:
- Y^ là biến phụ thuộc Winnings.
- X1, X2, X3, X4 lần lượt là các biến độc lập Poles, Wins, Top 5, Top 10. lOMoAR cPSD| 61601590 a. Câu 1:
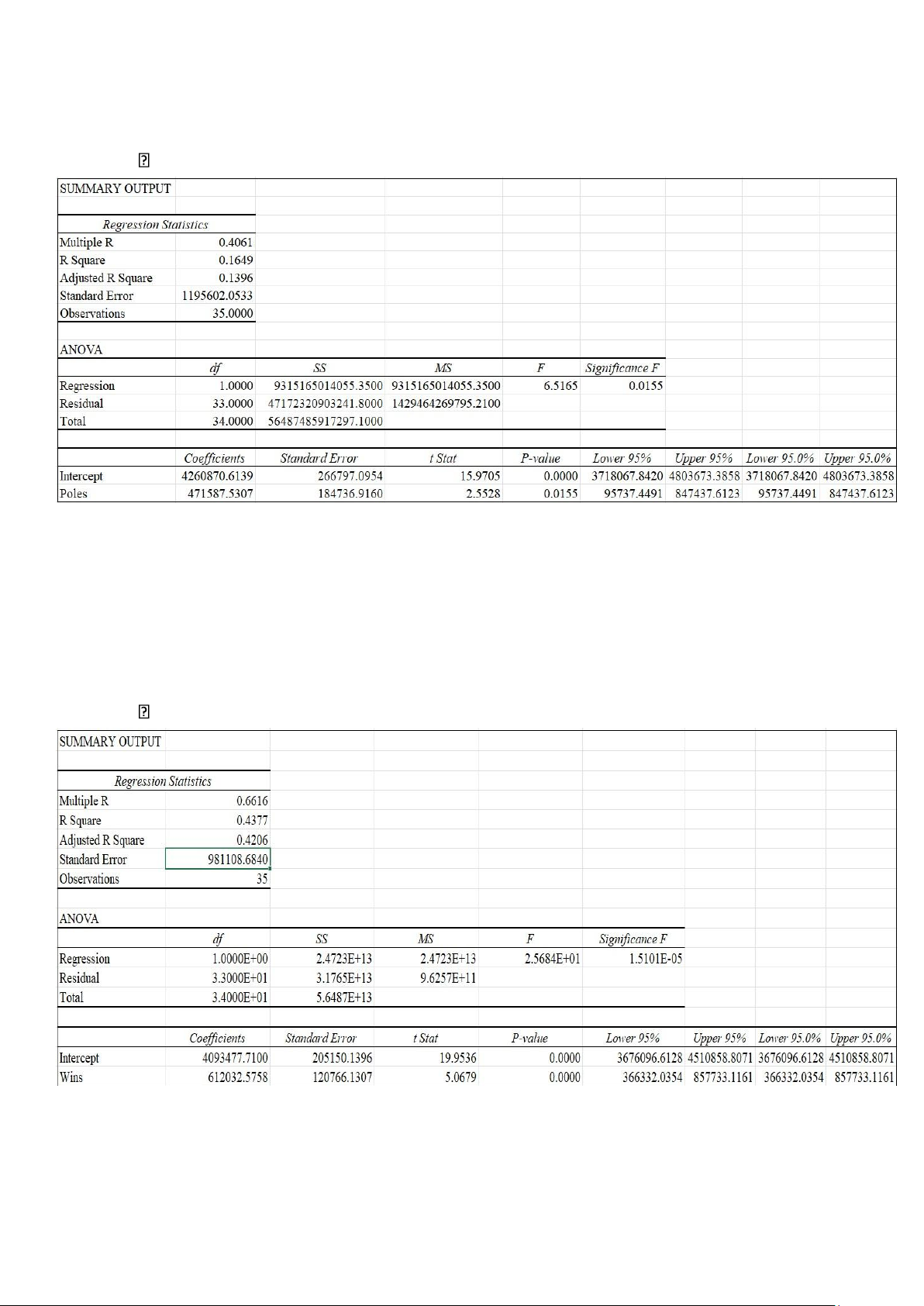
 Sự ảnh hưởng của biến độc lập X1 đến biến phụ thuộc Y^: - Phương trình hồi quy:
Y^ = 4260870.6139 + 471587.5307xX1
- Với R Square = 0.1649 ➪ Biến độc lập X1 giải thích được 16.49% sự biến
động của biến phụ thuộc Y^.
 Sự ảnh hưởng của biến độc lập X2 đến biến phụ thuộc Y^: - Phương trình hồi quy:
Y^ = 4093477.71 + 612032.5758xX2 lOMoAR cPSD| 61601590
- Với R Square = 0.4377 ➪ Biến độc lập X2 giải thích được 43.77% sự
biến động của biến phụ thuộc Y^.
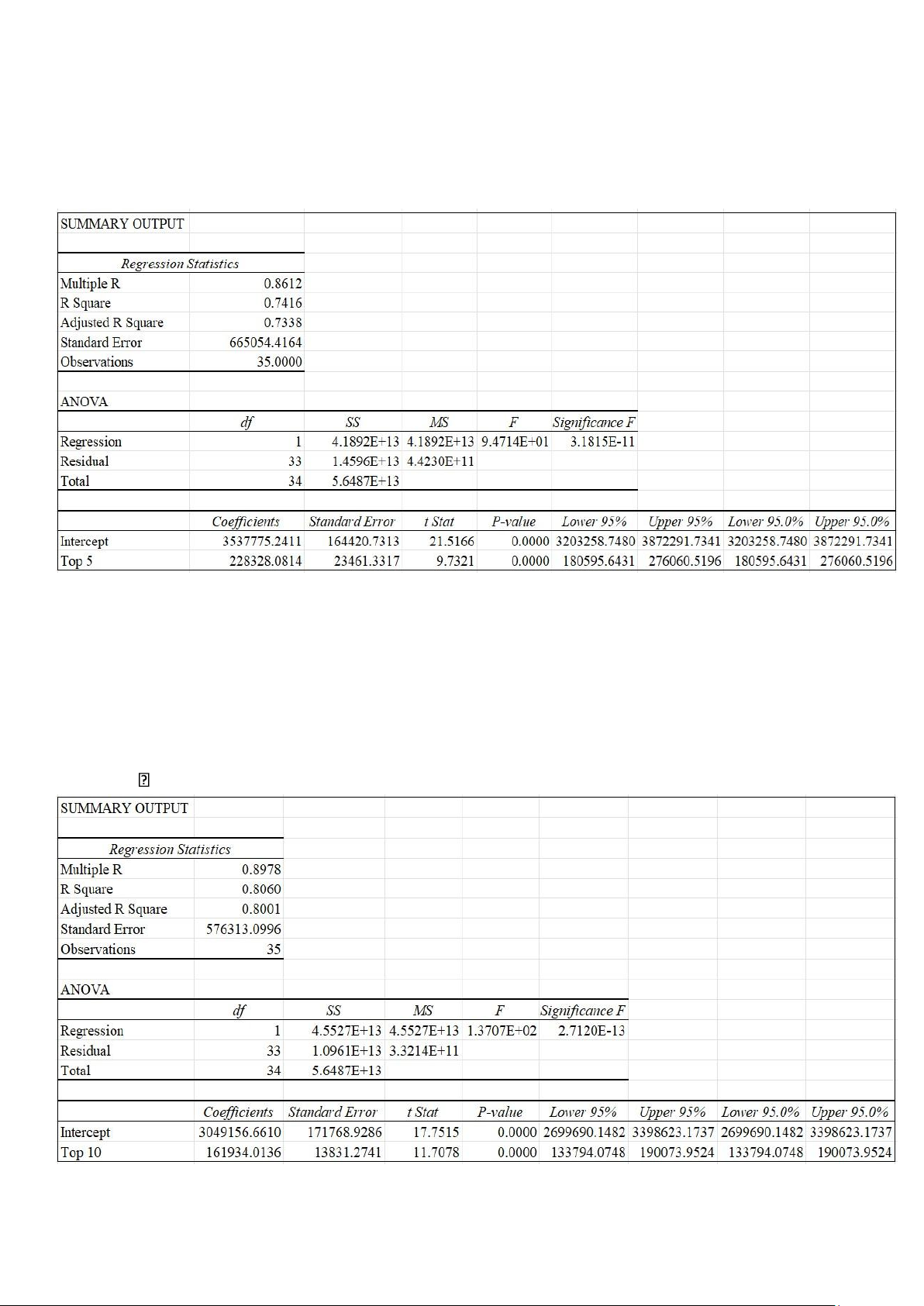
- Sự ảnh hưởng của biến độc lập X3 đến biến phụ thuộc Y^. - Phương trình hồi quy:
Y^ = 3537775.2411 + 228328.0814xX3
- Với R Square = 0.7416 ➪ Biến độc lập X3 giải thích được 74.16% sự
biến động của biến phụ thuộc Y^.
 Sự ảnh hưởng của biến độc lập X3 đến biến phụ thuộc Y^ lOMoAR cPSD| 61601590 - Phương trình hồi quy:
Y^ = 3049156.661 + 161934.0136xX4
- Với R Square = 0.8060 -> Biến độc lập X4 giải thích được 80.60% sự
biến động của biến phụ thuộc Y^
 Vậy, do Biến độc lập X4 (Top 10) có R Square lớn nhất và P-value của biến X4
<< 0.05 nên ta có thể kết luận biến X4 dự đoán chiến thắng tốt nhất trong 4 biến. b. Câu 2: - Phương trình hồi quy:
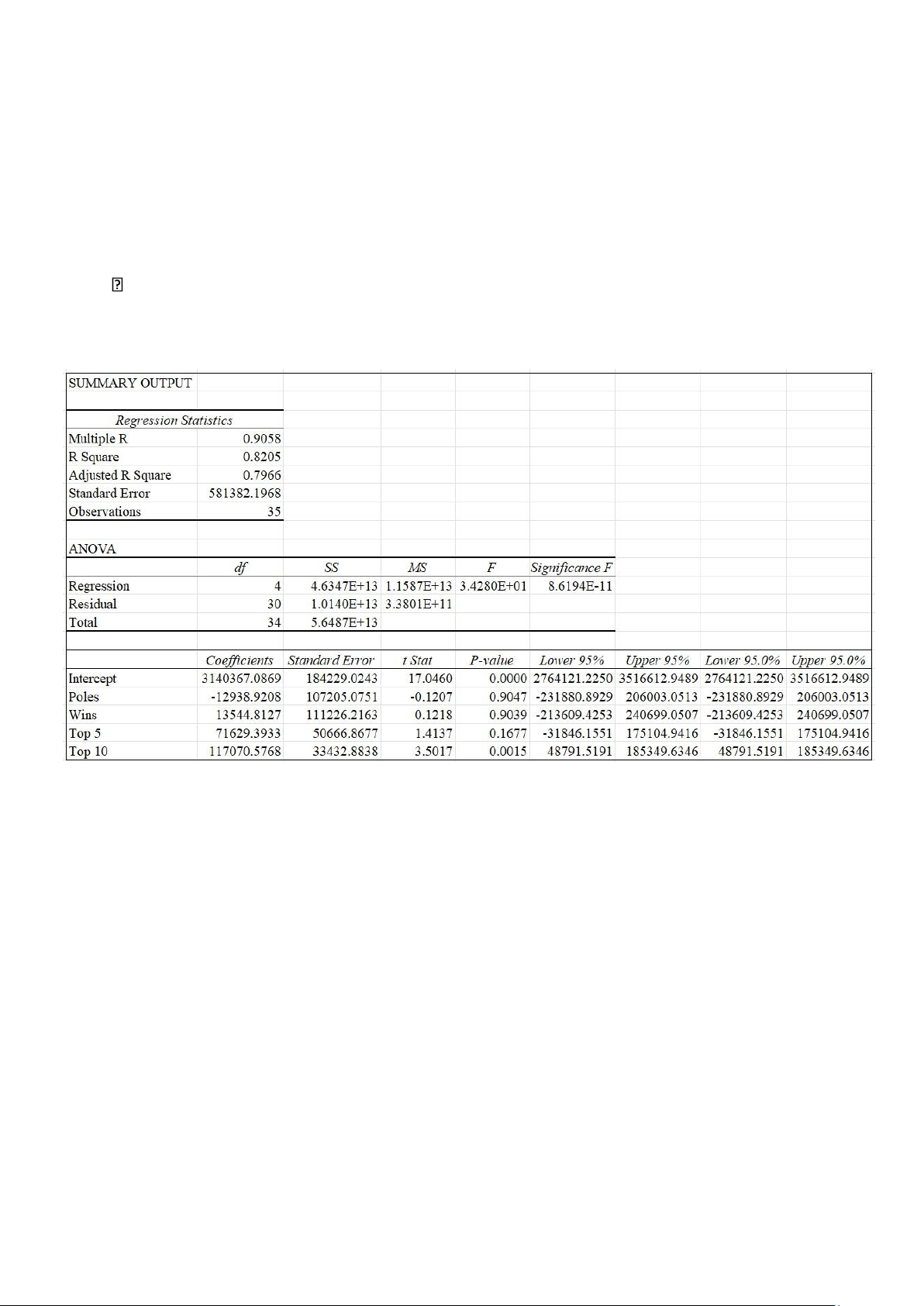
Y^ = 3140367.0869 - 12938.9208X1 +13544.8127X2 + 71629.3933X3 + 117070.5768X4
- Từ phương trình hồi quy ta có thể đưa ra kết luận:
+ X1 cứ tăng 1 thì Y^ giảm trung bình 12938.9208 và ngược lại.
+ X2 cứ tăng 1 thì Y^ tăng trung bình 13544.8127 và ngược lại.
+ X3 cứ tăng 1 thì Y^ tăng trung bình 71629.3933 và ngược lại.
+ X4 cứ tăng 1 thì Y^ tăng trung bình 117070.5768 và ngược lại.
- R Square = 0.8205 => cho thấy 82,05% biến thiên của biến phụ thuộc
Winnings có thể được giải thích bởi mối liên hệ tuyến tính giữa các biến
phục thuộc Winnings với 4 biến độc lập Poles, Wins, Top5, Top10. lOMoAR cPSD| 61601590
- Adjusted R Square = 0.7966 => cho thấy 79.66% sự biến thiên của biến
phụ thuộc có thể giải thích bởi mô hình hồi quy bội.
 Đánh giá ý nghĩa toàn diện mô hình
- H0: R2 = 0 - H1: R2 ≠ 0
- F = MSR/MSE = 11586832038700.5/ 338005258749.844 = 34.28
- Với mức ý nghĩa là α=0,05 và n=35, k=4  (Fk ; ;0,05) = 2,69
n−k−1 α¿ = (F430
 F > (Fkn−k−1;α¿
➤ Bác bỏ giả thuyết H0  Mô hình hồi quy bội với các biến độc lập Poles,
Wins, Top 5, Top 10 có thể giải thích một cách có ý nghĩa cho biến thiên của biến phụ thuộc Winnings.
 Đánh giá ý nghĩa của từng biến độc lập riêng biệt.  Biến X1 (Pole)
- H0: 𝛽1 = 0 - H1: 𝛽1 ≠ 0 - t(n-k-1, α/2) = 2.042
- t1 = (b1 – 0)/(S(b1)) = -12938.9208/107205.0751 = -0.12
- |t1| < t(n-k-1, α/2) => chấp nhận giả thuyết H0
 Biến X1 không có ý nghĩa giải thích cho Winnings.  Biến X2 (Wins)
- H0: 𝛽2 = 0 - H1: 𝛽2 ≠ 0 - t(n-k-1, α/2) = 2.042
- t2 = (b2 – 0)/(S(b2)) = 13544.8127/111226.2163 = 0.12
- |t2| < t(n-k-1, α/2) => chấp nhận giả thuyết H0
 Biến X1 không có ý nghĩa giải thích cho Winnings.  Biến X3 (Top 5)
- H0: 𝛽3 = 0 - H1: 𝛽3 ≠ 0 - t(n-k-1, α/2) = 2.042
- t3 = (b3 – 0)/(S(b3)) = 71629.3933/50666.8677 = 1.41
- |t3| < t(n-k-1, α/2) => chấp nhận giả thuyết H0
 Biến X3 không có ý nghĩa giải thích cho Winnings.  Biến X4 (Top 10) lOMoAR cPSD| 61601590
- H0: 𝛽4 = 0 - H1: 𝛽4 ≠ 0
- t(n-k-1, α/2) = 2.042
- t4 = (b4 – 0)/(S(b4)) = 117070.5768/33432.8838 = 3.5 -
|t4| > t(n-k-1, α/2) => bác bỏ giả thuyết H0
 Biến X4 có ý nghĩa giải thích cho Winnings. c. Câu 3: Giả sử:
- Y^ là biến phụ thuộc Winnings.
- X1, X2, X3, X4 lần lượt là các biến độc lập Poles, Wins, Top 2-5, Top 6-10 lOMoAR cPSD| 61601590 - Phương trình hồi quy:
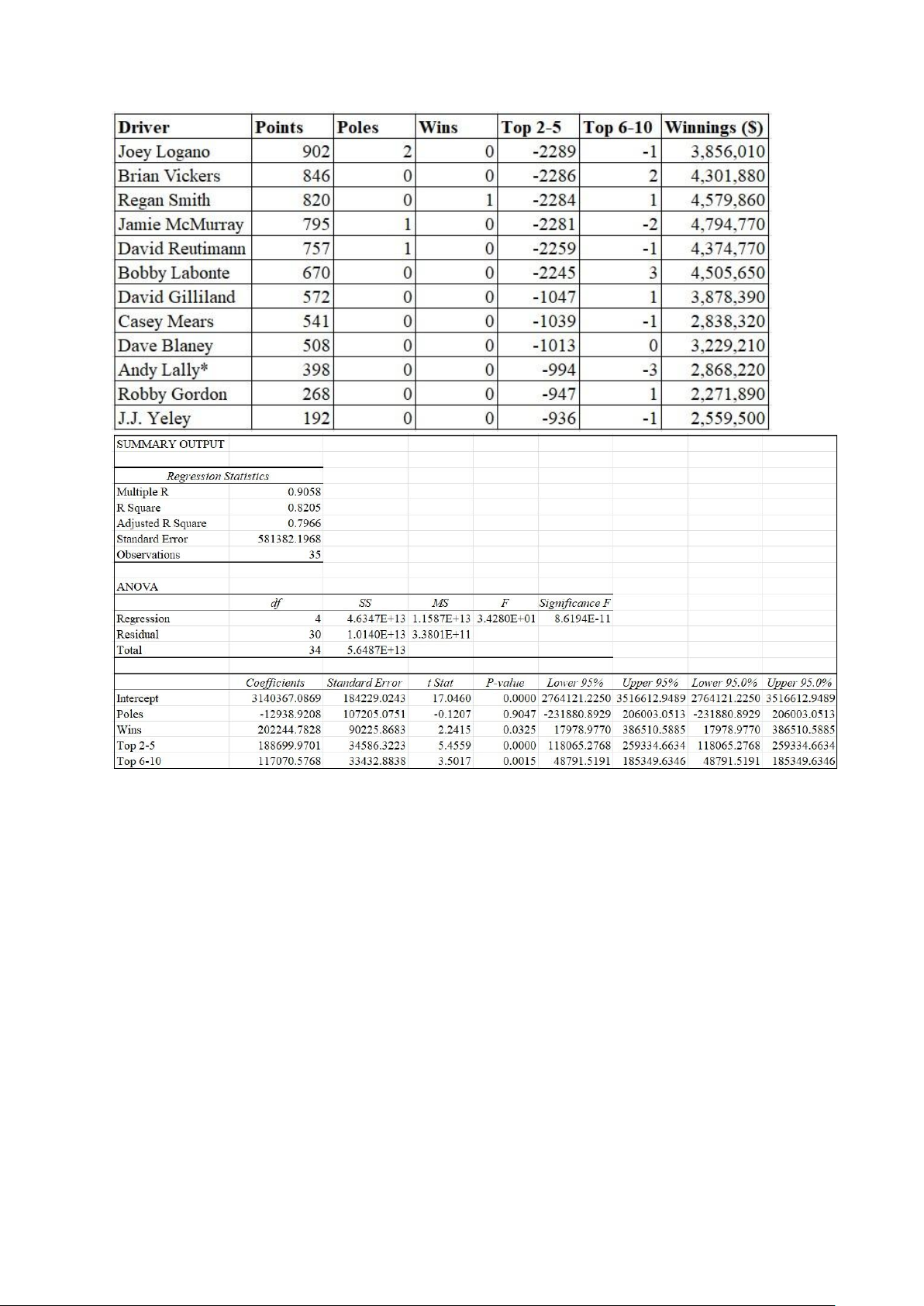
Y^ = 3140367.0869 – 12938.9208X1 + 202244.7828X2 + 188699.9701X3 + 117070.5768X4
- Từ phương trình hồi quy ta có thể đưa ra kết luận:
+ X1 cứ tăng 1 thì Y^ giảm trung bình 12938.9208 và ngược lại.
+ X2 cứ tăng 1 thì Y^ tăng trung bình 202244.7828 và ngược lại.
+ X3 cứ tăng 1 thì Y^ tăng trung bình 188699.9701 và ngược lại.
+ X4 cứ tăng 1 thì Y^ tăng trung bình 117070.5768 và ngược lại.
- R Square = 0.8205 => cho thấy 82,05% biến thiên của biến phụ thuộc
Winnings có thể được giải thích bởi mối liên hệ tuyến tính giữa các biến
phục thuộc Winnings với 4 biến độc lập Poles, Wins, Top 2-5, Top 6-10.
- Adjusted R Square = 0.7966 => cho thấy 79.66% sự biến thiên của biến
phụ thuộc có thể giải thích bởi mô hình hồi quy bội. lOMoAR cPSD| 61601590
 Đánh giá ý nghĩa toàn diện mô hình - H0: R2 = 0 - H1: R2 ≠ 0
- F = MSR/MSE = 11586832038700.5/ 338005258749.844 = 34.28
- Với mức ý nghĩa là α=0,05 và n=35, k =4 => (Fk ; ;0,05) = 2,69
n−k−1 α¿ = (F430
=> F > (Fkn−k−1;α¿ => bác bỏ giả thuyết H0
=> Mô hình hồi quy bội với các biến độc lập Poles, Wins, Top 2-5,
Top 6-10 có thể giải thích một cách có ý nghĩa cho biến thiên của biến phụ thuộc Winnings.
 Đánh giá ý nghĩa của từng biến độc lập riêng biệt.  Biến X1 (Pole) - H0: 𝛽1 = 0 - H1: 𝛽1 ≠ 0
- t(n-k-1, α/2) = 2.042
- t1 = (b1 – 0)/(S(b1)) = -12938.9208/107205.0751 = -0.12
- |t1| < t(n-k-1, α/2) => chấp nhận giả thuyết H0
=> biến X1 không có ý nghĩa giải thích cho Winnings.  Biến X2 (Wins)
- H0: 𝛽2 = 0 - H1: 𝛽2 ≠ 0
- t(n-k-1, α/2) = 2.042
- t2 = (b2 – 0)/(S(b2)) = 202244.7828/90225.8683 = 2.24
- |t2| > t(n-k-1, α/2) => bác bỏ giả thuyết H0
=> biến X1 có ý nghĩa giải thích cho Winnings.
 Biến X3 (Top 2-5)
- H0: 𝛽3 = 0 - H1: 𝛽3 ≠ 0
- t(n-k-1, α/2) = 2.042
- t3 = (b3 – 0)/(S(b3)) = 188699.9701/34586.3223 = 5.45
- |t3| > t(n-k-1, α/2) => bác bỏ giả thuyết H0
=> biến X3 có ý nghĩa giải thích cho Winnings.
 Biến X4 (Top 6-10)
- H0: 𝛽4 = 0 - H1: 𝛽4 ≠ 0
- t(n-k-1, α/2) = 2.042
- t4 = (b4 – 0)/(S(b4)) = 117070.5768/33432.8838 = 3.5
- |t4| > t(n-k-1, α/2) => bác bỏ giả thuyết H0
=> biến X4 có ý nghĩa giải thích cho Winnings. lOMoAR cPSD| 61601590 d. Câu 4:
Vậy ta thấy mô hình hồi quy ở câu 3 có 3 biến độc lập có ý nghĩa giải thích
cho Winnings trong khi mô hình hồi quy ban đầu chỉ có duy nhất 1 biến độc lập
có ý nghĩa giải thích cho Winnings, do đó nên chọn mô hình hồi quy ở câu 3 để
dự đoán cho biến phụ Winnings.