Tiểu luận: Ứng dụng đạo hàm trong các bài toán kinh tế môn Toán kinh tế | Học viện Công Nghệ Bưu Chính Viễn Thông
Tiểu luận: Ứng dụng đạo hàm trong các bài toán kinh tế môn Toán kinh tế. Tài liệu được sưu tầm, biên soạn dưới dạng file PDF gồm 26 trang, giúp các bạn học tốt, ôn tập hiệu quả, đạt kết quả cao trong các bài thi, bài kiểm tra sắp tới. Mời bạn đón xem!
Môn: Toán kinh tế (BSA1241) 10 tài liệu
Trường: Học viện Công Nghệ Bưu Chính Viễn Thông 1.2 K tài liệu
Tác giả:
Preview text:
lOMoAR cPSD| 59031616
HỌC VIỆN CÔNG NGHỆ BƯU CHÍNH VIỄN THÔNG
KHOA QUẢN TRỊ KINH DOANH 2 ( CỦA PTIT) oOo BỘ MÔN : TOÁN TÊN TIỂU LUẬN
ỨNG DỤNG CỦA ĐẠO HÀM TRONG CÁC BÀI TOÁN KINH TẾ Nhóm thực hiện: Nhóm 11 Lớp : D23CQMR01-N
Giảng viên hướng dẫn: Lê Thanh Phong lOMoAR cPSD| 59031616 Lời nói đầu
Là sinh viên, chắc hẳn bạn đã quá quen thuộc với thuật ngữ “đạo hàm” nhưng không
phải ai cũng biết đến những ý nghĩa, ứng dụng thực tế mà “đạo hàm” mang lại. Sự
phát triển của cây cối hay tốc độ gia tăng dân số của một vùng miền,...đều liên quan
đến ứng dụng đạo hàm. Khi một hiện tượng, sự vật, sự việc biến đổi, chúng có thể
thay đổi nhanh hoặc chậm và đạo hàm sẽ cho biết tốc độ, đặc tính thay đổi của các
đối tượng trên. Chính vì lẽ đó, đạo hàm đã trở thành một trong những công cụ hỗ trợ
một cách tối ưu nhất để giải quyết các bài toán trong nhiều lĩnh vực khác nhau, đặc
biệt trong lĩnh vực kinh tế.
Với mong muốn tìm hiểu chi tiết hơn về vấn đề này nên nhóm 11 chúng em đã chọn
đề tài: “Ứng dụng của đạo hàm trong các bài toán về kinh tế” Lời cảm ơn
Trong suốt khoảng thời gian học tập và tìm hiểu về môn Toán Cao Cấp, em đã không
chỉ đúc kết được rất nhiều kiến thức hay mà còn nhận được nhiều sự giúp đỡ và tâm
huyết từ thầy Lê Thanh Phong.
Cuối cùng, chúng em cũng đã hoàn thành được bài tiểu luận thuộc đề tài “Ứng dụng
của đạo hàm trong các bài toán về kinh tế”. Vì đây là lần đầu tiên chúng em làm tiểu
luận nên không thể nào tránh khỏi nhiều thiếu sót. Em mong rằng sẽ nhận được những
lời góp ý của thầy để những bài tiểu luận của em ngày càng hoàn thiện hơn. Lời cam đoan
Chúng em xin cam đoan đây là công trình nghiên cứu của riêng nhóm 11. Các nội dung
trong đề tài “Ứng dụng của đạo hàm trong các bài toán về kinh tế” của chúng em là
trung thực và chưa từng được phát hành dưới mọi hình thức trước đó. Những số liệu,
các bảng biểu từ các nguồn khác nhau đều được trình bày rõ nguồn gốc. Nếu phát hiện
có sự gian lận, chúng em xin hoàn toàn chịu trách nhiệm về bài tiểu luận của mình. lOMoAR cPSD| 59031616 MỤC LỤC Phần I. Mở đầu
1. Mục đích – yêu cầu:
Phần II. Nội dung bài tiểu luận 1. Cơ sở lý luận: 5
1.1. Định nghĩa của đạo hàm: 5
1.2. Các công thức của đạo hàm: 5
1.2.1. Công thức đạo hàm tổng hiệu tích thương
1.2.2. Đạo hàm của các hàm số cơ bản 1.2.3. Đạo hàm cấp cao
2. Ứng dụng của đạo hàm: 8
2.1. Ứng dụng đạo hàm trong hàm số
2.2. Ứng dụng đạo hàm trong vật lý (sgk Giải Tích 11).9
3. Đạo hàm trong các bài toán kinh tế 10
3.1. Ý nghĩa của đạo hàm trong kinh tế: 11
3.2. Các bài toán kinh tế 11 PHẦN 1: MỞ ĐẦU
1. Mục đích – yêu cầu:
1.1. Mục đích:
Để đi sâu tìm hiểu và đưa các vấn đề cần phải giải quyết đối với ứng dụng của đạo
hàm trong các bài toán kinh tế.
1.2. Yêu cầu :
- Nắm được các vấn đề liên quan đến đaọ hàm.
- Ứng dụng được đạo hàm vào giải các bài toán kinh tế.
1.3. Đối tượng nghiên cứu: đạo hàm và các bài toán kinh tế
1.4. Phạm vi nghiên cứu:
Bài tiểu luận này được tiến hành nghiên cứu từ tuần 7 - tuần 8 tại Học Viện Công Nghệ
Bưu Chính Viễn Thông PTITHCM.
PHẦN 2: NỘI DUNG BÀI TIỂU LUẬN lOMoAR cPSD| 59031616
1. Cơ sở lý luận:
1.1. Định nghĩa của đạo hàm:
Cho y = f(x) xác định trên miền D, x
gọi là số gia của x tại ,
0∈ D,∆ x=x−x0
x0 Δy=f ( x ) −f (x .
0)=f (x0+Δx) gọi là số gia của y tại x0 lim Δ y Nếu
hữu hạn thì giới hạn đó gọi là đạo hàm của y = f(x) tại x0 là Δx f ' (x0)= ∆ x .
1.2. Các công thức của đạo hàm:
1.2.1. Công thức đạo hàm của tổng, hiệu, tích, thương:
(u+v )'=u'+v' ' '
(u.v)'=u . v−2u. v v y'x=y'u.u'x
(k .u)'=k .u' k ' k .u' (u) u2 =
1.2.2. Đạo hàm của hàm số sơ cấp: (C )'=0
(xa)'=a.xa−1,vớia∈ R (uα)'
=α.ua−1.u', với α ϵ R x
(√ u)'= u' 2√u 1 x2 1 ' u' =− (u) u2
,vớinϵ N∗,n>1 n n−1 n√x ' u' ∗ lOMoAR cPSD| 59031616 = n
n−1 ,vớinϵ N ,n>1 n√u
(sin x )'=cosx
(sinu)'=u' .cosu
(cosx )'=−sinx
(cosu )'=−u' .sinu x
( tanu )'=u' .¿
(cot x )'=−¿
(cotu)'=−u' .¿
(e x)'=ex
(eu)'=u' .eu
(ax )'=ax .lna
(au)'=u' .au.lna ( 1 lnx)'= x (lnu) = ( '
uu' loga x)'= x.1lna ' (logau)'= u u.lna ax+b ' ad−bc =
(cx+d ) (cx+d)2
a x2+bx+c '
ae x2+2af . x+(bf −ce) ( ex+f ) (ex+f )2 = | | | | 2 ' aa12 bb12
. x2+2|aa12 cc12 +|bb12 cc21
a1 x +b1x+c1 (a )
2 2+b2x+c2
(a2 x2+b2x+c2)2 = x lOMoAR cPSD| 59031616
1.2.3. Đạo hàm cấp cao:
(xm)( n)=m(m−1)(m−2) (m−n+1) .xm− nnếum≥n
(xm)( n)=0nếu m<n( lna . xn
(ln x)(n)=(−1)( n− 1) .( n−1)!x− n
(ekx)(n)=kn.ekx
(ax )(n)=(lna)n .ax
( sinax)(n)=an.sin (ax+n. )
(cosax)(n)=an .cos (ax+n. )
(ax1+b )(n)=(−1)n.an.n!
(ax+1b)n+1
Ví dụ: Tính đạo hàm các hàm số sau:
a) y=x4+2√x Giải: y' √x
b) y=sin(¿2 x+1)+cos (1− x)¿
Giải: y'=2cos(2 x+1 )+sin(1−x)
c) y=log (2sin x−1) Giải: y'=
d) y=( x2+1).22x
Giải: y'=(x2+1)' .22x +(x2+1).(22x )' y'=2 x.22x +(x2+1).2.22x .ln2 Ví dụ: Cho hàm số:
f ( x )=log2(x2−x).Tính f ' (2)
Giải: f ' ( x )= . ⇒f ' (2)= 2.= .log2e.
2. Ứng dụng của đạo hàm:
2.1.Ứng dụng của đạo hàm trong hàm số:
Như đã tiếp xúc với các bài toán liên quan đến đạo hàm các hàm số. Ta đã
làm quen nhiều đến các dạng bài tập về xét tính đơn điệu của hàm số, xác
định các cực trị của hàm số đã cho,…
Xét tính đơn điệu của hàm số: lOMoAR cPSD| 59031616
Định lý sau được thừa nhận: Cho hàm y=f(x) có đạo hàm trên K nếu f ' ( x
)>0 với mọi x thuộc K thì hàm số f(x) đồng biến trên K nếu f ' ( x)<0 với
mọi x thuocj K thì hàm số f(x) nghịch biến trên K giả sử hàm số y=f(x)
có đạo hàm trên K. Nếu f ' ( x)>0 (f ' ( x)≤0 ∀ x∈K , f ( x )=0 tại môt số hữu hạn
điểm thì hàm số đồng biến hoặc nghịch biến trên K.
Điều kiện để hàm số có cực trị:
Định lý sau được thừa nhận: Giả sử hàm y=f(x) liên tục trên
K=(x0−ℎ;x0+ℎ)và có đạo hàm trên K hoặc trên K ∖{x0},ℎ>0. Nếu f ' ( x )>0 trên
khoảng (x0;x0+ℎ) thì x0 là một điểm cực tiểu của hàm số f(x).
Tìm cực trị:
Định lý sau được thừa nhận: Giả sử hàm y=f(x) có đạo hàm cấp 2 trong
khoảng K kể trên và h>0 thì: nếu f ' (x0)=0,f ' (x0)>0⇒ x0min nếu f ' (x0)=0,f '
(x0)<0⇒ x0max
(sgk Giải Tích 11).
Vẽ đồ thị hàm số
Sơ đồ bài toán khảo sát và vẽ đồ thị hàm số
• Bước 1. Tìm tập xác định của hàm số;
• Bước 2. Tính đạo hàm y' = f'(x) ;
• Bước 3. Tìm nghiệm của phương trình ;
• Bước 4. Tính giới hạn
và tìm tiệm cận đứng, ngang (nếu có);
• Bước 5. Lập bảng biến thiên;
• Bước 6. Kết luận tính biến thiên và cực trị (nếu có);
• Bước 7. Tìm các điểm đặc biệt của đồ thị (giao với trục Ox, Oy, các điểm đối xứng, ...);
• Bước 8. Vẽ đồ thị.
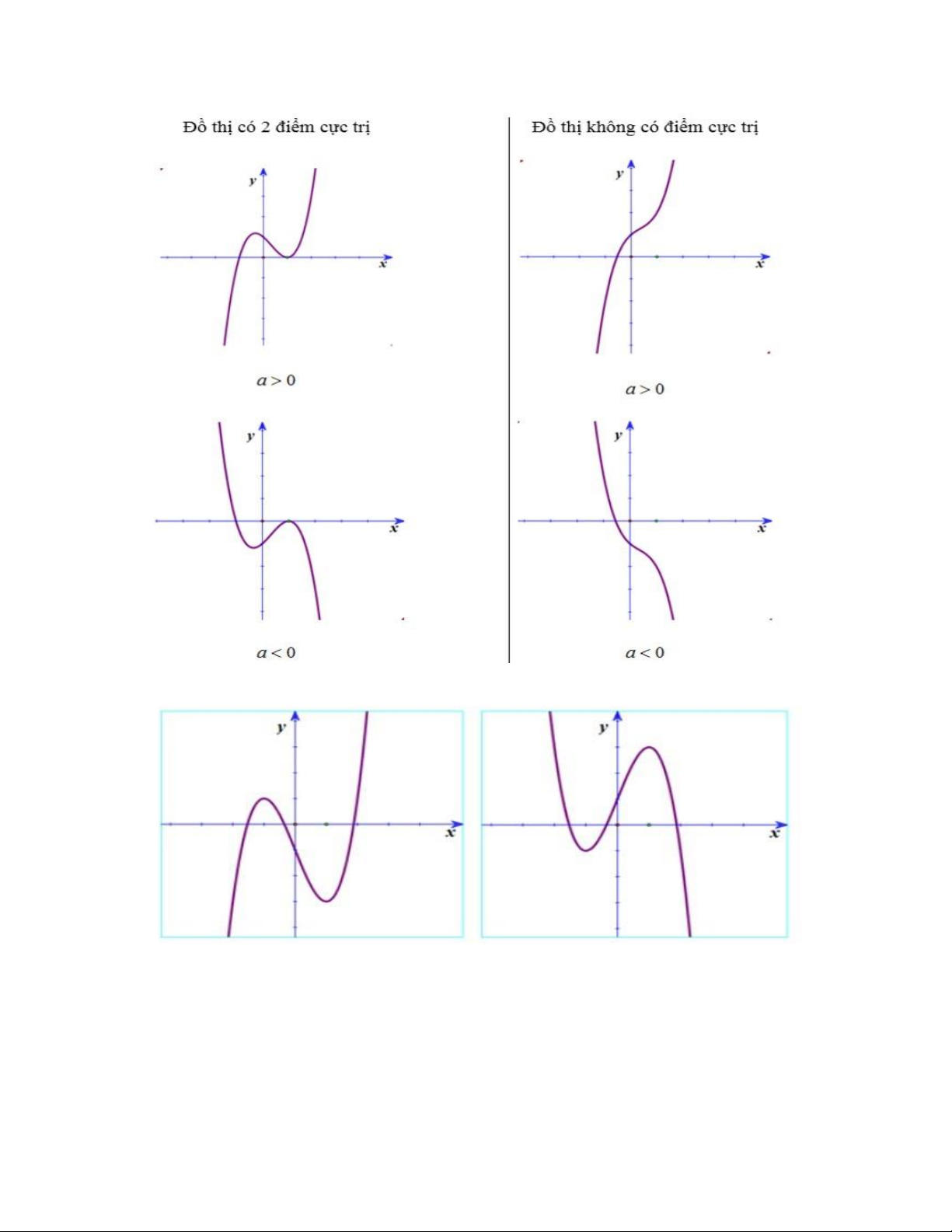
*Các dạng đồ thị của hàm số bậc 3 y= ax3 + bx2 + cx + d (a ≠ 0) lOMoAR cPSD| 59031616
- Lưu ý: Đồ thị hàm số có 2 điểm cực trị nằm 2 phía so với trục Oy khi ac < 0
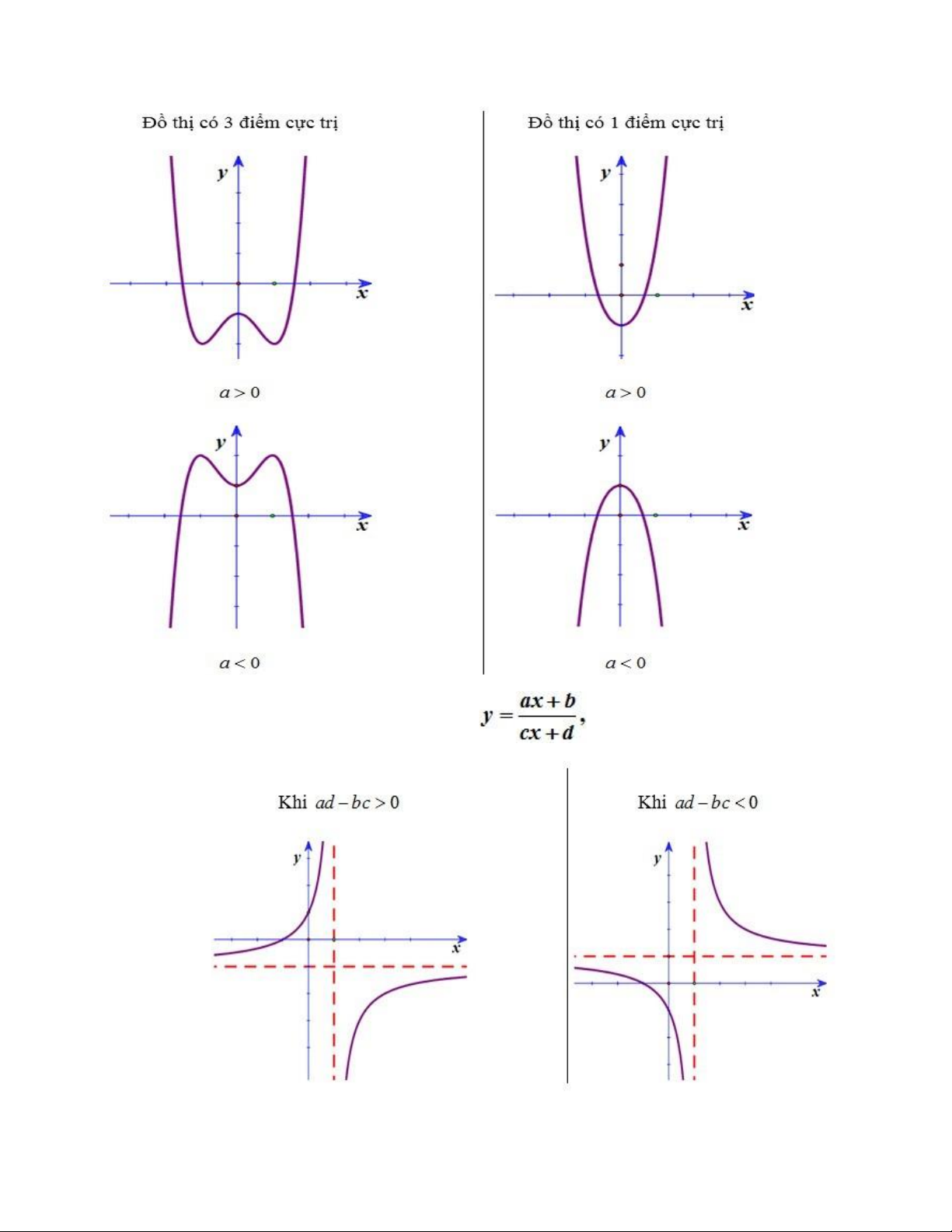
3. Các dạng đồ thị của hàm số bậc 4 trùng phương y = ax4 + bx2 + c (a ≠ 0) lOMoAR cPSD| 59031616
4 . Các dạng đồ thị của hàm số nhất biến
( ab - bc ≠ 0)
Biến đổi đồ thị Cho hàm số y = f(x) có đồ thị (C) . Khi đó, với số a > 0 ta có: lOMoAR cPSD| 59031616
• Hàm số y = f(x) + a có đồ thị (C') là tịnh tiến (C) theo phương của Oy lên trên a đơnvị.
• Hàm số y = f(x) - a có đồ thị (C') là tịnh tiến (C) theo phương của Oy xuống dưới ađơn vị.
• Hàm số y = f(x + a) có đồ thị (C') là tịnh tiến (C) theo phương của Ox qua trái a đơnvị.
• Hàm số y = f(x - a) có đồ thị (C') là tịnh tiến (C) theo phương của Ox qua phải ađơn vị.
• Hàm số y = -f(x) có đồ thị (C') là đối xứng của (C) qua trục Ox.
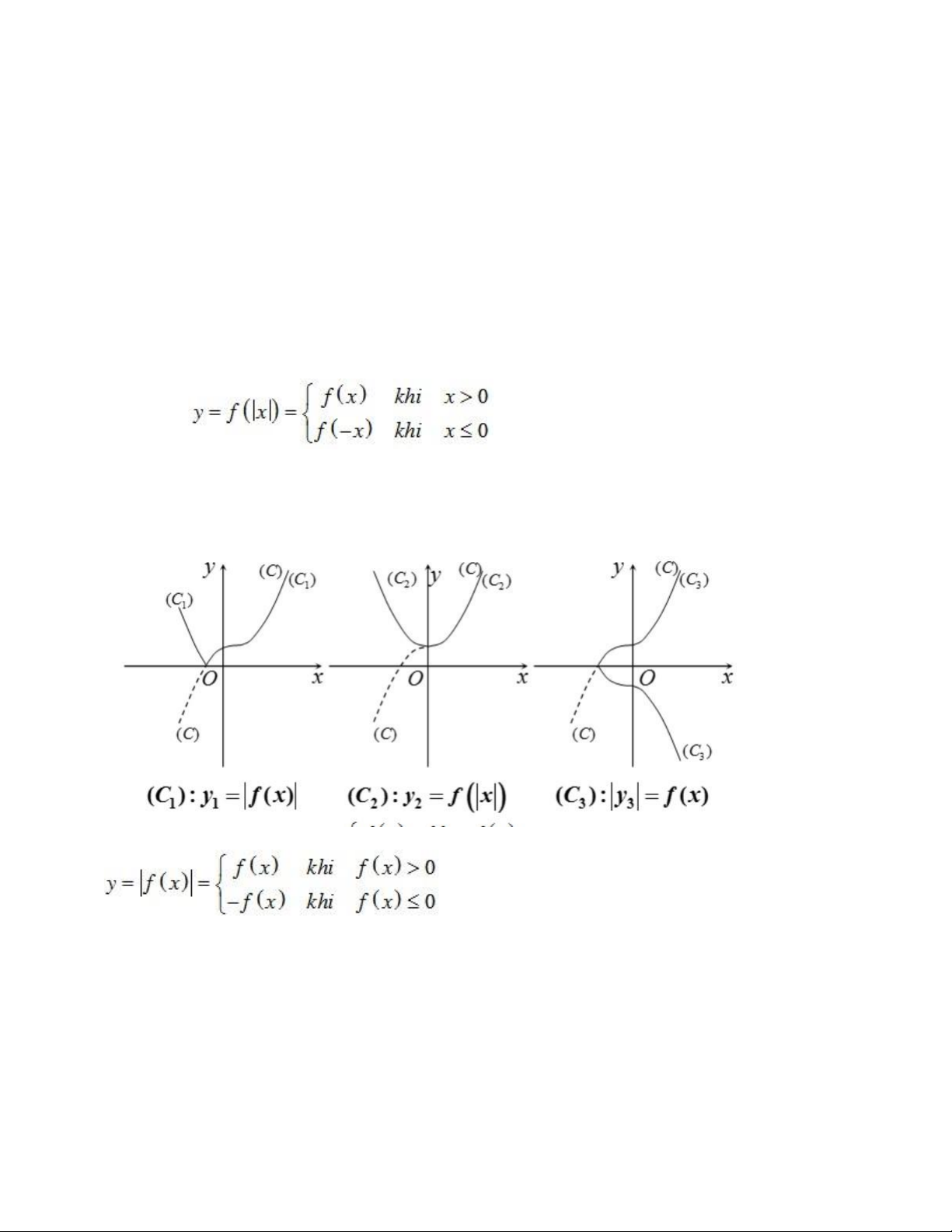
• Hàm số y = f(-x) có đồ thị (C') là đối xứng của (C) qua trục Oy. • Hàm số
có đồ thị (C') bằng cách:
- Giữ nguyên phần đồ thị (C) nằm bên phải trục Oy và bỏ phần (C) nằm bên trái Oy.
- Lấy đối xứng phần đồ thị (C) nằm bên phải trục Oy qua Oy. • Hàm số
có đồ thị (C') bằng cách:
- Giữ nguyên phần đồ thị (C) nằm trên Ox.
- Lấy đối xứng phần đồ thị (C) nằm dưới Ox qua Ox và bỏ phần đồ thị (C) nằm dướiOx.
2.2. Ứng dụng của đạo hàm trong vật lý:
Giải thích sự biến thiên của vận tốc tức thời, gia tốc tức thời, cường độ
tức thời của dòng điện,… mà ta gặp trong quá trình học vật lý. Vận tốc tức lOMoAR cPSD| 59031616
thời của một vật chuyển động thẳng có phương trình dạng s=s(t ) là một
hàm số có đạo hàm thì được xác định bằng:
lim s(t )−s (t0)
v(t0)=s' (t0)=
t→t0 t−t0Trong đó nếu t→t0⇔|t−t0| sẽ có độ chính xác cao.
Gia tốc tức thời:
Với đạo hàm cấp hai f '' (t) là gia tốc tức thời của chuyển động s=f (t ) tại thời điểm t.
Cường độ tức thời của dòng điện:
Điện lượng Q truyền trong dây dẫn là một hàm số thời gian của t hay Q=Q (t ) với
cường độ trung bình của dòng điện trong khoảng thời gian |t−t0| là I= Q(t ) ( ) −Q t0 t−t0
hoặc đơn giản chỉ là I (t0)=Q' (t0).
2.3. Ứng dụng của đạo hàm trong hình học:
Các bài toán về xác định tiếp tuyến của đường cong phẳng, phương
trình tiếp tuyến thường được thấy trong chương trình THPT.
Đạo hàm của hàm số y=f ( x) tại x là hệ số góc của tiếp tuyến 0 M0T của (C)
tại điểm M0(x0;f (x0)). Chứng minh: Giả sử ta có điểm M ¿ là điểm di chuyển
trên (C). Ta có M0H=Δx, HM=Δy. Hệ số góc của cát tuyến M0Mlà
tanφ== . Khi M dần tới thuyết, f(x) có đạo hàm tại x nên tồn tại giới hạn 0 MHM0HΔyΔx
M0¿thì Δx→0 và ngược lại. Theo giả f ' (x thì cát tuyến
0)= lim ΔyΔx=¿ Mlim→ M0 tanφ¿. Vậy khiM → M0 M0M dần tới vị Δx →0
trí giới hạn là đường thẳng ) M lim tanφ=f ' .
0T, có hệ số góc bằng M → M (x 0 0 Đường thẳng M của (C). Vậy
0T là tiếp tuyến tại M0
f ' (x0) là hệ số góc của
tiếp tuyến tại M của đồ thị (C). 0
2.4. Ứng dụng của đạo hàm để khảo sát và vẽ đồ thị hàm số: lOMoAR cPSD| 59031616
Dùng để tính các giá trị đồng biến, nghịch biến, tính đơn điệu của hàm
số, vì lẽ đó, các bài toán trong thực tế được tính toán một cách dễ dàng, thuận tiện hơn.
2.5. Ứng dụng của đạo hàm trong kinh tế:
Đặc biệt, đạo hàm còn được sử dụng phổ biến để giải quyết các bài toán
kinh tế. Để từ đó, các cá nhân, tổ chức, doanh nghiệp có thể lập được
những chiến lược đúng đắn vào các cuộc đầu tư, kinh doanh,…
2.6. Ứng dụng của đạo hàm trong đời sống:
2.6.1. Ứng dụng của đạo hàm trên đồng hồ công tơ xe máy:
Giúp xác định được quãng đường (km) mà xe đang chạy. Trường hợp,
kim chỉ giá trị 0 thì quãng đường không tăng không giảm, hoặc đang ngừng chuyển động.
2.6.2. Ứng dụng của đạo hàm trong xây dựng:
Giúp các nhà thầu, kĩ sư tính toán chi phí xây dung, thiết kế công
trình kiến trúc sao cho sự sai số là ít nhất. Áp dụng như bài toán cực tiểu của hàm số.
2.6.3. Tính thời gian của các vận động viên thể thao (chạy, bơi) tiếp sức:
Lúc này, tổng thời gian được coi là hàm số f(x) và đây là một bài
toán cực trị. Tìm thời gian cực tiểu dựa vào đạo hàm của hàm số đó.
2.6.4. Tính tốc độ sinh trưởng của sinh vật:
Các khảo sát về tốc độ, quá trình về sự phát triển, sinh trưởng và sinh
sản của sinh vật sẽ được tiến hành một cách dễ dàng hơn. Từ đó, đưa
ra những khuyến cáo, những biện pháp hợp lí đối với từng đối tượng nghiên cứu.
3. Đạo hàm trong các bài toán kinh tế
3.1. Ý nghĩa của đạo hàm trong kinh tế:
- Tính tốc độ tăng trưởng kinh tế nhằm đưa ra những quyết định đầu tư đúng đắn.
- Dự đoán được tốc độ tăng trưởng của doanh nghiệp trong tương lai lOMoAR cPSD| 59031616
- Dự đoán hàm cần tính đạt giá trị lớn nhất hay giá trị nhỏ nhất ở đâu nhằm tối ưu hóa các hoạt động. -
3.2. Các bài toán kinh tế
3.2.1. Hàm một biến
Hiện nay các sản phẩm có mặt trên thị trường nhìn chung đều bị chi phối bởi 2 yếu tố chính:
- Giá của sản phẩm: p ( hay còn gọi là hàm cầu ) -> hàm giảm theo x
- Số lượng sản phẩm bán ra: x
Khi đó với x sản phẩm được bán ra thị trường với giá mỗi sản phẩm là p thì tổng danh
thu sẽ được tính theo công thức: R(x) = p.x
Hàm R(x) lúc này sẽ được gọi là hàm doanh thu. Đạo hàm R’ của hàm doanh thu được
gọi là hàm doanh thu cận biên, tượng trưng cho tốc độ thay đổi theo số sản phẩm x được bán ra.
Khi doanh nghiệp thay đổi một lượng sản phẩm thì doanh thu cũng sẽ thay đổi.
Gọi C(x) là hàm chi phí sản xuất trên x sản phẩm thì tổng lợi nhuận thu được sẽ được tính theo công thức: P(x) = R(x) - C(x)
Hàm P(x) lúc này sẽ được gọi là hàm lợi nhuận. Đạo hàm P’ của hàm lợi nhuận được
gọi là hàm lợi nhuận biên.
Nhiều quyết định kinh tế được đưa ra khi phân tích hàm chi phí sản xuất C(x), hàm
doanh thu R(x) Một quy tắc cơ bản là
- Nếu hàm lợi nhuận > 0 thì tăng sản xuất là có lợi.
- Nếu hàm lợi nhuận < 0 thì giảm sản xuất là có lợi.
Ví dụ: Một của hiệu bán 200 đầu đĩa/tuần với giá 350$. Thông tin từ một cuộc
khảo sát thị trường cho biết nếu người mua được giảm 10$, thì số lượng đầu đĩa
bán ra sẽ tăng thêm 20 chiếc/tuần. Tìm hàm cầu và hàm doanh thu. Để tối đa hoá
doanh thu thì cửa hàng cần đưa ra mức giảm giá là bao nhiêu? lOMoAR cPSD| 59031616
Giải: Nếu x là số đầu đĩa được bán mỗi tuần thì doanh số tăng thêm mỗi tuần là x-200.
Với mỗi 20 đơn vị bán thêm được thì giá sản phẩm lại giảm đi 10$. Vậy cứ bán thêm
được một sản phẩm thì giá sẽ giảm đi (1/20)×10 và hàm cầu sẽ bằng:
p(x)=350-10/20 (x-200)=450-1/2 x Hàm doanh thu là R(x)=xp(x)=450x-1/2 x^2
Vì R' (x)=450-x, chúng ta thấy rằng R'(x)=0 khi x=450. Giá trị x này cho ta một cực
đại tuyệt đối theo Tiêu chuẩn đạo hàm cấp 1 (hoặc đơn giản chỉ cần quan sát ta thấy
đồ thị R là một parabol hướng xuống). Giá trị tương ứng là: p(450)=450-1/2 (450)=250
Do đó, số tiền giảm giá là 350-225=125. Vậy, để tối đa hoá doanh thu cửa hàng nên giảm giá 125$.
Ví Dụ 2: Một nhà sản xuất camera ước tính khi x ( trăm ) camera được sản xuất
thì tổng lợi nhuận thu được sẽ là:
P(x) = -0,0035x3 + 0,07x2 + 25x - 200 ngàn đô la
1. Tìm lợi nhuận cận biên
2. Tìm lợi nhuận cận biên khi x=10, x=50,x=80
3. Giải thích các kết quả này Giải
1. Lợi nhuận cận biên P’(x)= -0,0105x2 + 14x +25
2. P’(10) = 25,35; P’(50) = 5,75; P’(80) = -31
3. P’(10) = 25,35 nghĩa là khi lợi nhuận tăng lên xấp xỉ 25,35, ngàn đô la khi mức sản
xuất tăng từ 10 lên 11 ( trăm ) camera. Một số bài tập
Bài 1: Cho biết hàm sản xuất ngắn hạn Q = 15√3 L. Hãy tính MPPL khi L = 8 và
khi L = 1000 và giải thích ý nghĩa của kết quả tìm được? Q = f(L) L: Lao động Giải Q = 15 MPPL )’ = 15.(L1/3) 15 -2/3 lOMoAR cPSD| 59031616 = 3 .L = 5.L-2/3
=> MPPL (8) = 5.8-2/3 = 1.25
Tại mức lao động L = 8 khi lao động tăng 1 đơn vị ( 8 -> 9) thì sản lượng tăng 1 lượng 1.25.
MPPL (1000) = 5.1000-2/3 = 0.05
Tại mức lao động L = 1000 khi lao động tăng 1 đơn vị ( 1000 -> 1001) thì sản
lượng tăng 1 lượng 0.05.
Bài 2: Cho biết hàm cầu đối với sản phẩm của nhà sản xuất độc quyền với giá p
tính bằng USD: Q = 500 - 0.2p. Hãy tính MR tại mức sản lượng Q = 90 và giải
thích ý nghĩa. MR = TR’ Giải Hàm doanh thu: TR = p.Q ;
p = D-1(Q) : hàm cầu ngược Qđ = Q(p) = 500 - 0.2p
<=> p = 2500 - 5Q = D-1(Q) => TR = (2500 - 5Q).Q Doanh thu cận biên:
MR = TR’(Q) => MR = 2500 - 10Q (Q = 90) MR (90) = 2500 - 10.90 = 1600
Tại mức Q0 = 90 khi sản lượng tăng thêm 1 đơn vị (90 -> 91) thì doanh thu sẽ tăng thêm 1600.
Bài 3: Cho biết hàm cầu đối với sản xuất 1 loại hàng hóa như sau: Q = 3200 - 0.5p2
a) Tính hệ số co dãn của cầu theo giá ở mức giá p < 80.
b) Tính hệ số co dãn của cầu theo giá tại các mức giá p = 20, p = 50 và giải thích ý nghĩa. Giải Qđ = Q(p) = 3200 - 0.5p2 P
Hệ số co dãn của cầu theo giá: Ɛd = D’(p).D(p) − p = 3200−0.5 p lOMoAR cPSD| 59031616 Ɛd (20) = = - 3.33%
Tại mức giá p0 = 20, nếu giá tăng 1% thì lượng cầu giảm 3.33%.
Bài 4: Hãy xác định mức sản lượng tối ưu của nhà sản xuất, cho biết hàm doanh
thu và hàm chi phí như sau: TR = 4000Q - 33Q2,
TC = 2Q3 - 3Q2 + 400Q + 5000 Q: sản lượng Giải Hàm lợi nhuận: Π(Q) = TR(Q) - TC(Q) = - 2Q3 - 30Q2 + 3600Q - 5000 Π’(Q0) = 0 Π(Q) đạt max tại Q0 <=> Π”(Q0) = 0 Π’(Q)= -6Q2 - 60Q + 3600 Π”(Q) = 0 <=> Q = 20 (nhận) => Q = - 30 (loại)
Π”(Q) = (- 6Q2 - 60Q + 3600)’ = - 12Q - 60 Π”(20) = - 12.20 - 60 = - 400 < 0
Suy ra Π đạt max tại Q = 20 => Πmax = 39000
Bài 5: Một nhà sản xuất độc quyền bán sản phẩm trên thị trường có hàm cầu
ngược là p = 1400 - 7.5Q.
a) Tính hệ co dãn của cầu theo giá ở mỗi mức giá p
b) Xác định mức sản lượng cho lợi nhuận tối đa, cho biết hàm chi phí cận biên là MC = 3Q2 -12Q + 140 Giải P a) Ɛd = D’(p).D(p),
Qd = D(p): hàm cầu <=> p = D-1(Q): hàm cầu ngược P = 1400 - 7.5Q 1 => Q = - 7.5p lOMoAR cPSD| 59031616 p => Ɛd = 1 − p 7.5 − p = 1400− p b) TR - TC Π MC = TC’ Hàm doanh thu: TR(Q) = p.Q
= (1400 - 7.5Q).Q => Doanh thu cận biên: MR = TR’(Q) = 1400 - 15Q
Điều kiện cần để tối đa lợi nhuận là: doanh thu cận biên phải bằng chi phí cận biên. <=> MR = MC
<=> 1400 - 15Q = 3Q2 -12Q + 140 Điều kiện đủ:
Π”(Q) = MR’(Q) - MC’(Q)
Π = TR - TC => Π’ = TR’ - TC’ = MR - MC => Π” = MR’ - MC’
Bài 6: Giả sử hàm sản xuất của một doang nghiệp là:
Q = f(L) = 5 √ L L: số công nhân
Ở mức L = 100 đơn vị lao động = 100 công nhân thì Q = 5 = 50 đơn vị sản phẩm Giả i
Sản phẩm biên tế của lao động tại L = 100 là 5 dQ = f’(L) 2√100 dL 5 = 2√L = 0.25 khi L =100
Điều này có nghĩa là: khi tăng mức sử dụng lao đông từ 100 -> 101 thì sản lượng sẽ
tăng thêm 0.25 đơn vị sản phẩm. Thử xét: lOMoAR cPSD| 59031616 L 100 110 120 150 200 400 1.000 MQ 0.25 0.23 0.22 0.2 0.17 0.125 0.079 Nhận xét:
MQ là một hàm số giảm dần, đến một số lượng công nhân nhất định nào đó,
việc tuyển thêm công nhân không còn hiệu quả, chỉ tăng thêm chi phí lOMoAR cPSD| 59031616
Bài 7: (Tối đa hóa sản lượng trong điều kiện ngân sách cố định) Một doanh
nghiệp cạnh tranh thuần túy có hàm sản xuất là Q = K(L + 5). Biết rằng giá thuê
một đơn vị vốn là wK = 5USD, giá thuê nhân công giá wL = 10USD và doanh
nghiệp sản xuất trong điều kiện ngân sách cố định B = 950USD. Xác định lượng
cầu Marshall của vốn và nhân công mà doanh nghiệp cần sử dụng để tối đa hóa sản lượng. Giải
Gọi K là lượng vốn, L là lượng nhân công mà doanh nghiệp cần sử dụng. Khi dó điều
kiện ngân sách cố định B = 950USD trở thành 5K + 10L = 950 K + 2L – 190 = 0
Vấn đề kinh tế của doanh nghiệp được đưa về bài toán: chọn K, L (K > 0, L > 0) để
hàm Q = K(L + 5) cực đại trong điều kiện K + 2L – 190 = 0.
Ta có hàm điều kiện = (K, L) = K + 2L – 190.
Vì điều kiện giải được ngay K = 190 – 2L nên ta dùng phương pháp thế.
Thay vào Q ta được Q = (190 – 2L).(L + 5) = – 2L2 + 180L + 950 (hàm 1 biến L)
Ta có Q’(L) = – 4L + 180; Q”(L) = – 4 < 0 (với mọi L > 0).
Bởi thế Q chỉ có thể đạt cực đại. Q’(L) = 0 <=> – 4L + 180 = 0
<=> L = 45 (> 0)
K = 190 – 2.45 = 100 (> 0).
Do đó Q đạt cực đại tại L = 45, tương ứng K = 100 với
Qmax = Q(100, 45) =100(45 + 5) = 5000
Bài 8: Một sản phẩm trên thị trường có hàm cầu là:
Q= 1.000 - 14P, Q là sản lượng, P là giá bán.
Tìm MR khi P = 40 và P = 30 Giải
Hàm doanh thu là: TR = PQ = P(1.000 – 14P) = 1.000P – 14P2 MR = 1.000 – 28 P
*Khi P = 40, MR = 1000 – 28(40) = - 120 26 Downloaded by Canh Gia (canhgia23@gmail.com) lOMoAR cPSD| 59031616
Nghĩa là khi doanh nghiệp tăng giá từ 40 lên 41 (tăng 1 đơn vị tiền tệ), thì
doanh thu sẽ giảm 120 đơn vị tiền tệ.
*Khi P = 30, MR = 1.000 – 28(40) = 160
Nghĩa là khi doanh nghiệp tăng giá từ 30 lên 31 (tăng 1 đơn vị tiền tệ), thì
doanh thu sẽ tăng 160 đơn vị tiền tệ.
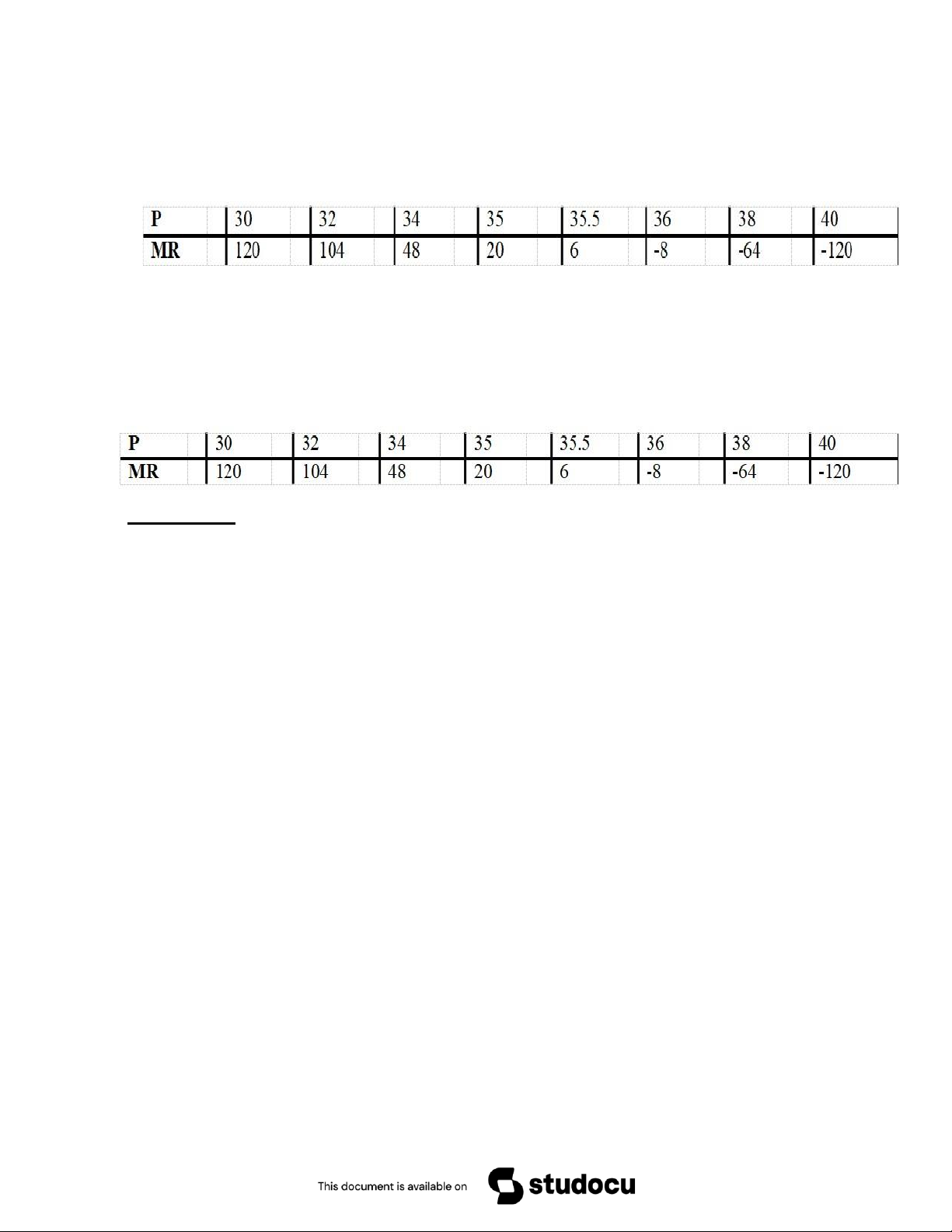
Ta tính MR ở một số mức khác nhau: Nhận xét:
MR là một hàm số giảm, Có một mức giá MR = 0. 27 Downloaded by Canh Gia (canhgia23@gmail.com)