Tìm điều kiện để Phương trình – Hệ phương trình có nghiệm – Đặng Thành Nam

Tài liệu gồm 40 trang hướng dẫn giải các bài toán tìm điều kiện của tham số để phương trình – hệ phương trình có nghiệm, tài liệu do thầy Đặng Thành Nam biên soạn.

Dạng toán tìm điều kiện của tham số để phương trình, hệ phương trình có nghiệm thường xuất hiện trong đề thi TSĐH dưới dạng áp dụng phương pháp xét tính đơn điệu của hàm số để tìm miền giá trị của hàm số, từ đó suy ra giá trị cần tìm của tham số m. Đây là loại bài toán không khó và chiếm một điểm trong đề thi, nên nhớ áp xét tính đơn điệu của hàm số.

77 39 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung Toán 10

Môn: Toán 10

Thông tin:

40 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
Chuyên đề 2: Điều kiện để phương trình, hệ phương trình có nghiệm
102
Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
Email : dangnamneu@gmail.com
Yahoo: changtraipkt
Mobile: 0976266202
CHUYÊN ĐỀ 2:
ĐIỀU KIỆN ĐỂ PHƯƠNG TRÌNH, HỆ
PHƯƠNG TRÌNH CÓ NGHIỆM
Chuyên đề 2: Điều kiện để phương trình, hệ phương trình có nghiệm
103
Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
104
Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
Email : dangnamneu@gmail.com
Yahoo: changtraipkt
Mobile: 0976266202
Dạng toán tìm điều kiện của tham số để phương trình, hệ phương trình có nghiệm thường xuất
hiện trong đề thi TSĐH dưới dạng áp dụng phương pháp xét tính đơn điệu của hàm số để tìm
miền giá trị của hàm số, từ đó suy ra giá trị cần tìm của tham số m. Đây là loại bài toán không
khó và chiếm một điểm trong đề thi, nên nhớ áp xét tính đơn điệu của hàm số.
Phương pháp
+ Điều kiện cho trước ở đây được rút ra từ tập xác định của hàm số hoặc được xác định từ điều
kiện nghiệm của phương trình mà đề bài yêu cầu. Ta quy ước điều kiện cho trước này là miền
D
.
+ Để giải quyết dạng bài toán này ta dùng phương pháp hàm số, mục đích là biểu diễn tham số
theo hàm của một ẩn trên miền
D
, sau đó tìm GTLN,GTNN của hàm số đó trên
D
.
+ Phương trình, bất phương trình dưới dạng sau thì điều kiện của tham số là:
(i).
( ) ( ), min ( ) ( ) max ( )
t D
t D
g m f t t D f t g m f t
.
(ii). ( ) ( ),
g m f t t D
có nghiệm
( ) min ( )
t D
t D g m f t
.
(iii). ( ) ( ),
g m f t t D
có nghiệm
( ) max ( )
t D
.
(iv). ( ) ( ),
g m f t t D
có nghiệm với mọi t thuộc
D
khi và chỉ khi
( ) ax ( )
t D
g m m f t
.
(v). ( ) ( ),
g m f t t D
có nghiệm với mọi t thuộc
D
khi và chỉ khi
( ) min ( )
t D
g m f t
.
Các hướng giải quyết bài toán loại này:
(i). Xét tính đơn điệu của hàm trực tiếp theo ẩn
x
.
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
105
Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
(ii). Nếu xuất hiện biểu thức đối xứng
ax
(ax )( )
b cx d
b cx d
, thì
đặt ax
t b cx d
.
(iii). Nếu xuất hiện
2 2
; ( ) ( )
a bx c bx a bx c bx a c
,
thì đặt
sin
os
a bx a c
c bx a cc
Và sử dụng hệ thức
2
2
2
2t
2
sin
1 t
2
1 t
2
os
1 t
2
an
an
an
c
an
, tiếp tục đặt
2
t tan
.
(iv). Nhân hai vế với hệ thức liên hợp nếu có.
BÀI TẬP MẪU
Bài 1. Tìm các giá trị thực của tham số m để phương trình sau có nghiệm
6 2 (4 )(2 2) 4( 4 2 2)( )
x x x m x x x R
Lời giải:
+Điều kiện:
1 4
x
.
Đặt
4 2 2
t x x
Xét hàm số
( ) 4 2 2
t x x x
liên tục trên đoạn
1,4
. Ta có
1 2
'( ) '( ) 0 2 4 2 2 3
2 4 2 2 2
t x t x x x x
x x

.
Ta có:
1,4
(1) (3) (4)
1,4
min ( ) (1) 3
3; 3; 6
( ) (3) 3
x
x
t x t
t t t
maxt x t
Phương trình đã cho trở thành:
2 2
4 4 4 4
t m t m t t
.
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
106
Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
Xét hàm số
2
(
4
) 4f
t t
t
Ta có
( ) 2 4
f t t
( ) 0 2 ( 3) 7 4 3; (2) 0; (3) 1
f t t f f f
( ) ( )
0 ( ) 1 min ax 0 1
f t f t
f t m m m
Vậy giá trị cần tìm của m là
0 1
m
.
Bài 2. Tìm các giá trị thực của tham số m để phương trình sau có nghiệm thực
2
9
1 4 3
4
x x x x m
Lời giải:
+Điều kiện:
4 1
x
.
Khi đó phương trình tương đương với:
3
1 4
2
m x x x
.
Đặt
3 5 5 5 5
( ) ,( )
2 2 2 2 2
t x m f t t t t t
.
Xét hàm số
5 5 5 5
( ) ,( )
2 2 2 2
f t t t t t
, ta có
( ) ( )
f t f t
nên hàm số
f(t) chẵn, nên ta chỉ cần chỉ cần xét f(t) trên
5
0;
2
. Khi đó
5 5
( )
2 2
f t t t t
.
+Ta có:
1 1
( ) 1 ( ) 0
5 5
2 2
2 2
f t f t
t t
5 5 5 5
2 ( )( ) 0(*)
2 2 2 2
t t t t
Giải phương trình (*):
+Đặt
2
5 5 5 5
( 0) 5 2 ( )( )
2 2 2 2
u t t u u t t
Khi đó phương trình (*) trở thành:
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
107
Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
2 2 2
1 21 1 21 25
5 0 ( ) 5 2
2 2 4
u u u t
39 21
8
t
.
Ta có:
5 5 39 21 9 21 39 21
(0) 10; ( ) 5 ; ( )
2 2 8 2 8
f f f
.
Từ đó suy ra :
5
0;
2
5
0;
2
min ( ) (
39 21 9 21 39 21
( )
8 2 8
0) 10
m ( )
x
x
f x f
ax f x f
.
Vậy giá trị cần tìm của m là:
9 21 39 21
10
2 8
m
.
Bài 3. Tìm các giá trị thực của tham số m để phương trình sau đây có nghiệm thực
3
2 3 2 3 6 5 8 0
x m x m
Lời giải:
+Điều kiện:
5
6
m
x .
Đặt
3
3
2
3 2 3 2
6 5
6 5
u x m u x m
v x m
v x m
.
Từ đó suy ra:
3 2
2 (1);2 3 8 0(2)
u v m u v
Từ (1) và (2) ta suy ra
3 2
8 3
2( )
2
v
m v
.
Xét hàm số
3 2
8 3
( ) 2( )
2
v
f v v
liên tục trên đoạn
0;

.
Ta có
2
8 3
'( ) 9( ) 2 0, 0
2
v
f v v v
. Suy ra hàm số
( )
f v
nghịch biến trên đoạn
0;

.
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
108
Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
Mặt khác
lim ( ) ; (0) 128
v
f v f

 .
( ) 128, 0
f v v
để phương trình có nghiệm thì
128
m
.
Vậy giá trị cần tìm của m là:
,128
 .
Bài 4. Tìm các giá trị của tham số m để phương trình sau có đúng 2 nghiệm thực phân biệt:
4 4
2 2 2 6 2 6
x x x x m
Lời giải:
Điều kiện:
0 6
x
.
Xét hàm số
4 4
2 2 2 6 2( 6)f xx
x x x
lien tục trên đoạn
0;6
.
Ta có
3 3
4 4
1 1 1 1
'( )
2 6
2 (2 ) 2 (6 )
f x
x x
x x
3 3
4 4
1 1 1 1
'( ) 0 0
2 6
2 (2 ) 2 (6 )
f x
x x
x x
3 3
4 4
1 1 1 1 1
( ) ( ) 0
2
2 6
(2 ) (6 )
x x
x x
4 4 4 4 4 4
4
1 1 1 1 1 1 1 1 1 1
( )( ) ( )( ) 0
2
2 6 2 2 (6 ) 6 2 6 2 6x x x x x x x x x x
4 4 4 4
4
1 1 1 1 1 1 1
( )( ) 0
2 6 2 2 2 2 (6 ) 2 6 2 6x x x x x x x x
4 4
1 1
2 6 2
2 6
x x x
x x
.
Ta có
4
4
(0) 2 6 2 6
(2) 6 3 2
(6) 12 12
f
f
f
Lập bảng biến thiên của hàm số
( )
f x
trên đoạn
0;6
, ta suy ra để phương trình có đúng 2
nghiệm thực thì :
4
2 6 2 6 6 3 2
m .
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
109
Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
Bài 5. Tìm m để phương trình sau có nghiệm thực:
24
3 1 1 1
x m x x
Lời giải:
+Điều kiện:
1
x
.
Phương trình đã cho tương đương với
4
1 1
3 (*)
1 1
x x
m
x x
.
Ta đặt
4
1
1
x
t
x
, xét hàm số
4
1
( )
1
x
t x
x
trên đoạn
1;

.
Ta có
3
4
2
1 1
'( ) ( ) 0, 1
2( 1) 1
x
t x x
x x
Mặt khác ta có:
4
1
lim lim 1
0 1
1
(1) 0
x x
x
t
t
x
t
 
.
Phương trình (*) trở thành:
2
3
m t t
.
Xét hàm số
2
( ) 3
f t t t
liên tục trên đoạn
0;1
.
Ta có
1
( ) 1 6 ( ) 0
6
f t t f t t
.
Ta có:
0;1
0;1
(0) 0
min ( ) (1) 2
1 1
( )
1 1
6 12
m ( ) ( )
6 12
(1) 2
t
t
f
f t f
f
ax f t f
f
.
Vậy để phương trình có nghiệm thì
1
2
12
m
.
Bài 6. Tìm m để phương trình sau có nghiệm thực:
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
110
Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
2 2
1 1
x x x x m
Lời giải:
Xét hàm số
2 2
( ) 1 1
f x x x x x
liên tục và xác định trên
.
Ta có
2 2
2 1 2 1
'( )
2 1 2 1
x x
f x
x x x x
.
Suy ra
2 2
'( ) 0 (2 1) 1 (2 1) 1
f x x x x x x x
2 2 2 2
(2 1) ( 1) (2 1) ( 1) 0.
x x x x x x x
Thử lại thấy
0
x
không thỏa mãn, vậy
'( )
f x
không đổi dấu trên tập xác định. Mặt khác lại có
'(0) 1 '( ) 0,f f x x
. Vậy
( )
f x
đồng biến trên
.
Ta có
2 2
2 2
2
lim ( ) lim( 1 1) lim
1 1
x x x
x
f x x x x x
x x x x
  
2 2
2
lim 1
1 1 1 1
1 1
x
x x x x

.
Và tương tự ta có,
lim ( ) 1
x
f x

.
Từ đó suy ra :
1 ( ) 1
f x
.
Vậy để phương trình có nghiệm thì
1 1
m
.
Bài 7. Tìm m để phương trình sau có nghiệm thực:
3
3(3 2) 3 2 2(6 5 ) 6 5 48
x x x x x m
.
Lời giải:
Xét hàm số
3
3(3 2) 3 2 2(6 5 ) 6 5)
8
(
4
x x x xf x
x
liên tục trên đoạn
6
0;
5
.
Ta có
3
'( ) 12 3 2 18 6 5 48
f x x x
3
'( ) 0 2 3 2 3 6 5 8 0(*)
f x x x .
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
111
Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
Giải phương trình (*):
Đặt
3
3
3 2
2
3 2 3 2
5 3 8(1)
6 5
6 5
u x u x
u v
v x
v x
.
Và từ (*) ta có
2 3 8 0(2)
u v
.
Từ (1) và (2) ta suy ra:
3 2 2
8 2
5 3( ) 8 ( 2)(15 26 20) 0
3
u
u u u u
3
2 3 2 2 2
u x x
.
Vậy
'( ) 0 2
f x x
.
Ta có
3 3
6
0;
5
( 2) 272
6 48 288 6 48 288
( ) min ( ) ( ) .
5 5 5 5
5 5 5 5
lim ( )
x
x
f
f f x f
f x


Vậy để phương trình có nghiệm thì
3
48 288
5
5 5
m
.
Bài 8.Tìm m để phương trình sau đây có nghiệm thực:
(4 3) 3 (3 4) 1 1 0
m x m x m
Lời giải:
+ Điều kiện:
3 1
x
.
Phương trình đã cho tương đương với
(4 3 3 1 1) 1 4 1 3 3
m x x x x
1 4 1 3 3
(*)
4 3 3 1 1
x x
m
x x
.
Ta có
2 2
( 1 ) ( 3) 4
x x
, nên ta đặt
1 2sin
,(0 )
2
3 2cos
x
x
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
112
Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
Sử dụng
2
2 2
2tan 1 tan
2 2
sin ;cos
1 tan 1 tan
2 2
và đặt
2
tan (0 1)
2
t t
.
Khi đó (*) trở thành:
2 2 2
2 2 2
1 16 6(1 ) 5 16 7
8(1 ) 12 1 7 12 9
t t t t t
m
t t t t t
.
Xét hàm số
2
2
5 16 7
( )
7 12 9
t t
f t
t t
liên tục trên đoạn
0;1
.
Ta có
2
2 2
52 8 60
'( ) '( ) 0, [0;1]
( 7 12 9)
t t
f t f t t
t t
. Suy ra hàm số
( )
f t
đồng biến trên
0;1
.
Suy ra
0;1
0;1
7
min ( ) (0)
9
9
m ( ) (1)
7
x
x
f x f
ax f x f
Vậy để phương trình có nghiệm thì
7 9
9 7
m
.
Bài 9. Tìm những giá trị thực dương của tham số m để phương trình sau đây có nghiệm thực
không vượt quá
6
.
2 2 1 3 6 6 2 1 3 2
x x x m x x x
.
Lời giải:
Điều kiện
1
2
x
.
Khi đó phương trình tương đương với
2 6 2 1 3 (*)
x x x m
Với những giá trị thực dương của tham số m nên để phương trình (*) có nghiệm thì
2 1 3 0 5
x x
Vậy ta xét hàm số
( ) 2 6 2 1 3
f x x x x
trên khoảng
5;6
Ta có
'( ) 0, 5;6
f x x . Và
(5) 0; (6) 6 2 11 3
f f
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
113
Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
Vậy
0 6 2 11 3
m
là giá trị cần tìm.
Bài 10. Xác định tất cả các giá trị thực của tham số m để hệ sau đây có nghiệm thực:
3 3
3 3
1 1
5
1 1
15 10
x y
x y
x y m
x y
Lời giải:
Hệ phương trình đã cho tương đương với:
3 3
1 1
5
1 1 1 1
( ) ( ) 3( ) 3( ) 15 10
x y
x y
x y x y m
x y x y
3 3
1 1
5
1 1
( ) ( ) 15 5
x y
x y
x y m
x y
3
1 1
5
1 1 1 1 1 1
( ) 3( )( )( ) 15 5
x y
x y
x y x y x y m
x y x y x y
1 1
5
1 1
( )( ) 8
x y
x y
x y m
x y
Đặt
1
( ; 2)
1
u x
x
u v
v y
y
,
u v
là nghiệm của phương trình:
2
5 (8 ) 0
t t m
(1)
Yêu cầu bài toán tương đương với phương trình (1) có 2 nghiệm phân biệt thỏa mãn
2
t
.
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
114
Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
Từ (1) ta có:
2
5
( ) 5 8( 2) '( ) 2 5 '( ) 0
2
m f t t t t f t t f t t
.
Ta có:
5 7
( 2) 22; (2) 2; ( ) ;lim ( )
2 4
x
f f f f x

.
+Để (1) có 2 nghiệm phân biệt (
2
t
)thì đường thẳng
y m
cắt đồ thị hàm số
( )
y f t
tại 2
điểm phân biệt. Lập bảng biến thiên hàm số
( )
f t
,dựa vào bảng biến thiên
7
2 22
4
m m

là giá trị cần tìm.
Bài 11. Tìm tất cả các giá trị thực của tham số m để hệ phương trình sau có nghiệm thực:
2
4
(3 ) 2 2 2 1 0(1)
(*)
3 1 10 2 2 1(2)
x x y y
y m x y
Lời giải:
+ Điều kiện:
2; 1
x y
.
Khi đó phương trình (1) tương đương với:
(1 2 ) 2 (1 2 1) 2 1
x x y y
( 2 ) ( 2 1)
f x f y
, trong đó
( ) (1 ) ( 0)
f t t t t
.
Ta có
1
'( ) 0, 0
2
t
f t t t
t
hàm số
( )
f t
đồng biến trên
0;

( 2 ) ( 2 1) 2 2 1 3 2 1 2( 1)
f x f y x y x y y
.
Thay
3 2
x y
vào (2) ta được :
2
4
3 1 2 1 2 1(1)
y m y y . Do vậy ta chỉ cần tìm m để
phương trình (1) có nghiệm
1
y
.
Chia cả hai vế của (1) cho
4
1
y
ta được:
4
1 1
3 2 2 ( )
1 1
y y
m i
y y
, đặt
4
1
0 1
1
y
t t
y
.
Khi đó phương trình (i) trở thành:
2
3
2
m t t
.
Xét hàm số
2
( ) 3
f t t t
liên tục trên đoạn
0;1
.
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
115
Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
Ta có
1
'( ) 3 1 '( ) 0
3
f t t f t t
.
Lại có:
1 1 1 1 1
(0) 0; ( ) ; (1) ( )
3 6 2 6 2
f f f f t
.
Vậy để phương trình có nghiệm thì
1 1
6 2
m
.
Bài 12. Tìm m để hệ phương trình sau có nghiệm:
3 2
2
2 ( 2)
(*)
1 2
x y x xy m
x x y m
Lời giải:
Hệ phương trình đã cho tương đương với:
2
2
( )(2 )
2 1 2
x x x y m
x x x y m
Ta đặt
2
1
4
2
u x x
v x y
Khi đó hệ trở thành:
2
(2 1) 0(1)
1 2
1 2
uv m
u m u m
u v m
v m u
Vậy hệ có nghiệm khi và chỉ khi (1) có nghiệm thỏa mãn
1
4
u
Với
1
4
u
, Từ(1)
2
2
(2 1)
2 1
u u
m u u u m
u
.
Xét hàm số
2
( )
2 1
u u
f u
u
liên tục trên đoạn
1
;
4

.
Ta có:
2
2
2 2 1 1 3
'( ) '( ) 0
(2 1) 2
u u
f u f u u
u
.
Lại có:
1 5 1 3 2 3
( ) ; ( ) ; lim ( )
4 8 2 2
u
f f f u


.
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
116
Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
Lập bảng biến thiên của hàm số
( )
f u
ta suy ra để hệ có nghiệm thì
2 3
2
m
.
Bài 13. Xác định tham số m để hệ phương trình sau có nghiệm:
3 32 4 2
3 3 3 3
8 2 2 4 4
( 1)
(*)
( 1) ( 1) 2
m x x x xy
m x x x m x y x
Lời giải:
+Nếu
3 3
4 4
0
0
0 (*)
2
xy
x
m
y
x y x
+Nếu
0;
m
Đặt
3
t x
, khi đó
0
t
không là nghiệm của hpt;và hệ phương trình trở thành:
6 4 2 3
8 6 2 4 4
( 1)
( 1) ( 1) 2
m t t t yt
m t t t m t yt
6 4 2 3
8 6 4 2 4
( 1) (1)
( 1) (2 1) (2)
m t t t yt
m t t t t y t
+Do
0
t
không là nghiệm của hpt, nên chia 2 vế của (1) cho
3
t
và của (2) cho
4
t
, ta được:
3
3
4 2
4 2
1 1
( )
1 1
( 1) 2 1
m t t y
t t
m t t y
t t
3 3 4 2 2 2 2
3 4 2 2
1 1 1 1 1 1 1
( ) 3( ); ( ) 2; ( ) 2
t t t t t t t
t t t t t t t
Đặt
1
( 2)
u t u
t
, Khi đó HPT trở thành:
4 2
4 2
3 3
2 2 2
3
3
( ) ( )
( 2) 2 2 1 2 1 ( 1) 2 1
( )
(
3 2
[ ] u 3
1) 2 ( ) 1(3)
2
u 3 2
m u y m u y
m u u y m y
m u y
m m
u u u
u
u
u uu
+ Hệ có nghiệm khi và chỉ khi (3) có nghiệm
2
u
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
117
Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
4 2 3 4 3 2
3 2
1
(3) ( 3 1 2 4 ) 1 ( ) 2 3 4 1
'( ) 4 6 6 4; '( ) 0 2( 2)
m u u u u f u u u u u
m
f u u u u f u u u
Lập bảng biến thiên của
( )
f u
ta suy ra (3) có nghiệm thỏa mãn
( 2)
u
khi và chỉ khi:
0
1
3
1
3
m
m
m
Vậy giá trị cần tìm của m là:
0
1
3
m
m
.
Bài 14. Tìm m để phương trình sau có nghiệm thực:
1
( 4 5 ) 2 1 3(*)
2
m x x x x x
Lời giải:
Điều kiện:
1 4
x
.
Khi đó phương trình tương đương với:
2 1 3
1
4 5
2
x x
m
x x x
Xét hàm số
2 1 3 ( )
( )
1
( )
4 5
2
x x u x
f x
v x
x x x
liên tục trên đoạn
1;4
.
Trong đó:
( ) 2 1 3 0
,(1 4)
1
( ) 4 5 0
2
u x x x
x
v x x x x
.
Ta có
2
'( ) ( ) '( ) ( )
'( )
( )
u x v x v x u x
f x
v x
Mặt khác, ta có:
1 1
'( ) 0;
2 1
u x
x x
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
118
Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
1 1 1 1 1 1 1 1
'( ) 0( 5 2)
2 2 2
2 4 2 5 2 5 2 5 5
v x x
x x x x x
Từ đó suy ra :
'( ) 0
f x
. Hàm số
( )
f x
đồng biến trên đoạn
1;4
.
1;4 1;4
10 7 3
min ( ) (1) ; ( ) (4) , [1;4]
3
5 2 3
x x
f x f max f x f x
.
Vậy để phương trình có nghiệm thì
10 7 3
3
5 2 3
m
.
Bài 15. Xác định m để phương trình sau có nghiệm
12 ( 5 4 )
x x x m x x
Lời giải:
+ Điều kiện
0 4
x
.
Nhân cả 2 vế của phương trình với
( 5 4 )
x x
, phương trình trở thành
( 12)( 5 4 )
m x x x x x
.
Xét hàm số
( ) ( 12)( 5 4 ) ( ). ( )
f x x x x x x u x v x
.
Trong đó:
3 1
'( ) 0
2
( ) 12 0
2 12
5 4
( ) 5 4 0
'( ) 0
2 5 4
u x x
u x x x x
x
x x
v x x x
v x
x x
Từ đó suy ra:
'( ) '( ) ( ) '( ) ( ) 0
f x u x v x v x u x
. Hàm số
( )
f x
đồng biên trên đoạn
0;4
.
Suy ra
0;4
0;4
min( ) (0) 2 15 4 3; ( ) (4) 12, 0;4
x
x
x f max f x f x
.
Vậy phương trình có nghiệm khi và chỉ khi
2 15 4 3 12
m
.
Bài 16. Xác định m để bất phương trình sau có nghiệm:
3 3
3 1 ( 1)
x x m x x
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
119
Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
Lời giải:
Điều kiện:
1
x
.
Khi đó nhân cả 2 vế của bất phương trình với
3
( 1) 0
x x
, bất phương trình trở thành:
3 3 3 3
( 3 1)( 1) ( 1) ( 1)
x x x x m x x x x m
3 3
( ) ( 3 1)( 1)
f x x x x x m
.
Suy ra để bất phương trình có nghiệm là
1;
min ( )
x
m f x

.
Xét hàm số
3 3
( ) ( 3 1)( 1) ( ). ( )
f x x x x x u x v x
,
trong đó:
3
3
( ) 3 1 0
, 1
( ) ( 1) 0
u x x x
x
v x x x
.
Ta có
2 2
3 1 1
'( ) 3 3 0; '( ) ( )( 1) 0
2
1
u x x v x x x
x x
.
'( ) '( ) ( ) '( ) ( ) 0
f x u x v x v x u x
. Hàm số
( )
f x
đồng biến trên khoảng
1;

.
1;
min ( ) (1) 1, 1
x
f x f x

.
+ Để bpt có nghiệm khi và chỉ khi
min ( ) 1
m f x
.
Vậy giá trị cần tìm của m là:
( 1; )

.
Bài 17. Tìm m để hệ phương trình sau
2 1 2 1
2
7 7 2012 2012(1)
( 2) 2 3 0(2)
x x x
x
x m x m
có nghiệm
Lời giải:
+Điều kiện:
1
x
, Khi đó ta có:
2 1 2 1
(1) 7 7 2012 2012
x x x
x
2 1 2 1
7 1006(2 1) 7 1006(2 1)
x x x
x x x
(2 1) (2 1)(*)
f x x f x
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
120
Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
Với
( ) 7 1006
t
f t t
, ta có
'( ) 7 ln7 1006 0
t
f t
, suy ra
( )
f t
đồng biến trên R, và từ
(*) 2 1 2 1
x x x
1 1
x
.
Vậy hệ phương trình có nghiệm khi và chỉ khi (2) có nghiệm
[ 1;1]
x
2
( 2) 2 3 0
x m x m
có nghiệm
[ 1;1]
x
2
2 3
( ) ; [ 1;1]
2
x x
m g x x
x
[ 1;1]
min ( )
x
m g x
Ta có:
2
2
4 1
'( ) '( ) 0 2 3 [ 1;1]
( 2)
x x
g x g x x
x
[ 1;1]
( 1) 2; (2 3) 2 2 3; (1) 2 min ( ) ( 1) 2
x
g g g g x g
.
Vậy
2
m
là giá trị cần tìm.
Bài 18. Biết rằng
2
( ) 3 2 6 2 4 4 10 3 , 2 2
f t t t t t t
, xác định giá trị của m
để phương trình sau có nghiệm:
0
( ) ; [ 2;2]
x
m f t dt x
Lời giải:
Ta có:
0
( ) ( ) ; [ 2;2]
x
m F x f t dt x
2
'( ) ( ) '( ) 0 3 2 6 2 4 4 10 3
F x f x F x x x x x
2
3( 2 2 2 ) 4 4 10 3 (*)
x x x x
Đặt
2 2 2
2 2 2 2 4 4 4(2 ) 10 3 4 4
u x x u x x x x x
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
121
Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
Khi đó phương trình (*) trở thành:
2
0 2 2 2
6
3
3
5
2 2 2 3
u x x
u u x
u
x x
Ta tìm GTLN và GTNN của
( ), [ 2;2]
F x x
, ta có:
2 2
2
0 0
( 2) ( ) (3 2 6 2 4 4 10 3 ) 58 12 2 4
F f x dx x x x x dx
6
5
2
0
6
( ) (3 2 6 2 4 4 10 3 )
5
F x x x x dx
5 246 3 3
32 8arcsin 4sin(2arcsin )
5 25 5 5
.
2
2
0
(2) (3 2 6 2 4 4 10 3 ) 2 12 2 4
F x x x x dx
[ 2;2] [ 2;2]
min ( ) (2) 2 12 2 4 ;max ( ) ( 2) 58 12 2 4 ;
x x
F x F F x F
2 12 2 4 58 12 2 4
m
.
Bài 19. Xác định giá trị của tham số m để bất phương trình sau có nghiệm thuộc đoạn
[ 3; 3]
2
2
2
1 2
2 4 *
4
1
x x
x m
x
x
Lời giải:
BPT(*)
2
2
2
1 2
( ) 2 4
4
1
x x
m f x x
x
x
Vậy
(*)
có nghiệm thuộc đoạn
[ 3; 3]
khi và chỉ khi
[ 3; 3]
max ( )
x
m f x
Ta chứng minh:
( ) 0 [ 3; 3]
f x x , thật vậy với
[ 3; 3]
x thì ta có
2
2
2
1 2
( ) 2 4
4
1
x x
f x x
x
x
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
122
Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
2
2
2
1 2
2( 1) ( 3) (1 )
4
1
x x
x
x
x
2 2
2
2 2 2
2( 3) ( 3)
( 3)
( 1)( 4) 4 1(2 1)
x x
x
x x x x x x
2
2 2 2
2 1
( 3)( 1 ) 0, [ 3; 3]
( 1)( 4) 4 1(2 1)
x x
x x x x x x
Vậy giá trị
cần tìm của m là:
( ;0)

.
Bài 20. Tìm giá trị nhỏ nhất của tham số m để bất phương trình sau luôn đúng
2 2 4 2 2
( 1 1) 2 1 2(*)
m x x x x x x
Lời giải:
+Điều kiện
: 1 1
x
+ Đặt
2 2 2 4
1 0 1 2 1 1
t x x t x x t
;
+
2 2 2
1 2( 1 ) 2 1 2
t x x x x t
BPT(*)
2
2
1
( 1) 1 ( )
1
t t
m t t t m f t
t
BPT(*) có luôn có nghiệm khi và chỉ khi
[1; 2]
max ( )
t
m f t
.
Ta có
2
2
[1; 2]
2
'( ) 0, [1; 2] max ( ) ( 2) 2 2 1
( 1)
t
t t
f t t f t f
t
.
Vậy giá trị cần tìm của m là:
2 2 1
m
.
2
2
2
2 2 2
1
1
( 3)
4
2( ) ( 3)
1 1(2 1)
1
4
x x
x
x
x
x x x x
x
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
123
Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
Vậy giá trị nhỏ nhất của tham số m cần tìm là:
2 2 1
m
.
Bài 21. Xác định giá trị tham số m để hệ phương trình sau có nghiệm thực
2 2
2 2
3 2
1 1
3 1
( ) 2 3 ( ) 1 2 2 0(1)
2 2
log (3 1) log ( 2 )(2)
m m
x x x x x x
x m x
Lời giải:
Đặt
2 2 2
2 2
2 2
2
1 0 1
2
2
2 3
2 3 0
u x u x
v u
x
v x x
v x x
Thay vào (1), ta được:
2 2 2 2 2 2
( 1) ( 1) 0
2 2
v u
v u v u v u
2
( )( 1) 0 0 1
v u u v v u x
.
Điều kiện:
2
1 1 0
m m
. Khi đó phương trình (2) tương đương với
3
2
3
2
0
( ) 3 2 1; 1( 0)
0 3 1 2
m
m f x x x x m
x m x
.
Vậy hệ phương trình có nghiệm khi và chỉ khi (2) có nghiệm
1
x
, điều này tương đương với
[ 1; ]
min ( )
x
m f x

.
Ta có:
3
2
'( ) 2 '( ) 0 1
f x f x x
x
.
Lập bảng biến thiên của hàm số
( )
f x
ta suy ra
[ 1; ]
min ( ) (0) 1 1
x
f x f m

.
Vậy giá trị cần tìm của m là:
(1; )

.
Bài 22. Xác định giá trị tham số m để hệ phương trình sau có nghiệm
2
3 2
3 4 0(1)
3 15 0(2)
x x
x x x m m
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
124
Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
Lời giải:
Ta có
(1) ( 1)( 4) 0 1 4
x x x
.
2 3
(2) 15 ( ) 3
m m f x x x x
.
Vậy hệ phương trình có nghệm khi và chỉ khi, bất phương trình (2) có nghiệm thuộc đoạn
[ 1;4]
, khi và chỉ khi
2
[ 1;4]
15 max ( )
x
m m f x
.
Xét hàm số
3 2
3
3 2
3 ( 1 0)
( ) 3
3 (0 4)
x x x
f x x x x
x x x
.
Ta có
2
2
3 6 ( 1 0)
'( ) '( ) 0 0; 2
3 6 (0 4)
x x x
f x f x x x
x x x
.
Ta có
( 1) 2; (0) 0; ( 2) 4; (2) 4; (4) 16
f f f f f
.
Từ đó suy ra:
[ 1;4]
max ( ) (4) 16
x
f x f
.
Vậy hệ bất phương trình có nghiệm khi và chỉ khi
2
15 16 16 1
m m m
.
Vậy
16,1
m là giá trị cần tìm.
Bài 23. Tìm m để phương trình
2
1 cos
mx x
có đúng 1 nghiệm thuộc
0;
2
.
Lời giải:
+ Phương trình đã cho tương đương với
2 2
2
2
2 2
2sin sin
cos 1 sin
2 2
2 ; 0;
2 4
2
x x
x t x
m m t
x x t
x
Xét hàm số
2
sin
( ) ; 0;
2 4
t x
f t t
t
.
+ Ta có
2 2
sin cos sin sin cos ( tan )
'( ) 2 2 0
t t t t t t t t
f t
t t t t
, vì với
0;
4
t
thì
sin cos 0,tan
t t t t
.
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
125
Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
+ Như vậy
( )
f t
đồng biến trên đoạn
0;
4
suy ra để phương trình có nghiệm thì
2
1 4
(0) 2 ( )
4 2
f m f m
là giá trị cần tìm.
Bài 24. Tìm tất cả các giá trị của
m
để hệ phương trình
2 2
2 2
2 1 (1)
x xy y
x xy y m
có nghiệm
Lời giải:
Từ hai phương trình trong hệ ta suy ra
2 2
2 2
(*)
2
x xy y
m
x xy y
+ Nếu
1
0
2
y m
và hệ có nghiệm
;0 , .
x x
+ Nếu
0
y
chia cả tử và mẫu của (*) cho
y
và đặt
x
t
y
, khi đó ta được
2
2
1
(**)
2 1
t t
m
t t
. Từ (1) ta có:
2
2
1 1
2 1 0 1
2
t t t t
y
.
Vậy hệ có nghiệm khi và chỉ khi phương trình (**) có nghiệm
1
; 1 ; .
2
t
 
Xét hàm số
2
2
1
( )
2 1
t t
f t
t t
trên khoảng
1
; 1 ; .
2
 
Ta có
2
2
2
3 7
6 2
'( ) , '( ) 0
3 7
2 1
t
t t
f t f t
t
t t
Lập bảng biến thiên suy ra giá trị của m là
14 5 7
.
28 11 7
m
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
126
Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
Bài 25. Tìm m để hệ phương trình
3 3 2
2 2 2
3 3 2 0(1)
1 3 2 0(2)
x y y x
x x y y m
có nghiệm thực.
Lời giải:
Điều kiện
1 1
0 2
x
y
Đặt
1 0;2
t x t , khi đó phương trình (1) trở thành
3 2 3 2
3 3 (*)
t t y y , xét hàm số
3 2
( ) 3
f u u u
trên đoạn
0;2
, ta có
2
'( ) 3 6 0, 0;2
f u u u u , suy ra
( )
f u
nghịch biến trên đoạn
0;2
Do đó phương trình (*) tương đương với
( ) ( ) 1
f t f y t y y x
Khi đó
2 2 2 2 2
1 3 2 0 2 1 0( )
x x y y m x x m i
Đặt
2 2
1 0;1 ( ) 2 1
v x v i v v m
.
Xét hàm số
2
( ) 2 1
g v v v
lien tục trên đoạn
0;1
, ta có
'( ) 2 2 0, 0;1
g v v v
Suy ra
0;1
0;1
min ( ) (0) 1; ( ) (1) 2
v
v
g v g max g v g
Vậy hệ phương trình có nghiệm khi và chỉ khi
1 2
m
.
Bài 26. Tìm m để hệ bất phương trình sau có nghiệm
2 2
2 2
5 4 2 3
2 1
7 4 2
2 5
x xy y
m
x xy y
m
Lời giải:
Hệ phương trình đã cho tương đương với:
2 2
2 2
5 4 2 3
18
21 12 6 3
2 5
x xy y
x xy y
m
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
127
Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
Cộng theo vế hai phương trình trong hệ trên ta suy ra:
2
2 2
18
4 2 16 16 4
2 5
x y x xy y
m
Suy ra để hệ có nghiệm thì cần
5
2 5 0
2
m m
.
Bây giờ ta chứng minh với
5
2
m
thì hệ có nghiệm.
Thật vậy, xét hệ phương trình sau:
2 2
2 2
1
5 4 2 3
7
(*)
2
21 12 6 3
7
x
x xy y
x xy y
y
, suy ra hệ này có nghiệm.
Giả sử
0 0
,
x y
là nghiệm của hệ phương trình (*), khi đó ta có
2 2
0 0 0 0
2 2
0 0 0 0
5 4 2 3
5
,
18
2
21 4 6 3 3
2 5
x x y y
m
x x y y
m
Suy ra
0 0
,
x y
cũng là nghiệm của hệ đã cho.
Từ đó suy ra
5
2
m
là những giá trị cần tìm.
Bài 27. Tìm m để hệ phương trình sau có nghiệm duy nhất:
2 3 2
2 3 2
3 2
3 2
x y y my
y x x mx
Lời giải:
(i). Điều kiện cần:
Giả sử hệ phương trình có nghiệm
0 0
,
x y
, khi đó
0 0
,
y x
cũng là nghiệm của hệ nên để hệ có
nghiệm duy nhất thì trước hết
0 0
x y
.
Thay vào hệ ta được
0
3 2
0 0 0
2
0 0
0
5 0
5 0(*)
x
x x mx
x x m
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
128
Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
Hệ có nghiệm duy nhất thì (*) hoặc vô nghiệm hoặc có nghiệm kép
0
x
, điều này tương đương
với
25 4 0
25
25 4 0
4
0
m
m
m
m
.
(ii). Điều kiện đủ:
Với
25
4
m , khi đó hệ phương trình tương đương với
2
2 2
2
2 2
3 2 1 1 0
, 0
3 2 1 1 0
x y y y m y y m
x y
y x x x m x x m
.
Cộng theo vế hai phương trình của hệ ta được:
2 2
5 5 0
x x x m y y y m
2 2
5 25 5 25
0 0
2 4 2 4
x x m y y m x y
.
Kết luận vậy
25
4
m là những giá trị cần tìm.
Bài 28. Tìm m để phương trình sau có nghiệm
2
1 4 1 1 1
x m x m x
Lời giải:
Điều kiện:
1 1 0
x x
Nhận thấy
1
x
không là nghiệm của phương trình, khi đó chia hai vế của phương trình cho
1
x
và có
1
1
1 1
x
x
x x
, ta được
2
1 1 4
4 1
1 1 1
x x t t
m m m
x x t
, với
1
1
x
t
x
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
129
Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
Ta có
0
t
. Xét hàm số
2
4
( )
1
t t
f t
t
có
2
2
2 3
'( ) 0, 0; ; 1
1
t t
f t t t
t

Từ đó suy ra ( ) (1) 3; lim ( )
t
f t f f t


Vậy phương trình có nghiệm khi và chỉ khi
3
m
Bài 29. Tìm m để phương trình sau có nghiệm
4 2
8 2 2 2 4
x x m x m x m
Lời giải:
Phương trình tương đương với
4 2
4 2 2
2
8 2 4
8 2 4 2 4
2 4
x x x x
x x x x m x x m
x x
2 2
2 2
2 2
2.
2 4 2 4
x x x x
x x x x
Do đó ta đặt
2
2
2
2 4
x x
t
x x
; khi đó
2
m t t
Trước hết ta tìm tập giá trị của
t
, ta có
2
2
2
4 2 2
1 3
'( ) 0
1 3
2 4
x x
x
t x
x
x x
Từ đó suy ra
2 3 2 3
1 ,1
3 3
t
Vậy ta xét hàm số ( ) 2
f t t t
đồng biến trên
2 3 2 3
1 ,1
3 3
Giá trị cần tìm của tham số m thỏa mãn
2 3 2 3 2 3 2 3
2 1 1 ;2 1 1
3 3 3 3
m
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
130
Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
Bài 30. Tìm m để phương trình sau có nghiệm duy nhất trong đoạn
1
;1
2
2 3 2
3 1 2 2 1
x x x m
Lời giải:
Xét hàm số
2 3 2
( ) 3 1 2 2 1
f x x x x
trên đoạn
1
;1
2
Ta có
2
2 3 2 2 3 2
3 3 4 3 3 4
'( )
1 2 1 1 2 1
x x x x
f x x
x x x x x x
Do
2 3 2
1 3 3 4
;1 3 4 0 0
2
1 2 1
x
x x
x x x
Vậy
'( ) 0 0
f x x
Ta có bảng biến thiên của hàm số
( )
f x
trên đoạn
1
;1
2
Dựa vào bảng biến thiên suy ra để phương trình có nghiệm duy nhất khi và chỉ khi
1
22 3 3
4
2
m
m
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
131
Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
Bài 31. Tìm m để hệ sau có nghiệm
2 3
3 3
log log 2 2
x y xy
x y xy m
Lời giải:
Đặt
2 3
log ; log 2
a x y b xy
khi đó ta có
2
a b
Lại có
2
2
2
4 2 4 3 2 4 3 2 12 8.3 36 0
a b a a a
x y xy
Xét hàm số
( ) 12 8.3 36
a a
f a
đồng biến; lại có
(1) 0
f
vậy
1
a
Biến đổi phương trình thứ hai của hệ:
3
3
2 2
3 2 3 3 2 .2 3 2
a a a a
m x y xy x y xy
Xét hàm số
3
2 2
( ) 2 3 3 2 .2 3 2
a a a a
f a
trên
1,

Ta có
2 2 1 1
'( ) 8 ln8 6.2 ln 2 27. .ln 9. .ln 0
3 3 3 3
a a
a a
f a
với mọi a
Suy ra
( ) (1) 1
f a f
Vậy giá trị cần tìm của m là
1
m
.
Bài 32. Tìm m để hệ sau có nghiệm
2 2
2
2
2 2 2
x xy y x m
x xy x m
Lời giải:
Hệ bất phương trình tương đương với
2 2 2 2
2 2
2 2
2 2 2
2 2
2 2 2 2 2 2
2 2 2 2 2 3
2 2 2 1 3
x xy y x m x xy y x m
x xy x m x xy x m
x xy y x x xy x m
x y x m
Suy ra để hệ có nghiệm thì trước tiên
3 0 0
m m
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
132
Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
Ngược lại với
0
m
; thì hệ luôn có nghiệm
1
1;
2
. Vậy
0
m
là giá trị cầ tìm.
Bài 33. Tìm m để hệ phương trình
2 5
5 1
xy y x y
x y m
có nghiệm
Lời giải:
Điều kiện:
1 0
5
1
y x
x
y
Khi đó phương trình thứ nhất của hệ biến đổi thành:
2 1 1 4 (1)
y y x x
Nếu
1; 0
x y
thì ta có (1) tương đương với
2
1 4
x y
vô nghiệm, nên hệ vô nghiệm
Vậy
1 5;0 1
x y
và (1) tương đương với
2
1 4 1 4
x y x y
, đặt
2
0;1 4 5
t y x t t
Thay vào phương trình thứ hai của hệ ta được
2 2
4 1 (*)
m t t t
Xét hàm số
2 2
( ) 4 1
f t t t t
liên tục trên đoạn
0;1
Ta có
2 2
2 2
2
'( ) 0 2 1 4
4 1
t t
f t t t t t t
t t t
2
2
3 4 4 0 0;1
3
t t t
Ta có
2 5
(0) 1; (1) 3;
3 3
f f f
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
133
Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
Vậy để hệ có nghiệm khi và chỉ khi phương trình (*) có nghiệm, tương đương với m thuộc tập
giá trị của hàm số
( )
f t
trên đoạn
0;1
từ đó suy ra
5
, 3
3
m
là giá trị cần tìm.
Bài 34. Tìm giá trị lớn nhất của tham số m để hệ phương trình sau đây có nghiệm
2 2
3 3 3
1x y
x y x y m
Lời giải:
Ta có
3 3 2 2
1 2
x y x y x y x xy y x y xy
Suy ra
2 2
6
2 1 2 2 2
m x y xy xy xy xy
nhưng do
2 2
1 1
2 2
xy x y
nên
theo bất đẳng thức cô sic ho 3 số không âm ta được:
3 3
6
1 2 2 2 5 5
1 2 2 2
3 3 3
xy xy xy
m xy xy xy m
Ngược lại, với
5
3
m thì dấu bằng của bất đẳng thức xảy ra khi đó
2 2
1
; 1
3
xy x y
. rõ
rang hệ này có nghiệm.
Vậy giá trị cần tìm của m là
5
3
.
BÀI TẬP ĐỀ NGHỊ
1.1. Tìm m để phương trình sau có nghiệm thực:
24
1
x x m
1.2. Tìm tham số m để phương trình sau có đúng một nghiệm:
44
13 1 0
x x m x
1.3. Xác định m để phương trình sau có nghiệm:
2 2 4 2 2
( 1 1 2) 2 1 1 1
m x x x x x
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
134
Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
1.4. Tìm m để phương trình sau có nghiệm
2 24 4
( 2 2 4) 2 2 4
m x x x x
1.5. Tìm m để phương trình sau
2
2
1 1 0
3
m
x x x x
có nghiệm thực
1.6. Cho phương trình
2
2 2 (2 )
2
x
x x x m
x
Tìm m để phương trình có 2 nghiệm phân biệt.
1.7. Cho phương trình
2 3 2 (3 5)
x x m x
.
Tìm m để phương trình có nghiệm.
1.8. Xác định giá trị của m để phương trình sau có nghiệm
4
2 2
2 1 1
x x x x m
1.9. Định m để phương trình sau có nghiệm
3 2 2 2
(1 )
x x x m x
1.10. Xác định giá trị tham số m để phương trình sau có nghiệm
2 2 2 2 2 2 2
( 1) ( 1) ( 1)
x x x x m x x
1.11. Tìm m để phương trình sau đây có nghiệm thực:
2
(1 2( 1))
x x m x x
1.12. Tìm m để phương trình sau có nghiệm:
( 1 2) 2 1 4
m x x x x
1.13. Tìm m để phương trình sau có nghiệm thực
3
24 12 6 0
x m m x
1.14. Tìm giá trị tham số m để phương trình sau có 2 nghiệm thực phân biệt
2
2 2 1
x mx x
1.15. Xác định giá trị của tham số m để phương trình sau có nghiệm
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
135
Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
3 2 3 2 2
1
x mx x m x mx x m m x
1.16. Xác định m để phương trình có đúng 2 nghiệm thực:
3 2 4 6 4 5
x x x x m
1.17. Tìm m để phương trình sau có nghiệm
3
2 1
2
log ( 4 ) log (2 2 1) 0
x mx x m
1.18. Cho phương trình
2 2
3 3
log log 1 2 1 0(
x x m m
là tham số)
Xác định m để phương trình có ít nhất 1 nghiệm thuộc đoạn
3
[1;3 ]
1.19. Xác định giá trị của tham số m để phương trình sau có nghiệm thực:
3 3 2
12( 2) 2 4 (3 2) 6 9 36
x x x x x x m
1.20. Chứng minh rằng với mọi giá trị thực dương của tham số m phương trình sau luôn có 2
nghiệm phân biệt:
2
2 8 ( 2)
x x m x
1.21. Tìm để bất phương trình sau có nghiệm
[0;1+ 3]
x :
2
( 2 2 1) (2 ) 0
m x x x x
1.22. Tìm m để bất phương trình sau có nghiệm
3
3 2
3 1
x x m x x x
1.23. Tìm tất cả m để bất phương trình
3
3
1
3 2x mx
x
thỏa mãn với
1
x
1.24. Tìm m để bất phương trình
2
1
2
log ( 3) 1
m
m
x
đúng với mọi
x
1.25. Tìm m để phương trình sau có nghiệm thuộc đoạn
[2;4]
2
( )
x
m f t dt
; trong đó
( ) 3(2 2) 2 6( 2)
f t t t t t
1.26. Tìm giá trị lớn nhất của tham số m để bất phương trình sau có nghiệm thực
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
136
Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
3 2 3
4
2
( 1) sin
( 1) 2
m x
m x m
x
1.27. Tìm m để bất phương trình sau có nghiệm thuộc đoạn
1
;1
2
3 32 2
3 3
1 2 1 2 2 1
m x x x x
1.28. Tìm m để phương trình sau đây có nghiệm
2 ( 1) 2
m x y y x
1.29. Tìm m để hệ phương trình sau có nghiệm duy nhất:
2 0
1
x y m
x xy
1.30. Tìm m để hệ phương trình sau có nghiệm thực:
1
1 3
x y
x x y y m
1.31. Tìm m để hệ phương trình sau có nghiệm thực:
2
4
8
4
(4 1) ( 3) 5 2 0
5 2 5 2 2 6 2 6
x x y y
y y x x m
1.32. Tìm m để hệ phương trình sau đây có nghiệm thực
,
x y
dương:
2 3 2
4 2
5
4
5
(1 2 )
4
x y x y xy xy m
x y xy x m
1.33. Tìm m để hệ phương trình sau có nghiệm thực:
3 3 2
2 2 2
3 3 2 0
1 3 2 0
x y y x
x x y y m
1.34. Tìm giá trị của tham số m để hệ phương trình sau có nghiệm:
2 2
2
2
1
( )
xy
x y
x y
x y m x y
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
137
Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
1.35. Chứng minh rằng với mọi
0
a
, hệ phương trình sau có nghiệm duy nhất
ln(1 ) ln( )
x y
e e x x y
y x a
1.36. Chứng minh rằng hệ phương trình
2
2
2011
1
2011
1
x
y
y
e
y
x
e
x
có đúng 2 nghiệm thỏa mãn
0; 0
x y
1.37. Tìm
m
để phương trình sau có hai nghiệm phân biệt
2 2
10 8 4 2 1 1
x x m x x
1.38. Cho bất phương trình
2
(1)
1
x
mx x
x
(i). Giải bất phương trình (1) khi
2
m
.
(ii). Tìm giá trị
m
lớn nhất sao cho bất phương trình (1) nghiệm đúng với mọi
x
.
1.39. Chứng minh rằng với mọi tham số
m
phương trình
3 2
9 1 0
x x m x
luôn có 3 nghiệm.
1.40. Chứng minh rằng với mọi m phương trình sau luôn có nghiệm
2
2
2
2
log 2 2 1
2 1
x mx
x x mx
x
.
1.41. Tìm m để phương trình sau có nghiệm thực
2 2
2 2 2 4 2 2
2012 2012 2
x mx x mx m
x mx m
.
1.42. Tìm m để tồn tại cặp số
,
x y
không đồng thời bằng 0 và thỏa mãn phương trình:
2 2
4 3 3 4 1 0
m x m y m x y
.
1.43. Tìm tất cả các giá trị thực của tham số
m
đê hệ phương trình sau có nghiệm
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
138
Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
2 2
2 2
1 1
4
2 1
1
x m y m
x y
x y xy
1.44. Tìm tất các các giá trị của tham số
m
để hệ sau có nghiệm
2 3
3 3
log log 2 2
x y xy
x y xy m
1.45. Tìm tất cả các giá trị thực của tham số m để hệ sau có nghiệm
2 2 2
2
x y m x y m
x y m
1.46. Tìm tất cả các giá trị của tham số
m
để phương trình sau có nghiệm duy nhất
2
2
3
14 1 1
2
3 96
x
m x
x
x
1.47. Tìm các giá trị của tham số
m
để hệ sau có nghiệm
2 2
2
6
1 1 1
2 3 1 1
x x y y
x y x y m x y
1.48. Tìm tất cả các giá trị của tham số
m
để bất phương trình sau có nghiệm
2 3
2 4 1 4x m x m x x x
1.49. Tìm
m
để phương trình sau có nghiệm thực
2 2 4 2 2
7 1 1 1 2
x m x x x x m x x
1.50. Tìm tất cả các giá trị của tham số
m
để mọi nghiệm của phương trình
3
2
2
log 9
3
log 3
x
x
cũng là nghiệm của phương trình:
2 2 2 2
m m
x x
1.51. Tìm tất cả các giá trị thực của tham số
m
để phương trình
2 2 2 2 2
1 log 1 2 1 log 1 4 0
x x m x x m
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
139
Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
có đúng hai nghiệm thực thỏa mãn điều kiện
1 3
x
.
1.52. Tìm
m
để phương trình sau có nghiệm
2
2 2 2
1 4 2 2 2 2 1 ln 2
x x x x x x x m
1.53. Tìm những giá trị thực của tham số
m
để phương trình sau có nghiệm
2 2
1 1 1 1
9 2 .3 2 1 0
x x
m m
1.54. Tìm tất cả các giá trị của tham số m để phương trình sau có nghiệm
3 2 3 0
m x m x m
1.55. Tìm m để phương trình sau có nghiệm thực
5 2
4
34 1 33 1
x x m x x
1.56. Tìm m để bất phương trình sau có nghiệm
2 2
4
2 17 2 1 2 17 1 0
m x x m x x m
1.57. Tìm tất cả các giá trị không âm của tham số m để phương trình sau có nghiệm
2 1
x m x x
1.58. Tìm tham số m để phương trình sau có nghiệm
4
1
1 1 1
1
x x m x x x
x
1.59. Tìm m để phương trình
4 4
2 sin cos cos4 2sin 2 0
x x x x m
có ít nhất một nghiệm
thuộc đoạn
0;
2
.
1.60. Tìm m để phương trình:
2
12 4 3 3 24 3 1 2 4 3
x x x m x x
có nghiệm
1.61. Tìm m để hệ phương trình
1 15
2
x y
x y
x y m
có nghiệm
1.62. Tìm m để hệ sau có nghiệm
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
140
Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
2 2 2 2
2 2
4 3 2 9 8
11 2 2 2 5 2
x y x xy y x y y
x y y m y x
1.63. Tìm m để hệ sau có nghiệm
3 2
2
2 2 2 3
3
x y x xy m
x x y m
1.64. Tìm m để phương trình sau có nghiệm duy nhất trong đoạn
1
;1
2
2 3 2
3 1 2 2 1
x x x m
1.65. Tìm m để hệ sau có nghiệm
2 3
3 3
log log 2 2
x y xy
x y xy m
1.66. Tìm m để phương trình sau có nghiệm thực
2 3
4 2 1 3 8 2
x mx x x
1.67. Tìm m để bất phương trình
6 4 3
3 2 1 0
x mx x
với mọi
1
x
1.68. Tìm m để hệ phương trình sau có nghiệm duy nhất
7 11 4 4 3 10 3
7 11 4 4 3 10 3
x y m m
y x m m
1.69. Tìm m để hệ sau vô nghiệm
2
4 4 1
4 5 4 6 4
x y
m x m x y
1.70. Tìm m để hệ sau có nghiệm
4 4
2
2 2
2 2
1
1
x y
x y
x y m
x y x y
1.71. Tìm m để hệ sau có ba nghiệm phân biệt
2
1 2
x y m
x y xy m y
1.72. Tìm m để hệ sau có nghiệm
2 2 2
2
2
x m y m
x y m
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
141
Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
1.73. Tìm tất cả các giá trị thực của m để hệ sau có nghiệm
2 2
2
6 4 6 3 9 2 5 16 3 3 5
7 31
12 3 2 8 2 5 1 9
3 4
x y x y x xy y x y
x y x y m m
1.74. Tìm m để phương trình sau có nghiệm
2
5 1 7
1 1
6 2
x m
x x
1.75. Tìm m để bất phương trình sau dung với mọi
0;1
x
1
2
2
6 1 6 2 1
6
0
2012
x x
x
x m m
ex x
1.76. Tìm m để hệ phương trình
2 2
4 2
2 5
x y
x y xy
m x y x y x y
có nghiệm
,
x y
thỏa
mãn
, 1
x y
.
| 1/40
| | Tải xuống

Có thể bạn quan tâm:

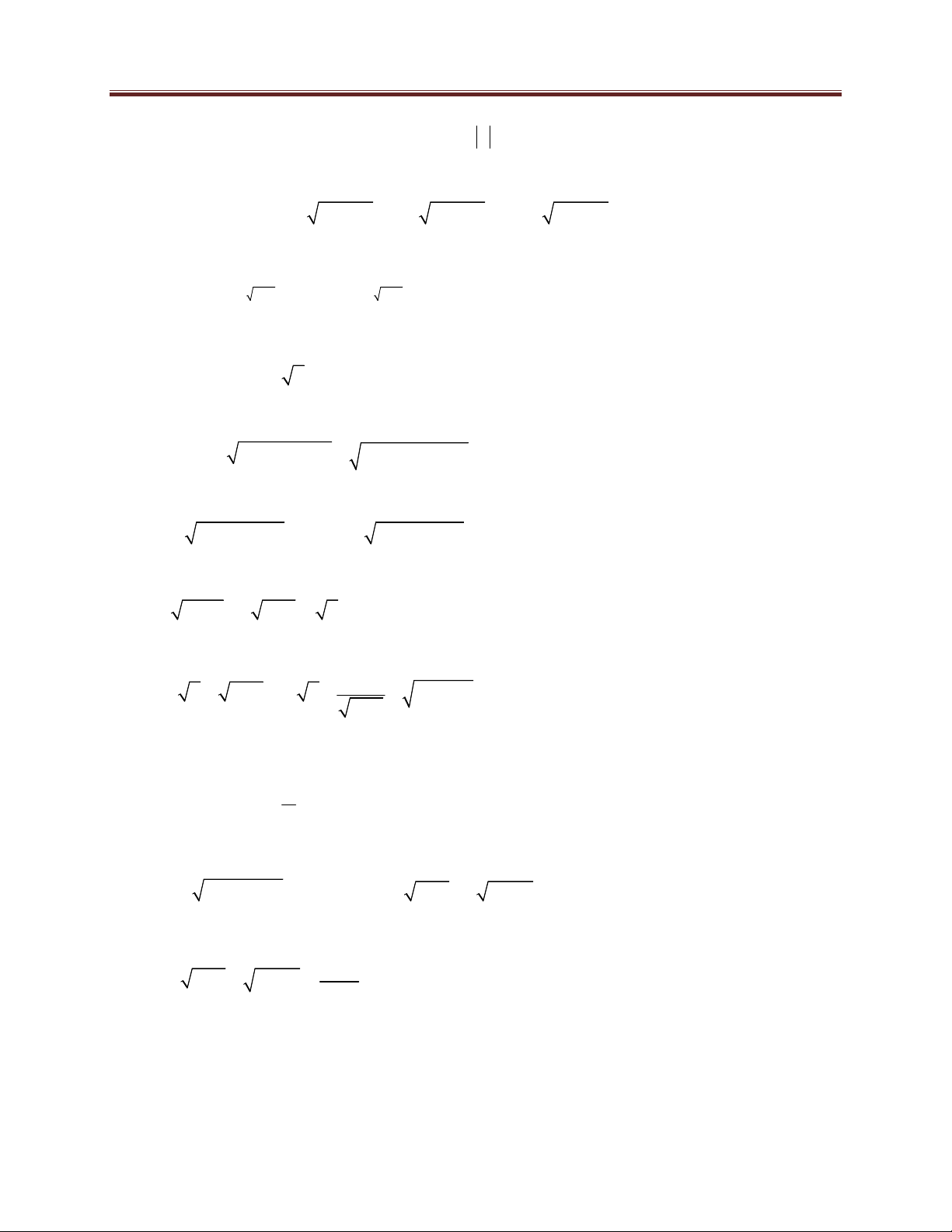
Preview text:

Chuyên đề 2: Điều kiện để phương trình, hệ phương trình có nghiệm Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam Email : dangnamneu@gmail.com Yahoo: changtraipkt Mobile: 0976266202 CHUYÊN ĐỀ 2:
ĐIỀU KIỆN ĐỂ PHƯƠNG TRÌNH, HỆ
PHƯƠNG TRÌNH CÓ NGHIỆM 102 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
Chuyên đề 2: Điều kiện để phương trình, hệ phương trình có nghiệm 103 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam Email : dangnamneu@gmail.com Yahoo: changtraipkt Mobile: 0976266202
Dạng toán tìm điều kiện của tham số để phương trình, hệ phương trình có nghiệm thường xuất
hiện trong đề thi TSĐH dưới dạng áp dụng phương pháp xét tính đơn điệu của hàm số để tìm
miền giá trị của hàm số, từ đó suy ra giá trị cần tìm của tham số m. Đây là loại bài toán không
khó và chiếm một điểm trong đề thi, nên nhớ áp xét tính đơn điệu của hàm số. Phương pháp
+ Điều kiện cho trước ở đây được rút ra từ tập xác định của hàm số hoặc được xác định từ điều
kiện nghiệm của phương trình mà đề bài yêu cầu. Ta quy ước điều kiện cho trước này là miền D .
+ Để giải quyết dạng bài toán này ta dùng phương pháp hàm số, mục đích là biểu diễn tham số
theo hàm của một ẩn trên miền D , sau đó tìm GTLN,GTNN của hàm số đó trên D .
+ Phương trình, bất phương trình dưới dạng sau thì điều kiện của tham số là:
(i). g(m)  f (t), t D  m in f (t)  g(m)  m ax f (t) . t Dt D
(ii). g(m)  f (t), t D có nghiệm t D g( )
m  min f (t) . t D
(iii). g(m)  f (t), t D có nghiệm t D g(m)  m ax f (t) . t D
(iv). g(m)  f (t), t D có nghiệm với mọi t thuộc D khi và chỉ khi g(m)  a
m x f (t) . t D
(v). g(m)  f (t), t D có nghiệm với mọi t thuộc D khi và chỉ khi g(m)  min f (t) . tD
Các hướng giải quyết bài toán loại này:
(i). Xét tính đơn điệu của hàm trực tiếp theo ẩn x . 104 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
 ax  b cx d
(ii). Nếu xuất hiện biểu thức đối xứng  , thì
 (ax  b)(cx d ) 
đặt t  ax  b cx d .
(iii). Nếu xuất hiện 2 2
a bx; c bx  ( a bx )  ( c bx )  a c ,  2 t an  2 sin  2   1 t ana bx
a c sin  2 thì đặt 
Và sử dụng hệ thức 
, tiếp tục đặt t tan .  c bx a c os c  2  2 1 t an  2 o c s  2 1 t an   2
(iv). Nhân hai vế với hệ thức liên hợp nếu có. BÀI TẬP MẪU
Bài 1. Tìm các giá trị thực của tham số m để phương trình sau có nghiệm
6  x  2 (4  x)(2x  2)  m  4( 4  x  2x  2)(x R) Lời giải:
+Điều kiện: 1  x  4 . Đặt t
4  x  2x  2
Xét hàm số t(x) 
4  x  2x  2 liên tục trên đoạn 1, 4. Ta có 1 2 t '(x)  
 t '(x)  0  2 4  x  2x  2  x  3. 2 4  x 2 2x  2
min t(x)  t(1)  3 x   1,4 Ta có: t  3;t  3;t  6  (1) (3) (4)
maxt(x)  t(3)  3 x 1,4 
Phương trình đã cho trở thành: 2 2
t  4  m  4t m t  4t  4 . 105 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM Xét hàm số 2
f (t)  t  4t  4 Ta có f (
t)  2t  4 f (
t)  0  t  2  f ( 3)  7  4 3; f (2)  0; f (3)  1
 0  f (t)  1  min  m max  0  m  1 f (t ) f (t )
Vậy giá trị cần tìm của m là 0  m  1 .
Bài 2. Tìm các giá trị thực của tham số m để phương trình sau có nghiệm thực 9 2
1 x  4  x x  3x   m 4 Lời giải: +Điều kiện: 4   x  1 . 3
Khi đó phương trình tương đương với: m  1 x  4  x x  . 2 3 5 5 5 5
Đặt t x
m f (t)   t
t t , (  t  ) . 2 2 2 2 2 5 5 5 5
Xét hàm số f (t)   t
t t , (
t  ) , ta có f ( t
 )  f (t) nên hàm số 2 2 2 2  5  5 5
f(t) chẵn, nên ta chỉ cần chỉ cần xét f(t) trên 0; 
. Khi đó f (t)   t   t t . 2    2 2 1  1 5 5 5 5 +Ta có: f (  t)   1  f (  t)  0   t
t  2 (  t)(  t)  0(*) 5 5 2 2 2 2 2  t 2  t 2 2 Giải phương trình (*): 5 5 5 5 +Đặt 2 u   t
t (u  0)  u  5  2 (  t)(  t) 2 2 2 2
Khi đó phương trình (*) trở thành: 106 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM 1 21 1 21 25 39  21 2 2 2
u  5  u  0  u   ( )  5  2  t t  . 2 2 4 8 5 5 39  21 9  21 39  21
Ta có: f (0)  10; f ( )  5  ; f ( )   . 2 2 8 2 8 Từ đó suy ra :
 min f (x)  f (0)  10  5  x 0;  2      . 39  21 9  21 39  21
m ax f (x)  f ( )     5 x 0; 8 2 8  2     9  21 39  21
Vậy giá trị cần tìm của m là: 10  m   . 2 8
Bài 3. Tìm các giá trị thực của tham số m để phương trình sau đây có nghiệm thực 3
2 3x  2m  3 6x  5m  8  0 Lời giải: 5m +Điều kiện: x  . 6 3 3 u
  3x  2m
u  3x  2m Đặt    . 2
v  6x  5m
v  6x  5m   Từ đó suy ra: 3 2
2u v m(1); 2u  3v  8  0(2) 8  3v Từ (1) và (2) ta suy ra 3 2  m  2( )  v . 2 8  3v Xét hàm số 3 2 f (v)  2(
)  v liên tục trên đoạn 0;  . 2 8  3v Ta có 2 f '(v)  9(
)  2v  0, v
  0 . Suy ra hàm số f (v) nghịch biến trên đoạn 0;  . 2 107 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
Mặt khác lim f (v)  ; f (0)  128 . v
f (v)  128, v
  0  để phương trình có nghiệm thì m  128 .
Vậy giá trị cần tìm của m là: ,128.
Bài 4. Tìm các giá trị của tham số m để phương trình sau có đúng 2 nghiệm thực phân biệt: 4 4
2x  2x  2 6  x  2 6  x m Lời giải:
Điều kiện: 0  x  6 . Xét hàm số 4 4 f (x) 
2x  2x  2 6  x  2 6  x lien tục trên đoạn 0;6 . 1 1 1 1
Ta có f '(x)     3 3 4 4 2 (2x) 2x 2 (6  x) 6  x 1 1 1 1
f '(x)  0      0 3 3 4 4 2 (2x) 2x 2 (6  x) 6  x 1 1 1 1 1  (  )  (  )  0 3 3 4 4 2 (2x) (6  x) 2x 6  x 1 1 1 1 1 1 1 1 1 1  (  )(   )  (  )(  )  0 4 4 4 4 4 4 4 2 2x 6  x 2x 2x(6  x) 6  x 2x 6  x 2x 6  x 1 1 1 1 1 1 1  (  )(     )  0 4 4 4 4 4 2x 6  x 2 2x 2 2x(6  x) 2 6  x 2x 6  x 1 1  
 2x  6  x x  2 . 4 4 2x 6  x 4
f (0)  2 6  2 6  
Ta có  f (2)  6  3 2  4 f (6)  12  12  
Lập bảng biến thiên của hàm số f (x) trên đoạn 0;6 , ta suy ra để phương trình có đúng 2 nghiệm thực thì : 4
2 6  2 6  m  6  3 2 . 108 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
Bài 5. Tìm m để phương trình sau có nghiệm thực: 4 2
3 x 1  m x 1  x 1 Lời giải:
+Điều kiện: x  1.
Phương trình đã cho tương đương với x 1 x 1 4 3  m  (*) . x 1 x 1 x 1 x 1 Ta đặt 4 t  , xét hàm số 4 t(x) 
trên đoạn 1; . x 1 x  1 3 1 x 1 Ta có 4 t '(x)  ( )  0, x   1 2 2(x 1) x 1  x 1 4  lim t  lim  1
Mặt khác ta có: x x  x  1  0  t  1. t  (1)  0 
Phương trình (*) trở thành: 2
m t  3t . Xét hàm số 2
f (t)  t  3t liên tục trên đoạn 0;  1 . 1 Ta có f (
t)  1 6t f (
t)  0  t  . 6   f (0)  0
min f (t)  f (1)  2   t   0;  1  1 1  Ta có:  f ( )    1 1 . 6 12 
m ax f (t)  f ( )  t   0;  1  6 12  f (1)  2   1
Vậy để phương trình có nghiệm thì 2   m  . 12
Bài 6. Tìm m để phương trình sau có nghiệm thực: 109 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM 2 2 x x 1 
x x 1  m Lời giải: Xét hàm số 2 2 f (x) 
x x  1  x x 1 liên tục và xác định trên  . 2x 1 2x 1
Ta có f '(x)   . 2 2 2 x x 1 2 x x 1 Suy ra 2 2
f '(x)  0  (2x 1) x x  1  (2x 1) x x 1 2 2 2 2
 (2x 1) (x x 1)  (2x 1) (x x 1)  x  0.
Thử lại thấy x  0 không thỏa mãn, vậy f '(x) không đổi dấu trên tập xác định. Mặt khác lại có
f '(0)  1  f '(x)  0, x
   . Vậy f (x) đồng biến trên  . 2x Ta có 2 2
lim f (x)  lim ( x x  1  x x 1)  lim x x x 2 2 x x 1  x x 1 2  lim  1  . x 1 1 1 1  1   1  2 2 x x x x
Và tương tự ta có, lim f (x)  1. x Từ đó suy ra : 1
  f (x)  1.
Vậy để phương trình có nghiệm thì 1   m  1 .
Bài 7. Tìm m để phương trình sau có nghiệm thực: 3
3(3x  2) 3x  2  2(6  5x) 6  5x  48x m . Lời giải:  6  Xét hàm số 3
f (x)  3(3x  2) 3x  2  2(6  5x) 6  5x  48x liên tục trên đoạn 0;  . 5    Ta có 3
f '(x)  12 3x  2 18 6  5x  48 3
f '(x)  0  2 3x  2  3 6  5x  8  0(*) . 110 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM Giải phương trình (*): Đặt 3 3 u    3x  2 u    3x  2 3 2   
 5u  3v  8(1) . 2
v  6  5x
v  6  5x  
Và từ (*) ta có 2u  3v  8  0(2) . Từ (1) và (2) ta suy ra: 8  2u 3 2 2 5u  3(
)  8  (u  2)(15u  26u  20)  0 3 3
u  2  3x  2  2   x  2  .
Vậy f '(x)  0  x  2  .  f ( 2  )  272   6 48 288 6 48 288 Ta có  f ( )  
 min f (x)  f ( )   . 3  6 3 5 5 5 5  x 0; 5 5 5 5   5   
 lim f (x)   x 48 288
Vậy để phương trình có nghiệm thì m   . 3 5 5 5
Bài 8.Tìm m để phương trình sau đây có nghiệm thực: (4m  3) x  3  (3m  4) 1 x m 1  0 Lời giải: + Điều kiện: 3   x  1.
Phương trình đã cho tương đương với (
m 4 x  3  3 1 x 1)  1 4 1 x  3 x  3
1 4 1 x  3 x  3  m  (*) .
4 x  3  3 1 x 1 
 1 x  2sin Ta có 2 2
( 1 x )  ( x  3)  4 , nên ta đặt  , (0   ) 2
x  3  2 cos  111 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM 2 2 tan 1 tan Sử dụng 2 2 sin ;cos và đặt 2 t  tan (0  t  1) . 2 2 2 1 tan 1 tan 2 2 2 2 2
1 t 16t  6(1 t )
5t  16t  7
Khi đó (*) trở thành: m   . 2 2 2
8(1 t )  12t 1 t
7t 12t  9 2
5t 16t  7
Xét hàm số f (t) 
liên tục trên đoạn 0;  1 . 2
7t 12t  9 2
52t  8t  60
Ta có f '(t) 
f '(t)  0,t [0;1] . Suy ra hàm số f (t) đồng biến trên 0;  1 . 2 2
(7t 12t  9)  7
min f (x)  f (0)  x    0;  1 9 Suy ra  9
m ax f (x)  f (1)   x   0;  1  7 7 9
Vậy để phương trình có nghiệm thì  m  . 9 7
Bài 9. Tìm những giá trị thực dương của tham số m để phương trình sau đây có nghiệm thực không vượt quá 6 .
x  22x  
1  3 x  6  m   x  6 2x   1  3 x  2 . Lời giải: 1 Điều kiện x  . 2
Khi đó phương trình tương đương với
x  2  x  6 2x 13  m(*)
Với những giá trị thực dương của tham số m nên để phương trình (*) có nghiệm thì
2x 1  3  0  x  5
Vậy ta xét hàm số f (x)   x  2  x  6 2x 1   3 trên khoảng 5; 6
Ta có f '(x)  0, x
 5;6 . Và f (5)  0; f (6)  6 2  11  3 112 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
Vậy 0  m  6 2  11  3 là giá trị cần tìm.
Bài 10. Xác định tất cả các giá trị thực của tham số m để hệ sau đây có nghiệm thực:  1 1 x   y   5   x y  1 1 3 3 x   y   15m 10 3 3  x y Lời giải:  1 1 x   y   5   x y
Hệ phương trình đã cho tương đương với:  1 1 1 1 3 3
(x  )  ( y  )  3(x  )  3( y  ) 15m 10  x y x y   1 1 x   y   5   x y   1 1 3 3
(x  )  ( y  ) 15m  5  x y   1 1 x   y   5   x y   1 1 1 1 1 1 3
(x   y  )  3(x  )(y  )(x   y  ) 15m  5  x y x y x y   1 1 x   y   5   x y   1 1
(x  )( y  )  8  mx y   1 u x    x Đặt  ( u ; v  2) 1 v y   y
u, v là nghiệm của phương trình: 2
t  5t  (8  m)  0 (1)
Yêu cầu bài toán tương đương với phương trình (1) có 2 nghiệm phân biệt thỏa mãn t  2 . 113 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM 5 Từ (1) ta có: 2
m f (t)  t  5t  8( t  2)  f '(t)  2t  5  f '(t)  0  t  . 2 5 7 Ta có: f ( 2
 )  22; f (2)  2; f ( ) 
; lim f ( x)   . 2 4 x
+Để (1) có 2 nghiệm phân biệt ( t  2 )thì đường thẳng y m cắt đồ thị hàm số y f (t) tại 2
điểm phân biệt. Lập bảng biến thiên hàm số
f (t) ,dựa vào bảng biến thiên 7 
m  2  22  m   là giá trị cần tìm. 4
Bài 11. Tìm tất cả các giá trị thực của tham số m để hệ phương trình sau có nghiệm thực:
(3  x) 2  x  2 y 2y 1  0(1)   (*) 2 4 3 
y 1  m 10  2x  2 y 1(2) 
Lời giải:
+ Điều kiện: x  2; y  1 .
Khi đó phương trình (1) tương đương với: (1 2  x) 2  x  (1 2 y 1) 2 y 1
f ( 2  x )  f ( 2 y 1) , trong đó f (t)  (1 t) t (t  0) . 1 t
Ta có f '(t)  t   0, t
  0  hàm số f (t) đồng biến trên 0;  2 t
f ( 2  x )  f ( 2 y 1)  2  x
2 y 1  x  3  2 y  1  2( y  1) .
Thay x  3  2 y vào (2) ta được : 2 4
3 y 1  2m y 1  2 y 1(1) . Do vậy ta chỉ cần tìm m để
phương trình (1) có nghiệm y  1.
Chia cả hai vế của (1) cho 4 y  1 ta được: y 1 y 1 y 1 3  2m  24
(i) , đặt t  4  0  t  1 . y 1 y 1 y 1 3
Khi đó phương trình (i) trở thành: 2 m t t . 2 Xét hàm số 2
f (t)  t  3t liên tục trên đoạn 0;  1 . 114 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM 1
Ta có f '(t)  3t 1  f '(t)  0  t  . 3 1 1 1 1  1
Lại có: f (0)  0; f ( )  ; f (1)    f (t)  . 3 6 2 6 2 1  1
Vậy để phương trình có nghiệm thì  m  . 6 2
Bài 12. Tìm m để hệ phương trình sau có nghiệm: 3 2 
2x  ( y  2)x xy m  (*) 2
x x y  1 2m Lời giải: 2 
(x x)(2x y)  m
Hệ phương trình đã cho tương đương với:  2
x x  2x y  1 2m   1 2 u
  x x  Ta đặt  4
v  2x y  2 uv m
u  (2m 1)u m  0(1)
Khi đó hệ trở thành:   
u v  1 2m
v  1 2m u  1 
Vậy hệ có nghiệm khi và chỉ khi (1) có nghiệm thỏa mãn u  4 1  2 u u Với u  , Từ(1) 2
m(2u 1)  u   u m  . 4 2u 1 2 u   u  1 
Xét hàm số f (u) 
liên tục trên đoạn  ;    . 2u  1  4  2 2u  2u 1 1   3
Ta có: f '(u)  
f '(u)  0  u  . 2 (2u  1) 2 1  5  1   3 2  3 Lại có: f ( )  ; f ( ) 
; lim f (u)   . 4 8 2 2 u 115 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM 2  3
Lập bảng biến thiên của hàm số f (u) ta suy ra để hệ có nghiệm thì m  . 2
Bài 13. Xác định tham số m để hệ phương trình sau có nghiệm: 2 3 4 3 2   ( m x x x 1)  xy  (*) 3 8 2 3 2 3 4 3 4  ( m x x
x 1)  (m 1) x  2 y x Lời giải: xy  0  x  0
+Nếu m  0  (*)     3 4 3 4
 x  2 y x y     +Nếu m  0; Đặt 3 t
x , khi đó t  0 không là nghiệm của hpt;và hệ phương trình trở thành: 6 4 2 3   (
m t t t  1)  yt  8 6 2 4 4  (
m t t t 1)  (m 1)t  2 yt  6 4 2 3  (
m t t t  1)  yt (1)  8 6 4 2 4 (
m t t t t 1)  (2 y 1)t (2) 
+Do t  0 không là nghiệm của hpt, nên chia 2 vế của (1) cho 3 t và của (2) cho 4 t , ta được:  1 1 3 ( m t
t  )  y  3  t t  1 1 4 2  ( m t   t  1)  2 y  1 4 2   t t 1 1 1 1 1 1 1 3 3 4 2 2 2 2 t
 (t  )  3(t  );t   (t  )  2; t   (t  )  2 3 4 2 2 t t t t t t t 1
Đặt u t  ( u  2) , Khi đó HPT trở thành: t 3 3  (
m u  3u u)  y
m(u  2u)  y    2 2 2 4 2 [
m (u  2)  2  u  2 1]  2 y  1
m(u  3u  1)  2 y 1   3  (
m u  2u)  y   4 2 3 (
m u  3u 1)  2m(u  2u) 1(3) 
+ Hệ có nghiệm khi và chỉ khi (3) có nghiệm u  2 116 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM 1 4 2 3 4 3 2
(3)  m(u  3u 1 2u  4u)  1 
f (u)  u  2u  3u  4u  1 m 3 2
f '(u)  4u  6u  6u  4; f '(u)  0  u  2( u  2)
Lập bảng biến thiên của f (u) ta suy ra (3) có nghiệm thỏa mãn ( u  2) khi và chỉ khi: m  0 1 3     1  mm   3 m  0
Vậy giá trị cần tìm của m là:  1 . m    3
Bài 14. Tìm m để phương trình sau có nghiệm thực: 1 ( m
4  x  5  x x)  2 x x 1  3(*) 2
Lời giải:
Điều kiện: 1  x  4 . 2 x x 1  3
Khi đó phương trình tương đương với: m  1
4  x  5  x x 2 2 x x 1  3 u(x)
Xét hàm số f (x)  
liên tục trên đoạn 1;4. 1 v(x)
4  x  5  x x 2 u
 (x)  2 x x 1  3  0  Trong đó:  , (1  x  4) 1 . v(x) 
4  x  5  x x  0   2
u '(x)v(x)  v '(x)u(x)
Ta có f '(x)  2 v (x) 1 1
Mặt khác, ta có: u '(x)    0; x 2 x 1 117 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM 1 1 1 1 1  1 1 1 v '(x)          0( 5  x  2) 2 4  x 2 5  x 2 2 2 5  x 2 5  x 2 5  x
Từ đó suy ra :  f '(x)  0 . Hàm số f (x) đồng biến trên đoạn 1;4. 10 7  3
 min f (x)  f (1) 
; max f (x)  f (4)  , x [1; 4] . x   1;4 x   1;4 5  2 3 3 10 7  3
Vậy để phương trình có nghiệm thì  m  . 5  2 3 3
Bài 15. Xác định m để phương trình sau có nghiệm x x x 12  ( m
5  x  4  x )
Lời giải:
+ Điều kiện 0  x  4 .
Nhân cả 2 vế của phương trình với ( 5  x  4  x ) , phương trình trở thành m  (x x
x 12)( 5  x  4  x ) .
Xét hàm số f (x)  (x x
x 12)( 5  x  4  x )  u(x).v(x) .  3 1 u '(x)  x   0 u  (x) x x x 12 0       2  2 x 12 Trong đó:   
v(x)  5  x  4  x  0
5  x  4  x  v '(x)   0  
2 5  x 4  x Từ đó suy ra:
f '(x)  u '(x)v(x)  v '(x)u(x)  0 . Hàm số f (x) đồng biên trên đoạn 0; 4 .
Suy ra min (x)  f (0)  2 15  4 3; max f (x)  f (4)  12, x  0;  4 . x   0;4 x   0;4
Vậy phương trình có nghiệm khi và chỉ khi 2 15  4 3  m  12 .
Bài 16. Xác định m để bất phương trình sau có nghiệm: 3 3
x  3x 1  m( x x 1) 118 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM Lời giải:
Điều kiện: x  1.
Khi đó nhân cả 2 vế của bất phương trình với 3 ( x
x 1)  0 , bất phương trình trở thành: 3 3 3 3
(x  3x 1)( x
x 1)  m( x x 1) ( x x 1)  m 3 3
f (x)  (x  3x 1)( x x 1)  m .
Suy ra để bất phương trình có nghiệm là m  min f (x) . x   1; Xét hàm số 3 3
f (x)  (x  3x 1)( x
x 1)  u(x).v(x) , 3 u
 (x)  x  3x 1  0  trong đó:  , x   1. 3
v(x)  ( x x 1)  0  3 1 1 Ta có 2 2
u '(x)  3x  3  0; v '(x)  (  )( x x 1)  0 . 2 x x 1
f '(x)  u '(x)v(x)  v '(x)u(x)  0 . Hàm số f (x) đồng biến trên khoảng 1; .
min f (x)  f (1)  1  , x   1. x   1;
+ Để bpt có nghiệm khi và chỉ khi m  min f (x)  1.
Vậy giá trị cần tìm của m là: ( 1  ; ) .
Bài 17. Tìm m để hệ phương trình sau 2xx 1  2 x 1 7 7     2012x  2012(1)  có nghiệm 2
x  (m  2)x  2m  3  0(2)  Lời giải:
+Điều kiện: x  1  , Khi đó ta có: 2 xx 1  2 x 1 (1) 7 7     2012x  2012 2 xx 1  2 x 1 7 1006(2x x 1) 7       1006(2  x 1)  f (2x
x 1)  f (2  x 1)(*) 119 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM Với ( )  7t f t 1006t , ta có '( ) 7t f t  ln 7 1006  0 , suy ra f (t) đồng biến trên R, và từ (*)  2x x  1  2  x 1  1   x  1.
Vậy hệ phương trình có nghiệm khi và chỉ khi (2) có nghiệm x [ 1;1] 2
x  (m  2) x  2m  3  0 có nghiệm x [ 1;1] 2 x  2x  3
m g(x)  ; x [ 1;1] x  2
m  min g(x) x [  1  ;1] 2 x  4x  1
Ta có: g '(x) 
g '(x)  0  x  2  3 [ 1;1] 2 (x  2) g( 1  )  2
 ; g(2  3)  2  2 3; g(1)  2  min g(x)  g( 1  )  2. x [  1  ;1]
Vậy m  2 là giá trị cần tìm. Bài 18. Biết rằng 2
f (t)  3 2  t  6 2  t  4 4  t 10  3t, 2  t  2 , xác định giá trị của m
để phương trình sau có nghiệm: x m
f (t)dt; x [  2; 2]  0 Lời giải: x
Ta có: m F (x) 
f (t)dt; x [  2; 2]  0 2
F '(x)  f (x)  F '(x)  0  3 2  x  6 2  x  4 4  x  10  3x 2
 3( 2  x  2 2  x )  4 4  x  10  3x(*) Đặt 2 2 2 u
2  x  2 2  x u  2  x  4 4  x  4(2  x)  10  3x  4 4  x 120 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM u   0
 2  x  2 2  x 6
Khi đó phương trình (*) trở thành: 2 3u u     x   u  3 5 
 2  x  2 2  x  3 
Ta tìm GTLN và GTNN của F (x), x [  2; 2] , ta có: 2  2  2 F ( 2  ) 
f (x)dx  (3 2  x  6 2  x  4 4  x 10  3x)dx  58 12 2  4   0 0 6 5 6 2
F ( )  (3 2  x  6 2  x  4 4  x 10  3x)dx  5 0 5 246 3 3  32   8 arcsin  4 sin(2 arcsin ) . 5 25 5 5 2 2
F (2)  (3 2  x  6 2  x  4 4  x 10  3x)dx  2 12 2  4  0
 min F (x)  F (2)  2 12 2  4; m axF (x)  F ( 2
 )  58 12 2  4; x [  2;2] x [  2;2]
 2 12 2  4m  58 12 2  4.
Bài 19. Xác định giá trị của tham số m để bất phương trình sau có nghiệm thuộc đoạn [ 3; 3] 2 x x  1 2 2 2  x  4   m  * 2 x  4 x 1 Lời giải: 2 x x  1 2 BPT(*) 2
m f (x)  2  x  4  2 x  4 x 1
Vậy (*) có nghiệm thuộc đoạn [ 3; 3] khi và chỉ khi m  max f (x) x [   3; 3 ]
Ta chứng minh: f (x)  0 x
 [  3; 3] , thật vậy với x
 [  3; 3] thì ta có 2 x x  1 2 2 f (x)  2  x  4  2 x  4 x  1 121 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM 2 x x  1 2 2  2(
1)  (x  3)  (1 ) 2 x  4 x  1 2
x x 1 1 2 (x  3) x  4 2  2( )  (x  3)  2 2 2 x x 1 x 1(2  x 1)  1 x  4 2 2 2(x  3) (x  3) 2   (x  3)  2 2 2
(x x 1)(x  4)  x  4 x  1(2  x 1) 2 1 2  (x  3)( 1 )  0, x
 [  3; 3]Vậy giá trị 2 2 2
(x x 1)(x  4)  x  4 x 1(2  x  1) cần tìm của m là: ( ;  0) .
Bài 20. Tìm giá trị nhỏ nhất của tham số m để bất phương trình sau luôn đúng 2 2 4 2 2 (
m x  1 x 1)  2 x x x  1 x  2(*) Lời giải: +Điều kiện : 1   x  1 + Đặt 2 2 2 4
t x  1 x  0  t  1 2 x x  1  t  1; + 2 2 2
t x  1 x
2(x 1 x )  2  1  t  2 2 t t 1 BPT(*) 2
m(t 1)  t t 1  m f (t)  t 1
BPT(*) có luôn có nghiệm khi và chỉ khi m  max f (t) . t [  1; 2 ] 2 t  2t
Ta có f '(t)   0, t
 [1; 2]  max f (t)  f ( 2)  2 2 1. 2 (t 1) t [  1; 2 ]
Vậy giá trị cần tìm của m là: m  2 2 1 . 122 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
Vậy giá trị nhỏ nhất của tham số m cần tìm là: m  2 2 1.
Bài 21. Xác định giá trị tham số m để hệ phương trình sau có nghiệm thực  3 1 2 2
(x  ) x  2x  3  (x  ) x 1  2x  2  0(1)  2 2  3 2 log (3 x 1)  log (m  2x)(2) 2 2  m 1  m 1  Lời giải: 2 2 2  2 2 u   x 1  0  u x 1 v u  2  Đặt     x  2 2 2     
v x  2x  3 2 v x 2x 3 0   Thay vào (1), ta được: v u 2 2 2 2 2 2 (v u 1)
 (v u 1)
v u  0 2 2 2
 (v u)(u v 1)  0  v u  0  x  1. Điều kiện: 2
m 1  1  m  0 . Khi đó phương trình (2) tương đương với m  0  3 2 
m f (x)  3 x  2x 1; x  1(m  0) . 3 2
0  3 x  1  m  2x
Vậy hệ phương trình có nghiệm khi và chỉ khi (2) có nghiệm x  1
 , điều này tương đương với
m  min f ( x) . x [  1  ;] 2
Ta có: f '(x)  2 
f '(x)  0  x  1  . 3 x
Lập bảng biến thiên của hàm số f (x) ta suy ra min f (x)  f (0)  1  m  1 . x [  1  ;]
Vậy giá trị cần tìm của m là: (1; ) .
Bài 22. Xác định giá trị tham số m để hệ phương trình sau có nghiệm 2
x  3x  4  0(1)   3 2
x  3 x x m 15m  0(2)  123 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM Lời giải:
Ta có (1)  (x  1)(x  4)  0  1   x  4 . 2 3
(2)  m 15m f (x)  x  3 x x .
Vậy hệ phương trình có nghệm khi và chỉ khi, bất phương trình (2) có nghiệm thuộc đoạn
[ 1; 4] , khi và chỉ khi 2
m  15m  max f (x) . x [  1  ;4] 3 2 
x  3x (1  x  0) Xét hàm số 3
f (x)  x  3 x x   . 3 2
x  3x (0  x  4)  2 
3x  6x(1  x  0)
Ta có f '(x)  
f '(x)  0  x  0; x  2  . 2
3x  6x(0  x  4)  Ta có f ( 1
 )  2; f (0)  0; f ( 2
 )  4; f (2)  4  ; f (4)  16.
Từ đó suy ra: max f (x)  f (4)  16 . x [  1  ;4]
Vậy hệ bất phương trình có nghiệm khi và chỉ khi 2
m 15m  16  1  6  m  1.
Vậy m 16,  1 là giá trị cần tìm. 
Bài 23. Tìm m để phương trình 2
mx 1  cos x có đúng 1 nghiệm thuộc 0;   .  2  Lời giải:
+ Phương trình đã cho tương đương với 2 x 2 x 2 2  sin sin cos x 1  sin 2 2 t xm    2  m   ; t   0; 2 2 2     x xx   t  2  4     2  2  sin t x
Xét hàm số f (t)  ;t   0;     .  t  2  4 
 sin t t cos t  sin t
 sin t  cos t(t  tan t)   + Ta có f '(t)  2  2  0   , vì với t  0; thì 2   2    t tt t  4 
sin t cos t  0, tan t t . 124 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
+ Như vậy f (t) đồng biến trên đoạn 0; 
 suy ra để phương trình có nghiệm thì  4  1  4 
f (0)  2m f ( )   m  là giá trị cần tìm. 2 4 2
Bài 24. Tìm tất cả các giá trị của m để hệ phương trình 2 2 
2x xy y  1 (1)  có nghiệm 2 2
x xy y m Lời giải:
Từ hai phương trình trong hệ ta suy ra 2 2
x xy y m  (*) 2 2
2x xy y 1
+ Nếu y  0  m  và hệ có nghiệm  ; x 0 , x  .  2 x
+ Nếu y  0 chia cả tử và mẫu của (*) cho y và đặt t  , khi đó ta được y 2 t t 1 1  1  m  (**) . Từ (1) ta có: 2
2t t 1   0  t   t  1  . 2     2 2t t 1 y  2   1 
Vậy hệ có nghiệm khi và chỉ khi phương trình (**) có nghiệm t  ;    1  ;  .    2  2 t t 1  1 
Xét hàm số f (t)  trên khoảng  ;    1  ;  . 2   2t t 1  2  2 t  6t  2 t   3   7
Ta có f '(t)  
, f '(t)  0  
2t t  2 2 1 t   3   7  14  5 7
Lập bảng biến thiên suy ra giá trị của m là m  . 28 11 7 125 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
Bài 25. Tìm m để hệ phương trình 3 3 2
x y  3y  3x  2  0(1)   có nghiệm thực. 2 2 2
x  1 x  3 2 y y m  0(2)  Lời giải:  1   x  1 Điều kiện  0  y  2 
Đặt t x 1  t 0; 2 , khi đó phương trình (1) trở thành 3 2 3 2
t  3t y  3y (*) , xét hàm số 3 2
f (u)  u  3u trên đoạn 0; 2 , ta có 2
f '(u)  3u  6u  0, u
 0; 2 , suy ra f (u) nghịch biến trên đoạn 0; 2
Do đó phương trình (*) tương đương với f (t)  f ( y)  t y y x 1 Khi đó 2 2 2 2 2
x  1 x  3 2 y y m  0  x  2 1 x m  0(i) Đặt 2 v
x v   2 1
0;1  (i)  v  2v 1  m . Xét hàm số 2
g(v)  v  2v 1lien tục trên đoạn 0; 
1 , ta có g '(v)  2v  2  0, v  0;  1
Suy ra min g(v)  g(0)  1
 ; max g(v)  g(1)  2 v   0;  1 v   0;  1
Vậy hệ phương trình có nghiệm khi và chỉ khi 1   m  2 .
Bài 26. Tìm m để hệ bất phương trình sau có nghiệm 2 2 5
x  4xy  2 y  3   2m 1 2 2
7x  4xy  2 y    2m  5 Lời giải: 2 2  5
x  4xy  2 y  3  
Hệ phương trình đã cho tương đương với:  18 2 2
21x  12xy  6 y  3    2m  5 126 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
Cộng theo vế hai phương trình trong hệ trên ta suy ra: 18 4x  2y2 2 2
 16x 16xy  4 y   2m  5 5
Suy ra để hệ có nghiệm thì cần 2m  5  0  m   . 2 5
Bây giờ ta chứng minh với m   thì hệ có nghiệm. 2
Thật vậy, xét hệ phương trình sau:  1 2 2 x   5 
x  4xy  2 y  3   7  (*)  
, suy ra hệ này có nghiệm. 2 2
21x  12xy  6 y  3 2   y     7
Giả sử  x , y là nghiệm của hệ phương trình (*), khi đó ta có 0 0  2 2 5
x  4x y  2 y  3 0 0 0 0  5  , 18 m   2 2
21x  4x y  6 y  3  3  2  0 0 0 0  2m  5
Suy ra  x , y cũng là nghiệm của hệ đã cho. 0 0  5
Từ đó suy ra m  
là những giá trị cần tìm. 2
Bài 27. Tìm m để hệ phương trình sau có nghiệm duy nhất: 2 3 2 3 
x y  2 y my  2 3 2 3
y x  2x mx Lời giải:
(i). Điều kiện cần:
Giả sử hệ phương trình có nghiệm  x , y , khi đó  y , x cũng là nghiệm của hệ nên để hệ có 0 0  0 0 
nghiệm duy nhất thì trước hết x y . 0 0  x  0 0 Thay vào hệ ta được 3 2
x  5x mx  0  0 0 0  2
x  5x m  0(*)  0 0 127 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
Hệ có nghiệm duy nhất thì (*) hoặc vô nghiệm hoặc có nghiệm kép x  0 , điều này tương đương với
  25  4m  0  25
  25  4m  0  m   .  4  m  0 
(ii). Điều kiện đủ: 25 Với m
, khi đó hệ phương trình tương đương với 4 3
x y y  2y m  y   y  2 2 2 1  m   1  0 
x, y  0 . 3
y x x  2x m  x x  2 2 2 1  m   1  0 
Cộng theo vế hai phương trình của hệ ta được: x  2
x x m  y  2 5
y  5 y m  0 2 2  5 25   5 25       x x   m   
  y y   m   
  0  x y  0 .  2 4   2 4          25
Kết luận vậy m
là những giá trị cần tìm. 4
Bài 28. Tìm m để phương trình sau có nghiệm
x     mx    m   2 1 4 1 1 x 1 Lời giải:
Điều kiện:  x   1  x   1  0
Nhận thấy x  1 không là nghiệm của phương trình, khi đó chia hai vế của phương trình cho x 1 x 1 x 1 và có  , ta được x 1 x 1 2 x 1 x  1 t t  4 x 1
 4  m  m   1  m  , với t x 1 x 1 1 t x 1 128 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM 2 t t  4 2 t  2t  3
Ta có t  0 . Xét hàm số f (t)  có f '(t) 
 0,t  0;  ;t  1 2   t 1 t   1
Từ đó suy ra f (t)  f (1)  3; lim f (t)   t 
Vậy phương trình có nghiệm khi và chỉ khi m  3
Bài 29. Tìm m để phương trình sau có nghiệm 4
x x  m   2 8
2 x  2m  2 x  4m Lời giải:
Phương trình tương đương với 4 2
x  8x  2x  4x 4 2
x  8x  2x  4x m 2
x  2x  4  m  2 x  2x  4 2 2 x  2x x  2x   2. 2 2 x  2x  4 x  2x  4 2 x  2x Do đó ta đặt t
; khi đó m t  2t 2 x  2x  4
Trước hết ta tìm tập giá trị của t , ta có 4   2
x  2x  2  x  1 3 t '(x)   0  
x  2x  42 2 x  1 3   2 3 2 3 
Từ đó suy ra t  1   ,1  3 3    2 3 2 3 
Vậy ta xét hàm số f (t)  2t t đồng biến trên 1   ,1  3 3    2 3 2 3 2 3 2 3     
Giá trị cần tìm của tham số m thỏa mãn m  2 1   1 ; 21   1   3  3  3   3        129 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM  1 
Bài 30. Tìm m để phương trình sau có nghiệm duy nhất trong đoạn  ;1  2    2 3 2
3 1 x  2 x  2x 1  m Lời giải:  1  Xét hàm số 2 3 2
f (x)  3 1 x  2 x  2x 1 trên đoạn  ;1  2    2 3x 3x  4x  3 3x  4 
Ta có f '(x)    x    2 3 2 2 3 2 1 x x  2x 1  1 x
x  2x  1  1  3 3x  4
Do x   ;1  3x  4  0    0   2 3 2  2  1 x x  2x 1
Vậy f '(x)  0  x  0  1 
Ta có bảng biến thiên của hàm số f (x) trên đoạn  ;1  2   
Dựa vào bảng biến thiên suy ra để phương trình có nghiệm duy nhất khi và chỉ khi m  1   22  3 3  4   m   2 130 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
Bài 31. Tìm m để hệ sau có nghiệm log x y  log xy  2  2  2   3    3 3
x y xy mLời giải: Đặt a  log
x y ;b  log
xy  2 khi đó ta có a b  2 2   3   2 2 Lại có    a   b   2 4 2 4 3 2 4 3 a 2 12a 8.3a x y xy            36  0 Xét hàm số ( ) 12a 8.3a f a  
 36 đồng biến; lại có f (1)  0 vậy a  1
Biến đổi phương trình thứ hai của hệ: 3  3    a   2 aa  2 3 2 3 3 2 .2 3 a m x y xy x y xy             2 3 Xét hàm số  a   2 aa  2 ( ) 2 3 3 2 .2 3 a f a      
 2 trên 1,  a a a a  2  2  1  1
Ta có f '(a)  8 ln 8  6.2 ln 2  27. .ln  9. .ln  0     với mọi a  3  3  3  3
Suy ra f (a)  f (1)  1
Vậy giá trị cần tìm của m là m  1.
Bài 32. Tìm m để hệ sau có nghiệm 2 2 
x xy  2 y x m  2
x  2xy  2x m  2  Lời giải:
Hệ bất phương trình tương đương với 2 2 2 2
x xy  2 y x m
x xy  2 y x m    2  2
x  2xy  2x  2  m
 x  2xy  2x  2  m   2   2 2
x xy  2 y x   2
x  2xy  2x  2  3m
2 x  2 y 2  2 x  2 1  3m  
Suy ra để hệ có nghiệm thì trước tiên 3m  0  m  0 131 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM  1 
Ngược lại với m  0 ; thì hệ luôn có nghiệm 1; 
 . Vậy m  0 là giá trị cầ tìm.  2 
Bài 33. Tìm m để hệ phương trình
2 xy y x y  5   có nghiệm
 5  x  1 y m Lời giải:
y x   1  0 
Điều kiện: x  5  y 1 
Khi đó phương trình thứ nhất của hệ biến đổi thành: y  2 y x   1   x   1  4 (1)
Nếu x  1; y  0 thì ta có (1) tương đương với
  x  y 2 1
 4 vô nghiệm, nên hệ vô nghiệm
Vậy 1  x  5; 0  y  1 và (1) tương đương với
x   y2 1  4  x 1 
y  4 , đặt t y   2
0;1  x t  4t  5
Thay vào phương trình thứ hai của hệ ta được 2 2 m
4t t  1 t (*) Xét hàm số 2 2 f (t) 
4t t  1 t liên tục trên đoạn0;  1 2  t t
Ta có f '(t)  
 0   2  t 2 2
1 t t 4t t 2 2 4t t 1 t 2 2
 3t  4t  4  0  t  0;  1 3  2  5
Ta có f (0)  1; f (1)  3; f     3  3 132 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
Vậy để hệ có nghiệm khi và chỉ khi phương trình (*) có nghiệm, tương đương với m thuộc tập  5 
giá trị của hàm số f (t) trên đoạn 0; 
1 từ đó suy ra m  
, 3 là giá trị cần tìm. 3  
Bài 34. Tìm giá trị lớn nhất của tham số m để hệ phương trình sau đây có nghiệm 2 2 x y  1   3 3 3
x y x y m   Lời giải: Ta có 3 3
x y x y x y  2 2
1  x xy y   x y 2  xy 2 2 1 1 Suy ra 6
m   x y 2  xy  1 2xy 2  xy 2  xy nhưng do xy   2 2
x y   nên 2 2
theo bất đẳng thức cô sic ho 3 số không âm ta được: 3 3
 1 2xy  2  xy  2  xy   5  5 6
m  1 2xy 2  xy 2  xy    m       3   3  3 5 1
Ngược lại, với m
thì dấu bằng của bất đẳng thức xảy ra khi đó 2 2
xy   ; x y  1 . rõ 3 3 rang hệ này có nghiệm. 5
Vậy giá trị cần tìm của m là . 3
BÀI TẬP ĐỀ NGHỊ 1.1.
Tìm m để phương trình sau có nghiệm thực: 4 2 x 1  x m 1.2.
Tìm tham số m để phương trình sau có đúng một nghiệm: 4 4
x 13x m x 1  0 1.3.
Xác định m để phương trình sau có nghiệm: 2 2 4 2 2 ( m
1 x  1 x  2)  2 1 x  1 x  1 x 133 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM 1.4.
Tìm m để phương trình sau có nghiệm 4 2 4 2 ( m
x  2  2 x  4) 
x  2  2 x  4 1.5.
Tìm m để phương trình sau 2m 2 1
x x x  1 x  0 có nghiệm thực 3 1.6. Cho phương trình 2  x
2  x  2  x  (2  x)  m 2  x
Tìm m để phương trình có 2 nghiệm phân biệt. 1.7. Cho phương trình
2x  3  2  x m(3x  5) .
Tìm m để phương trình có nghiệm. 1.8.
Xác định giá trị của m để phương trình sau có nghiệm 4 2 2
2 x x 1  x x 1  m 1.9.
Định m để phương trình sau có nghiệm 3 2 2 2
x x x m(1 x )
1.10. Xác định giá trị tham số m để phương trình sau có nghiệm 2 2 2 2 2 2 2
x  ( x x 1)  (x  1)  m(x x 1)
1.11. Tìm m để phương trình sau đây có nghiệm thực: 2 x x  (
m 1 2( x x 1))
1.12. Tìm m để phương trình sau có nghiệm: ( m
x  1 x  2)  2 x  1 x  4
1.13. Tìm m để phương trình sau có nghiệm thực
3 x  24m  12m x  6  0
1.14. Tìm giá trị tham số m để phương trình sau có 2 nghiệm thực phân biệt 2
x mx  2  2x 1
1.15. Xác định giá trị của tham số m để phương trình sau có nghiệm 134 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM 3 2 3 2 2
x mx x m  x mx x m m x 1
1.16. Xác định m để phương trình có đúng 2 nghiệm thực:
x  3  2 x  4 
x  6 x  4  5  m
1.17. Tìm m để phương trình sau có nghiệm 3
log (x  4mx)  log (2x  2m 1)  0 2 1 2
1.18. Cho phương trình 2 2 log x  log
x 1  2m 1  0(m là tham số) 3 3
Xác định m để phương trình có ít nhất 1 nghiệm thuộc đoạn 3 [1;3 ]
1.19. Xác định giá trị của tham số m để phương trình sau có nghiệm thực: 3 3 2
12(x  2) x  2  4 (3x  2)  6x  9x  36x m
1.20. Chứng minh rằng với mọi giá trị thực dương của tham số m phương trình sau luôn có 2 nghiệm phân biệt: 2
x  2x  8  m(x  2)
1.21. Tìm để bất phương trình sau có nghiệm x [0;1+ 3] : 2 ( m
x  2x  2 1)  x(2  x)  0
1.22. Tìm m để bất phương trình sau có nghiệm x x   mx x x3 3 2 3 1
1.23. Tìm tất cả m để bất phương trình 1 3
x  3mx  2  
thỏa mãn với x  1  3 x
1.24. Tìm m để bất phương trình 2 log
(x  3)  1 đúng với mọi x   m 1  m2
1.25. Tìm m để phương trình sau có nghiệm thuộc đoạn[2; 4] x m f (t)dt
; trong đó f (t)  3(2  t  2)  2t t  6(t  2) 2
1.26. Tìm giá trị lớn nhất của tham số m để bất phương trình sau có nghiệm thực 135 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM m  x 3 2 4 3 m (x 1)   m sin 2 (x 1) 2  1  
1.27. Tìm m để bất phương trình sau có nghiệm thuộc đoạn ;1  2    3 3 3 2 3 2 m  1 x  2 
x 1  2x  2x 1
1.28. Tìm m để phương trình sau đây có nghiệm
m  2x( y 1)  y x  2
1.29. Tìm m để hệ phương trình sau có nghiệm duy nhất:
2x y m  0   x xy  1 
1.30. Tìm m để hệ phương trình sau có nghiệm thực:
x y  1  
x x y y  1 3m
1.31. Tìm m để hệ phương trình sau có nghiệm thực: 2
(4x 1)x  ( y  3) 5  2 y  0   8 4 4
 5  2 y  5  2 y  2 6  x  2 6  x m
1.32. Tìm m để hệ phương trình sau đây có nghiệm thực x, y dương:  5  2 3 2
x y x y xy xy   m   4  5  4 2
x y xy(1 2x)   m   4
1.33. Tìm m để hệ phương trình sau có nghiệm thực: 3 3 2
x y  3y  3x  2  0   2 2 2
x  1 x  3 2 y y m  0 
1.34. Tìm giá trị của tham số m để hệ phương trình sau có nghiệm:  2xy 2 2 x y   1  x y   2 x y  ( m x y)  136 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
1.35. Chứng minh rằng với mọi a  0 , hệ phương trình sau có nghiệm duy nhất x y
e e  ln(1 x)  ln(x y) 
y x a
1.36. Chứng minh rằng hệ phương trình  y x e  2011  2  y 1 
có đúng 2 nghiệm thỏa mãn x  0; y  0 xy e  2011  2  x 1
1.37. Tìm m để phương trình sau có hai nghiệm phân biệt 2 x x
mx   2 10 8 4 2 1 x 1
1.38. Cho bất phương trình x 2  mx x(1) 1 x
(i). Giải bất phương trình (1) khi m  2 .
(ii). Tìm giá trị m lớn nhất sao cho bất phương trình (1) nghiệm đúng với mọi x   .
1.39. Chứng minh rằng với mọi tham số m phương trình 3
x x m  2 9 x   1  0 luôn có 3 nghiệm.
1.40. Chứng minh rằng với mọi m phương trình sau luôn có nghiệm 2  x mx 2    2 log 
  2x x mx  2 1. 2  2x 1   
1.41. Tìm m để phương trình sau có nghiệm thực 2 2 x 2 mx2
2 x 4 mxm2 2 2012  2012
x  2mx m .
1.42. Tìm m để tồn tại cặp số  x, y không đồng thời bằng 0 và thỏa mãn phương trình:
m   x   m   y  m   2 2 4 3 3 4 1 x y  0.
1.43. Tìm tất cả các giá trị thực của tham số m đê hệ phương trình sau có nghiệm 137 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM  1 1 2 2  x   m y   m  4 2 2  x y  2 1    1  x y xy
1.44. Tìm tất các các giá trị của tham số m để hệ sau có nghiệm log x y  log xy  2  2  2   3    3 3
x y xy m
1.45. Tìm tất cả các giá trị thực của tham số m để hệ sau có nghiệm 
x y m
x y m  2  2 2 2
x y m
1.46. Tìm tất cả các giá trị của tham số m để phương trình sau có nghiệm duy nhất 2 14x 1 1   m   2x 2 3 3 96x x
1.47. Tìm các giá trị của tham số m để hệ sau có nghiệm  2  x  1 x   2
y  1 y  1 
 2x y  3 x y  2 6 1
mx y 1 
1.48. Tìm tất cả các giá trị của tham số m để bất phương trình sau có nghiệm 2
x  m   x   m   3 2 4 1
x  4x x 
1.49. Tìm m để phương trình sau có nghiệm thực 2 2 4 2
x   m x x  
x x   m  2 7 1 1
x x 1  2 log  3 9  x 2 
1.50. Tìm tất cả các giá trị của tham số m để mọi nghiệm của phương trình  3 log 3  x 2   m m
cũng là nghiệm của phương trình:  2  x   2  x  2 2
1.51. Tìm tất cả các giá trị thực của tham số m để phương trình  2 x   2  2 x    m  2 x    2 1 log 1 2 1 log x   1  m  4  0 138 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
có đúng hai nghiệm thực thỏa mãn điều kiện 1  x  3 .
1.52. Tìm m để phương trình sau có nghiệm 2  x   2  x x   2
x x    2 1 4 2 2 2 2 1 ln
x  2x   m
1.53. Tìm những giá trị thực của tham số m để phương trình sau có nghiệm 2  x     2 1 1 1 1 9 2 .3  x m  2m 1  0
1.54. Tìm tất cả các giá trị của tham số m để phương trình sau có nghiệm
m  3 x  2  mx  3  m  0
1.55. Tìm m để phương trình sau có nghiệm thực 5 2 4
x  34x m   x  
1  x  33  1
1.56. Tìm m để bất phương trình sau có nghiệm 2
m x  2x 17  2m   4 2 1
x  2x 17  m 1  0
1.57. Tìm tất cả các giá trị không âm của tham số m để phương trình sau có nghiệm
x m  2 x 1  x
1.58. Tìm tham số m để phương trình sau có nghiệm    x x 1 1 4 m x   x   x   1  1   x 1 
1.59. Tìm m để phương trình  4 4
2 sin x  cos x  cos 4x  2sin 2x m  0 có ít nhất một nghiệm   thuộc đoạn 0;  . 2   
1.60. Tìm m để phương trình: 2
12 4  x  3x  3x  24  m 3 x 1  2 4  3x có nghiệm
1.61. Tìm m để hệ phương trình  x yx 1  y 15   2 có nghiệm
x y m
1.62. Tìm m để hệ sau có nghiệm 139 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
x y 2 2
x xy y  4  3   2 2
x  2 y   9 y  8  
 11 22x y 2 2
y  2m  5  2 y x
1.63. Tìm m để hệ sau có nghiệm 3 x    y  2 2
x  2xy  2m  3  2
x  3x y m   1 
1.64. Tìm m để phương trình sau có nghiệm duy nhất trong đoạn  ;1  2    2 3 2
3 1 x  2 x  2x 1  m log x y  log xy  2  2  2   3  
1.65. Tìm m để hệ sau có nghiệm  3 3
x y xy m
1.66. Tìm m để phương trình sau có nghiệm thực 2 3
4x  2mx 1  3 8x  2x
1.67. Tìm m để bất phương trình 6 4 3
x  3mx  2x 1  0 với mọi x  1
1.68. Tìm m để hệ phương trình sau có nghiệm duy nhất
 7  x  11 y  4  m  4  3 10  3m  
 7  y  11 x  4  m  4  3 10  3m
1.69. Tìm m để hệ sau vô nghiệm
 4  x  4  y  1   2 m
4  x  5m 4  x  6 4  y
1.70. Tìm m để hệ sau có nghiệm 4 4 x y  1 
 x y 2 2 2 1 2 2   x y   m x y x y
x y m
1.71. Tìm m để hệ sau có ba nghiệm phân biệt    x   2
1 y xy m y  2    x m y m  2
1.72. Tìm m để hệ sau có nghiệm  2 2 2
x y  2m  140 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam
ĐIỀU KIỆN PT-HPT CÓ NGHIỆM
1.73. Tìm tất cả các giá trị thực của m để hệ sau có nghiệm
 6x  4y  6 x  3y  9  2   2 2
5x  16xy  3y  3 5x y   7 31 12 x 3yx 2y 8 2 m  2 5 1 9m            3 4   5 1 7
1.74. Tìm m để phương trình sau có nghiệm x 1  1  m 2 6x 2 x
1.75. Tìm m để bất phương trình sau dung với mọi x 0;  1  1 x   x   x 2 6   m   1 6   2m 1  6x   0 2
ex  x  2012
x y  4  2xy
1.76. Tìm m để hệ phương trình 
có nghiệm  x, y thỏa
2xy m   2 2
x y x y  5  x y 
mãn x, y  1 . 141 Dang Thanh Nam
Auditing 51a, National economics University, Ha Noi, Viet Nam