Tìm hiểu về hệ trục tọa độ | Đại học Sư phạm Hà Nội

Tìm hiểu về hệ trục tọa độ | Đại học Sư phạm Hà Nội với những kiến thức và thông tin bổ ích giúp sinh viên tham khảo, ôn luyện và phục vụ nhu cầu học tập của mình cụ thể là có định hướng, ôn tập, nắm vững kiến thức môn học và làm bài tốt trong những bài kiểm tra, bài tiểu luận, bài tập kết thúc học phần, từ đó học tập tốt và có kết quả cao cũng như có thể vận dụng tốt những kiến thức mình đã học vào thực tiễn cuộc sống.

15 8 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Nhập môn lý thuyết ma trận

Trường: Đại học Sư Phạm Hà Nội

Thông tin:

32 trang 2 tháng trước

Tác giả:

Profile Kim Oanh
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 1
TOÁN 10 HỆ TRỤC TỌA ĐỘ
TRUY CẬP ĐỂ ĐƯỢC NHIỀU HƠN https://diendangiaovientoan.vn/tai-lieu-tham-khao-d8.html
0H1-2
MỤC LỤC
Phần A. Câu hỏi ................................................................................................................................................... 1
Dạng 1. Sử dụng các kiến thức về trục, tọa độ vectơ trên trục và tọa độ của một điểm trên trục để giải một số
bài toán................................................................................................................................................................. 1
Dạng 2. Tọa độ vectơ ........................................................................................................................................... 3
Dạng 2.1 Sử dụng các công thức tọa độ của tổng, hiệu, tích vectơ với một số để giải toán ............................ 3
Dạng 2.2 Điều kiện 2 véc tơ cùng phương, thẳng hàng, bằng nhau ................................................................ 4
Dạng 2.3 Biểu diễn một vectơ theo 2 vectơ không cùng phương .................................................................... 6
Dạng 3. Tọa độ điểm ............................................................................................................................................ 6
Dạng 3.1 Xác định tọa độ trung điểm, tọa độ trọng tâm, tọa độ điểm đối xứng ............................................ 6
Dạng 3.2 Xác định tọa độ điểm thỏa mãn điều kiện cho trước ....................................................................... 8
Dạng 3.3 Một số bài toán GTLN-GTNN của biểu thức chứa véctơ ............................................................. 11
Phần B. LỜI GIẢI THAM KHẢO .................................................................................................................... 13
Dạng 1. Sử dụng các kiến thức về trục, tọa độ vectơ trên trục và tọa độ của một điểm trên trục để giải một số
bài toán............................................................................................................................................................... 13
Dạng 2. Tọa độ vectơ ......................................................................................................................................... 14
Dạng 2.1 Sử dụng các công thức tọa độ của tổng, hiệu, tích vectơ với một số để giải toán .......................... 14
Dạng 2.2 Điều kiện 2 véc tơ cùng phương, thẳng hàng, bằng nhau .............................................................. 15
Dạng 2.3 Biểu diễn một vectơ theo 2 vectơ không cùng phương .................................................................. 16
Dạng 3. Tọa độ điểm .......................................................................................................................................... 17
Dạng 3.1 Xác định tọa độ trung điểm, tọa độ trọng tâm, tọa độ điểm đối xứng .......................................... 17
Dạng 3.2 Xác định tọa độ điểm thỏa mãn điều kiện cho trước ..................................................................... 20
Dạng 3.3 Một số bài toán GTLN-GTNN của biểu thức chứa véctơ ............................................................. 27
Phần A. Câu hỏi
Dạng 1. Sử dụng các kiến thức về trục, tọa độ vectơ trên trục và tọa độ của một điểm trên
trục để giải một số bài toán
Câu 1. Trên trục
'x Ox
cho 2 điểm A, B lần lượt có tọa độ là a, b. M là điểm thỏa mãn
, 1
MA kMB k
 
. Khi đó tọa độ của điểm là: M
A.
1
ka b
k
B.
1
kb a
k
C.
1
a kb
k
D.
1
kb a
k
Câu 2. Trên trục
ø ù
;O i
cho ba điểm A, B, C. Nếu biết
5, 7
AB AC
thì
bằng:
A.
2
B. 2 4 3 C. D.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 2
Câu 3. Tên trục
ø ù
;O i
cho hai điểm lần lượt có tọa độ 1 và 5. Khi đó tọa độ điểm thỏa mãn A, B M
2 3 0
MA M B
 
là:
A. B. C. D. 10 11 12 13
Câu 4. Trên trục
'x Ox
cho bốn điểm có tọa độ lần lượt là A, B, C, D
3;5; 7;9
. Mệnh đề nào sau đây
sai?
A.
2AB
B.
10
AC
C.
16
CD
D.
8
AB AC
Câu 5. Trên trục
'x Ox
có vectơ đơn vị
i
. Mệnh đề nào sau đây sai?
A.
A
x
là tọa độ điểm
.
A
A OA x i

B.
,
B C
x x
là tọa độ của điểm và thì B C
B C
BC x x
C.
AC CB AB
D. M AB là trung điểm của
2
OA OB
OM
Câu 6. Trên trục
'x Ox
, cho tọa độ của lần lượt là A, B
2;3
. Khi đó tọa độ điểm thỏa mãn: M
2
.OM MA MB
là:
A. B. 6
6
C.
6
D.
4
Câu 7. Trên trục
'x Ox
cho tọa độ các điểm A, B lần lượt là . Khi đó tọa độ điểm a, b
'A
đối xứng với A
qua là: B
A.
b a
B.
2
a b
C. 2
a b
D. 2
b a
Câu 8. Trên trục
ø ù
;O i
tìm tọa độ của điểm sao cho x M
2 0
MA MC
 
, với có tọa độ tương ứng A, C
là
1
và 3
A.
5
3
x
B.
2
3
x
C.
2
5
x
D.
5
2
x
Câu 9. Trên trục
ø ù
;O i
cho 4 điểm có tọa độ lần lượt là . Gọi A, B, C, D a, b, c, d E, F, G, H (có tọa độ
lần lượt là ) theo thứ tự là trung điểm của , , e, f, g, h AB, BC CD DA. Xét các mệnh đề:
I.
e f g h a b c d
II.
EG EF EH
  
III.
0
AE CF
 
Trong các mệnh đề trên mệnh đề nào đúng?
A. B. C. D. Chỉ I II và III I, II, III Chỉ III
Câu 10. Cho 4 điểm trên trục A, B, C, D
ø ù
;O i
thỏa mãn
CA DA
CB DB
. Khi sso mệnh đề nào sau đây là
đúng?
A.
2 1 1
AC AB AD
B.
2 1 1
AB AC DA
C.
2 1 1
AB AC AD
D.
2 1 1
AD AB AC
Câu 11. Trên trục
ø ù
cho bốn điểm bất kì. Đẳng thức nào sau đây là đúng? A, B, C, D
A.
. . . 0
AB CD AC DB AD BC
B.
. . . 0
AB DB AC BC AD CD
C.
. . . 0
AB AC AD BC BC CD
D.
. . . 0
BD BC AD AC CB CA
Câu 12. Trên trục
ø ù
;O i
cho ba điểm có tọa độ lần lượt là A, B, C
5;2;4
. Khi đó tọa độ điểm thảo M
mãn
2 3 4 0
MA MC MB
  
là:
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 3
A.
10
3
B.
10
9
C.
5
3
D.
5
4
Câu 13. Trên trục
'x Ox
cho tọa độ các điểm B, C lần lượt là
2
m
và
2
3 2
m m
. Tìm để đoạn thẳng m
BC có độ dài nhỏ nhất.
A.
2
m
B.
1
m
C.
1
m
D.
2
m
Câu 14. Trên trục
'x Ox
cho 4 điểm , Gọi lần lượt là trung điểm của A B, C, D. I, J, K, L AC, DB,
AD, BC. Mệnh đề nào sau đây là sai?
A.
2AD CB IJ
 
B.
2AC DB KI
  
C. D. Trung điểm các đoạn và trùng nhau IJ KL
2AB CD IK
  
Câu 15. Trên trục
'x Ox
cho 3 điểm , có tọa độ lần lượt là A B, C
2;1; 2
. Khi đó tọa độ điểm nguyên M
dương thỏa mãn
1 1 1
MA MB MC
là:
A. B. C. D. 0 4 2 3
Câu 16. Trên trục
'x Ox
cho 4 điểm , Đẳng thức nào sau đây là đúng? A B, C, D.
A.
2 2 2
. . . . . 0
DA BC DB CA DC AB BC CA AB
B.
2 2 2
. . . 0
DA BC DB CA DC AB
C.
2 2 2
. . . 0
AB BC CD DB DB CA
D.
. . . . 0
DA BC DB CA CD AB BC AB
Dạng 2. Tọa độ vectơ
Dạng 2.1 Sử dụng các công thức tọa độ của tổng, hiệu, tích vectơ với một số để giải toán
Câu 17. (Kiểm tra HKI - Phan Đình Tùng - Hà Nội năm học 2018-2019) Trong hệ trục tọa độ
ø ù
; ,O i j
, tọa độ của véc tơ
2 3i j
là:
A.
ø ù
2;3
. B.
ø ù
0;1
. C.
ø ù
1;0
. D.
ø ù
3;2
.
Câu 18. (HKI - Sở Vĩnh Phúc - 2018-2019) Trên mặt phẳng với hệ tọa độ
Oxy
cho vectơ
3 4u i j
.
Tọa độ của vectơ
u
là
A.
ø ù
3; 4
u
. B.
ø ù
3;4
u
. C.
ø ù
3; 4
u
. D.
ø ù
3;4
u
.
Câu 19. Trong hệ tọa độ
Oxy
cho
1
5 .
2
u i j
Tọa độ của vecto
u
là
A.
1
;5 .
2
u
B.
1
; 5 .
2
u
C.
ø ù
1;10 .
u
D.
ø ù
1; 10 .
u
Câu 20. Trong hê truc toa đô
Oxy
, cho hai điêm
ø ù
1;1
M ,
ø ù
4; 1
N
. Tinh đô dai vectơ
MN

.
A.
13
MN

. B.
5
MN

. C.
29
MN

. D.
3
MN

.
Câu 21. Trong hệ trục tọa độ
Oxy
, cho hai điểm
ø ù ø ù
2; 1 , 4;3
A B . Tọa độ của véctơ
AB
bằng
A.
ø ù
8; 3
AB

. B.
ø ù
2; 4
AB

. C.
ø ù
2;4
AB

. D.
ø ù
6;2
AB

.
Câu 22. Trong hệ trục toạ độ
Oxy
, toạ độ của vectơ
8 3a j i
bằng
A.
ø ù
3;8
a
. B.
ø ù
3; 8
a
. C.
ø ù
8;3
a
. D.
ø ù
8; 3
a
.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 4
Câu 23. Trong mặt phẳng
Oxy
, cho hai điểm
ø ù
1;3
B
và
ø ù
3;1
C . Độ dài vectơ
BC
bằng
A.
6
. B.
2 5
. C.
2
. D.
5
.
Câu 24. (Kiểm tra HKI - Phan Đình Tùng - Hà Nội năm học 2018-2019) Trong mặt phẳng với hệ
trục tọa độ
Oxy
, cho điểm
ø ù
1;3
A và
ø ù
0;6
B . Khẳng định nào sau đây đúng?
A.
ø ù
5; 3
AB
. B.
ø ù
1; 3
AB
. C.
ø ù
3; 5
AB

. D.
ø ù
1;3
AB

.
Câu 25. Xác định tọa độ của vectơ
3c a b
biết
ø ù ø ù
2; 1 , 3;4
a b
A.
ø ù
11;11
c
B.
ø ù
11; 13
c
C.
ø ù
11;13
c
D.
ø ù
7;13
c
Câu 26. Cho
ø ù ø ù ø ù
2;1 , 3; 4 , 7;2
a b c
. Tìm vectơ
x
sao cho
2 3x a b c
.
A.
ø ù
28;2
x
B.
ø ù
13;5
x
C.
ø ù
16; 4
x
D.
ø ù
28;0
x
Câu 27. Vectơ
ø ù
5;0
a
biểu diễn dạng
. .a x i y j
được kết quả nào sau đây?
A. 5
a i j
B.
5a i
C.
5a i j

D.
5a i j
Câu 28. Xác định tọa độ vectơ
5 2c a b
biết
ø ù ø ù
3; 2 , 1;4
a b
A.
ø ù
2; 11
c
B.
ø ù
2;11
c
C.
ø ù
2;11
c
D.
ø ù
11; 2
c
Câu 29. Cho
ø ù ø ù ø ù
3; 1 , 0;4 , 5;3
a b c
. Tìm vectơ
x
sao cho
2 3 0
x a b c
.
A.
ø ù
18; 0
B.
ø ù
8;18
C.
ø ù
8;18
D.
ø ù
8; 18
Câu 30. Cho điểm
ø ù
2;3
A và vectơ
3 2AM i j

.Vectơ nào trong hình là vectơ
AM

?
A.
1
V
B.
2
V
C.
3
V
D.
4
V
Dạng 2.2 Điều kiện 2 véc tơ cùng phương, thẳng hàng, bằng nhau
Câu 31. (KTNL GV BẮC GIANG NĂM 2018-2019) Trong mặt phẳng với hệ trục tọa độ , cho
hai vectơ và Khẳng định nào sau đây là đúng?
.
A. và
cùng hướng và ngược hướng.
.
B.
C. D. . .
Câu 32. Cho
ø ù ø ù
1
3; 2 , 5;4 , ;0
3
A B C
. Tìm
x
thỏa mãn
AB x AC
 
.
A.
3
x
B.
3
x
C.
2
x
D.
4
x
Câu 33. Trong các cặp vectơ sau, cặp vectơ nào không cùng phương?
ø ù
; ,O i j
2
a i j
ø ù
4;2
b
a
b
a
b
ø ù
1; 2
a
ø ù
2;1
a
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 5
A.
ø ù ø ù
2;3 ; 10; 15
a b
B.
ø ù ø ù
0;5 ; 0;8
u v
C.
ø ù ø ù
2;1 ; 6;3
m n
D.
ø ù ø ù
3;4 ; 6;9
c d
Câu 34. Cho
ø ù ø ù ø ù
1;1 , 1;3 , 2;0
A B C . Tìm sao cho x
AB xBC
 
A.
2
3
x
B.
2
3
x
C.
3
2
x
D.
3
2
x
Câu 35. (THPT Nhữ Văn Lan - Hải Phòng - Học kỳ I - 2019) Trong mặt phẳng tọa độ
Oxy
,
(5;2)
a
,
(10;6 2 )b x
. Tìm
x
để
;a b
cùng phương?
A.
1.
B.
1.
C.
2.
D.
2.
Câu 36. Trong các cặp vectơ sau, cặp vectơ nào không cùng phương?
A.
ø ù ø ù
2;3 , 6;9
a b
B.
ø ù ø ù
0;5 , 0; 1
u v
C.
ø ù ø ù
2;1 , 1; 2
m b
D.
ø ù ø ù
3;4 , 6; 8
c d
Câu 37. Cho
ø ù ø ù
2 2
3;2 , 5 3;
u m m v m m
. Vectơ
u v
khi và chỉ khi thuộc tập hợp: m
A.
2
B.
0;2
C.
0;2;3
D.
Câu 38. Cho 2 vectơ
ø ù ø ù
2 1 3
u m i m j
và
2 3v i j
. Tìm để hai vectơ cùng phương. m
A.
5
11
m
B.
11
5
m
C.
9
8
m
D.
8
9
m
Câu 39. Trong mặt phẳng , cho Oxy
ø ù ø ù ø ù
1; 2 ; 2;5 2 ; 3; 4
A m B m C m . Tìm để m A, B, C thẳng hàng.
A.
3
m
B.
2
m
C.
2
m
D.
1
m
Câu 40. Trong hệ trục Oxy, cho 4 điểm
ø ù ø ù ø ù ø ù
3; 2 , 7;1 , 0;1 , 8; 5
A B C D
. Mệnh đề nào sau đây đúng?
A.
,AB CD
 
đối nhau B.
,AB CD
 
ngược hướng
C.
,AB CD
 
cùng hướng thẳng hàng D. A, B, C, D
Câu 41. Cho
ø ù ø ù
4; , 2 6;1
a m v m
. Tập giá trị của để hai vectơ m
a
và
b
cùng phương là:
A.
1;1
B.
1; 2
C.
2; 1
D.
2;1
Câu 42. Cho 4 điểm
ø ù ø ù ø ù
1; 2 , 0;3 , 3;4 ,
A B C
ø ù
1;8
D . Ba điểm nào trong bốn điểm dã cho thẳng
hàng?
A. B. C. D. A, B, C B, C, D A, B, D A, C, D
Câu 43. Cho 2 vectơ
a
và
b
không cùng phương. Hai vectơ nào sau đây cùng phương?
A. 2
u a b
và
1
3
2
v a b
B.
2
3
3
u a b
và
2 9v a b
C.
3
3
5
u a b
và
3
2
5
v a b
D.
3
2
2
u a b
và
1 1
3 4
v a b
Câu 44. (ĐỘI CẤN VĨNH PHÚC LẦN 1 2018-2019) Trong mặt phẳng với hệ tọa độ Oxy cho
ø ù ø ù
1;2 , 2;5 2A m B m
và
ø ù
3;4
C m . Tìm giá trị m để A, B, C thẳng hàng.
A.
2
m
.
B.
2
m
.
C.
1
m
.
D.
3
m
.
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 6
Dạng 2.3 Biểu diễn một vectơ theo 2 vectơ không cùng phương
Câu 45. Vectơ
ø ù
2; 1
a
biểu diễn dưới dạng
a xi y j
được kết quả nào sau đây?
A. 2
a i j
B.
2a i j
C. 2
a i j
D.
2a i j
Câu 46. Trong mặt phẳng tọa độ
Oxy
cho
(2;1), (3;4), (7;2)
a b c
. Cho biết
c ma nb
khi đó.
A.
22 3
;
5 5
m n
. B.
22 3
;
5 5
m n
. C.
1 3
;
5 5
m n
. D.
22 3
;
5 5
m n
.
Câu 47. Trong mặt phẳng
,Oxy
cho các điểm
ø ù ø ù ø ù ø ù
4;2 , 2;1 , 0;3 , 3;7
A B C M
. Giả sử
ø ù
. . , .
AM x AB y AC x y
  
Khi đó
x y
bằng
A.
12
5
. B.
5
. C.
12
5
. D.
5
.
Câu 48. Trong mặt phẳng
Oxy
;cho các véc tơ
ø ù
2; 1
a
;
ø ù
0;4
b
và
ø ù
3;3
c
. Gọi
m
và
n
là hai
số thực sao cho
c ma nb
. Tính giá trị biểu thức
2 2
P m n
.
A.
225
64
P
. B.
100
81
P
. C.
97
64
P
. D.
193
64
P
.
Câu 49. Cho
ø ù
2;1
a
,
ø ù
3; 4
b
,
ø ù
4; 9
c
. Hai số thực
m
,
n
thỏa mãn
ma nb c
. Tính
2 2
m n
?
A.
5
. B.
3
. C.
4
. D.
1
.
Câu 50. Trong mặt phẳng , cho Oxy
ø ù ø ù ø ù
2;1 ; 3;4 ; 7;2
a b c
. Tìm , n đểm
c ma nb
.
A.
22 3
,
5 5
m n
B.
1 3
,
5 5
m n
C.
22 3
,
5 5
m n
D.
22 3
,
5 5
m n
Câu 51. Cho các vectơ
ø ù ø ù
4; 2 , 1; 1 ,
a b
ø ù
2;5
c
Phân tích vectơ
a
và
c
ta được:
A.
1 1
8 4
b a c
B.
1 1
8 4
b a c
C.
1
4
8
b a c
D.
1 1
8 4
b a c
Câu 52. Cho vectơ
ø ù ø ù
2;1 , 3;4 ,
a b
ø ù
7;2
c
. Khi đó
c ma nc
. Tính tổng
m n
bằng:
A. B. 5
3,8
C.
5
D.
3,8
Câu 53. Trong mặt phẳng tọa độ , cho 4 điểm Oxy
ø ù ø ù ø ù ø ù
1; 2 , 0;3 , 3;4 , D 1;8
A B C . Phân tích
CD

qua
AB
và
AC

. Đẳng thức nào sau đây đúng?
A.
2 2
CD AB AC
  
B.
2
CD AB AC
  
C.
2
CD AB AC
  
D.
1
2
2
CD AB AC
  
Dạng 3. Tọa độ điểm
Dạng 3.1 Xác định tọa độ trung điểm, tọa độ trọng tâm, tọa độ điểm đối xứng
Câu 54. (THPT Nhữ Văn Lan - Hải Phòng - Học kỳ I - 2019) Trong mặt phẳng tọa độ
Oxy
, cho điểm
ø ù
;M x y
. Tìm tọa độ của điểm
1
M
đối xứng với
M
qua trục hoành?
A.
ø ù
1
;M x y
. B.
ø ù
1
;
M x y
. C.
ø ù
1
;M x y
. D.
ø ù
1
;
M x y
.
Câu 55. (THPT Nhữ Văn Lan - Hải Phòng - Học kỳ I - 2019) Trong măt phăng toa đô
Oxy
, cho
ABC
biết
ø ù ø ù ø ù
2; 3 , 4; 7 , 1;5
A B C . Toa đô trong tâm
G
cua
ABC
là
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 7
A.
ø ù
7;15
.
B.
7
;5
3
. C.
ø ù
7;9
.
D.
7
;3
3
.
Câu 56. (THPT Nhữ Văn Lan - Hải Phòng - Học kỳ I - 2019) Trong mặt phẳng tọa độ
Oxy
, cho
ø ù ø ù
2; 3 , 4;7
A B
. Tìm tọa độ trung điểm
I
của
AB
.
A.
ø ù
3;2
. B.
ø ù
2;10
. C.
ø ù
6;4
. D.
ø ù
8; 21
.
Câu 57. Cho
ABC
có
ø ù
4;9
A ,
ø ù
3;7
B ,
ø ù
1;C x y
. Để
ø ù
; 6
G x y
là trọng tâm
ABC
thì giá trị
x
và
y
là
A.
3, 1x y
. B.
3, 1
x y
. C.
3, 1x y
. D.
3, 1
x y
.
Câu 58. Trong hệ tọa độ , cho Oxy
ø ù ø ù
2; 3 ; 4;7
A B . Tìm tọa độ trung điểm của đoạn I AB.
A.
ø ù
6;4
I B.
ø ù
2;10
I C.
ø ù
3;2
I D.
ø ù
8; 21
I
Câu 59. Trên mặt phẳng tọa độ
Oxy
, cho tam giác
ABC
có
ø ù
2;1
A
,
ø ù
1; 2
B
,
ø ù
3;2
C
. Tọa độ trọng
tâm
G
của tam giác
ABC
là
A.
2 1
;
3 3
G
. B.
2 2
;
3 3
G
. C.
1 1
;
3 3
G
. D.
2 1
;
3 3
G
.
Câu 60. Trong mặt phẳng với hệ tọa độ
Oxy
, cho tam giác
ABC
có ba đỉnh
ø ù
1;2
A
,
ø ù
2;0
B
,
ø ù
3;1 .
C Toạ độ trọng tâm
G
của tam giác
ABC
là
A.
2
;1
3
G
.
B.
2
; 1
3
G
. C.
4
;1
3
G
.
D.
4
; 1
3
G
.
Câu 61. Trong hệ tọa độ Oxy, cho
ø ù ø ù ø ù
4;1 ; 2;4 ; 2; 2
A B C
. Tìm tọa độ điểm sao cho C là trọng tâm D
ABD
A.
ø ù
8;11
D B.
ø ù
12;11
D C.
ø ù
8; 11
D D.
ø ù
8; 11
D
Câu 62. Trong hệ tọa độ , cho Oxy
ABC
có
ø ù
3;5
A ,
ø ù ø ù
1; 2 , 5;2
B C . Tìm tọa độ trọng tâm của tam G
giác.
A.
ø ù
3;4
G B.
ø ù
4;0
G C.
ø ù
2;3
G D.
ø ù
3;3
G
Câu 63. Trong mặt phẳng tọa độ
Oxy
cho bốn điểm
ø ù ø ù ø ù ø ù
A 3;-5 ,B -3;3 ,C -1;-2 ,D 5; -10 .
Hỏi
1
;-3
3
G
là trọng tâm của tam giác nào dưới đây?
A.
ABC
. B.
BCD
. C.
ACD
. D.
ABD
.
Câu 64. Trong mặt phẳng tọa độ
Oxy
cho tam giác
ABC
có
ø ù ø ù ø ù
3;4 , 6;1 , 7;3
D E F lần lượt là trung
điểm các cạnh
, ,AB BC CA
.Tính tổng tung độ ba đỉnh của tam giác
ABC
.
A.
16
3
. B.
8
3
. C.
8
. D.
16
.
Câu 65. Trong mặt phẳng toạ độ , cho Oxy
ABC
có
ø ù ø ù ø ù
2;3 , 0;4 , 1;6
M N P lần lượt là trung điểm
của các cạnh BC, CA, AB. Tìm tọa độ đỉnh A.
A.
ø ù
1;5
A B.
ø ù
3;7
A C.
ø ù
2; 7
A
D.
ø ù
1; 10
A
Câu 66. Cho tam giác
ABC
. Biết trung điểm của các cạnh
BC
,
CA
,
AB
có tọa độ lần lượt là
ø ù
1; 1
M
,
ø ù
3;2
N
,
ø ù
0; 5
P
. Khi đó tọa độ của điểm
A
là:
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 8
A.
ø ù
2; 2
. B.
ø ù
5;1
. C.
ø ù
5;0
. D.
ø ù
2; 2
.
Câu 67. Trong mặt phẳng tọa độ , cho Oxy
MNP
có
ø ù ø ù
1; 1 ; 5; 3
M N
và thuộc trục . Trọng tâm P Oy
G của tam giác nằm trên trục Ox P. Tọa độ của điểm là:
A.
ø ù
0;4
P B.
ø ù
2;0
P C.
ø ù
2;4
P D.
ø ù
0;2
P
Câu 68. Trong hệ tọa độ , cho Oxy
ø ù
3; 4
M
. Gọi
1 2
,M M
làn lượt là hình chiếu vuông góc của trên M
Ox, Oy. Khẳng định nào đúng?
A.
1
3
OM
B.
2
4
OM
C.
ø ù
1 2
3;4
OM OM
 
D.
ø ù
1 2
3; 4
OM OM
 
Câu 69. Trong hệ tọa độ , cho Oxy
ø ù ø ù ø ù
2;0 ; 2;2 ; 1;3
M N P lần lượt là trung điểm các cạnh BC, CA,
AB của
ABC
.Tọa độ điểm là: B
A.
ø ù
1;1
B B.
ø ù
1; 1
B
C.
ø ù
1;1
B D.
ø ù
1; 1
B
Câu 70. Trong mặt phẳng
Oxy
, cho tam giác
MNP
có
ø ù
1; 1
M
,
ø ù
5; 3
N
và
P
là điểm thuộc trục
Oy
, trọng tâm
G
của tam giác
MNP
nằm trên trục
Ox
. Tọa độ điểm
P
là
A.
ø ù
2; 4
. B.
ø ù
0; 4
. C.
ø ù
0; 2
. D.
ø ù
2; 0
.
Dạng 3.2 Xác định tọa độ điểm thỏa mãn điều kiện cho trước
Câu 71. (THPT Nhữ Văn Lan - Hải Phòng - Học kỳ I - 2019) Trong mặt phẳng tọa độ
Oxy
, cho
ø ù ø ù ø ù
1 1 1 3 5 2A ; ,B ; ,C ;
. Tìm tọa độ điểm
D
sao cho
ABCD
là hình bình hành.
A.
ø ù
3 0;
. B.
ø ù
5 0;
. C.
ø ù
7 0;
. D.
ø ù
5 2
;
.
Câu 72. Trong mặt phẳng tọa độ
Oxy
, cho hình bình hành
ABCD
có
ø ù ø ù ø ù
2;3 , 0;4 , 5; 4
A B C
. Tọa
độ đỉnh
D
là
A.
ø ù
3; 2
. B.
ø ù
3;7
. C.
ø ù
7;2
. D.
ø ù
3; 5
.
Câu 73. Trong mặt phẳng
Oxy
;cho hai điểm
ø ù ø ù
1; 4 , 4;2
A B . Tọa độ giao điểm của đường thẳng đi
qua hai điểm
,A B
với trục hoành là
A.
ø ù
9;0
. B.
ø ù
0;9
. C.
ø ù
9;0
. D.
ø ù
0; 9
.
Câu 74. (HKI - Sở Vĩnh Phúc - 2018-2019) Trên mặt phẳng với hệ tọa độ
Oxy
cho hai điểm
ø ù ø ù
1;1 , 2;4
A B
. Tìm tọa độ điểm
M
để tứ giác
OBMA
là một hình bình hành.
A.
( 3; 3)
M
. B.
(3; 3)
M
. C.
(3;3)
M . D.
( 3;3)
M
.
Câu 75. Trong hệ tọa độ Oxy, cho 3 điểm
ø ù ø ù ø ù
2;1 ; 0; 3 ; 3;1
A B C . Tìm tọa độ điểm để là hình D ABCD
bình hành.
A.
ø ù
5;5
D B.
ø ù
5; 2
D
C.
ø ù
5; 4
D
D.
ø ù
1; 4
D
Câu 76. (THPT MINH CHÂU HƯNG YÊN NĂM 2018 – 2019) Trong mặt phẳng
Oxy
cho tam giác
ABC
có
ø ù ø ù ø ù
2;1 , 1;2 , 3;0
A B C
. Tứ giác
ABCE
là hình bình hành khi tọa độ
E
là cặp số
nào sau đây?
A.
ø ù
6; 1
B.
ø ù
0;1
C.
ø ù
1; 6
D.
ø ù
6;1
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 9
Câu 77. Trong mặt phẳng với hệ tọa độ Oxy, cho ba điểm
ø ù ø ù ø ù
2;5 , 1;1 , 3;3
A B C
, một điểm E thỏa
mãn 3 2
AE AB AC

. Tọa độ của E là
A.
ø ù
3;3
. B.
ø ù
3; 3
. C.
ø ù
3; 3
. D.
ø ù
2; 3
.
Câu 78. Trong hệ tọa độ , cho Oxy
ø ù ø ù
3;1 , 1;4 ,
A B
ø ù
5;3
C . Tìm tọa độ điểm sao cho là hình D ABCD
bình hành.
A.
ø ù
1; 0
D B.
ø ù
1; 0
D C.
ø ù
0; 1
D
D.
ø ù
0;1
D
Câu 79. (THPT NGUYỄN TRÃI-THANH HOÁ - Lần 1.Năm 2018&2019) Trong mặt phẳng với hệ
tọa độ
Oxy
cho tam giác
ABC
có trọng tâm
2
; 0
3
G
, biết
ø ù
1; 1
M
là trung điểm của cạnh
BC
. Tọa độ đỉnh
A
là
A.
ø ù
2; 0
. B.
ø ù
2; 0
. C.
ø ù
0; 2
. D.
ø ù
0; 2
.
Câu 80. Trên mặt phẳng tọa độ
Oxy
, cho
ø ù
2;3
A
,
ø ù
2;1
B
. Điểm
C
thuộc tia
Ox
sao cho tam giác
ABC
vuông tại
C
có tọa độ là:
A.
ø ù
3;0
C
. B.
ø ù
3;0
C
. C.
ø ù
1;0
C
. D.
ø ù
2;0
C
.
Câu 81. (THPT Nhữ Văn Lan - Hải Phòng - Học kỳ I - 2019) Trong mặt phẳng tọa độ
Oxy
, cho
ø ù
3;3
A
,
ø ù
1; 9
B
,
ø ù
5; 1
C
. Gọi
I
là trung điểm của
AB
. Tìm tọa độ
M
sao cho
1
2
AM CI


.
A.
ø ù
5;4
. B.
ø ù
1;2
. C.
ø ù
6; 1
. D.
ø ù
2;1
.
Câu 82. Trong mặt phẳng toạ độ , cho Oxy
ABC
có
ø ù ø ù ø ù
3;3 , 1; 4 , 2; 5
A B C
. Tọa độ điểm thỏa mãn M
2 4
MA BC CM
  
là:
A.
1 5
;
6 6
M
B.
1 5
;
6 6
M
C.
1 5
;
6 6
M
D.
5 1
;
6 6
M
Câu 83. Trong hệ tọa độ , cho Oxy
ø ù ø ù
2; 3 , 3;4
A B . Tìm tọa độ điểm M trên trục hoành sao cho A, B, M
thẳng hàng.
A.
ø ù
1; 0
M B.
ø ù
4;0
M
C.
5
;0
3
M
D.
17
;0
7
M
Câu 84. Trong hệ tọa độ , cho Oxy
ø ù ø ù
2;1 , 1; 3
A B
. Tìm tọa độ giao điểm I của hai đường chéo hình bình
hành OABC.
A.
1 2
;
3 3
I
B.
5 1
;
2 2
I
C.
ø ù
2;6
I D.
1 3
;
2 2
I
Câu 85. Trong hệ tọa độ , cho Oxy
ø ù ø ù
1;3 , 4;0
A B . Tìm tọa độ điểm thỏa mãn M
3 0
MA MB MC
 
A.
ø ù
1;18
M B.
ø ù
1;18
M C.
ø ù
18;1
M D.
ø ù
1; 18
M
Câu 86. Trong hệ tọa độ , cho 3 điểm Oxy
ø ù ø ù ø ù
2;5 ; 1;1 ; 3;3
A B C . Tìm điểm thuộc mặt phẳng tọa độ E
thỏa mãn
3 2
AE AB AC
 
?
A.
ø ù
3; 3
E
B.
ø ù
3;3
E C.
ø ù
3; 3
E
D.
ø ù
2; 3
E
Câu 87. Trong hệ tọa độ , cho Oxy
ø ù ø ù
2;1 ; 6; 1
A B
. Tìm điểm trên sao cho thẳng hàng. M Ox A, B, M
A.
ø ù
2;0
M B.
ø ù
8;0
M C.
ø ù
4;0
M D.
ø ù
4;0
M
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong
10
Câu 88. Trong hệ tọa độ , cho Oxy
ABC
có
ø ù ø ù ø ù
3;4 , 2;1 , 1; 2
A B C
. Tìm điểm có tung độ dương M
trên đường thẳng sao cho 3BC
ABC ABM
S S
.
A.
ø ù
2;2
M B.
ø ù
3;2
M C.
ø ù
3;2
M D.
ø ù
3;3
M
Câu 89. Trong hệ tọa độ , cho 3 điểm Oxy
ø ù ø ù ø ù
1; 1 , 0;1 , 3;0
A B C . Xác định tọa độ giao điểm của I
AD D BC và với BG thuộc và
2 5
BD DC
, là trọng tâm G
ABC
A.
5
;1
9
I
B.
1
;1
9
I
C.
35
;2
9
I
D.
35
;1
9
I
Câu 90. Trong mặt phẳng với hệ tọa độ
Oxy
, cho tam giác
ABC
có ba đỉnh
ø ù
1;2
A
,
ø ù
2;0
B
,
ø ù
3;1 .
C
Toạ độ tâm đường tròn ngoại tiếp
I
của tam giác
ABC
là
A.
11 13
;
14 14
I
. B.
11 13
;
14 14
I
. C.
11 13
;
14 14
I
. D.
11 13
;
14 14
I
.
Câu 91. Tam giác
ABC
có đỉnh
ø ù
1;2
A , trực tâm
ø ù
3;0
H , trung điểm của
BC
là
ø ù
6;1
M . Bán kính
đường tròn ngoại tiếp tam giác
ABC
là
A.
5
. B.
5
C.
3
. D.
4
.
Câu 92. Gọi điểm M là giao điểm của đường thẳng AB và trục hoành biết
ø ù
1; 2
A và
ø ù
2;5
B . Biết hoành
độ điểm có dạng M
m
n
trong đó
m
n
tối giản và ,m n
. Tính
2 2
m n
.
A. B. C. D. 34 41 25 10
Câu 93. Trong hệ tọa độ , cho Oxy
ABC
biết
ø ù ø ù ø ù
2;0 , 1;1 , 1; 2
A B C
. Các điểm
', ', 'C A B
lần lượt
chia các đoạn thẳng theo tỉ số là
AB, BC, CA
1
1; ; 2
2
. Khi đó đẳng thức nào sau đây đúng?
A.
' ' 2 ' 'A C B C
 
B.
' ' 3 ' 'A C B C
 
C.
' 3 ' 'A C B C
 
D.
' 4 ' 'A C B C
 
Câu 94. Trong hệ tọa độ , cho 4 điểm Oxy
ø ù
0;1
A ;
ø ù ø ù ø ù
1;3 ; 2;7 ; 0;3
B C D . Tìm giao điểm của 2 đường
thẳng và AC BD.
A.
2
;3
3
B.
1
; 3
3
C.
4
;13
3
D.
2
;3
3
Câu 95. Trong hệ tọa độ , cho ba điểm Oxy
ø ù
6;3
A ;
ø ù ø ù
3;6 ; 1; 2
B C
. Biết điểm trên cạnh sao E BC
cho
2
BE EC
. nằm trên đường thẳng và thuộc trục . Tìm giao điểm của và D AB Ox DE AC.
A.
7 1
;
2 2
I
B.
3 1
;
2 2
I
C.
7 1
;
4 2
I
D.
7 1
;
2 2
I
Câu 96. Hình vuông
DABC
có
ø ù
2;1
A
,
ø ù
4;3
C
. Tọa độ của đỉnh
B
có thể là:
A.
ø ù
2;3
. B.
ø ù
1; 4
. C.
ø ù
4; 1
. D.
ø ù
3;2
.
Câu 97. Các điểm
, ,A B N
thẳng hàng
,BA BN
 
cùng phương
0.
x
Trong mặt phẳng tọa độ
Oxy
cho tam giác
.ABC
Biết
ø ù ø ù
3; 1 , 1;2
A B và
ø ù
1; 1
I
là trọng tâm tam giác
.ABC
Trực tâm
H
của tam giác
ABC
có tọa độ
ø ù
;a b
. Tính
3a b
.
A.
2
3
3
a b
. B.
4
3
3
a b
. C.
3 1
a b
. D.
3 2
a b
.
| 1/32
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 TOÁN 10 HỆ TRỤC TỌA ĐỘ
TRUY CẬP https://diendangiaovientoan.vn/tai-lieu-tham-khao-d8.html ĐỂ ĐƯỢC NHIỀU HƠN 0H1-2 MỤC LỤC
Phần A. Câu hỏi ................................................................................................................................................... 1
Dạng 1. Sử dụng các kiến thức về trục, tọa độ vectơ trên trục và tọa độ của một điểm trên trục để giải một số
bài toán................................................................................................................................................................. 1
Dạng 2. Tọa độ vectơ ........................................................................................................................................... 3
Dạng 2.1 Sử dụng các công thức tọa độ của tổng, hiệu, tích vectơ với một số để giải toán ............................ 3
Dạng 2.2 Điều kiện 2 véc tơ cùng phương, thẳng hàng, bằng nhau ................................................................ 4
Dạng 2.3 Biểu diễn một vectơ theo 2 vectơ không cùng phương .................................................................... 6
Dạng 3. Tọa độ điểm ............................................................................................................................................ 6
Dạng 3.1 Xác định tọa độ trung điểm, tọa độ trọng tâm, tọa độ điểm đối xứng ............................................ 6
Dạng 3.2 Xác định tọa độ điểm thỏa mãn điều kiện cho trước ....................................................................... 8
Dạng 3.3 Một số bài toán GTLN-GTNN của biểu thức chứa véctơ ............................................................. 11
Phần B. LỜI GIẢI THAM KHẢO .................................................................................................................... 13
Dạng 1. Sử dụng các kiến thức về trục, tọa độ vectơ trên trục và tọa độ của một điểm trên trục để giải một số
bài toán............................................................................................................................................................... 13
Dạng 2. Tọa độ vectơ ......................................................................................................................................... 14
Dạng 2.1 Sử dụng các công thức tọa độ của tổng, hiệu, tích vectơ với một số để giải toán .......................... 14
Dạng 2.2 Điều kiện 2 véc tơ cùng phương, thẳng hàng, bằng nhau .............................................................. 15
Dạng 2.3 Biểu diễn một vectơ theo 2 vectơ không cùng phương .................................................................. 16
Dạng 3. Tọa độ điểm .......................................................................................................................................... 17
Dạng 3.1 Xác định tọa độ trung điểm, tọa độ trọng tâm, tọa độ điểm đối xứng .......................................... 17
Dạng 3.2 Xác định tọa độ điểm thỏa mãn điều kiện cho trước ..................................................................... 20
Dạng 3.3 Một số bài toán GTLN-GTNN của biểu thức chứa véctơ ............................................................. 27 Phần A. Câu hỏi
Dạng 1. Sử dụng các kiến thức về trục, tọa độ vectơ trên trục và tọa độ của một điểm trên
trục để giải một số bài toán  
Câu 1. Trên trục x 'Ox cho 2 điểm A, B lần lượt có tọa độ là a, b. M là điểm thỏa mãn MA  kM , B k  1
. Khi đó tọa độ của điểm M là:     A. ka b B. kb a C. a kb D. kb a k 1 k 1  k 1  k 1   Câu 2. Trên trục ø ;
O iù cho ba điểm A, B, C. Nếu biết AB  5, AC  7 thì CB bằng: A. 2 B. 2 C. 4 D. 3
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 1
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489  Câu 3. Tên trục ø ;
O i ù cho hai điểm A, B lần lượt có tọa độ 1 và 5. Khi đó tọa độ điểm M thỏa mãn    2MA  3M B  0 là: A. 10 B. 11 C. 12 D. 13
Câu 4. Trên trục x 'Ox cho bốn điểm A, B, C, D có tọa độ lần lượt là 3;5; 7;
 9. Mệnh đề nào sau đây sai? A. AB  2 B. AC  10 C. CD  16 D. AB  AC  8  
Câu 5. Trên trục x 'Ox có vectơ đơn vị i . Mệnh đề nào sau đây sai?  
A. x là tọa độ điểm A  OA  x .i A A
B. x , x là tọa độ của điểm B và C thì BC  x  x B C B C C. AC CB  AB  D. OA OB
M là trung điểm của AB  OM  2
Câu 6. Trên trục x 'Ox , cho tọa độ của A, B lần lượt là 2
 ;3 . Khi đó tọa độ điểm M thỏa mãn: 2 OM  M . A MB là: A. 6 B. 6 C. 6 D. 4
Câu 7. Trên trục x 'Ox cho tọa độ các điểm A, B lần lượt là a, b. Khi đó tọa độ điểm A' đối xứng với A qua B là: a  b A. b  a B. C. 2a  b D. 2b  a 2     Câu 8. Trên trục ø ;
O i ù tìm tọa độ x của điểm M sao cho MA 2MC  0 , với A, C có tọa độ tương ứng là 1  và 3 5 2 2 5 A. x  B. x  C. x  D. x  3 3 5 2  Câu 9. Trên trục ø ;
O i ù cho 4 điểm A, B, C, D có tọa độ lần lượt là a, b, c, d. Gọi E, F, G, H (có tọa độ
lần lượt là e, f, g, h) theo thứ tự là trung điểm của AB, BC, CD, DA. Xét các mệnh đề:
I. e  f  g  h  a  b  c  d    II. EG  EF  EH    III. AE  CF  0
Trong các mệnh đề trên mệnh đề nào đúng? A. Chỉ I B. II và III C. I, II, III D. Chỉ III 
Câu 10. Cho 4 điểm A, B, C, D trên trục ø ; O i ù thỏa mãn CA DA  
. Khi sso mệnh đề nào sau đây là CB DB đúng? 2 1 1 2 1 1 2 1 1 2 1 1 A.   B.   C.   D.   AC AB AD AB AC DA AB AC AD AD AB AC
Câu 11. Trên trục øù cho bốn điểm A, B, C, D bất kì. Đẳng thức nào sau đây là đúng? A. A . B CD  A . C DB A . D BC  0
B. AB.DB  AC.BC  AD.CD  0 C. A . B AC  A . D BC  B . C CD  0
D. BD.BC  AD.AC CB.CA  0  Câu 12. Trên trục ø ;
O i ù cho ba điểm A, B, C có tọa độ lần lượt là 5
 ;2;4 . Khi đó tọa độ điểm M thảo    
mãn 2MA  3MC  4MB  0 là:
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 2
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 10 10 5 5 A. B. C. D. 3 9 3 4
Câu 13. Trên trục x 'Ox cho tọa độ các điểm B, C lần lượt là m  2 và 2
m  3m  2. Tìm m để đoạn thẳng
BC có độ dài nhỏ nhất. A. m 2 B. m1 C. m  1 D. m 2 
Câu 14. Trên trục x 'Ox cho 4 điểm A, B, C,
D. Gọi I, J, K, L lần lượt là trung điểm của AC, DB,
AD, BC. Mệnh đề nào sau đây là sai?       A. AD  CB  2IJ B. AC  DB  2KI   
C. Trung điểm các đoạn IJ và KL trùng nhau D. AB CD  2IK
Câu 15. Trên trục x 'Ox cho 3 điểm A, B, C có tọa độ lần lượt là 2;1;2 . Khi đó tọa độ điểm M nguyên 1 1 1 dương thỏa mãn   là: MA MB MC A. 0 B. 4 C. 2 D. 3
Câu 16. Trên trục x 'Ox cho 4 điểm A, B, C,
D. Đẳng thức nào sau đây là đúng? 2 2 2
A. DA .BC  DB .CA DC . AB B . C C . A AB  0 2 2 2
B. DA .BC  DB .CA DC . AB  0 2 2 2
C. AB .BC  CD .DB  DB .CA  0 D. D . A BC D . B CA C . D AB B . C AB 0 Dạng 2. Tọa độ vectơ
Dạng 2.1 Sử dụng các công thức tọa độ của tổng, hiệu, tích vectơ với một số để giải toán  
Câu 17. (Kiểm tra HKI - Phan Đình Tùng - Hà Nội năm học 2018-2019) Trong hệ trục tọa độ ø ; O i, j ù  
, tọa độ của véc tơ 2i  3 j là: A. ø2;3ù. B. ø0;1ù. C. ø1;0ù. D. ø3;2 ù.   
Câu 18. (HKI - Sở Vĩnh Phúc - 2018-2019) Trên mặt phẳng với hệ tọa độ Oxy cho vectơ u  3i  4 j . 
Tọa độ của vectơ u là     A. u  ø3; 4  ù . B. u  ø3;4ù . C. u  ø3;4ù. D. u  ø3;4ù.    
Câu 19. Trong hệ tọa độ 1 Oxy cho u 
i 5 .j Tọa độ của vecto u là 2   1   1   A.   u  ;5 .  B. u  ;5 . C. u  ø1;10 ù. D. u  ø1; 10  ù. 2       2 
Câu 20. Trong hê truc toa đô Oxy , cho hai điêm M ø1;1ù , Nø4; ù
1 . Tinh đô dai vectơ MN . A. MN  13 . B. MN  5 . C. MN  29 . D. MN  3. 
Câu 21. Trong hệ trục tọa độ Oxy , cho hai điểm Aø2; ù 1 ,B ø4; ù
3 . Tọa độ của véctơ AB bằng     A. AB  ø8; 3ù. B. AB  ø 2  ;  4ù . C. AB  ø2; 4ù . D. AB  ø6;2ù .   
Câu 22. Trong hệ trục toạ độ Oxy , toạ độ của vectơ a  8 j  3i bằng     A. a  ø 3  ;8 ù. B. a  ø3; 8ù . C. a  ø8;3ù. D. a  ø8; 3 ù .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 3
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 
Câu 23. Trong mặt phẳng Oxy , cho hai điểm Bø 1  ;3ù và Cø3;1ù bằng . Độ dài vectơ BC A. 6. B. 2 5 . C. 2 . D. 5 .
Câu 24. (Kiểm tra HKI - Phan Đình Tùng - Hà Nội năm học 2018-2019) Trong mặt phẳng với hệ
trục tọa độ Oxy, cho điểm Aø1; ù
3 và B ø0;6ù. Khẳng định nào sau đây đúng?     A. AB  ø5;  ù 3 . B. AB  ø1; 3  ù . C. AB  ø3; ù 5 . D. AB  ø 1; ù 3 .     
Câu 25. Xác định tọa độ của vectơ c  a  3b biết a  ø2; 1  ù, b  ø3;4 ù     A. c ø  11 ù ;11 B. c  ø11; 13  ù C. c  ø11;13ù D. c  ø7;13ù        
Câu 26. Cho a  ø2;1 ù, b  ø3; 4 ù, c  ø 7
 ;2 ù . Tìm vectơ x sao cho x  2a  b  3c .     A. x  ø28;2ù B. x  ø13;5ù C. x  ø16;4ù D. x  ø28;0 ù    
Câu 27. Vectơ a  ø5;0 ù biểu diễn dạng a  . x i  .
y j được kết quả nào sau đây?            A. a  5i  j B. a  5i C. a  i  5 j D. a  i   5 j     
Câu 28. Xác định tọa độ vectơ c  5a  2b biết a  ø3; 2  ù, b ø1;4 ù     A. c ø 2; ù 11 B. c  ø 2  ù ;11 C. c  ø 2 ù ;11 D. c  ø11;2ù          Câu 29. Cho a  ø3; 1
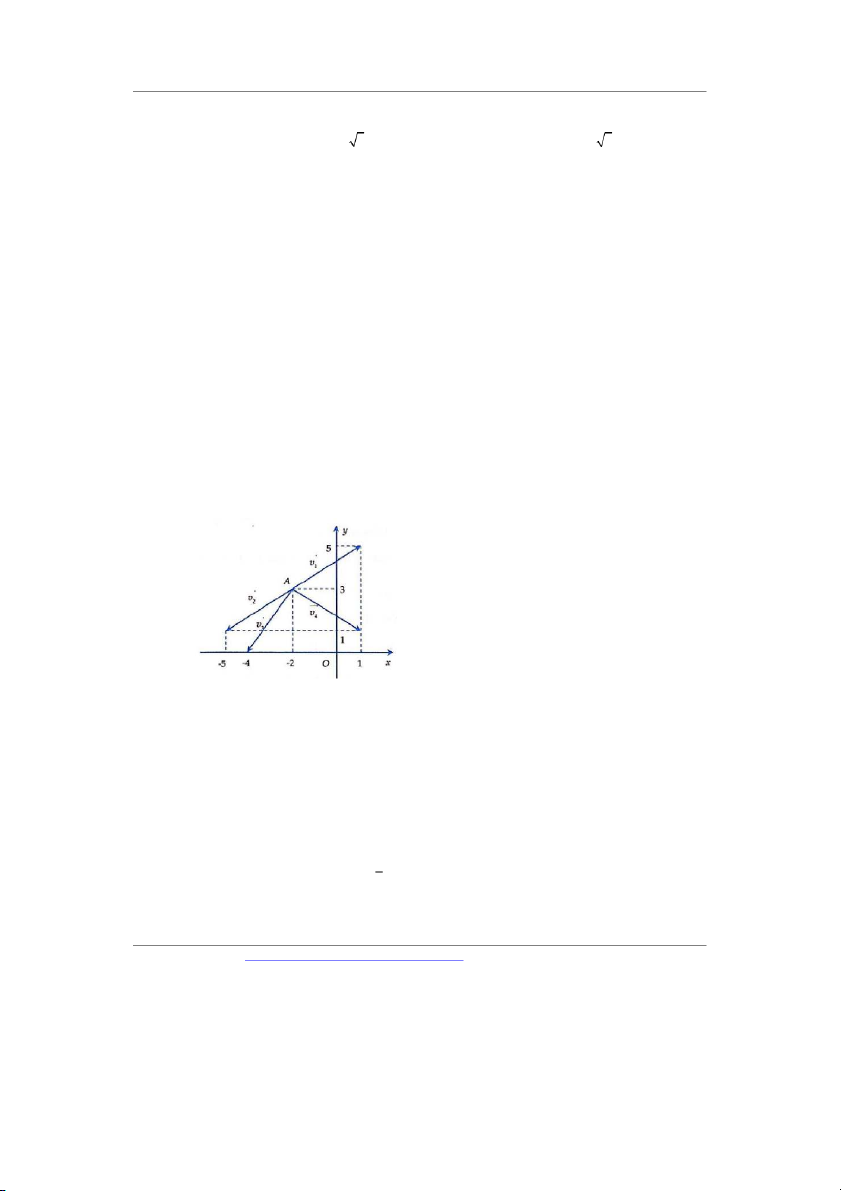
 ù, b  ø0;4 ù, c  ø5;3 ù . Tìm vectơ x sao cho x  a  2b  3c  0 . A. ø18;0ù B. ø 8  ;18 ù C. ø8;18 ù D. ø8;18 ù     Câu 30. Cho điểm Aø 2
 ;3ù và vectơ AM  3i  2 j .Vectơ nào trong hình là vectơ AM ?     A. B. C. D. 1 V 2 V 3 V 4 V
Dạng 2.2 Điều kiện 2 véc tơ cùng phương, thẳng hàng, bằng nhau  
Câu 31. (KTNL GV BẮC GIANG NĂM 2018-2019) Trong mặt phẳng với hệ trục tọa độ ø ; O i, j ù , cho    
hai vectơ a  2i  j và b ø 4
 ; 2ù Khẳng định nào sau đây là đúng? .     A. a và b cùng hướng a và b ngược hướng. . B.   C. a ø  1  ; 2ù . D. a  ø2; ù 1 .       Câu 32. Cho   A  ø  ù B  ø ù 1 3; 2 , 5; 4 ,C  ;0 
. Tìm x thỏa mãn AB  x AC . 3    A. x  3 B. x  3  C. x  2 D. x  4 
Câu 33. Trong các cặp vectơ sau, cặp vectơ nào không cùng phương?
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 4
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489     A. a ø2;3ù; b ø 10  ; 15  ù
B. u  ø0;5ù;v  ø0;8ù     C. m ø 2  ;1ù; n ø 6  ;3ù D. c  ø3; ù 4 ;d  ø6;9ù   Câu 34. Cho Aø 1  ;1ù, B ø1;3ù, C ø 2
 ;0 ù. Tìm x sao cho AB  xBC 2 2 3 3 A. x  B. x   C. x  D. x   3 3 2 2 
Câu 35. (THPT Nhữ Văn Lan - Hải Phòng - Học kỳ I - 2019) Trong mặt phẳng tọa độ Oxy , a  (5;2)   
, b  (10;6 2x) . Tìm x để ; a b cùng phương? A. 1. B. 1. C. 2. D. 2.
Câu 36. Trong các cặp vectơ sau, cặp vectơ nào không cùng phương?    
A. a  ø2;3ù, b ø6;9ù B. u  ø0;5ù,v  ø0; 1  ù     C. m ø 2
 ;1ù, b ø1;2ù D. c  ø3; ù 4 ,d  ø 6; ù 8     Câu 37. Cho u  ø 2 m  m ù v  ø 2 3; 2 ,
5m 3; m ù . Vectơ u  v khi và chỉ khi m thuộc tập hợp: A.   2 B. 0;  2 C. 0;2;  3 D.   3      
Câu 38. Cho 2 vectơ u  ø2m 1ù i ø3 mù j và v  2i  3 j . Tìm m để hai vectơ cùng phương. 5 11 9 8 A. m B. m  C. m  D. m  11 5 8 9
Câu 39. Trong mặt phẳng Oxy, cho ø A m 1  ;2 ù; ø B 2;5 2  ù m ; Cø m 3
 ;4ù . Tìm m để A, B, C thẳng hàng. A. m 3 B. m  2 C. m  2 D. m  1
Câu 40. Trong hệ trục Oxy, cho 4 điểm Aø3; 2  ù, B ø7; ù 1 ,C ø0;1ù, D ø 8  ; 5
 ù . Mệnh đề nào sau đây đúng?     A. AB,CD đối nhau B. AB,CD ngược hướng  
C. AB,CD cùng hướng D. A, B, C, D thẳng hàng    
Câu 41. Cho a  ø4; mù, v  ø2 m 6;1 ù. Tập giá trị của m để hai vectơ a và b cùng phương là: A.  1  ;  1 B.  1  ;  2 C.  2  ;   1 D.  2  ;  1 Câu 42. Cho 4 điểm Aø1; 2
 ù, B ø0;3ù,C ø3;4ù, D ø 1
 ;8 ù. Ba điểm nào trong bốn điểm dã cho thẳng hàng? A. A, B, C B. B, C, D C. A, B, D D. A, C, D  
Câu 43. Cho 2 vectơ a và b không cùng phương. Hai vectơ nào sau đây cùng phương?     1    2     
A. u  2a  b và v  a  3b
B. u  a 3b và v  2a  9b 2 3  3     3    3   1  1 
C. u  a  3b và v  2a b
D. u  2a  b và v   a  b 5 5 2 3 4
Câu 44. (ĐỘI CẤN VĨNH PHÚC LẦN 1 2018-2019) Trong mặt phẳng với hệ tọa độ Oxy cho A øm 1  ;2 ù, B ø2;5 2
 m ù và Cøm 3;4ù . Tìm giá trị m để A, B, C thẳng hàng. A. m  2 . B. m  2. C. m  1. D. m  3 .
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 5
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Dạng 2.3 Biểu diễn một vectơ theo 2 vectơ không cùng phương     Câu 45. Vectơ a  ø2; 1
 ù biểu diễn dưới dạng a  xi  y j được kết quả nào sau đây?             A. a  2i  j B. a  i  2 j C. a  2  i  j D. a  i   2 j      
Câu 46. Trong mặt phẳng tọa độ Oxy cho a  (2;1), b  (3;4), c  (7;2). Cho biết c  ma  nb khi đó. 22 3 22 3 1  3 22 3  A. m  ; n  . B. m   ; n   . C. m  ; n  . D. m  ; n  . 5 5 5 5 5 5 5 5
Câu 47. Trong mặt phẳng Oxy, cho các điểm Aø4;2ù,B ø2; ù 1 ,C ø0; ù 3 ,M ø3;7ù. Giả sử   
AM  x.AB  y .AC ø x,y  ù . Khi đó x  y bằng A. 12 . B. 5. C. 12  . D. 5 . 5 5   
Câu 48. Trong mặt phẳng Oxy ;cho các véc tơ a  ø2; 1
 ù;b  ø0;4 ù và c  ø3;3ù . Gọi m và n là hai   
số thực sao cho c  ma  nb . Tính giá trị biểu thức 2 2 P  m  n . 225 100 97 193 A. P  . B. P  . C. P  . D. P  . 64 81 64 64      
Câu 49. Cho a  ø2; 1ù , b  ø 3; 4ù, c ø 4
 ; 9 ù . Hai số thực m , n thỏa mãn ma  nb  c . Tính 2 2 m  n ? A. 5. B. 3. C. 4 . D. 1.      
Câu 50. Trong mặt phẳng Oxy, cho a  ø2;1 ù;b  ø3;4 ù;c ø7;2 ù. Tìm m, n để c  ma  nb . 22 3 1 3 22 3 22 3 A. m   ,n   B. m  , n   C. m  ,n   D. m  ,n  5 5 5 5 5 5 5 5     
Câu 51. Cho các vectơ a  ø4; 2  ù, b  ø 1  ; 1  ù, c ø 2; ù
5 Phân tích vectơ a và c ta được:  1  1   1  1   1    1  1  A. b   a  c B. b  a  c C. b   a 4c D. b   a c 8 4 8 4 8 8 4      
Câu 52. Cho vectơ a  ø2;1 ù, b  ø3;4 ù, c  ø7;2ù . Khi đó c  ma  nc . Tính tổng m  n bằng: A. 5 B. 3,8 C. 5 D. 3  ,8 
Câu 53. Trong mặt phẳng tọa độ Oxy, cho 4 điểm Aø1; 2  ù , Bø0; ù 3 , C ø 3  ;4ù ,Dø 1; ù 8 . Phân tích CD  
qua AB và AC . Đẳng thức nào sau đây đúng?            1  A. CD  2 AB  2 AC B. CD  2 AB  AC
C. CD  2 AB  AC D. CD 2 AB AC 2 Dạng 3. Tọa độ điểm
Dạng 3.1 Xác định tọa độ trung điểm, tọa độ trọng tâm, tọa độ điểm đối xứng
Câu 54. (THPT Nhữ Văn Lan - Hải Phòng - Học kỳ I - 2019) Trong mặt phẳng tọa độ Oxy , cho điểm
M ø x; yù . Tìm tọa độ của điểm M đối xứng với 1 M qua trục hoành? A. M ; . B. M ; . C. M  ; . D. M  ;  . 1 ø x y ù 1 ø x y ù 1 ø x y ù 1ø x y ù
Câu 55. (THPT Nhữ Văn Lan - Hải Phòng - Học kỳ I - 2019) Trong măt phăng toa đô Oxy , cho A  BC biết Aø2;  ù
3 , Bø4;7ù,Cø1;5ù . Toa đô trong tâm G cua A  BC là
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 6
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 A. ø7;15ù. B. 7 ;5     . C. ø7;9 ù. D. 7 ;3 . 3     3   
Câu 56. (THPT Nhữ Văn Lan - Hải Phòng - Học kỳ I - 2019) Trong mặt phẳng tọa độ Oxy , cho Aø 2; ù
3 ,B ø4;7ù . Tìm tọa độ trung điểm I của AB . A. ø3;2 ù. B. ø2;10 ù. C. ø6;4 ù. D. ø8; 21ù. Câu 57. Cho A
 BC có Aø4;9ù, Bø3;7ù , C øx 1  ; yù . Để Gø ; x y  6ù là trọng tâm A  BC thì giá trị x và y là A. x  3, y  1. B. x  3  , y  1  . C. x  3, y  1. D. x  3, y  1.
Câu 58. Trong hệ tọa độ Oxy, cho Aø2; ù
3 ;B ø 4;7ù . Tìm tọa độ trung điểm I của đoạn AB. A. I ø6;4ù B. I ø2;10ù C. I ø3;2ù D. I ø8; 2  ù 1
Câu 59. Trên mặt phẳng tọa độ Oxy , cho tam giác ABC có Aø2;1ù , B ø 1  ; 2  ù , Cø 3
 ;2ù . Tọa độ trọng
tâm G của tam giác ABC là  2 1  2 2  1 1  2 1 A.     G  ;   . B. G  ;   . C. G  ;   . D. G ;   .  3 3  3 3  3 3   3 3 
Câu 60. Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có ba đỉnh Aø 1  ;2 ù , Bø2;0ù , C ø 3  ; ù
1 . Toạ độ trọng tâm G của tam giác ABC là  2  2  4  4 A.     G  ;1  . B. G ; 1  . C. G  ;1 . D. G ; 1  . 3           3   3   3 
Câu 61. Trong hệ tọa độ Oxy, cho Aø 4  ;1ù; Bø2;4ù; C ø2; 2
 ù. Tìm tọa độ điểm D sao cho C là trọng tâm A  BD A. D ø8;11ù B. D ø12;11ù C. D ø8;11ù D. D ø 8  ; 1  1ù
Câu 62. Trong hệ tọa độ Oxy, cho ABC có Aø3;5ù, B ø1; 2 ù, C ø5;2 ù. Tìm tọa độ trọng tâm G của tam giác. A. G ø3;4ù B. Gø4;0ù C. G ø2;3ù D. Gø3; ù 3
Câu 63. Trong mặt phẳng tọa độ Oxy cho bốn điểm A ø3;-5 ù,B ø-3;3 ù,C ø-1;-2 ù,D ø5;-10 ù. Hỏi  1  G ;-3 
là trọng tâm của tam giác nào dưới đây? 3    A. ABC . B. BCD . C. ACD. D. ABD .
Câu 64. Trong mặt phẳng tọa độ Oxy cho tam giác ABC có D ø3;4 ù, E ø6;1ù, F ø7;3 ù lần lượt là trung
điểm các cạnh AB, BC,CA .Tính tổng tung độ ba đỉnh của tam giácABC . A. 16 . B. 8 . C. 8 . D. 16 . 3 3
Câu 65. Trong mặt phẳng toạ độ Oxy, cho ABC có M ø2;3ù, N ø0;4ù , Pø1;6ù lần lượt là trung điểm
của các cạnh BC, CA, AB. Tìm tọa độ đỉnh A. A. Aø1;5ù B. Aø 3  ;7 ù C. Aø 2  ; 7  ù D. Aø1;10ù
Câu 66. Cho tam giác ABC . Biết trung điểm của các cạnh BC , CA , AB có tọa độ lần lượt là M ø1; 1  ù , N ø3;2ù , Pø0; ù
5 . Khi đó tọa độ của điểm A là:
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 7
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489 A. ø2; 2  ù . B. ø5;1ù. C. ø 5;0ù. D. ø2; 2 ù.
Câu 67. Trong mặt phẳng tọa độ Oxy, cho MNP có M ø1; ù 1 ; N ø5; ù
3 và P thuộc trục Oy. Trọng tâm
G của tam giác nằm trên trục Ox. Tọa độ của điểm P là: A. P ø0;4 ù B. P ø2;0ù C. P ø2;4 ù D. P ø0;2ù
Câu 68. Trong hệ tọa độ Oxy, cho M ø3;4ù . Gọi M ,1 M làn lượt là hình chiếu vuông góc của M trên 2
Ox, Oy. Khẳng định nào đúng? A. OM  3  B. OM  4 1 2    
C. OM  OM  3; 4 D. OM  OM  3;4 1 2 ø ù 1 2 ø ù
Câu 69. Trong hệ tọa độ Oxy, cho M ø2;0ù; Nø 2;2ù; Pø 1
 ;3ù lần lượt là trung điểm các cạnh BC, CA,
AB của ABC .Tọa độ điểm B là: A. B ø1;1ù B. B ø 1  ; 1  ù C. B ø 1  ;1 ù D. B ø1; ù 1
Câu 70. Trong mặt phẳng Oxy , cho tam giác MNP có M ø1; 1ù , Nø 5;  ù
3 và P là điểm thuộc trục
Oy , trọng tâm G của tam giác MNP nằm trên trục Ox . Tọa độ điểm P là A. ø2; 4ù. B. ø0; 4ù. C. ø0; 2ù. D. ø2; 0ù.
Dạng 3.2 Xác định tọa độ điểm thỏa mãn điều kiện cho trước
Câu 71. (THPT Nhữ Văn Lan - Hải Phòng - Học kỳ I - 2019) Trong mặt phẳng tọa độ Oxy , cho A ø 1  1
; ù,B ø1;3ù,C ø5;2 ù . Tìm tọa độ điểm D sao cho ABCD là hình bình hành. A. ø3;0 ù. B. ø5;0 ù. C. ø7;0ù. D. ø5;2 ù.
Câu 72. Trong mặt phẳng tọa độ Oxy , cho hình bình hành ABCD có ø A 2  ;3ù, Bø0;4ù, Cø5; 4  ù . Tọa độ đỉnh D là A. ø3; 2 ù. B. ø3;7 ù. C. ø 7;2 ù. D. ø3; 5  ù.
Câu 73. Trong mặt phẳng Oxy ;cho hai điểm ø A 1; 4ù , ø B 4;  ù
2 . Tọa độ giao điểm của đường thẳng đi qua hai điểm , A B với trục hoành là A. ø 9  ;0 ù. B. ø0;9 ù . C. ø9;0 ù. D. ø0; 9 ù.
Câu 74. (HKI - Sở Vĩnh Phúc - 2018-2019) Trên mặt phẳng với hệ tọa độ Oxy cho hai điểm
Aø1;1ù, B ø2; 4ù . Tìm tọa độ điểm M để tứ giác OBMA là một hình bình hành. A. M (3; 3)  . B. M (3; 3)  . C. M (3;3). D. M ( 3  ;3) .
Câu 75. Trong hệ tọa độ Oxy, cho 3 điểm Aø2; ù 1 ;B ø0; ù 3 ;C ø3; ù
1 . Tìm tọa độ điểm D để ABCD là hình bình hành. A. D ø5;5ù B. D ø5; 2  ù C. D ø5; 4  ù D. D ø1;4ù
Câu 76. (THPT MINH CHÂU HƯNG YÊN NĂM 2018 – 2019) Trong mặt phẳng Oxy cho tam giác ABC có A ø2; ù 1 ,B ø 1
 ;2ù,C ø3;0ù . Tứ giác ABCE là hình bình hành khi tọa độ E là cặp số nào sau đây? A. ø6;1ù B. ø0;1ù C. ø1;6ù D. ø6;1ù
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 8
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 77. Trong mặt phẳng với hệ tọa độ Oxy, cho ba điểm A ø2;5ù ,B ø1; ù
1 ,C ø3;3ù, một điểm E thỏa   
mãn AE  3AB  2AC . Tọa độ của E là A. ø 3  ;3 ù. B. ø3;3ù . C. ø3;3 ù. D. ø2;3 ù .
Câu 78. Trong hệ tọa độ Oxy, cho ø A 3  ;1ù, Bø1; 4ù, C ø5; ù
3 . Tìm tọa độ điểm D sao cho ABCD là hình bình hành. A. D ø 1;0ù B. D ø1;0 ù C. D ø0; 1  ù D. D ø0;1ù
Câu 79. (THPT NGUYỄN TRÃI-THANH HOÁ - Lần 1.Năm 2018&2019) Trong mặt phẳng với hệ  2 tọa độ 
Oxy cho tam giác ABC có trọng tâm G ; 0  , biết M ø1; 1
 ù là trung điểm của cạnh 3   
BC . Tọa độ đỉnh A là A. ø2; 0ù. B. ø 2  ; 0 ù . C. ø0; 2  ù . D. ø0; 2ù.
Câu 80. Trên mặt phẳng tọa độ Oxy , cho ø A 2; ù 3 , B ø 2
 ;1ù. Điểm C thuộc tia Ox sao cho tam giác
ABC vuông tại C có tọa độ là: A. C ø3; ù 0 . B. C ø3; ù 0 . C. C ø1;0ù. D. C ø2;0ù .
Câu 81. (THPT Nhữ Văn Lan - Hải Phòng - Học kỳ I - 2019) Trong mặt phẳng tọa độ Oxy , cho
A ø3;3 ù, B ø 1; 9 ù, C ø5; 1ù. Gọi I là trung điểm của AB . Tìm tọa độ M sao cho 1 AM CI . 2 A. ø5; ù 4 . B. ø1; ù 2 . C. ø 6; 1ù . D. ø2; ù 1 .
Câu 82. Trong mặt phẳng toạ độ Oxy, cho ABC có    A ø 3
 ;3 ù, B ø1;4 ù, C ø2; 5
 ù . Tọa độ điểm M thỏa mãn 2MA BC  4CM là:  1 5   1 5   1 5   5 1  A. M  ;  B. M  ;   C. M ;    D. M ;     6 6   6 6   6 6   6 6 
Câu 83. Trong hệ tọa độ Oxy, cho Aø2; 3
 ù, Bø3;4ù . Tìm tọa độ điểm M trên trục hoành sao cho A, B, M thẳng hàng.  5   17  A. M ø1;0ù B. M ø4;0ù C. M  ;0  D. M ;0 3       7 
Câu 84. Trong hệ tọa độ Oxy, cho Aø2; ù 1 ,B ø1;  ù
3 . Tìm tọa độ giao điểm I của hai đường chéo hình bình hành OABC.  1 2   5 1   1 3  A. I   ;  B. I  ;  C. I ø2;6ù D. I ;    3 3   2 2   2 2    
Câu 85. Trong hệ tọa độ Oxy, cho Aø1; ù
3 ,B ø 4;0ù. Tìm tọa độ điểm M thỏa mãn MA  MB 3MC  0 A. M ø1;18ù B. M ø 1  ;18ù C. M ø 1  8;1ù D. M ø1;18ù
Câu 86. Trong hệ tọa độ Oxy, cho 3 điểm A ø2;5ù;B ø1; ù 1 ;C ø3; ù
3 . Tìm điểm E thuộc mặt phẳng tọa độ   
thỏa mãn AE  3AB  2AC ? A. E ø3; ù 3 B. E ø 3; ù 3 C. E ø3;3ù D. E ø 2  ; 3  ù
Câu 87. Trong hệ tọa độ Oxy, cho Aø2; ù 1 ;B ø6; ù
1 . Tìm điểm M trên Ox sao cho A, B, M thẳng hàng. A. M ø2;0ù B. M ø8; ù 0 C. M ø 4  ;0 ù D. M ø4;0ù
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 9
CÁC DẠNG TOÁN THƯỜNG GẶP ĐT:0946798489
Câu 88. Trong hệ tọa độ Oxy, cho ABC có Aø3;4 ù, B ø2;1ù, C ø 1  ; 2
 ù . Tìm điểm M có tung độ dương
trên đường thẳng BC sao cho S  3S . ABC ABM A. M ø2;2ù B. M ø3;2ù C. M ø 3  ;2 ù D. M ø3; ù 3
Câu 89. Trong hệ tọa độ Oxy, cho 3 điểm ø A 1  ; 1  ù, ø
B 0;1ù, Cø3;0 ù . Xác định tọa độ giao điểm I của
AD và BG với D thuộc BC và 2BD  5DC , G là trọng tâm ABC  5   1   35   35  A. I ;1  B. I ;1 C. I ; 2 D. I ;1 9           9   9   9 
Câu 90. Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có ba đỉnh Aø 1  ;2 ù , Bø2;0ù , C ø 3  ; ù
1 . Toạ độ tâm đường tròn ngoại tiếp I của tam giác ABC là  11 13  11 13  11 13  11 13 A.     I ;  . B. I ; . C. I  ; . D. I  ;  . 14 14           14 14   14 14   14 14 
Câu 91. Tam giác ABC có đỉnh ø A 1
 ;2ù , trực tâm H ø3;0ù , trung điểm của BC là M ø6; ù 1 . Bán kính
đường tròn ngoại tiếp tam giác ABC là A. 5. B. 5 C. 3. D. 4 .
Câu 92. Gọi điểm M là giao điểm của đường thẳng AB và trục hoành biết A ø1; 2ù và Bø2;5 ù . Biết hoành m m độ điểm M có dạng
trong đó tối giản và m,n   . Tính 2 2 m  n . n n A. 34 B. 41 C. 25 D. 10
Câu 93. Trong hệ tọa độ Oxy, cho ABC biết Aø2;0ù , Bø1; ù
1 , C ø1;2ù . Các điểm C ', A', B ' lần lượt 1
chia các đoạn thẳng AB, BC, CA theo tỉ số là 1  ; ; 2
 . Khi đó đẳng thức nào sau đây đúng? 2         A. A'C '  2B 'C ' B. A'C '  3  B 'C ' C. A'C  3B 'C ' D. A'C  4  B 'C '
Câu 94. Trong hệ tọa độ Oxy, cho 4 điểm Aø0;1ù ; Bø1;3ù; C ø2;7ù; Dø0;3ù . Tìm giao điểm của 2 đường thẳng AC và BD.  2  1  4  2 A.       ;3  B. ; 3    C.  ;13  D.  ;3   3  3   3   3 
Câu 95. Trong hệ tọa độ Oxy, cho ba điểm Aø6;3ù ; B ø 3  ;6 ù;C ø1; 2
 ù. Biết điểm E trên cạnh BC sao
cho BE  2 EC . D nằm trên đường thẳng AB và thuộc trục Ox. Tìm giao điểm của DE và AC.  7 1  3 1   7 1  7 1 A.     I   ; B. I  ; C. I  ; D. I  ; 2 2        2 2   4 2   2 2  Câu 96. Hình vuông AB D
C có Aø2;1ù ,C ø 4;3ù . Tọa độ của đỉnh B có thể là: A. ø2;3ù. B. ø1;4ù. C. ø4;1ù . D. ø3;2 ù .  
Câu 97. Các điểm A, B, N thẳng hàng  BA, BN cùng phương  x  0. Trong mặt phẳng tọa độ Oxy cho tam giác ABC. Biết ø A 3; 1  ù, ø B 1  ;2ù và I ø1; ù
1 là trọng tâm tam giác ABC. Trực tâm H
của tam giác ABC có tọa độ øa; b ù. Tính a  3b . 2 4 A. a  3b  . B. a  3b   . C. a  3b  1 . D. a  3b  2  . 3 3
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 10