

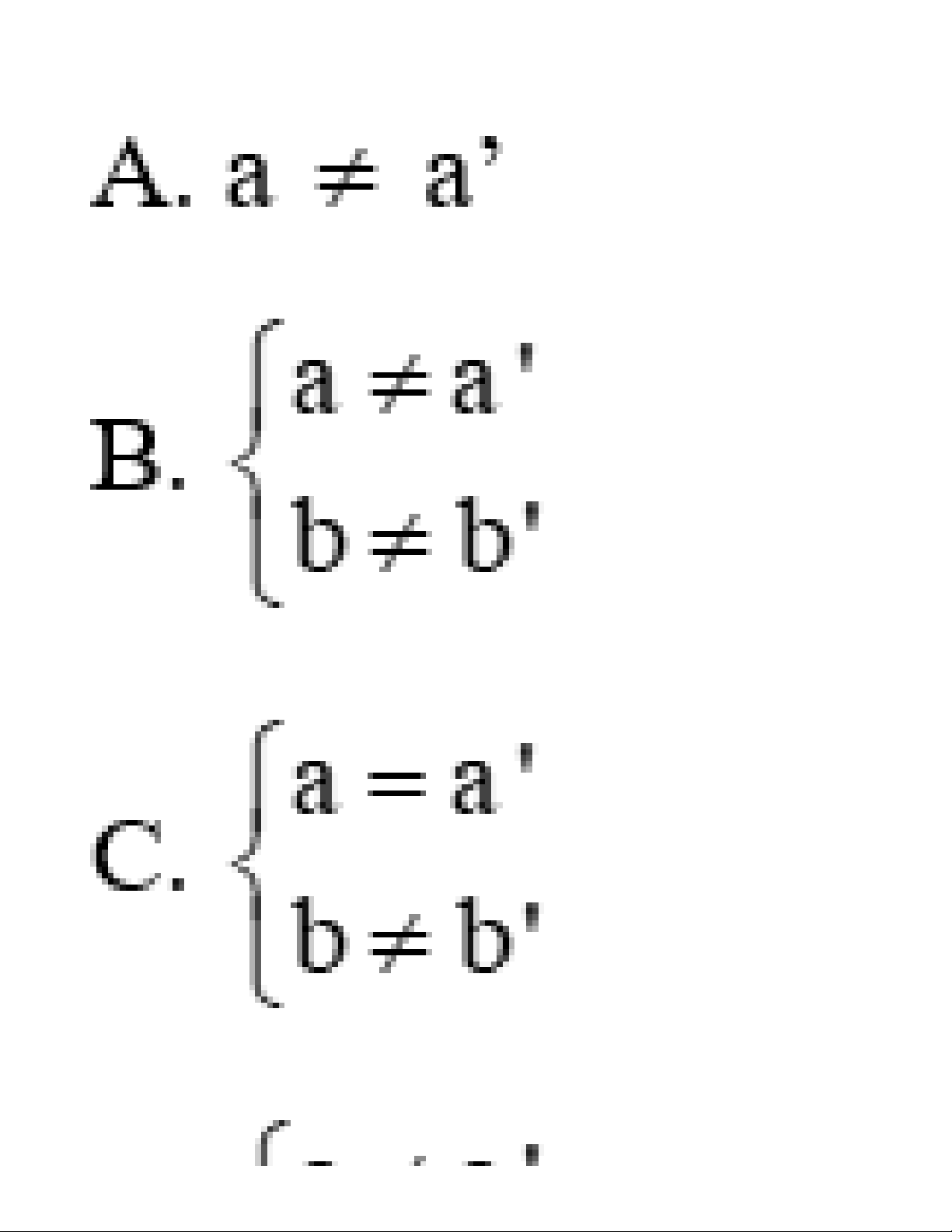
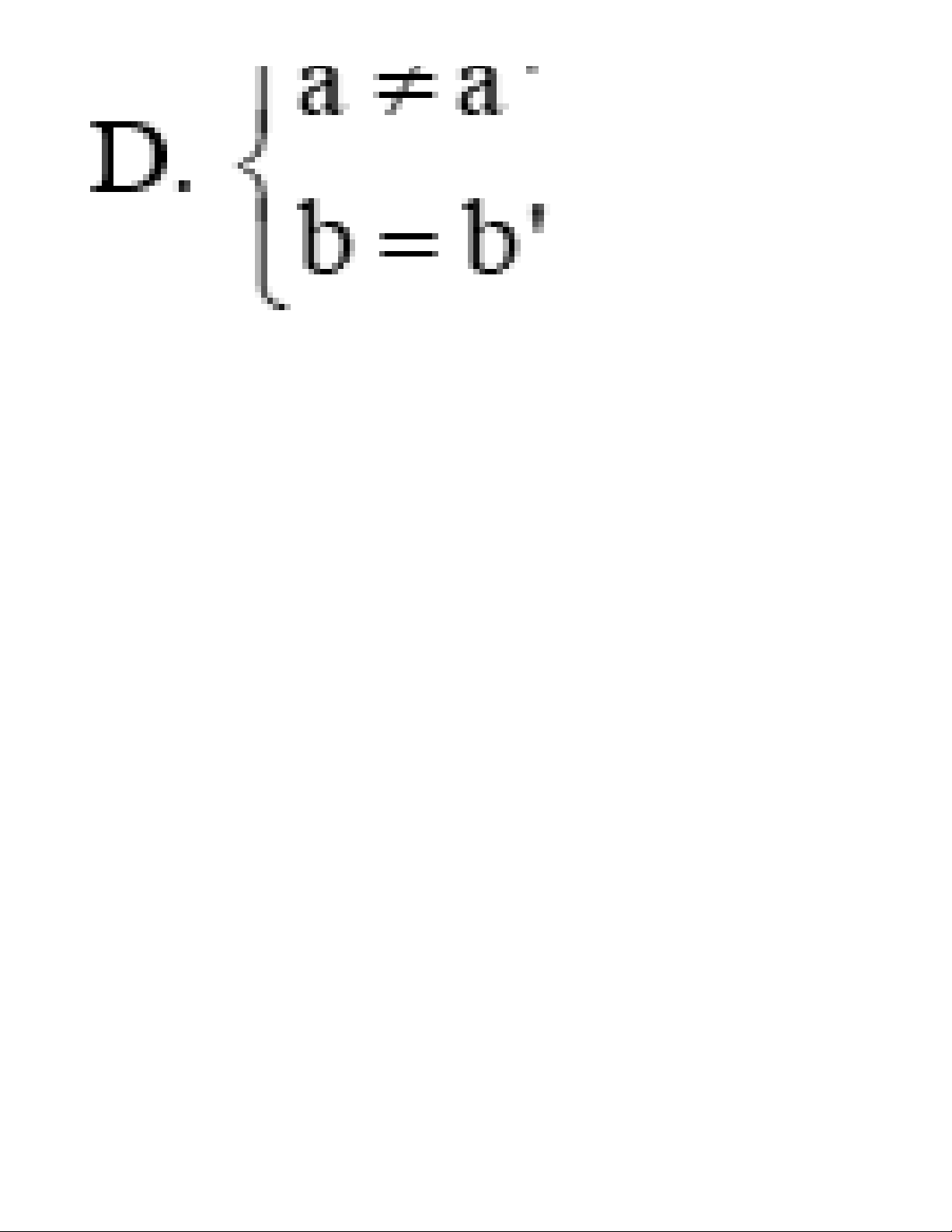
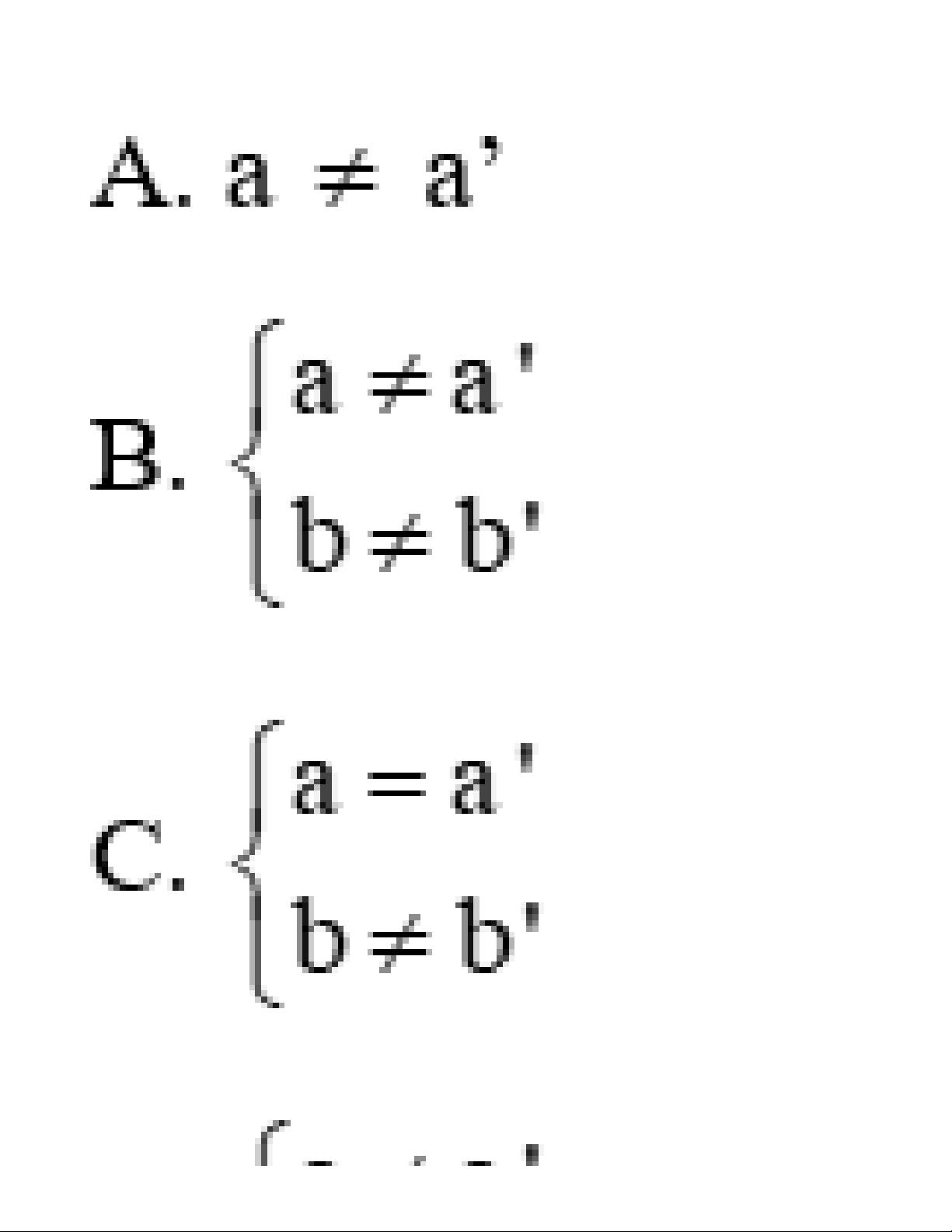
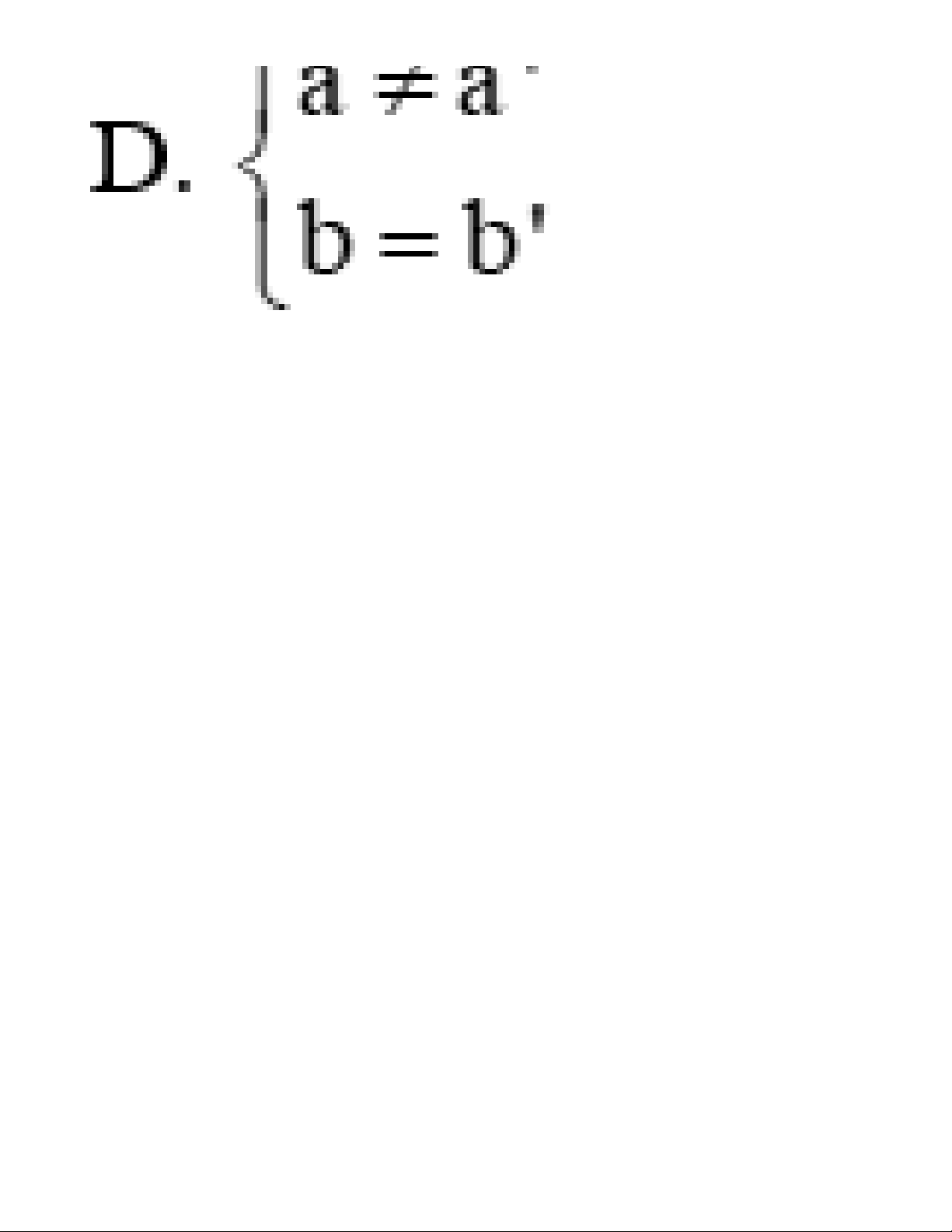
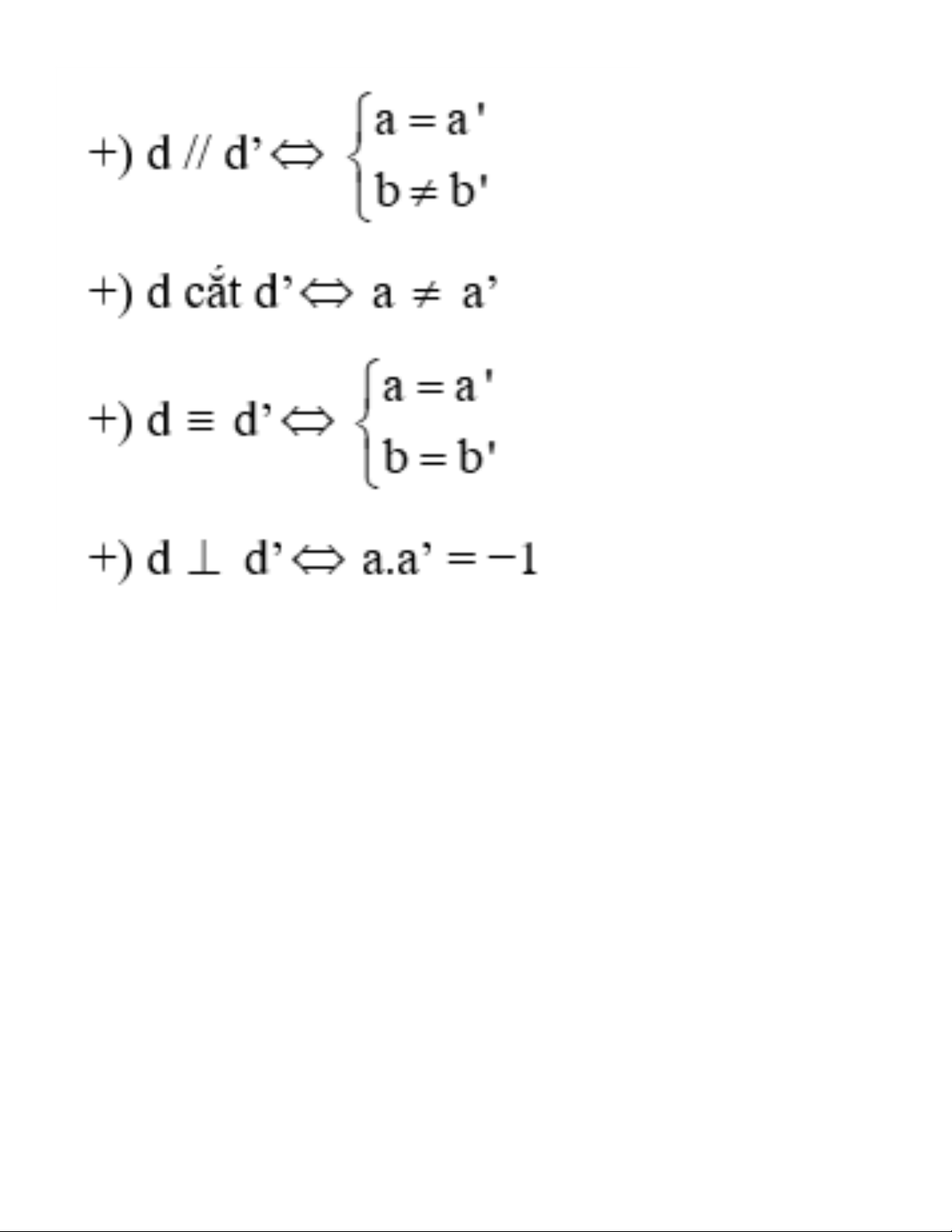

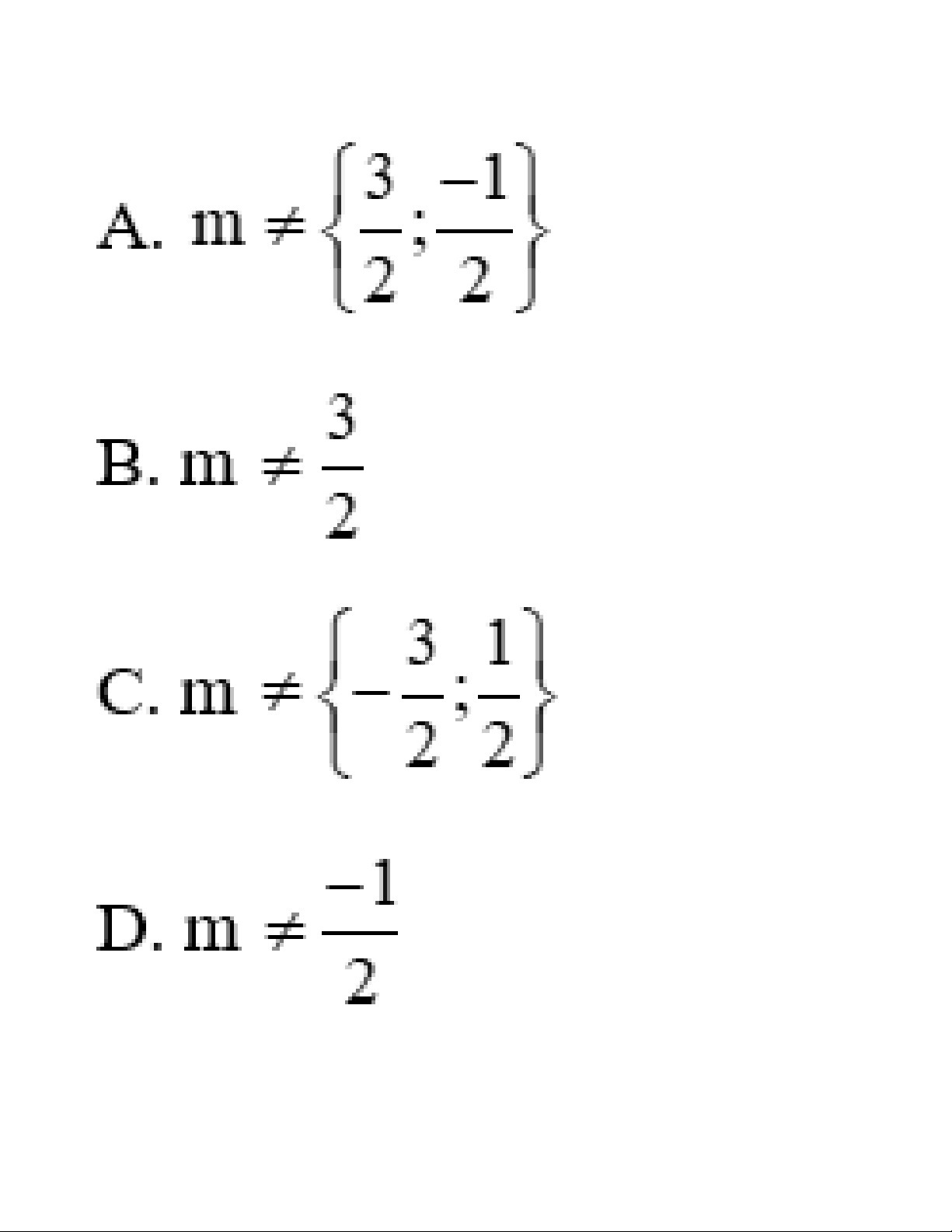
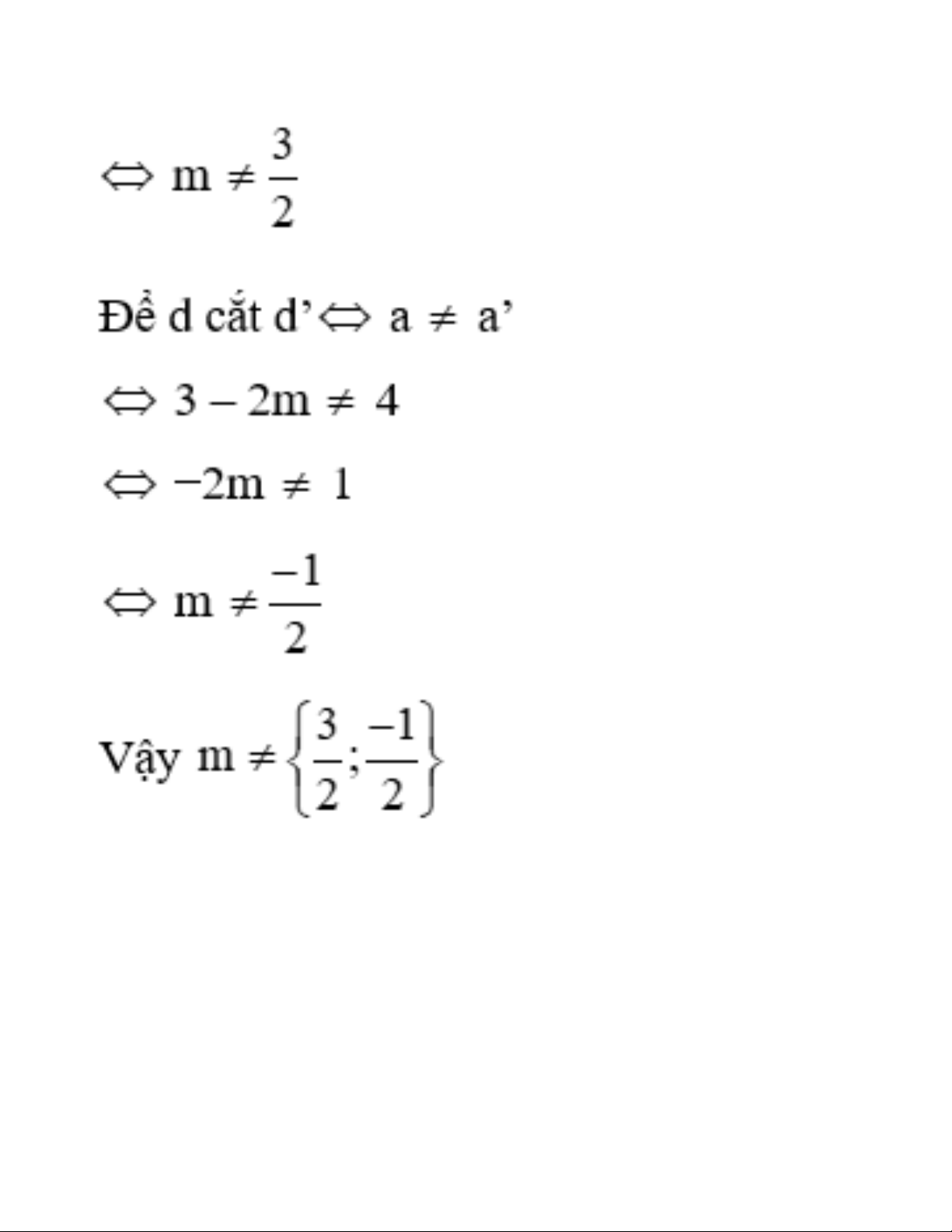


Preview text:
Tìm m để hai đường thẳng song song, cắt nhau, trùng nhau! vuông góc
1. Lý thuyết tìm m để hai đường thẳng song song, cắt nhau trùng nhau và vuông góc
Hai đường thẳng trùng nhau là hai đường thẳng có mọi điểm chung.
Hai đường thẳng phân biệt là hai đường thẳng chỉ có một điêm chung hoặc không có điểm chung nào.
Nếu hai đường thẳng chỉ có một điểm chung, ta nói rằng hai đường thẳng đó cắt nhau.
Điểm chung được gọi là giao điểm của hai đường thẳng.
Nếu hai đường thẳng không có điểm chung nào, ta nói rằng hai đường thẳng đó song song với nhau.
Ta viết a//b hay b//aHai đường thẳng vuông góc với nhau: a.a’ = -1.Hai đường thẳng song song với nhau: a = a’ và b ≠ b’.
Hai đường thẳng cắt nhau: a ≠ a’.Hai đường thẳng trùng nhau: a = a’ và b = b’.
Hai đường thẳng được cho là vuông góc với nhau khi chỉ số a x a’= -1. Khi đó, chúng gặp nhau và tạo thành
1 góc 90 độ. Trường hợp song song là khi chỉ số a = a’ và b ≠ b’, trong trường hợp này thì 2 đường thẳng
không có điểm chung và không giao nhau tại 1 số thời điểm. Khi chỉ số a ≠ a’ sẽ dẫn đến trường hợp 2
đường thẳng giao nhau. Trùng nhau ở trường hợp a = a’.
2. Các dạng toán thường gặp về đường thẳng song song, cắt
nhau, trùng nhau và vuông góc
Dạng 1: Chỉ ra vị trí tương đối của hai đường thẳng cho trước. Tìm tham số m để các đường thẳng thỏa
mãn vị trí tương đối cho trước. Phương pháp:
Cho hai đường thẳng d:y=ax+b(a≠0) và d′:y=a′x+b′(a′≠0) +) d//d′⇔{a=a′; b≠b′ +) d cắt d′⇔a≠a′ +) d≡d′⇔{a=a′b=b′
Dạng 2: Viết phương trình đường thẳng Phương pháp:
+) Sử dụng vị trí tương đối của hai đường thẳng để xác định hệ số.
Ngoài ra ta còn sử dụng các kiến thức sau
+) Ta có y=ax+b với a≠0,b≠0 là phương trình đường thẳng cắt trục tung tại điểm A(0;b), cắt trục hoành tại điểm B(−b/a;0)
+) Điểm M(x0;y0) thuộc đường thẳng y=ax+b khi và chỉ khi y0=ax0+b
Dạng 3: Tìm điểm cố định mà đường thẳng d luôn đi qua với mọi tham số m Phương pháp:
Gọi M(x;y) là điểm cần tìm khi đó tọa độ điểm M(x;y) thỏa mãn phương trình đường thẳng d
Đưa phương trình đường thẳng d về phương trình bậc nhất ẩn m.
Từ đó để phương trình bậc nhất ax+b=0 luôn đúng thì a=b=0
Giải điều kiện ta tìm được x,y
Khi đó M(x;y) là điểm cố định cần tìm.
3. Bài tập vận dụng tìm m để hai đường thẳng cắt nhau, song
song, trùng nhau và vuông góc Phần I: Trắc nghiệm
Câu 1: Hai đường thẳng d: y = ax + b (a ≠ 0) và d’: y = a’x + b’ (a’ ≠ 0) cắt nhau khi Lời giải:
Cho hai đường thẳng d: y = ax + b (a ≠ 0) và d’: y = a’x + b’ (a’ ≠ 0) d cắt d’ ⇔ a ≠ a’ Đáp án cần chọn là: A
Câu 2: Hai đường thẳng d: y = ax + b (a ≠ 0) và d’: y = a’x + b’ (a’ ≠ 0) trùng nhau khi: Lời giải:
Cho hai đường thẳng d: y = ax + b (a ≠ 0) và d’: y = a’x + b’ (a’ ≠ 0)
d trùng d’ ó a=a’; b=b’ Đáp án cần chọn là: D
Câu 3: Hai đường thẳng d: y = ax + b (a ≠ 0) và d’: y = a’x + b’ (a’ ≠ 0) có a = a’ và b ≠ b’. Khi đó: A. d // d’ B. d ≡ d’ C. d cắt d’ D. d ⊥ d’ Lời giải:
Cho hai đường thẳng d: y = ax + b (a ≠ 0) và d’: y = a’x + b’ (a’ ≠ 0) Đáp án cần chọn là: A
Câu 4: Hai đường thẳng d: y = ax + b (a ≠ 0) và d’: y = a’x + b’ (a’ ≠ 0) có a ≠ a’. Khi đó: A. d // d’ B. d ≡ d’ C. d cắt d’ D. d ⊥ d’ Lời giải:
Cho hai đường thẳng d: y = ax + b (a ≠ 0) và d’: y = a’x + b’ (a’ ≠ 0) +) d cắt d’ ⇔ a ≠ a’ Đáp án cần chọn là: C
Câu 5: Cho hai đường thẳng d: y = x + 3 và d’: y = −2x. Khi đó: A. d // d’ B. d ≡ d’ C. d cắt d’ D. d ⊥ d’ Lời giải:
Ta thấy d: y = x + 3 có a = 1 và d’: y = −2x có a’ = −2
⇒ a ≠ a’ (1 ≠ −2) nên d cắt d’ Đáp án cần chọn là: C
Câu 6: Cho hai đồ thị của hàm số bậc nhất là hai đường thẳng d: y = (m + 2)x – m và d’: y = −2x − 2m + 1.
Với giá trị nào của m thì d cắt d’? A. m ≠ −2 B. m ≠ −4 C. m ≠ {−2; −4} D. m ≠ {2; −4} Lời giải:
+) Ta thấy d: y = (m + 2)x – m có a = m + 2 và d’: y = −2x − 2m + 1 có a’ = −2
+) Để y = (m + 2)x – m là hàm số bậc nhất thì m + 2 ≠ 0 ⇔ m ≠ −2.
+) Để d cắt d’⇔ a ≠ a’ m + 2 ⇔ −2 ⇔ m −4 Vậy m ⇔ {−2; −4} Đáp án cần chọn là: C
Câu 7: Cho hai đồ thị của hàm số bậc nhất là hai đường thẳng d: y = (3 – 2m)x – 2 và d’: y = 4x − m + 2. Với
giá trị nào của m thì d cắt d’? Lời giải:
Ta thấy d: y = (3 – 2m)x – 2 có a = 3 – 2m và d’: y = 4x − m + 2 có a’ = 4
Để d: y = (3 – 2m)x – 2 là hàm số bậc nhất thì 3 – 2m Đáp án cần chọn là: A Phần II: Tự luận
Bài 1: Cho hai hàm số y = kx + m -2 và y = (5 - k).x + (4 - m). Tìm m, k để đồ thị của hai hàm số a, Trùng nhau b, Song song với nhau c, Cắt nhau
Bài 2: Cho hàm số y = (2m - 3)x + m - 5. Tìm m để đồ thị hàm số:
a, Tạo với 2 trục tọa độ một tam giác vuông cân
b, Cắt đường thẳng y = 3x - 4 tại một điểm trên Oy
c, Cắt đường thẳng y = -x - 3 tại một điểm trên Ox
Bài 3: Cho hai đường thẳng (d1): y = (m + 1)x + 2 và (d2): y = 2x + 1. Tìm m để hai đường thẳng cắt nhau
tại một điểm có hoành độ và tung độ trái dấu
Bài 4: Tìm m để đồ thị của hàm số y = (m - 2)x + m + 3 và các đồ thị của các hàm số y = -x + 2 và y = 2x - 1 đồng quy
Bài 5: Cho hàm số y = 2x + 3k và y = (2m + 1)x + 2l - 3. Tìm điều kiện của m và k để đồ thị của hai hàm số là:
a, Hai đường thẳng cắt nhau
b, Hai đường thẳng song song với nhau
c, Hai đường thẳng trùng nhau
Bài 6: Cho hàm số y = mx + 4 và y = (2m - 3)x - 2. Tìm m để đồ thị của hai hàm số đã cho là:
a, Hai đường thẳng song song với nhau
b, Hai đường thẳng cắt nhau
c, Hai đường thẳng trùng nhau
d, Hai đường thẳng cắt nhau tại 1 điểm trên trục tung
Bài 7: Cho hai hàm số y = 2x + m - 3 và y = 5x + 5 - 3m. Tìm m để đồ thị của hai hàm số trên cắt nhau tại
một điểm trên trục tung
Bài 8: Cho hai hàm số y = (m - 1)x + 3 và y = (3 - m)x + 1
a, Với giá trị nào của m thì đồ thị của hai hàm só là hai đường thẳng song song với nhau
b, Với giá trị nào của m thì đồ thị của 2 hàm số là hai đường thẳng cắt nhau
Bài 9: Cho hàm số y = mx - 2 (m khác 0). Xác định giá trị của m để đồ thị hàm số cắt hai trục tọa độ tạo
thành tam giác có diện tích bằng 1.
Bài 10: Cho hàm số y = x + m. Tìm m để đồ thị hàm số song song với đường thẳng x - y + 3 = 0
Bài 11: Tìm m để đường thẳng y = x + m2 + 1 và đường thẳng y = 5 + (m - 1)x cắt nhau tại
a, Một điểm trên trục hoành
b, Một điểm trên trục tung
Bài 12: Cho hai hàm số bậc nhất y = (m - 1)x + 3 và y = (3 - m)x + 1
a, Với giá trị nào của m thì đồ thị của hai hàm số là hai đường thẳng song song với nhau
b, Với giá trị nào của m thì đồ thị của hai hàm số là hai đường thẳng cắt nhau
Bài 13: Cho đường thẳng (d1): y = x + 2 và đường thẳng (d2): y = -2x + 2
a, Tìm tọa độ giao điểm của (d1) và (d2) bằng phép tính
b, Gọi giao điểm của (d1) và (d2) với trục Ox lần lượt là A và B. Tính diện tích và chu vi của tam giác ABC
Bài 14: Cho hàm số y = (2m - 1)x + n. Tìm m và n để đồ thị hàm số trên song song với đường thẳng y = 2x và đi qua A (1; 2)
Bài 15: Cho hàm số y = (m -1)x + 5 có đồ thị là đường thẳng (d) và đường thẳng (d1): y = -x + 3, (d2): y = x -
1. Tìm m để ba đường thẳng (d1), (d2), (d3) đồng quy




