Tìm tập xác định của hàm số lũy thừa – mũ – lôgarit có chứa tham số

Tài liệu gồm 16 trang, được biên soạn bởi quý thầy, cô giáo Nhóm Toán VDC & HSG THPT, hướng dẫn phương pháp giải bài toán Tìm tập xác định của hàm số lũy thừa – mũ – lôgarit có chứa tham số; đây là dạng toán thường gặp trong chương trình Toán 12 phần Giải tích chương 2.

41 21 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 6: Hàm số mũ và hàm số lôgarit (KNTT)

Môn: Toán 11

Thông tin:

16 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT-VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 1
TÌM TẬP XÁC ĐỊNH CỦA HÀM SỐ LŨY THỪA, HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT
CÓ CHỨA THAM SỐ
HÀM SỐ LŨY THỪA
PHƯƠNG PHÁP
1. Định nghĩa: Hàm số
y x
với
,
được gọi là hàm số lũy thừa.
2. Tập xác định
Tập xác định của hàm số
y x
là:
với
là số nguyên dương
\ 0
với
là số nguyên âm hoặc bằng 0.
0;

với
không nguyên.
3. Đạo hàm
Hàm số
y x
với
có đạo hàm với mọi
0
x
và
1
' .
x x
4. Tính chất của hàm số lũy thừa trên khoảng
0;

0
y x
0;x

Đồ thị hàm số luôn đi qua điểm
1;1
Khi
1
0 ' ' . 0
y x x
0;x

hàm số luôn đồng biến
Trong trường hợp này
0
lim ; lim 0
x
x
x x


do đó đồ thị hàm số không có đường tiệm cận
Khi
1
0 ' ' . 0
y x x
0;x

hàm số luôn nghịch biến
Trong trường hợp này
0
lim 0; lim
x
x
x x


do đó đồ thị hàm số nhận trục
Ox
là đường tiệm
cận ngang và trục
Oy
là đường tiệm cận đứng.
5. Đồ thị hàm số lũy thừa
a
y x
trên khoảng
0;

Đồ thị hàm số
y x
luôn đi qua điểm
1;1 .
I
Câu 1. Có bao nhiêu giá trị nguyên âm của tham số
m
để hàm số
2
3 2
2
y x mx x
xác định trên
miền
0;2022 .
A.
4
. B.
3
. C.
2
. D.
1
.
Lời giải
Chọn C
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT-VD_VDC
Trang 2 TÀI LIỆU ÔN THI THPT QUỐC GIA
Hàm số xác định trên miền
3 2
0;2022 2 0 0;2022
x mx x x
2
1
2 0;2022
m x x
x
.
Xét hàm số
2
1
2 0;2022
f x x x
x
Ta có
3
2
' 2 0 1
f x x
x
Ta có bảng biến thiên
Dựa vào bảng biến thiên ta có
3.
m
Do đó có 2 giá trị nguyên âm thỏa mãn.
Câu 2. Tìm tập hợp các giá trị thực của tham số
m
để hàm số
1
2
2
2 2
y x mx
xác định với mọi
x
?
A.
4;4
. B.
2;2
. C.
4;4
. D.
2;2
.
Lời giải
Chọn A
Hàm số
1
2
2
2 2
y x mx
xác định với mọi
x
2 2
2 2 0 16 0 4;4
x mx x m m
.
Câu 3. Có bao nhiêu giá trị
m
nguyên,
0;2021
m
sao cho hàm số
4 1
m
y x
đồng biến trên
; 2

?
A.
2021
. B.
1
. C.
2
. D.
2020
.
Lời giải
Chọn A
Ta có
4 2
4 1 .
m
y m x
.
Nhận thấy
4 2
0 ; 2
m
x x

.
Vậy hàm số đã cho đồng biến trên
; 2

1
4 1 0
4
m m
.
Vì
m
nguyên,
0;2021
m
. nên
1;2;...;2021
m
.
Vậy có 2021 giá trị.
Câu 4. Tìm tập hợp các giá trị thực của tham số
m
để hàm số
2
1
2
1
m
y x
nghịch biến trên khoảng
1;

.
A.
1;1
. B.
1;

. C.
1;1
. D.
2;2
.
Lời giải
Chọn A
Ta có
2
2
2 2
2 . 1 1
m
y x m x
.
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT-VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 3
Nhận thấy
2
2
2
2 . 1 0 1;
m
x x x

.
Vậy hàm số đã cho nghịch biến trên
1;

2
1 0 1;1
m m
.
Câu 5. Có bao nhiêu giá trị nguyên của
2021;2021
m
để hàm số
2021
4 3 2
2 3 2 2y x x m x m x m
có tập xác định là
D
.
A.
2022
. B.
2023
. C.
2019
. D.
2020
.
Lời giải
Chọn A
Để hàm số có tập xác định là
thì
4 3 2
2 3 2 2 0,x x m x m x m x
4 3 2 2
2 3 2 2 1 ,x x x x m x x x
4 3 2
2
2 3 2 2
,
1
x x x x
m x
x x
2
2
1
1 ,
1
m x x x
x x
Ta có:
2
2
1
1 2,
1
x x x
x x
.
2
2
1
1 2
1
x x
x x
khi
0; 1
x x
Vậy
2
m
, vì
2021;2021
m
2021 2
m
nên có
2022
giá trị.
Câu 6. Cho hàm số
2022
3 2
3
2021
15 78 141 5 2 9f x x x x m x m với
m
là tham số. Có bao
nhiêu số nguyên
m
thuộc đoạn
2020 ; 2020
để hàm số xác định trên đoạn
2 ; 4
?
A.
2020
. B.
2024
. C.
2021
. D.
2022
.
Lời giải
Chọn A
Hàm số xác định trên đoạn
2 ; 4
khi
3 2
3
15 78 141 5 2 9 0
x x x m x m
3 2
3
2 9 5 2 9 15 80 150
x m x m x x x
3 2
3
2 9 5 2 9 15 80 150
x m x m x x x
3
3
2 9 5 2 9 5 5 5
x m x m x x
3
3
3 3
2 9 5 2 9 5 5 5
x m x m x x
3
2 9 5
g x m g x
với
3
( ) 5
g t t t
.
Vì
g t
đồng biến trên
nên
3
3 3
2 9 5 2 9 5 5 2 9
g x m g x x m x m x x
.
Do đó,
3 2
3
15 78 141 5 2 9 0, 2 ; 4
x x x m x m x
khi và chỉ khi
2 ; 4
max
m h x
với
3
5 2 9
h x x x
.
Ta có
2
3 5 2
h x x
6 5 6 30 0, 2 ; 4
h x x x x
.
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT-VD_VDC
Trang 4 TÀI LIỆU ÔN THI THPT QUỐC GIA
h x
nghịch biến trên
2 ; 4
4 1 0, 2 ; 4
h x h x
.
h x
đồng biến trên
2 ; 4
Vì thế
2 ; 4
max 4 0
h x h
.
Vậy
0
m
nên số nguyên
m
thuộc đoạn
2020 ; 2020
thỏa mãn đề bài gồm
2020
số
nguyên.
Câu 7. Cho hàm số
3
2
2cos sin 5
cos 2
x m x
y
x
. Có bao nhiêu giá trị nguyên của tham số thuộc
đoạn
10;10
để hàm số có tập xác định là
?
A.
5
. B.
9
. C.
15
. D.
16
.
Lời giải
Chọn B
Hàm số có tập xác định là
khi
2cos sin 5
0, (1)
cos 2
x m x
x
x
Vì cos 2 0,x x
nên từ
1 2cos sin 5 0,x m x x
2
4 cos 5 0,m x x
Với
2 2
2
cos ;sin
4 4
m
m m
2
4 cos 5 0,m x x
khi
2 2
4 5 0 25 4
m m
21 21
m
Vậy có
9
giá trị nguyên của tham số
m
thỏa yêu cầu đề bài.
Câu 8. Gọi
S
là tập hợp các giá trị nguyên của tham số
m
để hàm số
2021
2 2 2
2 2f x m x m m x m xác định với mọi số thực
x
. Tổng các phần tử của
S
là
A.
1
3
. B.
0
. C.
2
. D.
2
3
.
Lời giải
Chọn C
Hàm số
2021
2 2 2
2 2f x m x m m x m xác định với mọi số thực
x
.
2 2 2
2 2 0,m x m m x m x
.
Trường hợp 1:
2 0 2
m m
. Khi đó
2 2 2
2 2 4 0,m x m m x m x
hàm số
xác định với mọi số thực
1
.
Trường hợp 2:
2 0 2
m m
.
Khi đó
f x
xác định với mọi
2
2 2
2
2 0
0
2 4 2 0
m
m
x
m m m m
.
m
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT-VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 5
2
4 3 2 3 2 4 2
2
2
2 2
4 0 2 2
4 4 4 8 0 4 0
0 0
2 2; 0
m
m
m m
m m
m m m m m m m
m m
m m
.
Do
1;1
m m
.
2
Từ
1
và
2
1;1; 2
S
.
Tổng các phần tử của
S
là
2
.
Câu 9. Tích của giá trị nguyên lớn nhất và giá trị nguyên nhỏ nhất của
m
để hàm số
2 2 2
1 8 9
f x m x mx m
xác định với mọi
0;x

bằng
A.
2
. B.
3
. C.
0
. D.
2
.
Lời giải
Chọn A
Hàm số
2 2 2
1 8 9
f x m x mx m
xác định với mọi
0;x

.
2 2 2
1 8 9 0, 0; 1
m x mx m x 
+)
2
1
1 0
1
m
m
m
Với
1
m
bất phương trình (1) có dạng
8 8 0 1
x x
. Do đó
1
m
không thoả mãn.
Với
1
m
bất phương trình (1) có dạng
8 8 0 1
x x
. Do đó
1
m
là một giá trị
thỏa
2 2 2
1 8 9 0, 0;m x mx m x
.
+)
2
1 0 1
m m
. Khi đó vế trái là tam thức bậc hai có
4 2
6 9 0
m m m
nên
tam thức luôn có 2 nghiệm
1 2
x x
.
Suy ra mọi
0;x

đều là nghiệm của bất phương trình
2 2 2
1 8 9 0
m x mx m
khi và
chỉ khi
2
2
1 2
2
1 2
2
1 2
2
1
1
1 0
0 1
1 0
8
0 3 1
1
1
0
9
3 1
0
1
1 3
m
m
m
m
m
m
x x m
m
m
x x
m
m
x x
m
m
.
Từ đó suy ra
3; 1
m
. Giá trị nguyên lớn nhất của
m
là
1
và giá trị nguyên nhỏ nhất của
m
là
2
. Tích của giá trị nguyên lớn nhất và giá trị nguyên nhỏ nhất của
m
là 2.
Câu 10. Trong
2004;2022
có bào nhiêu giá trị nguyên của tham số
m
để hàm số
2
(2 1) 1
y mx m x m
xác định
2;5
x
A.
2021
. B.
2022
. C.
2023
. D.
2020
.
Lời giải
Chọn A
Để hàm số
2
(2 1) 1
y mx m x m
xác định
2;5
x
thì
2
(2 1) 1 0, 2;5
mx m x m x
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT-VD_VDC
Trang 6 TÀI LIỆU ÔN THI THPT QUỐC GIA
Trường hợp 1:
0
m
Ta có
1 0 1
x x
nên
0
m
không thỏa yêu cầu bài toán.
Trường hợp 2:
0
m
Vì
2
(2 1) 4 ( 1) 1 0
m m m
nên phương trình luôn có 2 nghiệm
1 2
2 1 1 1 1 2 1 1
1 ; 1
2 2
m m m
x x
m m m m
Nếu
0
m
thì
1
1 1
m
, YCBT
1 1
1 2 1 1
m
m m
.
Nếu
0
m
thì
1
1 1
m
nên
2
1
(2 1) 1 0 ;1
m
mx m x m x
m
không thỏa yêu cầu
bài toán.
Vậy
1
m
thì hàm số xác định
2;5
x
. Mà
2004;2022
m
và
m
nên có 2021 số
nguyên
m
thỏa bài toán.
HÀM SỐ MŨ
PHƯƠNG PHÁP
1. Định nghĩa: Cho số thực dương
1
a
. Hàm số
x
y a
được gọi là hàm số mũ cơ số
.
a
2. Tập xác định:
( )
P x
y a
xác định khi
( )
P x
xác định. Đối với
y a
thì có
.
D
Tập giá trị của hàm số mũ là
(0; ).
T
3. Đạo hàm:
( ) .ln
( ) .ln . ( ) .
( ) .
x x
u u x x
u u
a a a
a a a u e e
e u e
Công thức thừa nhận
0
1
lim 1.
t
t
e
t
4. Đồ thị hàm số mũ:
x
y a
Đồ thị hàm số nhận trục hoành làm tiệm ngang.
Đồ thị hàm số đi qua điểm
(0;1)
và
(1; ),
a
nằm về phía bên trên trục hoành
( )
x
y a x
.
Câu 11. Có bao nhiêu giá trị nguyên của
0;2022
m
để hàm số
3 2
1
2021
x x mx
y
nghịch biến trên
1;2
.
A.
2021
. B.
2015
. C.
2020
. D.
2014
.
Lời giải
Chọn B
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT-VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 7
3 2
2 1
' 3 2 .2021 .ln 2021
x x mx
y x x m
Hàm số nghịch biến trên
1;2
' 0 1;2
y x
2
3 2 0 1;2
x x m x
2
3 2 1;2x x m x
Đặt
2
( ) 3 2f x x x
; '( ) 6 2f x x .
Bảng biến thiên:
Từ bảng biến thiên suy ra
( ) 8 1;2
f x x
.
Do đó ycbt 8m .
Vì
m
nguyên và
0;2022m
nên có 2015 giá trị
m
thỏa mãn.
Câu 12. Số giá trị nguyên của tham số
m
thuộc đoạn
2020;2021
sao cho hàm số
4
2
1
x
x m
y
e
nghịch biến trên khoảng
0;2
là
A. 2021. B. 2022 . C. 2020 . D. 2019 .
Lời giải
Chọn B
Ta có:
4 4
2 2
1 4 1 1
. .ln
2
x x
x m x m
x
y y
e x m e e
.
Để hàm số nghịch biến trên khoảng
0;2
thì
' 0, 0;2y x
4
2
0
0, 0;2
4 1 1
. .ln 0, 0;2
2
x
x m
x
x
x
x m e e
4
0, 0;2
2
x
x
x m
2
2 4
0, 0;2
2
m
x
x m
2 2
2 4 0 1 2
2 0 0
2 0
2 2 1
m m
m m
m m
x m m
m m
.
Mặt khác,
2020;2021m
2020;0 1;2m
.
Vì
1;0; 1; 2;...; 2020
m m
. Có 2022 giá trị nguyên của
m
.
Câu 13. Có bao nhiêu giá trị nguyên của tham số
m
thuộc đoạn
10;10
để hàm số
2 3 2
1
2 3
3
e
m m x mx x
y
đồng biến trên
?
A. 21. B.
19
. C.
20
. D.
18
.
Lời giải
Chọn B
Ta có
2 3 2
1
2 3
2 2
3
2 2 3 e
m m x mx x
y m m x mx
.
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT-VD_VDC
Trang 8 TÀI LIỆU ÔN THI THPT QUỐC GIA
Hàm số đồng biến trên
2 2
2 2 3 0,g x m m x mx x
.
• Nếu
0m
, ta có
3 0,g x x
nên
0m
thỏa mãn.
• Nếu
2m
, hàm số
4 3g x x
. Bảng xét dấu
Suy ra
3
0
4
g x x
nên
2m
không thỏa mãn.
• Với
0
2
m
m
. Ta có
2
2 2
0
2 0
2
0
0,
3
3 2 0
0
3
m
m m
m
m
g x x
m
m m m
m
m
.
Do đó
10, 9, 1,0 3,4,5, 9,10m
. Vậy có
19
giá trị
m
thỏa mãn yêu cầu bài
toán.
Câu 14. Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
3 2 2
1
6 2022
3 2
2
m
x x m x
y
đồng biến trên
khoảng
2;3
?
A. 1. B. 2 . C. vô số. D.
0
.
Lời giải
Chọn B
Ta có
3 2 2
1
6 2022
2 2
3 2
6 2 ln 2
m
x x m x
y x mx m
.
+Hàm số đồng biến trên
2 2 2
6 0, 0 25 0 0g x x mx m x m m
+ Phương trình
2 2
2
0 6 0
3 .
x m
g x x mx m
x m
.
Ta xét các trường hợp:
TH1:
2 3 0m m m
. Khi đó
2
0
g x x
,
x
. Do đó nhận
0m
.
TH2:
2 3 0m m m
. Ta có bảng biến thiên
Từ bảng biến thiên, suy ra hàm số đồng biến trên
; 3m
và
2 ;m
.
Hàm số đã cho đồng biến trên khoảng
2;3
khi
2;3 ; 3
3 3 1
1.
2 2 1
2;3 2 ;
m
m m
m
m m
m


So với điều kiện, ta nhận
0 1m
.
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT-VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 9
TH3:
2 3 0m m m
. Ta có bảng biến thiên
Từ bảng biến thiên, suy ra hàm số đồng biến trên
;2
m

và
3 ;m
.
Hàm số đã cho đồng biến trên khoảng
2;3
khi
3
2;3 ;2
2 3
2
2
.
2
3 2
3
2;3 3 ;
3
m
m
m
m
m
m
m

So với điều kiện, ta nhận
2
0
3
m
.
Vậy
2
1
3
m
thỏa yêu cầu bài toán.
Do
m
nên
0;1
m
.
Câu 15. Gọi
S
là tập hợp các giá trị nguyên dương của
m
để hàm số
3 2
3 2 1 12 5 2
10
x m x m x
y
đồng
biến trên khoảng
2;
. Số phần tử của
S
bằng
A.
1
. B.
2
. C. 3 . D. 0 .
Lời giải
Chọn D
Ta có
3 2
3 2 1 12 5 2
2
3 6 2 1 12 5 10 ln10
x m x m x
y x m x m
.
Hàm số đồng biến trên
2;
khi
2
2
2
0 2;
3 6 2 1 12 5 0 2;
12 1 3 6 5 2;
3 6 5
2 1 1 0 .
12 12
y x
x m x m x
m x x x x
x x
m x x
x



Đặt
2
3 6 5
2;
12 12
x x
g x x
x

.
Ta có
2
2
36 72 12
12 12
x x
g x
x
.
2
3 6
1. loai
3
0 36 72 12 0
3 6
loai
3
x
g x x x
x
Ta có bảng biến thiên
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT-VD_VDC
Trang 10 TÀI LIỆU ÔN THI THPT QUỐC GIA
Từ bảng biến thiên suy ra
5
12
m
Mà
m
nên không có giá trị
m
thoả mãn.
HÀM SỐ LÔGARIT
1. Định nghĩa
- Hàm số dạng log ,( 0; 1)
a
y x a a được gọi là hàm số logarit cơ số
a
.
2. Tập xác định và tập giá trị
- Tập xác định:
(0; )D 
- Tập giá trị: T
.
3. Tính đơn điệu và đồ thị
- Khi 1a thì hàm số log
a
y x đồng biến trên
D
,
khi đó nếu log ( ) log ( ) ( ) ( )
a a
f x g x f x g x
- Khi
0 1a
thì hàm số log
a
y x nghịch biến trên D ,
khi đó nếu: log ( ) log ( ) ( ) ( )
a a
f x g x f x g x
Câu 16. Có bao nhiêu giá trị nguyên của
m
thuộc khoảng ( 2019;2019) để hàm số
2 2 2
2
2( 1) 2 4 log 2 1y x m x m x m m x m x
có tập xác định là D
.
A.
2020
. B.
2021
. C.
2018
. D.
2019
.
Lời giải
Chọn D
Hàm số xác định với mọi x
thì
2 2
2
2( 1) 2 4 0
2 1 0
x m x m m
x m x
luôn đúng với mọi x
Ta có:
2
2 2
2( 1) 2 4 1 3 0,x m x m m x m x
Ta có:
2 2
2 1 0, 2 1 ,x m x x x x m x
.
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT-VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 11
Xét hàm số
2
( ) 2 1f x x x với
x
có
2
2 1
( ) 1 ; ( ) 0
2
2 1
x
f x f x x
x
.
Từ bảng biến thiên ta thấy để
2
2
2 1 ,
2
x x m x m
. Kết hợp điều kiện
{ 2018, 2017, 2016, , 1,0}
( 2019;2019)
m
m
m
.
Kết luận: có 2019 giá trị của
m
thỏa mãn bài toán.
Câu 17. Tìm tất cả các giá trị của
m
để hàm số
2
ln 2 1y x mx m
xác định với mọi
1;2x
.
A.
1
3
m
. B.
3
4
m
. C.
3
4
m
. D.
1
3
m
.
Lời giải
Chọn B
Hàm số xác định với mọi
1;2x
khi
2
2 1 0, 1; 2x mx m x
.
2
2 1 0, 1;2f x x mx m x
.
0f x
có 2 nghiệm thỏa mãn
1 2
1 2x x .
1 0
3 0
3
4 3 0
4
2 0
f
m
m
m
f
Câu 18. Tìm tất cả các giá trị của
m
để hàm số
2
2021
log 2021
2
x
x
y x m
xác định với mọi giá trị
x
thuộc
0;
A.
9m
. B.
1m
. C.
0 1m
. D.
2m
.
Lời giải
Chọn B
Hàm số đã cho xác định
0;x
2
2021 0, 0;
2
x
x
x m x 
2
2021 , 0;
2
x
x
x m x  .
YCBT
0;
min
x
m f x

.
Đặt
2
2021 , 0;
2
x
x
f x x x 
2021 ln 2021 1
x
f x x
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT-VD_VDC
Trang 12 TÀI LIỆU ÔN THI THPT QUỐC GIA
2
2021 ln 2021 1 0, 0;
x
f x x

Khi đó
f x
đồng biến trên
0;x

và
0 ln 2021 1 0
f
Suy ra
f x
đồng biến trên
0;x

và
0 1
f
Vậy
1
m
thì thỏa YCBT.
Câu 19. Tập hợp tất cả các giá trị của tham số
m
để hàm số
2 2
2022
3 5
log 2 4 5
x
y
x x m m
xác
định với mọi
x
là
A.
;1 3;
 
. B.
(1;3) \ 2
. C.
;1

. D.
1;3 \ 2
.
Lời giải
Chọn A
Xét hàm số
2 2
2022
3 5
log 2 4 5
x
y
x x m m
ĐKXĐ:
2 2
2 2
2 2
2 2
2022
2 4 5 0
2 4 5 0
log 2 4 5 0
2 4 5 1
x x m m
x x m m
x x m m
x x m m
.
Nên điều kiện để hàm số xác định với mọi
x
là
2 2
2 2
2 4 5 0
2 4 4 0
x x m m
x x m m
với
x
.
Điều này xảy ra khi và chỉ khi :
2
1
2
2
1 4 5 0
1 4 4 0
m m
m m
2
2
4 4 0
4 3 0
m m
m m
2
2
2
1
4 3 0
3
m
m
m
m m
m
.
Vậy
;1 3; \ 2
m 
.
Câu 20. Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số
2
ln 2 4
y x mx
xác định với
mọi
x
?
A.
2.
B.
3.
C.
4.
D.
5.
Lời giải
Chọn B
Hàm số xác định
2
2 4 0, x x mx x
.
2
1 0
0
2 2
0
4 16 0
a
m
m
.
Do
m
nên
1;0;1
m
.
Câu 21. Có tất cả bao nhiêu giá trị nguyên của tham số m nằm trong khoảng
2021; 2021
để hàm số
2
2
log 2 2 2 3
y m x m x m
có tập xác định
D
.
A.
2020.
B.
1010
C.
2023
D.
4046
Lời giải
Chọn C
Hàm số xác định trên
2
2 2 2 3 0,m x m x m x
(*).
Trường hợp 1:
2 0 2
m m
, ta có
(*) 1 0, x
(đúng), suy ra
2
m
thỏa mãn.
Trường hợp 2:
2
m
.
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT-VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 13
(*)
2
2 0
2
2
2 0
4 2 4 2 3 0
a m
m
m
m
m m m
.
Vậy với
2
m
thì hàm số có tập xác định
D
.
Suy ra có
2023
giá trị nguyên của tham số m nằm trong khoảng
2021; 2021
thỏa mãn.
Câu 22. Có tất cả bao nhiêu giá trị nguyên của tham số
m
để hàm số
5
3
log 2 1
y m x
x m
xác
định trên khoảng
2;3
?
A.
1.
B.
2.
C.
3.
D.
4.
Lời giải
Chọn B
Hàm số xác định
0
2 1 0 2 1
x m x m
m x x m
.
Xét các trường hợp sau:
+) Nếu 2 1 1m m m D
, suy ra không thỏa mãn.
+) Nếu
2 1 1 ;2 1
m m m D m m
Hàm số đã cho xác định trên khoảng
2;3
khi và chỉ khi
2;3
D
2
2 3 2 1 1 2
1
m
m m m
m
.
Vì
m
nguyên nên
1;2
m
.
Câu 23. Tìm tất cả giá trị thực của tham số
m
để hàm số
2
3
log ( 1)
y x m x m
xác định trên
1;4
.
A.
3
1
4
m
. B.
1
m
. C.
1
m
. D.
3
4
m
.
Lời giải
Chọn B
Để hàm số
2
3
log ( 1)
y x m x m
xác định trên
1;4
thì
2
( 1) 0, x 1;4 ( 1)( ) 0, x 1;4
x m x m x x m
.
Do
1 4
x
nên có các trường hợp sau \
TH1:
1
1
1
x
m
x m
vậy hàm số xác định trên
1;4
.
TH2:
1
m
thì
2
( 1) 0 1
x x
vậy hàm số xác định trên
1;4
.
TH3:
1
1
1
x
m
x m
như vậy hàm số không xác định trên
1;4
(loại).
Kết luận:
1
m
.
Câu 24. Tìm tổng tất cả giá trị nguyên của tham số
2;8
m
để hàm số
4 2
2
log
y x x m
xác
định trên
.
A.
36
. B.
35
. C.
28
. D.
21
.
Lời giải
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT-VD_VDC
Trang 14 TÀI LIỆU ÔN THI THPT QUỐC GIA
Chọn A
Hàm số xác định trên
khi
4 2 4 2
0, ,x x m x x x m x
.
Xét hàm số
4 2
,y x x x
có
3
0
1
4 2 0
2
1
2
x
y x x x
x
.
Ta có bảng biến thiên
Vậy để hàm số xác định trên
thì
1 1
( ) , in ( ) m
4 4
f x m x M f x m m
.
Vậy tổng tất cả các giá trị nguyên của
2;8
m
là:
1 2 3 4 5 6 7 8 36
.
Câu 25. Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
5
1
log 3 1
7 5
x m
m x
y
xác định trên
1;3
.
A.
0
. B.
1
. C.
2
. D.
4
.
Lời giải
Chọn A
Để hàm số xác định ta có .
7 5
3 1
x m
x m
TH1:
3 1 7 5 1
m m m
TXĐ của hàm số là
D
(loại).
TH2:
3 1 7 5 1
m m m
TXĐ của hàm số là
3 1;7 5
D m m
.
Để hàm số xác định trên
1;3
thì
1;3
D
1;3 3 1;7 5
m m
3 1 1 3 7 5
m m
0
8
7
m
m
(vô nghiệm).
Vậy không có giá trị nào của
m
để hàm số xác định trên
1;3
.
Câu 26. Có bao nhiêu số nguyên dương
m
để hàm số
3 2
( ) ln 3 32
f x x m x m
xác định trên khoảng
0;

?
A. 3. B. 4. C. 6. D. 5.
Lời giải
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT-VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 15
Chọn A
Cách 1: Cô lập thông thường
Hàm số
3 2
( ) ln 3 32
f x x m x m
xác định trên khoảng
0;

3 2
3 32 0
x m x m
,
0
x
Xét
3 2
3 32
g x x m x m
,
2 2
3 3
g x x m
,
0
x m
g x
x m
Vì
m
nguyên dương nên ta có bảng biến thiên sau
Suy ra
0, 0
g x x
3
4
2 32 0
0 4
m
m m
m
Vì
m
nguyên dương nên
1,2,3
m
. Vậy có 3 số nguyên dương
m
.
Cách 2: Sử dụng bất đẳng thức
Ta có điều kiện xác định của hàm số trên là:
3 2
3 32 0
x m x m
trên khoảng
0;

2 3 2 2 2
32 16 16
3 32 3
m m m
m x x m m x x g x
x x x
Để hàm số
f x
xác định trên khoảng
0;

thì
2
3 min
m g x
Mà
3
2 2
2
3
16 16 16 16
3 .. 3 16
m m m m
g x x x m
x x x x
nên suy ra
2
2
3
2 3
4
3
0
3 16 16 4 0
4
m
m
m
m m m m m
Vì
m
nguyên dương nên
1,2,3
m
. Vậy có 3 số nguyên dương
m
.
Ghi chú: Do hàm số trên xác định trên khoảng
0;

nên nó chính là dấu hiệu rõ cho việc sử
dụng bất đẳng thức Cosi.
Câu 27. Cho hàm số
2
12
log 2
x x m
f x
. Có bao nhiêu giá trị nguyên của tham số
100;100
m
thỏa mãn hàm số đã cho nghịch biến trên
6;

?
A. 64. B. 65. C. 36. D. 0.
Lời giải
Chọn A
Ta có:
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT-VD_VDC
Trang 16 TÀI LIỆU ÔN THI THPT QUỐC GIA
2
2
2
12
2 2
2
2
1 12 2
log 2
log 12
log 12 . 12 ln 2
x x m
x
f x f x
x x m
x x m x x m
Do đó để hàm số đã cho nghịch biến trên
6;

thì
2
12 0 6;x x m x
2
6;
max 12 36
m x x

Ngoài ra ta còn một điều kiện nữa rất dễ sót đó chính là
2
2
log 12 0 6;x x m x

2
2
2
1 12 6;
1 12 6; 37
1 12 6;
m x x x
m x x x m
m x x x


.
Như vậy có tất cả 64 giá trị nguyên
m
thỏa mãn bài toán.
_______________ TOANMATH.com _______________
| 1/16
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT-VD_VDC
TÌM TẬP XÁC ĐỊNH CỦA HÀM SỐ LŨY THỪA, HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT CÓ CHỨA THAM SỐ HÀM SỐ LŨY THỪA PHƯƠNG PHÁP
1. Định nghĩa: Hàm số y x  với   ,
 được gọi là hàm số lũy thừa. 2. Tập xác định
Tập xác định của hàm số y x  là:
  với  là số nguyên dương   \ 
0 với  là số nguyên âm hoặc bằng 0.
 0; với  không nguyên. 3. Đạo hàm Hàm số y x 
với    có đạo hàm với mọi x  0 và x   1 ' .x  
4. Tính chất của hàm số lũy thừa trên khoảng 0;  y x 
 0 x 0;
 Đồ thị hàm số luôn đi qua điểm 1;  1  Khi  y x   1 0 ' ' .x     
 0 x 0; hàm số luôn đồng biến
Trong trường hợp này lim x  ; lim x  0 do đó đồ thị hàm số không có đường tiệm cận x x 0    Khi  y x   1 0 ' ' .x     
 0 x 0; hàm số luôn nghịch biến
Trong trường hợp này lim x  0; lim x   do đó đồ thị hàm số nhận trục Ox là đường tiệm x x 0  
cận ngang và trục Oy là đường tiệm cận đứng.
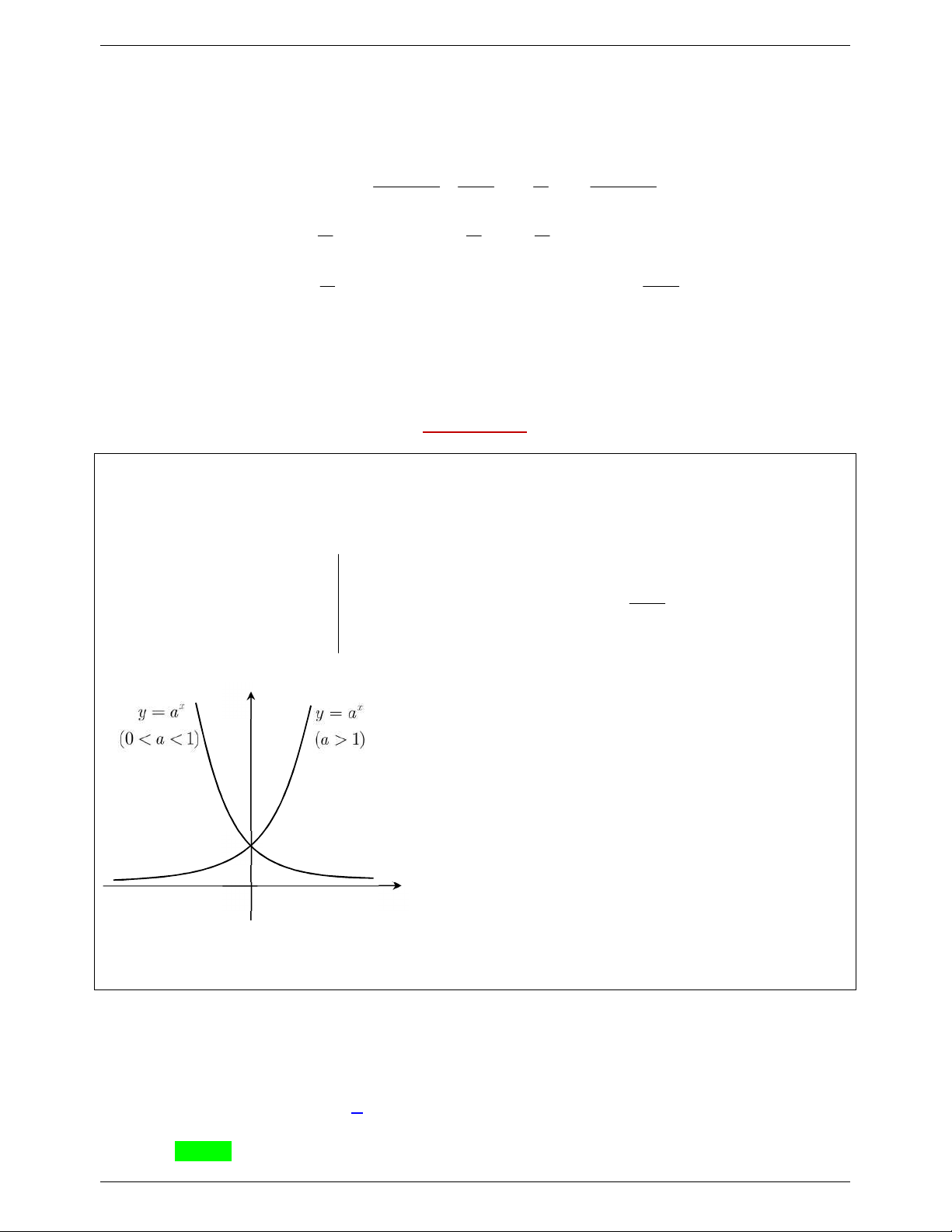
5. Đồ thị hàm số lũy thừa a
y  x trên khoảng 0; Đồ thị hàm số y x 
luôn đi qua điểm I 1;  1 .
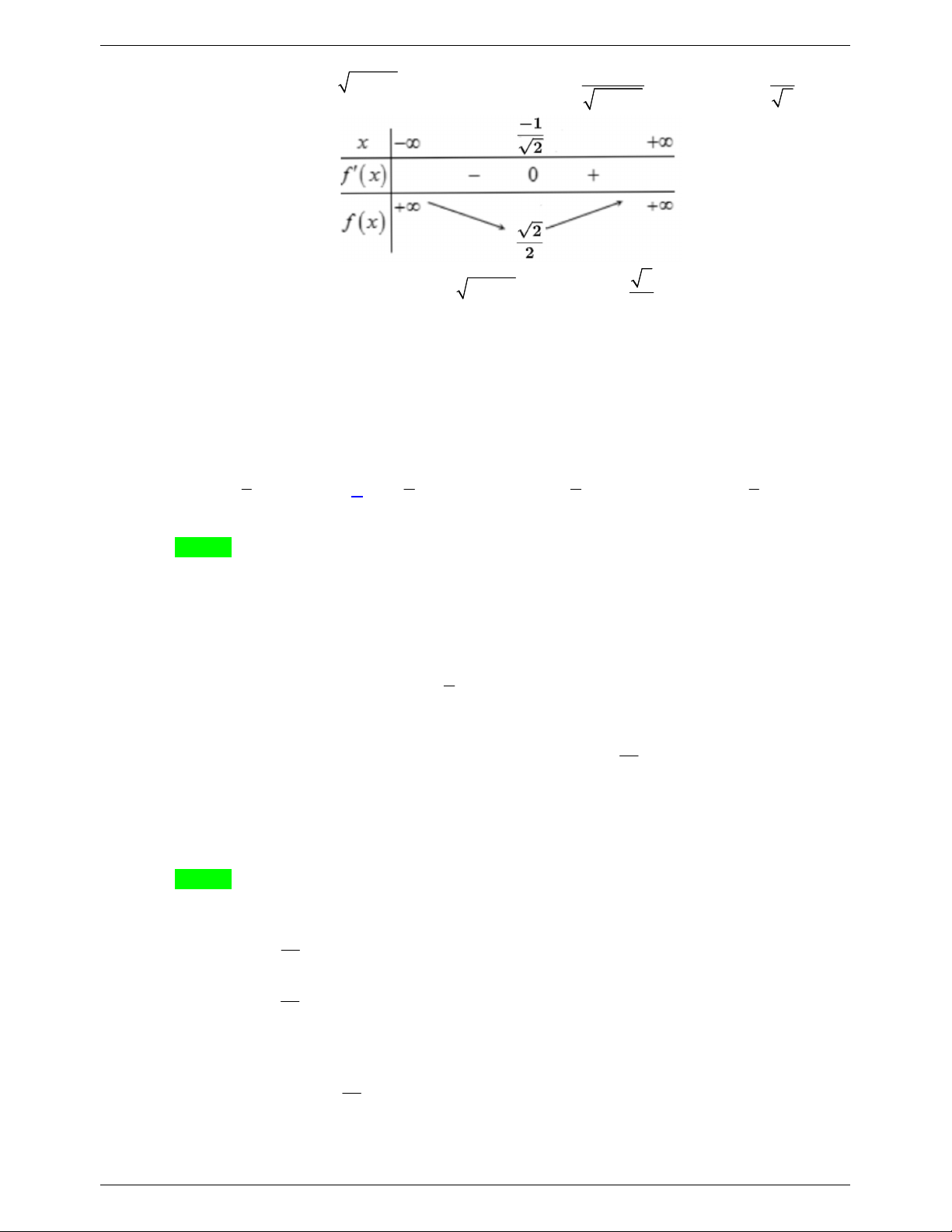
Câu 1. Có bao nhiêu giá trị nguyên âm của tham số m để hàm số y   x  mx  x 2 3 2 2 xác định trên miền 0;2022. A. 4 . B. 3. C. 2 . D. 1. Lời giải Chọn C
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 1
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT-VD_VDC
Hàm số xác định trên miền   3 2
0; 2022  2x  mx  x  0 x  0;2022 1  m  2  x  x   0;2022 . 2   x 1
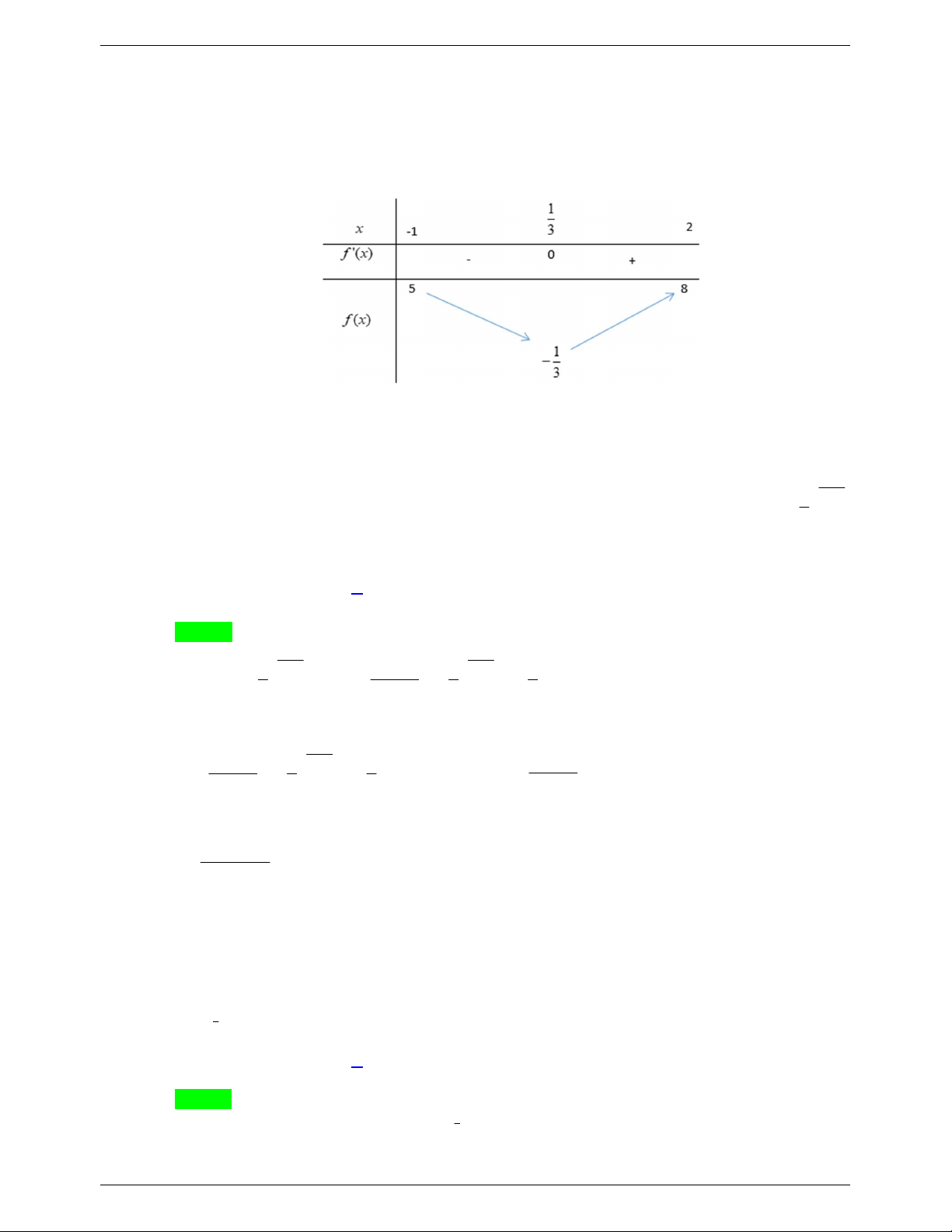
Xét hàm số f  x  2  x  x   0;2022 2   x 2 Ta có f ' x  2    0  x 1 3 x Ta có bảng biến thiên
Dựa vào bảng biến thiên ta có m  3. Do đó có 2 giá trị nguyên âm thỏa mãn. Câu 2.
Tìm tập hợp các giá trị thực của tham số m để hàm số y   x  mx  1 2 2 2 2 xác định với mọi x   ? A. 4;4 . B. 2;2 . C. 4; 4. D. 2;2. Lời giải Chọn A
Hàm số y   x  mx  1 2 2 2
2 xác định với mọi x   2 2
2x  mx  2  0 x    m 16  0  m  4; 4 .
Câu 3. Có bao nhiêu giá trị m nguyên, m  0;202  1 sao cho hàm số 4m 1 y x   đồng biến trên ; 2? A. 2021. B. 1. C. 2 . D. 2020 . Lời giải Chọn A Ta có   4 2 4 1 . m y m x     . Nhận thấy 4m2 x
 0 x ; 2 . 1
Vậy hàm số đã cho đồng biến trên ; 2  4m 1  0  m  . 4
Vì m nguyên, m  0;202 
1 . nên m 1; 2;...; 202  1 . Vậy có 2021 giá trị. 
Câu 4. Tìm tập hợp các giá trị thực của tham số m
m để hàm số y  x   2 1 2 1
nghịch biến trên khoảng 1;. A. 1;  1 . B. 1; . C. 1;  1 . D. 2;2 . Lời giải Chọn A 
Ta có y  x m  x   2m 2 2 2 2 . 1 1 . Trang 2
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT-VD_VDC 2 m 2 Nhận thấy x  2 2 . x   1
 0 x 1; .
Vậy hàm số đã cho nghịch biến trên 1; 2
 m 1  0  m 1;  1 .
Câu 5. Có bao nhiêu giá trị nguyên của m  2021;202  1 để hàm số
y  x  x    m x  m   x  m   2021 4 3 2 2 3 2 2
có tập xác định là D   . A. 2022 . B. 2023. C. 2019 . D. 2020 . Lời giải Chọn A
Để hàm số có tập xác định là  thì 4 3 x  x    m 2 2 3
x  m  2 x  m  2  0,x   4 3 2
 x  x  x  x   m 2 2 3 2 2 x  x   1 , x   4 3 2 x  2x  3x  2x  2  m  , x    2 x  x 1 1 2  m  x  x 1 , x    2 x  x 1 1 1 Ta có: 2 x  x 1  2, x   . 2 x  x 1  2 khi x  0; x 1 2 x  x 1 2 x  x 1
Vậy m  2 , vì m  2021; 202 
1  2021  m  2 nên có 2022 giá trị. Câu 6.
Cho hàm số f  x  x  x  x   m  x   m 2022 3 2 3 2021 15 78 141 5 2 9
với m là tham số. Có bao
nhiêu số nguyên m thuộc đoạn 2020 ; 2020 để hàm số xác định trên đoạn 2 ; 4? A. 2020 . B. 2024 . C. 2021. D. 2022 . Lời giải Chọn A
Hàm số xác định trên đoạn 2 ; 4 khi 3 2 3
x 15x  78x 141 m  5 2x  9  m  0 3 3 2
 2x  9  m  5 2x  9  m  x 15x  80x 150 3 3 2
 2x  9  m  5 2x  9  m  x 15x  80x 150  x   m  x   m   x  3 3 2 9 5 2 9 5  5x  5   x   m3  x   m   x  3 3 3 2 9 5 2 9 5  5 x  5
 g  3 2x 9 m  g x 5 với 3 g(t)  t  5t .
Vì g t đồng biến trên  nên
g  x   m  g x   
x   m  x   m   x  3 3 3 2 9 5 2 9 5 5  2x  9 . Do đó, 3 2 3
x 15x  78x 141 m  5 2x  9  m  0, x
 2 ; 4 khi và chỉ khi m  max hx 2; 4
với h x   x  3 5  2x  9 .
Ta có h x   x  2 3 5  2
 h x  6 x  5  6x  30  0,x 2 ; 4.
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 3
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT-VD_VDC
 hx nghịch biến trên 2 ; 4
 h x  h4 1  0,x 2 ; 4 .
 hx đồng biến trên 2 ; 4
Vì thế max h x  h4  0 . 2; 4
Vậy m  0 nên số nguyên m thuộc đoạn 2020 ; 2020 thỏa mãn đề bài gồm 2020 số nguyên. 3 2
 2cos x  msin x  5 
Câu 7. Cho hàm số y  
 . Có bao nhiêu giá trị nguyên của tham số m thuộc  cos x  2 
đoạn 10;10 để hàm số có tập xác định là  ? A. 5 . B. 9 . C. 15. D.16 . Lời giải Chọn B 2cos x  msin x  5
Hàm số có tập xác định là  khi  0, x    (1) cos x  2 Vì cos x  2  0, x   nên từ  
1  2 cos x  m sin x  5  0,x   2
 4  m cos  x    5  0,x   2 m Với cos  ;sin  2 2 4  m 4  m 2
 4  m cos x     5  0,x   khi 2 2
 4  m  5  0  25  4  m   21  m  21
Vậy có 9 giá trị nguyên của tham số m thỏa yêu cầu đề bài. Câu 8. Gọi
S là tập hợp các giá trị nguyên của tham số m để hàm số
f  x    m x m  m x  m  2021 2 2 2 2 2
xác định với mọi số thực x . Tổng các phần tử của S là 1 2 A. . B. 0 . C. 2 . D. . 3 3 Lời giải Chọn C
Hàm số f  x    m x m  m x  m  2021 2 2 2 2 2
xác định với mọi số thực x .    m 2 x   2 m  m 2 2 2 x  m  0, x   .
Trường hợp 1: 2  m  0  m  2 . Khi đó   m 2 x   2 m  m 2 2 2 x  m  4  0, x   hàm số
xác định với mọi số thực   1 .
Trường hợp 2: 2  m  0  m  2 .    m  2 2 m 0 
Khi đó f  x xác định với mọi x       .   0 m  2m2 2 2  4m m  2  0 Trang 4
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT-VD_VDC m  2 m  2 m  2 m  2   2    
 m  4  0  2  m  2 4 3 2 3 2 4 2
m  4m  4m  4m 8m  0 m  4m  0  . m 0   m  0    2  m  2;m  0
Do m    m 1;  1 . 2 Từ  
1 và 2  S  1;1;  2 .
Tổng các phần tử của S là 2 .
Câu 9. Tích của giá trị nguyên lớn nhất và giá trị nguyên nhỏ nhất của m để hàm số f  x   2 m   2 2
1 x  8mx  9  m xác định với mọi x 0; bằng A. 2 . B. 3 . C. 0 . D. 2  . Lời giải Chọn A Hàm số f  x   2 m   2 2
1 x 8mx  9  m xác định với mọi x 0; .   2 m   2 2
1 x 8mx  9  m  0, x  0;  1 m  1 +) 2 m 1  0   m  1
Với m  1 bất phương trình (1) có dạng 8x  8  0  x  1. Do đó m  1 không thoả mãn.
Với m  1 bất phương trình (1) có dạng 8x  8  0  x  1. Do đó m  1 là một giá trị thỏa  2 m   2 2
1 x  8mx  9  m  0, x  0; . +) 2 m 1  0  m  1
 . Khi đó vế trái là tam thức bậc hai có 4 2
  m  6m  9  0 m  nên
tam thức luôn có 2 nghiệm x  x . 1 2
Suy ra mọi x 0; đều là nghiệm của bất phương trình  2 m   2 2
1 x  8mx  9  m  0 khi và m 1   2    m  1 m 1 0   2 m 1  0  8m 0  m 1 chỉ khi   x  x   0    3   m  1  . 1 2 2  x  x  0 m 1   m  1  1 2 2  9  m 3  m  1 x x   0  1 2 2   m 1  1    m  3
Từ đó suy ra m  3; 
1 . Giá trị nguyên lớn nhất của m là 1
 và giá trị nguyên nhỏ nhất của m là 2
 . Tích của giá trị nguyên lớn nhất và giá trị nguyên nhỏ nhất của m là 2.
Câu 10. Trong 2004;2022 có bào nhiêu giá trị nguyên của tham số m để hàm số  y   2
mx  (2m 1)x  m  
1 xác định x  2;5 A. 2021. B. 2022 . C. 2023. D. 2020 . Lời giải Chọn A  Để hàm số y   2
mx  (2m 1)x  m  
1 xác định x  2;5 thì 2
mx  (2m 1)x  m 1  0,x  2;5
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 5
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT-VD_VDC
 Trường hợp 1: m  0
Ta có x 1  0  x  1 nên m  0 không thỏa yêu cầu bài toán.
 Trường hợp 2: m  0 Vì 2
  (2m 1)  4m(m 1)  1  0 nên phương trình luôn có 2 nghiệm 2m 11 m 1 1 2m 11 x   1 ; x  1 1 2 2m m m 2m 1 1 1  Nếu m  0 thì 1 1, YCBT  1  2  1  m 1. m m m 1  m 1   Nếu m  0 thì 1 1 nên 2
mx  (2m 1)x  m 1  0  x  ;1   không thỏa yêu cầu m  m  bài toán.
Vậy m  1 thì hàm số xác định x  2;5 . Mà m 2004;2022 và m   nên có 2021 số nguyên m thỏa bài toán. HÀM SỐ MŨ PHƯƠNG PHÁP
1. Định nghĩa: Cho số thực dương a  1. Hàm số x
y  a được gọi là hàm số mũ cơ số a. 2. Tập xác định: P( x) y  a
xác định khi P(x) xác định. Đối với y a  thì có D  .
Tập giá trị của hàm số mũ là T  (0; ). ( x a ) x  a .ln a t e 1 3. Đạo hàm: ( u a ) u   a .ln . a u  ( x e ) x  e
. Công thức thừa nhận lim 1. t0 t ( u e ) u . u  e 4. Đồ thị hàm số mũ: x y  a
 Đồ thị hàm số nhận trục hoành làm tiệm ngang.
 Đồ thị hàm số đi qua điểm (0;1) và (1;a), nằm về phía bên trên trục hoành ( x y  a x   ) .
Câu 11. Có bao nhiêu giá trị nguyên của m 0;2022 để hàm số 3 2 1 2021x x mx y     nghịch biến trên 1;2. A. 2021. B. 2015 . C. 2020 . D. 2014 . Lời giải Chọn B Trang 6
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT-VD_VDC y  x x m 3 2 2 x x mx 1 ' 3 2 .2021     .ln 2021
Hàm số nghịch biến trên  1
 ;2  y '  0 x 1;2 2
 3x  2x  m  0 x 1;2 2
 3x  2x  m x 1;2 Đặt 2
f (x)  3x  2x ; f '(x)  6x  2 . Bảng biến thiên:
Từ bảng biến thiên suy ra f (x)  8 x 1;2 . Do đó ycbt  m  8 .
Vì m nguyên và m 0;2022 nên có 2015 giá trị m thỏa mãn. x4 x2  1 m 
Câu 12. Số giá trị nguyên của tham số m thuộc đoạn 2020;202 
1 sao cho hàm số y     e 
nghịch biến trên khoảng 0;2 là A. 2021 . B. 2022 . C. 2020 . D. 2019 . Lời giải Chọn B x4 x4  x2m x     2 1 4   1 m x   1  Ta có: y   y  . .ln         .  e   x  2m   e   e 
Để hàm số nghịch biến trên khoảng 0;2 thì y '  0,x 0;2 x4   x   2 x 4   1 m   1   x  4   . .ln  0,x        0;2   0, x     0;2  x  2m   e   e      x  2m  0, x    0;2 0 m  2 m  2 2  m  4           2m 4 0 1 m 2 0, x   0;2  
 2m  0  m  0  . 2     x  2m x  2m   m  0 2m  2 m  1
Mặt khác, m 2020;202 
1  m 2020;01;2 .
Vì m    m 1;0;1;2;...;202 
0 . Có 2022 giá trị nguyên của m .
Câu 13. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn 10;10 để hàm số 1 2 m 2m 3 2 x mx 3x 3 y  e đồng biến trên  ? A. 21. B. 19 . C. 20 . D. 18 . Lời giải Chọn B 1 2 3 2 m 2m x mx 3x Ta có y   2 m  m 2   3 2 x  2mx  3  e  .
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 7
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT-VD_VDC
Hàm số đồng biến trên   g  x   2 m  m 2 2 x  2mx  3  0, x   .
• Nếu m  0 , ta có g  x  3  0,x   nên m  0 thỏa mãn.
• Nếu m  2 , hàm số g  x  4x  3. Bảng xét dấu Suy ra g  x 3
 0  x  nên m  2 không thỏa mãn. 4 m  0 • Với  . Ta có m  2 m  0 2          g  x m 2m 0 m 2 m 0  0, x        . 2  m  3   2 m  2m  0 m  0 m  3  m  3
Do đó m 10, 9,1,  0 3, 4,5,9,1 
0 . Vậy có 19 giá trị m thỏa mãn yêu cầu bài toán. 1 3 m 2 2 x  x 6m x2022
Câu 14. Có bao nhiêu giá trị nguyên của tham số m để hàm số 3 2 y  2 đồng biến trên khoảng 2;3? A. 1. B. 2 . C. vô số. D. 0 . Lời giải Chọn B 1 m x  x 6m x2022 Ta có y   2 2 x  mx  m  3 2 2 3 2 6  2 ln 2 .
+Hàm số đồng biến trên   g  x 2 2 2
 x  mx  6m  0,x      0  25m  0  m  0 x  2m + Phương trình g  x 2 2
 0  x  mx  6m  0   . x  3 . m Ta xét các trường hợp:
TH1: 2m  3m  m  0 . Khi đó g  x 2
 x  0 , x   . Do đó nhận m  0 .
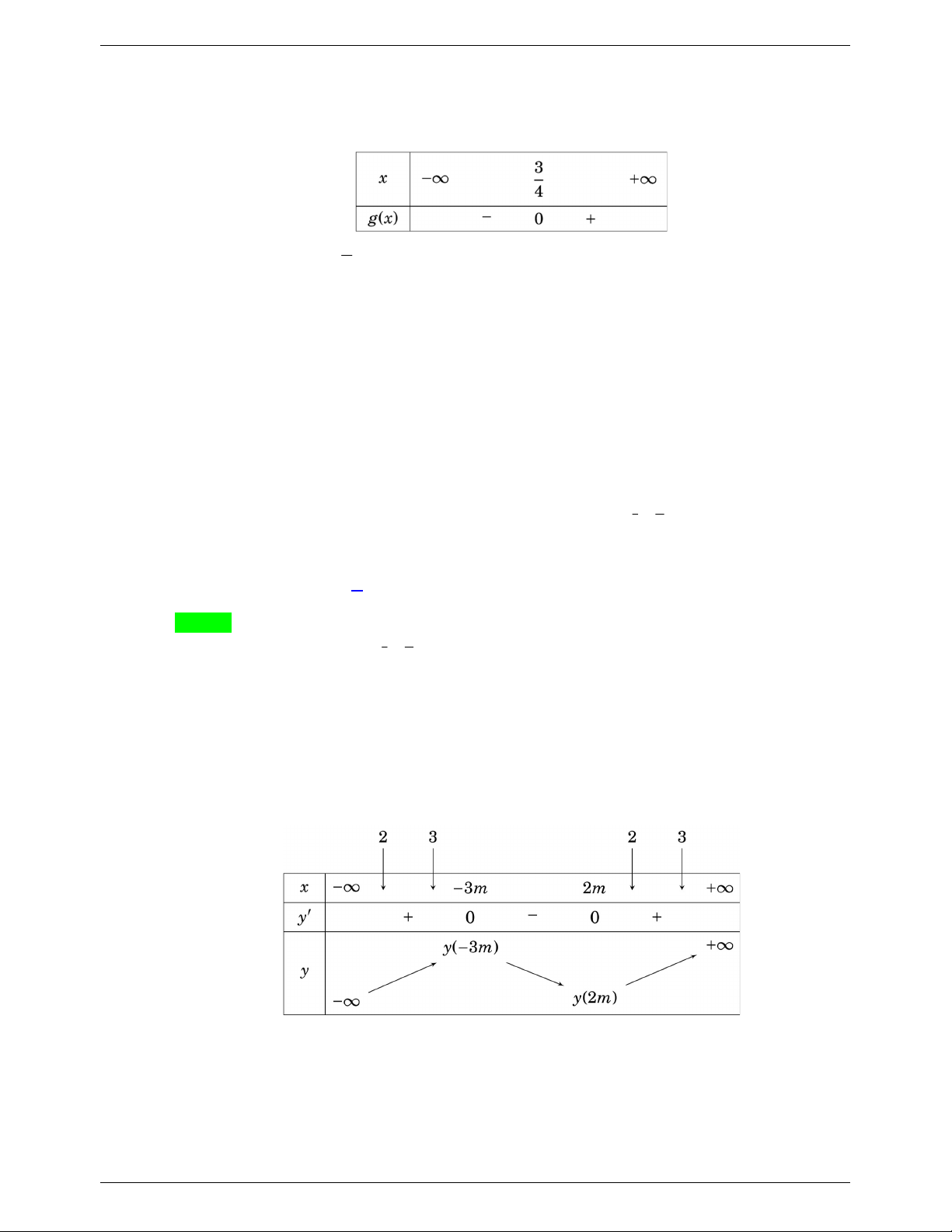
TH2: 2m  3m  m  0 . Ta có bảng biến thiên
Từ bảng biến thiên, suy ra hàm số đồng biến trên ;3m và 2 ; m  .
Hàm số đã cho đồng biến trên khoảng 2;3 khi 2;3   ;  3  m  3  m  3 m  1      m    2;3  2 ; m  1. 2m  2 m 1
So với điều kiện, ta nhận 0  m  1 . Trang 8
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT-VD_VDC
TH3: 2m  3m  m  0 . Ta có bảng biến thiên
Từ bảng biến thiên, suy ra hàm số đồng biến trên ;2m và 3 ; m  .
Hàm số đã cho đồng biến trên khoảng 2;3 khi  3 2;3   ;  2  m m  2m  3  2 2        m   2;3  3 ; m  .  3  m  2 2 3 m    3 2 
So với điều kiện, ta nhận  m  0. 3 2
Vậy   m 1 thỏa yêu cầu bài toán. 3
Do m   nên m0;  1 . Câu 15. Gọi 3 2
S là tập hợp các giá trị nguyên dương của m để hàm số  3 2  1 12 5 2 10x m x m x y       đồng
biến trên khoảng 2;  . Số phần tử của S bằng A. 1. B. 2 . C. 3 . D. 0 . Lời giải Chọn D Ta có 2
y  3x  62m   3 x   m  2 3 2 1 x 12m5x2 1 x 12m  5 10  ln10   .
Hàm số đồng biến trên 2; khi y  0 x  2; 2  3x  62m   1 x 12m  5  0 x  2;  12m1 x 2  3x  6x  5 x  2; 2 3  x  6x  5  m 
x2 1 x  1 0. 1  2x 12 2 3x  6x  5 Đặt g  x  x2; . 12x 12 2 36x  72x 12 Ta có g x  .  1  2x 122  3  6 x  1.loai g x 2 3
 0  36x  72x 12  0    3  6 x  loai  3 Ta có bảng biến thiên
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 9
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT-VD_VDC 5
Từ bảng biến thiên suy ra m  12 Mà m 
 nên không có giá trị m thoả mãn. HÀM SỐ LÔGARIT 1. Định nghĩa
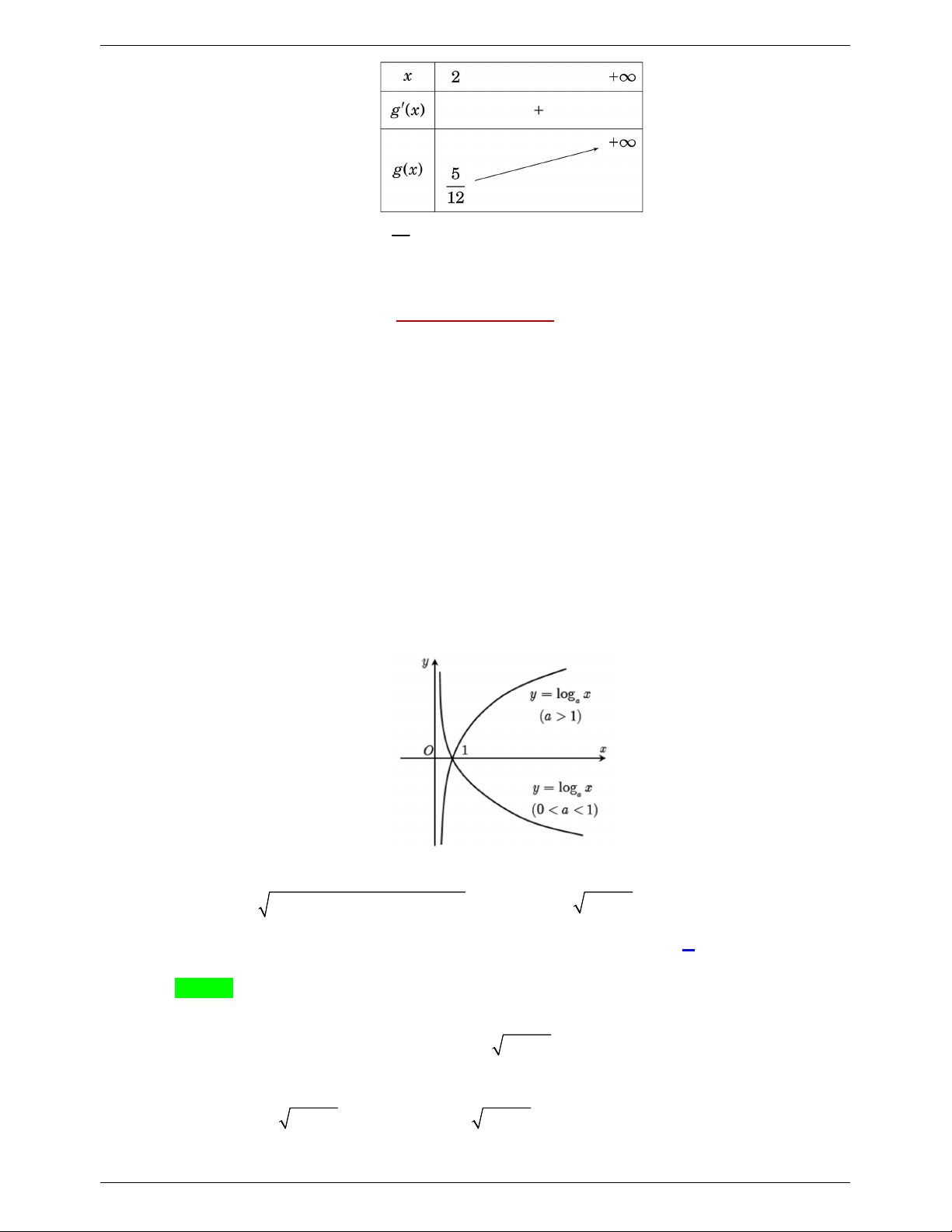
- Hàm số dạng y  log x,(a  0; a  1) được gọi là hàm số logarit cơ số a . a
2. Tập xác định và tập giá trị
- Tập xác định: D  (0; ) 
- Tập giá trị: T   .
3. Tính đơn điệu và đồ thị
- Khi a  1 thì hàm số y  log x đồng biến trên D , a
khi đó nếu log f (x)  log g(x)  f (x)  g(x) a a
- Khi 0  a  1 thì hàm số y  log x nghịch biến trên D , a
khi đó nếu: log f (x)  log g(x)  f (x)  g(x) a a
Câu 16. Có bao nhiêu giá trị nguyên của m thuộc khoảng ( 2  019;2019) để hàm số 2 2
y  x  m  x  2(m 1)x  m  2m  4  log  2
x  m  2x 1 có tập xác định là D   . 2  A. 2020 . B. 2021 . C. 2018 . D. 2019 . Lời giải Chọn D 2 2
x  2(m 1)x  m  2m  4  0 
Hàm số xác định với mọi x   thì 
luôn đúng với mọi x   2
x  m  2x 1  0
Ta có: x  m  x  m  m   x   m   2 2 2 2( 1) 2 4 1   3  0, x     Ta có: 2 2 x  m  2x 1  0, x
    x  2x 1  , m x    . Trang 10
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT-VD_VDC  2x  1  Xét hàm số 2
f (x)  x  2x 1 với x   có f (x) 1 ; f (x)  0  x  . 2 2x 1 2 2
Từ bảng biến thiên ta thấy để 2 x  2x 1  , m x   
 m . Kết hợp điều kiện 2 m    m{2018, 2017, 2  016,, 1  ,0}. m (2019; 2019)
Kết luận: có 2019 giá trị của m thỏa mãn bài toán.
Câu 17. Tìm tất cả các giá trị của m để hàm số y   2 ln x  mx  2m  
1 xác định với mọi x 1;2 . 1 3 3 1 A. m   . B. m  . C. m  . D. m   . 3 4 4 3 Lời giải Chọn B
Hàm số xác định với mọi x  1; 2 khi 2
x  mx  2m 1  0,x 1;2 .  f x 2
 x  mx  2m 1  0,x  1;2 .
 f  x  0 có 2 nghiệm thỏa mãn x 1 2  x . 1 2  f    1  0 3m  0 3        f   m 2  0 4m  3  0 4 2  x 
Câu 18. Tìm tất cả các giá trị của m để hàm số y  log  2021x  x 
 m xác định với mọi giá trị 2021   2  x thuộc 0; A. m  9 . B. m  1. C. 0  m  1 . D. m  2 . Lời giải Chọn B
Hàm số đã cho xác định x 0; 2 x  2021x  x   m  0, x  0; 2 2 x  2021x  x   , m x  0; . 2
YCBT  m  min f  x . x   0; 2 x
Đặt f  x  2021x  x  , x 0; 2     2021x f x ln 202  1 1 x
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 11
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT-VD_VDC     x f x   2 2021 ln 2021 1  0, x  0;
Khi đó f  x đồng biến trên x 0; và f 0  ln 202  1 1  0
Suy ra f  x đồng biến trên x 0; và f 0 1
Vậy m  1 thì thỏa YCBT. 3x  5
Câu 19. Tập hợp tất cả các giá trị của tham số m để hàm số y  xác log  2 2 x  2x  m  4m  5 2022 
định với mọi x   là A. ;  1  3; . B. (1;3) \   2 . C. ;  1 . D. 1;3 \  2 . Lời giải Chọn A 3x  5 Xét hàm số y  log  2 2 x  2x  m  4m  5 2022  2 2 2 2
x  2x  m  4m  5  0 
x  2x  m  4m  5  0 ĐKXĐ:    . log   2 2 x  2x  m  4m  5 2 2  0
x  2x  m  4m  5  1 2022 2 2
x  2x  m  4m  5  0
Nên điều kiện để hàm số xác định với mọi x   là  với x   . 2 2
x  2x  m  4m  4  0
Điều này xảy ra khi và chỉ khi :   m  2 1   2 m  4m  5  0 2 1  m  4m  4  0 m  2        m 1 .   1 2 2   2 m  4m  4  0 m  4m 3  0 m  4m  3  0  2  m  3 Vậy m  ;  1  3;  \  2 .
Câu 20. Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số y   2
ln x  2mx  4 xác định với mọi x   ? A. 2. B. 3. C. 4. D. 5. Lời giải Chọn B Hàm số xác định 2
x    x  2mx  4  0, x    . a  0 1   0      2  m  2 . 2   0 4m 16  0
Do m   nên m 1;0;  1 .
Câu 21. Có tất cả bao nhiêu giá trị nguyên của tham số m nằm trong khoảng 2021; 202  1 để hàm số y  log m 2 2
x  2 m  2 x  m  3 2  
 có tập xác định D   . A. 2020. B.1010 C. 2023 D. 4046 Lời giải Chọn C
Hàm số xác định trên   m   2
2 x  2m  2 x  m  3  0,x   (*).
Trường hợp 1: m  2  0  m  2 , ta có (*)  1  0, x
  (đúng), suy ra m  2 thỏa mãn.
Trường hợp 2: m  2 . Trang 12
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT-VD_VDC a  m  2  0  m  2 (*)      m   .   4  m  2 2
2  4m  2m  3  0 m  2  0
Vậy với m  2 thì hàm số có tập xác định D   .
Suy ra có 2023giá trị nguyên của tham số m nằm trong khoảng 2021; 202  1 thỏa mãn. 3
Câu 22. Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số y   log 2m 1 x xác 5 x  m
định trên khoảng 2;3? A.1. B. 2. C. 3. D. 4. Lời giải Chọn B  x  m  0 x  m Hàm số xác định     . 2m 1 x  0  x  2m 1
Xét các trường hợp sau:
+) Nếu 2m 1 m  m  1
  D   , suy ra không thỏa mãn.
+) Nếu 2m 1  m  m  1  D  m;2m   1
Hàm số đã cho xác định trên khoảng 2;3 khi và chỉ khi 2;3  D m  2
 m  2  3  2m 1    1  m  2 . m  1
Vì m nguyên nên m  1;  2 .
Câu 23. Tìm tất cả giá trị thực của tham số m để hàm số y  log  2
x  (m 1)x  m xác định trên 3  1;4 . 3 3 A.   m 1. B. m  1 . C. m  1. D. m   . 4 4 Lời giải Chọn B
Để hàm số y  log  2
x  (m 1)x  m xác định trên 1; 4 thì 3  2
x  (m 1)x  m  0, x  1;4  (x 1)(x  m)  0, x 1;4 .
Do 1  x  4 nên có các trường hợp sau \ x  1 TH1: m  1 
vậy hàm số xác định trên 1;4 . x  m 1 TH2: m  1thì 2
(x 1)  0  x  1vậy hàm số xác định trên 1;4 . x  1 TH3: m  1 
như vậy hàm số không xác định trên 1;4 (loại). x  m 1 Kết luận: m  1.
Câu 24. Tìm tổng tất cả giá trị nguyên của tham số m 2;8 để hàm số y  log  4 2 x  x  m xác 2  định trên  . A. 36 . B. 35 . C. 28 . D. 21. Lời giải
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 13
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT-VD_VDC Chọn A
Hàm số xác định trên  khi 4 2 4 2 x  x  m  0, x
    x  x  m,x .  x  0   1  Xét hàm số 4 2 y  x  x , x    có 3
y  4x  2x  0  x   . 2   1 x   2 Ta có bảng biến thiên Vậy để hàm số xác định trên  thì 1  1 f (x)   , m x
   M in f (x)  m   m  m  .  4 4
Vậy tổng tất cả các giá trị nguyên của m 2;8 là: 1 2  3  4  5  6  7  8  36 .
Câu 25. Có bao nhiêu giá trị nguyên của tham số m để hàm số 1 y   log
x  3m 1 xác định trên 1;3 . 5   7m  5  x A. 0 . B. 1. C. 2 . D. 4 . Lời giải Chọn A
Để hàm số xác định ta có . x  7m  5  x  3m 1
TH1: 3m 1  7m  5  m  1  TXĐ của hàm số là D   (loại).
TH2: 3m 1  7m  5  m  1  TXĐ của hàm số là D  3m 1;7m  5 .
Để hàm số xác định trên 1;3 thì 1;3  D  1;3  3m 1;7m  5 m  0 
 3m 1  1  3  7m  5   8 (vô nghiệm). m   7
Vậy không có giá trị nào của m để hàm số xác định trên 1;3 .
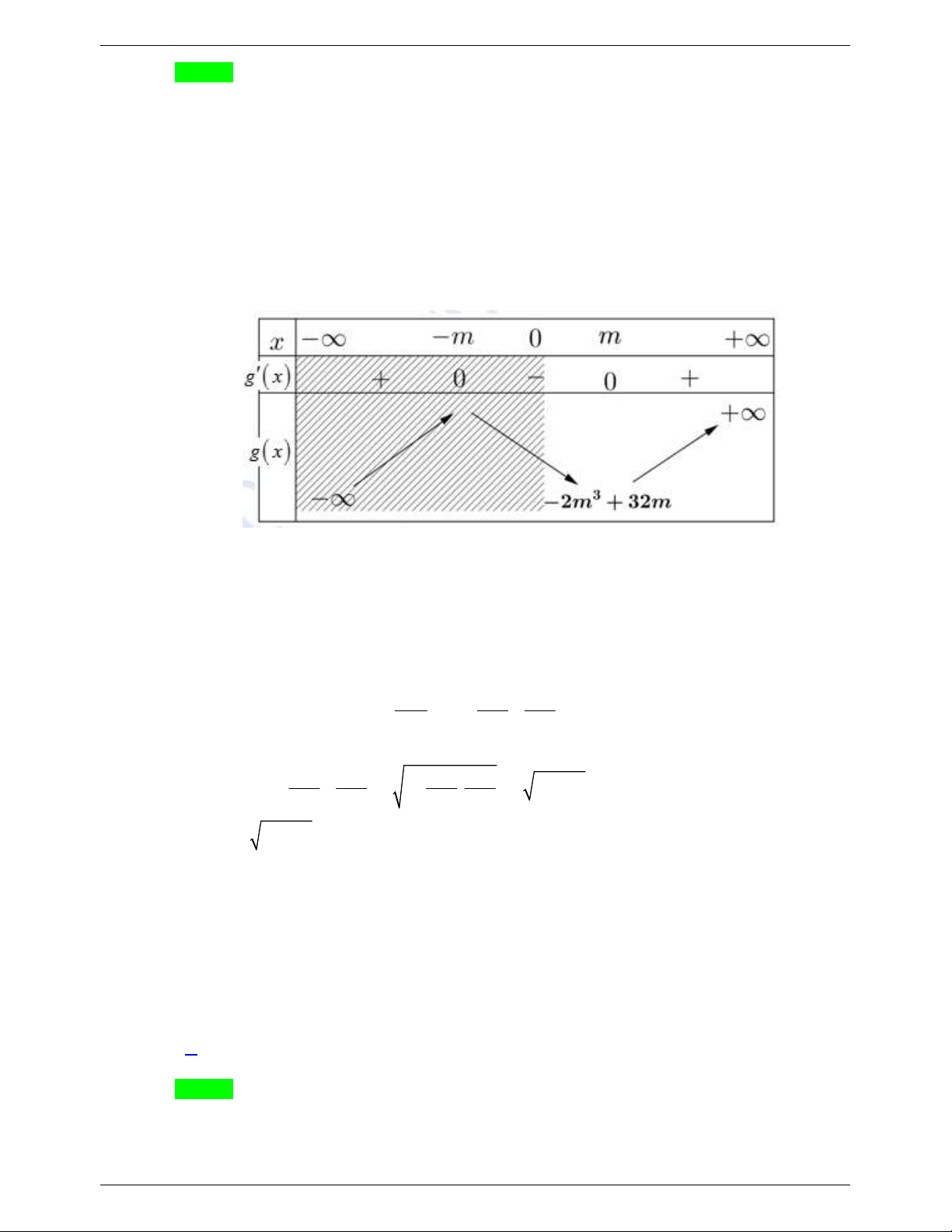
Câu 26. Có bao nhiêu số nguyên dương m để hàm số f x   3 2
( ) ln x  3m x  32m xác định trên khoảng 0;? A. 3. B. 4. C. 6. D. 5. Lời giải Trang 14
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT-VD_VDC Chọn A
Cách 1: Cô lập thông thường Hàm số f x   3 2
( ) ln x  3m x  32m xác định trên khoảng 0; 3 2
 x  3m x  32m  0 , x  0 Xét g  x 3 2  x  3m x  32m ,  gx 2 2  3x  3m ,    x  m g x  0   x  m
Vì m nguyên dương nên ta có bảng biến thiên sau
Suy ra g  x  0,x  0 m  4  3
 2m  32m  0   0  m  4
Vì m nguyên dương nên m 1, 2, 
3 . Vậy có 3 số nguyên dương m .
Cách 2: Sử dụng bất đẳng thức
Ta có điều kiện xác định của hàm số trên là: 3 2
x  3m x  32m  0 trên khoảng 0; 32m 16m 16m 2 3 2 2 2
3m x  x  32m  3m  x   x    g  x x x x
Để hàm số f  x xác định trên khoảng 0; thì 2 3m  min g  x 16m 16m 16m 16m Mà g  x 2 2 3  x    3 x . .  3 16m2 3 nên suy ra x x x x m  4 2  3m  3 16m2 3  m  16m  m 2 3 m  4  0   0  m  4
Vì m nguyên dương nên m 1, 2, 
3 . Vậy có 3 số nguyên dương m .
Ghi chú: Do hàm số trên xác định trên khoảng 0; nên nó chính là dấu hiệu rõ cho việc sử
dụng bất đẳng thức Cosi.
Câu 27. Cho hàm số f  x  log
2 . Có bao nhiêu giá trị nguyên của tham số m 100;100 2 x 1  2 xm
thỏa mãn hàm số đã cho nghịch biến trên 6; ? A. 64. B. 65. C. 36. D. 0. Lời giải Chọn A Ta có:
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 15
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT-VD_VDC   1 12  2x f x  log 2   f  x  2 x 1  2xm log  2 x 12x  m   log   2x 12xm 2.   2 2 x 12x  m ln 2 2 
Do đó để hàm số đã cho nghịch biến trên 6; thì 2
x 12x  m  0 x  6;   m  max  2 12x  x   36 6;
Ngoài ra ta còn một điều kiện nữa rất dễ sót đó chính là log  2 x 12x  m  0 x   6; 2    2 m  112x  x x  6; 2  m  112x  x x  6;    m  37 . 2
m  112x  x x   6;
Như vậy có tất cả 64 giá trị nguyên m thỏa mãn bài toán.
_______________ TOANMATH.com _______________ Trang 16
TÀI LIỆU ÔN THI THPT QUỐC GIA