




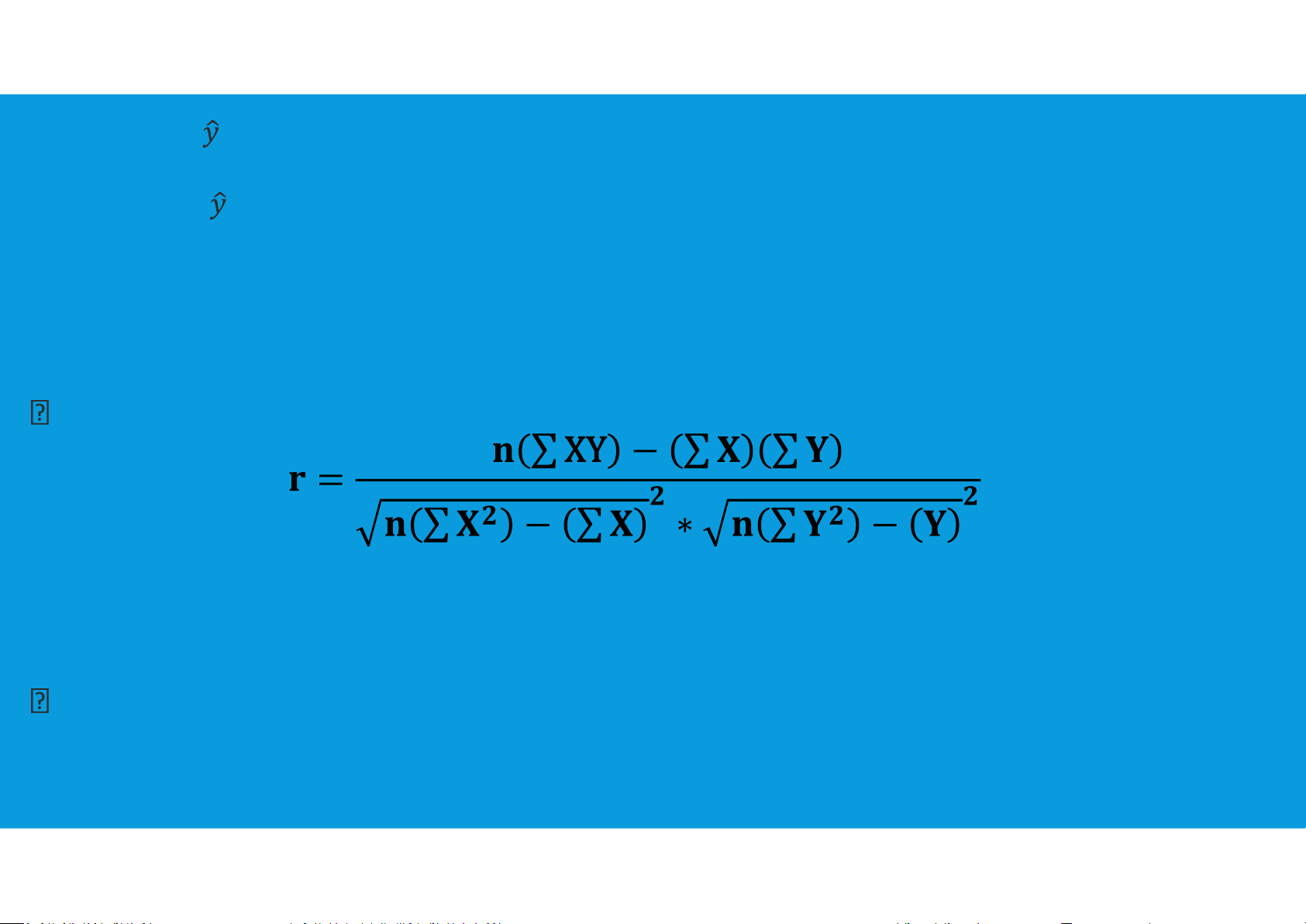






Preview text:
APPLIED STATISTICS COURSE CODE: ENEE1006IU Lecture 15:
Chapter 8: Time series analysis and forecasting
(3 credits: 2 is for lecture, 1 is for lab-work)
Instructor: TRAN THANH TU Email: tttu@hcmiu.edu.vn tttu@hcmiu.edu.vn 1
CHAPTER 8: TIME SERIES ANALYSIS AND FORECASTING •8.1. Time series patterns •8.2. Forecast accuracy •8.3. Trend projection
•8.4. Time series decomposition tttu@hcmiu.edu.vn 2 LINEAR MODEL
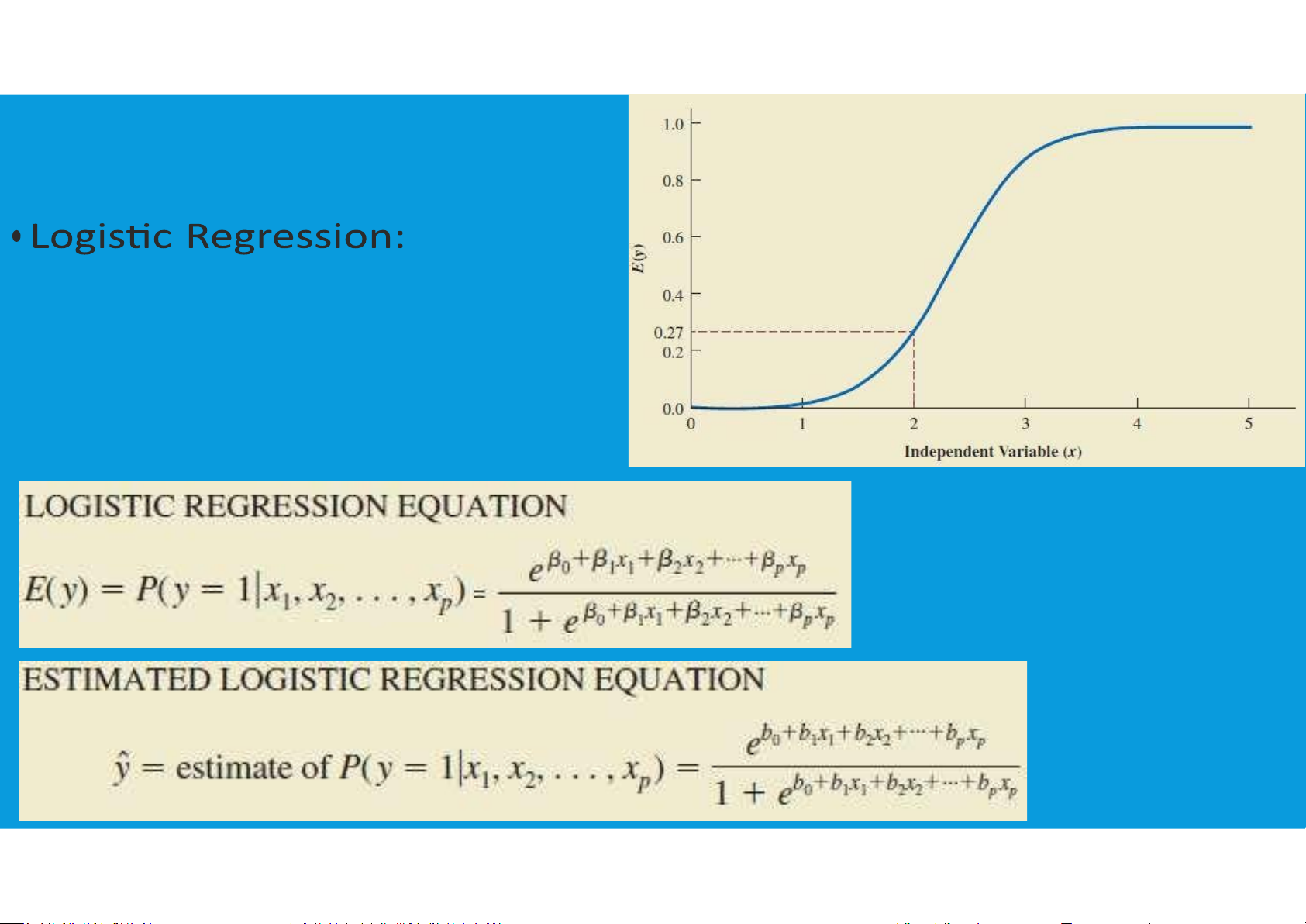
Each of the independent variables zj (where j = 1, 2, . . . , p) is a function of x1, x2, . . . , xk (the variables for which data are collected).
In some cases, each zj may be a function of only one x variable. straight-line relationship
simple first-order model with one predictor variable curvilinear relationship
second-order model with one predictor variable interaction
second-order model with two predictor variable tttu@hcmiu.edu.vn 3 tttu@hcmiu.edu.vn 4
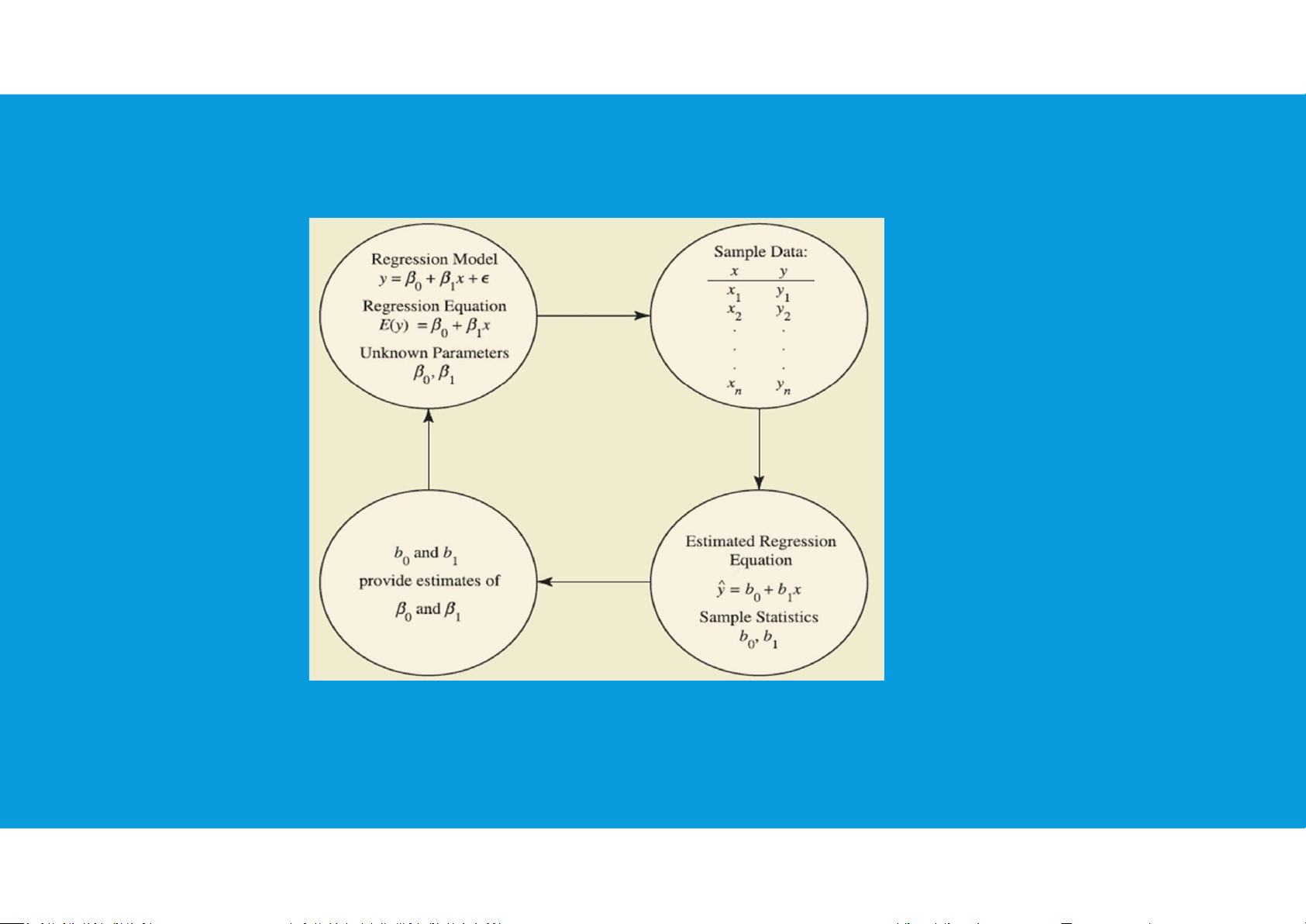
LINEAR REGRESSION ESTIMATION PROCESS Simple regression tttu@hcmiu.edu.vn 5
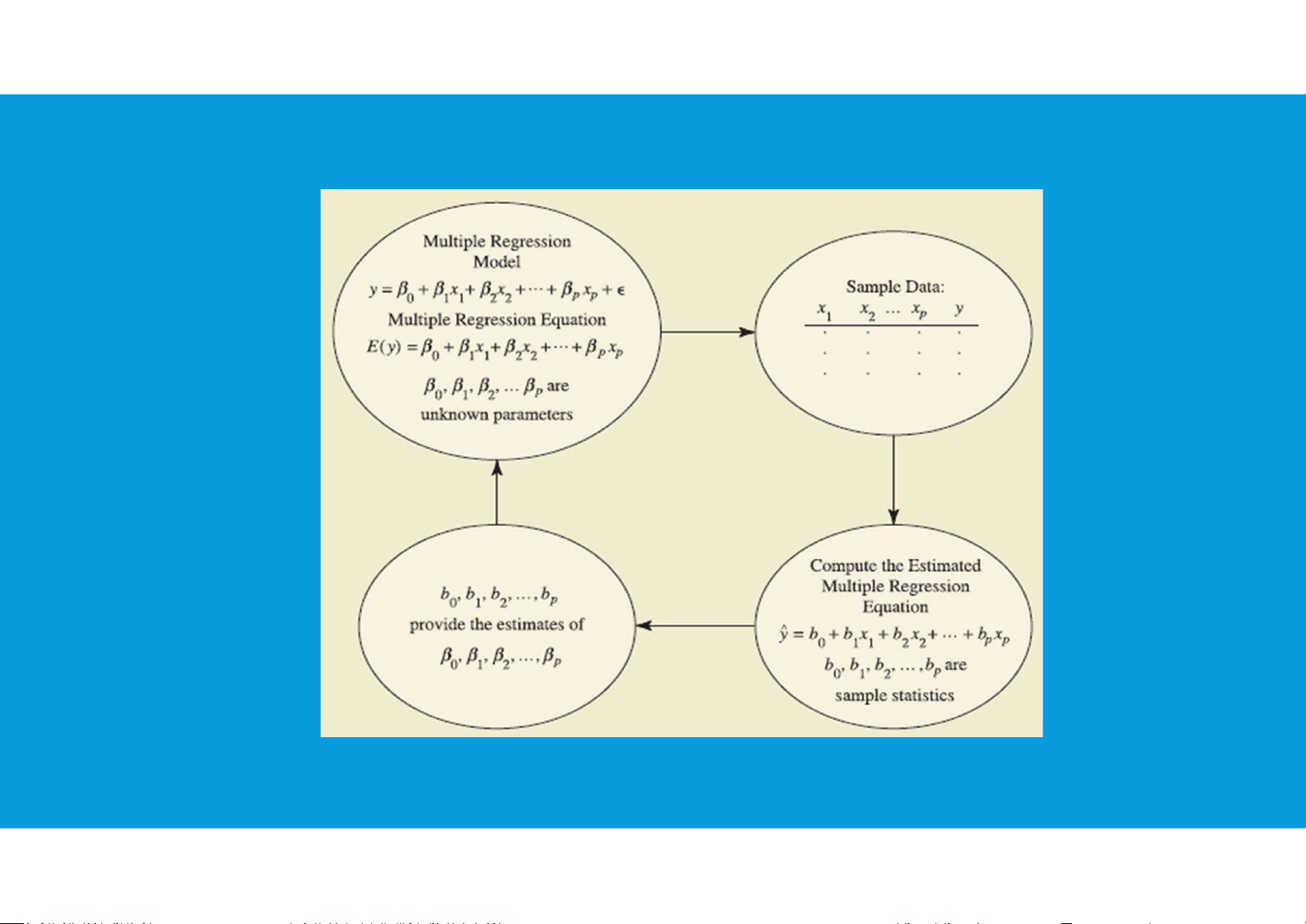
LINEAR REGRESSION ESTIMATION PROCESS Multiple regression tttu@hcmiu.edu.vn 6 8.3. TREND PROJECTION
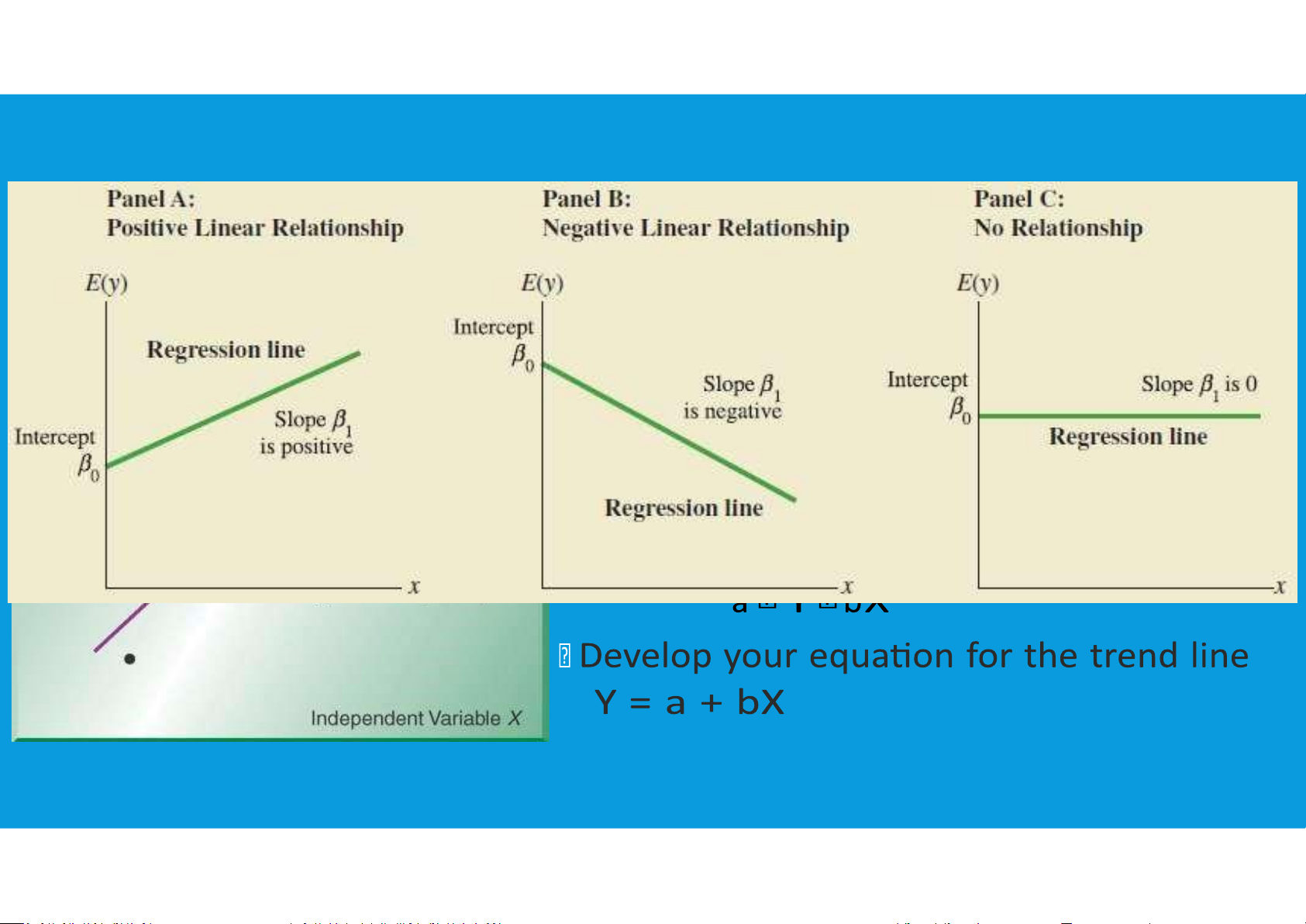
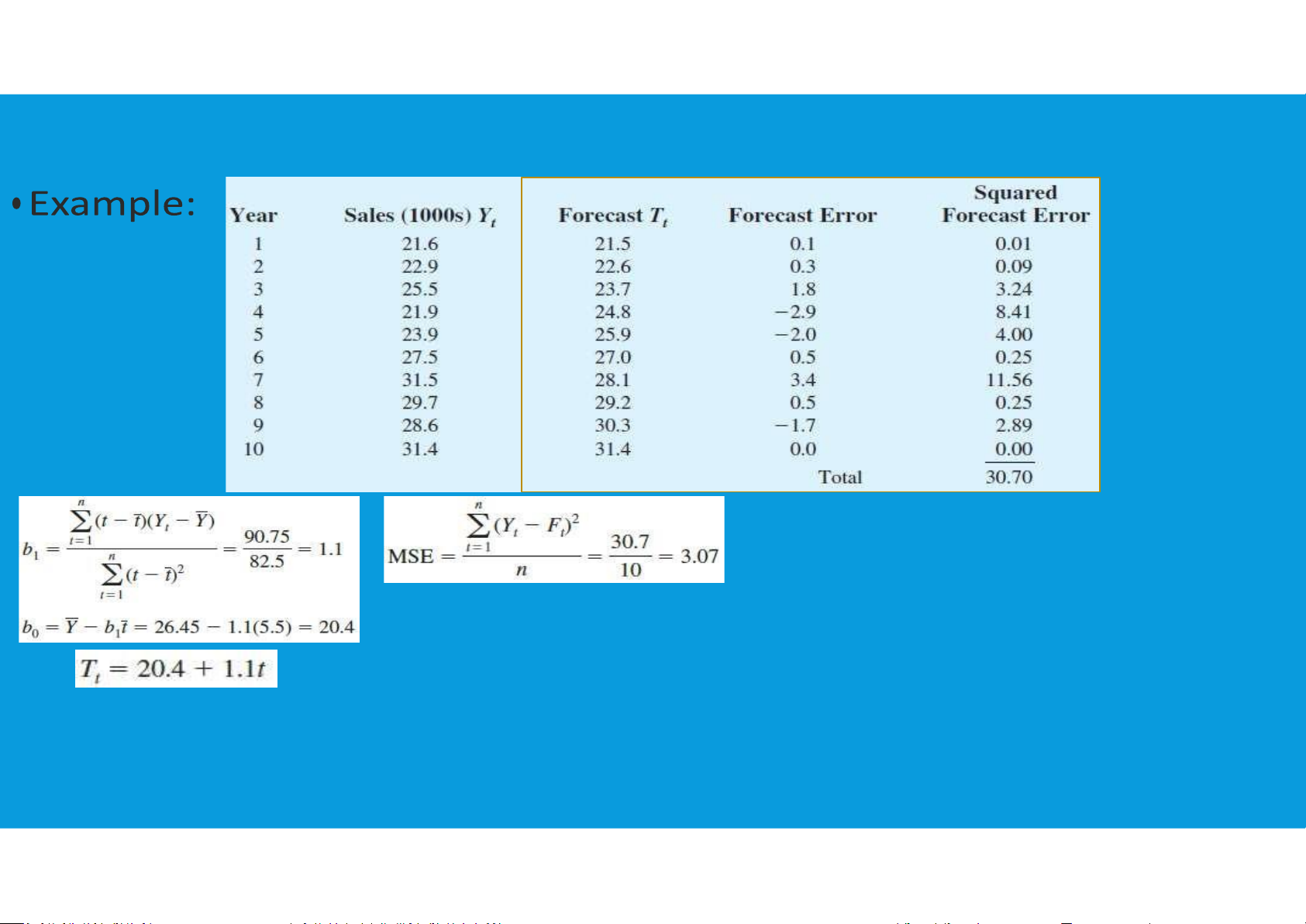
•Linear Trend Regression: A time series technique that computes a forecast with
trend by drawing a straight line through a set of data using tttu@hcmiu.edu.vn 7 8.3. TREND PROJECTION tttu@hcmiu.edu.vn 8 8.3. TREND PROJECTION
•Nonlinear Trend Regression: a curvilinear function appears to be needed to model the long-term trend: Quadratic trend equation: Exponential trend equation: tttu@hcmiu.edu.vn 9 tttu@hcmiu.edu.vn 10 i i i i i i i i i tttu@hcmiu.edu.vn 11
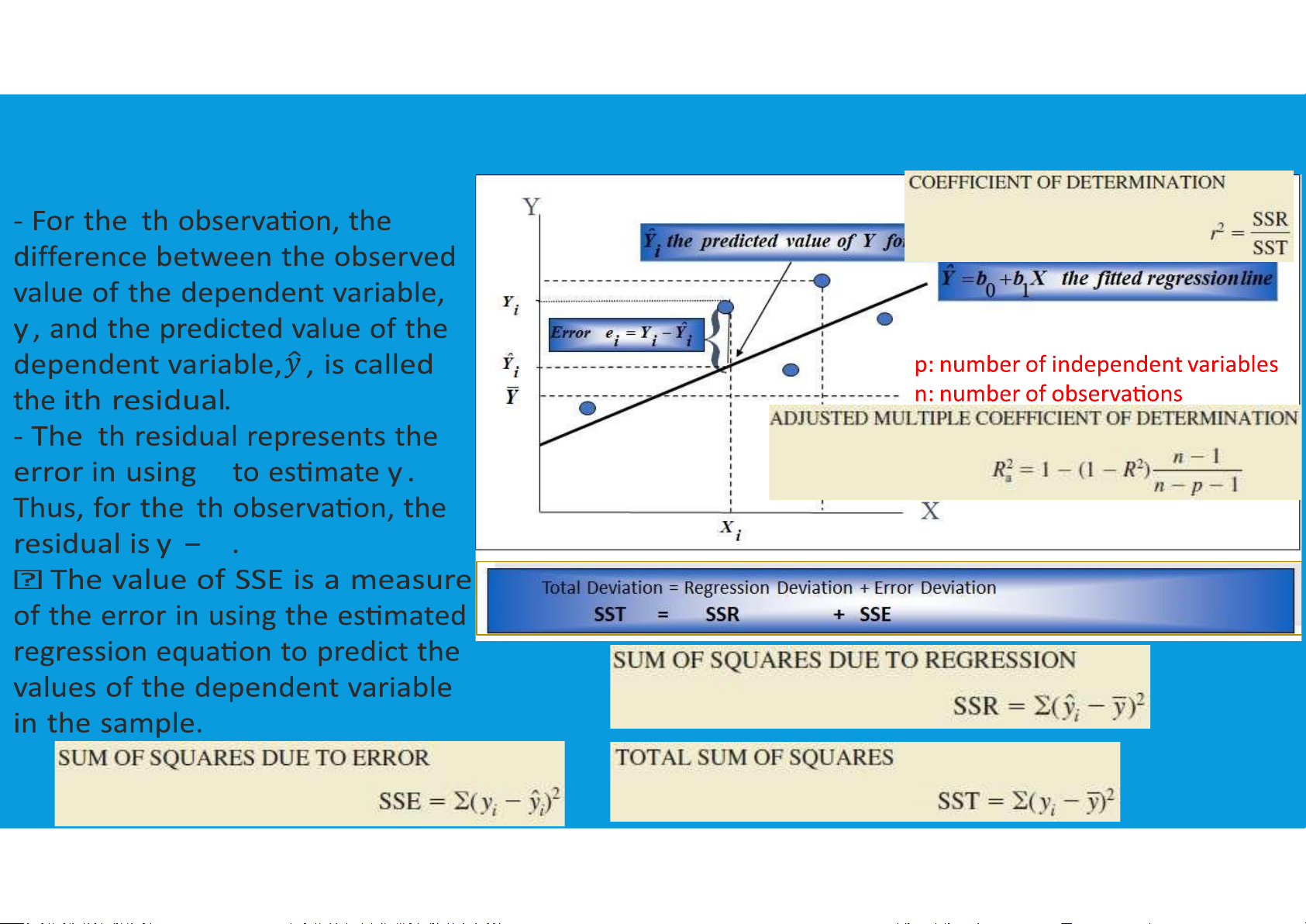
DECOMPOSITION OF THE TOTAL DEVIATION IN A LINEAR
CORRELATION COEFFICIENT - HOW GOOD IS THE FIT?
•Correlation coefficient (r) measures the direction and strength of the linear
relationship between two variables.
The closer the r value is to 1.0 the better the regression line fits the data points.
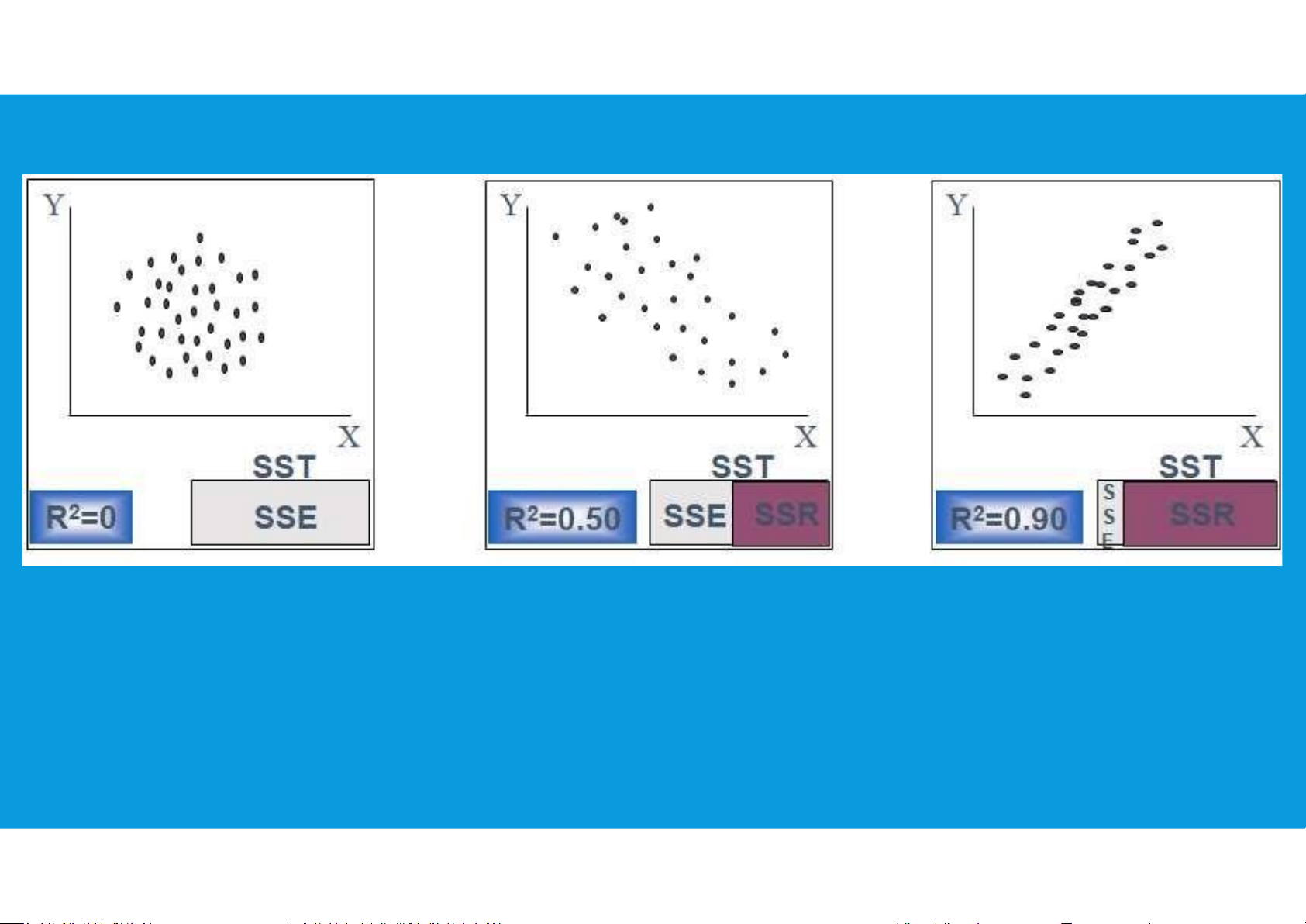
•Coefficient of determination (r2) measures the amount of variation in the
dependent variable about its mean that is explained by the regression line.
provides a measure of the goodness of fit for the estimated regression equation
•Values of (r2) close to 1.0 are desirable. tttu@hcmiu.edu.vn 12 HOW GOOD IS THE REGRESSION tttu@hcmiu.edu.vn 13 RESIDUAL ANALYSIS i i tttu@hcmiu.edu.vn 14
DETECTING OUTLIERS AND INFLUENTIAL OBSERVATIONS
•Outliers: The presence of one or more outliers in a data set tends to increase s,
the standard error of the estimate increase , , the standard deviation of residual i
•Influential observations: the value of the independent variable may have a strong
influence on the regression results tttu@hcmiu.edu.vn 15
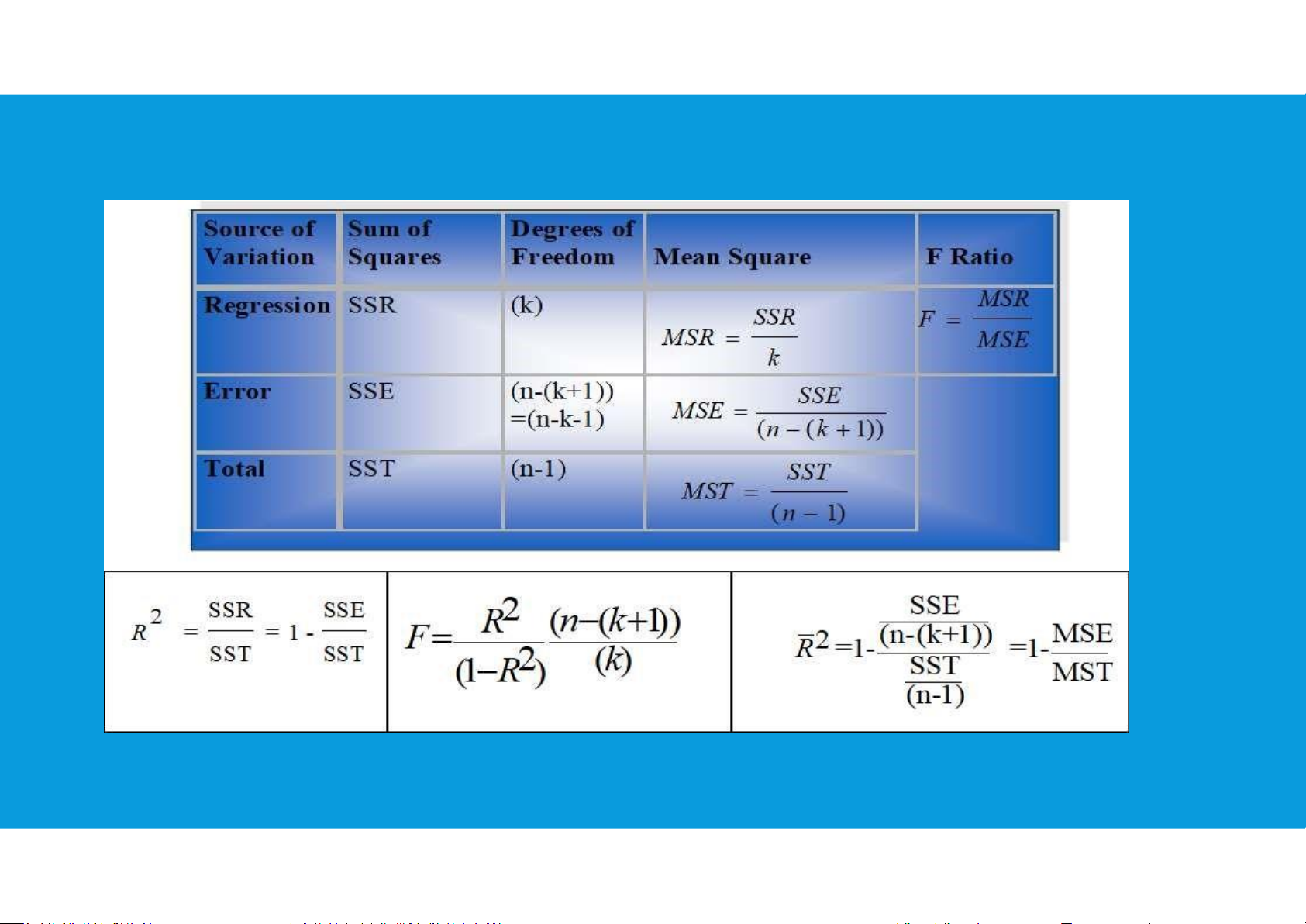
THE F TEST OF A MULTIPLE REGRESSION MODEL tttu@hcmiu.edu.vn 16
DECOMPOSITION OF THE SUM OF SQUARES AND THE ADJUSTED COEFFICIENT OF DETERMINATION tttu@hcmiu.edu.vn 17
MEASURES OF PERFORMANCE IN MULTIPLE REGRESSION AND THE ANOVA TABLE tttu@hcmiu.edu.vn 18
8.4. TIME SERIES DECOMPOSITION
•Time series decomposition can be used to separate or decompose a time series
into seasonal, trend, and irregular components.
get a better understanding of the time series
an additive model is appropriate in situations where the seasonal fluctuations do
not depend upon the level of the time series. tttu@hcmiu.edu.vn 19
8.4. TIME SERIES DECOMPOSITION
•If the seasonal fluctuations change over time, growing larger as the sales volume
increases because of a long-term linear trend, then a multiplicative model should be used tttu@hcmiu.edu.vn 20




