Tín hiệu và hệ thống kỳ 2020 môn Lý thuyết mạch | Đại học Bách Khoa, Đại học Đà Nẵng

Bài giảng: Tín hiệu và hệ thống kỳ 20202 Đào Lê Thu Thảo,
TLTK: Signal and System, Oppehiem and Wilsky. 30% 70% thi chung Nội dung:
1. Tín hiệu và hệ thống trong miền thời gian.
2. Tín hiệu và hệ thống trong miền tần số à phép biên đổi F.
3. Tín hiệu và hệ thống trong miền tần số phức à phép biến
đổi Laplace, biến đổi Z. 4 nội dung, 1.1, 2.3 ….
+++++++++++++++++++++++++++++++++++++
2. Tín hiệu và hệ thống trong miền tần số:
2.1. Khai triển chuỗi Fourier cho tín hiệu liên tục: PB:
Những tín hiệu tần hoàn thì có thể khai triển thành các
hàm sincos có tần số là bội số của tần số tín hiệu gốc.
x(t)=x(t+k.To) To: chu kỳ cơ sở 1 (*)
Hệ số Ck được gọi là hệ số Fourier (**)
Nếu y(t) tuần hoàn cùng chu kỳ To: thì chúng có cùng 1
không gian vecto của cth (*) chung nhau , chỉ khác nhau
ở hệ số Fourier là Dk nên trong nhiều trường hợp nếu xét
ở cùng chu kỳ tuần hoàn thì chỉ cần nhắc tới hệ số Fourier là đủ:
Nhìn vào hệ số Fourier: (**) Ck là số phức: Phầần biên ộ ộ ớ Phầần pha, góc l ch ệ đ , đ l n pha c a vector ủ vector
Tại tần số kwo có lượng đóng góp về mặt biên độ là |Ck| và đóng góp pha là φk.
người ta vẽ đồ thị của |Ck| và φk. và gọi là đồ thị phổ rời rạc: (k.wo) 2 VD: x(t)= cos(2П.t)
a/ tìm khai triển FS dạng (*)
b/ Vẽ đồ thị phổ bd và pha (*) AD công thức Euler: x(t)=cos(2Пt)= k.wo=2П à k=1 - k.wo=2П à k=-1 Vậy C j.0 1= ½ . e C- j.0 1= ½ . e |Ck| 1/2 1/2 k φk k VD: x(t)= sin(2П.t) 3
a/ tìm khai triển FS dạng (*)
b/ Vẽ đồ thị phổ bd và pha (*) x(t)=sin(2Пt)=
từ phần hàm e mũ (không gian vector) k.wo=2П à k=1 hài bậc 1
- k.wo=2П à k=-1 hài bậc k Vậy C j.(-П/2) 1= 1/2j = ½ . e C- j.(-П/2 +П) 1= -1/(2j)= ½ . e |Ck| 1/2 1/2 k -1 1 φk П/2 k -П/2
VD: x(t)= 1+ 2.cos(3Пt) + sin(2П.t) 4
a/ tìm khai triển FS dạng (*)
b/ Vẽ đồ thị phổ bd và pha
Chú ý: phải tìm chu kỳ cơ bản cho tín hiệu à tìm chu kỳ là bội số của các dddh
cos(3Пt) à T1=2 woT=2kП T=2kП/wo sin(2П.t) à T2=1
Bội số nhỏ nhất: To=2 à wo=2Pi/2=П
Sau đó, lại AD cth Euler ( tại vì ở đây các hàm toàn sincos)
Còn nếu là hàm bất kỳ khác thì phải dung định nghĩa (phtri** để tính Ck)
x(t)= 1+ 2.cos(3Пt) + sin(2П.t) k=0 k=3 k=-3 k=2 k=-2 Co= thành phầần DC 5 |Ck| 1 1 1 1/2 1/2 k 2 -2 3 -3 2П 3П rad/s φk П/2 k -П/2
VD : chuỗi xung lấy mẫu sampling TS chu kỳ lấy mẫu
VD : chuỗi xung lấy mẫu sampling 6 τ/2 τ/2
Dựa vào công thức ** để tính Ck k ≠ 0 Xét riêng k=0 thì:
= diện tích trung bình trog 1 chu kỳ của tín hiệu
Vậy: với tín hiệu xung vuông tiêu chuẩn: 7
Co= diện tích hình chữ nhật = A.τ/To
Tuy nhiên, ta sử dụng công thức tổng quát mọi k. Và ta đã biết hàm
Kiểm tra với k=0: sinc(x) = 1 khi x->0
Co= đúng như tính diện tích.
Lấy ví dụ với To=3 τ=1 A=1
ta sẽ tính riêng từng giá trị Ck
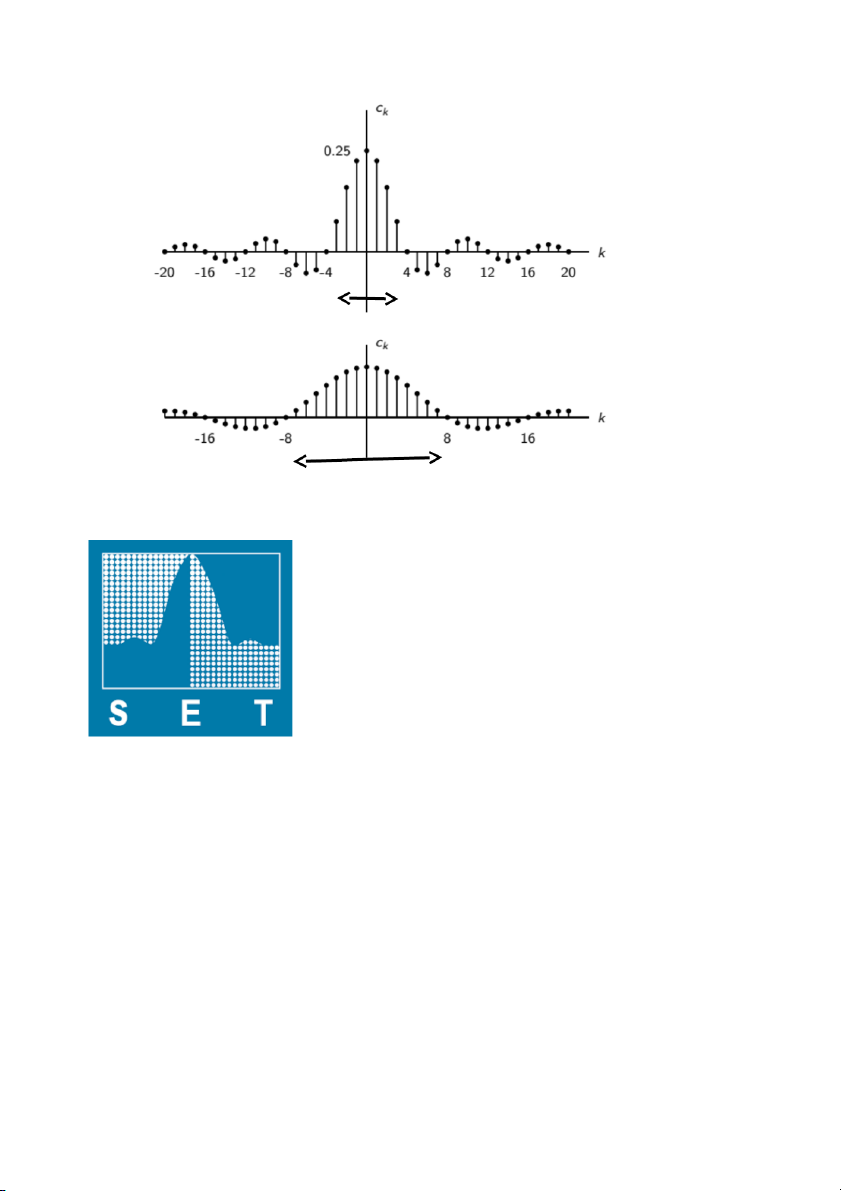
Hàm sinc là hà chẵn, nên đối xứng qua trục tung Ck k= biên độ pha Co 0 1/3=0.333 0 C1 1 0.28 0 C2 2 0.14 0 C3 3 0 0 C4 4 0.07 П C5 5 0.056 П C6 6 0 0 8 |Ck| 1/3 0.28 0.14 k 1 2 3 4 5 φk П П k VD 9 τ/2TO đ r ộ ng ộ lớ đ r ộ ng ph ộ ổ h đ r ộ ng ộ bé h τ/2TO đ r ộ ng ph ộ ổ ộ
độ rộng xung liên quan đến tốc độ truyền của bit
đường bao la hàm sinc(x)= sin(x)/x VD:
x(t)= -1+ 2j.cos((2π/3).t) - 3sin((π/5).t) 10
Khai triển chuỗi F dạng phức và vẽ đồ thị phổ rr. a/ Tìm chu kỳ cơ bản:
T1=3 T2=10 à chu kỳ chung: To=30 k=0 k=10 k=-10 k=-3 k=3 Co= thành phầần DC |Ck| 1 1 1 1/2 1/2 k -3 3 10 -10 φk П П П/2 k -П/2 Tính chất chuỗi Fourier: xTo(t) à Ck yTo(t) à Dk a/ Tuyến tính: 11
A.xTo(t) + B.yTo(t) à A.Ck +B.Dk b/ Dịch thời gian: xTo(t-to) à
VD: Biết hệ số F của xung vuông tiêu chuẩn độ rộng τ (đi từ
-τ/2 đến τ/2) , cao A, chu kỳ cơ bản To:
Tìm, hệ số Fourier Dk của chuỗi xung rect, rộng τ (đi từ 0 đến
τ), cao A, chu kỳ cơ bản To: Giải:
chính là chuỗi xung vuông tiêu chuẩn dịch thời gian sang phải: τ/2 c/ Đảo trục thời gian xTo(-t) à C(-k) Đổi biến 12 VD:
tính chẵn lẻ của chuỗi;
x(t)=x(-t) à Ck=C(-k) đối xứng trục tung cả phổ biên đô và phổ pha
x(t)=-x(-t) à Ck = -C(-k) đối xứng qua tâm d/ tính đối xứng: x*(t) à hệ số ntn?
Lấy liên hợp phức 2 vế VD: Với hàm thực: x(t)=x*(t) FS cả 2 vế: Ck = C*(-k) Vậy: 13
Hệ quả: Tìm khai triển chuỗi Fourier dạng thực x(t)=x*(t) Vậy: AD công thức (*) (***)
(***): chuỗi Fourier dạng thực.
Phổ vẽ được thì còn gọi là phổ 1 phía e/ Quan hệ Parseval: Từ đó suy ra: 14
Công suất trung bình trong 1 chu kỳ = tổng các bình phương vạch phổ VD:
x(t)= 2-cos(3π/5.t) + 3 sin(5π/4 t)
a/ Khai triển chuỗi F dạng phức
b/ Khai triển chuỗi F dạng thực
x(t)= 2+ 2.1/2 cos(3π/5 t) -3j. cos(5π/4 t) c/ Vẽ đồ thị phổ d/ tính cs trung bình
Cs trung bình = 22 + 2. (1/2)2 + 2. (3/2)2 =… 15 16
2.2. Biến đổi Fourier cho tín hiệu liên tục:
Xét tin hiệu không tuần hoàn = x(t) x(t)= (*) (**) Gọi phần mầu vàng X(k.ω0) = (1) thay vào phtrinh (*) (2)
Tiến hành cho Toà vô cùng k.wo à w liên tục
1/To à df vi phân của tần số Hz liên tục (1) (2)
Phương trình (1) và (2) là 2 phương trình của cặp biến đổi Fourier (1): biến đổi thuận: (2): biến đổi ngược: 17 FT{.} Fourier transform. ĐK Dirichlet
+ x(t) phải có hữu hạn các điểm cực trị trong bất kỳ khoảng thgian hữu hạn này.
+ x(t) phải có hữu hạn các điểm gián đoạn (nhảy bậc) trong bất
kỳ khoảng thgian hữu hạn này với khoảng nhảy bậc hữu hạn.
+ : thường có 2 loại: bị chặn 2 đầu và bị chặn 1 đầu và tiến
về 0 khi t tiến ra vô cùng. VD: tìm FT{.} a/ x(t)=δ(t) b/ x(t)= α thực
c/ x(t) = một xung vuông tiêu chuẩn: =A khi |t| <=τ/2 Giải: a/ thay vào định nghĩa
Vậy ta có thể vẽ được đồ thị của X(jw)= phổ biên độ và phổ
pha ( theo tần số liên tục) 18 |X(jw)| 1 w -3 3 10 -10 φ(jw) П w b/ x(t)= α thực
Xét α<0 thì không tồn tại “=” à không tồn tại FT Xét: α>0 thì e-α.∞=0 X(jw) = 1/(α+jw)
x(t)= là hàm suy giảm bị chặn 1 đầu 19 |X(jw)| 1/α w 0 φ(jw) П/2 w -П/2
c/ x(t) = một xung vuông tiêu chuẩn: =A khi |t| <=τ/2 Kiểm tra tại w=0:
Ý nghĩa: tại w=0, phổ khi đó là thành phần 1 chiều và có giá
trj bằng diện tích của hình học tạo bởi tín hiệu so với trục hoành
X(0) của xung vuông = S hình chữ nhật= Aτ = thay w=0 vào phtrinh 20 A t -τ/2 τ/2 |X(jw)|
cắắt trục hoành: ωτ/2=kП ω = 2kП/τ 2П/τ 4П/τ 6П/τ w 0 φ(jw) П w
Độ rộng của phổ tỷ lệ nghịch độ rộng của xung. 2.2.1. Tính chất FT: a/ Tính tuyến tính 21 b/ Tính dịch thời gian
Chỉ bị sai pha, biên độ không thay đổi
Phần hay đổi tuyến tính: pha=-w.to xung vuông tiêu chuẩn: VD: FT{ A.rect(t/τ)}= 22 A t 0 τ |X(jw)|
cắắt trục hoành: ωτ/2=kП ω = 2kП/τ 2П/τ 4П/τ 6П/τ w 0 φ(jw) -ωτ/2 П w c/ Dịch tần số:
Cặp công thức đối ngẫu với nhau: 23 VD: FT{δ(t-to)}= FT{x(t).cos(wot)}= Định lý điều chế: |X(jw)| xAM(t)=x(t).cos(ωct) W |X(jw)| wc - W wc + W c(t)=cos(ωct) wc ωC l n ớ FT{x(t).cos(wot)}=
= ½. X(j(w-wo)) + ½. X(j(w+wo)) VD: 24
x(t)=1+ 3cos((3П/2)t +П/4) – sin(П/3 t) |X(jw)| xAM(t)=x(t).cos(ωct) W |X(jw)| wc wc - W wc + W c(t)=cos(ωct) ωC l n ớ VD: 25 x(t)=1+ 3cos((3П/2)t +П/4) xAM(t)=x(t).cos(ωct) Ck Ck wc 0 3П/2 wc - W wc + W pha П/4 pha wc П/4 wc - W wc + W c(t)=cos(ωct) ωC l n >= 2. ớ W VD: FT{.} x1(t)= e-αt.u(t) α>0 à
x2(t)= e-αt.cos(ωot).u(t) α>0 à
x3(t)= e-3t+4.cos(5t).u(t) α>0
x4(t)= e-3t+4.cos(5t).u(t-1) α>0
= e-3(t-1)+1.cos(5(t-1)+5).u(t-1) đặt t-1=t’ 26
= e. e-3t’.cos(5t’+5).u(t’) của t’
Phải đưa về t bằng tính chất dịch thời gian: x1(t)= e-αt.u(t) à
x1(t)= e-αt.u(t). e-j.wo.t à
x1(t-to)= e-α(t-to).u(t-to). e-j.wo.(t-to) à x1(-t)= e-α(-t).u(-t) à
x5(t)= e-t.cos(5t+1).u(t) α>0
x6(t)= e-t.sin(5t+1).u(t-2) α>0 =
x7(t)= e-|t|.sin(3t)= e-t.sin(3t).u(t) + et.sin(3t).u(-t) α>0 27
et.sin(3t).u(-t) = e-(-t).sin(-3(-t)).u(-t) à
tính chất đảo trục thời gian: x(-t) à X(j(-w)) d/ Co giãn e/ Đối xứng
VD: phổ của tín hiệu thực: x(t)=x*(t) f/ Đối ngẫu VD 28 (X(jw))
cắắt trục hoành: ωτ/2=kП ω = 2kП/τ Aτ X(jw)=Aτ.sinc(w.τ/2) A t w -τ/2 τ/2
(X(t)) cắắt trục hoành: tW/2=kП t = 2kП/W AW/2П X(t)=(AW/2П).sinc(t.W/2) A w t -W/2 W/2 Đã biết: δ(t)à 1 1 à 2П.δ(w) δ(t-to)à e-jw.to
Vậy: ĐK Dirichlet chỉ là đk cần cos(wot) à sin(wot) à 29
Vậy có thể tìm phổ của tín hiệu tuần hoàn: à ??? Biết: và Ta co : (1) trong đó, thay vào (1)
Thực hiện biến đổi F cả 2 vế:
Vậy phổ của tín hiệu tuần hoàn là hàm của các xung dirac tại
rời rạc tần số, có độ lớn là giá trị của phổ G tại điểm đó.
VD: Chuỗi xung vuông tiêu chuẩn:
Biết 1 xung tiêu chuẩn có phổ là hàm G(jw)= 30 Ôn tập GK: Hàm h(t) bị chặn t=[0,3]
Hàm x(t) bị chặn t=[1,∞)
Giữ lại hàm h(τ) τ=[0,3]
còn đảo trục thời gian của x(-τ) thì τ=(-∞,-1]
dịch hàm x(t-τ) τ=(-∞,t-1] TH1: t-1 <0 loại
TH2: 0< t-1 <3 t=2 là ở TH này y(t=2)= =con số g/ Tích phân và vi phân 31
Vi phân tích phân trong miền t sẽ trở thành phép tính
nhân chia trong miền tần số: lợi cho việc tính toán trên miền tần số.
thể hiện rõ ưu việt trong các bài toàn mạch điện h/ Quan hệ Parseval
E(jw)= |X(jw)|2 là hàm mật độ phổ năng lượng. Ω
i/ Tích chập- tích thường x1(t)*x2(t) à X1(jw).X2(jw)
x1(t).x2(t) à (1/2П) . X1(jw)*X2(jw) 32 33