Giải Toán 8 Bài 2: Tứ giác Bài tập 1
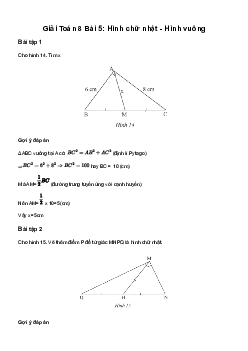
Tìm số đo các góc chưa biết của tứ giác trong Hình 11 Bài giải
Tổng các góc trong tứ giác bằng nên ta có: a) Trong tứ giác ABCD: b) Trong tứ giác MNPQ: c) Trong tứ giác STUV: d) Trong tứ giác EFGH: Bài tập 2
Góc kề bù với một góc của tứ giác được gọi là góc ngoài của tứ giác đó.
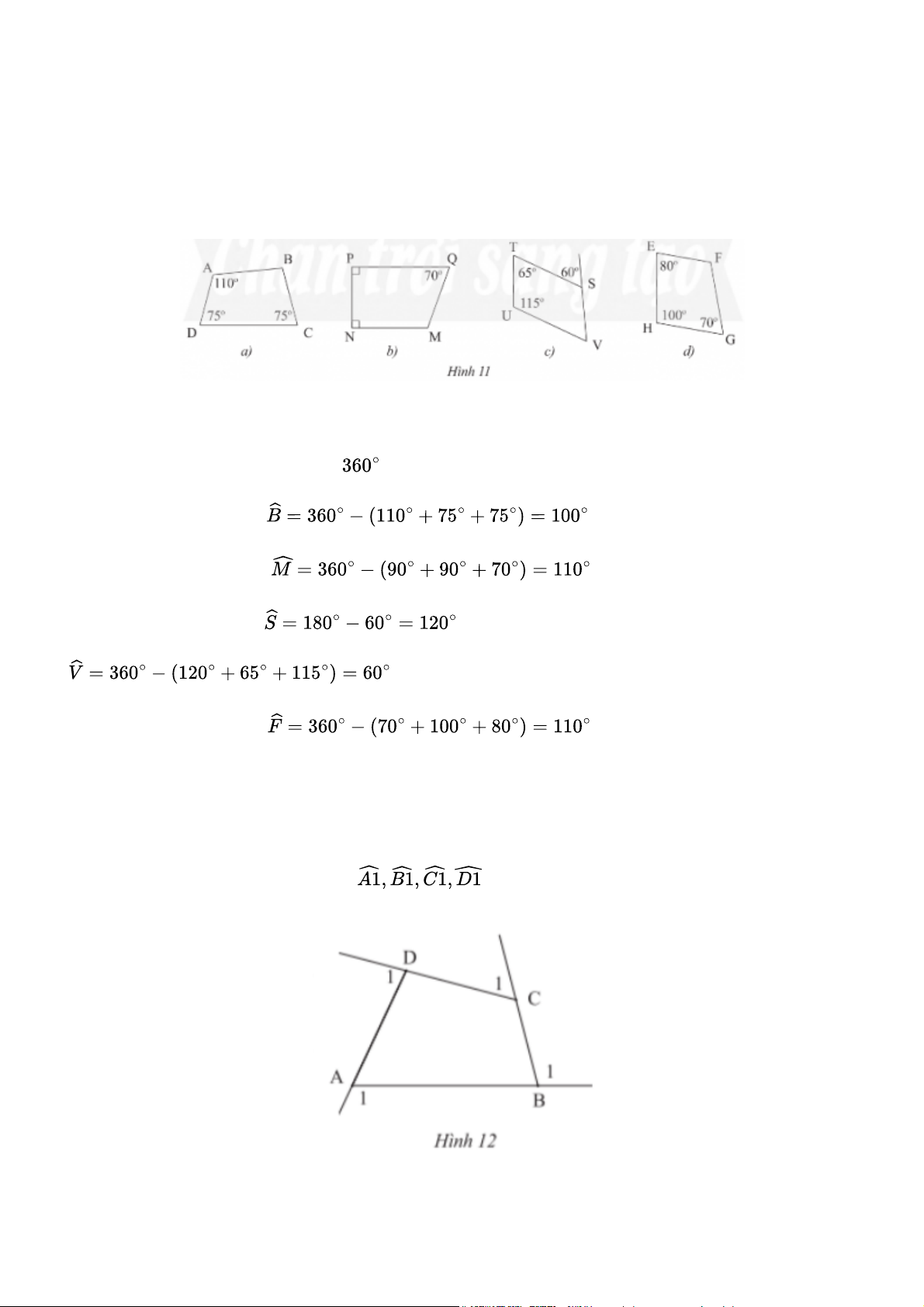
Hãy tính tổng số đo bốn góc ngoài
của tứ giác ABCD ở Hình 12. Bài giải Ta có: º º º º º º º º º º º º º
Mà theo định lý tổng bốn góc trong một tứ giác bằng 360º ta có: º =4 x 180º - 360º = 360º Bài tập 3 Tứ giác ABCD có
, góc ngoài tại đỉnh B bằng . Tính số đo góc D Bài giải Ta có:
Do tổng các góc của một tứ giác bằng nên ta có: Bài tập 4
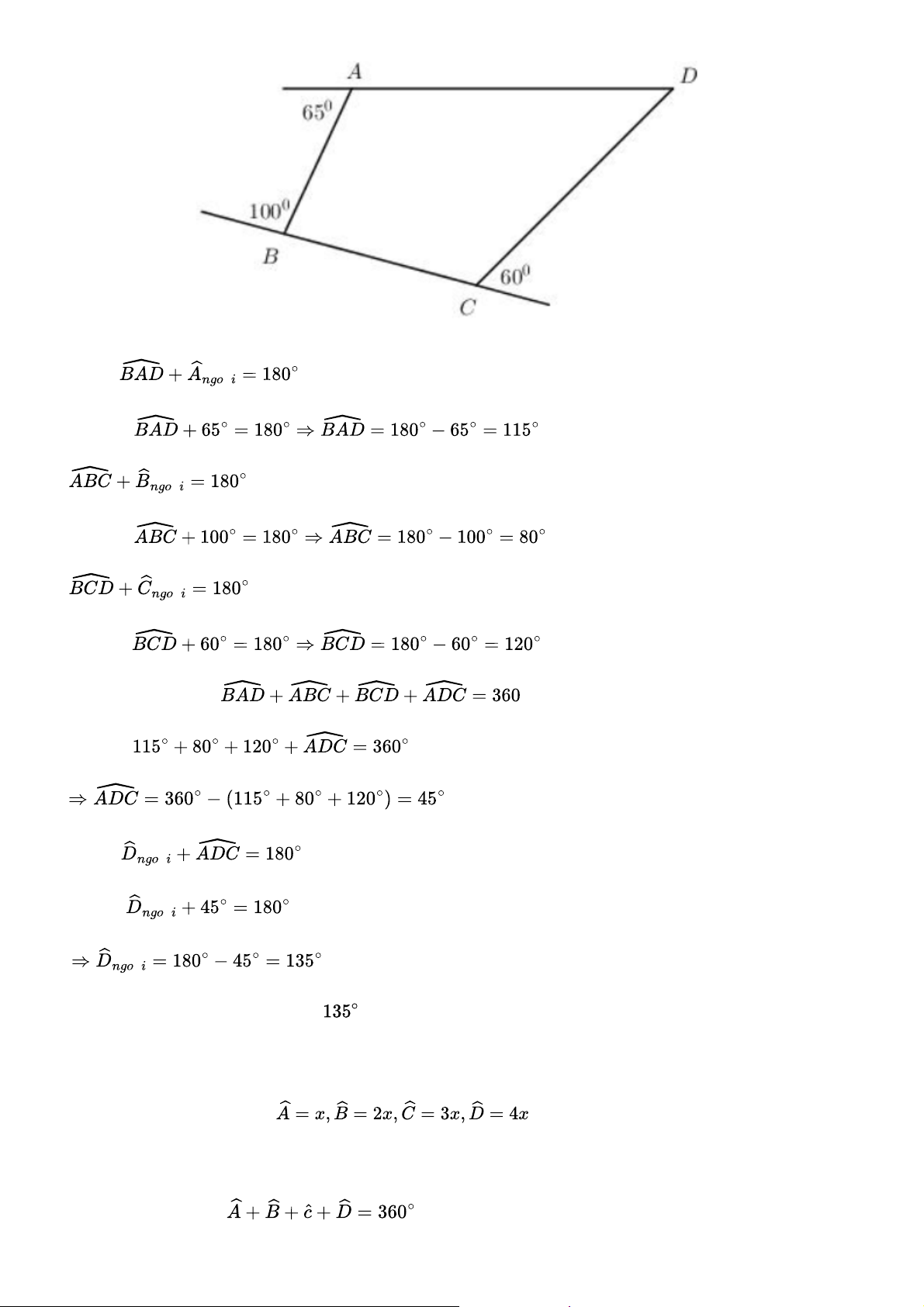
Tứ giác ABCD có góc ngoài tại đỉnh A bằng
, góc ngoài tại đỉnh B bằng góc ngoài tại đỉnh C bằng
. Tính số đo góc ngoài tại đỉnh D Bài giải Ta có: à (hai góc kề bù) Do đó: à (hai góc kề bù) Do đó: à (hai góc kề bù) Do đó: Tứ giác ABCD có Do đó: Ta có à (hai góc kề bù) Do đó à à
Vậy góc ngoài tại đỉnh D bằng Bài tập 5 Tứ giác ABCD có số đo
. Tính số đo các góc của tứ giác đó. Bài giải Tứ giác ABCD có: hay Vậy Bài tập 6
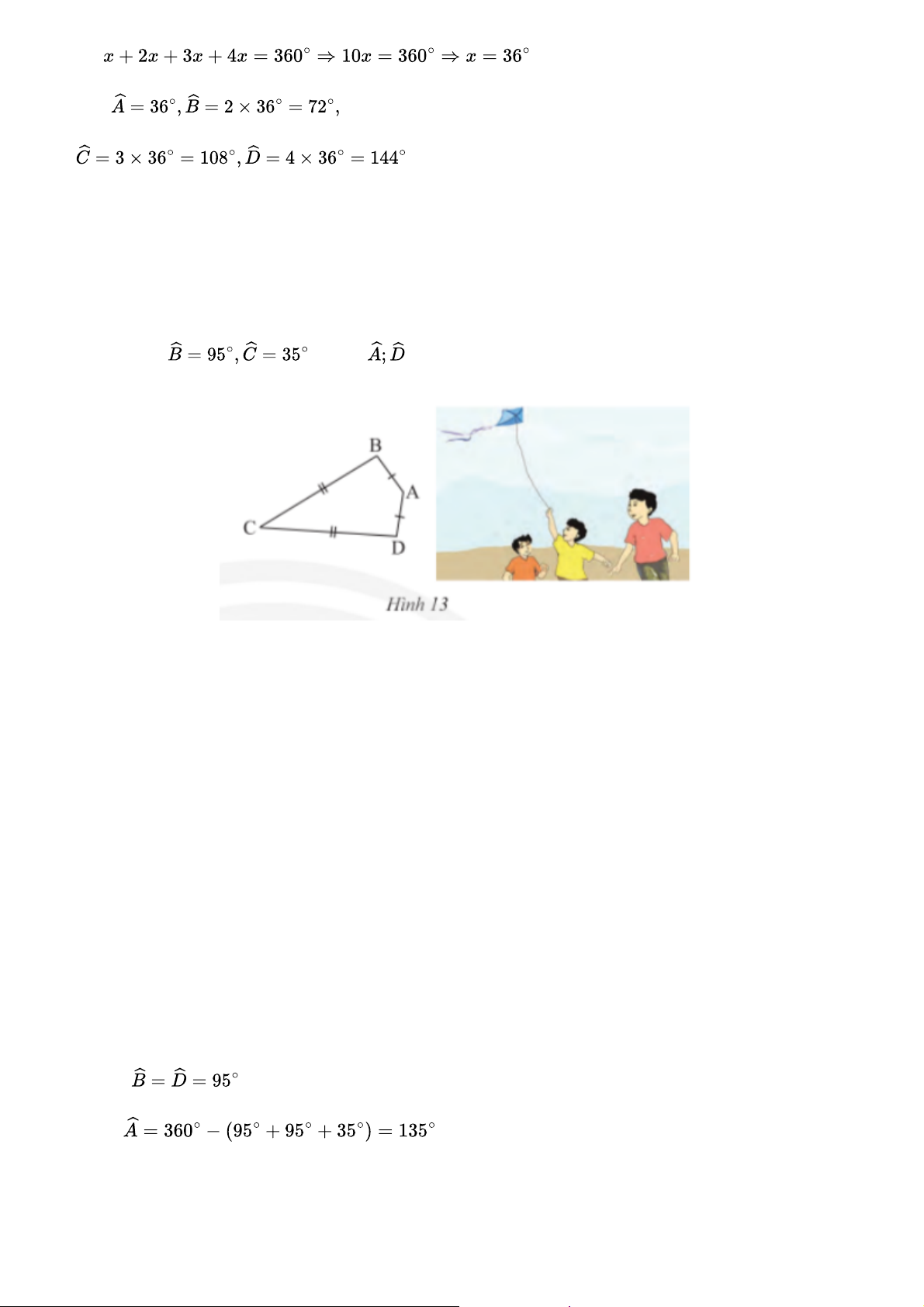
Ta có tứ giác ABCD với AB = AD, CB = CD (Hình 13) là hình "cái diều".
a) Chứng minh rằng AC là đường trung trực của BD b) Cho biết . Tính Bài giải
a) Ta có: AB = AD (gt) => A thuộc đường trung trực của BD
CB = CD (gt) => C thuộc đường trung trực của BD.
Vậy AC là đường trung trực của BD.
b) Xét ∆ ABC và ∆ADC có: AB = AD (gt) CB = CD (gt) AC chung nên ∆ ABC = ∆ADC (c.c.c) Suy ra Ta có: Bài tập 7
Trên bản đồ, tứ giác BDNQ với các đỉnh là các thành phố Buôn Ma Thuột, Đà Lạt, Nha Trang, Quy Nhơn.
a) Tìm các cạnh kề và cạnh đối của cạnh BD
b) Tìm các đường chéo của tứ giác Bài giải
a) Cạnh kề cạnh BD: DN, BQ Cạnh đối cạnh BD: NQ
b) Các đường chéo: BN, DQ