Toán 8 Bài 3: Hình thang - Hình thang cân - Chân trời sáng tạo
Toán 8 Bài 3: Hình thang - Hình thang cân Chân trời sáng tạo được biên soạn dưới dạng file PDF cho học sinh tham khảo, ôn tập đầy đủ kiến thức đẻ chuẩn bị tốt cho kỳ thi sắp tới. Mời bạn đọc đón xem.
Chủ đề: Chương 3: Định lý Pythagore - Các loại tức giác thường gặp (CTST)
Môn: Toán 8
Sách: Chân trời sáng tạo
Thông tin:
Tác giả:
Thông tin :
Chủ đề:
Chương 3: Định lý Pythagore - Các loại tức giác thường gặp (CTST)
Môn:
Sách:
Tác giả:
Preview text:
Giải Toán 8 Bài 3: Hình thang - Hình thang cân Bài tập 1
Tìm x và y ở các hình sau. Gợi ý đáp án MN // PQ suy ra à c) Ta có: hay d) Ta có: hay Bài tập 2
Cho tứ giác ABCD có AB = CD, BD là tia phân giác góc B. Chứng minh rằng ABCD là hình thang Gợi ý đáp án
Xét tam giác ABD có AB=AD(gt) ⇒ΔABD cân tại A ⇒ Mà
(BD là tia phân giác của góc B) Do đó Mà so le trong ⇒AD//BC Vậy ABCD là hình thang. Bài tập 3
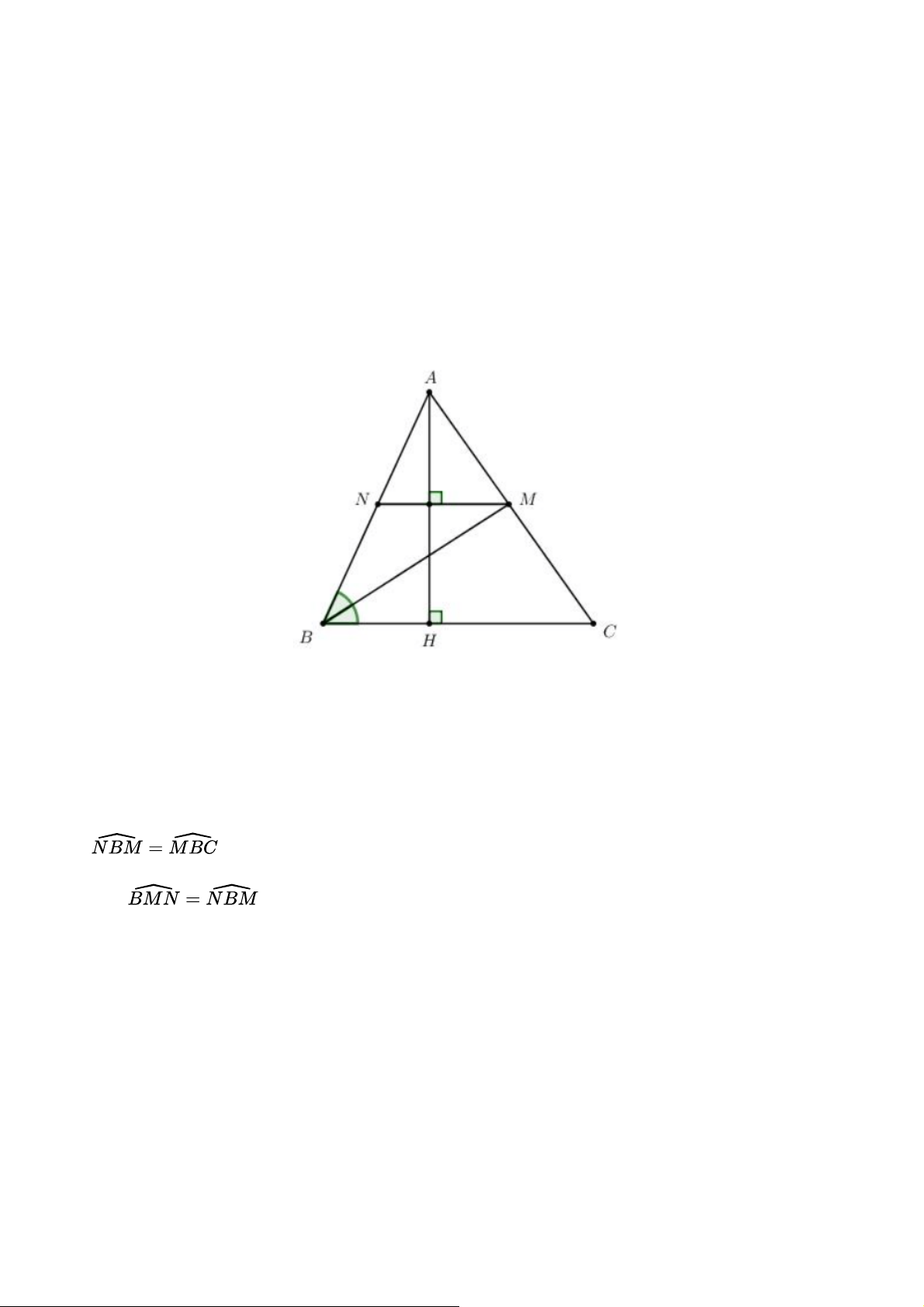
Cho tam giác nhọn ABC có AH là đường cao. Tia phân giác của góc B cắt AC tại M. Từ M kẻ
đường thẳng vuông góc với AH cắt AB tại N.
a) Chứng minh rằng tứ giác BCMN là hình thang.
b) Chứng mình rằng BN = MN. Gợi ý đáp án a) Ta có: MN⊥AH(gt)
Và BC⊥AH (AH là đường cao của tam giác ABC) ⇒MN//BC Suy ra BCMN là hình thang b)
(BM là tia phân giác góc B) Suy ra ⇒ ΔBMN cân tại N. Vậy BN=MN Bài tập 4
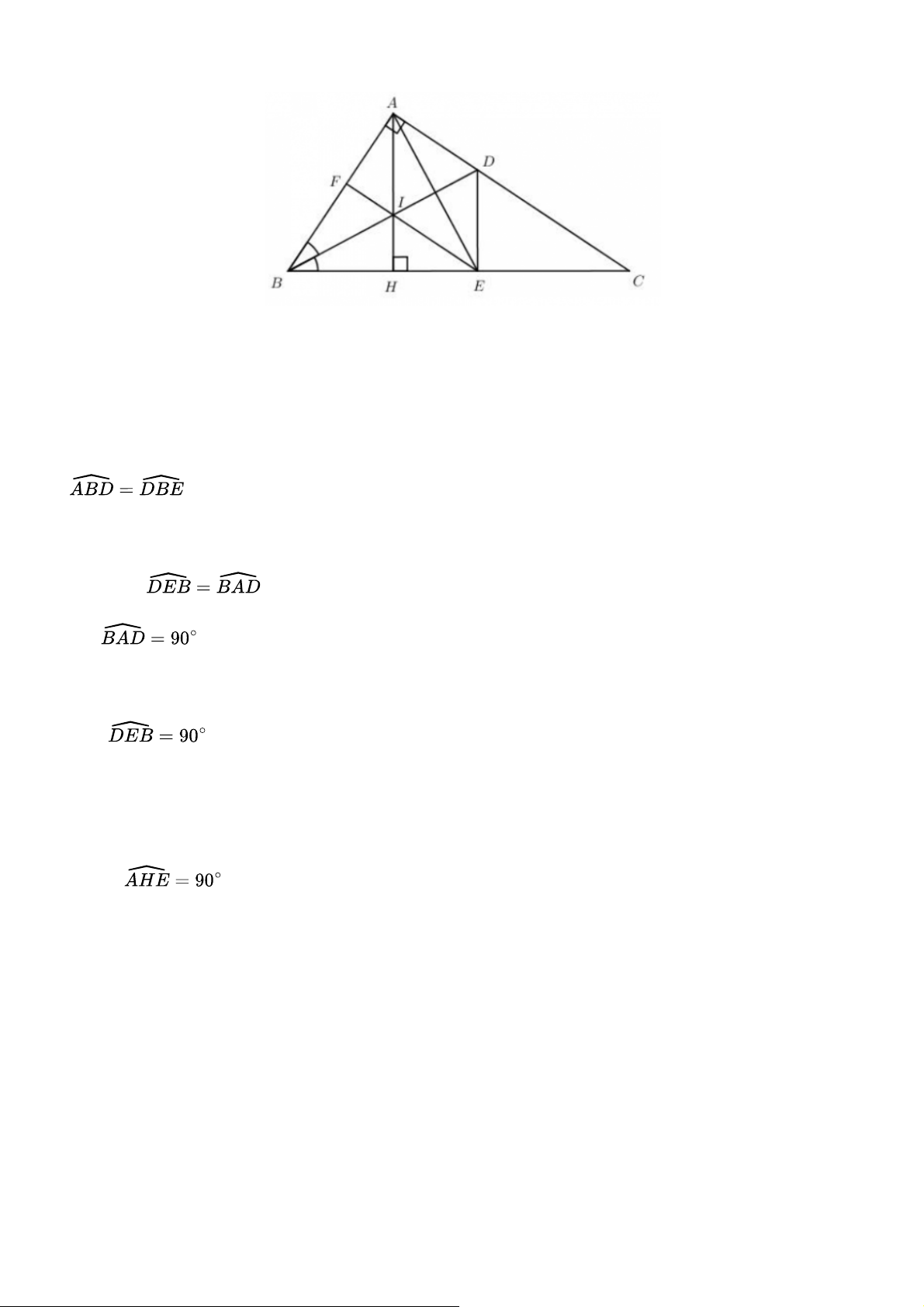
Cho tam giác ABC vuông tại A (AB < AC). Tia phân giác của góc B cắt AC tại D. Trên BC lấy điểm E sao cho BE = BA.
a) Chứng minh rằng: Δ A B D = Δ E B D
b) Kẻ đường cao AH của tam giác ABC. Chứng mình rằng tứ giác ADEH là hình thang vuông.
c) Gọi I là giao điểm của AH với BD, đường thẳng EI cắt AB tại F. Chứng minh rằng tứ giác ACEF là hình thang vuông. Gợi ý đáp án
a) Xét ΔABD và ΔEBD ta có: AB = BE (gt) BD là cạnh chung
(BD là tia phân giác của góc B) Do đó ΔABD = ΔEBD(c.g.c) b) Ta có: (ΔEBD=ΔABD) Mà (ΔABD vuông tại A) Nên ⇒DE⊥BC
Mặt khác AH⊥BC (gt) do đó DE // AH
⇒ Tứ giác ADEH là hình thang Lại có (AH⊥BC)
Vậy tứ giác ADEH là hình thang vuông.
c) Ta có BE=BA(gt)⇒ cân tại B.
Mà BD là tia phân giác của góc B. Do đó BD là đường cao của tam giác BAE.
ΔBAEcó AH, BD là hai đường cao cắt nhau tại I ⇒I là trực tâm của tam giác BAE.
⇒ EFlà đường cao của tam giác BAE ⇒ EF⊥AB Mà AC⊥AB⇒EF//AC
Vậy tứ giác ACEF là hình thang. Mà
. Do đó tứ giác ACEF là hình thang vuông. Bài tập 5
Tứ giác nào trong Hình 15 là hình thang cân? Gợi ý đáp án a) Ta có: . Mà
là hai góc trong cùng phía suy ra GH // KI ⇒ GHKI là hình thang
Suy ra GHIK không là hình thang cân b) Ta có: à (hai góc kề bù) Do đó Ta có: . Mà
là hai góc trong cùng phía suy ra MQ // PN ⇒MQPN là hình thang Lại có:
Do đó MQPN là hình thang cân c) Ta có: à à . Mà à và
à là hai góc trong cùng phía
suy ra AB // CD⇒ABCD là hình thang
Lại có AC = BD suy ra ABCD là hình thang cân Bài tập 6
Cho hình thang ABCD có AB // CD. Qua giao điểm E của AC và BD, ta vẽ đường thẳng song
song với AB cắt AD, BC lần lượt tại F và G (Hình 16). Chứng minh rằng EG là tia phân giác góc CEB. Gợi ý đáp án
Xét tam giác ACD và BDC ta có: AD = BC (gt) AC = BD (gt) CD chung Suy ra (c.c.c) Ta có: FG // CD suy ra (đồng vị), (so le trong) Suy ra
hay EG là tia phân giác góc CEB.