Giải Toán 8 Chân trời sáng tạo trang 88 - Trắc nghiệm Bài tập 1
Bạn Nam dùng 6 đoạn tre vót thẳng để làm khung diều hình thoi. Trong đó 2 đoạn tre dài 60 cm
và 80 cm để làm đường chéo của cái diều, 4 đoạn tre còn lại là 4 cạnh của cái diều. Khi đó
tổng độ dài 4 đoạn tre dùng làm cạnh của cái diều hình thoi là A. 5 m B. 1 m C. 1.5 m D. 2 m Gợi ý đáp án
Độ dài 1 đoạn tre còn lại là: (cm)
Tổng độ dài 4 đoạn tre còn lại: 50 x 4 = 200 (cm) = 2 m Đáp án: D Bài tập 2
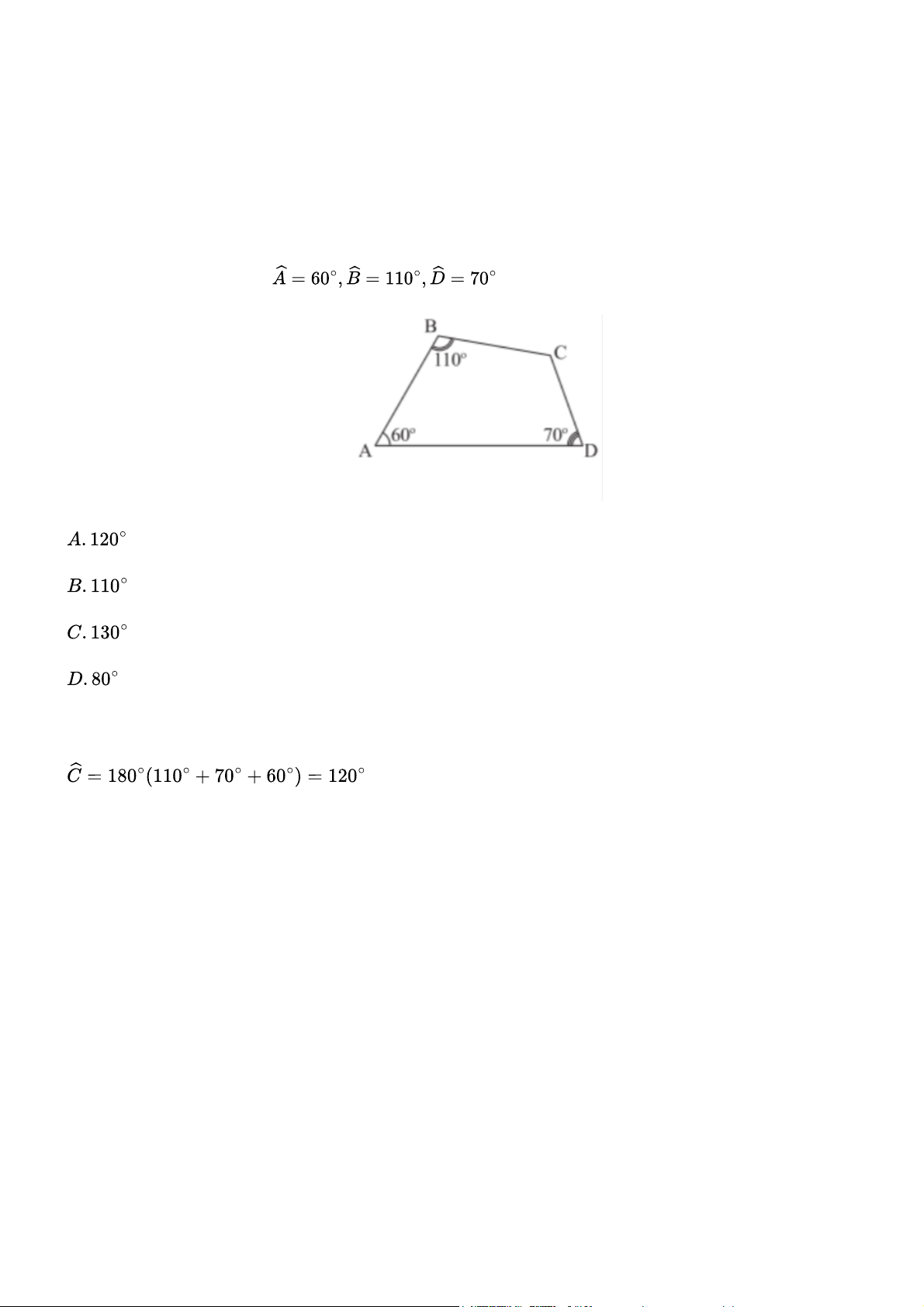
Cho hình thang cân ABCD (AB // CD) có . Số đo góc C là: A. Gợi ý đáp án Đáp án: A Bài tập 3
Trong khẳng định sau, khẳng định nào sai?
A. Tứ giác có ba góc vuông là hình chữ nhật
B. Hình bình hành có một góc vuông là hình chữ nhật
C. Hình bình hành có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình chữ nhật
D. Tứ giác có các cạnh đối bằng nhau là hình bình hành. Gợi ý đáp án Đáp án: C Bài tập 4
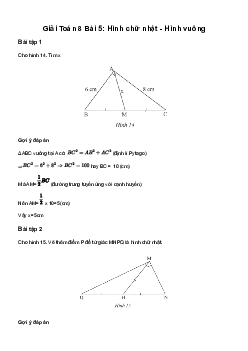
Cho tam giác ABC vuông tại A, đường trung tuyến AM. BIết AB = 8 cm, AC = 15 cm. Độ dài đoạn AM là: A. 8.5 cm B. 8 cm C. 7 cm D. 7.5 cm Gợi ý đáp án Ta có: suy ra BC = 17 cm AM = = 8.5 cm Đáp án: A Bài tập 5
Cho hình thoi ABCD có cạnh bằng 13 cm, độ dài đường chéo AC = 10 cm. Độ dài đường chéo BD là A. 24 cm B. 12 cm C. 16 cm D. 20 cm Gợi ý đáp án Đáp án: A Bài tập 6
Trong các khẳng định sau, khẳng định nào đúng?
A. Hình chữ nhật có hai đường chéo bằng nhau là hình vuông
B. Hình thoi có hai đường chéo vuông góc là hình vuông
C. Hình thoi có một góc vuông là hình vuông
D. Hình chữ nhật có một góc vuông là hình vuông Gợi ý đáp án Đáp án: C Bài tập 6 Cho tứ giác ABCD, biết . Khi đó số đo góc C là Gợi ý đáp án Đáp án: A
Giải Toán 8 Chân trời sáng tạo trang 89 - Tự luận Bài tập 8
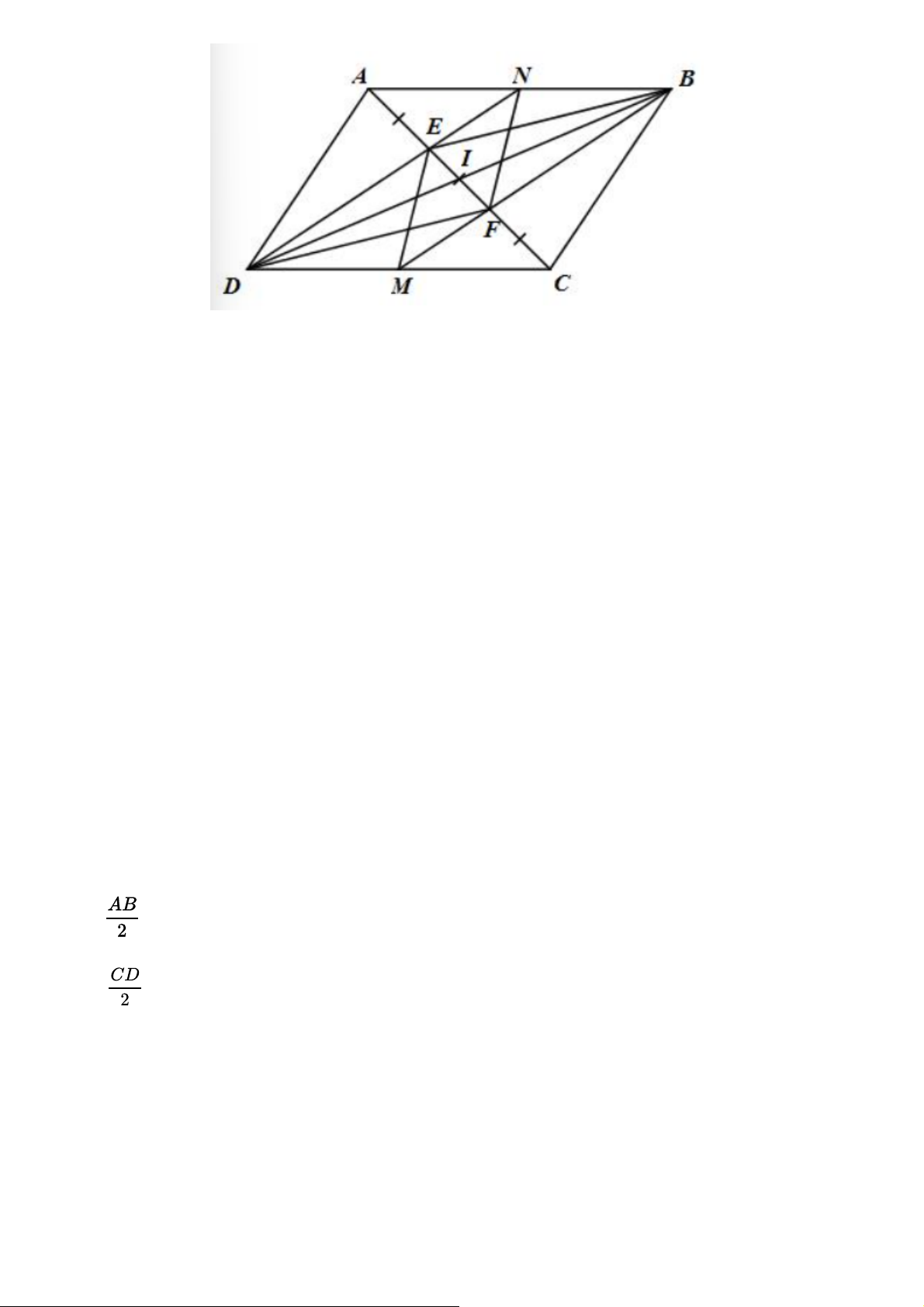
Cho hình bình hành ABCD. Các điểm E, F thuộc đường chéo AC sao cho AE = EF = FC. Gọi M
là giao điểm của BF và CD, N là giao điểm của DE và AB. Chứng minh rằng:
a) M, N theo thứ tự là trung điểm của CD, AB b) EMFN là hình bình hành Gợi ý đáp án
a) Gọi I là tâm đối xứng của hình bình hành ABCD
⇒I là trung điểm của AC và BD ⇒IA=IC ⇒IA–AE=IC–FC (vì AE=FC)
⇒EI=FI⇒I là trung điểm của EF.
Tứ giác DEBF có DB và EF cắt nhau tại I (I là tâm đối xứng, E,F∈AC)
I là trung điểm của BD và I là trung điểm của EF.
Do đó tứ giác DEBF là hình bình hành ⇒DE//BF⇒EN//BF (N∈DE)
Mà E là trung điểm của AF (AE=EF) nên N là trung điểm của AB.
ΔDEC có MF//DE(DE//BF,M∈BF) và F là trung điểm của EC (EF=FC)
⇒M là trung điểm của CD. b) Ta có AN=
(N là trung điểm của AB) MC=
(M là trung điểm của CD)
AB=CD (ABCD là hình bình hành) ⇒AN=MC
Xét tam giác AEN và tam giác MFC ta có : AE=FC(gt) AN=MC (gt)
(hai góc so le trong và AB // CD) Do đó ΔAEN=ΔCFM(c.g.c)
Tứ giác EMFN có EN // MF (DE//BF,N∈DF,M∈BF)
Và EN=MF(ΔAEN=ΔCFM). Do đó tứ giác EMFN là hình bình hành. Bài tập 9
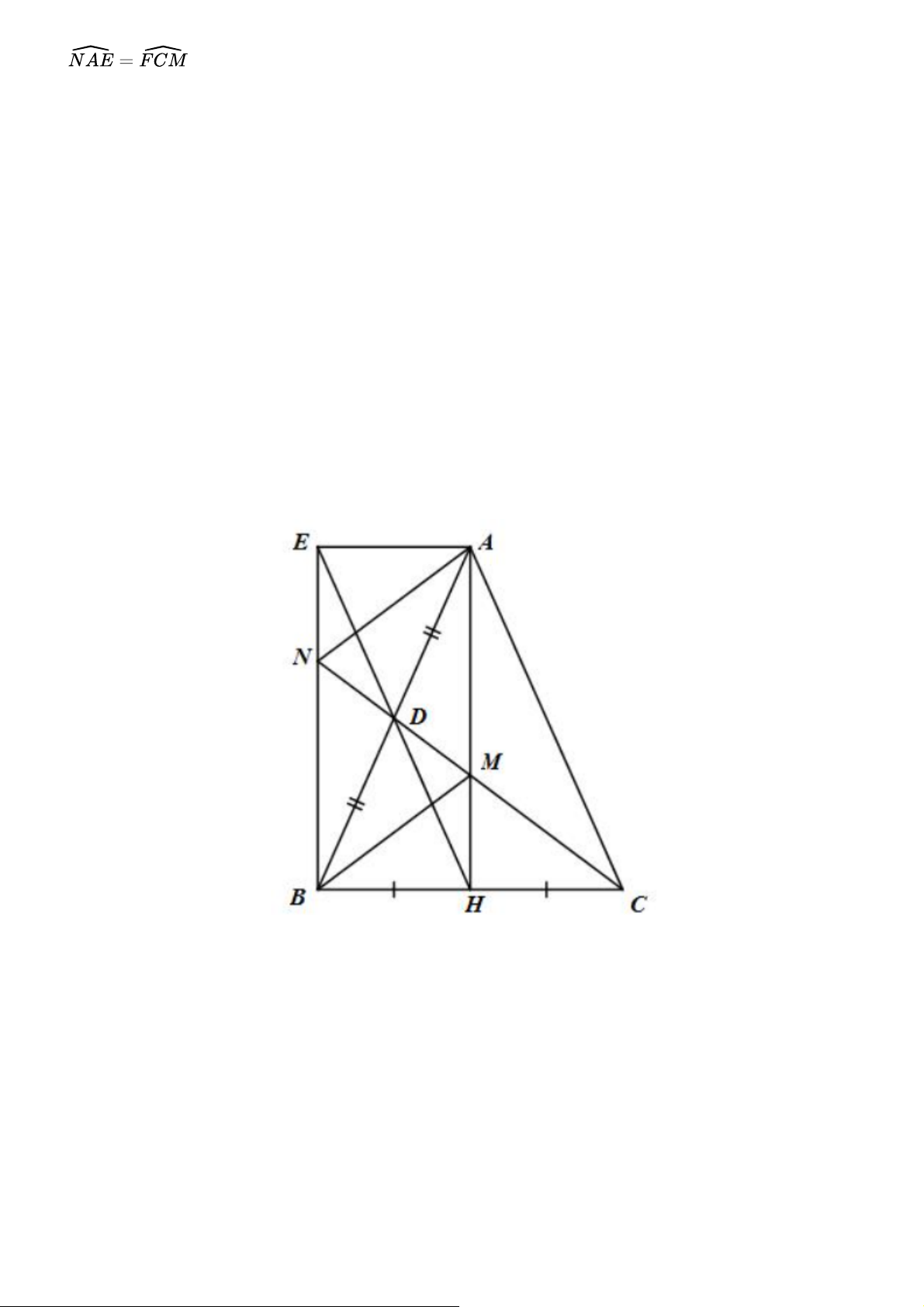
Cho tam giác ABC cân tại A. Gọi H, D lần lượt là trung điểm của các cạnh BC và AB.
a) Chứng minh rằng tứ giác ADHC là hình thang.
b) Gọi E là điểm đối xứng với H qua D. Chứng minh rằng tứ giác AHBE là hình chữ nhật.
c) Tia CD cắt AH ở M và cắt BE ở N. Chứng minh tứ giác AMBN là hình bình hành. Gợi ý đáp án
a) Ta có D, H lần lượt là trung điểm của AB và BC.
⇒DH là đường trung bình của tam giác ABC.
⇒DH//AC⇒ Tứ giác ADHC là hình thang.
b) ΔABC cân tại A có AH là đường trung tuyến (H là trung điểm của BC)
⇒AH là đường cao của tam giác ABC. ⇒AH⊥BC tại H.
Tứ giác AHBE có AB và EH cắt nhau tại D (gt)
D là trung điểm của AB (gt)
D là trung điểm của EH (E là điểm đối xứng với H qua D),
(hai góc so le trong và EB // AH) Và
(hai góc đối đỉnh), do đó ΔEND=ΔHDM(g.c.g)
⇒ND=MD⇒D là trung điểm của NB (D∈NM)
Mặt khác D là trung điểm của AB (gt) và NM, AB cắt nhau tại D (gt)
Do đó tứ giác AMBN là hình bình hành (dấu hiệu nhận biết hình bình hành) Bài tập 10
Cho tam giác ABC vuông tại A (AB < AC). Gọi M, N, E lần lượt là trung điểm của AB, AC, BC.
a) Chứng minh tứ giác ANEB là hình thang vuông.
b) Chứng minh tứ giác ANEM là hình chữ nhật.
c) Đường thẳng song song với BN kẻ từ M cắt tia EN tại F. Chứng minh rằng tứ giác AFCE là hình thoi.
d) Gọi D là điểm đối xứng của E qua M. Chứng minh rằng A là trung điểm của DF. Bài tập 11
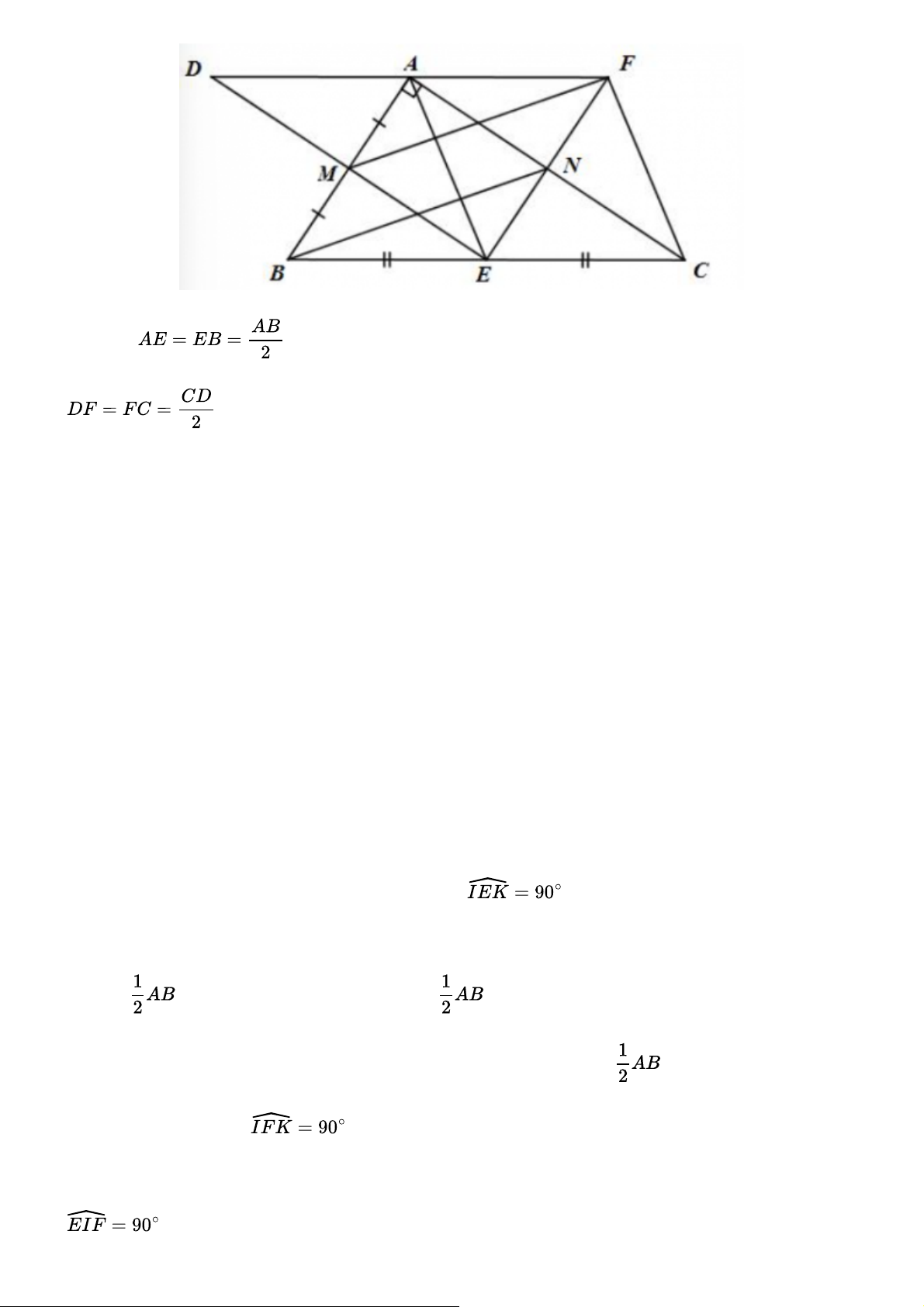
Cho hình bình hành ABCD có AB = 2AD. Gọi E, F lần lượt là trung điểm của AB và CD. Gọi I là
giao điểm của AF và DE, K là giao điểm của BF và CE. Chứng minh rằng:
a) Tứ giác AECF là hình bình hành.
b) Tứ giác AEFD là hình gì? Vì sao?
c) Chứng minh tứ giác EIFK là hình chữ nhật.
d) Tìm điều kiện của hình bình hành ABCD để tứ giác EIFK là hình vuông. Gợi ý đáp án a) Ta có
(E là trung điểm của AB),
(F là trung điểm của CD)
Và AB=CD(ABCD là hình bình hành) ⇒AE=CF=EB=DF
Tứ giác AECF có AE // CF (AB // CD, E∈AB, F∈CD) và AE=CF ⇒AECF là hình bình hành.
b) Ta có : AB=2AD(gt) và AB=2AE (E là trung điểm của AB) => AD = AE
Tứ giác AEFD có AE // DF và AE=DF(chứng minh câu a)
⇒ Tứ giác AEFD là hình bình hành
Mà AE=AD (chứng minh trên) nên AEFD là hình thoi.
c) Ta có AF⊥DE tại I (AEFD là hình bình hành)
Và AF//EC(AECF là hình bình hành) ⇒EC⊥DE⇒
Ta có EF=AE(AEFD là hình thoi) Và AE=
(E là trung điểm của AB) ⇒EF=
ΔAFBcó FE là đường trung tuyến (E là trung điểm của AB) và EF= ⇒ΔAFB vuông tại F ⇒ Tứ giác EIFK có: (IE⊥IFtại I)
Do đó tứ giác EIFK là hình chữ nhật.
d) Ta có tứ giác EIFK là hình chữ nhật.
I là trung điểm của ED (tứ giác AEFD là hình bình hành)
Tương tự K là trung điểm của EC.
Do đó IK là đường trung bình của tam giác ECD ⇒IK⊥CD
Mặt khác AD // EF (tứ giác AEFD là hình bình hành)
Do đó tứ giác EIFK là hình vuông.
⇔ Hình chữ nhật EIFK có IK⊥EF⇔IK⊥AD⇔AD⊥CD
⇔ Hình bình hành ABCD có
Vậy điều kiện của hình bình hành ABCD là
để tứ giác EIFK là hình vuông. Bài tập 12
a) Ta có MN⊥CE(gt); AB⊥CE(gt)⇒MN//AB
Mà AB // CD (ABCD là hình bình hành) nên MN // CD Tứ giác MNCD có MN // CD
Và MD // CN (AD // BC, M∈AD,N∈BC)
Do đó tứ giác MNCD là hình bình hành.
b) Gọi F là giao điểm của MN và EC
Hình thang AECD (EC // CD) có MF//AE//CD
Và M là trung điểm của AD (gt)
⇒F là trung điểm của EC.
ΔMEC có MF là đường trung tuyến (F là trung điểm của EC)
Và MF là đường cao (MF⊥EC)⇒ΔMEC cân tại M. c) Ta có AD=2AB(gt)
AD=2MD (M là trung điểm của AD)
Và AB=CD (ABCD là hình bình hành) ⇒MD=CD
Hình bình hành MNCD có MD=CD nên là hình thoi.
⇒CM là đường phân giác ⇒ Mà
(hai góc so le trong và AE // MF) Và
(hai góc so le trong và MF // CD) Nên Ta có
(CM là tia phân giác của ) Và
(ABCD là hình bình hành) ⇒