















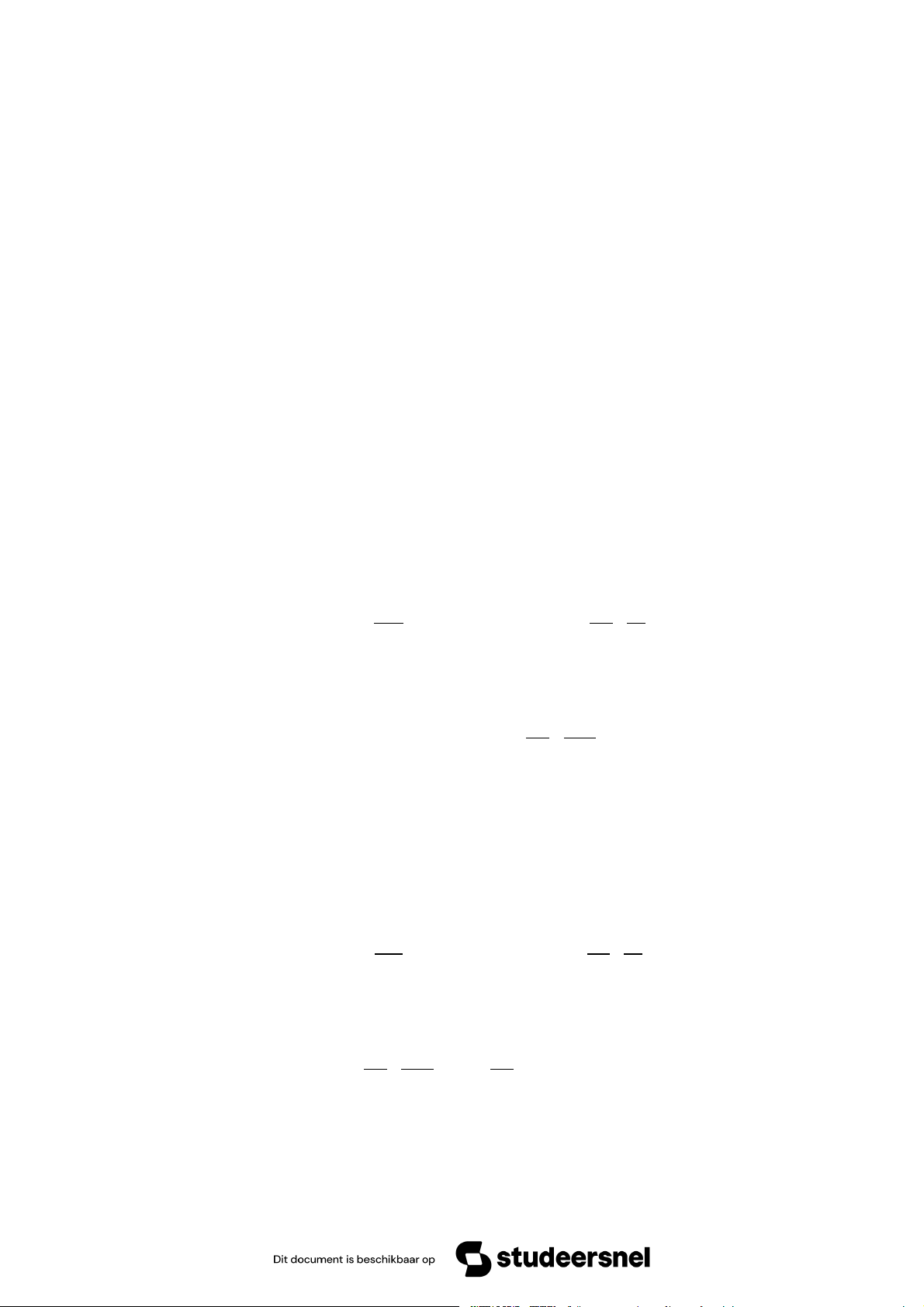

Preview text:
CHƯƠNG 6. HÀM SỐ HAI BIẾN SỐ
Ở những chương trước, chúng ta đã nghiên cứu hàm y = f(x) với x là biến
số và gọi là hàm một biến. Tuy nhiên trong thực tế, một đại lượng biến thiên
không chỉ phụ thuộc vào một mà vào hai hay nhiều đại lượng biến thiên khác,
do vậy ta phải nghiên cứu hàm số nhiều biến số. Nói chung việc nghiên cứu hàm
nhiều biến khá phức tạp, nên ở chương này chỉ dừng lại nghiên cứu hàm hai
biến, song từ việc nghiên cứu hàm hai biến ta có thể suy ra các tính chất của hàm nhiều biến.
Đan xen với các nội dung toán học, chúng tôi trình bày một số mô hình
toán kinh tế, với mục đích giúp sinh viên làm quen với việc sử dụng công cụ
toán học trong phân tích kinh tế
6.1. CÁC KHÁI NIỆM CƠ BẢN
6.1.1. Định nghĩa hàm số hai biến số Định nghĩa 6.1.
Cho D là một tập con của mặt phẳng xOy.
Một qui tắc đặt tương ứng mỗi điểm M(x, y)∈D với một và chỉ một số thực z=f(x,y) f: D R (x,y)
z = f (x, y)
được gọi là một hàm số hai biến số xác định trên D.
Trong đó: + D gọi là miền xác định của hàm số z = f (x, y)
+ x, y là các biến độc lập
+ z = f (x, y) hay z = f (M ) được gọi là giá trị của hàm số tại điểm M(x,y) Ví dụ 1.
1. z = 1- x2 - y2
2. z =arcsin(x - y +1)
là các hàm số hai biến x và y
6.1.2. Miền xác định của hàm số hai biến số
a. Tập hợp trong không gian R2
Định nghĩa 6.2. Trong không gian vectơ 2 chiều
R2 ={ M (x, y) x, y ∈ R }
Khoảng cách giữa hai điểm M(x1,y1) và N(x2,y2), ký hiệu là d(M,N), được xác
định theo công thức:
d(M , N ) = (x - x )2 + (y - y )2 2 1 2 1
• Hình cầu tâm Mo, bán kính r ( r > 0) trong R2, kí hiệu là S(M0,r):
S(M 0,r) ={ M ∈R2 d(M,M 0) ∈ r}
S(M0, r) còn được gọi là r lân cận của điểm Mo
• Mọi tập con của R2 chứa một r - lân cận của điểm M0 được gọi là một lân
cận của điểm M là điểm trong của D nếu tồn tại một r lân cận nào đó của M nằm hoàn toàn trong D
• D là tập mở nếu mọi điểm của D đều là điểm trong của D
• M là điểm biên của D nếu mọi r lân cận của M vừa chứa điểm thuộc D
vừa chứa điểm không thuộc D. Tập tất cả các điểm biên của D gọi là biên của D.
• Tập D được gọi là đóng nếu D chứa mọi điểm biên của nó. Ví dụ :
+ D ={ M ∈R2 d(M,M 0) ∈ r} là tập mở và được gọi là hình cầu mở tâm M0 bán kính r
+ L ={M ∈ R2 d(M,M 0) r} là tập đóng và được gọi là hình cầu đóng tâm M0 bán kính r
b. Miền xác định của hàm số hai biến số
Cho hàm số z = f (x, y) . Miền xác định của z là tập hợp tất cả các cặp
(x, y)∈ R2 làm cho biểu thức f (x, y) có nghĩa và được ký hiệu là Df
Quy ước: Nếu hàm số được cho bởi biểu thức z = f (x, y) = f (M ) mà
không nói gì thêm về miền xác định của hàm số thì ta hiểu miền xác định của z
là tập hợp những điểm M sao cho biểu thức f(M) có nghĩa, hay
Df = { M(x, y) ∈R2| biểu thức z = f (x, y) có nghĩa}
Ví dụ 1: Hàm số z =x2 + y2 được xác định với 6(x, y)∈ R2
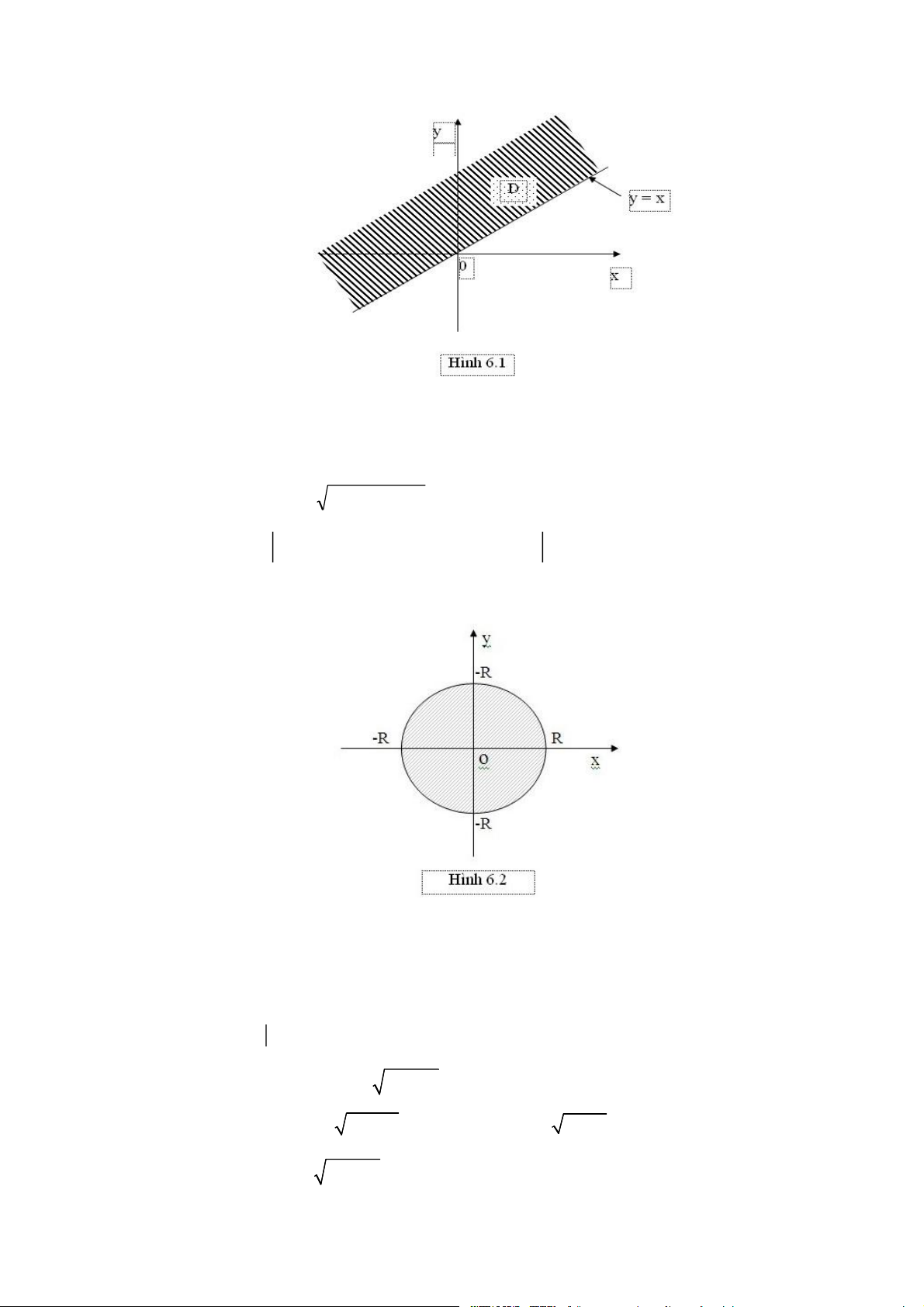
Ví dụ 2: Hàm số z = y - x được xác định trong miền
D ={(x, y) ∈ R2 y - x ?0} ={(x, y) ∈ R2 y ?x} 255
là nửa mặt phẳng phía trên đường thẳng y =x , kể cả đường thẳng này (Hình 6.1)
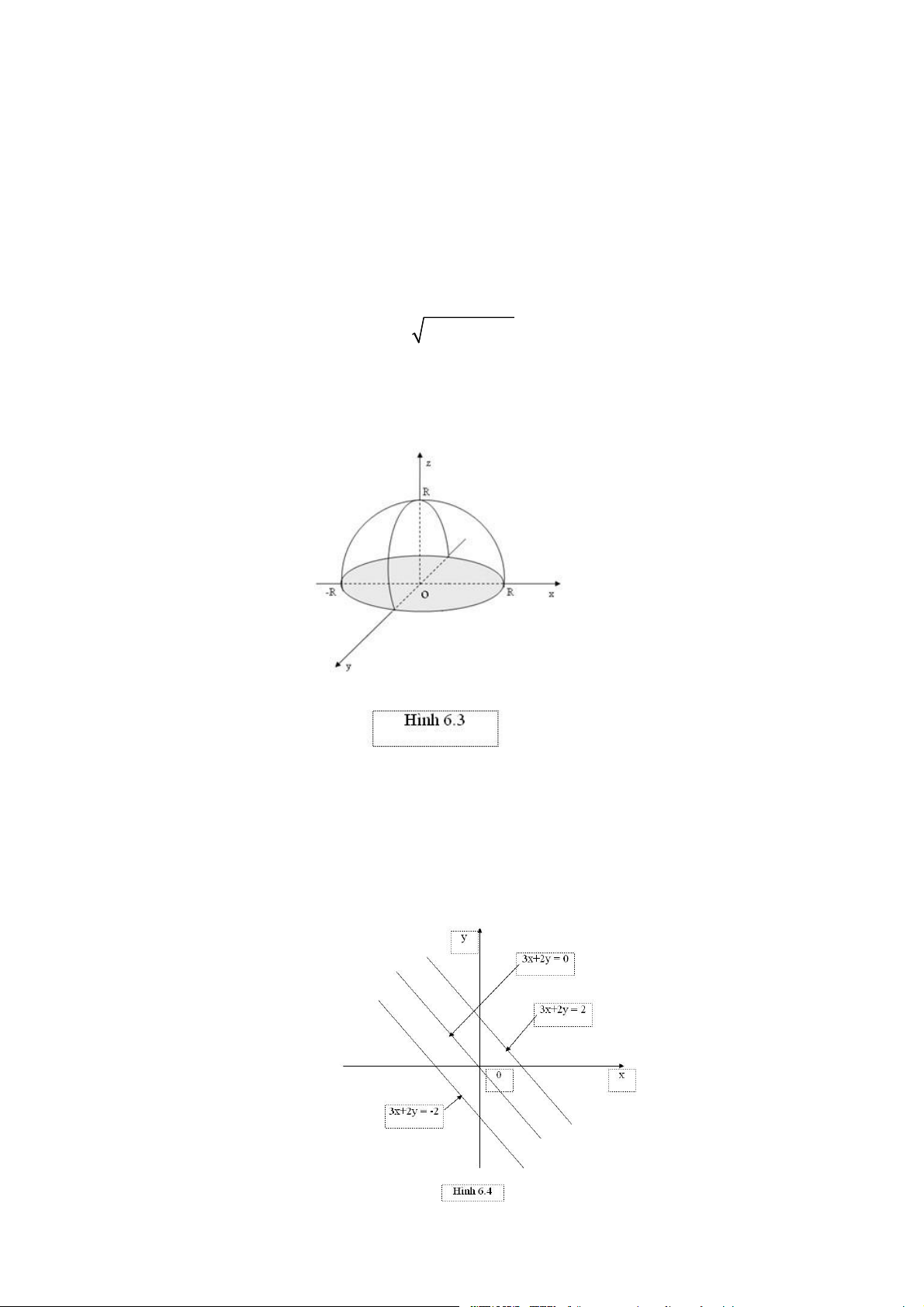
Ví dụ 3: Hàm số z = R2 - x2 - y2 được xác định trong miền
D ={ (x, y)∈R2 R2 - x2 - y2 ?0} ={ (x, y)∈R2 x2 + y2 R2}
là hình cầu đóng tâm O, bán kính R (Hình 6.2)
c. Miền giá trị và đồ thị của hàm số hai biến số
+ Miền giá trị của hàm số z = f (x, y) là tập hợp tất cả các giá trị của hàm số khi
M (x, y) thay đổi trong miền xác định, ký hiệu Df , và
Df ={ z = f (x, y) 6(x, y) ∈ D}
Ví dụ 1: Cho hàm số z = x2 + y2 . Giá trị của hàm số tại các điểm M0(0;0);
M1(4;3) là: z0 = f (0,0) = 02 +02 =0 ; z1 = f (4,3) = 16+9 =5
Ví dụ 2: Hàm số z = x2 + y2 có miền giá trị là: Df =[ 0;+∞3
Ví dụ 3: Hàm số z =sin(x2 + y2) có miền giá trị là Df =[ - 1;1]
+ Đồ thị của hàm hai biến
Trên hệ trục tọa độ Oxyz, tập hợp tất cả các điểm có tọa độ (x, y, z) với
(x, y) ∈D và z ∈D f gọi là đồ thị của hàm hai biến z = f (x, y)
Nói chung đồ thị của hàm số z = f (x, y) tạo thành một mặt S nào đó trong không gian ba chiều Oxyz.
Ví dụ 4: Đồ thị của hàm số: z = R2 - x2 - y2 là nửa mặt cầu nằm phía trên mặt phẳng xOy (Hình 6.3)
d. Đường mức
Cho hàm số z = f (x, y) xác định trên miền D và z0 là một giá trị cố định cho trước của hàm số.
Định nghĩa 6.3. Đường
mức của hàm số z = f (x, y)
là tập hợp tất cả các điểm M (x,y) thỏa mãn điều kiện f(x,y) =z0
Ví dụ 1: Cho hàm số z =3x +2y
Các đường mức của hàm số ứng với các giá trị z0 =- 2; z0 =0 ; z0 =2 lần lượt là
3x + 2y =- 2; 3x + 2y =0; 3x + 2y =2 (Hình 6.4) 257
Ví dụ 2: Hãy viết phương trình đường mức đi qua điểm A(0,1) của hàm số x2 + y2 z = 2x+6y A(0,1) 02 +12 1
Giá trị của hàm số tại điểm là: z = 0 = f (0,1) =2.0 +6.1 6
Phương trình đường mức của hàm số tại giá trị z 1 = là: 0 6 x2 + y2 1 1 1 =
6x2 +6y2 - 2x - 6y =0 (x - )2 + (y- )2 =10 2x + 6y 6 6 2 36
Vậy đường mức của hàm số tại giá trị z 1
= là đường tròn tâm I(1 ; 1) và bán 0 6 6 2 10 kính R = 6
6.1.3. Một số hàm số thường gặp trong phân tích kinh tế.
a. Hàm sản xuất
+ Hàm sản xuất là hàm số biểu diễn sự phụ thuộc của sản lượng hàng hóa
( tổng số lượng sản phẩm hiện vật) của một doanh nghiệp vào lượng sử dụng các
yếu tố đầu vào của sản xuất. Nếu trong hoạt động sản xuất, các nhà kinh tế chỉ
quan tâm đến 2 yếu tố sản xuất quan trọng nhất là vốn (capital) và lao động
(labor) thì hàm sản xuất có dạng: Q = f(K, L)
trong đó: Q là sản lượng ; K là vốn; L là lao động,
Q = f(K, L) > 0 6K > 0, L > 0
Các dạng hàm sản xuất phổ biến là: + Dạng tuyến tính: Q = a + bK+cL
+Hàm sản xuất dạng hàm Cobb-Douglas:
Q = a.KαLβ với a, α, β là các hằng số dương
b. Hàm chi phí, hàm doanh thu và hàm lợi nhuận + Hàm chi phí
Trong kinh tế, chi phí sản xuất giữ một vai trò quan trọng và là vấn đề quan
tâm của các doanh nghiệp, của người tiêu dùng và của cả xã hội nói chung.Chi
phí sản xuất là số tiền mà doanh nghiệp phải chi để mua các yếu tố đầu vào cần
thiết cho quá trình sản xuất nhằm thu được lợi nhuận.
Gọi wK là giá thuê một đơn vị vốn ( chẳng hạn như tiền thuê một giờ sử
dụng xưởng máy), wL là giá thuê một đơn vị lao động ( chẳng hạn như tiền phải
trả cho một giờ lao động của một công nhân), C0 là chi phí cố định, thì chi phí
sản xuất theo các yếu tố sản xuất, kí hiệu TC, là hàm số có dạng: TC = wK .K + wL .L + C0 + Hàm doanh thu
Doanh thu là số tiền mà doanh nghiệp thu được sau khi bán các sản phẩm và
dịch vụ của mình. Giả sử doanh nghiệp cạnh tranh có hàm sản xuất Q = f( K,L )
và giá thị trường của sản phẩm là P thì tổng doanh thu của doanh nghiệp là hàm
số của 2 biến số K , L như sau: TR = P.Q = P. f( K,L) + Hàm lợi nhuận
Lợi nhuận là mục tiêu kinh tế cao nhất, là sự chênh lệch giữa tổng doanh thu
và tổng chi phí. Nếu tính theo các yếu tố sản xuất thì hàm lợi nhuận là hàm số
của các yếu tố sản xuất, kí hiệu là TP, có dạng:
TP = TR – TC = P. f(K, L) – ( wK .K + wL .L + C0)
Ví dụ: Một công ty cạnh tranh sản xuất một loại sản phẩm có hàm sản xuất
Q = 25. K0.5. L0.5 với Q, K, L
Hãy lập hàm doanh thu, hàm chi phí và hàm lợi nhuận của công ty theo K và
L, biết giá bán sản phẩm trên thị trường là 4$, giá tư bản wK là 15$, giá lao động
wL là $8 và chi phí cố định của công ty là $50.
Giải. Hàm doanh thu của công ty là:
TR = P.Q = 4. 25. K0.5. L0.5 = 100 K0.5. L0.5
Hàm chi phí của công ty là: TC = wK .K + wL .L + C0 = 18K + 8L + 50
Hàm lợi nhuận của công ty là:
TP = TR – TC = P. f(K, L) – ( wK .K + wL .L + C0)
= 100K0.5. L0.5 - (18K + 8L + 50 ) 259
c. Hàm chi phí khi doanh nghiệp cùng sản xuất nhiều loại sản phẩm khác nhau
Giả sử một doanh nghiệp sản xuất hai loại sản phẩm Q1 và Q2. Để sản xuất Q1
đơn vị sản phẩm 1 và Q2 đơn vị sản phẩm 2 thì doanh nghiệp phải bỏ ra một
khoản chi phí TC. Khi đó chi phí của doanh nghiệp được xác định là hàm số của 2 biến Q1 và Q2: TC = TC(Q1, Q2)
e. Hàm lợi ích
Giả sử cơ cấu tiêu dùng của người tiêu dùng gồm có 2 mặt hàng x và y. Mỗi
giỏ hàng là một bộ số thực (x, y), trong đó x là lượng hàng hóa thứ nhất và y là
lượng hàng hóa thứ hai (x ≥ 0, y ≥ 0) do người mua thiết lập. Hàm lợi ích là hàm
số đặt tương ứng với mỗi giỏ hàng (x,y) một giá trị U nhất định theo qui tắc: giỏ
hàng nào được ưa chuộng hơn thì gán cho giá trị lợi ích lớn hơn, kí hiệu là:U=
U( x,y) ( U(x,y) >0 với x ?0, y ?0) .
Một trong những hàm lợi ích hay được sử dụng là hàm dạng Cobb-Douglas: U(x,y) = a. xα .yβ
(a, α , β là các hằng số dương).
6.2. GIỚI HẠN VÀ TÍNH LIÊN TỤC CỦA HÀM SỐ HAI BIẾN SỐ
6.2.1. Giới hạn của hàm hai biến số
a. Giới hạn của dãy điểm trong mặt phẳng:
Cho dãy điểm {Mn(xn,yn)} ∈D ( với D∈ R2 ). Ta nói dãy điểm {Mn} hội tụ tới
M0 khi n ⟶ ∞ nếu lim d(Mn ,M0) =0 n⟶ ∞
Kí hiệu: lim Mn =M0 hay M n⟶ ∞
n ⟶ M 0 khi n ⟶ ∞
Nhận xét: M ⟶ M - d(M ,M ) = xn ⟶ x0 (x ⟶ 0 -
n - x0 )2 + ( ym - y0)2 n 0 n 0 y y n ⟶ 0
Như vậy, sự hội tụ của dãy điểm trong không gian R2 chính là sự hội tụ theo tọa độ. 1 n lim M
Ví dụ 1: Cho dãy điểm M n( ;
) . Tìm n⟶∞ n n n +1 J
Ta có: lim x =lim 1 =0 và lim y =lim n =1 n⟶ ∞ n n⟶ ∞ n n⟶ ∞ n n⟶ ∞ n +1 260
Vậy dãy điểm { M } hội tụ về điểm M (0,1) khi n ⟶ ∞ hay lim M (1 ; n ) =M (0,1) n n⟶ ∞ n n n +1 3 2n - 1 lim M
Ví dụ 2: Cho dãy điểm Mn( ;
) .Tìm n⟶∞ n n n +1 J Ta có: lim x 3 =lim =0 và lim y 2n - 1 =lim =2 n⟶ ∞ n n⟶ ∞ n n⟶ ∞ n n⟶ ∞ n +1
Vậy dãy điểm { Mn} hội tụ về điểm M (0,2)
b. Giới hạn của hàm số hai biến số.
Cho hàm số z =f(x, y) xác định trong miền D ∈R2 , M0∈R2, { Mn (xn, yn)} là
một dãy điểm trong miền D. Với hàm số z = f (x,y), mỗi dãy điểm
M1(x1, y1) ; M2(x2, y2) ;…; Mn (xn, yn) ;… (1)
cho tương ứng với một dãy số
z1 = f (M1) ; z2 = f (M2) ; …; zn = f (Mn ) ;… (2)
Khi đó, dãy số (2) được gọi là dãy các giá trị của hàm z tương ứng với dãy
điểm (1) lấy từ miền xác định D.
Định nghĩa 6.4. Nếu với mọi dãy điểm (1) lấy từ miền xác định D M0(x0, y0) của
hàm số z = f (x, y) và hội tụ tại điểm M0(x0, y0), mà dãy số (2) tương ứng luôn
luôn có giới hạn L thì số L được gọi là giới hạn của hàm số đã cho khi M ⟶ M0
hay (x, y) ⟶ (x0, y0) và ký hiệu:
lim f (x, y) =L x f (M ) ⟶ x =L 0 hay lim y⟶ y M ⟶ M 0 0
Cũng như khi xét giới hạn của hàm số một biến, có thể chứng minh rằng
định nghĩa trên tương đương với định nghĩa sau:
Định nghĩa 6.5. Hằng số L được gọi là giới hạn của hàm số z = f (x, y) khi
(x, y) ⟶ (x0, y0) nếu với mọi ε > 0 bé tùy ý cho trước, đều tồn tại số ơ > 0 sao cho
0 ∈ x - x0 ∈ơ và 0 ∈ y - y0 ∈ơ thì f (x, y) - L ∈ε Chú ý:
- Khái niệm giới hạn vô hạn cho hàm hai biến cũng được định nghĩa tương tự
như đối với hàm một biến.
- Việc chứng minh các định lý sau về giới hạn của tổng, tích, thương đối với các
hàm số hai biến cũng tương tự như khi chứng minh cho hàm một biến 261
Định lý 6.1: Nếu lim f (x, y) =m lim g(x, y) =n x⟶ a và x⟶a thì: y⟶ b y⟶ b
lim[ f (x, y) g(x,y ]) =lim f (x, y) lim g(x,y) =m n + x⟶ a x⟶ a x⟶ a y⟶ b y⟶ b y⟶ b
lim[ f (x, y).g(x,y)] =lim f (x, y).lim g(x,y) =m.n + x⟶ a x⟶ a x⟶ a y⟶ b y⟶ b y⟶ b
lim f (x, y)
f (x, y) x⟶ a m + lim = y⟶b = với (n 0) x⟶ a g(x, y) lim g(x, y) n y⟶ b x⟶ a y⟶ b
Định lý 6.2. (Nguyên lý kẹp) Giả sử g(x, y) f (x, y) h(x, y) với 6(x, y) thuộc
lim g(x, y) =lim h(x, y) =L
lim f (x, y) =L
lân cận của điểm M(x0,y0) và x⟶x0 x⟶ x0
. Khi đó: x⟶x0 y⟶ y0 y⟶ y0 y⟶ y0
Ví dụ 1: Tìm giới hạn
lim(x2 - 2x + y2 - 6y + 4) x⟶1 y⟶ 3 Giải:
+ Tập xác định của hàm số f (x, y) =(x2 - 2x + y2 - 6y + 4) là R2
+ Với mọi dãy điểm { Mn(xn, yn)} hội tụ đến điểm M0(1,3) , ta luôn có: d =d(M 2 2 n , M 0 ) =
(xn - 1) +( yn - 3) ⟶ 0 khi n ⟶ ∞ + Ta có
lim f (M ) =lim(x 2 - 2x + y 2 - 6y + 4) n x⟶ 1 x⟶ 1 n n n n y⟶ 3 y⟶ 3
=lim (x - 1)2 +( y - 3)2 - 6 =lim(d 2 - 6) =- 6 x⟶1 L n n d ⟶ 0 y⟶ 3
Vậy theo định nghĩa 6.4 ta có lim(x2 - 2x + y2 - 6y +4) x⟶1 = - 6 y⟶ 3 x2 + y2
Ví dụ 2: Tìm giới hạn lim x⟶ 0 y⟶ 0 x2 + y2 +1 - 1 Giải. x2 + y2
+ Hàm số f (x, y) =
không xác định tại điểm O(0,0) x2 + y2 +1 - 1
+ Với mọi dãy điểm { Mn (xn, yn)} hội tụ đến điểm M0(0,0) , ta luôn có: d =d(M 2 2 2 2 n , M 0 ) = (x x
n - 0) +( yn - 0)
= n + yn ⟶ 0 khi n ⟶ ∞ + Ta có 262 lim f (M x 2 + y 2 d2 ) =lim n n =lim
=lim d( d2 +1 +1) =lim( +1) =2 d 2 +1 x⟶ 0 n x⟶ 0 d ⟶ 0 d ⟶ 0 x 2 d2 (d2 n + y 2 n +1 +1 - 1 +1) - 1 d ⟶ 0 y⟶ 0 y⟶ 0 - 1 x2 Vậy lim + y2 =2 x⟶ 0 y⟶ 0 x2 + y2 +1 - 1 lim 2xy
Ví dụ 3: Giới hạn x⟶0 x2 + y2 có tồn tại hay không? y⟶ 0 Giải.
Giới hạn này không tồn tại vì xét hai dãy điểm cùng hội tụ đến O(0,0) { (x , y )} 1 1
= ( ; ) ⟶ (0,0) khi n ⟶ ∞ n n n n J { (x' , y' )}
1 1 ) ⟶ (0,0) khi n⟶ ∞ n n = ( ; 2 n n J
nhưng các dãy giá trị tương ứng của hàm số lại hội tụ đến hai giá trị khác nhau 1 1 1 2. . 2. 2
f (x , y ) = n n = n ⟶ 1 n n 1 1 1 khi n ⟶ ∞ 2. n2 + n2 n2 1 1 2 2. .
f (x ' , y ' ) = n n2 = n3 ⟶ 0 khi n ⟶ ∞ n n 1 1 1 1 + + n2 n4 n2 n4 x3 + 2y3
Ví dụ 4: Tìm giới hạn lim
x⟶ 0 x2 + y2 y⟶ 0 Giải. x3 + 2y3
+Hàm số f (x, y) = x2 + y2 không xác định tại điểm O(0,0). x3 + 2y3 x3 2y3 + Ta có: 0 +
x + 2 y ; 6x 0, y 0. x2 + y2 x2 + y2 x2 + y2 x3 + 2y3
+ Vì lim( x +2 y ) =0 x⟶ 0
nên theo định lí 6.2 (nguyên lý kẹp) ta có lim =0 y⟶ 0
x⟶ 0 x2 + y2 y⟶ 0 x3 + 2y3 Vậy lim =0
x⟶ 0 x2 + y2 y⟶ 0
c. Các giới hạn lặp 263
Giới hạn theo định nghĩa trên được gọi là giới hạn bội hoặc giới hạn kép (các
quá trình x ⟶ x0 và y ⟶ y0 diễn ra đồng thời, không phụ thuộc lẫn nhau). Ngoài
giới hạn kép, ta có thể xét các giới hạn lặp theo cách thức sau:
+ Với y y0 cố định y, ta tính trước giới hạn lim f (x, y) =φ(y) , sau đó tính giới x⟶ x0
hạn lim φ(y) =E y⟶ y0
Trong trường hợp này, ta viết: lim lim f (x, y) =E
y⟶ y0 x⟶ x0
Tương tự, ký hiệu lim lim f (x, y) =F
x⟶ x0 y⟶ y0
Có nghĩa: lim f (x, y) = (x) và lim (x) =F y⟶ y0 x⟶ x0
Nói chung, giới hạn kép L và các giới hạn lặp E, F là các giới hạn có giá trị khác
nhau, thậm chí các giới hạn lặp E và F cũng có thể khác nhau. x - y
Ví dụ: Cho hàm số f (x, y) = x+ y
+ Khi (x, y) ⟶ (0,0) hàm số trên không có giới hạn kép 1 1 2 1
Thật vậy: Xét hai dãy điểm { n n } = ( ; ) và { (x'n, y'n)} = ( ; ) n n J n n J
đều hội tụ đến điểm O(0,0) khi n ⟶ ∞, trong khi đó các dãy giá trị tương ứng
của hàm số lại hội tụ tới những giới hạn khác nhau 1 1 2 1 1 -
f (x , y ) = n n ⟶ 0 khi n ⟶ ∞ và - f (x ' 1
n , y 'n ) = n
n =n ⟶ khi n⟶ ∞ n n 1 1 2 + + 1 3 3 n n n n n
Do đó: lim f (x, y) x⟶ 0 không tồn tại y⟶ 0
+ Các giới hạn lặp tồn tại nhưng có giá trị khác nhau
E =lim(lim f (x, y)) =lim(lim x - y) =lim - y =- 1 y⟶ 0 x⟶ 0
y⟶ 0 x⟶ 0 x + y y⟶ 0 y
F =lim(lim f (x, y)) =lim(lim x - y) =lim x =1 x⟶ 0 y⟶ 0
x⟶ 0 y⟶ 0 x + y x⟶ 0 x
6.2.2. Tính liên tục của hàm hai biến số
a. Các định nghĩa về tính liên tục
Định nghĩa 6.6. Hàm số z = f (x, y) được gọi là liên tục điểm (x0, y0)∈ D nếu:
lim f (x, y) = f (x0, y0) x⟶ x0 y⟶ y0 264
và điểm (x0, y0) gọi là điểm liên tục của hàm số
Ví dụ: Hàm số z =3x 2 +2xy + y2 liên tục tại M(1,1)
lim(3x2 + 2xy + y2) =6 = f (1,1) vì x⟶1 y⟶ 1
Nhận xét: Cũng như đối với hàm một biến, để xét tính liên tục của hàm số hai
biến tại M(x0, y0) , chúng ta phải kiểm tra ba điều kiện sau:
• Hàm số xác định tại (x0, y0)
lim f (x, y) =b
• Tồn tại giới hạn x⟶x0 y⟶ y0
• b = f (x0, y0)
Định nghĩa 6.7. Hàm số z = f (x, y) được gọi là liên tục trên miền D nếu nó liên
tục tại mọi điểm (x0, y0)∈ D
Định nghĩa 6.8. Nếu tại điểm (x0, y0) hàm số z = f (x, y) không liên tục thì hàm
f (x, y) gọi là gián đoạn tại (x0, y0) và điểm (x0, y0) gọi là điểm gián đoạn của hàm số
b. Các phép tính về hàm liên tục
Nếu các hàm f (x, y) và g(x, y) liên tục tại điểm (x0, y0) thì:
• f (x, y) g(x, y) liên tục tại (x0, y0)
• f (x, y).g(x, y) liên tục tại (x0, y0) f (x, y) •
g(x, y) liên tục tại (x0, y0) (với g(x0, y0) 0 ) ∣ xy α
khi (x, y) (0,0) 2 2
Ví dụ: Khảo sát tính liên tục của hàm số f (x, y) = x + y ∣0
khi (x, y) =(0, 0)
trong đó α là một hằng số dương. Giải:
Hàm f (x, y) liên tục tại mọi điểm (x, y) (0,0) vì là thương của hai hàm liên tục mà mẫu khác 0 Xét tại điểm O(0,0)
Theo bất đẳng thức Cauchy, ta có: 1
xy ? (x2 + y2 ) ⟶ f (x, y)
1 (x2 + y2)α-1 2 2α Do đó: 265
• Nếu α >1 thì lim f (x, y) =0 , vậy f (x, y) liên tục tại O(0,0) ( x, y)⟶ (0,0) x2α 1
• Nếu α 1, ta có: f (x, x) = =
không dần tới 0 khi x ⟶ 0 , suy ra 2x2 2x2(1- α )
hàm f (x, y) không liên tục tại O(0,0)
6.3. Đạo hàm và vi phân 6.3.1. Đạo hàm riêng
a. Định nghĩa.
Cho hàm số z = f(x,y) xác định trong một miền D, M0 (x0, y0) là một điểm của D
+Cố định y = y0 và cho x một số gia ∆x thì số gia theo biến x của hàm số tương ứng là:
∆xz = f (x0 + ∆x, y0 ) – f(x0,y0)
Nếu lim Δxz = lim f (x0 + Δx,y0) - f (x0,y0) tồn tại giới hạn thì giới hạn đó Δx⟶ 0 Δx Δx⟶ 0 Δx
được gọi là đạo hàm riêng của hàm số z theo biến x tại điểm M0 (x0, y0) và kí
hiệu là:f ' (x ,y ) , ∂f (x0,y0) , ∂z (x0,y0) hay z' (x ,y ) x 0 0 ∂x ∂x x 0 0
+ Tương tự, đạo hàm riêng của hàm số z = f(x,y) theo biến y tại điểm M0 (x0, y0)
là giới hạn (nếu có) của tỷ số lim Δyz = lim f (y0,y0 + Δy) - f (x0, y0) Δy⟶ 0 Δy Δy⟶ 0 Δy ∂f ∂z
và kí hiệu là:f ' (x ,y ) , (x0, y0) , (x0, y0) hay z' (x ,y ) y 0 0 ∂y ∂y y 0 0
b. Cách tính đạo hàm riêng
• Để tìm đạo hàm riêng của hàm z = f(x,y) theo biến x tại điểm M0 (x0, y0) ,
ta coi y như hằng số và lấy đạo hàm như hàm số một biến đối với biến x.
• Để tìm đạo hàm riêng của hàm z = f(x,y) theo biến y tại điểm M0 (x0, y0) ,
ta coi x như hằng số và lấy đạo hàm như hàm số một biến đối với biến y.
Ví dụ 1: Tính các đạo hàm riêng của hàm số z = 5x2 + 2xy2 - 7y2 + 1 Ta có z’x = 10x + 2y2 z’y = 4xy – 14y2 266
Ví dụ 2: Tính z’x và z’y tại điểm M(1, 2) của hàm số z = 3 x2y3 + x+ y Ta có
z’x = 6 xy3 +1 ⟶ z’x(1, 2) = 6.1.8 + 1 = 49
z’y = 9 xy2 + 1 ⟶ z’y(1, 2) = 9.1.4 + 1 = 37
Ví dụ 3: Tính đạo hàm riêng của hàm số z = xy (x > 0) Ta có : z’x = y. xy- 1 y z ’ = xy.ln x
c. Đạo hàm riêng của hàm số hợp Trường hợp 1:
Cho hàm số z =f (u, v) là hàm hai biến khả vi,với u= u(x), v = v(x) là các hàm khả vi. Khi đó:
∂z ∂f ∂f ∂u ∂ f ∂ v ' ' ' ' = = . + . =f (u,v).u (x) + f (u,x).v (x) ∂x ∂x ∂u ∂x ∂v ∂x u x v x
Đặc biệt nếu z =f (x, y) và y = thì ∂z ∂f = =f ' (x, y) + f ' (x, y).y' φ(y) ∂x ∂x x y x Trường hợp 2:
Cho hàm số z =f (u, v) trong đó u, v lại là các hàm số của hai biến x và y :
u = u(x, y), v = v(x, y). Khi đó: ∂z ∂f
= =∂f .∂u + ∂f .∂v =f ' (u,v).u' (x,y) + f ' (u,x).v' (x, y) ∂x ∂x ∂u ∂x ∂v ∂x u x v x ∂z ∂f
= =∂f .∂u + ∂f .∂v =f ' (u,v).u' (x,y) + f ' (u,v).v' (x, y) ∂y ∂y ∂u ∂y ∂v ∂y u y v y
Ví dụ: Tính đạo hàm riêng cấp 1 của hàm số hợp sau
f(u, v) = ln(u2 + v2), u = x+y, v = xy
Giải. Theo công thức đạo hàm của hàm số hợp, ta có ∂f 2u
=∂f . ∂u + ∂f . ∂v = .1 2v + .y
∂x ∂u ∂x ∂v ∂x u 2 + v2 u2 + v2 2(x + y) 2(xy)
2(x + y + xy2 ) = + .y =
(x + y)2 + (xy)2 (x + y)2 + (xy)2
(x + y)2 + (xy)2 267 Tương tự, ta có ∂f
∂f ∂u ∂f ∂v 2u 2v = . + . = .1+ .x
∂y ∂u ∂y ∂v ∂y u 2 + v2 u 2 + v2 2(x + y) 2(xy)
2(x + y + x2 y) = + .x =
(x + y)2 + (xy)2 (x + y)2 + (xy)2
(x + y)2 + (xy)2
6.3.2. Vi phân toàn phần
Nếu hàm số z = f( x,y ) xác định trong miền D.
Tại điểm: M0( x0, y0) ∈D , cho x một số gia Δx và y một số gia Δy sao cho
M(x0 + Δx; y0 + Δy) thuộc miền D.
Biểu thức Δz =f(x0 + Δx;y0 + Δy) - f(x0, y0) được gọi là số gia toàn phần của hàm số z = f( x,y ).
Định nghĩa 6.9. Nếu số gia Δz biểu diễn dưới dạng:
Δz =AΔx + BΔy +α (Δx) + p (Δy)
trong đó A, B chỉ phụ thuộc vào điểm M0( x0, y0) còn α(Δx);p(Δy) là các vô cùng
bé khi M ⟶ M0 ( tức làΔx ⟶ 0, Δy ⟶ 0 ) thì ta nói hàm số z khả vi tại M0( x0, y0) và biểu thức: dz = df = A.Δx + B.Δy
được gọi là vi phân toàn phần của hàm số z = f( x,y ) tại điểm M0
Định nghĩa 6.10. Hàm số z = f( x,y ) được gọi là khả vi trong miền D nếu nó
khả vi tại mọi điểm của miền D
Định lý 6.3. Nếu hàm z = f( x,y) khả vi tại điểm M( x ,y ), thì tồn tại f '(x, y) và x
f ' (x, y) y đồng thời
dz =f 'x(x,y).Δx + f 'y(x,y).Δy =f 'x(x,y).dx+f 'y(x,y).dy
Ví dụ: Tính vi phân toàn phần của hàm số z =ln(x + y2) Ta có: z' 1 = ; ' z 2y = x x + y2 y x + y2 1 2y Vậy dz = dy x + y2 dx + x+y2 268
Nhận xét: Từ định nghĩa ta thấy hàm hai biến số z = f( x,y ) có các đạo hàm
riêng tại một điểm thì chưa chắc khả vi tại điểm đó, mà chỉ khi có đạo hàm
riêng liên tục thì hàm số mới khả vi. Ngược lại, một hàm 2 biến số khả vi tại
một điểm thì có các đạo hàm riêng tại điểm đó. Vì vậy, đối với hàm 2 biến, khái
niệm hàm số khả vi và hàm số có đạo hàm riêng là không tương đương. Đây là
điểm khác nhau căn bản của hàm số hai biến số so với hàm một biến số.
6.3.3. Đạo hàm riêng cấp cao và vi phân cấp cao
a. Đạo hàm riêng cấp cao
Cho hàm số z =f( x, y), các đạo hàm riêng z’x, z’y được gọi là các đạo hàm
riêng cấp một của hàm số z =f( x, y).
Nói chung các đạo hàm riêng( nếu tồn tại) này lại là các hàm số của hai biến số
x và y. Nếu các hàm số này có đạo hàm riêng thì các đạo hàm riêng đó được gọi
các đạo hàm riêng cấp hai của hàm số z.
Khi đó ta có bốn đạo hàm riêng cấp hai của hàm số z và được kí hiệu như là: ∂ ∂z ∂2z ∂ ∂z ∂2z ∂ ∂z ∂2z ( ) = =z' ; ( ) = =z' ; ( ) = =z' ; 2 ∂x ∂x ∂x2 x ∂y ∂x ∂x∂y xy ∂x ∂y ∂y∂x yx ∂ ∂z ∂2z ( ) = =z' ∂y ∂y ∂y2 y2 2 2
Ví dụ 1: Tính các đạo hàm riêng cấp hai của hàm số z = x y + y
Các đạo hàm riêng cấp một của hàm số z là:
z' =∂z =2xy z z' ∂ 2 x ∂x ; y = =x + 2y ∂y
Các đạo hàm riêng cấp hai của hàm số z là: ∂2z ∂2z ∂2z ∂2z z' = z ' z' z' = =2 x2 xy = =2x; yx = =2x ; y ∂x2 =2y ; ∂x∂y ∂x∂y 2 ∂y2 269 ∂2z ∂2z
Ví dụ 2: Cho hàm số z =arctan x + =0
y chứng minh rằng: ∂x2 ∂y2
Các đạo hàm riêng cấp một của hàm số z là: ∂z y ∂z - x z' = = = = x
∂x x2 + y2 ; z'y ∂y x2 + y2
Các đạo hàm riêng cấp hai của hàm số z là: ∂2z 2xy = - 2xy ; ∂2z =
∂x2 x2 + y2
∂y2 x2 + y2 ∂2z ∂2z Vậy + =0 ∂x2 ∂y2
Tương tự như trên ta có: đạo hàm riêng của các đạo hàm riêng cấp hai được gọi
là các đạo hàm riêng cấp 3, đạo hàm riêng của đạo hàm riêng cấp (n-1) được gọi
là đạo hàm riêng cấp n của hàm số z = f(x,y).
Định lí 6.4.(Schwarz). Nếu trong một lân cận U nào đó của điểm M0(x0,y0,) ,
hàm số z = f(x,y) có các đạo hàm riêngf'x, f'y, f ’xy, f ’yx và nếu các đạo hàm f ’xy,
f ’yx liên tục tại M0 thì f ’xy = f ’yx tại M0
Trong giáo trình này chúng ta chỉ dừng lại nghiên cứu các hàm số thỏa mãn định lí trên.
b. Vi phân cấp cao.
Nếu hàm số z = f(x,y) khả vi tại điểm (x, y) thì dz = z’xdx + z’ydy
được gọi là vi phân toàn phần cấp một của hàm số z. Vi phân toàn phần của vi
phân toàn phần cấp một dz nếu tồn tại, được gọi là vi phân toàn phần cấp hai của 2
z, kí hiệu là d z và được tính theo công thức:
d 2z =d(dz) =d( f ' dx dy) dx2 dxdy d y2 x + f 'y =f' + 2f' + f' x2 xy y2 270
Tổng quát, ta định nghĩa được vi phân toàn phần cấp n (n ≥ 2) của hàm số n n-1
z = f(x,y) như sau: d z= d(d z) 2 x
Ví dụ: Tính vi phân cấp hai d z của hàm số z = e siny
Các đạo hàm riêng cấp một của hàm số z là:
z' =ex sin y ; z' =excosy x y
Các đạo hàm riêng cấp hai của hàm số z là: x x x
z ' =e sin y ; z' =e cosy ; z' 2 =- e sin y 2 x xy y
Vậy vi phân toàn phần cấp hai của hàm số là:
d 2z =ex sin ydx2 + 2excosydxdy - ex sin ydy2
=ex (sin ydx2 + 2cosydxdy-sin ydy2)
6.3.4. Ứng dụng của đạo hàm riêng trong phân tích kinh tế
a. Đạo hàm riêng và giá trị cận biên
Xét hàm số z = f(x,y) biểu diễn sự phụ thuộc của biến kinh tế z vào các biến kinh tế x và y. Khi đó:
+ Đạo hàm riêng z'x tại điểm M(x,y) trong kinh tế được gọi là giá trị cận biên
của hàm z theo biến x tại điểm M. Giá trị cận biên của hàm z theo biến x tại
điểm M(x,y) biểu diễn xấp xỉ lượng thay đổi giá trị của biến phụ thuộc z khi
biến x tăng thêm 1 đơn vị trong khi cố định biến y .
+ Tương tự: Đạo hàm riêng zy' tại điểm M(x,y) được gọi là giá trị cận biên của
hàm số z theo biến y tại điểm M. Giá trị cận biên của hàm số z theo biến y tại
điểm M(x,y) biểu diễn xấp xỉ lượng thay đổi giá trị của biến phụ thuộc z khi
biến y tăng thêm 1 đơn vị trong khi cố định biến x .
Sau đây ta xét giá trị cận biên của một số hàm thường gặp trong kinh tế:
1. Hàm sản xuất Q = f(K, L)
Các đạo hàm riêng:Q'K =∂Q ; Q'L =∂Q ∂K ∂L 271
được gọi tương ứng là sản lượng cận biên của Q theo vốn và sản lượng cận biên
của Q theo lao động tại điểm (K,L)
Ý nghĩa: Tại điểm M0( K0, L0)
• Q'K (K0, L0) mô tả sự thay đổi của sản lượng khi lượng vốn tăng từ K0 lên
(K0 +1) đơn vị với điều kiện L = L0
• Q'L(K0, L0) mô tả sự thay đổi của sản lượng khi lượng lao động tăng từ L0
lên (L0 +1) đơn vị với điều kiện K = K0
Ví dụ: Một doanh nghiệp có hàm sản xuất Q =25.K0,5L0,5.
Trong đó: K, L, Q là mức sử dụng vốn, mức sử dụng lao động và sản lượng. Giả
sử doanh nghiệp đó đang sử dụng 25 đơn vị vốn và 100 đơn vị lao động, hãy
tính sản lượng cận biên theo vốn, sản lượng cận biên theo lao động và giải thích ý nghĩa. Giải:
+ Sản lượng cận biên theo vốn là: ∂Q - 0,5 0,5 25 / L 0,5 Q'K = =25.0,5.K L = ∣ ∣ ∂K 2 K J Với K = 25 và L =100 thì: 25/100 0,5
Q'K(K =25,L =100) = 2 ∣ 25 ∣ =25 J
Điều này có nghĩa là: Nếu doanh nghiệp nâng mức sử dụng vốn K từ 25 lên 26
đơn vị và giữ nguyên mức sử dụng L =100 lao động thì sản lượng sẽ tăng thêm
khoảng 25 đơn vị sản phẩm.
+ Sản lượng cận biên theo lao động là: ∂Q 0,5 - 0,5 25/ K 0,5 Q'L = =25.0,5.K L = ∣ ∣ ∂L 2 L J Với K = 25 và L =100 thì: 25 / 0,5 25 25
Q'L(K =25,L =100) = 2 ∣100 J∣ = =6,25 4
Điều này có nghĩa là: Nếu doanh nghiệp nâng mức sử dụng lao động L từ
100 lên 101 đơn vị và giữ nguyên mức sử dụng vốn thì sản lượng sẽ tăng thêm
khoảng 6,25 đơn vị sản phẩm. 272
2. Hàm chi phí theo các yếu tố sản xuất TC=TC (K,L)
Các đạo hàm riêng : TC'K =∂TC ; TC'L =∂TC ∂K ∂L
được gọi tương ứng là chi phí cận biên theo vốn và chi phí cận biên theo lao
động. Nếu giá thuê một đơn vị vốn là wK và giá vốn thuê một đơn vị lao động wL thì TC(K,L) =wKK + wLL TC' ; K =∂TC =wK TC'L =∂TC =wL ta có ∂K ∂L
Ý nghĩa: Ở mọi mức sử dụng các yếu tố đầu vào, chi phí cận biên theo vốn bằng
giá thuê một đơn vị vốn, chi phí cận biên theo lao động bằng giá thuê một đơn vị lao động.
3. Hàm lợi ích U= f(x,y) Các đạo hàm riêng: U' U' x =∂U ; y =∂U ∂x ∂y
được gọi tương ứng là lợi ích cận biên của hàm lợi ích theo hàng hóa x, lợi ích
cận biên của hàng hóa theo hàng hóa y.
Ý nghĩa: Tại một mức sử dụng giỏ hàng M0(x0, y0)
+ Giá trị U'x biểu diễn xấp xỉ lợi ích tăng thêm khi người tiêu dùng có thêm
một đơn vị hàng hóa thứ nhất và giữ nguyên lượng hàng hóa thứ hai.
+ Giá trị U'y biểu diễn xấp xỉ lợi ích tăng thêm khi người tiêu dùng có thêm
một đơn vị hàng hóa thứ hai và giữ nguyên lượng hàng hóa thứ nhất.
Ví dụ: Giả sử hàm lợi ích của người tiêu dùng đối với hai loại hàng hóa là 3 1 U =2x 2y2 .
trong đó: x là lượng hàng hóa 1; y là lượng hàng hóa 2 ; U là lợi ích của người tiêu dùng hàng ngày.
Gỉa sử người tiêu dùng đang sử dụng 64 đơn vị hàng hóa 1 và 25 đơn vị hàng
hóa 2 trong một ngày. Xác định lợi ích cận biên của các hàng hóa tại điểm đó và giải thích ý nghĩa. Giải:
Hàm số biểu diễn lợi ích cận biên theo hàng hóa 1 là: 273



