Toán cho Vật Lý: Vectơ và phép tính vectơ trong chương 1 | Học viện Kỹ thuận Quân sự

lOMoARcP SD| 58886 076
Chuyên đề: Toán cho Vật lí phổ thông chuyên (Ver.1) Chương 1: VECTƠ 1.1. KHÁI NIỆM VECTƠ 1.1.1. Vectơ là gì?
Vectơ là một đoạn thẳng có hướng, nghĩa là trong hai điểm nút
của đoạn thẳng ta đã chỉ rõ điểm nào là điểm đầu, điểm nào là điểm cuối.
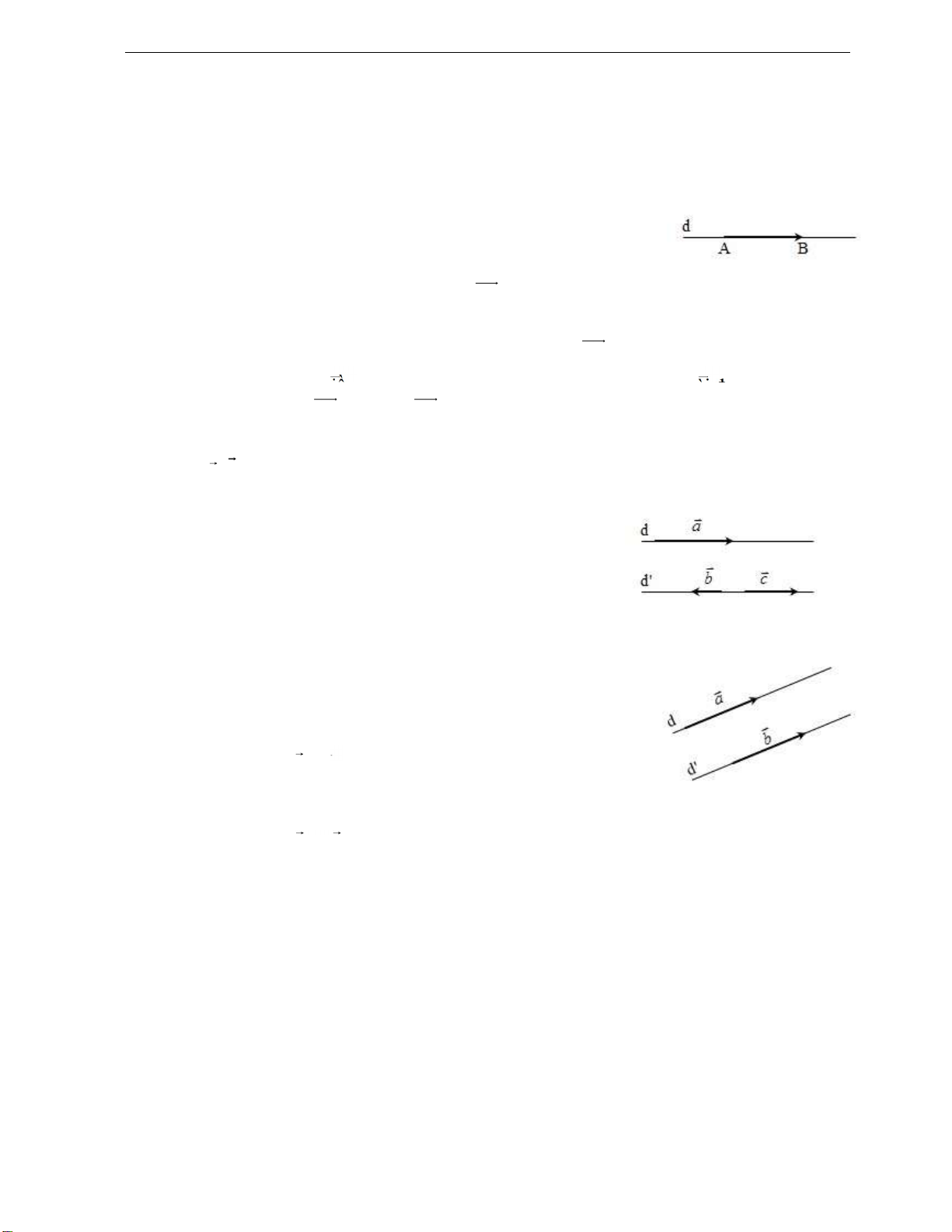
Trên hình biểu diễn vectơ AB. Kí hiệu AB .
A gọi là gốc của vectơ, B là ngọn của vectơ.
Đường thẳng d i qua A và B gọi là giá của vectơ AB . Phương của ường thẳng d gọi là
phương của vectơ AB . Chiều từ A sang B gọi là chiều của vectơ AB . Độ dài đoạn
AB gọi là ộ lớn vectơ AB , kí hiệu | AB |.
Để thuận tiện, ta có thể kí hiệu vectơ dưới dạng các chữ cái thường có dấu mũi tên trên đầu: a,b ,…
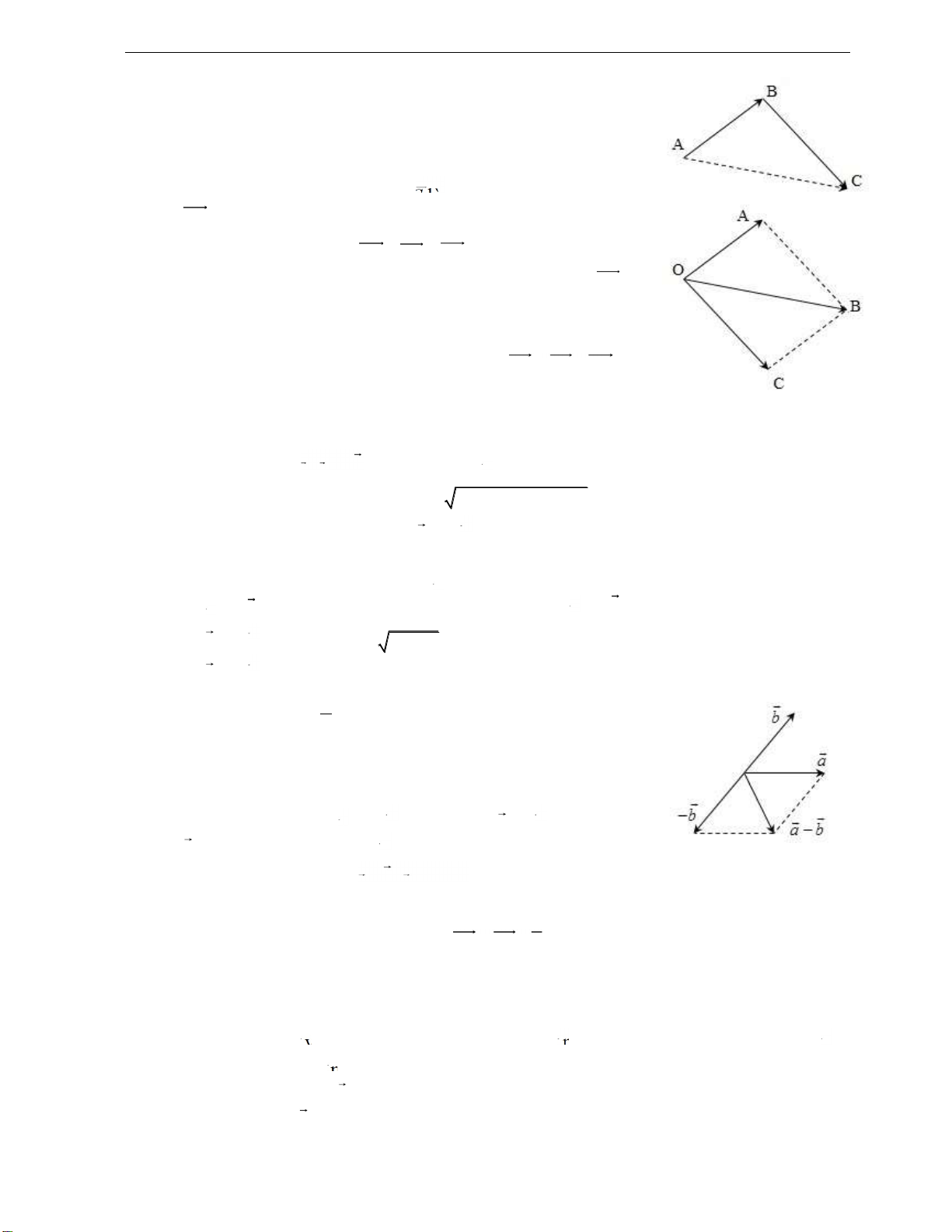
1.1.2. Hai vectơ cùng phương
Hai vectơ ược gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
Hai vectơ cùng phương thì có thể cùng chiều hoặc ngược chiều nhau.
1.1.3. Hai vectơ bằng nhau, ối nhau
Hai vectơ ược gọi là bằng nhau khi chúng có cùng phương, chiều và ộ lớn Kí hiệu: a = b
Hai vectơ ược gọi là ối nhau khi chúng có cùng phương, cùng
ộ lớn nhưng ngược chiều. Kí hiệu: ac 1.2. CÁC PHÉP TOÁN VECTƠ 1.2.1. Phép cộng vectơ lOMoARcP SD| 58886 076
Chuyên ề: Toán cho Vật lí phổ thông chuyên (Ver.1)
a. Định nghĩa phép cộng vectơ
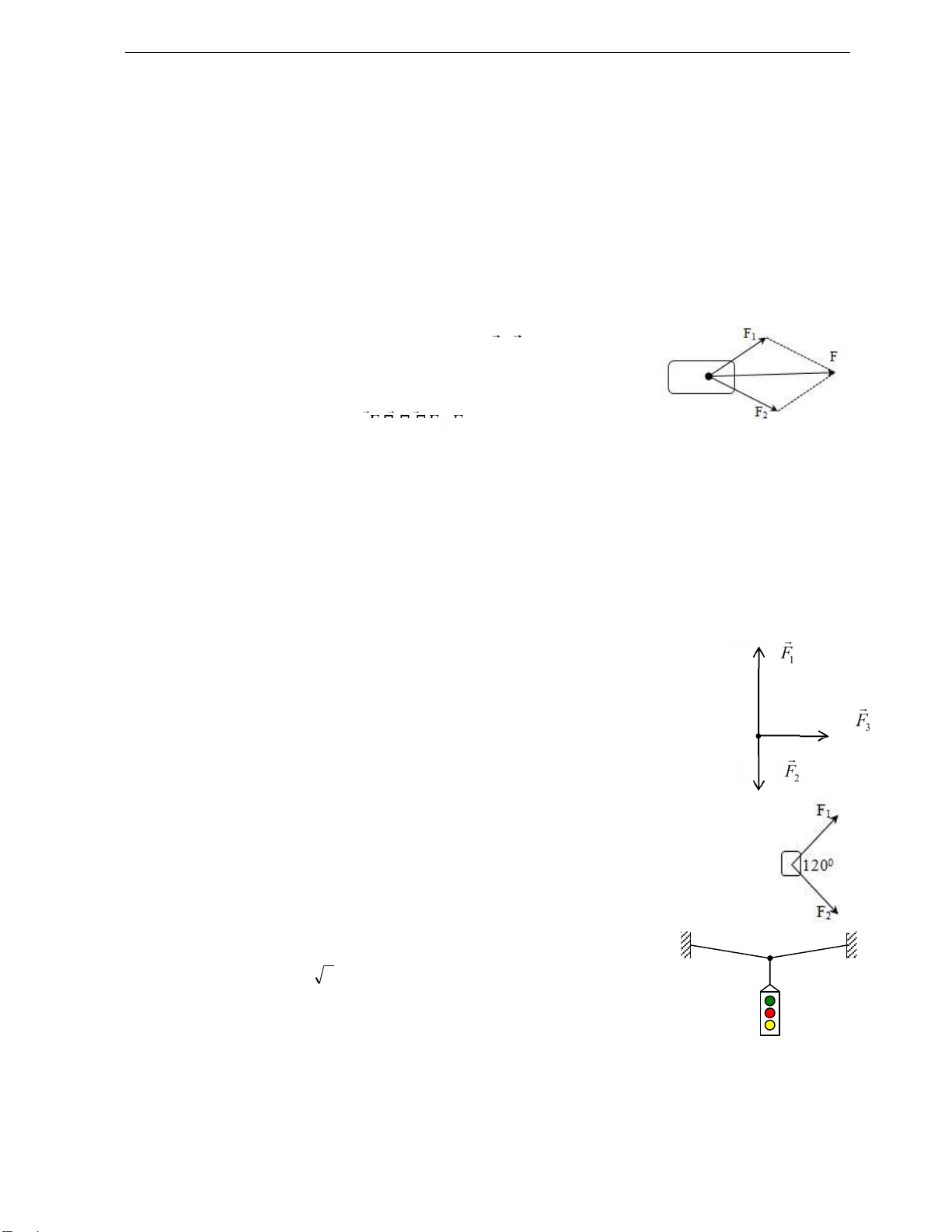
Khi ta tịnh tiến một chất điểm từ A ến B rồi từ B ến C
thì kết quả thu ược giống như ta tịnh tiến chất điểm trực tiếp từ A ến C.
Về mặt toán học ta nói vectơ AC là tổng của vectơ AB và vectơ BC AC = AB +BC
Quy tắc cộng vectơ trên ược gọi là quy tắc ba điểm, áp
dụng cho ba điểm A, B, C bất kì.
b. Quy tắc hình bình hành
Nếu OABC là một hình bình hành thì ta có OB OA
OC  c. Công thức tính ộ lớn vectơ tổng
Xét tổng vectơ: c a b  thì ộ lớn của c ược xác ịnh bằng công thức: c  a2  b2 2abcos
Với  là góc hợp bởi hai vectơ a và b . Một
số trường hợp ặc biệt:
+ a và b cùng chiều: c = a + b; c cùng chiều với a và b
+ a và b ngược chiều: c = |a – b|
+ a và b vuông góc: c  a2 b2  + a = b: c 2asin 2 1.2.2. Phép trừ vectơ
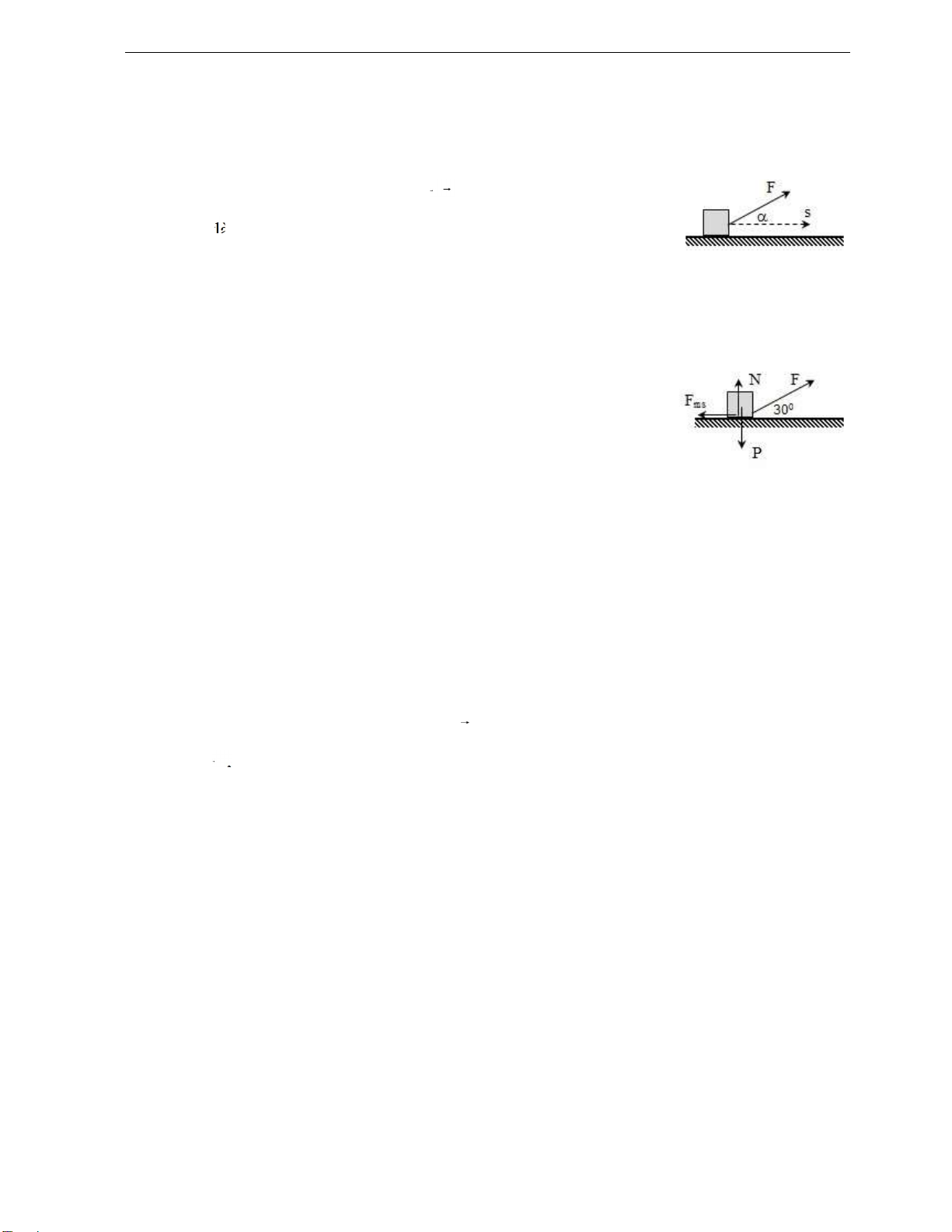
Hiệu của hai vectơ a và b , kí hiệu là a - b , là tổng của vectơ a
và vectơ ối của vectơ b . a b a   ( b)
Quy tắc ba điểm: Với bất kì ba điểm A, B, C ta luôn có: AB CB CA 
1.2.3. Tích của vectơ với một số a. Định nghĩa
Tích của vectơ a với một số thực k, kí hiệu là ka là một vectơ cùng phương với a và:
+ Cùng chiều với a nếu k > 0,
+ Ngược chiều với a nếu k < 0, + Có ộ lớn | ka| = ka lOMoARcP SD| 58886 076
Chuyên đề: Toán cho Vật lí phổ thông chuyên (Ver.1) b. Các tính chất
Với mọi vectơ a b, và số thực k, l ta luôn có: + k la  (kl a) + k l a  kala
+ k a b  ka kb
+ ka 0 khi và chỉ khi k = 0 hoặc a 0 c.
Điều kiện hai vectơ cùng phương
Điều kiện cần và ủ ể hai vectơ a và b cùng phương là tồn tại một số thực k ≠ 0 sao cho a kb
Hệ quả: Điều kiện cần và ủ ể ba điểm A, B, C thẳng hàng là tồn tại một số thực k ≠ 0 sao cho AB kAC
d. Biểu diễn một vectơ qua hai vectơ không cùng phương
Với hai veccto a và b không cùng phương bất kì, ta luôn có thể xác
ịnh một vectơ x dưới dạng: x ma nb 
1.2.4. Tích vô hướng của hai vectơ a. Góc giữa hai vectơ
Tại một điểm O, ta dựng hai vectơ OA a vàOB b thì góc AOB ược gọi là góc giữa hai
vectơ a và b , kí hiệu là (a,b )
b. Định nghĩa tích vô hướng
Tích vô hướng giữa hai vectơ a và b , kí hiệu ab. , là một số thực ược xác ịnh bởi: ab a b. | |.| |.cos( ,a b)
Hệ quả: Bình phương vô hướng cuẩ một vectơ bằng bình phương ộ dài của vectơ ó a2 aa. .cos00 a2 c. Các tính chất
Với các vectơ a, b , c và số thực k bất kì, ta luôn có: + ab ba.  . + ab.   0a b
+ k ab . ka b kb a
+ a b c  ab ac lOMoARcP SD| 58886 076
Chuyên ề: Toán cho Vật lí phổ thông chuyên (Ver.1)
1.2. ỨNG DỤNG CỦA VECTƠ TRONG VẬT LÍ
Trong Vật lí, các ại lượng chỉ có ộ lớn mà không có phương chiều ược gọi là ại lượng
ại số. Ví dụ: khối lượng, nhiệt ộ,… Các ại lượng có cả phương chiều và ộ lớn ược gọi là các
ại lượng vectơ. Ví dụ: lực, vận tốc,…
Các ại lượng vectơ ược cộng, trừ, nhân,… như các vectơ. 1.2.1. Vectơ lực
a. Tổng hợp và phân tích lực
Tổng hợp lực là thay thế nhiều lực tác dụng lên vật bằng một lực duy nhất có tác dụng tương ương các lực kia
Nếu một vật chịu tác dụng của các lực F F1, 2,..., thì lực tổng
hợp ược xác ịnh bằng phép cộng vectơ: F   F1 F2 ...
Điều kiện ể một vật nằm cân bằng là tổng hợp lực tác dụng lên nó bằng 0.
Trong một số trường hợp ta phải phân tích một lực thành hai thành phần theo phương
Ox, Oy vuông góc nhau ể xét tác dụng của lực lên vật. Các lực thành phần này cũng ược
phân tích theo quy tắc hình bình hành.
VD1: Cho hai lực có ộ lớn lần lượt là F1 = 3N, F2 = 4N. Tính ộ lớn hợp lực của hai lực
ó trong các trường hợp sau:
a. Hai lực cùng giá, cùng chiều.
b. Hai lực cùng giá, ngược chiều.
c. Hai lực có giá vuông góc.
d. Hướng của hai lực tạo với nhau góc 600.
VD2: Một chất điểm chịu các lực tác dụng có hướng như hình vẽ
và ộ lớn lần lượt là F1 = 60 N, F2 = 30 N, F3 = 40 N. Xác ịnh hướng và
ộ lớn lực tổng hợp tác dụng lên chất điểm.
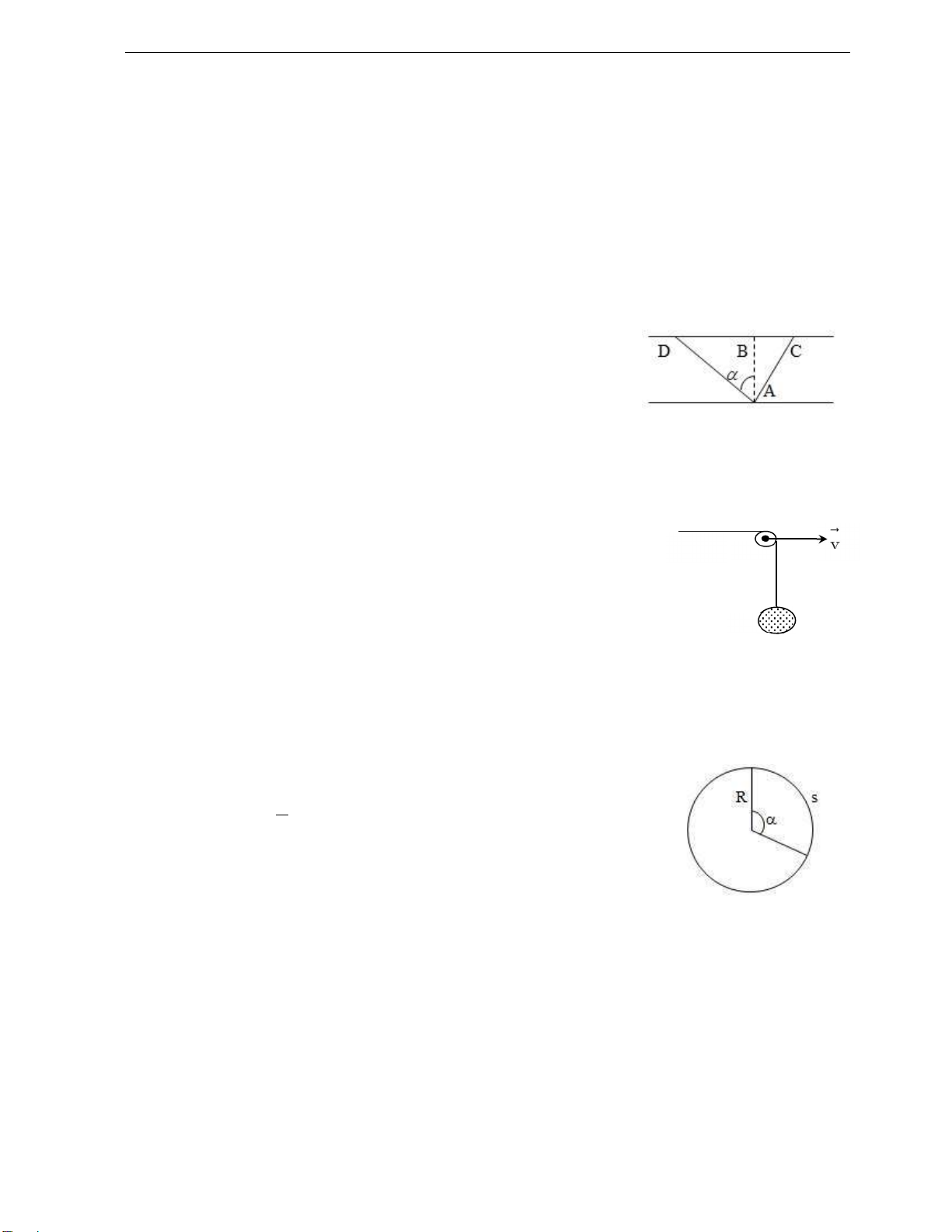
VD3: Hai con kiến cùng kéo một hạt ường về tổ, lực kéo của
chúng có ộ lớn như nhau nhưng theo hai phương khác nhau như hình
vẽ. Xác ịnh chiều chuyển ộng của viên ường. Trong trường hợp này hai
con cùng kéo có lợi hơn một con hay không?    
VD4: Hợp lực F của 2 lực F1 và F2 tạo với hướng của lực F1 góc
450 và có ộ lớn 8 2 N và ộ lớn của F1 = 8N. Xác ịnh hướng và ộ lớn của lực F2 .
VD5: Một èn giao thông ược treo chính giữa đoạn dây căng ngang và mỗi phần chịu
một lực căng như nhau 200 N. Biết góc tạo bởi hai dây 1500. Tính trọng lượng của èn. lOMoARcP SD| 58886 076
Chuyên đề: Toán cho Vật lí phổ thông chuyên (Ver.1) b. Công của một lực
Ở lớp 8 ta đã biết công của một lực khi kéo vật di chuyển cùng chiều lực kéo là A = F.s.
Tuy nhiên trong nhiều trường hợp, chiều lực kéo và chiều chuyển ộng của vật không trùng
nhau. Khi ó, công thức tính công của lực là: A Fs .
Với slà vectơ có ộ lớn bằng quđãng ường i ược của vật và chiều là
chiều chuyển ộng của vật.
Công của lực là ại lượng ại số:
+ A > 0: lực óng vai trò làm vật chuyển ộng, gọi là lực phát ộng.
+ A < 0: lực óng vai trò cản trở chuyển ộng, gọi là lực cản.
+ A = 0: lực không sinh công
VD6: Một vật nằm trên mặt sàn nằm ngang chịu tác dụng của lực
kéo F = 10N, trọng lực P = 10N, lực ma sát Fms = 1N và phản lực của
sàn N như hình vẽ. Xác ịnh công của lực F, P và Fms khi vật i ược một đoạn dài 2m.
VD7: Một xe ô tô có trọng lượng P = 104 N chạy trên một dốc dài 100m và nghiêng 50
so với phương ngang. Xác ịnh công của trọng lực trong hai trường hợp xe lên dốc và xuống dốc. 1.2.2. Vectơ vận tốc
Vận tốc của một vật ược xác ịnh bằng một vectơ có phương chiều là phương chiều của
chuyển ộng, ộ lớn là tốc ộ chuyển ộng của vật.
Khi vật tham gia cùng lúc nhiều chuyển ộng, ví dụ người i trên tàu ang chuyển ộng, thì
vectơ vận tốc của vật ược tổng hợp bằng phép tổng hợp vectơ.
Quy tắc ba điểm trong tổng hợp vận tốc: v13  v12 v23 Với
vxy là vận tốc của vật x so với vật y
VD8: Hai đầu máy xe lửa cùng chạy trên một đoạn ường sắt thẳng với vận tốc 40km/h
và 60km/h. Xác ịnh vận tốc tương ối (cả hướng lẫn ộ lớn) của đầu máy thứ nhất so với đầu
máy thứ hai trong hai trường hợp.
a. Hai đầu máy chuyển ộng ngược chiều.
b. Hai đầu máy chuyển ộng cùng chiều.
VD9: Một chiếc phà chạy xuôi dòng từ A ến B mất 3 giờ; khi chạy về mất 6 giờ. Hỏi
phà tắt máy trôi theo dòng nước thì mất trong bao lâu?
VD10: Hai bến sông A và B cách nhau 70 km. Khi xuôi dòng từ A ến B, cano ến sớm
hơn 48 min so với khi ngược dòng từ B ến A. Vận tốc cano khi nước ứng yên là 30 km/h.
Tính vận tốc của dòng nước. ĐS: 5km/h.
VD11: Một oàn xe cơ giới có ội hình dài 1200m, hành quân với vận tốc 18km/h. Người
chỉ huy ngồi trên chiếc xe i đầu, trao cho một chiến sĩ i moto với một mệnh lệnh chuyển
xuống xe cuối oàn. Người chiến sĩ hoàn thành nhiệmvụ và quay trở lại báo cáo với người chỉ lOMoARcP SD| 58886 076
Chuyên ề: Toán cho Vật lí phổ thông chuyên (Ver.1)
huy, tất cả mất một thời gian là 1 min 40s.Tính vận tốc của chiến sĩ i mô tô, biết rằng người
ấy i theo cả hai chiều với cùng một vận tốc so với ất.
VD12: Hai xe ô tô chạy trên 2 ường thẳng vuông gócc với nhau, sau khi gặp nhau tại
ngđã tư, một xe chạy về hướng ông xe kia chạy về hướng bắc với cùng vận tốc 40km/h.
a. Tính vận tốc tương ối của xe thứ nhất so với xe thứ 2.
b. Người ngồi trên xe thứ 2 quan sát thì thấy người ngồi trên xe thứ nhất chạy theo hướng nào?
c. Tính khoảng cách 2 xe sau nữa giờ kể từ khi gặp nhau ở ngđã tư. VD13: Một
thuyền xuất phát từ A và mũi thuyền hướng về B với AB
vuông góc với bờ sông. Do nước chảy nên thuyền ến bờ bên
kia tại C với BC = 100m và thời gian t = 50s. a.
Tính vận tốc dòng nước. b.
Biết AB = 200m. Tính vận tốc thuyền khi nước yên lặng. c.
Muốn thuyền ến bờ bên kia tại B thì mũi thuyền phải hướng ến D ở bờ bên kia.
Tính khoảng cách giữa B và D. Biết vận tốc dòng nước và của thuyền khi nước yên lặng
như đã tính ở hai câu trên.
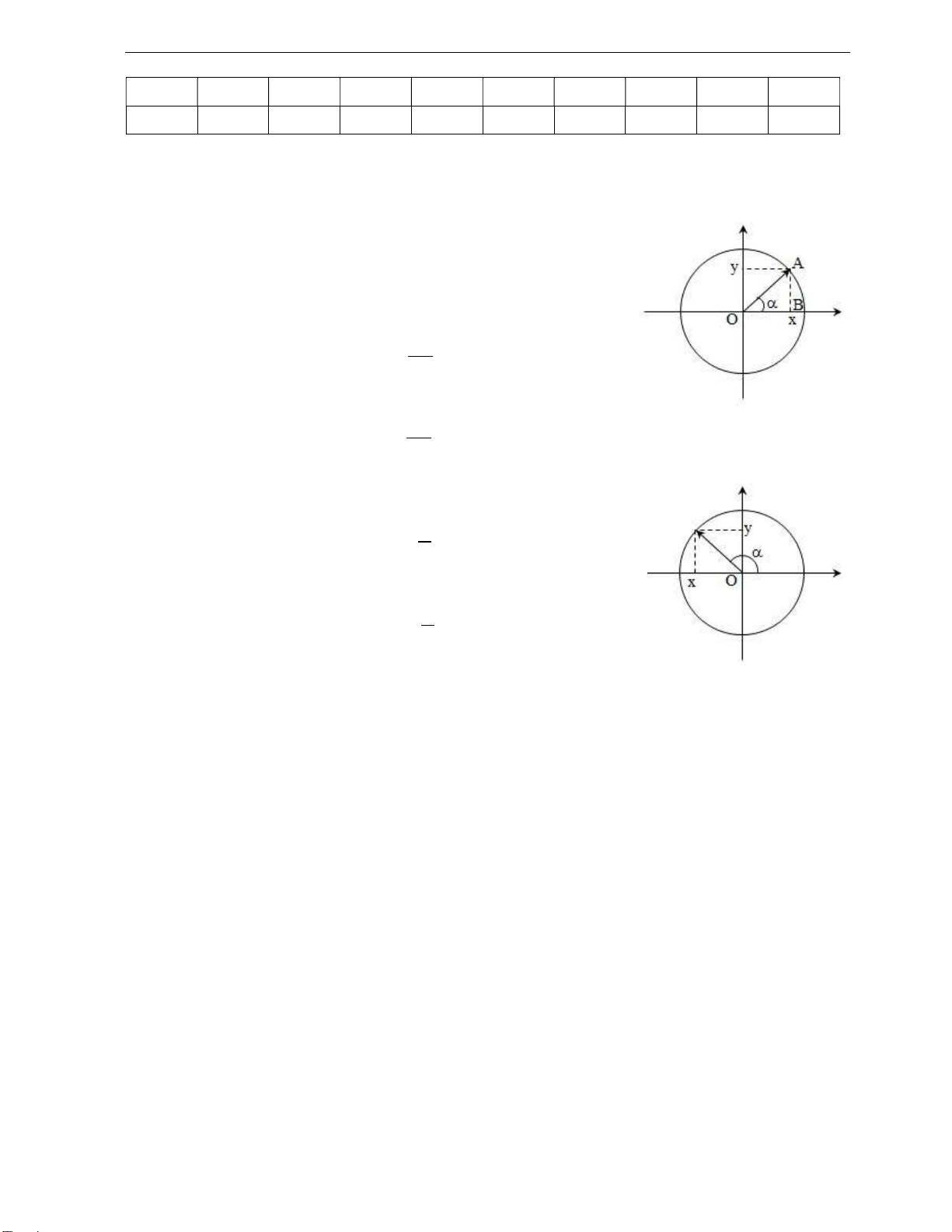
VD14: Một quả cđầu M ược treo vào inh A vắt qua ròng rọc di
ộng B như hình vẽ. B chuyển ộng ều trên ường thẳng nằm ngang qua A
A với vận tốc v hướng ra xa A như hình vẽ. Xác ịnh vận tốc của M ối với các hệ qui chiếu:
a. ắn với ròng rọc? b. ắn với tường? CHƯƠNG 2: LƯỢNG GIÁC 2.1. ĐƠN VỊ GÓC RADIAN
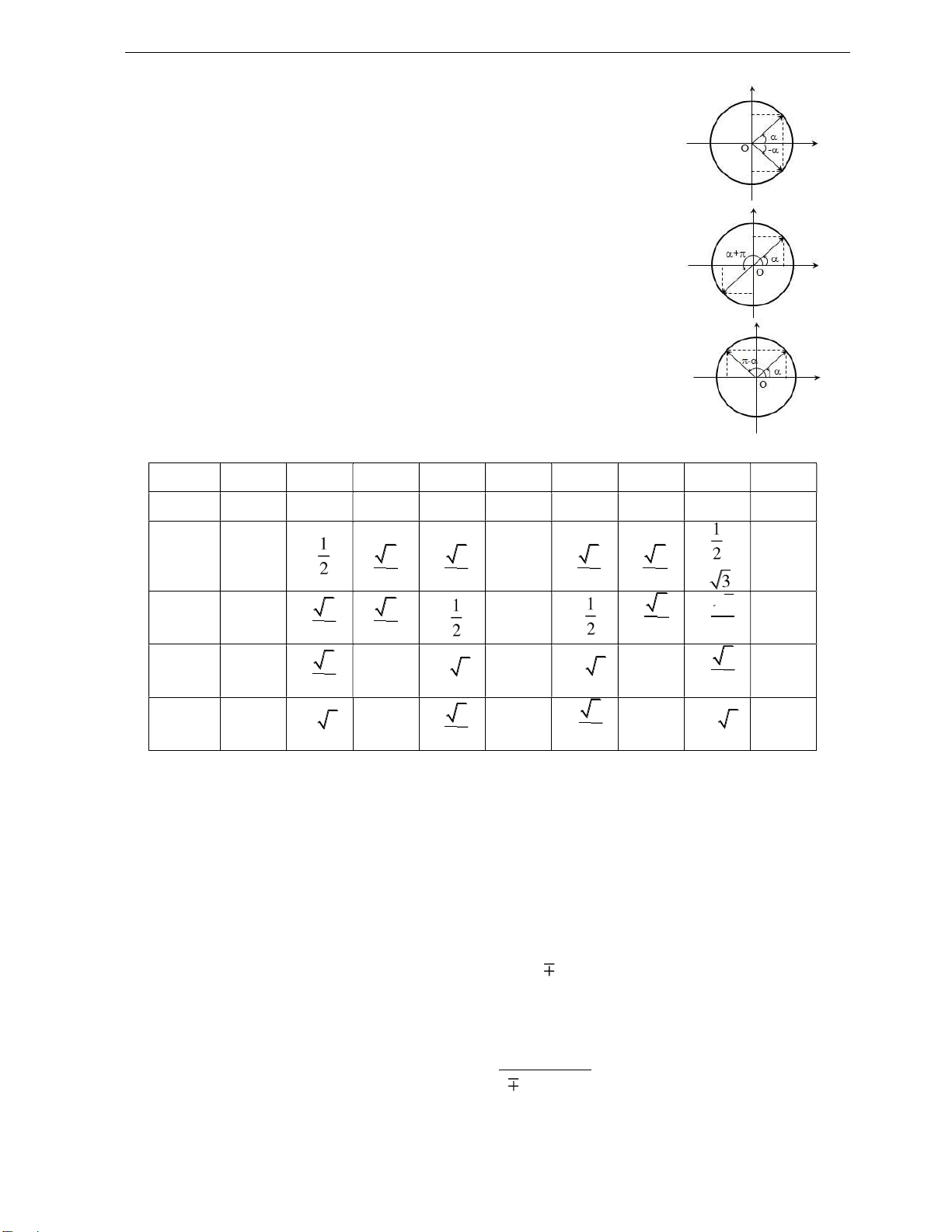
Ta đã biết một cung tròn bán kính R và số o góc  thì có ộ dài xác
ịnh bởi công thức: 0 s 2R. 0 360
Để tiện cho việc tính toán ta ặt ơn vị o góc radian, kí hiệu rad, như sau:  rad = 1800 2 rad = 3600
Với  tính theo ơn vị rad, ộ dài cung ược xác ịnh bằng biểu thức: s = R.
Ngoài ra ơn vị rad còn có nhiều ưu thế khác trong các phép toán về hình học, lượng
giác và các biểu thức vật lí nên ược sử dụng rộng rđãi. Trong các phần sau, nếu không nói gì
thêm thì các số o góc ược tính theo ơn vị rad. Bảng quy ổi một số góc thông dụng lOMoARcP SD| 58886076
Chuyên đề: Toán cho Vật lí phổ thông chuyên (Ver.1) 0 00 300 450 600 900 1200 1350 1500 1800  rad 0 /6 /4 /3 /2 2/3 3/4 5/6 
2.2. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC BẤT KÌ
2.2.1. Giá trị lượng giác cá góc từ 0 ến 2
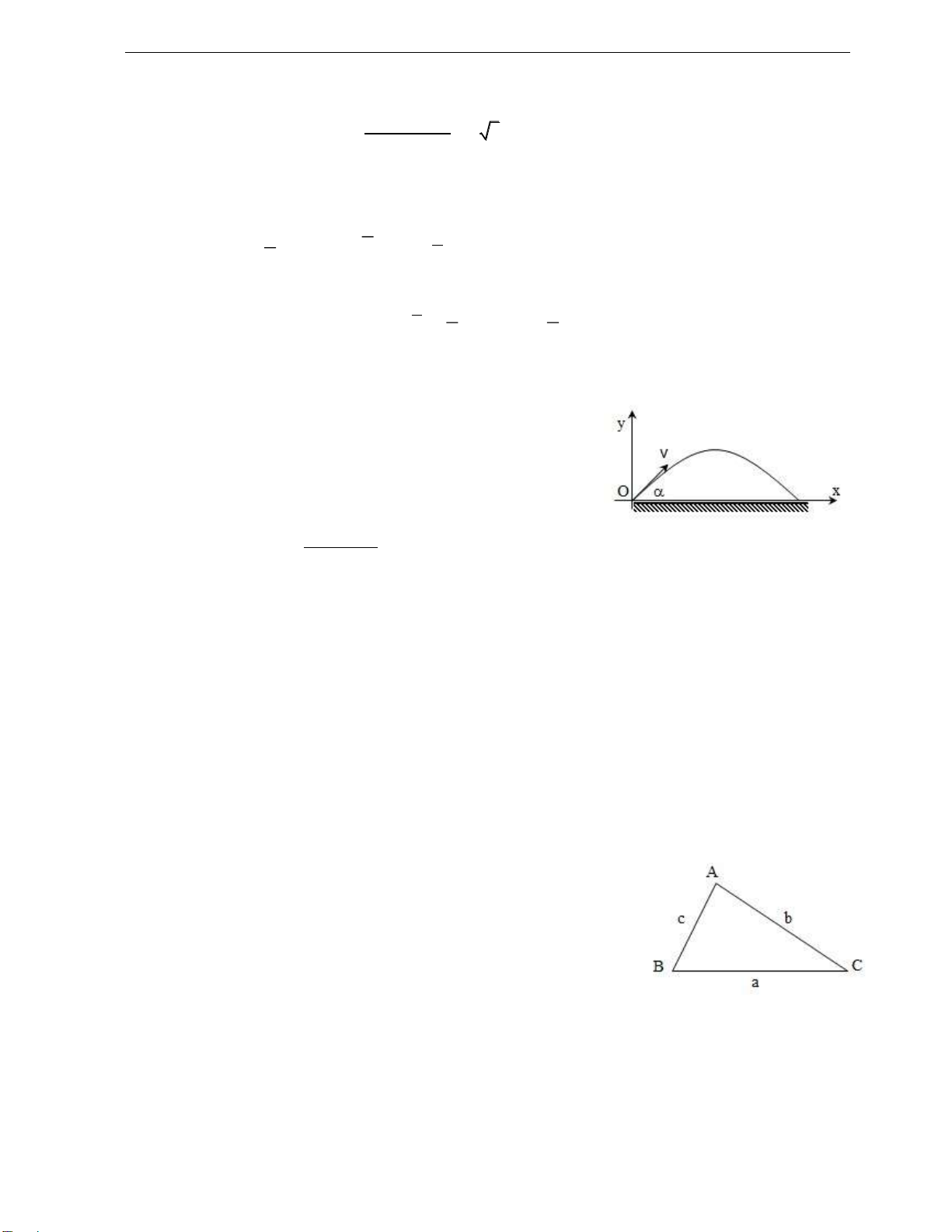
Ta đã biết các giá trị lượng giác của góc  như trên hình ược
xác ịnh bằng các công thức: sin AB OA cos OB OA
Để mở rộng các giá trị lượng giác cho các góc bất kì ta xác ịnh giá trị lượng giác thông
qua tọa ộ điểm A như sau: sin y R cos x R
Khi ó giá trị lượng giác có thể có giá trị âm, dương, hoặc bằng 0.
2.2.3. Giá trị lượng giác của một góc bất kì
Ta thấy mọi tính chất của góc sẽ lặp lại khi ta tăng, giảm số o góc một lượng 2
sin( ± 2) = sin cos( ± 2) = cos tan( ± 2) =
tan tan( ± 2) = tan
2.3.4. Giá trị lượng giác của các góc có quan hệ ặc biệt lOMoARcP SD| 58886 076
Chuyên ề: Toán cho Vật lí phổ thông chuyên (Ver.1) a. Góc ối nhau sin(-) = -sin cos(-) = cos tan(-) = -tan cot(-) = -cot b. Góc bù nhau
sin( - ) = sin cos( - ) = -cos tan( - ) = -tan
cot( - ) = -cot c. Góc hơn kém nhau 
sin( + ) = -sin cos( + ) = -cos tan( + ) = tan cot( + ) = cot d. Góc phụ nhau
sin(/2 - ) = cos cos(/2 - ) = sin tan(/2 - ) = cot cot(/2 - ) = tan
e. Bảng lượng giác các góc ặc biệt
Bảng giá trị lượng giác của một số góc ặc biệt: 0 00 300 450 600 900 1200 1350 1500 1800  rad 0 /6 /4 /3 /2 2/3 3/4 5/6  sin 0 2 3 1 3 2 0 2 2 2 2 2 cos 1 3 2 0 - - -1 2 2 - 2 2 3 tan 0 3 1 3 | - 3 -1 - 0 3 3 3 cot | 3 1 3 0 - -1 - 3 | 3 3
Học sinh tự tính giá trị các góc ặt biệt từ  ến 2.
2.2. CÔNG THỨC LƯỢNG GIÁC 2.2.1. Công thức cộng
Công thức cộng cho hàm sin và cos như sau:
sin(a b ) sin cosa bsin cosb a
cos(a b ) cos cosa b sin sina b
Từ các công thức trên ta có thể suy ra công thức cộng cho hàm tan như sau: tan(a b ) tanatanb 1 tan tana b
Bằng cách cho b = a vào các công thức trên, học sinh tự chứng minh các công thức sau: lOMoARcP SD| 58886 076
Chuyên đề: Toán cho Vật lí phổ thông chuyên (Ver.1) a. sin2a = 2sinacosa b. sin3a = 3sina – 4sin3a
c. cos2a = cos2a – sin2a = 1 – 2sin2a = 2cos2a – 1 d. cos3a = 4cos3a – 3cosa
2.2.2. Công thức biến ổi tổng – tích
a. Biến ổi tích thành tổng
cosacosb cos(a b ) cos(a b )
sinasinb 1cos(a b ) cos(a b )
sinacosb sin(a b ) sin(a b )
b. Biến ổi tổng thành tích cosacosb 2cos a b a b (  )cos(  ) 2 2 cosacosb2sin a b a b (  )sin(  ) 2 2 sinasinb 2sin a b a b (  )cos(  ) 2 2 sinasinb 2cos a b a b (  )sin(  ) 2 2
2.2.3. Bài tập vận dụng
VD1: Chứng minh các ẳng thức sau: 
a. sinacosa  2sin(a ) 4 
b. sinacosa  2sin(a ) 4
4 a 11tantanaa c. tan     VD2: Biết sin 1 a và a  ,
 , hđãy tính các giá trị lượng giác của các góc 2a và 3  2  a . lOMoARcP SD| 58886076
Chuyên ề: Toán cho Vật lí phổ thông chuyên (Ver.1) 2
VD3: Chứng minh rằng sinasinb  3 nếu a + b = /3 và cosa ≠ cosb.
cosacosb VD4: Chứng minh rằng:   
a. sinasina sin a  1sin3a  3   3  4
acosa 1 cos3a b.cosacos  3   3  4
VD5: Một vật nhỏ ược ném lên từ một điểm O trên mặt
ất với vận tốc đầu v theo phương hợp với phương ngang một
góc  (0 <  < /2). Nếu bỏ qua sức cản của không khí thì
quỹ ạo của vật là một ường cong parabol ược xác ịnh bởi phương trình: y  2 g 2x2 (tan2)x 2v cos 
trong ó g = 9,81 (m/s2) gọi là gia tốc trọng trường, có giá trị như nhau với mọi vật.
a. Tính tầm bay xa của vật (là khoảng cách từ O ến điểm vật chạm ất) theo .
b. Với cùng một vận tốc ném v, hđãy xác ịnh giá trị  ể tầm bay xa của vật ạt cực ại.
c. Hai vật cùng ược ném lên từ một điểm với cùng vận tốc ném nhưng theo các góc
ném lần lượt là  và . Tìm mối quan hệ giữa  và  ể hai vật rơi xuống cùng một vị trí.
2.3. HỆ THỨC LƯỢNG TRONG TAM GIÁC 2.3.1. Định lí côsin
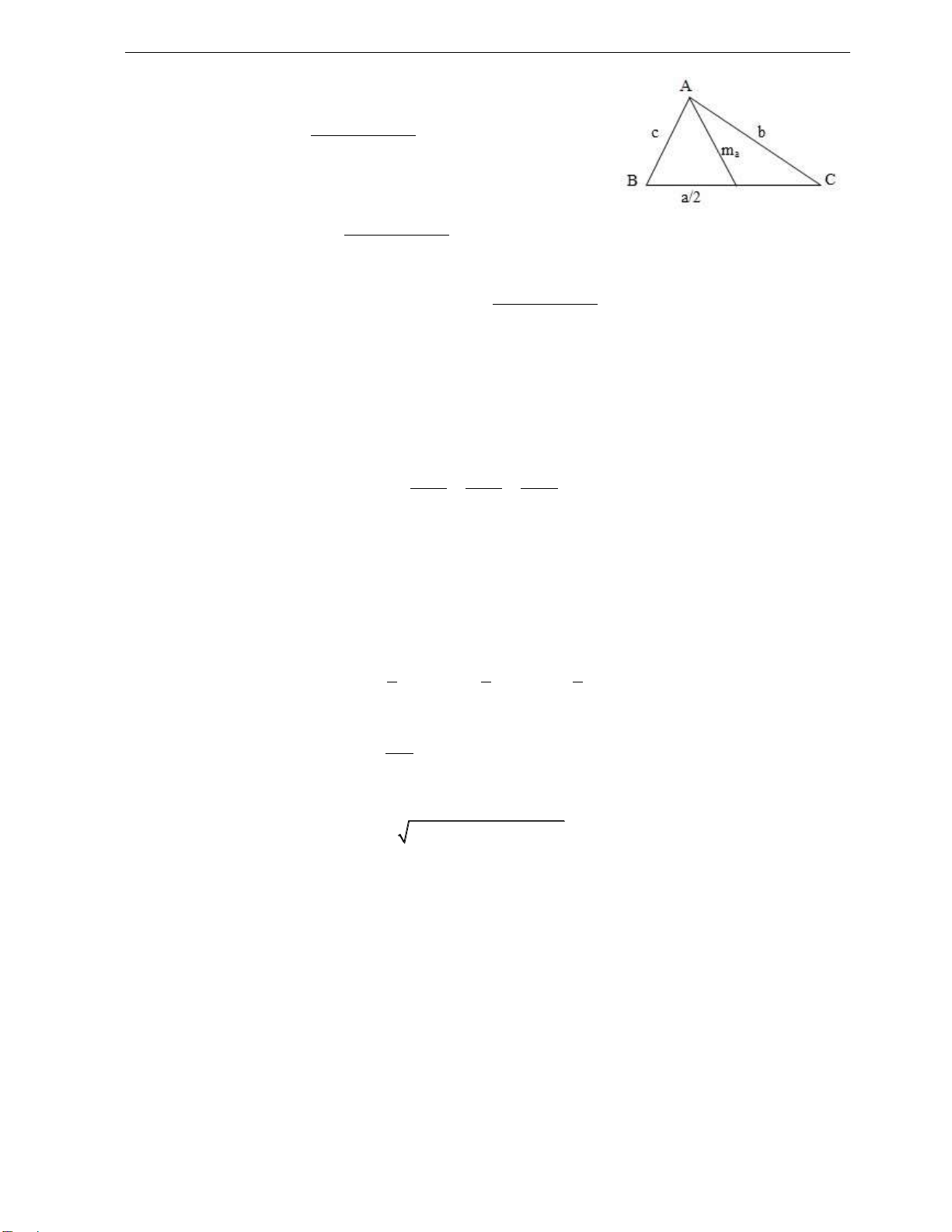
Trong tam giác ABC bất kì, ặt BC = a, CA = b, AB = c thì ta có: a2 = b2 + c2 – 2bc.cosA b2 =a2 + c2 – 2ac.cosB c2 = b2 + a2 – 2bc.cosC
Học sinh có thể chứng minh ịnh lí trên dựa vào tích vô hướng của hai vecto
Hệ quả: Gọi ma, mb, mc là ộ dài các ường trung tuyến dựng từ A, B, C của tam giác ABC thì ta có lOMoARcP SD| 58886076
Chuyên đề: Toán cho Vật lí phổ thông chuyên (Ver.1)  2 2b c2  2 a2 ma  4  2 2a c2  2 b2 mb  4  2 2a b2  2 c2 mc  4 2.3.2. Định lí sin
Trong tam giác ABC bất kì, ặt BC = a, CA = b, AB = c và R là bán kính ường tròn ngoại tiếp tam giác thì ta có: a b c    2R sin A sin B sinC
2.3.4. Các công thức tnhs diện tích tam giác
Trong tam giác ABC bất kì, ặt BC = a, CA = b, AB = c, R là bán kính ường tròn ngoại
tiếp tam giác, r là bán kính ường tròn nội tiếp tam giác và p là nửa chu vi tam giác thì diện
tích tam giác ABC ược tính theo các công thức sau:
S  1 absinC  1 acsin B 1 bcsin A 2 2 2 S  abc 4R S  pr
S  p p a p b p c(  )(  )(  )
2.3.5. Bài tập vận dụng
VD6: Cho tam giác ABC có A = 1200, AC = 8cm, AC = 5cm. Tính số o các góc và chiều dài các cạnh còn lại.
VD7: Tính diện tích một tam giác có chiều dài các cạnh lần lượt là 7m, 9m và 12m.
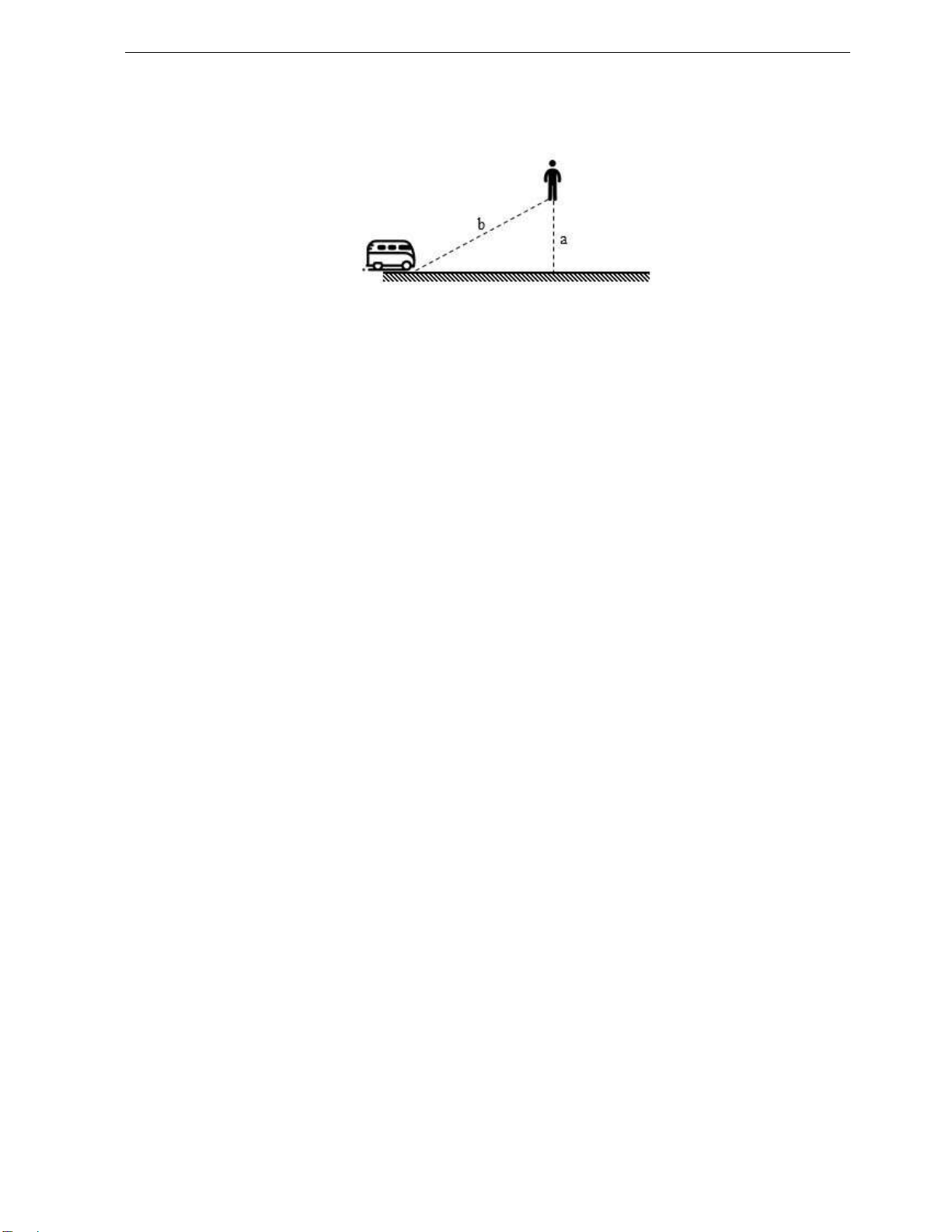
VD8: Bác Ba ang ra ường quốc lộ ón xe khách i Sài òn thăm con. Khi bác Ba còn cách
ường quốc lộ một khoảng a = 60m thì bác thấy một chiếc xe khách cách mình một khoảng b
= 400m ang i tới với vận tốc v1 = 16m/s. a.
Bác Ba có thể chạy với vận tốc v2 = 4m/s. Hỏi bác Ba phải chạy theo phương nào
ể có thể tới ược ường quốc lộ kịp lúc xe khách tới. lOMoARcP SD| 58886076
Chuyên ề: Toán cho Vật lí phổ thông chuyên (Ver.1) b.
Cùng i ón xe với bác Ba có cô Chín nhưng cô Chín chạy không nhanh bằng
bác Ba. Tính vận tốc tối thiểu cô Chín phải chạy ể ón ược xe. Nếu chạy với vận tốc ó thì cô
Chín phải chạy theo phương nào? lOMoARcP SD| 58886 076
Chuyên đề: Toán cho Vật lí phổ thông chuyên (Ver.1) Chương 3: LOGARIT
3.1. NHẮC LẠI VỀ LŨY THỪA 3.1.1. Định nghĩa
a. Lũy thừa với số mũ nguyên
Cho n là một số nguyên dương và a là một số thực tùy ý. Lũy thừa bậc n của a là tích của n thừa số a. an aa a. ... n Với a ≠ 0 a0 = 1 an  1n a b. Căn bậc n
Cho số thực b và số nguyên dương n. Số a ược gọi là căn bậc n của số b nếu an = b. Kí hiệu: a n b
c. Lũy thừa với số mũ hữu tỉ Cho số thực a dương và số hửu tỉ r  m , với m ,n .
Lũy thừa của a với số mũ r n ược xác ịnh như sau: m ar  an n am
3.1.2. Tính chất của lũy thừa
Cho a, b là các số thực dương, m, n là các số thực tùy ý, khí ó ta có: a a am n.  m n amn am n a a  m n amn abm a bm m 3.2. LOGARIT 3.2.1. Định nghĩa lOMoARcP SD| 58886076
Chuyên ề: Toán cho Vật lí phổ thông chuyên (Ver.1)
Cho hai số dương a và b với a ≠ 1. Số n thỏa mđãn ẳng thức an = b ược gọi là logarit
cơ số a của b và kí hiệu là logab nloga b ax b Ví dụ: a. log28 = 3 vì 23 = 8; b. log327 = 3 vì 33 = 27 3.2.2. Các tính chất a. Tính chất cơ bản log 1 b a  0 loga a1 alog  a b loga ax x
b. Logarit của một tích log ( . ) xy x a  loga loga y c. Logarit của một
thương  x loga   log x a loga y  y
d. Logarit của một lũy thừa log  a bnnloga b e. Đổi cơ số
loga b logc b  1 logc a logb a
3.2.3. Logarit thập phân và logarit tự nhiên
Trong vật lí ta chủ yếu gặp các bài toán logarit thập phân và logarit tự nhiên. Trong
phần này ta chỉ tập trung vào hai loại logarit này. a. Logarit thập phân
Logarit thập phân là logarit cơ số 10. log10b thường ược viết là logb (không viết cơ số
thì mặc ịnh là cơ số 10), hay lgb. b. Logarit tự nhiên
Trong toán học, người ta thấy có một số vô tỉ e 2,718 có nhiều tính chất ặc biệt (sẽ
ề cập ở phần “Đạo hàm”), ta gọi e là cơ số tự nhiên
Logarit tự nhiên là logarit cơ số e. logeb thường ược viết là lnb, ọc là loga-nêbe của b. c. Tính chất
Logarit thập phân và logarit tự nhiên cũng có các tính chất như các loagarit cơ số khác: log1 0 ln1 0 log10 1 lne1 10logb b elnb b lOMoARcP SD| 58886 076
Chuyên đề: Toán cho Vật lí phổ thông chuyên (Ver.1) log10x x lnex x  x log  log  x ln  ln xlog y xln y  y  y logbnnlogb lnbnn bln
3.2.4. Bài tập vận dụng
VD1: Giải các phương trình sau: a. 32x-1 + 32x = 108 b. 22x+1 + 22x-1 + 2x = 28 c. 64x – 8x – 56 = 0 d. 3.4x – 2.6x = 9x
VD2: Giải các phương trình sau:
a. log(x – 1) – log(2x – 11) = log2
b. log(x2 – 6x + 7) = log(x – 3)
c. log(x2 – 4x – 1) = log8x – log4x
d. 1 log(x2 + x – 5) = log5x + log 1 2 5x
VD3: Độ to của âm thanh mà tai chúng ta nghe thấy ược xác ịnh bằng ại lượng mức
cường ộ âm L tính theo ơn vị ê-xi-ben (dB) theo công thức: L10log I (dB) I0
Với I (W/m2) là cường ộ âm tại vị trí ang xét, I0 là cường ộ âm tối thiểu mà tai người
nghe ược, thường ược lấy cỡ 10-12 W/m2.
Biết rằng một nguồn âm có công suất P thì cường ộ âm I ở vị trí cách nguồn một khoảng
R ược xác ịnh bằng công thức: I  P 2 4R
a. Hđãy tính mức cường ộ âm do một nguồn có công suất 20W tạo ra tại một điểm cách nó 20m.
b. Tai con người chỉ chịu ược mức cường ộ âm tối a 130dB. Hỏi phải ứng cách
xa nguồn âm trên một khoảng tối thiểu bằng bao nhiêu ể không bị au tai.
VD4: Tại hai điểm A và B trên cùng một phương truyền âm thanh, người ta o ược mức
cường ộ âm lần lượt là LA = 60dB và LB = 20dB. Tính mức cường ộ âm tại trung điểm M của AB.
VD5: Trong thực tế, âm thanh khi truyền i trong không khí thì bị hấp thụ một phần năng
lượng. Cho rằng cứ truyền i 1m, năng lượng âm bị giảm 5% so với ban đầu. Công suất âm
thanh cực ại của một máy nghe nhạc gia ình là 10W, nếu mở to hết cỡ thì mức cường ộ âm ở
khoảng cách 6 m là bao nhiêu? Lấy I0 = 10-12 W/m2. lOMoARcP SD| 58886076
Chuyên ề: Toán cho Vật lí phổ thông chuyên (Ver.1)
VD6: Một vật khối lượng m, ược thả rơi không vận tốc đầu trong không khí. Nếu lực
cản của không khí có ộ lớn tỉ lệ thuận với vận tốc của vật (Fc = kv) thì biểu thức xác ịnh vận
tốc v của vật sau thời gian rơi t là: mg   ktm  v 1e  k  
trong ó g = 9,81 m/s2 là gia tốc rơi tự do. Cho m = 1kg, k = 0,1. a.
Tìm vận tốc tối a mà vật có thể ạt tới.
b. Tính thời gian ể vật ạt ược vận tốc bằng nửa vận tốc tối a ở trên.