Toàn tập góc và khoảng cách vận dụng cao

Tài liệu gồm 62 trang, được biên soạn bởi thầy giáo Lương Tuấn Đức (Giang Sơn), tuyển tập hệ thống bài tập trắc nghiệm chuyên đề góc và khoảng cách vận dụng cao (VDC) lớp 11 THPT.

95 48 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 7: Quan hệ vuông góc trong không gian (KNTT)

Môn: Toán 11

Thông tin:

62 trang 9 tháng trước

Tác giả:

Profile Kim Oanh
1
THÂN TẶNG QUÝ THẦY CÔ VÀ CÁC EM HỌC SINH TOÀN QUỐC
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM CHUYÊN ĐỀ
GÓC, KHOẢNG CÁCH VẬN DỤNG CAO
LỚP 11 THPT
CREATED BY GIANG SƠN; TEL 0333275320
TP.THÁI BÌNH; 20/8/2021
TOÀN TẬP
GÓC, KHOẢNG CÁCH VẬN DỤNG CAO
PHIÊN BẢN 2021
2
TOÀN TẬP
GÓC, KHOẢNG CÁCH VẬN DỤNG CAO
__________________________________________________________________________________________________
VẬN DỤNG CAO GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG – P1
VẬN DỤNG CAO GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG – P2
VẬN DỤNG CAO GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG – P3
VẬN DỤNG CAO GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG – P4
VẬN DỤNG CAO GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG – P5
VẬN DỤNG CAO GÓC NHỊ DIỆN – P1
VẬN DỤNG CAO GÓC NHỊ DIỆN – P2
VẬN DỤNG CAO GÓC NHỊ DIỆN – P3
VẬN DỤNG CAO GÓC NHỊ DIỆN – P4
VẬN DỤNG CAO GÓC NHỊ DIỆN – P5
VẬN DỤNG CAO GÓC NHỊ DIỆN – P6
VẬN DỤNG CAO KHOẢNG CÁCH GIỮA ĐIỂM VÀ MẶT PHẲNG – P1
VẬN DỤNG CAO KHOẢNG CÁCH GIỮA ĐIỂM VÀ MẶT PHẲNG – P2
VẬN DỤNG CAO KHOẢNG CÁCH GIỮA ĐIỂM VÀ MẶT PHẲNG – P3
VẬN DỤNG CAO KHOẢNG CÁCH GIỮA ĐIỂM VÀ MẶT PHẲNG – P4
VẬN DỤNG CAO KHOẢNG CÁCH GIỮA ĐIỂM VÀ MẶT PHẲNG – P5
VẬN DỤNG CAO KHOẢNG CÁCH GIỮA ĐIỂM VÀ MẶT PHẲNG – P6
VẬN DỤNG CAO KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG CHÉO NHAU – P1
VẬN DỤNG CAO KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG CHÉO NHAU – P2
VẬN DỤNG CAO KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG CHÉO NHAU – P3
VẬN DỤNG CAO KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG CHÉO NHAU – P4
VẬN DỤNG CAO KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG CHÉO NHAU – P5
VẬN DỤNG CAO KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG CHÉO NHAU – P6
VẬN DỤNG CAO KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG CHÉO NHAU – P7
VẬN DỤNG CAO KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG CHÉO NHAU – P8
VẬN DỤNG CAO KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG CHÉO NHAU – P9
VẬN DỤNG CAO KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG CHÉO NHAU – P10
VẬN DỤNG CAO KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG CHÉO NHAU – P11
VẬN DỤNG CAO KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG CHÉO NHAU – P12
VẬN DỤNG CAO KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG CHÉO NHAU – P13
VẬN DỤNG CAO KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG CHÉO NHAU – P14
3
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN CỔ ĐIỂN LỚP 11 – 12 THPT
(LỚP BÀI TOÁN GÓC GIỮA ĐƯỜNG VÀ MẶT PHẲNG – P1)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho hình chóp S.ABCD có đáy là tam giác vuông đỉnh B, AB = a, SA vuông góc với đáy là SA = a. Tính
tan của góc giữa SA và mặt phẳng (SBC).
A. 2 B. 1 C. 3 D. 0,5
Câu 2. Cho khối chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy và khoảng cách từ A đến
mặt phẳng (SBC) bằng
2
2
a
. Tính sin của góc giữa đường thẳng SA và mặt phẳng (SBD).
A.
3
3
B.
2
3
C.
4
D.
2
2
Câu 3. Hình chóp S.ABCD có đáy là hình chữ nhật, AB = a, AD = 2a, SA vuông góc với đáy và mặt phẳng
(SCD) tạo với đáy một góc
30
o
. Tính cosin của góc giữa đường thẳng SC và mặt phẳng (SBD).
A.
35
38
B.
2
3
C.
23
38
D.
13
31
Câu 4. Cho hình chóp S.ABC có SA = 3a và SA vuông góc với đáy (ABC), AB = BC = 2a,
·
120
ABC
o
. Tính sin
của góc giữa đường thẳng SA và mặt phẳng (SBC).
A. 0,5 B.
3
4
C.
2
2
D.
5
5
Câu 5. Cho hình chóp S.ABC có đáy là hình vuông cạnh 2a, hình chiếu vuông góc của S lên mặt đáy trùng với
trung điểm H của AB. Biết SD = 3a, tính cosin của góc giữa đường thẳng SA và mặt phẳng (SBD).
A.
145
15
B. 0,5 C.
10
15
D.
2 5
15
Câu 6. Hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B,
3 , 2 ,
AD a AB BC a SA a
. Biết
rằng SA vuông góc với đáy (ABCD). Tính sin của góc giữa đường thẳng SB và mặt phẳng (SCD).
A.
3
205
B.
5
205
C.
10
35
D.
3
3
Câu 7. Cho hình chóp S.ABC có đáy là tam giác vuông tại B có AB = a, BC = 2a. Tam giác SAC cân tại S và
thuộc mặt phẳng vuông góc với đáy. Biết SB = 1,5a, tính cosin của góc giữa đường thẳng SA và mặt phẳng
(SBC).
A.
145
15
B. 0,5 C.
10
15
D.
2 5
15
Câu 8. Cho hình chóp S.ABC có đáy là tam giác vuông,
·
30
ABC
o
, SBC là tam giác đều cạnh à và mặt bên
(SBC) vuông góc với đáy. Gọi M là điểm thỏa mãn
2 0
MC MB
uuuur uuur r
và
là góc giữa đường thẳng SM với mặt
phẳng (SAB). Khi đó
sin
gần nhất giá trị nào sau đây
A. 0,2 B. 0,3 C. 0,4 D. 0,45
Câu 9. Hình chóp S.ABC có đáy là tam giác đều cạnh a, hình chiếu vuông góc H của đỉnh S trên cạnh AC là
điểm H sao cho HA = 2HC. Tính cosin của góc giữa đường thẳng SG và mặt phẳng (SBC) với G là trọng tâm
tam giác ABC và SH = 0,5a.
A.
559
26
B.
129
26
C.
3 13
26
D.
10
15
Câu 10. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SD = 1,5a. Tam giác SAB cân tại S và thuộc mặt
phẳng vuông góc với đáy. Gọi M là trung điểm của SB, cosin của góc giữa đường thẳng AM và mặt phẳng
(SBD) gần nhất giá trị nào sau đây
A. 0,25 B. 0,67 C. 0,52 D. 0,73
Câu 11. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a,
·
60 ,
BAD SA a
o
và SA vuông góc với mặt
phẳng đáy. Tính cosin của góc giữa đường thẳng SB và mặt phẳng (SCD).
A.
145
15
B.
154
14
C.
21
7
D.
21
14
Câu 12. Cho khối lăng trụ đứng
.
ABC A B C
có đáy là tam giác đều cạnh a, đường thẳng A’C tạo với mặt
phẳng đáy một góc
60
o
. Tính cosin của góc giữa đường thẳng C’B với mặt phẳng
( )
A BC
.
4
A.
85
10
B.
10
15
C.
13
15
D.
11
5
Câu 13. Cho khối lăng trụ đứng
.
ABC A B C
có đáy ABC là tam giác vuông tại A,
3;
AB a AC A A a
.
Tính sin của góc tạo bởi đường thẳng A’B và mặt phẳng
( )
BCC B
.
A.
60
o
B.
30
o
C.
45
o
D.
75
o
Câu 14. Cho hình chóp S.ABC có các tam giác ABC và SBC là tam giác đều và nằm trong hai mặt phẳng vuông
góc với nhau. Góc giữa đường thẳng SA và mặt phẳng (ABC) là
A.
60
o
B.
30
o
C.
45
o
D.
75
o
Câu 15. Hình chóp S.ABC có SA vuông góc với (ABC), SA = a, tam giác ABC đều cạnh a. Gọi
là góc giữa SC
và mặt phẳng (SAB). Khi đó
tan
bằng
A.
3
5
B. 2 C.
6
2
D.
23
4
Câu 16. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh SA vuông góc với đáy (ABCD) và
6
SA a
. Tính sin của góc tạo bởi AC và mặt phẳng (ABC).
A.
1
3
B.
1
6
C.
1
7
D.
3
7
Câu 17. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại B và C, cạnh SA vuông góc với đáy
(ABCD) và
·
2 ; ; 2 ; 30
CD AB AD a SA a ADC
o
. Khi đó
·
sin ,( )
SD SBC
gần nhất giá trị nào sau đây
A. 0,25 B. 0,71 C. 0,34 D. 0,36
Câu 18. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B với AD = 2AB = 2BC = 2a, SA
vuông góc với mặt phẳng đáy, SA = 2a. Tính sin của góc giữa đường thẳng SD và mặt phẳng (SAC).
A. 0,5 B.
3
4
C.
2
2
D.
5
5
Câu 19. Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông tâm O cạnh a, cạnh bên tạo với đáy một góc
60
o
. Điểm M thuộc cạnh SB sao cho
3
SM SB
. Khi đó sin của góc giữa OM và mặt phẳng (SCD) gần nhất
giá trị nào sau đây ?
A. 0,03 B. 0,2 C. 0,09 D. 0,15
Câu 20. Cho hình chóp đều S.ABCD có tất cả các cạnh bằng a. Gọi G là trọng tâm tam giác SCD, tan của góc
giữa đường thẳng AG và mặt phẳng (SCD) bằng
A.
17
7
B.
5
3
C.
5
D.
17
______________________________________
5
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN LỚP 12 THPT
(LỚP BÀI TOÁN GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG – P2)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại A cạnh AB = a, SA vuông góc với mặt phẳng và
2
SA a
. Gọi M là trung điểm của SA, tính
sin
biết
là góc giữa BM và mặt phẳng (SBC).
A.
2
2 15
B.
1
15
C.
2
15
D.
1
2 15
Câu 2. Cho hình lập phương ABCD.A’B’C’D’. Gọi M, N lần lượt là trung điểm của cạnh AC, B’C’. Tính
sin
với
là góc giữa đường thẳng MN và mặt phẳng (A’B’C’D’).
A.
5
sin
5
B.
2 5
sin
5
C.
2
sin
2
D.
1
sin
2
Câu 3. Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, tam giác SAB là tam giác đều và nằm trong mặt
phẳng vuông góc với đáy. Gọi M, N lần lượt là trung điểm của SC và AD. Góc giữa đường thẳng MN và mặt
phẳng (ABCD) bằng
A.
0
45
B.
60
o
C.
90
o
D.
30
o
Câu 4. Cho hình chóp
.
S ABCD
có
SA
vuông góc với mặt phẳng đáy,
ABCD
là hình chữ nhật có
3
AD a
;
5
AC a
, góc giữa hai mặt phẳng
SCD
và
ABCD
bằng
0
45
. Khi đó côsin của góc giữa đường
thẳng
SD
và mặt phẳng
SBC
bằng
A.
7
5
. B.
4
5
. C.
2 2
5
. D.
17
5
.
Câu 5. Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông tâm O, cạnh a. Gọi M, N lần lượt là trung điểm
của SA và BC. Góc giữa đường thẳng MN và mặt phẳng (ABCD) bằng
60
o
. Tính cosin của góc giữa đường
thẳng MN và mặt phẳng (SBD).
A.
41
4
B.
5
5
C.
2 5
5
D.
2 41
7
Câu 6. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng
2
a
và cạnh bên bằng
3
a
. Gọi M, N theo thứ
tự là trung điểm của các cạnh SB, CD. Tính sin của góc tạo bởi đường thẳng MN và mặt phẳng (SBC).
A.
2 15
15
B.
14
14
C.
3 105
105
D.
2 70
35
Câu 7. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, SA vuông góc với (ABCD). Biết
rằng AD = 2AB = 2BC = 2SA = 2a. Gọi
là góc giữa đường thẳng SA và (SAC). Khi đó
A.
10
cos
5
B.
10
sin
5
C.
tan 2
D.
tan 3
Câu 8. Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a, M là trung điểm của cạnh SD. Tính tan
của góc giữa đường thẳng BM và mặt phẳng (ABCD) bằng
A.
1
3
B.
2
3
C.
3
D.
2
2
Câu 9. Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a. Gọi M là điểm nằm trên SD sao cho
SM = 2MD. Giá trị tan của góc giữa đường thẳng BM và mặt phẳng (ABCD) bằng
A. 0,2 B.
1
3
C.
3
D.
5
5
Câu 10. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Tam giác SAB cân tại S và (SAB) vuông
góc với mặt phẳng (ABCD). Giả sử thể tích của khối chóp S.ABCD bằng
3
4
3
a
. Tính cosin góc giữa đường
thẳng SC và mặt phẳng (ABCD).
A.
3
cos
2
B.
30
cos
6
C.
14
cos
4
D.
5
cos
3
Câu 11. Cho hình lập phương ABCD.A
1
B
1
C
1
C
1
có cạnh a. Gọi I là trung điểm của BD. Tính góc giữa hai đường
thẳng A
1
D và B
1
I.
A.
0
45
B.
60
o
C.
90
o
D.
30
o
6
Câu 12. Cho tứ diện S.ABC có
; 2
SA SB SC AB AC a BC a
. Góc giữa hai đường thẳng AB và
SC bằng
A.
120
o
B.
60
o
C.
90
o
D.
30
o
Câu 13. Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB = a và
6
2
a
AD , mặt bên SAB là tam giác
đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Góc giữa đường thẳng SB và mặt phẳng (SCD)
bằng
A.
0
45
B.
60
o
C.
90
o
D.
30
o
Câu 14. Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm I, cạnh a,
·
60
BAD
o
,
3
2
a
SA SB SC .
Gọi
là góc giữa đường thẳng SD và mặt phẳng (SBC). Tính
sin
.
A.
5
3
B.
2
3
C.
1
3
D.
2 2
3
Câu 15. Cho hình chóp S.ABCD có cạnh đáy bằng a, tâm O. Gọi M, N lần lượt trung điểm của SA, BC. Biết rằng
góc giữa MN và (ABCD) bằng
60
o
. Cosin của góc giữa MN và mặt phẳng (SBD) bằng
A.
5
5
B.
41
41
C.
2 5
5
D.
2 41
41
Câu 16. Hình lăng trụ tam giác ABC.A’B’C’ có đáy là tam giác đều cạnh a,
6
A A a
. Hình chiếu vuông góc H
của A trên mặt phẳng (A’B’C’) trùng với trọng tâm tam giác A’B’C’. Tính cosin của góc giữa cạnh bên và mặt đáy
hình lăng trụ.
A.
2
3
B.
2
6
C.
15
15
D.
3
6
Câu 17. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B, AB = a, SA vuông góc với AB, SC vuông góc
với BC, SB = 2a. Gọi M, N lần lượt là trung điểm SA, BC. Tính cosin của góc giữa đường MN với mặt (ABC).
A.
6
3
B.
2 6
5
C.
10
5
D.
2
11
Câu 18. Cho hình chóp tứ giác đều
.
S ABCD
có cạnh đáy bằng
a 2
và cạnh bên bằng
2a
. Góc giữa đường
thẳng
SB
với mặt phẳng
SAC
bằng
A.
0
60
. B.
0
30
. C.
0
90
. D.
0
45
.
Câu 19. Cho hình chóp
.
S ABCD
có
SA ABCD
và
SA a 3
. Đáy
ABCD
là hình chữ nhật có
,
AB a AD a 3
. Gọi
M
là trung điểm của
CD
, góc giữa
SA
và mặt phẳng
SBM
bằng
.
tan
bằng:
A.
2
15
. B.
4
15
. C.
2
13
. D.
4
13
.
Câu 20. Cho hình chóp
. D
S ABC
có đáy
D
ABC
là hình thang vuông tại
A
và
B
,
=2 2 2
AD AB BC a
,
2
SA a
và
SA
vuông góc với
D
ABC
. Gọi
M
là trung điểm của
SB
và
là góc tạo bởi đường thẳng
MD
và mặt phẳng
D
SC
. Khi đó
sin
bằng:
A.
10
24
B.
10
12
. C.
15
24
. D.
15
12
.
Câu 21. Cho hình chóp
.
S ABCD
có
SA ABCD
,
2
SA a
,
ABCD
là hình thang vuông tại
,
A B
và
2 2 2
AB BC AD a
. Gọi
O AC BD
,
M
là trung điểm
SB
. Tính
sin
góc giữa
OM
và
SCD
.
A.
2 35
35
. B.
35
35
. C.
3 35
70
. D.
35
70
.
______________________________________
7
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN LỚP 12 THPT
(LỚP BÀI TOÁN GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG – P3)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho hình vuông
ABCD
và tam giác đều
SAB
cạnh
a
nằm trong hai mặt phẳng vuông góc với nhau.
Tính sin góc giữa đường thẳng
SC
và mặt phẳng
SAD
.
A.
3
3
. B.
2
2
. C.
6
4
. D.
3
4
.
Câu 2. Cho hình lăng trụ tam giác đều .
ABC A B C
có cạnh đáy bằng
a
, cạnh bên
AA a
. Gọi
M
,
N
lần
lượt là trung điểm của
BB
,
B C
. Lấy điểm
P
thuộc
A B
sao cho
4
a
PB
. Tính
tan
góc giữa đường thẳng
AP
và mặt phẳng
MNP
A.
2
. B.
1
2
. C.
1
3
. D.
3
.
Câu 3. Cho hình chóp .
S ABCD
có
ABCD
là hình vuông,
SAB
là tam giác đều và nằm trong mặt phẳng
vuông góc với đáy. Gọi
M
là trung điểm
BC
. Gọi
góc hợp bởi đường thẳng
SA
và mặt phẳng
SDM
.
Tính
.
A.
30
. B.
60
. C.
55
. D.
45
.
Câu 4. Cho hình lăng trụ đều .
ABC A B C
có tất cả các cạnh bằng
1
. Điểm
M
và
N
lần lượt là trung điểm các
đoạn
AC
,
BB
. Côsin góc giữa đường thẳng
MN
và
BA C
bằng
A.
21
14
. B.
7
14
. C.
3
21
. D.
21
21
.
Câu 5. Cho hình lăng trụ
. ' ' '
ABC A B C
có
10
'
4
a
AA
,
2
AC a
,
BC a
,
·
0
135
ACB
. Hình chiếu vuông
góc của
C
lên mặt phẳng
( )
ABC
trùng với trung điểm
M
của
AB
. Tính góc tạo bởi đường thẳng
C M
với
mặt phẳng
ACC A
A.
0
90
. B.
0
60
. C.
0
45
. D.
0
30
.
Câu 6. Cho lăng trụ đứng
. ’ ’ ’
ABC A B C
có đáy
ABC
cân đỉnh
·
,A ABC
,
'
BC
tạo đáy góc
. Gọi
I
là trung
điểm của
’
AA
, biết
·
0
90
BIC
. Tính
2 2
tan tan
A.
1
2
. B.
2
. C.
3
. D.
1
.
Câu 7. Cho hình lăng trụ đứng
. ' ' '
ABC A B C
có đáy là tam giác vuông cân tại
A
,
AC b
, các cạnh bên có
độ dài bằng
b
. Tính góc giữa đường thẳng
AB
và mặt phẳng
' ' .
AB C
A.
3
2
. B.
3
3
. C. .
1
2
D.
6
3
.
Câu 8. Cho hình lăng trụ
.
ABC A B C
có đáy
ABC
là tam giác vuông tại
B
,
·
, 30
AB a ACB
,
M
là trung
điểm cạnh
AC
. Góc giữa cạnh bên và mặt đáy của lăng trụ bằng
60
. Hình chiếu vuông góc của đỉnh
A
lên
mặt phẳng
ABC
là trung điểm
H
của
BM
. Gọi
là góc tạo bởi
A H
với
A ACC
. Tính
sin
?
A.
1
3
. B.
3
4
. C.
2
5
. D.
3
6
.
Câu 9. Cho hình hộp chữ nhật
.
ABCD A B C D
có đáy
ABCD
là hình vuông cạnh bằng
2 2
,
4
AA
. Tính
góc giữa đường thẳng
A C
với mặt phẳng
AA B B
.
A.
30
. B.
90
. C.
60
. D.
45
.
Câu 10. Cho hình lập phương
.
ABCD A B C D
. Tính góc tạo bởi đường thẳng
AB
và mặt phẳng
BDD B
.
A.
60
. B.
90
. C.
45
. D.
30
.
Câu 11. Cho hình hộp chữ nhật
. ' ' ' '
ABCD A B C D
nội tiếp mặt cầu
S
có bán kình
17
2
R
Gọi
,
I J
là
8
trung điểm
,
BC CD
và
là góc giữa đường thẳng
'
AC
và mặt phẳng
'IJ
C
. Giá trị lớn nhất của sin
là
A.
3
5
. B.
3
5
. C.
4
5
. D.
4
5
.
Câu 12. Cho hình lập phương
.
ABCD A B C D
có cạnh bằng
a
và
I AC BD
. Gọi
,
M N
lần lượt là trung
điểm của
C D
,
AA
. Gọi
là góc tạo bởi đường thẳng
IN
và mặt phẳng
ACM
. Tính
sin
.
A.
3
9
. B.
2
2
. C.
5 3
9
. D.
3
24
.
Câu 13. Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông tại
A
.
BC a
.
3
3
a
SA SB SC
. Góc giữa
đường thẳng
SA
và
ABC
bằng
A.
30
. B.
45
. C.
60
. D.
90
.
Câu 14. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
. Tam giác
SAB
đều và nằm trong mặt
phẳng vuông góc với đáy. Gọi
là góc giữa đường thẳng
SC
và
ABCD
. Giá trị của
tan
bằng:
A.
1
. B.
15
5
. C.
15
3
. D.
5
2
.
Câu 15. Cho hình chóp .
S ABCD
có đáy
ABCD
là hình thang vuông tại
A
và
B
;
SAB
là tam giác cân tại
S
;
3 3 3
AD BC AB a
. Gọi
M
là điểm thuộc đoạn
AD
sao cho 3
AD MD
. Biết rằng
SCM
là tam giác đều.
Gọi
là góc giữa đường thẳng
SB
và mặt phẳng
SAD
. Khi đó
cos
nhận giá trị là
A.
2 7
7
. B.
21
7
. C.
42
14
. D.
154
14
.
Câu 16. Cho tứ diện
OABC
có
, ,
OA OB OC
đôi một vuông góc với nhau và
OA O B OC
. Gọi
M
là trung
điểm của
BC
(tham khảo hình vẽ bên dưới). Góc giữa hai đường thẳng
OM
và
AB
bằng
A.
0
45
B.
0
90
C.
0
30
D.
0
60
Câu 17. Cho tứ diện
ABCD
với
·
·
0
3
, 60 ,
2
AC AD CAB DAB CD AD
. Gọi
là góc giữa hai đường thẳng
AB
và
CD
. Chọn khẳng định đúng về góc
.
A.
3
4
cos
B.
0
30
C.
0
60
D.
1
4
cos
Câu 18. Cho hình hộp chữ nhật .
ABCD A B C D
, biết đáy
ABCD
là hình vuông. Tính góc giữa
A C
và
BD
.
A.
90
. B.
30
. C.
60
. D.
45
.
Câu 19. Cho tứ diện
ABCD
có
2
AB CD a
. Gọi
M
,
N
lần lượt là trung điểm
AD
và
BC
. Biết
3
MN a
,
góc giữa hai đường thẳng
AB
và
CD
bằng.
A.
0
45
. B.
0
90
. C.
0
60
. D.
0
30
.
Câu 20. Cho hình lập phương .
ABCD A B C D
; gọi
M
là trung điểm của
B C
. Góc giữa hai đường thẳng
AM
và
BC
bằng
A.
45
. B.
90
. C.
30
. D.
60
.
Câu 21. Cho hình chóp
.
S ABC
có độ dài các cạnh
SA SB SC AB AC a
và
2
BC a
. Góc giữa hai
đường thẳng
AB
và
SC
là?
A.
45
. B.
90
. C.
60
. D.
30
.
9
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN LỚP 12 THPT
(LỚP BÀI TOÁN GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG – P4)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho hình lăng trụ tam giác đều
.
ABC A B C
có
AB a
và
2
AA a
. Góc giữa hai đường thẳng
AB
và
BC
bằng
A.
60
. B.
45
. C.
90
. D.
30
.
Câu 2. Cho tứ diện
ABCD
có
DA DB DC AC AB a
,
·
45
ABC
. Tính góc giữa hai đường thẳng
AB
và
DC
.
A.
60
. B.
120
. C.
90
. D.
30
.
Câu 3. Cho hình lập phương
.
ABCD A B C D
. Gọi
M
,
N
lần lượt là trung điểm của
AD
,
.
BB
Cosin của góc
hợp bởi
MN
và
'
AC
bằng
A.
3
3
. B.
2
3
. C.
5
3
. D.
2
4
.
Câu 4. Cho hình chóp
.
S ABCD
có đáy là hình chữ nhật,
2
AB a
,
BC a
. Hình chiếu vuông góc
H
của đỉnh
S
trên mặt phẳng đáy là trung điểm của cạnh
AB
, góc giữa đường thẳng
SC
và mặt phẳng đáy bằng
0
60
.
Tính cosin góc giữa hai đường thẳng
SB
và
AC
A.
2
7
. B.
2
35
. C.
2
5
. D.
2
7
.
Câu 5. Cho hình chóp tứ giác đều
.
S ABCD
có đáy
ABCD
là hình vuông,
E
là điểm đối xứng của
D
qua trung
điểm
SA
. Gọi
M
,
N
lần lượt là trung điểm của
AE
và
BC
. Góc giữa hai đường thẳng
MN
và
BD
bằng
A.
90
. B.
60
. C.
45
. D.
75
.
Câu 6. Cho hình chóp đều
.
S ABCD
có tất cả các cạnh đều bằng
a
. Gọi
M
,
N
lần lượt là trung điểm của
AD
và
SD
. Số đo của góc giữa hai đường thẳng
MN
và
SC
là
A.
45
. B.
60
. C.
30
. D.
90
.
Câu 7. Cho hình lăng trụ
.
ABC A B C
có đáy
ABC
là tam giác vuông tại
A
,
AB a
,
3
AC a
. Hình chiếu
vuông góc của
A
lên mặt phẳng
ABC
là trung điểm
H
của
BC
,
3
A H a
. Gọi
là góc giữa hai đường
thẳng
A B
và
B C
. Tính
cos
.
A.
1
cos
2
. B.
6
cos
8
. C.
6
cos
4
. D.
3
cos
2
.
Câu 8. Cho tứ diện đều
ABCD
,
M
là trung điểm của cạnh
BC
. Tính giá trị của
cos ,
AB DM
.
A.
3
2
. B.
3
6
. C.
1
2
. D.
2
2
.
Câu 9. Lăng trụ .
ABC A B C
có đáy
ABC
là tam giác đều cạnh
a
, tam giác
A BC
đều nằm trong mặt phẳng
vuông góc với
ABC
.
M
là trung điểm cạnh
CC
. Tính cosin góc
giữa hai đường thẳng
AA
và
BM
.
A.
2 22
os
11
c
. B.
33
os
11
c
. C.
11
os
11
c
. D.
22
os
11
c
.
Câu 10. Cho hình lăng trụ tam giác đều .
ABC MNP
có tất cả các cạnh bằng nhau. Gọi
I
là trung điểm cạnh
AC
. Côsin của góc giữa hai đường thẳng
NC
và
BI
bằng
A.
6
4
. B.
15
5
. C.
6
2
. D.
10
4
.
Câu 11. Cho tứ diện đều
ABCD
,
M
là trung điểm của cạnh
BC
. Khi đó
cos ,
AB DM
bằng
A.
2
2
. B.
3
6
. C.
1
2
. D.
3
2
.
Câu 12. Cho hình chóp
.
S ABCD
có đáy là hình vuông cạnh
3
a
,
SA
vuông góc với mặt phẳng đáy và
2
SA a
. Góc giữa
SC
và mặt phẳng
( )
ABCD
bằng
A.
0
45
. B.
0
60
. C.
0
30
. D.
0
90
.
Câu 13. Cho hình chóp
.
S ABC
có
SA
vuông góc với mặt phẳng
,
ABC
2,
SA a tam giác
ABC
vuông cân tại
B
và
2
AC a
(minh họa nhứ hình bên). Góc giữa đường thẳng
SB
và mặt phẳng
ABC
bằng
A.
30 .
B.
45 .
C.
60 .
D.
90 .
10
Câu 14. Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông tại
B
,
AB a
,
2
BC a
,
SA
vuông góc với
mặt phẳng đáy và
15
SA a
.Góc giữa đường thẳng
SC
và mặt phẳng đáy bằng
A.
45
. B.
30
. C.
60
. D.
90
.
Câu 15. Cho hình chóp .
S ABC
có đáy là tam giác vuông tại
B
,
3 , 3 ,
AB a BC a
SA
vuông góc với mặt
phẳng đáy và
2
SA a
. Góc giữa đường thẳng
SC
và mặt phẳng đáy bằng
A.
60
o
. B.
0
45
. C.
0
30
. D.
0
90
.
Câu 16. Cho hình chóp
.
S ABC
và có đáy
ABC
là tam giác vuông tại
,
B
, 3 ;
AB a BC a
SA
vuông góc với
mặt phẳng đáy và
30
SA a
. Góc giữa đường thẳng
SC
và mặt đáy bằng
A.
45
. B.
90
. C.
60
. D.
30
.
Câu 17. Cho hình chóp .
S ABC
có đáy
ABC
là tam giác vuông tại
B
,
AB a
;
2
BC a
;
SA
vuông góc với
mặt phẳng đáy và
SA a
. Góc giữa đường thẳng
SC
và đáy bằng
A.
0
90
. B.
0
45
. C.
0
60
. D.
0
30
.
Câu 18. Cho hình hộp chữ nhật
.
ABCD A B C D
có
, 6
AB BC a AA a
.Góc giữa đường thẳng
A C
và
mặt phẳng
ABCD
bằng:
A.
60
. B.
90
. C.
30
. D.
45
.
Câu 19. Cho hình hộp chữ nhật
D. ' ' ' '
ABC A B C D
có
AB a
,
D 2 2
A a
,
' 3
AA a
(tham khảo hình bên).
Góc giữa đường thẳng
'
A C
và mặt phẳng
D
ABC
bằng
A.
45
. B.
90
. C.
60
. D.
30
.
Câu 20. Cho hình hộp chữ nhật .
ABCD A B C D
, có
AB AA a
,
2
AD a
(tham khảo hình vẽ). Góc giữa
đường thẳng
A C
và mặt phẳng
ABCD
bằng
A.
30
o
. B.
45
o
. C.
90
o
. D.
60
o
.
Câu 21. Cho hình hộp chữ nhật
.
ABCD A B C D
có
, 3 , 2 3
AB a AD a AA a
. Góc giữa đường thẳng
A C
và mặt phẳng
ABCD
bằng
A.
45
. B.
30
. C.
60
. D.
90
.
Câu 22. Cho hình chóp
.
S ABC
có đáy là tam giác vuông tại
C
,
AC a
,
2
BC a
,
SA
vuông góc với mặt
phẳng đáy và
SA a
. Góc giữa đường thẳng
SB
và mặt phẳng đáy bằng
A.
60
B.
90
C.
30
D.
45
Câu 23. Cho hình chóp .
S ABC
có
SA
vuông góc với mặt phẳng
ABC
,
2
SA a
, tam giác
ABC
vuông tại
B
,
AB a
và
3
BC a
. Góc giữa đường thẳng
SC
và mặt phẳng
ABC
bằng
A.
30
. B.
60
. C.
45
. D.
90
.
Câu 24. Cho khối chóp .
S ABC
có
SA ABC
, tam giác
ABC
vuông tại
B
,
2
AC a
,
BC a
,
2 3
SB a
.
Tính góc giữa
SA
và mặt phẳng
SBC
.
A.
45
. B.
30
. C.
60
. D.
90
.
Câu 25. Cho hình chóp
SABCD
có đáy là hình thang vuông tại
1
và
B
.
, 2
AB BC a AD a
. Biết
SA
vuông
góc với đáy
( )
ABCD
và
SA a
. Gọi
,
M N
lần lượt là trung điểm
,
SB CD
. Tính sin góc giữa đường thẳng
MN
và mặt phẳng
( )
SAC
A.
5
5
B.
55
10
C.
3 5
10
D.
2 5
5
Câu 26. Cho hình chóp
.
S ABCD
có đáy là hình vuông cạnh
a
,
SA
vuông góc với mặt phẳng đáy và
2
SA a
. Góc giữa đường thẳng
SC
và mặt phẳng đáy bằng
A.
45
B.
60
C.
30
D.
90
Câu 27. Cho hình chóp
.
S ABCD
có đáy hình vuông. Cho tam giác
SAB
vuông tại
S
và góc
SBA
bằng
0
30
.
Mặt phẳng
SAB
vuông góc mặt phẳng đáy. Gọi
,
M N
là trung điểm
,
AB BC
. Tìm cosin góc tạo bởi hai
đường thẳng
,
SM DN
.
A.
2
5
. B.
1
5
. C.
1
3
. D.
2
3
.
______________________________________
11
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN LỚP 12 THPT
(LỚP BÀI TOÁN GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG – P5)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho hình chóp .
S ABCD
có đáy là hình vuông cạnh
a
,
SA
vuông góc với mặt phẳng đáy và
2
SB a
.
Góc giữa đường thẳng
SB
và mặt phẳng đáy bằng
A.
45
B.
60
C.
90
D.
30
Câu 2. Cho hình chóp .
S ABC
có
SA
vuông góc với mặt phẳng
ABC
,
2
SA a
, tam giác
ABC
vuông tại
,
B
3
AB a
và
BC a
.Góc giữa đường thẳng
SC
và mặt phẳng
ABC
bằng:
A.
0
45
. B.
0
30
. C.
0
60
. D.
0
90
.
Câu 3. Cho hình chóp tứ giác đều
.
S ABCD
có tất cả các cạnh bằng
a
. Gọi
M
là trung điểm của
SD
(tham
khảo hình vẽ bên). Tang của góc giữa đường thẳng
BM
và mặt phẳng
ABCD
bằng
A
B
C
D
S
M
A.
2
2
B.
3
3
C.
2
3
D.
1
3
Câu 4. Cho hình chóp .
S ABC
có
SA
vuông góc với mặt phẳng
ABC
,
2
SA a
, tam giác
ABC
vuông cân tại
B
và
2
AB a
.Góc giữa đường thẳng
SC
và mặt phẳng
ABC
bằng
A.
30
o
. B.
90
o
. C.
60
o
. D.
45
o
.
Câu 5. Cho hình chóp tứ giác đều .
S ABCD
có tất cả các cạnh bằng
2
a
. Gọi
M
là trung điểm của
SD
Tính
tan
của góc giữa đường thẳng
BM
và mặt phẳng
ABCD
.
A.
2
2
. B.
3
3
. C.
2
3
. D.
1
3
.
Câu 6. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
và
SA ABCD
. Biết
6
3
a
SA
. Tính
góc giữa
SC
và
ABCD
.
A.
30
B.
60
C.
75
D.
45
Câu 7. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA
vuông góc với đáy và
3
SA a
.
Gọi
là góc giữa
SD
và
SAC
. Giá trị
sin
bằng
A.
2
4
. B.
2
2
. C.
3
2
. D.
2
3
.
Câu 8. Cho hình chóp tam giác
.
S ABC
có đáy là tam giác đều cạnh
a
. Tam giác
SAB
cân tại
S
và thuộc mặt
phẳng vuông góc với đáy. Biết
SC
tạo với mặt phẳng đáy một góc
60
, gọi
M
là trung điểm của
BC
. Gọi
là
góc giữa đường thẳng
SM
và mặt phẳng
ABC
. Tính
cos
.
A.
6
cos
3
. B.
3
cos
3
. C.
3
cos
10
. D.
1
cos
10
.
Câu 9. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật,
, 3
AB a AD a
. Mặt bên
SAB
là tam giác
đều và nằm trong mặt phẳng vuông góc với mặt đáy. Cosin của góc giữa đường thẳng
SD
và mặt phẳng
SBC
bằng
A.
13
4
B.
3
4
C.
2 5
5
D.
1
4
Câu 10. Cho hình chóp .
S ABC
có đáy là tam giác vuông tại
C
,
CH
vuông góc với
AB
tại
H
,
I
là trung điểm
của đoạn
HC
. Biết
SI
vuông góc với mặt phẳng đáy,
·
90
ASB
. Gọi
O
là trung điểm của đoạn
AB
,
O
là
12
tâm mặt cầu ngoại tiếp tứ diện
SABI
. Góc tạo bởi đường thẳng
OO
và mặt phẳng
ABC
bằng
A.
60
. B.
30
. C.
90
. D.
45
.
Câu 11. Cho hình chóp tứ giác đều
.
S ABCD
có
AB a
,
O
là trung điểm
AC
và
SO b
. Gọi
là đường
thẳng đi qua
C
,
chứa trong mặt phẳng
ABCD
và khoảng cách từ
O
đến
là
14
6
a
. Giá trị lượng
giác
cos ,SA
bằng
A.
2 2
2
3 4 2
a
b a
. B.
2 2
2
3 2 4
a
a b
. C.
2 2
3 2 4
a
a b
. D.
2 2
3 4 2
a
b a
.
Câu 12. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình thoi cạnh
a
và
·
60
ABC . Hình chiếu vuông góc của
điểm
S
lên mặt phẳng
ABCD
trùng với trọng tâm của tam giác
ABC
, gọi
là góc giữa đường thẳng
SB
và
mặt phẳng
SCD
, tính
sin
biết rằng
SB a
.
A.
sin
3
2
. B.
sin
1
4
. C.
sin
1
2
. D.
sin
2
2
.
Câu 13. Cho hình chóp .
S ABCD
có đáy là hình vuông cạnh
a
,
SA ABCD
,
SA x
. Xác định
x
để hai mặt
phẳng
SBC
và
SCD
hợp với nhau góc
60
.
A.
2
x a
. B.
x a
. C.
3
2
a
x
. D.
2
a
x
.
Câu 14. Cho hình chóp
.
S ABC
có đáy là tam giác vuông tại
B
, cạnh bên
S
A
vuông góc với mặt đáy,
2a
AB
,
·
0
60
BAC
và
2
SA a
. Góc giữa đường thẳng
SB
và mặt phẳng
( )
SAC
bằng
A.
0
45
. B.
0
60
. C.
0
30
. D.
0
90
.
Câu 15. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
, cạnh bên
SA
vuông góc với mặt phẳng
đáy,
2
SA a
. Gọi
M
,
N
lần lượt là hình chiếu vuông góc của điểm
A
trên các cạnh
SB
,
SD
. Góc giữa mặt
phẳng
AMN
và đường thẳng
SB
bằng
A.
o
45
. B.
o
90
. C.
o
120
. D.
o
60
.
Câu 16. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật,
AB a
,
3
BC a
,
SA a
và
SA
vuông
góc với đáy
ABCD
. Tính
sin
, với
là góc tạo bởi giữa đường thẳng
BD
và mặt phẳng
SBC
.
A.
7
sin
8
. B.
3
sin
2
. C.
2
sin
4
. D.
3
sin
5
.
Câu 17. Cho hình chóp
.
S ABC
có đáy là tam giác vuông tại
B
, cạnh bên
SA
vuông góc với mặt phẳng đáy,
2
AB a
,
·
0
60
BAC
và
2
SA a
. Góc giữa đường thẳng
SB
và mặt phẳng
SAC
bằng
A.
0
30
. B.
0
45
. C.
0
60
. D.
0
90
.
Câu 18. Cho hình chóp tứ giác đều
.
S ABCD
có cạnh đáy bằng
a
, tâm
O
. Gọi
M
và
N
lần lượt là trung điểm
của
SA
và
BC
. Biết rằng góc giữa
MN
và
ABCD
bằng
0
60
, cosin góc giữa
MN
và mặt phẳng
SBD
bằng:
A.
41
41
. B.
5
5
. C.
2 5
5
. D.
2 41
41
.
Câu 19. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình bình hành,
2
AB a
,
BC a
,
·
120
ABC
. Cạnh bên
3
SD a
và
SD
vuông góc với mặt phẳng đáy. Tính
sin
của góc tạo bởi
SB
và mặt phẳng
SAC
A.
3
4
. B.
3
4
. C.
1
4
. D.
3
7
.
Câu 20. Cho hình lăng trụ đứng
.
ABC A B C
có
, 120
AB AC a BAC
. Gọi
,
M N
lần lượt là trung điểm
của
B C
và
CC
. Biết thể tích khối lăng trụ .
ABC A B C
bằng
3
3
4
a
. Gọi
là góc giữa mặt phẳng
AMN
và
mặt phẳng
ABC
. Khi đó
A.
3
cos
2
. B.
1
cos
2
. C.
13
cos
4
. D.
3
cos
4
.
13
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN LỚP 12 THPT
(LỚP BÀI TOÁN GÓC NHỊ DIỆN – P1)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có AD = 2a, AB = a, cạnh SA vuông góc với đáy
và SA = a. Tính sin của góc giữa hai mặt phẳng (SBC) và (SCD).
A. 0,5 B.
15
5
B.
2 2
5
D.
2
4
Câu 2. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, SA vuông góc với mặt phẳng
(ABCD), AB = BC = a và AD = 2a. Nếu góc giữa SC và mặt phẳng (ABCD) bằng
45
o
thì cosin của góc giữa
(SAD) và (SCD) bằng
A. 0,5 B.
2
3
C.
4
D.
5
6
Câu 3. Cho hình chóp S.ABCD có đáy là hình vuông ABCD tâm O cạnh a. Biết SA vuông góc với đáy (ABCD),
tính độ dài cạnh SA theo a để góc giữa hai mặt phẳng (SBC) và (SCD) bằng
60
o
.
A. SA = a B. SA = 2a B. SA =
3
a
D. SA =
2 3
a
Câu 4. Cho hình chóp S.ABCD có đáy ABCD là hình vuông,
3
SA AB
, SA vuông góc với đáy. Tính cosin
của góc giữa hai mặt phẳng (SBC) và (SDC).
A.
1
4
B.
2
3
C.
4
D.
2
2
Câu 5. Cho khối chóp S.ABC có ABC là tam giác vuông cân tại A,
·
·
90
SBA SCA
o
, góc giữa hai mặt phẳng
(SAB) và (SAC) bằng
60
o
. Tính thể tích khối chóp S.ABC.
A.
3
a
B.
3
3
a
C.
3
2
a
D.
3
6
a
Câu 6. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B với BA = BC = 5a,
·
·
90
SAB SCB
o
.
Biết góc giữa hai mặt phẳng (SBC) và (SBA) bằng
9
: cos
16
. Thể tích khối chóp S.ABC bằng
A.
3
125 7
18
a
B.
3
125 7
9
a
C.
3
50
9
a
D.
3
50
3
a
Câu 7. Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), đáy ABC là tam giác vuông tại B có các
yếu tố
; 3
AB a BC a
. Tính góc giữa hai mặt phẳng (SAC) và (SBC) khi
2
2
a
SA .
A.
60
o
B.
30
o
C.
45
o
D.
75
o
Câu 8. Cho hình chóp S.ABC có ABCD là hình thoi tâm O, đường thẳng vuông góc với mặt phẳng (ABCD) và
6
;
3
a
AB SB a SO
. Tìm cosin của góc giữa hai mặt phẳng (SAB) và (SAD).
A. 0 B.
1
3
C.
1
7
D.
3
7
Câu 9. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AC = 2a, tam giác SAB và tam giác SCB
lần lượt vuông tại A và C. Khoảng cách từ C đến mặt phẳng (ABC) bằng a. Tính cosin của góc giữa hai mặt
phẳng (SAB) và (SCB).
A.
2
3
B.
2 2
3
C.
3
D.
1
3
Câu 10. Cho hình chóp S.ABCD có đáy ABCD là nửa lục giác đều nội tiếp đường tròn đường kính AB = 2a,
cạnh SA vuông góc với đáy và SA =
3
a
. Tính cosin của góc giữa hai mặt phẳng (SAD) và (SBC).
A.
2
2
B.
2
3
C.
2
4
D.
2
5
Câu 11. Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, SA vuông góc với đáy (ABCD). Gọi N là trung
điểm của SA, mặt phẳng (NCD) cắt khối chóp theo một thiết diện có diện tích là
2
2 3
S a
. Tính góc giữa hai
mặt phẳng (NCD) và (ABCD).
14
A.
60
o
B.
30
o
C.
45
o
D.
75
o
Câu 12. Cho lăng trụ đứng
.
ABC A B C
có đáy ABC là tam giác cân với AB = AC = a,
·
120
BAC
o
, cạnh bên
B B a
. Tính cosin góc giữa hai mặt phẳng (AB’I) và (ABC), trong đó I là trung điểm của C’C.
A.
30
10
B.
15
10
C.
2
3
D.
11
5
Câu 13. Cho lăng trụ đứng
.
ABCD A B C D
có đáy ABCD là hình vuông cạnh a và chiều cao
6
A A a
. Trên
C’C lấy điểm M, trên D’D lấy điểm N sao cho
2
C M MC
và
2
DN ND
. Tính cosin của góc giữa hai mặt
phẳng (B’MN) và (ABCD).
A.
1
21
B.
3
4
C.
2
2
D.
5
5
Câu 14. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, D, AB là đáy lớn và tam giác ABC cân
tại C với AC = a. Các mặt phẳng (SAB), (SAC) cùng vuông góc với mặt phẳng đáy, cạnh bên
3
SC a
và tạo
với mặt phẳng (SAB) một góc bằng
30
o
. Góc giữa hai mặt phẳng (SAB) và (SAC) bằng
A.
60
o
B.
30
o
C.
45
o
D.
75
o
Câu 15. Hình chóp S.ABCD có đáy là hình thoi có
·
120
BAD
o
, hình chiếu vuông góc của điểm H trên mặt
phẳng đáy trùng với trọng tâm của tam giác ABC, biết đường cao của khối chóp là
6
3
a
SH và tam giác SBD
vuông tại S. Tính cosin của góc giữa hai mặt phẳng (SAD), (SCD).
A. 0 B.
15
10
C.
2
3
D.
3
6
Câu 16. Hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = 2,
2 3
BC , cạnh bên SA vuông góc với
đáy (ABC) và
3
2
SA . Gọi M là trung điểm của AB, tính tan của góc giữa hai mặt phẳng (SMC), (ABC).
A.
4
13
B.
13
4
C. 1 D.
2
2
Câu 17. Cho lăng trụ đứng
.
ABC A B C
có đáy ABC là tam giác vuông, AB = BC = a, biết góc giữa hai mặt
phẳng (ACC’) và (AB’C’) bằng
60
o
. Khi đó sin của góc giữa hai mặt phẳng (AB’C’) và (A’B’C’) bằng
A.
4
13
B.
13
4
C. 1 D.
2
2
Câu 18. Cho hình chóp S.ABCD có đáy ABCD là hình vuông, cạnh bên SA = a và vuông góc với đáy (ABCD).
Góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng
. Tính cosin của góc giữa hai mặt phẳng (SBC),
(SCD) biết rằng
cot 2
.
A. 0,5 B.
1
3
C.
2
3
D.
1
6
______________________________________
15
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN LỚP 12 THPT
(LỚP BÀI TOÁN GÓC NHỊ DIỆN – P2)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho tứ diện ABCD có
· ·
·
90 ; ; 5; 135
DAB CBD AB a AC a ABC
o o
. Biết góc giữa hai mặt
phẳng (ABD) và (BCD) bằng
30
o
. Thể tích của tứ diện ABCD bằng
A.
3
2 3
a
B.
3
2
a
C.
3
3 2
a
D.
3
6
a
Câu 2. Cho hình chóp đều
S.ABCD
có cạnh đáy bằng
2
a
, cạnh bên bằng
2a. Gọi
là góc tạo bởi hai mặt
phẳng (SAC) và (SCD). Tính
cos
A.
21
2
B.
21
14
C.
21
3
D.
21
7
Câu 3. Cho hình chóp S.ABC có SA vuông góc với đáy, SA = 2BC và
·
120
BAC
o
. Hình chiếu vuông góc của
A lên các đoạn SB và SC lần lượt là M và N. Góc của hai mặt phẳng (ABC) và (AMN) bằng
A.
15
o
B.
30
o
C.
60
o
D.
45
o
Câu 4. Cho tứ diện
ABCD
có
ACD BCD
,
AC AD BC BD a
,
2
CD x
. Giá trị của
x
để hai mặt
phẳng
ABC
và
ABD
vuông góc với nhau là:
A.
2
3
a
. B.
3
3
a
. C.
3
2
a
. D.
5
3
a
.
Câu 5. Cho tứ diện ABCD có
2;
AC AD a BC BD a
. Khoảng cách từ điểm B đến mặt phẳng (ACD)
bằng
3
3
a
và thể tích tứ diện ABCD bằng
3
15
27
a
. Góc giữa hai mặt phẳng (ACD) và (BCD) bằng
A.
15
o
B.
30
o
C.
60
o
D.
45
o
Câu 6. Cho tứ diện
ABCD
có
ACD BCD
,
AC AD BC BD a
,
2
CD x
. Giá trị của
x
để hai mặt
phẳng
ABC
và
ABD
vuông góc với nhau là:
A.
2
3
a
. B.
3
3
a
. C.
3
2
a
. D.
5
3
a
.
Câu 7. Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác cân đỉnh A,
·
3; 30
BC a ABC
o
. Gọi M là
điểm thỏa mãn
2 3
CM CC
uuuur uuuur
. Tính sin của góc giữa hai mặt phẳng (ABC), (AB’M).
A.
66
22
B.
481
22
C.
22
D.
418
22
Câu 8. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB = a, AD = 2a. Biết rằng SA vuông góc với
(ABCD), SA = 2a. Tính tan của góc giữa hai mặt phẳng (SBD), (SBC).
A.
1
5
B.
3
2
C.
2
D.
5
Câu 9. Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a. Gọi M, N lần lượt là trung điểm của
SA, SB, G là trọng tâm tam giác SAC. Khi đó cosin của góc tạo bởi hai mặt phẳng (GMN) và (GAB) bằng
A.
6 2
11
B. 0,5 C.
2
D.
7
11
Câu 10. Cho hình chóp S.ABC có SC vuông góc với (ABC) và tam giác ABC vuông tại B. Biết
; 3
AB a AC a
và góc giữa hai mặt phẳng (SAB), (SAC) bằng
6
: cos
19
. Tính độ dài SC theo a.
A.
6
SC a
B.
2 6
SC a
C.
7
SC a
D.
6
SC a
Câu 11. Cho hình chóp S.ABC có (SAC) vuông góc với đáy, SA = AB = a, AC = 2a,
·
·
90
ASC ABC
o
. Tính
cosin của góc giữa hai mặt phẳng (SAB) và (SBC).
16
A.
105
35
B.
4 70
35
C.
70
35
D.
4 105
35
Câu 12. Cho hình chóp S.ABC có đường cao SA, tam giác ABC cân tại A và
·
; 120
AB a BAC
o
. Biết thể tích
khối chóp là
3
3
24
a
, góc giữa hai mặt phẳng (SBC) và (ABC) bằng
A.
60
o
B.
30
o
C.
45
o
D.
90
o
Câu 13. Cho hình chóp tứ giác đều S.ABCD. Mặt phẳng (P) chứa đường thẳng AC và vuông góc với mặt phẳng
(SCD) cắt đường thẳng SD tại E. Gọi V và V
1
lần lượt là thể tích khối chóp S.ABCD và D.ACE biết V = 5V
1
. Tính
cosin của góc tạo bởi mặt bên và mặt đáy của hình chóp S.ABCD.
A. 0,5 B.
3
2
C.
1
2 2
D.
2
3
Câu 14. Cho hình chóp S.ABCD đáy là hình thoi tâm O và SO vuông góc với (ABCD),
6
3
a
SO , SB = BC =
a. Số đó góc giữa hai mặt phẳng (SBC) và (SCD) là
A.
60
o
B.
30
o
C.
45
o
D.
90
o
Câu 15. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và SA = SB = SC = SD = a. Khi đó cosin của
góc giữa hai mặt phẳng (SAB) và (SAD) bằng
A. 0,25 B.
1
3
C.
2
D.
1
3
Câu 16. Cho hình chóp S.ABC có
·
·
2; ; 3; 90
AB a AC a BC a SBA SCA
o
và hai mặt phẳng (SAC),
(SAB) tạo với nhau một góc
1
: cos
3
. Tính thể tích của khối chóp S.ABC
A.
3
2
12
a
B.
3
2
2
a
C.
3
2
3
a
D.
3
2
6
a
Câu 17. Cho hình chóp S.ABCD có ABCD là hình vuông cạnh a, SA vuông góc với đáy (ABCD). Tính SA theo a
để góc giữa hai mặt phẳng (SBC), (SCD) bằng
60
o
.
A. SA = a B. SA = 2a C. SA = 3a D. SA = 1,5a
Câu 18. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật biết AB = 2a, AD = a, SA = 3a và SA vuông góc
với mặt phẳng đáy. Gọi M là trung điểm của CD, điểm E thuộc cạnh SA sao cho SE = 2a. Cosin của góc giữa
hai mặt phẳng (SAC) và (BME) là
A.
210
15
B.
30
30
C.
15
15
D.
870
30
Câu 19. Cho hình chóp
.
S ABC
có SA vuông góc với mặt đáy,
SA BC
và
·
120
BAC
. Hình chiếu vuông góc
của
A
lên các cạnh
SB
và
SC
lần lượt là
M
và
N
. Góc giữa hai mặt phẳng
ABC
và
AMN
bằng
A.
45
. B.
60
. C.
15
. D.
30
.
______________________________________
17
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN LỚP 12 THPT
(LỚP BÀI TOÁN GÓC NHỊ DIỆN – P3)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Hình lăng trụ đứng ABC.A’B’C’ có
·
; 120
AB AC a BAC
o
và có thể tích
3
3
4
a
. bằng Gọi M, N lần
lượt là trung điểm của B’C’ và CC’. Gọi
là góc giữa hai mặt phẳng (AMN), (ABC). Khi đó
A.
3
cos
2
B.
1
cos
2
C.
13
cos
4
D.
3
cos
4
Câu 2. Hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Số đo góc giữa hai mặt phẳng (A’BC) và (A’DC) bằng
A.
45
. B.
60
. C.
90
o
. D.
30
.
Câu 3. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SAB là tam giác đều và nằm trong
mặt phẳng vuông góc với mặt phẳng (ABCD). Gọi G là trọng tâm của tam giác SAB và M, N lần lượt là trung
điểm của SC, SD. Tính cosin của góc giữa hai mặt phẳng (GMN) và (ABCD).
A.
2 39
39
B.
13
13
C.
6
D.
2 39
13
Câu 4. Cho hình chóp đều S.ABCD có cạnh đáy bằng
2
a
, biết cạnh bên tạo với đáy bằng
60
o
. Tính tan của
góc tạo bởi hai mặt phẳng (SAC), (SCD).
A.
2 3
3
B.
3
2
C.
21
3
D.
21
7
Câu 5. Cho hình chóp S.ABC có đáy là tam giác vuông tại A với AB = a, AC = 2a. Mặt phẳng (SBC) vuông góc
với mặt phẳng (ABC). Mặt phẳng (SAB), (SAC) cùng tạo với mặt phẳng (ABC) một góc
60
o
. Tính tan của góc
tạo bởi hai mặt phẳng (SAB), (SBC).
A.
51
17
B.
51
3
C.
17
3
D.
3 17
17
Câu 6. Cho tứ diện ABCD có
3
;
2
a
AB a AC BC AD BD . Gọi M, N là trung điểm của AB, CD. Góc
giữa hai mặt phẳng (ABD), (ABC) là
. Tính
cos
biết mặt cầu đường kính MN tiếp xúc với cạnh AD.
A.
2 3
B.
2 3 3
C.
3 2 3
D.
2 1
Câu 7. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với
; 1,5 ; 3
AB a SA a AD a
, SA vuông
góc với đáy, M là trung điểm của cạnh SD. Tính tan của góc tạo bởi hai mặt phẳng (SAC), (MAC).
A. 1 B.
3
C.
2
D.
1
3
Câu 8. Cho hình lăng trụ đứng ABC.A’B’C’ có A’A = AB = AC = 1 và
·
120
BAC
o
. Gọi I là trung điểm cạnh C’C.
Tính cosin của góc tạo bởi hai mặt phẳng (ABC), (AB’I).
A.
370
20
B.
70
10
C.
30
20
D.
30
10
Câu 9. Cho lăng trụ đều ABC.A’B’C’ có tất cả các cạnh đều bằng 2a. Gọi M, N lần lượt là trung điểm cạnh A’B’,
BB’. Tính cosin của góc hợp bởi hai mặt phẳng (MC’N), (ACC’A’).
A.
2
4
B.
6
4
C.
3
4
D. 0,75
Câu 10. Cho hình chóp S.ABCD có ABCD là hình chữ nhật có AB = a, AD = 2a. Biết SA vuông góc với mặt
phẳng (ABCD), SA = 2a. Tính tan của góc giữa hai mặt phẳng (SBD), (SBC).
A.
1
5
B.
2
3
C.
2
D.
5
Câu 11. Tứ diện ABCD có BC = 3, CD = 4,
·
·
·
90
ABC BCD ADC
o
, góc giữa hai đường thẳng AD, BC
bằng
60
o
. Cosin của góc giữa hai mặt phẳng (ABC), (ACD) bằng
A.
3
43
B.
4
43
C.
1
43
D.
2
43
18
Câu 12. Cho khối lăng trụ đứng ABCD.A’B’C’D’ có đáy là hình vuông cạnh a, cạnh bên
6
2
a
A A
. Góc giữa
hai mặt phẳng (A’BD), (C’BD) bằng
A.
90
o
B.
60
o
C.
45
o
D.
30
o
Câu 13. Cho hình lập phương ABCD.A’B’C’D’ có tâm O, gọi I là tâm của hình vuông ABCD và M là điểm thuộc
OI sao cho
1
2
MO MI
. Khi đó cosin của góc tạo bởi hai mặt phẳng (MC’D’) và (MAB) bằng
A.
7
85
B.
6 13
65
C.
6
85
D.
17 3
65
Câu 14. Cho hình chóp S.ABCD có đáy ABCD là hình vuông, mặt bên SAB là tam giác vuông tại S và nằm trong
mặt phẳng vuông góc với đáy,
·
60
SBA
o
. Tính
2
cos
với
là góc giữa hai mặt phẳng (SBC), (SDC).
A.
15
19
B.
16
19
C.
4
19
D.
15
76
Câu 15. Cho lăng trụ ABC.A’B’C’ có A’.ABC là hình chóp tam giác đều,
7
;
12
AB a A A a
. Tính góc giữa
hai mặt phẳng (ABB’A’), (ABC).
A.
75
o
B.
60
o
C.
45
o
D.
30
o
Câu 16. Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, SA vuông góc với (ABC),
3
SA a
. Cosin của
góc giữa hai mặt phẳng (SAB), (SBC) là
A.
1
5
B.
2
5
C.
2
D. 0,5
Câu 17. Lăng trụ ABC.A’B’C’ có đáy ABC là tam giác vuông cân cạnh huyền
2 2
AB ,
A A A B A C
và
khoảng cách giữa hai mặt phẳng đáy bằng
3
a
. Tính góc giữa hai mặt phẳng (B’BC) và (ABC).
A.
75
o
B.
60
o
C.
45
o
D.
30
o
Câu 18. Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = BC = a, góc giữa đường thẳng AC’ và mặt phẳng
(BCC’B’) bằng
30
o
. Tính cosin của góc giữa hai mặt phẳng (ABC’) và (AB’C’).
A.
1
3
B.
2 2
3
C.
2
2
D.
1
6
Câu 19. Hình chóp S.ABC có ABC là tam giác đều cạnh a,
3
SA a
và SA vuông góc với (ABC). Tính số đo
gần đúng của góc nhị diện (SAB), (SBC).
A. 63 độ B. 65 độ C. 70 độ D. 72 độ
Câu 20. Cho hình chóp S.ABCD có SA vuông góc với (ABCD), ABCD là hình thang vuông tại A, D, AB = 2CD,
AD = CD = a, SA = x. Tìm x để số đo góc giữa hai mặt phẳng (SAB), (SBC) bằng
60
o
.
A. x = 0,5a B. x = a c.
3
x a
D.
2
x a
______________________________________
19
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN LỚP 12 THPT
(LỚP BÀI TOÁN GÓC NHỊ DIỆN – P4)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho hình chóp tứ giác đều
.
S ABCD
, cạnh bên bằng cạnh đáy và bằng
a
. Gọi
M
là trung điểm của
SC
. Tính góc giữa hai mặt phẳng
MBD
và
ABCD
.
A.
90
. B.
30
. C.
60
. D.
45
.
Câu 2. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình thang vuông tại
A
và
B
,
SA
vuông góc với mặt phẳng
ABCD
,
, 2
AB BC a AD a
. Biết góc giữa
SC
và mặt phẳng
ABCD
bằng
45
. Tính góc giữa mặt
phẳng
SAD
và
SCD
.
A.
90
. B.
30
. C.
60
. D.
45
.
Câu 3. Hình chóp đều
.
S ABCD
có
ABCD
là hình vuông cạnh
a
, tâm
O
. Góc giữa
SB
và mặt phẳng
( )
SAC
bằng
0
60
. Gọi
M
là trung điểm của
SB
. Tính
sin
của góc giữa mặt phẳng
( )
AMO
và mặt phẳng
( )
SAB
.
A.
1
5
. B.
1
2 5
. C.
2
5
D.
3
2 5
.
Câu 4. Cho hình chóp
SABCD
có đáy
ABCD
là hình thang vuông tại
A
và
B
với
AB BC a
,
2
AD a
,
SA ABCD
,
2
SA a
. Tính góc giữa hai mặt phẳng
SCD
và
SAB
.
A.
30
. B.
45
. C.
90
. D.
60
.
Câu 5. Cho hai tam giác đều
DAC
và
BAC
lần lượt nằm trong hai mặt phẳng vuông góc với nhau. Gọi
là
góc giữa hai mặt phẳng
DAB
và
DBC
. Tính giá trị
cos
.
A.
3
5
. B.
5
. C.
1
5
. D.
3
5
.
Câu 6. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA ABCD
. Góc giữa
SB
và mặt
phẳng
SAD
là
30
. Gọi các điểm
,
E F
lần lượt đối xứng với
,
B C
qua
,
A D
. Tính
sin
góc giữa hai mặt
phẳng
SCF
và
SEF
.
A.
15
4
. B.
21
7
. C.
21
3
. D.
15
5
.
Câu 7. Cho hình chóp
.
S ABCD
có đáy là hình chữ nhật,
2 ,
AB a
2 3
AD a
. Mặt bên
SAB
là tam giác đều
và nằm trong mặt phẳng vuông góc với đáy. Gọi
là góc giữa hai mặt phẳng
SAD
và
SCD
. Tính
sin
.
A.
2
5
. B.
5
2
. C.
2 5
5
. D.
42
7
.
Câu 8. Trong mặt phẳng
P
, cho tam giác đều
ABC
cạnh
a
. Trên các đường thẳng vuông góc với
P
tại
B
và
C
, lấy về cùng phía với mp
P
các điểm
D
,
E
sao cho
3
3
a
BD
,
3
CE a
. Gọi
là góc giữa hai
mặt phẳng
P
và
ADE
. Tính
cos
.
A.
37
cos
37
. B.
2 259
cos
37
. C.
14 7
cos
3
. D.
3 37
cos
37
.
Câu 9. Cho hình lăng trụ đều .
ABC A B C
có cạnh đáy bằng
a
, cạnh bên bằng
3
2
a
. Góc giữa hai mặt phẳng
AB C
và
A BC
bằng
A.
60
. B.
90
. C.
45
. D.
30
.
Câu 10. Cho hình lăng trụ đứng
.
ABCD A B C D
có đáy
ABCD
là hình thoi,
AB a
,
3
2
a
AA
,
·
60
BAD
.
Góc giữa hai mặt phẳng
ABCD
và
A D BC
bằng
A.
60
. B.
90
. C.
45
. D.
30
.
Câu 11. Lăng trụ đều
.ABC
B
A
C
có cạnh đáy bằng
2
.
a
Gọi
,
M
N
lần lượt là trung điểm của
,
AB
.
BC
20
Khoảng cách từ điểm
A
đến mặt phẳng
A MN
bằng
.
2
2
a
Tính côsin của góc giữa
A AB
và
A MN
.
A.
1
.
2
B.
6
.
2
C.
6
.
6
D.
6
.
3
Câu 12. Cho hình lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác cân với
AB AC a
và
·
120
BAC
,
cạnh bên
BB a
. Gọi
I
là trung điểm
CC
. Tính cosin góc tọa bởi hai mặt phẳng
ABC
và
AB I
.
A.
3
21
. B.
30
10
. C.
21
10
. D.
3
3
.
Câu 13. Cho hình hộp
ABCD.A B C D
có đáy
ABCD
là hình vuông cạnh bằng
2a
, cạnh bên bằng
a 5
. Hình
chiếu vuông góc của
A
trên mặt phẳng
ABCD
là trùng với giao điểm của hai đường chéo
AC
và
BD
. Góc
giữa mặt phẳng
ABB A
và mặt đáy của hình hộp bằng
A.
0
30
. B.
0
60
. C.
0
45
. D.
0
75
.
Câu 14. Cho hình hộp chữ nhật
.
ABCD A B C D
có
2
AB a
,
3
AD a
,
4
AA a
. Gọi
là góc giữa hai mặt
phẳng
AB D
và
A C D
. Giá trị của
cos
bằng.
A.
29
61
. B.
27
34
. C.
2
2
. D.
3
2
.
Câu 15. Cho hình lăng trụ
.
ABC A B C
có đáy là tam giác đều, cạnh bên
2
AA a
. Hình chiếu vuông góc của
A
lên mặt phẳng
ABC
trùng với trung điểm của đoạn
BG
(với
G
là trọng tâm tam giác
ABC
). Biết khoảng
cách giữa
AB
và
A I
bằng
3
12
a
. Tính cosin của góc
giữa hai mặt phẳng
ABC
và
ABB A
.
A.
1
cos
95
. B.
1
cos
165
. C.
1
cos
134
. D.
1
cos
126
.
Câu 16. Cho hình lăng trụ
. ' ' ' '
ABCD A B C D
cạnh bên
2
a
và hình chiếu
'
A
lên mặt đáy là điểm
I
sao cho
3
BI ID
uur uur
; đáy là hình chữ nhật
ABCD
có tâm
O
và
, 3
AB a AD a
. Tính cosin của góc
giữa hai mặt
phẳng
ABCD
và
' '
CDD C
.
A.
1
cos
3
. B.
165
cos
55
. C.
2 165
cos
55
. D.
1
cos
6
.
Câu 17. Cho hình lập phương
.
ABCD A B C D
có cạnh
a
. Số đo góc giữa hai mặt
BA C
và
DA C
bằng?
A.
30
. B.
45
. C.
90
. D.
60
.
Câu 18. Cho hình chóp .
S ABC
có đáy
ABC
là tam giác vuông cân tại
B
,
SA a
và
SA ABC
,
AB BC a
. Góc giữa hai mặt phẳng
SAC
và
SBC
bằng?
A.
45
. B.
30
. C.
60
. D.
90
.
Câu 19. Tính
sin
với
là góc giữa hai mặt phẳng
AB D
và
BA C
của hình lập phương
.
ABCD A B C D
cạnh a.
A.
2 2
sin
3
. B.
3
sin
2
. C.
3
sin
3
. D.
2
sin
3
.
Câu 20. Cho hình chóp
.
S ABC
, đáy
ABC
là tam giác vuông cân tại
B
,
BA BC a
,
M
là trung điểm của
AC
. Gọi
N
là hình chiếu của
S
trên
ABC
sao cho
3
BM MN
uuuur uuuur
và
SB a
. Tính giá trị lượng giác
sin
của
góc giữa hai mặt phẳng
SBN
và
SBC
?
A.
5
10
B.
3 5
10
. C.
10
10
. D.
3 10
10
.
Câu 21. Cho hình chóp
.
S ABCD
với
ABCD
là hình thang vuông tại
A
và
D
có
2
AD CD a
,
4
AB a
và
2 5
SB a
. Gọi
M
là trung điểm của
CD
. Biết hình chiếu
H
của đỉnh
S
xuống
( )
ABCD
nằm trên
AD
và
BC
vuông góc với
SM
, tính sin của góc giữa 2 mặt phẳng
( )
SHB
và
( )
SBC
.
A
238
17
. B.
51
17
. C.
85
17
. D.
2 51
17
.
21
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN LỚP 12 THPT
(LỚP BÀI TOÁN GÓC NHỊ DIỆN – P5)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Lăng trụ tam giác đều
.
ABC A B C
có
2 3
AB và
2.
AA
Gọi
, ,
M N P
lần lượt là trung điểm các
cạnh
,
A B A C
và
BC
(tham khảo hình vẽ bên). Côsin của góc tạo bởi hai mặt phẳng
AB C
và
MNP
là
P
N
M
C'
B'
A'
C
B
A
A.
17 13
65
B.
18 13
65
C.
6 13
65
D.
13
65
Câu 2. Cho hình lập phương
.
ABCD A B C D
có tâm
O
. Gọi
I
là tâm của hình vuông
A B C D
và
M
là điểm
thuộc đoạn thẳng
OI
sao cho
2
MO MI
(tham khảo hình vẽ). Khi đó côsin của góc tạo bởi hai mặt phẳng
( )
MC D
và
( )
MAB
bằng
A.
7 85
85
B.
17 13
65
C.
6 13
65
D.
6 85
85
Câu 3. Cho hình chóp .
S ABC
có
SA
vuông góc với mặt phẳng
3
,
2
a
ABC SA
, tam giác
ABC
đều cạnh
bằng
a
(minh họa như hình dưới). Góc tạo bởi giữa mặt phẳng
SBC
và
ABC
bằng
A.
0
90
. B.
0
30
. C.
0
45
. D.
0
60
.
Câu 4. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật,
AB a
,
2
AD SA a
,
SA ABCD
. Tính
tang của góc giữa hai mặt phẳng
SBD
và
( )
ABCD
.
A.
5
2
. B.
5
. C.
1
5
. D.
2
5
.
Câu 5. Cho hình chóp
SABCD
có đáy
ABCD
là hình thoi tâm
O
, đường thẳng
SO
vuông góc với mặt phẳng
ABCD
. Biết
AB SB a
,
6
3
a
SO
. Tìm số đo của góc giữa hai mặt phẳng
SAB
và
.
SAD
A.
30
B.
45
C.
60
D.
90
Câu 6. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông có độ dài đường chéo bằng
2
a
và
SA
vuông
góc với mặt phẳng
ABCD
. Gọi
là góc giữa hai mặt phẳng
SBD
và
ABCD
. Nếu
tan 2
thì góc
giữa
SAC
và
SBC
bằng.
A.
0
30
. B.
0
90
C.
0
60
. D.
0
45
.
Câu 7. Cho hình hộp chữ nhật
. ' ' ' '
ABCD A B C D
có mặt
ABCD
là hình vuông,
6
'
2
AB
AA
. Xác định góc
giữa hai mặt phẳng
'
A BD
và
'
C BD
.
A.
0
30
. B.
0
45
. C.
0
60
. D.
0
90
.
Câu 8. Cho hình lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác cân, với
AB AC a
và góc
·
120
BAC
,
cạnh bên
AA a
. Gọi
I
là trung điểm của
CC
. Cosin của góc tạo bởi hai mặt phẳng
ABC
và
AB I
bằng
22
A.
11
11
. B.
33
11
. C.
10
10
. D.
30
10
.
Câu 9. Cho hình chóp
.
S ABC
có
SA a
,
SA ABC
, tam giác
ABC
vuông cân đỉnh
A
và
2
BC a
. Gọi
M
,
N
lần lượt là trung điểm của
SB
,
SC
. Côsin của góc tạo bởi hai mặt phẳng
MNA
và
ABC
bằng
A.
2
4
. B.
2
6
. C.
3
2
. D.
3
3
.
Câu 10. Cho hình chóp
.
S ABCD
có
ABCD
là hình thoi cạnh bằng
a
và góc
A
bằng
60
, cạnh
SC
vuông góc
với đáy và
6
2
a
SC
. Giá trị lượng giác cô-sin của góc giữa hai mặt phẳng
SBD
và
SCD
bằng
A.
6
6
. B.
5
5
. C.
2 5
5
. D.
30
6
.
Câu 11. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình thoi cạnh
a
,
BD a
. Cạnh
SA
vuông góc với mặt đáy
và
6
2
a
SA . Tính góc giữa hai mặt phẳng
SBC
và
SCD
.
A.
60
. B.
120
. C.
45
. D.
90
.
Câu 12. Cho hình chóp .
S ABC
có đáy
ABC
là tam giác vuông cân tại
B
,
2
AC a
, tam giác
SAB
và tam giác
SCB
lần lượt vuông tại
A
,
C
. Khoảng cách từ
S
đến mặt phẳng
ABC
bằng
2
a
. Côsin của góc giữa hai
mặt phẳng
SAB
và
SCB
bằng
A.
1
2
. B.
1
3
. C.
1
2
. D.
1
3
.
Câu 13. Cho hình lăng trụ đứng
.
ABC A B C
có
AB AC a
, góc
·
120
BAC
,
AA a
. Gọi
M
,
N
lần lượt
là trung điểm của
B C
và
CC
. Số đo góc giữa mặt phẳng
AMN
và mặt phẳng
ABC
bằng
A.
60
. B.
30
. C.
3
arcsin
4
. D.
3
arccos
4
.
Câu 14. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
, cạnh bên
2
SA a
và vuông góc với
mặt phẳng đáy. Gọi
M
là trung điểm cạnh
SD
. Tang của góc tạo bởi hai mặt phẳng
AMC
và
SBC
bằng
A.
5
5
.
B.
3
2
. C.
2 5
5
. D.
2 3
3
.
Câu 15. Tứ diện
ABCD
có
AC AD BC BD a
,
2
CD x
,
ACD BCD
. Tìm
x
để
ABC ABD
?
D
C
B
A
A.
x a
. B.
2
2
a
x
. C.
2
x a
. D.
3
3
a
x
.
Câu 17. Cho hình lăng trụ đứng .
ABC A B C
có
1
AA AB AC
và
·
0
120
BAC
. Gọi
I
là trung điểm cạnh
CC
. Côsin góc giữa hai mặt phẳng
ABC
và
AB I
bằng
A.
370
20
. B.
70
10
. C.
30
20
. D.
30
10
.
Câu 18. Cho hình chóp
.
S ABCD
có đáy là hình thoi cạnh
·
0
, 120 ,
a ABC SA
vuông góc với mặt phẳng
.
ABCD
Biết góc giữa hai mặt phẳng
SBC
và
SCD
bằng
0
60 ,
khi đó
A.
6
.
4
a
SA
B.
6.
SA a
C.
6
2
a
SA
. D.
3
2
a
SA
.
23
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN CỔ ĐIỂN LỚP 11 – 12 THPT
(LỚP BÀI TOÁN KHOẢNG CÁCH ĐIỂM ĐẾN MẶT PHẲNG – P1)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho khối tứ diện
ABCD
có thể tích
3
32cm
V ;
BCD
vuông cân có cạnh huyền
4 2cm
CD
. Khoảng
cách từ
A
đến
BCD
bằng:
A.
8cm
. B.
4cm
. C.
9cm
. D.
12cm
.
Câu 2. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình bình hành tâm
O
. Thể tích khối chóp bằng
3
4
a
. Tính
khoảng cách từ tâm
O
đến mặt bên (SBC) của hình chóp biết rằng tam giác
SBC
cân tại S và
·
0
, 45
SB a BSC
.
A.
6 2
a
. B.
6
a
. C.
3 2
a
. D.
3
a
.
Câu 3. Cho lăng trụ đứng
. ' ' '
ABC A B C
có
·
0
1, 2, ' 3, 120
AB AC AA BAC . Gọi
,
M N
lần lượt là các điểm
trên cạnh
', '
BB CC
sao cho
3 ' , 2 '
BM B M CN C N
. Tính khoảng cách từ
M
đến mặt phẳng
( ' )
A BN
?
A.
9 138
.
184
B.
3 138
.
46
C.
9 3
.
16 46
D.
9 138
.
46
Câu 4. Cho hình chóp
S.ABCD
có đáy
ABCD
là hình thang vuông tại
A
và
D
. Độ dài
AB AD 2
a
,
CD
a
; góc giữa hai mặt phẳng
SBC
và
ABCD
bằng 60
0
. Gọi
I
là trung điểm
AD
, hai mặt phẳng
SBI
và
SCI
cùng vuông góc với mặt phẳng
ABCD
. Tính khoảng cách từ điểm
A
đến mặt phẳng
SBC
.
A.
15
5
a
. B.
3 15
10
a
. C.
15
10
a
. D.
2 15
5
a
.
Câu 5. Cho hình chóp .
S ABC
. Tam giác
ABC
vuông tại
A
,
1cm
AB
,
3cm
AC
. Tam giác
SAB
,
SAC
lần
lượt vuông góc tại
B
và
C
. Khối cầu ngoại tiếp hình chóp .
S ABC
có thể tích bằng
3
5 5
cm
6
. Tính
khoảng cách từ
C
tới
SAB
A.
5
cm
2
. B.
5
cm
4
. C.
3
cm
2
. D.
1cm
.
Câu 6. Cho hình chóp .
S ABC
có tam giác
ABC
vuông tại
A
góc
·
0
30
ABC
, tam giác
SBC
là tam giác đều
cạnh
a
và mặt phẳng
( )
SAB
vuông góc với mặt phẳng
( )
ABC
. Khoảng cách từ
A
đến mặt phẳng
( )
SBC
bằng
A.
6
5
a
. B.
6
3
a
. C.
3
5
a
. D.
6
6
a
.
Câu 7. Cho hình chóp S.ABC có mặt bên (SAB) vuông góc với mặt đáy và tam giác SAB đều cạnh 2a. Biết tam
giác ABC vuông tại C và cạnh
3
AC a
. Tính khoảng cách từ C đến (SAB).
A.
3
.
2
a
B.
3
.
4
a
C.
3.
a
D.
3
.
3
a
Câu 8. Cho hình chóp .
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA ABCD
. Tính khoảng cách từ
điểm
B
đến
mp
SAC
.
A.
2
a
. B.
2
2
a
. C.
2
3
a
. D.
2
4
a
.
Câu 9. Cho hình chóp S.ABCD có đáy là hình chữ nhật với diện tích đáy bằng
2
6
a
, hình chiếu của đỉnh S trên
mặt phẳng đáy trùng với điểm H thuộc cạnh AD với
2
AH DH
. Biết
SH a
và diện tích tam giác SAD bằng
2
a
. Tính theo a khoảng cách từ trung điểm M của đoạn SB đến mp (SAD).
A.
2 .
a
B.
.
a
C.
3
.
4
a
D.
3
.
2
a
Câu 10. Cho hình chóp .
S ABC
có tam giác
ABC
là tam giác vuông tại
A
,
3
AC a
,
·
30
ABC
. Góc giữa
SC
và mặt phẳng
ABC
bằng
0
60
. Cạnh bên
SA
vuông góc với đáy. Khoảng cách từ
A
đến
SBC
là
24
A.
6
35
a
. B.
3
35
a
. C.
2 3
35
a
. D.
3
5
a
.
Câu 11. Cho hình chóp .
S MNPQ
có đáy là hình chữ nhật với
3 2
PQ a
,
SM
vuông góc với mặt phẳng đáy,
3
SM a
. Khoảng cách từ điểm
M
đến mặt phẳng
SNP
bằng
A.
3
a
. B.
2 6
a
. C.
2 3
a
. D.
6
a
.
Câu 12. Hình chóp .
S ABCD
có đáy
ABCD
là hình chữ nhật,
2 , .
AB a AD a
Hình chiếu của
S
lên mặt
phẳng
ABCD
là trung điểm H của
,
AB SC
tạo với đáy góc
0
45 .
Khoảng cách từ
H
đến mặt phẳng
SCD
là:
A.
6
.
3
a
B.
6
.
6
a
C.
6
.
4
a
D.
3
.
3
a
Câu 13. Cho hình chóp
.
S ABCD
có đường cao
2
SA a
, đáy
ABCD
là hình thang vuông ở
A
và
D
,
2 ,
AB a AD CD a
. Khoảng cách từ điểm
A
đến mặt phẳng
SBC
bằng
A.
2
.
3
a
B.
2
.
2
a
C.
2
.
3
a
D.
2.
a
Câu 14. Cho hình chóp tứ giác .
S ABCD
có đáy
ABCD
là hình bình hành tâm
;
O
mặt phẳng
SAC
vuông
góc với mặt phẳng
SBD
. Biết khoảng cách từ
O
đến các mặt phẳng
, ,
SAB SBC SCD
lần lượt là
1; 2; 5
. Tính khoảng cách
d
từ
O
đến mặt phẳng
SAD
.
A.
19
20
d
. B.
20
19
d
. C.
2
d
. D.
2
2
d
.
Câu 15. Cho hình chóp
.
S ABCD
có đáy là hình chữ nhật, cạnh
2 2 .
AB AD a
Tam giác
SAB
đều và nằm
trong mặt phẳng vuông góc với đáy
ABCD
Tính khoảng cách từ điểm
A
đến mặt phẳng
SBD
.
A.
3
4
a
. B.
3
2
a
. C.
2
a
. D.
a
.
Câu 16. Cho hình chóp .
S ABC
có
SA
vuông góc với mặt phẳng đáy. Biết góc
·
o
30
BAC ,
SA a
và
BA BC a
. Gọi
D
là điểm đối xứng với
B
qua
AC
. Khoảng cách từ
B
đến mặt phẳng
SCD
bằng
A.
21
7
a
. B.
2
2
a
. C.
2 21
7
a
. D.
21
14
a
.
25
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN CỔ ĐIỂN LỚP 11 – 12 THPT
(LỚP BÀI TOÁN KHOẢNG CÁCH ĐIỂM ĐẾN MẶT PHẲNG – P2)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho hình chóp
.
S ABCD
đáy là hình vuông
ABCD
cạnh
a
, cạnh bên
SA
vuông góc với mặt phẳng
( )
ABCD
và
2
SD a
. Tính khoảng cách từ
S
đến mặt phẳng
( ).
ABCD
A.
5.
a
B.
.
2
a
C.
3 .
a
D.
3.
a
Câu 2. Cho hình chóp tứ giác đều .
S ABCD
có các cạnh đáy đều bằng
a
và các cạnh bên đều bằng
2
a
. Tính
khoảng cách từ
S
đến mặt phẳng
( ).
ABCD
A.
14
2
a
. B.
14
4
a
. C.
2
a
. D.
7
2
a
.
Câu 3. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông tâm
O
,
SA ABCD
. Gọi
I
là trung điểm của
SC
. Khoảng cách từ
I
đến mặt phẳng
ABCD
bằng độ dài đoạn thẳng nào?
A.
IB
. B.
IC
. C.
IA
. D.
IO
.
Câu 4. Cho hình chóp
.
S ABCD
đáy là hình vuông
ABCD
cạnh
a
, cạnh bên
SA
vuông góc với mặt phẳng
( )
ABCD
và
2
SD a
. Tính khoảng cách từ
S
đến mặt phẳng
( ).
ABCD
A.
5.
a
B.
.
2
a
C.
3 .
a
D.
3.
a
Câu 5. Cho hình chóp
.
S ABC
có
ABC
là tam giác vuông tại
B
,
SA ABC
. Khoảng cách từ điểm
A
đến
mặt phẳng
SBC
là
A. Độ dài đoạn
AC
. C. Độ dài đoạn
AH
trong đó
H
là hình chiếu vuông góc của
A
trên
SB
.
B. Độ dài đoạn
AB
. D. Độ dài đoạn
AM
trong đó
M
là trung điểm của
SC
.
Câu 6. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
và
SA
vuông góc với mặt đáy. Biết
10
SB a
. Gọi
I
là trung điểm của
SC
. Khoảng cách từ điểm
I
đến mặt phẳng
ABCD
bằng
A.
3
a
. B.
3
2
a
. C.
10
2
a
. D.
2
a
.
Câu 7. Cho hình chóp
SABC
có đáy là tam giác vuông tại
A
,
AB a
,
3
AC a
,
SA
vuông góc với mặt
phẳng đáy và
2
SA a
. Khoảng cách từ điểm
đến mặt phẳng
SBC
bằng
A.
57
19
a
. B.
2 57
19
a
. C.
2 3
19
a
. D.
2 38
19
a
.
Câu 8. Cho hình chóp
.
S ABC
, tam giác
ABC
vuông cân tại
A
,
( )
SA ABC
,
2
SA a
,
2
AB a
. Tính khoảng cách
từ
A
tới mặt phẳng
( )
SBC
.
A.
3
7
a
. B.
2
5
a
. C.
5
a
. D.
2 3
7
a
.
Câu 9. Cho hình chóp
.
S ABC
có
SA ABC
,
2
SA AB a
, tam giác
ABC
vuông tại
B
(tham khảo hình
vẽ). Khoảng cách từ
A
đến mặt phẳng
SBC
bằng
A.
3
a
. B.
a
. C.
2
a
. D.
2
a
.
Câu 10. Cho hình chóp .
S ABC
có đáy
ABC
là tam giác vuông tại
B
,
AB a
,
2
BC a
, đường thẳng
SA
vuông góc với mặt phẳng đáy và góc giữa đường thẳng
SC
và mặt phẳng đáy bằng
0
30
. Gọi
h
là khoảng cách
từ điểm
S
đến mặt phẳng
ABC
. Mệnh đề nào dưới đây là đúng?
A.
2
a
h
. B.
3
h a
. C.
3
h a
. D.
h a
.
Câu 11. Cho hình chóp tứ giác đều .
S ABCD
có cạnh đáy bằng
a
và chiều cao bằng
2.
a
Tính khoảng cách
d
từ tâm
O
của đáy
ABCD
đến một mặt bên theo
.
a
A.
5
.
2
a
d
B.
3
.
2
a
d
C.
2 5
.
3
a
d
D.
2
.
3
a
d
26
Câu 12. Cho hình chóp
.
S ABCD
có đáy là hình vuông cạnh
a
,
SA
vuông góc với mặt phẳng
ABCD
và
SA a
. Khoảng cách từ điểm
A
đến mặt phẳng
SBC
bằng:
A.
2
a
. B.
2
a
. C.
2
2
a
. D.
3
2
a
.
Câu 13. Cho tứ diện
.
O ABC
có
, ,
OA OB OC
đôi một vuông góc với nhau
3.
OA OB OC
Khoảng cách từ
O
đến
( )
mp ABC
là.
A.
1
3
. B.
1
. C.
1
2
. D.
1
3
.
Câu 14. Cho hình chóp
.
S ABC
có đáy là tam giác vuông cân tại
B
,
2 2
SA AC a
và
SA
vuông góc với đáy.
Khoảng cách từ
A
đến mặt phẳng
SBC
là
A.
2 6
3
a
. B.
4 3
3
a
. C.
6
3
a
. D.
3
3
a
.
Câu 15. Cho hình chóp .
S ABC
có đáy là tam giác vuông tại
A
,
AB a
,
3
AC a
,
SA
vuông góc với mặt
phẳng đáy và
2
SA a
. Khoảng cách từ điểm
đến mặt phẳng
SBC
bằng
A.
57
19
a
. B.
2 57
19
a
. C.
2 3
19
a
. D.
2 38
19
a
.
Câu 16. Cho tứ diện đều
ABCD
có cạnh bằng
a
. Khoảng cách từ
A
đến mặt phẳng
BCD
bằng:
A.
3
4
a
. B.
3
3
a
. C.
6
3
a
. D.
6
2
a
.
Câu 17. Cho hình chóp tứ giác đều .
S ABCD
có đáy
ABCD
là hình vuông cạnh
2
a
, tâm
O
,
SO a
(tham
khảo hình vẽ bên). Khoảng cách từ
O
đến mặt phẳng
SCD
bằng
A.
5
5
a
. B.
2
2
a
. C.
3
a
. D.
6
3
a
.
Câu 18. Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông tại
B
và cạnh bên
SB
vuông góc với mặt phẳng
đáy. Biết
3 , 4 , 2
SB a AB a BC a
. Khoảng cách từ
B
đến mặt phẳng
( )
SAC
bằng
A.
12 61
61
a
. B.
3 14
14
a
. C.
4
5
a
. D.
12 29
29
a
.
Câu 19. Cho hình chóp
.
S ABCD
có đáy
ABC
là tam giác vuông tại
A
.
·
30
ABC
, tam giác
SBC
là tam giác
đều cạnh
a
và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính khoảng cách
h
từ điểm
C
đến mặt
phẳng
SAB
.
A.
2 39
13
a
h
. B.
39
52
a
h
. C.
39
13
a
h
. D.
39
26
a
27
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN CỔ ĐIỂN LỚP 11 – 12 THPT
(LỚP BÀI TOÁN KHOẢNG CÁCH ĐIỂM ĐẾN MẶT PHẲNG – P3)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho tứ diện đều
.
S ABCD
có tất cả các cạnh đều bằng
2
a
, gọi
M
là điểm thuộc cạnh AD sao
cho
2
DM MA
. Tính khoảng cách từ
M
đến mặt phẳng
BCD
.
A.
2 6
9
a
. B.
6
a
. C.
4 6
9
a
. D.
2 6
3
a
.
Câu 2. Cho hình chóp tam giác đều
.
S ABC
có tất cả các cạnh đều bằng
a
, gọi
G
là trọng tâm
ABC
. Khoảng
cách từ
G
đến mặt phẳng
ABC
bằng
A.
3
6
a
. B.
6
6
a
. C.
6
9
a
. D.
6
12
a
.
Câu 3. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
và
SA
vuông góc với mặt đáy. Biết
10
SB a
. Gọi
I
là trung điểm của
SD
. Khoảng cách từ điểm
I
đến mặt phẳng
ABCD
bằng
A.
3
a
. B.
3
2
a
. C.
10
2
a
. D.
2
a
.
Câu 4. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông tâm
O
cạnh bằng
4
a
; Hình chiếu vuông góc của
S
trên mặt đáy trùng với trung điểm
H
của
OA
; góc giữa
SCD
và đáy là
45
. Tính khoảng cách từ điểm
B
đến mặt phẳng
SCD
.
A.
2 2
a
. B.
2
a
. C.
2
2
a
. D.
2
4
a
.
Câu 5. Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
2
a
, cạnh bên
SA
vuông góc với mặt đáy,
3
SA a
; gọi
M
là trung điểm của
AC
. Tính khoảng cách từ
M
đến mặt phẳng
SBC
.
A.
3
,
3
a
d M SBC
. B.
6
,
2
a
d M SBC
.
C.
6
,
4
a
d M SBC
. D.
3
,
2
a
d M SBC
.
Câu 6. Cho hình chóp tứ giác đều
.
S ABCD
có đáy là hình vuông cạnh
a
. Gọi
M
là trung điểm của
SD
.
Khoảng cách từ
M
đến mặt phẳng
SAC
bằng
A.
2
2
a
. B.
2
4
a
. C.
2
a
. D.
4
a
.
Câu 7. Cho hình chóp .
S ABCD
có đáy
ABCD
là hình vuông cạnh bằng 1. Hai mặt phẳng
SAB
và
SAC
cùng vuông góc với mặt phẳng đáy,
1
SA
. Gọi
M
là trung điểm
SD
. Khoảng cách từ
M
đến mặt phẳng
SBC
bằng
A.
1
. B.
2
4
. C.
1
2
. D.
2
2
.
Câu 8. Hình chóp .
S ABCD
có đáy là hình thoi tâm
O
cạnh
2
a
,
·
60
ABC
, hình chiếu vuông góc của
S
lên
ABCD
trùng với trung điểm
I
của
BO
,
3
SI a
. Khoảng cách từ
B
đến mặt phẳng
SCD
bằng
A.
3 3
5
a
. B.
2 3
5
a
. C.
3
5
a
. D.
4 3
5
a
.
Câu 9. Cho hình chóp S.ABC có SA vuông góc với mặt phẳng đáy. Biết
·
30 ; ;
BAC SA a BA BC a
o
. Gọi
D là điểm đối xứng của B qua CA. Tính khoảng cách từ B đến mặt phẳng (SCD).
A.
17
51
a
B.
21
7
a
C.
51
51
a
D.
17
68
a
Câu 10. Cho hình lăng trụ tam giác đều
. ' ' '
ABC A B C
có tất cả các cạnh đều bằng
a
. Khoảng cách từ
A
đến
mặt phẳng
'
A BC
bằng
28
A.
3
4
a
. B.
21
7
a
. C.
2
2
a
. D.
6
4
a
.
Câu 11. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình thang vuông tại
C
và
D
,
·
30
ABC
. Biết
AC a
,
2
a
CD
,
3
2
a
SA và cạnh
SA
vuông góc với mặt phẳng đáy. Khoảng cách từ
B
đến mặt phẳng
SCD
bằng
A.
6
a
. B.
6
2
a
. C.
6
4
a
. D.
3
2
a
.
Câu 12. Cho hình chóp .
S ABCD
có đáy là hình thoi cạnh
2
a
, góc
·
0
60
BAD
,
SAB
là tam giác đều nằm trên
mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách từ
đến mặt phẳng
SCD
là?
A.
3
2
a
. B.
3
2
a
. C.
2
a
. D.
6
a
.
Câu 13. Cho hình chóp
.
S ABCD
có đáy là hình thoi cạnh
·
0
, 60 ,
a BAD SA a
và
SA
vuông góc với mặt phẳng
đáy. Khoảng cách từ
B
đến mặt phẳng
( )
SCD
bằng
A.
21
.
7
a
B.
15
7
a
. C.
21
.
3
a
D.
15
3
a
.
Câu 14. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA ABCD
và
3
SA a
. Gọi
I
là
hình chiếu của
A
lên
S
C
. Từ I lần lượt vẽ các đường thẳng song song với
SB, SC
cắt
BC
,
CD
tại
P, Q
. Gọi
E, F
lần lượt là giao điểm của
PQ
với
,
AB AD
. Tính khoảng cách từ
E
đến
SBD
.
A.
3 21
11
a
B.
21
9
a
C.
3 21
7
a
D.
21
7
a
Câu 15. Cho hình chóp tứ giác đều .
S ABCD
có cạnh đáy bằng
2
a
, tâm
O
,
SO a
. Khoảng cách từ
O
đến mặt phẳng
SCD
bằng
A.
2
2
a
. B.
3
a
. C.
5
5
a
. D.
6
3
a
.
Câu 16. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật. Mặt bên
SAB
là tam giác đều và nằm trong
mặt phẳng vuông góc với đáy. Gọi
M
là trung điểm của
SA
biết
3,
AD a AB a
. Khi đó khoảng cách từ
C
đến
MBD
là:
A.
2 15
10
a
. B.
39
13
a
. C.
2 39
13
a
. D.
39
26
a
.
Câu 17. Cho hình lăng trụ đứng
.
ABC A B C
có
·
; 2 ; 120
AB a AC a BAC
o
. Gọi
M
là trung điểm của
cạnh
CC
thì
·
90
BMA
o
. Tính khoảng cách từ điểm
A
đến mặt phẳng
BMA
.
A.
5
7
a
. B.
5
5
a
. C.
7
7
a
. D.
5
3
a
Câu 18. Cho hình chóp
.
S ABC
có
·
·
·
0
60 , 3, 6, 9
ASB ASC CSB SA SB SC
. Tính khoảng cách
d
từ
C
đến
SAB
.
A.
3 6
d
. B.
9 6
d
. C.
27 2
2
d . D.
2 6
d
.
29
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN CỔ ĐIỂN LỚP 11 – 12 THPT
(LỚP BÀI TOÁN KHOẢNG CÁCH ĐIỂM ĐẾN MẶT PHẲNG – P4)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho hình chóp S.ABCD có đáy là hình vuông, AB = a, SA vuông góc với mặt phẳng đáy và SA = 2a. Gọi
M là trung điểm của CD, khoảng cách giữa điểm M và mặt phẳng (SBD) bằng
A.
2
3
a
B.
2
a
C.
2
a
D.
3
a
Câu 2. Cho hình chóp S.ABCD có đáy ABCD là hình vuông, tam giác SAB đều và nằm trong mặt phẳng vuông
góc với đáy. Gọi M là trung điểm của cạnh CD. Biết khoảng cách từ A đến mặt phẳng (SBM) bằng
3
2
19
a
. Thể
tích khối chóp S.ABCD bằng
A.
3
3
6
a
B.
3
3
12
a
C.
3
2 3
18
a
D.
3
3
a
Câu 3. Cho hình chóp S.ABCD có SA = a, SA vuông góc với mặt phẳng (ABCD), đáy là hình vuông ABCD. Gọi
M, N lần lượt là trung điểm của AD, DC và góc giữa (SBM) và (ABCD) bằng
30
o
. Tính khoảng cách từ D đến
mặt phẳng (SBM) bằng
A.
2
2
a
B.
2
a
C.
3
2
a
D.
2
3
a
Câu 4. Cho hình chóp đều S.ABC có
·
·
·
60 ; 90 ; 120
ASB BSC CSA
o o o
và SA = a, SB = 2a, SC = 5a. Tính
khoảng cách từ C đến mặt phẳng (SAB).
A.
5 6
3
a
B.
5 6
6
a
C.
5 2
3
a
D.
5 3
3
a
Câu 5. Cho hình lăng trụ đứng ABC.A’B’C’ có
·
; 2 ; 120
AB a AC a BAC
o
. Gọi M là trung điểm của cạnh
CC’ thì
·
90
BMA
o
. Tính khoảng cách từ điểm A đến mặt phẳng (BMA’).
A.
5
7
a
B.
5
5
a
C.
7
7
a
D.
5
3
a
Câu 6. Cho hình chóp S.ABCD có
·
·
·
; 60 ; 90 ; 120
SA SB SC a ASB ASC BSC
o o o
. Khoảng cách từ
điểm B đến mặt phẳng (SAC) bằng
A.
3
3
a
B.
2
3
a
C.
2
2
a
D.
3
2
a
Câu 7. Hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB đều và nằm trong mặt phẳng
vuông góc với mặt đáy (ABCD); N là trung điểm cạnh AD. Tính khoảng cách từ điểm B đến mặt phẳng (SCN).
A.
2
2
a
B.
2
4
a
C.
3 2
4
a
D.
3 2
8
a
Câu 8. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD),
3
SA a
. Gọi O là giao điểm của AC và BD, với E là điểm đối xứng với O qua trung điểm của SA. Tính
khoảng cách từ điểm S đến mặt phẳng (EAB).
A.
3
2
a
B.
39
13
a
C.
39
2
a
D.
39
3
a
Câu 9. Hình chóp S.ABCD có đáy là hình thang vuông tại A và D, SA vuông góc với (ABCD). Góc giữa SB và
mặt phẳng đáy bằng
45
o
, E là trung điểm của SD, AB = 2a, AD = DC = a. Tính khoảng cách từ B đến mặt
(ACE).
A.
4
3
a
B. a C.
2
3
a
D. 0,75a
Câu 10. Hình chóp S.ABC có SA vuông góc với mặt phẳng đáy (ABC). Biết
·
30 ; ;
BAC SA a BA BC a
o
.
Gọi D là điểm đối xứng của B qua AC. Khoảng cách từ B đến mặt phẳng (SCD) bằng
A.
17
51
a
B.
21
7
a
C.
51
51
a
D.
17
68
a
30
Câu 11. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, cạnh
; 2
AB a AD a
. Hình chiếu
vuông góc của S trên mặt phẳng (ABCD) là trung điểm của đoạn OA. Góc giữa SC và mặt phẳng (ABCD) bằng
30
o
. Tính khoảng cách từ C đến mặt phẳng (SAB).
A.
9 22
44
a
B.
3 22
11
a
C.
22
11
a
D.
3 22
44
a
Câu 12. Cho hình chóp S.ABC có SA = a, tam giác ABC đều, tam giác SAB vuông cân tại S và nằm trong mặt
phẳng vuông góc với mặt phẳng đáy. Tính khoảng cách từ B đến mặt phẳng (SAC).
A.
42
7
a
B.
42
14
a
C.
42
12
a
D.
42
6
a
Câu 13. Cho hình chóp S.ABC có đáy là tam giác vuông tại A, AC = a, I là trung điểm của SC. Hình chiếu vuông
góc của S lên (ABC) là trung điểm H của BC. Mặt phẳng (SAB) tạo với (ABC) một góc
60
o
. Tính khoảng cách từ
I đến mặt phẳng (SAB).
A.
3
4
a
B.
3
5
a
C.
5
4
a
D.
2
3
a
Câu 14. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và
·
60
BAD
o
. Hình chiếu vuông góc của S
trên mặt phẳng (ABCD) trùng với trọng tâm của tam giác ABC. Góc giữa hai mặt phẳng (SAB), (ABCD) bằng
60
o
. Tính khoảng cách từ B đến mặt phẳng (SCD).
A.
21
14
a
B.
21
7
a
C.
3 7
14
a
D.
3 7
7
a
Câu 15. Cho tứ diện ABCD có AB = CD = 4, AC = BD = 5, AD = BC = 6. Tính khoảng cách từ điểm A đến mặt
phẳng (BCD).
A.
3 6
7
B.
3 2
5
C.
3 42
7
D.
7
2
Câu 16. Cho hình chóp tam giác đều S.ABC có độ dài cạnh đáy bằng a, cạnh bên bằng
3
a
. Gọi O là tâm của
đáy ABC, tính tổng
( ,( )) ( ,( ))
d A SBC d O SBC
.
A.
2 2
11
a
B.
2 2
33
a
C.
8 2
33
a
D.
8 2
11
a
Câu 17. Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB = 2AD = 2a. Tam giác SAB đều và nằm trong mặt
phẳng vuông góc với đáy (ABCD). Tính khoảng cách từ điểm A đến mặt phẳng (SBD).
A. 0,5a B. a C.
3
2
a
D.
3
4
a
Câu 18. Cho hình lăng trụ đứng ABC.A
1
B
1
C
1
có
·
1
; 2 5; 120
AB a A A a BAC
o
. Gọi I, K lần lượt là trung
điểm của C
1
C, B
1
B. Tính khoảng cách từ điểm I đến mặt phẳng (A
1
BK).
A.
15
a
B.
5
6
a
C.
15
3
a
D.
5
3
a
______________________________________
31
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN CỔ ĐIỂN LỚP 11 – 12 THPT
(LỚP BÀI TOÁN KHOẢNG CÁCH ĐIỂM ĐẾN MẶT PHẲNG – P5)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho hình hộp ABCD.A’B’C’D’ có đáy ABCD là hình vuông cạnh a, tâm O. Hình chiếu vuông góc của A’
lên mặt phẳng (ABCD) trùng với O. Biết tam giác AA’C vuông cân tại A’. Tính khoảng cách từ D đến mặt phẳng
(ABB’A’).
A.
6
6
a
B.
2
6
a
C.
2
3
a
D.
6
3
a
Câu 2. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, mặt bên SAB là tam giác đều và nằm trong mặt
phẳng vuông góc với đáy. Gọi M là trung điểm của SA biết
3;
AD a AB a
. Tính khoảng cách từ C đến mặt
phẳng (MBD).
A.
15
5
a
B.
39
13
a
C.
2 39
13
a
D.
39
26
a
Câu 3. Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình bình hành tâm O, mặt phẳng (SAC) vuông góc với
mặt phẳng (SBD). Biết khoảng cách từ O đến các mặt phẳng (SAB), (SBC), (SCD) lần lượt là
1;2; 5
. Tính
khoảng cách từ O đến mặt phẳng (SAD).
A.
2 95
19
B.
95
10
C.
2
D.
2
2
Câu 4. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại B và C, CD = 2AB, AD = a,
·
30
ADC
o
,
SA vuông góc với mặt đáy và SA = 2a. Tính khoảng cách từ D đến mặt phẳng (SBC).
A.
2 57
19
a
B.
57
19
a
C.
3 57
19
a
D.
3
a
Câu 5. Cho hình lăng trụ tam giác ABC.A’B’C’ có
2 3; 2
AB A A
. Gọi M, N, P lần lượt là trung điểm các
cạnh A’B’, A’C’ và BC. Tính khoảng cách từ A đến mặt phẳng (MNP).
A.
17
65
B. 2,4 C.
6 13
65
D.
13
65
Câu 6. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy và SA = 2a, M là trung điểm
của SD. Tính khoảng cách d giữa đường thẳng SB và mặt phẳng (ACM).
A. 1,5a B. a C.
2
3
a
D.
3
a
Câu 7. Cho hình lập phương ABCD.A’B’C’D’ cạnh a, tính khoảng cách giữa hai mặt phẳng (AB’C) và (A’DC’).
A.
3
a
B.
3
a
C.
2
a
D.
3
3
a
Câu 8. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB vuông cân tại S và nằm trong
mặt phẳng vuông góc với đáy, gọi I là trung điểm của AB và M là trung điểm của BC. Tính khoảng cách từ I đến
mặt phẳng (SMD).
A.
6
6
a
B.
30
12
a
C.
13
26
a
D.
3 14
28
a
Câu 9. Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi I, J lần lượt là trung điểm của BC, AD. Tính khoảng
cách d giữa hai mặt phẳng (AIA’) và (CJC’).
A.
10
a B.
2 5
a
C.
5
5
a
D.
3 5
5
a
Câu 10. Cho khối lăng trụ ABC.A’B’C’ có thể tích bằng
3
a
. Gọi M, N lần lượt là trung điểm của A’B’, C’C. Tính
khoảng cách từ A đến mặt phẳng (BMN) biết rằng BMN là tam giác đều cạnh 2a.
A.
3
a
B.
3
a
C.
3
3
a
D.
3
2
a
Câu 11. Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Trên A’A, B’B lấy lần lượt các điểm M, N sao cho
0,75 ; 0,5
AM a BN a
. Tính khoảng cách từ điểm B’ đến mặt phẳng (MNC) là
A.
2
21
a
B.
2 21
63
a
C.
21
a
D.
41
8
a
32
Câu 12. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a,
·
60
BAD
o
. Hình chiếu của S lên mặt phẳng
(ABCD) là trọng tâm tam giác ABC. Góc giữa (ABCD) và (SAB) bằng
60
o
. Tính khoảng cách từ B đến mặt
phẳng (SCD).
A.
3 17
14
a
B.
3 7
14
a
C.
3 17
4
a
D.
3 7
4
a
Câu 13. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a,
·
60
BAC
o
. Hình chiếu của đỉnh S trên mặt
phẳng (ABCD) trùng với trọng tâm tam giác ABC, góc tạo bởi hai mặt phẳng (SAC), (ABCD) là
60
o
. Tính
khoảng cách từ B đến mặt phẳng (SCD).
A.
3
2 7
a
B.
9
2 7
a
C.
2 7
a
D.
3
7
a
Câu 14. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, D và AB = AD = 2a, DC = a. Điểm I là
trung điểm đoạn AD, hai mặt phẳng (SIB), (SIC) cùng vuông góc với mặt phẳng (ABCD). Mặt phẳng (SBC) tạo
với mặt phẳng (ABCD) một góc
60
o
. Tính khoảng cách từ D đến (SBC).
A.
15
5
a
B.
9 15
10
a
C.
2 15
5
a
D.
9 15
20
a
Câu 15. Cho tứ diện ABCD có
·
·
·
90 ; 60 ; 120 ;
BAC CAD BAD AB AC a
o o o
. Tính khoảng cách từ C
đến mặt phẳng (ABD).
A.
3
2
a
B.
6
3
a
C.
6
2
a
D.
2
2
a
Câu 16. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AB = 3a, AD = DC = a, gọi I là
trung điểm của AD, biết hai mặt phẳng (SBI), (SCI) cùng vuông góc với đáy và mặt phẳng (SBC) tạo với đáy một
góc
60
o
. Tính khoảng cách từ trung điểm cạnh SD đến mặt phẳng (SBC).
A.
17
5
a
B.
6
19
a
C.
3
15
a
D.
15
20
a
Câu 17. Cho hình chóp S.ABCD có đáy là hình thoi tâm O cạnh a,
·
60
BAD
o
. Đường thẳng SO vuông góc với
mặt đáy (ABCD) và SO = 0,75a. Khoảng cách từ O đến mặt phẳng (SBC) bằng
A. 0,75a B. 0,375a C.
3
4
a
D.
3
a
Câu 18. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với đáy (ABC), góc giữa
đường thẳng SB và mặt phẳng (ABC) bằng
60
o
. M là trung điểm của cạnh AB. Tính khoảng cách từ B đến mặt
phẳng (SMC).
A.
39
13
a
B. a C. 0,5a D.
3
a
______________________________________
33
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN CỔ ĐIỂN LỚP 11 – 12 THPT
(LỚP BÀI TOÁN KHOẢNG CÁCH ĐIỂM ĐẾN MẶT PHẲNG – P6)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A,
·
30
ABC
o
, tam giác SBC đều cạnh a và
nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính khoảng cách từ C đến mặt phẳng (SAB).
A.
39
26
a
B.
15
16
a
C.
39
13
a
D.
15
8
a
Câu 2. Cho hình chóp S.ABCD có đáy ABCD là hình vuông với AB = 2a, tam giác SAB vuông tại S, mặt phẳng
(SAB) vuông góc với (ABCD). Biết góc tạo bởi đường thẳng SD và mặt phẳng (SBC) bằng
1
:sin
3
. Tính
khoảng cách từ C đến mặt phẳng (SBD) theo a.
A.
3
a
B.
2
3
a
C.
3
4
a
D. a
Câu 3. Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của A’ lên
(ABC) trùng với trung điểm của BC. Tính khoảng cách từ A’ đến (BCC’B’) biết góc giữa hai mặt phẳng (ABB’A’)
và (A’B’C’) bằng
60
o
.
A.
3 7
14
a
B.
3
4
a
C.
21
14
a
D. 0,75a
Câu 4. Cho hình hộp đứng ABCD.A’B’C’D’ có đáy là hình vuông, tam giác A’AC vuông cân, A’C = 2. Tính
khoảng cách từ điểm A đến mặt phẳng (BCA’).
A.
3
2
B.
2
3
C.
6
3
D.
6
6
Câu 5. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của AD, BC.
Biết khoảng cách từ M đến mặt phẳng (SBD) bằng
6
7
a
. Tính khoảng cách từ điểm N đến mặt phẳng (SBD).
A.
12
7
a
B.
4
7
a
C.
6
7
a
D.
3
7
a
Câu 6. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên (SAB) là tam giác đều và nằm
trong mặt phẳng vuông góc với đáy (ABCD). Lấy điểm I trên đoạn SB sao cho IB = 2SI. Tính khoảng cách h từ
điểm I đến mặt phẳng (SCD).
A.
21
a
B.
21
7
a
C.
2
21
a
D.
21
14
a
Câu 7. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh SA vuông góc với mặt đáy, góc giữa
SC và mặt phẳng đáy bằng
60
o
. Gọi I là trung điểm của đoạn thẳng SB. Tính theo a khoảng cách từ điểm S đến
mặt phẳng (ADI).
A.
6
a
B.
42
7
a
C.
7
2
a
D.
7
a
Câu 8. Cho hình chóp S.ABCD có đáy là hình vuông tại A và D, AB = 2AD = 2CD = 2a. Cạnh bên SA vuông góc
với đáy và SA = a. Gọi M là trung điểm của SD, N là điểm thỏa mãn
3
SB SN
uur uuur
, tính khoảng cách từ C đến mặt
phẳng (AMN).
A.
2
a
B.
2
3
a
C.
3
3
a
D.
2 3
3
a
Câu 9. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a, từ S hạ SN, SM vuông góc với AC và AB tại
N, M. Biết NC = 2NA, MA = MB, G là trọng tâm tam giác SAB. Tính khoảng cách từ G đến mặt phẳng (SAC).
A.
21
98
a
B.
2 5
9
a
C.
7
2 2
a
D.
3
15
a
Câu 10. Cho lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy bằng 1, cạnh bên
3
A A
. Tính khoảng cách d từ
điểm A lên mặt phẳng (A’BC).
A.
3
2
B.
2 15
5
C.
15
5
D.
3
4
34
Câu 11. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a và cạnh bên SA vuông góc với mặt phẳng
đáy. Gọi E là trung điểm của CD, biết thể tích khối chóp S.ABCD bằng
3
3
a
. Tính khoảng cách từ A đến mặt
phẳng (SBE) theo a.
A.
3
3
a
B.
3
a
C.
2
3
a
D.
2
3
a
Câu 12. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB là tam giác đều và nằm trong mặt
phẳng vuông góc với mặt phẳng đáy. Tính khoảng cách từ A đến mặt phẳng (SBD).
A.
21
28
a
B.
21
7
a
C.
21
14
a
D.
2
2
a
Câu 13. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, mặt phẳng (SAC) vuông góc với mặt
phẳng (SBD). Biết khoảng cách từ O đến các mặt phẳng (SAB), (SBC), (SCD) lần lượt là
1;2; 5
. Tính khoảng
cách d từ O đến các mặt phẳng (SAD).
A.
19
20
B.
20
19
C.
2
2
D.
2
Câu 14. Cho lăng trụ ABCD.A’B’C’D’ có đáy ABCD là hình vuông cạnh 2a,
3
A A a
, hình chiếu của A’ lên
mặt phẳng ABCD trùng với trung điểm I của AB. Gọi K là trung điểm của BC. Tính khoảng cách từ I đến mặt
phẳng (A’KD).
A.
3 2
19
a
B.
3 38
19
a
C.
4 2
3
a
D.
3 2
8
a
Câu 15. Cho hình chóp S.BACD có đáy ABCD là hình vuông, SA vuông góc với đáy, mặt bên (SCD) hợp với
đáy góc
60
o
, M là trung điểm của BC. Biết thể tích khối chóp S.ABCD bằng
3
3
3
a
. Tính khoảng cách từ M đến
mặt phẳng (SCD).
A.
3
6
a
B.
3
a
C.
3
4
a
D.
3
2
a
Câu 16. Cho hình chóp S.ABCD có đáy là hình thang vuông tại A, D, SA vuông góc với (ABCD). Góc giữa SB
và mặt phẳng đáy bằng
45
o
. E là trung điểm của SD, AB = 2a, AD = DC = a. Tính khoảng cách từ điểm B đến
mặt phẳng (ACE).
A. a B.
2
3
a
C. 0,75a D.
4
3
a
Câu 17. Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều cạnh 2a, góc giữa A’B và mặt phẳng
(AA’C’C) bằng
45
o
. Gọi I là trung điểm của AC. Tính khoảng cách từ C’ đến mặt phẳng (A’BI).
A.
2 6
3
a
B.
6
a
C.
6
3
a
D.
6
2
a
35
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN CỔ ĐIỂN LỚP 11 – 12 THPT
(LỚP BÀI TOÁN KHOẢNG CÁCH HAI ĐƯỜNG CHÉO NHAU – P1)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B có AD = 2°; AB = BC = a,
cạnh SA vuông góc với đáy và
2
SA a
. Khoảng cách giữa hai đường phẳng SB và DC bằng
A.
10
5
a
. B.
7
3
a
. C.
6
3
a
. D.
11
5
a
.
Câu 2. Cho tứ diện đều
ABCD
có cạnh bằng a. Khoảng cách giữa hai đường thẳng
AB
và
CD
bằng
A.
2
3
a
. B.
2
2
a
. C.
3
2
a
. D.
3
3
a
.
Câu 3. Cho hình chóp
.
S ABCD
có đáy là hình vuông cạnh
a
, tam giác
SAB
đều và nằm trong mặt
phẳng vuông góc với đáy. Khoảng cách giữa hai đường thẳng
SA
và
BC
bằng
A.
a
. B.
5
2
a
. C.
3
2
a
. D.
2
a
.
Câu 4. Cho hình chóp S.ABCD có đáy là hình thoi cạnh 2a và đường chéo
2 3
BD a
, cạnh bên SA
vuông góc với mặt đáy. Biết góc tạo bởi SC và mặt phẳng đáy bằng
0
45
. Tìm khoảng cách giữa hai
đường thẳng
,
BD SC
.
A.
2
2
a
. B.
3
2
a
. C.
2
3
a
. D.
3
3
a
.
Câu 5. Cho tứ diện
OABC
có
, ,
OA OB OC
đôi một vuông góc với nhau và
, 2 .
OA a OB OC a
Gọi
M
là trung điểm của cạnh
BC
. Khoảng cách giữa hai đường thẳng
OM
và
AC
bằng:
A.
2
2
a
. B.
2 5
5
a
. C.
a
. D.
6
3
a
.
Câu 6. Cho hình chóp tứ giác đều .
S ABCD
có đáy bằng
2
a
,
SA
tạo với đáy một góc
30
. Tính theo
a
khoảng cách
d
giữa hai đường thẳng
SA
và
CD
.
A.
2 10
5
a
d
. B.
3 14
5
a
d
. C.
4 5
5
a
d
. D.
2 15
5
a
d
.
Câu 7. Cho hình chóp
.
S ABCD
có đáy là hình chữ nhật
ABCD
có
2 , 4 , ( )
AB a AD a SA ABCD
,
cạnh
SC
tạo với đáy một góc
0
60
. Gọi
M
là trung điểm của
,
BC N
là điểm nằm trên cạnh
AD
sao cho
DN a
. Khoảng cách giữa
MN và SB
là
A.
2 95
19
a
B.
8
19
a
C.
2 285
19
a
D.
285
19
a
Câu 8. Cho hình chóp .
S ABC
có đáy là tam giác đều cạnh bằng
a
. Gọi
I
là trung điểm của
AB
, hình
chiếu của
S
lên mặt phẳng
ABC
là trung điểm của
CI
, góc giữa
SA
và mặt đáy bằng
45
. Gọi
G
là
trọng tâm
SBC
. Khoảng cách giữa hai đường thẳng
SA
và
CG
bằng:
A.
21
14
a
. B.
14
8
a
. C.
77
22
a
. D.
21
7
a
.
Câu 9. Cho hình lăng trụ tam giác đều
.
ABC A B C
có
2 3
AB
và
2
AA
. Gọi
M
,
N
,
P
lần lượt là
trung điểm các cạnh
A B
,
A C
và
BC
. Khoảng cách từ
A
đến
MNP
bằng
A.
17
65
. B.
6 13
65
. C.
13
65
. D.
12
5
.
Câu 10. Cho lăng trụ đứng
.
ABC A B C
có
·
, 2 , 120
AC a BC a ACB
. Gọi
M
là trung điểm của
BB
.
Tính khoảng cách giữa hai đường thẳng
AM
và
CC
theo
a
.
A.
3
7
a
. B.
3
a
. C.
7
7
a
. D.
3
7
a .
Câu 11. Cho hình lập phương .
ABCD A B C D
có cạnh bằng
a
. Gọi
K
là trung điểm của
DD
. Tính
khoảng cách giữa hai đường thẳng
CK
,
A D
.
36
A.
a
. B.
3
8
a
. C.
2
5
a
. D.
3
a
.
Câu 12. Cho lăng trụ
.
ABC A B C
có đáy
ABC
là tam giác đều có cạnh bằng 4. Hình chiếu vuông góc
của
A
trên
mp( )
ABC
trùng với tâm của đường tròn ngoại tiếp
ABC
. Gọi
M
là trung điểm cạnh
AC
.
Khoảng cách giữa hai đường thẳng
BM
và
B C
bằng
A.
2
. B.
2
. C.
1
. D.
2 2
.
Câu 13. Cho hình lập phương
1 1 1 1
.
ABCD A B C D
. Khoảng cách giữa
AD
và
1
BB
là độ dài đoạn thẳng?
A.
1
AC
. B.
BD
. C.
1
AB
. D.
DC
.
Câu 14. Hình lập phương .
D A B C D
ABC
cạnh
a
. Tính khoảng cách giữa hai đường
AB
và
CD
.
A.
2
.
2
a
B.
.
a
C.
2.
a
D.
2 .
a
Câu 15. Cho hình hộp chữ nhật
.
EFGH E F G H
có
3 , 4 , 12 ,
EF a EH a EE a
với
0 a
¡
. Khoảng
cách giữa hai đường thẳng
EF
và
GH
bằng
A.
12
a
. B.
3
a
. C.
2
a
. D.
4
a
.
Câu 16. Cho hình lập phương
.
ABCD A B C D
cạnh
.
a
Tính khoảng cách giữa hai đường
AB
và
CD
.
A.
2
.
2
a
B.
.
a
C.
2 .
a
D.
2 .
a
Câu 17. Hình lập phương
. ' ' ' '
ABCD A B C D
có cạnh bằng
a
. Khoảng cách giữa hai đường thẳng
BD
và
' '
A C
bằng
A.
a
. B.
2
a
. C.
3
2
a
. D.
3
a
.
Câu 18. Cho hình lăng trụ
.
ABC A B C
có tất cả các cạnh đều bằng
a
. Góc tạo bởi cạnh bên và mặt
phẳng đáy bằng
30
. Hình chiếu
H
của
A
trên mặt phẳng
A B C
là trung điểm của
B C
. Tính theo
a
khoảng cách giữa hai mặt phẳng đáy của lăng trụ
.
ABC A B C
.
A.
2
a
. B.
3
a
. C.
3
2
a
. D.
2
2
a
.
Câu 19. Cho lăng trụ đứng
.
ABC A B C
có tất cả các cạnh đều bằng
2
a
. Khoảng cách giữa hai đường
thẳng
BC
và
AA
bằng
A.
2 5
3
a
. B.
2
5
a
. C.
3
2
a
. D.
3
a
.
Câu 20. Cho hình lăng trụ tam giác đều
. ' ' '
ABC A B C
có tất cả các cạnh đều bằng
a
. Khoảng cách từ
A
đến mặt phẳng
'
A BC
bằng
A.
3
4
a
. B.
21
7
a
. C.
2
2
a
. D.
6
4
a
.
______________________________________
37
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN CỔ ĐIỂN LỚP 11 – 12 THPT
(LỚP BÀI TOÁN KHOẢNG CÁCH HAI ĐƯỜNG CHÉO NHAU – P2)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho lăng trụ đều
.
ABC A B C
có cạnh đáy bằng a và có thể tích bằng
3
3
4
a
. Tính khoảng cách giữa hai
đường thẳng AB và A’C.
A.
2
a
B.
15
5
a
C.
2
5
a
D.
5
5
a
Câu 2. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AB = 3a, AD = DC = a. Gọi I là
trung điểm của AD, biết hai mặt phẳng (SBI), (SCI) cùng vuông góc với đáy và mặt phẳng (SBC) tạo với đáy một
góc
60
. Gọi M là điểm trên AB sao cho AM = 2a. Tính khoảng cách giữa hai đường thẳng MD và SC.
A.
17
5
a
B.
15
10
a
C.
6
9
a
D.
3
15
a
Câu 3. Cho lăng trụ tam giác đều
.
ABC A B C
có AB = a, A’A = 2a. Tính khoảng cách giữa hai đường thẳng
AB’ và A’C.
A.
2
5
a
B.
3
2
a
C.
5
a
D.
2
17
a
Câu 4. Cho hình chóp S.ABCD có đáy là hình thang vuông tại B và C, AB = 3a, BC = CD = a, SA vuông góc với
mặt phẳng đáy. Góc giữa SC và mặt phẳng đáy bằng
30
. Gọi M là điểm thuộc cạnh AB sao cho 3AM = 2AB.
Khoảng cách giữa hai đường thẳng SB và DM bằng
A.
3 370
37
a
B.
370
37
a
C.
37
13
a
D.
3 37
13
a
Câu 5. Cho lăng trụ đứng
.
ABC A B C
có tất cả các cạnh bằng a. Tính theo a khoảng cách giữa hai đường
thẳng A’B’ và BC’.
A. a B.
3
7
a
C.
21
7
a
D.
2
2
a
Câu 6. Cho hình chóp S.ABC có đáy là tam giác đều cạnh 2a. Hình chiếu vuông góc của S trên mặt phẳng
(ABC) là trung điểm H của cạnh AB. Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng
30
. Tính khoảng
cách giữa hai đường thẳng BC và SA.
A.
2
7
a
B.
7
a
C.
21
7
a
D.
2 21
7
a
Câu 7. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, tam giác ABC là tam giác đều cạnh à và
thuộc mặt phẳng vuông góc với đáy. Tính khoảng cách giữa hai đường thẳng SA và BC.
A.
3
4
a
B.
3
2
a
C.
2
a
D.
3
2
a
Câu 8. Cho lăng trụ đứng
.
ABC A B C
có tất cả các cạnh bằng a. Tính khoảng cách giữa hai đường thẳng AC
và B’B.
A.
3
2
a
B.
2
5
a
C.
a
D.
5
3
a
Câu 9. Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O có
2 ; 2 3
AC a BD a
. Hình chiếu vuông
góc của đỉnh S xuống mặt đáy trùng với trung điểm của OB. Biết tam giác SBD vuông tại S. Khoảng cách giữa
hai đường thẳng AC và SB là
A. 0,75a B. 1,5a C.
3
2
a
D. 0,375a
Câu 10. Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a, gọi M, N lần lượt là trung điểm của AB và
AD. Hình chiếu vuông góc của S trên mặt phẳng đáy trùng với giao điểm H của CM và BN. Biết SH = a, tính
khoảng cách giữa hai đường thẳng SC và BN.
A.
2
3
a
B.
3
a
C.
3
4
a
D.
4
7
a
Câu 11. Hình hộp chữ nhật
.
ABCD A B C D
có đáy ABCD là hình vuông cạnh
2
a
. Biết
2
A A a
, tính
38
khoảng cách giữa hai đường thẳng BD và CD’.
A.
2
a
B. 2a C.
2
a
D.
5
5
a
Câu 12. Hình chóp S.ABCD có đáy là tam giác đều cạnh a, góc giữa SC và đáy (ABC) bằng
45
. Hình chiếu
vuông góc của S lên mặt phẳng (ABC) là điểm H thuộc AB sao cho HA = 2HB. Biết
7
3
a
CH , tính khoảng
cách giữa hai đường thẳng SA, BC.
A.
210
15
a
B.
210
45
a
C.
210
30
a
D.
210
20
a
Câu 13. Cho hình lăng trụ đứng
.
ABC A B C
có đáy ABC là tam giác vuông tại A, AB = a. Khoảng cách giữa
hai đường thẳng AC và B’B là
A. a B.
2
2
a
C.
3
2
a
D.
2
a
Câu 14. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy (ABCD)
và SA = a, khoảng cách giữa hai đường thẳng BD và SC là
A.
3
2
a
B.
2
3
a
C.
6
6
a
D. 2a
Câu 15. Hình chóp S.ABCD có đáy là hình thang, AB = 2a, AD = DC = CD = a, SA = 3a và SA vuông góc với
mặt phẳng đáy. Gọi M là trung điểm của AB, khoảng cách giữa hai đường thẳng SB và DM bằng
A. 1,5a B. 0,75a C.
3
13
a
D.
6
13
a
Câu 16. Cho hình chóp S.ABC có đáy là tam giác vuông tại A, AB = 2a, AC = 4a, SA vuông góc với mặt phẳng
đáy và SA = a. Gọi M là trung điểm của AB. Khoảng cách giữa hai đường thẳng SM và BC là
A. 0,5a B.
3
a
C.
6
3
a
D.
2
3
a
Câu 17. Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, cạnh a,
60
BAD
. Tính khoảng cách giữa
hai đường thẳng AD và SB.
A.
2 57
19
a
B.
57
19
a
C.
2
a
D.
3
2
a
Câu 18. Cho hình hộp chữ nhật
.
ABCD A B C D
. Khoảng cách giữa AB và B’C’ là
2
5
a
, khoảng cách giữa BC
và AB’ là
2
5
a
, khoảng cách giữa AC và BD’ là
3
a
. Thể tích khối hộp đó là
A. 8
3
a
B. 4
3
a
C. 2
3
a
D.
3
a
______________________________________
39
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN CỔ ĐIỂN LỚP 11 – 12 THPT
(LỚP BÀI TOÁN KHOẢNG CÁCH HAI ĐƯỜNG CHÉO NHAU – P3)
_______________________________________________
Câu 1. Cho lăng trụ
.
ABC A B C
có đáy
ABC
là tam giác đều có cạnh bằng 4. Hình chiếu vuông góc của
A
trên
( )
mp ABC
trùng với tâm của đường tròn ngoại tiếp
ABC
. Gọi
M
là trung điểm cạnh
AC
. Khoảng cách
giữa hai đường thẳng
BM
và
B C
bằng
A.
2
. B.
2
. C.
1
. D.
2 2
.
Câu 2. Cho hình lập phương
.
ABCD A B C D
cạnh
a
. Gọi
,
M N
lần lượt là trung điểm của
BC
và
DD
. Tính
theo
a
khoảng cách giữa hai đường thẳng
MN
và
BD
.
A.
3
a
. B.
3
2
. C.
3
3
. D.
3
6
a
.
Câu 3. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
. Đường thẳng
SA
vuông góc với mặt
phẳng
ABCD
và
SA a
. Tính khoảng cách
d
giữa hai đường thẳng
SB
và
CD
.
A.
2
d a
. B.
3
d a
. C.
2
d a
. D.
d a
.
Câu 4. Cho hình chóp .
S MNPQ
có đáy là hình vuông,
3
MN a
, với
0 a
¡
, biết
SM
vuông góc với đáy,
6
SM a
. Khoảng cách giữa hai đường thẳng
NP
và
SQ
bằng
A.
6
a
. B.
3
a
. C.
2 3
a
. D.
3 2
a
.
Câu 5. Cho hình chóp .
S ABCD
có đáy là hình vuông với đường chéo
2
AC a
,
SA
vuông góc mặt phẳng
ABCD
. Khoảng cách giữa hai đường thẳng
SB
và
CD
là:
A.
3
a
. B.
2
a
. C.
2
a
. D.
3
a
.
Câu 6. Cho tứ diện đều
ABCD
có cạnh bằng 3cm,
M
là trung điểm
CD
. Khoảng cách giữa
AC
và
BM
là
A.
2 11
cm
11
. B.
3 22
cm
11
. C.
3 2
cm
11
. D.
2
cm
11
.
Câu 7. Cho tứ diện đều
ABCD
có cạnh bằng a. Khoảng cách giữa hai đường thẳng
AB
và
CD
bằng
A.
2
3
a
. B.
2
2
a
. C.
3
2
a
. D.
3
3
a
.
Câu 8. Cho hình chóp tứ giác
.
S ABCD
có đáy là hình chữ nhật cạnh
2
AD a
,
SA ABCD
và
SA a
.
Khoảng cách giữa hai đường thẳng
AB
và
SD
bằng
A.
3
3
a
. B.
6
4
a
. C.
2 5
5
a
. D.
6
a
.
Câu 9. Cho hình chóp
.
S ABCD
có đáy là hình vuông cạnh
a
, tam giác
SAB
đều và nằm trong mặt phẳng
vuông góc với đáy. Khoảng cách giữa hai đường thẳng
SA
và
BC
bằng
A.
a
. B.
5
2
a
. C.
3
2
a
. D.
2
a
.
Câu 10. Cho hình chóp .
S ABCD
có đáy là hình vuông cạnh
a
, tam giác
SAD
đều và nằm trong mặt phẳng
vuông góc với đáy .Tính khoảng cách
d
giữa hai đường thẳng
SA
và
BD
.
A.
21
14
a
d
. B.
2
2
a
d
. C.
21
7
a
d
. D.
d a
.
Câu 11. Cho khối chóp
.
S ABCD
có thể tích bằng
3
2
a
và đáy ABCD là hình bình hành. Biết diện tích tam giác
SAB bằng
2
.
a
Tính khoảng cách giữa hai đường thẳng
SB
và
.
CD
A.
.
a
B.
3
.
2
a
C.
3 .
a
D.
2
.
2
a
Câu 12. Cho hình chóp tứ giác đều
.
S ABCD
có tất cả các cạnh đều bằng
a
. Tính khoảng cách giữa hai đường
thẳng
AD
và
SB
.
A.
6
2
a
. B.
6
3
a
. C.
3
3
a
. D.
3
2
a
.
Câu 13. Cho hình chóp
.
S ABC
có đáy
ABC
vuông cân tại
A
,
2
AB a
, tam giác
SBC
đều nằm trong mặt
phẳng vuông góc với mặt đáy. Tính khoảng cách giữa
AC
và
SB
.
40
A.
21
14
a
. B.
2 21
3
a
. C.
21
7
a
. D.
2 21
7
a
.
Câu 14. Cho hình chóp tứ giác đều
.
S ABCD
có đáy bằng
2
a
,
SA
tạo với đáy một góc
30
. Tính theo
a
khoảng cách
d
giữa hai đường thẳng
SA
và
CD
.
A.
2 10
5
a
d
. B.
3 14
5
a
d
. C.
4 5
5
a
d
. D.
2 15
5
a
d
.
Câu 15. Cho tứ diện
OABC
có
, ,
OA OB OC
đôi một vuông góc với nhau và 2 ,
OC a OA OB a
. Gọi
M
là
trung điểm của
AB
. Tính khoảng cách giữa hai đường thẳng
OM
và
AC
.
A.
2
3
a
. B.
2 5
5
a
. C.
2
3
a
. D.
2
2
a
.
Câu 16. Cho tứ diện đều
ABCD
có cạnh bằng
a
. Khoảng cách giữa hai đường thẳng
AB
và
CD
bằng:
A.
3
2
a
. B.
3
a
. C.
2
a
. D.
2
2
a
.
Câu 17. Cho lăng trụ đứng tam giác
.A'B'C'
ABC
tam giác vuông cân tại
, 2
A AB a
. Khoảng cách giữa hai
đường thẳng
'
AA
và
BC
là ?
A.
', 2
d AA BC a
. B.
', 2
d AA BC a
. C.
',
d AA BC a
. D.
1
',
2
d AA BC a
.
Câu 18. Cho lăng trụ đứng .
ABC A B C
có
·
, 2 , 120
AC a BC a ACB
. Gọi
M
là trung điểm của
BB
. Tính
khoảng cách giữa hai đường thẳng
AM
và
CC
theo
a
.
A.
3
7
a
. B.
3
a
. C.
7
7
a
. D.
3
7
a
.
Câu 19. Cho lăng trụ đứng
.
ABC A B C
, đáy
ABC
là tam giác vuông ở
A
,
2
AB a
,
AC a
,
4
AA a
.
M
là
điểm thuộc cạnh
AA
sao cho 3
MA MA
. Tính khoảng cách giữa hai đường chéo nhau
BC
và
C M
.
A.
6
7
a
d . B.
4
7
a
d . C.
4
3
a
d . D.
8
7
a
d .
Câu 20. Cho hình lăng trụ tam giác đều
.
ABC A B C
có
,
AB a
2 .
AA a
Tính khoảng cách giữa hai đường
thẳng
AB
và
.
A C
A.
3
.
2
a
B.
2 5
.
5
a
C.
5.
a
D.
2 17
.
17
a
Câu 21. Cho khối hộp
.
ABCD A B C D
có thể tích bằng
6
,
A BC
là tam giác đều có cạnh bằng
2.
Khoảng
cách từ điểm
B
đến mặt phẳng
A BC
bằng
A.
3
. B.
3
2
. C.
3
3
. D.
3
6
.
Câu 22. Cho hình chóp .
S ABC
có đáy
ABC
là tam giác vuông tại
B
,
AB a
, cạnh bên
SA
vuông góc với
đáy và
2
SA a
. Gọi
E
là trung điểm của
AB
. Khoảng cách giữa đường thẳng
SE
và đường thẳng
BC
bằng bao nhiêu ?
A.
3
3
a
. B.
3
2
a
. C.
2
a
. D.
2
3
a
.
41
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN CỔ ĐIỂN LỚP 11 – 12 THPT
(LỚP BÀI TOÁN KHOẢNG CÁCH HAI ĐƯỜNG THẲNG CHÉO NHAU – PHẦN 4)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Bài 1. Hình chóp có đáy ABCD là hình vuông cạnh a,
17
2
a
SD , hình chiếu vuông góc của S lên mặt phẳng
(ABCD) là trung điểm của đoạn AB. Gọi K là trung điểm của AD. Tính khoảng cách giữa hai đường SD, HK.
A.
3
5
a
B.
3
7
a
C.
21
5
a
D.
2
6
a
Bài 2. Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, đường thẳng SA vuông góc với mặt phẳng đáy,
SA = 2a. Gọi N là trung điểm của AD. Tính khoảng cách d giữa hai đường thẳng SN và CD.
A.
2
5
a
B.
5
a
C.
2
a
D.
2
3
a
Bài 3. Cho khối chóp S.ABCD có thể tích bằng
3
a
. Mặt bên SAB là tam giác đều cạnh a và thuộc mặt phẳng
vuông góc với đáy, biết đáy ABCD là hình bình hành. Tính theo a khoảng cách d giữa SA và CD.
A.
2 3
a
B.
3
a
C.
2
a
D. 0,5a
Bài 4. Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại A, BC = 2a, tam giác SBC là tam giác đều và
nằm trong mặt phẳng vuông góc với mặt đáy. Tính khoảng cách d giữa hai đường thẳng SA và BC.
A.
6
2
a
B.
3
2
a
C.
6
a
D.
3
a
Bài 5. Cho hình chóp S.ABCD, có đáy ABCD là hình vuông cạnh a, hình chiếu vuông góc của S lên mặt phẳng
ABCD là điểm H thuộc cạnh AB sao cho HB = 2HA, cạnh SC tạo với mặt đáy (ABCD) một góc bằng
60
. Tính
khoảng cách d giữa hai đường thẳng AD và SC.
A.
13
3
129
a
B.
4 13
3 129
a
C.
13
2
129
a
D.
13
6
129
a
Bài 6. Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông, AB = AC = a, cạnh bên
2
BB a
. Gọi M
là trung điểm AC, tính khoảng cách giữa hai đường thẳng A’C và BM.
A.
4
7
a
B.
7
a
C.
3
7
a
D.
2
7
a
Bài 7. Tứ diện OABC có đáy OBC là tam giác vuông tại O, OB = a,
3
OC a
và đường cao
3
OA a
. Gọi
M là trung điểm của BC, tính khoảng cách giữa hai đường thẳng AB và OM.
A.
3
5
a
B.
15
15
a
C.
15
5
a
D.
5
a
Bài 8. Hình chóp S.ABC có tam giác ABC vuông cân tại A, BC = 2a, tam giác ABC đều và nằm trong mặt phẳng
vuông góc với đáy, khoảng cách giữa hai đường thẳng SA và BC là
A.
6
2
a
B.
3
2
a
C.
6
a
D.
3
a
Bài 9. Hình chóp tứ giác đều S.ABCD có cạnh bên tạo với mặt đáy góc
60
và độ dài cạnh đáy bằng a. Tính
khoảng cách giữa hai đường thẳng AD, SC.
A.
42
7
a
B.
2 42
7
a
C.
3 42
7
a
D.
42
14
a
Bài 10. Hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, tam giác SAD đều và nằm trong mặt phẳng
vuông góc với đáy, tính khoảng cách giữa hai đường thẳng AD, SB.
A.
14
7
a
B.
2 14
7
a
C.
14
3
a
D.
2 21
7
a
Bài 11. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Hình chiếu vuông góc của S lên mặt phẳng
(ABCD) là trung điểm H của AB, tam giác SAB vuông cân tại S,
3, 3
SH a CH a
. Tính khoảng cách giữa
hai đường thẳng SD, CH.
42
A.
2 66
11
a
B.
4 66
11
a
C.
66
11
a
D.
66
22
a
Bài 12. Hình chóp S.ABCD có đáy là hình vuông tâm O cạnh a, SO vuông góc với mặt phẳng (ABCD) và SO =
a. Khoảng cách giữa SC và AB là
A.
3
15
a
B.
5
5
a
C.
2 3
15
a
D.
2 5
5
a
Bài 13. Hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = 3a, BC = 4a. Cạnh bên SA vuông góc với
đáy, góc tạo bởi SC và mặt phẳng đáy là
60
. Gọi M là trung điểm của AC, tính khoảng cách giữa AB và SM.
A.
10 237
79
a
B.
3
a
C. 2,5a D.
5 3
a
Bài 14. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, G là trọng tâm tam giác ABC, góc giữa đường
thẳng SA với mặt phẳng (ABC) bằng
60
. Khoảng cách giữa hai đường thẳng GC và SA là
A.
5
5
a
B. 0,2a C.
5
10
a
D.
2
5
a
Bài 15. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, góc giữa mặt bên và mặt đáy bằng
60
. Gọi
M là trung điểm của BC. Tính khoảng cách giữa hai đường thẳng AM và SC.
A.
3
2
a
B.
3
4
a
C.
6
2
a
D.
6
3
a
Bài 16. Cho lăng trụ đứng
.
ABC A B C
có đáy ABC là tam giác vuông,
AB BC a
, cạnh bên
2
AA a
.
Gọi M là trung điểm của BC, tính khoảng cách giữa hai đường thẳng
,
AM B C
.
A.
7
7
a
B.
2
2
a
C.
3
3
a
D.
5
5
a
Bài 17. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 2a, BC = a. Các cạnh bên của hình chóp
bằng nhau và bằng
2
a
. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD. Gọi K là điểm trên cạnh AD
sao cho KD = 2KA. Tính khoảng cách giữa hai đường MN và SK.
A.
21
7
a
B.
3
7
a
C.
2
3
a
D. 1,5a
Bài 18. Cho khối chóp S.ABC có SA vuông góc với đáy, tam giác ABC vuông cân tại B, SA = a, SB hợp với đáy
(ABC) một góc
30
. Tính khoảng cách giữa AB và SC.
A.
3
2
a
B. 1,5a C.
2
a
D.
3
a
Bài 19. Hình chóp S.ABCD có đáy ABCD là hình vuông với
2
a
AC
. Cạnh bên SA vuông góc với mặt phẳng
đáy (ABC), SB hợp với mặt phẳng đáy một góc
60
. Tính khoảng cách giữa hai đường thẳng AD, SC.
A.
2
a
B.
3
2
a
C.
3
4
a
D. 0,5a
43
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN CỔ ĐIỂN LỚP 11 – 12 THPT
(LỚP BÀI TOÁN KHOẢNG CÁCH HAI ĐƯỜNG CHÉO NHAU – P5)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho khối lăng trụ
.
ABC A B C
có thể tích bằng
3
a
. Gọi
M
,
N
lần lượt là trung điểm của
A B
,
CC
.Tính khoảng cách từ
đến mặt phẳng
BMN
biết rằng
BMN
là tam giác đều cạnh
2
a
.
A.
3
a
. B.
3
a
. C.
3
3
a
. D.
3
2
a
.
Câu 2. Cho hình lăng trụ đứng
1 1 1
.
ABC A B C
có
AB a
,
2
AC a
,
1
2 5
AA a
và
·
0
120
BAC . Gọi
,
K I
lần
lượt là trung điểm của
1 1
,
CC BB
. Khoảng cách từ
I
đến mặt phẳng
1
A BK
bằng
A.
15
a
. B.
5
6
a
. C.
15
3
a
. D.
5
3
a
.
Câu 3. Cho hình lập phương
.
ABCD A B C D
cạnh
.
a
Gọi
,
M N
lần lượt là trung điểm của
AC
và
B C
.
Khoảng cách giữa hai đường thẳng
MN
và
B D
bằng
A.
5
5
a
B.
3
a
C.
3
a
D.
5
a
Câu 4. Cho .
S ABCD
có đáy là hình vuông cạnh
a
,
SA ABCD
và
3
SA a
. Gọi
M
là trung điểm của
AD
.
Khoảng cách giữa hai đường thẳng
BM
và
SD
bằng
A.
a
. B.
57
3
a
. C.
57
19
a
. D.
2
a
.
Câu 5. Cho hình chóp
.
S ABC
có đáy ABC là tam giác vuông cân tại
,
A
mặt bên
( )
SBC
là tam giác đều cạnh
a
và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách giữa hai đường thẳng
SA
và
BC
bằng
A.
3
4
a
. B.
2
4
a
. C.
5
4
a
. D.
3
3
a
.
Câu 6. Cho hình chóp .
S ABC
có đáy
ABC
là tam giác đều cạnh bằng
.
a
Mặt bên
SAB
là tam giác cân tại
,
S
cạnh bên
SC
hợp với mặt đáy
ABC
một góc
45
, mặt bên
SAB
vuông góc với mặt đáy
ABC
và
I
là
trung điểm của
.
AB
Khoảng cách giữa hai đường thẳng
SA
và
CI
bằng
A.
2
.
6
a
B.
3
.
8
a
C.
6
.
3
a
D.
3
.
4
a
Câu 7. Cho hình chóp
.
S ABCD
có
ABCD
là hình vuông cạnh
a
và
SA
vuông góc với mặt đáy. Biết
2
SA a
.
Khoảng cách giữa hai đường thẳng
AB
và
SC
bằng
A.
2
a
. B.
2 5
5
a
. C.
5
2
a
. D.
2
a
.
Câu 8. Cho hình chóp .
S ABC
có đáy là tam giác đều cạnh bằng
4
. Góc giữa
SC
và mặt phẳng
ABC
là
45
. Hình chiếu của
S
lên mặt phẳng
ABC
là điểm
H
thuộc cạnh
AB
sao cho
2
HA HB
. Tính khoảng
cách giữa hai đường thẳng
SA
và
BC
.
A.
4 210
45
. B.
210
5
. C.
4 210
15
. D.
2 210
15
.
Câu 9. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
, tâm
O
,
SA ABCD
,
6
SA a
(như
hình vẽ). Tính khoảng cách giữa
SB
và
AC
.
A.
7
d ,
3
a
AC SB
. B.
78
d ,
3
a
AC SB
.
C.
87
d ,
13
a
AC SB
D.
78
d ,
13
a
AC SB
.
Câu 10. Cho hình chóp tứ giác đều
SABCD
có đáy
ABCD
là hình vuông cạnh
a
, cạnh bên
2
SA a
; Tính
khoảng cách giữa hai đường thẳng
AB
và
SC
.
44
A.
14
2 15
a
. B.
2 14
15
a
. C.
3
5
a
. D.
14
15
a
.
Câu 11. Cho hình chóp .
S ABCD
có
ABCD
là hình vuông cạnh
a
và
SA
vuông góc với mặt đáy. Biết
2
SA a
.
Khoảng cách giữa hai đường thẳng
AB
và
SC
bằng:
A.
2
a
. B.
2 5
5
a
. C.
5
2
a
. D.
2
a
.
Câu 12. Cho hình chóp
.
S ABCD
đáy là hình thoi cạnh
,
a
góc
·
60
BAC
, tam giác
SAB
cân tại
S
nằm trong
mặt phẳng vuông góc với đáy. Mặt phẳng
( )
SCD
tạo với đáy góc
30
. Tính khoảng cách
d
giữa hai đường
thẳng
SB
và
.
AD
A.
21
14
d a
. B.
3
5
d a
. C.
2 3
5
d a
. D.
21
7
d a
.
Câu 13. Cho tứ diện
OABC
có , ,
OA OB OC
đôi một vuông góc với nhau và
, 2 .
OA a OB OC a
Gọi
M
là
trung điểm của cạnh
BC
. Khoảng cách giữa hai đường thẳng
OM
và
AC
bằng:
A.
2
2
a
. B.
2 5
5
a
. C.
a
. D.
6
3
a
.
Câu 14. Cho hình chóp
.
S ABC
có đáy là tam giác đều cạnh bằng
a
. Gọi
I
là trung điểm của
AB
, hình chiếu
của
S
lên mặt phẳng
ABC
là trung điểm của
CI
, góc giữa
SA
và mặt đáy bằng
45
(tham khảo hình vẽ
bên). Gọi
G
là trọng tâm
SBC
. Khoảng cách giữa hai đường thẳng
SA
và
CG
bằng
A.
21
14
a
. B.
14
8
a
. C.
77
22
a
. D.
21
7
a
.
Câu 15. Cho hình chóp
.
S ABC
có
13, 14, 15
AB BC CA
. Hình chiếu vuông góc của
S
trên mặt phẳng
ABC
là điểm
H
thuộc cạnh
AC
sao cho
2
HA HC
. Gọi
G
là trọng tâm tam giác
SBC
. Biết
12
SH
tính
khoảng cách giữa hai đường thẳng
AB
và
HG
.
A.
336 1717
1717
. B.
336
1717
. C.
84 1717
1717
. D.
336 17
1717
.
Câu 16. Cho hình chóp
.
S ABCD
có đáy là hình thoi cạnh
2
AB BD
, hai đường chéo cắt nhau tại
O
. Hình
chiếu vuông góc của
S
trên mặt phẳng
ABCD
là trung điểm
H
của
BO
. Gọi
G
là trọng tâm tam giác
ADC
.
Biết
SC
tạo với mặt phẳng đáy góc
45
, tính khoảng cách giữa hai đường thẳng
SA
và
CG
.
A.
2 2373
113
. B.
4 2373
113
. C.
6 2373
113
. D.
2373
113
.
Câu 17. Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông đỉnh
A
, cạnh huyền
BC a
. Gọi
I
là trung
điểm của
BC
và
3
2
a
SA SB SC
. Góc tạo bởi
SI
và mặt phẳng
SAC
bằng
0
30
. Tính cosin của góc tạo
bởi
SA
và mặt phẳng
SBC
.
A.
57
8
. B.
19
5
. C.
19
6
. D.
57
9
.
Câu 18. Cho hình chóp
.
S ABCD
có đáy là hình bình hành và
11,
SA SB SC
·
0
30 ,
SAB
·
0
60
SBC và
·
0
45 .
SCA Tính khoảng cách
d
giữa hai đường thẳng
AB
và
SD
.
A.
4 11.
d
B.
2 22.
d
C.
22
.
2
d
D.
22.
d
______________________________________
45
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN CỔ ĐIỂN LỚP 11 – 12 THPT
(LỚP BÀI TOÁN KHOẢNG CÁCH HAI ĐƯỜNG CHÉO NHAU – P6)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật,
SA ABCD
,
3 , 4
AB a AD a
. Đường
thẳng
SC
tạo với mặt phẳng
ABCD
góc
60
. Gọi
M
là trung điểm của cạnh
BC
,
O
là giao điểm của
AC
và
BD
. Khoảng cách giữa hai đường thẳng
DM
và
SO
bằng
A.
15 22
22
a
. B.
15 22
44
a
. C.
15 22
77
a
. D.
15 22
88
a
.
Câu 2. Cho tứ diện
SABC
có các cạnh
, ,
SA SB SC
đôi một vuông góc với nhau và
, 2 ,
SA a SB a
3
SC a
.
Gọi
I
là trung điểm của
BC
. Tính khoảng cách giữa hai đường thẳng
SC
và
AI
theo
.
a
A.
a
. B.
2
a
. C.
3 2
2
a
. D.
2
2
a
.
Câu 3. Cho hình chóp .
S ABCD
có đáy
ABCD
là hình chữ nhật cạnh
AB a
,
2
AD a
. Mặt phẳng
SAB
và
SAC
cùng vuông góc với
ABCD
. Gọi
H
là hình chiếu vuông góc của
A
trên
SD
. Tính khoảng cách giữa
AH
và
SC
biết
AH a
.
A.
19
19
a
. B.
2 19
19
a
. C.
73
73
a
. D.
2 73
73
a
.
Câu 4. Cho hình chóp đều .
S ABC
có cạnh đáy bằng
2 3
a
, chiều cao bằng
4
a
. Gọi
, ,
M N P
lần lượt là trung
điểm của các cạnh
, ,
SA AB SC
. Tính khoảng cách giữa hai đường thẳng
BM
và
.
NP
A.
21
7
a
. B.
2
a
. C.
2
2
a
. D.
5
2
a
.
Câu 5. Cho hình chóp đáy là hình vuông cạnh
17
,
2
a
a SD
, hình chiếu vuông góc của
S
lên mặt phẳng
ABCD
là điểm
H
trung điểm của đoạn
AB
. Gọi
K
là trung điểm của đoạn
AD
. Tính khoảng cách giữa hai
đường thẳng
HK
và
SD
theo
a
.
A.
3
5
a
B.
3
45
a
C.
3
15
a
. D.
3
25
a
.
Câu 6. Cho hình chóp
.
S ABC
có đáy là tam giác đều cạnh
a
,
I
là trung điểm của
AB
, hình chiếu
S
lên mặt
đáy là trung điểm
H
của
CI
, góc giữa
SA
và đáy là
45
. Khoảng cách giữa
SA
và
CI
bằng:
A.
2
a
. B.
3
2
a
. C.
77
22
a
. D.
7
4
a
.
Câu 7. Cho tứ diện đều
ABCD
cạnh
1
AB
. Gọi
M
,
N
,
P
lần lượt là trung điểm các cạnh
AB
,
BC
,
AD
.
Tính khoảng cách giữa hai đường thẳng
CM
và
NP
.
A.
10
10
. B.
10
20
. C.
3 10
10
. D.
3 10
20
.
Câu 8. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình thoi cạnh
a
,
µ
0
60
D
và
SA
vuông góc với
ABCD
. Biết
thể tích của khối chóp
.
S ABCD
bằng
3
2
a
. Tính khoảng cách
k
từ
A
đến mặt phẳng
SBC
.
A.
3
5
a
k
B.
3
5
k a
C.
2
5
a
k
D.
2
3
k a
Câu 9. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật,
3, 2
AB a BC a
. Cạnh bên
SA a
và SA
vuông góc với mặt phẳng đáy. Khoảng cách giữa SB và DC bằng:
A.
2
a
. B.
2
3
a
. C.
3
a
. D.
3
2
a
Câu 10. Cho hình chóp .
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
. Gọi
M
và
N
lần lượt là trung điểm của
các cạnh
AB
và
AD
;
H
là giao điểm của
CN
với
DM
. Biết
SH
vuông góc với mặt phẳng
ABCD
và
3
SH a
.Tính khoảng cách giữa hai đường thẳng
DM
và
SC
theo
a
.
46
A.
2 3
19
a
. B.
2 3
19
a
. C.
3
19
. D.
3 3
19
a
.
Câu 11. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
. Gọi
M
và
N
lần lượt là trung điểm của
các cạnh
AB
và
AD
;
H
là giao điểm của
CN
với
DM
. Biết
SH
vuông góc với mặt phẳng
ABCD
và
3
SH a
.Tính khoảng cách giữa hai đường thẳng
DM
và
SC
theo
a
.
A.
2 3
19
a
. B.
2 3
19
a
. C.
3
19
. D.
3 3
19
a
.
Câu 12. Cho hình tứ diện OABC có đáy OBC là tam giác vuông tại O,
, 3
OB a OC a
. Cạnh OA vuông góc
với mặt phẳng (OBC),
3
OA a
, gọi M là trung điểm của BC. Tính khoảng cách h giữa hai đường thẳng AB và
OM.
A.
5
5
a
h
. B.
3
2
a
h
. C.
15
5
a
h
. D.
3
15
a
h
.
Câu 13. Cho hình chóp .
S ABC
, có đáy là tam giác đều cạnh
2
a
,
2
SA a
,
SA
vuông góc với mặt phẳng đáy (
minh họa như hình vẽ). Gọi
,
M N
lần lượt là trung điểm của
,
AB AC
. Khoảng cách giữa hai đường thẳng
MN
và
SC
bằng.
A.
21
7
a
. B.
21
14
a
. C.
2 57
19
a
. D.
57
19
a
.
Câu 14. Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
a
. Cạnh bên
3
SA a
và vuông góc với mặt
đáy
ABC
. Tính khoảng cách
d
từ
A
đến mặt phẳng
SBC
A.
2 13
13
a
d
B.
13
39
a
d
C.
13
13
a
d
D.
3 13
13
a
d
Câu 15. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình thang vuông tại A, B
và
2 , ; ( ), 2
AD a AB BC a SA ABCD SA a
. Khoảng cách giữa
SB
và
DC
bằng
A.
10
5
a
. B.
7
a
. C.
5
a
. D.
11
5
a
.
Câu 16. Cho hình chóp
.
S ABCD
có đáy là hình thang vuông tại
A
và
B
. Biết
, 2
AB BC a AD a
và
SA
vuông góc với mặt phẳng
ABCD
và
2
SA a
. Gọi
M
là trung điểm
AD
. Khoảng cách giữa hai
đường thẳng
BM
và
SC
bằng
A.
2
a
B.
a
C.
2
2
a
D.
2
a
Câu 17. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình thang vuông tại
A
và
B
có
2
AD a
,
AB BC a
và
SA ABCD
,
2
SA a
. Khoảng cách giữa hai đường phẳng
SB
và
DC
bằng
A.
10
5
a
. B.
7
3
a
. C.
6
3
a
. D.
11
5
a
.
Câu 18. Cho hình chóp đều .
S ABC
có thể tích bằng
3
3
24
a
, mặt bên tạo với đáy một góc
60
. Khi đó
khoảng cách từ
A
đến mặt phẳng
SBC
bằng
A.
3
2
a
. B.
2
2
a
. C.
3
a
. D.
3
4
a
.
47
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN CỔ ĐIỂN LỚP 11 – 12 THPT
(LỚP BÀI TOÁN KHOẢNG CÁCH HAI ĐƯỜNG CHÉO NHAU – P7)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho hình chóp
.
S ABCD
có đáy là hình thang vuông tại
A
và
D
. Biết
2 ,
AB a
,
AD DC a
cạnh bên
SA
vuông góc với mặt phẳng
ABCD
và
3
SA a
. Gọi
M
là trung
điểm
.
AB
Khoảng cách giữa hai đường thẳng
DM
và
SB
bằng
A.
3 22
22
a
B.
3 22
11
a
C.
6 22
11
a
D.
22
22
a
Câu 2. Cho hình chóp đều
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
, cạnh bên bằng
2
a
. Tính
theo
a
khoảng cách giữa hai đường thẳng
AD
và
SB
.
A.
42
7
a
. B.
21
7
a
. C.
42
14
a
. D.
21
14
a
.
Câu 3. Cho hình chóp
.
S ABCD
có đáy là hình chữ nhật cạnh
2 2
AB AD a
. Tam giác
SAB
đều và
nằm trong mặt phẳng vuông góc với đáy
ABCD
. Tính khoảng cách từ
A
đến mặt phẳng
SBD
.
A.
2
a
. B.
3
2
a
. C.
3
4
a
. D.
a
.
Câu 4. Cho hình chóp
.
S ABC
có đáy tam giác đều
ABC
cạnh là
a
, cạnh bên
SA a
,
SA ABC
,
I
là
trung điểm của
BC
. Khoảng cách giữa hai đường thẳng
SI
và
AB
là
A.
57
19
a
. B.
23
7
a
. C.
17
7
a
. D.
17
4
a
.
Câu 5. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình thoi cạnh
a
. Tam giác
ABC
đều, hình chiếu vuông
góc
H
của đỉnh
S
lên mặt phẳng
ABCD
trùng với trọng tâm của tam giác
ABC
. Đường thẳng
SD
hợp
với mặt phẳng
ABCD
góc
0
30
. Tính khoảng cách từ
B
đến mặt phẳng
SCD
theo
a
.
A.
2 21
21
a
. B.
21
7
a
. C.
17
4
a
D.
17
7
a
Câu 6. Cho hình chóp .
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
, cạnh bên
SA
vuông góc với mặt
phẳng đáy. Gọi
M
là trung điểm của
CD
. Biết khoảng cách giữa hai đường thẳng
BC
và
SM
bằng
3
4
a
. Tính thể tích của khối chóp đã cho theo
a
.
A.
3
3
4
a
. B.
3
3
2
a
. C.
3
3
6
a
. D.
3
3
12
a
.
Câu 7. Cho hình chóp
.
S ABC
có đáy là tam giác vuông đỉnh
B
,
AB a
,
SA
vuông góc với mặt phẳng
đáy và
2
SA a
. Khoảng cách từ
A
đến mặt phẳng
SBC
bằng:
A.
2 5
5
a
B.
5
3
a
C.
2 2
3
a
D.
5
5
a
Câu 8. Cho tứ diện
OABC
có
OA
,
OB
,
OC
đôi một vuông góc với nhau và
OA OB a
,
2
OC a
. Gọi
M
là trung điểm của
AB
. Khoảng cách giữa hai đường thẳng
OM
và
AC
bằng
A.
2
3
a
B.
2 5
5
a
C.
2
2
a
D.
2
3
a
Câu 9. Cho hình chóp .
S ABC
có đáy
ABC
là tam giác đều cạnh
a
,
SA ABC
, góc giữa đường
thẳng
SB
và mặt phẳng
ABC
bằng
60
. Khoảng cách giữa hai đường thẳng
AC
và
SB
bằng
A.
2
2
a
. B.
15
5
a
. C.
2
a
. D.
7
7
a
.
Câu 10. Cho hình lập phương
.
ABCD A B C D
có cạnh là
6
. Khi đó, khoảng cách giữa hai đường
thẳng chéo nhau
AB
và
BC
là
A.
3 3.
B.
2 3.
C.
3 2.
D.
2 6.
48
Câu 11. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB là tam giác đều và nằm trong mặt
phẳng vuông góc với mặt phẳng đáy. Khoảng cách từ A đến mặt phẳng
SBD
bằng
A.
21
.
14
a
B.
21
.
7
a
C.
2
.
2
a
D.
21
.
28
a
Câu 12. Cho khối chóp .
S ABC
có
SAB ABC
,
SAC ABC
,
SA a
,
2
AB AC a
,
2 2
BC a
. Gọi
M
là trung điểm của
BC
. Khoảng cách giữa hai đường thẳng
SM
và
AC
bằng
A.
2
a
. B.
2
a
. C.
a
. D.
2
a
.
Câu 13. Hình chóp
.
S ABC
có đáy là tam giác vuông cân tại
,
B
.
AB a
Cạnh bên
SA
vuông góc với mặt
phẳng đáy, góc tạo bởi hai mặt phẳng
ABC
và
SBC
bằng
60
. Tính khoảng cách giữa hai đường AB, SC.
A.
a
. B.
3
3
a
. C.
2
2
a
. D.
3
2
a
.
Câu 14. Cho hình chóp
.
S ABCD
có đáy là hình thang, 2 ,
AB a AD DC CB a
.
SA
vuông góc với mặt
phẳng đáy và
3
SA a
. Gọi
M
là trung điểm của
AB
. Khoảng cách giữa hai đường thẳng
SB
và
CM
bằng
A.
3
4
a
. B.
3
2
a
. C.
3 13
13
a
. D.
6 13
13
a
.
Câu 15. Cho hình chóp
.
S A B C D
có đáy
AB C D
là hình vuông cạnh
a
. Gọi
M
và
N
lần lượt là trung điểm
của các cạnh
AB
và
A D
;
H
là giao điểm của
C N
với
DM
. Biết
SH
vuông góc với mặt phẳng
ABCD
và
3
SH a
.Tính khoảng cách giữa hai đường thẳng
DM
và
SC
theo
.
A.
2 3
19
a
. B.
2 3
19
a
. C.
3
19
a
. D.
3 3
19
a
.
Câu 16. Cho hình lăng trụ đứng
. ' ' ' '
ABCD A B C D
có đáy
ABCD
là hình thoi. Biết
2,
AC
' 3
AA . Tính góc
giữa hai mặt phẳng
' '
AB D
và
' '
CB D
.
A.
0
45
. B.
0
90
. C.
0
30
. D.
0
60
.
Câu 17. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình thang,
2
AB a
,
AD DC BC a
.
SA
vuông góc
với mặt phẳng
ABCD
và
3
SA a
. Gọi
M
là trung điểm
AB
. Khoảng cách giữa hai đường thẳng
SM
và
BC
bằng:
A.
3
13
a
. B.
3
2
a
. C.
6
13
a
. D.
3
4
a
.
Câu 18. Cho hình chóp .
S ABC
có đáy
ABC
là tam giác đều cạnh
a
, cạnh bên
SA
vuông góc với đáy. Biết
hình chóp
.
S ABC
có thể tích bằng
3
a
. Tính khoảng cách
d
từ điểm
A
đến mặt phẳng
SBC
.
A.
6a 195
65
d
. B.
4a 195
65
d
. C.
4a 195
195
d
. D.
8a 195
195
d
.
Câu 19. Cho lăng trụ tam giác đều .
ABC A B C
có
AB a
,
2
AA a
. Khoảng cách giữa
AB
và
CC
bằng
A.
2 5
5
a
. B.
a
. C.
3
a
. D.
3
2
a
.
49
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN CỔ ĐIỂN LỚP 11 – 12 THPT
(LỚP BÀI TOÁN KHOẢNG CÁCH HAI ĐƯỜNG CHÉO NHAU – P8)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho hình chóp
.
S ABCD
có đáy là hình vuông cạnh
2 .
a
Biết các mặt bên của hình chóp cùng tạo với đáy
các góc bằng nhau và thể tích của khối chóp bằng
3
4 3
.
3
a
Khoảng cách giữa hai đường thẳng
SA
và
CD
bằng
A.
2 .
a
B.
3 .
a
C.
5.
a D.
3 2 .
a
Câu 2. Cho hình chóp
.
S ABCD
có đáy là hình thang vuông tại
A
và
B
. Biết
, 2
AB BC a AD a
và
SA
vuông góc với mặt phẳng
ABCD
và
2
SA a
. Gọi
M
là trung điểm
AD
. Khoảng cách giữa hai đường
thẳng
BM
và
SC
bằng
A.
.
2
a
B.
.
a
C.
2
.
2
a
D.
2 .
a
Câu 3. Cho hình chóp .
S ABC
có đáy
ABC
là tam giác vuông tại
, 3 , 4 .
B AB a BC a
Cạnh bên
SA
vuông góc
với đáy. Góc tạo bởi giữa
SC
và đáy bằng
60
. Gọi
M
là trung điểm của
AC
(tham khảo hình vẽ bên dưới).
Khoảng cách giữa hai đường thẳng
AB
và
SM
bằng
A.
3
a
. B.
5 3
a
. C.
5
2
a
. D.
10 3
79
a
.
Câu 4. Cho hình chóp .
S ABCD
, đáy là hình thang vuông tại
A
và
B
, biết
AB BC a
,
2
AD a
,
3
SA a
và
SA ABCD
. Khoảng cách giữa hai đường thẳng
AC
và
SD
bằng
A.
6
5
a
. B.
30
5
a
. C.
3
2
a
. D.
15
5
a
.
Câu 5. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật
3 ,
AB a AD a
. SA vuông góc với mặt phẳng
đáy,
2
SA a
. Gọi M là điểm thuộc đoạn thẳng DC sao cho
3
DC DM
( minh họa như hình vẽ bên). Khoảng
cách giữa hai đường BM và SD bằng
A.
2
3
a
. B.
6
6
a
. C.
6
3
a
. D.
3
a
.
Câu 6. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình thang vuông tại
A
và
B
,
,
AB BC a
2
AD a
,
SA a
và vuông góc với
ABCD
. Tính khoảng cách giữa hai đường thẳng
SD
và
AC
.
A.
3
3
a
. B.
3
2
a
. C.
6
2
a
. D.
6
3
a
.
Câu 7. Cho lăng trụ đều
. ' ' '
ABC A B C
có
1,
AB
' 0 .
AA m m
Hỏi
m
bằng bao nhiêu để góc giữa
'
AB
và
'
BC
bằng 60
0
?
A.
2.
m
B.
1
m
. C.
3.
m D.
5.
m
Câu 8. Cho hình chóp
.
S ABCD
có đáy ABCD là hình vuông,
3
AB a
, vuông góc với mặt phẳng đáy và
4
SA a
. Gọi M, N lần lượt là trung điểm của CD và AB. Khoảng cách giữa hai đường thẳng SC và AM
bằng:
A.
12 89
89
a
B.
6 2
7
a
. C.
12 89
49
a
. D.
6 2
14
a
.
Câu 10. Cho hình chóp S.ABC có đáy
ABC
là tam giác vuông tại
B
,
,
BA a BC a
3 4
mặt phẳng
SBC
vuông góc với mặt phẳng
ABC
.Biết
SB a
2 3
và
·
SBC
= 30
0
. Khoảng cách từ điểm
B
đến
mặt phẳng
SAC
bằng
A.
6 7
21
a
. B.
3 7
56
a
. C.
3 7
14
a
. D.
6 7
7
a
.
Câu 11. Cho hình chóp .
S ABCD
có đáy
ABCD
là hình vuông cạnh bằng
3
. Hai mặt phẳng
SAB
và
SAC
cùng vuông góc với mặt phẳng đáy. Góc giữa
SB
và mặt phẳng đáy bằng
60
. Gọi
M
,
N
là
các điểm lần lượt thuộc cạnh đáy
BC
và
CD
sao cho
2
BM MC
và
2
CN ND
. Tính khoảng cách
giữa hai đường thẳng chéo nhau
DM
và
.
SN
50
A.
3 3
730
. B.
3 3
370
. C.
3
370
. D.
3
730
.
Câu 12. Cho hình thoi
ABCD
tâm
O
cạnh
a
và
AC a
. Từ trung điểm
H
của
AB
, dựng
SH ABCD
với
SH a
. Khoảng cách từ
A
đến mặt phẳng
SBC
bằng
A.
8 3
15
a
. B.
2 57
19
a
. C.
2 66
23
a
. D.
10 5
27
a
.
Câu 13. Cho hình chóp tứ giác đều
.
S ABCD
có cạnh đáy bằng
a
. Gọi
M
,
N
lần lượt là trung điểm của
SA
và
BC
. Biết góc giữa
M N
và mặt phẳng
ABC
bằng
60
. Khoảng cách giữa hai đường thẳng
BC
và
DM
bằng
A.
15
62
a
. B.
30
31
a
. C.
15
68
a
. D.
15
17
a
.
Câu 14. Cho hình chóp
.
S ABCD
có đáy là hình vuông cạnh
3
a
,
SA
vuông góc với mặt phẳng đáy và
SA a
. Gọi
M
là điểm thào mãn
2 0
MB MC
 
. Khoảng cách giữa hai đường thẳng
SC
và
DM
bằng:
A.
154
77
a
. B.
3 154
154
a
. C.
6 154
77
a
. D.
2 154
77
a
.
Câu 15. Cho hình lập phương .
ABCD A B C D
cạnh
a
. Tính khoảng cách từ
B
tới đường thẳng
DB
.
A.
3
6
a
. B.
6
3
a
. C.
3
3
a
. D.
6
6
a
.
Câu 16. Cho khối chóp
.
S ABC
có
SAB ABC
,
SAC ABC
,
SA a
,
2
AB AC a
,
2 2
BC a
.
Gọi
M
là trung điểm của
BC
. Khoảng cách giữa hai đường thẳng
SM
và
AC
bằng
A.
2
a
. B.
2
a
. C.
a
. D.
2
a
.
Câu 17. Cho hình chóp .
S ABC
có đáy
ABC
là tam giác đều cạnh
a
,
SA ABC
, góc giữa đường
thẳng
SB
và mặt phẳng
ABC
bằng
60
. Khoảng cách giữa hai đường thẳng
AC
và
SB
bằng
A.
2
2
a
. B.
15
5
a
. C.
2
a
. D.
7
7
a
.
Câu 18. Cho hình chóp .
S ABC
, có
SA SB SC
, đáy là tam giác đều cạnh
a
. Biết thể tích khối chóp
.
S ABC
bằng
3
3
3
a
. Khoảng cách giữa hai đường thẳng
SA
và
BC
bằng:
A.
4
7
a
B.
3 13
13
a
C.
6
7
a
D.
3
4
a
______________________________________
51
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN CỔ ĐIỂN LỚP 11 – 12 THPT
(LỚP BÀI TOÁN KHOẢNG CÁCH HAI ĐƯỜNG CHÉO NHAU – P9)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho hình chóp .
S ABC
có đáy
ABC
là tam giác vuông tại
B
,
3
AC a
,
3
BC a
,
SA
vuông
góc với mặt phẳng đáy và
3 2
SA a
. Điểm
G
là trọng tâm tam giác
SAC
( minh họa như hình bên).
Khoảng cách giữa hai đường thẳng
SC
và
BG
bằng
A.
42
7
a
. B.
6
a
. C.
4 6
3
a
. D.
6
3
a
.
Câu 2. Cho hình chóp .
S ABCD
có đáy là hình thang,
2 ,
AB a AD D C CB a
.
SA
vuông góc với mặt
phẳng đáy và
3
SA a
. Gọi
M
là trung điểm của
AB
. Khoảng cách giữa hai đường thẳng
SB
và
CM
bằng
A.
3
4
a
. B.
3
2
a
. C.
3 13
13
a
. D.
6 13
13
a
.
Câu 3. Cho hình chóp .
S ABCD
có đáy là hình bình hành
·
2 , , 120
o
AB a AD a BAD
,
SA
vuông góc với
mặt phẳng đáy và
3
SA a
. Gọi
M
là trung điểm của
AB
. Khoảng cách giữa 2 đường
DM
và
SB
bằng
A.
3 10
10
a
. B.
3 10
20
a
. C.
10
a
. D.
3 10
a
.
Câu 4. Cho hình chóp .
S ABCD
có đáy
ABCD
là hình chữ nhật với
AB a
,
2
AD a
. Hình chiếu vuông
góc của
S
trên mặt phẳng đáy là trung điểm
H
của
AD
, góc giữa
SB
và mặt phẳng đáy
( )
ABCD
là
0
45
. Tính khoảng cách giữa hai đường thẳng
SD
và
BH
theo a
A.
2
3
a
B.
3
a
. C.
2
3
a
D.
2
5
a
.
Câu 5. Cho hình lăng trụ đứng
. ' ' ' '
ABCD A B C D
có đáy
ABCD
là hình thoi. Biết
2,
AC
' 3
AA
. Tính
góc giữa hai mặt phẳng
' '
AB D
và
' '
CB D
.
A.
0
45
. B.
0
90
. C.
0
30
. D.
0
60
.
Câu 6. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật có
2
AB a
,
4
AD a
,
SA ABCD
,
cạnh
SC
tạo với đáy góc
60
. Gọi
M
là trung điểm của
BC
,
N
là điểm trên cạnh
AD
sao cho
DN a
. Khoảng cách giữa
MN
và
SB
là
A.
2 285
19
a
. B.
285
19
a
. C.
2 95
19
a
. D.
8
19
a
.
Câu 7. Cho hình chóp .
S ABC
có đáy
ABC
là tam giác đều cạnh
a
,
SA ABC
, góc giữa đường
thẳng
SB
và mặt phẳng
ABC
bằng
60
. Khoảng cách giữa hai đường thẳng
AC
và
SB
bằng
A.
2
2
a
. B.
15
5
a
. C.
2
a
. D.
7
7
a
.
Câu 8. Cho hình chóp
.
S ABCD
, đáy là hình thang vuông tại
A
và
B
, biết
AB BC a
,
2
AD a
,
3
SA a
và
SA ABCD
. Khoảng cách giữa hai đường thẳng
AC
và
SD
bằng
A.
6
5
a
. B.
30
5
a
. C.
3
2
a
. D.
15
5
a
.
Câu 9. Cho hình chóp
.
S ABCD
có đáy là hình vuông
ABCD
tâm cạnh
AB a
, đường cao
SO
vuông
góc với mặt đáy và
SO a
. Khoảng cách giữa
SC
và
AB
là
A.
2 5
7
a
. B.
5
7
a
C.
2 5
5
a
.
D.
5
5
a
.
Câu 10. Cho hình chóp
.
S ABCD
, đáy là hình thang vuông tại
A
và
B
, biết
AB BC a
,
2
AD a
,
3
SA a
và
SA ABCD
. Khoảng cách giữa hai đường thẳng
AC
và
SD
bằng
52
A.
6
5
a
. B.
30
5
a
. C.
3
2
a
. D.
15
5
a
.
Câu 11. Cho hình chóp .
S ABCD
có đáy
ABCD
là hình thang vuông tại
A
và
D
,
AD DC
,
2
AB AD
,
mặt bên
SBC
là tam giác đều cạnh
2
a
và thuộc mặt phẳng vuông góc với mặt phẳng
ABCD
. Tính
khoảng cách giữa hai đường thẳng
BC
và
SA
theo
a
.
A.
6
7
a
B.
2
7
a
C.
2 7
21
a
D.
2 21
7
a
Câu 12. Cho hình lập phương .
ABCD A B C D
có cạnh bằng
a
. Gọi
K
là trung điểm của
DD
. Khoảng
cách giữa hai đường thẳng
CK
và
A D
bằng
A.
3
3
a
B.
3
2
a
C.
2 3
3
a
D.
3
a
Câu 13. Cho hình chóp S.ABCD có ABCD là nửa lục giác đều cạnh a, hai mặt phẳng (ABCD) và (SAD)
vuông góc nhau,SAD cân tại S. Góc tạo bởi SB và mặt phẳng (ABCD) bằng 60
0
. Tính theo a khoảng
cách từ AD đến (SBC).
A.
3 15
5
a
. B.
15
5
a
. C.
15
5
. D.
3
2
a
.
Câu 14. Cho hình chóp tứ giác đều có cạnh đáy bằng
2
a
, cạnh bên bằng
3
a
. Gọi
là góc giữa mặt
bên và mặt đáy, mệnh đề nào dưới đây đúng?
A.
2
cos
4
. B.
10
cos
10
. C.
2
cos
2
. D.
14
cos
2
.
Câu 15. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình thang cân, đáy lớn
AB
. Biết rằng
AD DC CB a
,
2
AB a
, cạnh bên
SA
vuông góc với đáy và mặt phẳng
SBD
tạo với đáy góc
45
.
Gọi
I
là trung điểm của cạnh
AB
. Tính khoảng cách
d
từ
I
đến mặt phẳng
SBD
.
A.
4
a
d
. B.
2
a
d
. C.
2
4
a
d
. D.
2
2
a
d
.
Câu 16. Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông tại
B
,
2
BC a
,
SA
vuông góc với mặt
phẳng đáy và
2 3
SA a
. Gọi
M
là trung điểm
AC
. Khoảng cách giữa hai đường thẳng AB và SM là
A.
39
13
a
B.
2
13
a
C.
2 3
13
a
D.
2 39
13
a
Câu 17. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình thoi tâm
O
, cạnh
a
, góc
0
60
BAD
. Đường
thẳng
SO
tạo với mặt phẳng
ABCD
một góc
0
60
. Hình chiếu vuông góc của
S
trên mặt
phẳng
ABCD
là điểm
H
thuộc đoạn
BD
sao cho
4
BD BH
. Tính khoảng cách từ điểm
B
tới mặt
phẳng
SCD
. Tính
BE
theo
a
.
A.
3 39
52
a
. B.
2 39
13
a
. C.
3 39
13
a
. D.
39
13
a
.
53
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN CỔ ĐIỂN LỚP 11 – 12 THPT
(LỚP BÀI TOÁN KHOẢNG CÁCH HAI ĐƯỜNG CHÉO NHAU – P10)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình thang vuông tại
A
và
D
,
3 , .
AB a AD DC a
Gọi
I
là trung điểm của
AD
, biết hai mặt phẳng
SBI
và
SCI
cùng vuông góc với đáy và mặt
phẳng
SBC
tạo với đáy một góc
0
60 .
Gọi
M
điểm trên
AB
sao cho
2
AM a
, tính khoảng cách giữa
MD
và
SC
.
A.
17
5
a
. B.
15
10
a
. C.
6
19
a
. D.
3
15
a
.
Câu 2. Cho hình chóp
S.ABC
có đáy
ABC
là tam giác vuông cân tại
B
;
ABC
và
SA ABC
;
AB BC
a
. Tính góc giữa hai mặt phẳng
SAC
và
SBC
.
A.
3
13
a
. B.
13
3
a
. C.
13
3
a
. D.
3
13
a
.
Câu 3. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông tâm
O
cạnh
a
,
SO
vuông góc với mặt
phẳng
ABCD
và
SO a
. Khoảng cách giữa
SC
và
AB
bằng.
A.
5
5
a
. B.
2 5
5
a
. C.
3
15
a
. D.
2 3
15
a
.
Câu 4. Cho hình chóp
.
S ABCD
đáy là hình thoi cạnh
a
tâm
O
,
·
30
ADC
,
SA a
,
( )
SA ABCD
. Tính
khoảng cách từ
O
đến
( )
mp SCD
theo
a
.
A.
5
2
a
. B.
5
a
. C.
5
5
a
. D.
5
10
a
.
Câu 5. Cho khối chop S.ABCD có thể tích bằng 8. Gọi M,N lần lượt là trung điểm của SB,SC và ABCD
là hình bình hành (như hình vẽ). Biết diện tích của tứ giác AMND bằng 2. Tính khoảng cách h từ đỉnh
S đến mặt phẳng (AMND)
A.
3
2
h
B.
8
3
h
. C.
9
2
h
. D.
3
h
.
Câu 6. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình thoi cạnh
a
, tam giác
ABC
đểu, hình chiếu
vuông góc
H
của đỉnh S trên mặt phẳng
ABCD
trùng với trọng tâm của tam giác
ABC
. Đường
thẳng SD hợp với mặt phẳng
ABCD
góc
o
30
. Tính khoảng cách d từ B đến mặt phẳng
SCD
theo
a
.
A.
3
d a
. B.
2 21
21
a
d
. C.
21
7
a
d
. D.
2 5
3
a
d
.
Câu 7. Cho hình chóp .
S ABCD
, đáy là hình thang vuông tại
A
và
B
, biết
AB BC a
,
2
AD a
,
3
SA a
và
SA ABCD
. Gọi
M
và
N
lần lượt là trung điểm của
SB
,
SA
. Tính khoảng cách từ
M
đến
NCD
theo
a
.
A.
66
22
a
. B.
2 66
a . C.
66
11
a
. D.
66
44
a
.
Câu 8. Cho hình chóp .
S ABCD
có đáy là hình thang vuông tại
A
và
B
. Biết
SA ABCD
và
2 ;
AD a AB BC SA a
. Tính khoảng cách giữa hai đường thẳng
SB
và
CD
.
A.
3
3
a
. B.
3
2
a
. C.
3
4
a
. D.
3 3
4
a
.
Câu 9. Cho lăng trụ tam giác đều .
ABC A B C
có tất cả các cạnh đều bằng
a
. Khoảng cách giữa hai
đường thẳng
BC
và
AB
bằng
A.
21
7
a
B.
3
2
a
C.
7
4
a
D.
2
2
a
Câu 10. Cho hình chóp
.
S ABCD
có đáy là hình thang vuông tại
A
và
B
. Biết
, 2
AB BC a AD a
và
54
SA
vuông góc với mặt phẳng
ABCD
và
2
SA a
. Gọi
M
là trung điểm
AD
. Khoảng cách giữa hai
đường thẳng
BM
và
SC
bằng
A.
2
a
B.
a
C.
2
2
a
D.
2
a
Câu 11. Cho tứ diện
ABCD
có
2 ,
AC AD BC BD a ACD BCD
. Biết góc giữa hai mặt phẳng
ABC
và
ABD
là
0
60
. Độ dài cạnh
CD
bằng
A.
7
7
CD a
. B.
2 7
7
CD a
. C.
3 7
7
CD a
. D.
4 7
7
CD a
.
Câu 12. Cho khối chóp .
S ABC
có
,
SAB ABC
, , 2 ,
SAC ABC SA a AB AC a
2 2.
BC a
Gọi
M
là trung điểm của
BC
. Khoảng cách giữa hai đường thẳng
SM
và
AC
bằng
A.
2
a
. B.
2
a
. C.
a
. D.
2
a
.
Câu 13. Cho hình chóp .
S ABCD
có đáy
ABCD
là hình chữ nhật,
, 3
AB a AD a
. Mặt bên
SAB
là
tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Cosin của góc giữa đường thẳng
SD
và
mặt phẳng
SBC
bằng
A.
13
4
B.
3
4
C.
2 5
5
D.
1
4
Câu 14. Cho hình chóp .
S ABCD
có đáy
ABCD
là hình chữ nhật,
, 3
AB a AD a
. Mặt bên
SAB
là
tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Cosin của góc giữa đường thẳng
SD
và
mặt phẳng
SBC
bằng
A.
13
4
B.
3
4
C.
2 5
5
D.
1
4
Câu 15. Cho hình chóp .
S ABC
có đáy
ABC
là tam giác đều cạnh
a
,
SA ABC
, góc giữa đường
thẳng
SB
và mặt phẳng
ABC
bằng
60
. Khoảng cách giữa hai đường thẳng
AC
và
SB
bằng
A.
2
2
a
. B.
15
5
a
. C.
3
7
a
. D.
7
7
a
.
Câu 16. Cho hình chóp
.
S ABCD
có đáy là hình thang vuông tại
A
và
B
. Biết
, 2
AB BC a AD a
và
SA
vuông góc với mặt phẳng
ABCD
và
2
SA a
. Gọi
M
là trung điểm
AD
. Khoảng cách giữa hai
đường thẳng
BM
và
SC
bằng
A.
2
a
B.
a
C.
2
2
a
D.
2
a
Câu 17. Cho hình chóp .
S ABCD
có đáy là hình vuông cạnh
2
a
,
SA
vuông góc với mặt phẳng đáy và
SA = a. Gọi
M
là trung điểm
.
AB
Khoảng cách giữa hai đường thẳng
SB
và
DM
bằng:
A.
2 21
21
a
B.
21
8
a
C.
4 21
21
a
D.
a
______________________________________
55
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN CỔ ĐIỂN LỚP 11 – 12 THPT
(LỚP BÀI TOÁN KHOẢNG CÁCH HAI ĐƯỜNG CHÉO NHAU – P11)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho hình chóp S.ABCD có đáy là nửa lục giác đều nội tiếp đường tròn đường kính AD = 2a, SA vuông
góc với (ABCD), SA = 1,5a. Tính khoảng cách giữa hai đường thẳng BD, SC.
A.
2
4
a
B.
5 2
4
a
C.
3 2
4
a
D.
5 2
12
a
Câu 2. Cho hình chóp
.
S ABCD
có đáy là hình vuông cạnh
.
a
Đường thẳng
SA
vuông góc với mặt phẳng đáy,
.
SA a
Khoảng cách giữa hai đường thẳng
SB
và
CD
nhận giá trị nào trong các giá trị sau?
A.
.
a
B.
2.
a C.
3.
a D.
2 .
a
Câu 3.
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B,
2; 3
AB a BC a
. Cạnh bên SA vuông
góc với đáy. Góc giữa đường thẳng SC và mặt phẳng đáy bằng
30
o
. Gọi M là trung điểm của AC khoảng cách
giữa hai đường thẳng AB và SM bằng
A.
2 51
17
a
B.
435
29
a
C.
21
a D.
3
17
a
Câu 4.
Cho hình hộp đứng ABCD.A’B’C’D’ có
12 6
5 ; 6 ; 7 ;
7
AB a AD a BD a A A a
. Khoảng cách giữa
hai đường thẳng A’B và B’C là
A.
12
7
a
B.
12 2
7
a
C.
12 6
7
a
D.
12 3
7
a
Câu 5. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 2a, AD = 4a, SA vuông góc với (ABCD).
Cạnh SC tạo với mặt phẳng đáy góc
30
o
. Gọi M là trung điểm của BC, N là điểm trên cạnh AD sao cho DN = a.
A.
35
14
a
B.
35
7
a
C.
2 35
7
a
D.
3 35
7
a
Câu 6. Cho hình chóp S.ABCD có SA vuông góc với đáy (ABCD), ABCD là hình chữ nhật,
3; 2
AB a AD a
. Tính khoảng cách giữa hai đường thẳng SD, BC.
A.
2
3
a
B.
3
a
C. 0,75a D.
3
2
a
Câu 7. Cho lăng trụ đứng tam giác ABC.A’B’C’ có đáy là một tam giác vuông cân tại B, AB = A’A = 2a. M là
trung điểm BC. Khoảng cách giữa hai đường thẳng AM và B’C bằng
A. 0,5a B.
2
3
a
C.
7
7
a
D.
3
a
Câu 8. Cho hình chóp S.ABCD có đáy là hình thang vuông tại B và C với AB = 4a, BC = 2a, CD = a. Gọi M, N
lần lượt là trung điểm của AB và BC. Hai mặt phẳng (SMN) và (SBD) cùng vuông góc với mặt phẳng đáy và
cạnh bên SB hợp với đáy một góc
45
o
. Khoảng cách giữa SN và BD bằng
A. 0,5a B. 0,4a C. 0,2a D. 0,1a
Câu 9. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, AD = 2a, SA vuông góc với mặt phẳng
(ABCD), SA = 2a. Gọi M là trung điểm của SB. Khoảng cách giữa hai đường thẳng AM và SC bằng
A. 1,4a B.
2
3
a
C.
5 3
3
a
D.
2 5
5
a
Câu 10. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hình chiếu vuông góc của điểm S trên mặt
phẳng (ABCD) trùng với trọng tâm của tam giác BCD. Góc giữa mặt phẳng (SBC) và mặt phẳng đáy (ABCD)
bằng
30
o
. Tính khoảng cách giữa hai đường thẳng AD và SC.
A.
6
a
B. 0,5a C. 1,5a D. a
Câu 11. Hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB đều và nằm trong mặt phẳng
vuông góc với mặt phẳng (ABCD). Gọi M là trung điểm của SD. Khoảng cách giữa hai đường thẳng AM và SC
là
A.
3
2
a
B.
5
5
a
C. a D. 0,5a
56
Câu 12. Cho hình lập phương ABCD.A’B’C’D’ có cạnh a. Khoảng cách giữa hai đường thẳng AC và DC’ bằng
A. a B.
3
2
a
C.
3
3
a
D.
3
a
Câu 13. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, SD vuông góc với mặt phẳng (ABCD),
AD = a,
·
120
AOB
o
. Góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng
45
o
. Khoảng cách giữa hai
đường thẳng SB và AC bằng
A.
6
2
a
B.
6
3
a
C.
6
4
a
D.
6
6
a
Câu 13. Cho hình chóp S.ABCD có đáy là hình vuông cạnh 4a, hai mặt phẳng (SAB) và (SAC) cùng vuông góc
với mặt phẳng đáy, góc giữa mặt phẳng (SCD) với mặt phẳng đáy bằng
45
o
. Gọi M là trung điểm của SB.
Khoảng cách giữa hai đường thẳng AM và SD bằng
A.
3
3
a
B.
4 3
3
a
C.
2 3
3
a
D.
3
a
Câu 14. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Mặt bên (SAB) là tam giác đều và nằm
trong mặt phẳng vuông góc với đáy. Trên cạnh SB lấy điểm M sao cho SB = 3SM. Tính khoảng cách giữa hai
đường thẳng AM và SD.
A.
3 165
55
a
B.
3 31
31
a
C.
93
31
a
D.
3 93
31
a
Câu 15. Cho hình chóp S.ABCD có đáy là hình thang, AB = 2a, AD = DC = CB = a và SA vuông góc với mặt
phẳng đáy. Gọi M là trung điểm của cạnh AB. Khoảng cách giữa hai đường thẳng CM và SD bằng
A.
3
2
a
B. 1,5a C.
3
a
D. 0,75a
Câu 16. Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông cân tại B, AB = 2a, cạnh bên
2 2
A A a
. Gọi M là trung điểm của cạnh BC. Khoảng cách giữa hai đường thẳng AM và B’C bằng
A.
2 14
7
a
B.
7
7
a
C.
2 7
7
a
D.
4 7
7
a
Câu 17. Cho hình chóp S.ABC có SA vuông góc với (ABC), SA = 2a, đáy ABC là tam giác vuông cân tại B với
BC = 2a. Gọi M là trung điểm của cạnh AC. Khoảng cách giữa hai đường thẳng SM và BC bằng
A.
2 5
5
a
B.
5
5
a
C.
2 5
a
D.
5
2
a
Câu 18. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 6a, cạnh bên SA vuông góc với mặt phẳng
đáy, SA = 2a. Gọi G là trọng tâm tam giác ABC. Tính khoảng cách giữa hai đường thẳng SG, BC.
A.
2 3
a
B.
3
a
C.
3
2
a
D.
3 3
2
a
57
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN CỔ ĐIỂN LỚP 11 – 12 THPT
(LỚP BÀI TOÁN KHOẢNG CÁCH HAI ĐƯỜNG CHÉO NHAU – P12)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho hình lăng trụ ABC.A”B’C’ có tất cả các cạnh bằng a. Gọi M là trung điểm của cạnh BC. Khoảng cách
giữa hai đường thẳng AM và B’C là
A. a B.
2
4
a
C.
2
2
a
D.
2
a
Câu 2. Cho hình chóp S.ABCD có ABCD là hình vuông tâm O cạnh a. Hình chiếu vuông góc của S lên mặt
phẳng (ABCD) là trung điểm của AO. Mặt phẳng (SBC) tạo với mặt đáy một góc
45
o
. Tính khoảng cách giữa
hai đường thẳng SD và AC.
A.
38
17
a
B.
51
13
a
C.
13
3
a
D.
3 34
34
a
Câu 3. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, M là trung điểm BC, hình chiếu vuông góc
của S lên mặt phẳng (ABC) trùng với trung điểm của AM. Cho biết
; 3
AB a AC a
và mặt phẳng (SAB) tạo
với mặt phẳng (ABC) một góc
30
o
. Tính khoảng cách giữa hai đường thẳng SA và BC.
A.
3
2
a
B.
3
8
a
C. 1,5a D. 0,75a
Câu 4. Cho hình chóp S.ABCD có đáy là hình thoi cạnh a,
·
120
ABC
o
, SA vuông góc với mặt phẳng (ABCD).
M là điểm đối xứng của A qua D. Góc giữa đường thẳng SC với mặt phẳng (ABCD) bằng
45
o
. Khoảng cách
giữa hai đường thẳng BD và SM bằng
A.
6
2
a
B.
3
2
a
C.
6
4
a
D.
3
4
a
Câu 5. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, BC = 2a, SA vuông góc với mặt phẳng
đáy và
3
SA a
. Gọi M là trung điểm của CD, khoảng cách giữa hai đường thẳng SM và BD bằng
A.
5
4
a
B.
2
4
a
C.
30
4
a
D.
3 2
8
a
Câu 6. Cho hình chóp S.ABCD có đáy là hình thang,
·
·
90 ; 2 ;
CBA BAD AB BC a AD a
o
. Biết SA =
SB và
·
90
SCD
o
. Cạnh bên SA tạo với mặt đáy
0
45
. Tính khoảng cách giữa hai đường thẳng AB và SC bằng
A.
2 5
3
a
B.
357
21
a
C.
306
18
a
D.
2 357
21
a
Câu 7. Cho hình lăng trụ ABC.A’B’C’ có các mặt bên đều là hình vuông cạnh a. Gọi D là trung điểm của cạnh
BC. Tính khoảng cách giữa hai đường thẳng A’B và DC’ theo a.
A.
3
6
a
B.
2
6
a
C.
2
4
a
D.
3
4
a
Câu 8. Cho hình hộp ABCD.A’B’C’D’ có tất cả các cạnh đều bằng 1 và các góc phẳng đỉnh A đều bằng
60
o
.
Tính khoảng cách giữa hai đường thẳng AB’ và A’C’.
A.
22
11
B.
2
11
C.
2
11
D.
3
11
Câu 9. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = 2a, AD = 3a. Tam giác SAB cân tại S và
nằm trong mặt phẳng vuông góc với mặt phẳng đáy, góc giữa mặt phẳng (SCD) và mặt đáy là
45
o
. Gọi H là
trung điểm cạnh AB. Tính khoảng cách giữa hai đường thẳng SD, CH.
A.
3 10
109
a
B.
3 85
17
a
C.
3 11
11
a
D.
3 14
7
a
Câu 10. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông cạnh a, M và N lần lượt là trung điểm các
cạnh AB, AD; H là giao điểm của CN với DM. Biết SH vuông góc với mặt phẳng (ABCD) và
3
SH a
. Tính
khoảng cách giữa hai đường thẳng DM, SC.
A.
59
2
19
a B.
3
2
a
C.
2 57
19
a
D. a
58
Câu 11. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hình chiếu vuông góc của S trên mặt
phẳng (ABCD) là trung điểm của cạnh AB, góc giữa (SAC) và đáy bằng
45
o
. Gọi M là trung điểm của SD.
Khoảng cách giữa hai đường thẳng AM và SC bằng
A. a B.
2
4
a
C.
5
10
a
D.
5
5
a
Câu 12. Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc với nhau và AD = 2, AB = AC = 1. Gọi I là trung
điểm của đoạn thẳng BC, khoảng cách giữa hai đường thẳng AI và BD bằng
A. 1,5 B.
2
3
C.
2
D.
5
2
Câu 13. Cho S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD) và
3
SA a
. Gọi M
là trung điểm của AD. Tính khoảng cách giữa hai đường thẳng BM, SD.
A. a B. 0,5a C.
57
3
a
D.
57
19
a
Câu 14. Cho lăng trụ ABC.A’B’C’ có đáy ABC là tam giác vuông tại A,
; 3
AB a AC a
. Hình chiếu vuông
góc của A’ trên mặt phẳng (ABC) là trọng tâm tam giác ABC và
241
6
a
A A
. Gọi M là trung điểm AC, tính
khoảng cách giữa hai đường thẳng MC’ và AB’ bằng
A. 0,6a B.
15
669
a
C.
5
669
a
D.
5 3
669
a
Câu 15. Cho hình chóp tứ giác đều S.ABCD có AB = a, SA tạo với mặt phẳng đáy một góc
45
o
. Gọi M là trung
điểm của đoạn thẳng AB. Tính khoảng cách giữa hai đường thẳng SM và CD.
A.
6
3
a
B.
2
2
a
C.
3
2
a
D. 0,5a
Câu 16. Hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác cân tại A,
·
120 ; 2 ; 2
BAC AB a A A a
o
.
Gọi M là trung điểm của cạnh BC. Tính khoảng cách giữa hai đường thẳng C’M và AB.
A.
2 66
11
a
B.
66
22
a
C.
22
11
a
D.
66
11
a
Câu 17. Cho hình lăng trụ ABC.A’B’C’ có cạnh bên bằng
2
a
, đáy ABC là tam giác vuông tại B,
3;
BC a AB a
. Biết hình chiếu vuông góc của đỉnh A’ lên mặt đáy là điểm M thỏa mãn
3
AM AC
uuuur uuur
.
Khoảng cách giữa hai đường thẳng A’A và BC bằng
A.
210
15
a
B.
210
45
a
C.
714
17
a
D.
714
51
a
______________________________________
59
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN CỔ ĐIỂN LỚP 11 – 12 THPT
(LỚP BÀI TOÁN KHOẢNG CÁCH HAI ĐƯỜNG CHÉO NHAU – P13)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, AD = 2a, SA vuông góc với (ABCD), SA
= 2a. Gọi M là trung điểm của SB. Khoảng cách giữa hai đường thẳng AM và SC bằng
A.
7
5
a
B.
2
3
a
C.
5 3
3
a
D.
2 5
3
a
Câu 2. Cho hình chóp S.ABCD có SA vuông góc với (ABCD),
6
SA a
, ABCD là nửa lục giác đều nội tiếp
đường tròn đường kính AD = 2a. Tính khoảng cách từ B đến mặt phẳng (SCD) bằng
A.
6
2
a
B.
3
2
a
C.
2
2
a
D.
3
4
a
Câu 3. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = 3a, BC = 4a. Cạnh bên SA vuông góc
với đáy. Góc giữa SC và mặt phẳng đáy bằng
60
o
. Gọi M là trung điểm của AC, tính khoảng cách giữa hai
đường thẳng AB và SM.
A. 2,5a B.
3
a
C.
3
10
79
a D.
5 3
a
Câu 4. Cho hình lăng trụ tam giác ABC.A’B’C’ có độ dài cạnh bên bằng
7
a
, đáy ABC là tam giác vuông tại A,
AB = a,
3
AC a
. Biết hình chiếu vuông góc của A’ trên mặt phẳng (ABC) là trung điểm của BC. Khoảng
cách giữa hai đường thẳng A’A và B’C’ bằng
A.
2
3
a
B.
6
4
a
C.
6
3
a
D.
3
4
a
Câu 5. Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = 2a, AD = A’A = a. Khoảng cách giữa hai đường thẳng
AC và DC’ bằng
A.
2
3
a
B.
3
2
a
C.
3
3
a
D.
3
2
a
Câu 6. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B có AD = 2a, AB = BC = a và SA
vuông góc với (ABCD),
2
SA a
. Tính khoảng cách giữa hai đường thẳng SB và DC.
A.
10
5
a
B.
7
3
a
C.
6
3
a
D.
11
5
a
Câu 7. Cho hình chóp S.ABCD có đáy là hình thang, AB = 2a, AD = DC = CB = a, SA vuông góc với mặt phẳng
đáy. Gọi M là trung điểm của AB. Khoảng cách giữa hai đường thẳng CM và SD bằng
A. 0,75a B. 1,5a C.
3
a
D.
3
2
a
Câu 8. Cho hình lăng trụ đứng ABC.A’B’C’ có độ dài cạnh bên bằng 2a, đáy là tam giác ABC vuông cân tại C,
CA = CB = a. Gọi M là trung điểm của cạnh A’A. Tính khoảng cách giữa hai đường thẳng AB và MC’.
A.
3
3
a
B.
3
a
C.
3
2
a
D.
2
3
a
Câu 9. Cho hình chóp tứ giác đều S.ABCD có AB = a, góc giữa đường thẳng SA và mặt phẳng (ABCD) bằng
45
o
. Gọi M là trung điểm AB. Khoảng cách giữa hai đường thẳng SM và CD bằng
A.
6
3
a
B.
2
2
a
C.
2
a
D.
3
2
a
Câu 10. Cho lăng trụ đều ABC.A’B’C’ có tất cả các cạnh bằng a, gọi M là trung điểm BC. Khoảng cách giữa hai
đường thẳng AM và B’C bằng
A. a B.
2
4
a
C.
2
a
D.
2
2
a
Câu 11. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 6a, cạnh bên SA vuông góc với mặt phẳng
đáy, SA = 2a. Gọi G là trọng tâm tam giác ABC. Khoảng cách giữa hai đường thẳng SG và BC bằng
A.
2 3
a
B.
3
a
C.
3 3
2
a
D.
3
2
a
Câu 12. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA = 2a và vuông góc với (ABCD). Gọi M
60
là trung điểm của SD. Tính khoảng cách giữa hai đường thẳng SB, CM.
A.
3
a
B.
2
2
a
C.
2
3
a
D.
6
a
Câu 13. Hình chóp S.ABCD có đáy ABCD là hình bình hành và SA = SB = SC = a,
·
·
·
30 ; 60 ; 45
SAB SBC SCA
o o o
. Tính khoảng cách giữa hai đường thẳng AB và SD.
A.
4
11
a
B.
22
a
C.
22
11
a
D.
2 22
11
a
Câu 14. Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Hình chiếu vuông góc của S trên mặt
phẳng (ABCD) là điểm H thuộc đoạn BD sao cho HD = 3HB. Biết góc giữa mặt phẳng (SCD) và mặt phẳng đáy
là
45
o
. Tính khoảng cách hai đường thẳng SA và BD.
A.
2 38
17
a
B.
2 13
3
a
C.
2 51
13
a
D.
3 34
17
a
Câu 15. Hình chóp S.ABC có đáy ABC là tam giác vuông tại A,
·
4 3; 30
AC a ASB
o
. Góc giữa hai mặt
phẳng (SAB), (ABC) bằng
30
o
. Biết I là trung điểm của SA đồng thời là tâm mặt cầu ngoại tiếp hình chóp
S.ABC. Gọi
là góc giữa IB và mặt (SAC). Khi
21
sin
7
thì khoảng cách hai đường thẳng AC và SB bằng
A.
14 3
5
a
B.
8 3
3
a
C.
3 3
a
D.
4 3
a
Câu 16. Cho hình chữ nhật ABCD.A’B’C’D’ có cạnh bằng AB = 2a, AD = AA’ = a như hình vẽ. Tính khoảng cách
giữa hai đường thẳng BD và AD’.
A. a B. 0,5a C.
3
a
D.
2
3
a
Câu 17. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt phẳng (ABC), góc
giữa đường thẳng SB và mặt phẳng (ABC) bằng
60
o
. Khoảng cách giữa hai đường thẳng AC và SB bằng
A. 2a B.
2
2
a
C.
15
5
a
D.
7
7
a
Câu 18. Cho khối chóp S.ABCD có thể tích bằng
3
2
a
và đáy ABCD là hình bình hành. Biết diện tích tam giác
SAB bằng
2
a
. Tính khoảng cách giữa hai đường thẳng SA, CD.
A. a B. 6a C. 3a D. 1,5a
Câu 19. Cho lăng trụ tam giác đều ABC.A’B’C’ có cạnh bên bằng cạnh đáy. Đường thẳng MN (với M thuộc
đường thẳng A’C, N thuộc đường thẳng BC’) là đường vuông góc chung của A’C và BC’. Tính tỉ số
NB
NC
.
A. 1 B. 1,5 C.
2
3
D.
5
2
______________________________________
61
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN CỔ ĐIỂN LỚP 11 – 12 THPT
(LỚP BÀI TOÁN KHOẢNG CÁCH HAI ĐƯỜNG CHÉO NHAU – P14)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho hình chóp ABCD.A’B’C’D’ có
·
·
·
1; 60
AB AD A A BAD BAA DAA
o
. Tính khoảng cách
giữa hai đường thẳng AB’ và A’C’.
A.
2
11
B.
8
11
C.
3
11
D.
2
11
Câu 2. Cho hình lăng trụ đều ABC.A’B’C’ có tất cả các cạnh có độ dài bằng 2. Tính khoảng cách giữa hai
đường thẳng AC’ và A’B.
A.
2
5
B.
3
2
C.
1
2
D.
3
5
Câu 3. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với (ABC), góc giữa hai đường
thẳng SB và mặt phẳng (ABC) bằng
60
o
. Tính khoảng cách giữa hai đường thẳng AC, SB.
A.
15
5
a
B.
2
2
a
C.
7
7
a
D. 2a
Câu 4. Cho hình chóp S.ABCD có đáy là hình thoi tâm O, cạnh bằng
3
a
,
·
60
BAD
o
, SA vuông góc với mặt
phẳng đáy, SA = 3a. Tính khoảng cách giữa hai đường thẳng SO và AD.
A.
5
a
B.
17
a
C.
3
17
a
D.
3
5
a
Câu 5. Cho hình chóp S.ABCD có cạnh đáy bằng 2a, cạnh SA tạo với mặt phẳng đáy một góc
30
o
, khoảng
cách giữa hai đường thẳng SA và CD bằng
A.
2 15
5
a
B.
3 14
5
a
C.
2 10
5
a
D.
4 5
5
a
Câu 6. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với đáy và SA = 3a. Gọi E, F,
G lần lượt là trung điểm của các cạnh AB, AC, SC. Tính khoảng cách giữa hai đường EF, BG.
A.
3 13
26
a
B.
13
6
a
C.
13
3
a
D.
3 13
13
a
Câu 7. Cho hình tứ diện đều ABCD có cạnh bằng a, M là trung điểm của cạnh AD, tính khoảng cách giữa hai
đường thẳng AB, CM.
A.
33
11
a
B.
33
a
C.
22
a
D.
22
11
a
Câu 8. Cho hình chóp S.ABC có đáy là tam giác vuông tại A, AB = 4a, AC = 3a. Biết
·
2 3; 30
SA a SAB
o
và
hai mặt phẳng (SAB), (ABC) vuông góc. Tính khoảng cách từ A đến mặt phẳng (SBC).
A.
3 7
14
a
B.
8 7
3
a
C.
6 7
7
a
D.
3 7
2
a
Câu 9. Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau, OA = OB = a, OC = 2a. Gọi M là trung
điểm của AB, khoảng cách giữa hai đường thẳng OM và AC bằng
A.
2
3
a
B.
2 5
5
a
C.
2
2
a
D.
3
a
Câu 10. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, AB = BC = a, AD = 2a, SA = a và
SA vuông góc với đáy (ABCD). Tính khoảng cách giữa hai đường thẳng SD, AC.
A.
6
3
a
B.
3
2
a
C.
3
3
a
D.
6
2
a
Câu 11. Cho hình chóp S.ABCD có đáy là hình thang có đáy lớn AB, SA vuông góc với mặt phẳng đáy, AD =
CD = CB = 0,5AB = 2a,
3
SA a
. Khoảng cách giữa hai đường thẳng SD và CB bằng
A.
6
a
B.
3
2
a
C.
2
3
a
D.
6
2
a
Câu 12. Cho hình chóp S.ABCD có đáy là hình thang, AB = 2a, AD = DC = CB = a, SA vuông góc với đáy và SA
= 2a. Khoảng cách giữa hai đường thẳng SC, BD.
62
A. 1,5a B. 1,2a C. 0,5a D. 0,4a
Câu 13. Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB = a, AD = 2a, H là điểm thuộc AC sao cho 3AH =
AC, SH vuông góc với (ABCD), SH = 2a. Gọi G là trọng tâm tam giác SAD. Khoảng cách giữa hai đường thẳng
CG, SB khi đó bằng
A.
6
3
a
B.
6
6
a
C.
3
3
a
D.
2
2
a
Câu 14. Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, SA vuông góc với mặt phẳng đáy, góc giữa mặt
phẳng (SBC) và mặt đáy là
60
o
. Gọi M, N lần lượt là trung điểm của AB, AC. Tính khoảng cách giữa hai đường
thẳng SB, MN.
A. 0,375a B. 0,75a C.
6
a
D.
6
2
a
Câu 15. Cho hình chóp S.ABCD có đáy là hình thoi cạnh a,
·
6
120 ;
4
a
BAD SA
o
và vuông góc với đáy. Gọi
G
1
, G
2
lần lượt là trọng tâm các tam giác ABC, SAB. Tính khoảng cách giữa hai đường thẳng CD, G
1
G
2
.
A. 0,5a B. 0,25a C.
6
a
D.
3
a
Câu 16. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, D, AB = 2a, AD = DC = a, SA vuông
góc với mặt phẳng đáy và SA = 4a. Gọi M là điểm trên SD sao cho SM = 2MD, O là giao điểm của AC và BD.
Tính khoảng cách giữa hai đường thẳng BC, OM.
A. 0,75a B. 2,25a C.
4
9
a
D.
4
3
a
Câu 17. Cho hình lăng trụ tam giác ABC.A’B’C’ có độ dài cạnh bên bằng
7
a
, đáy ABC là tam giác vuông tại
A,
; 3
AB a AC a
. Hình chiếu vuông góc của A’ trên mặt phẳng (ABC) là trung điểm của BC. Tính khoảng
cách giữa hai đường thẳng A’A và B’C’.
A.
3
2
a
B.
2
3
a
C.
3
2
a
D.
3
2
a
Câu 18. Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại A. Gọi E là trung điểm của AB. Cho
biết AB = 2a, C’C = 4a và
13
BC a . Tính khoảng cách giữa hai đường thẳng A’B và CE.
A.
12
7
a
B.
4
7
a
C.
3
7
a
D.
6
7
a
Câu 19. Cho lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy bằng a và chiều cao 2a. Gọi M, N lần lượt là trung
điểm BC và A’C’. Tính khoảng cách giữa hai đường thẳng AM và B’N.
A. 2a B. a C.
2
a
D.
3
a
______________________________________
| 1/62
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


THÂN TẶNG QUÝ THẦY CÔ VÀ CÁC EM HỌC SINH TOÀN QUỐC
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM CHUYÊN ĐỀ
GÓC, KHOẢNG CÁCH VẬN DỤNG CAO LỚP 11 THPT
CREATED BY GIANG SƠN; TEL 0333275320 TP.THÁI BÌNH; 20/8/2021 TOÀN TẬP
GÓC, KHOẢNG CÁCH VẬN DỤNG CAO PHIÊN BẢN 2021 1 TOÀN TẬP
GÓC, KHOẢNG CÁCH VẬN DỤNG CAO
__________________________________________________________________________________________________
VẬN DỤNG CAO GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG – P1
VẬN DỤNG CAO GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG – P2
VẬN DỤNG CAO GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG – P3
VẬN DỤNG CAO GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG – P4
VẬN DỤNG CAO GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG – P5
VẬN DỤNG CAO GÓC NHỊ DIỆN – P1
VẬN DỤNG CAO GÓC NHỊ DIỆN – P2
VẬN DỤNG CAO GÓC NHỊ DIỆN – P3
VẬN DỤNG CAO GÓC NHỊ DIỆN – P4
VẬN DỤNG CAO GÓC NHỊ DIỆN – P5
VẬN DỤNG CAO GÓC NHỊ DIỆN – P6
VẬN DỤNG CAO KHOẢNG CÁCH GIỮA ĐIỂM VÀ MẶT PHẲNG – P1
VẬN DỤNG CAO KHOẢNG CÁCH GIỮA ĐIỂM VÀ MẶT PHẲNG – P2
VẬN DỤNG CAO KHOẢNG CÁCH GIỮA ĐIỂM VÀ MẶT PHẲNG – P3
VẬN DỤNG CAO KHOẢNG CÁCH GIỮA ĐIỂM VÀ MẶT PHẲNG – P4
VẬN DỤNG CAO KHOẢNG CÁCH GIỮA ĐIỂM VÀ MẶT PHẲNG – P5
VẬN DỤNG CAO KHOẢNG CÁCH GIỮA ĐIỂM VÀ MẶT PHẲNG – P6
VẬN DỤNG CAO KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG CHÉO NHAU – P1
VẬN DỤNG CAO KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG CHÉO NHAU – P2
VẬN DỤNG CAO KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG CHÉO NHAU – P3
VẬN DỤNG CAO KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG CHÉO NHAU – P4
VẬN DỤNG CAO KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG CHÉO NHAU – P5
VẬN DỤNG CAO KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG CHÉO NHAU – P6
VẬN DỤNG CAO KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG CHÉO NHAU – P7
VẬN DỤNG CAO KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG CHÉO NHAU – P8
VẬN DỤNG CAO KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG CHÉO NHAU – P9
VẬN DỤNG CAO KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG CHÉO NHAU – P10
VẬN DỤNG CAO KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG CHÉO NHAU – P11
VẬN DỤNG CAO KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG CHÉO NHAU – P12
VẬN DỤNG CAO KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG CHÉO NHAU – P13
VẬN DỤNG CAO KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG CHÉO NHAU – P14 2
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN CỔ ĐIỂN LỚP 11 – 12 THPT
(LỚP BÀI TOÁN GÓC GIỮA ĐƯỜNG VÀ MẶT PHẲNG – P1)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho hình chóp S.ABCD có đáy là tam giác vuông đỉnh B, AB = a, SA vuông góc với đáy là SA = a. Tính
tan của góc giữa SA và mặt phẳng (SBC). A. 2 B. 1 C. 3 D. 0,5
Câu 2. Cho khối chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy và khoảng cách từ A đến a 2 mặt phẳng (SBC) bằng
. Tính sin của góc giữa đường thẳng SA và mặt phẳng (SBD). 2 3 2 3 2 A. B. C. D. 3 3 4 2
Câu 3. Hình chóp S.ABCD có đáy là hình chữ nhật, AB = a, AD = 2a, SA vuông góc với đáy và mặt phẳng
(SCD) tạo với đáy một góc 30o . Tính cosin của góc giữa đường thẳng SC và mặt phẳng (SBD). 35 2 23 13 A. B. C. D. 38 3 38 31
Câu 4. Cho hình chóp S.ABC có SA = 3a và SA vuông góc với đáy (ABC), AB = BC = 2a, · ABC  120o . Tính sin
của góc giữa đường thẳng SA và mặt phẳng (SBC). 3 2 5 A. 0,5 B. C. D. 4 2 5
Câu 5. Cho hình chóp S.ABC có đáy là hình vuông cạnh 2a, hình chiếu vuông góc của S lên mặt đáy trùng với
trung điểm H của AB. Biết SD = 3a, tính cosin của góc giữa đường thẳng SA và mặt phẳng (SBD). 145 10 2 5 A. B. 0,5 C. D. 15 15 15
Câu 6. Hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, AD  3a, AB  BC  2a, SA  a . Biết
rằng SA vuông góc với đáy (ABCD). Tính sin của góc giữa đường thẳng SB và mặt phẳng (SCD). 3 5 10 3 A. B. C. D. 205 205 35 3
Câu 7. Cho hình chóp S.ABC có đáy là tam giác vuông tại B có AB = a, BC = 2a. Tam giác SAC cân tại S và
thuộc mặt phẳng vuông góc với đáy. Biết SB = 1,5a, tính cosin của góc giữa đường thẳng SA và mặt phẳng (SBC). 145 10 2 5 A. B. 0,5 C. D. 15 15 15
Câu 8. Cho hình chóp S.ABC có đáy là tam giác vuông, ·
ABC  30o, SBC là tam giác đều cạnh à và mặt bên uuuur uuur r
(SBC) vuông góc với đáy. Gọi M là điểm thỏa mãn 2MC  MB  0 và  là góc giữa đường thẳng SM với mặt
phẳng (SAB). Khi đó sin gần nhất giá trị nào sau đây A. 0,2 B. 0,3 C. 0,4 D. 0,45
Câu 9. Hình chóp S.ABC có đáy là tam giác đều cạnh a, hình chiếu vuông góc H của đỉnh S trên cạnh AC là
điểm H sao cho HA = 2HC. Tính cosin của góc giữa đường thẳng SG và mặt phẳng (SBC) với G là trọng tâm tam giác ABC và SH = 0,5a. 559 129 3 13 10 A. B. C. D. 26 26 26 15
Câu 10. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SD = 1,5a. Tam giác SAB cân tại S và thuộc mặt
phẳng vuông góc với đáy. Gọi M là trung điểm của SB, cosin của góc giữa đường thẳng AM và mặt phẳng
(SBD) gần nhất giá trị nào sau đây A. 0,25 B. 0,67 C. 0,52 D. 0,73
Câu 11. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, ·
BAD  60o, SA  a và SA vuông góc với mặt
phẳng đáy. Tính cosin của góc giữa đường thẳng SB và mặt phẳng (SCD). 145 154 21 21 A. B. C. D. 15 14 7 14
Câu 12. Cho khối lăng trụ đứng ABC.AB C
  có đáy là tam giác đều cạnh a, đường thẳng A’C tạo với mặt
phẳng đáy một góc 60o . Tính cosin của góc giữa đường thẳng C’B với mặt phẳng ( ABC) . 3 85 10 13 11 A. B. C. D. 10 15 15 5
Câu 13. Cho khối lăng trụ đứng ABC.AB C
  có đáy ABC là tam giác vuông tại A, AB  a 3; AC  AA  a .
Tính sin của góc tạo bởi đường thẳng A’B và mặt phẳng (BCC B  ) . A. 60o B. 30o C. 45o D. 75o
Câu 14. Cho hình chóp S.ABC có các tam giác ABC và SBC là tam giác đều và nằm trong hai mặt phẳng vuông
góc với nhau. Góc giữa đường thẳng SA và mặt phẳng (ABC) là A. 60o B. 30o C. 45o D. 75o
Câu 15. Hình chóp S.ABC có SA vuông góc với (ABC), SA = a, tam giác ABC đều cạnh a. Gọi  là góc giữa SC
và mặt phẳng (SAB). Khi đó tan bằng 3 6 23 A. B. 2 C. D. 5 2 4
Câu 16. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh SA vuông góc với đáy (ABCD) và
SA  a 6 . Tính sin của góc tạo bởi AC và mặt phẳng (ABC). 1 1 1 3 A. B. C. D. 3 6 7 7
Câu 17. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại B và C, cạnh SA vuông góc với đáy (ABCD) và ·
CD  2AB; AD  a;SA  2a; ADC  30o. Khi đó ·
sin SD,(SBC) gần nhất giá trị nào sau đây A. 0,25 B. 0,71 C. 0,34 D. 0,36
Câu 18. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B với AD = 2AB = 2BC = 2a, SA
vuông góc với mặt phẳng đáy, SA = 2a. Tính sin của góc giữa đường thẳng SD và mặt phẳng (SAC). 3 2 5 A. 0,5 B. C. D. 4 2 5
Câu 19. Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông tâm O cạnh a, cạnh bên tạo với đáy một góc
60o . Điểm M thuộc cạnh SB sao cho 3SM  SB . Khi đó sin của góc giữa OM và mặt phẳng (SCD) gần nhất giá trị nào sau đây ? A. 0,03 B. 0,2 C. 0,09 D. 0,15
Câu 20. Cho hình chóp đều S.ABCD có tất cả các cạnh bằng a. Gọi G là trọng tâm tam giác SCD, tan của góc
giữa đường thẳng AG và mặt phẳng (SCD) bằng 17 5 5 A. B. C. D. 17 7 3 5
______________________________________ 4
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN LỚP 12 THPT
(LỚP BÀI TOÁN GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG – P2)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại A cạnh AB = a, SA vuông góc với mặt phẳng và
SA  a 2 . Gọi M là trung điểm của SA, tính sin biết  là góc giữa BM và mặt phẳng (SBC). 2 1 2 1 A. B. C. D. 2 15 15 15 2 15
Câu 2. Cho hình lập phương ABCD.A’B’C’D’. Gọi M, N lần lượt là trung điểm của cạnh AC, B’C’. Tính sin với
 là góc giữa đường thẳng MN và mặt phẳng (A’B’C’D’). 5 2 5 2 1 A. sin  B. sin  C. sin  D. sin  5 5 2 2
Câu 3. Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, tam giác SAB là tam giác đều và nằm trong mặt
phẳng vuông góc với đáy. Gọi M, N lần lượt là trung điểm của SC và AD. Góc giữa đường thẳng MN và mặt phẳng (ABCD) bằng A. 0 45 B. 60o C. 90o D. 30o
Câu 4. Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng đáy, ABCD là hình chữ nhật có
AD  3a ; AC  5a , góc giữa hai mặt phẳng SCD và  ABCD bằng 0
45 . Khi đó côsin của góc giữa đường
thẳng SD và mặt phẳng SBC bằng 7 4 2 2 17 A. . B. . C. . D. . 5 5 5 5
Câu 5. Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông tâm O, cạnh a. Gọi M, N lần lượt là trung điểm
của SA và BC. Góc giữa đường thẳng MN và mặt phẳng (ABCD) bằng 60o . Tính cosin của góc giữa đường
thẳng MN và mặt phẳng (SBD). 41 5 2 5 2 41 A. B. C. D. 4 5 5 7
Câu 6. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a 2 và cạnh bên bằng a 3 . Gọi M, N theo thứ
tự là trung điểm của các cạnh SB, CD. Tính sin của góc tạo bởi đường thẳng MN và mặt phẳng (SBC). 2 15 14 3 105 2 70 A. B. C. D. 15 14 105 35
Câu 7. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, SA vuông góc với (ABCD). Biết
rằng AD = 2AB = 2BC = 2SA = 2a. Gọi  là góc giữa đường thẳng SA và (SAC). Khi đó 10 10 A. cos  B. sin  C. tan  2 D. tan  3 5 5
Câu 8. Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a, M là trung điểm của cạnh SD. Tính tan
của góc giữa đường thẳng BM và mặt phẳng (ABCD) bằng 1 2 3 2 A. B. C. D. 3 3 3 2
Câu 9. Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a. Gọi M là điểm nằm trên SD sao cho
SM = 2MD. Giá trị tan của góc giữa đường thẳng BM và mặt phẳng (ABCD) bằng 1 3 5 A. 0,2 B. C. D. 3 3 5
Câu 10. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Tam giác SAB cân tại S và (SAB) vuông 3 4a
góc với mặt phẳng (ABCD). Giả sử thể tích của khối chóp S.ABCD bằng
. Tính cosin góc giữa đường 3
thẳng SC và mặt phẳng (ABCD). 3 30 14 5 A. cos  B. cos  C. cos  D. cos  2 6 4 3
Câu 11. Cho hình lập phương ABCD.A1B1C1C1 có cạnh a. Gọi I là trung điểm của BD. Tính góc giữa hai đường thẳng A1D và B1I. A. 0 45 B. 60o C. 90o D. 30o 5
Câu 12. Cho tứ diện S.ABC có SA  SB  SC  AB  AC  ;
a BC  a 2 . Góc giữa hai đường thẳng AB và SC bằng A. 120o B. 60o C. 90o D. 30o a 6
Câu 13. Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB = a và AD 
, mặt bên SAB là tam giác 2
đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Góc giữa đường thẳng SB và mặt phẳng (SCD) bằng A. 0 45 B. 60o C. 90o D. 30o a 3
Câu 14. Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm I, cạnh a, ·
BAD  60o, SA  SB  SC  . 2
Gọi  là góc giữa đường thẳng SD và mặt phẳng (SBC). Tính sin . 5 2 1 2 2 A. B. C. D. 3 3 3 3
Câu 15. Cho hình chóp S.ABCD có cạnh đáy bằng a, tâm O. Gọi M, N lần lượt trung điểm của SA, BC. Biết rằng
góc giữa MN và (ABCD) bằng 60o . Cosin của góc giữa MN và mặt phẳng (SBD) bằng 5 41 2 5 2 41 A. B. C. D. 5 41 5 41
Câu 16. Hình lăng trụ tam giác ABC.A’B’C’ có đáy là tam giác đều cạnh a, AA  a 6 . Hình chiếu vuông góc H
của A trên mặt phẳng (A’B’C’) trùng với trọng tâm tam giác A’B’C’. Tính cosin của góc giữa cạnh bên và mặt đáy hình lăng trụ. 2 2 15 3 A. B. C. D. 3 6 15 6
Câu 17. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B, AB = a, SA vuông góc với AB, SC vuông góc
với BC, SB = 2a. Gọi M, N lần lượt là trung điểm SA, BC. Tính cosin của góc giữa đường MN với mặt (ABC). 6 2 6 10 2 A. B. C. D. 3 5 5 11
Câu 18. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a 2 và cạnh bên bằng 2a. Góc giữa đường
thẳng SB với mặt phẳng SAC bằng A. 0 60 . B. 0 30 . C. 0 90 . D. 0 45 .
Câu 19. Cho hình chóp S.ABCD có SA   ABCD và SA  a 3 . Đáy ABCD là hình chữ nhật có
AB  a, AD  a 3 . Gọi M là trung điểm của CD, góc giữa SAvà mặt phẳng SBM  bằng . tan bằng: 2 4 2 4 A. . B. . C. . D. . 15 15 13 13
Câu 20. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B , AD = 2AB  2BC  2a ,
SA  2 a và SA vuông góc với ABCD . Gọi M là trung điểm của SB và  là góc tạo bởi đường thẳng MD
và mặt phẳng SCD . Khi đó sin bằng: 10 10 15 15 A. B. . C. . D. . 24 12 24 12
Câu 21. Cho hình chóp S.ABCD có SA   ABCD , SA  a 2 , ABCD là hình thang vuông tại , A B và
2AB  2BC  AD  2a . Gọi O  AC  BD , M là trung điểm SB . Tính sin góc giữa OM và SCD . 2 35 35 3 35 35 A. . B. . C. . D. . 35 35 70 70
______________________________________ 6
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN LỚP 12 THPT
(LỚP BÀI TOÁN GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG – P3)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho hình vuông ABCD và tam giác đều SAB cạnh a nằm trong hai mặt phẳng vuông góc với nhau.
Tính sin góc giữa đường thẳng SC và mặt phẳng SAD . 3 2 6 3 A. . B. . C. . D. . 3 2 4 4
Câu 2. Cho hình lăng trụ tam giác đều ABC.A B  C
  có cạnh đáy bằng a , cạnh bên AA  a . Gọi M , N lần a
lượt là trung điểm của BB , B C
 . Lấy điểm P thuộc A B
  sao cho PB  . Tính tangóc giữa đường thẳng 4
AP và mặt phẳng MNP 1 1 A. 2 . B. . C. . D. 3. 2 3
Câu 3. Cho hình chóp S.ABCD có ABCD là hình vuông, S
 AB là tam giác đều và nằm trong mặt phẳng
vuông góc với đáy. Gọi M là trung điểm BC . Gọi  góc hợp bởi đường thẳng SA và mặt phẳng SDM  . Tính  . A. 30 . B. 60. C. 55 . D. 45.
Câu 4. Cho hình lăng trụ đều ABC.A B  C
  có tất cả các cạnh bằng 1. Điểm M và N lần lượt là trung điểm các
đoạn AC , BB . Côsin góc giữa đường thẳng MN và  BAC bằng 21 7 3 21 A. . B. . C. . D. . 14 14 21 21 a 10
Câu 5. Cho hình lăng trụ AB . C A' B'C ' có AA'  , AC  a 2 , BC  a , · 0
ACB 135 . Hình chiếu vuông 4
góc của C lên mặt phẳng ( ABC ) trùng với trung điểm M của AB . Tính góc tạo bởi đường thẳng C M  với mặt phẳng  ACC A   A. 0 90 . B. 0 60 . C. 0 45 . D. 0 30 .
Câu 6. Cho lăng trụ đứng AB . C ’ A ’ B ’ C có đáy ABC cân đỉnh · ,
A ABC   , BC ' tạo đáy góc  . Gọi I là trung điểm của A ’ A , biết · 0 BIC  90 . Tính 2 2 tan   tan  1 A. . B. 2 . C. 3 . D. 1. 2
Câu 7. Cho hình lăng trụ đứng  ABC.A' B 'C ' có đáy là tam giác vuông cân tại A , AC  b , các cạnh bên có
độ dài bằng b . Tính góc giữa đường thẳng AB và mặt phẳng AB 'C '. 3 3 1 6 A. . B. . C. . D. . 2 3 2 3
Câu 8. Cho hình lăng trụ AB . C A B  C
  có đáy ABC là tam giác vuông tại B , ·
AB  a, ACB  30 , M là trung
điểm cạnh AC . Góc giữa cạnh bên và mặt đáy của lăng trụ bằng 60 . Hình chiếu vuông góc của đỉnh A lên
mặt phẳng  ABC là trung điểm H của BM . Gọi  là góc tạo bởi A H  với  A A  CC . Tính sin ? 1 3 2 3 A. . B. . C. . D. . 3 4 5 6
Câu 9. Cho hình hộp chữ nhật ABC . D A B  C  D
  có đáy ABCD là hình vuông cạnh bằng 2 2 , AA  4. Tính
góc giữa đường thẳng A C
 với mặt phẳng  AAB B  . A. 30 . B. 90 . C. 60 . D. 45 .
Câu 10. Cho hình lập phương ABC . D  A  B C 
D . Tính góc tạo bởi đường thẳng AB và mặt phẳng BDD B   . A. 60 . B. 90 . C. 45 . D. 30 . 17
Câu 11. Cho hình hộp chữ nhật ABC .
D A'B 'C 'D ' nội tiếp mặt cầu S  có bán kình R  Gọi I , J là 2 7
trung điểm BC ,CD và  là góc giữa đường thẳng AC ' và mặt phẳng C 'IJ  . Giá trị lớn nhất của sin là 3 3  4 4  A. . B. . C. . D. . 5 5 5 5
Câu 12. Cho hình lập phương ABC . D A B  C  D
  có cạnh bằng a và I  AC BD. Gọi M , N lần lượt là trung điểm của C D
  , AA . Gọi  là góc tạo bởi đường thẳng IN và mặt phẳng  ACM . Tính sin . 3 2 5 3 3 A. . B. . C. . D. . 9 2 9 24 a 3
Câu 13. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A . BC  a . SA  SB  SC  . Góc giữa 3
đường thẳng SA và  ABC bằng A. 30 . B. 45. C. 60. D. 90 .
Câu 14. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Tam giác SAB đều và nằm trong mặt
phẳng vuông góc với đáy. Gọi  là góc giữa đường thẳng SC và  ABCD. Giá trị của tan bằng: 15 15 5 A. 1. B. . C. . D. . 5 3 2
Câu 15. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B ; SAB là tam giác cân tại S ;
AD  3BC  3AB  3a . Gọi M là điểm thuộc đoạn AD sao cho AD  3MD . Biết rằng SCM là tam giác đều.
Gọi  là góc giữa đường thẳng SB và mặt phẳng SAD . Khi đó cos nhận giá trị là 2 7 21 42 154 A. . B. . C. . D. . 7 7 14 14
Câu 16. Cho tứ diện OABC có O , A O ,
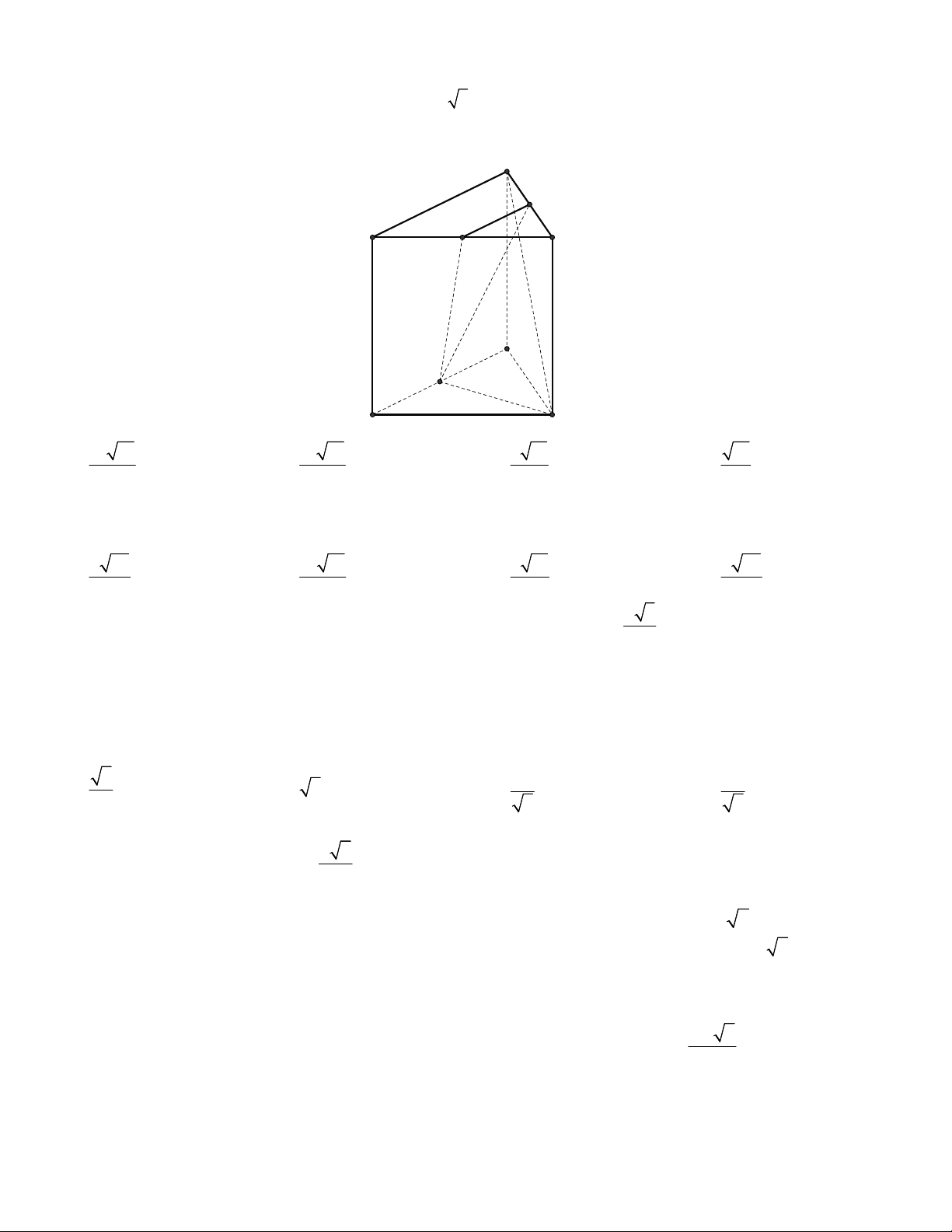
B OC đôi một vuông góc với nhau và OA  OB  OC . Gọi M là trung
điểm của BC (tham khảo hình vẽ bên dưới). Góc giữa hai đường thẳng OM và AB bằng A. 0 45 B. 0 90 C. 0 30 D. 0 60 3
Câu 17. Cho tứ diện ABCD với · · 0
AC  AD,CAB  DAB  60 ,CD  AD . Gọi  là góc giữa hai đường thẳng 2
AB và CD . Chọn khẳng định đúng về góc  . 3 1 A. cos  B. 0 30 C. 0 60 D. cos  4 4
Câu 18. Cho hình hộp chữ nhật ABC . D A B  C  D
  , biết đáy ABCD là hình vuông. Tính góc giữa AC và BD . A. 90 . B. 30 . C. 60 . D. 45.
Câu 19. Cho tứ diện ABCD có AB  CD  2a . Gọi M , N lần lượt là trung điểm AD và BC . Biết MN  a 3 ,
góc giữa hai đường thẳng AB và CD bằng. A. 0 45 . B. 0 90 . C. 0 60 . D. 0 30 .
Câu 20. Cho hình lập phương ABC . D AB C  D
  ; gọi M là trung điểm của B C
 . Góc giữa hai đường thẳng AM và BC bằng A. 45. B. 90 . C. 30 . D. 60 .
Câu 21. Cho hình chóp S.ABC có độ dài các cạnh SA  SB  SC  AB  AC  a và BC  a 2 . Góc giữa hai
đường thẳng AB và SC là? A. 45. B. 90 . C. 60 . D. 30 . 8
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN LỚP 12 THPT
(LỚP BÀI TOÁN GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG – P4)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho hình lăng trụ tam giác đều ABC.A B  C
  có AB  a và AA  2 a . Góc giữa hai đường thẳng AB và BC bằng A. 60 . B. 45 . C. 90 . D. 30 .
Câu 2. Cho tứ diện ABCD có DA  DB  DC  AC  AB  a , ·
ABC  45 . Tính góc giữa hai đường thẳng AB và DC . A. 60 . B. 120 . C. 90 . D. 30 .
Câu 3. Cho hình lập phương ABC . D A B  C  D
  . Gọi M , N lần lượt là trung điểm của AD , BB . Cosin của góc
hợp bởi MN và AC ' bằng 3 2 5 2 A. . B. . C. . D. . 3 3 3 4
Câu 4. Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB  2a , BC  a . Hình chiếu vuông góc H của đỉnh
S trên mặt phẳng đáy là trung điểm của cạnh AB , góc giữa đường thẳng SC và mặt phẳng đáy bằng 0 60 .
Tính cosin góc giữa hai đường thẳng SB và AC 2 2 2 2 A. . B. . C. . D. . 7 35 5 7
Câu 5. Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông, E là điểm đối xứng của D qua trung
điểm SA . Gọi M , N lần lượt là trung điểm của AE và BC . Góc giữa hai đường thẳng MN và BD bằng A. 90 . B. 60 . C. 45 . D. 75 .
Câu 6. Cho hình chóp đều S.ABCD có tất cả các cạnh đều bằng a . Gọi M , N lần lượt là trung điểm của AD
và SD . Số đo của góc giữa hai đường thẳng MN và SC là A. 45 . B. 60 . C. 30 . D. 90 .
Câu 7. Cho hình lăng trụ ABC.A B  C
  có đáy ABC là tam giác vuông tại A , AB  a , AC  a 3 . Hình chiếu
vuông góc của A lên mặt phẳng  ABC  là trung điểm H của BC , AH  a 3 . Gọi  là góc giữa hai đường thẳng A B  và B C  . Tính cos . 1 6 6 3 A. cos  . B. cos  . C. cos  . D. cos  . 2 8 4 2
Câu 8. Cho tứ diện đều ABCD , M là trung điểm của cạnh BC . Tính giá trị của cos AB, DM  . 3 3 1 2 A. . B. . C. . D. . 2 6 2 2
Câu 9. Lăng trụ ABC.AB C
  có đáy ABC là tam giác đều cạnh a , tam giác A B
 C đều nằm trong mặt phẳng
vuông góc với  ABC  . M là trung điểm cạnh CC . Tính cosin góc  giữa hai đường thẳng AA và BM . 2 22 33 11 22 A. o c s  . B. o c s  . C. o c s  . D. o c s  . 11 11 11 11
Câu 10. Cho hình lăng trụ tam giác đều ABC.MNP có tất cả các cạnh bằng nhau. Gọi I là trung điểm cạnh
AC . Côsin của góc giữa hai đường thẳng NC và BI bằng 6 15 6 10 A. . B. . C. . D. . 4 5 2 4
Câu 11. Cho tứ diện đều ABCD , M là trung điểm của cạnh BC . Khi đó cos  AB, DM  bằng 2 3 1 3 A. . B. . C. . D. . 2 6 2 2
Câu 12. Cho hình chóp S.ABCD có đáy là hình vuông cạnh 3a , SA vuông góc với mặt phẳng đáy và
SA  2a . Góc giữa SC và mặt phẳng (ABCD) bằng A. 0 45 . B. 0 60 . C. 0 30 . D. 0 90 .
Câu 13. Cho hình chóp S.ABC có SA vuông góc với mặt phẳng  ABC, SA  a 2, tam giác ABC vuông cân tại
B và AC  2a (minh họa nhứ hình bên). Góc giữa đường thẳng SB và mặt phẳng  ABC  bằng A. 30. B. 45. C. 60. D. 90. 9
Câu 14. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , AB  a , BC  2a , SA vuông góc với
mặt phẳng đáy và SA  15a .Góc giữa đường thẳng SC và mặt phẳng đáy bằng A. 45 . B. 30 . C. 60 . D. 90 .
Câu 15. Cho hình chóp S.ABC có đáy là tam giác vuông tại B , AB  3a, BC  3a, SA vuông góc với mặt
phẳng đáy và SA  2a . Góc giữa đường thẳng SC và mặt phẳng đáy bằng A. 60o . B. 0 45 . C. 0 30 . D. 0 90 .
Câu 16. Cho hình chóp S.ABC và có đáy ABC là tam giác vuông tại B, AB  a, BC  3 ; a SA vuông góc với
mặt phẳng đáy và SA  30a . Góc giữa đường thẳng SC và mặt đáy bằng A. 45 . B. 90 . C. 60 . D. 30 .
Câu 17. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , AB  a ; BC  a 2 ; SA vuông góc với
mặt phẳng đáy và SA  a . Góc giữa đường thẳng SC và đáy bằng A. 0 90 . B. 0 45 . C. 0 60 . D. 0 30 .
Câu 18. Cho hình hộp chữ nhật ABC . D AB C  D
  có AB  BC  a, AA  6a .Góc giữa đường thẳng A C  và
mặt phẳng  ABCD bằng: A. 60 . B. 90 . C. 30 . D. 45 .
Câu 19. Cho hình hộp chữ nhật ABCD.A' B 'C ' D ' có AB  a , D
A  2 2a , AA'  3a (tham khảo hình bên).
Góc giữa đường thẳng A'C và mặt phẳng  ABCD bằng A. 45 . B. 90 . C. 60 . D. 30 .
Câu 20. Cho hình hộp chữ nhật ABC . D  A BC  D , có AB  A 
A  a , AD  a 2 (tham khảo hình vẽ). Góc giữa đường thẳng 
A C và mặt phẳng  ABCD bằng A. 30o. B. 45o . C. 90o. D. 60o .
Câu 21. Cho hình hộp chữ nhật ABC . D AB C
 D có AB  a, AD  3a, AA  2 3a . Góc giữa đường thẳng A C
 và mặt phẳng  ABCD bằng A. 45 . B. 30 . C. 60 . D. 90 .
Câu 22. Cho hình chóp S.ABC có đáy là tam giác vuông tại C , AC  a , BC  2a , SA vuông góc với mặt
phẳng đáy và SA  a . Góc giữa đường thẳng SB và mặt phẳng đáy bằng A. 60 B. 90 C. 30 D. 45
Câu 23. Cho hình chóp S.ABC có SA vuông góc với mặt phẳng  ABC , SA  2a , tam giác ABC vuông tại B ,
AB  a và BC  3a . Góc giữa đường thẳng SC và mặt phẳng  ABC bằng A. 30 . B. 60 . C. 45 . D. 90 .
Câu 24. Cho khối chóp S.ABC có SA ABC, tam giác ABC vuông tại B , AC  2a , BC  a, SB  2a 3 .
Tính góc giữa SA và mặt phẳng SBC. A. 45. B. 30 . C. 60 . D. 90 .
Câu 25. Cho hình chóp SABCD có đáy là hình thang vuông tại 1và B . AB  BC  a, AD  2a . Biết SA vuông
góc với đáy ( ABCD) và SA  a . Gọi M , N lần lượt là trung điểm SB,CD . Tính sin góc giữa đường thẳng MN và mặt phẳng (SAC) 5 55 3 5 2 5 A. B. C. D. 5 10 10 5
Câu 26. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , SA vuông góc với mặt phẳng đáy và
SA  2a . Góc giữa đường thẳng SC và mặt phẳng đáy bằng A. 45 B. 60 C. 30 D. 90
Câu 27. Cho hình chóp S.ABCD có đáy hình vuông. Cho tam giác SAB vuông tại S và góc SBA bằng 0 30 .
Mặt phẳng SAB vuông góc mặt phẳng đáy. Gọi M , N là trung điểm AB, BC . Tìm cosin góc tạo bởi hai
đường thẳng SM , DN  . 2 1 1 2 A. . B. . C. . D. . 5 5 3 3
______________________________________ 10
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN LỚP 12 THPT
(LỚP BÀI TOÁN GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG – P5)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , SA vuông góc với mặt phẳng đáy và SB  2a .
Góc giữa đường thẳng SB và mặt phẳng đáy bằng A. 45 B. 60 C. 90 D. 30
Câu 2. Cho hình chóp S.ABC có SA vuông góc với mặt phẳng  ABC , SA  2a , tam giác ABC vuông tại B,
AB  a 3 và BC  a .Góc giữa đường thẳng SC và mặt phẳng  ABC bằng: A. 0 45 . B. 0 30 . C. 0 60 . D. 0 90 .
Câu 3. Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a . Gọi M là trung điểm của SD (tham
khảo hình vẽ bên). Tang của góc giữa đường thẳng BM và mặt phẳng  ABCD bằng S M A D B C 2 3 2 1 A. B. C. D. 2 3 3 3
Câu 4. Cho hình chóp S.ABC có SA vuông góc với mặt phẳng  ABC , SA  2a , tam giác ABC vuông cân tại
B và AB  a 2 .Góc giữa đường thẳng SC và mặt phẳng  ABC bằng A. 30o . B. 90o . C. 60o . D. 45o .
Câu 5. Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng 2a . Gọi M là trung điểm của SD Tính
tan của góc giữa đường thẳng BM và mặt phẳng  ABCD . 2 3 2 1 A. . B. . C. . D. . 2 3 3 3 a 6
Câu 6. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a và SA   ABCD . Biết SA  . Tính 3
góc giữa SC và  ABCD  . A. 30 B. 60 C. 75 D. 45
Câu 7. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với đáy và SA  a 3 .
Gọi  là góc giữa SD và SAC . Giá trị sin bằng 2 2 3 2 A. . B. . C. . D. . 4 2 2 3
Câu 8. Cho hình chóp tam giác S.ABC có đáy là tam giác đều cạnh a . Tam giác SAB cân tại S và thuộc mặt
phẳng vuông góc với đáy. Biết SC tạo với mặt phẳng đáy một góc 60 , gọi M là trung điểm của BC . Gọi  là
góc giữa đường thẳng SM và mặt phẳng  ABC . Tính cos . 6 3 3 1 A. cos  . B. cos  . C. cos  . D. cos  . 3 3 10 10
Câu 9. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB  a, AD  a 3 . Mặt bên SAB là tam giác
đều và nằm trong mặt phẳng vuông góc với mặt đáy. Cosin của góc giữa đường thẳng SD và mặt phẳng SBC bằng 13 3 2 5 1 A. B. C. D. 4 4 5 4
Câu 10. Cho hình chóp S.ABC có đáy là tam giác vuông tại C , CH vuông góc với AB tại H , I là trung điểm
của đoạn HC . Biết SI vuông góc với mặt phẳng đáy, ·
ASB  90 . Gọi O là trung điểm của đoạn AB , O là 11
tâm mặt cầu ngoại tiếp tứ diện SABI . Góc tạo bởi đường thẳng OO và mặt phẳng  ABC bằng A. 60 . B. 30 . C. 90 . D. 45 .
Câu 11. Cho hình chóp tứ giác đều S.ABCD có AB  a , O là trung điểm AC và SO  b . Gọi  là đường a 14
thẳng đi qua C ,  chứa trong mặt phẳng  ABCD và khoảng cách từ O đến  là . Giá trị lượng 6
giác cosSA, bằng 2a 2a a a A. . B. . C. . D. . 2 2 3 4b  2a 2 2 3 2a  4b 2 2 3 2a  4b 2 2 3 4b  2a
Câu 12. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và ·
ABC  60 . Hình chiếu vuông góc của
điểm S lên mặt phẳng  ABCD trùng với trọng tâm của tam giác ABC , gọi  là góc giữa đường thẳng SB và
mặt phẳng SCD , tính sin biết rằng SB  a . 3 1 1 2 A. sin  . B. sin   . C. sin   . D. sin  . 2 4 2 2
Câu 13. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , SA   ABCD , SA  x . Xác định x để hai mặt
phẳng SBC và SCD hợp với nhau góc 60 . 3a a A. x  2a . B. x  a . C. x  . D. x  . 2 2
Câu 14. Cho hình chóp S.ABC có đáy là tam giác vuông tại B , cạnh bên SA vuông góc với mặt đáy, AB  2a , · 0
BAC  60 và SA  a 2 . Góc giữa đường thẳng SB và mặt phẳng (SAC) bằng A. 0 45 . B. 0 60 . C. 0 30 . D. 0 90 .
Câu 15. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA vuông góc với mặt phẳng
đáy, SA  a 2 . Gọi M , N lần lượt là hình chiếu vuông góc của điểm A trên các cạnh SB , SD . Góc giữa mặt
phẳng  AMN  và đường thẳng SB bằng A. o 45 . B. o 90 . C. o 120 . D. o 60 .
Câu 16. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB  a , BC  a 3 , SA  a và SA vuông
góc với đáy ABCD . Tính sin  , với  là góc tạo bởi giữa đường thẳng BD và mặt phẳng SBC  . 7 3 2 3 A. sin  . B. sin  . C. sin  . D. sin  . 8 2 4 5
Câu 17. Cho hình chóp S.ABC có đáy là tam giác vuông tại B , cạnh bên SA vuông góc với mặt phẳng đáy, AB  2a , · 0
BAC  60 và SA  a 2 . Góc giữa đường thẳng SB và mặt phẳng SAC bằng A. 0 30 . B. 0 45 . C. 0 60 . D. 0 90 .
Câu 18. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a , tâm O . Gọi M và N lần lượt là trung điểm
của SA và BC . Biết rằng góc giữa MN và  ABCD bằng 0
60 , cosin góc giữa MN và mặt phẳng SBD bằng: 41 5 2 5 2 41 A. . B. . C. . D. . 41 5 5 41
Câu 19. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, AB  2a , BC  a , · ABC  120 . Cạnh bên
SD  a 3 và SD vuông góc với mặt phẳng đáy. Tính sin của góc tạo bởi SB và mặt phẳng SAC 3 3 1 3 A. . B. . C. . D. . 4 4 4 7
Câu 20. Cho hình lăng trụ đứng ABC.AB C
  có AB  AC  a, BAC 120. Gọi M , N lần lượt là trung điểm 3 3a của B C
 và CC . Biết thể tích khối lăng trụ ABC.AB C   bằng
. Gọi  là góc giữa mặt phẳng  AMN  và 4
mặt phẳng  ABC  . Khi đó 3 1 13 3 A. cos  . B. cos  . C. cos  . D. cos  . 2 2 4 4 12
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN LỚP 12 THPT
(LỚP BÀI TOÁN GÓC NHỊ DIỆN – P1)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có AD = 2a, AB = a, cạnh SA vuông góc với đáy
và SA = a. Tính sin của góc giữa hai mặt phẳng (SBC) và (SCD). 15 2 2 2 A. 0,5 B. B. D. 5 5 4
Câu 2. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, SA vuông góc với mặt phẳng
(ABCD), AB = BC = a và AD = 2a. Nếu góc giữa SC và mặt phẳng (ABCD) bằng 45o thì cosin của góc giữa (SAD) và (SCD) bằng 2 3 5 A. 0,5 B. C. D. 3 4 6
Câu 3. Cho hình chóp S.ABCD có đáy là hình vuông ABCD tâm O cạnh a. Biết SA vuông góc với đáy (ABCD),
tính độ dài cạnh SA theo a để góc giữa hai mặt phẳng (SBC) và (SCD) bằng 60o . A. SA = a B. SA = 2a B. SA = a 3 D. SA = 2a 3
Câu 4. Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA  3AB , SA vuông góc với đáy. Tính cosin
của góc giữa hai mặt phẳng (SBC) và (SDC). 1 2 3 2 A. B. C. D. 4 3 4 2
Câu 5. Cho khối chóp S.ABC có ABC là tam giác vuông cân tại A, · ·
SBA  SCA  90o, góc giữa hai mặt phẳng
(SAB) và (SAC) bằng 60o . Tính thể tích khối chóp S.ABC. 3 a 3 a 3 a A. 3 a B. C. D. 3 2 6
Câu 6. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B với BA = BC = 5a, · · SAB  SCB  90o . 9
Biết góc giữa hai mặt phẳng (SBC) và (SBA) bằng  : cos 
. Thể tích khối chóp S.ABC bằng 16 125 7 125 7 50 50 A. 3 a B. 3 a C. 3 a D. 3 a 18 9 9 3
Câu 7. Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), đáy ABC là tam giác vuông tại B có các a 2 yếu tố AB  ;
a BC  a 3 . Tính góc giữa hai mặt phẳng (SAC) và (SBC) khi SA  . 2 A. 60o B. 30o C. 45o D. 75o
Câu 8. Cho hình chóp S.ABC có ABCD là hình thoi tâm O, đường thẳng vuông góc với mặt phẳng (ABCD) và a 6 AB  SB  a; SO 
. Tìm cosin của góc giữa hai mặt phẳng (SAB) và (SAD). 3 1 1 3 A. 0 B. C. D. 3 7 7
Câu 9. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AC = 2a, tam giác SAB và tam giác SCB
lần lượt vuông tại A và C. Khoảng cách từ C đến mặt phẳng (ABC) bằng a. Tính cosin của góc giữa hai mặt phẳng (SAB) và (SCB). 2 2 2 5 1 A. B. C. D. 3 3 3 3
Câu 10. Cho hình chóp S.ABCD có đáy ABCD là nửa lục giác đều nội tiếp đường tròn đường kính AB = 2a,
cạnh SA vuông góc với đáy và SA = a 3 . Tính cosin của góc giữa hai mặt phẳng (SAD) và (SBC). 2 2 2 2 A. B. C. D. 2 3 4 5
Câu 11. Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, SA vuông góc với đáy (ABCD). Gọi N là trung
điểm của SA, mặt phẳng (NCD) cắt khối chóp theo một thiết diện có diện tích là 2 S  2a 3 . Tính góc giữa hai
mặt phẳng (NCD) và (ABCD). 13 A. 60o B. 30o C. 45o D. 75o
Câu 12. Cho lăng trụ đứng ABC.AB C
  có đáy ABC là tam giác cân với AB = AC = a, · BAC  120o, cạnh bên B B
  a . Tính cosin góc giữa hai mặt phẳng (AB’I) và (ABC), trong đó I là trung điểm của C’C. 30 15 2 11 A. B. C. D. 10 10 3 5
Câu 13. Cho lăng trụ đứng ABC . D AB C  D
  có đáy ABCD là hình vuông cạnh a và chiều cao A A   6a . Trên
C’C lấy điểm M, trên D’D lấy điểm N sao cho C M
  2MC và DN  2ND. Tính cosin của góc giữa hai mặt phẳng (B’MN) và (ABCD). 1 3 2 5 A. B. C. D. 21 4 2 5
Câu 14. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, D, AB là đáy lớn và tam giác ABC cân
tại C với AC = a. Các mặt phẳng (SAB), (SAC) cùng vuông góc với mặt phẳng đáy, cạnh bên SC  a 3 và tạo
với mặt phẳng (SAB) một góc bằng 30o . Góc giữa hai mặt phẳng (SAB) và (SAC) bằng A. 60o B. 30o C. 45o D. 75o
Câu 15. Hình chóp S.ABCD có đáy là hình thoi có ·
BAD  120o, hình chiếu vuông góc của điểm H trên mặt a 6
phẳng đáy trùng với trọng tâm của tam giác ABC, biết đường cao của khối chóp là SH  và tam giác SBD 3
vuông tại S. Tính cosin của góc giữa hai mặt phẳng (SAD), (SCD). 15 2 3 A. 0 B. C. D. 10 3 6
Câu 16. Hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = 2, BC  2 3 , cạnh bên SA vuông góc với 3 đáy (ABC) và SA 
. Gọi M là trung điểm của AB, tính tan của góc giữa hai mặt phẳng (SMC), (ABC). 2 4 13 2 A. B. C. 1 D. 13 4 2
Câu 17. Cho lăng trụ đứng ABC.A B  C
  có đáy ABC là tam giác vuông, AB = BC = a, biết góc giữa hai mặt
phẳng (ACC’) và (AB’C’) bằng 60o . Khi đó sin của góc giữa hai mặt phẳng (AB’C’) và (A’B’C’) bằng 4 13 2 A. B. C. 1 D. 13 4 2
Câu 18. Cho hình chóp S.ABCD có đáy ABCD là hình vuông, cạnh bên SA = a và vuông góc với đáy (ABCD).
Góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng  . Tính cosin của góc giữa hai mặt phẳng (SBC),
(SCD) biết rằng cot  2 . 1 2 1 A. 0,5 B. C. D. 3 3 6
______________________________________ 14
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN LỚP 12 THPT
(LỚP BÀI TOÁN GÓC NHỊ DIỆN – P2)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho tứ diện ABCD có · · o ·
DAB  CBD  90 ; AB  a; AC  a 5; ABC  135o. Biết góc giữa hai mặt
phẳng (ABD) và (BCD) bằng 30o . Thể tích của tứ diện ABCD bằng 3 a 3 a 3 a 3 a A. B. C. D. 2 3 2 3 2 6
Câu 2. Cho hình chóp đều S.ABCD có cạnh đáy bằng a 2 , cạnh bên bằng 2a. Gọi  là góc tạo bởi hai mặt
phẳng (SAC) và (SCD). Tính cos 21 21 21 21 A. B. C. D. 2 14 3 7
Câu 3. Cho hình chóp S.ABC có SA vuông góc với đáy, SA = 2BC và ·
BAC  120o. Hình chiếu vuông góc của
A lên các đoạn SB và SC lần lượt là M và N. Góc của hai mặt phẳng (ABC) và (AMN) bằng A. 15o B. 30o C. 60o D. 45o
Câu 4. Cho tứ diện ABCD có  ACD   BCD , AC  AD  BC  BD  a , CD  2x . Giá trị của x để hai mặt
phẳng  ABC và  ABD vuông góc với nhau là: a 2 a 3 a 3 a 5 A. . B. . C. . D. . 3 3 2 3
Câu 5. Cho tứ diện ABCD có AC  AD  a 2; BC  BD  a . Khoảng cách từ điểm B đến mặt phẳng (ACD) a 3 3 a 15 bằng
và thể tích tứ diện ABCD bằng
. Góc giữa hai mặt phẳng (ACD) và (BCD) bằng 3 27 A. 15o B. 30o C. 60o D. 45o
Câu 6. Cho tứ diện ABCD có  ACD   BCD , AC  AD  BC  BD  a , CD  2x . Giá trị của x để hai mặt
phẳng  ABC và  ABD vuông góc với nhau là: a 2 a 3 a 3 a 5 A. . B. . C. . D. . 3 3 2 3
Câu 7. Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác cân đỉnh A, ·
BC  a 3; ABC  30o. Gọi M là uuuur uuuur
điểm thỏa mãn 2CM  3CC. Tính sin của góc giữa hai mặt phẳng (ABC), (AB’M). 66 481 3 418 A. B. C. D. 22 22 22 22
Câu 8. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB = a, AD = 2a. Biết rằng SA vuông góc với
(ABCD), SA = 2a. Tính tan của góc giữa hai mặt phẳng (SBD), (SBC). 1 3 2 A. B. C. D. 5 5 2 3
Câu 9. Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a. Gọi M, N lần lượt là trung điểm của
SA, SB, G là trọng tâm tam giác SAC. Khi đó cosin của góc tạo bởi hai mặt phẳng (GMN) và (GAB) bằng 6 2 3 7 A. B. 0,5 C. D. 11 2 11
Câu 10. Cho hình chóp S.ABC có SC vuông góc với (ABC) và tam giác ABC vuông tại B. Biết 6 AB  ;
a AC  a 3 và góc giữa hai mặt phẳng (SAB), (SAC) bằng  : cos  . Tính độ dài SC theo a. 19 A. SC  a 6 B. SC  2a 6 C. SC  a 7 D. SC  6a
Câu 11. Cho hình chóp S.ABC có (SAC) vuông góc với đáy, SA = AB = a, AC = 2a, · · ASC  ABC  90o. Tính
cosin của góc giữa hai mặt phẳng (SAB) và (SBC). 15 105 4 70 70 4 105 A. B. C. D. 35 35 35 35
Câu 12. Cho hình chóp S.ABC có đường cao SA, tam giác ABC cân tại A và · AB  ;
a BAC  120o . Biết thể tích 3 khối chóp là 3
a , góc giữa hai mặt phẳng (SBC) và (ABC) bằng 24 A. 60o B. 30o C. 45o D. 90o
Câu 13. Cho hình chóp tứ giác đều S.ABCD. Mặt phẳng (P) chứa đường thẳng AC và vuông góc với mặt phẳng
(SCD) cắt đường thẳng SD tại E. Gọi V và V1 lần lượt là thể tích khối chóp S.ABCD và D.ACE biết V = 5V1. Tính
cosin của góc tạo bởi mặt bên và mặt đáy của hình chóp S.ABCD. 3 1 2 A. 0,5 B. C. D. 2 2 2 3 a 6
Câu 14. Cho hình chóp S.ABCD đáy là hình thoi tâm O và SO vuông góc với (ABCD), SO  , SB = BC = 3
a. Số đó góc giữa hai mặt phẳng (SBC) và (SCD) là A. 60o B. 30o C. 45o D. 90o
Câu 15. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và SA = SB = SC = SD = a. Khi đó cosin của
góc giữa hai mặt phẳng (SAB) và (SAD) bằng 1 3 1 A. 0,25 B. C. D.  3 2 3
Câu 16. Cho hình chóp S.ABC có · ·
AB  a 2; AC  a; BC  a 3; SBA  SCA  90ovà hai mặt phẳng (SAC), 1
(SAB) tạo với nhau một góc  : cos 
. Tính thể tích của khối chóp S.ABC 3 2 2 2 2 A. 3 a B. 3 a C. 3 a D. 3 a 12 2 3 6
Câu 17. Cho hình chóp S.ABCD có ABCD là hình vuông cạnh a, SA vuông góc với đáy (ABCD). Tính SA theo a
để góc giữa hai mặt phẳng (SBC), (SCD) bằng 60o . A. SA = a B. SA = 2a C. SA = 3a D. SA = 1,5a
Câu 18. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật biết AB = 2a, AD = a, SA = 3a và SA vuông góc
với mặt phẳng đáy. Gọi M là trung điểm của CD, điểm E thuộc cạnh SA sao cho SE = 2a. Cosin của góc giữa
hai mặt phẳng (SAC) và (BME) là 210 30 15 870 A. B. C. D. 15 30 15 30 Câu 19. Cho hình chóp .
S ABC có SA vuông góc với mặt đáy, SA  BC và ·
BAC 120 . Hình chiếu vuông góc
của A lên các cạnh SB và SC lần lượt là M và N . Góc giữa hai mặt phẳng  ABC và AMN  bằng A. 45. B. 60 . C. 15 . D. 30 .
______________________________________ 16
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN LỚP 12 THPT
(LỚP BÀI TOÁN GÓC NHỊ DIỆN – P3)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ 3 3a
Câu 1. Hình lăng trụ đứng ABC.A’B’C’ có ·
AB  AC  a; BAC  120ovà có thể tích . bằng Gọi M, N lần 4
lượt là trung điểm của B’C’ và CC’. Gọi  là góc giữa hai mặt phẳng (AMN), (ABC). Khi đó 3 1 13 3 A. cos  B. cos  C. cos  D. cos  2 2 4 4
Câu 2. Hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Số đo góc giữa hai mặt phẳng (A’BC) và (A’DC) bằng A. 45. B. 60 . C. 90o . D. 30 .
Câu 3. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SAB là tam giác đều và nằm trong
mặt phẳng vuông góc với mặt phẳng (ABCD). Gọi G là trọng tâm của tam giác SAB và M, N lần lượt là trung
điểm của SC, SD. Tính cosin của góc giữa hai mặt phẳng (GMN) và (ABCD). 2 39 13 3 2 39 A. B. C. D. 39 13 6 13
Câu 4. Cho hình chóp đều S.ABCD có cạnh đáy bằng a 2 , biết cạnh bên tạo với đáy bằng 60o . Tính tan của
góc tạo bởi hai mặt phẳng (SAC), (SCD). 2 3 3 21 21 A. B. C. D. 3 2 3 7
Câu 5. Cho hình chóp S.ABC có đáy là tam giác vuông tại A với AB = a, AC = 2a. Mặt phẳng (SBC) vuông góc
với mặt phẳng (ABC). Mặt phẳng (SAB), (SAC) cùng tạo với mặt phẳng (ABC) một góc 60o . Tính tan của góc
tạo bởi hai mặt phẳng (SAB), (SBC). 51 51 17 3 17 A. B. C. D. 17 3 3 17 a 3
Câu 6. Cho tứ diện ABCD có AB  a; AC  BC  AD  BD 
. Gọi M, N là trung điểm của AB, CD. Góc 2
giữa hai mặt phẳng (ABD), (ABC) là  . Tính cos biết mặt cầu đường kính MN tiếp xúc với cạnh AD. A. 2  3 B. 2 3  3 C. 3  2 3 D. 2 1
Câu 7. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB  ; a SA  1,5 ; a AD  a 3 , SA vuông
góc với đáy, M là trung điểm của cạnh SD. Tính tan của góc tạo bởi hai mặt phẳng (SAC), (MAC). 5 1 A. 1 B. 3 C. D. 2 3
Câu 8. Cho hình lăng trụ đứng ABC.A’B’C’ có A’A = AB = AC = 1 và ·
BAC  120o. Gọi I là trung điểm cạnh C’C.
Tính cosin của góc tạo bởi hai mặt phẳng (ABC), (AB’I). 370 70 30 30 A. B. C. D. 20 10 20 10
Câu 9. Cho lăng trụ đều ABC.A’B’C’ có tất cả các cạnh đều bằng 2a. Gọi M, N lần lượt là trung điểm cạnh A’B’,
BB’. Tính cosin của góc hợp bởi hai mặt phẳng (MC’N), (ACC’A’). 2 6 3 A. B. C. D. 0,75 4 4 4
Câu 10. Cho hình chóp S.ABCD có ABCD là hình chữ nhật có AB = a, AD = 2a. Biết SA vuông góc với mặt
phẳng (ABCD), SA = 2a. Tính tan của góc giữa hai mặt phẳng (SBD), (SBC). 1 2 3 A. B. C. D. 5 5 3 2
Câu 11. Tứ diện ABCD có BC = 3, CD = 4, · · ·
ABC  BCD  ADC  90o, góc giữa hai đường thẳng AD, BC
bằng 60o . Cosin của góc giữa hai mặt phẳng (ABC), (ACD) bằng 3 4 1 2 A. B. C. D. 43 43 43 43 17 a 6
Câu 12. Cho khối lăng trụ đứng ABCD.A’B’C’D’ có đáy là hình vuông cạnh a, cạnh bên AA  . Góc giữa 2
hai mặt phẳng (A’BD), (C’BD) bằng A. 90o B. 60o C. 45o D. 30o
Câu 13. Cho hình lập phương ABCD.A’B’C’D’ có tâm O, gọi I là tâm của hình vuông ABCD và M là điểm thuộc 1 OI sao cho MO 
MI . Khi đó cosin của góc tạo bởi hai mặt phẳng (MC’D’) và (MAB) bằng 2 7 6 13 6 17 3 A. B. C. D. 85 65 85 65
Câu 14. Cho hình chóp S.ABCD có đáy ABCD là hình vuông, mặt bên SAB là tam giác vuông tại S và nằm trong
mặt phẳng vuông góc với đáy, · SBA  60o. Tính 2
cos  với  là góc giữa hai mặt phẳng (SBC), (SDC). 15 16 4 15 A. B. C. D. 19 19 19 76 7
Câu 15. Cho lăng trụ ABC.A’B’C’ có A’.ABC là hình chóp tam giác đều, AB  a; AA  a . Tính góc giữa 12
hai mặt phẳng (ABB’A’), (ABC). A. 75o B. 60o C. 45o D. 30o
Câu 16. Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, SA vuông góc với (ABC), SA  a 3 . Cosin của
góc giữa hai mặt phẳng (SAB), (SBC) là 1 2 2 A. B. C. D. 0,5 5 5 3
Câu 17. Lăng trụ ABC.A’B’C’ có đáy ABC là tam giác vuông cân cạnh huyền AB  2 2 , AA  AB  AC và
khoảng cách giữa hai mặt phẳng đáy bằng a 3 . Tính góc giữa hai mặt phẳng (B’BC) và (ABC). A. 75o B. 60o C. 45o D. 30o
Câu 18. Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = BC = a, góc giữa đường thẳng AC’ và mặt phẳng
(BCC’B’) bằng 30o . Tính cosin của góc giữa hai mặt phẳng (ABC’) và (AB’C’). 1 2 2 2 1 A. B. C. D. 3 3 2 6
Câu 19. Hình chóp S.ABC có ABC là tam giác đều cạnh a, SA  a 3 và SA vuông góc với (ABC). Tính số đo
gần đúng của góc nhị diện (SAB), (SBC). A. 63 độ B. 65 độ C. 70 độ D. 72 độ
Câu 20. Cho hình chóp S.ABCD có SA vuông góc với (ABCD), ABCD là hình thang vuông tại A, D, AB = 2CD,
AD = CD = a, SA = x. Tìm x để số đo góc giữa hai mặt phẳng (SAB), (SBC) bằng 60o . A. x = 0,5a B. x = a c. x  a 3 D. x  a 2
______________________________________ 18
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN LỚP 12 THPT
(LỚP BÀI TOÁN GÓC NHỊ DIỆN – P4)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho hình chóp tứ giác đều S.ABCD , cạnh bên bằng cạnh đáy và bằng a . Gọi M là trung điểm của
SC . Tính góc giữa hai mặt phẳng MBD và  ABCD . A. 90 . B. 30 . C. 60 . D. 45 .
Câu 2. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B , SA vuông góc với mặt phẳng
 ABCD , AB  BC  a, AD  2a . Biết góc giữa SC và mặt phẳng  ABCD bằng 45. Tính góc giữa mặt
phẳng SAD và SCD . A. 90 . B. 30 . C. 60 . D. 45 . Câu 3. Hình chóp đều .
S ABCD có ABCD là hình vuông cạnh a , tâm O . Góc giữa SB và mặt phẳng (SAC) bằng 0
60 . Gọi M là trung điểm của SB . Tính sin của góc giữa mặt phẳng ( AMO) và mặt phẳng (SAB) . 1 1 2 3 A. . B. . C. D. . 5 2 5 5 2 5
Câu 4. Cho hình chóp SABCD có đáy ABCD là hình thang vuông tại A và B với AB  BC  a , AD  2a ,
SA   ABCD  , SA  a 2 . Tính góc giữa hai mặt phẳng SCD  và SAB  . A. 30. B. 45. C. 90 . D. 60.
Câu 5. Cho hai tam giác đều DAC và BAC lần lượt nằm trong hai mặt phẳng vuông góc với nhau. Gọi  là
góc giữa hai mặt phẳng  DAB  và  DBC  . Tính giá trị cos . 3 1 1 3 A. . B. . C.  . D.  . 5 5 5 5
Câu 6. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA ABCD. Góc giữa SB và mặt
phẳng SAD là 30. Gọi các điểm E, F lần lượt đối xứng với B,C qua A, D . Tính sin góc giữa hai mặt
phẳng SCFvà SEF. 15 21 21 15 A. . B. . C. . D. . 4 7 3 5
Câu 7. Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB  2a, AD  2a 3 . Mặt bên SAB là tam giác đều
và nằm trong mặt phẳng vuông góc với đáy. Gọi  là góc giữa hai mặt phẳng SAD và SCD . Tính sin  . 2 5 2 5 42 A. . B. . C. . D. . 5 2 5 7
Câu 8. Trong mặt phẳng P , cho tam giác đều ABC cạnh a . Trên các đường thẳng vuông góc với P tại B a 3
và C , lấy về cùng phía với mp P các điểm D , E sao cho BD 
, CE  a 3 . Gọi  là góc giữa hai 3
mặt phẳng P và  ADE . Tính cos . 37 2 259 14 7 3 37 A. cos  . B. cos  . C. cos  . D. cos  . 37 37 3 37 3a
Câu 9. Cho hình lăng trụ đều ABC.A B  C
  có cạnh đáy bằng a , cạnh bên bằng
. Góc giữa hai mặt phẳng 2  AB C
  và  ABC  bằng A. 60. B. 90. C. 45. D. 30 . 3a
Câu 10. Cho hình lăng trụ đứng ABC . D A B  C  D
  có đáy ABCD là hình thoi, AB  a , AA  , · BAD  60. 2
Góc giữa hai mặt phẳng  ABCD  và  AD B  C  bằng A. 60. B. 90. C. 45. D. 30 . Câu 11. Lăng trụ đều B A C.A B  C
  có cạnh đáy bằng 2a. Gọi M , N lần lượt là trung điểm của AB, BC. 19 a 2
Khoảng cách từ điểm A đến mặt phẳng  A M  N bằng
. Tính côsin của góc giữa  A A  B và  A M  N . 2 1 6 6 6 A. . B. . C. . D. . 2 2 6 3
Câu 12. Cho hình lăng trụ đứng AB . C A B  C
  có đáy ABC là tam giác cân với AB  AC  a và ·BAC  120,
cạnh bên BB  a. Gọi I là trung điểm CC . Tính cosin góc tọa bởi hai mặt phẳng  ABC và  AB I  . 3 30 21 3 A. . B. . C. . D. . 21 10 10 3
Câu 13. Cho hình hộp ABCD.A B  C  D
  có đáy ABCD là hình vuông cạnh bằng 2a , cạnh bên bằng a 5 . Hình
chiếu vuông góc của A trên mặt phẳng ABCD  là trùng với giao điểm của hai đường chéo AC và BD. Góc
giữa mặt phẳng ABBA và mặt đáy của hình hộp bằng A. 0 30 . B. 0 60 . C. 0 45 . D. 0 75 .
Câu 14. Cho hình hộp chữ nhật ABC . D A B  C  D
  có AB  2a , AD  3a , AA  4a . Gọi  là góc giữa hai mặt phẳng  AB D   và  AC D
 . Giá trị của cos bằng. 29 27 2 3 A. . B. . C. . D. . 61 34 2 2
Câu 15. Cho hình lăng trụ AB . C A B  C
  có đáy là tam giác đều, cạnh bên AA  2a . Hình chiếu vuông góc của
A lên mặt phẳng  ABC trùng với trung điểm của đoạn BG (với G là trọng tâm tam giác ABC ). Biết khoảng a 3 cách giữa AB và A I  bằng
. Tính cosin của góc  giữa hai mặt phẳng  ABC  và  ABB A   . 12 1 1 1 1 A. cos  . B. cos  . C. cos  . D. cos  . 95 165 134 126
Câu 16. Cho hình lăng trụ ABC .
D A' B'C ' D' cạnh bên 2a và hình chiếu A' lên mặt đáy là điểm I sao cho uur uur
3BI  ID ; đáy là hình chữ nhật ABCD có tâm O và AB  a, AD  a 3 . Tính cosin của góc  giữa hai mặt
phẳng  ABCD  và CDD 'C ' . 1 165 2 165 1 A. cos  . B. cos  . C. cos  . D. cos  . 3 55 55 6
Câu 17. Cho hình lập phương ABC . D AB C  D
  có cạnh a . Số đo góc giữa hai mặt BAC  và DAC  bằng? A. 30 . B. 45. C. 90 . D. 60.
Câu 18. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B , SA  a và SA   ABC  ,
AB  BC  a . Góc giữa hai mặt phẳng SAC  và SBC  bằng? A. 45. B. 30 . C. 60. D. 90 .
Câu 19. Tính sin với  là góc giữa hai mặt phẳng  AB D   và BA C
  của hình lập phương ABC . D A B  C  D   cạnh a. 2 2 3 3 2 A. sin  . B. sin  . C. sin  . D. sin  . 3 2 3 3
Câu 20. Cho hình chóp S.ABC , đáy ABC là tam giác vuông cân tại B , BA  BC  a , M là trung điểm của uuuur uuuur
AC . Gọi N là hình chiếu của S trên  ABC sao cho BM  3MN và SB  a . Tính giá trị lượng giác sin của
góc giữa hai mặt phẳng SBN  và SBC ? 5 3 5 10 3 10 A. B. . C. . D. . 10 10 10 10
Câu 21. Cho hình chóp S.ABCD với ABCD là hình thang vuông tại A và D có AD  CD  2a , AB  4a và
SB  2 5a . Gọi M là trung điểm của CD . Biết hình chiếu H của đỉnh S xuống (ABC ) D nằm trên AD và BC
vuông góc với SM , tính sin của góc giữa 2 mặt phẳng (SHB) và (SBC) . 238 51 85 2 51 A . B. . C. . D. . 17 17 17 17 20
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN LỚP 12 THPT
(LỚP BÀI TOÁN GÓC NHỊ DIỆN – P5)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Lăng trụ tam giác đều ABC.AB C
  có AB  2 3 và AA  2. Gọi M , N, P lần lượt là trung điểm các cạnh A B  , A C
  và BC (tham khảo hình vẽ bên). Côsin của góc tạo bởi hai mặt phẳng  AB C   và MNP là C' N M B' A' C P B A 17 13 18 13 6 13 13 A. B. C. D. 65 65 65 65
Câu 2. Cho hình lập phương ABC . D A B  C  D
  có tâm O . Gọi I là tâm của hình vuông A B  C  D   và M là điểm
thuộc đoạn thẳng OI sao cho MO  2MI (tham khảo hình vẽ). Khi đó côsin của góc tạo bởi hai mặt phẳng (MC D  ) và (MAB) bằng 7 85 17 13 6 13 6 85 A. B. C. D. 85 65 65 85 a
Câu 3. Cho hình chóp S.ABC có SA vuông góc với mặt phẳng  ABC  3 , SA  , tam giác ABC đều cạnh 2
bằng a (minh họa như hình dưới). Góc tạo bởi giữa mặt phẳng SBC và  ABC bằng A. 0 90 . B. 0 30 . C. 0 45 . D. 0 60 .
Câu 4. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB  a , AD  SA  2a , SA   ABCD . Tính
tang của góc giữa hai mặt phẳng SBD và ( ABCD) . 5 1 2 A. . B. 5 . C. . D. . 2 5 5
Câu 5. Cho hình chóp SABCD có đáy ABCD là hình thoi tâm O , đường thẳng SO vuông góc với mặt phẳng  a 6
ABCD. Biết AB  SB  a , SO 
. Tìm số đo của góc giữa hai mặt phẳng SAB và SAD. 3 A. 30 B. 45 C. 60 D. 90
Câu 6. Cho hình chóp S.ABCD có đáy ABCD là hình vuông có độ dài đường chéo bằng a 2 và SA vuông
góc với mặt phẳng  ABCD . Gọi  là góc giữa hai mặt phẳng SBD và  ABCD . Nếu tan  2 thì góc
giữa SAC  và SBC bằng. A. 0 30 . B. 0 90 C. 0 60 . D. 0 45 . 6
Câu 7. Cho hình hộp chữ nhật ABCD.A ' B 'C ' D ' có mặt ABCD là hình vuông, '  AB AA . Xác định góc 2
giữa hai mặt phẳng  A' BD và C ' BD . A. 0 30 . B. 0 45 . C. 0 60 . D. 0 90 .
Câu 8. Cho hình lăng trụ đứng ABC.A B  C
  có đáy ABC là tam giác cân, với AB  AC  a và góc · BAC  120 ,
cạnh bên AA  a . Gọi I là trung điểm của CC . Cosin của góc tạo bởi hai mặt phẳng  ABC  và  AB I  bằng 21 11 33 10 30 A. . B. . C. . D. . 11 11 10 10
Câu 9. Cho hình chóp S.ABC có SA  a , SA   ABC  , tam giác ABC vuông cân đỉnh A và BC  a 2 . Gọi
M , N lần lượt là trung điểm của SB , SC . Côsin của góc tạo bởi hai mặt phẳng MNA và  ABC  bằng 2 2 3 3 A. . B. . C. . D. . 4 6 2 3
Câu 10. Cho hình chóp S.ABCD có ABCD là hình thoi cạnh bằng a và góc A bằng 60 , cạnh SC vuông góc a 6 với đáy và SC 
. Giá trị lượng giác cô-sin của góc giữa hai mặt phẳng SBD và SCD bằng 2 6 5 2 5 30 A. . B. . C. . D. . 6 5 5 6
Câu 11. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a , BD  a . Cạnh SA vuông góc với mặt đáy a 6 và SA 
. Tính góc giữa hai mặt phẳng SBC  và SCD . 2 A. 60 . B. 120 . C. 45 . D. 90 .
Câu 12. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B , AC  2a , tam giác SAB và tam giác
SCB lần lượt vuông tại A , C . Khoảng cách từ S đến mặt phẳng  ABC  bằng 2a. Côsin của góc giữa hai
mặt phẳng SAB và SCB bằng 1 1 1 1 A. . B. . C. . D. . 2 3 2 3
Câu 13. Cho hình lăng trụ đứng ABC.A B  C
  có AB  AC  a , góc ·
BAC  120 , AA  a . Gọi M , N lần lượt là trung điểm của B C
  và CC . Số đo góc giữa mặt phẳng AMN  và mặt phẳng  ABC bằng 3 3 A. 60 . B. 30 . C. arcsin . D. arccos . 4 4
Câu 14. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA  2a và vuông góc với
mặt phẳng đáy. Gọi M là trung điểm cạnh SD . Tang của góc tạo bởi hai mặt phẳng  AMC  và SBC  bằng 5 3 2 5 2 3 A. . . C. . D. . 5 B. 2 5 3
Câu 15. Tứ diện ABCD có AC  AD  BC  BD  a , CD  2x ,  ACD   BCD . Tìm x để  ABC   ABD ? B D A C a 2 a 3 A. x  a . B. x  . C. x  a 2 . D. x  . 2 3
Câu 17. Cho hình lăng trụ đứng ABC.AB C
 có AA  AB  AC 1 và · 0
BAC  120 . Gọi I là trung điểm cạnh
CC . Côsin góc giữa hai mặt phẳng  ABC và  AB I  bằng 370 70 30 30 A. . B. . C. . D. . 20 10 20 10
Câu 18. Cho hình chóp S.ABCD có đáy là hình thoi cạnh · 0
a, ABC  120 , SA vuông góc với mặt phẳng
 ABCD.Biết góc giữa hai mặt phẳng SBCvà SCDbằng 0 60 , khi đó a 6 a 6 a 3 A. SA  . B. SA  a 6. C. SA  . D. SA  . 4 2 2 22
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN CỔ ĐIỂN LỚP 11 – 12 THPT
(LỚP BÀI TOÁN KHOẢNG CÁCH ĐIỂM ĐẾN MẶT PHẲNG – P1)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho khối tứ diện ABCD có thể tích 3 V  32cm ; B
 CD vuông cân có cạnh huyền CD  4 2cm . Khoảng
cách từ A đến  BCD bằng: A. 8cm . B. 4cm . C. 9cm . D. 12cm .
Câu 2. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O . Thể tích khối chóp bằng 3 4a . Tính
khoảng cách từ tâm O đến mặt bên (SBC) của hình chóp biết rằng tam giác SBC cân tại S và · 0 SB  , a BSC  45 . A. 6 2a . B. 6a . C. 3 2a . D. 3a .
Câu 3. Cho lăng trụ đứng ABC.A' B 'C 'có · 0
AB 1, AC  2, AA'  3, BAC 120 . Gọi M , N lần lượt là các điểm
trên cạnh BB ',CC ' sao cho BM  3B ' M ,CN  2C ' N . Tính khoảng cách từ M đến mặt phẳng ( A ' BN ) ? 9 138 3 138 9 3 9 138 A. . B. . C. . D. . 184 46 16 46 46
Câu 4. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D . Độ dài AB  AD  2a ,
CD  a ; góc giữa hai mặt phẳng SBC và ABCD bằng 600. Gọi I là trung điểm AD , hai mặt phẳng SBI
và SCI cùng vuông góc với mặt phẳng ABCD . Tính khoảng cách từ điểm A đến mặt phẳng SBC . 15a 3 15a 15a 2 15a A. . B. . C. . D. . 5 10 10 5
Câu 5. Cho hình chóp S.ABC . Tam giác ABC vuông tại A , AB  1cm , AC  3cm . Tam giác SAB , SAC lần 5 5
lượt vuông góc tại B và C . Khối cầu ngoại tiếp hình chóp S.ABC có thể tích bằng 3 cm . Tính 6
khoảng cách từ C tới SAB 5 5 3 A. cm . B. cm . C. cm . D. 1cm . 2 4 2
Câu 6. Cho hình chóp S.ABC có tam giác ABC vuông tại A góc · 0
ABC  30 , tam giác SBC là tam giác đều
cạnh a và mặt phẳng (SAB) vuông góc với mặt phẳng ( ABC) . Khoảng cách từ Ađến mặt phẳng (SBC) bằng a 6 a 6 a 3 a 6 A. . B. . C. . D. . 5 3 5 6
Câu 7. Cho hình chóp S.ABC có mặt bên (SAB) vuông góc với mặt đáy và tam giác SAB đều cạnh 2a. Biết tam
giác ABC vuông tại C và cạnh AC  a 3 . Tính khoảng cách từ C đến (SAB). a 3 a 3 a 3 A. . B. . C. a 3. D. . 2 4 3
Câu 8. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA   ABCD . Tính khoảng cách từ
điểm B đến mpSAC . a a 2 a 2 a 2 A. . B. . C. . D. . 2 2 3 4
Câu 9. Cho hình chóp S.ABCD có đáy là hình chữ nhật với diện tích đáy bằng 2
6a , hình chiếu của đỉnh S trên
mặt phẳng đáy trùng với điểm H thuộc cạnh AD với AH  2DH . Biết SH  a và diện tích tam giác SAD bằng 2
a . Tính theo a khoảng cách từ trung điểm M của đoạn SB đến mp (SAD). 3a 3a A. 2 . a B. . a C. . D. . 4 2
Câu 10. Cho hình chóp S.ABC có tam giác ABC là tam giác vuông tại A , AC  a 3 , · ABC 30  . Góc giữa
SC và mặt phẳng ABC bằng 0
60 . Cạnh bên SA vuông góc với đáy. Khoảng cách từ A đến SBC là 23 a 6 a 3 2a 3 3a A. . B. . C. . D. . 35 35 35 5
Câu 11. Cho hình chóp S.MNPQ có đáy là hình chữ nhật với PQ  3a 2 , SM vuông góc với mặt phẳng đáy,
SM  3a . Khoảng cách từ điểm M đến mặt phẳng SNP bằng A. a 3 . B. 2a 6 . C. 2a 3 . D. a 6 .
Câu 12. Hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB  2a, AD  .
a Hình chiếu của S lên mặt
phẳng  ABCD là trung điểm H của AB, SC tạo với đáy góc 0
45 . Khoảng cách từ H đến mặt phẳng SCD là: a 6 a 6 a 6 a 3 A. . B. . C. . D. . 3 6 4 3
Câu 13. Cho hình chóp S.ABCD có đường cao SA  2a , đáy ABCD là hình thang vuông ở A và D ,
AB  2a, AD  CD  a . Khoảng cách từ điểm A đến mặt phẳng SBC  bằng 2a 2a 2a A. . B. . C. . D. a 2. 3 2 3
Câu 14. Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình bình hành tâm O; mặt phẳng SAC  vuông
góc với mặt phẳng SBD  . Biết khoảng cách từ O đến các mặt phẳng SAB,SBC ,SCD lần lượt là
1; 2; 5 . Tính khoảng cách d từ O đến mặt phẳng SAD  . 19 20 2 A. d  . B. d  . C. d  2 . D. d  . 20 19 2
Câu 15. Cho hình chóp S.ABCD có đáy là hình chữ nhật, cạnh AB  2 AD  2a. Tam giác SAB đều và nằm
trong mặt phẳng vuông góc với đáy  ABCD Tính khoảng cách từ điểm A đến mặt phẳng SBD . a 3 a 3 a A. . B. . C. . D. a . 4 2 2
Câu 16. Cho hình chóp S.ABC có SA vuông góc với mặt phẳng đáy. Biết góc · o BAC  30 , SA  a và
BA  BC  a . Gọi D là điểm đối xứng với B qua AC . Khoảng cách từ B đến mặt phẳng SCD bằng 21 2 2 21 21 A. a . B. a . C. a . D. a . 7 2 7 14 24
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN CỔ ĐIỂN LỚP 11 – 12 THPT
(LỚP BÀI TOÁN KHOẢNG CÁCH ĐIỂM ĐẾN MẶT PHẲNG – P2)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho hình chóp S.ABCD đáy là hình vuông ABCD cạnh a , cạnh bên SA vuông góc với mặt phẳng
(ABCD) và SD  2a . Tính khoảng cách từ S đến mặt phẳng (ABCD). a A. a 5. B. . C. 3a. D. a 3. 2
Câu 2. Cho hình chóp tứ giác đều S.ABCD có các cạnh đáy đều bằng a và các cạnh bên đều bằng 2a . Tính
khoảng cách từ S đến mặt phẳng (ABCD). a 14 a 14 7a A. . B. . C. a 2 . D. . 2 4 2
Câu 3. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O , SA   ABCD . Gọi I là trung điểm của
SC . Khoảng cách từ I đến mặt phẳng  ABCD bằng độ dài đoạn thẳng nào? A. IB . B. IC . C. IA . D. IO .
Câu 4. Cho hình chóp S.ABCD đáy là hình vuông ABCD cạnh a , cạnh bên SA vuông góc với mặt phẳng
(ABCD) và SD  2a . Tính khoảng cách từ S đến mặt phẳng (ABCD). a A. a 5. B. . C. 3a. D. a 3. 2
Câu 5. Cho hình chóp S.ABC có ABC là tam giác vuông tại B , SA   ABC  . Khoảng cách từ điểm A đến mặt phẳng SBC là A. Độ dài đoạn AC .
C. Độ dài đoạn AH trong đó H là hình chiếu vuông góc của A trên SB . B. Độ dài đoạn AB .
D. Độ dài đoạn AM trong đó M là trung điểm của SC .
Câu 6. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a và SA vuông góc với mặt đáy. Biết
SB  a 10 . Gọi I là trung điểm của SC . Khoảng cách từ điểm I đến mặt phẳng  ABCD bằng 3a a 10 A. 3a . B. . C. . D. a 2 . 2 2
Câu 7. Cho hình chóp SABC có đáy là tam giác vuông tại A , AB  a , AC  a 3 , SA vuông góc với mặt
phẳng đáy và SA  2a . Khoảng cách từ điểm A đến mặt phẳng SBC  bằng a 57 2a 57 2a 3 2a 38 A. . B. . C. . D. . 19 19 19 19
Câu 8. Cho hình chóp S.ABC , tam giác ABC vuông cân tại A , SA  ( ABC) , SA  2a , AB  2a . Tính khoảng cách
từ A tới mặt phẳng (SBC) . a 3 2a a 2 3a A. . B. . C. . D. . 7 5 5 7
Câu 9. Cho hình chóp S.ABC có SA   ABC  , SA  AB  2a , tam giác ABC vuông tại B (tham khảo hình
vẽ). Khoảng cách từ A đến mặt phẳng SBC bằng A. a 3 . B. a . C. 2a . D. a 2 .
Câu 10. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , AB  a , BC  a 2 , đường thẳng SA
vuông góc với mặt phẳng đáy và góc giữa đường thẳng SC và mặt phẳng đáy bằng 0
30 . Gọi h là khoảng cách
từ điểm S đến mặt phẳng  ABC  . Mệnh đề nào dưới đây là đúng? a A. h  . B. h  3a . C. h  a 3 . D. h  a . 2
Câu 11. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng a 2. Tính khoảng cách d
từ tâm O của đáy ABCD đến một mặt bên theo a. a 5 a 3 2a 5 a 2 A. d  . B. d  . C. d  . D. d  . 2 2 3 3 25
Câu 12. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , SA vuông góc với mặt phẳng  ABCD và
SA  a . Khoảng cách từ điểm A đến mặt phẳng SBC  bằng: a a 2 a 3 A. a 2 . B. . C. . D. . 2 2 2 Câu 13. Cho tứ diện . O ABC có O ,
A OB,OC đôi một vuông góc với nhau OA  OB  OC  3. Khoảng cách từ O đến mp(ABC) là. 1 1 1 A. . B. 1. C. . D. . 3 2 3
Câu 14. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B , 2SA  AC  2a và SA vuông góc với đáy.
Khoảng cách từ A đến mặt phẳng SBC là 2a 6 4a 3 a 6 a 3 A. . B. . C. . D. . 3 3 3 3
Câu 15. Cho hình chóp S.ABC có đáy là tam giác vuông tại A , AB  a , AC  a 3 , SA vuông góc với mặt
phẳng đáy và SA  2a . Khoảng cách từ điểm A đến mặt phẳng SBC  bằng a 57 2a 57 2a 3 2a 38 A. . B. . C. . D. . 19 19 19 19
Câu 16. Cho tứ diện đều ABCD có cạnh bằng a . Khoảng cách từ A đến mặt phẳng  BCD bằng: a 3 a 3 a 6 a 6 A. . B. . C. . D. . 4 3 3 2
Câu 17. Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh 2a , tâm O , SO  a (tham
khảo hình vẽ bên). Khoảng cách từ O đến mặt phẳng SCD bằng 5a 2a 6a A. . B. . C. 3a . D. . 5 2 3
Câu 18. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B và cạnh bên SB vuông góc với mặt phẳng
đáy. Biết SB  3a, AB  4a, BC  2a . Khoảng cách từ B đến mặt phẳng (SAC) bằng 12 61a 3 14a 4a 12 29a A. . B. . C. . D. . 61 14 5 29
Câu 19. Cho hình chóp S.ABCD có đáy ABC là tam giác vuông tại A . ·
ABC 30, tam giác SBC là tam giác
đều cạnh a và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính khoảng cách h từ điểm C đến mặt phẳng SAB . 2a 39 a 39 a 39 a 39 A. h  . B. h  . C. h  . D. 13 52 13 26 26
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN CỔ ĐIỂN LỚP 11 – 12 THPT
(LỚP BÀI TOÁN KHOẢNG CÁCH ĐIỂM ĐẾN MẶT PHẲNG – P3)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho tứ diện đều S.ABCD có tất cả các cạnh đều bằng 2a , gọi M là điểm thuộc cạnh AD sao
cho DM  2MA . Tính khoảng cách từ M đến mặt phẳng  BCD . 2a 6 4a 6 2a 6 A. . B. a 6 . C. . D. . 9 9 3
Câu 2. Cho hình chóp tam giác đều S.ABC có tất cả các cạnh đều bằng a , gọi G là trọng tâm ABC . Khoảng
cách từ G đến mặt phẳng  ABC  bằng a 3 a 6 a 6 a 6 A. . B. . C. . D. . 6 6 9 12
Câu 3. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a và SA vuông góc với mặt đáy. Biết
SB  a 10 . Gọi I là trung điểm của SD . Khoảng cách từ điểm I đến mặt phẳng  ABCD bằng 3a a 10 A. 3a . B. . C. . D. a 2 . 2 2
Câu 4. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh bằng 4a ; Hình chiếu vuông góc của
S trên mặt đáy trùng với trung điểm H của OA ; góc giữa SCD và đáy là 45. Tính khoảng cách từ điểm B
đến mặt phẳng SCD . 2a 2a A. 2 2a . B. 2a . C. . D. . 2 4
Câu 5. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a , cạnh bên SA vuông góc với mặt đáy,
SA  a 3 ; gọi M là trung điểm của AC . Tính khoảng cách từ M đến mặt phẳng SBC . a a A. d M SBC 3 ,  . B. d M SBC  6 ,  . 3 2 a a C. d M SBC  6 ,  . D. d M SBC  3 ,  . 4 2
Câu 6. Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông cạnh a . Gọi M là trung điểm của SD .
Khoảng cách từ M đến mặt phẳng SAC  bằng a 2 a 2 a a A. . B. . C. . D. . 2 4 2 4
Câu 7. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 1. Hai mặt phẳng SAB và SAC 
cùng vuông góc với mặt phẳng đáy, SA  1. Gọi M là trung điểm SD . Khoảng cách từ M đến mặt phẳng SBC bằng 2 1 2 A. 1. B. . C. . D. . 4 2 2
Câu 8. Hình chóp S.ABCD có đáy là hình thoi tâm O cạnh 2a , ·
ABC  60 , hình chiếu vuông góc của S lên
 ABCD trùng với trung điểm I của BO, SI  a 3 . Khoảng cách từ B đến mặt phẳng SCD bằng 3a 3 2a 3 a 3 4a 3 A. . B. . C. . D. . 5 5 5 5
Câu 9. Cho hình chóp S.ABC có SA vuông góc với mặt phẳng đáy. Biết · BAC  30o; SA  ; a BA  BC  a . Gọi
D là điểm đối xứng của B qua CA. Tính khoảng cách từ B đến mặt phẳng (SCD). 17 21 51 17 A. a B. a C. a D. a 51 7 51 68
Câu 10. Cho hình lăng trụ tam giác đều ABC.A' B 'C ' có tất cả các cạnh đều bằng a . Khoảng cách từ A đến
mặt phẳng  A' BC  bằng 27 a 3 a 21 a 2 a 6 A. . B. . C. . D. . 4 7 2 4
Câu 11. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại C và D , ·
ABC  30. Biết AC  a , a CD  a 3 , SA 
và cạnh SA vuông góc với mặt phẳng đáy. Khoảng cách từ B đến mặt phẳng SCD 2 2 bằng a 6 a 6 a 3 A. a 6 . B. . C. . D. . 2 4 2
Câu 12. Cho hình chóp S.ABCD có đáy là hình thoi cạnh 2a , góc · 0
BAD  60 , SAB là tam giác đều nằm trên
mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách từ B đến mặt phẳng SCD là? a 3 3a a 6 A. . B. . C. . D. a 6 . 2 2 2
Câu 13. Cho hình chóp S.ABCD có đáy là hình thoi cạnh · 0
a, BAD  60 , SA  a và SA vuông góc với mặt phẳng
đáy. Khoảng cách từ B đến mặt phẳng (SCD) bằng a 21 a 15 a 21 a 15 A. . B. . C. . D. . 7 7 3 3 Câu 14. Cho hình chóp .
S ABCD có đáy ABCD là hình vuông cạnh a , SA   ABCD và SA  a 3 . Gọi I là
hình chiếu của A lên SC . Từ I lần lượt vẽ các đường thẳng song song với SB, SC cắt BC , CD tại P, Q . Gọi
E, F lần lượt là giao điểm của PQ với AB, AD . Tính khoảng cách từ E đến SBD. 3a 21 a 21 3a 21 a 21 A. B. C. D. 11 9 7 7
Câu 15. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a , tâm O , SO  a . Khoảng cách từ O
đến mặt phẳng SCD bằng 2a 5a 6a A. . B. 3a . C. . D. . 2 5 3
Câu 16. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Mặt bên SAB là tam giác đều và nằm trong
mặt phẳng vuông góc với đáy. Gọi M là trung điểm của SA biết AD  a 3, AB  a . Khi đó khoảng cách từ C đến MBD là: 2a 15 a 39 2a 39 a 39 A. . B. . C. . D. . 10 13 13 26
Câu 17. Cho hình lăng trụ đứng ABC.A B  C   có ·
AB  a; AC  2a; BAC  120o . Gọi M là trung điểm của cạnh CC thì ·
BMA  90o. Tính khoảng cách từ điểm A đến mặt phẳng BMA . a 5 a 5 a 7 a 5 A. . B. . C. . D. 7 5 7 3
Câu 18. Cho hình chóp S.ABC có · · · 0
ASB  ASC  CSB  60 , SA  3, SB  6, SC  9 . Tính khoảng cách d từ C đến SAB . 27 2 A. d  3 6 . B. d  9 6 . C. d  . D. d  2 6 . 2 28
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN CỔ ĐIỂN LỚP 11 – 12 THPT
(LỚP BÀI TOÁN KHOẢNG CÁCH ĐIỂM ĐẾN MẶT PHẲNG – P4)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho hình chóp S.ABCD có đáy là hình vuông, AB = a, SA vuông góc với mặt phẳng đáy và SA = 2a. Gọi
M là trung điểm của CD, khoảng cách giữa điểm M và mặt phẳng (SBD) bằng 2a a a a A. B. C. D. 3 2 2 3
Câu 2. Cho hình chóp S.ABCD có đáy ABCD là hình vuông, tam giác SAB đều và nằm trong mặt phẳng vuông 3
góc với đáy. Gọi M là trung điểm của cạnh CD. Biết khoảng cách từ A đến mặt phẳng (SBM) bằng 2a . Thể 19
tích khối chóp S.ABCD bằng 3 3a 3 3a 3 2 3a A. B. C. D. 3 3a 6 12 18
Câu 3. Cho hình chóp S.ABCD có SA = a, SA vuông góc với mặt phẳng (ABCD), đáy là hình vuông ABCD. Gọi
M, N lần lượt là trung điểm của AD, DC và góc giữa (SBM) và (ABCD) bằng 30o . Tính khoảng cách từ D đến mặt phẳng (SBM) bằng a 2 a 3 a 2 A. B. a 2 C. D. 2 2 3
Câu 4. Cho hình chóp đều S.ABC có · o · o ·
ASB  60 ; BSC  90 ;CSA  120ovà SA = a, SB = 2a, SC = 5a. Tính
khoảng cách từ C đến mặt phẳng (SAB). 5a 6 5a 6 5a 2 5a 3 A. B. C. D. 3 6 3 3
Câu 5. Cho hình lăng trụ đứng ABC.A’B’C’ có ·
AB  a; AC  2a; BAC  120o . Gọi M là trung điểm của cạnh CC’ thì ·
BMA  90o. Tính khoảng cách từ điểm A đến mặt phẳng (BMA’). a 5 a 5 a 7 a 5 A. B. C. D. 7 5 7 3
Câu 6. Cho hình chóp S.ABCD có · o · o ·
SA  SB  SC  a; ASB  60 ; ASC  90 ; BSC  120o. Khoảng cách từ
điểm B đến mặt phẳng (SAC) bằng a 3 a 2 a 2 a 3 A. B. C. D. 3 3 2 2
Câu 7. Hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB đều và nằm trong mặt phẳng
vuông góc với mặt đáy (ABCD); N là trung điểm cạnh AD. Tính khoảng cách từ điểm B đến mặt phẳng (SCN). a 2 a 2 3 2a 3 2a A. B. C. D. 2 4 4 8
Câu 8. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD),
SA  a 3 . Gọi O là giao điểm của AC và BD, với E là điểm đối xứng với O qua trung điểm của SA. Tính
khoảng cách từ điểm S đến mặt phẳng (EAB). a 3 a 39 a 39 a 39 A. B. C. D. 2 13 2 3
Câu 9. Hình chóp S.ABCD có đáy là hình thang vuông tại A và D, SA vuông góc với (ABCD). Góc giữa SB và
mặt phẳng đáy bằng 45o , E là trung điểm của SD, AB = 2a, AD = DC = a. Tính khoảng cách từ B đến mặt (ACE). 4a 2a A. B. a C. D. 0,75a 3 3
Câu 10. Hình chóp S.ABC có SA vuông góc với mặt phẳng đáy (ABC). Biết ·
BAC  30o; SA  a; BA  BC  a .
Gọi D là điểm đối xứng của B qua AC. Khoảng cách từ B đến mặt phẳng (SCD) bằng a 17 a 21 a 51 a 17 A. B. C. D. 51 7 51 68 29
Câu 11. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, cạnh AB  ; a AD  a 2 . Hình chiếu
vuông góc của S trên mặt phẳng (ABCD) là trung điểm của đoạn OA. Góc giữa SC và mặt phẳng (ABCD) bằng
30o . Tính khoảng cách từ C đến mặt phẳng (SAB). 9 22 3 22 22 3 22 A. a B. a C. a D. a 44 11 11 44
Câu 12. Cho hình chóp S.ABC có SA = a, tam giác ABC đều, tam giác SAB vuông cân tại S và nằm trong mặt
phẳng vuông góc với mặt phẳng đáy. Tính khoảng cách từ B đến mặt phẳng (SAC). a 42 a 42 a 42 a 42 A. B. C. D. 7 14 12 6
Câu 13. Cho hình chóp S.ABC có đáy là tam giác vuông tại A, AC = a, I là trung điểm của SC. Hình chiếu vuông
góc của S lên (ABC) là trung điểm H của BC. Mặt phẳng (SAB) tạo với (ABC) một góc 60o . Tính khoảng cách từ I đến mặt phẳng (SAB). 3 3 5 2 A. a B. a C. a D. a 4 5 4 3
Câu 14. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và ·
BAD  60o . Hình chiếu vuông góc của S
trên mặt phẳng (ABCD) trùng với trọng tâm của tam giác ABC. Góc giữa hai mặt phẳng (SAB), (ABCD) bằng
60o . Tính khoảng cách từ B đến mặt phẳng (SCD). 21 21 3 7 3 7 A. a B. a C. a D. a 14 7 14 7
Câu 15. Cho tứ diện ABCD có AB = CD = 4, AC = BD = 5, AD = BC = 6. Tính khoảng cách từ điểm A đến mặt phẳng (BCD). 3 6 3 2 3 42 7 A. B. C. D. 7 5 7 2
Câu 16. Cho hình chóp tam giác đều S.ABC có độ dài cạnh đáy bằng a, cạnh bên bằng a 3 . Gọi O là tâm của đáy ABC, tính tổng d ( , A (SBC))  d (O,(SBC)) . 2a 2 2a 2 8a 2 8a 2 A. B. C. D. 11 33 33 11
Câu 17. Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB = 2AD = 2a. Tam giác SAB đều và nằm trong mặt
phẳng vuông góc với đáy (ABCD). Tính khoảng cách từ điểm A đến mặt phẳng (SBD). a 3 a 3 A. 0,5a B. a C. D. 2 4
Câu 18. Cho hình lăng trụ đứng ABC.A o 1B1C1 có · AB  ;
a A A  2a 5; BAC  120 . Gọi I, K lần lượt là trung 1
điểm của C1C, B1B. Tính khoảng cách từ điểm I đến mặt phẳng (A1BK). a 5 a 15 a 5 A. a 15 B. C. D. 6 3 3
______________________________________ 30
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN CỔ ĐIỂN LỚP 11 – 12 THPT
(LỚP BÀI TOÁN KHOẢNG CÁCH ĐIỂM ĐẾN MẶT PHẲNG – P5)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho hình hộp ABCD.A’B’C’D’ có đáy ABCD là hình vuông cạnh a, tâm O. Hình chiếu vuông góc của A’
lên mặt phẳng (ABCD) trùng với O. Biết tam giác AA’C vuông cân tại A’. Tính khoảng cách từ D đến mặt phẳng (ABB’A’). a 6 a 2 a 2 a 6 A. B. C. D. 6 6 3 3
Câu 2. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, mặt bên SAB là tam giác đều và nằm trong mặt
phẳng vuông góc với đáy. Gọi M là trung điểm của SA biết AD  a 3; AB  a . Tính khoảng cách từ C đến mặt phẳng (MBD). a 15 a 39 2a 39 a 39 A. B. C. D. 5 13 13 26
Câu 3. Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình bình hành tâm O, mặt phẳng (SAC) vuông góc với
mặt phẳng (SBD). Biết khoảng cách từ O đến các mặt phẳng (SAB), (SBC), (SCD) lần lượt là 1; 2; 5 . Tính
khoảng cách từ O đến mặt phẳng (SAD). 2 95 95 2 A. B. C. 2 D. 19 10 2
Câu 4. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại B và C, CD = 2AB, AD = a, · ADC  30o ,
SA vuông góc với mặt đáy và SA = 2a. Tính khoảng cách từ D đến mặt phẳng (SBC). 2 57 57 3 57 A. a B. a C. a D. 3a 19 19 19
Câu 5. Cho hình lăng trụ tam giác ABC.A’B’C’ có AB  2 3; A A
  2 . Gọi M, N, P lần lượt là trung điểm các
cạnh A’B’, A’C’ và BC. Tính khoảng cách từ A đến mặt phẳng (MNP). 17 6 13 13 A. B. 2,4 C. D. 65 65 65
Câu 6. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy và SA = 2a, M là trung điểm
của SD. Tính khoảng cách d giữa đường thẳng SB và mặt phẳng (ACM). 2a a A. 1,5a B. a C. D. 3 3
Câu 7. Cho hình lập phương ABCD.A’B’C’D’ cạnh a, tính khoảng cách giữa hai mặt phẳng (AB’C) và (A’DC’). a a 3 A. B. a 3 C. a 2 D. 3 3
Câu 8. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB vuông cân tại S và nằm trong
mặt phẳng vuông góc với đáy, gọi I là trung điểm của AB và M là trung điểm của BC. Tính khoảng cách từ I đến mặt phẳng (SMD). a 6 a 30 a 13 3 14a A. B. C. D. 6 12 26 28
Câu 9. Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi I, J lần lượt là trung điểm của BC, AD. Tính khoảng
cách d giữa hai mặt phẳng (AIA’) và (CJC’). a 5 3a 5 A. a 10 B. 2a 5 C. D. 5 5
Câu 10. Cho khối lăng trụ ABC.A’B’C’ có thể tích bằng 3
a . Gọi M, N lần lượt là trung điểm của A’B’, C’C. Tính
khoảng cách từ A đến mặt phẳng (BMN) biết rằng BMN là tam giác đều cạnh 2a. a a 3 a 3 A. B. a 3 C. D. 3 3 2
Câu 11. Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Trên A’A, B’B lấy lần lượt các điểm M, N sao cho
AM  0,75a; BN  0,5a . Tính khoảng cách từ điểm B’ đến mặt phẳng (MNC) là 2a 2a 21 a a 41 A. B. C. D. 21 63 21 8 31
Câu 12. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, ·
BAD  60o . Hình chiếu của S lên mặt phẳng
(ABCD) là trọng tâm tam giác ABC. Góc giữa (ABCD) và (SAB) bằng 60o . Tính khoảng cách từ B đến mặt phẳng (SCD). 3a 17 3a 7 3a 17 3a 7 A. B. C. D. 14 14 4 4
Câu 13. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, ·
BAC  60o . Hình chiếu của đỉnh S trên mặt
phẳng (ABCD) trùng với trọng tâm tam giác ABC, góc tạo bởi hai mặt phẳng (SAC), (ABCD) là 60o . Tính
khoảng cách từ B đến mặt phẳng (SCD). 3a 9a a 3a A. B. C. D. 2 7 2 7 2 7 7
Câu 14. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, D và AB = AD = 2a, DC = a. Điểm I là
trung điểm đoạn AD, hai mặt phẳng (SIB), (SIC) cùng vuông góc với mặt phẳng (ABCD). Mặt phẳng (SBC) tạo
với mặt phẳng (ABCD) một góc 60o . Tính khoảng cách từ D đến (SBC). a 15 9a 15 2a 15 9a 15 A. B. C. D. 5 10 5 20
Câu 15. Cho tứ diện ABCD có · o · o ·
BAC  90 ;CAD  60 ; BAD  120o; AB  AC  a . Tính khoảng cách từ C đến mặt phẳng (ABD). a 3 a 6 a 6 a 2 A. B. C. D. 2 3 2 2
Câu 16. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AB = 3a, AD = DC = a, gọi I là
trung điểm của AD, biết hai mặt phẳng (SBI), (SCI) cùng vuông góc với đáy và mặt phẳng (SBC) tạo với đáy một
góc 60o . Tính khoảng cách từ trung điểm cạnh SD đến mặt phẳng (SBC). a 17 a 6 a 3 a 15 A. B. C. D. 5 19 15 20
Câu 17. Cho hình chóp S.ABCD có đáy là hình thoi tâm O cạnh a, ·
BAD  60o . Đường thẳng SO vuông góc với
mặt đáy (ABCD) và SO = 0,75a. Khoảng cách từ O đến mặt phẳng (SBC) bằng a 3 a A. 0,75a B. 0,375a C. D. 4 3
Câu 18. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với đáy (ABC), góc giữa
đường thẳng SB và mặt phẳng (ABC) bằng 60o . M là trung điểm của cạnh AB. Tính khoảng cách từ B đến mặt phẳng (SMC). a 39 A. B. a C. 0,5a D. a 3 13
______________________________________ 32
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN CỔ ĐIỂN LỚP 11 – 12 THPT
(LỚP BÀI TOÁN KHOẢNG CÁCH ĐIỂM ĐẾN MẶT PHẲNG – P6)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, ·
ABC  30o, tam giác SBC đều cạnh a và
nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính khoảng cách từ C đến mặt phẳng (SAB). 39 15 39 15 A. a B. a C. a D. a 26 16 13 8
Câu 2. Cho hình chóp S.ABCD có đáy ABCD là hình vuông với AB = 2a, tam giác SAB vuông tại S, mặt phẳng 1
(SAB) vuông góc với (ABCD). Biết góc tạo bởi đường thẳng SD và mặt phẳng (SBC) bằng  : sin  . Tính 3
khoảng cách từ C đến mặt phẳng (SBD) theo a. a 2a 3a A. B. C. D. a 3 3 4
Câu 3. Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của A’ lên
(ABC) trùng với trung điểm của BC. Tính khoảng cách từ A’ đến (BCC’B’) biết góc giữa hai mặt phẳng (ABB’A’)
và (A’B’C’) bằng 60o . 3a 7 a 3 a 21 A. B. C. D. 0,75a 14 4 14
Câu 4. Cho hình hộp đứng ABCD.A’B’C’D’ có đáy là hình vuông, tam giác A’AC vuông cân, A’C = 2. Tính
khoảng cách từ điểm A đến mặt phẳng (BCA’). 3 2 6 6 A. B. C. D. 2 3 3 6
Câu 5. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của AD, BC. 6a
Biết khoảng cách từ M đến mặt phẳng (SBD) bằng
. Tính khoảng cách từ điểm N đến mặt phẳng (SBD). 7 12a 4a 6a 3a A. B. C. D. 7 7 7 7
Câu 6. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên (SAB) là tam giác đều và nằm
trong mặt phẳng vuông góc với đáy (ABCD). Lấy điểm I trên đoạn SB sao cho IB = 2SI. Tính khoảng cách h từ
điểm I đến mặt phẳng (SCD). a a 21 2a a 21 A. B. C. D. 21 7 21 14
Câu 7. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh SA vuông góc với mặt đáy, góc giữa
SC và mặt phẳng đáy bằng 60o . Gọi I là trung điểm của đoạn thẳng SB. Tính theo a khoảng cách từ điểm S đến mặt phẳng (ADI). a 42 a 7 A. a 6 B. C. D. a 7 7 2
Câu 8. Cho hình chóp S.ABCD có đáy là hình vuông tại A và D, AB = 2AD = 2CD = 2a. Cạnh bên SA vuông góc uur uuur
với đáy và SA = a. Gọi M là trung điểm của SD, N là điểm thỏa mãn SB  3SN , tính khoảng cách từ C đến mặt phẳng (AMN). a 2 a 3 2a 3 A. a 2 B. C. D. 3 3 3
Câu 9. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a, từ S hạ SN, SM vuông góc với AC và AB tại
N, M. Biết NC = 2NA, MA = MB, G là trọng tâm tam giác SAB. Tính khoảng cách từ G đến mặt phẳng (SAC). 21 2a 5 7a a 3 A. a B. C. D. 98 9 2 2 15
Câu 10. Cho lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy bằng 1, cạnh bên A A
  3 . Tính khoảng cách d từ
điểm A lên mặt phẳng (A’BC). 3 2 15 15 3 A. B. C. D. 2 5 5 4 33
Câu 11. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a và cạnh bên SA vuông góc với mặt phẳng 3 a
đáy. Gọi E là trung điểm của CD, biết thể tích khối chóp S.ABCD bằng
. Tính khoảng cách từ A đến mặt 3 phẳng (SBE) theo a. a 3 a 2a a 2 A. B. C. D. 3 3 3 3
Câu 12. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB là tam giác đều và nằm trong mặt
phẳng vuông góc với mặt phẳng đáy. Tính khoảng cách từ A đến mặt phẳng (SBD). a 21 a 21 a 21 a 2 A. B. C. D. 28 7 14 2
Câu 13. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, mặt phẳng (SAC) vuông góc với mặt
phẳng (SBD). Biết khoảng cách từ O đến các mặt phẳng (SAB), (SBC), (SCD) lần lượt là 1; 2; 5 . Tính khoảng
cách d từ O đến các mặt phẳng (SAD). 19 20 2 A. B. C. D. 2 20 19 2
Câu 14. Cho lăng trụ ABCD.A’B’C’D’ có đáy ABCD là hình vuông cạnh 2a, A A
  a 3 , hình chiếu của A’ lên
mặt phẳng ABCD trùng với trung điểm I của AB. Gọi K là trung điểm của BC. Tính khoảng cách từ I đến mặt phẳng (A’KD). 3a 2 3 38a 4 2a 3 2a A. B. C. D. 19 19 3 8
Câu 15. Cho hình chóp S.BACD có đáy ABCD là hình vuông, SA vuông góc với đáy, mặt bên (SCD) hợp với 3 a 3
đáy góc 60o , M là trung điểm của BC. Biết thể tích khối chóp S.ABCD bằng
. Tính khoảng cách từ M đến 3 mặt phẳng (SCD). a 3 a 3 a 3 A. B. a 3 C. D. 6 4 2
Câu 16. Cho hình chóp S.ABCD có đáy là hình thang vuông tại A, D, SA vuông góc với (ABCD). Góc giữa SB
và mặt phẳng đáy bằng 45o . E là trung điểm của SD, AB = 2a, AD = DC = a. Tính khoảng cách từ điểm B đến mặt phẳng (ACE). 2a 4a A. a B. C. 0,75a D. 3 3
Câu 17. Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều cạnh 2a, góc giữa A’B và mặt phẳng
(AA’C’C) bằng 45o . Gọi I là trung điểm của AC. Tính khoảng cách từ C’ đến mặt phẳng (A’BI). 2a 6 a 6 a 6 A. B. a 6 C. D. 3 3 2 34
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN CỔ ĐIỂN LỚP 11 – 12 THPT
(LỚP BÀI TOÁN KHOẢNG CÁCH HAI ĐƯỜNG CHÉO NHAU – P1)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B có AD = 2°; AB = BC = a,
cạnh SA vuông góc với đáy và SA  a 2 . Khoảng cách giữa hai đường phẳng SB và DC bằng a 10 a 7 a 6 a 11 A. . B. . C. . D. . 5 3 3 5
Câu 2. Cho tứ diện đều ABCD có cạnh bằng a. Khoảng cách giữa hai đường thẳng AB và CD bằng a 2 a 2 a 3 a 3 A. . B. . C. . D. . 3 2 2 3
Câu 3. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , tam giác SAB đều và nằm trong mặt
phẳng vuông góc với đáy. Khoảng cách giữa hai đường thẳng SA và BC bằng a 5 a 3 A. a . B. . C. . D. a 2 . 2 2
Câu 4. Cho hình chóp S.ABCD có đáy là hình thoi cạnh 2a và đường chéo BD  2a 3 , cạnh bên SA
vuông góc với mặt đáy. Biết góc tạo bởi SC và mặt phẳng đáy bằng 0
45 . Tìm khoảng cách giữa hai đường thẳng BD, SC . a 2 a 3 a 2 a 3 A. . B. . C. . D. . 2 2 3 3
Câu 5. Cho tứ diện OABC có OA, OB , OC đôi một vuông góc với nhau và OA  a, OB  OC  2 . a Gọi
M là trung điểm của cạnh BC . Khoảng cách giữa hai đường thẳng OM và AC bằng: a 2 2a 5 a 6 A. . B. . C. a. D. . 2 5 3
Câu 6. Cho hình chóp tứ giác đều S.ABCD có đáy bằng 2a , SA tạo với đáy một góc 30 . Tính theo
a khoảng cách d giữa hai đường thẳng SA và CD . 2 10a 3 14a 4 5a 2 15a A. d  . B. d  . C. d  . D. d  . 5 5 5 5
Câu 7. Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD có AB  2a, AD  4a, SA  (ABCD) ,
cạnh SC tạo với đáy một góc 0
60 . Gọi M là trung điểm của BC, N là điểm nằm trên cạnh AD sao cho
DN  a . Khoảng cách giữa MN và SB là A. 2a 95 B. 8a C. 2a 285 D. a 285 19 19 19 19
Câu 8. Cho hình chóp S.ABC có đáy là tam giác đều cạnh bằng a. Gọi I là trung điểm của AB , hình
chiếu của S lên mặt phẳng  ABC là trung điểm của CI , góc giữa SA và mặt đáy bằng 45 . Gọi G là
trọng tâm SBC . Khoảng cách giữa hai đường thẳng SA và CG bằng: a 21 a 14 a 77 a 21 A. . B. . C. . D. . 14 8 22 7
Câu 9. Cho hình lăng trụ tam giác đều ABC.A B  C
  có AB  2 3 và AA  2 . Gọi M , N , P lần lượt là
trung điểm các cạnh AB , AC và BC . Khoảng cách từ A đến MNP bằng 17 6 13 13 12 A. . B. . C. . D. . 65 65 65 5
Câu 10. Cho lăng trụ đứng ABC.A B  C   có ·
AC  a, BC  2a, ACB  120 . Gọi M là trung điểm của BB .
Tính khoảng cách giữa hai đường thẳng AM và CC theo a . 3 7 3 A. a . B. a 3 . C. a . D. a . 7 7 7
Câu 11. Cho hình lập phương ABC . D A B  C  D
  có cạnh bằng a. Gọi K là trung điểm của DD. Tính
khoảng cách giữa hai đường thẳng CK , A D  . 35 3a 2a a A. a. B. . C. . D. . 8 5 3
Câu 12. Cho lăng trụ ABC.A B  C
  có đáy ABC là tam giác đều có cạnh bằng 4. Hình chiếu vuông góc
của A trên mp(ABC) trùng với tâm của đường tròn ngoại tiếp  ABC . Gọi M là trung điểm cạnh AC .
Khoảng cách giữa hai đường thẳng BM và B C  bằng A. 2 . B. 2 . C. 1. D. 2 2 .
Câu 13. Cho hình lập phương ABC .
D A B C D . Khoảng cách giữa AD và BB là độ dài đoạn thẳng? 1 1 1 1 1 A. AC . B. BD . C. AB . D. DC . 1 1
Câu 14. Hình lập phương ABC . D AB C  D
  cạnh a . Tính khoảng cách giữa hai đường AB và CD . a 2 A. . B. a. C. a 2. D. 2a. 2
Câu 15. Cho hình hộp chữ nhật EFGH.E F  G  H
  có EF  3a, EH  4a, EE 12a, với 0  a  ¡ . Khoảng
cách giữa hai đường thẳng EF  và GH  bằng A. 12a . B. 3a . C. 2a . D. 4a .
Câu 16. Cho hình lập phương ABC . D AB C  D
  cạnh a. Tính khoảng cách giữa hai đường AB và CD . 2a A. . B. . a C. 2 . a D. 2a. 2
Câu 17. Hình lập phương ABC .
D A ' B 'C ' D ' có cạnh bằng a . Khoảng cách giữa hai đường thẳng BD và A'C ' bằng 3 A. a . B. 2a. C. a . D. 3a . 2
Câu 18. Cho hình lăng trụ ABC.A B  C
  có tất cả các cạnh đều bằng a . Góc tạo bởi cạnh bên và mặt
phẳng đáy bằng 30 . Hình chiếu H của A trên mặt phẳng  AB C
  là trung điểm của B C   . Tính theo
a khoảng cách giữa hai mặt phẳng đáy của lăng trụ ABC.A B  C  . a a a 3 a 2 A. . B. . C. . D. . 2 3 2 2
Câu 19. Cho lăng trụ đứng ABC.A B  C
  có tất cả các cạnh đều bằng 2a . Khoảng cách giữa hai đường thẳng BC và AA bằng 2a 5 2a a 3 A. . B. . C. . D. a 3 . 3 5 2
Câu 20. Cho hình lăng trụ tam giác đều ABC.A' B 'C ' có tất cả các cạnh đều bằng a . Khoảng cách từ
A đến mặt phẳng  A' BC  bằng a 3 a 21 a 2 a 6 A. . B. . C. . D. . 4 7 2 4
______________________________________ 36
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN CỔ ĐIỂN LỚP 11 – 12 THPT
(LỚP BÀI TOÁN KHOẢNG CÁCH HAI ĐƯỜNG CHÉO NHAU – P2)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ 3 3a
Câu 1. Cho lăng trụ đều ABC.A B  C
  có cạnh đáy bằng a và có thể tích bằng
. Tính khoảng cách giữa hai 4
đường thẳng AB và A’C. a 15 2a a 5 A. a 2 B. C. D. 5 5 5
Câu 2. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AB = 3a, AD = DC = a. Gọi I là
trung điểm của AD, biết hai mặt phẳng (SBI), (SCI) cùng vuông góc với đáy và mặt phẳng (SBC) tạo với đáy một
góc 60 . Gọi M là điểm trên AB sao cho AM = 2a. Tính khoảng cách giữa hai đường thẳng MD và SC. a 17 a 15 a 6 a 3 A. B. C. D. 5 10 9 15
Câu 3. Cho lăng trụ tam giác đều ABC.A B  C
  có AB = a, A’A = 2a. Tính khoảng cách giữa hai đường thẳng AB’ và A’C. 2a a 3 2a A. B. C. a 5 D. 5 2 17
Câu 4. Cho hình chóp S.ABCD có đáy là hình thang vuông tại B và C, AB = 3a, BC = CD = a, SA vuông góc với
mặt phẳng đáy. Góc giữa SC và mặt phẳng đáy bằng 30 . Gọi M là điểm thuộc cạnh AB sao cho 3AM = 2AB.
Khoảng cách giữa hai đường thẳng SB và DM bằng 3a 370 a 370 a 37 3a 37 A. B. C. D. 37 37 13 13
Câu 5. Cho lăng trụ đứng ABC.AB C
  có tất cả các cạnh bằng a. Tính theo a khoảng cách giữa hai đường thẳng A’B’ và BC’. 3a a 21 a 2 A. a B. C. D. 7 7 2
Câu 6. Cho hình chóp S.ABC có đáy là tam giác đều cạnh 2a. Hình chiếu vuông góc của S trên mặt phẳng
(ABC) là trung điểm H của cạnh AB. Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng 30 . Tính khoảng
cách giữa hai đường thẳng BC và SA. 2a a a 21 2a 21 A. B. C. D. 7 7 7 7
Câu 7. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, tam giác ABC là tam giác đều cạnh à và
thuộc mặt phẳng vuông góc với đáy. Tính khoảng cách giữa hai đường thẳng SA và BC. a 3 a 3 a 3a A. B. C. D. 4 2 2 2
Câu 8. Cho lăng trụ đứng ABC.A B  C
  có tất cả các cạnh bằng a. Tính khoảng cách giữa hai đường thẳng AC và B’B. a 3 2a a a 5 A. B. C. D. 2 5 5 3
Câu 9. Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O có AC  2a; BD  2a 3 . Hình chiếu vuông
góc của đỉnh S xuống mặt đáy trùng với trung điểm của OB. Biết tam giác SBD vuông tại S. Khoảng cách giữa
hai đường thẳng AC và SB là a 3 A. 0,75a B. 1,5a C. D. 0,375a 2
Câu 10. Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a, gọi M, N lần lượt là trung điểm của AB và
AD. Hình chiếu vuông góc của S trên mặt phẳng đáy trùng với giao điểm H của CM và BN. Biết SH = a, tính
khoảng cách giữa hai đường thẳng SC và BN. 2a a 3a 4a A. B. C. D. 3 3 4 7
Câu 11. Hình hộp chữ nhật ABC . D AB C  D
  có đáy ABCD là hình vuông cạnh a 2 . Biết A A   2a , tính 37
khoảng cách giữa hai đường thẳng BD và CD’. 2a a 5 A. a 2 B. 2a C. D. 5 5
Câu 12. Hình chóp S.ABCD có đáy là tam giác đều cạnh a, góc giữa SC và đáy (ABC) bằng 45 . Hình chiếu a 7
vuông góc của S lên mặt phẳng (ABC) là điểm H thuộc AB sao cho HA = 2HB. Biết CH  , tính khoảng 3
cách giữa hai đường thẳng SA, BC. a 210 a 210 a 210 a 210 A. B. C. D. 15 45 30 20
Câu 13. Cho hình lăng trụ đứng ABC.A B  C
  có đáy ABC là tam giác vuông tại A, AB = a. Khoảng cách giữa
hai đường thẳng AC và B’B là a 2 a 3 A. a B. C. D. a 2 2 2
Câu 14. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy (ABCD)
và SA = a, khoảng cách giữa hai đường thẳng BD và SC là a 3 a 2 a 6 A. B. C. D. 2a 2 3 6
Câu 15. Hình chóp S.ABCD có đáy là hình thang, AB = 2a, AD = DC = CD = a, SA = 3a và SA vuông góc với
mặt phẳng đáy. Gọi M là trung điểm của AB, khoảng cách giữa hai đường thẳng SB và DM bằng 3a 6a A. 1,5a B. 0,75a C. D. 13 13
Câu 16. Cho hình chóp S.ABC có đáy là tam giác vuông tại A, AB = 2a, AC = 4a, SA vuông góc với mặt phẳng
đáy và SA = a. Gọi M là trung điểm của AB. Khoảng cách giữa hai đường thẳng SM và BC là a a 6 2a A. 0,5a B. C. D. 3 3 3
Câu 17. Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, cạnh a, 
BAD  60 . Tính khoảng cách giữa
hai đường thẳng AD và SB. 2a 57 a 57 2a a 3 A. B. C. D. 19 19 5 2 2a
Câu 18. Cho hình hộp chữ nhật ABC . D AB C  D
  . Khoảng cách giữa AB và B’C’ là , khoảng cách giữa BC 5 2a a và AB’ là
, khoảng cách giữa AC và BD’ là
. Thể tích khối hộp đó là 5 3 A. 8 3 a B. 4 3 a C. 2 3 a D. 3 a
______________________________________ 38
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN CỔ ĐIỂN LỚP 11 – 12 THPT
(LỚP BÀI TOÁN KHOẢNG CÁCH HAI ĐƯỜNG CHÉO NHAU – P3)
_______________________________________________
Câu 1. Cho lăng trụ ABC.A B  C
  có đáy ABC là tam giác đều có cạnh bằng 4. Hình chiếu vuông góc của A
trên mp( ABC ) trùng với tâm của đường tròn ngoại tiếp  ABC . Gọi M là trung điểm cạnh AC . Khoảng cách
giữa hai đường thẳng BM và B C  bằng A. 2 . B. 2 . C. 1. D. 2 2 .
Câu 2. Cho hình lập phương ABC . D AB C  D
  cạnh a . Gọi M , N lần lượt là trung điểm của BC và DD. Tính
theo a khoảng cách giữa hai đường thẳng MN và BD . 3a 3a 3a A. 3a . B. . C. . D. . 2 3 6
Câu 3. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Đường thẳng SA vuông góc với mặt
phẳng  ABCD và SA  a . Tính khoảng cách d giữa hai đường thẳng SB và CD . A. d  2a . B. d  a 3 . C. d  a 2 . D. d  a .
Câu 4. Cho hình chóp S.MNPQ có đáy là hình vuông, MN  3a , với 0  a  ¡ , biết SM vuông góc với đáy,
SM  6a . Khoảng cách giữa hai đường thẳng NP và SQ bằng A. 6a . B. 3a . C. 2a 3 . D. 3a 2 .
Câu 5. Cho hình chóp S.ABCD có đáy là hình vuông với đường chéo AC  2a , SA vuông góc mặt phẳng
 ABCD . Khoảng cách giữa hai đường thẳng SB và CD là: a a A. . B. . C. a 2 . D. a 3 . 3 2
Câu 6. Cho tứ diện đều ABCD có cạnh bằng 3cm, M là trung điểm CD . Khoảng cách giữa AC và BM là 2 11 3 22 3 2 2 A. cm . B. cm . C. cm . D. cm . 11 11 11 11
Câu 7. Cho tứ diện đều ABCD có cạnh bằng a. Khoảng cách giữa hai đường thẳng AB và CD bằng a 2 a 2 a 3 a 3 A. . B. . C. . D. . 3 2 2 3
Câu 8. Cho hình chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh AD  2a , SA   ABCD và SA  a .
Khoảng cách giữa hai đường thẳng AB và SD bằng a 3 a 6 2a 5 A. . B. . C. . D. a 6 . 3 4 5
Câu 9. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , tam giác SAB đều và nằm trong mặt phẳng
vuông góc với đáy. Khoảng cách giữa hai đường thẳng SA và BC bằng a 5 a 3 A. a . B. . C. . D. a 2 . 2 2
Câu 10. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , tam giác SAD đều và nằm trong mặt phẳng
vuông góc với đáy .Tính khoảng cách d giữa hai đường thẳng SA và BD . a 21 a 2 a 21 A. d  . B. d  . C. d  . D. d  a . 14 2 7
Câu 11. Cho khối chóp S.ABCD có thể tích bằng 3
2a và đáy ABCD là hình bình hành. Biết diện tích tam giác SAB bằng 2
a . Tính khoảng cách giữa hai đường thẳng SB và C . D 3a a 2 A. a. B. . C. 3a. D. . 2 2
Câu 12. Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a . Tính khoảng cách giữa hai đường thẳng AD và SB . a 6 a 6 a 3 a 3 A. . B. . C. . D. . 2 3 3 2
Câu 13. Cho hình chóp S.ABC có đáy ABC vuông cân tại A , AB  a 2 , tam giác SBC đều nằm trong mặt
phẳng vuông góc với mặt đáy. Tính khoảng cách giữa AC và SB . 39 a 21 2a 21 a 21 2a 21 A. . B. . C. . D. . 14 3 7 7
Câu 14. Cho hình chóp tứ giác đều S.ABCD có đáy bằng 2a , SA tạo với đáy một góc 30 . Tính theo a
khoảng cách d giữa hai đường thẳng SA và CD . 2 10a 3 14a 4 5a 2 15a A. d  . B. d  . C. d  . D. d  . 5 5 5 5
Câu 15. Cho tứ diện OABC có O ,
A OB, OC đôi một vuông góc với nhau và OC  2a,OA  OB  a . Gọi M là
trung điểm của AB . Tính khoảng cách giữa hai đường thẳng OM và AC . 2a 2a 5 a 2 a 2 A. . B. . C. . D. . 3 5 3 2
Câu 16. Cho tứ diện đều ABCD có cạnh bằng a . Khoảng cách giữa hai đường thẳng AB và CD bằng: a 3 a 2 A. . B. a 3 . C. a 2 . D. . 2 2
Câu 17. Cho lăng trụ đứng tam giác ABC.A'B'C' tam giác vuông cân tại ,
A AB  2a . Khoảng cách giữa hai
đường thẳng AA ' và BC là ?
A. d  AA ', BC   2a . B. d  AA', BC   2a . C. d  AA', BC   a . D. d  AA BC  1 ',  a . 2
Câu 18. Cho lăng trụ đứng ABC.A B  C   có ·
AC  a, BC  2a, ACB  120 . Gọi M là trung điểm của BB . Tính
khoảng cách giữa hai đường thẳng AM và CC theo a . 3 7 3 A. a . B. a 3 . C. a . D. a . 7 7 7
Câu 19. Cho lăng trụ đứng ABC.A B  C
 , đáy ABC là tam giác vuông ở A , AB  2a , AC  a , AA  4a . M là
điểm thuộc cạnh AA sao cho MA  3MA . Tính khoảng cách giữa hai đường chéo nhau BC và C M  . 6a 4a 4a 8a A. d  . B. d  . C. d  . D. d  . 7 7 3 7
Câu 20. Cho hình lăng trụ tam giác đều ABC.A B  C
  có AB  a, AA  2 .
a Tính khoảng cách giữa hai đường thẳng AB và A C  . a 3 2 5 2 17 A. . B. . a C. a 5. D. . a 2 5 17
Câu 21. Cho khối hộp ABC . D AB C  D
  có thể tích bằng 6 , ABC là tam giác đều có cạnh bằng 2. Khoảng
cách từ điểm B đến mặt phẳng  ABC bằng 3 3 3 A. 3 . B. . C. . D. . 2 3 6
Câu 22. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , AB  a , cạnh bên SA vuông góc với
đáy và SA  a 2 . Gọi E là trung điểm của AB . Khoảng cách giữa đường thẳng SE và đường thẳng BC bằng bao nhiêu ? a 3 a 3 a a 2 A. . B. . C. . D. . 3 2 2 3 40
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN CỔ ĐIỂN LỚP 11 – 12 THPT
(LỚP BÀI TOÁN KHOẢNG CÁCH HAI ĐƯỜNG THẲNG CHÉO NHAU – PHẦN 4)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ a 17
Bài 1. Hình chóp có đáy ABCD là hình vuông cạnh a, SD 
, hình chiếu vuông góc của S lên mặt phẳng 2
(ABCD) là trung điểm của đoạn AB. Gọi K là trung điểm của AD. Tính khoảng cách giữa hai đường SD, HK. a 3 a 3 a 21 a 2 A. B. C. D. 5 7 5 6
Bài 2. Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, đường thẳng SA vuông góc với mặt phẳng đáy,
SA = 2a. Gọi N là trung điểm của AD. Tính khoảng cách d giữa hai đường thẳng SN và CD. 2a 2a A. B. a 5 C. a 2 D. 5 3
Bài 3. Cho khối chóp S.ABCD có thể tích bằng 3
a . Mặt bên SAB là tam giác đều cạnh a và thuộc mặt phẳng
vuông góc với đáy, biết đáy ABCD là hình bình hành. Tính theo a khoảng cách d giữa SA và CD. 2a A. 2 3a B. 3a C. D. 0,5a 3
Bài 4. Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại A, BC = 2a, tam giác SBC là tam giác đều và
nằm trong mặt phẳng vuông góc với mặt đáy. Tính khoảng cách d giữa hai đường thẳng SA và BC. a 6 a 3 A. B. C. a 6 D. a 3 2 2
Bài 5. Cho hình chóp S.ABCD, có đáy ABCD là hình vuông cạnh a, hình chiếu vuông góc của S lên mặt phẳng
ABCD là điểm H thuộc cạnh AB sao cho HB = 2HA, cạnh SC tạo với mặt đáy (ABCD) một góc bằng 60 . Tính
khoảng cách d giữa hai đường thẳng AD và SC. 13 4a 13 13 13 A. 3a B. C. 2a D. 6a 129 3 129 129 129
Bài 6. Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông, AB = AC = a, cạnh bên BB  a 2 . Gọi M
là trung điểm AC, tính khoảng cách giữa hai đường thẳng A’C và BM. 4a a 3a 2a A. B. C. D. 7 7 7 7
Bài 7. Tứ diện OABC có đáy OBC là tam giác vuông tại O, OB = a, OC  a 3 và đường cao OA  a 3 . Gọi
M là trung điểm của BC, tính khoảng cách giữa hai đường thẳng AB và OM. a 3 a 15 a 15 a A. B. C. D. 5 15 5 5
Bài 8. Hình chóp S.ABC có tam giác ABC vuông cân tại A, BC = 2a, tam giác ABC đều và nằm trong mặt phẳng
vuông góc với đáy, khoảng cách giữa hai đường thẳng SA và BC là a 6 a 3 a A. B. C. a 6 D. 2 2 3
Bài 9. Hình chóp tứ giác đều S.ABCD có cạnh bên tạo với mặt đáy góc 60 và độ dài cạnh đáy bằng a. Tính
khoảng cách giữa hai đường thẳng AD, SC. a 42 2a 42 3a 42 a 42 A. B. C. D. 7 7 7 14
Bài 10. Hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, tam giác SAD đều và nằm trong mặt phẳng
vuông góc với đáy, tính khoảng cách giữa hai đường thẳng AD, SB. a 14 2a 14 a 14 2a 21 A. B. C. D. 7 7 3 7
Bài 11. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Hình chiếu vuông góc của S lên mặt phẳng
(ABCD) là trung điểm H của AB, tam giác SAB vuông cân tại S, SH  a 3,CH  3a . Tính khoảng cách giữa hai đường thẳng SD, CH. 41 2a 66 4a 66 a 66 a 66 A. B. C. D. 11 11 11 22
Bài 12. Hình chóp S.ABCD có đáy là hình vuông tâm O cạnh a, SO vuông góc với mặt phẳng (ABCD) và SO =
a. Khoảng cách giữa SC và AB là a 3 a 5 2a 3 2a 5 A. B. C. D. 15 5 15 5
Bài 13. Hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = 3a, BC = 4a. Cạnh bên SA vuông góc với
đáy, góc tạo bởi SC và mặt phẳng đáy là 60 . Gọi M là trung điểm của AC, tính khoảng cách giữa AB và SM. 10a 237 A. B. a 3 C. 2,5a D. 5a 3 79
Bài 14. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, G là trọng tâm tam giác ABC, góc giữa đường
thẳng SA với mặt phẳng (ABC) bằng 60 . Khoảng cách giữa hai đường thẳng GC và SA là a 5 a 5 a 2 A. B. 0,2a C. D. 5 10 5
Bài 15. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, góc giữa mặt bên và mặt đáy bằng 60 . Gọi
M là trung điểm của BC. Tính khoảng cách giữa hai đường thẳng AM và SC. a 3 a 3 a 6 a 6 A. B. C. D. 2 4 2 3
Bài 16. Cho lăng trụ đứng ABC.AB C
  có đáy ABC là tam giác vuông, AB  BC  a , cạnh bên AA  a 2 .
Gọi M là trung điểm của BC, tính khoảng cách giữa hai đường thẳng AM , B C  . a 7 a 2 a 3 a 5 A. B. C. D. 7 2 3 5
Bài 17. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 2a, BC = a. Các cạnh bên của hình chóp
bằng nhau và bằng a 2 . Gọi M, N lần lượt là trung điểm của các cạnh AB, CD. Gọi K là điểm trên cạnh AD
sao cho KD = 2KA. Tính khoảng cách giữa hai đường MN và SK. a 21 a 3 a 2 A. B. C. D. 1,5a 7 7 3
Bài 18. Cho khối chóp S.ABC có SA vuông góc với đáy, tam giác ABC vuông cân tại B, SA = a, SB hợp với đáy
(ABC) một góc 30 . Tính khoảng cách giữa AB và SC. a 3 2a A. B. 1,5a C. D. a 3 2 3 a
Bài 19. Hình chóp S.ABCD có đáy ABCD là hình vuông với AC 
. Cạnh bên SA vuông góc với mặt phẳng 2
đáy (ABC), SB hợp với mặt phẳng đáy một góc 60 . Tính khoảng cách giữa hai đường thẳng AD, SC. a a 3 a 3 A. B. C. D. 0,5a 2 2 4 42
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN CỔ ĐIỂN LỚP 11 – 12 THPT
(LỚP BÀI TOÁN KHOẢNG CÁCH HAI ĐƯỜNG CHÉO NHAU – P5)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho khối lăng trụ ABC.A B  C
  có thể tích bằng 3
a . Gọi M , N lần lượt là trung điểm của
AB , CC .Tính khoảng cách từ A đến mặt phẳng BMN  biết rằng BMN là tam giác đều cạnh 2a . a a 3 a 3 A. . B. a 3 . C. . D. . 3 3 2
Câu 2. Cho hình lăng trụ đứng ABC.A B C có AB  a , AC  2a , AA  2a 5 và · 0 BAC 120 . Gọi K, I lần 1 1 1 1
lượt là trung điểm của CC , BB . Khoảng cách từ I đến mặt phẳng  A BK bằng 1  1 1 a 5 a 15 a 5 A. a 15 . B. . C. . D. . 6 3 3
Câu 3. Cho hình lập phương ABC . D AB C  D   cạnh .
a Gọi M , N lần lượt là trung điểm của AC và B C   .
Khoảng cách giữa hai đường thẳng MN và B D   bằng a 5 a A. B. 3a C. D. a 5 5 3
Câu 4. Cho S.ABCD có đáy là hình vuông cạnh a , SA   ABCD và SA  a 3 . Gọi M là trung điểm của AD .
Khoảng cách giữa hai đường thẳng BM và SD bằng a 57 a 57 a A. a . B. . C. . D. . 3 19 2
Câu 5. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại ,
A mặt bên (SBC) là tam giác đều cạnh
a và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách giữa hai đường thẳng SA và BC bằng a 3 a 2 a 5 a 3 A. . B. . C. . D. . 4 4 4 3
Câu 6. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng a. Mặt bên SAB là tam giác cân tại
S, cạnh bên SC hợp với mặt đáy  ABC một góc 45, mặt bên SAB vuông góc với mặt đáy  ABC và I là trung điểm của A .
B Khoảng cách giữa hai đường thẳng SA và CI bằng a 2 a 3 a 6 a 3 A. . B. . C. . D. . 6 8 3 4
Câu 7. Cho hình chóp S.ABCD có ABCD là hình vuông cạnh a và SA vuông góc với mặt đáy. Biết SA  2a .
Khoảng cách giữa hai đường thẳng AB và SC bằng a 2a 5 a 5 A. . B. . C. . D. a 2 . 2 5 2
Câu 8. Cho hình chóp S.ABC có đáy là tam giác đều cạnh bằng 4 . Góc giữa SC và mặt phẳng  ABC  là
45. Hình chiếu của S lên mặt phẳng  ABC  là điểm H thuộc cạnh AB sao cho HA  2HB . Tính khoảng
cách giữa hai đường thẳng SA và BC . 4 210 210 4 210 2 210 A. . B. . C. . D. . 45 5 15 15
Câu 9. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , tâm O , SA   ABCD , SA  a 6 (như
hình vẽ). Tính khoảng cách giữa SB và AC . a a A.  AC SB 7 d ,  . B.  AC SB 78 d ,  . 3 3 a a C.  AC SB 87 d ,  D.  AC SB 78 d ,  . 13 13
Câu 10. Cho hình chóp tứ giác đều SABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA 2a ; Tính
khoảng cách giữa hai đường thẳng AB và SC . 43 a 14 2a 14 a 3 a 14 A. . B. . C. . D. . 2 15 15 5 15
Câu 11. Cho hình chóp S.ABCD có ABCD là hình vuông cạnh a và SA vuông góc với mặt đáy. Biết SA  2a .
Khoảng cách giữa hai đường thẳng AB và SC bằng: a 2a 5 a 5 A. . B. . C. . D. a 2 . 2 5 2
Câu 12. Cho hình chóp S.ABCD đáy là hình thoi cạnh a, góc ·
BAC  60 , tam giác SAB cân tại S nằm trong
mặt phẳng vuông góc với đáy. Mặt phẳng (SCD) tạo với đáy góc 30 . Tính khoảng cách d giữa hai đường thẳng SB và A . D 21 3 2 3 21 A. d  a . B. d  a . C. d  a . D. d  a . 14 5 5 7
Câu 13. Cho tứ diện OABC có OA, OB , OC đôi một vuông góc với nhau và OA  a, OB  OC  2 . a Gọi M là
trung điểm của cạnh BC . Khoảng cách giữa hai đường thẳng OM và AC bằng: a 2 2a 5 a 6 A. . B. . C. a . D. . 2 5 3
Câu 14. Cho hình chóp S.ABC có đáy là tam giác đều cạnh bằng a . Gọi I là trung điểm của AB , hình chiếu
của S lên mặt phẳng  ABC  là trung điểm của CI , góc giữa SA và mặt đáy bằng 45 (tham khảo hình vẽ
bên). Gọi G là trọng tâm SBC . Khoảng cách giữa hai đường thẳng SA và CG bằng a 21 a 14 a 77 a 21 A. . B. . C. . D. . 14 8 22 7
Câu 15. Cho hình chóp S.ABC có AB  13, BC  14,CA  15 . Hình chiếu vuông góc của S trên mặt phẳng
 ABC là điểm H thuộc cạnh AC sao cho HA  2HC . Gọi G là trọng tâm tam giác SBC . Biết SH 12 tính
khoảng cách giữa hai đường thẳng AB và HG . 336 1717 336 84 1717 336 17 A. . B. . C. . D. . 1717 1717 1717 1717
Câu 16. Cho hình chóp S.ABCD có đáy là hình thoi cạnh AB  BD  2 , hai đường chéo cắt nhau tại O . Hình
chiếu vuông góc của S trên mặt phẳng  ABCD là trung điểm H của BO . Gọi G là trọng tâm tam giác ADC .
Biết SC tạo với mặt phẳng đáy góc 45 , tính khoảng cách giữa hai đường thẳng SA và CG . 2 2373 4 2373 6 2373 2373 A. . B. . C. . D. . 113 113 113 113
Câu 17. Cho hình chóp S.ABC có đáy ABC là tam giác vuông đỉnh A , cạnh huyền BC  a . Gọi I là trung a 3
điểm của BC và SA  SB  SC 
. Góc tạo bởi SI và mặt phẳng SAC bằng 0
30 . Tính cosin của góc tạo 2
bởi SA và mặt phẳng SBC . 57 19 19 57 A. . B. . C. . D. . 8 5 6 9
Câu 18. Cho hình chóp S.ABCD có đáy là hình bình hành và SA  SB  SC  11, · 0 SAB  30 , · 0 SBC  60 và · 0
SCA  45 . Tính khoảng cách d giữa hai đường thẳng AB và SD . 22 A. d  4 11. B. d  2 22. C. d  . D. d  22. 2
______________________________________ 44
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN CỔ ĐIỂN LỚP 11 – 12 THPT
(LỚP BÀI TOÁN KHOẢNG CÁCH HAI ĐƯỜNG CHÉO NHAU – P6)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA   ABCD , AB  3a, AD  4a . Đường
thẳng SC tạo với mặt phẳng  ABCD góc 60. Gọi M là trung điểm của cạnh BC , O là giao điểm của AC
và BD . Khoảng cách giữa hai đường thẳng DM và SO bằng 15a 22 15a 22 15a 22 15a 22 A. . B. . C. . D. . 22 44 77 88
Câu 2. Cho tứ diện SABC có các cạnh S ,
A SB, SC đôi một vuông góc với nhau và SA  a, SB  2a, SC  3a .
Gọi I là trung điểm của BC . Tính khoảng cách giữa hai đường thẳng SC và AI theo . a 3a 2 a 2 A. a . B. a 2 . C. . D. . 2 2
Câu 3. Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật cạnh AB  a , AD  2a . Mặt phẳng SAB và
SAC cùng vuông góc với  ABCD . Gọi H là hình chiếu vuông góc của A trên SD . Tính khoảng cách giữa AH và SC biết AH  a . 19 2 19a 73 2 73 A. a . B. . C. a . D. a . 19 19 73 73
Câu 4. Cho hình chóp đều S.ABC có cạnh đáy bằng 2a 3 , chiều cao bằng 4a . Gọi M , N, P lần lượt là trung điểm của các cạnh S ,
A AB, SC . Tính khoảng cách giữa hai đường thẳng BM và N . P a 21 a 2 a 5 A. . B. a 2 . C. . D. . 7 2 2 a 17
Câu 5. Cho hình chóp đáy là hình vuông cạnh a, SD 
, hình chiếu vuông góc của S lên mặt phẳng 2
ABCD là điểm H trung điểm của đoạn AB . Gọi K là trung điểm của đoạn AD . Tính khoảng cách giữa hai
đường thẳng HK và SD theo a . a 3 a 3 a 3 a 3 A. B. C. . D. . 5 45 15 25
Câu 6. Cho hình chóp S.ABC có đáy là tam giác đều cạnh a , I là trung điểm của AB , hình chiếu S lên mặt
đáy là trung điểm H của CI , góc giữa SA và đáy là 45 . Khoảng cách giữa SA và CI bằng: a a 3 a 77 a 7 A. . B. . C. . D. . 2 2 22 4
Câu 7. Cho tứ diện đều ABCD cạnh AB  1. Gọi M , N , P lần lượt là trung điểm các cạnh AB , BC , AD .
Tính khoảng cách giữa hai đường thẳng CM và NP . 10 10 3 10 3 10 A. . B. . C. . D. . 10 20 10 20
Câu 8. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, µ 0
D  60 và SA vuông góc với  ABCD . Biết 3 a
thể tích của khối chóp S.ABCD bằng
. Tính khoảng cách k từ A đến mặt phẳng SBC  . 2 3 3 2 2 A.  a k B. k  a C.  a k D. k  a 5 5 5 3
Câu 9. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB  a 3, BC  a 2 . Cạnh bên SA  a và SA
vuông góc với mặt phẳng đáy. Khoảng cách giữa SB và DC bằng: 2a a 3 A. a 2 . B. . C. a 3 . D. 3 2
Câu 10. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Gọi M và N lần lượt là trung điểm của
các cạnh AB và AD ; H là giao điểm của CN với DM . Biết SH vuông góc với mặt phẳng  ABCD và
SH  a 3 .Tính khoảng cách giữa hai đường thẳng DM và SC theo a . 45 2 3a 2 3a 3a 3 3a A. . B. . C. . D. . 19 19 19 19
Câu 11. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Gọi M và N lần lượt là trung điểm của
các cạnh AB và AD ; H là giao điểm của CN với DM . Biết SH vuông góc với mặt phẳng  ABCD và
SH  a 3 .Tính khoảng cách giữa hai đường thẳng DM và SC theo a . 2 3a 2 3a 3a 3 3a A. . B. . C. . D. . 19 19 19 19
Câu 12. Cho hình tứ diện OABC có đáy OBC là tam giác vuông tại O, OB  a, OC  a 3 . Cạnh OA vuông góc
với mặt phẳng (OBC), OA  a 3 , gọi M là trung điểm của BC. Tính khoảng cách h giữa hai đường thẳng AB và OM. a 5 a 3 a 15 a 3 A. h  . B. h  . C. h  . D. h  . 5 2 5 15
Câu 13. Cho hình chóp S.ABC , có đáy là tam giác đều cạnh 2a , SA  2a , SA vuông góc với mặt phẳng đáy (
minh họa như hình vẽ). Gọi M , N lần lượt là trung điểm của A ,
B AC . Khoảng cách giữa hai đường thẳng MN và SC bằng. a 21 a 21 2a 57 a 57 A. . B. . C. . D. . 7 14 19 19
Câu 14. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a . Cạnh bên SA  3a và vuông góc với mặt
đáy  ABC . Tính khoảng cách d từ A đến mặt phẳng SBC 2a 13 a 13 a 13 3a 13 A. d  B. d  C. d  D. d  13 39 13 13
Câu 15. Cho hình chóp S.ABCD có đáy
ABCD là hình thang vuông tại A, B
và AD  2a, AB  BC  a; SA  ( ABCD), SA  a 2 . Khoảng cách giữa SB và DC bằng a 10 a 11 A. . B. a 7 . C. a 5 . D. . 5 5
Câu 16. Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B . Biết AB  BC  a, AD  2a và
SA vuông góc với mặt phẳng  ABCD và SA  a 2 . Gọi M là trung điểm AD . Khoảng cách giữa hai
đường thẳng BM và SC bằng a 2a A. B. a C. D. 2a 2 2
Câu 17. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B có AD  2a ,
AB  BC  a và SA ABC 
D , SA  a 2 . Khoảng cách giữa hai đường phẳng SB và DC bằng a 10 a 7 a 6 a 11 A. . B. . C. . D. . 5 3 3 5 3 a 3
Câu 18. Cho hình chóp đều S.ABC có thể tích bằng
, mặt bên tạo với đáy một góc 60 . Khi đó 24
khoảng cách từ A đến mặt phẳng SBC bằng a 3 a 2 3a A. . B. . C. a 3 . D. . 2 2 4 46
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN CỔ ĐIỂN LỚP 11 – 12 THPT
(LỚP BÀI TOÁN KHOẢNG CÁCH HAI ĐƯỜNG CHÉO NHAU – P7)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và D . Biết
AB  2a, AD  DC  a, cạnh bên SA vuông góc với mặt phẳng  ABCD và SA  3a . Gọi M là trung
điểm AB. Khoảng cách giữa hai đường thẳng DM và SB bằng 3a 22 3a 22 6a 22 a 22 A. B. C. D. 22 11 11 22
Câu 2. Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên bằng a 2 . Tính
theo a khoảng cách giữa hai đường thẳng AD và SB . a 42 a 21 a 42 a 21 A. . B. . C. . D. . 7 7 14 14
Câu 3. Cho hình chóp S.ABCD có đáy là hình chữ nhật cạnh AB  2AD  2a . Tam giác SAB đều và
nằm trong mặt phẳng vuông góc với đáy  ABCD . Tính khoảng cách từ A đến mặt phẳng SBD . a a 3 a 3 A. . B. . C. . D. a . 2 2 4
Câu 4. Cho hình chóp S.ABC có đáy tam giác đều ABC cạnh là a , cạnh bên SA  a , SA   ABC , I là
trung điểm của BC . Khoảng cách giữa hai đường thẳng SI và AB là a 57 a 23 a 17 a 17 A. . B. . C. . D. . 19 7 7 4
Câu 5. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a . Tam giác ABC đều, hình chiếu vuông
góc H của đỉnh S lên mặt phẳng ABCD trùng với trọng tâm của tam giác ABC . Đường thẳng SD hợp
với mặt phẳng  ABCD góc 0
30 . Tính khoảng cách từ B đến mặt phẳng SCD theo a . 2a 21 a 21 a 17 a 17 A. . B. . C. D. 21 7 4 7
Câu 6. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA vuông góc với mặt
phẳng đáy. Gọi M là trung điểm của CD . Biết khoảng cách giữa hai đường thẳng BC và SM bằng
a 3 . Tính thể tích của khối chóp đã cho theo a. 4 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 4 2 6 12
Câu 7. Cho hình chóp S.ABC có đáy là tam giác vuông đỉnh B , AB  a , SA vuông góc với mặt phẳng
đáy và SA  2a . Khoảng cách từ A đến mặt phẳng SBC bằng: 2 5a 5a 2 2a 5a A. B. C. D. 5 3 3 5
Câu 8. Cho tứ diện OABC có OA , OB , OC đôi một vuông góc với nhau và OA  OB  a , OC  2a . Gọi
M là trung điểm của AB . Khoảng cách giữa hai đường thẳng OM và AC bằng 2a 2 5a 2a 2a A. B. C. D. 3 5 2 3
Câu 9. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA   ABC , góc giữa đường
thẳng S B và mặt phẳng  ABC bằng 60 . Khoảng cách giữa hai đường thẳng AC và SB bằng a 2 a 15 a 7 A. . B. . C. 2a. D. . 2 5 7
Câu 10. Cho hình lập phương ABC . D AB C  D
  có cạnh là 6 . Khi đó, khoảng cách giữa hai đường
thẳng chéo nhau AB và BC là A. 3 3. B. 2 3. C. 3 2. D. 2 6. 47
Câu 11. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB là tam giác đều và nằm trong mặt
phẳng vuông góc với mặt phẳng đáy. Khoảng cách từ A đến mặt phẳng SBD bằng 21a 21a 2a 21a A. . B. . C. . D. . 14 7 2 28
Câu 12. Cho khối chóp S.ABC có SAB   ABC , SAC   ABC , SA  a , AB  AC  2a , BC  2a 2 . Gọi
M là trung điểm của BC . Khoảng cách giữa hai đường thẳng SM và AC bằng a a A. . B. . C. a . D. a 2 . 2 2
Câu 13. Hình chóp S.ABC có đáy là tam giác vuông cân tại B, AB  a. Cạnh bên SA vuông góc với mặt
phẳng đáy, góc tạo bởi hai mặt phẳng  ABC  và SBC bằng 60 . Tính khoảng cách giữa hai đường AB, SC. a 3 a 2 a 3 A. a . B. . C. . D. . 3 2 2
Câu 14. Cho hình chóp S.ABCD có đáy là hình thang, AB  2a, AD  DC  CB  a . SA vuông góc với mặt
phẳng đáy và SA  3a . Gọi M là trung điểm của AB . Khoảng cách giữa hai đường thẳng SB và CM bằng 3a 3a 3 13a 6 13a A. . B. . C. . D. . 4 2 13 13
Câu 15. Cho hình chóp S .A BC D có đáy ABC D là hình vuông cạnh a . Gọi M và N lần lượt là trung điểm
của các cạnh AB và A D ; H là giao điểm của C N với DM . Biết SH vuông góc với mặt phẳng  ABCD  và
SH  a 3 .Tính khoảng cách giữa hai đường thẳng DM và SC theo a . 2 3a 2 3a 3a 3 3a A. . B. . C. . D. . 19 19 19 19
Câu 16. Cho hình lăng trụ đứng ABC .
D A' B 'C ' D ' có đáy ABCD là hình thoi. Biết AC  2, AA'  3 . Tính góc
giữa hai mặt phẳng  AB ' D ' và CB ' D ' . A. 0 45 . B. 0 90 . C. 0 30 . D. 0 60 . Câu 17. Cho hình chóp .
S ABCD có đáy ABCD là hình thang, AB  2a , AD  DC  BC  a . SA vuông góc
với mặt phẳng  ABCD và SA  3a . Gọi M là trung điểm AB . Khoảng cách giữa hai đường thẳng SM và BC bằng: 3a 3a 6a 3a A. . B. . C. . D. . 13 2 13 4
Câu 18. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với đáy. Biết
hình chóp S.ABC có thể tích bằng 3
a . Tính khoảng cách d từ điểm A đến mặt phẳng SBC  . 6a 195 4a 195 4a 195 8a 195 A. d  . B. d  . C. d  . D. d  . 65 65 195 195
Câu 19. Cho lăng trụ tam giác đều AB . C A B  C
 có AB  a , AA  2a . Khoảng cách giữa AB và CC bằng 2a 5 a 3 A. . B. a . C. a 3 . D. . 5 2 48
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN CỔ ĐIỂN LỚP 11 – 12 THPT
(LỚP BÀI TOÁN KHOẢNG CÁCH HAI ĐƯỜNG CHÉO NHAU – P8)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2 .
a Biết các mặt bên của hình chóp cùng tạo với đáy 3
các góc bằng nhau và thể tích của khối chóp bằng 4 3a . Khoảng cách giữa hai đường thẳng SA và CD bằng 3 A. 2 . a B. 3 . a C. a 5. D. 3 2 . a
Câu 2. Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B . Biết AB  BC  a, AD  2a và SA
vuông góc với mặt phẳng  ABCD và SA  a 2 . Gọi M là trung điểm AD . Khoảng cách giữa hai đường thẳng BM và SC bằng a 2a A. . B. . a C. . D. 2 . a 2 2
Câu 3. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB  3a, BC  4 . a Cạnh bên S A vuông góc
với đáy. Góc tạo bởi giữa SC và đáy bằng 60 . Gọi M là trung điểm của AC (tham khảo hình vẽ bên dưới).
Khoảng cách giữa hai đường thẳng AB và SM bằng 5a 10a 3 A. a 3 . B. 5a 3 . C. . D. . 2 79
Câu 4. Cho hình chóp S.ABCD , đáy là hình thang vuông tại A và B , biết AB  BC  a , AD  2a , SA  a 3
và SA   ABCD . Khoảng cách giữa hai đường thẳng AC và SD bằng a 6 a 30 a 3 a 15 A. . B. . C. . D. . 5 5 2 5
Câu 5. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB  3 ,
a AD  a. SA vuông góc với mặt phẳng
đáy, SA  2a . Gọi M là điểm thuộc đoạn thẳng DC sao cho DC  3DM ( minh họa như hình vẽ bên). Khoảng
cách giữa hai đường BM và SD bằng 2a a 6 a 6 a A. . B. . C. . D. . 3 6 3 3
Câu 6. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B , AB  BC  a, AD  2a ,
SA  a và vuông góc với  ABCD . Tính khoảng cách giữa hai đường thẳng SD và AC . a 3 a 3 a 6 a 6 A. . B. . C. . D. . 3 2 2 3
Câu 7. Cho lăng trụ đều ABC.A' B 'C ' có AB 1, AA'  mm  0. Hỏi m bằng bao nhiêu để góc giữa AB ' và BC ' bằng 600? A. m  2. B. m  1. C. m  3. D. m  5.
Câu 8. Cho hình chóp S.ABCD có đáy ABCD là hình vuông, AB  3a , vuông góc với mặt phẳng đáy và
SA  4a . Gọi M, N lần lượt là trung điểm của CD và AB. Khoảng cách giữa hai đường thẳng SC và AM bằng: 12a 89 6a 2 12a 89 6a 2 A. B. . C. . D. . 89 7 49 14
Câu 10. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , BA  3a, BC  4a mặt phẳng
SBCvuông góc với mặt phẳng ABC.Biết SB 2a 3 và ·SBC = 300. Khoảng cách từ điểm Bđến mặt phẳng SACbằng 6a 7 3a 7 3a 7 6a 7 A. 21 . B. 56 . C. 14 . D. 7 .
Câu 11. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 3 . Hai mặt phẳng SAB và
SAC cùng vuông góc với mặt phẳng đáy. Góc giữa SB và mặt phẳng đáy bằng 60. Gọi M , N là
các điểm lần lượt thuộc cạnh đáy BC và CD sao cho BM  2MC và CN  2ND . Tính khoảng cách
giữa hai đường thẳng chéo nhau DM và SN. 49 3 3 3 3 3 3 A. . B. . C. . D. . 730 370 370 730
Câu 12. Cho hình thoi ABCD tâm O cạnh a và AC  a . Từ trung điểm H của AB , dựng
SH   ABCD với SH  a . Khoảng cách từ A đến mặt phẳng SBC  bằng 8a 3 2a 57 2a 66 10a 5 A. . B. . C. . D. . 15 19 23 27
Câu 13. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a . Gọi M , N lần lượt là trung điểm của
SA và BC . Biết góc giữa M N và mặt phẳng  ABC bằng 60 . Khoảng cách giữa hai đường thẳng BC và DM bằng 15 30 15 15 A. a . B. a . C. a . D. a . 62 31 68 17
Câu 14. Cho hình chóp S.ABCD có đáy là hình vuông cạnh 3a , SA vuông góc với mặt phẳng đáy và   
SA  a . Gọi M là điểm thào mãn MB  2MC  0. Khoảng cách giữa hai đường thẳng SC và DM bằng: 154 3 154a 6 154 2 154 A. a . B. . C. a . D. a . 77 154 77 77
Câu 15. Cho hình lập phương ABC . D A B  C  D
  cạnh a . Tính khoảng cách từ B tới đường thẳng DB. a 3 a 6 a 3 a 6 A. . B. . C. . D. . 6 3 3 6
Câu 16. Cho khối chóp S.ABC có SAB   ABC , SAC   ABC , SA  a , AB  AC  2a , BC  2a 2 .
Gọi M là trung điểm của BC . Khoảng cách giữa hai đường thẳng SM và AC bằng a a A. . B. . C. a . D. a 2 . 2 2
Câu 17. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA   ABC , góc giữa đường
thẳng SB và mặt phẳng  ABC bằng 60 . Khoảng cách giữa hai đường thẳng AC và SB bằng a 2 a 15 a 7 A. . B. . C. 2a. D. . 2 5 7
Câu 18. Cho hình chóp S.ABC , có SA  SB  SC , đáy là tam giác đều cạnh a. Biết thể tích khối chóp 3 a 3 S.ABC bằng
. Khoảng cách giữa hai đường thẳng SA và BC bằng: 3 3 13a a 3 A. 4 a B. C. 6 a D. 7 13 7 4
______________________________________ 50
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN CỔ ĐIỂN LỚP 11 – 12 THPT
(LỚP BÀI TOÁN KHOẢNG CÁCH HAI ĐƯỜNG CHÉO NHAU – P9)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , AC  3a , BC  a 3 , SA vuông
góc với mặt phẳng đáy và SA  3a 2 . Điểm G là trọng tâm tam giác SAC ( minh họa như hình bên).
Khoảng cách giữa hai đường thẳng SC và BG bằng a 42 4a 6 a 6 A. . B. a 6 . C. . D. . 7 3 3 Câu 2. Cho hình chóp .
S ABCD có đáy là hình thang, AB  2a, AD  DC  CB  a . SA vuông góc với mặt
phẳng đáy và SA  3a . Gọi M là trung điểm của AB . Khoảng cách giữa hai đường thẳng SB và CM bằng 3 13a 6 13a A. 3a . B. 3a . C. . D. . 4 2 13 13 Câu 3. Cho hình chóp .
S ABCD có đáy là hình bình hành ·  2 ,  , 120o AB a AD a BAD , SA vuông góc với
mặt phẳng đáy và SA  3a . Gọi Mlà trung điểm của AB . Khoảng cách giữa 2 đường DM và SB bằng 3 10a 3 10a A. . B. . C. 10a. D. 3 10a . 10 20
Câu 4. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB  a , AD  2a . Hình chiếu vuông
góc của S trên mặt phẳng đáy là trung điểm H của AD , góc giữa SB và mặt phẳng đáy (ABCD) là 0
45 . Tính khoảng cách giữa hai đường thẳng SD và BH theo a 2a a 2 2 A. B. . C. a D. a . 3 3 3 5
Câu 5. Cho hình lăng trụ đứng ABC .
D A' B 'C ' D ' có đáy ABCD là hình thoi. Biết AC  2, AA'  3 . Tính
góc giữa hai mặt phẳng  AB ' D ' và CB ' D ' . A. 0 45 . B. 0 90 . C. 0 30 . D. 0 60 . Câu 6. Cho hình chóp .
S ABCD có đáy ABCD là hình chữ nhật có AB  2a, AD  4a , SA   ABCD,
cạnh SC tạo với đáy góc 60. Gọi M là trung điểm của BC , N là điểm trên cạnh AD sao cho
DN  a. Khoảng cách giữa MN và SB là 2a 285 a 285 2a 95 8a A. . B. . C. . D. . 19 19 19 19
Câu 7. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , SA   ABC , góc giữa đường
thẳng SB và mặt phẳng  ABC bằng 60 . Khoảng cách giữa hai đường thẳng AC và SB bằng a 2 a 15 a 7 A. . B. . C. 2a . D. . 2 5 7
Câu 8. Cho hình chóp S.ABCD , đáy là hình thang vuông tại A và B , biết AB  BC  a , AD  2a , SAa 3 và SA ABC 
D . Khoảng cách giữa hai đường thẳng AC và SD bằng a 6 a 30 a 3 a 15 A. . B. . C. . D. . 5 5 2 5
Câu 9. Cho hình chóp S.ABCD có đáy là hình vuông ABCD tâm cạnh AB  a , đường cao SO vuông
góc với mặt đáy và SO  a . Khoảng cách giữa SC và AB là 2a 5 a 5 2a 5 a 5 A. . B. C. . D. . 7 7 5 5
Câu 10. Cho hình chóp S.ABCD , đáy là hình thang vuông tại A và B , biết AB  BC  a , AD  2a ,
SA  a 3 và SA   ABCD . Khoảng cách giữa hai đường thẳng AC và SD bằng 51 a 6 a 30 a 3 a 15 A. . B. . C. . D. . 5 5 2 5
Câu 11. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D , AD  DC , AB  2AD ,
mặt bên SBC  là tam giác đều cạnh 2a và thuộc mặt phẳng vuông góc với mặt phẳng  ABCD. Tính
khoảng cách giữa hai đường thẳng BC và SA theo a . 6a 2a 2 7a 2 21a A.  B.  C.  D.  7 7 21 7
Câu 12. Cho hình lập phương ABC . D A B  C  D
  có cạnh bằng a . Gọi K là trung điểm của DD. Khoảng
cách giữa hai đường thẳng CK và AD bằng a 3 a 3 2a 3 a A. B. C. D. 3 2 3 3
Câu 13. Cho hình chóp S.ABCD có ABCD là nửa lục giác đều cạnh a, hai mặt phẳng (ABCD) và (SAD)
vuông góc nhau,SAD cân tại S. Góc tạo bởi SB và mặt phẳng (ABCD) bằng 600. Tính theo a khoảng cách từ AD đến (SBC). 3a 15 a 15 15 a 3 A. . B. . C. . D. . 5 5 5 2
Câu 14. Cho hình chóp tứ giác đều có cạnh đáy bằng 2a , cạnh bên bằng 3a . Gọi  là góc giữa mặt
bên và mặt đáy, mệnh đề nào dưới đây đúng? 2 10 2 14 A. cos  . B. cos  . C. cos  . D. cos  . 4 10 2 2
Câu 15. Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, đáy lớn AB . Biết rằng
AD  DC  CB  a , AB  2a , cạnh bên SA vuông góc với đáy và mặt phẳng SBD tạo với đáy góc 45 .
Gọi I là trung điểm của cạnh AB . Tính khoảng cách d từ I đến mặt phẳng SBD . a a a 2 a 2 A. d  . B. d  . C. d  . D. d  . 4 2 4 2
Câu 16. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , BC  2a , SA vuông góc với mặt
phẳng đáy và SA  2a 3 . Gọi M là trung điểm AC . Khoảng cách giữa hai đường thẳng AB và SM là 2a 2a 39 A. a 39 B. C. 2a 3 D. 13 13 13 13
Câu 17. Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, cạnh a , góc 0 BAD  60 . Đường
thẳng SO tạo với mặt phẳng  ABCD một góc 0
60 . Hình chiếu vuông góc của S trên mặt
phẳng  ABCD là điểm H thuộc đoạn BD sao cho BD  4BH . Tính khoảng cách từ điểm B tới mặt
phẳng SCD . Tính BE theo a . 3a 39 2a 39 3a 39 a 39 A. . B. . C. . D. . 52 13 13 13 52
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN CỔ ĐIỂN LỚP 11 – 12 THPT
(LỚP BÀI TOÁN KHOẢNG CÁCH HAI ĐƯỜNG CHÉO NHAU – P10)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D , AB  3a, AD  DC  a.
Gọi I là trung điểm của AD , biết hai mặt phẳng SBI  và SCI  cùng vuông góc với đáy và mặt
phẳng SBC tạo với đáy một góc 0
60 . Gọi M điểm trên AB sao cho AM  2a , tính khoảng cách giữa MD và SC . a 17 a 15 a 6 a 3 A. . B. . C. . D. . 5 10 19 15
Câu 2. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B; ABC và SA  ABC ;
AB  BC  a . Tính góc giữa hai mặt phẳng SAC và SBC . 3a 13a 13a 3a A. . B. . C. . D. . 13 3 3 13
Câu 3. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a, SO vuông góc với mặt
phẳng  ABCD và SO  a . Khoảng cách giữa SC và AB bằng. a 5 2a 5 a 3 2a 3 A. . B. . C. . D. . 5 5 15 15 Câu 4. Cho hình chóp .
S ABCDđáy là hình thoi cạnh a tâm O, ·ADC 30 
, SA  a , SA  (ABCD) . Tính
khoảng cách từ O đến mp(SCD) theo a. a 5 a a 5 a 5 A. . B. . C. . D. . 2 5 5 10
Câu 5. Cho khối chop S.ABCD có thể tích bằng 8. Gọi M,N lần lượt là trung điểm của SB,SC và ABCD
là hình bình hành (như hình vẽ). Biết diện tích của tứ giác AMND bằng 2. Tính khoảng cách h từ đỉnh S đến mặt phẳng (AMND) 3 8 9 A. h  B. h  . C. h  . D. h  3. 2 3 2
Câu 6. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a , tam giác ABC đểu, hình chiếu
vuông góc H của đỉnh S trên mặt phẳng  ABCD trùng với trọng tâm của tam giác ABC . Đường
thẳng SD hợp với mặt phẳng  ABCD góc o
30 . Tính khoảng cách d từ B đến mặt phẳng SCD theo a . 2a 21 a 21 2a 5 A. d  a 3 . B. d  . C. d  . D. d  . 21 7 3
Câu 7. Cho hình chóp S.ABCD , đáy là hình thang vuông tại A và B , biết AB  BC  a , AD  2a ,
SA  a 3 và SA   ABCD . Gọi M và N lần lượt là trung điểm của SB , SA . Tính khoảng cách từ M đến  NCD theo a . a 66 a 66 a 66 A. . B. 2a 66 . C. . D. . 22 11 44
Câu 8. Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B . Biết
SA   ABCDvà AD  2a; AB  BC  SA  a . Tính khoảng cách giữa hai đường thẳng SB và CD . a 3 a 3 a 3 3a 3 A. . B. . C. . D. . 3 2 4 4
Câu 9. Cho lăng trụ tam giác đều ABC.AB C
  có tất cả các cạnh đều bằng a . Khoảng cách giữa hai
đường thẳng BC và AB bằng A. a 21 B. a 3 C. a 7 D. a 2 7 2 4 2
Câu 10. Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B . Biết AB  BC  a, AD  2a và 53
SA vuông góc với mặt phẳng  ABCD và SA  a 2 . Gọi M là trung điểm AD . Khoảng cách giữa hai
đường thẳng BM và SC bằng a 2a A. B. a C. D. 2a 2 2
Câu 11. Cho tứ diện ABCD có AC  AD  BC  BD  2a, ACD  BCD . Biết góc giữa hai mặt phẳng
 ABC và  ABD là 0
60 . Độ dài cạnh CD bằng 7 2 7 3 7 4 7 CD  a CD  a CD  a CD  a A. 7 . B. 7 . C. 7 . D. 7 .
Câu 12. Cho khối chóp S.ABC có SAB  ABC, SAC  ABC, SA  , a AB  AC  2 , a BC  2a 2. Gọi
M là trung điểm của BC . Khoảng cách giữa hai đường thẳng SM và AC bằng a a A. . B. . C. a. D. a 2 . 2 2
Câu 13. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB  a, AD  a 3 . Mặt bên SAB là
tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Cosin của góc giữa đường thẳng SD và
mặt phẳng SBC bằng 13 3 2 5 1 A. B. C. D. 4 4 5 4
Câu 14. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB  a, AD  a 3 . Mặt bên SAB là
tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Cosin của góc giữa đường thẳng SD và
mặt phẳng SBC bằng 13 3 2 5 1 A. B. C. D. 4 4 5 4
Câu 15. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA   ABC , góc giữa đường
thẳng SB và mặt phẳng  ABC bằng 60 . Khoảng cách giữa hai đường thẳng AC và SB bằng a 2 a 15 a 3 a 7 A. . B. . C. . D. . 2 5 7 7
Câu 16. Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B . Biết AB  BC  a, AD  2a và
SA vuông góc với mặt phẳng  ABCD và SA  a 2 . Gọi M là trung điểm AD . Khoảng cách giữa hai
đường thẳng BM và SC bằng a 2a A. B. a C. D. 2a 2 2
Câu 17. Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a , SA vuông góc với mặt phẳng đáy và
SA = a. Gọi M là trung điểm A .
B Khoảng cách giữa hai đường thẳng SB và DM bằng: 2 21 21 4 21 A. a B. a C. a D. a 21 8 21
______________________________________ 54
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN CỔ ĐIỂN LỚP 11 – 12 THPT
(LỚP BÀI TOÁN KHOẢNG CÁCH HAI ĐƯỜNG CHÉO NHAU – P11)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho hình chóp S.ABCD có đáy là nửa lục giác đều nội tiếp đường tròn đường kính AD = 2a, SA vuông
góc với (ABCD), SA = 1,5a. Tính khoảng cách giữa hai đường thẳng BD, SC. a 2 5a 2 3a 2 5a 2 A. B. C. D. 4 4 4 12 Câu 2. Cho hình chóp .
S ABCD có đáy là hình vuông cạnh .
a Đường thẳng SA vuông góc với mặt phẳng đáy, S A  .
a Khoảng cách giữa hai đường thẳng SB và CD nhận giá trị nào trong các giá trị sau? A. . a B. a 2. C. a 3. D. 2 . a
Câu 3. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB  a 2; BC  a 3 . Cạnh bên SA vuông
góc với đáy. Góc giữa đường thẳng SC và mặt phẳng đáy bằng 30o . Gọi M là trung điểm của AC khoảng cách
giữa hai đường thẳng AB và SM bằng 2a 51 a 435 a 3 A. B. C. a 21 D. 17 29 17 12 6
Câu 4. Cho hình hộp đứng ABCD.A’B’C’D’ có AB  5a; AD  6a; BD  7a; AA  a . Khoảng cách giữa 7
hai đường thẳng A’B và B’C là 12a 12 2a 12 6a 12 3a A. B. C. D. 7 7 7 7
Câu 5. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 2a, AD = 4a, SA vuông góc với (ABCD).
Cạnh SC tạo với mặt phẳng đáy góc 30o . Gọi M là trung điểm của BC, N là điểm trên cạnh AD sao cho DN = a. a 35 a 35 2a 35 3a 35 A. B. C. D. 14 7 7 7
Câu 6. Cho hình chóp S.ABCD có SA vuông góc với đáy (ABCD), ABCD là hình chữ nhật,
AB  a 3; AD  a 2 . Tính khoảng cách giữa hai đường thẳng SD, BC. 2a a 3 A. B. a 3 C. 0,75a D. 3 2
Câu 7. Cho lăng trụ đứng tam giác ABC.A’B’C’ có đáy là một tam giác vuông cân tại B, AB = A’A = 2a. M là
trung điểm BC. Khoảng cách giữa hai đường thẳng AM và B’C bằng 2a a 7 A. 0,5a B. C. D. a 3 3 7
Câu 8. Cho hình chóp S.ABCD có đáy là hình thang vuông tại B và C với AB = 4a, BC = 2a, CD = a. Gọi M, N
lần lượt là trung điểm của AB và BC. Hai mặt phẳng (SMN) và (SBD) cùng vuông góc với mặt phẳng đáy và
cạnh bên SB hợp với đáy một góc 45o . Khoảng cách giữa SN và BD bằng A. 0,5a B. 0,4a C. 0,2a D. 0,1a
Câu 9. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, AD = 2a, SA vuông góc với mặt phẳng
(ABCD), SA = 2a. Gọi M là trung điểm của SB. Khoảng cách giữa hai đường thẳng AM và SC bằng 2a 5 3a 2 5a A. 1,4a B. C. D. 3 3 5
Câu 10. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hình chiếu vuông góc của điểm S trên mặt
phẳng (ABCD) trùng với trọng tâm của tam giác BCD. Góc giữa mặt phẳng (SBC) và mặt phẳng đáy (ABCD)
bằng 30o . Tính khoảng cách giữa hai đường thẳng AD và SC. a A. B. 0,5a C. 1,5a D. a 6
Câu 11. Hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB đều và nằm trong mặt phẳng
vuông góc với mặt phẳng (ABCD). Gọi M là trung điểm của SD. Khoảng cách giữa hai đường thẳng AM và SC là a 3 a 5 A. B. C. a D. 0,5a 2 5 55
Câu 12. Cho hình lập phương ABCD.A’B’C’D’ có cạnh a. Khoảng cách giữa hai đường thẳng AC và DC’ bằng a 3 a 3 a A. a B. C. D. 2 3 3
Câu 13. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, SD vuông góc với mặt phẳng (ABCD), AD = a, ·
AOB  120o . Góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng 45o . Khoảng cách giữa hai
đường thẳng SB và AC bằng a 6 a 6 a 6 a 6 A. B. C. D. 2 3 4 6
Câu 13. Cho hình chóp S.ABCD có đáy là hình vuông cạnh 4a, hai mặt phẳng (SAB) và (SAC) cùng vuông góc
với mặt phẳng đáy, góc giữa mặt phẳng (SCD) với mặt phẳng đáy bằng 45o . Gọi M là trung điểm của SB.
Khoảng cách giữa hai đường thẳng AM và SD bằng a 3 4a 3 2a 3 a A. B. C. D. 3 3 3 3
Câu 14. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Mặt bên (SAB) là tam giác đều và nằm
trong mặt phẳng vuông góc với đáy. Trên cạnh SB lấy điểm M sao cho SB = 3SM. Tính khoảng cách giữa hai đường thẳng AM và SD. 3 165a 3 31 93a 3 93 A. B. a C. D. a 55 31 31 31
Câu 15. Cho hình chóp S.ABCD có đáy là hình thang, AB = 2a, AD = DC = CB = a và SA vuông góc với mặt
phẳng đáy. Gọi M là trung điểm của cạnh AB. Khoảng cách giữa hai đường thẳng CM và SD bằng a 3 A. B. 1,5a C. a 3 D. 0,75a 2
Câu 16. Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông cân tại B, AB = 2a, cạnh bên
AA  2a 2 . Gọi M là trung điểm của cạnh BC. Khoảng cách giữa hai đường thẳng AM và B’C bằng 2a 14 a 7 2a 7 4a 7 A. B. C. D. 7 7 7 7
Câu 17. Cho hình chóp S.ABC có SA vuông góc với (ABC), SA = 2a, đáy ABC là tam giác vuông cân tại B với
BC = 2a. Gọi M là trung điểm của cạnh AC. Khoảng cách giữa hai đường thẳng SM và BC bằng 2a 5 a 5 a 5 A. B. C. 2a 5 D. 5 5 2
Câu 18. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 6a, cạnh bên SA vuông góc với mặt phẳng
đáy, SA = 2a. Gọi G là trọng tâm tam giác ABC. Tính khoảng cách giữa hai đường thẳng SG, BC. a 3 3a 3 A. 2a 3 B. a 3 C. D. 2 2 56
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN CỔ ĐIỂN LỚP 11 – 12 THPT
(LỚP BÀI TOÁN KHOẢNG CÁCH HAI ĐƯỜNG CHÉO NHAU – P12)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho hình lăng trụ ABC.A”B’C’ có tất cả các cạnh bằng a. Gọi M là trung điểm của cạnh BC. Khoảng cách
giữa hai đường thẳng AM và B’C là a 2 a 2 A. a B. C. D. a 2 4 2
Câu 2. Cho hình chóp S.ABCD có ABCD là hình vuông tâm O cạnh a. Hình chiếu vuông góc của S lên mặt
phẳng (ABCD) là trung điểm của AO. Mặt phẳng (SBC) tạo với mặt đáy một góc 45o . Tính khoảng cách giữa
hai đường thẳng SD và AC. a 38 a 51 a 13 3a 34 A. B. C. D. 17 13 3 34
Câu 3. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, M là trung điểm BC, hình chiếu vuông góc
của S lên mặt phẳng (ABC) trùng với trung điểm của AM. Cho biết AB  ;
a AC  a 3 và mặt phẳng (SAB) tạo
với mặt phẳng (ABC) một góc 30o . Tính khoảng cách giữa hai đường thẳng SA và BC. a 3 3a A. B. C. 1,5a D. 0,75a 2 8
Câu 4. Cho hình chóp S.ABCD có đáy là hình thoi cạnh a, ·
ABC  120o , SA vuông góc với mặt phẳng (ABCD).
M là điểm đối xứng của A qua D. Góc giữa đường thẳng SC với mặt phẳng (ABCD) bằng 45o . Khoảng cách
giữa hai đường thẳng BD và SM bằng a 6 a 3 a 6 a 3 A. B. C. D. 2 2 4 4
Câu 5. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, BC = 2a, SA vuông góc với mặt phẳng
đáy và SA  a 3 . Gọi M là trung điểm của CD, khoảng cách giữa hai đường thẳng SM và BD bằng a 5 a 2 a 30 3 2a A. B. C. D. 4 4 4 8
Câu 6. Cho hình chóp S.ABCD có đáy là hình thang, · ·
CBA  BAD  90o; AB  BC  2 ; a AD  a . Biết SA = SB và ·
SCD  90o . Cạnh bên SA tạo với mặt đáy 0
45 . Tính khoảng cách giữa hai đường thẳng AB và SC bằng 2 5 357 306 2 357 A. a B. a C. a D. a 3 21 18 21
Câu 7. Cho hình lăng trụ ABC.A’B’C’ có các mặt bên đều là hình vuông cạnh a. Gọi D là trung điểm của cạnh
BC. Tính khoảng cách giữa hai đường thẳng A’B và DC’ theo a. a 3 a 2 a 2 a 3 A. B. C. D. 6 6 4 4
Câu 8. Cho hình hộp ABCD.A’B’C’D’ có tất cả các cạnh đều bằng 1 và các góc phẳng đỉnh A đều bằng 60o .
Tính khoảng cách giữa hai đường thẳng AB’ và A’C’. 22 2 2 3 A. B. C. D. 11 11 11 11
Câu 9. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = 2a, AD = 3a. Tam giác SAB cân tại S và
nằm trong mặt phẳng vuông góc với mặt phẳng đáy, góc giữa mặt phẳng (SCD) và mặt đáy là 45o . Gọi H là
trung điểm cạnh AB. Tính khoảng cách giữa hai đường thẳng SD, CH. 3 10 3 85 3 11 3 14 A. a B. a C. a D. a 109 17 11 7
Câu 10. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông cạnh a, M và N lần lượt là trung điểm các
cạnh AB, AD; H là giao điểm của CN với DM. Biết SH vuông góc với mặt phẳng (ABCD) và SH  a 3 . Tính
khoảng cách giữa hai đường thẳng DM, SC. 59 a 3 2 57a A. 2a B. C. D. a 19 2 19 57
Câu 11. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hình chiếu vuông góc của S trên mặt
phẳng (ABCD) là trung điểm của cạnh AB, góc giữa (SAC) và đáy bằng 45o . Gọi M là trung điểm của SD.
Khoảng cách giữa hai đường thẳng AM và SC bằng a 2 a 5 a 5 A. a B. C. D. 4 10 5
Câu 12. Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc với nhau và AD = 2, AB = AC = 1. Gọi I là trung
điểm của đoạn thẳng BC, khoảng cách giữa hai đường thẳng AI và BD bằng 2 2 5 A. 1,5 B. C. D. 3 5 2
Câu 13. Cho S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD) và SA  a 3 . Gọi M
là trung điểm của AD. Tính khoảng cách giữa hai đường thẳng BM, SD. a 57 a 57 A. a B. 0,5a C. D. 3 19
Câu 14. Cho lăng trụ ABC.A’B’C’ có đáy ABC là tam giác vuông tại A, AB  ;
a AC  a 3 . Hình chiếu vuông a 241
góc của A’ trên mặt phẳng (ABC) là trọng tâm tam giác ABC và AA 
. Gọi M là trung điểm AC, tính 6
khoảng cách giữa hai đường thẳng MC’ và AB’ bằng 15 5 5 3 A. 0,6a B. a C. a D. a 669 669 669
Câu 15. Cho hình chóp tứ giác đều S.ABCD có AB = a, SA tạo với mặt phẳng đáy một góc 45o . Gọi M là trung
điểm của đoạn thẳng AB. Tính khoảng cách giữa hai đường thẳng SM và CD. a 6 a 2 a 3 A. B. C. D. 0,5a 3 2 2
Câu 16. Hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác cân tại A, · BAC  120o; AB  2 ; a A A   a 2 .
Gọi M là trung điểm của cạnh BC. Tính khoảng cách giữa hai đường thẳng C’M và AB. 2 66a 66a 22a 66a A. B. C. D. 11 22 11 11
Câu 17. Cho hình lăng trụ ABC.A’B’C’ có cạnh bên bằng a 2 , đáy ABC là tam giác vuông tại B, uuuur uuur
BC  a 3; AB  a . Biết hình chiếu vuông góc của đỉnh A’ lên mặt đáy là điểm M thỏa mãn 3AM  AC .
Khoảng cách giữa hai đường thẳng A’A và BC bằng a 210 a 210 a 714 a 714 A. B. C. D. 15 45 17 51
______________________________________ 58
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN CỔ ĐIỂN LỚP 11 – 12 THPT
(LỚP BÀI TOÁN KHOẢNG CÁCH HAI ĐƯỜNG CHÉO NHAU – P13)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, AD = 2a, SA vuông góc với (ABCD), SA
= 2a. Gọi M là trung điểm của SB. Khoảng cách giữa hai đường thẳng AM và SC bằng 7a 2a 5 3a 2 5a A. B. C. D. 5 3 3 3
Câu 2. Cho hình chóp S.ABCD có SA vuông góc với (ABCD), SA  a 6 , ABCD là nửa lục giác đều nội tiếp
đường tròn đường kính AD = 2a. Tính khoảng cách từ B đến mặt phẳng (SCD) bằng a 6 a 3 a 2 a 3 A. B. C. D. 2 2 2 4
Câu 3. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = 3a, BC = 4a. Cạnh bên SA vuông góc
với đáy. Góc giữa SC và mặt phẳng đáy bằng 60o . Gọi M là trung điểm của AC, tính khoảng cách giữa hai đường thẳng AB và SM. 3 A. 2,5a B. a 3 C. 10a D. 5a 3 79
Câu 4. Cho hình lăng trụ tam giác ABC.A’B’C’ có độ dài cạnh bên bằng a 7 , đáy ABC là tam giác vuông tại A,
AB = a, AC  a 3 . Biết hình chiếu vuông góc của A’ trên mặt phẳng (ABC) là trung điểm của BC. Khoảng
cách giữa hai đường thẳng A’A và B’C’ bằng a 2 a 6 a 6 a 3 A. B. C. D. 3 4 3 4
Câu 5. Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = 2a, AD = A’A = a. Khoảng cách giữa hai đường thẳng AC và DC’ bằng 2a a 3 a 3 3a A. B. C. D. 3 2 3 2
Câu 6. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B có AD = 2a, AB = BC = a và SA
vuông góc với (ABCD), SA  a 2 . Tính khoảng cách giữa hai đường thẳng SB và DC. a 10 a 7 a 6 a 11 A. B. C. D. 5 3 3 5
Câu 7. Cho hình chóp S.ABCD có đáy là hình thang, AB = 2a, AD = DC = CB = a, SA vuông góc với mặt phẳng
đáy. Gọi M là trung điểm của AB. Khoảng cách giữa hai đường thẳng CM và SD bằng a 3 A. 0,75a B. 1,5a C. a 3 D. 2
Câu 8. Cho hình lăng trụ đứng ABC.A’B’C’ có độ dài cạnh bên bằng 2a, đáy là tam giác ABC vuông cân tại C,
CA = CB = a. Gọi M là trung điểm của cạnh A’A. Tính khoảng cách giữa hai đường thẳng AB và MC’. a 3 a a 3 2a A. B. C. D. 3 3 2 3
Câu 9. Cho hình chóp tứ giác đều S.ABCD có AB = a, góc giữa đường thẳng SA và mặt phẳng (ABCD) bằng
45o . Gọi M là trung điểm AB. Khoảng cách giữa hai đường thẳng SM và CD bằng a 6 a 2 a a 3 A. B. C. D. 3 2 2 2
Câu 10. Cho lăng trụ đều ABC.A’B’C’ có tất cả các cạnh bằng a, gọi M là trung điểm BC. Khoảng cách giữa hai
đường thẳng AM và B’C bằng a 2 a 2 A. a B. C. a 2 D. 4 2
Câu 11. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 6a, cạnh bên SA vuông góc với mặt phẳng
đáy, SA = 2a. Gọi G là trọng tâm tam giác ABC. Khoảng cách giữa hai đường thẳng SG và BC bằng 3a 3 a 3 A. 2a 3 B. a 3 C. D. 2 2
Câu 12. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA = 2a và vuông góc với (ABCD). Gọi M 59
là trung điểm của SD. Tính khoảng cách giữa hai đường thẳng SB, CM. a a 2 2a a A. B. C. D. 3 2 3 6
Câu 13. Hình chóp S.ABCD có đáy ABCD là hình bình hành và SA = SB = SC = a, · o · o ·
SAB  30 ; SBC  60 ; SCA  45o . Tính khoảng cách giữa hai đường thẳng AB và SD. 4a a a 22 2a 22 A. B. C. D. 11 22 11 11
Câu 14. Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Hình chiếu vuông góc của S trên mặt
phẳng (ABCD) là điểm H thuộc đoạn BD sao cho HD = 3HB. Biết góc giữa mặt phẳng (SCD) và mặt phẳng đáy
là 45o . Tính khoảng cách hai đường thẳng SA và BD. 2a 38 2a 13 2a 51 3a 34 A. B. C. D. 17 3 13 17
Câu 15. Hình chóp S.ABC có đáy ABC là tam giác vuông tại A, ·
AC  4a 3; ASB  30o. Góc giữa hai mặt
phẳng (SAB), (ABC) bằng 30o . Biết I là trung điểm của SA đồng thời là tâm mặt cầu ngoại tiếp hình chóp 21
S.ABC. Gọi  là góc giữa IB và mặt (SAC). Khi sin 
thì khoảng cách hai đường thẳng AC và SB bằng 7 14 3 8 3 A. a B. a C. 3 3a D. 4 3a 5 3
Câu 16. Cho hình chữ nhật ABCD.A’B’C’D’ có cạnh bằng AB = 2a, AD = AA’ = a như hình vẽ. Tính khoảng cách
giữa hai đường thẳng BD và AD’. 2a A. a B. 0,5a C. a 3 D. 3
Câu 17. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt phẳng (ABC), góc
giữa đường thẳng SB và mặt phẳng (ABC) bằng 60o . Khoảng cách giữa hai đường thẳng AC và SB bằng a 2 a 15 a 7 A. 2a B. C. D. 2 5 7
Câu 18. Cho khối chóp S.ABCD có thể tích bằng 3
2a và đáy ABCD là hình bình hành. Biết diện tích tam giác SAB bằng 2
a . Tính khoảng cách giữa hai đường thẳng SA, CD. A. a B. 6a C. 3a D. 1,5a
Câu 19. Cho lăng trụ tam giác đều ABC.A’B’C’ có cạnh bên bằng cạnh đáy. Đường thẳng MN (với M thuộc NB
đường thẳng A’C, N thuộc đường thẳng BC’) là đường vuông góc chung của A’C và BC’. Tính tỉ số NC . 2 5 A. 1 B. 1,5 C. D. 3 2
______________________________________ 60
VẬN DỤNG CAO, PHÂN LOẠI HÌNH HỌC KHÔNG GIAN CỔ ĐIỂN LỚP 11 – 12 THPT
(LỚP BÀI TOÁN KHOẢNG CÁCH HAI ĐƯỜNG CHÉO NHAU – P14)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Câu 1. Cho hình chóp ABCD.A’B’C’D’ có · · · AB  AD  A A
  1;BAD  BAA  DAA  60o. Tính khoảng cách
giữa hai đường thẳng AB’ và A’C’. 2 8 3 2 A. B. C. D. 11 11 11 11
Câu 2. Cho hình lăng trụ đều ABC.A’B’C’ có tất cả các cạnh có độ dài bằng 2. Tính khoảng cách giữa hai
đường thẳng AC’ và A’B. 2 3 1 3 A. B. C. D. 5 2 2 5
Câu 3. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với (ABC), góc giữa hai đường
thẳng SB và mặt phẳng (ABC) bằng 60o . Tính khoảng cách giữa hai đường thẳng AC, SB. a 15 a 2 a 7 A. B. C. D. 2a 5 2 7
Câu 4. Cho hình chóp S.ABCD có đáy là hình thoi tâm O, cạnh bằng a 3 , ·
BAD  60o, SA vuông góc với mặt
phẳng đáy, SA = 3a. Tính khoảng cách giữa hai đường thẳng SO và AD. a a 3a 3a A. B. C. D. 5 17 17 5
Câu 5. Cho hình chóp S.ABCD có cạnh đáy bằng 2a, cạnh SA tạo với mặt phẳng đáy một góc 30o , khoảng
cách giữa hai đường thẳng SA và CD bằng 2 15 3 14 2 10 4 5 A. a B. a C. a D. a 5 5 5 5
Câu 6. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với đáy và SA = 3a. Gọi E, F,
G lần lượt là trung điểm của các cạnh AB, AC, SC. Tính khoảng cách giữa hai đường EF, BG. 3a 13 a 13 a 13 3a 13 A. B. C. D. 26 6 3 13
Câu 7. Cho hình tứ diện đều ABCD có cạnh bằng a, M là trung điểm của cạnh AD, tính khoảng cách giữa hai đường thẳng AB, CM. a 33 a a a 22 A. B. C. D. 11 33 22 11
Câu 8. Cho hình chóp S.ABC có đáy là tam giác vuông tại A, AB = 4a, AC = 3a. Biết · SA  2a 3; SAB  30ovà
hai mặt phẳng (SAB), (ABC) vuông góc. Tính khoảng cách từ A đến mặt phẳng (SBC). 3 7 8 7 6 7 3 7 A. a B. a C. a D. a 14 3 7 2
Câu 9. Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau, OA = OB = a, OC = 2a. Gọi M là trung
điểm của AB, khoảng cách giữa hai đường thẳng OM và AC bằng a 2 2 5a a 2 a A. B. C. D. 3 5 2 3
Câu 10. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, AB = BC = a, AD = 2a, SA = a và
SA vuông góc với đáy (ABCD). Tính khoảng cách giữa hai đường thẳng SD, AC. a 6 a 3 a 3 a 6 A. B. C. D. 3 2 3 2
Câu 11. Cho hình chóp S.ABCD có đáy là hình thang có đáy lớn AB, SA vuông góc với mặt phẳng đáy, AD =
CD = CB = 0,5AB = 2a, SA  a 3 . Khoảng cách giữa hai đường thẳng SD và CB bằng a 3 a 2 a 6 A. a 6 B. C. D. 2 3 2
Câu 12. Cho hình chóp S.ABCD có đáy là hình thang, AB = 2a, AD = DC = CB = a, SA vuông góc với đáy và SA
= 2a. Khoảng cách giữa hai đường thẳng SC, BD. 61 A. 1,5a B. 1,2a C. 0,5a D. 0,4a
Câu 13. Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB = a, AD = 2a, H là điểm thuộc AC sao cho 3AH =
AC, SH vuông góc với (ABCD), SH = 2a. Gọi G là trọng tâm tam giác SAD. Khoảng cách giữa hai đường thẳng CG, SB khi đó bằng a 6 a 6 a 3 a 2 A. B. C. D. 3 6 3 2
Câu 14. Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, SA vuông góc với mặt phẳng đáy, góc giữa mặt
phẳng (SBC) và mặt đáy là 60o . Gọi M, N lần lượt là trung điểm của AB, AC. Tính khoảng cách giữa hai đường thẳng SB, MN. a 6 A. 0,375a B. 0,75a C. a 6 D. 2 o a
Câu 15. Cho hình chóp S.ABCD có đáy là hình thoi cạnh a, · 6 BAD  120 ; SA 
và vuông góc với đáy. Gọi 4
G1, G2 lần lượt là trọng tâm các tam giác ABC, SAB. Tính khoảng cách giữa hai đường thẳng CD, G1G2. a a A. 0,5a B. 0,25a C. D. 6 3
Câu 16. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, D, AB = 2a, AD = DC = a, SA vuông
góc với mặt phẳng đáy và SA = 4a. Gọi M là điểm trên SD sao cho SM = 2MD, O là giao điểm của AC và BD.
Tính khoảng cách giữa hai đường thẳng BC, OM. 4a 4a A. 0,75a B. 2,25a C. D. 9 3
Câu 17. Cho hình lăng trụ tam giác ABC.A’B’C’ có độ dài cạnh bên bằng a 7 , đáy ABC là tam giác vuông tại A, AB  ;
a AC  a 3 . Hình chiếu vuông góc của A’ trên mặt phẳng (ABC) là trung điểm của BC. Tính khoảng
cách giữa hai đường thẳng A’A và B’C’. a 3 2 3 3a A. B. a C. a D. 2 3 2 2
Câu 18. Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại A. Gọi E là trung điểm của AB. Cho
biết AB = 2a, C’C = 4a và BC  a 13 . Tính khoảng cách giữa hai đường thẳng A’B và CE. 12a 4a 3a 6a A. B. C. D. 7 7 7 7
Câu 19. Cho lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy bằng a và chiều cao 2a. Gọi M, N lần lượt là trung
điểm BC và A’C’. Tính khoảng cách giữa hai đường thẳng AM và B’N. A. 2a B. a C. a 2 D. a 3
______________________________________ 62