













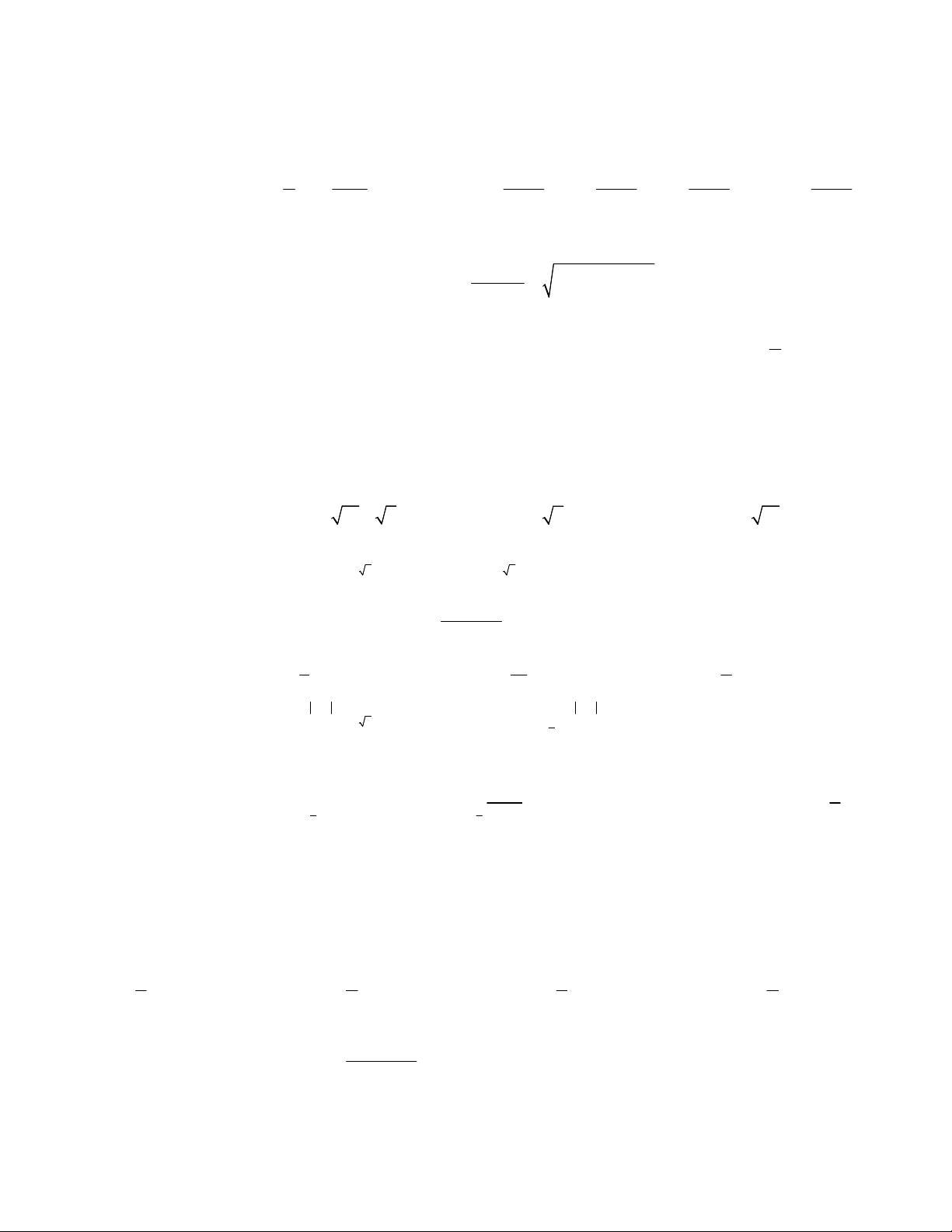
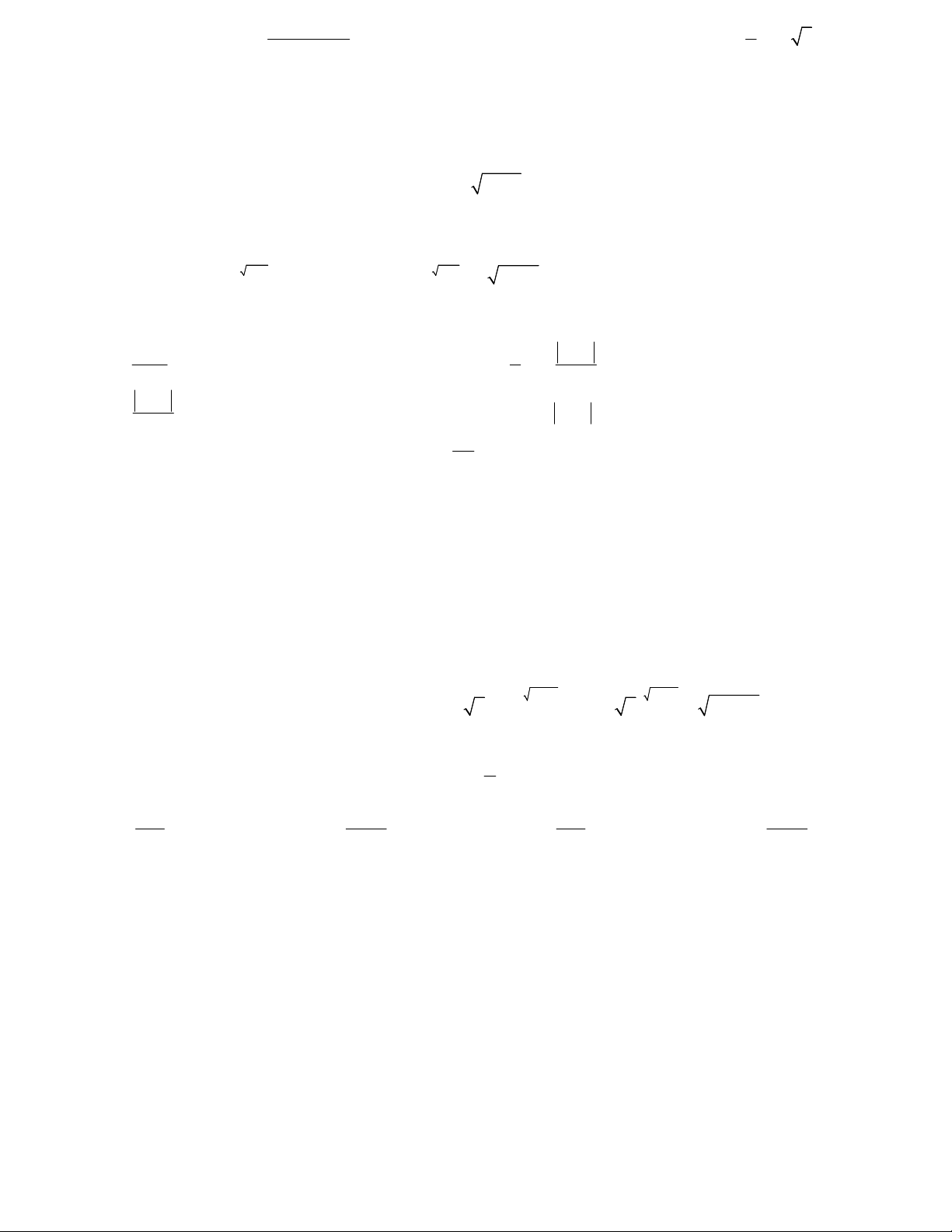































































Preview text:
THÂN TẶNG QUÝ THẦY CÔ VÀ CÁC EM HỌC SINH TOÀN QUỐC
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM CHUYÊN ĐỀ
LŨY THỪA, MŨ, LOGARIT LỚP 12 THPT
CREATED BY GIANG SƠN; TEL 0333275320 TP.THÁI BÌNH; 20/8/2021 TOÀN TẬP
PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH,
HỆ MŨ LOGARIT VẬN DỤNG CAO (55 PHẦN) PHIÊN BẢN 2021 1 TOÀN TẬP
PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH,
HỆ MŨ LOGARIT VẬN DỤNG CAO
__________________________________________________________________________________________________
VẬN DỤNG CAO, PHÂN LOẠI PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH, HỆ MŨ LOGARIT
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P1
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P2
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P3
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P4
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P5
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P6
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P7
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P8
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P9
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P10
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P11
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P12
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P13
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P14
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P15
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P16
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P17
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P18
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P19
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P20
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P21
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P22
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P23
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P24
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P25
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P26
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P27
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P28
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P29
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P30
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P31
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P32
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P33
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P34
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P35
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P36
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P37
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P38
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P39
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P40 2
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P41
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P42
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P43
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P44
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P45
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P46
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P47
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P48
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P49
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P50
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P51
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P52
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P53
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P54
LỚP BÀI TOÁN PT, BPT, HỆ MŨ LOGARIT VẬN DỤNG CAO P55 3 4
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 1)
__________________________________________________ 2 2 2
Câu 1. Phương trình x 3x2 x 6 x5 2 x 3x7 4 4 4
1có bốn nghiệm phân biệt a,b,c,d theo thứ tự tăng dần.
Tính giá trị biểu thức a 2b 3c 4d . A. 10 B. 3 C. 4 D. 5
Câu 2. Tồn tại bao nhiêu giá trị nguyên m nhỏ hơn 10 để phương trình sau có ba nghiệm phân biệt x 2 x 1 m 2 m m x 2 27 .3 2 5 .3 m 5m . A. 6 B. 5 C. 4 D. 7
Câu 3. Tồn tại bao nhiêu giá trị nguyên của tham số m để phương trình sau có ba nghiệm phân biệt x x m 2 m m x 2 125 4 .25 4 5 .5 2m 10m 0 . A. 6 B. 5 C. 3 D. 7
Câu 4. Phương trình log 2 x x 2
1 log x 2x x có bao nhiêu nghiệm thực ? 3 3 A. 2 B. 1 C. 3 D. 4
Câu 5. Tồn tại bao nhiêu số nguyên m nhỏ hơn 10 để phương trình có hai nghiệm phân biệt ? 12x 3.6x 1 .2x m 3m 3 0 . A. 4 B. 10 C. 6 D. 7
Câu 6. Tìm tất cả các giá trị m để phương trình 6x 3.2x m
m 0 có nghiệm thuộc khoảng (0;1). A. (– 4;– 2) B. [– 4;– 3] C. [– 4;– 2] D. (– 4;– 1) Câu 7. Phương trình 2x 1 x 1 3 3
3x 7 2 x có một phương trình hệ quả là A. 3x 3x 6 B. 3x 4x 7 C. 3x 2x 5 D. 3x 3 x x x 1 1 1
Câu 8. Phương trình 3 4 5
có bao nhiêu nghiệm thực ? 2x 3x 4x A. 2 B. 1 C. 3 D. 4
Câu 9. Phương trình log sin x log sin x có bao nhiêu nghiệm thực trong khoảng (– 5;5) ? 3 2 A. 2 B. 1 C. 4 D. 3
Câu 10. Phương trình x 2 2
log x 1 4 x 1 log x 1 16 có tổng các nghiệm bằng 3 3 82 11 A. 1 B. C. 2 D. 81 81
Câu 11. Tồn tại bao nhiêu giá trị nguyên của tham số m để phương trình sau có ba nghiệm phân biệt x x
2 x 2 27 5 .18 6 2 .12 3 6 .8x m m m m m 0 . A. 6 B. 5 C. 0 D. 7
Câu 12. Tồn tại bao nhiêu giá trị nguyên của tham số m để phương trình sau có ba nghiệm phân biệt x x m 2 m m x 2 2.8 5 .4 2 6 2 m 6m . A. 6 B. 5 C. 3 D. 7 2 x x 1 Câu 13. Phương trình 2 log
x 3x 2 có bao nhiêu nghiệm thực ? 2 2 2x 4x 3 A. 3 B. 1 C. 4 D. 2 Câu 14. Phương trình x x 3 2
3 3 8 x có bao nhiêu nghiệm thực ? A. 3 B. 2 C. 4 D. 1 3 2 x 3x 3x 5 3
Câu 15. Tính tổng tất cả các nghiệm của phương trình log x 2 1 x 6x 7 là 2 x 1 A. 0 B. – 2 C. 2 3 D. 2 3 3 3 3
Câu 16. Tổng các nghiệm thực x của phương trình 4x 2 2x 4 4x 2x 6 là A. 2,5 B. 1,75 C. 3,5 D. 1,5 Câu 17. Phương trình x x 3 2 2
3.2019 3.2019 8 x 4 1 x có bao nhiêu nghiệm thực ? A. 3 B. 2 C. 4 D. 1 5
Câu 18. Cho phương trình log m 6x log 2
3 2x x 0 , m là tham số. Có bao nhiêu giá trị nguyên 0,5 2
dương của m để phương trình có nghiệm thực. A. 15 B. 18 C. 13 D. 17
Câu 19. Tìm tất cả các giá trị thực của tham số m để phương trình 2
4log x 2log x 3 m 0 2 2 có nghiệm 1 thuộc đoạn ;4 . 2 11 11 A. [2;3] B. [2;6] C. ;15 D. ;9 4 4
Câu 20. Tìm điều kiện tham số m để bất phương trình x x x 12 m log 3 có nghiệm. 5 4x A. m 2 3 B. m 12log 5 2 m 12log 5 m 3 C. 3 D. 2 3
Câu 21. Tìm điều kiện m để phương trình log 2
1 x log x m 4 0 có hai nghiệm thực phân biệt. 3 1 3 21 1 21 1 A. 5 m B. m 2 C. 5 m D. m 0 4 4 4 4
Câu 22. Tìm tập hợp tất cả các giá trị tham số m để bất phương trình log 2 x 3x m log x 1 3 1 có tập 3
nghiệm chứa khoảng 1; . A. 3; B. 2; C. ; 0 D. ; 1
Câu 23. Tìm điều kiện tham số m để phương trình log 4x 3 log x 1 m có nghiệm. 2 2 A. m 4 B. 2 m 3 C. 0 m 2 D. m 2 Câu 24. Phương trình 2
log x 3log x 2m 7 0 có hai nghiệm thực thỏa mãn x 3 x 3 72 . Giá trị 1 2 3 3
tham số m thu được thuộc khoảng nào sau đây ? 7 7 21 7 A. 0; B. ;0 C. 7; D. ;7 2 2 2 2
Câu 25. Tồn tại bao nhiêu giá trị nguyên m nhỏ hơn 12 để phương trình sau có ba nghiệm phân biệt x x
2 x 2 3 27 4 .36 3 5 .48 5 .4 x m m m m m 0 . A. 6 B. 5 C. 4 D. 7
Câu 26. Tìm tập hợp tất cả các giá trị thực của tham số m để phương trình 2x 2 .4x 8x m 0 có nghiệm thuộc khoảng (0;1). 7 7 7 7 A. 2; B. 1; C. 1; D. 2; 2 2 2 2
Câu 27. Có bao nhiêu giá trị nguyên m để phương trình x x 1 2 4 . m 2
2m 5 có hai nghiệm thực ? A. 1 B. 5 C. 2 D. 4
_________________________________ 6
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 2)
__________________________________________________
Câu 1. Phương trình 2 log cot x log cos x có bao nhiêu nghiệm dương nhỏ hơn 20 ? 3 2 A. 5 B. 6 C. 3 D. 4
Câu 2. Tồn tại bao nhiêu giá trị nguyên dương nhỏ hơn 10 của m để phương trình sau có nghiệm thực x x 2
3 3 x 2x m 5 . A. 6 B. 7 C. 9 D. 8 2 sin x
Câu 3. Tập hợp [a;b] gồm tất cả các giá trị m để phương trình
x x m có nghiệm. Tính giá 2 trị biểu thức 2 a 4b . A. 6,5 B. 7 C. 8,5 D. 5,25
Câu 4. Tồn tại bao nhiêu giá trị nguyên của tham số m để phương trình có hai nghiệm thực phân biệt. log x 1 log x log 2 2x 7x m . 2 2 2 A. 4 giá trị B. 3 giá trị C. 10 giá trị D. 8 giá trị.
Câu 5. Có bao nhiêu số nguyên m nhỏ hơn 10 để phương trình x 2 m m x 3 2 4 4
5 2 5m 5m 25m 0 có
hai nghiệm phân biệt đều lớn hơn 2 ? A. 6 B. 8 C. 7 D. 9 Câu 6. Phương trình log 3 x x
log x có bao nhiêu nghiệm thực ? 2 log6 6 A. 2 B. 1 C. 4 D. 3
Câu 7. Tồn tại bao nhiêu giá trị nguyên của tham số m để hệ phương trình sau có nghiệm 2 log 2x y 1 m 4 2 log x m 4 0 2 2 2 x y 1 3x2 y e e x y 1 A. 3 B. 4 C. 5 D. 6 2 2
Câu 8. Phương trình x 5x6 1x 65 2 2
2.2 x 1có bao nhiêu nghiệm dương ? A. 2 B. 1 C. 3 D. 4
Câu 9. Tồn tại bao nhiêu giá trị nguyên của tham số m để phương trình sau có nghiệm thực.
2log cos x sin x 6 log
3sin x 2cos x m 1 . 7 7 A. 4 giá trị B. 9 giá trị C. 10 giá trị D. 8 giá trị. 2 x x Câu 10. Phương trình 2 2cos
2x 2x có bao nhiêu nghiệm không âm ? 6 A. 3 B. 1 C. 2 D. 4 5x 3x
Câu 11. Tính tổng tất cả các nghiệm của phương trình x 1 ln
5 5.3x 30x 10 0 . 6x 2 A. 1 B. 2 C. – 1 D. 3 9
Câu 12. Bất phương trình 2x x 2 log 2
log x 2x 3 có nghiệm x . Giả sử S p;q là tập a a 4
nghiệm của bất phương trình đã cho. Tìm p 2q 5 . A. 14 B. 12 C. 13 D. 10
Câu 13. Ký hiệu S a;b là tập hợp tất cả các giá trị m để phương trình log x 3
9 9m x có hai nghiệm 3
thực phân biệt. Tính giá trị của biểu thức 3 a 72b . A. 4 B. 2 C. 1 D. 5
Câu 14. Có bao nhiêu số nguyên m để phương trình 3 3 3 27 3 27.2x 2x m m có nghiệm thực ? A. Vô số B. 4 C. 8 D. 6
Câu 15. Tồn tại bao nhiêu giá trị nguyên của tham số m để phương trình sau có nghiệm thực
ln m 2sin x lnm 3sin x sin x . A. 3 B. 4 C. 5 D. 6
Câu 16. Cho phương trình mcos x sin x 21 sin x e e
2 sin x mcos x với m là tham số thực. Gọi S là tập hợp tất 7
cả các giá trị của m để phương trình có nghiệm. Khi đó S có dạng ;a ;
b , tính T 10a 20b . A. 1 B. 0 C. 10 3 D. 3 10
Câu 17. Phương trình sau có nghiệm thực khi m thuộc đoạn [a;b]. Tính 8a 16b . sin xcos xm sin 2 x3m 1 e e
sin 2x sin x cos x 4m 1. A. 10 B. 9 2 2 C. 10 3 2 D. 4 2
Câu 18. Tồn tại bao nhiêu giá trị nguyên m lớn hơn – 10 để bất phương trình sau nghiệm đúng với mọi giá trị x sin x4 cos xm e e
cos x sin x m 4 . A. 13 B. 14 C. 15 D. 12
Câu 19. Có bao nhiêu giá trị nguyên m 1
5;15 để phương trình 3x m log x m có nghiệm ? 3 A. 16 B. 9 C. 14 D. 15 2 2
Câu 20. Tìm số nghiệm của phương trình 2 x x 2
x x x 3x6 2 x x x x3 2 2 9 3 .8 3 6 .8 . A. 1 B. 3 C. 2 D. 4
Câu 21. Có bao nhiêu giá trị nguyên m 2
5;25 để phương trình 7x m log x m có nghiệm ? 7 A. 25 B. 9 C. 24 D. 26
Câu 22. Phương trình log 2 log 4x 3 2 2
có tổng các nghiệm bằng x A. 5 B. 6 C. 3 D. 4
Câu 23. Tồn tại bao nhiêu số nguyên m 3
0;30 để phương trình x x x m2 4 4 4 có nghiệm A. 2 B. 1 C. 4 D. 3
Câu 24. Tồn tại bao nhiêu giá trị nguyên dương của tham số m để phương trình sau có nghiệm thực 2 2 2 sin x cos x cos 5 6 7 x log m . 2 A. 62 B. 63 C. 64 D. 6 2 2 2
Câu 25. Có bao nhiêu giá trị nguyên dương m để bất phương trình cos x sin x sin 3 2 .3 x m có nghiệm. A. 1 B. 3 C. 2 D. 4 Câu 26. Cho phương trình .4x sin 4 4x a x
; a là tham số thực. Tồn tại duy nhất giá trị a a0 để phương
trình đã cho có nghiệm thực duy nhất. Tính giá trị của log a 2 0 . A. B. 1 C. 2 D. 2 1
Câu 27. Cho phương trình 6x .6x a
cos x 1296 . Tồn tại duy nhất một giá trị a để phương trình đã cho
có nghiệm duy nhất x . Nghiệm x nằm trong khoảng nào ? 0 0 A. (1;2) B. (1;4) C. (4;7) D. (3;5)
_________________________________ 8
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 3)
__________________________________________________ 2 2 2
Câu 1. Biết tập hợp tất cả các giá trị của tham số m để bất phương trình sin x cos x cos 4 5 .7 x m có nghiệm là a a nửa khoảng ;
với a, b nguyên dương và phân số tối giản. Tính giá trị của S a b . b b A. S 13 B. S 15 C. S 9 D. S 11
Câu 2. Tồn tại bao nhiêu giá trị nguyên dương của tham số m để phương trình sau có nghiệm thực 2 2 sin x cos x cos 2 3 13 8.7 x log m . 3 A. 18 B. 14 C. 45 D. 60
Câu 3. Tồn tại bao nhiêu giá trị nguyên m để phương trình 3 3 3 3.4x 4x m m có nghiệm thực ? A. Vô số B. 4 C. 8 D. 6
Câu 4. Có bao nhiêu giá trị nguyên của tham số m nhỏ hơn 10 để phương trình sau có nghiệm thực x x m m e e . A. 10 B. 9 C. 7 D. 6
Câu 5. Cho phương trình ẩn x: 4x 4 6 .6 x a
cos x 36 . Tồn tại bao nhiêu giá trị thực của tham số a thuộc
đoạn [– 2018;2018] để phương trình đã cho có đúng một nghiệm thực ? A. 2 B. 3 C. 1 D. 2018
Câu 6. Tồn tại bao nhiêu giá trị nguyên của tham số m để phương trình sau có nghiệm thực 2 sin x 2 2 2 ln
sin x cos x m 1 0 . 2 m 3 cos x A. 7 B. 6 C. 5 D. 3
Câu 7. Tồn tại duy nhất một giá trị thực của m để phương trình 9x 2 .6x .4x m m
0 có hai nghiệm thực phân biệt x , x 1
2 có tổng bằng 2. Giá trị tham số m thu được nằm trong khoảng nào ? 17 5 8 17 11 A. (2;3) B. ; C. ; D. ;2 16 4 9 16 8
Câu 8. Tìm tập hợp tất cả các giá trị thực của tham số m để phương trình 3x 4x 2 .5x m 0 có nghiệm
thực thuộc khoảng (0;2). A. [3;4] B. [2;4] C. (2;4) D. (3;4)
Câu 9. Tồn tại bao nhiêu giá trị nguyên lớn hơn 5 của tham số m để phương trình sau có nghiệm thực sin x cos x 2 ln
sin 2x m 6 sin x cos x . sin 2x m 4 A. 2 B. 6 C. 5 D. 3
Câu 10. Tìm số nghiệm của phương trình x x x x x x 2 2 2 3 5 x 8x3 5 2 8 3 .8 3 5 .8 . A. 4 B. 3 C. 1 D. 2
Câu 11. Tồn tại bao nhiêu giá trị nguyên của tham số m để phương trình sau có nghiệm thực x x m5 x x m5 x x m5 sin 3cos 2cos sin 2 2sin cos . A. 4 B. 6 C. 5 D. 7 Câu 12. Phương trình 2 3 3x 2x log 2
x 1 log x có bao nhiêu nghiệm thực ? 2 2 A. 3 B. 1 C. 4 D. 2 Câu 12. Phương trình 2
log x m 2 log x 3m 1 0 có hai nghiệm thực có tích bằng 27. Mệnh đề nào 3 3 dưới đây đúng ? A. m 2 ; 1 B. m 0;2 C. Không tồn tại m. D. m 2;4 x x x 1 2 3
Câu 13. Phương trình 5.3 3.4 3.5
có bao nhiêu nghiệm thực ? 20x 30x 40x A. 2 B. 1 C. 3 D. 4
Câu 14. Tìm tập hợp tất cả các giá trị m để phương trình 3x .2x m
m 2 0 có nghiệm thuộc khoảng (0;2). 9 1 7 1 7 1 7 1 7 A. ; B. ; C. ; D. ; 2 5 2 5 3 5 3 5
Câu 15. Gọi S là tập hợp các giá trị tham số m để phương trình sau có ba nghiệm phân biệt log
mx 6x 2log 14x 29x 2 0 2 3 2 1 2
Số các giá trị nguyên của S là A. 20 B. 30 C. 0 D. Vô số
Câu 16. Tìm điều kiện m để phương trình log 2
1 x log x m 4 0 3 1
có hai nghiệm thực phân biệt. 3 21 1 21 1 A. 5 m B. m 2 C. 5 m D. m 0 4 4 4 4 2 Câu 17. Phương trình x3 x 5 x6 2 3
có hai nghiệm x , x x x . Lựa chọn phát biểu đúng 1 2 1 2 A. 3x 2x log 8 B. 2x 3x log 8 1 2 3 1 2 3 C. 2x 3x log 54 D. 3x 2x log 54 1 2 3 1 2 3
Câu 18. Tìm tất cả các giá trị m để bất phương trình 2
log 2x 2 m 1 log x 2 0 có nghiệm thuộc khoảng 2 2 2;. 3 3 A. ; 0 B. ;0 C. ; D. 0; 4 4
Câu 19. Tìm tập hợp giá trị m để phương trình 4log x 2 log x m 0 2 1
có nghiệm thuộc khoảng (0;1). 2 1 1 1 A. 0; B. ; C. ; D. ; 0 4 4 4
Câu 20. Tồn tại bao nhiêu số nguyên của tham số m lớn hơn – 5 để phương trình sau có nghiệm duy nhất x x 5 1 . 5 1 2x m A. 0 B. 5 C. 2 D. 3
Câu 21. Tìm tập hợp tất cả các giá trị thực m để phương trình có nghiệm thuộc nửa khoảng 1; .
log 5x 1 log 2.5x 2 m . 2 4 1 A. 1; B. 6; C. 3; D. ; 4
Câu 22. Tìm tập hợp giá trị m để phương trình 6x 2 .3x m
m 0 có nghiệm thực thuộc khoảng (0;1). 3 27 3 3 27 3 A. ; B. ;3 C. ; D. ;3 2 5 2 2 5 2
________________________________ 10
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 4)
__________________________________________________
Câu 1. Có bao nhiêu số nguyên m để hàm số f x x mx 2018 2019 2 6 xác định trên R ? A. 6 B. 7 C. 9 D. 10 Câu 2. Phương trình 3x 722 3x
2018 1296 có bao nhiêu nghiệm nguyên ? A. 2 B. 1 C. 3 D. 4
Câu 3. Tìm tập hợp tất cả các giá trị m để hàm số 8x .2x y m
1đồng biến trên . 1 A. ; 1 B. ; 0 C. ;5 D. 5; 3
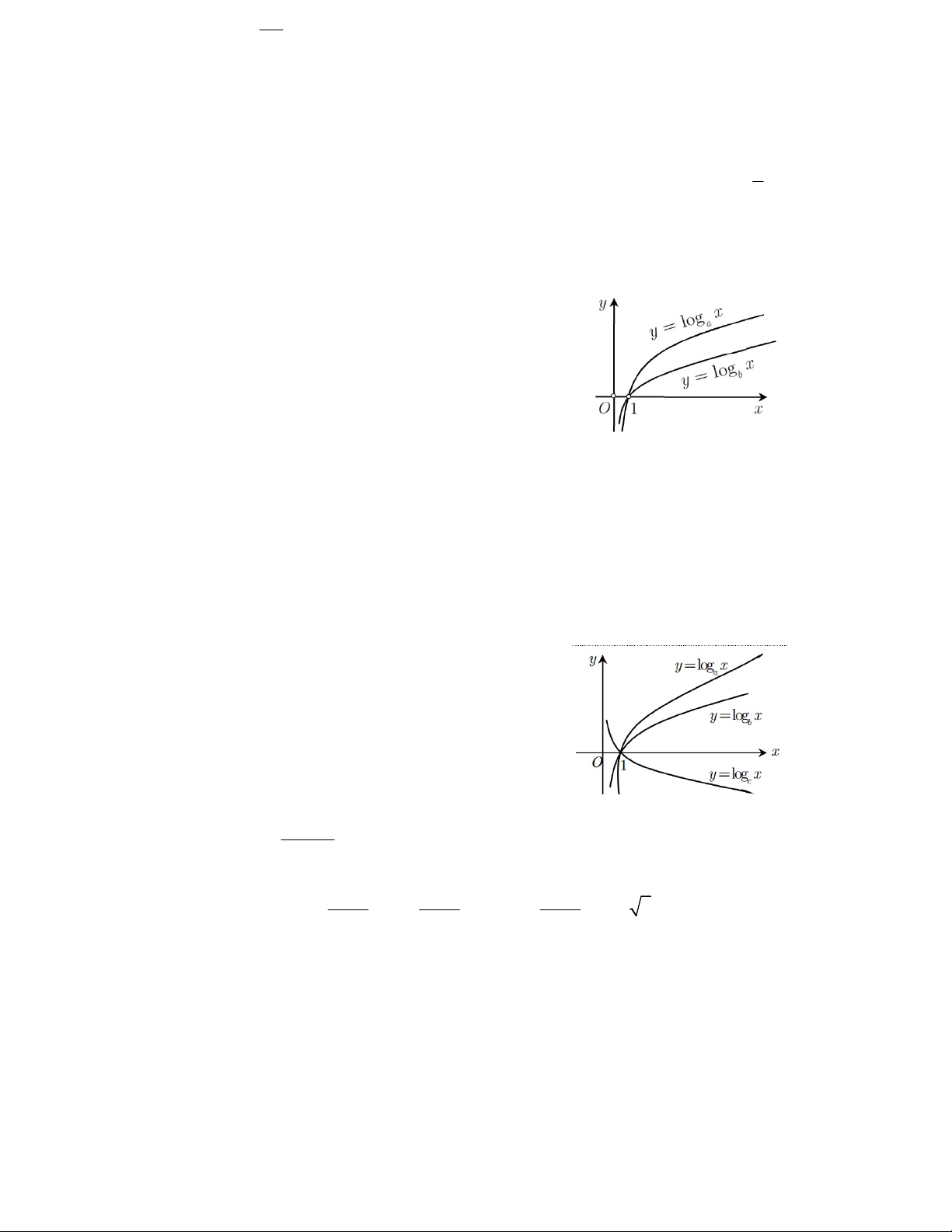
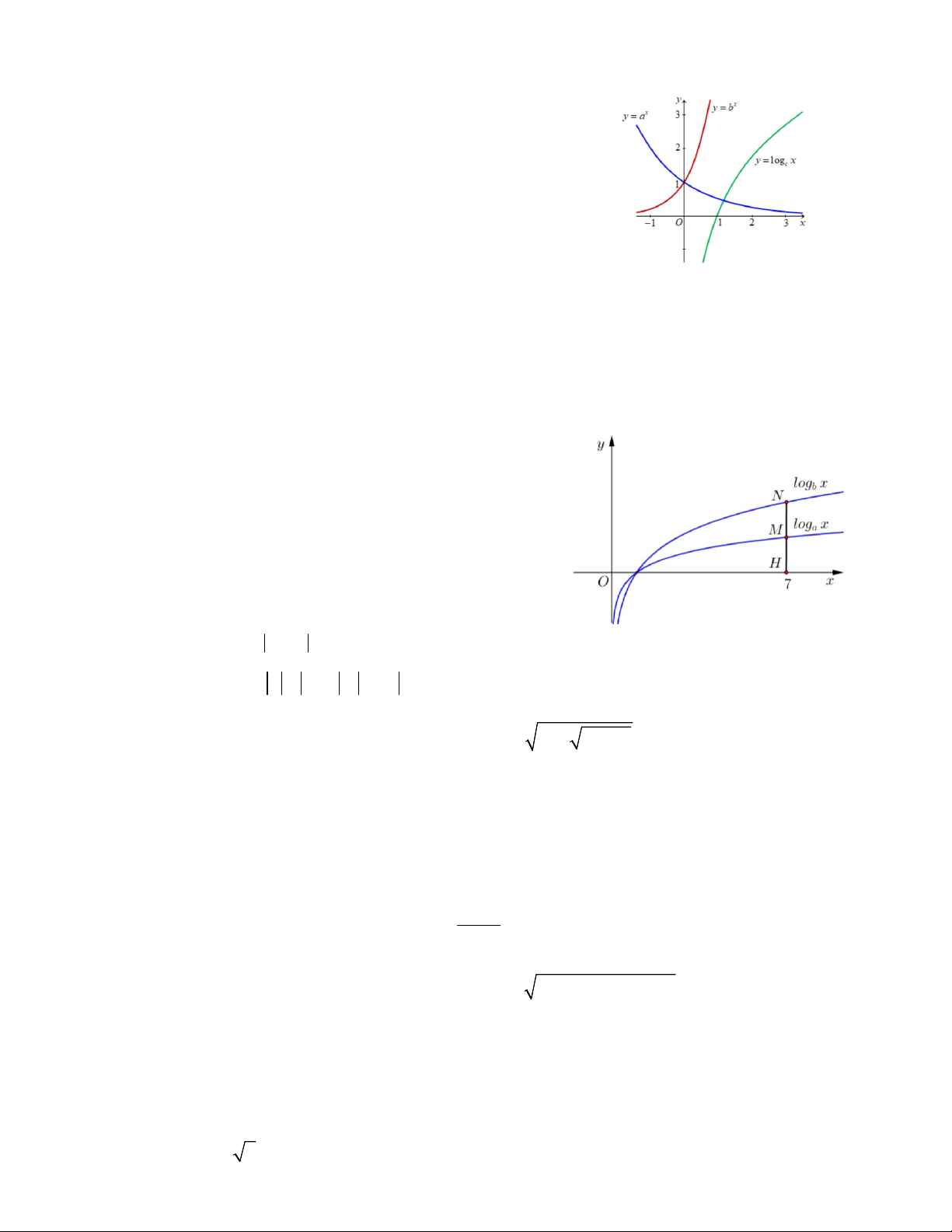
Câu 4. Hình vẽ bên là hai đồ thị C : y log ; x C : x y a . 1 b 2 Mệnh đề nào đúng ?
A. a > 1; b > 1. B. 0 < a < 1, 0 < b < 1.
C. 0 < a < 1 < b. D. 0 < b < 1 < a.
Câu 5. Tìm giá trị nhỏ nhất của tham số m để hàm số y log 2
x mx 2m 1 xác định trên [1;2]. 3 A. 0,25 B. 0,5 C. 0,75 D. 1 Câu 6. Phương trình x x 2
2 1 2 2 x 2x y có bao nhiêu cặp nghiệm (x;y) ? A. 2 B. 3 C. 1 D. Vô nghiệm 3 x 1 x e m e 1 1972
Câu 7. Tìm điều kiện tham số m để hàm số y
đồng biến trên khoảng (1;2). 1973 A. 3 4 3e 1 m 3e 1 B. 2 3 3e 1 m 3e 1 C. 4 m 3e 1 D. 2 m 3e 1
Câu 8. Tồn tại bao nhiêu số nguyên m lớn hơn – 10 để hàm số y 2 ln x
1 mx 1đồng biến trên . A. 5 B. 7 C. 9 D. 10
Câu 9. Tìm số nghiệm thực của phương trình log2 3 log2 7 x x x 2 . A. 3 B. 1 C. 2 D. 4
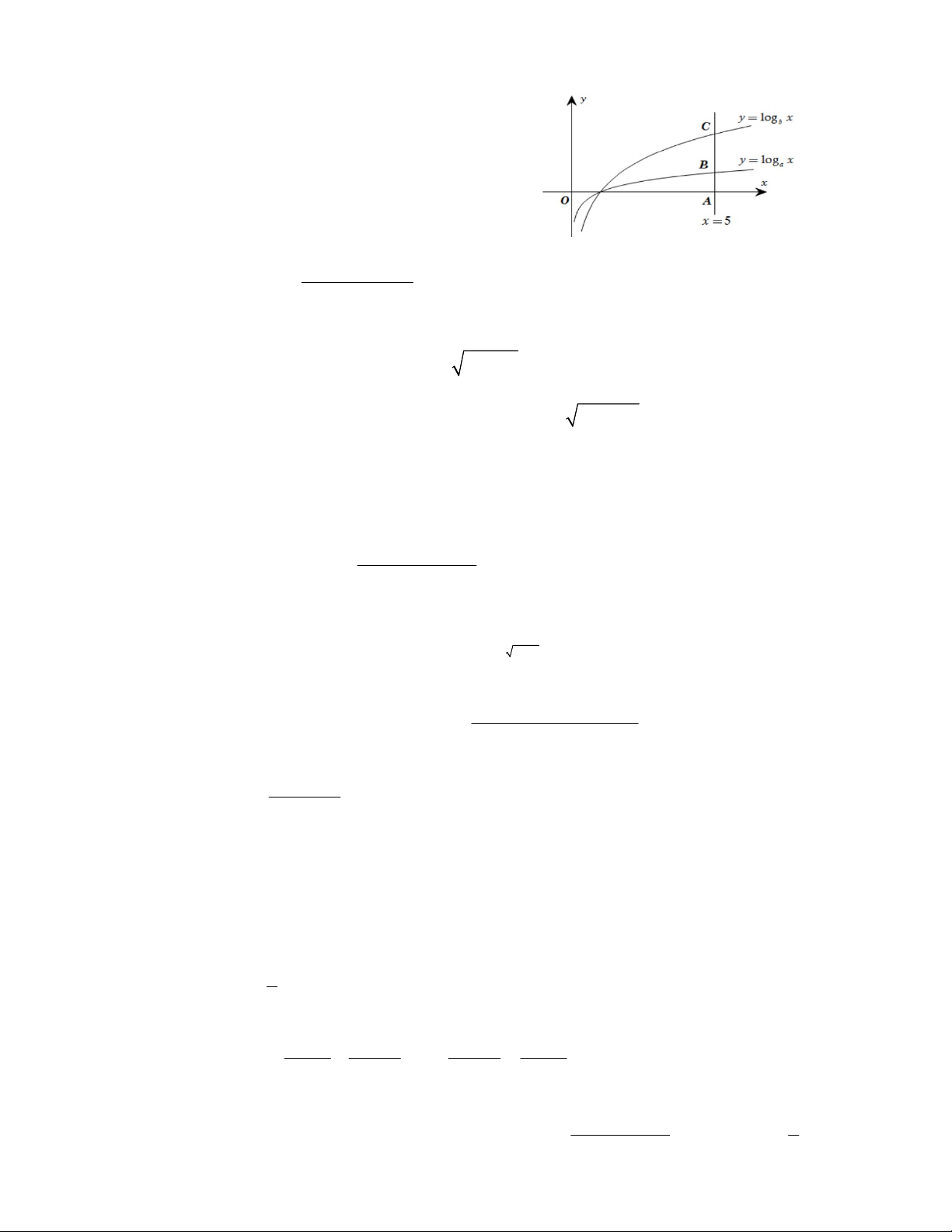
Câu 10. Cho hình vẽ bên. Mệnh đề nào đúng ?
A. a < c < b B. a < b < c
C. b < c < a D. c < a < b 2
Câu 11. Tính trung bình cộng các nghiệm thực của phương trình x x x8 2 2 2 8 2x x . A. 2 B. 1 C. 3 D. 1,5 x 1
Câu 12. Có bao nhiêu số nguyên m thuộc [– 20;20] để hàm số y xác định x m 2ln 2 x 4x 6 m trên miền 1; ? A. 21 B. 20 C. 4 D. 3 mx 1 6
Câu 13. Có bao nhiêu số nguyên m để hàm số xm y e
nghịch biến trên 2; ? A. 6 B. 5 C. 7 D. 9 11 2 x 1 Câu 14. Phương trình 3 .
x 5 x 15 có một nghiệm x log b 1 a 8,1 b 8;a,b . Tính a + b. a A. 10 B. 8 C. 13 D. 5 Câu 15. Cho hàm số sin 5 x y
. Phương trình y 5cos x ln 5 có bao nhiêu nghiệm trong khoảng (0;10) ? A. 1 B. 3 C. 4 D. 2 3
Câu 16. Tìm giá trị nhỏ nhất của m để phương trình x 3x3 e
m có nghiệm x 0;2. 1 A. m = 2e B. m = 3e C. m = e D. m = e
Câu 17. Ký hiệu S là tập hợp tất cả các giá trị thực m để phương trình 2 2
log x 4log x m 2m 0 có hai 2 2
nghiệm phân biệt x , x thỏa mãn 2 2
x x 68 . Tính tổng bình phương các phần tử của S. 1 2 1 2 A. 15 B. 10 C. 18 D. 26
Câu 18. Cho hình vẽ bên. Mệnh đề nào đúng ?
A. a > b > 1 B. 1 > a > b
C. b > a > 1 D. a > 1 > b
Câu 19. Có bao nhiêu số nguyên m < 2018 để phương trình log 2018x m log 1009x có nghiệm. 6 4 A. 2019 B. 2018 C. 2017 D. 2020 2
Câu 20. Tìm tập hợp tất cả các giá trị m để phương trình log2 x m log2 x 2 3 2 3 3
m 3 0 có hai nghiệm
phân biệt mà tích của chúng lớn hơn 2.
A. 1; \ 0 B. 1; C. 0; D. \ 1 ; 1
Câu 21. Tồn tại bao nhiêu số nguyên m trong khoảng (– 5;15) để bất phương trình sau nghiệm đúng với mọi số thực x: 1 log 2 x 1 log 2 mx 4x m . 5 5 A. 2 B. 1 C. 3 D. 11
Câu 22. Cho hình vẽ bên. Mệnh đề nào đúng ?
A. 0 < c < 1 < a < b. B. 0 < a < b < 1 < c.
C. 0 < c < a < 1 < b. D. 0 < c < 1 < b < a. x
Câu 23. Cho hàm số g x 81
. Với mọi số thực x, phần nguyên của x được ký hiệu [x], tức là số nguyên 81x 9
lớn nhất không vượt quá x. Tìm phần nguyên của số 1 2 2016 Q g g ... g g 3. 2017 2017 2017 A. Q 112 B. Q 113 C. Q 115 D. Q 120
_________________________________ 12
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 5)
__________________________________________________
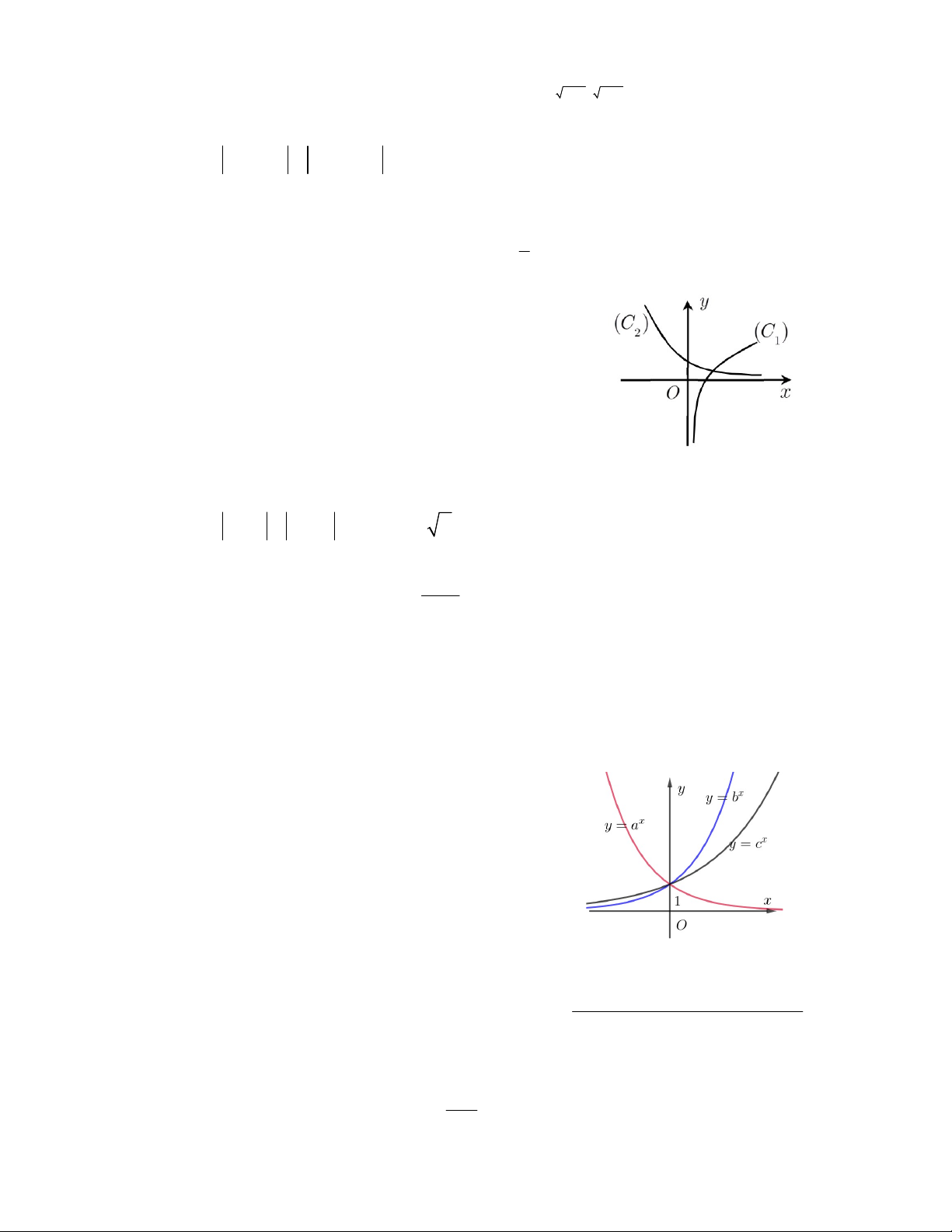
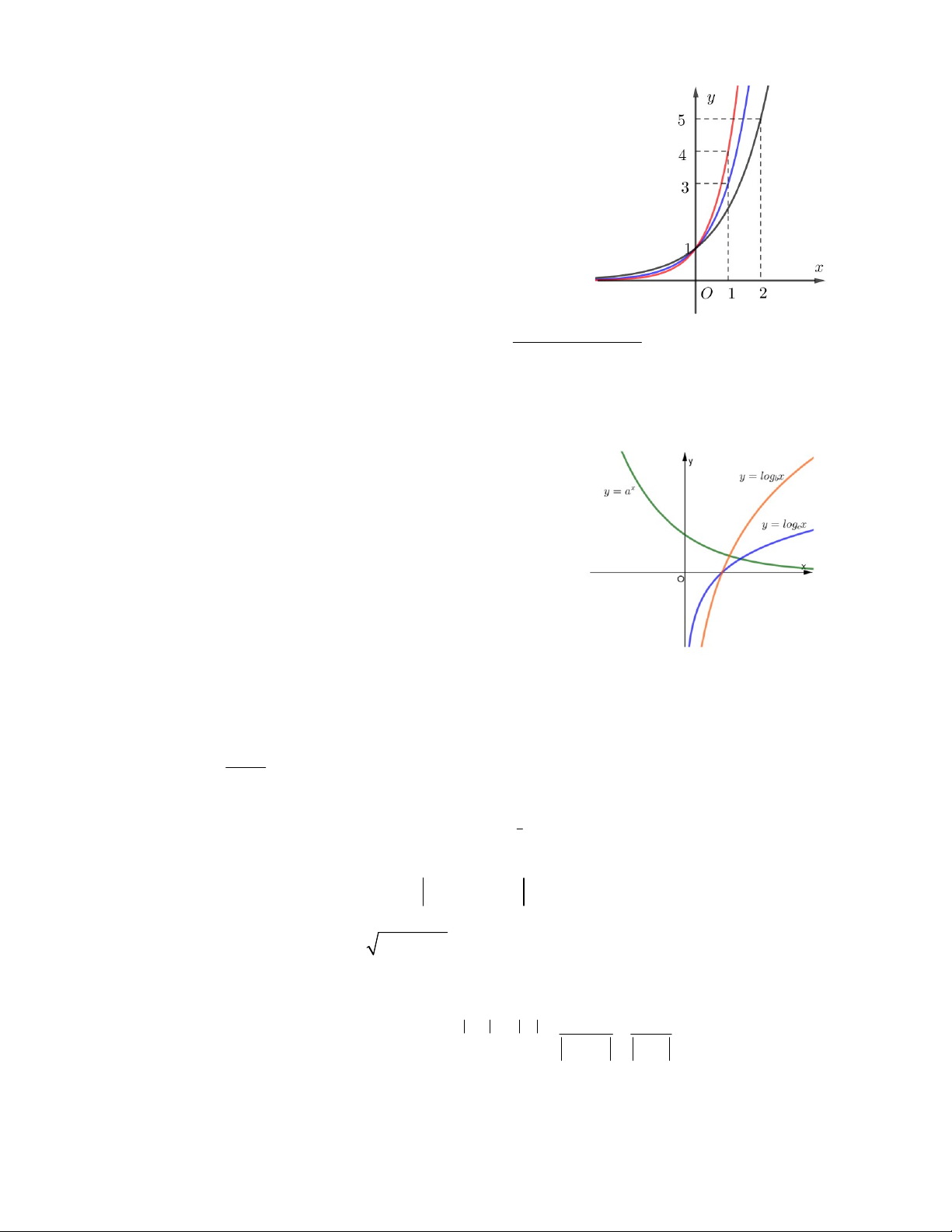
Câu 1. Hình vẽ bên là đồ thị các hàm số x ; x ; x y a y c y b .
Nghiệm của phương trình x x x a c b là A. x = 0 B. x = 2 C. x = 1 D. x = 3
Câu 2. Tồn tại bao nhiêu giá trị nguyên của tham số m để phương trình sau có nghiệm thực
ln m 2sin x lnm 7sin x 5sin x . A. 35 B. 141 C. 52 D. 66
Câu 3. Có bao nhiêu số nguyên dương m để hàm số 2
y x 8ln x m
1 đồng biến trên tập xác định của nó A. 2 B. 1 C. 3 D. 4 Câu 4. Phương trình sin x 1sin 4 2
x cos xy 2 y 0 có nghiệm x ; y . Tính tổng các giá trị x , y khi 0 0 0 0 x y 10 . 0 0 A. 4 B. 2 C. 3 D. 6
Câu 5. Có bao nhiêu giá trị nguyên của tham số m nhỏ hơn 10 để phương trình sau có nghiệm thực x x m m e e . A. 10 B. 9 C. 7 D. 6
Câu 6. Cho hình vẽ bên. Mệnh đề nào sau đây đúng ?
A. a > 1; 0 < b < 1. B. 1 > a > 0; b > 1.
C. 0 < a < 1; b < 1. D. a > 1; b > 1. x
Câu 7. Cho hàm số f x 2016
. Tìm số nguyên dương n lớn nhất sao cho 2016x 2016 n 1 2 2015 2016 3 f f ... f f . 2017 2017 2017 2017 A. n 4 B. n 5 C. n 6 D. n 7 1 1 1 m 2 2 x m
Câu 8. Cho hàm số f x x 1 e . Biết rằng
1. 2... 2017 n f f f
e với là phân số tối giản. Tính n
giá trị của biểu thức 2 m n . A. 2018 B. 1 C. – 2018 D. – 1
Câu 9. Tập hợp S a;b bao gồm tất cả các giá trị m để phương trình sau có nghiệm thực m sin x4 cos x 2 m 3sin xm cos x5 e e
m 4cos x 3 msin x 2m 5 Tính a b 20 . A. 4 B. 2 C. 5 D. 3 4x 2x
Câu 10. Có bao nhiêu giá trị nguyên m thuộc (– 2018;2018) để hàm số y 2 . m
m 2 x 1đồng ln 4 ln 2 biến trên khoảng ; ? A. 2018 B. 2019 C. 2020 D. 4034 13
Câu 11. Cho hình vẽ bên. Mệnh đề nào sau đây đúng ?
A. b < c < a. B. c < a < b
C. a < b < c D. b < a < c
Câu 12. Tính tích các nghiệm của phương trình 8.3x 3.2x 24 6x . A. 3 B. 2 C. 4 D. 6
Câu 13. Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình sau có nghiệm thực ? 2 4m 2 sin cos x xm 5 5e 5e 5cos2x m . A. 12 B. 10 C. 11 D. 15 log2 x log2 x Câu 14. Phương trình x 2 3 1 3 1
1 x có bao nhiêu nghiệm thực ? A. 2 B. 1 C. 3 D. 0
Câu 15. Tìm giá trị lớn nhất của tham số m để phương trình ln m ln m cos x cos x có nghiệm thực ? e 1 A. 1 B. e C. D. e – 1 2
Câu 16. Cho 0 a,b,c 1 và ba đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng ?
A. 1 < c < a < b B. c < a < b < 1
C. c < 1 < b < a D. c < 1 < a < b
Câu 17. Có bao nhiêu giá trị nguyên m 1
8;18 để phương trình 2x m log x m có nghiệm ? 2 A. 19 B. 9 C. 17 D. 18 2 2
Câu 18. Tính tổng các nghiệm của phương trình x x 32 x 2 2x3 2 9 6 4 3xx x 5x . A. 6 B. 7 C. 8 D. 4
Câu 19. Tồn tại bao nhiêu giá trị nguyên m lớn hơn – 10 để phương trình sau có nghiệm 2 3x cos 2x m . A. 10 B. 12 C. 15 D. 14
Câu 20. Phương trình log 8
3x 1 y 1 y 3 6log x có bao nhiêu cặp nghiệm thực (x;y) ? 4 4 A. 3 B. 2 C. 1 D. 4 2
Câu 21. Tìm tất cả các giá trị m để phương trình x
m có hai nghiệm phân biệt. log x 1 3 A. 1 m 0 B. m > – 1 C. Không tồn tại m D. – 1 < m < 0
_________________________________ 14
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 6)
__________________________________________________
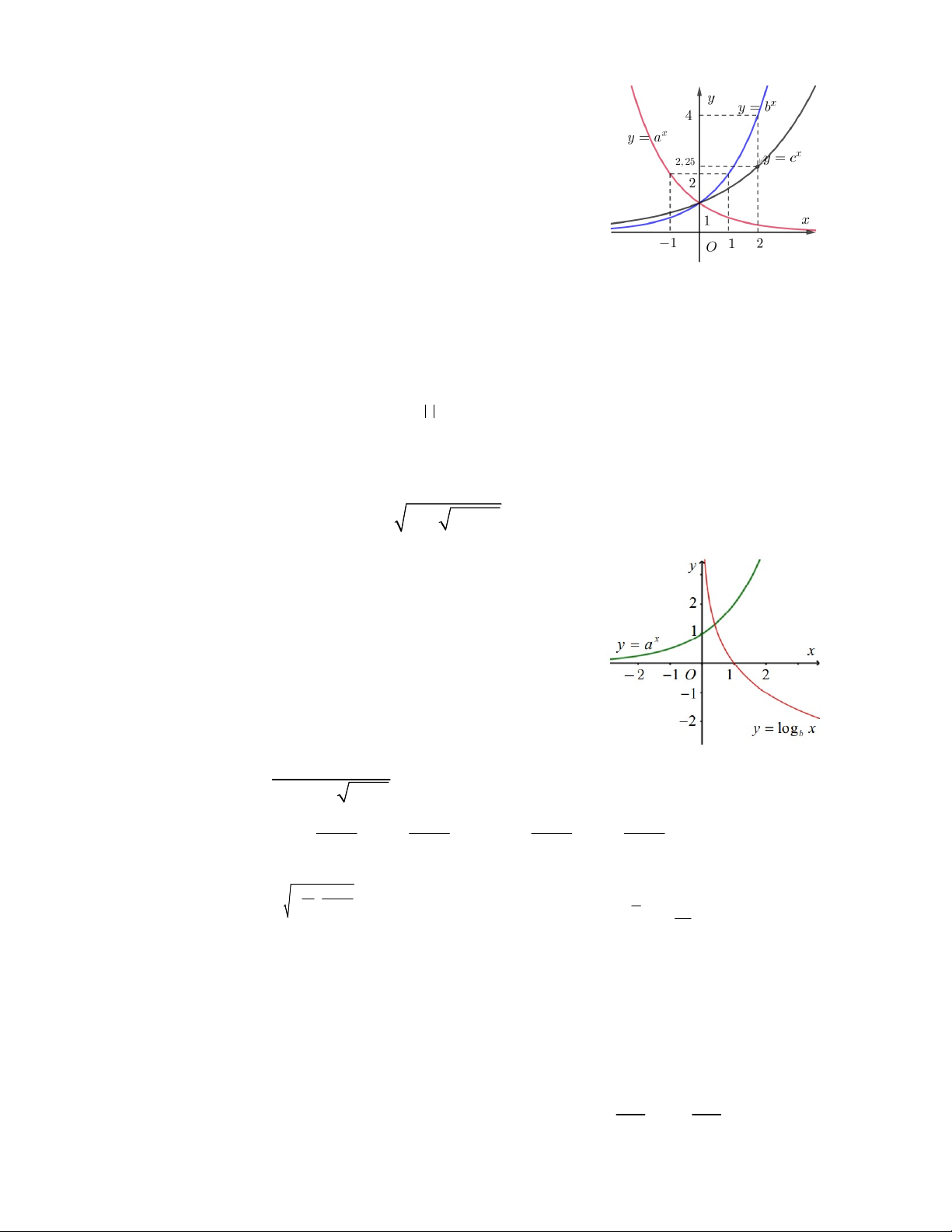
Câu 1. Đối với góc phần tư thứ nhất, theo thứ tự từ trái sang phải
trong hình bên là đồ thị các hàm số x ; x ; x y a y c y b .
Nghiệm của phương trình x x 2x a c b là A. x = 0 B. x = 1 C. x = 2 D. x = 3 2 x 2mx m 2
Câu 2. Có bao nhiêu giá trị nguyên m để hàm số f x log xác định trên ? 3 6 sin x 2cos x A. 3 B. 2 C. 1 D. 4
Câu 3. Tìm giá trị bé nhất của m để hàm số y 2 ln 16x 1 m
1 x m 2 nghịch biến trên ? A. m = 2 B. m = 4 C. m = 5 D. m = 3
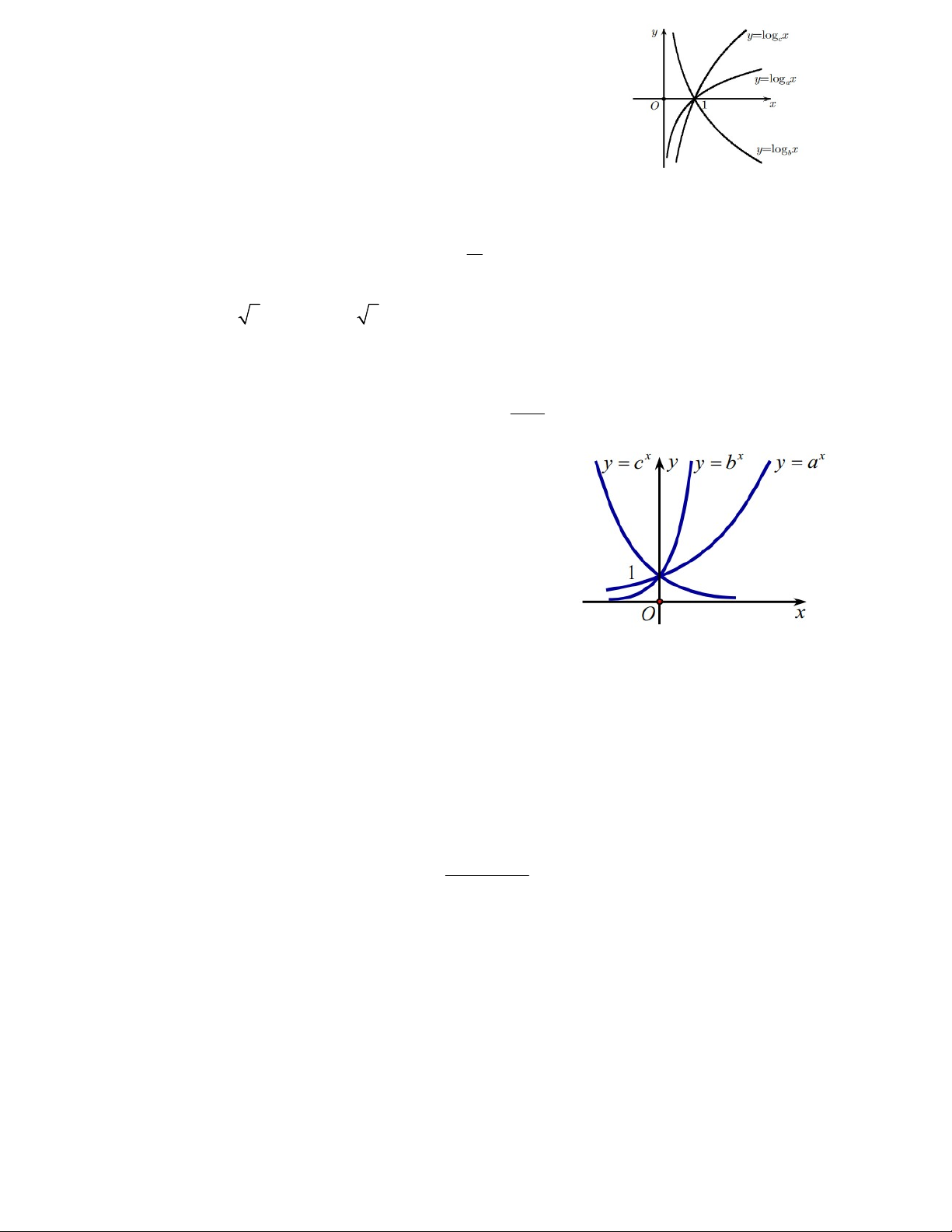
Câu 4. Cho hình vẽ bên với các đồ thị hàm số x
y a ; y log x; y log x . Mệnh đề nào sau đây đúng ? b c
A. c > b > a B. b > a > c
C. a > b > c D. b > c > a
Câu 5. Phương trình x log x log x 2 2
1 x có bao nhiêu nghiệm thực lớn hơn 1,5 ? 3 3 A. 3 B. 4 C. 2 D. 1
Câu 6. Đồ thị hàm số y = g (x) đối xứng với đồ thị của hàm số x
y a a 1,a 0 qua điểm I (1;1). Tính giá trị 1 biểu thức g 2 log . a 2018 A. 2016 B. – 2020 C. 2020 D. – 2016 1 3 2 x mx 2m3 x5
Câu 7. Tồn tại bao nhiêu giá trị nguyên m để hàm số f x 3 e
2019 đồng biến trên ? A. 10 B. 4 C. 12 D. 5
Câu 8. Có bao nhiêu giá trị m để hàm số 2 x 4 x f x e
e m có giá trị nhỏ nhất trên đoạn [0;ln4] bằng 6. A. 3 B. 4 C. 1 D. 2
Câu 9. Cho dãy số u thỏa mãn 1u8 1 u 8 4 1 u 4 1 5 u e e e
e và u u 3 với n nguyên dương. Giá trị lớn n n 1 n
nhất của n để log u ln 2018 bằng 3 n A. 1420 B. 1419 C. 1417 D. 1418
Câu 10. Tính tổng các nghiệm thực của phương trình 2x 5 x 1 1 1 e e . 2x 5 x 1 A. 5 B. 6 C. 7 D. 4 15
Câu 11. Cho hình vẽ bên. Mệnh đề nào sau đây đúng ?
A. c > b > a B. b > a > c
C. a > b > c D. b > c > a
Câu 12. Tìm giá trị tham số m để hai đường cong sau tiếp xúc nhau
: 3x 3x 2 2 3 ; : 3x C y m m m C y 1. 1 2 5 2 10 5 2 10 5 2 2 5 3 2 A. B. C. D. 3 3 3 3 x x 8 Câu 13. Phương trình 2 1 3 2 2 2
có bao nhiêu nghiệm thực ? log 2 4x 4x 4 3 A. 3 B. 2 C. 1 D. Vô nghiệm
Câu 14. Tồn tại bao nhiêu giá trị nguyên dương của tham số m để phương trình sau có nghiệm thực 2 2 sin x cos x cos 2 4 15 9.6 x log m 1 . 3 A. 69 B. 90 C. 42 D. 112 ln x 6 Câu 15. Cho hàm số y
. Gọi S là tập hợp tất cả các giá trị nguyên dương của m để hàm số đã cho ln x 2m
đồng biến trên khoảng (1;e). Tìm số phần tử của S. A. 1 B. 2 C. 4 D. 3
Câu 16. Cho phương trình 3x .3x a
cos x 9 . Có bao nhiêu giá trị thực của tham số a thuộc đoạn [–
2018;2018] để phương trình đã cho có đúng một nghiệm thực ? A. 2 B. 3 C. 1 D. 2018
Câu 17. Cho phương trình 4x 4 6 .6 x a
cos x 36 . Có bao nhiêu giá trị thực a thuộc đoạn [– 2018;2018]
để phương trình đã cho có đúng một nghiệm thực ? A. 2 B. 3 C. 1 D. 2018
Câu 18. Gọi S là tập hợp các giá trị của tham số thực m để hàm số 2
y x ln x m 2 đồng biến trên tập
xác định của nó. Biết S ;
a b , tính tổng K a b . A. K 5 B. K 5 C. K 0 D. K 2
Câu 19. Tồn tại bao nhiêu giá trị nguyên dương của tham số m để phương trình sau có nghiệm thực 2 2 sin x cos x cos 2 2 9 4 x log m . 2 A. 4096 B. 4091 C. 1300 D. 1250 x a b
Câu 20. Cho hai số thực dương x, y thỏa mãn log x log y log x y . Khi đó , a và b đều 9 6 4 y 2 nguyên dương. Tính a + b. A. a + b = 11 B. a + b = 4 C. a + b = 6 D. a + b = 8 1
Câu 21. Có bao nhiêu số nguyên m 2
0;20 để hàm số y xác định với x > 0. 2 m log x 4log x m 3 3 3 A. 35 B. 20 C. 16 D. 38
_________________________________ 16
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 7)
__________________________________________________
Câu 1. Cho hình vẽ bên với các đồ thị hàm số x y a ; x y b ; y log x c
Mệnh đề nào sau đây đúng ?
A. a < b = c B. b > a > c
C. a > c > b D. b > c > a log x log 5 7 y,
Câu 2. Hệ phương trình
có nghiệm duy nhất (x;y). Tính P = 7x – 5y + 1. 7x log7 5ylog5 A. P = 3 B. P = 2 C. P = 13 D. P = 6
Câu 3. Cho dãy số u thỏa mãn 3 2
log u 2log u log u 2 0 và u
2u 10, n nguyên dương. Tìm n 1 1 1 n 1 n
giá trị nhỏ nhất của n sao cho 100 u 10 10 . n A. 226 B. 325 C. 225 D. 326
Câu 4. Cho hàm số y log x; y log x a b
có đồ thị như hình vẽ
bên. Đường thẳng x = 7 cắt trục hoành và các đồ thị hàm số
y log x; y log x lần lượt tại H, M, N. Biết rằng 2HM = HN. a b
Mệnh đề nào sau đây đúng ? A. a = 7b B. 2 a b C. a = 2b D. 7 a b 2 x 2x3 log 3 5 y4 3 5 ,
Câu 5. Hệ phương trình
có hai nghiệm x ; y . Tính 2 x 3 y . 0 0 0 0
4 y y 1 y 3 8. A. 5 B. 7 C. 6 D. 4
Câu 6. Có bao nhiêu số nguyên m nhỏ hơn 10 để phương trình x x
m m e e có nghiệm thực ? A. 10 B. 9 C. 7 D. 6
Câu 7. Cho dãy số u thỏa mãn 2
log u logu 6 0 và u
u 5, n nguyên dương. Giá trị lớn nhất n 1 1 n 1 n
của n để u 500 bằng bao nhiêu ? n A. 80 B. 100 C. 99 D. 82
Câu 8. Cho dãy số u thỏa mãn 3 2 u e ;u
u , k là số tự nhiên thỏa mãn 765
u u ...u e . Giá trị của k là n 1 n 1 n 1 2 k A. 6 B. 7 C. 8 D. 9 4x 1
Câu 9. Tìm điều kiện tham số m để phương trình log m có nghiệm. 2 4x 1 A. – 1 < m < 1 B. m < 0 C. – 1 < m < 0 D. m 1
Câu 10. Cho dãy số u thỏa mãn log u 2log u 2 1 logu 2logu 1 và u 3u , n nguyên 5 2 5 2 n n n 1
dương. Giá trị lớn nhất của n để 100 u 7 bằng n A. 192 B. 191 C. 176 D. 177
Câu 11. Có bao nhiêu số nguyên m [– 2018;2018] để hàm số f x x
1 ln x 2 m x đồng biến trên khoảng 2 0;e . A. 2022 B. 2014 C. 2023 D. 2016
Câu 12. Giá trị m a b a,b là giá trị nhỏ nhất của tham số m để phương trình sau có nghiệm 17 3 x 3 x 1 2.2 4 3.2 2x m m .
Tính giá trị biểu thức a 2b 7 . A. 10 B. 15 C. 18 D. 12 Câu 13. Cho phương trình .5x sin 5 5x a x
; a là tham số thực. Phương trình đã cho tồn tại nghiệm duy nhất x sin x cos x sin x 0 . Tính . 0 0 0 2 A. 1 B. 2 C. 4 D. 3 Câu 14. Phương trình x2 x x2 3.25 3 10 .5
3 xcó tổng các nghiệm gần nhất với giá trị nào A. 8 B. 3 C. 10 D. 12
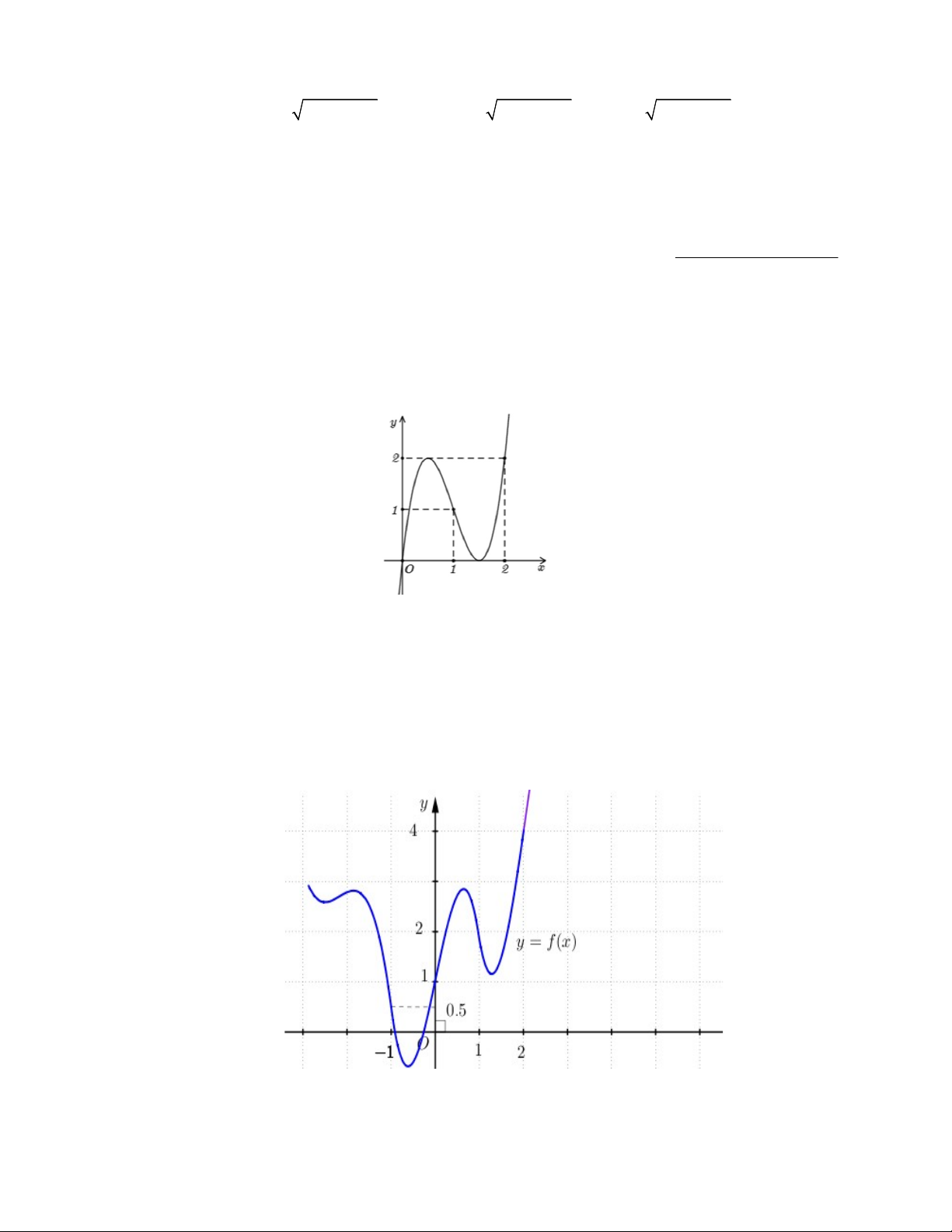
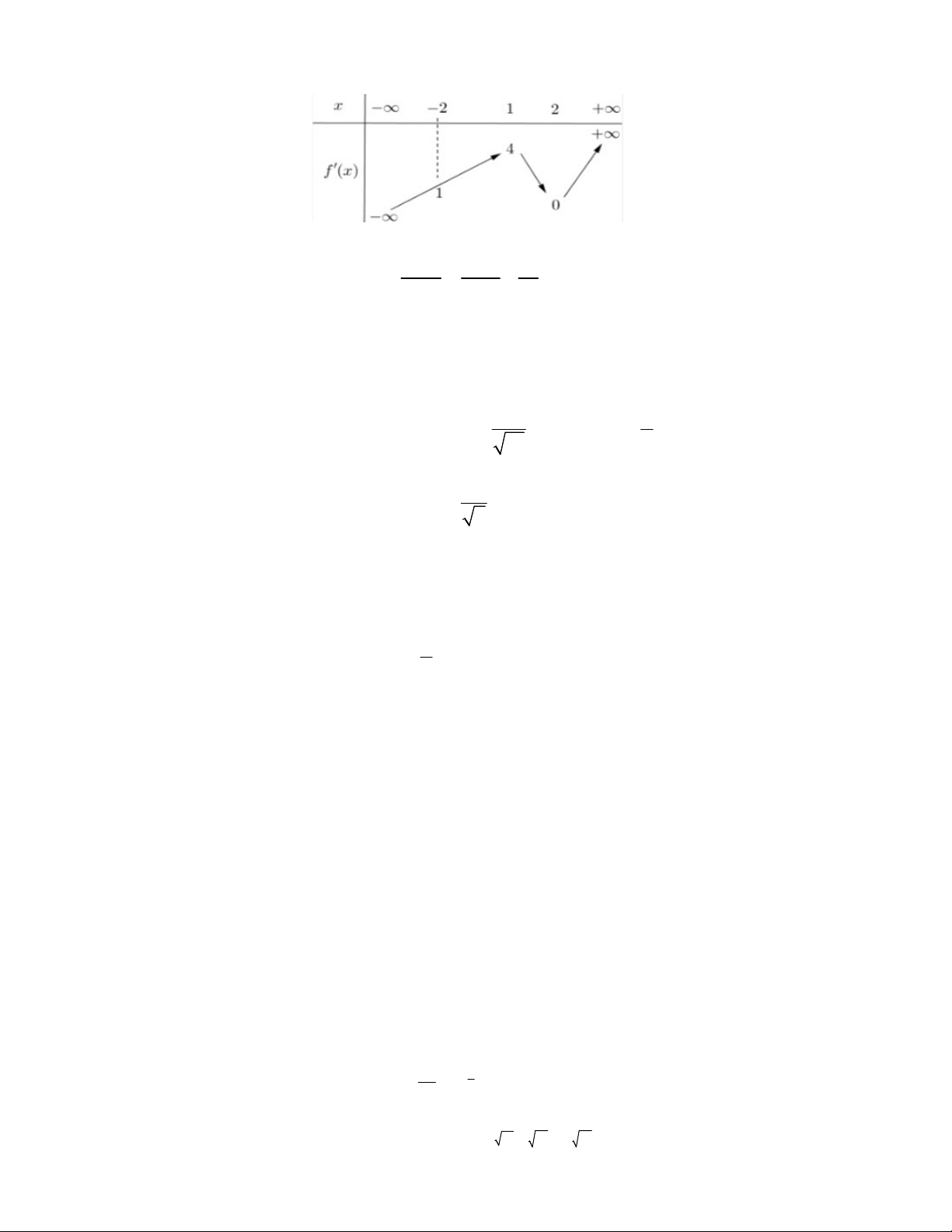
Câu 15. Cho hàm số y f x có đồ thị như hình vẽ bên. Hàm số 2 f x 1 f x g e 6
có bao nhiêu điểm cực trị ? A. 3 B. 6 C. 4 D. 5 3
Câu 16. Phương trình log 4 2 x 3x 3x m log
4 x log x 1 có ba nghiệm thực phân biệt khi 5 125 5
m thuộc khoảng (a;b). Mệnh đề nào sau đây đúng ? a 2 A. ab 4 B. a b 1 C. b 2a 6 D. b 5 2 x x 1 2 x 1 7 7 2012x 2012,
Câu 17. Tồn tại bao nhiêu số nguyên m < 100 để hệ có nghiệm ? 2
x (m 2)x 2m 3 0. A. 100 B. 105 C. 102 D. 90 2 x Câu 18. Phương trình 3
3x ln(x 1) 4 0 có bao nhiêu nghiệm thực ? 2 A. 3 B. 2 C. 1 D. 4
Câu 19. Có bao nhiêu số nguyên a thuộc (– 200;200) để phương trình x xa e e
ln(x a) ln(x a 1) có nghiệm thực duy nhất. A. 399 B. 199 C. 200 D. 398
Câu 20. Cho các số thực dương a, b khác 1. Biết rằng bất kỳ
đường thẳng nào song song với trục hoành mà cắt các đường thẳng x ; x
y a y b , trục tung lần lượt tại M, N và A thì ta luôn có
AN = 2AM (hình vẽ bên). Mệnh đề nào sau đây đúng ? A. 2a = b B. 2 ab 1 C. 2 a b D. 2ab = 1
_________________________________ 18
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 8)
__________________________________________________
Câu 1. Biết rằng a là số thực dương để x a 9x 1, x
. Mệnh đề nào sau đây đúng ? A. a 3 4 10 ;10 4 B. a 2 3 10 ;10 C. a 2 0;10 D. a 1 0 ;
Câu 2. Có bao nhiêu số nguyên m < 10 để hàm số y 2 ln x mx
1 đồng biến trên 0; ? A. 10 B. 11 C. 8 D. 9 1
Câu 3. Cho dãy số u thỏa mãn log u
2017 2018 2logu logu
2logu và u u , n là số n 2018 1 2018 1 n 1 2 n
nguyên dương. Tìm giá trị lớn nhất của n để 1917 u 5 . n A. 232 B. 233 C. 234 D. 235
Câu 4. Tính tổng các nghiệm của phương trình 2
log x x 12 log x 11 x . 3 3 A. 18 B. 10 C. 12 D. 6
Câu 5. Tồn tại bao nhiêu giá trị nguyên m lớn hơn – 10 để phương trình sau có nghiệm 2 x 2 65.13
x 4cos3x 3 m 1. A. 10 B. 11 C. 13 D. 12 log 2 log 3 log 4 ... log n
Câu 6. Gọi a là giá trị nhỏ nhất của hàm số f n 3
3 3 3 * ;n ,n 2. Có bao 9n
nhiêu số tự nhiên n để f (n) = a ? A. 2 B. 4 C. 1 D. Vô số
Câu 7. Biết a là số thực dương sao cho bất đẳng thức 3x x 6x 9x a
đúng với mọi số thực x. Mệnh đề nào sau đây đúng ? A. a (10;12] B. a (16;18] C. a (14;16] D. a (12;14]
Câu 8. Tính tổng các nghiệm của phương trình 7x 1 6log 6x 1 . 7 A. 2 B. 3 C. 1 D. 0 1
Câu 9. Cho hàm số f x ln 1
thỏa mãn f 2 f 3 ... f 2018 ln a ln b ln c ln d , trong 2 x
đó a, b, c, d là các số nguyên dương tăng dần, a, c, d đều là số nguyên tố. Tính P = a + b + c + d. A. 1986 B. 1698 C. 1689 D. 1968
Câu 10. Giả sử a, b là các số thực sao cho 3 3 3z 2 .10 .10 z x y a b
đúng với mọi số thực dương x, y, z thỏa mãn điều kiện x y z 2 2 log
;log x y z 1. Giá trị của a + b là A. 15,5 B. 14,5 C. – 15,5 D. – 12,5
Câu 11. Tồn tại bao nhiêu giá trị nguyên m để phương trình sau có 4 nghiệm thực phân biệt ? 2 2 3 x 3 x 2 log
m 2.6 5 m 3.6 x . 6 A. 4 B. 3 C. 1 D. 2 log 2 2 x y 1 log xy , 2 2
Câu 12. Biết hệ phương trình có hai nghiệm ; x y a;b, ; c d ;a c . 2 2 3x xyy 81. Tính b + 2d. A. b + 2d = 4 B. b + 2d = 3 C. b + 2d = 2 D. b + 2d = 5
Câu 13. Gọi a là số thực lớn nhất sao cho 2 x x a 2 2 ln x x 1 0, x
. Mệnh đề nào đúng ? A. a (2;3] B. a 8; C. a (6;7] D. a (– 6;– 5]
Câu 14. Tìm điều kiện tham số m để hàm số y 2 ln x x
1 mln x đồng biến trên khoảng (0;4). 2 2 28 A. m 1 B. m 1 C. m D. m 0 3 3 13 19 2
Câu 15. Tìm điều kiện tham số m để hàm số log 2018x x y x
m xác định với mọi x không âm. 2018 2 A. m > 9 B. m < 1 C. 0 < m < 1 D. m < 2
Câu 16. Có bao nhiêu số nguyên m để phương trình sau có hai nghiệm phân biệt x , x với tổng bình phương 1 2 các nghiệm bằng 3: log . 2 2 2x x 4m 2m 2 2 log x mx 2m 0 2 5 52 A. 1 B. 0 C. 3 D. 2
Câu 17. Cho dãy số u thỏa mãn log u 2 log u 2logu 2logu và u 2u , n nguyên dương. n 1 1 10 10 n 1 n
Giá trị lớn nhất của n để 100 u 5 bằng n A. 248 B. 246 C. 247 D. 290
Câu 18. Tìm điều kiện tham số m để phương trình 4x 2x 4 3m 2x
1 có hai nghiệm phân biệt. A. 1 m log 4 B. 1 m log 4 C. log 3 m 1 D. log 3 m 2 3 3 4 4
Câu 19. Có bao nhiêu số nguyên dương khác 1 của m để phương trình sau có nghiệm x lớn hơn 2 log 2 x x 1.log 2
x x 1 log x x m 2 1 2 5 A. Vô số B. 3 C. 2 D. 1
Câu 20. Biết rằng a là số thực dương để x a 2018x 1, x
. Hỏi log(a) gần nhất với giá trị nào ? A. 2018 B. 876 C. 1010 D. 502
Câu 21. Tập hợp S a;b bao gồm tất cả các giá trị m để phương trình sau có nghiệm thực m sin x4 cos x2m 3sin xm cos x5 e e
m 4cos x 3 msin x 2m 5 Tính a b 20 . A. 4 B. 2 C. 5 D. 3 2 m 2 1
Câu 22. Tìm điều kiện tham số m để hàm số y log x 2 đồng biến trên đoạn ;100 . log x m 10 3 m 1 A. m B. C. m 2 D. m 2 2 m 2
Câu 23. Tính tích các nghiệm của phương trình log 2 x 2x 1 log 2 x 2x . 3 2 A. – 2 B. 1 C. – 1 D. 4
Câu 24. Cho dãy số u có số hạng đầu u 1và thỏa mãn 2
log 5u log 7u log 5 log 7 .Biết 2 1 2 2 2 2 2 n 1 2 2 u
7u với n 1. Giá trị nhỏ nhất của n để u 1111111bằng n 1 n n A. 11 B. 8 C. 9 D. 10 mlog x 2
Câu 25. Có bao nhiêu số nguyên m lớn hơn – 40 để hàm số 2 y
nghịch biến với mọi x > 4 ? log x m 1 2 A. 37 B. 20 C. 16 D. 32
_________________________________ 20
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 9)
__________________________________________________
Câu 1. Giả sử a là số thực dương sao cho x 4.5x 220x 15x a , x
. Khi đó số nghiệm thực của phương trình 3 x 2018x a là A. 3 B. 2 C. 1 D. Vô số 1 2x 1 2 3 2016
Câu 2. Cho hàm số f x log . Ký hiệu M f f f ... f . 2 2 1 x 2017 2017 2017 2017
Biết rằng M là một số tự nhiên, hỏi M có bao nhiêu ước nguyên dương ? A. 10 B. 12 C. 8 D. 30 x 2 1 2
Câu 3. Có bao nhiêu số nguyên m để phương trình log 8 7 2 3 x m có nghiệm ? 2 x A. 6 B. 3 C. 2 D. 2 3
Câu 4. Tồn tại bao nhiêu số nguyên m để hàm số y log
mx 3m 5 xác định với mọi x ? 2 m 4 2 A. 5 B. 4 C. 3 D. 2 x
Câu 5. Giả sử a là số thực dương để a 4 2 10x 39, x
. Giá trị log(a) gần nhất với A. 4,3 B. 6,1 C. 3,2 D. 2,5
Câu 6. Trong tất cả các cặp số (x;y) thỏa mãn log
4x 4 y 4 1. Tìm giá trị của tham số m thỏa mãn 2 2 x y 2 đẳng thức 2 2
x y 2x 2 y 2 m 0 . A. m = 4 B. m = 10 2 C. m = 7 1 D. m 10 2
Câu 7. Có bao nhiêu số nguyên m nhỏ hơn 8 để phương trình sau có nghiệm duy nhất log x m 1 log . 2 mx x 0 3 2 2 3 2 2 A. 5 B. 4 C. 6 D. 7 2x 1
Câu 8. Tính tổng các nghiệm của phương trình 2 log 3x 8x 5 . 3 3x 2 1 8 11 2 A. 4 B. C. D. 3 7 3 2
Câu 9. Biết rằng phương trình 4 xm log 2 3 2x x x x
log 2 xm 2 0 có nghiệm khi và chỉ khi m > 2 2 2 1 2
a hoặc m < b. Tính a + b. A. a + b = 2 B. a + b = 4 C. a + b = 5 D. a + b = 2,5 1 5
Câu 10. Phương trình m 1 log x 22 2 4 m 5 log
4m 4 0 có nghiệm thực trong đoạn ;4 1 1 x2 4 2 2
khi m thuộc đoạn [p;q]. Tính p + 3q. A. p + 3q = 5 B. p + 3q = 4 C. p + 3q = 8 D. p + 3q = 10
Câu 11. Tìm tất cả các giá trị của tham số m để phương trình 2x mx 1 có hai nghiệm phân biệt. A. 0 m ln 2 B. Mọi giá trị m C. m ln 2 D. 0 < m < ln2
Câu 12. Tìm điều kiện tham số m để hàm số 2 2. x f x mx x
e đồng biến trên khoảng (1;2). 5 4 5 4 A. m B. m C. m D. m 8 3 8 3 2 2 2 x y x 2017 2016 , Câu 13. Hệ phương trình 2 y 2017
có bao nhiêu nghiệm thực 3
log x 2y 6 2log x y 2 1. 3 2 A. 3 B. 2 C. 1 D. 0 2 2
Câu 14. Tìm số nghiệm nguyên của bất phương trình 2x 1 5x 1 00 x 1 0 x50 2 2 2 x 25x 150 0 . A. 6 B. 4 C. 5 D. 3 21 2 4x 4x 1 1 Câu 15. Phương trình 2 log
4x 1 6x có hai nghiệm x , x thỏa mãn x 2x a b , trong 1 2 7 2x 1 2 4
đó a và b là hai số nguyên dương. Tính a + b. A. 16 B. 11 C. 14 D. 13
Câu 16. Có bao nhiêu giá trị nguyên m để phương trình 1x 1x 2x 2 4 4 1 2 2 x m 168mcó nghiệm thuộc đoạn [0;1]. A. 2 B. 5 C. 4 D. 3
Câu 17. Cho hai số thực a, b thỏa mãn f x 2017 a 2x x 2018 ln 1 bxsin x 2 . Biết log 6 5 c f 6, tính giá trị của biểu thức log 5 6 c P f với 0 c 1. A. P = – 2 B. P = 6 C. P = 4 D. P = 2 Câu 18. Phương trình 2x 1 1 x 3x 1 1 2 0, 25 1 0,5 2
2x 1 có tổng các nghiệm bằng A. 4 B. 8 C. 3 D. 6
Câu 19. Giả sử có hệ thức 2 2
a b 11ab (a và b là hai số dương khác nhau). Khẳng định nào sau đây đúng ? a b 1 a b A. 2 log log a log b B. log log a log b 2 2 2 3 2 2 2 2 3 a b C. 2 log log a log b
D. 2 log a b log a log b 2 2 2 3 2 2 2 2017 z
Câu 20. Cho các số thực x, y, z thỏa mãn 3x 5y 15 xy . Ký hiệu S = xy + yz + xz. Chọn mệnh đề đúng A. 1 < S < 2016 B. 0 < S < 2017 C. 2016 < S < 2017 D. 0 < S < 2018
Câu 21. Có bao nhiêu số nguyên âm m để phương trình 3 2
log x 3x 8x 14 m log x 1 có hai nghiệm phân biệt ? A. 1 B. 0 C. 2 D. 3
Câu 22. Có bao nhiêu số nguyên m để bất đẳng thức 2 x 2 ln 5 ln 1
ln mx 4x m đúng với mọi m ? A. 3 B. 4 C. 1 D. 2
Câu 23. Có bao nhiêu giá trị nguyên dương của tham số m để bất phương trình sau nghiệm đúng với mọi x thuộc khoảng (2;4): 2 log x 2 m 3 2
1 log x m 2m m 0 . 4 2 A. 0 B. 2 C. 1 D. 3 2 2 1 x 3x x 3x
Câu 24. Tính tích tất cả các nghiệm của phương trình 2 2 1 3 2 2 x 3x 1. A. – 3 B. – 1 C. 2 D. 4 1 x
Câu 25. Tìm tất cả các giá trị thực của m để hàm số y mlog x
đồng biến trên nửa khoảng (0;2]. 2 2 ln 2 2ln 2 ln 2 2ln 2 A. m B. m C. m D. m e e e e ______________________ 22
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 10)
__________________________________________________
Câu 1. Có bao nhiêu số nguyên m lớn hơn – 12 để hàm số y log
2sin x 3cos x m xác định với 2 m 2m5 mọi x ? A. 7 B. 8 C. 6 D. 5 Câu 2. Cho hàm số x
y e sin x . Lựa chọn mệnh đề đúng
A. y 2 y 2 y 0
B. y 2 y y 0
C. y 2 y 2 y 0 D. y y 3y 0
Câu 3. Tồn tại bao nhiêu số nguyên m để phương trình 3 3 3 27 3 27.2x 2x m m có nghiệm thực ? A. Vô số B. 4 C. 8 D. 6
Câu 4. Tồn tại giá trị m m để phương trình 1 m log x 4m 2 log x m có nghiệm duy nhất. 0 2 2
Mệnh đề nào sau đây đúng ? A. m [3;5] B. m [6;9] C. m (0;3) D. m 10 0 0 0 0
Câu 5. Tồn tại duy nhất giá trị m = a để phương trình log 2x 1 m 1 log 2 m 4x 4x có nghiệm 2 3
duy nhất. Giá trị a thuộc khoảng nào sau đây ? A. (0;4) B. (4;6) C. (6;9) D. (9;14)
Câu 6. Tính tổng các số tự nhiên m để phương trình 2
log x 3mlog (3x) 2m 2m 1 0có hai nghiệm 3 3 10
phân biệt mà tổng hai nghiệm không nhỏ hơn . 3 A. 6 B. 1 C. 0 D. 10 2 mx 2mx m 6
Câu 7. Tồn tại bao nhiêu số nguyên m thuộc khoảng (– 10;10) để hàm số y ln xác định 10 sin 2x 3cos 2x với mọi x. A. 15 B. 8 C. 9 D. 10 Câu 8. Cho hàm số 4 x 2 x y e e
. Tính y 13y 5y theo y. A. 6y B. 5y C. 7y D. 8y
Câu 9. Tồn tại bao nhiêu số nguyên m để phương trình 2
log x 4log x m 3 0 có hai nghiệm phân biệt 3 3
x x thỏa mãn điều kiện x 81x . 1 2 2 1 A. 4 B. 5 C. 3 D. 6
Câu 10. Tồn tại bao nhiêu số nguyên a < 50 để bất phương trình 2x 60x 10x 2x a
nghiệm đúng với mọi số thực x ? A. 46 B. 49 C. 30 D. 27
Câu 11. Tồn tại bao nhiêu số nguyên m thuộc [– 2020;2020] để bất phương trình sau nghiệm đúng với mọi x 2 x 2x m thuộc [0;4]: 2 log x 4x 3 m . 2 2 x x 1 A. 2023 B. 1 C. 2 D. 2012
Câu 12. Hàm số y = f (x) thỏa mãn f ( x) 2 2019
x x 2019 . Có tất cả bao nhiêu giá trị nguyên m thỏa mãn
điều kiện f (log m) f (log 2019) ? m A. 66 B. 65 C. 63 D. 64 1 Câu 13. Hàm số y log
có đồ thị (H), hàm số y = f (x) có đồ thị (H’). Hai đồ thị trên đối xứng nhau gốc tọa 2018 x
độ. Khi đó hàm số y f (x) nghịch biến trên khoảng A. ( ; 1 ) B. (– 1;0) C. (0;1) D. (1;)
Câu 14. Kết quả đạo hàm cấp 2018 của hàm số 10 20 ( ) x f x e là A. 200 f (x) B. 10! f (x) C. 102018201009 f (x) D. 102018 f (x)
Câu 15. Có tất cả bao nhiêu số nguyên dương m để phương trình 2 (4log log 5) 4x x x m 0 có đúng 2 2 hai nghiệm phân biệt ? 23 A. 14 B. 15 C. Vô số D. 16
Câu 16. Tiếp tuyến của đồ thị của hàm số x
y x tại điểm có hoành độ bằng 2 cắt trục tung tại điểm M. Tung độ
điểm M gần nhất giá trị nào ? A. – 9,54 B. – 10,51 C. – 7,56 D. – 2,75
Câu 17. Có bao nhiêu số nguyên m > – 20 để phương trình 2
log (x 4) (m 5)log (x 4) 2m 1 0 có 3 3
hai nghiệm phân biệt a, b thỏa mãn ab 4(a b) 65 . A. 10 B. 12 C. 20 D. 21 x 1
Câu 18. Tổng các nghiệm phương trình 5x.8 x 500 gần nhất với giá trị nào ? A. 2,56 B. 2,89 C. 3,54 D. 4,23 x 1 1
Câu 19. Có bao nhiêu số nguyên dương m để phương trình 5x.8 x m có tổng các nghiệm lớn hơn ? 2020 A. 8 B. 7 C. 6 D. 10 2
Câu 20. Tồn tại bao nhiêu số nguyên m để phương trình x 2x 2 log ( . m 4
9) x 2x 3 log 3 có hai 2 2 nghiệm phân biệt ? A. 12 B. 11 C. 4 D. 13 Câu 21. Cho hàm số 3 ( ) 2m f x x x
. Tồn tại bao nhiêu số nguyên m để phương trình f ( f (x)) x có nghiệm trên [1;2]. A. 0 B. 4 C. 2 D. 3 2 x 1
Câu 22. Tồn tại bao nhiêu giá trị nguyên dương m để phương trình 3 .
x 5 x m có hai nghiệm phân biệt a, b
thỏa mãn điều kiện ln(a b ab) 3 . A. 5 B. 6 C. 18 D. 10 mx 1 6
Câu 23. Tồn tại bao nhiêu số nguyên m để hàm số 3 8 x m y e
4 x 2020nghịch biến trên (2;) ? A. 7 B. 6 C. 5 D. 9
Câu 24. Tồn tại bao nhiêu số nguyên m thuộc [– 100;100] để phương trình sau có đúng hai nghiệm phân biệt 2 (log 3log 2) 9x ( 1).3x x x m m 0 . 2 2 A. 103 B. 102 C. 101 D. 100
Câu 25. Tìm điều kiện tham số m để bất phương trình sau có nghiệm 2 2
2log (sin x m ) 4log sin x 2sin x cos 2x 2m 1 0 . 3 3 1 A. m 2; 2 B. m C. Không tồn tại m. D. m = 0 4
_________________________________ 24
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 11)
__________________________________________________ 2
Câu 1. Tổng các nghiệm của phương trình x 4 2 2 .5 x 1 . A. log25 B. 2log25 C. 2 D. 2log25 – 1
Câu 2. Tồn tại bao nhiêu số nguyên m thuộc (– 10;100) để phương trình 2
log x (m 1)log x m 2 0 có 3 2 nghiệm ? A. 109 B. 100 C. 10 D. 6
Câu 3. Tồn tại bao nhiêu số nguyên m thuộc (– 19;20) để phương trình 2
log x (m 2)log x m 4 0 có 3 2
hai nghiệm phân biệt x , x thỏa mãn x x 9 . 1 2 1 2 A. 20 B. 23 C. 17 D. 19 x3
Câu 4. Tồn tại bao nhiêu số nguyên m để phương trình x 1
2 .5 x m có hai nghiệm phân biệt mà tổng bình
phương hai nghiệm không vượt quá 15 ? A. 5 B. 4 C. 8 D. 7 2
Câu 5. Khoảng (a;b) là điều kiện tham số m để phương trình x 4 2 2
.5 x m có hai nghiệm phân biệt mà tổng
của chúng nhỏ hơn 0,5. Giá trị b – a gần nhất với số nào A. 0,49 B. 0,48 C. 0,47 D. 0,51
Câu 6. Tồn tại bao nhiêu số nguyên m để phương trình 3 4 x x
me có hai nghiệm phân biệt. A. 2 B. 3 C. 4 D. Vô số
Câu 7. Tồn tại bao nhiêu số nguyên m để phương trình 2 x (5 2 2) x me x m
e 10x 4 0 có ba nghiệm phân biệt ? A. 10 B. 2 C. 3 D. 4 3 2 x 3x 3x 3m 8
Câu 8. Tồn tại bao nhiêu số nguyên m để phương trình 3 log
x 3x 3m 2 có hai 2 2 x 2x 3 nghiệm phân biệt. A. 1 B. 2 C. 3 D. 0 2
Câu 9. Tồn tại bao nhiêu số nguyên m để phương trình x 1 2x x 1 5 .2
10.8mx có hai nghiệm phân biệt x , x thỏa 1 2
mãn điều kiện 2 x x x x 12 . 1 2 1 2 A. 3 B. 2 C. 4 D. 5
Câu 10. Tồn tại bao nhiêu số tự nhiên m để phương trình 3m m 2 2
e e 2(x 1 x )(1 x 1 x ) có nghiệm A. 2 B. 0 C. Vô số D. 1 Câu 11. Tập hợp S ( ;
a b) gồm tất cả các giá trị m để phương trình 2x 3 4x m 1 có hai nghiệm thực
phân biệt. Tính giá trị biểu thức 2a + 3b. A. 29 B. 28 C. 32 D. 36 Câu 12. Phương trình 2
log x (m 2)log x n 5 0 (n là tham số nguyên) có hai nghiệm phân biệt mà tích 3 3
của chúng bằng 27. Giá trị nguyên nhỏ nhất của n là A. 3 B. 4 C. 2 D. 5 1
Câu 13. Tìm giá trị nhỏ nhất m để hàm số 2
y log (x 3x m) 1 có tập xác định ¡ . 2 2 x 2 x me x A. 4,25 B. 4,75 C. 2,25 D. 4
Câu 14. Cho ba số thực dương a, b, c khác 1 thỏa mãn log b 2log c 4 log a và a + 2b + 3c = 48. Tính a b c abc. A. 324 B. 243 C. 521 D. 512 1 Câu 15. Cho f (x)
. Tìm số nguyên n nhỏ nhất sao cho 2018x 2018 5n 2018 f ( 2 017) f ( 2
016) ... f (0) f (1) ... f (2018). A. n = 5 B. n = 6 C. n = 7 D. n = 8 3 5
Câu 16. Cho a, b, c, d là các số nguyên dương thỏa mãn log b ;log d
và a – c = 9. Tính b – d. a 2 c 4 25 A. 93 B. 85 C. 71 D. 76
Câu 17. Có bao nhiêu số nguyên m thuộc miền [– 2019;2019] để phương trình sau có nghiệm 2
log x 2log x m log x m . 2 2 2 A. 2021 B. 2019 C. 4038 D. 2020 Câu 18. Phương trình 2 2
3log 2x (m 3)x 1 m log (x x 1 3m) 0 27
có hai nghiệm phân biệt a, b 1 3
thỏa mãn điều kiện |a – b| < 15. Số giá trị nguyên của tham số m thu được là A. 12 B. 11 C. 13 D. 14
Câu 19. Tính tổng các nghiệm phân biệt của hai phương trình 2 2
x 7x 3 ln(x 4); x 11x 21 ln(6 x) . A. 2 B. 4 C. 8 D. 6 Câu 20. Phương trình 2 3
3x 6x ln(x 1) 1 0 có bao nhiêu nghiệm phân biệt ? A. 2 B. 1 C. 3 D. 4 2 2 2
Câu 21. Tìm điều kiện tham số để bất phương trình 2 x x 2 x x 2 .9 (2 1).6 .4 x x m m m 0nghiệm đúng với 1 mọi giá trị x . 2 A. m < 1,5 B. m 1,5 C. m 0 D. m < 0 2 x
Câu 22. Tồn tại bao nhiêu số nguyên dương m để hàm số y
mx ln(x 1) đồng biến trên (1;) ? 2 A. 4 B. 1 C. 3 D. 2
Câu 23. Tìm tập hợp các giá trị của a để bất phương trình log x 3x 3 ( 0 a 1). a A. (2;3) B. (1;2) C. (3;5] D. (5; ) 1
Câu 24. Tồn tại bao nhiêu số nguyên m để hàm số y log(mx m 2) xác định trên ; . 2 A. 4 B. 5 C. 3 D. Vô số x
Câu 25. Các số thực dương x, y, z thỏa mãn log x log y log z log
3 . Tính giá trị biểu thức 6 3 2 5 yz log6 5 log3 5 log2 5 P x 2y 3z . A. 20 B. 24 C. 26 D. 30 Câu 26. Phương trình 2
log x (m 2)log x 2m 0 có hai nghiệm phân biệt a, b thỏa mãn a b 60 . Số 2 2
các giá trị nguyên m < 100 thỏa mãn bài toán là A. 93 B. 98 C. 92 D. 97
_________________________________ 26
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 12)
__________________________________________________
Câu 1. Tồn tại bao nhiêu số nguyên m để hệ phương trình sau có số nghiệm tối đa 1 993y 9x 4 m 10
9log x 1993xy x log (1993y) 4 4 A. 6 B. 7 C. 3 D. 10
Câu 2. Biết rằng a là số thực dương để bất phương trình x4 a
1993x 7971nghiệm đúng với x ¡ . Khi đó giá trị biểu thức 4 log
(9a) gần nhất số nào sau đây 1993 A. 1993 B. 1050 C. 1975 D. 1945
Câu 3. Tồn tại bao nhiêu số nguyên dương m không vượt quá 2020 để phương trình sau có nghiệm m x 2 2 2ln ( 1)cos
tan x m 2m 0 . A. 2018 B. 2019 C. 2020 D. 2021 2 2 log (x 2x y ) 1
Câu 4. Có tất cả bao nhiêu cặp số nguyên (x;y) thỏa mãn 2 1 ? 2 2 log (x y 1) 2 A. 5 B. 4 C. 2 D. 6
Câu 5. Cho phương trình 4x 3x log (m x) 2m 2 0 , m là tham số. Gọi S là tập hợp tất cả các giá 4
trị nguyên của m để phương trình đã cho có nghiệm thuộc 1;
1 . Số phần tử của S là A. 3. B. 6. C. 5. D. Vô số 2 log a log b log c b Câu 6. Cho log x ; 0 y x . Tính y theo p,q,r . p q r ac p r A. 2 y q pr . B. y . C. y 2q p r . D. y 2q pr . 2q
Câu 7. Có bao nhiêu số nguyên m thuộc (– 2019;2020) sao cho hệ phương trình sau có nghiệm 2 2 2 x 2 y x 2 y 2 yx 2 4 9.3 (4 9 ).7 ,
2x 1 2y 2x m. A. 2017 B. 2021 C. 2019 D. 2020
Câu 8. Có bao nhiêu cặp số nguyên x, y thỏa mãn 0 x 2020 và log (3 3) 2 9y x x y ? 3 A. 2019 B. 6 C. 2020 D. 4
Câu 9. Có bao nhiêu cặp số nguyên dương (x;y) với x 2020 thỏa mãn 2(3 ) 3(1 9x x y ) log (2x 1) ? 3 A. 4 B. 3 C. 2020 D. 1010
Câu 10. Có bao nhiêu giá trị nguyên dương c để tồn tại các số thực a > 1, b > 1 thỏa mãn 5b a log a log b log ? 9 12 16 c A. 5 B. 2 C. 3 D. 4
Câu 11. Tồn tại bao nhiêu số hữu tỷ a thuộc [– 1;1] sao cho tồn tại số thực b thỏa mãn 2a 4a 1 1 2 2 log (1 a b 2b) . 2 4a 1 2a 1 2a 4a 2 A. 0 B. 3 C. 1 D. Vô số
Câu 12. Tồn tại bao nhiêu cặp số (x;y) với 0 x 2020; y ¥ thỏa mãn 2 2 y 2 2
log (3x 6x 6) 3 y x 2x 1 ? 3 A. 5 B. 6 C. 7 D. 4
Câu 13. Tồn tại bao nhiêu số nguyên m để 3 3
max ln x 3ln x m min ln x 3ln x m 3 ? 2 2 1 ;e 1 ;e A. 1 B. 2 C. 0 D. 3 x
Câu 14. Tồn tại bao nhiêu cặp số nguyên (x;y) thỏa mãn y 2x 1
0 x 2020; 2.4 1 2 2log ? 2 y 27 A. 2020 B. 2019 C. 63 D. 31 * y ¥ ;0 x 2020
Câu 15. Có bao nhiêu cặp số (x;y) thỏa mãn đồng thời 2 2 y 2 2
ln (x x 1)e e y x . x A. 3 B. 2 C. 4 D. Vô số
Câu 16. Có bao nhiêu cặp số nguyên dương (x;y) thỏa mãn x 2 4 3 2 2 y 2020; log
4y 8y (x 4x)y 1. 2 y 1 A. 2019.2020 B. 20202 C. 1993 D. 4
Câu 17. Có bao nhiêu cặp số nguyên (x;y) thỏa mãn x y 0; 20 x 20 thỏa mãn điều kiện 2 2
log (x 2 y) x 2y 3xy x y 0 ? 3 A. 19 B. 6 C. 10 D. 41
Câu 18. Có bao nhiêu cặp số nguyên (x;y) với 1 y 2020 thỏa mãn điều kiện x x x 1 2 x 1 2 (4y 2x)
log (4 2 y 4y ) log (2 y) . 3 3 2 4y A. 9 B. 10 C. 11 D. 12 log (x y) m
Câu 19. Tồn tại bao nhiêu giá trị m để hệ phương trình 3
có đúng hai nghiệm nguyên ? 2 2 2 log (x y ) 2m A. 3 B. 2 C. 1 D. Vô số 2 2x 3x y
Câu 20. Có bao nhiêu cặp số nguyên (x;y) với y 0;2017thỏa mãn 2 log x 8x 2 2y . 2 2 5x 2x 3 A. 44 B. 22 C. 42 D. 21 log (x y) 0 2019
Câu 21. Khi hệ bất phương trình
có nghiệm duy nhất thì giá trị m thu được thuộc khoảng x y 2xy m 1 1 1 A. ;0 B. (0;1) C. (1;2) D. 1; 3 3
Câu 22. Tồn tại bao nhiêu cặp số nguyên dương (x;y) với 0 < x < 500 thỏa mãn phương trình 2 2 2 2
log (2x 2x 2) 2 y y x x . 2 A. 4 B. 2 C. 3 D. 1
Câu 23. Cho hai số thực x > y thỏa mãn 2 ln( ) 2 x y x y x
y e e 2 . Hỏi giá trị biểu thức 5x + 3y nằm trong
khoảng giá trị nào sau đây 1 1 3 A. (0;1) B. (1;2) C. 1; D. ; 2 2 10
_______________________________________ 28
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 13)
__________________________________________________
Câu 1. Có bao nhiêu số nguyên m để phương trình sau có hai nghiệm đều lớn hơn – 2: log (x 3) mlog 9 16 . 3 x3 A. 15 B. 17 C. 14 D. 16
Câu 2. Tính tổng các số nguyên dương n thỏa mãn 4n 3viết trong hệ thập phân là số có 2020 chữ số. A. 6711 B. 6709 C. 6707 D. 6705
Câu 3. Tồn tại bao nhiêu số nguyên m để tập nghiệm của bất phương trình sau chứa khoảng (1;3) 2 2
log (x 2x 2) 1 log (x 6x 5 m) 7 7 A. 35 B. 36 C. 34 D. Vô số x x
Câu 4. Có bao nhiêu cặp số nguyên (a;b) thỏa mãn 1 < a < b < 100 và phương trình b a a b có nghiệm nhỏ hơn 1 ? A. 4751 B. 4656 C. 2 D. 4750
Câu 5. Cho a là hằng số dương khác 1 thỏa mãn 2cos2x 2 a 4cos x 1với x
¡ . Giá trị của a thuộc khoảng nào sau đây A. (2;3) B. (43;5) C. (0;2) D. (4;)
Câu 6. Có bao nhiêu số nguyên x sao cho tồn tại số thực y thỏa mãn 2 2
log (x y) log (x y ) ? 3 4 A. 3 B. 2 C. 1 D. Vô số 2
Câu 7. Biết rằng phương trình x 2 x3 2
.5 .7x m có hai nghiệm phân biệt x , x thỏa mãn x x x x 4 . Giá 1 2 1 2 1 2
trị tham số m nằm trong khoảng nào A. (1;2) B. (2;3) C. (3;4) D. (4;5) 2
Câu 8. Khi phương trình 3x 2 2
.5 xm 2 có hai nghiệm phân biệt a, b thỏa mãn a b 2 2 thì giá trị m thu
được thuộc khoảng giá trị nào A. [2;3) B. (1;2) C. (0;1) D. (– 3;0) x
Câu 9. Tồn tại bao nhiêu số nguyên m để phương trình 2 4log x .
m log 1 0 có hai nghiệm phân biệt a, b 25 5
thỏa mãn điều kiện ab 50 ab 625 0 . A. 0 B. 1 C. 2 D. 3 Câu 10. Cho phương trình 2 2
log x (5m 1)log x 4m m 0 với m là tham số. Biết phương trình có hai 2 2
nghiệm phân biệt x , x thỏa mãn x x 165 . Giá trị của x x bằng 1 2 1 2 1 2 A. 16 B. 119 C. 120 D. 159 1 1 1 1
Câu 11. Cho các số thực dương x, y, z thỏa mãn và log (xyz) 2020 . log x log y log z 2020 2 2 2 2
Tính giá trị của biểu thức log xyz(x y z) xy yz xz 1 . 2 A. 20202 B. 1010 C. 4040 D. 2020 x 2020
Câu 12. Có bao nhiêu cặp số nguyên dương (x;y) thỏa mãn 2 3 3
x y x (3x 1) (x 1)3y x A. 7 B. 6 C. 15 D. 13
Câu 13. Gọi S là tập hợp tất cả các giá trị m để phương trình x x x x 1 2 16 6.8 8.4 . m 2 m 0 có hai nghiệm
phân biệt. Khi đó S có số tập con là A. 16 tập con B. 8 tập con C. 4 tập con D. Vô số tập con x Câu 14. Cho hàm số 2019 f (x) 2019ln e
e . Tính f (1) f (2) ... f (2018). A. 2018 B. 1009 C. 1008,5 D. 1009,5 x 1
Câu 15. Tìm số nghiệm x thuộc [0;100] của phương trình cos( ) 1 2
cos( x) log (3cos( x) 1) . 4 2 A. 51 B. 49 C. 50 D. 52
Câu 16. Tìm số nghiệm nguyên của bất phương trình 2 2
ln(x 3x 1) x 3x 0 . A. 0 B. 2 C. 1 D. 3 29
Câu 17. Có bao nhiêu giá trị nguyên m để tập nghiệm của bất phương trình sau chứa đúng hai số nguyên ? 2
ln(x 2x m) 2ln(2x 1) 0 . A. 10 B. 8 C. 11 D. 9 a a Câu 18. Cho a, ,
b c là các số thực khác 0 thỏa mãn 6a 9b 24c . Tính T . b c 11 A. 3 . B. 3 . C. 2 . D. . 12 x 2 3 1
Câu 19. Cho hai hàm số y ln và y
4m 2020 . Tổng tất cả các giá trị nguyên của tham x x 2 x
số m để đồ thị hai hàm số cắt nhau tại một điểm duy nhất bằng A. 506 B. 1011 C. 2020 D. 1010
Câu 20. Có bao nhiêu m nguyên dương để tập nghiệm của bất phương trình 2x2 x m2 3 3 3 1 3m 0 có
không quá 30 nghiệm nguyên? A. 28 . B. 29 . C. 30 . D. 31. x
Câu 21. Cho hàm số f (x) ln
. Tính tổng f (1) f (2) ... f (2021). x 2 2022 2021 4035 A. 2021 B. C. D. 2023 2022 2021
Câu 22. Cho các hàm số y log x 1 và y log x 4 có đồ thị như hình vẽ. 2 2
Diện tích của tam giác ABC bằng 7 21 21 A. 21. B. . C. . D. . 4 2 4
Câu 23. Có tất cả bao nhiêu số nguyên dương m để bất phương trình x 2 x 1 8 3.2
9.2x m 5 0 1 nghiệm
đúng với mọi x 1, 2 A. Vô số. B. 4 . C. 5 . D. 6 . 30
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 14)
__________________________________________________
Câu 1. Cho đồ thị như hình vẽ. Biết rằng CB = 2AB. Mệnh đề nào sau đây đúng A. a = 5b B. 2 a b C. 3 a b D. 3 a b
Câu 2. Có bao nhiêu cặp số thực (x;y) thỏa mãn đẳng thức 2 2 x 4xy 6y 2 2 2 log
2log (2 2x 2y 2xy x y ) . 2 2 2 9 x 2xy 3y A. 3 B. 2 C. 0 D. 1
Câu 3. Tồn tại bao nhiêu số nguyên m thuộc [– 2020;2020] để phương trình sau có đúng hai nghiệm 2 (2 2 ) 3 x x x m 0. A. 2094 B. 2093 C. 2092 D. 2095
Câu 4. Tồn tại bao nhiêu số tự nhiên m để phương trình log 3x x m
100 0 có đúng một nghiệm ? 2 A. 1 B. 0 C. 3 D. 8
Câu 5. Có tất cả bao nhiêu số nguyên m thỏa mãn – 10 < m < 10 để phương trình x 1
2 log (x 2m) m có 4 nghiệm ? A. 4 B. 9 C. 10 D. 5
Câu 6. Tồn tại bao nhiêu số nguyên âm m để phương trình sau có nghiệm 2 3x 3x m 1 2 log x 5x m 2 . 2 2 2x x 1 A. 6 B. 5 C. Vô số D. 4
Câu 7. Gọi S là tập hợp tất cả các giá trị m sao cho 10m ¢ và phương trình sau có nghiệm duy nhất 2 2 2log (2x 5x 4) log (x 2x 6) . mx5 mx5
Tìm số phần tử của S. A. 16 B. 15 C. 13 D. 14 (2 log y)(1 log 2)
Câu 8. Tồn tại bao nhiêu cặp số nguyên (x;y) thỏa mãn 6 3 log 5 và 2 x y 0 ? 3 log x 5 A. 40 B. 35 C. 34 D. 27 2 x
Câu 9. Cho hàm số f (x) . 1 2019x
Tính giá trị biểu thức P f (cos1o) f (cos 2o) ... f (cos178o) f (cos179o) . A. 45,5 B. 89,5 C. 90,5 D. 44,5
Câu 10. Biết rằng phương trình 3
log x (m 5) log x (6m 5)log x 9m 3 0 có ba nghiệm thực phân 3 3 3
biệt sao cho tích của chúng bằng 729. Tổng các nghiệm khi đó bằng A. 1 B. 12 C. 39 D. 6
Câu 11. Có tất cả bao nhiêu số nguyên m thuộc khoảng (1;20) để bất phương trình log x log m có tập hợp m x 1 nghiệm chứa khoảng x ;1 ? 3 A. 17 B. 0 C. 18 D. 16 1 1 1 276
Câu 12. Tính 3n + 2 biết rằng ... ,x 0, x 1. log x log x log x x n log 2 2 2 2 2 A. 68 B. 71 C. 74 D. 77 sin x msin 4 6 x 1
Câu 13. Tìm tất cả các giá trị m để giá trị lớn nhất của hàm số f (x) không nhỏ hơn ? sin x 1sin 9 4 x 3 31 2 2 13 A. m log B. m log C. m log D. m log 3 6 3 6 3 6 18 6
Câu 14. Khoảng (a;b) là tập hợp các giá trị m để phương trình 2 2
log cos x m log(cos x) m 4 0có
nghiệm. Tính giá trị biểu thức 2 2 a b . A. 6 B. 4 C. 8 D. 5
Câu 15. Có tất cả bao nhiêu số thực m thuộc [– 1;1] để phương trình sau có nghiệm (x;y) duy nhất 2 2 log
(x y ) log (2x 2 y 2) . 2 2 m 1 A. 3 B. 2 C. 1 D. 0
Câu 16. Biết rằng phương trình 9x (2 3).3x m
81 0 có hai nghiệm phân biệt mà tổng bình phương hai
nghiệm bằng 10. Giá trị tham số m thu được thuộc khoảng A. (5;10) B. (0;5) C. (10;15) D. 15;
Câu 17. Tồn tại bao nhiêu số nguyên m để phương trình x x 2
log (3 2m) log (3 m ) có nghiệm ? 3 5 A. 3 B. 4 C. 2 D. 5
Câu 18. Cho x, y là hai số dương thỏa mãn 5x + y = 4. Tính tổng tất cả các giá trị nguyên m để phương trình 2 x 2y m sau có nghiệm: 2 log
x 3x y m 1 0 . 3 x y A. 10 B. 5 C. 9 D. 2 b
Câu 19. Cho hai số dương a, b thỏa mãn log a log b log (4a 5b) 1. Ký hiệu T thì 4 6 9 a 1 2 1 A. 1 < T < 2 B. T C. – 2 < T < 0 D. 0 T 2 3 2
Câu 20. Tồn tại bao nhiêu số nguyên m để phương trình sau có đúng hai nghiệm phân biệt thuộc [1;81] 2
log (9x) (m 5)log x 3m 10 . 3 3 A. 3 B. 5 C. 4 D. 2
Câu 21. Tồn tại bao nhiêu bộ số nguyên (x;y) thỏa mãn 1 x 20;1 y 20 và 2y 2x 1 (xy 2x 4y 8)log
(2x 3y xy 6).log . 3 2 y 2 x 3 A. 2017 B. 4034 C. 2 D. 2017.2020
Câu 22. Có bao nhiêu cặp số nguyên (x;y) thỏa mãn đồng thời: x 3
0 y 2020; 3 3x 6 9y log y . 3 A. 2020 B. 9 C. 7 D. 8
Câu 23. Bất phương trình log 11 log x ax x ax có nghiệm duy nhất. a 2 3 10 4 2 .log ( 3 12) 0 3 1 3a 7
Giá trị tham số a thu được thuộc khoảng A. (0;1) B. (1;2) C. (– 1;0) D. (2;)
_________________________________ 32
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 15)
__________________________________________________ Câu 1. Cho hàm số 2 ( ) 4ln( 1 ) 9( x x f x x x e e
) . Tồn tại bao nhiêu số nguyên m để phương trình
sau có hai nghiệm phân biệt: ( x
f me ) f (2 x) 0 . A. 0 B. 1 C. 2 D. 3 Câu 2. Cho hàm số 2 ( ) ln( 1 ) ( x x f x x x e e ) . Hỏi phương trình (3x f
) f (2x 1) 0 có bao nhiêu nghiệm thực ? A. 3 B. 0 C. 2 D. 1 Câu 3. Cho hàm số f x 2 ( ) ln
x 1 x. Có tất cả bao nhiêu giá trị nguyên m thỏa mãn bất phương trình
f (log m) f (log 2019) 0 ? m A. 63 B. 64 C. 65 D. 66 Câu 4. Cho hàm số f x 2 ( ) ln
x 1 x. Tính giá trị biểu thức 2 2
a b khi a và b là hai số thực dương a, b 1
thỏa mãn f (a) f (b 2) 0; 4ab 2(a b) . ab A. 1 B. 4 C. 2 D. 3
Câu 5. Cho các số thực dương a, b thỏa mãn đẳng thức ln( ) 2 aeb ab a e
b(a e) . Giá trị biểu thức
ln(2a 3b) nằm trong khoảng nào sau đây ? A. (2;3) B. (1;2) C. (0;1) D. (3;4) Câu 6. Cho hàm số 2 ( ) 1( x x f x e x e e
) . Tồn tại bao nhiêu số nguyên dương m thỏa mãn bất phương 12 trình f (m 7) f 0 . m 1 A. 4 B. 6 C. 3 D. 5 4 Câu 7. Cho hàm số 2 ( ) ln( 1 ) 1993( x x f x x x e e
) . Tìm tập nghiệm của bất phương trình 9
f (a 1) f (ln a) 0 . A. [0;1] B. (0;1] C. 0; D. 0; Câu 6. Cho hàm số ( ) 2x 2 x f x
. Ký hiệu m là số lớn nhất trong các số nguyên m thỏa mãn bất phương 0 trình 12
f (m) f (2m 2 ) 0 , khi đó m nằm trong khoảng nào sau đây 0 A. [1513;2019) B. [1009;1513) C. [505;1009) D. [1;505)
Câu 7. Cho hàm số ( ) 1993x 1993 x f x
. Gọi m là giá trị lớn nhất của tham số m để phương trình sau có 0
hai nghiệm phân biệt: (4 9) ( .1993x f x f m
) 0 . Giá trị m gần nhất số nào sau đây 0 A. 5140343 B. 9681010 C. 1975542 D. 1945722
Câu 8. Cho hàm số ( ) 1993x 1993 x f x
. Biết rằng tồn tại duy nhất bộ số (x;y) thỏa mãn bất phương trình ( xy ) ( x f e y x
f e ln x 1) 0 . Giá trị biểu thức P 2x 5y nằm trong khoảng nào ? A. (1;2) B. (2;3) C. (3;4) D. (5;6) Câu 9. Cho hàm số x 2 3
f (x) 2e log(m x 1 mx) . Tồn tại bao nhiêu số nguyên m để bất phương trình
sau nghiệm đúng với mọi giá trị x: f (x) f (x) 0 . A. 21 B. 4 C. Vô số D. 22 1
Câu 10. Cho hai số thực dương a, b thỏa mãn 3 ab
ln(ae ) a . Giá trị của biểu thức P 2a b bằng ab A. 3 B. 1 C. 2 D. 4 3 x 2019x Câu 11. Cho hàm số 2
f (x) x 1 x và bất phương trình (x m) f (x m) 0 . 3 f (x 2019x)
Ký hiệu M là giá trị nguyên nhỏ nhất của m để bất phương trình nghiệm đúng với x
4;16, M có số ước nguyên dương là 33 A. 16 B. 14 C. 20 D. 24 Câu 12. Cho hàm số 2
f (x) x x 1 . Có bao nhiêu giá trị nguyên m nhỏ hơn 10 để bất phương trình sau
nghiệm đúng với mọi giá trị x: x ( x
e f e ). f (m x) x m . A. 10 B. 11 C. 12 D. 9 Câu 13. Cho hàm 4 x 2 9 f (x) 4e
9log(m x 1 mx) 1993. Bất phương trình f (x) f (x) 0nghiệm
đúng với mọi giá trị x thì số nguyên m lớn nhất thu được có căn bậc 10 gần nhất với số nào A. 20 B. 12 C. 13 D. 18
Câu 14. Cho hai số thực x, y thỏa mãn x 2
(x ln 2 2 )(1 y ) 2 y . Giá trị của tổng x y bằng A. 1 B. 2 C. – 1 D. 4
Câu 15. Cho hai số thực dương a, b thỏa mãn điều kiện 4 2 2 1
993ae ln(1993a) 4 (4a 9b ) 12ab . Khi đó giá trị biểu thức 12
10 ab gần nhất số nào sau đây A. 45 B. 56 C. 17 D. 29 2 m x
Câu 16. Cho hàm số f (x) log
. S là tập hợp tất cả các giá trị m để f (a) f (b) 3với mọi số thực a, 3 1 x
b thỏa mãn điều kiện ab e
e(a b) . Tính tích các phần tử của S. A. 27 B. – 27 C. 3 3 D. – 3 3 x e
Câu 17. Cho các số thực x, y dương thỏa mãn
ey x y 2 ln(x y) . Giá trị biểu thức 3x 2y nằm ey x e trong khoảng nào sau đây A. (16;17) B. (15;16) C. (17;18) D. (19;20)
Câu 18. Cho các số thực dương a, b thỏa mãn điều kiện (ea ln a 1)(1 ab) 2 ab . Giá trị biểu thức
2a 3b nằm trong khoảng nào sau đây A. (8;9) B. (6;7) C. (7;8) D. (9;10) x y e e(x y), Câu 19. Cho hệ
với m là tham số lớn hơn 1. x m 1993y 1994
Khi hệ có nghiệm duy nhất thì giá trị log m thu được gần nhất với A. 866 B. 968 C. 722 D. 542 Câu 20. Cho hàm số x x 2
f (x) 1993 1993 ln( 4x 1 2x) . Tồn tại bao nhiêu số nguyên m để bất
phương sau nghiệm đúng với x f 3 2 x x x m 2 (0;1) : 2 3
f (2x x 5) 0 . A. 7 B. 3 C. 9 D. 8 Câu 21. Cho hàm số 3 3
( ) 1993 4 1993 4 (9x 9x f x x x
) 2019x . Tồn tại bao nhiêu số nguyên âm
m để bất phương trình f (3sin x 4 cos x) f (m) 0 có nghiệm ? A. 6 B. 5 C. 4 D. 3
_________________________________ 34
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 16)
__________________________________________________ 1
Câu 1. Tìm tổng tất cả các nghiệm của phương trình 2
log (x 3) log (x 1) x x 4 2 x 3 . 2 2 2 A. 1 B. 2 C. – 1 D. 1 2
Câu 2. Tìm số giá trị nguyên của tham số m thuộc (– 10;10) để phương trình sau có đúng hai nghiệm phân biệt 2 2 2 x x x 1 ( 10 1) ( 10 1) 2.3 . A. 14 B. 13 C. 15 D. 16
Câu 3. Tồn tại bao nhiêu số nguyên m thuộc [– 100;100] để phương trình sau có hai nghiệm phân biệt 2 log 3log 2 9x ( 1)3x x x m m 0 . 2 2 A. 103 B. 102 C. 101 D. 100
Câu 4. Tồn tại bao nhiêu số nguyên dương m để phương trình sau có đúng hai nghiệm phân biệt 2 2x mx 1 2 log
2x mx 1 x 2 . 2 x 2 A. 4 B. 1 C. 2 D. 3
Câu 5. Tồn tại bao nhiêu số nguyên m thuộc [– 20;20] để phương trình sau có nghiệm thuộc (0;2) ? 2 2 2 x 2 x x 2 x x 2 .9 (2 1).6 .4 x m m m 0 . A. 15 B. 13 C. 12 D. 11
Câu 6. Cho các số thực x, y lớn hơn 1 thỏa mãn log . x log (6 y) 2log .
x log (2y). 3 log (2xy) 4,5. 3 3 3 3 3
Giá trị của biểu thức x 2 y gần nhất với số nào sau đây A. 7 B. 8 C. 10 D. 9
Câu 7. Có bao nhiêu cặp số nguyên (x;y) thỏa mãn y y 1 2 x 2021; 2 log (x 2 ) 2x y ? 2 A. 2020 B. 9 C. 2019 D. 10 2 2
Câu 8. Tồn tại bao nhiêu số nguyên m thuộc [– 10;10] để phương trình x x 1 16 2.4 10 m có đúng hai
nghiệm thực phân biệt ? A. 7 B. 9 C. 8 D. 1
Câu 9. Tìm số nghiệm thực của phương trình x 2 3 5
2018 x 2016 2017 2018 ? A. 3 B. 1 C. 4 D. 2 2 2 2
Câu 10. Cho các số thực dương x, y, z thỏa mãn log3 7 log7 11 lo 1 g 1 25 x y z 11. Tính log3 7 log7 11 lo 1 g 1 25 x y z . A. 469 B. 2020 C. 2019 D. 76 11 2 2 2 Câu 11. Phương trình x 2 x x 2 x 1 2 x 4 x2 9.9 (2m 1).15 (4m 2).5
0có đúng hai nghiệm thực phân biệt
khi và chỉ khi m thuộc khoảng (a;b). Tính 2a + b. A. 2 B. 0 C. 1 D. 3
Câu 12. Khoảng k; là tập hợp tất cả các giá trị m để bất phương trình 2
log (2x) 2(m 1)log x 2 0 2 2
có nghiệm x 2 . Tính giá trị biểu thức 2 16k 4k . A. 1993 B. 12 C. 60 D. 10 5x 3x 2x e e e
Câu 13. Cho hàm số f x 2 m 16 x e 3m 4 x e 14 2 x e 2020 5 3 2
Gọi S là tập hợp tất cả các giá trị của tham số m để hàm số trên đồng biến trên ¡ . Tổng tất cả các phần tử thuộc S bằng 7 1 3 A. . B. . C. 2 . D. . 8 2 8 2 2
Câu 14. Tồn tại bao nhiêu số nguyên m để phương trình sin x 1cos 2 2 x m có nghiệm ? A. 3 B. 2 C. 1 D. 4 x b a
Câu 15. Cho hai số thực dương x, y thỏa mãn log x log y log (x y) và với a, b nguyên 9 12 16 y 2
dương. Tính giá trị biểu thức ab. A. 6 B. 5 C. 8 D. 4 35 9 y 4x
Câu 16. Tồn tại bao nhiêu bộ số ( ; x y; z) thỏa mãn *
x 1; y 1; z ; log x log y log . 9 6 4 z A. 6 B. 5 C. 4 D. 3 3 2 3 a ab b
Câu 17. Cho hai số thực dương a, b thỏa mãn log (2a 3b) log a log b . Tính . 4 10 25 3 2 3 a ab b 25 5 25 25 A. B. C. D. 29 6 27 28 c
Câu 18. Cho các số thực a, b, c lớn hơn 1 thỏa mãn 2 log b log . c log 9log c 4log b . a b b 2 a a b
Tính giá trị biểu thức 2 log b log c . a b A. 1 B. 0,5 C. 2 D. 3
Câu 19. Cho ba số thực dương x, y, z thỏa mãn log x log y log z log (x y z) . Khi đó giá trị 5 12 84 85 biểu thức log
2020 nằm trong khoảng nào sau đây xyz 1 3 3 1 A. ; B. (– 1;0) C. ;2 D. 0; 2 2 2 2 3 2 2
Câu 20. Tập hợp các giá trị m để phương trình x x 2 xm x x 3 1993 1993
x 3x m 0có ba nghiệm phân
biệt có dạng (a;b). Tính giá trị tổng a 2b . A. 0 B. 2 C. – 2 D. 1 3x 2x
Câu 21. Tồn tại bao nhiêu số nguyên m trên khoảng – 50;50) để bất phương trình m nghiệm đúng với 3x 2x mọi giá trị x dương. A. 98 B. 50 C. 49 D. 51
Câu 22. Tồn tại bao nhiêu cặp số nguyên (x;y) thỏa mãn đồng thời x x 2 x 3 3 0 x 2020; 8 3 .
x 4 (3x 1).2 ( y 1)x ( y 1)x . A. 2021 B. 6 C. 2020 D. 11
Câu 23. Tồn tại b bao nhiêu số nguyên m để hệ phương trình sau có nghiệm 5 x7 y 3x5 y2 3 3 2(x y 1) 0, 2 2
ln (4x 3y 3) (m 2)ln x m 1 0. A. 2019 B. 6 C. 2020 D. 4
Câu 24. Tồn tại bao nhiêu số nguyên m để phương trình ( 2 1)x ( 2 1)x m
8có hai nghiệm dương phân biệt ? A. 8 B. 7 C. 10 D. 9
_________________________________ 36
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 17)
__________________________________________________ 2 2 2
Câu 1. Có bao nhiêu số nguyên dương m để bất phương trình sin x cos x cos 2019 2018 .2019 x m có nghiệm ? A. 1 B. 2020 C. 2019 D. 2018
Câu 2. Tính tổng các giá trị m thu được khi tồn tại duy nhất một cặp số (x;y) thỏa mãn 2 2
log (x y 2) 2 log (x y 1) 2 2 3 x 4y . m A. 20 B. 14 C. 46 D. 28 Câu 3. Cho hàm số 2
f (x) ln(x x) . Tính giá trị biểu thức f (1) f (2) f (2019) e e ... e . 2020 2019 2019 A. B. – C. D. 2019 e 2019 2020 2020
Câu 4. Tìm tất cả các giá trị m để tập nghiệm của bất phương trình sau chứa đúng hai số nguyên 2
log (x 3x m) 2log (x 1) . 2 2 A. (3;4] B. (4;5] C. (2;3] D. ; 2 2 x 4x3 1
Câu 5. Tìm điều kiện tham số m để phương trình 4 2
m m 1có bốn nghiệm phân biệt. 5 A. (0;1] B. – 1;1] C. ; 1 D. (1;0) U (0;1) 2
Câu 6. Tính tổng các giá trị m để phương trình x 2x 1 3 xm log
2 x m 2 có ba nghiệm phân biệt. 2 x 2 x3 A. 3 B. 2 C. – 3 D. 2
Câu 7. Tập hợp tất cả các giá trị tham số m để phương trình x 2x 1 2 x 3 8 . m 2
(2m 1).2 m m 0 có ba
nghiệm thực phân biệt là khoảng (a;b). Tính ab. 3 2 2 3 4 A. B. C. D. 2 2 3 3 Câu 8. Cho hàm số 2 ( ) log 4 2 ( x x f x a x ab e e
) 6 thỏa mãn f (log(log e)) 4 . Giá trị của biểu thức f (log(ln10)) bằng A. 2 B. 8 C. 3 D. 4 2a 6b 12c
Câu 9. Cho các số thực a, b, c thỏa mãn . Giá trị a + b + c bằng 2 2 2
(a 2) (b 2) (c 2) 18 A. 0 B. 3 C. 4 D. 2 2x 6 8
Câu 10. Tồn tại bao nhiêu cặp số nguyên (x;y) trong đó 0 x 2020 và log y 2 2y ? 2 x 1 x 1 A. 1 B. 2 C. 2018 D. 2020
Câu 11. Tồn tại bao nhiêu số nguyên m để bất phương trình sau nghiệm đúng với mọi giá trị x thực 2 2
2 log (x 1) log (mx 2x m) . 3 3 A. 7 B. 5 C. 6 D. 8
Câu 12. Tính tổng các nghiệm của phương trình log (cos x) 2 log (cot x) trên đoạn [5;25]. 2 3 40 70 A. 13 B. 7 C. D. 3 3
Câu 13. Tìm số giá trị nguyên m thuộc [– 20;20] để phương trình sau có nghiệm 2 2 2
log (x m x x 4) (2m 9)x 1 (1 2m) x 4 . 2 A. 12 B. 23 C. 25 D. 10 Câu 14. Cho hàm số 2
f (x) ln( x 1 x) . Tập nghiệm của bất phương trình f (a 1) f (ln a) 0 là A. [0;1] B. (0;1] C. 1; D. (0; ) 37 2xy 2y x 2y,
Câu 15. Tồn tại bao nhiêu số nguyên m để hệ phương trình có nghiệm duy nhất x 2 y 2
2 1 (m 2).2 . 1 y A. 0 B. 1 C. 3 D. 2
Câu 16. Phương trình log x 3x 2 2 2 2 x 3x 1 5
2có hai nghiệm phân biệt x , x x x thỏa mãn 1 2 1 2 3 a b điều kiện x 2x
với a, b nguyên dương. Tính a – 2b. 1 2 2 A. 5 B. – 1 C. 1 D. 9
Câu 17. Tồn tại bao nhiêu số nguyên m thuộc – 2;7] để phương trình 2 2 3 .2 x m x
7 có hai nghiệm phân biệt ? A. 5 B. 8 C. 7 D. 6 2 1 2x 1 x
Câu 18. Tính tích tất cả các nghiệm thực của phương trình 2 log 2 x 5 . 2 2x A. 0 B. 2 C. 1 D. 0,5 x 2x 1 mx 2m 1
Câu 19. Tồn tại bao nhiêu số nguyên m [– 2019;2019] để phương trình 2019 0 có x 1 x 2
ba nghiệm thực phân biệt ? A. 4038 B. 2019 C. 2017 D. 4039
Câu 20. Tìm điều kiện tham số m sao cho 6x (2 ).3x m m 0, x (0;1) . A. m < 1,5 B. 0 m 1,5 C. m 1,5 D. m 3 m 1
Câu 21. Tìm tập hợp tất cả các giá trị m để hàm số y ln(3x 1) 2 đồng biến trên ; . x 2 2 7 4 1 A. ; B. ; C. ; D. ; 9 3 3 3 2 Câu 22. Phương trình x mx 1
2 .3 6có hai nghiệm mà tổng của chúng bằng log 81. Giá trị tham số m thu được 2 nằm trong khoảng nào A. (– 7;– 2) B. (– 2;5) C. (6;7) D. (5;6)
Câu 23. Tồn tại bao nhiêu số nguyên m lớn hơn – 20 để phương trình sau có nghiệm lớn hơn 1 2
x log (x m) (2x 1)log (x m) 2 0 . 2 2 A. 23 B. 22 C. 20 D. 18
Câu 24. Tồn tại bao nhiêu số tự nhiên x thỏa mãn ln x ln(x 1) ln(x 2) ... ln(x 2019) ln(2020!) ? A. 1 B. 2019 C. 0 D. 2020 2
Câu 25. Tồn tại bao nhiêu số nguyên dương m để phương trình x
m có nghiệm duy nhất ? log(x 1) A. 1 B. 0 C. 2 D. Vô số
Câu 26. Có tất cả bao nhiêu cặp số nguyên dương (a;b) thỏa mãn đẳng thức 3 2 2
log (a b) (a b) 3(a b ) 3ab(a b 1) 1. 3 A. 2 B. 3 C. 1 D. Vô số
_________________________________ 38
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 18)
__________________________________________________
Câu 1. Có bao nhiêu số nguyên m (– 5;5) để hàm số 3 2
y x 3x 3mln x 2 nghịch biến trên (0; ) ? A. 3 B. 2 C. 4 D. 5 3
Câu 2. Tồn tại bao nhiêu số nguyên dương m để bất phương trình sau nghiệm đúng với mọi x 0;log ? 4 2 3 .16x (2 1).12x .9x m m m 0 . A. 6 B. 2 C. 5 D. 0 0 x 2020
Câu 3. Tồn tại bao nhiêu cặp số nguyên (x;y) thỏa mãn đồng thời 2 x y 2
2.625 10.125 3y 4x 1 A. 2020 B. 674 C. 2021 D. 1347 1 x 2020
Câu 4. Tồn tại bao nhiêu cặp số nguyên (x;y) thỏa mãn y y 1
2 y 2x log (x 2 ) 2 A. 2021 B. 10 C. 11 D. 2020 2 16(a 8)
Câu 5. Tồn tại bao nhiêu cặp số nguyên (a;b) thỏa mãn điều kiện 2 2 log b 4b a 2 2 (b 2) A. 1 B. 2 C. 3 D. 4
Câu 6. Tập hợp (a;b) bao gồm tất cả các giá trị m để phương trình sau có ba nghiệm phân biệt 3 x2 m3x 3 2 2
1 2x 2(x 6x 9x m) .
Tính giá trị biểu thức 2 2 a ab b . A. 112 B. 124 C. 64 D. 156
Câu 7. Cho hàm số ( ) 1993x 1993 x f x
. Tồn tại bao nhiêu số nguyên dương m thỏa mãn bất phương trình
f (4m) f (9m 1993) 0? A. 153 B. 69 C. 96 D. 72
Câu 8. Tính tổng các giá trị m thu được khi tồn tại duy nhất một cặp số (x;y) thỏa mãn 2 2
log (x y 2) 2 log (x y 1) 2 2 3 x 4y . m A. 20 B. 14 C. 46 D. 28
Câu 9. Tồn tại bao nhiêu cặp số nguyên dương (x;y) thỏa mãn đồng thời 6 1 x 10 2 2 y 2 2
log(10x 20x 20) 10 y x 2x 1 A. 3 B. 4 C. 2 D. 1
Câu 10. Tồn tại bao nhiêu số nguyên m thuộc [– 100;100] để phương trình 2019x mx 1có hai nghiệm phân biệt ? A. 94 B. 92 C. 184 D. 93
Câu 11. Đường thẳng x k cắt đồ thị hàm số y log x và đồ thị hàm số y log x 4 . Khoảng cách giữa 5 5 1
các giao điểm là . Biết k a b , trong đó a,b là các số nguyên. Khi đó tổng a b bằng 2 A. 7 . B. 6 . C. 8 . D. 5 . Câu 12. Tập hợp (a;b) gồm tất cả các giá trị m để phương trình
( 5).3x (2 2).2 .x 3x (1 ).4x m m m
0 có hai nghiệm phân biệt. Tính a + b. A. 4 B. 5 C. 6 D. 8
Câu 13. Có bao nhiêu số nguyên m thuộc (– 10;10) để phương trình sau có hai nghiệm phân biệt mà tích hai nghiệm > 2 2 log2 x log2 x 2 3 2(m 3)3 m 3 0. A. 9 B. 16 C. 10 D. 11
Câu 14. Tồn tại bao nhiêu số nguyên m để phương trình sau có ít nhất một nghiệm thuộc [1;2] ? 39 4 8
2log x 2log x 2m 2018 0 . 2 2 A. 7 B. 9 C. 8 D. 6 2 1 2x 4x 6
Câu 15. Tính tổng các giá trị m để phương trình 2 log
x 2(x x m ) có đúng ba nghiệm 2 2 x m 1 phân biệt. A. 2 B. 3 C. 1 D. 0
Câu 16. Tồn tại bao nhiêu số nguyên m thuộc (– 10;10) để phương trình sau có hai nghiệm phân biệt 2
log ( 1) log 9( 1) m x x x 3 9 . A. 1 B. 0 C. 11 D. 10
Câu 17. Tồn tại bao nhiêu số nguyên dương m để tập nghiệm bất phương trình x2 (3
3)(3x 2m) 0 chứa không quá 9 số nguyên ? A. 3281 B. 3283 C. 3280 D. 3279 2
Câu 18. Tìm số nghiệm thực của phương trình x 1 2 2 .log ( 1 ) 4x x x log (3x) . 2 2 A. 0 B. 1 C. 2 D. 3
Câu 19. Tìm tập hợp tất cả các giá trị m để bất phương trình 12x (2 ).6x 3x m 0 đúng x 0 . A. m < 4 B. m > 4 C. m 4 D. 0 < m 4 sin x sin x
Câu 20. Tính tổng tất cả các nghiệm của phương trình 7 4 3 7 4 3 4 trên 2 ;2 . 3 A. B. 0 C. D. 2 2
Câu 21. Tồn tại bao nhiêu số nguyên m thuộc [– 10;10] để phương trình sau có nghiệm nhỏ hơn – 1 2 log x 1 log (mx m) . 2 2 A. 10 B. 9 C. 1 D. 20 Câu 22. Phương trình x 1 4 (8 5).2x m
2m 1 0 có hai nghiệm phân biệt với tích của chúng bằng – 1. Khi
đó m thuộc khoảng nào sau đây A. (– 5;– 3) B. (– 3;0) C. (0;1) D. (1;3)
Câu 23. Tính tổng tất cả các giá trị nguyên m để bất phương trình sau nghiệm đúng với mọi giá trị x 2 2
ln(7x 7) ln(mx 4x m) . A. 0 B. 35 C. 12 D. 14
Câu 24. Tìm điều kiện tham số m để tổng các nghiệm của phương trình sau đạt giá trị nhỏ nhất 2 2 1mxx 2 mx(1m) 2 2
1 2x m(m 1)x 2.2 (x mx 1)2 x m x . A. 0 B. 2 C. – 0,5 D. 0,5 40
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 19)
__________________________________________________ 2x 1
Câu 1. Cho hàm số f (x) log
. Tính f ( f (1)) f ( f (2)) ... f ( f (40)) . 2 2x 1 A. 410 B. 820 C. 40 D. 1640
Câu 2. Có bao nhiêu giá trị nguyên m để phương trình sau có nghiệm thực: 2
log (x 3x 2m) log (x m) . 2 2 A. 10 B. 9 C. Vô số D. 8
Câu 3. Tập hợp [a;b) bao gồm tất cả các giá trị m để phương trình 2
ln(3x mx 1) ln(x 4x 3) có
nghiệm. Giá trị biểu thức a + b là 22 10 A. 4 B. 7 C. D. 3 3 3 5
Câu 4. 4 số nguyên dương a,b,c, d với a 1, c 1thỏa mãn log b ;log d
và a c 9 . Tính b – d. a 2 c 4 A. 93 B. 21 C. 9 D. 13 2 2
Câu 5. Phương trình 4xy 3x y có bao nhiêu nghiệm (x;y) với x là số nguyên ? A. 2 B. 1 C. 3 D. 4
Câu 6. Tồn tại bao nhiêu số nguyên m để bất phương trình sau nghiệm đúng với mọi x thuộc (0;4) 2 2
log (x 2) 1 log (x 2x m) . 1 1 2 2 A. Vô số B. 4 C. 5 D. 3 2 2
Câu 7. Tính tổng các giá trị m để phương trình x 4x5m 2 2 log (m 1) . 2 x 4x5 A. 1 B. 0 C. – 2 D. 7
Câu 8. Có bao nhiêu số nguyên dương m để hàm 3 2
y x 9x (m 2002)x 12ln x nghịch biến trên (0;3) ? A. 2019 B. 2022 C. 2020 D. 2021 2 2
Câu 9. Phương trình 4x9 y 4 x 9 4 9
y có bao nhiêu nghiệm với (x;y) với y là số nguyên ? A. 2 B. 1 C. 3 D. 4 2 5 mx m 1
Câu 10. Cho hai hàm số f (x) ; g(x)
. Có bao nhiêu số nguyên m để đồ thị hai 5x ln(x 1) x 1
hàm số cắt nhau tại đúng ba điểm phân biệt ? A. 11 B. 8 C. 10 D. 9
Câu 11. Tồn tại bao nhiêu số nguyên a thuộc (– 2019;2019) để phương trình sau có đúng hai nghiệm phân biệt 1 1 x a . ln(x 5) 3x 1 A. 2015 B. 2014 C. 2022 D. 0
Câu 12. Biết rằng tồn tại duy nhất cặp số thực (x;y) thỏa mãn x y 1 2 2 (x y)e
log (2y y 1) 0 . Giá trị 2
biểu thức 5x – 3y khi đó bằng A. 0 B. – 1 C. 1 D. 2
Câu 13. Biết các số thực x, y thỏa mãn 2y x 4 y x 4
3 (3 3 ) 81(3 3 y ) . Giá trị biểu thức x + 6y bằng A. 1 B. 2 C. 3 D. 4
Câu 14. Bất phương trình x 1 2 .log .2x x m
log x m 0 . Số giá trị nguyên dương m để bất phương trình 4 2
đã cho nghiệm đúng với mọi x 4; là A. 3 B. 1 C. 2 D. Vô số
Câu 15. Tồn tại bao nhiêu cặp số nguyên (x;y) với – 5 < y < 5 thỏa mãn phương trình 2 2 4 x 4 x2 y 1 log (4x 4x 3) 2020 .log 2 y 2 0 3 1 3 A. 1 B. 5 C. 8 D. 0
Câu 16. Có bao nhiêu cặp số nguyên (x;y) thỏa mãn 3 y 2019;2020 và 1 1
log x x log (y x) . 4 2 2 4 41 A. 84567 B. 93781 C. 90787 D. 60608
Câu 17. Cho các số không âm a, b thỏa mãn ab 2b2a 4 a b 1; 2 2
1 log 34 2a b . Có bao nhiêu 2
số tự nhiên không vượt quá tổng a + b ? A. 0 B. 1 C. 2 D. 4 y
Câu 18. Có bao nhiêu số nguyên dương x sao cho tồn tại số thực y thỏa mãn log ( 2y ) log (3y x 2 ) ? 2 3 A. 2 B. Vô số C. 0 D. 1
Câu 19. Tìm điều kiện tham số m để phương trình sau có nghiệm duy nhất 3 x2 m3x 3 2 x2 x 1 2 (x 6x 9x m).2 2 1. m 4 A. m 4 B. 4 m 8 C. m 8 D. m 8
Câu 20. Phương trình (4 15)x (2 1)(4 15)x m
6 0 có hai nghiệm phân biệt x , x thỏa mãn 1 2
x 2x , khi đó giá trị tham số m thu được thuộc khoảng nào 1 2 A. (3;5) B. (– 1;1) C. (1;3) D. ( ; 1 ) Câu 21. Phương trình 2 2
log (x 1) 4log (x 1) 4m 8 0với 0 a 1 có hai nghiệm x , x thỏa mãn a a 1 2
điều kiện x x x x 15 . Mệnh đề nào dưới đây đúng ? 1 2 1 2 3 3 5 5 A. a 0; B. a ;2 C. a 2; D. a ;4 2 2 2 2 2
Câu 22. Tồn tại bao nhiêu cặp số nguyên (x;y) thỏa mãn x( x y) x y 3 4.2 2
2x 6 2(x 1)(y 1) ? A. 1 B. 2 C. 3 D. 4 Câu 23. Cho hàm số ( ) 2x 2 x f x
. Gọi m là số lớn nhất trong các số nguyên m thỏa mãn điều kiện 0 12
f (m) f (2m 2 ) 0 . Khi đó m thuộc khoảng nào sau đây ? 0 A. [1513;2019) B. [1009;1513) C. [505;1009) D. [1;505)
Câu 24. Tồn tại bao nhiêu số nguyên m để phương trình 2 x 4 2 9.3 (4 2 1 3 3).3x m x x m 1 0có đúng
ba nghiệm thực phân biệt ? A. Vô số B. 3 C. 1 D. 2
Câu 25. Giả sử m là số thực thỏa mãn giá trị nhỏ nhất của hàm số ( ) 31x 3x f x
mx trên ¡ là 2. Khi đó m thuộc khoảng nào A. (– 10;– 5) B. (– 5;0) C. (0;5) D. (5;10)
Câu 26. S là tập hợp các giá trị nguyên của tham số m để phương trình 5x 10 25x m 4 có nghiệm duy
nhất. Số tập hợp con của S là A. 3 B. 4 C. 16 D. 15
_________________________________ 42
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 20)
__________________________________________________
Câu 1. Tồn tại bao nhiêu giá trị nguyên m thuộc đoạn [0;18] để phương trình sau có đúng một nghiệm dương
(x 2).log (x m) x 1. 4 A. 16 B. 19 C. 17 D. 18
Câu 2. Tính tổng tất cả các nghiệm nguyên của bất phương trình 2 2
log (x 3) log x x 4x 1 0 . 2 2 A. 4 B. 6 C. 5 D. 3 1
Câu 3. Cho hàm số ( ) ln 2x 2x f x x
. Tính tổng bình phương các giá trị m để phương trình sau có đúng ba 1 nghiệm thực phân biệt: 2 f
f (x 4x 7) 0 . 4 x m 3 A. 10 B. 14 C. 13 D. 5
Câu 4. Tồn tại bao nhiêu số nguyên m thuộc [– 2019;2019] để phương trình sau có đúng hai nghiệm phân biệt 2020 2020 9 .(ln 2020 x ) .ln 2020 x x x e m x e x . x A. 2016 B. 2015 C. 2020 D. 2019 Câu 5. Cho hàm số 5 5 3
f (x) x (x 2) (x 3) . Tính tổng tất cả các giá trị nguyên m để phương trình ( x
f me ) f (x 5) có hai điểm phân biệt. A. 1540 B. 1485 C. 28 D. 136
Câu 6. Tồn tại bao nhiêu số nguyên m để bất phương trình 3 3 2 x (m 4m)x .
m ln(x 1) nghiệm đúng với mọi số thực x ? A. 2 B. 1 C. 3 D. Vô số
Câu 7. Có bao nhiêu số nguyên x để tồn tại duy nhất cặp (x;y) thỏa mãn 2
log (2 x 2xy x ) log y ? 3 3 A. 4 B. 3 C. 5 D. 2 5 3 2 ( x 5x 4 x) log 3 5 3 5 ( y 4)
Câu 8. Tồn tại bao nhiêu cặp số thực (x;y) thỏa mãn hệ 2
4 y y 1 (y 3) 8 A. 1 B. 2 C. 5 D. Vô số Câu 9. Cho hàm số 7 ( ) 3 3m f x x x
. Tồn tại bao nhiêu số nguyên m để phương trình f ( f (x)) x có nghiệm thuộc [1;3]. A. 7 B. 8 C. 9 D. 10 Câu 10. Cho hàm số 2 ( ) x
f x e x x . Tồn tại bao nhiêu giá trị nguyên m để phương trình sau có nghiệm
thuộc khoảng 0;ln10 : f f x m 2 ( ) x m . A. 7 B. 8 C. 6 D. 5
Câu 11. Tồn tại bao nhiêu số tự nhiên n có bốn chữ số thỏa mãn n n 2020 2020 2020 (2 3 ) (2 3 )n ? A. 8999 B. 2019 C. 1010 D. 7979
Câu 12. Có bao nhiêu số nguyên âm m để phương trình 3x 2 log (9x m) 7x m có hai nghiệm phân biệt. 3 A. 8 B. 9 C. 10 D. 11 b 16
Câu 13. Cho hai số dương a, b khác 1 thỏa mãn log b ;log a . Tính a + b. a 2 4 b A. 16 B. 12 C. 10 D. 18 Câu 14. Cho hàm số 2 ( ) x
f x e x m m . Có bao nhiêu giá trị nguyên của tham số m để phương trình sau
có nghiệm thuộc 0;ln10: 2 2
f ( f (x) m ) x m . A. 2 B. Vô số C. 0 D. 4 2 2
Câu 15. Tồn tại bao nhiêu giá trị nguyên m để phương trình 4 xx 4 9
4.3 xx 2m 1 0 có nghiệm ? A. 27 B. 25 C. 23 D. 24 2
Câu 16. Tập hợp tất cả các giá trị x không thỏa mãn bất phương trình x 4 2 x2 9 (x 4).2019 1là khoảng
(a;b). Tính giá trị biểu thức b – a. A. 5 B. – 1 C. – 5 D. 4 43
Câu 17. Có bao nhiêu giá trị nguyên m để phương trình 5 3log (8 ) 2x x x m
mcó hai nghiệm phân biệt. 2 A. 17 B. 15 C. 16 D. 18 1
Câu 18. Cho hàm số f (x) ln 1
, biết rằng f (2) f (3) ... f (2018) ln a ln b ln c ln d với a, 2 x
b, c, d là các số nguyên dương, trong đó a, c, d là các số nguyên tố tăng dần. Tính P a b c d . A. 1986 B. 1698 C. 1689 D. 1968
Câu 19. Có bao nhiêu giá trị nguyên m để phương trình sau có hai nghiệm phân biệt x , x thỏa mãn 1 2 2 2 x x 1 1 2 2 2 2 2
3log (2x x 2m 3m ) log
x (2 m)x m m 0 . 8 1 2 A. 1 B. 2 C. 5 D. 11
Câu 20. T = [c;d] là tập hợp tất cả các giá trị a để phương trình sau có nghiệm 2 2 2 2 4 2 2
2(1 a )x 2a log (x 3x 3) x log (3x 6x 2a 3) 4 . 2 2 Giá trị biểu thức 3 3 5
(d c ) thuộc khoảng nào A. (650;750) B. (1000;1500) C. (550;650) D. (200;450)
Câu 21. Tồn tại bao nhiêu số nguyên m thuộc – 10;10) để hai đồ thị hàm số sau cắt nhau, trong đó có đúng hai x(m 1) 2m ln( x 1 ) 1 1 x 1
giao điểm có hoành độ dương: y và y . x 2 2 2x 1 x 3 A. 19 B. 8 C. 10 D. 12
Câu 22. Tồn tại bao nhiêu số nguyên dương m để phương trình (3.2 .
x log 12log 2x 4) 5x x x m 0 có
đúng hai nghiệm thực phân biệt ? A. 23 B. 22 C. 25 D. 24
Câu 23. Tồn tại bao nhiêu số nguyên y để tồn tại số thực x thỏa mãn 2 2
log (x 2 y) log (x y ) ? 3 2 A. 2 B. 1 C. Vô số D. 3 axy 1 Câu 24. Cho log 12 ; x log 24 y; log 168
với a, b, c là các số nguyên. Tính a 2b 3c . 7 12 54 bxy cx A. 4 B. 10 C. 19 D. 15
Câu 25. Tập hợp S = [a;b] bao gồmcác giá trị tham số m để bất phương trình sau đúng với mọi giá trị x 0;2: 2 2 log
x 2x m 4 log (x 2x m) 5. 2 4
Tính giá trị biểu thức a + b. A. 4 B. 2 C. 0 D. 6
Câu 26. Tồn tại bao nhiêu số nguyên m < 10 để hàm số 2
y ln(x mx 1) đồng biến trên (0;) ? A. 10 B. 11 C. 8 D. 9
_________________________________ 44
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 21)
__________________________________________________
Câu 1. Tồn tại bao nhiêu bộ số nguyên (x;y;z) thỏa mãn 2 2 2
log (x y z 3) log (xy 3y 2z) ? 3 3 A.2 B. 1 C. 4 D. 3 2
Câu 2. Cho a > 4. Gọi P là tích tất cả các nghiệm của phương trình ln x ln(ex) a a a 0 . Khi đó A.P = ae B. P = a C. P = e D. e P a
Câu 3. Tìm số nghiệm của phương trình 2x 3.5x 17x . A.2 B. 1 C. 3 D. 4
Câu 4. Tìm số nghiệm của phương trình x x x x 1 6 5 4 3 A.3 B. 2 C. 1 D. 4
Câu 5. Có bao nhiêu số nguyên m 2 021;202
1 để phương trình 2x 3x 6x 11xm có nghiệm x 6 ;4 A.2 B. 1 C. 0 D. 5
Câu 6. Tập nghiệm bất phương trình 2x 3x 5x 10x
chứa bao nhiêu số nguyên lớn hơn – 9 A.9 B. 10 C. 6 D. 5
Câu 7. Có bao nhiêu số nguyên m 2 021;202 1 để x x x 3
3 4 5 (x m 1) đúng với x 6 A.2261 B. 2262 C. 2260 D. 2021
Câu 8. Có bao nhiêu số nguyên m 2 021;202 1 để x x x 2
4 5 2 (m x ) đúng với x 2 A.2036 B.2035 C. 2037 D. 2023
Câu 9. Tìm số nghiệm của phương trình 2.3x 4x 5x 7x 8x A.2 B. 1 C. 3 D. 0
Câu 10. Có bao nhiêu số nguyên m 2 021;202
1 để phương trình 4x 5x .7x 9x m có nghiệm x 8 ; 4 A.89 B. 88 C. 90 D. 67
Câu 11. Tìm số tự nhiên lớn nhất x sao cho 2021! chia hết cho 19x . A. x = 111 B. x = 110 C. x = 109 D. x = 108
Câu 12. Tồn tại bao nhiêu cặp số nguyên (x;y) thỏa mãn y 2 3 x 5x 7 ? A. 4 B. 2 C. 3 D. 1
Câu 13. Tồn tại bao nhiêu cặp số nguyên (x;y) thỏa mãn đẳng thức 3 1993.3y x 2021 ? A. 4 B. 2 C. 3 D. 1
Câu 14. Có bao nhiêu cặp số tự nhiên (m;n) thỏa mãn 2 11 39 51.49m n n A.2 B. 1 C. 3 D. 4
Câu 15. Có bao nhiêu cặp số tự nhiên (m;n) thỏa mãn 2 1 3m n n A.3 B. 2 C. 1 D. 0 2 2 2
Câu 16. Tính tổng các giá trị m để phương trình 2 x 3x2 x 3x2 x 4 . m 3 3 . m 3
1có đúng ba nghiệm phân biệt 85 A.109 B. 81 C. – 7 D. 81
Câu 17. Tồn tại số thực dương a sao cho 3cos2x 2 a 2cos x, x . Khi đó 5 7 1 3 7 9 3 5 A. a ; B. a ; C. a ; D. a ; 2 2 2 2 2 2 2 2 Câu 18. Cho hàm số ( ) 3x 3 x f x
. Tính tích các giá trị m sao cho 2
f (3log m) f (log m 2) 0 . 2 2 A.0,25 B. 0,125 C. 2 D. 0,5 2 x
Câu 19. Cho hai số thực dương x, y khác 1 thỏa mãn log x log 16; xy 64 . Tính log 2 y 2 y A.12,5 B. 12,5 C. 25 D. 20 Câu 20. Phương trình log
x log (x 1) ... log (x 2020) 0 có bao nhiêu nghiệm 0,3 0,3 0,3 A.0 B. 1 C. 2 D. 3
Câu 21. Phương trình ln(2x 1) log(x 3) ln(x 4) 2022x 1 0 có bao nhiêu nghiệm 45 A.0 B. 1 C. 2 D. 5
Câu 22. Tìm số nghiệm của phương trình x x 6 ln x ln(2x 5) e e 0. A.0 B. 1 C. 2 D. 3 2
Câu 23. Tìm số nghiệm của phương trình ln ln( 2) 2 3x x x x 2x 1 0 . A.0 B. 1 C. 2 D. 5 2
Câu 24. Tìm số nghiệm không nhỏ hơn 1 của phương trình x 2
ln x ln(x 1) 2x 3 x 2x 0 A.0 B. 1 C. 2 D. 3
Câu 25. Tìm số nghiệm phương trình 2x 5x 2 5x . A.2 B. 1 C. 3 D. 4
Câu 26. Tìm số nghiệm phương trình log x log (2x 1) 2 3 A.3 B. 2 C. 1 D. 0
Câu 27. Tìm m để tổng các nghiệm phương trình sau đạt giá trị nhỏ nhất 2 2 1mxx 2 mx(1m) 2 2
1 2x m(m 1)x 2 2 (x mx 1)2 x m x . A.0 B. 2 C. – 0,5 D. 0,5 2
Câu 28. Có bao nhiêu số nguyên m để phương trình x 1 x 2 2 .2 1 ( )log 2m x x m có nghiệm trên [0;9] 2 A.8 B. 9 C. 10 D. 12
Câu 29. Tìm điều kiện m để phương trình 2
log x 4log x 5 m(log x 1) có nghiệm thuộc 27; 3 3 3 A.0 < m < 2 B. 0 m 2 C. 0 m 1 D. 0 m 1
Câu 30. Tìm số nghiệm của phương trình log (6x 1) log (10x 9) 5 7 A.0 B. 2 C. 1 D. 2 a 2b
Câu 31. Cho hai số thực dương a, b thỏa mãn log a log b log (b a) . Tính giá trị T 4 25 10 3a b 9 2 5 14 3 5 6 2 5 17 7 5 A. B. C. D. 2 2 3 2 7 y x
Câu 32. Cho a, b > 0 thỏa mãn log x log y 2log 5x
. Giá trị biểu thức P x y thuộc 3 5 5 y khoảng nào dưới A.(0;2) B. (3;6) C. (6;10) D. (2;3)
Câu 33. Tìm tập hợp các giá trị m để phương trình x 2 1 2020 ( 2) 2020x m
m 2 0 . Tập hợp tất
cả các giá trị của m để phương trình đã cho có 2 nghiệm phân biệt thuộc [0;2] là A.[2;2021] B. [1;2] C. (2;2021] D. 2; Câu 34. Cho phương trình 2
log 9x (m 5)log x 3m 10 0 . Có bao nhiêu số nguyên m để phương 3 3
trình đã cho có hai nghiệm phân biệt thuộc [1;81] A.2 B. 3 C. 4 D. 5
Câu 35. Có bao nhiêu số nguyên x thỏa mãn log x 2 log 3x 4 3 5 A.5 B. 7 C. 8 D. 9
Câu 36. Cho hai số thực dương x, y thỏa mãn log (x 1) log y log (2x y) . Tính 3 2 x 2y 11y 2 5 11 A.18 B. 17 C. 32 D. – 5
Câu 37. Ba số thực dương x, y thỏa mãn log x log y log z log (2x 2 y z) . Tính 2 2x y z 2 3 5 15 A.11 B. 8 C. 6 D. 9
Câu 38. Xét các số nguyên dương a , b sao cho phương trình 2
a ln x b ln x 5 0 có hai nghiệm phân biệt x , x và phương trình 2
5log x b log x a 0 có hai nghiệm phân biệt x , x thỏa mãn x x x x . Tính giá 1 2 3 4 1 2 3 4 trị nhỏ nhất S của S 2a 3b . min A. S 17 B. S 30 C. S 25 D. S 33 min min min min
Câu 39. Cho dãy số u thỏa mãn log u 2 log u 2log u 2log u và u 2u với mọi n 1. Giá trị n 1 1 10 10 n 1 n nhỏ nhất của n để 100 u 5 bằng n A. 247 . B. 248 . C. 229 . D. 290 .
_________________________________ 46
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 22)
__________________________________________________
Câu 1. Có bao nhiêu giá trị nguyên m 2
0;20 để phương trình 5x m log (x m) có nghiệm 5 A.20 B. 19 C. 9 D. 21 x 1 2 1 Câu 2. Cho hàm số y
. Có bao nhiêu giá trị nguyên m 5
0;50 để hàm số nghịch biến trên 1; 1 2x m A.48 B. 47 C. 50 D. 49 2 2 2
Câu 3. Cho a, b, c dương thỏa mãn log2 5 log4 6 log7 3 a 4; b 16; c 49 . Tính log2 5 log4 6 log7 3 a b c . A.126 B. 88 C. 5 2 3 D. 3 2 3
Câu 4. Tìm tập hợp giá trị m để phương trình x sin x cos 2 2 .x2x m 2 cos x m có nghiệm 4 1 1 A. m 1 ; 1 B. m 2 C. m ; D. m 2; 2 2 2 2 2
Câu 5. Số nguyên dương m lớn nhất để phương trình 1 1x 1 1 25 ( 2).5 x m
2m 1 0 có nghiệm là A.20 B. 30 C. 25 D. 35
Câu 6. Tìm tập hợp các giá trị m để phương trình 2 2 2
log cos x mlog cos x 4 m vô nghiệm. A. m 2;2 B. m 2; 2 C. m 2;2 D. m 2; 2
Câu 7. Có bao nhiêu giá trị nguyên m 2019;2019 để phương trình 2
log x 2log x m log x m có 2 2 2 nghiệm. A.2021 B. 2019 C. 4038 D. 2020
Câu 8. Tìm tập hợp các giá trị m để hàm số 2
y ln(x 1) mx 1đồng biến trên R A. 1; 1 B. 1; 1 C. 1; 1 D. ; 1
Câu 9. Tồn tại bao nhiêu cặp số nguyên dương (x;y) thỏa mãn 1994 1994 4691 x y 469 (x y) A.2 B. 1 C. 3 D. 4
Câu 10. Tìm số giá trị nguyên m < 10 để hàm số 2
y ln(x mx 1) đồng biến trên 0; A.10 B. 11 C. 8 D. 9
Câu 11. Có bao nhiêu giá trị nguyên dương m khác 1 để phương trình sau có nghiệm x lớn hơn 2 log 2 x x 1.log 2
x x 1 log x x m 2 1 2 5 A.3 B. 2 C. 1 D. Vô số x a b
Câu 12. Cho hai số dương x, y thỏa mãn log x log y log x y6 6 4 . Tính a + b khi , trong 4 2 2 y 2
đó a và b là hai số nguyên. A.6 B. 5 C. 7 D. 4 1 x x a b
Câu 13. Nghiệm dương của phương trình log 2x 3x 2 1 2 3 2 1 2có dạng (a, b, c là các 2 2 c
số tự nhiên). Tính a + b + c. A.20 B. 23 C. 24 D. 42
Câu 14. Tính ab bc 1 khi bộ ba số nguyên dương (a;b;c) thỏa mãn
log1 log(1 3) log 1 3 5 ... log1 3 5 ... 19 2log5050 a blog 2 clog3. A.37 B. 21 C. 25 D. 10 a 4b a
Câu 15. Cho hai số dương a, b thỏa mãn log a log b log . Tính 100 40 16 12 b A.4 B. 12 C. 6 D. 2 1 1
Câu 16. Giả sử p, q là các số thực dương thỏa mãn log p log p log ( p q) . Tính . 3 6 2 2 2 a b A.18 B. 45 C. 27 D. 36 47
Câu 17. Có bao nhiêu cặp số nguyên (x;y) thỏa mãn ( 1999)( 1975) 3y x x 81 A.4 B. 2 C. 3 D. 1 x
Câu 18. Cho x, y dương thỏa mãn log x log y log (2x y) . Tính . 9 6 4 y 3 A.2 B. 0,5 C. log 2 D. log 3 2 2 2
Câu 19. Xác định điều kiện tham số m để phương trình x x 2 9 2( 2).6 ( 4 3)4x m m m 0 có hai nghiệm phân biệt A. m 2 B. m 3 C. m 1 D. m 2 1
Câu 20. Tìm điều kiện tham số m để hàm số 2
y ln(x 4) mx 3 nghịch biến trên R. 2 1 1 1 A. m 4 B. m C. m D. m 4 4 4 4 2 a b
Câu 21. Tồn tại bao nhiêu cặp số tự nhiên (a;b;c) thỏa mãn 2021c 2 a b 1 A.3 B. 2 C. 10 D. 8 3 2 x 6 x (2m 1 ) x 1 1
Câu 22. Số giá trị nguyên dương của tham số m để hàm số y đồng biến trên (1;3) 3 A.9 B. 6 C. 5 D. Vô số
Câu 23. Có bao nhiêu số hữu tỉ a thuộc đoạn 1 ;
1 sao cho tồn tại số thực b thỏa mãn a a log 2 4 1 1 2 2 1 a b 2b . 2 4a 1 2a 1 2a 4a 2 A. 0 . B. 3. C. 1. D. Vô số.
Câu 24. Có bao nhiêu cặp số nguyên x; y thoả mãn x y 0; 20 x 20 và log x 2 y 2 2
x 2 y 3xy x y 0 ? 2 A. 19. B. 6 C. 10. D. 41. a Câu 25. Cho hàm số x4 7 ( ) 3 ( 1).2 x f x x
6x 3. Giả sử m (phân số tối giản, a và b nguyên 0 b
dương) là giá trị nhỏ nhất của m để phương trình 2
f (7 4 6x 9x ) 2m 1 0có số nghiệm nhiều nhất.
Tính giá trị của biểu thức 2 a b . A.11 B. 7 C. – 1 D. 9
Câu 26. Tìm tất cả các giá trị của m để phương trình 2 2
log x log x 3 m có nghiệm x 1;8. 2 2 A. 2 m 6 B. 3 m 6 C. 6 m 9 D. 2 m 3.
Câu 27. Tìm số nghiệm nguyên dương của phương trình 10(2x 1) x(13x 3) A.3 B. 2 C. 1 D. 4
Câu 28. Có bao nhiêu giá trị nguyên của tham số m để phương trình 2
log (4x) m log x 2m 4 0 có 2 2
nghiệm thuộc đoạn 1;8 ? A. 1. B. 2 . C. 5 . D. 3.
Câu 29. Tìm tất cả các giá trị thực của tham số m để phương trình 4x 1 .2x m
2 0 có hai nghiệm x , x 1 2 thoả mãn x x 1. 1 2 A. m R .
B. m 1 2 2;m 1 2 2 . C. m 1 2 2 . D. m 1 2 2 .
Câu 30. Có bao nhiêu cặp số nguyên dương ; x y thỏa mãn xy 2
x x x y 3 3 3 1
1 3 x , với x 2020 ? A. 13 . B. 15 . C. 6 . D. 7 .
Câu 31. Có bao nhiêu số tự nhiên n để 3n 144 là số chính phương A.3 B. 2 C. 1 D. 4 48
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 24)
__________________________________________________
Câu 1. Tập hợp S = [a;b] bao gồm tất cả các giá trị thực a để mỗi nghiệm của bất phương trình 2
log (5x 8x 3) 2 đều là nghiệm của bất phương trình 2 4
x 2x a 1 0 . Tính 2 2 a b . x A.0,4 B. 0,2 C. 0,8 D. 1,2 Câu 2. Cho hàm số 3
f (x) x 3x ; cấp số cộng u thỏa mãn u u 0 ; cấp số nhân v thỏa mãn n n 2 1 f u 2 f u 2 1 v v 1. Biết rằng 2 1
f (log v ) 2 f log v 2 2 2 1
Tìm số nguyên dương nhỏ nhất n 1để v 2019u n n A.17 B. 18 C. 16 D. 15
Câu 3. Tồn tại bao nhiêu số nguyên m thuộc (– 1993;1993) để phương trình sau có nghiệm duy nhất Cho hàm số 3 f x a 2 ( ) log
x 1 x bsin xcos2x 20. Tính ln 2019 f (2020 ) khi ln 2020 f (2019 ) 2021 A.2001 B. 1981 C. – 1981 D. – 2001
Câu 4. Tìm số nghiệm x 5
;2017 của phương trình 2
2017sin x sin x 2 cos x A.2023 B. 2017 C. 2022 D. Vô nghiệm
Câu 5. Tính tổng các giá trị nguyên m 1
0;10để bất phương trình sau có nghiệm 2 2x x m 1 2 log 2x 4x 5 2m 3 2 x x 1 A.20 B. 10 C. 15 D. 5
Câu 6. Có bao nhiêu số nguyên dương m để bất phương trình x2 2
2 2x m 0có tập nghiệm không chứa quá 6 số nguyên A.62 B. 33 C. 32 D. 31
Câu 7. Có bao nhiêu số nguyên dương y sao cho ứng với mỗi y có không quá 50 số nguyên x thỏa mãn x y x 1 1 3 3 3 0 A.1866 B. 2188 C. 2364 D. 2187
Câu 8. Có tất cả bao nhiêu số nguyên dương y sao cho tập nghiệm của bất phương trình sau chứa tối đa 1000
số nguyên: log x 2 log x y 0 2 2 A.8 B. 10 C. 9 D. 11
Câu 9. Có bao nhiêu số nguyên dương y sao cho ứng với mỗi số y có không quá 4031 số nguyên x thỏa mãn 2 2
log x 3y log x 2y 0 2 2 A.4 B. 6 C. 8 D. 5
Câu 10. Tìm số nghiệm của phương trình x 2 x 1 1 e log 2 0 A.4 B. 3 C. 2 D. 0
Câu 11. Tìm điều kiện tham số m để phương trình 4x 2x 2m
1 0có hai nghiệm âm phân biệt 3 3 3 A. log m 0 B. log 2 m 0 C. log m 0 D. m 1 2 4 3 2 4 4 4 2 2
Câu 12. Có bao nhiêu giá tri thực m để phương trình x 3x2 4x 63 .3 3 3 x m
m có ba nghiệm phân biệt A.4 B. 2 C. 3 D. 1
Câu 13. Gọi m là giá trị nhỏ nhất của m để bất phương trình sau nghiệm đúng với mọi giá trị thuộc tập xác định 0 (x 3)log x 2 2 mx (2m 1)x 3 3 a Biết rằng m
(a, b, c tự nhiên và c 8 ). Tính a + b + c 0 b ln c A.3 B. 7 C. 10 D. 15 n n
Câu 1. Cho các số dương m, n, p thỏa mãn 4m 10n 25p . Tính 2m 2 p 49 A.1 B. 2,5 C. 2 D. 0,1 Câu 14. Cho hàm số ( ) 2019x 2019 x f x
. Số nguyên m lớn nhất thỏa mãn f (m) f (2m 2019) 0 là A. – 673 B. – 674 C. 673 D. 674
Câu 15. Tìm tập hợp các giá trị tham số m để phương trình 2
log 3x log x m 1có đúng hai nghiệm phân 3 3 biệt thuộc (0;1). 9 1 9 9 A. m B. 0 m C. 0 m D. m 4 4 4 4
Câu 16. Tập hợp các giá trị m để bất phương trình 2 2 log x log x 3 m 2 log x 3 có nghiệm 2 1 4 2 x 8 2;
là (a;b]. Khẳng định nào sau đây đúng A.2a + b = 3 B. 2a + b = 4 C. 2a + b = 0 D. 2a + b = 5
Câu 17. Tìm m để phương trình 2
log x 3log x 2m 7 có hai nghiệm a, b thỏa mãn (a 3)(b 3) 72 3 3 A.m = 4,5 B. m = 3 C. Không tồn tại D. m = 30,5 2 1 2x 1 x
Câu 18. Tính tích tất cả các nghiệm của phương trình 2 log 2 x 5 2 2x A.0 B. 2 C. 1 D. 0,5
Câu 19. Có bao nhiêu số nguyên dương m không vượt quá 2020 để phương trình sau có nghiệm (m2) sin x2 cos x 1 2(sin x3cos x2) 2019 2019
3msin x 15 24cos x A.2016 B. 2017 C. 2018 D. 2019
Câu 20. Có bao nhiêu giá trị nguyên m để phương trình 4 log
2x 1 log mx 1 có hai nghiệm phân biệt 2 2 A.3 B. 5 C. 4 D. 8
Câu 21. Tập hợp các giá trị m để phương trình 2 log (4 x ) log
(2x m 1) 0 có hai nghiệm phân 2019 1 2019
biệt là khoảng (a;b). Tính 2a + b A.18 B. 16 C. 8 D. 20
Câu 22. Cho n là số nguyên dương và 0 a 1, tìm n sao cho 2 2 2 2 2
log 2019 2 log 2019 3 log 2019 ... n log n 2019 1008 .2017 log 2019 3 a a a n a A.2017 B. 2018 C. 2019 D. 2016
Câu 23. Gọi a, b lần lượt là hai nghiệm dương của hai phương trình 2018 2017 x x ... x 1 0 2019 2018 x x ... x 1 0
Mệnh đề nào sau đây đúng A.b > a + 1 B. a > b + 1 C. alnb > blna D. blna > alnb 2
Câu 24. Tính tổng các giá trị m để phương trình x 2x 1 2 3 xm log
2 x m 2 có đúng ba nghiệm 2 x 2 x3 phân biệt A.3 B. 2 C. – 3 D. – 2
Câu 25. Phương trình 4x (2 3)2x m
64 0 có hai nghiệm a, b thỏa mãn a 2b 2 24. Giá trị tham
số m thu được thuộc khoảng 3 3 21 29 11 19 A. 0; B. ;0 C. ; D. ; 2 2 2 2 2 2
Câu 26. Hai hàm số y log ;
x y f (x) có đồ thị đối xứng nhau qua a
đường thẳng x y 0 như hình vẽ bên. Tính giá trị f ( log 3) . a 1 1
A. – 3 B. – 9 C. D. 3 9
___________________________________ 50
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 26)
__________________________________________________
Câu 1. Tìm số nghiệm thuộc 0;2019 của phương trình cos x 2 2.2019 cos x 5 sin x A.2018 B. 2017 C. 4036 D. 2019
Câu 2. Có bao nhiêu số tự nhiên n < 100 để 2n 1là một số nguyên tố A.6 B. 7 C. 5 D. 4 n
Câu 3. Dãy số u thỏa mãn 2 log u 4log u n
u và số hạng thứ 4 lớn hơn 8 10 . Số tự n n 2 4 16log 0 n 3 nhiên n thỏa mãn 2019 u 10 khi đó bằng n A.2017 B. 2016 C. 2009 D. 2008
Câu 4. Tìm số nghiệm của phương trình x x x 2
8 (x 1)4 (3x 1)2 3x 4x 1 0 A.2 B. 3 C. 4 D. 1
Câu 5. Có bao nhiêu cặp số tự nhiên (m;n) thỏa mãn 2 3 5 15.11m n n A.2 B. 1 C. 3 D. 4 n
Câu 6. Tồn tại bao nhiêu số nguyên tố có dạng 2 2 5 A.4 B. Vô số C. 1 D. 2 2 n1
Câu 7. Có bao nhiêu cặp số tự nhiên (m;n) thỏa mãn 2 2 3 9m A.0 B. 2 C. 1 D. 3 x x x
Câu 8. Tìm số nghiệm của phương trình 9 log 2 x 1 9 9 2x 1 9 3 2020 2020 2020 A.4 B. 1 C. 3 D. 2
Câu 9. Tìm số nghiệm của phương trình 2 x 4 2
log x log x ... log x log x 0 2 3 19 20 A.1 B. 2 C. 3 D. 4
Câu 10. Có bao nhiêu số nguyên dương m nhỏ hơn 2018 để phương trình log 2x m m 2x có nghiệm 2 A.2017 B. 2016 C. 1005 D. 1004
Câu 11. Có bao nhiêu số nguyên m mà m 10 để phương trình x 1
2 log (x 2m) m có nghiệm 4 A.9 B. 10 C. 5 D. 4
Câu 12. Có bao nhiêu số nguyên dương m để phương trình (mx e) ln x 1 0 có hai nghiệm phân biệt. A. 7 B. 6 C. 8 D. 9 3 2 x 3x 3x 5
Câu 13. Tính tổng tất cả các nghiệm của phương trình 3 2 log
(x 1) x 6x 7 2 x 1 A.0 B. – 2 C. 3 2 D. 5 1
Câu 14. Khi phương trình 2 x 1 1 x 1 2 2
m 0 có nghiệm duy nhất thì giá trị m thu được thuộc khoảng A.[3;4) B. (0;1) C. [1;2) D. (– 4;0)
Câu 15. Tìm tập hợp các giá trị m để phương trình 2
(m 1) log x 2log x m 2 có hai nghiệm thực a, b 2 2
thỏa mãn 0 a 1 b . A. 1 ;2 B. 2; C. 3;5 D. ; 1
Câu 16. Hàm số y f (x) liên tục trên R và có bảng biến thiên như hình vẽ
Tìm số nghiệm thực của phương trình log f (x) log 2 f (x) 1 . 2 6 A.3 B. 4 C. 5 D. 6
Câu 17. Tìm điều kiện tham số m để phương trình sau có nghiệm dương duy nhất 2x m log mx 2 ( 1) x 1 2 log 2 x x 1 2 2 A.m > 0 B. 0 < m < 1 C. 1 < m < 2 D. m > 2 51
Câu 18. Tìm số giá trị nguyên m < 2018 để phương trình log 2018x m log 2019x có nghiệm 6 4 A.2020 B. 2017 C. 2019 D. 2018
Câu 19. Cho dãy số u thỏa mãn ln u 2 3 ln u 3ln u 3ln u và u
3u với mọi n nguyên dương. n 1 1 5 5 n 1 n
Gọi n là số nguyên lớn nhất để 10 u 3 , tính 2 n 6 . n A.22 B. 150 C. 175 D. 250 2
Câu 20. Có tất cả các số nguyên dương x thỏa mãn x 2 cos 2.2 sin 2 y x y A.0 B. 6 C. 1 D. 3
Câu 21. Có bao nhiêu số nguyên dương n để 3n 63là số chính phương A.4 B. 2 C. 1 D. 3
Câu 22. Phương trình 2x 2x 2 cos x có 2019 nghiệm thực. Tìm số nghiệm của phương trình
2x 2x 4 2cosx . A.2019 B. 2018 C. 4037 D. 4038 4b a
Câu 23. Hai số dương a, b thỏa mãn log a log b log
. Tính log a 2b 5 log b . 6 4 25 2 6 A.1 B. 2 C. 4 D. 3
Câu 24. Tính a + b với a, b là số nguyên trong nghiệm duy nhất x a b 2 của phương trình 2 1 x 1 log 2log . 2018 2019 x x 2 2 x A.5 B. – 1 C. 2 D. 1
Câu 25. Tính tổng tất cả các số nguyên dương m để mọi nghiệm bất phương trình 4 x x 1 0 đều là
nghiệm của bất phương trình 2 2
log (x 4x m) log (x 1) 1. 5 5 A.13 B. 21 C. 11 D. 28
Câu 26. Có bao nhiêu số tự nhiên n để 2012 2015 2 2 2n là số chính phương A.2 B. 1 C. 3 D. 4 x x
Câu 27. Phương trình 2 3 (1 2a)2 3 4có 2 nghiệm phân biệt với hiệu của chúng bằng log 3 . Khi đó a thuộc miền 2 3 3 3 3 A. ; B. ; C. ; D. 0; 2 2 2 2
Câu 28. Có bao nhiêu số nguyên m < 100 để phương trình x x3 2 .5
m có 2 nghiệm phân biệt A.50 B. 26 C. 20 D. 18
Câu 29. Tìm tập hợp các giá trị m để bất phương trình 2 2
log x (2m 5) log x m 5m 4 0nghiệm đúng 2 2
với mọi giá trị thuộc [2;4) A.[0;1) B. [– 2;0) C. (0;1] D. (– 2;0] x 1 4 4
Câu 30. Có bao nhiêu số nguyên dương x thỏa mãn sin ycos y 2 log x 4 sin 2y 2 2 A.Vô số B. 3 C. 2 D. 1 m Câu 31. Cho hàm số ( ) 2020x 2020 x f x
. Số nguyên lớn nhất để f (m 1) f 2020 0 là 2020 A.2018 B. 2019 C. 2017 D. 2020
Câu 32. Tìm tập hợp tất cả các giá trị thực của tham số m để phương trình mx ln x 0 có hai nghiệm phân biệt thuộc khoảng 2; 3 ln 2 ln 3 ln 2 ln 3 ln 2 1 ln 3 1 A. ; B. ; ; C. ; D. ; 2 3 2 3 2 e 3 e Câu 33. Cho phương trình 2
log x log 3x 1 log m ( m là tham số thực). Có tất cả bao nhiêu giá trị 9 3 3
nguyên của tham số m để phương trình đã cho có nghiệm? A. 2. B. 4. C. 3. D. Vô số.
___________________________________ 52
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 27)
__________________________________________________ 3x 3
Câu 1. Tìm điều kiện tham số m để hàm số y
nghịch biến trên 1; 1 3x m 1 A. ;3 B. 3; C. 3; D. ; 3 3 2 1 1 3 2 x x m x mx x
Câu 2. Có bao nhiêu số nguyên dương m nhỏ hơn 20 để phương trình 2 x x e có 4 x 1 nghiệm thực dương A.19 B. 18 C. 16 D. 17
Câu 3. Tồn tại bao nhiêu số tự nhiên m thỏa mãn 239 30 30 239 33m A.3 B. 2 C. 1 D. 0 Câu 4. Cho phương trình 2
log 2x m 2 log x m 2 0 ( m là tham số thực). Tập hợp tất cả các giá trị 2 2
của m để phương trình đã cho có hai nghiệm phân biệt thuộc đoạn 1;2 là A. 1; 2 . B. 1; 2. C. 1; 2 . D. 2; . Câu 5. Cho hàm số 2
3log 2x m 3 x 1 m log
2x x13m 0. Số các giá trị nguyên của m để 27 1 3
phương trình đã cho có hai nghiệm phân biệt x , x thỏa mãn x x 15 là: 1 2 1 2 A. 14 B. 11 C. 12 D. 13
Câu 6. Xét các số nguyên dương a, b sao cho phương trình 2
a ln x b ln x 5 0 có hai nghiệm phân biệt x , x và phương trình 2
5 log x b log x a 0 có hai nghiệm phân biệt x , x thỏa mãn x x x x . Tìm giá trị 1 2 3 4 1 2 3 4
nhỏ nhất của S 2a 3b A. S 33 . B. S 30 . C. S 17 . D. S 25 . min min min min
Câu 7. Có bao nhiêu giá trị nguyên dương của tham số m để phương trình 2 2x mx 1 2 log
2x mx 1 x 2 có hai nghiệm phân biệt? 2 x 2 A. 3 . B. 1. C. 4. D. 2 .
Câu 8. Cho phương trình x me 10x mlog mx 2logx 1 0
. ( m là tham số ). Có tất cả bao nhiêu giá
trị nguyên của m để phương trình đã cho có ba nghiệm thực phân biệt? A. Vô số. B. 10 . C. 11. D. 5 .
Câu 9. Có bao nhiêu số tự nhiên m thỏa mãn 101 101 101 7 13 19 2021.41m A.3 B. 5 C. Vô số D. 2 2
Câu 10. Cho phương trình 4 xm.log 2 3 2 xx x x
.log 2 x m 2 0 với m là tham số. Tổng tất cả 2 2 2 1 2
các giá trị của tham số m để phương trình đã cho có ba nghiệm phân biệt là A. 4 . B. 1. C. 2 . D. 3 . Câu 11. Cho phương trình 2
log 9x m 5 log x 3m 10 0 (với m là tham số thực). Số giá trị nguyên của 3 3
tham số m để phương trình đã cho có hai nghiệm phân biệt thuộc 1;8 1 là A. 3 B. 5 C. 4 . D. 2 . 2
Câu 12. Tập nghiệm của bất phương trình x 9 2 x 1 3 (x 9)5
1là khoảng (a;b). Tính b – a. A.6 B. 3 C. 8 D. 4 x 1 log x
Câu 13. Bất phương trình 1010
có bao nhiêu nghiệm nguyên 2018 x 1 A.31 B. 32 C. 1010 D. 1009 2
Câu 14. Tính tổng các nghiệm của phương trình x x 2 2 .5 x 1 A. 2 log 2 B. 2 log 2 C. 2 log 2 D. 2 log 5 5 5 5 2
Câu 15. Có bao nhiêu cặp số tự nhiên (m;n) thỏa mãn 2 3 4 8.7m n n A.3 B. 2 C. 1 D. 4 53
Câu 16. Giá trị m nhỏ nhất để phương trình x x 2 x 3 3 27 3 .
x 9 (3x 1)3 (m 1)x (m 1)x có nghiệm dương
là a e ln b với a, b nguyên. Tính 17a + 3b. A.26 B. 54 C. 48 D. 18 Câu 17. Phương trình 2
log x (m 2)log x 3m 1có tích hai nghiệm phân biệt bằng 27. Giá trị m thu được 3 3 đều thuộc khoảng A.(4;5) B. (8;10) C. (20;28) D. (0;2) 1 1 x
Câu 18. Phương trình 2x 3 1 x 2 1
2x 1có nghiệm là nghiệm lớn hơn 1, trong đó a, b, c 3
nguyên dương. Tính a + b + c. A.6 B. 0 C. 2 D. 4
Câu 19. Có bao nhiêu số nguyên m 5
;5 để bất phương trình 2
log x log 4x 1 log m có nghiệm 4 2 2 A.3 B. 2 C. 4 D. 0
Câu 20. Tìm tổng bình phương các giá trị m để giá trị nhỏ nhất của hàm số 3x 3 x y e e m trên đoạn [0;ln2] bằng 6 A.160 B. 128 C. 80 D. 78
Câu 21. Có bao nhiêu cặp số nguyên (x;y) thỏa mãn 2 24 44 5y x x A.3 B. 2 C. 1 D. 4 1 Câu 22. Cho f (x) ln 1
. Tính 2m – n biết m, n nguyên dương và nguyên tố cùng nhau trong trường 2 x m
hợp f 2 f 3 ... f 2019 f 2020 n A.2 B. 4 C. – 2 D. – 4
Câu 23. Số nguyên dương x lớn nhất thỏa mãn 3log 3 1 x x 2log
x là số dạng abcd . Tính giá trị 3 2
biểu thức a b c d A.4 B. 18 C. 20 D. 19
Câu 24. Tìm miền của tham số m để phương trình 2 log x log x 3 m có ba nghiệm phân biệt 2 2 A.(0;2) B. m = 2 C. m < 2 D. m 0; 2
Câu 25. Có bao nhiêu số nguyên m 2
0;20 để bất phương trình sau có nghiệm 2 2 2
(m 1) ln(x 1) (m 2m 2)log(2x x ) 0 A.13 B. 12 C. 1 D. 0
Câu 26. Phương trình 9x 2(2 1)3x m
3(4m 1) 0 có hai nghiệm a, b thỏa mãn (a 2)(b 2) 12 . Khi đó m thuộc khoảng 1 1 A.(3;9) B. 9; C. ;3 D. ;2 4 2 2 2 2
Câu 27. Tìm tập hợp giá trị m để bất phương trình sin x cos x cos 4 5 .7 x m có nghiệm 6 6 6 6 A. m B. m C. m D. m 7 7 7 7
Câu 28. Tồn tại bao nhiêu số nguyên dương x nhỏ hơn 2021 để 400 7 3x là số tròn chục A.505 B. 420 C. 722 D. 938 4x Câu 29. Cho hàm số 2 f (x)
3x 2x . Có tất cả bao nhiêu giá trị nguyên m để phương trình ln 2
f (x 2019) m có nhiều nghiệm nhất A.2 B. 0 C. 1 D. 3
Câu 30. Cấp số nhân u có công bội bằng 2 và các số hạng của dãy thỏa mãn n log u 2
2 log u log u 2log u 10 2 1 2 4 2 3 2 2
Số nguyên n lớn nhất thỏa mãn u 2019 là n A.12 B. 7 C. 10 D. 6 54
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 28)
__________________________________________________ Câu 1. Cho phương trình 2 ln 2 mx x x
x e m2x2 0 . Khoảng a;b là tập hợp tât cả các giá trị của b
tham số m để phương trình đã cho có đúng hai nghiệm thuộc khoảng 4 1;e . Tính . a b 2 b c 3 b e b 4 A. . B. . C. . D. . 2 a e a 2 a 3 3 a e a 4b a
Câu 2. Cho hai số a, b thỏa mãn log a log b log . Tính 100 40 16 12 b A.4 B. 12 C. 6 D. 2
Câu 3. Cho hàm số y log 2.log (2 x) m . Hỏi có bao nhiêu giá trị nguyên dương của tham số m để x 4
phương trình f ( x 2 x ) 0 có tổng tất cả các nghiệm bằng 2. A.0 B. 1 C. 2 D. 3
Câu 4. Có bao nhiêu số nguyên m thuộc khoảng ( 2
020;2020) để phương trình log (mx) 3log (x 1) có 2 2 nghiệm thực duy nhất ?
A. 2018. B. 2020. C. 2021. D. 2019.
Câu 5. Tìm tất cả các giá trị thực của tham số m để phương trình 2
log x m 2 log x 3m 1 0 có hai 3 3
nghiệm x , x phân biệt thỏa mãn x .x 27 . 1 2 1 2 A. m 2 . B. m 1 . C. m 1. D. m 2 . 1 1
Câu 6. Cho các số a,b 0 thỏa mãn log a log b log a b . Giá trị bằng 3 6 2 2 2 a b A. 18. B. 27. C. 36. D. 45.
Câu 7. Có bao nhiêu số nguyên y để tồn tại số thực x thỏa mãn log 3x 4y log 2 2 x y ? 11 4 A. 3 . B. 2 . C. 1. D. vô số.
Câu 8. Gọi S là tập hợp tất cả các giá trị của tham số m sao cho hệ bất phương trình sau có nghi ệm duy nhất: 2 2 2 x y 2x6 y6 2020 2020 2020 x 2 1 y 32 4
x 2 y 2 1 3 e 2 2 x y 2x 6y 11 m m e
Tổng tất cả các phần tử thuộc tập hợp S là: A. 44 8 10 . B. 88 . C. 2 10 2 . D. 2 10 2 .
Câu 9. Tồn tại bao nhiêu số nguyên m để phương trình 1994 x208 1994 x208 36 6.6
2m 1có 4 nghiệm phân biệt A.1 B. 2 C. 3 D. 5
Câu 10. Tồn tại bao nhiêu số nguyên m để phương trình 2x (2 3)2x m
2m 0 có hai nghiệm phân biệt
x , x thỏa mãn điều kiện x x 5 ? 1 2 1 2 A. 13 B. Vô số C. 11 D. 10 log (x y) m
Câu 11. Có bao nhiêu giá trị m để hệ phương trình 3
có đúng hai nghiệm nguyên 2 2 log (x y ) 2m 2 A.1 B. 0 C. 2 D. 3
Câu 12. Có bao nhiêu số nguyên x 0 để 2 2
log (x y ) 4 đúng với mọi số thực y 0; x 2 A.2 B. 1 C. 4 D. 3 2 1 2x 1 1
Câu 13. Tính tổng các nghiệm phương trình log x 2 x 3 log 1 2 x 2 . 2 2 2 x x 1 13 1 13 A.2 B. – 2 C. D. 2 2
Câu 14. Có bao nhiêu số nguyên m để phương trình 2
log (9 x ) log (2x m 1) 0 có 2 nghiệm phân biệt 2 1 2 55 A.17 B. 3 C. 15 D. 5 2 2 1 x 1 x
Câu 15. Tập hợp các giá trị m để phương trình (m 1) 2m 0
có nghiệm là a 2 b;0 4 4
với a, b nguyên dương. Tính b – a. A.1 B. – 11 C. 11 D. – 1
Câu 16. Có bao nhiêu cặp số nguyên không âm (x;y) thỏa mãn x 3 3 y 1 A.3 B. 2 C. 1 D. 4 m ln x 2
Câu 17. Có bao nhiêu số nguyên không dương m để hàm số y đồng biến trên 2 e ; ln x m 3 A.2 B. Vô số C. 0 D. 1 Câu 18. Cho hàm số 3 2
f (x) x 12x 2018x 2019 . Có bao nhiêu số nguyên m 1 2;12thỏa mãn bất phương trình f log
log m 1 2019 f f 0 . 0,2 2 A.9 B. 10 C. 11 D. 12 Câu 19. Phương trình 2 2 2
log (x 1) mlog (x 1) 8 m 0 có đúng ba nghiệm phân biệt. Khi đó m thuộc 2 2 khoảng A.(1;9) B. (9;15) C. (15;21) D. (21;28) Câu 20. Cho hàm số ( ) 3x 3 x f x
. Tính tích các giá trị m để f 3log m f 2 log m 2 0 . 2 2 A.2 B. 0,125 C. 0,25 D. 0,5
Câu 21. Có bao nhiêu giá trị nguyên m 2
5;25để phương trình 3x 2 xln 3 xln 9 e 2e e m 0 có nghiệm duy nhất A.41 B. 22 C. 21 D. 25
Câu 22. Có bao nhiêu giá trị nguyên m để có đúng 4 bộ số thực (x;y) thỏa mãn hệ 2 2 x y 2x 4y 5 2 log (26x 53).log 8log m 0 3 3 3 729 2 2
(x 12) (y 2) 196 A.80 B. 79 C. 81 D. 77
Câu 23. Tìm tập hợp các giá trị m để phương trình cos x cos x 1 4
2 + 2m 1 0 có đúng ba nghiệm x ; 2 7 7 A.(1;2) B. (0;1) C. 1; D. ;1 8 8 1 Câu 24. Cho x 0;
thỏa mãn log(sin x) log(cos x) 1
; log(sin x cos x) (log n 1) . Tìm n. 2 2 A.11 B. 12 C. 10 D. 15
Câu 25. Có bao nhiêu cặp số thực (x;y) trong đó y nguyên dương thỏa mãn 2 3x 3x y 1 2 2 x x 1 log 2 2 x 4 1 2 x y 2 2x x 1 A.4 B. 5 C. 6 D. 7
Câu 26. Có bao nhiêu cặp số tự nhiên (m;n) thỏa mãn 2 5 16 30.13m n n A.3 B.2 C. 1 D. 4
Câu 27. Tìm số nghiệm nguyên của phương trình 9 9 9 2012 x y z 2009 A.4 B. 3 C. 2 D. 1
Câu 28. Cho x, y dương thỏa mãn x y 1; log . 3 3 x y xy 3 3 2 log (x y ) log xy 1 3 1 3 1 3 3 3 x y Tính . xy A. 3 B. 2 3 C. 3 D. 1 3
Câu 29. Có bao nhiêu số nguyên m để phương trình 4 8
2log x 2log x 2m 2020 0 có ít nhất một 2 2 nghiệm thuộc [1;2] A.7 B. 9 C. 8 D. 6 56
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 29)
__________________________________________________
Câu 1. Có bao nhiêu số nguyên m 2
0;20để tồn tại hệ sau có nghiệm nguyên dương x 6 x( y 1) 6 log log (4x 8) 2 2 y y 2
log (x 2) mlog (1 y) m 0 2 2 A.12 B. 9 C. 11 D. 10
Câu 2. Tìm số nghiệm của phương trình 2 log x 2x log 2 x 2x 2 3 2 A.4 B. 3 C. 1 D. 2
Câu 3. Có bao nhiêu số nguyên x sao cho ứng với mỗi x thì mọi giá trị thực của y đều thỏa mãn 2 2 2 2
log ( y 2xy 2x 1) 1 log ( y 2 y 4).log ( y 4) . 5 3 5 A.5 B. 3 C. 6 D. 4
Câu 4. Có bao nhiêu số nguyên x sao cho tồn tại ba số thực y, z,t thỏa mãn log 2 2
x y log xz yt log 2 2 z t 4 5 6 A. 2 B. 4 C. 3 . D. 1.
Câu 5. Có tất cả bao nhiêu cặp số nguyên (x;y) thỏa mãn 0 x 3456 thỏa mãn 5y x log (5x 10) y log 5 2 A.7 B. 4 C. 5 D. 6
Câu 6. Có bao nhiêu số nguyên x để ứng với mỗi x tồn tại đúng 8 giá trị nguyên của y thỏa mãn bất phương trình x (2x ) y e y ye log y x . 2 A.1 B. 2 C. 3 D. 4
Câu 7. Có bao nhiêu số nguyên a không nhỏ hơn 3 sao cho tồn tại số thực x thỏa mãn log a x a 3log2021 2021 x 3 A.2019 B. 2018 C. 2020 D. 2003
Câu 8. Tìm số giá trị nguyên m để tồn tại các số thực x, y thỏa mãn đẳng thức 2 2 x y m x y xym 2 2 e e
x y x y xy 2m 2 . A.6 B. 9 C. 8 D. 7
Câu 9. Có tất cả bao nhiêu giá trị nguyên y để tương ứng với mỗi y tồn tại không quá 63 số nguyên x thỏa mãn 2 2 log (x y ) log
( y y 64) log (x y) . 2020 2021 4 A.301 B. 302 C. 602 D. 2
Câu 10. Tìm điều kiện tham số m để phương trình sau có nghiệm lớn hơn 1 2 1 x m 3 2 x 2x3 3 3 3.27
log (x m) 1 3 log (x 2x) 1 3 3 A.m < 1 B. m > 1 C. m > 3 D. – 1 < m < 1 1
Câu 11. Có bao nhiêu số nguyên m để hàm số y log(mx m 2) xác định trên ; 2 A.4 B. 5 C. Vô số D. 3
Câu 12. Có bao nhiêu số nguyên m để hàm số y log
(4mx 5m 1995) xác định trên 1; 2020 A. 1995 B. 1992 C. 1994 D. 2020
Câu 13. Tồn tại bao nhiêu cặp số nguyên (x;y) thỏa mãn x y 2020 1994 log x ? 2020 y A. 2 B. 3 C. 1 D. 4 1
Câu 14. Có bao nhiêu giá trị nguyên y, y 3 sao cho tồn tại đúng hai số thực x lớn hơn thỏa mãn 2021 ln x y y xy x e xy A.2028 B. 2026 C. 2027 D. 2025
Câu 15. Có bao nhiêu cặp giá trị nguyên (x;y) không âm thỏa mãn 57 2 2 x y 3x 5y 27 2 2 log
x y 6x 10y 25 0 . 9x 15y 2 A.25 B. 29 C. 30 D. 26
Câu 16. Tồn tại giá trị m m để bất phương trình 4x 5x 7x 2mx 3 nghiệm đúng với mọi x thuộc R. Khi 0 đó a thuộc khoảng nào A.(0;1) B. (1;2) C. (2;4) D. (4;5)
Câu 17. Có bao nhiêu cặp số nguyên dương ;
x yvới x 2020 thỏa mãn: 23 31 9x x y log 2x 1 1 3 A. 4 . B. 3 . C. 2020 . D. 1010 .
Câu 18. Có bao nhiêu giá trị nguyên của tham số m 0;10 để tập nghiệm của bất phương trình 2 2
log x 3log x 7 m 2
log x 7 chứa khoảng 256; ? 2 1 4 2 A. 8 . B. 7 . C. 10 . D. 9 .
Câu 19. Có bao nhiêu cặp số nguyên ;
x y thỏa mãn 2 x 20210 và log y 1 2 2y x y 2x ? 2 A. 2020. B. 10. C. 14. D. 2019.
Câu 20. Tồn tại bao nhiêu cặp số nguyên ;
x ythỏa mãn đẳng thức 2log 2 1 7x 24x y y ? 1995 A. 2 B. 1 C. 3 D. 4
Câu 21. Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc đoạn 7; 7
để tập giá trị của hàm số mx2 1 x1 f (x) 2 chứa đoạn ;16 ? 2 A. 6 . B. 8 . C. 7 . D. 9 . 2 x x 1 2 x 1 7 7 2020x 2020
Câu 22. Điều kiện của m để hệ bất phương trình có nghiệm là : 2 x m 2 x 2m3 0 A. m 3 . B. 2 m 1. C. 1 m 2. D. m 2 . x
Câu 23. Gọi S là tập nghiệm của phương trình x x 2 2 2 3
m 0 (với m là tham số thực). Có tất cả bao
nhiêu giá trị nguyên của m 2
020;2020 để tập hợp S có hai phần tử? A. 2094. B. 2092. C. 2093. D. 2095. 2
Câu 24. Cho hai số thực bất kỳ a 1, b 1. Gọi x , x là hai nghiệm phương trình x x 1 a b 1. Trong trường 1 2 2 x x hợp biểu thức 1 2 S
6x 6x đạt giá trị nhỏ nhất, khẳng định nào dưới đây đúng? 1 2 x x 1 2 1 1 3 3 3 3 A. 3 a b . B. 6 a b . C. 3 a b . D. 6 a b .
Câu 25. Có bao nhiêu số nguyên m để phương trình 3 x x
me có hai nghiệm phân biệt A.Vô số B. 7 C. 6 D. 5
Câu 26. Tính tổng các giá trị nguyên m để phương trình x 2 3 ( )3x m m
2m có đúng hai nghiệm phân biệt 1 nhỏ hơn log3 A.28 B. 27 C. 20 D. 21 x
Câu 27. Có bao nhiêu số nguyên dương m để phương trình 2 m ln (2 m)ln x 4 có nghiệm x 1 ; e e A.0 B. 4 C. 3 D. 2 y
Câu 28. Cho x, y dương thỏa mãn log x log y log (x y) . Tính 10 15 5 x 2 1 A.1,5 B. 0,5 C. D. 3 3
_________________________________ 58
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 30)
__________________________________________________ x a b
Câu 1. Gọi x , y các số thực dương thỏa mãn điều kiện log x log y log x y và , với 9 6 4 y 2
a, b là hai số nguyên dương. Tính 2 2 T a b . A. T 26. B. T 29. C. T 20. D. T 25. b
Câu 2. Cho các số thực dương a, b thỏa mãn log a log b log 4a5b 1
. Đặt T . Khẳng định nào 4 6 9 a sau đây đúng? 1 2 1 A. 1 T 2 . B. T . C. 2 T 0. D. 0 T . 2 3 2 x x 1 Câu 3. Phương trình 2 1 3 .4
0 có hai nghiệm x , x . Tính T x .x x x . 3x 1 2 1 2 1 2 A. T log 4 . B. T log 4 . C. T 1 . D. T 1. 3 3
Câu 4. Tổng tất cả các nghiệm thực của phương trình x x 1 15 . x 5 5 27x 23 bằng. A. 1 . B. 2 . C. 1. D. 0 .
Câu 5. Cho số thực sao cho phương trình 2x 2x 2cosx có đúng 2019 nghiệm thực. Số nghiệm của
phương trình 2x 2x 4 2cos x là A. 2019 . B. 2018 . C. 4037 . D. 4038 . 2 4x 4x1 1
Câu 6. Biết x , x là hai nghiệm của phương trình 2 log
4x 1 6x và x 2x a b 1 2 4 1 2 7 2x
với a , b là hai số nguyên dương. Tính a b. A. a b 13 . B. a b 11. C. a b 16 . D. a b 14 .
Câu 7. Phương trình x x 1 x 1 2 2 4 2
x có tổng các nghiệm bằng A. 7 B. 3 C. 5 D. 6
Câu 8. Tìm số nghiệm của phương trình x 2 x 1 1 e log 2 0 . A. 4 . B. 3 . C. 2 . D. 0 . 11
Câu 9. Tính số nghiệm của phương trình cot 2x x trong khoảng ;2019 . 12 A. 2019 . B. 2018 . C. 1 . D. 2020 .
Câu 10. Hỏi phương trình 3.2x 4.3x 5.4x 6.5x
có tất cả bao nhiêu nghiệm thực ? A. 0 . B. 1. C. 3 . D. 2 . Câu 11. Phương trình sin x 2 2019
sin x 2 cos x có bao nhiêu nghiệm thực trên 5 ;2019 ? A. 2025 . B. 2017 . C. 2022 . D. Vô nghiệm.
Câu 12. Số nghiệm của phương trình log7 4 3 x x là A. 1. B. 0 . C. 2 . D. 3. x y xy xy 1
Câu 13. Cho các số thực x , y với x 0 thỏa mãn 3 1 e e x y 1 1 1 e 3y . Gọi m là giá x3 e y
trị nhỏ nhất của biểu thức T x 2 y 1 . Mệnh đề nào sau đây là đúng? A. m 2;3 . B. m 1 ; 0 . C. m 0; 1 . D. m 1;2 .
Câu 14. Số nghiệm của phương trình x x x x x x 2 2 2 3 5 x 8 x3 5 2 8 3 .8 3 5 .8 là A. 4 . B. 3 . C. 1. D. 2 . 2 2 2
Câu 15. Tích tất cả các giá trị của x thỏa mãn phương trình 3x 3 4x 4 3x 4x 7 bằng A. 2. B. 1. C. 4. D. 3. Câu 16. Phương trình x 2x 1 2 e e
1 x 2 2x 1 có nghiệm trong khoảng nào? 5 3 3 1 A. 2; . B. ; 2 . C. 1; . D. ;1 . 2 2 2 2 59 5x 3x
Câu 17. Tính tổng S tất cả các nghiệm của phương trình: x 1 ln
5 5.3x 30x 10 0 . 6x 2 A. S 1. B. S 2 . C. S 1 . D. S 3
Câu 18. Tích tất cả các nghiệm của phương trình 2 log x log x 1 1 2 2 1 5 1 5 1 A. 2 2 . B. 1. C. 2 2 . D. . 2 x a b
Câu 19. Gọi x , y các số thực dương thỏa mãn điều kiện log x log y log x y và , với 9 6 4 y 2
a, b là hai số nguyên dương. Tính 2 2 T a b . A. T 26. B. T 29. C. T 20. D. T 25. b
Câu 20. Cho các số thực dương a, b thỏa mãn log a log b log 4a5b 1
. Đặt T . Khẳng định nào 4 6 9 a sau đây đúng? 1 2 1 A. 1 T 2 . B. T . C. 2 T 0. D. 0 T . 2 3 2 Câu 21. Cho phương trình 2
log 2x m 2 log x m 2 0 ( m là tham số thực). Tập hợp tất cả các giá trị 2 2
của m để phương trình đã cho có hai nghiệm phân biệt thuộc đoạn 1;2 là A. 1; 2 . B. 1; 2. C. 1; 2 . D. 2; . Câu 22. Cho phương trình 2
log x log 5x 1 log m ( m là tham số thực). Có tất cả bao nhiêu giá trị 9 3 3
nguyên của m để phương trình đã cho có nghiệm? A. 4. B. 6. C. Vô số. D. 5. x
Câu 23. Có bao nhiêu giá trị nguyên dương của tham số m để phương trình 2 m ln 2mln x4 có e 1
nghiệm thuộc vào đoạn ;1 ? e A. 1. B. 2 . C. 3 . D. 4 .
Câu 24. Tìm tất cả các giá trị thực m để phương trình log 1 log 9 2 1 m x x x 3 9
có hai nghiệm phân biệt.
A. m 1;0 . B. m 2;0 . C. m 1 ; . D. m 1 ;0. 2 4x 4x 1 1
Câu 25. Biết x , x là hai nghiệm của phương trình 2 log
4x 1 6x và x 2x a b 1 2 1 2 7 2x 4
với a , b là hai số nguyên dương. Tính a . b A. a b 16 . B. a b 11. C. a b 14 . D. a b 13. 2 x
Câu 26. Số nghiệm của phương trình x 2 ln x 2 2018 là 2 A. 3 . B. 1. C. 4 . D. 2 . 2 2 2
Câu 27. Gọi S là tập nghiệm của của phương trình: x 3x2 x 6x5 2x 3x7 4 4 4 1. Khi đó S là A. 1; 2 . B. 1; 2; 1 . C. 1;2; 1 ; 5 . D. . 2
Câu 28. Số giao điểm của các đồ thị hàm số 1 3x y và y 5 là A. 0 . B. 3 . C. 2 . D. 1. 2
Câu 29. Cho hai số thực a 1, b 1. Gọi x , x là hai nghiệm của phương trình x x 1
a .b 1. Trong trường hợp 1 2 2 x .x biểu thức 1 2 S
4x 4x đạt giá trị nhỏ nhất, mệnh đề nào sau đây là đúng? 1 2 x x 1 2 A. a b . B. . a b 4 . C. . a b 2 . D. a b .
Câu 30. Cho x , y , z là các số thực thỏa mãn 2x 3y 6z. Giá trị của biểu thức M xy yz xz là: A. 0. B. 6. C. 3. D. 1.
_________________________________ 60
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 31)
__________________________________________________ 5b a a
Câu 1. Cho a , b là các số dương thỏa mãn log a log b log . Tính giá trị . 9 16 12 2 b a 3 6 a a a 3 6 A. . B. 7 2 6 . C. 7 2 6 . D. . b 4 b b b 4 m m
Câu 2. Hai số thực dương , m n thỏa mãn log
log n log m n . Tính giá trị của biểu thức P . 4 6 9 2 n 1 A. P 2 . B. P 1 . C. P 4 . D. P . 2 p Câu 3. Giả sử ,
p q là các số thực dương thỏa mãn log p log q log
p q . Tính giá trị của . 16 20 25 q 1 8 1 4 A. 1 5 . B. . C. 1 5 . D. . 2 5 2 5
Câu 4. Có bao nhiêu cặp số tự nhiên (x;y) thỏa mãn 3x 2y 1 A.3 B. 4 C. 5 D. 2
Câu 5. Hỏi phương trình x x x 3 2 3 6 ln
1 1 0 có bao nhiêu nghiệm phân biệt? A. 2 . B. 1. C. 3 . D. 4
Câu 6. Có bao nhiêu số nguyên m < 30 để hàm số y log (mx m 6) 5 xác định trên 2; 3 A.27 B 26 C. 25 D. 4
Câu 7. Số nghiệm của phương trình x 1 ln 1 là: x 2 A. 1. B. 0 . C. 3 . D. 2 .
Câu 8. Giải phương trình log . x log x .
x log x 3 log x 3log x x . Ta có tổng tất cả các nghiệm bằng 2 3 3 2 3 A. 35 . B. 5 . C. 10 . D. 9 . 1
Câu 9. Tính tổng tất cả các nghiệm của phương trình log x 3 log x 2
1 x x 4 2 x 3 . 2 2 2 A. S 2 . B. S 1. C. S 1 . D. S 1 2 . 2 x 1 x 1
Câu 10. Biết phương trình log 2log
có một nghiệm dạng x a b 2 trong đó a,b là 5 3 x 2 2 x
các số nguyên. Tính 2a b . A. 3 . B. 8 . C. 4 . D. 5 .
Câu 11. Cho a, b, c dương khác 1 thỏa mãn log x 2log x 3log x, x 0, x 1. Tính 2 log ab c a a b c 14 A.6 B. 5,5 C. 6,5 D. 3 2
Câu 12. Số nghiệm thực của phương trình x 1 2 log 2 1 4x x x log 3x . 2 2 A. 0 . B. 1. C. 2 . D. 3 . 2 1 2x 1 1 Câu 13. Cho phương trình
log x 2 x 3 log 1
2 x 2 , gọi S là tổng tất cả các 2 2 2 x x
nghiệm của nó. Khi đó, giá trị của S là 1 13 1 13 A. S 2 . B. S . C. S 2 . D. S . 2 2 1 2 2x 1 x
Câu 14. Tính tích tất cả các nghiệm thực của phương trình 2 log 2 x 5. 2 2x 1 A. 0 . B. 2 . C. 1. D. . 2 61 x
Câu 15. Tổng tất cả các nghiệm của phương trình log 10 2019 2019x 4 bằng 2 A. log 16 2log 16 log 10 2log 10 2019 . B. 2019 . C. 2019 . D. 2019 . 1 x
Câu 16. Biết rằng 2 x log 1 4 y 2 y 1
x . Tính giá trị của biểu thức 2 2 P x y xy 1. 2 với 0 A. 3 . B. 1. C. 2 . D. 4 .
Câu 17. Phương trình 4xlog8 x log84x x 4 có tập nghiệm là 1 1 1 1 A. 2; 8 . B. ;8 . C. ; . D. 2; . 2 2 8 8
Câu 18. Số nghiệm của phương trình sin 2x cos x 1 log sin x trên khoảng 0; là: 2 2 A. 4 . B. 3 . C. 2 . D. 1.
Câu 19. Cho x, y, z > 0 thỏa mãn 3x 4y 12z ; xy yz xz 4 . Giá trị của z thuộc khoảng 1 1 3 3 A. ;1 B. 0; C. 1; D. ;3 2 2 2 2
Câu 20. Có tất cả bao nhiêu số nguyên x để tồn tại ít nhất một số thực y thỏa mãn
log 2x y log 2 2 x y 2 3 A.21 B. 20 C. 22 D. 23
Câu 21. Phương trình log 2 x 2x 3 2
x x 7 log x 1 có số nghiệm là T và tổng các nghiệm là S . 3 3 Khi đó T S bằng A. 2 . B. 4 . C. 3 . D. 1. 2 4x 4x 1 1
Câu 22. Hai nghiệm x , x x x của phương trình 2 log
4x 1 6x và x 3x a 2 b 1 2 1 2 1 2 7 2x 4
với a, b là các số nguyên dương. Tính a b A. a b 14 . B. a b 16 . C. a b 17 . D. a b 15 .
Câu 23. Có tất cả bao nhiêu cặp số nguyên dương (x;y) thỏa mãn x 2 y2 9 5 104 A.3 B. 0 C. 1 D. 2 2 x 1 x 1
Câu 24. Cho biết phương trình log 2log
có nghiệm duy nhất x a b 2 . Hỏi m 5 3 x 2 2 x mx a 2
thuộc khoảng nào dưới đây để hàm số y
có giá trị lớn nhất trên đoạn 1; 2 bằng 2 . x m A. m 7; 9 . B. m 6; 7 . C. m 2; 4 . D. m 4; 6 .
Câu 25. Nghiệm của phương trình 25x 23 5x x
2x 7 0 nằm trong khoảng nào sau đây? A. 5;10 . B. 0;2 . C. 1;3 . D. 0; 1
Câu 26. Có bao nhiêu bộ số nguyên dương (x;y;z) thỏa mãn 3x 4y 5z . A.3 B. 2 C. 1 D. 4
Câu 27. Số nghiệm nguyên không âm của bất phương trình x 1 x x 1 15.2 1 2 1 2 bằng bao nhiêu? A. 3. B. 0. C. 1. D. 2. x 1 Câu 28. Cho phương trình 3 1 x 3 8 8. 0,5 3.2 125 24.0,5x x x . Khi đặt t 2 , phương trình đã cho 2x
trở thành phương trình nào dưới đây? A. 3 8t 3t 12 0 . B. 3 2 8t 3t t 10 0 . C. 3 8t 125 0 . D. 3 8t t 36 0 .
Câu 29. Xét phương trình log x 1 log x 2 3 . Mệnh đề nào sau đây đúng? 2 3
A. Phương trình trên vô nghiệm.
B. Phương trình trên có nghiệm bé hơn 1.
C. Phương trình trên có nghiệm lớn hơn 1 và một nghiệm bé hơn 1.
D. Phương trình trên chỉ có nghiệm hơn 1.
__________________________________ 62
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 32)
__________________________________________________ Câu 1. Cho phương trình 2
log x 4log 4x 1 log m 9 3 3
( m là tham số thực). Có tất cả bao nhiêu giá trị
nguyên của m để phương trình đã cho có nghiệm? A. 5 . B. 3 . C. Vô số. D. 4 . 1 5
Câu 2. Tìm m để phương trình :m 1 log x 22 2 4 m 5 log
4m 4 0 có nghiệm trên , 4 . 1 1 x2 2 2 2 7 7 A.Mọi giá trị m. B. 3 m . C. m . D. 3 m . 3 3
Câu 3. Có bao nhiêu số nguyên m để phương trình log 3x 2m log x 2 3 m có nghiệm? 3 5 A. 3 . B. 4 . C. 2 . D. 5 . n n
3 5 3 5
Câu 4. Có bao nhiêu số tự nhiên n < 1000 để a
2 là số chính phương n 2 2 A.500 B. 320 C. 180 D. 450
Câu 5. Gọi m là giá trị thực nhỏ nhất của tham số m sao cho phương trình 0 m 2
1 log x 3 m 5 log x 3 m 1 0 có nghiệm thuộc 3;6 . Khẳng định nào sau đây là đúng? 1 1 3 3 4 10 5 A. Không tồn tại m . B. m 1; . C. m 2; . D. m 5; . 0 0 3 0 3 0 2
Câu 6. Có bao nhiêu cặp số nguyên không (x;y) với x 0;2018 thỏa mãn log 2 2 3 8y x x y 2 A.2 B. 3 C. 4 D. 5
Câu 7. Cho phương trình m ln x
1 x 2 0 . Biết rằng tập hợp tất cả các giá trị của tham số m để phương
trình đã cho có hai nghiệm x , x thỏa mãn 0 x 2 4 x là khoảng ;
a . Khi đó a thuộc khoảng nào 1 2 1 2 dưới đây? A. 3,7;3,8 . B. 3,6;3,7 . C. 3,8;3,9 . D. 3,5;3,6 .
Câu 8. Hàm số bậc ba y f x có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của m 5 ; 5 sao cho phương trình 3 log f x 2 1 log f x 1 2m 8 log
f x 1 2m 0 có nghiệm x 1 ; 1 ? 2 2 1 2 A. 7 . B. 5 . C. 6 . D. vô số.
Câu 9. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình 4x 2 .2x m m 6 0 có hai
nghiệm thực x , x sao cho x x 3 . Tập hợp S có bao nhiêu phần tử? 1 2 1 2 A. Vô số. B. 3 . C. 2 . D. 1.
Câu 10. Có bao nhiêu cặp số nguyên dương (m;n) để 2 .
m 5n 25 là số chính phương A.Vô số B. 4 C. 2 D. 8
Câu 11. Giá trị thực của tham số m để phương trình 4x 2 3.2x m
64 0 có hai nghiệm thực x , x thỏa 1 2
mãn x 2 x 2 24 thuộc khoảng nào sau đây? 1 2 3 3 21 29 11 19 A. 0; . B. ;0 . C. ; . D. ; . 2 2 2 2 2 2 63
Câu 12. Cho hàm số y f x liên tục trên R và có đồ thị như hình vẽ 2
Tập hợp tất cả các giá trị thực của m để phương trình x
f e m có đúng 2 nghiệm thực là A. 0;4. B. 0; 4 . C. 0 4; . D. 4; . 2 2
Câu 13. Tìm tập hợp tất cả các giá trị tham số m để phương trình x 2x 1 x 2x2 4 . m 2
3m 2 0 có 4 nghiệm phân biệt. A. 1; . B. ; 1 2; . C. 2; . D. 2; .
Câu 14. Cho phương trình 2 2log x 2 x
3log2 x 2 3 m 0 ( m là tham số thực). Có tất cả bao nhiêu giá trị
nguyên dương của m để phương trình đã cho có đúng hai nghiệm phân biệt? A. vô số. B. 81. C. 79. D. 80.
Câu 15. Có bao nhiêu bộ (x; y) với x, y nguyên và 1 x, y 2020 thỏa mãn xy x y 2 y 2x 1 2 4 8 log 2x 3y xy 6 log ? 3 2 y 2 x 3 A. 2017 . B. 4034 . C. 2 . D. 2017.2020 .
Câu 16. Biết a,b là các số thực sao cho 3 3 3z 2 .10 .10 z x y a b
, đồng thời x, y, z là các số các số thực 1 1
dương thỏa mãn logx y z và 2x 2 log
y z 1. Giá trị của thuộc khoảng 2 2 a b A. (1;2) . B. (2;3) . C. (3; 4) . D. (4;5) .
Câu 17. Có bao nhiêu số tự nhiên n < 1994 để 2n 2
3 3 1 là một hợp số. A.1328 B. 1430 C. 1527 D. 1288 9
Câu 18. Cho các số thực x , y thỏa mãn x 1 , y 1 và log x log 6 y 2 log x log 2 y 3 log 2xy . Giá 3 3 3 3 3 2
trị của biểu thức P x 2y gần với số nào nhất trong các số sau A. 7 . B. 8. C. 10 . D. 9 .
Câu 19. Cho các đồ thị như hình vẽ bên. Khẳng định nào sau đây đúng
A. b > a > d > c B. a > b > d > c
C. a > c > b > d D. c > d > b > a
Câu 20. Có bao nhiêu giá trị nguyên của tham số m để phương trình 2 2 4 x x 4 9
4.3 xx 2m 1 0 có nghiệm? A. 27 . B. 25 . C. 23. D. 24 .
Câu 21. Gọi a;b là tập các giá trị của tham số m để phương trình 2 2 x 8 x e
e m 0 có đúng hai nghiệm
thuộc khoảng 0;ln 5 . Tổng a b là A. 2. B. 4. C. 6 . D. 14 .
Câu 22. Có bao nhiêu cặp số nguyên dương ;
x y với x 2020 thỏa mãn 23 31 9y x y log 2x 1 3 A. 1010 . B. 2020 . C. 3 . D. 4 .
_________________________________ 64
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 34)
__________________________________________________
Câu 1. Có bao nhiêu giá trị nguyên của tham số m 1
0;10 để bất phương trình sau nghiệm đúng với mọi x: x x
6 2 7 2 3 7 1 2x m m 0 A. 10 . B. 9 . C. 12 . D. 11.
Câu 2. Cho hàm số y f x . Hàm số y f ' x có bảng biến thiên như sau: Bất phương trình x
f x e m đúng với mọi x 1; 1 khi và chỉ khi. A. m f 1 1 B. m f 1 1 C. m f 1 e D. m f 1 e e e
Câu 3. Cho hàm số y f x liên tục trên và có bảng xét dấu đạo hàm như sau Bất phương trình 2 x
f x e m đúng với mọi x 1; 1 khi và chỉ khi A. m f 0 1. B. m f 1 . e C. m f 0 1. D. m f 1 . e
Câu 4. Cho hàm số y f x liên tục trên R và có đồ thị như hình vẽ
Tổng tất cả các giá trị nguyên của tham số m để bất phương trình f x 2
f x f x 2 9.6 4 .9 m 5m f x .4 đúng x ¡ là A. 10 B. 4 C. 5 D. 9
Câu 5. Cho hàm số y f x . Hàm số y f x có bảng biến thiên như sau: Bất phương trình 2 3. x f x e m có nghiệm x 2 ;2 khi và chỉ khi: A. m f 2 3 B. m f 4 2 3e C. m f 4 2 3e D. m f 2 3 65
Câu 6. Tất cả giá trị của tham số thực m x x
sao cho bất phương trình 9 2m
1 .3 3 2m 0 có nghiệm
đúng với mọi số thực x là 3 3 A. m . B. m 2 . C. m . D. m . 2 2
Câu 7. Bất phương trình x m x 1 4 1 2
m 0 nghiệm đúng với mọi x 0 . Tập tất cả cá giá trị của m là A. ; 12. B. ; 1 . C. ; 0 . D. 1;16 . 3
Câu 8. Cho hàm số f x cos 2x . Bất phương trình 2019 f
x m đúng với mọi x ; khi và chỉ khi 12 8 A. 2018 m 2 . B. 2018 m 2 . C. 2019 m 2 . D. 2019 m 2 .
Câu 9. Cho hàm số y f x . Hàm số y f x có bảng biến thiên như sau:
Bất phương trình 2x f x
m đúng với mọi x 1 ; 1 khi và chỉ khi: A. m f 1 2 . B. m f 1 2 . C. m f 1 1 . D. m f 1 1 . 2 2
Câu 10. Số giá trị nguyên dương của m để bất phương trình 2 2 x 3 xm x 3xm 2x 2 x3 9 2.3 3 có nghiệm là A. 4 . B. 8 . C. 1. D. 6 .
Câu 11. Gọi S là tập hợp tất cả các giá trị của tham số m để bất phương trình 2 m 4 3 x x m 3 2 x x x 1 x e
0 đúng với mọi x thực. Số tập con của S là A. 2. B. 4. C. 3. D. 1. x x
Câu 12. Cho bất phương trình x 1 .
m 3 3m 24 7 4 7 0, với m là tham số thực. Tìm tất cả các
giá trị thực của tham số m để bất phương trình đã cho nghiệm đúng với mọi x (; 0] . 2 2 3 2 2 3 2 2 3 2 2 3 A. m . B. m . C. m . D. m . 3 3 3 3
Câu 13. Có bao nhiêu số nguyên dương m để tập nghiệm của bất phương trình x2 3
33x 2m 0 chứa không quá 9 số nguyên? A. 1094. B. 3281. C. 1093. D. 3280.
Câu 14. Có bao nhiêu m nguyên dương để bất phương trình 2x2 x m2 3 3 3
1 3m 0 có không quá 30 nghiệm nguyên? A. 28. B. 29. C. 30. D. 31. 2 x x 1 2 x 1 7 7 2020x 2020
Câu 15. Điều kiện của m để hệ bất phương trình có nghiệm là : 2 x
m 2 x 2m3 0 A. m 3 . B. 2 m 1. C. 1 m 2. D. m 2 .
Câu 16. Tìm điều kiện của m để bất phương trình 2x 3 5 2x m nghiệm đúng với mọi x ;log 5 . 2 A. m 4 . B. m 2 2 . C. m 4 . D. m 2 2 .
Câu 17. Tìm tất cả các giá trị của m để bất phương trình 2 x x m m 2 2 2 1 x 2 x 1 x 2 x 1 .4 1 2 .10 . m 25 0 nghiệm 1 đúng với mọi x ; 2 . 2 100 1 100 A. m 0 . B. m . C. m . D. m . 841 4 841
Câu 18. Có bao nhiêu số nguyên x sao cho ứng với mỗi x có không quá 728 số nguyên y thỏa mãn log 2 x y log (x y) ? 4 3 A. 59 . B. 58 . C. 116 . D. 115 . 66
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 35)
__________________________________________________
Câu 1. Cho hàm số f x có đồ thị như hình vẽ bên.
Bất phương trình x 3 x f e
m e 2019 có nghiệm x 0; 1 khi và chỉ khi 4 4 2 f e A. m . B. m . C. m . D. m . 1011 3e 2019 1011 3e 2019
Câu 2. Phương trình log x 2 1 2 log
4 x log 4 x3 có bao nhiêu nghiệm? 4 2 8 A. Vô nghiệm. B. Một nghiệm. C. Hai nghiệm. D. Ba nghiệm.
Câu 3. Cho phương trình log 2 x x 1.log 2 x x 1 2
log x x 1 . Biết phương trình có một 2 3 6 1
nghiệm là 1 và một nghiệm còn lại có dạng log c log b b c x a a
(với a, c là các số nguyên tố và a c ). Khi 2 đó giá trị của 2 a 2b 3c bằng: A. 0 . B. 3 . C. 6 . D. 4 .
Câu 4. Cho hàm số y f x liên tục trên đoạn 1;9 và có đồ thị là đường cong trong hình vẽ dưới đây
Có bao nhiêu giá trị nguyên m để bất phương trình sau nghiệm đúng với mọi giá trị thuộc 1;9 ? f x 2
f x f x f x 2 16.3 2 8 .4 m 3m f x .6 A. 32 . B. 31. C. 5. D. 6 . 2 2
Câu 5. Có bao nhiêu giá trị nguyên m để bất phương trình 3x x 92x m 0 có 5 nghiệm nguyên? A. 65021 . B. 65024 C. 65022 . D. 65023 .
Câu 6. Có bao nhiêu số nguyên x sao cho ứng với mỗi x có không quá 242 số nguyên y thỏa mãn log 2 x y log x y ? 4 3 A. 55 . B. 28 . C. 29 . D. 56 . Câu 7. Cho phương trình 2
log x log 5x 1 log m ( m là tham số thực). Có tất cả bao nhiêu giá trị 9 3 3
nguyên của m để phương trình đã cho có nghiệm? A. 4. B. 6. C. Vô số. D. 5.
Câu 8. Tìm tập S tất cả các giá trị thực của tham số m để tồn tại duy nhất cặp số ; x y thỏa mãn 2 log
4x 4 y 6 m 1 và 2 2
x y 2x 4 y 1 0 . 2 2 x y 2 67 A. S 1 ; 1 B. S 5 ;1;1; 5 C. S 5 ; 5
D. S 7; 5; 1;1;5; 7
Câu 9. Tìm tham số m để tồn tại duy nhất cặp số ;
x y thỏa mãn đồng thời các điều kiện sau log x y 0 2019
và x y 2xy m 1 1 1 A. m . B. m 0 . C. m 2 . D. m . 2 3
Câu 10. Số các giá trị nguyên m để phương trình log (x 1) log (mx 8) có hai nghiệm phân biệt là 2 2 A. 5. B. Vô số. C. 4 . D. 3 . x
Câu 11. Có bao nhiêu giá trị nguyên dương của tham số m để phương trình 2 m ln 2mln x4 có e 1
nghiệm thuộc vào đoạn ;1 ? e A. 1. B. 2 . C. 3 . D. 4 .
Câu 12. Tìm tất cả các giá trị thực của tham số m để phương trình log 1 log 9 2 1 m x x x 3 9 có hai nghiệm phân biệt. A. m 1;0 . B. m 2;0 . C. m 1 ; . D. m 1 ;0.
Câu 13. Số các giá trị nguyên nhỏ hơn 2018 của tham số m để phương trình log 2018x m log 1009x 6 4 có nghiệm là A. 2018 . B. 2017 . C. 2020 . D. 2019 .
Câu 14. Giả sử phương trình 2
log x (m 2)log x 2m 0 có hai nghiệm thực phân biệt x , x thỏa mãn 2 2 1 2
x x 6. Giá trị biểu thức x x là 1 2 1 2 A. 4. B. 3. C. 8. D. 2.
Câu 15. Trong tất cả các cặp x; y thỏa mãn log
4x 4 y 4 1. Tìm m để tồn tại duy nhất cặp x; y 2 2 x y 2 sao cho 2 2
x y 2x 2 y 2 m 0 . A. m 2 10 2 . B. m 10 2 . C. m 10 2 . D. m 2 10 2 .
Câu 16. Gọi S là tập tất cả các giá trị nguyên của tham số m với m 64 để phương trình
log x m log 2 x 0 có nghiệm. Tính tổng tất cả các phần tử của S . 1 5 5 A. 2018. B. 2016. C. 2015. D. 2013. Câu 17. Cho phương trình 2
log x log 6x 1 log m ( m là tham số thực). Có tất cả bao nhiêu giá trị 9 3 3
nguyên của m để phương trình đã cho có nghiệm? A. 7 . B. 6 . C. 5 . D. Vô số.
Câu 18. Cho phương trình log
. Hỏi có bao nhiêu giá trị 2 2 2x x 4m 2m 2 2 log x mx 2m 0 2 5 52
nguyên của tham số m để phương trình đã cho có hai nghiệm 2 2 x x 3 ? 1 2 A. 1 B. 0 C. 3 D. 4
Câu 19. Tìm m để phương trình 2 2
log x log x 3 m có nghiệm x [1;8] . 2 2 A. 6 m 9 B. 2 m 3 C. 2 m 6 D. 3 m 6 Câu 20. Cho phương trình 2
log x 2log x m log x m * . Có bao nhiêu giá trị nguyên của tham số 2 2 2 m 2
019;2019 để phương trình (*) có nghiệm? A. 2021. B. 2019 . C. 4038 . D. 2020 .
Câu 21. Hỏi có bao nhiêu giá trị m nguyên trong 2
017;2017 để phương trình logmx 2logx 1 có nghiệm duy nhất? A. 4014. B. 2018. C. 4015. D. 2017 .
Câu 22. Tìm tất cả các giá trị của m để phương trình ln m ln m sin x sin x có nghiệm. 1 1 A. 1 m e1. B. 1 m e1. C. 1 m 1. D. 1 m e1. e e 68
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 36)
__________________________________________________
Câu 1. Tập nghiệm của bất phương trình log 2 2 x x 2 4 x 2
2x x 2 1 là a; b . 2 Khi đó . a b bằng 15 12 16 5 A. . B. . C. . D. . 16 5 15 12
Câu 2. Có bao nhiêu số nguyên x sao cho ứng với mỗi x có không quá 127 số nguyên y thỏa mãn log 2 x y log x y ? 3 2 A. 89 . B. 46 . C. 45 . D. 90 .
Câu 3. Bất phương trình 3
x 9xln x 5 0 có bao nhiêu nghiệm nguyên? A. 4. B. 7. C. 6. D. Vô số.
Câu 4. Tính tổng tất cả các nghiệm nguyên của bất phương trình log 2 x 3 2
log x x 4x 1 0 . 2 2 A. 4 . B. 6 . C. 5 . D. 3 . 2 2 x x 1
Câu 5. Bất phương trình log
x 2 x 1 có tập nghiệm là S ;
a b. Tính T 20a 10 . b 2 16x 3 A. T 45 10 2 . B. T 46 10 2 . C. T 46 11 2 . D. T 47 11 2 .
Câu 6. Tập nghiệm của bất phương trình 2x9 2 x x 1 3 9 .5
1 là khoảng a;b . Tính b a A. 6 . B. 3 . C. 8 . D. 4 . 2x 4x 4x 2 2 3 3 4 3 7 3 x 2 Câu 7. Bất phương trình có bao nhiêu nghiệm? 2 2 2 x x x 4x 2 2 3 2 3 3 4 3 2 3 x A. Vô số. B. 1. C. 2. D. 3
Câu 8. Số nghiệm nguyên thuộc đoạn 2 0; 2
0 của bất phương trình: 2x 1 x 2 2
9.2 4 x 2x 3 0 là A. 38 . B. 36 . C. 37 . D. 19 . 2
Câu 9. Tập hợp tất cả các số thực x không thỏa mãn bất phương trình x 4 2 x x2 9 4 .2019 1 là khoảng a;b. Tính b a. A. 5 . B. 4 . C. 5 . D. 1. 2
Câu 10. Tập nghiệm của bất phương trình x 9 2 x x 1 3 9 .5
1 là khoảng a;b. Tính b a . A. 6. B. 3. C. 8. D. 4.
Câu 11. Có bao nhiêu giá trị nguyên của x trong đoạn 0;2020 thỏa mãn bất phương trình sau 16x 25x 36x 20x 24x 30x . A. 3 . B. 2000 . C. 1. D. 1000 . x x 1
Câu 12. Tập nghiệm của bất phương trình 2 x 1 (3 9)(3 ) 3
1 0 chứa bao nhiêu số nguyên ? 27 A. 2. B. 3. C. 4. D. 5.
Câu 13. Tập nghiệm của bất phương trình 9x 2 5.3x x 92x 1 0 là A. 0; 1 2; . B. ; 1 2; . C. 1; 2. D. ; 02; .
Câu 14. Tập nghiệm của bất phương trình x2 x2 2.7 7.2
351. 14x có dạng là đoạn S ; a b. Giá trị b 2a
thuộc khoảng nào dưới đây? 2 49 A. 3; 10 . B. 4; 2 . C. 7;4 10 . D. ; . 9 5 1 Câu 15. Cho f x 2 x 1 .5 ; 5x g x 4 .
x ln 5 . Tập nghiệm của bất phương trình f x g x là 2 A. x 0 . B. x 1. C. 0 x 1. D. x 0 .
Câu 16. Bất phương trình x2 x2 2.5 5.2
133. 10x có tập nghiệm là S ;
a b thì biểu thức A 1000b 4a 1 có giá trị bằng 69 A. 3992 . B. 4008 . C. 1004 . D. 2017 . 1 11 x 1 2 2x 11
Câu 17. Số nghiệm nguyên thuộc khoảng 0;12 của bất phương trình 3 x 3 x log là: 2 2 x x 1 A. 7 . B. 8 . C. 5 . D. 11.
Câu 18. Tìm tất cả giá trị của tham số m để bất phương trình 2x 2 log 2 3 log x mx 1 có tập nghiệm R. A. 2 m 2 . B. m 2 2 . C. 2 2 m 2 2 . D. m 2 .
Câu 19. Xét các số nguyên dương a, b sao cho phương trình 2
a ln x b ln x 5 0 có hai nghiệm phân biệt x , x và phương trình 2
5log x b log x a 0 có hai nghiệm phân biệt x , x sao cho x x x x . Tìm giá trị 1 2 3 4 1 2 3 4
nhỏ nhất của S 2a 3b . A. 30 . B. 25 . C. 33 . D. 17 .
Câu 20. Cho x, y là hai số thực dương thỏa mãn 5x y 4 . Tổng tất cả giá trị nguyên của tham số m để 2 x 2y m phương trình 2 log
x 3x y m 1 0 có nghiệm là 3 x y A. 10. B. 5. C. 9. D. 2.
Câu 21. Có bao nhiêu cặp số nguyên x; y thỏa mãn 0 x 2020 và log 3 3 2 9y x x y ? 3 A. 2019 . B. 6 . C. 2020 . D. 4 .
Câu 22. Tồn tại bao nhiêu số nguyên dương n để 2n 3n 4n T là số chính phương A.3 B. 2 C. 1 D. 0
Câu 23. Có bao nhiêu số nguyên x sao cho tồn tại số thực y thỏa mãn log (x y) log 2 2 x y ? 3 4 A. 3 . B. 2 . C. 1. D. Vô số. x x
Câu 24. Tìm tập hợp các giá trị m để phương trình 42 3 2 3 m 3 0có 2 nghiệm phân biệt A.(7;8) B. (7;9) C. ; 3 D. ; 1 7;
Câu 25. Tìm tập hợp các giá trị m để phương trình 2
log 3x (m 2)log x m 2 có hai nghiệm phân biệt 3 3 1 thuộc ;3 3 A.(0;2) B. [0;2] C. [2;2) D. 2;
Câu 26. Tìm điều kiện tham số m để phương trình 2
log 3x (2m 2)log x 2m 2 có hai nghiệm phân biệt 3 3 thuộc [3;9] 3 3 3 3 A. 1; B. 1; C. 1; D. ; 2 2 2 2
Câu 27. Tính tổng các giá trị nguyên của m để phương trình 2 log 2020x (m 2)log x m 2 có hai 2020 2020 nghiệm phân biệt thuộc 2 1 ;2020 A.2 B. 4 C. 6 D. 3
Câu 28. Có bao nhiêu số nguyên m để phương trình 2 log x 3m log 3x 2
2m 2m 1 0 có hai nghiệm 3 3 phân biệt thuộc [1;3] A.2 B. 1 C. 0 D. 3
Câu 29. Có bao nhiêu số nguyên m để phương trình 2
2log x (m 4)log x 3m 2 0có hai nghiệm phân 3 3 biệt thuộc đoạn [1;3] A.2 B. 1 C. 3 D. 0
Câu 30. Tìm điều kiện tham số m để bất phương trình 9x 6x 2.4x .2x 3x 2x m nghiệm đúng x 0; 1 7 7 7 A. m B. m C. m D. Mọi giá trị m 2 2 4
Câu 31. Có tất cả bao nhiêu số nguyên x để tồn tại ít nhất một số thực y thỏa mãn
log 2x y log 2 2 x y 2 3 A.21 B. 20 C. 22 D. 23 70
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 37)
__________________________________________________
Câu 1. Có bao nhiêu số nguyên m 1
0;10 để phương trình log x 4 2
log x m có ba nghiệm phân 1 4 2 biệt A.5 B. 3 C. 11 D. 12 3 3
Câu 2. Tính tổng các giá trị nguyên m để phương trình 3x 1 8x30m x 6 x 1 0m 2m e e
e 1có 3 nghiệm phân biệt A.110 B. 106 C. 24 D. 126 2 Câu 3. Phương trình log5 x log5 x 2 3 2(m 3)3
m 3 0 có 2 nghiệm phân biệt mà tích hai nghiệm lớn hơn 5.
Số giá trị nguyên m thỏa mãn bài toán là A.2019 B. 2020 C. 2021 D. 2022 p
Câu 4. Cho p, q dương thỏa mãn log p log q log ( p q) . Tính . 16 20 25 q 5 1 5 1 A.1,6 B. 0,8 C. D. 2 2
Câu 5. Tập hợp a; bao gồm tất cả các giá trị m để phương trình sau có hai nghiệm phân biệt x , x thỏa 1 2
mãn 0 x 2 4 x 1 2 2
m ln (x 1) (x 2 m)ln(x 1) x 2 .
Khi đó a thuộc khoảng nào sau đây A.(3,8;3,9) B. (3,7;3,8) C. (3,6;3,7) D. (3,5;3,6)
Câu 6. Tìm số giá trị nguyên m 2
0;20 để phương trình sau có nghiệm log 2 2 x m x x 4 2
(2m 9)x 1 (1 2m) x 4 2 A.12 B. 23 C. 25 D. 0
Câu 7. Có bao nhiêu số nguyên a thuộc [0;2020] để ứng với mỗi giá trị a tồn tại số thực a để ba số sau theo thứ a
tự lập thành một cấp số cộng: x 1 1 5 5 x; ; 25x 25x 2 A.2007 B. 2009 C. 2010 D. 2008 2 2 2 Câu 8. Phương trình x 2 x x 2 x 1 2 x 4 x2 9.9 (2m 1).15 (4m 2).5
0có đúng hai nghiệm phân biệt khi
m a;bvới a là phân số tối giản. Tính 2a + b. A.2 B. 0 C. 1 D. 3
Câu 9. Có bao nhiêu cặp số nguyên dương (x;y) với y không vượt quá 1000 thỏa mãn x 1 4 3 2 2 2 log 9y 6y x y 2xy 3y 1 A.1501100 B. 1501300 C. 1501400 D. 1501500
Câu 10. Có bao nhiêu cặp số nguyên (x;y) với x 0;2020thỏa mãn 39y 2y 3 x log (x 1) 2 3 A.2 B. 4 C. 5 D. 3 m ln x 2 Câu 11. Hàm số y
có tổng giá trị lớn nhất, giá trị nhỏ nhất trên miền [1;e] bằng 2. Khi đó ln x 1 A.0 < m < 10 B. 6 < m < 11 C. m + 2 < 0 D. 0 m 2 2
Câu 12. Tổng tất cả các giá trị của m sao cho phương trình x 1 2 .log 2
x 2x 3 4 xm.log 2 x m 2 có 2 2
đúng ba nghiệm phân biệt là: 3 A. 2. B. . C. 0. D. 3. 2
Câu 13. Có bao nhiêu cặp số nguyên dương ,
m n sao cho m n 14 và ứng với mỗi cặp , m n tồn tại đúng
ba số thực a 1; 1 thỏa mãn m a n 2 2 ln a a 1 ? A. 14 . B. 12 . C. 11. D. 13 .
Câu 14. Cho phương trình 5x m log x m . Có bao nhiêu giá trị m nguyên trong khoảng 2 0;20 để 5
phương trình trên có nghiệm? 71 A. 15 . B. 19 . C. 14. D. 17 . Câu 15. Cho phương trình 2
log x 2 log x 4 1 log x m , với m là tham số thực. Số các giá trị nguyên 2 2 2 thuộc đoạn 2
019;2019 của m để phương trình đã cho có nghiệm là A. 2021. B. 2024. C. 2023. D. 2020. 9
Câu 16. Tìm hai chữ số tận cùng của số 9 9 A.19 B. 89 C. 81 D. 49 3 2
Câu 17. Tìm số nghiệm của phương trình x 2x 3x x 1 2 .3 1 A.2 B. 1 C. 0 D. 3 3 2
Câu 18. Có bao nhiêu số nguyên dương m < 100 để phương trình x 2x 3x 3x 1 2 .3 5 có nghiệm ? A.4 B. 99 C. 36 D. 45 Câu 19. Cho 2a 3; 3b 4; 4c 5; 5d 6 . Tính 2abcd . A.2 B. 6 C. log 6 D. log 2 2 6
Câu 20. Tìm số nguyên dương n để các số viết dạng thập phân của 2n;5n đứng cạnh nhau ta được số tự nhiên có 2012 chữ số. A.n = 2012 B. n = 2010 C. n = 2011 D. n = 2009 1 1 1
Câu 21. Cho ba số thực x, y, z khác 0 thỏa mãn 2x 5y 10z . Tính . x y z A.3 B. 0 C. 1 D. 3 a b
Câu 22. Cho a, b, c dương thỏa mãn 2018a 2019b 2020c . Tính b c A. log 2019 B. log 2019 log 2020 2018 2018 2019 C. log 2020 log 2020 D. log (2019.2020) 2018 2019 2018 2 2 2
Câu 23. Có bao nhiêu số tự nhiên m bốn chữ số để phương trình sin x cos x cos 2017 20018 .2019 x m có nghiệm A.1019 B. 1018 C. 2018 D. 2019
Câu 24. Có bao nhiêu số nguyên dương n để 2n 1là một số chính phương A.3 B. 2 C. 4 D. 1
Câu 25. Có bao nhiêu số nguyên dương m để hệ phương trình sau có nghiệm 3x5 y 1 0 x3 y9 e e 1 2x 2y 2 2
log (3x 2y 4) (m 6)log (x 5) m 9 0 5 5 A.3 B. 4 C. 5 D. 6
Câu 26. Có bao nhiêu giá trị nguyên m để phương trình 2
log x 4log x m 3 có hai nghiệm phân biệt đều 3 3 lớn hơn 1 A.6 B. 4 C. 3 D. 5
Câu 27. Có bao nhiêu số nguyên m 2020;2020 để phương trình sau có đúng hai nghiệm
3x 4m 1.log x xm 1 4 2 21 2m 0 2 A.7 B. 2011 C. 8 D. 2012
Câu 28. Có bao nhiêu số nguyên x sao cho ứng với mỗi x có không quá 255 số nguyên y thỏa mãn log 2 x y log x y ? 3 2 A. 80 . B. 79 . C. 157 . D. 158 m 1
Câu 29. Tìm tập hợp tất cả các giá trị m để hàm số y ln(3x 1) 2 nghịch biến trên ;3 x 2 27 4 3 4 27 1 A. ; B. ; C. ; D. ; 8 3 2 3 8 2 mx
Câu 30. Cho hàm số f (x) log
. Với mọi số thực a, b thuộc (0;2) có tổng bằng 2 ta có 2 2 x
f (a) f (b) 3. Số giá trị m thỏa mãn là A.0 B. 1 C. 2 D. 3 72
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 38)
__________________________________________________
Câu 1. Tìm điều kiện tham số m để phương trình 2
(3x 5)log x m (9x 19)log x m 12 có nghiệm 3 3 thuộc 2; . 53 53 A. ; B. ;79 C. 79; D. ; 79 27 27 5x 2
Câu 2. Tìm điều kiện tham số m để hàm số y đồng biến trên ; 0 5x m A. m 2 B. m 2 C. 2 m 1 D. 2 m 1
Câu 3. Có bao nhiêu số nguyên dương m để bất phương trình 2 2
log x log x 3 m 2 log x 3 có 2 1 4 2
nghiệm duy nhất không nhỏ hơn 32 A.0 B. 2 C. 1 D. 3
Câu 4. Tìm điều kiện tham số m sao cho bất phương trình log log 3x 1 log m đúng x 0 0,02 2 0,02 A.m < 2 B. 0 < m < 1 C. m > 1 D. m 1
Câu 5. Có bao nhiêu giá trị nguyên thuộc (1;2018) của a sao cho phương trình sau có nghiệm lớn hơn 3 log 2 x x 1.log 2
x x 1 log x x a 2 1 2 2017 A.20 B. 17 C. 19 D. 18
Câu 6. Gọi m là giá trị nhỏ nhất để bất phương trình sau có nghiệm 0 x
1 log 2 x 2log m 4 2 x 2x 2 log x 1 2 2 2 2 Khi đó m thuộc miền 0 A.(9;10) B. (8;9) C. 10; 9 D. 9;8 x x
Câu 7. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình 2 1 m 2 1 8 có
hai nghiệm dương phân biệt. Số phần tử của S bằng A. 8. B. 7. C. 10. D. 9. 2 2 x x
Câu 8. Tìm số giá trị nguyên của tham số 2
m 10;10 để phương trình m x 1 10 1 10 1 2.3 có
đúng hai nghiệm phân biệt? A. 14 . B. 15 . C. 13 . D. 16 . x x
Câu 9. Cho phương trình 4 15 2m
1 4 15 6 0 ( m là tham số ). Biết phương trình có hai
nghiệm phân biệt x , x thỏa mãn x 2x 0 . Khi đó m thuộc khoảng nào sau đây? 1 2 1 2 A. 3;5 . B. 1 ; 1 . C. 1;3 . D. ; 1 .
Câu 10. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình 5x 10 25x m 4 có
nghiệm duy nhất. Số tập con của S là A.8 B. 16 C. 32 D. 4 3 2 2
Câu 11. Cho phương trình: x x 2xm x x 3 2 2
x 3x m 0 . Tập các giá trị để bất phương trình có ba nghiệm
phân biệt có dạng a;b . Tổng a 2b bằng: A. 1. B. 2. C. 4. D. 0.
Câu 12. Có bao nhiêu số nguyên m để phương trình 2 9.3 x 4 2 4 2 1 3 33x m x x m 1 0 có đúng 3 nghiệm thực phân biệt? A. Vô số. B. 3. C. 1. D. 2.
Câu 13. Cho phương trình 2 2 log log 1 5x x x
m 0 ( m là tham số thực). Có tất cả bao nhiêu giá trị 3 3
nguyên dương của m để phương trình đã cho có đúng hai nghiệm phân biệt? A. Vô số. B. 124. C. 123. D. 125. 73 sin( x )
Câu 14. Tính tổng tất cả các nghiệm của phương trình 4 e
tan x thuộc đoạn 0;50 2671 1853 2475 2653 A. . B. . C. . D. . 2 2 2 2
Câu 15. Có bao nhiêu giá trị nguyên m 2
019;2020 sao cho hệ phương trình sau có nghiệm 2 x y 2 x y 2 2 2 2 yx 2 4 9.3 4 9 .7 ? 2x 1 2y 2x m A. 2017 . B. 2021. C. 2019 . D. 2020 .
Câu 16. Cho phương trình 5x m log x m với m là tham số. Có bao nhiêu giá trị nguyên của 5 m 2
0;20 để phương trình đã cho có nghiệm? A. 19 B. 9 C. 21 D. 20 2 2
Câu 17. Tổng tất cả các giá trị của tham số m để phương trình x 4x5m 2 2 log m 1 có đúng 1 2 x 4 x6 nghiệm là A. 2 . B. 1. C. 4 . D. 0 .
Câu 18. Có bao nhiêu cặp số nguyên dương ;
m n sao cho m n 10 và ứng với mỗi cặp ; m n tồn tại đúng
3 số thực a 1; 1 thỏa mãn m a n 2 2 ln a a 1 ? A. 7 . B. 8 . C. 10 . D. 9 .
Câu 19. Giả sử a,b là các số thực sao cho 3 3 3z 2 .10 .10 z x y a b
đúng với mọi các số thực dương x, y, z
thỏa mãn log(x y) z và 2 2
log(x y ) z 1. Giá trị của a b bằng 25 31 31 29 A. . B. . C. . D. . 2 2 2 2
Câu 20. Cho phương trình log x x x
, gọi S là tập hợp tất cả các giá trị nguyên m mx 2 6 12 log 2 5 mx5
để phương trình đã cho có nghiệm duy nhất. Tìm số phần tử của S . A. 2 . B. 0 . C. 3 . D. 1.
Câu 21. Tìm tất cả các giá trị của tham số thực m để phương trình 4log x 2 log x m 0 có hai nghiệm 2 1 2
phân biệt thuộc khoảng 0; 1 . 1 1 1 1 A. 0 m B. 0 m C. m D. m 0 4 4 4 4 x
Câu 22. Có bao nhiêu giá trị của tham số m để phương trình 2 4 log x m log
2 0 có hai nghiệm phân 36 6 6
biệt x , x thỏa mãn x .x 72 x .x 1296 0 1 2 1 2 1 2 A. 0. B. 1. C. 2. D. 3.
Câu 23. Tính a + b với [a;b) là tập hợp giá trị m để phương trình x mx 2 ln 3 1
ln x 4x 3 có nghiệm. 10 22 A. . B. 4. C. . D. 7. 3 3
Câu 24. Cho a,b là các số thực dương lớn hơn 1, thay đổi thỏa mãn a b 2019 để phương trình 5log .
x log x 4log x 3log x 2019 0 luôn có hai nghiệm phân biệt x ; x . Biết giá trị lớn nhất của a b a b 1 2 3 m 4 n ln x .x bằng ln ln
; với m, n là các số nguyên dương. Tính S m 2n 1 2 5 7 5 7 A. 22209 . B. 20190 . C. 2019 . D. 14133 .
Câu 25. Biết rằng điều kiện cần và đủ của tham số m để phương trình log 2x m m 2x có nghiệm là 2 a
m với a,b là hai số nguyên dương và b 7 . Hỏi 2
a b b bằng bao nhiêu? b A. 31. B. 32 . C. 21 . D. 23 .
_________________________________ 74
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 39)
__________________________________________________
Câu 1. Tìm tất cả các giá trị của tham số m để phương trình 2
x x m 2x x m 2 2 2 1 2 x 4 x2 4.4 2 2 6 6 3 3 0 có
hai nghiệm thực phân biệt.
A. 4 3 2 m 4 3 2
B. m 4 3 2 hoặc m 4 3 2 1 1 C. m 1 hoặc m D. 1 m 2 2
Câu 2. Có tất cả bao nhiêu số nguyên m để phương trình 4x .2x m
2m 2019 0 có hai nghiệm trái dấu? A. 1008 . B. 1007 . C. 2018 . D. 2017 . x x
Câu 3. Cho phương trình 4 15 2m
1 4 15 6 0 . Để phương trình có hai nghiệm phân biệt
x , x thỏa mãn x 2x 0 . Ta có m thuộc khoảng nào? 1 2 1 2 A. 3;5 . B. 1 ; 1 . C. 1;3 . D. ; 1 .
Câu 4. Có bao nhiêu cặp số nguyên dương (x;y) thỏa mãn 2 4 3x y 1 A.2 B. 1 C. 3 D. 4 x x
Câu 5. Phương trình 2 3 1 2a2 3 4 0 có 2 nghiệm phân biệt x , x thỏa mãn 1 2 x x log
3 . Khi đó a thuộc khoảng 1 2 2 3 3 3 3 A. ; . B. 0; . C. ; . D. ; . 2 2 2
Câu 6. Biết rằng m m là giá trị của tham số 9x 2 2 1 3x m 3 4m 1 0 có hai 0 m sao cho phương trình
nghiệm thực x , x thỏa mãn x 2 x 2 12 . Khi đó m thuộc khoảng nào sau đây 1 2 1 2 0 A. (3;9) . B. 9; + . C. 1;3 . D. -2;0 . 1 x 1 x Câu 7. Phương trình . m 2m 1 0
có nghiệm khi m nhận giá trị: 9 3 1 1 A. m . B. m 4 2 5 . 2 2 1 C. m 4 2 5 .
D. m m 4 2 5 . 2
Câu 8. Số các giá trị nguyên của tham số m để phương trình: 1.16x 2 2 3.4x m m 6m 5 0 có hai nghiệm trái dấu là A. 4 . B. 8 . C. 1. D. 2 .
Câu 9. Phương trình 4x 1 2 .x .
m cos( x) có nghiệm duy nhất. Số giá trị của tham số m thỏa mãn là A. Vô số B. 1 C. 2 D. 0
Câu 10. Cho phương trình 2x .2x
m .cos x 4 , với m là tham số. Gọi m là giá trị của m sao cho phương 0
trình trên có đúng một nghiệm thực. Khẳng định nào sau đây là đúng? A. m 5 ; 1 . m 5 . m 1 ;0 . m 0. 0 B. C. 0 D. 0 0
Câu 11. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m sao cho phương trình x x 1 2 16 . m 4
5m 44 0 có hai nghiệm đối nhau. Hỏi S có bao nhiêu phần tử? A. 2 . B. 0 . C. 1. D. 3 .
Câu 12. Tìm tất cả các giá trị thực của tham số m để phương trình 3m m e e 2 x x 2 2 1 1 x 1 x có nghiệm. 1 1 1 1 A. 0; . B. 0; ln 2 . C. ; ln 2 . D. ln 2; . e 2 2 2 2 2 x x
Câu 13. Tìm số giá trị nguyên của tham số m 1
0;10 để phương trình m 2 x 1 10 1 10 1 2.3 có
đúng hai nghiệm phân biệt. A. 14. B. 15. C. 13. D. 16 . 75
Câu 14. Tìm hai chữ số tận cùng của số 1000 2 A.76 B. 32 C. 92 D. 84 3
Câu 15. Tổng tất cả các giá trị nguyên của m để phương trình x3 m3x 3 2 x3 3 9 24 .3 3x x x x m 1 có 3 nghiệm phân biệt. A. 34 . B. 27 . C. 38 . D. 45 . Câu 16. Cho hàm số x4 7 3 1 .2 x f x x
– 6x 3 , khi phương trình f 2
7 4 6x 9x 3m 1 0 có số a a
nghiệm nhiều nhất thì giá trị nhỏ nhất của tham số m có dạng (trong đó a,b và là phân số tối giản). b b Tính T a b . A. T 7 . B. T 11. C. T 8. D. T 13 . 2 2
Câu 17. Có bao nhiêu giá trị nguyên của tham số m để phương trình 1 1x 1 1 9 3 .3 x m 2m 1 0 có nghiệm thực? A. 5 . B. 7 . C. Vô số. D. 3 .
2xy 2y x 2y
Câu 18. Cho hệ phương trình
, m là tham số. Gọi S là tập các giá trị m 2x 1 1 2 m 2 y 2 .2 . 1 y nguyên để hệ
1 có một nghiệm duy nhất. Tập S có bao nhiêu phần tử? A. 0 . B. 1. C. 3 . D. 2 .
Câu 19. Có bao nhiêu giá trị nguyên của tham số m 2
019;2019 để phương trình x mx m x 2 1 2 1 2019
0 có đúng 3 nghiệm thực phân biệt? x 1 x 2 A. 4038. B. 2019. C. 2017. D. 4039.
Câu 20. Có bao nhiêu cặp số nguyên x; y thỏa mãn 0 y 2020 và x 3
3 3x 6 9y log y . 3 A. 2020 B. 9. C. 7 . D. 8 .
Câu 21. Gọi S là tập hợp các giá trị của tham số m sao cho hai phương trình 2 2 1 3m x và x 2
m 3 2x x 1 có nghiệm chung. Tính tổng các phần tử của S. 5 A. 6 B. 3 . C. 1. D. . 2 2 2
Câu 22. Tìm điều kiện của tham số a để phương trình sau có nghiệm: 1 1x 1 1 9 2 .3 x a 2a 1 0. Hãy
chọn đáp án đúng nhất? 64 64 50 50 A. 4 a . B. 2 a . C. 3 a . D. 1 a . 7 9 3 3
Câu 23. Cho phương trình 2 4log log 5 7x x x
m 0 ( m là tham số thực). Có tất cả bao nhiêu giá trị 2 2
nguyên dương của m để phương trình đã cho có đúng hai nghiệm phân biệt? A. 49 . B. 47 . C. Vô số. D. 48 .
Câu 24. Cho phương trình 5x m log
x m 0 với m là tham số. Có bao nhiêu giá trị nguyên của tham số 1 5 m 2
0;20 để phương trình đã cho có nghiệm thực? A. 20 . B. 21 . C. 18 . D. 19 .
Câu 25. Có bao nhiêu cặp số nguyên dương (m, n) sao cho m n 12 và ứng với mỗi cặp (m, n) tồn tại đúng 3
số thực a (1,1) thỏa mãn m 2 2a n ln(a a 1) ? A. 12 . B. 10 . C. 11. D. 9 .
Câu 26. Tìm hai chữ số cuối cùng của 106 2012 41 57 A.94 B. 42 C. 36 D. 58
Câu 27. Có tất cả bao nhiêu giá trị m 1 ; 1 sao cho phương trình 2 2 log x y log 2x 2 y 2 có 2 m 1 2 nghiệm nguyên ; x y duy nhất? A. 3 . B. 2 . C. 1. D. 0 .
_________________________________ 76
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 40)
__________________________________________________
Câu 1. Tập hợp các giá trị thực của tham số m để phương trình log 2 4 x log 2x m 1 0 có hai 2019 1 2019
nghiệm thực phân biệt là T ;
a b . Tính S 2a b . A. 18 . B. 8 . C. 20 . D. 16 .
Câu 2. Có bao nhiêu số nguyên m để phương trình log x 3 m log
9 16 có hai nghiệm thỏa mãn 3 x3 2 x x . 1 2 A. 17 . B. 16. C. 14 . D. 15.
Câu 3. Tìm tất cả các giá trị của tham số a để phương trình 2 3
log x a log x a 1 0 có nghiệm duy nhất. 3 3 A. Không tồn tại a . B. a 1 hoặc a 4 2 10 . C. a 1. D. a 1.
Câu 4. Gọi m là giá trị nhỏ nhất của m sao cho phương trình sau có nghiệm thuộc 2; 4 0 m 2 1 log x 2 m 5 log x 2 m 1 0 1 1 2 2
Khẳng định nào dưới đây đúng? 4 10 16 5 A. m 1; . B. m 2; . C. m 4; . D. m 5 ; . 0 3 0 3 0 3 0 2
Câu 5. Tìm các giá trị thực của tham số m để phương trình 2
log x 3log x 2m 7 0 có hai nghiệm thực x , 3 3 1
x thỏa mãn x 3 x 3 72 . 1 2 2 9 61 A. m . B. m 3 . C. Không tồn tại. D. m . 2 2
Câu 6. Số các giá trị nguyên nhỏ hơn 2020 của tham số m để phương trình log 2020x m log 1010x 6 4 có nghiệm là A. 2022 . B. 2020 . C. 2019 . D. 2021.
Câu 7. Có bao nhiêu số nguyên m để phương trình x x 2 x x x 3 m 3 8 3 .4 3 1 .2 1 x m 1 x có đúng
hai nghiệm phân biệt thuộc 0;10 . A. 101 B. 100 C. 102 D. 103
Câu 8. Tìm tất cả các giá trị thực của tham số m để phương trình 3m m e e 2 x x 2 2 1 1 x 1 x có nghiệm. 1 1 1 1 A. 0; ln 2 B. ; ln 2 C. 0; D. ln 2; 2 2 e 2
Câu 9. Gọi A là tập tất cả các giá trị thực của tham số m sao cho tập nghiệm của phương trình .2x 1 .2x x x x m m
1 có hai phần tử. Số phần tử của A bằng A. 2. B. 3. C. 1. D. Vô số.
Câu 10. Giá trị của m để phương trình x x 1 4 2
m 0 có nghiệm duy nhất là: A. m 2 . B. m 0. C. m 1. D. m 1 .
Câu 11. Gọi S là tổng các giá trị nguyên của tham số m để phương trình x x3 2 4 7 2 m 6m có nghiệm
x 1;3 . Chọn đáp án đúng. A. S 3 5. B. S 20 . C. S 25 . D. S 2 1. 2 2
Câu 12. Tập các giá trị của m để phương trình 1 1x 1 1 4 2 2 x m
2m 1 0 có nghiệm là 9 9 A. ; . B. 4; . C. ;4 . D. 4; . 2 2
Câu 13. Có bao nhiêu số nguyên a trên đoạn 1
0;10 để phương trình xa x e
e ln 1 x a ln1 x có nghiệm duy nhất. A. 2 . B. 10 . C. 1. D. 20 77
Câu 14. Có bao nhiêu số nguyên m thuộc 2
020;2020 để phương trình x
e ln x 2m 2m có nghiệm? A. 2019 . B. 2020 . C. 2021 . D. 4039 .
Câu 15. Có bao nhiêu giá trị nguyên của m để phương trình log mx log x 1 vô nghiệm? 2 2 A. 4 . B. 6 . C. 3 . D. 5 .
Câu 16. Số các giá trị nguyên nhỏ hơn 2020 của tham số m để phương trình log 2020x m log 1010x 6 4 có nghiệm là A. 2020. B. 2021. C. 2019. D. 2022. Câu 17. Cho phương trình 2 log x5m 2
1 log x 4m m 0 . Biết phương trình có 2 nghiệm phân biệt 2 2
x ,x thỏa x x 165. Giá trị của x x bằng 1 2 1 2 1 2 A. 16. B. 119 . C. 120. D. 159 . x x Câu 18. Gọi ;
a b là tập hợp tất cả các giá trị thực của tham số m để phương trình 2
2e 8e m 0 có đúng
hai nghiệm thuộc khoảng 0;ln
5 . Giá trị của tổng a b là A. 2 . B. 4 . C. 6 . D. 1 4.
Câu 19. Giả sử x ; y là một nghiệm của phương trình x 1 x x 1 y x x 1 4 2 sin 2 1 2 2 2sin 2 y 1 . 0 0
Mệnh đề nào sau đây đúng? A. x 7 . B. 2 x 4 . C. 4 x 7 . D. 5 x 2 . 0 0 0 0
Câu 20. Giá trị của tham số m thuộc khoảng nào sau đây để phương trình x x 1 4 . m 2 2m 0 có hai nghiệm
x , x thoả mãn x x 3 . 1 2 1 2 9 A. m ;5 . B. m 2 ; 1 . C. m 1;3 . D. m 3;5 . 2 x 1
Câu 21. Cho a, b là các số thực thỏa mãn a 0 và a 1, biết phương trình a 2 cos bx có 7 nghiệm x a
phân biệt. Tìm số nghiệm thực phân biệt của phương trình 2x 2 x a
a cosbx 2 1 0 . A. 28 . B. 14 . C. 0 . D. 7 .
Câu 22. Tìm tập hợp các giá trị m để phương trình 6x 3 2x m
m 0 có nghiệm thuộc khoảng 0; 1 . A. 3;4. B. 2; 4. C. 2; 4. D. 3;4. 2
Câu 23. Tìm tập hợp các giá trị của tham số m để phương trình (ẩn x ): log2 x m log2 x 2 3 2 3 .3 m 3 0 có
hai nghiệm phân biệt thỏa mãn: x x 2 . 1 2 A. 1; \ 0 . B. 0; . C. \ 1 ; 1 . D. 1 ; .
Câu 24. Cho phương trình 2 2log log 1 4x x x
m 0 ( m là tham số thực). Có tất cả bao nhiêu giá trị 3 3
nguyên dương của m để phương trình có đúng hai nghiệm phân biệt? A. 64 . B. Vô số. C. 62 . D. 63.
Câu 25. Cho phương trình 7x m log x m với m là tham số. Có bao nhiêu giá trị nguyên của 7 m 2
5;25 để phương trình đã cho có nghiệm? A. 9 B. 25 C. 24 D. 26 2
Câu 26. Tổng tất cả các giá trị của tham số m để phương trình x 2x 1 2 3 xm log 2 x m 2 có đúng 2 x 2 x3 ba nghiệm phân biệt là: A. 2 . B. 3 . C. 1. D. 0 .
Câu 27. Có bao nhiêu số nguyên y để tồn tại số thực x thỏa mãn log 3x 4y log 2 2 x y ? 11 4 A. 3 B. 2 C. 1 D. vô số. 2 x 2x3 l og 5
Câu 28. Có bao nhiêu cặp số thực ;
x y thỏa mãn đồng thời các điều kiện 3 y4 3 5 và y y y 2 4 1 3 8 ? A. 1. B. 3 . C. 4 . D. 2 .
_________________________________ 78
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 41)
__________________________________________________ 2 2
Câu 1. Tính tổng các giá trị m để phương trình x 4 x 4 2 25 (m 3)5
m 9m có hai nghiệm phân biệt A.10 B. 2 C. 3 D. 4
Câu 2. Tìm tập hợp các giá trị m để phương trình ln(1 2x m
) x m có nghiệm âm A. ln 2; B. 0; C. (1;e) D. ; 0
Câu 3. Có bao nhiêu số nguyên m để phương trình 2
log (2x m) 2log x x 4x 2m 1có hai nghiệm 2 2 thực phân biệt A.2 B. 3 C. 1 D. 4
Câu 4. Tìm điều kiện tham số m để phương trình sin x 5 cos x m 5 3 log m 5 có nghiệm sin x 5 cos x 1 0 A. m 6 B. m 5 C. m 5 6 D. 6 m 5
Câu 5. Tìm tổng 8 chữ số tận cùng của 1995 5 . A.38 B. 26 C. 40 D. 14 2 2
Câu 6. Tính tổng các giá trị m để phương trình x 4x5m 2 2 log
(m 1) có đúng một nghiệm 2 x 4 x6 A.1 B. 0 C. – 2 D. 4 2 1 2x 4x 6
Câu 7. Tính tổng các giá trị m để phương trình 2 log
x 2 x x m có đúng ba nghiệm 2 2 x m 1 phân biệt A.2 B. 3 C. 1 D. 0
Câu 8. Có bao nhiêu số nguyên m 2
019;2để phương trình sau có đúng hai nghiệm
x 1log 4x 1 log 2x 1 2x m 3 5 A.2 B. 2022 C. 1 D. 2021 2
Câu 9. Tính tổng các giá trị m để phương trình x 2x 1 2 3 xm log
2 x m 2 có đúng ba nghiệm phân 2 x 2 x3 biệt A.3 B. – 2 C. – 3 D. 2
Câu 10. Có bao nhiêu cặp số tự nhiên (x;y) sao cho (2 1)(3 2) 100y x x A.2 B. 1 C. 3 D. 4 Câu 11. Cho hàm số 2
f (x) ln(x x 1) . Có bao nhiêu số nguyên m thỏa mãn 1 f (log m) f log 0 m 2019 A.65 B. 66 C. 64 D. 63
Câu 12. Tính tổng các giá trị m để 2 m 4 x 2 ln
16 3m(ln x 4) 14(ln x 2) 0 đúng với mọi x không âm 3 7 A.0,5 B. – 2 C. D. 8 8
Câu 13. Đoạn [a;b] bao gồm tất cả các giá trị m để bất phương trình sau nghiệm đúng x 0;2 2 2 log
x 2x m 4 log (x 2x m) 5 2 4 Tính a + b. A.4 B. 2 C. 0 D. 6 2 3ln x 2ln x 12
Câu 14. Có bao nhiêu số nguyên m để bất phương trình
2 nghiệm đúng x 0 2 ln x (m 1) ln x 4 A.4 B. 5 C. 3 D. 7
Câu 15. Tồn tại bao nhiêu cặp số tự nhiên (x;y) để 3 4 5x(x 4) 2 y . A.1 B. 2 C. 3 D. 0 79 3 (xyz)
Câu 16. Có bao nhiêu bộ số nguyên (x;y;z) để 5 5 5 x y z và là số nguyên. 125 A.Vô số B. 4 C. 5 D. 1
Câu 17. Tìm số cặp số nguyên (x;y) thỏa mãn 2 4 x 27y 7 . A.3 B. 1 C. 2 D. 0 Câu 18. Phương trình 2 sin 100 x x
có bao nhiêu nghiệm 2 ;3 A.1 B. 2 C. 3 D. 4
Câu 19. Có bao nhiêu cặp số (x;y) sao cho y nguyên thuộc 2 023;202 3 thỏa mãn log 5 2x y y 5 2x 2 A.2019 B. 2021 C. 4041 D. 2021 2
ln x mln x m 4 0
Câu 20. Hệ bất phương trình x 3 có nghiệm khi 0 2 x m 6 A. B. m 3 C. m 3 D. m 6 m 3
Câu 21. Có bao nhiêu cặp số nguyên (x;y) thỏa mãn 2xy 4 x y7 (4 7 )(2 1)(
) 2 (2 ) 7 y xy y x e e x y y e A.5 B. 6 C. 7 D. 8 1 2
Câu 22. Có bao nhiêu số nguyên y sao cho x ;3 thỏa mãn 3x xy 9 27 (1 ).27 x xy 3 A.27 B. 9 C. 11 D. 12
Câu 23. Có bao nhiêu số nguyên y 2027 sao cho với mỗi giá trị của y tồn tại nhiều hơn hai số thực x thỏa 2 mãn điều kiện 2 2 x y 2 ( )2027 (2 )2027xx x y x x x x y . A.2026 B. 2027 C. 2028 D. 2029
Câu 24. Có bao nhiêu cặp số nguyên dương (x;y) thỏa mãn log x, log y ,log x,log y đều là số nguyên đồng thời
log x log y log x log y 100 A.3 B. 2 C. 0 D. 1
Câu 25. Có bao nhiêu giá trị nguyên z để có đúng hai bộ (x;y;z) thỏa mãn 2 2 3 3
log (2x y ) log (x 2 y ) log z 3 7 A.2 B. 211 C. 99 D. 4
Câu 26. Tính a b khi phương trình 2 2
log x (5m 1)log x 4m m 0có hai nghiệm phân biệt a, b với 2 2 tổng bằng 165. A.16 B. 119 C. 120 D. 159
Câu 27. Có bao nhiêu số nguyên m để phương trình log (x 3) m log
9 16 có hai nghiệm phân biệt lớn 3 x3 hơn – 2 A.17 B. 16 C. 14 D. 15 2
Câu 28. Có bao nhiêu số nguyên m nhỏ hơn 30 để phương trình x x2 2 .7 m có nghiệm. A.17 B. 16 C. 12 D. 10
Câu 29. Có bao nhiêu số nguyên dương m để phương trình x 1 x 1 2.4 5.2 m 0 có nghiệm A.3 B. 0 C. 1 D. 4 2 x2m
Câu 30. Tìm tập nghiệm S của phương trình x 1
3 .5 xm 15 với m khác 2 là A. 2;m log 5 B. 2;m log 5 C. 2 D. 2;m log 5 3 3 3
Câu 31. Tìm số nghiệm của phương trình x 2 3 5
2025 x 2023 2024 2025 A.1 B. 2 C. 3 D. 4
_______________________________ 80
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 42)
__________________________________________________ 2 2
Câu 1. Tính tổng tất cả các nghiệm của phương trình sin x cos 2017
2017 x cos 2x trên 0; 3 A. B. C. D. 4 2 4 2
Câu 2. Tính tổng lập phương hai nghiệm của phương trình x 1 2 x 1 3 (x 1)3 1là A.2 B. 0 C. 8 D. – 8
Câu 3. Tồn tại bao nhiêu giá trị m để phương trình .2x ( 1) (2x x x x m m
1) có hai nghiệm phân biệt A.1 B. 3 C. 2 D. Vô số y
Câu 4. Có bao nhiêu cặp số nguyên (x;y) thỏa mãn log x 2x 5 2 2 8 2 2 y 8y 7 4 A.6 B. 1 C. 2 D. 3 2
Câu 5. Có bao nhiêu cặp số nguyên (x;y) thỏa mãn 4 2 y 2019 log (x 2x 2020) 2y 2018 2019 A.1 B. 2 C. 3 D. 0
Câu 6. Có bao nhiêu cặp số nguyên (x;y) thỏa mãn log 2 2
x y 4 log x 2y 1; 2x y 2 2 A.2 B. 5 C. 4 D. 3
Câu 7. Tính tổng các nghiệm phương trình x 1 x 1 2 x(2 4) 2 x A.5 B. 3 C. 6 D. 7 2 2
Câu 8. Tìm số nghiệm phương trình 2 2 x 3x6 2 x x3
2x 2x 9 (x x 3).8 (x 3x 6).8 A.1 B. 3 C. 2 D. 4 2
Câu 9. Tìm số nghiệm của phương trình 2 x 3x 2 x3 2 2014 2024
2x 3x x 1 0 là A.3 B. 0 C. 1 D. 2
Câu 10. Tổng lập phương tất cả các nghiệm thực của phương trình x x 1 15 . x 5 5 27x 23 A.5 B. 6 C. 8 D. 0 2 2
Câu 11. Tìm số nghiệm của phương trình x 2024 x 2023 2 2 e . x 2023 x 2024 A.0 B. 2 C. 4 D. 1 2 2 2 cos x 2 cos 2024 2024 2024 x
Câu 12. Tính tổng các nghiệm phương trình cos 2 . x 643 643 643 3 A. x B. x C. x D. x 4 2 4
Câu 13. Hỏi phương trình 2 3
3x 6x ln(x 1) 1 0 có bao nhiêu nghiệm phân biệt A.2 B. 1 C. 3 D. 4
Câu 14. Tổng S gồm các giá trị nguyên m để phương trình x x3 2 4 7 2
m 6m có nghiệm 1;3 là A.20 B. 25 C. – 21 D. – 35
Câu 15. Tính tổng các giá trị m sao cho hai phương trình 2 m 2 2 2x 1 3 ;
m 3x 2x x 1có nghiệm chung A.6 B. 3 C. 1 D. 2,5
Câu 16. Có bao nhiêu số nguyên dương a nhỏ hơn 2021 để tồn tại số nguyên x thỏa mãn a x3 2 a a a x3 2 2 1 2 2 1 A.12 B. 15 C. 10 D. 14
Câu 17. Có bao nhiêu cặp số nguyên dương (x;y) với x 2024 thỏa mãn xy 2 y 3 3
x (3x 1) (x 1).3 x A.13 B. 15 C. 6 D. 7
Câu 18. Có bao nhiêu cặp số nguyên (x;y) với 0 x 2021 thỏa mãn log ( 1) 3 1 27y x x y 3 A.2021 B. 2020 C. 4 D. 3
Câu 19. Có bao nhiêu số nguyên x để tồn tại số thực y thỏa mãn log x y log 2 2 x 2y 3 4 A.3 B. 2 C. Vô số D. 1
Câu 20. Có bao nhiêu số nguyên dương x để tồn tại số nguyên dương y thỏa mãn điều kiện 81 1 log (2 2 1)( 2 ) x y x 2 3.9 27 y x y x y 1. 3 A.3 B. 2 C. 0 D. 1
Câu 21. Có bao nhiêu số nguyên x sao cho tồn tại số thực y thỏa mãn log 2x y log 2 2 4x y 5 6 A.1 B. 0 C. 2 D. 3
Câu 22. Có bao nhiêu cặp số nguyên (x;y) với x 2;2, y 0; thỏa mãn log 2x y y 2x 2 A.2 B. 0 C. 3 D. 1
Câu 23. Số cặp số nguyên (x;y) thỏa mãn log x y 2 log x y 2 log 2 4x 13 2 y là 2 2 2 A.14 B. 12 C. 10 D. 15 x x x 131x
Câu 24. Tìm số nghiệm của phương trình 2 5 2 44log 2 5x 2 3 3 A.2 B. 1 C. 3 D. 4 2x 1
Câu 25. Có bao nhiêu cặp số nguyên (x;y) thỏa mãn 0 y 2020 và log 1 2x y 3 y A.2019 B. 10 C. 4 D. 2020 xy 5
Câu 26. Có bao nhiêu cặp số nguyên (x;y) thỏa mãn log x y a a log 0 1 2 a 2 A.4 B. 8 C. 2 D. 3
Câu 27. Có tất cả bao nhiêu số nguyên y 2
020;2020 sao cho tồn tại duy nhất số thực x thỏa mãn log x log x y 2 3 A.2019 B. 2021 C. 2020 D. 2022 n
Câu 28. Có bao nhiêu số hữu tỷ dạng (n nguyên) nhỏ hơn 5 trong tập nghiệm bất phương trình 3 log 3 x log x 1 5 3 2 2 2 A.10 B. 12 C. 8 D. 6
Câu 29. Có bao nhiêu số nguyên x sao cho tồn tại y thỏa mãn log x y log 4 4 x y 3 6 A.0 B. 2 C. 4 D. 8
Câu 30. Có bao nhiêu số nguyên x sao cho tồn tại số thực y thỏa mãn
log x y 2 log 2 2 x y 2x 2 y 2 3 4 A.0 B. 2 C. 4 D. 8
Câu 31. Có bao nhiêu cặp số nguyên (x;y) thỏa mãn 3 x 27 và 2 log 3 3 1 4 8 4y x x y 4 2 A.2019 B. 3 C. 2020 D. 2
Câu 32. Có bao nhiêu số thực y 0;6 sao cho tồn tại ít nhất một số thực x thỏa mãn x x 1 4 2
2(2x 1)sin(2x y 1) 2 0 A.3 B. 4 C. 5 D. Vô số
Câu 33. Có bao nhiêu cặp số (x;y) với x, y là các số nguyên dương thỏa mãn 2x log 2 y 615 2 y x 615. 2 A.1 B. 2 C. 3 D. Vô số
Câu 34. Có bao nhiêu bộ (x;y) với x, y là các số nguyên thỏa mãn 1 x, y 1024 và 2xy log x x(x y) 2 2 4 A.1 B. 3 C. 11 D. 22
Câu 35. Có bao nhiêu cặp số (a;b) thỏa mãn đồng thời 2 2 a b 1 và 2 2 2 2 2 2 b (a b 4) 4a a b 3 log 2 2 a b 2 2 a 2b A.10 B. 6 C. 7 D. 8 82
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 43)
__________________________________________________ 2 x3 2
Câu 1. Tìm số nghiệm của phương trình x 2 3 .4 x 18 A.2 B. 3 C. 4 D. 1
Câu 2. S là tập hợp các giá trị nguyên m để phương trình 5x 10 25x m
4 . Số tập con của S là A.3 B. 4 C. 16 D. 15 2 2
Câu 3. Tìm tập hợp giá trị m để phương trình 1 1x 1 1 4 ( 2).2 x m
2m 1 0 có nghiệm 9 9 A. ; B. 4; C. ; 4 D. 4; 2 2 x
Câu 4. Có bao nhiêu giá trị m để phương trình 2 4log x mlog
2 0 có hai nghiệm phân biệt x , x thỏa 36 6 6 1 2
mãn điều kiện x x 72 x x 1296 0 . 1 2 1 2 A.0 B. 1 C. 2 D. 3
Câu 5. Tập hợp các giá trị m để phương trình 2
ln(3x mx 1) ln(x 4x 3) có nghiệm là miền [a;b). Tính giá trị tổng a + b. 10 22 A.4 B. 7 C. D. 3 3 m
Câu 6. Có bao nhiêu số nguyên m không nhỏ hơn 2 để tồn tại số thực x thỏa mãn x m ln ln 4 4 x A.8 B. 9 C. 1 D. Vô số
Câu 7. Tồn tại bao nhiêu bộ số tự nhiên (x;y;z;t) thỏa mãn đẳng thức 2x3y 5z 7t . A.4 B. 2 C. 1 D. 3 log m
Câu 8. Có bao nhiêu số nguyên m lớn hơn 1 để tồn tại số thực x thỏa mãn log x m 3 5 5 x 3 A.4 B. 3 C. 5 D. 8 2
Câu 9. Tính tổng tất cả các giá trị m để phương trình (x 1 ) 2 2
log (x 2x 3) 4 xm.log 2 x m 2 2 2 A.2 B. 0 C. 3 D. 1,5
Câu 10. Có bao nhiêu số nguyên y lớn hơn – 2021 để với mỗi giá trị y tồn tại nhiều hơn hai số thực x thỏa mãn 2 2 2 x y 2 ( ).2020 (2 )2020xx x y x x x x y A.2020 B. 2019 C. 2021 D. 2022
Câu 11. Có bao nhiêu cặp số (x;y) nguyên không âm thỏa mãn 21 1 2y 2 2 2 2
log (x 2y) 2log (x y x 2xy) 2(x y) 4x 4y 2 2 A.3 B. 2 C. 4 D. 5
Câu 12. Phương trình 2 log (cot x) log cos x có bao nhiêu nghiệm thuộc 0;2020 3 2 A.2020 B. 2019 C. 1009 D. 1010
Câu 13. Tồn tại bao nhiêu bộ số nguyên không âm (a;b;c) thỏa mãn a b 2 2 3 9 c . A.4 B. 3 C. 2 D. 1
Câu 14. Có bao nhiêu giá trị nguyên y thỏa mãn 5x log (x y) y trong đó y 2020 . 5 A.2020 B. 2019 C. 1010 D. 1018
Câu 15. Có bao nhiêu giá trị m nguyên dương để bất phương trình 2 log10x log x 3 . m log100x luôn đúng
với mọi x không nhỏ hơn 1 A.3 B. 1 C. Vô số D. 2
Câu 16. Có bao nhiêu cặp số nguyên (x;y) với x 2020 thỏa mãn log x log (x y) 1 4log y 2 2 4 A.2020 B. 1010 C. 2019 D. 1011
Câu 17. Có bao nhiêu bộ số nguyên không âm (m;n) thỏa mãn 9m 7n 2. A.2 B. 1 C. 3 D. 4 a b
Câu 18. Biết a, b, c là các số thực dương thỏa mãn 2018a 2019b 2020c . Tính . b c A. log 2019 log 2020 B. log 2019 2018 2019 2018 83 C. log 2020 D. log (2019.2020) 2018 2018
Câu 19. Hai số nguyên không âm x, y thỏa mãn log
x y log x y . Tính x + y. 2 3 A.1 B. 4 C. 3 D. 7
Câu 20. Có bao nhiêu cặp số nguyên dương (x;y) với y không vượt quá 1000 thỏa mãn x 1 4 3 2 2 2 log
9y 6y x y 2xy . 3y 1 A.1501100 B. 1501300 C. 1501400 D. 1501500
Câu 21. Dãy số u có số hạng đầu tiên u 1thỏa mãn 2
log 5u log 7u log 5 log 7; u 7u , 2 1 2 2 1 2 2 n 1 2 2 n 1 n
trong đó n nguyên dương. Tìm giá trị nhỏ nhất n để u 1111111. n A.11 B. 8 C. 9 D. 10
Câu 22. Dãy số u thỏa mãn log 2u 63 2log u 8n 8 với mọi n nguyên dương. 3 5 4 n n u .S 148
Ký hiệu S u u ... u . Tìm số nguyên dương lớn nhất n thỏa mãn n 2n . n 1 2 n u S 75 2n n A.18 B. 17 C. 16 D. 19
Câu 23. Cho cấp số cộng u có tất cả các số hạng đều dương thỏa mãn n u u ... u 4(u u ... u ) 1 2 2018 1 2 1009
Tìm giá trị nhỏ nhất của 2 2 2
P log u log u log u . 3 2 3 5 3 14 A.2 B. 3 C. – 2 D. – 3
Câu 24. Có bao nhiêu cặp số nguyên dương (x;y) thỏa mãn 2x 5 11y . A.2 B. 1 C. 3 D. 4 2x y 100
Câu 25. Có bao nhiêu cặp số nguyên dương (x;y) thỏa mãn hệ 2 (x 4 y) 2 log 4(x y) 1 5 2 2 x 4y A.5 B. 6 C. 7 D. 10
Câu 26. Có bao nhiêu số nguyên x sao cho tồn tại số thực dương y thỏa mãn 2 1
log (x 2y) log (x y ) 3 2 16 A.Vô số B. 2 C. 1 D. 4
Câu 27. Có bao nhiêu số nguyên y sao cho tồn tại số thực x thỏa mãn log 4444 4x 2x 2 2 y 2 2
2.2 x y 2x 2020 2 A.13 B. 9 C. 11 D. 7
Câu 28. Có bao nhiêu bộ số nguyên (x;y) thỏa mãn x 1 xy2022 4 2log (xy 2021) 2 2log (2x 1) 2 2 A.12 B. Vô số C. 1 D. 3 6x 2y 1 3y 2x 4
Câu 29. Có bao nhiêu cặp số nguyên dương (x;y) thỏa mãn log log 2 3 2x y 1 y 1 A.1 B. 0 C. 2 D. Vô số 3 3 x y
Câu 30. Có bao nhiêu bộ số thực (x;y) với x y là số nguyên dương thỏa mãn log log (x y) 2 2 2 3 x y A.8 B. 12 C. 6 D. 10
Câu 31. Có bao nhiêu cặp số (x;y) nguyên với 3 y 2019;2020 thỏa mãn 1 1
log x x log (y x) 4 2 2 4 A.84567 B. 93781 C. 90787 D. 60608
Câu 32. Có bao nhiêu số nguyên dương x sao cho tồn tại số thực y lớn hơn 1 thỏa mãn 2 xy x y 2 y x 3 2 1 .log y log . x A.4 B. 2 C. 3 D. Vô số
_________________________________ 84
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 44)
__________________________________________________ 2
Câu 1. Có bao nhiêu số nguyên m nhỏ hơn 10 để phương trình x x e cos x m x có nghiệm 2 A.8 B. 5 C. 19 D. 25
Câu 2. Tìm số nghiệm nguyên nhỏ hơn 100 của bất phương trình log (1 x x) log x . 7 4 A.96 B. 92 C. 16 D. 6
Câu 3. Có bao nhiêu số nguyên m để phương trình 3 3 3
m 3 m 9cos x 12cos x cos3x có nghiệm A.2 B. 3 C. 5 D. 7 2016 1945
Câu 4. Tìm hai chữ số tận cùng của hiệu 9 9 2 2 . A.40 B. 32 C. 26 D. 54 2xy 1
Câu 5. Tồn tại bao nhiêu bộ số tự nhiên (x;y;z) thỏa mãn 7z . (x 1)( y 1) A.1 B. 2 C. 3 D. 6 2 2 1
994a a 1995b b
Câu 6. Tồn tại bao nhiêu cặp số tự nhiên (a;b) thỏa mãn
a b 5a 5b 2 A.2 B. 1 C. 5 D. 0 x 1 4 4
Câu 7. Có bao nhiêu số nguyên dương x thỏa mãn sin ycos y 2 log x 4 sin 2y 2 2 A.3 B. 1 C. 2 D. Vô số
Câu 8. Có bao nhiêu cặp số nguyên không âm (x;y) thỏa mãn log (33x 31) y log 2 . 1994 1994 A.3 B. 2 C. 10 D. 8
Câu 9. Tính tổng hai chữ số tận cùng của số 2009 2008 2008 2009 . A.13 B. 14 C. 15 D. 12
Câu 10. Tồn tại bao nhiêu cặp số nguyên (m;n) để 5 5
mn 2019; m n 2019 là hai lập phương của hai số nguyên nào đó A.4 B. 1 C. 0 D. 2
Câu 11. Giả sử n là số nguyên dương sao cho 3n 7n 1
1. Tìm số dư của khi 2n 17n 2018n chia cho 11. A.9 B. 10 C. 8 D. 5 0 y 100
Câu 12. Có bao nhiêu cặp số nguyên (x;y) thỏa mãn 6 4 2 2 3 2
x 6x y 12x y 19y 3x y 3y 0 A.10 B. 100 C. 20 D. 21
Câu 13. Có bao nhiêu số nguyên dương x thỏa mãn x 2 2
2.2 x sin y 2cos y A.4 B. 3 C. 1 D. 0
Câu 14. Có bao nhiêu cặp số (x;y) thuộc [1;2020] thỏa mãn y là số nguyên và ln y x x y e A.2021 B. 2020 C. 7 D. 6
Câu 15. Có bao nhiêu số nguyên x sao cho tồn tại số thực y thỏa mãn log x y 2 log 2 2 x y 3 2 A.3 B. 2 C. 1 D. Vô số
Câu 16. Có bao nhiêu số nguyên x sao cho tồn tại số thực y thỏa mãn 2 2
log (x y 3) log (x y 2x 4y 5) 4 5 A.3 B. 2 C. 1 D. Vô số 2 2
Câu 17. Có bao nhiêu số nguyên x sao cho tồn tại số thực dương y thỏa mãn biểu thức 2x y 2.2yx A.1 B. 2 C. 3 D. 4 2 2 2
Câu 18. Tìm số nghiệm thuộc 2
017;2017của phương trình sin x cos x sin 2 2 4.3 x A.1284 B. 4034 C. 1285 D. 4035 2 x
Câu 19. Tìm số nghiệm của phương trình 2
x ln(x 2) 2018 2 A.3 B. 1 C. 4 D. 2 85
Câu 20. Tìm số nghiệm phương trình 3
x 7x a 0khi phương trình 9x 9 .3x a
cos x có nghiệm duy nhất. A.2 B. 3 C. 1 D. 4
Câu 21. Có bao nhiêu giá trị nguyên m để tồn tại cặp số (x;y) thỏa mãn hệ 2 x y 1 3x2 y e e x y 1 2 log 2x y
1 m 4log 2x y 2 1 m 4 0 2 2 A.3 B. 4 C. 5 D. 6
Câu 22. Có bao nhiêu số nguyên dương m để phương trình 2x 3 4x m 1 có nghiệm duy nhất A.3 B. 1 C. 2 D. Vô số y
Câu 23. Có bao nhiêu cặp số nguyên dương (x;y) thỏa mãn log (x 1)( y 1) 1 4 (x 1)( y 1) . 2 A.1 B. 2 C. 3 D. 8 2 2
Câu 24. Có bao nhiêu số nguyên x sao cho tồn tại số thực y thỏa mãn 4xy 3x y A.4 B. 2 C. 3 D. Vô số
Câu 25. Có bao nhiêu số nguyên dương x không lớn hơn 2020 để tồn tại số nguyên dương y thỏa mãn 2 (4 y 3 y 1 )log x 3y 1 10 . 4 A.2020 B. 1347 C. 673 D. Vô số 3x 2 y
Câu 26. Có bao nhiêu số nguyên x sao cho tồn tại số thực dương y thỏa mãn 2 2 log log (x y ) 5 4 2 2 x 4y A.1 B. 2 C. 3 D. Vô số log (x y) m
Câu 27. Có bao nhiêu giá trị m để hệ 3
có hai nghiệm nguyên (x;y) 2 2 log (x y ) 2m 2 A.3 B. 2 C. 1 D. Vô số 2 2
Câu 28. Có bao nhiêu số tự nhiên y và số thực x thỏa mãn x 2 y x 3 2020 3 y A.1 B. 2 C. 0 D. 4
Câu 29. Có bao nhiêu cặp số nguyên (x;y) là nghiệm phương trình 2 y x x 2x 9 2 ( 1) ( x 1 ) 2 log 256.2 log (x 1) . 3 3 y A.0 B. 3 C. 4 D. 5
Câu 30. Có bao nhiêu giá trị nguyên không âm m để phương trình log m x log 4 2 m x có nghiệm 2 3 A.2 B. 3 C. 4 D. Vô số 2 2 3alog 2 x 3(1 log2 x) a 1
Câu 31. Tính tổng các giá trị a để bất phương trình 2 2 (2x) 2 đúng x 0 . A.2,5 B. 1,5 C. 2 D. 3 Câu 32. Cho hàm số f x 2 ( ) ln
x 1 x. Tìm tập nghiệm của bất phương trình f (x a) f (lna) 0. A.[0;1] B. (0;1] C. 0; D. 0; 2 2 log (x 2x y ) 1
Câu 33. Có tất cả bao nhiêu cặp số nguyên (x;y) thỏa mãn 2 1 2 2 log (x y 1) 2 A.2 B. 5 C. 6 D. 4
Câu 34. Trong hệ tọa độ Oxy có bao nhiêu điểm M ; x y với x, y ; 6
x 6; y 0thỏa mãn điều kiện 36 2 2 y 3 36 x 39 2 log . 2 3 x 2 3 y A.4 B. 1 C. 3 D. 2
Câu 35. Cho cấp số nhân a có a a ,q r . Biết log a log a ... log a 2020 . Hỏi có n 1 8 1 8 2 8 12
bao nhiêu cặp số (a;r) thỏa mãn A.92 B. 91 C. 45 D. 46
_________________________________ 86
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 45)
__________________________________________________
Câu 1. Có bao nhiêu cặp số nguyên (x;y) thỏa mãn x y 0; 2 0 x 20và log x 2y 2 2
x 2y 3xy x y . 2 A.19 B. 16 C. 10 D. 41
Câu 2. Có bao nhiêu cặp số nguyên (a;b) thỏa mãn đồng thời 2 2 2 2 b (a b 4) 4a 2 2 2 2
a b 1; a b 3 log 2 2 a b 2 2 a 2b A.10 B. 6 C. 7 D. 8 a a 3 Câu 3. Cho dãy số a a với *
n . Tìm số nguyên dương n nhỏ nhất lớn hơn 1 n n 1 : 1; 5 n 1 1 3n 2 để a là số nguyên. n A.n = 123 B. n = 41 C. n = 39 D. n = 49 2u u u 2 4e 2e 4 u eu u e e 3 Câu 4. Cho dãy số u
. Tìm giá trị nhỏ nhất của n để u 1 n 9 9 2 1 1 9 : u u 3 n n 1 n A.n = 725 B. n = 682 C. n = 681 D. n = 754
Câu 5. Có bao nhiêu cặp số nguyên (a;b) thỏa mãn đồng thời 16 b 64 2 2 0 a b 16; a b log . 2 a 2 b A.10 B. 6 C. 7 D. 8
Câu 6. Có bao nhiêu số thực x sao cho tồn tại số nguyên y thỏa mãn 2 x 3 2 y(x x) 3 x log log (4x 4x 8) . 2 2 y y A.2 B. 3 C. 4 D. Vô số
Câu 7. Có bao nhiêu số nguyên y để tồn tại số thực x thỏa mãn log 4x 3y log 2 2 x y 7 2 A.1 B. 2 C. 0 D. 3
Câu 8. Có bao nhiêu số nguyên x sao cho tồn tại số thực y thỏa mãn 2 2
log (x 2y 2) log (x 4 y 2x 4 y 2) . 3 4 A.0 B. 2 C. 4 D. 8 3x 1
Câu 9. Có bao nhiêu cặp số nguyên (x;y) thỏa mãn 0 x 2020 và log 2 2 3x y 2 y A.2019 B. 7 C. 2020 D. 4 x y xy xy 1
Câu 10. Có bao nhiêu cặp số nguyên (x;y) thỏa mãn 3 1 1 5 5 x( y 1) 1 5 3y x3 5 y A.2 B. 1 C. 4 D. 3 x y 20
Câu 11. Có bao nhiêu cặp số nguyên dương (x;y) thỏa mãn 2 2 log
x y 2x 4y 42 2 2 2 x y 6y A.1 B. 2 C. 3 D. 4 log a 1 log b 2 3
Câu 12. Có bao nhiêu cặp số nguyên dương (a;b) thỏa mãn 2 2 2 a b 2020 * log a 2 A.1 B. 2 C. 0 D. 3 2 2
Câu 13. Có bao nhiêu cặp số nguyên (x;y) thỏa mãn x y 2 2
2.625 6250.1253 9 y 4x 5 A.1 B. 2 C. 0 D. 3
Câu 14. Có bao nhiêu bộ (x;y) với x, y là các số nguyên thỏa mãn 1 x, y 243 và 9log 2 9 3xy x 9x(x y) 3 A.1 B. 3 C. 12 D. 243 2 2 2
Câu 15. Có bao nhiêu cặp số nguyên (a;b) thỏa mãn a 2b ab 2 2 1 1 abb e e a ab b e 0 87 A.4 B. 2 C. 9 D. 6 3 2
Câu 16. Có bao nhiêu cặp số nguyên (x;y) thỏa mãn điều kiện x x 2 y ( x 2) 2 .8 x (x y) 32.2 2y 3x 5 A.4 B. 2 C. 1 D. 3
Câu 17. Có bao nhiêu cặp số nguyên (x;y) không âm thỏa mãn điều kiện 2 2 x y 11 2 2 log
x y 6x 8y 9 0 6x 8y 2 A.25 B. 24 C. 36 D. 35 2 2 2 2
Câu 18. Có bao nhiêu cặp số nguyên (a;b) thỏa mãn 2a b a b log 4a b 1 2 a b A.24 B. 25 C. 36 D. 35
Câu 19. Có bao nhiêu số hữu tỷ a 1;
1 sao cho tồn tại số thực b thỏa mãn a a 2 2 2 4 1 1 log 1 a b 2b . 2 4a 1 2a 1 2a 4a 2 A.0 B. 3 C. 1 D. Vô số 1
Câu 20. Có bao nhiêu cặp số nguyên dương (x;y) thỏa mãn log 2x 5 y 1 log 21 1 5 5 log 5 2 2 x yx x A.2 B. 3 C. 4 D. 1 1 10x 2 y
Câu 21. Có bao nhiêu cặp số nguyên (x;y) với x, y thỏa mãn m log log và m là số 2 3 2 x 2 2 y 1 nguyên A.0 B. 1 C. 2 D. 3 2
Câu 22. Có bao nhiêu cặp số nguyên (a;b) thỏa mãn (ab) 2 2 4.2
8ab a b a b 3(a b) 2 ab A.12 B. 10 C. 14 D. 9 1 x
Câu 23. Cho số dương x và số thực y thỏa mãn 2 x log 2 81 y . Tính 2x + 3y. 3 A.2 B. 3 C. 0 D. 1
Câu 24. Các số thực dương x, y thỏa mãn log 2 4 8 3 y x x . Tính 2x + y. 2 2 log3 (2 ) A.3 B. 0 C. 2 D. 4 2 2 x y 2 2 e (x y )e
Câu 25. Có bao nhiêu giá trị nguyên của tham số để tồn tại hai cặp số (x;y) thỏa mãn hệ x y m 0 A.3 B. 0 C. 2 D. 4
Câu 26. Có bao nhiêu số nguyên x không vượt quá 2021 để ứng với mỗi x tồn tại hai số thực y thỏa mãn 2 y 3 log 2 x y y 1 3 3.2 x y 2 . A.2021 B. 2020 C. 2019 D. 2022
Câu 27. Cho x, y thỏa mãn ( 1) x y
e x ln( y 1) 1. Tìm giá trị lớn nhất của x – y A.0 B. – 1 C. 1 D. – 2
Câu 28. Có bao nhiêu cặp số nguyên (x;y) thỏa mãn x 2
0 y 2020; 4 8(x 1) 4y 2log y 2 A.4 B. 7 C. 6 D. 5
Câu 29. Ký hiệu S 1n 2n 3n 4n . Tìm chữ số tận cùng của S S . n 1994 2021 A.0 B. 4 C. 2 D. 6 2x 1
Câu 30. Có bao nhiêu cặp số nguyên (x;y) thỏa mãn 0 y 2020; log y 1 2x 3 y A.19 B. 12 C. 2020 D. 11 x2 y
Câu 31. Có bao nhiêu bộ số nguyên (x;y) thỏa mãn xy 1 1 3 2 2xy 2x 4y 3 A.4 B. 2 C. 3 D. 1
Câu 32. Có bao nhiêu số nguyên x để tồn tại y 1;2020 và thỏa mãn x 1 y ln y e y(x 2) . A.8 B. 7 C. 6 D. 5 88
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 46)
__________________________________________________ Câu 1. Cho hàm số 3
f (x) x 2020x 2020sin x và tập nghiệm của bất phương trình log x f
e 2020 2020 f (2020) f f 0 2
Là S ln a;ln b. Tính b – a. A.1 B. 2 C. 3 D. 4
Câu 2. Có bao nhiêu giá trị m mà 10m thỏa mãn phương trình sau có duy nhất nghiệm 2 2 2log (2x 5x 4) log (x 2x 6) mx5 mx5 A.15 B. 14 C. 13 D. 16 4x 1
Câu 3. Trong các cặp số nguyên dương (x;y) thỏa mãn 2 1 y 2020; log
y 2y 116x , tìm tổng 3 y
giá trị lớn nhất, giá trị nhỏ nhất mà y có thể đạt được. A.103 B. 3010 C. 1030 D. 301 2x 6 8
Câu 4. Có bao nhiêu cặp số nguyên (x;y) và 0 x 2020 thỏa mãn log y 2 2y 2 x 1 x 1 A.2018 B. 2 C. 2020 D. 1 2 1 x x 2020
Câu 5. Có bao nhiêu bộ hai số nguyên (x;y) thỏa mãn hệ 2
log x log(x 1) x x y 10y A.8 B. 4 C. 2 D. 10 x y xy xy 1
Câu 6. Có bao nhiêu cặp số nguyên (x;y) thỏa mãn 3 1 1 e e x(y 1) 1 e x3 y e A.10 B. 7 C. 4 D. 3 x x 2
Câu 7. Có bao nhiêu cặp số nguyên dương (x;y) thỏa mãn 2 . y 2 log 1 2y 3x 2 y A.1 B. 2 C. 10 D. 4
Câu 8. Có tất cả bao nhiêu cặp số nguyên không âm (x;y) thỏa mãn
log 2x y xy 2y2 8 (x 2)(y 2) 2 A.1 B. 2 C. 3 D. Vô số
Câu 9. Có bao nhiêu cặp số nguyên (x;y) thỏa mãn 1 x 2020; y 2 và 2 log ( ) 2x x x xy x xy x 2 A.6 B. 2021 C. 2020 D. 11
Câu 10. Có bao nhiêu cặp số nguyên (x;y) với 10 y 15 thỏa mãn x y log
x(x 9) y( y 9) xy . 3 2 2 x y xy 2 A.13 B. 16 C. 15 D. 14 y
Câu 11. Có bao nhiêu cặp số nguyên (x;y) thỏa mãn log x 2x 3 2 2019 4 2 2y 2018 2 A.1 B. 0 C. 2 D. 3
Câu 12. Có bao nhiêu số nguyên y không vượt quá 2021 để với mỗi y tồn tại hai số thực x thỏa mãn 2 x y 3 e
x(y ln x) x x . A.2020 B. 2021 C. 2022 D. 2019
Câu 13. Có bao nhiêu giá trị nguyên thuộc (1;2018) của a để phương trình sau có nghiệm lớn hơn 3 log 2 x x 1.log 2
x x 1 log x x a 2 1 2 2017 A.20 B. 19 C. 18 D. 17
Câu 14. Có bao nhiêu giá trị m nguyên dương khác 1 để phương trình sau có nghiệm lớn hơn 2 log 2 x x 1.log 2
x x 1 log x x m 2 1 2 5 A.3 B. 2 C. 1 D. Vô số
Câu 15. Có tất cả bao nhiêu số dương a thỏa mãn log a log a log a log . a log . a log a 2 3 5 2 3 5 A.3 B. 1 C. 2 D. 0 89 11 log x log x m
Câu 16. Có bao nhiêu số nguyên dương m 2
018;2018để bất phương trình x 10 10 10 10 đúng x 0;100 . A.2018 B. 4026 C. 2013 D. 4036
Câu 17. Cho hai số a 1;b 1. Phương trình x x
a b b ax có nhiều nhất bao nhiêu nghiệm A.0 B. 1 C. 2 D. 3 x 1 3
Câu 19. Có bao nhiêu số nguyên m 2
018;2018để bất phương trình 1 2 2 x mcó đúng hai 8 2 nghiệm thực phân biệt A.2013 B. 2012 C. 4024 D. 2014
Câu 20. Tìm tập hợp giá trị a để bất phương trình sau có nghiệm duy nhất. log 11 log x ax a x ax a
2 3 10 4log3 2 3 12 0 3 1 7 A. 1 ;0 B. (1;2) C. (0;1) D. 2;
Câu 21. Tìm tập hợp giá trị m để bất phương trình (3 1).12x (2 ).6x 3x m m
0 nghiệm đúng x 0 1 1 A. 2; B. ; 2 C. ; D. 2; 3 3
Câu 22. Tìm tập hợp giá trị a để bất phương trình 2x 3x ax 2 nghiệm đúng với mọi x A.(1;3) B. (0;1) C. ; 0 D. 3;
Câu 23. Có bao nhiêu giá trị nguyên m 1
0;10để phương trình sau có nghiệm 1 m 1 m 2 2
2(x 1 x )(1 x 1 x ) 2 8 A.13 B. 12 C. 11 D. 10
Câu 24. Có bao nhiêu giá trị nguyên m 2 020;202
1 để phương trình sau có ba nghiệm phân biệt 2 1 1 x (m 2)x 2m 1 ln(x 5) 3x 3 x 2 A.4042 B. 2027 C. 0 D. 2016 2 3 2 2 ln(2x 2)
ln 2x 2 (x 3x m)
Câu 25. Có bao nhiêu giá trị nguyên m để phương trình có ba 2 2 3 2 ln(x 2)
ln x 2 (x 3x m) nghiệm phân biệt A.1 B. 2 C. 3 D. Vô số
Câu 26. Cho hàm số f (x) có đạo hàm ( ) ( 1) x f x x
e , có bao nhiêu giá trị nguyên m 2 020;202 1 để hàm số 2
f (x) f (ln x) mx mx 2nghịch biến trên 2020 ; e e . A.2018 B. 2019 C. 2020 D. 2021
Câu 27. Tính tổng các giá trị m để hệ phương trình sau có nghiệm duy nhất 2 2020 2 2 x y 2 x6 y6 2020 2020 2 2
(x 1) (y 3) 4 2 2 ( x 1 ) ( y3) e 2 2
x y 2x 6 y 11 m m e A.88 B. 44 C. 2 10 2 D. 2 10 2
Câu 28. Dãy số u có tất cả các số hạng đều dương thỏa mãn n 2 2 2 2 4 u u ... u u u 1 và u 2u . 1 2 n n 1 n2 3 n 1 n
Số tự nhiên n nhỏ nhất để 100 u 5 là n A.232 B. 233 C. 234 D. 235
Câu 29. Dãy số u thỏa mãn ln 2 2
u u 10 ln 2u 6u . Tìm giá trị n nhỏ nhất để u 5050 1 2 1 2 n n A.100 B. 99 C. 101 D. 102 90
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 47)
__________________________________________________ 2xy 2y x 2y
Câu 1. Cho hệ phương trình , m là tham số. 2x 1 m 2 1 2 y 2 .2 . 1 y
Gọi S là tập các giá trị m nguyên để
1 có một nghiệm duy nhất. Tập S có bao nhiêu phần tử? A. 0 . B. 1. C. 3 . D. 2 .
Câu 2. Có tất cả bao nhiêu bộ số tự nhiên (x;y;z) thỏa mãn x y 2 2 3 z A.2 B. 3 C. 1 D. 4 2 Câu 3. Phương trình 2021( x 6 x4) 10 2022
có một nghiệm x a b . Tính 2 ab a . 4 x 4 x A.5 B. 11 C. 8 D. 6 2 2 b a Câu 4. Phương trình 4x 5x 4 x 5x 1 2 4 . x 3 4.3
(4x 1) 9 có nghiệm dương x trong đó a, b, c nguyên c dương. Tính a + b – c. A.38 B. 17 C. 13 D. 28 2 2
Câu 5. Tính tổng bình phương các nghiệm phương trình x 2 x 2
16 (x 3)4 2x 2 0 . A.1 B. 0 C. 0,5 D. 2
Câu 6. Tìm số nghiệm phương trình 2
x 2022xln x x 2021 0 A.1 B. 2 C. 3 D. 4
Câu 7. Có bao nhiêu cặp số (x;y) thuộc đoạn [1;2020] thỏa mãn y nguyên và ln ln x y x e y e A.6 B. 7 C. 2021 D. 2020
log (x 2y)log (2x 4y 1)
Câu 8. Có bao nhiêu cặp số tự nhiên (x;y) thỏa mãn đồng thời 2 3 log (x y) y 2 3 A.7 B. 6 C. 10 D. 8 Câu 9. Phương trình 3 3 log ( 1) 27 8y x y
1 x có bao nhiêu cặp nghiệm nguyên (x;y) với 1992 2020 x 8 ;8 2 A.26 B. 28 C. 24 D. 30 2 x 3x 2 Câu 10. Phương trình 2 log
x 4x 3 có hai nghiệm a, b. Tính 2 2 a b 3ab . 2 2 3x 5x 8 A.31 B. 1 C. – 1 D. – 31
Câu 11. Tính tổng các nghiệm phương trình x2 x2 3.25 (3x 10)5 3 x là A.2 B. log 3 C. 4 log 3 D. 2 log 3 5 5 5
Câu 12. Tổng các nghiệm của phương trình 9x 2( 2)3x x 2x 5 là A.5 B. 1 C. – 1 D. 4
Câu 13. Tập nghiệm của bất phương trình 9x 2 5.3x x 92x 1 0 là A. 0; 1 2; . B. ; 1 2; . C. 1;2. D. ; 02; .
Câu 14. Tập nghiệm của bất phương trình 25x 4 6.5x x 20x 5 0 là A. 0; 1 . B. 1; . C. ;0 . D. ; 1 .
Câu 15. Bất phương trình 2x x x2 2 . x 2 2x 3 2
x * có tập nghiệm là S ; a b ; c tính T a 2b c . 4 2 8 A. log . B. log . C. log . D. log 3 . 2 3 2 3 2 3 2
Câu 16. Cho bất phương trình 3.4x 7 9.2x x 14x 6 0
1 . Số nghiệm nguyên thuộc 2 022;2022 của bất phương trình 1 là A. 1011. B. 2022. C. 4042. D. 2021.
Câu 17. Cho bất phương trình 2x e x x 2 2 1 e x x 0
1 . Số nghiệm nguyên thuộc 2 0;20 của bất 91 phương trình 1 là A. 41. B. 40. C. 20. D. 19.
Câu 18. Số nghiệm nguyên thuộc đoạn 2
0;20 của bất phương trình sau: 4 x2 3x 1 2 x x
2x 2x x x 2 2 18.2 8 2 3 85 .2 9 4 2
3 2 2 8 x 2x 3 0 là A. 36 . B. 38 . C. 18 . D. 17 .
Câu 19. Tính tổng bình phương các nghiệm nguyên của phương trình 2 2 x x x x xx 2 2 3 2 2 3 3 2 x x 32x 2 x3 2 9 4 3 6 11 6 2 9 4 3xx x x x x A.5 B. 25 C. 13 D. 14 4 2 x x x cos 2022
Câu 20. Tính tổng các nghiệm 2
021;2021 của phương trình sin sin 2021 2 sin x 2sin x 2023 A.2021 B. 1011,5 C. 1010 D. 1010,5 Câu 21. Cho hàm số 3
f (x) x 3x 2 . Phương trình sau có bao nhiêu nghiệm 2 f x f (x) 1 f ( x) 1 f ( x) 1 f ( x) .5 3 f (x) 3.5 f (x) 2.5 3 . A.3 B. 4 C. 5 D. 7
Câu 22. Cho hàm số f (x) có đồ thị như hình vẽ. 2 2
Tìm số nghiệm của phương trình f x 2 f x 2 4 f (x) 7 2 12 4 f x A.6 B. 8 C. 7 D. 9 2 x y 1 2 x y 1 2 x y 1 2 x y 1 2 x y 1 2 x y 1 2 2 3 3 5 5
Câu 23. Hệ phương trình có nghiệm duy nhất ; x y. 2
y(x 3x 3) 2 0
Khi đó x + y gần nhất với A.3,4 B. – 3,4 C. – 3,5 D. 3,5
Câu 24. Cho hàm số y f (x) liên tục trên R có đồ thị như hình vẽ.
Tập nghiệm của bất phương trình 4x 1 .2x x f x x
1 f x 0 * là A. ; 02; . B. 0; 1 . C. ; 1 2; . D. 1 ; 2.
_________________________________ 92
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 48)
__________________________________________________
Câu 1. Tồn tại bao nhiêu cặp số tự nhiên (m ;n) để 2 11 39 65.7m n n A.1 B. 2 C. 3 D. 4
Câu 2. Có bao nhiêu số nguyên m để phương trình log 3x 2m log 2 3x m có nghiệm 3 5 A.3 B. 4 C. 2 D. 4 2
Câu 3. Có bao nhiêu số nguyên m < 100 để phương trình x x2 3 .4
m có hai nghiệm phân biệt A.89 B. 37 C. 52 D. 76 3 2
Câu 4. Có bao nhiêu số nguyên m 1
2;12để phương trình x x 3 4 .5 xm m có nghiệm A.10 B. 12 C. 7 D. 18
Câu 5. Cho các số nguyên dương x, y không lớn hơn 4022. Mỗi giá trị của y luôn có ít nhất 2021 giá trị của x
thỏa mãn bất phương trình 2xy y x2 3
3 log y 3 y 3x . Hỏi có bao nhiêu giá trị của y x A.2000 B. 2001 C. 2021 D. 2022
Câu 6. Có bao nhiêu số nguyên x để không có quá 25 giá trị nguyên y thỏa mãn 3 6 4 2
log x log x y y 2 y 1 . 2 2 A.4215 B. 4214 C. 8413 D. 8412
Câu 7. Có bao nhiêu giá trị nguyên tham số a thuộc 1
0;10để phương trình sau có nghiệm duy nhất xa x e
e ln(1 x a) ln(1 x). A.2 B. 10 C. 1 D. 20
Câu 8. Tính tổng các nghiệm nguyên của bất phương trình log x log x 2 7 3 A.2176 B. 1128 C. 1196 D. 1176
Câu 9. Có tất cả bao nhiêu giá trị thực m để phương trình sau có nghiệm (x;y) duy nhất log
x y log 2x 4y 5 m 1 1m 2 2 2 A.2 B. 3 C. 1 D. 6
Câu 10. Có bao nhiêu số nguyên m 2 000;2000để log b log 2 a b a a b m log b 1với a 1;b 1 a A.2199 B. 1999 C. 2000 D. 2001
Câu 11. Có tất cả bao nhiêu giá trị nguyên m để bất phương trình sau có nghiệm sin x3cos xm 1 sin x3cos 3 4
xm 6sin x 18cos x 6m 7 A.7 B. 9 C. 11 D. 5
Câu 12. Hàm số f (x) có f x 2 3
(x m 2)(x 4 m ) ln(x 1) với x 1
, trong đó m là tham số. Có
bao nhiêu giá trị nguyên m để hàm số f (x) đạt cực tiểu tại x = 0 A.2 B. 3 C. 4 D. 5
Câu 13. Hai số thực x, y 1thỏa mãn 2 log 2x 2 2log 2 y 1 2
log x 1 . Tính log x y . 2 2 2 2 A.1 B. 2 C. log 3 D. log 5 2 2
Câu 14. Hỏi có bao nhiêu giá trị nguyên m 2022;2022 để bất phương trình sau có nghiệm 2 x mx4 2 2 2 2e
2x 4mx 10 (x 2mx 4) A.4040 B. 4041 C. 4042 D. 5
Câu 15. Hai số x y 1thỏa mãn 4 log 12 2xy x y 1 log x y 2
5 2log x y 2 2 2 2 Khi đó 3 3
P a b có đặc điểm A.P = 2 B. P = 3 C. P = 1 D. P < 1
Câu 16. Hai số thực x, y không âm thỏa mãn x y 2 y 2x 2 1; 2 2 9.2 x y x y . Có bao nhiêu số nguyên
dương không vượt quá x + y. A.1 B. 2 C. 5 D. 0
Câu 17. Có bao nhiêu cặp số tự nhiên (m;n) thỏa mãn ( 1)( 2)( 3)( 3) 2 100y x x x x x A.2 B. 0 C. 4 D. 10 93 Câu 18. Cho hàm số x 1 x 1 f (x) 2 2
. Tìm điều kiện m để bất phương trình f 3
x m 3x 3có nghiệm x 0;2. A. m 1 B. m 21 C. m < 21 D. m > 1
Câu 19. Có bao nhiêu giá trị nguyên x để bất phương trình sau luôn đúng với mọi y thực 2 2
log 2x 2xy y 2(x y) 1 log
2y 2.log 2y 2y 4 3 2 3 A.3 B. 1 C. 4 D. 2 10
Câu 20. Cho a, b dương thỏa mãn 2a b 2 . Có bao nhiêu số nguyên x sao cho tồn tại y 1; thỏa mãn 3 axby x . b 9y 3 . a 3 . 2 A.4 B. 2 C. 7 D. 6 2 y
Câu 21. Hai số dương x, y thỏa mãn 2 2 2
log x log y log x 2 log . Có bao nhiêu số nguyên 2 4 2 2 x
dương không vượt quá 8xy. A.2 B. 4 C. 6 D. 8
Câu 22. Tập nghiệm của bất phương trình log 2 x x 2 4 x2 2
2x x 2 1là a; b 2 15 16 5 A.2,4 B. C. D. 16 15 12
Câu 23. Có bao nhiêu số nguyên dương y để tồn tại số thực x lớn hơn 7 thỏa mãn log y log x 7 log 7 11 11 y A.10 B. 9 C. 8 D. 11
Câu 24. Bất phương trình 2 2
ln(1 x ) x có bao nhiêu nghiệm nguyên 2 021;2022 A.4042 B. 4040 C. 4041 D. 4039 2 2 x y a
Câu 25. Hai số x, y 0 thỏa mãn xy 1 x2 y 1 3x4y3 1xy 2x3 2 2 2 2 2 y . Khi đó (phân số 4 b tối giản), tính a + b A.4 B. 5 C. 6 D. 7 1 y 1 x
Câu 26. Hai số thực x, y thỏa mãn 4x 4 2 2 y 4 . Tính x + y. A.1 B. 2 C. 1,5 D. 2,5
Câu 27. Có bao nhiêu giá trị nguyên m 2 021;202 1 để bất phương trình x 1x x 1 27 .3 .3 27 x m m có nghiệm A.2018 B. 2019 C. 2017 D. 2020 1
Câu 28. Có tất cả bao nhiêu giá trị nguyên m 3
0;30để bất phương trình sau nghiệm đúng x 2 x x
3 5 3 5 1 .2x m m A.36 B. 34 C. 35 D. 37 2 2
Câu 29. Có bao nhiêu giá trị nguyên m 2
0;20 để bất phương trình sin x 1 cos 3 (2 1).3 x m 4 nghiệm
đúng với mọi giá trị thực x A.18 B. 20 C. 21 D. 19 2
Câu 30. Tìm điều kiện tham số m để bất phương trình 2 2 x x2 2 4 4 8 4 2 2 2 m x x m x 2x nghiệm
đúng với mọi giá trị thực x. 1 1 3 1 A. m B. m C. m D. m 8 8 8 7
Câu 31. Có bao nhiêu giá trị nguyên m 2
021;2022để bất phương trình 9x ( 2)3x m m 3 0nghiệm
đúng với mọi số thực x. A.2020 B. 2019 C. 2018 D. 2017
_________________________________ 94
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 49)
__________________________________________________
Câu 1. Có bao nhiêu cặp số nguyên (a ;b) thỏa mãn 0 a,b 100 sao cho đồ thị hai hàm số sau cắt nhau tại 1 1 1 1
đúng hai điểm phân biệt: y ; y . x x a b b a A.9704 B. 9702 C. 9698 D. 9700
Câu 2. Có bao nhiêu giá trị nguyên dương m để bất phương trình 2 log 2x 3 4 m log x 1 2 8 nghi ệm
đúng với mọi giá trị x lớn hơn 16 A.2 B. 3 C. 1 D. 4
Câu 3. Hai số thực x, y không âm thỏa mãn log log 2 2
x 9y 6xy 2x 6y 2 log log 2 2
9x y 6xy 6x 2 y 3 2 3 3 2 m Biết rằng 2
xy được viết dưới dạng phân số tối giản
(m, n tự nhiên). Tính m + n. n A.8 B. 9 C. 10 D. 11 Câu 4. Tính 2 2
sin(x y x y ) khi hai số x, y thỏa mãn 0 x y thỏa mãn 4 2
tan(x y)sin(xy) cot(x y)cos(xy) 2 2 log (4 x y ) . 2 3 2 A.0 B. 1 C. D. 2 2
log (x y) log (xy 2) 2
Câu 5. Tìm giá trị nhỏ nhất m để hệ phương trình 2 3 có nghiệm 3 3 x y 2xy m A.1 B. 2 C. 3 D. 4
Câu 6. Có bao nhiêu số nguyên m 1
0;10 để bất phương trình 3 x x 4 2mlog 2 có nghiệm 4 4x A.8 B. 5 C. 6 D. 7 2 x 2x5 log 3 5 3 5 y 4
Câu 7. Có tất cả bao nhiêu cặp số thực (x;y) thỏa mãn hệ 2
4 y y 1 ( y 3) 8 A.3 B. 2 C. 1 D. 0
Câu 8. Hàm số chẵn f x sao cho f 0 0 và phương trình 4x 4x f (x)có 10 nghiệm phân biệt. Tìm số x
nghiệm thực của phương trình x x 2 4 4 f 2 . 2 A.10 B. 20 C. 5 D. 15
Câu 9. Đồ thị các hàm số x ; x y a
y a ; y 2(a 1) đôi một cắt nhau tại ba điểm A, B, C phân biệt, không
thẳng hàng. Biết tam giác ABC đều, khẳng định nào dưới đây đúng A. a [3;4) B. a [2;3) C. a [4;5) D. a (1;2)
Câu 10. Số giá trị nguyên m để bất phương trình 1 log 2 x 1 log 2
mx 2x m nghiệm đúng với mọi 3 3 số thực x là A.1 B. 2 C. 4 D. 6
Câu 11. Cho hai số dương a, x khác 1. Tính tổng các số nguyên dương n sao cho 1 1 1 1 4095 ... log x log x log x log x x n log 2 3 a a a a a A.8010 B. 4005 C. 8090 D. 4095 2
Câu 12. Cho 0 a 1, phương trình a a x a có bao nhiêu nghiệm a 2x 4x 2 2 1 log ( 1) loga a A.0 B. 1 C. 3 D. 4
Câu 13. Có bao nhiêu giá trị nguyên m thỏa mãn bất phương trình sau nghiệm đúng x 1 , biết 2m e 95 x 2 2
2019 log x (m m)x (2019 m m) 2 A.122 B. 100 C. 98 D. 123
Câu 14. Hai số dương a, b phân biệt thỏa mãn 2 ; a b
ab e b a . Tìm số giá trị nguyên m 0;6để bất phương
trình sau nghiệm đúng với mọi giá trị x dương 2 m 3 2 2 m x x x x 2 a b a b
2(m 3m) 4 x 3 2 A.4 B. 5 C. 2 D. 1 2 a 2 ( 1) ( 1)y x b 2
Câu 15. Tìm a để hệ phương trình có nghiệm với mọi b 2 a bxy x y 1 A.a = 1 B. a = 2 C. a = 3 D. a = – 1 bx 2 2 2 (a 1)by a
Câu 16. Tìm a để hệ phương trình ẩn (x;y) có nghiệm với mọi b: 3 2 (a 1)x y 1 A.a = 1 B. a = 2 C. a = 3 D. a = – 1
Câu 17. Tìm a để phương trình log 2 2 2
a x 5ax 6 a log
3 a 1 nghiệm đúng với mọi x 2 2 2 x A.a = 5 B. a = 4 C. a = 2 D. a = 6
Câu 18. Có bao nhiêu giá trị nguyên m để bất phương trình sau nghiệm đúng với mọi x log 2 2 x 2mx 2m 1 1 log 2 x 2x 3.log 2 x 3 3 2 3 A.2 B. 3 C. 1 D. 4
Câu 19. Biết là một số thực để bất phương trình ax 2
9 (ax) 18x 1 sau luôn đúng. Khi đó A. (2;6] B. 12; C. (0;2] D. (6;10]
Câu 20. Có bao nhiêu số nguyên dương y sao cho ứng với mỗi giá trị y có không quá 10 số nguyên x thỏa mãn
log x x 11 y log x 0 3 3 A.0 B. 1 C. 2 D. 3 1 2 2x 9
Câu 21. Cho hai số dương x, y thỏa mãn y 2x và log log log (xy) . Giá trị 2x2y P x 2 2 2 x y 16 thuộc miền A.[4;5] B. [1;2] C. [2;3] D. [6;7]
Câu 22. Hai số thực x, y thỏa mãn 2 x 3; 2 y 5. Có bao nhiêu bộ số (x;y) thỏa mãn
log 3 sin(xy) cos x 3 6 A.4 B. 2 C. 3 D. 1
Câu 23. Có bao nhiêu số nguyên dương m để bất phương trình 2x2 x m2 3 3 3
1 3m 0 có không quá 30 nghiệm nguyên A.28 B. 29 C. 30 D. 31
Câu 24. Tồn tại duy nhất một giá trị a để phương trình sin x 2 2
sin x cos x sin x a có nghiệm duy nhất,
hỏi a có tất cả bao nhiêu ước số nguyên A.2 B. 8 C. Không có D. Vô số
Câu 25. Có bao nhiêu số nguyên dương x sao cho tồn tại số nguyên dương y thỏa mãn 1 x y 1 x 2 ln ( 1)( 2 ) 2 8 y x y x y ln 3 A.1 B. 2 C. 2020 D. 2021
Câu 26. Có bao nhiêu cặp số thực dương (a;b) thỏa mãn log a là số nguyên dương thỏa mãn 2 log a 1 log b 2 3 2 2 2 a b 2020 A.8 B. 6 C. 7 D. 5 y
Câu 27. Có tất cả bao nhiêu số nguyên dương x để tồn tại số thực y thỏa mãn log 2y log 3y x 2 2 3 A.2 B. Vô số C. 0 D. 1 96
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 50)
__________________________________________________ 2
Câu 1. Có bao nhiêu giá trị nguyên của x thỏa mãn bất phương trình x 25 2 x x2021 3 25 .4 1 A. 10 . B. 11. C. 8 . D. 9 . x 1 6 3 10
Câu 2. Giải bất phương trình
ta được tập nghiệm S a;b . Tính giá trị P 10b 3a x 2x 1 A. P 5 . B. P 4 . C. P 2 . D. P 0 . 1 2 x 2x 1
Câu 3. Tập nghiệm của bất phương trình 0 là 2x 1 A. 0; 1 . B. 0; 1 . C. 1;0 . D. 0; 2. 2 2 2
Câu 4. Bất phương trình sin x cos x sin 2 3 4.3 x
có bao nhiêu nghiệm nguyên trên 2021 ;2022 . A. 4043. B. 2021. C. 4044 . D. 2022 .
Câu 5. Có bao nhiêu bộ số tự nhiên (m;n) thỏa mãn n m 2 10 6 4n A.3 B. 2 C. 1 D. 4 2 Câu 6. Cho hàm số x 1 2 2x 2 x f x
. Tính tổng các giá trị x nguyên dương thỏa mãn bất phương trình f x 228 22 f 0 . x 9 A. S 36 . B. S 45 . C. 30 . D. 8 .
Câu 7. Có bao nhiêu cặp số nguyên x; y thỏa mãn bất phương trình 2 2 2 x xy y x y x y2 5 2 2 3 2 .2 3 ? A. 0 . B. 1. C. 2 . D. 3 .
Câu 8. Có bao nhiêu số nguyên trong đoạn 0;202
1 thỏa mãn bất phương trình : x x x 2 2 x 6x2 2 x x 3x4 3 2 3 4 .2021 6 2 .2021 A. 2016 . B. 2017 . C. 2020 . D. 2021. 100
Câu 9. Tìm số dư khi chia 3 9 cho 19. A.2 B. 1 C. 3 D. 4 2
Câu 10. Tính tổng các nghiệm phương trình 2021x x 1 x x 2 2021
2021 .x 2021 2021 .x . A.2 B. 2021 C. 2022 D. 2023 2 2
Câu 11. Có bao nhiêu giá trị nguyên m để phương trình 1 1x 1 1 4 ( 2).2 x m
2m 1 0 có bốn nghiệm phân biệt A.0 B. 2 C. 3 D. 4
Câu 12. Tồn tại bao nhiêu bộ số nguyên dương (x;y;z) thỏa mãn 5 4y 2013z x A.3 B. 2 C. 1 D. 4
Câu 13. Tìm số nghiệm của phương trình 6 4 x 3 x 2 6 8 (15 3.4 ) 6.2 .x x x x x x 10 0 A.1 B. 0 C. 2 D. 3 f 2.5x Câu 14. Cho hàm số ( ) 2020x 2020 x f x
. Nghiệm của phương trình thuộc khoảng f x 1 3.5 1 nào dưới đây A.(1;5) B. (0;3) C. 1; 1 D. 2; 1
Câu 15. Có bao nhiêu số nguyên m để phương trình sau có ba nghiệm phân biệt x x 2 x 2 27 2 .18 ( 1).12 ( ).8 x m m m m m 0 A.1 B. 2 C. 3 D. 4
Câu 16. Tập hợp (a;b) gồm tất cả các giá trị m để phương trình ( 5)3x (2 2)2x 3x (1 ).4x m m m 0 có
hai nghiệm phân biệt. Tính a + b. A.4 B. 5 C. 6 D. 8
Câu 17. Tính tổng các giá trị nguyên m để phương trình sau có nghiệm 2 2 2 x 2 x2,5 x x 1 ,25 (m 2).3 2(m 1).3 2m 6 97 A.18 B. 12 C. 20 D. 14
Câu 18. Tồn tại bao nhiêu bộ số (x;y;z) thỏa mãn y 1 z 1 (x 1) 1 (x 2) A.3 B. 2 C. 1 D. 6 x x
Câu 19. Phương trình 2 3 1 2a2 3 4 0có hai nghiệm phân biệt mà hiệu hai nghiệm bằng log
3 . Khi đó giá trị a thuộc khoảng 2 3 3 3 3 A. ; B. 0; C. ; D. ; 2 2 2
Câu 20. Tìm điều kiện tham số m để phương trình 6x ( 3)3x 9.2x m
9m 27 0 có nghiệm thuộc (0;2) A.Mọi giá trị m B. 3 < m < 7 C. 1 < m < 3 D. – 1 < m < 2
Câu 21. Tìm tập hợp giá trị m để phương trình 3m m 2 x x 2 10 10 2 1 1 x 1 x có nghiệm 1 1 1 1 A. 0; log 2 B. log 2; C. 0; D. ; log 2 2 2 10 2 3 2 2
Câu 22. Tập hợp (a;b) gồm tất cả các giá trị m để phương trình x x 2xm x x 3 e e
x 3x m 0có ba
nghiệm phân biệt. Tính a + 2b A.1 B. 0 C. 2 D. – 2
Câu 23. Có bao nhiêu giá trị nguyên m để phương trình x3 5x x3 5 4 16.2 x 8 m có nghiệm A.65 B. 64 C. 11 D. 12
Câu 24. Tồn tại bao nhiêu cặp số nguyên dương (a;b) thỏa mãn 5a 1 3 . a b . A.2 B. 1 C. 3 D. 4 2
Câu 25. Tim tập hợp giá trị m để phương trình log2 x log2 x 2 3 2(m 3).3
m 3 0 có hai nghiệm phân biệt mà
tích hai nghiệm lớn hơn 4 m 6 A. m 6 B. m 1 C. D. m 6 m 6
Câu 26. Có bao nhiêu số nguyên dương n để tồn tại các số nguyên dương x, y, k (k 1) thỏa mãn (x, y) 1 3n k k x y A.3 B. 1 C. 2 D. 6 2 m
Câu 27. Có bao nhiêu số nguyên m để phương trình x 2mx 4m 3 2 3 2
có đúng hai nghiệm phân biệt x m thuộc 6 ;0 A.0 B. 1 C. 2 D. 3 2 x x
Câu 28. Cho hàm số f x 2 2 3 7 4 3 ln
x 1 x. Tìm các giá trị của tham số m để bất
phương trình f x m f 2 3 2
x 2x 2 0 nghiệm đúng với mọi giá trị x. 3 1 3 1 A. m . B. m . C. m . D. m . 2 2 2 2
Câu 29. Biết rằng a là số thực dương sao cho bất phương trình log 3x x log 6x 9x a 0 nghiệm 2 5 52
đúng với mọi x. Mệnh đề nào sau đây đúng? A. a 12;14 . B. a 10;12 . C. a 14;16 . D. a 16;1 8 .
Câu 30. Có bao nhiêu số nguyên m 2
022;2022 sao cho thỏa mãn bất phương trình sau luôn đúng, x 0, x 1 ? ln x 1 ln x m x 1 x x 1 x A. 2. B. 1. C. Vô số. D. 0.
_________________________________ 98
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 52)
__________________________________________________
Câu 1. Hàm số f x có đạo hàm liên tục trên R và có bảng biến thiên như hình dưới
Tính tổng các số nguyên m để hàm số sau nghịch biến trên 1; 1 2 2020 2 x x f (x) f (x 1) ln 3x 4ln(2 x) m 2 x 2 A.81810 B. 5151 C. 1275 D. 127765
Câu 2. Gọi A thuộc đồ thị hàm số 2x y
, B thuộc đồ thị hàm số 2 x y
, C và D là hai điểm thuộc trục hoành
sao cho tứ giác ABCD là hình thang cân với đáy lớn AB, AB = 2CD và có chu vi bằng 20 đơn vị. Diện tích của
hình thang ABCD nằm trong khoảng nào dưới đây A.(20;25) B. (27;33) C. (34;39) D. (41;45) b a
Câu 3. Hai số a, b thỏa mãn b a 1và 2 log a 16log 4 . Tính log . b a 4 3 2 a b A.0 B. 2 C. 3 D. 1 1
Câu 4. Có bao nhiêu số nguyên x sao cho tồn tại y ;2 thỏa mãn 2 8 (1 2 )8y y xy xy 2 A.1 B. 0 C. 2 D. 3 y
Câu 5. Có bao nhiêu cặp số nguyên (x ;y) thỏa mãn log x 2x 3 2 8 2 2 7 y 3y 2 A.6 B. 5 C. 2 D. 4
Câu 6. Tìm tập hợp các giá trị m để phương trình sau có ba nghiệm phân biệt thuộc [1;625] 3 x log 5x 2 6log
(11 m)log x m 3 0. 5 5 5 5 A.(1;2) B. [1;2] C. (1;2] D. 2;
Câu 7. Có bao nhiêu giá trị nguyên m để phương trình 4x 3x log (m x) 2m 2 0 có nghiệm 4 x 1 ; 1 A.3 B. 6 C. 5 D. Vô số
Câu 8. Có bao nhiêu số nguyên dương y để bất phương trình 2x 202 1 2x x
y 0 có đúng 5 nghiệm nguyên dương x A.35 B. 32 C. 40 D. 45
Câu 9. Cho a, b nguyên dương thỏa mãn log 1000 log log 2
0 . Giá trị lớn nhất của ab là 2 2 a 2 b A.500 B. 375 C. 125 D. 250
Câu 10. Cho số dương a 1, biết khi a a thì bất đẳng thức a x
x a đúng với mọi số thực x lớn hơn 1. Khi đó 0 A. 1 a 2 B. 2 e a e C. 2 a 3 D. 2 3 e a e 0 0 0 0 3 2 3 2
x 3x 4x 4 y 3y 4y
Câu 11. Tìm số nghiệm của hệ y 1 3
y x 4 log (2 x) 3 A.2 B. 3 C. 1 D. 4 1 1
Câu 12. Tìm số nghiệm của phương trình 1 1 x x x x A.2 B. 1 C. 3 D. 6 3 2 3 2 3 2 2 x .4 y .16 y 128
Câu 13. Có tất cả bao nhiêu bộ số thực (x;y;z) thỏa mãn 2 4 2 2 4 2
(xy z ) 4 (xy z ) 99 A.2 B. 1 C. 4 D. 3 2 2 9 x 4y 5
Câu 14. Hệ phương trình
có nghiệm (x;y) thỏa mãn 3x 2 y 5 .
log (3x 2 y) log (3x 2y) 1 m 3
Giá trị lớn nhất của m là A.5 B. – 5 C. log 3 D. log 5 5 3
Câu 15. Tồn tại bao nhiêu cặp số tự nhiên (p;q) với p nguyên tố thỏa mãn 2 3 p p 1 q A.3 B. 1 C. 8 D. 2 m
Câu 16. Số thực a nhỏ nhất để 2
ln(x 1) x ax đúng với mọi số thực x là
với m, n là các số nguyên n m dương và
là phân số tối giản. Tính 2m + 3n. n A.5 B. 8 C. 7 D. 11 2 x m
Câu 17. Số thực a nhỏ nhất để 3 ln(x 1) x
ax đúng với mọi số thực x là (phân số tối giản), m và n 2 n
nguyên dương. Tính 2m + 3n. A.8 B. 20 C. 11 D. 34
Câu 18. Tất cả các nghiệm của phương trình thỏa mãn điều kiện nào sau đây x 2021 2021 4041 2021x log 2021(2x 1) 2021 A. 2 x 1 0 B. 2 x 3x 0 C. 2 x x 0 D. 2 x 2x 3 0
Câu 19. Phương trình log 2 x 2x 3 2
1 x x 4x 2 0có 1 nghiệm dương dạng a b c với a, b hữu 2
tỷ, c nguyên tố. Tính 2a 3b c . A.8 B. 15,5 C. 6,25 D. 8,5 3 x 6 x4 Câu 20. Phương trình 3 2 4 3 .2 x x x 24x 32 có nghiệm 3 3
x a b c (với a, b, c hữu tỷ). Tính 2abc. A.28 B. 24 C. 54 D. 50
Câu 21. Có bao nhiêu cặp số nguyên dương (x;y) thỏa mãn 2010 2009 2008 5 x x x ... x 2 y A.4 B. 2 C. 1 D. 0
Câu 22. Tính 2a + 8b với a, b lần lượt là nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình
2sin x3cos x 2cosx cosx cos x 1sin 2 2 sin 1 .2 4.25 2 x x cosx A.0 B. C. 2 D. x
Câu 23. Tìm số nghiệm dương của phương trình 4 4 x 2 8 x 3x 6 6 21 2 4 3 x 2 3 3x 24 3x A.0 B. 1 C. 2 D. 3
Câu 24. Có bao nhiêu cặp số nguyên dương (x;y) với x 2020 thỏa mãn 23 3(1 9y x y ) log (2x 1) 3 A.3 B. 1010 C. 4 D. 2020 x 1 (3x 1)log (3x 1)
Câu 25. Tính tổng số nghiệm của phương trình 4 4 2x 1 log 2 2 x A.2 B. 1 C. 3 D. 4
Câu 26. Tồn tại bao nhiêu số tự nhiên n để 2
3n n là số chính phương A.2 B. 3 C. 1 D. 5
Câu 27. S là tổng tất cả các nghiệm nguyên không vượt quá 2022 của bất phương trình 3 2
log (x 3x 25) log (x 1) 3log (x 1) 1. 3 3 3
Tìm chữ số hàng đơn vị của S A.3 B. 8 C. 0 D. 5 2 2
Câu 28. Số nghiệm nguyên của bất phương trình 2x 1 5x 1 00 x 1 0x50 2 2 2
x 25x 150 0 là A. 4 . B. 6. C. 3 . D. 5 . 2 x x 8
Câu 29. Cho bất phương trình 2 x
x x . Số nghiệm nguyên dương của bất phương trình x 1 3 2 đã cho là A. 0 . B. 3 C. 1. D. 2 . 100
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 53)
__________________________________________________ 3 3 x 1 log x 1 2 x x 1 2 2
Câu 1. Tìm số nghiệm dương của phương trình 2 1 log 2 2 2 x A.0 B. 3 C. 2 D. 1 7x 3x
Câu 2. Tìm số nghiệm của phương trình x 1 log
7 7.3x 56x 14 2021 8x 2 A.0 B. 1 C. 3 D. 2
Câu 3. Có bao nhiêu bộ số (m;n) thỏa mãn 2 1 3.5m n n A.3 B. 1 C. 2 D. 4
Câu 4. Có bao nhiêu cặp số nguyên (x;y) thỏa mãn đẳng thức y
log 2x y 4x y 2 4 2 2 4 2 2 2 4
27 (2 2x )(y 2) 3 A.2 B. 4 C. 8 D. 0
Câu 5. Tìm số nghiệm của phương trình 2 lg x lg . x log (4x) 2log x 0 2 2 A.0 B. 1 C. 2 D. 3
Câu 6. Tìm số nghiệm của phương trình 2
log x (x 1)log x 2x 6 0 2 2 A.0 B. 1 C. 2 D. 3
Câu 7. Tính tổng các nghiệm phương trình 2
(x 1)log (x 1) (x 2)log (x 1) 3 3 3 4 2 A.1 B. 2 C. D. 3 3
Câu 8. Có bao nhiêu giá trị m 2
0;20 mà 4m để phương trình sau có nghiệm x x 1 x 1 9 3 2 (3 1) 3x m m . A.79 B. 82 C. 81 D. 80
Câu 9. Có bao nhiêu cặp số tự nhiên (m;n) thỏa mãn đẳng thức 3 9 27 17.9m n n . A.2 B. 1 C. 3 D. 0
Câu 10. Tính tổng các nghiệm của phương trình 3x 2x 4 3(x 2) A.1 B. 0 C. 2 D. 3 2005 2005 2005 p
Câu 11. Có bao nhiêu số nguyên tố p để là số nguyên p 2005 A.2 B. 4 C. 1 D. 3
Câu 12. Tìm số nghiệm thực của phương trình 9x 9 6 .3x cos x A.1 B. 2 C. 3 D. Vô nghiệm 3 cos x cos 1 1 x
Câu 13. Tìm số nghiệm của phương trình cos3x trên [0;2021] 16 8 A.1932 B. 1930 C. 1925 D. 1927 2 ( x2) 1 3 1
Câu 14. Tính tổng các nghiệm của phương trình x6 x 1 9.3 (x 4)(2 x) 2 x8 x 4 5 27 5.5 x A.3 B. – 3 C. – 6 D. 37
Câu 15. Có tất cả bao nhiêu bộ số tự nhiên (a;b;c;d) thỏa mãn 11a5b 3c2d 1 A.4 B. 3 C. 2 D. 1 2 4 2
Câu 16. Tính tổng bình phương các nghiệm của phương trình x 2 x x 1 2 2 5 5 (x 1) A.1 B. 5 C. 2 D. 0
Câu 17. Tìm số nghiệm thực của phương trình 3.2x 4.3x 5.4x 6.5x A.1 B. 5 C. 2 D. 0 2
Câu 18. Có bao nhiêu số nguyên x 1 0;10thỏa mãn x sin
3.3 2 1 cos(2 ) 3 y x y A.2 B. 3 C. 1 D. 0 101
Câu 19. Có bao nhiêu cặp số nguyên (x;y) thỏa mãn x, y 1;14 và 2 2
x 1 2( y 1) 2(x 2) y 2 y A.8 B. 4 C. 1 D. 7 x x 13
Câu 20. Tìm số nghiệm thuộc 0;3 của phương trình sin cos cos x sin 14 14 .7 .2 x 2 A.3 B. 4 C. 2 D. 5 2 2
Câu 21. Mệnh đề nào sau đây đúng đối với phương trình x x x x 4 2 2 2 2 2 3x x 2xln 2
A. Phương trình có hai nghiệm trái dấu thuộc 1; 1
B. Tổng các nghiệm thuộc 1; 1 bằng 1
C. Tổng các nghiệm thuộc 1; 1 bằng 0
D. Phương trình vô nghiệm. 2
Câu 22. Tìm điều kiện của a, b để phương trình ax bx 6 x 2 e
e (6 b)x ax có hai nghiệm phân biệt a 0 A. b 6 B. a 0 C. Mọi a, b D. b 6 4 x 2
Câu 23. Tập nghiệm của bất phương trình 2 5 5x 2 0 là 2 5 x 5x x log 2 x log 2 A. 0 x log 2 . B. 0 x log 2 . C. 5 . D. 5 . 5 5 x 0 x 0 Câu 24. Phương trình 2 2 x 8 2 x 1 2 2021
2021 x 2x 8 1 có nghiệm duy nhất x a b với a,b . Tính
giá trị biểu thức b a. A. 9 . B. 11. C. 11. D. 9 . 2 2
Câu 25. Tìm số nghiệm của phương trình sin x cos x
cos 2x trong khoảng 0;10 . A. 19 . B. 15 . C. 20 . D. 17 .
Câu 26. Có bao nhiêu cặp số nguyên x; y thỏa mãn 0 y 2021 và 2 x 1 2 2021 2021y x y 1. A. 45 . B. 89 . C. 11. D. 20 . 2
Câu 27. Có bao nhiêu số nguyên dương x thỏa mãn x 2 sin 2 2 .cos 2 y .2x y x A.2 B. 1 C. 0 D. 3
Câu 28. Có bao nhiêu cặp số nguyên dương (x;y) thỏa mãn x 2022 và 4 3 y y 2
x 2x 2.3 9 3x 2x A.19 B. 15 C. 13 D. 6 2 3 3 2
Câu 29. Có bao nhiêu cặp số nguyên dương (x;y) thỏa mãn y 1994 và 3
5 x x y 4 3x y 4 27x A.10 B. 13 C. 3 D. 9
Câu 30. Cho hàm số f x 2
log x 1 x 2x 2 . Có bao nhiêu giá trị nguyên của tham số m thuộc 1
0;10 để bất phương trình f x m f 2 2
x 4x 6 0 nghiệm đúng với mọi x thuộc 1 ; 1 ? A. 8 . B. 4 . C. 11. D. 3 .
Câu 31. Hỏi có tất cả bao nhiêu giá trị thực của tham số m để bất phương trình sau có nghiệm thực x ? 2 m 4m 4log 2 2 x 2mx m 2 1 m log 2 x 1 0 2 3 A. 1. B. 2 . C. 3 . D. 6 .
Câu 32. Gọi S là tập chứa tất cả các giá trị nguyên của tham số m để bất phương trình 2
ln x 4x 3 log m có
đúng 3 nghiệm nguyên, vậy tổng phần tử của S là A. 108 . B. 5 . C.Vô số D. 89 .
Câu 33. Cho a,b là các số nguyên dương nhỏ hơn 2022 . Biết rằng với mỗi giá trị của b luôn có ít nhất 1000
giá trị của a thỏa mãn ab2 2 2ba .log
b 4b 1. Số giá trị b là a 1 A. 1021. B. 1022 . C. 1020 . D. 1023 .
_________________________________ 102
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 54)
__________________________________________________ Câu 1. Cho hàm số 2 3log 2x
2m 3 x 1 2m log
2x x16m 0. Số các giá trị nguyên của m để 8 1 2
phương trình đã cho có hai nghiệm phân biệt x , x thỏa mãn x x 15 là: 1 2 1 2 1 3 2 3 1 3 2 3 3 A. m . m . C. m . D. m . 2 B. 2 2 2 4 Câu 2. Cho phương trình 2
log x log 5x 1 log m 0 ( m là tham số thực). Có tất cả bao nhiêu số nguyên 4 2 2
của m để phương trình đã cho có nghiệm? 3 A. m 0 . B. m 5 . C. 0 m 5 . D. m . 4
Câu 3. Cho hai số thực a,b 1 thỏa mãn a b 2021. Gọi ,
m n là hai nghiệm của phương trình
log x log x 2log x 2 0. Giá trị nhỏ nhất của biểu thức mn 4a bằng a b a A. 8080 . B. 2032 . C. 1015 . D. 3626 .
Câu 4. Có bao nhiêu số nguyên m 20; 20 để phương trình log x log m x 2 có nghiệm thực 2 3 A. 15 . B. 14 . C. 24 . D. 21.
Câu 5. Có bao nhiêu số nguyên m thuộc khoảng 10;10 để phương trình x 1 3 log x 3m m có nghiệm? 27 A. 9 . B. 8 . C. 10 . D. 7 .
Câu 6. Cho phương trình log x m log
2 x 0 (1). Với m là giá trị của tập S m | m 49; m ¢ để 2 1 2
phương trình (1) có nghiệm. Tính tổng lập phương tất cả các phần tử của S A. 1382975 . B. 1382976 . C. 1382977 . D. 1382978 .
Câu 7. Cho phương trình ln ln
cos x m m cos x (1)
. Tìm tất cả các giá trị của m để phương trình (1) có nghiệm. A. 1 1 m e 1 1 1 B. e 1 m e 1 C. 1 m 1 D. 1 m e 1
Câu 8. Cho phương trình mcos2xsin2x 21sin 2 x 3 3
2 sin 2x m cos 2x với m là tham số. Hỏi có bao nhiêu giá trị
m nguyên dương bé hơn 2021 để phương trình có nghiệm. A. 2019 . B. 2018 . C. 2020 . D. 2021.
Câu 9. Có bao nhiêu số nguyên m thuộc khoảng 2022;2022 để phương trình 10x log x 3m 3m có nghiệm? A. 2020 . B. 4042 . C. 4040 . D. 2021.Có bao nhiêu
Câu 10. Có bao nhiêu số nguyên m 2021; 2022 để phương trình 2
log x 2 log x m log x m * có 2 2 2 nghiệm? A. 2021. B. 2022 . C. 4042 . D. 2024 .
Câu 11. Tìm tất cả các giá trị của m để phương trình ln m ln m cos x cos x có nghiệm. 1 1 A. 1 m e 1. B. 1 m e 1. C. 1 m 1. D. 1 m e 1. e e
Câu 12. Có bao nhiêu giá trị m nguyên trong 2017;2017 để phương trình log mx 2log x 1 có nghiệm duy nhất? A. 2017 . B. 4014 . C. 2018 . D. 4015 . 2
Câu 13. Cho phương trình 4 xm.log 2 3 2 xx x x
.log 2 x m 2 0 với m là tham số. Tổng tất cả 2 2 2 1 2
các giá trị của tham số m để phương trình đã cho có ba nghiệm phân biệt là A. 3 . B. 2 . C. 4 . D. 1.
Câu 14. Gọi S là tập chứa tất cả các giá trị thực của tham số m để tồn tại đúng một bộ số thực ; x y thỏa mãn 2
log x y 4m log 2 2
x y 15 3m 0 . Tính tổng bình phương giá trị tất cả các phần tử của tập S đó 2 2 144 45 225 41 A. B. C. D. 289 4 256 16
Câu 15. Gọi S là tập chứa tất cả các giá trị thức của tham số m để tồn tại duy nhất bộ ba số thực x; y; z thỏa 103 mãn điều kiện 2 log 2 2 2
2x y z 2m log 4x 2y 2z 0 . Tích tất cả các phần tử của tập S tương ứng 2 2 bằng: A. 0 . B. 16 . C. 6 . D. 12 . 2 Câu 16. Cho hai số thực , x y thỏa mãn hệ thức 2 2 y x log
x . Hỏi có bao nhiêu số nguyên m 40; 40 2 y 1
để tồn tại duy nhất một số thực x thỏa mãn hệ thức 2 2
4 y 10x mx 1 0 ? A. 51. B. 52 . C. 53 . D. 31.
Câu 17. Cho các số thực x, y, z thỏa mãn log 2 2 2x y log 3 3
x 2 y log z . Có bao giá trị nguyên của 3 7
z để có đúng hai cặp x, y thỏa mãn đẳng thức trên. A. 2 . B. 211. C. 99 . D. 4.
Câu 18. Cho phương trình
2x xm 2 2 4 2 2 x 4 2 2 2 4 1 2 mx x mx x x m
1 0 . Hỏi có tất cả bao nhiêu
giá trị thực của tham số m để phương trình đã cho có 3 nghiệm thực x? A. 4. B. 5 . C. 2. D. 3.
Câu 19. Tổng tất cả các số nguyên a để tồn tại số thực b thỏa mãn 4b 2 2 3b a a A. 7 B. 0 C. 3 D. 2
Câu 20. Cho phương trình 4x 4 .2x a log 2
2x x b . Có bao nhiêu bộ số a,b thỏa mãn điều kiện 2 100a , 100b , 1
00 a,b 100 sao cho phương trình có nghiệm duy nhất A. 15 B. 6 C. 3 D. 4 2
Câu 21. Cho phương trình sau: 2log xlogx 1log 2 4 x 9x 2 3x m
2m 0 (với m là tham số thực). Gọi S là
tập hợp tất cả các giá trị nguyên dương của m để phương trình đã cho có đúng hai nghiệm phân biệt. Tổng của
phần tử nhỏ nhất và phần tử lớn nhất của S bằng A. 100 3 1. B. 100 3 1 . C. 99 3 . D. 99 3 1. x m
Câu 22. Cho hàm số f (x)
. Gọi S là tập hợp các số nguyên dương m 7 sao cho với mọi bộ số thực 2x 1 a,b,c 2;
3 thì ln f (a) , ln f (b) , ln f (c) là độ dài ba cạnh của một tam giác. Tổng các phần tử của S là A. 10 . B. 15 . C. 16 . D. 14 .
Câu 23. Cho hàm số f (x) log 2.log 2 x m . Hỏi có bao nhiêu giá trị nguyên dương của tham số m để x 4
phương trình f x 2 x 0 có tổng tất cả các nghiệm bằng 2 . A. 0 B. 1 C. 2 D. 3 2 x Câu 24. Cho phương trình 2 log
3mlog x 2m 2m 1 0
. Có bao nhiêu giá trị nguyên của tham số 3 3 3 m lớn hơn 2
021 sao cho phương trình đã cho có hai nghiệm phân biệt x , x thoả x x 10 ? 1 2 1 2 A. 2020 . B. 2019 . C. 2020 . D. 2021.
Câu 25. Hỏi có tất cả bao nhiêu giá trị nguyên của tham số m 24;24 để ba số hạng sau theo thứ tự tạo
thành 1 cấp số cộng, với x 1;2 : x m 3x 2x 1 9.2 1 ; ; 2 3.2 A. 2 . B. 1. C. 17 . D. 7 .
Câu 26. Có bao nhiêu giá trị nguyên m 18;18 để phương trình 2 2 x 1 .2x m
3m 1 0 có hai nghiệm
thỏa 0 x 1 3 x 1 2 A. 8 . B. 18. C. 11. D. 12.
Câu 27. Có bao nhiêu số nguyên m 2022;2022 sao cho phương trình sau có hai nghiệm sao cho thỏa mãn 0 x x 8 : 2 log x 2m 1 log 2 x 2m 3 0 . 2 2 1 2 A. 2021. B. 2019 . C. 18. D. 2023.
Câu 28. Hỏi có tất cả bao nhiêu giá trị nguyên của tham số m 2
0;20 để phương trình sau có nghiệm log 2 2
x m x x 4 2m 9 x 1 1 2m 2 x 4 2 A. 12 . B. 23. C. 25 . D.10 .
_________________________________ 104
VẬN DỤNG CAO, PHÂN LOẠI HÀM SỐ MŨ, HÀM SỐ LOGARIT LỚP 12 THPT
(LỚP BÀI TOÁN PT, BPT, HPT – PHẦN 55)
__________________________________________________
Câu 1. Tìm m để bất phương trình 2
log 2x 2(m 1) log x 2 0 có nghiệm x ( 2; ). 2 2 3 3 A. m (0;) . B. m ;0 . C. m ; . D. m (;0) . 4 4
Câu 2. Tập nghiệm của bất phương trình 3x 3 3 5 x 33x 5x 0 là A. ;0. B. ;0 . C. 0; . D. 0; .
Câu 3. Có bao nhiêu số nguyên m để bất phương trình 2 x 2 ln5 ln 1
ln mx 4x m có tập nghiệm R? A.1 . B. 2 . C. 3 . D. 4 .
Câu 4. Có bao nhiêu số nguyên m thuộc 2 021;202
1 sao cho bất phương trình sau nghiệm đúng với mọi x trên đoạn 0; 3 : 1 log 3 2
x x 3x m log 2 3x 1 3 3 A. 2020 . B. 2018 . C. 2022 . D. 4040 .
Câu 5. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m thuộc 2 021;202
1 sao cho bất phương trình 2
3log 2x 12log x 1 m 0 nghiệm đúng với mọi x trên khoảng 2; . Tính số phần tử của tập hợp S . 2 2 A. 2018 . B. 2020 . C. 2022 . D. 4040 .
Câu 6. Tìm điều kiện tham số m để bất phương trình log (5x 1).log (2.5x 2) m có nghiệm x 1. 2 2 A.Mọi giá trị m. B. m 6 . C. m 6 . D. m 6 .
Câu 7. Tìm tất cả các giá trị thực của tham số m để bất phương trình log x
1 log 3x xm có nghiệm. 1 1 2 2 A. m 2 . B. Mọi m. C. m 2 . D. Không tồn tại m . 2 x x 1
Câu 8. Cho hàm số f x
. Tìm tất cả các giá trị thực của tham số m để bất phương trình sau có 2 x 1 2 f x f x 4
nghiệm x 0; : 4 2 log f x m . 5 f x 9 1 9 1 A. m . B. m . C. m . D. m . 8 2 8 2
Câu 9. Cho các bất phương trình 2 log x 4x m 2 log 2 x 4x m 8
1 và 3 x x 1 0 2 . 2 4
Có tất cả bao nhiêu giá trị nguyên của m thỏa mãn mọi nghiệm của bất phương trình 2 đều là nghiệm của bất phương trình 1 . A. 254 . B. 255 . C. 256 . D. 257 . 2
Câu 10. Cho bất phương trình x2 2 .log 2
x 4x 6 4 xm log 2 x m 2 với m là tham số thực. Biết 2 2
rằng tập hợp tất cả các giá trị nguyên của m để bất phương trình có nghiệm đúng với mọi x 0;2 là đoạn ;ab. Khi đó 2 2 a b bằng: A. 4 . B. 8 . C. 16. D. 0 .
Câu 11. Có tất cả bao nhiêu bộ số nguyên ; a ; b ; c d với a, , b c,d 3 ;
3 thỏa mãn điều kiện bất phương trình 2 3 x x x 4 3 2 ln 1
ax bx cx dx nghiệm đúng với x 1 ;? 2 3 A. 43 B. 71 C. 37 D. 47 2
Câu 12. Tìm số nghiệm nguyên của bất phương trình x x 3x 2 2 2x 2 x 3. A. 5 . B. 6 . C. 7 . D. 8 .
Câu 13. Tìm số nghiệm nguyên dương của bất phương trình sau: x 3x 1 3 5 1 2 x 2 3x 1 3x 6x . 5 105 A. 2022 . B. 1. C. 2 . D. 2021 .
Câu 14. Tổng các nghiệm nguyên dương nhỏ hơn 6 của bất phương trình 27x 8x 3.4x 2.3x 5.2x 3 0 là A. 15 . B. 12 . C. 13 . D. 19 .
Câu 15. Tìm số nghiệm nguyên thuộc 2021;2022 của bất phương trình 3 2x 1 2x 3 3 2 2022 2022
2x 1 x 6x 15x 11 0 A. 2024 . B. 2023 . C. 2021 . D. 2022 .
Câu 16. Cho hai bất phương trình 2 2 5 x x x 5 x x
x 23 xx 32 2 2 3 4 2 3 2 1 2
x m 2 x 2m 4 0 2
Có bao nhiêu giá trị nguyên của tham số m 2021;202
1 để mọi nghiệm của bất phương trình (1) đều là
nghiệm của bất phương trình (2). A. 2019 . B. 2020 . C. 2021 . D. 2018 .
Câu 17. Có bao nhiêu cặp nghiệm nguyên x; y thỏa mãn x y 2 2 2 10x 8 xy2 y 4 2 2 3 .3 4 x 2xy y ? A. 8 . B. 6 . C. 5 . D. 9 . 1992 1990
Câu 18. Tìm số tự nhiên k lớn nhất để 1991 1991 1990 1992 chia hết cho 1991k A.k = 1991 B. k = 1990 C. k = 1992 D. k = 1993 2
Câu 19. Tính tổng các nghiệm nguyên dương của bất phương trình sau x 1 2 x2 5 2x 4x 6 25 A. 6 . B. 5 . C. 3 . D. 7 . 2
Câu 20. Hãy xác định số nghiệm nguyên âm của bất phương trình sau: x 3x7 x 1 0 2 9.3 3 2x 8x 30 A. 2 . B. 3 . C. 6 . D. 9 .
Câu 21. Tính tích của nghiệm nguyên âm lớn nhất và nghiệm nguyên dương nhỏ nhất của bất phương trình sau 2 x 1 2 x2 4 2x 4x 6 16 A. 8 . B. 3 . C. 3 . D. 2 .
Câu 22. Có bao nhiêu bộ số tự nhiên (x;y) thỏa mãn 3x 2x.y 1 A.3 B. 1 C. 2 D. 4 2
Câu 23. Tính tổng các nghiệm nguyên của bất phương trình x 5x 2 5x2 2 2021 2021
x 5x 2 5x 2 . A. 55 . B. 5 . C. 6 . D. 25 .
Câu 24. Có bao nhiêu số tự nhiên n để n 2 2 1n A.2 B. 1 C. 3 D. 4
Câu 25. Có bao nhiêu số nguyên x thỏa mãn bất phương trình 2 1 x 3x 1 0 x 1 2 2
2 2 x 3x 10 2x 4 . A. 9 . B. 5 . C. 4 . D. 15 . 3 x 6x4
Câu 26. Bất phương trình 2 3 2 4 3 2 x x x
24x 32 có tập nghiệm là S 3 3 a ;b c d ,
với a,b,c, d . Tính giá trị của biểu thức T 4abcd . A. T 75 . B. T 80 . C. T 81 . D. T 82 . 3 2 x 1 6x 48x36
Câu 27. Bất phương trình 1 2 3 2 .2 x x x x
có tập nghiệm S a ;b c d với a,b,c,d và
c 1. Tính giá trị của biểu thức S a b c d . A. 17 . B. 16 . C. 15 . D. 18 .
Câu 28. Có bao nhiêu giá trị nguyên dương của tham số m nhỏ hơn 2018 để phương trình x 2 2 2 x m m có nghiệm thực? A. 2017 . B. 2018 . C. 2016 . D. 2015 .
Câu 29. Có bao nhiêu bộ số (a;b;p) với a, b nguyên dương, p nguyên tố thỏa mãn 2a b 19a p A.1 B. 2 C. 3 D. 4 2 2
Câu 30. Có bao nhiêu số nguyên x sao cho tồn tại số thực dương y thỏa mãn 2x y 2.2yx ? A. 1. B. 2 . C. 3 . D. 4 .
Câu 31. Có bao nhiêu số nguyên x 2021; 2022 thỏa mãn 6x 4 x 3x 2x x2 2 2 2 2 2 3 0 A. 2021 . B. 2020 . C. 2022 . D. 2019 .
_________________________________ 106




