



Preview text:
Bài 2
2.1. Phép thử và biến cố
Loại bài tập: Phân loại biến cố, phân biệt biến cố và bnn
VD: Một người mua 10 sản phẩm từ cửa hàng. Đại lượng nào sau đây không phải biến cố?
A) Người đó mua được hơn 10 chính phẩm ()
B) Số chính phẩm người đó mua được tối thiểu là 10 = mua được 10 cp (biến cố ngẫu nhiên)
C) Số chính phẩm mà người đó mua được (biến ngẫu nhiên rời rạc)
D) Người đó mua được tối đa là 10 chính phẩm (biến cố chắc chắn)
2.2. Xác suất của biến cố A là P(A)
Xác suất có điều kiện của A khi B đã xảy ra là P(A|B)
2.3. Tính xác suất theo định nghĩa
Định nghĩa cổ điển về XS:
Định nghĩa thống kê về XS:
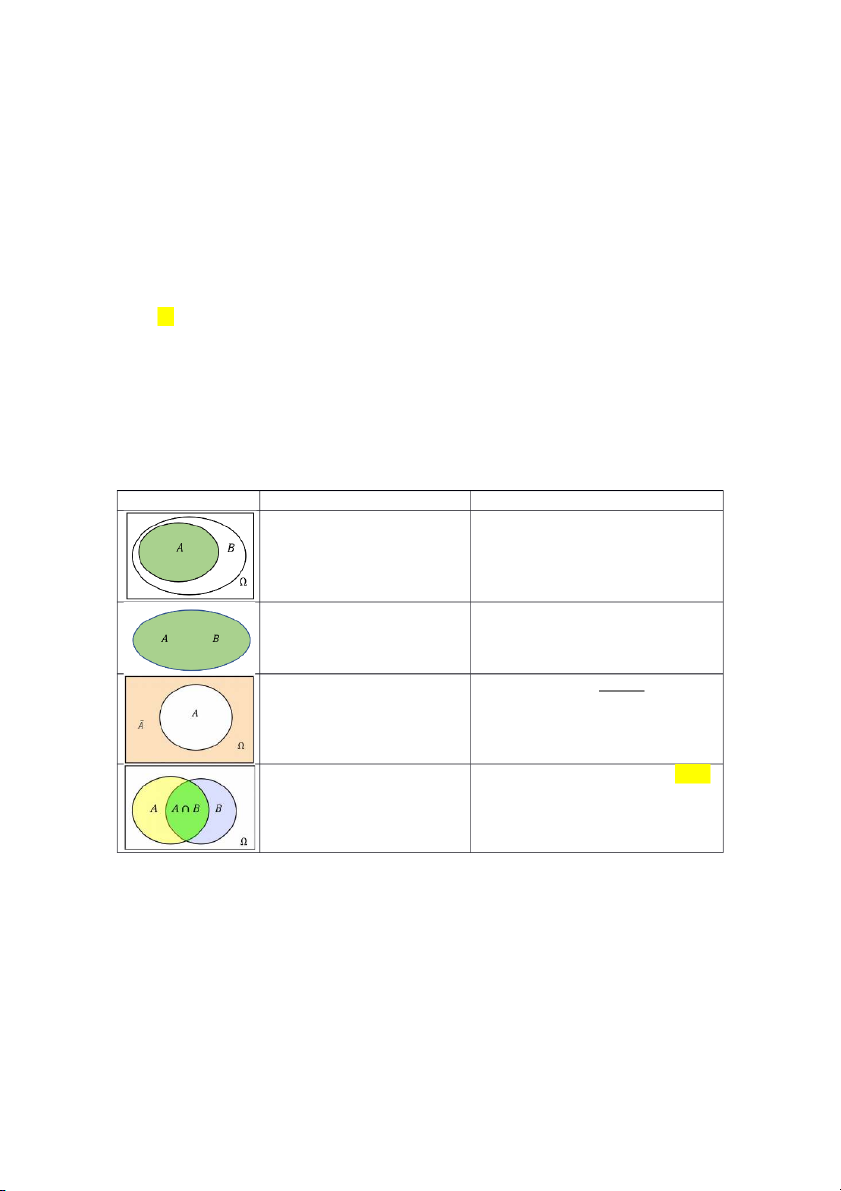
2.4. Liên hệ giữa các biến cố Hình ảnh Tập hợp Biến cố Tập con: A thuận lợi cho B: Hai tập bằng nhau: 2 biến cố bằng nhau: là phần bù của
và là hai biến cố đối lập C/m được: Giao của 2 tập hợp:
Tích của 2 biến cố xảy ra khi tất cả
các thành phần đều xảy ra: hoặc Hợp của 2 tập hợp:
Tổng của 2 biến cố xảy ra khi có ít
nhất một trong các thành phần xảy ra hoặc Hai tập hợp không giao
Hai biến cố xung khắc nếu không nhau: đồng thời xảy ra Hiệu 2 tập hợp:
Độc lập: không ảnh hưởng đến nhau về mặt xác suất
BT: Đọc tên biến cố; biểu diễn biến cố thành các thành phần; kiểm tra tính độc lập, xung khắc; …
VD: Đấu thầu 2 dự án, XS thắng thầu lần lượt là 0,5 và 0,6. XS không thắng thầu dự án
nào là 0,3. A= thắng dự án 1; B= thắng 2 1. Chọn phát biểu đúng
A. A và B độc lập và xung khắc
B. A và B độc lập và không xung khắc
C. A và B phụ thuộc và xung khắc
D. A và B phụ thuộc và không xung khắc
2. Tìm xs thắng dự án 2 biết rằng thắng dự án 1 A. 0,8 B. 0,4 C. 0,67 D. 0,6
2.5. Tính xác suất theo công thức
Công thức XS của biến cố tích Ví dụ 2.11.
Xác suất một sinh viên thi đạt hai môn A và B lần lượt là 0,6 và 0,8. Nếu sinh viên đó thi
đạt môn A thì xác suất để anh ta thi đạt môn B là 0,7.
A = “Thi đạt môn A” và B = “Thi đạt môn B”
a) Tính xác suất sinh viên thi đạt cả hai môn.
b) Các biến cố A và B có độc lập không?
C1: A và B không độc lập C2: A và B ko độc lập
C3: A và B không độc lập
c) Hãy tính xác suất sinh viên đó thi đạt môn A biết rằng anh ta đã thi đạt môn B. Hướng dẫn lập bảng Ví dụ 2.12.
Hộp gồm 16 bóng trắng và 4 bóng đen. Lấy lần lượt có hoàn lại 5 quả bóng. Tính xác
suất để lấy được 5 quả bóng màu trắng.
Lần thứ i lấy được quả bóng trắng
Lấy có hoàn lại nên độc lập toàn phần
Công thức XS của biến cố tổng Ví dụ 2.11. (tiếp)
Xác suất một sinh viên thi đạt hai môn A và B lần lượt là 0,6 và 0,8. Nếu sinh viên đó thi
đạt môn A thì xác suất để anh ta thi đạt môn B là 0,7. Join probability = đạt môn B đạt môn A
Cách 1: áp dụng công thức Cách 2: áp dụng Cách 3: áp dụng
d) Tính xác suất sinh viên thi đạt ít nhất một môn. Cần C1: C2: C2:
e) Tính xác suất có ít nhất một môn không đạt. Cần C1: C2: C4: hay Công thức Bernoulli
Ví dụ 2.13. Phép thử có nhiều bước lặp lại Coi như nhiều phép thử độc lập
Một người đi bán hàng ở 3 nơi độc lập, xác suất bán được ở mỗi nơi đều bằng 0,6. Tính
xác suất người đó bán được hàng ở đúng 2 nơi.
Gọi “bán được hàng ở nơi thứ i” (i=1,2,3)
“bán được hàng ở đúng 2 nơi”
Trình bày theo công thức Bernoulli
+ Coi việc đi chào hàng ở một chỗ là 1 phép thử có 3 phép thử
+ Trong mỗi phép thử, quan tâm ”bán được hàng” có xảy ra hay không + Trong mỗi phép thử:
Bài toán thỏa mãn lược đồ bernoulli với
XS bán được hàng ở đúng 2 nơi là:
BT2. Sinh viên học 6 môn học với XS qua mỗi môn đều là 0,8. Tìm XS sinh viên không qua đúng 2 môn. BL
Bài toán thỏa mãn lược đồ bernoulli với XS ko qua đúng 2 môn là:
BT1. Chào hàng ở 3 nơi với XS bán được hàng ở nơi 1 là 0,6. Nếu bán được ở nơi trước
thì XS bán được ở nơi tiêp theo là 0,7. Nếu không bán được ở nơi trước thì XS bán được
ở nơi tiêp theo là 0,45. Tìm XS bán được hàng ở đúng 2 nơi.
Gợi ý: nên vẽ sơ đồ cây (xem ảnh)
Công thức XS đầy đủ
Ví dụ 2.14. Phép thử có 2 bước không lặp lại của nhau Hai hộp giống nhau:
Hộp loại I chứa 20 sản phẩm, trong đó có 6 phế phẩm;
Hộp loại II chứa 20 sản phẩm, trong đó có 5 phế phẩm.
Chọn ngẫu nhiên một hộp và từ đó chọn 1 sản phẩm. là nhóm đầy đủ a)
Tính xác suất để đó là chính phẩm.
Theo công thức Xs đầy đủ: b)
Biết chọn được chính phẩm. Tính xác suất đã lấy được hộp loại I. Hướng dẫn lập bảng: hộp 1 hộp 2 Tổng c)
Lô hàng có 100 hộp sản phẩm, trong đó có 40 hộp loại I, còn lại là hộp loại
II. Làm lại câu a, b trong trường hợp này. hộp 1 hộp 2 Tổng
Ví dụ 2.15. Phép thử có 1 bước, 1 phần tử có 2 đặc điểm
Một công ty có 70% nhân viên là nam, còn lại là nữ.
Trong số nhân viên nam: 40% đã có bằng đại học, còn lại chưa có bằng đại học.
Trong số nhân viên nữ: 20% đã có bằng đại học, còn lại chưa có bằng đại học.
a) Chọn 1 nhân viên bất kì, tìm xác suất người đó có bằng đại học.
b) Chọn 1 nhân viên có bằng đại học bất kì, tìm xác suất người đó là nữ.
c) Trong số nhân viên có bằng đại học, chọn 3 người, tìm xác suất chọn được đúng 1 nhân viên nữ. nam nữ Tổng
a) Từ bảng P(có bằng ĐH) = 0,34
b) Từ bảng P(nữ | có ĐH) = 0,176
c) Bài toán thỏa mãn lược đồ Bernoulli với
XS chọn được đúng 1 nữ là BÀI 3
Lý thuyết: trang 82 đến 87
3.2. Bảng phân phối xác suất: chỉ dùng cho bnn rời rạc Ví dụ 3.2.
a) Hộp có 16 chính phẩm và 4 phế phẩm. Lấy đồng thời 2 sản phẩm. Lập bảng
PPXS của số chính phẩm lấy được. Số CP lấy được P
b) Học sinh làm đề thi có 2 câu hỏi độc lập với xác suất là đúng mỗi câu đều là 0,4.
Lập bảng PPXS của số câu trả lời đúng.
BT thỏa mãn lược đồ Bernoulli với số câu đúng P
Ví dụ 3.3. Tại 1 phân xưởng mỗi ngày có 4 máy cùng loại hoạt động. Bảng sau là PPXS
của số máy hỏng trong 1 ngày: X 0 1 2 3 4 P 0,6 0,2 0,12 0,07 0,01
a) Tìm xác suất một ngày bất kì có ít nhất là 2 máy hỏng.
b) Số máy hỏng trong các ngày khác nhau là độc lập với nhau. Tìm xác suất trong 3
ngày liên tiếp không có máy nào hỏng = XS ba ngày liền đều không có máy hỏng
C1: A = ngày 1 không có máy hỏng,
B = ngày 1 không có máy hỏng,
C = ngày 1 không có máy hỏng, XS cần tìm:
C2: Bài toán thỏa mãn lược đồ Bernoulli với
XS trong 3 ngày liên tiếp không có máy nào hỏng:




