-
Thông tin
-
Quiz
Tóm tắt công thức môn xác suất thống kê| Đại học Kinh tế Quốc Dân
Đại học Kinh tế Quốc dân với những kiến thức và thông tin bổ ích giúp các bạn định hướng và họp tập dễ dàng hơn. Mời bạn đọc đón xem. Chúc bạn ôn luyện thật tốt và đạt điểm cao trong kì thi sắp tới
Môn: Xác suất thống kê (XSTK021) 145 tài liệu
Trường: Đại học Kinh Tế Quốc Dân 3 K tài liệu
Thông tin:
Tác giả:
Preview text:
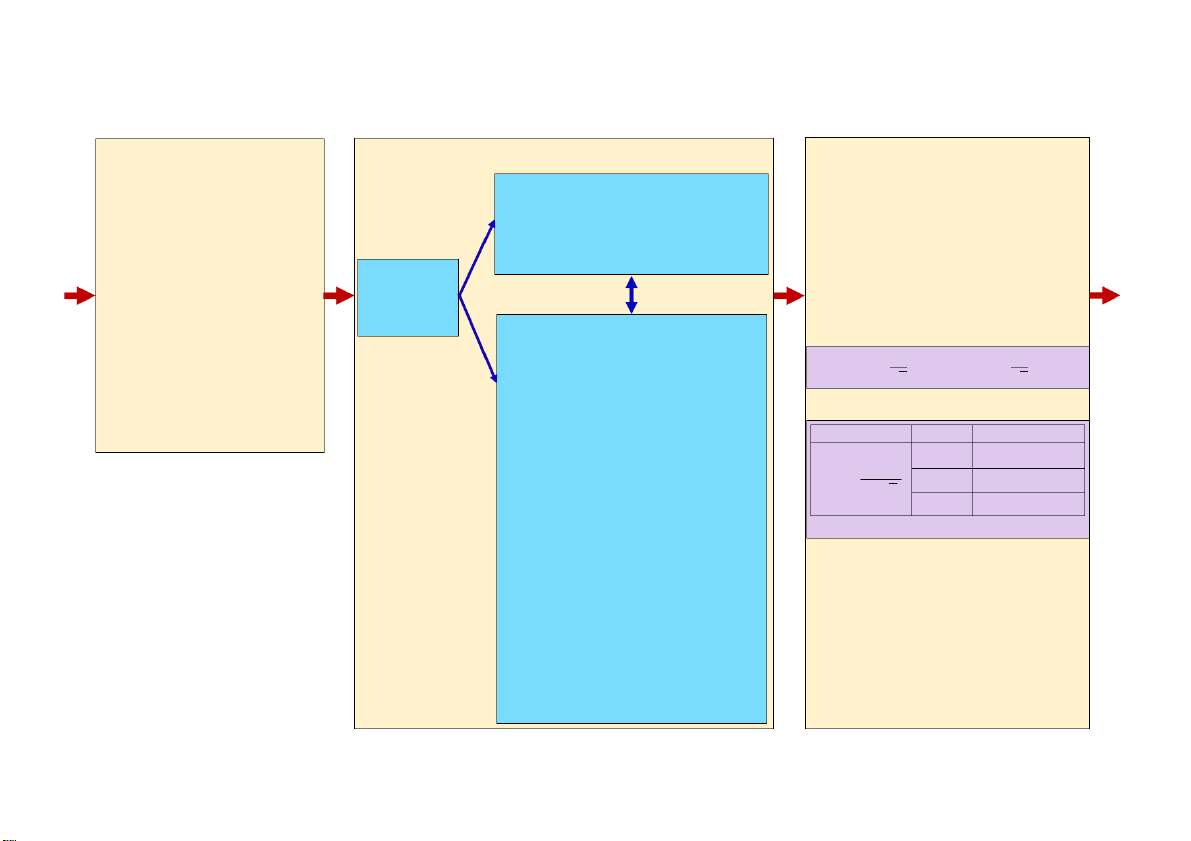
LÝ THUYẾT XÁC SUẤT VÀ THỐNG KÊ TOÁN
THỐNG KÊ MÔ TẢ
LÝ THUYẾT XÁC SUẤT
THỐNG KÊ SUY DIỄN ▪ Tổng thể
▪ Tổng thể và Biến ngẫu nhiên gốc 𝑋
▪ Biến cố, liên hệ giữa các biến cố ▪ Quan sát
▪ Mẫu ngẫu nhiên và mẫu cụ thể
▪ Xác suất của biến cố
▪ Biến, phân loại biến, thang đo
▪ Phân phối của thống kê trên mẫu
▪ Điều tra tổng thể hay điều tra • Tính theo định nghĩa
▪ Bài toán ước lượng mẫu?
• Tính theo công thức (cộng, nhân, ..) ▪ Bài toán kiểm định Phép thử ▪ (Mẫu)
▪ 𝑋 ∼ 𝑁(𝜇, 𝜎2) (thử nghiệm ▪ Thu thập dữ liệu
• 𝑥 là ước lượng điểm tốt nhất của 𝜇 / quan sát) ▪ Xử lý dữ liệu
Biến ngẫu nhiên
• Khoảng tin cậy cho 𝜇 ▪ Mô tả dữ liệu ▪ BNN 1 chiều rời rạc
𝑃 (𝑋 − 𝑡(𝑛−1) 𝑆 (𝑛−1) 𝑆 𝛼
< 𝜇 < 𝑋 + 𝑡𝛼 ) = 1 − 𝛼 • Dùng bảng • Bảng PPXS, hàm PPXS 2 √𝑛 1 √𝑛 • Dùng đồ thị • Tham số đặc trưng
• Kiểm định 𝐻0: 𝜇 = 𝜇0
• Dùng thống kê bằng số
• 𝐴(𝑝), 𝐵(𝑛, 𝑝), 𝑃(𝜆), … 𝐻0 và TK kđ 𝐻1 Bác bỏ 𝐻0 khi ▪ BNN 1 chiều liên tục 𝐻0: 𝜇 = 𝜇0 𝜇 ≠ 𝜇0 |𝑇 (𝑛−1) 𝑞𝑠| > 𝑡𝛼/2
• Hàm mật độ XS, hàm PPXS 𝑥 − 𝜇 𝑇 0 (𝑛−1) 𝑞𝑠 = 𝜇 > 𝜇0 𝑇 • Tham số đặc trưng 𝑠/√𝑛 𝑞𝑠 > 𝑡𝛼 𝜇 < 𝜇 (𝑛−1) 0 𝑇
• 𝑈(𝑎, 𝑏), 𝑵(𝝁, 𝝈𝟐), 𝜒2, 𝑇, 𝐹, … 𝑞𝑠 < −𝑡𝛼
𝑃 − 𝑣𝑎𝑙𝑢𝑒 < 𝛼 ⇔ bác bỏ 𝐻0 ▪ BNN 2 chiều rời rạc
• ƯL và kiểm định cho 𝜎2
• Bảng XS đồng thời (𝑋, 𝑌) • 𝑋 2 2
1 ∼ 𝑁(𝜇1, 𝜎1 ), 𝑋2 ∼ 𝑁(𝜇2, 𝜎2 )
• Bảng XS biên, kì vọng, phương sai
• Khoảng tin cậy cho 𝜇1 − 𝜇2 • Bảng XS điều kiện
• Kiểm định 𝐻0: 𝜇1 − 𝜇2 = 0
• Kì vọng điều kiện, hàm hồi quy
• ƯL và kiểm định cho 𝜎2 2 1 /𝜎2
• Hiệp phương sai, hệ số tương quan
• BNN gốc phân phối Không – Một ▪ BNN 2 chiều liên tục
• Kiểm định phi tham số ▪ BNN n – chiều • Vấn đề khác 1
THỐNG KÊ MÔ TẢ Ví dụ 1.
• Làm báo cáo về nhân sự của công ty
• Làm danh sách sản phẩm trong kho
• Tình hình các xã trong 1 huyện
• Nghiên cứu các công ty khởi nghiệp trong lĩnh vực CNTT
• Nghiên cứu các công ty đang niêm yết trên HOSE về … … Cần xác định
▪ Tổng thể? 1 phần tử? 1 quan sát?
▪ Biến? phân loại? đo thế nào?
▪ Có điều tra toàn bộ tổng thể được không? (Nếu không thì điều tra mẫu)
▪ Nếu điều tra mẫu thì điều tra bao nhiêu quan sát? (Dùng TK suy diễn để trả lời)
▪ Lập kế hoạch → Thu thập dữ liệu → Xử lí dữ liệu
▪ Mô tả dữ liệu (tổng thể/mẫu): bằng bảng, bằng đồ thị, bằng thống kê mô tả số. ▪ …
1. Khái niệm cơ bản
Tổng thể là tập hợp tất cả các phần tử cần quan tâm. Có kích thước 𝑁 – hữu hạn hoặc vô hạn.
Quan sát là tập hợp các kết quả của các phép đo được áp dụng cho một phần tử bất kì.
Biến là một đặc điểm/tính chất của các phần tử.
Thang đo gồm: định danh (nominal) → thứ bậc (ordinal) → khoảng (interval) → tỉ lệ (ratio)
Phân loại biến:
Biến định tính: chia tập hợp (tổng thể, mẫu) thành các nhóm, không có đơn vị đo lường
- Biến nhị phân: chỉ có 2 nhóm, ví dụ giới tính (nam, nữ), thích/không thích, …
- Biến định danh: mỗi nhóm được gắn tên và không thể sắp xếp thứ tự, ví dụ quê quán của sinh viên
- Biến thứ bậc: mỗi nhóm được gắn tên (số hoặc chữ) và có thể sắp thứ tự, VD size quần áo, giầy dép
Biến định lượng: có đơn vị đo lường
- Biến định lượng rời rạc: nhận các giá trị tách rời nhau, ví dụ tuổi, điểm thi THPT môn toán, …
- Biến định lượng liên tục: nhận các giá trị lấp đầy ít nhất một khoảng trên trục số, ví dụ thời gian hoàn
thành một bài thi của sinh viên, kết quả phép đo chiều cao của một ngọn núi, …
2. Mô tả dữ liệu
a. Dùng bảng
b. Dùng đồ thị (xem slide)
c. Dùng thống kê mô tả bằng số
Thống kê mô tả bằng số tính từ dữ liệu của tổng thể gọi là tham số
Thống kê mô tả bằng số tính từ dữ liệu của mẫu gọi là thống kê
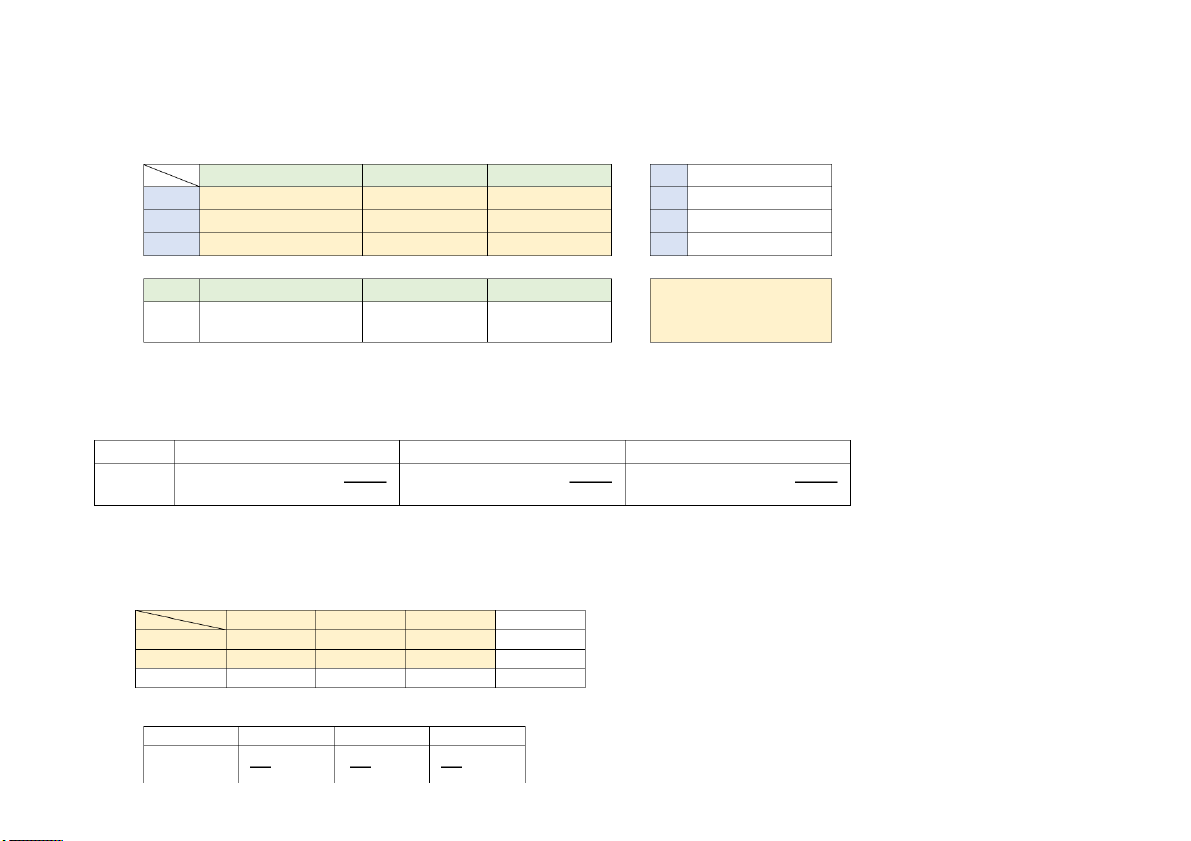
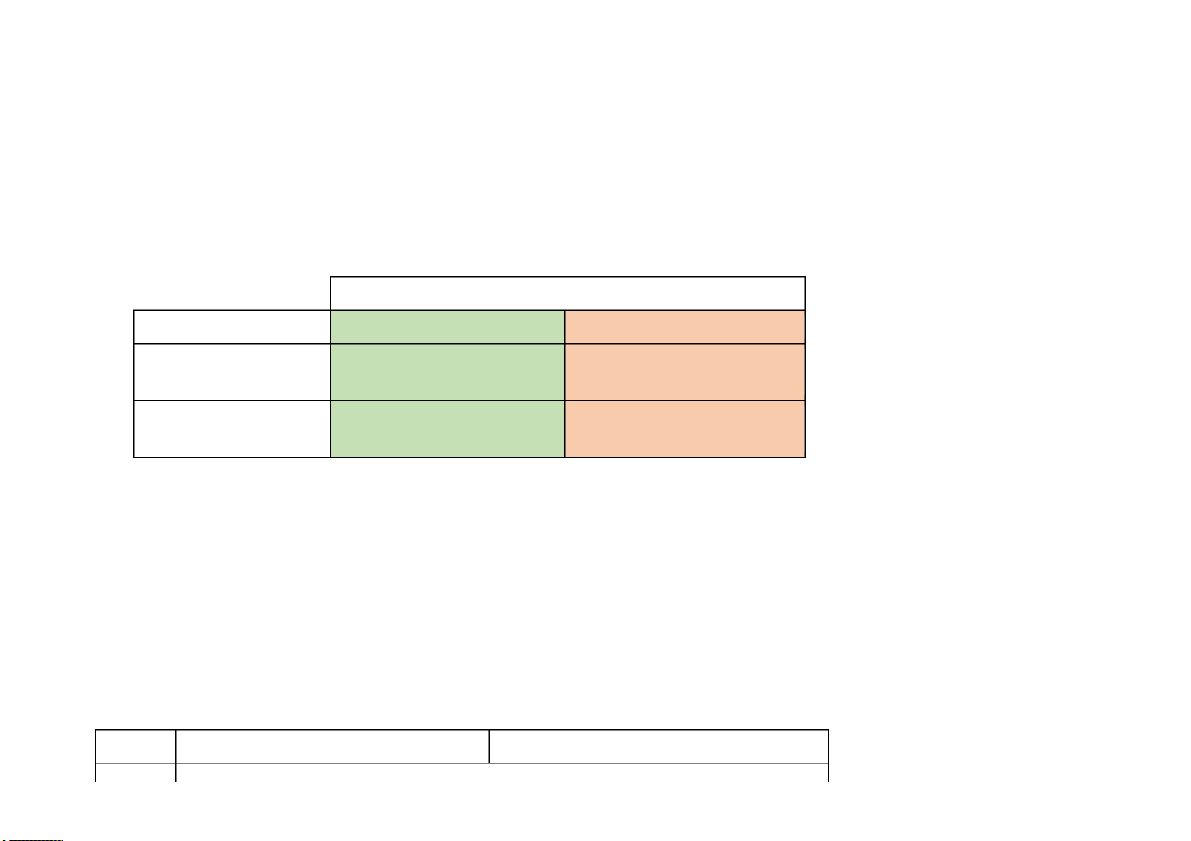
Bảng các thống kê mô tả của số liệu về 1 biến Tên thống kê mô tả
Tổng thể Mẫu {𝑥1,𝑥2,… ,𝑥𝑁}
{𝑥1,𝑥2,… ,𝑥𝑛} Trung bình (mean) ∑𝑥 ∑𝑥 𝜇 = 𝑖 𝑖 𝑁 𝑥 = 𝑛 Trung vị = Q2 Tự đọc 2 Mốt Tự đọc Q1, Q3 Phương sai (variance) ∑(𝑥 ∑(𝑥 𝜎2 = 𝑖 − 𝜇)2 𝑖 − 𝑥)2 𝑁 𝑠2 = 𝑛 − 1 Độ lệch chuẩn (SD) 𝜎 = √𝜎2 𝑠 = √𝑠2 Hệ số biến thiên 𝜎 𝑠 𝐶𝑉 = 𝜇 × 100% 𝐶𝑉 = 𝑥 × 100% Khoảng biến thiên Tự đọc Khoảng tứ phân vị Tự đọc Hệ số bất đối xứng ∑(𝑥 ∑(𝑥 𝛼 𝑖 − 𝜇)3/𝑁 𝑖 − 𝑥)3/𝑛 3 = 𝜎3 𝑎3 = 𝑠3 Hệ số nhọn ∑(𝑥 ∑(𝑥 𝛼 𝑖 − 𝜇)4/𝑁 𝑖 − 𝑥)4/𝑛 4 = 𝜎4 𝑎4 = 𝑠4
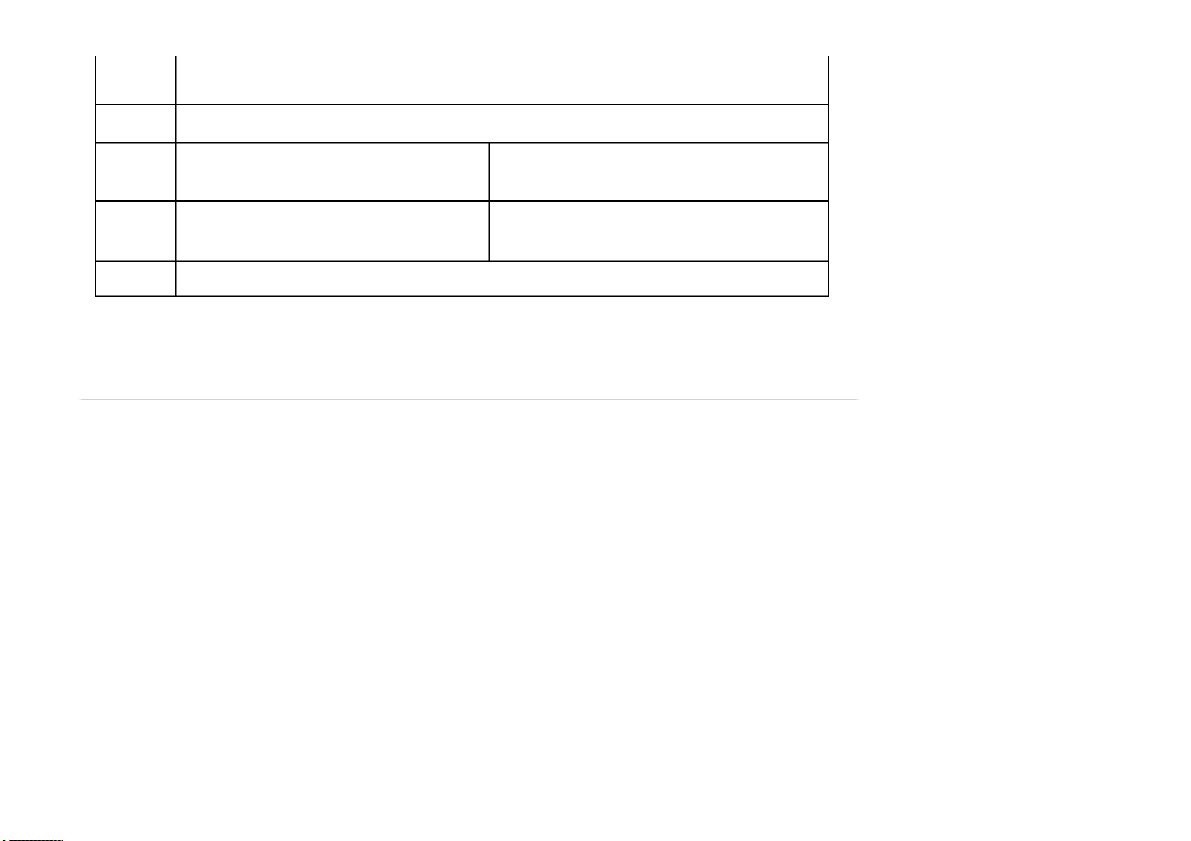
Thống kê mô tả liên quan số liệu 2 biến (liên hệ tương quan) Tên đại lượng Tổng thể Mẫu Hiệp phương sai ∑(𝑥 ∑(𝑥 )( 𝐶𝑜𝑣(𝑋, 𝑌) =
𝑖 − 𝜇𝑋)(𝑦𝑖 − 𝜇𝑌) ( )
𝑖 − 𝑥 𝑦𝑖 − 𝑦) 𝑁 𝑐𝑜𝑣 𝑋, 𝑌 = 𝑛 − 1
Chú ý: 𝐶𝑜𝑣(𝑋, 𝑋) = 𝜎2 2 𝑋
Chú ý: 𝐶𝑜𝑣(𝑋, 𝑋) = 𝑠𝑋 Hệ số tương quan 𝐶𝑜𝑣(𝑋, 𝑌) 𝐶𝑜𝑣(𝑋, 𝑌) (Correlation) 𝜌𝑋,𝑌 = 𝜎 𝑟𝑋,𝑌 = 𝑋𝜎𝑌 𝑠𝑋𝑠𝑌
Nhận xét Corr, tính giá trị tuyệt đối |𝐶𝑜𝑟𝑟| 0 0,4 0,7 0,8 0,95 1 Nhận xét TQ yếu TQ trung bình TQ khá chặt TQ chặt TQ rất chặt
LÝ THUYẾT XÁC SUẤT
Phép thử (thử nghiệm, quan sát): thực hiện các điều kiện cơ bản để quan sát các hiện tượng xảy ra.
Biến cố: là sự kiện, hiện tượng có thể xảy ra (có thể không xảy ra) trong kết quả của phép thử.
Biến ngẫu nhiên: là 1 biến số mà trong kết quả của phép thử nó chỉ nhận đúng 1 giá trị trong các giá trị có thể có của nó.
1. BIẾN CỐ
Gồm: biến cố không thể có, biến cố chắc chắn, biến cố ngẫu nhiên
Xác suất (probability) của biến cố A là 𝑃(𝐴), là con số đặc trưng cho khả năng khách quan xuất hiện
biến cố 𝐴 khi thực hiện phép thử
Xác suất có điều kiện (condition probability) của 𝐴 với điều kiện 𝐵 là 𝑃(𝐴|𝐵), là xác suất của biến cố
𝐴 được tính với điều kiện biến cố 𝐵 đã xảy ra.
Liên hệ giữa 2 biến cố (với nhiều biến cố tương tự) Liên hệ Kí hiệu Khái niệm A thuận lợi cho B
𝐴 ⊂ 𝐵 khi A xảy ra thì B cũng xảy ra Bằng nhau
A = B Khi A thuận lợi cho B và B thuận lợi cho A Tích A.B
A.B xảy ra khi cả A và B cùng xảy ra 𝐴 ∩ 𝐵 3 Độc lập
Biến cố này xảy ra hay không không ảnh hưởng đến xác suất của biến cố kia Tổng
A + B A + B xảy ra khi có ít nhất 1 trong 2 biến cố thành phần xảy ra 𝐴 ∪ 𝐵 Xung khắc
Là hai biến cố không đồng thời xảy ra trong kết quả của phép thử
Chú ý: A, B xung khắc ⇔ 𝐴. 𝐵 = ∅
A, B xung khắc → phụ thuộc
A, B độc lập → không x. khắc Nhóm đầy đủ các
Là nhóm 𝑛 ≥ 2 biến cố mà sau khi thực hiện phép thử sẽ xảy ra đúng 1 biến cố biến cố trong nhóm Đối lập
A và 𝐴 Là 2 biến cố tạo thành nhóm đầy đủ
Các công thức xác suất của biến cố
• Công thức cổ điển: 𝑃(𝐴) = Số kết cục sơ cấp thuận lợi cho A (giả thiết: các kết cục sơ cấp là đồng khả năng)
Số kết cục sơ cấp của phép thử
• Công thức nhân: A, B bất kì: P(AB) = P(A)P(B|A); 𝑃(𝐵|𝐴) = 𝑃(𝐴𝐵) 𝑃(𝐴)
A, B độc lập ⇔ P(AB) = P(A)P(B)
• Công thức cộng: A, B bất kì: P(A+B) = P(A) + P(B) – P(AB)
A, B xung khắc ⇒ P(A+B) = P(A) + P(B) (không suy ngược lại được)
• Công thức Bernoulli: thực hiện n phép thử độc lập, xác suất xuất hiện biến cố A trong mỗi lần thử
đều là p. Xác suất sau n phép thử, biến cố A xuất hiện đúng k lần là:
𝑃(𝑥|𝑛, 𝑝) = 𝐶𝑥𝑛𝑝𝑥(1 − 𝑝)𝑛−𝑥; x = 0;1;…;n
• Công thức đầy đủ, Bayes:
Với H1, …, Hn là nhóm đầy đủ các biến cố, A xảy ra cùng với Hi nào đó thì:
CT đầy đủ: 𝑃(𝐴) = ∑𝑛𝑖=1 𝑃(𝐻𝑖)𝑃(𝐴|𝐻𝑖)
CT Bayes: 𝑃(𝐻𝑖|𝐴) = 𝑃(𝐻𝑖)𝑃(𝐴|𝐻𝑖)
∑𝑛𝑗=1 𝑃(𝐻𝑗)𝑃(𝐴|𝐻𝑗)
2. BIẾN NGẪU NHIÊN 1 CHIỀU
Có 2 loại biến ngẫu nhiên (BNN, bnn) là bnn rời rạc và bnn liên tục
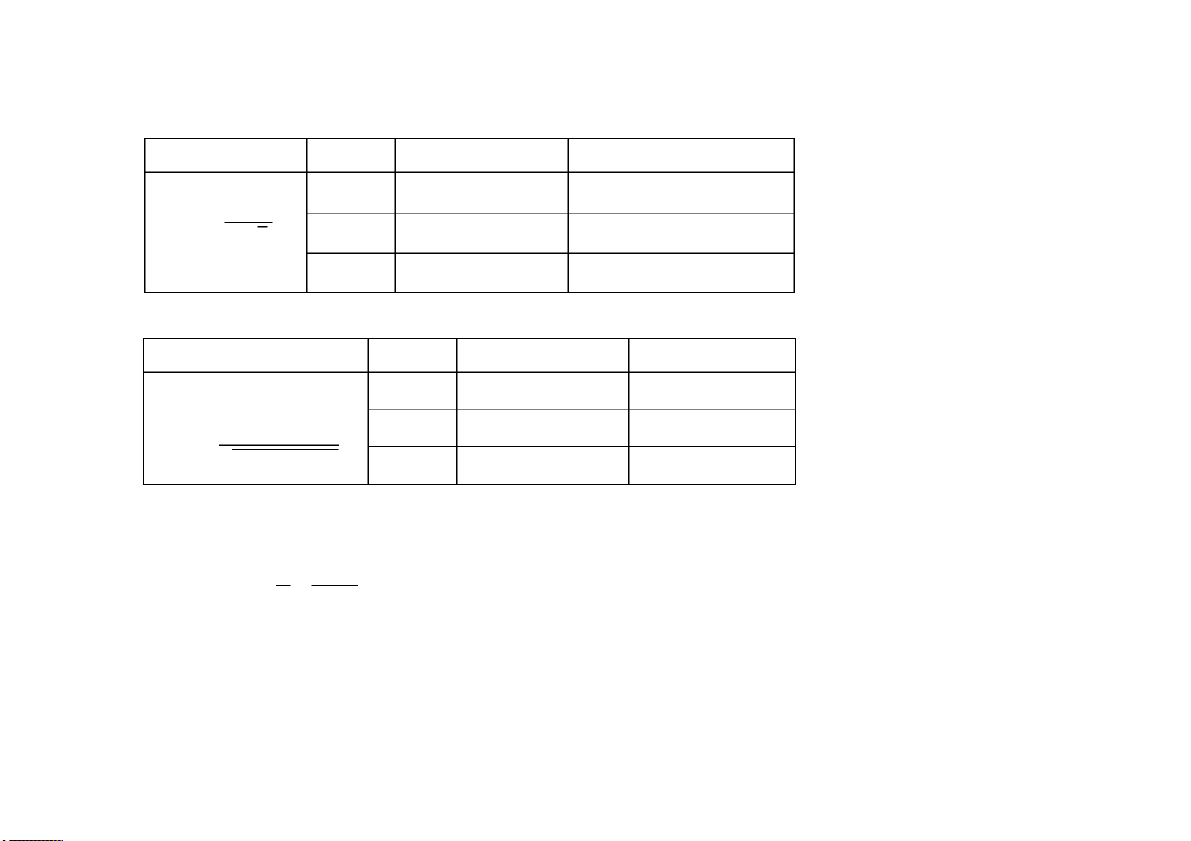
BNN rời rạc BNN liên tục
Định nghĩa Là BNN có tập giá trị đếm được
Là BNN có tập giá trị lấp đấy (𝑎, 𝑏) ⊂ 𝑅 Phân phối Bảng PPXS
Hàm mật độ XS: 𝑓(𝑥) = 𝐹′(𝑥) xác suất X (PPXS) P p1 p2 … pn a) 𝑓(𝑥 + ) ∞ ≥ 0, ∀𝑥 b) ∫ 𝑓(𝑥)𝑑𝑥 a) 𝑝 = 1 𝑖 ≥ 0 −∞ b) ∑ 𝑏 𝑖 𝑝𝑖 = 1
c) 𝑃(𝑎 < 𝑥 < 𝑏) = ∑
c) 𝑃(𝑎 < 𝑋 < 𝑏) = ∫𝑎 𝑓(𝑥)𝑑𝑥 𝑖 < <𝑏 𝑝𝑖
Hàm PPXS: 𝐹(𝑥) = 𝑃(𝑋 < 𝑥)
Hàm PPXS: 𝐹(𝑥) = 𝑃(𝑋 < 𝑥) Tham số
Kì vọng toán (trung bình):
Kì vọng toán (trung bình): đặc trưng 𝐸(𝑋) = ∑ +∞ 𝑖 𝑥𝑖𝑝𝑖
𝐸(𝑋) = ∫ 𝑥𝑓(𝑥)𝑑𝑥 −∞
T/c: E(a.X+b.Y+c) = a.E(X) + b.E(Y) + c; X và Y độc lập thì E(X.Y) = E(X).E(Y)
Phương sai: 𝑉(𝑋) = 𝐸(𝑋2) − [𝐸(𝑋)]2
Phương sai: 𝑉(𝑋) = 𝐸(𝑋2) − [𝐸(𝑋)]2 4 𝐸( +∞
𝑋2) = ∑ 𝑥2𝑖𝑝𝑖
𝐸(𝑋2) = ∫ 𝑥2𝑓(𝑥)𝑑𝑥 𝑖 −∞
T/c: X và Y độc lập thì V(a.X+b.Y+c) = a2V(X) + b2V(Y)
X và Y không độc lập thì V(a.X+b.Y+c) = a2V(X) + b2V(Y) + 2ab.Cov(X,Y)
Giá trị tới hạn mức 𝛼 của bnn 𝑋, kí hiệu 𝑥 , là giá tr th 𝛼
ị ỏa mãn 𝑃(𝑋 > 𝑥𝛼) = 𝛼 PPXS
Không – Một (Bernoulli): A(p) Đều: U(a,b) thông dụng
𝑃(𝑋 = 𝑥) = 𝑝𝑥(1 − 𝑝)1−𝑥; 𝑥 = 0; 1
0 𝑛ế𝑢 𝑥 ∉ (𝑎, 𝑏)
𝐸(𝑋) = 𝑝; 𝑉(𝑋) = 𝑝(1 − 𝑝) 𝑓(𝑥) = { 1 X 0 1
𝑏 − 𝑎 𝑛ế𝑢 𝑥 ∈ (𝑎, 𝑏) P 1-p p 𝑎 + 𝑏 (𝑏 − 𝑎)2
𝐸(𝑋) = 2 ; 𝑉(𝑋) = 12 Nhị thức: B(n,p)
Chuẩn: 𝑵(𝝁, 𝝈𝟐) 𝑃(𝑋 = 𝑥) = 𝐶𝑥 𝑛−𝑥 𝑛 𝑝𝑥(1 − 𝑝) ; 𝑥 = 0, 𝑛 𝑥−𝜇 2
𝐸(𝑋) = 𝑛𝑝; 𝑉(𝑋) = 𝑛𝑝(1 − 𝑝) 𝑒−( ) 2𝜎2 • 𝑓(𝑥) = 1 𝜎√2𝜋 𝑀𝑜𝑑𝑒: 𝑚 ) = 𝑚𝑑 = 𝑚 ) = 𝜎2 0 ∈ 𝑁; • 𝐸(𝑋 0 = 𝜇; 𝑉(𝑋
𝑛𝑝 + 𝑝 − 1 ≤ 𝑚 𝛼
(𝑆𝑘𝑒𝑤𝑛𝑒𝑠𝑠) 0 ≤ 𝑛𝑝 + 𝑝 3 = 0
; 𝛼4 = 3(𝐾𝑢𝑟𝑡𝑜𝑠𝑖𝑠)
• 𝑋1, … , 𝑋𝑛 độc lập, cùng phân phối
• 𝑃(𝑋 < 𝑏) = Φ (𝑏−𝜇 ) 𝐴(𝑝) thì ∑𝑋 𝜎 𝑖 ∼ 𝐵(𝑛, 𝑝)
𝑡𝑐: Φ(−𝑢) + Φ(𝑢) = 1
• 𝑋 ∼ 𝐵(𝑛, 𝑝) với 𝑛 ≥ 100 thì coi như
𝑢 ≥ 5 thì coi như Φ(𝑢) = 1
𝑋 ∼ 𝑁(𝜇 = 𝑛𝑝; 𝜎2 = 𝑛𝑝(1 − 𝑝)) • 𝑋 ∼ 𝑁(𝜇 2 2
1, 𝜎1 ); 𝑌 ∼ 𝑁(𝜇2, 𝜎2 ) và độc lập
với nhau thì 𝑍 = 𝑎𝑋 + 𝑏𝑌 ∼ 𝑁(𝑎𝜇1 + 𝑏𝜇 2 2 2 2, 𝑎 𝜎1 + 𝑏2𝜎2 ) Poisson: 𝑃(𝜆) Lũy thừa: 𝐸(𝜆) 𝑒−𝜆𝜆𝑥 𝑃(𝑋 = 𝑥) =
𝑓(𝑥) = {𝜆𝑒−𝜆𝑥 nếu 𝑥 ≥ 0 𝑥! ; 𝑥 = 0,1,2, … 0 nếu 𝑥 < 0
𝐸(𝑋) = 𝜆; 𝑉(𝑋) = 𝜆; 𝜆 − 1 ≤ 𝑚 1 1 0 ≤ 𝜆
𝐸(𝑋) = 𝜆; 𝑉(𝑋) =𝜆2
Khi – bình phương: 𝝌𝟐(𝒏)
• 𝑋1, … , 𝑋𝑛 là n bnn độc lập, cùng PP chuẩn
hóa 𝑁(0,1) thì bnn 𝑋 = ∑𝑋2𝑖 ∼ 𝜒2(𝑛) 2(𝑛) 2
• Giá trị tới hạn: 𝜒𝛼 ; 𝜒𝑛,𝛼 Student
• 𝑈 ∼ 𝑁(0,1); 𝑉 ∼ 𝜒2(𝑛) và độc lập thì 𝑈 𝑇 = (𝑛) ∼ 𝑇(𝑛) ; 𝑡 • Giá trị tới hạn: √ 𝑡 𝑉/𝑛𝑛,𝛼 Fisher – Snedecor
• 𝑈 ∼ 𝜒2(𝑛1), 𝑉 ∼ 𝜒2(𝑛2), độc lập thì 𝑈/𝑛 𝐹 = 1
𝑉/𝑛 ∼ 𝐹(𝑛1, 𝑛2) 2 (𝑛1,𝑛
• Giá trị tới hạn: 𝑓 2) 𝛼 5
3. BIẾN NGẪU NHIÊN HAI CHIỀU RỜI RẠC
Xét đồng thời 2 bnn rời rạc thì có bnn 2 chiều rời rạc
a. Bảng PPXS đồng thời và bảng PPXS biên X Y y1 y2 y3 → X P(x) x1 p11 p12 p13 → x1 P(x1) = p11+12+p13 x2 p21 p22 p23 → x2 P(x2) x3 p31 p32 p33 → x3 P(x3) ↓ ↓ ↓ ↓ Y y 3 3 1 y2 y3 P(y) P(y1) = p11+ p21+ p31 P(y2) P(y3) ∑ ∑ 𝑝𝑖𝑗 = 1 𝑖=1 𝑗=1
Từ bảng PP biên có thể tính E(X), E(Y), V(X), V(Y).
𝑋 và 𝑌 độc lập ⇔ 𝑝𝑖𝑗 = 𝑃(𝑥𝑖)𝑃(𝑦𝑗),∀𝑖, 𝑗
Nếu tồn tại 𝑖, 𝑗 để 𝑝𝑖𝑗 ≠ 𝑃(𝑥𝑖)𝑃(𝑦𝑗) thì nói 𝑋 và 𝑌 phụ thuộc.
b. Bảng PPXS có điều kiện của Y khi X = x1. Chỉ xét dòng x1, ta có (Y|X=x1) y1 y2 y3 P 𝑝 𝑝 𝑝 𝑃(𝑌 = 𝑦 11 12 13
1|𝑋 = 𝑥1) = 𝑃(𝑥1) 𝑃(𝑌 = 𝑦2|𝑋 = 𝑥1) = 𝑃(𝑥1) 𝑃(𝑌 = 𝑦3|𝑋 = 𝑥1) = 𝑃(𝑥1)
Từ bảng này có thể tính E(Y|X= x1) viết gọn là E(Y|x1), tính được V(Y|x1).
Tương tự có thể tạo các bảng (Y|X=xi); (X|Y=yj) và tính các kì vọng, phương sai điều kiện
c. Kì vọng điều kiện và Hàm hồi quy
Ví dụ. Cho 𝑋 là thu nhập, 𝑌 là chi tiêu (đơn vị: triệu đồng) của cá nhân. Cho bảng PPXS đồng thời của (𝑋, 𝑌) như sau: 𝑋 𝑌 5 8 10 Tổng 10 0,1 0,2 0,1 0,4 15 0,1 0,2 0,3 0,6 Tổng 0,2 0,4 0,4 1
Tìm hàm hồi quy:
Bảng PPXS có điều kiện của 𝑌 khi (𝑋 = 1 ) 0 (𝑌|𝑋 = 1 ) 0 5 8 10 𝑃 0,1 0,2 0,1
𝐸(𝑌|𝑋 = 10) = 5 × 0,25 + 8 × 0,5 + 10 × 0,25 = 7,75 (tr.đ) ( ) Bảng P 𝑌|P(X 𝑋 S c = ó1 đ
5 i)ề u kiện 5c ủa 𝑌 khi (𝑋8 = 1 ) 5 10 𝑃 0,1/0,6 0,2/0,6
0,3/0,6 𝐸(𝑌|𝑋 = 15) = 5 × 0,1 + 8 × 0,2 + 10 × 0,3 = 8,5 (tr.đ) 0,6 0,6 0,6
Có: 𝐸(𝑌|𝑋 = 10) = 7,75 𝐸(𝑌|𝑋 = 15) = 8,5
⇒ 𝐸(𝑌|𝑋 = 𝑥) = 𝑓(𝑥) = 𝑎𝑥 + 𝑏 = 0,1 𝑥
5 + 6,25: là hàm hồi quy của 𝑌 theo 𝑋, cho biết trung bình của 𝑌
thay đổi thế nào khi 𝑋 thay đổi
(7,75 = 𝑎. 10 + 𝑏; 8,5 = 𝑎. 15 + 𝑏, giải hệ pt, tìm được 𝑎 = 0,1 ; 5 𝑏 = 6,2 ) 5
+ 𝐸(𝑌|𝑋 = 0) = 𝐸(𝑌|0) = 0,15 × 0 + 6,25 = 6,25: nếu không có thu nhập thì chi tiêu trung bình là 6,25 tr.đ
+ 𝐸(𝑌|𝑥 + 1) − 𝐸(𝑌|𝑥) = 0,15(𝑥 + 1) + 6,25 − 0,1 𝑥
5 − 6,25 = 0,15 > 0: khi thu nhập tăng thêm 1 tr.đ thì
chi tiêu trung bình tăng thêm 0,15 tr.đ
Tg tự: 𝐸(𝑋|𝑌 = 5) = 1 ,
2 5; 𝐸(𝑋|𝑌 = 8) = 12,5; 𝐸(𝑋|𝑌 = 10) = 13,75 → 𝐸(𝑋|𝑦) = 𝑓(𝑦) = 𝑎𝑦2 + 𝑏𝑦 + 𝑐 6
d. Hiệp phương sai: 𝑛 𝑚
𝐶𝑜𝑣(𝑋, 𝑌) = 𝐸([𝑋 − 𝐸(𝑋)][𝑌 − 𝐸(𝑌)]) = 𝐸(𝑋𝑌) − 𝐸(𝑋)𝐸(𝑌) = ∑ ∑ 𝑥𝑖𝑦𝑗𝑃(𝑥𝑖,𝑦𝑗) − 𝐸(𝑋)𝐸(𝑌) 𝑖=1 𝑗=1
Có đơn vị đo là tích đơn vị đo của X và đơn vị đo của Y
𝐶𝑜𝑣(𝑋, 𝑌) = 𝐶𝑜𝑣(𝑌, 𝑋)
𝑋, 𝑌 độc lập 𝐶𝑜𝑣(𝑋, 𝑌) = 0
Cho biết X và Y có tương quan với nhau không: 𝐶𝑜𝑣(𝑋, 𝑌) > 0 thì 𝑋, 𝑌 có “tương quan dương”
𝐶𝑜𝑣(𝑋, 𝑌) < 0 thì 𝑋, 𝑌 có “tương quan âm”
e. Hệ số tương quan: 𝜌𝑋,𝑌 = 𝐶𝑜𝑣(𝑋,𝑌) ⇔ 𝐶𝑜𝑣(𝑋, 𝑌) = 𝜌𝑋,𝑌𝜎 𝜎 𝑋𝜎 𝑋.𝜎𝑌 𝑌
Hệ số tương quan không có đơn vị đo
Tính chất của hệ số tương quan: –1 X,Y 1 X,Y = Y,X
X,Y > 0: tương quan dương, X,Y < 0: tương quan âm
X,Y = 0: không tương quan (chưa chắc đã độc lập)
𝑋, 𝑌 độc lập X,Y = 0
X,Y = 1: 𝑋, 𝑌 có quan hệ hàm số bậc 1 với nhau
THỐNG KÊ SUY DIỄN
Tổng thể: là tập hợp có nhiều phần tử đồng nhất theo một dấu hiệu nghiên cứu.
• Dấu hiệu nghiên cứu: định tính hoặc định lượng → đại diện và lượng hóa bởi biến ngẫu nhiên gốc (𝑋).
• Trung bình tổng thể = 𝜇 = 𝐸(𝑋); Phương sai tổng thể = 𝜎2 = 𝑉(𝑋)
→ Nghiên cứu tham số của tổng thể đồng nhất với nghiên cứu tham số của bnn gốc 𝑋
VD: Cho tổng thể pp Chuẩn = Cho tổng thể với BNN gốc pp theo quy luật Chuẩn
• Nếu điều tra được tổng thể thì có thể mô tả số liệu tổng thể bằng bảng, đồ thị và tính được các tham số
của tổng thể (chính là các thống kê mô tả của tổng thể - bài 1)
• Thực tế không điều tra tổng thể → điều tra mẫu
Mẫu ngẫu nhiên: trước khi điều tra thì có mẫu ngẫu nhiên (𝑋1, … , 𝑋𝑛) ⇔ {𝑋1, … , 𝑋𝑛 độc lập với nhau
𝑋1,… , 𝑋𝑛 có cùng PPXS với X
• Trung bình mẫu = 𝑋 = ∑𝑋𝑖 là bnn, là thống kê, hàm ước lượng; )2
𝐸(𝑋) = 𝜇; 𝑉(𝑋) = 𝜎2𝑛 𝑛(𝑋
• Phương sai mẫu = 𝑆2 = ∑ 𝑖−𝑋 = 𝑛 2
(∑𝑋𝑖 − 𝑋2) là bnn, là thống kê, hàm ước lượng; 𝐸(𝑆2) = 𝜎2 𝑛−1 𝑛−1 𝑛 −𝜇 −𝜇
• Nếu bnn gốc 𝑋 ∼ 𝑁(𝜇, 𝜎2) thì 𝑋 ∼ 𝑁 (𝜇, 𝜎2) ; 𝑍 = 𝑋 𝜎 𝑆 𝑛
∼ 𝑁(0,1); 𝑇 = 𝑋 ∼ 𝑇(𝑛 − 1) 𝑛−1 𝑆2 √𝑛 √𝑛 𝜒2 = ( ) ∼ 𝜒2(𝑛 − 1) 𝜎2
Áp dụng: Tính XS 𝑃(𝑎 < 𝑋 < 𝑏) =?
Tìm a (hoặc b) để 𝑃(𝑋 > 𝑎) = 1 − 𝛼 (hoặc 𝑃(𝑋 < 𝑏) = 1 − 𝛼) (suy đoán mẫu • Nếu 𝑋 2 2
1 ∼ 𝑁(𝜇1, 𝜎1 ), 𝑋2 ∼ 𝑁(𝜇2, 𝜎2) thì …
• Nếu 𝑋 ∼ 𝐴(𝑝) thì … 7
1. BÀI TOÁN ƯỚC LƯỢNG
Giả sử biến ngẫu nhiên gốc có phân phối xác suất đã biết (thường gặp là A(p), N(µ, σ2) ).
Ước lượng: xác định một cách gần đúng giá trị của tham số θ của tổng thể.
a. Cách 1: Ước lượng điểm chủ trương tìm 𝜃 là ước lượng của 𝜃
+ Nếu xét (tính) trên mẫu cụ thể thì 𝜃 là một số, gọi là ước lượng điểm (estimate) của 𝜃.
+ Nếu xét trên mẫu ngẫu nhiên thì 𝜃 là một biến ngẫu nhiên, gọi là hàm ước lượng (estimator).
Các tính chất của hàm ước lượng
+ Ước lượng không chệch: 𝐸(𝜃) = 𝜃.
+ Tính hiệu quả: ước lượng không chệch có phương sai nhỏ nhất trong lớp các ước lượng không chệch
trên cùng 1 mẫu gọi là ước lượng hiệu quả.
+ Tính vững: nếu 𝜃 hội tụ theo xác suất đến 𝜃 thì nó là ước lượng vững của 𝜃.
• Nếu 𝑋 ∼ 𝑁(𝜇, 𝜎2) thì chứng minh được 𝑋 là ước lượng không chệch, hiệu quả và vững của 𝜇; do đó
𝑥 là ước lượng tối nhất của 𝜇
• Nếu 𝑋 ∼ 𝑁(𝜇, 𝜎2) thì 𝑆2 là ước lượng không chệch (nhưng không phải hiệu quả) của 𝜎2, 𝑀𝑆 = 𝑋 2
− 𝑋2 là ước lượng vững của 𝜎2
Phương pháp ước lượng hợp lí tối đa
Biến ngẫu nhiên gốc X biết PPXS → biết hàm mật độ XS của X là 𝑓(𝑥, 𝜃).
Với mẫu cụ thể 𝑤 = (𝑥1, … , 𝑥 , tìm hàm h p lí trên m u: 𝑛) ợ ẫ
𝐿(𝑤, 𝜃) = 𝐿(𝑥1,…, 𝑥𝑛,𝜃) = 𝑓(𝑥2,𝜃) … 𝑓(𝑥1,𝜃). 𝑓(𝑥𝑛,𝜃)
Nếu hàm hợp lí 𝐿 đạt cực đại tại 𝜃 thì 𝜃 là ước lượng hợp lí tối đa của tham số 𝜃.
Cách giải: tìm nghiệm của đạo hàm bậc 1 của ln (𝐿), kí hiệu là 𝜃
Chứng minh đạo hàm bậc 2 của ln (𝐿) âm tại nghiệm tìm được
b. Cách 2: Ước lượng bằng khoảng tin cậy chủ trương tìm khoảng (𝑔1, 𝑔2) chưa 𝜃 với độ tin cậy (khá lớn) cho trước.
+ Khoảng ngẫu nhiên (𝐺1, 𝐺2) là khoảng tin cậy với độ tin cậy 1 − 𝛼 của tham số 𝜃 nếu thỏa mãn
𝑃(𝐺1 < 𝜃 < 𝐺2) = 1 − 𝛼
Với mẫu cụ thể, 𝐺1, 𝐺2 nhận giá trị cụ thể là 𝑔1, 𝑔2
(1 − 𝛼) gọi là độ tin cậy (ĐTC)
𝐼 = 𝐺2 − 𝐺1 gọi là độ dài khoảng tin cậy (KTC)
+ Cách xây dựng KTC cho 𝜇 và công thức xác định kích thước mẫu tối thiểu.
Ví dụ. xây dựng KTL cho 𝜇 khi chưa biết 𝜎2, tổng thể phân phối Chuẩn
Chọn thống kê 𝑇 = 𝑋−𝜇 𝑆 ∼ 𝑇(𝑛 − 1) √𝑛
Với ĐTC (1 − 𝛼) chọn 𝛼 (𝑛−1) (𝑛−1)
1 > 0; 𝛼2 > 0 và 𝛼1 = 𝛼2 = 𝛼 → 𝑡1−𝛼 < 𝑡 (do ĐTC lớn) 1 𝛼2 𝑃(𝑡(𝑛−1) (𝑛−1) 1−𝛼 < 𝑇 < 𝑡 ) = 1 − 𝛼 1 𝛼2 8
𝑃 (−𝑋 − 𝑡(𝑛−1) 𝑆 (𝑛−1) 𝑆 𝛼
< −𝜇 < −𝑋 + 𝑡 ) = 1 − 𝛼 1 √𝑛 𝛼2 √𝑛
𝑃 (+𝑋 + 𝑡(𝑛−1) 𝑆 (𝑛−1) 𝑆 𝛼
> +𝜇 > +𝑋 − 𝑡 ) = 1 − 𝛼 1 √𝑛 𝛼2 √𝑛
BT ước lượng trung bình tổng thể (𝜇) khi chưa biết phương sai tổng thể (𝜎2): 𝑆 𝑆 𝑋− 𝑡 (𝑛−1) (𝑛−1) 𝛼 . < 𝜇 < 𝑋 + 𝑡 . 2 √𝑛 𝛼1 √𝑛
KTC tối đa: 𝜇 < 𝑋 + 𝑡(𝑛−1) 𝛼 . 𝑆 √𝑛
KTC tối thiểu: 𝑋 − 𝑡(𝑛−1) 𝛼 . 𝑆 < 𝜇 √𝑛
KTC đối xứng: 𝑋 − 𝑡(𝑛−1) (𝑛−1)
𝛼/2 . 𝑆 < 𝜇 < 𝑋 + 𝑡 . 𝑆 √𝑛 𝛼/2 √𝑛
Độ dài KTC đối xứng: 𝐼 = 2𝑡(𝑛−1) 𝛼/2 . 𝑆 √𝑛
Sai số của ước lượng (sai số biên, ME): 𝜀 = 𝐼 = 𝑡 (𝑛−1). 𝑆 2 𝛼/2 √𝑛
Bài toán tìm kích thước mẫu tối thiểu để …: 4𝑆2 𝐼 ≤ 𝐼 (𝑛−1) 0 ⇔ 𝑛0 ≥ ]2 𝐼2 [𝑡𝛼/2 0 𝑆2 𝜀 ≤ 𝜀 (𝑛−1)
0 ⇔ 𝑛0 ≥ 𝜀2 [𝑡𝛼/2 ]2 0
2. BÀI TOÁN KIỂM ĐỊNH GIẢ THUYẾT
Giả thuyết thống kê: là giả thuyết về
+ Tham số đặc trưng của biến ngẫu nhiên
+ Phân phối xác suất của BNN
+ Sự độc lập của các BNN
Giả thuyết gốc: 𝐻0 (kđ tham số thì 𝐻0 là phát biểu chứa dấu bằng (=, ≥, ≤) )
Giả thuyết đối: 𝐻1 (kđ tham số thì 𝐻0 là phát biểu không chứa dấu bằng (≠, <, >) )
Viết cặp giả thuyết cho các phát biểu sau
• Chiều cao trung bình của nam thanh niên ở VN bằng 168 cm g g
• Phương sai về cân nặng của sản phẩm nhỏ hơn 25 g2
• Độ lệch chuẩn về thu nhập của hộ gia đình không vượt quá 3 triệu
• Tỉ lệ phế phẩm của lô hàng ít hơn 5%
• Ở VN, tỉ lệ nam cao hơn tỉ lệ nữ (giả sử giới tính gồm nam và nữ)
• Điểm trung bình của ca thi sáng cao hơn ca thi chiều
• Độ phân tán của thời gian hoàn thành bài thi trắc nghiệm cao hơn so với bài thi tự luận.
Thống kê kiểm định (tiêu chuẩn kiểm định) là thống kê 𝐺 trên mẫu ngẫu nhiên (𝑋1, 𝑋2, … , 𝑋𝑛) sao
cho phân phối xác suất của 𝐺 là xác định khi 𝐻0 đúng.
Phương pháp kiểm định
▪ Giả sử 𝐻0 đúng, từ phân phối của 𝐺, tìm một biến cố 𝐴 (liên quan 𝐺) có XS nhỏ → coi như biến cố
𝐴 không xảy ra khi thử (theo nguyên lí XS nhỏ). 9
▪ Thực hiện phép thử thì thu được mẫu cụ thể, tìm được 𝐺𝑞𝑠
• Nếu 𝐴 xảy ra → giả sử 𝐻0 đúng là không chính xác→ bác bỏ 𝐻0.
• Nếu 𝐴 không xảy ra → chưa có cơ sở để kết luận 𝐻0 đúng
Các loại sai lầm
▪ Phương pháp kiểm định ⇒ Nếu 𝐴 xảy ra thì bác bỏ 𝐻0, trong khi thực tế 𝐻0 có thể đúng ⇒ Có thể
mắc sai lầm, gọi là sai lầm loại I.
▪ Sai lầm loại I (type I error): bác bỏ giả thuyết 𝐻0 trong khi 𝐻0 đúng
▪ Sai lầm loại II (type II error): không bác bỏ giả thuyết 𝐻0 trong khi 𝐻0 sai
Tình huống thực tế Quyết định 𝑯𝟎 đúng 𝑯𝟎 sai Bác bỏ 𝐻0
Sai lầm loại I Đúng, không sai lầm
Xác suất kí hiệu là 𝛼 Xác suất = 1 − 𝛽 Không bác bỏ 𝐻0 Đúng, không sai lầm
Sai lầm loại II Xác suất = 1 − 𝛼
Xác suất kí hiệu là 𝛽
▪ Khi 𝛼 giảm thì 𝛽 tăng và ngược lại.
Mức ý nghĩa (significant level) là mức xác suất mắc sai lầm loại I, hay mức ý nghĩa là 𝜶.
Thường dùng mức ý nghĩa 0,05; 0,1; 0,01 (hay 5%, 10% 1%)
Miền bác bỏ (reject area) giả thuyết 𝐻0 với mức ý nghĩa 𝛼, kí hiệu 𝑊𝛼, là miền trên trục số thỏa mãn
𝑃(𝐺 ∈ 𝑊𝛼|𝐻0) = 𝛼
Từ phương pháp kiểm định → 𝐴 = (𝐺 ∈ 𝑊𝛼)
𝑊𝛼 được xác định bởi các giá trị tới hạn của thống kê 𝐺 (critical value)
𝑷 − 𝒗𝒂𝒍𝒖𝒆, còn gọi là mức ý nghĩa quan sát được, là mức xác suất mà nếu mức ý nghĩa (𝛼) vượt qua
nó thì giả thuyết 𝐻0 bị bác bỏ.
Hay: 𝑃 − 𝑣𝑎𝑙𝑢𝑒 là mức xác suất thấp nhất để bác bỏ 𝐻0
Hai cách kiểm định
Dùng miền bác bỏ (hay giá trị tới hạn)
Dùng 𝑷 − 𝒗𝒂𝒍𝒖𝒆 Bước 1
phát biểu chứa dấu bằng ( ) ế ế {𝐻0: =, ≥, ≤ 𝐻 há biể khô hứ dấ bằ ( ) Bước 2
Xác định tiêu chuẩn kiểm định (tra công thức) + mẫu cụ thể → giá trị quan sát 𝐺𝑞𝑠 Bước 3
Tìm miền bác bỏ (tra công thức) và tra
Tính 𝑃 − 𝑣𝑎𝑙𝑢𝑒 theo công thức
giá trị tới hạn tương ứng → 𝑊𝛼
XSTK: tra tài liệu TH; KTL: cho sẵn Bước 4
+ 𝐺𝑞𝑠 ∈ 𝑊𝛼 ⇒ bác bỏ 𝐻0
+ 𝑃 − 𝑣𝑎𝑙𝑢𝑒 < 𝛼 ⇒ bác bỏ 𝐻0
+ 𝐺𝑞𝑠 ∉ 𝑊𝛼 ⇒ không bác bỏ 𝐻0
+ 𝑃 − 𝑣𝑎𝑙𝑢𝑒 > 𝛼 ⇒ không bác bỏ 𝐻0 Bước 5
Tính xác suất mắc sai lầm loại II 10
Kiểm định trung bình (một) tổng thể
𝑯𝟎, thống kê KĐ 𝑯𝟏
Bác bỏ 𝑯 khi 𝟎 𝑷 − 𝒗𝒂𝒍𝒖𝒆 𝑯𝟎:𝝁 = 𝝁𝟎 𝜇 ≠ 𝜇0 |𝑇 (𝑛−1)
2 × 𝑃[𝑇(𝑛 − 1) > |𝑇𝑞𝑠|] 𝑥 − 𝜇 𝑞𝑠| > 𝑡𝛼/2 𝑇 0 𝑞𝑠 = 𝑠/√𝑛 𝜇 > 𝜇 (𝑛−1) 0 𝑇𝑞𝑠 > 𝑡 ) 𝛼
𝑃[𝑇(𝑛 − 1 > 𝑇𝑞𝑠] 𝜇 < 𝜇0 𝑇 (𝑛−1) 𝑞𝑠 < −𝑡 ) 𝛼
𝑃[𝑇(𝑛 − 1 < 𝑇𝑞𝑠]
Kiểm định trung bình hai tổng thể (chưa biết 2 phương sai và 2 phương sai khác nhau)
𝑯𝟎, thống kê KĐ 𝑯𝟏
Bác bỏ 𝑯 khi 𝟎 𝑷 − 𝒗𝒂𝒍𝒖𝒆 𝑯𝟎:𝝁𝟏 = 𝝁𝟐 𝜇1 ≠ 𝜇2
|𝑇𝑞𝑠| > 𝑧𝛼/2
2 × 𝑃(𝑍 > |𝑇𝑞𝑠|)
𝒏𝟏 > 𝟑𝟎,𝒏𝟐 > 𝟑𝟎 𝑥 𝜇 T 1 − 𝑥2 1 > 𝜇2 𝑇𝑞𝑠 > 𝑧𝛼 𝑃(𝑍 > 𝑇𝑞𝑠) qs = √𝑠2 2 1 /𝑛1 + 𝑠2 /𝑛2 𝜇1 < 𝜇2 𝑇𝑞𝑠 < −𝑧𝛼 𝑃(𝑍 < 𝑇𝑞𝑠)
Kiểm định Jarque-Bera về phân phối Chuẩn
𝐻0: biến 𝑋 phân phối Chuẩn
𝐻1: biến 𝑋 không phân phối Chuẩn 2
Thống kê: 𝐽𝐵𝑞𝑠 = 𝑛 (𝑎3 + (𝑎4−3)2) 6 24
Trong đó 𝑎3, 𝑎4 là hệ số bất đối xứng và hệ số nhọn của mẫu
Miền bác bỏ: 𝑊 2(2)
𝛼 = {𝐽𝐵: 𝐽𝐵 > 𝜒𝛼 }
Các kiểm định khác: tự đọc
+ Kiểm định phương sai, tỷ lệ của một tổng thể, hai tổng thể
+ Kiểm định sự độc lập của hai dấu hiệu định tính 11