











Preview text:
- 1 - Tóm tắt công thức
Tóm tắt công thức Xác Suất - Thống Kê I. Phần Xác Suất 1. Xác suất cổ điển Công th c
ứ cộng xác suất: P(A+B)=P(A)+P(B)-P(AB). A ắ ừng đôi 1, A2,…, An xung kh c t
P(A1+A2+…+An)=P(A1)+P(A2)+…+P(An). Ta có
o A, B xung khắc P(A+B)=P(A)+P(B).
o A, B, C xung khắc từng đôi P(A+B+C)=P(A)+P(B)+P(C). o
P(A) 1 P(A). P (AB ) P (AB ) Công th c
ứ xác suất có điều kiện: P(A / B)
, P(B / A) . P(B) P(A) Công th c
ứ nhân xác suất: P(AB)=P(A).P(B/A)=P(B).P(A/B). A độ ậ ớ 1, A2,…, An c l p v i nhau
P(A1.A2.….An)=P(A1).P(A2).….P( An). Ta có
o A, B độc lập P(AB)=P(A).P(B).
o A, B, C độc lập với nhau P(A.B.C)=P(A).P(B).P(C). Công th c ứ Bernoulli: B(k; ; n p) k k n k C ất để ế n p q , với p=P(A): xác su bi n cố A
xảy ra ở mỗi phép thử và q=1-p. Công th c
ứ xác suất đầy đủ - Công thức Bayes
o Hệ biến cố gồm n phần t A ử đượ ọ ộ 1, A2,…, An c g i là m t phép phân A
.A i
j;i, j 1 ,n hoạch của i j
A A ... 1 2 n A
o Công thức xác suất đầy đủ: n P(B) P
(A ).P(B / A ) P ( i i 1
A ).P(B / 1 A ) P( 2
A ).P(B / A2) ... P(A ).P(B / A ) n n i 1 o Công th c ứ Bayes:
P (A ).P (B / A ) P(A / B) i i i P(B)
với P(B) P(A ).P(B / A ) P(A ).P(B / A ) ... P(A ).P(B / A ) 1 1 2 2 n n 2. Biến ngẫu nhiên
a. Biến ngẫu nhiên rời rạc
Luật phân phối xác suất X x 1 x2 … xn P p1 p2 … pn
với p P(X x ),i 1,n. i i Ta có: n p 1 { P a f(X) b}= i và pi i 1
af(x b i - 1 - XSTK - 2 - Tóm tắt công thức
Hàm phân phối xác suất F ( ) x ( P X ) x p X i x x i Mode
ModX x p max{p :i 1,n} 0 0 i Median p 0,5 i (
P X x ) 0, 5 e x x MedX i e x e
P(X x ) 0,5 p e i 0,5 x x i e Kỳ vọng n EX (x . p )
i i 1x. 1p 2x. 2p ... x .n np i 1 n ( E ( X ))
(( x ). p ) ( i i 1 x ). 1 p ( 2 x ). 2 p ... ( x ). n n p i 1 Phương sai 2 2
VarX E (X ) (EX ) n với 2 2 2 2 2 E (X ) (x .p ) i i 1x . 1 p
x2 .p2 ... x . n p n i 1
b. Biến ngẫu nhiên liên tục. f(x) là hàm mật xá độ c suất của X ( ) 1 f x dx , b { P a X b} f ( ) x .dx a
Hàm phân phối xác suất x F ( ) x ( P X ) x f ( ) t dt X Mode
ModX x Hàm mật độ xác suất f(x) của X đạt c i ực đạ tại x0. 0 Median x 1 e 1
MedX x F ( x ) f ( ) x dx e X e . 2 2 Kỳ vọng EX
x.f (x)dx . ( E ( X )) ( ) x . f ( ) x dx - 2 - XSTK - 3 - Tóm tắt công thức Phương sai 2 2
VarX E (X ) (EX ) với 2 2 EX
x .f (x )dx . c. Tính chất
- E (C ) C ,V
ar (C ) 0, C là một hằng số. - 2
E (kX ) kEX ,V
ar (kX ) k VarX
- E(aX bY ) aEX bEY - Nếu c X, Y độ lập thì 2 2
E (XY ) EX .EY ,V
ar (aX bY ) a VarX b VarY
- (X ) VarX : Độ lệch chuẩn của X, có cùng thứ nguyên với X và EX.
3. Luật phân phối xác suất a. Phân phối Chuẩn 2
(X ~ N ( ; ))
X ( ) , EX=ModX=MedX= , 2 VarX 2 ( x ) 1 2 Hàm mđxs 2 f ( , x , ) e Với 0, 1: 2 2 x 1 2 f (x) e (Hàm Gauss) 2 2 t x b a 1 (
P a X b) ( ) ( ) với 2 ( ) x e dt (Hàm Laplace) 2 0 Cách s d
ử ụng máy tính bỏ túi để tính giá trị hàm Laplace, hàm phân phối
xác suất của phân phối chuẩn chuẩn tắc Tác vụ Máy CASIO 570MS Máy CASIO 570ES
Khởi động gói Thống kê Mode…(tìm)…SD Mode…(tìm)…STAT 1-Var Tính 2 x t 1 2 ( ) x e dt Shift 3 2 x ) = Shift 1 7 2 x ) = 2 0 2 t x 1 2 F (x) e dt Shift 3 1 x ) = Shift 1 7 1 x ) = 2
Thoát khỏi gói Thống kê Mode 1 Mode 1
Lưu ý: F( ) x 0,5 ( ) x
b. Phân phối Poisson ( X ~ ( P ) )
X ( ) , EX VarX . M
odX=k -1 k k ( P X=k)=e , k k ! - 3 - XSTK - 4 - Tóm tắt công thức
c. Phân phối Nhị thức (X ~ B(n; p))
X () {0..n}, EX=np, VarX=npq, ModX=k (n 1)p 1 k (n 1)p (
P X=k)=Ck. k p . n k q , q p 0 k ,
n k n Nếu (n 30; 0
,1 p 0,9; np 5, nq 5) thì 2 X ~ ( B ; n ) p N( ; ) với
n.p, npq 1 k P(X=k) f ( ), 0
k n, k b a P(a X) ( )
Nếu (n 30, p np 5) thì X ~ B( ;
n p) P( ) với np k P(X=k) e , k k!
Nếu (n 30, p 0,9, nq 5) n k P(X=k) e , k
với nq (n k )!
d. Phân phối Siêu bội (X ~ H (N ;N ;n )) A X ( )
{max{0; n (N N )}..min{n;N }} A A N n N EX=np, VarX=npq với A p , q=1-p. N 1 N (N 1)(n 1) 2 (N 1)(n 1) 2 A ModX k 1 A k . N 2 N 2 k nk C C N N N P(X=k)= A A , k X ( ) n CN N N Nếu
20 thì X ~ H (N ;N ;n) B(n; p) ớ A A v i p . n N
P(X=k) C k. k p . n k q , k
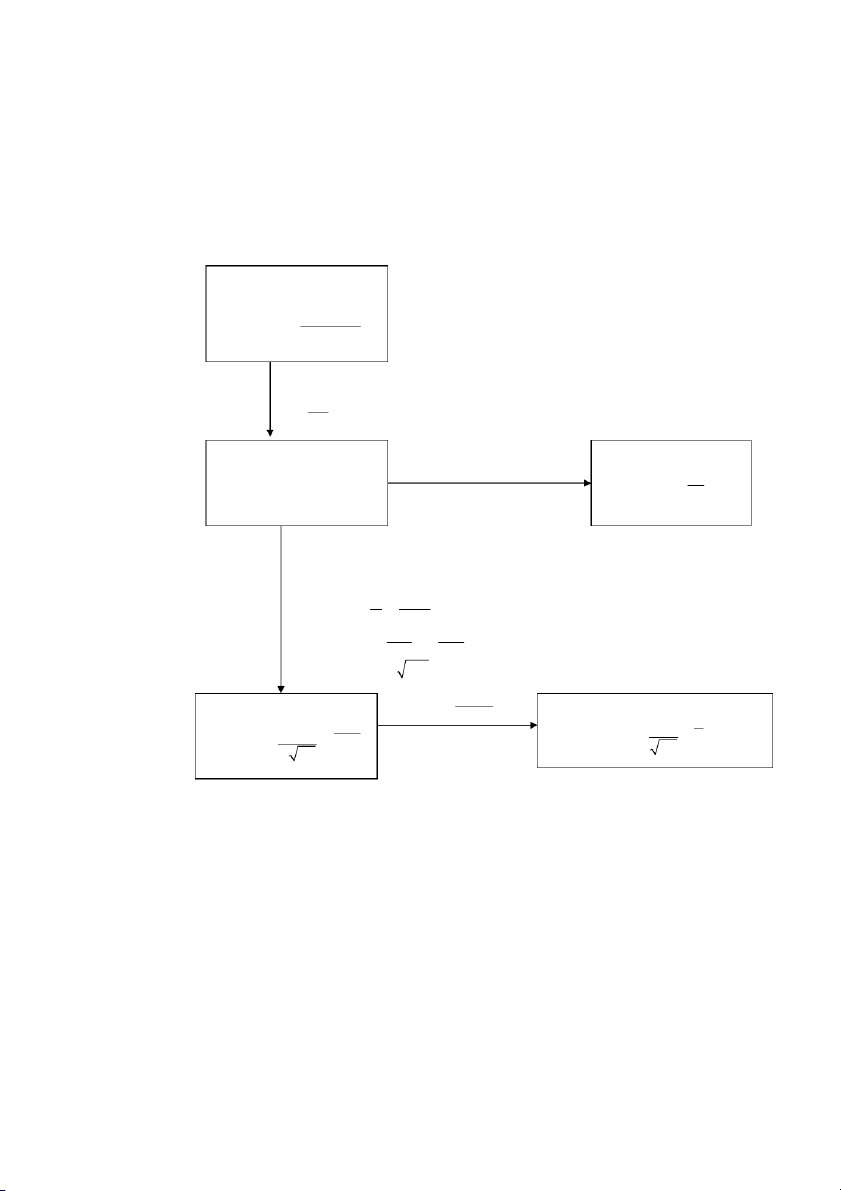
X (), q 1 p . n - 4 - XSTK - 5 - Tóm tắt công thức Sơ đồ tóm t t
ắ các dạng phân ph i ố xác su t ấ thông dụng: Siêu bội: X~H(N;NA;n) k C . n k C ( P X ) N N N A A k n CN N>20n N p= A , q=1-p N n30, np<5 p Nhị thức: X~B(n;p) 0,1 Poisson: X~ P() =np k k k n k ( P X k) e ( P X ) k
C . p . q n k!
n30, np 5, nq 5 0,1
1 k ( P X k) f ( ) b a
P (a X b ) ( ) ( )
với np, npq X Y N Chuẩn: X~ 2 ( ; )
Chuẩn chuẩn tắc: Y~ N(0;1) 2 2 y ( x ) 1 1 2 2 2 f (y ) .e f ( ; x ; ) .e 2 2 - 5 - XSTK - 6 - Tóm tắt công thức II. Phần Thống Kê. 1. Lý thuyết mẫu. a. Các công th n. ức cơ bả
Các giá trị đặc trưng
Mẫu ngẫu nhiên
Mẫu cụ thể Giá trị trung bình X ... X x ... x 1 n X 1 n x n n
Phương sai không hiệu chỉnh 2 2
(X X ) ... (X X ) 2 2
(x x) ... (x x) 2 1 ˆ 2 1 S n ˆ s x n X n n Phương sai hiệu chỉnh 2 2
(X X ) ... (X X ) 2 2
(x x) ... (x x) 2 1 S n 2 1 s n X n 1 x n 1
b. Để dễ xử lý ta viết số liệu của mẫu cụ thể dưới dạng tần số như sau: x x x … x i 1 2 k n n n n … i 1 2 k Khi đó
Các giá trị đặc trưng
Mẫu cụ thể
x n ... x n Giá trị trung bình 1 1 k k x n
Phương sai không hiệu chỉnh 2 2
(x x) n ... (x x) n 2 1 1 ˆ s k k x n 2 2
(x x) n ... (x x) Phương sai hiệ n u chỉnh 2 1 1 s k k x n 1
c. Cách sử dụng máy tính bỏ túi để tính các giá trị đặc trưng mẫu
- Nếu số liệu thống kê thu thập theo miền [ ;
a b) hay (a;b] thì ta s d ử ụng giá a b
trị đại diện cho miền đó là để tính toán. 2 Tác vụ Dòng CASIO MS Dòng CASIO ES
Bật chế độ nhập tần số Không cần Shift Mode 4 1
Khởi động gói Thống kê Mode…(tìm)…SD Mode…(tìm)…STAT 1-Var
x Shift , n M+ 1 1 X FREQ
x Shift , n M+ x = n = k k 1 1 Nhập số liệu
Nếu n 1 thì chỉ cần x = n = i k k nhấn x M+ i - 6 - XSTK - 7 - Tóm tắt công thức Xóa màn hình hiển thị AC AC Xác định: Kích thước mẫu (n) Shift 1 3 = Shift 1 5 1 = Giá trị trung bình (x ) Shift 2 1 = Shift 1 5 2 =
Độ lệch chuẩn không hiệu chỉnh ( ˆs ) Shift 2 2 = Shift 1 5 3 = x
Độ lệch chuẩn hiệu Shift 2 3 = Shift 1 5 4 = chỉnh (s ) x
Thoát khỏi gói Thống kê Mode 1 Mode 1 2. Ước lượng khoảng.
a) Khoảng tin cậy cho giá trị trung bình.
Trường hợp 1. ( đã biết)
Ước lượng đối xứng. 1 (z )
z z .
x ;x ) 2 n 2 2 2
Ước lượng chệch trái.
(z ) 0, 5 z z . ; x ) n
Ước lượng chệch phải.
(z ) 0, 5 z z .
x ) n
Trường hợp 2. ( chưa biết, n 30)
Ước lượng đối xứng. 1 s (z )
z z .
x ;x ) 2 n 2 2 2
Ước lượng chệch trái. s
(z ) 0, 5 z z . ; x ) n
Ước lượng chệch phải. s
(z ) 0, 5 z z .
x ) n
Trường hợp 3. ( chưa biết, n<30)
Ước lượng đối xứng. s 1 t t .
x ; x ) 2 (n1; ) (n1; ) n 2 2
Ước lượng chệch trái. s 1 t t .
;x ) ( n 1 ;) ( n 1 ; ) n - 7 - XSTK - 8 - Tóm tắt công thức
Ước lượng chệch phải. s 1 t t .
x ; ) ( n 1 ; ) ( n 1 ;) n
b) Khoảng tin cậy cho tỉ lệ.
Ước lượng đối xứng. 1 f (1 f ) (z )
z z .
f ; f ) 2 n 2 2 2
Ước lượng chệch trái. f (1 f )
(z ) 0, 5 z z . ; f ) n
Ước lượng chệch phải. f (1 f )
(z ) 0, 5 z z . f ) n
c) Khoảng tin cậy cho phương sai.
Trường hợp 1. ( chưa biết)
- Nếu đề bài chưa cho s mà cho mẫu cụ thể thì phải xác định s (bằng máy tính).
Ước lượng không chệch. 2 1 2 , 1 1 2 2 (n 1 ; ) 1 2 ( n 1 ;1 ) 2 2 2 2 (n 1)s (n 1) s ( ; ) 2 1
Ước lượng chệch trái. 2 2 (n 1)s 1 (0; ) 1 (n 1 ;1) 1
Ước lượng chệch phải. 2 2 ( n1) s
1 ( ; ) 2 (n1; ) 2
Trường hợp 2. ( đã biết) k - Tính 2 2
(n 1)s n .(x ) i i i 1
Ước lượng không chệch. 2 1 2 , 2 1 1 1 2 (n ; ) 2 ( ; n1 ) 2 2 2 2 (n 1)s (n 1) s ( ; ) 2 1 - 8 - XSTK - 9 - Tóm tắt công thức
Ước lượng chệch trái. 2 2 (n 1)s 1 1 ( ; n 1 ) (0; ) 1
Ước lượng chệch phải. 2 2 (n 1)s
1 ( ; ) 2 (n;) 2 3. Kiểm định tham số.
a) Kiểm định giá trị trung bình.
Trường hợp 1. ( đã biết)
H : , 1 H : o o o 1 x (z ) z , o z . n 2 2 2
- Nếu z z : Bác bỏ H ấ ậ o, ch p nh n H1. 2
- Nếu z z : Chấp nhận Ho. 2
H : ,H 1 : o o o x
(z ) 0, 5 z , o z . n - Nếu z z : Bác bỏ H ấ ậ o, ch p nh n H1. - Nếu z z : Chấp nhận Ho.
H : ,H 1 : o o o x
(z ) 0, 5 z , o z . n
- Nếu z z : Bác bỏ H ấ ậ o, ch p nh n H1.
- Nếu z z : Chấp nhận Ho.
Trường hợp 2. ( chưa biết, n 30 )
H : , 1 H : o o o 1 x (z ) z , o z . n 2 s 2 2
- Nếu z z : Bác bỏ H ấ ậ o, ch p nh n H1. 2
- Nếu z z : Chấp nhận Ho. 2
H : , 1 H : o o o x
(z ) 0, 5 z , o z . n s - 9 - XSTK - 10 - Tóm tắt công thức - Nếu z z : Bác bỏ H ấ ậ o, ch p nh n H1. - Nếu z z : Chấp nhận Ho.
H : ,H 1 : o o o x
(z ) 0, 5 z , o z . n s
- Nếu z z : Bác bỏ H ấ ậ o, ch p nh n H1.
- Nếu z z : Chấp nhận Ho.
Trường hợp 3. ( chưa biết, n<30)
H : , 1 H : o o o x t , o t . n 2 ( n 1 ; ) s 2 - Nếu t t : Bác bỏ H ấ ậ o, ch p nh n H1. (n 1 ; ) 2 - Nếu t t : Chấp nhận Ho. (n 1 ; ) 2
H : ,H 1 : o o o x t , o t . ( n 1 ;) n s
- Nếu t t ỏ ấ ( n 1 ; )
: Bác b Ho, ch p nhận H1.
- Nếu t t(n 1 ; ) : Chấp nhận Ho.
H : , 1 H : o o o x o ( t n 1 ;) , t . n s - Nếu t ỏ ấ ậ ( t n 1 ; )
: Bác b Ho, ch p nh n H1. - Nếu t t ấ ậ (n 1 ; ) : Ch p nh n Ho. b) Kiểm định tỉ lệ.
H : p p , H p p 1 : o o o 1 k f p (z )
z ,f , o z . n 2 n p (1 p ) 2 2 o o
- Nếu z z : Bác bỏ H ấ ậ o, ch p nh n H1. 2
- Nếu z z : Chấp nhận Ho. 2
H : p p , H 1 : o o p po k f p
(z ) 0, 5 z ,f , o z . n n p (1 p ) o o - 10 - XSTK - 11 - Tóm tắt công thức - Nếu z z : Bác bỏ H ấ ậ o, ch p nh n H1. - Nếu z z : Chấp nhận Ho.
H : p p , H p p 1 : o o o k f p
(z ) 0, 5 z ,f , o z . n n p (1 p ) o o
- Nếu z z : Bác bỏ H ấ ậ o, ch p nh n H1.
- Nếu z z : Chấp nhận Ho.
c) Kiểm định phương sai.
Trường hợp 1. ( chưa biết)
- Nếu đề chưa cho s mà cho mẫu cụ thể thì phải s d
ử ụng máy tính để xác định s. 2 2 2 2 H : , 1 H : o o o 2 2 2 (n 1)s 1 2 1 , 2 2 2 , ( 1 ;1 ) 2 2 n 2 (n 1 ; ) 2 2 o 2 2 2 - Nếu : Bác bỏ H ấ ậ 0, ch p nh n H1. 2 2 1 - Nế 2 2 2 u ấ ậ 1 2 : Ch p nh n Ho. 2 2 2 2 H : , 1 H : o o o 2 2 2 (n 1) s 1 2 1 (n 1 ;1) , 2 o - Nế 2 2 u ỏ ấ ậ 1 : Bác b H0, ch p nh n H1. - Nế 2 2 u ấ ậ 1 : Ch p nh n Ho. 2 2 2 2 H : , 1 H : o o o 2 2 2 2 (n 1) s 2 (n 1 ;), 2 o - Nế 2 2 u ỏ ấ ậ 2 : Bác b H0, ch p nh n H1. - Nế 2 2 u ấ ậ 2 : Ch p nh n Ho.
4. Kiểm định so sánh tham số.
a) Kiểm định so sánh giá trị trung bình.
Trường hợp 1. ( , đ 1 2 ã biết)
H : ,H : o 1 2 1 1 2 1 1 x x2 (z ) z , z 2 2 2 2 2 1 2 1 n n2 - 11 - XSTK - 12 - Tóm tắt công thức
- Nếu z z : Bác bỏ H ấ ậ o, ch p nh n H1. 2
- Nếu z z : Chấp nhận Ho. 2 H : 1 2 , 1 H : o 1 2 1 x 2 x
(z ) 0, 5 z ,z 2 2 1 2 1 n 2 n - Nếu z z : Bác bỏ H ấ ậ o, ch p nh n H1. - Nếu z z : Chấp nhận Ho. H : 1 2 , 1 H : o 1 2 1 x 2 x
(z ) 0, 5 z ,z 2 2 1 2 n n 1 2
- Nếu z z : Bác bỏ H ấ ậ o, ch p nh n H1.
- Nếu z z : Chấp nhận Ho.
Trường hợp 2. ( chưa biế 1, 2 t, 1 n 2 n 30) H : 1 2 , 1 H : o 1 2 1 1 x 2 x (z ) z , z 2 2 2 2 2 1 s 2 s 1 n 2 n
- Nếu z z : Bác bỏ H ấ ậ o, ch p nh n H1. 2
- Nếu z z : Chấp nhận Ho. 2 H : 1 2 , 1 H : o 1 2 1 x 2 x
(z ) 0, 5 z ,z 2 2 1 s s2 n1 n2 - Nếu z z : Bác bỏ H ấ ậ o, ch p nh n H1. - Nếu z z : Chấp nhận Ho.
H : ,H : o 1 2 1 1 2 1 x 2 x
(z ) 0, 5 z ,z 2 2 1 s s2 n1 n2 - 12 - XSTK - 13 - Tóm tắt công thức
- Nếu z z : Bác bỏ H ấ ậ o, ch p nh n H1.
- Nếu z z : Chấp nhận Ho.
Trường hợp 3. ( chưa biế 1 2 t, 1 n , n 2 30 ) H : 1 2 , 1 H : o 1 2 2 2
(n 1).s ( n 1). 1 x 2 x s t ,t 2 1 1 2 2 , với s 2 ( 1 n 2 n 2; ) 2 1 1 n n 2 2 s ( ) 1 2 n1 n2 - Nếu t t : Bác bỏ H ấ ậ o, ch p nh n H1. ( 1 n n2 2; ) 2 - Nếu t t : Chấp nhận Ho. ( 1 n 2 n 2; ) 2 H : 1 2 , 1 H : o 1 2 x 2 2 1 x 2 2 (n1 1).s1 (n 2 1).s 2 (
t n n 2;) , t , với s 1 2 n n 2 1 1 2 s ( ) 1 2 1 n 2 n
- Nếu t t
: Bác bỏ Ho, chấp nhận H1. ( 1 n 2 n 2; ) 2
- Nếu t t : Chấp nhận Ho. ( 1 n 2 n 2; ) 2 H : 1 2 , 1 H : o 1 2 x 2 2 1 x 2 2 (n1 1).s1 (n 2 1).s 2 (
t n n 2;) , t , với s 1 2 n n 2 1 1 2 s ( ) 1 2 1 n 2 n - Nếu t t : Bác bỏ H ấ ậ o, ch p nh n H1. (n n 2; ) 1 2 2 - Nếu t t : Chấp nhận Ho. (n n 2; ) 1 2 2
b) Kiểm định so sánh tỉ lệ. 1 k k2 1 k k2 f 1 , f 2 , f 1 n 2 n 1 n 2 n H : 1 p
p2 , H1 : p p o 1 2 1 f 1 f 2 (z ) z , z 2 1 1 2 2 f (1 f ).( ) n1 n2
- Nếu z z : Bác bỏ H ấ ậ o, ch p nh n H1. 2
- Nếu z z : Chấp nhận Ho. 2 - 13 - XSTK - 14 - Tóm tắt công thức H : 1 p
p2 , H1 : p p o 1 2 f 1 f 2
(z ) 0, 5 z ,z 1 1 f (1 f ).( ) n1 n2 - Nếu z z : Bác bỏ H ấ ậ o, ch p nh n H1. - Nếu z z : Chấp nhận Ho. H : 1 p
p2 , H1 : p p o 1 2 f 1 f 2
(z ) 0, 5 z ,z 1 1 f (1 f ).( ) n n 1 2
- Nếu z z : Bác bỏ H ấ ậ o, ch p nh n H1.
- Nếu z z : Chấp nhận Ho.
c. Kiểm định so sánh phương sai. - chưa biế ừ ẫu (sử 1, 2 t nên tính s1 và s2 t m
dụng máy tính) nếu đề bài chưa cho. 2 2 2 2 :
,H : o H 1 2 1 1 2 2 s - 1 f , 1 f f ( 1 n 1; 2 n 1;1 ) , 2 f f ( 1 n 1; 2 n 1; ) 2 s 2 2 2 f 1f - Nếu : Bác bỏ H ấ ậ o, ch p nh n H1. f f 2 - Nếu ấ ậ 1 f f f2: Ch p nh n Ho. 2 2 2 2 : 1 2 , 1 : o H H 1 2 2 s - 1 f
, f f n n 1 ( 1 1; 2 1;1 ) 2 s2 - Nếu f ỏ ấ ậ 1
f : Bác b Ho, ch p nh n H1. - Nếu ấ ậ 1 f f : Ch p nh n Ho. 2 2 2 2 :
,H : o H 1 2 1 1 2 2 s - 1 f , 2 f f ( 1 n 1; 2 n 1;) 2 s2 - Nếu f ỏ ấ ậ 2
f : Bác b Ho, ch p nh n H1. - Nếu f ấ ậ 2 f : Ch p nh n Ho.
5. Hệ số tương quan mẫu và phương t ì
r nh hồi quy tuyến tính mẫu. - 14 - XSTK - 15 - Tóm tắt công thức n n n n x y x y i i i i
a. Hệ số tương quan mẫu: i 1 i 1 i 1 r n n n n 2 2 2 2 n x ( x ) n y ( y ) i i i i i 1 i 1 i 1 i 1
Phương trình hồi quy tuyến tính mẫu: y A B x với x n n n n n n x y x y y B .x i i i i i i i1 i 1 i 1 B và i 1 i 1 A . n n 2 2 n n x (x ) i i i 1 i 1 b. Trong trường hợp s d ử ụng bảng tần số: x x x … x i 1 2 k y y y … y i 1 2 k n n n … n i 1 2 k
Ta tính theo công thức thu gọn như sau: k k k nn x y n x n y i i i i i i i Hệ số tương quan mẫu: i1 i1 i1 r k k k k 2 2 2 2 n n x (n x ) n n y ( n y ) i i i i i i i i i 1 i 1 i 1 i 1
Phương trình hồi quy tuyến tính mẫu: y A B x với x k k k k k n n x y n x n y n y B.n x i i i i i i i i i i i i1 i 1 i 1 B và i1 i1 A . k k 2 2 n nn x (n x ) i i i i i 1 i 1 - 15 - XSTK - 16 - Tóm tắt công thức c. S d
ử ụng máy tính bỏ túi để tính hệ số tương quan mẫu và phương trình hồi quy tuyến tính mẫu: Tác vụ Dòng CASIO MS Dòng CASIO ES
Bật chế độ nhập tần số Không cần Shift Mode 4 1 Khởi động gói Hồi quy Mode…(tìm)…REG Mode…(tìm)…STAT tuyến tính Lin A+BX
x , y Shift , n M+ 1 1 1 X Y FREQ
x , y Shift , n M+ x = y = n = 1 1 1 k k k Nhập số liệu
n 1 thì chỉ cần nhấn x = y = n = i k k k x , y M+ i i Xóa màn hình hiển thị AC AC Xác định: Hệ số tương quan Shift 2 3 = Shift 1 7 3 = mẫu (r) Hệ số hằng: A Shift 2 1 = Shift 1 7 1 = Hệ số ẩn (x): B Shift 2 2 = Shift 1 7 2 = Thoát khỏi gói Hồi quy Mode 1 Mode 1
Lưu ý: Máy ES nếu đã kích hoạt chế độ nhập tần số ở phần Lý thuyết mẫu rồi thì
không cần kích hoạt nữa.
………………………………………. - 16 - XSTK




