Tóm tắt kiến thức Toán ôn thi THPT Quốc gia – Hoàng Xuân Nhàn

Tài liệu gồm 41 trang, được biên soạn bởi thầy giáo Hoàng Xuân Nhàn, tóm tắt kiến thức môn Toán THPT (10 – 11 – 12), giúp học sinh ôn thi THPT Quốc gia môn Toán. Mời mọi người đón xem.

19 10 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu ôn thi THPTQG môn Toán

Môn: Toán

Thông tin:

41 trang 6 tháng trước

Tác giả:

Profile Nguyễn Vân
1
Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
I. CÔNG THỨC LƯỢNG GIÁC
1. Hệ thức Cơ bản:
22
sin cos 1


cos
cot
sin
tan .cot 1

2
2
1
1 tan
cos

2
2
1
1 cot
sin

sin( 2 ) sin
cos( 2 ) cos
k
k
k



tan( ) tan
cot( ) cot
k
k
k



2. Cung Liên kết:
Đối:
;
Bù:
;

Phụ:
;
2
Khác pi:
;
Khác
:;
22
Pi

sin( ) sin

sin( ) sin

sin cos
2





sin( ) sin
sin cos
2





cos( ) cos


cos( ) cos
cos sin
2





cos( ) cos
cos sin
2




tan( ) tan

tan( ) tan
tan cot
2





tan( ) tan

tan cot
2




cot( ) cot

cot( ) cot
cot tan
2





cot( ) cot

cot tan
2




Cos đối
Sin bù
Phụ chéo
Khác Pi: tang,
cotang
Khác pi/2: sin bạn cos,
cos thù sin
3. Công thức Cộng:
sin( ) sin .cos cos .sin
sin( ) sin .cos cos .sin
a b a b a b
a b a b a b
cos( ) cos .cos sin .sin
cos( ) cos .cos sin .sin
a b a b a b
a b a b a b
tan tan
tan( )
1 tan .tan
ab
ab
ab

tan tan
tan( )
1 tan .tan
ab
ab
ab

2
Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
4. Công thức Nhân đôi, Nhân ba:
sin2 2sin .cos
22
22
cos2 cos sin
2cos 1 1 2sin


2
2tan
tan2
1 tan
3
sin3 3sin 4sin

3
cos3 4cos 3cos

3
2
3tan tan
tan3
1 3tan

5. Công thức Hạ bậc:
2
1 cos2
sin
2
2
1 cos2
cos
2
2
1 cos2
tan
1 cos2
6. Biến đổi Tổng thành Tích:
cos cos 2cos .cos
22
a b a b
ab


cos cos 2sin .sin
22
a b a b
ab

sin sin 2sin .cos
22
a b a b
ab


sin sin 2cos .sin
22
a b a b
ab


sin( )
tan tan
cos .cos
ab
ab
ab

sin( )
tan tan
cos .cos
ab
ab
ab

sin cos 2.sin 2.cos
44

sin cos 2sin 2 cos
44

7. Công thức biến đổi tích thành tổng
1
cos .cos cos( ) cos( )
2
a b a b a b
1
sin .sin cos( ) cos( )
2
a b a b a b
1
sin .cos sin( ) sin( )
2
a b a b a b
II. PHƯƠNG TRÌNH LƯỢNG GIÁC
2
sin sin ( )
2
u v k
u v k
u v k


2
cos cos
2
u v k
u v k
u v k

Nếu
sin 1;1um
và
3 2 1
1; ; ; ;0
2 2 2
m





thì:
arcsin 2
sin
arcsin 2
u m k
um
u m k



()k
Nếu
cos 1;1um
và
3 2 1
1; ; ; ;0
2 2 2
m





thì:
cos arccos 2u m u m k
()k
Nếu
sin 1;1um
thì:
sinu m u
Nếu
cos 1;1um
thì:
cosu m u
Đặc biệt:
sin 1 2
2
sin 1 2
2
sin 0
u u k
u u k
u u k
k
Đặc biệt:
cos 1 2
cos 1 2
cos 0
2
u u k
u u k
u u k

k
tan tanu v u v k
k
cot cotu v u v k
k
Nếu
3
tan 3; 1; ;0
3
um





thì:
Nếu
3
cot 3; 1; ;0
3
um





thì:
3
Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
tan arctanu m u m k
k
cot cotu m u arc m k
k
Lưu ý: Điều kiện để hàm
tanu
có nghĩa là
,
2
u k k
. Tuy vậy, phương trình
tanum
luôn có nghiệm, vì vậy không cần đặt điều kiện.
Lưu ý: Điều kiện để hàm
cotu
có nghĩa là
,u k k

. Tuy vậy, phương trình
cotum
luôn có
nghiệm, vì vậy không cần đặt điều kiện cho nó.
Kỹ thuật 1: Làm mất dấu TRỪ
sin sin( )
cos cos( )
tan tan( )
cot cot( )



Ví dụ:
sin sin 0 sin sin sin sin( )
4 4 4
2
4
( ).
8
2 (voâ nghieäm)
4
x x x x x x
x x k
x k k
x x k
Kỹ thuật 2: Biến đổi CHÉO
sin cos
2
cos sin
2
tan cot
2
cot tan
2




















Ví dụ:
22
2
sin2 cos sin2 sin
2
22
2
x x k
x x x x
x x k







2
63
( ).
2
2
k
x
k
xk




Phương trình
sin cosa x b x c
(với
2 2 2
a b c
)
Phương trình
22
sin sin cos cosa x b x x c x d
sin cosa x b x c
2 2 2 2 2 2
22
sin cos
sin .cos cos .sin
a b c
xx
a b a b a b
c
xx
ab

(với
2 2 2 2
cos , sin
ab
a b a b



)
sin( ) sin .........x

với
22
sin
c
ab
Trường hợp 1: Xét
2
cos 0 sin 1xx
. Ta có hệ
sau:
2
2
2
sin 1
sin 1
.............(1)
sin
x
x
ad
a x d


Trường hợp 2: Xét
cos 0x
, chia hai vế phương trình
cho
2
cos x
, ta có:
22
tan tan (1 tan ) .........a x b x c d x
(2)
Hợp nghiệm của (1), (2) ta có tập nghiệm của phương
trình đã cho.
Lưu ý: Phương trình
sin cosa x b x c
chỉ có nghiệm khi và chỉ khi
2 2 2
a b c
.
[
III. TỔ HỢP – XÁC SUẤT
QUY TẮC CỘNG
QUY TẮC NHÂN
Nếu phép đếm được chia ra nhiều trường hợp, ta
sẽ cộng các kết quả lại.
Nếu phép đếm được chia ra làm nhiều giai đoạn bắt buộc, ta
sẽ nhân các kết quả của mỗi giai đoạn ấy.
4
Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
HOÁN VỊ
TỔ HỢP
CHỈNH HỢP
Sắp xếp (đổi chỗ) của
n
phần tử khác nhau, ta có số
cách xếp là
!
n
Pn
với
n
.
! 1.2..... 1n n n
.
Quy ước sốc:
0! 1.
Chọn
k
phần tử từ
n
phần tử
(không sắp xếp thứ tự), ta có số cách
chọn là
k
n
C
.
!
!!
k
n
n
C
n k k
với
*
,
.
0
kn
kn

Chọn
k
phần tử từ
n
phần tử (có sắp
xếp thứ tự), ta được số cách chọn là
k
n
A
.
!
!
k
n
n
A
nk
với
*
,
.
0
kn
kn

Một số tính chất:
k n k
nn
CC
11
1
k k k
n n n
C C C


!
kk
nn
A k C
XÁC
SUẤT
Công thức:
()
()
()
nX
PX
n
Trong đó:
( ):nX
số phần tử của tập biến cố
;X
( ):n
số phần tử không gian mẫu;
()PX
là xác suất để biến cố
X
xảy ra với
X 
.
Tính chất:
0 ( ) 1PX
.
( ) 0; ( ) 1PP
.
( ) 1 ( )P X P X
với
X
là biến cố đối của
X
.
Nếu A, B là hai biến cố xung khắc với nhau
thì
P A B P A P B
.
Nếu A và B là hai biến cố độc lập với nhau thì
..P A B P A P B
.
IV. KHAI TRIỂN NHỊ THỨC NEWTƠN
Khai triển dạng
liệt kê:
(với
*
n
)
0 1 1 2 2 2 1 1
.........
n
n n n n n n n
n n n n n
a b C a C a b C a b C ab C b
.
Đặc biệt:
0 1 2 2 1 1
1 .........
n
n n n n
n n n n n
x C C x C x C x C x

(*).
Hệ quả 1:
0 1 2 1
......... 2
n n n
n n n n n
C C C C C
(tức là thay
1x
vào (*)).
Hệ quả 2: Với
n
chẵn, chỉ cần thay
1x 
vào (*), ta có:
0 1 2 1 0 2 4 1 3 1
......... 0 ...... ......
n n n n
n n n n n n n n n n n n
C C C C C C C C C C C C

Khai triển tổng
quát:
(với
*
n
)
Khai triển:
0
n
n
k n k k
n
k
a b C a b

. Số hạng tổng quát:
1
k n k k
kn
T C a b
Phân biệt hệ số và số hạng:
( 1) .
k k n k k
n
HEÄ SOÁ
SOÁ HAÏNG
C a b x
. Số hạng không chứa
x
ứng với
0.
V. CẤP SỐ CỘNG – CẤP SỐ NHÂN
CẤP SỐ CỘNG
CẤP SỐ NHÂN
1. Định nghĩa:
Dãy số
n
u
được gọi là cấp số cộng khi và
chỉ khi
1nn
u u d

với
*
n
, d là hằng
số.
Cấp số cộng như trên có số hạng đầu
1
,u
công sai
.d
2. Số hạng tổng quát:
1
( 1)
n
u u n d
với
*
.n
3. Tính chất các số hạng:
1. Định nghĩa:
Dãy số
n
u
được gọi là cấp số nhân khi và chỉ khi
1
.
nn
u u q
với
*
n
, q là hằng số.
Cấp số nhân như trên có số hạng đầu
1
,u
công bội
q
.
2. Số hạng tổng quát:
1
1
.
n
n
u u q
với
*
.n
3. Tính chất các số hạng:
2
11
.
k k k
u u u

với
k
và k
2.
4. Tổng n số hạng đầu tiên:
5
Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
11
2
k k k
u u u


với
*
k
và k
2.
4. Tổng n số hạng đầu tiên:
1
12
()
... .
2
n
nn
u u n
S u u u
1
12
(1 )
...
1
n
nn
uq
S u u u
q
với
1.q
VI. GIỚI HẠN DÃY SỐ - HÀM SỐ
1. Giới hạn dãy số
1.1. Dãy số có giới hạn 0:
▪
1
lim 0
n
▪
1
lim 0
n
▪
3
1
lim 0
n
▪
1
lim 0
n
▪
lim 0
n
q
với
1q
.
1.2. Dãy số có giới hạn hữu hạn:
Cho
lim
n
ua
. Ta có:
▪
lim
n
ua
và
33
lim ua
▪
lim
n
ua
với
0.a
Cho
lim
n
ua
,
lim
n
vb
. Ta có:
▪
lim
nn
u v a b
▪
lim . .
nn
u v a b
▪
lim
n
n
u
a
vb
với
0b
▪
lim . .
n
k u k a
1.3. Tổng của cấp số nhân lùi vô hạn:
2
1
1 1 1
...
1
u
S u u q u q
q
.
1.4. Dãy số có giới hạn vô cùng:
Quy tắc 1: Cho
lim , lim .
nn
uv
Tính
lim
nn
uv
.
lim
n
u
lim
n
v
lim
nn
uv












Quy tắc 2: Cho
lim , lim 0.
nn
u v a
Tính
lim
nn
uv
.
lim
n
u
Dấu của a
lim
nn
uv

+


–


+


–

Quy tắc 3: Cho
lim 0, lim 0.
nn
u a v
Tính
lim
n
n
u
v
.
Dấu của a (tử)
Dấu của
n
v
(mẫu)
lim
n
n
u
v
+
+

+
–

–
+

–
–

6
Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
2. Giới hạn hàm số:
2.1. Giới hạn tại vô cực:
Cho k dương, ta có:
▪
1
lim 0
k
x
x

▪
lim
k
x
x


▪
,
lim
,
k
x
k chaün
x
k leû
2.2. Giới hạn hữu hạn:
Cho
00
lim , lim
x x x x
f x a g x b


. Ta có:
▪
0
lim
xx
f x a
▪
0
3
3
lim
xx
f x a
▪
0
lim
xx
f x a
với
0a
▪
0
lim
xx
f x g x a b


▪
0
lim . .
xx
f x g x ab


▪
0
lim . .
xx
k f x k a


với k là hằng số
▪
0
lim
xx
fx
a
g x b
với b khác 0
2.3. Quy tắc tìm giới hạn vô cực:
Quy tắc 1: Cho
00
lim , lim 0
x x x x
f x g x a


. Tính
0
lim .
xx
f x g x


.
0
lim
xx
fx
Dấu của a
0
lim
xx
f x g x


.

+


–


+


–

Quy tắc 2: Cho
00
lim 0, lim 0
x x x x
f x a g x

. Tính
0
lim
xx
fx
gx
.
Dấu của a
Dấu của
gx
0
lim
xx
fx
gx
.
+
+

+
–

–
+

–
–

2.4. Bổ trợ các công thức để khử dạng vô định:
2
12
ax bx c a x x x x
với
12
,xx
là nghiệm của tam thức bậc hai.
12
1 2 1
1 1 ... 1
...
n n n
n n n n n
x x x x
a b a b a a b b

2
ab
ab
ab

2
ab
ab
ab

3
3
2
2
33
ab
ab
a a b b


3
3
2
2
33
ab
ab
a a b b


7
Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
3. Điều kiện giới hạn
và điều kiện liên
tục:
3.1. Điều kiện tồn tại giới hạn:
Giới hạn bên phải
Giới hạn bên trái
Điều kiện để hàm số có
giới hạn tại
0
x
.
Ký hiệu
0
lim
xx
fx
0
lim
xx
fx
00
lim lim
x x x x
f x f x


Khi đó:
0
0
0
lim lim
lim
xx
xx
xx
f x f x
fx
Nghĩa là
0
0
xx
xx

0
0
xx
xx

3.2. Điều kiện liên tục của hàm số:
Hàm số
fx
liên tục tại
0
00
0 0 0
lim lim lim
xx
x x x x
x f x f x f x f x f x


Mọi hàm số đa thức, phân thức hữu tỉ, hàm lượng giác đều liên tục trên tập xác định
của chúng.
Hàm số
fx
liên tục trên khoảng
;ab
nếu nó liên tục với mọi
0
;.x x a b
Hàm số
fx
liên tục trên
( ) lieân tuïc treân ( ; )
;
lim ( ) ( ); lim ( ) ( )
x a x b
f x a b
ab
f x f a f x f b
.
3.3. Điều kiện có nghiệm của phương trình:
Nếu hàm số
fx
liên tục trên
;ab
và
.0f a f b
thì phương trình
0fx
có ít nhất một nghiệm trên
;ab
.
VII. ĐẠO HÀM
1. Định nghĩa đạo hàm tại một điểm:
0
0
0
0
lim
xx
f x f x
fx
xx
.
2. Bảng đạo hàm cơ bản và mở rộng:
0k
(với
k
là hằng số)
1
()xx

1
( ) .
MR
u u u



1
2
x
x
2
MR
u
u
u

2
11
xx




2
1
MR
u
uu



xx
ee
.
MR
uu
e e u

ln
xx
a a a
.ln .
MR
uu
a a a u

1
ln x
x
ln
MR
u
u
u

1
log
ln
a
x
xa
log
ln
MR
a
u
u
ua

sin cosxx
sin cos
MR
u u u
cos sinxx

cos sin
MR
u u u
2
2
1
tan 1 tan
cos
xx
x
2
2
tan 1 tan
cos
MR
u
u u u
u

2
2
1
cot 1 cot
sin
xx
x
2
2
cot 1 cot
sin
MR
u
u u u
u

8
Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
3. Quy tắc tìm đạo hàm:
▪
u v u v

▪
( . ) .k u k u

▪
( . )u v u v uv

▪
2
u u v uv
vv




▪
.
x u x
f f u
với
x
u
x
f laø ñaïo haøm cuûa f theo bieán x
f laø ñaïo haøm cuûa f theo bieán u
u laø ñaïo haøm cuûa u theo bieán x
.
4. Đạo hàm cấp cao và vi phân:
Đạo hàm cấp cao
Vi phân
;f x f x f x f x


41
;...;
nn
f x f x f x f x






.
.
.
df x f x dx
dy y dx
du u dx
VIII. KHẢO SÁT HÀM SỐ VÀ BÀI TOÁN LIÊN QUAN
XÉT TÍNH ĐƠN ĐIỆU
HÀM BẬC BA
32
y ax bx cx d
( 0)a
HÀM NHẤT BIẾN
( 0, 0)
ax b
y ad bc c
cx d
Bước 1: Tìm tập xác định
D
.
Bước 2: Tính
()y f x

;
cho
0y
12
, ...
Tìm nghieäm
xx
Tìm thêm
các giá trị
x
mà
y
không
xác định.
Bước 3: Lập bảng biến
thiên. (Nên chọn giá trị x đại
diện cho từng khoảng thay
vào
y
để tìm dấu của
y
trên khoảng đó).
Bước 4: Dựa vào bảng biến
thiên để kết luận về sự đồng
biến, nghịch biến của hàm
số.
Đạo hàm
2
32y ax bx c
.
Hàm số đồng biến trên tập xác
định
0,yx
0
0
a

.
Hàm số nghịch biến trên tập xác
định
0,yx
0
0
a

.
Đạo hàm
2
()
ad bc
y
cx d
.
Hàm số đồng biến trên từng
khoảng xác định
0.ad bc
Hàm số nghịch biến trên từng
khoảng xác định
0.ad bc
Lưu ý: Nếu
a
chứa tham số m thì
ta xét
0a
, tìm m. Thay m tìm được
để kiểm tra dấu
y
, xem y có đơn
điệu trên không?
Lưu ý: Nếu đề cho đồng biến
(nghịch biến) trên
( ; )

thì ta xét điều
kiện:
( ; )
d
c


.
ĐIỀU KIỆN CỰC TRỊ
CỰC TRỊ HÀM BẬC BA
32
y ax bx cx d
( 0)a
CỰC TRỊ HÀM BẬC BỐN
42
y ax bx c
( 0)a
Hàm số có điểm cực trị là
00
( ; )xy
0
00
( ) 0
()
yx
y x y
.
(giả thiết là hàm số liên tục
tại
0
x
).
Đạo hàm
2
32y ax bx c
.
Hàm số có hai cực trị (tức là có
CĐ-CT)
0
(*)
0
y
a

.
Hàm số có hai điểm cực trị trái dấu
12
00x x ac
.
Hàm số có hai điểm cực trị cùng
dấu
0, 0
0
y
a
ac
.
Đạo hàm
3
42y ax bx

.
Điều kiện cực trị
Ba cực trị
0ab
Một cực trị
22
0
0
ab
ab

Có cực trị
22
0ab
Cho
,,A B C
là ba điểm cực trị, ta có:
3
3
8
cos
8
ba
BAC
ba
Nếu
0
0
( ) 0
( ) 0
fx
fx

thì hàm
số
()fx
đạt cực đại tại
0
.xx
9
Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
Nếu
0
0
( ) 0
( ) 0
fx
fx

thì hàm
số
()fx
đạt cực tiểu tại
0
.xx
Phương trình đường thẳng đi qua
hai điểm cực trị:
( ). ( )
( ) .
18
f x f x
y f x
a

Lưu ý: Nếu tọa độ hai cực trị đã
rõ ràng ta nên gọi đường thẳng
y ax b
rồi thay tọa độ hai điểm
đó vào
Giải hệ tìm a, b.
5
3
32
ABC
b
S
a
.
TÌM MAX-MIN TRÊN ĐOẠN
Tìm Max-Min của
()fx
trên đoạn
;ab
TÌM MAX-MIN TRÊN KHOẢNG
Tìm Max-Min của
()fx
trên khoảng
( ; )ab
Bước 1: Tính
()y f x

.
Tìm các nghiệm
( ; )
i
x a b
khi cho
( ) 0fx
.
Tìm
( ; )
j
x a b
mà
y
không xác định.
Bước 2: Tính các giá trị
( ), ( )f a f b
và
( ),
i
fx
()
j
fx
(nếu có).
Bước 3: So sánh tất cả giá trị trong bước 2 để
kết luận về giá trị lớn nhất, nhỏ nhất.
Bước 1: Tính
()y f x

.
Tìm các nghiệm
( ; )
i
x a b
khi cho
( ) 0fx
. Tìm
( ; )
j
x a b
mà
y
không xác định.
Bước 2: Cần tính
lim , lim
x a x b
yy


. (Nếu thay
( ; )ab
bằng
( ; ) 
thì ta tính thêm
lim
x
y

).
Bước 3: Lập bảng biến thiên và suy ra giá trị lớn nhất, nhỏ
nhất trên khoảng.
ĐẶC BIỆT
Nếu hàm
()fx
đồng biến trên
[ ; ]ab
thì
[ ; ]
[ ; ]
max ( ) ( )
min ( ) ( )
x a b
x a b
f x f b
f x f a
Nếu hàm
()fx
nghịch biến trên
[ ; ]ab
thì
[ ; ]
[ ; ]
max ( ) ( )
min ( ) ( )
x a b
x a b
f x f a
f x f b
TIỆM CẬN ĐỨNG
TIỆM CẬN NGANG
Định nghĩa:
0
xx
y


(x hữu hạn, y vô
hạn), ta có tiệm cận đứng
0
xx
. Lưu ý:
điều kiện
0
xx
có thể được thay bằng
0
xx

(giới hạn bên trái) hoặc
0
xx

(giới hạn bên phải).
Cách tìm TCĐ: Nếu
0
xx
là một nghiệm
của mẫu số mà không phải là nghiệm của
tử số thì
0
xx
chính là một TCĐ của đồ thị.
(với tập xác định có dạng
01
\ ; ;...D K x x
).
Định nghĩa:
0
x
yy


(x vô hạn, y hữu hạn), ta có tiệm
cận ngang
0
yy
.
Cách tìm TCN: Đơn giản nhất là dùng CASIO
Bước 1: Nhập hàm số vào máy.
Bước 2:
10^10
NEXT NEXT
CALC X 
10^10
NEXT NEXT
CALC X 
Bước 3: Nếu kết quả thu được là hữu hạn (tức là
0
y
) thì ta
kết luận TCN:
0
yy
.
Đồ thị hàm số
ax b
y
cx d
với
( 0, 0)c ad bc
có một TCĐ:
d
x
c

, một TCN:
.
a
y
c
Nên nhớ, mỗi đồ thị chỉ có tối đa là 2 tiệm cận ngang.
10
Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
SỰ TƯƠNG GIAO GIỮA HAI ĐỒ THỊ
Xét hai đồ thị
1
( ): ( )C y f x
và
2
( ): ( )C y g x
.
Phương pháp chung tìm giao điểm hai đồ thị
Bước 1 : Lập phương trình hoành độ giao
điểm của
12
( )&( )CC
:
( ) ( )f x g x
. (*)
Bước 2 : Giải phương trình (*) để tìm các nghiệm
12
, ,...xx
(nếu có), suy ra
12
, ...yy
Điều kiện để
1
()C
và
2
()C
có n
điểm chung là phương trình (*) có
n nghiệm khác nhau.
Điều kiện để
1
()C
tiếp xúc
2
()C
là phương trình (*) có nghiệm kép hoặc
hệ sau có nghiệm :
( ) ( )
( ) ( )
f x g x
f x g x

.
Tìm tham số để
( ):
:
ax b
Cy
cx d
d y x


cắt nhau tại hai điểm phân biệt
Bước 1 : Viết phương trình hoành độ giao
điểm :
ax b
x
cx d


, đưa phương trình về
dạng
2
( ) 0
d
g x Ax Bx C x
c



.
Bước 2 : Giải hệ
0
0?
0
Tìm
g
A
m
d
g
c





Tìm tham số để
32
( ):
:
C y ax bx cx d
d y x


cắt nhau tại ba điểm phân biệt
(Ta chỉ áp dụng cho trường hợp phương trình hoành độ giao điểm có nghiệm đẹp)
Bước 1 : Viết phương trình hoành độ giao
điểm :
32
ax bx cx d x

, đưa
phương trình về dạng
2
0
()
( ) 0
gx
x x Ax Bx C




.
(có vận dụng kỹ năng chia Hoocner)
Bước 2 : Giải hệ điều kiện :
0
0
0?
( ) 0
Tìm
g
A
m
gx

Lưu ý : Để tìm nghiệm đẹp
0
xx
, ta nhập vào máy chức
năng giải phương trình bậc ba với
100m
.
PHƯƠNG TRÌNH TIẾP TUYẾN
DẠNG 1
Viết phương trình tiếp tuyến của
đồ thị
( ): ( )C y f x
tại điểm
00
( ; ) ( )M x y C
DẠNG 2
Viết phương trình tiếp tuyến của đồ thị
( ): ( )C y f x
biết tiếp tuyến có hệ số
góc k.
DẠNG 3
Viết phương trình tiếp tuyến của đồ thị
( ): ( )C y f x
biết tiếp tuyến đi qua
( ; )
AA
A x y
.
Bước 1: Tính đạo hàm
y
, từ
đó có hệ số góc
0
( ).k y x
Bước 2 : Viết phương trình tiếp
tuyến của đồ thị dạng
00
()y k x x y
.
Bước 1: Gọi
00
( ; )M x y
là tiếp điểm
và tính đạo hàm
y
.
Bước 2: Cho
0
()y x k
, tìm được
tiếp điểm
00
( ; ).xy
Bước 3: Phương trình tiếp tuyến :
00
()y k x x y
.
Bước 1: Tiếp tuyến có dạng :
0 0 0
( )( )y y x x x y
(*) với
00
( ).y f x
Bước 2: Thay tọa độ điểm
A
vào
(*)
để tìm được
0
.x
Bước 3: Thay
0
x
vào (*) để viết phương
trình tiếp tuyến.
Đặc biệt : Nếu tiếp tuyến song song đường thẳng
y ax b
thì nó có hệ số góc
,ka
nếu tiếp tuyến vuông góc đường
11
Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
thẳng
y ax b
thì nó có hệ số góc
1
k
a

( 0)a
; nếu tiếp tuyến tạo với
Ox
góc
thì nó có hệ số góc
tank

.
ĐIỂM ĐẶC BIỆT THUỘC ĐỒ THỊ
Tâm đối xứng (hay điểm uốn) của đồ thị bậc ba
32
y ax bx cx d
( 0)a
Bước 1: Tính
2
32
62
y ax bx c
y ax b


.
Bước 2: Cho
00
0
3
Tìm nghieäm
b
y x y
a
. Ta có tâm
đối xứng (tức điểm uốn):
00
( ; ).I x y
Cần nhớ: Tâm đối xứng của đồ thị bậc ba
cũng là trung điểm của hai điểm cực trị (nếu có).
Tâm đối xứng của đồ thị hàm nhất biến
( 0, 0)
ax b
y c ad bc
cx d
Tìm tiệm cận đứng
d
x
c

và tiệm cận
ngang
a
y
c
, suy ra được tâm đối xứng của
đồ thị là:
;
da
I
cc



(là giao điểm 2 tiệm cận
tìm được).
Điểm có tọa độ nguyên thuộc đồ thị hàm nhất biến
( 0, 0)
ax b
y c ad bc
cx d
Cách 1: Tự luận
Cách 2: Trắc nghiệm
Bước 1: Chia đa thức cho đa thức, ta viết
lại hàm số
y
cx d

.
Bước 2: Yêu cầu bài toán
cx d
là
ước số nguyên của
.......
Tìm ñöôïc
x
x
, suy
ra các giá trị
y
tương ứng. Từ đây tìm
được các điểm có tọa độ nguyên thuộc đồ
thị.
Thực hiện trên máy tính bỏ túi như sau:
7MODE 
( ) : 19
aX b
F X START
cX d

:1END
:1STEP
. Ta dò tìm những hàng có
()FX
nguyên thì nhận làm điểm cần tìm. Làm tương tự khi cho
:0START
:18END
:1STEP
, ta sẽ bổ sung thêm các
điểm nguyên còn lại. Lưu ý: Học sinh muốn đạt được tính chính xác
cao hơn thì có thể dò trên nhiều khoảng, mỗi khoảng có
START
và
END
cách nhau 19 đơn vị. (Máy tính đời mới sẽ có bộ nhớ lớn hơn).
NHẬN DIỆN ĐỒ THỊ HÀM SỐ
1. Hàm số bậc ba
32
0y ax bx cx d a
2
32
A B C
y a x b x c

Hệ số
Dấu hiệu đồ thị
Kết luận
a
Nhánh phải đồ thị đi lên
0a
Nhánh phải đồ thị đi xuống
0a
d
Giao điểm với Oy nằm trên điểm O
0d
12
Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
Giao điểm với Oy nằm dưới điểm O
0d
Giao điểm với Oy trùng với điểm O
0d
b, c
Đồ thị không có điểm cực trị nào
2
2
30
y
B AC b ac

Đồ thị có hai điểm cực trị
2
2
30
y
B AC b ac

Tâm đối xứng nằm bên phải Oy
2
0 0 0
3
Bb
ab
Aa
Tâm đối xứng nằm bên trái Oy
2
0 0 0.
3
Bb
ab
Aa
Hai điểm cực trị nằm cùng phía Ox
12
0 0 0 0
3
Cc
x x ac
Aa
Hai điểm cực trị nằm khác phía Ox
12
0 0 0 0
3
Cc
x x ac
Aa
Chú ý: Đôi khi, ta thấy đồ thị đi qua điểm
00
;xy
cho trước, ta thay tọa độ này vào hàm số để có 1 phương
trình. Điều này đúng cho mọi hàm số.
2. Hàm số bậc bốn trùng phương
42
0y ax bx c a
32
4 2 2 2y ax bx x ax b

Hệ số
Dấu hiệu đồ thị
Kết luận
a
Nhánh phải đồ thị đi lên
0a
Nhánh phải đồ thị đi xuống
0a
c
Giao điểm với Oy nằm trên điểm O
0c
Giao điểm với Oy nằm dưới điểm O
0c
Giao điểm với Oy trùng với điểm O
0c
b
Đồ thị hàm số có ba cực trị
0ab
Đồ thị hàm số có một cực trị
0, 0ab a
3. Hàm số nhất biến
0, 0
ax b
y c ad bc
cx d
2
ad bc
y
cx d

Hệ số
Dấu hiệu đồ thị
Kết luận
c và d
Tiệm cận đứng nằm bên phải Oy
00
d
cd
c
Tiệm cận đứng nằm bên trái Oy
00
d
cd
c
a và c
Tiệm cận ngang nằm phía trên Ox
00
a
ac
c
Tiệm cận ngang nằm phía dưới Ox
00
a
ac
c
a và b
Giao điểm của đồ thị với Ox nằm bên phải gốc O
00
b
ab
a
Giao điểm của đồ thị với Ox nằm bên trái gốc O
00
b
ab
a
13
Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
b
Đồ thị đi qua gốc O(0;0)
0b
b và d
Giao điểm của đồ thị với Oy nằm trên gốc O
00
b
bd
d
Giao điểm của đồ thị với Oy nằm dưới gốc O
00
b
bd
d
a, b, c, d
Mỗi nhánh đồ thị đi lên (từ trái sang phải)
0ad bc
Mỗi nhánh đồ thị đi xuống (từ trái sang phải)
0ad bc
PHÉP SUY ĐỒ THỊ TỪ ĐỒ THỊ CÓ SẴN
1. Phép tịnh tiến và đối xứng đồ thị
Cho hàm
()y f x
có đồ thị (C)
Đồ thị cần tìm
Cách biến đổi
Minh họa
1
( ): ( )C y f x a
Tịnh tiến đồ thị
()C
theo phương
Oy
lên phía trên
a
đơn vị.
2
( ): ( )C y f x a
Tịnh tiến đồ thị
()C
theo phương
Oy
xuống phía dưới
a
đơn vị.
3
( ): ( )C y f x a
Tịnh tiến đồ thị
()C
theo phương
Ox
qua trái
a
đơn vị.
4
( ): ( )C y f x a
Tịnh tiến đồ thị
()C
theo phương
Ox
qua phải
a
đơn vị.
14
Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
5
( ): ( )C y f x
Lấy đối xứng
()C
qua
Ox
.
6
( ): ( )C y f x
Lấy đối xứng
()C
qua
Oy
.
2. Đồ thị hàm chứa giá trị tuyệt đối
a) Từ đồ thị
( ): ( )C y f x
ta suy ra đồ thị
1
( ): ( )C y f x
.
Ta có
( ) neáu ( ) 0
( ) .
( ) neáu ( ) 0
f x f x
y f x
f x f x
Bước 1: Giữ nguyên phần đồ thị
()C
nằm phía trên
Ox
, ta được
()C
.
Bước 2: Lấy đối xứng phần đồ thị
()C
phía dưới
Ox
qua
Ox
, ta được
()C

.
Kết luận: Đồ thị
1
( ): ( )C y f x
là hợp của
()C
với
( ).C

Xem ví dụ minh họa sau:
b) Từ đồ thị hàm số
( ): ( )C y f x
ta suy ra đồ thị
2
( ) : .C y f x
Ta có
( ) neáu 0
( ) .
( ) neáu 0
f x x
y f x
f x x
Bước 1: Giữ nguyên phần đồ thị
()C
nằm bên phải trục
Oy
, ta được
( ).C
Bước 2: Lấy đối xứng phần đồ thị
()C
qua trục
Oy
, ta được
()C

.
(Đây là tính chất đối xứng của đồ thị hàm số chẵn)
Kết luận: Đồ thị
2
( ):C y f x
là hợp của
()C
với
( ).C

Xem ví dụ minh họa sau:
15
Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
CÔNG THỨC BỔ TRỢ CHO QUÁ TRÌNH GIẢI TOÁN HÀM SỐ
Bổ trợ về tam thức bậc hai
Cho phương trình
2
0 (*)ax bx c
(*) có hai nghiệm phân biệt
0
0
a

(*)
có hai nghiệm trái dấu
.0ac
.
Định lí Vi-ét :
12
12
b
S x x
a
c
P x x
a

AÙp duïng
2 2 2 3 3 3 2 2
1 2 1 2 1 2
2 ; 3 ; ( ) 4 ;x x S P x x S SP x x S P
22
1 2 1 2
( ) 4x x x x S P
. Trong trắc nghiệm, ta nên dùng công thức :
12
xx
a

.
(*)
có hai nghiệm dương phân biệt
0, 0
.
0, 0
a
SP

(*)
có hai nghiệm âm phân biệt
0, 0
0, 0
a
SP

.
Bổ trợ hình học giải tích phẳng
Nếu
ABC
có
12
12
( ; )
( ; )
AB b b
AC c c
thì
1 2 2 1
1
2
ABC
S b c b c

ABC
tại
.0A AB AC
1 1 2 2
0bc b c
.
22
( ) ( ) .
B A B A
AB x x y y
Khoảng cách từ điểm
( ; )
MM
M x y
đến
:0ax by c
là
22
;
MM
ax by c
dM
ab


.
Đặc biệt:
; , ;
MM
d M Ox y d M Oy x
.
IX. LŨY THỪA – MŨ VÀ LOGARIT
1. Công thức lũy thừa
Cho các số dương
,ab
và
,mn
. Ta có:
0
1a
. ...........
n
n thöøa soá
a a a a
với
*
n
1
n
n
a
a
( ) ( )
m n mn n m
a a a
.
m n m n
a a a
m
mn
n
a
a
a
()
n n n
a b ab
n
n
n
aa
bb



1
2
*
1
3
3
( , )
n
m
n
m
aa
a a m n
aa



16
Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
2. Công thức logarit:
Cho các số
, 0, 1a b a
và
,mn
. Ta có:
log
a
b a b
10
lg log logb b b
ln log
e
bb
log 1 0
a
log 1
a
a
log
n
a
an
1
log log
m
a
a
bb
m
log log
n
aa
b n b
log log
m
n
a
a
n
bb
m
log ( ) log log
a a a
bc b c
log log log
a a a
b
bc
c




log
log log
a
bb
b
ca
ab
ac
log .log log
a b a
b c c
,
1b
log
log
log
a
b
a
c
c
b
,
1b
1
log
log
a
b
b
a
,
1b
BÀI TOÁN NGÂN HÀNG
1. Công
thức tính
lãi đơn
Nếu ta gởi tiền vào ngân hàng theo hình thức tiền lãi chỉ được tính dựa vào tiền gốc ban đầu (tức là
tiền lãi của kỳ hạn trước không gộp vào vốn để tính lãi cho kỳ hạn kế tiếp), đây gọi là hình thức lãi
đơn. Ta có:
(1 )T A nr
với A: tiền gởi ban đầu; r: lãi suất; n: kỳ hạn gởi; T: tổng số tiền nhận sau
kỳ hạn n. Lưu ý: r và n phải khớp đơn vị; T bao gồm cả A, muốn tính số tiền lời ta lấy T – A.
2. Công
thức lãi
kép
Nếu ta gởi tiền vào ngân hàng theo hình thức: hàng tháng tiền lãi phát sinh sẽ được cộng vào tiền
gốc cũ để tạo ra tiền gốc mới và cứ tính tiếp như thế, đây gọi là hình thức lãi kép.
Ta có:
(1 )
n
T A r
với A: tiền gởi ban đầu; r: lãi suất; n: kỳ hạn gởi; T: tổng số tiền nhận sau kỳ
hạn n. Lưu ý: r và n phải khớp đơn vị; T bao gồm cả A, muốn tính số tiền lời ta lấy T – A.
3. Mỗi tháng gởi
đúng số tiền giống
nhau theo hình
thức lãi kép
Nếu đầu mỗi tháng khách hàng luôn gởi vào ngân hàng số tiền A đồng với lãi kép
%r
/tháng
thì số tiền họ nhận được cả vốn lẫn lãi sau n tháng là:
1 1 1
n
A
T r r
r


.
4. Gởi tiền vào ngân
hàng rồi rút ra hàng
tháng số tiền cố định
Nếu khách hàng gởi vào ngân hàng số tiền A đồng với lãi suất
%r
/tháng. Vào ngày ngân
hàng tính lãi mỗi tháng thì rút ra X đồng. Số tiền thu được sau n tháng là:
11
1
n
n
r
T A r X
r

5. Vay vốn và trả góp
(tương tự bài toán 4)
Nếu khách hàng vay ngân hàng số tiền A đồng với lãi suất r%/tháng. Sau đúng một tháng
kể từ ngày vay bắt đầu hoàn nợ, hai lần hoàn nợ cách nhau đúng một tháng, mỗi lần hoàn
nợ đúng số tiền X đồng. Số tiền khách hàng còn nợ sau n tháng là:
11
1
n
n
r
T A r X
r

3. Hàm số lũy thừa, mũ và logarit:
HÀM LŨY THỪA
HÀM SỐ MŨ
HÀM SỐ LOGARIT
Dạng:
yx
yu
với
u
là đa
thức đại số.
Dạng:
x
u
ya
ya
với
0
.
1
a
a
Tập xác định:
.D
Đạo hàm:
Dạng:
log
log
a
a
yx
yu
với
0
.
1
a
a
Đặc biệt:
ln ;a e y x
10 log lga y x x
.
Điều kiện xác định:
0u
.
17
Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
Tập xác định:
Nếu
.
ÑK
u
Nếu
0.
0
ÑK
u
Nếu
0.
ÑK
u
Đạo hàm:
1
1
.
y x y x
y u y u u





ln
ln .
xx
uu
y a y a a
y a y a a u



.
Đặc biệt:
()
( ) .
xx
uu
ee
e e u

với
2,71828...e
Sự biến thiên:
x
ya
.
Nếu
1a
thì hàm đồng biến
trên . Nếu
01a
thì hàm
nghịch biến trên .
Đạo hàm:
1
log
ln
log
ln
a
a
y x y
xa
u
y u y
ua


.
Đặc biệt:
1
(ln )
(ln )
x
x
u
u
u
.
Sự biến thiên:
log
a
yx
. Nếu
1a
:
hàm đồng biến trên
(0; )
. Nếu
01a
: hàm nghịch biến trên
(0; ).
4. Đồ thị hàm số mũ và logarit:
ĐỒ THỊ HÀM SỐ MŨ
ĐỒ THỊ HÀM SỐ LOGARIT
Ta thấy:
0 1; 0 1
xx
a a b b
.
Ta thấy:
1; 1.
xx
c c d d 
So sánh a với b: Đứng trên cao, bắn mũi tên từ trái
sang phải, trúng
x
a
trước nên
ab
.
So sánh c với d: Đứng trên cao, bắn mũi tên từ trái
sang phải, trúng
x
c
trước nên
.cd
Vậy
0 1 .b a d c
Ta thấy:
log 0 1; log 0 1
ab
x a x b 
.
Ta thấy:
log 1; log 1.
cd
x c x d
So sánh a với b: Đứng trên cao, bắn mũi tên từ phải
sang trái, trúng
log
b
x
trước:
.ba
So sánh c với d: Đứng trên cao, bắn mũi tên từ phải
sang trái, trúng
log
d
x
trước:
.dc
Vậy
01a b c d
.
5. Phương trình mũ và logarit:
Phương trình mũ
Phương trình Logarit
1. Dạng cơ bản:
( ) ( )
( ) ( )
f x g x
a a f x g x
1. Dạng cơ bản:
log ( ) log g( ) ( ) ( ) 0
aa
f x x f x g x
2. Dạng logarit hóa:
()
( ) ( )
( ) log
( , 0, 1)
( ) ( ).log
fx
a
f x g x
a
a b f x b
a b a
a b f x g x b

2. Dạng mũ hóa:
log ( ) ( )
b
a
f x b f x a
(không cần điều kiện)
18
Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
3. Dạng đặt ẩn phụ:
Đặt
()
0
fx
ta
Đưa phương trình đã cho về bậc
n
theo
t
giải tìm
t
.
Với
t
có được, thay vào
()fx
ta
để tìm
x
.
a) Phương trình
2 ( ) ( )
. . 0
f x f x
ma na p
• Đặt
()
0
fx
ta
.
• PT:
2
0mt nt p
.
b) Phương trình
( ) ( ) ( )
. . . 0
g x g x g x
ma nb pc
• Nhận dạng:
2 ( ) ( ) 2 ( )
( . ) . 0
f x f x f x
ma n ab pb
• Chia hai vế PT cho
2 ( )
0
fx
b
, ta được
2 ( ) ( )
0
f x f x
aa
m n p
bb
. (Xem a))
Chú ý: Ta có thể chia PT cho bất kỳ hàm mũ nào
trong ba hàm
( ) ( ) ( )
;;
g x g x g x
abc
, kết quả không
thay đổi.
c) Phương trình
( ) ( )
.( ) ( )
f x f x
m a b n a b p
• Nhận dạng:
2
( )( ) 1a b a b a b
• Đặt
( ) ( )
1
( ) , 0 ( )
f x f x
t a b t a b
t
• PT:
2
0
n
mt p mt pt n
t
3. Dạng đặt ẩn phụ:
Đặt
log ( )
a
t f x
Đưa pt đã cho về bậc
n
theo
t
giải tìm
t
.
Có
t
, thay vào
log ( )
a
t f x
để tìm
x
.
a) Phương trình
2
log ( ) log ( ) 0
aa
m f x n f x p
• Đặt
log ( )
a
t f x
• PT:
2
0mt nt p
b) Phương trình
()
.log ( ) .log 0
a f x
m f x n a p
• ĐK:
( ) 0, ( ) 1f x f x
• Đặt
()
1
log ( ) log
a f x
t f x a
t
• PT:
2
00
n
mt p mt pt n
t
c) Phương trình đơn giản chứa
log ( )
log ( )
a
b
fx
gx
• Đặt
log ( ) ( )
t
a
t f x f x a
• Thay trở lại phương trình, ta có một phương
trình mới đơn giản hơn (chứa ít logarit hơn).
6. Bất phương trình mũ và logarit:
Bất Phương trình mũ
Bất Phương trình Logarit
Dạng cơ bản:
1
( ) ( )
01
( ) ( )
( ) ( )
( ) ( )
a
f x g x
a
f x g x
a a f x g x
a a f x g x

Dạng cơ bản:
1
01
log ( ) log ( ) ( ) ( ) 0
log ( ) log ( ) 0 ( ) ( )
a
aa
a
aa
f x g x f x g x
f x g x f x g x

Lưu ý: Cách nhận dạng bất phương trình mũ-logarit cũng giống với cách nhận dạng phương trình mũ-
logarit. Học sinh tham khảo kỹ mục 5 để có phương pháp giải bất phương trình một cách hiệu quả.
X. NGUYÊN HÀM – TÍCH PHÂN
1. Công thức nguyên hàm:
( ) ( ) ( ) ( )f x dx F x C F x f x
. ( ) ( )k f x dx k f x dx

( ) ( ) ( ) ( )f x g x dx f x dx g x dx
( ) ( )f x dx f x C

1)
kdx kx C
22dx x C
( 3) 3dx x C
2)
1
1
x
x dx C

1
1 ( )
( ) .
1
MR
ax b
ax b dx C
a

4
3
4
x
x dx C
3
1
2
3
2
2
3/ 2 3
x
xdx x dx C x C

11 11
10
1 (1 2 ) (1 2 )
(1 2 ) .
2 11 22
xx
x dx C C


19
Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
3)
1 1 1
ln ln
MR
dx x C dx ax b C
x ax b a


11
ln 1 3
1 3 3
dx x C
x

4)
22
1 1 1 1 1
.
()
MR
dx C dx C
x x ax b a ax b



2
1 1 1 1
.
(2 3) 2 2 3 4 6
dx C C
x x x
3
2
2
1 1 1
10 ln 10
3
x
x dx x x C
x x x



55
4
11
ln
5
xx
dx x dx x C
xx




5)
1
MR
x x ax b ax b
e dx e C e dx e C
a



1
1
x x x
e dx e C e C
6)
ln
x
x
a
a dx C
a

1
.
ln
bx c
MR
bx c
a
a dx C
ba

5
5
ln5
x
x
dx C
2
9
39
ln9
x
xx
dx dx C

2 5 2 5
25
1 3 3
3.
2 ln3 2ln3
xx
x
dx C C

1 2 1 2 1
1
2 2 2
2
x x x x x x
e e dx e e dx e e C

1
1 1 6
2 .3 2 .3 . 6
3 3 3ln6
x
x x x x x
dx dx dx C
7)
sin cosxdx x C
1
sin( ) cos( )
MR
ax b dx ax b C
a

4;
2
1
sin 4 cos 4
2 4 2
ab
x dx x C

8)
cos sinxdx x C
1
cos( ) sin( )
MR
ax b dx ax b C
a

1;
3
1
cos sin sin
3 1 3 3
ab
x dx x C x C
3sin 2cos 3cos 2sinx x dx x x C
2
1 1 1
sin 1 cos2 sin2
2 2 2
xdx x dx x x C




9)
2
2
1
1 tan tan
cos
dx x dx x C
x

2
11
tan
cos
MR
dx ax b C
ax b a

2
1
1 tan tan
MR
ax b dx ax b C
a



2
22
1 2cos 1
2 tan 2
cos cos
x
dx dx x x C
xx




2
11
tan3
cos 3 3
dx x C
x

2
2;
1
1 tan 2 tan 2
2
ab
x dx x C





10)
2
2
1
1 cot cot
sin
dx x dx x C
x

2
11
cot
sin
MR
dx ax b C
ax b a

2
1
1 cot cot
MR
ax b dx ax b C
a



22
22
sin 1 1
cot
sin sin 2
x x x
dx x dx x C
xx




2
11
cot8
sin 8 8
dx x C
x
2
1
1 cot 3 cot3
3
x dx x C
22
2 2 2 2 2 2
1 sin cos 1 1
tan cot
sin cos sin cos cos sin
xx
dx dx dx x x C
x x x x x x



20
Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
2. Tích phân:
a) Định nghĩa:
b
a
b
a
f x dx F x F b F a
với
Fx
là một nguyên hàm của
fx
trên
;ab
.
b) Tính chất:
0
a
a
f x dx
ba
ab
f x dx f x dx

bb
aa
kf x dx k f x dx

(k là hằng số)
b b b
a a a
f x g x dx f x dx g x dx


c b c
a a b
f x dx f x dx f x dx
b b b
a a a
f x dx f t dt f u du
Nếu
0, ;f x x a b
thì
0.
b
a
f x dx
Nếu
,;f x g x x a b
thì
.
bb
aa
f x dx g x dx

Đặc biệt:
Nếu hàm
y f x
là hàm số lẻ trên
;aa
thì
0.
a
a
f x dx
Nếu hàm
y f x
là hàm số chẵn trên
;aa
thì
0
2
aa
a
f x dx f x dx

.
3. Phương pháp tính tích phân:
a) Phương pháp tích phân từng phần:
Quy tắc chung:
.
bb
aa
b
a
I u dv uv vdu

. Ta xét các dạng phổ biến sau:
Dạng
..
b
a
P x Q x dx
với
Px
là đa thức đại số,
Qx
là hàm lượng giác hoặc hàm
mũ.
PP
u P x
dv Q x dx

du P x dx
v Q x dx

.
Lưu ý:
v Q x dx
nên kết
quả có dạng
R x C
, ta chủ
Minh họa:
2
0
2 1 sinI x xdx

.
Đặt
21
sin
ux
dv xdx

0
2
sin cos
choïn C
du dx
v xdx x
.
Ta có:
.
bb
aa
b
a
I u dv uv vdu

2
0
2
0
2 1 cos 2cos ......x x xdx
1
2
0
1
x
J x e dx
.
Đặt
22
2
0
1
1
2
xx
x
choïn C
du dx
ux
v e dx e
dv e dx
.
21
Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
động chọn 1 giá trị
C
có lợi cho
tính toán sau này.
1
22
0
1
0
11
1 ......
22
xx
J x e e dx
Dạng
..
b
a
P x Q x dx
với
Px
là đa thức đại số hoặc
phân thức,
Qx
là hàm
logarit.
PP
u Q x
dv P x dx

du Q x dx
v P x dx

.
Minh họa:
2
1
ln
e
I x xdx
.
Đặt
23
2
1
ln
3
du dx
ux
x
dv x dx x
v x dx


.
3 3 3
2
11
1
11
ln . ......
3 3 3 3
ee
e
x x e
I x dx x dx
x

2
1
ln
1
e
x
J
x
.
Đặt
2
1
1
ln
1
1
1
11
( 1)
choïn C
du dx
ux
x
x
dv dx
v
xx
x
.
1
11
1
ln . ln 1 ...
1 1 1
e
ee
x x e
J x dx x
x x x e
b) Phương pháp tích phân đổi biến:
Đổi biến loại 1: Xét tích phân dạng
.
b
a
I f u x u x dx


.
PP
Đặt
t u x dt u x dx
. Đổi cận:
xa
1
,t u a
xb
2
t u b
.
Khi đó tích phân cần tính là:
2
1
t
t
I f t dt
. Ta xét các dạng phổ biến sau:
1) Dạng
1
()
b
nn
a
I f x x dx
.
PP
n
tx

(hoặc
n
tx
)
1
2
3
0
1
1
I x dx
x
Đặt
3 2 2
1
13
3
t x dt x dx x dx dt
.
Đổi cận:
0 1, 1 2x t x t
.
Ta có:
2
1
11
. ......
3
I dt
t

2) Dạng
..
b
n
a
I f u u dx
.
PP
n
n
t u t u
.
7
3
2
0
1.I x xdx
Đặt
3
2 3 2 2
1 1 3 2t x t x t dt xdx
2
3
2
xdx t dt
. Đổi cận:
0 1, 7 2x t x t
.
22
Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
22
23
11
33
. ......
22
I t t dt t dt

3) Dạng
2
11
..
b
a
I f dx
xx



.
1
.
PP
t
x


hay
11
;
n
tt
xx

v.v…
4
2
1
11
1.I dx
xx

Đặt
2
2
1 1 1
1 1 2t t tdt dx
x x x
.
Ta có:
3
2
2
0
2 . ......I t dt
4) Dạng
1
..
b
a
I f x dx
x
.
PP
tx

hay
...tx
4
2
1
11
.
1
I dx
x
x
Đặt
11
12
2
t x dt dx dt dx
xx
.
Ta có:
3
2
2
1
.2 ......I dt
t

.
5) Dạng
..
b
xx
a
I f e e dx
.
PP
x
te

hay
x
te
.
2
1
0
1
x
x
e
I dx
e
1
0
1
x
x
x
e
I e dx
e

.
Đặt
1
1
x
x
x
dt e dx
te
et

. Khi đó:
1
2
1
e
t
I dt
t
.
1
2
1
1 ......
e
I dt
t



6) Dạng
1
ln . .
b
a
I f x dx
x
.
ln
PP
tx

hay
lntx
.
2
1
2ln 1
e
x
I dx
x
2
1
1
2ln 1 .
e
I x dx
x

.
Đặt
1
lnt x dt dx
x
.
Khi đó
2
2
0
2
0
2 1 ......I t dt t t
7) Dạng
(sin ).cos
b
a
I f x xdx
sin
PP
tx

hay
sintx
.
2
0
cos
1 2sin
x
I dx
x
Đặt
1
1 2sin 2cos cos
2
t x dt xdx dt xdx
.
Khi đó
3
1
1
3
1
2
ln ......
1
2
dt
It
t
.
8) Dạng
(cos ).sin
b
a
I f x xdx
.
cos
PP
tx

hay
costx
2
0
cos2 cos 1 sinI x x xdx
2
2
0
2cos cos sinI x x xdx
.
Đặt
cos sin sint x dt xdx dt xdx
.
Khi đó:
01
22
10
2 ( ) 2 ......I t t dt t t dt

23
Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
9) Dạng
2
1
(tan )
cos
b
a
I f x dx
x
.
tan
PP
tx

hay
tantx
.
3
3
2
0
tan
cos
x
I dx
x
Đặt
2
1
tan
cos
t x dt dx
x
.
Khi đó:
3
3
0
......I t dt
10) Dạng
2
1
(cot )
sin
b
a
I f x dx
x
.
cot
PP
tx

hay
cottx
.
2
3
2
4
cot 1
cot .sin
x
I dx
xx
2
3
2
4
cot 1 1
.
cot sin
x
I dx
xx

.
Đặt
22
11
cot
sin sin
t x dt dx dt dx
xx
.
1
2
3
1
1
......
t
I dt
t
11) Dạng
2
2
sin
cos sin2 .
cos2
b
a
x
I f x x dx
x





.
2
2
sin
sin 2 .
cos sin 2 .
cos2 2sin 2 .
PP
tx
dt x dx
t x dt x dx
t x dt x dx

2
4
0
sin 3 sin2I x xdx

Đặt
2
sin 2sin (sin ) sin2t x dt x x dx xdx
.
Ta có:
1
2
0
3 ......I t dt
Đổi biến loại 2: Xét tích phân dạng
b
a
I f x dx
trong đó
fx
phức tạp và không thể tính nguyên hàm
trực tiếp. Đổi biến loại 2 là ta đặt:
x u t dx u t dt
. Ta xét 4 dạng phổ biến sau:
1) Dạng
2
1
22
()
x
x
I f a x dx
.
sin
PP
x a t
(hay
cosx a t
).
2
2
0
1
4
I dx
x
Đặt
2sin 2cosx t dx tdt
. Đổi cận:
0 0,xt
2.
2
xt
Ta có:
2 2 2
0
4 4 4sin 4cos 2cosx t t t
do
0; .
2
t



Ta có:
22
00
2cos
.
2cos 2
tdt
I dt
t


2) Dạng
2
1
22
()
x
x
I f a x dx
hay
2
1
22
1
x
x
f dx
ax



.
tan
PP
x a t
.
3
2
0
1
9
I dx
x
Đặt
2
3tan 3(1 tan )x t dx t dt
.
Đổi cận:
0 0, 3
4
x t x t
.
Khi đó:
2 2 2
9 9tan 9 9(tan 1)x t t
.
24
Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
Vậy
2
44
2
00
3(1 tan ) 1
.
9(tan 1) 3 12
t dt
I dt
t


3) Dạng
2
1
22
()
x
x
I f x a dx
sin
PP
a
x
t

hay
cos
a
x
t
2
4
2
4x
I dx
x
Đặt
2
2 2sin
cos cos
t
x dx dt
tt
.
Đổi cận:
2 0, 4 .
3
x t x t
Khi đó:
2
2
33
2
00
4
4
2sin
cos
. 2 tan .
2
cos
cos
t
t
I dt t dt
t
t



3
2
0
3
0
12
2 1 . 2 tan 2 3 .
cos 3
dt t t
t



4) Dạng
2
1
x
x
ax
I f dx
ax




cos2
PP
x a t
.
2
0
2
2
x
I dx
x
Đặt
2cos2 4sin2 . 8sin .cos .x t dx t dt t t dt
Đổi cận:
0 , 2 0.
4
x t x t
Ta có:
2 2 2cos2 1 cos2 sin
.
2 2 2cos2 1 cos2 cos
x t t t
x t t t
2
44
00
sin
8 sin .cos 8 sin ......
cos
t
I t tdt tdt
t


4. Ứng dụng tích phân để tính diện tích – thể tích:
Hình phẳng giới hạn bởi các đường
()y f x
, trục
Ox
,
,x a x b
thì có diện tích:
()
b
a
S f x dx
Hình phẳng giới hạn bởi các đường
()y f x
,
()y g x
,
,x a x b
thì có diện tích:
( ) ( )
b
a
S f x g x dx
Khi xoay hình phẳng
()
,
y f x
x a x b

quanh
Ox
, ta
được khối trụ tròn có thể tích
2
()
b
a
V f x dx
Khi xoay hình phẳng
()
()
,
y f x
y g x
x a x b

quanh
Ox
, được
khối trụ tròn có thể tích
22
( ) ( )
b
a
V f x g x dx

.
25
Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
Xét hình khối được giới hạn bởi hai mặt phẳng
,x a x b
. Khi cắt khối này ta được thiết diện có diện tích
()Sx
(là hàm liên tục trên [a;b]). Thể tích khối này trên
;ab
là:
()
b
a
V S x dx
.
5. Công thức chuyển động:
Xét hàm quảng đường
( ),St
hàm vận tốc
()vt
và hàm gia tốc
()at
. Ba hàm này sẽ biến thiên theo
t
.
( ) ( ) ( ) ( )S t v t dt v t S t
( ) ( ) ( ) ( )v t a t dt a t v t
[
XI. SỐ PHỨC VÀ CÁC YẾU TỐ LIÊN QUAN
Số phức có dạng:
z a bi
với
2
,
1
ab
i

(i: là đơn vị ảo). Ký hiệu tập số phức: .
Thành phần
Hình học
Minh họa
Phần thực: a.
Nếu
0a
thì
z bi
được gọi là
số thuần ảo.
Phần ảo: b.
Nếu
0b
thì
za
là số thực.
Khi
0ab
thì
0z
vừa là số
thuần ảo vừa là số thực.
Điểm
( ; )M a b
biểu diễn
cho
z
trên hệ trục
.Oxy
Mô-đun:
22
z OM a b
.
Số phức liên hợp – Hai số
phức bằng nhau
Căn bậc hai
Phương trình bậc hai
Cho
z a bi
và
z a b i

Khi đó:
Số phức liên hợp của
z
là
z a bi
.
aa
zz
bb

.
0
0
0
a
z
b

.
Căn bậc hai của
0a
là
.a
Căn bậc hai của
0a
là
ia
.
Căn bậc hai của số phức
z a bi
là hai số phức dạng
w x yi
với
22
2
x y a
xy b

.
Phương trình
2
0za
có hai
nghiệm phức
.za
Phương trình
2
0za
có hai
nghiệm phức
z i a
.
Phương trình
2
0az bz c
( 0)a
với
0
sẽ có hai nghiệm phức là:
1,2
2
bi
z
a

.
Công thức bổ trợ
Cho hai số phức
12
,zz
, có:
▪
1 2 1 2
.z z z z
. ▪
1
1
22
z
z
zz
với
2
0.z
▪
12
z z MN
với M, N theo thứ tự là hai điểm biểu diễn cho
12
,zz
.
Dấu hiệu cơ bản nhận biết tập hợp điểm M biểu diễn cho số phức z
0ax by c
KL
Tập hợp điểm M một là đường thẳng.
22
2
22
2 2 0
x a y b R
x y ax by c
KL
Tập hợp điểm M là đường tròn có tâm
;I a b
, bán kính
22
R a b c
.
22
2
22
2 2 0
x a y b R
x y ax by c
KL
Tập hợp điểm M là hình tròn tâm
;I a b
, bán kính
22
R a b c
.
26
Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
2
2
KL
y ax bx c
x ay by c

Tập hợp điểm M là đường parabol.
22
22
1
xy
ab

KL
Tập hợp điểm M là đường elip.
Đặc biệt: Nhận biết ngay không cần biến đổi.
0z a bi m
KL
Tập hợp điểm M là đường tròn có tâm
;I a b
, bán kính
Rm
.
1 1 2 2
1 1 2 2
; , ;A a b B a b
z a bi z a b i MA MB
KL
Tập hợp điểm M là đường trung trực đoạn thẳng AB.
1 1 1 2 2 2
12
1 1 2 2 1 2
00
; , ;
2
22
F a b F a b
F F a
z a b i z a b i a MF MF a
KL
Tập hợp điểm M là đường elip với hai tiêu điểm
12
,.FF
XII. KHỐI ĐA DIỆN VÀ THỂ TÍCH CỦA CHÚNG
A – MỘT SỐ HÌNH PHẲNG CƠ BẢN:
1. Tam giác vuông:
▪
2 2 2
Pitago
AB AC BC
▪
2
.AB BH BC
▪
2
.AC CH BC
▪
2
.AH BH CH
▪
2 2 2
1 1 1
AH AB AC

22
.AB AC
AH
AB AC

1
.
2
ABC
S AB AC
1
.
2
AH BC
▪
sin
AC
B
BC
(đối/huyền) ▪
cos
AB
B
BC
(kề/huyền) ▪
tan
AC
B
AB
(đối/kề) ▪
cot
AB
B
AC
(kề/đối)
2. Tam giác đều:
Giả sử tam giác
ABC
đều có cạnh
;a
trọng tâm
;G
các đường cao (trùng
với trung tuyến) gồm
AH
,
.BK
▪ Đường cao:
( ) 3 3
.
22
caïnh a
AH BK
▪
2 2 3 3 1 1 3 3
. ; . .
3 3 2 3 3 3 2 6
a a a a
AG AH GH AH
▪ Diện tích:
22
( ) 3 3
.
44
ABC
caïnh a
S
3. Tam giác thường:
Giả sử tam giác
ABC
có
,,a BC b AC c AB
; các đường cao
,,
a b c
h h h
lần lượt ứng với cạnh
, , .abc
Ký hiệu
,Rr
lần lượt là bán kính
đường tròn ngoại tiếp và nội tiếp ∆.
▪ Định lí Sin:
2
sin sin sin
a b c
R
A B C
.
▪ Định lí Cô-sin:
2 2 2
2 .cosa b c bc A
;
2 2 2 2 2 2
2 .cos ; 2 .cos .b a c ac B c a b ab C
▪ Diện tích:
1 1 1
. . . ;
2 2 2
ABC a b c
S h a h b h c
1 1 1
.sin .sin .sin
2 2 2
ABC
S ab C ac B bc A
;
A
C
B
H
a
a
a
G
K
H
B
C
A
27
Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
I
4
ABC
abc
S pr
R

;
( )( )( )
2
ABC
Coâng thöùc Heâ Roâng
a b c
S p p a p b p b vôùi p
(nửa chu vi).
4. Hình vuông:
Cho hình vuông
ABCD
có cạnh
;a
hai điểm
,MN
lần lượt là trung điểm
của
,;CD AD
I
là tâm hình vuông.
▪ Đường chéo:
( ) 2 2
AC BD
AC BD caïnh a
.
2
2
a
IA IB IC ID
nên
I
là tâm đường tròn ngoại tiếp hình vuông.
▪ Diện tích:
22
()
ABCD
S caïnh a
; chu vi:
4.pa
▪ Vì
ABN ADM
, ta chứng minh được:
.AM BN
5. Hình chữ nhật:
Cho hình chữ nhật
ABCD
tâm
I
có
,.AB a AD b
▪ Đường chéo:
22
AC BD a b
.
22
1
2
IA IB IC ID a b
nên
I
là tâm đường tròn đi qua bốn điểm
, , , .A B C D
▪ Diện tích:
.
ABCD
S ab
; chu vi:
2( ).p a b
6. Hình thoi:
Cho hình thoi
ABCD
có tâm
,I
cạnh bằng
.a
▪ Đường chéo:
;AC BD
2 2 .sin 2 .sin .AC AI AB ABI a ABI
▪ Diện tích:
1
.
2
ABCD
S AC BD
;
2 2 2
ABCD ABC ACD ABD
S S S S
.
Đặc biệt: Nếu hình thoi có góc
0
60BD
(
0
120AC
) thì ta chia hình
thoi ra làm hai tam giác đều:
;ABC ACD
AC a
và
2
3
;
4
ABC ACD
a
SS


2
3
2.
2
ABCD ABC
a
SS

B – THỂ TÍCH KHỐI CHÓP:
7. Hình chóp:
1
.
3
ñ
V h S
7.1. Hình chóp tam giác đều
▪ Tất cả cạnh bên bằng nhau.
▪ Đáy là tam giác đều cạnh
.a
▪
()SH ABC
với
H
là trọng tâm (cũng
là trực tam) ∆
.ABC
▪
2
2
3
13
.
4
34
Theå tích
ñ
a
a
S
Vh
SH h
Góc giữa cạnh bên và mặt
đáy:
,( )SA ABC SAH
,( )SC ABC SCH
Góc giữa mặt bên và mặt đáy:
( ),( )SAB ABC SMH
( ),( )SBC ABC SNH
.
7.2. Tứ diện đều:
S
đ
h
A
B
C
D
S
H
28
Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
▪ Đây cũng là hình chóp tam
giác đều, đặc biệt là cạnh bên
bằng cạnh đáy. Thể tích:
3
2
12
a
V
.
7.3. Hình chóp tứ giác đều:
▪ Tất cả cạnh bên bằng nhau.
▪ Đáy là hình vuông cạnh
.a
▪
()SO ABCD
với
O
là tâm hình vuông
.ABCD
▪
2
2
1
.
3
Theå tích
ñ
Sa
V h a
SO h
.
Góc giữa cạnh bên và mặt
đáy:
,( )SA ABCD SAO
,( )SB ABCD SBO
.
Góc giữa mặt bên và mặt đáy:
( ),( )SAB ABCD SMO
( ),( )SBC ABCD SNO
.
7.4. Hình chóp có cạnh bên SA
vuông góc với mặt phẳng đáy.
Đáy là tam giác
Đáy là tứ giác đặc biệt
▪
1
.
3
Theå tích
ABC
ñ ABC
h SA
V SA S
SS
▪ Góc giữa cạnh bên và mặt đáy:
,( )
,( )
SB ABC SBA
SC ABC SCA
.
▪
1
.
3
Theå tích
ABCD
ñ ABCD
h SA
V SA S
SS
.
▪ Góc giữa cạnh bên và mặt đáy:
,( )
,( )
SB ABCD SBA
SC ABCD SCA
.
7.5. Hình chóp có mặt bên
(SAB) vuông góc với mặt
phẳng đáy.
Đáy là tam giác
Đáy là tứ giác đặc biệt
▪ Đường cao
h SH
cũng là
đường cao của ∆SAB.
▪ Góc giữa cạnh bên và mặt đáy:
,( )
,( )
SA ABC SAH
SC ABC SCH
.
▪ Đường cao
h SH
cũng là đường cao
của ∆SAB.
▪ Góc giữa cạnh bên và mặt đáy:
,( )
,( )
SA ABCD SAH
SC ABCD SCH
.
29
Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
C – TỈ SỐ THỂ TÍCH KHỐI CHÓP
Cho hình chóp có đáy là
tam giác ABC. Các điểm
M, N, P nằm trên cạnh
SA, SB, SC. Ta có:
.
.
..
S MNP
S ABC
V
SM SN SP
V SA SB SC
.
Đặc biệt:
MA
Đặc biệt
,M A N B
.
.
.
S ANP
S ABC
V
SN SP
V SB SC
.
.
S ABP
S ABC
V
SP
V SC
Hình chóp có đáy là
hình bình hành với
,
SM
x
SA
,
SN
y
SB
,
SP
z
SC
SQ
t
SD
.
Khi đó:
.
.
4
S MNPQ
S ABCD
V
xyz xyt xzt yzt
V
và
1 1 1 1
.
x z y t
Hình chóp có đáy là đa
giác bất kỳ. Chẳng hạn:
(MNPQR) (ABCDE)
và tỉ số:
SM
x
SA
SN
SB
SP SQ SR
SC SD SE
Khi đó:
.
3
.
S MNPQR
S ABCDE
V
x
V
D – THỂ TÍCH KHỐI LĂNG TRỤ:
1. Hình lăng trụ thường:
Hai đáy là hai hình giống nhau
và nằm trong hai mặt phẳng
song song.
Các cạnh bên song song và
bằng nhau. Các mặt bên là các
hình bình hành.
Thể tích:
.
ñ
V h S
.
Đáy là tam giác
Đáy là tứ giác
..
ABC A B C
V AH S AH S


..
ABCD A B C D
V AH S AH S

2. Hình lăng trụ đứng:
Các cạnh bên cùng vuông góc
với hai mặt đáy nên mỗi cạnh
bên cũng là đường cao của lăng
trụ.
Lăng trụ tam giác đều: Là
lăng trụ đứng và có hai đáy là
hai tam giác đều bằng nhau.
Đáy là tam giác
Đáy là tứ giác
Thể tích:
.
ñ
V h S
với
h AA BB CC

.
Thể tích:
.
ñ
V h S
với
h AA BB CC DD
.
30
Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
3. Hình hộp:
Là lăng trụ có tất cả các mặt là
hình bình hành.
Thể tích:
.
ñ
V h S
.
3.1 Hình hộp chữ nhật:
Là lăng trụ đứng có đáy là hình
chữ nhật.
V abc
với
,,a b c
là ba kích
thước của hình hộp chữ nhật.
3.2. Hình lập phương:
Là hình hộp chữ nhật có tất cả các cạnh
bằng nhau.
3
Va
với
a
là cạnh của hình lập
phương.
4. Tỉ số thể tích đối với lăng trụ:
Lăng trụ có đáy tam giác
,,
AM BN CP
x y z
AA BB CC
Lăng trụ đáy là hình bình hành, hình chữ nhật, hình
thoi, hình vuông
(Lăng trụ này chính là hình hộp thường hoặc hình hộp
chữ nhật, hình lập phương)
Ta có:
.
.
3
ABC MNP
ABC A B C
V
x y z
V

,,,
AM BN CP DQ
x y z t
AA BB CC DD
Ta có:
.
.
4
ABCD MNPQ
ABCD A B C D
V
x y z t
V
và
x z y t
E – BÀI TOÁN KHOẢNG CÁCH
1. Hình chóp có cạnh bên vuông góc với mặt
đáy là tam giác
2. Hình chóp có cạnh bên vuông góc với mặt đáy
là hình vuông, hình chữ nhật
22
.
,
SA AK
d A SBC AH
SA AK

.
22
.
,,
SA AB
d A SBC AH d D SBC
SA AB
.
22
.
,,
SA AD
d A SCD AK d B SCD
SA AD
.
31
Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
,d B SAC BM
;
,d C SAB CN
.
,.d SA BC AK
22
.
,,
SA AE
d A SBD AF d C SBD
SA AE
.
, ; , .d AD SB AH d AB SD AK
, , , .d AD SC d AD SBC d A SBC AH
, , , .d AB SC d AB SCD d A SCD AK
3. Hình chóp tam giác đều
4. Hình chóp tứ giác đều
22
.
,
SO OK
d O SBC OH
SO OK

,,d O SAB d O SAC
.
, 3 , 3d A SBC d O SBC OH
,,d B SAC d C SAB
.
, , ,d SA BC IK d SB AC d SC AB
.
22
.
,
SO OK
d O SCD OH
SO OK

, , ,d O SAB d O SBC d O SAD
.
, 2 , 2 ,d A SCD d O SCD OH d A SBC
, , ...d B SAD d B SCD
, , , 2d AB SC d AB SCD d A SCD OH
, , , ...d AB SD d AD SB d AD SC
F – MẶT TRỤ, MẶT NÓN – MẶT CẦU
MẶT NÓN
Các yếu tố mặt nón:
Một số công thức:
Hình thành: Quay
vuông
SOM
quanh trục
SO
, ta được
mặt nón như hình bên với:
h SO
r OM
.
Đường cao:
h SO
. (
SO
cũng
được gọi là trục của hình nón).
Bán kính đáy:
.r OA OB OM
Đường sinh:
.l SA SB SM
Góc ở đỉnh:
.ASB
Thiết diện qua trục:
SAB
cân
tại
.S
Góc giữa đường sinh và mặt
đáy:
.SAO SBO SMO
Chu vi đáy:
2.pr
Diện tích đáy:
2
đ
.Sr
Thể tích:
đ
2
11
. . .
33
V h S h r

(liên tưởng đến thể tích khối chóp).
Diện tích xung quanh:
.
xq
S rl
Diện tích toàn phần:
2
.
tp xq
S S S rl r

đ
h
l
l
l
r
O
A
B
S
M
32
Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
MẶT TRỤ
Các yếu tố mặt trụ:
Một số công thức:
Hình thành: Quay hình chữ
nhật
ABCD
quanh đường trung
bình
OO
, ta có mặt trụ như
hình bên.
Đường cao:
.h OO
Đường sinh:
.l AD BC
Ta
có:
.lh
Bán kính đáy:
.r OA OB O C O D

Trục (∆) là đường thẳng đi qua
hai điểm
,.OO
Thiết diện qua trục: Là hình chữ
nhật
.ABCD
Chu vi đáy:
2.pr
Diện tích đáy:
2
đ
.Sr
Thể tích khối trụ:
2
..V h S h r

đ
.
Diện tích xung quanh:
2 . .
xq
S r h
Diện tích toàn phần:
đ
2
2 2 . 2 .
tp xq
S S S r h r
MẶT CẦU
Một số công thức:
Mặt cầu ngoại tiếp đa diện
Mặt cầu nội tiếp đa diện
Hình thành: Quay đường tròn
tâm
I
, bán kính
2
AB
R
quanh
trục
AB
, ta có mặt cầu như hình
vẽ.
Tâm
,I
bán kính
R IA IB IM
.
Đường kính
2AB R
.
Thiết diện qua tâm mặt cầu: Là
đường tròn tâm
I
, bán kính
R
.
Diện tích mặt cầu:
2
4SR
.
Thể tích khối cầu:
3
4
3
R
V
.
Mặt cầu ngoại tiếp
đa diện là mặt cầu
đi qua tất cả đỉnh
của đa diện đó.
Mặt cầu nội tiếp
đa diện là mặt cầu
tiếp xúc với tất cả
các mặt của đa
diện đó.
CÁCH TÌM BÁN KÍNH MẶT CẦU NGOẠI TIẾP HÌNH CHÓP THƯỜNG GẶP
1. Hình chóp có các đỉnh nhìn một cạnh dưới một
góc vuông.
2. Hình chóp đều.
Xét hình chóp có
()SA ABC
và
0
90ABC
.
Ta có
0
90SAC SBC
nên mặt cầu ngoại tiếp
Xét hình chóp có
()SA ABCD
và
ABCD
là hình chữ nhật
hoặc hình vuông.
Ta có:
SAC SBC
0
90SDC
Xét hình chóp tam giác
đều có cạnh bên bằng
b
và đường cao
SH h
.
Bán kính mặt cầu ngoại
tiếp hình chóp trên là
Xét hình chóp tứ giác đều có
cạnh bên bằng b và chiều
cao
SO h
.
Bán kính mặt cầu ngoại tiếp
hình chóp trên là
2
2
b
R
h
.
33
Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
hình chóp có tâm
I
là
trung điểm
SC
, bán
kính
.
2
SC
R
Suy ra mặt cầu ngoại tiếp
hình chóp có tâm
I
là
trung điểm
SC
, bán kính
.
2
SC
R
2
2
b
R
h
.
3. Hình chóp có cạnh bên vuông góc với mặt phẳng
đáy.
4. Hình chóp có mặt bên vuông góc với mặt đáy.
Xét hình chóp có
SA
(đáy) và
SA h
; bán
kính đường tròn ngoại tiếp
của đáy là
ñ
r
.
Khi đó mặt cầu ngoại tiếp
hình chóp có bán kính
2
2
2
ñ
h
Rr
.
Nếu đáy là tam giác đều
cạnh
a
thì
3
3
ñ
a
r
.
Nếu đáy là hình vuông
cạnh
a
thì
2
2
ñ
a
r
.
Nếu đáy là hình chữ nhật
cạnh
,ab
thì
22
2
ñ
ab
r
.
Xét hình chóp có mặt bên
()SAB
(đáy), bán kính ngoại tiếp
đáy là
ñ
r
, bán kính ngoại tiếp
SAB
là
b
r
,
()d AB SAB
(đáy). (đoạn giao tuyến)
Khi đó bán kính mặt cầu ngoại tiếp hình chóp là
2
22
4
ñb
d
R r r
.
XIII. HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN
1. Hệ trục tọa độ Oxyz:
Hệ trục gồm ba trục
,,Ox Oy Oz
đôi một vuông góc nhau.
Trục
:Ox
trục hoành, có vectơ đơn vị
(1;0;0)i
.
Trục
Oy
: trục tung, có vectơ đơn vị
(0;1;0)j
.
Trục
:Oz
trục cao, có vectơ đơn vị
(0;0;1).k
Điểm
(0;0;0)O
là gốc tọa độ.
2. Tọa độ vectơ: Vectơ
( ; ; )u xi y j zk u x y z
.
Cho
1 2 3 1 2 3
( ; ; ), ( ; ; )a a a a b b b b
. Ta có:
1 1 2 2 3 3
( ; ; )a b a b a b a b
a
cùng phương
b
()a kb k R
11
3
12
2 2 1 2 3
1 2 3
33
, ( , , 0).
a kb
a
aa
a kb b b b
b b b
a kb
1 2 3
( ; ; )ka ka ka ka
11
22
33
ab
a b a b
ab
1 1 2 2 3 3
. . . .a b a b a b a b
222
1 2 2
a a a a
2
2 2 2 2
1 2 3
a a a a a
34
Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
1 1 2 2 3 3
. 0 0a b a b a b a b a b
1 1 2 2 3 3
2 2 2 2 2 2
1 2 3 1 2 3
.
cos( , )
.
.
a b a b a b
ab
ab
ab
a a a b b b


3. Tọa độ điểm:
( ; ; ) ( ; ; )M x y z OM x y z
. Cho
( ; ; ) , ( ; ; ) , ( ; ; )
A A A B B B C C C
A x y z B x y z C x y z
, ta có:
( ; ; )
B A B A B A
AB x x y y z z
2 2 2
( ) ( ) ( )
B A B A B A
AB x x y y z z
Toạ độ trung điểm M của đoạn thẳng AB:
; ; .
2 2 2
A B A B A B
x x y y z z
M



Toạ độ trọng tâm G của tam giác ABC:
; ; .
3 3 3
A B C A B C A B C
x x x y y y z z z
G



QUY TẮC CHIẾU ĐẶC BIỆT
Chiếu điểm trên trục tọa độ
Chiếu điểm trên mặt phẳng tọa độ
Điểm
1
()
( ; ; ) ( ;0;0)
Chieáu vaøo Ox
M M M M
Giöõ nguyeân x
M x y z M x
Điểm
2
()
( ; ; ) (0; ;0)
Chieáu vaøo Oy
M M M M
Giöõ nguyeân y
M x y z M y
Điểm
3
()
( ; ; ) (0; 0; )
Chieáu vaøo Oz
M M M M
Giöõ nguyeânz
M x y z M z
Điểm
1
( , )
( ; ; ) ( ; ;0)
Chieáu vaøo Oxy
M M M M M
Giöõ nguyeân x y
M x y z M x y
Điểm
2
( , )
( ; ; ) (0; ; )
Chieáu vaøo Oyz
M M M M M
Giöõ nguyeân y z
M x y z M y z
Điểm
3
( , )
( ; ; ) ( ;0; )
Chieáu vaøo Oxz
M M M M M
Giöõ nguyeânx z
M x y z M x z
Đối xứng điểm qua trục tọa độ
Đối xứng điểm qua mặt phẳng tọa độ
1
( ; , )
( ; ; ) ( ; ; )
Ñoái xöùng qua Ox
M M M M M M
Giöõ nguyeân x ñoåi daáu y z
M x y z M x y z
2
( ; , )
( ; ; ) ( ; ; )
Ñoái xöùng qua Oy
M M M M M M
Giöõ nguyeân y ñoåi daáu x z
M x y z M x y z
3
( ; , )
( ; ; ) ( ; ; )
Ñoái xöùng qua Oz
M M M M M M
Giöõ nguyeânz ñoåi daáu x y
M x y z M x y z
1
( , ; )
( ; ; ) ( ; ; )
Ñoái xöùng qua Oxy
M M M M M M
Giöõ nguyeân x y ñoåi daáu z
M x y z M x y z
2
( , ; )
( ; ; ) ( ; ; )
Ñoái xöùng qua Oxz
M M M M M M
Giöõ nguyeân x z ñoåi daáu y
M x y z M x y z
3
( , ; )
( ; ; ) ( ; ; )
Ñoái xöùng qua Oyz
M M M M M M
Giöõ nguyeân y z ñoåi daáu x
M x y z M x y z
4. Tích có hướng của hai vectơ:
Định nghĩa: Cho
1 2 3
( , , )a a a a
,
1 2 3
( , , )b b b b
, tích có hướng của
a
và
b
là:
2 3 3 1
12
2 3 3 2 3 1 1 3 1 2 2 1
2 3 3 1
12
, ; ; ; ;
a a a a
aa
a b a b a b a b a b a b a b
b b b b
bb





.
Tính chất:
[ , ]a b a
[ , ]a b b
[ , ] . .sin ,a b a b a b
Điều kiện cùng phương của hai vectơ
&ab
là
,0ab


với
0 (0;0;0).
Điều kiện đồng phẳng của ba vectơ
,ab
và
c
là
[ , ]. 0.a b c
Diện tích hình bình hành ABCD:
,.
ABCD
S AB AD


Diện tích tam giác ABC:
1
,.
2
ABC
S AB AC


Thể tích khối hộp:
. ' ' ' '
[ , ]. ' .
ABCD A B C D
V AB AD AA
Thể tích tứ diện:
1
,.
6
ABCD
V AB AC AD


.
5. Phương trình mặt cầu:
Dạng 1:
2 2 2 2
( ):( ) ( ) ( )S x a y b z c R
()
2
( ; ; )
Maët caàu S coù
taâm I a b c
RR
Dạng 2:
2 2 2
( ): 2 2 2 0S x y z ax by cz d
()
2 2 2
( ; ; )
Maët caàu S coù
taâm I a b c
R a b c d
Phương trình
2 2 2
2 2 2 0x y z ax by cz d
là phương trình mặt cầu
2 2 2
0a b c d
.
Bài toán 5.1. Viết phương trình mặt cầu tâm I và đi qua
Bài toán 5.2. Viết phương trình mặt cầu có đường kính AB.
35
Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
điểm M.
Bước 1: Tính bán kính
R IM
.
Bước 2: Viết phương trình mặt cầu dạng 1.
Bước 1: Tìm tâm I là trung điểm AB. Bán kính
2
AB
R IA IB
.
Bước 2: Viết phương trình mặt cầu dạng 1.
6. Phương trình mặt phẳng:
Lưu ý: Vectơ pháp tuyến (VTPT) của mặt phẳng là
vectơ khác
0
nằm trên đường thẳng vuông góc với mặt
phẳng đó.
Mặt phẳng
0 0 0
qua ( ; ; )
()
( ; ; )
M x y z
P
VTPT n a b c
thì phương trình
0 0 0
( ): ( ) ( ) ( ) 0P a x x b y y c z z
(*)
Ngược lại, một mặt phẳng bất kỳ đều có phương trình dạng
0ax by cz d
, mặt phẳng này có
( ; ; )VTPT n a b c
vôùi
2 2 2
0a b c
.
Đặc biệt:
( ) ( ) ( )
( ): 0 (1;0;0), ( ): 0 (0;1;0), ( ): 0 (0;0;1)
VTPT VTPT VTPT
Oyz Oxz Oxy
Mp Oyz x n mp Oxz y n mp Oxy z n   
Bài toán 6.1. Viết phương trình mặt phẳng (P) qua M
và song song với mặt phẳng (Q) cho trước.
Mặt phẳng (P) qua M, có VTPT là
( ) ( )PQ
nn
nên
phương trình được viết theo (*).
Bài toán 6.2. Viết phương trình mặt phẳng (P) qua M và
vuông góc với với đường thẳng d cho trước.
Mặt phẳng (P) qua M , có VTPT
()Pd
nu
nên phương trình
được viết theo (*).
Bài toán 6.3. Viết phương trình mặt phẳng trung trực
của đoạn thẳng AB.
Bước 1: Tìm trung điểm I của đoạn AB và tính
AB
.
Bước 2: Phương trình
qua
mp( )
VTPT
I
P
n AB
.
Bài toán 6.4. Viết phương trình mặt phẳng đi qua ba điểm
A, B, C.
Bước 1: Tính tọa độ
,AB AC
và suy ra
,AB AC


.
Bước 2: Phương trình
qua
mp( )
VTPT ,
A
P
n AB AC


.
Bài toán 6.5. Viết phương trình mặt phẳng qua M và chứa
đường thẳng d với
Md
.
Bước 1: Chọn điểm
Ad
và một VTCP
.
d
u
Tính
,
d
AM u


.
Bài toán 6.6. Viết phương trình mặt phẳng cắt Ox,
Oy, Oz lần lượt tại
( ;0;0), (0; ;0),A a B b
(0;0; )Cc
với
. . 0a b c
.
Phương trình mặt
phẳng được viết
theo đoạn chắn
( ): 1.
x y z
P
a b c
36
Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
Bước 2: Phương trình
qua
mp( )
VTPT ,
d
M
P
n AM u


Khoảng cách từ điểm đến mặt phẳng
Khoảng cách giữa hai mặt phẳng song song
Cho
0 0 0
( ; ; )
( ): 0
M x y z
mp P ax by cz d
.
Khi đó:
0 0 0
2 2 2
,( )
ax by cz d
d M P
abc

.
Cho hai mặt phẳng
1
2
( ): 0
( ): 0
P ax by cz d
Q ax by cz d
.
Khi đó:
12
2 2 2
( ),( )
dd
d P Q
abc

với
12
dd
.
Góc giữa hai mặt phẳng
Vị trí tương đối giữa hai mặt phẳng
Cho hai mặt phẳng (P), (Q) có phương trình:
1 1 1 1
2 2 2 2
( ): 0
( ): 0
P a x b y c z d
Q a x b y c z d
.
Góc giữa
( )&( )PQ
được tính:
1 2 1 2 1 2
2 2 2 2 2 2
1 1 1 2 2 2
.
cos ( ),( )
.
.
PQ
PQ
nn
a a bb c c
PQ
nn
a b c a b c


Chú ý:
00
0 ( ),( ) 90PQ
.
Cho hai mặt phẳng (P), (Q) có phương trình:
1 1 1 1
2 2 2 2
( ): 0
( ): 0
P a x b y c z d
Q a x b y c z d
. Ta có:
1 1 1 1
2 2 2 2
( ) ( )
a b c d
PQ
a b c d
.
1 1 1 1
2 2 2 2
( ) ( )
a b c d
PQ
a b c d
.
( )&( )PQ
cắt nhau
1 1 1 2 2 2
: : : :a b c a b c
.
1 2 1 2 1 2
( ) ( ) 0P Q a a bb c c
.
Lưu ý: Các tỉ số trên có nghĩa khi mẫu khác 0.
Ví trị tương đối giữa mặt phẳng và mặt cầu
Cho mặt phẳng
( ): 0P ax by cz d
và mặt cầu
()S
có tâm
I
và bán kính R.
Trường hợp 1:
,( )d I P R
()P
và
()S
không có điểm chung.
Trường hợp 2:
,( )d I P R
()P
và
()S
có một
điểm chung. Khi đó ta nói
()P
tiếp xúc
()S
hoặc
()P
là tiếp diện của
( ).S
Ta có:
()IM P
với
M
là tiếp điểm.
Trường hợp 3:
,( )d I P R
()P
cắt
()S
theo giao
tuyến là một đường tròn.
Đường tròn giao tuyến có tâm H (là trung điểm AB), bán kính
22
r R IH
với
,( ) .IH d I P
7. Phương trình đường thẳng:
Đường thẳng
1 2 3
qua ( ; ; )
VTCP ( ; ; )
A A A
A x y z
d
u u u u
Vectơ chỉ phương (VTCP) của đường thẳng d là vectơ khác
Phương trình tham số
1
2
3
:
A
A
A
x x u t
d y y u t
z z u t



với t là tham số.
37
Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
0
, có giá trùng với d hoặc song song với d.
Phương trình chính tắc
1 2 3
:
A A A
x x y y z z
d
u u u

với
1 2 3
. . 0u u u
.
Lưu ý: Nếu có cặp vectơ khác
0
không cùng phương sao cho
ad
bd
thì
d
có VTCP là:
,
d
u a b


.
7.1. Ví trị tương đối giữa hai đường thẳng:
Xét vị trí tương đối của hai đường thẳng với
1
1
qua
VTCP
M
d
u
,
2
2
qua
VTCP
N
d
u
.
Bước I
Bước II
Kết luận
Hai đường thẳng
song song hoặc trùng nhau.
1
,0u MN


1
,0u MN


Hai đường thẳng
cắt nhau hoặc chéo nhau.
cắt
chéo nhau
7.2. Ví trị tương đối giữa đường thẳng và mặt phẳng:
Xét vị trí tương đối giữa đường thẳng và mặt phẳng .
Bước I:
Bước II:Giải PT (*), ta gặp 1
trong 3 trường hợp sau
Kết luận
Thay phương trình tham số vào phương
trình , ta được PT (*):
PT (*) vô nghiệm
PT (*) có 1 nghiệm
0
tt
cắt tại một điểm
PT (*) có vô số nghiệm t.
7.3. Khoảng cách từ điểm đến đường thẳng:
Cho điểm
M
và đường thẳng
d
(có phương
trình tham số hoặc chính tắc).
Bước 1: Chọn điểm
Ad
và một VTCP
d
u
.
Bước 2:
,
,
d
d
u AM
d M d
u


.
7.4. Khoảng cách giữa hai đường thẳng:
Trường hợp 1: Hai đường thẳng song song
12
,.dd
Bước 1: Chọn điểm M (đẹp) thuộc
1
.d
Bước 2:
1 2 2
,,d d d d M d
. (xem 7.3)
Trường hợp 2: Hai đường thẳng chéo nhau
12
,.dd
Bước 1: Ghi rõ
1
1
...
...
qua A
d
VTCP u
,
2
2
...
...
qua B
d
VTCP u
.
Bước 2: Tính:
12
12
12
,.
,.
,
u u AB
d d d
uu




12
,dd
12
,0uu
12
,dd
12
dd
12
dd
12
,0uu
12
,dd
12
, . 0u u MN
1
d
2
d
12
, . 0u u MN
12
&dd
01
02
03
:
x x u t
d y y u t
z z u t
( ) : 0P ax by cz d
d
()P
0 1 0 2 0 3
( ) ( ) ( ) 0a x u t b y u t c z u t d
()dP
d
()P
()dP
38
Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
7.5. Góc giữa hai đường thẳng:
Cho hai đường thẳng
12
,dd
lần lượt có VTCP là
12
,uu
.
Ta có:
12
12
12
.
cos ,
.
uu
dd
uu
.
7.6. Góc giữa đường thẳng và mặt phẳng:
Cho đường thẳng d có VTCP
u
và măt phẳng
()P
có VTPT
n
.
Ta có:
.
sin ,( )
.
un
dP
un
.
8. Hình chiếu và điểm đối xứng:
Bài toán
Phương pháp
8.1. Tìm hình chiếu
của điểm trên mặt
phẳng .
Gọi d là đường thẳng
qua
()
A
P
Viết pt tham số của d
với VTCP của d cũng là VTPT của (P).
Gọi
()H d P
. Thay pt tham số của d vào pt mp (P) ta
tìm được tọa độ H.
8.2. Tìm điểm đối
xứng với qua .
Ta có H là trung điểm
2
2
2
A H A
A H A
A H A
x x x
AA y y y
z z z


.
8.3. Tìm hình chiếu
của điểm trên
đường thẳng d.
Cách 1
Gọi
()H theo t
(dựa vào pt tham số của d).
.0
d
AH d AH u
Tìm được
Tọa độ H.
Cách 2
Gọi
qua
()
()
A
P
Pd
Viết pt
mp( )P
.
Gọi
()H d P
. Thay pt tham số của d vào
pt mp (P) ta tìm được tọa độ H.
8.4. Tìm điểm đối
xứng với qua
đường thẳng d.
Ta có H là trung điểm
2
2
2
A H A
A H A
A H A
x x x
AA y y y
z z z


.
8.5. Viết phương
trình đường thẳng
d
là hình chiếu
của đường thẳng
d
trên mp
()P
.
Trường hợp 1:
d song song mp
(P).
Lập phương trình mp(Q) biết
(Q) chứa d và
( ) ( )QP
:
(Q) qua điểm
Ad
.
(Q) có VTPT
,
Q d P
n u n


.
Lập phương trình
d
là giao
tuyến hai mp (P) và (Q):
Chọn hai điểm M, N thuộc
d
bằng cách thay
0,
Tìm
x y z
và thay
0,
Tìm
y x z
(đối với hệ
hai pt (P), (Q)).
Viết pt d qua M, N.
Trường hợp 2:
d cắt mp (P) tại một
điểm.
[
A
()P
A
A
()P
A
.......t
A
A
39
Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
XIV. GẮN TỌA ĐỘ VÀO HÌNH HỌC KHÔNG GIAN
1. Gắn tọa độ đối với hình chóp
1.1.Hình chóp có cạnh bên (SA) vuông góc với mặt đáy:
Đáy là tam giác đều
Gọi O là trung điểm BC. Chọn hệ
trục như hình vẽ,
1AB a
.
Tọa độ các điểm là:
31
(0;0;0), 0; ;0 , ;0;0 ,
22
O A B







13
;0;0 , 0; ;
22
SA
C S OH







.
Đáy là tam giác cân tại A
Gọi O là trung điểm BC. Chọn hệ
trục như hình vẽ,
1a
.
Tọa độ các điểm là:
(0;0;0), 0; ;0 , ;0;0 ,O A OA B OB
;0;0 , 0; ;
SA
C OC S OA OH



.
Đáy là tam giác cân tại B
Gọi O là trung điểm AC. Chọn hệ
trục như hình vẽ,
1a
.
Tọa độ các điểm:
0;0;0O
,
;0;0 , 0, ;0 ,A OA B OB
;0;0 , ;0;
SA
C OC S OA OH



.
Đáy là tam giác vuông tại B
Chọn hệ trục như hình vẽ,
1a
.
Tọa độ các điểm:
0;0;0BO
,
0; ;0 , ,0;0 ,A AB C BC
0; ;
SA
S AB BH



.
Đáy là tam giác vuông tại A
Chọn hệ trục như hình vẽ,
1a
.
Tọa độ các điểm:
0;0;0AO
,
0; ;0 , ;0;0 ,B OB C AC
0;0;S SA
.
Đáy là tam giác thường
Dựng đường cao BO của
.ABC
Chọn hệ trục như hình vẽ,
1a
.
Tọa độ các điểm:
0;0;0O
,
;0;0 , 0, ;0 ,A OA B OB
;0;0 , ;0;
SA
C OC S OA OH



.
Đáy là hình vuông, hình chữ nhật
Đáy là hình thoi
Chọn hệ trục như hình vẽ,
1.a
Đáy là hình thang vuông
40
Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
Chọn hệ trục như hình vẽ,
1.a
Tọa độ
0;0;0AO
,
0; ;0 ,B AB
; ;0 , ;0;0 , 0;0;C AD AB D AD S SA
.
Tọa độ
0;0;0O
,
;0;0 ,A OA
0; ;0 , ;0;0B OB C OC
0; ;0 , ;0;
SA
D OD S OA OH



.
Chọn hệ trục như hình vẽ,
1.a
Tọa độ
0;0;0AO
,
0; ;0 , ; ;0 ,B AB C AH AB
;0;0 , 0;0; .D AD S SA
1.2.Hình chóp có mặt bên (SAB) vuông góc với mặt đáy
Đáy là tam giác, mặt bên là tam
giác thường
Vẽ đường cao CO trong
ABC
.
Chọn hệ trục như hình, a = 1.
Ta có:
0;0;0 , 0; ;0 ,O A OA
0; ;0 , ;0;0 , 0; ;
SH
B OB C OC S OH OK



Đáy là tam giác cân tại C (hoặc
đều), mặt bên là tam giác cân tại S
(hoặc đều)
Gọi O là trung điểm BC, chọn hệ
trục như hình, a = 1.
Ta có:
0;0;0 , 0; ;0 ,O A OA
0; ;0 , ;0;0 , 0;0;B OB C OC S SO
Đáy là hình vuông-hình chữ nhật
Dựng hệ trục như hình, chọn a = 1.
Ta có:
0;0;0 , ;0;0A O B AB
; ;0 , 0; ;0 , ;0;
SH
C AB AD D AD S AH AK



1.3.Hình chóp đều
Hình chóp tam giác đều
Gọi O là trung điểm một cạnh đáy. Dựng hệ trục như
hình vẽ và a = 1. Tọa độ điểm:
0;0;0 ,O
3
0; ;0
2
AB
A




,
;0;0
2
BC
B



,
;0;0
2
BC
C



,
3
0; ;
6
SH
OH
AB
S OK





.
Hình chóp tứ giác đều
Chọn hệ trục như hình với a = 1. Tọa độ điểm:
0;0;0 ,O
2
;0;0 ,
2
OA
AB
A





2
0; ;0
2
OB
AB
B





,
2
;0;0 ,
2
OA
AB
C






2
0; ;0
2
OB
AB
D




0;0;S SO
.
2. Gắn tọa độ đối với hình lăng trụ
2.1. Lăng trụ đứng
Hình lập phương, hình hộp chữ nhật
Dựng hệ trục như hình vẽ với a = 1. Tọa độ điểm:
Lăng trụ đứng đáy là hình thoi
Gọi O là tâm hình thoi đáy, ta dựng hệ trục như hình
với
41
Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
0;0;0 ,AO
0; ;0 ,B AB
; ;0C AD AB
,
;0;0D AD
,
0;0; ,A AA

0; ; ,B AB AA

;;C AD AB AA

,
;0; .D AD AA

0;0;0 ,O
;0;0 ,A OA
0; ;0 ,B OB
;0;0 ,C OC
0; ;0 ,D OD
;0; ,A OA AA

0; ; ,B OB AA

;0; ,C OC CC

0; ;D OD DD

Lăng trụ tam giác đều
Gọi O là trung điểm một
cạnh đáy, chọn hệ trục
như hình vẽ với a = 1. Ta
có:
0;0;0 ,O
;0;0 ,
2
AB
A



;0;0 ,
2
AB
B



0; ;0 ,C OC
;0; ,A OA AA

;0; ,
2
AB
B BB




0; ; .C OC CC

Lăng trụ đứng có đáy tam giác thường
Vẽ đường cao CO
trong tam giác ABC
và chọn hệ trục như
hình vẽ với a = 1.
Tọa độ điểm là:
0;0;0 ,O
;0;0 ,A OA
;0;0 ,B OB
0; ;0 ,C OC
;0; ,A OA AA

;0; ,B OB BB

0; ; .C OC CC

2.2.Lăng trụ nghiêng:
Lăng trụ nghiêng có đáy là tam giác đều, hình chiếu của
đỉnh trên mặt phẳng đối diện là trung điểm một cạnh tam
giác đáy
Dựng hệ trục như hình vẽ, ta dễ dàng xác định được các
điểm
, , , ,O A B C A
.
Tìm tọa độ các điểm còn lại thông qua hệ thức vectơ
bằng nhau:
AA BB CC

.
Lăng trụ nghiêng có đáy là hình vuông hoặc hình
chữ nhật, hình chiếu của một đỉnh là một điểm
thuộc cạnh đáy không chứa đỉnh đó
Dựng hệ trục như hình vẽ, ta dễ dàng xác định được
các điểm
, , , , ,O A B C D A
.
Tìm tọa độ các điểm còn lại thông qua hệ thức vectơ
bằng nhau:
AA BB CC DD
.
| 1/41
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

I. CÔNG THỨC LƯỢNG GIÁC
1. Hệ thức Cơ bản: sin cos  2 2 sin   cos  1  tan   cot   tan.cot  1 cos sin  k    k   1 1    2 1 tan   1 cot    s
 in(  k2 )  sin     k   2  2 tan( ) tan cos  2 sin   
cos(  k2 )  cos 
cot(  k )  cot  2. Cung Liên kết: Pi
Đối: ;  
Bù: ;   Phụ: ; 
Khác pi: ;    Khác : ;  2 2 2       sin(   )  sin sin( )  sin sin   cos  
sin( )   sin sin   cos    2   2        cos(   )  cos
cos( )   cos cos   sin   cos( )  cos cos    sin    2   2        tan(   )   tan
tan( )   tan tan   cot   tan( )  tan tan    cot    2   2        cot(   )   cot
cot( )   cot cot   tan   cot( )  cot cot    tan    2   2 
Khác pi/2: sin bạn cos, Cos đố Khác Pi: tang, i Sin bù Phụ chéo cotang cos thù sin
3. Công thức Cộng:
 sin(a b)  sin .
a cos b  cos . a sin b
 cos(a b)  cos .
a cos b  sin . a sin b
 sin(a b)  sin . a cos b  cos . a sin b
 cos(a b)  cos . a cos b  sin . a sin b tan a  tan b tan a  tan b tan(a b)  tan(a b)  1 tan . a tan b 1 tan . a tan b
1 Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
4. Công thức Nhân đôi, Nhân ba: 2 2
cos 2  cos   sin  2 tan  sin 2  2sin.cos tan 2  2 2
 2cos  1 1 2sin  2 1 tan  3    3 3 tan tan
sin 3  3sin  4sin  3
cos3  4cos  3cos tan 3  2 1 3 tan 
5. Công thức Hạ bậc: 1 cos 2 1 cos 2 1 cos 2 2 sin    2 cos    2 tan   2 2 1 cos 2
6. Biến đổi Tổng thành Tích: a b a b a b a b
cos a  cos b  2 cos .cos
cos a  cos b   2sin .sin 2 2 2 2 a b a b a b a b
sin a  sin b  2sin .cos
sin a  sin b  2 cos .sin 2 2 2 2 sin(a b) sin(a b)
tan a  tan b
tan a  tan b  cos . a cos b cos . a cos b             sin   cos  2.sin    2.cos      
sin  cos  2 sin      2 cos     4   4   4   4 
7. Công thức biến đổi tích thành tổng 1 1 1 cos . a cos b
cos(a b)  cos(a b) sin .asinb  cos(a b) cos(a b) sin . a cos b
sin(a b) sin(a b) 2 2 2
II. PHƯƠNG TRÌNH LƯỢNG GIÁC
u v k2
u v k2
 sin u  sin v  (k  ) 
 cosu  cos v  k   
u    v k2
u  v k2
Nếu sin u m  1   ;1 và  3 2 1   3 2 1  m   1  ; ;  ;  ;0 thì:
Nếu cos u m  1   ;1 và m   1  ; ;  ;  ;0 thì:  2 2 2    2 2 2  
u  arcsin m k2
cos u m u   arccos m k 2 (k  )
sin u m   (k  )
u    arcsin m k2
Nếu sin u m  1  
;1 thì: sin u m u 
Nếu cos u m  1  
;1 thì: cos u m u  
sin u  1  u   k2 2
cos u  1  u k 2  Đặc biệt: sin u  1
  u    k2 k  
Đặc biệt: cosu  1
  u    k2 k   2 
sin u  0  u k
cos u  0  u   k 2
 tanu  tan v u v k k  
 cot u  cot v u v k k    3   3 
Nếu tan u m   3; 1  ; ;0 thì:
Nếu cot u m   3; 1  ; ;0 thì:  3    3  
2 Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
tan u m u  arctan m k k  
cot u m u arc cot m k k  
Lưu ý: Điều kiện để hàm tanu có nghĩa là Lưu ý:
Điều kiện để hàm cot u có nghĩa là u
k , k  . Tuy vậy, phương trình tan u m u k, k  . Tuy vậy, phương trình cot u m luôn có 2
nghiệm, vì vậy không cần đặt điều kiện cho nó.
luôn có nghiệm, vì vậy không cần đặt điều kiện.
Kỹ thuật 1: Làm mất dấu TRỪ Ví dụ:  sin  sin(   ) sin x sin x 0 sin x sin x sin x sin( ) x  cos  cos( ) 4 4 4  tan  tan(   ) x x 2 k  cot  cot(   ) 4 x k (k ). 8 x x 2 k (voâ nghieäm) 4
Kỹ thuật 2: Biến đổi CHÉO    sin   cos     2     Ví dụ: cos  sin        k2  2  2x   x k2     x    2 6 3  
 sin 2x  cos x  sin 2x  sin  x        (k ). tan   cot     2                  2  2x x k 2    x k 2   2   2    cot   tan     2 
Phương trình asin x bcos x c (với 2 2 2
a b c ) Phương trình 2 2
a sin x bsin x cos x c cos x d
a sin x b cos x c
Trường hợp 1: Xét 2
cos x  0  sin x 1. Ta có hệ a b c  sin x  cos x  2 2 s  in x 1   2 2 2 2 2 2 sin x 1 a b a b a b sau:     .............(1) 2 a x da d c sin  sin . x cos  cos . x sin  2 2  a b
Trường hợp 2: Xét cos x  0 , chia hai vế phương trình a b cho 2 cos x , ta có: (với cos  , sin   ) 2 2 2 2 2 2      a b a b
a tan x b tan x c d(1 tan ) x .........(2)
 Hợp nghiệm của (1), (2) ta có tập nghiệm của phương  c
sin(x )  sin   ......... với sin   trình đã cho. 2 2 a b
Lưu ý: Phương trình asin x bcos x c chỉ có nghiệm khi và chỉ khi 2 2 2
a b c . [
III. TỔ HỢP – XÁC SUẤT QUY TẮC CỘNG QUY TẮC NHÂN
Nếu phép đếm được chia ra nhiều trường hợp, ta Nếu phép đếm được chia ra làm nhiều giai đoạn bắt buộc, ta
sẽ cộng các kết quả lại.
sẽ nhân các kết quả của mỗi giai đoạn ấy.
3 Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com HOÁN VỊ TỔ HỢP CHỈNH HỢP
 Sắp xếp (đổi chỗ) của n
phần tử khác nhau, ta có số
Chọn k phần tử từ n phần tử
 Chọn k phần tử từ n phần tử (có sắp
(không sắp xếp thứ tự), ta có số cách
xếp thứ tự), ta được số cách chọn là
cách xếp là P n! với n chọn là k C . k A . n n n . n * k  ,nn * k  ,nk ! k !
n!  1.2.....n   1 n .  C   .  A   . nn  với k !k !  n 0  k nn  với k ! 0  k n  Quy ước sốc: 0!1.
Một số tính chất:   k n k C C   k k 1 k 1 C CC k
A k ! k C n n n n n 1  n nTính chất: n X Công thức: ( ) P( X )  ( n ) 
0  P( X )  1 . XÁC Trong đó: (
n X ) : số phần tử của tập biến cố
P()  0; P()  1 . X ; ( n )
 :số phần tử không gian mẫu; P(X ) SUẤT  
là xác suất để biến cố ( P X ) 1 (
P X ) với X là biến cố đối của X .
X xảy ra với X   .
 Nếu A, B là hai biến cố xung khắc với nhau
 Nếu A và B là hai biến cố độc lập với nhau thì
thì P A B  P A  P B . P  .
A B  P A.P B .
IV. KHAI TRIỂN NHỊ THỨC NEWTƠN na b 0 n 1 n 1  2 n2 2 n 1  n 1
C a C a b C a b .........  n n
C ab C b . n n n n n Khai triển dạng n Đặc biệt:     x 0 1 2 2 n 1 n 1 1
C C x C x  ......... n n
C x C x (*). liệt kê: n n n n n nn nHệ quả 1: 0 1 2 1
C C C  .........  C
C  2 (tức là thay x 1 vào (*)). n n n n n (với * n )
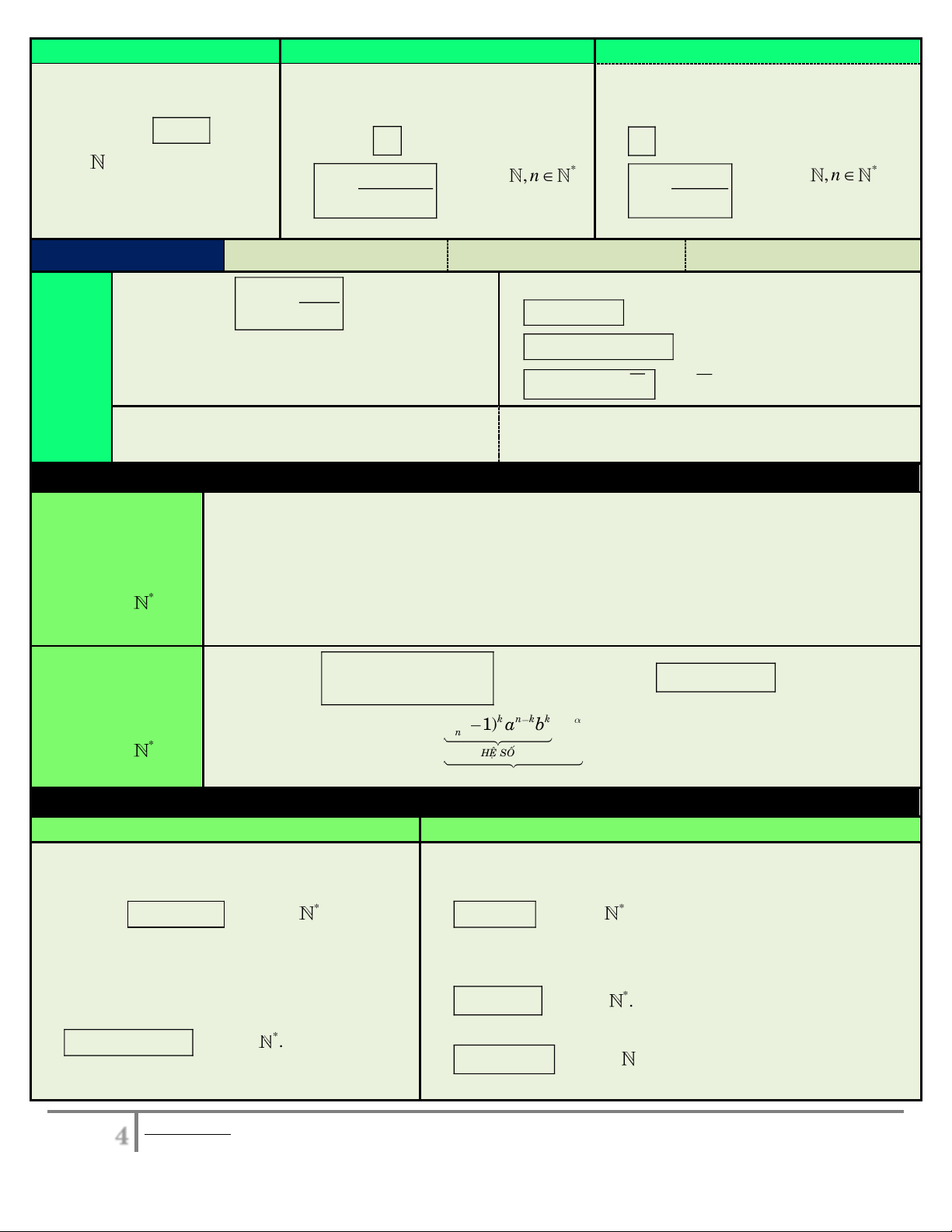
Hệ quả 2: Với n chẵn, chỉ cần thay x  1  vào (*), ta có: 0 1 2 n 1  n 0 2 4 n 1 3 n 1 C C C ......... C C 0 C C C ...... C C C ......C               n n n n n n n n n n n n n n k nk k k nk k Khai triển tổng
 Khai triển: a b  C a b . Số hạng tổng quát: T C a b n k 1  nquát: k 0 k k n k k
 Phân biệt hệ số và số hạng: C ( 1) a b . x   n
. Số hạng không chứa x ứng với 0. (với * n ) HEÄ SOÁ SOÁ HAÏNG
V. CẤP SỐ CỘNG – CẤP SỐ NHÂN CẤP SỐ CỘNG CẤP SỐ NHÂN 1. Định nghĩa: 1. Định nghĩa:
 Dãy số u được gọi là cấp số cộng khi và
 Dãy số u được gọi là cấp số nhân khi và chỉ khi n n  chỉ khi u
u d với * n  , d là hằng uu .q với * n  , q là hằng số. n 1  n n 1  n số.
Cấp số nhân như trên có số hạng đầu u , công bội q . 1
Cấp số cộng như trên có số hạng đầu u , 1
2. Số hạng tổng quát: công sai d.  1 u u . n q   với * n  .
2. Số hạng tổng quát: n 1
3. Tính chất các số hạng:
u u  (n 1)d với * n  . n 1  2 
3. Tính chất các số hạng: u .u u với k và k 2. k 1  k 1  k
4. Tổng n số hạng đầu tiên:
4 Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com  uu  2u với * k và k 2. nk 1  k 1  k u (1 q )       1 S u u ... u q 4. Tổng n 1 2 n
n số hạng đầu tiên: 1 với 1. q
(u u )n  1
S u u  ... nu  . n 1 2 n 2
VI. GIỚI HẠN DÃY SỐ - HÀM SỐ
1.1. Dãy số có giới hạn 0: ▪ 1 1 1 1 lim  0 ▪ lim  0 ▪ lim  0 ▪ lim  0  n n 3 n n ▪ lim n
q  0 với q  1 .
1.2. Dãy số có giới hạn hữu hạn:
Cho limu a . Ta có: n
▪ lim u a và 3 3 lim u a
▪ lim u a với a  0. n n
Cho limu a , limv b . Ta có: n n
▪ lim u v a b
▪ lim u .v a b n n  . n n u a
▪ lim n  với b  0
▪ lim k.u k a n  . v b n u
1.3. Tổng của cấp số nhân lùi vô hạn: 2 1
S u u q u q  ...  . 1 1 1 1 q
1.4. Dãy số có giới hạn vô cùng:
Quy tắc 1: Cho limu   ,  limv   .
 Tính limu v . n n n n limu lim v lim u v n n n n
1. Giới hạn dãy số            
Quy tắc 2: Cho limu   ,
 limv a  0. Tính limu v . n n n n limu Dấu của lim u v n an n   +   –   +   –  Quy tắc 3: u
Cho limu a  0, limv  0. Tính lim n . n n vn u Dấu của a (tử) Dấu của v (mẫu) lim n n vn + +  + –  – +  – – 
5 Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
2.1. Giới hạn tại vô cực: Cho k dương, ta có: k chaün k , ▪ 1 lim  0 ▪ lim k x   ▪ lim x k x x x x , k leû
2.2. Giới hạn hữu hạn:
Cho lim f x  a, lim g x  b . Ta có: x  0 x x 0 x
▪ lim f x  a ▪ f x 3 3 lim  a
▪ lim f x  a với a  0 x   0 x x 0 x x 0 x ▪ lim  f
 x  g x  a b  ▪ lim  f
 x.g x  . a bx  0 x x 0 x f x ▪ a lim k. f
x  k.a
với k là hằng số ▪ lim  với b khác 0 xx 0 x g x 0 x b
2.3. Quy tắc tìm giới hạn vô cực:
Quy tắc 1: Cho lim f x   ,
 lim g x  a  0. Tính lim  f x.g x   . x   0 x x 0 x x 0 x lim f x Dấu của a
lim  f xg x   . x 0 x x 0 x  +   – 
2. Giới hạn hàm số:  +   –  f x
Quy tắc 2: Cho lim f x  a  0, lim g x  0 . Tính lim . x  x 0 x g x 0 x x 0 x f x Dấu của a
Dấu của g x lim . x 0 x g x + +  + –  – +  – – 
2.4. Bổ trợ các công thức để khử dạng vô định: 2
ax bx c a x x x x với n
x 1   x   1  n 1 n2 xx ...  1   2  1
x , x là nghiệm của tam thức bậc hai. n n n 1  n2 n 1  1 2
a b  a ba
a b ... b  2 a b 2 a b a b a b a b a b 3 a b 3 a b 3 a b  3 a b  2
a a b   b 2 2 3 3 2 3
a a b   3 b
6 Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
3.1. Điều kiện tồn tại giới hạn:
Điều kiện để hàm số có
Giới hạn bên phải Giới hạn bên trái giới hạn tại x . 0 Ký hiệu lim f x lim f x
lim f x  lim f x   x    0 x x 0 x x  0 x x 0 x Khi đó: x   x x   x
lim f x  lim f xNghĩa là 0 0 xx     0 x x0 x xx x  0  0
 lim f x  x 0 x
3. Điều kiện giới hạn 3.2. Điều kiện liên tục của hàm số:
và điều kiện liên
 Hàm số f x liên tục tại x f x  lim f x  lim f x f x  lim f x 0  0        0    tục: xx xx xx 0 0 0
 Mọi hàm số đa thức, phân thức hữu tỉ, hàm lượng giác đều liên tục trên tập xác định của chúng.
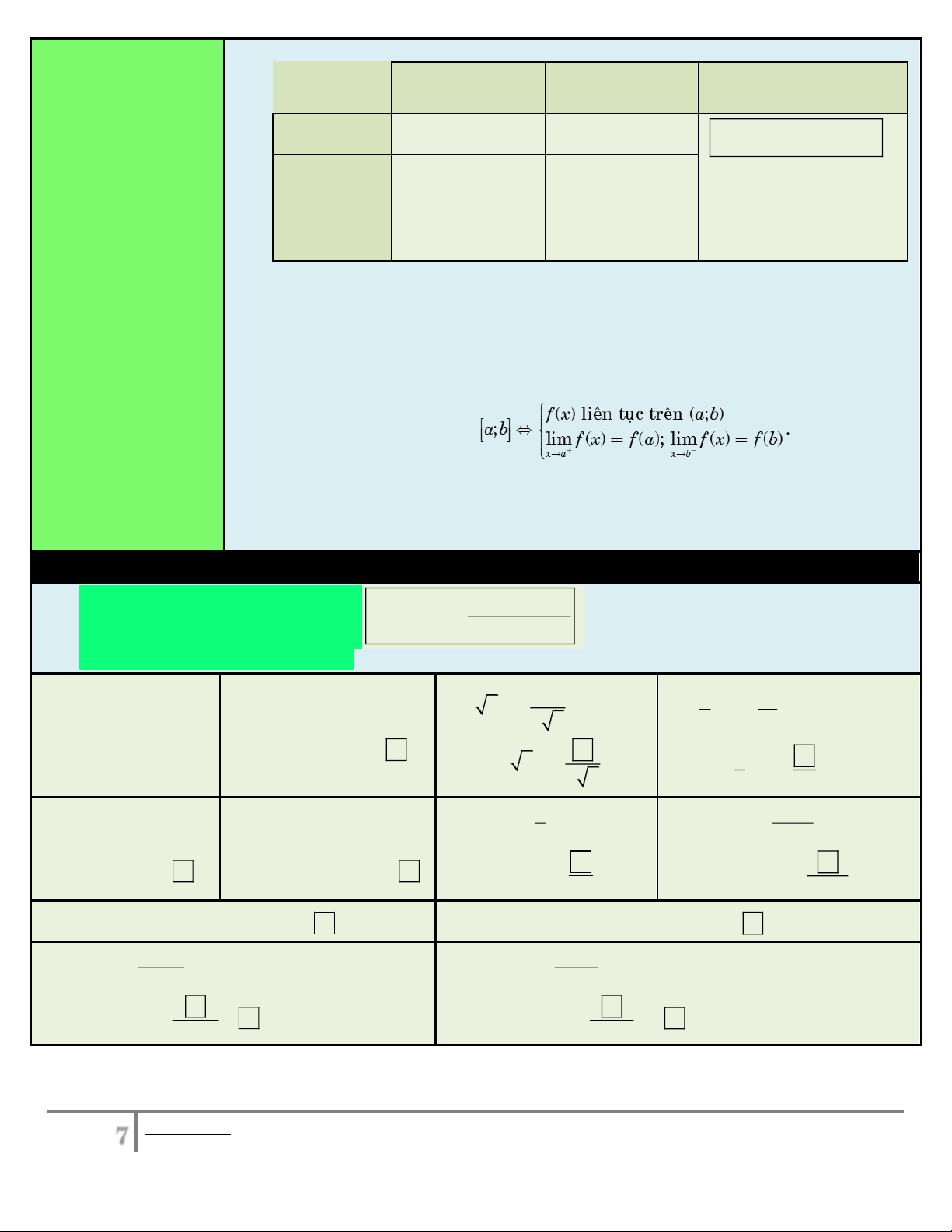
 Hàm số f x liên tục trên khoảng a;b nếu nó liên tục với mọi x x a;b . 0   f ( )
x lieân tuïc treân ( ; a ) b
 Hàm số f x liên tục trên ; a b lim f ( ) x f ( ); a lim f ( ) x f ( ) b . x a x b
3.3. Điều kiện có nghiệm của phương trình:
Nếu hàm số f x liên tục trên a;b và f a. f b  0 thì phương trình f x  0
có ít nhất một nghiệm trên a;b . VII. ĐẠO HÀM f x f x
1. Định nghĩa đạo hàm tại một điểm: f  x  lim . 0     0 x  0 x x x0
2. Bảng đạo hàm cơ bản và mở rộng:       1 1      x  1     2 k  0  1
(x )   x 2 xx x
(với k là hằng số) MR   1  (
u )  u   . u  u  MR     u   u MR 1    2 u   2  u u           1 ln x   x a  1 log  x x ee   x x aa ln a x x ln a     MR  u u u u ee . uMR  u u aa .ln . a uMR     ln u   MR log u au u ln a     
sin x  cos x MR
sinu  u cosu
 cos x  sin x MR
cosu   u sinu 1 1    tan x 2  1 tan x  cot x     2 1 cot x 2  2 cos x sin x uuMR    tan u    u  2 1 tan u MR
cot u     u  2 1 cot u 2  2  cos u sin u
7 Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
3. Quy tắc tìm đạo hàm: ▪  
u v  u  v
▪ (k.u)  k.u ▪ ( . u v)  u v  uv 
f laø ñaïo haøm cuûa f theo bieán x      x ▪ u u v uv   
▪ f   f .u với f laø ñaïo haøm cuûa f theo bieán u . 2  u v v x u x
u laø ñaïo haøm cuûa u theo bieán x x
4. Đạo hàm cấp cao và vi phân: Đạo hàm cấp cao Vi phân  
df x  f  x.dx
f   x   f  x ; f  x   f   x    
dy y .dx   
4                1 ;...; n n f x f x f x   fx  
du u .dx
VIII. KHẢO SÁT HÀM SỐ VÀ BÀI TOÁN LIÊN QUAN HÀM BẬC BA HÀM NHẤT BIẾN
XÉT TÍNH ĐƠN ĐIỆU
ax b 3 2
y ax bx cx d (a 0) y
(ad bc 0, c 0)
cx d
Bước 1: Tìm tập xác định D  Đạo hàm 2
y  3ax  2bx c . .
 Hàm số đồng biến trên tập xác
Bước 2: Tính y  f (  ) x ;  định ad bc
y  0, x  
 Đạo hàm y  . cho 2 y  0   (cx d ) a  0 Tìm nghieäm x , x ...   .
 Hàm số đồng biến trên từng 1 2 Tìm thêm   0
các giá trị x mà y không
khoảng xác định     ad bc 0.
Hàm số nghịch biến trên tập xác xác định. định
 Hàm số nghịch biến trên từng
y  0, x  
Bước 3: Lập bảng biến     khoảng xác định ad bc 0. a  0
thiên. (Nên chọn giá trị x đại   .
diện cho từng khoảng thay   0
vào y để tìm dấu của y trên khoảng đó).
Lưu ý: Nếu a chứa tham số m thì
Lưu ý: Nếu đề cho đồng biến
Bước 4: Dựa vào bảng biến
ta xét a  0 , tìm m. Thay m tìm được
(nghịch biến) trên (;  ) thì ta xét điều
thiên để kết luận về sự đồng
để kiểm tra dấu y , xem y có đơn d    
biến, nghịch biến của hàm kiện: điệu ( ; ) . trên không? c số.
CỰC TRỊ HÀM BẬC BA
CỰC TRỊ HÀM BẬC BỐN
ĐIỀU KIỆN CỰC TRỊ 3 2
y ax bx cx d (a 0) 4 2
y ax bx c (a 0)
 Hàm số có điểm cực trị là     Đạo hàm 2
y  3ax  2bx c .  Đạo hàm 3 y 4ax 2bx .
y (x )  0
 Điều kiện cực trị (x ; y ) 0   .
 Hàm số có hai cực trị (tức là có 0 0
y(x )  yBa cực trị ab  0 0 0 a  0
(giả thiết là hàm số liên tục CĐ-CT)   (*)   . ab  0  0  Một cực trị  tại y x ). 2 2    0
 Hàm số có hai điểm cực trị trái dấu a b 0
f (x )  0
x x  0  ac  0 . Có cực trị 2 2 a b  0 1 2  Nếu 0  thì hàm f (  x )  0
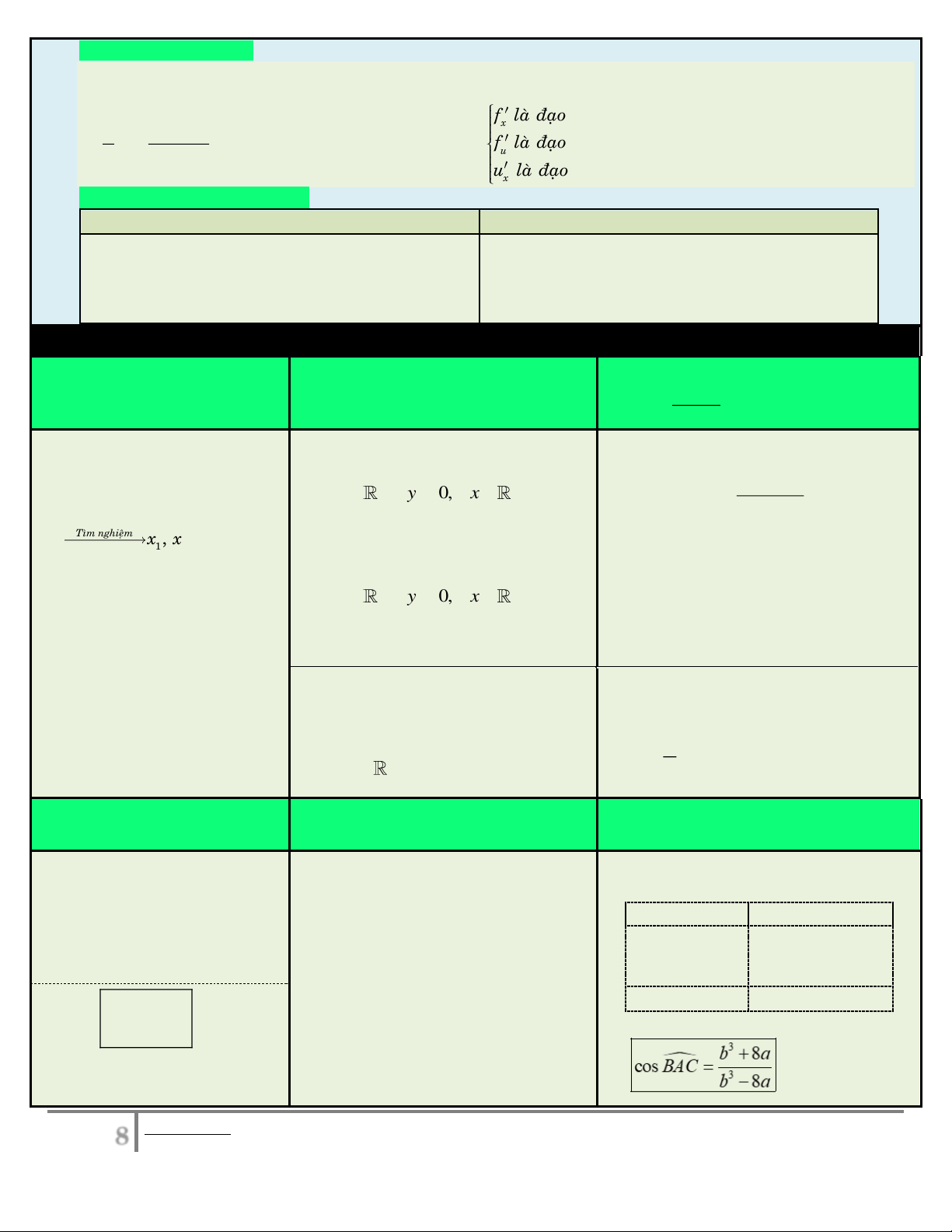
 Hàm số có hai điểm cực trị cùng  Cho , A ,
B C là ba điểm cực trị, ta có:  0 a  0,   3  0 b  8a
số f (x) đạt cực đại tại dấu y   . cos BAC x x . ac  0 3 b  8a 0
8 Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
f (x )  0
 Phương trình đường thẳng đi qua 5  Nếu 0  b thì hàm hai điểm cực trị: S  . f  (  x )  0  ABC  3  0 32a f (
x). f (x) số  
f (x) đạt cực tiểu tại y f (x) . 18a x x . 0
Lưu ý: Nếu tọa độ hai cực trị đã
rõ ràng ta nên gọi đường thẳng
y ax b rồi thay tọa độ hai điểm đó vào 
Giải hệ tìm a, b.
TÌM MAX-MIN TRÊN ĐOẠN
TÌM MAX-MIN TRÊN KHOẢNG
Tìm Max-Min của f (x) trên đoạn a;b
Tìm Max-Min của f (x) trên khoảng ( ; a ) b Bước 1:   
Tính y  f (  ) x .
Bước 1: Tính y f ( ) x . 
Tìm các nghiệm x ( ; a ) b khi cho   f (
x)  0. Tìm các nghiệm x ( ; a )
b khi cho f (x)  0 . Tìm x ( ; a b) j i i Tìm x  ( ;
a b) mà y không xác định.
mà y không xác định. jBước 2:  . (Nếu thay
Tính các giá trị f ( ) a , f ( ) b và
Bước 2: Cần tính lim y, lim y ( ; a ) b bằng   xa xb
f (x ), f (x ) (nếu có). ( ;   )
 thì ta tính thêm lim y ). i j x
Bước 3: So sánh tất cả giá trị trong bước 2 để
Bước 3: Lập bảng biến thiên và suy ra giá trị lớn nhất, nhỏ
kết luận về giá trị lớn nhất, nhỏ nhất. nhất trên khoảng.
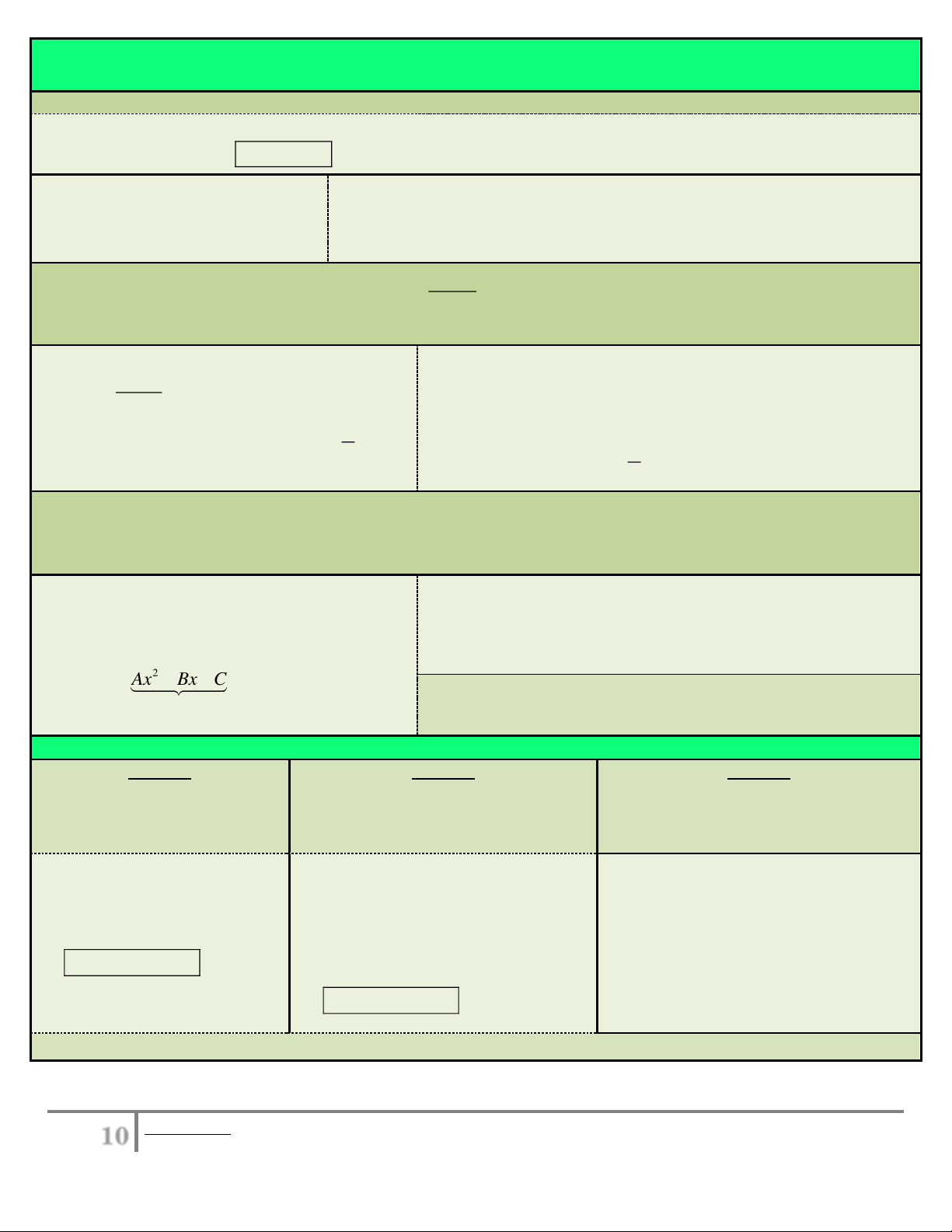
 Nếu hàm f (x) đồng biến trên [ ; a ] b thì
 Nếu hàm f (x) nghịch biến trên [ ; a ] b thì
max f (x)  f (b)    max f (x) f (a) x [  a;b]   x [  a;b] 
min f (x)  f (a)    min f (x) f (b)  x [  a;b]
x [a;b] ĐẶC BIỆT TIỆM CẬN ĐỨNG TIỆM CẬN NGANG x   x x    Định nghĩa: 0 
(x hữu hạn, y vô  Định nghĩa:
(x vô hạn, y hữu hạn), ta có tiệm y   y   y  0
hạn), ta có tiệm cận đứng x x . Lưu ý:
cận ngang y y . 0 0 điều kiện x 
x có thể được thay bằng
Cách tìm TCN: Đơn giản nhất là dùng CASIO 0
Bước 1: Nhập hàm số vào máy. x x 
 (giới hạn bên trái) hoặc x x   0 0 Bước 2: NEXT NEXT     (giới hạn bên phải). CALC X 10 ^10  NEXT NEXT Cách tìm TCĐ:     
Nếu x x là một nghiệm CALC X 10 ^10 0
của mẫu số mà không phải là nghiệm của
Bước 3: Nếu kết quả thu được là hữu hạn (tức là y ) thì ta 0
tử số thì x x chính là một TCĐ của đồ thị.
kết luận TCN: y y . 0 0
(với tập xác định có dạng D K \ x ; x ;... ). 0 1    a Đồ thị hàm số ax b y c ad bc  có một TCĐ: d x  
, một TCN: y  . cx  với ( 0, 0) d c c
Nên nhớ, mỗi đồ thị chỉ có tối đa là 2 tiệm cận ngang.
9 Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
SỰ TƯƠNG GIAO GIỮA HAI ĐỒ THỊ
Xét hai đồ thị (C ) : y f (x) và (C ) : y ( g x) . 1 2
Phương pháp chung tìm giao điểm hai đồ thị
Bước 1 : Lập phương trình hoành độ giao
Bước 2 : Giải phương trình (*) để tìm các nghiệm x , x ,... 1 2
điểm của (C ) &(C ) : f (x)  g(x) . (*) 1 2
(nếu có), suy ra y , y ... 1 2
 Điều kiện để (C ) và (C ) có n
 Điều kiện để (C ) tiếp xúc (C ) là phương trình (*) có nghiệm kép hoặc 1 2 1 2
điểm chung là phương trình (*) có
f (x)  g(x)
n nghiệm khác nhau. hệ sau có nghiệm :  .
f (x)  g (x) 
ax b
(C) : y
Tìm tham số để
cx d cắt nhau tại hai điểm phân biệt
d : y  x  
Bước 1 : Viết phương trình hoành độ giao    điểm ax b :
  x   , đưa phương trình về A  0  cx d   Tìm     
Bước 2 : Giải hệ 0 m ? g dạng d 2
g(x)  Ax Bx C  0 x     .   c   d  g   0     c 3 2
(C) : y ax bx cx d
Tìm tham số để
cắt nhau tại ba điểm phân biệt
d : y   x  
(Ta chỉ áp dụng cho trường hợp phương trình hoành độ giao điểm có nghiệm đẹp)
Bước 1 : Viết phương trình hoành độ giao A  0 điểm : 3 2
ax bx cx d   x   , đưa 
Bước 2 : Giải hệ điều kiện :   0 Tìm m? phương trình về dạng g    g(x )  0  0 2
(x x )  Ax Bx C   0 . 0   
Lưu ý : Để tìm nghiệm đẹp x x , ta nhập vào máy chức g ( x)  0
(có vận dụng kỹ năng chia Hoocner)
năng giải phương trình bậc ba với m 100 .
PHƯƠNG TRÌNH TIẾP TUYẾN DẠNG 1 DẠNG 2 DẠNG 3
Viết phương trình tiếp tuyến của
Viết phương trình tiếp tuyến của đồ thị
Viết phương trình tiếp tuyến của đồ thị
đồ thị (C) : y f ( ) x tại điểm
(C) : y f ( )
x biết tiếp tuyến có hệ số
(C) : y f ( )
x biết tiếp tuyến đi qua
M (x ; y ) (C) góc k. ( A x ; y ) . 0 0 A A
Bước 1: Tính đạo hàm y , từ
Bước 1: Gọi M (x ; y ) là tiếp điểm
Bước 1: Tiếp tuyến có dạng : 0 0
đó có hệ số góc k y (  x ).     và tính đạo hàm y
y (x )(x x ) y (*) với 0 y . 0 0 0
Bước 2 : Viết phương trình tiếp  Bước 2:  Cho y (
x )  k , tìm được y f (x ). 0 0
tuyến của đồ thị dạng 0
tiếp điểm (x ; y ). 
Bước 2: Thay tọa độ điểm A vào (*)
y k(x x )  y . 0 0 0 0
Bước 3: Phương trình tiếp tuyến :
để tìm được x . 0
y k(x x )  y .
Bước 3: Thay x vào (*) để viết phương 0 0 0 trình tiếp tuyến.
Đặc biệt : Nếu tiếp tuyến song song đường thẳng y ax b thì nó có hệ số góc k  ,
a nếu tiếp tuyến vuông góc đường
10 Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com 1
thẳng y ax b thì nó có hệ số góc k  
(a  0) ; nếu tiếp tuyến tạo với Ox góc thì nó có hệ số góc k   tan . a
ĐIỂM ĐẶC BIỆT THUỘC ĐỒ THỊ
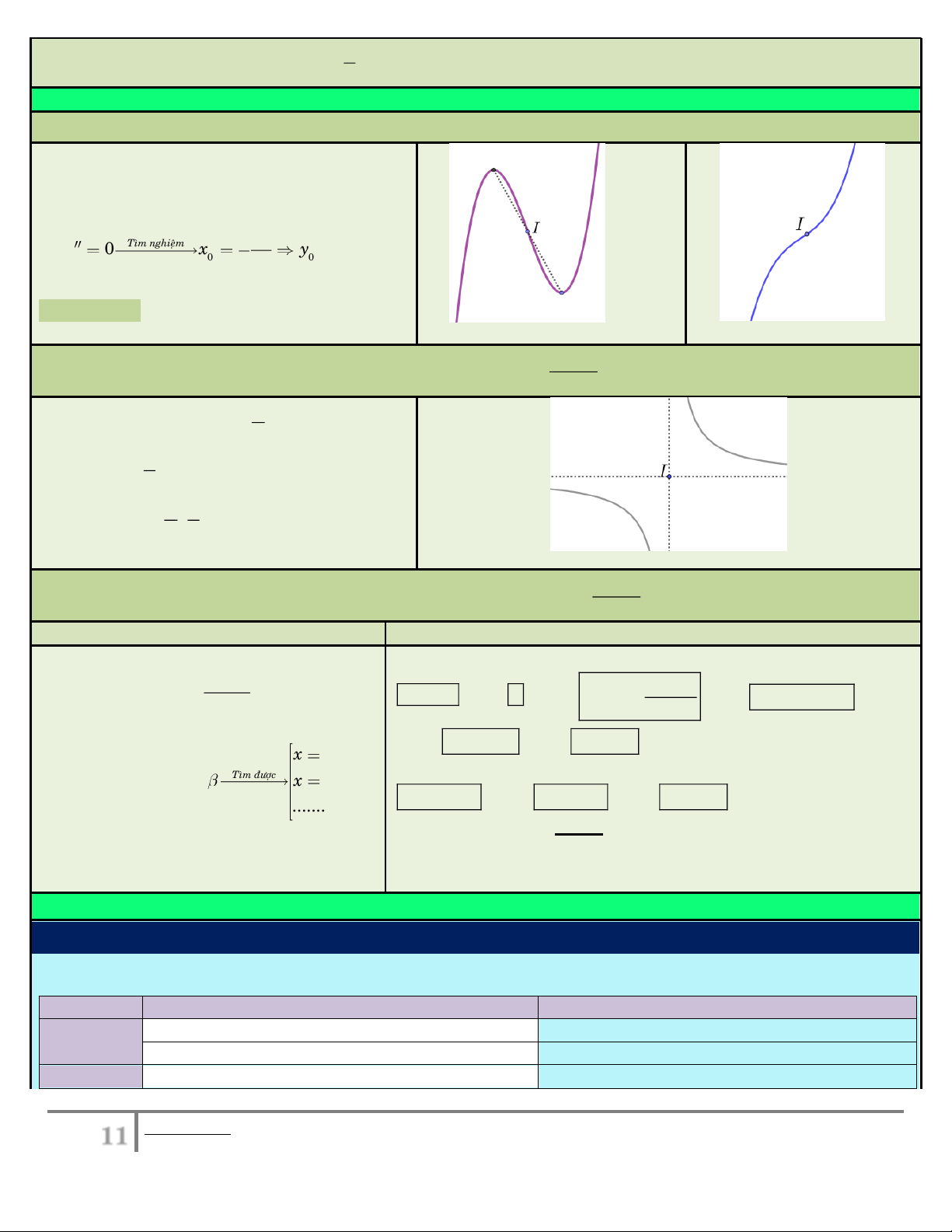
Tâm đối xứng (hay điểm uốn) của đồ thị bậc ba 3 2
y ax bx cx d (a 0) 2
y  3ax  2bx c
Bước 1: Tính  .
y  6ax  2bBước 2: Cho 0 Tìm nghieäm b y x y 0 0 3a . Ta có tâm
đối xứng (tức điểm uốn): I(x ; y ). 0 0
Cần nhớ: Tâm đối xứng của đồ thị bậc ba
cũng là trung điểm của hai điểm cực trị (nếu có). 
Tâm đối xứng của đồ thị hàm nhất biến ax b y
(c 0, ad bc 0) cx d  Tìm tiệm cận đứng d x   và tiệm cận c a ngang y
, suy ra được tâm đối xứng của c   đồ thị d a là: I  ; 
 (là giao điểm 2 tiệm cận  c c  tìm được).
Điểm có tọa độ nguyên thuộc đồ thị hàm nhất biến ax b y
(c 0, ad bc 0) cx d Cách 1: Tự luận
Cách 2: Trắc nghiệm
Bước 1: Chia đa thức cho đa thức, ta viết Thực hiện trên máy tính bỏ túi như sau:  lại hàm số  y    aX b MODE   7   F(X )    START : 19 cx  . d cX d
Bước 2: Yêu cầu bài toán  cx d là     
. Ta dò tìm những hàng có x END : 1 STEP : 1 F( X ) ước số nguyên của Tìm ñöôïc x
nguyên thì nhận làm điểm cần tìm. Làm tương tự khi cho , suy ....... START : 0   END : 18 
STEP : 1 , ta sẽ bổ sung thêm các ra các giá trị
điểm nguyên còn lại. Lưu ý: Học sinh muốn đạt được tính chính xác
y tương ứng. Từ đây tìm
cao hơn thì có thể dò trên nhiều khoảng, mỗi khoảng có
được các điểm có tọa độ nguyên thuộc đồ START và thị.
END cách nhau 19 đơn vị. (Máy tính đời mới sẽ có bộ nhớ lớn hơn).
NHẬN DIỆN ĐỒ THỊ HÀM SỐ 1. Hàm số bậc ba 3 2
y ax bx cx d a 0 2 
y  3a x 2b x c A B C Hệ số
Dấu hiệu đồ thị Kết luận
Nhánh phải đồ thị đi lên a  0 a
Nhánh phải đồ thị đi xuống a  0 d
Giao điểm với Oy nằm trên điểm O d  0
11 Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
Giao điểm với Oy nằm dưới điểm O d  0
Giao điểm với Oy trùng với điểm O d  0
Đồ thị không có điểm cực trị nào         B 2 2 AC b 3ac 0 y
Đồ thị có hai điểm cực trị         B 2 2 AC b 3ac 0 y B 2b
Tâm đối xứng nằm bên phải Oy   0    0  ab  0 A 3a b, c B 2b
Tâm đối xứng nằm bên trái Oy   0    0  ab  0. A 3a C c
Hai điểm cực trị nằm cùng phía Ox x x  0   0   0  ac  0 1 2 A 3a C c
Hai điểm cực trị nằm khác phía Ox x x  0   0   0  ac  0 1 2 A 3a
Chú ý: Đôi khi, ta thấy đồ thị đi qua điểm x ; y cho trước, ta thay tọa độ này vào hàm số để có 1 phương 0 0
trình. Điều này đúng cho mọi hàm số. 2.
Hàm số bậc bốn trùng phương 4 2
y ax bx c a 0 3 
y  ax bx x 2 4 2 2
2ax b Hệ số
Dấu hiệu đồ thị Kết luận
Nhánh phải đồ thị đi lên a  0 a
Nhánh phải đồ thị đi xuống a  0
Giao điểm với Oy nằm trên điểm O c  0 c
Giao điểm với Oy nằm dưới điểm O c  0
Giao điểm với Oy trùng với điểm O c  0
Đồ thị hàm số có ba cực trị ab  0 b
Đồ thị hàm số có một cực trị
ab  0, a  0
ax b 3.
Hàm số nhất biến y
c 0, ad bc 0cx d
ad bc   y  
cx d 2 Hệ số
Dấu hiệu đồ thị Kết luận d
Tiệm cận đứng nằm bên phải Oy   0  cd  0 c c và d d
Tiệm cận đứng nằm bên trái Oy   0  cd  0 c a
Tiệm cận ngang nằm phía trên Ox  0  ac  0 c a và c a
Tiệm cận ngang nằm phía dưới Ox  0  ac  0 c b
Giao điểm của đồ thị với Ox nằm bên phải gốc O   0  ab  0 a a và b b
Giao điểm của đồ thị với Ox nằm bên trái gốc O   0  ab  0 a
12 Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com b b
Đồ thị đi qua gốc O(0;0) 0 b
Giao điểm của đồ thị với Oy nằm trên gốc O  0  bd  0 d b và d
Giao điểm của đồ thị vớ b
i Oy nằm dưới gốc O  0  bd  0 d
Mỗi nhánh đồ thị đi lên (từ trái sang phải) ad bc  0 a, b, c, d
Mỗi nhánh đồ thị đi xuống (từ trái sang phải) ad bc  0
PHÉP SUY ĐỒ THỊ TỪ ĐỒ THỊ CÓ SẴN
1. Phép tịnh tiến và đối xứng đồ thị
Cho hàm y f ( )
x có đồ thị (C) Đồ thị cần tìm Cách biến đổi Minh họa
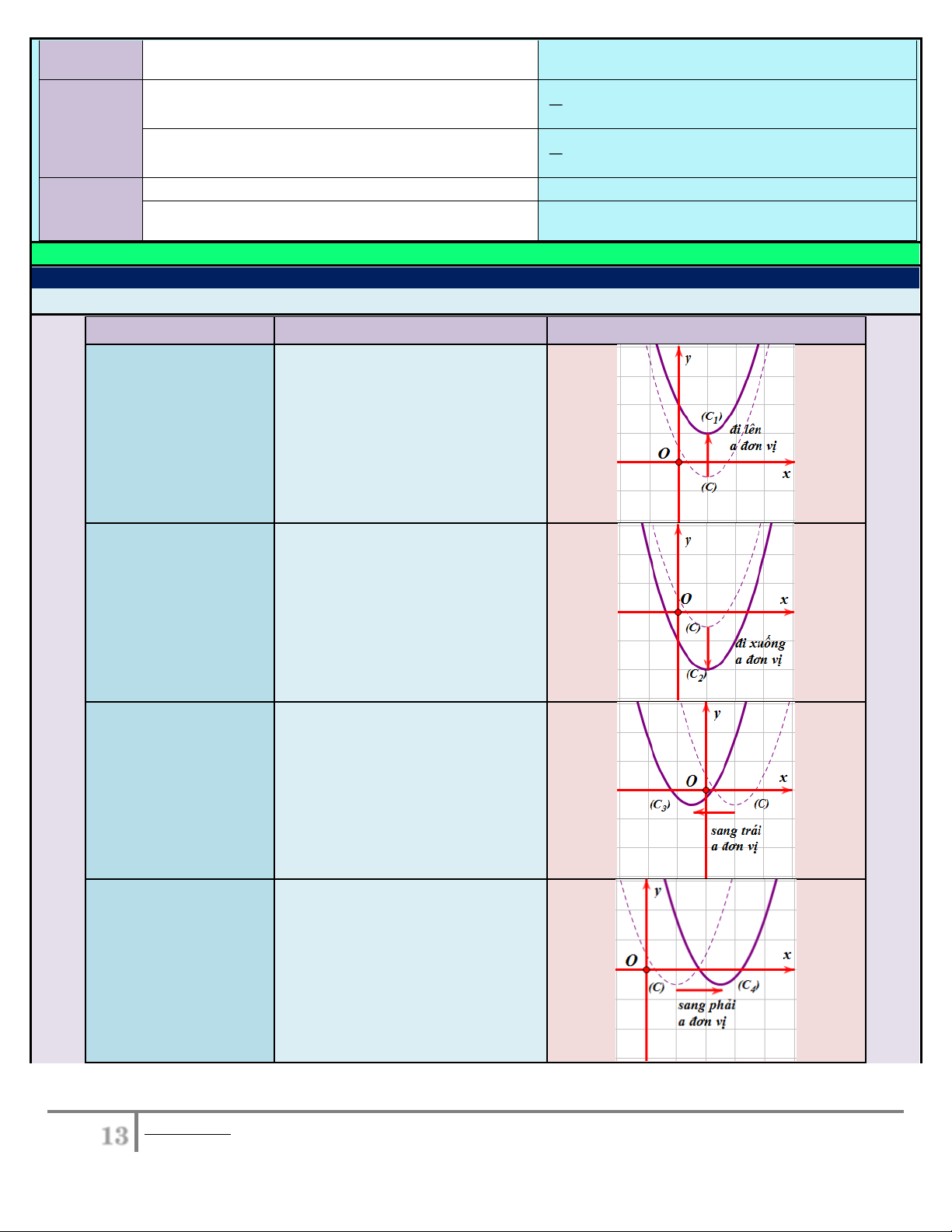
Tịnh tiến đồ thị (C) theo phương
(C ) : y f ( ) x a 1
Oy lên phía trên a đơn vị.
Tịnh tiến đồ thị (C) theo phương
(C ) : y f ( ) x a 2
Oy xuống phía dưới a đơn vị.
Tịnh tiến đồ thị (C) theo phương
(C ) : y f (x a) 3
Ox qua trái a đơn vị.
Tịnh tiến đồ thị (C) theo phương
(C ) : y f (x a) 4
Ox qua phải a đơn vị.
13 Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
(C ) : y   f ( ) x
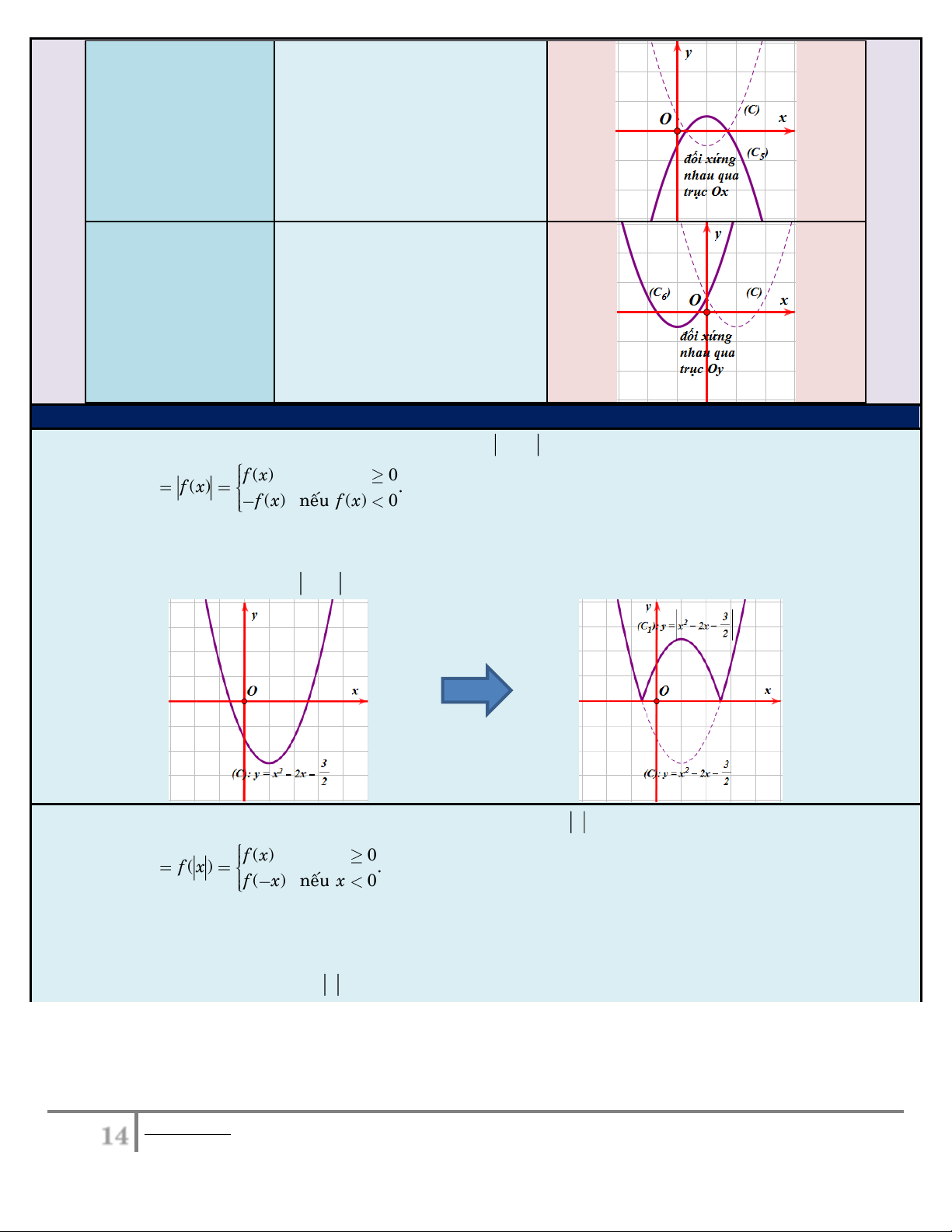
Lấy đối xứng (C) qua Ox . 5
(C ) : y f ( ) x
Lấy đối xứng (C) qua Oy . 6
2. Đồ thị hàm chứa giá trị tuyệt đối
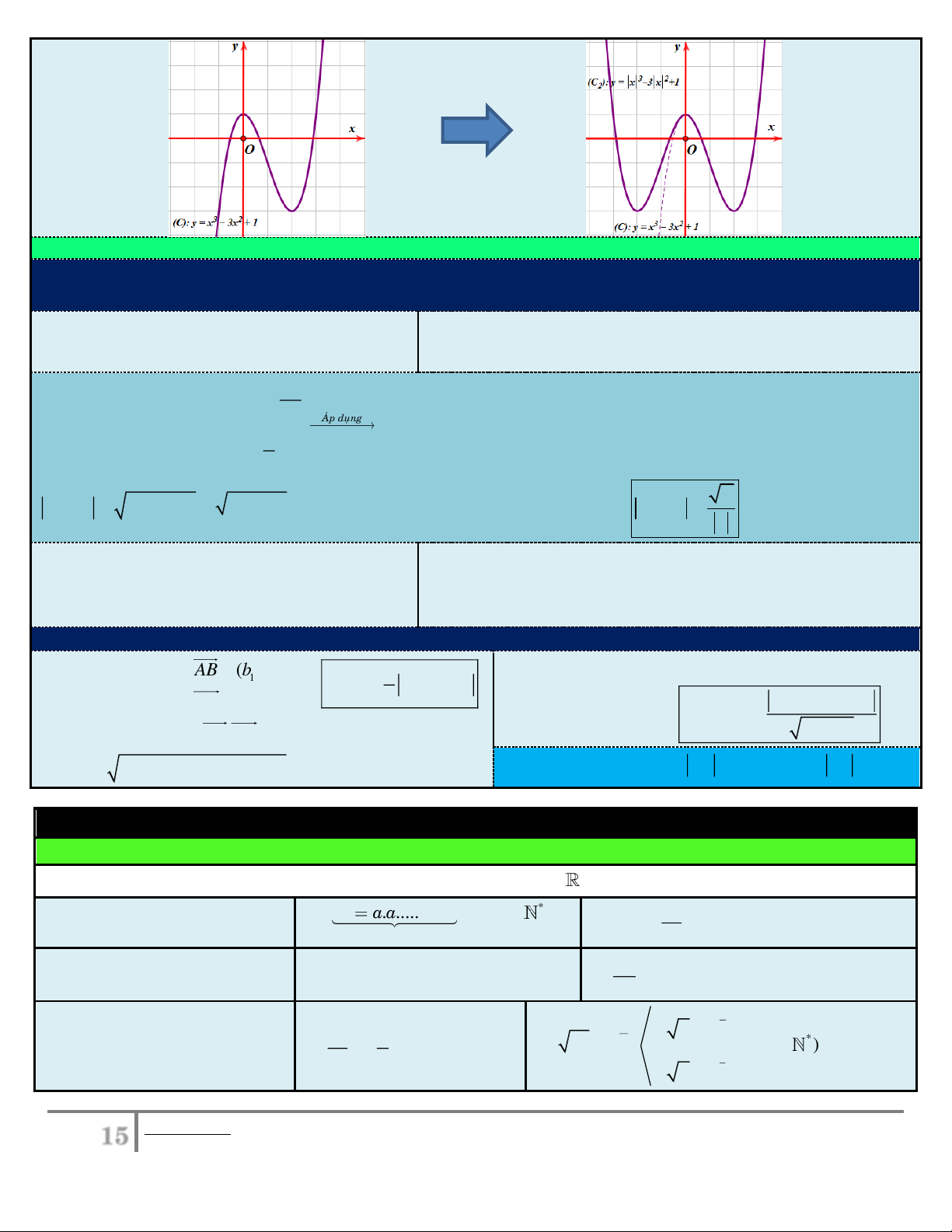
a) Từ đồ thị (C) : y f ( x) ta suy ra đồ thị (C ) : y f ( x) . 1 f ( ) x neáu f ( ) x 0 Ta có y f ( ) x . f ( ) x neáu f ( ) x 0
Bước 1: Giữ nguyên phần đồ thị (C) nằm phía trên Ox , ta được (C )  .
Bước 2: Lấy đối xứng phần đồ thị (C) phía dưới Ox qua Ox , ta được (C)  .
Kết luận: Đồ thị (C ) : y f (x) là hợp của (C )
 với (C). Xem ví dụ minh họa sau: 1
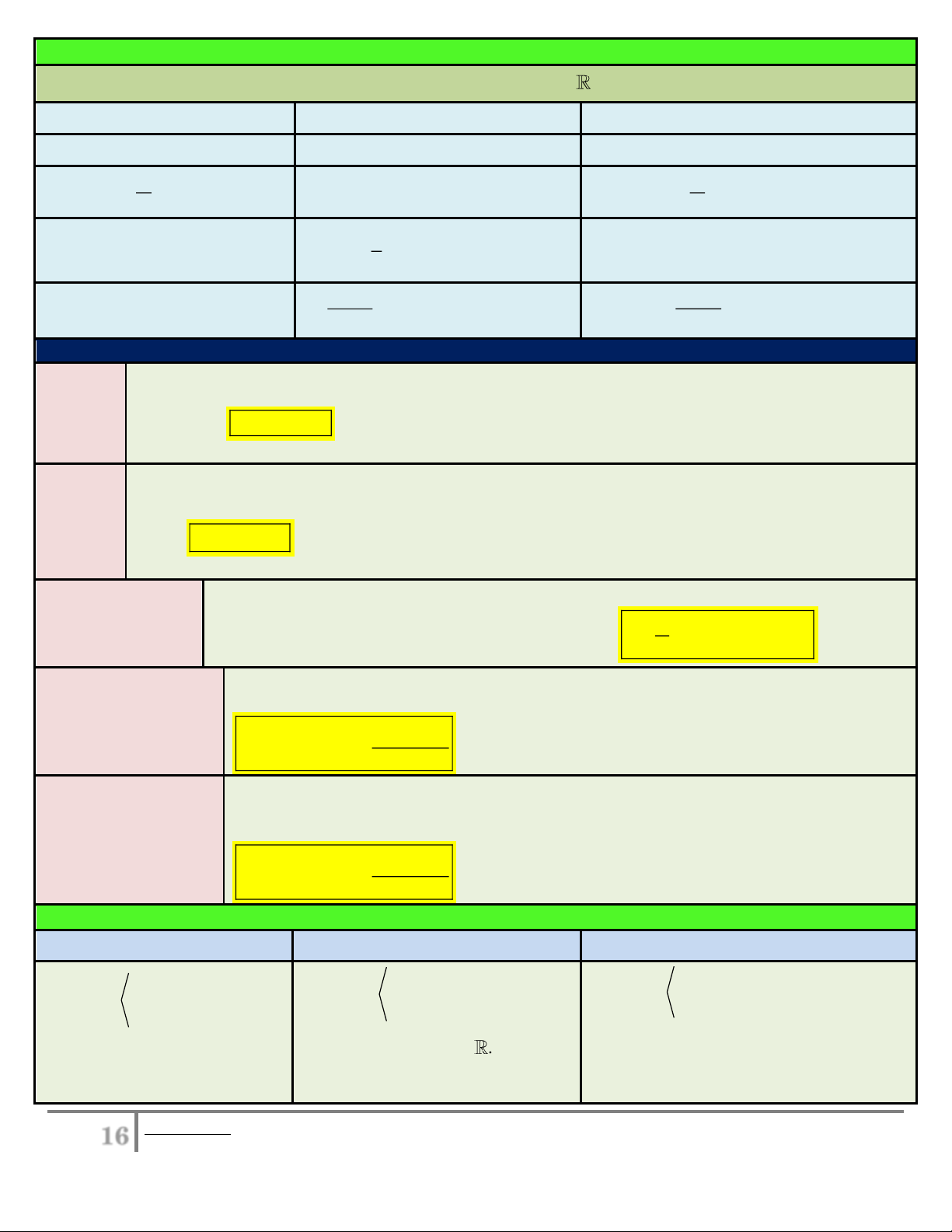
b) Từ đồ thị hàm số (C) : y f ( )
x ta suy ra đồ thị (C ) : y f x . 2   f ( ) x neáu x 0 Ta có y f ( x) . f ( ) x neáu x 0
Bước 1: Giữ nguyên phần đồ thị (C) nằm bên phải trục Oy , ta được (C )  .
Bước 2: Lấy đối xứng phần đồ thị (C )
 qua trục Oy , ta được (C) .
(Đây là tính chất đối xứng của đồ thị hàm số chẵn)
Kết luận: Đồ thị (C ) : y f x là hợp của (C )
 với (C). Xem ví dụ minh họa sau: 2  
14 Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
CÔNG THỨC BỔ TRỢ CHO QUÁ TRÌNH GIẢI TOÁN HÀM SỐ
Bổ trợ về tam thức bậc hai Cho phương trình 2
ax bx c  0 (*) a  0
 (*) có hai nghiệm phân biệt  
 (*) có hai nghiệm trái dấu  . a c  0 .   0  b
S x x   1 2   a Định lí Vi-ét :  AÙp duïng 2 2 2 3 3 3 2 2
x x S  2 ;
P x x S  3S ;
P (x x )  S  4 ; P c  1 2 1 2 1 2 P x x  1 2  a  2 2
x x  (x x )  S  4P . Trong trắc nghiệm, ta nên dùng công thức : x x  . 1 2 1 2 1 2 a
 (*) có hai nghiệm dương phân biệt
 (*) có hai nghiệm âm phân biệt a  0,   0      a 0, 0  .   .
S  0, P  0
S  0, P  0
Bổ trợ hình học giải tích phẳng
AB  (b ;b )
 Khoảng cách từ điểm M (x ; y ) đến  1 M M Nếu ABC  có 1 2  thì Sb c b c ABC 1 2 2 1
AC  (c ; c )  2
ax by c 1 2
 : ax by c  0 là d M; M M  .  2 2 ABC
 tại A A .
B AC  0  b c b c  0 . a b 1 1 2 2  2 2
AB  (x x )  ( y y ) .  
 Đặc biệt: d M ;Oxy
, d M ;Oy x . MM B A B A
IX. LŨY THỪA – MŨ VÀ LOGARIT
1. Công thức lũy thừa Cho các số dương , a b và , m n  . Ta có: n a a a an 1  . ........... với * n  0 a  1  a n thöøa soá n a ma ( m)n mn   ( n)m a a am  . n m n a a a    m na n a 1 n n   n 2  a aa a n n  ( )n a b ab m n *      m a a ( , m n  ) n bb  1 3 3  a a
15 Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
2. Công thức logarit: Cho các số ,
a b  0, a  1 và , m n . Ta có:  
log b    a b
 lgb  logb  log b
 lnb  log b a 10 e  log 1  0  log a 1  log n a n a a a 1 n  log b b  log n
b n log b  log n b b m log m loga a m a a a a m   loga b abb log (b )
c  log b  log c
 log    log b  log c   a a a a a ac  log c log b b a ac log c 1  log .
b log c  log c , b   1  a
 log c , b   1  log b  , b   1 a b a log b b a log a a b BÀI TOÁN NGÂN HÀNG
Nếu ta gởi tiền vào ngân hàng theo hình thức tiền lãi chỉ được tính dựa vào tiền gốc ban đầu (tức là 1. Công
tiền lãi của kỳ hạn trước không gộp vào vốn để tính lãi cho kỳ hạn kế tiếp), đây gọi là hình thức lãi
thức tính đơn. Ta có: T  (
A 1 nr) với A: tiền gởi ban đầu; r: lãi suất; n: kỳ hạn gởi; T: tổng số tiền nhận sau lãi đơn
kỳ hạn n. Lưu ý: r và n phải khớp đơn vị; T bao gồm cả A, muốn tính số tiền lời ta lấy T – A.
Nếu ta gởi tiền vào ngân hàng theo hình thức: hàng tháng tiền lãi phát sinh sẽ được cộng vào tiền 2. Công
gốc cũ để tạo ra tiền gốc mới và cứ tính tiếp như thế, đây gọi là hình thức lãi kép. thức lãi kép Ta có:  (1 )n T A r
với A: tiền gởi ban đầu; r: lãi suất; n: kỳ hạn gởi; T: tổng số tiền nhận sau kỳ
hạn n. Lưu ý: r và n phải khớp đơn vị; T bao gồm cả A, muốn tính số tiền lời ta lấy T – A. 3. Mỗi tháng gởi
Nếu đầu mỗi tháng khách hàng luôn gởi vào ngân hàng số tiền A đồng với lãi kép r% /tháng
đúng số tiền giống A n nhau theo hình
thì số tiền họ nhận được cả vốn lẫn lãi sau n tháng là: T
1 r 11 r   . thức lãi kép r
Nếu khách hàng gởi vào ngân hàng số tiền A đồng với lãi suất r% /tháng. Vào ngày ngân
4. Gởi tiền vào ngân
hàng tính lãi mỗi tháng thì rút ra X đồng. Số tiền thu được sau n tháng là:
hàng rồi rút ra hàng n  
tháng số tiền cố định n 1 r 1
T A1 r     X r
Nếu khách hàng vay ngân hàng số tiền A đồng với lãi suất r%/tháng. Sau đúng một tháng
kể từ ngày vay bắt đầu hoàn nợ, hai lần hoàn nợ cách nhau đúng một tháng, mỗi lần hoàn
5. Vay vốn và trả góp nợ đúng số tiền X đồng. Số tiền khách hàng còn nợ sau n tháng là:
(tương tự bài toán 4) n  
T A  r n 1 r 1 1  X r
3. Hàm số lũy thừa, mũ và logarit: HÀM LŨY THỪA HÀM SỐ MŨ HÀM SỐ LOGARIT x    y  log x   y x y a a 0 a 0 a   Dạng: với u là đa  Dạng: với  . Dạng:  .  u  a  1 y  với log ua  1 y u y a a      
Đặc biệt: a e y ln x ;
Tập xác định: D  . thức đại số. a 10 
y  log x  lg x .  Đạo hàm:
Điều kiện xác định: u  0 .
16 Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
Tập xác định: x x y a 
y  a ln aĐạo hàm: . 1 u u            Nếu ÑK u . y a y a ln . a u y log x y a x ln a . ( x e ) x   e uĐặc biệt: với
y  log u   y  Nếu ÑK u 0. a u u    u ln a 0 (e ) e . u 1 e 2,71828...   (ln x) Đặc biệt: x . Nếu ÑK u 0.   Sự biến thiên: x y a . u (ln u)  uĐạo hàm:
Nếu a  1 thì hàm đồng biến
Sự biến thiên: y  log x . Nếu a  1 : a hàm đồng biến trên   (0; )  . Nếu 1 y x 
y   x  trên
. Nếu 0  a 1 thì hàm
0  a  1 : hàm nghịch biến trên   1 y u 
y  u  . u nghịch biến trên . (0; )  .
4. Đồ thị hàm số mũ và logarit:
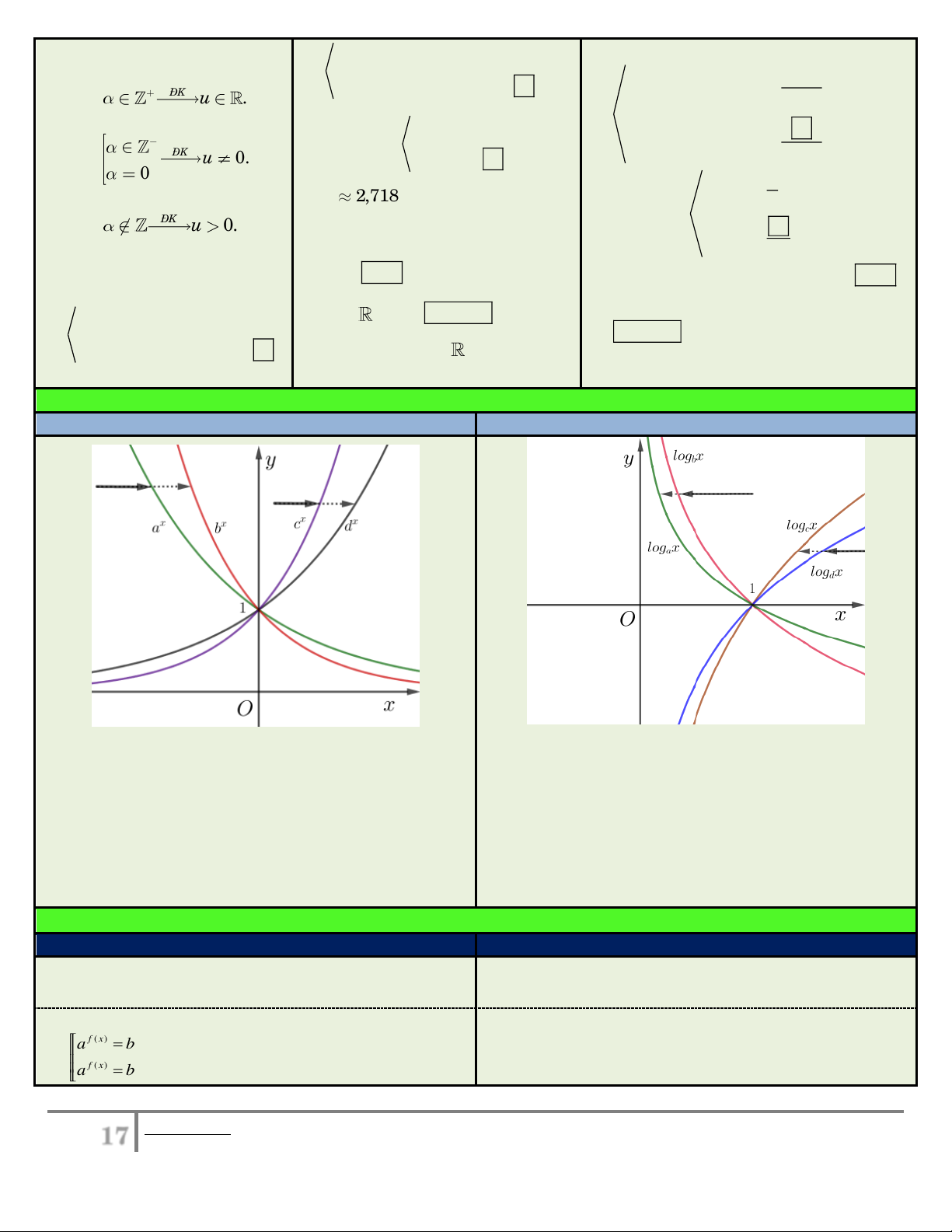
ĐỒ THỊ HÀM SỐ MŨ
ĐỒ THỊ HÀM SỐ LOGARIT
 Ta thấy: x  0  1; x a a
b  0  b 1.
 Ta thấy: log x  0  a 1; log x  0  b 1. a b
 Ta thấy: x  1; x c c
d  d 1.
 Ta thấy: log x  c 1; log x  d 1. c d
So sánh a với b: Đứng trên cao, bắn mũi tên từ trái
So sánh a với b: Đứng trên cao, bắn mũi tên từ phải
sang phải, trúng x
a trước nên a b .
sang trái, trúng log x trước: b  . a b
So sánh c với d: Đứng trên cao, bắn mũi tên từ trái
So sánh c với d: Đứng trên cao, bắn mũi tên từ phải
sang phải, trúng x
c trước nên c d.
sang trái, trúng log x trước: d  . c d
 Vậy 0  b a 1 d  . c
 Vậy 0  a b 1 c d .
5. Phương trình mũ và logarit: Phương trình mũ
Phương trình Logarit 1. Dạng cơ bản:
1. Dạng cơ bản: f (x) g (x) aaf ( ) x g( ) x log f ( ) x  log g( ) x f ( ) x g( ) x  0 a a
2. Dạng logarit hóa:    f ( x)
2. Dạng mũ hóa: log f (x) b f (x) b a a
b f (x)  log b a a
(a, b  0, a  1) (không cần điều kiện) f ( x) g ( x) ab
f (x)  g(x).log b a
17 Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
3. Dạng đặt ẩn phụ:  Đặt f ( x) t a  0
 Đưa phương trình đã cho về bậc n theo t  
3. Dạng đặt ẩn phụ: giải tìm t .
 Đặt t  log f ( ) x a
 Với t có được, thay vào f ( x) t a để tìm x .
 Đưa pt đã cho về bậc n theo t   giải tìm t . a) Phương trình 2 f ( x) f ( x) . m a  . n ap  0
 Có t , thay vào t  log f ( )
x để tìm x . a • Đặt f ( x) t a  0 . a) Phương trình 2 m log
f (x)  n log f (x)  p  0 a a • PT: 2
mt nt p  0 .
• Đặt t  log f ( ) x a b) Phương trình g ( x) g ( x) g ( x) . m a  . n b  . p c  0 • PT: 2
mt nt p  0 • Nhận dạng: 2 f ( x) f ( x) 2 f ( x) ma  ( n . a ) b  . p b  0 b) Phương trình .
m log f (x)  . n log
a p  0 a f ( x)
• Chia hai vế PT cho 2 f (x) b  0 , ta được
• ĐK: f (x)  0, f (x) 1 2 f ( x) f ( x)  a   a mnp  0     . (Xem a)) 1     b   b
• Đặt t log f (x) log a a f ( x) t
Chú ý: Ta có thể chia PT cho bất kỳ hàm mũ nào n
trong ba hàm  g(x) g(x) g(x) a ;b ; c , kết quả không • PT: 2 mt
p  0  mt pt n  0 t thay đổi. log f (x) a c) Phương trình f ( x) f ( x) .
m (a b)
n(a b)  p
c) Phương trình đơn giản chứa log g(x) b • Nhận dạng: 2
(a b)(a b)  a b  1
• Đặt t  log f (x)  f (x) ta a • Đặ f x 1 t ( ) f ( x)
t  (a b) , t  0   (a b)
• Thay trở lại phương trình, ta có một phương t
trình mới đơn giản hơn (chứa ít logarit hơn). • PT: n 2 mt
p mt pt n  0 t
6. Bất phương trình mũ và logarit:
Bất Phương trình mũ
Bất Phương trình Logarit  Dạng cơ bản: a 1  f ( x) g ( x)  aa
f (x)  g(x) a 1   Dạng cơ bản:
 log f (x)  log g(x)  f (x)  g(x)  0 a a 0a 1  f ( x) g ( x)  aa
f (x)  g(x) 0a 1 
 log f (x)  log g(x)  0  f (x)  g(x) a a
Lưu ý: Cách nhận dạng bất phương trình mũ-logarit cũng giống với cách nhận dạng phương trình mũ-
logarit. Học sinh tham khảo kỹ mục 5 để có phương pháp giải bất phương trình một cách hiệu quả.
X. NGUYÊN HÀM – TÍCH PHÂN
1. Công thức nguyên hàm:
f (x)dx F (x)  C F (
x)  f (x) 
k. f (x)dx k f (x)dx  
   f (x) g(x)dx f (x)dx g(x)dx    f (
x)dx f (x)  C
1) kdx kx C  
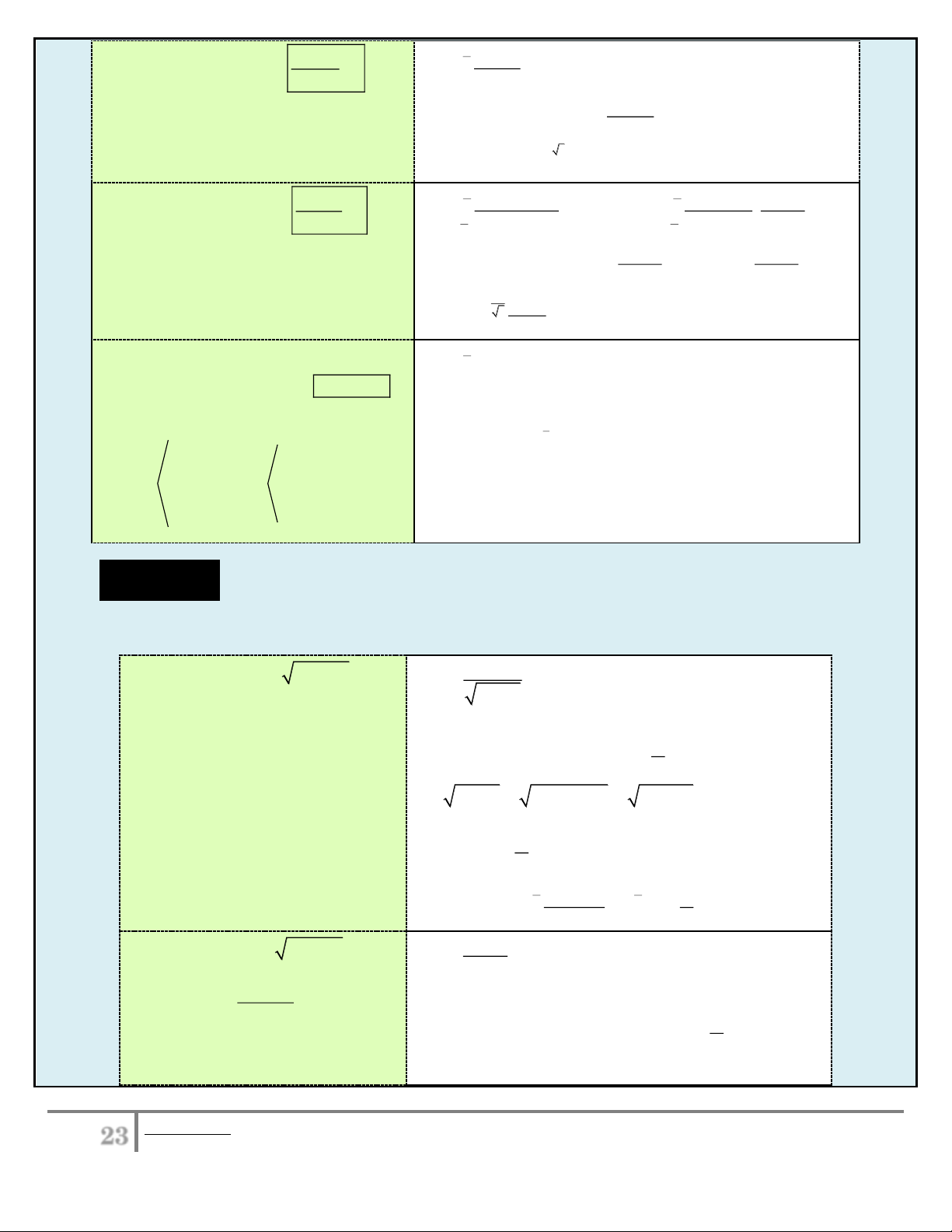
2dx  2x C   ( 3  )dx  3  x C   1  3 2)  x 4 x dx   Cx 1 2  3     x 2 3 1 x dx C   2 xdx x dx   C x C   4  3 / 2 3 1   ax b MR 1 ( )
 (ax b) dx  .  C  11 11   a  1  1 (1 2x) (1 2x) 10 (1 2x) dx  .  C   C  2  11 2  2
18 Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com 3) 1 1 1 MR 1 1
dx  ln x C  dx
ln ax b C    dx  ln 1 3x Cx ax b a 1 3x 3  4) 1 1  1 1 1  1 MR 1 1 1 dx    C  dx  .  C    dx  .  C    C  2 2 x x (ax b) a ax b 2 (2x  3) 2 2x  3 4x  6 3  1 1  x 1 5 5 x 1  1  x  2 x   10 dx
 ln x  10x C     4 dx x dx   ln x C     2  x x  3 x xx  5 5) x 1 x x MR axb 1    ax b
e dx e C  e dx eC    x x e dx e
C  e Ca 1  x x x 6) a x x 9 x 5 x a dx   C   5 dx   C   2 3 dx  9 dx   C   ln a ln 5 ln 9  1 bxc a 2 x5 2 x5 MR bx c  a dx  .  C   x 1 3 3 2 5 3 dx  .  C   Cb ln a 2 ln 3 2 ln 3 x xx xx 1   x xx x 1 1 x 6   1  2    2 1 2  2 x 1   2 x e e dx e e dx e e C  1 2 .3 dx  2 .3 . dx  6 dx   C    2 3 3 3ln 6
7) sin xdx  cos x C         1 sin 4x dx   cos 4x   C          MR 1  2 4 2
sin(ax b)dx  
cos(ax b)  Ca
a4; b  2 8)        
cos xdx  sin x C    1 cos  x dx  sin
x C  sin  x C         3  1   3   3  MR 1
 cos(ax b)dx  sin(ax b)  C   a a 1;  b 3 1 1  1     2
3sin x  2 cos xdx  3
 cos x  2sin x C  sin xdx  
 1cos2xdx x sin2x C   2 2  2  2 1 2 cos x  1       9) 1  dx 2 dx tan x 2x C     dx     2
1 tan x dx  tan x C 2 2   2  cos x cos x cos x 1 1 MR 1 1     dx
tan ax b Cdx tan 3x C  2 2
cos ax b   a cos 3x 3   1 MR 1 2  1   tan 
axbdx  tanaxbC        2 1 tan 
 2xdx  tan  2xC a   2  
a  2; b    2 2 10) 1 x sin x 1  1  x dx     2
1 cot x dx   cot x C dx x dx   cot x C   2    sin x 2 2 sin x  sin x  2 MR 1 1  dx  
cot ax b C  1 1    2  dx cot 8x C
sin ax b   a 2 sin 8x 8 1 MR 1 2  1   cot 
axbdx   cotaxbC      2
1 cot 3xdx   cot 3x C a 3 2 2 1 sin x  cos x  1 1   dx dx  
dx  tan x  cot x C      2 2 2 2 2 2 sin x cos x sin x cos x
 cos x sin x
19 Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com 2. Tích phân: b b a) Định nghĩa: f
 xdx F x  F bF a với F x là một nguyên hàm của f x trên a;b. a a b) Tính chất: a b a f
 xdx  0 f
 xdx   f  xdx a a b b b b b kf  xb dx k f
 xdx (k là hằng số)  f
  x gxdx f
 xdxg  xdx a a a a a c b b b f  xb dx f  xc dx f  xdx f
 xdx f
 tdt f  udu a a b a a a b
Nếu f x  0, x
 a;b thì f
 xdx  0. a b b
Nếu f x  g x, x
 a;b thì f
 xdx g
 xd .x a a Đặc biệt: a
Nếu hàm y f x là hàm số lẻ trên a; a thì f
 xdx  0. aa a
Nếu hàm y f x là hàm số chẵn trên a; a thì f
 xdx  2 f
 xdx . a 0
3. Phương pháp tính tích phân:
a) Phương pháp tích phân từng phần: b b b Quy tắc chung: I  . u dv uv vdu  
. Ta xét các dạng phổ biến sau: a a a bMinh họa: Dạng
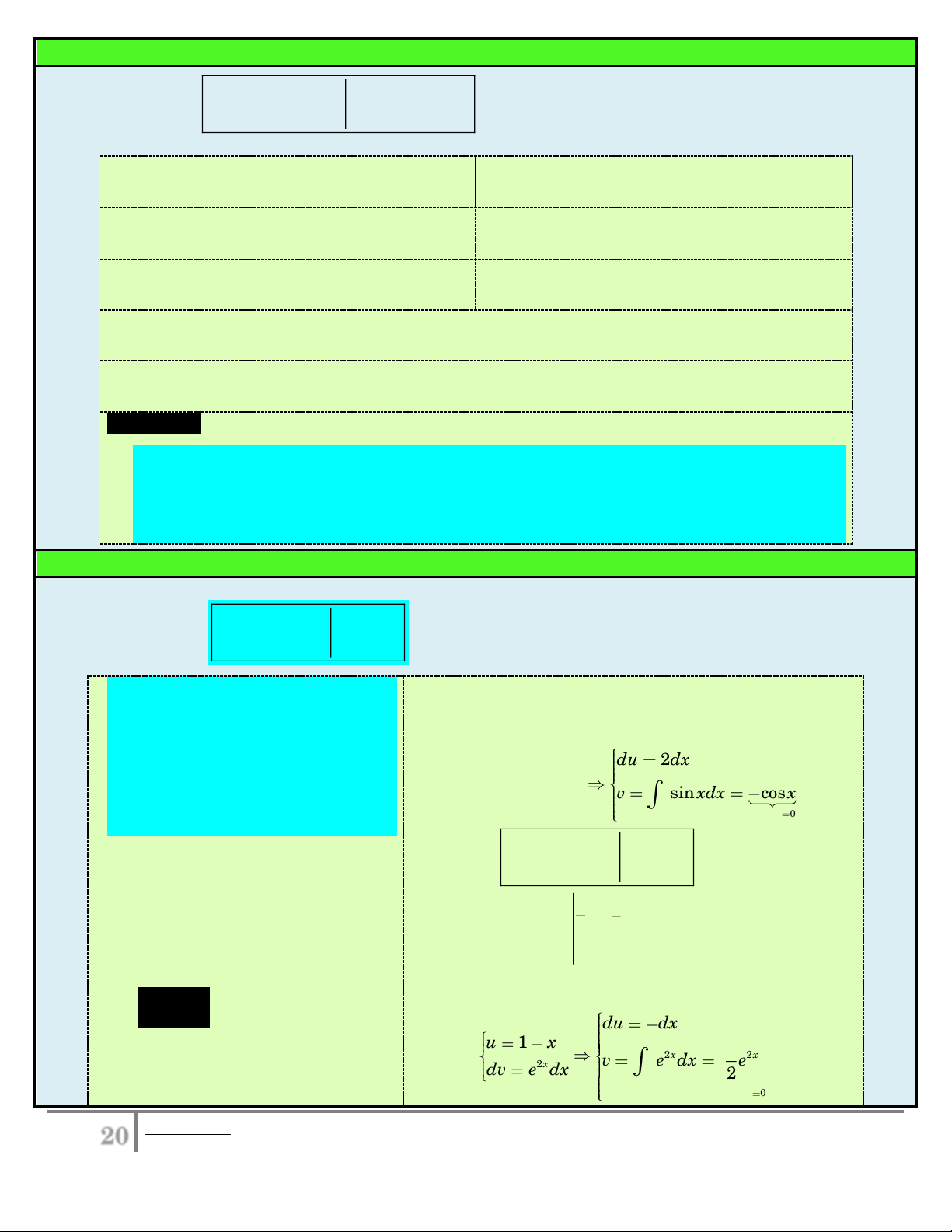
P x.Q x.dx với a  2 I  2x    1 sin xdx .
P x là đa thức đại số, Q x 0 du 2dx u   2x 1
là hàm lượng giác hoặc hàm Đặt 
dv  sin xdx v sin xdx cosx . mũ. choïn C 0 u   P  xb b b Ta có: I  . u dv uv vdu   PP  a a adv Q  xdx   
du P xdx    2x   2    1 cos x 2 2 cos xdx ......  0
v Q xdx   . 0 1   1   2x J x e dx .
Lưu ý: v Q
 xdx nên kết 0 du dx u 1 x x 1
quả có dạng R x  C , ta chủ Đặt 2 2x . 2x v e dx e dv e dx 2 choïn C 0
20 Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
động chọn 1 giá trị C có lợi cho 1  1  1 1 x 1 2 2 x J x ee dx  ......  tính toán sau này. 0 2 0 2 bMinh họa: Dạng
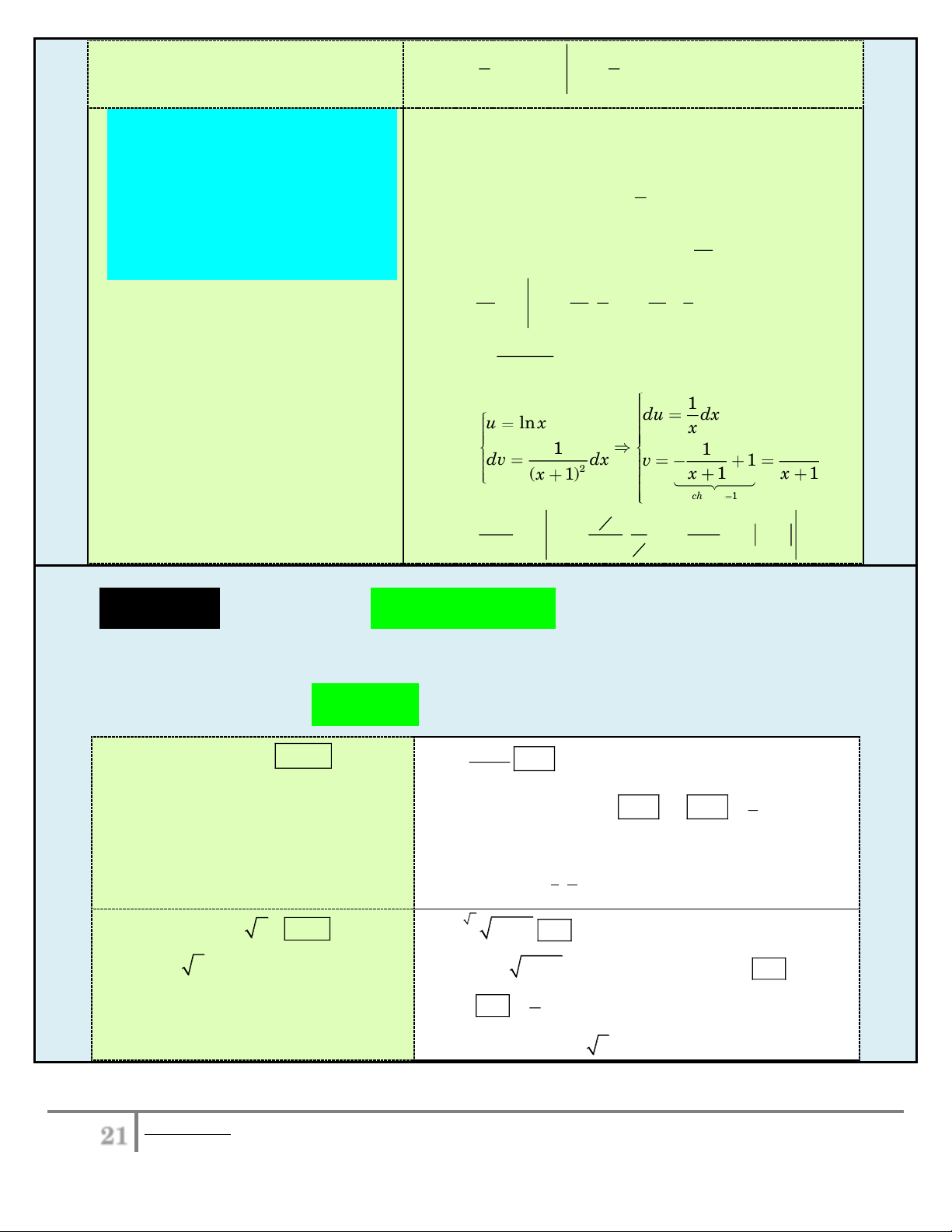
P x.Q x.dx với a e  2 I x ln xdx  . 1
P x là đa thức đại số hoặc  1 du dx u   ln x  x
phân thức, Q x là hàm Đặt    . 2 3 dv x dx x  2 v x dx   logarit.  3 3 3 3 u   Q  xx e e x 1 e 1 e 2      PP  I ln x . dx x dx ......   1 1  3 1 3 x 3 3 dv P  xdx e ln x
du QxdxJ   .   x  2 1  1
v P xdx   . 1 ln du dx u x x Đặt 1 1 x dv dx . v 1 2 (x 1) x 1 x 1 choïn C 1 x e e x 1 e e J  ln x  . dx   ln x 1  ...  1 x 1 1 x 1 x e 1 1
b) Phương pháp tích phân đổi biến: b
Đổi biến loại 1: Xét tích phân dạng I f u
  x.u
 xdx . a PP
 Đặt t u x  dt u xdx . Đổi cận: x a t u a , x b t u b . 2   1   Khi đó tích phân cầ t n tính là: 2 I f
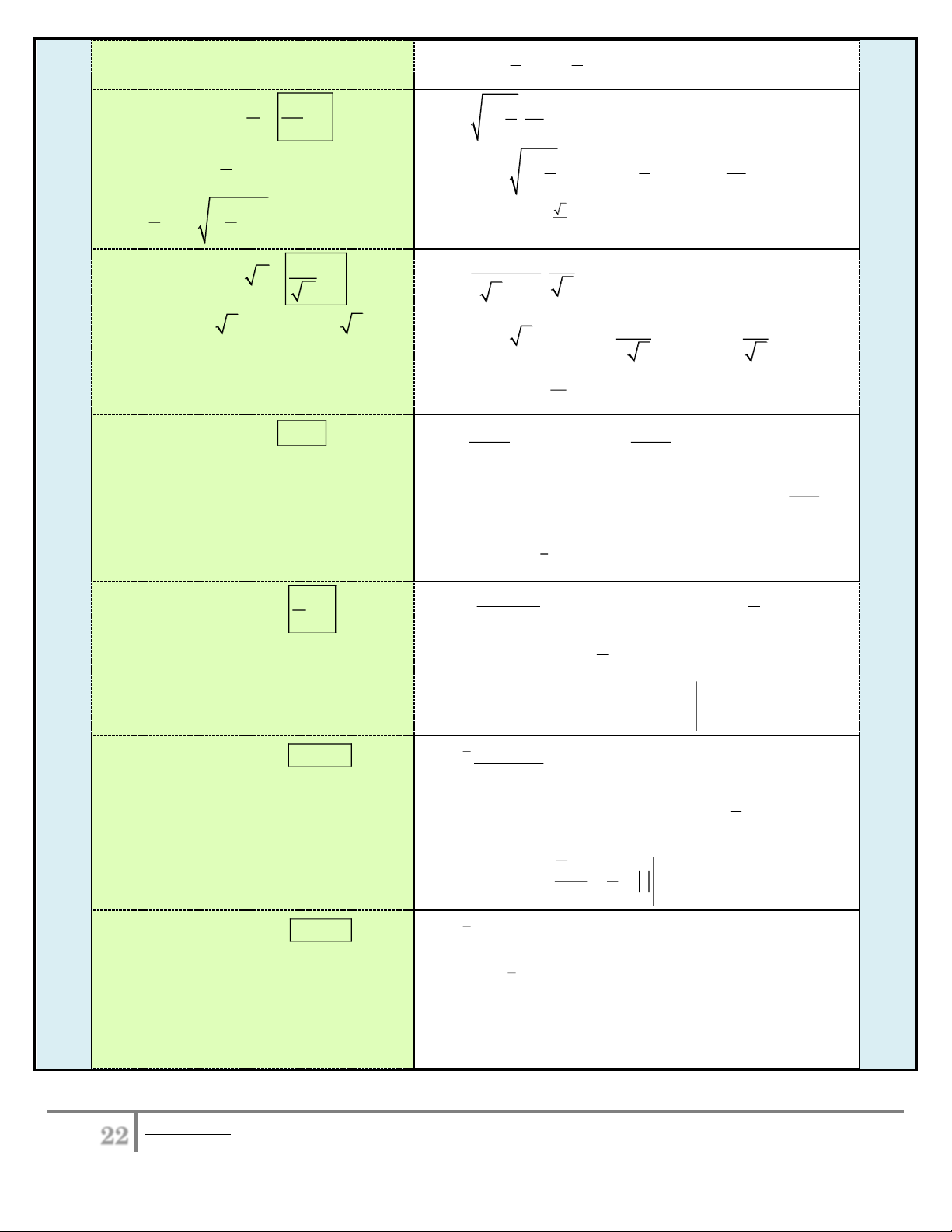
 tdt . Ta xét các dạng phổ biến sau: 1 t b  1 1 1) Dạng n n 1 I
f ( x ) x dx. 2 I x dxa 3 0 x 1 PP n
t x   (hoặc n
t x )  1 Đặt 3 2 2
t x 1  dt  3 x dx x dx dt . 3
 Đổi cận: x  0  t 1, x 1 t  2.  2 1 1 Ta có: I  . dt  ......  1 t 3 b 7 2) Dạng I f
 n u udx . 3 2 I x 1. xdxa. . 0 PP n n
t u t u .  Đặt 3 2 3 2 2 t
x 1  t x 1 3t dt  2 xdx 3 2
xdx t dt . Đổi cận: 2
x  0  t  1, x  7  t  2 .
21 Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com  2 2 3 3 2 3 I t. t dt t dt  ......   1 1 2 2 b1 1 4 1 1 3) Dạng I f . .dx    . I  1 . dx2 a
x x 2 1 x x PP 1
t  .   hay  1 1 1 Đặt 2 t  1
t 1  2tdt dx . x 2 x x x 1 1  3 ; n t t     v.v…  2 2   x x Ta có: I 2 t .dt ......  0 b 4 1 1 4) Dạng I f x dx. I  . dx  2 a   1 . . 1 x   1 x x PP
t   x   hay t x...  1 1
Đặt t x 1  dt dx  2dt dx . 2 x x  3 1 Ta có: I  .2dt  ......  . 2 2 t b 2 x x 5) Dạng I f
  xe. xe.dx . 1 e 1 e I dxx   I e dx  . a 0 x e 1 0 x e 1 PP x
t e   hay x t e . x     dt e dx e 1  t 1 Đặt x
t e 1   . Khi đó: I dt  . x
e t 1 2 te 1   1  I  1 dt  ......    2  t  2  2 b e 2 ln x 1 e 1 6) Dạng I f
  x1 ln . .dx . I dx    I  2ln x    1 . dx . a x 1 x 1 x PP  1
t   ln x   hay t  ln x .
 Đặt t  ln x dt dx . x  2 2
Khi đó I   2t   1 dt   2
t t   ...... 0 0 b7) Dạng I
f (sin x). cos xdx cos x 2 I dxa 0 1 2sin x PP
t  sin x   hay t  sin x .  1
Đặt t  1 2sin x dt  2 cos xdx
dt  cos xdx . 2 1 dt  3 1 3 Khi đó 2 I   ln t  ......  . 1 t 2 1 b8) Dạng I
f (cos x). sin xdx. 2 I
cos2x cos x    1 sin xdx a 0 PP
t  cos x   hay t  cos x   I    2 2
2cos x  cos xsin xdx . 0
 Đặt t  cos x dt  sin xdx  dt  sin xdx .  0 1
Khi đó: I    2
2t t (dt)    2
2t t dt  ...... 1 0
22 Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com  3 b 1 tan x 9) Dạng I
f (tan x) dx. 3 I dx2 a cos x 2 0 cos x PP
t  tan x   hay t  tan x .  1
Đặt t  tan x dt dx . 2 cos x  3 Khi đó: 3 I t dt  ......  0  2  2 b 1 cot x 1 cot x 1 1 10) Dạng I
f (cot x) dx. 3 I dx  3   I  . dx  . 2   a sin x 2 cot . x sin x 2 cot x sin x 4 4 PP
t  cot x   hay t  cot x .  1 1
Đặt t  cot x dt   dx  dt dx . 2 2 sin x sin x 1 2   t 1 3 I   dt  ...... 1 t 2   sin x I    2 4
sin x  3sin 2xdx b   0 11) Dạng 2 I f
 cos x sin2x.dx . a    Đặt 2
t  sin x dt  2sin ( x sin ) x d
x  sin 2xdx . cos 2x   1  2    2 Ta có: I
 t 3dt ...... t  sin x dt  sin 2 . x dx 0 PP 2
 t  cos x dt  sin 2 . x dx t  cos 2x dt  2  sin 2 . x dx b
Đổi biến loại 2: Xét tích phân dạng I f
 xdx trong đó f x phức tạp và không thể tính nguyên hàm a
trực tiếp. Đổi biến loại 2 là ta đặt: x u t   dx ut dt . Ta xét 4 dạng phổ biến sau: x2 2 1 1) Dạng 2 2 I
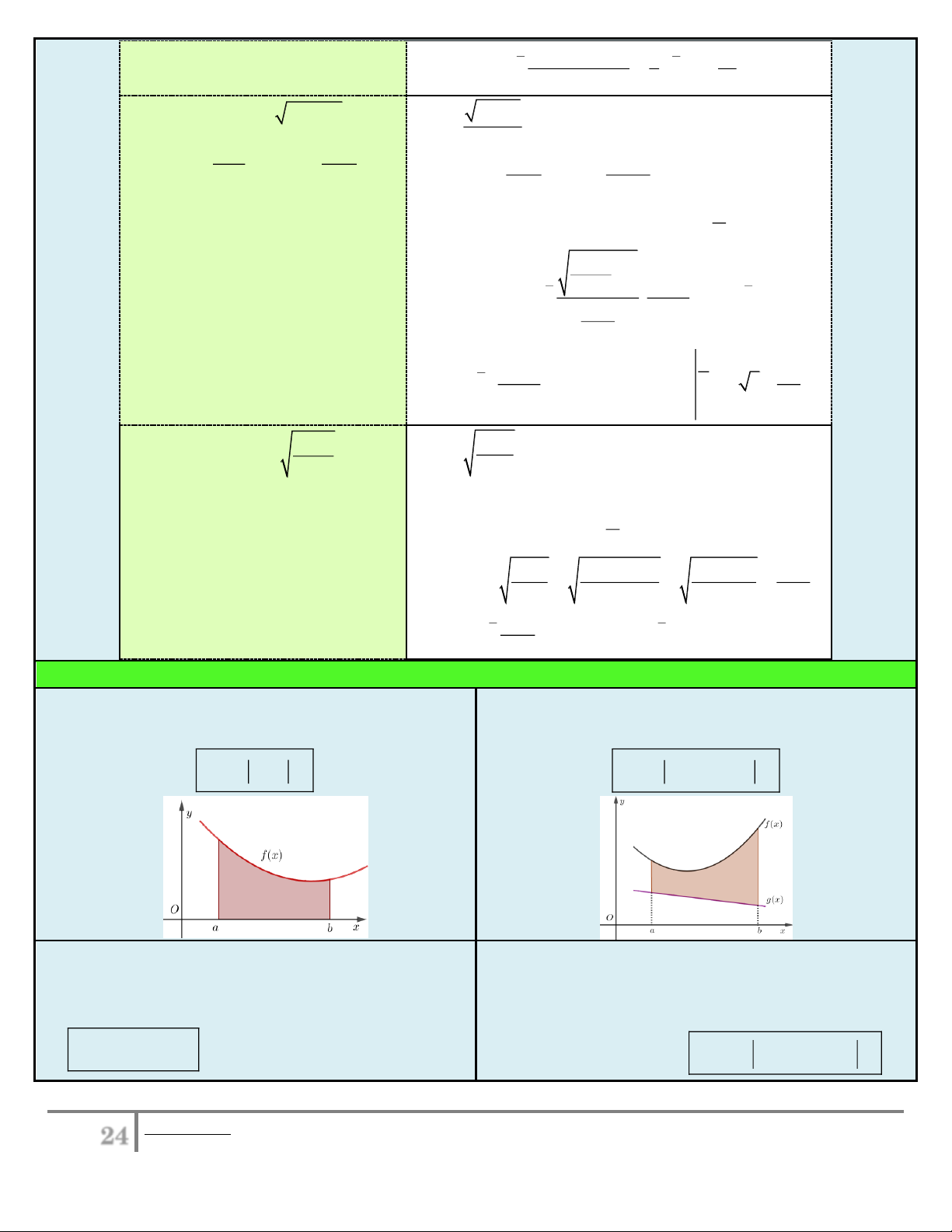
f ( a x )dx. I dxx1 0 2 4  x PP
x asint (hay x a cost ).  Đặt x  2sint dx  2costdt . Đổi cận: 
x  0  t  0, x  2  t  . Ta có: 2 2 2 2
4  x  4  4sin t  4 cos t  2 cos t 0    do t  0; .    2     2 cos tdt  Ta có: 2 2 I   dt  .   0 0 2 cos t 2 x2 3 1 2) Dạng 2 2 I
f ( a x )dx I dxx 2 1 0 x  9 x   2 1      hay f dx    . Đặt 2 x 3tan t dx 3(1 tan t)dt . 2 2 x   1 a x    Đổ x   t x   t PP  i cận: 0 0, 3 .
x a tan t . 4  Khi đó: 2 2 2
x  9  9 tan t  9  9(tan t 1) .
23 Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com  2     3(1 tan t)dt 1 Vậy 4 4 I   dt  .   2 0 0 9(tan t 1) 3 12 x2 2 3) Dạng 2 2 I
f ( x a )dx 4 x  4  x I dx1 2 x a a PP  x
hay x  2 2sin t sin t cos t  Đặt x   dx dt . 2 cos t cos t  
Đổi cận: x  2  t  0, x  4  t  . 3 4   4   2 cos t 2sin t Khi đó: 2 3 3 I  . dt  2 tan t.dt   2 0 0 2 cos t cos t    1  2 3  2
1 .dt  2 tan t t    3  2 3  . 2   0  cos t  3 0    x 2 2  x 2 a x 4) Dạng I f    dx   I dxx  0  1 a x   2 x        PP  Đặ
x a cos 2t . t x 2cos 2t dx 4sin 2 . t dt 8sin . t cos . t dt  
Đổi cận: x  0  t
, x  2  t  0. 4 2  x 2  2 cos 2t 1 cos 2t sin t Ta có:    . 2  x 2  2 cos 2t 1 cos 2t cos t    sin t 2 4 4 I  8
sin t.cos tdt  8 sin tdt  ......   0 0 cos t
4. Ứng dụng tích phân để tính diện tích – thể tích:
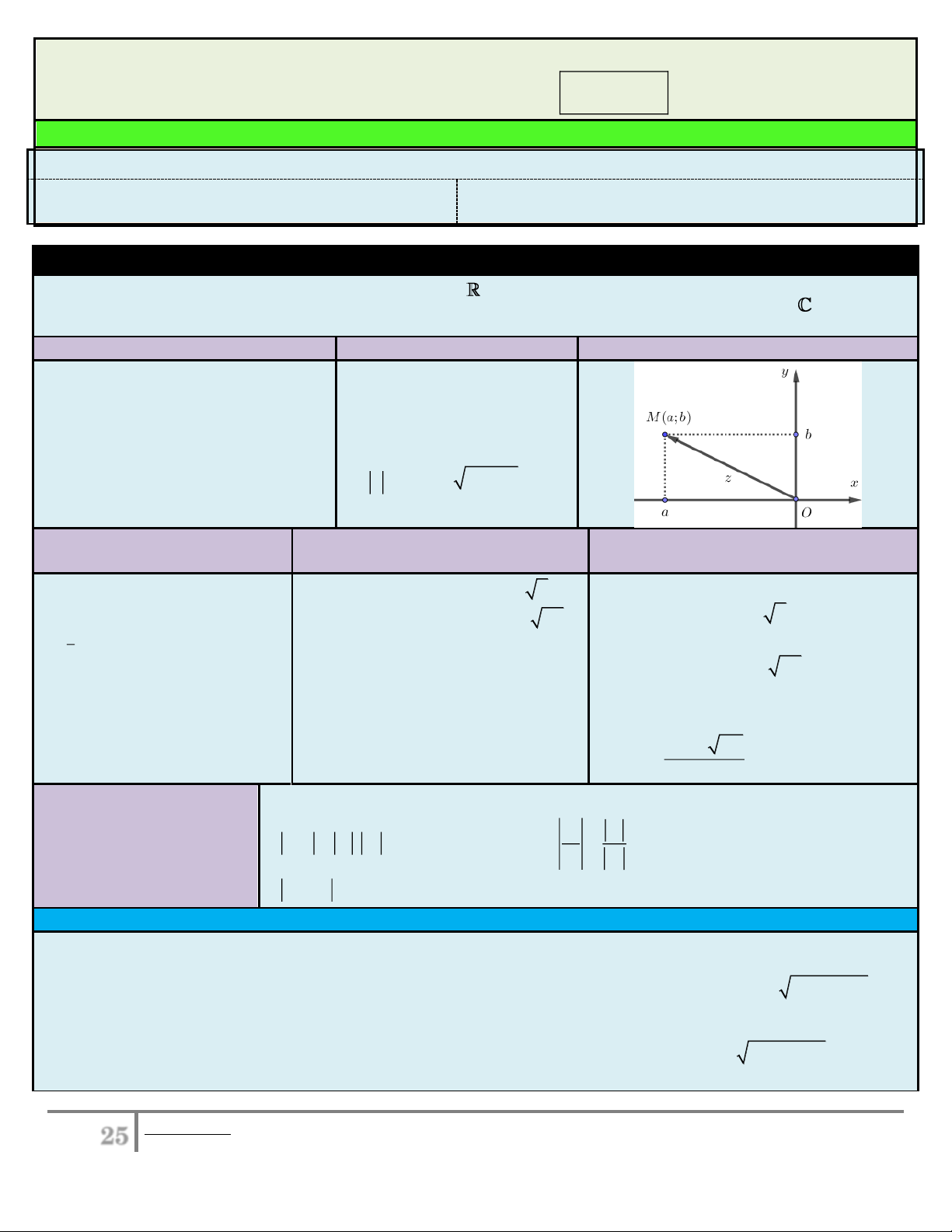
 Hình phẳng giới hạn bởi các đường y f (x) , trục
 Hình phẳng giới hạn bởi các đường y f (x) ,
Ox , x a, x b thì có diện tích:
y g(x) , x a, x b thì có diện tích: b b S f (x) dxS
f (x)  g(x) dxa a
y f (x)
y f (x)  Khi xoay hình phẳng  quanh Ox , ta  x  , a x b
 Khi xoay hình phẳng y g(x) quanh Ox , được 
được khối trụ tròn có thể tích
x a, x bb 2 b V   f (x)dx
khối trụ tròn có thể tích 2 2 V  
f (x)  g (x) dx  . a a
24 Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
 Xét hình khối được giới hạn bởi hai mặt phẳng x a, x b . Khi cắt khối này ta được thiết diện có diện tích b
S(x) (là hàm liên tục trên [a;b]). Thể tích khối này trên a;b là: V S(x)dx  . a
5. Công thức chuyển động:
Xét hàm quảng đường S(t), hàm vận tốc v(t) và hàm gia tốc a(t) . Ba hàm này sẽ biến thiên theo t .  S(t) 
v(t)dt v(t)  S (  t)   v(t) 
a(t)dt a(t)  v (  t)  [
XI. SỐ PHỨC VÀ CÁC YẾU TỐ LIÊN QUAN
a, b
Số phức có dạng: z a bi với
(i: là đơn vị ảo). Ký hiệu tập số phức: . 2
i  1 Thành phần Hình học Minh họa
Phần thực: a.
Nếu a  0 thì z bi được gọi là  Điểm M ( ; a ) b biểu diễn số thuần ảo.
cho z trên hệ trục Ox . y
Phần ảo: b.Mô-đun:
Nếu b  0 thì z a là số thực. 2 2    
Khi a b  0 thì z  0 vừa là số z OM a b .
thuần ảo vừa là số thực.
Số phức liên hợp – Hai số Căn bậc hai phức bằng nhau
Phương trình bậc hai
Cho z a bi và z  a  b i
 Căn bậc hai của a  0 là  a.  Phương trình 2
z a  0 có hai Khi đó:  
nghiệm phức z   a. 
 Căn bậc hai của a  0 là i a .
Số phức liên hợp của z là
 Căn bậc hai của số phức  Phương trình 2
z a  0 có hai
z a bi .
z a bi là hai số phức dạng nghiệm phức     z i a . a a  2 2
z z   .
x y a  Phương trình 2
az bz c  0 (a  0) b   b
w x yi với  . 2xy b
với   0 sẽ có hai nghiệm phức là: a  0  z  0   .
b i   b   0 z . 1,2 2a
Cho hai số phức z , z , có: 1 2 z z Công thức bổ trợ 1
▪ z z z . z . ▪ 1  với z  0. 1 2 1 2 z z 2 2 2
▪ z z MN với M, N theo thứ tự là hai điểm biểu diễn cho z , z . 1 2 1 2
Dấu hiệu cơ bản nhận biết tập hợp điểm M biểu diễn cho số phức z
ax by c  0 KL
 Tập hợp điểm M một là đường thẳng.
xa2 y b2 2  R   KL
 Tập hợp điểm M là đường tròn có tâm I a;b , bán kính 2 2
R a b c . 2 2
x y  2ax  2by c  0
xa2 y b2 2  R   KL
 Tập hợp điểm M là hình tròn tâm I a;b , bán kính 2 2
R a b c . 2 2
x y  2ax  2by c  0
25 Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com 2
y ax bx cKL
 Tập hợp điểm M là đường parabol. 2
x ay by c 2 2  x y  1 KL
 Tập hợp điểm M là đường elip. 2 2 a b
Đặc biệt: Nhận biết ngay không cần biến đổi.
z  a bi  m  0 KL
 Tập hợp điểm M là đường tròn có tâm I a;b , bán kính R m .
z a bi z a b i MA MB KL
 Tập hợp điểm M là đường trung trực đoạn thẳng AB. 1 1   2 2   A 1 a ; 1 b , B 2 a ; 2 b
z a bi z a b i  2a MF MF  2a KL
 Tập hợp điểm M là đường elip với hai tiêu điểm F , F . 1 1   2 2  1 2 1 2 0 0 1 F  1 a ; 1 b , 2 F  2 a ; 2 b   1 F 2 F 2a
XII. KHỐI ĐA DIỆN VÀ THỂ TÍCH CỦA CHÚNG
A – MỘT SỐ HÌNH PHẲNG CƠ BẢN: 1. Tam giác vuông: Pitago 1 ▪ 2 2 2  AB ACBC ▪ 2
AB BH.BC S A . B AC ABCA 2 ▪ 2
AC CH.BC ▪ 2
AH BH.CH 1  AH.BC 2 B C ▪ 1 1 1   A . B ACAH  2 2 2 H AH AB AC 2 2 AB AC ▪ AC AB AC AB sin B  (đối/huyền) ▪ cos B  (kề/huyền) ▪ tan B  (đối/kề) ▪ cot B  (kề/đối) BC BC AB AC 2. Tam giác đều:
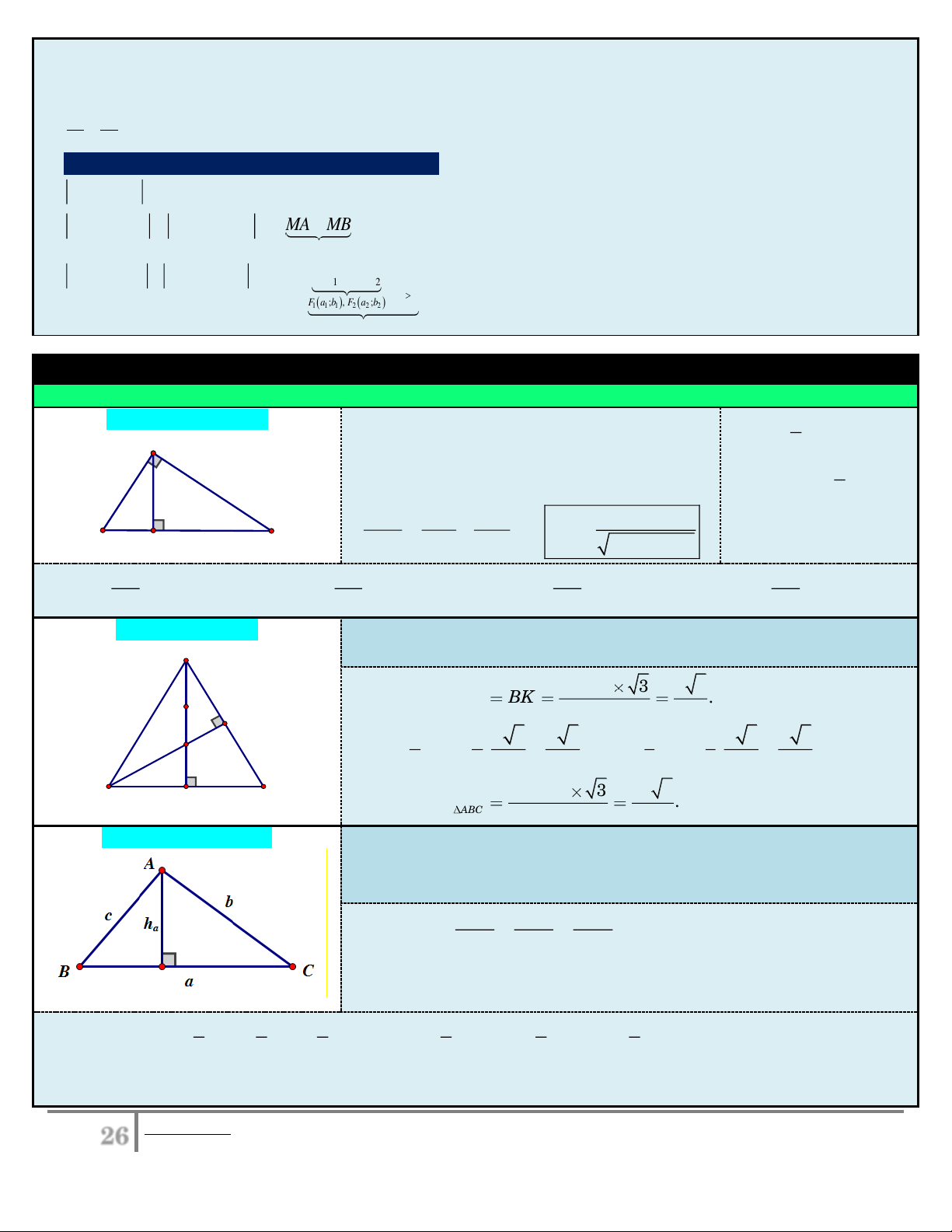
Giả sử tam giác ABC đều có cạnh ; a trọng tâm ;
G các đường cao (trùng A
với trung tuyến) gồm AH , BK. (caïn ) h 3 a 3 a ▪ Đường cao: AH BK . 2 2 a K G ▪ 2 2 a 3 a 3 1 1 a 3 a 3 AG AH  .  ; GH AH  .  . 3 3 2 3 3 3 2 6 C 2 2 B H (caïn ) h 3 a 3 a ▪ Diện tích: S . ABC 4 4
3. Tam giác thường:
Giả sử tam giác ABC có a BC, b AC, c AB ; các đường cao
h , h , h lần lượt ứng với cạnh , a , b . c Ký hiệu ,
R r lần lượt là bán kính a b c
đường tròn ngoại tiếp và nội tiếp ∆. ▪ Định lí Sin: a b c    2R . sin A sin B sin C ▪ Định lí Cô-sin: 2 2 2
a b c  2b . c cos A ; 2 2 2 2 2 2
b a c  2a . c cos ;
B c a b  2a . b cos . C ▪ Diện tích: 1 1 1 1 1 1 S
h .a h .b h .c ; Sa . b sin C a . c sin B b . c sin A ; ABC  2 a 2 b 2 c ABC 2 2 2
26 Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com abc a b c S   pr ; S ( p p ) a (p ) b (p ) b vôùi p (nửa chu vi). ABC  4R ABC 2
Coâng thöùc Heâ Roâng 4. Hình vuông:
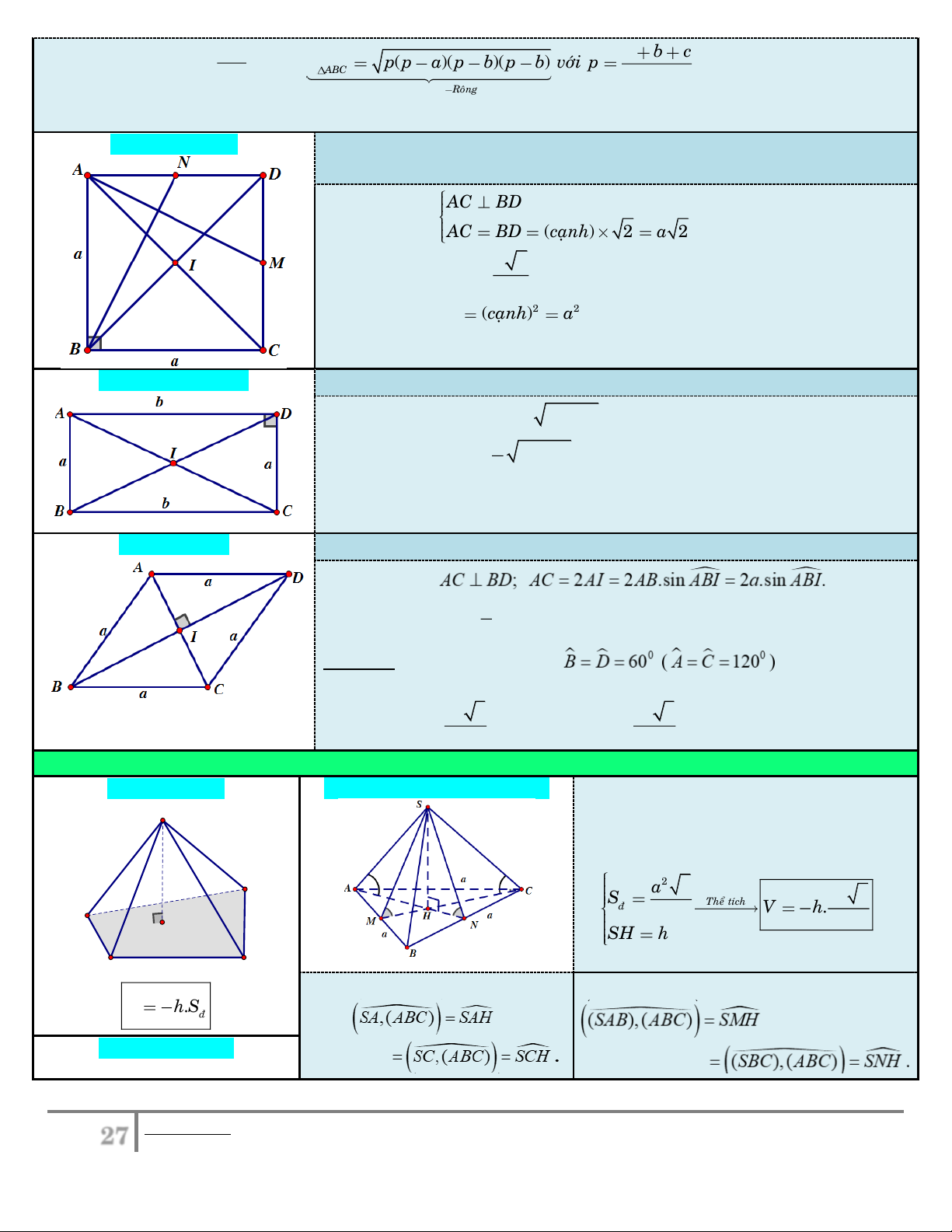
Cho hình vuông ABCD có cạnh ;
a hai điểm M , N lần lượt là trung điểm của C , D A ;
D I là tâm hình vuông. AC BD ▪ Đường chéo: . AC BD (caïn ) h 2 a 2 I a 2     IA IB IC ID
nên I là tâm đường tròn ngoại tiếp hình vuông. 2 ▪ Diện tích: 2 2 S (caïn ) h aABCD ; chu vi: p 4 . a ▪ Vì ABN A
DM , ta chứng minh được: AM BN. 5. Hình chữ nhật:
Cho hình chữ nhật ABCD tâm I có AB  , a AD  . b ▪ Đường chéo: 2 2
AC BD a b . 1 2 2
IA IB IC ID
a b nên I là tâm đường tròn đi qua bốn điểm 2 , A , B C, . D ▪ Diện tích: S  .
a b ; chu vi: p  2(a  ) b . ABCD 6. Hình thoi:
Cho hình thoi ABCD có tâm I , cạnh bằng . a
▪ Đường chéo: AC B ;
D AC  2AI  2A .
B sin ABI  2 . a sin ABI. ▪ Diện tích: 1 S
AC.BD ; S  2S  2S  2S . ABCD    2 ABCD ABC ACD ABD
Đặc biệt: Nếu hình thoi có góc 0 B D  60 ( 0
A C 120 ) thì ta chia hình
thoi ra làm hai tam giác đều: ABC AC ;
D AC a và 2 a 3 2 a 3 SS  ; S  2S  . ABCACD  4 ABCD ABC 2
B – THỂ TÍCH KHỐI CHÓP: 7. Hình chóp:
7.1. Hình chóp tam giác đều
▪ Tất cả cạnh bên bằng nhau. S
▪ Đáy là tam giác đều cạnh . a
▪ SH  (ABC) với H là trọng tâm (cũng là trực tam) ∆ . ABC h 2 D a 3 2 S Theå tích 1 a 3 ▪ ñ V . A 4 h H 3 4 SH h Sđ B C 1
Góc giữa cạnh bên và mặt
Góc giữa mặt bên và mặt đáy: V . h S 3 ñ
đáy: S ,
A ( ABC)  SAH
(SAB),(ABC)SMH
7.2. Tứ diện đều:
 SC,(ABC)  SCH
 (SBC),(ABC)  SNH .
27 Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
▪ Đây cũng là hình chóp tam
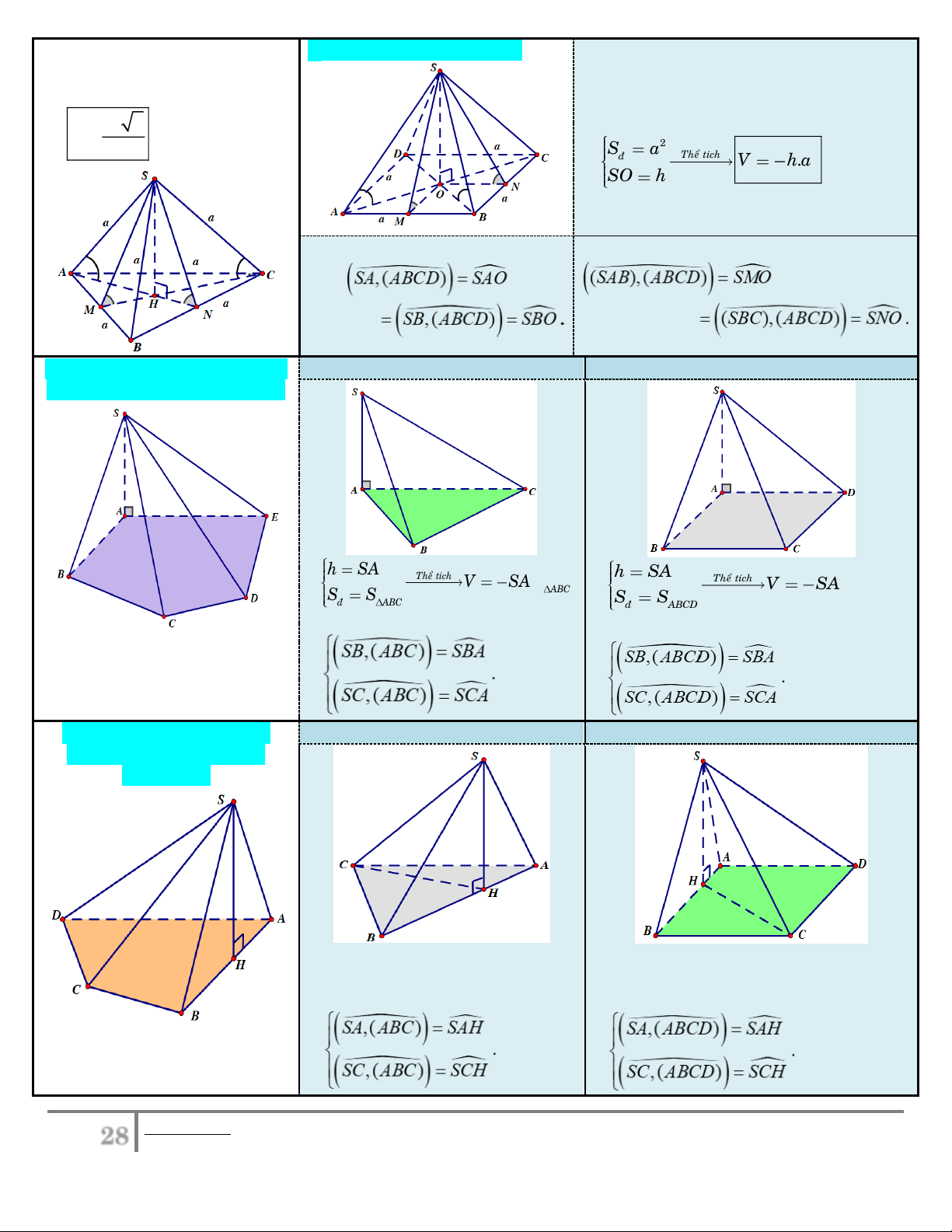
7.3. Hình chóp tứ giác đều:
▪ Tất cả cạnh bên bằng nhau.
giác đều, đặc biệt là cạnh bên
▪ Đáy là hình vuông cạnh . a
bằng cạnh đáy. Thể tích:
▪ SO  (ABC )
D với O là tâm hình vuông 3 a 2 ABC . D V  . 2 12 S a ñ Theå tích 1 ▪ 2 V . h a . SO h 3
Góc giữa cạnh bên và mặt
Góc giữa mặt bên và mặt đáy: đáy: S ,
A ( ABCD)  SAO
(SAB),(ABCD)SMO  S ,
B ( ABCD)  SBO .
 (SBC),(ABCD)  SNO .
7.4. Hình chóp có cạnh bên SA Đáy là tam giác
Đáy là tứ giác đặc biệt
vuông góc với mặt phẳng đáy. h SA Theå tích 1 ▪ V S . A S h SA Theå tích 1 V S . A S S S 3 ABC ▪ ABCD . ñ ABC S S 3 ñ ABCD
▪ Góc giữa cạnh bên và mặt đáy:
▪ Góc giữa cạnh bên và mặt đáy: SB,(ABC)   SBASB,(ABCD)   SBA  .  .  SC,(ABC) SC,(ABCD)    SCASCA
7.5. Hình chóp có mặt bên Đáy là tam giác
Đáy là tứ giác đặc biệt
(SAB) vuông góc với mặt phẳng đáy.
▪ Đường cao h SH cũng là
▪ Đường cao h SH cũng là đường cao
đường cao của ∆SAB. của ∆SAB.
▪ Góc giữa cạnh bên và mặt đáy:
▪ Góc giữa cạnh bên và mặt đáy:
S ,A(ABC)    SAH
S ,A(ABCD)  SAH  .  .  SC,(ABC) SC,(ABCD)     SCHSCH
28 Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
C – TỈ SỐ THỂ TÍCH KHỐI CHÓP
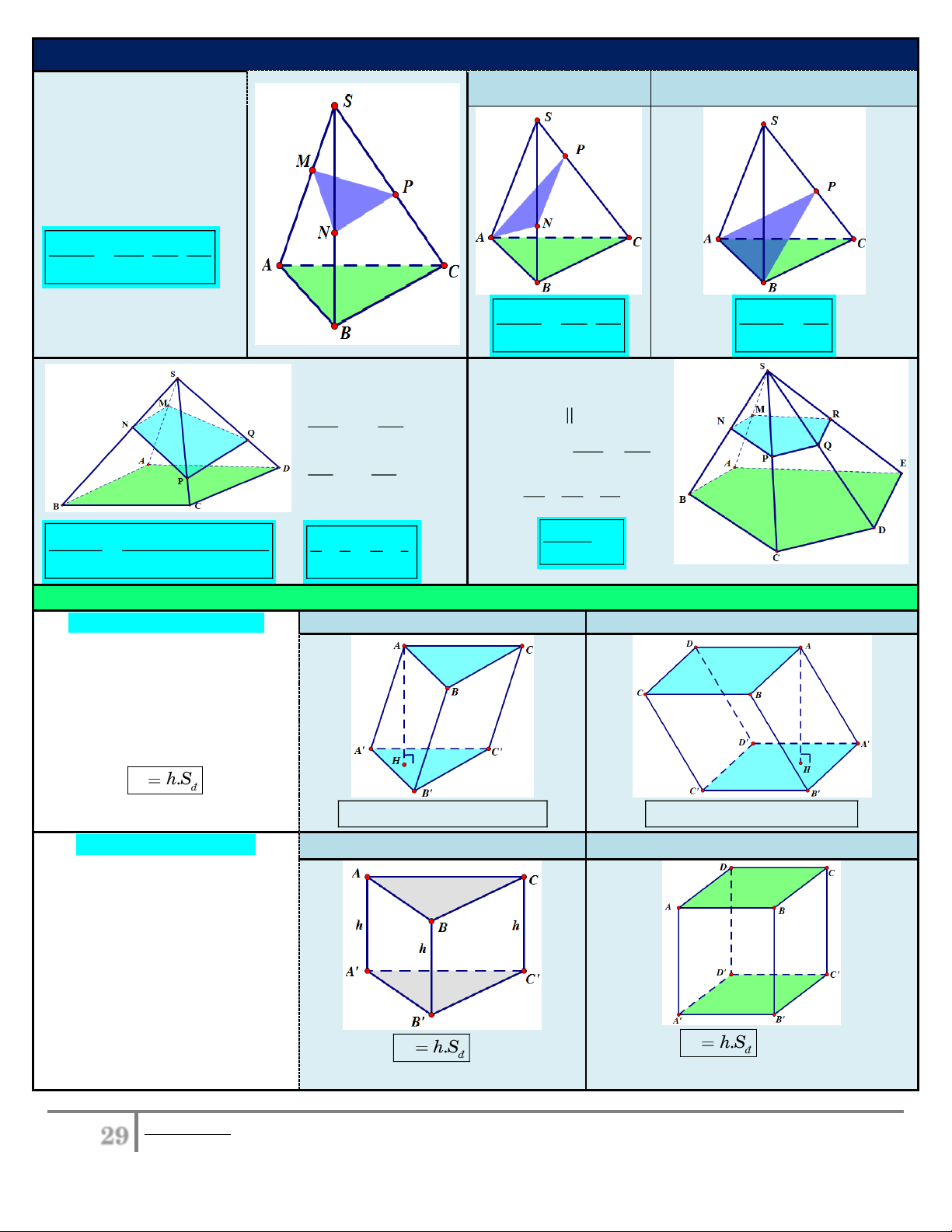
Đặc biệt: M A Đặc biệt M  , A N B Cho hình chóp có đáy là
tam giác ABC. Các điểm
M, N, P nằm trên cạnh SA, SB, SC. Ta có: V SM SN SP S .MNP  . . . V SA SB SC S . ABC V SN SP V SP S . ANP  . S .ABP V SB SC V SC S .ABC S . ABC
Hình chóp có đáy là Hình chóp có đáy là đa hình bình hành với
giác bất kỳ. Chẳng hạn: SM SN (MNPQR) (ABCDE) x,  y, SA SB SM và tỉ số: x SNSP SQ SA SB z,  t . SC SD SP SQ SR    Khi đó: SC SD SE V   
Khi đó: VS.MNPQR 3 S .MNPQ xyz xyt xzt yzt  1 1 1 1  x và    . V V 4 x z y t S . ABCDE S . ABCD
D – THỂ TÍCH KHỐI LĂNG TRỤ:
1. Hình lăng trụ thường: Đáy là tam giác Đáy là tứ giác
 Hai đáy là hai hình giống nhau
và nằm trong hai mặt phẳng song song.
 Các cạnh bên song song và
bằng nhau. Các mặt bên là các hình bình hành.  Thể tích: V . h Sñ .
V AH .SAH.S
V AH.SAH.S ABC ABC   ABCD AB CD  
2. Hình lăng trụ đứng: Đáy là tam giác Đáy là tứ giác
 Các cạnh bên cùng vuông góc
với hai mặt đáy nên mỗi cạnh
bên cũng là đường cao của lăng trụ.
Lăng trụ tam giác đều: Là
lăng trụ đứng và có hai đáy là
hai tam giác đều bằng nhau.  Thể tích: V . h S  Thể tích: V . h S với ñ với ñ        
h AA  BB  CC . h AA BB CC DD .
29 Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com 3. Hình hộp:
3.1 Hình hộp chữ nhật:
3.2. Hình lập phương:
 Là lăng trụ đứng có đáy là hình
 Là hình hộp chữ nhật có tất cả các cạnh
 Là lăng trụ có tất cả các mặt là chữ nhật. bằng nhau. hình bình hành.
V abc với , a , b c là ba kích 3
V a với a là cạnh của hình lập  Thể tích: V . h S thước ñ .
của hình hộp chữ nhật. phương.
4. Tỉ số thể tích đối với lăng trụ:
Lăng trụ có đáy tam giác
Lăng trụ đáy là hình bình hành, hình chữ nhật, hình AM BN CP thoi, hình vuông x  , y  , z AABBCC
(Lăng trụ này chính là hình hộp thường hoặc hình hộp
chữ nhật, hình lập phương) AM BN CP DQ x  , y  , z  , t AABBCCDD V
x y z V    Ta có: ABC.MNPx y z t Ta có: ABCD.MNPQ
và x z y t V    3 ABC.A B C V     4 ABCD. A B C D
E – BÀI TOÁN KHOẢNG CÁCH
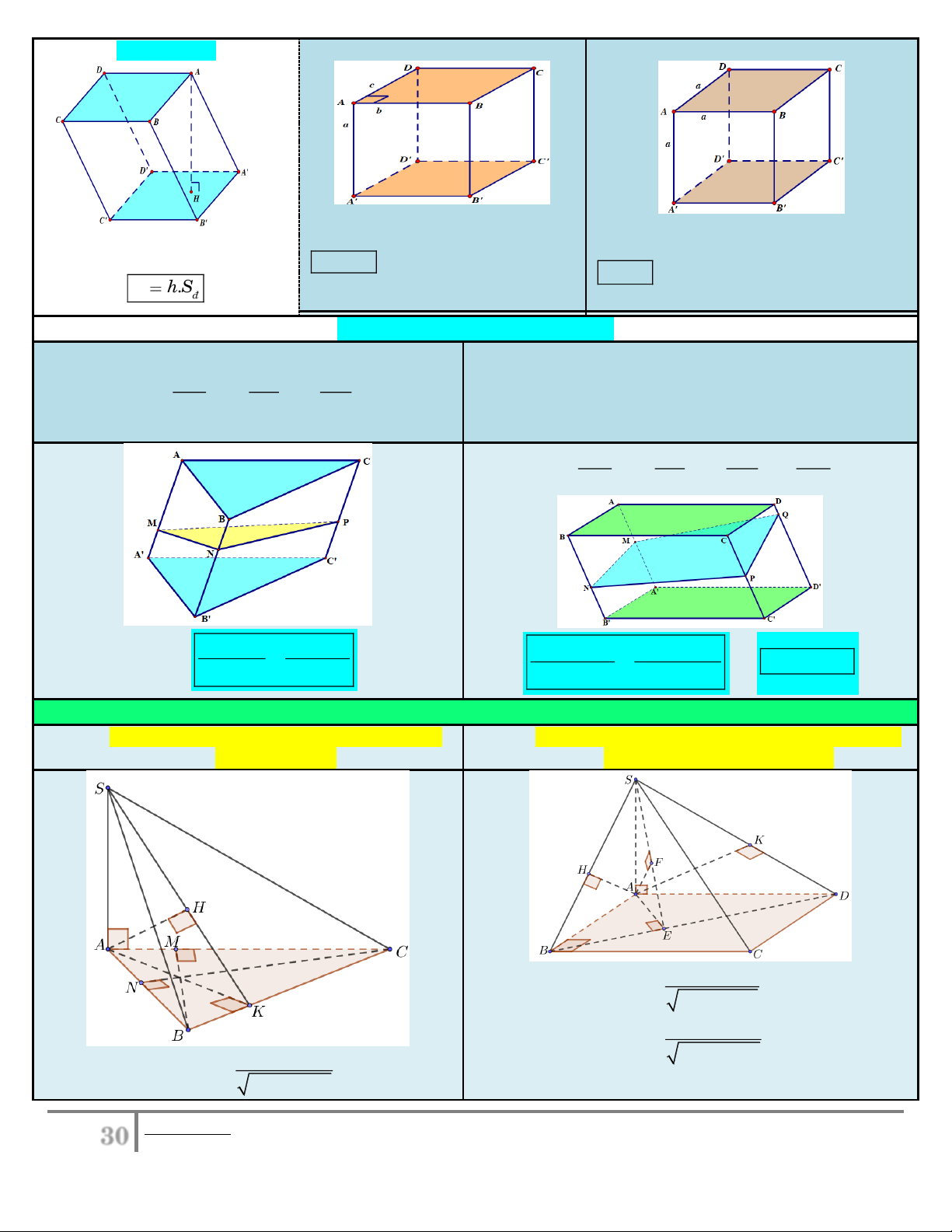
1. Hình chóp có cạnh bên vuông góc với mặt
2. Hình chóp có cạnh bên vuông góc với mặt đáy đáy là tam giác
là hình vuông, hình chữ nhật . SA ABd  ,
A SBC   AH
d D,SBC. 2 2 SA AB S . A ADd  ,
A SCD  AK
d B,SCD . S . A AK 2 2 SA ADd  ,
A SBC   AH  . 2 2 SA AK
30 Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
d B,SAC  BM ; d C,SAB  CN . S . A AEd  ,
A SBD  AF
d C,SBD.  2 2 d  ,
SA BC   AK. SA AE
d AD, SB  AH; d AB, SD  AK.
d AD, SC  d AD,SBC  d  ,
A SBC   AH.
d AB, SC   d AB,SCD  d  ,
A SCD  AK.
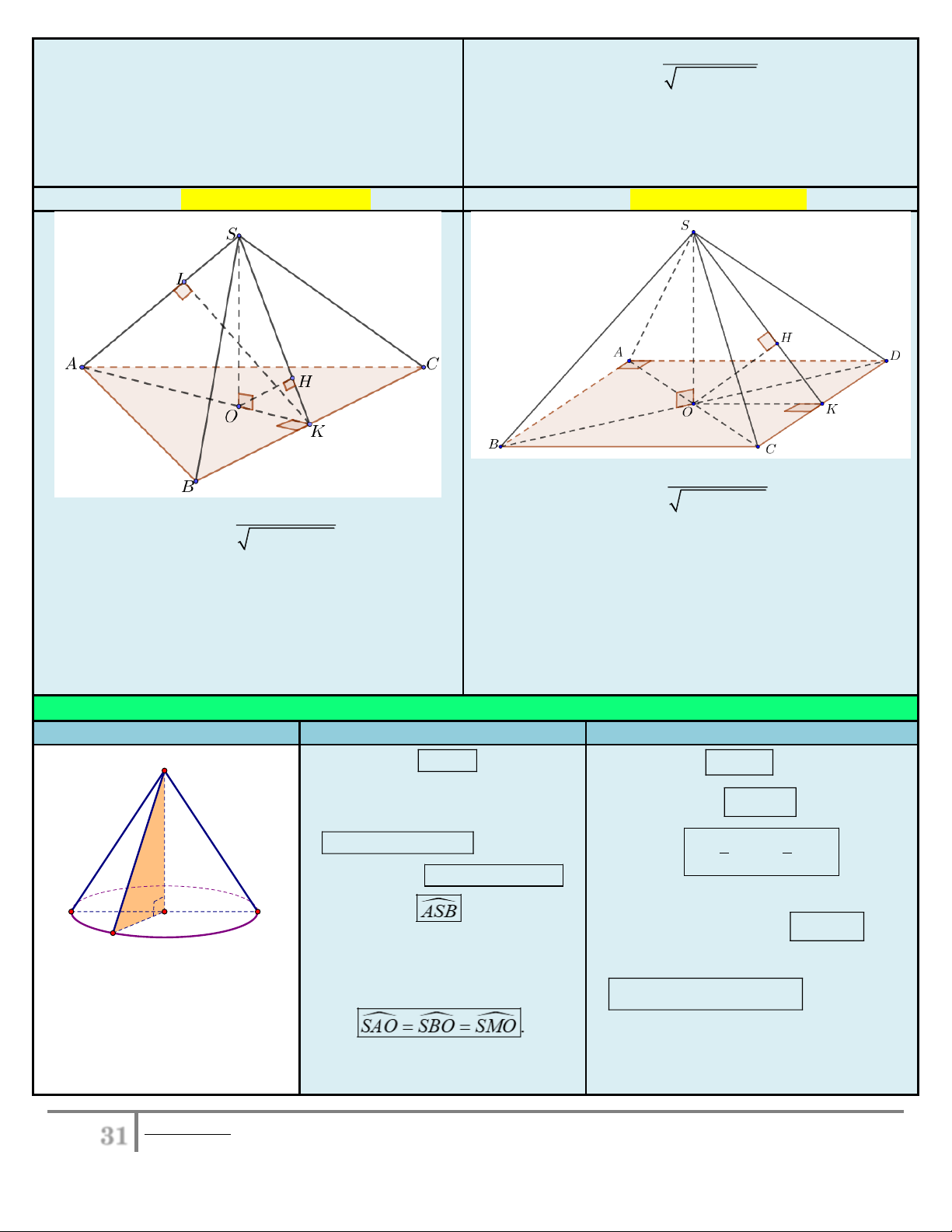
3. Hình chóp tam giác đều
4. Hình chóp tứ giác đều SO OK d O, SCD  .      OH 2 2  S . O OK SO OK
d O,SBC  OH
d O,SAB  d O,SBC  d O,SAD . 2 2 SO OK
d O,SAB  d O,SAC .  d  ,
A SCD  2d O,SCD  2OH d  , A SBC  
d B,SAD  d B,SCD d  ,
A SBC   3d O,SBC   3OH  ...
d B,SAC  d C,SAB .  d AB,SC  d AB,SCD  d  ,
A SCD  2OH d  ,
SA BC   IK d SB, AC   d SC, AB .
d AB, SD  d AD, SB  d AD, SC  ...
F – MẶT TRỤ, MẶT NÓN – MẶT CẦU MẶT NÓN
Các yếu tố mặt nón:
Một số công thức: S
Đường cao: h SO . ( SO cũng
Chu vi đáy: p  2 r .
được gọi là trục của hình nón).  Diện tích đáy    : 2 S r Bán kính đáy: đ . l h
r OA OB OM . l  1 1 Thể tích: 2 V  . h S   đ . h r . l  3 3
Đường sinh: l SA SB SM .
(liên tưởng đến thể tích khối chóp). A B r
Góc ở đỉnh: ASB . O
Diện tích xung quanh: S   rl . M   xq
Thiết diện qua trục: SAB cân 
Diện tích toàn phần:
Hình thành: Quay  vuông tại S. 2
SOM quanh trục SO , ta được
Góc giữa đường sinh và mặt
S S S   rl   r . tp xq đ
mặt nón như hình bên với:
đáy: SAO SBO SMO . h SO  . r OM
31 Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com MẶT TRỤ
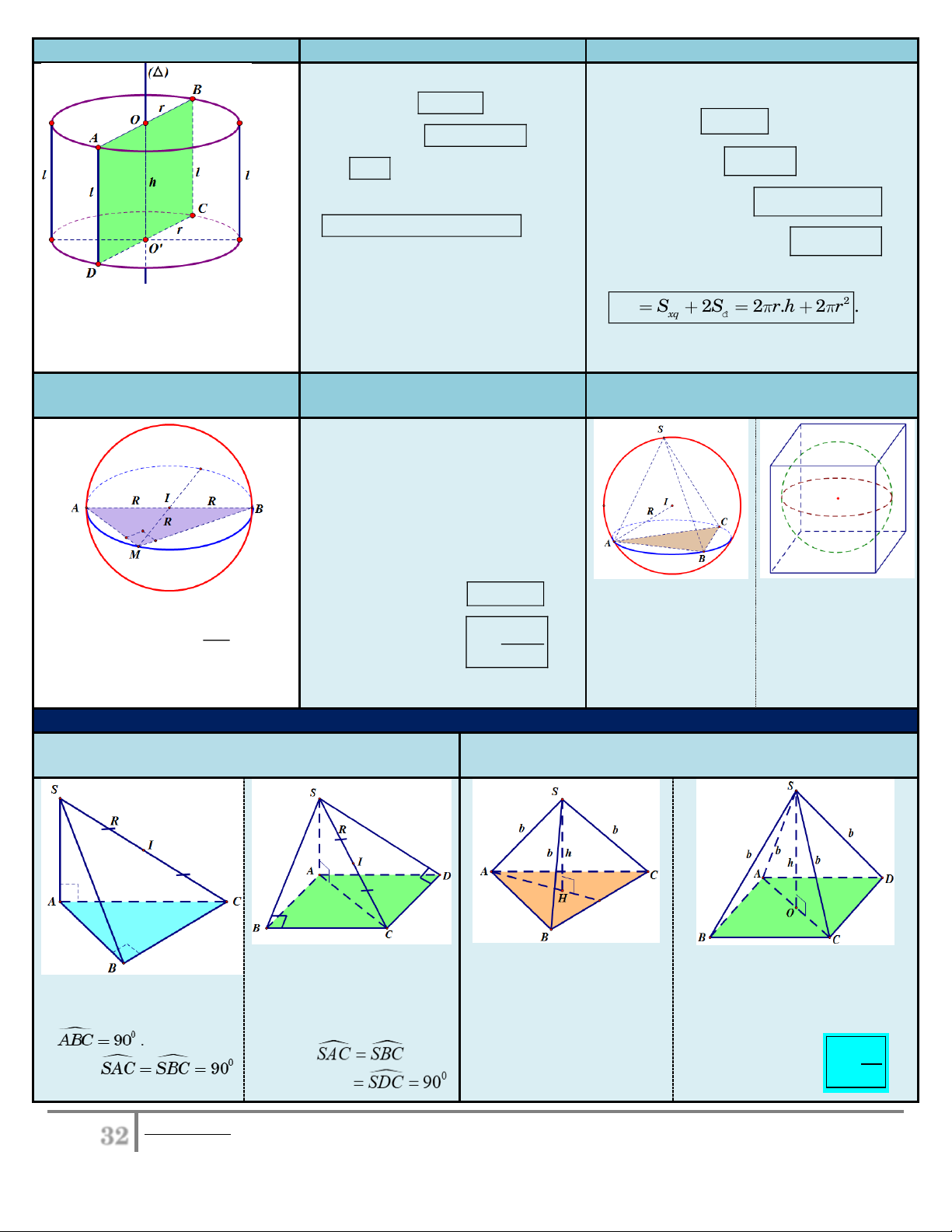
Các yếu tố mặt trụ:
Một số công thức:
Đường cao: h OO .
Chu vi đáy: p  2 r .
Đường sinh: l AD BC . Ta  Diện tích đáy   có: l h . : 2 Sđ r .  Bán kính đáy:
Thể tích khối trụ: 2 V  . h S  . h r . đ
r OA OB O C   O D  .
Diện tích xung quanh: S  2 r.h .  xq
Trục (∆) là đường thẳng đi qua hai điểm , O O . 
Diện tích toàn phần:
Hình thành: Quay hình chữ 2 S S 2S 2 . r h 2 r . nhật
Thiết diện qua trục ABCD : Là hình chữ quanh đường trung tp xq đ
bình OO , ta có mặt trụ như nhật ABC . D hình bên.
Mặt cầu ngoại tiếp đa diện MẶT CẦU
Một số công thức:
Mặt cầu nội tiếp đa diện
Tâm I, bán kính
R IA IB IM .
Đường kính AB  2R .
Thiết diện qua tâm mặt cầu: Là
đường tròn tâm I , bán kính R .
Mặt cầu ngoại tiếp Mặt cầu nội tiếp
Diện tích mặt cầu: 2 S  4 R .
Hình thành: Quay đường tròn
đa diện là mặt cầu
đa diện là mặt cầu AB 3  đi qua tất cả đỉnh
tâm I , bán kính R  quanh tiếp xúc với tất cả  4 R
Thể tích khối cầu: V  . 2 3 của đa diện đó. các mặt của đa
trục AB , ta có mặt cầu như hình diện đó. vẽ.
CÁCH TÌM BÁN KÍNH MẶT CẦU NGOẠI TIẾP HÌNH CHÓP THƯỜNG GẶP
1. Hình chóp có các đỉnh nhìn một cạnh dưới một 2. Hình chóp đều. góc vuông.  Xét hình chóp có
 Xét hình chóp tam giác
 Xét hình chóp tứ giác đều có  
đều có cạnh bên bằng b cạnh bên bằng và b và chiều Xét hình chóp có SA ( ABC ) D
và đường cao SH h .  .
SA  (ABC) và
ABCD là hình chữ nhật cao SO h hoặc hình vuông.
 Bán kính mặt cầu ngoại
 Bán kính mặt cầu ngoại tiếp 0 ABC  90 . tiếp hình chóp trên là  2
Ta có: SAC SBC b   Ta có 0
SAC SBC  90 hình chóp trên là R . 0 2h
nên mặt cầu ngoại tiếp  SDC  90
32 Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
hình chóp có tâm I là
Suy ra mặt cầu ngoại tiếp 2 b
trung điểm SC , bán
hình chóp có tâm I là R  . 2h SC
trung điểm SC , bán kính kính R  . 2 SC R  . 2
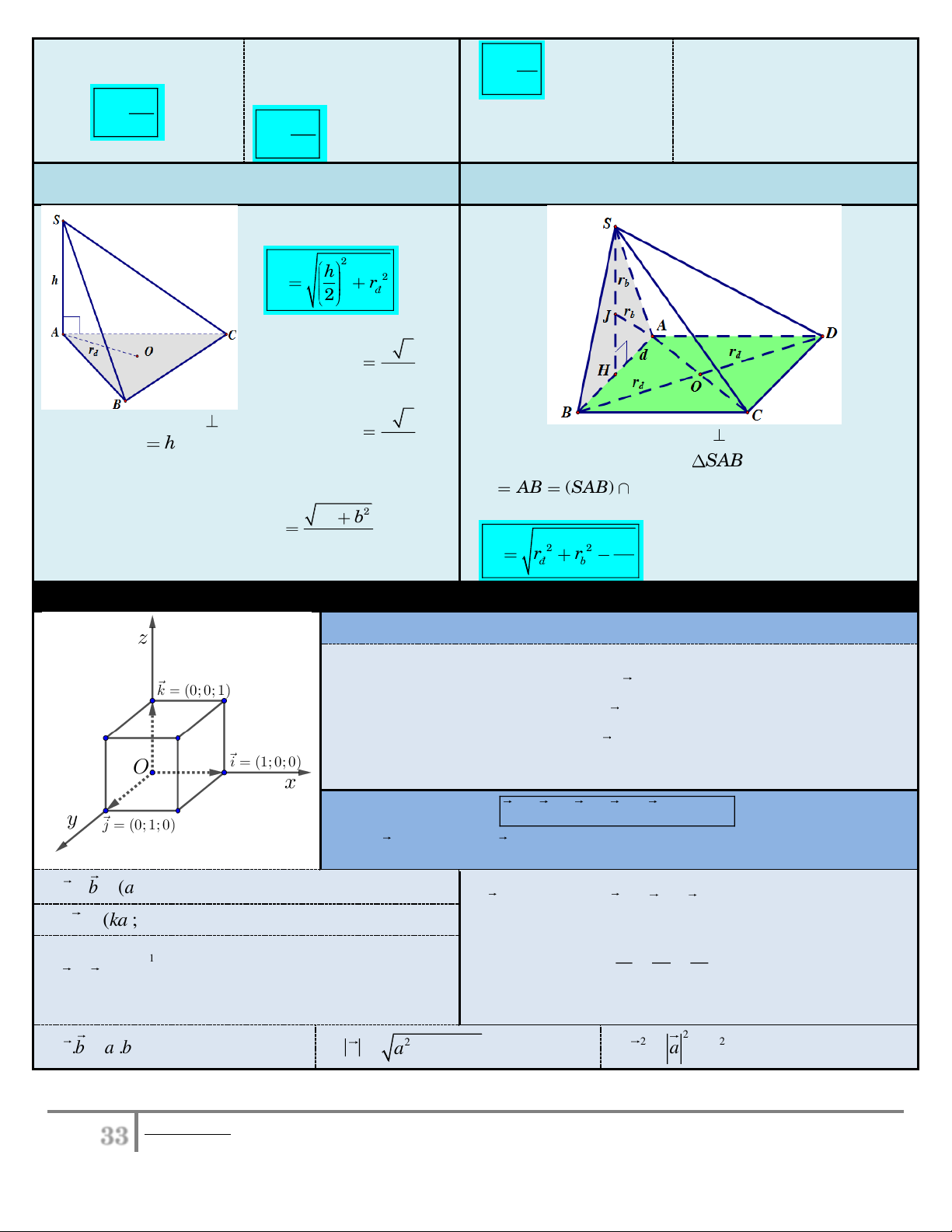
3. Hình chóp có cạnh bên vuông góc với mặt phẳng đáy.
4. Hình chóp có mặt bên vuông góc với mặt đáy.
 Khi đó mặt cầu ngoại tiếp hình chóp có bán kính 2 h 2 R r . 2 ñ
 Nếu đáy là tam giác đều a 3
cạnh a thì rñ . 3
 Nếu đáy là hình vuông
 Xét hình chóp có SA a 2 cạnh a thì r . SAB (đáy) và SA h
 Xét hình chóp có mặt bên (
) (đáy), bán kính ngoại tiếp ; bán ñ 2
kính đường tròn ngoại tiếp  Nếu đáy là hình chữ nhật
đáy là r , bán kính ngoại tiếp SAB r ñ là b , của đáy là r cạnh , a b thì d AB (SA ) B ñ .
(đáy). (đoạn giao tuyến) 2 2 a b
 Khi đó bán kính mặt cầu ngoại tiếp hình chóp là rñ 2 . 2 2 2 d R r r ñ b 4 .
XIII. HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN
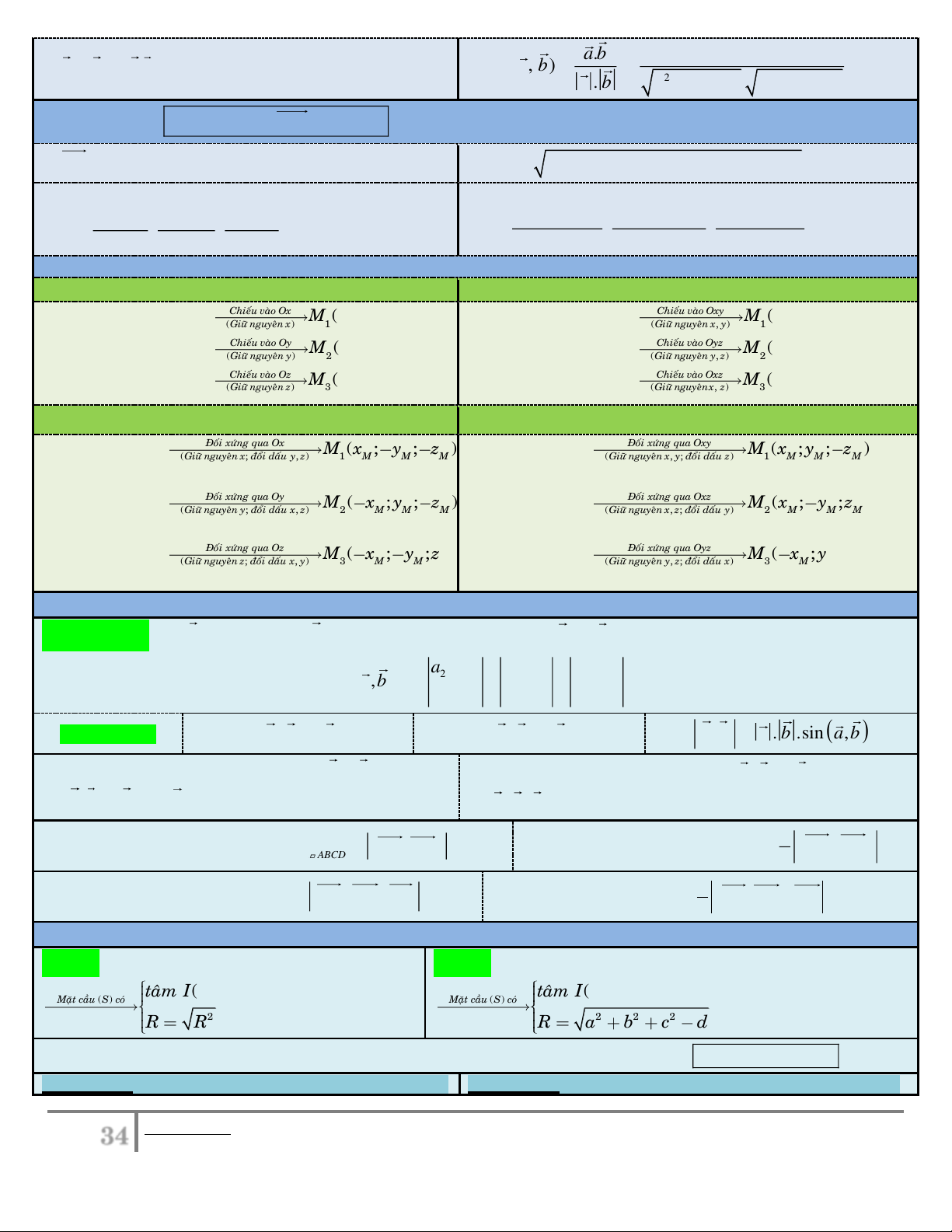
1. Hệ trục tọa độ Oxyz:
 Hệ trục gồm ba trục O ,
x Oy, Oz đôi một vuông góc nhau.
 Trục Ox : trục hoành, có vectơ đơn vị i  (1;0;0) .
 Trục Oy : trục tung, có vectơ đơn vị j  (0;1;0) .
 Trục Oz : trục cao, có vectơ đơn vị k  (0;0;1).  Điểm (0
O ;0;0) là gốc tọa độ.
2. Tọa độ vectơ: Vectơ u xi y j zk u  ( ; x ; y z) .
Cho a  (a ; a ; a ), b  (b ;b ;b ) . Ta có: 1 2 3 1 2 3
a b  (a b ; a b ; a b ) 1 1 2 2 3 3
a cùng phương b a kb (k R)
ka  (ka ; ka ; ka ) 1 2 3 a kb 1 1 a ba a a 1 1 1 2 3   a kb   
, (b , b , b  0). 2 2 1 2 3
a b  a b b b b 2 2  1 2 3 a kb  3 3 a b  3 3 2
a.b a .b a .b a .b 2 2 2 2  2 2 2 a
a a a
a a a a a 1 1 2 2 3 3  1 2 2 1 2 3
33 Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com . a b
a b a b a b
a b  .
a b  0  a b a b a b  0    1 1 2 2 3 3 cos(a, b) 1 1 2 2 3 3 2 2 2 2 2 2 a . b
a a a . b b b 1 2 3 1 2 3
3. Tọa độ điểm: M ( ; x ;
y z)  OM  ( ; x ; y z) . Cho (
A x ; y ; z ) , (
B x ; y ; z ) , C(x ; y ; z ) , ta có: A A A B B B C C C
AB  (x x ; y y ; z z )        B A B A B A 2 2 2 AB (x x ) ( y y ) (z z ) B A B A B A
 Toạ độ trung điểm M của đoạn thẳng AB:
 Toạ độ trọng tâm G của tam giác ABC:
x x y y z z
x x x y y y z z z A B M  ; A B ; A B . A B C G  ; A B C ; A B C .  2 2 2   3 3 3 
QUY TẮC CHIẾU ĐẶC BIỆT
Chiếu điểm trên trục tọa độ
Chiếu điểm trên mặt phẳng tọa độ
 Điểm M(x ; y ;z ) Chieáu vaøo Ox M (x ;0;0)
 Điểm M(x ; y ;z ) Chieáu vaøo Oxy M (x ; y ;0) M M M (Giöõ nguyeân x) 1 M M M M
(Giöõ nguyeân x, y) 1 M M
 Điểm M(x ; y ;z ) Chieáu vaøo Oy M (0; y ;0)
 Điểm M(x ; y ;z ) Chieáu vaøo Oyz M (0; y ;z ) M M M (Giöõ nguyeân y) 2 M M M M (Giöõ nguyeân , y z) 2 M M
 Điểm M(x ; y ;z ) Chieáu vaøo Oz M (0;0;z )
 Điểm M(x ; y ;z ) Chieáu vaøo Oxz
M (x ;0;z ) M M M (Giöõ nguyeân z) 3 M M M M
(Giöõ nguyeânx, z) 3 M M
Đối xứng điểm qua trục tọa độ
Đối xứng điểm qua mặt phẳng tọa độ
M(x ; y ;z ) Ñoái xöùng qua Ox
M (x ; y ; z )  M(x ; y ;z ) Ñoái xöùng qua Oxy
M (x ; y ; z ) M M M (Giöõ nguyeân ; x ñoåi daáu , y z) 1 M M M M M M (Giöõ nguyeân x, ; y ñoåi daáu z) 1 M M M
M(x ; y ;z ) Ñoái xöùng qua Oy
M ( x ; y ; z )  M(x ; y ;z ) Ñoái xöùng qua Oxz
M (x ; y ;z ) M M M (Giöõ nguyeân ;
y ñoåi daáu x, z) 2 M M M M M M (Giöõ nguyeân x, ; z ñoåi daáu y) 2 M M M
M(x ; y ;z ) Ñoái xöùng qua Oz
M ( x ; y ;z )  M(x ; y ;z ) Ñoái xöùng qua Oyz
M ( x ; y ;z ) M M M (Giöõ nguyeân ;
z ñoåi daáu x, y) 3 M M M M M M (Giöõ nguyeân , y ; z ñoåi daáu x) 3 M M M
4. Tích có hướng của hai vectơ:
Định nghĩa: Cho a  (a , a , a ) , b  (b , b , b ) , tích có hướng của a và b là: 1 2 3 1 2 3  a a a a a a  2 3 3 1 1 2
a,b   ; ;
  a b a b ;a b a b ;a b a b . 2 3 3 2 3 1 1 3 1 2 2 1  b b b b b b  2 3 3 1 1 2  
[a,b]  a . b .sin a,b Tính chất: [ , a ] b a [ , a ] b b
 Điều kiện cùng phương của hai vectơ a & b là
 Điều kiện đồng phẳng của ba vectơ a, b và c là a,b  0   với 0  (0; 0; 0). [ , a ] b .c  0. 1
Diện tích hình bình hành    ABCD: S
 AB, AD .
Diện tích tam giác ABC: SAB, AC . ABCD ABC  2 1
Thể tích khối hộp: V  [A , B AD].AA' .
Thể tích tứ diện: V
 AB, AC.AD
ABCD.A' B 'C ' D ' ABCD   . 6
5. Phương trình mặt cầu: Dạng 1: 2 2 2 2 (S) : (x  ) a  ( y  ) b  (z  ) cR Dạng 2: 2 2 2
(S) : x y z  2ax  2by  2cz d  0 taâm I( ; a ; b ) c taâm I( ; a ; b ) c
Maët caàu (S) coù
Maët caàu (S) coù 2 R R 2 2 2 R a b c d  Phương trình 2 2 2
x y z  2ax  2by  2cz d  0 là phương trình mặt cầu 2 2 2
a b c d  0 .
Bài toán 5.1. Viết phương trình mặt cầu tâm I và đi qua
Bài toán 5.2. Viết phương trình mặt cầu có đường kính AB.
34 Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
điểm M.
Bước 1: Tìm tâm I là trung điểm AB. Bán kính
Bước 1: Tính bán kính R IM . AB R   IA IB .
Bước 2: Viết phương trình mặt cầu dạng 1. 2
Bước 2: Viết phương trình mặt cầu dạng 1.
6. Phương trình mặt phẳng:
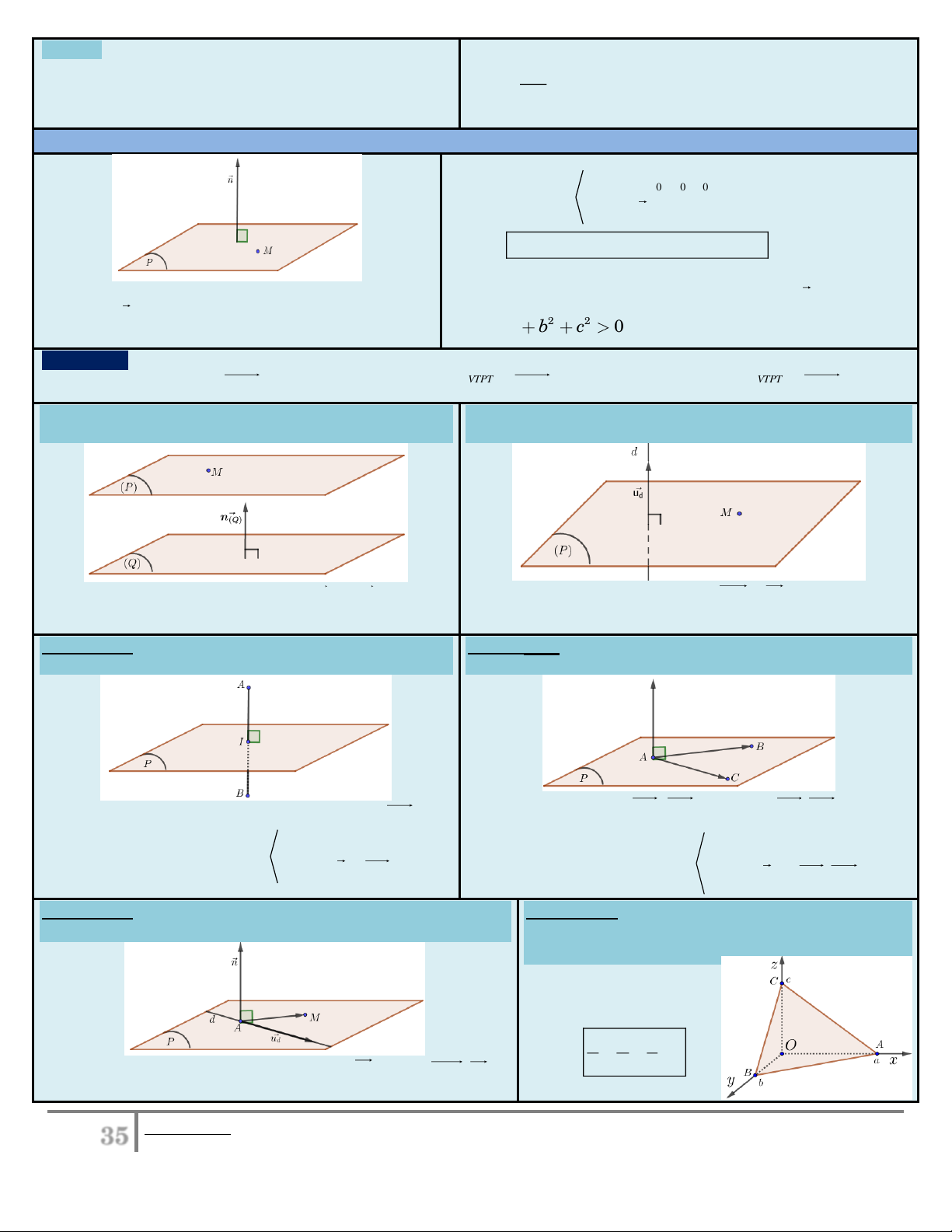
qua M (x ; y ; z )  Mặt phẳng 0 0 0 (P) thì phương trình VTPT n  ( ; a ; b c)
(P) : a(x x )  b( y y )  c(z z )  0 (*) 0 0 0
 Ngược lại, một mặt phẳng bất kỳ đều có phương trình dạng
Lưu ý: Vectơ pháp tuyến (VTPT) của mặt phẳng là
ax by cz d  0 , mặt phẳng này có VTPT n  ( ; a ; b c)
vectơ khác 0 nằm trên đường thẳng vuông góc với mặt vôùi 2 2 2 a b c 0 . phẳng đó.  Đặc biệt:
Mp(Oyz) : x  0 VTPT  n
 (1;0;0), mp(Oxz) : y  0 VTPT  n
 (0;1;0), mp(Oxy) : z  0 VTPT  n  (0;0;1) (Oyz ) (Oxz) (Oxy)
Bài toán 6.1. Viết phương trình mặt phẳng (P) qua M
Bài toán 6.2. Viết phương trình mặt phẳng (P) qua M và
và song song với mặt phẳng (Q) cho trước.
vuông góc với với đường thẳng d cho trước.
 Mặt phẳng (P) qua M, có VTPT là nn nên
 Mặt phẳng (P) qua M , có VTPT n
u nên phương trình ( P) (Q) ( P) d
phương trình được viết theo (*). được viết theo (*).
Bài toán 6.3. Viết phương trình mặt phẳng trung trực
Bài toán 6.4. Viết phương trình mặt phẳng đi qua ba điểm
của đoạn thẳng AB. A, B, C.    
Bước 1: Tìm trung điểm I của đoạn AB và tính AB .
Bước 1: Tính tọa độ AB, AC và suy ra AB, AC   . qua I qua A
Bước 2: Phương trình mp(P) .
Bước 2: Phương trình mp(P) . VTPT n AB
VTPT n   A , B AC  
Bài toán 6.5. Viết phương trình mặt phẳng qua M và chứa
Bài toán 6.6. Viết phương trình mặt phẳng cắt Ox,
đường thẳng d với M d .
Oy, Oz lần lượt tại ( A ; a 0;0), ( B 0; ;
b 0), C(0;0;c)
với a. .
b c 0 .  Phương trình mặt phẳng được viết theo đoạn chắn x y z (P) :   1.
Bước 1: Chọn điểm Ad và một VTCP u . Tính  AM ,u a b c d d   .
35 Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com qua M
Bước 2: Phương trình mp(P)
VTPT n   AM ,u d  
Khoảng cách từ điểm đến mặt phẳng
Khoảng cách giữa hai mặt phẳng song song
M (x ; y ; z )
(P) : ax by cz d  0  0 0 0 Cho  .  Cho hai mặt phẳng 1  .
mp(P) : ax by cz d  0
(Q) : ax by cz d  0  2
ax by cz d d d
 Khi đó: d M ,(P) 0 0 0  .
 Khi đó: d (P),(Q) 1 2 
với d d . 1 2 2 2 2
a b c 2 2 2
a b c
Góc giữa hai mặt phẳng
Vị trí tương đối giữa hai mặt phẳng
Cho hai mặt phẳng (P), (Q) có phương trình:
 Cho hai mặt phẳng (P), (Q) có phương trình:
(P) : a x b y c z d  0  1 1 1 1
(P) : a x b y c z d  0  . Ta có: 1 1 1 1      .
(Q) : a x b y c z d 0  2 2 2 2
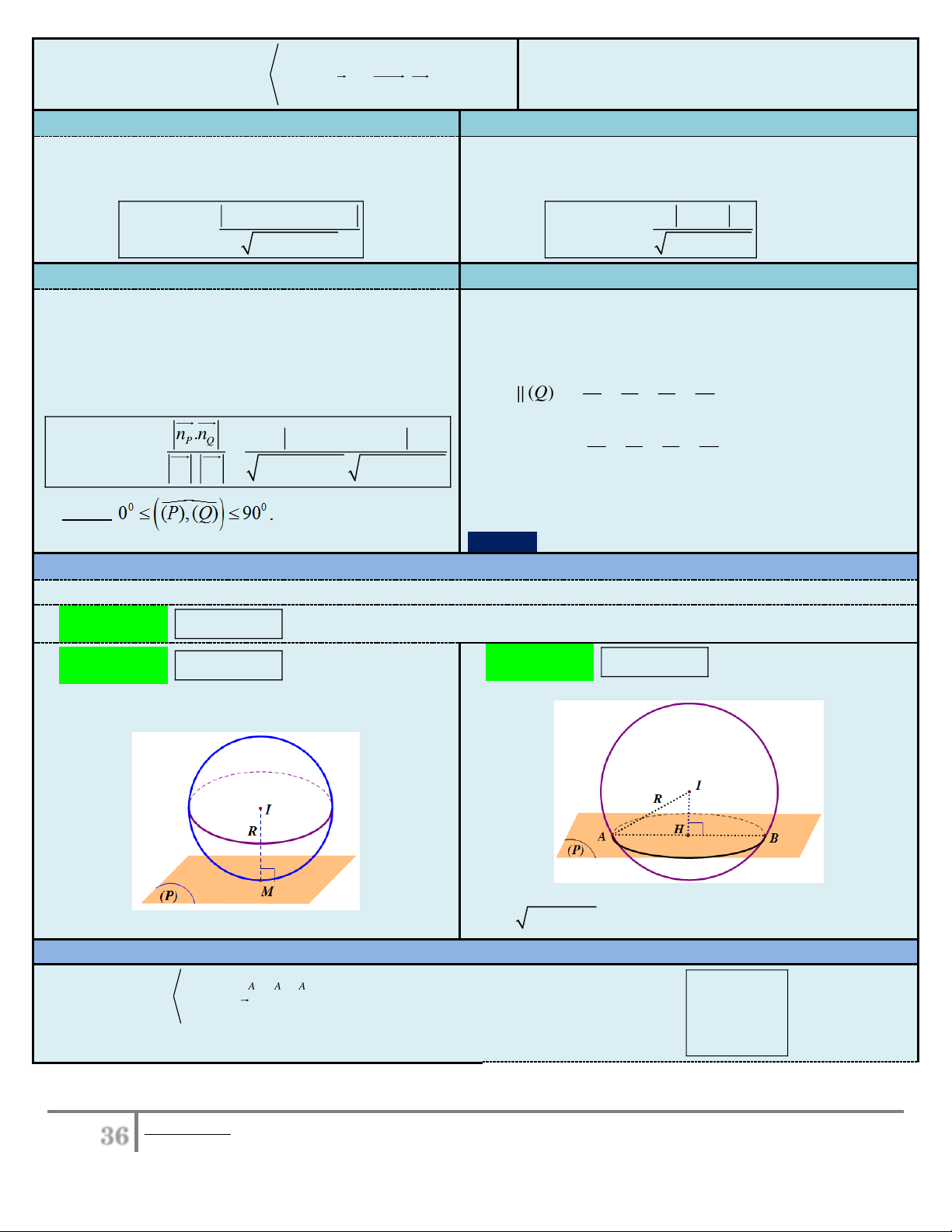
(Q) : a x b y c z d  0  2 2 2 2 a b c d      Góc giữa ( ) P & ( ) Q được tính:  1 1 1 1 (P) (Q) . a b c d 2 2 2 2 n n   a b c d P Q a a b b c c
cos (P), (Q) . 1 2 1 2 1 2    1 1 1 1 (P)  (Q)     . 2 2 2 2 2 2 n . n a b c d
a b c . a b c 2 2 2 2 P Q 1 1 1 2 2 2  ( ) P & ( )
Q cắt nhau  a : b : c a : b : c . 1 1 1 2 2 2
Chú ý: 0   P Q  0 0 ( ), ( )  90 .  ( ) P  ( )
Q a a b b c c  0. 1 2 1 2 1 2
Lưu ý: Các tỉ số trên có nghĩa khi mẫu khác 0.
Ví trị tương đối giữa mặt phẳng và mặt cầu Cho mặt phẳng ( )
P : ax by cz d  0 và mặt cầu (S) có tâm I và bán kính R.
Trường hợp 1: d I,(P)  R  ( )
P và (S) không có điểm chung.
Trường hợp 2: d I,(P)  R  ( )
P và (S) có một Trường hợp 3: d I , (P)  R  ( )
P cắt (S) theo giao
điểm chung. Khi đó ta nói ( )
P tiếp xúc (S) hoặc ( ) P
tuyến là một đường tròn.
là tiếp diện của (S).
Đường tròn giao tuyến có tâm H (là trung điểm AB), bán kính Ta có: IM  ( )
P với M là tiếp điểm. 2 2 r
R IH với IH d I , (P).
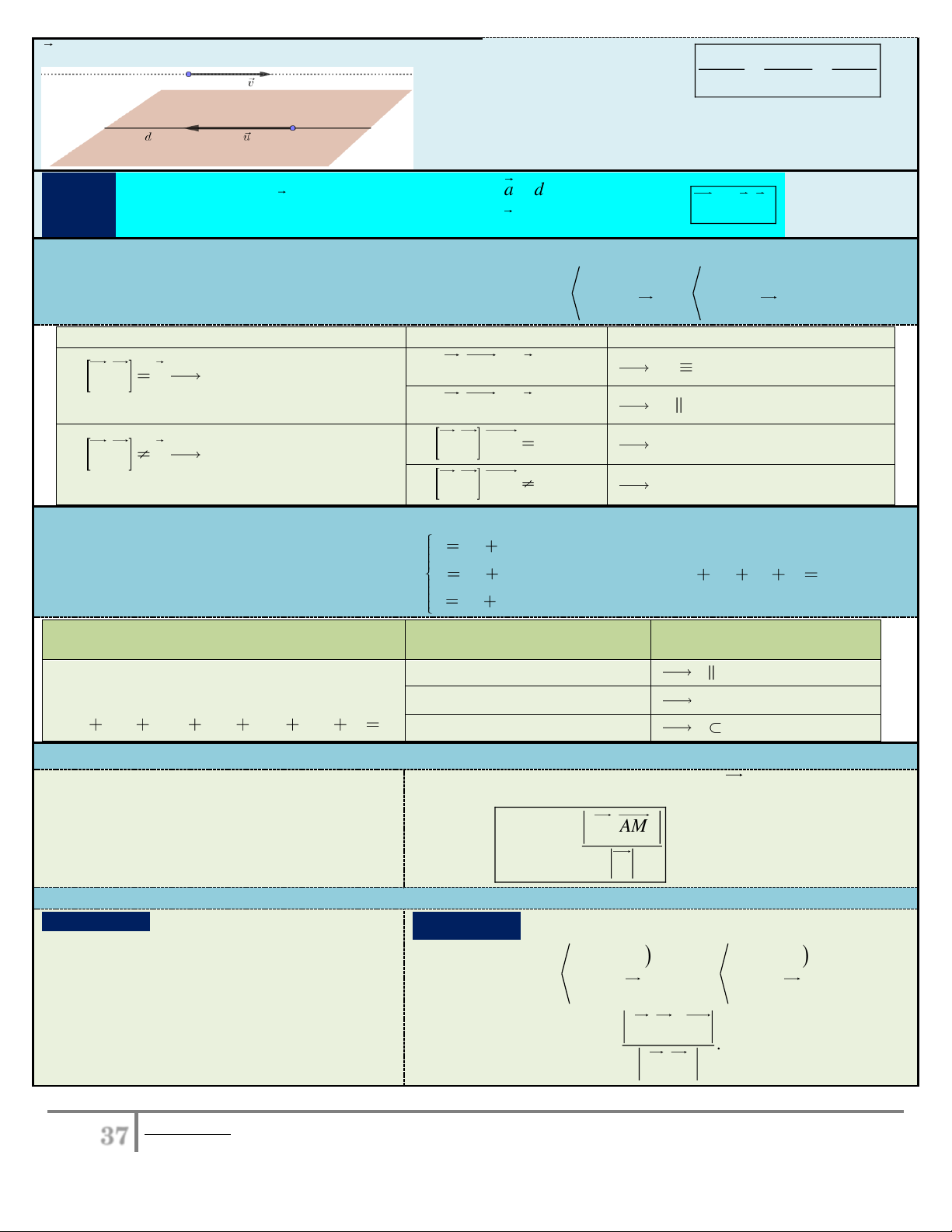
7. Phương trình đường thẳng: qua (
A x ; y ; z )
x x u tA A A Đường thẳng d A 1 
VTCP u  (u ;u ;u )
 Phương trình tham số d : y y u t với t là tham số. 1 2 3 A 2
Vectơ chỉ phương (VTCP) của đường thẳng d là vectơ khác
z z u tA 3
36 Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
0 , có giá trùng với d hoặc song song với d. x x y y z z
 Phương trình chính tắc d : A A A   u u u 1 2 3
với u .u .u  0 . 1 2 3 a d
Lưu ý: Nếu có cặp vectơ khác 0 không cùng phương sao cho 
thì d có VTCP là: u  a,bd   . b   d
7.1. Ví trị tương đối giữa hai đường thẳng: qua M qua N
Xét vị trí tương đối của hai đường thẳng d , d với d , d . 1 2 1 2 VTCP u VTCP u 1 2 Bước I Bước II Kết luận    d d   u , MN 0 u ,u 0
Hai đường thẳng d , d 1   1 2 1 2 1 2
song song hoặc trùng nhau.
 u , MN   0 d d 1   1 2
u ,u .MN 0 d d  cắt u ,u 0
Hai đường thẳng d , d 1 2 1 2 1 2 1 2
cắt nhau hoặc chéo nhau.
u ,u .MN 0
d & d chéo nhau 1 2 1 2
7.2. Ví trị tương đối giữa đường thẳng và mặt phẳng: x x u t 0 1
Xét vị trí tương đối giữa đường thẳng d : y y
u t và mặt phẳng ( ) P : ax by cz d 0 . 0 2 z z u t 0 3
Bước II:Giải PT (*), ta gặp 1 Bước I: Kết luận
trong 3 trường hợp sau d (P)
Thay phương trình tham số d vào phương  PT (*) vô nghiệm
trình (P) , ta được PT (*):
 PT (*) có 1 nghiệm t t
d cắt (P) tại một điểm 0 ( a x u ) t ( b y u ) t ( c z u ) t d 0 0 1 0 2 0 3
 PT (*) có vô số nghiệm t. d (P)
7.3. Khoảng cách từ điểm đến đường thẳng:
Bước 1: Chọn điểm Ad và một VTCP u . d
 Cho điểm M và đường thẳng d (có phương u AM
trình tham số hoặc chính tắc).   d
Bước 2: d M d  , ,  . ud
7.4. Khoảng cách giữa hai đường thẳng:
Trường hợp 1: Hai đường thẳng song song
Trường hợp 2: Hai đường thẳng chéo nhau d , d . 1 2
d , d . 1 2 qua A... qua B ...
Bước 1: Chọn điểm M (đẹp) thuộc d .
Bước 1: Ghi rõ d , d . 1 1 2 VTCP u  ... VTCP u  ... 2   1  
Bước 2: d d , d d M , d . (xem 7.3) 1 2   2 
u ,u .AB  
Bước 2: Tính: d d , d  1 2  . 1 2 u ,u  1 2  
37 Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
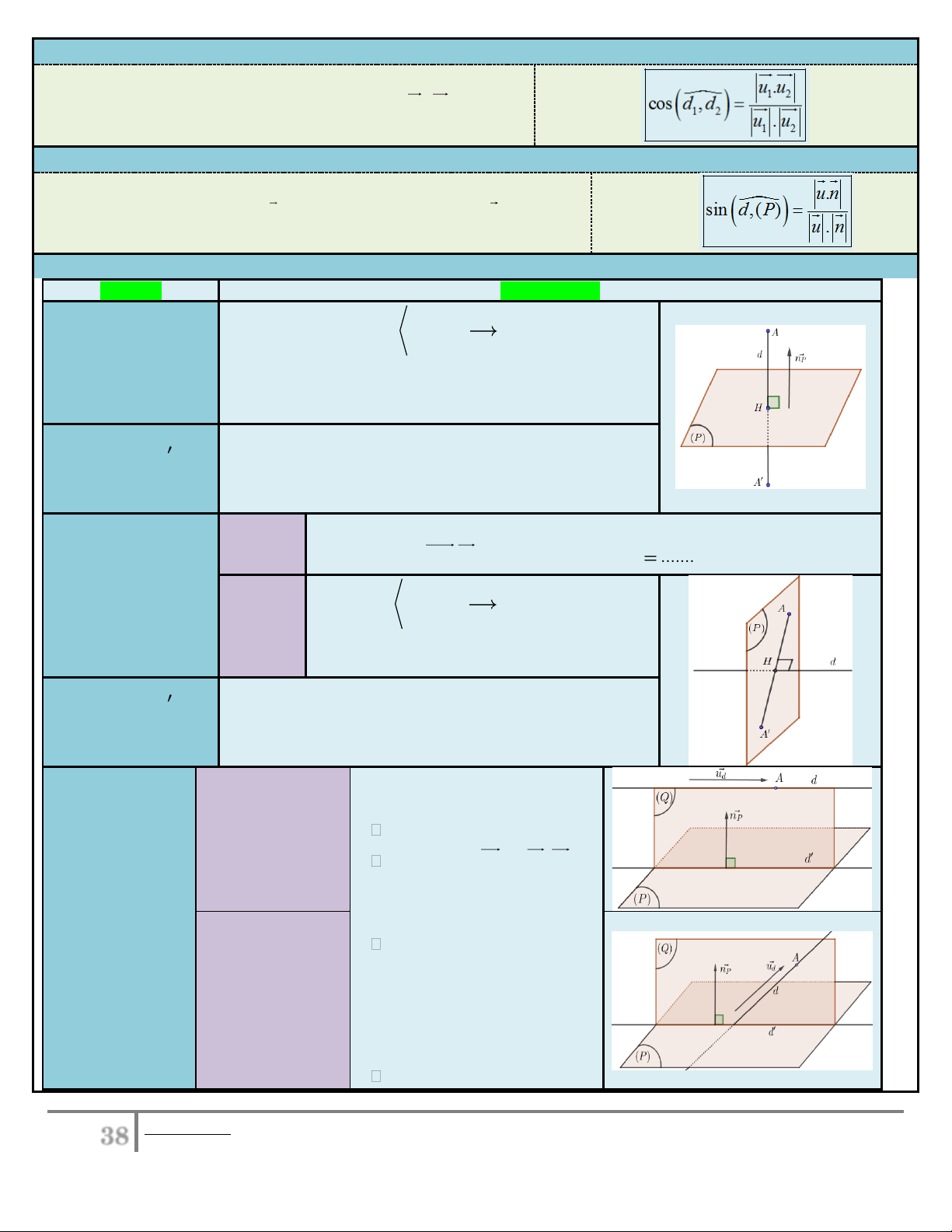
7.5. Góc giữa hai đường thẳng: u .u
 Cho hai đường thẳng d , d lần lượt có VTCP là u , u . 
 Ta có: cosd ,d  . 1 2  1 2 1 2 1 2 u . u 1 2
7.6. Góc giữa đường thẳng và mặt phẳng: u n
 Cho đường thẳng d có VTCP u và măt phẳng ( ) P có VTPT n .   Ta có: d P  . sin , ( )  . u . n
8. Hình chiếu và điểm đối xứng: Bài toán Phương pháp qua A
 Gọi d là đường thẳng
8.1. Tìm hình chiếu 
Viết pt tham số của d (P)
của điểm A trên mặt
với VTCP của d cũng là VTPT của (P). phẳng (P) .
 Gọi H d ( )
P . Thay pt tham số của d vào pt mp (P) ta
tìm được tọa độ H. x    2x x A H A
8.2. Tìm điểm A đối       xứng với
 Ta có H là trung điểm AA y  2 y y . A qua (P) . A H Az     2z z A H A
 Gọi H (theo t) (dựa vào pt tham số của d). Cách 1
AH d AH u    t ....... . 0 Tìm được  Tọa độ H. d
8.3. Tìm hình chiếu của điểm A trên qua A  Gọi (P) đường thẳng d. (P)  Viết pt mp( ) P . d Cách 2
 Gọi H d ( )
P . Thay pt tham số của d vào
pt mp (P) ta tìm được tọa độ H. x    2x x
8.4. Tìm điểm A đối A H A  xứng với A qua
 Ta có H là trung điểm AA  y    2 y y . A H A đường thẳng d. z     2z z A H A
 Lập phương trình mp(Q) biết
(Q) chứa d và ( ) Q  ( ) P : Trường hợp 1:
(Q) qua điểm Ad . d song song mp (P).
(Q) có VTPT n  u , n Q d P   . 8.5. Viết phương trình đường thẳng
 Lập phương trình d là giao
d  là hình chiếu
tuyến hai mp (P) và (Q): của đường thẳng
Chọn hai điểm M, N thuộc d d trên mp ( ) P . bằng cách thay Trường hợp 2:  0 Tìm x  , y z và thay
d cắt mp (P) tại một điểm.  0 Tìm y  ,
x z (đối với hệ
hai pt (P), (Q)).
Viết pt d qua M, N. [
38 Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
XIV. GẮN TỌA ĐỘ VÀO HÌNH HỌC KHÔNG GIAN
1. Gắn tọa độ đối với hình chóp
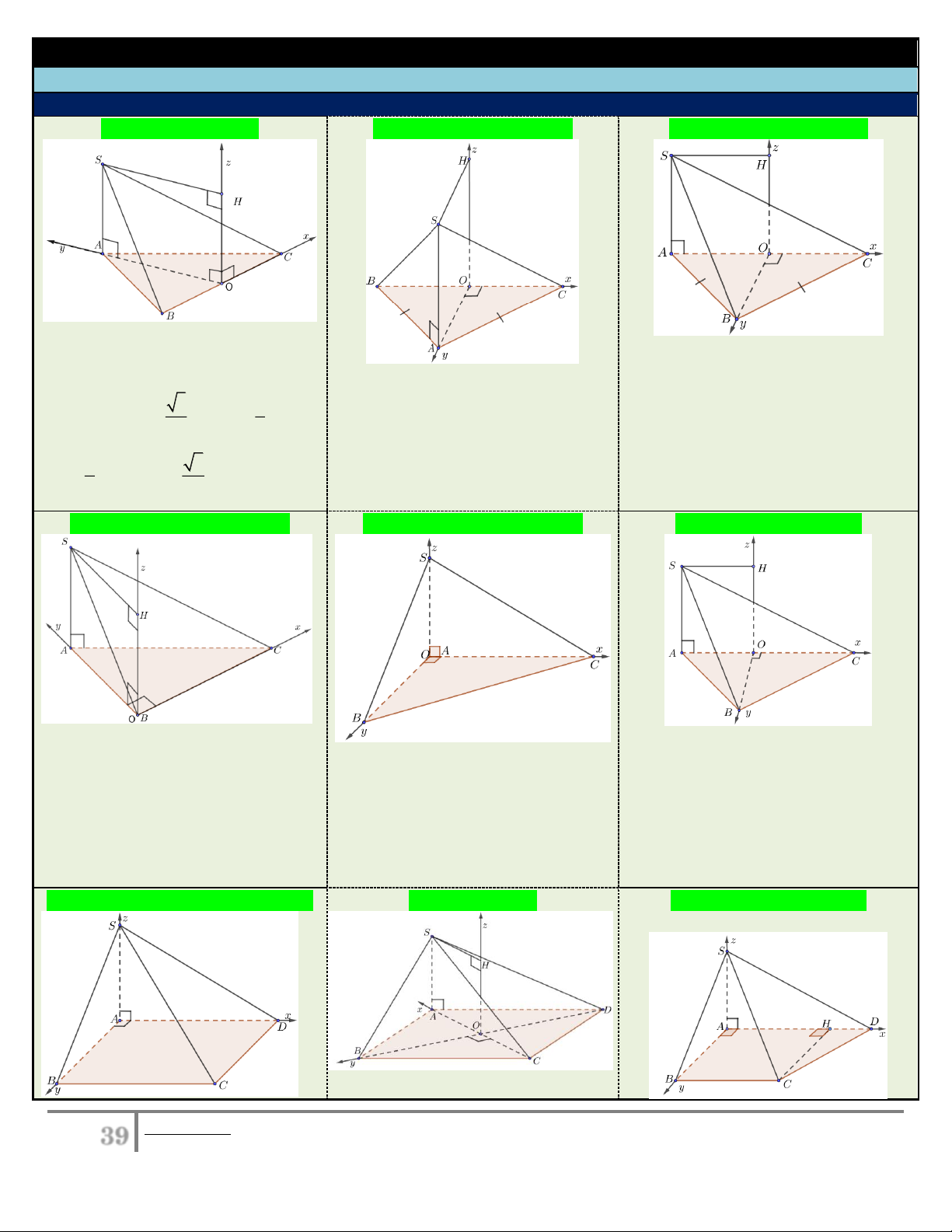
1.1.Hình chóp có cạnh bên (SA) vuông góc với mặt đáy:
Đáy là tam giác đều
Đáy là tam giác cân tại A
Đáy là tam giác cân tại B
 Gọi O là trung điểm BC. Chọn hệ trục như hình vẽ,  AB a 1 Gọi .
O là trung điểm AC. Chọn hệ  trục như hình vẽ,
Tọa độ các điểm là:
 Gọi O là trung điểm BC. Chọn hệ a  1.  trục như hình vẽ,
 Tọa độ các điểm: O0;0;0 , 3   1  a  1. O(0;0;0), A0; ;0, B  ;0;0 ,    
 Tọa độ các điểm là: AO  ;
A 0; 0, B 0,O ; B 0 2    2  ,
O(0; 0; 0), A0;O ;
A 0, B O  ; B 0; 0,    1   3 
C OC;0;0, S O  ; A 0;OH C ; 0; 0 , S   0; ;OH    .   .    C OC;0;0 2  2 , S 0;O ; A OH .       SA SA    SA
Đáy là tam giác vuông tại B
Đáy là tam giác vuông tại A
Đáy là tam giác thường
 Chọn hệ trục như hình vẽ, a 1.
 Dựng đường cao BO của . ABC
 Tọa độ các điểm: B O 0;0;0 ,
 Chọn hệ trục như hình vẽ, a 1.
Chọn hệ trục như hình vẽ, a 1.
 Tọa độ các điểm: A O 0;0;0 , A0; ;
AB 0, C BC, 0;0,
 Tọa độ các điểm: O0;0;0 , B 0; ;
OB 0, C AC;0;0   , AO  ;
A 0; 0, B 0,O ; B 0, S 0; A ; B BH   . S 0;0; SA  .   SA
C OC;0;0, S O  ; A 0;OH .    SA
Đáy là hình vuông, hình chữ nhật Đáy là hình thoi
Đáy là hình thang vuông
 Chọn hệ trục như hình vẽ, a 1.
39 Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
 Chọn hệ trục như hình vẽ, a 1.
 Tọa độ O 0;0;0 , AO ; A 0; 0,
 Chọn hệ trục như hình vẽ, a 1.
 Tọa độ A O 0;0;0 , B0; ; AB 0,
 Tọa độ A O 0;0;0 , B 0;O ;
B 0, C OC;0;0 C A ; D A ;
B 0, D A ;
D 0;0, S 0;0; SA .   B 0; ;
AB 0, C AH ; ; AB 0, D 0; O  ; D 0, S O ; A 0;OH   .  D  ;
AD 0; 0, S 0;0; SA. SA
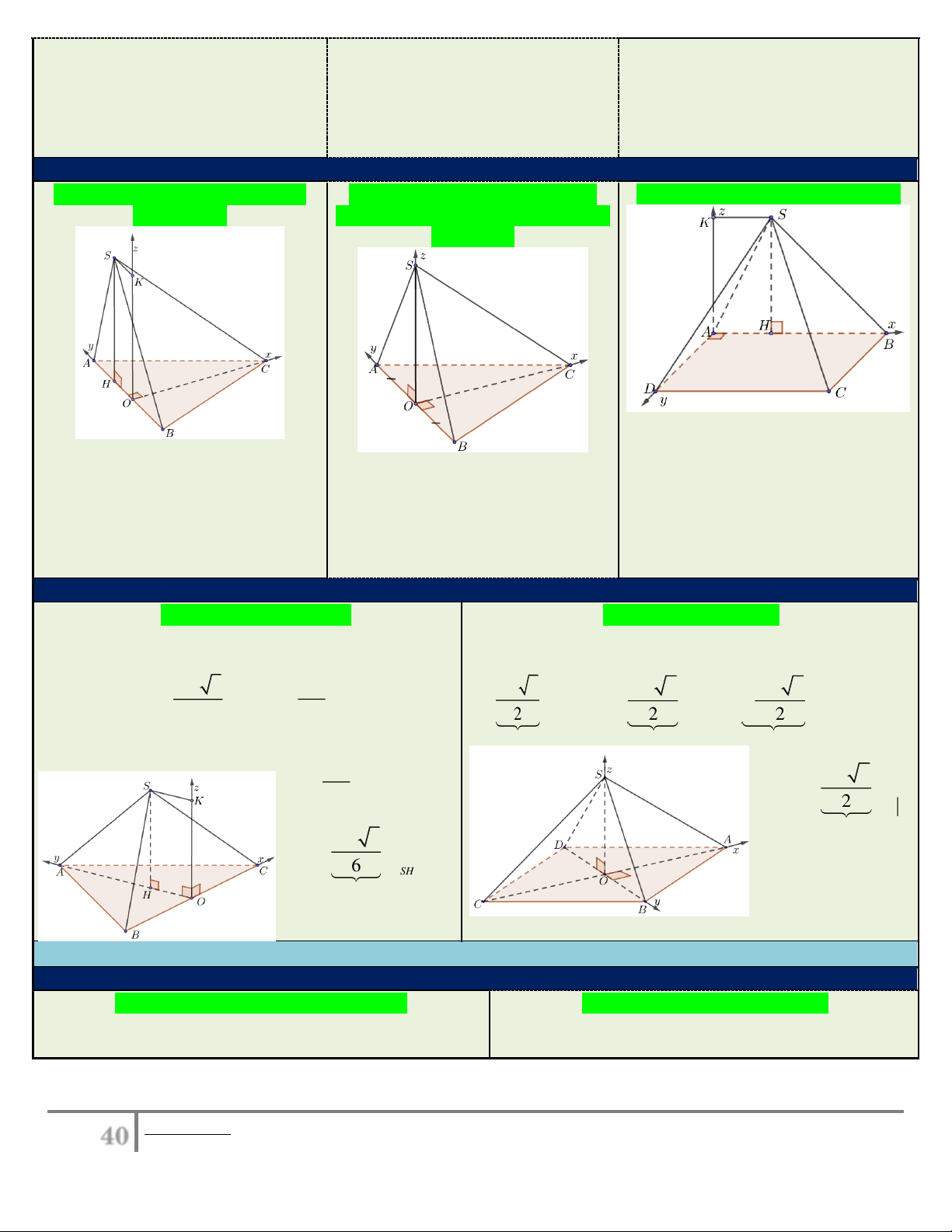
1.2.Hình chóp có mặt bên (SAB) vuông góc với mặt đáy
Đáy là tam giác, mặt bên là tam
Đáy là tam giác cân tại C (hoặc
Đáy là hình vuông-hình chữ nhật giác thường
đều), mặt bên là tam giác cân tại S (hoặc đều)
 Dựng hệ trục như hình, chọn a = 1.
 Vẽ đường cao CO trong ABC  .
 Ta có: A O0;0;0, BA ; B 0;0
 Gọi O là trung điểm BC, chọn hệ
Chọn hệ trục như hình, a = 1. trục như hình,    a = 1. C A ; B A ;
D 0, D 0; A ; D 0
Ta có: O 0;0;0, A0; ; OA 0, , S AH ;0; AK  
 Ta có: O0;0;0, A0; ; OA 0,  SH    B 0; O  ;
B 0, C OC;0;0, S 0;OH;OK   B 0;  ;
OB 0, C OC;0;0, S 0;0; SO  SH 1.3.Hình chóp đều
Hình chóp tam giác đều
Hình chóp tứ giác đều
Gọi O là trung điểm một cạnh đáy. Dựng hệ trục như
Chọn hệ trục như hình với a = 1. Tọa độ điểm:O0;0;0,
hình vẽ và a = 1. Tọa độ điểm:      
AB 3   BC   AB 2   AB 2   AB
O 0;0;0, A 0; ; 0    , B  ; 0; 0   , A ;0;0 ,   B 0; ;0   , 2 C  ;0;0 ,   2    2  2   2   2    OA   OB   OA     BCC ; 0; 0   ,  AB 2    2  D 0; ;0   2      OB   AB 3  S 0;0; SOS 0; ;OK   . . 6 SH    OH
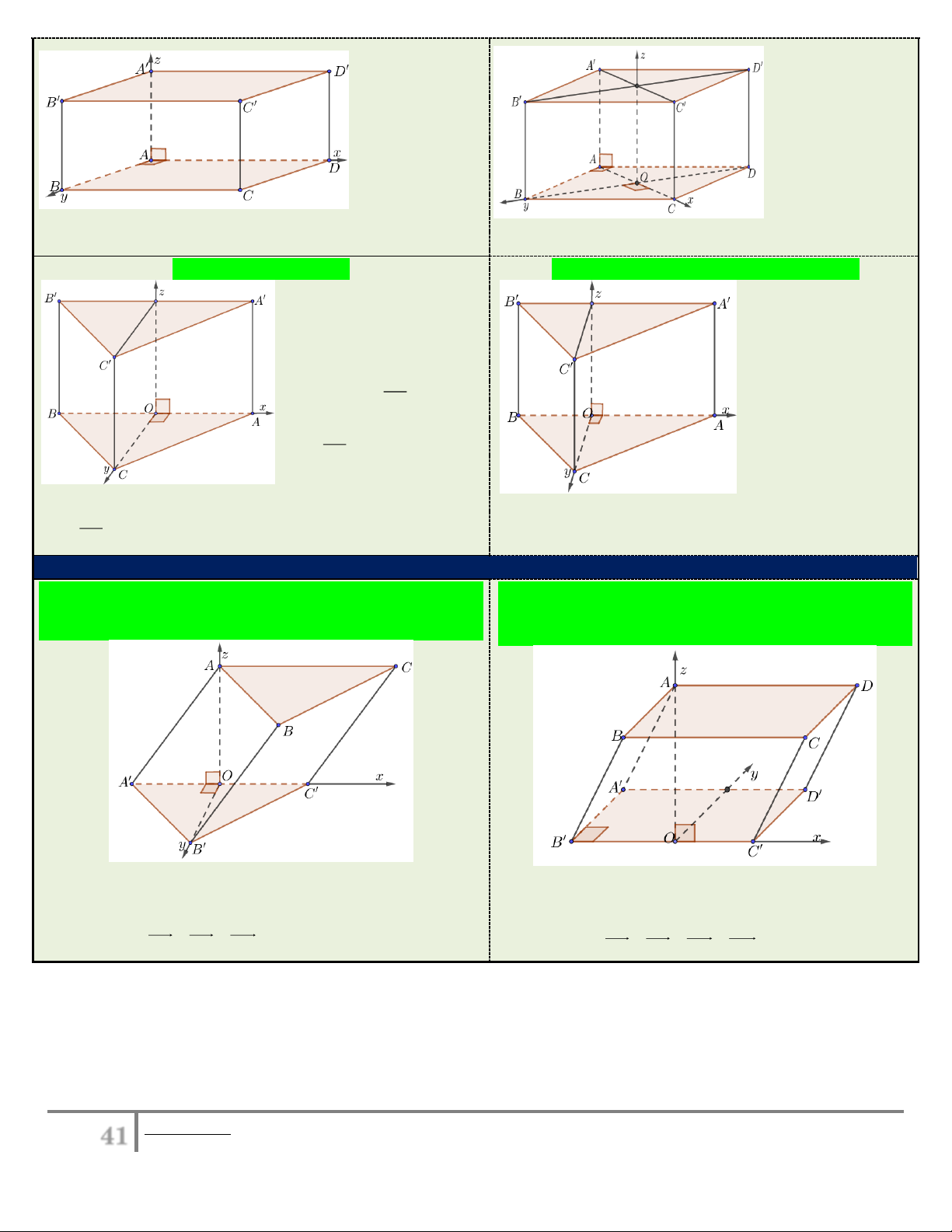
2. Gắn tọa độ đối với hình lăng trụ
2.1. Lăng trụ đứng
Hình lập phương, hình hộp chữ nhật
Lăng trụ đứng đáy là hình thoi
Dựng hệ trục như hình vẽ với a = 1. Tọa độ điểm:
Gọi O là tâm hình thoi đáy, ta dựng hệ trục như hình với
40 Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com
A O 0;0;0, O 0;0;0, B 0; ; AB 0, AO ; A 0;0, C  ; AD AB; 0 , B 0; ; OB 0, D A ; D 0; 0 , C OC;0;0,
A0;0; AA, D 0; O  ; D 0, B0; A ; B AA, A ; OA 0; AA, C A ; D A ;
B AA , D AD;0; AA. B0;O ;
B AA, COC;0;CC, D0; OD; DD
Lăng trụ tam giác đều
Lăng trụ đứng có đáy tam giác thường
Gọi O là trung điểm một Vẽ đường cao CO
cạnh đáy, chọn hệ trục trong tam giác ABC
như hình vẽ với a = 1. Ta và chọn hệ trục như có:
hình vẽ với a = 1.  AB  Tọa độ điểm là: O 0;0;0, A ;0;0 ,    2 
O 0;0;0, AO ; A 0;0,  ABB  ; OB  0;0, B  ;0;0 , 
C 0;OC;0,  2  C 0;OC;0, A ; OA 0; AA, A ; OA 0; AA,  ABB  ;0; BB , 
C0;OC;CC. B O  ;
B 0; BB, C0;OC;CC.  2 
2.2.Lăng trụ nghiêng:
Lăng trụ nghiêng có đáy là tam giác đều, hình chiếu của
Lăng trụ nghiêng có đáy là hình vuông hoặc hình
đỉnh trên mặt phẳng đối diện là trung điểm một cạnh tam
chữ nhật, hình chiếu của một đỉnh là một điểm giác đáy
thuộc cạnh đáy không chứa đỉnh đó
 Dựng hệ trục như hình vẽ, ta dễ dàng xác định được các  Dựng hệ trục như hình vẽ, ta dễ dàng xác định được điểm ,
O A , B , C , A. các điểm ,
O A , B , C , D , A .
 Tìm tọa độ các điểm còn lại thông qua hệ thức vectơ
 Tìm tọa độ các điểm còn lại thông qua hệ thức vectơ
bằng nhau: AA  BB  CC .
bằng nhau: AA  BB  CC  DD.
41 Bieân soaïn: Hoaøng Xuaân Nhaøn______________Email goùp yù: thayxuannhan@gmail.com