lOMoARcPSD|36340008
CHƯƠNG 1. BIẾN CỐ VÀ XÁC SUẤT CỦA BIẾN CỐ Thuật ngữ:
Complement event: biến cố đối lập (phần bù)
Union events: biến cố tổng (hợp của các biến cố)
Intersection events: biến cố tích (giao của các biến cố)
Collectively exhaustive events (nhóm biến cố mà hợp/ tổng của nó là toàn bộ không gian mẫu)
Partition: nhóm biến cố đầy đủ - xung khắc từng đôi và hợp của chúng là toàn bộ không gian mẫu
Mutually exclusive events: các biến cố xung khắc (loại trừ lẫn nhau)
Prior probability: xác suất tiên nghiệm - xác suất ước tính ban đầu
Posterior probability: xác suất hậu nghiệm - xác suất tính lại sau khi có thêm thông tin
TÓM TẮT NỘI DUNG CHÍNH CHƯƠNG 1
- Phép thử: Việc thực hiện một nhóm các điều kiện cơ bản để nghiên cứu xem một
hiện tượng nào đó có xảy ra hay không
- Biến cố: các sự kiện liên quan tới kết quả xảy ra sau khi thực hiện phép thử
- Phân loại biến cố: biến cố chắc chắn, biến cố không thể có, biến cố ngẫu nhiên
- Kết cục duy nhất: trong kết quả của phép thử nhất định sẽ xảy ra 1 và chỉ 1 trong các
kết cục đó, nếu xảy ra kết cục nào đó thì không xảy ra bất kỳ kết cục nào khác
- Kết cục đồng khả năng: khả năng xảy ra của các kết cục là như nhau trong kết quả của 1 phép thử
- Biến cố sơ cấp (kết cục duy nhất): biến cố tạo nên từ một kết cục duy nhất mà
không thể phân chia thành các kết cục nhỏ hơn.
- Không gian mẫu: tập hợp tất cả các biến cố sơ cấp của 1 phép thử
- Hai cách tiếp cận về xác suất: xác suất theo quan điểm chủ quan và khách quan
- Xác suất của biến cố: con số đặc trưng cho khả năng khách quan để xuất hiện biến
cố trong kết quả của phép thử 0
- Tính xác suất theo phương pháp cổ điển:
Page 1 of 6
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
Trong đó là số biến cố sơ cấp đồng khả năng và duy nhất, là số biến cố sơ cấp thuận
lợi cho biến cố A xảy ra.
- Để tính xác suất theo phương pháp cổ điển cần phải đếm số kết cục: suy luận trực
tiếp, liệt kê, dùng sơ đồ Venn, dùng các công thức của giải tích tổ hợp (hoán vị, chỉnh hợp, tổ hợp)
- Tính xác suất theo định nghĩa thống kê: lấy tần suất xuất hiện biến cố A làm xấp xỉ
cho xác suất khi số phép thử đủ lớn. Phương pháp này chỉ áp dụng cho các hiện tượng
ngẫu nhiên mà tần suất ổn định và phải thực hiện phép thử với số lần đủ lớn.
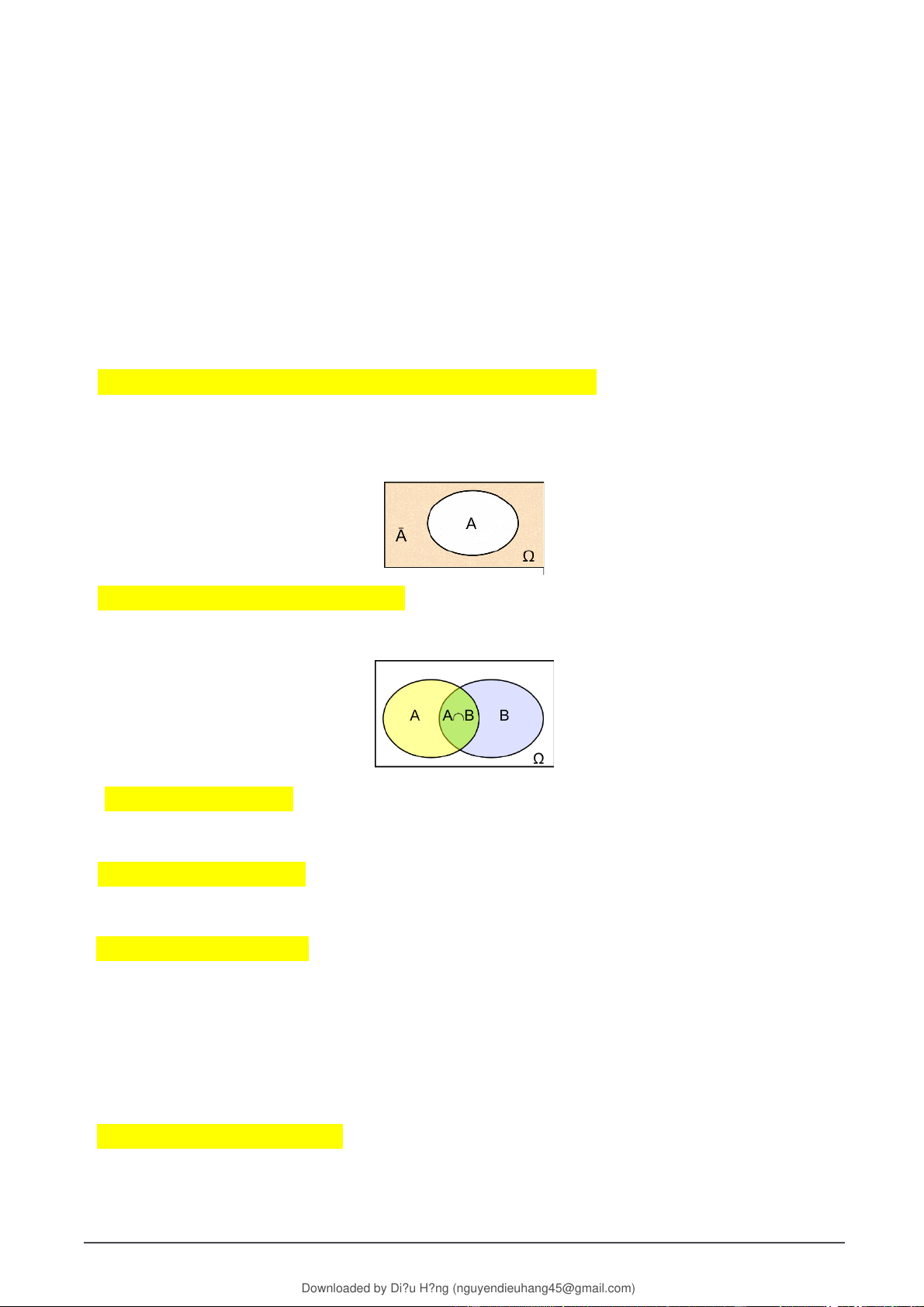
- Phần bù của biến cố A (biến cố đối lập của biến cố A) được kí hiệu là , là biến cố
mà nếu không xảy ra A thì sẽ xảy ra và ngược lại. lấp đầy toàn bộ không gian mẫu và
không có phần giao nhau, ) = 1
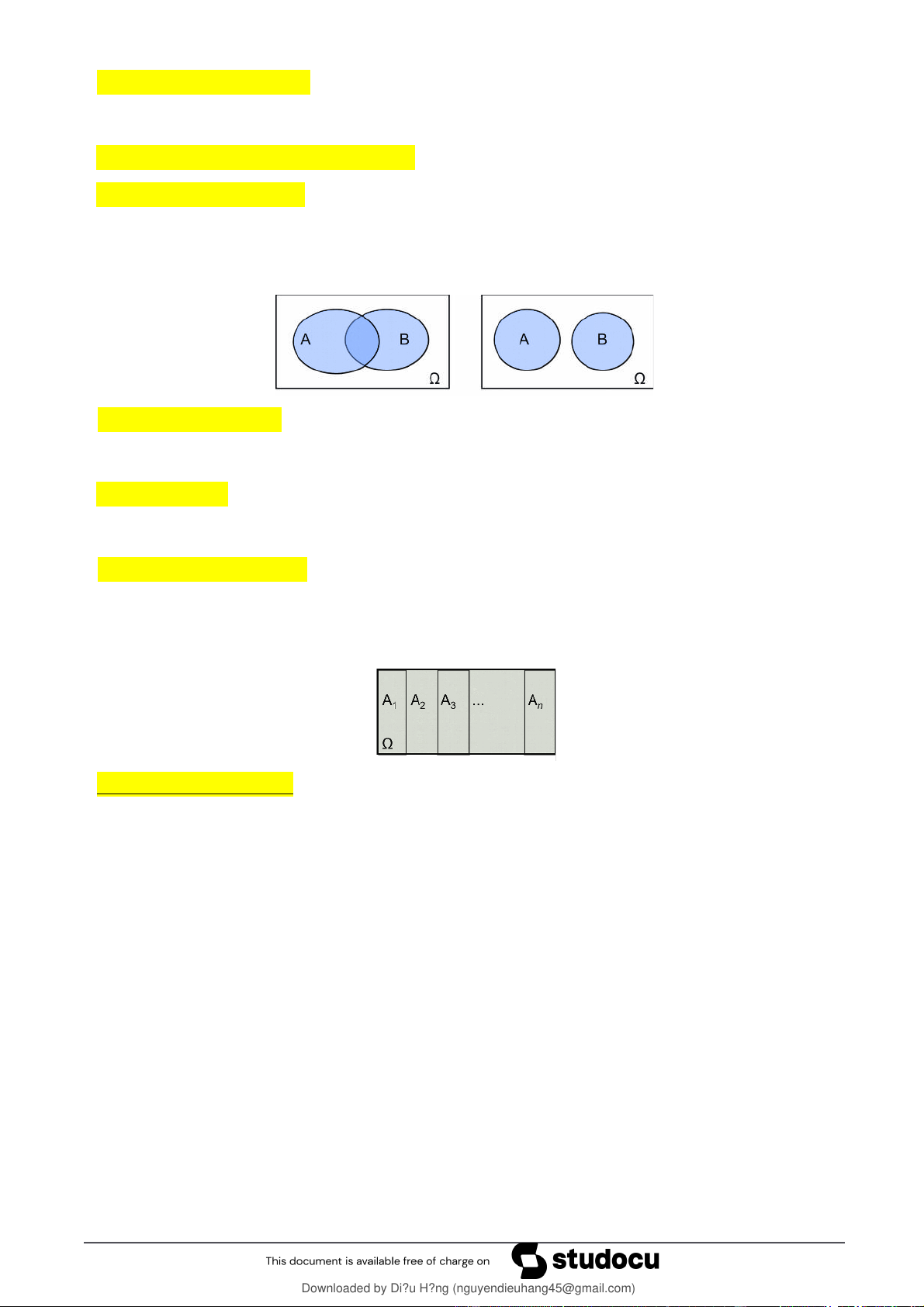
- Giao (tích) của 2 biến cố A và B: A.B hay là biến cố xảy ra khi và chỉ khi A và B cùng đồng thời xảy ra.
- Hai biến cố độc lập: việc xảy ra hay không xảy ra của biến cố này không làm ảnh
hưởng đến khả năng xảy ra của biến cố kia.
- Xác suất có điều kiện: Xác suất xảy ra biến cố A tính trong điều kiện biến cố B đã
xảy ra, kí hiệu . Nếu A, B độc lập thì
- Quy tắc nhân xác suất: Nếu A, B độc lập thì
Nếu độc lập toàn phần (mỗi biến cố độc lập với một tổ hợp bất kỳ của các biến cố còn lại) thì
- Hợp (tổng) của hai biến cố: là biến cố xảy ra khi và chỉ khi A xảy ra, hoặc B xảy ra, hoặc cả 2 cùng xảy ra.
Page 2 of 6
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
- Hai biến cố xung khắc: là hai biến cố không thể cùng đồng thời xảy ra trong kết quả
1 phép thử. A và B xung khắc thì
- Nhóm biến cố xung khắc từng đôi: hai biến cố bất kỳ là xung khắc
- Quy tắc cộng xác suất:
Nếu A và B là xung khắc thì:
Nếu xung khắc từng đôi thì
- Xác suất đồng thời: là xác suất để 2 biến cố cùng xảy ra, là xác suất phần giao của
hai biến cố đó. Xác suất này có mặt trong bảng xác suất đồng thời.
- Xác suất biên: xác suất xảy ra của biến cố có trong bảng xác suất đồng thời, được xét một cách riêng lẻ
- Nhóm biến cố đầy đủ: nhóm biến cố xung khắc từng đôi và hợp của chúng là một
biến cố chắc chắn (hợp của chúng lấp đầy không gian mẫu). là nhóm biến cố đầy đủ.
Nếu là nhóm biến cố đầy đủ thì - C
ông thức Bernoulli : công thức tính xác suất để khi thực hiện phép thử, thì biến cố
A sẽ xảy ra lần, nếu như xác suất xảy ra A trong mỗi lần thử đều là
- Xác suất tiên nghiệm: xác suất ước tính ban đầu của biến cố
- Xác suất hậu nghiệm: xác suất của biến cố được tính lại dựa trên các thông tin có thêm được
- Công thức xác suất đầy đủ: xảy ra đồng thời với nhóm biến cố đầy đủ . Khi đó xác
suất của A được tính như sau:
- Định lí Bayes: dùng để tính xác suất hậu nghiệm
Page 3 of 6
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
1. Các mệnh đề sau đây đúng hay sai, giải thích?
a) Biến cố đối lập của tổng 2 biến cố chính là tích các biến cố đối lập của 2 biến cố đó.
b) Số cách lấy ra 1 tập con gồm x phần tử từ 1 tập hợp có n phần tử cũng bằng
số cách lấy ra (n-x) phần tử từ n phần tử đó, với .
c) Nếu A và B là hai biến cố mà, xác suất xảy ra A tính trong điều kiện B đã xảy
ra bằng xác suất xảy ra B tính trong điều kiện A đã xảy ra, thì xác suất xảy ra
A bằng với xác suất xảy ra B.
d) Nếu một biến cố và biến cố đối lập của nó có xác suất xảy ra bằng nhau, thì
xác suất xảy ra biến cố đó phải bằng 0,5.
e) Nếu và là hai biến cố độc lập thì và cũng độc lập.
f) Nếu và là hai biến cố xung khắc thì và cũng là hai biến cố xung khắc.
2. Các mệnh đề sau đây đúng hay sai, giải thích?
a) Xác suất của tổng hai biến cố không thể bé hơn xác suất của tích hai biến cố đó.
b) Xác suất của tổng hai biến cố không thể lớn hơn tổng xác suất của hai biến cố đó.
c) Xác suất của tích hai biến cố không thể lớn hơn xác suất của từng biến cố thành phần.
d) Biến cố A và biến cố đối lập của nó là xung khắc.
e) Nếu hai biến cố là xung khắc thì hợp của chúng là toàn bộ không gian mẫu.
f) Nếu hai biến cố mà hợp của chúng là toàn bộ không gian mẫu thì chúng là hai biến cố xung khắc.
3. Các mệnh đề sau đây đúng hay sai, giải thích?
a) Xác suất xảy ra biến cố A trong điều kiện biến cố B đã xảy ra ít nhất phải
bằng với xác suất xảy ra biến cố A.
b) Biến cố A và biến cố đối lập của nó là độc lập với nhau.
c) Xác suất xảy ra biến cố A tính trong điều kiện biến cố B đã xảy ra, ít nhất
phải bằng với xác suất của tích hai biến cố A và B.
d) Xác suất của một tích hai biến cố không thể lớn hơn tích xác suất của 2 biến cố đó.
Page 4 of 6
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
e) Xác suất hậu nghiệm của một biến cố luôn lớn hơn hoặc bằng xác suất tiên nghiệm của nó. Bài tập.
1. Một lô hàng cùng loại gồm có 7 sản phẩm nhập khẩu và 5 sản phẩm sản xuất
trong nước. Lấy ngẫu nhiên 4 sản phẩm từ lô hàng. Xác suất lấy được 2 sản
phẩm sản xuất trong nước và 2 sản phẩm nhập khẩu là: A. 0,42 B. 0,58 C. 0,48 D. 0,52
2. Một người thi tuyển dụng vào một cơ quan, ở vòng thi cuối phải qua phỏng
vấn của Trưởng phòng và Phó trưởng phòng của đơn vị tuyển dụng đó,
một cách độc lập. Nếu cả trưởng phòng và phó phòng đều đồng ý thì người
đó sẽ được tiếp nhận. Khả năng để người này được Trưởng phòng đồng ý
là 0,6; được phó phòng đồng ý là 0,7. Hãy tính xác suất để:
- Người đó được tiếp nhận
- Người đó chỉ được 1 người đồng ý
- Cả hai người không đồng ý nhận
- Có ít nhất một người đồng ý tiếp nhận
3. Một nhà máy sản xuất sản phẩm qua 2 khâu ở 2 phân xưởng độc lập với nhau,
với xác suất sản phẩm bị lỗi ở các khâu tương ứng là 0,03 và 0,05. Sản phẩm bị
coi là phế phẩm nếu như có lỗi ở ít nhất một khâu sản xuất. Xác suất để lấy
ngẫu nhiên 1 sản phẩm thì được phế phẩm là: A. 0,079 B. 0,921 C. 0,08 D. 0,92
4. Trong một tháng nào đó, thì khả năng xăng tăng giá là 0,3; khả năng gas
tăng giá là 0,2; khả năng cả xăng và gas cùng tăng giá là 0,1. Hãy tính xác
suất để trong tháng đó:
- Xăng tăng giá nhưng gas không tăng giá
Page 5 of 6
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008
- Chỉ xăng hoặc gas tăng giá
- Có ít nhất 1 mặt hàng tăng giá
- Gas tăng giá trong trường hợp xăng đã tăng giá
- Xăng tăng giá trong trường hợp gas không tăng giá
5. Một nhân viên tiếp thị đi tiếp xúc và chào bán hàng cho các khách hàng tiềm
năng, khả năng để mỗi khách hàng tiềm năng sẽ mua hàng đều là 0,4. Hãy tính
xác suất để khi người đó đi chào hàng cho 10 người thì:
- Bán được hàng cho 3 người
- Bán được hàng cho không quá 8 người
- Bán được hàng cho ít nhất 1 người
6. Ở một địa phương nằm trong vùng đang có lây lan dịch Covid19, các chuyên gia
đánh giá 10% người dân có nguy cơ lây nhiễm cao, 60% có nguy cơ lây nhiễm
mức trung bình và 30% có nguy cơ lây nhiễm thấp. Xác suất để những người
thuộc các nhóm này bị lây nhiễm Covid19 tương ứng là 0,8; 0,5 và 0,05. Lấy
ngẫu nhiên một người dân ở địa phương này, tính xác suất để người đó bị lây nhiễm Covid19. A. 0,395 B. 0,605 C. 0,02 D. 0,98
7. Với thông tin của bài 6 ở trên, giả sử lấy ngẫu nhiên 1 người của địa phương này
và làm test thì thấy người này bị nhiễm Covid19. Tính xác suất để người đó
thuộc nhóm có nguy cơ lây nhiễm thấp.
Page 6 of 6
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com)