Tóm tắt lý thuyết chương 2 Biến ngẫu nhiên - Xác suất thống kê (MI2020) | Trường Đại học Bách khoa Hà Nội
Biến ngẫu nhiên là một hàm số gán giá trị thực cho mỗi kết cục của một phép thử ngẫu nhiên.
Preview text:
lOMoAR cPSD| 45254322
TÓM TẮT LÝ THUYẾT CHƯƠNG 2. BIẾN NGẪU NHIÊN
2.1 Khái niệm biến ngẫu nhiên
- Biến ngẫu nhiên là một hàm số gán giá trị thực cho mỗi kết cục của một phép thử ngẫu nhiên.
- Biến ngẫu nhiên rời rạc là BNN nhận hữu hạn hoặc vô hạn đếm được giá trị.
- Biến ngẫu nhiên liên tục là BNN nhận vô hạn không đếm được giá trị trong một khoảng liên tục.
2.2 Phân bố xác suất của biến ngẫu nhiên rời rạc
- Bảng phân bố xác suất của BNN rời rạc X X … x1 x2 x3 … P(X = )x i p1 p2 p3
- X nhận các giá trị x1, x2, x3,...
- Xác suất pi = P(X = xi) thuộc [0, 1] - ng Tổ
∑ pi = ∑P(X = xi) = 1 i i
2.3 Phân bố xác suất của biến liên tục
- Hàm mật độ xác suất của BNN liên tục là hàm fX(x) thoả mãn các điều kiện:
• fX(x) ≥ 0, với mọi x ∈ R •
(diện tích giới hạn bởi Ox và y = fX(x) bằng 1)
• P(X = a) = 0,∀a ∈ R . b
• P(a ≤ X ≤ b) = P(a < X ≤ b) = P(a ≤ X < b) = P(a < X < b) =
fX(x)dx (diện tích giới
a hạn bởi Ox và y = fX(x), x = a, x = b)
2.3 Hàm phân bố xác suất của BNN
- Hàm phân bố xác suất của biến ngẫu nhiên X là hàm: FX(x) = P(X < x) - Tính
chất của hàm phân bố xác suất:
• 0 ≤ FX(x) ≤ 1,∀x ∈ R
• FX(−∞) = lim FX(x) = 0 và FX(+∞) = lim FX(x) = 1 x→−∞ x→+∞
• FX(x) là hàm không giảm trên R.
• P(a ≤ X < b) = FX(b) − FX(a) lOMoAR cPSD| 45254322
• Với X là BNN rời rạc thì: FX(x) = ∑ P(X = xi) xi<x
• Với X là BNN liên tục thì: FX
fX(u)du và fX(x) = FX′ (x)
2.4 Các số đặc trưng của BNN
2.4.1 Các số đặc trưng đo trung tâm của BNN - Kỳ
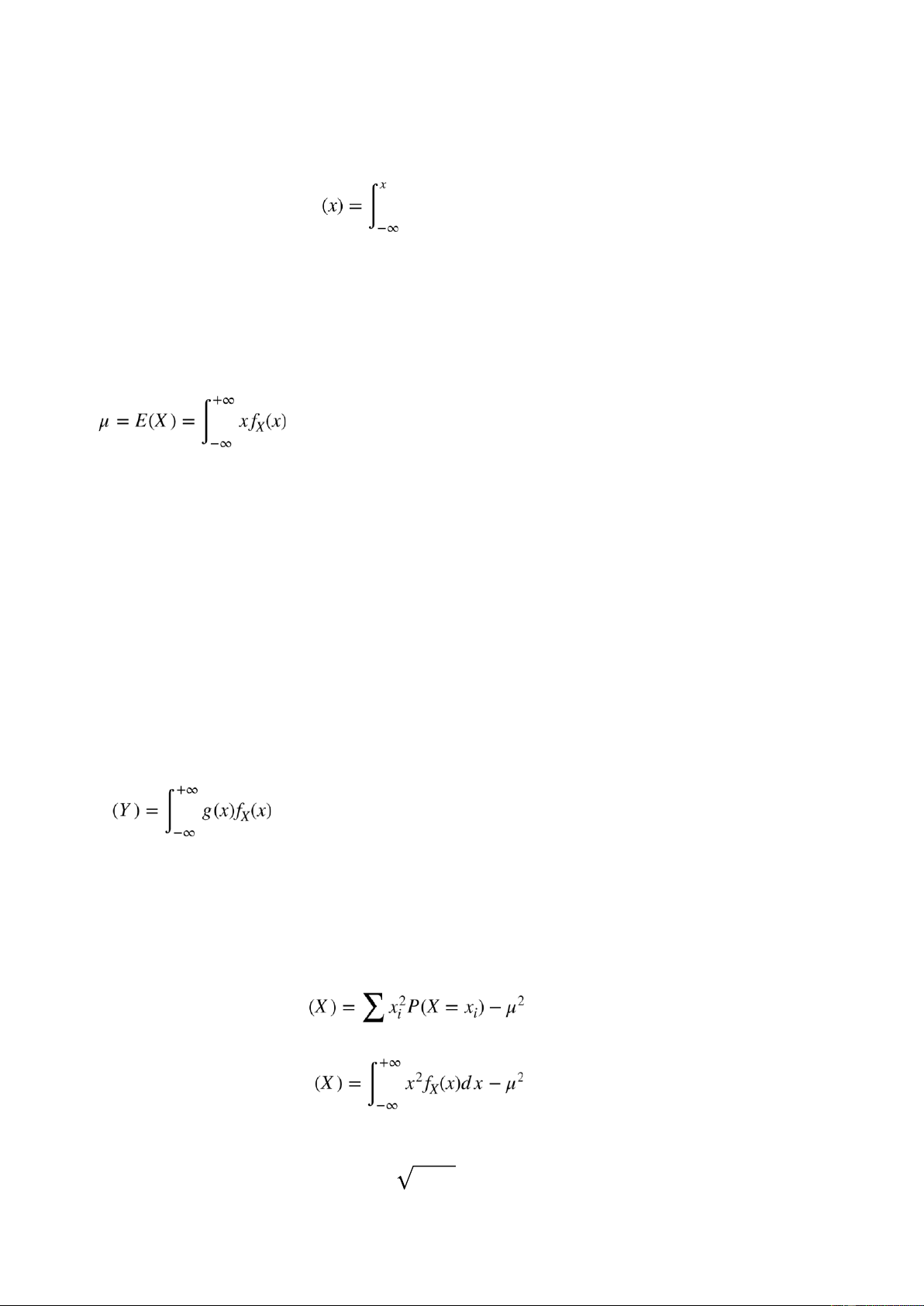
vọng (giá trị trung bình) của BNN X là: • μ = E(X) =
∑xiP(X = xi) nếu X là BNN rời rạc i •
dx nếu X là BNN liên tục.
- Trung vị của BNN X là giá trị x0.5 thoả mãn x0.5 = inf{x : FX(x) ≥ 0.5} hoặc x0.5 = sup{x : FX(x) ≤ 0.5}.
Nếu X là BNN liên tục thì x0.5 thoả mãn FX(x0.5) = 0.5
- Mode của BNN X là giá trị mà P(X = x) (với X là BNN rời rạc) hoặc fX(x) (với X là BNN liên tục)
đạt giá trị lớn nhất.
- Tính chất: E(X + Y) = E(X) + E(Y); E(aX + b) = aE(X) + b; E(XY) = E(X)E(Y) nếu X, Y độc lập (chương 3). - Xét Y = g(X) thì:
• E(Y ) = ∑g(xi)P(X = xi) nếu X là BNN rời rạc i • E
dx nếu X là BNN liên tục.
2.4.2 Các số đặc trưng đo độ phân tán của BNN
- Phương sai của BNN X là V(X) = E{[X − E(X)]2}. - Tính chất:
• Công thức rút gọn: V(X) = E(X2) − [E(X)]2
• Nếu X là BNN rời rạc thì V i
• Nếu X là BNN liên tục thì V
• V(aX + b) = a2V(X); V(X + Y) = V(X - Y) = V(X) + V(Y) nếu X, Y độc lập (chương 3).
- Độ lêch chuẩn của BNN X là σ(X) = V(X)
2.4.3 Số đặc trưng đo vị trí tương đối
- Phân vị mức α ∈ (0,1) là giá trị xα thoả mãn xα = inf{x : FX(x) ≥ α} hoặc xα = sup{x : FX(x) ≤ α}. lOMoAR cPSD| 45254322
2.4 Một số phân bố xác suất quan trọng
2.4.1 Phân bố nhị thức và phân bố Poa-xông
- Dãy phép thử Bernoulli là dãy gồm n phép thử thoả mãn các điều kiện:
• n phép thử độc lập.
• Xét sự kiện A xảy ra ở mỗi phép thử (kí hiệu là thành công).
• Xác suất thành công (sự kiện A xảy ra) là trong mp ỗi phép thử. Vậy xác suất không
thành công là q = 1- trong mp ỗi lần thử.
Phân bố nhị thức B(n, p) Phân bố Poa-xông
ĐN: X là số lần thành công trong n lần thử
ĐN: X là số lần thành công trong một Bernoulli
khoảng thời gian nhất định.
X nhận các giá trị: 0, 1, 2, …, n
X nhận các giá trị: 0, 1, 2, 3, …,
P(X = k) = C k
n pk(1 − p)n−k λk
P(X = k) = e−λ k!
E(X) = np; V(X) = npq; σ(X) = npq
E(X) = V(X) = λ
2.4.2 Phân bố đều trên [a, b]
- Biến X có phân bố đều trên đoạn [a, b] nếu hàm mật độ xác suất của X là: 1
nếu a ≤ x ≤ b fX(x) =b − a 0 trái lại
- Tính chất cảu phân bố đều: Nếu X ∼ U([a,b]) thì: a + b • E(X) = 2 (b − a)2 • V(X) = 12
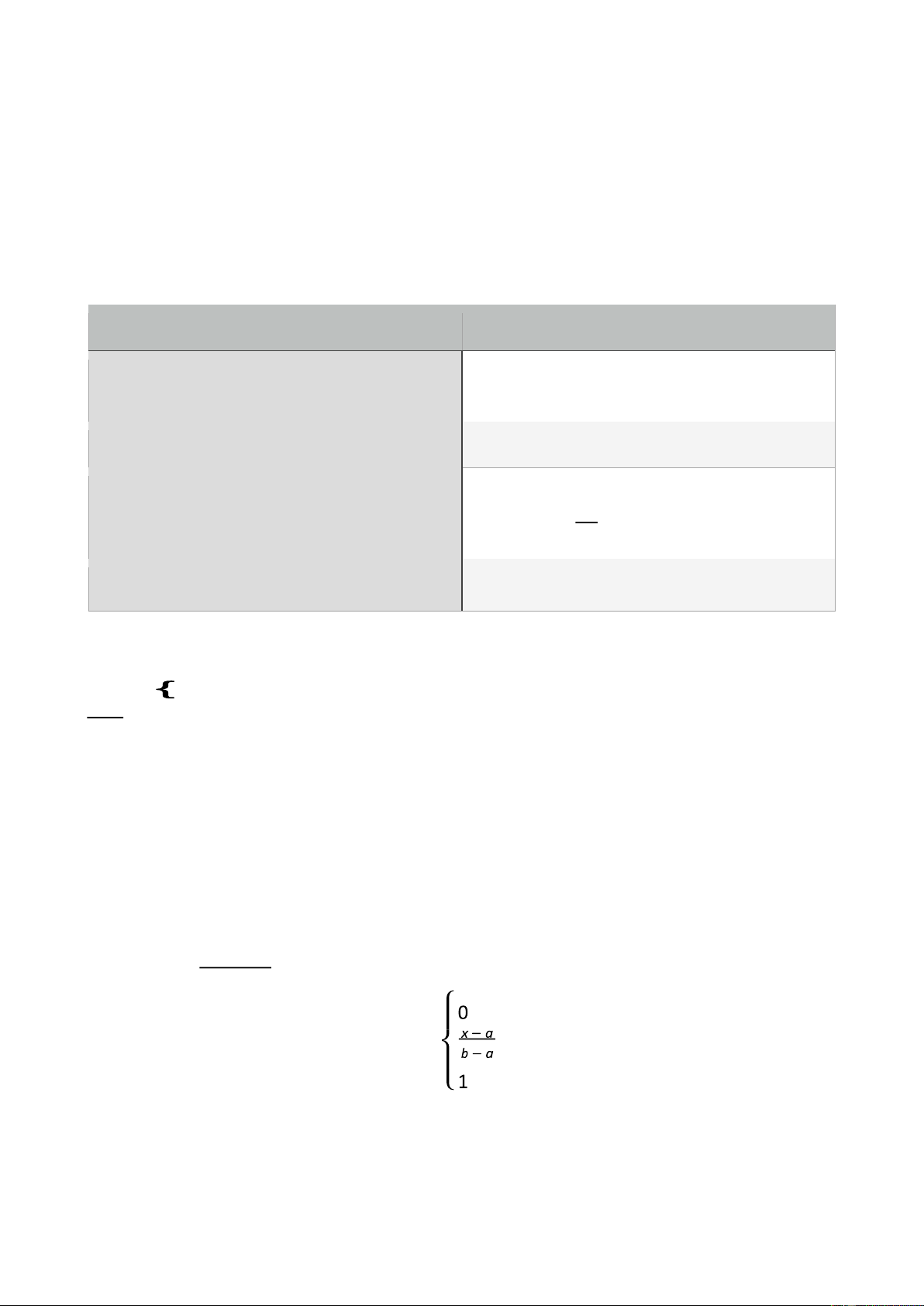
nếu x ≤ a
Hàm phân bố xác suất của X là: FX(x)
=nếu a < x < b •
nếu x ≥ b 2.4.3 Phân bố mũ
- Biến X có phân bố mũ với tham số λ > 0 nếu hàm mật độ xác suất của X là:
λe−λx nếu x ≥ 0 fX(x) = { 0 nếu x < 0 lOMoAR cPSD| 45254322
- Tính chất của phân bố mũ: Nếu X ∼ℰ(λ) thì • E(X) = • V(X) = 0 if x ≤ 0
• Hàm phân bố xác suất của X là: FX(x) = {1 − e−λx if x > 0
2.4.4 Phân bố chuẩn
- Biến X có phân bố chuẩn với tham số kỳ vọng và phμ ương sai σ2 nếu hàm mật độ xác suất của X là: 1 2
−(x −μ) fX(x) =
- Nếu μ = 0,σ = 1 thì X có phân bố chuẩn tắc, ký hiệu là Z. Hàm mật độ xác suất của Z 1 z2 là: và hàm phân b ố xác su ấ t c ủ a Z là: v ớ i . ϕ ϕ
Chú ý: Φ(−x) = 1 −Φ(x) and ϕ(−x) = −ϕ(x).
- Tính chất của phân bố chuẩn: Nếu X ∼𝒩(μ,σ) thì: • E(X) = μ •
V(X) = σ2 và σ(X) = σ 1 − x −μ
Hàm mật độ xác suất của X là: f 2 X(x) = 2σ = φ( ) • σ σ x −μ •
Hàm phân bố xác suất của X
là: FX(x) = Φ( σ ) = 0.5 + ϕ( σ ) a −μ a −μ •
P(X < a) = FX(a) = Φ( σ ) = 0.5 + ϕ( σ ) lOMoAR cPSD| 45254322 a −μ a −μ •
P(X > a) = 1 − FX(a) = 1 −Φ(
σ ) = 0.5 −ϕ( σ ) b −μ a −μ b −μ a −μ •
P(a < X < b) = FX(b) − FX(a) = Φ( σ ) −Φ( σ ) = ϕ( σ ) −ϕ( σ )
2.4.5 Xấp xỉ phân bố nhị thức
Cho X có phân bố nhị thức B(n, p).
- Nếu n lớn và p rất nhỏ thì X ∼ B(n, p) ≈ Y ∼ P(λ) with λ = np (np)k
Khi đó: P(X = k) ≈ e−np k!
- Nếu n lớn và p gần 0.5 thì X ∼ B(n, p) ≈ Y ∼ N(μ,σ2) with μ = np;σ2 = npq. Khi đó k + 0.5 − np k + 0.5 − np
• P(X ≤ k) ≈ P(Y < k + 0.5) = Φ( ) = 0.5 + ϕ( ) k k
• P(k1 ≤ X ≤ b) ≈ P(k1− 0.5 < Y < k2 + 0.5) = Φ() =
ϕ( k2 + 0.5 − np ) −ϕ( k1− 0.5 − np )