

Preview text:
lOMoAR cPSD| 45254322 TÓM TẮT CHƯƠNG 3
ƯỚC LƯỢNG THAM SỐ
3.1 Ước lượng điểm
- Ước lượng điểm của gi trị trung b nh tổng thể (gi trị kỳ vọng) l trung b nh mμ ẫu ¯
= X1 + X2 + … + Xn (l ước lượng kh ng chệch,
vững v hiệu quả) X n
- Ước lượng điểm của phương sai tổng thể σ2 l phương sai mẫu (đ hiệu chỉnh): n n S2 X 2
i − nX¯ 2) (l ước lượng kh ng chệch, vững) i=1 i=1
Khi đ ước lượng điểm của độ lệch chuẩn tổng thể l σ độ lệch chuẩn mẫu S X
- Ước lượng điểm của tỷ lệ (x c suất) trong tp ổng thể l tỷ lệ trong mẫu p̂ = , với X l n số
lần th nh c ng trong một mẫu k ch thước (n l ước lượng kh ng chệch, vững v hiệu quả).
3.2 Khoảng ước lượng (tin cậy) của gi trị trung b nh tổng thể μ
Quan sát một mẫu ngẫu nhiên (X1, X2,…, Xn) từ tổng thể X với trung bình μ = E(X) v phương
sai σ2 = V(X).
- Trường hợp 1: dữ liệu X ∼ N(μ;σ2) với phương sai σ2 đ biết: thống k X¯ −μ
Z =∼ N(0,1) n n khoảng ước lượng (đối xứng) vμ ới độ tin cậy 1 −α l : σ σ
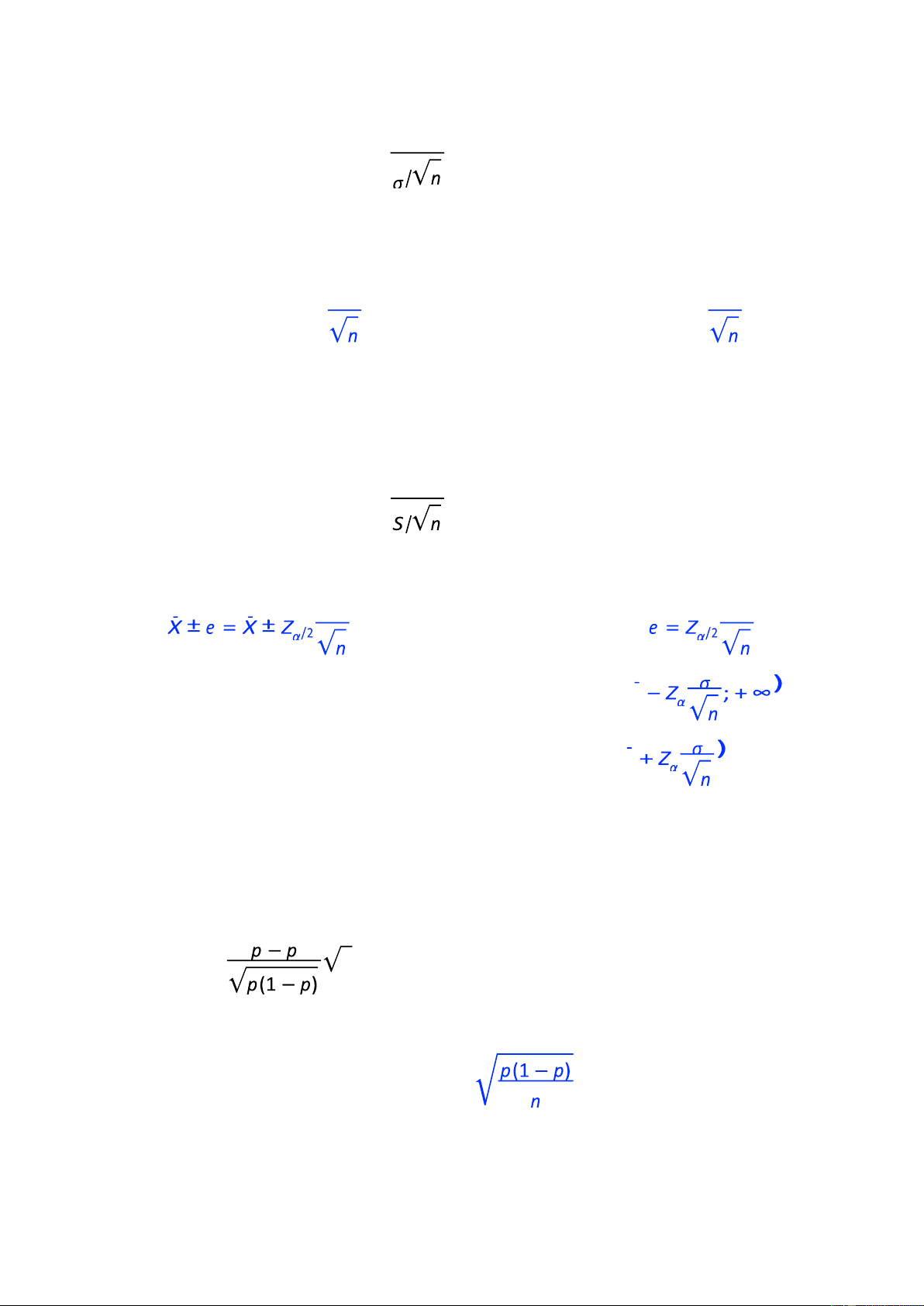
X¯ ± e = X¯ ± Zα/2 , trong đ
sai số (độ ch nh x c) l e = Zα/2
- Trường hợp 2: dữ liệu X ∼ N(μ;σ2) với phương sai σ2 chưa biết: thống k X¯ −μ T = ∼
tn−1 n n khoảng ước lượng (đối xứng) vμ ới độ tin cậy 1 −α l : S
X¯ ± e = X¯ ± tα/2
S trong đ sai số (độ ch nh x c) l e = tα/2
v bậc tự do l d . f = n − 1 lOMoAR cPSD| 45254322
- Trường hợp 3: kh ng biết dữ liệu X ∼ N(μ;σ2) với phương sai σ2 đ biết, k ch thước X¯ −μ mẫu đủ lớn ≈
n > 30: thống k Z =
N(0,1) n n khoảng ước lượng (đối xứng) μ với độ tin cậy − 1 α l : σ σ
X¯ ± e = X¯ ± Zα/2 , trong đ
sai số (độ ch nh x c) l e = Zα/2
- Trường hợp 4: kh ng biết dữ liệu X ∼ N(μ;σ2) với phương sai σ2 chưa biết, k ch thước ≈
X¯ −μ mẫu đủ lớn n > 30: thống k T = N(0,1) n n
khoảng ước lượng (đối xứng) μ với độ tin cậy − 1 α l : S S
, trong đ độ chnh xc ướ c l ượ ng l
Ch ý: Khoảng ước lượng tối thiểu của v
μ ới độ tin cậy 1 −α l : (X v
khoảng ước lượng tối đa của vμ ới độ tin cậy 1 −α l : (−∞; X
(với trường hợp 1 v tương tự cho c c trường hợp kh c)
3.3 Khoảng ước lượng (tin cậy) của gi trị tỷ lệ (x c suất) p
Gọi p l tỷ lệ trong tổng thể; x t một mẫu k ch thước n đủ lớn, gọi l tp ỷ lệ trong mẫu. Ta c thống k Z = n ≈ N(0,1)
N n khoảng ước lượng (đối xứng) của p với độ tin cậy 1 −α l :
p̂ ± e = p̂ ± Zα/2
Khoảng ước lượng tối thiểu của p với độ tin cậy 1 −α l : lOMoAR cPSD| 45254322 (p̂− Zα
;1) (0; p̂ + Zα )
Khoảng ước lượng tối đa của p với độ tin cậy 1 −α l :
3.4 K ch thước mẫu cần thiết
- K ch thước mẫu cần thiết để ước lượng gi trị trung b nh vμ ới độ tin cậy 1 −α v độ
Zα/2σ 2 ch nh x c l e n = ) e
- K ch thước mẫu cần thiết để ước lượng gi trị tỷ lệ vp ới độ tin cậy 1 −α v độ ch nh x c Zα/2 2 e l n = ( ) p̂q e
Nếu kh ng bip ết th chọn p̂ = q̂ = .




