




Preview text:
lOMoAR cPSD| 45254322 TÓM TẮT CHƯƠNG 5
QUY HOẠCH THỰC NGHIỆM
5.1 Phương ph p b nh phương cực tiểu
Bài toán: ta cần nghiên cứu một đại lượng y trong một hệ thống nào đó. Giả sử y phụ thuộc
vào các yếu tố độc lập và các tác động ngẫu nhiên không điều khiển được .
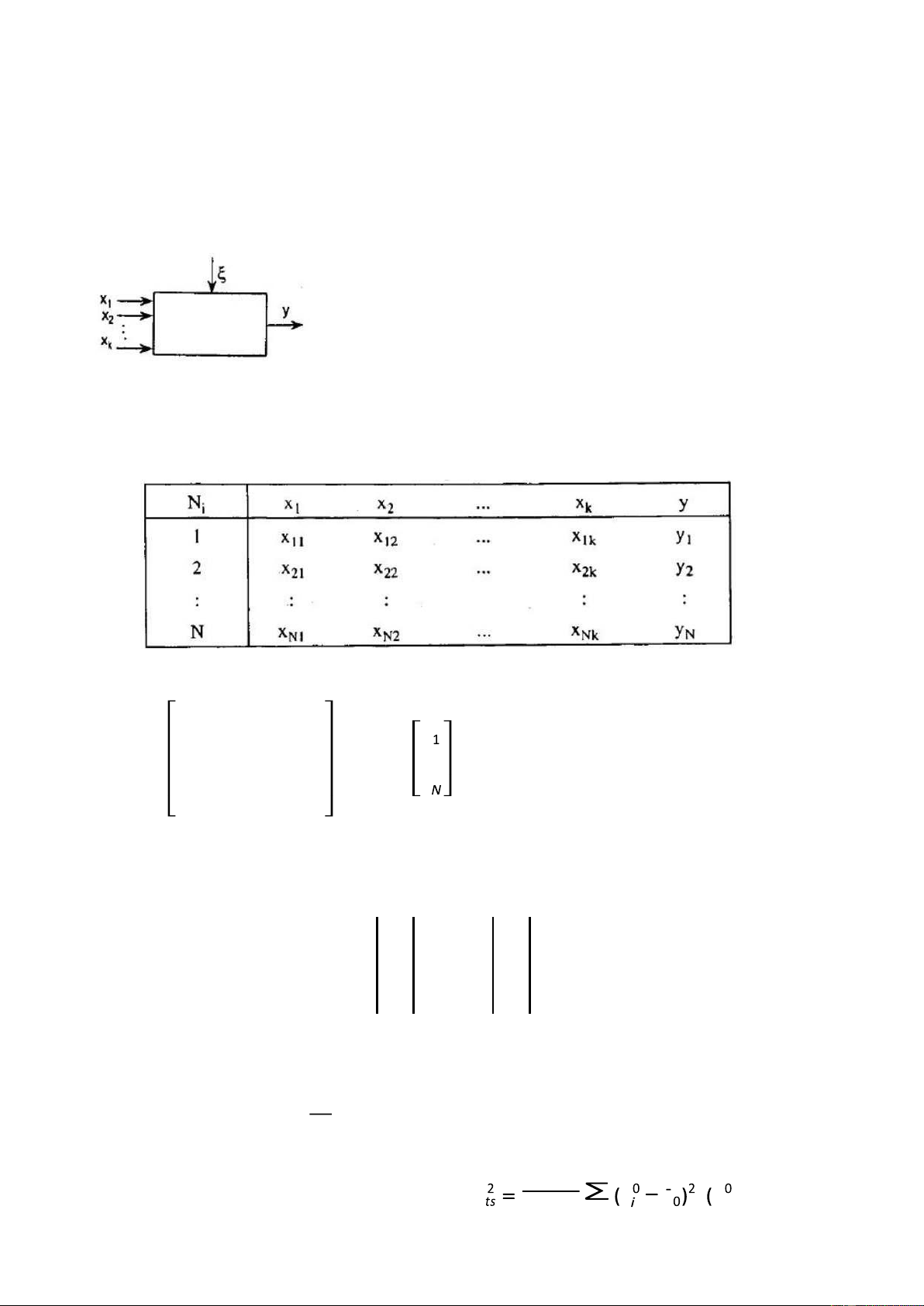
X t m h nh hồi quy tuyến t nh: y = β0 + β1x1 + … + βkxk + ξ, với giả thiết ξ ∼ N(0;σ2). Giả sử
ta thực hiện N th nghiệm thu được dữ liệu như sau:
1 x11 … x1k 1 x21 … y
x2k v Y =. ⋮ y Đặt X = ⋮ ⋮ ⋮ ⋮ 1 xN1 … xNk β0 b0
C ng thức 1: Ước lượng của β ==
(XtX)−1XtY ⋮ B = ⋮ βk bk
C ng thức 2: Kiểm định sự c ý nghĩa của hệ số hồi quy với H0 : βj = 0 b j
Ti u chuẩn kiểm định l tbj = ∼ td.f khi H0 đng. sbj n0 , 2 2 0
j = sts (C−1)jj, với C−1 = (XtX)−1 v s 1
y y y 1,…,yn 0) l trong đ sb n0 − 1 i=1 lOMoAR cPSD| 45254322
c c gi trị quan s t của y lặp lại tại 1 điểm th nghiệm; d . f = n0 − 1
Quy tắc kiểm định: Ta b c bỏ H0 nếu |tbj| > td.f;1−α
C ng thức 3: Kiểm định sự ph hợp của m h nh với H0 : m h nh ph hợp 2 sdu
Ti u chuẩn kiểm định l = F
2 ∼ FN−k−1;n0−1 khi H0 đng. sts N 2 =
1 ∑(yi − yî )2 trong đ sdu N − k − 1 i=1
Quy tắc kiểm định: Ta b c bỏ F
H0 nếu F > N−k−1;n0−1;1−α
5.2 Phương ph p quy hoạch trực giao
1 x11 … x1k 1
x21 … x2k
- Quy hoạch trực giao: l phương ph p quy hoạch m ma trận X = ⋮ ⋮ ⋮ ⋮ 1 xN1 … xNk
thoả m n điều kiện: 2 cột bất kỳ của X trực giao nhau (t ch v hướng của 2 cột bất kỳ của X = 0).
Khi đ C−1 = (XtX)−1 với (C−1)ij = 0 nếu i ≠ j v (C−1)jj = ∥xj∥−2. < xj,y > ∑Ni=1 xijyi
C ng thức 1: C ng thức t nh hệ số hồi quy b j ; j = 0, 1, , k
C ng thức 2: Kiểm định sự c ý nghĩa của hệ số hồi quy với H0 : βj = 0 bj
Ti u chuẩn kiểm định l tbj = ∼ td.f khi H0 đng. sbj 2 n0 2 y y j = sts y v 1 , s 0
1,…,yn 0) l c c gi trị quan
s t trong đ sb ∑Ni=1 xij2 n0 − 1 i=1 lOMoAR cPSD| 45254322
của y lặp lại tại 1 điểm th nghiệm; d . f = n0 − 1
Quy tắc kiểm định: Ta b c bỏ H0 nếu |tbj| > td.f;1−α
C ng thức 3: Kiểm định sự ph hợp của m h nh với H0 : m h nh ph hợp 2 sdu
Ti u chuẩn kiểm định l = F
2 ∼ FN−k−1;n0−1 khi H0 đng. sts 1 N du ∑ i i
trong đ s2 =(y − ŷ )2 N − k − 1 i=1
Quy tắc kiểm định: Ta b c bỏ F
H0 nếu F > N−k−1;n0−1;1−α
5.2.1 Phương ph p quy hoạch trực giao cấp 1
- Phương ph p quy hoạch trực giao cấp 1: l phương ph p quy hoạch trực giao (tức l 2
cột bất kỳ của X trực giao nhau: t ch v hướng của 2 cột bất kỳ của X = 0) v ∥xj∥2 = N. -
Trong hệ thống x t biến y phụ thuộc c c biến độc lập Z1,…, Zk với Zi ≤ Zj ≤ Zj. X t th
0 Zi + Zj ; thực nghiệm tại c c gi trị bi
n Zi, Zj v lặp lại n0 lần th nghiệm tại t m Zj Zj − Zj0 Zj − Zi
hiện đổi biến Xj = với ΔZj = v x t m h nh: ΔZj 2
y = β0 + β1X1 + … + βkXk + ξ.
- Khi đ ma trận X thoả m n điều kiện của Quy hoạch trực giao cấp 1. < xj,y > ∑Ni=1 xijyi
C ng thức 1: C ng thức t nh hệ số hồi quy bj ; j = 0, 1, , k N
C ng thức 2: Kiểm định sự c ý nghĩa của hệ số hồi quy với H0 : βj = 0 bj
Ti u chuẩn kiểm định l tbj = ∼ td.f khi H0 đng. sbj lOMoAR cPSD| 45254322 2 n0 , 2 y j y y = sts v s 1 0
1,…,yn 0) l c c gi trị quan s t của y trong đ sb N n0 − 1 i=1
lặp lại tại 1 điểm th nghiệm; d . f = n0 − 1
Quy tắc kiểm định: Ta b c bỏ H0 nếu |tbj| > td.f;1−α
C ng thức 3: Kiểm định sự ph hợp của m h nh với H0 : m h nh ph hợp 2 sdu
Ti u chuẩn kiểm định l = F
2 ∼ FN−k−1;n0−1 khi H0 đng. sts N 2 =
1 ∑(yi − yî )2 trong đ sdu N − k − 1 i=1
Quy tắc kiểm định: Ta b c bỏ F
H0 nếu F > N−k−1;n0−1;1−α
5.2.2 Phương ph p quy hoạch trực giao cấp 2
Trong hệ thống x t biến y phụ thuộc c c biến độc lập Z1,…, Zk với Zi ≤ Zj ≤ Z j. Thực hiện Zj − Zj0 Zj − Zi đổi biến Xj = với ΔZj = . ΔZj 2 C c tham số của m h nh:
+) k l số biến độc lập +) n 0
0 l số lần lặp th nghiệm tại t m Zj
+) N = 2k + n0 + 2k l tổng số th nghiệm: gồm 2k th nghiệm tại bi n Zi, Z j ; n0 lần th nghiệm
tại t m v 2k th nghiệm tại c c trục Xj với toạ độ l ∓a. k k 1 k + 2a1).
1 = 1 ∑(yi − yî )2 nghĩa (số biến độc
lập trong m h nh), trong đ sdu N − r − 1 lOMoAR cPSD| 45254322
+) tham số a = v λ =(2 N
X t m h nh bậc 2 đầy đủ với X 2
j′ = Xj − λ:
y = β0 + ∑βjXj + ∑βijXiXj + ∑βjjXj′ + ξ.
Phương ph p quy hoạch trực giao cấp 2: l phương ph p quy hoạch trực giao với N =
2k + n0 + 2k th nghiệm với c c tham số như ở tr n.
Ta c C = XtX với Cmn = < Xm, Xn > = 0 nếu m ≠ n v N nếu m = 0
2k + 2a2 nếu m = 1,...,k Cmm
=k nếu m = ij
2a4 nếu m = jj 2 < Xm,y > < Xm,y >
C ng thức 1: C ng thức t nh hệ số hồi quy bm = = n n
< Xm, Xm > Cmm ∑yi < Xj,y >
< XiXj,y > b0 = = ¯y; bj =
2k + 2a2 , j=1, , k; bij = 2k với i < j v N
< Xj′, y > bjj = 4 . 2a
C ng thức 2: Kiểm định sự c ý nghĩa của hệ số hồi quy với H0 : βm = 0 với
m = 0,1,...,k;ij; jj bm
Ti u chuẩn kiểm định l tbm =
∼ td.f khi H0 đng. sbm s 2 n trong đ 1 s2 = ts v
y y y s 0 , ,…,y0 ) l
c c gi trị quan s t của y bm 1 n0 Cmm n0 − 1 i=1 i=1 Quy
tắc kiểm định: Ta b c bỏ F
H0 nếu F > N−r−1;n0−1;1−α. lOMoAR cPSD| 45254322
lặp lại tại 1 điểm th nghiệm; d . f = n0 − 1
Quy tắc kiểm định: Ta b c bỏ H0 (tức l hệ số bm c ý nghĩa ở mức ) nα ếu |tbm| > td.f;1−α C
ng thức 3: Kiểm định sự ph hợp của m h nh với H0 : m h nh ph hợp sdu2
Ti u chuẩn kiểm định l F =
2 ∼ FN−r−1;n0−1 khi H0 đng với l sr
ố hệ số hồi quy c ý sts N