Tóm tắt lý thuyết môn Toán 12 – Nguyễn Ngọc Dũng

Tóm tắt lý thuyết môn Toán 12 – Nguyễn Ngọc Dũng được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

23 12 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung

Môn: Toán 12

Thông tin:

39 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
NGUYỄN NGỌC DŨNG
TOÁN THẦY DŨNG
TQB
π
π
π
π
π
π
π
π
π
π
π
π
π
π
π
π
π
π
π
π
x
y
O
a
b
y = f(x)
y = g(x)
S =
b
Z
a
(f(x) − g(x)) dx.
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TOÁN
TÓM TẮT LÝ THUYẾT
TÓM TẮT LÝ THUYẾT
12
2023 - 2024
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
MỤC LỤC
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
i
MỤC LỤC
I Giải tích 1
Chương1. Khảo sát hàm số 3
Bài số 1. Tính đơn điệu của hàm số. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
Bài số 2. Cực trị của hàm số. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
Bài số 3. Giá trị lớn nhất - giá trị nhỏ nhất. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
Bài số 4. Đường tiệm cận. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
Bài số 5. Đồ thị hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
Bài số 6. Phương trình tiếp tuyến. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
Chương2. Mũ - Luỹ thừa - Lôgarit 11
Bài số 1. Công thức mũ và lôgarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
Bài số 2. Phương trình mũ - Lôgarit. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
Bài số 3. Bất phương tình mũ - Lôgarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
Bài số 4. Đạo hàm và đồ thị. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
Chương3. Nguyên hàm - Tích phân 15
Chương4. Số phức 18
II Hình học
20
Chương5. Khối đa diện 21
Chương6. Nón - Trụ - Cầu 28
Chương7. Phương pháp tọa độ trong không gian 31
i/37
i/37
NGUYỄN NGỌC DŨNG – 0976.071.956
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
PHẦN
GIẢI TÍCH
I
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
2
Bảng đạo hàm
Cho c là hằng số, u = u(x), v = v(x).
CÔNG THỨC ĐẠO HÀM CÔNG THỨC ĐẠO HÀM HÀM HỢP
1) c
′
= 0; x
′
= 1; (ax)
′
= a
2) x
n
= nx
n−1
3) (
√
x)
′
=
1
2
√
x
4)
Å
1
x
ã
′
=
−1
x
2
;
c
x
′
=
−c
x
2
5)
Å
1
x
n
ã
′
=
−n
x
n+1
6) (c · u)
′
= c · u
′
2’) u
n
= nu
n−1
· u
′
3’) (
√
u)
′
=
1
2
√
u
· u
′
4’)
Å
1
u
ã
′
=
−1
u
2
· u
′
,
c
u
′
=
−c
u
2
· u
′
5’)
Å
1
u
n
ã
′
=
−n
u
n+1
· u
′
QUY TẮC TÍNH ĐẠO HÀM
1) (u · v)
′
= u
′
v + v
′
u; 2)
u
v
′
=
u
′
v − v
′
u
v
2
ĐẠO HÀM CỦA HÀM LƯỢNG GIÁC
1) (sin x)
′
= cos x;
2) (cos x)
′
= −sin x;
3) (tan x)
′
=
1
cos
2
x
= 1 + tan
2
x;
4) (cot x)
′
= −
1
sin
2
x
= −(1 + cot
2
x).
1’) (sin u)
′
= u
′
· cos u;
2’) (cos u)
′
= −u
′
· sin u;
3’) (tan u)
′
=
u
′
cos
2
u
= u
′
· (1 + tan
2
u);
4’) (cot u)
′
= −
u
′
sin
2
u
= −u
′
· (1 + cot
2
u).
ĐẠO HÀM CỦA HÀM MŨ - LÔGARIT
1) (e
x
)
′
= e
x
;
2) (a
x
)
′
= a
x
· ln a;
3) (ln x)
′
=
1
x
;
4) (log
a
x)
′
=
1
x · ln a
.
1’) (e
u
)
′
= e
u
· u
′
;
2’) (a
u
)
′
= a
u
· ln a · u
′
;
3’) (ln u)
′
=
u
′
u
;
4’) (log
a
u)
′
=
u
′
u · ln a
.
Công thức tính nhanh đạo hàm
Với a, b, c, d ∈ R. Ta kí hiệu
a b
c d
= ad − bc (chéo trừ chéo). Khi đó
Å
ax + b
cx + d
ã
′
=
ad − bc
(cx + d)
2
.•
Å
a
1
x
2
+ b
1
x + c
1
a
2
x
2
+ b
2
x + c
2
ã
′
=
a
1
b
1
a
2
b
2
x
2
+ 2
a
1
c
1
a
2
c
2
x +
b
1
c
1
b
2
c
2
(a
2
x
2
+ b
2
x + c
2
)
2
.•
2/37 2/37
NGUYỄN NGỌC DŨNG – 0976.071.956
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
Chương 1. Khảo sát hàm số Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
3
KHẢO SÁT HÀM SỐ
1
Chûúng
KHẢO SÁT HÀM SỐ
TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
1
Baâi söë
Hàm số y = f(x) đồng biến trên K ⇔ f
′
(x) ≥ 0, ∀x ∈ K.
Hàm số y = f(x) nghịch biến trên K ⇔ f
′
(x) ≤ 0, ∀x ∈ K.
A–PHƯƠNG PHÁP CHUNG
B1. Tìm TXĐ.
B2. Tính y
′
; cho y
′
= 0 → tìm nghiệm.
B3. Lập BBT. Dựa vào BBT kết luận.
B–PHÂN LOẠI BÀI TẬP
Hàm bậc ba y = ax
3
+ bx
2
+ cx + d Hàm nhất biến y =
ax + b
cx + d
- Không chứa m.
- Chứa m (xét riêng trường hợp a = 0).
+ Hàm số đồng biến trên R
⇔ y
′
≥ 0, ∀x ∈ R ⇔
®
a > 0
∆
y
′
≤ 0.
+ Hàm số nghịch biến trên R
⇔ y
′
≤ 0, ∀x ∈ R ⇔
®
a < 0
∆
y
′
≤ 0.
+ Hàm số đơn điệu trên (a; b) cho trước:
B1. Tính y
′
.
(Nếu ĐB → y
′
≥ 0; Nếu NB → y
′
≤ 0).
B2. Cô lập m.
B3. ≤ thì ≤ min; ≥ thì ≥ max.
(dùng máy tính kiểm tra kết quả).
TXĐ: D = R \
ß
−d
c
™
; y
′
=
ad − bc
(cx + d)
2
.
Hàm số đồng biến trên từng khoảng xác
định ⇔ ad − bc > 0.
Hàm số nghịch biến trên từng khoảng xác
định ⇔ ad − bc < 0.
Hàm số đồng biến trên (a; b)
⇔
ad − bc > 0
−d
c
/∈ (a; b)
Hàm số nghịch biến trên (a; b)
⇔
ad − bc < 0
−d
c
/∈ (a; b)
3/37 3/37
NGUYỄN NGỌC DŨNG – 0976.071.956
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
2. Cực trị của hàm số
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
4
CỰC TRỊ CỦA HÀM SỐ
2
Baâi söë
A–PHƯƠNG PHÁP CHUNG
B1. Tìm TXĐ.
B2. Tính y
′
; cho y
′
= 0 → tìm nghiệm.
B3. Lập BBT. Dựa vào BBT kết luận.
B–PHÂN LOẠI BÀI TẬP
Hàm bậc ba y = ax
3
+ bx
2
+ cx + d Hàm trùng phương y = ax
4
+ bx
2
+ c
Hàm số có 2 cực trị (hoặc có cực trị) ⇔
∆
′
y
′
> 0.
Hàm số không có cực trị ⇔ ∆
′
y
′
≤ 0.
Hàm số đạt cực tiểu tại x
0
⇔
®
y
′
(x
0
) = 0
y
′′
(x
0
) > 0
Hàm số đạt cực đại tại x
0
⇔
®
y
′
(x
0
) = 0
y
′′
(x
0
) < 0
Vi-ét: (y
′
= 3ax
2
+ 2bx + c)
S = x
1
+ x
2
=
−B
A
=
−2b
3a
P = x
1
· x
2
=
C
A
=
c
3a
x
2
1
+ x
2
2
= S
2
− 2P
Phương trình đường thẳng nối hai điểm
cực trị là y = f(x) −
f
′
(x).f
′′
(x)
18a
Nếu a chứa m thì xét riêng trường hợp
a = 0.
Hàm số có 3 điểm cực trị ⇔ ab < 0.
x
y
O
a > 0
x
y
O
a < 0
Hàm số có 1 điểm cực trị ⇔ ab ≥ 0
x
y
O
a > 0
x
y
O
a < 0
Dựa vào đồ thị suy ra trường hợp cực đại
hoặc cực tiểu.
Hàm nhất biến y =
ax + b
cx + d
KHÔNG có cực trị.
4/37 4/37
NGUYỄN NGỌC DŨNG – 0976.071.956
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
Chương 1. Khảo sát hàm số Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
5
GIÁ TRỊ LỚN NHẤT - GIÁ TRỊ NHỎ NHẤT
3
Baâi söë
Tìm Max - Min của hàm số y = f(x) liên tục trên [a; b].
B1. Tính đạo hàm f
′
(x).
B2. Giải phương trình f
′
(x) = 0 được các nghiệm x
1
; x
2
... ∈ [a; b].
B3. Tính các giá trị f(x
1
); f(x
2
); ...f(a); f(b) rồi so sánh để lấy Max - Min.
Nếu xét trên (a; b) mà Max - Min đạt được tại hai cận a hoặc b thì sẽ không tồn tại Max - Min.
ĐƯỜNG TIỆM CẬN
4
Baâi söë
lim
x→±∞
y = a thì y = a là TCN.
(Tính giới hạn tại vô cực: Bấm CALC x = ±10
10
)
lim
x→x
±
0
y = ±∞ thì x = x
0
là TCĐ.
(Tìm nghiệm của mẫu x
0
, sau đó tính giới hạn bằng cách bấm CALC x = x
0
± 10
−10
)
Đối với hàm phân thức hữu tỷ y =
P (x)
Q(x)
(đa thức chia đa thức):
Về tiệm cận ngang:
Nếu bậc tử nhỏ hơn bậc mẫu thì tiệm cận ngang là đường thẳng y = 0.
Nếu bậc tử bằng bậc mẫu thì tiệm cận ngang là đường thẳng y =
a
b
với a là hệ số bậc cao
nhất của tử, b là hệ số bậc cao nhất của mẫu.
Nếu bậc tử lớn hơn bậc mẫu thì đồ thị hàm số không có tiệm cận ngang.
Về tiệm cận đứng:
Nếu x = x
0
là nghiệm của mẫu mà không phải nghiệm của tử thì x = x
0
là tiệm cận
đứng.
Nếu x
0
là nghiệm của mẫu và cũng là nghiệm của tử thì:
+ Nếu bội nghiệm x
0
ở mẫu lớn hơn bội nghiệm x
0
ở tử thì x = x
0
là tiệm cận đứng.
+ Nếu bội nghiệm x
0
ở mẫu nhỏ hơn hoặc bằng bội nghiệm x
0
ở tử thì x = x
0
không là
tiệm cận đứng.
5/37
5/37
NGUYỄN NGỌC DŨNG – 0976.071.956
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
5. Đồ thị hàm số
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
6
ĐỒ THỊ HÀM SỐ
5
Baâi söë
A–ĐỒ THỊ HÀM SỐ y = ax
3
+ bx
2
+ cx + d (a = 0)
1 Các dạng đồ thị
Số nghiệm của y
′
Dấu của a
a > 0 a < 0
Phương trình y
′
= 0
có hai nghiệm phân biệt
(∆
y
′
> 0)
x
y
O
I
x
y
O
I
Phương trình y
′
= 0
có nghiệm kép
(∆
y
′
= 0)
x
y
O
I
x
y
O
I
Phương trình y
′
= 0
vô nghiệm
(∆
y
′
< 0)
x
y
O
I
x
y
O
I là tâm đối xứng của đồ thị hàm số đã cho
2 Xét dấu các hệ số a, b, c, d
Dấu của a Dấu của b Dấu của c Dấu của d
- Nhánh phải đi lên → a > 0.
- Nhánh phải đi xuống → a < 0.
x
CĐ
+ x
CT
cùng dấu
−→
−b
a
x
CĐ
· x
CT
cùng dấu
−→
c
a
Giao với trục tung
x = 0, y = d.
Nếu tâm đối xứng thuộc trục Oy thì b = 0
Nếu đồ thị có một điểm cực trị thuộc trục Oy thì c = 0
6/37 6/37
NGUYỄN NGỌC DŨNG – 0976.071.956
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
Chương 1. Khảo sát hàm số Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
7
B–ĐỒ THỊ HÀM TRÙNG PHƯƠNG
Số điểm cực trị
Dấu của a
a > 0 a < 0
Hàm số có 3 điểm cực trị ⇔ ab < 0
x
y
O
x
y
O
Hàm số có 1 điểm cực trị ⇔ ab ≥ 0
x
y
O
x
y
O
Dấu của d dựa vào giao điểm với trục tung: x = 0 thì y = d.
C–ĐỒ THỊ HÀM SỐ y =
ax + b
cx + d
(c = 0, ad − bc = 0)
1 Các dạng của đồ thị
ad − bc > 0 ad − bc < 0
x
y
O
I
x
y
O
I
I là tâm đối xứng của đồ thị hàm số đã cho
2 Phương pháp đọc đồ thị hàm số y =
ax + b
cx + d
(c = 0, ad − bc = 0)
Các đường tiệm cận Giao điểm với các trục tọa độ Tính đơn điệu của hàm số
- Tiệm cận ngang y =
a
c
.
- Tiệm cận đứng x = −
d
c
.
- Giao với Ox → x = −
b
a
, y = 0.
- Giao với Oy → x = 0, y =
b
d
.
- Đồng biến → ad − bc > 0.
- Nghịch biến → ad − bc < 0.
D–CÁC PHÉP BIẾN ĐỔI ĐỒ THỊ
7/37 7/37
NGUYỄN NGỌC DŨNG – 0976.071.956
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
5. Đồ thị hàm số
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
8
1 Từ đồ thị (C) : y = f(x) suy ra đồ thị (C
′
) : y = |f(x)|
B1. Giữ lại phần đồ thị nằm phía trên trục Ox của (C).
B2. Lấy đối xứng phần đồ thị nằm phía dưới Ox của (C) qua trục Ox, sau đó xóa nó đi.
x
y
O
(C)
x
y
O
(C
′
)
Số điểm cực trị của hàm số y = |f(x)| bằng a + b, với
a là số điểm cực trị của hàm số y=f(x);
b là số giao điểm (không tính tiếp xúc) của đồ thị y = f(x) với trục Ox.
2 Từ đồ thị (C) : y = f(x) suy ra đồ thị (C
′
) : y = f(|x|)
B1. Giữ lại phần đồ thị nằm bên phải và xóa hẳn phần đồ thị nằm bên trái trục Oy của (C).
B2. Lấy đối xứng phần đồ thị nằm bên phải Oy của (C) qua trục Oy.
x
y
O
(C)
x
y
O
(C
′
)
Số điểm cực trị của hàm y = f (|x|) bằng 2a + 1, với a là số điểm cực trị dương của hàm số
f(x).
3 Từ đồ thị (C) : y = f(x) suy ra đồ thị (C
′
) : y = |f(|x|)|
B1. Giữ lại phần đồ thị nằm bên phải và xóa hẳn phần đồ thị (C) nằm bên trái Oy.
B2. Lấy đối xứng phần đồ thị nằm bên phải qua trục Oy, ta được đồ thị (C
1
).
B3. Giữ lại phần đồ thị của (C
1
) nằm phía trên Ox.
B4. Lấy đối xứng phần đồ thị nằm phía dưới trục Ox của (C
1
) qua trục Ox.
x
y
O
(C)
x
y
O
(C
1
)
x
y
O
(C
′
)
8/37 8/37
NGUYỄN NGỌC DŨNG – 0976.071.956
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
Chương 1. Khảo sát hàm số Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
9
4 Từ đồ thị (C) : y = f(x) suy ra đồ thị (C
′
) : y = f(x − a) (xét a > 0)
Tịnh tiến đồ thị (C) : y = f(x) sang phải a đơn vị ta được đồ thị (C
′
) : y = f(x − a).
Tịnh tiến đồ thị (C) : y = f(x) sang trái a đơn vị ta được đồ thị (C
′
) : y = f(x + a).
x
y
O
(C)
x
y
O
(C
′
)
5 Từ đồ thị (C) : y = f(x) suy ra đồ thị (C
′
) : y = f(x) + b (xét b > 0)
Tịnh tiến đồ thị (C) : y = f(x) lên trên b đơn vị ta được đồ thị (C
′
) : y = f(x) + b.
Tịnh tiến đồ thị (C) : y = f(x) xuống dưới b đơn vị ta được đồ thị (C
′
) : y = f(x) − b.
x
y
O
(C)
x
y
O
(C
′
)
6 Từ đồ thị (C) : y = f(x) · g(x) suy ra đồ thị (C
′
) : y = |f(x)| · g(x)
B1. Xét dấu f(x).
B2. Giữ nguyên phần đồ thị của (C) mà f(x) ≥ 0 .
B3. Lấy đối xứng phần còn lại của (C) (phần f(x) < 0) qua trục Ox (phần dưới đối xứng lên trên,
phần trên đối xứng xuống dưới).
Hình ảnh minh họa dưới đây giả sử (C) : y = (x − a) · g(x), với f(x) = x − a.
x
y
O
y = (x − a) · g(x)
a x
y
O
y = |x − a| · g(x)
a
9/37 9/37
NGUYỄN NGỌC DŨNG – 0976.071.956
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
6. Phương trình tiếp tuyến Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
10
PHƯƠNG TRÌNH TIẾP TUYẾN
6
Baâi söë
Tiếp tuyến tại điểm thuộc đồ thị Tiếp tuyến có hệ số góc
Phương pháp:
• Xác định x
0
; y
0
. Tính đạo hàm y
′
.
• Phương trình tiếp tuyến
y = y
′
(x
0
)(x − x
0
) + y
0
Cách xác định x
0
, y
0
:
Giao với trục hoành thì y = 0.
Giao với trục tung thì x = 0.
Giao với đường bất kì thì dùng phương trình
hoành độ giao điểm.
Phương pháp:
• Xác định hệ số góc k.
• Giải phương trình f
′
(x) = k để tìm x
0
⇒ y
0
.
• Phương trình tiếp tuyến
y = k(x − x
0
) + y
0
Cách tìm hệ số góc:
Nếu tt ∥ (d) : y = ax + b thì k = a.
Nếu tt ⊥ (d) : y = ax + b thì k =
−1
a
.
10/37 10/37
NGUYỄN NGỌC DŨNG – 0976.071.956
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
Chương 2. Mũ - Luỹ thừa - Lôgarit Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
11
MŨ - LUỸ THỪA - LÔGARIT
2
Chûúng
MŨ - LUỸ THỪA - LÔGARIT
CÔNG THỨC MŨ VÀ LÔGARIT
1
Baâi söë
A–CÔNG THỨC MŨ VÀ LÔGARIT
CÔNG THỨC MŨ
a
−n
=
1
a
n
• a
n
· a
m
= a
n+m
•
a
n
a
m
= a
n−m
•
(a · b)
n
= a
n
· b
n
•
a
b
n
=
a
n
b
n
• (a
n
)
m
= a
n·m
•
n
√
a = a
1
n
•
n
√
a
n
√
b
=
n
…
a
b
•
n
p
k
√
a = a
1
n
·
1
k
=
nk
√
a•
CÔNG THỨC LÔGARIT
log
a
1 = 0• log
a
a = 1• log
a
b =
1
log
b
a
• a
log
a
b
= b•
log
a
b
n
=
ñ
n log
a
b nếu n lẻ
n log
a
|b| nếu n chẵn
• log
a
n
b =
1
n
log
a
b nếu n lẻ
1
n
log
|a|
b nếu n chẵn
•
log
a
(bc) = log
a
|b| + log
a
|c|• log
a
b
c
= log
a
|b| − log
a
|c|•
a
log
b
c
= c
log
b
a
• log
a
b · log
b
c = log
a
c• log
a
b =
log
c
b
log
c
a
•
Quy ước: log = log
10
và ln = log
e
.
MỐI LIÊN HỆ GIỮA MŨ VÀ LÔGARIT
log
a
x = b ⇔ x = a
b
;• a
x
= b ⇔ x = log
a
b.•
B–TẬP XÁC ĐỊNH CỦA HÀM SỐ y = x
a
a ∈ Z
+
thì x ∈ R;• a ∈ Z
−
hoặc a = 0 thì x = 0;• a /∈ Z thì x > 0.•
PHƯƠNG TRÌNH MŨ - LÔGARIT
2
Baâi söë
Khi giải phương trình lôgarit, để an tâm ta luôn đặt điều kiện trước.
A–PHƯƠNG TRÌNH CƠ BẢN (1 = a > 0, b > 0)
a
f(x)
= b ⇔ f(x) = log
a
b.• log
a
f(x) = b ⇔ f(x) = a
b
.•
11/37 11/37
NGUYỄN NGỌC DŨNG – 0976.071.956
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
3. Bất phương tình mũ - Lôgarit Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
12
Ví dụ 1. 2
2x−1
= 3 ⇔ 2x − 1 = log
2
3 ⇔ x =
log
2
3 + 1
2
.
B–ĐƯA VỀ CÙNG CƠ SỐ (1 = a > 0, b > 0)
a
f(x)
= a
g(x)
⇔ f(x) = g(x)• log
a
f(x) = log
a
g(x) ⇔
®
f(x) = g(x)
f(x) > 0 (hoặc g(x) > 0)
•
Ví dụ 1. log
2
(x
2
− 1) = log
2
2x ⇔
®
x
2
− 1 = 2x
2x > 0
⇔
ñ
x = 1 +
√
2
x = 1 −
√
2
x > 0
⇔ x = 1 +
√
2.
C–MŨ HÓA - LÔGARIT HÓA
• a
f(x)
= b
g(x)
⇔ log
a
a
f(x)
= log
a
b
g(x)
⇔ f(x) = g(x) log
a
b.
• log
a
f(x) = log
b
g(x) ⇔ a
log
a
f(x)
= a
log
b
g(x)
⇔ f(x) = g(x)
log
b
a
.
Ví dụ 1. log
3
x = log
5
x. (∗)
Điều kiện: x > 0.
(∗) ⇔ 3
log
3
x
= 3
log
5
x
⇔ x = x
log
5
3
⇔ 1 =
x
log
5
3
x
= x
log
5
3−1
⇔ x = 1.
D–ĐẶT ẨN PHỤ
Đặt t = f(x), với f(x) là biểu thức giống nhau trong phương trình.
Ví dụ 1. 2
2x
− 5 · 2
x
+ 6 = 0. (∗)
Đặt t = 2
x
(t > 0).
(∗) ⇔ t
2
− 5t + 6 = 0 ⇔
ñ
t = 2
t = 3
⇔
ñ
2
x
= 2
2
x
= 3
⇔
ñ
x = 1
x = log
2
3
BẤT PHƯƠNG TÌNH MŨ - LÔGARIT
3
Baâi söë
A–BẤT PHƯƠNG TRÌNH CƠ BẢN
a > 1 thì cùng chiều;• 0 < a < 1 thì đổi chiều.•
B–BẤT PHƯƠNG TRÌNH MŨ a
x
> b:
Xét b > 0 (do a
x
luôn dương nên trường hợp b ≤ 0 tự suy luận):
Với a > 1 thì a
x
> b ⇔ x > log
a
b.• Với 0 < a < 1 thì a
x
> b ⇔ x < log
a
b.•
12/37 12/37
NGUYỄN NGỌC DŨNG – 0976.071.956
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
Chương 2. Mũ - Luỹ thừa - Lôgarit Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
13
C–BẤT PHƯƠNG TRÌNH LÔGARIT log
a
x > b:
Với a > 1 thì log
a
x > b ⇔ x > a
b
.• Với 0 < a < 1 thì log
a
x > b ⇔ 0 < x < a
b
.•
Ví dụ 1. Giải bất phương trình 3
x
2
−2x
< 27.
A. (3; +∞). B. (−1; 3).
C. (−∞; −1) ∪ (3; +∞). D. (−∞; −1).
Ví dụ 2. Tập nghiệm của bất phương trình log
1
2
(x − 1) > −1 là
A. [1; 3]. B. (3; +∞). C. (1; 3). D. (−∞; 3).
D–ĐƯA VỀ CÙNG CƠ SỐ
⋆ Với a > 1 thì
a
f(x)
> a
g(x)
⇔ f(x) > g(x).• log
a
f(x) > log
a
g(x) ⇔ f(x) > g(x).•
⋆ Với 0 < a < 1 thì
a
f(x)
> a
g(x)
⇔ f(x) < g(x).• log
a
f(x) > log
a
g(x) ⇔ f(x) < g(x).•
Ví dụ 1. Giải bất phương trình 5
x
2
+x
≤ 25
x+1
.
Ví dụ 2. Tập nghiệm S của bất phương trình log
2
(x − 3) + log
2
x ≥ 2 là
A. S = [4; +∞). B. S = (3; +∞).
C. S = (3; 4]. D. S = (−∞; −1] ∪ [4; +∞).
E–MŨ HÓA - LÔGARIT HÓA
⋆ Với a > 1 thì
a
f(x)
> b
g(x)
⇔ f(x) > g(x) log
a
b.• log
a
f(x) > log
b
g(x) ⇔ f(x) > g(x)
log
b
a
.•
⋆ Với 0 < a < 1 thì
a
f(x)
> b
g(x)
⇔ f(x) < g(x) log
a
b.• log
a
f(x) > log
b
g(x) ⇔ f(x) < g(x)
log
b
a
.•
Ví dụ 1. Giải bất phương trình 5
x
· 8
x−1
x
≤ 500 ta được kết quả là
A. x ≤ log
5
2. B. x ≤ −log
5
2 hoặc 0 < x ≤ 3.
C. −log
5
2 ≤ x ≤ 3. D. x ≥ 3.
F–ĐẶT ẨN PHỤ
Tương tự như phương trình mũ - lôgarit.
Ví dụ 1. Tập nghiệm của bất phương trình
Ä
p
6 +
√
35
ä
x
− 12
Ä
p
6 −
√
35
ä
x
≥ 1 là
13/37 13/37
NGUYỄN NGỌC DŨNG – 0976.071.956
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
4. Đạo hàm và đồ thị
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
14
A. S =
h
log
√
6+
√
35
4; +∞
. B. S =
log
√
6+
√
35
4; +∞
.
C. S =
−∞; log
√
6+
√
35
4;
. D. S =
−∞; log
√
6+
√
35
4;
i
.
Ví dụ 2. Tìm tập nghiệm S của bất phương trình log
2
2
x − 5 log
2
x + 4 ≥ 0.
A. S = (−∞; 2] ∪ [16; +∞). B. S = [2; 16].
C. S = (0; 2] ∪ [16; +∞). D. S = (−∞; 1] ∪ [4; +∞).
ĐẠO HÀM VÀ ĐỒ THỊ
4
Baâi söë
A–BẢNG ĐẠO HÀM
Hàm sơ cấp Hàm hợp (u = u(x))
1. (x
α
)
′
= αx
α−1
, (α ∈ R, x > 0) 1’. (u
α
)
′
= αu
α−1
.u
′
2. (e
x
)
′
= e
x
2’. (e
u
)
′
= e
u
.u
′
3. (a
x
)
′
= a
x
ln a, (a > 0, a = 1) 3’. (a
u
)
′
= a
u
ln a.u
′
4. (ln x)
′
=
1
x
, (x > 0) 4’. (ln u)
′
=
u
′
u
5. (log
a
x)
′
=
1
x ln a
, (a > 0, a = 1, x > 0) 5’. (log
a
u)
′
=
u
′
u ln a
6. (log
a
|x|)
′
=
1
x ln a
, (a > 0, a = 1) 6’. (log
a
|u|)
′
=
u
′
u ln a
B–ĐỒ THỊ
Hàm số lũy thừa y = x
α
Hàm số mũ y = a
x
Hàm số lôgarit y = log
a
x
1
1
O
x
y
α > 1
0 < α < 1
α = 1
α = 0
α < 0
Nếu α > 0 thì hàm số đồng
biến, α < 0 thì hàm số
nghịch biến.
Đồ thị hàm số lũy thừa y =
x
α
luôn đi qua điểm (1; 1).
y
x
O
1
Đồ thị của hàm số mũ y =
a
x
luôn đi qua điểm (0; 1)
và luôn nằm phía trên trục
hoành.
y
x
O
1
Đồ thị của hàm số lôgarit
y = log
a
x luôn đi qua điểm
(1; 0) và luôn nằm bên phải
trục tung.
14/37 14/37
NGUYỄN NGỌC DŨNG – 0976.071.956
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
Chương 3. Nguyên hàm - Tích phân Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
15
NGUYÊN HÀM - TÍCH PHÂN
3
Chûúng
NGUYÊN HÀM - TÍCH PHÂN
F (x) =
Z
f(x) dx ⇒ F
′
(x) = f(x).•
Z
b
a
f(x) dx = F (b) − F (a).•
A–BẢNG NGUYÊN HÀM
HÀM SƠ CẤP HÀM MỞ RỘNG (u = u(x) = mx + n)
A. HÀM CƠ BẢN
1.
Z
k dx = kx + C, với k là hằng số nào đó.
2.
Z
x
α
dx =
x
α+1
α + 1
+ C,α = −1 2’.
Z
(mx+n)
α
dx =
1
m
·
(mx + n)
α+1
α + 1
+C,α = −1
3.
Z
1
x
dx = ln |x| + C 3’.
Z
1
mx + n
dx =
1
m
· ln |mx + n| + C
4.
Z
1
x
2
dx = −
1
x
+ C 4’.
Z
1
(mx + n)
2
dx = −
1
m
·
1
mx + n
+ C
B. HÀM LƯỢNG GIÁC
1.
Z
cos x dx = sin x + C 1’.
Z
cos(mx + n) dx =
1
m
sin(mx + n) + C
2.
Z
sin x dx = −cos x + C 2’.
Z
sin(mx + n) dx = −
1
m
cos(mx + n) + C
3.
Z
1
cos
2
x
dx = tan x + C 3’.
Z
1
cos
2
(mx + n)
dx =
1
m
tan(mx + n) + C
4.
Z
1
sin
2
x
dx = −cot x + C 4’.
Z
1
sin
2
(mx + n)
dx = −
1
m
cot(mx + n) + C
C. HÀM MŨ
1.
Z
e
x
dx = e
x
+ C 1’.
Z
e
mx+n
dx =
1
m
· e
mx+n
+ C
2.
Z
a
x
dx =
a
x
ln a
+ C 2’.
Z
a
mx+n
dx =
1
m
·
a
mx+n
ln a
+ C
Nếu F (x) và G(x) là nguyên hàm của f(x) thì F (x) = G(x) + c.
CÔNG THỨC GIẢI NHANH
Z
1
(ax + b) (cx + d)
dx =
1
ad − cb
ln
ax + b
cx + d
+ C
Z
1
x
2
− a
2
dx =
1
2a
ln
x − a
x + a
+ C
15/37 15/37
NGUYỄN NGỌC DŨNG – 0976.071.956
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
16
Z
tan xdx = −ln |cos x| + C
Z
cot xdx = ln |sin x| + C
Z
1
sin x
dx = ln
tan
x
2
+ C
Z
1
cos x
dx = ln
tan
x
2
+
π
4

+ C
Z
√
x
2
+ a dx =
x
2
√
x
2
+ a +
a
2
ln
x +
√
x
2
+ a
+ C
Z
dx
√
x
2
+ a
= ln
x +
√
x
2
+ a
+ C
P (x)
Q(x)
= Thương +
dư
mẫu
.
B–TÍNH CHẤT CỦA TÍCH PHÂN
b
Z
a
f
′
(x) dx = f(b) − f(a).a)
a
Z
a
f(x) dx = 0.b)
b
Z
a
f(x) dx = −
a
Z
b
f(x) dxc)
b
Z
a
f(x) dx =
b
Z
a
f(t) dtd)
b
Z
a
kf(x) dx = k
b
Z
a
f(x) dxe)
b
Z
a
k dx = k(b − a), k = const.f)
b
Z
a
[f(x) ± g(x)] dx =
b
Z
a
f(x) dx±
b
Z
a
g(x) dxg)
b
Z
a
f(x) dx =
c
Z
a
f(x) dx +
b
Z
c
f(x) dxh)
C–CÔNG THỨC LƯỢNG GIÁC
tan x =
sin x
cos x
a) cot x =
cos x
sin x
b) tan x · cot x = 1c)
sin
2
x + cos
2
x = 1d) 1 + tan
2
x =
1
cos
2
x
e) 1 + cot
2
x =
1
sin
2
x
f)
sin 2a = 2 sin a cos ag) cos 2a = cos
2
a − sin
2
a = 1 − 2 sin
2
a = 2 cos
2
a − 1h)
sin
2
a =
1 − cos 2a
2
i) cos
2
a =
1 + cos 2a
2
j)
D–DIỆN TÍCH HÌNH PHẲNG
1 Hình phẳng giới hạn bởi một đường cong
Diện tích S của hình phẳng giới hạn bởi y = f(x), trục Ox, x = a, x = b
được tính theo công thức
S =
b
Z
a
|f(x)|dx.
y = f(x)
x
b
a
O
y
16/37 16/37
NGUYỄN NGỌC DŨNG – 0976.071.956
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
Chương 3. Nguyên hàm - Tích phân Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
17
2 Hình phẳng giới hạn bởi hai đường cong
Diện tích S của hình phẳng giới hạn bởi y = f(x), y = g(x), x = a,
x = b được tính theo công thức
S =
b
Z
a
f(x) − g(x)
dx
x
y
O
b
a
E–THỂ TÍCH VẬT THỂ
1 Thể tích vật thể bất kì
Thể tích của vật thể giới hạn bởi hai mặt phẳng (P ) và (Q)
tính bởi công thức
V =
b
Z
a
S(x) dx, với S(x) là thiết diện tại x.
xa
b
x
2 Thể tích khối tròn xoay
2.1. Quay một đường quanh trục Ox
Thể tích vật thể tròn xoay sinh bởi miền D giới hạn bởi y = f(x), trục
Ox, x = a, x = b (a < b) quay quanh trục Ox được tính bởi công thức
V = π
b
Z
a
f
2
(x) dx.
x
y
O
a
b
y = f(x)
2.2. Quay hai đường quanh trục Ox
Thể tích vật thể tròn xoay sinh bởi miền (D) giới hạn bởi y =
f (x), y = g (x), x = a, x = b quay quanh trục Ox được tính bởi
công thức
V = π
b
Z
a
f
2
(x) − g
2
(x)
dx.
x
y
O
a
b
y = f(x)
y = g(x)
17/37 17/37
NGUYỄN NGỌC DŨNG – 0976.071.956
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
18
SỐ PHỨC
4
Chûúng
SỐ PHỨC
A–CÁC YẾU TỐ VÀ TÍNH CHẤT CỦA SỐ PHỨC
+ Số phức là số có dạng z = a + bi, với i
2
= −1.
+ a được gọi là phần thực, b được gọi là phần ảo, i được gọi là đơn vị ảo.
+ z là số thực ⇔ b = 0; z là số thuần ảo ⇔ a = 0;
a + bi = c + di ⇔ a = c và b = d.+ |z| = |a + bi| =
√
a
2
+ b
2
.+
z = a + bi = a − bi.+ z = z.+ |z| = |z|.+
⋆ Công thức mô-đun số phức:
|z
1
z
2
| = |z
1
||z
2
|.•
z
1
z
2
=
|z
1
|
|z
2
|
.• |z|
2
= |z
2
|;•
|z
1
− z
2
|
2
+ |z
1
+ z
2
|
2
= 2(|z
1
|
2
+ |z
2
|
2
) (Công thức trung tuyến).•
⋆ Công thức số phức liên hợp:
z = z;• z
−1
= (z)
−1
, ∀z = 0;• z ·z = |z|
2
;•
z
1
· z
2
= z
1
· z
2
;• z
1
± z
2
= z
1
± z
2
;•
Å
z
1
z
2
ã
=
z
1
z
2
, z
2
= 0.•
B–PHƯƠNG TRÌNH BẬC HAI TRÊN TẬP SỐ PHỨC
Xét phương trình bậc hai Ax
2
+ Bx + C = 0, (A = 0). Với thức ∆ = B
2
− 4AC. Khi đó
Nếu ∆ > 0 thì phương trình có hai nghiệm thực phân biệt
z
1
=
−B +
√
∆
2A
, z
2
=
−B −
√
∆
2A
.
Nếu ∆ < 0 thì phương trình có hai nghiệm phức phân biệt
z
1
=
−B + i
p
|∆|
2A
, z
2
=
−B − i
p
|∆|
2A
.
Hai nghiệm phức có tính chất:
z
1
= z
2
; z
2
= z
1
; |z
1
| = |z
2
|; |z
1
+ a| = |z
2
+ a|, ∀a ∈ R; |z
1
|
2
= |z
2
|
2
= z
1
z
2
.
Nếu ∆ = 0 thì phương trình (1) có nghiệm kép
z
1
= z
2
= −
B
2A
.
Định lý Vi-ét:
z
1
+ z
2
= −
B
A
z
1
z
2
=
C
A
.
18/37 18/37
NGUYỄN NGỌC DŨNG – 0976.071.956
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
Chương 4. Số phức Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
19
C–CĂN BẬC HAI CỦA SỐ PHỨC
Cho số phức w. Mỗi số phức z thỏa mãn z
2
= w được gọi là một căn bậc hai của w.
Hai căn bậc hai của một số phức là hai số đối nhau.
Bấm máy căn bậc hai số phức z = a + bi (chuyển sang Mode 1):
B1: Nhập Pol(a, b);
B2: Nhập Rec
√
x,
y
2
.
D–QUỸ TÍCH
Điểm M(a; b) là điểm biểu diễn số phức z = a + bi.
O
x
y
b
a
M
CÁC TẬP HỢP ĐIỂM QUAN TRỌNG
1. |z − (a + bi)| = r: Đường tròn tâm I(a, b) bán kính r.
2. |z − (a
1
+ b
1
i)| = |z − (a
2
+ b
2
i)|: Đường trung trực của AB với A(a
1
, b
1
), B(a
2
, b
2
).
3. |z − (a
1
+ b
1
i)| + |z − (a
2
+ b
2
i)| = 2a:
Đoạn thẳng AB với A(a
1
, b
1
), B(a
2
, b
2
) nếu 2a = AB.
Elip (E) nhận A, B làm hai tiêu điểm với độ dài trục lớn là 2a nếu 2a > AB.
Đặc biệt |z + c| + |z − c| = 2a: Elip (E) :
x
2
a
2
+
y
2
b
2
= 1 với b =
√
a
2
− c
2
.
MỘT SỐ PHƯƠNG TRÌNH QUAN TRỌNG
1. ax + by + c = 0: Phương trình đường thẳng nhận (a, b) làm vtpt.
2. (x − x
0
)
2
+ (y − y
0
)
2
= R
2
: Phương trình đường tròn tâm (x
0
, y
0
), bán kính R.
3.
x
2
a
2
+
y
2
b
2
= 1: Phương trình Elip với độ dài trục lớn 2a và độ dài trục nhỏ 2b.
19/37 19/37
NGUYỄN NGỌC DŨNG – 0976.071.956
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
PHẦN
HÌNH HỌC
II
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
Chương 5. Khối đa diện Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
21
KHỐI ĐA DIỆN
5
Chûúng
KHỐI ĐA DIỆN
A–THỂ TÍCH KHỐI ĐA DIỆN
V
chóp
=
1
3
· S
đáy
· h =
1
3
· S
đáy
· d(đỉnh, đáy) V
lăng trụ
= S
đáy
· h = S
đáy
· d(đỉnh, đáy)
V
hộp chữ nhật
= a · b · c V
lập phương
= a
3
B–HÌNH CHÓP ĐẶC BIỆT
1 Hình chóp đều
Là hình chóp có:
Đáy là đa giác đều• Hình chiếu của đỉnh lên đáy trùng với tâm đáy.•
Có hai hình chóp đều thường gặp:
Hình chóp tam giác đều Hình chóp tứ giác đều
B
A C
S
Đáy là tam giác đều;
Hình chiếu của S trùng trọng tâm G của
đáy.
B C
A D
S
Đáy là hình vuông;
Hình chiếu của S trùng với giao điểm hai
đường chéo của hình vuông.
Tính chất:
Các cạnh bên bằng nhau• Các mặt bên là các tam giác cân bằng nhau.•
2 Tứ điện đều
Là tứ diện có các cạnh bằng nhau, do đó mặt bên là những tam giác đều.
21/37
21/37
NGUYỄN NGỌC DŨNG – 0976.071.956
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
22
C–KĨ NĂNG XÁC ĐỊNH GÓC VÀ KHOẢNG CÁCH
XÁC ĐỊNH GÓC
Góc giữa đường và mặt Góc giữa hai mặt phẳng
A
H B
α
Tìm hình chiếu của AB lên (α) là HB. Khi đó
[AB, (P )] = (AB, HB) =
’
ABH.
d
a
b
P
Q
Tìm hai đường thẳng vuông góc giao tuyến.
[(P ), (Q)] = (a, b)
XÁC ĐỊNH KHOẢNG CÁCH
Tính trực tiếp Tính gián tiếp
Quy tắc ba đường:
A
S
H
B
C
K
1
2
3
α
d (A, (SBC)) = AK.
H
A
K
B
P
AB ∥ (P ) ⇒ d (A, (P )) = d (B, (P )).
I H
A
B
K
P
AB cắt (P ) tại I ⇒
d (A, (P ))
d (B, (P ))
=
IA
IB
.
1 Chóp S.ABC có SA ⊥ (ABC)
22/37 22/37
NGUYỄN NGỌC DŨNG – 0976.071.956
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
Chương 5. Khối đa diện Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
23
GÓC KHOẢNG CÁCH
B
A C
S
M
[SB, (ABC)] =
’
SBA
[SC, (ABC)] =
’
SCA
[(SBC), (ABC)] =
’
SMA
Nếu △ABC vuông tại B hoặc tại
C thì M trùng B hoặc trùng C.
B
A
C
S
H
• d [B, (SAC)] = BH
B
A
C
S
K
• d [C, (SAB)] = CK
B
A
C
S
M
I
• d [A, (SBC)] = AI
2 Chóp S.ABCD có SA ⊥ (ABCD)
GÓC KHOẢNG CÁCH
B
C
A D
S
H
[SB, (ABCD)] =
’
SBA
[SC, (ABCD)] =
’
SCA
[(SD), (ABCD)] =
’
SDA
[(SBD), (ABCD)] =
’
SHA
B C
A
D
S
I
H
M
N
d [A, (SBC)] = AN
d [A, (SCD)] = AM
d [A, (SBD)] = AH
23/37 23/37
NGUYỄN NGỌC DŨNG – 0976.071.956
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
24
D–CÁC CÔNG THỨC HÌNH HỌC PHẲNG
1 Diện tích
1.1. Diện tích tam giác
Tam giác vuông Tam giác đều Tam giác thường
a
b
S =
1
2
a · b
60
◦
60
◦
60
◦
S =
cạnh
2
·
√
3
4
Đường cao = cạnh ·
√
3
2
B
A
CH
h
c
a
b
S =
1
2
a · h =
1
2
b · c · sin A
=
abc
4R
= pr
=
»
p(p − a)(p − b)(p − c)
1.2. Diện tích tứ giác
Hình vuông
B
A
C
D
AC = (cạnh) ×
√
2.
S = (cạnh)
2
.
Hình chữ nhật
B
A
C
D
AC =
»
(dài)
2
+ (rộng)
2
S = (dài) × (rộng).
Hình thang
B
A
C
D
H
S =
1
2
(AD + BC) · AH
Hình bình hành
a
hb
α
S = a · h = a · b · sin α
Hình thoi
S =
1
2
tích hai đường chéo
2 Các định lý hay dùng
24/37 24/37
NGUYỄN NGỌC DŨNG – 0976.071.956
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
Chương 5. Khối đa diện Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
25
2.1. Hệ thức lượng tam giác vuông
BC
2
= AB
2
+ AC
2
• AB
2
= BH · BC•
AC
2
= CH · CB• AH
2
= BH · CH•
AH · BC = AB · AC•
1
AH
2
=
1
AB
2
+
1
AC
2
•
AH =
AB · AC
√
AB
2
+ AC
2
•
B
A
CH M
2.2. Tam giác bất kỳ
Định lý côsin: BC
2
= AB
2
+ AC
2
−2 ·AB ·AC ·cos A.
Công thức tính góc: cos A =
AB
2
+ AC
2
− BC
2
2 · AB · AC
.
Định lý sin:
AB
sin C
=
AC
sin B
=
BC
sin A
= 2R.
Định lý trung tuyến: AM
2
=
AB
2
+ AC
2
2
−
BC
2
4
.
B
A
CM
2.3. Phương tích
Nếu ABCD là tứ giác nội tiếp thì
IA · ID = IB ·IC;
JA · JB = JD · JC;
OA · OC = OD · OB.
B
A
C
D
I
J
O
2.4. Định lý Menelaus và định lý Ceva
B
A
C
M
N
K
(M, N, K thẳng hàng)
B
A
C
M
N
K
(AK, BN, CM đồng quy)
MA
MB
×
KB
KC
×
NC
NA
= 1
E–TỈ SỐ THỂ TÍCH
25/37 25/37
NGUYỄN NGỌC DŨNG – 0976.071.956
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
26
1 Khối chóp
Chóp tam giác
A
B
C
S
M
N
P
V
S.MNP
V
S.ABC
=
SM
SA
·
SN
SB
·
SP
SC
Chóp tứ giác
(A
1
B
1
C
1
D
1
) ∥ (ABCD) và
SA
1
SA
=
SB
1
SB
=
SC
1
SC
=
SD
1
SD
= k:
S
A
D
C
B
A
1
D
1
C
1
B
1
V
S.A
1
B
1
C
1
D
1
V
S.ABCD
= k
3
2 Lăng trụ tam giác
Chóp so với lăng trụ tam giác
V
chóp(4)
=
V
3
; V
chóp(5)
=
2V
3
Ví dụ. V
A
′
B
′
BC
=
V
3
; V
A
′
B
′
ABC
=
2V
3
.
Lăng trụ tam giác
M
N
P
A
B
C
A
′
B
′
C
′
V
A
′
C
′
B
′
.MNP
V
A
′
B
′
C
′
.ABC
=
1
3
·
Å
A
′
M
A
′
A
+
C
′
N
C
′
C
+
B
′
P
B
′
B
ã
3 Khối hộp
Chóp so với khối hộp
D
A
B
A
′
C
D
′
C
′
B
′
V
chóp(4)
2 đường chéo của
2 mặt song song
=
V
3
;
V
chóp(4)
(trường hợp còn lại) =
V
6
Ví dụ. V
A
′
C
′
BD
=
V
3
; V
A
′
C
′
D
′
D
=
V
6
.
Mặt phẳng cắt các cạnh của hình hộp
D
A
B
A
′
C
D
′
C
′
B
′
M
N
P
Q
DM
DD
′
= x
BP
BB
′
= y
⇒ V
2
=
x + y
2
· V
(chỉ quan tâm tới hai cạnh đối nhau)
26/37 26/37
NGUYỄN NGỌC DŨNG – 0976.071.956
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
Chương 5. Khối đa diện Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
27
27/37 27/37
NGUYỄN NGỌC DŨNG – 0976.071.956
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
28
NÓN - TRỤ - CẦU
6
Chûúng
NÓN - TRỤ - CẦU
A–KHỐI NÓN
1 Các công thức
Đường sinh: l
2
= r
2
+ h
2
Chu vi đáy: P = 2πr
Diện tích đáy: S = πr
2
Diện tích xung quanh: S
xq
= πrl
Diện tích toàn phần:
S
tp
= S
xq
+ S
đáy
= πrl + πr
2
= πr(r + l)
Thể tích: V =
1
3
S
đáy
· h =
1
3
πr
2
h
O
BA
S
h
r
2 Thiết diện không qua trục của hình nón
Thiết diện là △SAB cân tại S.
OH là khoảng các từ O đến (P ).
’
SMO là góc giữa (P ) và mặt đáy hình nón.
△OAB cân tại O có OM vừa là đường cao, vừa là
đường trung tuyến.
O
S
A
B
M
H
B–KHỐI TRỤ
Diện tích xung quanh hình trụ: S
xq
= 2πrh
Diện tích toàn phần hình trụ: S
tp
= S
xq
+ 2 · S
đáy
= 2πrh + 2πr
2
Thể tích khối trụ: V = Bh = πr
2
h
C–KHỐI CẦU
28/37 28/37
NGUYỄN NGỌC DŨNG – 0976.071.956
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
Chương 6. Nón - Trụ - Cầu Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
29
1 Diện tích và thể tích
Diện tích: S = 4πr
2
.• Thể tích: V =
4
3
πr
3
•
2 Mặt cầu ngoại tiếp
2.1. Mặt cầu ngoại tiếp hình nón
Tâm I của mặt cầu là tâm đường tròn ngoại tiếp △SAB.
Bán kính mặt cầu là bán kính đường tròn ngoại tiếp △SAB.
I
S
BA
2.2. Mặt cầu ngoại tiếp hình trụ
Tâm của mặt cầu là trung điểm đoạn thẳng nối tâm của hai đáy hình
trụ (I là trung điểm EF ).
Bán kính R = IB =
1
2
BD.
I
E
F
B
D
2.3. Mặt cầu ngoại tiếp hình chóp có cạnh bên vuông góc đáy
Dựng trục đường tròn ∆ của đáy (vuông góc với đáy tại tâm đường
tròn ngoại tiếp).
Dựng đường trung trực d của đường cao.
Tìm giao điểm của ∆ với d, đó chính là tâm I.
Bán kính R = IA =
√
AM
2
+ AH
2
=
Å
h
2
ã
2
+ r
2
(r là bán kính đáy).
A B
C
S
H
D E
M
I
2.4. Hình chóp đều
Gọi K là trung điểm SA
Dựng đường trung trực của SA cắt SO tại I.
Do tứ giác KIOA nội tiếp (có hai góc đối vuông) nên
SI · SO = SK · SA ⇔ R = SI =
SA · SK
SO
=
SA
2
2SO
.
A B
CD
S
K
I
O
29/37 29/37
NGUYỄN NGỌC DŨNG – 0976.071.956
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
30
2.5. Mặt cầu ngoại tiếp hình chóp có mặt bên (SAC) vuông góc với mặt đáy
Gọi K là tâm △ABC, J là tâm của △SAC.
Tính bán kính r = SJ đường tròn ngoại tiếp ∆SAC.
Bán kính mặt cầu ngoại tiếp là R = SI thỏa R
2
= SJ
2
+ IJ
2
.
Với IJ = DK.
A B
C
S
K
D
J
I
30/37 30/37
NGUYỄN NGỌC DŨNG – 0976.071.956
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
Chương 7. Phương pháp tọa độ trong không gian Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
31
PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG
GIAN
7
Chûúng
PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG
GIAN
A–TỌA ĐỘ TRONG KHÔNG GIAN
a) Trong mặt phẳng Oxyz;
#»
i ,
#»
j ,
#»
k là các vectơ đơn vị, với
#»
i = (1; 0; 0),
#»
j = (0; 1; 0),
#»
k = (0; 0; 1) và
#»
i ·
#»
j =
#»
i ·
#»
k =
#»
j ·
#»
k = 0
b) Tọa độ vectơ:
#»
u = (x; y; z) ⇔
#»
u = x ·
#»
i + y ·
#»
j + z ·
#»
k .
c) Tọa độ điểm: M(x; y; z) ⇔
# »
OM = (x; y; z) ⇔
# »
OM = x ·
#»
i + y ·
#»
j + z ·
#»
k .
d)
# »
AB = (x
B
− x
A
; y
B
− y
A
; z
B
− z
A
).
e) AB =
# »
AB
=
p
(x
B
− x
A
)
2
+ (y
B
− y
A
)
2
+ (z
B
− z
A
)
2
.
f) Các công thức quan trọng: Cho
#»
u = (a; b; c),
#»
v = (a
′
; b
′
; c
′
). Khi đó
#»
u ±
#»
v = (a ± a
′
; b ± b
′
; c ± c
′
) k
#»
u = (ka; kb; kc)
#»
u ·
#»
v = aa
′
+ bb
′
+ cc
′
cos (
#»
u ,
#»
v ) =
#»
u ·
#»
v
|
#»
u | · |
#»
v |
=
aa
′
+ bb
′
+ cc
′
√
a
2
+ b
2
+ c
2
·
√
a
′2
+ b
′2
+ c
′2
|
#»
u | =
√
a
2
+ b
2
+ c
2
#»
u ·
#»
v = 0 ⇔
#»
u ⊥
#»
v ⇔ aa
′
+ bb
′
+ cc
′
= 0
#»
u =
#»
v ⇔
a = a
′
b = b
′
c = c
′
#»
u cùng phương
#»
v ⇔
a
a
′
=
b
b
′
=
c
c
′
g) M là trung điểm của AB ⇔
x
M
=
x
A
+ x
B
2
y
M
=
y
A
+ y
B
2
z
M
=
z
A
+ z
B
2
.
h) G là trọng tâm của △ABC ⇔
x
G
=
x
A
+ x
B
+ x
C
3
y
G
=
y
A
+ y
B
+ y
C
3
z
G
=
z
A
+ z
B
+ z
C
3
.
i) G là trọng tâm của tứ diện ABCD ⇔
x
G
=
x
A
+ x
B
+ x
C
+ x
D
4
y
G
=
y
A
+ y
B
+ y
C
+ y
D
4
z
G
=
z
A
+ z
B
+ z
C
+ z
D
4
.
31/37 31/37
NGUYỄN NGỌC DŨNG – 0976.071.956
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
32
j) Tích có hướng:
Cho
#»
a = (x; y; z);
#»
b = (x
′
, y
′
, z
′
). Tích có hướng của hai vectơ
#»
a và
#»
b là:
î
#»
a ;
#»
b
ó
=
Ç
y z
y
′
z
′
; −
x z
x
′
z
′
;
x y
x
′
y
′
å
k) Tính chất tích có hướng:
[
#»
u ,
#»
v ] vuông góc với
#»
u và
#»
v .• |[
#»
u ,
#»
v ]| = |
#»
u | · |
#»
v |· sin (
#»
u ,
#»
v ).•
[
#»
u ,
#»
v ] = 0 ⇔
#»
u và
#»
v cùng phương.•
l) Một số ứng dụng của tích có hướng:
Ba vectơ
#»
a ,
#»
b ,
#»
c đồng phẳng khi và chỉ khi
î
#»
a ,
#»
b
ó
·
#»
c = 0.
A, B, C, D tạo thành tứ diện ⇔
î
# »
AB,
# »
AC
ó
·
# »
AD = 0.
Diện tích hình bình hành ABCD là S
ABCD
=
î
# »
AB,
# »
AD
ó
.
Diện tích tam giác ABC là S
ABC
=
1
2
î
# »
AB,
# »
AC
ó
.
Thể tích hình hộp là V
ABCD.A
′
B
′
C
′
D
′
=
î
# »
AB,
# »
AD
ó
·
# »
AA
′
.
Thể tích hình tứ diện là V
ABCD
=
1
6
î
# »
AB,
# »
AC
ó
·
# »
AD
.
B–MẶT CẦU - MẶT PHẲNG - ĐƯỜNG THẲNG
1 Mặt cầu
a) Mặt cầu tâm I(a; b; c) và bán kính R có
Phương trình tổng quát (x − a)
2
+ (y − b)
2
+ (z − c)
2
= R
2
.
Phương trình khai triển x
2
+ y
2
+ z
2
− 2ax − 2by − 2cz + d = 0.
b) Phương trình x
2
+ y
2
+ z
2
− 2ax − 2by − 2cz + d = 0 là phương trình mặt cầu khi và chỉ khi
a
2
+ b
2
+ c
2
− d > 0.
Khi đó, tâm và bán kính mặt cầu lần lượt là I(a, b, c); R =
√
a
2
+ b
2
+ c
2
− d.
2 Mặt phẳng
a) VTPT của mặt phẳng (α) là vectơ khác
#»
0 và vuông góc với (α).
b) Mặt phẳng (α):
®
Đi qua M (x
0
, y
0
, z
0
)
VTPT
#»
n = (A, B, C)
⇒ (α): A (x − x
0
) + B (y − y
0
) + C (z − z
0
) = 0.
c) Mặt phẳng (α) cắt Ox tại A(a; 0; 0), cắt Oy tại B(0; b; 0), cắt Oz tại C(0; 0; c) thì
(α):
x
a
+
y
b
+
z
c
= 1.
d) Nếu
#»
a và
#»
b là cặp VTCP của (α) thì
î
#»
a ,
#»
b
ó
là VTPT của (α).
32/37 32/37
NGUYỄN NGỌC DŨNG – 0976.071.956
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
Chương 7. Phương pháp tọa độ trong không gian Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
33
e) Nếu (α) ⊥ AB thì
# »
AB là VTPT.
f) Nếu (α) ⊥ Ox thì
#»
i = (1; 0; 0) là VTPT.
g) Nếu (α) chứa 3 điểm A, B, C thì
# »
AB,
# »
AC là cặp VTCP ⇒
î
# »
AB,
# »
AC
ó
là VTPT của (α).
h) Nếu (α) chứa M và chứa Oy thì có cặp VTCP là
# »
OM và
#»
j = (0; 1; 0).
i) Nếu (α) ∥ (β) thì
# »
n
(α)
=
# »
n
(β)
.
j) Nếu (α) ⊥ (β) thì
# »
u
(α)
=
# »
n
(β)
.
3 Đường thẳng
a) VTCP của đường thẳng (d) là vectơ khác
#»
0 và song song với (d).
b) Đường thẳng (d) đi qua M (x
0
, y
0
, z
0
) và VTCP
#»
u = (a, b, c) có
Phương trình tham số
x = x
0
+ at
y = y
0
+ bt
z = z
0
+ ct
(t ∈ R).
Phương trình chính tắc
x − x
0
a
=
y − y
0
b
=
z − z
0
c
, với abc = 0.
c) Nếu
#»
a và
#»
b là cặp VTPT của (d) thì
î
#»
a ,
#»
b
ó
là VTCP của (d).
d) Nếu d đi qua A, B hoặc d ∥ AB thì
# »
AB là VTCP của d.
e) Nếu d ⊥ AB thì
# »
AB là VTPT của d.
f) Nếu d ⊥ ∆ thì
#»
n
d
=
# »
u
∆
.
g) Nếu d ⊥ (α) thì
#»
u
d
=
# »
n
(α)
.
h) Nếu d ∥ (α) hoặc d ⊂ (α) thì
#»
n
d
=
# »
n
(α)
.
4 Phương trình mặt phẳng liên quan đến đường thẳng
a) (α) chứa M và đường thẳng d thì (α):
(
#»
n =
î
#»
u
d
,
# »
AM
ó
Đi qua M
với A ∈ d.
b) (α) chứa hai đường thẳng cắt nhau d
1
, d
2
thì (α):
®
#»
n = [
# »
u
d
1
,
# »
u
d
1
]
Đi qua A
với A ∈ d
1
.
c) (α) chứa hai đường thẳng song song d
1
, d
2
thì (α):
(
#»
n =
î
# »
u
d
1
,
# »
AB
ó
Đi qua A
với A ∈ d
1
, B ∈ d
2
.
d) (α) chứa đường thẳng d
1
và song song với d
2
thì (α):
®
#»
n = [
# »
u
d
1
,
# »
u
d
1
]
Đi qua A
với A ∈ d
1
.
5 Góc và khoảng cách
5.1. Góc giữa hai mặt phẳng
cos ((P ), (Q)) =
# »
n
(P )
·
# »
n
(Q)
# »
n
(P )
·
# »
n
(Q)
=
|aa
′
+ bb
′
+ cc
′
|
√
a
2
+ b
2
+ c
2
·
√
a
′2
+ b
′2
+ c
′2
33/37 33/37
NGUYỄN NGỌC DŨNG – 0976.071.956
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
34
5.2. Góc giữa hai đường thẳng
cos (d
1
, d
2
) =
# »
u
d
1
·
# »
u
d
2
|
# »
u
d
1
| · |
# »
u
d
2
|
=
|aa
′
+ bb
′
+ cc
′
|
√
a
2
+ b
2
+ c
2
·
√
a
′2
+ b
′2
+ c
′2
5.3. Góc giữa đường thẳng và mặt phẳng
sin (d, (P )) =
#»
u
d
·
# »
n
(P )
|
#»
u
d
| ·
# »
n
(P )
=
|aa
′
+ bb
′
+ cc
′
|
√
a
2
+ b
2
+ c
2
·
√
a
′2
+ b
′2
+ c
′2
5.4. Khoảng cách từ điểm tới mặt phẳng
d (M, (P )) =
ax
M
+ by
M
+ cz
M
+ d
√
a
2
+ b
2
+ c
2
5.5. Khoảng cách từ điểm tới đường thẳng
Với d đi qua A và có VTCP là
#»
u
d
thì
d (M, (d)) =
î
#»
u
d
,
# »
AM
ó
|
#»
u
d
|
.
5.6. Khoảng cách giữa hai đường thẳng chéo nhau
Với
®
d
1
đi qua A, VTCP là
# »
u
d
1
d
2
đi qua B, VTCP là
# »
u
d
2
thì
d (d
1
, d
2
) =
[
# »
u
d
1
,
# »
u
d
2
] ·
# »
AB
|[
# »
u
d
1
,
# »
u
d
2
]|
.
6 Vị trí tương đối
6.1. Vị trí tương đối giữa hai mặt phẳng
Cho (P ): Ax + By + Cz + D = 0 và (Q) : A
′
x + B
′
y + C
′
z + D
′
= 0. Khi đó
A
A
′
=
B
B
′
=
C
C
′
=
D
D
′
⇔ (P ) ≡ (Q);•
A
A
′
=
B
B
′
=
C
C
′
=
D
D
′
⇔ (P ) ∥ (Q);•
A : B : C = A
′
: B
′
: C
′
⇔ (P ) cắt (Q);• A · A
′
+ B ·B
′
+ C · C
′
= 0 ⇔ (P ) ⊥ (Q).•
Nếu mẫu số bằng 0 thì tử số cũng phải bằng 0.
6.2. Vị trí tương đối giữa đường thẳng và mặt phẳng
Xét hệ gồm phương trình đường thẳng d và phương trình mặt phẳng (P ).
Nếu hệ vô nghiệm thì d ∥ (P ).
Nếu hệ có đúng 1 nghiệm thì d cắt (P ).
Nếu hệ vô số nghiệm thì d ⊂ (P ).
34/37 34/37
NGUYỄN NGỌC DŨNG – 0976.071.956
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
Chương 7. Phương pháp tọa độ trong không gian Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
35
6.3. Vị trí tương đối giữa hai đường thẳng
Cho (d) :
®
qua A
vtcp
#»
u
và (d
′
) :
®
qua B
vtcp
#»
u
′
. Khi đó:
a) Nếu
#»
u cùng phương
#»
u
′
thì d và d
′
song song hoặc trùng nhau (dùng tỉ lệ).
Nếu A ∈ d
′
thì d và d
′
trùng nhau.
Nếu A /∈ d
′
thì d và d
′
song song.
b) Nếu
#»
u không cùng phương
#»
u
′
thì d và d
′
cắt nhau hoặc chéo nhau.
Nếu
î
#»
u ,
#»
u
′
ó
·
# »
AB = 0 thì d và d
′
cắt nhau.
Nếu
î
#»
u ,
#»
u
′
ó
·
# »
AB = 0 thì d và d
′
chéo nhau.
Có thể dùng hệ phương trình để biện luận vị trí tương đối hoặc kết hợp vừa hệ vừa vectơ.
6.4. Vị trí tương đối giữa mặt phẳng, đường thẳng và mặt cầu
Cho mặt phẳng (P ) và mặt cầu (S) tâm I bán kính R. Khi đó
d [I, (P )] = R ⇔ (P ) tiếp xúc với (S);
d [I, (P )] < R ⇔ (P ) cắt (S);
d [I, (P )] > R ⇔ (P ) nằm ngoài (S).
Trong trường hợp (P ) cắt (S) thì
Giao tuyến là đường tròn tâm H, bán kính r = HM.
R
2
= d
2
+ r
2
với d = OH.
E
I
6.5. Hình chiếu của điểm M trên đường thẳng d
Gọi H là hình chiếu của M lên d ⇒ H (x
0
+ at, y
0
+ bt).
MH ⊥ d ⇒
# »
MH ·
#»
u
d
= 0 ⇒ t = . . . ⇒ H(. . . , . . .).
d
# »
u
d
M
H
7 Phương trình đường thẳng trong mối liên hệ với mặt phẳng hoặc đường thẳng khác
Đối với bài toán tương giao có yếu tố cắt nhau giữa các đường thẳng thì ta gọi tên giao điểm
và dựa vào các tính chất để lập hệ phương trình liên quan đến giao điểm vừa gọi.
7.1. Đường thẳng ∆ đi qua M, cắt và vuông góc với d
Gọi N = ∆ ∩ d ⇒ N (x
0
+ at, y
0
+ bt).
MN ⊥ d ⇒
# »
MN ·
#»
u
d
= 0 ⇒ t = . . . ⇒ N(. . . , . . .).
Viết phương trình đường thẳng ∆ đi qua M, N.
d
∆
#»
u
d
M
N
35/37 35/37
NGUYỄN NGỌC DŨNG – 0976.071.956
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
36
7.2. Đường thẳng ∆ đi qua M, cắt d
1
và vuông góc với d
2
Gọi N = ∆ ∩ d
1
⇒ N (x
0
+ at, y
0
+ bt) .
MN ⊥ d
2
⇒
# »
MN ·
# »
u
d
2
= 0 ⇒ t = . . . ⇒ N(. . . , . . .).
Viết phương trình đường thẳng ∆ đi qua M, N.
d
2
d
1
∆
M
N
7.3. Đường thẳng ∆ đi qua M, song song với (P ) và cắt d
Gọi N = ∆ ∩ d ⇒ N (x
0
+ at, y
0
+ bt) .
MN ∥ (P ) ⇒
# »
MN ⊥
#»
n
p
⇒
# »
MN ·
#»
n
p
= 0
⇒ t = ... ⇒ N(..., ...).
Viết phương trình đường thẳng ∆ đi qua M, N.
M
N
d
∆
P
# »
n
P
7.4. Đường thẳng ∆ qua M đồng thời cắt cả d
1
và d
2
Gọi
®
A = ∆ ∩ d
1
B = ∆ ∩ d
2
⇒
®
A(x
1
+ at, y
1
+ bt)
A(x
2
+ a
′
t
′
, y
2
+ b
′
t
′
)
.
Do A, B, M thẳng hàng nên
# »
AB cùng phương
# »
AM
⇒
# »
AM = k
# »
AB.
Giải hệ tìm được k, t, t
′
⇒ A, B.
Viết phương trình đường thẳng ∆ đi qua A, B hoặc M.
M
A
B
d
1
d
2
∆
7.5. Đường thẳng ∆ nằm trong (P ) đồng thời cắt cả d
1
và d
2
Gọi
®
A = d
1
∩ (P )
B = d
2
∩ (P )
⇒
®
A (x
1
+ at; y
1
+ bt)
B (x
2
+ a
′
t
′
; y
2
+ b
′
t
′
)
.
Thay A, B vào phương trình (P ) tìm được t, t
′
và A, B.
Viết phương trình ∆ đi qua A, B.
A
B
d
1
d
2
∆
7.6. Đường thẳng ∆ vuông góc đồng thời cắt cả d
1
và d
2
(đường vuông góc chung)
36/37 36/37
NGUYỄN NGỌC DŨNG – 0976.071.956
MATH.ND
0976071956
? Lớp TOÁN THẦY DŨNG ?
Thầy NGUYỄN NGỌC DŨNG - THPT TẠ QUANG BỬU
Chương 7. Phương pháp tọa độ trong không gian Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
37
Gọi
®
A = ∆ ∩ d
1
B = ∆ ∩ d
2
⇒
®
A(x
1
+ at, y
1
+ bt)
A(x
2
+ a
′
t
′
, y
2
+ b
′
t
′
)
.
Tính VTCP của ∆:
# »
u
∆
= [
# »
u
d
1
,
# »
u
d
2
] .
Do AB cùng phương với
# »
u
∆
nên
# »
AB = k
# »
u
∆
.
Giải hệ tìm được k, t, t
′
⇒ A, B.
Viết phương trình đường thẳng ∆ đi qua A và nhận VTCP là
# »
u
∆
.
A
B
d
1
d
2
∆
8 Hình chiếu vuông góc
8.1. Hình chiếu của điểm M trên mặt phẳng (P )
Gọi H là hình chiếu của M lên (P ) thì MH ⊥ (P ).
Lập phương trình MH đi qua M và có VTCP là
# »
n
(P )
.
Tọa độ H là giao điểm của (P ) và MH (giải hệ).
M
H
P
# »
n
(P )
37/37 37/37
NGUYỄN NGỌC DŨNG – 0976.071.956
| 1/39
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

NGUYỄN NGỌC DŨNG TOÁN THẦY DŨNG TQB TO T ÁN O 12 TÓM TẮT LÝ L THUYẾT 2023 - 2024 y y = f (x) y = g(x) x O a b b Z S = (f (x) − g(x)) dx. a π π π π π π π π π π π π π π π 0976071956 π MATH.ND π ? Lớp TOÁN THẦY DŨNG ? π π π i MỤC LỤC
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM MỤC LỤC I Giải tích 1 Chương 1. Khảo sát hàm số 3 Bài số 1.
Tính đơn điệu của hàm số. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 BỬU Bài số 2.
Cực trị của hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4 G Bài số 3.
Giá trị lớn nhất - giá trị nhỏ nhất . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5 Bài số 4.
Đường tiệm cận . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5 AN Bài số 5.
Đồ thị hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 QU Bài số 6.
Phương trình tiếp tuyến . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10 TẠ Chương 2.
Mũ - Luỹ thừa - Lôgarit 11 Bài số 1.
Công thức mũ và lôgarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 Bài số 2.
Phương trình mũ - Lôgarit. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 THPT - Bài số 3.
Bất phương tình mũ - Lôgarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12 G Bài số 4.
Đạo hàm và đồ thị . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14 0976071956 Chương 3.
Nguyên hàm - Tích phân 15 DŨN Chương 4. Số phức MATH.ND 18 II Hình học 20 GỌC N Chương 5. Khối đa diện 21 ? Lớp TOÁN THẦY DŨNG ? Chương 6. Nón - Trụ - Cầu 28 Chương 7.
Phương pháp tọa độ trong không gian 31 GUYỄN N Thầy i/37 i/37 NGUYỄN NGỌC DŨNG – 0976.071.956 PHẦN I GIẢI TÍCH BỬU G AN 37 QU TẠ 39 34 36 17 44 THPT 16 8 - 3025 43 20 14 G 13 18 0976071956 28 DŨN 3 4 1 9 MATH.ND 49 32 45 GỌC 31 33 N 6 ? Lớp TOÁN THẦY DŨNG ? 7 26 27 19 35 41 47 40 12 42 10 GUYỄN 50 15 N 22 48 23 46 2 11 29 38 Thầy 24 21 5 2
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM Bảng đạo hàm
Cho c là hằng số, u = u(x), v = v(x). CÔNG THỨC ĐẠO HÀM
CÔNG THỨC ĐẠO HÀM HÀM HỢP
1) c′ = 0; x′ = 1; (ax)′ = a 2) xn = nxn−1 2’) un = nun−1 · u′ √ 1 √ 1 Thầy 3) ( x)′ = √ 3’) ( u)′ = √ · u′ 2 x 2 u Å 1 ã′ −1 Å ã′ c ′ −c 1 −1 c ′ −c 4) = ; = 4’) = · u′, = · u′ x x2 x x2 u u2 u u2 N Å 1 ã′ −n Å 1 ã′ −n GUYỄN 5) = 5’) = · u′ xn xn+1 un un+1 6) (c · u)′ = c · u′ QUY TẮC TÍNH ĐẠO HÀM u ′ u′v − v′u
1) (u · v)′ = u′v + v′u; 2) = v v2 N
ĐẠO HÀM CỦA HÀM LƯỢNG GIÁC GỌC 1) (sin x)′ = cos x;
1’) (sin u)′ = u′ · cos u; 2) (cos x)′ = − sin x;
2’) (cos u)′ = −u′ · sin u; 1 u′ 3) (tan x)′ = = 1 + tan2 x; 3’) (tan u)′ = = u′ · (1 + tan2 u); DŨN cos2 x cos2 u 1 u′ 4) (cot x)′ = − = − (1 + cot2 x). 4’) (cot u)′ = − = −u′ · (1 + cot2 u). sin2 x sin2 u G
ĐẠO HÀM CỦA HÀM MŨ - LÔGARIT 1) (ex)′ = ex; 0976071956 1’) (eu)′ = eu · u′; - THPT 2) (ax)′ = ax · ln a;
2’) (au)′ = au · ln a · u′; 1 u′ 3) (ln x)′ = ; 3’) (ln u)′ = ; x MATH.ND u 1 u′ 4) (log x)′ = . T a 4’) (log u)′ = . x · ln a a Ạ u · ln a QU ? Lớp Công TO thức ÁN THẦ tính Y DŨNG
nhanh đạo?hàm AN a b
Với a, b, c, d ∈ R. Ta kí hiệu
= ad − bc (chéo trừ chéo). Khi đó G c d BỬU a1 b1 a1 c1 b1 c1 x2 + 2 x + Å ax + b ã′ ad − bc Å a ã′ a a b 2 b2 2 c2 2 c2 • = 1x2 + b1x + c1 . • = . cx + d (cx + d)2 a2x2 + b2x + c2 (a2x2 + b2x + c2)2 2/37 2/37 NGUYỄN NGỌC DŨNG – 0976.071.956 3
Chương 1. Khảo sát hàm số
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM Chûúng 1 KHẢO SÁT HÀM SỐ KHẢO SÁT HÀM SỐ Baâi söë 1
TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
○ Hàm số y = f (x) đồng biến trên K ⇔ f ′(x) ≥ 0, ∀x ∈ K. BỬU
○ Hàm số y = f (x) nghịch biến trên K ⇔ f ′(x) ≤ 0, ∀x ∈ K. G AN
A – PHƯƠNG PHÁP CHUNG B1. Tìm TXĐ. QU
B2. Tính y′; cho y′ = 0 → tìm nghiệm. TẠ
B3. Lập BBT. Dựa vào BBT kết luận. THPT
B – PHÂN LOẠI BÀI TẬP - G ax + b Hàm bậc ba y = ax3 + bx2 0976071956 + cx + d Hàm nhất biến y = cx + d ß −d ™ ad − bc DŨN - Không chứa m. TXĐ: D = R \ ; y′ = . c (cx + d)2
- Chứa m (xét riêng trường hợp a MA = 0). TH.ND
○ Hàm số đồng biến trên từng khoảng xác
+ Hàm số đồng biến trên R định ⇔ ad − bc > 0. GỌC ®a > 0 N ⇔ y′ ≥ 0, ∀x ∈ R ⇔
○ Hàm số nghịch biến trên từng khoảng xác ? ∆y Lớp ′ ≤ 0. TOÁN THẦY DŨNG định ⇔ ad − ? bc < 0.
+ Hàm số nghịch biến trên R ® ○ a < 0
Hàm số đồng biến trên (a; b) ⇔ y′ ≤ 0, ∀x ∈ R ⇔  ∆ ad − bc > 0 y′ ≤ 0.  GUYỄN ⇔ −d
+ Hàm số đơn điệu trên (a; b) cho trước: / ∈ (a; b) N  c B1. Tính y′.
○ Hàm số nghịch biến trên (a; b)
(Nếu ĐB → y′ ≥ 0; Nếu NB → y′ ≤ 0). ad − bc < 0 Thầy  B2. Cô lập m. ⇔ −d /∈ (a; b)
B3. ≤ thì ≤ min; ≥ thì ≥ max.  c
(dùng máy tính kiểm tra kết quả). 3/37 3/37 NGUYỄN NGỌC DŨNG – 0976.071.956 4 2. Cực trị của hàm số
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM Baâi söë 2
CỰC TRỊ CỦA HÀM SỐ
A – PHƯƠNG PHÁP CHUNG B1. Tìm TXĐ.
B2. Tính y′; cho y′ = 0 → tìm nghiệm. Thầy
B3. Lập BBT. Dựa vào BBT kết luận. N
B – PHÂN LOẠI BÀI TẬP GUYỄN
Hàm bậc ba y = ax3 + bx2 + cx + d
Hàm trùng phương y = ax4 + bx2 + c
○ Hàm số có 2 cực trị (hoặc có cực trị) ⇔ ∆′y′ > 0. N
○ Hàm số có 3 điểm cực trị ⇔ ab < 0.
○ Hàm số không có cực trị ⇔ ∆′ GỌC y′ ≤ 0. y y
○ Hàm số đạt cực tiểu tại x0 ®y′(x0) = 0 ⇔ x DŨN y′′(x O 0) > 0 x O
○ Hàm số đạt cực đại tại x0 a > 0 a < 0 G ®y′(x0) = 0 ⇔ y′′(x 0976071956 - 0) < 0
○ Hàm số có 1 điểm cực trị ⇔ ab ≥ 0 THPT
○ Vi-ét: (y′ = 3ax2 + 2bx + c) MATH.ND y y −B −2b S = x = T 1 + x2 = Ạ A 3a x C c O QU P = x1 · x2 = = x ? Lớp A TO 3a ÁN THẦY DŨNG ? O x2 + x2 = S2 − 2P 1 2 AN a > 0 a < 0
○ Phương trình đường thẳng nối hai điểm G f ′(x).f ′′(x)
Dựa vào đồ thị suy ra trường hợp cực đại cực trị là y = f (x) − hoặc cực tiểu. BỬU 18a
Nếu a chứa m thì xét riêng trường hợp a = 0. ax + b Hàm nhất biến y = KHÔNG có cực trị. cx + d 4/37 4/37 NGUYỄN NGỌC DŨNG – 0976.071.956 5
Chương 1. Khảo sát hàm số
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM Baâi söë 3
GIÁ TRỊ LỚN NHẤT - GIÁ TRỊ NHỎ NHẤT
Tìm Max - Min của hàm số y = f (x) liên tục trên [a; b].
B1. Tính đạo hàm f ′(x).
B2. Giải phương trình f ′(x) = 0 được các nghiệm x1; x2... ∈ [a; b].
B3. Tính các giá trị f (x1); f (x2); ...f (a); f (b) rồi so sánh để lấy Max - Min.
Nếu xét trên (a; b) mà Max - Min đạt được tại hai cận a hoặc b thì sẽ không tồn tại Max - Min. BỬU Baâi söë 4 ĐƯỜNG TIỆM CẬN G AN QU ○ lim y = a thì y = a là TCN. x→±∞ TẠ
(Tính giới hạn tại vô cực: Bấm CALC x = ±1010)
○ lim y = ±∞ thì x = x0 là TCĐ. THPT x→x± 0 - G
(Tìm nghiệm của mẫu x0, sau đó tính giới hạn bằng cách bấm CALC x = x0 ± 10−10) 0976071956 DŨN P (x)
Đối với hàm phân thức hữu tỷ y MA = (đa thức chia đa thức): Q(TH.ND x) Về tiệm cận ngang: GỌC
○ Nếu bậc tử nhỏ hơn bậc mẫu thì tiệm cận ngang là đường thẳng y = 0. N a ○ Nếu bậc tử b ? ằng b Lớp ậc mẫu TO thì ÁN tiệm c THẦ ận ngang Y là DŨNG đường thẳng ? y =
với a là hệ số bậc cao b
nhất của tử, b là hệ số bậc cao nhất của mẫu.
○ Nếu bậc tử lớn hơn bậc mẫu thì đồ thị hàm số không có tiệm cận ngang. GUYỄN Về tiệm cận đứng: N
○ Nếu x = x0 là nghiệm của mẫu mà không phải nghiệm của tử thì x = x0 là tiệm cận đứng. Thầy
○ Nếu x0 là nghiệm của mẫu và cũng là nghiệm của tử thì:
+ Nếu bội nghiệm x0 ở mẫu lớn hơn bội nghiệm x0 ở tử thì x = x0 là tiệm cận đứng.
+ Nếu bội nghiệm x0 ở mẫu nhỏ hơn hoặc bằng bội nghiệm x0 ở tử thì x = x0 không là tiệm cận đứng. 5/37 5/37 NGUYỄN NGỌC DŨNG – 0976.071.956 6 5. Đồ thị hàm số
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM Baâi söë 5 ĐỒ THỊ HÀM SỐ
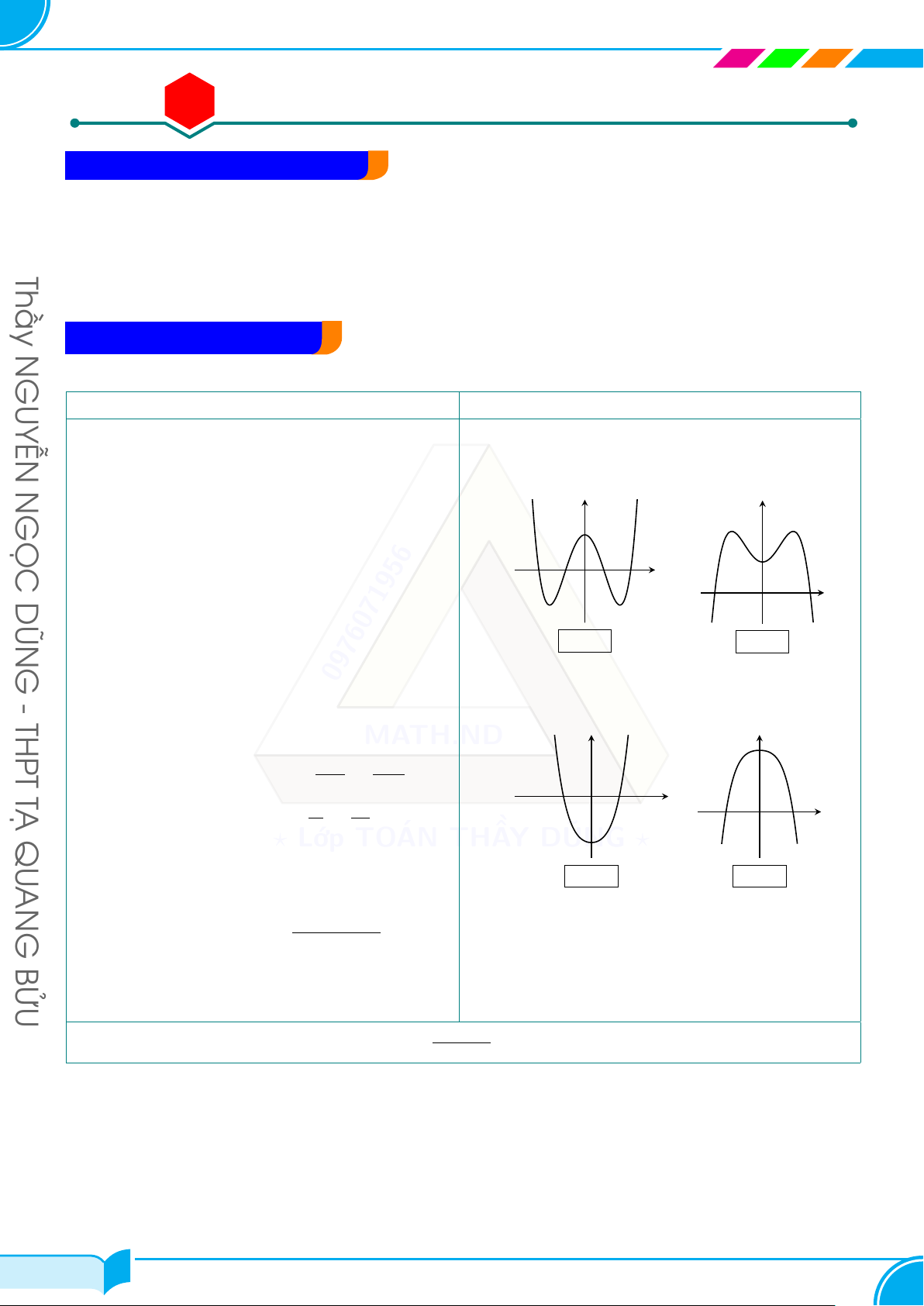
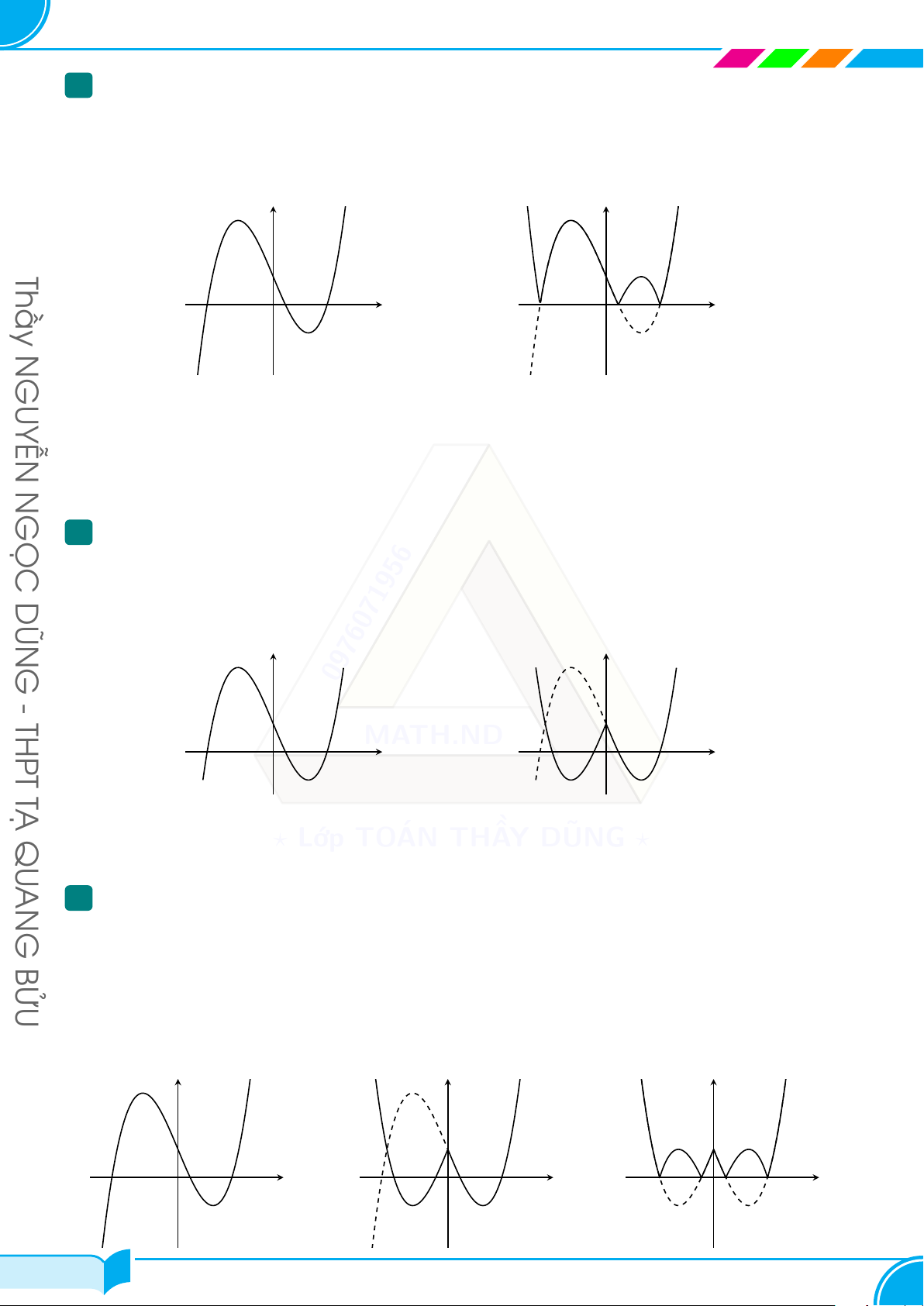
A – ĐỒ THỊ HÀM SỐ y = ax3 + bx2 + cx + d (a ̸= 0) 1 Các dạng đồ thị Thầy Dấu của a a > 0 a < 0 Số nghiệm của y′ Phương trình y′ = 0 y y có hai nghiệm phân biệt N (∆y′ > 0) GUYỄN I I x O x O y y N Phương trình y′ = 0 GỌC có nghiệm kép I (∆y′ = 0) I DŨN x O x O y y G Phương trình y′ = 0 vô 0976071956 nghiệm - I I THPT (∆y′ < 0) MATH.ND x O x O TẠ
I là tâm đối xứng của đồ thị hàm số đã cho QU ? Lớp TOÁN THẦY DŨNG ? 2
Xét dấu các hệ số a, b, c, d AN G Dấu của a Dấu của b Dấu của c Dấu của d cùng dấu −b cùng dấu c BỬU
- Nhánh phải đi lên → a > 0. xCĐ + xCT −→ xCĐ · xCT −→ Giao với trục tung a a
- Nhánh phải đi xuống → a < 0. x = 0, y = d.
Nếu tâm đối xứng thuộc trục Oy thì b = 0
Nếu đồ thị có một điểm cực trị thuộc trục Oy thì c = 0 6/37 6/37 NGUYỄN NGỌC DŨNG – 0976.071.956 7
Chương 1. Khảo sát hàm số
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
B – ĐỒ THỊ HÀM TRÙNG PHƯƠNG Dấu của a a > 0 a < 0 Số điểm cực trị y y
Hàm số có 3 điểm cực trị ⇔ ab < 0 x O x O BỬU y y G
Hàm số có 1 điểm cực trị ⇔ ab ≥ 0 x AN O x O QU TẠ
Dấu của d dựa vào giao điểm với trục tung: x = 0 thì y = d. ax + b THPT
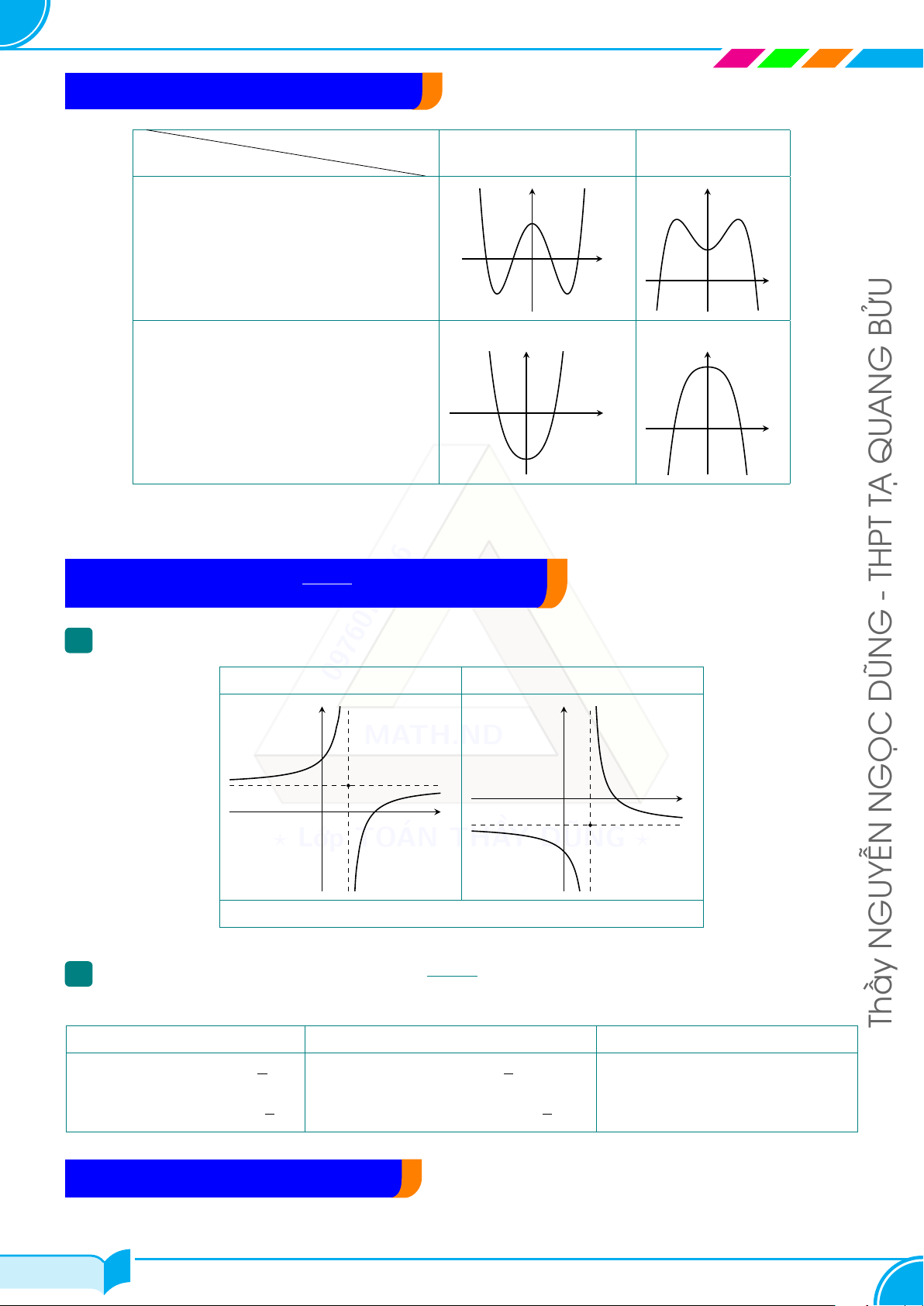
C – ĐỒ THỊ HÀM SỐ y = (c ̸= 0, ad − bc ̸= 0) cx + d - G 1
Các dạng của đồ thị ad − 0976071956 bc > 0 ad − bc < 0 DŨN y y MATH.ND I x GỌC O N x ? Lớp O TOÁN THẦY DŨNG I ?
I là tâm đối xứng của đồ thị hàm số đã cho GUYỄN N ax + b 2
Phương pháp đọc đồ thị hàm số y = (c ̸= 0, ad − bc ̸= 0) cx + d Thầy Các đường tiệm cận
Giao điểm với các trục tọa độ
Tính đơn điệu của hàm số a b - Tiệm cận ngang y = .
- Giao với Ox → x = − , y = 0.
- Đồng biến → ad − bc > 0. c a d b
- Nghịch biến → ad − bc < 0.
- Tiệm cận đứng x = − . - Giao với Oy → x = 0, y = . c d
D – CÁC PHÉP BIẾN ĐỔI ĐỒ THỊ 7/37 7/37 NGUYỄN NGỌC DŨNG – 0976.071.956 8 5. Đồ thị hàm số
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM 1
Từ đồ thị (C) : y = f (x) suy ra đồ thị (C′) : y = |f (x)|
B1. Giữ lại phần đồ thị nằm phía trên trục Ox của (C).
B2. Lấy đối xứng phần đồ thị nằm phía dưới Ox của (C) qua trục Ox, sau đó xóa nó đi. y y (C) (C′) Thầy x O x O N GUYỄN
Số điểm cực trị của hàm số y = |f (x)| bằng a + b, với
○ a là số điểm cực trị của hàm số y=f(x); N
○ b là số giao điểm (không tính tiếp xúc) của đồ thị y = f (x) với trục Ox. GỌC 2
Từ đồ thị (C) : y = f (x) suy ra đồ thị (C′) : y = f (|x|)
B1. Giữ lại phần đồ thị nằm bên phải và xóa hẳn phần đồ thị nằm bên trái trục Oy của (C). DŨN
B2. Lấy đối xứng phần đồ thị nằm bên phải Oy của (C) qua trục Oy. y y G 0976071956 (C) (C′) - THPT MATH.ND x O x O TẠ QU
Số điểm cực trị của hàm y = f (|x|) bằng 2a + 1, với a là số điểm cực trị dương của hàm số f (x). ? Lớp TOÁN THẦY DŨNG ? AN 3
Từ đồ thị (C) : y = f (x) suy ra đồ thị (C′) : y = |f (|x|)| G
B1. Giữ lại phần đồ thị nằm bên phải và xóa hẳn phần đồ thị (C) nằm bên trái Oy. BỬU
B2. Lấy đối xứng phần đồ thị nằm bên phải qua trục Oy, ta được đồ thị (C1).
B3. Giữ lại phần đồ thị của (C1) nằm phía trên Ox.
B4. Lấy đối xứng phần đồ thị nằm phía dưới trục Ox của (C1) qua trục Ox. y y y (C) (C1) (C′) x O x O x O 8/37 8/37 NGUYỄN NGỌC DŨNG – 0976.071.956 9
Chương 1. Khảo sát hàm số
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM 4
Từ đồ thị (C) : y = f (x) suy ra đồ thị (C′) : y = f (x − a) (xét a > 0)
○ Tịnh tiến đồ thị (C) : y = f (x) sang phải a đơn vị ta được đồ thị (C′) : y = f (x − a).
○ Tịnh tiến đồ thị (C) : y = f (x) sang trái a đơn vị ta được đồ thị (C′) : y = f (x + a). y y (C) (C′) x O x O BỬU G 5
Từ đồ thị (C) : y = f (x) suy ra đồ thị (C′) : y = f (x) + b (xét b > 0) AN
○ Tịnh tiến đồ thị (C) : y = f (x) lên trên b đơn vị ta được đồ thị (C′) : y = f (x) + b.
○ Tịnh tiến đồ thị (C) : y = f (x) xuống dưới b đơn vị ta được đồ thị (C′) : y = f (x) − b. QU y TẠ y (C′) (C) THPT - G x O 0976071956 x O DŨN MATH.ND 6
Từ đồ thị (C) : y = f (x) · g(x) suy ra đồ thị (C′) : y = |f (x)| · g(x) GỌC B1. Xét dấu f (x). N
B2. Giữ nguyên phần đồ ?thịLớp của ( TO C) màÁN f (x) THẦ ≥ 0 . Y DŨNG ?
B3. Lấy đối xứng phần còn lại của (C) (phần f (x) < 0) qua trục Ox (phần dưới đối xứng lên trên,
phần trên đối xứng xuống dưới). GUYỄN
Hình ảnh minh họa dưới đây giả sử (C) : y = (x − a) · g(x), với f (x) = x − a. N y y y = (x − a) · g(x) y = |x − a| · g(x) Thầy a x O a x O 9/37 9/37 NGUYỄN NGỌC DŨNG – 0976.071.956 10
6. Phương trình tiếp tuyến
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM Baâi söë 6
PHƯƠNG TRÌNH TIẾP TUYẾN
Tiếp tuyến tại điểm thuộc đồ thị
Tiếp tuyến có hệ số góc Phương pháp: Phương pháp:
• Xác định x0; y0. Tính đạo hàm y′.
• Xác định hệ số góc k. Thầy
• Phương trình tiếp tuyến
• Giải phương trình f ′(x) = k để tìm x0 ⇒ y0. y = y′(x
• Phương trình tiếp tuyến 0)(x − x0) + y0 N GUYỄN y = k(x − x Cách xác định x 0) + y0 0, y0:
○ Giao với trục hoành thì y = 0. Cách tìm hệ số góc:
○ Giao với trục tung thì x = 0.
○ Nếu tt ∥ (d): y = ax + b thì k = a. N
○ Giao với đường bất kì thì dùng phương trình −1 GỌC
○ Nếu tt ⊥ (d) : y = ax + b thì k = . hoành độ giao điểm. a DŨN G 0976071956 - THPT MATH.ND TẠ QU ? Lớp TOÁN THẦY DŨNG ? AN G BỬU 10/37 10/37 NGUYỄN NGỌC DŨNG – 0976.071.956 11
Chương 2. Mũ - Luỹ thừa - Lôgarit
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM Chûúng 2
MŨ - LUỸ THỪA - LÔGARIT
MŨ - LUỸ THỪA - LÔGARIT Baâi söë 1
CÔNG THỨC MŨ VÀ LÔGARIT
A – CÔNG THỨC MŨ VÀ LÔGARIT BỬU G CÔNG THỨC MŨ 1 an • a−n = an · am = an+m • = an−m • AN an am a n an (a · b)n = an · bn • • = (an)m = an·m • QU b bn √ √ n … √ √ 1 a a 1 n a = a n p k · 1 n • • √ = n • a = a n k = nk a TẠ n b b CÔNG THỨC LÔGARIT 1 THPT • log 1 = 0 • log a = 1 • log b = • aloga b = b a a a log a - b  1 G ñn log b nếu n lẻ log b nếu n lẻ a a • log bn = • log n  a an b = n log |b| nếu n chẵn  1 a 0976071956 log n |a| b nếu n chẵn DŨN b
• log (bc) = log |b| + log |c| • log = log |b| − log |c| a a a MATH.ND a c a a log b alog c b c = clogb a • • log b · log c = log c • log b = a b a a GỌC log a c N
Quy ước: log = log ?và ln = log . 10 Lớp TO e ÁN THẦY DŨNG ?
MỐI LIÊN HỆ GIỮA MŨ VÀ LÔGARIT • log x = b ⇔ x = ab; • ax = b ⇔ x = log b. a a GUYỄN N
B – TẬP XÁC ĐỊNH CỦA HÀM SỐ y = xa • a ∈ + − Z thì x ∈ R;
• a ∈ Z hoặc a = 0 thì x ̸= 0; • a / ∈ Z thì x > 0. Thầy Baâi söë 2
PHƯƠNG TRÌNH MŨ - LÔGARIT
Khi giải phương trình lôgarit, để an tâm ta luôn đặt điều kiện trước.
A – PHƯƠNG TRÌNH CƠ BẢN (1 ̸= a > 0, b > 0)
• af(x) = b ⇔ f (x) = log b.
• log f (x) = b ⇔ f (x) = ab. a a 11/37 11/37 NGUYỄN NGỌC DŨNG – 0976.071.956 12
3. Bất phương tình mũ - Lôgarit
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM log 3 + 1
cVí dụ 1. 22x−1 = 3 ⇔ 2x − 1 = log 3 ⇔ x = 2 . 2 2
B – ĐƯA VỀ CÙNG CƠ SỐ (1 ̸= a > 0, b > 0) ®f (x) = g(x)
• af(x) = ag(x) ⇔ f (x) = g(x) • log f (x) = log g(x) ⇔ a a Thầy
f (x) > 0 (hoặc g(x) > 0) √  ñx = 1 + 2 ®  N x2 − 1 = 2x  √ √
cVí dụ 1. log (x2 − 1) = log 2x ⇔ ⇔ ⇔ x = 1 + 2. 2 2 x = 1 − 2 GUYỄN 2x > 0  x > 0
C – MŨ HÓA - LÔGARIT HÓA N
• af(x) = bg(x) ⇔ log af(x) = log bg(x) ⇔ f (x) = g(x) log b. GỌC a a a
• log f (x) = log g(x) ⇔ aloga f(x) = alogb g(x) ⇔ f (x) = g(x)logb a. a b c DŨN
Ví dụ 1. log x = log x. (∗) 3 5 Điều kiện: x > 0. xlog5 3 G
(∗) ⇔ 3log3 x = 3log5 x ⇔ x = xlog5 3 ⇔ 1 = = xlog5 3−1 ⇔ x = 1. 0976071956 x - THPT D – ĐẶT ẨN PHỤ MATH.ND T
Đặt t = f (x), với f (x) là biểu thức giống nhau trong phương trình. Ạ QU
cVí dụ 1. 22x − 5 · 2x + 6 = 0. (∗) Đặt t = 2x (t > 0). ? Lớp TOÁN THẦY DŨNG ? AN ñt = 2 ñ2x = 2 ñx = 1
(∗) ⇔ t2 − 5t + 6 = 0 ⇔ ⇔ ⇔ G t = 3 2x = 3 x = log 3 2 BỬU Baâi söë 3
BẤT PHƯƠNG TÌNH MŨ - LÔGARIT
A – BẤT PHƯƠNG TRÌNH CƠ BẢN
• a > 1 thì cùng chiều;
• 0 < a < 1 thì đổi chiều.
B – BẤT PHƯƠNG TRÌNH MŨ ax > b:
Xét b > 0 (do ax luôn dương nên trường hợp b ≤ 0 tự suy luận):
• Với a > 1 thì ax > b ⇔ x > log b.
• Với 0 < a < 1 thì ax > b ⇔ x < log b. a a 12/37 12/37 NGUYỄN NGỌC DŨNG – 0976.071.956 13
Chương 2. Mũ - Luỹ thừa - Lôgarit
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
C – BẤT PHƯƠNG TRÌNH LÔGARIT loga x > b:
• Với a > 1 thì log x > b ⇔ x > ab.
• Với 0 < a < 1 thì log x > b ⇔ 0 < x < ab. a a
cVí dụ 1. Giải bất phương trình 3x2−2x < 27. A. (3; +∞). B. (−1; 3).
C. (−∞; −1) ∪ (3; +∞). D. (−∞; −1).
cVí dụ 2. Tập nghiệm của bất phương trình log 1 (x − 1) > −1 là 2 A. [1; 3]. B. (3; +∞). C. (1; 3). D. (−∞; 3). BỬU G
D – ĐƯA VỀ CÙNG CƠ SỐ AN ⋆ Với a > 1 thì QU
• af(x) > ag(x) ⇔ f (x) > g(x).
• log f (x) > log g(x) ⇔ f (x) > g(x). a a TẠ ⋆ Với 0 < a < 1 thì
• af(x) > ag(x) ⇔ f (x) < g(x).
• log f (x) > log g(x) ⇔ f (x) < g(x). a a THPT -
cVí dụ 1. Giải bất phương trình 5x2+x ≤ 25x+1. G
cVí dụ 2. Tập nghiệm S của 0976071956
bất phương trình log (x − 3) + log x ≥ 2 là 2 2 A. S = [4; +∞). B. S = (3; +∞). DŨN C. S = (3; 4]. MATH.ND
D. S = (−∞; −1] ∪ [4; +∞). GỌC
E – MŨ HÓA - LÔGARIT HÓA N ⋆ Với a > 1 thì ? Lớp TOÁN THẦY DŨNG ?
• af(x) > bg(x) ⇔ f (x) > g(x) log b.
• log f (x) > log g(x) ⇔ f (x) > g(x)logb a. a a b ⋆ Với 0 < a < 1 thì GUYỄN
• af(x) > bg(x) ⇔ f (x) < g(x) log b.
• log f (x) > log g(x) ⇔ f (x) < g(x)logb a. a a b N c x−1
Ví dụ 1. Giải bất phương trình 5x · 8 x ≤ 500 ta được kết quả là A. x ≤ log 2.
B. x ≤ − log 2 hoặc 0 < x ≤ 3. Thầy 5 5
C. − log 2 ≤ x ≤ 3. 5 D. x ≥ 3. F – ĐẶT ẨN PHỤ
Tương tự như phương trình mũ - lôgarit. √ √ Äp äx Äp äx
cVí dụ 1. Tập nghiệm của bất phương trình 6 + 35 − 12 6 − 35 ≥ 1 là 13/37 13/37 NGUYỄN NGỌC DŨNG – 0976.071.956 14 4. Đạo hàm và đồ thị
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM h A. S = log√ √ 4; +∞ . B. S = log√ √ 4; +∞ . 6+ 35 6+ 35 i C. S = −∞; log√ √ 4; . D. S = −∞; log√ √ 4; . 6+ 35 6+ 35
cVí dụ 2. Tìm tập nghiệm S của bất phương trình log2 x − 5 log x + 4 ≥ 0. 2 2
A. S = (−∞; 2] ∪ [16; +∞). B. S = [2; 16]. Thầy
C. S = (0; 2] ∪ [16; +∞).
D. S = (−∞; 1] ∪ [4; +∞). Baâi söë 4
ĐẠO HÀM VÀ ĐỒ THỊ N GUYỄN
A – BẢNG ĐẠO HÀM Hàm sơ cấp Hàm hợp (u = u(x)) N
1. (xα)′ = αxα−1, (α ∈ R, x > 0)
1’. (uα)′ = αuα−1.u′ GỌC 2. (ex)′ = ex 2’. (eu)′ = eu.u′
3. (ax)′ = ax ln a, (a > 0, a ̸= 1) 3’. (au)′ = au ln a.u′ 1 u′ 4. (ln x)′ = , (x > 0) 4’. (ln u)′ = DŨN x u 1 u′ 5. (log x)′ =
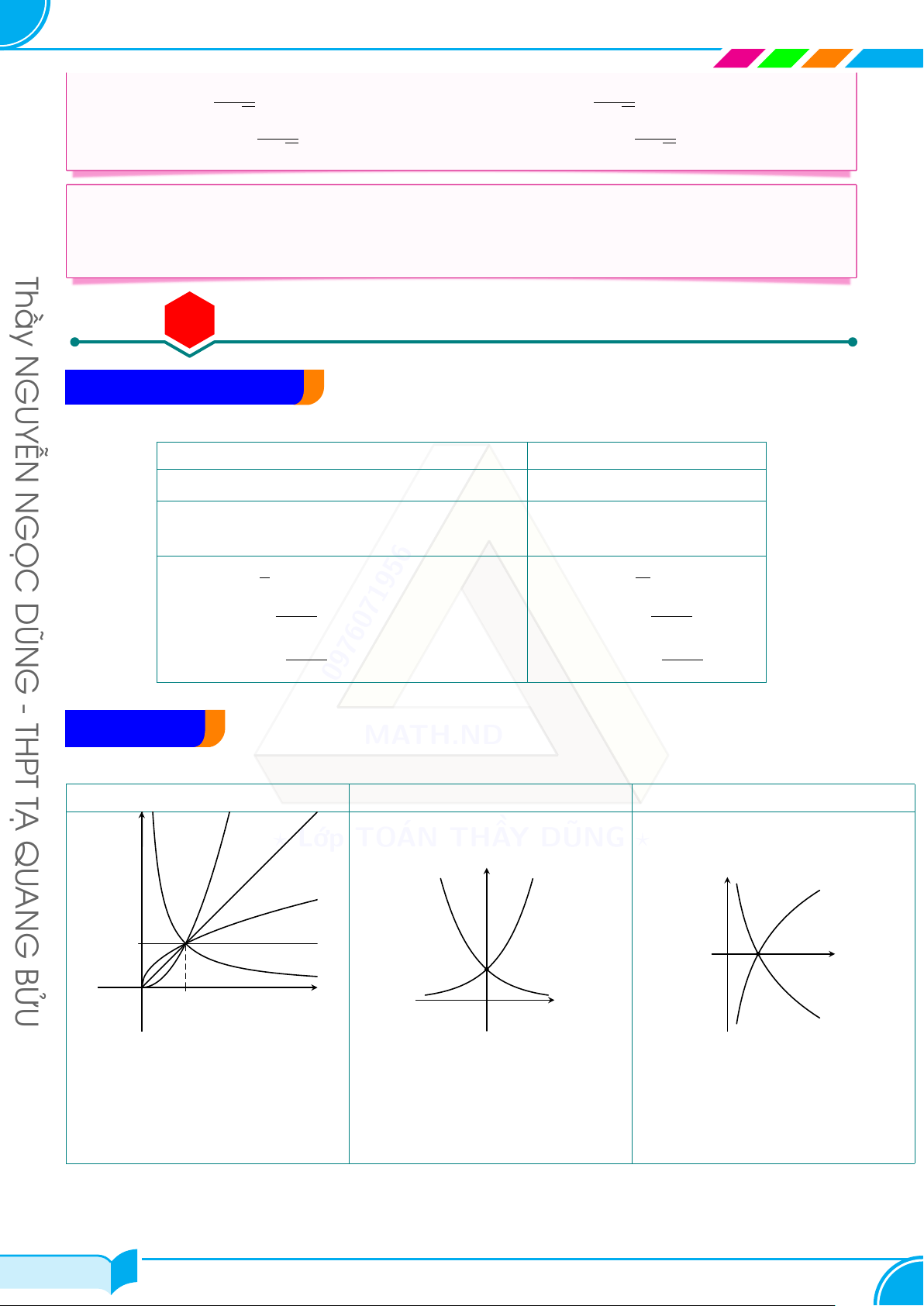
, (a > 0, a ̸= 1, x > 0) 5’. (log u)′ = a x ln a a u ln a G 1 u′ 6. (log |x|)′ = , (a > 0, a ̸= 1) 6’. (log |u|)′ = a x ln a 0976071956 a u ln a - THPT B – ĐỒ THỊ MATH.ND TẠ Hàm số lũy thừa y = xα Hàm số mũ y = ax Hàm số lôgarit y = log x a QU y
α > 1 ? Lớp TOÁN THẦY DŨNG ? α = 1 AN y y 0 < α < 1 G α = 0 1 1 BỬU α < 0 1 x O O 1 x x O
Nếu α > 0 thì hàm số đồng
Đồ thị của hàm số mũ y =
Đồ thị của hàm số lôgarit
biến, α < 0 thì hàm số
ax luôn đi qua điểm (0; 1)
y = log x luôn đi qua điểm a nghịch biến.
và luôn nằm phía trên trục
(1; 0) và luôn nằm bên phải
Đồ thị hàm số lũy thừa y = hoành. trục tung.
xα luôn đi qua điểm (1; 1). 14/37 14/37 NGUYỄN NGỌC DŨNG – 0976.071.956 15
Chương 3. Nguyên hàm - Tích phân
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM Chûúng 3
NGUYÊN HÀM - TÍCH PHÂN
NGUYÊN HÀM - TÍCH PHÂN Z Z b • F (x) = f (x) dx ⇒ F ′(x) = f (x). • f (x) dx = F (b) − F (a). a BỬU G
A – BẢNG NGUYÊN HÀM AN QU HÀM SƠ CẤP
HÀM MỞ RỘNG (u = u(x) = mx + n) A. HÀM CƠ BẢN TẠ Z 1.
k dx = kx + C, với k là hằng số nào đó. Z xα+1 Z 1 (mx + n)α+1 2. xα dx = + C,α ̸= −1 2’. (mx+n)α dx = · +C,α ̸= −1 THPT α + 1 m α + 1 Z Z - 1 1 1 3. dx = ln |x| + C 3’. dx = · ln |mx + n| + C x mx + n m G Z 1 1 Z 1 1 1 4. dx = − + C 4’. dx = − · + C x2 x 0976071956 (mx + n)2 m mx + n B. HÀM LƯỢNG GIÁC DŨN Z Z 1 1. cos x dx = sin x + C MATH.ND 1’. cos(mx + n) dx = sin(mx + n) + C m Z Z 1 2. sin x dx = − cos x + C 2’. sin(mx + n) dx = − cos(mx + n) + C m GỌC Z 1 Z 1 1 N 3. dx = tan x + C 3’. dx = tan(mx + n) + C cos2x ? Lớp TOÁN THẦY DŨNG cos2(mx + n) ? m Z 1 Z 1 1 4. dx = − cot x + C 4’. dx = − cot(mx + n) + C sin2x sin2(mx + n) m C. HÀM MŨ Z Z GUYỄN 1 1. ex dx = ex + C 1’. emx+n dx = · emx+n + C N m Z ax Z 1 amx+n 2. ax dx = + C 2’. amx+n dx = · + C ln a m ln a Thầy
Nếu F (x) và G(x) là nguyên hàm của f (x) thì F (x) = G(x) + c. CÔNG THỨC GIẢI NHANH Z 1 1 ax + b Z 1 1 x − a dx = ln + C dx = ln + C (ax + b) (cx + d) ad − cb cx + d x2 − a2 2a x + a 15/37 15/37 NGUYỄN NGỌC DŨNG – 0976.071.956 16
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM Z Z tan xdx = − ln |cos x| + C cot xdx = ln |sin x| + C Z 1 Z x 1 x π dx = ln tan + C dx = ln tan + + C sin x 2 cos x 2 4 Z √ x √ a Z √ dx √ x2 + a dx = x2 + a + ln x + x2 + a + C √ = ln x + x2 + a + C 2 2 x2 + a Thầy P (x) dư = Thương + . Q(x) mẫu N GUYỄN
B – TÍNH CHẤT CỦA TÍCH PHÂN b a Z Z a) f ′(x) dx = f (b) − f (a). b) f (x) dx = 0. a a N b a b b GỌC Z Z Z Z c) f (x) dx = − f (x) dx d) f (x) dx = f (t) dt a b a a b b b Z Z Z DŨN e) kf (x) dx = k f (x) dx f) k dx = k(b − a), k = const. a a a G b b b b c b Z Z Z Z Z Z g) [f (x) ± g(x)] dx = f (x0976071956 ) dx± g(x) dx h) f (x) dx = f (x) dx + f (x) dx - THPT a a a a a c MATH.ND
C – CÔNG THỨC LƯỢNG GIÁC TẠ sin x cos x a) tan x = b) cot x = c) tan x · cot x = 1 QU cos x ? Lớp TOÁN THẦ sin x Y DŨNG ? 1 1 AN d) sin2 x + cos2 x = 1 e) 1 + tan2 x = f) 1 + cot2 x = cos2 x sin2 x G g) sin 2a = 2 sin a cos a
h) cos 2a = cos2 a − sin2 a = 1 − 2 sin2 a = 2 cos2 a − 1 1 − cos 2a 1 + cos 2a BỬU i) sin2 a = j) cos2 a = 2 2
D – DIỆN TÍCH HÌNH PHẲNG 1
Hình phẳng giới hạn bởi một đường cong
Diện tích S của hình phẳng giới hạn bởi y = f (x), trục Ox, x = a, x = b y
được tính theo công thức b Z S = |f (x)|dx. y = f (x) a O a x b 16/37 16/37 NGUYỄN NGỌC DŨNG – 0976.071.956 17
Chương 3. Nguyên hàm - Tích phân
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM 2
Hình phẳng giới hạn bởi hai đường cong
Diện tích S của hình phẳng giới hạn bởi y = f (x), y = g(x), x = a, y
x = b được tính theo công thức b Z S = f (x) − g(x)dx a O b x a
E – THỂ TÍCH VẬT THỂ BỬU 1
Thể tích vật thể bất kì G
Thể tích của vật thể giới hạn bởi hai mặt phẳng (P ) và (Q) AN tính bởi công thức b QU Z V =
S(x) dx, với S(x) là thiết diện tại x. TẠ a a x x b THPT 2
Thể tích khối tròn xoay -
2.1. Quay một đường quanh trục Ox G
Thể tích vật thể tròn xoay sinh bở0976071956
i miền D giới hạn bởi y = f (x), trục y
Ox, x = a, x = b (a < b) quay quanh trục Ox được tính bởi công thức y = f (x) DŨN b Z MATH.ND V = π f 2(x) dx. x O a b a GỌC N ? Lớp TOÁN THẦY DŨNG ?
2.2. Quay hai đường quanh trục Ox
Thể tích vật thể tròn xoay sinh bởi miền (D) giới hạn bởi y = y
f (x), y = g (x), x = a, x = b quay quanh trục Ox được tính bởi y = f (x) GUYỄN công thức N b Z y = g(x) V = π f 2(x) − g2(x)dx. x O a b a Thầy 17/37 17/37 NGUYỄN NGỌC DŨNG – 0976.071.956 18
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM Chûúng 4 SỐ PHỨC SỐ PHỨC Thầy
A – CÁC YẾU TỐ VÀ TÍNH CHẤT CỦA SỐ PHỨC
+ Số phức là số có dạng z = a + bi, với i2 = −1. N
+ a được gọi là phần thực, b được gọi là phần ảo, i được gọi là đơn vị ảo. GUYỄN
+ z là số thực ⇔ b = 0; z là số thuần ảo ⇔ a = 0; √
+ a + bi = c + di ⇔ a = c và b = d. + |z| = |a + bi| = a2 + b2. + z = a + bi = a − bi. + z = z. + |z| = |z|. N
⋆ Công thức mô-đun số phức: GỌC z |z • |z 1 1| 1z2| = |z1||z2|. • = . • |z|2 = |z2|; z2 |z2|
• |z1 − z2|2 + |z1 + z2|2 = 2(|z1|2 + |z2|2) (Công thức trung tuyến). DŨN
⋆ Công thức số phức liên hợp: • z = z;
• z−1 = (z)−1 , ∀z ̸= 0; • z · z = |z|2; G Å z ã z • z 1 1 1 · z2 = z1 · z2; 0976071956 • z1 ± z2 = z1 ± z2; • = , z2 ̸= 0. z z - 2 2 THPT
B – PHƯƠNG TRÌNH BẬC HAI MA TRÊN TTH.ND ẬP SỐ PHỨC T
Xét phương trình bậc hai Ax2 + Bx + C = 0, (A ̸= 0). Với thức ∆ = B2 − 4AC. Khi đó Ạ
○ Nếu ∆ > 0 thì phương trình có hai nghiệm thực phân biệt QU ? Lớp TOÁN √ √ −B + THẦ ∆ Y DŨNG −B − ∆ ? z1 = , z2 = . AN 2A 2A
○ Nếu ∆ < 0 thì phương trình có hai nghiệm phức phân biệt G −B + ip|∆| −B − ip|∆| BỬU z1 = , z2 = . 2A 2A
Hai nghiệm phức có tính chất:
z1 = z2; z2 = z1; |z1| = |z2|; |z1 + a| = |z2 + a|, ∀a ∈ R; |z1|2 = |z2|2 = z1z2.
○ Nếu ∆ = 0 thì phương trình (1) có nghiệm kép B z1 = z2 = − . 2A Định lý Vi-ét:  B z  1 + z2 = − A C  z1z2 = . A 18/37 18/37 NGUYỄN NGỌC DŨNG – 0976.071.956 19 Chương 4. Số phức
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
C – CĂN BẬC HAI CỦA SỐ PHỨC
○ Cho số phức w. Mỗi số phức z thỏa mãn z2 = w được gọi là một căn bậc hai của w.
○ Hai căn bậc hai của một số phức là hai số đối nhau.
○ Bấm máy căn bậc hai số phức z = a + bi (chuyển sang Mode 1): B1: Nhập Pol(a, b); √ y B2: Nhập Rec x, . 2 BỬU D – QUỸ TÍCH G
Điểm M (a; b) là điểm biểu diễn số phức z = a + bi. y AN M b QU O a x TẠ
CÁC TẬP HỢP ĐIỂM QUAN TRỌNG THPT -
1. |z − (a + bi)| = r: Đường tròn tâm I(a, b) bán kính r. G
2. |z − (a1 + b1i)| = |z − (a2 + b2i)|: Đường trung trực của AB với A(a1, b1), B(a2, b2).
3. |z − (a1 + b1i)| + |z − (a2 + 0976071956 b2i)| = 2a: DŨN
○ Đoạn thẳng AB với A(a1, b1), B(a2, b2) nếu 2a = AB. ○ Elip (E) nhận A, B làm MA hai TH.ND
tiêu điểm với độ dài trục lớn là 2a nếu 2a > AB. x2 y2 √
Đặc biệt |z + c| + |z − c| = 2a: Elip (E) : + = 1 với b = a2 − c2. GỌC a2 b2 N ? Lớp TOÁN THẦY DŨNG ?
MỘT SỐ PHƯƠNG TRÌNH QUAN TRỌNG
1. ax + by + c = 0: Phương trình đường thẳng nhận (a, b) làm vtpt. GUYỄN
2. (x − x0)2 + (y − y0)2 = R2: Phương trình đường tròn tâm (x0, y0), bán kính R. N x2 y2 3. +
= 1: Phương trình Elip với độ dài trục lớn 2a và độ dài trục nhỏ 2b. a2 b2 Thầy 19/37 19/37 NGUYỄN NGỌC DŨNG – 0976.071.956 PHẦN II Thầy HÌNH HỌC N GUYỄN 37 10 41 N 24 5 GỌC 4 12 26 22 28 31 14 45 15 DŨN 33 7 G 50 0976071956 30 - THPT 1 MATH.ND 48 35 17 42 38 6 T 19 46 Ạ 21 2 40 QU ? Lớp TOÁN THẦ 39 Y DŨNG ? 25 AN 16 11 29 49 3436 27 G 23 43 BỬU 13 44 820 32 3 9 18 47 21 Chương 5. Khối đa diện
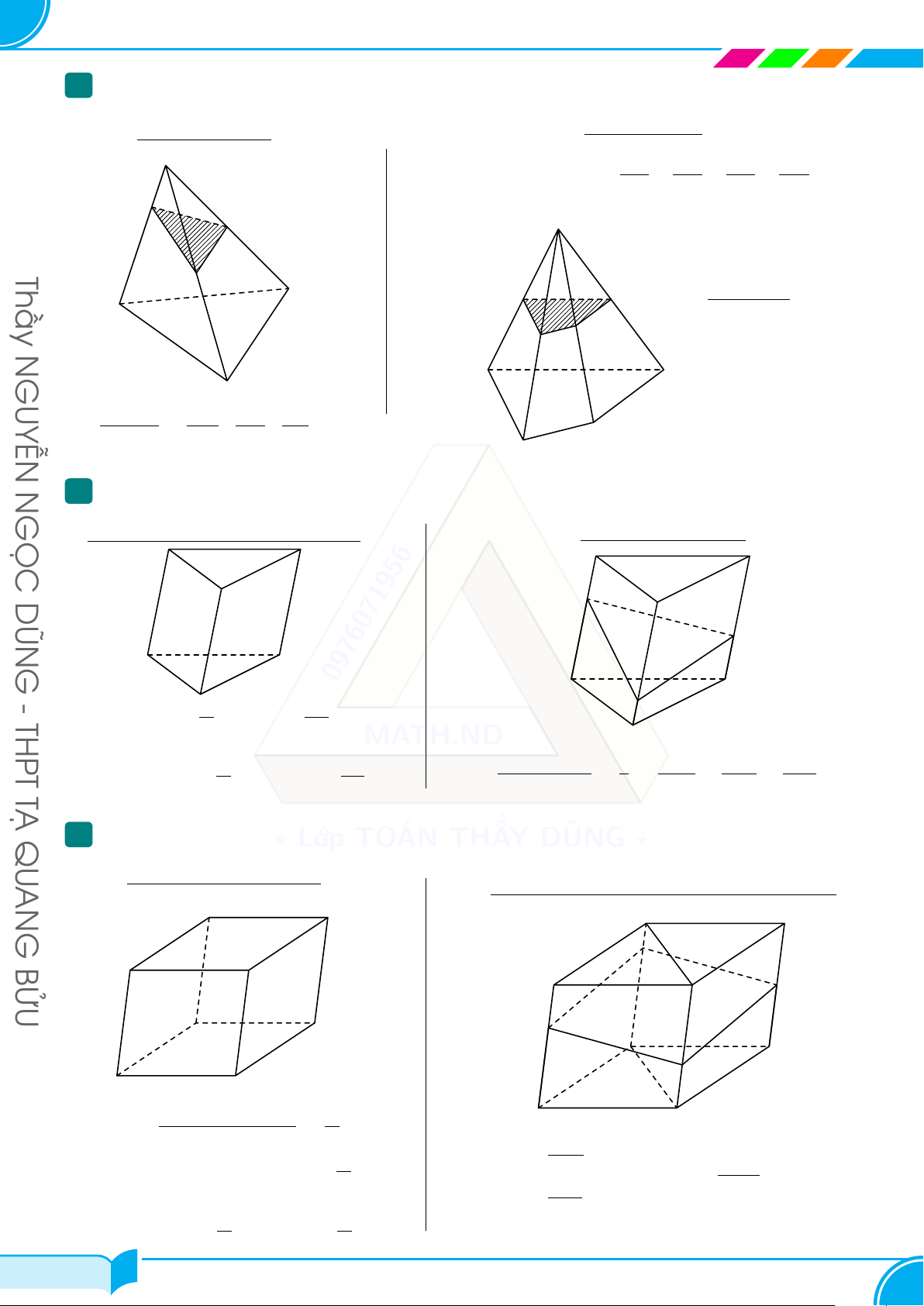
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM Chûúng 5 KHỐI ĐA DIỆN KHỐI ĐA DIỆN
A – THỂ TÍCH KHỐI ĐA DIỆN 1 1 ✓ V = · S · h = · S · d(đỉnh, đáy) ✓ V = S · h = S · d(đỉnh, đáy) chóp 3 đáy 3 đáy lăng trụ đáy đáy BỬU ✓ V = a · b · c V = a3 ✓ hộp chữ nhật lập phương G AN
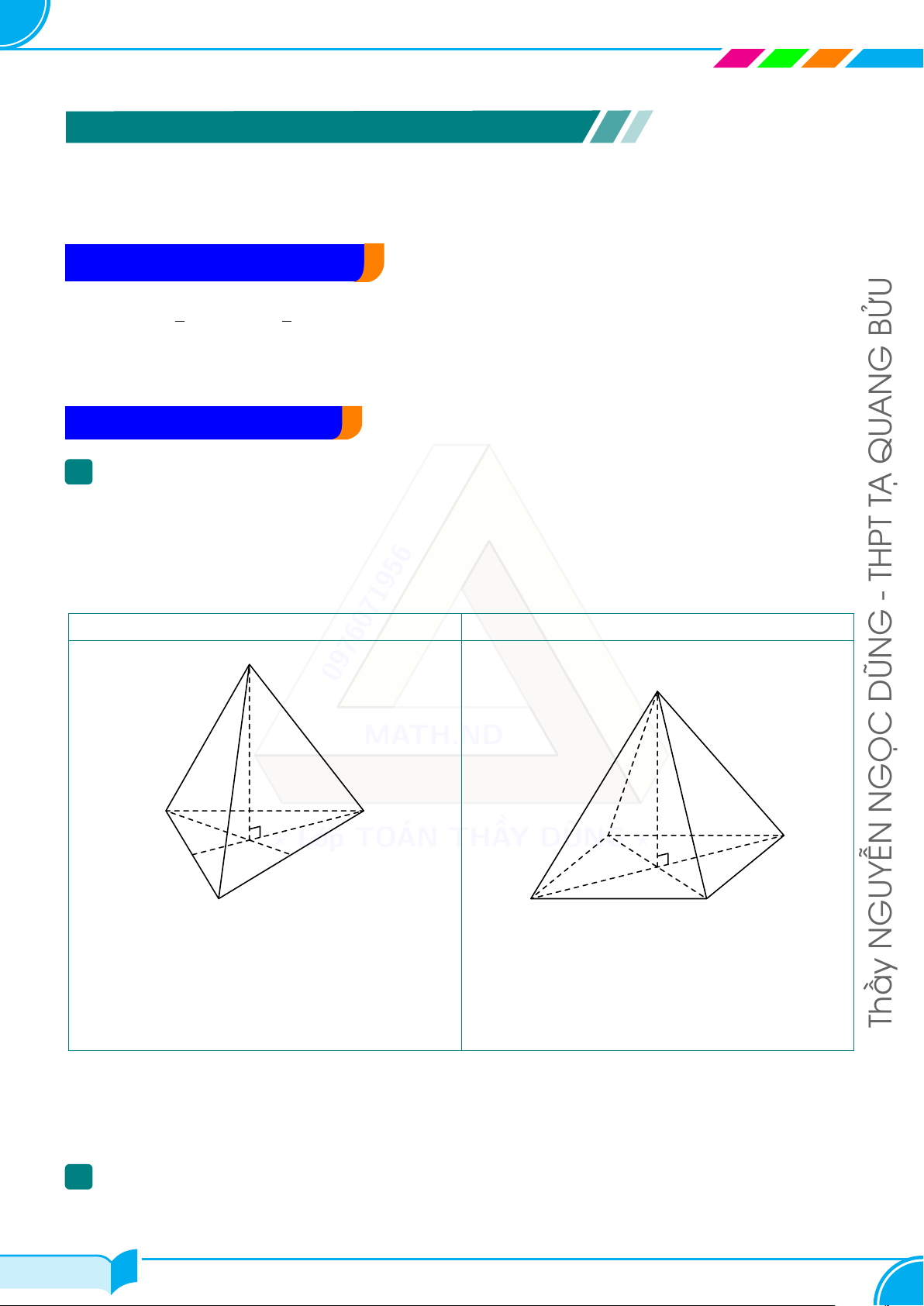
B – HÌNH CHÓP ĐẶC BIỆT QU 1 Hình chóp đều Là hình chóp có: TẠ • Đáy là đa giác đều
• Hình chiếu của đỉnh lên đáy trùng với tâm đáy. THPT
Có hai hình chóp đều thường gặp: - Hình chóp tam giác đều Hình chóp tứ giác đều G S 0976071956 S DŨN MATH.ND GỌC A C N A D ? Lớp TOÁN THẦY DŨNG ? B B C GUYỄN N
○ Đáy là tam giác đều; ○ Đáy là hình vuông;
○ Hình chiếu của S trùng trọng tâm G của
○ Hình chiếu của S trùng với giao điểm hai đáy.
đường chéo của hình vuông. Thầy Tính chất:
• Các cạnh bên bằng nhau
• Các mặt bên là các tam giác cân bằng nhau. 2 Tứ điện đều
Là tứ diện có các cạnh bằng nhau, do đó mặt bên là những tam giác đều. 21/37 21/37 NGUYỄN NGỌC DŨNG – 0976.071.956 22
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
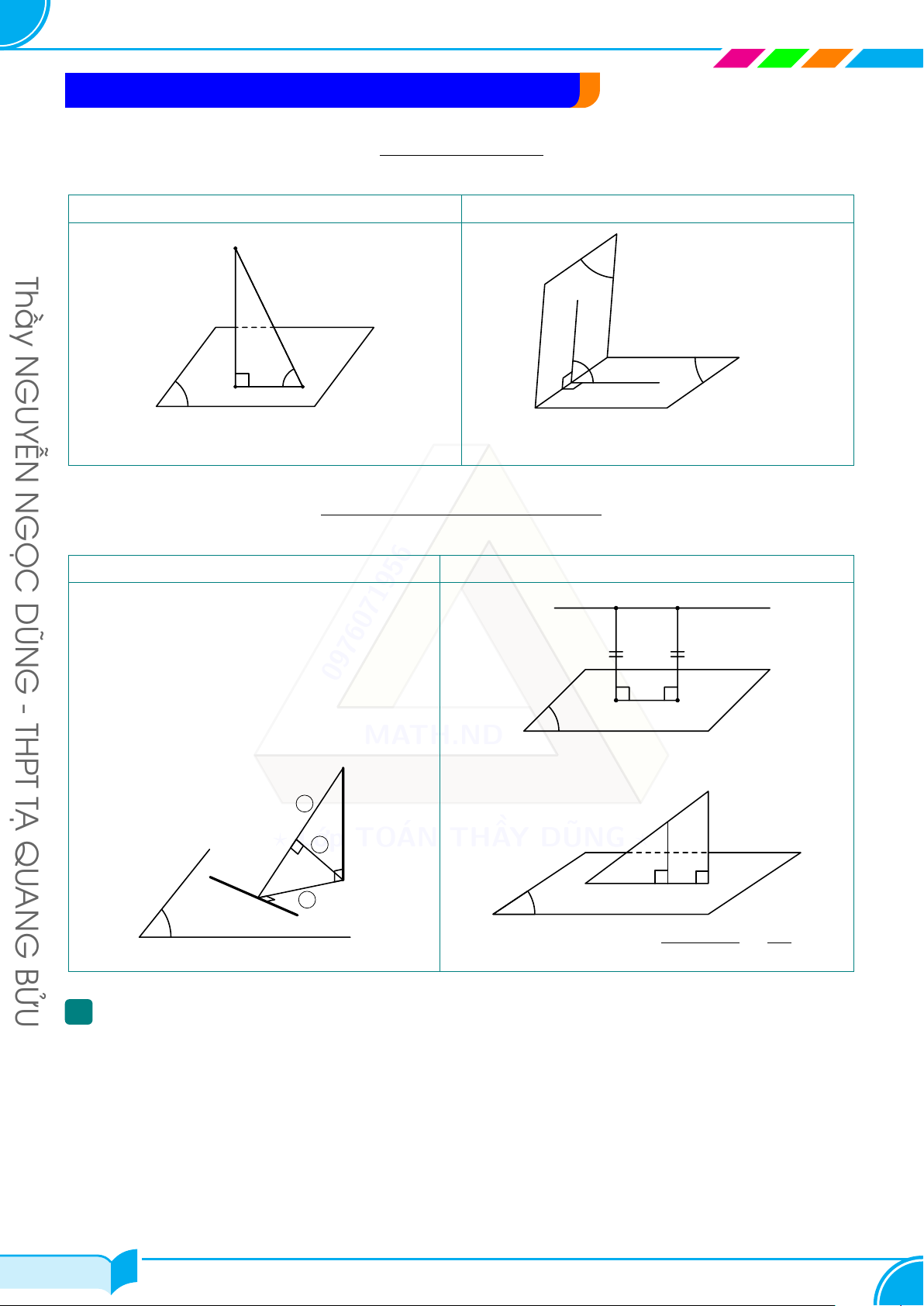
C – KĨ NĂNG XÁC ĐỊNH GÓC VÀ KHOẢNG CÁCH XÁC ĐỊNH GÓC
Góc giữa đường và mặt Góc giữa hai mặt phẳng A Thầy P a N GUYỄN d Q H B b α
Tìm hình chiếu của AB lên (α) là HB. Khi đó
Tìm hai đường thẳng vuông góc giao tuyến. [AB, (P )] = (AB, HB) = [(P ), (Q)] = (a, b) ’ ABH. N GỌC XÁC ĐỊNH KHOẢNG CÁCH Tính trực tiếp Tính gián tiếp DŨN B A G 0976071956 - THPT K H Quy tắc ba đường: MATH.ND P S
AB ∥ (P ) ⇒ d (A, (P )) = d (B, (P )). T A Ạ 2 B QU ? K Lớp 3 TOÁN THẦY DŨNG ? AN C A 1 I K H P G H α B d (A, (P )) IA AB cắt (P ) tại I ⇒ = . BỬU d (A, (SBC)) = AK. d (B, (P )) IB 1
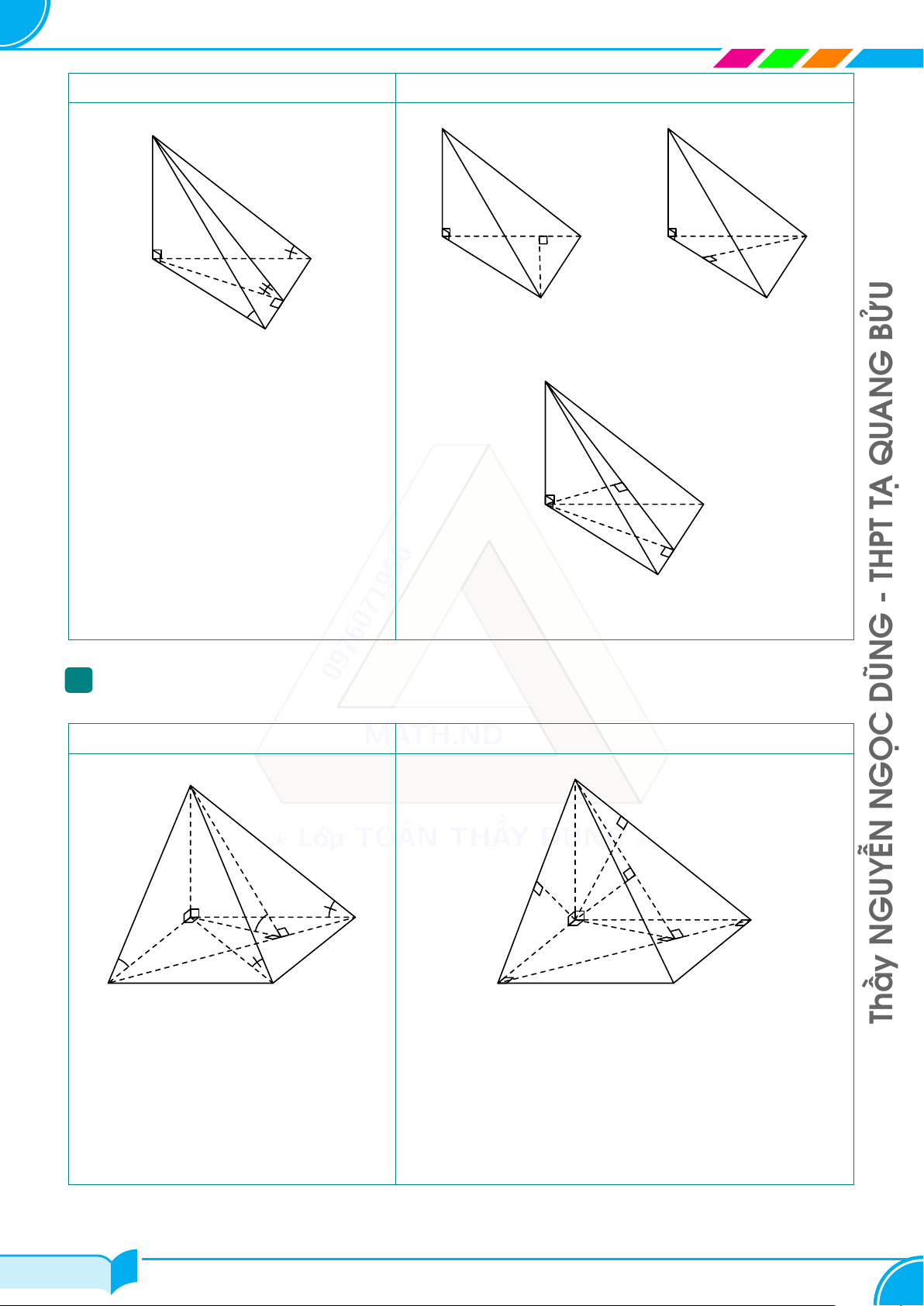
Chóp S.ABC có SA ⊥ (ABC) 22/37 22/37 NGUYỄN NGỌC DŨNG – 0976.071.956 23 Chương 5. Khối đa diện
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM GÓC KHOẢNG CÁCH S S S A H C A C A C K M B B B • d [B, (SAC)] = BH • d [C, (SAB)] = CK BỬU S ○ [SB, (ABC)] = ’ SBA ANG ○ [SC, (ABC)] = ’ SCA ○ [(SBC), (ABC)] = ’ SM A I QU A C
Nếu △ABC vuông tại B hoặc tại TẠ
C thì M trùng B hoặc trùng C. M THPT B - • d [A, (SBC)] = AI 2
Chóp S.ABCD có SA ⊥ 0976071956 (ABCD) DŨNG GÓC MATH.ND KHOẢNG CÁCH S S M NGỌC ? Lớp TOÁN THẦY DŨNG ? H N A D D A NGUYỄN H I B C B C Thầy ○ [SB, (ABCD)] = ’ SBA ○ d [A, (SBC)] = AN ○ [SC, (ABCD)] = ’ SCA ○ d [A, (SCD)] = AM ○ [(SD), (ABCD)] = ’ SDA ○ d [A, (SBD)] = AH ○ [(SBD), (ABCD)] = ’ SHA 23/37 23/37 NGUYỄN NGỌC DŨNG – 0976.071.956 24
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
D – CÁC CÔNG THỨC HÌNH HỌC PHẲNG 1 Diện tích
1.1. Diện tích tam giác Tam giác vuông Tam giác đều Tam giác thường A Thầy 60◦ c h b N a GUYỄN 60◦ 60◦ b B H a C 1 S = a · b √ 2 cạnh2 · 3 1 1 ○ S = S = a · h = b · c · sin A N 4 2 2 GỌC √ abc 3 = = pr ○ Đường cao = cạnh · 4R 2 » = p(p − a)(p − b)(p − c) DŨN
1.2. Diện tích tứ giác G Hình vuông 0976071956Hình chữ nhật Hình thang - THPT A D A D A D MATH.ND TẠ QU B H C ? Lớp TO B ÁN THẦY DŨNG C ? 1 S = (AD + BC) · AH B C AN 2 » 2 2 √ ○ AC = (dài) + (rộng) ○ AC = (cạnh) × 2. G ○ S = (dài) × (rộng). ○ S = (cạnh)2. BỬU Hình bình hành Hình thoi b h α a 1 S = tích hai đường chéo 2 S = a · h = a · b · sin α 2
Các định lý hay dùng 24/37 24/37 NGUYỄN NGỌC DŨNG – 0976.071.956 25 Chương 5. Khối đa diện
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
2.1. Hệ thức lượng tam giác vuông A BC2 = AB2 + AC2 • • AB2 = BH · BC • AC2 = CH · CB • AH2 = BH · CH 1 1 1 • AH · BC = AB · AC • = + AH2 AB2 AC2 AB · AC • AH = √ B H M C AB2 + AC2
2.2. Tam giác bất kỳ BỬU G
○ Định lý côsin: BC2 = AB2 + AC2 − 2 · AB · AC · cos A. A AB2 + AC2 − BC2 AN
○ Công thức tính góc: cos A = . 2 · AB · AC QU AB AC BC ○ Định lý sin: = = = 2R. sin C sin B sin A TẠ AB2 + AC2 BC2
○ Định lý trung tuyến: AM 2 = − . B M C 2 4 2.3. Phương tích THPT - J
Nếu ABCD là tứ giác nội tiếp thì G D ○ IA · ID = IB · IC; 0976071956 A O DŨN ○ JA · JB = JD · JC; MATH.ND ○ OA · OC = OD · OB. I B C GỌC
2.4. Định lý Menelaus và định lý Ceva N A ? Lớp TOÁN THẦY DŨNGA ? M N N M GUYỄN N B C K B K C (M, N, K thẳng hàng) (AK, BN, CM đồng quy) M A KB N C Thầy × × = 1 M B KC N A
E – TỈ SỐ THỂ TÍCH 25/37 25/37 NGUYỄN NGỌC DŨNG – 0976.071.956 26
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM 1 Khối chóp Chóp tam giác Chóp tứ giác S SA1 SB1 SC1 SD1 (A1B1C1D1) ∥ (ABCD) và = = = = k: SA SB SC SD M P S Thầy N VS.A C A 1 B1 C1 D1 1 B1 = k3 A VS.ABCD N D1 C1 GUYỄN A B B VS.MNP SM SN SP = · · C VS.ABC SA SB SC D N GỌC 2 Lăng trụ tam giác
Chóp so với lăng trụ tam giác Lăng trụ tam giác A′ B′ DŨN M C′ P G 0976071956 A - B THPT V 2V V = ; V = N chóp(4) 3 chóp(5) 3 MATH.ND C V 2V V Å ã A′C′B′.M N P 1 A′M C′N B′P = · + + T Ví dụ. VA′B′BC = ; VA′B′ABC = . V 3 A′A C′C B′B Ạ 3 3 A′B′C′.ABC QU 3 Khối hộp ? Lớp TOÁN THẦY DŨNG ? AN Chóp so với khối hộp
Mặt phẳng cắt các cạnh của hình hộp A′ G B′ A′ B′ Q BỬU D′ C′ D′ P C′ A B A M B D N C 2 đường chéo của V D V = ; C chóp(4) 2 mặt song song 3 DM  V = x   x + y V (trường hợp còn lại) = DD′ chóp(4) ⇒ V · V 6 BP 2 = 2 = y   V V BB′ Ví dụ. V
(chỉ quan tâm tới hai cạnh đối nhau) A′C′BD = ; VA′C′D′D = . 3 6 26/37 26/37 NGUYỄN NGỌC DŨNG – 0976.071.956 27 Chương 5. Khối đa diện
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM BỬU G AN QU TẠ THPT - G 0976071956 DŨN MATH.ND GỌC N ? Lớp TOÁN THẦY DŨNG ? GUYỄN N Thầy 27/37 27/37 NGUYỄN NGỌC DŨNG – 0976.071.956 28
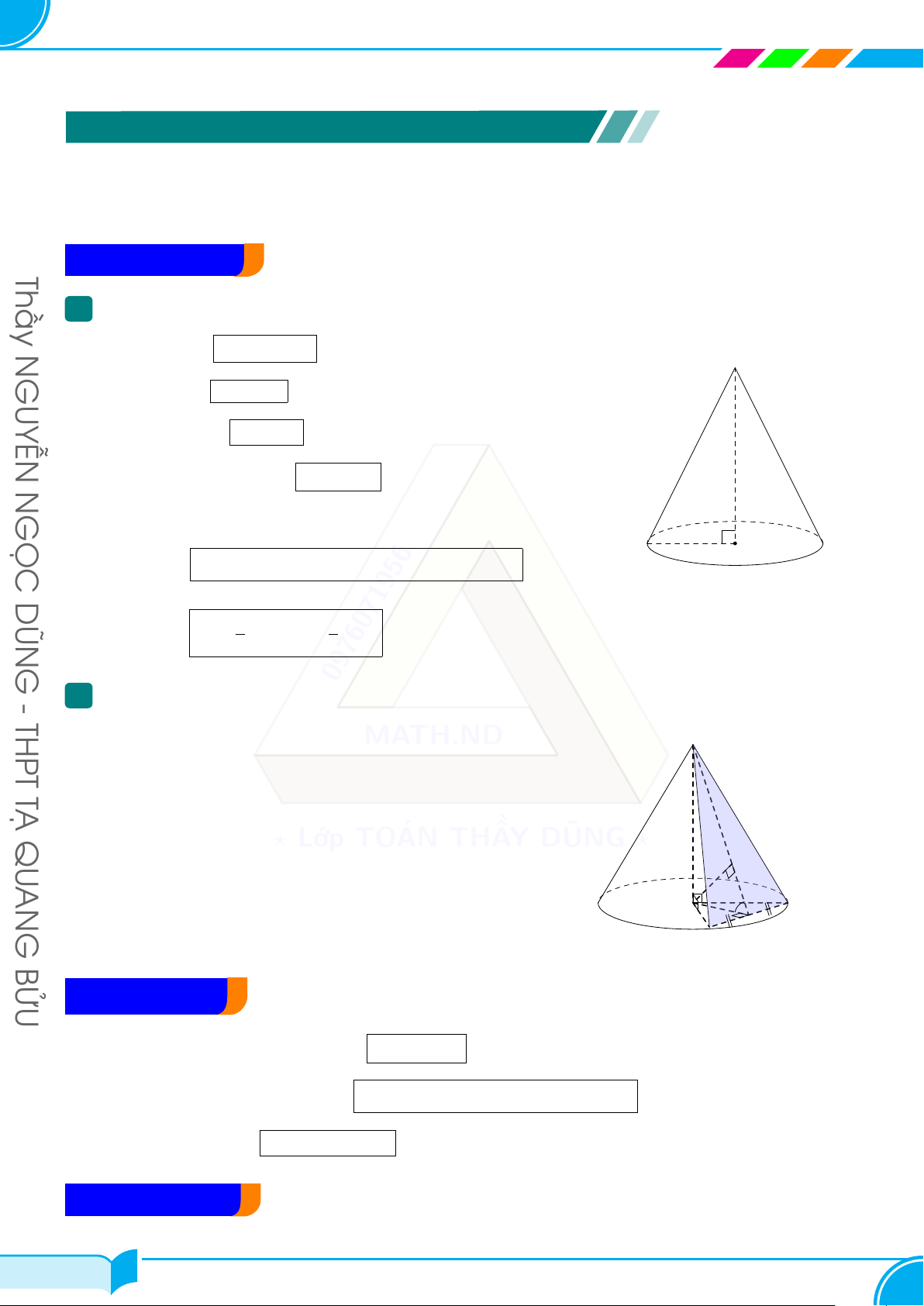
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM Chûúng 6 NÓN - TRỤ - CẦU NÓN - TRỤ - CẦU Thầy A – KHỐI NÓN 1 Các công thức N
○ Đường sinh: l2 = r2 + h2 GUYỄN S ○ Chu vi đáy: P = 2πr
○ Diện tích đáy: S = πr2 h N
○ Diện tích xung quanh: Sxq = πrl GỌC ○ Diện tích toàn phần: A B r S O tp = Sxq + S = πrl + πr2 = πr(r + l) đáy DŨN 1 1 ○ Thể tích: V = S · h = πr2h đáy G 3 3 0976071956 - THPT 2
Thiết diện không qua trục của hình nón MATH.ND S
○ Thiết diện là △SAB cân tại S. TẠ
○ OH là khoảng các từ O đến (P ). QU ○ ’ SM O là góc giữa ( ? P ) Lớp và mặt TO đáy ÁN hình THẦ nón. Y DŨNG ? AN H
○ △OAB cân tại O có OM vừa là đường cao, vừa là đường trung tuyến. G O A M B BỬU B – KHỐI TRỤ
○ Diện tích xung quanh hình trụ: Sxq = 2πrh
○ Diện tích toàn phần hình trụ: Stp = Sxq + 2 · S = 2πrh + 2πr2 đáy
○ Thể tích khối trụ: V = Bh = πr2h C – KHỐI CẦU 28/37 28/37 NGUYỄN NGỌC DŨNG – 0976.071.956 29
Chương 6. Nón - Trụ - Cầu
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM 1
Diện tích và thể tích 4 • Diện tích: S = 4πr2 . Thể tích: V = πr3 • 3 2
Mặt cầu ngoại tiếp
2.1. Mặt cầu ngoại tiếp hình nón
○ Tâm I của mặt cầu là tâm đường tròn ngoại tiếp △SAB. S
○ Bán kính mặt cầu là bán kính đường tròn ngoại tiếp △SAB. BỬU G I AN A B QU
2.2. Mặt cầu ngoại tiếp hình trụ TẠ
○ Tâm của mặt cầu là trung điểm đoạn thẳng nối tâm của hai đáy hình F
trụ (I là trung điểm EF ). D 1 ○ Bán kính R = IB = BD. I THPT 2 - G B 0976071956 E
2.3. Mặt cầu ngoại tiếp hình chóp có cạnh bên vuông góc đáy DŨN
○ Dựng trục đường tròn ∆ của đá MA y TH.ND
(vuông góc với đáy tại tâm đường S tròn ngoại tiếp). GỌC
○ Dựng đường trung trực d của đường cao. M N ○ Tìm giao điểm của ? ∆ vLớp ới d, TO đó ch ÁN ính là THẦ tâm I. Y DŨNG ? I A B √ Å hã2 ○ Bán kính R = IA = AM 2 + AH2 = + r2 2 D H E (r là bán kính đáy). GUYỄN C N 2.4. Hình chóp đều
○ Gọi K là trung điểm SA S Thầy
○ Dựng đường trung trực của SA cắt SO tại I.
○ Do tứ giác KIOA nội tiếp (có hai góc đối vuông) nên K SA · SK SA2
SI · SO = SK · SA ⇔ R = SI = = . SO 2SO I A B O D C 29/37 29/37 NGUYỄN NGỌC DŨNG – 0976.071.956 30
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
2.5. Mặt cầu ngoại tiếp hình chóp có mặt bên (SAC) vuông góc với mặt đáy
○ Gọi K là tâm △ABC, J là tâm của △SAC. S
○ Tính bán kính r = SJ đường tròn ngoại tiếp ∆SAC.
○ Bán kính mặt cầu ngoại tiếp là R = SI thỏa R2 = SJ2 + IJ2. Với IJ = DK. J I Thầy A B D K N GUYỄN C N GỌC DŨN G 0976071956 - THPT MATH.ND TẠ QU ? Lớp TOÁN THẦY DŨNG ? AN G BỬU 30/37 30/37 NGUYỄN NGỌC DŨNG – 0976.071.956 31
Chương 7. Phương pháp tọa độ trong không gian
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM Chûúng
PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG 7 GIAN
PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN
A – TỌA ĐỘ TRONG KHÔNG GIAN #» #» #»
a) Trong mặt phẳng Oxyz; i , j , k là các vectơ đơn vị, với BỬU #» #» #» #» #» #» #» #» #» G
i = (1; 0; 0), j = (0; 1; 0), k = (0; 0; 1) và i · j = i · k = j · k = 0 #» #» #» #» AN
b) Tọa độ vectơ: u = (x; y; z) ⇔ #» u = x · i + y · j + z · k . # » # » #» #» #»
c) Tọa độ điểm: M (x; y; z) ⇔ OM = (x; y; z) ⇔ OM = x · i + y · j + z · k . QU # »
d) AB = (xB − xA; yB − yA; zB − zA). TẠ # »
e) AB = AB = p(xB − xA)2 + (yB − yA)2 + (zB − zA)2. THPT #» #»
f) Các công thức quan trọng: Cho u = (a; b; c), v = (a′; b′; c′). Khi đó - #» #» u ± #»
v = (a ± a′; b ± b′; c ± c′) k u = (ka; kb; kc) G #» #» #» #» u · #» v aa′ + bb′ + cc′ u · #» v = aa′ + bb′ + cc′ 0976071956 cos ( u , v ) = = √ √ | #» u | · | #» v | a2 + b2 + c2 · a′2 + b′2 + c′2 √ DŨN | #» u | = a2 + b2 + c2 #» u · #» v = 0 ⇔ #» u ⊥ #»
v ⇔ aa′ + bb′ + cc′ = 0 a = a′   MATH.ND #» #» #» #» a b c u = v ⇔ b = b′ u cùng phương v ⇔ = = a′ b′ c′  c = c′ GỌC N ? Lớp TO  xA + xB  ÁN THẦY DŨNG ? x  M =  2    y
g) M là trung điểm của AB ⇔ y A + yB M = . 2    z  A + zB GUYỄN z  M = 2 N  xA + xB + xC x  G =  3    yA + yB + yC Thầy
h) G là trọng tâm của △ABC ⇔ yG = . 3    z  A + zB + zC z  G = 3  xA + xB + xC + xD x  G =  4    y
i) G là trọng tâm của tứ diện ABCD ⇔ y A + yB + yC + yD G = . 4    z  A + zB + zC + zD z  G = 4 31/37 31/37 NGUYỄN NGỌC DŨNG – 0976.071.956 32
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM j) Tích có hướng: #» #» #» #»
Cho a = (x; y; z); b = (x′, y′, z′). Tích có hướng của hai vectơ a và b là: Ç å î #» #»ó y z x z x y a ; b = ; − ; y′ z′ x′ z′ x′ y′
k) Tính chất tích có hướng: #» #» #» #» #» #» #» #» Thầy
• [ u , v ] vuông góc với u và v . • |[ u , v ]| = | #» u | · | #» v | · sin ( u , v ). #» #» #» • [ u , v ] = 0 ⇔ #» u và v cùng phương. N
l) Một số ứng dụng của tích có hướng: GUYỄN #» î #»ó ○ #» #» #»
Ba vectơ a , b , c đồng phẳng khi và chỉ khi a , b · #» c = 0. î # » # »ó # »
○ A, B, C, D tạo thành tứ diện ⇔ AB, AC · AD ̸= 0. î # » # »ó
○ Diện tích hình bình hành ABCD là S ABCD = AB, AD . N 1 î # » # »ó GỌC
○ Diện tích tam giác ABC là S ABC = AB, AC . 2 î # » # »ó # »
○ Thể tích hình hộp là V ABCD.A′B′C′D′ = AB, AD · AA′ . 1 î # » # »ó # » DŨN
○ Thể tích hình tứ diện là VABCD = AB, AC · AD . 6 G
B – MẶT CẦU - MẶT PHẲNG - ĐƯỜNG THẲNG 0976071956 - THPT 1 Mặt cầu
a) Mặt cầu tâm I(a; b; c) và bán MA kính R TH.ND có ○ T
Phương trình tổng quát (x − a)2 + (y − b)2 + (z − c)2 = R2. Ạ
○ Phương trình khai triển x2 + y2 + z2 − 2ax − 2by − 2cz + d = 0. QU ? Lớp TOÁN THẦY DŨNG ?
b) Phương trình x2 + y2 + z2 − 2ax − 2by − 2cz + d = 0 là phương trình mặt cầu khi và chỉ khi AN a2 + b2 + c2 − d > 0. G √
Khi đó, tâm và bán kính mặt cầu lần lượt là I(a, b, c); R = a2 + b2 + c2 − d. BỬU 2 Mặt phẳng #»
a) VTPT của mặt phẳng (α) là vectơ khác 0 và vuông góc với (α). ®Đi qua M (x0, y0, z0) b) Mặt phẳng (α) : #»
⇒ (α) : A (x − x0) + B (y − y0) + C (z − z0) = 0. VTPT n = (A, B, C)
c) Mặt phẳng (α) cắt Ox tại A(a; 0; 0), cắt Oy tại B(0; b; 0), cắt Oz tại C(0; 0; c) thì x y z (α) : + + = 1. a b c #» #» î #» #»ó
d) Nếu a và b là cặp VTCP của (α) thì a , b là VTPT của (α). 32/37 32/37 NGUYỄN NGỌC DŨNG – 0976.071.956 33
Chương 7. Phương pháp tọa độ trong không gian
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM # »
e) Nếu (α) ⊥ AB thì AB là VTPT. #»
f) Nếu (α) ⊥ Ox thì i = (1; 0; 0) là VTPT. # » # » î # » # »ó
g) Nếu (α) chứa 3 điểm A, B, C thì AB, AC là cặp VTCP ⇒ AB, AC là VTPT của (α). # » #»
h) Nếu (α) chứa M và chứa Oy thì có cặp VTCP là OM và j = (0; 1; 0). # » # »
i) Nếu (α) ∥ (β) thì n(α) = n(β). # » # »
j) Nếu (α) ⊥ (β) thì u(α) = n(β). 3 Đường thẳng BỬU #»
a) VTCP của đường thẳng (d) là vectơ khác 0 và song song với (d). G #»
b) Đường thẳng (d) đi qua M (x0, y0, z0) và VTCP u = (a, b, c) có AN x = x0 + at   ○ Phương trình tham số y = y0 + bt (t ∈ R). QU  z = z0 + ct TẠ x − x y − y z − z ○ 0 0 0 Phương trình chính tắc = = , với abc ̸= 0. a b c #» #» î #» #»ó
c) Nếu a và b là cặp VTPT của (d) thì a , b là VTCP của (d). THPT - # »
d) Nếu d đi qua A, B hoặc d ∥ AB thì AB là VTCP của d. G # »
e) Nếu d ⊥ AB thì AB là VTPT của d. #» # » 0976071956
f) Nếu d ⊥ ∆ thì nd = u∆. DŨN #» # »
g) Nếu d ⊥ (α) thì ud = n(α). MATH.ND #» # »
h) Nếu d ∥ (α) hoặc d ⊂ (α) thì nd = n(α). GỌC N 4
Phương trình mặt phẳng liên quan đến đường thẳng ? Lớp TOÁN( THẦ #» î #»Y # DŨNG »ó ? n = ud, AM
a) (α) chứa M và đường thẳng d thì (α) : với A ∈ d. Đi qua M ® #» # » # » n = [ud , u ] 1 d1 GUYỄN
b) (α) chứa hai đường thẳng cắt nhau d1, d2 thì (α) : với A ∈ d1. Đi qua A N ( #» î # » # »ó n = ud , AB
c) (α) chứa hai đường thẳng song song d 1 1, d2 thì (α) : với A ∈ d1, B ∈ d2. Đi qua A Thầy ® #» # » # » n = [ud , ud ]
d) (α) chứa đường thẳng d 1 1
1 và song song với d2 thì (α) : với A ∈ d1. Đi qua A 5 Góc và khoảng cách
5.1. Góc giữa hai mặt phẳng # » n(P ) · # » n(Q) |aa′ + bb′ + cc′| cos ((P ), (Q)) = = √ √ # » # » n(P ) · n(Q) a2 + b2 + c2 · a′2 + b′2 + c′2 33/37 33/37 NGUYỄN NGỌC DŨNG – 0976.071.956 34
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
5.2. Góc giữa hai đường thẳng # » u · # » u |aa′ + bb′ + cc′| cos (d d1 d2 1, d2) = = √ √ | # » ud | · | # » u | a2 + b2 + c2 · a′2 + b′2 + c′2 1 d2
5.3. Góc giữa đường thẳng và mặt phẳng #» ud · # » n(P ) |aa′ + bb′ + cc′| sin (d, (P )) = = √ √ | #» # » u d| · n(P ) a2 + b2 + c2 · a′2 + b′2 + c′2 Thầy
5.4. Khoảng cách từ điểm tới mặt phẳng axM + byM + czM + d √ N d (M, (P )) = a2 + b2 + c2 GUYỄN
5.5. Khoảng cách từ điểm tới đường thẳng #»
Với d đi qua A và có VTCP là ud thì î #» # »ó u d, AM d (M, (d)) = . N | #» ud| GỌC
5.6. Khoảng cách giữa hai đường thẳng chéo nhau ® # » d1 đi qua A, VTCP là ud Với 1 # » thì DŨN d2 đi qua B, VTCP là ud2 # » # » # » [u d , ud ] · AB 1 2 G d (d1, d2) = . | # » # » [u , u ]| 0976071956 d1 d2 - THPT 6
Vị trí tương đối MATH.ND
6.1. Vị trí tương đối giữa hai mặt phẳng
Cho (P ) : Ax + By + Cz + D = 0 và (Q) : A′x + B′y + C′z + D′ = 0. Khi đó TẠ A B C D A B C D QU • = = = ⇔ (P ) ≡ (Q); • = = ̸= ⇔ (P ) ∥ (Q); A′ B′ C′ D′? Lớp TOÁN THẦY A′ DŨNG B′ C′ ?D′ AN
• A : B : C ̸= A′ : B′ : C′ ⇔ (P ) cắt (Q);
• A · A′ + B · B′ + C · C′ = 0 ⇔ (P ) ⊥ (Q). G
Nếu mẫu số bằng 0 thì tử số cũng phải bằng 0.
6.2. Vị trí tương đối giữa đường thẳng và mặt phẳng BỬU
Xét hệ gồm phương trình đường thẳng d và phương trình mặt phẳng (P ).
○ Nếu hệ vô nghiệm thì d ∥ (P ).
○ Nếu hệ có đúng 1 nghiệm thì d cắt (P ).
○ Nếu hệ vô số nghiệm thì d ⊂ (P ). 34/37 34/37 NGUYỄN NGỌC DŨNG – 0976.071.956 35
Chương 7. Phương pháp tọa độ trong không gian
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
6.3. Vị trí tương đối giữa hai đường thẳng ®qua A ®qua B Cho (d) : #» và (d′) : #». Khi đó: vtcp u vtcp u′ #» #»
a) Nếu u cùng phương u′ thì d và d′ song song hoặc trùng nhau (dùng tỉ lệ).
○ Nếu A ∈ d′ thì d và d′ trùng nhau. ○ Nếu A /
∈ d′ thì d và d′ song song. #» #»
b) Nếu u không cùng phương u′ thì d và d′ cắt nhau hoặc chéo nhau. î #» # » ○ #» Nếu
u , u′ó · AB = 0 thì d và d′ cắt nhau. BỬU î #» # » ○ #» Nếu
u , u′ó · AB ̸= 0 thì d và d′ chéo nhau. G
Có thể dùng hệ phương trình để biện luận vị trí tương đối hoặc kết hợp vừa hệ vừa vectơ. AN
6.4. Vị trí tương đối giữa mặt phẳng, đường thẳng và mặt cầu QU
Cho mặt phẳng (P ) và mặt cầu (S) tâm I bán kính R. Khi đó
○ d [I, (P )] = R ⇔ (P ) tiếp xúc với (S); TẠ
○ d [I, (P )] < R ⇔ (P ) cắt (S); I
○ d [I, (P )] > R ⇔ (P ) nằm ngoài (S). THPT -
Trong trường hợp (P ) cắt (S) thì E G
○ Giao tuyến là đường tròn tâm H, bán kính r = HM . 0976071956 ○ R2 = d2 + r2 với d = OH. DŨN
6.5. Hình chiếu của điểm M trên đường thẳng d MATH.ND
○ Gọi H là hình chiếu của M lên d ⇒ H (x0 + at, y0 + bt). M # » # » ud GỌC ○ M H ⊥ d ⇒ M H · #»
ud = 0 ⇒ t = . . . ⇒ H(. . . , . . .). N H ? Lớp TOÁN THẦY DŨNG ? d 7
Phương trình đường thẳng trong mối liên hệ với mặt phẳng hoặc đường thẳng khác GUYỄN
Đối với bài toán tương giao có yếu tố cắt nhau giữa các đường thẳng thì ta gọi tên giao điểm N
và dựa vào các tính chất để lập hệ phương trình liên quan đến giao điểm vừa gọi.
7.1. Đường thẳng ∆ đi qua M , cắt và vuông góc với d Thầy
○ Gọi N = ∆ ∩ d ⇒ N (x0 + at, y0 + bt). ∆ # » M ○ M N ⊥ d ⇒ M N · #»
ud = 0 ⇒ t = . . . ⇒ N (. . . , . . .). #» ud
○ Viết phương trình đường thẳng ∆ đi qua M , N . N d 35/37 35/37 NGUYỄN NGỌC DŨNG – 0976.071.956 36
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM
7.2. Đường thẳng ∆ đi qua M , cắt d1 và vuông góc với d2
○ Gọi N = ∆ ∩ d1 ⇒ N (x0 + at, y0 + bt) . ∆ # » M ○ M N ⊥ d2 ⇒ MN · # »
ud = 0 ⇒ t = . . . ⇒ N (. . . , . . .). 2 d1 N
○ Viết phương trình đường thẳng ∆ đi qua M, N . Thầy d2 N
7.3. Đường thẳng ∆ đi qua M, song song với (P ) và cắt d GUYỄN
○ Gọi N = ∆ ∩ d ⇒ N (x0 + at, y0 + bt) . d # » # » # » ○ M N n ∥ (P ) ⇒ M N ⊥ #» np ⇒ M N · #» np = 0 M P ⇒ t = ... ⇒ N (..., ...). N ∆ N ○ GỌC
Viết phương trình đường thẳng ∆ đi qua M, N . P DŨN
7.4. Đường thẳng ∆ qua M đồng thời cắt cả d1 và d2 ® A = ∆ ∩ d ® 1 A(x1 + at, y1 + bt) G ○ Gọi ⇒ . B = ∆ ∩ d ∆ 2 A(x2 0976071956 + a′t′, y2 + b′t′) - # » # » d1 THPT
○ Do A, B, M thẳng hàng nên AB cùng phương AM # » # » A ⇒ AM = kAB. MATH.ND
○ Giải hệ tìm được k, t, t′ ⇒ A, B. M TẠ
○ Viết phương trình đường thẳng ∆ đi qua A, B hoặc M . B QU ? Lớp TOÁN THẦY DŨNG ? AN d2
7.5. Đường thẳng ∆ nằm trong (P ) đồng thời cắt cả d1 và d2 G ® A = d ®A (x ○ 1 ∩ (P ) 1 + at; y1 + bt) Gọi ⇒ . BỬU B = d d d2 2 ∩ (P )
B (x2 + a′t′; y2 + b′t′) 1
○ Thay A, B vào phương trình (P ) tìm được t, t′ và A, B.
○ Viết phương trình ∆ đi qua A, B. B ∆ A
7.6. Đường thẳng ∆ vuông góc đồng thời cắt cả d1 và d2 (đường vuông góc chung) 36/37 36/37 NGUYỄN NGỌC DŨNG – 0976.071.956 37
Chương 7. Phương pháp tọa độ trong không gian
Lớp Toán Thầy DŨNG — Tạ Quang Bửu, P5, Q8, HCM ® A = ∆ ∩ d ®A(x ○ 1 1 + at, y1 + bt) Gọi ⇒ . B = ∆ ∩ d ∆ 2
A(x2 + a′t′, y2 + b′t′) d1 ○ # » # » # »
Tính VTCP của ∆ : u∆ = [ud , u ] . A 1 d2 # » ○ # » # »
Do AB cùng phương với u∆ nên AB = ku∆.
○ Giải hệ tìm được k, t, t′ ⇒ A, B.
○ Viết phương trình đường thẳng ∆ đi qua A và nhận VTCP là B # » u∆. d2 BỬU 8
Hình chiếu vuông góc G
8.1. Hình chiếu của điểm M trên mặt phẳng (P ) AN
○ Gọi H là hình chiếu của M lên (P ) thì M H ⊥ (P ). M QU ○ # »
Lập phương trình M H đi qua M và có VTCP là n(P ). # » TẠ n
○ Tọa độ H là giao điểm của (P ) và M H (giải hệ). (P ) H THPT P - G 0976071956 DŨN MATH.ND GỌC N ? Lớp TOÁN THẦY DŨNG ? GUYỄN N Thầy 37/37 37/37 NGUYỄN NGỌC DŨNG – 0976.071.956