Tóm tắt lý thuyết và bài tập trắc nghiệm logarit

Sau một khoảng thời gian nghỉ học kéo dài do ảnh hưởng của tình hình dịch bệnh, thì hiện tại, nhiều trường THPT trên toàn quốc đã bắt đầu cho học sinh đi học trở lại. 

126 63 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 6: Hàm số mũ và hàm số lôgarit (KNTT)

Môn: Toán 11

Thông tin:

15 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
Trang 1/15
CHỦ ĐỀ 2. LOGARIT
A. KIẾN THỨC CƠ BẢN
1. Đinh nghia:
Cho hai sô dương
,ab
vơi
1≠a
. Sô
α
thoa man đăng thưc
α
=ab
đươc goi la lôgarit cơ sô
a
cua
b
va ki hiêu la
log
a
b
. Ta viêt:
2. Cac tinh chât: Cho
, 0, 1>≠ab a
, ta co:
•
log 1, log 1 0
= =
aa
a
•
log
, log ( )
α
α
= =
a
b
a
ab a
3. Lôgarit cua môt tich: Cho 3 sô dương
12
,,ab b
vơi
1a ≠
, ta co
•
12 1 2
log ( . ) log log= +
a aa
bb b b
4. Lôgarit cua môt thương: Cho 3 sô dương
12
,,ab b
vơi
1≠a
, ta co
•
1
12
2
log log log= −
a aa
b
bb
b
• Đăc biêt : vơi
, 0, 1>≠ab a
1
log log= −
aa
b
b
5. Lôgarit cua luy thưa: Cho
, 0, 1>≠ab a
, vơi moi
α
, ta co
•
log log
α
α
=
aa
bb
• Đăc biêt:
1
log log
=
n
aa
bb
n
6. Công thưc đôi cơ sô: Cho 3 sô dương
,,abc
vơi
1, 1≠≠
ac
, ta co
•
log
log
log
=
c
a
c
b
b
a
• Đăc biêt :
1
log
log
=
a
c
c
a
va
1
log log
α
α
=
a
a
bb
vơi
0
α
≠
.
Lôgarit thâp phân và Lôgarit tư nhiên
Lôgarit thâp phân la lôgarit cơ sô 10. Viêt :
10
log log lg= =b bb
Lôgarit tư nhiên la lôgarit cơ sô
e
. Viêt :
log ln=
e
bb
B. KỸ NĂNG CƠ BẢN
1. Tính giá trị biểu thức
2. Rút gọn biểu thức
3. So sánh hai biểu thức
4. Biểu diễn giá trị logarit qua một hay nhiều giá trị logarit khác
C. KỸ NĂNG SỬ DỤNG MÁY TÍNH
1. Tính giá trị của một biểu thức chứa logarit
Ví dụ : Cho
0, 1aa>≠
, giá trị của biểu thức
log 4
a
a
bằng bao nhiêu ?
A. 16 B. 4 C. 8 D. 2
Ví dụ : Giá trị của biểu thức
2 22 2
2log 12 3log 5 log 15 log 150A = + −−
bằng:
A. 2 B. 3 C. 4 D. 5
2. Tính giá trị của biểu thức Logarit theo các biểu thức logarit đã cho
Ví dụ: Cho log
23
5 a; log 5 b= =
. Khi đó
6
log 5
tính theo a và b là
A.
1
ab+
B.
ab
ab+
C. a + b D.
22
ab+
3. Tìm các khẳng định đúng trong các biểu thức logarit đã cho.
Ví dụ: Cho
0, 0ab
>>
thỏa điều kiện
22
7a b ab+=
.Khẳng định nào sau đây đúng:
Trang 2/15
A.
(
) ( )
1
3log log log
2
ab a b
+= +
B.
3
log( ) (log log )
2
ab a b
+= +
C.
2(log logb) log(7a )ab+=
D.
1
log (log log )
32
ab
ab
+
= +
4. So sánh lôgarit với một số hoặc lôgarit với nhau
Ví dụ: Trong 4 số
2 0,5
33
log 5 log 2
log 4 2log 2
11
3 ;3 ; ;
4 16



số nào nhỏ hơn 1
A.
3
log 4
3
B.
3
2log 2
3
C.
2
log 5
1
4



D.
0,5
log 2
1
16



D. BÀI TẬP TRẮC NGHIỆM
Câu 1. Với giá trị nào của
x
thì biểu thức
2
( ) log (2 1)fx x= −
xác định?
A.
1
;
2
x

∈ +∞


. B.
1
;
2
x

∈ −∞


. C.
1
\
2
x

∈


. D.
x ( 1; )∈ − +∞
.
Câu 2. Với giá trị nào của
x
thì biểu thức
2
( ) ln(4 )
fx x= −
xác định?
A.
( 2; 2)x ∈−
. B.
[ 2; 2]x ∈−
. C.
\[ 2;2]
x ∈−
. D.
\ ( 2; 2)
x
∈−
.
Câu 3. Với giá trị nào của
x
thì biểu thức
1
2
1
( ) log
3
x
fx
x
−
=
+
xác định?
A.
[ 3;1]
x ∈−
. B.
\ [ 3;1]x ∈−
. C.
\ ( 3;1)
x ∈−
. D.
( 3;1)x ∈−
.
Câu 4. Với giá trị nào của
x
thì biểu thức:
xác định?
A.
02x<<
. B.
2
x >
. C.
11x−< <
. D.
3x <
.
Câu 5. Với giá trị nào của
x
thì biểu thức:
32
5
( ) log ( 2 )fx x x x= −−
xác định?
A.
(0;1)
x ∈
. B
(1; )x ∈ +∞
.
C.
( 1; 0) (2; )x ∈ − ∪ +∞
. D.
(0; 2) (4; )x ∈ ∪ +∞
.
Câu 6. Cho
0, 1aa>≠
, giá trị của biểu thức
log 4
a
Aa=
bằng bao nhiêu?
A.8. B.16. C.4. D.2.
Câu 7. Giá trị của biểu thức
2 22 2
2log 12 3log 5 log 15 log 150B = + −−
bằng bao nhiêu?
A.5. B.2. C.4. D.3.
Câu 8. Giá trị của biểu thức
2 22 2
22log 12 3log 5 log 15 log 150P = + −−
bằng bao nhiêu?
A. 2 . B. 3. C. 4 . D. 5.
Câu 9. Cho
0, 1aa>≠
, biểu thức
3
log
a
Da=
có giá trị bằng bao nhiêu?
A.3. B.
1
3
. C.
3−
. D.
1
3
−
.
Câu 10. Giá trị của biểu thức
3
77 7
1
log 36 log 14 3log 21
2
C = −−
bằng bao nhiêu ?
A.
2−
. B.2. C.
1
2
−
. D.
1
2
.
Câu 11. Cho
0, 1aa>≠
, biểu thức
2
4log 5
a
Ea=
có giá trị bằng bao nhiêu?
A.
5
. B.
625
. C.
25
. D.
8
5
.
Câu 12. Trong các số sau, số nào lớn nhất?
A.
3
5
log
6
. B.
3
5
log
6
. C.
1
3
6
log
5
. D.
3
6
log
5
.
Câu 13. Trong các số sau, số nào nhỏ nhất ?
A.
5
1
log
12
. B.
1
5
log 9
. C.
1
5
log 17
. D.
5
1
log
15
.
Trang 3/15
Câu 14. Cho
0, 1aa>≠
, biểu thức
22 2
(ln log ) ln log
aa
Aa e a e=+ +−
có giá trị bằng
A.
2
2ln 2a +
. B.
4ln 2a
+
. C.
2
2ln 2
a
−
. D.
2
ln 2a +
.
Hướng dẫn giải
Câu 15. Cho
0, 1aa>≠
, biểu thức
32
2ln 3log
ln log
a
a
Ba e
ae
= + −−
có giá trị bằng
A.
4ln 6log 4
a
a +
. B.
4ln
a
. C.
3
3ln
log
a
a
e
−
. D.
6log
a
e
.
Câu 16. Cho
0, 0ab>>
, nếu viết
(
)
2
3
5
3
3 33
log log log
5 15
xy
ab a b= +
thì
xy+
bằng bao nhiêu?
A.3. B.5. C.2. D.4.
Câu 17. Cho
0, 0ab>>
, nếu viết
0,2
10
5 55
6
5
log log log
a
x ay b
b
−

= +


thì
xy
bằng bao nhiêu ?
A.
3
. B.
1
3
. C.
1
3
−
. D.
3−
.
Câu 18. Cho
3 39
3
log 3log 2 log 25 log 3x =+−
. Khi đó giá trị của
x
là :
A.
200
3
. B.
40
9
. C.
20
3
. D.
25
9
.
Câu 19. Cho
7 7 49
1
log 2log 6logab
x
= −
. Khi đó giá trị của
x
là :
A.
26ab−
. B.
2
3
a
x
b
=
. C.
23
x ab
=
. D.
3
2
b
x
a
=
.
Câu 20. Cho
, , 0; 1abc a>≠
và số
α
∈
, Trong các khẳng định sau, khẳng định nào sai?
A.
log
c
a
ac=
. B.
log 1
a
a =
.
C.
log log
aa
bb
α
α
=
. D.
log ( ) log log
a aa
bc b c
−= −
.
Câu 21. Cho
, , 0; 1abc a>≠
, Trong các khẳng định sau, khẳng định nào sai?
A.
1
log
log
a
b
b
a
=
. B.
.
C.
log log
c
a
a
bc b
=
. D.
log ( . ) log log
a aa
bc b c
= +
.
Câu 22. Cho
,, 0abc>
và
,1ab≠
, Trong các khẳng định sau, khẳng định nào sai?
A.
log
a
b
ab
=
. B.
log log
aa
b c bc= ⇔=
.
C.
log
log
log
a
b
a
c
c
b
=
. D.
log log
aa
b c bc> ⇔>
.
Câu 23. Cho
,, 0abc>
và
1a >
. Trong các khẳng định sau, khẳng định nào sai?
A.
log log
aa
b c bc< ⇔<
. B.
log log
aa
b c bc> ⇔>
.
C.
log
a
bc bc>⇔>
. D.
bc
a a bc> ⇔>
.
Câu 24. Cho
,, 0abc>
và
1a <
.Trong các khẳng định sau, khẳng định nào sai?
A.
log log
aa
b c bc> ⇔<
. D.
23
aa<
.
C.
log log
aa
b c bc< ⇔>
. D.
log 0 1
a
bb>⇔<
.
Câu 25. Số thực
a
thỏa điều kiện
32
log (log ) 0a =
là:
A.
1
3
. B. 3. C.
1
2
. D. 2.
Câu 26. Biết các logarit sau đều có nghĩa. Khẳng định nào sau đây là khẳng định đúng ?
A.
log log
aa
b c bc= ⇔=
. B.
log log
aa
b c bc> ⇔>
Trang 4/15
C.
log log
aa
b c bc> ⇔<
. D.
log log 0 0
aa
b c bc
+ <⇔+<
.
Câu 27. Cho
,, 0
abc>
và
1a ≠
. Khẳng định nào sau đây là khẳng định sai ?
A.
log ( ) log log
a aa
bc b c= +
. B.
log ( ) log log
a aa
b
bc
c
= −
.
C.
log
c
a
bc ba=⇔=
. D.
log ( ) log log
a aa
bc b c+= +
.
Câu 28. Số thực
x
thỏa mãn điều kiện
248
log log log 11xxx
++=
là :.
A. 64. B.
11
6
2
. C.8. D. 4.
Câu 29. Số thực
x
thỏa mãn điều kiện
3
log 2 2 4
x
=
là
A.
3
2
. B. .
3
1
2
C. 4. D. 2.
Câu 30. Cho
,0ab>
và
,1ab≠
. Biểu thức
2
2
2
log
log
a
a
b
Pb
a
= +
có giá trị bằng bao nhiêu?
A. 6. B.3. C.4. D.2.
Câu 31. Cho
,0ab>
và
,1ab
≠
, biểu thức
34
log .log
b
a
P ba=
có giá trị bằng bao nhiêu?
A.6. B.24. C.12. D. 18.
Câu 32. Giá trị của biểu thức
8 16
3log 3 2log 5
4
+
là:
A. 20. B.40. C. 45. D. 25 .
Câu 33. Giá trị của biểu thức
(
)
3
5
log
a
P a aa=
là
A.
53
30
. B.
37
10
. C.20. D.
1
15
.
Câu 34. Giá trị của biểu thức
3 4 5 16
log 2.log 3.log 4...log 15A =
là:
A.
1
2
. B.
3
4
. C.
1
. D.
1
4
.
Câu 35. Giá trị của biểu thức
35
32 3
1
4
log
a
aa a
aa




là:.
A.
1
5
. B.
3
4
. C.
211
60
−
. D.
91
60
.
Câu 36. Trong 2 số
3
log 2
và
2
log 3
, số nào lớn hơn 1?.
A.
2
log 3
. B.
3
log 2
. C. Cả hai số . D. Đáp án khác.
Câu 37. Cho 2 số
1999
log 2000
và
2000
log 2001
. Khẳng định nào sau đây là khẳng định đúng?
A.
1999 2000
log 2000 log 2001>
. B. Hai số trên nhỏ hơn 1.
C. Hai số trên lớn hơn 2. D.
1999 2000
log 2000 log 2001≥
.
Câu 38. Các số
3
log 2
,
2
log 3
,
3
log 11
được sắp xếp theo thứ tự tăng dần là:
A.
33 2
log 2, log 11, log 3
. B.
323
log 2, log 3, log 11
.
C.
233
log 3, log 2, log 11
. D.
3 32
log 11, log 2, log 3
.
Câu 39. Số thực
x
thỏa mãn điều kiện
( )
3
log 2 3x +=
là:
A.
5
. B.
25−
. C.
25
. D.
3−
.
Câu 40. Số thực
x
thỏa mãn điều kiện
39
3
log log
2
xx+=
là :
A.
3−
. B.
25
. C.
3
. D.
9
.
Câu 41. Cho
( )
3 33
log 4log 7 log , 0x a b ab=+>
. Giá trị của
x
tính theo
,
ab
là:
A.
ab
. B.
4
ab
. C.
47
ab
. D.
7
b
.
Trang 5/15
Câu 42. Cho
( )
(
)
22
22
log 1 log 0x y xy xy+=+ >
. Chọn khẳng định đúng trong các khẳng định sau ?
A.
xy>
. B.
xy=
. C.
xy<
. D.
2
xy=
.
Câu 43. Cho
( )
( )
14
4
1
log log =1 0,yx y y x
y
−− > >
. Chọn khẳng định đúng trong các khẳng định sau?
A.
34xy=
. B.
3
4
xy
= −
. C.
3
4
xy=
. D.
34xy= −
.
Câu 44. Chọn khẳng định đúng trong các khẳng định sau?
A.
(
)
22
log 2log 0
aa
x xx= >
. B.
log log log
a aa
xy x y= +
.
C.
(
)
log log log 0
a aa
xy x y xy=+>
. D.
( )
log log log 0
a aa
xy x y xy=+>
.
Câu 45. Cho
,0>xy
và
22
4 12
+=x y xy
. Khẳng định nào sau đây là khẳng định đúng ?
A.
2 22
2
log log log
4
+

= −


xy
xy
. B.
2 22
1
log ( 2 ) 2 (log log )
2
+=+ +xy x y
.
C.
2 22
log ( 2 ) log log 1
+= + +xy x y
. D.
2 22
4log ( 2 ) log log+= +
xy x y
.
Câu 46. Cho
,0ab>
và
22
7+=a b ab
. Khẳng định nào sau đây là khẳng định đúng ?
A.
2log( ) log logab a b+= +
. B.
4log log log
6
+

= +


ab
ab
.
C.
1
log (log log )
32
+

= +


ab
ab
. D.
log 3(log log )
3
+

= +


ab
ab
.
Câu 47. Cho
2
log 6 = a
. Khi đó giá trị của
3
log 18
được tính theo
a
là:
A.
a
. B.
1
a
a
+
. C.
23+a
. D.
21
1
a
a
−
−
.
Câu 48. Cho
2
log 5 = a
. Khi đó giá trị của
4
log 1250
được tính theo
a
là :
A.
14
2
− a
. B.
2(1 4 )+ a
. C.
14+ a
. D.
14
2
+ a
.
Câu 49. Biết
7
log 2 = m
, khi đó giá trị của
49
log 28
được tính theo
m
là:
A.
2
4
+m
. B.
1
2
+ m
. C.
14
2
+ m
. D.
12
2
+ m
.
Câu 50. Biết
25
log 5, log 3= =ab
; khi đó giá trị của
10
log 15
được tính theo
a
là:
A.
1
+
+
ab
a
. B.
1
1
+
+
ab
a
. C.
1
1
−
+
ab
a
. D.
( 1)
1
+
+
ab
a
.
Câu 51. Cho
33
log 15; log 10= =ab
. Khi đó giá trị của
3
log 50
được tính theo
,ab
là :
A.
2( 1)ab−−
. B.
2( 1)ab+−
. C.
2( 1)ab++
. D.
2( 1)ab−+
.
Câu 52. Biết
5
log 3
= a
, khi đó giá trị của
15
log 75
được tính theo
a
là:
A.
2
1
+
+
a
a
. B.
12
1
+
+
a
a
. C.
1
2
+
+
a
a
. D.
2
.
Câu 53. Biết
4
log 7 = a
, khi đó giá trị của
2
log 7
được tính theo
a
là:
A.
2
a
. B.
1
2
a
. C.
1
4
a
. D.
4a
.
Câu 54. Biết
5
log 3 = a
, khi đó giá trị của
3
27
log
25
được tính theo
a
là:
A.
3
2a
. B.
3
2
a
. C.
32−a
a
. D.
32−
a
a
.
Câu 55. Biết
25
log 5, log 3= =ab
. Khi đó giá trị của
24
log 15
được tính theo
a
là :
Trang 6/15
A.
1+ab
b
. B.
1
1
+
+
ab
a
. C.
1
1
+
+
b
a
. D.
( 1)
3
+
+
ab
ab
.
Câu 56. Cho
12
log 27 = a
. Khi đó giá trị của
6
log 16
được tính theo
a
là:
A.
( )
43
3
+
−
a
a
. B.
( )
43
3
−
+
a
a
. C.
4
3 −
a
a
. D.
2
3 +
a
a
.
Câu 57. Cho
lg3 , lg 2= =ab
. Khi đó giá trị của
125
log 30
được tính theo
a
là:
A.
( )
1
31
+
−
a
b
. B.
( )
43
3
−
−
a
b
. C.
3 +
a
b
. D.
3 +
a
a
.
Câu 58. Cho
log 3=
a
b
. Giá trị của biểu thức
3
log=
b
a
b
A
a
được tính theo
a
là:
A.
3
3
−
. B.
3
4
. C.
1
3
D.
3
4
−
.
Câu 59. Cho
27 8 2
log 5 , log 7 , log 3= = =abc
. Giá trị của
6
log 35
được tính theo ,,
abc
là:
A.
1−
ac
c
. B.
1+
ac
b
. C.
( )
3a
1
+
+
cb
c
. D.
33
3
+
+
ac b
a
.
Câu 60. Cho
2000!=x
. Giá trị của biểu thức
2 3 2000
11 1
...
log log log
= + ++
A
xx x
là:
A.
1
. B.
1−
. C.
1
5
. D.
2000
.
Câu 61. Biết
7 12
log 12, log 24= =ab
. Khi đó giá trị của
54
log 168
được tính theo a là:
D.
(8 5 )
1
−
+−
ab
ab a
. B.
1
(8 5 )
+−
−
ab a
ab
. C.
(8 5 )
1
−
+
ab
ab
. A.
1
(8 5 )
+
−
ab
ab
.
Câu 62. Biết
log 2,log 3= = −
aa
bc
. Khi đó giá trị của bieeur thức
23
4
a
log
a
b
c
bằng:
A.
20
. B.
2
3
−
. C.
1−
. D.
3
2
.
Câu 63. Biết
log 3,log 4= = −
aa
bc
. Khi đó giá trị của biểu thức
( )
22
3
log
a
a bc
bằng:
A.
16 3
3
−
. B.
5−
. C.
16−
. D.
48
−
.
Câu 64. Rút gọn biểu thức
3
5
log=
a
A a aa
, ta được kết quả là:
A.
37
10
. B.
35
10
. C.
3
10
. D.
1
10
.
Câu 65. Rút gọn biểu thức
53
32
1
4
log
=
a
aa a
B
aa
, ta được kết quả là :
A.
91
60
−
. B.
60
91
. C.
16
5
. D.
5
16
−
.
Câu 66. Biết
23
log 5, log 5= =ab
. Khi đó giá trị của
6
log 5
được tính theo
,ab
là :
A.
+
ab
ab
. B.
1
+ab
. C.
+ab
. D.
22
+ab
.
Câu 67. Cho
237
log 3; log 5; log 2= = =abc
. Khi đó giá trị của biểu thức
140
log 63
được tính theo
,,abc
là:
A.
21
21
−
++
ac
abc c
. B.
21
21
++
+
abc c
ac
. C.
21
21
+
++
ac
abc c
. D.
1
21
+
++
ac
abc c
.
Trang 7/15
Câu 68. Cho
55
log 2; log 3= =ab
. Khi đó giá trị của
5
log 72
được tính theo
,ab
là :
A.
32+ab
. B.
32
+ab
. C.
32−ab
. D.
6ab
.
Câu 69. Biết
12 24
log 18, log 54= =ab
. Khẳng định nào sau đây là khẳng định đúng?
A.
5( ) 1+ −=−ab a b
. B.
51
++=ab a b
.
C.
5( ) 1+ −=ab a b
. D.
50+−=ab a b
.
Câu 70. Biết
( )
( )
342
log log log 0=y
, khi đó giá trị của biểu thức
21Ay= +
là:
A.33. B. 17. C. 65. D. 133.
Câu 71. Cho
5
log 0>
x
. Khẳng định nào sau đây là khẳng định đúng?
A.
log 5 log 4
xx
≤
. B.
log 5 log 6
xx
>
. C.
5
log log 5
x
x
=
. D.
56
log logxx>
.
Câu 72. Cho
01<<x
. Khẳng định nào sau đây là khẳng định đúng?
A.
3
3
1
2
log 5 log 5 0+<
x
B.
3
1
log 5 log
2
>
xx
C.
5
11
log log .
22
<
x
D.
3
1
log . log 5 0
2
>
xx
Câu 73. Trong bốn số
2 0,5
33
log 5 log 2
log 4 2log 2
11
3 ,3 , ,
4 16



số nào nhỏ hơn 1?
A.
0,5
log 2
1
16



. B.
3
2log 2
3
. C.
3
log 4
3
. D.
2
log 5
1
4



.
Câu 74. Gọi
0,5 0,5
log 4 log 13
3 ; N = 3
=
M
. Khẳng định nào sau đây là khẳng định đúng?
A.
1MN
<<
. B.
1
NM
<<
. C.
1
MN<<
. D.
1NM
<<
.
Câu 75. Biểu thức
22
log 2sin log cos
12 12
ππ

+


có giá trị bằng:
A.
2−
. B.
1−
. C.1. D.
2
log 3 1
−
.
Câu 76. Với giá trị nào của
m
thì biểu thức
5
( ) log ( )= −fx x m
xác định với mọi
( 3; )∈ − +∞x
?
A.
3>−m
. B.
3<−m
. C.
3≤−m
. D.
3≥−
m
.
Câu 77. Với giá trị nào của
m
thì biểu thức
1
2
( ) log (3 )( 2 )= −+fx x x m
xác định với mọi
[ 4;2]∈−x
?
A.
2
≥m
. B.
3
2
≥m
. C.
2>m
. D.
1≥−
m
.
Câu 78. Với giá trị nào của
m
thì biểu thức
3
( ) log ( )( 3 )
= −−fx m x x m
xác định với mọi
( 5; 4]∈−x
?
A.
0≠m
. B.
4
3
>m
. C.
5
3
<−
m
. D.
∈∅m
.
Câu 79. Với mọi số tự nhiên n, Khẳng định nào sau đây là khẳng định đúng?
A.
22
log log ... 2
n
n =

c¨n bËc hai
. B.
22
log log ... 2
n
n = −

c¨n bËc hai
.
C.
22
2 log log ... 2
ncăn
n = +

bËc hai
. D.
22
2 log log ... 2
ncăn
n = −

bËc hai
.
Câu 80. Cho các số thực
,,abc
thỏa mãn:
37
11
log 7 log 11
log 25
27, 49, 11
= = =ab c
. Giá trị của biểu thức
2
2
2 (log 11)
(log 25)
7
11
3
(log 7)
= ++Aa b c
là:
A. 519. B.729. C. 469. D.129.
Câu 81. Kết quả rút gọn của biểu thức
( )
log log 2 log log log= ++ −
a b a ab a
C ba b b b
là:
Trang 8/15
A.
3
log
a
b
. B.
. log
a
b
. C.
( )
3
log
a
b
. D.
log
a
b
.
Câu 82. Cho
,, 0abc>
đôi một khác nhau và khác 1, Khẳng định nào sau đây là khẳng định đúng?
A.
222
log ;log ;log 1=
ab c
bca
cab
bca
. B.
222
log ;log ;log 1>
ab c
bca
cab
bca
.
C.
222
log ;log ;log 1
>−
ab c
bca
cab
bca
. D.
222
log ;log ;log 1<
ab c
bca
cab
bca
.
Câu 83. Gọi
(; )xy
là nghiệm nguyên của phương trình
23
+=xy
sao cho
Pxy
= +
là số dương nhỏ
nhất. Khẳng định nào sau đây đúng?
A.
23
log log
+
xy
không xác định. B.
2
log ( ) 1+=xy
.
C.
2
log ( ) 1+>xy
. D.
2
log ( ) 0
+>
xy
.
Câu 84. Có tất cả bao nhiêu số dương
a
thỏa mãn đẳng thức
2 3 5 235
log log log log .log .log++=a a a aaa
A. 3. B.1. C.2. D. 0.
E. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI BÀI TẬP TRẮC NGHIỆM
I – ĐÁP ÁN 1.2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
A
A
B
A
C
B
D
B
B
A
C
D
C
A
C
D
C
B
D
D
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
C
D
C
B
D
A
D
A
A
D
B
C
B
D
B
A
A
B
C
C
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
C
B
B
C
B
C
D
D
D
D
B
A
A
C
D
B
A
A
C
A
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
D
A
B
A
A
A
C
A
C
D
B
A
D
B
B
C
C
D
B
C
81
82
83
84
C
A
A
A
II –HƯỚNG DẪN GIẢI
Câu 1. Biểu thức
()fx
xác định
1
2 10
2
xx⇔ −> ⇔ >
. Ta chọn đáp án A
Câu 2. Biểu thức
()fx
xác định
2
4 0 ( 2; 2)xx⇔ − > ⇔ ∈−
. Ta chọn đáp án A
Câu 3. Biểu thức
()fx
xác định
1
0 ( ; 3) (1; )
3
x
x
x
−
⇔ > ⇔ ∈ −∞ − ∪ +∞
+
. Ta chọn đáp án B
Câu 4. Biểu thức
()fx
xác định
2
2 0 (0;2)xx x⇔ − >⇔∈
. Ta chọn đáp án A.
Câu 5. Biểu thức
()fx
xác định
32
- 2 0 ( 1; 0) ( 2; )xx x x⇔ − > ⇔ ∈ − ∪ +∞
. Ta chọn đáp án C.
Câu 6. Ta có
1/ 2
log 4
log 4
2log 4 log 16
16
a
a aa
Aa a a a= = = = =
. Ta chọn đáp án B
Câu 7. Ta nhập vào máy tính biểu thức
2 22 2
2log 12 3log 5 log 15 log 150+ −−
, bấm =, được kết quả
3B
=
Ta chọn đáp án D
Câu 8. +Tự luận
23
2 22 2 2 2 2
23
2
2log 12 3log 5 log 15 log 150 log 12 log 5 log (15.150)
12 .5
log 3
15.150
P = + −− = +−
= =
Trang 9/15
Đáp án B.
+Trắc nghiệm: Nhập biểu thức vào máy tính và nhấn calc ta thu được kết quả bằng 3.
Câu 9. Ta có
3
11
log log
33
a
a
Da a
= = =
. Ta chọn đáp án B
Câu 10. Ta nhập vào máy tính biểu thức:
3
77 7
1
log 36 log 14 3log 21
2
−−
bấm = , được kết quả
2C
= −
.
Ta chọn đáp án A
Câu 11. Ta có
2
4
log 5
4log 5
log 25
2
25
a
aa
Ea a a= = = =
. Ta chọn đáp án C
Câu 12. + Tự luận: Đưa về cùng 1 cơ số và so sánh
Ta thấy
331
3
3
656 5
log log log log
565 6
>==
.Ta chọn đáp án D
+ Trắc nghiệm: Sử dụng máy tính, lấy 1 số bất kỳ trừ đi lần lượt các số còn lại, nếu kết quả
0>
thì giữ nguyên số bị trừ và thay đổi số trừ là số mới; nếu kết quả
0<
thì đổi số trừ thành số
bị trừ và thay số trừ là số còn lại; lặp lại đến khi có kết quả.
Câu 13. + Tự luận : Đưa về cùng 1 cơ số và so sánh
Ta thấy
115 15 1
55 5 5
11
log 17 log 15 log log 12 log log 9
15 12
<=<=<
.Ta chọn đáp án C.
+ Trắc nghiệm: Sử dụng máy tính, lấy 1 số bất kỳ trừ đi lần lượt các số còn lại, nếu kết quả
0<
thì giữ nguyên số bị trừ và thay đổi số trừ là số mới; nếu kết quả
0>
thì đổi số trừ thành số
bị trừ và thay số trừ là số còn lại; lặp lại đến khi có kết quả.
Câu 14. +Tự luận :
Ta có
2 22 2 2 2
ln 2ln .log log ln log 2ln 2ln 2ln 2
aa a
Aaaeeaeaea
=+ + +− = + = +
. Ta chọn đáp
án A
+Trắc nghiệm : Sử dung máy tính, Thay
2a =
rồi lấy biểu thức đã cho trừ đi lần lượt các
biểu thức có trong đáp số, nếu kết quả nào bằng 0 thì đó là đáp số.
Câu 15. +Tự luận :
Ta có
3
2ln 3log 3log 2ln 0 3ln
log
aa
a
B a e ea a
e
=+ − −==−
. Ta chọn đáp án C
+Trắc nghiệm : Sử dung máy tính, Thay
2
a =
rồi lấy biểu thức đã cho trừ đi lần lượt các
biểu thức có trong đáp số, nếu kết quả nào bằng 0 thì đó là đáp số.
Câu 16. Ta có:
(
)
2
2
3
5
33
15
3 3 33
22
log log ( ) log log 4
5 15
ab ab a b x y
= = + ⇒+=
. Ta chọn đáp án D
Câu 17. Ta có :
0,2
1
10
2
6
5 5 55
6
5
11
log log ( . ) 2log log .
63
a
a b a b xy
b
−
−

= =− + ⇒=−


. Ta chọn đáp án C
Câu 18. Ta có:
3 333 3
40 40
log log 8 log 5 log 9 log
99
xx= + − = ⇒=
. Ta chọn đáp án B
Câu 19. Ta có:
23
23
7 7 49 7 7 7
32
1
log 2log 6log log log log
ab
a ba b x
x ba
= − = − = ⇒=
. Ta chọn đáp án D
Câu 20. Câu D sai, vì không có tính chất về logarit của một hiệu
Trang 10/15
Câu 21. Câu C sai, vì
1
log log
c
a
a
bb
c
=
Câu 22. Câu D sai, vì khẳng định đó chỉ đúng khi
1a >
, còn khi
0 1 log log
aa
a b c bc< <⇒ > ⇔ <
Câu 23. Câu C sai, vì
log
c
a
bc ba
>⇔>
Câu 24. Câu D sai, vì
23
2 3 ( 0 1)a a do a
< ⇒ > <<
Câu 25. Ta có
32 2
log (log ) 0 log 1 2a aa=⇒ =⇒=
. Ta chọn đáp án D
Câu 26. Đáp án A đúng với mọi
,,
abc
khi các logarit có nghĩa
Câu 27. Đáp án D sai, vì không có logarit của 1 tổng.
Câu 28. Sử dụng máy tính và dùng phím CALC : nhập biểu thức
248
log log log 1XXX++−
vào máy
và gán lần lượt các giá trị của x để chọn đáp án đúng. Với
64
x
=
thì kquả bằng 0. Ta chọn D là
đáp án đúng.
Câu 29. Sử dụng máy tính và dùng phím CALC : nhập biểu thức
3
log 2 2 4
x
−
vào máy và gán lần lượt
các giá trị của x để chọn đáp án đúng. Với .. thì kquả bằng 0. Ta chọn A là đáp án đúng.
Câu 30. +Tự luận : Ta có
2
2
2
2
log 4log 2log 2
log
aa
a
a
b
a
Pb b
ab
= +=+ =
. Ta chọn đáp án A.
+Trắc nghiệm : Sử dụng máy tính, thay
2ab
= =
, rồi nhập biểu thức
2
2
2
log
log
a
a
b
b
a
+
vào
máy bấm =, được kết quả
2
P =
. Ta chọn đáp án D.
Câu 31. + Tự luận : Ta có
34
log .log 2.3.4 24
b
a
P ba= = =
. Ta chọn đáp án A.
+Trắc nghiệm : Sử dụng máy tính Casio, Thay
2ab= =
, rồi nhập biểu thức
34
log .log
b
a
ba
vào máy bấm =, được kết quả
24P
=
. Ta chọn đáp án B.
Câu 32. + Tự luận :
( )
8 16
22
2
3log 3 2log 5
log 3 log 5
4 2 .2 45
+
= =
+ Trắc nghiệm : Sử dụng máy tính, rồi nhập biểu thức
8 16
3log 3 2log 5
4
+
vào máy, bấm =, được kết
quả bằng 45. Ta chọn đáp án C.
Câu 33. +Tự luận :
( )
37
3
5
10
37
log log
10
aa
a aa a= =
+Trắc nghiệm : Sử dụng máy tính, Thay
2a =
, rồi nhập biểu thức
( )
3
5
log
a
a aa
vào máy
bấm =, được kết quả
37
10
P
=
. Ta chọn đáp án B.
Câu 34. +Tự luận :
16 15 5 4 3 16
1
log 15.log 14...log 4.log 3.log 2 log 2
4
A = = =
+Trắc nghiệm : Sử dụng máy tính Casio, rồi nhập biểu thức
3 4 5 16
log 2.log 3.log 4...log 15
vào
máy bấm =, được kết quả
1
4
A =
. Ta chọn đáp án D.
Câu 35. +Tự luận :
91
35
32 3
60
1
4
91
log log
60
a
a
aa a
a
aa

=−=−



Trang 11/15
+Trắc nghiệm : Sử dụng máy tính, Thay
2a
=
, rồi nhập biểu thức
35
32 3
1
4
log
a
aa a
aa




vào
máy bấm =, được kết quả
211
60
−
. Ta chọn đáp án C.
Câu 36. Ta có:
33 22
log 2 log 3 1, log 3 log 2 1<= >=
Câu 37.
22
2000 2000
2000 1999.2001 log 2000 log 2001.1999
>⇒ >
2000 2000 1999 2000
2 log 2001 log 1999 log 2000 log 2001⇒> + ⇒ >
Câu 38. Ta có
3 3 223
log 2 log 3=1=log 2< log 3 log 11<<
Câu 39.
( )
3
3
log 2 3 2 3 25xxx+ =⇔+= ⇔=
Câu 40.
39 3 3
3 13
log log log log 3
2 22
xx x x x+ =⇔ + =⇔=
Câu 41. Ta có
47 47
3 33
4log 7 log log ( )a b ab x ab+ = ⇒=
. Ta chọn đáp án C.
Câu 42. Ta có:
( ) ( )
22 22 22
2 22 2
log 1 log log log 2 2xxy xy xy xy xy y xy+=+ ⇔ += ⇔+= ⇔=
Câu 43.
( )
1 44
4
13
log log =1 log 1
4
y
yx x y
y yx
− − ⇔ =⇔=
−
Câu 44. Do
, 0 log log log
a aa
x y xy x y>⇒ = +
, ta chọn đáp án D.
Câu 45. Ta có : Chọn B là đáp án đúng, vì
( )
22 2 2
22
2 22 2 22
4 12 ( 2 ) 16x log (x 2 y) log 16x
1
2log ( 2 ) 4 log log log ( 2 ) 2 log log
2
+ = ⇔+ = ⇔ + =
⇔ +=+ + ⇔ +=+ +
x y xy x y y y
xy x y xy x y
Câu 46. Ta có: Chọn C là đáp án đúng, vì
22 2 2
7 ( ) 9 log( ) log9
1
2log( ) log9 log log log (log log )
32
+= ⇔+= ⇔ +=
+
⇔ += + + ⇔ = +
a b ab a b ab a b ab
ab
ab ab ab
Câu 47. +Tự luận : Ta có :
22 2 3
1
log 6 log (2.3) 1 log 3 log 2
1
== =+⇒=
−
a
a
Suy ra
2
33 3
1 21
log 18 log (2.3 ) log 2 2 2
11
a
aa
−
= = += +=
−−
. Ta chọn đáp án A.
+Trắc nghiệm:
Sử dụng máy tính: Gán
2
log 6
cho A
Lấy
3
log 18
trừ đi lần lượt các đáp số ở A, B, C, D. Kết quả nào bẳng 0 thì đó là đáp án.
Ta chọn đáp án D
Câu 48. +Tự luận : Ta có :
2
44
4 22
2
1 1 14
log 1250 log (2.5 ) log (2.5 ) 2log 5
22 2
+
= = =+=
a
. Ta chọn đáp
án A.
+Trắc nghiệm:
Sử dụng máy tính: Gán
2
log 5
cho A
Lấy
4
log 1250
trừ đi lần lượt các đáp số ở A, B, C, D. Kết quả nào bằng 0 thì đó là đáp án.
Ta chọn đáp án D
Trang 12/15
Câu 49. Sử dụng máy tính: gán
7
log 2
cho A
Lấy
49
log 28
trừ đi lần lượt các đáp số ở A, B, C, D. Kết quả nào bẳng 0 thì đó là đáp án.
Ta chọn đáp án D
Câu 50. Sử dụng máy tính: gán lần lượt
25
log 5; log 3
cho A, B
Lấy
10
log 15
trừ đi lần lượt các đáp số ở A, B, C, D. Kết quả nào bẳng 0 thì đó là đáp án.
Ta chọn đáp án D
Câu 51. +Tự luận : Ta có :
33 33
log 15 log (3.5) 1 log 5 log 5 1= = =+⇒=−aa
.
Khi đó :
3 33
3
log 50 2log (5.10) 2(log 5 log 10) 2( 1 )= = + = −+
ab
Ta chọn đáp án B.
+Trắc nghiệm
Sử dụng máy tính: gán lần lượt
33
log 15;log 10
cho A, B.
Lấy
3
log 50
trừ đi lần lượt các đáp số ở A, B, C, D. Kết quả nào bẳng 0 thì đó là đáp án.
Ta chọn đáp án B.
Câu 52. Sử dụng máy tính: Gán
5
log 3
cho A
Lấy
15
log 75
trừ đi lần lượt các đáp số ở A, B, C, D. Kết quả nào bẳng 0 thì đó là đáp án.
Ta chọn đáp án A.
Câu 53. Ta có:
2 24
1
log 7 2. log 7 2log 7 2
2
= = =
a
. Ta chọn đáp án A.
Câu 54. Ta có:
3 33 3
27 2 3a 2
log log 27 log 25 3 2log 5 3
25
−
= − =− =−=
aa
. Ta chọn đáp án C.
Câu 55. Sử dụng máy tính: Gán lần lượt
25
log 5;log 3
cho A, B
Lấy
24
log 15
trừ đi lần lượt các đáp số ở A, B, C, D. Kết quả nào bẳng 0 thì đó là đáp án.
Ta chọn đáp án D.
Câu 56. Ta có:
( )
22
12 2 6
22
43
log 27 3log 3 2a
log 27 log 3 log 16
log 12 2 log 3 3 3
−
= = = ⇒=⇒ =
+ −+
a
a
aa
.
Câu 57. Ta có:
( ) ( )
125
lg30 1 lg3 1
log 30
lg125 3 1 lg 2 3 1
++
= = =
−−
a
b
.
Câu 58. Ta có :
3
3
3
1
3
2
3
log 3
3
α
α
−
= ⇔ = = ⇒ = ⇒=−
a
bb
b aa a A
a
a
.
Câu 59.
Ta có
27 3 8 3 2
3
log 5 log 5 3 , log 7 log 7 log 5 3=⇒ = =⇒=⇒=
b
a a b ac
c
( )
6
3a
log 35
1
+
⇒=
+
cb
c
.
Câu 60. Ta có:
( )
log 2 log 3 ... log 2000 log 1.2.3...2000 log 1= + ++ = = =
xx x x x
Ax
Câu 61. Sử dụng máy tính: Gán lần lượt
7 12
log 12;log 24
cho A, B
Lấy
54
log 168
trừ đi lần lượt các đáp số ở A, B, C, D. kết quả nào bẳng 0 thì đó là đáp án.
Ta chọn đáp án D.
Trang 13/15
Câu 62. Ta có
23
234
4
a
log log log log 2 3.2 4.( 3) 20= + − =+ − −=
a a aa
b
abc
c
. Ta chọn đáp án A.
Câu 63. Ta có
( )
22
3
11
log 2log log 2log 2 .3 2.( 4) 5
33
= + + =+ + −=−
a a aa
a bc a b c
. Ta chọn đáp án B.
Câu 64. Thay
ae=
, rồi sử dụng máy tính sẽ được kết quả
37
10
A =
. Ta chọn đáp án A.
Câu 65. Thay
ae=
, rồi sử dụng máy tínhsẽ được kết quả
91
60
B = −
. Ta chọn đáp án A
Câu 66. Ta có:
23
6
5 5 55 23
1 1 1 log 5.log 5
log 5
log 6 log (2.3) log 2 log 3 log 5 log 5
= = = = =
+ ++
ab
ab
.
Câu 67. Sử dụng máy tính: gán lần lượt
237
log 3;log 5;log 2
cho A, B, C
Lấy
140
log 63
trừ đi lần lượt các đáp số ở A, B, C, D. kết quả nào bẳng 0 thì đó là đáp án.
Ta chọn đáp án C.
Câu 68. Sử dụng máy tính: gán lần lượt
55
log 2;log 3
cho A, B
Lấy
5
log 72
trừ đi lần lượt các đáp số ở A, B, C, D. kết quả nào bẳng 0 thì đó là đáp án.
Ta chọn đáp án A.
Câu 69. Sử dụng máy tính Casio, gán lần lượt
12 24
log 18;log 54
cho A và B.
Với đáp án C nhập vào máy :
5( ) 1AB A B+ −−
, ta được kết quả bằng
0
. Vậy C là đáp án
đúng.
Câu 70. Vì
( )
(
)
342
log log log 0=
y
nên
4
42 2
log (log ) 1 log 4 2 2 1 33=⇒ = ⇒ = ⇒ +=y yy y
.
Đáp án A.
Câu 71. Vì
5
log 0 1
>⇒>xx
. Khi đó
56
log log>xx
. Chọn đáp án D.
Câu 72. Sử dụng máy tính Casio, Chọn
0,5x =
và thay vào từng đáp án, ta được đáp án A.
Câu 73. +Tự luận:
Ta có:
2
2
3 33
22
log 5
log 4 2log 2 log 4
2log 5 log 5
2
11
3 4;3 3 4; 2 2 5
4 25
−
−
−

= = = = = = =


,
( )
0,5
4
2
2
log 2
log 2
log 2
44
1
2 2 2 16
16
−
−

= = = =


.
Chọn : Đáp án D.
Trắc nghiệm: nhập vào máy tính từng biểu thức tính kết quả, chọn kết quả nhỏ hơn 1.
Câu 74. +Tự luận:
Ta có
0,5 0,5
log 13 log 4
0,5 0,5
log 13 log 4 0 3 3 1 1< < ⇒ < <⇒ < <NM
.
Chọn : Đáp án B.
+ Trắc nghiệm: Nhập các biểu thức vào máy tính, tính kết quả rồi so sánh, ta thấy đáp án B
đúng.
Câu 75. Ta có
2 2 2 22
1
log 2sin log cos log 2sin .cos log sin log 1
12 12 12 12 6 2
π π ππ π
 
+= ===−
 
 
Chọn: Đáp án B.
Trang 14/15
Câu 76. Biểu thức
()fx
xác định
⇔
0xm x m− >⇔>
.
Để
()fx
xác định với mọi
( 3; )∈ − +∞x
thì
3
m
≤−
Ta chọn đáp án C.
Câu 77. Thay
2
m =
vào điều kiện
(3 )( 2 ) 0xx m−+>
ta được
(3 )( 4) 0 ( 4;3)xx x− + > ⇔ ∈−
mà
[ 4; 2] ( 4;3)− ⊄−
nên các đáp án B, A, D loại. Ta chọn đáp án đúng là C.
Câu 78. - Thay
2m =
vào điều kiện
( )( 3 ) 0m xx m
−−>
ta được
(2 )( 6) 0 (2;6)xx x− − >⇔∈
mà
( 5; 4] (2; 6)−⊄
nên các đáp án B, A loại.
- Thay
2m = −
vào điều kiện
( )( 3 ) 0m xx m−−>
ta được
( 2 )( 6) 0 ( 6; 2)xx x− − + > ⇔ ∈− −
mà
( 5;4] ( 6; 2)− ⊄− −
nên các đáp án C loại. Do đó Ta chọn đáp án đúng là D.
Câu 79. +Tự luận:
Đặt
22
-log log ... 2 .
n
m=

c¨n bËc hai
Ta có:
2
2
log ... 2 2 ... 2 2
−
−
=⇔=
m
m
.
Ta thấy :
2
11
1
2
22
2
2 2 , 2 2 ,....., ... 2 2 2
−
 
 
 
= = = =
n
n
.
Do đó ta được:
22
−−
= ⇔=
mn
mn
. Vậy
22
log log ... 2
n
n
= −

c¨n bËc hai
. Đáp án B.
+Trắc nghiệm: Sử dụng máy tính Casio, lấy n bất kì, chẳng hạn
3n =
.
Nhập biểu thức
22
log log 2−
( có 3 dấu căn ) vào máy tính ta thu được kết quả bằng – 3.
Vậy chọn B.
Câu 80. Ta có
(
) ( )
( )
( )
log 25
11
11
37
3 7 37
11
1
log 25
log 7 log 11
log 7 log 11 log 7 log 11
log 25
32
2
27 49 11 7 11 25 469+ + = + + =++ =ab c
Suy ra : Đáp án C.
Câu 81.
( )
log log 2 log log log
a b a ab a
C ba b b b
= ++ −
( ) ( )
(
)
2
2
3
2
log 1 log 1
log log
log log log log
log 1 log log 1 log
aa
aa
a a aa
a a aa
bb
bb
b b bb
b b bb
++

= −= =

++

Câu 82. *
12
22
log log log log log log
−

= =−⇒ =− =


aa a a a a
bc cb c c
cb bc b b
*
log .log .log 1 log .log log 1=⇔==
abc ab a
bca ba a
* Từ 2 kết quả trên ta có :
2
222
log log log log .log log 1

= =


abc a bc
bca b ca
cab b ca
bca c ab
Chọn : Đáp án A.
Câu 83. Vì
0xy
+>
nên trong hai số
x
và
y
phải có ít nhất một số dương mà
30xy x+=−>
nên suy ra
3x <
mà
x
nguyên nên
0; 1; 2;...x = ±±
+ Nếu
2x =
suy ra
1y = −
nên
1xy+=
+ Nếu
1x =
thì
1y =
nên
2xy+=
Trang 15/15
+ Nếu
0x =
thì
3y =
nên
3xy+=
+ Nhận xét rằng :
2
x
<
thì
1xy+>
. Vậy
xy
+
nhỏ nhất bằng 1.
Suy ra: Chọn đáp án A.
Câu 84.
23252 2355
(*) log log 2.log log 2.log log .log 5.log .loga a a a aa
⇔+ + =
(
)
(
)
35
3
2
2 3 5 235
2
2 3 5 35
2
1 log 2 log 2
35
2
log 5
5
3 5 35
3
log . 1 log 2 log 2 log .log 5.log
log . 1 log 2 log 2 log 5.log 0
1
1
log 0
1 log 2 log 2
log
1 log 2 log 2 log 5.log 0
5
log 5
a aa
aa
a
a
a
a
a
a
++
±
⇔ ++ =
⇔ ++− =
=
=
=
⇔ ⇔⇔
++
= ±
++− =
=
Chọn: Đáp án A.
| 1/15
| | Tải xuống

Có thể bạn quan tâm:

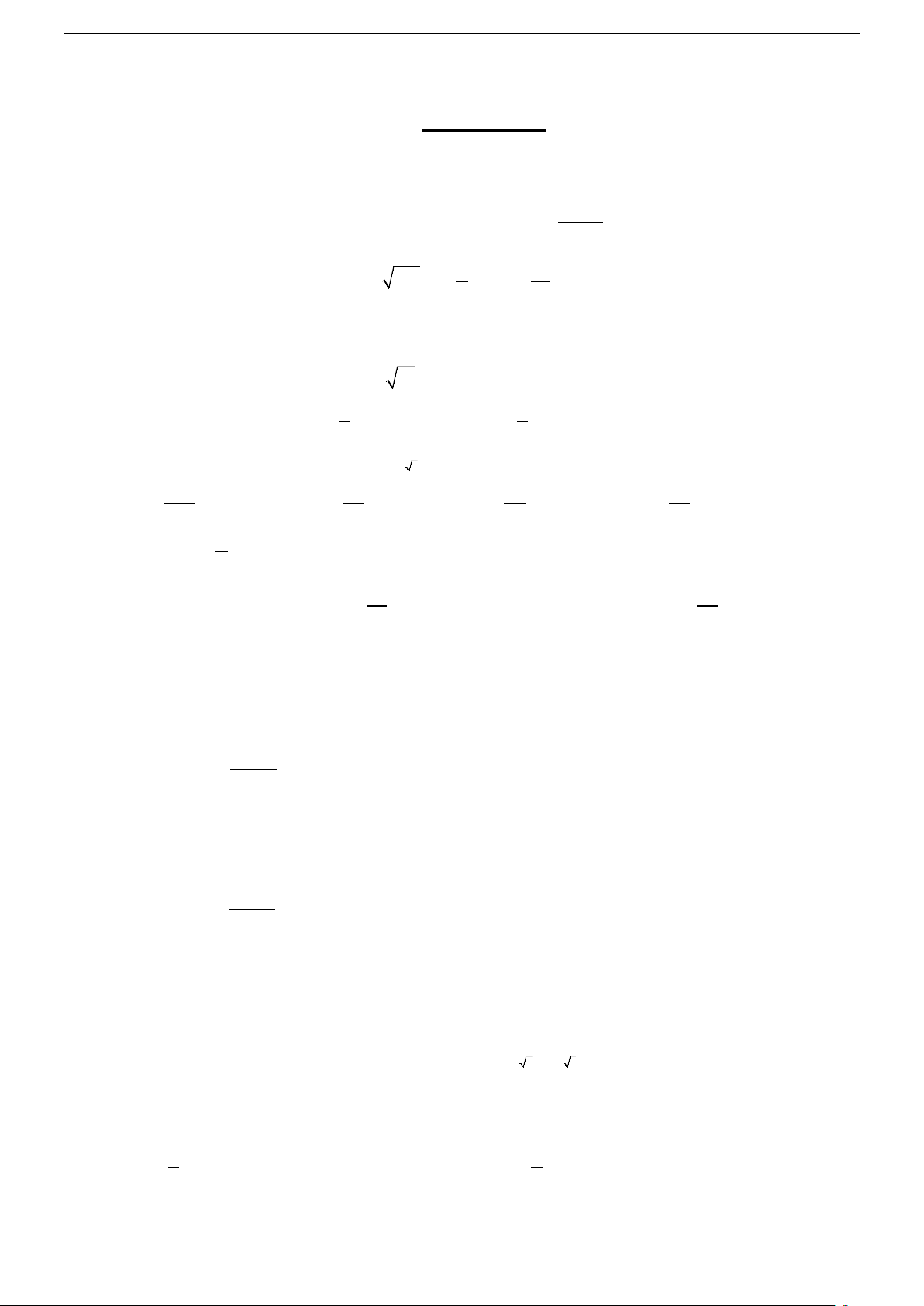
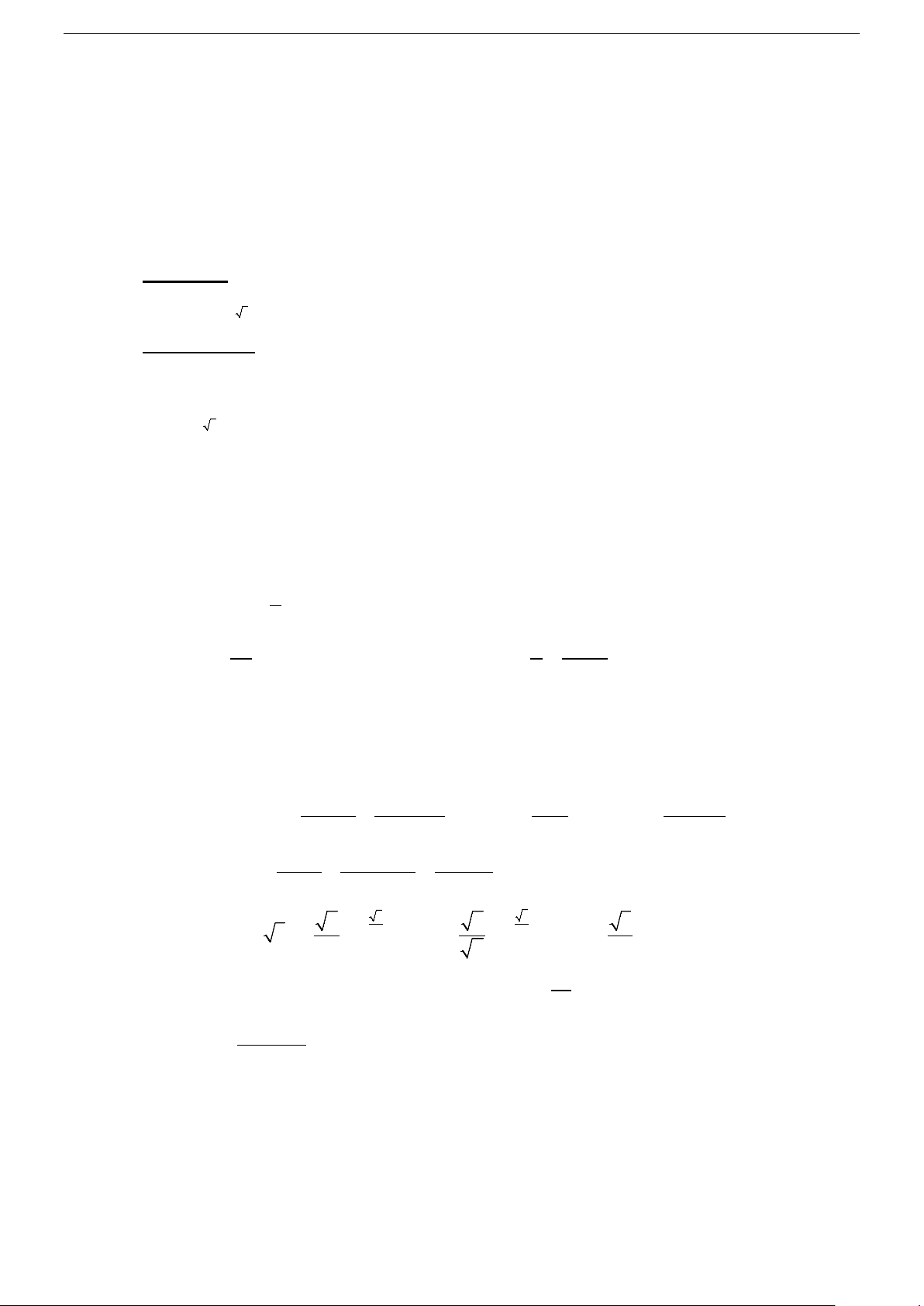
Preview text:

CHỦ ĐỀ 2. LOGARIT
A. KIẾN THỨC CƠ BẢN 1. Định nghĩa:
Cho hai số dương a, b với a ≠ 1. Số α thỏa mãn đẳng thức α
a = b được gọi là lôgarit cơ số a
của b và kí hiệu là log b . Ta viết: log α α =
b ⇔ a = b a . a
2. Các tính chất: Cho a, b > 0, a ≠1, ta có: • log a =1, log 1 = a a 0 • logab a = b, log a a ( α ) = α
3. Lôgarit của một tích: Cho 3 số dương a, b , b với a ≠ 1, ta có 1 2
• log (b .b ) = log b + b a a log 1 2 1 a 2
4. Lôgarit của một thương: Cho 3 số dương a, b , b với a ≠1, ta có 1 2 • b1 log = log b − b a a log 1 a 2 b2
• Đặc biệt : với a, b > 0, a ≠ 1 1 log = − b a loga b
5. Lôgarit của lũy thừa: Cho a, b > 0, a ≠1, với mọi α , ta có • log α b = α b a loga • Đặc biệt: n 1 log b = b a loga n
6. Công thức đổi cơ số: Cho 3 số dương a, ,
b c với a ≠ 1,c ≠ 1, ta có • log log b = b c a log a c • Đặc biệt : 1 log c = và 1 log b = b với α ≠ 0 . α log a log a a α a c
Lôgarit thập phân và Lôgarit tự nhiên
 Lôgarit thập phân là lôgarit cơ số 10. Viết : log b = logb = lgb 10
 Lôgarit tự nhiên là lôgarit cơ số e . Viết : log b = b e ln
B. KỸ NĂNG CƠ BẢN
1. Tính giá trị biểu thức
2. Rút gọn biểu thức
3. So sánh hai biểu thức
4. Biểu diễn giá trị logarit qua một hay nhiều giá trị logarit khác
C. KỸ NĂNG SỬ DỤNG MÁY TÍNH
1. Tính giá trị của một biểu thức chứa logarit
Ví dụ : Cho a > 0,a ≠ 1, giá trị của biểu thức log 4 a a bằng bao nhiêu ? A. 16 B. 4 C. 8 D. 2
Ví dụ : Giá trị của biểu thức A = 2log 12 + 3log 5 − log 15 − log 150 bằng: 2 2 2 2 A. 2 B. 3 C. 4 D. 5
2. Tính giá trị của biểu thức Logarit theo các biểu thức logarit đã cho
Ví dụ: Cho log 5 = a; log 5 = b . Khi đó log 5 tính theo a và b là 2 3 6 A. 1 B. ab C. a + b D. 2 2 a + b a + b a + b
3. Tìm các khẳng định đúng trong các biểu thức logarit đã cho.
Ví dụ: Cho a > 0,b > 0 thỏa điều kiện 2 2
a + b = 7ab .Khẳng định nào sau đây đúng: Trang 1/15 A. (a +b) 1 3log
= (log a + logb) B. 3
log(a + b) = (log a + logb) 2 2 +
C. 2(log a + logb) = log(7ab) D. a b 1 log
= (log a + logb) 3 2
4. So sánh lôgarit với một số hoặc lôgarit với nhau log2 5 log0,5 2
Ví dụ: Trong 4 số log     3 4 2log3 2 1 1 3 ;3 ;   ; số nào nhỏ hơn 1 4 16     log2 5 log0,5 2 A. log  1   1  3 4 3 B. 2log32 3 C.  D. 4      16 
D. BÀI TẬP TRẮC NGHIỆM
Câu 1. Với giá trị nào của x thì biểu thức f (x) = log (2x −1) xác định? 2 A. 1 x  ;  ∈ +∞     . B. 1 x  ∈ ; −∞ . C. 1 x ∈ \ . D. x ∈( 1; − +∞). 2        2  2
Câu 2. Với giá trị nào của x thì biểu thức 2
f (x) = ln(4 − x ) xác định? A. x ∈( 2; − 2).
B. x ∈[ − 2;2].
C. x ∈ \[ − 2;2] . D. x∈ \ ( 2; − 2) . Câu 3. −
Với giá trị nào của x thì biểu thức x 1 f (x) = log xác định? 1 3+ x 2
A. x ∈[ − 3;1].
B. x ∈ \[ −3;1] .
C. x ∈ \ ( 3 − ;1) . D. x ∈( 3 − ;1) .
Câu 4. Với giá trị nào của x thì biểu thức: 2
f (x) = log (2x − x ) xác định? 6
A. 0 < x < 2. B. x > 2 . C. 1 − < x <1. D. x < 3.
Câu 5. Với giá trị nào của x thì biểu thức: 3 2
f (x) = log (x − x − 2x) xác định? 5 A. x ∈(0;1).
B x ∈(1;+∞) . C. x ∈( 1; − 0) ∪ (2;+∞) .
D. x ∈(0;2) ∪ (4;+∞).
Câu 6. Cho a > 0,a ≠1, giá trị của biểu thức log 4 a A = a bằng bao nhiêu? A.8. B.16. C.4. D.2.
Câu 7. Giá trị của biểu thức B = 2log 12 + 3log 5 − log 15 − log 150 bằng bao nhiêu? 2 2 2 2 A.5. B.2. C.4. D.3.
Câu 8. Giá trị của biểu thức P = 22log 12 + 3log 5− log 15− log 150 bằng bao nhiêu? 2 2 2 2 A. 2 . B. 3. C. 4 . D. 5.
Câu 9. Cho a > 0,a ≠1, biểu thức D = log a có giá trị bằng bao nhiêu? 3 a A.3. B. 1 . C. 3 − . D. 1 − . 3 3
Câu 10. Giá trị của biểu thức 1 3
C = log 36 − log 14 − 3log 21 bằng bao nhiêu ? 7 7 7 2 A. 2 − . B.2. C. 1 − . D. 1 . 2 2
Câu 11. Cho a > 0,a ≠1, biểu thức 4log 2 5 a E = a
có giá trị bằng bao nhiêu? A.5. B. 625. C. 25 . D. 8 5 .
Câu 12. Trong các số sau, số nào lớn nhất? A. 5 log . B. 5 log . C. 6 log . D. 6 log . 3 6 3 6 1 5 3 5 3
Câu 13. Trong các số sau, số nào nhỏ nhất ? A. 1 log . B. log 9 . C. log 17 . D. 1 log . 5 12 1 1 5 15 5 5 Trang 2/15
Câu 14. Cho a > 0,a ≠1, biểu thức 2 2 2
A = (ln a + log e + a −
e có giá trị bằng a ) ln loga A. 2 2ln a + 2. B. 4ln a + 2. C. 2 2ln a − 2 . D. 2 ln a + 2 . Hướng dẫn giải
Câu 15. Cho a > 0,a ≠1, biểu thức 3 2
B = 2ln a + 3log e − − có giá trị bằng a ln a log e a
A. 4ln a + 6log . B. 4ln a . C. 3 3ln a − . D. 6log e. a 4 log e a a
Câu 16. Cho a > 0,b > 0 , nếu viết log (5 3 x = log y a b
a + log b thì x + y bằng bao nhiêu? 3 )23 3 3 5 15 A.3. B.5. C.2. D.4. 0 − ,2 10  
Câu 17. Cho a > 0,b > 0 , nếu viết log a  
= x log a + y log b thì xy bằng bao nhiêu ? 5 5 5 6 5  b A.3. B. 1 . C. 1 − . D. 3 − . 3 3
Câu 18. Cho log x = 3log 2 + log 25 − log 3. Khi đó giá trị của x là : 3 3 9 3 A. 200 . B. 40 . C. 20 . D. 25 . 3 9 3 9 Câu 19. Cho 1 log
= 2log a − 6log b . Khi đó giá trị của x là : 7 7 49 x 2 3
A. 2a − 6b . B. a x = . C. 2 3 x = a b . D. b x = . 3 b 2 a
Câu 20. Cho a,b,c > 0;a ≠1 và số α ∈ , Trong các khẳng định sau, khẳng định nào sai? A. log c a = c . B. log a = . a 1 a C. log bα = α b .
D. log b − c = b − c . a ( ) loga log a loga a
Câu 21. Cho a,b,c > 0;a ≠1, Trong các khẳng định sau, khẳng định nào sai? A. 1 log b = . B. log b c = c . a .logb log a log a a b
C. log b = c b . D. log b c = b + c . a ( . ) loga log c log a a a
Câu 22. Cho a,b,c > 0 và a,b ≠1, Trong các khẳng định sau, khẳng định nào sai? A. logab a = b . B. log b =
c ⇔ b = c . a loga C. log log c a c = . D. log b >
c ⇔ b > c . a log b log b a a
Câu 23. Cho a,b,c > 0 và a >1. Trong các khẳng định sau, khẳng định nào sai? A. log b <
c ⇔ b < c . B. log b >
c ⇔ b > c . a log a loga a
C. log b > c ⇔ b > c . D. b c
a > a ⇔ b > c . a
Câu 24. Cho a,b,c > 0 và a <1.Trong các khẳng định sau, khẳng định nào sai? A. log b >
c ⇔ b < c . D. 2 3 a < a . a loga C. log b <
c ⇔ b > c .
D. log b > ⇔ b < . a 0 1 a loga
Câu 25. Số thực a thỏa điều kiện log (log a) = 0 là: 3 2 A. 1 . B. 3. C. 1 . D. 2. 3 2
Câu 26. Biết các logarit sau đều có nghĩa. Khẳng định nào sau đây là khẳng định đúng ? A. log b =
c ⇔ b = c . B. log b >
c ⇔ b > c a log a loga a Trang 3/15 C. log b >
c ⇔ b < c . D. log b +
c < ⇔ b + c < . a loga 0 0 a loga
Câu 27. Cho a,b,c > 0 và a ≠1. Khẳng định nào sau đây là khẳng định sai ? A. log bc = b + c . B. log b = b − c . a ( ) loga log a ( ) loga loga a c C. log c
b = c ⇔ b = a .
D. log b + c = b + c . a ( ) loga log a a
Câu 28. Số thực x thỏa mãn điều kiện log x + log x + log x =11 là :. 2 4 8 11 A. 64. B. 6 2 . C.8. D. 4.
Câu 29. Số thực x thỏa mãn điều kiện 3 log = là x 2 2 4 A. 3 2 . B. . 1 C. 4. D. 2. 3 2
Câu 30. Cho a,b > 0 và a,b ≠1. Biểu thức 2 2 P = log b +
có giá trị bằng bao nhiêu? a log a a 2 b A. 6. B.3. C.4. D.2.
Câu 31. Cho a,b > 0 và a,b ≠1, biểu thức 3 4
P = log b .log a có giá trị bằng bao nhiêu? a b A.6. B.24. C.12. D. 18.
Câu 32. Giá trị của biểu thức 3log83 2lo 16g5 4 + là: A. 20. B.40. C. 45. D. 25 .
Câu 33. Giá trị của biểu thức P = ( 3 5 log a a a là a ) A. 53 . B. 37 . C.20. D. 1 . 30 10 15
Câu 34. Giá trị của biểu thức A = log 2.log 3.log 4...log 15 là: 3 4 5 16 A. 1 . B. 3 . C. 1. D. 1 . 2 4 4  3 3 2 5 3 
Câu 35. Giá trị của biểu thức log a a a   là:. 1  4  a a a   A. 1 . B. 3 . C. 211 − . D. 91 . 5 4 60 60
Câu 36. Trong 2 số log 2 và log 3, số nào lớn hơn 1?. 3 2 A. log 3. B. log 2 . C. Cả hai số . D. Đáp án khác. 2 3
Câu 37. Cho 2 số log 2000 và log
2001. Khẳng định nào sau đây là khẳng định đúng? 1999 2000 A. log 2000 > log 2001.
B. Hai số trên nhỏ hơn 1. 1999 2000
C. Hai số trên lớn hơn 2. D. log 2000 ≥ log 2001. 1999 2000
Câu 38. Các số log 2 , log 3, log 11 được sắp xếp theo thứ tự tăng dần là: 3 2 3
A. log 2, log 11, log 3 .
B. log 2, log 3, log 11. 3 3 2 3 2 3
C. log 3, log 2, log 11.
D. log 11, log 2, log 3. 2 3 3 3 3 2
Câu 39. Số thực x thỏa mãn điều kiện log x + 2 = 3 là: 3 ( ) A. 5. B. 25 − . C. 25. D. 3 − .
Câu 40. Số thực x thỏa mãn điều kiện 3
log x + log x = là : 3 9 2 A. 3 − . B. 25 . C. 3. D. 9.
Câu 41. Cho log x = 4log a + 7log b a,b > 0 . Giá trị của x tính theo a,b là: 3 3 3 ( ) A. ab . B. 4 a b . C. 4 7 a b . D. 7 b . Trang 4/15 Câu 42. Cho log ( 2 2
x + y =1+ log xy xy > 0 . Chọn khẳng định đúng trong các khẳng định sau ? 2 ) 2 ( )
A. x > y .
B. x = y .
C. x < y . D. 2 x = y . Câu 43. Cho 1
log y − x − log
=1 y > 0, y > x . Chọn khẳng định đúng trong các khẳng định sau? 1 ( ) 4 ( ) y 4
A. 3x = 4y . B. 3 x = − y . C. 3 x = y . D. 3x = 4 − y . 4 4
Câu 44. Chọn khẳng định đúng trong các khẳng định sau? A. 2 x = x x > . B. log xy = x + y . a loga loga a a ( 2 log 2log 0) C. log xy = x + y xy > . D. log xy = x + y xy > . a loga loga ( 0) a loga loga ( 0)
Câu 45. Cho x, y > 0 và 2 2
x + 4y =12xy . Khẳng định nào sau đây là khẳng định đúng ?  x + A 2y 1 . log  = log x−   log y .
B. log (x + 2y) = 2 + (log x + log y) . 2 2 2  4  2 2 2 2
C. log (x + 2y) = log x + log y +1.
D. 4log (x + 2y) = log x + log y . 2 2 2 2 2 2
Câu 46. Cho a,b > 0 và 2 2
a + b = 7ab . Khẳng định nào sau đây là khẳng định đúng ?  a + A b
. 2log(a + b) = log a + logb . B. 4log  = loga+   logb .  6   a +  a + C b  1 b . log = (log a +    logb). D. log = 3(log a +   logb) .  3  2  3 
Câu 47. Cho log 6 = a . Khi đó giá trị của log 18 được tính theo a là: 2 3 A. a a − a . B. . C. 2a + 3. D. 2 1. a +1 a −1
Câu 48. Cho log 5 = a . Khi đó giá trị của log 1250 được tính theo a là : 2 4 − + A 1 4a 1 4a . . B. 2(1+ 4a) . C.1+ 4a . D. . 2 2
Câu 49. Biết log 2 = m , khi đó giá trị của log 28 được tính theo m là: 7 49 m + + + + A 2 1 m 1 4m 1 2m . . B. . C. . D. . 4 2 2 2
Câu 50. Biết a = log 5,b = log 3 ; khi đó giá trị của log 15 được tính theo a là: 2 5 10 a + ab + ab − a b + A b 1 1 ( 1) . . B. . C. . D. . a +1 a +1 a +1 a +1
Câu 51. Cho a = log 15;b = log 10 . Khi đó giá trị của log 50 được tính theo a,b là : 3 3 3
A. 2(a − b −1) .
B. 2(a + b −1) .
C. 2(a + b +1).
D. 2(a − b +1) .
Câu 52. Biết log 3 = a , khi đó giá trị của log 75 được tính theo a là: 5 15 + + + A 2 a 1 2a 1 a . . B. . C. . D. 2 . 1+ a a +1 2 + a
Câu 53. Biết log 7 = a , khi đó giá trị của log 7 được tính theo 4 2 a là: A. 2a . B. 1 a . C. 1 a . D. 4a . 2 4 Câu 54. 27
Biết log 3 = a , khi đó giá trị của log
được tính theo a là: 5 3 25 a − A. 3 a a . B. 3 . C. 3 2 . D. . 2a 2 a 3a − 2
Câu 55. Biết a = log 5,b = log 3 . Khi đó giá trị của log 15 được tính theo a là : 2 5 24 Trang 5/15 ab + ab + b + a b + A. 1 . B. 1 . C. 1 . D. ( 1) . b a +1 a +1 3+ ab
Câu 56. Cho log 27 = a . Khi đó giá trị của log 16 được tính theo 12 6 a là: 4(3+ a) 4(3− a) A 4a 2a . . B. . C. . D. . 3− a 3+ a 3− a 3+ a
Câu 57. Cho lg3 = a, lg 2 = b . Khi đó giá trị của log 30 được tính theo 125 a là: + 4(3− a) A a a . 1 a . B. . C. . D. . 3(1− b) 3− b 3+ b 3+ a 3 Câu 58. Cho b log b =
. Giá trị của biểu thức A = log
được tính theo a là: a 3 b a a A. 3 − . B. 3 . C. 1 D. 3 − . 3 4 3 4
Câu 59. Cho log 5 = a, log 7 = b, log 3 = c . Giá trị của log 35 được tính theo a, , b c là: 27 8 2 6 3(ac + b) ac + A ac ac 3 3b . . B. . C. . D. . 1− c 1+ b 1+ c 3+ a
Câu 60. Cho x = 2000!. Giá trị của biểu thức 1 1 1 A = + + ...+ là: log x log x log x 2 3 2000 A 1 .1. B. 1 − . C. . D. 2000 . 5
Câu 61. Biết a = log 12,b = log 24 . Khi đó giá trị của log 168 được tính theo a là: 7 12 54 a − a − D (8 5b) ab + − (8 5b) ab + . . B. 1 a . C. . A. 1 . 1+ ab − a a(8 − 5b) 1+ ab a(8 − 5b) 2 3
Câu 62. Biết log b = 2,log c = 3
− . Khi đó giá trị của bieeur thức a log b bằng: a a a 4 c A 2 3 . 20 . B. − . C. 1 − . D. . 3 2
Câu 63. Biết log b = 3,log c = 4
− . Khi đó giá trị của biểu thức log a bc bằng: a ( 2 3 2 ) a a A. 16 3 − . B. 5 − . C. 16 − . D. 48 − . 3
Câu 64. Rút gọn biểu thức 3 5
A = log a a a , ta được kết quả là: a A 37 35 3 1 . . B. . C. . D. . 10 10 10 10 5 3 3 2
Câu 65. Rút gọn biểu thức = log a a a B
, ta được kết quả là : 1 4 a a a A 91 60 16 5 . − . B. . C. . D. − . 60 91 5 16
Câu 66. Biết a = log 5,b = log 5 . Khi đó giá trị của log 5 được tính theo a,b là : 2 3 6 A ab 1 . . B. .
C. a + b . D. 2 2 a + b . a + b a + b
Câu 67. Cho a = log 3;b = log 5;c = log 2 . Khi đó giá trị của biểu thức log 63 được tính theo a, , b c 2 3 7 140 là: ac − abc + c + ac + ac + A 2 1 2 1 2 1 1 . . B. . C. . D. . abc + 2c +1 2ac +1 abc + 2c +1 abc + 2c +1 Trang 6/15
Câu 68. Cho a = log 2;b = log 3. Khi đó giá trị của log 72 được tính theo a,b là : 5 5 5
A.3a + 2b . B. 3 2 a + b .
C.3a − 2b . D. 6ab .
Câu 69. Biết a = log 18,b = log 54 . Khẳng định nào sau đây là khẳng định đúng? 12 24
A. ab + 5(a − b) = 1 − .
B.5ab + a + b =1.
C. ab + 5(a − b) =1.
D.5ab + a − b = 0 .
Câu 70. Biết log log log y = 0 , khi đó giá trị của biểu thức A = 2y +1 là: 3 ( 4 ( 2 )) A.33. B. 17. C. 65. D. 133.
Câu 71. Cho log x > 0 . Khẳng định nào sau đây là khẳng định đúng? 5 A. log ≤ . B. log > . C. log x = log .
D. log x > log x . x 5 x 5 logx 6 x 5 logx 4 5 5 6
Câu 72. Cho 0 < x <1. Khẳng định nào sau đây là khẳng định đúng? A. 1 3 log 5 + log 5 < B. 3 log 5 > x log x 0 3 1 x 2 2 C. 1 1 log < D. 1 3 log . log 5 > x x 0 x log . 5 2 2 2 log2 5 log0,5 2
Câu 73. Trong bốn số log     3 4 2log3 2 1 1 3 , 3 ,   ,
số nào nhỏ hơn 1? 4 16     log0,5 2 log2 5 A.  1   1   . B. 2log32 3 . C. log34 3 . D. . 16       4  Câu 74. Gọi log0,5 4 log0,513 M = 3 ; N = 3
. Khẳng định nào sau đây là khẳng định đúng?
A. M <1< N .
B. N < M <1.
C. M < N <1.
D. N <1< M .  π   π
Câu 75. Biểu thức log 2sin  log cos  + có giá trị bằng: 2 2 12 12      A. 2 − . B. 1 − . C.1. D. log 3 −1. 2
Câu 76. Với giá trị nào của m thì biểu thức f (x) = log (x − m) xác định với mọi x∈( 3 − ;+∞) ? 5 A. m > 3 − . B. m < 3 − . C. m ≤ 3 − . D. m ≥ 3 − .
Câu 77. Với giá trị nào của m thì biểu thức f (x) = log (3− x)(x + 2m) xác định với mọi x∈[ − 4;2] ? 1 2 A 3 . m ≥ 2. B. m ≥ . C. m > 2 . D. m ≥ 1 − . 2
Câu 78. Với giá trị nào của m thì biểu thức f (x) = log (m − x)(x −3m) xác định với mọi x∈( 5; − 4] ? 3 A 4 5 . m ≠ 0 . B. m > . C. m < − . D. m∈∅ . 3 3
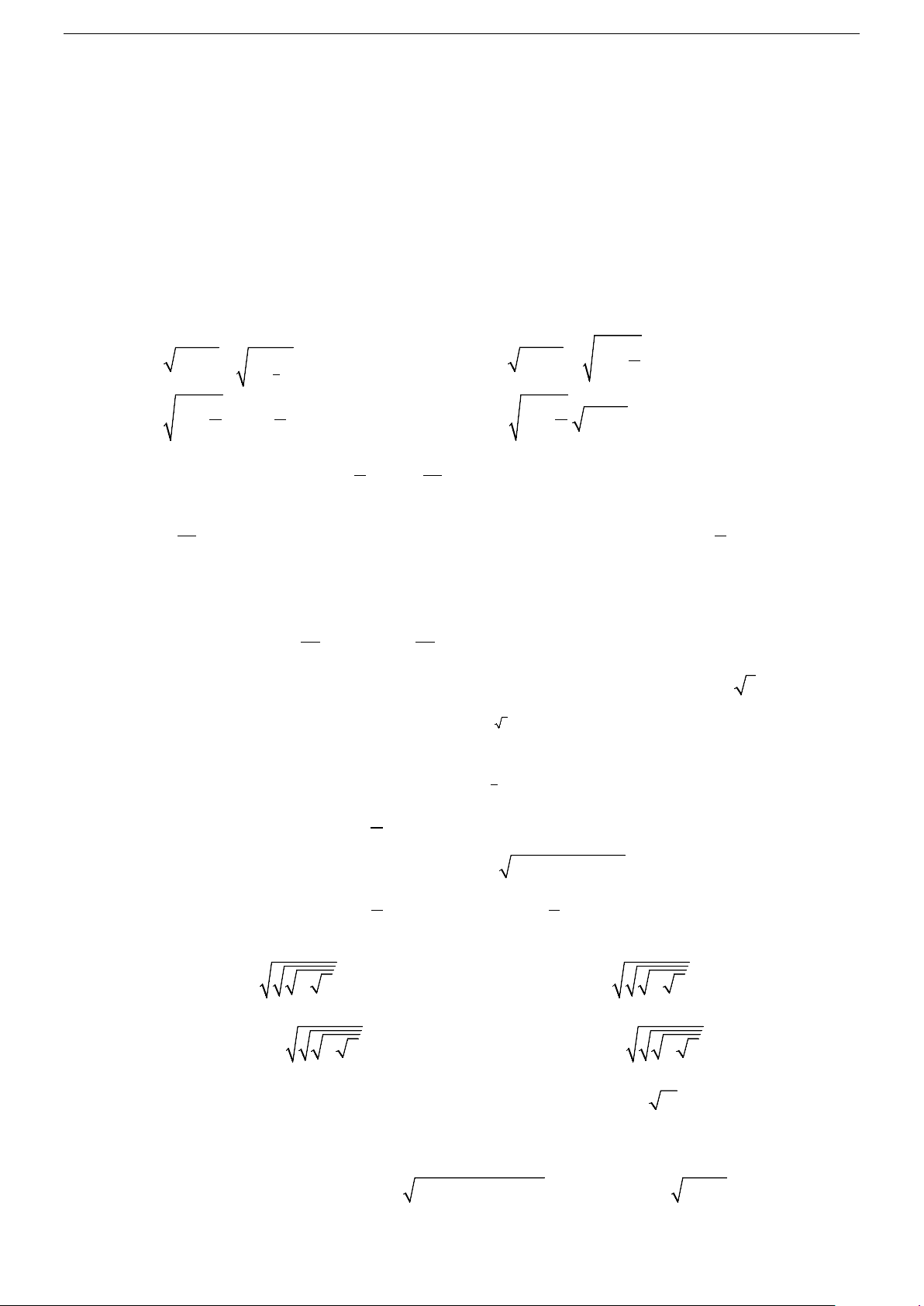
Câu 79. Với mọi số tự nhiên n, Khẳng định nào sau đây là khẳng định đúng? A. n = log log ... 2 .
B. n = −log log ... 2 . 2 2  2 2  n c¨n bËc hai n c¨n bËc hai
C. n = 2 + log log ... 2 .
D. n = 2 − log log ... 2 . 2 2  2 2  n căn bËc hai n căn bËc hai
Câu 80. Cho các số thực a, , b c thỏa mãn: log37 log711 l 11 og 25 a = 27,b = 49,c
= 11 . Giá trị của biểu thức 2 2 2 (log 11) 7 (log 25) 11 (log3 7) A = a + b + c là: A. 519. B.729. C. 469. D.129.
Câu 81. Kết quả rút gọn của biểu thức C = log b + log a + 2 (log b − b b là: a b a logab ) loga Trang 7/15 A. 3 log b . B. . log b . C.( b . D. log b . a )3 log a a a
Câu 82. Cho a, ,
b c > 0 đôi một khác nhau và khác 1, Khẳng định nào sau đây là khẳng định đúng? A. 2 c 2 a 2 log ;log ;log b = . B. 2 c 2 a 2 log ;log ;log b > . a b c 1 a b c 1 b c a b c a b c a b c a C. 2 c 2 a 2 log ;log ;log b > 1 − . D. 2 c 2 a 2 log ;log ;log b < . a b c 1 a b c b c a b c a b c a b c a Câu 83. Gọi ( ;
x y) là nghiệm nguyên của phương trình 2x + y = 3 sao cho P = x + y là số dương nhỏ
nhất. Khẳng định nào sau đây đúng?
A. log x + log y không xác định.
B. log (x + y) =1. 2 3 2
C. log (x + y) >1.
D. log (x + y) > 0 . 2 2 Câu 84. Có tất cả bao nhiêu số dương a thỏa mãn đẳng thức
log a + log a + log a = log . a log . a log a 2 3 5 2 3 5 A. 3. B.1. C.2. D. 0.
E. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI BÀI TẬP TRẮC NGHIỆM I – ĐÁP ÁN 1.2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
A A B A C B D B B A C D C A C D C B D D
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
C D C B D A D A A D B C B D B A A B C C
41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
C B B C B C D D D D B A A C D B A A C A
61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80
D A B A A A C A C D B A D B B C C D B C 81 82 83 84 C A A A
II –HƯỚNG DẪN GIẢI
Câu 1. Biểu thức f (x) xác định 1
⇔ 2x −1 > 0 ⇔ x > . Ta chọn đáp án A 2
Câu 2. Biểu thức f (x) xác định 2
⇔ 4 − x > 0 ⇔ x ∈( 2;
− 2) . Ta chọn đáp án A Câu 3. −
Biểu thức f (x) xác định x 1 ⇔ > 0 ⇔ x ∈( ; −∞ 3
− ) ∪ (1;+∞) . Ta chọn đáp án B 3+ x
Câu 4. Biểu thức f (x) xác định 2
⇔ 2x − x > 0 ⇔ x ∈(0;2) . Ta chọn đáp án A.
Câu 5. Biểu thức f (x) xác định 3 2
⇔ x - x − 2x > 0 ⇔ x ∈( 1;
− 0) ∪ (2;+∞) . Ta chọn đáp án C. Câu 6. Ta có log 4 log 1/2 4 a a 2loga 4 loga16 A = a = a = a = a = 16 . Ta chọn đáp án B
Câu 7. Ta nhập vào máy tính biểu thức 2log 12 + 3log 5 − log 15 − log 150 , bấm =, được kết quả 2 2 2 2 B = 3 Ta chọn đáp án D Câu 8. +Tự luận 2 3
P = 2log 12 + 3log 5 − log 15 − log 150 = log 12 + log 5 − log (15.150) 2 2 2 2 2 2 2 2 3 12 .5 = log = 3 2 15.150 Trang 8/15 Đáp án B.
+Trắc nghiệm: Nhập biểu thức vào máy tính và nhấn calc ta thu được kết quả bằng 3. Câu 9. Ta có 1 1
D = log a = log a = . Ta chọn đáp án B 3 a 3 a 3
Câu 10. Ta nhập vào máy tính biểu thức: 1 3
log 36 − log 14 − 3log 21 bấm = , được kết quả C = 2 − . 7 7 7 2 Ta chọn đáp án A 4 Câu 11. Ta có 4log 5 loga 5 2 a loga 25 2 E = a = a = a = 25 . Ta chọn đáp án C
Câu 12. + Tự luận: Đưa về cùng 1 cơ số và so sánh Ta thấy 6 5 6 5 log > log = log = log .Ta chọn đáp án D 3 3 1 3 5 6 5 6 3
+ Trắc nghiệm: Sử dụng máy tính, lấy 1 số bất kỳ trừ đi lần lượt các số còn lại, nếu kết quả
> 0 thì giữ nguyên số bị trừ và thay đổi số trừ là số mới; nếu kết quả < 0 thì đổi số trừ thành số
bị trừ và thay số trừ là số còn lại; lặp lại đến khi có kết quả.
Câu 13. + Tự luận : Đưa về cùng 1 cơ số và so sánh Ta thấy 1 1 log 17 < log 15 = log < log 12 = log
< log 9 .Ta chọn đáp án C. 1 1 5 1 5 1 15 12 5 5 5 5
+ Trắc nghiệm: Sử dụng máy tính, lấy 1 số bất kỳ trừ đi lần lượt các số còn lại, nếu kết quả
< 0 thì giữ nguyên số bị trừ và thay đổi số trừ là số mới; nếu kết quả > 0 thì đổi số trừ thành số
bị trừ và thay số trừ là số còn lại; lặp lại đến khi có kết quả.
Câu 14. +Tự luận : Ta có 2 2 2 2 2 2 A = ln a + 2ln . a log e + e + a − e = a + e = a + . Ta chọn đáp a loga ln loga 2ln 2ln 2ln 2 án A
+Trắc nghiệm : Sử dung máy tính, Thay a = 2 rồi lấy biểu thức đã cho trừ đi lần lượt các
biểu thức có trong đáp số, nếu kết quả nào bằng 0 thì đó là đáp số.
Câu 15. +Tự luận : Ta có 3
B = 2ln a + 3log e − e − a = = a − . Ta chọn đáp án C a 3loga 2ln 0 3ln log e a
+Trắc nghiệm : Sử dung máy tính, Thay a = 2 rồi lấy biểu thức đã cho trừ đi lần lượt các
biểu thức có trong đáp số, nếu kết quả nào bằng 0 thì đó là đáp số.
Câu 16. Ta có: log (5 3ab)2 2 3 3 2 2 15
= log (a b) = log a +
log b ⇒ x + y = 4 . Ta chọn đáp án D 3 3 3 3 5 15 0 − ,2 10 1   Câu 17. Ta có : a 2 − 1 1 6 log  
= log (a .b ) = 2
− log a + log b ⇒ .
x y = − . Ta chọn đáp án C 5 5 5 5 6 5  b  6 3 Câu 18. Ta có: 40 40
log x = log 8 + log 5 − log 9 = log ⇒ x = . Ta chọn đáp án B 3 3 3 3 3 9 9 2 3 Câu 19. Ta có: 1 2 3 log = 2log − 6log = log − log = log a b a b a b ⇒ x = . Ta chọn đáp án D 7 7 49 7 7 7 3 2 x b a
Câu 20. Câu D sai, vì không có tính chất về logarit của một hiệu Trang 9/15
Câu 21. Câu C sai, vì 1 log b = b c log a a c
Câu 22. Câu D sai, vì khẳng định đó chỉ đúng khi a >1, còn khi 0 < a <1⇒ log b >
c ⇔ b < c a loga
Câu 23. Câu C sai, vì log c
b > c ⇔ b > a a
Câu 24. Câu D sai, vì 2 3
2 < 3 ⇒ a > a (do 0 < a <1)
Câu 25. Ta có log (log a) = 0 ⇒ log a =1⇒ a = 2. Ta chọn đáp án D 3 2 2
Câu 26. Đáp án A đúng với mọi a,b,c khi các logarit có nghĩa
Câu 27. Đáp án D sai, vì không có logarit của 1 tổng.
Câu 28. Sử dụng máy tính và dùng phím CALC : nhập biểu thức log X + log X + log X −1 vào máy 2 4 8
và gán lần lượt các giá trị của x để chọn đáp án đúng. Với x = 64 thì kquả bằng 0. Ta chọn D là đáp án đúng.
Câu 29. Sử dụng máy tính và dùng phím CALC : nhập biểu thức 3 log
− vào máy và gán lần lượt x 2 2 4
các giá trị của x để chọn đáp án đúng. Với .. thì kquả bằng 0. Ta chọn A là đáp án đúng.
Câu 30. +Tự luận : Ta có 2 2 = log + = 4log + 2log a P b b = 2 . Ta chọn đáp án A. a 2 log a a a b a 2 b
+Trắc nghiệm : Sử dụng máy tính, thay a = b = 2 , rồi nhập biểu thức 2 2 log b + vào a log a a 2 b
máy bấm =, được kết quả P = 2 . Ta chọn đáp án D.
Câu 31. + Tự luận : Ta có 3 4
P = log b .log a = = . Ta chọn đáp án A. a b 2.3.4 24
+Trắc nghiệm : Sử dụng máy tính Casio, Thay a = b = 2 , rồi nhập biểu thức 3 4 log b .log a a b
vào máy bấm =, được kết quả P = 24 . Ta chọn đáp án B. 2
Câu 32. + Tự luận : 3log83+2lo 16g5 = ( log23 log2 5 4 2 .2 ) = 45
+ Trắc nghiệm : Sử dụng máy tính, rồi nhập biểu thức 3log83 2lo 16 g 5 4 +
vào máy, bấm =, được kết
quả bằng 45. Ta chọn đáp án C.
Câu 33. +Tự luận : log a a a = a = a ( ) 37 3 5 37 10 loga 10
+Trắc nghiệm : Sử dụng máy tính, Thay a = 2 , rồi nhập biểu thức ( 3 5 log a a a vào máy a ) bấm =, được kết quả 37 P = . Ta chọn đáp án B. 10
Câu 34. +Tự luận : 1
A = log 15.log 14...log 4.log 3.log 2 = log 2 = 16 15 5 4 3 16 4
+Trắc nghiệm : Sử dụng máy tính Casio, rồi nhập biểu thức log 2.log 3.log 4...log 15 vào 3 4 5 16
máy bấm =, được kết quả 1
A = . Ta chọn đáp án D. 4  3 3 2 5 3 91 
Câu 35. +Tự luận : a a a 91 60 log   = − log a = − 1  4 a a a  60 a   Trang 10/15  3 3 2 5 3 
+Trắc nghiệm : Sử dụng máy tính, Thay a = 2 , rồi nhập biểu thức log a a a   vào 1  4  a a a  
máy bấm =, được kết quả 211 − . Ta chọn đáp án C. 60
Câu 36. Ta có: log 2 < log 3 =1, log 3 > log 2 =1 3 3 2 2 Câu 37. 2 2 2000 >1999.2001⇒ log 2000 > log 2001.1999 2000 2000 ⇒ 2 > log 2001+ log 1999 ⇒ log 2000 > log 2001 2000 2000 1999 2000
Câu 38. Ta có log 2 < log 3=1=log 2< log 3 < log 11 3 3 2 2 3
Câu 39. log (x + 2) 3
= 3 ⇔ x + 2 = 3 ⇔ x = 25 3 Câu 40. 3 1 3
log x + log x = ⇔ log x + log x = ⇔ x = 3 3 9 3 3 2 2 2 Câu 41. Ta có 4 7 4 7
4log a + 7log b = log (a b ) ⇒ x = a b . Ta chọn đáp án C. 3 3 3
Câu 42. Ta có: log ( 2 2
x + y ) =1+ log xy ⇔ log ( 2 2 x + y ) 2 2
= log 2xy ⇔ x + y = 2xy ⇔ x = y 2 2 2 2 Câu 43. 1 y 3
log y − x − log =1 ⇔ log
= 1 ⇔ x = y 1 ( ) 4 4 y y − x 4 4
Câu 44. Do x , y > 0 ⇒ log xy = x +
y , ta chọn đáp án D. a loga loga
Câu 45. Ta có : Chọn B là đáp án đúng, vì 2 2 2 2
x + 4y =12xy ⇔ (x + 2y) =16xy ⇔ log (x+ 2 y) = log 16xy 2 2 1
⇔ 2log (x + 2y) = 4 + log x + log y ⇔ log (x + 2y) = 2 + log x + log y 2 2 2 2 ( 2 2 ) 2
Câu 46. Ta có: Chọn C là đáp án đúng, vì 2 2 2 2
a + b = 7ab ⇔ (a + b) = 9ab ⇔ log(a + b) = log9ab a + b 1
⇔ 2log(a + b) = log9 + log a + logb ⇔ log
= (log a + logb) 3 2 1
Câu 47. +Tự luận : Ta có : a = log 6 = log (2.3) =1+ log 3 ⇒ log 2 = 2 2 2 3 a −1 − Suy ra 2 1 2a 1
log 18 = log (2.3 ) = log 2 + 2 = + 2 = . Ta chọn đáp án A. 3 3 3 a −1 a −1 +Trắc nghiệm:
Sử dụng máy tính: Gán log 6 cho A 2
Lấy log 18 trừ đi lần lượt các đáp số ở A, B, C, D. Kết quả nào bẳng 0 thì đó là đáp án. 3 Ta chọn đáp án D 1 1 1+ 4
Câu 48. +Tự luận : Ta có : 4 4
log 1250 = log (2.5 ) = log (2.5 ) = + 2log 5 = a . Ta chọn đáp 2 4 2 2 2 2 2 2 án A. +Trắc nghiệm:
Sử dụng máy tính: Gán log 5 cho A 2
Lấy log 1250 trừ đi lần lượt các đáp số ở A, B, C, D. Kết quả nào bằng 0 thì đó là đáp án. 4 Ta chọn đáp án D Trang 11/15
Câu 49. Sử dụng máy tính: gán log 2 cho A 7
Lấy log 28 trừ đi lần lượt các đáp số ở A, B, C, D. Kết quả nào bẳng 0 thì đó là đáp án. 49 Ta chọn đáp án D
Câu 50. Sử dụng máy tính: gán lần lượt log 5; log 3 cho A, B 2 5
Lấy log 15 trừ đi lần lượt các đáp số ở A, B, C, D. Kết quả nào bẳng 0 thì đó là đáp án. 10 Ta chọn đáp án D
Câu 51. +Tự luận : Ta có : a = log 15 = log (3.5) =1+ log 5 ⇒ log 5 = a −1. 3 3 3 3
Khi đó : log 50 = 2log (5.10) = 2(log 5 + log 10) = 2(a −1+ b) Ta chọn đáp án B. 3 3 3 3 +Trắc nghiệm
Sử dụng máy tính: gán lần lượt log 15;log 10 cho A, B. 3 3
Lấy log 50 trừ đi lần lượt các đáp số ở A, B, C, D. Kết quả nào bẳng 0 thì đó là đáp án. 3 Ta chọn đáp án B.
Câu 52. Sử dụng máy tính: Gán log 3 cho A 5
Lấy log 75 trừ đi lần lượt các đáp số ở A, B, C, D. Kết quả nào bẳng 0 thì đó là đáp án. 15 Ta chọn đáp án A. 1
Câu 53. Ta có:log 7 = 2. log 7 = 2log 7 = 2a 2 2 4 . Ta chọn đáp án A. 2 27 2 3a − 2 Câu 54. Ta có: log
= log 27 − log 25 = 3− 2log 5 = 3− = 3 3 3 3 . Ta chọn đáp án C. 25 a a
Câu 55. Sử dụng máy tính: Gán lần lượt log 5;log 3 cho A, B 2 5
Lấy log 15 trừ đi lần lượt các đáp số ở A, B, C, D. Kết quả nào bẳng 0 thì đó là đáp án. 24 Ta chọn đáp án D. log 27 3log 3 2a 4 3− a 2 2 ( )
Câu 56. Ta có: a = log 27 = = ⇒ log 3 = ⇒ log 16 = . 12 2 6 log 12 2 + log 3 3− a 3+ a 2 2 + + Câu 57. Ta có: lg30 1 lg3 1 log 30 = = = a . 125
lg125 3(1− lg 2) 3(1− b) 3 3 3 Câu 58. Ta có : b 1 − α α b 3 2 3 log b = 3 ⇔ = a = a ⇒ = a ⇒ A = − . a a a 3 3b
Câu 59. Ta có log 5 = a ⇒ log 5 = 3a, log 7 = b ⇒ log 7 = ⇒ log 5 = 3ac 27 3 8 3 2 c 3(ac + b) ⇒ log 35 = . 6 1+ c
Câu 60. Ta có: A = log 2 + log 3+...+ log 2000 = log (1.2.3...2000) = log x = x x x x x 1
Câu 61. Sử dụng máy tính: Gán lần lượt log 12;log 24 cho A, B 7 12
Lấy log 168 trừ đi lần lượt các đáp số ở A, B, C, D. kết quả nào bẳng 0 thì đó là đáp án. 54 Ta chọn đáp án D. Trang 12/15 2 3 Câu 62. Ta có a b 2 3 4 log
= log a + log b − log c = 2 + 3.2 − 4.( 3 − ) = . Ta chọn đáp án A. a a a a 20 4 c Câu 63. 1 1 Ta có log ( 2 3 2
a bc ) = 2log a + log b + c a 2log = a 2 + .3+ 2.( 4) − = 5 − a a . Ta chọn đáp án B. 3 3
Câu 64. Thay a = e , rồi sử dụng máy tính sẽ được kết quả 37 A = . Ta chọn đáp án A. 10
Câu 65. Thay a = e , rồi sử dụng máy tínhsẽ được kết quả 91 B = − . Ta chọn đáp án A 60 Câu 66. ab 1 1 1 log 5.log 5 Ta có: 2 3 log 5 = = = = = . 6
log 6 log (2.3) log 2 + log 3 log 5 + log 5 a + b 5 5 5 5 2 3
Câu 67. Sử dụng máy tính: gán lần lượt log 3;log 5;log 2 cho A, B, C 2 3 7
Lấy log 63 trừ đi lần lượt các đáp số ở A, B, C, D. kết quả nào bẳng 0 thì đó là đáp án. 140 Ta chọn đáp án C.
Câu 68. Sử dụng máy tính: gán lần lượt log 2;log 3 cho A, B 5 5
Lấy log 72 trừ đi lần lượt các đáp số ở A, B, C, D. kết quả nào bẳng 0 thì đó là đáp án. 5 Ta chọn đáp án A.
Câu 69. Sử dụng máy tính Casio, gán lần lượt log 18;log 54 cho A và B. 12 24
Với đáp án C nhập vào máy : AB + 5(A − B) −1, ta được kết quả bằng 0 . Vậy C là đáp án đúng.
Câu 70. Vì log log log y = 0 nên 4
log (log y) =1⇒ log y = 4 ⇒ y = 2 ⇒ 2y +1 = 33. 3 ( 4 ( 2 )) 4 2 2 Đáp án A.
Câu 71. Vì log x > 0 ⇒ x >1 . Khi đó log x > log x . Chọn đáp án D. 5 5 6
Câu 72. Sử dụng máy tính Casio, Chọn x = 0,5 và thay vào từng đáp án, ta được đáp án A.
Câu 73. +Tự luận: log2 5 Ta có:  1 2 log −  − − 1 3 4 2log3 2 log3 4 2log2 5 log2 5 2 3 = 4;3 = 3 = 4; =  2 = 2 = 5 =  ,  4  25 log0,5 2  1  = ( 4 2− )−log 2 4 2 log2 2 4 = 2 = 2 =   16 . 16  Chọn : Đáp án D.
Trắc nghiệm: nhập vào máy tính từng biểu thức tính kết quả, chọn kết quả nhỏ hơn 1.
Câu 74. +Tự luận: Ta có log0,513 log0,5 4 log 13 < log 4 < 0 ⇒ 3 < 3
< 1⇒ N < M <1. 0,5 0,5 Chọn : Đáp án B.
+ Trắc nghiệm: Nhập các biểu thức vào máy tính, tính kết quả rồi so sánh, ta thấy đáp án B đúng.  π   π   π π   π Câu 75. Ta có  1 log 2sin +  log cos =  log  2sin .cos =  log sin =  log = 1 − 2 2 2 2 2  12   12   12 12   6  2 Chọn: Đáp án B. Trang 13/15
Câu 76. Biểu thức f (x) xác định ⇔ x − m > 0 ⇔ x > m .
Để f (x) xác định với mọi x ∈( 3 − ;+∞) thì m ≤ 3 − Ta chọn đáp án C.
Câu 77. Thay m = 2 vào điều kiện (3− x)(x + 2m) > 0 ta được (3− x)(x + 4) > 0 ⇔ x∈( 4; − 3) mà [ − 4;2] ⊄ ( 4;
− 3) nên các đáp án B, A, D loại. Ta chọn đáp án đúng là C.
Câu 78. - Thay m = 2 vào điều kiện (m − x)(x −3m) > 0 ta được (2 − x)(x − 6) > 0 ⇔ x∈(2;6) mà ( 5
− ;4] ⊄ (2;6) nên các đáp án B, A loại. - Thay m = 2
− vào điều kiện (m − x)(x − 3m) > 0 ta được ( 2
− − x)(x + 6) > 0 ⇔ x∈( 6 − ; 2) − mà ( 5 − ;4] ⊄ ( 6 − ; 2)
− nên các đáp án C loại. Do đó Ta chọn đáp án đúng là D. Câu 79. +Tự luận: Đặt -log log ... 2 = . m Ta có: 2 log ... 2 2 ... 2 2 − − = ⇔ = m m . 2 2  2 n c¨n bËc hai 2 1  1   1 n Ta thấy :     2  2   2  2 2 = 2 , 2 = 2 ,....., ... 2 = 2 = 2 −n .
Do đó ta được: 2−m 2−
= n ⇔ m = n . Vậy n = −log log ... 2 . Đáp án B. 2 2  n c¨n bËc hai
+Trắc nghiệm: Sử dụng máy tính Casio, lấy n bất kì, chẳng hạn n = 3.
Nhập biểu thức −log log
2 ( có 3 dấu căn ) vào máy tính ta thu được kết quả bằng – 3. 2 2 Vậy chọn B. Câu 80. Ta có ( log 7 a ) 1 log 7 log 11 log 25 3 + ( log 11 b ) 7 3 7 + ( l 11 og 25 c )log 2511 log3 7 log711 = + + ( ) 11 3 2 2 27 49 11 = 7 +11 + 25 = 469 Suy ra : Đáp án C.
Câu 81. C = log b + a + b − b b a logb 2 (loga logab ) loga (log b +  b b +   a )2 1 log b a (loga ) 2 1 log = log b −  log a b =   b = b a a loga ( loga )3 2 log b + b b +    b a 1 loga loga 1 loga  1 − 2 Câu 82. * bc c 2 bc  2 log = c a log = − a log ⇒ a log = − a log =    a  log cb b c b a b * log . b log .
c log a =1 ⇔ log .
b log a = log a = a b c a b a 1
* Từ 2 kết quả trên ta có : 2 c a b b c a  2 2 2 log a logb log = c
 loga .logb logc  = 1 b c a c a b b c ab c a  Chọn : Đáp án A.
Câu 83. Vì x + y > 0 nên trong hai số x và y phải có ít nhất một số dương mà
x + y = 3− x > 0 nên suy ra x < 3 mà x nguyên nên x = 0; 1 ± ; 2; ± . .
+ Nếu x = 2 suy ra y = 1
− nên x + y =1
+ Nếu x =1 thì y =1 nên x + y = 2 Trang 14/15
+ Nếu x = 0 thì y = 3 nên x + y = 3
+ Nhận xét rằng : x < 2 thì x + y >1 . Vậy x + y nhỏ nhất bằng 1. Suy ra: Chọn đáp án A.
Câu 84. (*) ⇔ log a + log 2.log a + log 2.log a = log . a log 5.log . a log a 2 3 2 5 2 2 3 5 5 ⇔ log . a (1+ log 2 + log 2) 2 = log . a log 5.log a 2 3 5 2 3 5 ⇔ log . a ( 2
1+ log 2 + log 2 − log 5.log a = 0 2 3 5 3 5 ) a =1 a =1 log a = 0 2    1+ log 2 + log 2  ⇔ ⇔ ⇔ 1+log3 2+log5 2 2 3 5
1+ log 2 + log 2 − log 5.log a =  0 log a ± = ±  log3 5 3 5 3 5 5  log 5 a = 5  3 Chọn: Đáp án A. Trang 15/15
Document Outline

  • DS_C2_LOGARIT
    • A. KIẾN THỨC CƠ BẢN
    • B. KỸ NĂNG CƠ BẢN
    • C. KỸ NĂNG SỬ DỤNG MÁY TÍNH
    • D. BÀI TẬP TRẮC NGHIỆM
    • E. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI BÀI TẬP TRẮC NGHIỆM