














Preview text:
CHỦ ĐỀ 2. MẶT CẦU – MẶT NÓN – MẶT TRỤ
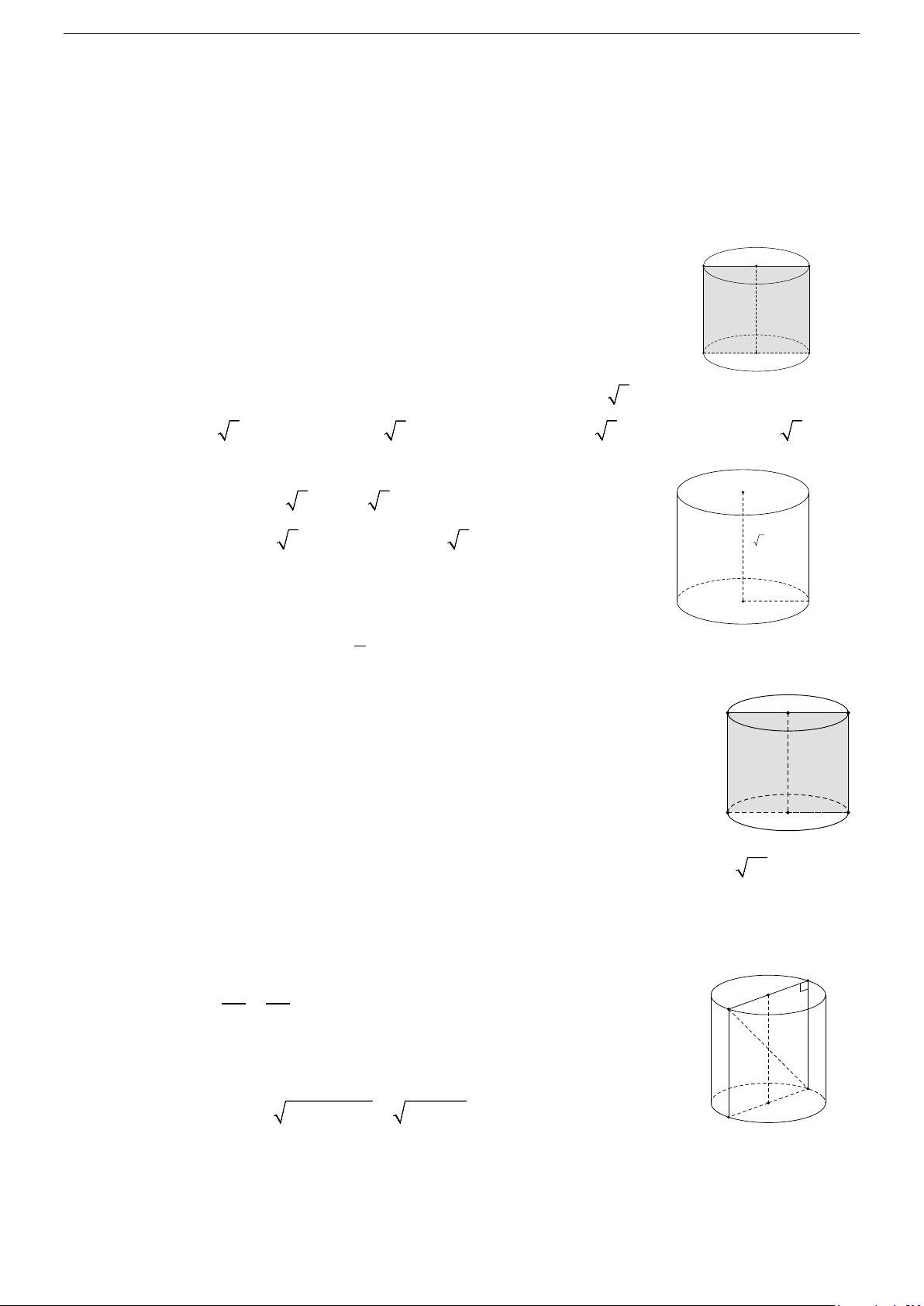
A. KIẾN THỨC CƠ BẢN I. MẶT NÓN Hình 1 Hình 2
1/ Mặt nón tròn xoay
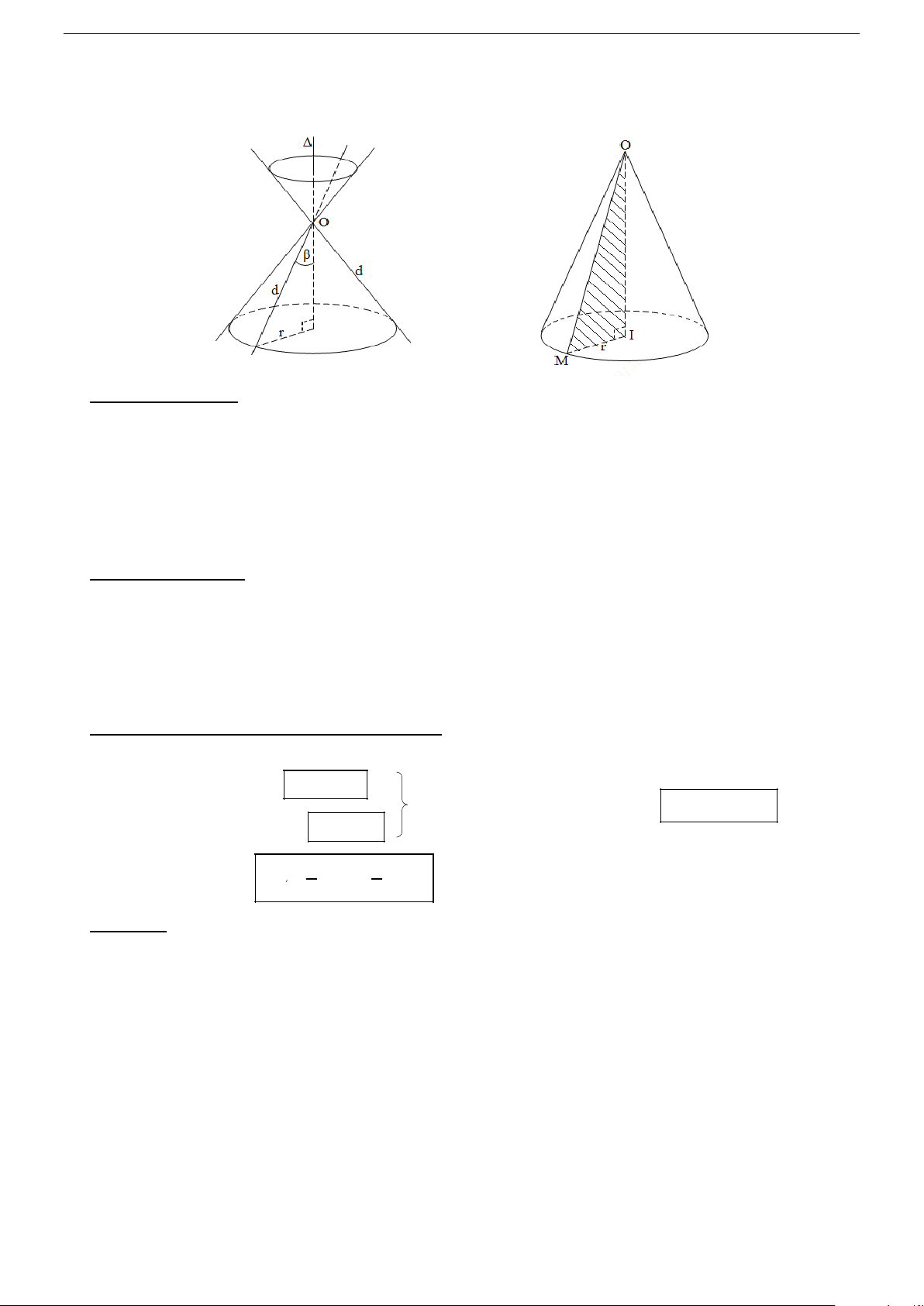
Trong mặt phẳng (P) , cho 2 đường thẳng d , ∆ cắt nhau tại O và chúng tạo thành góc β với 0 0
0 < β < 90 . Khi quay mp (P) xung quanh trục ∆ với góc β không thay đổi được gọi là mặt nón tròn
xoay đỉnh O (hình 1).
Người ta thường gọi tắt mặt nón tròn xoay là mặt nón.
Đường thẳng ∆ gọi là trục, đường thẳng d được gọi là đường sinh và góc 2β gọi là góc ở đỉnh.
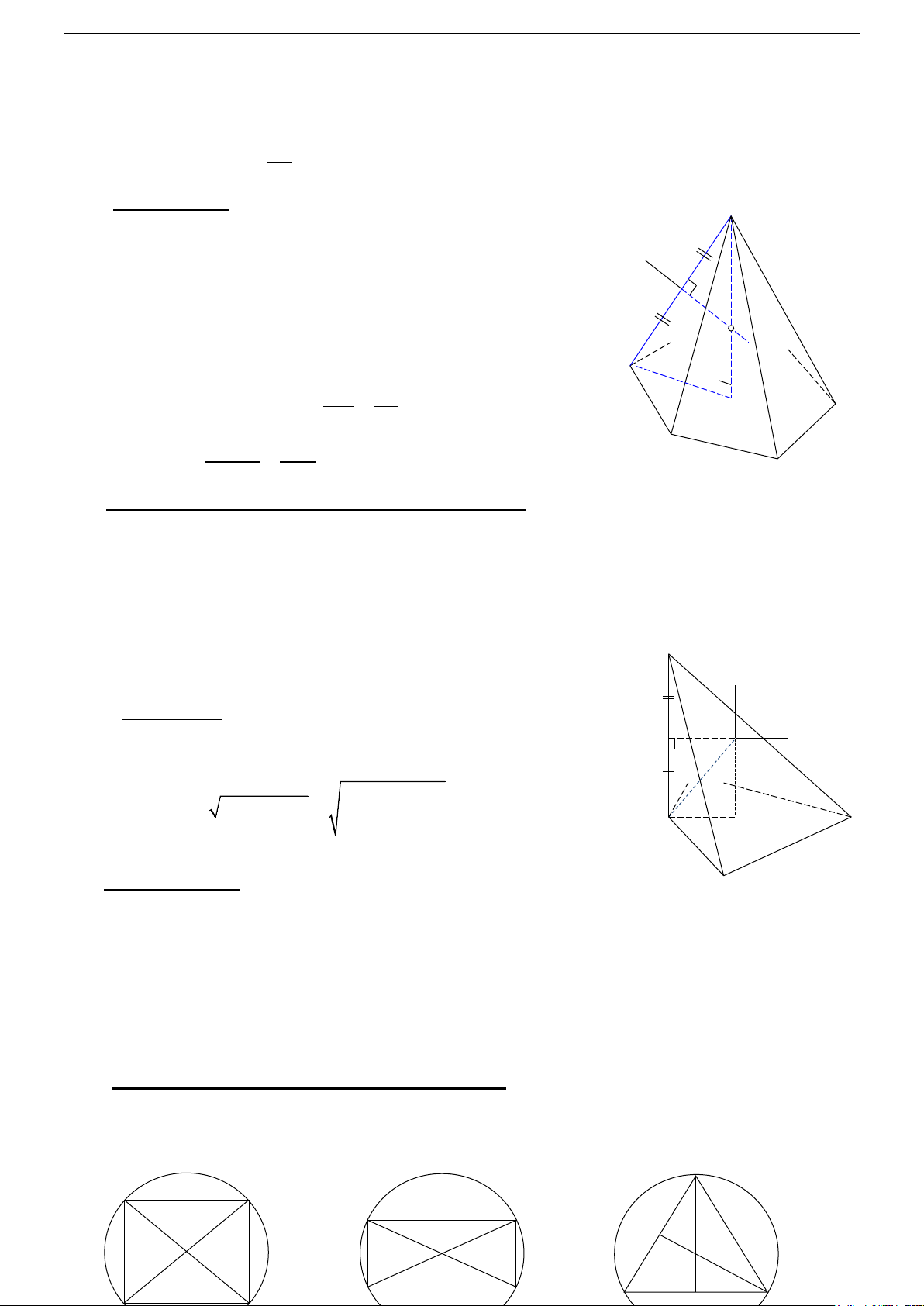
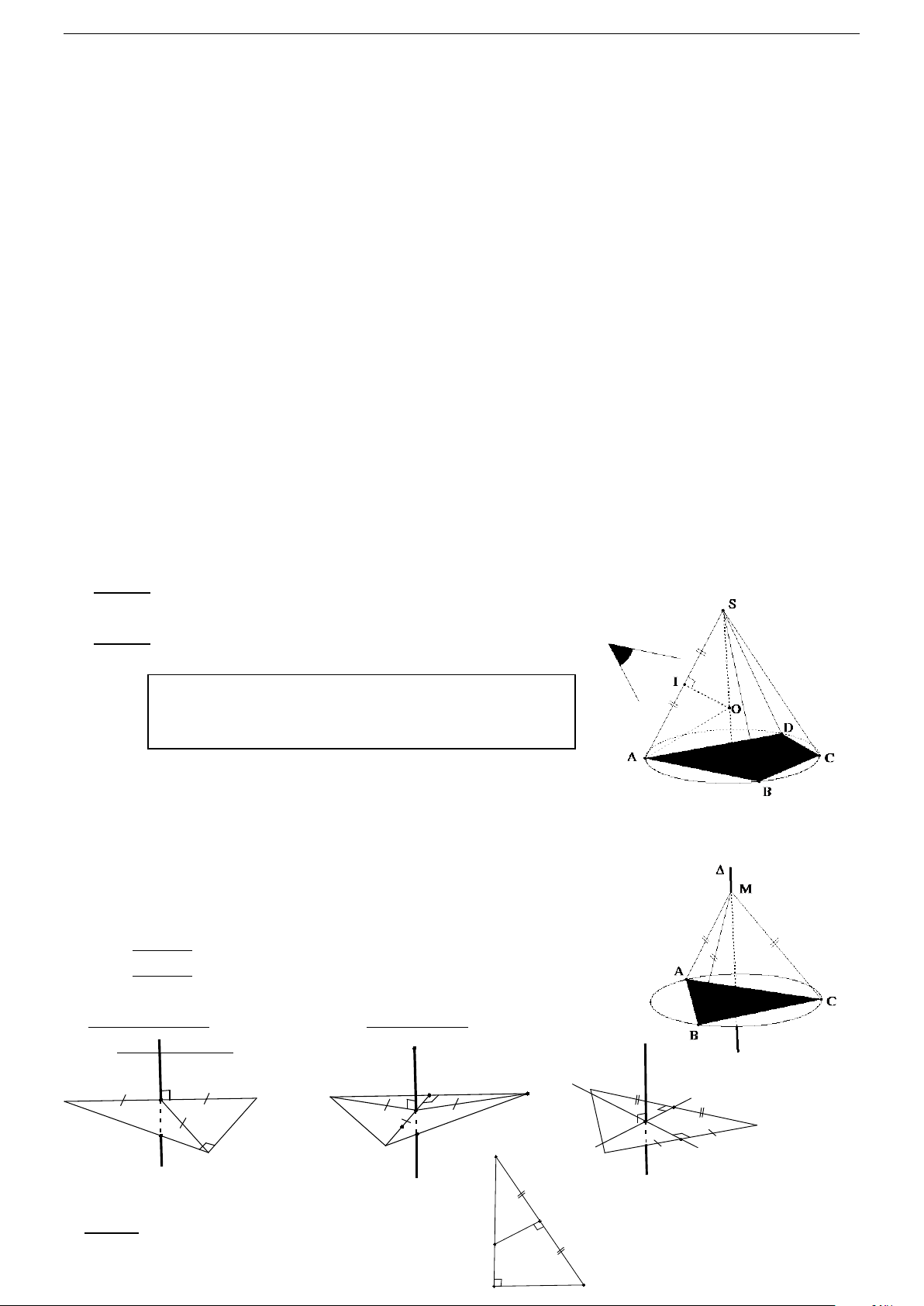
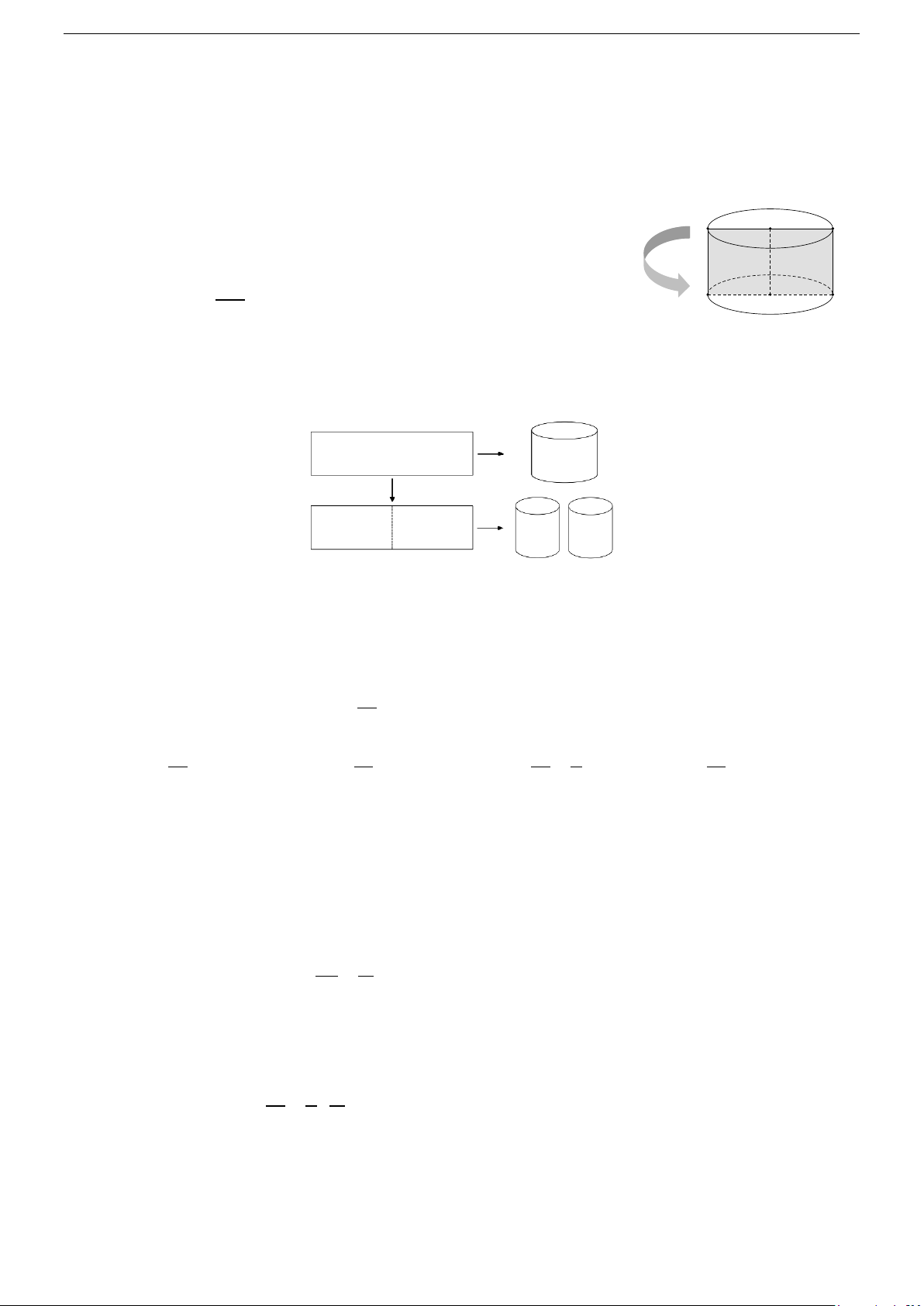
2/ Hình nón tròn xoay Cho OI
∆ M vuông tại I quay quanh cạnh góc vuông OI thì đường gấp khúc OIM tạo thành một hình,
gọi là hình nón tròn xoay (gọi tắt là hình nón) (hình 2).
Đường thẳng OI gọi là trục, O là đỉnh, OI gọi là đường cao và OM gọi là đường sinh của hình nón.
Hình tròn tâm I , bán kính r = IM là đáy của hình nón.
3/ Công thức diện tích và thể tích của hình nón
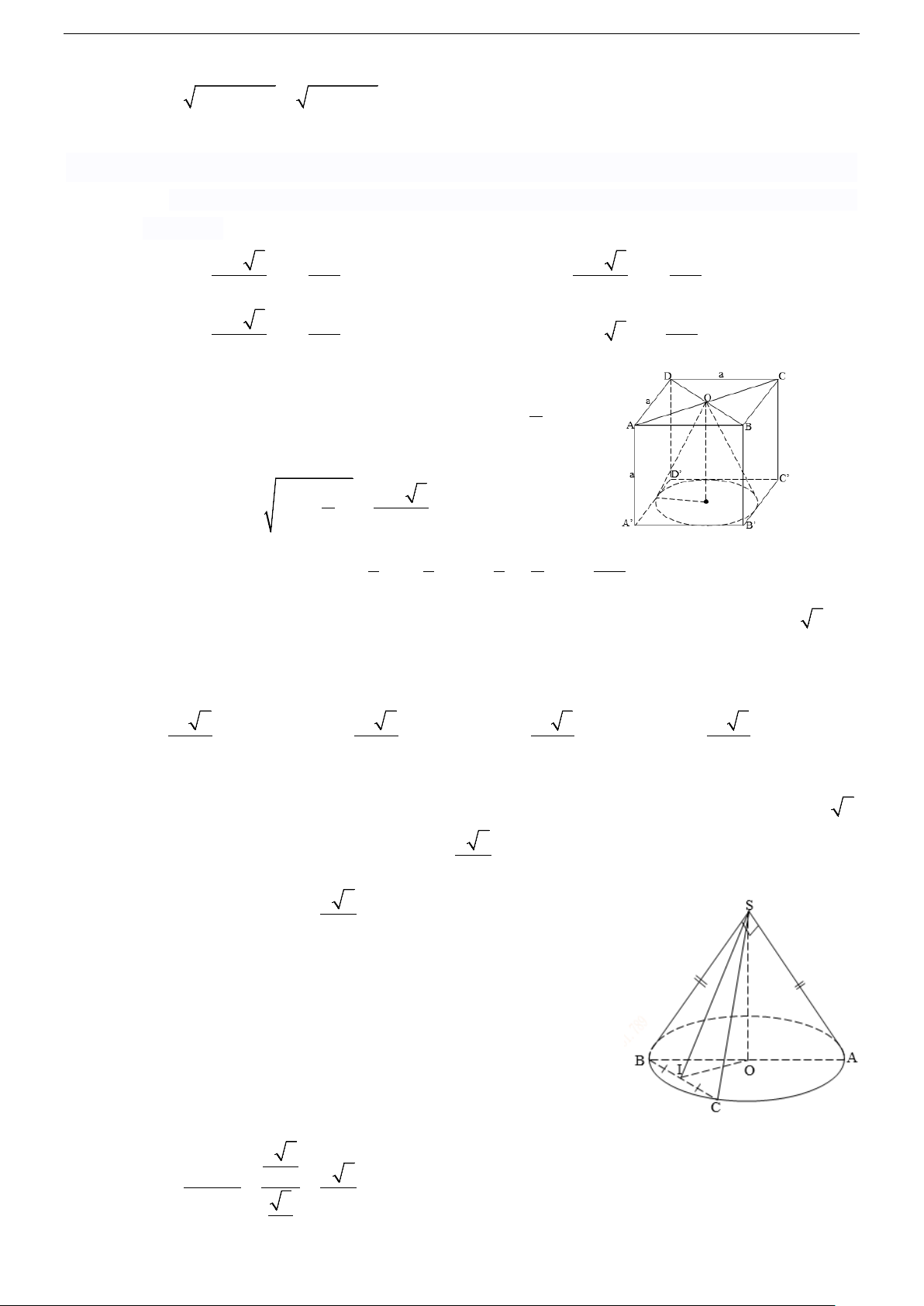
Cho hình nón có chiều cao là h , bán kính đáy r và đường sinh là l thì có:
Diện tích xung quanh: S = π r l xq . .
Diện tích toàn phần hình nón: S S S . tp xq ð
Diện tích đáy (hình tròn): 2 S = π r ð . 1 1
Thể tích khối nón: 2
V = S h = π r h . non ð . . . 3 3 4/ Tính chất:
TH1: Nếu cắt mặt nón tròn xoay bởi mp(P) đi qua đỉnh thì có các trường hợp sau xảy ra:
+ Nếu mp(P) cắt mặt nón theo 2 đường sinh⇒Thiết diện là tam giác cân.
+ Nếu mp(P) tiếp xúc với mặt nón theo một đường sinh. Trong trường hợp này, người ta gọi đó
là mặt phẳng tiếp diện của mặt nón.
TH2: Nếu cắt mặt nón tròn xoay bởi mp (Q) không đi qua đỉnh thì có các trường hợp sau xảy ra:
+ Nếu mp(Q) vuông góc với trục hình nón⇒giao tuyến là một đường tròn.
+ Nếu mp(Q) song song với 2 đường sinh hình nón⇒giao tuyến là 2 nhánh của 1 hypebol.
+ Nếu mp(Q) song song với 1 đường sinh hình nón⇒giao tuyến là 1 đường parabol. II. MẶT TRỤ Trang 1/44
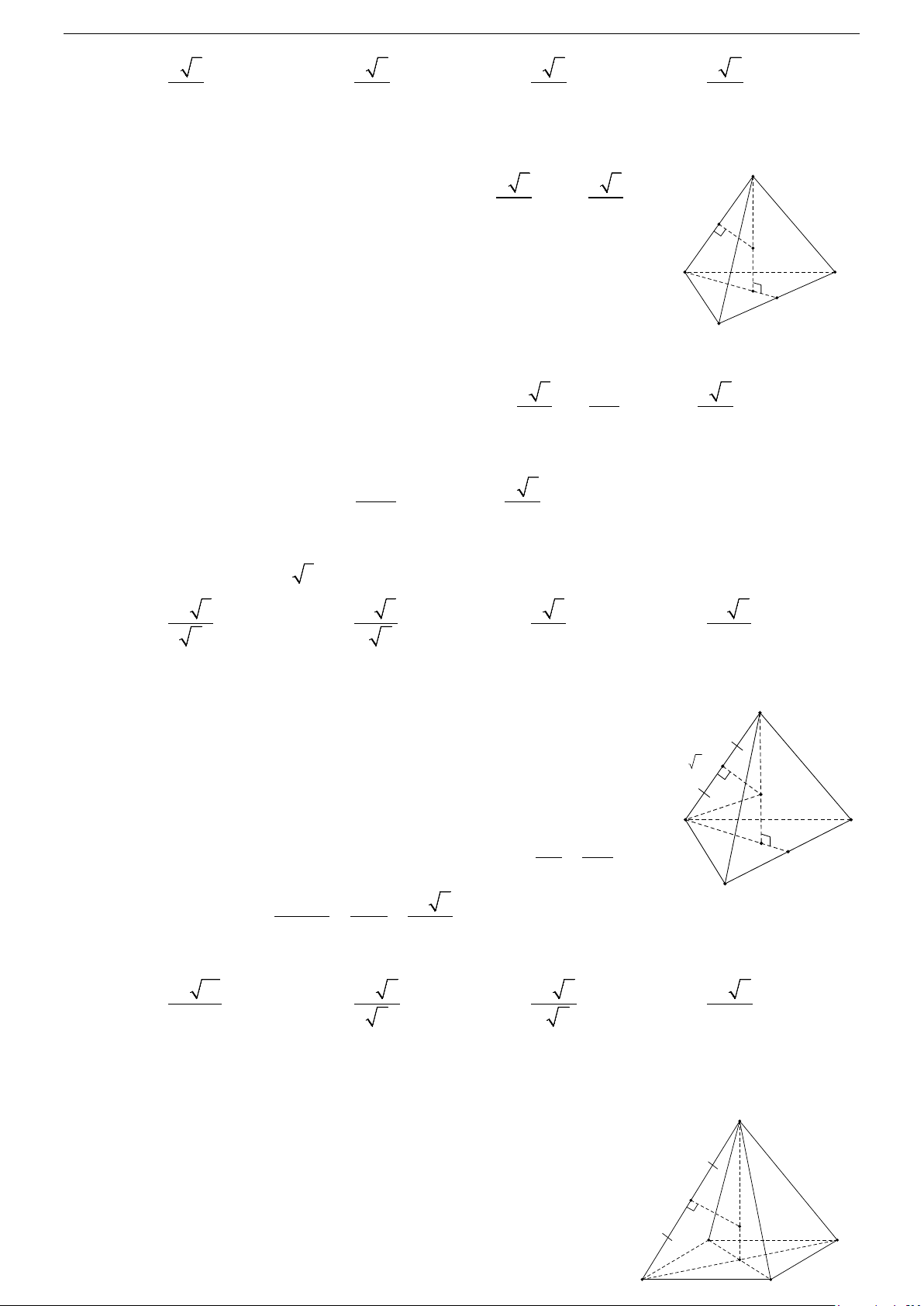
1/ Mặt trụ tròn xoay
Trong mp (P) cho hai đường thẳng ∆ và l song song nhau, cách nhau ∆
một khoảng r . Khi quay mp (P) quanh trục cố định ∆ thì đường r l
thẳng l sinh ra một mặt tròn xoay được gọi là mặt trụ tròn xoay hay A
gọi tắt là mặt trụ. D
Đường thẳng ∆ được gọi là trụC.
Đường thẳng l được gọi là đường sinh.
Khoảng cách r được gọi là bán kính của mặt trụ.
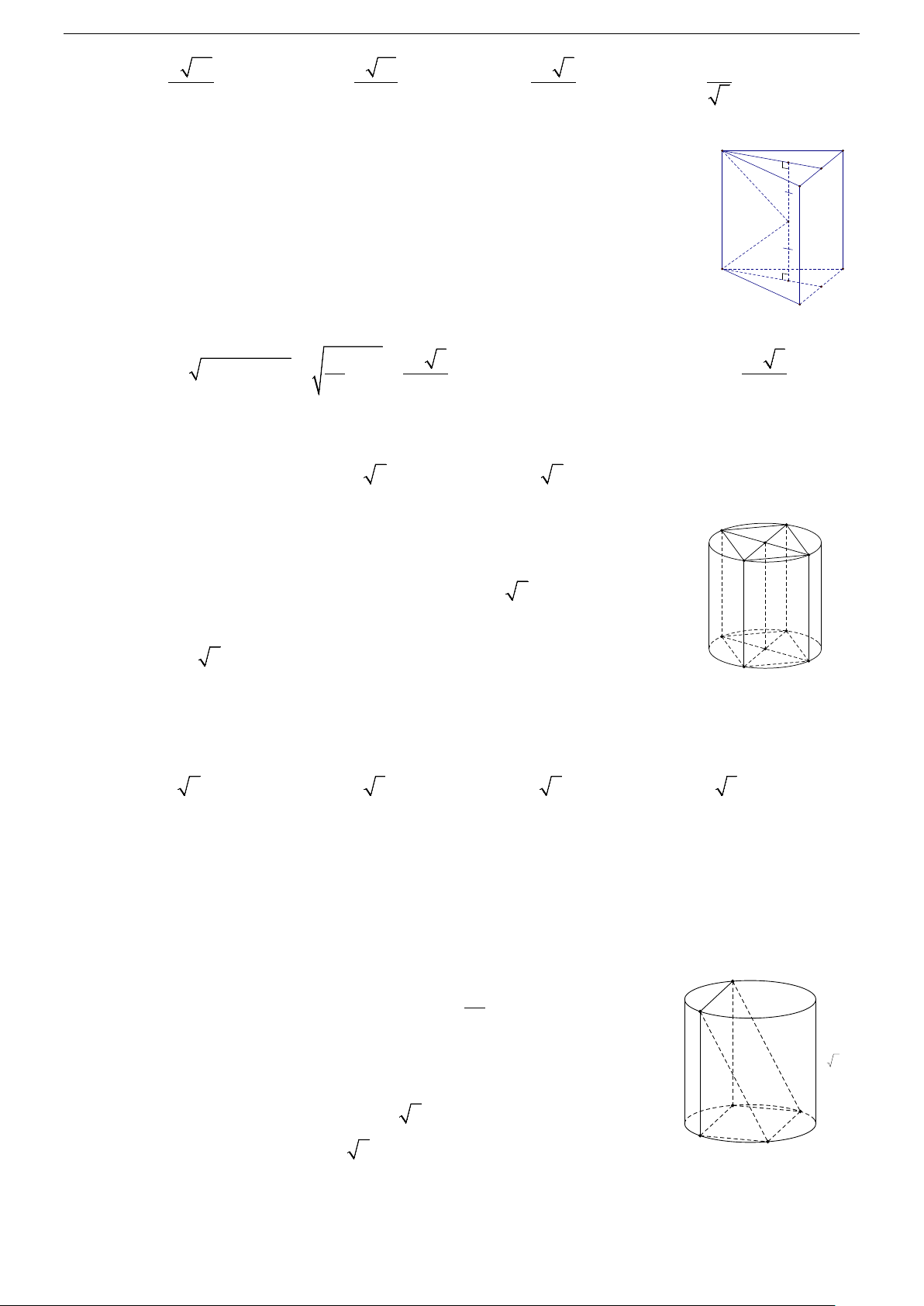
2/ Hình trụ tròn xoay
Khi quay hình chữ nhật ABCD xung quanh đường thẳng chứa một
cạnh, chẳng hạn cạnh AB thì đường gấp khúc ABCD tạo thành một B
hình, hình đó được gọi là hình trụ tròn xoay hay gọi tắt là hình trụ. r C
Đường thẳng AB được gọi là trụC.
Đoạn thẳngCD được gọi là đường sinh.
Độ dài đoạn thẳng AB = CD = h được gọi là chiều cao của hình trụ.
Hình tròn tâm A , bán kính r = AD và hình tròn tâm B , bán kính r = BC được gọi là 2 đáy của hình trụ.
Khối trụ tròn xoay, gọi tắt là khối trụ, là phần không gian giới hạn bởi hình trụ tròn xoay kể cả hình trụ.
3/ Công thức tính diện tích và thể tích của hình trụ
Cho hình trụ có chiều cao là h và bán kính đáy bằng r , khi đó:
Diện tích xung quanh của hình trụ: S = π rh xq 2
Diện tích toàn phần của hình trụ: 2 S = S + S = π rh + π r tp xq 2. Ðay 2 2
Thể tích khối trụ: 2 V = . B h = π r h 4/ Tính chất:
Nếu cắt mặt trụ tròn xoay (có bán kính là r ) bởi một mp (α ) vuông góc với trục ∆ thì ta được
đường tròn có tâm trên ∆ và có bán kính bằng r với r cũng chính là bán kính của mặt trụ đó.
Nếu cắt mặt trụ tròn xoay (có bán kính là r ) bởi một mp (α ) không vuông góc với trục ∆ nhưng
cắt tất cả các đường sinh, ta được giao tuyến là một đường elíp có trụ nhỏ bằng 2r và trục lớn
bằng 2r , trong đó ϕ là góc giữa trục ∆ và mp (α ) với 0 0 0 < ϕ < 90 . sinϕ
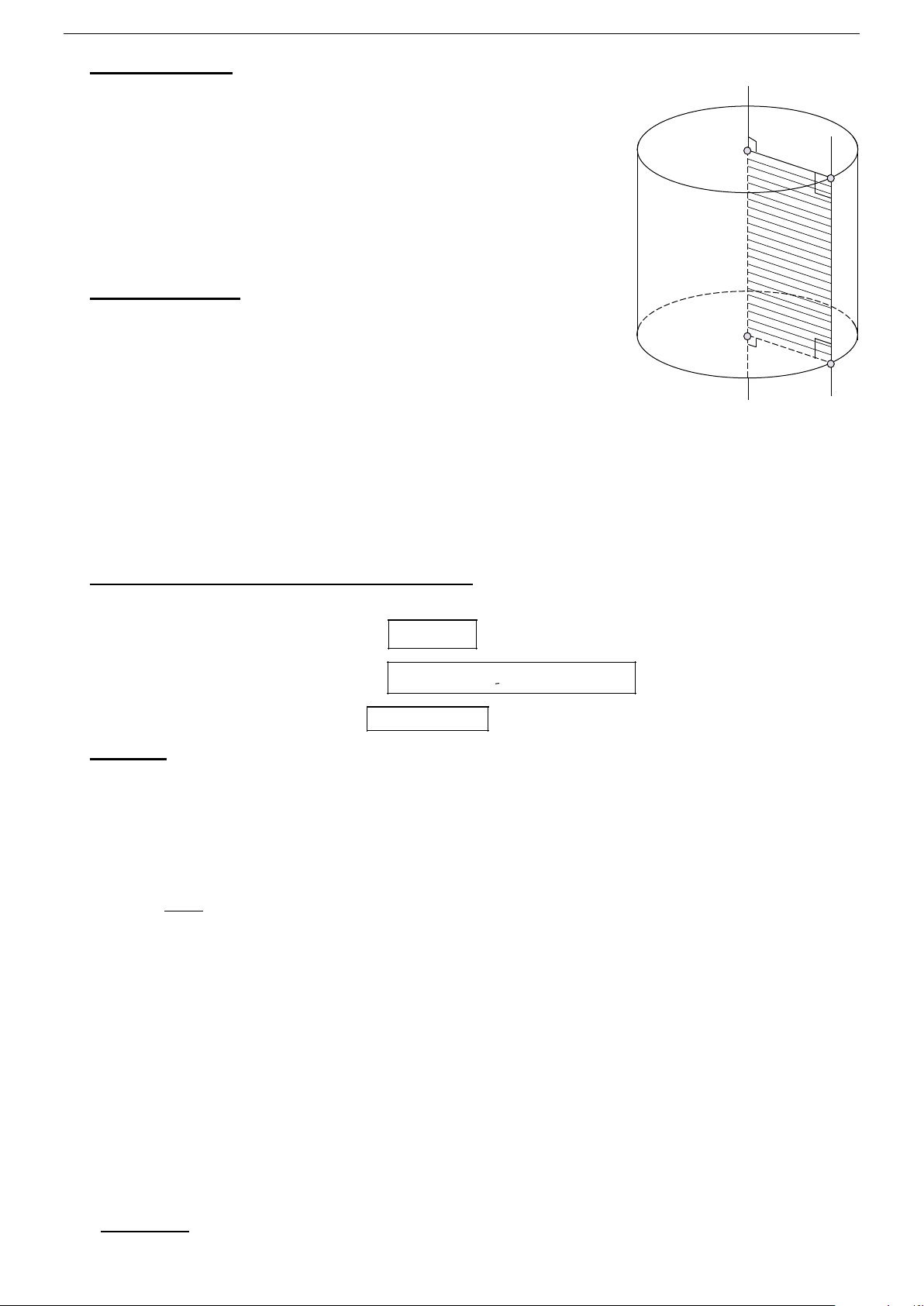
Cho mp (α ) song song với trục ∆ của mặt trụ tròn xoay và cách ∆ một khoảng d .
+ Nếu d < r thì mp (α ) cắt mặt trụ theo hai đường sinh ⇒ thiết diện là hình chữ nhật.
+ Nếu d = r thì mp (α ) tiếp xúc với mặt trụ theo một đường sinh.
+ Nếu d > r thì mp (α ) không cắt mặt trụ. III. MẶT CẦU 1/ Định nghĩa Trang 2/44
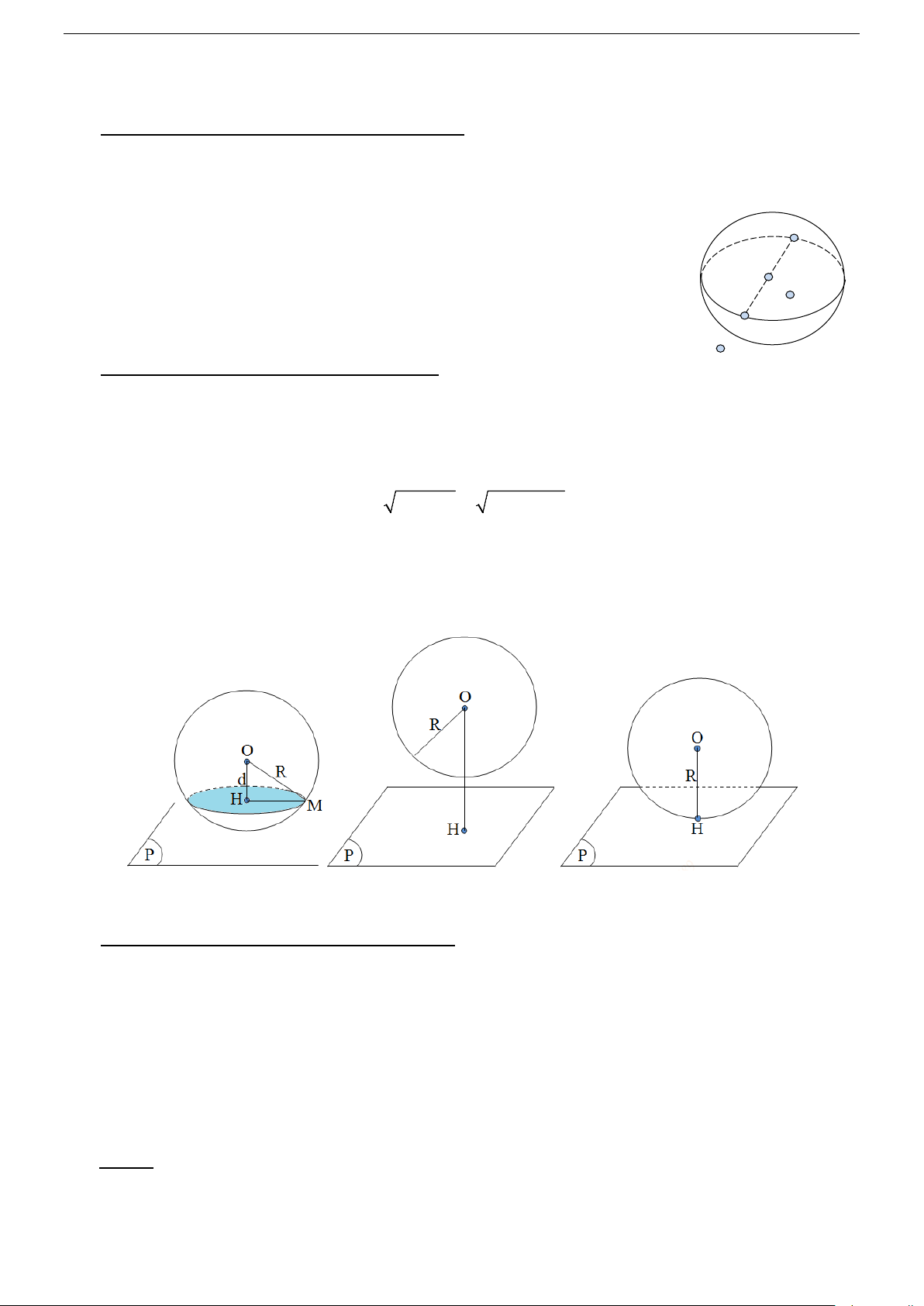
Tập hợp các điểm M trong không gian cách điểm O cố định một khoảng R gọi là mặt cầu tâm O ,
bán kính R , kí hiệu là: S (O; R) . Khi đó S (O; R) = {M | OM = R}
2/ Vị trí tương đối của một điểm đối với mặt cầu
Cho mặt cầu S (O; R) và một điểm A bất kì, khi đó:
Nếu OA = R ⇔ A∈ S (O; R) . Khi đó OA gọi là bán kính mặt cầu. Nếu OA và OB là hai bán
kính sao cho OA = OB −
thì đoạn thẳng AB gọi là một đường kính của B mặt cầu.
Nếu OA < R ⇔ Anằm trong mặt cầu. O
Nếu OA > R ⇔ Anằm ngoài mặt cầu. A A
⇒ Khối cầu S (O; R) là tập hợp tất cả các điểm M sao cho OM ≤ R . A
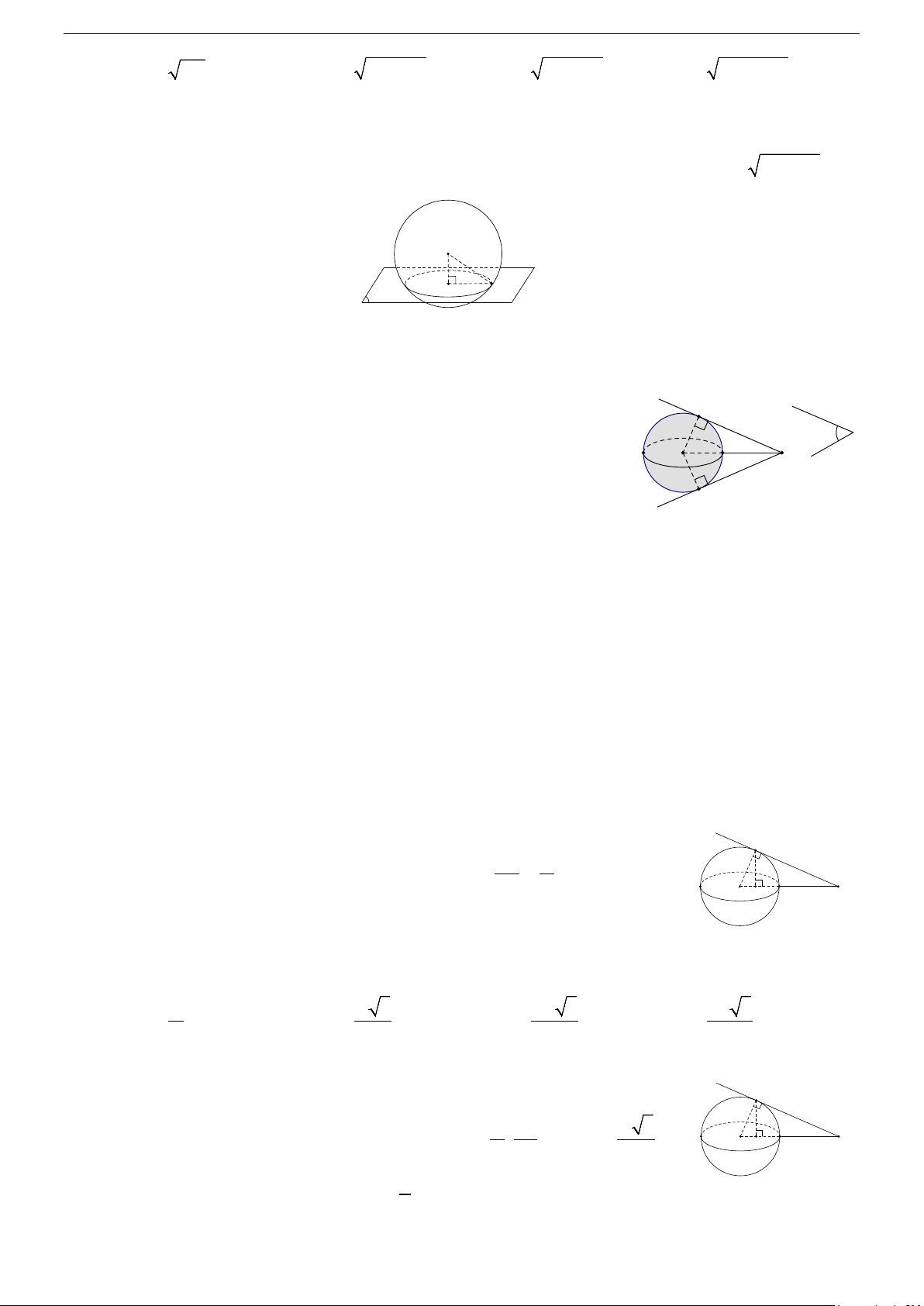
3/ Vị trí tương đối của mặt phẳng và mặt cầu
Cho mặt cầu S (O; R) và một mp (P) . Gọi d là khoảng cách từ tâm O của mặt cầu đến mp (P) và
H là hình chiếu của O trên mp (P) ⇒ d = OH .
Nếu d < R ⇔ mp (P) cắt mặt cầu S (O; R) theo giao tuyến là đường tròn nằm trên mp (P) có
tâm là H và bán kính 2 2 2 2
r = HM = R − d = R − OH (hình a).
Nếu d > R ⇔ mp (P) không cắt mặt cầu S (O; R) (hình b).
Nếu d = R ⇔ mp (P) có một điểm chung duy nhất. Ta nói mặt cầu S (O; R) tiếp xúc mp (P) .
Do đó, điều kiện cần và đủ để mp (P) tiếp xúc với mặt cầu S (O; R) là d (O,(P)) = R (hình c). d d = Hình a Hình b Hình c
4/ Vị trí tương đối của đường thẳng và mặt cầu
Cho mặt cầu S (O; R) và một đường thẳng ∆ . Gọi H là hình chiếu củaO trên đường
thẳng ∆ và d = OH là khoảng cách từ tâmO của mặt cầu đến đường thẳng ∆ . Khi đó: d
Nếu d > R ⇔ ∆ không cắt mặt cầu S (O; R) . d =
Nếu d < R ⇔ ∆ cắt mặt cầu S (O; R) tại hai điểm phân biệt.
Nếu d = R ⇔ ∆ và mặt cầu tiếp xúc nhau (tại một điểm duy nhất). Do đó: điều kiện cần và đủ để
đường thẳng ∆ tiếp xúc với mặt cầu là d = d (O, ∆) = R .
Định lí: Nếu điểm A nằm ngoài mặt cầu S (O; R) thì:
Qua A có vô số tiếp tuyến với mặt cầu S (O; R) .
Độ dài đoạn thẳng nối A với các tiếp điểm đều bằng nhau. Trang 3/44
Tập hợp các điểm này là một đường tròn nằm trên mặt cầu S (O; R) .
5/ Diện tích và thể tích mặt cầu
• Diện tích mặt cầu: 2 S = π R .
• Thể tích mặt cầu: 4 3 V = π R . C 4 C 3
B. KỸ NĂNG CƠ BẢN
I. Mặt cầu ngoại tiếp khối đa diện
1/ Các khái niệm cơ bản
Trục của đa giác đáy: là đường thẳng đi qua tâm đường tròn ngoại tiếp của đa giác đáy và vuông
góc với mặt phẳng chứa đa giác đáy.
⇒ Bất kì một điểm nào nằm trên trục của đa giác thì cách đều các đỉnh của đa giác đó.
Đường trung trực của đoạn thẳng: là đường thẳng đi qua trung điểm của đoạn thẳng và vuông
góc với đoạn thẳng đó.
⇒ Bất kì một điểm nào nằm trên đường trung trực thì cách đều hai đầu mút của đoạn thẳng.
Mặt trung trực của đoạn thẳng: là mặt phẳng đi qua trung điểm của đoạn thẳng và vuông góc với đoạn thẳng đó.
⇒ Bất kì một điểm nào nằm trên mặt trung trực thì cách đều hai đầu mút của đoạn thẳng.
2/ Tâm và bán kính mặt cầu ngoại tiếp hình chóp
Tâm mặt cầu ngoại tiếp hình chóp: là điểm cách đều các đỉnh của hình chóp. Hay nói cách khác,
nó chính là giao điểm I của trục đường tròn ngoại tiếp mặt phẳng đáy và mặt phẳng trung trực của
một cạnh bên hình chóp.
Bán kính: là khoảng cách từ I đến các đỉnh của hình chóp.
3/ Cách xác định tâm và bán kính mặt cầu của một số hình đa diện cơ bản
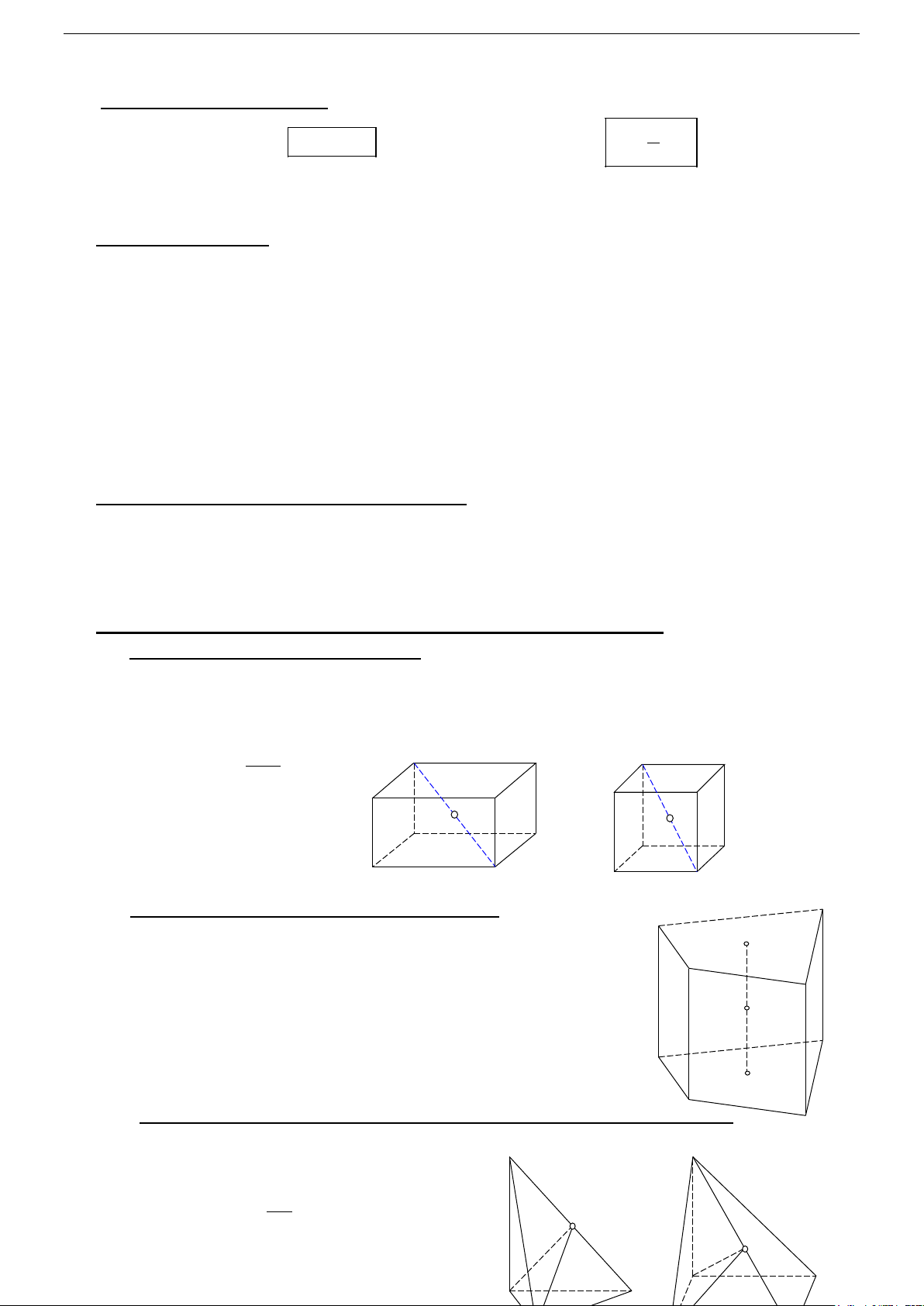
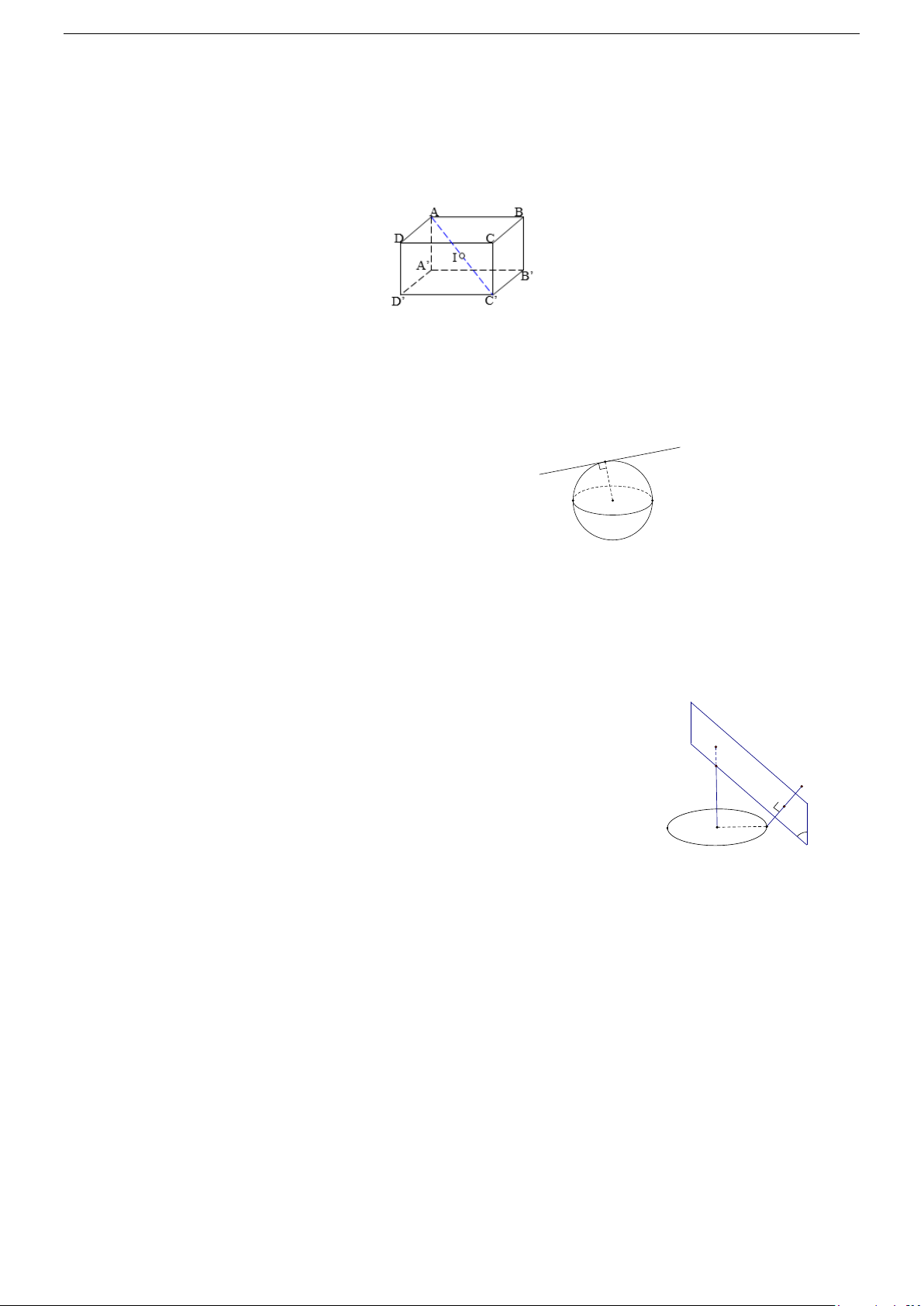
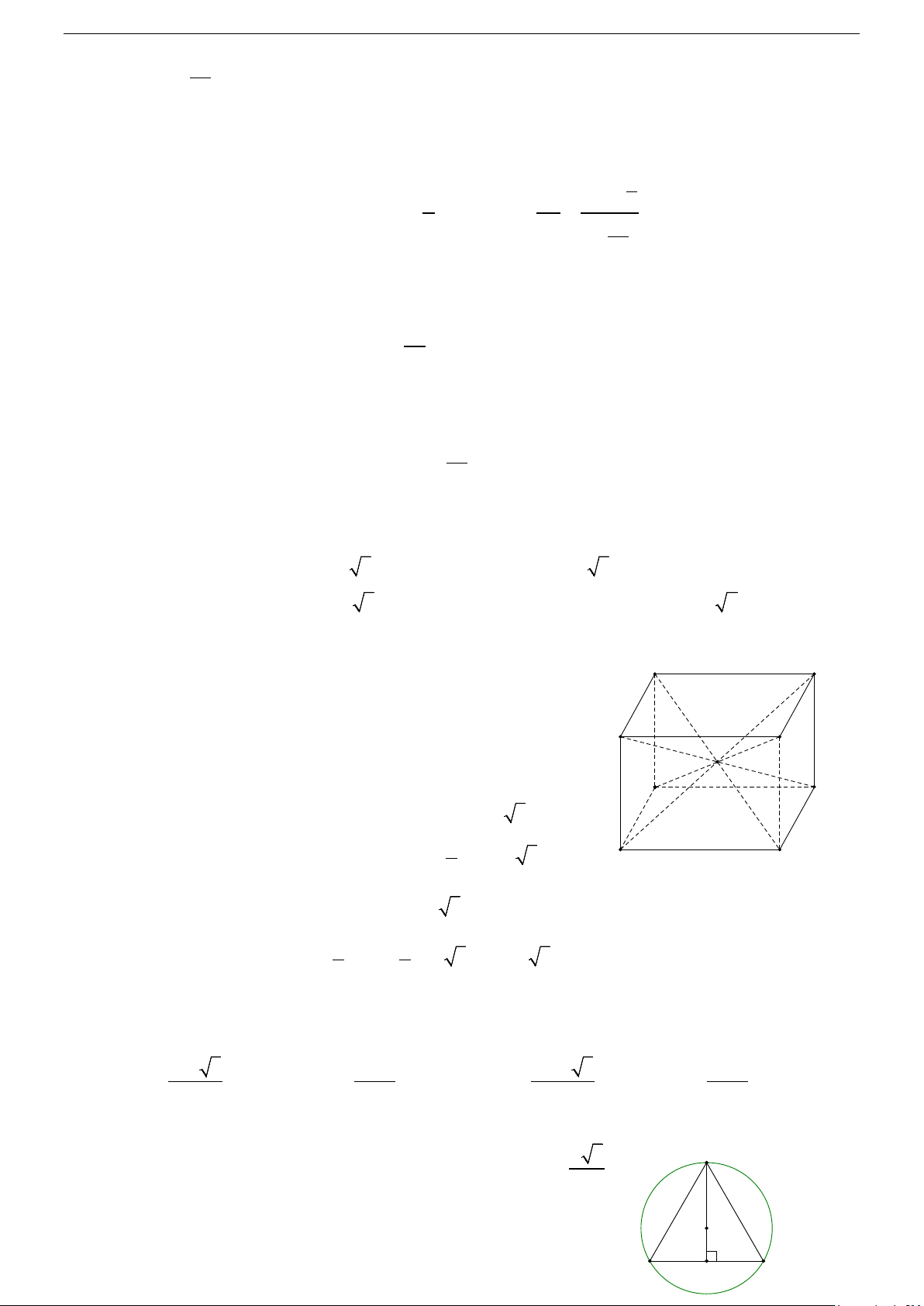
a/ Hình hộp chữ nhật, hình lập phương.
- Tâm: trùng với tâm đối xứng của hình hộp chữ nhật (hình lập phương).
⇒ Tâm là I , là trung điểm của AC ' .
- Bán kính: bằng nửa độ dài đường chéo hình hộp chữ nhật (hình lập phương). ⇒ Bán kính: AC ' R = . A B A 2 D C I A’ I B’ D’ C’ C’
b/ Hình lăng trụ đứng có đáy nội tiếp đường tròn. An
Xét hình lăng trụ đứng ' ' ' '
A A A ...A A A A A , trong đó có 2 đáy A1 n . ... 1 2 3 1 2 3 n O
A A A ...A và ' ' ' '
A A A ...A nội tiếp đường tròn (O) và (O '). Lúc đó, A2 1 2 3 n 1 2 3 n A3
mặt cầu nội tiếp hình lăng trụ đứng có: I
- Tâm: I với I là trung điểm của OO ' . A’n - Bán kính: '
R = IA = IA = ... = IA . A’ 1 2 n 1 O’ A’2
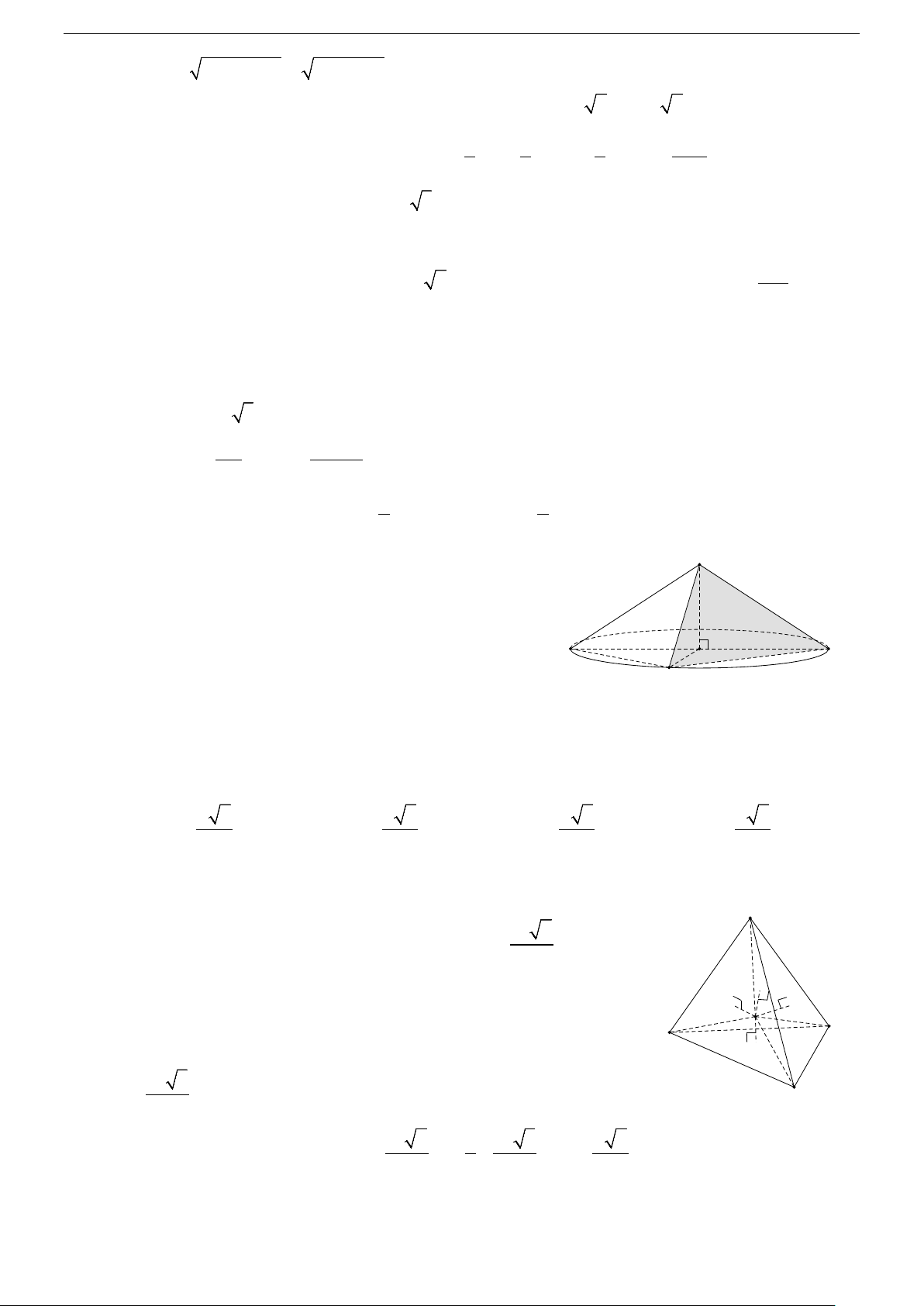
c/ Hình chóp có các đỉnh nhìn đoạn thẳng nối 2 đỉnh còn lại dưới 1 góc vuông. A’3
- Hình chóp S.ABC có SAC = 0 SBC = 90 . S S
+ Tâm: I là trung điểm của SC . + Bán kính: SC R =
= IA = IB = IC . 2 I I A Trang 4/ 44 A C
- Hình chóp S.ABCD có SAC = SBC = 0 SDC = 90 .
+ Tâm: I là trung điểm của SC . + Bán kính: SC R =
= IA = IB = IC = ID . 2
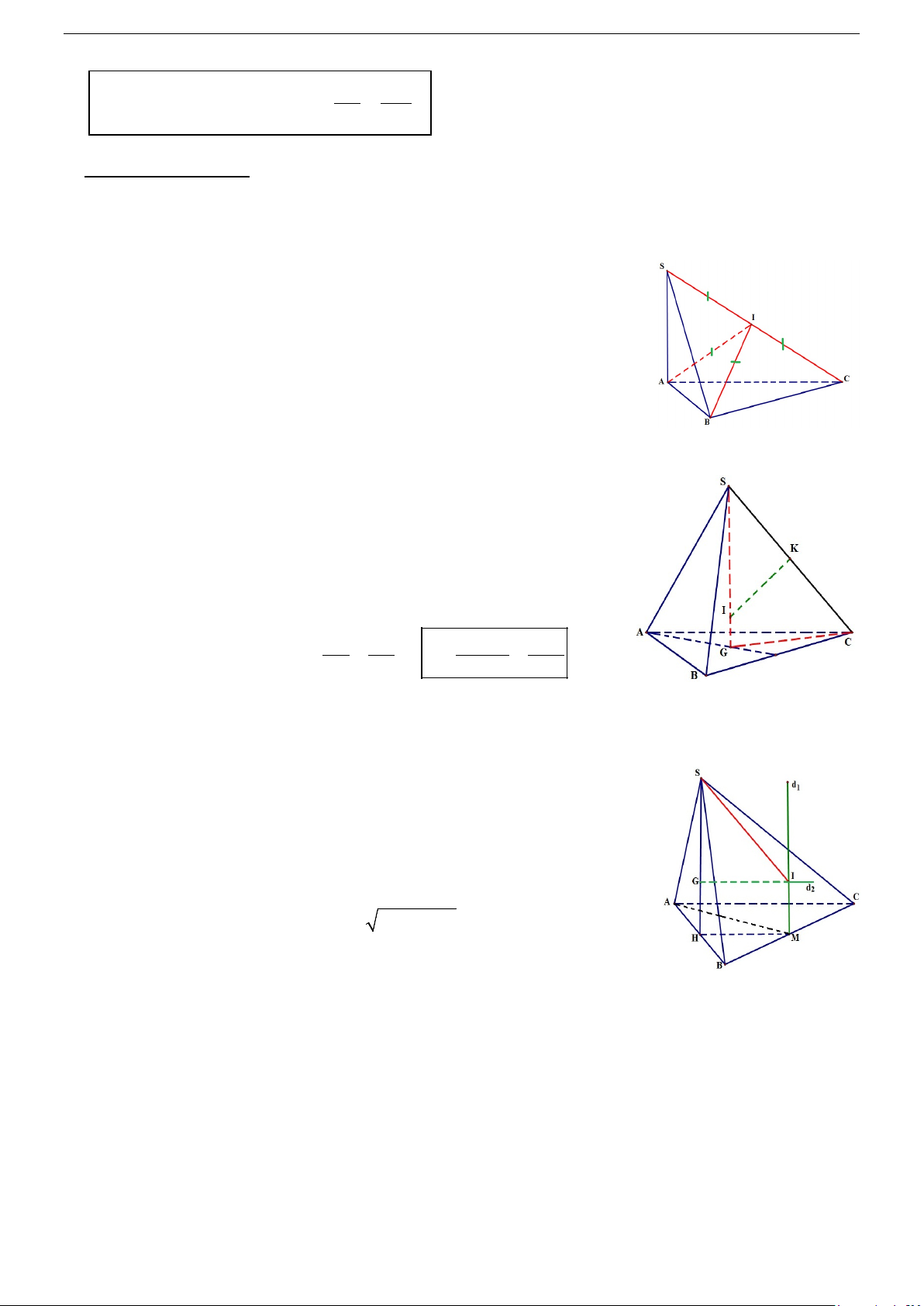
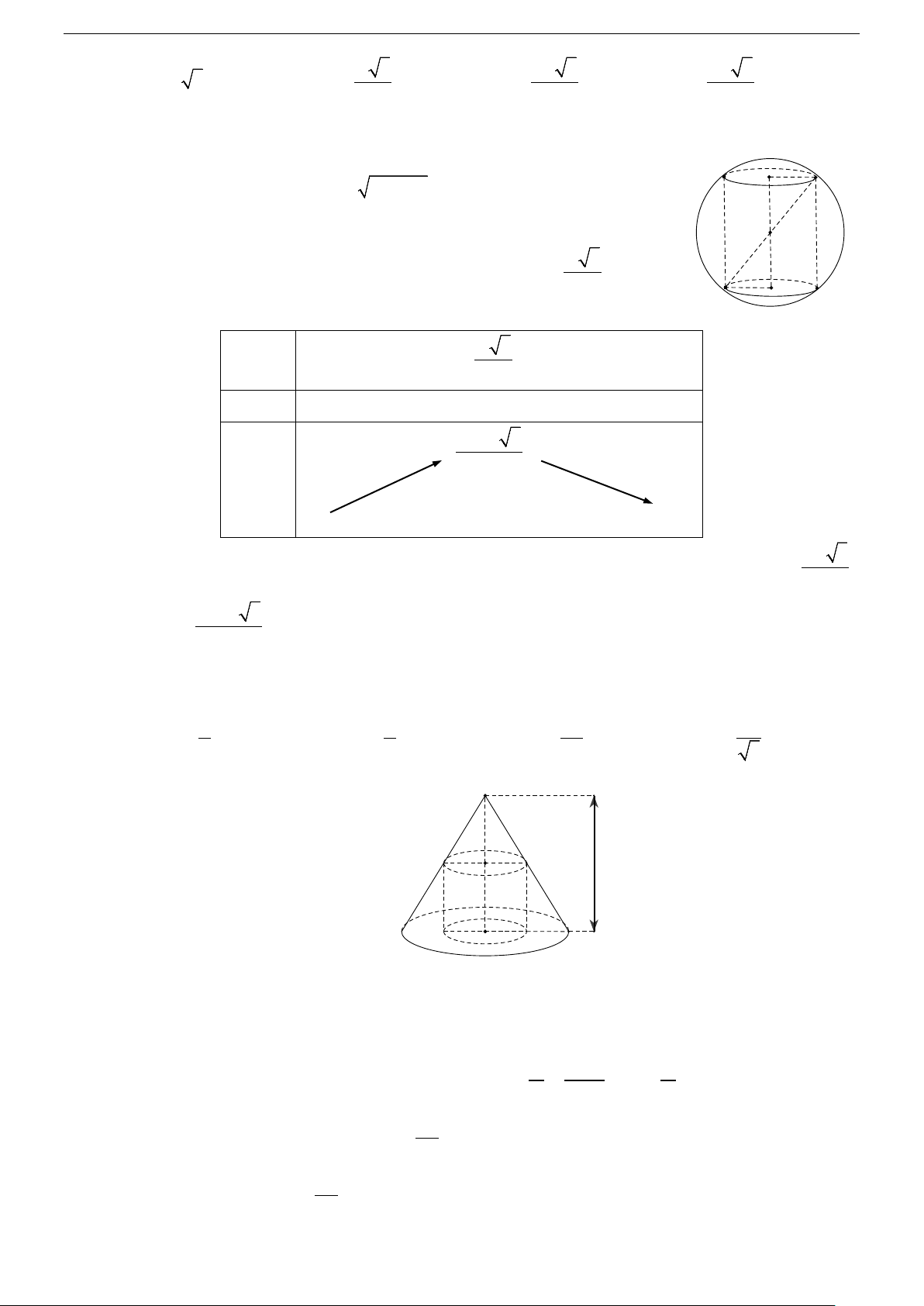
d/ Hình chóp đều. S
Cho hình chóp đều S.ABC...
- Gọi O là tâm của đáy⇒ SO là trục của đáy. ∆
- Trong mặt phẳng xác định bởi SO và một cạnh bên, M
chẳng hạn như mp (SAO) , ta vẽ đường trung trực của cạnh SA
là ∆ cắt SA tại M và cắt SO tại I ⇒ I là tâm của mặt cầu. I - Bán kính: A Ta có: SM SI SM ∆ I SO ∆ A ⇒ = ⇒ Bán kính là: O D SO SA B 2 SM.SA SA R = IS = =
= IA = IB = IC = ... SO 2SO C
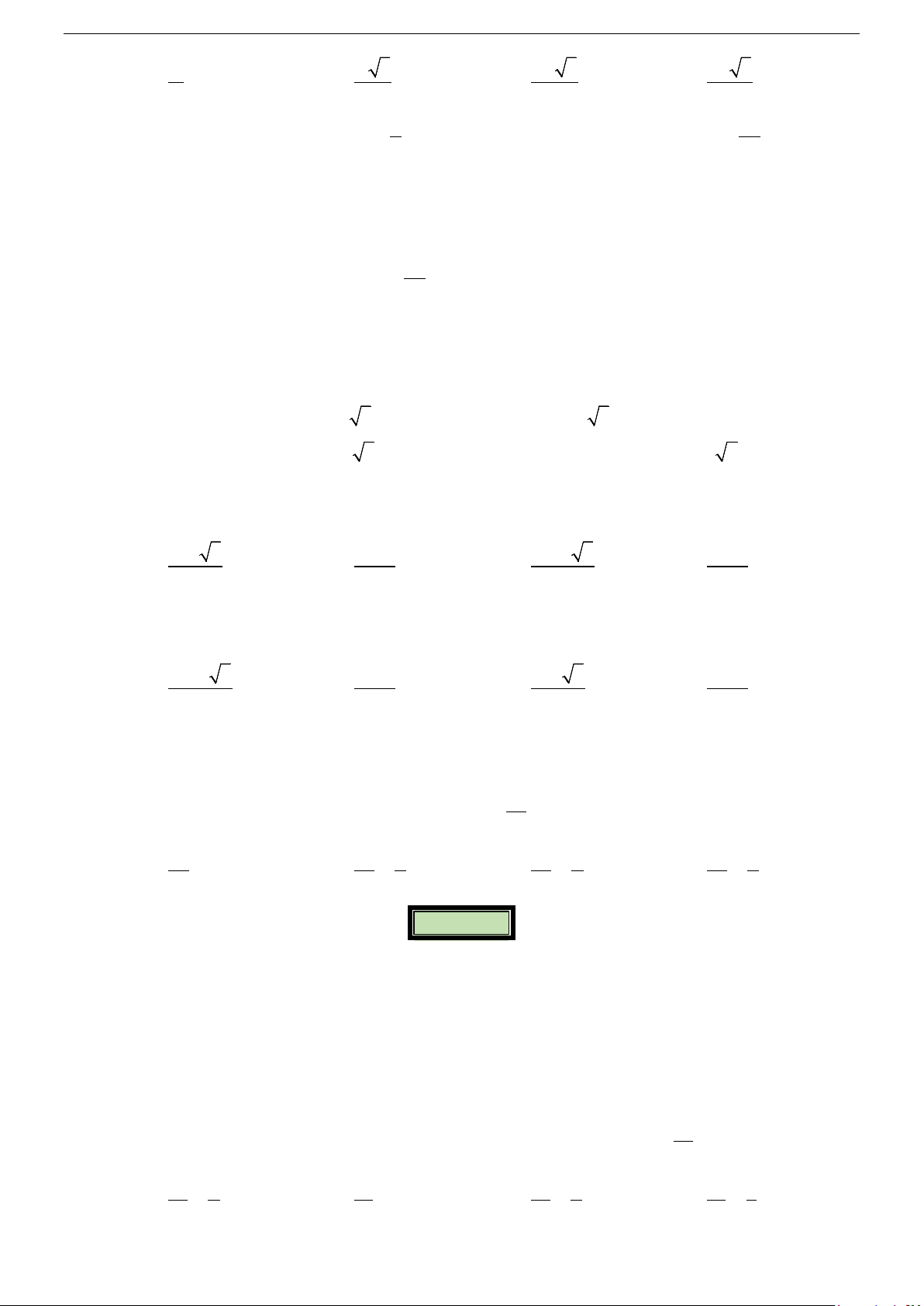
e/ Hình chóp có cạnh bên vuông góc với mặt phẳng đáy.
Cho hình chóp S.ABC... có cạnh bên SA ⊥ đáy ( ABC...) và đáy ABC... nội tiếp được trong
đường tròn tâm O . Tâm và bán kính mặt cầu ngoại tiếp hình chóp S.ABC... được xác định như sau:
- Từ tâm O ngoại tiếp của đường tròn đáy, ta vẽ đường thẳng d vuông góc với mp ( ABC...) tại O .
- Trong mp (d, SA) , ta dựng đường trung trực ∆ của cạnh SA , cắt SA tại M , cắt d tại I . S
⇒ I là tâm mặt cầu ngoại tiếp hình chóp
và bán kính R = IA = IB = IC = IS = ... d - Tìm bán kính:
Ta có: MIOB là hình chữ nhật. M ∆ I Xét M
∆ AI vuông tại M có: 2 2 2 2 SA R AI MI MA AO = = + = + . 2 O A C
f/ Hình chóp kháC. B
- Dựng trục ∆ của đáy.
- Dựng mặt phẳng trung trực (α ) của một cạnh bên bất kì.
- (α ) ∩ ∆ = I ⇒ I là tâm mặt cầu ngoại tiếp hình chóp.
- Bán kính: khoảng cách từ I đến các đỉnh của hình chóp.
g/ Đường tròn ngoại tiếp một số đa giác thường gặp.
Khi xác định tâm mặt cầu, ta cần xác định trục của mặt phẳng đáy, đó chính là đường thẳng vuông
góc với mặt phẳng đáy tại tâm O của đường tròn ngoại tiếp đáy. Do đó, việc xác định tâm ngoại O
là yếu tố rất quan trọng của bài toán. O O O Trang 5/44
II. KỸ THUẬT XÁC ĐỊNH MẶT CẦU NGOẠI TIẾP HÌNH CHÓP.
Cho hình chóp S.A A ...A (thoả mãn điều kiện tồn tại mặt cầu ngoại tiếp). Thông thường, để xác định 1 2 n
mặt cầu ngoại tiếp hình chóp ta thực hiện theo hai bước:
Bước 1: Xác định tâm của đường tròn ngoại tiếp đa giác đáy. Dựng ∆ : trục đường tròn ngoại tiếp đa giác đáy.
Bước 2: Lập mặt phẳng trung trực (α) của một cạnh bên.
Lúc đó : - Tâm O của mặt cầu: ∆ ∩ mp(α) = {O}
- Bán kính: R = SA(= SO) . Tuỳ vào từng trường hợp.
Lưu ý: Kỹ năng xác định trục đường tròn ngoại tiếp đa giác đáy.
1. Trục đường tròn ngoại tiếp đa giác đáy: là đường thẳng đi qua tâm đường tròn ngoại tiếp đáy và
vuông góc với mặt phẳng đáy.
Tính chất: M
∀ ∈ ∆ : MA = MB = MC
Suy ra: MA = MB = MC ⇔ M ∈ ∆
2. Các bước xác định trục:
- Bước 1: Xác định tâm H của đường tròn ngoại tiếp đa giác đáy.
- Bước 2: Qua H dựng ∆ vuông góc với mặt phẳng đáy.
VD: Một số trường hợp đặc biệt A. Tam giác vuông B. Tam giác đều C. Tam gi ∆ ác bất kì ∆ ∆ B H B C B C H C H A A S A
3. Lưu ý: Kỹ năng tam giác đồng dạng M O Trang 6/44 I A SM ∆
O đồng dạng với SO SM SI ∆ A ⇒ = . SA SI
4. Nhận xét quan trọng:
MA = MB = MC ∃M , S :
⇒ SM là trục đường tròn ngoại tiếp ABC ∆ .
SA = SB = SC
5. Ví dụ: Tìm tâm và bán kính mặt cầu ngoại tiếp hình chóp
Dạng 1: Chóp có các điểm cùng nhìn một đoạn dưới một góc vuông. SA ⊥ ( ABC) BC ⊥ AB (gt)
Ví dụ: Cho S.ABC :
. Theo đề bài: A ∆ BC ⊥ B BC ⊥ SA (SA ⊥ ( ABC))
⇒ BC ⊥ (SAB) ⇒ BC ⊥ SB
Ta có B và A nhìn SC dưới một góc vuông
⇒ nên B và A cùng nằm trên một mặt cầu có đường kính là SC.
Gọi I là trung điểm SC ⇒ I là tâm MCNT khối chóp S.ABC và bán kính R = SI .
Dạng 2: Chóp có các cạnh bên bằng nhau.
Ví dụ: Cho hình chóp tam giác đều S.ABC .
+ Vẽ SG ⊥ ( ABC) thì G là tâm đường tròn ngoại tiếp A ∆ BC .
+ Trên mặt phẳng (SGC) , vẽ đường trung trực của SC , đường này cắt
SG tại I thì I là tâm mặt cầu ngoại tiếp S.ABC và bán kính R = IS . 2 + Ta có ∆ ∆ ( − ) SG SC SC.SK SC SGC SKI g g ⇒ = ⇒ R = = SK SI SG 2SG
Dạng 3: Chóp có một mặt bên vuông góc với đáy.
Ví dụ: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A . Mặt bên (SAB) ⊥ ( ABC) và S ∆ AB
đều. Gọi H, M lần lượt là trung điểm của AB, AC .
Ta có M là tâm đường tròn ngoại tiếp A
∆ BC (do MA = MB = MC ).
Dựng d là trục đường tròn ngoại tiếp A
∆ BC ( d qua M và song song SH ). 1 1
Gọi G là tâm đường tròn ngoại tiếp S
∆ AB và d là trục đường tròn ngoại 2 tiếp S
∆ AB , d cắt d tại I ⇒ I là tâm mặt cầu ngoại tiếp khối chóp S.ABC 2 1
⇒ Bán kính R = SI . Xét 2 2 SG
∆ I → SI = GI + SG . Trang 7/44
C. BÀI TẬP TRẮC NGHIỆM MẶT CẦU
Câu 1. Cho một mặt cầu có diện tích là S , thể tích khối cầu đó là V . Tính bán kính R của mặt cầu. A. 3V R = . B. S R = . C. 4V R = . D. V R = . S 3V S 3S
Câu 2. Cho mặt cầu S(O; R) và điểm A cố định với OA = d . Qua A , kẻ đường thẳng ∆ tiếp xúc với
mặt cầu S(O; R) tại M . Công thức nào sau đây được dùng để tính độ dài đoạn thẳng AM ? A. 2 2 2R − d . B. 2 2 d − R . C. 2 2 R − 2d . D. 2 2 d + R .
Câu 3. Một hình hộp chữ nhật có ba kích thước là a, ,
b c . Gọi (S) là mặt cầu đi qua 8 đỉnh của hình
hộp chữ nhật đó. Tính diện tích của hình cầu (S) theo a, , b c . A. 2 2 2
π (a + b + c ) . B. 2 2 2
2π (a + b + c ) . π C. 2 2 2
4π (a + b + c ) . D. 2 2 2
(a + b + c ) . 2
Câu 4. Một hình hộp chữ nhật có ba kích thước là a, ,
b c . Gọi (S) là mặt cầu đi qua 8 đỉnh của hình
hộp chữ nhật đó. Tâm của mặt cầu (S) là
A. một đỉnh bất kì của hình hộp chữ nhật.
B. tâm của một mặt bên của hình hộp chữ nhật.
C. trung điểm của một cạnh của hình hộp chữ nhật.
D. tâm của hình hộp chữ nhật.
Câu 5. Cho mặt cầu S(O; R) và đường thẳng ∆ . Biết khoảng cách từ O tới ∆ bằng d . Đường thẳng
∆ tiếp xúc với S(O; R) khi thỏa mãn điều kiện nào trong các điều kiện sau ?
A. d = R .
B. d > R .
C. d < R .
D. d ≠ R .
Câu 6. Cho đường tròn (C) và điểm A nằm ngoài mặt phẳng chứa (C) . Có tất cả bao nhiêu mặt cầu
chứa đường tròn (C) và đi qua A ? A. 2. B. 0. C. 1. D. vô số.
Câu 7. Cho hai điểm ,
A B phân biệt. Tập hợp tâm những mặt cầu đi qua A và B là
A. mặt phẳng trung trực của đoạn thẳng AB . B. đường thẳng trung trực của AB .
C. mặt phẳng song song với đường thẳng AB . D. trung điểm của đoạn thẳng AB .
Câu 8. Cho mặt cầu S(O; R) và mặt phẳng (α) . Biết khoảng cách từ O tới (α) bằng d . Nếu d < R
thì giao tuyến của mặt phẳng (α) với mặt cầu S(O; R) là đường tròn có bán kính bằng bao nhiêu? A. Rd . B. 2 2 R + d . C. 2 2 R − d . D. 2 2 R − 2d .
Câu 9. Từ điểm M nằm ngoài mặt cầu S(O; R) có thể kẻ được bao nhiêu tiếp tuyến với mặt cầu? A. Vô số. B. 0. C. 1. D. 2.
Câu 10. Một đường thẳng d thay đổi qua A và tiếp xúc với mặt cầu S(O; R) tại M . Gọi H là hình
chiếu của M lên đường thẳng OA . M thuộc mặt phẳng nào trong những mặt phẳng sau đây?
A. Mặt phẳng qua H và vuông góc với OA . B. Mặt phẳng trung trực của OA .
C. Mặt phẳng qua O và vuông góc với AM . D. Mặt phẳng qua A và vuông góc với OM .
Câu 11. Một đường thẳng thay đổi d qua A và tiếp xúc với mặt cầu S(O; R) tại M . Gọi H là hình
chiếu của M lên đường thẳng OA . Độ dài đoạn thẳng MH tính theo R là: Trang 8/44 A. R . B. R 3 . C. 2R 3 . D. 3R 3 . 2 3 3 4
Câu 12. Thể tích của một khối cầu là 1 3
113 cm thì bán kính nó là bao nhiêu ? (lấy 22 π ≈ ) 7 7 A. 6cm . B. 2cm . C. 4cm . D. 3cm .
Câu 13. Khinh khí cầu của nhà Mông–gôn–fie (Montgolfier) (người Pháp) phát minh ra khinh khí cầu
dùng khí nóng. Coi khinh khí cầu này là một mặt cầu có đường kính 11m thì diện tích của mặt
khinh khí cầu là bao nhiêu? (lấy 22 π ≈
và làm tròn kết quả đến chữ số thập phân thứ hai). 7 A. 2 379,94 (m ) . B. 2 697,19 (m ) . C. 190,14cm . D. 2 95,07 (m ) .
Câu 14. Cho hình lập phương ABC .
D A' B 'C ' D ' có độ dài mỗi cạnh là 10cm . Gọi O là tâm mặt cầu đi
qua 8 đỉnh của hình lập phương. Khi đó, diện tích S của mặt cầu và thể tích V của hình cầu là: A. 2 3
S = 150π (cm );V = 125 3 (cm ) . B. 2 3
S = 100 3π (cm );V = 500(cm ) . C. 2 3
S = 300π (cm );V = 500 3 (cm ) . D. 2 3
S = 250π (cm );V = 500 6 (cm ) .
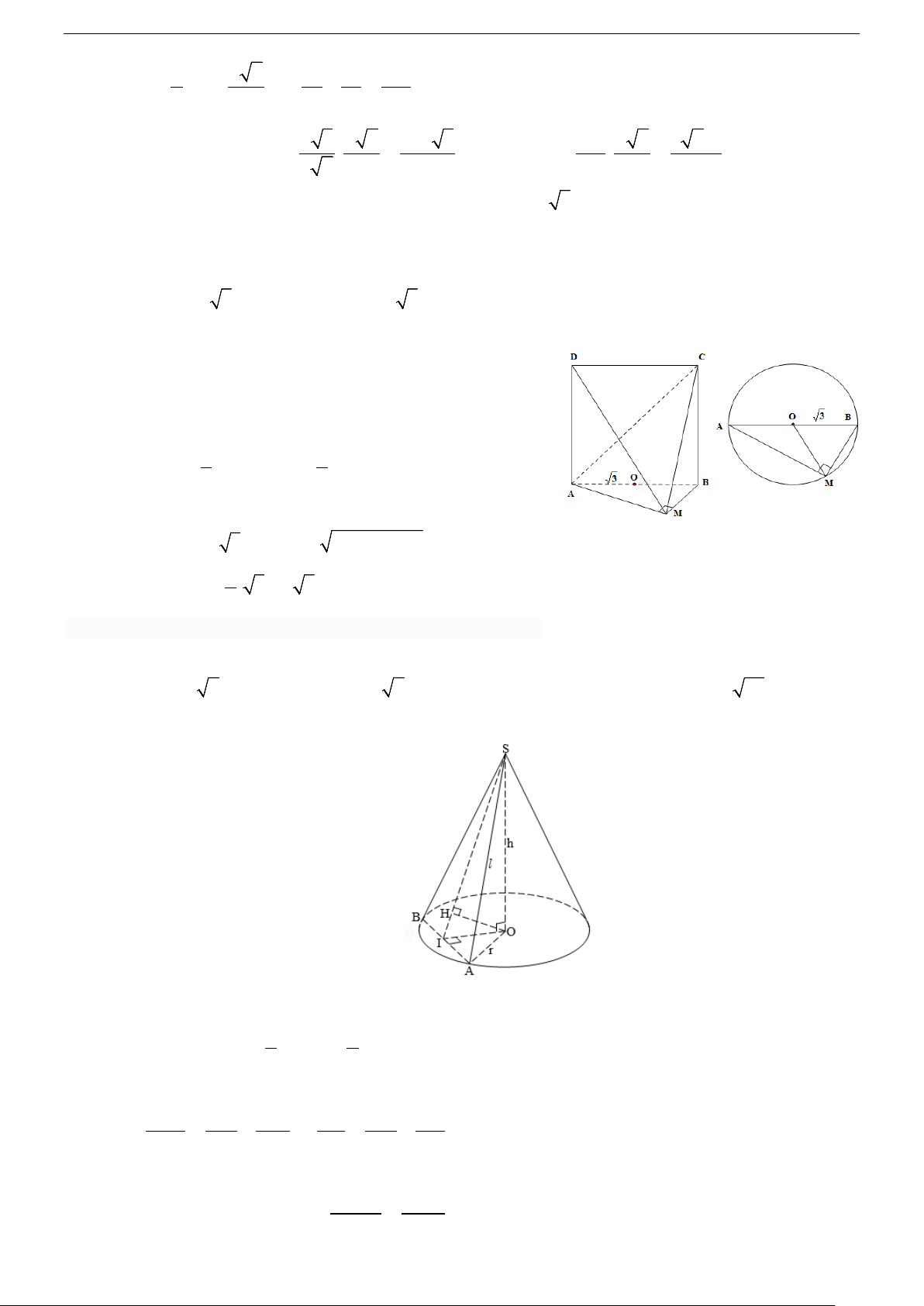
Câu 15. Cho đường tròn (C) ngoại tiếp một tam giác đều ABC có cạnh bằng a , chiều cao AH . Quay
đường tròn (C) xung quanh trục AH , ta được một mặt cầu. Thể tích của khối cầu tương ứng là: 3 π 3 π 3 π 3 π A. a 3 . B. 4 a . C. 4 a 3 . D. 4 a . 54 9 27 3
Câu 16. Cho đường tròn (C) ngoại tiếp một tam giác đều ABC có cạnh bằng a , chiều cao AH . Quay
đường tròn (C) xung quanh trục AH , ta được một mặt cầu. Thể tích của khối cầu tương ứng là: 3 π 3 π 3 π 3 π A. 4 a 3 . B. 4 a . C. a 3 . D. 4 a . 27 9 54 3
Câu 17. Cho tam giác ABC vuông tại A có BC = 2a và 0
B = 30 . Quay tam giác vuông này quanh
trục AB , ta được một hình nón đỉnh B . Gọi S là diện tích toàn phần của hình nón đó và S là 1 2
diện tích mặt cầu có đường kính AB . Khi đó, tỉ số S1 là: S2 A. S S 1 S 2 S 3 1 = 1. B. 1 = . C. 1 = . D. 1 = . S S 2 S 3 S 2 2 2 2 2 MẶT NÓN
Câu 18. Cho hình nón có thiết diện qua trục là một tam giác đều cạnh 2a , diện tích xung quanh là S 1
và mặt cầu có đường kính bằng chiều cao hình nón, có diện tích S . Khẳng định nào sau đây là 2 khẳng định đúng ?
A. 2S = 3S .
B. S = 4S .
C. S = 2S .
D. S = S . 2 1 1 2 2 1 1 2
Câu 19. Cho hình nón có thiết diện qua trục là một tam giác đều cạnh 2a , có thể tích V và hình cầu có 1
đường kính bằng chiều cao hình nón, có thể tích V . Khi đó, tỉ số thể tích V1 bằng bao nhiêu? 2 V2 A. V 2 V V 1 V 1 1 = . B. 1 = 1. C. 1 = . D. 1 = . V 3 V V 2 V 3 2 2 2 2 Trang 9/44
Câu 20. Tính diện tích xung quanh của hình trụ biết hình trụ có bán kính đáy a và đường cao là a 3 . A. 2 2π a . B. 2 2π a 3 . C. 2 π a . D. 2 π a 3 .
Câu 21. Một hình nón có thiết diện qua trục là một tam giác vuông cân có cạnh góc vuông bằng a .
Tính diện tích xung quanh của hình nón. 2 π 2 π 2 π A. a 2 . B. a 2 . C. 2 π a 2 . D. 2 a 2 . 4 2 3
Câu 22. Thiết diện đi qua trục của hình nón đỉnh S là tam giác vuông cân SAB có cạnh cạnh huyền
bằng a 2 . Diện tích toàn phần S của hình nón và thể tích V của khối nón tương ứng đã cho là tp 2 3 π + π 2 3 π π A. a (1 2) a 2 S = V = . B. a 2 a 2 S = V = . tp ; tp ; 2 12 2 4 3 π 2 3 π − π C. 2 a 2 S = π a + V = . D. a ( 2 1) a S = V = . tp ; tp (1 2); 6 2 12
Câu 23. Cho hình nón tròn xoay có đỉnh là S , O là tâm của đường tròn đáy, đường sinh bằng a 2 và
góc giữa đường sinh và mặt phẳng đáy bằng 0
60 . Diện tích xung quanh S của hình nón và thể xq
tích V của khối nón tương ứng là: 3 π 2 3 π π A. 2 a 6 S = π a V = . B. a a 3 S = V = . xq ; xq ; 12 2 12 3 π 3 π C. 2 a 6 S = π a V = . D. 2 a 6 S = π a V = . xq ; xq 2; 4 4
Câu 24. Một hình nón có đường kính đáy là 2a 3 , góc ở đỉnh là 0
120 . Tính thể tích của khối nón đó theo a . A. 3 3π a . B. 3 π a . C. 3 2 3π a . D. 3 π a 3 .
Câu 25. Trong không gian, cho tam giác ABC vuông tại A , AB = a và AC = 3a . Tính độ dài đường
sinh l của hình nón, nhận được khi quay tam giác ABC xung quanh trục AB .
A. l = a .
B. l = 2a .
C. l = 3a .
D. l = 2a . MẶT TRỤ
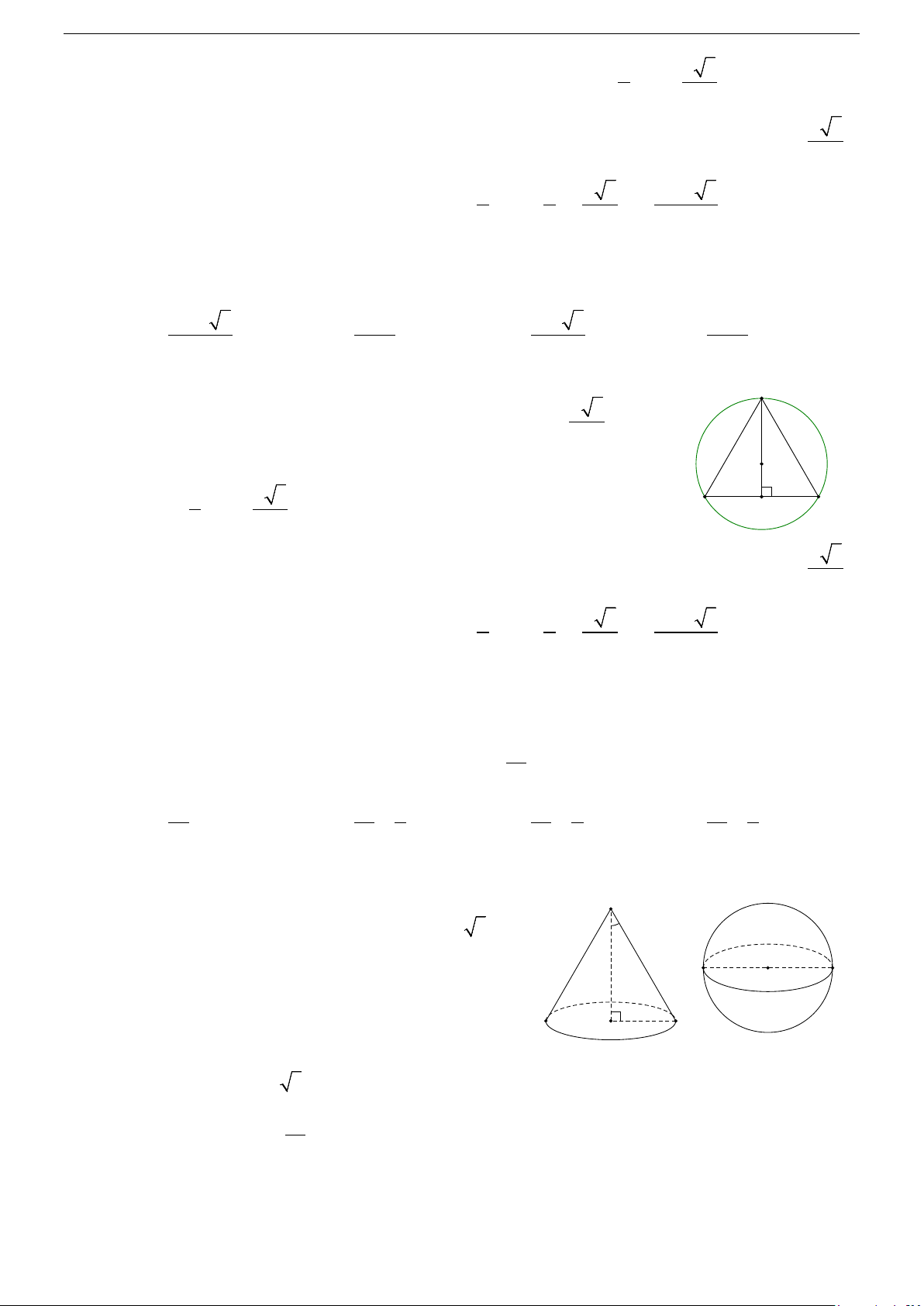
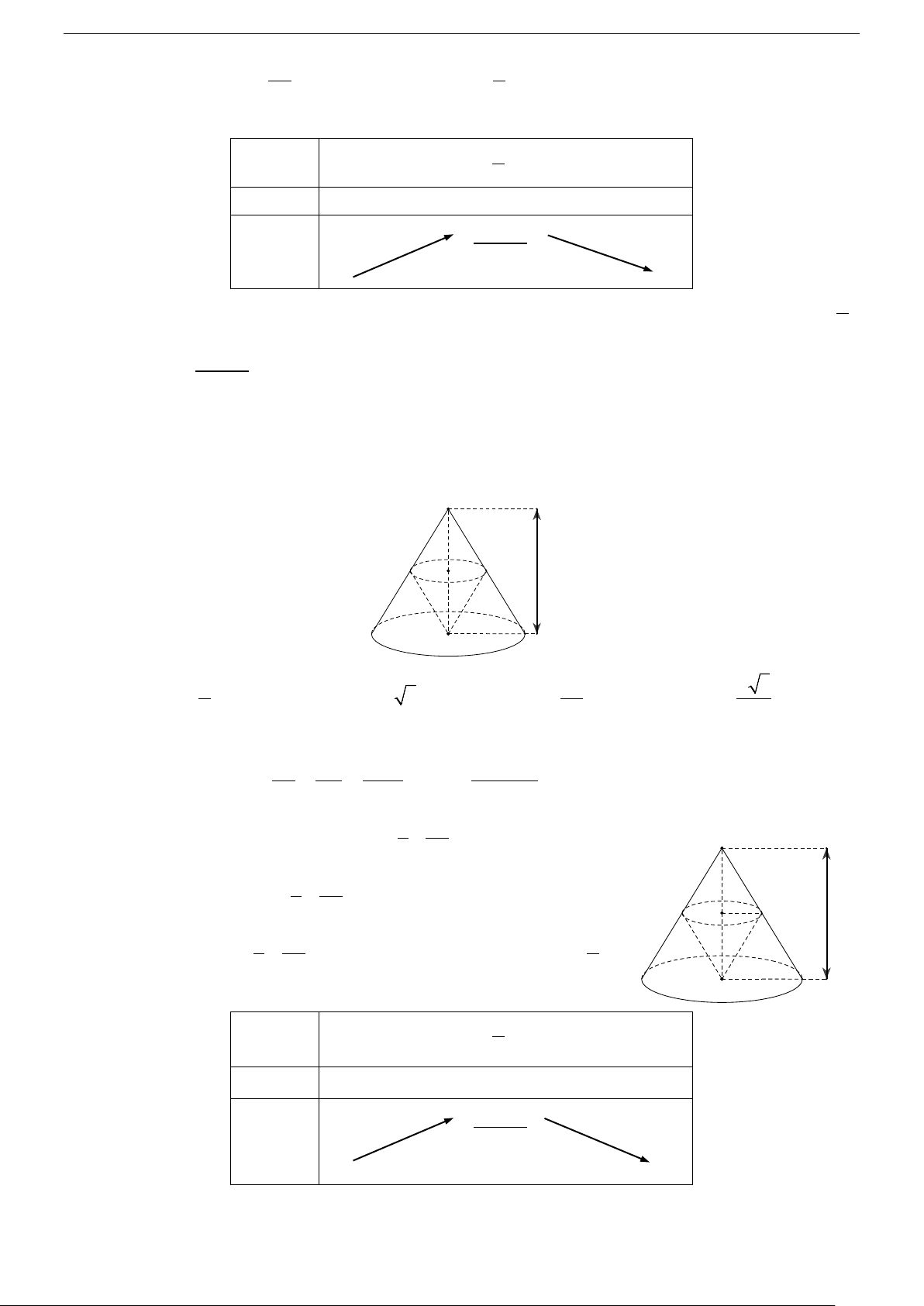
Câu 26. Cho một hình trụ có bán kính đáy R , chiều cao h và thể tích V ; một hình nón có đáy trùng 1
với một đáy của hình trụ, có đỉnh trùng với tâm đáy còn lại của hình trụ (hình vẽ bên dưới) và có thể tích V . 2
Khẳng định nào sau đây là khẳng định đúng ? h R
A. V = 3V .
B. V = 2V .
C. V = 3V .
D. V = V . 2 1 1 2 1 2 2 1
Câu 27. Tính thể tích V của khối trụ có bán kính đáy R , chiều cao là h . A. 2 V = π R h . B. 2 V = π Rh . C. 2 V = π Rh .
D. V = 2π Rh . Trang 10/44
Câu 28. Một hình trụ có bán kính đáy a , có thiết diện qua trục là một hình vuông. Tính diện tích xung quanh của hình trụ. A. 2 π a . B. 2 2π a . C. 2 3π a . D. 2 4π a .
Câu 29. Tính diện tích toàn phần của hình trụ có bán kính đáy a và đường cao a 3 . A. 2 2π a ( 3 − ) 1 . B. 2 π a 3 . C. 2 π a (1+ 3). D. 2 2π a (1+ 3).
Câu 30. Tính thể tích của khối trụ biết bán kính đáy của hình trụ đó bằng a và thiết diện đi qua trục là một hình vuông. A. 3 2π a . B. 2 3 π a . C. 3 4π a . D. 3 π a . 3
Câu 31. Tính thể tích của khối trụ biết chu vi đáy của hình trụ đó bằng 6π (cm) và thiết diện đi qua trục
là một hình chữ nhật có độ dài đường chéo bằng 10 (cm) . A. 3 48π (cm ) . B. 3 24π (cm ) . C. 3 72π (cm ) . D. 3 18π 3472π (cm ) .
Câu 32. Trong không gian, cho hình chữ nhật ABCD có AB = 1 và AD = 2 . Gọi M, N lần lượt là
trung điểm của AD và BC . Quay hình chữ nhật đó xung quanh trục MN, ta được một hình trụ.
Tính diện tích toàn phần S của hình trụ đó. tp A. S = π . B. S = π . C. S = π . D. S = π . tp 10 tp 4 tp 2 tp 6
Câu 33. Từ một tấm tôn hình chữ nhật kích thước 50cm x 240cm, người ta làm các thùng đựng nước
hình trụ có chiều cao bằng 50cm, theo hai cách sau (xem hình minh họa dưới đây):
- Cách 1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng.
- Cách 2: Cắt tấm tôn ban đầu thành hai tấm bằng nhau, rồi gò mỗi tấm đó thành mặt xung quanh của một thùng.
Kí hiệu V là thể tích của thùng gò được theo cách 1 và V là tổng thể tích của hai thùng gò 1 2
được theo cách 2. Tính tỉ số V1 . V2 A. V V V 1 V 1 = 1. B. 1 = 2 . C. 1 = . D. 1 = 4 . V V V 2 V 2 2 2 2 VẬN DỤNG THẤP
Câu 34. Tính bán kính của mặt cầu ngoại tiếp hình tứ diện đều cạnh a . A. a 3 . B. a 6 . C. a 6 . D. a 2 . 2 2 4 4
Câu 35. Tính bán kính của mặt cầu ngoại tiếp hình chóp tam giác đều S.ABC , biết các cạnh đáy có độ
dài bằng a , cạnh bên SA = a 3 . A. 2a 3 . B. 3a 3 . C. a 3 . D. 3a 6 . 2 2 2 8 8 Trang 11/44
Câu 36. Tính bán kính của mặt cầu ngoại tiếp hình chóp tứ giác đều có cạnh đáy bằng a , cạnh bên bằng 2a . A. 2a 14 . B. 2a 7 . C. 2a 7 . D. 2a 2 . 7 2 3 2 7
Câu 37. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác
đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối cầu ngoại tiếp hình chóp đã cho. π π π π A. 5 V = . B. 5 15 V = . C. 4 3 V = . D. 5 15 V = . 3 18 27 54
Câu 38. Một hình lăng trụ tam giác đều có cạnh đáy bằng a , cạnh bên bằng 2a . Tính bán kính mặt cầu
ngoại tiếp hình lăng trụ đó. A. a 39 . B. a 12 . C. 2a 3 . D. 4a . 6 6 3 3
Câu 39. Cho hình trụ có bán kính đáy là R , thiết diện qua trục là một hình vuông. Tính thể tích khối
lăng trụ tứ giác đều nội tiếp trong hình trụ đã cho theo R . A. 3 4R . B. 3 2 2R . C. 3 4 2R . D. 3 8R .
Câu 40. Cho hình trụ có bán kính đáy là 4 cm, một mặt phẳng không vuông góc với đáy và cắt hai mặt
đáy theo hai dây cung song song AB, A' B ' mà AB = A' B ' = 6cm (hình vẽ). Biết diện tích tứ giác
ABB ' A' bằng 60 cm2. Tính chiều cao của hình trụ đã cho. A. 6 2 cm. B. 4 3 cm. C. 8 2 cm. D. 5 3 cm.
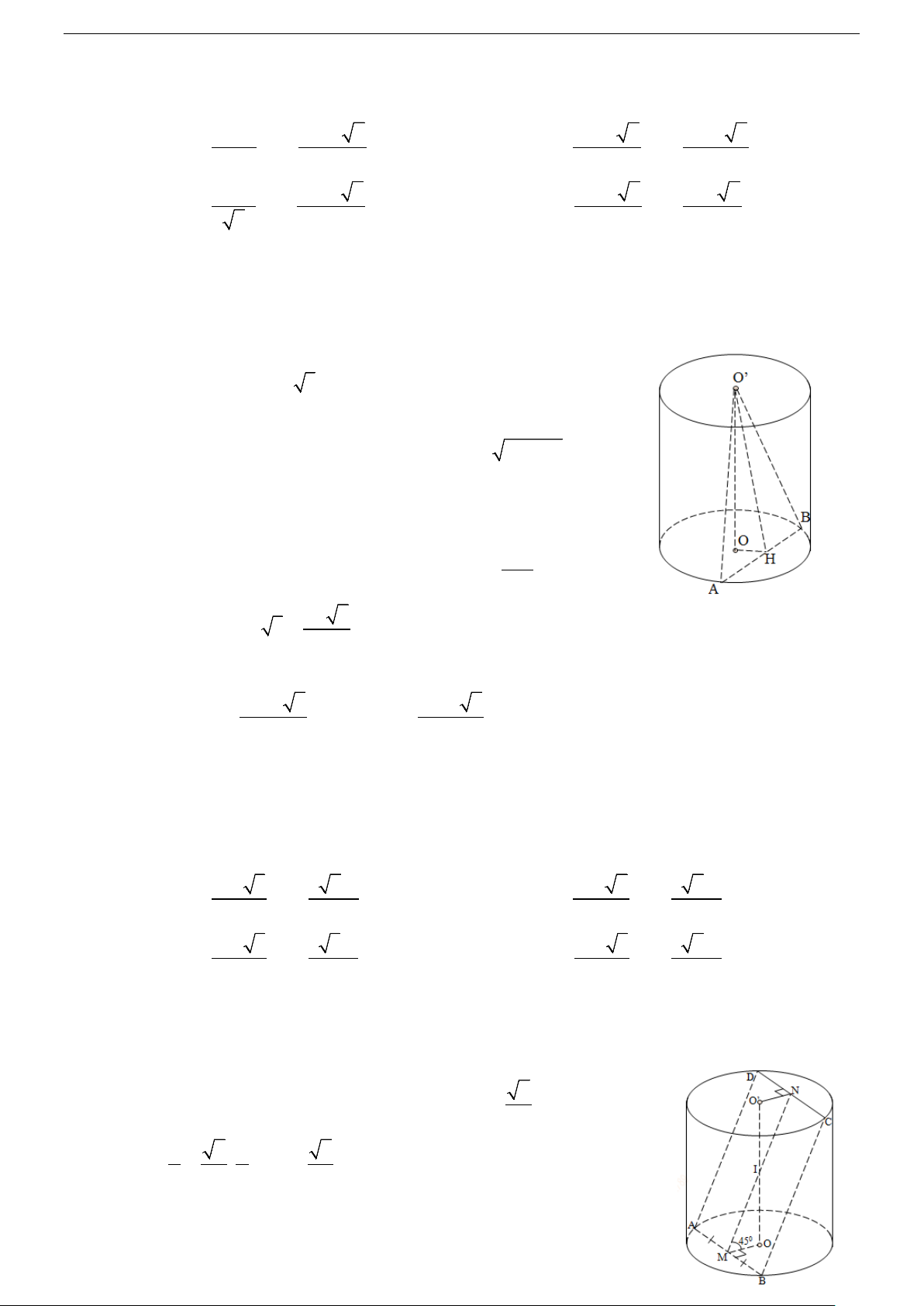
Câu 41. Cho hình trụ tròn xoay có hai đáy là hai hình tròn (O; R) và (O '; R) . Tồn tại dây cung AB
thuộc đường tròn (O) sao cho O
∆ ' AB là tam giác đều và mặt phẳng (O ' AB) hợp với mặt phẳng
chứa đường tròn (O) một góc 0
60 . Khi đó, diện tích xung quanh S hình trụ và thể tích V của xq
khối trụ tương ứng là: 2 3 π π 2 3 π π A. 4 R 2 R 7 S = V = . B. 6 R 7 3 R 7 S = V = . xq ; xq ; 7 7 7 7 2 3 π π 2 3 π π C. 3 R 2 R 7 S = V = . D. 3 R 7 R 7 S = V = . xq ; xq ; 7 7 7 7
Câu 42. Cho một hình trụ tròn xoay và hình vuông ABCD cạnh a có hai đỉnh liên tiếp , A B nằm trên
đường tròn đáy thứ nhất của hình trụ, hai đỉnh còn lại nằm trên đường tròn đáy thứ hai của hình
trụ. Mặt phẳng (ABCD) tạo với đáy hình trụ góc 0
45 . Diện tích xung quanh S hình trụ và thể xq
tích V của khối trụ là: 2 3 π 2 3 π A. a 3 3 2a S = V = . B. a 2 3 2a S = V = . xq ; xq ; 3 8 3 32 2 3 π 2 3 π C. a 3 3 3a S = V = . D. a 3 3 2a S = V = . xq ; xq ; 4 16 2 16
Câu 43. Cho hình trụ có thiết diện qua trục là hình vuông ABCD cạnh 2 3 cm với AB là đường kính
của đường tròn đáy tâm O . Gọi M là điểm thuộc cung AB sao cho 0
ABM = 60 . Khi đó, thể tích
V của khối tứ diện ACDM là: Trang 12/44 A. 3 V = 6 3 (cm ) . B. 3 V = 2 3 (cm ) . C. 3 V = 6(cm ) . D. 3 V = 3(cm ) .
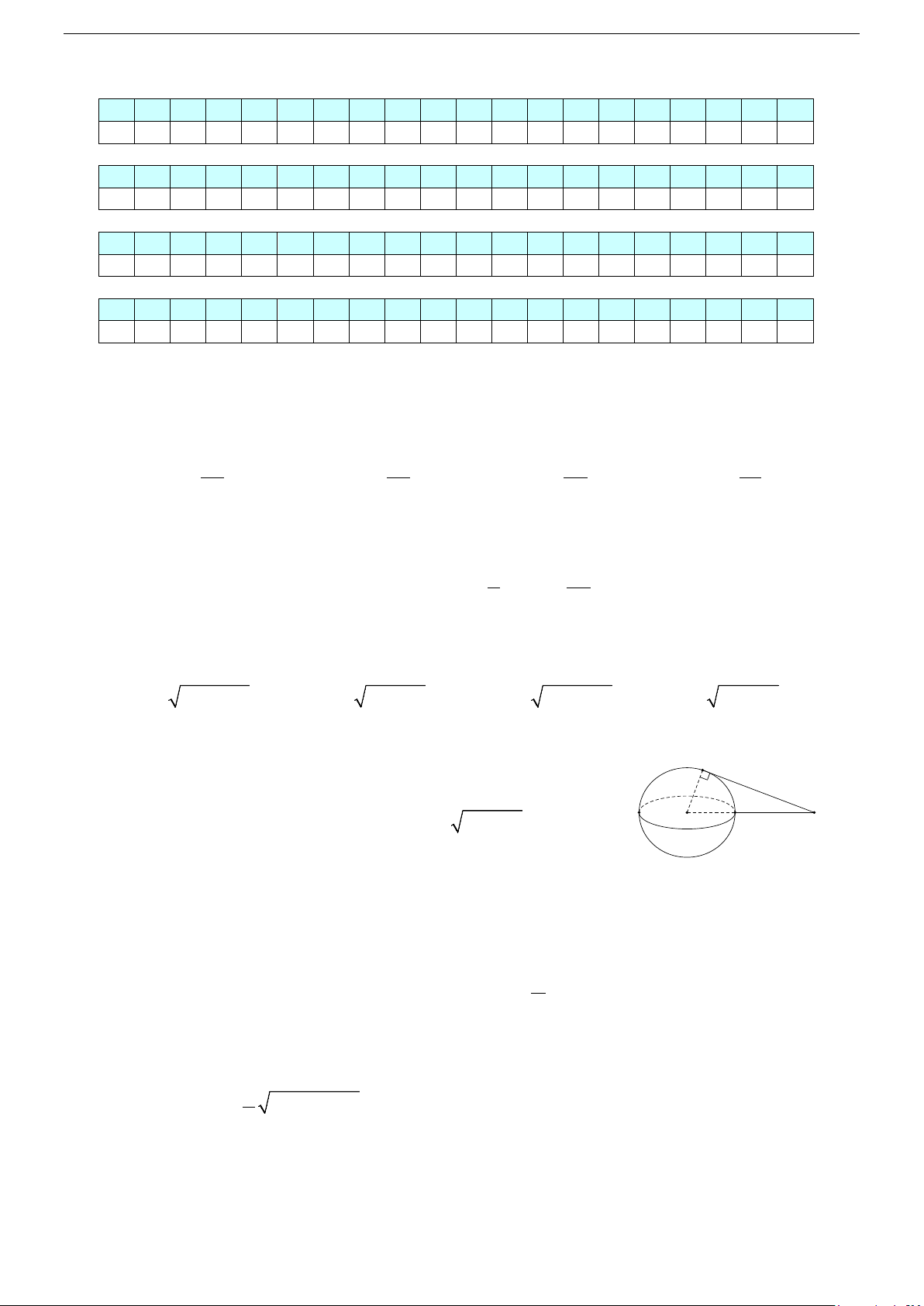
Câu 44. Một hình nón có chiều cao h = 20 cm, bán kính đáy r = 25cm. Một thiết diện đi qua đỉnh có
khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là 12cm. Tính diện tích thiết diện đó. A. 450 2 cm2. B. 500 2 cm2. C. 500cm2. D. 125 34 cm2.
Câu 45. Cho hình lập phương ABC . D ’ A ’ B C’ ’
D có cạnh là a . Hãy tính diện tích xung quanh S và xq
thể tích V của khối nón có đỉnh là tâm O của hình vuông ABCD và đáy là hình tròn nội tiếp hình vuông ’ A ’ B C’ ’ D . 2 3 π π 2 3 π π A. a 5 a S = V = . B. a 5 a S = V = . xq ; xq ; 2 12 4 4 2 3 π π 3 π C. a 3 a S = V = . D. 2 a S = π a V = . xq 5; xq ; 2 6 4
Câu 46. Thiết diện đi qua trục của hình nón đỉnh S là một tam giác vuông cân có cạnh cạnh huyền
bằng a 2 . Kẻ dây cung BC của đường tròn đáy hình nón, sao cho mp (SBC) tạo với mặt phẳng
chứa đáy hình nón một góc 0
60 . Diện tích tam giác SBC tính theo a là: 2 2 2 2 A. a 2 . B. a 2 . C. a 3 . D. a 6 . 3 6 2 3
Câu 47. Cho hình nón tròn xoay có đỉnh là S , O là tâm của đường tròn đáy, đường sinh bằng a 2 và
góc giữa đường sinh và mặt phẳng đáy bằng 0
60 . Gọi I là một điểm trên đường cao SO của hình
nón sao cho tỉ số SI 1
= . Khi đó, diện tích của thiết diện qua I và vuông góc với trục của hình OI 3 nón là: 2 π 2 π 2 π 2 π A. a 2 . B. a . C. a . D. a . 18 9 18 36
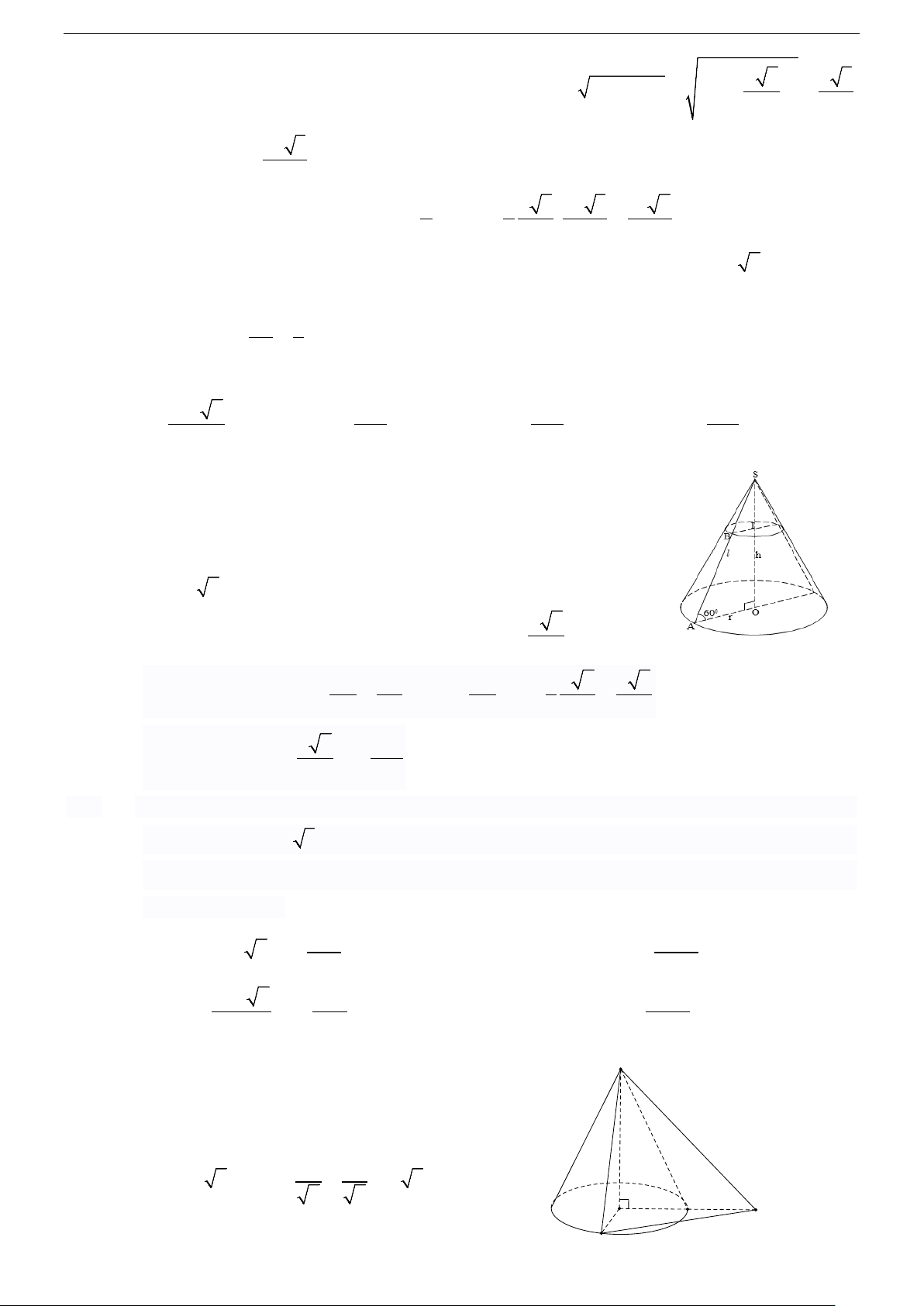
Câu 48. Cho hình nón đỉnh S với đáy là đường tròn tâm O bán kính R . Gọi I là một điểm nằm trên
mặt phẳng đáy sao cho OI = R 3 . Giả sử A là điểm nằm trên đường tròn (O; R) sao cho
OA ⊥ OI . Biết rằng tam giác SAI vuông cân tại S . Khi đó, diện tích xung quanh S của hình xq
nón và thể tích V của khối nón là: 3 π 3 π A. 2 R S = π R V = . B. 2 2 R S = π R V = . xq 2 ; xq 2; 3 3 2 3 π π 3 π C. R 2 R S = V = . D. 2 2 R S = π R V = . xq ; xq ; 2 6 3
Câu 49. Một hình nón đỉnh S có bán kính đáy bằng a 3 , góc ở đỉnh là 1200. Thiết diện qua đỉnh của
hình nón là một tam giác. Diện tích lớn nhất S của thiết điện đó là bao nhiêu ? max 2 A. 2 S = 2a . B. 2 S = a 2 . C. 2 S = 4a . D. 9a S = . max max max max 8 VẬN DỤNG CAO
Câu 50. Bán kính r của mặt cầu nội tiếp tứ diện đều cạnh a là A. a 6 r = . B. a 6 r = . C. a 6 r = . D. a 6 r = . 12 8 6 4 Trang 13/44
Câu 51. Chiều cao của khối trụ có thể tích lớn nhất nội tiếp trong hình cầu có bán kính R là A. R 3 . B. R 3 . C. 4R 3 . D. 2R 3 . 3 3 3
Câu 52. Cho hình nón có chiều cao h . Tính chiều cao x của khối trụ có thể tích lớn nhất nội tiếp trong hình nón theo h . A. h x = . B. h x = . C. 2h x = . D. h x = . 2 3 3 3
Câu 53. Cho hình nón đỉnh O , chiều cao là h . Một khối nón khác có đỉnh là tâm của đáy và có đáy là
là một thiết diện song song với đáy của hình nón đỉnh O đã cho (hình vẽ). Tính chiều cao x của
khối nón này để thể tích của nó lớn nhất, biết 0 < x < h . O h x A. h x = .
B. x = h 3 . C. 2h x = . D. h 3 x = . 3 3 3
Câu 54. Cho một hình nón có bán kính đáy là R , chiều cao là 2R , ngoại tiếp một hình cầu S(O;r) .
Khi đó, thể tích của khối trụ ngoại tiếp hình cầu S(O;r) là 3 π 3 π 3 π 3 π A. 16 R 4 R 16 R 4 R ( . B. . C. . D. . 3 5 − )3 1 1 + 2 5 (1+ 5) 2 5 −1
Câu 55. Trong số các hình trụ có diện tích toàn phần đều bằng S thì bán kính R và chiều cao h của
khối trụ có thể tích lớn nhất là: A. S 1 = ; S R h = . B. S = ; S R h = . 2π 2 2π 4π 4π C. 2S 2 = ; = 4 S R h . D. S = ; = 2 S R h . 3π 3π 6π 6π
BÀI TẬP TRẮC NGHIỆM TỰ RÈN LUYỆN (CÓ HƯỚNG DẪN)
Câu 56. Thiết diện qua trục của một hình nón tròn xoay là một tam giác vuông cân có điện tích bằng 2
2a . Khi đó thể tích của khối nón bằng: 3 π 3 π 3 π 3 π A. 2 2 a B. a C. 4 2 a D. 2 a 3 3 3 3
Câu 57. Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a . Gọi S là diện tích xung quanh của hình
trụ có hai đường tròn đáy lần lượt ngoại tiếp các hình vuông ABDC và A'B'C'D'. Khi đó S bằng: 2 π 2 π A. 2 S = π a B. 2 S = π a 2 C. a 2 S = D. a 2 S = 2 4 Trang 14/44
Câu 58. Một hình lập phương có diện tích mặt chéo bằng 2
a 2 . Gọi V là thể tích khối cầu và S là diện
tích mặt cầu ngoại tiếp hình lập phương nói trên. Khi đó tích S.V bằng: 2 5 π 2 5 π 2 5 π 2 5 π A. 3 3 . a S V = B. 3 . a S V = C. 3 . a S V = D. 3 6 . a S V = 2 2 2 2
Câu 59. Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, BC = a 3, AA' = a 5 . Gọi V là thể tích
hình nón sinh ra khi quay tam giác AA'C quanh trục AA'. Khi đó V bằng: 3 π 3 π 3 π 3 π A. 2 a 5 V = B. a 5 V = C. 4 a 5 V = D. 4 a 3 V = 3 3 3 5
Câu 60. Một hình trụ có diện tích xung quanh bằng 4π và có thiết diện qua trục là một hình vuông. Khi
đó thể tích khối trụ tương ứng bằng: A. π 2π B. 4π C. D. π 2
Câu 61. Tỉ số thể tích của khối lập phương và khối cầu ngoại tiếp khối lập phương đó bằng: A. 6 B. 2 3 C. 3 D. 2 3 3π π 3π 3π
Câu 62. Một hình nón có đường sinh hợp với đáy một góc α và độ dài đường sinh bằng l. Khi đó diện
tích toàn phần của hình nón bằng: A. α α 2 2 S = πl α B. 2 2 S = π l α tp 2 cos .sin tp 2 cos .cos 2 2 C. α α 2 2 S = πl α D. 1 2 2 S = πl α tp cos .cos tp cos .cos 2 2 2
Câu 63. Cho lăng trụ đều có tất cả các cạnh đều bằng A. Gọi V là thể tích hình trụ ngoại tiếp khối lăng
trụ nói trên. Khi đó V bằng: 3 π 3 π 3 π 3 π A. a 3 V = B. a V = C. 3 a 3 V = D. a V = 3 3 2 6
Câu 64. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và cạnh bên bằng a 6 . Khẳng định 3 nào sau đây sai?
A. Không có mặt cầu ngoại tiếp S.ABC.
B. Mặt cầu ngoại tiếp khối chóp có tâm là trọng tâm tam giác ABC.
C. Mặt cầu ngoại tiếp khối chóp có tâm là trực tâm tam giác ABC.
D. Mặt cầu ngoại tiếp khối chóp có bán kính a 3 R = 3
Câu 65. Một hình nón có bán kính đường tròn đáy bằng A. Thiết diện qua trục của hình nón là một tam
giác có góc ở đỉnh bằng 1200. Gọi V là thể tích khối nón. Khi đó V bằng: 3 π 3 π 3 π 3 π A. a V = B. a 3 V = C. a 3 V = D. a V = 6 3 9 3
Câu 66. Trong không gian cho hình vuông ABCD cạnh a . Gọi I và H lần lượt là trung điểm của các
cạnh AB và CD. Khi quay hình vuông đó xung quanh trục IH ta được một hình trụ tròn xoay.Khi
đó thể tích khối trụ tương ứng bằng: Trang 15/44 3 π 3 π 3 π 3 π A. a B. a C. 4 a D. a 2 4 12 3 4
Câu 67. Cho tứ diện S.ABC có đáy ABC là tam giác vuông tại B với AB = 3a, BC = 4a, SA ⊥ (ABC) ,
cạnh bên SC tạo với đáy góc 600. Khi đó thể tích khối cầu ngoại tiếp S.ABC là: 3 π 3 π 3 π 3 π A. a V = B. 50 a V = C. 5 a V = D. 500 a V = 3 3 3 3
Câu 68. Cho hình lăng trụ tứ giác đều ABCD.A′B′C′D′ có cạnh đáy bằng a , chiều cao 2a . Biết rằng O′
là tâm của A′B′C′D′ và (C) là đường tròn nội tiếp đáy ABCD. Diện tích xung quanh của hình nón
có đỉnh O′ và đáy (C). 2 π 2 π 2 π 2 π A. 3 a S = B. 5 a S = C. a S = D. 3 2 a S = xq 2 xq 2 xq 2 xq 2
Câu 69. Một hình trụ có hai đáy là hai đường tròn nội tiếp hai mặt của một hình lập phương có cạnh
bằng 1. Thể tích của khối trụ đó bằng: A. π π π B. C. D. π 4 3 2
Câu 70. Cho tứ diện S.ABC có 3 đường thẳng SA, SB, SC vuông góc với nhau từng đôi một, SA = 3,
SB = 4, SC = 5. Diện tích mặt cầu ngoại tiếp S.ABC bằng: A. 25π B. 50π C. 75π D. 100π
Câu 71. Thể tích khối lăng trụ tứ giác đều nội tiếp trong hình trụ có chiều cao h và bán kính đường tròn đáy R bằng: 2 A. 2 2R h B. 2 R h C. 2 2R h D. R h 2 Trang 16/44
D. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI BÀI TẬP TRẮC NGHIỆM I – ĐÁP ÁN 7.5
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
A B A D A C A C A A B D A C C A A D A B
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
B A A B D C A D D A C C B C D A D C A A
41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
B D D C A A C A A D A B A C D A B A C A
61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 D A B A C B D A A B A
II –HƯỚNG DẪN GIẢI
NHẬN BIẾT – THÔNG HIỂU * MẶT CẦU
Câu 1. Cho một mặt cầu có diện tích là S , thể tích khối cầu đó là V . Tính bán kính R của mặt cầu. A. 3V R = . B. S R = . C. 4V R = . D. V R = . S 3V S 3S Hướng dẫn giải:
Ta có công thức tính diện tích mặt cầu và thể tích hình cầu là: 2 4 3
S = 4π r ; V = π r ⇒ 3V = r . 3 S
Câu 2. Cho mặt cầu S(O; R) và điểm A cố định với OA = d . Qua A , kẻ đường thẳng ∆ tiếp xúc với
mặt cầu S(O; R) tại M . Công thức nào sau đây được dùng để tính độ dài đoạn thẳng AM ? A. 2 2 2R − d . B. 2 2 d − R . C. 2 2 R − 2d . D. 2 2 d + R . Hướng dẫn giải:
Vì ∆ tiếp xúc với S(O; R) tại M nên OM ⊥ ∆ tại M . M
Xét tam giác OMA vuông tại M , ta có: R 2 2 2 2 2 2 2
AM = OA − OM = d − R ⇒ AM = d − R . O A
Câu 3. Một hình hộp chữ nhật có ba kích thước là a, ,
b c . Gọi (S) là mặt cầu đi qua 8 đỉnh của hình
hộp chữ nhật đó. Tính diện tích của hình cầu (S) theo a, , b c . A. 2 2 2
π (a + b + c ) . B. 2 2 2
2π (a + b + c ) . π C. 2 2 2
4π (a + b + c ) . D. 2 2 2
(a + b + c ) . 2 Hướng dẫn giải:
Đường kính của mặt cầu (S) chính là đường chéo của hình hộp chữ nhật, nên mặt cầu (S) có bán kính 1 2 2 2 r =
a + b + c . Do đó diện tích mặt cầu (S) là: 2 2 2 2
S = 4π r = π (a + b + c ) . 2
Câu 4. Một hình hộp chữ nhật có ba kích thước là a, ,
b c . Gọi (S) là mặt cầu đi qua 8 đỉnh của hình
hộp chữ nhật đó. Tâm của mặt cầu (S) là
A. một đỉnh bất kì của hình hộp chữ nhật.
B. tâm của một mặt bên của hình hộp chữ nhật. Trang 17/44
C. trung điểm của một cạnh của hình hộp chữ nhật.
D. tâm của hình hộp chữ nhật. Hướng dẫn giải:
Tâm của hình hộp chữ nhật cách đều 8 đỉnh của hình hộp nên tâm của mặt cầu (S) chính là
tâm của hình hộp chữ nhật.
Câu 5. Cho mặt cầu S(O; R) và đường thẳng ∆ . Biết khoảng cách từ O tới ∆ bằng d . Đường thẳng
∆ tiếp xúc với S(O; R) khi thỏa mãn điều kiện nào trong các điều kiện sau ?
A. d = R .
B. d > R .
C. d < R .
D. d ≠ R . Hướng dẫn giải:
Đường thẳng ∆ tiếp xúc với S(O; R) khi d = R . M Δ d=R O
Câu 6. Cho đường tròn (C) và điểm A nằm ngoài mặt phẳng chứa (C) . Có tất cả bao nhiêu mặt cầu
chứa đường tròn (C) và đi qua A ? A. 2. B. 0. C. 1. D. vô số. Hướng dẫn giải:
Trên đường tròn (C) lấy điểm điểm M cố định. Gọi (α) là mặt 0
phẳng trung trực của AM và đường thẳng ∆ là trục của (C) . Gọi I 0
I giao điểm của (α) và ∆ thì mặt cầu tâm I thỏa mãn yêu cầu đề A Δ bài.
Ta sẽ chứng minh tâm I là duy nhất. Giả sử M là điểm bất kì α O M
khác nằm trên đường tròn (C) , gọi (α ') là mặt phẳng trung trực của AM và I ' = (α ') ∩ ∆ thì
mặt cầu tâm tâm I ' thỏa mãn yêu cầu đề bài. Ta có:
I ' A = I ' M = I ' M ⇒ I ' thuộc mặt phẳng trung trực (α) của AM nên I ' = (α) ∩ ∆ . 0 0
Từ đó suy ra I ' ≡ I . Vậy chỉ có duy nhất 1 mặt cầu thỏa mãn yêu cầu bài toán.
Câu 7. Cho hai điểm ,
A B phân biệt. Tập hợp tâm những mặt cầu đi qua A và B là
A. mặt phẳng trung trực của đoạn thẳng AB . B. đường thẳng trung trực của AB .
C. mặt phẳng song song với đường thẳng AB . D. trung điểm của đoạn thẳng AB . Hướng dẫn giải:
Gọi I là tâm mặt cầu đi qua hai điểm ,
A B cố định và phân biệt thì ta luôn có IA = IB . Do đó
I thuộc mặt phẳng trung trực của đoạn AB .
Câu 8. Cho mặt cầu S(O; R) và mặt phẳng (α) . Biết khoảng cách từ O tới (α) bằng d . Nếu d < R
thì giao tuyến của mặt phẳng (α) với mặt cầu S(O; R) là đường tròn có bán kính bằng bao nhiêu? Trang 18/44 A. Rd . B. 2 2 R + d . C. 2 2 R − d . D. 2 2 R − 2d . Hướng dẫn giải:
Gọi I là hình chiếu của O lên (α) và M là điểm thuộc đường giao tuyến của (α) và mặt cầu
S(O; R) . Xét tam giác OIM vuông tại I , ta có: OM = R và OI = d nên 2 2
IM = R − d . O
Câu 9. Từ điểm M nằm ngoài M
mặt cầu S(O; R) có thể kẻ được α I
bao nhiêu tiếp tuyến với mặt cầu ? A. Vô số. B. 0. C. 1. D. 2. Hướng dẫn giải:
+ Gọi (α) là mặt phẳng chứa đường thẳng MO thì dễ dàng T1
thấy rằng mp (α) luôn cắt mặt cầu S(O; R) theo giao tuyến (C) α
là đường tròn (C) có tâm O , bán kính R . Trong mp(α) , ta O M
thấy từ điểm M nằm ngoài (C) ta luôn kẻ được 2 tiếp tuyến T2
MT , MT với đường tròn (C) . Hai tiếp tuyến này cũng 1 2
chính là tiếp tuyến với mặt cầu S(O; R) .
+ Do có vô số mặt phẳng (α) chứa đường thẳng MO cắt mặt cầu S(O; R) theo các giao tuyến
là đường tròn (C) khác nhau nên cũng có vô số tiếp tuyến với mặt cầu được kẻ từ điểm M nằm ngoài mặt cầu.
Câu 10. Một đường thẳng d thay đổi qua A và tiếp xúc với mặt cầu S(O; R) tại M . Gọi H là hình
chiếu của M lên đường thẳng OA . M thuộc mặt phẳng nào trong những mặt phẳng sau đây?
A. Mặt phẳng qua H và vuông góc với OA . B. Mặt phẳng trung trực của OA .
C. Mặt phẳng qua O và vuông góc với AM . D. Mặt phẳng qua A và vuông góc với OM . Hướng dẫn giải:
Trong mặt phẳng (d,O) , xét tam giác OMA vuông tại M có MH là d M 2 đường cao. Ta có: 2 = . R R OM OH OA ⇒ OH = = . Do đó H cố 2R 2 O H A
định. Vậy M thuộc mặt phẳng vuông góc với OA tại H .
Câu 11. Một đường thẳng thay đổi d qua A và tiếp xúc với mặt cầu S(O; R) tại M . Gọi H là hình
chiếu của M lên đường thẳng OA . Độ dài đoạn thẳng MH tính theo R là: A. R . B. R 3 . C. 2R 3 . D. 3R 3 . 2 3 3 4 Hướng dẫn giải:
Trong mặt phẳng (d,O) , xét tam giác OMA vuông tại M có MH là d M đường cao. Ta có: 2 2 R 3R R 3
MH = HO.HA ⇒ MH = . ⇒ MH = . A 2 2 2 O H
Câu 12. Thể tích của một khối cầu là 1 3
113 cm thì bán kính nó là bao nhiêu ? 7 Trang 19/44 (lấy 22 π ≈ ) 7 A. 6cm . B. 2cm . C. 4cm . D. 3cm . Hướng dẫn giải: 1 3.113
Thể tích khối cầu bán kính R là 4 3 3 3V 7
V = π R ⇒ R = = = 27 ⇒ R = 3 (cm). 3 4π 22 4. 7
Câu 13. Khinh khí cầu của nhà Mông–gôn–fie (Montgolfier) (người Pháp) phát minh ra khinh khí cầu
dùng khí nóng. Coi khinh khí cầu này là một mặt cầu có đường kính 11m thì diện tích của mặt
khinh khí cầu là bao nhiêu? (lấy 22 π ≈
và làm tròn kết quả đến chữ số thập phân thứ hai). 7 A. 2 379,94 (m ) . B. 2 697,19 (m ) . C. 190,14cm . D. 2 95,07 (m ) . Hướng dẫn giải:
Diện tích của kinh khí cầu là 2 22 2 2 S = π d = .11 = 379,94 (m ) . 7
Câu 14. Cho hình lập phương ABC .
D A' B 'C ' D ' có độ dài mỗi cạnh là 10cm . Gọi O là tâm mặt cầu đi
qua 8 đỉnh của hình lập phương. Khi đó, diện tích S của mặt cầu và thể tích V của hình cầu là: A. 2 3
S = 150π (cm );V = 125 3 (cm ) . B. 2 3
S = 100 3π (cm );V = 500(cm ) . C. 2 3
S = 300π (cm );V = 500 3 (cm ) . D. 2 3
S = 250π (cm );V = 500 6 (cm ) . Hướng dẫn giải:
Dễ thấy tâm O của mặt cầu chính là tâm của hình lập A D phương.
Trong tam giác vuông AA'C có: 2 2 2
AC ' = AA' + A'C ' . B C
Trong tam giác vuông A' B 'C ' có: 2 2 2
A'C ' = A' B ' + B 'C ' . O A' D' Do đó 2
AC = 100 + 100 + 100 = 300 ⇒ AC = 10 3 (cm).
+ Bán kính mặt cầu tâm O là 1
R = OA = AC = 5 3 (cm) 2 B' C'
+ Diện tích mặt cầu: S = π R = π ( )2 2 2 4 4 . 5 3 = 300π (cm ) . + Thể tích khối cầu: 4 4
V = π R = π (5 3)3 3 3 = 500 3 (cm ) . 3 3
Câu 15. Cho đường tròn (C) ngoại tiếp một tam giác đều ABC có cạnh bằng a , chiều cao AH . Quay
đường tròn (C) xung quanh trục AH , ta được một mặt cầu. Thể tích của khối cầu tương ứng là: 3 π 3 π 3 π 3 π A. a 3 . B. 4 a . C. 4 a 3 . D. 4 a . 54 9 27 3 Hướng dẫn giải: A
AH là đường cao trong tam giác đều cạnh a nên a 3 AH = . 2 O B H C Trang 20/44
Gọi O là tâm mặt cầu ngoại tiếp ABC ∆
, thì O ∈ AH và 2 a 3 OA = AH = . 3 3
Bán kính mặt cầu được tạo thành khi quay đường tròn (C) quanh trục AH là a 3 R = OA = . 3 3 3 π
Vậy thể tích của khối cầu tương ứng là: 4 3 4 a 3 4 a 3
V = π R = π = (đvtt). 3 3 3 27
Câu 16. Cho đường tròn (C) ngoại tiếp một tam giác đều ABC có cạnh bằng a , chiều cao AH . Quay
đường tròn (C) xung quanh trục AH , ta được một mặt cầu. Thể tích của khối cầu tương ứng là: 3 π 3 π 3 π 3 π A. 4 a 3 . B. 4 a . C. a 3 . D. 4 a . 27 9 54 3 Hướng dẫn giải: A
AH là đường cao trong tam giác đều cạnh a nên a 3 AH = . 2
Gọi O là tâm mặt cầu ngoại tiếp ABC ∆
, thì O ∈ AH và O 2 a 3 OA = AH = . B H C 3 3
Bán kính mặt cầu được tạo thành khi quay đường tròn (C) quanh trục AH là a 3 R = OA = . 3 3 3 π
Vậy thể tích của khối cầu tương ứng là: 4 3 4 a 3 4 a 3
V = π R = π = (đvtt). 3 3 3 27
Câu 17. Cho tam giác ABC vuông tại A có BC = 2a và 0
B = 30 . Quay tam giác vuông này quanh
trục AB , ta được một hình nón đỉnh B . Gọi S là diện tích toàn phần của hình nón đó và S là 1 2
diện tích mặt cầu có đường kính AB . Khi đó, tỉ số S1 là: S2 A. S S 1 S 2 S 3 1 = 1. B. 1 = . C. 1 = . D. 1 = . S S 2 S 3 S 2 2 2 2 2 Hướng dẫn giải:
Xét tam giác ABC vuông tại A , ta có: B 0 0
AC = BC sin 30 = a; AB = BC cos30 = a 3 .
Diện tích toàn phần hình nón là: 300 A B O 2 2 2
S = S + S = π Rl + π R = π a a + π a = π a xq day .2 3 1 . B A C
Diện tích mặt cầu đường kính AB là:
S = π AB = π (a 3)2 2 2 = 3π a . 2
Từ đó suy ra, tỉ số S1 = 1. S2 * MẶT NÓN Trang 21/44
Câu 18. Cho hình nón có thiết diện qua trục là một tam giác đều cạnh 2a , diện tích xung quanh là S 1
và mặt cầu có đường kính bằng chiều cao hình nón, có diện tích S . Khẳng định nào sau đây là 2 khẳng định đúng ?
A. 2S = 3S .
B. S = 4S .
C. S = 2S .
D. S = S . 2 1 1 2 2 1 1 2 Hướng dẫn giải:
Bán kính đáy của hình nón là a . Đường sinh của hình nón là 2a . Do đó, ta có 2
S = π Rl = 3π a (1) 1 2a a 3
Mặt cầu có bán kính là a 3 , nên ta có 2 a a 2 a 3 2 S = 4π = 3π a (2) . 2 2
Từ (1) và (2) suy ra S = S . 1 2
Câu 19. Cho hình nón có thiết diện qua trục là một tam giác đều cạnh 2a , có thể tích V và hình cầu có 1
đường kính bằng chiều cao hình nón, có thể tích V . Khi đó, tỉ số thể tích V1 bằng bao nhiêu? 2 V2 A. V 2 V V 1 V 1 1 = . B. 1 = 1. C. 1 = . D. 1 = . V 3 V V 2 V 3 2 2 2 2 Hướng dẫn giải:
Hình nón có bán kính đáy là a , chiều cao a 3 . 3 π Do đó thể tích 1 2 a 3 V = π a a 3 = . 1 3 3 2a a 3
Hình cầu có bán kính a 3 nên có thể tích 2 3 3 4 a 3 π a 3 a a V = π = . 1 3 2 2 Từ đó suy ra V 2 1 = . V 3 2
Câu 20. Tính diện tích xung quanh của hình trụ biết hình trụ có bán kính đáy a và đường cao là a 3 . A. 2 2π a . B. 2 2π a 3 . C. 2 π a . D. 2 π a 3 . Hướng dẫn giải:
Hình trụ có bán kính đáy a và đường cao a 3 nên 2
S = π rh = π a a = π a . xq 2 2 . 3 2 3
Một hình nón có thiết diện qua trục là một tam giác vuông cân có cạnh góc vuông bằng a . Tính diện tích xung quanh của hình nón. 2 π 2 π 2 π A. a 2 . B. a 2 . C. 2 π a 2 . D. 2 a 2 . 4 2 3 Hướng dẫn giải: a a O Trang 22/44
Thiết diện qua trục là một tam giác vuông cạnh a nên đường sinh của hình nón là a và bán 2 π kính đáy là a 2 a 2 a 2 S = π a = . xq . 2 nên 2 2
Thiết diện đi qua trục của hình nón đỉnh S là tam giác vuông cân SAB có cạnh cạnh huyền bằng a 2 .
Diện tích toàn phần S của hình nón và thể tích V của khối nón tương ứng đã cho là tp 2 3 π + π 2 3 π π A. a (1 2) a 2 S = V = . B. a 2 a 2 S = V = . tp ; tp ; 2 12 2 4 3 π 2 3 π − π C. 2 a 2 S = π a + V = . D. a ( 2 1) a S = V = . tp ; tp (1 2); 6 2 12 Hướng dẫn giải:
+ Do thiết diện đi qua trục là tam giác SA
∆ B vuông cân tại đỉnh S
S , có cạnh huyền AB = a 2 nên suy ra bán kính đáy hình nón a a a 2 2 là a 2 r =
; đường sinh hình nón l = SA = SB = a ; đường cao 2 A a 2 O B 2 hình nón a 2 h = SO = . 2
+ Diện tích toàn phần hình nón là: 2 2 2 2 π π π 2 a 2 a 2 a 2 a a (1 + 2)
S = S + S = π rl + π r = π a + π = + = (đvdt). tp xq day 2 2 2 2 2 3 π
+ Thể tích khối nón tương ứng là: 1 1 2 a 2
V = Bh = π r h = (đvtt). 2 3 12
Cho hình nón tròn xoay có đỉnh là S , O là tâm của đường tròn đáy, đường sinh bằng a 2 và góc giữa
đường sinh và mặt phẳng đáy bằng 0
60 . Diện tích xung quanh S của hình nón và thể tích V xq
của khối nón tương ứng là: 3 π 2 3 π π A. 2 a 6 S = π a V = . B. a a 3 S = V = . xq ; xq ; 12 2 12 3 π 3 π C. 2 a 6 S = π a V = . D. 2 a 6 S = π a V = . xq ; xq 2; 4 4 Hướng dẫn giải:
Gọi A là một điểm thuộc đường tròn đáy hình nón. Theo giải S
thiết ta có đường sinh SA = a 2 và góc giữa đường sinh và mặt phẳng đáy là 0
SAO = 60 . Trong tam giác vuông SAO , ta a 2 a 2 có: 600 0 a 2 OA = SAcos60 = ; O 2 A 0 3 a 6 SO = . SA sin 60 = a 2. = . 2 2
Diện tích xung quanh hình nón a 2 2 S = π rl = π a = π a (đvdt). xq . . 2 2 Trang 23/44 2 3 π
Thể tích của khối nón tròn xoay 1 2 1 a 2 a 6 a 6
V = π r h = π . = (đvtt). 3 3 2 2 12
Một hình nón có đường kính đáy là 2a 3 , góc ở đỉnh là 0
120 . Tính thể tích của khối nón đó theo a . A. 3 3π a . B. 3 π a . C. 3 2 3π a . D. 3 π a 3 . Hướng dẫn giải:
Gọi S là đỉnh hình nón, O là tâm đáy, A là một điểm thuộc đường tròn đáy.
Theo giả thiết dễ suy ra đường tròn đáy có bán kính B
R = OA = a 3 (cm) 600 và góc 0 120 0 ASO =
= 60 . Xét tam giác SOA vuông tại O , ta 2 A a 3 C có OA a 3 SO = =
= a . Do đó chiều cao hình nón là h = a . 0 tan 60 3
Vậy thể tích khối nón là 1 2 1 2 3
V = π R h = π.3a .a = π a . 3 3
Trong không gian, cho tam giác ABC vuông tại A , AB = a và AC = 3a . Tính độ dài đường sinh l của
hình nón, nhận được khi quay tam giác ABC xung quanh trục AB .
A. l = a .
B. l = 2a .
C. l = 3a .
D. l = 2a . Hướng dẫn giải: B
Độ dài đường sinh l bằng độ dài cạnh BC của tam giác vuông ABC . a Theo
định lý Pytago thì A C a 3 2 2 2 2 2 2
BC = AB + AC = a + 3a = 4a ⇒ BC = 2a
Vậy độ dài đường sinh của hình nón là l = 2a. * MẶT TRỤ
Cho một hình trụ có bán kính đáy R , chiều cao h và thể tích V ; một hình nón có đáy trùng với một đáy 1
của hình trụ, có đỉnh trùng với tâm đáy còn lại của hình trụ (hình vẽ bên dưới) và có thể tích V . 2
Khẳng định nào sau đây là khẳng định đúng ? h R
A. V = 3V .
B. V = 2V .
C. V = 3V .
D. V = V . 2 1 1 2 1 2 2 1 Hướng dẫn giải:
Hình trụ có bán kính đáy R và chiều cao h nên thể tích 2 V = π R h . 1
Hình nón có bán kính đáy R và chiều cao h nên thể tích 1 2 V = π R h . 2 3
Từ đó suy ra V = 3V . 1 2 Trang 24/44
Tính thể tích V của khối trụ có bán kính đáy R , chiều cao là h . A. 2 V = π R h . B. 2 V = π Rh . C. 2 V = π Rh .
D. V = 2π Rh .
Hướng dẫn giải: Áp dụng công thức thể tích khối trụ, đáp án là 2 V = π R h .
Một hình trụ có bán kính đáy a , có thiết diện qua trục là một hình vuông. Tính diện tích xung quanh của hình trụ. A. 2 π a . B. 2 2π a . C. 2 3π a . D. 2 4π a . Hướng dẫn giải:
Một hình trụ có bán kính đáy a , có thiết diện qua trục là một hình
vuông nên chiều cao hình trụ bằng 2a . Do đó diện tích xung quanh hình 2a trụ là 2
S = π Rh = π a a = π a . xq 2 2 . .2 4 a
Tính diện tích toàn phần của hình trụ có bán kính đáy a và đường cao a 3 . A. 2 2π a ( 3 − ) 1 . B. 2 π a 3 . C. 2 π a (1+ 3). D. 2 2π a (1+ 3). Hướng dẫn giải: Ta có: 2 S = π a a = π a ; 2 S = π a . xq 2 . 3 2 3 day Do đó 2 2 2 S = π a + π a = π a + . a 3 tp 2 3 2 2 (1 3)
Tính thể tích của khối trụ biết bán kính đáy của hình trụ đó bằng a và thiết
diện đi qua trục là một hình vuông. a A. 3 2π a . B. 2 3 π a . C. 3 4π a . D. 3 π a . 3 Hướng dẫn giải:
Theo bài ra thiết diện qua trục của hình trụ là hình vuông nên hình trụ có
bán kính đáy là a , chiều cao 2a . Do đó thể tích khối trụ là: 2a 2 2 3
V = π R h = π a .2a = 2π a .
Tính thể tích của khối trụ biết chu vi đáy của hình trụ đó bằng 6π (cm) và thiết diện a
đi qua trục là một hình chữ nhật có độ dài đường chéo bằng 10 (cm) . A. 3 48π (cm ) . B. 3 24π (cm ) . C. 3 72π (cm ) . D. 3 18π 3472π (cm ) . Hướng dẫn giải:
Gọi O,O ' là hai tâm của đáy hình trụ và thiết diện qua trục là hình chữ nhật ABCD .
Do chu vi đáy của hình trụ đó bằng 6π (cm) nên bán kính đáy của hình B π O trụ là C 6 R = = = 3(cm) . A 2π 2π
Vì thiết diện đi qua trục là một hình chữ nhật ABCD có AC = 10 (cm)
và AB = 2R = 6(cm) nên chiều cao của hình trụ là: C 2 2 2 2
h = OO ' = BC = AC − AB = 10 − 6 = 8 (cm). O' D
Vậy thể tích khối trụ là: 2 2 3
V = π R h = π.3 .8 = 72π (cm ) . Trang 25/44
Trong không gian, cho hình chữ nhật ABCD có AB = 1 và AD = 2 . Gọi M, N lần lượt là trung điểm của
AD và BC . Quay hình chữ nhật đó xung quanh trục MN, ta được một hình trụ. Tính diện tích
toàn phần S của hình trụ đó. tp A. S = π . B. S = π . C. S = π . D. S = π . tp 10 tp 4 tp 2 tp 6 Hướng dẫn giải: Ta có 2 S = S + S
= π Rh + π R = π R h + R . A 1 M 1 D tp xq day 2 2 2 ( ) 2
Hình trụ đã cho có chiều cao là h = MN = AB = 1 và bán kính 1 đáy AD R =
= 1. Do đó diện tích toàn phần hình trụ là: B 2 N C S = π + = π tp 2 (1 1) 4
Từ một tấm tôn hình chữ nhật kích thước 50cm x 240cm, người ta làm các thùng đựng nước hình trụ có
chiều cao bằng 50cm, theo hai cách sau (xem hình minh họa dưới đây):
- Cách 1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng.
- Cách 2: Cắt tấm tôn ban đầu thành hai tấm bằng nhau, rồi gò mỗi tấm đó thành mặt xung quanh của một thùng.
Kí hiệu V là thể tích của thùng gò được theo cách 1 và V là tổng thể tích của hai thùng gò 1 2
được theo cách 2. Tính tỉ số V1 . V2 A. V V V 1 V 1 = 1. B. 1 = 2 . C. 1 = . D. 1 = 4 . V V V 2 V 2 2 2 2 Hướng dẫn giải:
Gọi R và r lần lượt là bán kính đáy của mỗi thùng đựng nước hình trụ được làm theo cách 1 và cách 2.
Gọi C và C lần lượt là chu vi đáy của mỗi thùng đựng nước hình trụ được làm theo cách 1 1 2 và cách 2. C = 2π R Ta có: 1 C R 1 ⇒ =
= 2 (vì cắt tấm tôn ban đầu thành hai tấm bằng nhau nên C = 2π r C r 2 2 C = 2C ). 1 2
Thùng làm theo cả hai cách đều có cùng chiều cao h nên ta có: 2 2 V = π R h 1 V 1 R 1 ⇒ = = 2. 2 V = 2π r h V 2 r 2 2 VẬN DỤNG THẤP
Tính bán kính của mặt cầu ngoại tiếp hình tứ diện đều cạnh a . Trang 26/44 A. a 3 . B. a 6 . C. a 6 . D. a 2 . 2 2 4 4 Hướng dẫn giải:
Cho tứ diện ABCD đều cạnh a . Gọi I là trung điểm cạnh BC , G D
là trọng tâm của tam giác ABC . Ta có a 3 a 3 AI = ; AG = và 2 3 J
DG là trục của tam giác ABC . Trong mp(DAG) kẻ trung trực của O
DA cắt DG tại O thì OD = OA = OB = OC nên O chính là tâm A C
mặt cầu ngoại tiếp tứ diện ABCD . Bán kính R của mặt cầu bằng G I
độ dài đoạn OD . B
Trong tam giác ADG vuông tại G , ta có: 2 2 2 2 2 2 2 2 2 a 3 6a
DA = DG + GA ⇒ DG = DA − GA = a − a 6 = ⇒ DG = . 3 9 3 Mặt khác do tứ giác AGOI nội tiếp nên ta có: 2 DA a 6
DJ.DA = DO.DG ⇒ DO = ⇒ R = DO = . 2DG 4
Tính bán kính của mặt cầu ngoại tiếp hình chóp tam giác đều S.ABC , biết các cạnh đáy có độ dài bằng
a , cạnh bên SA = a 3 . A. 2a 3 . B. 3a 3 . C. a 3 . D. 3a 6 . 2 2 2 8 8 Hướng dẫn giải:
Gọi H là tâm của tam giác đều ABC , ta có SH ⊥ (ABC) nên SH S
là trục của tam giác ABC . Gọi M là trung điểm của SA , trong
mp(SAH ) kẻ trung trực của SA cắt SH tại O thì a 3 M
OS = OA = OB = OC nên O chính là tâm mặt cầu ngoại tiếp hình O
chóp S.ABC . Bán kính mặt cầu là R = SO . A C
Vì hai tam giác SMO và SHA đồng dạng nên ta có SO SM = . a H SA SH I 2 B Suy ra SM.SA SA 3a 6 R = SO = = = . SH 2SH 8
Tính bán kính của mặt cầu ngoại tiếp hình chóp tứ giác đều có cạnh đáy bằng a , cạnh bên bằng 2a . A. 2a 14 . B. 2a 7 . C. 2a 7 . D. 2a 2 . 7 2 3 2 7 Hướng dẫn giải:
Cho hình chóp tứ giác đều S.ABCD . Gọi H là tâm đáy thì SH là trục của hình
vuông ABCD . Gọi M là trung điểm của SD , trong mp S
(SDH ) kẻ trung trực của đoạn SD cắt SH tại O thì
OS = OA = OB = OC = OD nên O chính là tâm của mặt cầu
ngoại tiếp hình chóp S.ABCD . Bán kính mặt cầu là R = SO . M 2a O A B H Trang 27/44 D a C 2 Ta có SO SM . SD SM SD SM ∆ O ∽ SH ∆ D ⇒ = ⇒ R = SO = = . SD SH SH 2SH 2 2 Với 2 2 2 2 a 7 = − = 4 a SH SD HD a − = a 7 ⇒ SH = . 2 2 2 2 Vậy SD 2a 14 R = = . 2SH 7
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác đều và nằm
trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối cầu ngoại tiếp hình chóp đã cho. π π π π A. 5 V = . B. 5 15 V = . C. 4 3 V = . D. 5 15 V = . 3 18 27 54 Hướng dẫn giải:
Gọi M là trung điểm của AB thì SM ⊥ AB (vì tam giác S
SAB đều). Mặt khác do (SAB) ⊥ (ABC) nên SM ⊥ (ABC) .
Tương tự: CM ⊥ (SAB) . K O
Gọi G và K lần lượt là tâm của các tam giác ABC và B SAB . M
Trong mặt phẳng (SMC) , kẻ đường thẳng Gx//SM và kẻ G A C O G ⊥ (SAB)
đường thẳng Ky//SM . Gọi O = Gx ∩ Ky , thì ta có: O K ⊥ (ABC)
Suy ra OG, OK lần lượt là trục của tam giác ABC và SAB .
Do đó ta có: OA = OB = OC = OD = OS hay O chính là tâm mặt cầu ngoại tiếp hình chóp S.ABC .
Tứ giác OKMN là hình chữ nhật có 3 MK = MG =
nên OKMN là hình vuông. Do đó 6 3 OK = . 6 Mặt khác 3 SK = . Xét tam giác SKO vuông tại K có 3 2 2 3 3 15
OS = OK + SK = + = . 36 9 6
Suy ra bán kính mặt cầu cần tìm là 15 R = OS =
. Vậy thể tích khối cầu cần tìm là: 6 3 4 π 3 4 15 5 15
V = π R = π. = . 3 3 6 54
Một hình lăng trụ tam giác đều có cạnh đáy bằng a , cạnh bên bằng 2a . Tính bán kính mặt cầu ngoại tiếp hình lăng trụ đó. Trang 28/44 A. a 39 . B. a 12 . C. 2a 3 . D. 4a . 6 6 3 3 Hướng dẫn giải:
Cho lăng trụ tam giác đều ABC.A' B 'C ' . Gọi G,G ' lần lượt là A' C' G'
tâm của hai đáy ABC và A' B 'C ' . Ta có GG ' chính là trục của các tam B'
giác ABC và A' B 'C ' . 2a O
Gọi O là trung điểm của GG ' thì O cách đều 6 đỉnh của hình lăng trụ
nên là tâm của mặt cầu ngoại tiếp hình lăng trụ. Bán kính mặt cầu là A C R = OA . G a B
Xét tam giác OAG vuông tại G , ta có: 2 2 2 a 2 2a 3
OA = AG + GO = + a =
. Vậy bán kính mặt cầu cần tìm là 2a 3 R = . 3 3 3
Cho hình trụ có bán kính đáy là R , thiết diện qua trục là một hình vuông. Tính thể tích khối lăng trụ tứ
giác đều nội tiếp trong hình trụ đã cho theo R . A. 3 4R . B. 3 2 2R . C. 3 4 2R . D. 3 8R . Hướng dẫn giải: C' Giả sử ABC .
D A' B 'C ' D ' là lăng trụ tứ giác đều nội tiếp trong hình trụ D' O'
thì BDD ' B ' là thiết diện qua trục của hình trụ đã cho nên B' A'
BD = BB ' = 2R và cạnh đáy hình lăng trụ là R 2 . Do đó thể tích khối 2R lăng trụ ABC .
D A' B 'C ' D ' là D C V = (R )2 3 2 .2R = 4R . R O B A
Cho hình trụ có bán kính đáy là 4 cm, một mặt phẳng không vuông góc với đáy và cắt hai mặt đáy theo
hai dây cung song song AB, A' B ' mà AB = A' B ' = 6cm (hình vẽ). Biết diện tích tứ giác
ABB ' A' bằng 60 cm2. Tính chiều cao của hình trụ đã cho. A. 6 2 cm. B. 4 3 cm. C. 8 2 cm. D. 5 3 cm. Hướng dẫn giải:
Dựng đường sinh B 'C và A' D , ta có tứ giác A' B 'CD là hình chữ nhật nên
CD//A' B ' và CD = A' B ' = 6cm . Vậy CD//AB và CD = AB = 6cm . Do đó tứ giác ABCD là
hình bình hành và nội tiếp được nên là hình chữ nhật. Từ đó AB ⊥ BC , mặt khác AB ⊥ B 'C
nên AB ⊥ (BCB ') ⇒ AB ⊥ BB '
Vậy ABB 'C ' là hình bình hành có một góc vuông nên là hình chữ B' nhật. Ta có S = AB BB nên 60 BB ' =
= 10cm . Xét tam giác A' ABB A . ' ' ' 6 BB 'C vuông tại C có 2 2 2
B 'C = BB ' − BC mà 6 2cm 2 2 2
BC = AC − AB = 64 − 36 = 28 nên C B 2
B 'C = 100 − 28 = 72 ⇒ B 'C = 6 2 cm . 6 cm
Vậy chiều cao hình trụ là 6 2 cm . D A
Cho hình trụ tròn xoay có hai đáy là hai hình tròn (O; R) và (O '; R) . Tồn tại dây cung AB thuộc đường
tròn (O) sao cho O
∆ ' AB là tam giác đều và mặt phẳng (O ' AB) hợp với mặt phẳng chứa Trang 29/44
đường tròn (O) một góc 0
60 . Khi đó, diện tích xung quanh S hình trụ và thể tích V của khối xq trụ tương ứng là: 2 3 π π 2 3 π π A. 4 R 2 R 7 S = V = . B. 6 R 7 3 R 7 S = V = . xq ; xq ; 7 7 7 7 2 3 π π 2 3 π π C. 3 R 2 R 7 S = V = . D. 3 R 7 R 7 S = V = . xq ; xq ; 7 7 7 7 Hướng dẫn giải: * Ta có:
OO ' ⊥ (OAB) . Gọi H là trung điểm
của AB thìOH ⊥ AB,
O ' H ⊥ AB ⇒ 0 OHO ' = 60 .
* Giả sử OH = x . Khi đó: 0 < x < R và 0
OO ' = x tan 60 = x 3 . * Xét O ∆ AH , ta có: 2 2 2
AH = R − x . * Vì O ∆ ' AB đều nên: 2 2
O ' A = AB = 2AH = 2 R − x ( ) 1 . * Mặt khác, AO ∆
O ' vuông tạiO nên: 2 2 2 2 2
AO ' = OO ' + R = 3x + R (2). * Từ ( ) 1 ,(2) ⇒ ( − ) 2 2 2 2 2 2 3 4 = 3 R R x
x + R ⇒ x = . 7 3R 7
⇒ h = OO ' = x 3 = . 7
* Vậy, nếu kí hiệu S là diện tích xung quanh vàV là thể tích của hình trụ thì, ta có: 2 3 6π R 7 π 2 3 R 7 S = 2π Rh = ; V = π R h = . 7 7
Cho một hình trụ tròn xoay và hình vuông ABCD cạnh a có hai đỉnh liên tiếp ,
A B nằm trên đường tròn đáy
thứ nhất của hình trụ, hai đỉnh còn lại nằm trên đường tròn đáy thứ hai của hình trụ. Mặt phẳng
(ABCD) tạo với đáy hình trụ góc 0
45 . Diện tích xung quanh S hình trụ và thể tích V của xq khối trụ là: 2 3 π 2 3 π A. a 3 3 2a S = V = . B. a 2 3 2a S = V = . xq ; xq ; 3 8 3 32 2 3 π 2 3 π C. a 3 3 3a S = V = . D. a 3 3 2a S = V = . xq ; xq ; 4 16 2 16 Hướng dẫn giải:
* Gọi M , N theo thứ tự là trung điểm của AB vàCD . Khi đó: OM ⊥ AB vàO ' N ⊥ DC .
Giả sử I là giao điểm của MN vàOO ' . Đặt R = , OA h = OO ' . * Trong I
∆ OM vuông cân tại I nên: 2 OM = OI = IM . 2 h 2 a 2 ⇒ = . ⇔ h = a . 2 2 2 2 * Ta có: 2 2 2 2
R = OA + AM + MO Trang 30/44 2 2 2 2 2 a a 2 a a 3a = + = + = . 2 4 4 8 8 2 2 3
a 3 a 2 π a 3 2 3a a 2 3 2a
⇒ S = π Rh = π = V = π R h = π = . xq 2 2 . ; . 2 2 2 2 8 2 16
Cho hình trụ có thiết diện qua trục là hình vuông ABCD cạnh 2 3 cm với AB là đường kính của đường
tròn đáy tâm O . Gọi M là điểm thuộc cung AB sao cho 0
ABM = 60 . Khi đó, thể tích V của
khối tứ diện ACDM là: A. 3 V = 6 3 (cm ) . B. 3 V = 2 3 (cm ) . C. 3 V = 6(cm ) . D. 3 V = 3(cm ) . Hướng dẫn giải:
Ta có: BM ⊥ AD, BM ⊥ AM ⇒ BM ⊥ (ADM )
BC//AD ⇒ BC//(ADM )
⇒ d[C,(ADM )] = d[B,(ADM )] = BM 1 1
⇒ V = .BM.S = (1). ∆ BM AM AD ADM . . . 3 6 Vì O ∆ BM đều 2 2
⇒ BM = 3 ⇒ AM = AB − BM = 3 (cm) 1 3
(1) ⇒ V = . 3.3.2 3 = 3(cm ) . 6
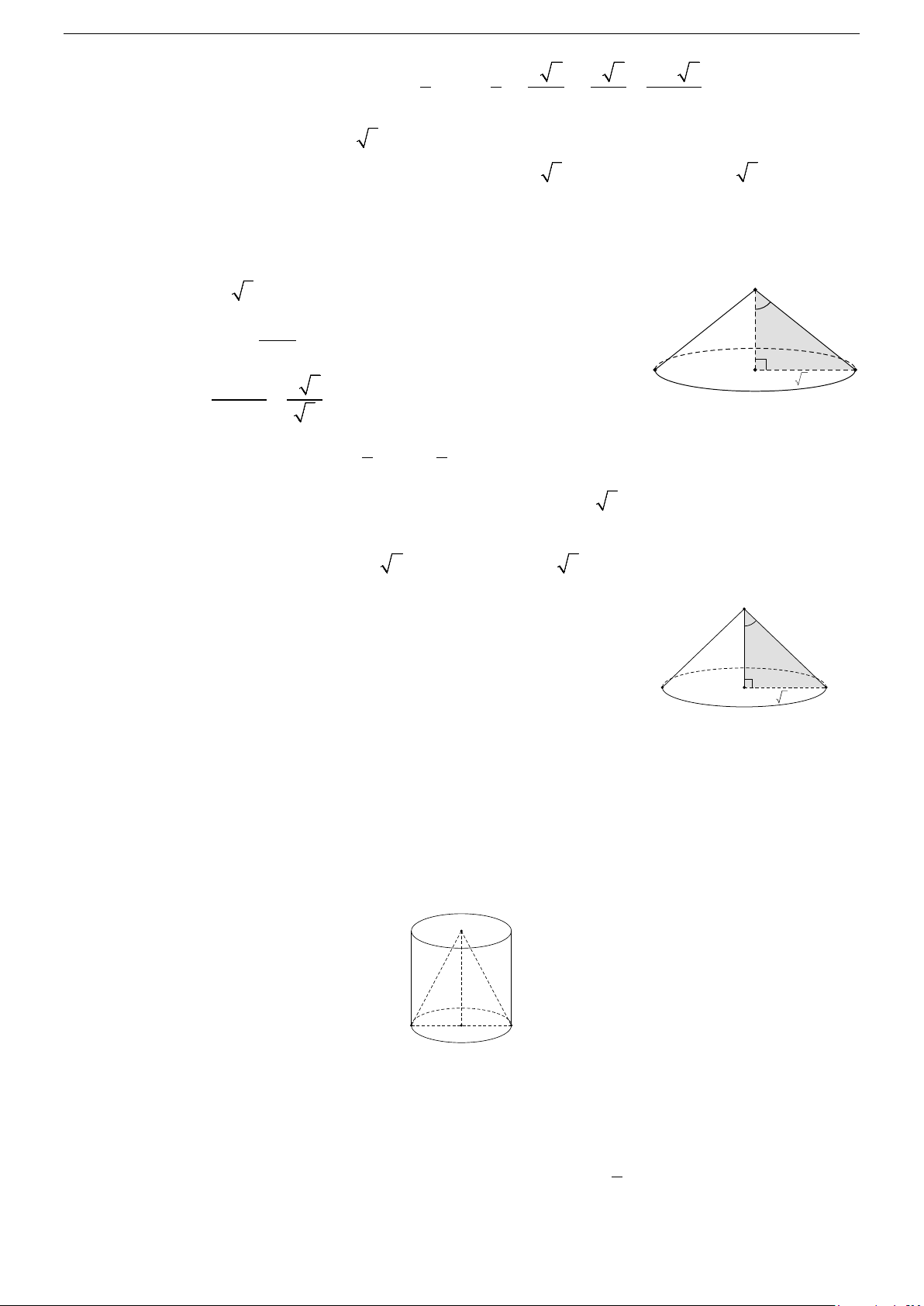
Một hình nón có chiều cao h = 20 cm, bán kính đáy r = 25cm. Một thiết diện đi qua đỉnh có khoảng cách
từ tâm của đáy đến mặt phẳng chứa thiết diện là 12cm. Tính diện tích thiết diện đó. A. 450 2 cm2. B. 500 2 cm2. C. 500cm2. D. 125 34 cm2. Hướng dẫn giải:
Tính diện tích thiết diện S SAB + Ta có 1 1 S = = = ∆ AB SI IA SI IA SI SAB . 2 . . 2 2
+ Xét tam giác vuông SOI , ta có: 1 1 1 1 1 1 = + ⇒ = + ⇒ OI = 15 (cm) . 2 2 2 2 2 2 OH OI OS 12 OI 20
+ Mặt khác, xét tam giác vuông SOI thì: OI.OS 20.15
OI.OS = SI.OH ⇒ SI = = = 25 (cm). OH 12 Trang 31/44
+ Trong tam giác vuông AIO , ta có: 2 2 2 2
IA = OA − OI = 25 −15 = 20 (cm). + Từ đó suy ra: S = = = (cm2). ∆ IA SI SAB . 20.25 500
Cho hình lập phương ABC . D ’ A ’ B C’ ’
D có cạnh là a . Hãy tính diện tích xung quanh S và thể tích V xq
của khối nón có đỉnh là tâm O của hình vuông ABCD và đáy là hình tròn nội tiếp hình vuông ’ A ’ B C’ ’ D . 2 3 π π 2 3 π π A. a 5 a S = V = . B. a 5 a S = V = . xq ; xq ; 2 12 4 4 2 3 π π 3 π C. a 3 a S = V = . D. 2 a S = π a V = . xq 5; xq ; 2 6 4 Hướng dẫn giải:
Khối nón có chiều cao bằng a và bán kính đáy a r = . 2 Diện tích xung quanh khối nón là 2 2 π 2 a a 5
S = π rl = π a a + = (đvdt) xq . . 2 2 2 3 π
Thể tích của khối nón là: 1 1 2 1 a a V Bh π r h π = = = a = (đvtt) 3 3 3 2 12
Thiết diện đi qua trục của hình nón đỉnh S là một tam giác vuông cân có cạnh cạnh huyền bằng a 2 . Kẻ
dây cung BC của đường tròn đáy hình nón, sao cho mp (SBC) tạo với mặt phẳng chứa đáy hình nón một góc 0
60 . Diện tích tam giác SBC tính theo a là: 2 2 2 2 A. a 2 . B. a 2 . C. a 3 . D. a 6 . 3 6 2 3 Hướng dẫn giải:
+ Do thiết diện đi qua trục là tam giác SA
∆ B vuông cân tại đỉnh S , có cạnh huyền AB = a 2
nên suy ra bán kính đáy hình nón là a 2 r =
; đường sinh hình nón l = SA = SB = a ; đường 2 cao hình nón a 2 h = SO = . 2
+ Gọi I là trung điểm BC thì OI ⊥ BC (1) BC ⊥ OI Ta lại có:
⇒ BC ⊥ (SOI ) ⇒ BC ⊥ SI (2) BC ⊥ SO
Gọi (α) là mặt phẳng chứa đáy thì (α) ∩ (SBC) = BC (3)
Từ (1), (2) và (3) suy ra ( α ) = SI OI = 0 ( ),(SBC) ( , ) SIO = 60 .
Xét tam giác SOI vuông tại O , ta có: a 2 SO 2 a 6 SI = = = . sin SIO 3 3 2 Trang 32/44 2
Xét tam giác SIB vuông tại I , ta có: 2 2 2 a 6 a 3
IB = SB − SI = a − = 3 3 2a 3 ⇒ BC = 2IB = . 3 2
Diện tích thiết diện SBC là: 1
1 a 6 2a 3 a 2 S = = = (đvdt). ∆ SI BC SBC . . 2 2 3 3 3
Cho hình nón tròn xoay có đỉnh là S , O là tâm của đường tròn đáy, đường sinh bằng a 2 và góc giữa
đường sinh và mặt phẳng đáy bằng 0
60 . Gọi I là một điểm trên đường cao SO của hình nón sao cho tỉ số SI 1
= . Khi đó, diện tích của thiết diện qua I và vuông góc với trục của hình OI 3 nón là: 2 π 2 π 2 π 2 π A. a 2 . B. a . C. a . D. a . 18 9 18 36 Hướng dẫn giải:
Gọi A là một điểm thuộc đường tròn đáy hình nón. Thiết diện qua I
và vuông góc với trục của hình nón là một hình tròn có bán kính như
hình vẽ. Gọi diện tích này là S . Theo giả thiết ta có đường sinh td
SA = a 2 và góc giữa đường sinh và mặt phẳng đáy là 0 SAO = 60 .
Trong tam giác vuông SAO có 0 a 2 OA = SAcos60 = . 2 Ta có SI ∆ B SI IB SI 1 a 2 a 2 ∽ SO ∆ A ⇒ = ⇒ IB = .OA = = SO OA SO 3 2 6 2 2 π ⇒ 2 a 2 a
S = π IB = π = . td . 6 18
Cho hình nón đỉnh S với đáy là đường tròn tâm O bán kính R . Gọi I là một điểm nằm trên mặt phẳng
đáy sao cho OI = R 3 . Giả sử A là điểm nằm trên đường tròn (O; R) sao cho OA ⊥ OI . Biết
rằng tam giác SAI vuông cân tại S . Khi đó, diện tích xung quanh S của hình nón và thể tích xq
V của khối nón là: 3 π 3 π A. 2 R S = π R V = . B. 2 2 R S = π R V = . xq 2 ; xq 2; 3 3 2 3 π π 3 π C. R 2 R S = V = . D. 2 2 R S = π R V = . xq ; xq ; 2 6 3 Hướng dẫn giải: S
+ Xét tam giác AOI vuông tại O , có: 2 2 2 2 2 2
IA = OA + OI = R + 3R = 4R ⇒ IA = 2R
+ Do tam giác SAI vuông cân tại S nên ta có: IA 2 = 2 R IA SA ⇒ SA = = = R 2 . 2 2 O I
+ Xét tam giác SOA vuông tại O , ta có: A Trang 33/44 2 2 2 2
SO = SA − OA = 2R − R = R .
+ Diện tích xung quanh của hình nón là: 2
S = π Rl = π R R = π R (đvdt). xq . 2 2 3 π
+ Thể tích của khối nón tương ứng là: 1 1 2 1 2 R
V = Bh = π R h = π R R = (đvtt). 3 3 3 3
Một hình nón đỉnh S có bán kính đáy bằng a 3 , góc ở đỉnh là 1200. Thiết diện qua đỉnh của hình nón là
một tam giác. Diện tích lớn nhất S của thiết điện đó là bao nhiêu ? max 2 A. 2 S = 2a . B. 2 S = a 2 . C. 2 S = 4a . D. 9a S = . max max max max 8 Hướng dẫn giải:
Giả sử O là tâm đáy và AB là một đường kính của đường tròn đáy hình nón. Thiết diện qua
đỉnh của hình nón là tam giác cân SAM . Theo giả thiết hình nón có bán kính đáy
R = OA = a 3 cm , 0 ASB = 120 nên 0
ASO = 60 . Xét tam giác SOA vuông tại O , ta có: 0 sin 60 OA OA = ⇒ SA = = 2a . 0 SA sin 60
Diện tích thiết diện là: 1 S = = = ∆ SA SM 1 ASM a a ASM a ASM SAM . .sin 2 .2 .sin 2 2 sin 2 2 Do 0 < sin ASM ≤ 1 nên S lớn nhất khi và chỉ S ∆SAM khi sin
ASM = 1 hay khi tam giác ASM vuông cân
tại đỉnh S (vì 0 0
ASB = 120 > 90 nên tồn tại tam O B
giác ASM thỏa mãn). A M
Vậy diện tích thiết diện lớn nhất là: 2 S = 2a max (đvtt). VẬN DỤNG CAO
Bán kính r của mặt cầu nội tiếp tứ diện đều cạnh a là A. a 6 r = . B. a 6 r = . C. a 6 r = . D. a 6 r = . 12 8 6 4 Hướng dẫn giải:
Gọi O là tâm mặt cầu nội tiếp tứ diện đều ABCD cạnh a . A 3
Ta tính được thể tích khối tứ diện đều là a 2 V = . ABCD 12 Mặt khác, ta lại có: V = V + V + V + V O ABCD O ABC O ACD O BCD O ABD (*) . . . . B
Mỗi hình tứ diện đỉnh O đều có chiều cao r và diện tích đáy là D 2 a 3 . C 4 3 2 Do đó, từ (*) ta suy ra: a 2 1 a 3 a 6 V = = r ⇒ r = . ABCD 4. . 12 3 4 12
Chiều cao của khối trụ có thể tích lớn nhất nội tiếp trong hình cầu có bán kính R là Trang 34/44 A. R 3 . B. R 3 . C. 4R 3 . D. 2R 3 . 3 3 3 Hướng dẫn giải:
Giả sử 2x là chiều cao hình trụ (0 < x < R) (xem hình vẽ)
Bán kính của khối trụ là 2 2
r = R − x . Thể tích khối trụ là: x 2 2
V = π (R − x )2x . Xét hàm số 2 2
V (x) = π (R − x )2x, 0 < x < R R O x Ta có 2 2 R 3
V '(x) = 2π (R − 3x ) = 0 ⇔ x = . 3 Bảng biến thiên: x 0 R 3 R 3 V '(x) + 0 − 3 π 4 R 3 V (x) 9 0 0
Dựa vào BBT, ta thấy thể tích khối trụ lớn nhất khi chiều cao của khối trụ là 2R 3 ; 3 3 4π R 3 V = . max 9
Cho hình nón có chiều cao h . Tính chiều cao x của khối trụ có thể tích lớn nhất nội tiếp trong hình nón theo h . A. h x = . B. h x = . C. 2h x = . D. h x = . 2 3 3 3 O B h J x I R r A Hướng dẫn giải:
Gọi r, R theo thứ tự là bán kính đáy hình nón và khối trụ cần tìm. O là đỉnh của hình nón, I
là tâm của đáy hình nón, J là tâm của đáy hình trụ và khác I . OA là một đường sinh của hình −
nón, B là điểm chung của OA với khối trụ. Ta có: r h x R =
⇒ r = (h − x) . R h h 2 Thể tích khối trụ là: 2 R 2
V = π xR = π x (h − x) 2 h 2 Xét hàm số R 2
V (x) = π x
(h − x) , 0 < x < h . 2 h Trang 35/44 2 Ta có '( ) R = π ( − )( − 3 ) = 0 h V x h x h x
⇔ x = hay x = . h 2 h 3 Bảng biến thiên: x h 0 h 3
V '(x) + 0 − 0 2 4π R h V (x) 27 0 0
Dựa vào BBT, ta thấy thể tích khối trụ lớn nhất khi chiều cao của khối trụ là h x = ; 3 2 4π R h V = . max 27
Cho hình nón đỉnh O , chiều cao là h . Một khối nón khác có đỉnh là tâm của đáy và có đáy là là một thiết
diện song song với đáy của hình nón đỉnh O đã cho (hình vẽ). Tính chiều cao x của khối nón
này để thể tích của nó lớn nhất, biết 0 < x < h . O h x A. h x = .
B. x = h 3 . C. 2h x = . D. h 3 x = . 3 3 3 Hướng dẫn giải: − −
Từ hình vẽ ta có JB OJ h x R(h x) = = ⇒ JB = . IA OI h h 2
Thể tích khối nón cần tìm là: 1 R 2 V = π
(h − x) x . O 2 3 h 2 Xét hàm số 1 R 2 V (x) = π
(h − x) x , 0 < x < h . 2 3 h J B h 2 Ta có 1 '( ) R = π ( − )( − 3 ) = 0 ⇔ = hay h V x h x h x x h x = . x 2 3 h 3 Bảng biến thiên: I R A x h 0 h 3
V '(x) + 0 − 0 2 4π R h V (x) 81 0 0 Trang 36/44
Dựa vào BBT, ta thấy thể tích khối nón cần tìm lớn nhất khi chiều cao của nó là h x = ; 3 2 4π R h V = . max 81
Cho một hình nón có bán kính đáy là R , chiều cao là 2R , ngoại tiếp một hình cầu S(O;r) . Khi đó, thể
tích của khối trụ ngoại tiếp hình cầu S(O;r) là 3 π 3 π 3 π 3 π A. 16 R 4 R 16 R 4 R ( . B. . C. . D. . 3 5 − )3 1 1 + 2 5 (1+ 5) 2 5 −1 Hướng dẫn giải: O
Giả sử hình nón có đỉnh O và đường kính đáy là AB . Ta có 2 2
OA = OB = R + (2R) = R 5 . 2R
Tam giác OAB có diện tích là 2 S = 2R , r O
chu vi là 2 p = 2R(1 + 5) . Do đó bán kính khối cầu S(O;r) là S 2R A R B r = = . p 1+ 5 3 π
Thể tích khối trụ cần tìm là: 2 3 16 R
V = π r h = π r = . tru 2 (1+ 5)3
Trong số các hình trụ có diện tích toàn phần đều bằng S thì bán kính R và chiều cao h của khối trụ có thể tích lớn nhất là: A. S 1 = ; S R h = . B. S = ; S R h = . 2π 2 2π 4π 4π C. 2S 2 = ; = 4 S R h . D. S = ; = 2 S R h . 3π 3π 6π 6π Hướng dẫn giải:
Gọi thể tích khối trụ là V , diện tích toàn phần của hình trụ là S . Ta có: 2 S = S
+ S = π R + π Rh . Từ đó suy ra: day xq 2 2 2 Cauchy 2 S 2 S 2 V 2 V V V 3 = R + Rh ⇔ = R + = R + + ≥ 3 hay 2 2π 2π π R 2π R 2π R 4π 2 3 3 27 V S S ≤ ⇔ V ≤ . 2 4π 2π 54π 3 2 π Vậy S V = . Dấu “=” xảy ra ⇔ 2 V R h Rh R = = = hay h = 2R . max 54π 2π R 2π R 2 Khi đó 2 = 6 S S π R ⇒ R = và = 2 = 2 S h R . 6π 6π
BÀI TẬP TRẮC NGHIỆM TỰ RÈN LUYỆN (CÓ HƯỚNG DẪN)
Thiết diện qua trục của một hình nón tròn xoay là một tam giác vuông cân có điện tích bằng 2 2a . Khi đó
thể tích của khối nón bằng: Trang 37/44 3 π 3 π 3 π 3 π A. 2 2 a B. a C. 4 2 a D. 2 a 3 3 3 3 Hướng dẫn giải Ta có: 1 2 2
S = l = 2a ⇒ l = 2a 2
Dùng định lý Pitago cho tam giác thiết diện ta được đường kính đường tròn đáy
d = 2a 2 ⇒ r = a 2 3 π Vậy 1 1 2 2 2 2 2 a
V = Bh = π r l − r = . 3 3 3
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a . Gọi S là diện tích xung quanh của hình trụ có hai
đường tròn đáy lần lượt ngoại tiếp các hình vuông ABDC và A'B'C'D'. Khi đó S bằng: 2 π 2 π A. 2 S = π a B. 2 S = π a 2 C. a 2 S = D. a 2 S = 2 4 Hướng dẫn giải
+) Đáy là hình vuông cạnh a ⇒ đường chéo bằng AC = a 2 ⇒ bán kính đường tròn ngoại tiếp đáy a 2 r = 2 .
+) Đường sinh l bằng cạnh của hình lập phương ⇒ l = a +) Vậy 2
S = π rl = π a ⇒ Chọn B. xq 2 2
Một hình lập phương có diện tích mặt chéo bằng 2
a 2 . Gọi V là thể tích khối cầu và S là diện tích mặt
cầu ngoại tiếp hình lập phương nói trên. Khi đó tích S.V bằng: 2 5 π 2 5 π 2 5 π 2 5 π A. 3 3 . a S V = B. 3 . a S V = C. 3 . a S V = D. 3 6 . a S V = 2 2 2 2 Hướng dẫn giải
+) Đặt AB = x ⇒ BD = x 2 +) Ta có: 2 a 3 S = a = x x
⇒ x = a ⇒ BD = a ⇒ R = . BDD B 2 . 2 ' 3 ' ' 2 3 π +) Khi đó ta có: 4 3 a 3 V = π R = và 2 2
S = 4π R = 3π a 3 2 2 5 π +) Vậy 3 3 a SV = ⇒ Chọn A. 2
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, BC = a 3, AA' = a 5 . Gọi V là thể tích hình nón
sinh ra khi quay tam giác AA'C quanh trục AA'. Khi đó V bằng: 3 π 3 π 3 π 3 π A. 2 a 5 V = B. a 5 V = C. 4 a 5 V = D. 4 a 3 V = 3 3 3 5 Hướng dẫn giải. Ta có: 2 2
r = AC = AB + BC = 2a 3 π Vậy: 1 1 2 V a
= Bh = π r AA' = 4 5 3 3 3 Trang 38/44
Một hình trụ có diện tích xung quanh bằng 4π và có thiết diện qua trục là một hình vuông. Khi đó thể
tích khối trụ tương ứng bằng: A. π 2π B. 4π C. D. π 2 Hướng dẫn giải
+) Theo đề ta có: S = π ⇒ π rl = π ⇒ rl = (*) xq 4 2 4 2
+) Thiết diện qua trục là hình vuông l
⇒ r = . Thay vào (*) ta được: l = 2 ⇒ r = 1 2 +) Vậy 2
V = π r l = 2π ⇒ Chọn A.
Tỉ số thể tích của khối lập phương và khối cầu ngoại tiếp khối lập phương đó bằng: A. 6 B. 2 3 C. 3 D. 2 3 3π π 3π 3π Hướng dẫn giải
+) Thể tích khối lập phương 3 V = a .
+) Đăt AB = a⇒ AC = a 2 ⇒ A'C = a 3 ⇒ Bán kính mặt cầu ngoại tiếp khối lập phương là 3 a 3 4 π 3 a 3 R = ⇒ V = π R = (**). 2 Câu 3 2 V
Từ (*) và (**) suy ra: lâp phuong 2 3 = ⇒ Chọn D V π CAU 3
Một hình nón có đường sinh hợp với đáy một góc α và độ dài đường sinh bằng l. Khi đó diện tích toàn
phần của hình nón bằng: A. α α 2 2 S = πl α B. 2 2 S = π l α tp 2 cos .sin tp 2 cos .cos 2 2 C. α α 2 2 S = πl α D. 1 2 2 S = πl α tp cos .cos tp cos .cos 2 2 2 Hướng dẫn giải
+) Ta có: r = cosα ⇒ r = l cosα l +) α 2 2 2 2 2 2 2
S = S + S = π rl + π r = πl α + π l α = π l α + α = π l α TP XQ Đ cos cos cos (1 cos ) 2 cos cos 2 +) Vậy chọn A.
Cho lăng trụ đều có tất cả các cạnh đều bằng A. Gọi V là thể tích hình trụ ngoại tiếp khối lăng trụ nói trên. Khi đó V bằng: 3 π 3 π 3 π 3 π A. a 3 V = B. a V = C. 3 a 3 V = D. a V = 3 3 2 6 Hướng dẫn giải
+) Gọi I, G lần lượt là trung điểm BC và trọng tâm tam giác ABC. +) Tam giác ABC đều a 3 2 a 3 a 3 ⇒ AI = ⇒ AG = . = = r 2 3 2 3 +) l = a . Trang 39/44 3 π +) Vậy 2 a V = π r l = ⇒ Chọn B. 3
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và cạnh bên bằng a 6 . Khẳng định nào sau đây 3 sai?
A. Không có mặt cầu ngoại tiếp S.ABC.
B. Mặt cầu ngoại tiếp khối chóp có tâm là trọng tâm tam giác ABC.
C. Mặt cầu ngoại tiếp khối chóp có tâm là trực tâm tam giác ABC.
D. Mặt cầu ngoại tiếp khối chóp có bán kính a 3 R = 3
Một hình nón có bán kính đường tròn đáy bằng A. Thiết diện qua trục của hình nón là một tam giác có
góc ở đỉnh bằng 1200. Gọi V là thể tích khối nón. Khi đó V bằng: 3 π 3 π 3 π 3 π A. a V = B. a 3 V = C. a 3 V = D. a V = 6 3 9 3 Hướng dẫn giải + ) r = a +) Góc ở đỉnh 0 a a 3 = 120 ⇒ h = = 0 tan 60 3 3 π +) 1 1 2 a 3
V = S h = π r h = ⇒ Chọn C. Đ . 3 3 9
Trong không gian cho hình vuông ABCD cạnh a . Gọi I và H lần lượt là trung điểm của các cạnh AB và
CD. Khi quay hình vuông đó xung quanh trục IH ta được một hình trụ tròn xoay.Khi đó thể tích
khối trụ tương ứng bằng: 3 π 3 π 3 π 3 π A. a B. a C. 4 a D. a 2 4 12 3 4 Hướng dẫn giải +) Ta có: a
r = và l = a 2 3 π +) 2 = . a V B h = π r l = 4
Cho tứ diện S.ABC có đáy ABC là tam giác vuông tại B với AB = 3a, BC = 4a, SA ⊥ (ABC) , cạnh bên
SC tạo với đáy góc 600. Khi đó thể tích khối cầu ngoại tiếp S.ABC là: 3 π 3 π 3 π 3 π A. a V = B. 50 a V = C. 5 a V = D. 500 a V = 3 3 3 3 Hướng dẫn giải +) Ta có: SA
∆ C vuông tại S(*). BC ⊥ AB +)
⇒ BC ⊥ (SAB) ⇒ BC ⊥ SB ⇒ S
∆ BC vuông tại B(**) BC ⊥ SA
+) Từ (*) và (**) ⇒ Tâm mặt cầu ngoại tiếp khối chóp S.ABC là trung điểm đoạn SC. +) Ta có: AC 2 2 AC 0 1 = + = 5 . = cos 60 = ⇒ = 2 = 10 SC AB BC a Mà SC AC a ⇒ R = = 5a SC 2 2 Trang 40/44 3 π +) Vậy 4 3 500 a V = π R = ⇒ Chọn D. 3 3
Cho hình lăng trụ tứ giác đều ABCD.A′B′C′D′ có cạnh đáy bằng a , chiều cao 2a . Biết rằng O′ là tâm
của A′B′C′D′ và (C) là đường tròn nội tiếp đáy ABCD. Diện tích xung quanh của hình nón có đỉnh O′ và đáy (C). 2 π 2 π 2 π 2 π A. 3 a S = B. 5 a S = C. a S = D. 3 2 a S = xq 2 xq 2 xq 2 xq 2 Hướng dẫn giải
+) ABCD.A'B'C'D' là lăng trụ tứ giác đều ⇒ đáy ABCD là hình vuông. Khi đó bán kính
đường tròn ngoại tiếp đáy là r = AC a 2 = . 2 2 2 +) Đường sinh 2 2 2 a 3a 2
l = O ' A = AA' + A'O = 4a + = . 2 2 2 π +) Vậy
a 2 3a 2 3 a S = π rl = π = ⇒ Chọn A. XQ . . 2 2 2
Một hình trụ có hai đáy là hai đường tròn nội tiếp hai mặt của một hình lập phương có cạnh bằng 1. Thể
tích của khối trụ đó bằng: A. π π π B. C. D. π 4 3 2 Hướng dẫn giải
+) Ta có:Đường tròn đáy nội tiếp hình vuông cạnh bằng 1 ⇒ bán kính 1 r = 2
+) Độ dài đường sinh = độ dài cạnh của hình lập phương ⇒ l = 1 2 π +) Vậy 2 1
V π r l π = = .1 = ⇒ Chọn A. 2 4
Cho tứ diện S.ABC có 3 đường thẳng SA, SB, SC vuông góc với nhau từng đôi một, SA = 3, SB = 4, SC
= 5. Diện tích mặt cầu ngoại tiếp S.ABC bằng: A. 25π B. 50π C. 75π D. 100π Hướng dẫn giải
+) Tam giác SBC vuông tại S nên từ trung điểm I của cạnh BC ta vẽ đường thẳng (d) vuông
góc với (SBC) (tức là d // SA), khi đó d chính là trục đường tròn ngoại tiếp tam giác SBC.
+) Trong mp được xác định bởi 2 đường thẳng song song d và SA ta dựng đường trung trực của
SA cắt d tại J. Khi đó J chính là tâm mặt cầu ngoại tiếp SABC⇒ SJ là bán kính. 2 2 2 +) 2 SA BC SA 5 2 SJ = SI + + = = 2 4 2 + 2 50 S = 4π R = 4π = 50π ⇒ Chọn B 4
Thể tích khối lăng trụ tứ giác đều nội tiếp trong hình trụ có chiều cao h và bán kính đường tròn đáy R bằng: 2 A. 2 2R h B. 2 R h C. 2 2R h D. R h 2 Trang 41/44 Hướng dẫn giải +) Ta có: 2 2 V = S
AA = AB OO = AB h (*) LTRU ABCD . ' . '
+) Tính AB: Ta có tam giác OAB vuông cân tại O nên AB = OA 2 = R 2 + Thay vào (*) ta được: 2 V = 2R h . Trang 42/44
Document Outline
- DS_C7_THE TICH KHOI NON TRU CAU
- A. KIẾN THỨC CƠ BẢN
- B. KỸ NĂNG CƠ BẢN
- C. BÀI TẬP TRẮC NGHIỆM
- D. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI BÀI TẬP TRẮC NGHIỆM




