Tổng hợp bài giảng VLĐC 2| Bài giảng VLĐC 2| Trường Đại học Bách Khoa Hà Nội

VẬT LÝ ĐẠI CƯƠNG II (PH1120)
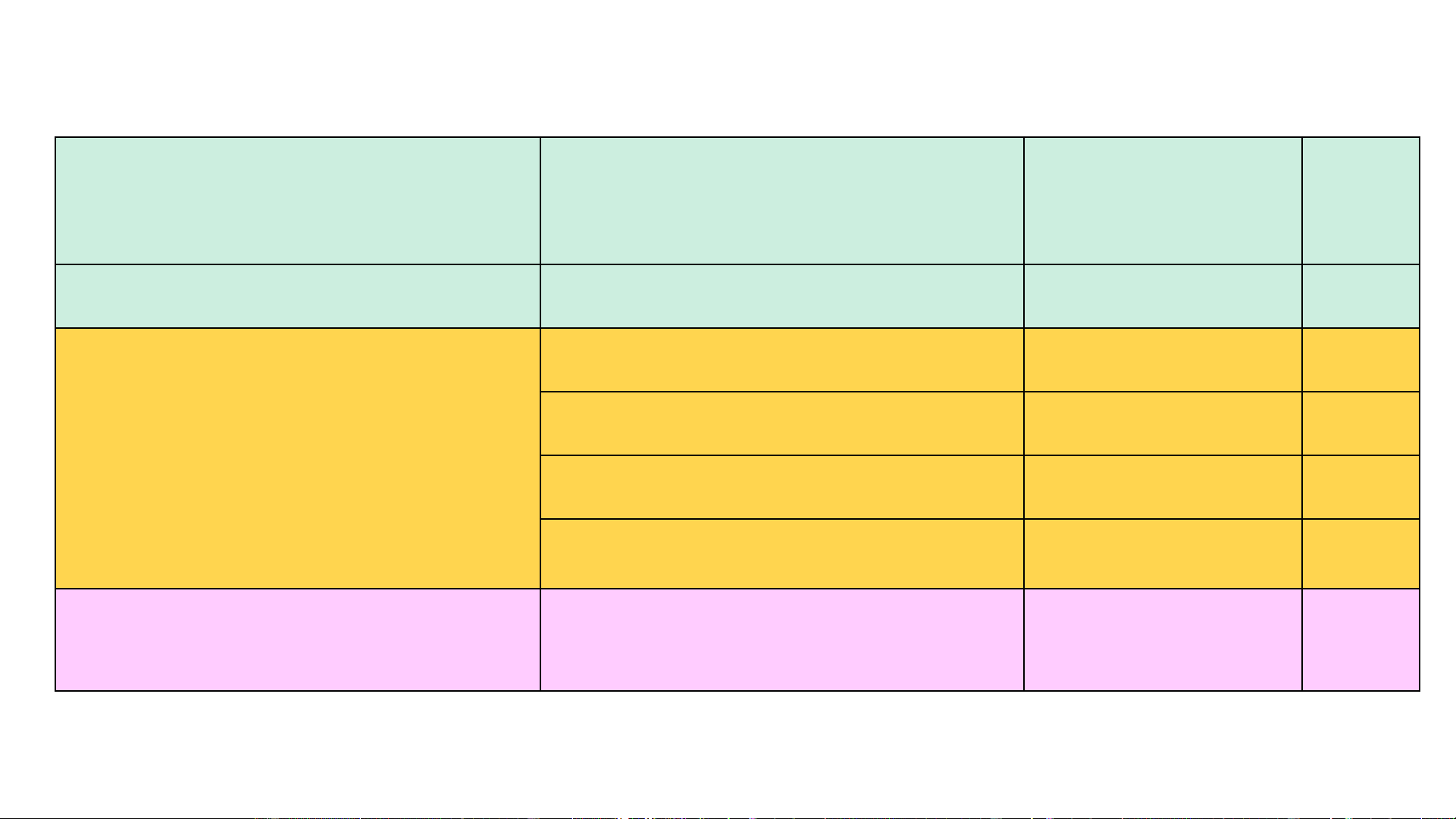
CÁCH ĐÁNH GIÁ HỌC PHẦN Phương Tỷ Điểm pháp đánh giá cụ thành phần Mô tả thể trọng [1] [2] [3] [5]
A1. Điểm quá trình (*) Đánh giá quá trình 30% A1.1. Kiểm tra giữa kỳ Trắc nghiệm 80% A1.2. Bài tập về nhà Tự luận 20%
A1.3. Thảo luận trên lớp Điểm thưởng + A2. Điểm cuối kỳ A2.1. Thi cuối kỳ Tự luận và trắc 70% nghiệm
* Điểm quá trình sẽ được điều chỉnh bằng cách cộng thêm điểm chuyên cần. Điểm
chuyên cần có giá trị từ –2 đến +1, theo Quy chế Đào tạo ĐH Bách khoa Hà Nội.
Yêu cầu bài tập về nhà
✓ Bài tập về nhà giao trên Asignmant;
✓ SV nộp bài tập trước 9h00 thứ năm trước tuần có tiết bài tập;
✓ Chụp ảnh bài tập làm theo thứ tự:
- Chụp bài trong sách bài tập trước (chụp theo đúng thứ tự); -Bài tập thêm chụp sau;
✓ Số bài tập ghi ra lề;
✓ Trang đầu tiên: tổng hợp các bài tập được giao và điền đáp số
Kết quả làm bài tập tuần 1 1.5:…………… Thêm 1:…………… 1.9:…………… Thêm 2 :…………… 1.11…………… Thêm 3…………… 1.12…………… Thêm 4 …………… 1.13…………… Thêm 5 …………… 1.16…………… 1.17…………….. 1.18……………. 1.19…………… Bài 1.5 Bài 1.9 Bài 1.11
CHƯƠNG I: ĐIỆN TRƯỜNG TĨNH
§1. NHỮNG KHÁI NIỆM MỞ ĐẦU 1. Hai loại điện tích
Điện tích nguyên tố:
✓ Electron -e=-1,6.10-19C, m =9,1.10-31kg; e
✓ Proton: +e, m =1,67.10-27kg p
Bình thường nguyên tử trung hòa điện.
✓Khi nguyên tử mất electron: nhiễm điện dương
✓Khi nguyên tử nhận thêm electron: nhiễm điện âm: lụa 2. Thuyết electron
Thuyết dựa vào sự chuyển dời của electron để giải thích các hiện tượng điện
gọi là thuyết electron
VD: Giải thích sự nhiễm điện của thủy tinh khi xát vào lụa: electron chuyển
dời từ thuỷ tinh sang lụa, thủy tinh mất electron và mang điện dương
Định luật bảo toàn điện tích: Tổng đại số điện tích trong một hệ cô lập là không đổi.
3. Phân biệt vật dẫn, điện môi
✓ Vật dẫn: là vật để cho điện tích chuyển động tự do trong toàn bộ thể tích của vật
✓ Điện môi: điện tích ở đâu sẽ định xử ở đó
§ 2. ĐỊNH LUẬT CULÔNG
I. Định luật Culông trong chân không
1. Khái niệm điện tích điểm
Là một vật mang điện có kích thước nhỏ không đáng kể so với khoảng
cách từ điện tích đó tới những điểm hoặc những vật mang điện khác mà ta khảo sát.
2. Phát biểu định luật
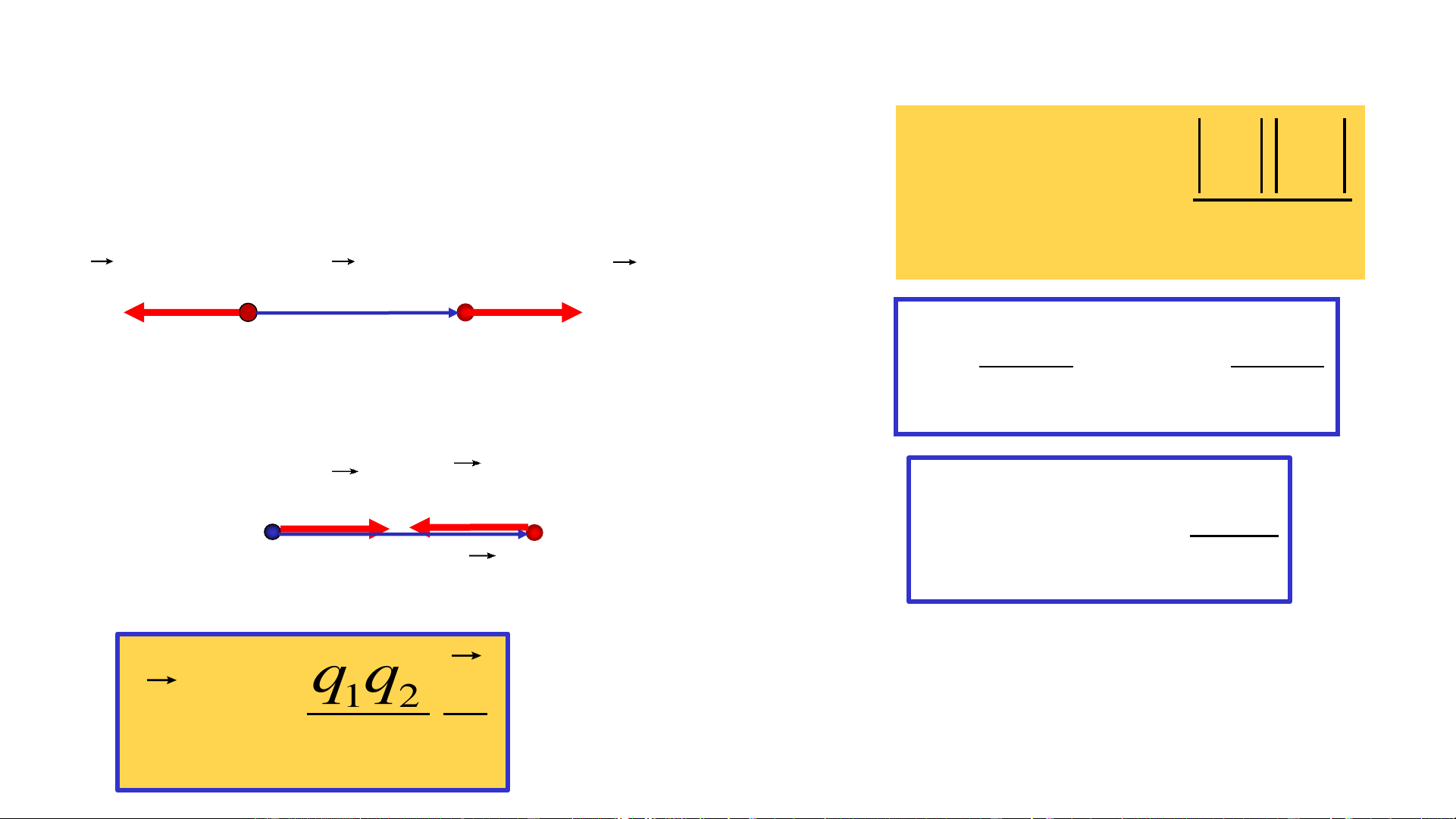
Lực tương tác tĩnh điện giữa hai điện tích điểm có phương nằm trên đường
thẳng nối hai điện tích, có chiều là lực đẩy nếu hai điện tích cùng dấu và có
chiều là lực hút nếu hai điện tích là trái dấu, có độ lớn tỷ lệ thuận với tích số
độ lớn của hai điện tích đó và tỷ lệ nghịch với bình phương khoảng cách giữa hai điện tích đó
3. Biểu diễn Định luật Culông dưới dạng vectơ q q 1 2 q q >0 1 2
F = F ' = k 2 r F ' r F 2 q q 1 Nm 9 1 2 k = = 9.10 2 4 C 0 q q <0 2 F ' F 1 2 − C q 12  = 8,86.10 1 q2 0 2 r Nm
𝜀0: Hằng số điện q q r 1 2 F = k Ԧ 𝐹 : Lực do 𝑞 2 1 tác dụng lên 𝑞2 r r
Ԧ𝑟 : Vecto hướng từ 𝑞1tới 𝑞2
II. Định luật Culông trong môi trường
: Hằng số điện môi, đặc trưng cho 1 q q r 1 2 F =
tính chất của môi trường, là đại lượng 2 4  r r 0 không thứ nguyên
III. Lực tương tác tĩnh điện giữa hai vật mang điện bất kỳ
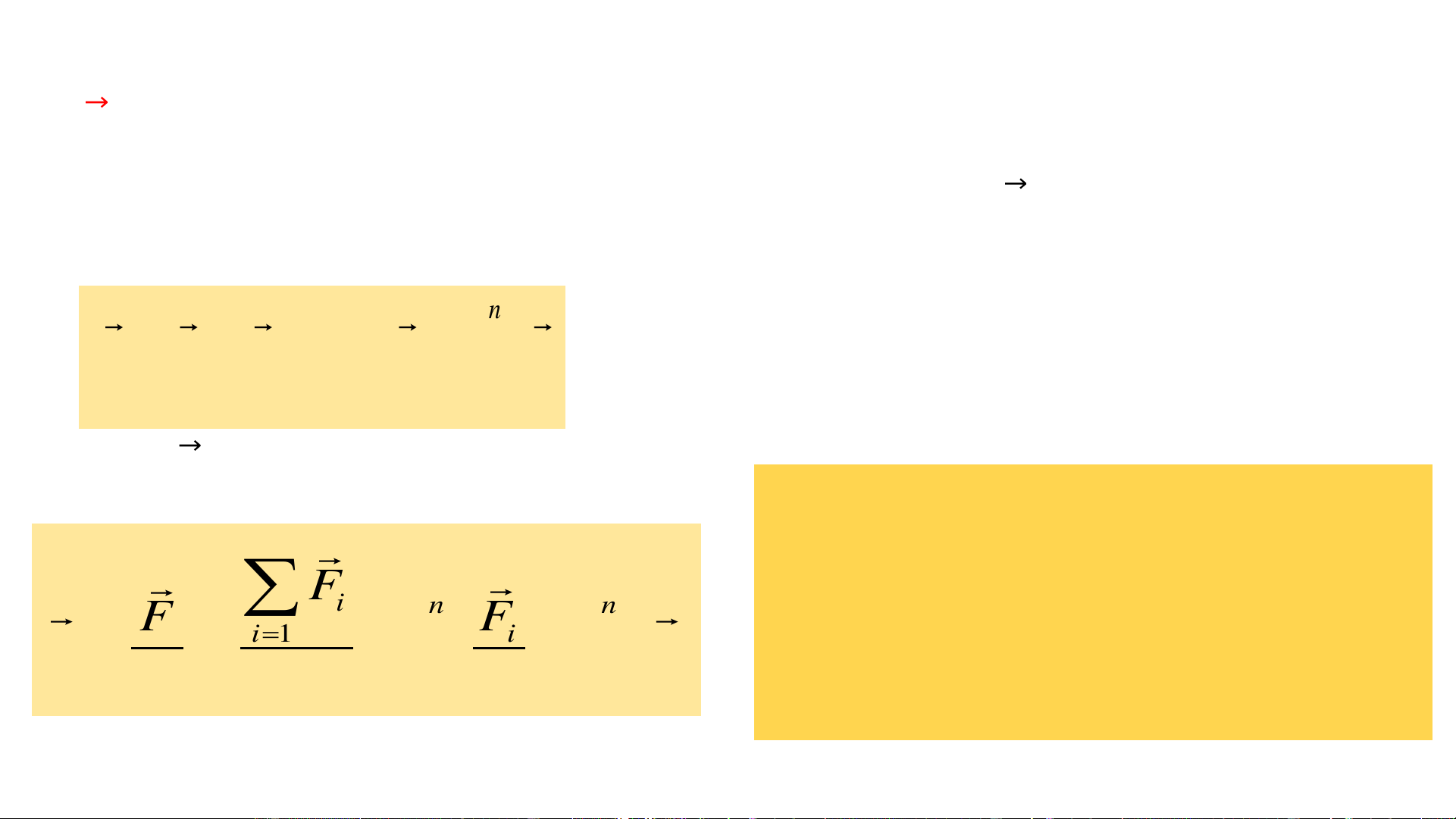
Có hệ điện tích điểm q , q , ..., q phân bố gián đoạn trong không gian và một 1 2 n
điện tích điểm q . Gọi Ԧ 𝐹
, q , ..., q tác dụng lên q . 0 1, Ԧ 𝐹2, … Ԧ
𝐹𝑛 là lực do q1 2 n 0
Lực tổng hợp tác dụng lên q là: 0
Để xác định lực tương tác tĩnh điện giữa 2 vật n
mang điện bất kỳ, ta coi mỗi vật mang điện như
F = F + F + ... + F = F
một hệ vô số các điện tích điểm. Khi đó lực tác 1 2 n i
dụng lên mỗi vật sẽ bằng tổng vectơ của tất cả i 1 =
các lực do hệ điện tích điểm của vật này tác
dụng lên mỗi điện tích điểm của vật kia
§3. KHÁI NIỆM VỀ ĐIỆN TRƯỜNG, VÉC TƠ CƯỜNG ĐỘ ĐIỆN TRƯỜNG
I. Khái niệm điện trường
✓ Không gian bao quanh mỗi điện tích có xuất hiện một dạng đặc biệt
của vật chất gọi là điện trường;
✓ Chính nhờ điện trường làm nhân tố trung gian, lực tương tác tĩnh
điện được truyền đi với vận tốc hữu hạn;
✓ Một tính chất cơ bản của điện trường là mọi điện tích đặt trong điện
trường đều bị điện trường đó tác dụng.
II. Véc tơ cường độ điện trường 1. Định nghĩa
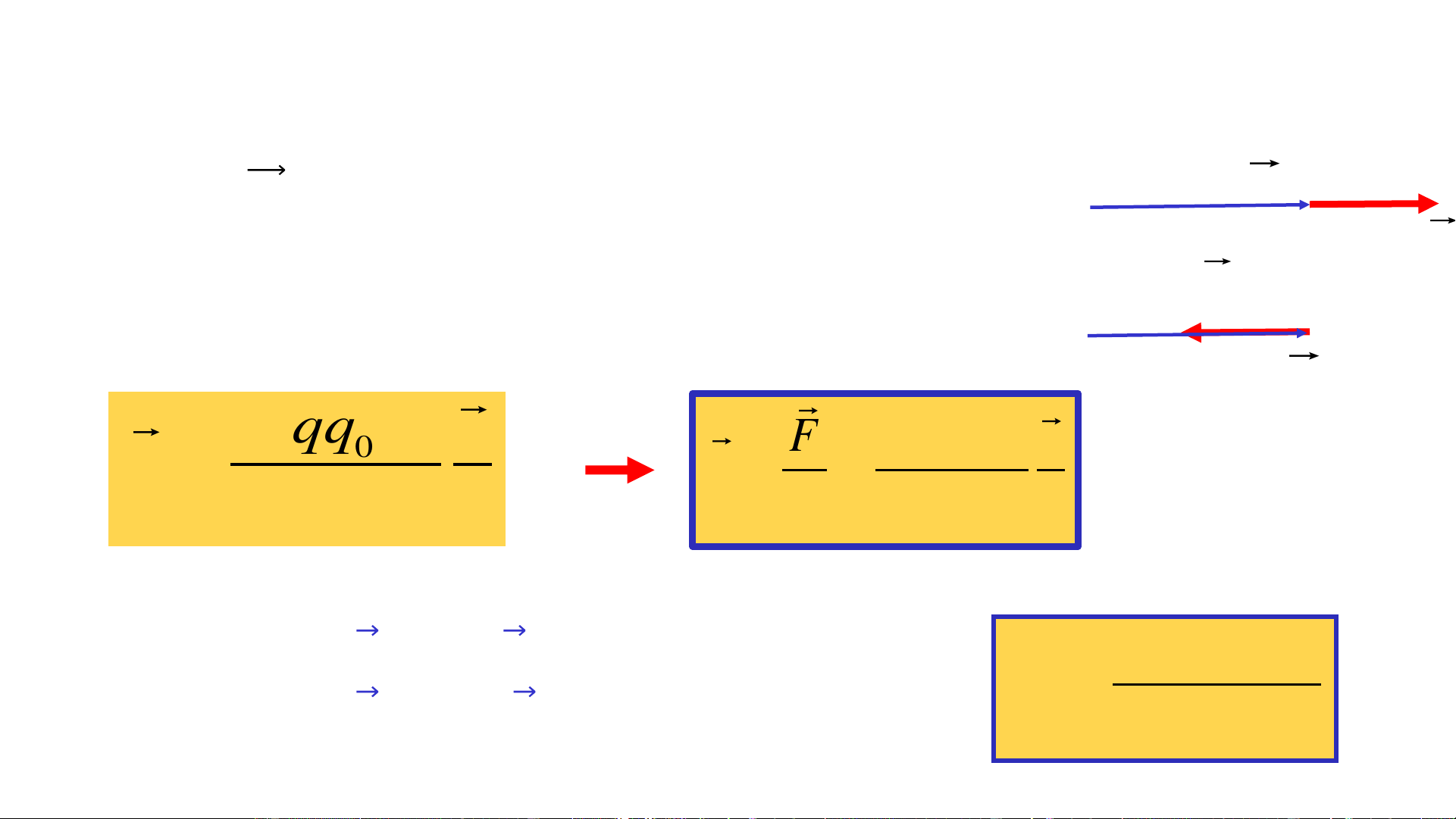
Giả sử có điện tích thử 𝑞0 đặt tại điểm M trong điện trường. 𝑞0 bị điện trường tác dụng một lực Ԧ
𝐹. Thực nghiệm chứng tỏ tỷ số 𝐹 không phụ thuộc vào 𝑞 𝑞 0 , chỉ phụ 0
thuộc vào vị trí điểm M. 𝑭
→ tại mỗi điểm xác định trong điện trường, tỷ số 𝑬 = =const. 𝒒𝟎
Vì vậy có thể dùng vectơ E để đặc trưng cho điện trường tại điểm đang xét về
phương diện tác dụng lực.
Đơn vị của E: V/m
E : vectơ cường độ điện trường
E= 𝐸 : cường độ điện trường
Nếu chọn 𝑞0=1C thì E =F
Định nghĩa:Véc tơ cường độ điện trường tại một điểm là đại lượng có giá trị bằng
lực tác dụng của điện trường lên một đơn vị điện tích dương đặt tại điểm đó
2. Véc tơ cường độ điện trường gây ra bởi điện tích điểm a. Biểu thức M
Xác định 𝐸 do điện tích điểm q gây ra tại điểm M r q 
cách q một khoảng là r. E Đặt 𝑞 E M
0 tại M. Lực do q tác dụng lên 𝑞0: q ⊝ r qq r 0 F q r F = E = = 2 2 4  r r q 4  r r 0 0 0 b. Nhận xét
✓ q>0 thì 𝐸 ↑↑ Ԧ𝑟 (𝐸 hướng ra xa q) | q | E = 2
✓ q<0 thì 𝐸 ↑↓ Ԧ𝑟 (𝐸 hướng về q) 4  r 0
3. Véc tơ cường độ điện trường gây bởi 1 vật mang điện
a. 𝐸 gây ra bởi hệ điện tích điểm
Xét một hệ điện tích điểm: q , q , ..., q Cần xác định 𝐸 tại M. 1 2 n.
Đặt q tại M. Lực tổng hợp tác dụng lên q là: 0 0 n
F = F + F + ...+ F =  F 1 2 n i i 1 =
Vectơ 𝐸 tổng hợp tại M bằng:
Nguyên lý chồng chất điện trường: n 
Véc tơ cường độ điện trường gây ra bởi Fi n n F F
một hệ điện tích điểm bằng tổng các i 1 = i E = = =  =  Ei
véc tơ cường độ điện trường gây ra q q = q 0 0 i 1 0 i 1 =
bởi từng điện tích điểm của hệ
b. Véc tơ cường độ điện trường gây ra bởi một vật mang điện
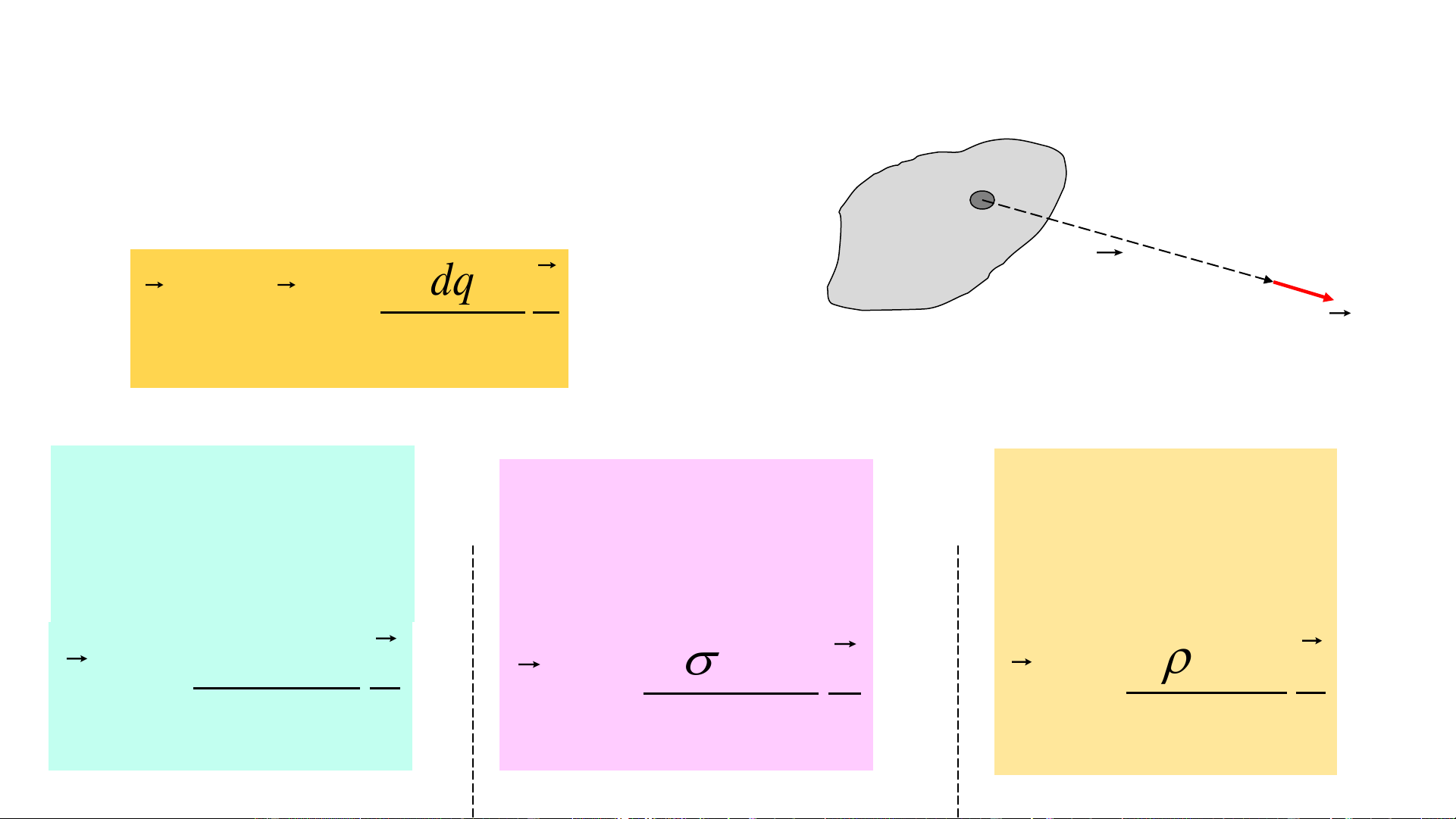
Chia vật mang điện thành nhiều phần
nhỏ chứa điện tích dq. Vật mang điện dq>0
được coi như 1 hệ vô số điện tích điểm M r dq r E = dE =   2 4  r r dE tbv tbv 0 Dây: (C/m) Mặt:  (C/m2) Khối:  (C/m3) dq= dl dq=  dS dq=  dV dl r  dS r dV r E =  E =  E =  2 4  r r 2 4  r r 2   (C ) 0 4 r r tbv 0 tbv 0 E III. Thí dụ 2 
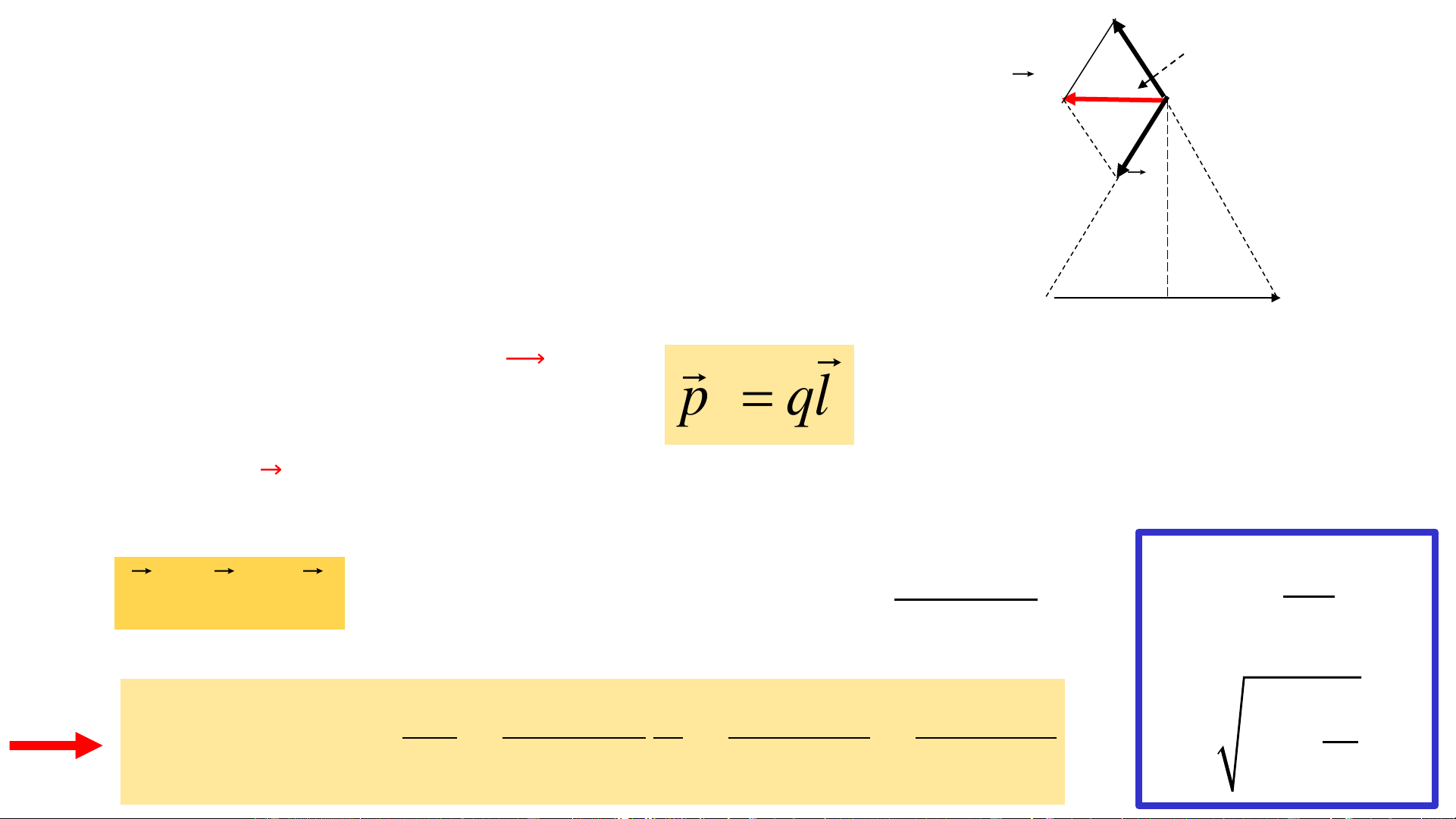
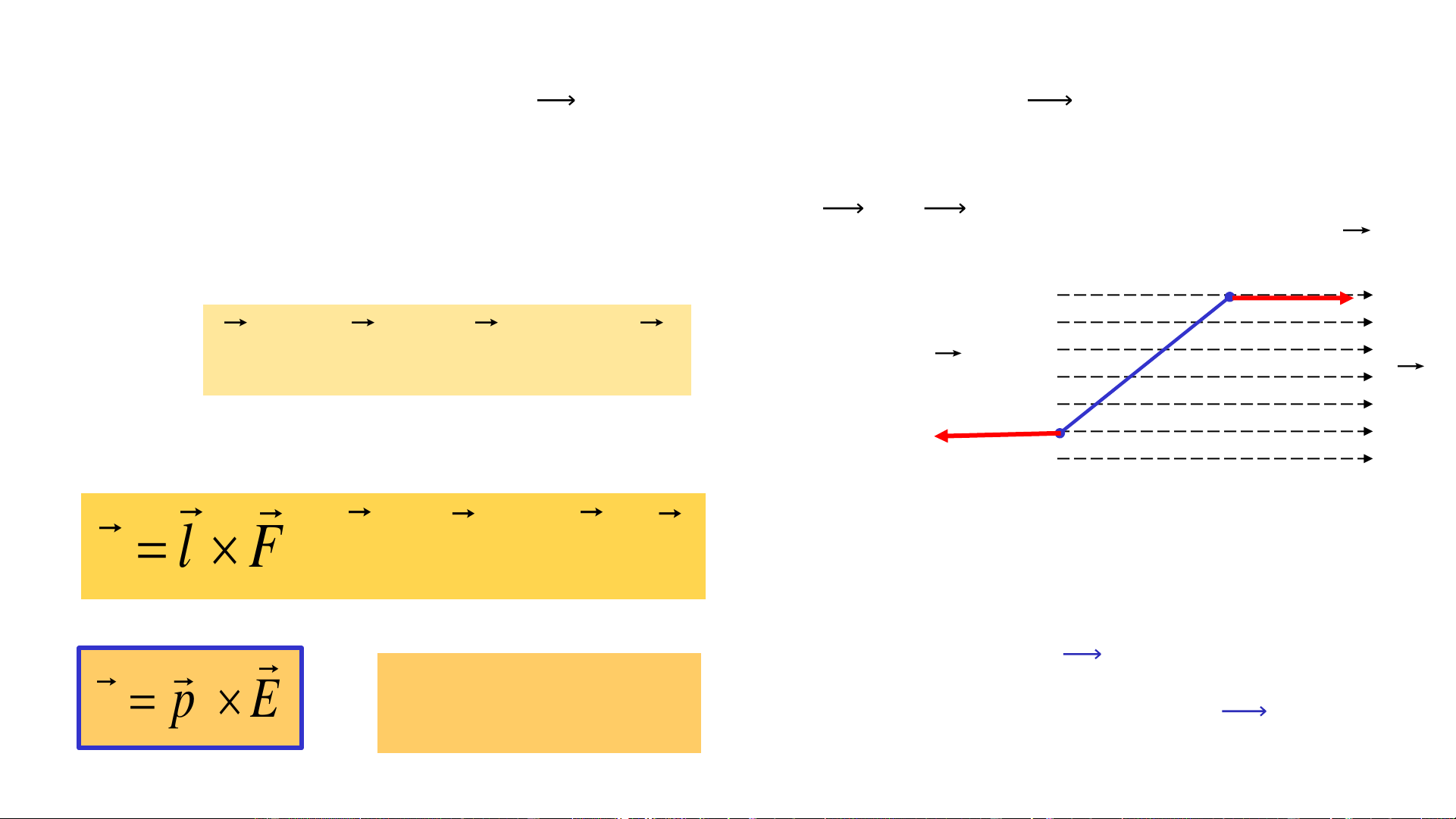
1. Lưỡng cực điện E M
a. Định nghĩa: Lưỡng cực điện là một hệ 2 điện tích điểm E
có độ lớn bằng nhau nhưng trái dấu +q và –q 1 r r r 1 2
cách nhau một khoảng l rất nhỏ so với khoảng cách 
từ lưỡng cực tới những điểm đang ⊝  xét của trường -q l +q
b. Mômen lưỡng cực điện (𝑃𝑒 ) p = ql
Ԧ𝑙: Hướng từ -q đến +q, có chiều dài e
bằng khoảng cách l giữa +q và -q
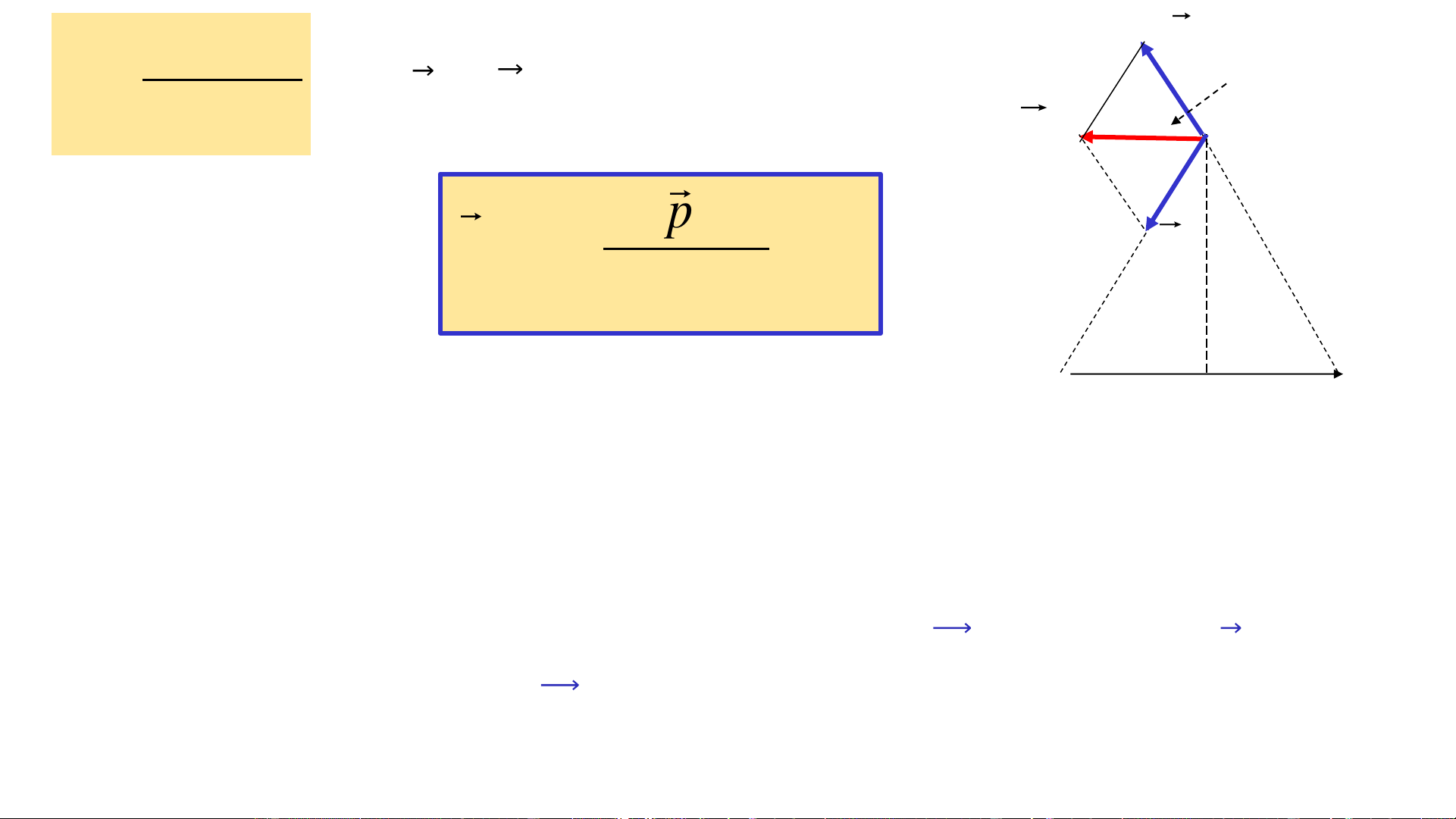
c. Xác định 𝐸 tại điểm M nằm trên trung trực của lưỡng cực q l E = E + E E = E = cos = 1 2 Vì 𝑟 1 2 1= 𝑟2 → 2 4  r 2r 0 1 1 E l q l ql P 2 1 l E = 2E cos e  = = = = 2 = +  1 r r r 2 3 3 r 4  r r 4  r 4  r 1 1 0 1 1 0 1 0 4 P E e 2 E =  3 Vì 𝐸 ↑↓ 𝑙 → 4  r 0 E M pe E = − (1) E1 M 3 4  r r r r 1 2 0 ⊝   -q l +q Nhận xét:
✓ (1) cho thấy E gây bởi lưỡng cực điện tỷ lệ thuận với mômen điện của nó và
tỷ lệ nghịch với lập phương khoảng cách từ tâm của lưỡng cực đến điểm đang xét;
✓ Ý nghĩa của việc sử dụng vectơ mômen điện: Biết 𝑃𝑒 ta có thể tính 𝐸 do
lưỡng cực gây ra → ta nói 𝑃𝑒 đặc trưng cho tính chất điện của lưỡng cực.
d. Tác dụng điện trường đều lên lưỡng cực điện
✓ Giả sử lưỡng cực điện 𝑃𝑒 đặt trong điện trường đều 𝐸0 và nghiêng với
đường sức điện trường một góc 𝜃
✓ Lưỡng cực chịu tác dụng của ngẫu lực: 𝐹1 và 𝐹2 +q F1 F = qE ; F = −qE l 1 0 2 0 F2 E0  Mômen của ngẫu lực: -q
 = l  F = l qE = ql  E 1 0 0
Dưới tác dụng của mômen ngẫu
lực, lưỡng cực điện bị quay theo  = chiều p  E  = qE l sin
sao cho 𝑃𝑒 tới trùng với e 0 0
hướng của diện trường 𝐸0
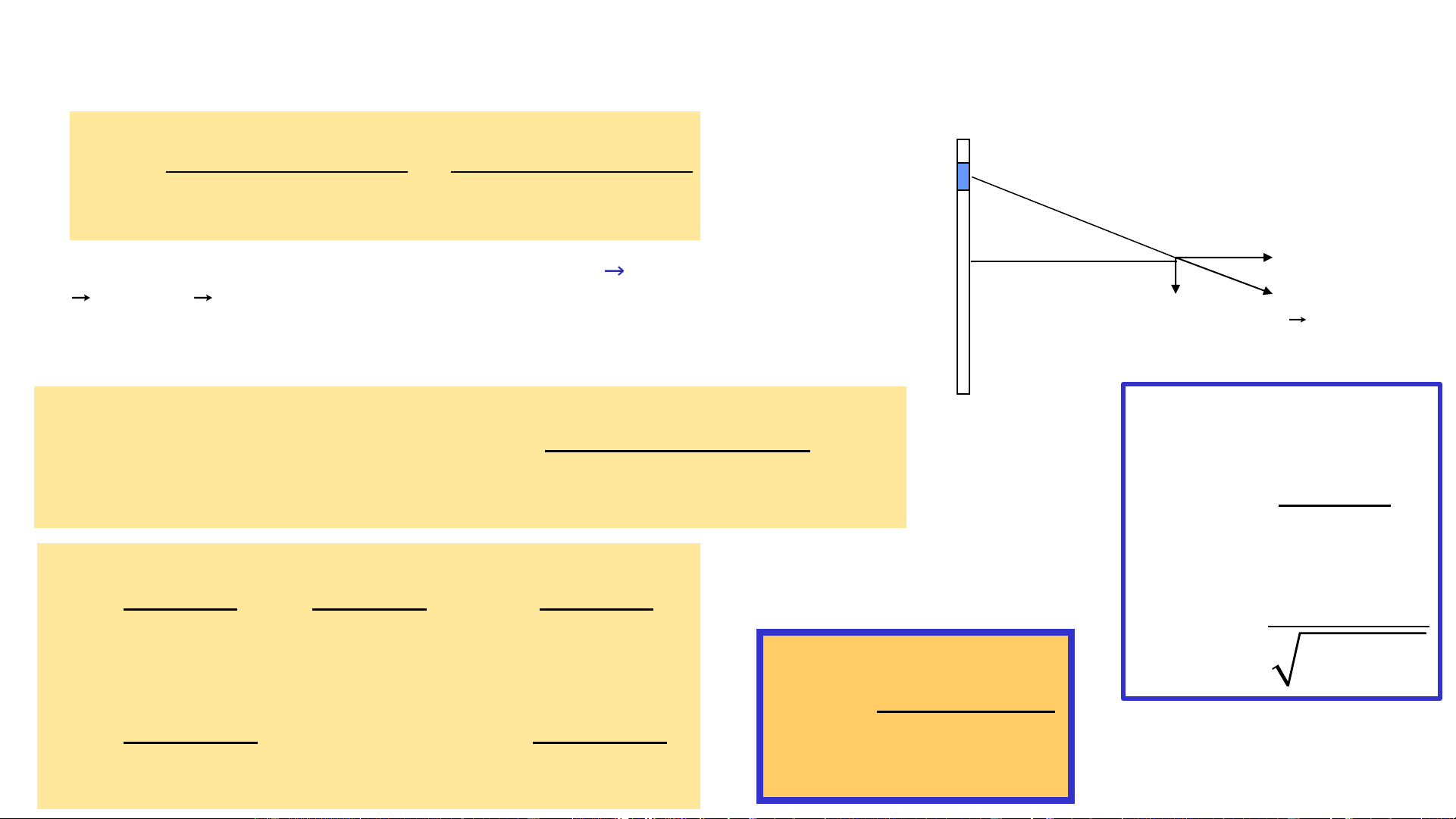
2.Véctơ cường độ điện trường gây ra bởi dây dẫn vô hạn tích điện đều dq dx = = dx + dE dq 2 2 2 2
4  (x + r )
4  (x + r ) 0 0 + M  x  E d + n r  E = dE 
Do đối xứng 𝐸 có hướng vuông góc với dây + dE // dE dx x = rtan E = dE = dEcos = cos    n 2 2
4  (x + r ) rd tbd tbd tbd 0 → dx = 2 cos   /2 2  rd cos  E = cos =  r 2 2  = 4  cos  r cos 0 − /2 |  | 2 2 r + x  /2   E = E = cosd =  2  r 4  r 2  r 0 0 − /2 0
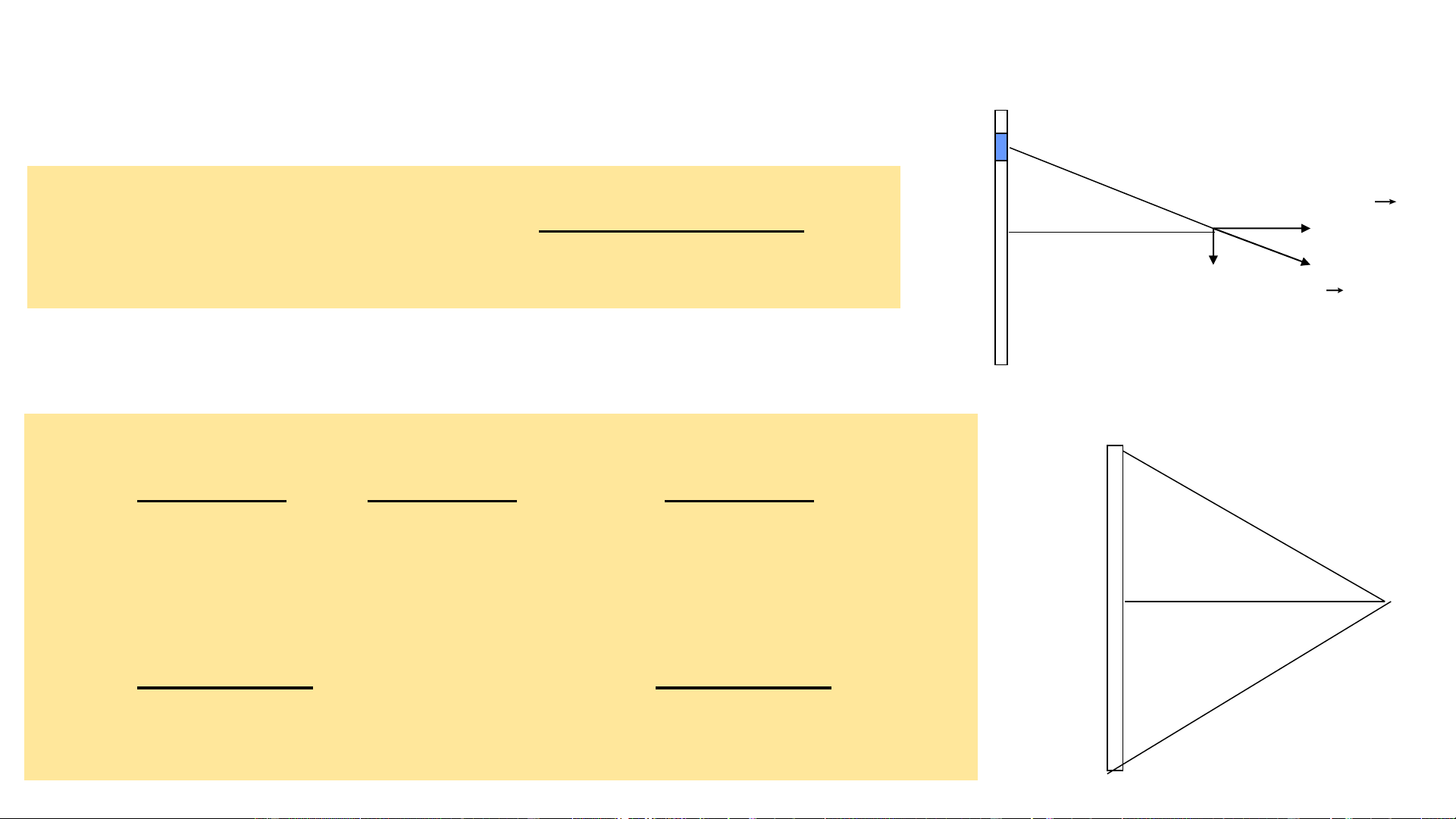
Véc tơ cường độ điện trường gây ra bởi 1 đoạn dây dẫn tích điện đều tại
điểm M nằm trên trung trực + dx dq dx + M x  E = dE = dEcos = cos    dE n n 2 2
4  (x + r ) + r tbd tbd tbd 0 + dE 0 2  rd cos  E = cos =  + 2 2 4  cos  r 0 − + 0  M 0  + 0   r E = cosd = sin  + 0 4  r 2  r 0 − 0 0