Tổng hợp bài tập - Click it if you want - Bussiness ( BUS123) | Đại học Hoa Sen

Ôn business statistics Chapter 1
Basic Exercises – chap 8 1.
Indicate whether each statement below is true or false. If false, explain why. a.
We can eliminate sampling error by selecting an unbiased sample. b.
The only truly representative sample is a census. c.
Randomization helps to ensure that our sample is representative. d.
Sampling error refers to sample to sample differences and is also known as sampling variability.
a) False. Sampling error is inevitable because a survey is given to several random samples
and samples are different from each other.
b) False. The census just includes the entire population and does not always give the best
possible information about the population c) True d) True 2.
Suppose that the administration of a large urban hospital is interested in obtaining
feedback from its employees regarding how their processes can be improved. For each of
the following, identify the sampling method.
a. There are six categories of employees (administration, physicians, nurses, medical
technologists, clerical and maintenance). Randomly select twenty individuals from each category.
b. Each employee has an ID number. Randomly select 150 numbers.
c. Randomly select a department within the hospital (e.g., Radiology) and survey all of the
employees who work in that department.
d. At the hospital cafeteria, select every fifth person who enters on a specific day. a) Stratified sampling b) Simple random sampling c) Cluster sampling d) Systematic sampling 3.
A consumer advocacy group is interested in gauging perceptions about food safety among
professionals in the food industry. Specifically, they wish to determine the percentage of
professional food preparers in the U.S. that believe food safety has improved. They use an
alphabetized list of members of the organization Chef’s Collaborative and select every 10th
member to include in the sample.
a. What is the population?
b. What is the sampling frame?
c. What is the population parameter of interest?
d. What sampling method is used?
a) U.S professionals in the food sector
b) Members of the organization Chef’s Collaborative
c) The Proportion of professional food preparers who believe food safety has improved d) Systematic sampling 4.
Indicate whether each statement below is true or false. If false, explain why.
a. A local television news program that asks viewers to call in and give their opinion on an
issue typically results in biased voluntary response sample.
b. Convenience samples are generally not representative of the population. c.
Measurement error is the same as sampling error.
d. A pilot test is useful for identifying poorly worded questions on a survey. a) TRUE b) True
c) False. Both of them are completely different because measurement error is the incorrect
answer or response, while the remaining one is sample-to-sample difference. d) TRUe ANSWERS 1. a.
false; unlike bias, sampling error cannot be avoided b.
false; a census is a covering of the entire population; a simple is a subset
of the population and if selected carefully can be representative of the population c. true d. true 2. a. stratified b. simple random c. cluster d. systematic 3. a.
professional food preparers in the U.S. b.
Chef’s Collaborative membership listing c.
proportion who believe that food safety has improved d. systematic 4. a. true b. true c.
false; measurement error refers to inaccurate responses d. true
Basic Exercises- chap 4 1.
Data from a sample of employees from a large multinational corporation were used to
estimate the following least squares regression equation:
Salary = 36775 + 1590 Years of Experience
a. What is the explanatory variable? \ Years of experience
b. What is the response variable? Salary
c. What does the slope mean in this context?
A slope of 1590 says that we can expect employees’ salary depends on a
experiencing year more to about $1590 more.
d. What does the y-intercept mean in this context? Is it meaningful?
The intercept of 36775 is the value of the line when the x-variable is zero.
I think it makes sense because maybe minimum annual wage is $35775. 2.
Based on the regression equation from the previous exercise,
Salary = 36775 + 1590 Years of Experience,
a. What is the predicted salary for an employee with 10 years of experience?
10-experiencing-year predicted salary = 36775 + its 1590*10 = $ 52675 $
e. If the salary for an employee with 10 years of experience turned out to be $56,500, what is the residual?
The residual e= 56500 – $ 52675 = $ 3825 $ f.
What is the predicted salary for an employee with 20 years of experience?
20-experiencing-year predicted salary = 36775 + $ 1590*20 = $ 68575 $
g. If the salary for an employee with 20 years of experience turned out to be $64,550, what is the residual?
The residual e = $64550 – $68575 = $-4025 3.
Based on the following data set and summary statistics: x y 6 20 9 18 12 10 15 8 18 9 25 4 Mean of x = 14.17 Standard deviation of x = 6.79 Mean of y = 11.50 Standard deviation of y = 6.19 Correlation r = -0.920.
a. What is the slope of the estimated regression equation?
The slope = (-0.92) = -0.8387
h. What is the intercept of the estimated regression equation?
The intercept = 11.5 – (-0.8387)*14.17 = 23.384 i.
What is the predicted value of when y
x is 25? = 23.384 + (-0.8387)*25 = 2.4165 j. What is its residual?
The residual e = 4 – 2.4165 = 1.5835 4.
A real estate agency fit a regression equation to determine the length of time a property is
on the market (number of months) before it sells based on asking price (in thousands of
dollars). The following results were obtained.
Time on Market = -0.64 + .041 Asking Price R2 = 50.5%
a. Interpret the meaning of R .
2 50.5% of the variation in the market-length time of a
property is accounted by the number of months.
k. Is the correlation between Time on Market and Asking Price positive or negative? How do you know?
The correlation between Time on market and asking price is positive because the
slop of the line represents the positiveness. (b1 = r*sy/sx) l.
What is the correlation between Time on Market and Asking Price?
The correlation between the time on market ad asking price is r = = 0.71. The
positive value of the square root is used, since the relationship is positive.
m. What proportion of the variability in Time on Market is not accounted for by Asking Price?
1-0.505= 0.495 or 49.5% is the variability in the time length has been left in the residuals 5.
For the regression model predicting Time on Market Asking Price using in the previous exercise, se = 7.459. a. What does se tell us?
Se of 7.459 means that there are 7.459 points vary around the regression line.
n. Using the model to predict number of months on the market for a home priced at
$550,000, the residual is 13.82. How many standard deviations away is the prediction from the actual value?
The predicted months = -0.64 + 0.041*550 = 21.91 months
The actual value = 13.82 + 21.91 = 35.73
The standard deviations == 7.459 => n= 5.433
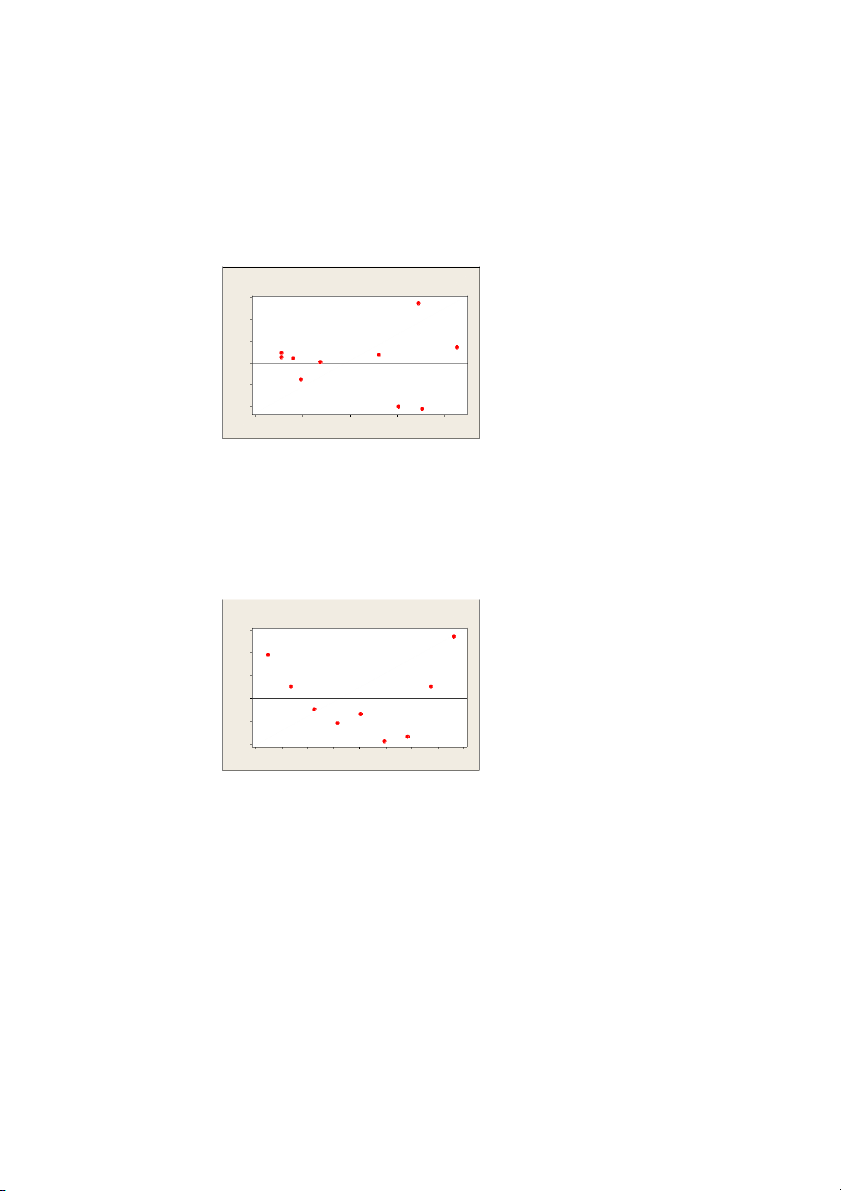
o. The residual plot is shown below. Based on this plot, is the equal spread condition satisfied? Explain.
The equal spread condition is not satisfied because the residual plot’s spreading is increasing. Versus Fits (response is Time on Market) 15 10 5 esidual R 0 -5 -10 5 10 15 20 25 Fitted Value 6.
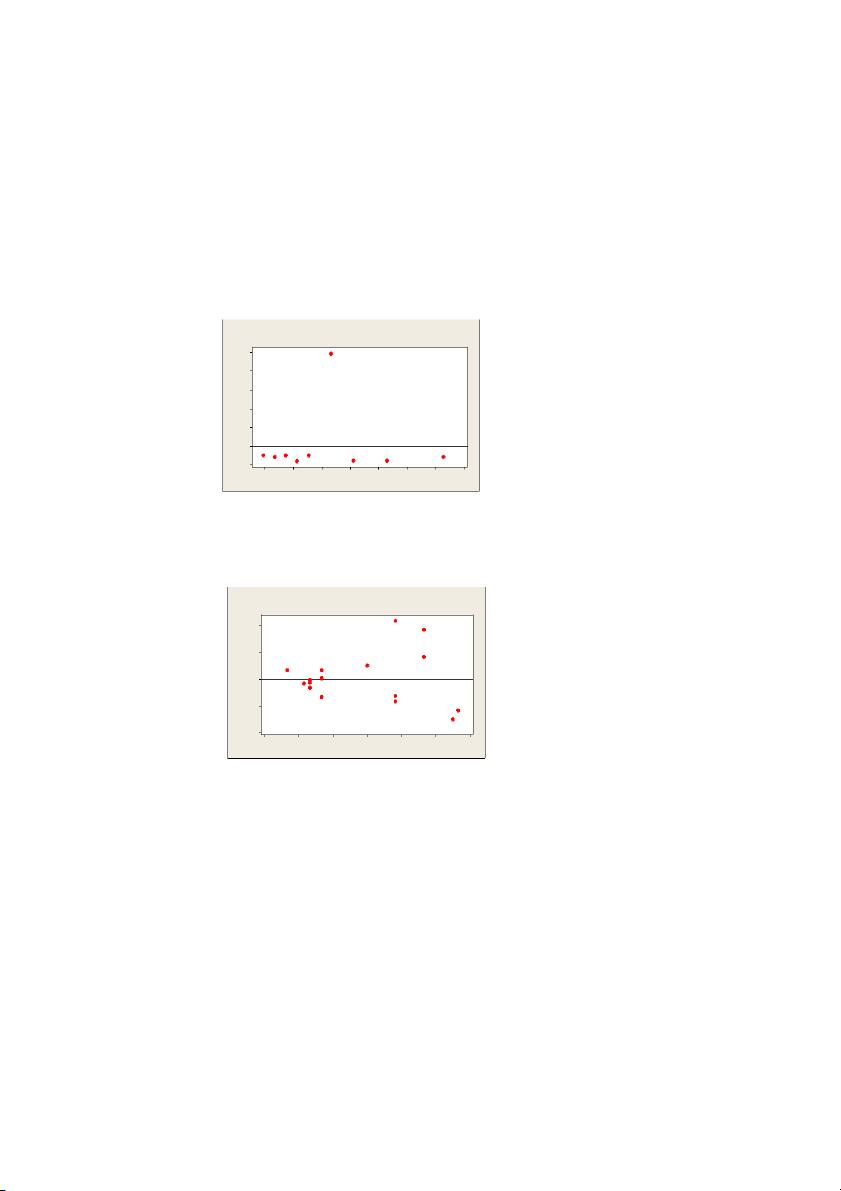
Below are residual plots (residuals plotted against predicted values) for three linear
regression models. Indicate which condition appears to be violated (linearity, outlier or equal spread) in each case.
a. Linearity curved shapre Versus Fits (response is y) 15 10 5 esidual R 0 -5 -10 -10 0 10 20 30 40 50 60 70 Fitted Value \ b. Outlier Versus Fits (response is y) 50 40 30 2esidual0 R 10 0 -10 15.0 17.5 20.0 22.5 25.0 27.5 30.0 32.5 Fitted Value c. equal spread Versus Fits (response is y) 200 100 esidual R 0 -100 -200 100 200 300 400 500 600 700 Fitted Value 2.a
Salary = 36775 + 1590 * 10 = 52675 b. 56500 - 52675 = 3825 c. 36775 + 1590 * 20 = 68575 d. 64550 - 68575 = -4025 3.a -0.8387
b. 11.5 - (-0.8387)*14.17 = 23.384 c. 23.384 - 0.8387*25 = 2.4165
d. residual e = 4 – 2.4165 = 1.5835
4.a. 50.5% of the variability in time on market can be explained by asking price.
b. positive, because the slope is positive
c.r = √(R^2 )=√(50.5%)=0.71 The positive value of the square root is used the relationship is positive d. 49.5%
5. a. It is the standard deviation in the residuals so it tells us how scattered the points are around the fitted line. b. 13.82/7.459 = 1.85 c. no 6. a linearity b. outlier c. equa spread
Basic Exercises- chap 7
1. Assuming that a variable follows the normal model, and using the 68-95-99.7 Rule, find the following. a.
The probability that an observation is within 2 standard deviations of the mean?
z = 2 => prob = 0.9772 => 97.72% => 100% - 97.72% = 2.28%
=> 100% - 2.28%*2 = 95.44% 1.a 95% b.
The probability that an observation is at least 2 standard deviations above the mean?
P(z>=2) = 100% – 97.72% = 2.28% b. 2.5% c.
The probability that an observation is at least 1 standard deviation below the mean?
P(z>=-1) = P(z=<1) (symmetric pattern) = 84.13%