
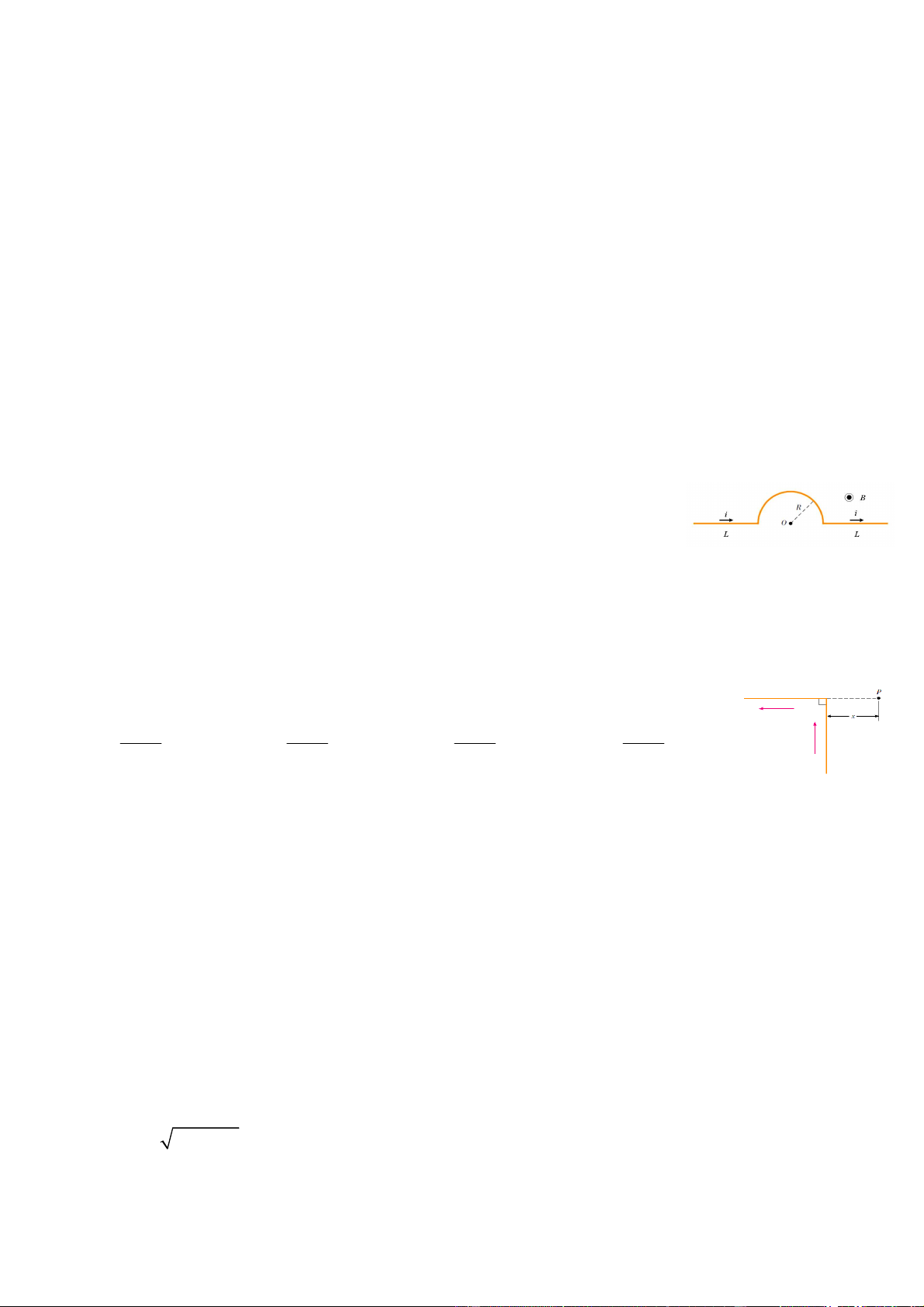










Preview text:
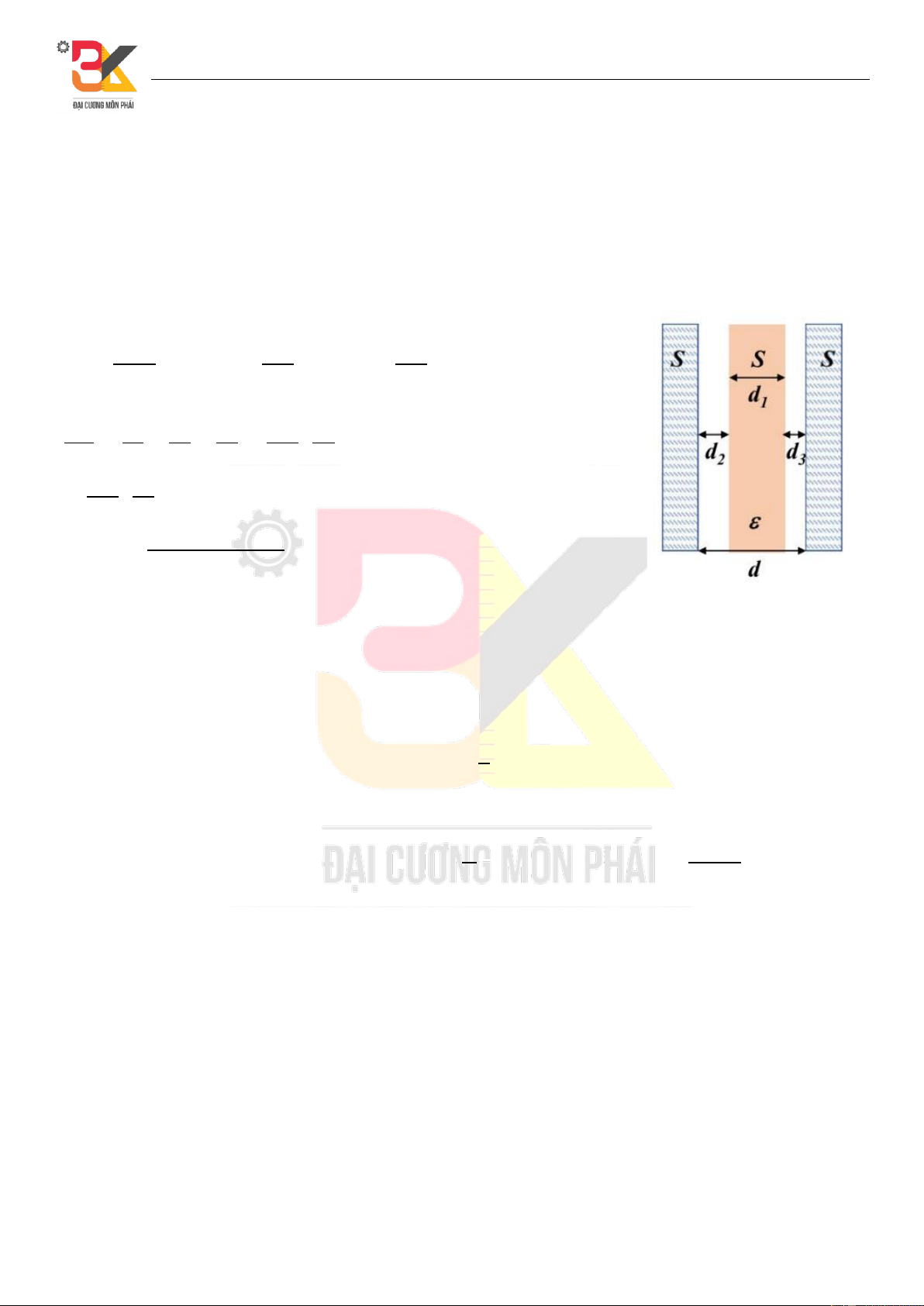
Câu 1. Một tụ phẳng có điện tích bằng A được lấp đầy hai chất điện môi như
hình vẽ (bề dày hai tấm điện môi bằng nhau). Tìm điện dung của tụ:
Câu 2 Một đoạn dây tích điện đều được uốn thành hình như hình vẽ. Biết
mật độ điện dài của sợi dây là λ = 4,43.10-9 C/m, tìm điện thế V tại điểm O.
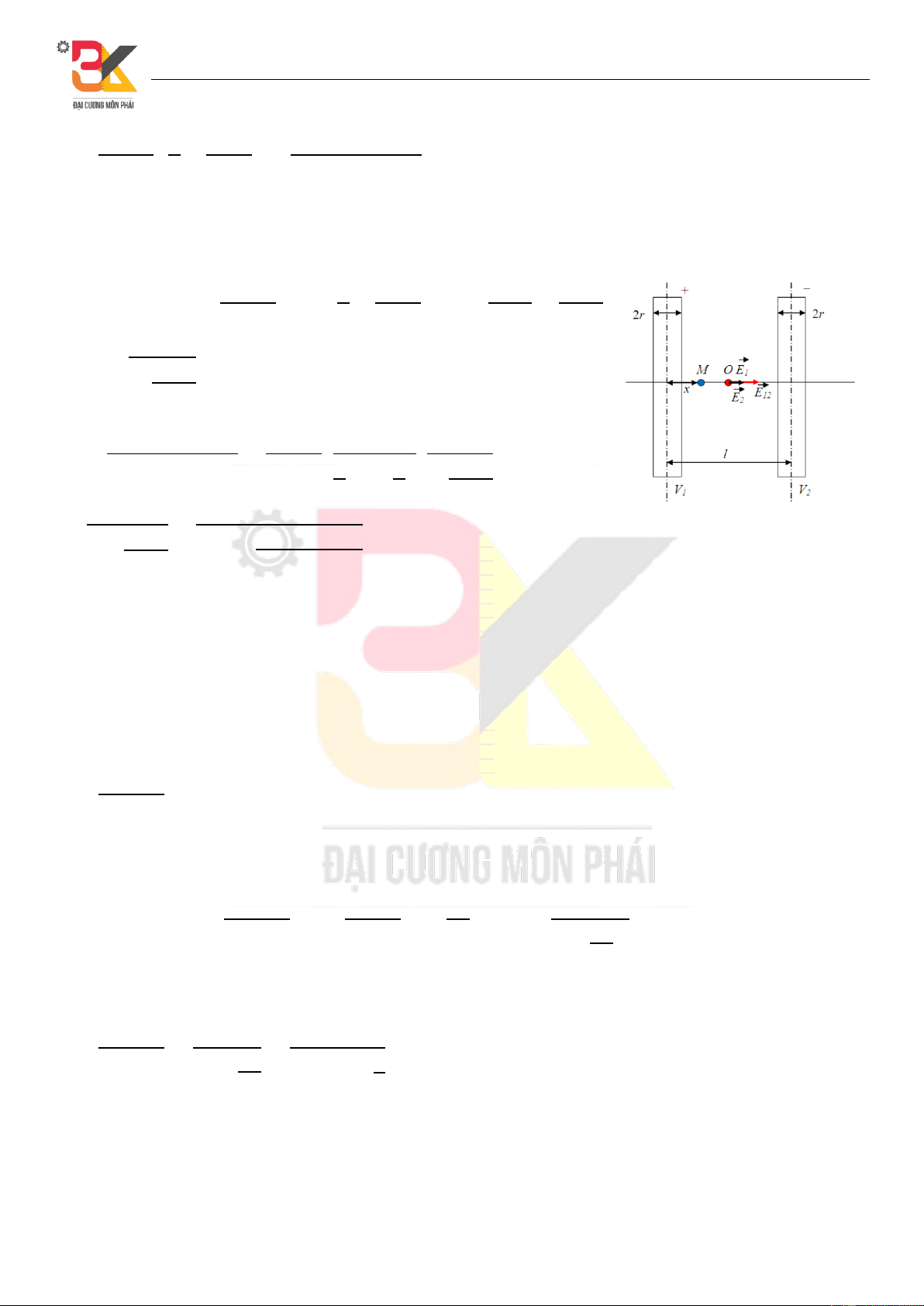
Câu 3. Giữa hai dây dẫn hình trụ song song cách nhau một khoảng l = 60
cm người ta đặt một hiệu điện thế U = 3000V. Bán kính tiết diện mỗi dây là r = 1 mm. Hãy xác định cường
độ điện trường tại trung điểm của khoảng cách giữa 2 sợi dây biết rằng các dây dẫn đặt trong không khí.
Câu 4. Hai bản kim loại lớn có diện tích 1,0 m2 nằm đối diện nhau. Chúng cách nhau 5,0cm và có điện tích
bằng nhau nhưng trái dấu ở trên các mặt trong của chúng. Nếu cường độ điện trường ở giữa hai bản bằng
55V/m thì độ lớn của các điện tích trên các bản bằng bao nhiêu? Bỏ qua các hiệu ứng mép.
Câu 5. Người ta đặt một hiệu điện thế U = 400 V giữa hai hình trụ dài đồng trục bằng kim loại mỏng bán
kính r1 = 2 cm và r2 = 10 cm. Tính mật độ điện dài trên hình trụ trong.
Câu 6. Cho một quả cầu tích điện đều với bán kính a. Hiệu điện thế giữa hai điểm cách tâm lần lượt a/2 và a
là U. Mật độ điện khối của quả cầu là:
Câu 7. Một tụ điện phẳng, diện tích bản cực S=140 cm2, khoảng cách giữa hai bản tụ d=0,5 cm. Giữa hai
bản cực là điện môi có hằng số điện môi ε=2. Tụ được tích điện đến hiệu điện thế U=300V. Nếu nối hai bản
tụ điện với điện trở R=100 Ω thành mạch kín thì nhiệt lượng tỏa ra trên điện trở khi tụ phóng hết điện là (cho ε=8,86.10-12 C/Nm2):
Câu 8. Một tụ điện phẳng có chứa điện môi ε = 3, khoảng cách giữa hai bản là 0,2 cm, hiệu điện thế giữa
hai bản là 600 V. Tính mật độ điện mặt trên chất điện môi.
Câu 9. Một quả cầu bán kính R = 10cm tích điện đều với mật độ điện tích ρ = 1,6.10-10C/cm3 đặt trong
không khí. Năng lượng điện trường bên ngoài quả cầu là (cho hằng số điện môi εo=1/(36π.109) C2/Nm2):
Câu 10. Electron chuyển động trong từ trường đều có cảm ứng từ B=2.10-6T theo phương vuông góc với
các đường cảm ứng từ. Quỹ đạo của electron là đường tròn có bán kính R=4 cm. Động năng của electron có
giá trị là (cho me=9,1.10-31kg, e=1,6.10-19C):
Câu 11. Cho một khung dây phẳng diện tích 20 cm2 quay trong một từ trường đều với vận tốc 5 vòng/s.
Trục quay nằm trong mặt phẳng của khung và vuông góc với các đường sức từ trường. Cường độ từ trường
bằng 2.104 A/m. Tìm giá trị lớn nhất của từ thông gửi qua khung dây.
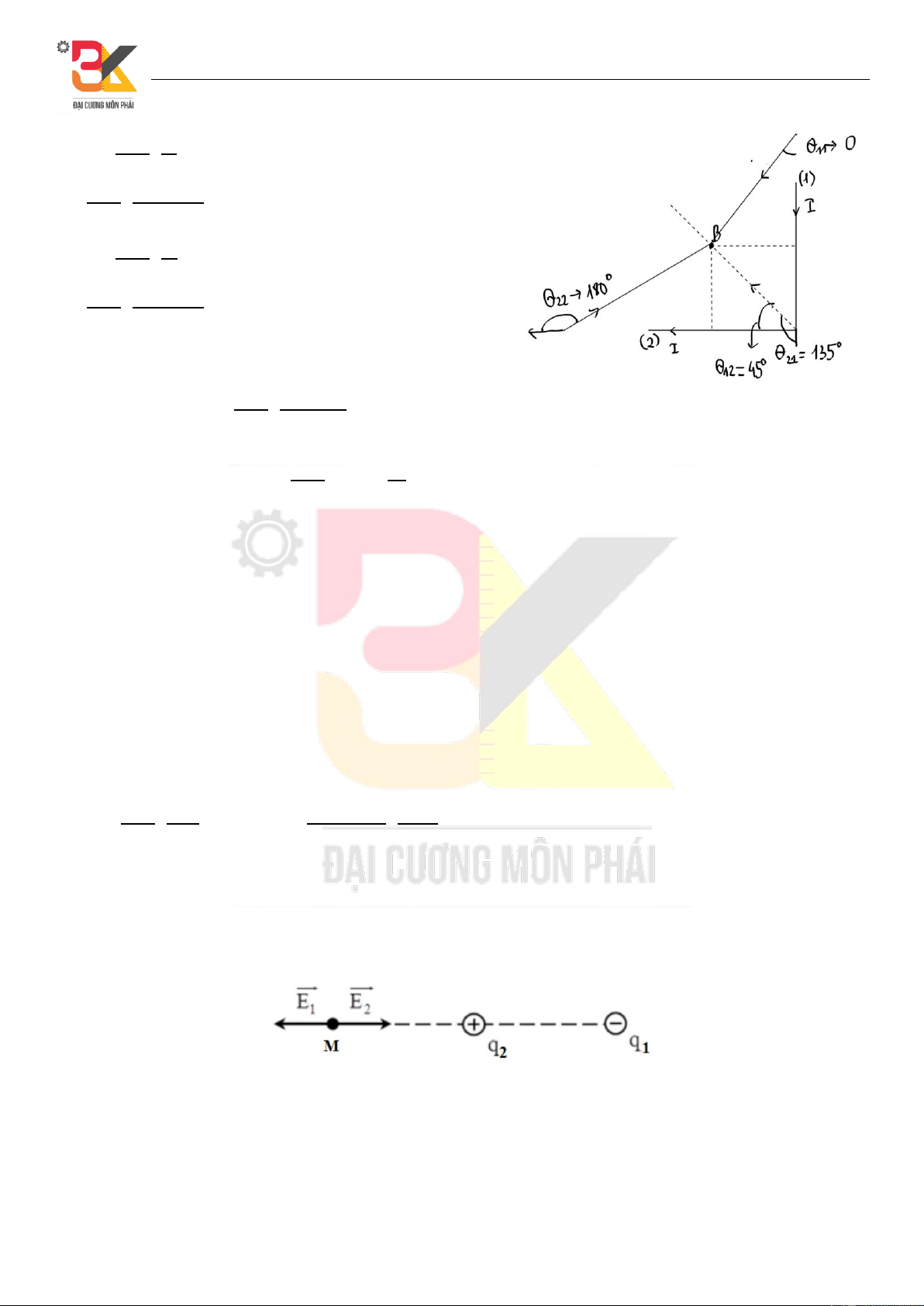
Câu 12. Hai dây dẫn dài song song, mang dòng điện I1 và I2 cùng chiều nhau. Xác định
độ lớn của từ trường tổng hợp tại điểm P. Biết I1 = 15A, I2 = 32A, d = 5,3cm.
Câu 13. Cho một dòng điện I = 10 A chạy qua một dây dẫn đặc hình trụ, bán kính tiết
diện thẳng góc R = 5 cm. Tính cường độ từ trường tại điểm nằm cách trục của dây là 2 cm.
Câu 14. Hai dây dẫn dài vô hạn đặt song song cách nhau một khoảng nào đó. Dòng điện chạy qua các dây
dẫn bằng nhau và cùng chiều. Tìm cường độ dòng điện chạy qua mỗi dây, biết rằng muốn dịch chuyển các
dây dẫn tới một khoảng cách lớn gấp đôi lúc đầu thì phải tốn một công bằng 6.10-5 J/m (công dịch chuyển 1 mét dài của dây dẫn).
Câu 15. Một đoạn dây mà phần giữa là một cung tròn đặt trong từ trường đều B
hướng từ mặt phẳng hình vẽ đi ra phía trước. Hỏi nếu có dòng điện I chay trên
dây thì lực từ tổng hợp F tác dụng lên nó là bao nhiêu?
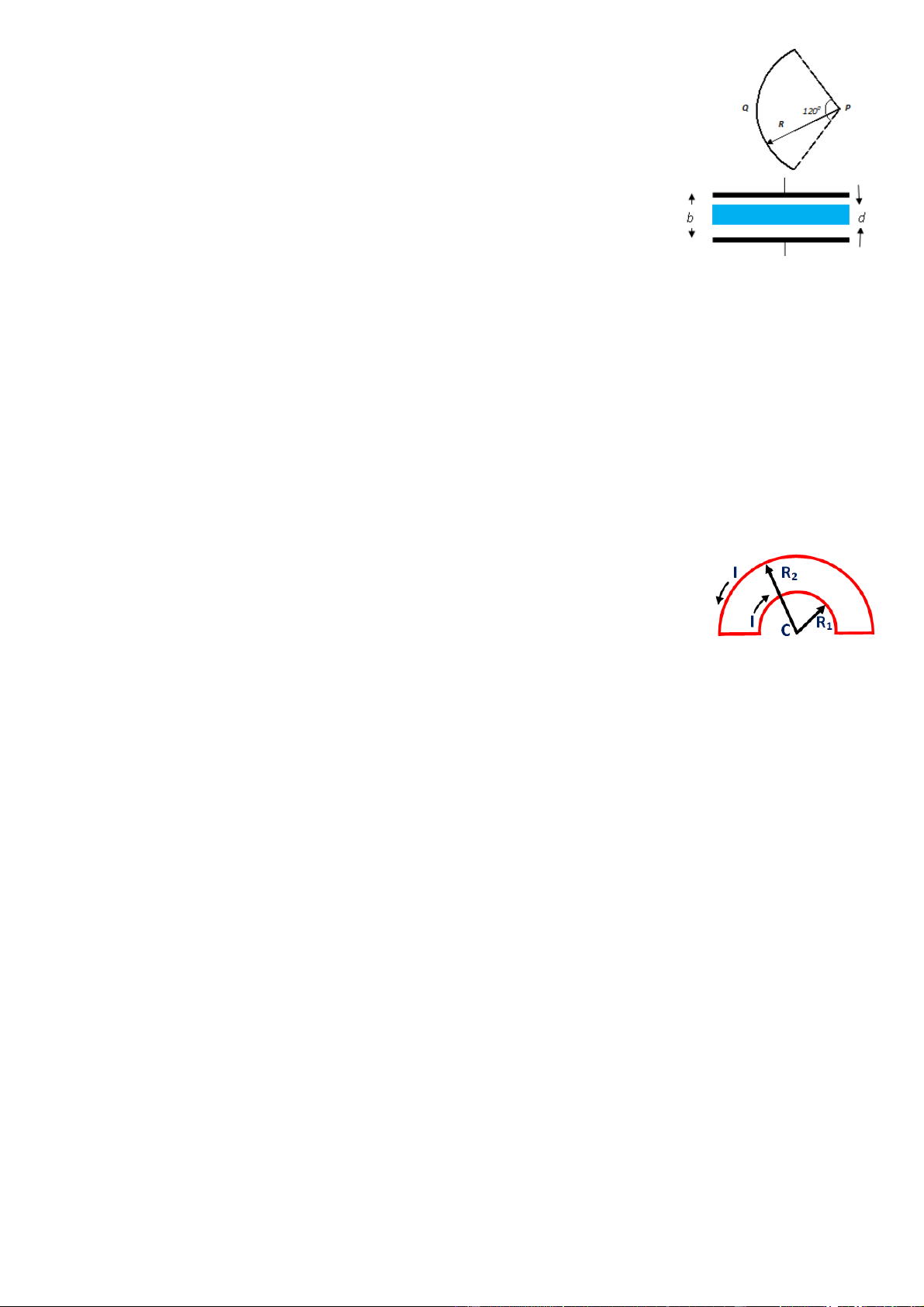
Câu 1. Một thanh nhựa, với điện tích Q được phân bố đều λ = 8,86.10-9 C/m, được uốn
cong thành một cung tròn bán kính R và góc ở tâm bằng 1200 như hình vẽ. Tìm điện thế
ở P là tâm của cung tròn đó. [A] 83,3 V [B] 75,0 V [C] 80,0 V [D] 41,7 V
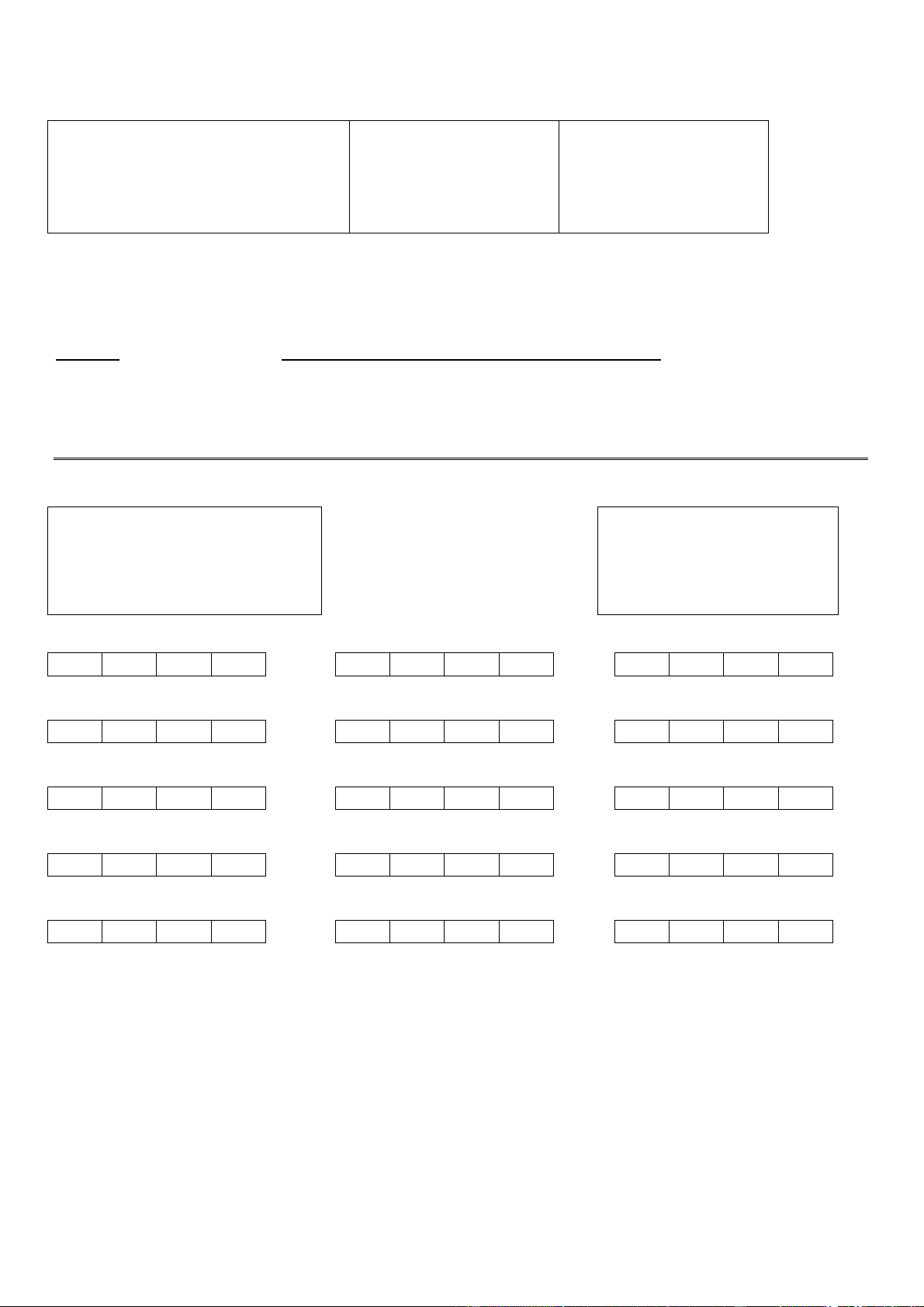
Câu 2. Một tụ điện phẳng có các bản với diện tích A và cách nhau d. Một hiệu
điện thế V được đặt vào giữa các bản tụ. Sau đó ắcquy được ngắt ra và một tấm
điện môi dày b và có hằng số điện môi K được đưa vào giữa các bản tụ (hình vẽ).
Cho A = 115cm2; d = 1,24cm; b = 0,78cm; K = 2,61; V0 = 85,5 V. Hiệu điện thế
giữa hai bản tụ sau khi đưa tấm điện môi vào:
Câu 3. Một quả cầu dẫn điện bán kính 10cm có một điện tích chưa biết. Nếu điện trường cách tâm quả cầu
15cm bằng 3,0x103V/m và hướng theo bán kính vào trong thì mật độ điện tích trên bề mặt quả cầu bằng bao nhiêu?
Câu 4. Tính điện thế tại một điểm nằm trên trục của đĩa tròn có bán kính là R = 40 cm mang điện tích đều
và cách tâm đĩa một khoảng h = 30 cm. Biết điện tích của đĩa là q = 1,256. 10-8 C.
Câu 5. Người ta đặt một hiệu điện thế U = 400 V giữa hai hình trụ dài đồng trục bằng kim loại mỏng bán
kính r1 = 2 cm và r2 = 10 cm. Tính mật độ điện dài trên hình trụ trong.
Câu 6. Hai điện tích điểm q1, q2 (q1=-4q2, q1<0), đặt tại hai điểm P, Q cách nhau một khoảng l=15 cm trong
không khí. Điểm M có cường độ điện trường bằng 0 cách q1 là:
Câu 7. Các bản cực của tụ điện phẳng không khí (ε =1) diện tích S hút nhau do tích điện trái dấu (q). Lực
này tạo nên một áp suất “tĩnh điện”, áp suất này bằng:
Câu 8. Một quả cầu có bán kính R = 3 cm, được tích điện đều trong khắp thể tích với mật
độ ρ=1,6.10-8 C/cm3. Tính năng lượng điện trường bên trong quả cầu, biết hằng số điện môi của quả cầu là ε = 2.
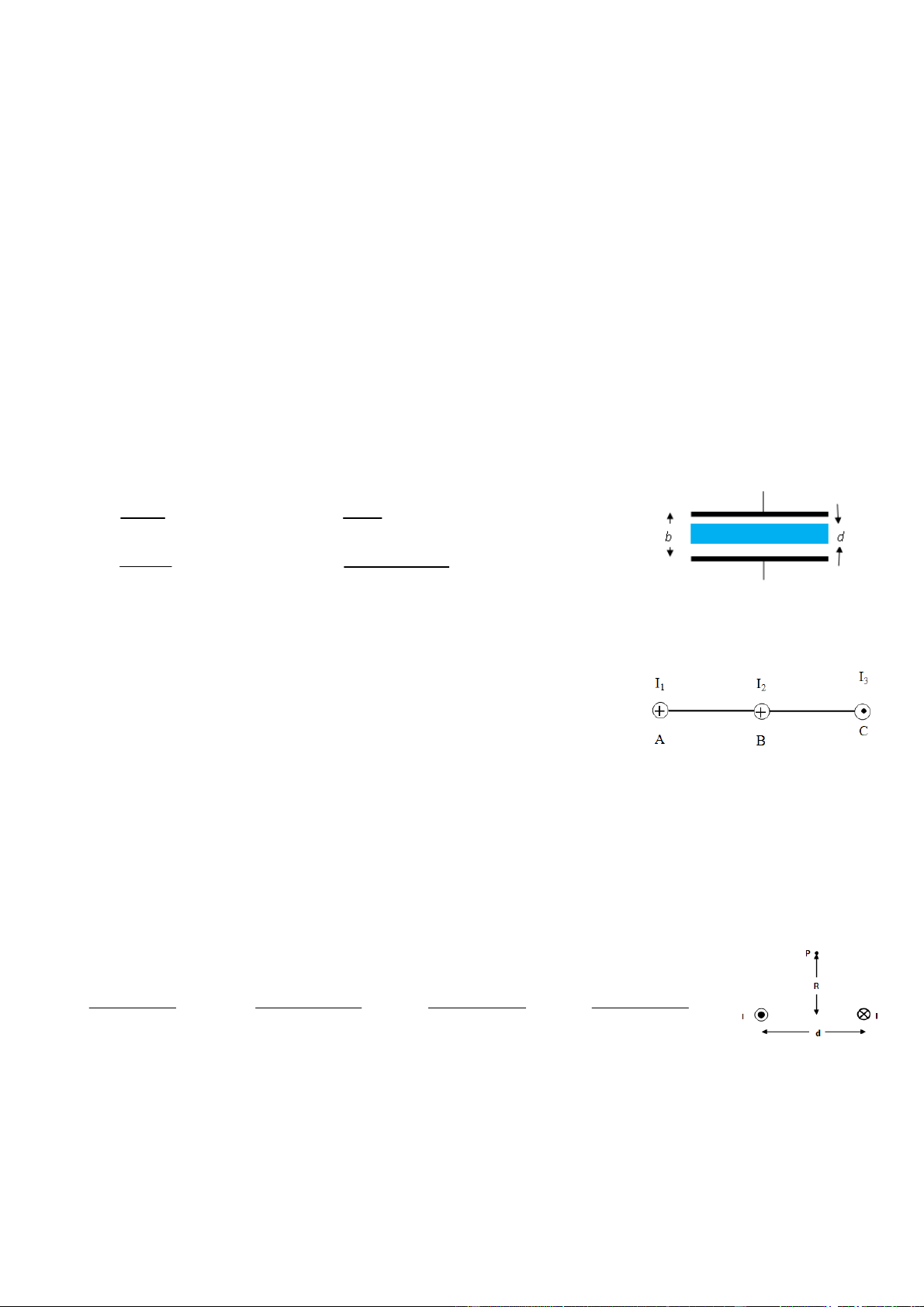
Câu 9. Một dây dẫn được uốn như hình vẽ. Xác định từ trường tổng hợp B tại điểm
C, biết I = 10A, R2 = 2R1 = 6,28cm.
Câu 10. Hai vòng dây dẫn bán kính giống nhau bán kính r0 = 10cm được đặt song song, trục trùng nhau và
mặt phẳng của chúng cách nhau một đoạn a = 20cm. Biết các dòng điện chạy trên các vòng dây bằng nhau
bằng 6A và cùng chiều, cảm ứng từ tại điểm giữa của đoạn thẳng nối hai tâm vòng dây là (µ0 = 4π.10-7 H/m): r ur
Câu 11. Một electron bay vào từ trường đều với vận tốc v có phương vuông góc với véctơ cảm ứng từ B .
Nhận xét nào dưới đây là không đúng:
[A] Chu kỳ quay của electron trên quỹ đạo không phụ thuộc vận tốc;
[B] Quỹ đạo của electrôn trong từ trường là đường tròn;
[C] Bán kính quỹ đạo của electron tỷ lệ thuận với vận tốc;
[D] Chu kỳ quay của electron trên quỹ đạo tỷ lệ nghịch với vận tốc;
Câu 12 Một vòng dây dẫn tròn bán kính R=4cm có dòng điện I=3A, được đặt sao cho mặt phẳng của vòng
dây vuông góc với đường sức của một từ trường đều có cảm ứng từ B=0,2T. Công phải tốn để quay vòng
dây về vị trí song song với đường sức từ là:
Câu 13. Cho một dòng điện I = 10 A chạy qua một dây dẫn đặc hình trụ, bán kính tiết diện thẳng góc R = 5
cm. Tính cường độ từ trường tại điểm nằm cách trục của dây là 2 cm.
Câu 14. . Một electron được gia tốc bằng một hiệu điện thế U = 6000 V bay vào một từ trường đều có cảm
ứng từ B = 1,3.10-2T. Hướng bay của electron hợp với đường sức từ một góc α = 60o, quỹ đạo của electron
khi đó là một đường đinh ốc. Bước của đường đinh ốc là (cho me=9,1.10-31kg, e=1,6.10-19C):
Câu 15. Một sợi dây dài 100cm nằm dọc theo trục x có dòng điện 0,50A chạy theo chiều dương của x và đặt
trong từ trường B = (3,0T)j+ (4,0T)k. Tính lực tác dụng lên dây đó. Biết i, j, k là các véc tơ đơn vị của 3 trục
tương ứng x,y,z trong hệ trục tọa độ Oxyz.
ĐỀ KIỂM TRA GIỮA KỲ MÔN VẬT LÝ ĐẠI CƯƠNG PHẦN II
Thời gian 45 phút (Không sử dụng tài liệu)
CHỮ KÝ (CÁC) CÁN BỘ COI THI ĐỀ SỐ 19 STT
HỌ VÀ TÊN SINH VIÊN:………………………………………………………………………………..
Lớp:……………………………………………………………… Số hiệu sinh viên:…………………...
Chó ý: ThÝ sinh ghi ®Çy ®ñ tªn, hä, líp, SHSVvà STT trong danh sách lớp vµo phÇn trªn tê giÊy nµy.
Khi tr¶ lêi thÝ sinh khoanh trßn mét « t−¬ng øng víi c©u tr¶ lêi ®óng trong sè bèn « cã kÝ hiÖu A, B, C, D
cña tõng c©u hái. Khi gi¶i c¸c bµi tËp thÝ sinh sö dông ph−¬ng ph¸p lµm trßn th«ng th−êng ®Ó lµm trßn ®¸p sè.
PhÇn tr¶ lêi tr¾c nghiÖm ĐIỂM
CHỮ KÝ CÁN BỘ CHẤM THI C©u 1 C©u 2 C©u 3 A B C D A B C D A B C D C©u 4 C©u 5 C©u 6 A B C D A B C D A B C D C©u 7 C©u 8 C©u 9 A B C D A B C D A B C D C©u 10 C©u 11 C©u 12 A B C D A B C D A B C D C©u 13 C©u 14 C©u 15 A B C D A B C D A B C D
Câu 1. Hai điện tích điểm q1, q2 (q1=-4q2, q1<0), đặt tại hai điểm P, Q cách nhau một khoảng l=10 cm trong
không khí. Điểm M có cường độ điện trường bằng 0 cách q1 là: [A] 20 cm; [B] 10 cm; [C] 15 cm; [D] 26 cm;
Câu 2 Hai bản kim loại lớn có diện tích 1,0 m2 nằm đối diện nhau. Chúng cách nhau 5,0cm và có điện tích
bằng nhau nhưng trái dấu ở trên các mặt trong của chúng. Nếu cường độ điện trường ở giữa hai bản bằng
55V/m thì độ lớn của các điện tích trên các bản bằng bao nhiêu? Bỏ qua các hiệu ứng mép. [A] 0,443.10-10 C; [B] 0,443.10-9 C; [C] 0,487.10-9 C; [D] 0,487.10-10 C;
Câu 3. Một mặt phẳng vô hạn tích điện đều với mật độ điện mặt σ = 1. 10-8 C/m2 và B là một quả cầu tích
điện cùng dấu với điện tích trên mặt phẳng. Sợi dây treo quả cầu lệch một góc 15o, biết khối lượng quả cầu
bằng m = 1g. Hỏi điện tích của quả cầu? [A] 6,49.10-6 C; [B] 4,66.10-6 C; [C] 4,81.10-6 C; [D] 5,66.10-6 C;
Câu 4. Một electrôn được bắn thẳng đến tâm của một bản kim loại rộng có điện tích âm dư với mật độ điện
tích mặt 2,0x10-6C/m2. Nếu động năng ban đầu của điện tử bằng 100 eV và nếu nó dừng (do lực đẩy tĩnh
điện) ngay khi đạt đến bản, thì nó phải được bắn cách bản bao nhiêu? [A] 8,86 mm; [B] 4,43 mm; [C] 0,886 mm; [D] 0,443 mm;
Câu 5. Giữa hai dây dẫn hình trụ song song cách nhau một khoảng l = 20 cm người ta đặt một hiệu điện thế
U = 2000V. Bán kính tiết diện mỗi dây là r = 1 mm. Hãy xác định cường độ điện trường tại trung điểm của
khoảng cách giữa 2 sợi dây biết rằng các dây dẫn đặt trong không khí. [A] 3780 V/m; [B] 3980 V/m; [C] 3880 V/m; [D] 4000 V/m;
Câu 6. Cho một tụ điện trụ, bán kính tiết diện mặt trụ trong và mặt trụ ngoài lần lượt là R1=1cm và R2=2cm,
hiệu điện thế giữa hai mặt trụ là U=350V. Cường độ điện trường tại điểm cách trục đối xứng của tụ một
khoảng r=1,5 cm có giá trị nào dưới đây: [A] 32,673 kV/m; [B] 33,663 kV/m; [C] 31,683 kV/m; [D] 36,633 kV/m;
Câu 7. Một pin ε, một tụ điện C, một điện kế số không G (số không ở giữa bảng chia độ), một khóa đóng
mở K được nối tiếp thành mạch kín. Khi đóng khóa K thì kim điện thế sẽ:
[A] Quay một góc rồi đứng yên ở đó; [B] Đứng yên;
[C] Quay một góc rồi trở về số không;
[D] Quay đi quay lại quanh số không;
Câu 8. Một tấm điện môi dày b, hằng số điện môi K, được đưa vào giữa các bản của một tụ điện phẳng có
khoảng cách giữa các bản bằng d (bKε A ε A [A] 0 C = [B] 0 C = d − b − d b Kε A Kε A [C] 0 C = 0 = + [D] C
Kd − b ( K − ) Kd b 1
Câu 9. Một tụ điện phẳng có chứa điện môi ε = 3, khoảng cách giữa hai bản là 0,2 cm, hiệu điện thế giữa
hai bản là 600 V. Tính mật độ điện mặt trên chất điện môi. [A] 4,3.10-6 C/m2; [B] 5,3.10-6 C/m2; [C] 3,3.10-6 C/m2; [D] 6, 3.10-6 C/m2;
Câu 10. Trên hình vẽ biểu diễn tiết diện của ba dòng điện thẳng song song
dài vô hạn. Cường độ các dòng điện lần lượt là I1=I2=I, I3=2I. Biết
AB=BC=6 cm. Trên đoạn AC, điểm M có cường độ từ trường tổng hợp bằng
không cách A một khoảng bằng: [A] 3,3 cm; [B] 3,1 cm; [C] 3,8 cm; [D] 4,0 cm;
Câu 11. Trong một từ trường đều cảm ứng từ B = 0.4 T và trong mặt phẳng vuông góc với các đường sức
từ, người ta đặt một dây dẫn uốn thành nửa vòng tròn. Dây dẫn dài 31,4 cm, có dòng điện I = 20 A chạy
qua. Tìm lực tác dụng của từ trường lên dây dẫn. [A] 1,3 N; [B] 1,4 N; [C] 0,8 N; [D] 1,6 N;
Câu 12 Một dây dẫn được uốn thành hình chữ nhật có các cạnh a=11 cm, b=16,0 cm, có dòng điện cường
độ I=5A chạy qua. Cường độ từ trường tại tâm của khung dây chữ nhật là: [A] 35,117 A/m; [B] 42,161 A/m; [C] 32,927 A/m; [D] 30,117 A/m;
Câu 13. Hai dây dẫn dài cách nhau d mang cùng dòng điện I nhưng trái chiều nhau như
cho trên hình vẽ. Xác định độ lớn của từ trường tổng cộng tại điểm P cách đều hai dây: 2µ id µ id 2µ id µ iR [A] ; [B] 0 ; [C]; 0 [D] 0 ; π ( 02 2 R + d ) π ( 2 2 2 4R + d ) π ( 2 2 4R + d ) π ( 2 2 4R + d )
Câu 14. Cho một khung dây phẳng diện tích 20 cm2 quay trong một từ trường đều với
vận tốc 5 vòng/s. Trục quay nằm trong mặt phẳng của khung và vuông góc với các đường sức từ trường.
Cường độ từ trường bằng 2.104 A/m. Tìm giá trị lớn nhất của từ thông gửi qua khung dây. [A] 5,02.10-5 Wb; [B] 6,21. 10-5 Wb; [C] 5,66. 10-5 Wb; [D] 7,07. 10-5 Wb;
Câu 15. Cho một vòng dây dẫn tròn bán kính R = 9 cm có dòng điện cường độ I = 10A chạy qua. Cảm ứng
từ B tại một điểm trên trục của vòng dây và cách tâm vòng dây một đoạn h = 12 cm là (hằng số từ 7 µ 4π .10− = H/m): 0 [A] 9,04.10-6 T; [B] 15,07. 10-6 T; [C] 13,66. 10-6 T; [D] 10,04. 10-6 T;
ĐỀ KIỂM TRA GIỮA KỲ MÔN VẬT LÝ ĐẠI CƯƠNG PHẦN II
Thời gian 45 phút (Không sử dụng tài liệu)
CHỮ KÝ (CÁC) CÁN BỘ COI THI ĐỀ SỐ 20
HỌ VÀ TÊN SINH VIÊN:………………………………………………………………………………..
Lớp:……………………………………………………………… Số hiệu sinh viên:…………………...
Chó ý: ThÝ sinh ghi ®Çy ®ñ tªn, hä, líp, SHSVvà STT trong danh sách lớp vµo phÇn trªn tê giÊy nµy.
Khi tr¶ lêi thÝ sinh khoanh trßn mét « t−¬ng øng víi c©u tr¶ lêi ®óng trong sè bèn « cã kÝ hiÖu A, B, C, D
cña tõng c©u hái. Khi gi¶i c¸c bµi tËp thÝ sinh sö dông ph−¬ng ph¸p lµm trßn th«ng th−êng ®Ó lµm trßn ®¸p sè.
PhÇn tr¶ lêi tr¾c nghiÖm ĐIỂM
CHỮ KÝ CÁN BỘ CHẤM THI C©u 1 C©u 2 C©u 3 A B C D A B C D A B C D C©u 4 C©u 5 C©u 6 A B C D A B C D A B C D C©u 7 C©u 8 C©u 9 A B C D A B C D A B C D C©u 10 C©u 11 C©u 12 A B C D A B C D A B C D C©u 13 C©u 14 C©u 15 A B C D A B C D A B C D
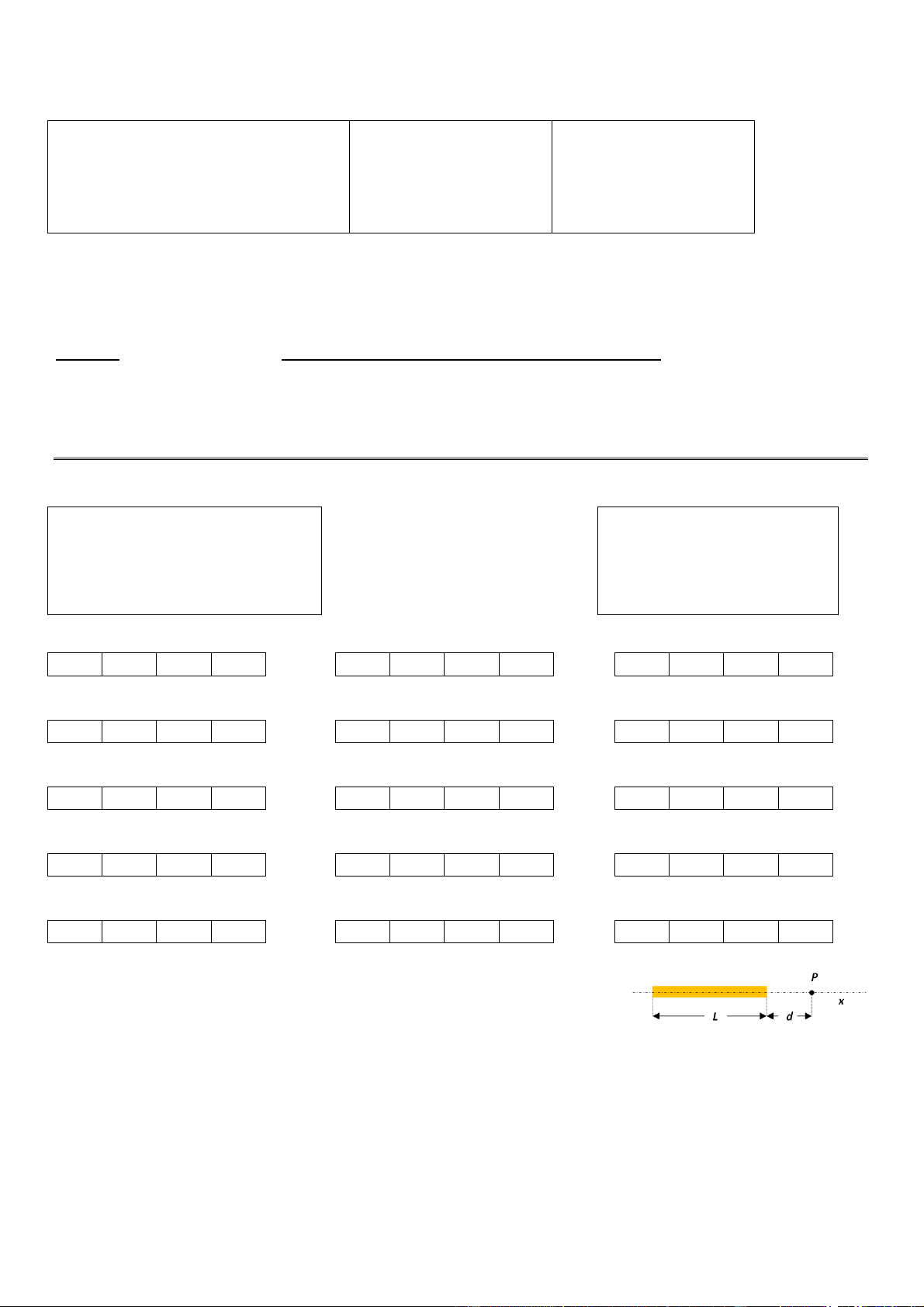
Câu 1. Tìm điện thế ở điểm P trên hình vẽ cách đầu phải của một thanh
nhưa có độ dài L = 2cm và điện tích toàn phần Q = 4,43.10-9C một
khoảng d = 1cm. Biết điện tích được phân bố đều trên thanh nhựa. [A] 2190 V; [B] 2150 V; [C] 2110 V; [D] 2230 V;
Câu 2 Cho một quả cầu bán kính 3 cm có điện tích q = 9,42.10-9 C, điện tích được phân bố đều trong thể
tích. Tính hiệu điện thế giữa hai điểm cách tâm lần lượt là 1,5 cm và 3 cm. [A] 1220 V; [B] 1000 V; [C] 1060 V; [D] 1300 V;
Câu 3. Giữa hai dây dẫn hình trụ song song cách nhau một khoảng l = 20 cm người ta đặt một hiệu điện thế
U = 4000V. Bán kính tiết diện mỗi dây là r = 2 mm. Hãy xác định cường độ điện trường tại trung điểm của
khoảng cách giữa 2 sợi dây biết rằng các dây dẫn đặt trong không khí. [A] 3680 V/m; [B] 8700 V/m; [C] 3780 V/m; [D] 7560 V/m;
Câu 4. Hai điện tích điểm q1=q2=4.10-8C đặt cách nhau d=6 cm trong không khí. Nếu cho điện tích q2 dịch
chuyển xa q1 thêm một khoảng a=4,5 cm thì công của lực điện trong dịch chuyển đó là (cho k = 1/(4πε0) =9.109 Nm2/C2): [A] -11,786.10-5 J; [B] -10,786.10-5 J; [C] -11,286.10-5 J; [D] -10,286.10-5 J;
Câu 5. Người ta đặt một hiệu điện thế U = 400 V giữa hai hình trụ dài đồng trục bằng kim loại mỏng bán
kính r1 = 2 cm và r2 = 10 cm. Tính mật độ điện dài trên hình trụ trong. [A] 1, 38.10-8 C/m; [B] 1,61.10-8 C/m; [C] 1, 51.10-8 C/m; [D] 2,31.10-8 C/m;
Câu 6. Một điện tích điểm tạo một điện thông -750 Vm đi qua một mặt Gauss hình cầu có bán kính bằng
10,0cm và có tâm nằm ở điện tích. Nếu bán kính của mặt Gauss tăng gấp đôi thì điện thông qua mặt đó bằng bao nhiêu? [A] Tăng 4 lần [B] Không đổi [C] Tăng 2 lần [D] Giảm 2 lần
Câu 7. Một tụ điện phẳng, diện tích bản cực S=140 cm2, khoảng cách giữa hai bản tụ d=0,5 cm. Giữa hai
bản cực là điện môi có hằng số điện môi ε=2. Tụ được tích điện đến hiệu điện thế U=300V. Nếu nối hai bản
tụ điện với điện trở R=100 Ω thành mạch kín thì nhiệt lượng tỏa ra trên điện trở khi tụ phóng hết điện là (cho ε=8,86.10-12 C/Nm2): [A] 2,083.10-6 J; [B] 2,333.10-6 J; [C] 2,233.10-6 J; [D] 2,283.10-6 J;
Câu 8. Một tụ điện phẳng có chứa điện môi ε = 3, khoảng cách giữa hai bản là 0,2 cm, hiệu điện thế giữa
hai bản là 600 V. Tính mật độ điện mặt trên chất điện môi. [A] 4,3.10-6 C/m2; [B] 3,3.10-6 C/m2; [C] 5,3.10-6 C/m2; [D] 6, 3.10-6 C/m2;
Câu 9. Một đoạn dây mà phần giữa là một cung tròn đặt trong từ trường đều B
hướng từ mặt phẳng hình vẽ đi ra phía trước. Hỏi nếu có dòng điện I chay trên dây
thì lực từ tổng hợp F tác dụng lên nó là bao nhiêu? [A] 2iB(L+πR); [B] 2iB(L+R); [C] iB(2L + πR); [D] iB(L + πR);
Câu 10. Electron chuyển động trong từ trường đều có cảm ứng từ B=2.10-6T theo phương vuông góc với
các đường cảm ứng từ. Quỹ đạo của electron là đường tròn có bán kính R=4 cm. Động năng của electron có
giá trị là (cho me=9,1.10-31kg, e=1,6.10-19C): [A] 8,902.10-23 J; [B] 9,152.10-23 J; [C] 9,052.10-23 J; [D] 9,002.10-23 J;
Câu 11. Một sợi dây dẫn dài vô hạn được uốn vuông góc như hình vẽ. Trên dây dẫn có
dòng điện I chạy qua. Xác định cảm ứng từ B tại điểm P cách góc 1 khoảng x. µ µI µ µI µ µI µ µI I [A] 0 B = ; [B] 0 B = ; [C] 0 B = ; [D] 0 B = ; 2x 2π x 4R 4π x I
Câu 12 Cho một vòng dây dẫn tròn bán kính R = 9 cm có dòng điện cường độ I = 6A
chạy qua. Cảm ứng từ B tại một điểm trên trục của vòng dây và cách tâm vòng dây một đoạn h = 15 cm là − (hằng số từ 7 µ = 4π.10 H/m): 0 [A] 5,71.10-6 T; [B] 6,21. 10-6 T; [C] 8,66. 10-6 T; [D] 8,04. 10-6 T;
Câu 13. Cho một dòng điện I = 10 A chạy qua một dây dẫn đặc hình trụ, bán kính tiết diện thẳng góc R = 5
cm. Tính cường độ từ trường tại điểm nằm cách trục của dây là 2 cm. [A] 11,74 A/m; [B] 12,04 A/m; [C] 12,74 A/m; [D] 12,34 A/m;
Câu 14. Hai dây dẫn dài vô hạn đặt song song cách nhau một khoảng nào đó. Dòng điện chạy qua các dây
dẫn bằng nhau và cùng chiều. Tìm cường độ dòng điện chạy qua mỗi dây, biết rằng muốn dịch chuyển các
dây dẫn tới một khoảng cách lớn gấp đôi lúc đầu thì phải tốn một công bằng 6.10-5 J/m (công dịch chuyển 1 mét dài của dây dẫn). [A] 20,8 A; [B] 22,7 A; [C] 17,8 A; [D] 21,4 A;
Câu 15. Điện trường không đổi E hướng theo trục z của hệ tọa độ Đềcác Oxyz; một từ trường B được đặt
hướng theo trục x. Điện tích q>0 có khối lượng m bắt đầu chuyển động theo trục y với vận tốc v. Bỏ qua lực
hút của trái đất lên điện tích. Quĩ đạo của điện tích là thẳng khi: [A]v= 2EB / m ; [B] v=E/B; [C] v=mEB; [D] v=EB/m; Câu 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Đề 11 A C B D A B C C B D D A C A B Đề 12 A C B D A B C C B D D A C A B Đề 13 A C B D A B C C B D D A C A B Đề 14 A C B D A B C C B D D A C A B Đề 15 A C B D A B C C B D D A C A B Đề 16 A C B D A B C C B D D A C A B Đề 17 A C B D A B C C B D D A C A B Đề 18 A C B D A B C C B D D A C A B Đề 19 A C B D A B C C B D D A C A B Đề 20 A C B D A B C C B D D A C A B
Đỗ Đức Phương – Nguyễn Hiếu
Giải chi tiết đề 18 Câu 1:
Hướng giải: Cường độ điện trường và điện thế tại điểm 𝑅 = 6𝑐𝑚 (𝑅1 < 𝑅 < 𝑅2) chỉ do mặt cầu trong (𝑅2) gây ra.
Cường độ điện trường: 𝑄 3.10−9 𝐸 = 2 = = 7484,7 (𝑉/𝑚) 4𝜋𝜀𝜀0𝑅2 4𝜋. 1. 10−12. 0,062 Điện thế: 𝑄 3.10−9 𝑉 = 2 = = 449,08 (𝑉) 4𝜋𝜀𝜀0𝑅 4𝜋. 1. 10−12. 0.06
Không có đáp án Câu 2:
Hướng giải: Điện thế tại mọi điểm trên quả cầu thứ nhất đều bằng nhau và điện thế này do
chính nó và quả cầu thứ 2 gây nên. 𝑄 𝑄 𝑉 1 2 1 = 𝑉11 + 𝑉21 = + 4𝜋𝜀𝜀0𝑅1 4𝜋𝜀𝜀0(𝑟 − 𝑅1) 5,9.10−9 −5,9.10−9 = + = 1004,05 (𝑉) 4𝜋. 1.8,86.10−12. 0,05
4𝜋. 1.8,86.10−12. (1 − 0,05) Đáp án B Câu 3:
Hướng giải: Muốn xác định được 𝑈 phải xác định được 𝜆 (mật độ điện dài). Ta sẽ xác định 𝜆
thông qua dữ kiện đề cho là vận tốc của hạt electron.
Định lý động năng: Công của lực điện trường bằng độ biến thiên động năng 𝑟2 1 1 𝐴 2 2
đ𝑖ệ𝑛 = Δ 𝑊đ ⟺ |𝑒| ∫ 𝐸 ⃗ 𝑑𝑟
⃗⃗ = 𝑚𝑣 − 𝑚𝑣 2 2 2 1 𝑟1
Do dịch chuyển từ 𝑟1 = 3𝑐𝑚 đến 𝑟2 = 6𝑐𝑚 nên 𝐸⃗ cùng hướng 𝑑𝑟 ⃗⃗ 𝑟2 1 1 𝐴 2 2
đ𝑖ệ𝑛 = ΔWđ ⟺ |𝑒| ∫ 𝐸𝑑𝑟 = 𝑚𝑣 − 𝑚𝑣 2 2 2 1 𝑟1
Điện trường giữa 2 mặt của tụ trụ chỉ do mặt bên trong gây ra: 1
Đỗ Đức Phương – Nguyễn Hiếu 𝜆 𝐸 = 2𝜋𝜀𝜀0𝑟 𝑟2 𝜆 1 1 ⇒ |𝑒| ∫
𝑑𝑟 = 𝑚𝑣2 − 𝑚𝑣2 2𝜋𝜀𝜀 2 1 0𝑟 2 2 𝑟1 0,06 𝜆 1 ⟺ 1,6.10−19 ∫
𝑑𝑟 = . 9,1.10−31(1,375.107)2 − 0 2𝜋. 1.8,86.10−12. 𝑟 2 0,03 𝐶 ⇒ 𝜆 = 4,318.10−8 ( ) 𝑚
Hiệu điện thế U giữa hai bản mặt tụ trụ: 𝑅 𝑅 0,08 𝜆 4,318.10−26
⇒ 𝑈 = ∫ 𝐸𝑑𝑟 = ∫ 𝑑𝑟 = ∫ 𝑑𝑟 = 1075,29 (𝑉) 2𝜋𝜀𝜀0𝑟 2𝜋. 1.8,86.10−12𝑟 𝑟 𝑟 0,02 Đáp án C Câu 4:
Hướng giải: Áp dụng định lý động năng sẽ tính được 𝑣2, nhưng trước đó phải xác định 𝑄 để
tính điện trường tại điểm nằm giữa 2 mặt cầu
Điện trường tại điểm nằm giữa 2 mặt cầu (𝑅1 < 𝑟 < 𝑅2) chỉ do mặt cầu trong gây ra: 𝑄 𝐸 = 4𝜋𝜀𝜀0𝑟2
Hiệu điện thế giữa 2 mặt của tụ điện cầu: 𝑅2 𝑅2 𝑄 𝑈 = ∫ 𝐸𝑑𝑟 = ∫ 𝑑𝑟 4𝜋𝜀𝜀0𝑟2 𝑅1 𝑅1 𝑈 4380 ⇒ 𝑄 = = = 6,502.10−9 (𝐶) 𝑅2 1 0,04 1 ∫ ∫ 𝑅1 4𝜋𝜀𝜀 0,01 0𝑟2 𝑑𝑟
4𝜋. 2.8,86.10−12. 𝑟2 𝑑𝑟
Định lý động năng: Công của lực điện trường bằng độ biến thiên động năng 𝑟2 1 1 𝐴 2 2
đ𝑖ệ𝑛 = Δ 𝑊đ ⟺ |𝑒| ∫ 𝐸 ⃗ 𝑑𝑟
⃗⃗ = 𝑚𝑣 − 𝑚𝑣 2 2 2 1 𝑟1
Do dịch chuyển từ 𝑟1 = 3𝑐𝑚 đến 𝑟2 = 2𝑐𝑚 nên 𝐸⃗ ngược hướng 𝑑𝑟 ⃗⃗ 2
Đỗ Đức Phương – Nguyễn Hiếu 𝑟2 1 1
⟺ |𝑒| ∫ −𝐸𝑑𝑟 = 𝑚𝑣2 − 𝑚𝑣2 2 2 2 1 𝑟1 0,02 6,502.10−9 1 ⇒ 1,6.10−19 ∫ −
𝑑𝑟 = . 9,1.10−31. 𝑣2 4𝜋. 1.8,86.10−12𝑟2 2 2 0,03 𝑚 ⇒ 𝑣2 = 1,85.107 ( ) 𝑠 Đáp án B Câu 5:
Hướng giải: Dùng mối liên hệ giữa điện thế và cường độ điện trường sau đó tích phân
Cường độ điện trường do mặt phẳng vô hạn gây ra tại 1 điểm: 𝜎 𝐸 = 2𝜀𝜀0
Hiệu điện thế giữa 2 điểm bất kì: 𝑑𝑉 = −𝐸⃗ 𝑑𝑟
⃗⃗ . Do xét hiệu điện thế giữa 2 điểm 𝑟𝐴 = 10𝑐𝑚 đến 𝑟𝐵 = 20𝑐𝑚 nên 𝑑𝑟 ⃗⃗ cùng hướng với 𝐸 ⃗ 𝑟𝐵 𝑟𝐵 0,2 𝜎 3.10−5
⇒ 𝑈 = ∫ 𝐸𝑑𝑟 = ∫ 𝑑𝑟 = ∫ 𝑑𝑟 = 169,3.103 (𝑉) 2𝜀𝜀0 2.1.8,86.10−12 𝑟𝐴 𝑟𝐴 0,1 Đáp án C Câu 6:
Hướng giải: Sử dụng công thức tính công
Cường độ điện trường do mặt phẳng vô hạn gây ra tại 1 điểm: 𝜎 𝐸 = 2𝜀𝜀0
Công của lực điện khi dịch chuyẻn 1 proton từ 𝑟𝐴 đến 𝑟𝐵 𝑟𝐵
𝐴 = 𝑞 ∫ 𝐸⃗ 𝑑𝑟 ⃗⃗ 𝑟𝐴
Do xét hiệu điện thế giữa 2 điểm 𝑟𝐴 = 10𝑐𝑚 đến 𝑟𝐵 = 20𝑐𝑚 nên 𝑑𝑟
⃗⃗ cùng hướng với 𝐸⃗ 3
Đỗ Đức Phương – Nguyễn Hiếu 𝑟𝐵 𝑟𝐵 𝑟𝐵 𝜎 3.10−5
⇒ 𝐴 = 𝑞 ∫ 𝐸𝑑𝑟 = 𝑞 ∫ 𝑑𝑟 = 1,6.10−19 ∫ 𝑑𝑟 = 2,7.10−14 (𝐽) 2𝜀𝜀0 2.1.8,86.10−12 𝑟𝐴 𝑟𝐴 𝑟𝐴
Không có đáp án Câu 7:
Hướng giải: Câu này quá dễ, không có gì phải lăn tăn cả
𝑈𝑂𝐵 = 𝑉𝑂 − 𝑉𝐵
Điện thế tại 1 điểm bất kì sẽ do 2 điện tích 𝑞1 và 𝑞2 gây ra. 𝑞 𝑞 𝑉 1 2 𝑂 = 𝑉1𝑂 + 𝑉2𝑂 = + 4𝜋𝜀𝜀0𝑂𝐶 4𝜋𝜀𝜀0𝑂𝐷 𝑞 𝑞 𝑉 1 2 𝐵 = 𝑉1𝐵 + 𝑉2𝐵 = + 4𝜋𝜀𝜀0𝐵𝐶 4𝜋𝜀𝜀0𝐵𝐷 𝑞 𝑞 𝑞 𝑞 ⇒ 𝑈 1 2 1 2 𝑂𝐵 = ( + ) − ( + ) 4𝜋𝜀𝜀0𝑂𝐶 4𝜋𝜀𝜀0𝑂𝐷 4𝜋𝜀𝜀0𝐵𝐶 4𝜋𝜀𝜀0𝐵𝐷 −10−8 10−8 ⇒ 𝑈𝑂𝐵 = ( + ) 4𝜋. 1.8,86.10−12. 0,05 4𝜋. 1.8,86.10−12. 0,05 −10−8 10−8 − ( + ) 4𝜋. 1.8,86.10−12. 0,06 4𝜋. 1.8,86.10−12. 0,1
⇒ 𝑈𝑂𝐵 = 598,77 (𝑉) Câu 8:
Hướng giải: Tương tự câu 8
𝑈𝑂𝐵 = 𝑉𝑂 − 𝑉𝐵
Điện thế tại 1 điểm bất kì sẽ do 2 điện tích 𝑞1 và 𝑞2 gây ra. 𝑞 𝑞 𝑉 1 2 𝑂 = 𝑉1𝑂 + 𝑉2𝑂 = + 4𝜋𝜀𝜀0𝑂𝐶 4𝜋𝜀𝜀0𝑂𝐷 𝑞 𝑞 𝑉 1 2 𝐵 = 𝑉1𝐵 + 𝑉2𝐵 = + 4𝜋𝜀𝜀0𝐵𝐶 4𝜋𝜀𝜀0𝐵𝐷 𝑞 𝑞 𝑞 𝑞 ⇒ 𝑈 1 2 1 2 𝑂𝐵 = ( + ) − ( + ) 4𝜋𝜀𝜀0𝑂𝐶 4𝜋𝜀𝜀0𝑂𝐷 4𝜋𝜀𝜀0𝐵𝐶 4𝜋𝜀𝜀0𝐵𝐷 4
Đỗ Đức Phương – Nguyễn Hiếu −10−8 10−8 ⇒ 𝑈𝑂𝐵 = ( + ) 4𝜋. 1.8,86.10−12. 0,05 4𝜋. 1.8,86.10−12. 0,05 −10−8 10−8 − ( + ) 4𝜋. 1.8,86.10−12. 0,06 4𝜋. 1.8,86.10−12. 0,1
⇒ 𝑈𝑂𝐵 = 598,77 (𝑉)
Công dịch chuyển 𝑞 từ O đến B:
𝐴𝑂𝐵 = 𝑞. 𝑈𝑂𝐵 = 10−9. 598,77 = 5,9877.10−7(𝐽)
Không có đáp án Câu 9:
Hướng giải: Dùng mối liên hệ giữa hiệu điện thế và cường độ điện trường
Do đang xét 2 điểm 𝑟1 = 10𝑐𝑚 và 𝑟2 = 𝑅 nên ta xét điện trường bên trong quả cầu đặc: 𝑄𝑟 𝐸 = 4𝜋𝜀𝜀0𝑅3
Hiệu điện thế giữa 2 điểm 𝑟1 và 𝑟2: 𝑑𝑉 = −𝐸⃗ 𝑑𝑟
⃗⃗ . Do đang xét 2 điểm 𝑟1 = 10𝑐𝑚 và 𝑟2 = 𝑅 nên 𝑑𝑟
⃗⃗ cùng hướng với 𝐸⃗ 𝑟2 𝑟2 0,15 𝑄𝑟 5.10−8𝑑𝑟
⇒ 𝑈 = ∫ 𝐸𝑑𝑟 = ∫ 𝑑𝑟 = ∫ 𝑑𝑟 = 415,8 (𝑉) 4𝜋𝜀𝜀0𝑅3 4𝜋. 2.8,86.10−120,153 𝑟1 𝑟1 0,1
Trong đề tính theo hằng số 𝑘 = 9.10^9 còn bài trên tính theo 𝜀0 nên sẽ có sự chênh lệch về
kết quả nhưng không đáng kể Đáp án A Câu 10:
Hướng giải: Xây dựng công thức hiệu điện thế giữa 2 mặt của tụ điện hình trụ phụ thuộc vào
mật độ điện dài 𝜆; Sử dụng mối liên hệ giữa mật độ điện dài 𝜆 và mật độ điện mặt 𝜎
Cường độ điện trường tại 1 điểm nằm giữa 2 mặt trụ: 𝜆 𝐸 = 2𝜋𝜀𝜀0𝑟
Hiệu điện thế giữa 2 mặt trụ: 𝑟2 𝑟2 𝜆 𝜆 𝑟 𝑈. 2𝜋𝜀𝜀 𝑈 = ∫ 𝐸𝑑𝑟 = ∫ 𝑑𝑟 = 𝑙𝑛 ( 2) ⇒ 𝜆 = 0 2𝜋𝜀𝜀 𝑟 0𝑟 2𝜋𝜀𝜀0 𝑟1 𝑙𝑛 ( 2) 𝑟1 𝑟1 𝑟1 5
Đỗ Đức Phương – Nguyễn Hiếu 𝜆
Mối liên hệ giữa 𝜆 và 𝜎 trong hình trụ: 𝜆. 𝑙 = 𝜎. 2𝜋𝑟1. 𝑙 ⇒ 𝜎 = 2𝜋𝑟1 𝑈. 2𝜋𝜀𝜀 1000.2𝜋. 1.8,86.10−12 𝐶 ⇒ 𝜎 = 0 𝑟 = = 1,6.10−7 ( ) 2𝜋𝑟 2 0,15 𝑚2 1 𝑙𝑛 (𝑟 ) 2𝜋. 0,05. 𝑙𝑛 ( ) 1 0,05 Đáp án D Câu 11:
Hướng giải: Dùng định lý Ampere cho dòng điện toàn phần tính được cường độ từ trường
Chọn đường cong kín (C) là đường tròn vuông góc với trục hình trụ, tâm nằm trên trục, bán
kính 𝑅′ = 𝑟 = 5𝑐𝑚.
Định lý Ampere về dòng điện toàn phần: ∮ 𝐻 ⃗ 𝑑𝑙 ⃗⃗ = ∑ 𝐼𝑖 (𝐶)
Do đường cong (C) là đường tròn nên mọi điểm trên đường cong cách đều trục của hình trụ
⇒ mọi điểm trên đường cong có cường độ từ trường bằng nhau và tại mọi điểm trên đường cong 𝐻
⃗ cùng hướng với 𝑑𝑙 ⃗⃗ 𝐼 𝐴
⇒ ∮ 𝐻𝑑𝑙 = 𝐼 ⇒ 𝐻. 2𝜋𝑅′ = 𝐼 ⇒ 𝐻 = = 31,8 ( ) 2𝜋𝑟 𝑚 (𝐶)
Nhận xét: Bài này xét điểm nằm ngoài trụ nên không quan tâm đến bán kính của trụ. Đáp án A Câu 12:
Hướng giải: Dùng công thức 𝜙 = ∫ 𝐵⃗ 𝑑𝑠 ⃗⃗
Chia hình vuông thành vô số hình chữ nhật chiều dài 𝑙, chiều rộng 𝑑𝑟 ⇒ 𝑑𝑆 = 𝑙𝑑𝑟
Cảm ứng từ gây bởi dây thẳng dài vô hạn tại 1 điểm trên hình chữ nhật là: 𝜇𝜇 𝐼 𝐵 = 0 . 2𝜋 𝑟 6
Đỗ Đức Phương – Nguyễn Hiếu 𝜇𝜇 𝐼 𝐵 = 0 . 2𝜋 𝑟 Do 𝐵 ⃗ ⇈ 𝑑𝑆
⃗⃗ ⇒ 𝜙 = ∫ 𝐵𝑑𝑆 𝑟+𝑙 𝜇𝜇 𝐼 𝜇𝜇 𝑟 + 𝑙 𝜙 = ∫ 0 . . 𝑙𝑑𝑟 = 0𝐼𝑙 . 𝑙𝑛 ( ) 2𝜋 𝑟 2𝜋 𝑟 𝑟 𝜙. 2𝜋 ⇒ 𝐼 = = 9,99 (𝐴) 𝑟 + 𝑙
𝜇𝜇0. 𝑙. 𝑙𝑛 ( 𝑟 ) Đáp án B Câu 13:
Hướng giải: Dùng công thức từ trường gây bởi dòng điện tròn 1 𝐼𝑅2 𝐻 = . 2 (𝑅2 + ℎ2)3/2
Cường độ từ trường tại điểm O1 sẽ gồm từ trường gây ra bởi dòng 𝐼1 và dòng 𝐼2 𝐻 ⃗⃗⃗⃗ ⃗⃗ ⃗⃗ 𝑂 = 𝐻 + 𝐻 1 1 2
Áp dụng quy tắc bàn tay phải, ta thấy 𝐻 ⃗⃗ ⃗⃗
1 và 𝐻2 ngược hướng ⇒ 𝐻𝑂 = |𝐻 1 1 − 𝐻2| ⇒ 𝐻𝑂 = |𝐻 1 1 − 𝐻2| 1 𝐼 1 𝐼. 𝑎2 𝐻1 = . , 𝐻 . 2 𝑎 2 = 2 (𝑎2 + 𝑏2)3/2 1 𝐼 1 𝐼. 𝑎2 𝐴 𝐻𝑂 = | . − . | = 16,16 ( ) 1 2 𝑎 2 (𝑎2 + 𝑏2)3/2 𝑚 Đáp án A Câu 14:
Hướng giải: Áp dụng công thức từ trường gây bởi dòng điện thẳng
Từ trường gây ra tại điểm O bằng từ trường do dây đứng (1) và từ trường do dây ngang (2) 𝐵 ⃗⃗⃗ ⃗⃗ ⃗⃗ 𝑂 = 𝐵1 + 𝐵2
Áp dụng quy tắc nắm bàn tay phải, ta thấy 𝐵 ⃗⃗ ⃗⃗
1 ⇈ 𝐵2 ⇒ 𝐵𝑂 = 𝐵1 + 𝐵2 7
Đỗ Đức Phương – Nguyễn Hiếu 𝜇𝜇 𝐼 𝐵 0 1 = . . (𝑐𝑜𝑠𝜃 4𝜋 𝑟 11 − 𝑐𝑜𝑠𝜃21) 𝜇𝜇 𝐼 = 0 .
. (𝑐𝑜𝑠0 − 𝑐𝑜𝑠135) 4𝜋 𝑂𝐵/√2 𝜇𝜇 𝐼 𝐵 0 2 = . . (𝑐𝑜𝑠𝜃 4𝜋 𝑟 12 − 𝑐𝑜𝑠𝜃22) 𝜇𝜇 𝐼 = 0 .
. (𝑐𝑜𝑠45 − 𝑐𝑜𝑠180) 4𝜋 𝑂𝐵/√2 𝜇𝜇 𝐼 ⇒ 𝐵 0 𝑂 = 𝐵1 + 𝐵2 = .
(𝑐𝑜𝑠0 − 𝑐𝑜𝑠135 + 𝑐𝑜𝑠45 − 𝑐𝑜𝑠180) 4𝜋 𝑂𝐵/√2 𝐵 𝐴 = 4,28.10−5 (𝑇) ⇒ 𝐻 𝑂 𝑂 = 38,4 ( ) 𝜇𝜇0 𝑚 Đáp án B Câu 15:
Hướng giải: Sử dụng công thức từ trường gây bởi dòng điện thẳng
Từ trường tại điểm M gồm từ trường do dòng 𝐼1 và từ trường do dòng 𝐼2 gây ra tại M 𝐵 ⃗⃗⃗ ⃗⃗⃗⃗ ⃗⃗⃗⃗ 𝑀 = 𝐵1𝑀 + 𝐵2𝑀
Áp dụng quy tắc nắm bàn tay phải, ta thấy 𝐵 ⃗⃗⃗⃗ ⃗⃗⃗⃗
1𝑀 ⇈ 𝐵2𝑀. Mà 𝐼1 = 𝐼2 và M cách đều 𝐼1, 𝐼2 nên
𝐵1𝑀 = 𝐵2𝑀 ⇒ 𝐵𝑀 = 2𝐵1𝑀 𝜇𝜇 𝐼 4𝜋. 10−7 10 𝐵 0 1 1𝑀 = . ⇒ 𝐵 . = 8.10−5 (𝑇) 2𝜋 𝐴𝑀 𝑀 = 2. 2𝜋 0,05 Đáp án C
Giải chi tiết đề 19 Câu 1:
Hướng giải: Sử dụng công thức lực tĩnh điện Lực tĩnh điện 𝑞 ⃗ ⃗⃗
1 tác dụng lên 𝑞3: 𝐹13 Lực tĩnh điện 𝑞 ⃗⃗⃗
2 tác dụng lên 𝑞3: 𝐹23 8
Đỗ Đức Phương – Nguyễn Hiếu 𝐹 ⃗ ⃗⃗ = −𝐹 ⃗⃗⃗
Điều kiện cân bằng: 𝐹 ⃗ ⃗⃗ ⃗⃗⃗ 13 23 13 + 𝐹23 = 0 ⃗ ⇒ { 𝐹 ⃗ ⃗⃗ ⃗⃗⃗ 13 = 𝐹23
Mà 𝑞1, 𝑞2 < 0 nên 𝑞3 nằm ngoài đoạn 𝑃𝑄 Ta có: |𝑞 |𝑞 𝑃𝑀 |𝑞 1 𝐹 1. 𝑞3| 2. 𝑞3| 1| 13 = 𝐹23 ⇔ 𝑘 = 𝑘 ⇔ = √ =
⇒ 𝑄𝑀 = 2𝑃𝑀 (1) 𝑃𝑀2 𝑄𝑀2 𝑄𝑀 |𝑞2| 2
Theo bài ra, ta có : 𝑄𝑀 − 𝑃𝑀 = 13 (𝑐𝑚)
Từ (1) và (2) ⇒ 𝑃𝑀 = 20 (𝑐𝑚); 𝑄𝑀 = 10 (𝑐𝑚) Đáp án A Câu 2:
Hướng giải: Sử dụng công thức điện dung của tụ điện phẳng
Hiệu điện thế giữa hai bản:
𝑈 = 𝐸. 𝑑 = 55.5.10−2 = 2,75 (𝑉) Điệ 𝜀𝜀
n dung của tụ điện được xác định theo công thức: 𝐶 = 𝑜𝑆 𝑑
Điện tích trên các bản tụ là: 𝜀𝜀 1.8,86.10−12. 1 𝑄 = 𝐶𝑈 = 𝑜𝑆 . 𝑈 = . 2,75 = 4,873.10−10 (𝐶) 𝑑 5.10−2 Đáp án C Câu 3:
Tại vị trí cân bằng: 𝐹 + 𝑇
⃗ + 𝑃⃗ = 0⃗ , trong đó: 𝑃 = 𝑚𝑔 { 𝜎𝑞 𝐹 = 𝐸. 𝑞 = 2𝜀𝜀𝑜 Từ hình vẽ, ta thấy: 𝐹 𝜎𝑞 tan 𝛼 . 2𝜀𝜀 tan 𝛼 = = ⇒ 𝑞 = 𝑜𝑚𝑔 𝑃 2𝜀𝜀𝑜𝑚𝑔 𝜎
tan 15𝑜 . 2.1.8,86.10−12. 10−3. 9,8 𝑞 =
= 4,66.10−6 (𝐶) 1.10−8 9
Đỗ Đức Phương – Nguyễn Hiếu Đáp án B Câu 4:
Hướng giải: Sử dụng định luật bảo toàn năng lượng, công thức tính cường độ điện trường
sinh ra bởi mặt phẳng tích điện đều
Công của lực điên biến đổi hoàn toàn thành động năng 1 2𝑊 𝑊 𝑑 𝑑 =
𝑚𝑣2 = |𝑒|𝑈 ⇒ 𝑈 = 2 |𝑒| Mặt khác, ta có: 𝑈 = 𝐸. 𝑑 2𝑊𝑑 𝑈 2𝑊
2.1,6.10−19. 100.1.8,6.10−12 { 𝜎 𝑒 𝑑. 𝜀𝜀𝑜 𝐸 = ⇒ 𝑑 = = 𝜎 = = = 0,000886 (𝑚) 𝜀𝜀 𝐸 𝑒𝜎 1,6.10−19. 2.10−6 𝑜 𝜀𝜀𝑜 Đáp án C Câu 5:
Hướng giải: Xác định mật độ điện dài 𝜆 thông qua biểu thức hiệu điện thế. Sau đó xây dựng
công thức 𝐸 tại 1 điểm bất kì nằm giữa 2 trụ rồi thay tọa độ điểm chính giữa 𝑥 = 𝑙/2 vào là xong.
Xét trường hợp tổng quát: nếu gọi khoảng cách từ điểm 𝑀 đến trục dây dẫn thứ nhất là 𝑥 thì
theo nguyên lý chồng chất điện trường, cường độ điện trường tại 𝑀 là: 10
Đỗ Đức Phương – Nguyễn Hiếu 1 𝜆 𝜆 𝜆𝑙 𝐸 = ( + ) = 2𝜋𝜀𝜀𝑜 𝑥 𝑙 − 𝑥
2𝜋𝜀𝜀𝑜𝑥(𝑙 − 𝑥)
Mặt khác: 𝑑𝑉 = −𝐸 ⃗ 𝑑𝑥
⃗⃗ . Do ta xét hiệu điện thế giữa 2 mặt, khi lấy tích phân cận sẽ lấy từ trụ
bên trái sang trụ bên phải nên 𝑑𝑥
⃗⃗ cùng hướng với 𝐸⃗ 𝜆 𝑙−𝑟 1 1 𝜆 𝑙 − 𝑟 ⇒ 𝑈 = ∫ 𝐸𝑑𝑥 = ∫ ( + ) 𝑑𝑥 = 𝑙𝑛 2𝜋𝜀𝜀𝑜 𝑥 𝑙 − 𝑥 𝜋𝜀𝜀 𝑟 𝑟 𝑜 𝜋𝜀𝜀 ⇒ 𝜆 = 𝑜𝑈 𝑙 − 𝑟 𝑙𝑛 𝑟
Tại điểm chính giữa: 𝑥 = 𝑙\2. Điện trường tại điểm này là: 𝜆𝑙 1 𝑙 𝜋𝜀𝜀 𝐸 = = . . 𝑜𝑈 2𝜋𝜀𝜀 𝑙 𝑙 𝑙 − 𝑟 𝑜𝑥(𝑙 − 𝑥) 2𝜋𝜀𝜀𝑜 ln 2 (𝑙 − 2) 𝑟 2𝑈 2.2000 = = ≈ 3778,36 (𝑉/𝑚) 𝑙 − 𝑟 0,2 − 0,001 𝑙. ln 0,2. 𝑙𝑛 𝑟 0,001 Đáp án A Câu 6:
Hướng giải: Xác định mật độ điện mặt thông qua biểu thức hiệu điện thế giữa 2 mặt của tụ
điện hình trụ, sau đó xác định cường độ điện trường tại điểm nằm giữa 2 mặt trụ (chỉ do mặt trong gây ra)
Cường độ điện trường giữa hai bản chỉ do mặt trụ bên trong gây ra: 𝜆 𝐸 = 2𝜋𝜀𝜀𝑜𝑟
Hiệu điện thế giữa 2 bản của tụ điện: 𝑅2 𝑅2 𝜆 𝜆 𝑅 𝑈. 2𝜋𝜀𝜀 𝑈 = ∫ 𝐸𝑑𝑟 = ∫ 𝑑𝑟 = . 𝑙𝑛 ( 2) ⇒ 𝜆 = 0 2𝜋𝜀𝜀 𝑅 𝑜𝑟 2𝜋𝜀𝜀𝑜 𝑅1 2 𝑅 𝑙𝑛 ( ) 1 𝑅1 𝑅1
Điện trường tại điểm cách trục 𝑟 = 1,5 𝑐𝑚: 𝜆 𝑈 350 𝐸 = = = ≈ 33662,88 (𝑉/𝑚) 2𝜋𝜀𝜀 𝑅 2 𝑜𝑟 𝑟. ln. 2 𝑅 0,015. 𝑙𝑛 1 1 Đáp án B Câu 7:
Hướng giải: Khi đóng khóa 𝐾 thì xảy ra quá trình nạp điện cho tụ, quá trình này đòi hỏi phải
có dòng nạp chạy trong mạch, mà có dòng nạp thì điện kế sẽ bị lệch. Khi tụ đã được nạp đầy, 11
Đỗ Đức Phương – Nguyễn Hiếu
dòng nạp này không còn tồn tại, lập tức kim của điện kế sẽ trở về vị trí 0 do không còn dòng nạp trong mạch. Đáp án C Câu 8:
Hướng giải: Khi đưa tấm điện môi vào thì hệ sẽ trở thành 3 tụ điện mắc nối tiếp.
Coi tụ điện như hệ ba tụ điện mắc nối tiếp với các điện dung: 𝜀𝜀 𝜀 𝜀 𝐶 𝑜𝑆 𝑜𝑆 𝑜𝑆 1 = 𝐶 𝐶 𝑑 2 = 3 = 1 𝑑2 𝑑3
Tính điện dung tương đương: 1 1 1 1 1 𝑑 = + + = ( 1 + 𝑑 𝐶 2 + 𝑑3) 𝑡𝑑 𝐶1 𝐶2 𝐶3 𝜀𝑜𝑆 𝜀 1 𝑑 = ( 1 + 𝑑 − 𝑑 𝜀 1) 𝑜𝑆 𝜀 𝜀𝜀 ⇒ 𝐶 𝑜𝑆 𝑡𝑑 = 𝜀𝑑 − 𝑑1(𝜀 − 1)
𝑆 ⇔ 𝐴; 𝜀 ⟺ 𝐾; 𝑑1 ⇔ 𝑏 Đáp án D Câu 9:
Hướng giải: Sử dụng công thức tính mật đọ điện mặt trên chất điện môi Cường độ 𝑈
điện trường trong chất điện môi: 𝐸 = 𝑑
Mật độ điện mặt trên chất điện môi: 𝑈 600
𝜎′ = (𝜀 − 1)𝜀𝑜𝐸𝑛 = (𝜀 − 1)𝜀𝑜𝐸 = (𝜀 − 1)𝜀𝑜 = (3 − 1). 8,86.10−12. 𝑑 0,002 Đáp án B Câu 10:
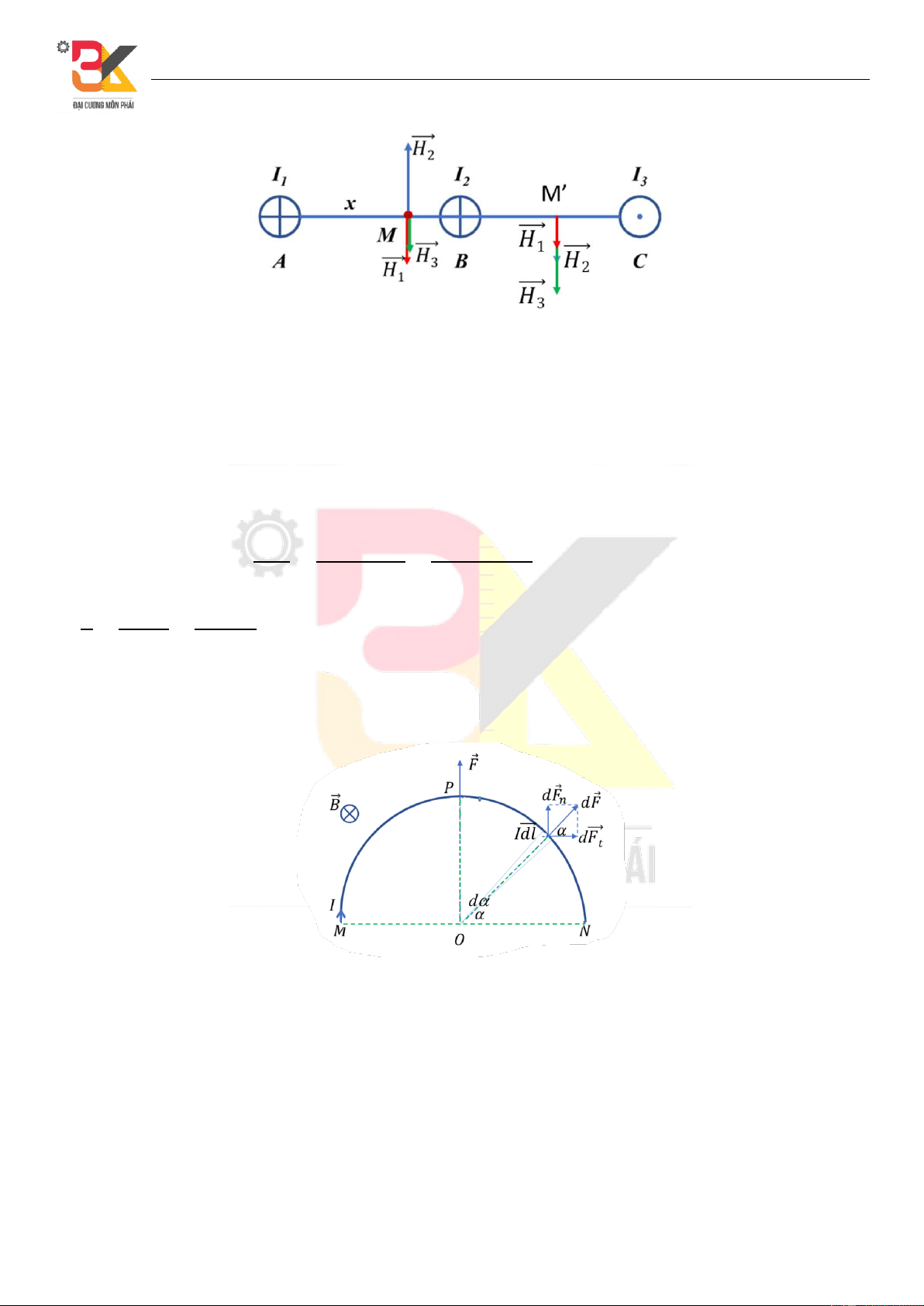
Hướng giải: Sử dụng công thức tính từ trường sinh ra bởi dòng điện thẳng dài Gọi 𝐻 ⃗⃗ ⃗⃗ ⃗⃗
1, 𝐻2 và 𝐻3 là các véc tơ cường độ từ trường do các dòng điện thẳng dài vô hạn 𝐼1, 𝐼2
và 𝐼3 gây ra tại 𝑀 ∈ 𝐴𝐶 có phương chiều xác định theo quy tắc vặn nút chai cho dòng điện thẳng như hình vẽ. 12
Đỗ Đức Phương – Nguyễn Hiếu
Theo nguyên lý chồng chất từ trường: Khi 𝑀′ ∈ 𝐵𝐶: 𝐻 ⃗ = 𝐻 ⃗⃗ ⃗⃗ ⃗⃗ 1 + 𝐻2 + 𝐻3 ≠ 0 ⃗
Khi 𝑀 ∈ 𝐴𝐵, ta có 𝐻 ⃗⃗ ⃗⃗ ⃗⃗
2 cùng phương ngược chiều với 𝐻1 và 𝐻3 nên tồn tại điểm 𝑀 ở đó 𝐻 ⃗ = 𝐻 ⃗⃗ ⃗⃗ ⃗⃗ 1 + 𝐻2 + 𝐻3 = 0 ⃗
Gọi 𝐴𝑀 = 𝑥 ta có : 𝐼 𝐼 2𝐼
𝐻 = 𝐻1 − 𝐻2 + 𝐻3 = − + = 0 2𝜋𝑥 2𝜋(𝑙 − 𝑥) 2𝜋(2𝑙 − 𝑥) 1 1 2 ⇒ − + = 0 ⇒ 𝑥 = 4 (𝑐𝑚) 𝑥 6 − 𝑥 12 − 𝑥 Đáp án D Câu 11:
Hướng giải: Chia vòng dây thành các phần tử 𝐼𝑑𝑙
⃗⃗ , tính lực từ do B tác dụng lên mỗi phần tử 𝐼𝑑𝑙 ⃗⃗ sau đó tích phân.
Chia dây dẫn 𝑆 thành các đoạn dây có chiều dài 𝑑𝑙 vô cùng nhỏ có dòng điện 𝐼 chạy qua. Từ
lực 𝑑𝐹 tác dụng lên phần tử dòng điện 𝐼𝑑𝑙 được xác định theo công thức: 𝑑𝐹 = 𝐼𝑑𝑙 ∧ 𝐵 ⃗
• Phương, chiều của từ lực dF⃗ được xác định theo quy tắc bàn tay trái như hình vẽ • Độ lớn dF = IBdl
Từ lực 𝐹 tác dụng lên dây dẫn là: 13