Thông tin
Quiz

Tổng hợp công thức Toán THPT – Nguyễn Thanh Tân

Tài liệu gồm 24 trang, được sưu tầm và biên soạn bởi thầy giáo Nguyễn Thanh Tân (giáo viên Toán trường THPT Nho Quan C, tỉnh Ninh Bình), tổng hợp công thức Toán THPT (lớp 10 – lớp 11 – lớp 12).

Chủ đề:

Tài liệu ôn thi THPTQG môn Toán 257 tài liệu

Môn:

Toán 1.9 K tài liệu

Thông tin:

24 trang 1 năm trước

Tác giả:

Nguyễn Vân

docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Tổng hợp công thức Toán THPT – Nguyễn Thanh Tân

62 31 lượt tải Tải xuống

Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT

Parabol

 

0y ax bx c a   

Đỉnh

;

2 4

a a

 



 

 

 



: Bề lõm quay lên



: Bề lõm quay xuống

Phương trình





0 0ax bx c a   

Có hai nghiệm phân biệt khi

 

, có nghiệm kép khi

 

, vô nghiệm khi

 

Nếu phương trình có hai nghiệm

1 2

,x x thì ta có định lí Vi-et:

   

1 2

S x x

và

 

1 2

P x x

Phương trình có hai nghiệm trái dấu khi

  

0 0

P ac

Phương trình có hai nghiệm cùng dấu khi



 







Phương trình có hai nghiệm phân biệt dương khi



 













, hai nghiệm phân biệt âm khi



 













Phương trình có hai nghiệm phân biệt

1 2

,x x thỏa mãn

  



 



  



  





1 2

x x



 

Phương trình có hai nghiệm phân biệt

1 2

,x x thỏa mãn

   

  



 



      





  





1 2 1 2

1 2

x x x x

x x

  

 

Phương trình có hai nghiệm phân biệt

1 2

,x x thỏa mãn

   

  



 



      





  





1 2 1 2

1 2

x x x x

x x

  

 

Chú ý:

chứa tham số thì xét riêng 

Nếu yêu cầu hai nghiệm (không phân biệt) thì

 

Phương trình chứa trị tuyệt đối

   







 



 



f x g x

   





   









 











 







0g x

f x g x

     

 a f x b g x h x

Dạng này ta chia trường

hợp để giải

Phương trình chứa căn









   

 

   

f x g x

f x or g x

f x g x





 













0 0

   

 

   







 









0g x

f x g x

   

  . . 0a f x b f x c

Đặt

 

  0t f x

Đưa về pt bậc 2 ẩn













 f x g x h x

PP: Tìm điều kiện và bình phương

2 vế, đưa về phương trình hệ quả

         

  

f x g x f x g x h x

PP: Đặt

   

 t f x g x

Một số dạng khác có thể sử

dụng nhân liên hợp, đưa về

hệ hoặc đánh giá…

Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT











f x g x

theo

đưa phương

trình đã cho về bậc hai theo ẩn

Phương trình trùng phương









4 2

0 0 1

ax bx c a   

PP: Đặt





     

2 2

0 0 2

t x at bt c





vô nghiệm







vô nghiệm, hoặc có 2 nghiệm âm





có đúng 1 nghiệm







có nghiệm kép bằng

hoặc có 1 nghiệm bằng

và 1 nghiệm âm





có đúng 2 nghiệm phân biệt







có nghiệm kép dương, hoặc có 1 nghiệm âm và 1 nghiệm dương





có đúng 3 nghiệm phân biệt







có một nghiệm dương và 1 nghiệm bằng





có 4 nghiệm phân biệt







có 2 nghiệm phân biệt dương

Hệ phương trình

Đối xứng loại I





 















; 0

f x y

g x y

Với









   















; ;

f x y f y x

g x y g y x

PP: Đặt

  

S x y P xy

với

điều kiện 

S P

Đối xứng loại II





 















; 0

f x y

f y x

PP: Trừ hai vế của phương trình

cho nhau, sau đó đưa về phương

trình tích

Hệ đẳng cấp bậc 2



  





  





2 2

1 1 1 1

2 2

2 2 2 2

a x b xy c y d

PP:

+ Giải hệ khi



+ Khi



đặt



y tx

chia vế

với vế của 2 phương trình cho

nhau, đưa về phương trình bậc

hai theo

Bất phương trình chứa trị tuyệt đối









f x g x











2 2

f x g x

 











f x g x





     











  





0g x

g x f x g x

   





 

   

















 

















 











g x

f x g x

Các dạng khác: Dùng định nghĩa trị tuyệt đối, chia khoảng để giải

Bất phương trình chứa căn

   





   

g x

f x g x







 









   





 

   























 























g x

f x

f x g x

g x

f x g x

   





 

   







  











f x

f x g x g x

f x g x

Các dạng khác: Đặt ẩn phụ, nhân liên hợp, đánh giá…

Ứng dụng dấu tam thức bậc hai

    



0,ax bx c x









 



    



0,ax bx c x









 



    



0,ax bx c x









 



    



0,ax bx c x









 



Công thức lượng giác





 

cos cos

 





 

  

sin sin





  

tan tan

 





  

cot cot

 





 

sin sin

  





  

cos cos

  





  

tan tan

  





  

cot cot

  

 

 

 

 

sin cos



 

 

 

 

 

cos sin



 

 

 

 

 

tan cot



 





  

sin sin

  





  

cos cos

  





 

tan tan

  

Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT



 

 

 

 

 

cot tan





 

cot cot

  

 

2 2

sin cos 1

 

 

1 tan

cos



 

1 cot

sin





tan .cot 1

 





  

cos cos .cos sin .sin

a b a b a b





  

cos cos .cos sin .sin

a b a b a b





  

sin sin .cos cos .sin

a b a b a b





  

sin sin .cos cos .sin

a b a b a b

 



 



tan tan

tan

1 tan .tan

a b

 

a b



 



tan tan

tan

1 tan .tan



sin 2 2sin .cos

a a a

 

   

2 2

cos2 cos sin

2cos 1 1 2sin

a a a

a a





2tan

tan2

1 tan

 

sin3 3sin 4sin

a a a

 

cos3 4cos 3cos

a a a







3tan tan

tan3

1 3tan

a a





1 cos2

cos





1 cos2

sin







1 cos2

tan

1 cos2





3cos cos3

cos

a a





3sin sin3

sin

a a

   

 

   

 

cos .cos cos cos

a b a b a b

   

 

   

 

sin .sin cos cos

a b a b a b

   

 

   

 

sin .cos sin sin

a b a b a b

 

 cos cos 2cos cos

2 2

a b a b

a b

 

  cos cos 2sin sin

2 2

a b a b

a b

 

 sin sin 2sin cos

2 2

a b a b

a b

a b a b

a b

 

 sin sin 2sin cos

2 2

 

  

 

 

sin cos 2 sin

a a a



 

  

 

 

sin cos 2 sin

a a a



Vectơ và các tính chất

 

  

AB BC AC

 

  

AB AC CB

Nếu

ABCD

là hình bình hành thì

 

  

AC AB AD

là trung điểm của đoạn

thì

 

  

IA IB và

 

  

MA MB MI

là trọng tâm tam giác

ABC

thì

  

   

GA GB GC và

  

   

MA MB MC MG

Ba điểm phân biệt

, ,

A B C

thẳng hàng





  

 

AB kAC k

Cho









1 1 2 2

; , ; ,

a x y b x y

 

 









   

 

1 2 1 2

;

a b x x y y









1 1

. ;

k a kx ky







 









 

1 2

x x

a b

y y

Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT

Vectơ



cùng phương với





 

  

1 1

2 2

x y





  



;

B A B A

AB x x y y

là trung điểm của

 

 ;

2 2

A B A B

I I

x x y y

x y

là trọng tâm tam giác

ABC

   

 ;

3 3

A B C A B C

G G

x x x y y y

x y

Điểm

chia đoạn

theo tỉ số

 

 

MA kMB

 



2 2

1 1

a x y





a b a b a b

x x y y



 

1 2 1 2

. . cos ,

     

 



 

 

 

1 2 1 2

2 2 2 2

1 1 2 2

cos ,

x x y y

a b

x y x y

   

 

1 2 1 2

a b x x y y

Một số kết quả cần nhớ

, ,

A B C

lập thành một tam giác





và



không cùng phương

là trực tâm của tam giác

ABC

. 0

AH BC

BH AC

















 

là tâm đường tròn ngoại tiếp tam giác

ABC

2 2

IA IB

IA IC

















là đường phân giác trong của

ABC



EB AB

  



Hệ thức lượng trong tam giác vuông Hệ thức lượng trong tam giác thường

  

2 2 2

2 .cos

a b c bc A

 



2 2 2

cos

b c a



 

2 2 2

2 4

b c a

  

sin sin sin

a b c

A B C



   

1 1

. .sin

2 2 4

ABC a

abc

S a h bc A pr













   

p p a p b p c

 

2 2 2

a b c



ah bc

;

 



h b c

Với

Đường trung tuyến xuất phát từ

đường cao xuất phát từ

 



a b c

p nửa chu vi tam giác

ABC

, :

R r

bán kính đường tròn ngoại tiếp và nội tiếp

b a b c a c

 

 

2 2

. ; .

 

2 2 2

1 1 1

h b c

Phương trình đường thẳng

Phương trình tham số đường thẳng



qua





0 0 0

;

M x y

có vtcp









;

u a b

là:



 





 





x x at

y y bt

Phương trình chính tắc đường thẳng



qua





0 0 0

;

M x y

có vtcp









;

u a b

là:

 



0 0

x x y y

a b

Phương trình tổng quát của đường thẳng



qua





0 0 0

;

M x y

có vtpt









;

n a b

là:









   

0 0

a x x b y y

Đường thẳng

  

ax by c

có vtpt







;

n a b

và có vtcp





 



;

u b a

Đặc biệt: Trục



: 0,

Ox y

trục



: 0.

Oy x

Cho

1 1 1 1 2 2 2 2

: 0; : 0

a x b y c a x b y c

       





0 0 0

;

M x y

     

1 1 1

1 2

2 2 2

a b c

    



1 1 1

1 2

2 2 2

a b c



cắt



 

1 1 1 2 2 2

: : : :

a b c a b c

     

1 2 1 2 1 2

a a b b







 

   

 

1 2

1 2 1 2

1 2

cos , cos ,

n n

 

 

 



1 0 1 0 1 0

0 1

2 2

1 1

;

a x b x c x

d M

a b

Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT

Phân giác của góc tạo bởi



và



là

a x b y c a x b y c

a b a b

   

 

 

1 1 1 2 2 2

2 2 2 2

1 1 2 2

Cho





    

: ; 0

f x y ax by c

A B

cùng phía với

  

. 0

A B

f f

A B

khác phía với

  

. 0

A B

f f

Phương trình đường tròn

   

   

2 2

x a y b R

có tâm





;

I a b

và có

bán kính

    

2 2

x y ax by c

có tâm

 

 

 

 

;

2 2

a b

và có bán

kính

 

 

   

 

 

2 2 2 2

4 4

a b a b

R c c

Phương trình đường elip

 

2 2

x y

a b





   

2 2 2

a b b a c











1 2

;0 , ;0

F c F c

: Các tiêu điểm



1 2

2 :

F F c

Tiêu cự











1 2

;0 , ;0

A a A a



1 2

2 :

A A a

Độ dài trục lớn











1 2

0; , 0;

B b B b



1 2

2 :

B B b

Độ dài trục bé

Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT

Phương trình lượng giác

Phương trình cơ bản

 



  

  



  



sin sin

u v k



 

   sin 1 2

u u k



     

sin 1 2

u u k



  

sin 0

u u k



 



 

  



  





cos cos

u v k



  

cos 1 2

u u k



    

cos 1 2

u u k

 

   cos 0

u u k



   

tan tan

u v u v k



   

cot cot

u v u v k



  

sin sin 0a x b x c

Đặt





   sin 1 1t x t

, đưa về giải phương trình bậc hai

( tương tự đối với cos ,x nếu đặt

tan,cot

thì không cần điều kiện t )

 sin cosa x b x c

Chia cả hai vế cho 

2 2

a b sau đó đưa về PTLG cơ bản

Chú ý: Phương trình có nghiệm

2 2 2

a b c

  

  

2 2

sin sin cos cos

a x b x x c x d

Xét

trường hợp

+ TH1:

  

cos 0 sin 1.

x x Thay vào phương trình và kết luận

+ TH2: cos 0 :x Chia cả hai vế của phương trình cho

cos x , đưa về

phương trình bậc hai của tanx

  

(sin cos ) sin cos

a x x b x x c

Đặt





    sin cos 2 2t x x t

, biểu diễn sin cosx x theo

đưa

phương trình đã cho về bậc hai theo t

Phương trình dạng dạng khác Phân tích thành nhân tử hoặc đánh giá

Hoán vị - chỉnh hợp – tổ hợp

Quy tắc cộng Quy tắc nhân

Một công việc được hoàn thành bởi một trong hai

hành động. Nếu hành động này có

cách thực

hiện, hành động kia có

cách thực hiện không

trùng với bất cứ cách nào của hành động thứ nhất

thì có m n cách hoàn thành công việc đó

Một công việc được hoàn thành bởi hai hành động

liên tiếp. Nếu có

cách thực hiện hành động thứ

nhất và ứng với mỗi cách đó có

cách thực hiện

hành động thứ hai thì có

.m n

cách hoàn thành

công việc đó

Hoán vị Chỉnh hợp Tổ hợp

Sắp xếp (đổi chỗ) của

phần tử khác

nhau có  !

P n cách

 

 ! 1 ...1n n n

Quy ước:

0! 1

Chọn

phần tử từ

phần tử sau đó

sắp thứ tự chúng có

A cách

 





n k

Chọn

phần tử từ

phần tử ta có số

cách chọn là

 





! !

n k k

Một số kết quả cần nhớ

Cho n điểm

trong không

gian, trong đó

không có 3

điểm nào thẳng

hàng

Số đường thẳng đi qua hai điểm:

Số vectơ khác



0 nối hai điểm bất kì:

Số tam giác tạo thành:

Nếu trong n điểm không có 4 điểm nào đồng thẳng thì số tứ diện được tạo thành:

Số đường chéo của đa giác: 

C n

Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT

Cho đa giác lồi

đỉnh

Nếu không có 3 đường chéo nào đồng quy thì số giao điểm giữa các đường chéo mà

giao điểm nằm trong đa giác là

Số tam giác có 3 đỉnh là đỉnh của đa giác:

Số tam giác có đúng 1 cạnh của đa giác, 2 cạnh còn lại là đường chéo:







n n

Số tam giác có 2 cạnh của đa giác, 1 cạnh còn lại là đường chéo:

Số tam giác có cạnh đều là đường chéo của đa giác:





  

C n n n

hoặc



Cho đa giác

đều

đỉnh

Số tam giác vuông được tạo thành:

với

chẵn; bằng

với

lẻ

Số tam giác tù được tạo thành:



với

chẵn; bằng



n C

với

lẻ

Số tam giác nhọn



số tam giác



( số tam giác vuông



số tam giác tù)

Cho đa giác

đều

đỉnh







Số hình chữ nhật:

Số tam giác vuông:

Cho đa giác

đều

đỉnh







Số tam giác đều:

Số tam giác cân không đều:

 



 

 

3 2

3 1

với

chẵn; bằng

 



 

 

3 1

với

lẻ

Xác suất

 





 





n A

P A





n A

số phần tử của biến cố







số phần tử không gian mẫu





P A

Xác suất của biến cố





 

0 1

P A









   

0, 1

P P









 1

P A P A

: b/cố đối của

Hai biến cố là xung khắc nếu

  

A B

Nếu

A B

xung khắc thì













  

P A B P A P B

Hai biến cố độc lập nếu việc xảy ra của

biến cố này không ảnh hưởng đến biến

cố khác. Nếu

A B

độc lập thì













P AB P A P B



TQ:

















   

P A B P A P B P AB

Nhị thức Niutơn

 





 



k n k k

a b C a b

Số hạng thứ





 

k n k k

k n

k T C a b





k n k

n n

C C

 



 

1 1

k k k

n n n

C C C



k k

n n

A k C

   

0 1

... 2

n n

n n n

C C C

 

     

0 1 2

... 1 0

n n n n

C C C C



      

0 2 2 1 3 2 1

2 2 2 2 2 2

... ...

n n

n n n n n n

C C C C C C

Cấp số

Cấp số cộng Cấp số nhân



 

1n n

u u d





  

u u n d

 





1 1

k k

u u





n n

u u q





u u q

 



1 1

k k k

u u u









 

 



 

     

1 2

2 1

...

2 2

n n

n u n d

n u u

S u u u





 

1 2

... 1

n n

u q

S u u u q



     



Tổng của cấp số nhân lùi vô hạn:

S u u u

     



1 2

... ...

Hàm số liên tục

Hàm số





y f x



liên tục tại

nếu









x x

f x f x





lim

     

x x x x

or f x f x f x

 

 

 

 

 

 

0 0

lim lim

Hàm số





y f x



liên tục trên đoạn

a b

 

 

;

nếu nó

liên tục trên khoảng





a b

;

và

















x a x b

f x f a f x f b

 

 

 lim ; lim

Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT

Nếu hàm số không liên tục tại

thì

được gọi là

điểm gián đoạn của hàm số





f x

Hàm số





y f x



liên tục trên

a b

 

 

;

và









f a f b



. 0

thì phương trình





f x



có ít nhất một nghiệm

thuộc khoảng





a b

;

Công thức đạo hàm

 





 



 

  

u v u v

 



 

 .

u v u v v u



 

 





 

 

u u v v u

Hàm thường Hàm hợp

 





kx k

 





ku k u

 







n n

x n x

 







. .

n n

u n u u



 

 

 

 

1 1



 

 

 

 

 





 





 





sin cos

x x

 





sin .cos

u u u

 



 

cos sin

x x

 



 

cos .sin

u u u

 



  

tan 1 tan

cos

x x

 





tan

cos

 



    

cot 1 cot

sin

x x

 



 

cot

sin

 





x x

e e

 





u u

e u e

 





.ln

x x

a a a

 





. ln

u u

a u a a

 





lnx

 





 





log

.ln

x a

 



log

.ln

u a

Phương trình tiếp tuyến

Phương trình tiếp tuyến của đồ thị hàm số





y f x



tại điểm





0 0

;

M x y









0 0 0

y f x x x y



  

Tiếp tuyến có hệ số góc

ta giải phương trình





f x k x



 

và

Tiếp tuyến song song với đường thẳng

y ax b

 







f x a x



 

và

Tiếp tuyến vuông góc với đường thẳng

y ax b

  

 

f x x



   và

Tiếp tuyến đi qua điểm





0 0

;

A x y

có hệ số góc

thỏa mãn hệ





   

0 0

k f x

f x k x x y











  





Tiếp tuyến có hệ số góc

tạo với đường thẳng

d y ax b

 

một góc



tan

k a









Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT

Quan hệ song song

Nếu

không nằm trên





và song song với

nằm trên





thì





a P



Nếu





d P



thì mọi mặt phẳng





chứa

mà cắt





thì cắt theo một giao tuyến song song với

Nếu hai mặt phẳng cắt nhau cùng song song với một đường thẳng thì giao tuyến của chúng song song

với đường thẳng đó

Ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến đó hoặc đồng quy, hoặc

song song với nhau

Nếu





chứa hai đường thẳng

a b

cắt nhau và cùng song song với mặt phẳng





thì









P Q



Nếu một đường thẳng nằm trên một trong hai mặt phẳng song song thì nó song song với mặt phẳng kia

Nếu hai mặt phẳng





và





song với nhau thì mọi mặt phẳng





đã cắt





thì phải cắt





và

giao tuyến của chúng song song với nhau

Quan hệ vuông góc

Một đường thẳng được gọi là vuông góc với một mặt phẳng nếu nó vuông góc với mọi đường thẳng nằm

trên mặt phẳng đó

Nếu đường thẳng

vuông góc với hai đường thẳng cắt nhau

và

cùng nằm trong





thì





d P



Định lí 3 đường vuông góc: Cho đường thẳng

không vuông góc với





và đường thẳng

nằm trong





điều kiện cần và đủ để

vuông góc với

là

vuông góc với hình chiếu



của

trên













P Q



nếu trong





chứa một đường thẳng

và





d Q



Nếu hai mặt phẳng vuông góc với nhau thì bất cứ đường thẳng nào nằm trong mặt phẳng này mà vuông

góc với giao tuyến thì vuông góc với mặt phẳng còn lại

Nếu









P Q



và





A P



thì đường thẳng

đi qua điểm

và vuông góc với





thì





a P



Nếu hai mặt phẳng cắt nhau và cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng cũng

vuông góc với mặt phẳng thứ ba

Góc giữa đường thẳng và đường thẳng, mặt phẳng, góc giữa hai mặt phẳng

Góc giữa đường thẳng

và

là góc giữa đường thẳng



và



cùng đi qua qua một điểm và lần lượt

song song với

và

Góc giữa đường thẳng

và





là góc giữa

và hình chiếu vuông góc



của

lên





Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó

Công thức dcm tính khoảng cách giữa hai đường thẳng chéo nhau

Cho hình chóp

S ABC

có đường cao

. Khi đó

 

2 2 2

1 1

d SA BC d m

 

Trong đó:





d d A BC



m SH



𝑐 =

đ𝑖ể𝑚 𝑐ℎâ𝑛

đ𝑖ể𝑚 𝑐ắ𝑡

𝐴𝐻

𝐴𝑀

Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT

Phép suy đồ thị: Cho hàm số





y f x

có đồ thị





, 0a 





y f x a 

Tịnh tiến

 

sang trái a đơn

vị





y f x a 

Tịnh tiến

 

sang phải a

đơn vị





y f x a 

Tịnh tiến

 

lên trên a đơn

vị





y f x a

 

Tịnh tiến

 

xuống dưới

đơn vị

 

y f x 

Lấy đối xứng

 

qua

 

y f x 

Lấy đối xứng

 

qua

Đồ thị

 

:f x

B1: Giữ nguyên phần đồ thị

 

nằm trên Ox

B2: Lấy đối xứng phần đồ đồ thị

 

nằm phía

dưới Ox qua ,Ox bỏ hết phần đồ thị phía dưới

Đồ thị





:f x

B1: Giữ nguyên phần đồ thị

 

nằm bên phải

,Oy bỏ hết phần đồ thị bên trái .Oy

B2: Lấy đối xứng phần đồ thị

 

nằm bên phải

Oy qua .Oy

Số điểm cực trị của hàm chứa dấu giá trị tuyệt đối

Số điểm cực trị của hàm

số

 

y f x

chính bằng

số điểm cực trị của hàm

số

 

f x

cộng với số

nghiệm đơn của phương

trình

 

 0.f x

Số điểm cực trị của

hàm số

 

y f x

chính bằng 

2 1,

trong đó n là số điểm

cực trị dương của hàm

số

 

f x

Nếu hàm số

 

y f x

có n điểm cực trị thì đồ thị

hàm số

 

y f x

và đường thẳng  0y có tối đa

1n giao điểm. Từ đó hàm số

 

y f x

có tối đa

2 1n điểm cực trị













3 2

0y f x ax bx cx d a C     

Điều kiện để hàm số có hai điểm cực trị:



   

3 0

b ac

Hàm số đồng biến (nghịch biến) trên



khi:









 







 





0 0

a a

Đồng biến (nghịch biến) trên đoạn có độ dài đúng bằng l khi:







 





 





2 1

0 0a a

x x l

Phương trình đường thẳng đi qua hai điểm cực trị:

 









 

 

f x f x

y f x

Định lí vi-et đối với 2 điểm cực trị:   

1 2

x x

và 

1 2

x x

Trong các tiếp tuyến của





tiếp tuyến tại điểm uốn là tiếp tuyến có hệ số góc nhỏ nhất khi  0,a và

là tiếp tuyến có hệ số góc lớn nhất khi  0a

Điều kiện để hàm số có hai điểm cực trị

1 2

x x

Trái dấu Cùng dấu Cùng dấu dương Cùng dấu âm





có hai nghiệm

phân biệt trái dấu





có hai nghiệm phân

biệt cùng dấu





có hai nghiệm

phân biệt cùng dương





có hai nghiệm

phân biệt cùng âm

Điều kiện để hàm số có hai điểm cực trị

nằm cùng phía với

trục Oy là phương

trình





có hai

nằm bên trái trục Oy là

phương trình



 0y có hai

nghiệm phân biệt âm

nằm bên phải trục

là phương trình





có hai nghiệm phân

biệt dương

nằm khác phía so với

trục Oy là phương trình



 0y có hai nghiệm trái

dấu

Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT

nghiệm phân biệt

cùng dấu

nằm cùng phía với

trục

là phương

trình







f x

có

nghiệm duy nhất

nằm cùng phía trên với trục

là phương trình







f x

có nghiệm duy

nhất và



nằm cùng phía dưới

trục

là phương

trình







f x

có

nghiệm duy nhất và



nằm khác phía với trục

là phương trình







f x

có bao nghiệm

phân biệt.

Chú ý: Hoành độ điểm uốn

là nghiệm của phương trình đạo hàm cấp hai của hàm bậc ba

Phương trình bậc ba có 3 nghiệm lập thành

cấp số cộng nếu có một nghiệm là

 

cấp số nhân nếu có một nghiệm là

 

Xác định dấu của các hệ số hàm số bậc ba theo thứ tự

a d b c

  

Nhìn nhánh ngoài cùng bên tay phải, nếu đi lên

thì



đi xuống thì



Quan sát giao của đồ thị với

cắt

phía

trên thì



cắt phía dưới thì



Sử dụng vi-ét   

1 2

x x

kết hợp với dấu

của

suy ra dấu của

sử dụng vi-ét 

1 2

x x

kết hợp với dấu của

suy ra ra dấu của

Định lí vi-ét cho phương trình bậc ba

3 2

y ax bx cx d

   

   

1 2 3

x x x

  

1 2 2 3 3 1

x x x x x x

 

1 2 3

x x x









4 2

y f x ax bx c a

    

Điều kiện đề hàm số có 3 điểm cực trị là



để có một cực trị là



Hàm số có đúng một

cực trị và cực trị là

cực tiểu:











Hàm số có đúng một cực

trị và cực trị là cực đại:











Hàm số có hai điểm cực

tiểu và một điểm cực đại:











Hàm số có một điểm

cực tiểu và hai điểm

cực đại:











Giả sử đồ thị hàm số có 3 điểm cực trị

 

   

 

    

   

   

0; , ; , ;

2 4 2 4

b b

A c B C

a a a a

và 3 điểm cực trị này

luôn tạo thành tam giác cân tại

Gọi

là diện tích



ABC

và





BAC



khi đó

a b



 

3 2

8 tan 0

 

3 2 5

32 0

a S b

Đồ thị hàm số cắt trục hoành tại bốn điểm có hoành độ lập thành cấp số cộng nếu 

9 100 .

b ac

Đồ thị hàm số cắt trục hoành tạo thành ba miền diện tích có diện tích phần trên và diện tích phần dưới

bằng nhau là 

5 36

b ac

Phương trình đường tròn ngoại tiếp



ABC

là

   

 

      

   

   

2 2

4 4

x y c y c

b a b a

Chú ý: Có thể dựa vào đồ thị hàm số bậc bốn trùng phương để dễ dàng nhớ các công thức hơn

   

0, 0



   



ax b

y c ad bc C

cx d

Tính chất của tiếp tuyến (gọi

là giao của hai đường tiệm cận)

Tiếp tuyến tại

thuộc

đồ thị hàm phân thức cắt

các tiệm cận tại

và

thì

là trung điểm của

Khoảng cách từ

tới

tiệm cận đứng

 

d cx d

Khoảng cách từ

tới tiệm cận ngang







ad bc

c cx d

Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT

Tổng khoảng cách ngắn

nhất từ điểm

đến hai

đường tiệm cận





min

ad bc

Diện tích tam giác

IAB

không đổi và

 

IAB

S ad bc

Khoảng cách ngắn nhất giữa hai điểm

P Q

bất kì

thuộc hai nhánh của đồ thị





min

2 2

ad bc

Điểm

thỏa mãn một trong các tính chất: Tổng khoảng cách đến hai đường tiệm cận đạt giá trị nhỏ

nhất, khoảng cách

ngắn nhất, khoảng cách từ

đến tiếp tuyến tại

đại giá trị lớn nhất, tiếp

tuyến tại

vuông góc với

tam giác

IAB

vuông cân, chu vi tam giác

IAB

nhỏ nhất,

nhỏ

nhất, bán kính đường tròn nội tiếp tam giác

IAB

lớn nhất, bán kính đường tròn ngoại tiếp tam giác

IAB

nhỏ nhất thì điểm

phải thỏa mãn tính chất







  

IA IB y x

M N

thuộc hai nhánh khác nhau của





sao cho

nhỏ nhất là thì hoành độ điểm

M N

thỏa

mãn





M N

thuộc hai nhánh khác nhau của





sao cho

tiếp tuyến của





tại

M N

song song và khoảng

cách giữa hai tiếp tuyến là lớn nhất thì hoành độ

điểm

M N

thỏa mãn





Cách nhận dạng đồ thị hàm phân thức bậc nhất/ bậc nhất

Tiệm cận ngang



Nếu tiệm cận

ngang nằm trên

thì



nằm dưới

thì



Tiệm cận đứng

 

Nếu tiệm cận đứng nằm

bên trái

thì



nằm bên phải

thì



Giao



: .

Oy y

Nếu giao

điểm này nằm trên

thì



nằm dưới

thì



Giao

 

: .

Ox x

Nếu giao điểm này

nằm bên trái

thì



nằm bên phải

thì



Cho hàm số





y f x



có giá trị lớn nhất và nhỏ nhất trên

lần lượt là

và

 

  

max

M m M m

f x

 









  









0 . 0

min

. 0

khi M m

f x

M m M m

khi M m

Cô lập

giải phương trình, bất phương trình







f x m

có nghiệm trên









f x m f x

  min max







f x m

nghiệm đúng





    min

x D m f x







f x m

có nghiệm trên





  max

D m f x







f x m

nghiệm đúng





    max

x D m f x







f x m

có nghiệm trên





  min

D m f x

Chú ý: Nếu có dấu bằng trong các bất phương trình thì ta thêm dấu bằng ở điều kiện tương ứng (nên xét

riêng tại dấu bằng xem có xảy ra không). Một số bài ta vẽ bảng biến thiên và dùng tương giao để giải

Đồ thị hàm lũy thừa

 

 



 

y f x









Điều kiện là







f x



 



0, :

 

Điều kiện là







f x







Điều kiện của hàm số là điều kiện





f x

Đồ thị hàm số



y x



luôn đi qua điểm





1;1

Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT

Đồ thị hàm số mũ



y a

có tập xác định





tập giá trị





 

0; .

Đồ thị hàm số



y a

luôn đi qua điểm





0;1

và có tiệm

cận ngang là trục hoành

Vẽ đường thẳng



để so sánh

, , ,

a b c d

( trên hình vẽ là

    

0 1

b a d c

)

Đồ thị hàm số logarit



log

y x

có tập xác định





 

0; ,

tập giá trị





Đồ thị hàm số 

log

y x

luôn đi qua điểm





1;0

và có tiệm

cận đứng là trục

Vẽ đường thẳng



để so sánh

, , ,

a b c d

( trên hình vẽ là

    

1 0

b a d c

)

Công thức mũ





, 0

a b



m n m n

a a a









m n

 



m m

ab a b

 



 

 

a a







m m n

a a



a a



a a





Công thức logarit





, 0, 1

a b a

 

  

log

b a b





log log

; 

ln log



log 1 0



log 1



log log

a a

b n b



log log

b b

 

 

 

 

log log log

a a a

b c

 

 

log

log 1

log

b c

 

 

log 1

log

b b





 

log log log

a a a

bc b c



log

a b



log log

b b

c a

a c

Bài toán lãi suất

Lãi đơn: Số tiền lãi của kì hạn trước không được tính vào vốn để tính lãi cho kì hạn tiếp

Lãi kép: Số tiền lãi của kì hạn trước nếu người gửi không rút ra thì được tính vào vốn để tính lãi cho kì

hạn sau đó

Bài toán 1: Gửi vào ngân hàng

đồng với lãi

kép

% /

kì hạn, số tiền nhận được sau

kì

hạn là

 

 

1 %

T T r

Bài toán 3: Gửi ngân hàng

đồng với lãi kép

% /

tháng, hàng tháng rút

đồng, số tiền còn lại sau

tháng là

 

 

  

1 % 1

1 % .

T T r t

Hết tiền khi



Bài toán tương đương: Vay ngân hàng số tiền

đồng

với lãi kép

% /

tháng, hàng tháng trả

đồng. Số tiền

còn nợ sau

tháng là

 

 

  

1 % 1

1 % .

T T r t

Trả hết nợ khi



Bài toán 2: Hàng tháng gửi

đồng vào ngân

hàng với lãi kép

% /

tháng, tổng số tiền nhận

được sau

tháng là

 

 

 

1 % 1

1 % .

T t r

Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT

Tính chất nguyên hàm

Nếu





F x

là một nguyên hàm của





f x

thì









F x f x













 



f x dx F x C











 



f x dx f x C

 







f x dx f x













kf x dx k f x dx k

 

 

















 

  

 

  

f x g x dx f x dx g x dx









 



f u du F u C

Nguyên hàm cần nhớ

dx C





 



kdx kx C

 



   





x dx C n

ax b

ax b dx C

a n



  





1 ( )

( )

dx x C

 



dx ax b C

ax b a

  





1 1

dx C

  



1 1

dx C

a ax b

ax b

   





1 1 1

( )

x x

e dx e C

 



ax b ax b

e dx e C

 

 



a dx C

 



mx n

a dx C

m a



 



xdx x C

  



sin cos

ax b dx ax b C

    



sin( ) cos( )

xdx x C

 



cos sin

ax b dx ax b C

   



cos( ) sin( )

dx x C

  



cot

sin

ax b C

ax b

   





cot( )

sin ( )

dx x C

 



tan

cos

ax b C

ax b

  





tan( )

cos ( )

xdx x C

  



tan ln cos

   

ax b dx ax b C

    



tan ln cos

xdx x C

 



cot ln sin

   

ax b dx ax b C

   



cot ln sin

dx x

 



ln tan

sin 2

 

dx ax b

ax b



 





ln tan

sin

dx x

  



ln cot

cos 2

 

dx ax b

ax b



  





ln cot

cos

Nguyên hàm mở rộng

  



 

 

 



dx ax b

ad bc cx d

ax b cx d



 





2 2

dx a x

a a x

a x





   





2 2

x x a C

x a

 





arctan

dx x

a a

a x

 





2 2

arcsin

dx x

a x

 





2 2

arccos

dx x

a a

x x a

    



2 2 2 2

arcsin

2 2

x a x

a x dx a x C

 

  





2 2

dx a x a

a x

x x a

Phương pháp đổi biến

Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT

Thường đặt dưới mẫu, dưới mũ, dưới căn, một số trường khác đặt nâng cao khác như sau

Dấu hiệu nhận biết Cách đặt



2 2

a x

 

  

 

 

sin , ; .

2 2

x a t t

 



2 2

x a

 

 

  

 

 

, ; \ 0

sin 2 2

x t

 



2 2

a x

 

  

 

 

tan , ;

2 2

x a t t

 

a x





hoặc

a x







cos2

x a t









 

x a b x





  

sin

x a b a t

Phương pháp từng phần

udv uv vdu

 

 

Thứ tự ưu tiên đặt

Log



đa



lượng



mũ

Một số tính chất cần nhớ

  



 

 

1 2

ax b A B

x x x x

   

1 2 3

ax bx c A B C

x x x x x x

 

  

  

     

 

  

 

  

2 2

1 2

1 2 1

ax bx c A B C

x x x x

x x x x x x

 

  

 

  

ax bx c A Bx C

x x mx nx p

Nguyên hàm hàm ẩn













f x dx d f x













f x dx f x C



 



         

f x f x f x f x f x

   

  

 

   

 

     

 

f x f x f x

f x

f x f x

 

 

 





 

  

 

 

   

 





f x

f x d f x C



 













 

d f x

f x C

f x

 



















f x p x f x h x



 

: Nhân cả hai vế với

 

p x dx



, đẳng thức trở thành

 

   

 

p x dx p x dx

f x e e h x



 

 



 

 

. .

Cho

y A y B



 





y a m



tính





y b

: . ,

20 20

b a b a

x x y y y

 



   

CALC

x a y m

 

ấn

" "



liên tục đến khi

x b



ta được giá trị





y b

Chú ý: Chuyển hết





f x



và





f x

sang vế phải, bậc của





f x



phải là bậc một

Một số tính chất của tích phân

     

f x dx F b F a

 



 

f x dx





 

f x dx





   

...

b b

a a

f x dx f t dt

 

 

   

b b

a a

kf x dx k f x dx



 

       

b b b

a a a

f x g x dx f x dx g x dx

 

  

 

  

     

b c b

a a c

f x dx f x dx f x dx

 

  





a b c

 

   

0, ; 0

f x x a b f x dx

 

    

 



       

, ;

b b

a a

f x g x x a b f x dx g x dx

 

    

 

 





f x

là hàm chẵn và liên tục trên

 



 

;

a a

thì

     

 

 

  

2 2

a a

f x dx f x dx f x dx

Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT





f x

là hàm lẻ và liên tục trên

 



 

;

a a

thì

 







f x dx

và

   



 

 

f x dx f x dx





f x

là hàm số chẵn và liên tục trên

;

a a

 



 

thì





 

a a

f x

dx f x dx







 





f x

liên tục trên

 

 

;

a b

thì

   

  

 

b b

a a

f x dx f a b x dx





f x

liên tục trên

 

 

;

a b

và thỏa mãn









 

    

 

, ;

f a b x f x x a b

thì

   





 

b b

a a

a b

xf x dx f x dx





f x

liên tục và









   

f a b x f x

thì

 





f x dx





f x

liên tục trên

 

 

0;2

thì

     

 

  

 

 

0 0

a a

f x dx f x f a x dx

f g

liên tục trên

 

 

;

a b

thì

 

  



 

max ,

b b

a a

f g f g

f g dx dx

 

  



 

min ,

b b

a a

f b f g

f g dx dx

Bất đẳng thức tích phân (Holder với

p q

 

       

2 2

b b b

a a a

f x g x dx f x dx g x dx

 



 

 

  

Kỹ thuật chọn hàm cơ bản trong tích phân

Nếu đề bài cho

 

f x dx C

 



chọn

 

f x

b a





Nếu đề bài cho

một điều kiện thì chọn





f x ax



hai điều kiện thì chọn





f x ax b

 

ba điều kiện thì chọn





f x ax bx c

  

Nếu đề bài cho hàm lẻ có

một điều kiện thì chọn





f x ax



hai điều kiện thì chọn





f x ax bx

 

Nếu đề bài cho hàm chẵn có

một điều kiện thì chọn





f x ax



hai điều kiện thì chọn





f x ax b

 

Một số kĩ thuật nâng cao

Điều kiện đề bài Phương pháp giải

















. . . .

A f x B u f u C f a b x g x



    

Nếu





f x

liên tục trên

;

a b

 

 

thì

   

b b

a a

f a b x dx f x dx

  

 

Nếu









u a a u b b

 

thì

   

b b

a a

f x dx g x dx

A B C



 

 

Nếu









u a b u b a

 

thì

   

b b

a a

f x dx g x dx

A B C



 

 













Af u Bf v g x

 

Đặt

t u



và

t v



để giải giải phương trình hai ẩn

(Nếu

u x



thì chỉ cần đặt

t v



)

Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT









f x f a b x k

  

 

dx b a

k f x



 









g f x x

 



 

với





g t

đơn điệu trên



Tính

 

f x dx



, ta đặt









y f x x g y

  

Tính diện tích hình phẳng

Theo

Điều kiện:

















 





: 0

y f x

Ox y

x a x b

 





S f x dx

Điều kiện:





 













 





y f x

y g x

x a x b

   

 



S f x g x dx

Điều kiện:

















 





: 0

x f y

Oy x

y a y b

 





S f y dy

Điều kiện:





 













 





x f y

x g y

y a y b

   





f y g y dy

Tính thể tích khối tròn xoay

Theo

Điều kiện:

















 





: 0

y f x

Ox y

x a x b

 





V f x dx



Điều kiện:





 













 





y f x

y g x

x a x b

   

 



2 2

V f x g x dx























   

, 0 ;

f x g x x a b

Điều kiện:

















 





: 0

x f y

Oy x

y a y b

 





V f y dy



Điều kiện:





 













 





x f y

x g y

y a y b

   

 



2 2

V f y g y dy























   

, 0 ;

f y g y y a b

Thể tích vật thể có diện tích thiết diện bằng





S x

 

V S x dx





Một số công thức tính nhanh

Đường thẳng



y n

cắt đường cong

  

4 2

y ax bx c

tại 4 điểm phân biệt và hình

phẳng giới hạn bởi hai đường này gồm phần phía

trên và phần phía dưới đường thẳng có diện tích

bằng nhau khi và chỉ khi





 

5 36

b a c n

Đường thẳng

 

y mx n

cắt đường cong

   

3 2

y ax bx cx d

tại ba điểm phân biệt và hình

phẳng giới hạn bới hai đường này gồm phần phía

trên và phía dưới đường thẳng có diện tích bằng

nhau khi và chi khi điểm uốn của đường cong bậc

ba thuộc đường thẳng

 

y mx n

Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT

Diện tích hình phẳng giới hạn bởi đường thẳng

 

y mx n

và parabol

  

y ax bx c

là

   





 

  

 



   

 

 

4 4

36 36

b m a c n

a a

Trong đó:



là của phương trình hoành độ

( Tức là của phương trình

   

ax bx c mx n

)

Số phức





,z a bi a b  



Phần thực,

phần ảo,

đơn vị ảo,

 

là số thực





là số thuần ảo





Số

vừa là số thực vừa là số ảo

Tính chất số phức :

z a bi z a b i

  

   

a a

z z

b b









 













;

M a b

là điểm biểu diễn

số phức

z a bi

 

là số phức

liên hợp của

z a b

 

2 2

là số thực

z z

 

là số ảo

z z

  

z z



;

z z z



1 2 1 2

z z z z

  

1 2 1 2

z z z z



1 2 1 2

z z z z



2 2

z z a b

 

1 1

z z

 



 

 

1 2 1 2 1 2

z z z z z z

    

Dạng lượng giác số phức









cos sin 0

z r i r

 

  

là dạng lượng giác của

z a bi

 



là một acgumen của





Ox OM





và

a b

r a b

r r

 

   

2 2

, cos , sin









1 1 1 1 2 2 2 2

cos sin , cos sinz r i z r i

   

   

   

1 1

1 2 1 2

2 2

cos sin

z r

   

 

   

 









1 2 1 2 1 2 1 2

cos sinz z r r i   

 

   

 

   

cos sin cos sin

r i r n i n

   

 

  

 

Một số đẳng thức mođun quan trọng





2 2 2

1 2 1 2 2 1 2 1 2

mz nz m z n z mn z z z z

    

với

m n









    

2 2 2 2

1 2 1 2 1 2

2z z z z z z

1 2 1 2 1 2

z z z z OM OM

 



2 1

1 2 1 2

1 2

. .

z z

z z z z

z z

  

với

1 2

z z



2 2

1 2 1 2

1 2

2 2

z z z z

z z z z z

 

 

 

     

 

 

Các công thức thể tích cơ bản

Thể tích chóp



V Bh

Thể tích lăng trụ



V Bh

Thể tích chóp cụt





 

  

V h B B B B

Công thức tính nhanh thể tích khối chóp đặc biệt

Nhận dạng Công thức tính nhanh

Tứ diện đều cạnh



Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT

Tứ diện gần đều có độ dài các cạnh đối là

, ,

a b c

   

      

2 2 2 2 2 2 2 2 2

6 2

V a b c b c a a c b

Chóp có ba mặt phẳng









SAB SAC

, ,





SBC

đôi một vuông góc và có diện tích

lần lượt là

1 2 3

, ,

S S S



1 2 3

2 . .

S S S

Tứ diện

ABCD

có

ABC ABD

S S S S

 

 

1 2

, ,

AB a



và

   









,ABC ABD





1 2

2 . sin

S S



Tứ diện

ABCD

có

 

AB a CD b

   



 

, ; ,d AB CD d AB CD





sin

V abd



Chóp

S ABC

có

  

, ,

SA a SB b SC c

   







  

, , ,SAB SAC ASB ASC

  



sin .sin .sin

abc

  

Chóp

S ABC

có

  

, ,

SA a SB b SC c



  

, ,ASB BSC CSA

  

    

2 2 2

1 2cos .cos .cos cos cos cos

abc

     

Chóp

S ABC

có

  

, ,

BC a CA b AB c

   







   







 

, , ,SBC ABC SAC ABC

 

   









,SAB ABC



 



 

3 .cot .cot .cot

ABC

a b c

  

Tỉ số thể tích

Chóp tam giác

S ABC

, ,

M N P

lần lượt thuộc

, ,

SA SB SC



. .

S MNP

S ABC

SM SN SP

V SA SB SC

Chóp tứ giác

S ABCD

Có

ABCD

là hình bình hành

, , ,

M N P Q

lần lượt thuộc

, , ,

SA SB SC SD

  



S MNPQ

S ABCD

x y z t

V xyzt

với

   ; ; ;

SA SB SC SD

x y z t

SM SN SP SQ

và

  

x z y t

Lăng trụ tam giác

ABC A B C

  

thể tích là

Thể tích tứ diện tạo bởi 4 đỉnh bất kì không đồng phẳng

là

Thể tích chóp tứ giác được tạo thành từ các đỉnh của lăng

trụ là

Gọi

, ,

M N P

lần lượt thuộc

  

, ,

AA BB CC

  

 



ABC MNP

ABC A B C

x y z

với   

  

; ;

AM BN CP

x y z

AA BB CC

Hình hộp

   

ABCD A B C D

có thể tích là

Thể tích tứ diện tạo bởi 4 đỉnh bất kì không đồng phẳng

là

Thể tích của tứ diện tạo bởi 2 đường chéo của 2 mặt

phẳng đối diện của hình hộp là

Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT

Gọi

, , ,

M N P Q

lần lượt thuộc

   

, , , .

AA BB CC DD

Khi đó

   

  



ABCD MNPQ

ABCD A B C D

x y z t

với    

   

, , ,

AM BN CP DQ

x y z t

AA BB CC DD

và

  

x z y t

Nón – Trụ – Cầu

Nón Nón cụt Trụ Cầu

 

2 2 2

l r h

, :

R r

bán kính đáy lớn và

đáy nhỏ



S rl



với



l h



S r





S rl







 

S rl R r

 

2 2

S rl r

 

 

S r l r

 









   

2 2

S R r l R r





V r h





V r





V r h



 

  

2 2

V h R r Rr



Với

AB CD

là hai đường bất kì

trên hai đáy thì

 





. . .sin ,

ABCD

V AB CD OO AB CD

Các vật thể tròn xoay trong không gian

Chỏm cầu





  

2 2

S Rh r h

 

 

 

   

 

 

2 2 2

3 6

h h

V h R h r



Hình trụ cụt





 

1 2

S R h h



 





 

 

1 2

h h

V R



Hình nêm loại 1



tan

V R



Hình nêm loại 2

 

 

 

 

tan

2 3

V R





Parabol



S Rh

 

 

 

 

a x

S R h



V R h



Elip



S ab



Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT



quay quanh a

V ab



quay quanh b

V a b

Hình xuyến

Diện tích hình vành khăn

 

 

2 2

S R r

Thể tích hình phao

  

  

V R r R r



Bán kính mặt cầu ngoại tiếp





và nội tiếp





của hình chóp, lăng trụ

Hình lập phương có cạnh bằng :x

R 

Hình hộp chữ nhật có các kích thước là , , :x y z

2 2 2

x y z

 



Chóp có chiều cao h và có cạnh bên vuông góc với đáy thì:

 

 

 

 

c d

R R

Chóp đều có chiều cao ,h cạnh bên bằng l thì:



Chóp có mặt bên vuông góc với đáy thì:

 

  

 

 

2 2

c d b

giao tuyen

R R R

d b

R R lần lượt là bán kính đường tròn ngoại tiếp đáy và mặt bên (mặt vuông góc với đáy)

Tổng quát: chóp có chân đường cao

H I

là tâm đường tròn ngoại tiếp đáy, gọi



IH d

thì

 

 

 

 

 

2 2 2

c d

h d R

R R

Mặt cầu ngoại tiếp tứ diện đều: 

R cạnh.

Mặt cầu ngoại tiếp tứ diện gần đều:   

2 2 2

R a b c

mặt cầu nội tiếp tứ diện gần đều: 

r cạnh.

Mặt cầu nội tiếp hình chóp: 



Trong đó:



tổng diện tích tất cả các mặt của chóp

Cách tính

Nếu đáy là tam giác

vuông thì



R .cạnh huyền

Nếu đáy là tam giác

đều thì 

R cạnh.

Nếu đáy là hình

vuông hoặc hình chữ

nhật thì



R .đường chéo

Nếu đáy là tam giác thường

thì áp dụng một trong hai

công thức

   

   

abc

p p a p b p c

hoặc

   2

sin sin sin

a b c

A B C

Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT

Tọa độ điểm và vec tơ

Hệ tọa độ trong không gian gồm ba trục

, ,

Ox Oy Oz

đôi một vuông góc với các vec-tơ đơn vị tương ứng

trên ba trục lần lượt là













  

  

1;0;0 , 0;1;0 , 0;0;1

i j k





; ;

u x y z





. . .

u x i y j z k

   

   





   



; ;

B A B A B A

AB x x y y z z





    

 

2 2 2

; ;

u x y z u x y z

ABCD

là hình bình

hành  

 

AB DC

là trung điểm của

thì

 

  

 

 

; ;

2 2 2

A B A B A B

x x y y z z

là trọng tâm



ABC

thì

 

     

 

 

; ;

3 3 3

A B C A B C A B C

x x x y y y z z z

Cho









1 1 1 2 2 2

; ; , ; ;

u x y z v x y z

 

 







     

. . .cos ,

u v u v u v

  

 

1 2 1 2 1 2

u v x x y y z z

. 0

u v u v

  

   





 



 

     

, . .sin ,

u v u v u v

1 1 1 1 1 1

2 2 2 2 2 2

, ; ;

y z z x x y

u v

y z z x x y

 

 



 

 

 

 





1 2 2 1 1 2 2 1 1 2 2 1

; ;

y z y z z x z x x y x y

   

, ,

w u w v w u v

 

   

 

      



và



cùng phương

 

 

 

 

, 0

u v

  

, ,

u v w

đồng phẳng

 

 

 

  

, . 0

u v w

, , ,

A B C D

là bốn đỉnh của tứ diện 

  

, ,

AB AC AD

không đồng phẳng

 

 

 

  

, . 0

AB AC AD

Diện tích, thể tích một số hình

Diện tích tam giác



 



 

 

ABC

S AB AC

Diện tích hình bình

hành

 



 

 

ABCD

S AB AD

Thể tích khối hộp

   

 





 

  

, .

ABCD A B C D

V AB AD AA

Thể tích tứ diện

 



 

  

, .

ABCD

V AB AC AD

Phương trình mặt cầu

     

2 2 2

x a y b z c R

     



Tâm





; ; ,

I a b c

bán kính

      

2 2 2

x y z ax by cz d



Tâm

 

 

  

 

; ; ,

2 2 2

a b c

 

   

   

 

 

2 2 2 2 2 2

4 4

a b c a b c

R d d

Phương trình mặt phẳng

Mặt phẳng đi qua





0 0 0

; ;

M x y z

có vtpt









; ;

n A B C













     

0 0 0

A x x B y y C z z





: 0

P Ax By Cz D

   

có vtpt

 





; ;

n A B C





Phương trình mặt chắn: Mặt phẳng







đi qua













;0;0 , 0; ;0 , 0;0;

A a B b C c

có phương trình

 

   

1 0

x y z

abc

a b c

Vậy để viết phương trình mặt phẳng ta cần tìm một vtpt và một điểm thuộc mặt phẳng

(một cặp vtcp của mặt phẳng tạo thành một vtpt của nó bằng việc lấy tích có hướng)

Các phương trình mặt phẳng đặc biệt





: 0

Oxy z







: 0

Oxz y







: 0

Oyz x



Vị trí tương đối: Cho





   

: 0

Ax By Cz D



và





    

   

: 0

A x B y C z D



Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT

   



    

   

A B C D

 

   



   

   



A B C D

 







cắt









  



: : : :

A B C A B C









   

    

AA BB CC

 

Khoảng cách từ điểm





0 0 0

; ;

M x y z

đến mặt phẳng





: 0

Ax By Cz D



   

 

  



 

0 0 0

2 2 2

;

Ax By Cz D

d M

A B C



Phương trình đường thẳng



đi qua điểm





0 0 0

; ;

M x y z

có vtcp





; ;

u a b c





Có phương trình tham số là

 

x x at

y y bt t

z z ct



 



   





 





Có phương trình chính tắc là

 

0 0 0

: 0

x x y y z z

abc

a b c

  

   

Vậy để viết phương trình đường thẳng ta cần tìm một vtcp và một điểm thuộc đường thẳng

Vị trí tương đối: Đường thẳng

đi qua điểm

và có vtcp



đi qua điểm

và có vtcp



và

đồng phẳng

 

 

 

  

1 2 1 2

, 0

u u M M

chéo

 

 

 

  

2 1 2 1 2

, 0

d u u M M

cắt



 





 





 





 



  

  

1 2

1 2 1 2

, 0

u u

u u M M

1 2

1 1 2

, 0

u u

d d

u M M



 





 





 





 



  



  

Khoảng cách, góc:

1 1 2 2

,M M

   

1 2

u u

 

lần lượt là hai vtcp của

1 2

 

 

 

 

 

 



1 1

MM u

d M

 

 

 

  

 

 

  

 

1 2 1 2

1 2

, .

u u M M

u u

 

1 2

1 2 1 2

1 2

cos , cos ,

u u

   

 

   

 

   





   

cos , cos ,

P Q

n n

P Q n n

n n

 

 

 





 

sin , cos ,

u n

P u n

u n



  

 

Hình chiếu vuông góc, điểm đối xứng đặc biệt

Hình chiếu vuông góc của điểm





0 0 0

; ;

M x y z

lên





Oxy

là





0 0

; ;0

H x y

Nhớ nhanh:

Khuyết vị trí nào

thì vị trí đó bằng





Oxz

là





0 0

;0;

H x z





Oyz

là





0 0

0; ;

H y z

là





;0;0

H x

là





0; ;0

H y

là





0;0;

H z

Điểm đối xứng với





0 0 0

; ;

M x y z

qua





Oxy

là





0 0 0

; ;

M x y z





Nhớ nhanh:

Khuyết vị trí nào

thì vị trí đó bằng

đối





Oxz

là





0 0 0

; ;

M x y z









Oyz

là





0 0 0

; ;

M x y z





là





0 0 0

; ;

M x y z



 

là





0 0 0

; ;

M x y z



 

là





0 0 0

; ;

M x y z



 

Một số công thức giải nhanh (

, ,

a b c

lần lượt là độ dài 3 cạnh tam giác

ABC

)

Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT

Tọa độ trực tâm

của tam giác

ABC

là nghiệm hệ:

. 0

, . 0

HA BC

HB AC

AB AC AH













 





 



 

  

Tọa độ tâm

đường tròn ngoại tiếp tam giác

ABC

là nghiệm hệ:

, . 0

IA IB

IA IC

AB AC IA













 





 



  

Tọa độ chân đường phân giác trong

của góc

thỏa mãn đẳng thức:

. . 0

b DB c DC

 

  

Tọa độ chân đường phân giác ngoài

của góc

thỏa mãn đẳng thức:

. 0

b EB cEC

 

  

Tâm

đường tròn nội tiếp tam giác

ABC

thỏa mãn đẳng thức:

. . . 0

a IA b IB c IC

  

   

Tọa độ hình chiếu vuông góc

của

lên





: 0

P ax by cz d

   

là





; ;

A A A

H at x bt y ct z

  

với

2 2 2

A A A

ax by cz d

a b c

  

 

 





đi qua

cắt các trục tọa độ tại













;0;0 , 0; ;0 , 0;0;

A a B b C c

(phương trình mặt chắn)

là trọng tâm

ABC



thì

3 , 3 , 3

M M M

a x b y c z

  

là trực tâm tam giác

ABC

thì

 

OM n



 

O ABC

nhỏ nhất khi

là trọng tâm

ABC



2 2 2

1 1

OA OB OC



 

nhỏ nhất khi

là trực tâm

ABC



Tâm mặt cầu ngoại tiếp

O ABC

là

; ;

2 2 2

a b c

 

 

 

Bán kính mặt cầu ngoại tiếp

O ABC

là

2 2 2

R a b c

  

Cực trị hình học

Oxyz

Viết





chứa

thỏa mãn

 







d P

là lớn nhất thì:

 

1 1 2

, ,

n u u u

 



 

 

   

Viết

chứa trong





sao cho

 



1 2

d d

nhỏ nhất thì:

   

1 2

, ,

P P

u n n u

 



 

 

   

Viết





chứa

sao cho

   







P Q

nhỏ nhất thì:

   

1 1

, ,

P Q

n u u n

 



 

 

   

Viết

nằm trong





và qua

sao cho





d M d

nhỏ nhất thì:

   

, ,

P P

u n n AM

 



 

 

   

Viết





chứa

sao cho









d M P

lớn nhất thì:

 

, ,

d d

n u u AM

 



 

 

   

với điểm

bất kì thuộc

Viết

nằm trong





và qua

sao cho





d M d

lớn nhất thì:

 

u n AM

 



 

 

  

Tâm tỉ cự: Điểm

thỏa mãn:

1 1 2 2

... 0

n n

a IA a IA a IA

   

   

đgl tâm tỉ cự của hệ điểm

1 2

, ,...,

A A A

Khi đó:

1 2

...

A A n A

a x a x a x

a a a

  



  

1 2

...

A A n A

a y a y a y

a a a

  



  

1 2

...

A A n A

a z a z a z

a a a

  



  

Cuốn công thức này của:………………………………………………………………..

Giáo viên: Nguyễn Thanh Tân

Bấm Tải xuống để xem toàn bộ.

| 1/24

| | Tải xuống

Preview text:

Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT  b   Parabol 2
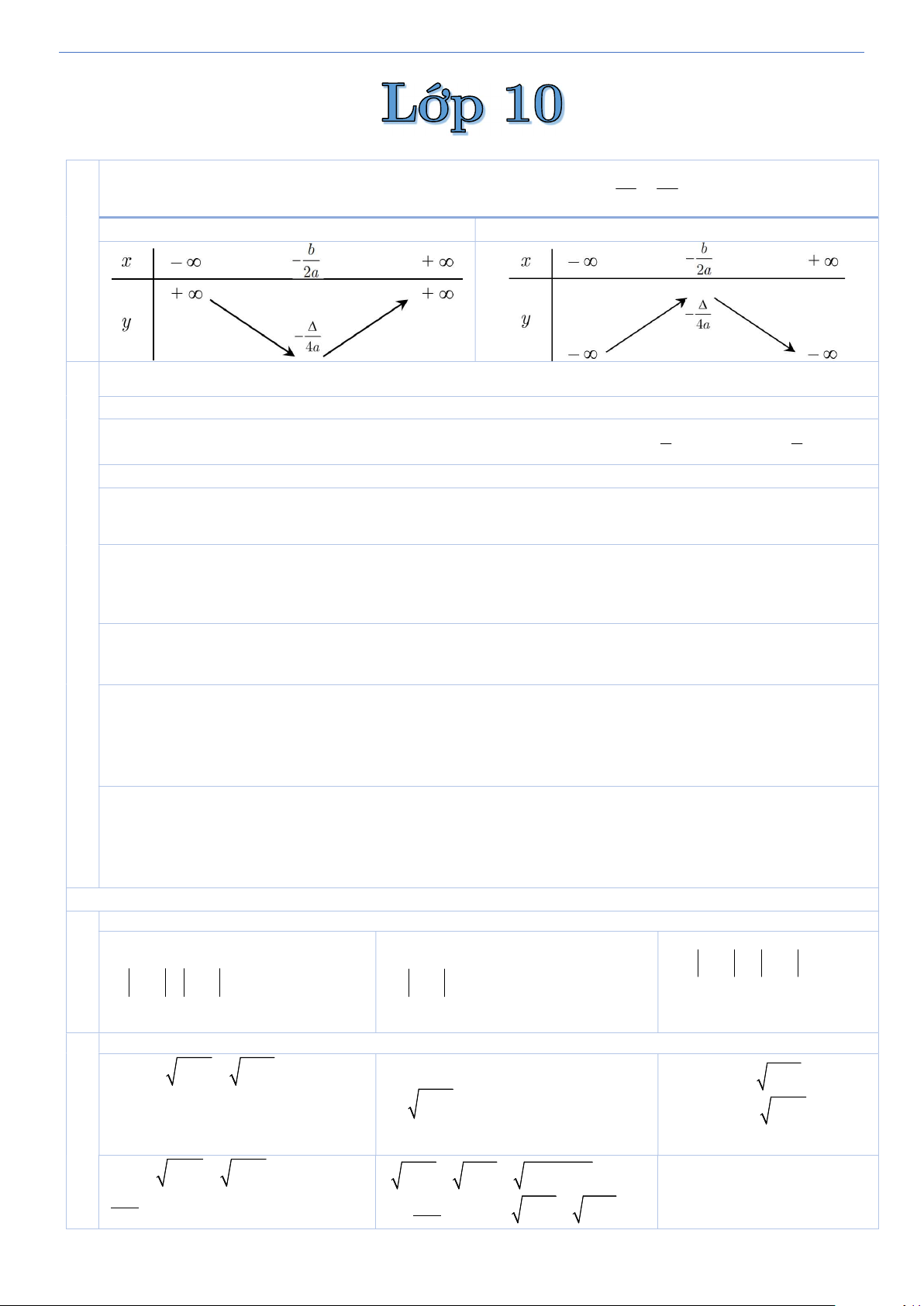
y  ax bx ca  0 Đỉnh I   ; 2a 4a    a0: Bề lõm quay lên a0: Bề lõm quay xuống 1 Phương trình 2
ax bx c  0 a  0
Có hai nghiệm phân biệt khi   0 , có nghiệm kép khi   0 , vô nghiệm khi   0 b c
Nếu phương trình có hai nghiệm x ,x thì ta có định lí Vi-et: S  x  x   và P  x .x  1 2 1 2 a 1 2 a
Phương trình có hai nghiệm trái dấu khi P  0 ac  0   0
Phương trình có hai nghiệm cùng dấu khi  P  0   0   0
Phương trình có hai nghiệm phân biệt dương khi  
S  0 , hai nghiệm phân biệt âm khi S  0 P    0 P   0 2    0
Phương trình có hai nghiệm phân biệt x ,x thỏa mãn x    x  1 2 1 2 x  x  0 1   2     0 
Phương trình có hai nghiệm phân biệt x ,x thỏa mãn x  x    x  x  0 1 2   1   2   1 2 x  x  0 1   2      0 
Phương trình có hai nghiệm phân biệt x ,x thỏa mãn   x  x  x  x  0 1 2   1   2   1 2 x  x  0 1   2   
Chú ý: a chứa tham số thì xét riêng a  0. Nếu yêu cầu hai nghiệm (không phân biệt) thì   0
Phương trình chứa trị tuyệt đối g x  0  
a f x  b g x   h x  3   f x g x f x  g x          f x gx     f x   g x  f x   Dạng này ta chia trường  g x  f x  hợp để giải  g x Phương trình chứa căn f x   g x  a.f x  b. f x   c 0 g x    0  
f x   0or g x    0 f x gx      Đặt t  f x   0   2 f x   g x  4 f  x   g x  Đưa về pt bậc 2 ẩn t
f x   g x   h x 
f x   g x   f x g x   h x  Một số dạng khác có thể sử
PP: Tìm điều kiện và bình phương
dụng nhân liên hợp, đưa về
PP: Đặt t  f x   g x 
2 vế, đưa về phương trình hệ quả hệ hoặc đánh giá… 1
Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT
 f x g x  theo t, đưa phương
trình đã cho về bậc hai theo ẩn t.
Phương trình trùng phương 4 2
ax  bx c  0a  0 1 PP: Đặt t  2 x   2 0 at bt c  0 2
1 vô nghiệm  2 vô nghiệm, hoặc có 2 nghiệm âm
1 có đúng 1 nghiệm 2 có nghiệm kép bằng 0, hoặc có 1 nghiệm bằng 0 và 1 nghiệm âm
1 có đúng 2 nghiệm phân biệt 2 có nghiệm kép dương, hoặc có 1 nghiệm âm và 1 nghiệm dương
5 1 có đúng 3 nghiệm phân biệt 2 có một nghiệm dương và 1 nghiệm bằng 0
1 có 4 nghiệm phân biệt 2 có 2 nghiệm phân biệt dương Hệ phương trình Đối xứng loại I Hệ đẳng cấp bậc 2 f x;y   2 2  0 Đối xứng loại II a x b xy c y  d 1 1 1 1   2 2  f x;y  0 a x b xy c y d g x;y   0  2 2 2 2 6   PP: f x;y  f y;x   0  f y;x  Với x  + Giải hệ khi  0
PP: Trừ hai vế của phương trình  x y tx
g x;y   g y;x 
+ Khi  0, đặt  , chia vế
cho nhau, sau đó đưa về phương
PP: Đặt S  x  y,P  xy với
với vế của 2 phương trình cho trình tích
nhau, đưa về phương trình bậc điều kiện 2 S  4P hai theo t
Bất phương trình chứa trị tuyệt đối g x   0 f x   g x   f x   g x  g x   0 7 g x   0
f x   g x    2    2 f x  g x       f x   g x    
 g x   f x   g x      f x g x
      
Các dạng khác: Dùng định nghĩa trị tuyệt đối, chia khoảng để giải
Bất phương trình chứa căn g x   0  f x   0   0 f x  0  f x   g x  g  x    
f x   g x   
f x   g x   g x   0 f  x   g x  g x   0   f x    2  g x   2
f x   g x  8
Các dạng khác: Đặt ẩn phụ, nhân liên hợp, đánh giá…
Ứng dụng dấu tam thức bậc hai 2
ax bx c  0,x  2
ax bx c  0,x   2
ax bx c  0,x   2
ax bx c  0,x   a  0 a  0 a  0 a  0           0   0   0   0 Công thức lượng giác    cos  cos
sin    sin sin    cos  2 
sin    sin 9 sin  sin
cos    cos     cos    sin
tan  tan
tan    tan  2 
cos    cos cot  cot
cot    cot    tan     tan tan         cot  2  2
Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT   
cot    cot cot    tan  2 
cosa b  cosa.cosb  sina.sinb sin2a  2sina.cosa 2   2 sin cos  1 cos2a  2 cos a  2 sin a
cosa b  cosa.cosb  sina.sinb 1  2 2cos a 1  1  2 2sin a 1  2 tan   2 cos 
sina b  sina.cosb  cosa.sinb 2tana 1
sina b  sina.cosb  cosa.sinb tan2a  1  2 cot   1  2 tan a 2 sin  tana tanb a  a  3 sin3 3sin 4sin a tan.cot  1 tana b    1  tana.tanb a  3 cos3 4cos a  3cosa  tan tan 3 tan   a  b a b  3tana  tan a 1  tana.tanb tan3a  1  2 3tan a 2 1  cos2a cos a  2 2 1  cos2 sin a a 1 
cosa.cosb  cosa b  cosa   b 2  2 2 1  cos2a 1 tan a 
sina.sinb  cosa b  cosa   b 1  cos2a  2 3 3cosa  cos3 cos a a 1 
sina.cosb  sina b  sina   b 4  2 3 3sina  sin3a sin a  4 a b a b cosa  cosb  2cos cos 2 2 a b a b    cosa  cosb  2sin sin
sina  cosa  2 sin a   2 2  4  a b a b    sina  sinb  2sin cos
sina  cosa  2 sina  2 2   4  a b a b sina sinb     2sin cos 2 2 Vectơ và các tính chất
  
   AB  BC  AC AB  AC CB
Nếu ABCD là hình bình hành thì
  
I là trung điểm của đoạn AB thì       1 AC  AB  AD
IA  IB  0 và MA  MB  2MI
G là trọng tâm tam giác ABC thì
    Ba điểm phân biệt , A B,C thẳng hàng GA GB GC  0 và  
     AB  kAC k  0 MA  MB  MC  3MG  
Cho a  x ;y ,b  x ;y , k   1 1   2 2  2      x  x a b  x  x ;y y k.a  kx ;ky a  b   1 2 1 1  1 2 1 2  y   y 1 2 3
Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT  
Vectơb cùng phương với a  0  I là trung điểm của AB x y AB  x x ;y y x  x y  y B A B A   1  1 x y  0 x  A B ;y  A B 2 2  x y I 2 I 2 2 2
G là trọng tâm tam giác ABC
Điểm M chia đoạn AB theo tỉ số k  x  x  x y y  y   a  2 x  2 y x  A B C ;y  A B C  MA  kMB 1 1 G 3 G 3         a b.  a . b cosa,b   a.b x x y y   cosa,b      1 2 1 2 a b  x x  y y  0 2 2 2 2  x x  y y a . b x  y . x  y 1 2 1 2 1 2 1 2 1 1 2 2
Một số kết quả cần nhớ
H là trực tâm của tam giác ABC ,
A B,C lập thành một tam giác     A  H.BC  0
 AB vàAC không cùng phương
   B  H.AC  0 3
I là tâm đường tròn ngoại tiếp tam giác ABC
AE là đường phân giác trong của ABC  2 2 I  A  IB  EB AB      2 2 I  A  IC EC AC
Hệ thức lượng trong tam giác vuông
Hệ thức lượng trong tam giác thường 2 b  2 c  2 a 2 a  2 b  2 c  2bc.cosA cosA  2bc 2 b  2 2 a b c 2 c a m      2R a 2 4 sinA sinB sinC 1 1 abc S  a.h  bc.sinA   pr ABC a 4 2 2 4R
 p p ap bp c
Với m : Đường trung tuyến xuất phát từ A a 2  2  2 a b c ah  bc ; 2 h b.c
h : đường cao xuất phát từ A a a b c p  : nửa chu vi tam giác ABC 1 1 1 b2  a b c2 . ;  a c.   2 2 2 2 h b c ,
R r : bán kính đường tròn ngoại tiếp và nội tiếp
Phương trình đường thẳng  x  x at
Phương trình tham số đường thẳng  qua M x ;y có vtcp u  a;b là: 0 0  0 0   y  y   bt 0  x x y y
5 Phương trình chính tắc đường thẳng  qua M x ;y có vtcp u  a;b là: 0  0 0  0 0  a b 
Phương trình tổng quát của đường thẳng  qua M x ;y có vtpt n  a;b là: a x  x b y y 0 0     0   0  0 0   
Đường thẳng ax  by  c  0 có vtpt n a;b và có vtcp u   ; b a 
Đặc biệt: Trục Ox :y  0, trục Oy : x  0.
Cho  : a x  b y  c  0;  : a x  b y  c  0 , M x ;y 0  0 0  1 1 1 1 2 2 2 2 a b c a b c  cắt      1  1  1  1 2 1    1  1  1 1 2 a b c 2 a b c  a :b :c  a :b :c 6 2 2 2 2 2 2 1 1 1 2 2 2     n .n a x b x c x
    a a  b b  0 1 2  cos , cos n ,n d M ; 0 1      1 0 1 0 1 0 1 2  
 1 2    1 2 1 2 1 2 n . n 2 a  2 b 1 2 1 1 4
Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT
Phân giác của góc tạo bởi  và  là
 : f x;y ax by c  0 1 2 Cho   a x b y c a x b y c 1 1 1   2 2 2 + ,
A B cùng phía với   f .f  0 A B a2 b2 a2 b2 + ,
A B khác phía với   f .f  0 1 1 2 2 A B
Phương trình đường tròn  a b  2 x  2
y ax by c  0 có tâm I  ;  và có bán 2 2 7
        2 x a y b
R có tâm I a;b và có  2 2  bán kính R 2 a  2 b  2 a  2 b  kính R  c  c  0 4  4 
Phương trình đường elip 2 2 x y   1 a b  2 b  2 a  2 0; c  2 2 8 a b
F c;0 ,F c;0 : Các tiêu điểm A  ; a 0 ,A a;0 B 0;b ,B 0;b 1  2  1  2  1  2   F F  2c : Tiêu cự
A A  2a : Độ dài trục lớn
B B  2b : Độ dài trục bé 1 2 1 2 1 2 5
Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT
Phương trình lượng giác
sinu  1  u    k2 u  v  k 2 sinu  sinv    k   u    v  k2
sinu  1  u    k2 2 sinu  0  u  k Phương trình cơ bản cosu  1  u  k2 u  v  k2
cosu  1  u    k2 cosu  cosv     k  u  v  k2
cosu  0  u    k 2
tanu  tanv  u  v  k
cotu  cotv  u  v  k 1
Đặt t  sinx 1 t 1 , đưa về giải phương trình bậc hai 2 a sin x bsinx c  0
( tương tự đối với cosx, nếu đặt tan,cot thì không cần điều kiện t ) 2 2 a sinx bcosx  c
Chia cả hai vế cho a b sau đó đưa về PTLG cơ bản
Chú ý: Phương trình có nghiệm 2 2 2  a b  c Xét 2 trường hợp + TH1: x   2 cos 0
sin x  1. Thay vào phương trình và kết luận 2 a x b x x  2 sin sin cos
c cos x d + TH2: cosx  0: Chia cả hai vế của phương trình cho 2 cos x , đưa về
phương trình bậc hai của tanx t x x t x x t ( a sinx  sin  cos  2   2  cosx)bsinx cosx c Đặt 
, biểu diễn sin cos theo , đưa
phương trình đã cho về bậc hai theo t
Phương trình dạng dạng khác
Phân tích thành nhân tử hoặc đánh giá
Hoán vị - chỉnh hợp – tổ hợp Quy tắc cộng Quy tắc nhân
Một công việc được hoàn thành bởi một trong hai
Một công việc được hoàn thành bởi hai hành động
hành động. Nếu hành động này có m cách thực
liên tiếp. Nếu có m cách thực hiện hành động thứ
hiện, hành động kia có n cách thực hiện không
nhất và ứng với mỗi cách đó có n cách thực hiện
trùng với bất cứ cách nào của hành động thứ nhất
hành động thứ hai thì có . m n cách hoàn thành
thì có m  n cách hoàn thành công việc đó công việc đó 2 Hoán vị Chỉnh hợp Tổ hợp Chọn k phần tử từ
Sắp xếp (đổi chỗ) của n phần tử khác n phần tử sau đó
Chọn k phần tử từ n phần tử ta có số nhau có P  n ! cách sắp thứ tự chúng có cách chọn là k C n n k A n!  n n 1...1 cách n k n! C  n k n! Quy ước: 0!  1 A  n k!k! n n k!
Một số kết quả cần nhớ Cho n điểm
Số đường thẳng đi qua hai điểm: 2 C n trong không  gian, trong đó
Số vectơ khác 0 nối hai điểm bất kì: 2 A n không có 3 Số tam giác tạo thành: 3 C điểm nào thẳng n hàng C
Nếu trong n điểm không có 4 điểm nào đồng thẳng thì số tứ diện được tạo thành: 4 n
Số đường chéo của đa giác: 2 C n n 6
Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT
Nếu không có 3 đường chéo nào đồng quy thì số giao điểm giữa các đường chéo mà
giao điểm nằm trong đa giác là 4 C n
Số tam giác có 3 đỉnh là đỉnh của đa giác: 3 C n Cho đa giác lồi 3 n n  4 n
Số tam giác có đúng 1 cạnh của đa giác, 2 cạnh còn lại là đường chéo:   đỉnh
Số tam giác có 2 cạnh của đa giác, 1 cạnh còn lại là đường chéo: n n
Số tam giác có cạnh đều là đường chéo của đa giác: 3 C n n  4 n hoặc 2 C n  4 3 n
Số tam giác vuông được tạo thành: 2
4.C với n chẵn; bằng 0 với n lẻ n 2 Cho đa giác 2 2 đều n đỉnh
Số tam giác tù được tạo thành: n.C với n chẵn; bằng n.C với n lẻ n2 n 1 n 2
Số tam giác nhọn  số tam giác  ( số tam giác vuông  số tam giác tù) Cho đa giác Số hình chữ nhật: 2 C đều 2n đỉnh n n 2 Số tam giác vuông: 2 4.C n Cho đa giác Số tam giác đều: n đều 3n đỉnh  3n  2   3n 1   3n  1 3n  1 n
Số tam giác cân không đều: với n chẵn; bằng với n lẻ   1    2   2  Xác suất
Hai biến cố là xung khắc nếu A B   Nếu , A B xung khắc thì P A nA  0  P A 1 n 
P A B  P A  P B P   0,P  4  1
Hai biến cố độc lập nếu việc xảy ra của
n A: số phần tử của biến cố A P A
biến cố này không ảnh hưởng đến biến  1  P A
n : số phần tử không gian mẫu cố khác. Nếu , A B độc lập thì P A :
P AB   P A.P B
Xác suất của biến cố A A : b/cố đối của A TQ:
P A B  P A  P B P AB Nhị thức Niutơn  n 0 1 n n a bn k n    k k C a b k n k C C  ... C  2 C C n n n n n 5 n k 0 k k 1 k  C n C  1 C 0 C  1 C  2 C  ...  C n n n 1 n  0 n Số hạng thứ k n k 1: T  k k C a b n n n 1 k 1 n k A  k ! k C 0 2 2n 1 3 2n 
C C  ... C C C  ...  1 C n n 2n 2n 2n 2n 2n 2n Cấp số Cấp số cộng Cấp số nhân u u u  u d  u  u  n 1 d k  k  u u  u .q  u  1 u . n q 2 u  u .u n 1  n  1 1 1 n k 2 n 1 n n 1 k k 1 k 1 6 n u  u n 2u n 1 d u 1 n q 1   1 n        
S  u  u  ...  u   1
S  u  u  ...  u  q  1 n 1 2 n   n 1 2 n 2 2 1 q u
Tổng của cấp số nhân lùi vô hạn: S  u  u  ...  u  ...  1 1 2 n 1 q Hàm số liên tục
Hàm số y  f x  liên tục tại x nếu
Hàm số y  f x  liên tục trên đoạn a  b ;  nếu nó 0   7 lim f x   f x  
liên tục trên khoảng a b ;  và or lim f 
x  lim f x  f x 0     0  x x  0 x x x x  0 0 
lim f x   f a; lim f x   f b    x a  x b  7
Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT
Nếu hàm số không liên tục tại x thì x được gọi là 0 0
điểm gián đoạn của hàm số f x 
Hàm số y  f x  liên tục trên a  b ;  
 và f a f. b  0 thì phương trình f x   0 có ít nhất một nghiệm thuộc khoảng a b ;  Công thức đạo hàm    u  uv vu C   0
u v uv
u.v uv vu     v  2 v Hàm thường Hàm hợp kx k ku k.u  nx  n   1 n.x n  u  n   1 n.u .u   1  1   1  u          x  2 x  u  2 u    x  1    u u  2 x 2 u 8 sinx  cosx sinu u.cosu cosx  sinx
cosu  u.sinu  u x  1 tan  1  2 tan x  tanu    2 cos x 2 cos u  u x  1 cot  1 2 cot x    cotu     2 sin x 2 sin u  x   x e e  u   . u e u e  x   x a a .lna  u  . u a u a lna   1 lnx u  lnu    x u  x u log u a     a  1 log  x.lna u.lna
Phương trình tiếp tuyến
Phương trình tiếp tuyến của đồ thị hàm sốy  f x  Tiếp tuyến có hệ số góc k, ta giải phương trình
tại điểm M x ;y : y  f x x  x y
f x   k  x và y 0   0  0 0  0 0 0
Tiếp tuyến song song với đường thẳng y  ax b
Tiếp tuyến vuông góc với đường thẳng 9 1
 f x  a  x và y
y  ax b  f x     x và y 0 0 0 a 0
Tiếp tuyến đi qua điểm Ax ;y có hệ số góc k 0 0 
Tiếp tuyến có hệ số góc k tạo với đường thẳng k   f   x k a thỏa mãn hệ 
d :y  ax b một góc  :  tan 1  ka f
 x   k x  x  y 0  0 8
Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT Quan hệ song song
Nếu a không nằm trên P  và song song với b nằm trên P  thì a  P 
Nếu d  P  thì mọi mặt phẳng Q chứa a mà cắt P  thì cắt theo một giao tuyến song song với a
Nếu hai mặt phẳng cắt nhau cùng song song với một đường thẳng thì giao tuyến của chúng song song với đường thẳng đó
1 Ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến đó hoặc đồng quy, hoặc song song với nhau
Nếu P  chứa hai đường thẳng a,b cắt nhau và cùng song song với mặt phẳng Q thì P   Q
Nếu một đường thẳng nằm trên một trong hai mặt phẳng song song thì nó song song với mặt phẳng kia
Nếu hai mặt phẳng P  và Q song với nhau thì mọi mặt phẳng R đã cắt P  thì phải cắt Q và
giao tuyến của chúng song song với nhau Quan hệ vuông góc
Một đường thẳng được gọi là vuông góc với một mặt phẳng nếu nó vuông góc với mọi đường thẳng nằm trên mặt phẳng đó
Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong P  thì d  P 
Định lí 3 đường vuông góc: Cho đường thẳng a không vuông góc với P  và đường thẳng b nằm trong
P, điều kiện cần và đủ để b vuông góc với a là b vuông góc với hình chiếu a của a trên P
P Q nếu trong P chứa một đường thẳng d và d Q
Nếu hai mặt phẳng vuông góc với nhau thì bất cứ đường thẳng nào nằm trong mặt phẳng này mà vuông
góc với giao tuyến thì vuông góc với mặt phẳng còn lại
Nếu P   Q và AP  thì đường thẳng a đi qua điểm A và vuông góc với Q thì a  P 
Nếu hai mặt phẳng cắt nhau và cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng cũng
vuông góc với mặt phẳng thứ ba
Góc giữa đường thẳng và đường thẳng, mặt phẳng, góc giữa hai mặt phẳng
Góc giữa đường thẳng a và b là góc giữa đường thẳng a và b cùng đi qua qua một điểm và lần lượt song song với a và b
2 Góc giữa đường thẳng a và P  là góc giữa a và hình chiếu vuông góc a của a lên P 
Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó
Công thức dcm tính khoảng cách giữa hai đường thẳng chéo nhau
Cho hình chóp S.ABC có đường cao SH . Khi đó 2 1 1 c   2 d S , A BC  2 2 d m Trong đó: d d  , A BC  m  SH đ𝑖ể𝑚 𝑐ℎâ𝑛 𝐴𝐻 𝑐 = = đ𝑖ể𝑚 𝑐ắ𝑡 𝐴𝑀 9
Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT
Phép suy đồ thị: Cho hàm số y  f x  có đồ thị C  , a  0 y  f x a y  f x a y  f x  a y  f x  a y  f x  y  f  x  
Tịnh tiến C  Tịnh tiến C 
Tịnh tiến C  Tịnh tiến C  Lấy đối xứng Lấy đối xứng sang trái a đơn sang phải a lên trên a đơn xuống dưới a C  qua Ox C  qua Oy vị đơn vị vị đơn vị Đồ thị f  x  : Đồ thị f x  :
B1: Giữ nguyên phần đồ thị C  nằm bên phải
B1: Giữ nguyên phần đồ thị C  nằm trên Ox
Oy, bỏ hết phần đồ thị bên trái Oy. 1
B2: Lấy đối xứng phần đồ đồ thị C  nằm phía
B2: Lấy đối xứng phần đồ thị C  nằm bên phải
dưới Ox qua Ox, bỏ hết phần đồ thị phía dưới Ox. Oy qua Oy.
Số điểm cực trị của hàm chứa dấu giá trị tuyệt đối
Số điểm cực trị của hàm
Số điểm cực trị của
số y  f x  chính bằng hàm số y  f  x 
Nếu hàm số y  f x  có n điểm cực trị thì đồ thị
số điểm cực trị của hàm chính bằng 2n  1,
hàm số y  f x  và đường thẳng y  0 có tối đa
số f x  cộng với số trong đó n là số điểm
n 1 giao điểm. Từ đó hàm số y  f x  có tối đa nghiệm đơn của phương
cực trị dương của hàm 2n 1 điểm cực trị trình f x   0. số f x  y  f x  3 2
 ax  bx  cx d a  0 C 
Điều kiện để hàm số có hai điểm cực trị:   2 b  3ac  0 y a  0a   0
Hàm số đồng biến (nghịch biến) trên  khi:     0 y  a  0a   0
Đồng biến (nghịch biến) trên đoạn có độ dài đúng bằng l khi:   x  x  l 2  2 1 f  x .f  x
Phương trình đường thẳng đi qua hai điểm cực trị: y  f x       18a 2b c
Định lí vi-et đối với 2 điểm cực trị: x  x   và x x  1 2 3a 1 2 3a
Trong các tiếp tuyến của C , tiếp tuyến tại điểm uốn là tiếp tuyến có hệ số góc nhỏ nhất khi a  0, và
là tiếp tuyến có hệ số góc lớn nhất khi a  0
Điều kiện để hàm số có hai điểm cực trị x ,x 1 2 Trái dấu Cùng dấu Cùng dấu dương Cùng dấu âm 3 y  0 có hai nghiệm
y  0 có hai nghiệm phân y  0 có hai nghiệm y  0 có hai nghiệm phân biệt trái dấu biệt cùng dấu phân biệt cùng dương phân biệt cùng âm
Điều kiện để hàm số có hai điểm cực trị nằm bên phải trục Oy nằm khác phía so với nằm cùng phía với
nằm bên trái trục Oy là 4 trục Oy là phương trình trục Oy là phương
là phương trình y  0
phương trình y  0 có hai
y  0 có hai nghiệm trái trình y  0 có hai có hai nghiệm phân nghiệm phân biệt âm biệt dương dấu 10
Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT nghiệm phân biệt cùng dấu nằm cùng phía dưới nằm cùng phía với
nằm cùng phía trên với trục trục Ox là phương
nằm khác phía với trục trục Ox là phương Ox là phương trình trình f x   0 có Ox là phương trình trình f x   0 có
f x   0 có nghiệm duy nghiệm duy nhất và
f x   0 có bao nghiệm nghiệm duy nhất nhất và y  0 y  0 U U phân biệt.
Chú ý: Hoành độ điểm uốn x là nghiệm của phương trình đạo hàm cấp hai của hàm bậc ba U
Phương trình bậc ba có 3 nghiệm lập thành b
cấp số cộng nếu có một nghiệm là x   d x 3a
cấp số nhân nếu có một nghiệm là  3 a
Xác định dấu của các hệ số hàm số bậc ba theo thứ tự a  d  b  c
a : Nhìn nhánh ngoài cùng bên tay phải, nếu đi lên
d : Quan sát giao của đồ thị với O , y cắt Oy phía
thì a  0, đi xuống thì a  0
trên thì d  0, cắt phía dưới thì d  0 b c 5
b : Sử dụng vi-ét x  x   , kết hợp với dấu c : sử dụng vi-ét x x 
, kết hợp với dấu của a 1 2 3a 1 2 3a của a suy ra dấu của . b suy ra ra dấu của . c
Định lí vi-ét cho phương trình bậc ba 3 2 y  ax bx cx d b x c d  x  x   x x  x x  x x  x x x   1 2 3 a 1 2 2 3 3 1 a 1 2 3 a y  f x  4 2
 ax  bx  c a  0
Điều kiện đề hàm số có 3 điểm cực trị là ab  0, để có một cực trị là ab  0. Hàm số có đúng một
Hàm số có đúng một cực
Hàm số có hai điểm cực Hàm số có một điểm
cực trị và cực trị là
trị và cực trị là cực đại:
tiểu và một điểm cực đại: cực tiểu và hai điểm a   0 a  0 a  0 a  0 cực tiểu: cực đại: b       0 b  0 b  0 b  0 b b
Giả sử đồ thị hàm số có 3 điểm cực trị A0;c       ,B   ; ,C   ;  
và 3 điểm cực trị này 2a 4a   2a 4a  6    
luôn tạo thành tam giác cân tại .
A Gọi S là diện tích ABC và  BAC  ,  khi đó a 8 b3 2   tan  0 3 2 a S  5 32 b  0 2
Đồ thị hàm số cắt trục hoành tại bốn điểm có hoành độ lập thành cấp số cộng nếu 2 9b  100ac.
Đồ thị hàm số cắt trục hoành tạo thành ba miền diện tích có diện tích phần trên và diện tích phần dưới bằng nhau là 2 5b  36ac 2 2  2    2  
Phương trình đường tròn ngoại tiếp ABC là x  y   
 c y c    0  b 4a   b 4a 
Chú ý: Có thể dựa vào đồ thị hàm số bậc bốn trùng phương để dễ dàng nhớ các công thức hơn ax b y 
c  0,ad bc  0 C  cx  d
Tính chất của tiếp tuyến (gọi I là giao của hai đường tiệm cận) 7
Tiếp tuyến tại M thuộc Khoảng cách từ M tới
Khoảng cách từ M tới tiệm cận ngang
đồ thị hàm phân thức cắt tiệm cận đứng
các tiệm cận tại A và B ad bc 1 1 d  .
thì M là trung điểm của d  cx d M c cx d AB c M 11
Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT Tổng khoảng cách ngắn
nhất từ điểm M đến hai Diện tích tam giác
Khoảng cách ngắn nhất giữa hai điểm P,Q bất kì đường tiệm cận IAB không đổi và ad bc ad 2 bc S  ad bc .
thuộc hai nhánh của đồ thị PQ  2 2 d  2 min IAB 2 c 2 c min 2 c
Điểm M thỏa mãn một trong các tính chất: Tổng khoảng cách đến hai đường tiệm cận đạt giá trị nhỏ
nhất, khoảng cách IM ngắn nhất, khoảng cách từ I đến tiếp tuyến tại M đại giá trị lớn nhất, tiếp
tuyến tại M vuông góc với IM, tam giác IAB vuông cân, chu vi tam giác IAB nhỏ nhất, AB nhỏ
nhất, bán kính đường tròn nội tiếp tam giác IAB lớn nhất, bán kính đường tròn ngoại tiếp tam giác
IAB nhỏ nhất thì điểm M phải thỏa mãn tính chất IA  IB  yx   1 M
M,N thuộc hai nhánh khác nhau của C  sao cho
M,N thuộc hai nhánh khác nhau của C  sao cho MN
tiếp tuyến của C  tại M,N song song và khoảng
nhỏ nhất là thì hoành độ điểm M,N thỏa
cách giữa hai tiếp tuyến là lớn nhất thì hoành độ mãn y  1.
điểm M,N thỏa mãn y  1.
Cách nhận dạng đồ thị hàm phân thức bậc nhất/ bậc nhất Tiệm cận ngang d : b Ox x . a
Tiệm cận đứng x   : b Giao   y  : Giao Oy :y  . Nếu giao a Nếu tiệm cận c c d
Nếu tiệm cận đứng nằm Nếu giao điểm này điểm này nằm trên Ox ngang nằm trên Ox bên trái Oy thì cd  0, nằm bên trái Oy thì
thì bd  0, nằm dưới Ox thì ac  0, nằm dưới nằm bên phải Oy thì ab  0, nằm bên phải Ox thì bd  0. thì ac  0. cd  0 Oy thì ab  0.
Cho hàm số y  f x  có giá trị lớn nhất và nhỏ nhất trên D lần lượt là M và m 0 khi M.m  0 8 M m M m  max f x     
min f x    M m  M m D 2 D  khi M.m  0  2
Cô lập m giải phương trình, bất phương trình
f x   m có nghiệm trên D  min f x   m  max f x  D D 9
f x   m nghiệm đúng x D  m  min f x 
f x   m có nghiệm trên D  m  max f x  D D
f x   m nghiệm đúng x D  m  max f x 
f x   m có nghiệm trên D  m  min f x  D D
Chú ý: Nếu có dấu bằng trong các bất phương trình thì ta thêm dấu bằng ở điều kiện tương ứng (nên xét
riêng tại dấu bằng xem có xảy ra không). Một số bài ta vẽ bảng biến thiên và dùng tương giao để giải Đồ thị hàm lũy thừa
: Điều kiện là f x   0 
  0, : Điều kiện là f x   0  y  f x 
  : Điều kiện của hàm số là điều kiện f x  1
Đồ thị hàm số y  x  luôn đi qua điểm I 1;1 12
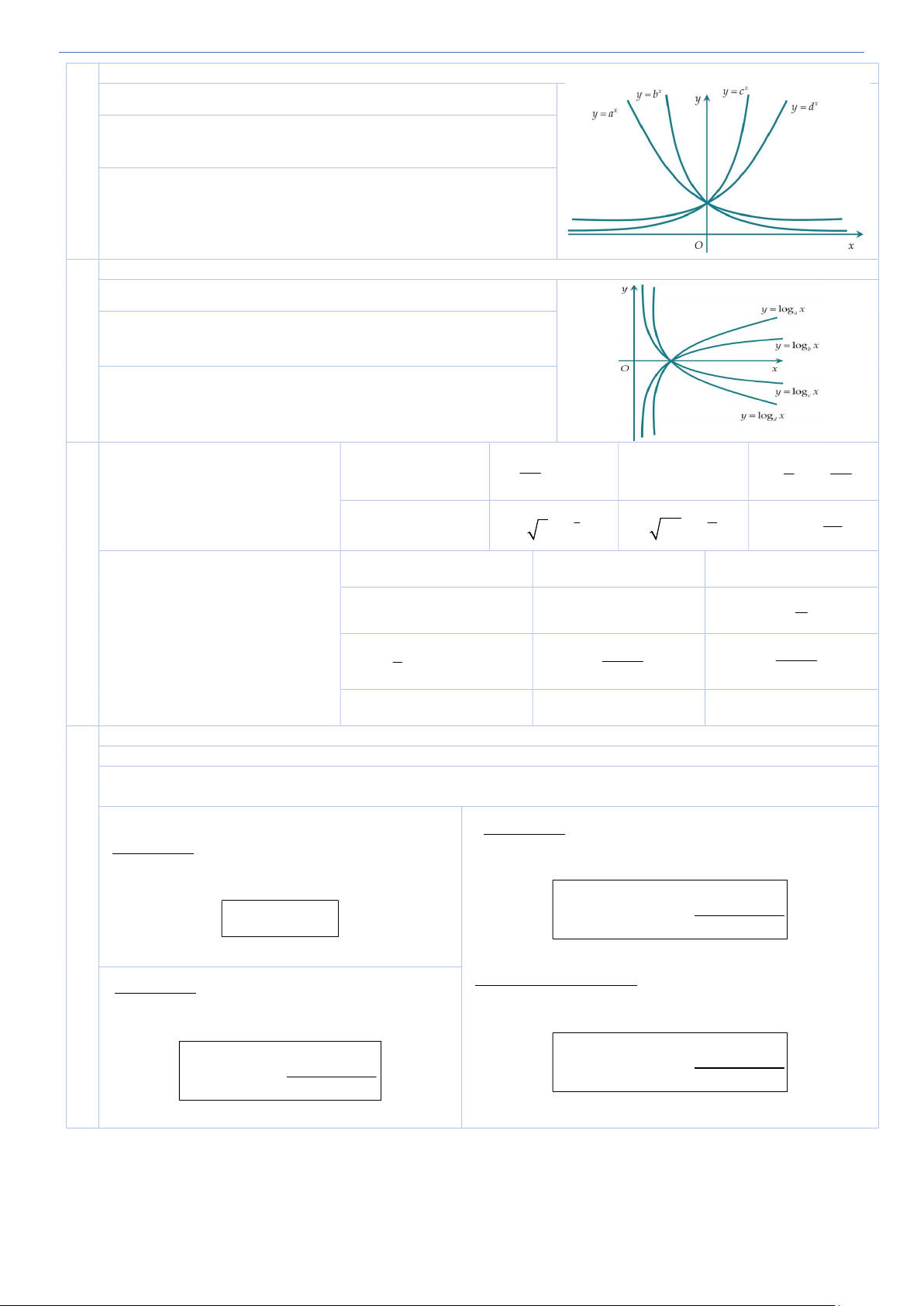
Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT Đồ thị hàm số mũ  x
y a có tập xác định D  , tập giá trị T  0;. Đồ thị hàm số  x
y a luôn đi qua điểm I 0;1 và có tiệm 2 cận ngang là trục hoành
Vẽ đường thẳng x  1 để so sánh a, , b , c d ( trên hình vẽ là
0  b a  1  d  c ) Đồ thị hàm số logarit
y  log x có tập xác định D  0;, tập giá trị T   a
Đồ thị hàm số y  log x luôn đi qua điểm I 1;0 và có tiệm a 3 cận đứng là trục Oy.
Vẽ đường thẳng y  1 để so sánh a, , b , c d ( trên hình vẽ là
b a  1 d c  0 ) m a a m m a m n m n m n a m    m. m ab a b    Công thức mũ a .a a     n a m b b    a,b  0  n m n 1 m 1  m.n a a   2 a a n m  n a a a  n a log b   a   b log  log ; ln  log log 1  0 10 e a 4 a log a  1 1 log n b  n log b log b b n  log Công thức logarit a a a a a n a,b  0,a  1  b  log b 1
log    log b  log c log b  c c log b  b a  1 a  1 a c  a a log a log a c b
log bc  log b  log c log log c log a a a a a b a b b a  b c Bài toán lãi suất
Lãi đơn: Số tiền lãi của kì hạn trước không được tính vào vốn để tính lãi cho kì hạn tiếp
Lãi kép: Số tiền lãi của kì hạn trước nếu người gửi không rút ra thì được tính vào vốn để tính lãi cho kì hạn sau đó
Bài toán 3: Gửi ngân hàng T đồng với lãi kép r% /
Bài toán 1: Gửi vào ngân hàng T đồng với lãi
tháng, hàng tháng rút t đồng, số tiền còn lại sau n
kép r% / kì hạn, số tiền nhận được sau n kì tháng là hạn là 1  r% n n 1 T T r T T r t n 1 %    . n 1 %n 5 r% Hết tiền khi T  0 n
Bài toán tương đương: Vay ngân hàng số tiền T đồng
Bài toán 2: Hàng tháng gửi t đồng vào ngân
với lãi kép r% / tháng, hàng tháng trả t đồng. Số tiền
hàng với lãi kép r% / tháng, tổng số tiền nhận còn nợ sau n tháng là được sau n tháng là n n r 1  r% 1 T T r t n 1 %n 1 % 1    . T t r n 1 %   . r% r% Trả hết nợ khi T  0. n 13
Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT Tính chất nguyên hàm
Nếu F x  là một nguyên hàm của f x  thì F x   f x  1      f x dx F x C       f x dx f x C      f x dx f x  kf
 xdx k f xdx k  0 
 f x gxdx   f xdx    gxdx      f u du F u C Nguyên hàm cần nhớ dx C 0 kdx  kx   C. n1 n1 n x x dx 1 (  )    C n  1 n ax b a ( x b) dx  C n  1 a n 1 dx  x C  1 ln dx  ax b C x  1 1 ln ax b a 1 1 1 1 dx 1   C  dx    C  x2 x a ( x  b 2) a ax  b x x e dx e C  ax b  ax b e dx  e C  1 a x mx n x a a dx  C  mx n a a dx  C lna  1 . m lna xdx   x C sin cos ax b dx   ax b C  1 sin( ) cos( ) a 2 xdx  x C cos sin ax b dx  ax b C  1 cos( ) sin( ) a 1 dx 1 dx  cotx C    cot a ( x  b)C  2 sin x 2 sin a ( x b) a 1 dx 1 dx  tanx C   tan a ( x  b)C  2 cos x 2 cos a ( x b) a xdx   x C tan ln cos  ax 1 tan
bdx   ln cosax b C a xdx  x C cot ln sin  ax 1 cot
bdx  ln sinax b C a dx x dx ax b  C  ln tan  C  1 ln tan sinx 2 sinax b a 2 dx x dx ax b   C  ln cot   C  1 ln cot cosx 2 cosax b a 2 Nguyên hàm mở rộng dx ax   1 b dx 1 a  x  ln C  ln C ax bcx d   ad bc cx d  2a  2x 2a a x dx   lnx  2x  2a C dx 1 x  arctan   C 2 2  2 3 x a a  x a a dx x  arcsin   C dx 1 x  arccos   C 2 a  2 x a 2 2 a a x x a 2 dx 1 a  2 x  2 a 2 x a x a  2 x dx  2 a  2 x  arcsin   C   ln   C 2 2 a 2  2 a x x x a Phương pháp đổi biến 14
Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT
Thường đặt dưới mẫu, dưới mũ, dưới căn, một số trường khác đặt nâng cao khác như sau Dấu hiệu nhận biết Cách đặt     2  2 a x x  a sint,t   ; .   2 2   4 a     2  2 x a x  , t    ;  \  0 sint  2 2      2  2 a x x  a tant,t  ;   2 2  a  x a  x hoặc x  a cos2t a  x a  x x ab x x  a  b a 2 sin t Phương pháp từng phần udv  uv  vdu  
Thứ tự ưu tiên đặtu : Log  đa  lượng  mũ
Một số tính chất cần nhớ ax b A B 2 ax bx c A B C     x  x x x x x x x x x x x x x x  x x  x x  x 1  2  3  1    2      5 1 2 1 2 3 2 ax bx c A B C 2 ax bx c A Bx C       2.  x x x x x x x x 2 2 x x mx nx p x x mx nx p 1 x x 2     2
  1      1   1 2 1 Nguyên hàm hàm ẩn
f x dx d f x  f 
 xdx  f xC f
 x  f x   f   xf x f   x  2 .  
 f x  f  x f x   f  d f x   x  2  n 1 f x    n f  xdf x    C  ln f x C   f f x     x  2  f  x n  1 6 
f x   px f x  h x  px dx p x dx p x dx
: Nhân cả hai vế với e
, đẳng thức trở thành f  x         e. e h  . x    b a   : b a x x y  y  .y , CALC x  , a y  m 20 20 Cho y  .
A y  B , y a  m, tính yb?
ấn "  " liên tục đến khi x  b ta được giá trị y b
Chú ý: Chuyển hết f x  và f x  sang vế phải, bậc của f x  phải là bậc một
Một số tính chất của tích phân
b f xdx FbFa a a a b b f  xdx  0 f  xdx  0 f
 xdx  f tdt ... a a a a b c b b b b b b f
 xdx  f xdx  f xdx 7 kf
 xdx k f xdx f
 x gxdx  f   xdx  g  xdx a a c a a a a a a b c b b f x  b  0, x   a  ;b  f    xdx  0 f x   g x , x    ; a b  f    xdx  g  xdx a a a a 0 a
f x  là hàm chẵn và liên tục trên a;a 
 thì f x dx  2 f x dx    2 f xdx a a 0 15
Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT a 0 a
f x  là hàm lẻ và liên tục trên a;a   thì f x dx   0 và f x dx     f xdx a a 0 a f x  a
f x  là hàm số chẵn và liên tục trên  a  ;a   thì dx  f x dx   x   b  a  1 0 b b
f x  liên tục trên a;b 
 thì f x dx  f a  b    x dx a a b b a b f x   liên tục trên a;b 
 và thỏa mãn f a  b  x   f x ,x  a;b   thì xf x dx   f xdx 2 a a b
f x  liên tục và f a b  x   f x  thì f x dx   0 a 2a a
f x  liên tục trên 0;2a 
 thì  f x dx    f x  f 2a   x dx 0 0 b b f g f g b b f b f g
f ,g liên tục trên a;b   thì maxf ,g    dx    dx , minf,g    dx  dx 2  2 a a a a 2 b b b  
Bất đẳng thức tích phân (Holder với p  q  2 ):  f  xgx 2 dx   f  x 2 dx. g  xdx    a  a a
Kỹ thuật chọn hàm cơ bản trong tích phân b
Nếu đề bài cho f x dx C   chọn   C f x  b a a
một điều kiện thì chọn f x  ax Nếu đề bài cho
hai điều kiện thì chọn f x  ax b 8
ba điều kiện thì chọn   2 f x ax bx c
Nếu đề bài cho hàm lẻ có
một điều kiện thì chọn f x  ax
hai điều kiện thì chọn   3 f x ax bx
Nếu đề bài cho hàm chẵn có
một điều kiện thì chọn   2 f x  ax
hai điều kiện thì chọn   2 f x ax b
Một số kĩ thuật nâng cao Điều kiện đề bài Phương pháp giải
Nếu f x  liên tục trên a  ;b   thì b f a bx b dx  f  xdx a a
Nếu u a a, u b b thì 9 .
A f x  B.u .f u C.f a b x   g x  b f x 1 b dx  g  xdx A  B C a a Nếu u a  , b u b a thì b f x 1 b dx  g  xdx A  B C a a Af u    Bf v  g x 
Đặt t u và t v để giải giải phương trình hai ẩn
(Nếu u  x thì chỉ cần đặt t  v ) 16
Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT b dx b a
f x  f a b x  2 .  k I    k  f x k a   2 b g f  x   x 
với g t  đơn điệu trên  Tính f x dx 
, ta đặt y  f x   x  g y a
Tính diện tích hình phẳng Theo Ox Theo Oy Điều kiện: y  f x  Điều kiện: x  f y y  f x   x  f y
Điều kiện: y  g x   1  
Điều kiện: x  g y Ox :y  0  Oy :x  0  x  a x  b  x  a,x   ,  y  a y  b  b y a,y  b    , b  b b S  f x    g x  dx b S   f x dx f y   g y dy a S   f y dy a a a
Tính thể tích khối tròn xoay Theo Ox Theo Oy Điều kiện: y  f x  Điều kiện: x  f y   y  f x   
Điều kiện: y  g x  x  f y
Điều kiện: x  g y   2     Ox :y  0 x  a x  b Oy :x  0 y  a y  b   ,  , x  a,x    b y a,y  b  b  b V   f x g x dx V   f y g y dy Oy    2 2   Ox    2 2   b b V   f x dx a V   f y dy a Oy  2   Ox  2   a
f x,gx0x a;b a
f y,gy0ya;b b 3
Thể tích vật thể có diện tích thiết diện bằng S x  : V  S  x dx a
Một số công thức tính nhanh
Đường thẳng y  n cắt đường cong  4  2 y ax
bx c tại 4 điểm phân biệt và hình
phẳng giới hạn bởi hai đường này gồm phần phía
trên và phần phía dưới đường thẳng có diện tích
bằng nhau khi và chỉ khi 2 5b  36a c n 4
Đường thẳng y  mx  n cắt đường cong  3  2 y ax
bx cx d tại ba điểm phân biệt và hình
phẳng giới hạn bới hai đường này gồm phần phía
trên và phía dưới đường thẳng có diện tích bằng
nhau khi và chi khi điểm uốn của đường cong bậc
ba thuộc đường thẳng y  mx  n 17
Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT
Diện tích hình phẳng giới hạn bởi đường thẳng
y  mx  n và parabol  2 y ax bx c là  3 2 3  b m 4a c n 2           S     4 36a  4 36a     
Trong đó:  là của phương trình hoành độ
( Tức là của phương trình 2 ax bx c  mx  n )
Số phức z  a  bi a,b   1 z là số thực  b  0
a : Phần thực, b : phần ảo, i : đơn vị ảo, 2 i  1 
z là số thuần ảo  a  0
Số 0 vừa là số thực vừa là số ảo
Tính chất số phức : z  a  bi, z  a  b i a   a M  ; a b z  z  là điểm biểu diễn z  a bi : là số phức b    b số phức z liên hợp của z z  a2 b2 z là số thực  z  z z là số ảo  z  z  2 z  z 2 ; z  z.z z  z  z  z z z  z z z z  z .z 1 2 1 2 1 2 1 2 1 2 1 2 z z  z  z 1 1 
z  z  z  z  z  z 2 2    1 2 1 2 1 2 z z z.z a b 1 1  z  2 2  2  z2
Dạng lượng giác số phức
z  r cos i sin r  0 là dạng lượng giác của z a bi  : 2 2 a b
là một acgumen của z,   Ox,OM  và r  a b , cos  , sin  r r 3 z r 1 1  cos 
  isin    1 2   1 2 z r  2 2
z  r cos i sin , z  r cos i sin 1 1  1 1  2 2  2 2 
z z  r r cos    i sin     1 2 1 2   1 2  1 2
 cos  sin n n r i   r  cosn isinn
Một số đẳng thức mođun quan trọng 2 2 2 2
mz  nz  m z  n z  mn z z  z z với , m n  1 2 1 2 2  1 2 1 2 2 2 2 2
 4 z  z  z  z  2 z z z z  z z  2OM OM 1 2 1 2   1 2  1 2 1 2 1 2 z z 2 2   2 1 z  z z  z z  z  .z  .z với z ,z  0 2 2 1 2 1 2 z  z  z  z  2  z    1 2 1 2 z z 1 2 1 2  2 2  1 2  
Các công thức thể tích cơ bản Thể tích chóp Thể tích chóp cụt 1 1 Thể tích lăng trụ V 1  Bh V  Bh
V  h B B B.B 3 3
Công thức tính nhanh thể tích khối chóp đặc biệt Nhận dạng Công thức tính nhanh 2 3 a 2 Tứ diện đều cạnh a V  12 18
Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT
Tứ diện gần đều có độ dài các cạnh đối là 1 V 
 2a  2b  2c 2b  2c  2a 2a  2c  2b a, , b c 6 2
Chóp có ba mặt phẳng SAB ,SAC , SBC  2S .S .S
đôi một vuông góc và có diện tích V  1 2 3 3 lần lượt là S ,S ,S 1 2 3 Tứ diện ABCD có S  S ,S  S , A  BC 1 ABD 2 2S .S sin V   1 2
AB  a và  ABC ,ABD    3a
Tứ diện ABCD có AB  a,CD  b 1 V  abd sin d AB,CD d;AB,CD     6
Chóp S.ABC có SA  a,SB  , b SC  c abc V  sin .  sin.sin  SAB,SAC     ,  ASB  ,ASC   6
Chóp S.ABC có SA  a,SB  , b SC  c abc 2 2 2    V  1  2cos .
 cos.cos  cos   cos   cos  ASB  ,  BSC  ,CSA   6
Chóp S.ABC có BC  a,CA  , b AB  c  2 SBC ,ABC   ,   SAC ,ABC      2S V  ABC
3a.cot b.cot c.cot  SAB,ABC   Tỉ số thể tích
M,N,P lần lượt thuộc S , A SB,SC : Chóp tam giác V S.ABC SM SN SP S .MNP  . . V SA SB SC S .ABC
M,N,P,Q lần lượt thuộc S , A SB,SC,SD VS.MNPQ x y  z t Chóp tứ giác S.ABCD  V 4xyzt
Có ABCD là hình bình hành S .ABCD SA SB SC SD với x  ;y  ;z  ;t  và x  z  y t SM SN SP SQ
Thể tích tứ diện tạo bởi 4 đỉnh bất kì không đồng phẳng V là 3
Thể tích chóp tứ giác được tạo thành từ các đỉnh của lăng 3 2V trụ là Lăng trụ tam giác 3 ABC.A B  C   thể tích là V
Gọi M,N,P lần lượt thuộc A  A ,BB,CC V x  y  z ABC .MNP  V 3 ABC .ABC  AM BN CP với x  ;y  ;z  AA BB CC 
Thể tích tứ diện tạo bởi 4 đỉnh bất kì không đồng phẳng V Hình hộp ABCD.  A BCD là 6 có thể tích là V
Thể tích của tứ diện tạo bởi 2 đường chéo của 2 mặt V
phẳng đối diện của hình hộp là 3 19
Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT
Gọi M,N,P,Q lần lượt thuộc A 
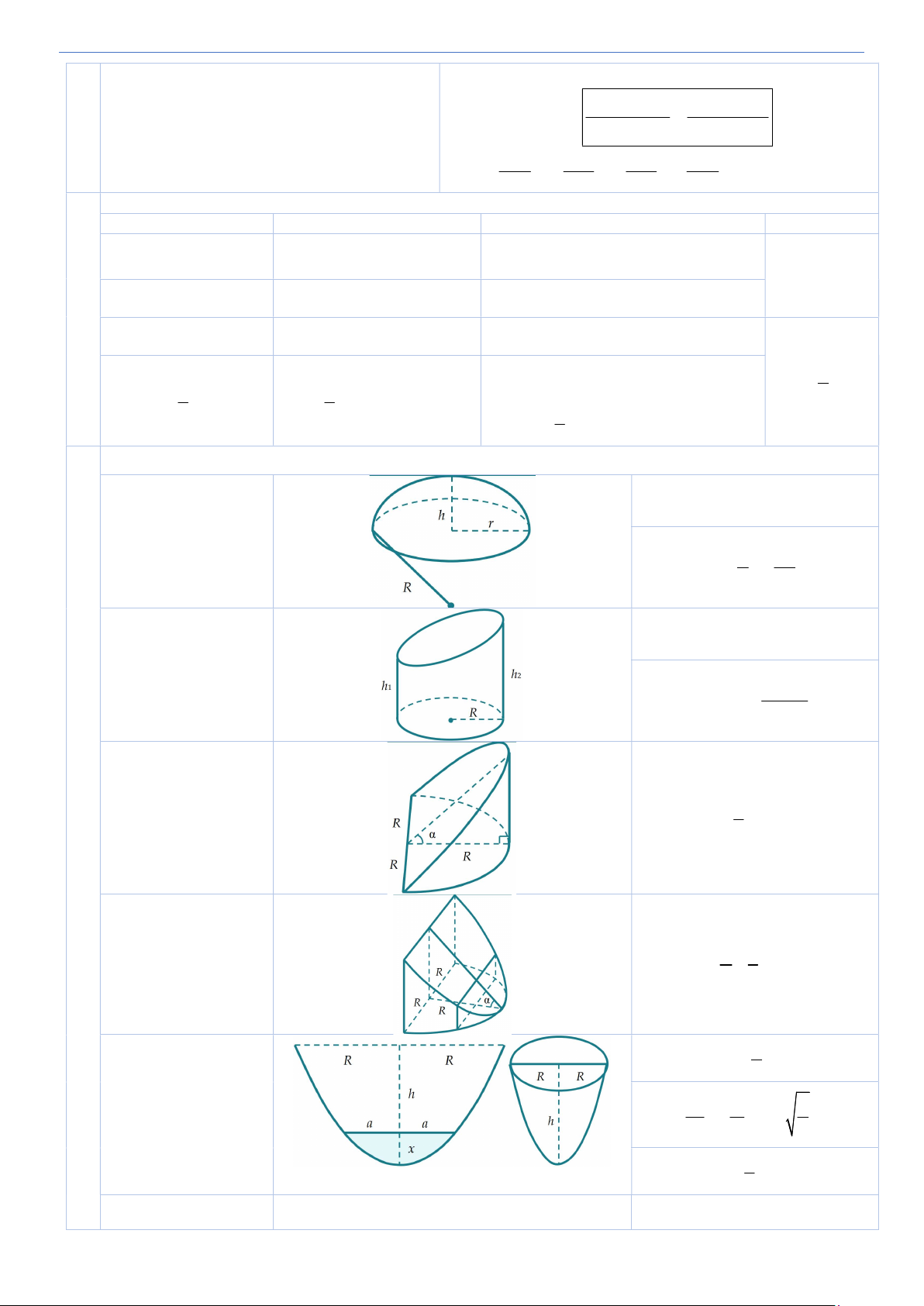
A ,BB,CC,DD. Khi đó VABCD.MNPQ x y  z t  V 4 ABCD.ABC D AM BN CP DQ với x  ,y  ,z  ,t  và x  z  y t AA BB CC  DD Nón – Trụ – Cầu Nón Nón cụt Trụ Cầu 2  2  2 l r h ,
R r : bán kính đáy lớn và S  2 r  l với l  h đáy nhỏ xq S  2 4 r  mc S  r  l S  rl R  r S  r  l  2 2 2 r  xp  xq tp 4 S  r l   2 r  S   R r l R r tp  2  2     tp  2 V r  h
Với AB,CD là hai đường bất kì 4 V  3 r  1 1 2 2 trên hai đáy thì 3 V  2 r  h V  h  R r Rr  3 3 1 V  AB.CD.OO.sin AB CD ABCD  ,  6
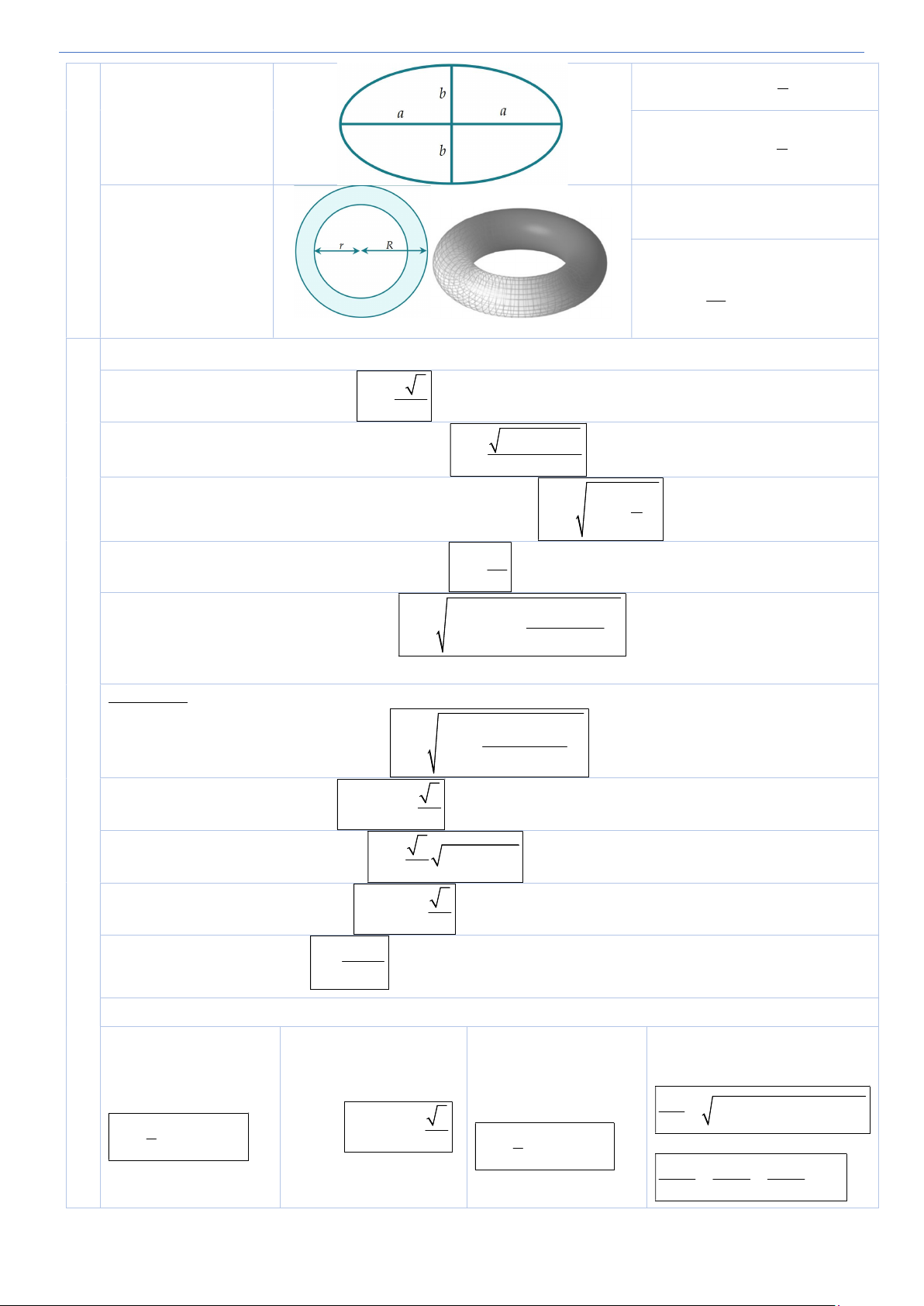
Các vật thể tròn xoay trong không gian S  R  h   2 r  2 2 h xq  Chỏm cầu 2  h  h V  h   R     2h  2 3r   3  6 S  R h h xq   1 2  Hình trụ cụt  h  h  V  2 R   1 2   2  2 Hình nêm loại 1 V  3 R tan 5 3   2  Hình nêm loại 2 V     3 R tan  2 3  4 S  Rh 3 3 S  a 3  x  Parabol 1       S R  h  2     1 V  2 R  h 2 Elip S  a  b 20
Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT 4 V  2 a  b quay quanh 2a 3 4 V  2 a  b quay quanh 2b 3
Diện tích hình vành khăn   2  2 S R r  Hình xuyến Thể tích hình phao 2
V   R rR r2 4
Bán kính mặt cầu ngoại tiếp R và nội tiếp r của hình chóp, lăng trụ c  c  x 3
Hình lập phương có cạnh bằng x : R  c 2 2 2 2 x  y  z
Hình hộp chữ nhật có các kích thước là x,y,z : R  c 3 2  h 2
Chóp có chiều cao h và có cạnh bên vuông góc với đáy thì: R  R  c d    2  2 l
Chóp đều có chiều cao h, cạnh bên bằng l thì: R  c 2h 2 2  giao tuyen 2
Chóp có mặt bên vuông góc với đáy thì: R  R  R  c d b    2 
R ,R lần lượt là bán kính đường tròn ngoại tiếp đáy và mặt bên (mặt vuông góc với đáy) d b
Tổng quát: chóp có chân đường cao H,I là tâm đường tròn ngoại tiếp đáy, gọi IH  d thì  2 2 h  2 d  2 R  R  2 R   d  c d  2h  6   6
Mặt cầu ngoại tiếp tứ diện đều: R  cạnh. c 4 2
Mặt cầu ngoại tiếp tứ diện gần đều: R  2 a  2 b  2 c c 3 6
mặt cầu nội tiếp tứ diện gần đều: r  cạnh. c 12 3V
Mặt cầu nội tiếp hình chóp: r  Trong đó: S
 : tổng diện tích tất cả các mặt của chóp c S m m Cách tính R d
Nếu đáy là tam giác thường
thì áp dụng một trong hai Nếu đáy là hình Nếu đáy là tam giác công thức Nếu đáy là tam giác vuông hoặc hình chữ vuông thì abc nhật thì
 p p ap bp c 1 3 4R R  .cạnh huyền đều thì R  cạnh. d 1 d 2 3 R  .đường chéo hoặc d 2 a b c    2R sinA sinB sinC 21
Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT
Tọa độ điểm và vec tơ
Hệ tọa độ trong không gian gồm ba trục Ox, Oy, Oz đôi một vuông góc với các vec-tơ đơn vị tương ứng   
trên ba trục lần lượt là i  1;0;0, j  0;1;0,k  0;0;1 u x;y;z    2 2 2 1    
AB  x x ;y y ;z z
u  x;y;z   u  x  y  z B A B A B A   u  x.i  y.j  z.k
I là trung điểm của AB thì
G là trọng tâm ABC thì ABCD là hình bình  
 x  x y  y z  z 
 x  x  x y  y  y z  z  z  A B A B A B hành  AB  DC I  ; ;  A B C G ; A B C ; A B C 2 2 2   3 3 3      
Cho u  x ;y ;z ,v  x ;y ;z 1 1 1   2 2 2         u.v  u . v .cosu,v u.v  x x  y y  z z       1 2 1 2 1 2     u,v    u . v .sinu,v u  v  u.v  0           y z z x x y  w  u, w  v  w  u  ,v    1 1 1 1 1 1 u  ,v   ; ;    u,v,w    đồng phẳng y z z x x y        2 2 2 2 2 2  u và v cùng phương    u v , .w  0 2
 y z y z ;z x z x ;x y x y  u v   1 2 2 1 1 2 2 1 1 2 2 1  ,    0
  
   ,
A B,C,D là bốn đỉnh của tứ diện  AB,AC,AD không đồng phẳng  AB AC  , .AD    0
Diện tích, thể tích một số hình Diện tích tam giác Diện tích hình bình Thể tích khối hộp Thể tích tứ diện 1   hành
  
1    S  AB,AC    V  AB,AD.AA V  AB,AC .AD ABC 2   S  AB,AD ABCD.ABC D   ABCD ABCD   6   Phương trình mặt cầu 2 x  2 y  2
z ax by cz d  0 2 2 2  a b c  2 3
x a y b z c R  Tâm I  ; ; ,  2 2 2 
 Tâm I a; ;bc, bán kính R 2 a  2 b  2 c  2 a  2 b  2 c  R  d  d  0 4  4  Phương trình mặt phẳng 
Mặt phẳng đi qua M x ;y ;z có vtpt n   ;
A B;C  Phương trình mặt chắn: Mặt phẳng  đi qua 0 0 0 
Ax  x   B y y  C z  z   0
Aa;0;0,B 0; ;b0,C 0;0;c có phương trình 0 0 0  
P :Ax By Cz  D  0 x y z có vtptn   ; A B;C    1 abc  0 P    a b c 4
Vậy để viết phương trình mặt phẳng ta cần tìm một vtpt và một điểm thuộc mặt phẳng
(một cặp vtcp của mặt phẳng tạo thành một vtpt của nó bằng việc lấy tích có hướng) Oxy:z  0
Các phương trình mặt phẳng đặc biệt Oxz:y  0 Oyz:x  0
Vị trí tương đối: Cho  :Ax  By Cz  D  0 và  :Ax  By C z  D  0 22
Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT  A B C D A B C D      
      A B C  D A B C  D
 cắt  A:B :C   A :B:C
    AABBCC  0
Khoảng cách từ điểm M x ;y ;z đến mặt phẳng :Ax  By Cz  D  0 0 0 0   Ax By Cz D d M;     0 0 0 2 A  2 B  2 C 
Phương trình đường thẳng  đi qua điểm M x ;y ;z có vtcp u  a;b;c  0 0 0  x   x at 0
Có phương trình chính tắc là 
Có phương trình tham số là  : y   y bt t   x x y y z  z 0   0 0 0  :   abc  0 z   z ct  a b c 0
Vậy để viết phương trình đường thẳng ta cần tìm một vtcp và một điểm thuộc đường thẳng 5  
Vị trí tương đối: Đường thẳng d đi qua điểm M và có vtcp u , d đi qua điểm M và có vtcp u . 1 1 1 2 2 2
  
  
d và d đồng phẳng  u u  , M M  0 d chéo d  u u  , M M  0 1 2  1 2  1 2 1 2  1 2  1 2       u ,u   0  u  ,u   0 d  1 2 1 2  cắt d    d d    1 2
   
    u ,u  1 2  M M  0  u  ,M M   0  1 2  1 2 1 1 2    
Khoảng cách, góc: M   ,M   , u ,u lần lượt là hai vtcp của  ,  1 1 2 2 1 2 1 2  
   MM ,u  u ,u .M M 1 2 1 2 d M,   d  , 1 2   1   1 1       u u ,u  1  1 2    6     u .u   n .n
cos ,   cosu ,u  1 2 
cos P , Q   cosn ,n  P Q  P Q 1 2 1 2         u . u     n . n 1 2 P Q      u .n sin ,  P   cosu ,n    P  P     u . n  P
Hình chiếu vuông góc, điểm đối xứng đặc biệt Oxy là H x ;y ;0 0 0  Oxz là H x ;0;z 0 0 
Hình chiếu vuông góc của điểm Oyz là H 0;y ;z Nhớ nhanh:    0 0 M x ;y ;z lên Khuyết vị trí nào 0 0 0  Ox là H x ;0;0 0  thì vị trí đó bằng 0 Oy là H 0;y ;0 0  7 Oz là H 0;0;z 0 
Oxy là Mx ;y ; z 0 0 0  Oxz là Mx ; y  ;z 0 0 0  Nhớ nhanh: Oyz là M x  ;y ;z 0 0 0 
Điểm đối xứng với M x ;y ;z qua Khuyết vị trí nào 0 0 0   thì vị trí đó bằng Ox là M x ; y  ; z  0 0 0  đối Oy là M  x  ;y ; z  0 0 0  Oz là M  x  ; y  ;z 0 0 0  8
Một số công thức giải nhanh (a,b,c lần lượt là độ dài 3 cạnh tam giácABC ) 23
Söu taàm vaø bieân soaïn : Nguyeãn Thanh Taân – THPT Nho Quan C Coâng thöùc toaùn THPT   H  . A BC  0
 
Tọa độ trực tâm H của tam giác ABC là nghiệm hệ: H  B.AC  0
    A  B,AC .AH  0   I  A IB 
Tọa độ tâm I đường tròn ngoại tiếp tam giác ABC là nghiệm hệ: I  A  IC
    A  B,AC .IA  0     
Tọa độ chân đường phân giác trong D của góc A thỏa mãn đẳng thức: b.DB c.DC  0   
Tọa độ chân đường phân giác ngoài E của góc A thỏa mãn đẳng thức: . b EB cEC  0    
Tâm I đường tròn nội tiếp tam giác ABC thỏa mãn đẳng thức: a.IA  . b IB c.IC  0
Tọa độ hình chiếu vuông góc H của A lên P  :ax by cz d  0 là H at  x ;bt  y ;ct  z A A A  ax by cz d với A A A t   2 2 2 a b c
M là trọng tâm ABC thì a  3x ,b  3y ,c  3z M M M  
M là trực tâm tam giác ABC thì OM  n P 
P đi qua M cắt các trục tọa độ tại V
nhỏ nhất khi M là trọng tâm ABC O.ABC
Aa;0;0,B 0; ;b0,C 0;0;c 1 1   
nhỏ nhất khi M là trực tâm ABC 2 2 2 OA OB OC
(phương trình mặt chắn) a b c 
Tâm mặt cầu ngoại tiếp O.ABC là I  ; ; 2 2 2    1
Bán kính mặt cầu ngoại tiếp O.ABC là 2 2 2 R  a b c C 2 Cực trị hình học Oxyz    
Viết P  chứa d thỏa mãn d , P là lớn nhất thì: n  u  , u  ,u  2    1 P 1 1 2    
  
Viết d chứa trong P  sao cho d ,d nhỏ nhất thì: u  n  , n  ,u  1 2   1 1  P    P 2  
  
Viết P  chứa d sao cho  P  Q  , nhỏ nhất thì: n  u  , u  ,n  1 P 1   1   Q 
     
9 Viết d nằm trong P  và qua A sao cho d M,d  nhỏ nhất thì: u  n   , n     ,AM d P P  
  
Viết P  chứa d sao cho d M,P  lớn nhất thì: n     
u u AM với điểm Abất kì thuộc d P  , , d d      
Viết d nằm trong P  và qua A sao cho d M,d  lớn nhất thì: u n      ,AM d P     
Tâm tỉ cự: Điểm I thỏa mãn: a IA  a IA  ... a IA  0 đgl tâm tỉ cự của hệ điểm A ,A ,...,A 1 1 2 2 n n 1 2 n a x a x  ... a x a y a y  ... a y a z a z  ... a z Khi đó: 1 1 A 2 2 A n n A x  , 1 1 A 2 2 A n n A y  , 1 1 A 2 2 A n n A z  I a a  ... a I a a  ... a I a a  ... a 1 2 n 1 2 n 1 2 n
Cuốn công thức này của:………………………………………………………………..
Giáo viên: Nguyễn Thanh Tân 24