











Preview text:
TỔNG HỢP CÔNG THỨC TOÁN THPT Th.S Nguyễn Viết Hiếu BRVT 089908.3939 viethieu220284@gmail.com Face:viethieu220284 Zalo:089908.3939 LỜI TỰA
Tác giả xin cám ơn quý thầy cô, các em học sinh đọc và nghiên
cứu tài liệu. Tác giả viết tài liệu với mong muốn góp một phần nhỏ
giúp các em học sinh trong việc học môn Toán ở THPT. Thông qua tài
liệu tác giả cũng mong nhận được sự chia sẽ từ quý thầy cô giảng dạy.
Viết tài liệu trong thời gian ngắn, kinh nghiệm chưa nhiều nên không
thể tránh được thiếu sót, tác giả rất mong nhận được sự đóng góp của quý độc giả. Xuyên Mộc, 9/2021 Face: viethieu220284 I. HÀM SỐ
Th.S Nguyễn Viết Hiếu 089908.3939
1.Sự đồng biến, nghịch biến của hàm số 2.Tìm điều kiện , a , b c để hàm số 2 0 b 3ac 0 y
Cho K là khoảng, nữa khoảng hoặc đoạn và 3 2 y
f x ax bx cx d
3.Tìm điều kiện để hàm số
hàm số y f x xác định trên K.
đồng biến, nghịch biến trên ax b f x
c 0;ad bc 0
+Định lí 1: Cho hàm số y f x có đạo f x 2 '
3ax 2bx c cx d hàm trên K.
đồng biến, nghịch biến.
+Hs y f x đồng biến trên
-Nếu f ' x 0, x
K thì hàm số đồng ad bc a b 0 f ' x biến trên K. cx d2 c 0
-Nếu f ' x 0, x
K thì hàm số nghịch
f ' x 0, x +Hs ax b f x đồng biến trên biến trên K. a 0 cx d
+Định lí 2: Cho hàm số y f x có đạo 0 từng khoảng xác định y hàm trên K. d
f 'x + 0, x ad bc 0
Hs y f x nghịch biến trên
-Nếu f ' x 0, x
K và f 'x 0 chỉ c a b 0
xảy ra tại hữu hạn điểm thì hàm số đồng +Hs ax b f x nghịch biến trên biến trên K. c 0 cx d từng khoảng xác định
-Nếu f ' x 0, x
K và f 'x 0 chỉ
f 'x 0, x a 0 d
xảy ra tại hữu hạn điểm thì hàm số nghịch
f ' x 0, x
ad bc 0 0 c biến trên K. y
4.Cho hs y f x liên tục trên ;
a b . b/ Có bao nhiêu giá trị nguyên âm của +Hs ax b f x
đb trên khoảng ; cx d 1
m f x, x ;
a b m max f x 3 tham số m để hs y x mx 5
f ' x 0, x
; ad bc 0 a;b 5x
m f x, x ;
a b m min f x đồ d
ng biến trên khoảng 0; ? d d a;b ;
or c c c
BT1a/Có bao nhiêu giá trị nguyên 1 2 y ' 3x m
của tham số m để hàm số 6 x +Hs ax b f x nb trên khoảng ; cx d x 2 Hs đb trên khoả y
đồng biến trên khoảng ng 0;
f ' x 0, x ;
ad bc 0 x 5m
y ' 0, x 0; 5m 2 d y ' , x 5 m 1 d ( ; 10) ? ; 2 m 3x , x 0; x5m2 c c 6 x Hs đồng biến trên ( ; 1 0) + Hs ax b f x
đồng biến trên ; 1 2 m max 3 x cx d y ' 0, x ( ; 10) 6 0; x
f ' x 0, x
; ad bc 0 5m ( ; 10) m 4 . d
KL: 4 số nguyên âm m thỏa. d d ;
or 5m 2 0 2 c c c m 2 5 m 10 5
Th.S Nguyễn Viết Hiếu 089908.3939 5.Cực trị của hàm số
+Định lí 1: Nếu hàm số y f x có
+Cho hs y f x đạt cực đại tại x x0
đạo hàm trên khoảng ; a b và đạt x x
0 là điểm cực đại của hàm số y f x
cực trị tại x ;
a b thì f ' x 0 . 0 0
y f x là giá trị cực đại (cực đại) của hs. 0 0
+Định lí 2: Giả sử hs y f x liên
M x ; y là điểm cực đại của đths y f x . 0 0 0
tục trên khoảng K x ; h x h 0 0
+Cho hs y f x đạt cực tiểu tại x x2
và có đạo hàm trên K hoặc trên x x
K \ x , với h 0 . 0
2 là điểm cực tiểu của hàm số y f x
y f x là giá trị cực tiểu (cực tiểu) của hs. 2 2
M x ; y là điểm cực tiểu của đths y f x . 2 2 2 Face: viethieu220284 Trang 1
Th.S Nguyễn Viết Hiếu 089908.3939 Face: viethieu220284
Th.S Nguyễn Viết Hiếu 089908.3939
+Định lí 3: Cho hàm số y f x có đạo
6. Cực trị hàm số bậc 3 A 0 +Hs có 2 điểm cực trị
hàm cấp 2 trên khoảng y '
0 có hai nghiệm phân biệt ; a b và 3 2 y
f x Ax Bx Cx D a 0 A 0 x ; a b . f ' x 2 0 3Ax 2Bx C 2 0 𝑓′(𝑥 y ' B 3AC 0 Nếu 2 {
0) = 0 thì hàm số y f x
ax bx c 𝑓′′(𝑥0) > 0 +Hs ko có cực trị 0 y '
đạt cực tiểu tại x . 0
+ Đths có 2 đ.cực trị nằm về 2 phía Oy 𝑓′(𝑥 Nếu y '
0 có hai nghiệm trái dấu {
0) = 0 thì hàm số y f x 𝑓′′(𝑥0) < 0 . a c 0
đạt cực đại tại x . 0
+Đths bậc 3 có hai điểm cực trị nằm về 2 phía trục Ox A 0 A 0
f(x) = 0 có 3 nghiệm phân biệt.
+ Pt đường thẳng đi qua 2 điểm cực trị b b
8.Giá trị lớn nhất, nhỏ nhất của hs
B1. Tìm đk hs có 2 điểm cực trị. B ; , C ;
+Cho hàm số y f x xác định trên
B2. C1: Lấy y chia cho y’ ta được 2a 4a 2a 4a tập hợp D.
thương là qx và dư là rx mx n với 2
b 4ac .
- Số M đgl giá trị lớn nhất của hs
Ptđt đi qua 2 điểm cực trị: y mx n
y f x trên D nếu
C2: Ptđt đi qua 2 điểm cực trị của f x đths: M , x D Th. . S N
x D : f x M 0 0
y f x
f ' x. f ' x gu y 18A ễ
Kí hiệu: M max f n x .
7.Cực trị hàm trùng phương D Viết
-Số m đgl giá trị nhỏ nhất của hs
𝑦 = 𝑎𝑥4 + 𝑏𝑥2 + 𝑐 (𝑎 ≠ 0) H iế
y f x trên D nếu 3 3
y ax bx x 2 ' 4 2 2 2ax b u 089908. Đặt b 8a 𝐵𝐴𝐶 ̂ = 𝛼, có cos 3 f
x m, x D x 0 b 8a . 3939 x
D : f x m 0 0 y ' 0 5 b b 2 x Diện tích S ABC bằng 3 2a 32a Th
Kí hiệu: m min f x . . +Đths trùng phương -Tam giác ABC vuông cân S N D gu
+Định lí: Mọi hàm số liên tục trên 3
b 8a 0
yễn đoạn ;ab đều có GTLN, GTNN trên -Tam giác ABC đều Viết đoạn đó. 3
b 24a 0 H i
+PP tìm GTLN, GTNN của hàm số ế
-Tam giác ABC có 𝐵𝐴𝐶 ̂ = 1200 u 089908.
y f x liên tục trên đoạn ; a b 3
3b 8a 0
B1: Tính f 'x. Tìm x ;x ;...;x
-Tam giác ABC có bán kính đường 1 2 n 3939 tròn ngoại tiếp: thuộc khoảng ;
a b thỏa f 'x 0 hay 3 A . B AC.BC b 8a
f ' x không xác định.
+Hs có 3 điểm cực trị R . a b 0 4S 8 a b
B2: Tính f a, f b, f x ,..., f x 1 n
( a,b trái dấu)
-Tam giác ABC có bán kính đường
+Hs có 1điểm cực trị
B3: Tìm số lớn nhất M, số nhỏ nhất m . a b 0 tròn nội tiếp:
+Hàm số có 1 điểm cực đại và 2 điểm trong các số ở B2. 2 2S b
Kết luận: M max f x , a 0 cực tiểu a;b r 3
AB BC AC b 0 b
m min f x 4 a 1 1 . a;b
+Hàm số có 1 điểm cực tiểu và hai 8a
+Ta có thể sử dụng BBT để tìm a 0 +Tam giác ABC cân tại A, điểm cực đại .
GTLN,GTNN của hàm số trên khoảng. b 0 4 b 8ba b AB AC ; BC 2
+Khi hs có 3 điểm cực trị ( ab 0 ) thì 2 16a 2a Zalo: 089908.3939
đths có 3 điểm cực trị A0;c , Face: viethieu220284 Trang 2
Th.S Nguyễn Viết Hiếu 089908.3939 Face: viethieu220284
Th.S Nguyễn Viết Hiếu 089908.3939
BT2:Tìm giá trị nhỏ nhất của hàm số +Đths nhất biến Đk: a 0 x . f x 3
x 24x trên đoạn 2;19. 2 ax b f x
c 0;ad bc 0 có Thể tích khối hộp: f x 2 ' 3x 24 cx d
V a 2x2 3 2 2 .x 4x 4ax a x
một đường tiệm cận ngang a y c f x x 2 2 ' 0 a a x 2 2 2;19
Có V 12 x x , 2 6
và một đường tiệm đứng d x . c
Ta có: f 2 40 ; f 19 6403 a
do đó V 0 x 10.Đồ thị hàm số f 2 2 3 2 2 6 +Đths bậc 3 3 2
y ax bx cx d a 0
Lập bảng biến thiên của hs V=V(x).
KL: min f x 3 2 2 . 2a a 2;19 maxV x 3 tại x .
BT3: Cho một tấm nhôm hình vuông a 0; 27 6
cạnh a . Người ta cắt ở bốn góc bốn 2
hình vuông bằng nhau, rồi gập tấm 9.Đường tiệm cận đứng, tiệm cận
nhôm lại như hình dưới đây để được ngang của đths y f x
một cái hộp không nắp. Tính cạnh của + y y là TCN của đths y f x nếu
hình vuông bị cắt sao cho thể tích của 0
thỏa ít nhất 1 trong hai đk: khối hộp lớn nhất. lim y y lim y y 0 x ; 0 x +Đường thẳng x x đgl tiệm cận 0
đứng của đths y f x nếu thỏa ít nhất 1 trong 4 đk: lim y ; lim y x x x x 0 0
Gọi x là cạnh hình vuông bị cắt. lim y ; lim y x x0 x x0
+Đths trùng phương (7. Cực trị hstp)
PTTT của đths y f x tại điểm 12a/Dựa vào đths y
f (x) , biện luận ax b f x m +Đths theo m số nghiệm pt ( ) . f x
c 0;ad bc 0
M x ; y là: y f 'x
x x y 0 0 0 0 0 cx d
Th. +Số no pt f (x) m là số giao điểm S N gu của đths y
f (x) và đth y m .
yễn +Lập BBT, vẽ đths y f (x) .
Viết +Dựa vào đths y f (x) biện luận. H iế BT5. Tìm m để pt 3 2x 6x m 0 u ad bc 0 ad bc 0 089908. có 1 nghiệm. ax 1
x là hoành độ tiếp điểm. BT4. Cho hs
+Số no pt đã cho là số giao điểm đths f x
a,b,c 0 bx c 3939 3 y y 2x 6x và đt y m .
0 là tung độ tiếp điểm.
có bảng biến thiên như sau:
f 'x là hệ số góc của tiếp +Xét hs 3 y 2x 6x 0 2 y ' 6x 6 tuyến tại
M x ; y . 0 0 y ' 0 x 1
Cho đường thẳng d: y ax b Lập BBT.
Tiếp tuyến có hệ số góc k Trong 3số , a ,
b c có bao nhiêu số dương? + pt 3 2x 6x m 0 có 1 nghiệm
f 'x k 0 -TCĐ: x 2 c 2b m 4 -TCN: y 1 a b
Tiếp tuyến song song với đt d m 4
-Hs đồng biến trên từng khoảng xác
f 'x a (viết pttt kiểm tra song 0 1
12b/ Tìm tọa độ giao điểm của 2đths
song hay trùng d, nếu trùng loại) định: ac b 0 b 0
y f x; y gx 2
Tiếp tuyến vuông góc với đt d KL:Trong 3 số , a ,
b c có 1 số dương.
B1: Lập pt hoành độ giao điểm của f 1 ' x 0 a
2đths: f x gx (*)
11.PT tiếp tuyến của đồ thị hàm số
12.Tương giao của hai đồ thị hàm số
B2: PT(*) vô nghiệm, 2đths ko cắt nhau
PT(*) có n nghiệm pb x ;x ;...;x 1 2 n Face: viethieu220284
Th.S Nguyễn Viết Hiếu 089908.3939 Trang 3 Face: viethieu220284
Th.S Nguyễn Viết Hiếu 089908.3939
KL: 2đths cắt nhau tại n điểm pb
Pt hoành độ giao điểm của d và 13.Đặc biệt 𝐴 (C):
1(𝑥1; 𝑓(𝑥1)), … , 𝐴𝑛(𝑥𝑛; 𝑓(𝑥𝑛))
+Cho hàm số y f x đồng biến trên
BT6. Tìm m để đths ax b 2 kx m Ax Bx C 0 (5) khoảng ;
a b và u,v ; a b f x 3 2
2x mx mx 2 cắt trục Ox tại cx d
f u f v
ba điểm phân biệt.
d cắt (C) tại hai điểm pb pt (5) u v
Giải: pt hoành độ giao điểm: d
f u f v u v có hai nghiệm pb khác . 3 2 2x mx mx 2 0 c
f u f v u v 𝑥 = 1 ↔ [
Khi d cắt (C) tại hai điểm phân biệt
2𝑥2 + (2 − 𝑚)𝑥 + 2 = 0(∗) 𝑀(𝑥 +Cho hàm số y
f x nghịch biến
1; 𝑘𝑥1 + 𝑚), 𝑁(𝑥2; 𝑘𝑥2 + 𝑚) Ycbt
pt (*) có 2 nghiệm pb khác 1
với x ; x là hai nghiệm phân biệt của trên khoảng ;
a b và u,v ; a b 1 2 m 2 . pt (5).
f u f v u v m 6 2 2 MN 1 k . x x 1 k .
f u f v u v
12c/Tương giao giữa đường thẳng d: 2 1 A
f u f v u v y kx m ax b và đths y
Th.S Nguyễn Viết Hiếu 089908.3939 cx d
+Cho hàm số y f x liên tục trên đoạn
m f x, x ;
a b m min f x 1 xy log
3xy x 2 y 4 a;b 3 ; a b. x 2 y
(Nếu tồn tại min f x ) a;b
log 3 3xy 3 3xy log x 2y x 2y 3 3
Pt f x m có nghiệm trên ; a b
m f x, x ;
a b m inf f x *
min f x m max f x . a;b a;b a;b
(Nếu không tồn tại min f x )
Xét hàm số f t log t t,t 0 . 3
m f x, x ;
a b m max f x a;b a;b
BT7. Xét các số thực dương x, y thỏa Có f t 1 ' 1 0, t 0 , nên
m f x, x ;
a b m min f x t ln 3 a;b 1 xy mãn log
3xy x 2y 4 . Tìm 3
hs y f t đồng biến trên 0; .
+Cho hs y f x liên tục trên khoảng x 2y
* f 33xy f x 2y (𝑎; 𝑏).
giá trị nhỏ nhất P
của P x y . min
m f x, x ;
a b m max f x (Câu 47 đề
3 3xy x 2y 101, THPTQuốc Gia 2017) a;b 9 11 19 9 11 19 3 x
(nếu tồn tại max f x ) y A. P B. P a;b min 3x 2 9 min 9
m f x, x ;
a b m sup f x 3 x
Suy ra: P x 18 11 29 2 11 3 a;b C. P D. P 3x 2 min min
(nếu không tồn tại max f x ) 9 3 2 11 3 a;b
Giải: Đk: x 0, y 0, xy 1 P . ĐA: D. min 3
BT8.Có bao nhiêu giá trị m nguyên để pt Đặt u sin , x 1 u 1, có pt 3 3 3
m 3 m 3sin x sin x có nghiệm
m u 3u
thực? (Câu 35, Đề MH2018) ycbt min 3
u 3u m max 3 u 3u 1 ; 1 1 ; 1 Giải: 2 m 2 3 3
m 3 m 3sin x sin x KL: 5 số nguyên m.
m3sin x 3 3
3 m 3sin x sin x 3sin x BT9. Cho hs f x , hs y f 'x
f 3 m 3sin x f sin x liên tục trên
và có đồ thị như hình
vẽ bên. Tìm tất cả m để bpt
(với f t 3
t 3t,t ,
f x x m nghiệm đúng với mọi f t 2 '
3t 3 0, t nên hs x 0; 2 .
Bpt f x x m no đúng x 0; 2 f t 3
t 3t đồng biến trên )
Giải: Xét hs g x f x x, x 0;2
m g(x), x 0;2 3
m 3sin x sin x
g ' x f ' x 1 0, x 0;2
m f 2 2 3
m sin x 3sin x
Hs y g x nghịch biến trên 0; 2 . Face: viethieu220284
Th.S Nguyễn Viết Hiếu 089908.3939 Trang 4 Face: viethieu220284
II.HÀM SỐ MŨ, HS LŨY THỪA, HS LOGARIT
Th.S Nguyễn Viết Hiếu 089908.3939
1.Lũy thừa mũ số nguyên a n le + log .
b log c log c 0 ,
a b 1;c 0 n n a b a Cho số thực
a và số nguyên dương n a a n chan + 1 0 ,ab 1 n log b a . a .
a ... .a (n thừa số a ) a log a
6.Tính chất lũy thừa với mũ số thực b log c log a n 1 0 b b
0 ,a ,bc a
1 a 0 a a
Cho a,b 0; , . + a c 1 n 0 a a 0 a 1
2.Lũy thừa mũ số hữu tỉ
a .a a a + log b b b b a . log log 1 2 a 1 a 2 m a b ;b 0 1 2 n m n a a *
a 0, m ;n
a a .
a b a .b b 0 a 1
3. Điều kiện xác định n A * n ; n 2 + 1 log log b log b a a 1 a 2 a a b b ;b 0 2 1 2 + n chẵn: Điều kiện A 0 b b a
+ n lẻ: Điều kiện A xác định +Nếu + b b a 0 1 log log a 1 thì
a a a 4. Phương trình n x b * b 0; n
+Nếu 0 a 1 thì
a a + n lẻ: n n
x b x b 1 a 7.Công thức logarit + log b 0 1 log b a a + n chẵn: n
x b(b 0) Vô nghiệm. + b 0; 0
a b log b 0 a 1;b 0 a n
x 0 x 0 0 a 1 a
+ log b có điều kiện b b + 0 1 log log 0 : n n b
x b x b a b 0 a a b 0; 0 5. Tính chất n * , n k ; , n k 2
+ log 1 0; log a 1 0 a 1 a a +Chú ý: log b ; * ; chẵn a n a a
+ log a 0 a 1; a 2 n .n n a b ab n
log b 2log b0 a 1;b 0 a a n b b log b + a a
b 0 a 1;b 0 2 log
b 2log b 0 a 1;b 0 a a
n a m n m a n k nk a a + log b log c b 0 ,
a c 1;b 0 a
Kí hiệu: log b logb lgb ; log b lnb log a 10 e c 8.Hàm số lũy thừa
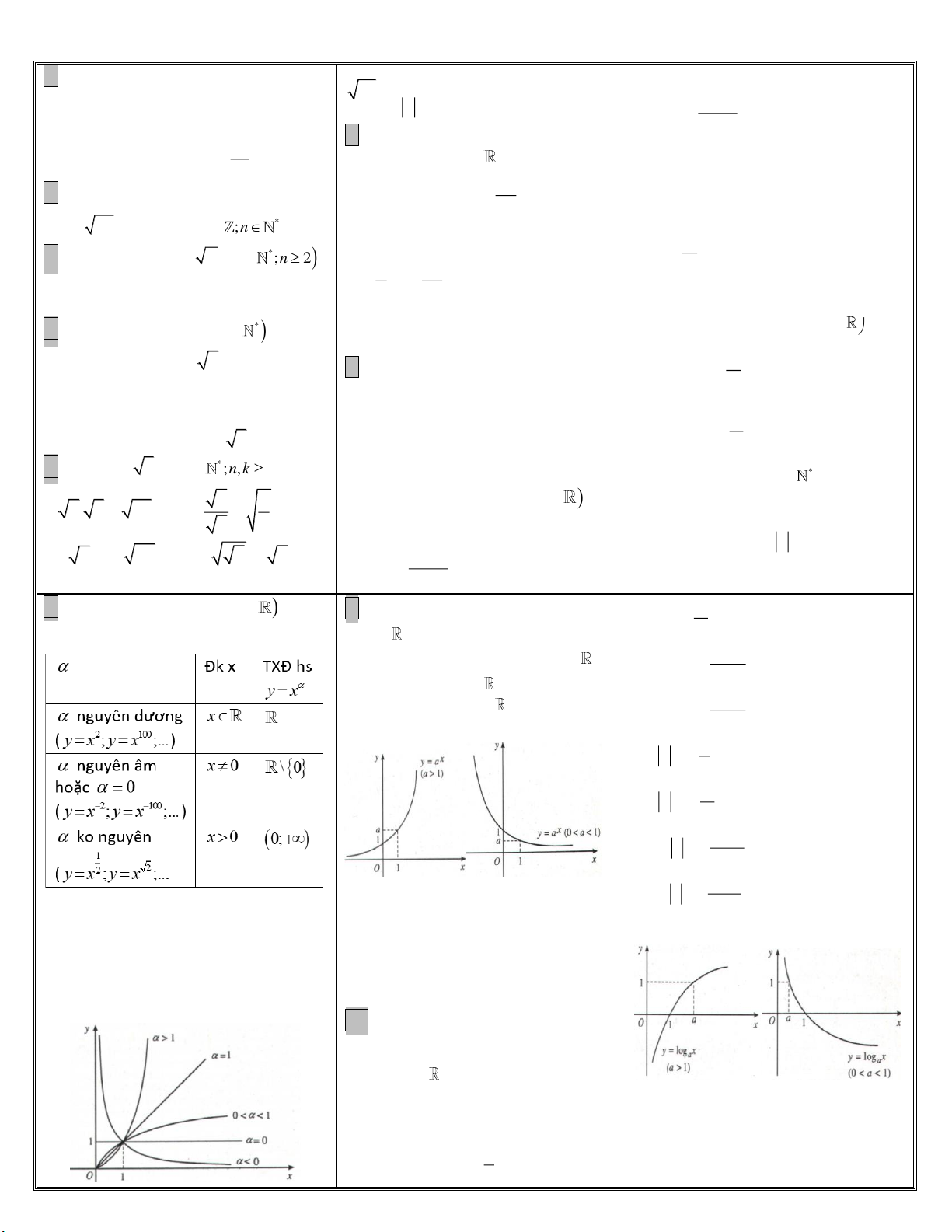
y x 9.Hàm số mũ x
y a 0 a 1 u ln u u 0 a/Txđ hs lũy thừa
y x tùy thuộc +TXĐ: u
+Tập giá trị: 0; (Vì x a 0, x ) x x a 1 log 0
+HS đồng biến trên khi a 1 . x ln a
+HS nghịch biến trên khi 0 a 1 . u log u u a 0 + Đths mũ x
y a 0 a 1 u ln a x 1 ln (x 0) x u ln u u 0 u x x a 1 log 0 x ln a
Trục Ox là TCN đths x u y a log u u a 0
b/Đạo hàm của hàm số lũy thừa + Đạo hàm hàm mũ: u ln a 0 a x 1 .x
+Đồ thị hs y log x 1 a x x e e u u e e .u u 1
.u .u x x a
a .ln a u . u a
u a .ln a c/Đồ thị hs lũy thừa
y x trên 0;
10.Hs logarit y log x 0 a 1 a +TXĐ: 0; +Tập giá trị:
+HS đồng biến trên 0; khi a 1.
+ Trục Oy là TCĐ đths y log x a +HS nb trên
+ Chú ý: Đồ thị các hs x y a và
0; khi 0 a 1 .
y log x (0 a 1) đối xứng nhau qua 1 a
+Đạo hàm: ln x x 0 đt y x . x Trang 5
Th.S Nguyễn Viết Hiếu 089908.3939 Face: viethieu220284
Th.S Nguyễn Viết Hiếu 089908.3939 11.a/Pt mũ cơ bản x
a b0 a 1 PP2: Đặt ẩn phụ c) x x 2 x 1 25 10 2 2 f x 25x 10x 2.4x 0 + b 0 : x
a b x
2 f x f x a a 2 a T
(Chia hai vế cho 25x hoặc 4x ) h.S N + b 0 : x
a b x log b a 2 x x f x f x 2 2 f x 5 5 gu
b/Phương pháp giải phương trình mũ 3 3 9 2 0 x 0 y ễ 2 2 n
PP1: Đưa về cùng cơ số 0 a 1
Bài 2. Giải các pt sau: Vi d/ 2 2 x x 2 x x ế x x 2 2 3 t f x g x a) 9 4.3 45 0 H a a
f x g x 2 2 2 x x x x i 2 ế 3 x 4.3x 45 0 2 2 3 u f x 089908. a
b(b 0) f x log b 2 2 x x 2 x x a 3x 9 VN 2 3.2 4 0 Bài 1. Giải pt a) 2 T x 3x 4 x log 5 5 5 125 2 h. 3939 S N 3 x x 3x 5 2 4 x 1 x 2 gu x x x x 2 1VN x 2
x 3x log 5 125 12 2 4 5 7 y b) ễ
5 24 5 24 98 x 2 n V e/ 2 2 x x x x 2 2 4.2
2 x 4 0 i x 2 x 1 ế 1 7 x t 5 24 b/ 98 x 1
8 0, 25. 2 (Đk: x 1) H iế x Đặt 2 2x x u ; 2 2 x v ; 2 . 2x x u v . 5 24 u
Pt trở thành: u.v 4u v 4 0 2x 1 7 3. x 2 089908. 2x x x 1 2 2 2
5 24 985 24 1 0
u
1 v 4 0
x 1 N 3939 2x 1 7x u 1 x 1 x 2 3. 2 2 x 1 2 x N v 4 x 0 7
PP3: Logarit hóa (Lấy logarit 2 vế)
PP4. Phương pháp hàm số
(HS 2t f t t đb trên ) 2 x
Bài 3. Giải pt a/ 3x.2x 1
Bài 4. Giải pt a) 3 11 x f 2
x x f 8 x
Lấy logarit cơ số 3 hai vế ta được pt: +Hs 3x f x đồng biến trên . x log 2 3x.2x log 1
+Hs g x 11 x nghịch biến trên 2
x x 8 4 x 3 3 x 2
+x=2 là 1 nghiệm của pt đã cho. x 0 x1 . x log 2 0
KL:x=2 là nghiệm duy nhất của pt.
12. a/Pt logarit log x b 0 a 1 3 a x log 3 2
b) 4x 6x 25x 2 log b
x b x a a x 1 x x b/
Xét hs f x 4 6 25x 2
5x.8 x 500 (Đk: x 0 )
b/ Phương pháp giải pt logarit 3x3 x3 f x x 2 x 2
4 ln 4 6 ln 6 0
PP1: Đưa về cùng cơ số x 3 2 x3
5 .2 x 5 .2 5 .2 x 1 log f x g x a a
loga 0
Ta có: x=0;x=2 là nghiệm. 1
Lấy logarit cơ số 5 hai vế ta được pt:
KL: Tập nghiệm S 0; 2
f x g x x 3 1 N 2
x 3 1 log 2 0 c) x x x 8 2 2 2
8 2x x
f (x) 0(g(x) 0) 5 x
x log 2 N 5 2 x x 2 x8 b 2
x x 2 8 x
+ log f x b f x a a
Bài 5.Giải pt: a/ log x log x log x 11 x x 1 x 1 3 9 27 b) log 3 1 .log 3 3 6 3 3 Đk: Đk: x>0 Đk: x 0 x 2
pt log x log x log x 11 2 3 3 3 3
pt log 3x 1 .log 3 3x 1 6 Đặt 2 u
x 3x 2,u 0 3 3
log x 6 x 729(N) 3 2 1 log 3x 1 log 3x 1 6 0 Pttt: log 2 .5u u 2 3 2 3 3
b/ log x 5 log x 2 3 2 2 5 Đk: x>5 28
x log 10; x log 1 u 3 3
Hs f u log u 2 .5 đồng biến 3 2
pt log x 5 x 2 3 27 2 5 PP3: Mũ hóa
trên 0; và f 1 2 x N
x 5 x 2 6 ( ) 3 2
Giải pt log 5 2x 2 x 2 x 3 (L)
+ u 1 là nghiệm duy nhất. PP2: Đặt ẩn phụ Đk: 5 2x 0 3 5
KL: Tập nghiệm S 1 2
x 0N Bài 6. Giải pt a) 1 2 pt x 2
5 2 2 x 5 log x 1 log x x 2 N
b) log x log x 1 3 2 3 Đk: 5 1 x
0; x 10 ; x 10
PP4: Hàm số biến thiên Đk: x 1 pt 2
log x 5log x 6 0
Bài 7. Giải các pt:
Hs f x log x log x 1 đồng 2 3 log x 2
x 100N x x 1 a)
biến trên 1; ; f 4 . log
x 3x 2 2 2 3 3 2 3 1 2 log x 3 x 1000 N 5
KL: x=4 là nghiệm duy nhất. Face: viethieu220284 Trang 6
Th.S Nguyễn Viết Hiếu 089908.3939 Face: viethieu220284 Zalo: 089908.3939
Th.S Nguyễn Viết Hiếu 089908.3939 2 x x x
d/Bpt logarit cơ bản log x b a a 0 1 x x 1 c) 1 2 2 log 5 5 2 2. 1 0 x Đk: x 0 2 2
Đk: 0 x 1
+ a 1 : log x b 0 b x a x a 5 1 pt x 1
2 log 2 x x log 1 x 2 2 + 0 a 1 : log b x b x a a 2 2 1 +Hs 2t f t
log t đồng biến trên
e/Công thức BPT mũ, logarit x log 2 5 x 2 5 f x g x 2 khoảng 0; 1 . + a 1 : a a
f x g(x) 1 VN 2
Pt f x f 1 x
f x g x f x g x
c/ log x 3 log x 2 1 2 2 a a ( ) log log 1 g(x) 0
x 1 x x Đk: x 3 2 f x gx
+ 0 a 1 : a
a f x g(x)
Bpt log x 3 x 2 1 2 13. BPT MŨ, BPT LOGARIT
x 3x 2 a/Bpt mũ cơ bản x f x g x
a b0 a 1 2 f x g x a a ( ) log log 2 + b 0 : x
a b x f (x) 0
x 5x 4 0
+ b 0;a 1: x
a b x log b Bài 8. Giải các bpt sau: 1 x 4 a 2 x 2 x 2
Đối chiếu điều kiện, tập nghiệm của +
b 0;0 a 1 : x
a b x log b a/ 3 1 x 2x 0 a
bpt là: S 3; 4 b/Bpt mũ cơ bản x 0 x 2
a b0 a 1 b/ log 2 x 2x 3 2 1 d/ log 5x 10 log x 6x 8 0,5 0,5 + b 0 : x
a b x 2
+ b 0;a 1: x
a b x log b 2 5x 10 0 a
x 2x 0 2 x 0 Đk: x 2 2
+ b 0;0 a 1 : x
a b x log b 2 x 6x 8 0 a
x 2x 8 2 x 4 c/Bpt logarit cơ bản 2
log x b0 a 1
Bpt 5x 10 x 6x 8 a c/ x 2 4 2.5 x 10x Đk: x 0 2 2.25x 10x 4x 0 x x 2 0 2 x 1 + a 1 : log b
x b x a
Đối chiếu điều kiện, tập nghiệm của a
Th.S Nguyễn Viết Hiếu 089908.3939
+ 0 a 1 : log x b 0 b x a bpt là: S 2 ; 1 a 14. Lãi suất kép Theo đề: n
A 1 r 2A
17.Độ pH của dung dịch pH log H
a/Một người gửi số tiền A đồng vào n log 2 9,51 (năm)
một ngân hàng với lãi suất r /năm. Biết 1r H
:nồng độ ion H trong dung dịch
rằng nếu không rút tiền ra khỏi ngân
Vì n là số tự nhiên nên ta chọn n 10
+ pH 7 : dung dịch có tính axit.
hàng thì cứ sau mỗi năm, số tiền lãi sẽ KL: 10 năm.
+ pH 7 : dung dịch có tính bazơ.
được nhập vào vốn ban đầu (người ta
15. Trong Vật lí, sự phân rã của các
+ pH 7 : dung dịch trung tính.
gọi đó là lãi kép). Hỏi người đó được
chất phóng xạ được biểu diễn bởi CT:
18. Độ chấn động M của một địa chấn
lĩnh bao nhiêu tiền sau n năm ( * n ), t
biên độ I được đo trong thang độ
nếu trong khoảng thời gian này không mt 1 T
Richte (Charles Francis Richter, nhà địa
rút tiền ra và lãi suất không thay đổi? m0 2
vật lí Mĩ, 1900 – 1985) xác định bởi:
Giải: Giả sử n 2 I
+Sau năm thứ 1, số tiền lĩnh là:
Trong đó: m là khối lượng chất phóng 0 M ln
( I là biên độ của dao 0
T A 1 r .
xạ ban đầu (tại thời điểm t 0 ) I0 1
+Sau năm thứ 2, số tiền lĩnh là:
+ mt là khối lượng chất phóng xạ tại
động bé hơn 1m trên máy đo địa
T T 1 r A1 r 2 thời điểm t.
chấn, đặt cách tâm địa chấn 100km, I 0 2 1
+ Tương tự, sau n năm, số tiền lĩnh là:
+ T là chu kì bán rã (tức là khoảng thời được lấy làm chuẩn).
gian để một nữa số nguyên tử của chất 19. Mức cường độ âm được tính theo T A r n n 1
phóng xạ bị biến thành chất khác). I
b/BT: Một người gửi 6 triệu đồng vào
16.Số các chữ số của số tự nhiên x
CT: L dB 10log (Graham Bell)
ngân hàng theo thể thức lãi kép, kì hạn I0
bằng : log x 1
1 năm với lãi suất 7,56% /năm. Hỏi sau
+ I là cường độ của âm, tức là năng
ít nhất bao nhiêu năm người gửi sẽ có
Với log x là phần nguyên của log x
lượng truyền đi bởi sóng âm trong 1
nhiều hơn 12 triệu đồng từ số tiền gởi
đơn vị thời gian và qua 1 đơn vị diện
Vd: Số các chữ số của 2008 2 bằng:
ban đầu (giả sử lãi suất không thay
tích bề mặt vuông góc với phương 2008 log2 1 2008log21 đổi)? Giải: 6
A 6.10 ; r 7,56% sóng truyền (đơn vị: 2 W / m ) 604,46 8 1 605 + 1 2 2 I 10
W / m là cường độ âm ở
Sau n năm, số tiền thu được n A 1 r 0 ngưỡng nghe. Face: viethieu220284 Trang 7
Th.S Nguyễn Viết Hiếu 089908.3939 Face: viethieu220284
III. NGUYÊN HÀM, TÍCH PHÂN, ỨNG DỤNG
Th.S Nguyễn Viết Hiếu 089908.3939 1/ 0dx C 20/ f
xdx FxC (F'x f x ) 39/ f '
xdx f xC 2/ b b
1dx x C 21/ k. f
xdx k f
xdx k 0 40/ (với k là hằng số). k. f
xdx k. f xdx a a 1 1 x 1 (ax b)
f x g x dx f x dx g x dx 3/ x dx C 1 22/ (ax b) dx . C 41/ 1 a 1 1 1 1 1 1 1 1 b b b 4/ dx C n 23/ dx . . C 42/ f
x gxdx f
xdx g
xdx n x n . ( 2) n 1 1 x
axbn a n
1 ax bn 1 a a a 1 1 1 b 5/
dx 2 x C 24/ dx
.2 ax b C b 43/ f
xdx Fx Fb Fa (Newton–Leibniz) x ax b a a a b b Th.S Nguyễn Viết Hiếu b
Th.S Nguyễn Viết Hiếu 089908.3939
44/ udv uv vdu
45/ udv uv vdu 089908.3939 a a a 1 n 1 1 n b a a n 6/ n n 1 dx x C 25/ dx . .n
ax b 1 C 46/ f
xdx f
xdx 47/ f
xdx 0 n x n 1 n ax b a n 1 a b a 2 1 2 b c b d7/ xdx x x C 26/ ax bdx . .
ax b. ax b C 48/ f
xdx f
xdx f
xdx (với a c b ) 3 a 3 a a c n 1 n 8/ n n xdx x x C
27/ n ax bdx .
ax b n ax b C 1 1 ax b 49/ dx ln C n 1 a n 1
ax bcx d ad bc cx d 1 1 1 9/
dx ln | x | C 28/ dx
ln ax b C 1 1 1 x a 50/ dx dx ln C x ax b a 2 2 x a
x ax a 2a x a 1 1 1 1 1 liên tục trên [ 10/ y f x
𝑎; 𝑏].Diện tích hình dx C 29/ dx C 51/Hs 2 x x ax b2 a ax b
phẳng giới hạn bởi đths y f x , trục Ox và hai đt 11/ x x
e dx e C axb 1 axb x ;
a x b được tính 30/ e dx e C b a x axb
bởi CT: S f A A ax b 1 x dx x c d a 12/ A dx C 31/ A dx . C ln A a ln A
(Chú ý với hình vẽ trên
13/ sin xdx cos x C 1 thì:
32/ sin(ax b)dx cos(ax b) C c d b a S
f (x)dx
f (x)dx f (x)dx 1 )
14/ cos xdx sin x C
33/ cos(ax b)dx
sin(ax b) C a c d a 1 1 1 15/ 52/Hs y f x
dx c otx C 34/
dx cot(ax b) C 2 sin x 2 sin (ax b) a
liên tục trên [𝑎; 𝑏]. 1 1 1 Diện tích hình 16/
dx tanx C 35/ dx
tan(ax b) C 2 2 phẳng giới hạn os c x cos (ax b) a
bởi đths y f x 1
17/ tan xdx ln cos x C 1 36/ tan
axbdx ln cosaxb C , đths y f x a 2 1 và hai đt
18/ cot xdx ln sin x C T 37/ cot
ax bdx ln sinax b C h. x ;
a x b được tính bởi công thức: S N a gu b dx 1 x dx 1 1 ax b y 19 / arctan C 38 / . arctan C ễ 2 2 2 2 ax b k a k k
S f x f x dx n x k k k 1 2 Vi a ế k 0 k 0 t Hi 53/Hàm số ế
y f x liên tục trên [𝑎; 𝑏]. Gọi (H) là hình phẳng giới u 089908.
hạn bởi đths y f x , trục Ox và hai đt x ; a x b .
Thể tích của khối tròn xoay thu được khi quay hình phẳng (H) quanh 3939 b
trục Ox là: V f
x 2 dx a Trang 8
55/ Một vật chuyển động với pt 57a/ HS 𝑦 = 𝑓(𝑥) là hàm
54/Cắt một vật thể T bởi hai mp (P) và (Q) vuông góc với
vận tốc v(t). Quãng đường vật chẵn và liên tục trên đoạn
trục Ox lần lượt tại x ; a x ( b a )
b . Một mp tùy ý vuông
di chuyển trong khoảng thời [−𝑎; 𝑎] thì
góc với Ox tại điểm x ( a x b ) cắt T theo thiết diện có gian từ t a đến t , b a b 𝑎 𝑎
diện tích là S(x). Giả sử S(x) liên tục trên đoạn
∫ 𝑓(𝑥)𝑑𝑥 = 2 ∫ 𝑓(𝑥) 𝑑𝑥 [𝑎; 𝑏]. Thể là: 𝑏
𝑆 = ∫ |𝑣(𝑡)|𝑑𝑡 b −𝑎 0 𝑎
57b/ Hs 𝑦 = 𝑓(𝑥) là hàm lẻ
tích của phần vật thể T được tính bởi CT: V S xdx
56/ PP tính nguyên hàm,TP PP1: Đổ và liên tục trên đoạn a i biến. [−𝑎; 𝑎] 𝑎
PP2: Tính nguyên hàm, TP
thì ∫ 𝑓(𝑥)𝑑𝑥 = 0 −𝑎 từng phần. Face: viethieu220284
Th.S Nguyễn Viết Hiếu 089908.3939 /2 B3.a Bài1.Tính: a) 2 x x 7dx B5. Tính a) ln xdx b/ sin x I e cos x dx Tính diện tích Đặt 2 2 2 u x 7 u x 7 0 1 hp giới u ln x dv dx Đặt t sin x dt cos xdx udu
xdx , Tích phân trở hạn bởi x 3 u đths 3
y x , trục hoành và 2 dv dx , chọn v . x thành: 2 u du C đường thẳng x 1;x 2 . 1 3 ln xdx x ln x x. dx 1 2 1 x t 1 t 17 2 2 2 3 x x 7dx (x 7) x 7 C I e dt e e 1 S x dx x ln x x C 3 0 4 0 1 1 1 b) 5 sin2x.cos xdx 3 x c/ I dx b) x I xe dx 4 2 Đặt t cos x dt sin xdx x 3x 2 0 0 Tích phân trở thành: Đặt 2 t x dt 2xdx u x du dx 7 2 x 6 t v e 2t dt C x dv e dx , chọn . 7 1 1
B3b) Tính diện tích hp giới 1 x x I xe e dx 1 7 2cos 1 t hạn bởi 2 đt x 0;x và 5 x sin2x.cos xdx C I dx 0 2 0 7 2 t 3t 2 đt2hs y
cos x ; y sin x 0 1 1 2 1 3
Th.S Nguyễn Viết Hiếu 089908.3939 dx ln3 ln2 S
sin x cos x dx 2 2
Th.S Nguyễn Viết Hiếu 089908.3939 2 t 2 t 1 2 0 0 x 1 B3c) Tính diện tích hình e c) 1 e 1 ln x dx dx d/ c)I dx x x x 2 I dx
phẳng giới hạn bởi 2đths e e 2 (e 1) 2 1 x 2 x 0 3 y x x và 2 y x x . 1 Đặt x 1 x t e dt e dx 1 Tích phân trở thành: Đặt x tan t,t ; x 0 u ln x du dx 2 2 Pt 3 2 x x x x x dt 1 x 1; 2 C 1 1 2 t t 1 dv dx , chọn v . 2 dx 1 tan t dt 37 2 3 2 x x 1 1 S
(x x) (x x )dx dx C 12 e e x x 1 1 2 e e 2 x e 1 4 2 4 2 1 tan t I ln x dx 1 I dt 1dt 2 x x e 2 1 tan t 4 1 1 0 0
Bài 2/ Tính các tích phân sau: 1
Bài 3d) Cho hp (H) giới hạn
B4/Tính thể tích V của phần vật thể 2 2 1 e/ I x 1 x dx bởi đths y sin x,Ox, 2 đt
giới hạn bởi hai mp x = 1 và x = 3, biết a/ 2
I x 1 x dx
rằng khi cắt vật thể bởi mp tùy ý vuông 0 x 0;x . Tính thể tích
góc với trục Ox tại điểm có hoành độ x 0
khối tròn xoay thu được khi Đặt x sin t,t ; 1 x 3 quay (H) quanh Ox.
thì được thiết diện là Đặt 2 t 1 x tdt xdx 2 2
một hình chữ nhật có độ dài hai cạnh 2 3x 2 dx cos tdt là 3x và . 1 3 0 1 3 124 t 1 2 2 2 2 V 3x 3x 2dx I t dx t dx 1 2 2 3 3 I sin 2tdt 3 2 1 1 0 4 16 0 V sin xdx 0 2 Face: viethieu220284 0 Trang 9 Face: viethieu220284 IV.SỐ PHỨC
Th.S Nguyễn Viết Hiếu 089908.3939
1.Số phức z a bi
(a bi) (c di) 5. 2 số phức z,w:
7. Số phức w đgl căn bậc hai của số phức ( 2 , a b ;i 1 ) 2 2
(a c) (b d )i .
z z z
z nếu w z .
a : phần thực của z.
(a bi) (c di) | . z w | | z | .| w |
+Số thực a 0 có 2 căn bậc hai a . T
b : phần ảo của z.
h.S N +Số 0 có 1 CBH là 0. i : đơn vị ảo.
(a c) (b d)i z | z |
w 0 guy +Số thực a 0 có 2 CBH là i a . 1 2 3 4 i ; i i 1
; i ;i i 1 (a bi).(c di) w | w | ễn V
+ Số phức liên hợp của z là iế 8. Ptbậc 2hệ số thực
(ac bd) (ad bc) .i | z | | z | t H
az bz c a a b c
z a bi 2 0 ( 0; , , ) i c di
(c di)(a bi)
z w z w ếu
+ Số phức nghịch đảo của 089908. 2 . z w . z w b 4ac 1 a b a bi (a bi)(a bi) z là: + 0, pt có 2 nghiệm thực .i 3939 2 2 2 2 z z z a b a b ac bd ad bc i ; w 0 b z
2.Cho 2 số phức: a bi 2 2 2 2 a b a b w w 1,2 2a
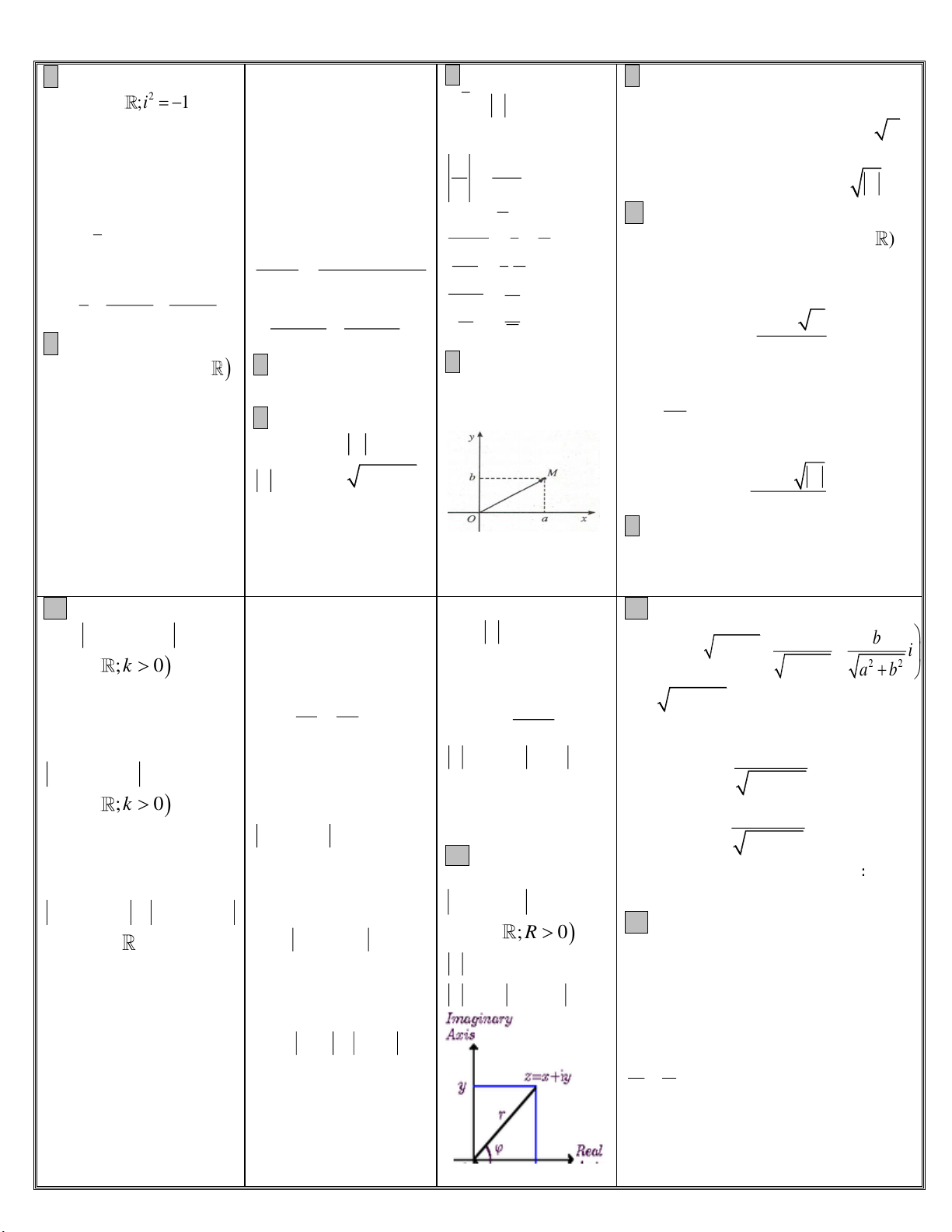
c di a,b,c,d 3. Điểm biểu diễn số 6.2 số phức z,w có 2
+ 0, pt có nghiệm kép thực
điểm bd lần lượt là M,
phức z a bi là M a;b a c b
a bi c di N thì: | z w | MN 4. Modun của số phức z b d 2a
z a bi là z .
+ , pt có 2 nghiệm phức 0 a 0
a bi 0 2 2 z OM a b b i b 0 z . 1,2 2a
a bi là số thực b 0
9. Pt bậc n hệ số phức
a bi thuần ảo a 0
Th.S Nguyễn Viết Hiếu 089908.3939 n n 1 a z a
z ... a z a 0 n n 1 1 0
, a 0 có n nghiệm. n
10. +Tập hợp điểm bdsp z -Nếu O là trung điểm Vd2: Cho số phức z
12. Dạng lượng giác của số phức
thỏa z a bi k
F F và F ; F thuộc
thỏa z 4 . Tìm tập 1 2 1 2 a b 2 2 Ox thì pt chính tắc của
hợp điểm bdsp w thỏa
z a bi a b . i
a,b ; k 0 là 2 2 2 2 đường Elip là: a b a b
w (3 4i)z i .
đường tròn tâm I ; a b , 2 2 x y 2 2
r a b là modun của z. 1 Giải: w i
bán kính R k. z 2 2 a b
là một argument của z thỏa 3 4i Th
+Tập hợp điểm bdsp z thỏa .S N 2 2 2 0 b ;
a a b c z 4 w i 20 a 08
z a bi k cos gu
Tập hợp điểm bdsp w 9908 2 2 yễ
Vd1a/Tập hợp điểm a b n
a,b ; k 0 . là hình 3939 V bdsp z thỏa
là đường tròn tâm i b ết I 0; 1 si n H
tròn tâm I ;
a b , bán kính z 1 2i 5 là
,bán kính R 20. 2 2 iế 11. Trong tất cả số a b u R k.
đường tròn tâm I 1; 2
phức z thỏa
Dạng lượng giác của số phức z là:
+ Tập hợp điểm bdsp z thỏa Bán kính R 5.
z r.cos i sin
z a bi R
z a bi z c di b/Tập hợp điểm bdsp z 13. Cho 3 số phức
a,b ; R 0 thì: a, , b , c d
là đường thỏa z 3 4i 2 là
z r.cos i sin
trung trực của đoạn thẳng hình tròn tâm I 3;4 , z OI R max
z r . cos i sin 1 1 1 1 PQ, với P ; a b;Q ;
c d bán kính R 2. z OI R min
z r . cos i sin 2 2 2 2
+Trong mp Oxy, cho hai c/Tập hợp điểm bdsp z điểm F ; F
thỏa thỏa z 3 z 2i là
z .z r .r .cos isin 1 2 1 2 1 2 1 2 1 2
F F 2c 0 . Tập hợp đường trung trực d của z r 1 1 1 2 .cos
isin 1 2 1 2
điểm M trong mp Oxy thỏa đoạn thẳng PQ với z r 2 2 P 3;0
MF MF 2a a c
; Q 0; 2 . n n
z r .cos n i sin n 1 2
là 1 đường Elip nhận Pt d: 6x 4y 5 0. (CT Moirve)
F ; F là 2 tiêu điểm.
Th.S Nguyễn Viết Hiếu 089908.3939 1 2 Face: viethieu220284 Trang 10 Face: viethieu220284
V.THỂ TÍCH KHỐI ĐA DIỆN
Th.S Nguyễn Viết Hiếu 089908.3939
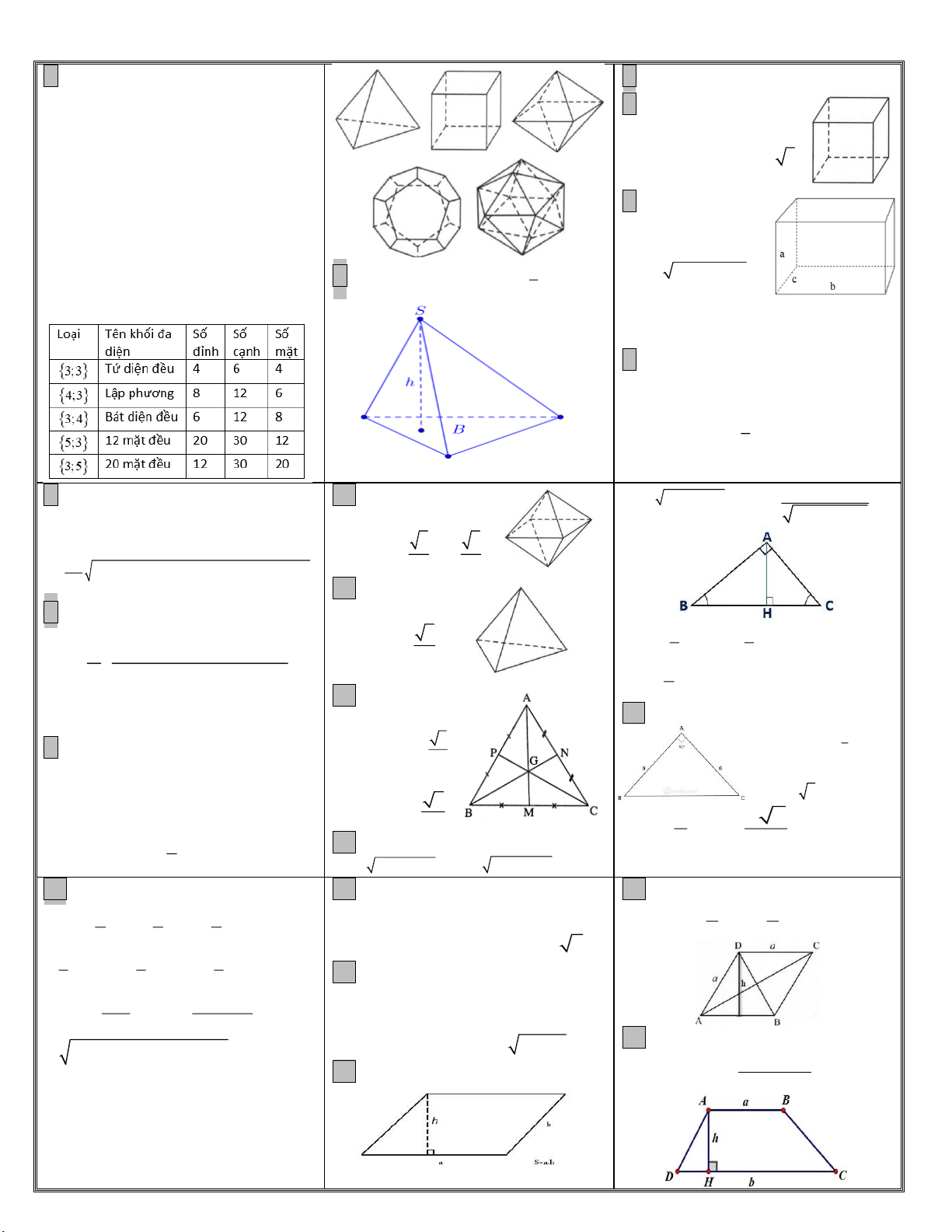
1. Hình đa diện, kh ối đa diện, khối đa
3. Thể tích khối lăng trụ: V S .h LT day
diện lồi, khối đa diện đều
4.Khối lập phương cạnh a
+Khối đa diện đều loại ; p q là khối V canh3 3 a KLP
đa diện lồi có các tính chất sau:
Độ dài đường chéo: a 3
a)Mỗi mặt của nó là một đa giác đều p cạnh.
b)Mỗi đỉnh của nó là đỉnh chung của 5. Khối hộp chữ đúng q mặt. nhật: V . a . b c KHCN
+Định lí: Chỉ có 5 loại khối đa diện đều. Độ dài đường Đó là loại 3; 3 , loại 3; 4 , loại 4;
3 , 2. Thể tích khối chóp: 1 chéo: 2 2 2 V .S .h a b c KC 3 day Với a, , b c lần lượt loại 3; 5 và loại 5; 3 .
là chiều dài, rộng, cao của hhcn.
6.Cho tứ diện ABCD có AB, AC, AD đôi
một vuông góc. Thể tích khối tứ diện ABCD là: 1 V A . B AC.AD ABCD 6
Th.S Nguyễn Viết Hiếu 089908.3939
7. Cho khối chóp S.ABC có SA a ; 10. Thể tích khối bát 2 2 . AB AC AB
BC AC ; AH 2 2 SB ;
b SC c ;𝐵𝑆𝐶 ̂ = 𝛼;𝐶𝑆𝐴 ̂ = 𝛽; diện đều cạnh a AB AC 𝐴𝑆𝐵
̂ = 𝛾. Thể tích khối chóp S.ABC là: V canh3 2 2 3 a abc 2 2 2 V
1 2cos.cos .cos cos cos cos 3 3 6 11. Thể tích khối
8. Thể tích khối chóp V tứ diện đều
S . A A ...A : 1 2 n 1 1 2 S .S .sin
V canh3 2 S A . B AC AH.BC S ABC 1 A 2 A 1 A 2 A ... V . n A 12 2 2 3 A A 1 AI
BC (I trung điểm BC) 1 2 12. ABC đều: 2
Biết SA A ; A A ...A + Diện tích: 14. ABC
vuông cân tại A (AB=AC=𝑎) 1 2 1 2 n D.tích: 1 2
9. Thể tích khối tứ diện có khoảng cách S a S canh ABC ABC 2 3 . 2 4
và góc giữa cặp cạnh đối diện + Độ dài đường Độ dài cạnh huyền: AD ;
a BC b ; d A ;
D BC d ; BC a 2 cao: canh 3 (𝐴𝐷; 𝐵𝐶 ̂ ) = 𝛼 . bằng: 2 1 a 2 AI BC 1 13. Tam giác ABC vuông A 2 2 V abd.sin ABCD 6 2 2 (I là trung điểm BC) BC AB AC ; 2 2 AC BC AB 15.Diện tích A
BC a BC;b AC;c AB 16. Hình vuông 19. Diện tích hình thoi 1 1 1 +Diện tích: 2 S canh 1 1 S . a h b.h c.h S . a h AC.BD ABC 2 a 2 b 2 c 2 2
+Độ dài đường chéo: canh 2 1 1 1 a . b sinC b . c sinA acsin B
17. Hình chữ nhật có chiều dài, chiều 2 2 2 rộng lần lượt là abc
a b c , a b . . p r vs p 4R 2 +Diện tích HCN: S = . a b 20. Diện tích hình thang:
p p a(p )
b p c +Độ dài đường chéo: 2 2 a b
a b.h
p: nữa chu vi tam giác ABC.
18. Diện tích hình bình hành: S . a h S 2
R: bán kính đtròn ngoại tiếp ABC .
r: bán kính đtròn nội tiếp ABC .
h ;h ;h lần lượt là độ dài đường cao a b c
kẻ từ A,B,C của ABC .
Th.S Nguyễn Viết Hiếu 089908.3939 Face: viethieu220284 Trang 11 Face: viethieu220284
Th.S Nguyễn Viết Hiếu 089908.3939
Th.S Nguyễn Viết Hiếu 089908.3939
21. Tỉ số thể tích khối chóp tam giác
23. Tỉ số thể tích hình lăng trụ
25.Tỉ số V hai khối chóp có chung V
SA' SB ' SC ' đường cao.
S . A' B 'C ' V 1 AM BN CP . . ABC.MNP V SA SB SC V 3 AA' BB ' CC ' V S AN AM S . ABC
ABC. A' B 'C ' S . AMN AMN . V S AC AB S . ABC ABC
22. Tỉ số thể tích khối chóp tứ giác, đáy ABCD là hình bình hành.
24. Tỉ số thể tích hình lăng trụ, đáy V
a b c d hình bình hành
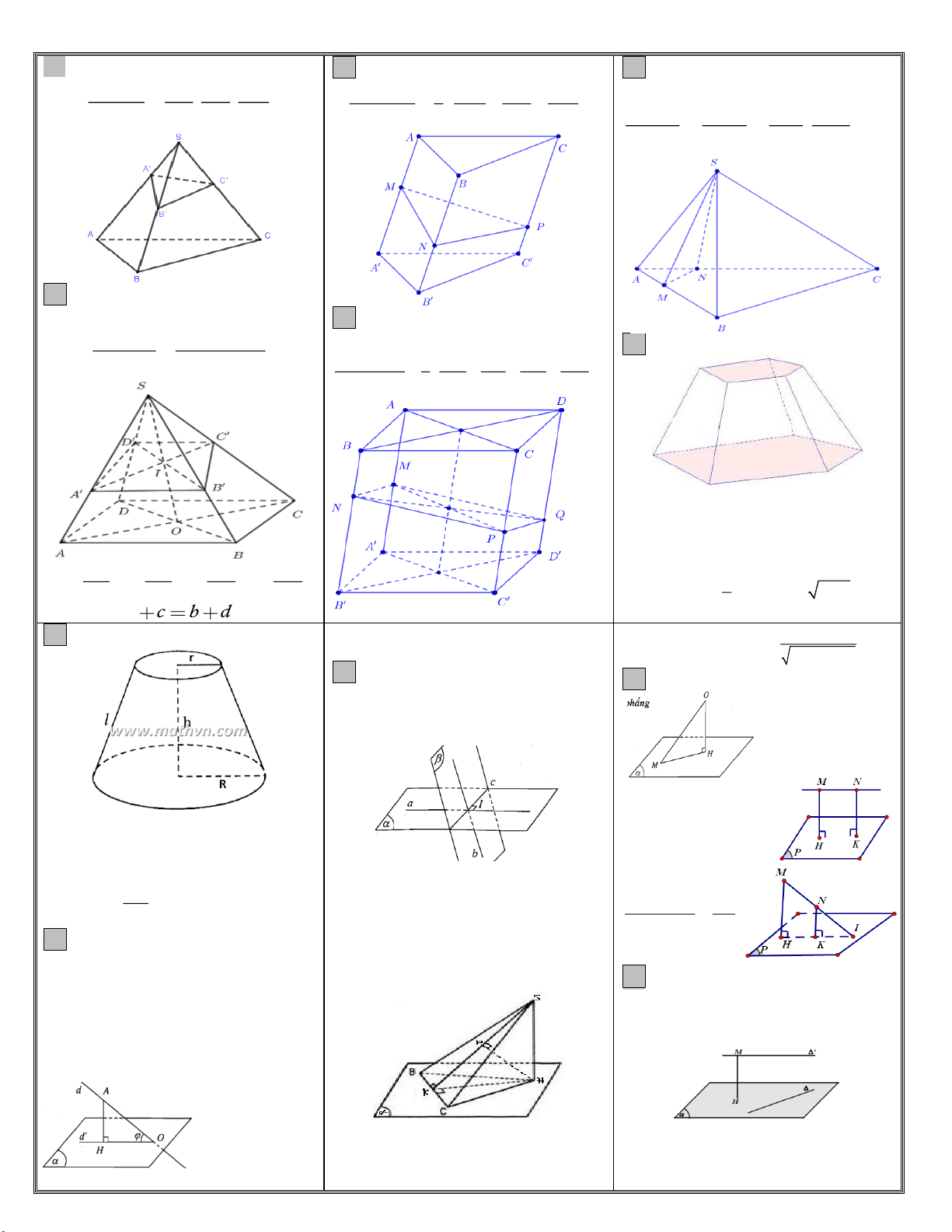
S . A' B 'C 'D'
26. Thể tích khối chóp cụt V 4abcd V AM BN CP DQ ABCD 1 .MNPQ S . ABCD V 4 AA' BB ' CC ' DD '
ABCD.A' B 'C 'D'
Gọi B và B’ lần lượt là diện tích của đáy
lớn và đáy nhỏ của hình chóp cụt, h là
chiều cao của nó (h là khoảng cách
giữa 2mp chứa 2 đáy). Thể tích khối SA SB SC SD a ;b ;c ; d 1 SA' SB ' SC ' SD '
chóp cụt: V hB B' . B B ' a c b d 3
Th.S Nguyễn Viết Hiếu 089908.3939
27. Thể tích khối nón cụt SH.HK + A ;
O AOH
d H;SBC HP 2 2 SH HK
29. Góc giữa 2 mặt phẳng
30. Khoảng cách từ điểm đến mp
+Góc giữa 2mp là góc giữa 2đường
+ d O; OH
thẳng lần lượt vuông góc 2mp đó.
+Cách xác định góc giữa 2mp cắt nhau H là hcvg của O trên . +MN // (P)
Gọi R, r, h lần lượt là bán kính đáy lớn,
d M;P d N;P
bán kính đáy nhỏ, chiều cao của hình nón cụt.
c ; Tìm mp c +MN cắt (P) tại I h V 2 2 R r . R r
d M;P
a ; b MI 3
d N;P NI
28.Góc giữa đường thẳng và mặt
; ; a b
phẳng: Cho đt d và mp .
+ SBC ; 𝐻𝐾𝑆 ̂
31. K/c giữa 2đt chéo nhau ; '
+Nếu d thì d 0 ; 90 CT1: d ;
' d M;
+Nếu d ko vuông thì
( chứa và song song ' )
d; d;d' Với d’ là hcvg của d trên mp .
SH ; BC . CT 2 : d ; ' HK
K, P lần lượt là hình chiếu vuông góc của H trên BC, SK.
(HK:đoạn vuông góc chung của ; ' ) Face: viethieu220284 Trang 12
Th.S Nguyễn Viết Hiếu 089908.3939 Face: viethieu220284 VI.KHỐI TRÒN XOAY
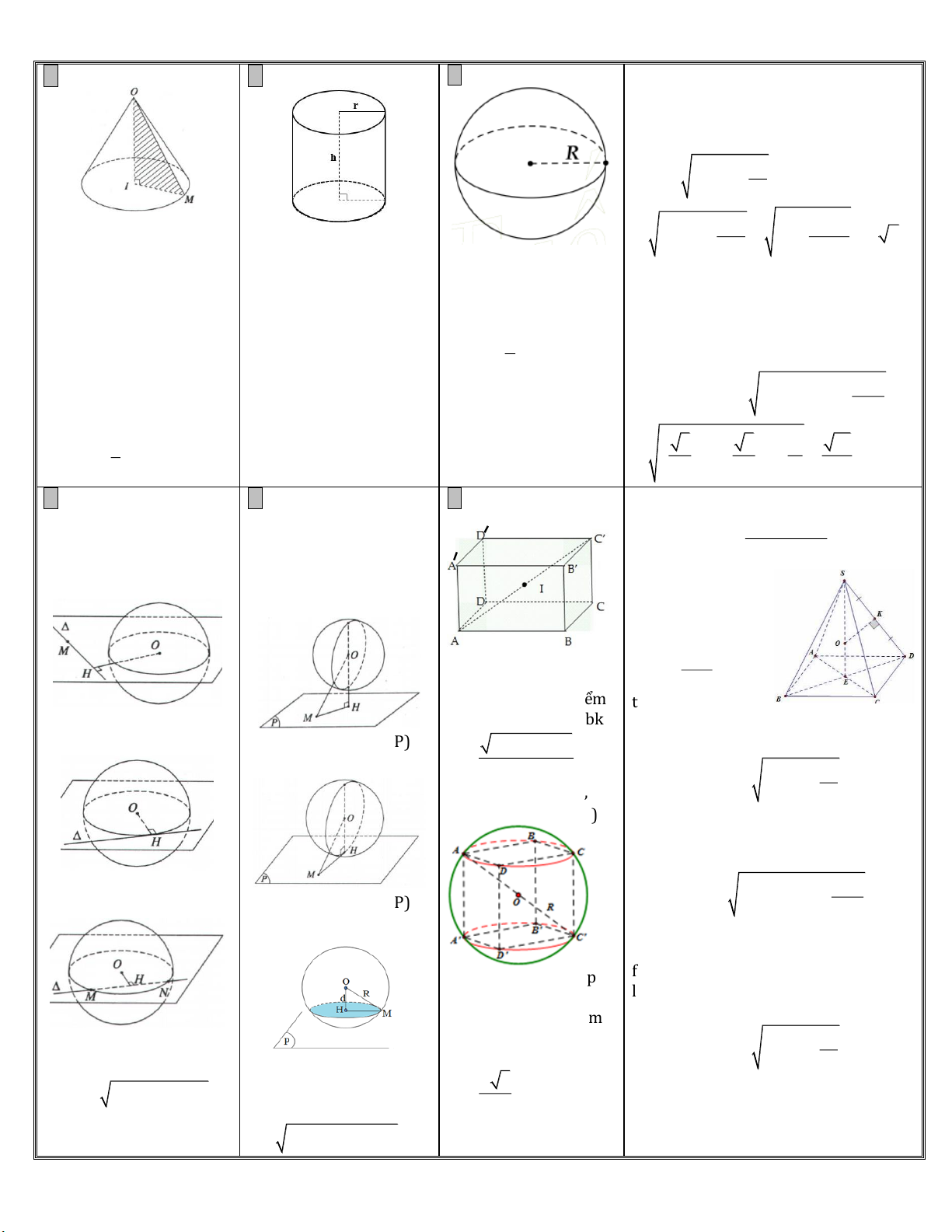
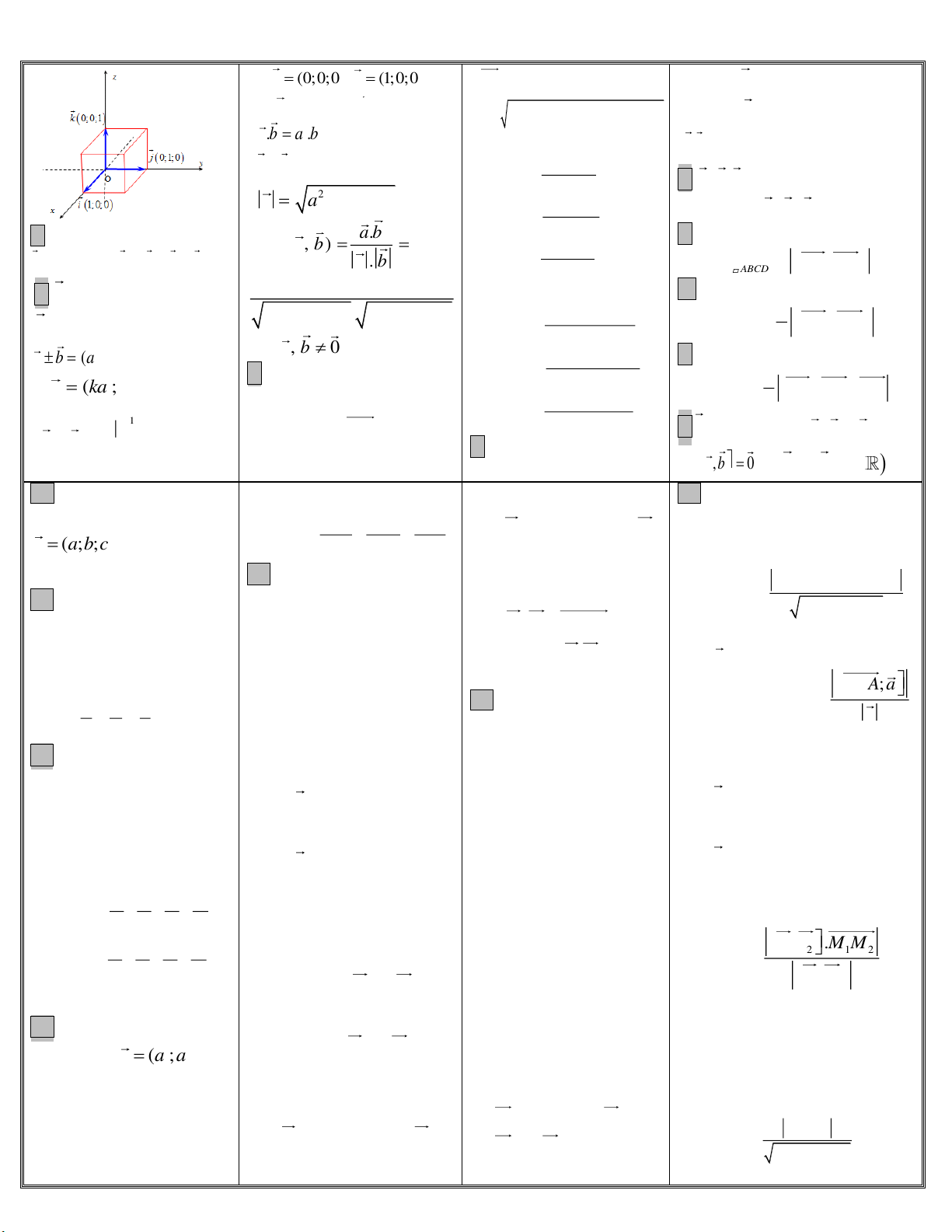
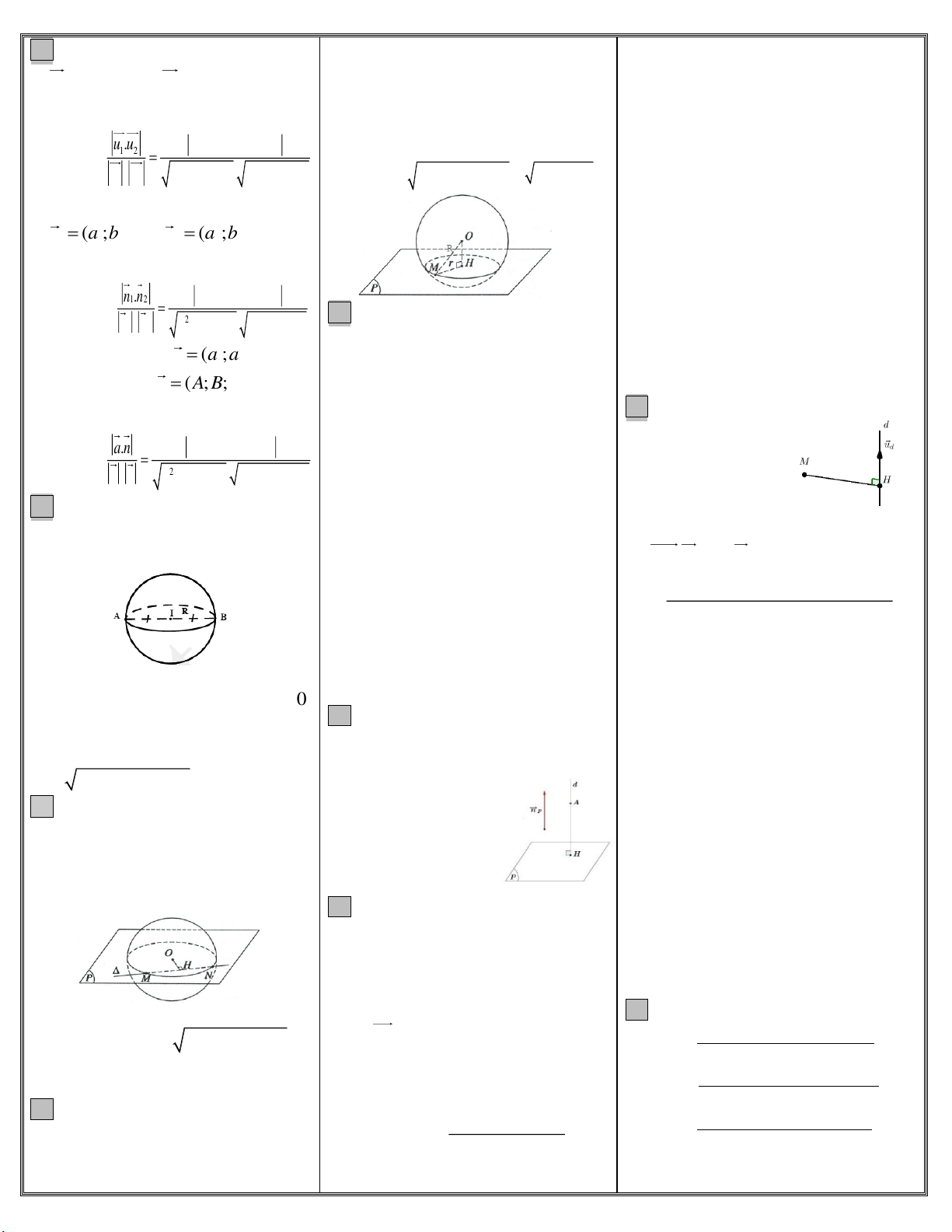
Th.S Nguyễn Viết Hiếu 089908.3939 1. Hình nón, khối nón 2. Hình trụ, khối trụ 3. Mặt cầu, khối cầu
BT1a)Cho hình chóp S.ABC có
SA ABC , tam giác ABC vuông tại B.
AC 2a SA 2a . Bán kính mặt cầu ngoại l l
tiếp h.chóp S.ABC bằng: h 2 h 2 R R Cau day 4 r
h:chiều cao của hình nón. SA 2a2 2 2 2
r: bán kính đáy hình nón. h:chiều cao hình trụ R a a 2 day 4 4 l: độ dài đường sinh
r: bán kính đáy hình trụ. R là bán kính mặt cầu
b) Cho hình chóp S.ABC có đáy ABC là tam h.nón.
l:độ dài đường sinh htrụ. + Diện tích mặt cầu:
giác đều cạnh bằng 1, mặt bên SAB là tam 2 2 2 2
l h r h l S 4 R
giác đều và nằm trong mp vuông góc với +Diện tích xung quanh +Diện tích xung quanh + Thể tích khối cầu:
đáy. Tính bán kính mặt cầu ngoại tiếp hình của hình nón:
chóp S.ABC.(Minh họa 2017) S rl. của hình trụ: S 2 rl. 4 xq 3 xq V R
+Bán kính mặt cầu ngoại tiếp hình chóp +Diện tích toàn phần: +Diện tích toàn phần: 3 2 2 AB 2 2 2
S rl r . S 2 rl 2 r . tp S.ABC bằng: R R R tp day ben 4 +Thể tích khối nón: +Thể tích khối trụ: Th.S Nguyễn Viết Hiếu 2 2 2 V r . h 089908.3939 2 3 3 1 15 1 2 KT V r . h . KN 3 3 3 4 6
4. VTTĐ của đt và mặt cầu 5. VTTĐ của mp và 6. Mặt cầu ngoại tiếp
c)Mặt cầu ngoại tiếp hình chóp đều có
Cho mặt cầu (S), tâm O, m.cầu hình đa diện canhben2
bán kính R và đt .Gọi H Cho mặt cầu (S), tâm O, bán kính R Cau là hcvg của O trên . bán kính R và mp(P).Gọi 2.chieu cao +Bán kính mặt d ;
O OH H là hcvg của O trên (P). cầu ngoại tiếp d ; O ( ) P OH hình chóp đều S.ABCD là: T a)Mặt cầu ngoại tiếp 2 SA h.S N ,E là HHCN ABCD.A’B’C’D’ RCau 2SE gu y có tâm I là trung điểm tâm đáy ABCD. ễ + d ; O R thì n
AC’,A’C, BD’,B’D và bk V
d)Bán kính mặt cầu ngoại tiếp hình chóp iế không cắt (S).
+ d O;P R thì (P) 2 2 2 t
a b c
có cạnh bên vuông góc mặt đáy là: H R không cắt (S). iếu 2 2 T h h 2 089908. .S N ( R R a, , b c 3 l chiều dài, Cau day 4 gu
rộng, cao của HHCN) yễ (h là chiều cao hình chóp). 3939 n V
e/ Bán kính mặt cầu ngoại tiếp hình iế
t chóp có mặt bên vuông góc mặt đáy là: Hi + d ;
O R thì tiếp ế 2 u AB 2 2 089908. R
R R xúc với (S) tại H.
+ d O;P R thì (P) Cau day ben 4 tiếp xúc (S) tại H. 3939
(với AB là giao tuyến mặt bên vuông góc mặt đáy và đáy). b)Mặt cầu ngoại tiếp
f/ Bán kính mặt cầu ngoại tiếp hình hình lập phương
lăng trụ đứng (hình lăng trụ có mặt cầu ngoại tiếp) là:
ABCD.A’B’C’D’ có tâm + 2 d ;
O R thì cắt O là trung điểm h 2 R R Cau day (S) tại 2 điểm pb MN. +
AC’,A’C,BD’,B’D và bk
d O; P R thì (P) 4 a 3
(h là chiều cao hình lăng trụ đứng) 2 2
MN 2 R d ; O
cắt (S) theo đường tròn R , với a là (C), tâm H, bk r: 2 (H là trung điểm MN) cạnh của h.lập phương Th.S Nguyễn Viết Hiếu 2 2
r R d ; O P ABCD.A’B’C’D’. 089908.3939 Face: viethieu220284 Trang 13 Face: viethieu220284 VII.KHÔNG GIAN OXYZ
Th.S Nguyễn Viết Hiếu 089908.3939
0 (0;0;0), i (1;0;0)
+ AB (x x ; y y ; z z )
a (a , a , a ) B A B A B A 1 2 3
j (0;1;0), k (0;0;1) 2 2 2
AB (x x ) (y y ) (z z )
b (b , b , b ) B A B A B A 1 2 3
+ a.b a .b a .b a .b 1 1 2 2 3 3
+ I là trung điểm AB
;ab (a b a b ; ab a b ;ab a b ) 2 3 3 2 1 3 3 1 1 2 2 1 + a b a b a b a b 0 x x 1 1 2 2 3 3 A B x I 5. , a , b c đồng phẳng 2 + 2 2 2 a
a a a 1 2 3 y y A B [ , a ] b .c 0 y I 1. Tọa độ vectơ a.b 2
6. Diện tích hình bình hành ABCD cos(a, b ) z z
u ;x y; z u xi y j zk a . b A B z I S
AB, AD 2 ABCD
2. a (a ; a ; a ), a b a b a b 1 1 2 2 3 3 +G là trọng tâm ABC
7. Diện tích tam giác ABC 1 2 3 2 2 2 2 2 2
a a a . b b b
x x x 1
b (b ;b ;b ), k R 1 2 3 1 2 3 A B C x S
AB, AC ABC 1 2 3 G 3 2
(với a, b 0 )
a b (a b ; a b ; a b )
y y y
8. Thể tích khối tứ diện ABCD 1 1 2 2 3 3 A B C
3. Tọa độ điểm:
C (x ; y ; z ) yG 1
+ ka (ka ; ka ; ka ) C C C 3 V
[AB, AC].AD 1 2 3 (
A x ; y ; z ), (
B x ; y ; z ) ABCD
z z z 6 A A A B B B A B C a b z 1 1 G 3
9. a cùng phương b b 0 + M ( ; x ; y z) OM ( ; x ; y z)
a b a b 2 2
4. Tích có hướng 2 vectơ
Th.S Nguyễn Viết Hiếu 089908.3939 a b
a,b 0 a kbk 3 3 10. Mp(P) đi qua
+Nếu a a a 0 thì pt chính + d chéo d
16.a/Khoảng cách từ điểm 1 2 3 1 2
M (x ; y ; z ) và có 1 vtpt
M x ; y ; z đến mp 0 0 0 0 0 0 0 0 x x y y z z tắc của d: 0 0 0 u kocung phuong u 1 2 n ( ; a ; b ) c . Pttq của (P): a a a
: Ax By Cz D 0 bằng: 1 2 3 He Ivonghiem
a x x b y y c z z 0 0 0 0 14. Cho 2đt
Ax By Cz D + d chéo d
d M ,() 0 0 0 0 11. Mp (P) đi qua 3 điểm
x x ta 1 2 1 1 2 2 2
A B C
A a;0;0 , B 0; ; b 0 ,
d : y y tb (tham số t) u , u .M M 0 1 2 1 2 1 1 1 b/Cho đt đi qua M 0 và có 1
C 0;0; c với , a , b c 0 .
z z tc
+ d d u .u 0
vtcp a . Khoảng cách từ điểm A 1 1 1 2 1 2 Pt (P) theo đoạn chắn:
x x sa M ; A a 2 2 x y z 15. VTTĐ giữa mp và đt đến đt : 0 d ( , A ) 1.
d : y y sb (tham số s) a 2 2 2 a b c : Ax By Cz D 0
z z sc
c/ Cho 2đt chéo nhau d và d 1 2
12.Cho 2 mp ; có pt 2 2
x x ta 0 1
+ d đi qua M (x ; y ; z ) và có 1
+ d đi qua M (x ; y ; z ) và có 1 1 1 1 1
: A x B y C z D 0 1 1 1 1 1
Đt d: y y ta 1 1 1 1 0 2 vtcp u1
(a ;b ; c ) . 1 vtcp u1
(a ;b ; c ) . 1 1 1
: A x B y C z D 0 1 1 1 z z ta 0 3 2 2 2 2
+ d đi qua M (x ; y ; z ) và có
+ d đi qua M (x ; y ; z ) và có 1 2 2 2 2 2 2 2 2 2 2 Xét pt (*):
+ ; cắt nhau (
A x ta ) (
B y ta ) C(z ta ) D 0 vtcp u 2
(a ;b ; c ) . 1 vtcp u2
(a ;b ; c ) . 0 1 0 2 0 3 2 2 2
A : B :C A : B :C 2 2 2 1 1 1 2 2 2 +d// (*) vô nghiệm.
Khoảng cách giữa 2 đt chéo nhau A B C D x ta x sa + 1 1 2 2 / / 1 1 1 1
+d (*) có vô số ng. d và d là: A B C D
Xét hệ (I) y tb y sb 1 2 2 2 2 2 1 1 2 2 A B C D + d cắt (*) có u ,u .M M 1 2 1 2 + 1 1 1 1 z tc z sc 1 1 2 2
d (d , d ) 1 2 A B C D nghiệm duy nhất. 2 2 2 2 u , u u ku
(Khi (*) có nghiệm duy 1 2
+ A A B B C C 0 + 1 2 d / /d 1 2 1 2 1 2 1 2 M d
nhất t t thì d cắt tại d/ Cho 2mp ; có: / / 0
13. Đt d đi qua M (x ; y ; z ) 1 2 0 0 0 0
điểm Ax t a ; y t a ;z t a ) : Ax By Cz D 0 0 0 1 0 0 2 0 0 3 u ku 1
và có 1 vtcp a (a ; a ; a ) . 1 2 3 + 1 2 d d 1 2
: Ax By Cz D 0 M d 2
x x a t 1 2 o 1 + d vuông góc + d cắt d
Khoảng cách giữa 2 mp ; là:
Ptts của d: y y a t 1 2 o 2 n cung phuong u d D D
z z a t u kocung phuong u
d (); 1 2 o 3 1 2 n k.u d 2 2 2
A B C He Iconghiem Face: viethieu220284 Trang 14
Th.S Nguyễn Viết Hiếu 089908.3939
17. a/Cho 2đt d và d có 2vtcp lần lượt + (P) tiếp xúc (S) d (O, P) R
b/Tìm điểm đối xứng A’ của A qua 1 2 mp(P).
là u a ;b ; c ,u a ;b ;c .Góc
+ (P) cắt (S) d (O, P) R . 1 1 1 1 2 2 2 2
+B1: Tìm hcvg H của A trên (P).
giữa 2 đt d và d được tính bởi CT:
(Khi (P) cắt (S) theo giao tuyến là đường +B2: H là trung điểm AA’. 1 2
tròn (C) có tâm H và bk r thì:
x 2x x A' H A u u
a a b b c c
H là hcvg của O trên (P). cos . . d ;d
y 2y y 1 2 1 2 1 2 1 2 1 2 A' H A 2 2 2 2 2 2 u . u
a b c . a b c 2 2 2 2 1 2 r R
d (O,P) R OH 1 1 1 2 2 2
z 2z z A' H A
b/cho 2mp ; có 2 vtpt lần lượt
Đặc biệt: Điểm Ax ; y ;z A A A
là n (a ;b ;c ) ; n (a ;b ;c ) . Góc 1 1 1 1 2 2 2 2
+Hcvg của A trên(Oxy) là H x ; y ;0 1 A A
giữa 2 mp ; được tính bởi CT:
+Hcvg của A trên(Oxz) là H x ;0; z 2 A A n n
a a b b c c
+Hcvg của A trên(Oyz) là H 0; y ; z 3 A A cos ; 1. 2 .1 2 1 2 1 2
21. Mp : Ax By Cz D 0 đặc biệt 2 2 2 2 2 2
Điểm đx của A qua(Oxy) là A x ; y ;z 1 A A A 1 n . n2
a b c . a b c 1 1 1 2 2 2
+ D 0 : đi qua gốc tọa độ O.
c/Cho đt d có 1vtcp a (a ; a ; a ) và
Điểm đx của A qua(Oxz) là A x ;y ;z 2 A A A 1 2 3
+ A 0 : chứa Ox hoặc // Ox.
mp có 1vtpt n ( ; A ; B C) . Góc
Điểm đx của A qua(Oyz) là A x ; y ;z 3 A A A
+ B 0 : chứa Oy hoặc // Oy.
giữa đt d và mp được tính bởi CT:
24. a/Tìm hcvg H của M x ; y ; z M M M
+ C 0 : chứa Oz hoặc // Oz.
x x a t a n
Aa Ba Ca o 1 sin d,() . 1 2 3
+ A B 0 : / /Oxy hoặc Oxy.
trên đt d : y y a t . 2 2 2 2 2 2 a . n
a a a . A B C o 2 1 2 3
+ A C 0 : / /Oxz hoặc Oxz .
z z a t
18. +Mặt cầu (S) có tâm I (x ; y ; z ) o 3 0 0 0
+ B C 0 : / /Oyz hoặc Oyz
B1: H d H x a t; y a t; z a t o 1 o 2 o 3 và bk R. Pt (S) là:
+Ptmp Oxy: z 0. +Ptmp Oxz: y 0 2 2 2 2
(x x ) ( y y ) (z z ) R
B2: MH.u 0 (u (a ; a ; a ) vtcp của d) 0 0 0 x t d d 1 2 3 Th. S N
a x x a y y a z z T 1 0 M 2 0 M 3 0 M
+Ptmp Oyz: x 0. +Pt Ox: y 0 . h. gu t S 2 2 2 y z 0 Ng ễ
a a a 1 2 3 n u V y i x 0 x 0 ễ KL: H n
x at; y a t;z a t ế o 1 o 2 o 3 t V +Pt Oy: H . +Pt Oz: . i +Pt mặt cầu (S): y t y 0 ết
b/Tìm điểm đối xứng M’ của M qua đt d iế u Hi 2 2 2 z 0 z t
x y z 2ax 2by 2cz d 0 089908.
B1: Tìm hcvg H của M trên d. ế T u h.
22. Điểm M trên đường thẳng, mp B2: H là trung điểm MM’ 08 S N (Đk: 2 2 2
a b c d 0 ). 9908 gu 3939
+ M Oxy M ; a ; b 0 x 2x x M ' H M y
Mặt cầu (S) có tâm I ( ; a ; b c) và bk ễ . n 3939
y 2y y V
+ M Oxz M ; a 0;b M ' H M iế 2 2 2 R
a b c d . t z 2z z H
+ M Oyz M 0; ; a b M ' H M
19. VTTĐ giữa đt và mặt cầu (S) có iế
Đặc biệt: Điểm Ax ; y ;z u A A A 089908. tâm O và bk R.
+ M Ox M t;0;0
+ ko cắt (S) d( , O ) R
+Hcvg của A trên Ox là: H x ;0;0 4 A
+ M Oy M 0;t;0 3939
+ tiếp xúc (S) d( , O ) R
+Hcvg của A trên Oy là: H 0; y ;0 5 A
+ M Oz M 0;0;t
+ cắt (S) d( , O ) R
+Hcvg của A trên Oz là: H 0;0; z 6 A
23. a/Tìm hcvg H của điểm
A x ; y ; z trên mp (P):
Điểm đx của A qua Ox là A x ;y ;z 4 A A A A A A
ax by cz d 0 .
Điểm đx của A qua Oy là A x ; y ;z 5 A A A
+Đt AH đi qua Ax ; y ;z và có
Điểm đx của A qua Oz là A x ;y ;z 6 A A A A A A
Khi cắt (S) tại 2 điểm M,N thì x x . a t
25. I là tâm đtròn nội tiếp ABC A 2 2 1vtcp n
;a ;bc . Pt AH: BC.x AC.x . AB x P
MN 2MH 2 R d (O, ) y y bt A B C A x I
AB AC BC
(H là hcvg của O trên ; H là trung
z z ct A
BC.y AC.y . AB y điểm MN). A B C
+ H AH H x at; y bt; z ct yI A A A
AB AC BC
20. VTTĐ giữa mp(P) và mặt cầu (S) có
ax by cz d
BC.z AC.z . AB z tâm O và bk R. A B C + H P A A A t z I 2 2 2
AB AC BC
+(P) ko cắt (S) d (O, P) R a b c
KL: H x at; y bt; z ct
Th.S Nguyễn Viết Hiếu 089908.3939 A A A Trang 15 Face: viethieu220284
VIII.PHÉP BIẾN HÌNH
Th.S Nguyễn Viết Hiếu 089908.3939 1. Phép tịnh tiến 2. Phép quay Q 3. Phép vị tự V k 0 O;k O;
T (M) M' MM ' v v OM OM ' V
M M ' OM ' kOM O;k Q (M) M' O; OM;OM '
T (M) M' T (M') M v v
+Phép tịnh tiến theo v biến đường
thẳng thành đường thẳng song song Q (M) M' Q (M') M V
M M ' V M ' M O;k 1
hoặc trùng với nó. O; O; O; k
Đt : ax by c 0 +Phép quay Q
biến đường thành O; +Phép vị tự V
biến đường thẳng O;k 2 '/ /
T () ' . Suy ra
thành đường thẳng vuông góc với nó.
thành đường thẳng song song hoặc v '
Đt : ax by c 0
trùng với nó. Đt : ax by c 0
Pt ' có dạng: ax by m 0 Q () ' V () ' O;k O;
+Phép tịnh tiến theo v biến đường 2 '/ /
tròn thành đường tròn có cùng bán Suy ra ' Suy ra '
kính, tâm biến thành tâm.
Pt ' có dạng: bx ay m 0
Đường tròn (C) tâm I a;b và bk R.
+Phép quay biến đường tròn thành đường Pt ' có dạng: ax by m 0
tròn có cùng bán kính, tâm biến thành +Phép vị tự V
biến đường tròn bk R T C C O;k v ' tâm.
Đtròn (C’) có tâm I’ và bk R’
thành đường tròn bk k R , tâm biến Q C C ' Th O; .S Nguy + R ' R thành tâm.
Đtròn (C’) có tâm I’ và bk R’ V C C ' O;k
+T (I) I ' I I' v ễ v R ' R n Vi
+Biểu thức tọa độ: M ;
x y, M 'x '; y ' Q (I) I '
Đtròn (C’) có tâm I’ và bk R’ ế O; t H R ' k R i
T (M) M' với v ; a b x ' x cos . y sin ếu v +Bttđ phép Q : 089908. O; V (I) I ' OI' kOI
x ' x a y ' xsin . y cos O;k Bttđ: x ' k x 3939
y ' y b + Bttđ V : O;k
Th.S Nguyễn Viết Hiếu 089908.3939 y ' ky
4. Phép dời hình là phép biến hình
+Phép dời hình biến tam giác ABC thành
5.Phép biến hình F đgl phép đồng dạng
bảo toàn khoảng cách giữa hai điểm
tam giác A’B’C’ thì nó cũng biến trọng
tỉ số k k 0 , nếu với hai điểm M, N bất kì.
tâm, trực tâm, tâm các đường tròn nội
bất kì và ảnh M’, N’ tương ứng của
+Phép đồng nhất, phép tịnh tiến, đối
tiếp, ngoại tiếp của tam giác ABC tương
chúng ta luôn có M ' N ' kMN
xứng trục, đối xứng tâm, phép quay
ứng thành trọng tâm, trực tâm, tâm các
+Phép dời hình là phép đồng dạng tỉ số
là những phép dời hình.
đường tròn nội tiếp, ngoại tiếp của tam k 1.
+Phép dời hình có được bằng cách giác A’B’C’.
+ Phép vị tự tỉ số k là phép đồng dạng tỉ
thực hiện liên tiếp 2 phép dời hình là
+Phép dời hình biến đa giác n cạnh thành một phép dời hình.
đa giác n cạnh, đỉnh biến thành đỉnh, cạnh số k . +T/c phép dời hình: biến thành cạnh.
+Phép đồng dạng tỉ số k:
-Biến 3 điểm thẳng hàng thành 3
+Hai hình đgl bằng nhau nếu có một phép -Biến 3 điểm thẳng hàng thành 3 điểm
điểm thẳng hàng và bảo toàn thứ tự
dời hình biến hình này thành hình kia.
thẳng hàng và bảo toàn thứ tự giữa các giữa các điểm ấy. điểm ấy.
-Biến đường thẳng thành đường
-Biến đường thẳng thành đường thẳng,
thẳng, biến tia thành tia, biến đoạn
biến tia thành tia, biến đoạn thẳng
thẳng thành đoạn thẳng bằng nó. thành đoạn thẳng.
-Biến tam giác thành tam giác bằng
-Biến tam giác thành tam giác đồng
nó, biến góc thành góc bằng nó.
dạng với nó, biến góc thành góc bằng
-Biến đtròn thành đường tròn có nó. cùng bán kính.
-Biến đường tròn bk R thành đường Face: viethieu220284 tròn có bán kính kR. Trang 16 Face: viethieu220284
Th.S Nguyễn Viết Hiếu 089908.3939
+Nếu một phép đồng dạng biến tam
6. Hình vẽ đẹp của họa sĩ + Hình đối xứng
giác ABC thành tam giác A’B’C’ thì nó Maurits Comelis Escher
cũng biến trọng tâm, trực tâm, tâm
các đường tròn nội tiếp, ngoại tiếp Th
của tam giác ABC tương ứng thành .S Ng
trọng tâm, trực tâm, tâm các đường uy
tròn nội tiếp, ngoại tiếp của tam giác ễn V A’B’C’. iết
+Phép đồng dạng biến đa giác n cạnh H iế
thành đa giác n cạnh, đỉnh biến u 089908.
thành đỉnh, cạnh biến thành cạnh.
+Hai hình đgl đồng dạng với nhau 3939 hocthoi.net
nếu có 1 phép đồng dạng biến hình này thành hình kia. Wikiwand.com
Th.S Nguyễn Viết Hiếu 089908.3939 + Hình Fractal
https://vuihocly.wordpress.com/2011/12/18/hin
scp-foundation-database.fandom.com/wiki/SCP-001 h-hoc-fractal/ khoahoc.tv Ảnh: Huanqiu
vi.mathigon.org/course/fractals/introduction
vi.mathigon.org/course/fractals/introduction
sprott.physics.wisc.edu/fractals/carlson
Th.S Nguyễn Viết Hiếu 089908.3939 Trang 17 Face: viethieu220284
IX. HÌNH HỌC KHÔNG GIAN
Th.S Nguyễn Viết Hiếu 089908.3939
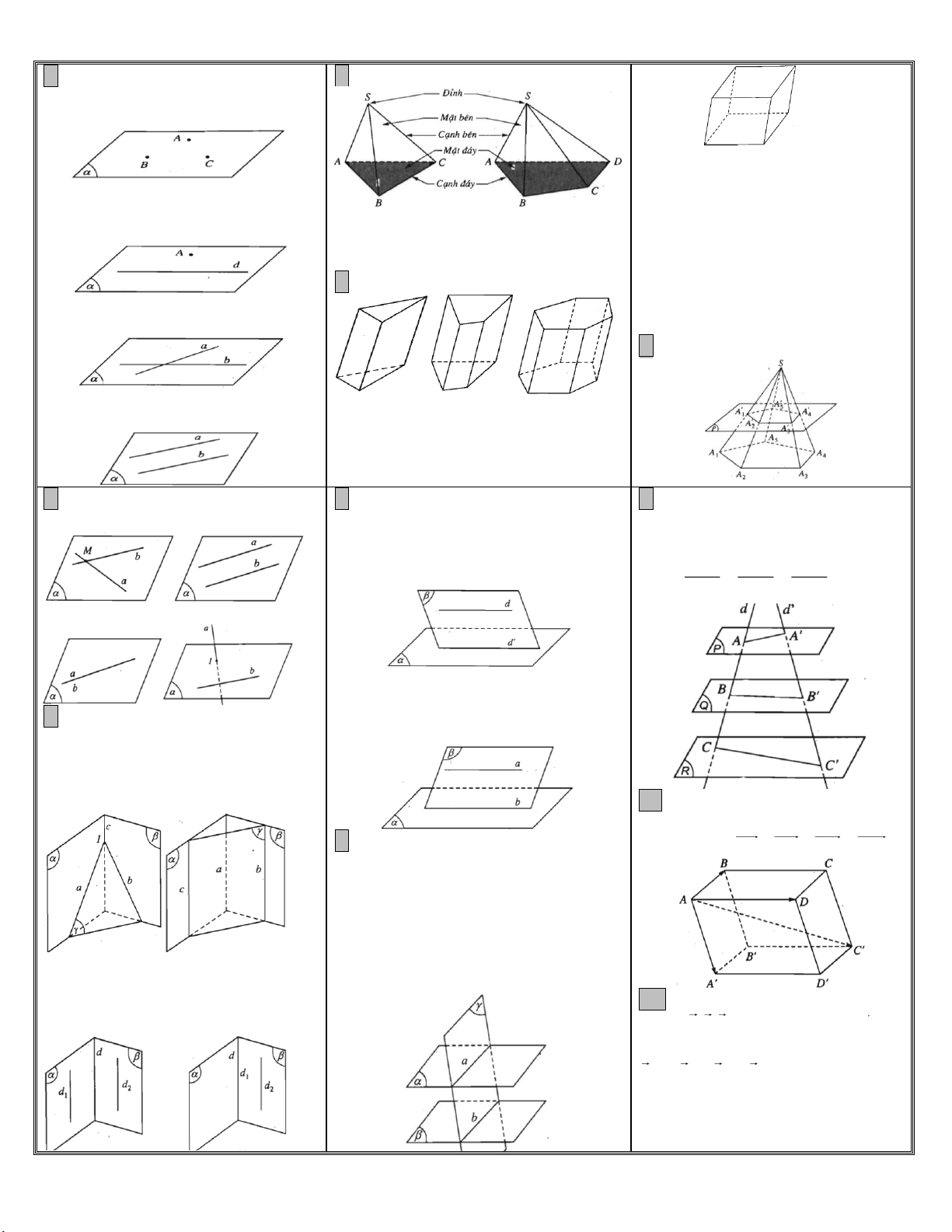
1.Cách xác định 1 mặt phẳng
2.Hình chóp, hình tứ diện
+Mp hoàn toàn được xác định khi biết
nó đi qua 3 điểm pb không thẳng hàng.
+Hình lăng trụ đứng là hình lăng trụ
có cạnh bên vuông góc mặt đáy.
+Mp hoàn toàn được xác định khi biết
+Hình lăng trụ đứng có đáy là hình
nó đi qua 1 điểm và chứa 1 đường
+Hình chóp đều là hình chóp có đáy là đa bình hành đgl hình hộp đứng.
thẳng không đi qua điểm đó.
giác đều và hình chiếu của đỉnh trên mặt
+ Hình lăng trụ đứng có đáy là hình
đáy trùng với tâm đa giác đáy.
chữ nhật đgl hình hộp chữ nhật. 3.Hình lăng trụ
+Hình lăng trụ đứng có đáy là hình
+Mp hoàn toàn được xác định khi biết
vuông và các mặt bên là hình vuông
nó chứa 2 đường thẳng cắt nhau. đgl hình lập phương.
4.Hình chóp cụt: A A A A A .A' A' A' A' A' 1 2 3 4 5 1 2 3 4 5
+Mp hoàn toàn được xác định khi biết
+Hình lăng trụ có đáy hình bình hành là
nó chứa 2 đường thẳng song song. hình hộp.
+Hình lăng trụ đều là hình lăng trụ đứng,
có đáy là đa giác đều. 5.4VTTĐ của 2đt ; a b trong không gian
7.Đường thẳng song song mặt phẳng 9.Định lí Thales
TH1: a cắt b tại M TH2: a / /b
+ Nếu đường thẳng d không nằm trong
+Ba mp đôi một song song chắn trên
mp và d song song với đt d’ nằm
2 cát tuyến bất kì những đoạn thẳng
trong thì d song song với . AB BC AC tỉ lệ.
A'B ' B 'C ' A'C '
TH3: a b TH4: a chéo b Th.S N gu 4 y 8 ễn 2 0
+Định lí: Cho đt a song song mp . Vi 2 ế 2 t u H
6.Định lí giao tuyến 3mp và hệ quả
Nếu mp chứa a và cắt theo giao iế hie u iet
+Nếu 3mp cắt nhau theo 3 giao tuyến
tuyến b thì b / /a . 089908. : v
phân biệt thì 3 giao tuyến ấy hoặc
đồng quy hoặc đôi 1 song song với 3939 Face nhau. 10.Vectơ trong không gian
Cho hình hộp ABCD.A’B’C’D’. 8.Hai mp song song
QT hình hộp: AB AD AA' AC '
+Nếu mp chứa 2 đường thẳng cắt
nhau a,b và a,b cùng song song với mp
thì / /.
+Định lí: Cho hai mp song song. Nếu một
+Nếu 2mp phân biệt lần lượt chứa 2đt
mp cắt mp này thì cũng cắt mp kia và hai
song song thì giao tuyến của chúng
giao tuyến song song với nhau.
(nếu có) cũng song song với hai đt đó
11. Trong kg cho 3 vectơ không đồng
hoặc trùng với một trong 2đt đó.
phẳng a,b,c . Khi đó mọi vectơ x ta
đều tìm được bộ 3 số m,n,p sao cho
x ma nb pc . Ngoài ra bộ 3 số m,n,p là duy nhất.
Th.S Nguyễn Viết Hiếu 089908.3939 Zalo: 089908.3939 Trang 18 Face: viethieu220284
Th.S Nguyễn Viết Hiếu 089908.3939
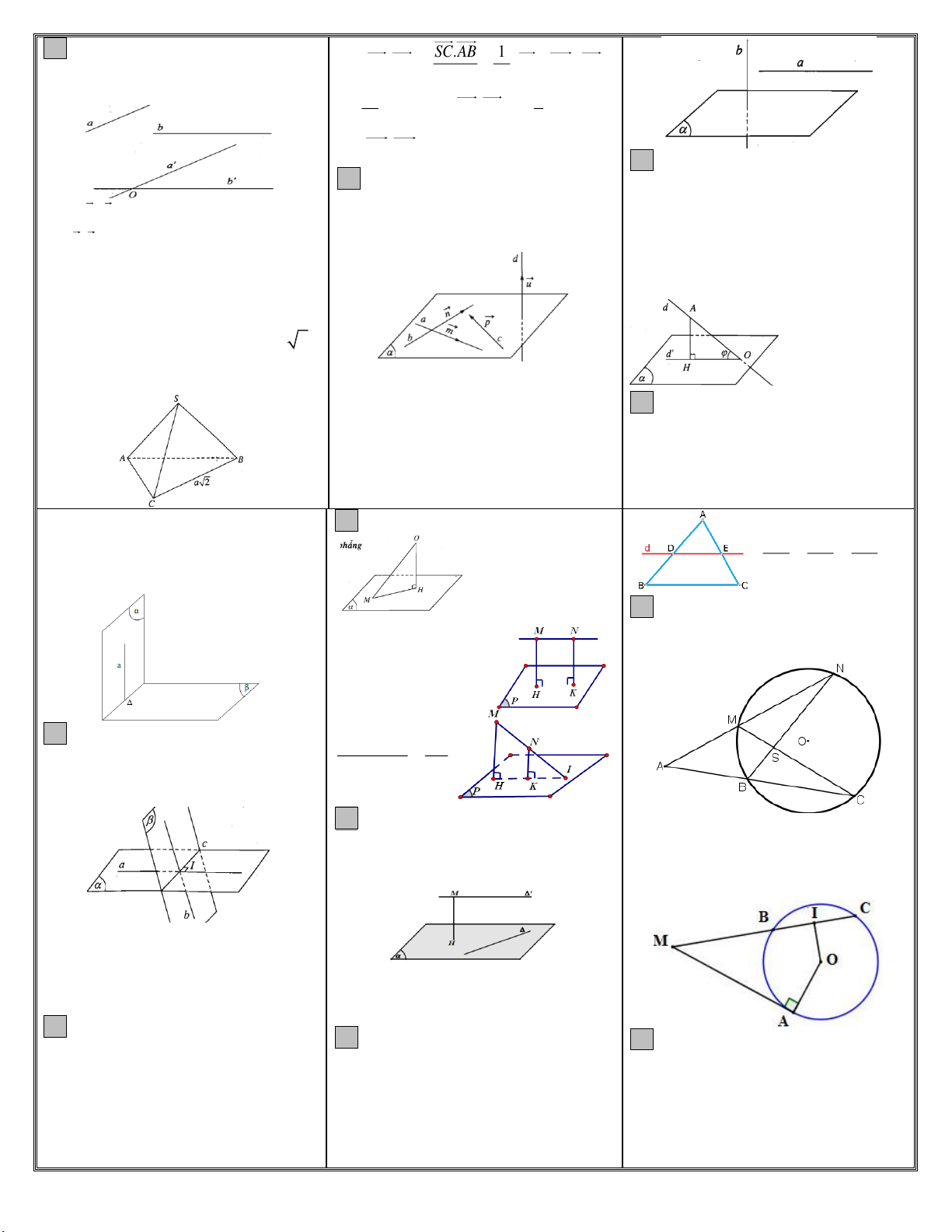
12.Góc giữa 2 đt a,b trong không gian
SC AB SC.AB 1 cos ;
SA AC .AB 2
là góc giữa 2 đt a ',b' cùng đi qua 1 SC.AB a
điểm và lần lượt song song với a,b . 1 1 .AS.A .
B cos AS; AB T 2 a 2 h.S N SC AB 0 SC AB 0 ; 120 ; 60 gu
14.Góc giữa đt và mặt phẳng yễn
13.Đt vuông góc mặt phẳng Viế Cho đt d và mp . t
+Nếu một đt vuông góc với hai đường H
+Cho u ; v lần lượt là vtcp của 2đt a,b i
thẳng cắt nhau cùng thuộc một mặt
+Nếu d thì d 0 ; 90 ếu 089908. và ; u v .
phẳng thì nó vuông góc với mp ấy.
+Nếu d ko vuông thì Nếu 0 0 0 90 thì ; a b 3939
d; d;d ' Nếu 0 0
90 180 thì a b 0 ; 180 Với d’ là hcvg
Vd.Cho hình chóp S.ABC có BC a 2 của d trên mp
SA SB SC AB AC a .Tính góc
+Mặt phẳng trung trực của đoạn thẳng giữa 2 đt AB và SC. .
là mp vuông góc với đoạn thẳng tại 15.Hai mp vuông góc
trung điểm của đoạn thẳng đó.
Định lí: Đk cần và đủ để hai mp vuông
+Định lí: Nếu một đường thẳng và 1mp
góc với nhau là mp này chứa 1 đường
(không chứa đt đó) cùng vuông góc với
thẳng vuông góc với mp kia.
một đường thẳng khác thì chúng song song với nhau.
+Định lí: nếu 2mp vuông góc với nhau
18. Khoảng cách từ điểm đến mp DE / /BC
thì bất cứ đường thẳng nào nằm trong
+ d O; OH AD AE DE
mp này và vuông góc với giao tuyến thì H là hcvg của O AB AC BC vuông góc với mp kia. trên .
21. Cho đường tròn (O); 2 cát tuyến
của đt (O) là AMN và ABC cắt nhau tại +MN // (P)
A. Ta có: AM .AN . AB AC
d M;P d N;P +MN cắt (P) tại I
16.Góc giữa 2 mặt phẳng
d M;P MI
+Góc giữa 2mp là góc giữa 2đt lần lượt
d N;P vuông góc 2mp đó. NI
+Cách xác định góc giữa 2mp cắt nhau Th.S N
19. K/c giữa 2đt chéo nhau ; ' gu
+Từ 1 điểm M nằm ngoài đường tròn CT1: d ;
' d M; yễ
(O), vẽ cát tuyến MBC và tiếp tuyến Mt n V
( chứa và song song ' ) i
tiếp xúc với (O) tại A. Ta có: ết 2 H M . B MC MA iế u 089908.
c ; Tìm mp c
a ; b 3939 CT 2 : d ; ' HK
; ; a b
(HK:đoạn vuông góc chung của ; ')
17.Diện tích hình chiếu của đa giác
20. Định lí Thales trong mặt phẳng
22. Trong tam giác vuông, đường trung
Cho đa giác (H) nằm trong mp có
+Nếu 1 đt song song với 1 cạnh của tam tuyến ứng với cạnh huyền bằng nữa
diện tích S và (H’) là hình chiếu vuông
giác và cắt 2 cạnh còn lại thì nó định ra cạnh huyền.
góc của (H) trên mp . Khi đó diện
trên 2 cạnh đó những đoạn thẳng
+Nếu một tam giác có đường trung
tích S’ của (H’) là: S ' S cos . tương ứng tỉ lệ.
tuyến ứng với một cạnh bằng nữa cạnh
Th.S Nguyễn Viết Hiếu 089908.3939
Với là góc giữa và .
ấy thì tam giác đó vuông. Face: viethieu220284 Trang 19
Th.S Nguyễn Viết Hiếu 089908.3939 Face: viethieu220284
X.ĐẠI SỐ TỔ HỢP
Th.S Nguyễn Viết Hiếu 089908.3939 1. Quy tắc cộng 3.Hoán vị
+Số các tổ hợp chập k 0 k n của
+ Một công việc được hoàn thành bởi + Cho tập hợp A có n phần tử n 1 . n k !
một trong hai hành động. Nếu hành
n phần tử là: C
Mỗi kết quả của sự sắp xếp thứ tự n n
k !.n k
động này có m cách thực hiện, hành !
phần tử của tập hợp A đgl một hoán vị
động kia có n cách thực hiện không k k
0 k n của n phần tử đó. Tính chất: A C .k! n n
trùng với bất kì cách nào của hành động k nk
thứ nhất thì công việc đó có m n cách +Số các hoán vị của n n 1 phần tử C C k n n n 0 thực hiện. là: P ! n 1.2.3...(n1).n k 1 k k C C C 1 k n n 1 n 1 n n
+ Quy tắc cộng phát biểu dưới dạng tập Quy ước: 0!1
6. Phép thử, biến cố, xác suất:
hợp: Nếu A, B là hai tập hợp hữu hạn 4. Chỉnh hợp
+Tập hợp tất cả các kết quả có thể xảy
không giao nhau A B thì + Cho tập hợp A có n phần tử n
1 . ra của một phép thử đgl không gian
n A B n A nB
mẫu của phép thử, kí hiệu .
Kết quả của việc lấy k phần tử khác +Biến cố là tập con của không gian mẫu.
+ Quy tắc cộng có thể mở rộng cho nhau từ n phần tử của A và sắp xếp nhiều hành động.
chúng theo thứ tự nào đó đgl một chỉnh +Tập là biến cố không thể (biến cố 2. Quy tắc nhân
hợp chập k của n phần tử đã cho. không).
+Tập là biến cố chắc chắn.
+ Một công việc được hoàn thành bởi +Số các chỉnh hợp chập k 1 k n +Cho A là 1 biến cố liên quan 1 phép
hai hành động liên tiếp. Nếu có m cách n k !
thực hiện hành động thứ nhất và ứng của n phần tử là: A
thử. Tập A \ A đgl biến cố đối của n n k
với mỗi cách đó có n cách thực hiện ! biến cố A.
hành động thứ hai thì có .
m n cách 5.Tổ hợp: + Cho tập hợp A có n phần tử + A B thì A, B đgl hai biến cố hoàn thành công việc. n
1 . Mỗi tập con gồm k phần tử của xung khắc.
+Quy tắc nhân có thể mở rộng cho
A đgl một tổ hợp chập k của n phần tử
nhiều hành động liên tiếp. đã cho.
Th.S Nguyễn Viết Hiếu 089908.3939
+Định nghĩa cổ điển của xác suất Tính chất xác suất:
Giả sử A là biến cố liên quan đến một phép thử với không gian mẫu chỉ có một
P 0; P 1
số hữu hạn kết quả đồng khả năng xuất hiện. Xác suất của biến cố A là:
0 P A 1, với mọi biến cố A P A n A
Nếu 2 biến cố A, B xung khắc thì n
P A B P A P B
Với n A là số phần tử của A hay số khả năng thuận lợi cho biến cố A.
P A 1 P A
n là số phần tử không gian mẫu.
7. Tam giác Pascal: Khai triển n x y * n
Th.S Nguyễn Viết Hiếu 089908.3939 n 1: 1 1
x y1 x y n 2 : 1 2 1 x y2 2 2
x 2xy y n 3 : 1 3 3 1 x y3 3 2 2 3
x 3x y 3xy y n 4 : 1 4 6 4 1 x y4 4 3 2 2 3 4
x 4x y 6x y 4xy y n 5 : 1 5 10 10 5 1 x y5 5 4 3 2 2 3 4 5
x 5x y 10x y 10x y 5xy y
8. Công thức nhị thức Newton n
a bn 0 n 1 n 1 2 n2 2 k nk k n 1 n 1
C a C a .b C a .b ... C a .b ... C . n n a b C b k n k C a . k b n n n n n n n k 0 (1)
Trong vế phải (1) có n
1 hạng tử; tính từ trái sang phải các hạng tử có: số mũ của a giảm dần từ n đến 0, số mũ của b
tăng dần từ 0 đến n và tổng số mũ của a , b bằng n. Số hạng tổng quát: k nk T C a . k b . k 1 n
Th.S Nguyễn Viết Hiếu 089908.3939 Face: viethieu220284 Trang 20 Đặc biệt: n + 2 n 1 2 2 0 1 2 2 1
C C C ... n C (*) 2n 2n 2n 2n n + n 0 1 2 2 1 1
C C C ... n C n n n n 2n k 0 1 0 1 2 3 1 C C C C ... C C C (**) n n n n k 2n 1 2 1 ... n 2 2 2 2 2n 2n 2n
+Cho tập hợp A có n phần tử * n Từ (*), (**) có:
Số tập con có 1 phần tử của A là: 1 C 0 2 4 2n 1 3 2n 1 2n 1
C C C
... C C C ... C 2 n 2n 2n 2n 2n 2n 2n 2n
Số tập con có k 0 k n phần tử n
+ 2 n 1 2 1 2 1 0 1 2 n n 1 2n 1 1 C C C ... C C ... C 2n 1 2n 1 2n 1 2n 1 2n 1 2n 1 của A là: k C . n n n n n Mà 0 2 1 1 2 1 C C ; C C ;...;C C 2n 1 2n 1 2n 1 2n 1 2n 1 2n 1
Số tất cả tập hợp con của A là: Suy ra: 2n 0 1 2 n n 1 2n 1 2 C C C ... C C ... C 2n 1 2n 1 2n 1 2n 1 2n 1 2n 1 n k C 2n n n n
+ Đa thức f x a bx 2 a a x a x ... a x 0 1 2 n k 0 n 0 1 2 k
Tổng tất cả các hệ số trong khai triển đa thức f x bằng: 0
1 1 C C C ... 1 k C n n n n n
T a a a ... a f 1 a b 0 1 2 n n ... 1 n Cn
BT1. Bạn H có 2 áo màu khác nhau và ba 2.Cho đa giác lồi (H) có n cạnh
+Tổng tất cả các hệ số từ khai triển biểu
quần kiểu khác nhau. Hỏi H có bao nhiêu ( n 4 ). thức x 17 3 4 là:
cách chọn 1 bộ quần áo?
+ Số vectơ khác 0 có điểm đầu và a a ... a a f 1 1 17 16 1 0 Giải: Hai áo được ghi
điểm cuối là hai đỉnh của (H) là: 2 A .
chữ a và b, ba quần n
4. Quy tắc cộng mở rộng cho 2 tập hữu được đánh số 1,2,3.
+ Số tam giác có 3 đỉnh là đỉnh của hạn A, B và AB Để chọn 1 bộ quần (H) là: 3 C . n
n A B n A n B n A B áo, ta phải thực hiện
+Số đoạn thẳng có 2 điểm đầu mút liên tiếp hai hành
(Quy tắc bao hàm và loại trừ) là 2 đỉnh của (H) là: 2 C . n động:
BT4. Một tổ 10 học sinh sẽ được chơi 2
+ Số đường chéo của đa giác (H) là: HĐ1: Chọn áo. Có hai
môn thể thao là cầu lông và bóng bàn. 2 cách chọn (chọn a C n
Có 5 bạn đăng kí chơi cầu lông, 4 bạn n hoặc b).
BT3. Từ khai triển biểu thức
đăng kí chơi bóng bàn, trong đó có 2
HĐ2: Chọn quần. Ứng với cách chọn áo có
bạn đăng kí chơi cả 2 môn. Hỏi có bao x 17 3 4
, hãy tính tổng tất cả các
ba cách chọn quần (Chọn 1, hoặc 2, hoặc 3).
nhiêu bạn đăng kí chơi thể thao? Bao
hệ số của đa thức nhận được.
Vậy số cách chọn 1 bộ quần áo là: 2.3 = 6
nhiêu bạn không đăng kí chơi thể thao? cách.
G: f x 3x 417 17
a .x ... a x a 17 1 0
Th.S Nguyễn Viết Hiếu 089908.3939
Giải: Kí hiệu X là tập hợp 10 học sinh trong BT5. Bài kiểm tra trắc nghiệm gồm nhau nếu việc xảy ra hay không xảy ra
tổ; A là tập hợp các học sinh đăng kí chơi 50 câu, mỗi câu có 4 phương án trả của biến cố này không làm ảnh hưởng
cầu lông; B là tập hợp các học sinh đăng kí lời và chỉ có 1 phương án trả lời tới xác suất xảy ra của biến cố kia. chơi bóng bàn.
đúng, điểm cho mỗi câu trả lời đúng + Nếu hai biến cố A, B độc lập với
là 0,2. Bạn H làm chắc chắn đúng 30 nhau thì A và B ; A và B; A và B
câu và 20 câu còn lại bạn chọn ngẫu cũng độc lập với nhau.
nhiên. Tính gần đúng xác suất bạn H + Quy tắc: Nếu hai biến cố A và B độc được đúng 7 điểm.
lập với nhau thì P .
A B P
A .PB Giải: .
A B A B
Số phần tử không gian mẫu: BT6. Một chiếc máy có hai động cơ I và n 20 4
II hoạt động độc lập với nhau. Xác suất
Gọi A là biến cố: “H được 7 điểm”.
để động cơ I và động cơ II chạy tốt lần
n X 10; n A 5; n B 4 n A 5 15 C .3 .
lượt là 0,8 và 0,7. Hãy tính xác suất để 20
n A B 2.
Vậy xác suất bạn H được đúng 7 cả 2 động cơ đều không chạy tốt.
A B là tập hợp các bạn đăng kí chơi thể điểm là:
Giải: Gọi A là bc “Động cơ I chạy tốt”, B thao.
là biến cố “Động cơ II chạy tốt”, D là P A 5 15 C .3 20
biến cố “Cả 2 động cơ đều không chạy
n A B n A n B n A B 7 20, 233% 20 4 tốt”.
Số bạn không đăng kí chơi thể thao là:
9.Quy tắc nhân xác suất:
P D P .
A B P A.PB 6%
n X n A B 3
+ Hai biến cố A và B đgl độc lập với Trang 21
Th.S Nguyễn Viết Hiếu 089908.3939
Face: viethieu220284 XI.CẤP SỐ CỘNG, CẤP SỐ NHÂN, GIỚI HẠN, ĐẠO HÀ Th M .
S Nguyễn Viết Hiếu 089908.3939 1.CẤP SỐ CỘNG 3.CẤP SỐ NHÂN
5.Giới hạn dãy số u
7.Tổng của CSN lùi vô hạn n
+ u là CSC (vô hạn) với
+ u là CSN (vô hạn) với công
u ,công bội q, q 1 bằng: n n n 1 lim 0, k công sai d: bội q: * u
u *q, n k n u n 1 n
S u u ... u ... 1 * u
u d, n lim k n , k 1 2 n 1 q n 1 n
+ u là CSN (hữu hạn, m phần n
+ u là CSC (hữu hạn, m
limC C, C hằng số.
8.Nếu limu a và n tử) với công bội q n
phần tử) với công sai d n u u * , q n 1 ,m 1 limq 0, q 1 un n 1 n
limv thì lim 0 . n u
u d, n 1 ,m 1 n v n 1 n
4.Tính chất CSN u , có số lim q , q 1 n n
2.Tính chất CSC u có số
6.Định lí về giới hạn hữu
+Nếu limu a 0 ; n
hạng đầu u , công bội q: n 1
hạng đầu u , công sai d hạn của dãy số
limv 0 và v 0, n thì 1 + 1 u u * n q n n n 1 Nếu limu ;
a limv b thì
+ u u n 1 d n n u n 1 + 2 u u *u , k 2 lim n . k k 1 k 1
limu v a b v n n u u n + k 1 k 1 u , k 2 ( u ;u ;u là 3 số hạng liên k k 1 k k 1
limu v a b
+Nếu limu a 0 ; n n 2 tiếp của CSN n u ) n ( u ;u ;u
limu *v a b
limv 0 và v 0, n thì n n n n k 1 k k 1 là 3 số hạng liên *
+ Tổng n số hạng đầu của CSN
tiếp của CSC u ) u n
u là: S u u ...u u a lim n . n lim n b 0
+ Tổng n số hạng đầu của CSC n 1 2 n vn Nếu q=1 thì S . n u v b n u
là: S u u ... u n 1
+ Nếu limu và n n 1 2 n n u 1 n q + Nếu u 0 và n 1
nu u n n 1 d
limv a 0 thì limu .v n n 1 n
Nếu q 1 thì S n nu n limu
a thì a 0 và n 1 1 q 2 2
+ Nếu limu và lim u a n n
Th.S Nguyễn Viết Hiếu 089908.3939
limv a 0 thì limu .v n n n
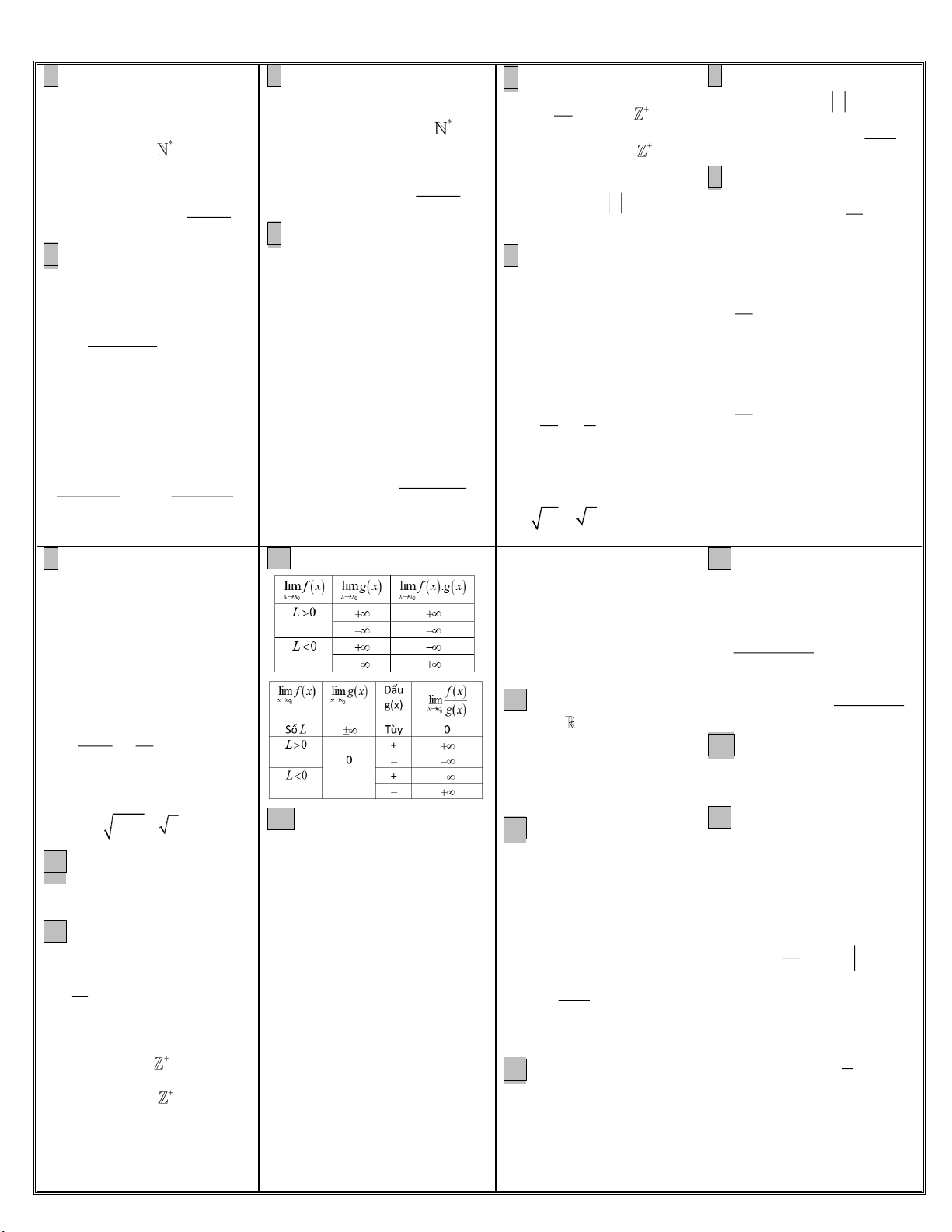
9.Định lí giới hạn hữu hạn hs
12. Giới hạn tích, thương hs
+Hs y f x liên tục trên 17.Đạo hàm
Nếu lim f x ;
L lim g x M đoạn ;
a b nếu nó liên tục Cho hs y
f x xác định trên xx xx 0 0
;ab và x ;ab . Nếu tồn tại 0 lim f
x g x L M trên khoảng ; a b và xx0
f x f x0
lim f x f a ; lim f x f b lim f
x g x L M lim hữu hạn thì xa x b x x xx 0 x x 0 . 0 lim f
x* g x L *M
14. +Hàm số đa thức liên f x f x
y 'x f ' x lim 0 0 0 xx0 xx x x tục trên . 0 0 f x L lim M
+Hàm số phân thức hữu tỉ
18. Định lí: Nếu hs y f x
xx g x 0 0 M
và các hàm lượng giác liên có đạo hàm tại x thì nó liên 0
Nếu f x 0; lim f x L thì
tục trên từng khoảng xác xx tục tại điểm đó. 0 định của chúng.
19. Pt tiếp tuyến của đths
L 0; lim f x L 13. Hàm số liên tục
15.Cho hs y f x và xx0
+Hs y f x xác định trên
y f x tại điểm M x ; y là: 0 0
y g x
10. lim f x L khi và chỉ khi
liên tục tại x . Khi 0
y f 'x
x x y 0 0 xx khoảng ; a b và x ; a b . 0 0 đó: 0
lim f x lim f x L
Hs y f x liên tục tại x
+ x là hoành độ tiếp điểm.
+ Các hs y f x gx ; 0 x 0 0 x x 0 x
+ y là tung độ tiếp điểm.
11.Giới hạn hàm số đặc biệt
lim f x f x
y f x.g x 0 0 liên tục tại xx0 d
lim C C , C hằng số. + f ' x f x 0
lim f x lim f x f x x . 0 x x0 0 x dx xx xx 1 0 0 f x lim 0 ,k nguyên dương.
là hệ số góc của tiếp tuyến. k + Hàm số y
f x liên tục trên +Hs y liên tục tại x x x g x 0
Chú ý: cho đt d: y ax b . lim k
x , k nguyên dương.
1 khoảng khi nó liên tục tại mọi +Tiếp tuyến vuông góc d x
điểm thuộc khoảng đó.
nếu g x 0 . 0 1 lim k x , k ,k chẵn.
“Đồ thị hs liên tục trên 1 khoảng 16. Nếu hs y f x liên f ' x 0 x
là một đường liền nét trên a lim k x , k , k lẻ. tục trên ; a b và +Tiếp tuyến //d x khoảng đó”.
f a. f b 0 thì pt f x 0
f 'x a 0
có ít nhất 1 nghiệm thuộc
(Tìm x , viết pttt, loại tt d ) 0 khoảng ;ab. Trang 22 Face: viethieu220284
20. CÔNG THỨC ĐẠO HÀM
Th.S Nguyễn Viết Hiếu 089908.3939
Th.S Nguyễn Viết Hiếu 089908.3939
Đạo hàm của hàm sơ cấp
Đạo hàm của hàm sơ cấp 1 ′ 1 1 ′ 𝑢′
(𝐶)′ = 0 (C là hằng số) ( ) = − (𝑥 ≠ 0) ( ) = − (𝑢 ≠ 0) 𝑥 𝑥2 𝑢 𝑢2 (𝑥)′ = 1 ′ 1 ′ ′ 𝑢′ 𝑢
𝑢′. 𝑣 − 𝑣′. 𝑢 (√𝑥) = (𝑥 > 0) (√𝑢) = (𝑢 > 0) ( ) = (𝑣 ≠ 0) 2√𝑥 2√𝑢 𝑣 𝑣2
(𝑥𝛼)′ = 𝛼. 𝑥𝛼−1
(𝑢𝛼)′ = 𝛼. 𝑢𝛼−1. ( 𝑢′
𝑢. 𝑣)′ = 𝑢′. 𝑣 + 𝑢. 𝑣′
(𝑢. 𝑣. 𝑤)′ = 𝑢′. 𝑣. 𝑤 + 𝑢. 𝑣′. 𝑤 + 𝑢. 𝑣. 𝑤′ ′ 1 𝑢′ ( ′ √ 𝑛 𝑥) = ( √ 𝑛 𝑢) =
(𝑘. 𝑢)′ = 𝑘. 𝑢′ (k là hằng số) 𝑛 √ 𝑛 𝑥𝑛−1 𝑛 √ 𝑛 𝑢𝑛−1
(𝑠𝑖𝑛𝑥)′ = 𝑐𝑜𝑠𝑥
(𝑠𝑖𝑛𝑢)′ = 𝑢′. 𝑐𝑜𝑠𝑢
21. Ý nghĩa vật lí của đạo hàm
(𝑐𝑜𝑠𝑥)′ = − 𝑠𝑖𝑛𝑥
(𝑐𝑜𝑠𝑢)′ = −𝑢′. 𝑠𝑖𝑛𝑢
Xét chuyển động thẳng có pt quãng 1 𝑢′
đường chuyển động theo thời gian t (𝑡𝑎𝑛𝑥)′ =
= 1 + 𝑡𝑎𝑛2𝑥 (𝑡𝑎𝑛𝑢)′ =
= 𝑢′(1 + 𝑡𝑎𝑛2𝑢) 𝑐𝑜𝑠2𝑥 𝑐𝑜𝑠2𝑢
là s st (Với s st là hàm số có (𝑐𝑜𝑠𝑥 ≠ 0) (𝑐𝑜𝑠𝑢 ≠ 0) đạo hàm cấp hai). ( 1 𝑐𝑜𝑡𝑥)′ = − −𝑢′
+Vận tốc tức thời của chuyển động tại 𝑠𝑖𝑛2𝑥 (𝑐𝑜𝑡𝑢)′ =
= −(1 + 𝑐𝑜𝑡2𝑥) (𝑠𝑖𝑛𝑥 ≠ 0) 𝑠𝑖𝑛2𝑢
thời điểm t là vt s' t 0 0
= −𝑢′(1 + 𝑐𝑜𝑡2𝑢) (𝑠𝑖𝑛𝑢 ≠ 0) 0
+ Gia tốc tức thời của chuyển động tại
Th.S Nguyễn Viết Hiếu 089908.3939
Th.S Nguyễn Viết Hiếu 089908.3939
thời điểm t là at s'' t . 0 0 0 (𝑒𝑥)′ = 𝑒𝑥
(𝑒𝑢)′ = 𝑢′. 𝑒𝑢
22.Vi phân: Cho hs y f x xác
(𝑎𝑥)′ = 𝑎𝑥. 𝑙𝑛𝑎 (0 < 𝑎 ≠ 1) (𝑎𝑢)′ = 𝑢′. 𝑎𝑢. 𝑙𝑛𝑎 (0 < 𝑎 ≠ 1) định trên ;ab và có đạo hàm tại 1 𝑢′
(𝑙𝑛𝑥)′ = (𝑥 > 0) (𝑙𝑛𝑢)′ = (𝑢 > 0) x ;
a b . Giả sử x là số gia của x. 𝑥 𝑢 1
Vi phân của hàm số y f x tại x ứng ( 𝑢′
𝑙𝑛|𝑥|)′ = (𝑥 ≠ 0) 𝑥 (𝑙𝑛|𝑢|)′ = (𝑢 ≠ 0) 𝑢
với số gia x là: dy df x f 'x. 1 x (𝑙𝑜𝑔 𝑢′
23. Ứng dụng vi phân tính gần 𝑎𝑥)′ = 𝑥. 𝑙𝑛𝑎 (𝑙𝑜𝑔𝑎𝑢)′ = 𝑢. 𝑙𝑛𝑎 đúng:
(𝑥 > 0, 0 < 𝑎 ≠ 1)
(𝑢 > 0, 0 < 𝑎 ≠ 1) 1
𝑓(𝑥0 + ∆𝑥) ≈ 𝑓(𝑥0) + 𝑓′(𝑥0). ∆𝑥 (𝑙𝑜𝑔 𝑢′ 𝑎|𝑥|)′ = 24. Đạo hàm cấp n: 𝑥. 𝑙𝑛𝑎 (𝑙𝑜𝑔𝑎𝑢)′ = 𝑢. 𝑙𝑛𝑎
(𝑥 ≠ 0, 0 < 𝑎 ≠ 1) n
(𝑢 ≠ 0, 0 < 𝑎 ≠ 1) f x n 1 f x a b Zalo 089908.3939
Th.S Nguyễn Viết Hiếu 089908.3939 ax b c d ad bc Đặc biệt: 2 2 cx d (cx d ) (cx d ) b c 2 adx 2aex 2 2 ax bx c d e adx 2aex be dc 2 2 dx e (dx e) (dx e) a b a c b c 2 x 2 x 2 ax bx c d e d f e f
(𝑎𝑒−𝑏𝑑)𝑥2+2(𝑎𝑓−𝑑𝑐)𝑥+(𝑏𝑓−𝑒𝑐) 2 2 2 dx ex f (dx ex f ) (𝑑𝑥2+𝑒𝑥+𝑓)2
23.Ứng dụng vi phân tính gần 1
3,99 f 4 0,0
1 f 4 f '4.0,0 1 y '
. Ta có công thức tính gần đúng
đúng giá trị của 3,99 . 2 x 1 Vậy: 3,99 4 .0,0 1 1,9975.
Xét hàm số y x, x 0 và x 4
𝑓(𝑥0 + ∆𝑥) ≈ 𝑓(𝑥0) + 𝑓′(𝑥0). ∆𝑥 2 4 0
0,01 là số gia của x 4 . x0 0 Face: viethieu220284
Th.S Nguyễn Viết Hiếu 089908.3939 T rang 23 Face: viethieu22028 X
4 II.TẬP HỢP, HÀM SỐ, PT, BẤT PT, THỐNG KÊ, LƯỢNG Th. GI S NguyÁ ễ C
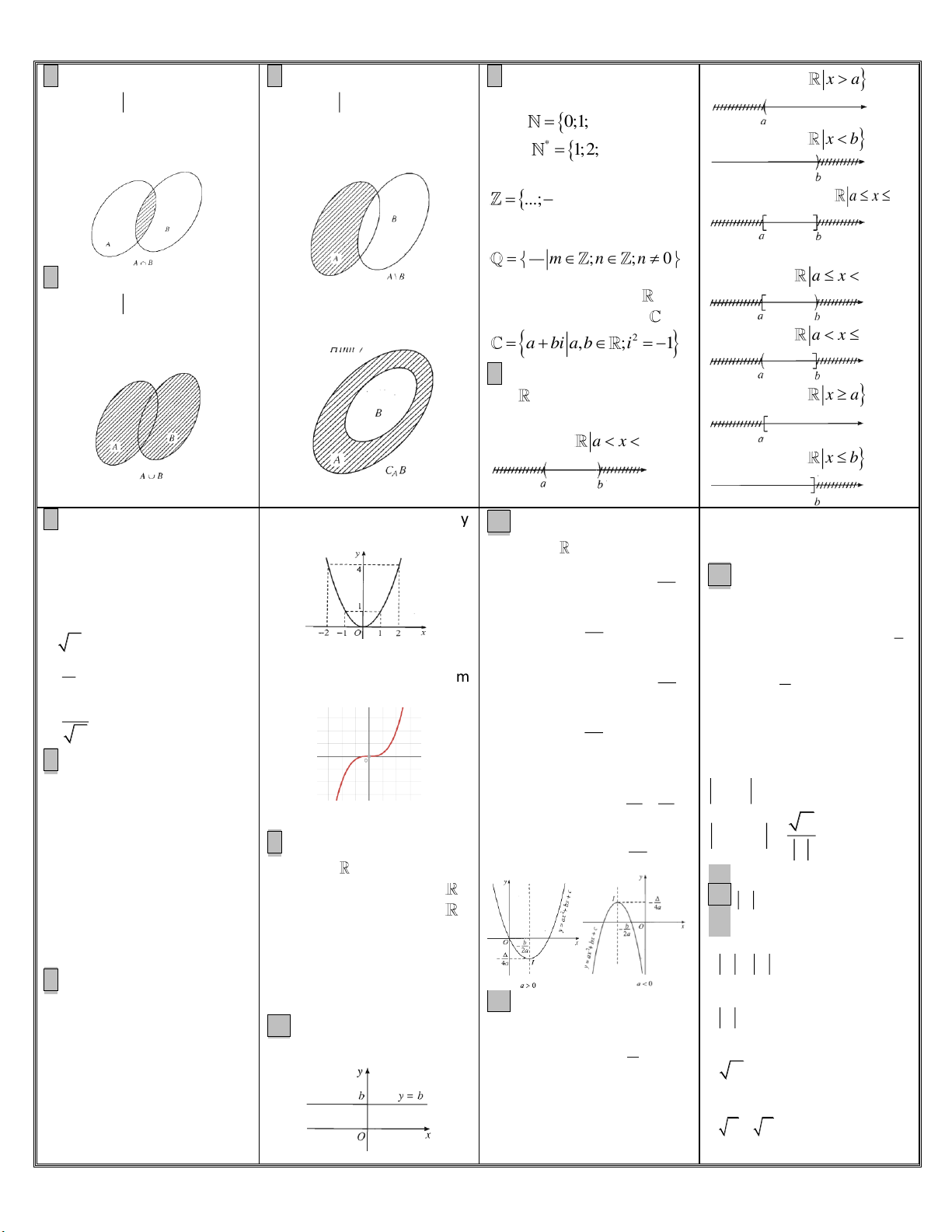
n Vi ết Hiếu 089908.3939 1. Giao của 2 tập hợp 3. Hiệu của 2 tập hợp 4. Các tập hợp số
;a x x a
A B x x A va x B
A \ B x x A va x B
+ Tập hợp các số tự nhiên 0;1;2;3;4;.. . x A x A ;
b x x
x A B
x A \ B b * 1;2;3;4;.. x B x B .
+Tập hợp các số nguyên ...; 3 ; 2 ; 1
;0;1;2;3;.. . + Đoạn a;b x a x b
+Tập hợp các số hữu tỉ m + Nữa khoảng
m ;n ;n 0 2. Hợp của 2 tập hợp n
a;b x a x b
+ Khi B A thì A \ B đgl +Tập hợp các số thực
A B x x A hoac x
B phần bù của B trong A, kí
+ Tập hợp các số phức x A
hiệu C B A \ B
a;b x a x 2 b
x A B A
a bi ,ab ;i 1 x B
5. Các tập con thường gặp của :
a; x x a + Khoảng
;ab x a x b ;
b x x b
Th.S Nguyễn Viết Hiếu 089908.3939
6. Tập xác định của hàm số
+Đồ thị hs chẵn nhận trục Oy T 11.Hsbậc 2: 2
y ax bx ca 0 a 0 h.S N +Pt có vô no
y f x là tập hợp tất cả số làm trục đối xứng + Txđ: D b 0 gu
thực x sao cho biểu thức yễ b n
+ a 0 : hs nb trên ;
13. Định lí Viet a 0
f x có nghĩa. Vi 2a ết +Nếu ptb2 2
ax bx c 0
+Chú ý: A, B là hai đa thức H b iế Hs đb trên ; u . b
A xác định A 0
có 2 no x ; x thì x x 1 2 1 2 (Đths 2 y x ) 089908. 2a a A
xác định B 0
+ Đồ thị hs lẻ nhận gốc O làm b c a B + 0 : hs đb trên ; 3939 và x .x tâm đối xứng. 2a 1 2 a A
xác định B 0 b
Chú ý: x x x x 2x x 1 2 1 22 2 2 B Hs nb trên ; . 1 2 2a
x x x x 3 3 3
3x x x x 1 2 1 2 1 2 1 2
7. Hs y f x đgl hàm đồng
+Đths bậc 2 là 1 đường 2 biến trên khoảng 2 ; a b nếu x x
x x 4x x 1 2 1 2 b
parabol có đỉnh I ; 1 2 T x ;x ;
a b thỏa x x (Đths 3 y x ) 2a 4a h. 1 2 1 2 S N x x
f x f x .
9. Hs bậc nhất y ax ba 0 b 1 2 gu 1 2
, trục đối xứng x . a y 2a ễn
+Hs y f x đgl hàm + Txđ: D B 0 Vi
+ a 0 : hs đồng biến trên ết
nghịch biến trên khoảng
14. A B A B H
+ a 0 : hs nghịch biến trên iế ; a b nếu x ;x ; a b A B u 1 2
+ Đths là 1 đường thẳng d đi 089908.
thỏa x x f x f x . A B 1 2 1 2
qua 2 điểm A0;b,B1;a b .
+ A B 3939
8. Hs y f x với tập xác
( a là hệ số góc của đường A B
định D gọi là hàm số chẵn
thẳng d: y ax b )
12.Pt ax b 0 A khi A 0 + A
nếu x D thì x D và
10.Đths hằng y b là một đt
+pt có no duy nhất a 0 A khi A 0
f x f x .
vuông góc Oy tại A0;b b
(No duy nhất x ) B 0 a
Hs y f x với tập xác định + A B 2 a 0 A B
D gọi là hàm số lẻ nếu +Pt có vô số no
B 0or A 0
x D thì x D và b 0
+ A B
f x f x . A B Trang 24
Th.S Nguyễn Viết Hiếu 089908.3939 Face: viethieu220284 Face: viethieu220284
Th.S Nguyễn Viết Hiếu 089908.3939 15.Pt bậc 2 2
ax bx c 0a 0 +pt có 2 no pb x ; x thỏa 17.Bđt Cauchy 1 2
+Pt có nghiệm 0
x x a b 1 2 + a ,b 0 thì ab
+Pt vô nghiệm 0 0 2 +Pt có 2 no pb 0
x x 0 (Dấu “=” xảy ra a b ) 1 2
+Pt có nghiệm kép 0 +pt có 2 no pb x ; x thỏa + 1 1 4 , ,ab 0 +Pt có 2 no dương pb 1 2 a b a b x x 1 2 + 1 1 1 9 , , a , b c 0 a b c
a b c 0 0 a b c b T + a , ,bc 0 thì 3 abc h.
x x 0 1 2
S x x 0 1 2 S 3 a Ng u
x x 0 1 2 (Dấu “=” xảy ra a b c ) c y
P x .x 0 ễ 18.Bđt Bunhiacopxki 1 2 n +pt có 2 no pb a x ; x thỏa 1 2 Viế + 2 t 2 2 2 2 2 2 ax by cz a b c
x y z +Pt có 2 no âm pb
x x 1 2 Hi ế 0 , a , b , c , x , y z u 0 08 9908
x x 0
Dấu “=” xảy ra khi a b c 1 2 x y z b
S x x 0 .3939
x x 0 x y x y2 2 2 1 2 1 2 a + , a ,b 0; ; x y a b a b c
P x .x 0 1 2 a
16.Tính chất đẳng thức
Dấu “=” xảy ra x y a b
+Pt có 2no trái dấu ac 0 2 2 2 + x y x y , x , y 2 2 18.Nhị thức bậc nhất + 2 2
A B A B Th. 23. Thống kê f x a 0 0, x S
f x ax ba 0 0 Ng +Tần số n, tần suất f
A B A B 0 u y
+Biểu đồ hình cột, hình quạt, ễn f x a 0 0, x + 2 2
A B A B V đường gấp khúc. 0 iế t
A B A B 0 Hi
+Số trung bình cộng x a ế f x 0 0, x A B n x n x ... n x u 1 1 2 2 k k 08 x
“phải cùng, trái trái” 0
+ A B 9908 n A B 19.Tam thức bậc hai A 0
f x f x ... f x 1 1 2 2 k k . A B 3939 f x 2
ax bx ca 0
21. A B B 0
+ A B
( n ; f lần lượt là tần số, tần i i + A B
0 (Pt f x 0 vô no) 2
suất của giá trị x ) A B i A B A B + là số + A B + A B n n ... n n A 0 1 2 k A B A B các số liệu thống kê. + + A B B 0
22. Trong mp Oxy, tập hợp các 0 (pt
f x 0 có n c n c ... n c 1 1 2 2 k k x 2
điểm có tọa độ là no của bpt n b A B nghiệm kép x )
ax by c đgl miền nghiệm
f c f c ... f c 2a A 0 1 1 2 2 k k
+ A B của nó.
( n ; f ;c lần lượt là tần số, A B i i i
+ Quy tắc biểu diễn miền
tần suất, giá trị đại diện của A 0 T
nghiệm của bpt ax by c h
+ A B . lớp ghép thứ i S N A B
B1: Vẽ đt : ax by c gu
+ n n ... n n là số 1 2 k
+ 0 (pt f x 0 có y ễ B2: Lấy 1 điểm M x ; y 0 0 0 B 0 n các số liệu thống kê) nghiệm 2no pb V
x ; x x x ) iế không thuộc . + Số trung vị M 1 2 1 2 A 0 e t + A B H B3. Tính ax by và so sánh
Sắp các số liệu thống kê 0 0 i B 0 ế u
ax by với c. thành 1 dãy không giảm 089908. 0 0 2 A B B4. KL: Nếu thì
(hoặc không tăng). Số trung
“Trong trái,ngoài cùng” ax by c 0 0 3939
vị của các số liệu thống kê
20. Tam thức không đổi dấu B 0
nữa mp bờ chứa M0 là miền no của bpt
đã cho là số đứng giữa dãy
ax by c . f x 2
ax bx ca 0 A 0
nếu số phần tử là lẻ và trung + Nếu thì nữa mp + A B ax by c a 0 0
bình cộng của 2 số đứng + f x 0 0, x B 0
bờ không chứa M là miền no 0
giữa dãy nếu số phần tử là 2 A B
của bpt ax by c chẵn. Face: viethieu220284 Trang 25 Th T .S N . gu S N yễ y n V n iế i t t H iế i u 089908. 3939 089908. Face: viethieu220284
Th.S Nguyễn Viết Hiếu 089908.3939
+Mốt của một bảng phân bố 1 + tan
xk tanxk
cosa b 2 cos . a cosb sin . a sinb
1 tan x cos x 0 2
tần số là giá trị có tần số lớn cos x
cot x k cot xk
cosa b cos . a cosb sin . a sinb
nhất và được kí hiệu là M . 1 O 2
1 cot x sin x 0 x khi k chan a b 2
+Phương sai của dãy số liệu sin x
x k sin sin
a b tan tan tan 1 tan . a tan b tan .
x cot x 1 (sin 2x 0) sin x khi k le
n x x2 ... n x x a b k k 2 1 1
tan a b tan tan 2 s
27.Cos đối, sinbù, phụ chéo
x k cosx khi kchan cos 1 tan . a tan b n
+ cosx cos x (cos đối) cos x khi k le 29.CT nhân đôi
f x x2 ... f x x k k 2 1 1
sinx sin x
+ sin x sin x sin x sin 2x 2sin . x cos x tanx
cos x cos x 2 2
cos 2x cos x sin x
n c x ... n c x tan x T 1 1 2 2 k k 2 + h s .S N 2 2
2cos x 1 1 2sin x
cot x cot x
tan x tanx n gu Áp dụng:
cot x cotx
+ sin x sin x (sin bù) y
f c x2 ... f c x ễ sin 4x 2sin 2 . x cos 2x k k 2 1 1 n
cos x cos x V + sin
x cos x i x x ế +Độ lệch chuẩn: 2 t s s . sin x 2sin .cos
tan x tan x 2 H 2 2 24. Độ và radian: i rad 0 180 ế 2 2 u cos6x cos
3xsin 3x
cot x cot x cos
x sin x 089908.
25. Cung có số đo rad của 2 2 2
2cos 3x 11 2sin 3x
đường tròn bán kính R có độ + sin x cos x (phụ chéo) 2 tan
x cot x 3939 x x 2 2 dài là: cos x cos sin l R . 2 T 2 2
26.CT lượng giác cơ bản h. cos x sin x S N x x 2 cot
x tan x 2 2 2cos 1 1 2sin 2 2
sin x cos x 1 gu 2 y 2 2 sin x ễn tan
x cot x 28. Công thức cộng 30. CT hạ bậc tan x cos x 0 Vi 2 cos x ế sin t
ab sin .acosbsin .bcosa 1 cos 2x H 2 sin x cos x cot x sin x 0 i cot x tan x ế
sina b sin . a cosb sin . b cosa 2 sin x u 2 089908. 1 cos 2x
sin u a 1 a cosu 1
u k2 k 2 35.CT đặc biệt 1 cos x 2 3939 38.PT
sin x cos x 2 sin x u arcsin a k 2 tan x a 1 cos 2x k 2 tan x 4 u
arcsin a k2 +Đk cos x 0 . 1 cos 2x
tan u tan v u v k 31.CT nhân 3 2 cos x +Đb: sinu 0
u k k 4 0 0 0
tan u tan u 1 k 80 3
cos 3x 4cos x 3cos x
sin u 1 u
k2 k
tanu a u arctan a k k 3
sin 3x 3sin x 4sin x
sin x cos x 2 sin x 2 4 32.CT bđ tổng thành tích
39.PT cot x a sin u 1
u k2 k u v u v +Đk sin x 0 . 2 cos x 2
cosu cos v 2cos .cos 4
cot u cot v u v k 2 2
37.PT cos x a 4 4 2 2 0 0 0 u v u v
sin x cos x 1 2sin . x cos x
+ Pt cos x a có nghiệm cot u cot u 1 k 80
cosu cos v 2sin .sin 2 2 1 3 1 2
cot u a u arccot a k k 1 sin 2x cos4x 1 a 1 a 1 u v u v 2 4 4 +Pt vô nghiệm
sin u sin v 2sin .cos cos x a
40. Pt a sin x b cos x c 6 6 2 2 2 2
sin x cos x 1 3sin . x cos x a 1 +Pt có nghiệm 2 2 2 a b c u v u v 3 5 3 a 1 2
sin u sin v 2cos .sin
1 sin 2x cos4x a 1 +Pt vô nghiệm 2 2 2 a b c 2 2 4 8 8 +PP giải khi 2 2 2 :
u v k2 a b c 33.CT BĐ tích thành tổng
36. Pt sin x a
cosu cosv k
u v k2 B1: Chia 2 vế cho 2 2 a b 1
+ Pt sin x a có nghiệm cos .
a cosb cos
a b cosa b a b c 0 0 2 1
a 1 a 1
u k360 sin x cos x 0
cosu cos 2 2 2 2 2 2 1 +Pt a b a b a b
sin x a vô nghiệm 0 0 sin .
a sin b cos
a b cosa b u k360 2 c a 1
sinx (*)
cos u a 1 a 1 1 a 1 2 2 a b sin .
a cosb sin
a b sina b a 1 2 u arccos a k 2 k a
u v k2 Với cos
sin u sin v k u arccos a k 2 34.CT x 2t 2 2
t tan . tan x u
v k2 a b 2 2 1 t
+Đb: cosu 0 u k k b 0 0 2t 2 1 t
u k360 2 sin sin x cos x 0
sinu sin 2 2 a b 2 1 t 2 1 t 0 0 0 u 180 k360
cosu 1 u k2 k B2: Giải (*). Face: viethieu220284 Trang 26
Th.S Nguyễn Viết Hiếu 089908.3939 Face: viethieu220284
Th.S Nguyễn Viết Hiếu 089908.3939
41.Giải pt đẳng cấp bậc 2 đối VdGiải 2 2
cos x 3 sin 2x 1 sin x
42.Hàm số y sin x
43.Hàm số y cos x với sinx và cosx
+ Ta có: cos x 0 ko thỏa pt. +TXĐ: D +TXĐ: D 2 2
a sin x bsin .
x cos x c cos x d +Xét cos x 0 , chia 2 vế pt +Tập giá trị: 1 ; 1 +Tập giá trị: 1 ; 1
B1: Kiểm tra cos x 0 thỏa pt cho 2 cos x ta được pt:
+Hs y sin x tuần hoàn
+Hs y cos x tuần hoàn chu
hay ko. Nếu cos x 0 thỏa thì 1 2 1 2 3 tan x tan x chu kì T 2 . kì T 2 . 2 KL x
k k là no của cos x
+Đồ thị hs y sin x :
+Đồ thị hs y cos x : 2 2
tan x 3 tan x 0
pt. Nếu cos x 0 ko thỏa, ta x k chuyển B2. tan x 0
B2: Xét cos x 0 . Chia 2 vế pt tan x 3
x k cho 2 3 cos x ta được pt: Vậy no của pt là 2 a x b
x c d 2 tan tan 1 tan x
x k ; x
k k
Giải pt trên.B3: Kết luận B1+B2.
Th.S Nguyễn Viết Hiếu 089908.3939 3
44. Hàm số y tan x
45. Hàm số y cot x 46. 2
sin x 1 cos x1 cos x
47.Hệ thức lượng tam giác V +TXĐ: D
\ k,k 2
cos x 1 sin x1 sin x +TXĐ: D
\ k ,k 2
sin a b +Tập giá trị: +Tập giá trị: cot a cot b sin . a sin b
+Hs y tan x tuần hoàn chu kì
+Hs y cot x tuần hoàn chu
sina b
cot a cot b T . kì T . ABC vuông tại A, đường sin . a sin b
+Đồ thị hàm số y tan x :
+Đồ thị hàm số y cot x : 4 4 cao AH.
cos x sin x cos 2x 2 2 2
BC AB AC x x x2 1 sin 2 sin cos 2
AB BH.BC ; 2
AC CH .CB x x x2 1 sin 2 sin cos 2
AH BH.CH 1 cos 2x AH .BC . AB AC 2 cot x 1 cos 2x 1 1 1 2 2 2 cos3x 3cos x AH AB AC 3 cos x 4 A . B AC AH
3sin x s in3x 2 2 3 sin x AB AC 4 AC AB +Định lí sin
r: bán kính đường tròn nội sin B cos B BC BC a b c tiếp ABC . 2R AC AB sin A sin B sin C 1 1 tan B cot B S . ab sin C . ac sin B AB AC
(R: bán kính đường tròn ABC 2 2
48.Hệ thức lượng trong ABC
ngoại tiếp tam giác ABC). 1 T . bc sin A + Độ dài trung tuyến h.S Nguy 2 2 2 2 b c 2 a S
p p a p b p c ABC 2 m ễ a 4 n V (CT Herong) iế 2 a c b t 49.Ứng dụng đo đạc 2 2 2 2 H
Áp dụng ĐL sin vào ABD : AB ; c AC ; b BC a mb i 4 ế
BT1. Đo chiều cao của tháp u AD AB
Độ dài trung tuyến AM;BN;CP 089908.
mà không đến được chân 2 a b c sin sin D 2 2 2 2
được kí hiệu LLL m ;m ;m m tháp. a b c c 4 0 3939
D 15 +Định lí Cosin
Giả sử CD h là chiều cao +Diện tích tam giác ABC 0 2 2 2
a b c 2b . c cos A
của tháp trong đó C là chân . AB sin 24.sin 48 1 1 1 AD 68,91 0 2 2 2
b a c 2a . c cos B S . a h . b h . c h
tháp. Chọn 2 điểm A,B trên sin D sin15 ABC 2 a 2 b 2 c 2 2 2
c a b 2a . b cos C
mặt đất sao cho ba điểm Trong tam giác vuông ACD :
( h ;h ;h LLL độ dài đường cao 2 2 2 a b c h CD A . D sin 61,4m
b c a
A,B và C thẳng hàng. Ta đo + cos A ABC kẻ từ đỉnh A, B,C)
khoảng cách AB và các góc 2bc abc 2 2 2 𝐶𝐴𝐷 ̂, 𝐶𝐵𝐷 ̂
a c b S S pr . Chẳng hạn ta ABC Th.S Nguyễn Viết Hiếu ABC cos B 4R
đo được AB 24m ; 2ac
a b c 089908.3939 2 2 2 (Với p là nữa chu 𝐶𝐴𝐷 ̂ 0 63
a b c cosC 2 𝐶𝐵𝐷 ̂ 0 48 2ab vi ABC ) Face: viethieu220284 Tran g 27
XIII. VECTƠ, CÁC PHÉP TOÁN VECTƠ, TÍCH VÔ HƯỚNG, Face: viethieu220284
Th.S Nguyễn Viết Hiếu 089908.3939 XIV.HÌNH OXY 1.Vectơ là 1
đoạn thẳng có 2. Hai vectơ a và b đgl bằng
4.Tính chất phép toán vectơ
MA MB 2MI hướng.
nhau nếu chúng cùng hướng
Với 3 vectơ a ; b ; c tùy ý,
+ Giá của vectơ là đường
và cùng độ dài, kí hiệu a b . với mọi số h,k ta có:
thẳng đi qua điểm đầu và
a b b a T
điểm cuối của vectơ đó. h.S N
a b c a b c +Hai vectơ đgl cùng gu
phương nếu giá của chúng yễ
a 0 0 a a n song song hoặc trùng nhau. V 7.Trọng tâm ABC iế
k a b
Với hbh ABCD có tâm O, ta có: ka kb t
+ G là trọng tâm ABC H i ; ế h k GA GB GC 0 u + AB DC AD BC
AB cùng phương, cùng a ha k a 089908. ; hướng với AO OC OD BO MA MB MC 3MG CD
hka hka +Vectơ không là vectơ có 3939 (M tùy ý)
điểm đầu và cuối trùng nhau.
1a a ; 1 a a
8. Đk cần và đủ để a và b
+ Vectơ không cùng phương, 5. Vectơ đối
b0 cùng phương là có 1
cùng hướng với mọi vectơ.
Cho a . Vectơ có cùng độ dài
+ PQ cùng phương, ngược
+ AA BB 0
số k để a k.b .
và ngược hướng với a đgl hướng với RS .
3. Quy tắc tổng hiệu 2 vectơ
9.Cho 3điểm phân biệt A,B,C
vectơ đối của a , kí hiệu a
+Khoảng cách giữa điểm
+QT 3 điểm: AB BC AC + A,B,C thẳng hàng
đầu và điểm cuối của vectơ AB BA
+QT trừ: AB AC CB
AB cùng phương AC là độ dài của vectơ. +QT hbh: Nếu ABCD là hình
6.Trung điểm đoạn thẳng AB
AB k AC k 0
+ I là trung điểm AB AB AB
bình hành thì AB AD AC
IA IB 0 10.Tích vô hướng 2vectơ
Điểm M x ; y OM x .i y .j 2 2
+Cho đường thẳng đi qua M M M M
AB x x y y B A B A .
a b a . b .cos ; a b + Cho
điểm M x ; y và có 1 vtcp 0 0 0
u u ;u ;v v ;v 1 2 1 2 BAC
AB AC A .BAC cos cos ;
u u ;u . Pt tham số của 1 2
+ Nếu a 0;b 0 thì:
u v u v ;u v 1 1 2 2 A . B AC
x x u t a b . a b 0
u v u v ;u v
14.Tích vô hướng trong Oxy 0 1 1 1 2 2 là: t +Bình phương vô hướng
Cho a a ;a ;b b ;b
y y u t 1 2 1 2
k.u ku ;ku ,k 0 2 1 2 2 2
của a là: a a
+ có 1 vtcp u u ;u ,u 0 1 2 u v + .
a b a b a b 1 1 1 1 1 2 2 u v u 2 2 AB AB u v + 2 2 a a a 2 2 thì có hệ số góc 2 k . 1 2 u
11. Tính chất tích vô hướng 1
+ u và v v 0 cùng phương
+Góc giữa 2 vectơ a;b 0 :
+Cho đường thẳng đi qua
Với 3 vectơ a ; b ; c tùy ý, u kv . a b a b a b
điểm M x ; y và có 1 vtpt 0 0 0 với mọi số k ta có: cosa;b 1 1 2 2
u kvk 1 1 u kv 2 2 2 2 a . b
a a . b b n ;
a b . Pt tổng quát của . a b . b a 2 2 1 2 1 2 13. Trong mp Oxy, cho tam Th .
a b c . a b . a c
15. Đường thẳng trong Oxy là: ax x b y y 0 . 0 0 S N
giác ABC có Ax ; y ; A A gu
+ u đgl vectơ chỉ phương
ka.b k. . a b . a kb y
Bx ; y ;Cx ; y ễ
của đường thẳng nếu n
+Đt có 1vtcp u u ;u 1 2 B B C C V 2 2 iế
u 0 và giá của u song song a a 0
+ AB x x ; y y t
thì có 1vtpt n u ; u . 2 1 B A B A H hoặc trùng . i 2 + I là trung điểm AB ế
+Đt có 1vtpt n u ;ab thì
a 0 a 0 089908.
+ u là 1 vtcp của thì x x A B
12.Hệ trục tọa độ Oxy x
có 1vtcp u ; b a . I
k.u k 0 2 là vtcp của . 3939
+ Đt có hệ số góc k thì y y A B + y
n đgl vectơ pháp tuyến I 2
của đường thẳng nếu
có 1vtcp u 1;k và 1
+G là trọng tâm tam giác ABC
u 0 và giá của u vuông góc vtpt n k; 1 .
x x x A B C x .
+Đt có hệ số góc k thì pt G 3
+ n là 1 vtpt của thì
có dạng: y kx m
i 1;0, j 0; 1
y y y A B C y
k.nk 0 là vtpt của . +Trục Ox: y 0. G
a a ;a a a .i a . j 3 1 2 1 2 +Trục Oy: x 0.
Th.S Nguyễn Viết Hiếu 089908.3939 Face: viethieu220284 Trang 28 Face: viethieu220284
Th.S Nguyễn Viết Hiếu 089908.3939
16.Đt đặc biệt trong Oxy
+(I) có 1 no duy nhất x ; y
và : a x b y c 0
20.Khoảng cách từ điểm 0 0 2 2 2 2
Đường thẳng : ax by c 0 Thì
M x ; y đến đt : ax by c 0 0 0 0
; cắt nhau tại M x ; y
có 1vtpt n a ;b 1 1 1 0 0 0 1 2 1
+ c 0 : đi qua gốc O(0;0).
+(I) có vô số no thì có 1vtpt
n a ;b ax by c 2 2 2
+ a 0 : / /Ox hoặc Ox . 1 2 2 d M ; 0 0 0 2 2 + +(I) vô nghiệm thì
b 0 : / /Oy hoặc Oy . / / Góc giữa 2đt tính bởi: a b 1 2 ; 1 2
17. Đường thẳng đi qua
Đặc biệt: Nếu a ;b ;c 0 thì 2 2 2 Th.S N n .n a a b b cos ; 1 2 1 2 1 2 1 2 hai điểm A ;0
a và B0;b với a b + cắt 1 1 . 2 2 2 2 gu n . n
a b . a b 1 2 a b 1 2 1 1 2 2 x y y 2 2 ễ
a,b 0 . Pt đt : 1. n V
n .n 0 a a bb 0 a b a b c 1 2 1 2 1 2 1 2 i + / / 1 1 1 ế 1 2 t
+ Khoảng cách giữa 2 đt song 18. VTTĐ của 2 đt a b c +Nếu : y k x m H 2 2 2 1 1 1 iế
song : ax by c 0
Cho 2 đt : a x b y c 0 a b c u
: y k x m 1 1 1 1 1 1 2 2 2 + 1 1 1 089908.
Và :ax by c 0 c c 2 2 2 1
và : a x b y c 0 1 2 a b c
có 1vtpt n k ; 1 1 1 2 2 2 2 2 2 2 1 3939 c c
a x b y c 0 19.Góc giữa 2đt
có 1vtpt n k ; 1 d ; 1 2 1 2 2 2 +Xét hệ: 1 1 1 I 2 2 2
a x b y c 0
Cho 2 đt : a x b y c 0 a b 2 2 2 1 1 1 1 n .n 0 k .k 1 1 2 1 2 1 2
21.Đường tròn (C) có tâm
22.VTTĐ giữa đường tròn (C) 23.Tiếp tuyến của đường 24. Trong mp cho hai điểm I ;
a b và có bk R. Pt đường
và đường thẳng :ax by c 0
tròn (C) có tâm I ; a b , bk R,
cố định F ;F và một độ dài 1 2
tròn (C): 2 2 2
không đổi 2a , lớn hơn x a y b R (C) có tâm I ; a b và bk R.
tại điểm M x ; y là . F F . 1 2 0 0 0
+ d I; R: ko cắt (C). + đi qua
Elip là tập hợp các điểm M
M x ; y và có 1 0 0 0 trong mp thỏa:
+ d I; R: tiếp xúc (C)
vtpt IM x ; a y b 0 0 0
MF MF 2a 1 2
+ d I; R : cắt (C) tại 2
+Pt : x a x x y b y y 0 0 0 0 0 điểm phân biệt A, B. +Pt đường tròn (C):
Gọi H là hcvg của I trên . 2 2
x y 2ax 2by c 0 H là trung điểm của AB. 2 2
AB 2HB 2 R d I; 2 2
a b c 0 . Đt (C) có tâm
+2 điểm F ;F là 2 tiêu điểm 1 2
của Elip. Độ dài F F 2c là 1 2 I ; a b và bk 2 2
R a b c tiêu cự của Elip.
25.PT chính tắc của Elip (E):
26.Dấu hiệu nhận biết hình +Hình thang cân có 1 góc 2 2 x y bình hành:
vuông là hình chữ nhật.
1 0 b a 2 2 +Hình bình hành có 1 góc a b
vuông là hình chữ nhật.
+Hình bình hành có 2 đường chéo bằng nhau là hcn.
+Tứ giác có 4 cạnh bằng
28.Dấu hiệu nhận biết hình nhau là hình thoi.
+Tứ giác có các cặp cạnh đối vuông
+Hình bình hành có hai cạnh 2 2 2
c a b 0ca song song là hbh.
+Hcn có hai cạnh kề bằng kề bằng nhau là hình thoi.
+Tứ giác có các cặp cạnh đối 2 2
c a b nhau là hình vuông. + Hình bình hành có hai bằng nhau là hbh.
đường chéo vuông góc là +Tiêu điểm:
+Hình chữ nhật có hai đường F ; c 0 , F ; c 0 1 2
+Tứ giác có hai cạnh đối
chéo vuông góc là h.vuông. hình thoi.
+Tiêu cự: F F 2c song song và bằng nhau là 1 2
+HCN có một đường chéo là +Hình bình hành có một +4 đỉnh: A ; a 0 , A ; a 0 hbh.
đường chéo là đường phân 1 2
đường phân giác của một góc
+Tứ giác có các góc đối bằng B 0; b ,B 0;b là hình vuông.
giác của một góc là hình thoi. 1 2 nhau là hbh.
+Hình thoi có 1 góc vuông là 30. Cho tam giác ABC. Gọi
+Độ dài trục lớn: A A 2a 1 2
+Tứ giác có hai đường chéo hình vuông.
D,E lần lượt là chân đường
+Độ dài trục nhỏ: B B 2b
cắt nhau tại trung điểm mỗi 1 2
+Hình thoi có hai đường chéo phân giác trong và ngoài của
+Đường thẳng : Ax By C 0 đường là hbh. bằng nhau là hình vuông. góc A của ABC . Ta có: tiếp xúc (E) khi
27.Dấu hiệu nhận biết hcn
29.Dấu hiệu nhận biết hình AB DB AB EB ; 2 2 2 2 2
+Tứ giác có 3góc vuông là hcn
A a B b C thoi AC DC AC EC Face: viethieu220284 Trang 29
Th.S Nguyễn Viết Hiếu 089908.3939 G. Polya (1887-1985)
Giải một bài toán như thế nào?
Theo G.Polya giải toán không chỉ đơn thuần là tìm ra đáp số của lời giải, mà “Giải
bài toán” là bao quát toàn bộ quá trình suy ngẫm, tìm tòi lời giải, tìm mối liên hệ
mật thiết giữa giả thiết kết luận, giải toán và tìm hướng phát triển cho lời giải.
4 bước giải toán theo G.Polya: 1.Understand, 2.Plan, 3.Solve, 4.Check. 1. UNDERSTAND
Đâu là ẩn? Đâu là dữ kiện? Đâu là điều kiện? Có thể thỏa mãn điều kiện bài toán hay
không? Điều kiện có đủ để xác định ẩn không? Hay chưa đủ? Hay thừa? Hay có mâu thuẫn?
Vẽ hình. Sử dụng kí hiệu thích hợp.
Phân biệt các phần khác nhau của điều kiện. Có thể diễn tả các điều kiện đó thành công thức không? 2. PLAN
Bạn đã gặp bài toán này lần nào chưa? Hay đã gặp bài toán này ở một dạng hơi khác?
Bạn có biết một bài toán nào liên quan không? Một định lí có thể dùng được không?
Xét kĩ cái chưa biết (ẩn) và thử nhớ lại một bài toán quen thuộc có cùng ẩn hay có ẩn tương tự.
Đây là một bài toán có liên quan mà bạn đã có lần giải rồi. Có thể sử dụng nó không?
Có thể sử dụng kết quả của nó không? Hay sử dụng phương pháp? Có cần phải đưa
thêm một số yếu tố phụ thì mới sử dụng được nó không?
Có thể phát biểu bài toán một cách khác không? Một cách khác nữa? Quay về định nghĩa.
Nếu bạn chưa giải được bài toán đã đề ra, thì hãy thử giải một bài toán có liên quan.
Bạn có thể nghĩ ra một bài toán có liên quan mà dễ hơn không? Một bài toán tổng
quát hơn? Một trường hợp riêng? Một bài toán tương tự? Bạn có thể giải một phần
bài toán không? Hãy giữ lại một phần của điều kiện, bỏ qua phần kia. Khi đó ẩn được
xác định đến một chừng mực nào đó; nó biến đổi như thế nào? Bạn có thể từ các dữ
kiện rút ra một yếu tố có ích không? Bạn có thể nghĩ ra những dữ kiện khác có thể
giúp bạn xác định được ẩn không? Có thể thay đổi ẩn, hay các dữ kiện, hay cả hai nếu
cần thiết, sao cho ẩn mới và các dữ kiện mới được gần nhau không?
Bạn đã sử dụng mọi dữ kiện hay chưa? Đã sử dụng toàn bộ điều kiện hay chưa? Đã
để ý đến mọi khái niệm chủ yếu trong bài toán chưa? 3. SOLVE
Khi thực hiện giải bạn hãy kiểm trạ lại từng bước giải.Bạn đã thấy rõ ràng là mỗi bước
đều đúng chưa? Bạn có thể chứng minh là nó đúng không? 4. CHECK
Bạn có thể kiểm tra lại kết quả? Bạn có thể kiểm tra lại toàn bộ quá trình giải bài toán không?
Có thể tìm được kết quả một cách khác không? Có thể thấy trực tiếp ngay kết quả không?
Bạn có thể sử dụng kết quả hay phương pháp giải cho một bài toán nào khác không?
Th.S Nguyễn Viết Hiếu 089908.3939 1. HÀM SỐ Trang 1
2. HÀM SỐ MŨ, HÀM SỐ LŨY THỪA, HÀM SỐ LOGARIT Trang 5
3. NGUYÊN HÀM, TÍCH PHÂN, ỨNG DỤNG Trang 9 4. SỐ PHỨC Trang 10
5. THỂ TÍCH KHỐI ĐA DIỆN Trang 11 6. KHỐI TRÒN XOAY Trang 13 7. KHÔNG GIAN OXYZ Trang 14 8. PHÉP BIẾN HÌNH Trang 16 9. HÌNH HỌC KHÔNG GIAN Trang 18 10. ĐẠI SỐ TỔ HỢP Trang 20
11. CẤP SỐ CỘNG, CẤP SỐ NHÂN, GIỚI HẠN, ĐẠO HÀM Trang 22
12. TẬP HỢP, HÀM SỐ, PHƯƠNG TRÌNH, BPT, THỐNG KÊ, LƯỢNG GIÁC Trang 24
13. VECTƠ, CÁC PHÉP TOÁN VECTƠ, TÍCH VÔ HƯỚNG Trang 28 14. HÌNH OXY Trang 28