Onthisinhvien.com 12 ngày chinh phục A+ Xác suất thống kê Lê Nguyễn Viết Duy
Chương 1: Biến cố và xác suất
• Với A và B là 2 biến cố không xung khắc ( độc lập hoặc phụ thuộc):
P(A + B) = P(A) + P(B) – P(AB) • Với A và B P •Với A và B l
ó các công thức đáng nhớ sau: ) ) 1) Công thức Bernoulli x n x
: P(x | n,p)  nCx.p .(1 p)    n  
2) Công thức xác suất đầy đủ:  i 1    P(A | H ).P(H ) 3) Công thức Bayes: i i P(H | A)  i  P(A)  
Chương 2 BNN rời rạc và QLPP xác suất
I. Biến ngẫu nhiên rời rạc
1) Bảng phân phối xác suất(Chỉ BNN rời rạc mới có)
•Cho biến NN rời rạc X nhận các giá trị x1,x2,…,xn với xác suất tương ứng p1,p2,…pn. X x1 x2 ………. xk ………. xn P p1 p2 ……….. pk ………… pn
2)Các tham số đặc trưng
•Kì vọng(trung bình) n
Kì vọng kí hiệu là E(X) và tính bằng: E(X) =
Đơn vị của kì vọng là đơn vị của X Tính chất:
1. E(C) = C C là hằng số 2. E(C + X) = C + E(X) 3. E(C.X) = C.E(X)
Onthisinhvien.com 12 ngày chinh phục A+ Xác suất thống kê Lê Nguyễn Viết Duy 4 ) = E(X) ± E(Y)
5. E(X,Y) = E(X).E(Y) ( Đây là trường hợp 2 biến X,Y độc lập còn nếu X,Y
phụ thuộc ta xem xét ở các bài sau •Phương sa n
-Công thức: V(X) = E(X ) – [E(X)] ( Trong đó E(X ) = )
-Đơn vị của phương sai là (đơn vị của X) v à V(X) ≥0 Tính chất: V(C) = 0 C là hằng số V(X + C) = V(X) V(C.X) = C . V(X)
= V(X) + V(Y)(V ới X và Y độc lập, nếu X và Y phụ thuộc ta xét sau)
•Độ lệch chuẩn Ϭ =
II. Quy luật Phân phối xác suất cho BNN rời rạc Nhị thức Poisson Ký hiệu X ~ B(n,p) X ~ P( Công thức x x 1 x P(X x) C .p .(1 p)       x    n P(X  x)   e  x! Kỳ vọng E(X) = np E(X) = Phương sai V(X) = np(1-p) V(X) = Mốt(Mode)
np + p -1 ≤ m0 ≤ np +   ≤ m0 ≤ Dấu hiệu
Đọc đầu bài thấy giống Khi đầu bài cho lượng Bernoulli trung bình mà không
cho biết p hay n thì ta dùng phân phối Poisso
1) Điều kiện xấp xỉ phân phối Nhị thức sang Poisson: n quá lớn np ≈ np(1-p)
Onthisinhvien.com 12 ngày chinh phục A+ Xác suất thống kê Lê Nguyễn Viết Duy
2) Phân phối Nhị thức tỉ lệ Cho X - B(n,p). Đặt =
Khi đó có phân phối Nhị thức tỉ lệ: 
• Ki vọng E( ) = p • Phương sai V( ) Chương 3: BNN liên QLPP xác suất
Biến ngẫu nhiên liên t
1) Hàm phân phối xác suất
-Hàm phân phối xác suất :       -Tính chất:
2) Hàm mật độ xác suất - Ký hiệu:
3) Tính chất hàm mật độ: •f(x) ≥ 0 x 0 •F(x0) = f (x)dx    • f (x)dx  = 1  b • P(a ≤ X ≤ b) = f (x)dx  a
II. Quy luật phân phối xác suất(BNN liên tục)
1. Quy luật phân phối xác suất Chuẩn
Phân phối Chuẩn Ký hiệu 2 X ~ N(, )
Kỳ vọn g E(X) =  (đọc là muy) Phương sai V(X) = 2  (đọc là sigma bình) Công thức     •PX   b b  (  )        •  P a   a X  1( )    
Onthisinhvien.com 12 ngày chinh phục A+ Xác suất thống kê Lê Nguyễn Viết Duy       •  P a  X   b a b  ( ) – ( )    
•(x)   (x) 0,5 0  
•Phân phối Nhị thức xấp xỉ phân phối Chuẩn
Cho X~B(n,p). Khi n ≥ 100 thì X~N(μ, 2  ) (Với μ = np; 2  = np(1-p))
•Phân phối Poisson xấp xỉ phân phối Chuẩn
Cho X~P( ). Khi n ≥ 20 thì X~N(μ, 2  ) (Với μ =; 2  = )
•“Sai lệch so với ….trung bình không quá ɛ” ta áp dụng công thức:
P(|X – μ| < ɛ) = 2 Φ(ɛ ) -1 𝜎
Chương 4: Tương quan BNN 2 chiều Hiệp phương sai Hệ số tương quan Kí hiệu
Cov(X,Y) = E(XY) – Ρ Cov(X,Y) E(X).E(Y) x,y=  . x y Ý nghĩa
Thể hiện tương quan tuyến
Đo mức độ chặt chẽ của tương tính giữa X và Y
quan tuyến tính giữa X và Y Cụ thể
Cov(X,Y) = 0 => X và Y
Ρx,y= 0 => X và Y không tương
không tương quan Cov(X,Y) quan
> 0 => X và Y tương quan
Ρx,y = ±1 => X và Y tương
dương Cov(X,Y) < 0 => X và quan hàm số Y tương quan âm tuyến tính
𝜌x,y → 0 => mức độ tương quan là thấp
𝜌x,y → ±1 => mức độ tương quan là cao Chú ý
V(aX+bY) = a 2.V(X) + b 2 .V(Y) + 2abCov(X,Y)
E(XY) = p11.x1. y1 + p12 .x2.y1 + ... + p21.x1 .y2 + ... + pmn.xn.ym
Chương 5: Tổng thể - Mẫu
1. Mẫu và tổng thể
-Dấu hiệu: Cân nặng của sinh viên trường N
-Tổng thể: Toàn bộ sinh viên trường N(xấp xỉ 22K người)
-Mẫu: Lấy ngẫu nhiên 100 sinh viên trường N(bất kể nam,nữ). 2. Các tham số
Onthisinhvien.com 12 ngày chinh phục A+ Xác suất thống kê Lê Nguyễn Viết Duy Tham số Tổng Mẫu thể Kích thước N n Trung bình m, μ (phân phối X , x chuẩn) Trung vị Md xd Mốt m0 x0 Phương sai σ2 S2, s2 Độ lệch Σ S, s chuẩn Hệ số  CV 100 cv s 100 biến  m  x thiên Hệ số α bất đối xứng 3 a3 Hệ số nhọn α4 a4 Tỉ lệ P = p = M/N m/n x= x d => a3 = 0 => đối xứng x> x d => a3 > 0
=> lệch phải (đồ thị kéo dài về phía +∞) x< x d => a3 < 0
=> lệch trái (đồ thị kéo dài về phía -∞)
3. Mẫu ngẫu nhiên, mẫu cụ thể
- Mẫu ngẫu nhiên: x1, x2, x3, ..., x n hay w = {xi, i=1,2,3,...n}
Ví dụ: Điều tra ngẫu nhiên cân nặng của 7 nữ sinh trường N,ta được mẫu liệt
kê sau: 45,47,50,47,47,51,50. - Mẫu cụ thể: X x1 x2 ... xk Ni n1 n2 ... nk
Ví dụ: Điều tra ngẫu nhiên cân nặng của 7 nữ sinh trường N ta thấy có 1 sv
nặng 45, 3 sv nặng 47, 2 sv nặng 50 và 1 sv nặng 51.Có bảng: Cân nặng 45 47 50 51 Tần số 1 3 2 1
4. Tính toán các tham số 1 n 1 n -Trung bình mẫu: x = x  hoặc x = n x  n i n i i i1 i1
45  47  50  47  47  51 50.
Ví dụ: Trung bình mẫu cân nặng: x = =48,143 7 x  x n n 1  -Trung vị mẫu: x = x ẻ x = 2 2 (n chẵn) d n 1  (n l ) d 2 2
Onthisinhvien.com 12 ngày chinh phục A+ Xác suất thống kê Lê Nguyễn Viết Duy
Ví dụ:Trung vị mẫu cân nặng: 45,47,50,47,47,51,50
Vì n=7 lẻ.Ta sắp xếp lại theo thứ tự từ lớn tới bé: 45,47,47,47,50,50,51 và ta lấy
số ở giữa là 47 => md = 47
- Mốt mẫu: x0 có số lần xuất hiện nhiều nhất
Ví dụ: Mốt mẫu trên là 47 n n 1 n 1 - Phương sai mẫu: 2 2 2 s  [x  (x) ] (Với 2 x = 2 x  hoặc 2x = 2 n x  ) n 1 i n i i i 1  n i1 m
- Tần suất mẫu: p = n
Ví dụ: Tìm tần suất các sv có cân nặng ≤ 50 => 6 p = 7
- Tứ phân vị: Chia tập dữ liệu ra thành 4 phần bằng nhau( sắp xếp từ nhỏ đến lớn)
- Hiệp phương sai mẫu: cov(X,Y)= n (xy x.y) n 1  cov(X,Y)
- Hệ số tương quan mẫu: rx,y = s .s x y
5. Suy diễn thống kê mẫu
•Suy đoán cho trung bình mẫu Suy đoán cho trung bình
Suy đoán cho tần suất(tỷ mẫu lệ) mẫu Giả thuyết
•Giả thiết có tổng thể X ~
• Giả thiết có tổng thể phân
N(μ;σ2 ) xác định (đã biết
phối A(p) xác định (đã biết μ và σ) p) •Trung bình mẫu ngẫu
•Với mẫu lớn (n ≥ 100), ta nhiên kích thước n lúc
có tần suất mẫu p ~ N(p; 2  p(1 p)
này: X ~ N ( ; ) ) n n •Chuẩn hóa bằng cách
đặt: Z = 𝑋 −𝜇 ~ N(0,1) 𝜎/√𝑛 Khoảng 2 phía μ 𝜎 - z √𝑝(1−𝑝)
α/2 < X < μ + 𝜎 zα/2 √𝑛 √𝑛 p -
zα/2 < p < p + √𝑛
√𝑝(1−𝑝) zα/2 √𝑛
Onthisinhvien.com 12 ngày chinh phục A+ Xác suất thống kê Lê Nguyễn Viết Duy Tối đa
X < μ + 𝜎 zα √𝑛
p < p +√𝑝(1−𝑝)zα √𝑛 Tối thiểu X > μ 𝜎 - zα √𝑝(1−𝑝) √ 𝑛 p > p - zα √𝑛 Chương 7: Ước lượng
1) Ước lượng điểm
- Không chệch: E(G1) = E(X) = m
- Hiệu quả: V nào mà nhỏ nhất trong số các V thì ước lượng đấy là hiệu quả
2. Ước lượng khoảng
Trung bình tổng thể Tỷ lệ tổng thể •Khoảng 2 phía S S (n 1  ) X  t <  < (n 1) X  t p(1 p) p(1 p)  /2 n /  2 n -z  p  p  z  /2  /2 n n •Tối đa S n 1   X  t  p(1 p)    n p p z /2 n •Tối thiểu S n 1   X  t  p(1  p)    n p z p  /2 n •Sai số ước lượng S (n 1)   p(1 p) (độ chính xác) t  /2 n  = z /2 n
•Độ dài khoảng tin I = 2 I = 2  cậy
Phương sai tổng thể •Khoảng 2 phía 2 (n 1)S 2 (n  1)S  2   2(n 1  )  2(n 1  )   /2 1 /2 •Tối đa 2 (n 1)S 2   2(n1) 1 •Tối thiểu 2 (n 1)S  2  2(n 1  ) 
Onthisinhvien.com 12 ngày chinh phục A+ Xác suất thống kê Lê Nguyễn Viết Duy
Chương 8: Kiểm định giả thuyết Cách làm 1:
- Bước 1: Viết cặp giả thuyết
***Lưu ý: H0 luôn nhận dấu = (lớn hơn hoặc bằng, nhỏ hơn hoặc bằng, =)
H1 trái với H0 (<, >, ≠)
- Bước 2: Tiêu chuẩn(Tqs, 2
 qs hoặc Fqs, Zqs) (Công thức tra bảng)
- Bước 3: Miền bác bỏ(Tra bảng tương ứng)
=> Kết luận: Thuộc miền bác bỏ => Bác bỏ H0, Chấp nhận H 1
Không thuộc miền bác bỏ => Chưa đủ cơ sở bác bỏ H0 Cách làm 2:
- Bước 1: Viết cặp giả thuyết
- Bước 2: Sử dụng P-Value
+) P-Value < α => Bác bỏ H0, chấp nhận H1
+) P-Value > α => Chưa đủ cơ sở bác bỏ H0
I) Kiểm định 1 tham số - Trung bình (<, >, =)
- Phương sai (<, >, =) -Tỷ lệ (<, >, =)
II) Kiểm định 2 tham số - Trung bình (<, >, =)
- Phương sai (<, >, =) 1 ***Lưu ý: (df1,df2) f  1 (df2 , 1 df ) f
Onthisinhvien.com 12 ngày chinh phục A+ Xác suất thống kê Lê Nguyễn Viết Duy -Tỷ lệ (<, >, =) n .p  n .p ***Lưu ý: 1 1 2 2 p  n  n 1 2
III) Kiểm định phi tham số
1) Kiểm định phân phối chuẩn(JB)
- B1: Cặp giả thuyết: H0: Biến X phân phối chuẩn
H1: Biến X Không phân phói chuẩn ( Slide trang 250) - B2: JBqs = Tra bảng 3 (X  X) / n Trong đó: a i 3 = 3 S 4 (X  X) / n a i 4 = 4 S
- B3: Miền bác bỏ(Tra bảng) - B4: Kết luận
2) Kiểm định tính độc lập
- B1: Cặp giả thuyết: H0: A và B độc lập
H1: A và B không độc lập (Slide trang 253)
- B2: Giá trị quan sát: Tra bản g
- B3: Miền bác bỏ(Tra bảng) - B4: Kết luận
***Nếu có thời gian thì đọc thêm Slide trang số:221, 214, 207, 199, 195, 179
Giả thuyết H1
Kiểm định T(1,2 trung bình)
Kiểm định Z(1,2 tỷ lệ) ≠
n < 31: P-Value = 2P(T(n-1) > |Tqs|) P-Value = 2P(Z > |Zqs|)
n > 31: P-Value = 2P( Z > |Tqs| ) >
n < 31: P-Value = P(T(n-1) > Tqs) P-Value = P(Z > Zqs)
n > 31: P-Value = P( Z > Tqs)
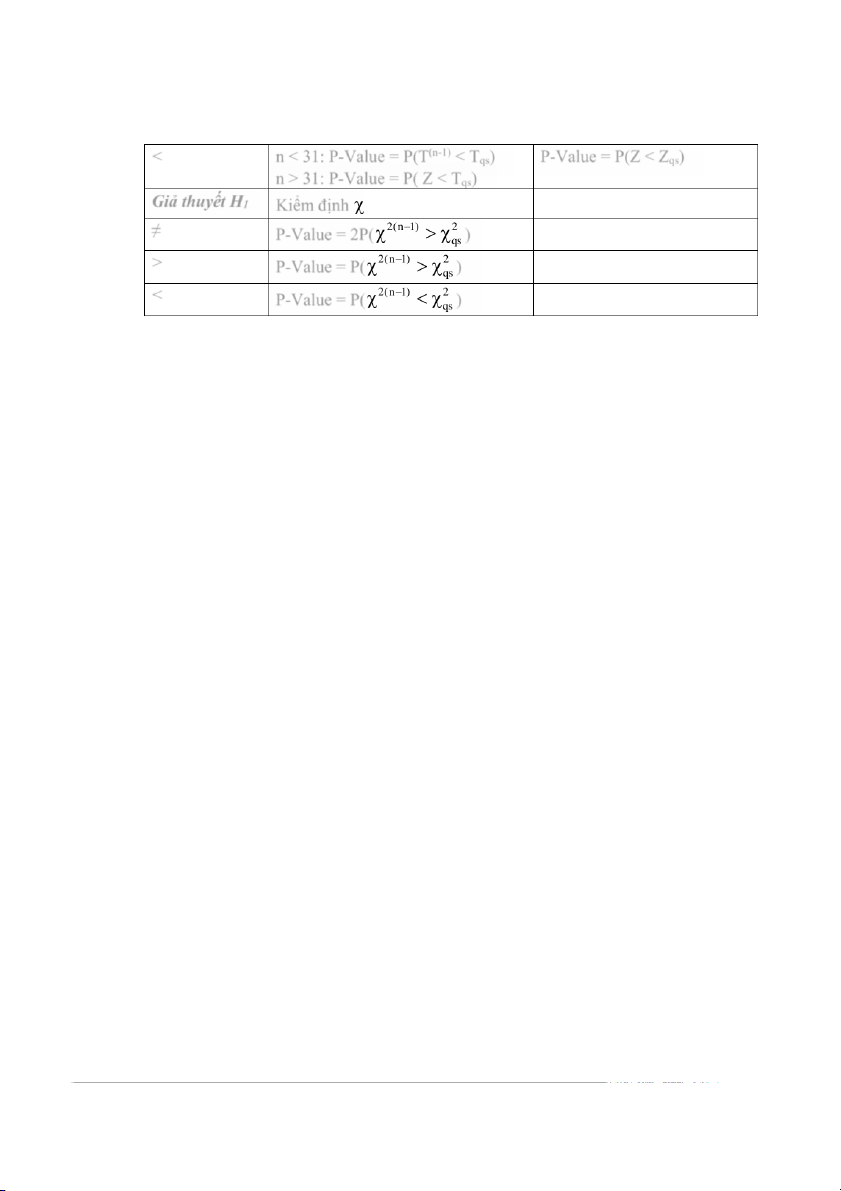
Onthisinhvien.com 12 ngày chinh phục A+ Xác suất thống kê Lê Nguyễn Viết Duy <
n < 31: P-Value = P(T(n-1) < Tqs) P-Value = P(Z < Zqs)
n > 31: P-Value = P( Z < Tqs) Giả thuyết H 2 1 Kiểm định ≠ P-Value = 2P( ) > P-Value = P( ) < P-Value = P( )