Tổng hợp kiến thức toán 10 bằng sơ đồ tư duy và hệ thống câu hỏi trắc nghiệm

CỘNG HÒA XÃ HỘI CHỦ NGHĨA VIỆT NAM
Độc lập – Tự do – Hạnh phúc    MÔ TẢ SÁNG KIẾN
Mã số: . . . . . . . . . . . . . . . . . . .
1. Tên sáng kiến:
CỦNG CỐ KIẾN THỨC TOÁN 10 BẰNG SƠ ĐỒ TƯ DUY VÀ
HỆ THỐNG CÂU HỎI TRẮC NGHIỆM
(Nguyễn Mộng Linh, Nguyễn Thị Minh Tuyền, Phạm Như Trinh,
@THPT Chê Guê-va-ra, Mỏ Cày Nam, Bến Tre)
2. Lĩnh vực áp dụng sáng kiến: Công tác chuyên môn
3. Mô tả bản chất của sáng kiến
3.1. Tình trạng giải pháp đã biết
- Về thực trạng của vấn đề:
Việc học sinh quên những kiến thức đã học ở lớp dưới là hiện tượng phổ
biến thường gặp hầu hết ở các khối lớp, tình trạng này không những làm hạn chế
việc tiếp thu bài mới, mà còn làm nản lòng ở một số em, dẫn đến hiện tượng
lười học, chán học, bỏ học hoặc nhẹ hơn là không giải quyết được các vấn đề một cách trọn vẹn.
Làm thế nào để học sinh có được một lượng kiến thức cơ bản, một số kĩ
năng cần thiết ở mỗi bộ môn, ở mỗi lớp, mỗi cấp học là hết sức cần thiết, để khi
lên lớp trên các em có đủ tự tin, đủ khả năng tiếp thu những kiến thúc mới, củng
cố và mở rộng kiến thức đã có. Từ đó, các em mới có thể nâng cao khả năng tự
học, mới có thể giải quyết được những vấn đề có tính lôgic, có tính khái quát, tổng hợp cao.
Qua nhiều năm giảng dạy nhận thấy, một số học sinh học rất chăm chỉ
nhưng vẫn học kém, nhất là môn toán, các em này thường học bài nào biết bài
đấy, học phần sau đã quên phần trước và không biết liên kết các kiến thức với
nhau, không biết vận dụng kiến thức đã học trước đó vào những phần sau. 1
Nguyên nhân chủ yếu là học sinh còn chưa biết cách học, mặc dù là môn tự
nhiên đa số học sinh chỉ học thuộc lòng nên vừa kết thúc mỗi kỳ kiểm tra, học
kỳ thi là học sinh quên hêt các kiến thức đã học. Vận dụng bản đồ tư duy trong
dạy học, học sinh sẽ học được phương pháp học, tăng tính độc lập, chủ động,
sáng tạo và phát triển tư duy.
Từ năm 2016_2017, Kiểm tra môn toán với hình thức trắc nghiệm khách
quan chính thức được áp dụng trong kì thi tốt nghiệp phổ thông quốc gia. Điều
đó là một thách thức lớn với học sinh và giáo viên. Làm thế nào để học sinh tự
ôn tập tốt ? và làm thế nào để giáo viên hướng dẫn các em hệ thống kiến thức tốt
để làm trắc nghiệm? Đó là điều trăn trở; Chúng tôi _ giáo viên phổ thông đã đưa
ra và áp dụng giảng dạy học sinh ôn tập bằng bản đồ tư duy và củng cố kiến
thức bằng hệ thống câu hỏi trắc nghiệm.
- Về nguyên nhân thực trạng:
Giáo viên vẫn quen giảng dạy và ôn tập theo hướng tự luận.
Học sinh không hệ thống được kiến thức mình đã học.
Trắc nghiệm khách quan, đòi hỏi học sinh phải nhớ lượng kiến thức lớn
và phải có kĩ năng làm trắc nghiệm.
- Giới hạn nghiên cứu của đề tài:
Chương II; chương III: đại số 10 Chương I : hình học 10
Sản phẩm tự ôn tập của học sinh bằng sơ đồ tư duy.
Ma trận tổng quát và đề kiểm tra học kì I khối 10 năm học 2017 – 2018.
Thống kê kết quả môn toán học kì I giữa lớp áp dụng giải pháp ôn tập
bằng sơ đồ tư duy, hệ thống câu hỏi trắc nghiệm và lớp ôn tập không áp dụng giải pháp.
3.2. Nội dung giải pháp đề nghị công nhận là sáng kiến
- Mục đích của giải pháp: nhằm tạo sự hứng thú và dễ hiểu cho học sinh
khi tiếp nhận kiến thức của bài. Từ đó, giúp học sinh tự hệ thống kiến thức bằng
sơ đồ tư duy và thực hành giải toán trắc nghiệm khách quan.
- Nội dung giải pháp: 2
* Những điểm khác biệt và tính mới của đề tài:
Giúp học sinh ôn tập kiến thức đã học một cách có hệ thống, trực quan, dễ
khắc sâu bằng việc vẽ bản đồ tư duy. Từ đó, học sinh có thể áp dụng vào việc
giải câu hỏi trắc nghiệm.
*Cách thức thực hiện: Được trình bày thông qua nội dung như sau
Chương 2 : HÀM SỐ BẬC NHẤT VÀ BẬC HAI
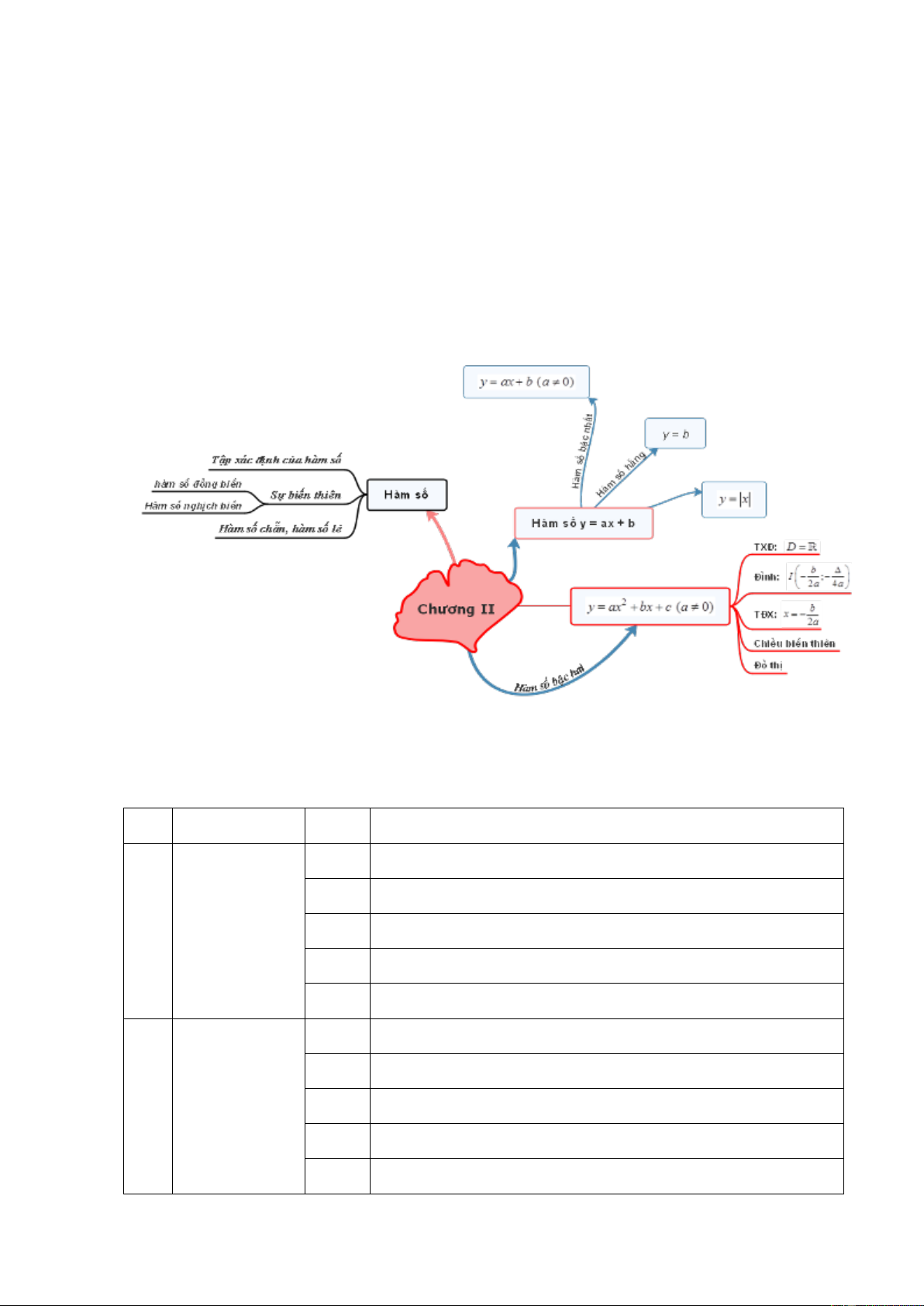
I. Hệ thống kiến thức bằng sơ đồ tư duy II.
Bảng mô tả chi tiết nội dung câu hỏi trắc nghiệm CHỦ ĐỀ CÂU MÔ TẢ 1 HÀM SỐ 1
Nhận biết: Tập xác định của hàm số 2
Thông hiểu: Tìm tập xác định của hàm số 3
Thông hiểu: Tìm tập xác định của hàm số 4
Nhận biết: đồ thị của hàm số 5
Vận dụng: Xét tính chẵn, lẻ của hàm số 2 HÀM SỐ 6
Nhận biết: hàm số bậc nhất y = ax + b 7
Nhận biết: sự biến thiên của hàm số bậc nhất 8
Thông hiểu: đồ thị của hàm số bậc nhất 9
Thông hiểu: Tìm hàm số bậc nhất 10
Vận dụng: Tìm hàm số bậc nhất 3 11
Vận dụng: đồ thị của hàm số chứa ẩn trong trị tuyệt đối 3 HÀM SỐ 12
Nhận biết: sự biến thiên của hàm số bậc hai BẬC HAI 13
Nhận biết: tính chất đồ thị hàm số bậc hai 14
Thông hiểu: lập bảng biến thiên của hàm số bậc hai 15
Thông hiểu: Tìm hàm số bậc hai 16
Vận dụng: Tìm hàm số bậc hai 17
Vận dụng: vẽ đồ thị hàm số bậc hai 18
Vận dụng: tính chất đồ thị hàm số bậc hai.
III. Câu hỏi trắc nghiệm ôn tập chương II
Câu 1: Hàm số nào sau đây xác định khi x  2 3 1 x A. y =
B. y = x − 2 C. y = +
D. y = x − 2 4 − 2x x x − 2
Câu 2: Tập xác định của hàm số 1 y = 3 x + 2 − là: x A. (− ;  2 −  B. 2; − +)
C.−2;+) \  0 D. \ 2; −  0
Câu 3: Hàm số y = x + 3 − 2 1− x có tập xác định là A. (−3; ) 1 B. −3;  1 C.  1
− ;+) D. (−  ;1 Câu 4: Cho hàm số 2
y = x − 3x + 4 . Điểm nào sau đây thuộc đồ thị hàm số A. M(2; 1) B. M(1; 2) C. M(-1; 3) D. M(0; 2)
Câu 5: Hàm số nào sau đây là hàm số chẵn A. 2
y = 2x + 3 x
B. y = 3x − 2
C. y = x + 4
D. y = ( x − )2 2
Câu 6: Hàm số nào sau đây là hàm số bậc nhất A. y = 2
B. y = x − 3
C. y = 3x D. 2 y = x
Câu 7: Giá trị nào của k thì hàm số y = (k −1)x + k − 2 nghịch biến trên tập xác định của hàm số.
A. k < 1 B. k > 1 C. k < 2 D. k > 2
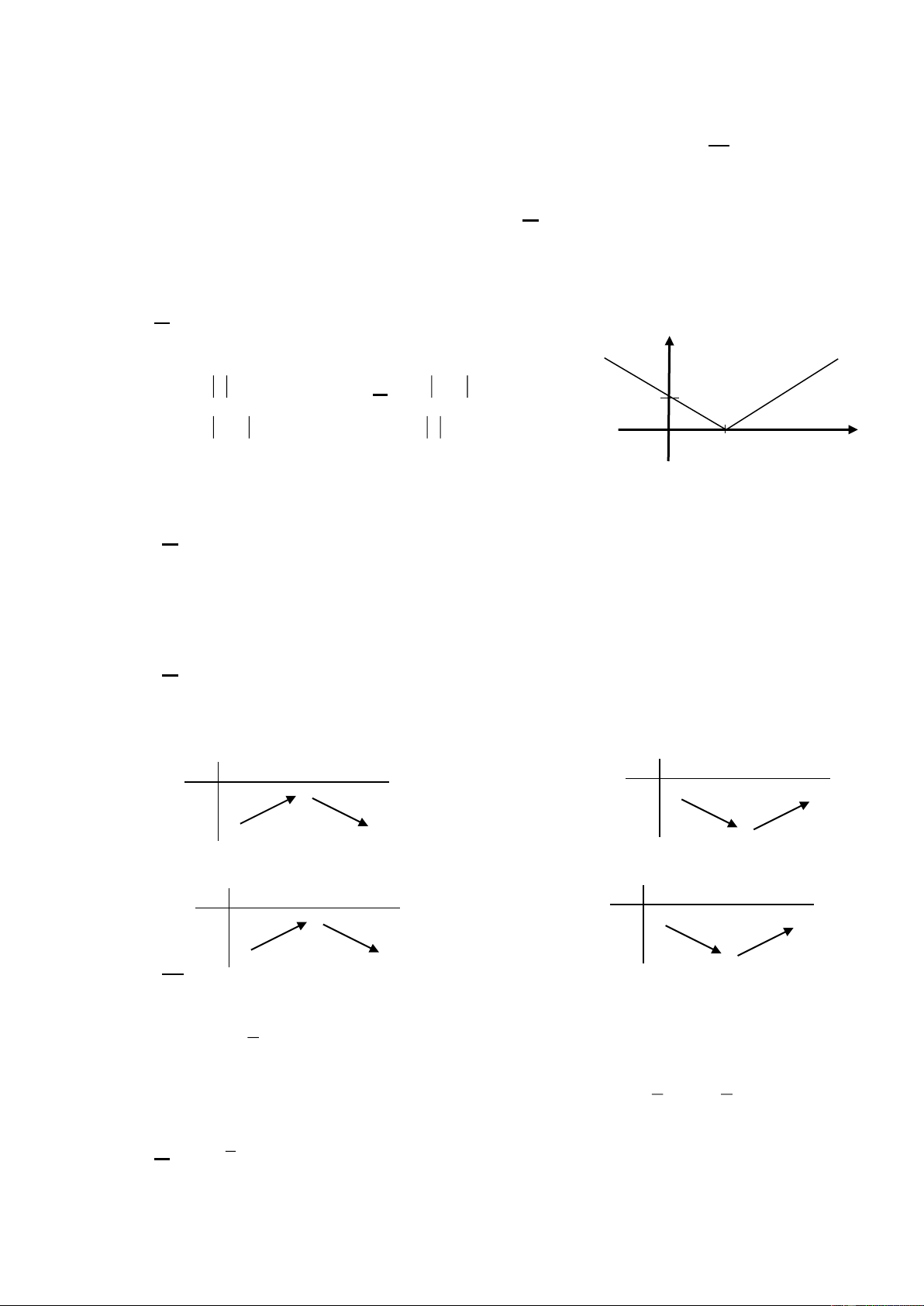
Câu 8: Đồ thị sau đây biểu diễn hàm số nào? 1 1 4
A. y = x +1 B. y = x −1 C. y = −x −1 D. y = −x +1
Câu 9: Đồ thị của hàm số nào sau đây đi qua 2 điểm ( A 1; 2) và ( B 0;-1)
A. y = x +1 B. y = x −1 C. y = 3x −1 D. y = 3 − x −1
Câu 10: Phương trình của đường thẳng d đi qua điểm (
A 2;1) và song song với
đường thẳng d’: y = 2x +3
A. y = 2x − 3 B. y = 2
− x − 2 C. y = 4 + 2x D. y = 2 + 2x
Câu 11: Đồ thị sau đây là đồ thị của hàm số nào?
A. y = x
B. y = x −1 1
C. y = x +1
D. y = x −1 1
Câu 12: Cho hàm số y = – x2 + 4x + 2. Khẳng định nào sau đây là đúng?
A. Hàm số nghịch biến trên (2; +∞) B. Hàm số nghịch biến trên(–∞; 2)
C. Hàm số đồng biến trên(-2; +∞) D. Hàm số nghịch biến trên(–∞;-2)
Câu 13: Cho hàm số 2
y = 2x − 4x +1 có đồ thị (P). Chọn khẳng định sai trong các khẳng định sau:
A. (P) là một đường parabol có trục đối xứng x = 2
B. (P) Có đỉnh I(1; -1)
C. Hàm số đồng biến trên (1; )
+ D. Hàm số nghịch biến trên ( ; − 1)
Câu 14 : Bảng biến thiên của hàm số y = –2x2 + 4x + 1 là bảng nào sau đây ? x –∞ 2 +∞ x –∞ 2 +∞ y y +∞ 1 +∞ –∞ A. –∞ B. 1 x –∞ 1 +∞ x –∞ 1 +∞ y y +∞ 3 +∞ –∞ C. –∞ D. 3
Câu 15: Biết rằng parabol 2
y = ax + bx + 2 đi qua điểm A(3,-4) và có trục đối xứng là 3 x = −
. Khi đó giá trị của a và b là: 2 1 3 A. a = 1, b = - 3
B. a = − , b = − 2 2 1
C. a = − , b = 1 − D. a = 2, b = 1 3 5
Câu 16: Biết rằng parabol 2
y = ax + bx + c có đỉnh I(1,4) và đi qua điểm D(3,0).
Khi đó giá trị của a,b và c là:
A. a = -1, b = 1, c = -1
B. a = -2, b = 4, c = 6 1 2
C. a = -1, b = 2, c = 3
D. a = − , b = − , c = 5 3 3
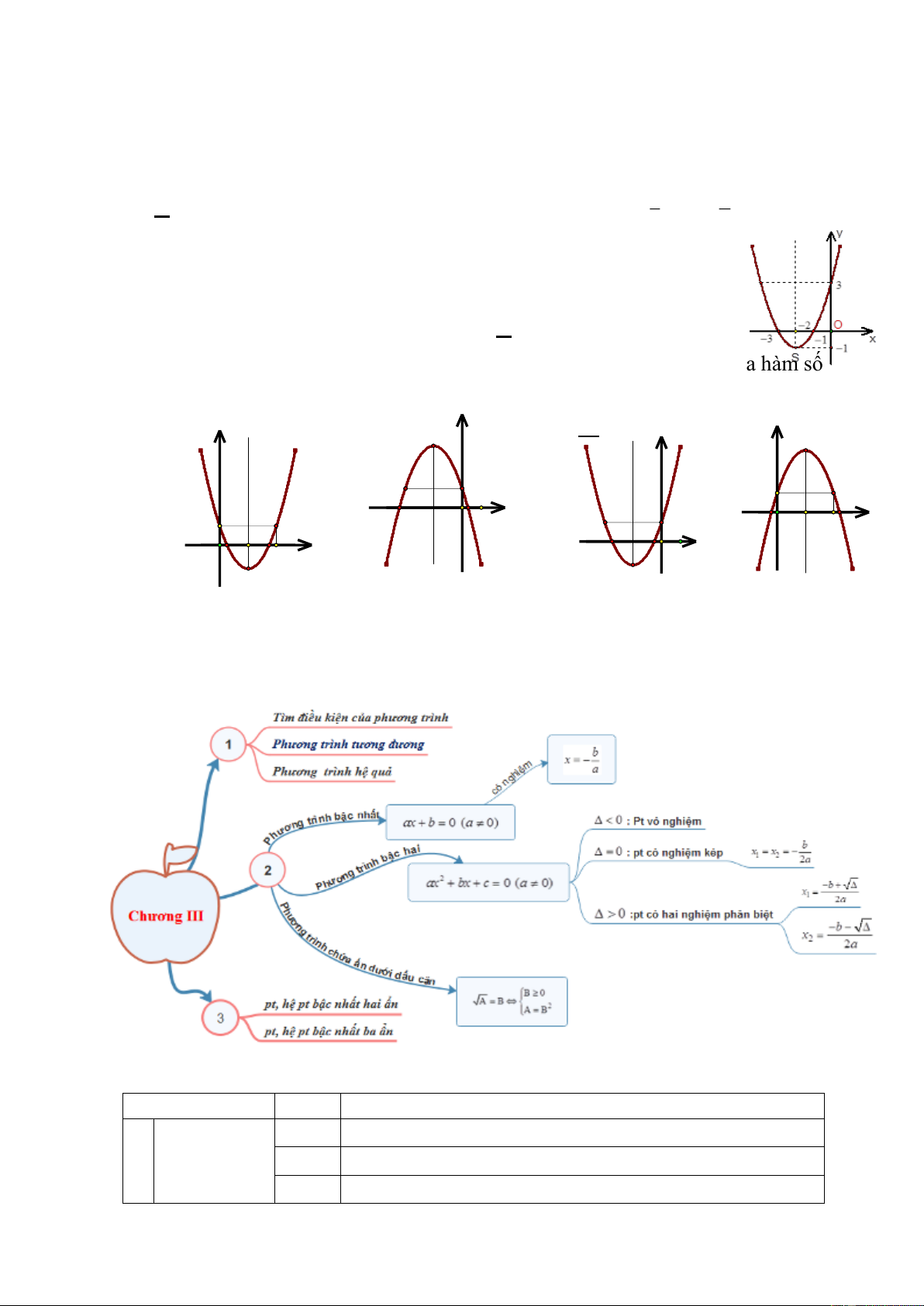
Câu 17: Trong các hàm số sau hàm số nào có đồ thị như hình vẽ A. 2
y = 2x + 8x + 3 B. 2
y = x − 4x + 3 C. 2
y = −x − 4x + 3 D. 2
y = x + 4x + 3
Câu 18: Cho hàm số 2
y = ax + bx + c có a  0;b  0;c  0 thì đồ thị (P) của hàm số
là hình nào trong các hình dưới đây y A. y B. C. D. y I y I x x x x I I
Chương III. PHƯƠNG TRÌNH. HỆ PHƯƠNG TRÌNH I.
Hệ thống kiến thức bằng sơ đồ tư duy
II. Bảng mô tả chi tiết nội dung câu hỏi trắc nghiệm CHỦ ĐỀ CÂU MÔ TẢ 1
Nhận biết: Điều kiện xác định của phương trình Đại cương về 1 phương trình 2
Thông hiểu: Tìm điều kiện của phương trình. 3
Thông hiểu: Xác định hai phương trình tương đương 6 4
Thông hiểu: Phương trình hệ quả 5
Vận dụng: Tìm nghiệm của phương trình 6
Vận dụng: Tìm điều kiện của tham số để hai phương trình tương đương 7
Nhận biết: Nghiệm của phương trình 8
Thông hiểu: Tìm số nghiệm của phương trình chứa ẩn dưới dấu căn. 9
Nhận biết: Giá trị tham số để phương trình vô Phương trình nghiệm quy về 10
Thông hiểu: Phương trình có hai nghiệm trái dấu 2 phương trình bậc nhất, bậc 11
Vận dụng: Tìm điều kiện của tham số để phương
trình bậc hai có hai nghiệm trái dấu hai 12
Vận dụng: Tìm điều kiện của tham số để phương
trình bậc hai có hai nghiệm phân biệt 13
Vận dụng: Tìm điều kiện của tham số để phương trình có nghiệm. Phương 14
Thông hiểu: Tìm nghiệm của hệ phương trình trình, hệ 15
Thông hiểu: Tìm nghiệm của hệ phương trình 3 phương trình 16
Vận dụng: Tìm giá trị biểu thức bậc nhất 17
Vận dụng: Giải toán bằng cách lập hệ phương trình nhiều ẩn 18
Vận dụng: Giải toán bằng cách lập hệ phương trình
III. Câu hỏi trắc nghiệm ôn tập chương III
Câu 1: Trong các phương trình sau phương trình nào có điều kiện là x 2 ? 1 1 A. x +
= 0 B. x + + x − 2 = 0 x − 2 x 1 1 C. x + = x − 2 D. x + = 2x −1 4 − x 2 − x
Câu 2: Điều kiện xác định của phương trình x − 3 = 6 − 2x là :
A. x  3 B. x  3 C. x  3 D. x = 3
Câu 3: Cặp phương trình nào sau đây tương đương ?
A. x = −x và x = −x B. x = −x và 2 x + x = 0
C. x +1 = x + x và 2
x + x = 0 D. x − x = −2 − x và 2 x(x − 4) = 0
Câu 4: Cho phương trình 2
2x − x = 0 . Tìm phương trình không phải là phương
trình hệ quả của phương trình đã cho: x A. 2 x − 2x +1 = 0
B. ( x − x)2 2 2 = 0 C. 3
4x − x = 0 D. 2x − = 0 1− x
Câu 5: Nghiệm phương trình 3x −12 + 2 = −x + 4 + 2x là :
A. x = 3 B. x = 4 C. Vô nghiệm D. x =1
Câu 6: Giá trị m để hai phương trình 2x −1 = 0 và ( 2
− m+ 4)x − 2m−5 = 0 tương đương là
A. m = -2 B. m = 1 C. m = 2 D. m = -1 7 x + − x
Câu 7: Nghiệm phương trình 3 1 4 2 − = 4 là : x − 2 x − 2 A. Vô nghiệm 7 B. x = 5
− C. x = 2 D. x = 5
Câu 8: Phương trình 2
x − 7x +10 = 3x −1 có bao nhiêu nghiệm : A. 1 B. 3 C. 0 D. 2
Câu 9: Cho phương trình ( 2
4m − 2) x = 1+ 2m − x . Với giá trị nào của m thì
phương trình đã cho vô nghiệm? 1 1
A. m =1 B. m = -2 C. m = D. m = − 2 4
Câu 10: Phương trình nào sau đây có hai nghiệm trái dấu: A. 2 2
(m + 2)x + 2mx +1 = 0 B. 2 2
(m +1)x + mx −1 = 0 C. 2
3x − 7x + 2 = 0 D. 2 2x + 7x + 5 = 0
Câu 11: Tìm k để phương trình 2
x − (k − 3)x − k + 6 = 0 có hai nghiệm trái dấu:
A. k  6 B. k  6 C. k  6 D. k  6
Câu 12: Phương trình 2
x − 4x + m − 2 = 0 có hai nghiệm phân biệt khi :
A. m < 6 B. m > 6 C. m  6 D. m  6
Câu 13: Phương trình 2 2
m x − 2(m −1)x +1 = 0 có nghiệm khi : 1 1 1 1
A. m  B. m  C. 0  m  D. m  2 2 2 2  x − y =
Câu 14: Nghiệm của hệ phương trình 3 4 2  là :  5 − x + 3y = 4
A. (-2;-2) B. (2;-2) C. (2;2) D. (-2;2)
−x − 3y + 4z = 0 
Câu 15: Nghiệm của hệ phương trình 3
 x + 4y − 2z = 5 là :
2x + y + 2z = 5 
A. (1;1;1) B. (0;1;2) C. (2;2;2) D. vô nghiệm  3
− x + 2y − z = 2 −  Câu 16: Gọi ( ;
x y; z ) là nghiệm của hệ phương trình 5
 x − 3y + 2z =10 .
2x − 2y −3z = 9 − 
Tính giá trị của biểu thức M = x + y + z . A. -1 B. 35 C. 15 D. 21
Câu 17: Một công ty Taxi có 85 xe chở khách gồm hai loại, xe chở được 4
khách và xe chở được 7 khách. Dùng tất cả các xe đó, tối đa mỗi lần công ty chở
được 445 khách. Hỏi công ty đó có mấy xe mỗi loại?
A. 45 xe 4 chỗ, 40 xe 7 chỗ. B. 50 xe 4 chỗ, 35 xe 7 chỗ.
C.35 xe 4 chỗ, 50 xe 7 chỗ. D. 40 xe 4 chỗ, 45 xe 7 chỗ.
Câu 18: Biết cách đây bốn năm tuổi mẹ gấp 5 lần tuổi con và sau hai năm nữa
tuổi mẹ gấp 3 lần tuổi con. Tính tuổi của mẹ và con hiện nay.
A. 33 tuổi và 10 tuổi B. 34 tuổi và 10 tuổi
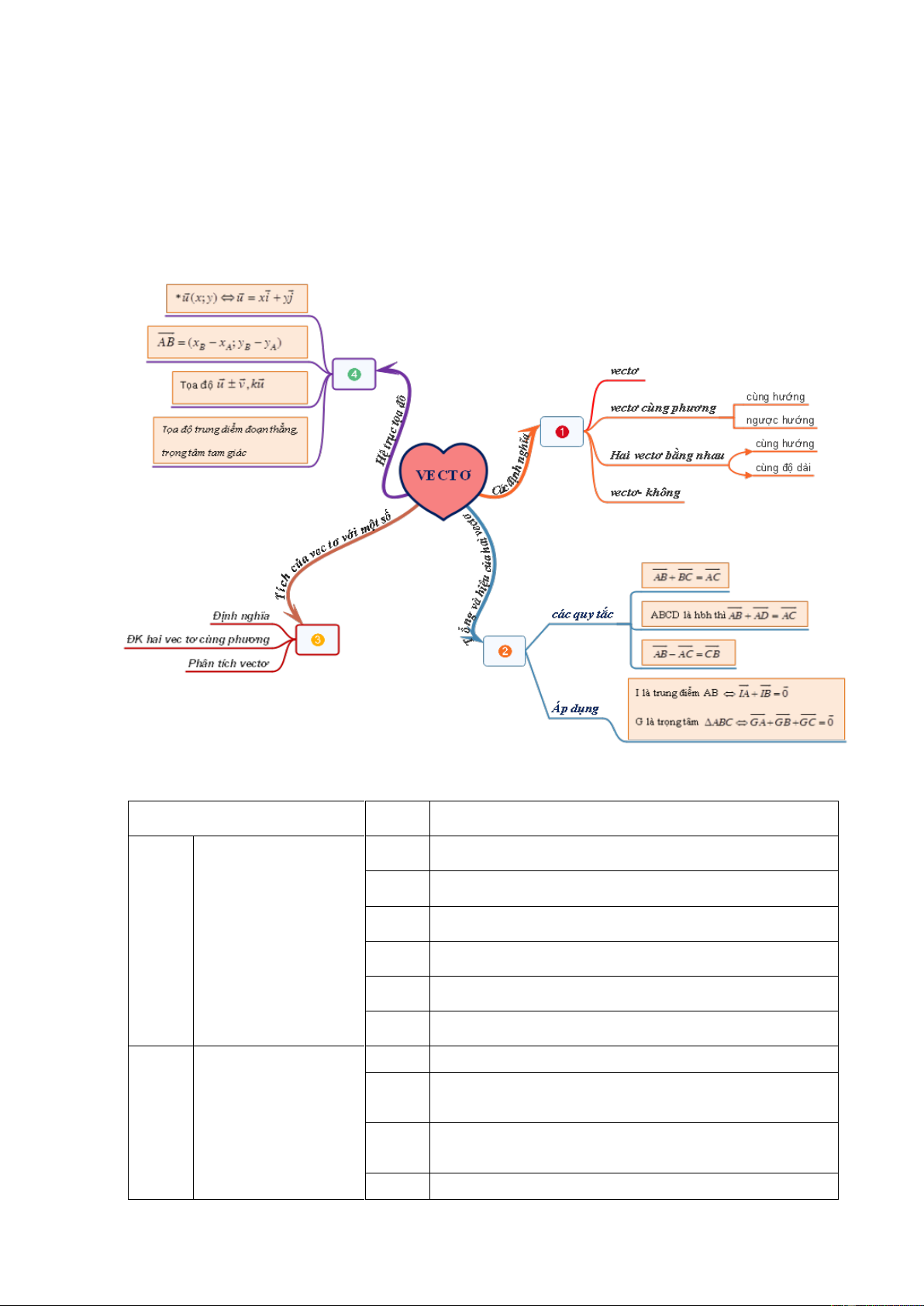
C. 36 tuổi và 10 tuổi D. 35 tuổi và 10 tuổi 8 Chương I. VÉC TƠ
I. Hệ thống kiến thức bằng sơ đồ tư duy
II. Bảng mô tả chi tiết nội dung câu hỏi trắc nghiệm CHỦ ĐỀ CÂU MÔ TẢ 1
Nhận biết: véc tơ cùng phương, cùng hướng 2
Nhận biết: véc tơ cùng phương, cùng hướng 3
Nhận biết: véc tơ _ không 1 Các định nghĩa 4
Thông hiểu: véc tơ, độ dài véc tơ 5
Vận dụng: hai véc tơ bằng nhau 6
Vận dụng: hai véc tơ bằng nhau 7
Nhận biết: Tổng hai véc tơ
Tổng và hiệu của
Nhận biết: tính chất trung điểm của đoạn 8 2 hai véc tơ
thẳng, trọng tâm của tam giác.
Thông hiểu: Tổng nhiều véc tơ, các quy tắc 9 véc tơ 10
Vận dụng: Tính độ dài véc tơ tổng 9 11
Nhận biết: quy tắc trừ 12
Thông hiểu: Tính tổng và hiệu các véc tơ 13
Vận dụng: Tính tổng và hiệu các véc tơ Tích véc tơ với 14
Nhận biết: Định nghĩa tích véctơ với một số. 3 một số 15
Thông hiểu: Tích véc tơ với một số 16
Vận dụng: Biểu diễn 1véc tơ theo 2 véc tơ 17
Nhận biết: Tính tọa độ véc tơ 18
Vận dụng: Tính tọa độ các véc tơ liên quan 4
Hệ trục tọa độ
Vận dụng: Phân tích véc tơ theo hai véc tơ 19 không cùng phương 20
Nhận biết: Tính tọa độ trọng tâm tam giác
III. Câu hỏi trắc nghiệm ôn tập chương I
Câu 1: Hãy chọn mệnh đề sai: Từ AB = CD suy ra:
A. AB và CD cùng phương
B. AB = CD
C. AB và CD cùng hướng
D. ABCD là hình bình hành
Câu 2: Cho 3 điểm A, B, C, bất kì trên một đường thẳng. Mệnh đề nào sau đây là đúng:
A. AB và AC ngược hướng
B. AB = BC
C. BA và BC cùng phương
D. CA và CB cùng hướng
Câu 3: Chọn mệnh đề sai trong các mệnh đề sau đây:
A. 0 cùng phương với mọi véc tơ
B. 0 cùng hướng với mọi véc tơ C. AB  0 D. AA = 0
Câu 4: Gọi M, N lần lượt là trung điểm của các cạnh AB, AC của tam giác đều
ABC. Đẳng thức nào dưới đây là đúng:
A. BC = 2 MN
B. MN = BC
C. MA = MB
D. AB = AC
Câu 5: Cho hình thoi ABCD cạnh a, góc BAD = 0
60 . Đẳng thức nào dưới đây đúng:
A. AB = AD
B. AB = a
C. BC = DA
D. BD = AC
Câu 6: Cho lục giác đều ABCDEF và O là tâm của nó. Đẳng thức nào dưới đây sai
A. OD = BC
B. OB = OE
C. AB = ED
D. AD = AF
Câu 7: O là tâm của hình bình hành ABCD. Hỏi AO + DO bằng véc tơ nào? A. BA B. AC C. BC D. DC
Câu 8: Mệnh đề nào sau đây sai:
A. Nếu ABCD là hình bình hành thì CB + CD = CA
B. Nếu G là trọng tâm của tam giác ABC thì GA+ GB + GC = 0
C. Nếu M là trung điểm cua đoạn thẳng AB thì MA+ MB = 0 10
D. Nếu 3 điểm phân biệt A, B, C nằm tùy ý trên đường thẳng thì AB + BC = AC
Câu 9: Cho tam giác ABC có AB = AC và đường cao AH. Đẳng thức nào sau đây đúng:
A. AB + AC = AH B. HA+ HB + HC = 0 C. HB + HC = 0
D. AB = AC
Câu 10: Cho hình thoi ABCD với AC = 2a , BD = a. Hỏi giá trị AC + BD bằng bao nhiêu? A. 5a B. 3a C. a 3 D. a 5
Câu 11: O là tâm của hình vuông ABCD. Hỏi OB − OC bằng véc tơ nào?
A. OD − OA B. DA C. BC D. AB
Câu 12: O là tâm hình bình hành ABCD, E và F lần lượt là trung điểm các cạnh
AB và BC. Đẳng thức nào sau đây sai:
A. DO = EB − EO
B. BE + BF − DO = 0
C. OA+ OC + OD + OE + 0F = 0
D. OC = EB + EO
Câu 13: Cho tam giác ABC vuông cân đỉnh A, đường cao AH. Đẳng thức nào sau đây sai:
A. AH − AB = AC − AH
B. AH = AB − AH
C. BC − BA = HC + HA
D. AH + HB = AH + HC
Câu 14: Hãy chọn mệnh đề đúng. Từ AB = 2 − CD suy ra:
A. AB và CD cùng hướng B. AB = 2 − CD 1 C. CD = AB
D. AB và CD cùng phương 2
Câu 15: Biết AB = 5
− AC suy ra đẳng thức nào sau đây đúng: 1 1 5
A. CB = 6CA
B. CA = − BC C. AC = AB
D. AB = − CB 6 5 6
Câu 16: Cho tam giác ABC, M là trung điểm của cạnh BC, gọi G và G’ lần lượt
là trọng tâm của tam giác ABM và AMC. Khi đó GG' bằng: 2 1 1 1 2 2 1 1
A. AC − AB
B. AC − AB
C. AC − AB
D. AC − AB 3 3 3 3 3 3 2 2
Câu 17: Trong mặt phẳng tọa độ Oxy cho ba điểm A(2; −3) , B (1; 4) , C ( 1 − ; 2 − ) .
Hỏi v = 2AB −3AC có tọa độ là cặp số nào? A. ( 7 − ;− ) 11 B. (7;1 ) 1 C. (11; −17) D. (−11;17)
Câu 18: Trong mặt phẳng tọa độ Oxy cho ba điểm A(2; ) 1 , B (3; − ) 1 , C (−2; 2) .
Gọi A’ là điểm đối xứng với A qua B, B’ là điểm đối xứng với B qua C. Khi đó
trung điểm M của đoạn thẳng A’B’ có tọa độ là cặp số nào?  3  11   3   11  A. ;1   B. ;1   C. − ;1   D. − ;1    2   2   2   2 
Câu 19: a = (2; )
1 ; b = (3; 4) ; c = (7; 2) . Tìm hai số m, n sao cho c = ma + nb 11 22 3 − 2 − 2 3 − 22 3 22 − 3 A. m = ; n = B. m = ; n = C. m = ; n = D. m = ; n = 5 5 5 5 5 5 5 5
Câu 20: Cho 3 điểm A(3; 4); B (2; ) 1 ;C ( 1 − ; 2
− ) . Tọa độ trọng tâm G của tam giác ABC là:  4   4   4 −   4 −  A. G ;1   B. G ; 1 −   C. G ; 1 −   D. G ;1    3   3   3   3 
3.3. Khả năng áp dụng của giải pháp
Đề tài có thể áp dụng để giảng dạy cho mọi trình độ của học sinh vì nó
giúp các em tiếp nhận kiến thức một cách nhẹ nhàng, logic và dễ hiểu.
3.4. Hiệu quả, lợi ích thu được hoặc dự kiến có thể thu được do áp dụng giải pháp
Khi áp dụng chúng tôi thấy kết quả chất lượng học kì I môn toán 10 cao
hơn. Từ đó, học sinh phấn chấn, thích thú hơn, không còn lo ngại cho rằng kiến
thức quá khó nữa. Học sinh tự học tốt hơn và kỹ năng giải trắc nghiệm tốt hơn.
Thống kê kết quả học kì I môn Toán:
THỐNG KÊ KẾT QUẢ HỌC KỲ 1 MÔN TOÁN NĂM HỌC 2017 - 2018 LỚP: 10C8 LỚP: 10C1
Ôn tập không sử dụng sơ đồ tư duy và
Ôn tập bằng sơ đồ tư duy và hệ thống
hệ thống câu hỏi trắc nghiệm
câu hỏi trắc nghiệm
Số học sinh đạt Giỏi 5 - 12.82%
Số học sinh đạt Giỏi 13 - 28.26% Số lượng - Tỉ lệ Khá 12 - 30.77% Số lượng - Tỉ (%) Khá 13 - 28.26% lệ (%) Trung 10 - 25.64% bình Trung 18 - 39.13% bình Yếu 9 - 23.08% Yếu 2 - 4.35% Kém 3 - 7.69% Kém 0 - 0%
3.5. Tài liệu kèm theo gồm: Phụ lục 1, phụ lục 2.
Bến Tre, ngày 19 tháng 3 năm 2018 12 Phụ lục 1
Sơ đồ tư duy của học sinh Đoàn Thị Hà My _ 10C2 13
Sơ đồ tư duy của học sinh Lê Thị Kim Tuyền _ 10C1 14 15
Phụ lục 2: MA TRẬN TỔNG QUÁT ĐỀ KIỂM TRA HỌC KÌ I MÔN TOÁN K10
Mức độ kiến thức đánh giá Tổng số STT Các chủ đề Vận Nhận Thông Vận câu dụng biết hiểu dụng hỏi cao 1 Hàm số 1 1 0 0 2 Câu: 2 Câu 1 2
Hàm số bậc nhất và 1 2 1 0 4 bậc hai Câu: 5 Câu: Câu 4 3,6 3
Đại cương về phương 2 1 0 0 3 trình Câu: 7,8 Câu: 9 4
Phương trình quy về pt 0 1 2 0 3
bậc nhất, bậc hai Câu: 11 Câu:10,12 5
Hệ phương trình bậc 1 0 0 1 2 nhất nhiều ẩn Câu: 13 Câu:14 6
Tổng và hiệu của hai 1 0 0 0 1 vectơ Câu: 16 7
Tích của vectơ với một 0 0 1 0 1 số Câu 17 8
Hệ trục tọa độ 0 1 1 0 2 Câu15 Câu 18 9 Góc giữa hai vectơ 0 1 0 0 1 Câu 19 10
Tích vô hướng giữa 0 0 1 0 1 hai vectơ Câu 20 Số câu 6 7 6 1 20 Tổng Tỷ lệ 30 % 35 % 30 % 5% 100% 16
ĐỀ KIỂM TRA HỌC KÌ I MÔN TOÁN KHỐI 10 NĂM HỌC 2017 - 2018
Câu 1: Tập xác định của hàm số y =
x + 2 + 2 − x là: A. D = (− ;  −  2 B. D = (− 2 ; 2 ) C. D = − 2 ; 2 D. D =  + ; 2 ) 2
x +2 khi x  3
Câu 2: Cho hàm số f (x) = 
, giá trị của f ( 3 − ) + f (7)là:
 x −3 khi x  3 A. 11 B. -5 C. 2 D. 13
Câu 3: Với giá trị nào của k thì hàm số y = (k − 3)x − 6k đồng biến trên R A. k  3 B. k  3 C. k  1 D. k 
Câu 4: Đường thẳng qua A(-1;3) và song song với d: y = 2x – 1 có phương trình A. y = 2x + 5 B. y = 2 − x +1 C. y = 5x D. y = 3x + 6 Câu 5: Cho hàm số 2
y = − x + 2x , khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên khoảng (1; +)
B. Hàm số nghịch biến trên khoảng ( ) ;1 −
C. Hàm số đồng biến trên khoảng (−;2)
D. Hàm số đồng biến trên khoảng (1; +)
Câu 6: Tọa độ giao điểm của đường thẳng y = x −1 và (P) 2
y = x − 2x −1 là: A. (0; ) 1 ;(3; 2) B. (1; − ) 1 ;(3; 2) C. (0; − )
1 ;(−3; 2) D. (0; − ) 1 ;(3; 2)
C©u 7: Cho phương trình x + 3 − x = 4 + 3 − x . Chọn khẳng định đúng:
A. Phương trình có nghiệm x = 4. B. Phương trình có nghiệm x = 3.
C. Phương trình vô nghiệm. D.Phương trình có vô số nghiệm.
C©u 8: Điều kiện của phương trình 2 x + x −1 = là: 5 − x
A. x  1 B. x  5 C. 1  x  5 D. x  5 2 x 9
Câu 9: Nghiệm của phương trình = là x − 2 x − 2 A. x= 3 B. x= -3 C. x= 3; x =- 3 D. x 
Câu 10: Phương trình 2
x + 3mx − 2m + 4 = 0 có 2 nghiệm trái dấu với giá trị của m là: A. m > 2 B. m < 2 C.m =2 D. m < 4
C©u 11: Phương trình 2
x − 2x + m = 0 có nghiệm khi: 17
A. m 1 B. m 1 C. m  1 − D. m  1 −
Câu 12: Tìm tất cả các giá trị của tham số a để cặp số ( x y) = ( 2 ;
2a ; 4a + 3) là một
nghiệm của phương trình 3x + 2y = 4 A. a = 1 − B. a = 1/ 3 C. a = − , 1 a = 1 − /3 D. a = , 1 a =1/ 3
x + y − z =1 
Câu 13: Gọi (x ; y ; z ) là nghiệm của hệ pt 3x − 2y + z = 8 . Tính tổng x + y + z . 0 0 0  0 0 0 2x + z = 4 A. 3 B. 1 C. -2 D. 2
Câu 14: Một người đi xe máy từ tỉnh A đến tỉnh B cách nhau 90km . Khi đến B
người đó nghỉ ngơi 30 phút rồi quay trở lại A với vận tốc lớn hơn vận tốc lúc đi là
9 km / h . Thời gian kể từ lúc đi từ A tới lúc trở về A là 5h. Vận tốc của xe máy lúc đi từ A đến B là:
A. 36km / h
B. 45km / h
C. 27km / h D. 32km / h
Câu 15: Cho hai vectơ a = (2; –4), b = (–5; 3). Tọa độ vectơ u = a 2 − b là : A. (7; –7)
B. (9; –11) C. (9; 5) D. (–1; 5)
Câu 16: Cho hình bình hành ABCD, tâm O. Chọn khẳng định sai:
A. AC − BD = 2AB
B. OA − OB = OD − OC
C. OA + OB + OD + OC = 0 D. AB + AD = 2AC
Câu 17: Cho hình bình hành ABCD tâm O.Ta có: BC = mOA + nOB khi đó giá trị của m, n lần lượt là: A. m = 1 − ;n = 1 − B. m = 1 − ;n =1 C. m = 1;n = 1 − D. m = 2 − ;n =1 Câu 18: Cho a x; 2 ,b 5;1 ,c x; 7 . c 2a 3b nếu: A. x –15 B. x 3 C. x 15 D. x 5
Câu 19: Cho hình vuông ABCD, giá trị cos (CB, CA) là : 1 1 2 2 A. B. – C. D. – 2 2 2 2
Câu 20: Cho hình vuông ABCD có cạnh bằng 3. I là trung điểm AB. Tích BI CA . bằng : 18 9 A. 6 2 B. C. 6 D. 9 2
II . PHẦN TỰ LUẬN (5 điểm)
Câu 1: ( 1.0 điểm) Giải các phương trình sau: x −1 − 3x +1 a) = (0.5đ) b) 2
3x + x + 5 = x + 2 (0.5đ) 2x − 3 x + 1
Câu 2: (2.5 điểm): Cho hàm số y = 2
x − 2x − 3 có đồ thị (P).
a) Xét sự biến thiên và vẽ đồ thị (P) của hàm số. (1.5đ)
b) Tìm m để đường thẳng d: y = mx − 2 2
m cắt (P) tại hai điểm phân biệt (1.0đ)
Câu 3: (1,0 điểm) Trong mặt phẳng tọa độ Oxy cho các điểm ( A 0;1), ( B 1;3), C( 2 − ;2)
a) Chứng minh rằng A, B, C là ba đỉnh của một tam giác.
b) Tìm toạ độ trung điểm BC và trọng tâm tam giác ABO.
c) Tìm tọa độ điểm M để tứ giác AMBC là hình bình hành.
Câu 4 (0.5 điểm). Cho tam giác ABC. Tìm tập hợp các điểm M thỏa mãn hệ thức:
(MA − MB).(MA + MB + MC) = 0
………..Hết ……….. 19