Tổng hợp lý thuyết lũy thừa – mũ – logarit – Lê Minh Tâm

Tài liệu gồm 125 trang, được biên soạn bởi thầy giáo Lê Minh Tâm, tổng hợp lý thuyết chung và hướng dẫn giải các dạng bài tập chuyên đề lũy thừa – mũ – logarit, giúp học sinh lớp 12 tham khảo khi học chương trình môn Toán 12 phần Giải tích chương 2.

118 59 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

TÀI LIỆU DÀNH CHO KHỐI 12

 
 
 
 
 
 
 
 Chủ đề 01. LŨY THỪA – HÀM SỐ LŨY THỪA 
 Dạng 1.1. Rút gọn và tính giá trị biểu thức ........................................................................... 6 
 Dạng 1.2. So sánh các biểu thức chứa lũy thừa ................................................................... 7 
 Dạng 1.3. Tập xác định hàm số lũy thừa ............................................................................... 8 
 Dạng 1.4. Đạo hàm số lũy thừa ................................................................................................ 9 
 Dạng 1.5. Đồ thị hàm số lũy thừa ........................................................................................... 10 
 Chủ đề 02. LOGARIT 
 Dạng 2.1. Tính giá trị biểu thức................................................................................................ 12 
 Dạng 2.2. Biểu diễn logarit ....................................................................................................... 13 
 Dạng 2.3. Mệnh đề đúng – sai ................................................................................................. 14 
 Chủ đề 03. HÀM SỐ MŨ – HÀM SỐ LOGARIT 
 Dạng 3.1. Tập xác định của hàm số logarit ........................................................................ 18 
 Dạng 3.2. Đạo hàm hàm số mũ – logarit ............................................................................. 20 
 Dạng 3.3. Khảo sát hàm số mũ – logarit .............................................................................. 21 
 Chủ đề 04. BÀI TOÁN LÃI SUẤT 
 Chủ đề 05. PHƯƠNG TRÌNH MŨ 
 Dạng 5.1. Phương trình mũ cơ bản ......................................................................................... 31 
 Dạng 5.2. Đưa về cùng cơ số ................................................................................................... 32 
 Dạng 5.3. Logarit hóa ............................................................................................................... 33 
 Dạng 5.4. Đặt ẩn phụ dễ thấy ................................................................................................ 34 
 Dạng 5.5. Đặt ẩn phụ với phương trình đẳng cấp ............................................................. 35 
 Dạng 5.6. Đặt ẩn phụ với tích hai cơ số bằng 1 .................................................................. 36 
 Dạng 5.7. Phương pháp hàm số ............................................................................................. 37 
 Dạng 5.8. Phương trình chứa tham số .................................................................................. 39 
 Chủ đề 06. PHƯƠNG TRÌNH LOGARIT 
 Dạng 6.1. Phương trình logarit cơ bản ................................................................................. 41 
 Dạng 6.2. Đưa về cùng cơ số .................................................................................................. 42 
 Dạng 6.3. Mũ hóa ....................................................................................................................... 43 
 Dạng 6.4. Đặt ẩn phụ dễ thấy ................................................................................................44 
 Dạng 6.5. Phương pháp hàm số ............................................................................................ 45 
 Dạng 6.6. Phương trình chứa tham số ................................................................................. 47   
Mục lục
 

Tổng Hợp Lý Thuyết  Năm học: 2023-2024 
 Biên soạn: Gv 
Lê Minh Tâm
 - 093.337.6281  Trang 2 
 Chủ đề 07. BẤT PHƯƠNG TRÌNH MŨ 
 Dạng 7.1. Bất phương trình mũ cơ bản ............................................................................... 50 
 Dạng 7.2. Đưa về cùng cơ số ................................................................................................... 51 
 Dạng 7.3. Đặt ẩn phụ ................................................................................................................. 52 
 Dạng 7.4. Logarit hóa ............................................................................................................... 53 
 Dạng 7.5. Chứa tham số .......................................................................................................... 54 
 Chủ đề 08. BẤT PHƯƠNG TRÌNH LOGARIT 
 Dạng 8.1. Bất phương trình logarit cơ bản ......................................................................... 56 
 Dạng 8.2. Đưa về cùng cơ số ................................................................................................... 57 
 Dạng 8.3. Đặt ẩn phụ.................................................................................................................58 
 Dạng 8.4. Mũ hóa ........................................................................................................................ 59 
 Dạng 8.5. Chứa tham số ........................................................................................................... 60 
 
 
   

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 3

A. LÝ THUYẾT CHUNG.

1. Lũy thừa:

1.1. Định nghĩa.

 Cho số thực b và số nguyên dương

 

2nn

Số a được gọi là căn bậc n của số b nếu

ab

Chú ý:

n lẻ

b

 Có duy nhất một căn bậc n của b, ký hiệu

n chẵn

0b 

 Không tồn tại căn bậc n của b

0b 

 Có một căn bậc n của b là 0

0b 

 Có hai bậc n của a là hai số đối nhau,

 Căn có giá trị dương ký hiệu là

, căn có giá trị âm ký hiệu là

b

1.2. Công thức.

Số mũ

Cơ số a

Lũy thừa

n

a

. ...

a a a a a

(n là thừa số a)

0

0a 

1aa

 

,nn  

0a 





 

  

0a 

 

a a a a b a b    

1.3. Tính chất.

⓵

.a a a





⓶





⓷

 

aa

⓸

 

.ab a b

⓹









⓺



   



   

   

⓻ Nếu

1a 

thì

aa  

. ⓼ Nếu

01a

thì

aa  

LŨY THỪA – HÀM SỐ LŨY THỪA

LŨY THỪA – MŨ – LOGARIT

CHÚ Ý

Các tính chất trên đúng trong trường hợp số mũ nguyên hoặc không.nguyên

Khi xét lũy thừa với số mũ 0 và số mũ nguyên âm thì cơ số phải khác 0.

Khi xét lũy thừa với số mũ không nguyên thì cơ số phải dương.

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 4

1.4. Tính chất căn bậc n.

Với

,,a b n

ta có

⓵

a a a

⓶

. , ;

n n n

ab a b a b

⓷

0,,

   

⓸

 

0,,

a a a n  

nguyên dương,

nguyên.

⓹

0, , ,

m nm

a a a n m  

nguyên dương.

⓺ Nếu



thì

0, , ,

a a a m n  

nguyên dương,

,pq

nguyên.

Đặc biệt:

.mn

aa

2. Hàm số lũy thừa:

2.1. Khái niệm.

 Hàm số

yx

với



được gọi là hàm số lũy thừa.

2.2. Tập xác định.

 Tập xác định của hàm số

yx

là:

⓵ Nếu là số nguyên dương

D 

⓶ Nếu nguyên âm hoặc bằng

 

0\D 

⓷ Nếu không nguyên

 

0;D  

※ Tổng quát: Tập xác định của hàm số

 

y f x

2.3. Đạo hàm.

 Hàm số

 

, yx

có đạo hàm

0x

và

 

.xx







2.4. Khảo sát hàm số lũy thừa

 

, yx

yx

với

0

yx

với

0

Tập khảo sát

 

0;

 

0;

Sự

biến

thiên

Đạo

hàm

00, .y x x





   

00, .y x x





   

Giới

hạn

0lim , lim .







  

0lim , lim .







  

Tiệm

cận

Không có.

Nhận

là tiệm cận ngang.

Nhận

là tiệm cận đứng.

Khi NGUYÊN DƯƠNG

Hàm số xác định xác định.

Khi NGUYÊN ÂM

Hàm số xác định .

Khi KHÔNG NGUYÊN

Hàm số xác định

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 5

Bảng biến thiên

Đồ thị

Đồ thị của hàm số lũy thừa

yx

luôn đi qua điểm

 

11;.I

Lưu ý:

 Khi khảo sát hàm số lũy thừa với số mũ cụ thể, ta phải xét hàm số đó trên toàn bộ tập

xác định của nó.

 Chẳng hạn:

, , y x y x y x



  

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 6

B. CÁC DẠNG BÀI TẬP.

 Dạng 1.1. Rút gọn và tính giá trị biểu thức

 Sử dụng phối hợp linh hoạt các tính chất của lũy thừa.

 Chọn

;ab

là các số thực dương và

;xy

là các số thực tùy ý, ta có:

⓵

.a a a





⓶





⓷

 

aa

⓸

 

.ab a b

⓹









⓺



   



   

   

⓻ Nếu

1a 

thì

aa  

. ⓼ Nếu

01a

thì

aa  

 Ví dụ 1.1.1

Đưa các biểu thức sau về dạng lũy thừa

⓵

 

0a a a 

⓶

0 75

⓷

 

0,.



Lời giải

⓵ . .................................................................................................................................................

⓶ ..................................................................................................................................................

⓷ ..................................................................................................................................................

 Ví dụ 1.1.2

Rút gọn các biểu thức sau đây:

⓵

 

5a 

⓶

 

81 0a b b 

⓷

   

11.x x x  

Lời giải

⓵ . .................................................................................................................................................

⓶ ..................................................................................................................................................

⓷ ..................................................................................................................................................

 Ví dụ 1.1.3

Cho

   

2 3 2 3,ab



   

. Tính

   

11.A a b



   

Lời giải

.......................................................................................................................................................

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 7

 Dạng 1.2. So sánh các biểu thức chứa lũy thừa

 Ta có hai cách làm như sau:

Đưa về cùng cơ số

Cho

:,a m n

. Khi đó

⓵ Với

1a 

a a m n   

;

⓶ Với

01a

a a m n   

Đưa về cùng số mũ

Với

0 ab

và

là số nguyên thì

⓵

a b m  

⓶

a b m  

 Ví dụ 1.2.1

So sánh các số sau:

⓵

300

và

400

⓶

 

5000

và

 

8000

Lời giải

⓵

300

và

400

⓶

 

5000

và

 

8000

 Ví dụ 1.2.2

So sánh các số sau:

⓵

và

. ⓶

100

và

⓷

 

31

và

 

31

. ⓸

34

và

 





Lời giải

⓵

và

⓶

100

và

⓷

 

31

và

 

31

⓸

34

và

 





 Ví dụ 1.2.3

So sánh 2 số

và

biết:

⓵



. ⓶

   

5 1 5 1

  

Lời giải

⓵



⓶

   

5 1 5 1

  

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 8

 Dạng 1.3. Tập xác định hàm số lũy thừa

 Tập xác định của hàm số

 

y f x

là:

⓵ là số nguyên dương

 

xác định.

⓶ nguyên âm hoặc bằng

 

0fx

⓷ không nguyên

 

0fx

 Ví dụ 1.3.1

Tìm tập xác định của hàm số

 

1yx





.

   

11;;    

 

11;

. D.

 

1\.

Lời giải

.......................................................................................................................................................

 Ví dụ 1.3.2

Tìm tập xác định của hàm số

 

2019

56y x x



  

   

23;;   

. B.

 

23;

 

23;;



   



. D.

 

23\;

Lời giải

.......................................................................................................................................................

 Ví dụ 1.3.3

Tìm tập xác định của hàm số

 

yx









. B.

;



 







. C.

;



  





. D.

.

Lời giải

.......................................................................................................................................................

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 9

 Dạng 1.4. Đạo hàm số lũy thừa

 Hàm số

 

, yx

có đạo hàm

0x

và

   

. . .x x u u u







  

 Ví dụ 1.4.1

Cho hàm số

   

23f x x

.Tính

 



. B.

. C.



. D.



Lời giải

.......................................................................................................................................................

 Ví dụ 1.4.2

Tìm đạo hàm của hàm số

 

13yx

trên khoảng

;









 

5 1 3'yx  

. B.

 

'yx

 

5 1 3'yx  

. D.

 

'yx

Lời giải

.......................................................................................................................................................

 Ví dụ 1.4.3

Tìm đạo hàm của hàm số

2yx

2x 

 





. B.





 





. D.

42'yx

Lời giải

.......................................................................................................................................................

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 10

 Dạng 1.5. Đồ thị hàm số lũy thừa

 Ta lưu ý các yếu tố trong sự biến thiên của hàm số lũy thừa

yx

với

0

0

Đạo hàm

0yx







00, .y x x





   

Giới hạn

0lim , lim .







  

0lim , lim .







  

Tiệm cận

Không có.

Nhận

là tiệm cận ngang.

Nhận

là tiệm cận đứng.

Đồ thị

Đồ thị của hàm số lũy thừa

yx

luôn đi qua điểm

 

11;.I

 Ví dụ 1.5.1

Hình vẽ bên là đồ thị các hàm số

yx

trên miền

 

0;

. Hỏi số

số nào nhận giá trị trong khoảng

 

01;

. B.

&ac

. D.

Lời giải

.......................................................................................................................................................

 Ví dụ 1.5.2

Cho hàm số

2023





. Mệnh đề nào đúng về đường tiệm cận của đồ thị hàm số?

A. Có một tiệm cận ngang và một tiệm cận đứng.

B. Không có tiệm cận ngang và có một tiệm cận đứng.

C. Có một tiệm cận ngang và không có tiệm cận đứng.

D. Không có tiệm cận.

Lời giải

.......................................................................................................................................................

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 11

A. LÝ THUYẾT CHUNG.

1. Định nghĩa.

Cho hai số dương

,ab

với

1a 

 Số thỏa mn đẳng thức

ab

được gọi là lôgarit cơ số

của

và k hiệu là

log

 Ta viết:

log .

b a b  

2. Tính chất.

3. Công thức.

 Cho 3 số dương

,,a b c

với

11;ac

và



, ta có các công thức sau:

 Logarit thập phân và Logarit tự nhiên

 Logarit thập phân là logarit cơ số 10. Viết :

log log lgb b b

 Logarit tự nhiên là logarit cơ số

. Viết :

log ln

bb

LOGARIT

LŨY THỪA – MŨ – LOGARIT

Cho

TÍNH CHẤT

Tích tổng – Thương hiệu

Đặc biệt: với

Lũy thừa

Đặc biệt:

Đổi cơ số

Đặc biệt: ;

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 12

B. CÁC DẠNG BÀI TẬP.

 Dạng 2.1. Tính giá trị biểu thức

 Áp dụng các tính chất – công thức để biến đổi:

Tính chất

⓵

1 1 0log , log

a 

⓶

 

log

, log

a b a

⓷

 

log . log log

a a a

b c b c

(Tích – tổng)

⓸

log log log

a a a



(Thương – hiệu)

Đặc biệt : với

01,,a b a

log log



Công thức bay

⓵

log log

bb

⓶

log log

bb

Đặc biệt:

log log



Đổi cơ số

⓵

log



⓶

log log .log

a a c

b c b

Đặc biệt :

log



 Ví dụ 2.1.1

Cho

01a

. Tính giá trị của biểu thức

4log

. B.

. C.

. D.

Lời giải

.......................................................................................................................................................

 Ví dụ 2.1.2

Tính giá trị của biểu thức

2 2 2 2

2 12 3 5 15 150log log log logA    

2

. B.

. C.

. D.

Lời giải

.......................................................................................................................................................

 Ví dụ 2.1.3

Rút gọn biểu thức

2 3 4

2 4 6 8

2 3 4log log log log

a a a

K b b b b   

ta được

4log

. B.

log

b

. C.

3log

. D.

log

Lời giải

.......................................................................................................................................................

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 13

 Dạng 2.2. Biểu diễn logarit

 Ta thực hiện theo các bước sau

 Bước 01. Biến đổi các biểu thức logarit phụ thuộc vào tham số

và

 Bước 02. Đặt các biểu thức logarit của các số nguyên tố là các ẩn

,,xyz

…. Từ đó ta

thu được phương trình hoặc hệ phương trình với các ẩn

,,xyz

…. Ta tìm

các ẩn này theo

,ab

 Bước 03. Giải hệ tìm được tìm

,,xyz

… theo

,ab

. Từ đó tnh được biểu thức theo các

tham số

,ab

Các công thức nền tảng là

log



và

log



 Ví dụ 2.2.1

Cho

14loga 

. Biểu diễn

16log

theo

1a 

. B.

. C.

3a

. D.

Lời giải

.......................................................................................................................................................

 Ví dụ 2.2.2

Cho

18loga 

và

60log .b 

Tính

2log

theo

và



. B.

a ab



. C.

  



. D.





Lời giải

.......................................................................................................................................................

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 14

 Dạng 2.3. Mệnh đề đúng – sai

 Ta lưu ý các công thức sau

Tính chất

⓵

1 1 0log , log

a 

⓶

 

log

, log

a b a

⓷

 

log . log log

a a a

b c b c

(Tích – tổng)

⓸

log log log

a a a



(Thương – hiệu)

Đặc biệt : với

01,,a b a

log log



Công thức bay

⓵

log log

bb

⓶

log log

bb

Đặc biệt:

log log



Đổi cơ số

⓵

log



⓶

log log .log

a a c

b c b

Đặc biệt :

log



 Ví dụ 2.3.1

Cho

0 1 1, , ; ; .a b c a b  

, Trong các khẳng định sau, khẳng định nào sai?

log



. B.

log .log log

a b a

b c c

log log

b c b

. D.

 

log . log log

a a a

b c b c

Lời giải

.......................................................................................................................................................

 Ví dụ 2.3.2

Cho

0,,a b c 

và

1,ab

, Trong các khẳng định sau, khẳng định nào sai?

log

ab

. B.

log log

b c b c  

log



. D.

log log

b c b c  

Lời giải

.......................................................................................................................................................

 Ví dụ 2.3.3

Cho

0,,a b c 

và

1,ab

, Trong các khẳng định sau, khẳng định nào sai?

log



. B.

log .log log

a b a

b c c

   

log . log

b c b c

. D.

log log log

a a a



Lời giải

.......................................................................................................................................................

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 15

 Ví dụ 2.3.4

Cho

00,ab

thỏa mãn

7a b ab

. Mệnh đề đúng trong các mệnh đề sau là:

   

27log log loga b ab

. B.

 

log log log





   

log log loga b a b  

. D.

   

log log loga b a b  

Lời giải

.......................................................................................................................................................

 Ví dụ 2.3.5

Với mọi số

0b 

thỏa mãn

9 10a b ab

thì đẳng thức đúng là.

 

23log log loga b a b  

. B.

 

log

log log





 

11log logab  

. D.

 

log log log





Lời giải

.......................................................................................................................................................

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 16

A. LÝ THUYẾT CHUNG.

1. Hàm số mũ.

Hàm số mũ

 

01, ,

y a a a  

Tập xác định

D 

Tập giá trị

 

0;,T  

nghĩa là khi giải phương trình mà đặt

 

ta

thì

0.t 

Đơn điệu

1a 

Hàm số

ya

đồng biến, khi đó:

   

f x g x

a a f x g x  

01a

Hàm số

ya

nghịch biến, khi đó:

   

f x g x

a a f x g x  

Đạo hàm

   

 

.ln . .ln

x x u u

a a a a u a a

e e e e u







  





  





Đồ thị

Nhận trục hoành làm đường tiệm cận ngang

 Nhận xét:

Đồ thị hàm số

 

y a a

đối xứng với đồ thị hàm số

 

y a a  

qua Oy.

HÀM SỐ MŨ – HÀM SỐ LOGARIT

LŨY THỪA – MŨ – LOGARIT

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 17

2. Hàm số logarit.

Hàm số logarit

 

0 1 0log , , ;

y x a a x   

Tập xác định

 

0;D   

Tập giá trị

T 

, nghĩa là khi giải PT mà đặt

log

tx

thì

không có điều kiện.

Đơn điệu

1a 

Hàm số

log

yx

đồng biến trên

, khi đó:

       

log log

f x g x f x g x  

01a

Hàm số

log

yx

nghịch biến trên

, khi đó:

       

log log

f x g x f x g x  

Đạo hàm

   

 

log log

.ln .ln

ln ln

ln , (ln )

x a u a

u n u

x x u







  



   



   

Đồ thị

Nhận trục tung làm đường tiệm cận đứng

 Nhận xét:

Đồ thị hàm số

 

1log

y x a

đối xứng với đồ thị hàm số

 

01log

y x a  

qua Ox.

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 18

B. CÁC DẠNG BÀI TẬP.

 Dạng 3.1. Tập xác định của hàm số logarit

 Điều kiện xác định của hàm số

 

log

y f x

 

















 Đặc biệt: với hàm số

 

log

y f x







ta lưu ý “mũ n” của

 

 Nếu

2n 

ĐKXĐ của hàm số

 

log

y f x







 



















 Nếu

2n 

ĐKXĐ của hàm số

 

log

y f x







 



















Tóm lại nếu

 

hoặc

 

có “mũ n” ta chú ý xem “n” chẵn hay lẻ.

 Ví dụ 3.1.1

Tìm tập xác định

của hàm số

 

21logyx



  





. B.



  





. C.

 

0;D  

. D.



   





Lời giải

.......................................................................................................................................................

 Ví dụ 3.1.2

Tìm tập xác định

của hàm số

 

32logy x x  

21,.D



  



   

21,,D      

 

21,D   

. D.

 

21,,D



     



Lời giải

.......................................................................................................................................................

 Ví dụ 3.1.3

Tập xác định của hàm số:

 

2logyx

là

A. B.

 

. C.

 

2;

. D.









Lời giải

.......................................................................................................................................................

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 19

 Ví dụ 3.1.4

Tập xác định của hàm số:

log







là



02;





 

02;

  

2 0 2;;



  



. D.

 

22;

Lời giải

.......................................................................................................................................................

 Ví dụ 3.1.5

Tập xác định của hàm số:

 

2021

3 2 3log ln

y x x x



    

là

       

1 1 0 0 1 2 3; ; ; ;D       

   

1 2 3;;D    

     

1 1 1 2 3; ; ;D      

. D.

 

1;D   

Lời giải

.......................................................................................................................................................

 Ví dụ 3.1.6

Tìm tất cả các giá trị thực của tham số

để hàm số

24ln( )y x mx  

có tập xác

định

D 

22m  











2m

. D.

22m  

Lời giải

.......................................................................................................................................................

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 20

 Dạng 3.2. Đạo hàm hàm số mũ – logarit

 Đạo hàm hàm số logarit:

   

 

log log

.ln .ln

ln ln

ln , (ln )

x a u a

u n u

x x u







  



   



   

 Đạo hàm hàm số mũ:

   

 

.ln . .ln

x x u u

a a a a u a a

e e e e u







  





  





 Ví dụ 3.2.1

Đạo hàm của hàm số

 

41logyx

là

 

4 1 3







 

4 1 3



















Lời giải

.......................................................................................................................................................

 Ví dụ 3.2.2

Hàm số





có đạo hàm là

 

4 1 2 ln2







2 ln2







 

4 1 2 2ln

y x x x





  

 

22ln2

y x x







Lời giải

.......................................................................................................................................................

 Ví dụ 3.2.3

Tnh đạo hàm của hàm số































Lời giải

.......................................................................................................................................................

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 21

 Dạng 3.3. Khảo sát hàm số mũ – logarit

 Ta cần lưu ý các vấn đề sau:

Hàm số Mũ

 

y a a  

Hàm số Logarit

 

10log

y x a  

Đơn điệu



1a 

HS đồng biến.



01a  

HS nghịch biến.



1a 

HS đồng biến.



01a  

HS nghịch biến.

Tiệm cận

Nhận

làm TCN.

Nhận

làm TCĐ.

Đồ thị

Nằm bên trên

Luôn đi qua điểm

 

01;

Nằm bên phải

Luôn đi qua điểm

 

10;

ĐTHS

 

y a a  

đối xứng

 

10log

y x a  

qua

yx

(đường

phân xác góc phần tư thứ nhất).

 Với bài toán xét thứ tự cơ số ta nhớ như sau:

Hàm số Mũ

 

y a a  

Hàm số Logarit

 

10log

y x a  

Cơ số

1

Càng gần

cơ số càng lớn.

Càng gần

cơ số càng lớn.

01a

Càng gần

cơ số càng bé.

Càng gần

cơ số càng bé.

Hình minh họa

 Ví dụ 3.3.1

Cho hàm số

logyx

. Mệnh đề nào dưới đây là mệnh đề sai?

A. Hàm số đ cho đồng biến trên tập xác định.

B. Đồ thị hàm số đ cho không có tiệm cận ngang.

C. Đồ thị hàm số đ cho có một tiệm cận đứng là trục

D. Hàm số đ cho có tập xác định

 

0\D 

Lời giải

.......................................................................................................................................................

 Ví dụ 3.3.2

Cho hàm số

logyx

. Mệnh đề nào dưới đây sai?

A. Đạo hàm của hàm số là

2lnyx





B. Đồ thị hàm số nhận trục

làm tiệm cận đứng.

C. Tập xác định của hàm số là

 

; 

D. Hàm số đồng biến trên khoảng

 

0;

Lời giải

.......................................................................................................................................................

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 22

 Ví dụ 3.3.3

Tìm mệnh đề đúng trong các mệnh đề sau:

A. Hàm số

log

yx

với

1a 

là một hàm số nghịch biến trên khoảng

 

0,

B. Đồ thị hàm số

log

yx

và

log

yx

với

01a

đối xứng với nhau qua Ox.

C. Hàm số

log

yx

với

01a

có tập xác định là .

D. Hàm số

log

yx

với

01a

là một hàm số đồng biến trên khoảng

 

0,

Lời giải

.......................................................................................................................................................

 Ví dụ 3.3.4

Đồ thị hàm số

 

1logyx

nhận đường thẳng nào dưới đây làm tiệm cận đứng ?

1x 

1y 

1x 

0x 

Lời giải

.......................................................................................................................................................

 Ví dụ 3.3.5

Hàm số nào sau đây nghịch biến trên tập xác định của nó?

 

y 

log

yx









logyx





Lời giải

.......................................................................................................................................................

 Ví dụ 3.3.6

Cho các hàm số

y a y b

và

yc

lần lượt có đồ

thị như hình vẽ bên dưới. Hãy so sánh

,,a b c

a b c

a b c

a b c

b a c

Lời giải

.......................................................................................................................................................

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 23

A. LÝ THUYẾT CHUNG.

1. Lãi đơn.

 Số tiền lãi chỉ tính trên số tiền gốc mà không tính trên số tiền lãi do số tiền gốc sinh ra.

 Công thức tnh li đơn:

 

1 .

V V r n

 Trong đó:

: Số tiền cả vốn lẫn lãi sau n kỳ hạn;

: Số tiền gửi ban đầu;

: Số kỳ hạn tính lãi;

: Lãi suất định kỳ, tính theo %.

2. Lãi kép.

 Số tiền lãi không chỉ tính trên số tiền gốc mà còn tính trên số tiền lãi do tiền gốc đó sinh

ra thay đổi theo từng định kỳ.

 Ta có các loại lãi kép sau:

2.1. Lãi kép, gửi một lần:

 

T T r

 Trong đó:

: Số tiền cả vốn lẫn lãi sau n kỳ hạn;

: Số tiền gửi ban đầu;

: Số kỳ hạn tính lãi;

: Lãi suất định kỳ, tính theo %.

2.2. Lãi kép liên tục:

T T e

 Trong đó:

: Số tiền cả vốn lẫn lãi sau n kỳ hạn;

: Số tiền gửi ban đầu;

: Số kỳ hạn tính lãi;

: Lãi suất định kỳ, tính theo %.

2.3. Lãi kép, gửi định kỳ.

2.3.1. Trường hợp gửi tiền định kì cuối tháng.

 Chứng minh

Tháng

Đầu tháng

Cuối tháng

Chưa gửi

 

1m r m

 

1m r m

   

11m r m r m   

Cứ cuối mỗi tháng gửi vào ngân hàng m triệu, lãi suất kép (tháng hoặc năm).

Hỏi sau

n (tháng hoặc năm) số tiền thu được là bao nhiêu?

Người ta chứng minh được số tiền thu được là: .

Bài toán 1

BÀI TOÁN LÃI SUẤT

LŨY THỪA – MŨ – LOGARIT

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 24

…

   

11...

m r m r m



    

 Vậy sau tháng n ta được số tiền

   

11...

T m r m r m



     

   

1 1 1...

m r r





     





 Ta thấy trong ngoặc là tổng

số hạng của cấp số nhân có

 

1 1 1, ,

u u r q r



    

 Biết rằng:

... .

S u u u



   



nên

 



  





 Chứng minh

 Áp dụng bài toán 1 ta có số tiền thu được là

 



  





 Mà đề cho số tiền đó chnh là A nên

 

m Ar

A r m



    







 Chứng minh

 Áp dụng bài toán 1 ta có số tiền thu được là

 



  





 Đề cho số tiền đó chnh là A nên:

 

1 1 1 1 1

log

m Ar Ar Ar

A r m r n

r m m







           











 Như vậy trong trường hợp 2.3.1 này ta cần nắm vững công thức bài toán 1 từ đó có thể dễ

dàng biến đổi ra các công thức ở bài toán 2, bài toán 3.

2.3.2. Trường hợp gửi tiền định kì đầu tháng.

 Chứng minh

 Ta xây dựng bảng sau:

Tháng

Đầu tháng

Cuối tháng

Cứ cuối mỗi tháng gửi vào ngân hàng m triệu, lãi suất kép (tháng hoặc năm). Sau n (tháng

hoặc năm) số tiền thu được là A triệu. Hỏi số tiền gửi mỗi tháng

m là bao nhiêu?

Người ta chứng minh được số tiền cần gửi mỗi tháng là: .

Bài toán 2

Cứ cuối mỗi tháng gửi vào ngân hàng m triệu, lãi suất kép (tháng hoặc năm). Sau n (tháng

hoặc năm) số tiền thu được là A triệu. Hỏi số tháng hoặc năm

n là bao nhiêu?

Người ta chứng minh được số tháng thu được đề bài cho là: .

Bài toán 3

Cứ đầu mỗi tháng gửi vào ngân hàng m triệu, lãi suất kép (tháng hoặc năm).

Hỏi sau

n (tháng hoặc năm) số tiền thu được là bao nhiêu?

Người ta chứng minh được số tiền thu được là: .

Bài toán 4

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 25

 

1mr

 

1m r m

   

11m r m r  

   

11m r m r m   

     

1 1 1m r m r m r    

…

   

11...

m r m r   

 Vậy sau tháng n ta được số tiền:

         

 

1 1 1 1 1... ...

T m r m r m r r m r





           





 Chứng minh

 Áp dụng bài toán 4. Ta có số tiền thu được là:

   

1 1 1

T r r



   





 Mà đề cho số tiền đó là A nên

   

1 1 1

m Ar

A r r m



     







  





 Chứng minh

 Áp dụng bài toán 4. Ta có: số tiền thu được là:

   

1 1 1

T r r



   





 Đề cho số tiền đó là A nên:

   

1 1 1

A r r



   





   

 

1 1 1

Ar Ar

     





  





 

log





  









 Như vậy trong trường hợp 2.3.2 ta cần nắm vững công thức bài toán 4 từ đó có thể dễ dàng

biến đổi ra các công thức ở bài toán 5, bài toán 6.

Cứ đầu mỗi tháng gửi vào ngân hàng m triệu, lãi suất kép (tháng hoặc năm). Sau n (tháng

hoặc năm) số tiền thu được là A triệu. Hỏi số tiền gửi mỗi tháng

m là bao nhiêu?

Người ta chứng minh được số tiền cần gửi mỗi tháng là: .

Bài toán 5

Cứ đầu mỗi tháng gửi vào ngân hàng m triệu, lãi suất kép (tháng hoặc năm). Sau n (tháng

hoặc năm) số tiền thu được là

A triệu. Hỏi số tháng hoặc năm n là bao nhiêu?

Người ta chứng minh được số tháng thu được đề bài cho là: .

Bài toán 6

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 26

2.3.3. Trường hợp vay nợ và trả tiền định kì đầu tháng.

 Chứng minh

 Ta xây dựng bảng sau:

Tháng

Đầu tháng

Cuối tháng

Am

      

1 1 1A m r A r m r     

   

11A r m r m   

     

111A r m r m r    

     

111A r m r m r m     

       

3 3 2

1 1 1 1A r m r m r m r      

…

       

1 1 1 1...

A r m r m r m r       

 Vậy sau tháng n ta còn nợ số tiền:

       

1 1 1 1...

T A r m r m r m r        

         

 

1 1 1 1 1...

n n n

A r m r r A r m r





          





3. Bài toán tăng trưởng dân số.

 Công thức tính:

 

X X r





 

,;m n m n





 Trong đó:

: tỉ lệ tăng dân số từ năm n đến năm m.

: dân số năm m.

: dân số năm n.

 Từ đó ra có công thức tính tỉ lệ tăng dân số là





 Ví dụ 4.1

Bà Hoa gửi

0 45,%

triệu vào tài khoản định kỳ tính lãi kép với lãi suất là

8%/

năm.

Tính số tiền li thu được sau

năm.

Lời giải

 Áp dụng công thức tính lãi kép, sau

năm số tiền cả gốc và lãi bà Hoa thu về là

   

1 100 1 0 08 215 892,,

Ar   

triệu đồng.

 Suy ra số tiền lãi bà Hoa thu về sau

năm là

215 892 100 115 892,,

triệu đồng.

 Ví dụ 4.2

Một người muốn gửi tiết kiệm ở ngân hàng và hi vọng sau 4 năm có được 850 triệu

đồng để mua nhà. Biết lãi suất ngân hàng mỗi tháng trong thời điểm hiện tại là

0 45,%

. Hỏi người đó mỗi tháng phải gửi vào ngân hàng tối thiểu bao nhiêu tiền

để đủ số tiền mua nhà ? (giả sử số tiền mỗi tháng là như nhau và li suất trong 4

năm là không thay đổi).

Lời giải

Vay ngân hàng A triệu đồng. Cứ đầu mỗi tháng (năm) trả ngân hàng m triệu, lãi suất kép

(tháng hoặc năm). Hỏi sau n (tháng hoặc năm) số tiền còn nợ là bao nhiêu?

Người ta chứng minh được số tiền còn nợ là: .

Bài toán 7

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 27

 Giả sử người này gửi tiền ở thời điểm

nào đó , kể từ thời điểm này sau 4 năm (48

tháng) ông muốn có số tiền 850 triệu.

 Như vậy rõ ràng ta có thể coi đây là bài toán gửi tiền định kì đầu tháng.

 Áp dụng bài toán 5 ta có số tiền phải gửi mỗi tháng là :

   

 

1 1 1





  





 Theo bài ra

48 0 45 850, , %,Anr  

 Thay vào

 



ta được

   

850 0 45

15 833

1 0 45 1 0 45 1

. , %

, % , %

m 



  





triệu đồng.

 Ví dụ 4.3

Một bà mẹ Việt Nam anh hùng được hưởng số tiền là 4 triệu đồng trên một tháng

(chuyển vào tài khoản của mẹ ở ngân hàng vào đầu tháng). Từ tháng 1 năm 2016 mẹ

không đi rút tiền mà để lại ngân hàng và được tính lãi suất

trên một tháng.

Đến tháng 12 năm 2016 mẹ rút toàn bộ số tiền (gồm số tiền của 12 tháng và số tiền đã

gửi tháng 1). Hỏi khi đó mẹ lĩnh về bao nhiêu tiền ? (kết quả làm tròn theo đơn vị

nghìn đồng).

Lời giải

 Nếu ban đầu gửi vào

đồng, từ đầu tháng sau gửi thêm

đồng (không đổi) vào

đầu mỗi tháng với lãi suất

trong

tháng thì tổng số tiền thu được là :

       

1 1 1 4 1 1 1 1 1 4 50 73

% % ,

A a r r

   

           

   

   

triệu đồng.



11n 

là tính từ đầu tháng 2 đến cuối tháng 12.

 Ví dụ 4.4

Đầu năm 2016, anh Hùng có xe công nông trị giá

100

triệu đồng. Biết mỗi tháng

thì xe công nông hao mòn mất

04,%

giá trị, đồng thời làm ra được

triệu đồng

(số tiền làm ra mỗi tháng là không đổi). Hỏi sau một năm, tổng số tiền (bao gồm giá tiền

xe công nông và tổng số tiền anh Hùng làm ra) anh Hùng có là bao nhiêu?

Lời giải

 Sau một năm số tiền anh Hùng làm ra là

6 12 72. 

triệu đồng

 Sau một năm giá trị xe công nông còn

100 1 0 4 95 3042( , %) ,

triệu đồng

 Vậy sau một năm số tiền anh Hùng có là

167 3042,

triệu đồng

 Ví dụ 4.5

Bác B gởi tiết kiệm số tiền ban đầu là

triệu đồng theo kỳ hạn

tháng với li suất

0 72,%

tháng. Sau một năm bác B rút cả vốn lẫn li và gởi theo kỳ hạn

tháng với li

suất

0 78,%

tháng. Sau khi gởi đúng một kỳ hạn

tháng do gia đình có việc bác gởi

thêm 3 tháng nữa thì phải rút tiền trước hạn cả gốc lẫn li được số tiền là

57 694 945 55. . ,

đồng (chưa làm trn). Biết rằng khi rút tiền trước hạn li suất được tnh theo li suất

không kỳ hạn, tức tnh theo hàng tháng. Trong số 3 tháng bác gởi thêm li suất là

Lời giải

 Số tiền bác B rút ra sau năm đầu:

 

50 000 000 1 0 0072 3. . * , *T 

 Số tiền bác B rút ra sau sáu tháng tiếp theo:

 

1 0 0078 6* , *TT

 Số tiền bác B rút ra sau ba tháng tiếp theo:

 

57 694 945 551 .* .,T T r  

57 694 94

01 0 004

5. . ,

, , %r

    

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 28

 Ví dụ 4.6

Bạn Nam là sinh viên của một trường Đại học, muốn vay tiền ngân hàng với lãi suất

ưu đi trang trải kinh phí học tập hàng năm. Đầu mỗi năm học, bạn ấy vay ngân hàng

số tiến 10 triệu đồng với lãi suất là

. Tính số tiền mà Nam nợ ngân hàng sau 4 năm,

biết rằng trong 4 năm đó, ngân hàng không thay đổi lãi suất ( kết quả làm trn đến

nghìn đồng).

Lời giải

 Tổng số tiền bạn Nam vay ( gốc và li) sau 4 năm là:

       

432

6 6 6 6

10 1 0 04 10 1 0 04 10 1 0 04 10 1 0 04, , , ,A        

         

 

1 1 0 04

10 1 0 04 1 1 0 04 1 0 04 1 0 04 10 1 0 04 44163256

1 1 0 04

, , , , , .





          







 Nên

44163000A 

đồng

 Ví dụ 4.7

Một giáo viên được nhận lương khởi điểm là

8 000 000..

đồng/tháng. Cứ sau hai năm

lương mỗi tháng của giáo viên đó được tăng thêm

10%

so với mức lương hiện tại.

Tính tổng số tiền

(đồng) giáo viên đó nhận được sau

năm làm việc.

Lời giải

 Lương 2 năm đầu tiên của giáo viên đó nhận được là

8 10 24 192 10. . .T 

(đồng)

 Theo công thức tnh li kép, lương 2 năm tiếp theo giáo viên đó nhận được:

 

24 8 10 1 10 212 2 10. . . % , .T   

(đồng)

 Lương 2 năm cuối cùng giáo viên đó nhận được:

 

24 8 10 1 10 232 32 10. . . % , .T   

(đồng)

 Tổng số tiền

(đồng) giáo viên đó nhận được sau 6 năm làm việc:

1 2 3

635 520 000,,T T T T   

(đồng).

 Ví dụ 4.8

Anh Hưng đi làm được lĩnh lương khởi điểm

4 000 000..

đồng/tháng. Cứ

năm, lương

của anh Hưng lại được tăng thêm

/1 tháng. Hỏi sau

năm làm việc anh Hưng

nhận được tất cả bao nhiêu tiền? (Kết quả làm trn đến hàng nghìn đồng).

Lời giải

 Gọi

là số tiền lương khởi điểm,

là lương được tăng thêm.

+ Số tiền lương trong ba năm đầu tiên:

36a

+ Số tiền lương trong ba năm kế tiếp:

 

36 36 1.a a r a r



  



+ Số tiền lương trong ba năm kế tiếp:

 

36 1ar

…

+ Số tiền lương trong ba năm cuối:

 

36 1ar

 Vậy sau

năm làm việc anh Hưng nhận được:

       

1 2 3 11

1 1 1 1 1 36 2 575 936983 2 575 937 000... . . . . . . .r r r r a



         





đồng.

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 29

 Ví dụ 4.9

Một người đem gửi tiền tiết kiệm vào một ngân hàng với lãi suất

một tháng. Biết

rằng cứ sau mỗi quý (

tháng) thì lãi sẽ được cộng dồn vào vốn gốc. Hỏi sau tối thiểu

bao nhiêu năm thì người đó nhận lại được số tiền bao gồm cả vốn lẫn lãi gấp ba lần số

tiền ban đầu

Lời giải

 Gọi

là số tiền người đó gửi ban đầu

 Số tiền nhận được cả gốc lẫn lãi sau

năm là

 

1 0 03,

Ta

   

3 1 0 03 3 4 1 03 3 9 29

4 1 03

, .ln , ln ,

ln ,

        

 Ví dụ 4.10

Một người vay ngân hàng một tỷ đồng theo phương thức trả góp để mua nhà. Nếu

cuối mỗi tháng, bắt đầu từ tháng thứ nhất người đó trả

triệu đồng và chịu lãi số

tiền chưa trả là

0 65,%

mỗi tháng (biết lãi suất không thay đổi) thì sau bao lâu người

đó trả hết số tiền trên?

Lời giải

 Gọi

là số tiền vay,

là số tiền gửi hàng tháng

là lãi suất mỗi tháng.

 Đến cuối tháng thứ

thì số tiền còn nợ là:

       

 

1 1 1 1 1...

n n n n

T A r a r r A r













          





 Hết nợ đồng nghĩa

0T 

 









   

 

1 log

a Ar a a

r r a Ar





    



 Áp dụng với

1A 

(tỷ),

0 04,a 

(tỷ),

0 0065,r 

ta được

27 37,n 

 Vậy cần trả

tháng.

 Ví dụ 4.11

Năm 2014, một người đ tiết kiệm được

triệu đồng và dùng số tiền đó để mua nhà

nhưng trên thực tế người đó phải cần

1 55, x

triệu đồng. Người đó quyết định gửi tiết

kiệm vào ngân hàng với lãi suất là

69,%

/ năm theo hình thức lãi kép và không rút

trước kỳ hạn. Hỏi năm nào người đó mua được căn nhà đó (giả sử rằng giá bán căn

nhà đó không thay đổi).

Lời giải

 Số tiền người gửi tiết kiệm sau

năm là

 

1 6 9,%

x 

 Ta cần tìm

để

 

1 6 9 1 55, % ,

xx

 

1 6 9 1 55, % ,

  

6 56, ...n

 Do đó, người gửi tiết kiệm cần gửi trọn

kỳ hạn, tức là

năm.

 Vậy đến năm 2021 người đó sẽ có đủ tiền cần thiết.

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 30

 Ví dụ 4.12

Một người gửi ngân hàng

100

triệu đồng theo hình thức lãi kép, lãi suất

05,%

một

tháng (kể từ tháng thứ 2, tiền li được tính theo phần trăm tổng tiền có được của tháng

trước đó và tiền lãi của tháng sau đó). Hỏi sau ít nhất bao nhiêu tháng, người đó có

nhiều hơn

125

triệu đồng?

Lời giải

 Số tiền cả vốn lẫn li người gởi sau

tháng:

 

100 1 0 005 100 1 005, . ,

S   

(triệu đồng)

1 005

100 100

, log

n   

 Để có số tiền

125S 

(triệu đồng) thì phải sau thời gian

1 005 1 005

125

44 74

100 100

log log ,

n 

(tháng)

 Vậy: sau ít nhất

tháng người đó có nhiều hơn

125

triệu đồng.

 Ví dụ 4.13

Ông Nam gởi

100

triệu đồng vào ngân hàng theo thể thức lãi kép kì hạn

năm với lãi

suất là

12%

một năm. Sau

năm ông Nam rút toàn bộ số tiền (cả vốn lẫn lãi). Tìm số

nguyên dương

nhỏ nhất để số tiền lãi nhận được lớn hơn

triệu đồng (giả sử lãi

suất hàng năm không thay đổi)

Lời giải

 Gọi

là tiền vốn lẫn lãi sau

tháng,

là số tiền ban đầu

 Tháng 1

 

1t 

 

1T a r

 Tháng 2

 

2t 

 

1T a r

……………….

 Tháng

   

n t n T a r  

 

   

140

100

1 33 815

1 1 1

ln ln

ln ln %

T a r t

     



(tháng)

 Để số tiền lãi nhận được lớn hơn 40 triệu thì

2 818

n 

 Vậy

3.n 

 Ví dụ 4.14

Tỉ lệ tăng dân số ở Việt Nam được duy trì ở mức 1,05%. Theo số liệu của Tổng cục

thống kê, dân số Việt Nam năm 2014 có 90.728.900 người. Với tốc độ tăng dân số

như thế đến năm 2030 thì dân số của Việt Nam là bao nhiêu?

Lời giải

 Từ năm

2014

đến năm

2030

cách nhau số năm là:

2030 2014 16

năm.

 Dân số Việt Nam năm

2030

 

90728900 1 1,05% 107232574A   

(người).

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 31

A. LÝ THUYẾT CHUNG.

 Phương trình mũ cơ bản:

 

01 ,

a b a a  

 Phương trình có một nghiệm duy nhất khi

0b 

 Phương trình vô nghiệm khi

0b 

B. CÁC DẠNG BÀI TẬP.

 Dạng 5.1. Phương trình mũ cơ bản

 Giải phương trình mũ cơ bản:

 

01 ,

a b a a  

 Khi đó

log

a b x b  

Lưu ý:

 Phương trình có một nghiệm duy nhất khi

0b 

 Phương trình vô nghiệm khi

0b 

 Ví dụ 5.1.1

Phương trình



có nghiệm là

3logx 

. B.

2logx 

. C.

3logx 

. D.

4logx 

Lời giải

.......................................................................................................................................................

 Ví dụ 5.1.2

Nghiệm của phương trình



là

x 

. B.

x 

. C.

x 

. D.

2x 

Lời giải

.......................................................................................................................................................

 Ví dụ 5.1.3

Nghiệm của phương trình

2 2 3 3

x x x x

  

là

logx 

. B.

1x 

. C.

0x 

. D.

logx 

Lời giải

.......................................................................................................................................................

PHƯƠNG TRÌNH MŨ

LŨY THỪA – MŨ – LOGARIT

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 32

 Dạng 5.2. Đưa về cùng cơ số

Với

0a 

1:a 

   

f x g x

aa

   

f x g x

 Ví dụ 5.2.1

Phương trình

x



có nghiệm là

1x 

. B.

2x 

. C.

2x 

. D.

1.x 

Lời giải

.......................................................................................................................................................

 Ví dụ 5.2.2

Tìm tập nghiệm của phương trình

 





 

4 3 4 3,

. B.

 

2 3 2 3,

 

4 3 4 3,   

. D.

 

2 3 2 3,   

Lời giải

.......................................................................................................................................................

 Ví dụ 5.2.3

Nghiệm của phương trình

125











là



. B.

. C.



. D.

Lời giải

.......................................................................................................................................................

 Ví dụ 5.2.4

Tìm tập hợp tất cả các nghiệm của phương trình

 



















. B.







. C.









. D.









Lời giải

.......................................................................................................................................................

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 33

 Dạng 5.3. Logarit hóa

 Phương trình

 

0 1 0,

log

f x b



  













 Phương trình

       

   

log log .log

f x g x f x g x

a a a

a b a b f x g x b    

hoặc

   

log log .log .

f x g x

b b b

a b f x a g x  

 Ví dụ 5.3.1

Tìm tập nghiệm

của phương trình

x



 

3S 

. B.

 

2S 

. C.

 

02;S 

. D.

 

12S 

Lời giải

.......................................................................................................................................................

 Ví dụ 5.3.2

Tìm tập nghiệm

của phương trình



S 

. B.

 

log log

log















 

log

log log















. D.

 

log log

log













Lời giải

.......................................................................................................................................................

 Ví dụ 5.3.3

Giải phương trình sau:

 

2 5 0 2 10. , .

x x x



x 

. B.

0x 

. C.

1x 

. D.

logx 

Lời giải

.......................................................................................................................................................

 Ví dụ 5.3.4

Cho phương trình

4 2 3 0.

xx

  

Khi đặt

t 

ta được phương trình nào sau đây

2 3 0tt

. B.

4 3 0t 

. C.

30tt  

. D.

2 3 0tt  

Lời giải

.......................................................................................................................................................

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 34

 Dạng 5.4. Đặt ẩn phụ dễ thấy

 Biến đổi quy về dạng:

 

0 0 1

f a a









   











 Thông thường sẽ gặp các cơ số:

4 2 0

25 5

;

 

  

 

 Ví dụ 5.4.1

Tập nghiệm của phương trình

9 5 3 6 0.

  

là

 

12;logS 

. B.

 

2logS 

. C.

 

1S 

. D.

 

S 

Lời giải

.......................................................................................................................................................

 Ví dụ 5.4.2

Số nghiệm của phương trình

4 4 9 2 8 0..

xx

  

(*) là:

. B.

. C.

. D.

Lời giải

.......................................................................................................................................................

 Ví dụ 5.4.3

Giải phương trình

2 15 2 8 0.

xx

  

 

x 

. B.

0x 

. C.

1x 

. D.

5x 

Lời giải

.......................................................................................................................................................

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 35

 Dạng 5.5. Đặt ẩn phụ với phương trình đẳng cấp

 Phương trình đẳng cấp có dạng:

0. . .m X n XY p Y  

 Khi đó với phương trình mũ đẳng cấp có dạng:

 

0. . . .

f x f x

m a n a b p b  

 Phương pháp làm như sau:

Chia 2 vế cho

 

2 fx

, đặt

 









 

2 2 2

. . .

f x f x

f x f x f x

m n p

b b b

  

   

0..

f x f x

m n p



   



   

   



   



0..m t n t p   

Chia 2 vế cho

 

2 fx

, đặt

 









 

2 2 2

. . .

f x f x

f x f x f x

m n p

a a a

  

   

0..

f x f x

m n p



   



   

   



   



0..m nt p t   

 Lưu ý:

Đây là dạng sẽ có trong bài “Bất phương trình mũ”, lúc giải BPT mũ ta cần chú ý đến cơ

số lớn hay bé hơn 1. Để giảm sai sót chúng ta hy “chia 2 vế” cho cơ số bé nhất !!!

 Ví dụ 5.5.1

Giải phương trình sau:

8 18 2 27.

x x x



(*)

1x 

. B.

2logx 

. C.

1x 

. D.

0x 

Lời giải

.......................................................................................................................................................

 Ví dụ 5.5.2

Số nghiệm của phương trình:

25 15 2 9.

x x x



(*) là:

. B.

. C.

. D.

Lời giải

.......................................................................................................................................................

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 36

 Dạng 5.6. Đặt ẩn phụ với tích hai cơ số bằng 1

 Phương trình đẳng cấp có dạng:

0. . .m X n XY p Y  

 Phương trình mũ ta xét có dạng:

   

 

0..

f x f x

m a n b p   

trong đó

1.ab

 Phương pháp làm như sau:

Vì

1.a b b

   

Đặt

   

f x f x

t a t b

   

Khi đó

 

00. . . .m t n p m t n p t

        

 Ví dụ 5.6.1

Tìm tích các nghiệm của phương trình

   

2 1 2 1 2 2 0

    

. B.

1

. C.

. D.

Lời giải

.......................................................................................................................................................

 Ví dụ 5.6.2

Phương trình

   

3 5 3 5 3 2.

   

có tổng các nghiệm là

. B.

. C.

1

. D.

Lời giải

.......................................................................................................................................................

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 37

 Dạng 5.7. Phương pháp hàm số

 Định lí. Nếu hàm số

 

y f x

là hàm số liên tục và đồng biến trên

 

;ab

 

y g x

là hàm số

liên tục và nghịch biến trên

 

;ab

thì phương trình

   

f x g x

có tối đa một nghiệm

trên

 

;ab

 Phương pháp làm như sau:

 Biến đổi phương trình đ cho về dạng

 

f x k

, với

là hằng số

 Chứng minh

 

là hàm đồng biến( nghịch biến) trên tập xác định.

 Tìm

sao cho

 

f x k

 Kết luận

là nghiệm duy nhất của phương trình

 

f x k

 Biến đổi phương trình đ cho về dạng

   

f x g x

, với

,DD

lần lượt là tập xác định

của hai hàm số

   

,f x g x

 Chứng minh

 

là hàm đồng biến và

 

nghịch biến trên tập

DD

(hay ngược lại)

 Tìm

sao cho

   

f x g x

 Kết luận

là nghiệm duy nhất của phương trình

   

f x g x

 Biến đổi phương trình đ cho về dạng

   

f u f v

, với hàm số

 

là hàm đồng

biến(hay nghịch biến).

 Phương trình

   

f u f v u v  

 Lưu ý:

⓵ Nếu

 

và

 

là hàm đồng biến(nghịch biến) trên

 

;ab

thì

   

f x g x

cũng là

hàm đồng biến (nghịch biến) trên

 

;ab

⓶ Hàm số

ya

đồng biến khi

1a 

và nghịch biến khi

01a

 Ví dụ 5.7.1

Phương trình

2016 2 2018 0

x  

có tất cả bao nhiêu nghiệm thực?

. B.

. D.

Lời giải

.......................................................................................................................................................

 Ví dụ 5.7.2

Tổng các nghiệm của phương trình

15 2

3 3 15 2

x x x



   

là:

6

. B.

1

. C.

. D.

Lời giải

.......................................................................................................................................................

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 38

 Ví dụ 5.7.3

Phương trình

 

1 2 1.

xx  

có bao nhiêu nghiệm thực

. B.

. C.

. D.

Lời giải

.......................................................................................................................................................

 Ví dụ 5.7.3

Phương trình

     

3 2 3 2 10

x x x

   

có tất cả bao nhiêu nghiệm thực?

. B.

. C.

. D.

Lời giải

.......................................................................................................................................................

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 39

 Dạng 5.8. Phương trình chứa tham số

 Để giải bài toán tìm tham số m trong phương trình mũ ta có hai cách phổ biến:

 Cô lập được tham số m.

 Ta dùng đồ thị hàm số để biện luận số nghiệm (bài toán tương giao).

 Không cô lập được tham số m và có liên quan đến Vi-ét.

 Đặt ẩn phụ đưa về phương trình bậc hai/bậc ba.

 Kết hợp định lý Vi-ét để giải quyết yêu cầu bài toán

 Ví dụ 5.8.1

Có bao nhiêu giá trị nguyên dương của tham số

để phương trình

16 2 12 2 9 0. ( ).

x x x

m   

có nghiệm dương?

. B.

. C.

. D.

Lời giải

.......................................................................................................................................................

 Ví dụ 5.8.2

Có bao nhiêu giá trị nguyên của tham số

để phương trình

9 4 3 2 1 0.

x x x x



   

có nghiệm?

. B.

. C.

. D.

Lời giải

.......................................................................................................................................................

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 40

 Ví dụ 5.8.3

Gọi

 

;ab

là tập các giá trị của tham số

để phương trình

2 8 0

e e m  

có

đúng hai nghiệm thuộc khoảng

 

05;ln

. Tổng

ab

là

. B.

. C.

6

. D.

14

Lời giải

.......................................................................................................................................................

 Ví dụ 5.8.4

Gọi

là tập hợp các giá trị nguyên của tham số

sao cho phương trình

25 5 7 7 0.



   

có hai nghiệm phân biệt.

Hỏi

có bao nhiêu phần tử.

. B.

. C.

. D.

Lời giải

.......................................................................................................................................................

 Ví dụ 5.8.5

Gọi

là tất cả các giá trị nguyên của tham số

sao cho phương trình

4 2 2 5 0.



   

có hai nghiệm phân biệt.

Hỏi

có bao nhiêu phần tử.

. B.

. C.

. D.

Lời giải

.......................................................................................................................................................

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 41

A. LÝ THUYẾT CHUNG.

 Phương trình logarit cơ bản:

   

01log ,

f x b a a  

 Lưu ý: khi giải phương trình logarit cần phải có điều kiện để logarit tồn tại.

B. CÁC DẠNG BÀI TẬP.

 Dạng 6.1. Phương trình logarit cơ bản

 Giải phương trình logarit cơ bản:

log

xb

 Khi đó

 

01log ,

x b x a a a    

 Ví dụ 6.1.1

Tìm tập nghiệm

của phương trình

 

22log x 

 

16S 

. B.

 

18S 

. C.

 

10S 

. D.

 

14S 

Lời giải

.......................................................................................................................................................

 Ví dụ 6.1.2

Phương trình

13log x 

có bao nhiêu nghiệm ?

. B.

. C.

. D.

Lời giải

.......................................................................................................................................................

 Ví dụ 6.1.3

Phương trình

 

28log x 

có tất cả bao nhiêu nghiệm thực?

Lời giải

.......................................................................................................................................................

PHƯƠNG TRÌNH LOGARIT

LŨY THỪA – MŨ – LOGARIT

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 42

 Dạng 6.2. Đưa về cùng cơ số

 Cho

10a

. Với điều kiện các biểu thức

 

và

 

xác định, ta thường đưa các phương

trình logarit về các dạng cơ bản sau:

 Loại 1:

 

log

f x b

f x a

















 Loại 2:

   

 

   

log log

f x g x

















 Ví dụ 6.2.1

Phương trình

     

1 3 7ln ln lnx x x    

có bao nhiêu nghiệm ?

. B.

. C.

. D.

Lời giải

.......................................................................................................................................................

 Ví dụ 6.2.2

Giải phương trình

 

2 1 1log logx x x   

A. vô nghiệm. B.

2.x 

02, .xx

3.x 

Lời giải

.......................................................................................................................................................

 Ví dụ 6.2.3

Số nghiệm của phương trình

 

12 2 1log .log

x 

là:

A. 0. B. 2. C. 3. D. 1

Lời giải

.......................................................................................................................................................

 Ví dụ 6.2.4

Tập nghiệm của phương trình

   

4 2 14 4log logxx   

là

 

5S 

. B.

 

5S 

. C.

 

5S 

. D.

 

S 

Lời giải

.......................................................................................................................................................

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 43

 Dạng 6.3. Mũ hóa

 Với điều kiện các biểu thức

 

và

 

xác định, ta thường đưa các phương trình logarit về

các dạng cơ bản sau:

     

 

01log

f x g x a

f x a







   









 Ví dụ 6.3.1

Tập nghiệm của phương trình

 

5 25 2log

xx



là:

 

1S 

. B.

 

5logS 

;

log













. D.

4log













Lời giải

.......................................................................................................................................................

 Ví dụ 6.3.2

Số nghiệm của phương trình

 

25 2log





là

. B.

. C.

. D.

Lời giải

.......................................................................................................................................................

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 44

 Dạng 6.4. Đặt ẩn phụ dễ thấy

 Giải phương trình

 

0log

f g x 

 

01a

 Bước 01. Đặt

 

log

t g x

 

 Bước 02. Tìm điều kiện của

(nếu có)

 Bước 03. Đưa về giải phương trình

 

0ft

đ biết cách giải.

 Bước 04. Thay vào

 

để tìm

 Ví dụ 6.4.1

Giải phương trình

4 3 0log logxx  

 

1S 

. B.

 

27S 

. C.

 

3 27;S 

. D.

 

3S 

Lời giải

.......................................................................................................................................................

 Ví dụ 6.4.2

Số nghiệm của phương trình

64 1log log

x 

là

. B.

. C.

. D.

Lời giải

.......................................................................................................................................................

 Ví dụ 6.4.3

Tích các nghiệm phương trình

1 5 0log logxx   

là

. B.

. C.

. D.

Lời giải

.......................................................................................................................................................

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 45

 Dạng 6.5. Phương pháp hàm số

 Định lí. Nếu hàm số

 

y f x

là hàm số liên tục và đồng biến trên

 

;ab

 

y g x

là hàm số

liên tục và nghịch biến trên

 

;ab

thì phương trình

   

f x g x

có tối đa một nghiệm

trên

 

;ab

 Phương pháp làm như sau:

 Biến đổi phương trình đ cho về dạng

 

f x k

, với

là hằng số

 Chứng minh

 

là hàm đồng biến( nghịch biến) trên tập xác định.

 Tìm

sao cho

 

f x k

 Kết luận

là nghiệm duy nhất của phương trình

 

f x k

 Biến đổi phương trình đ cho về dạng

   

f x g x

, với

,DD

lần lượt là tập xác định

của hai hàm số

   

,f x g x

 Chứng minh

 

là hàm đồng biến và

 

nghịch biến trên tập

DD

(hay ngược lại)

 Tìm

sao cho

   

f x g x

 Kết luận

là nghiệm duy nhất của phương trình

   

f x g x

 Biến đổi phương trình đ cho về dạng

   

f u f v

, với hàm số

 

là hàm đồng

biến(hay nghịch biến).

 Phương trình

   

f u f v u v  

 Lưu ý:

⓵ Nếu

 

và

 

là hàm đồng biến(nghịch biến) trên

 

;ab

thì

   

f x g x

cũng là

hàm đồng biến (nghịch biến) trên

 

;ab

⓶ Hàm số

ya

đồng biến khi

1a 

và nghịch biến khi

01a

 Ví dụ 6.5.1

Phương trình

   

21log logxx  

có bao nhiêu nghiệm?

. B.

. D.

Lời giải

.......................................................................................................................................................

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 46

 Ví dụ 6.5.2

Giải phương trình

   

2 3 4 2log logxx   

5x 

. B.

1x 

3x 

. D.

1x 

Lời giải

.......................................................................................................................................................

 Ví dụ 6.5.3

Giải phương trình

 

6 2 4log log ( )x x x x     

x 

. B.

1x 

4x 

. D.

3x 

Lời giải

.......................................................................................................................................................

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 47

 Dạng 6.6. Phương trình chứa tham số

 Để giải bài toán tìm tham số m trong phương trình logarit ta có hai cách phổ biến:

 Cô lập được tham số m.

 Ta dùng đồ thị hàm số để biện luận số nghiệm (bài toán tương giao).

 Không cô lập được tham số m và có liên quan đến Vi-ét.

 Đặt ẩn phụ đưa về phương trình bậc hai/bậc ba.

 Kết hợp định lý Vi-ét để giải quyết yêu cầu bài toán

 Ví dụ 6.6.1

Tìm tất cả các giá trị thực của tham số

để phương trình

10log logx m x  

có nghiệm duy nhất nhỏ hơn 1.

2m 

. B.

1m 

. C.

2m

. D.

1m 

Lời giải

.......................................................................................................................................................

 Ví dụ 6.6.2

Tìm tất cả các giá trị thực của tham số

để phương trình

2 7 0log logx m x m   

có hai nghiệm

,xx

thỏa mãn

81.xx

12m

. B.

0m 

. C.

2m 

. D.

4m 

Lời giải

.......................................................................................................................................................

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 48

 Ví dụ 6.6.3

Tìm tất cả các giá trị thực của tham số

để phương trình

   

21log logmx x

có nghiệm duy nhất.











. B.

1m 

. C.

2m

. D.











Lời giải

.......................................................................................................................................................

 Ví dụ 6.6.4

Tìm tất cả các giá trị thực của tham số

để phương trình

log







có nghiệm.











. B.

1m 

. C.

2m 

. D.











Lời giải

.......................................................................................................................................................

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 49

 Ví dụ 6.6.5

Tìm tất cả các giá trị thực của tham số

để phương trình

       

1 2 5 2 1 0log logm x m x m       

có nghiệm thuộc

 

24;











. B.

m  

. C.

17m  

. D.











Lời giải

.......................................................................................................................................................

 Ví dụ 6.6.6

Tìm tất cả các giá trị thực của tham số

để phương trình

   

12log logm x x



  



có nghiệm duy nhất.











. B.

13m

. C.











. D.











Lời giải

.......................................................................................................................................................

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 50

A. LÝ THUYẾT CHUNG.

Dạng 01.

 

01;

a b a a  

0b 

Tập nghiệm của bất phương trình là .

0b 

1a 

log

a b x b  

01a

log

a b x b  

Dạng 02.

 

01;

a b a a  

0b 

Tập nghiệm của bất phương trình là



0b 

1a 

log

a b x b  

01a

log

a b x b  

B. CÁC DẠNG BÀI TẬP.

 Dạng 7.1. Bất phương trình mũ cơ bản

 Xem lại mục “Lý thuyết chung”

 Bất phương trình mũ cơ bản:

 

01;

a b a a  

. Chú ý đến cơ số.

 Ví dụ 7.1.1

Tập nghiệm của bất phương trình



là

 

2;S  

. B.



2;S



  



. C.



2;S



 



. D.

 

12;S 

Lời giải

.......................................................................................................................................................

 Ví dụ 7.1.2

Tập nghiệm của bất phương trình









là

 

22;S 

. B.



2;S



  



. C.

 

0;S  

. D.

 

01;S 

Lời giải

.......................................................................................................................................................

 Ví dụ 7.1.3

Tập nghiệm của bất phương trình

xx



là



3;log







. B.

3;log









. C.



. D.

 

01;

Lời giải

.......................................................................................................................................................

BẤT PHƯƠNG TRÌNH MŨ

LŨY THỪA – MŨ – LOGARIT

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 51

 Dạng 7.2. Đưa về cùng cơ số

 Ta có hai chú ý như sau:

⓵ Với

   

f x g x

a a a f x g x   

⓶ Với

   

01,

f gxx

a a a f x g x    

 Ví dụ 7.2.1

Tìm tập nghiệm của bất phương trình:

5 25

x x x



 

1;S  

. B.

12;S







. C.

 

12;S 

. D.

 

0;S  

Lời giải

.......................................................................................................................................................

 Ví dụ 7.2.2

Tìm tập nghiệm của bất phương trình:

x









 

2;S   

. B.

 

0;S  

. C.

 

0;S   

. D.

 

;S    

Lời giải

.......................................................................................................................................................

 Ví dụ 7.2.3

Tìm số nghiệm nguyên dương của bất phương trình

. B.

. C.

. D.

Lời giải

.......................................................................................................................................................

 Ví dụ 7.2.4

Giải bất phương trình













ta được tập nghiệm:

;



 





. B.

 

1;

. C.

;









. D.

   

11;;   

Lời giải

.......................................................................................................................................................

5 125

xx









Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 52

 Dạng 7.3. Đặt ẩn phụ

 Phương pháp đặt ẩn phụ ta thường sử dụng một số phương pháp sau:

Ở đây ta xét bất phương trình dạng

 

0fx

, các trường hợp khác tiến hành tương tự.

⓵ Bất phương trình dạng

 

1 1 0

0... .

nx x

A a A a A a A



    

Đặt

0()

t a t

, ta thu được bất phương trình dạng

A t A t





0... A t A  

⓶ Bất phương trình dạng

 

Aa B ab Cb  

Chia cả hai vế cho

rồi đặt













, ta được

0. . .At Bt C  

⓷ Bất phương trình dạng

   

f x g x

Aa Bb C  

, trong đó

   

f x g x

a b k

Đặt

   

0( ) .

f x g x

a t t b k   

, ta thu được bất phương trình mới

At C

  

 Ví dụ 7.3.1

Nghiệm của bất phương trình





là

x 

hoặc

2x 

. B.

x

22ln lnx  

. D.

2lnx 

Lời giải

.......................................................................................................................................................

 Ví dụ 7.3.2

Bất phương trình

9 3 6 0

  

có tập nghiệm là

 

1;

. B.

   

23;;   

. C.

 

1;

. D.

 

23;

Lời giải

.......................................................................................................................................................

 Ví dụ 7.3.3

Tập hợp nghiệm của bất phương trình





là

 

01;.

. B.

 

12;.

. C.







. D.

 

23;.

Lời giải

.......................................................................................................................................................

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 53

 Dạng 7.4. Logarit hóa

 Phương trình

 

0 1 0,

log

f x b



  













 Phương trình

       

   

log log .log

f x g x f x g x

a a a

a b a b f x g x b    

hoặc

   

log log .log .

f x g x

b b b

a b f x a g x  

 Ví dụ 7.4.1

Tìm tập

của bất phương trình:

3 5 1.





30log ;







. B.



50log ;





. C.

 

30log ;

. D.

 

50log ;

Lời giải

.......................................................................................................................................................

 Ví dụ 7.4.2

Tìm tập

của bất phương trình:

 

log

x



 

5;

. B.

;









. C.

 

2;

. D.

 

1;

Lời giải

.......................................................................................................................................................

 Ví dụ 7.4.3

Giải bất phương trình:

27 2 72.





   

3 0 3log ; ;  

. B.



12;





 

22;

. D.

;









Lời giải

.......................................................................................................................................................

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 54

 Dạng 7.5. Chứa tham số

 Sử dụng PP giải BPT logarit kết hợp công thức, tnh chất của mũ, lũy thừa, logarit.

 Khai thác điều kiện bài toán.

 Xử lý bài toán và chọn giá trị m thỏa ĐK bài toán (cách “mò”).

 Ví dụ 7.5.1

Cho bất phương trình:

   

9 1 3 0 1.

mm   

. Tìm tất cả các giá trị của tham số

để bất phương trình

 

nghiệm đúng

1x

.m 

.m 

3 2 2.m 

3 2 2.m 

Lời giải

.......................................................................................................................................................

 Ví dụ 7.5.2

Tìm

để bất phương trình

 

9 2 1 6 4 0. . .

x x x

m m m   

nghiệm đúng với mọi

 

01;x

06m

6m

6m

0m

Lời giải

.......................................................................................................................................................

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 55

 Ví dụ 7.5.3

Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình sau có tập

nghiệm là









 

   

2 2 1 1 5 3 5 0



     

m 

m 

m 

m 

Lời giải

.......................................................................................................................................................

 Ví dụ 7.5.4

Tất cả các giá trị của

để bất phương trình

   

3 1 12 2 6 3 0

x x x

mm    

có

nghiệm đúng

0x

là:

 

2; 

2( ; ] 

;



 





;









Lời giải

.......................................................................................................................................................

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 56

A. LÝ THUYẾT CHUNG.

Dạng 01.

 

01log ;

x b a a  

1a 

log

x b x a  

01a

log

x b x a  

Dạng 02.

 

01log ;

x b a a  

1a 

log

x b x a  

01a

log

x b x a  

B. CÁC DẠNG BÀI TẬP.

 Dạng 8.1. Bất phương trình logarit cơ bản

 Ta có hai chú ý sau:



khi

log

khi

u a a



  





  





. 

0 0 1

khi

log

khi

u a a









   





 Ví dụ 8.1.1

Tập nghiệm của bất phương trình

 

2 1 1log x   

là:

;







. B.

;









. C.

;







. D.

;









Lời giải

.......................................................................................................................................................

 Ví dụ 8.1.2

Tập nghiệm của bất phương trình

 

2 1 2log x 

là:

1 25

2 32

x

. B.

x 

. C.

x 

. D.

x 

Lời giải

.......................................................................................................................................................

BẤT PHƯƠNG TRÌNH LOGARIT

LŨY THỪA – MŨ – LOGARIT

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 57

 Dạng 8.2. Đưa về cùng cơ số

 Dùng biến đổi logarit để đưa về cùng cơ số

khi > 1

log log

khi 0 < < 1

u v a













 Ví dụ 8.2.1

Bất phương trình

   

2 1 2log logxx  

có tập nghiệm

là











. B.

 

21;S 

. C.









. D.









Lời giải

.......................................................................................................................................................

 Ví dụ 8.2.2

Xác định tập nghiệm

của bất phương trình

 

44ln lnxx

   

12; \ .S  

 

2\.S 

 

2;.S  

 

1;.S  

Lời giải

.......................................................................................................................................................

 Ví dụ 8.2.3

Tập nghiệm của bất phương trình

 

2 3 1 2 1log logx x x   

là:

































Lời giải

.......................................................................................................................................................

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 58

 Dạng 8.3. Đặt ẩn phụ

 Tìm một

 

log

chung, đặt làm ẩn phụ

để đưa bất phương trình về bất phương trình ẩn

giải bất phương trình tìm

sau đó tìm

★ Chú ý: Nếu đặt

 

log log ,log ,log log ,log

a a a x

t x x t x t x x t a

       

 Ví dụ 8.3.1

Bất phương trình

0 2 0 2

log logxx  

có tập nghiệm là:

125 25









 

23;S 

. C.









. D.

 

03;S 

Lời giải

.......................................................................................................................................................

 Ví dụ 8.3.2

Nghiệm nguyên nhỏ nhất của bất phương trình

3 3 0log log



là:

3x 

1x 

. C.

2x 

. D.

4x 

Lời giải

.......................................................................................................................................................

 Ví dụ 8.3.3

Nếu đặt

logtx

thì bất phương trình

 

4 2 2

2 1 2

log log log log





  





trở thành bất phương trình nào?

13 36 0tt  

5 9 0tt  

13 36 0tt  

. D.

13 36 0tt  

Lời giải

.......................................................................................................................................................

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 59

 Dạng 8.4. Mũ hóa

 Với điều kiện các biểu thức

 

và

 

xác định, ta thường đưa các bất phương trình

logarit về các dạng cơ bản sau:

   

log

f x g x

 

khi a

f x a

khi a

f x a



































 Ví dụ 8.4.1

Bất phương trình

 

9 72 1log log



có tập nghiệm là:

73 2log ;S







. B.



72 2log ;S









73 2log ;S







. D.



2;S



 



Lời giải

.......................................................................................................................................................

 Ví dụ 8.4.2

Nghiệm nguyên lớn nhất của bất phương trình

 

4 3 2 1log .





là:

3x 

. B.

2x 

1x 

. D.

1x 

Lời giải

.......................................................................................................................................................

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 60

 Dạng 8.5. Chứa tham số

 Sử dụng PP giải BPT logarit kết hợp công thức, tnh chất của mũ, lũy thừa, logarit.

 Khai thác điều kiện bài toán.

 Xử lý bài toán và chọn giá trị m thỏa ĐK bài toán (cách “mò”).

 Ví dụ 8.5.1

Tìm tất cả các giá trị thực của tham số

để bất phương trình

 

51log

m

có

nghiệm

1x 

2m

. B.

2m

. C.

2m

. D.

2m

Lời giải

.......................................................................................................................................................

 Ví dụ 8.5.2

Tìm tất cả giá trị thực của tham số m để bất phương trình

 

41log x x m  

nghiệm đúng

x

7m 

. B.

7m

. C.

4m

. D.

47m

Lời giải

.......................................................................................................................................................

 Ví dụ 8.5.3

Tìm tất cả giá trị thực của tham số m để

 

4log logmx x

vô nghiệm?

44m  

. B.











. C.

4m 

. D.

44m  

Lời giải

.......................................................................................................................................................

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 61

 Ví dụ 8.5.4

Tìm tất cả các giá trị thực của tham số

sao cho khoảng

 

23;

thuộc tập nghiệm

của bất phương trình

   

1 4 1log log (1)x x x m    

12 13;m







. B.

12 13;m







. C.

13 12;m







. D.

13 12;m



  



Lời giải

.......................................................................................................................................................

 Ví dụ 8.5.5

Tìm

để bất phương trình

   

1 1 4log logx mx x m    

thoã mãn

x

10m  

. B.

10m  

. C.

23m

. D.

23m

Lời giải

.......................................................................................................................................................

 Ví dụ 8.5.6

Tìm tất cả các giá trị thực của tham số

để bất phương trình

 

0 02 2 0 02

log log log

m

có nghiệm với mọi

 

0;x 

01.m

1.m 

2.m

1.m 

Lời giải

.......................................................................................................................................................

TÀI LIỆU DÀNH CHO KHỐI 12

 
 
 
 
 
 
 
 Chủ đề 01. LŨY THỪA – HÀM SỐ LŨY THỪA 
 Dạng 1.1. Rút gọn và tính giá trị biểu thức ........................................................................... 6 
 Dạng 1.2. So sánh các biểu thức chứa lũy thừa ................................................................... 7 
 Dạng 1.3. Tập xác định hàm số lũy thừa ............................................................................... 8 
 Dạng 1.4. Đạo hàm số lũy thừa ................................................................................................ 9 
 Dạng 1.5. Đồ thị hàm số lũy thừa ........................................................................................... 10 
 Chủ đề 02. LOGARIT 
 Dạng 2.1. Tính giá trị biểu thức................................................................................................ 12 
 Dạng 2.2. Biểu diễn logarit ....................................................................................................... 13 
 Dạng 2.3. Mệnh đề đúng – sai ................................................................................................. 14 
 Chủ đề 03. HÀM SỐ MŨ – HÀM SỐ LOGARIT 
 Dạng 3.1. Tập xác định của hàm số logarit ........................................................................ 18 
 Dạng 3.2. Đạo hàm hàm số mũ – logarit ............................................................................. 20 
 Dạng 3.3. 
Khảo sát hàm số mũ – logarit .............................................................................. 21 
 Chủ đề 04. BÀI TOÁN LÃI SUẤT 
 Chủ đề 05. PHƯƠNG TRÌNH MŨ 
 Dạng 5.1. Phương trình mũ cơ bản ......................................................................................... 31 
 Dạng 5.2. Đưa về cùng cơ số ................................................................................................... 32 
 Dạng 5.3. Logarit hóa ............................................................................................................... 33 
 Dạng 5.4. Đặt ẩn phụ dễ thấy ................................................................................................ 34 
 Dạng 5.5. Đặt ẩn phụ với phương trình đẳng cấp ............................................................. 35 
 Dạng 5.6. Đặt ẩn phụ với tích hai cơ số bằng 1 .................................................................. 36 
 Dạng 5.7. Phương pháp hàm số ............................................................................................. 37 
 Dạng 5.8. Phương trình chứa tham số .................................................................................. 39 
 Chủ đề 06. PHƯƠNG TRÌNH LOGARIT 
 Dạng 6.1. Phương trình logarit cơ bản ................................................................................. 41 
 Dạng 6.2. Đưa về cùng cơ số .................................................................................................. 42 
 Dạng 6.3. Mũ hóa ....................................................................................................................... 43 
 Dạng 6.4. 
Đặt ẩn phụ dễ thấy ................................................................................................44 
 Dạng 6.5. Phương pháp hàm số ............................................................................................ 45 
 Dạng 6.6. Phương trình chứa tham số ................................................................................. 47   
Mục lục
 

Tổng Hợp Lý Thuyết  Năm học: 2023-2024 
 Biên soạn: Gv 
Lê Minh Tâm
 - 093.337.6281  Trang 2 
 Chủ đề 07. BẤT PHƯƠNG TRÌNH MŨ 
 Dạng 7.1. 
Bất phương trình mũ cơ bản ............................................................................... 50 
 Dạng 7.2. Đưa về cùng cơ số ................................................................................................... 51 
 Dạng 7.3. Đặt ẩn phụ ................................................................................................................. 52 
 Dạng 7.4. Logarit hóa ............................................................................................................... 53 
 Dạng 7.5. Chứa tham số .......................................................................................................... 54 
 Chủ đề 08. BẤT PHƯƠNG TRÌNH LOGARIT 
 Dạng 8.1. Bất phương trình logarit cơ bản ......................................................................... 56 
 Dạng 8.2. Đưa về cùng cơ số ................................................................................................... 57 
 Dạng 8.3. Đặt ẩn phụ.................................................................................................................58 
 Dạng 8.4. Mũ hóa ........................................................................................................................ 59 
 Dạng 8.5. Chứa tham số ........................................................................................................... 60 
 
 
   

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 3

A. LÝ THUYẾT CHUNG.

1. Lũy thừa:

1.1. Định nghĩa.

 Cho số thực b và số nguyên dương

 

2nn

Số a được gọi là căn bậc n của số b nếu

ab

Chú ý:

n lẻ

b

 Có duy nhất một căn bậc n của b, ký hiệu

n chẵn

0b 

 Không tồn tại căn bậc n của b

0b 

 Có một căn bậc n của b là 0

0b 

 Có hai bậc n của a là hai số đối nhau,

 Căn có giá trị dương ký hiệu là

, căn có giá trị âm ký hiệu là

b

1.2. Công thức.

Số mũ

Cơ số a

Lũy thừa

n

a

. ...

a a a a a

(n là thừa số a)

0

0a 

1aa

 

,nn  

0a 





 

  

0a 

 

a a a a b a b    

1.3. Tính chất.

⓵

.a a a





⓶





⓷

 

aa

⓸

 

.ab a b

⓹









⓺



   



   

   

⓻ Nếu

1a 

thì

aa  

. ⓼ Nếu

01a

thì

aa  

LŨY THỪA – HÀM SỐ LŨY THỪA

LŨY THỪA – MŨ – LOGARIT

CHÚ Ý

Các tính chất trên đúng trong trường hợp số mũ nguyên hoặc không.nguyên

Khi xét lũy thừa với số mũ 0 và số mũ nguyên âm thì cơ số phải khác 0.

Khi xét lũy thừa với số mũ không nguyên thì cơ số phải dương.

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 4

1.4. Tính chất căn bậc n.

Với

,,a b n

ta có

⓵

a a a

⓶

. , ;

n n n

ab a b a b

⓷

0,,

   

⓸

 

0,,

a a a n  

nguyên dương,

nguyên.

⓹

0, , ,

m nm

a a a n m  

nguyên dương.

⓺ Nếu



thì

0, , ,

a a a m n  

nguyên dương,

,pq

nguyên.

Đặc biệt:

.mn

aa

2. Hàm số lũy thừa:

2.1. Khái niệm.

 Hàm số

yx

với



được gọi là hàm số lũy thừa.

2.2. Tập xác định.

 Tập xác định của hàm số

yx

là:

⓵ Nếu là số nguyên dương

D 

⓶ Nếu nguyên âm hoặc bằng

 

0\D 

⓷ Nếu không nguyên

 

0;D  

※ Tổng quát: Tập xác định của hàm số

 

y f x

2.3. Đạo hàm.

 Hàm số

 

, yx

có đạo hàm

0x

và

 

.xx







2.4. Khảo sát hàm số lũy thừa

 

, yx

yx

với

0

yx

với

0

Tập khảo sát

 

0;

 

0;

Sự

biến

thiên

Đạo

hàm

00, .y x x





   

00, .y x x





   

Giới

hạn

0lim , lim .







  

0lim , lim .







  

Tiệm

cận

Không có.

Nhận

là tiệm cận ngang.

Nhận

là tiệm cận đứng.

Khi NGUYÊN DƯƠNG

Hàm số xác định xác định.

Khi NGUYÊN ÂM

Hàm số xác định .

Khi KHÔNG NGUYÊN

Hàm số xác định

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 5

Bảng biến thiên

Đồ thị

Đồ thị của hàm số lũy thừa

yx

luôn đi qua điểm

 

11;.I

Lưu ý:

 Khi khảo sát hàm số lũy thừa với số mũ cụ thể, ta phải xét hàm số đó trên toàn bộ tập

xác định của nó.

 Chẳng hạn:

, , y x y x y x



  

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 6

B. CÁC DẠNG BÀI TẬP.

 Dạng 1.1. Rút gọn và tính giá trị biểu thức

 Sử dụng phối hợp linh hoạt các tính chất của lũy thừa.

 Chọn

;ab

là các số thực dương và

;xy

là các số thực tùy ý, ta có:

⓵

.a a a





⓶





⓷

 

aa

⓸

 

.ab a b

⓹









⓺



   



   

   

⓻ Nếu

1a 

thì

aa  

. ⓼ Nếu

01a

thì

aa  

 Ví dụ 1.1.1

Đưa các biểu thức sau về dạng lũy thừa

⓵

 

0a a a 

⓶

0 75

⓷

 

0,.



Lời giải

⓵

1 3 3

2 2 4

.a a a a a a

   

  

   

   

. ⓶

 

0 75 3 3

2 4 2

16 2









  

⓷

5 15

15 15

5 15

b a b a b

a b a





  





 Ví dụ 1.1.2

Rút gọn các biểu thức sau đây:

⓵

 

5a 

⓶

 

81 0a b b 

⓷

   

11.x x x  

Lời giải

⓵

   

55aa  

⓶

4 2 2 2

81 9 9a b a b a b  

(do

0b 

⓷

   

8 2 2

1 1 1.x x x x x x     

(do

1 1 0xx    

 Ví dụ 1.1.3

Cho

   

2 3 2 3,ab



   

. Tính

   

11.A a b



   

Lời giải

 Ta có:

 

2 3 2 3



    



    



   

11A a b



    

       

1 1 1 1

1 1 6

2 3 1 2 3 1 3 3 3 3 1

3 3 3 3

   

             





Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 7

 Dạng 1.2. So sánh các biểu thức chứa lũy thừa

 Ta có hai cách làm như sau:

Đưa về cùng cơ số

Cho

:,a m n

. Khi đó

⓵ Với

1a 

a a m n   

;

⓶ Với

01a

a a m n   

Đưa về cùng số mũ

Với

0 ab

và

là số nguyên thì

⓵

a b m  

⓶

a b m  

 Ví dụ 1.2.1

So sánh các số sau:

⓵

300

và

400

⓶

 

5000

và

 

8000

Lời giải

⓵

300

và

400

Ta có

71

và

300 400

nên

300 400

77

⓶

 

5000

và

 

8000

Ta có



và

5000 8000

nên

   

5000 8000



 Ví dụ 1.2.2

So sánh các số sau:

⓵

và

. ⓶

100

và

⓷

 

31

và

 

31

. ⓸

34

và

 





Lời giải

⓵

và

15 3375 400 20  

Do đó

   

10 10

30 3 2 20

15 15 20 20 .  

⓶

100

và

10 3

2 1024 8000 20  

Do đó

   

10 10

100 10 3 30

2 2 20 2  

⓷

 

31

và

 

31

3 1 1

và

78

nên

   

3 1 3 1  

⓸

34

và

 





1

và

34 0

nên

 





 Ví dụ 1.2.3

So sánh 2 số

và

biết:

⓵



. ⓶

   

5 1 5 1

  

Lời giải

⓵



Ta có

1

nên

pq

⓶

   

5 1 5 1

  

Ta có

5 1 1

nên

pq

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 8

 Dạng 1.3. Tập xác định hàm số lũy thừa

 Tập xác định của hàm số

 

y f x

là:

⓵ là số nguyên dương

 

xác định.

⓶ nguyên âm hoặc bằng

 

0fx

⓷ không nguyên

 

0fx

 Ví dụ 1.3.1

Tìm tập xác định của hàm số

 

1yx





.

   

11;;    

 

11;

. D.

 

1\.

Lời giải

Chọn D

 Hàm số

 

1yx





xác định khi

1 0 1xx    

 Vậy

 

1\

là tập xác định của hàm số đã cho.

 Ví dụ 1.3.2

Tìm tập xác định của hàm số

 

2019

56y x x



  

   

23;;   

. B.

 

23;

 

23;;



    



. D.

 

23\;

Lời giải

Chọn C

 Hàm số

 

2019

56y x x



  

xác định khi và chỉ khi

5 6 0





   







 Vậy tập xác định của hàm số

 

2019

56y x x



  

là

 

23\ ; .

 Ví dụ 1.3.3

Tìm tập xác định của hàm số

 

yx









. B.

;



 







. C.

;



  





. D.

.

Lời giải

Chọn C

 Điều kiện xác định:

2 1 0

.xx   

 Vậy tập xác định cúa hàm số là

;



 





Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 9

 Dạng 1.4. Đạo hàm số lũy thừa

 Hàm số

 

, yx

có đạo hàm

0x

và

   

. . .x x u u u







  

 Ví dụ 1.4.1

Cho hàm số

   

23f x x

.Tính

 



. B.

. C.



. D.



Lời giải

Chọn B

 Tập xác định

;









 Ta có

   

23f x x



   

f x x









 





 Ví dụ 1.4.2

Tìm đạo hàm của hàm số

 

13yx

trên khoảng

;









 

5 1 3'yx  

. B.

 

'yx

 

5 1 3'yx  

. D.

 

'yx

Lời giải

Chọn A

 Với điều kiện

x 

, ta có

   

1 3 1 3y x x   

 Khi đó:

       

5 2 2

3 3 3

1 3 1 3 1 3 5 1 3

' . '.y x x x x



       





 Ví dụ 1.4.3

Tìm đạo hàm của hàm số

2yx

2x 

 





. B.





 





. D.

42'yx

Lời giải

Chọn A

 Có

 

   

4 2 4 2







Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 10

 Dạng 1.5. Đồ thị hàm số lũy thừa

 Ta lưu ý các yếu tố trong sự biến thiên của hàm số lũy thừa

yx

với

0

0

Đạo hàm

0yx







00, .y x x





   

Giới hạn

0lim , lim .







  

0lim , lim .







  

Tiệm cận

Không có.

Nhận

là tiệm cận ngang.

Nhận

là tiệm cận đứng.

Đồ thị

Đồ thị của hàm số lũy thừa

yx

luôn đi qua điểm

 

11;.I

 Ví dụ 1.5.1

Hình vẽ bên là đồ thị các hàm số

yx

trên miền

 

0;

. Hỏi số

số nào nhận giá trị trong khoảng

 

01;

. B.

&ac

. D.

Lời giải

Chọn D

 Nhìn vào hình vẽ, ta thấy đồ thị hàm số

là đường thẳng nên ta có được

1.b 

 Khi

1x 

thì

x x x

Do đó

01.c

 Ví dụ 1.5.2

Cho hàm số

2023





. Mệnh đề nào đúng về đường tiệm cận của đồ thị hàm số?

A. Có một tiệm cận ngang và một tiệm cận đứng.

B. Không có tiệm cận ngang và có một tiệm cận đứng.

C. Có một tiệm cận ngang và không có tiệm cận đứng.

D. Không có tiệm cận.

Lời giải

Chọn A

 Tập xác định:

 

0;D   

 Ta có

2023

lim lim





  

nên đồ thị có một tiệm cận đứng

0x 

 Mặt khác

2023

0lim lim

 



nên đồ thị có tiệm cận ngang

0y 

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 11

A. LÝ THUYẾT CHUNG.

1. Định nghĩa.

Cho hai số dương

,ab

với

1a 

 Số thỏa mãn đẳng thức

ab

được gọi là lôgarit cơ số

của

và k hiệu là

log

 Ta viết:

log .

b a b  

2. Tính chất.

3. Công thức.

 Cho 3 số dương

,,a b c

với

11;ac

và



, ta có các công thức sau:

 Logarit thập phân và Logarit tự nhiên

 Logarit thập phân là logarit cơ số 10. Viết :

log log lgb b b

 Logarit tự nhiên là logarit cơ số

. Viết :

log ln

bb

LOGARIT

LŨY THỪA – MŨ – LOGARIT

Cho

TÍNH CHẤT

Tích tổng – Thương hiệu

Đặc biệt: với

Lũy thừa

Đặc biệt:

Đổi cơ số

Đặc biệt: ;

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 12

B. CÁC DẠNG BÀI TẬP.

 Dạng 2.1. Tính giá trị biểu thức

 Áp dụng các tính chất – công thức để biến đổi:

Tính chất

⓵

1 1 0log , log

a 

⓶

 

log

, log

a b a

⓷

 

log . log log

a a a

b c b c

(Tích – tổng)

⓸

log log log

a a a



(Thương – hiệu)

Đặc biệt : với

01,,a b a

log log



Công thức bay

⓵

log log

bb

⓶

log log

bb

Đặc biệt:

log log



Đổi cơ số

⓵

log



⓶

log log .log

a a c

b c b

Đặc biệt :

log



 Ví dụ 2.1.1

Cho

01a

. Tính giá trị của biểu thức

4log

. B.

. C.

. D.

Lời giải

Chọn A

Ta có

2 4 4

4 16

log

log log

a a a   

 Ví dụ 2.1.2

Tính giá trị của biểu thức

2 2 2 2

2 12 3 5 15 150log log log logA    

2

. B.

. C.

. D.

Lời giải

Chọn C

 

2 3 2 3

2 2 2 2 2 2 2 2

18000

12 5 15 150 12 5 15 150 8 3

2250

log log log log log . log . log logA         

 Ví dụ 2.1.3

Rút gọn biểu thức

2 3 4

2 4 6 8

2 3 4log log log log

a a a

K b b b b   

ta được

4log

. B.

log

b

. C.

3log

. D.

log

Lời giải

Chọn A

2 3 4

2 4 6 8

2 3 4 2 4 6 8 4log log log log log log log log log

a a a a a a

a a a

K b b b b b b b b b        

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 13

 Dạng 2.2. Biểu diễn logarit

 Ta thực hiện theo các bước sau

 Bước 01. Biến đổi các biểu thức logarit phụ thuộc vào tham số

và

 Bước 02. Đặt các biểu thức logarit của các số nguyên tố là các ẩn

,,xyz

…. Từ đó ta

thu được phương trình hoặc hệ phương trình với các ẩn

,,xyz

…. Ta tìm

các ẩn này theo

,ab

 Bước 03. Giải hệ tìm được tìm

,,xyz

… theo

,ab

. Từ đó tnh được biểu thức theo các

tham số

,ab

Các công thức nền tảng là

log



và

log



 Ví dụ 2.2.1

Cho

14loga 

. Biểu diễn

16log

theo

1a 

. B.

. C.

3a

. D.

Lời giải

Chọn A

Ta có

 

49 7

2 2 2

1 2 2 2

16 2 2 2 2

7 14 2

log log log .

log log log

log

     



 Ví dụ 2.2.2

Cho

18loga 

và

60log .b 

Tính

2log

theo

và



. B.

a ab



. C.

  



. D.





Lời giải

Chọn C

Đầu tiên ta có hệ

5 5 5

18 2 2 3

60 2 2 3 1

log log log



  



   



Đặt

2logx 

và

3logy 

từ đó ta có hệ phương trình bậc nhất hai ẩn

x y a

x y b







  



log



  



















Nên

log



  





Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 14

 Dạng 2.3. Mệnh đề đúng – sai

 Ta lưu ý các công thức sau

Tính chất

⓵

1 1 0log , log

a 

⓶

 

log

, log

a b a

⓷

 

log . log log

a a a

b c b c

(Tích – tổng)

⓸

log log log

a a a



(Thương – hiệu)

Đặc biệt : với

01,,a b a

log log



Công thức bay

⓵

log log

bb

⓶

log log

bb

Đặc biệt:

log log



Đổi cơ số

⓵

log



⓶

log log .log

a a c

b c b

Đặc biệt :

log



 Ví dụ 2.3.1

Cho

0 1 1, , ; ; .a b c a b  

, Trong các khẳng định sau, khẳng định nào sai?

log



. B.

log .log log

a b a

b c c

log log

b c b

. D.

 

log . log log

a a a

b c b c

Lời giải

Chọn C

Câu C sai, vì

log log



 Ví dụ 2.3.2

Cho

0,,a b c 

và

1,ab

, Trong các khẳng định sau, khẳng định nào sai?

log

ab

. B.

log log

b c b c  

log



. D.

log log

b c b c  

Lời giải

Chọn D

Câu D sai, vì khẳng định đó chỉ đúng khi

1a 

, còn khi

01log log

a b c b c     

 Ví dụ 2.3.3

Cho

0,,a b c 

và

1,ab

, Trong các khẳng định sau, khẳng định nào sai?

log



. B.

log .log log

a b a

b c c

   

log . log

b c b c

. D.

log log log

a a a



Lời giải

Chọn C

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 15

Câu C sai, vì

 

log . log log

a a a

b c b c

 Ví dụ 2.3.4

Cho

00,ab

thỏa mãn

7a b ab

. Mệnh đề đúng trong các mệnh đề sau là:

   

27log log loga b ab

. B.

 

log log log





   

log log loga b a b  

. D.

   

log log loga b a b  

Lời giải

Chọn B

Ta có

7a b ab

 

a b ab ab



    

 

log log log log log

a b a b

ab a b





    





 Ví dụ 2.3.5

Với mọi số

0b 

thỏa mãn

9 10a b ab

thì đẳng thức đúng là.

 

23log log loga b a b  

. B.

 

log

log log





 

11log logab  

. D.

 

log log log





Lời giải

Chọn D

Ta có

9 10a b ab

9 6 16a ab b ab   

 

3 16a b ab  

 

log log





log log log



  

 

log log log



  

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 16

A. LÝ THUYẾT CHUNG.

1. Hàm số mũ.

Hàm số mũ

 

01, ,

y a a a  

Tập xác định

D 

Tập giá trị

 

0;,T  

nghĩa là khi giải phương trình mà đặt

 

ta

thì

0.t 

Đơn điệu

1a 

Hàm số

ya

đồng biến, khi đó:

   

f x g x

a a f x g x  

01a

Hàm số

ya

nghịch biến, khi đó:

   

f x g x

a a f x g x  

Đạo hàm

   

 

.ln . .ln

x x u u

a a a a u a a

e e e e u







  





  





Đồ thị

Nhận trục hoành làm đường tiệm cận ngang

 Nhận xét:

Đồ thị hàm số

 

y a a

đối xứng với đồ thị hàm số

 

y a a  

qua Oy.

HÀM SỐ MŨ – HÀM SỐ LOGARIT

LŨY THỪA – MŨ – LOGARIT

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 17

2. Hàm số logarit.

Hàm số logarit

 

0 1 0log , , ;

y x a a x   

Tập xác định

 

0;D   

Tập giá trị

T 

, nghĩa là khi giải PT mà đặt

log

tx

thì

không có điều kiện.

Đơn điệu

1a 

Hàm số

log

yx

đồng biến trên

, khi đó:

       

log log

f x g x f x g x  

01a

Hàm số

log

yx

nghịch biến trên

, khi đó:

       

log log

f x g x f x g x  

Đạo hàm

   

 

log log

.ln .ln

ln ln

ln , (ln )

x a u a

u n u

x x u







  



   



   

Đồ thị

Nhận trục tung làm đường tiệm cận đứng

 Nhận xét:

Đồ thị hàm số

 

1log

y x a

đối xứng với đồ thị hàm số

 

01log

y x a  

qua Ox.

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 18

B. CÁC DẠNG BÀI TẬP.

 Dạng 3.1. Tập xác định của hàm số logarit

 Điều kiện xác định của hàm số

 

log

y f x

 

















 Đặc biệt: với hàm số

 

log

y f x







ta lưu ý “mũ n” của

 

 Nếu

2n 

ĐKXĐ của hàm số

 

log

y f x







 



















 Nếu

2n 

ĐKXĐ của hàm số

 

log

y f x







 



















Tóm lại nếu

 

hoặc

 

có “mũ n” ta chú ý xem “n” chẵn hay lẻ.

 Ví dụ 3.1.1

Tìm tập xác định

của hàm số

 

21logyx



  





. B.



  





. C.

 

0;D  

. D.



   





Lời giải

Chọn D

Hàm số

 

21logyx

có nghĩa khi

2 1 0

xx    

Vậy TXĐ là



  





 Ví dụ 3.1.2

Tìm tập xác định

của hàm số

 

32logy x x  

21,.D



  



   

21,,D      

 

21,D   

. D.

 

21,,D



     



Lời giải

Chọn B

Điều kiện

   

3 2 0 2 1

x x D





          







 Ví dụ 3.1.3

Tập xác định của hàm số:

 

2logyx

là

A. B.

 

. C.

 

2;

. D.









Lời giải

Chọn B

Hàm số

 

2logyx

xác định nếu

 

2 0 2xx   

Vậy tập xác định

 

2\D 

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 19

 Ví dụ 3.1.4

Tập xác định của hàm số:

log







là



02;





 

02;

  

2 0 2;;



  



. D.

 

22;

Lời giải

Chọn A

ĐKXĐ:

 



log

;;

;



















    



  







   

  



























 Ví dụ 3.1.5

Tập xác định của hàm số:

 

2021

3 2 3log ln

y x x x



    

là

       

1 1 0 0 1 2 3; ; ; ;D       

   

1 2 3;;D    

     

1 1 1 2 3; ; ;D      

. D.

 

1;D   

Lời giải

Chọn A

ĐKXĐ:

       

1 1 0 0 1 2 3

3 2 0

; ; ; ;



















        







  





















 Ví dụ 3.1.6

Tìm tất cả các giá trị thực của tham số

để hàm số

24ln( )y x mx  

có tập xác

định

D 

22m  











2m 

. D.

22m  

Lời giải

Chọn D

Hàm số có tập xác định là

2 4 0, x mx x     

4 0 2 2' mm       

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 20

 Dạng 3.2. Đạo hàm hàm số mũ – logarit

 Đạo hàm hàm số logarit:

   

 

log log

.ln .ln

ln ln

ln , (ln )

x a u a

u n u

x x u







  



   



   

 Đạo hàm hàm số mũ:

   

 

.ln . .ln

x x u u

a a a a u a a

e e e e u







  





  





 Ví dụ 3.2.1

Đạo hàm của hàm số

 

41logyx

là

 

4 1 3







 

4 1 3



















Lời giải

Chọn D

Với

x 

. Áp dụng công thức

 

log





ta có

 

4 1 3







 Ví dụ 3.2.2

Hàm số





có đạo hàm là

 

4 1 2 ln2







2 ln2







 

4 1 2 2ln

y x x x





  

 

22ln2

y x x







Lời giải

Chọn B

Ta có:

 

2 2 2

2 2 2 2

2 2 2 4 1 2

ln2 ln2.

x x x x x x

y x x x

  



      

 Ví dụ 3.2.3

Tnh đạo hàm của hàm số































Lời giải

Chọn D

 

2 2 1 2 2

.ln . . .ln .







  



hay









Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 21

 Dạng 3.3. Khảo sát hàm số mũ – logarit

 Ta cần lưu ý các vấn đề sau:

Hàm số Mũ

 

y a a  

Hàm số Logarit

 

10log

y x a  

Đơn điệu



1a 

HS đồng biến.



01a  

HS nghịch biến.



1a 

HS đồng biến.



01a  

HS nghịch biến.

Tiệm cận

Nhận

làm TCN.

Nhận

làm TCĐ.

Đồ thị

Nằm bên trên

Luôn đi qua điểm

 

01;

Nằm bên phải

Luôn đi qua điểm

 

10;

ĐTHS

 

y a a  

đối xứng

 

10log

y x a  

qua

yx

(đường

phân xác góc phần tư thứ nhất).

 Với bài toán xét thứ tự cơ số ta nhớ như sau:

Hàm số Mũ

 

y a a  

Hàm số Logarit

 

10log

y x a  

Cơ số

1

Càng gần

cơ số càng lớn.

Càng gần

cơ số càng lớn.

01a

Càng gần

cơ số càng bé.

Càng gần

cơ số càng bé.

Hình minh họa

 Ví dụ 3.3.1

Cho hàm số

logyx

. Mệnh đề nào dưới đây là mệnh đề sai?

A. Hàm số đã cho đồng biến trên tập xác định.

B. Đồ thị hàm số đã cho không có tiệm cận ngang.

C. Đồ thị hàm số đã cho có một tiệm cận đứng là trục

D. Hàm số đã cho có tập xác định

 

0\D 

Lời giải

Chọn D

Điều kiện:

0x 

nên TXĐ

 

0;D  

 Ví dụ 3.3.2

Cho hàm số

logyx

. Mệnh đề nào dưới đây sai?

A. Đạo hàm của hàm số là

2lnyx





B. Đồ thị hàm số nhận trục

làm tiệm cận đứng.

C. Tập xác định của hàm số là

 

; 

D. Hàm số đồng biến trên khoảng

 

0;

Lời giải

Chọn C

Hàm số

logyx

xác định trên khoảng

 

0;

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 22

 Ví dụ 3.3.3

Tìm mệnh đề đúng trong các mệnh đề sau:

A. Hàm số

log

yx

với

1a 

là một hàm số nghịch biến trên khoảng

 

0,

B. Đồ thị hàm số

log

yx

và

log

yx

với

01a

đối xứng với nhau qua Ox.

C. Hàm số

log

yx

với

01a

có tập xác định là .

D. Hàm số

log

yx

với

01a

là một hàm số đồng biến trên khoảng

 

0,

Lời giải

Chọn B

Ta có:

log log log

y x x x



    

Đồ thị các hàm số

log

yx

và

log

yx

với

01a

đối xứng với nhau qua trục hoành.

 Ví dụ 3.3.4

Đồ thị hàm số

 

1logyx

nhận đường thẳng nào dưới đây làm tiệm cận đứng ?

1x 

1y 

1x 

0x 

Lời giải

Chọn C

Đồ thị hàm số

 

1logyx

có đường tiệm cận đứng là

1x 

 Ví dụ 3.3.5

Hàm số nào sau đây nghịch biến trên tập xác định của nó?

 

y 

log

yx









logyx





Lời giải

Chọn D

Hàm số

logyx





có cơ số





nên hàm số

logyx





nghịch biến trên TXĐ.

 Ví dụ 3.3.6

Cho các hàm số

y a y b

và

yc

lần lượt có đồ

thị như hình vẽ bên dưới. Hãy so sánh

,,a b c

a b c

a b c

a b c

b a c

Lời giải

Chọn D

Ta thấy

yb

là hàm số mũ nghịch biến nên

01b

y a y c

là hàm số mũ đồng biến nên

1,ac

Và đồ thị

yc

gần trục

hơn

ya

nên

ac

Từ đó

c a b

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 23

A. LÝ THUYẾT CHUNG.

1. Lãi đơn.

 Số tiền lãi chỉ tính trên số tiền gốc mà không tính trên số tiền lãi do số tiền gốc sinh ra.

 Công thức tnh lãi đơn:

 

1 .

V V r n

 Trong đó:

: Số tiền cả vốn lẫn lãi sau n kỳ hạn;

: Số tiền gửi ban đầu;

: Số kỳ hạn tính lãi;

: Lãi suất định kỳ, tính theo %.

2. Lãi kép.

 Số tiền lãi không chỉ tính trên số tiền gốc mà còn tính trên số tiền lãi do tiền gốc đó sinh

ra thay đổi theo từng định kỳ.

 Ta có các loại lãi kép sau:

2.1. Lãi kép, gửi một lần:

 

T T r

 Trong đó:

: Số tiền cả vốn lẫn lãi sau n kỳ hạn;

: Số tiền gửi ban đầu;

: Số kỳ hạn tính lãi;

: Lãi suất định kỳ, tính theo %.

2.2. Lãi kép liên tục:

T T e

 Trong đó:

: Số tiền cả vốn lẫn lãi sau n kỳ hạn;

: Số tiền gửi ban đầu;

: Số kỳ hạn tính lãi;

: Lãi suất định kỳ, tính theo %.

2.3. Lãi kép, gửi định kỳ.

2.3.1. Trường hợp gửi tiền định kì cuối tháng.

 Chứng minh

Tháng

Đầu tháng

Cuối tháng

Chưa gửi

 

1m r m

 

1m r m

   

11m r m r m   

Cứ cuối mỗi tháng gửi vào ngân hàng m triệu, lãi suất kép (tháng hoặc năm).

Hỏi sau

n (tháng hoặc năm) số tiền thu được là bao nhiêu?

Người ta chứng minh được số tiền thu được là: .

Bài toán 1

BÀI TOÁN LÃI SUẤT

LŨY THỪA – MŨ – LOGARIT

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 24

…

   

11...

m r m r m



    

 Vậy sau tháng n ta được số tiền

   

11...

T m r m r m



     

   

1 1 1...

m r r





     





 Ta thấy trong ngoặc là tổng

số hạng của cấp số nhân có

 

1 1 1, ,

u u r q r



    

 Biết rằng:

... .

S u u u



   



nên

 



  





 Chứng minh

 Áp dụng bài toán 1 ta có số tiền thu được là

 



  





 Mà đề cho số tiền đó chnh là A nên

 

m Ar

A r m



    







 Chứng minh

 Áp dụng bài toán 1 ta có số tiền thu được là

 



  





 Đề cho số tiền đó chnh là A nên:

 

1 1 1 1 1

log

m Ar Ar Ar

A r m r n

r m m







           











 Như vậy trong trường hợp 2.3.1 này ta cần nắm vững công thức bài toán 1 từ đó có thể dễ

dàng biến đổi ra các công thức ở bài toán 2, bài toán 3.

2.3.2. Trường hợp gửi tiền định kì đầu tháng.

 Chứng minh

 Ta xây dựng bảng sau:

Tháng

Đầu tháng

Cuối tháng

Cứ cuối mỗi tháng gửi vào ngân hàng m triệu, lãi suất kép (tháng hoặc năm). Sau n (tháng

hoặc năm) số tiền thu được là A triệu. Hỏi số tiền gửi mỗi tháng

m là bao nhiêu?

Người ta chứng minh được số tiền cần gửi mỗi tháng là: .

Bài toán 2

Cứ cuối mỗi tháng gửi vào ngân hàng m triệu, lãi suất kép (tháng hoặc năm). Sau n (tháng

hoặc năm) số tiền thu được là A triệu. Hỏi số tháng hoặc năm

n là bao nhiêu?

Người ta chứng minh được số tháng thu được đề bài cho là: .

Bài toán 3

Cứ đầu mỗi tháng gửi vào ngân hàng m triệu, lãi suất kép (tháng hoặc năm).

Hỏi sau

n (tháng hoặc năm) số tiền thu được là bao nhiêu?

Người ta chứng minh được số tiền thu được là: .

Bài toán 4

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 25

 

1mr

 

1m r m

   

11m r m r  

   

11m r m r m   

     

1 1 1m r m r m r    

…

   

11...

m r m r   

 Vậy sau tháng n ta được số tiền:

         

 

1 1 1 1 1... ...

T m r m r m r r m r





           





 Chứng minh

 Áp dụng bài toán 4. Ta có số tiền thu được là:

   

1 1 1

T r r



   





 Mà đề cho số tiền đó là A nên

   

1 1 1

m Ar

A r r m



     







  





 Chứng minh

 Áp dụng bài toán 4. Ta có: số tiền thu được là:

   

1 1 1

T r r



   





 Đề cho số tiền đó là A nên:

   

1 1 1

A r r



   





   

 

1 1 1

Ar Ar

     





  





 

log





  









 Như vậy trong trường hợp 2.3.2 ta cần nắm vững công thức bài toán 4 từ đó có thể dễ dàng

biến đổi ra các công thức ở bài toán 5, bài toán 6.

Cứ đầu mỗi tháng gửi vào ngân hàng m triệu, lãi suất kép (tháng hoặc năm). Sau n (tháng

hoặc năm) số tiền thu được là A triệu. Hỏi số tiền gửi mỗi tháng

m là bao nhiêu?

Người ta chứng minh được số tiền cần gửi mỗi tháng là: .

Bài toán 5

Cứ đầu mỗi tháng gửi vào ngân hàng m triệu, lãi suất kép (tháng hoặc năm). Sau n (tháng

hoặc năm) số tiền thu được là

A triệu. Hỏi số tháng hoặc năm n là bao nhiêu?

Người ta chứng minh được số tháng thu được đề bài cho là: .

Bài toán 6

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 26

2.3.3. Trường hợp vay nợ và trả tiền định kì đầu tháng.

 Chứng minh

 Ta xây dựng bảng sau:

Tháng

Đầu tháng

Cuối tháng

Am

      

1 1 1A m r A r m r     

   

11A r m r m   

     

111A r m r m r    

     

111A r m r m r m     

       

3 3 2

1 1 1 1A r m r m r m r      

…

       

1 1 1 1...

A r m r m r m r       

 Vậy sau tháng n ta còn nợ số tiền:

       

1 1 1 1...

T A r m r m r m r        

         

 

1 1 1 1 1...

n n n

A r m r r A r m r





          





3. Bài toán tăng trưởng dân số.

 Công thức tính:

 

X X r





 

,;m n m n





 Trong đó:

: tỉ lệ tăng dân số từ năm n đến năm m.

: dân số năm m.

: dân số năm n.

 Từ đó ra có công thức tính tỉ lệ tăng dân số là





 Ví dụ 4.1

Bà Hoa gửi

0 45,%

triệu vào tài khoản định kỳ tính lãi kép với lãi suất là

8%/

năm.

Tính số tiền lãi thu được sau

năm.

Lời giải

 Áp dụng công thức tính lãi kép, sau

năm số tiền cả gốc và lãi bà Hoa thu về là

   

1 100 1 0 08 215 892,,

Ar   

triệu đồng.

 Suy ra số tiền lãi bà Hoa thu về sau

năm là

215 892 100 115 892,,

triệu đồng.

 Ví dụ 4.2

Một người muốn gửi tiết kiệm ở ngân hàng và hi vọng sau 4 năm có được 850 triệu

đồng để mua nhà. Biết lãi suất ngân hàng mỗi tháng trong thời điểm hiện tại là

0 45,%

. Hỏi người đó mỗi tháng phải gửi vào ngân hàng tối thiểu bao nhiêu tiền

để đủ số tiền mua nhà ? (giả sử số tiền mỗi tháng là như nhau và lãi suất trong 4

năm là không thay đổi).

Lời giải

Vay ngân hàng A triệu đồng. Cứ đầu mỗi tháng (năm) trả ngân hàng m triệu, lãi suất kép

(tháng hoặc năm). Hỏi sau n (tháng hoặc năm) số tiền còn nợ là bao nhiêu?

Người ta chứng minh được số tiền còn nợ là: .

Bài toán 7

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 27

 Giả sử người này gửi tiền ở thời điểm

nào đó , kể từ thời điểm này sau 4 năm (48

tháng) ông muốn có số tiền 850 triệu.

 Như vậy rõ ràng ta có thể coi đây là bài toán gửi tiền định kì đầu tháng.

 Áp dụng bài toán 5 ta có số tiền phải gửi mỗi tháng là :

   

 

1 1 1





  





 Theo bài ra

48 0 45 850, , %,Anr  

 Thay vào

 



ta được

   

850 0 45

15 833

1 0 45 1 0 45 1

. , %

, % , %

m 



  





triệu đồng.

 Ví dụ 4.3

Một bà mẹ Việt Nam anh hùng được hưởng số tiền là 4 triệu đồng trên một tháng

(chuyển vào tài khoản của mẹ ở ngân hàng vào đầu tháng). Từ tháng 1 năm 2016 mẹ

không đi rút tiền mà để lại ngân hàng và được tính lãi suất

trên một tháng.

Đến tháng 12 năm 2016 mẹ rút toàn bộ số tiền (gồm số tiền của 12 tháng và số tiền đã

gửi tháng 1). Hỏi khi đó mẹ lĩnh về bao nhiêu tiền ? (kết quả làm tròn theo đơn vị

nghìn đồng).

Lời giải

 Nếu ban đầu gửi vào

đồng, từ đầu tháng sau gửi thêm

đồng (không đổi) vào

đầu mỗi tháng với lãi suất

trong

tháng thì tổng số tiền thu được là :

       

1 1 1 4 1 1 1 1 1 4 50 73

% % ,

A a r r

   

           

   

   

triệu đồng.



11n 

là tính từ đầu tháng 2 đến cuối tháng 12.

 Ví dụ 4.4

Đầu năm 2016, anh Hùng có xe công nông trị giá

100

triệu đồng. Biết mỗi tháng

thì xe công nông hao mòn mất

04,%

giá trị, đồng thời làm ra được

triệu đồng

(số tiền làm ra mỗi tháng là không đổi). Hỏi sau một năm, tổng số tiền (bao gồm giá tiền

xe công nông và tổng số tiền anh Hùng làm ra) anh Hùng có là bao nhiêu?

Lời giải

 Sau một năm số tiền anh Hùng làm ra là

6 12 72. 

triệu đồng

 Sau một năm giá trị xe công nông còn

100 1 0 4 95 3042( , %) ,

triệu đồng

 Vậy sau một năm số tiền anh Hùng có là

167 3042,

triệu đồng

 Ví dụ 4.5

Bác B gởi tiết kiệm số tiền ban đầu là

triệu đồng theo kỳ hạn

tháng với lãi suất

0 72,%

tháng. Sau một năm bác B rút cả vốn lẫn lãi và gởi theo kỳ hạn

tháng với lãi

suất

0 78,%

tháng. Sau khi gởi đúng một kỳ hạn

tháng do gia đình có việc bác gởi

thêm 3 tháng nữa thì phải rút tiền trước hạn cả gốc lẫn lãi được số tiền là

57 694 945 55. . ,

đồng (chưa làm tròn). Biết rằng khi rút tiền trước hạn lãi suất được tnh theo lãi suất

không kỳ hạn, tức tnh theo hàng tháng. Trong số 3 tháng bác gởi thêm lãi suất là

Lời giải

 Số tiền bác B rút ra sau năm đầu:

 

50 000 000 1 0 0072 3. . * , *T 

 Số tiền bác B rút ra sau sáu tháng tiếp theo:

 

1 0 0078 6* , *TT

 Số tiền bác B rút ra sau ba tháng tiếp theo:

 

57 694 945 551 .* .,T T r  

57 694 94

01 0 004

5. . ,

, , %r

    

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 28

 Ví dụ 4.6

Bạn Nam là sinh viên của một trường Đại học, muốn vay tiền ngân hàng với lãi suất

ưu đãi trang trải kinh phí học tập hàng năm. Đầu mỗi năm học, bạn ấy vay ngân hàng

số tiến 10 triệu đồng với lãi suất là

. Tính số tiền mà Nam nợ ngân hàng sau 4 năm,

biết rằng trong 4 năm đó, ngân hàng không thay đổi lãi suất ( kết quả làm tròn đến

nghìn đồng).

Lời giải

 Tổng số tiền bạn Nam vay ( gốc và lãi) sau 4 năm là:

       

432

6 6 6 6

10 1 0 04 10 1 0 04 10 1 0 04 10 1 0 04, , , ,A        

         

 

1 1 0 04

10 1 0 04 1 1 0 04 1 0 04 1 0 04 10 1 0 04 44163256

1 1 0 04

, , , , , .





          







 Nên

44163000A 

đồng

 Ví dụ 4.7

Một giáo viên được nhận lương khởi điểm là

8 000 000..

đồng/tháng. Cứ sau hai năm

lương mỗi tháng của giáo viên đó được tăng thêm

10%

so với mức lương hiện tại.

Tính tổng số tiền

(đồng) giáo viên đó nhận được sau

năm làm việc.

Lời giải

 Lương 2 năm đầu tiên của giáo viên đó nhận được là

8 10 24 192 10. . .T 

(đồng)

 Theo công thức tnh lãi kép, lương 2 năm tiếp theo giáo viên đó nhận được:

 

24 8 10 1 10 212 2 10. . . % , .T   

(đồng)

 Lương 2 năm cuối cùng giáo viên đó nhận được:

 

24 8 10 1 10 232 32 10. . . % , .T   

(đồng)

 Tổng số tiền

(đồng) giáo viên đó nhận được sau 6 năm làm việc:

1 2 3

635 520 000,,T T T T   

(đồng).

 Ví dụ 4.8

Anh Hưng đi làm được lĩnh lương khởi điểm

4 000 000..

đồng/tháng. Cứ

năm, lương

của anh Hưng lại được tăng thêm

/1 tháng. Hỏi sau

năm làm việc anh Hưng

nhận được tất cả bao nhiêu tiền? (Kết quả làm tròn đến hàng nghìn đồng).

Lời giải

 Gọi

là số tiền lương khởi điểm,

là lương được tăng thêm.

+ Số tiền lương trong ba năm đầu tiên:

36a

+ Số tiền lương trong ba năm kế tiếp:

 

36 36 1.a a r a r



  



+ Số tiền lương trong ba năm kế tiếp:

 

36 1ar

…

+ Số tiền lương trong ba năm cuối:

 

36 1ar

 Vậy sau

năm làm việc anh Hưng nhận được:

       

1 2 3 11

1 1 1 1 1 36 2 575 936983 2 575 937 000... . . . . . . .r r r r a



         





đồng.

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 29

 Ví dụ 4.9

Một người đem gửi tiền tiết kiệm vào một ngân hàng với lãi suất

một tháng. Biết

rằng cứ sau mỗi quý (

tháng) thì lãi sẽ được cộng dồn vào vốn gốc. Hỏi sau tối thiểu

bao nhiêu năm thì người đó nhận lại được số tiền bao gồm cả vốn lẫn lãi gấp ba lần số

tiền ban đầu

Lời giải

 Gọi

là số tiền người đó gửi ban đầu

 Số tiền nhận được cả gốc lẫn lãi sau

năm là

 

1 0 03,

Ta

   

3 1 0 03 3 4 1 03 3 9 29

4 1 03

, .ln , ln ,

ln ,

        

 Ví dụ 4.10

Một người vay ngân hàng một tỷ đồng theo phương thức trả góp để mua nhà. Nếu

cuối mỗi tháng, bắt đầu từ tháng thứ nhất người đó trả

triệu đồng và chịu lãi số

tiền chưa trả là

0 65,%

mỗi tháng (biết lãi suất không thay đổi) thì sau bao lâu người

đó trả hết số tiền trên?

Lời giải

 Gọi

là số tiền vay,

là số tiền gửi hàng tháng

là lãi suất mỗi tháng.

 Đến cuối tháng thứ

thì số tiền còn nợ là:

       

 

1 1 1 1 1...

n n n n

T A r a r r A r













          





 Hết nợ đồng nghĩa

0T 

 









   

 

1 log

a Ar a a

r r a Ar





    



 Áp dụng với

1A 

(tỷ),

0 04,a 

(tỷ),

0 0065,r 

ta được

27 37,n 

 Vậy cần trả

tháng.

 Ví dụ 4.11

Năm 2014, một người đã tiết kiệm được

triệu đồng và dùng số tiền đó để mua nhà

nhưng trên thực tế người đó phải cần

1 55, x

triệu đồng. Người đó quyết định gửi tiết

kiệm vào ngân hàng với lãi suất là

69,%

/ năm theo hình thức lãi kép và không rút

trước kỳ hạn. Hỏi năm nào người đó mua được căn nhà đó (giả sử rằng giá bán căn

nhà đó không thay đổi).

Lời giải

 Số tiền người gửi tiết kiệm sau

năm là

 

1 6 9,%

x 

 Ta cần tìm

để

 

1 6 9 1 55, % ,

xx

 

1 6 9 1 55, % ,

  

6 56, ...n

 Do đó, người gửi tiết kiệm cần gửi trọn

kỳ hạn, tức là

năm.

 Vậy đến năm 2021 người đó sẽ có đủ tiền cần thiết.

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 30

 Ví dụ 4.12

Một người gửi ngân hàng

100

triệu đồng theo hình thức lãi kép, lãi suất

05,%

một

tháng (kể từ tháng thứ 2, tiền lãi được tính theo phần trăm tổng tiền có được của tháng

trước đó và tiền lãi của tháng sau đó). Hỏi sau ít nhất bao nhiêu tháng, người đó có

nhiều hơn

125

triệu đồng?

Lời giải

 Số tiền cả vốn lẫn lãi người gởi sau

tháng:

 

100 1 0 005 100 1 005, . ,

S   

(triệu đồng)

1 005

100 100

, log

n   

 Để có số tiền

125S 

(triệu đồng) thì phải sau thời gian

1 005 1 005

125

44 74

100 100

log log ,

n 

(tháng)

 Vậy: sau ít nhất

tháng người đó có nhiều hơn

125

triệu đồng.

 Ví dụ 4.13

Ông Nam gởi

100

triệu đồng vào ngân hàng theo thể thức lãi kép kì hạn

năm với lãi

suất là

12%

một năm. Sau

năm ông Nam rút toàn bộ số tiền (cả vốn lẫn lãi). Tìm số

nguyên dương

nhỏ nhất để số tiền lãi nhận được lớn hơn

triệu đồng (giả sử lãi

suất hàng năm không thay đổi)

Lời giải

 Gọi

là tiền vốn lẫn lãi sau

tháng,

là số tiền ban đầu

 Tháng 1

 

1t 

 

1T a r

 Tháng 2

 

2t 

 

1T a r

……………….

 Tháng

   

n t n T a r  

 

   

140

100

1 33 815

1 1 1

ln ln

ln ln %

T a r t

     



(tháng)

 Để số tiền lãi nhận được lớn hơn 40 triệu thì

2 818

n 

 Vậy

3.n 

 Ví dụ 4.14

Tỉ lệ tăng dân số ở Việt Nam được duy trì ở mức 1,05%. Theo số liệu của Tổng cục

thống kê, dân số Việt Nam năm 2014 có 90.728.900 người. Với tốc độ tăng dân số

như thế đến năm 2030 thì dân số của Việt Nam là bao nhiêu?

Lời giải

 Từ năm

2014

đến năm

2030

cách nhau số năm là:

2030 2014 16

năm.

 Dân số Việt Nam năm

2030

 

90728900 1 1,05% 107232574A   

(người).

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 31

A. LÝ THUYẾT CHUNG.

 Phương trình mũ cơ bản:

 

01 ,

a b a a  

 Phương trình có một nghiệm duy nhất khi

0b 

 Phương trình vô nghiệm khi

0b 

B. CÁC DẠNG BÀI TẬP.

 Dạng 5.1. Phương trình mũ cơ bản

 Giải phương trình mũ cơ bản:

 

01 ,

a b a a  

 Khi đó

log

a b x b  

Lưu ý:

 Phương trình có một nghiệm duy nhất khi

0b 

 Phương trình vô nghiệm khi

0b 

 Ví dụ 5.1.1

Phương trình



có nghiệm là

3logx 

. B.

2logx 

. C.

3logx 

. D.

4logx 

Lời giải

Chọn C

Ta có

3 4 4 3log log

    

 Ví dụ 5.1.2

Nghiệm của phương trình



là

x 

. B.

x 

. C.

x 

. D.

2x 

Lời giải

Chọn A

Ta có:



4logx

logx  

 Ví dụ 5.1.3

Nghiệm của phương trình

2 2 3 3

x x x x

  

là

logx 

. B.

1x 

. C.

0x 

. D.

logx 

Lời giải

Chọn A

3 3 3

2 2 3 3 3 2 4 3

2 4 4

. . log

x x x x x x





        





PHƯƠNG TRÌNH MŨ

LŨY THỪA – MŨ – LOGARIT

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 32

 Dạng 5.2. Đưa về cùng cơ số

Với

0a 

1:a 

   

f x g x

aa

   

f x g x

 Ví dụ 5.2.1

Phương trình

x



có nghiệm là

1x 

. B.

2x 

. C.

2x 

. D.

1.x 

Lời giải

Chọn A

Ta có

2 1 2 1 3

2 0 2 2 1

  

      

 Ví dụ 5.2.2

Tìm tập nghiệm của phương trình

 





 

4 3 4 3,

. B.

 

2 3 2 3,

 

4 3 4 3,   

. D.

 

2 3 2 3,   

Lời giải

Chọn B

Ta có

   

 

2 4 2 2 1 2 4 1 0

x x x x







          







 Ví dụ 5.2.3

Nghiệm của phương trình

125











là



. B.

. C.



. D.

Lời giải

Chọn A

Ta có

 

125 5 5 2 1 3

25 5

x x x







         





 Ví dụ 5.2.4

Tìm tập hợp tất cả các nghiệm của phương trình

 



















. B.







. C.









. D.









Lời giải

Chọn C

Ta có

 













 

2 2 2.













 







 

2 11



      

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 33

 Dạng 5.3. Logarit hóa

 Phương trình

 

0 1 0,

log

f x b



  













 Phương trình

       

   

log log .log

f x g x f x g x

a a a

a b a b f x g x b    

hoặc

   

log log .log .

f x g x

b b b

a b f x a g x  

 Ví dụ 5.3.1

Tìm tập nghiệm

của phương trình

x



 

3S 

. B.

 

2S 

. C.

 

02;S 

. D.

 

12S 

Lời giải

Chọn B

x



18logx  

13x  

2x

 Ví dụ 5.3.2

Tìm tập nghiệm

của phương trình



S 

. B.

 

log log

log















 

log

log log















. D.

 

log log

log













Lời giải

Chọn B



4 3 4.log



 

34log .log

x

 

4 4 3

34.log log logxx  

 

log log

log

x



 Ví dụ 5.3.3

Giải phương trình sau:

 

2 5 0 2 10. , .

x x x



x 

. B.

0x 

. C.

1x 

. D.

logx 

Lời giải

Chọn D

 

2 5 0 2 10. , .

x



0 2 5 5log ,xx   

4 6 2logx  

.logx  

 Ví dụ 5.3.4

Cho phương trình

4 2 3 0.

xx

  

Khi đặt

t 

ta được phương trình nào sau đây

2 3 0tt

. B.

4 3 0t 

. C.

30tt  

. D.

2 3 0tt  

Lời giải

Chọn D

Phương trình

4 2 2 3 0.

   

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 34

 Dạng 5.4. Đặt ẩn phụ dễ thấy

 Biến đổi quy về dạng:

 

0 0 1

f a a









   











 Thông thường sẽ gặp các cơ số:

4 2 0

25 5

;

 

  

 

 Ví dụ 5.4.1

Tập nghiệm của phương trình

9 5 3 6 0.

  

là

 

12;logS 

. B.

 

2logS 

. C.

 

1S 

. D.

 

S 

Lời giải

Chọn A

9 5 3 6 0.

  

 

3 5 3 6 0.

   

 

3 5 3 6 0.

   

(**)

Đặt

t 

. Khi đó: (**)

5 6 0tt   

 





























logx













Vậy nghiệm của phương trình là

12logxx  

 Ví dụ 5.4.2

Số nghiệm của phương trình

4 4 9 2 8 0..

xx

  

(*) là:

. B.

. C.

. D.

Lời giải

Chọn C

(*)

4 2 18 2 8 0..

   

4 18 8 0











  



























Vậy phương trình có hai nghiệm

1x 

và

2x 

 Ví dụ 5.4.3

Giải phương trình

2 15 2 8 0.

xx

  

 

x 

. B.

0x 

. C.

1x 

. D.

5x 

Lời giải

Chọn C

 

2 2 15 2 8 0..

   

 

2 2 15 2 8 0..

   

2 15 8 0











  













     





















Vậy phương trình có nghiệm

1x 

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 35

 Dạng 5.5. Đặt ẩn phụ với phương trình đẳng cấp

 Phương trình đẳng cấp có dạng:

0. . .m X n XY p Y  

 Khi đó với phương trình mũ đẳng cấp có dạng:

 

0. . . .

f x f x

m a n a b p b  

 Phương pháp làm như sau:

Chia 2 vế cho

 

2 fx

, đặt

 









 

2 2 2

. . .

f x f x

f x f x f x

m n p

b b b

  

   

0..

f x f x

m n p



   



   

   



   



0..m t n t p   

Chia 2 vế cho

 

2 fx

, đặt

 









 

2 2 2

. . .

f x f x

f x f x f x

m n p

a a a

  

   

0..

f x f x

m n p



   



   

   



   



0..m n t p t   

 Lưu ý:

Đây là dạng sẽ có trong bài “Bất phương trình mũ”, lúc giải BPT mũ ta cần chú ý đến cơ

số lớn hay bé hơn 1. Để giảm sai sót chúng ta hãy “chia 2 vế” cho cơ số bé nhất !!!

 Ví dụ 5.5.1

Giải phương trình sau:

8 18 2 27.

x x x



(*)

1x 

. B.

2logx 

. C.

1x 

. D.

0x 

Lời giải

Chọn D

(*)

   

  

   

   

2 1 0



















  





    





Vậy phương trình có nghiệm

0x 

 Ví dụ 5.5.2

Số nghiệm của phương trình:

25 15 2 9.

x x x



(*) là:

. B.

. C.

. D.

Lời giải

Chọn C

(*)

   

   

   

   



















  



















    























Vậy phương trình có nghiệm

0x 

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 36

 Dạng 5.6. Đặt ẩn phụ với tích hai cơ số bằng 1

 Phương trình đẳng cấp có dạng:

0. . .m X n XY p Y  

 Phương trình mũ ta xét có dạng:

   

 

0..

f x f x

m a n b p   

trong đó

1.ab

 Phương pháp làm như sau:

Vì

1.a b b

   

Đặt

   

f x f x

t a t b

   

Khi đó

 

00. . . .m t n p m t n p t

        

 Ví dụ 5.6.1

Tìm tích các nghiệm của phương trình

   

2 1 2 1 2 2 0

    

. B.

1

. C.

. D.

Lời giải

Chọn B

Ta có:

  

2 1 2 1 1  

Đặt

 

t 

, điều kiện

0t 

. Suy ra

 



Phương trình trở thành:

2 2 0t

  

 

     

2 1 2 1 2 1 1

2 2 1 0

2 1 2 1 2 1 2 1 2 1 1





       



    



            



Vậy tích của hai nghiệm

 

1 1 1.xx    

 Ví dụ 5.6.2

Phương trình

   

3 5 3 5 3 2.

   

có tổng các nghiệm là

. B.

. C.

1

. D.

Lời giải

Chọn A

   

 

3 5 3 5

3 5 3 5 3 2 3

   



       

   

   

Thấy

3 5 3 5 3 5 3 5

2 2 2 2

xx

      

   

  

      

      

Đặt











3 5 1

2 t











 

3 5 3 5

3 3 1 0

3 5 3 5 3 5

2 2 2

t t t

































          











   

  







   



   



   



Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 37

 Dạng 5.7. Phương pháp hàm số

 Định lí. Nếu hàm số

 

y f x

là hàm số liên tục và đồng biến trên

 

;ab

 

y g x

là hàm số

liên tục và nghịch biến trên

 

;ab

thì phương trình

   

f x g x

có tối đa một nghiệm

trên

 

;ab

 Phương pháp làm như sau:

 Biến đổi phương trình đã cho về dạng

 

f x k

, với

là hằng số

 Chứng minh

 

là hàm đồng biến( nghịch biến) trên tập xác định.

 Tìm

sao cho

 

f x k

 Kết luận

là nghiệm duy nhất của phương trình

 

f x k

 Biến đổi phương trình đã cho về dạng

   

f x g x

, với

,DD

lần lượt là tập xác định

của hai hàm số

   

,f x g x

 Chứng minh

 

là hàm đồng biến và

 

nghịch biến trên tập

DD

(hay ngược lại)

 Tìm

sao cho

   

f x g x

 Kết luận

là nghiệm duy nhất của phương trình

   

f x g x

 Biến đổi phương trình đã cho về dạng

   

f u f v

, với hàm số

 

là hàm đồng

biến(hay nghịch biến).

 Phương trình

   

f u f v u v  

 Lưu ý:

⓵ Nếu

 

và

 

là hàm đồng biến(nghịch biến) trên

 

;ab

thì

   

f x g x

cũng là

hàm đồng biến (nghịch biến) trên

 

;ab

⓶ Hàm số

ya

đồng biến khi

1a 

và nghịch biến khi

01a

 Ví dụ 5.7.1

Phương trình

2016 2 2018 0

x  

có tất cả bao nhiêu nghiệm thực?

. B.

. D.

Lời giải

Chọn A

Xét hàm số :

 

2016 2 2018

f x x  

. Tập xác định:

Khi đó

 

2016 2016 2 0ln ,

f x x



    

. Do đó hàm số luôn đồng biến trên .

Mà

 

10f 

nên

1x 

là nghiệm duy nhất của phương trình.

 Ví dụ 5.7.2

Tổng các nghiệm của phương trình

15 2

3 3 15 2

x x x



   

là:

6

. B.

1

. C.

. D.

Lời giải

Chọn D

Phương trình

2 15

3 3 15

x x x



     

(1)

Xét hàm số :

 

3 ,

f t t t   

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 38

Khi đó

 

3 3 1 0ln ,

f t t



    

. Do đó hàm số luôn đồng biến trên .

Do đó phương trình (1)

 

15 15f x x f x x x x       













Vậy

3x 

5x 

là của phương trình.

 Ví dụ 5.7.3

Phương trình

 

1 2 1.

xx  

có bao nhiêu nghiệm thực

. B.

. C.

. D.

Lời giải

Chọn D

Vì

1x 

không là nghiệm của phương trình nên ta có

 

1 2 1 2



    



Hàm số

y 

đồng biến trên

Hàm số







nghịch biến trên

 

1;

và

 

1;

Do đó phương trình đã cho có hai nghiệm.

 Ví dụ 5.7.3

Phương trình

     

3 2 3 2 10

x x x

   

có tất cả bao nhiêu nghiệm thực?

. B.

. C.

. D.

Lời giải

Chọn A

     

3 2 3 2 10

x x x

   

3 2 3 2

10 10

   



  

   

   

Xét hàm số

 

3 2 3 2

10 10

   





   

   

Ta có:

 

21f 

Hàm số

 

nghịch biến trên do các cơ số

3 2 3 2

10 10

;





Vậy phương trình có nghiệm duy nhất là

2x 

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 39

 Dạng 5.8. Phương trình chứa tham số

 Để giải bài toán tìm tham số m trong phương trình mũ ta có hai cách phổ biến:

 Cô lập được tham số m.

 Ta dùng đồ thị hàm số để biện luận số nghiệm (bài toán tương giao).

 Không cô lập được tham số m và có liên quan đến Vi-ét.

 Đặt ẩn phụ đưa về phương trình bậc hai/bậc ba.

 Kết hợp định lý Vi-ét để giải quyết yêu cầu bài toán

 Ví dụ 5.8.1

Có bao nhiêu giá trị nguyên dương của tham số

để phương trình

16 2 12 2 9 0. ( ).

x x x

m   

có nghiệm dương?

. B.

. C.

. D.

Lời giải

Chọn A

Phương trình

16 2 12 2 9 0. ( ).

x x x

m   

có nghiệm

 

0;x  

Phương trình tương đương

 

2 2 0

. ( )

   

    

   

   

có nghiệm

 

0;x  

Đặt

 



  





   

2 2 0 1. ( ) , ;t t m t        

 

2 2 1. , ;t t m t      

Xét

2.y t t

Phương trình có nghiệm

 

1;t  

khi

2 1 3mm    

 Ví dụ 5.8.2

Có bao nhiêu giá trị nguyên của tham số

để phương trình

9 4 3 2 1 0.

x x x x



   

có nghiệm?

. B.

. C.

. D.

Lời giải

Chọn B

ĐKXĐ:

04;x







Đặt

4t x x

với

04;x







thì

02;t







Đặt

u 

với

02;t







thì

19;u







Khi đó, tìm

đề phương trình

4 2 1 0u u m   

có nghiệm thuộc đoạn

19;





2 4 1m u u    

, với

19;u







Xét hàm số

 

41f u u u   

 

2 4 0 2f u u u



      

Ta có,

 

14f 

 

25f 

 

9 44f 

Do đó, phương trình có nghiệm khi và chỉ khi

44 2 5 22

mm      

Vậy có

số nguyên của tham số

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 40

 Ví dụ 5.8.3

Gọi

 

;ab

là tập các giá trị của tham số

để phương trình

2 8 0

e e m  

có

đúng hai nghiệm thuộc khoảng

 

05;ln

. Tổng

ab

là

. B.

. C.

6

. D.

14

Lời giải

Chọn D

Đặt

te

;

 

05;lnx

tương ứng

 

15;t 

Phương trình thành

28t t m

Xét

 

28f t t t

với

 

15;t 

có

 

48f t t





Phương trình đã cho có 2 nghiệm pb thuộc

 

05;ln

Khi

 

f t m

có hai nghiệm

 

15;t 

86m    

 Ví dụ 5.8.4

Gọi

là tập hợp các giá trị nguyên của tham số

sao cho phương trình

25 5 7 7 0.



   

có hai nghiệm phân biệt.

Hỏi

có bao nhiêu phần tử.

. B.

. C.

. D.

Lời giải

Chọn C

Xét

 

25 5 7 7 0 1.



   

. Đặt

 

tt

   

1 5 7 7 0 2 t mt m    

YCBT



 

có hai nghiệm phân biệt



 

có hai nghiệm phân biệt

0,tt

 

25 4 7 7 0

0 5 0

7 7 0



  









   















2 21

m  

Mà

 

23;mm  

. Vậy có

giá trị nguyên của tham số

 Ví dụ 5.8.5

Gọi

là tất cả các giá trị nguyên của tham số

sao cho phương trình

4 2 2 5 0.



   

có hai nghiệm phân biệt.

Hỏi

có bao nhiêu phần tử.

. B.

. C.

. D.

Lời giải

Chọn B

1 2 2

4 2 2 5 0 4 2 2 2 5 0..

x x x x

m m m m



        

(1)

Đặt

20,

tt

. Phương trình (1) thành:

2 2 5 0.t mt m   

(2)

YCBT

2()

có 2 nghiệm dương phân biệt

0 2 5 0 5 5

0 2 0 0 5

2 5 0

m m m

S m m m

m hoac m







      





        

  

  









  





nguyên nên

2m

. Vậy S chỉ có một phần tử

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 41

A. LÝ THUYẾT CHUNG.

 Phương trình logarit cơ bản:

   

01log ,

f x b a a  

 Lưu ý: khi giải phương trình logarit cần phải có điều kiện để logarit tồn tại.

B. CÁC DẠNG BÀI TẬP.

 Dạng 6.1. Phương trình logarit cơ bản

 Giải phương trình logarit cơ bản:

log

xb

 Khi đó

 

01log ,

x b x a a a    

 Ví dụ 6.1.1

Tìm tập nghiệm

của phương trình

 

22log x 

 

16S 

. B.

 

18S 

. C.

 

10S 

. D.

 

14S 

Lời giải

Chọn B

Ta có

 

22log x 

 

24log log





































  







 Ví dụ 6.1.2

Phương trình

13log x 

có bao nhiêu nghiệm ?

. B.

. C.

. D.

Lời giải

Chọn C

Điều kiện:

1 0 1xx   

Phương trình tương đương với

1 8 9

1 8 7



  





    



 Ví dụ 6.1.3

Phương trình

 

28log x 

có tất cả bao nhiêu nghiệm thực?

Lời giải

Chọn B

 

28log x 

 



ĐK:

2 0 2xx    

 

1 2 2x  

 

24x  

4 2 2

x x x



    











PHƯƠNG TRÌNH LOGARIT

LŨY THỪA – MŨ – LOGARIT

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 42

 Dạng 6.2. Đưa về cùng cơ số

 Cho

10a

. Với điều kiện các biểu thức

 

và

 

xác định, ta thường đưa các phương

trình logarit về các dạng cơ bản sau:

 Loại 1:

 

log

f x b

f x a

















 Loại 2:

   

 

   

log log

f x g x

















 Ví dụ 6.2.1

Phương trình

     

1 3 7ln ln lnx x x    

có bao nhiêu nghiệm ?

. B.

. C.

. D.

Lời giải

Chọn C

Điều kiện

1x 

, phương trình

  

1 3 7

x x x





     







Kết hợp điều kiện ta có nghiệm của phương trình là

1x 

 Ví dụ 6.2.2

Giải phương trình

 

2 1 1log logx x x   

A. vô nghiệm. B.

2.x 

02, .xx

3.x 

Lời giải

Chọn C

Phương trình

 

1 1 2

log log

x x x x

x x x







       



   





 Ví dụ 6.2.3

Số nghiệm của phương trình

 

12 2 1log .log

x 

là:

A. 0. B. 2. C. 3. D. 1

Lời giải

Chọn D

Điều kiện :

01x

   

 

4 2 2

12 2 1 12 12 0

log .log log log

x x x x x





          









 Ví dụ 6.2.4

Tập nghiệm của phương trình

   

4 2 14 4log logxx   

là

 

5S 

. B.

 

5S 

. C.

 

5S 

. D.

 

S 

Lời giải

Chọn A

Điều kiện

4 14x  

Ta có:

   

4 2 14 4log logxx   

   

4 14 4log logxx    

  

4 14 4log xx   

10 56 3xx    

5x

So với điều kiện ta được

 

5S 

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 43

 Dạng 6.3. Mũ hóa

 Với điều kiện các biểu thức

 

và

 

xác định, ta thường đưa các phương trình logarit về

các dạng cơ bản sau:

     

 

01log

f x g x a

f x a







   









 Ví dụ 6.3.1

Tập nghiệm của phương trình

 

5 25 2log

xx



là:

 

1S 

. B.

 

5logS 

;

log













. D.

4log













Lời giải

Chọn C

Điều kiện

5 25 0

xx



 

5 25 2log

xx



5 25 4

xx

  

5 5 5 4 0.

   













4log













Kết hợp với điều kiện, ta được tập nghiệm của phương trình đã cho là

 

04;logS 

 Ví dụ 6.3.2

Số nghiệm của phương trình

 

25 2log





là

. B.

. C.

. D.

Lời giải

Chọn B

Điều kiện

25 2 0

xx



 

25 2log





25 2 10

x x x

  

25 2 4 10.

x x x

  

4 10

1 2 0

25 25

   

   

   

   

2 1 0

   

   

   

   

 



Đặt

 









. Khi đó

 



trở thành

2 1 0tt  

 

loai

thoa

















1 2 1

2 5 2



  





log logx  

Kết hợp với điều kiện, ta được tập nghiệm của phương trình đã cho là

2logS













Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 44

 Dạng 6.4. Đặt ẩn phụ dễ thấy

 Giải phương trình

 

0log

f g x 

 

01a

 Bước 01. Đặt

 

log

t g x

 

 Bước 02. Tìm điều kiện của

(nếu có)

 Bước 03. Đưa về giải phương trình

 

0ft

đã biết cách giải.

 Bước 04. Thay vào

 

để tìm

 Ví dụ 6.4.1

Giải phương trình

4 3 0log logxx  

 

1S 

. B.

 

27S 

. C.

 

3 27;S 

. D.

 

3S 

Lời giải

Chọn C

Điều kiện:

0x 

. Đặt

log xt

4 3 0tt   













 

3 27

log

;

log









   







 Ví dụ 6.4.2

Số nghiệm của phương trình

64 1log log

x 

là

. B.

. C.

. D.

Lời giải

Chọn C

Điều kiện :

01x

Phương trình

6 2 1log log

x  

. Đặt

logtx

 

0t 







  



    















log

























Kết hợp điều kiện, suy ra phương trình đã cho có tập nghiệm là









 Ví dụ 6.4.3

Tích các nghiệm phương trình

1 5 0log logxx   

là

. B.

. C.

. D.

Lời giải

Chọn D

Điều kiện:

0x 

. Đặt

1log xt

 

1t 

 





    









1 2 1 4

log

log log

log









       









Kết hợp điều kiện, suy ra phương trình đã cho có tập nghiệm là

 

33;S





Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 45

 Dạng 6.5. Phương pháp hàm số

 Định lí. Nếu hàm số

 

y f x

là hàm số liên tục và đồng biến trên

 

;ab

 

y g x

là hàm số

liên tục và nghịch biến trên

 

;ab

thì phương trình

   

f x g x

có tối đa một nghiệm

trên

 

;ab

 Phương pháp làm như sau:

 Biến đổi phương trình đã cho về dạng

 

f x k

, với

là hằng số

 Chứng minh

 

là hàm đồng biến( nghịch biến) trên tập xác định.

 Tìm

sao cho

 

f x k

 Kết luận

là nghiệm duy nhất của phương trình

 

f x k

 Biến đổi phương trình đã cho về dạng

   

f x g x

, với

,DD

lần lượt là tập xác định

của hai hàm số

   

,f x g x

 Chứng minh

 

là hàm đồng biến và

 

nghịch biến trên tập

DD

(hay ngược lại)

 Tìm

sao cho

   

f x g x

 Kết luận

là nghiệm duy nhất của phương trình

   

f x g x

 Biến đổi phương trình đã cho về dạng

   

f u f v

, với hàm số

 

là hàm đồng

biến(hay nghịch biến).

 Phương trình

   

f u f v u v  

 Lưu ý:

⓵ Nếu

 

và

 

là hàm đồng biến(nghịch biến) trên

 

;ab

thì

   

f x g x

cũng là

hàm đồng biến (nghịch biến) trên

 

;ab

⓶ Hàm số

ya

đồng biến khi

1a 

và nghịch biến khi

01a

 Ví dụ 6.5.1

Phương trình

   

21log logxx  

có bao nhiêu nghiệm?

. B.

. D.

Lời giải

Chọn A

Điều kiện











2x

. Đặt

   

21log logx x t   

















3 2 1 3 1 2 1

t t t t

   

        

   

   

 



Dễ thấy

1t 

là một nghiệm của

 



Xét

 

   



   

   

 

1 1 2 2

3 3 3 3

ln ln

   



   

   

   

 

ft

nghịch biến trên ,

 

1gt 

là hàm hằng

 



có một nghiệm duy nhất

1t 

4x

Kết hợp với điều kiện, ta được nghiệm của phương trình đã cho là

4x 

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 46

 Ví dụ 6.5.2

Giải phương trình

   

2 3 4 2log logxx   

5x 

. B.

1x 

3x 

. D.

1x 

Lời giải

Chọn B

Điều kiện của phương trình là















x  

Phương trình có một nghiệm

1x 

Xét

     

2 3 4log logf x x x   

trên

;



 





Ta có :

 

   

2 3 3 4 7ln ln



  



 

fx

đồng biến trên

;



 





;

 

2gx

là hàm hằng.

Nên phương trình đã cho có một nghiệm duy nhất

1x 

 Ví dụ 6.5.3

Giải phương trình

 

6 2 4log log ( )x x x x     

x 

. B.

1x 

4x 

. D.

3x 

Lời giải

Chọn C

Điều kiện:



  













 

6 2 4log logx x x x      

 

4 3 4 2

log log ( )

x x x



      



Vì

 

4 3 4 4log   

nên phương trình (2) có một nghiệm

 

43;x   

Xét hàm số

   

3logf x x x  

Ta có

 

1 0 3

f x x



     



nên

 

đồng biến trên tập xác định.

Do đó phương trình đã cho có một nghiệm duy nhất

4x 

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 47

 Dạng 6.6. Phương trình chứa tham số

 Để giải bài toán tìm tham số m trong phương trình logarit ta có hai cách phổ biến:

 Cô lập được tham số m.

 Ta dùng đồ thị hàm số để biện luận số nghiệm (bài toán tương giao).

 Không cô lập được tham số m và có liên quan đến Vi-ét.

 Đặt ẩn phụ đưa về phương trình bậc hai/bậc ba.

 Kết hợp định lý Vi-ét để giải quyết yêu cầu bài toán

 Ví dụ 6.6.1

Tìm tất cả các giá trị thực của tham số

để phương trình

10log logx m x  

có nghiệm duy nhất nhỏ hơn 1.

2m 

. B.

1m 

. C.

2m

. D.

1m 

Lời giải

Chọn A

Điều kiện:

0x 

. Vì phương trình có nghiệm nhỏ hơn 1 nên suy ra

01x

Đặt

log xt

, với

0 1 0xt   

. Phương trình

10 (*)t mt t m

      

Phương trình đã cho có nghiệm duy nhất nhở hơn 1



(*) có nghiệm duy nhất trên

 

0;

Xét

()f t t



trên

 

0;

, ta có:

( ; )

()

( ; )



  



   



   



Dựa vào bảng biến thiên ta được

2m

thỏa mãn đề bài toán.

 Ví dụ 6.6.2

Tìm tất cả các giá trị thực của tham số

để phương trình

2 7 0log logx m x m   

có hai nghiệm

,xx

thỏa mãn

81.xx

12m

. B.

0m 

. C.

2m 

. D.

4m 

Lời giải

Chọn D

Điều kiện:

0x 

. Giả sử phương trình có hai nghiệm

,xx

Đặt

logtx

, phương trình

2 7 0 (*)t mt m    

Phương trình đã cho có 2 nghiệm

,xx



(*) có hai nghiệm

,tt

8 28 0 mmm     

Theo Vi-et:

 

1 2 3 1 3 2 3 1 2 3

81 4log log log logt t x x m x x m m m         

(thỏa).

Vậy với

4m

là giá trị cần tìm.

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 48

 Ví dụ 6.6.3

Tìm tất cả các giá trị thực của tham số

để phương trình

   

21log logmx x

có nghiệm duy nhất.











. B.

1m 

. C.

2m

. D.











Lời giải

Chọn A

Điều kiện:

1x 

. Ta có

     

 

2 1 1log log

mx x mz x m



      

( vì

0x 

không thỏa).

Xét

1()

()





trên

10( ; )\{ } 

. Ta có:

( ; )

()

( ; )



   





  



    



Dựa vào bảng biến thiên, ta thấy phương trình có nghiệm duy nhất













 Ví dụ 6.6.4

Tìm tất cả các giá trị thực của tham số

để phương trình

log







có nghiệm.











. B.

1m 

. C.

2m

. D.











Lời giải

Chọn A

Điều kiện:

4 1 0 0

x   

Đặt

t 

, với

01xt  

. Phương trình trở thành

log (*)







Xét

( ) log







trên

 

1;

. Ta có

 

( ) ,

f t t



   



Suy ra hàm số

 

đồng biến trên khoảng

 

1;

Dựa vào bảng biến thiên, ta thấy phương trình có nghiệm

0m

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 49

 Ví dụ 6.6.5

Tìm tất cả các giá trị thực của tham số

để phương trình

       

1 2 5 2 1 0log logm x m x m       

có nghiệm thuộc

 

24;











. B.

m  

. C.

17m  

. D.











Lời giải

Chọn B

Đặt

 

2logtx

, do

2 4 0 2 2 1x x t        

Phương trình

     

1 5 1 0

m t m t m m



        



Để phương trình đã cho có nghiệm thuộc

 

24;



 

có nghiệm thuộc khoảng

 

1; 

Xét

 







với

1t 

. Ta có

 

;



   



  



    







Dựa vào bảng biến thiên, ta suy ra

m  

 Ví dụ 6.6.6

Tìm tất cả các giá trị thực của tham số

để phương trình

   

12log logm x x



  



có nghiệm duy nhất.











. B.

13m

. C.











. D.











Lời giải

Chọn C

     

1 2 1

m x x



  













. Do

0x 

không thỏa (1)

 



   

Xét

 





trên

   

2 0 0;;  

có:

 

1 0 2'f x x

    

Từ vào bảng biến thiên, ta thấy

 

f x m

có nghiệm duy nhất













Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 50

A. LÝ THUYẾT CHUNG.

Dạng 01.

 

01;

a b a a  

0b 

Tập nghiệm của bất phương trình là .

0b 

1a 

log

a b x b  

01a

log

a b x b  

Dạng 02.

 

01;

a b a a  

0b 

Tập nghiệm của bất phương trình là



0b 

1a 

log

a b x b  

01a

log

a b x b  

B. CÁC DẠNG BÀI TẬP.

 Dạng 7.1. Bất phương trình mũ cơ bản

 Xem lại mục “Lý thuyết chung”

 Bất phương trình mũ cơ bản:

 

01;

a b a a  

. Chú ý đến cơ số.

 Ví dụ 7.1.1

Tập nghiệm của bất phương trình



là

 

2;S  

. B.



2;S



  



. C.



2;S



 



. D.

 

12;S 

Lời giải

Chọn C

3 9 9 2log .

xx    

Vậy tập nghiệm là



2;S



 



 Ví dụ 7.1.2

Tập nghiệm của bất phương trình









là

 

22;S 

. B.



2;S



  



. C.

 

0;S  

. D.

 

01;S 

Lời giải

Chọn B

4 4 2

log .



     





Vậy tập nghiệm là



2;S



  



 Ví dụ 7.1.3

Tập nghiệm của bất phương trình

xx



là



3;log







. B.

3;log









. C.



. D.

 

01;

Lời giải

Chọn B

Ta có:

2 3 2 3 3 3 3

. log

x x x x





      





BẤT PHƯƠNG TRÌNH MŨ

LŨY THỪA – MŨ – LOGARIT

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 51

 Dạng 7.2. Đưa về cùng cơ số

 Ta có hai chú ý như sau:

⓵ Với

   

f x g x

a a a f x g x   

⓶ Với

   

01,

f gxx

a a a f x g x    

 Ví dụ 7.2.1

Tìm tập nghiệm của bất phương trình:

5 25

x x x



 

1;S  

. B.

12;S







. C.

 

12;S 

. D.

 

0;S  

Lời giải

Chọn B

1 2 2 2 2

5 25 5 5 2 2 2 0 1 122 ;

x x x x x x

x x x x x x S

   

     







      





 Ví dụ 7.2.2

Tìm tập nghiệm của bất phương trình:

x









 

2;S   

. B.

 

0;S  

. C.

 

0;S   

. D.

 

;S    

Lời giải

Chọn B









  





  



     

  





  





 Ví dụ 7.2.3

Tìm số nghiệm nguyên dương của bất phương trình

. B.

. C.

. D.

Lời giải

Chọn B

Ta có

  

2 3 1 3 0 1 3

5 125

x x x x x





           





Vì phương trình tìm nghiệm nguyên dương nên các nghiệm là

 

1 2 3;;x 

 Ví dụ 7.2.4

Giải bất phương trình













ta được tập nghiệm:

;



 





. B.

 

1;

. C.

;









. D.

   

11;;   

Lời giải

Chọn C

Ta có

2 1 2

3 3 2 1 1

x x x







       





5 125

xx









Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 52

 Dạng 7.3. Đặt ẩn phụ

 Phương pháp đặt ẩn phụ ta thường sử dụng một số phương pháp sau:

Ở đây ta xét bất phương trình dạng

 

0fx

, các trường hợp khác tiến hành tương tự.

⓵ Bất phương trình dạng

 

1 1 0

0... .

nx x

A a A a A a A



    

Đặt

0()

t a t

, ta thu được bất phương trình dạng

A t A t





0... A t A  

⓶ Bất phương trình dạng

 

Aa B ab Cb  

Chia cả hai vế cho

rồi đặt













, ta được

0. . .At Bt C  

⓷ Bất phương trình dạng

   

f x g x

Aa Bb C  

, trong đó

   

f x g x

a b k

Đặt

   

0( ) .

f x g x

a t t b k   

, ta thu được bất phương trình mới

At C

  

 Ví dụ 7.3.1

Nghiệm của bất phương trình





là

x 

hoặc

2x 

. B.

x

22ln lnx  

. D.

2lnx 

Lời giải

Chọn C

Ta có

 

5 1 5 1

2 5 2 0 2 2 2

2 2 2

ln ln

x x x x x x

e e e e e e x



               

 Ví dụ 7.3.2

Bất phương trình

9 3 6 0

  

có tập nghiệm là

 

1;

. B.

   

23;;   

. C.

 

1;

. D.

 

23;

Lời giải

Chọn D

 

9 3 6 0 3 3 6 0 2 3 3 1

x x x x x

x            

 Ví dụ 7.3.3

Tập hợp nghiệm của bất phương trình





là

 

01;.

. B.

 

12;.

. C.







. D.

 

23;.

Lời giải

Chọn C

Ta có

1 2 3 1 2

3 9 3

27 3



    

 

3 6 3 9 0.

   

 

3 3 0 3 3 0

x       

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 53

 Dạng 7.4. Logarit hóa

 Phương trình

 

0 1 0,

log

f x b



  













 Phương trình

       

   

log log .log

f x g x f x g x

a a a

a b a b f x g x b    

hoặc

   

log log .log .

f x g x

b b b

a b f x a g x  

 Ví dụ 7.4.1

Tìm tập

của bất phương trình:

3 5 1.





30log ;







. B.



50log ;





. C.

 

30log ;

. D.

 

50log ;

Lời giải

Chọn C

3 5 1.



 

5 5 5

3 5 0 3 0 3 0log . log log

x x x        

nên

 

30log ;S 

 Ví dụ 7.4.2

Tìm tập

của bất phương trình:

 

log

x



 

5;

. B.

;









. C.

 

2;

. D.

 

1;

Lời giải

Chọn B

Điều kiện:

3 1 0x

 

4 4 0 5 0 5

4 3 1 3 3 1 3

log

log log log log

x x x



        

 Ví dụ 7.4.3

Giải bất phương trình:

27 2 72.





   

3 0 3log ; ;  

. B.



12;





 

22;

. D.

;









Lời giải

Chọn A

Điều kiện

0x 

Bất phương trình

3 2 3 2..













   

32log log





 

32log



   

 

3 2 0logx



   





Xét

 

3 2 0

log









   













 

3log















Vậy tập nghiệm của bất phương trình là

   

3 0 3log ; ;  

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 54

 Dạng 7.5. Chứa tham số

 Sử dụng PP giải BPT logarit kết hợp công thức, tnh chất của mũ, lũy thừa, logarit.

 Khai thác điều kiện bài toán.

 Xử lý bài toán và chọn giá trị m thỏa ĐK bài toán (cách “mò”).

 Ví dụ 7.5.1

Cho bất phương trình:

   

9 1 3 0 1.

mm   

. Tìm tất cả các giá trị của tham số

để bất phương trình

 

nghiệm đúng

1x

.m 

.m 

3 2 2.m 

3 2 2.m 

Lời giải

Chọn A

Đặt

t 

. Vì

13xt  

Bất phương trình

 

10.t m t m   

3t



  



nghiệm đúng

3t

Xét

   

 

2 3 1 0 3

, , ' ,g t t t g t t

         



. Hàm số đồng biến trên









và

 

g 

Yêu cầu bài toán tương đương

mm    

 Ví dụ 7.5.2

Tìm

để bất phương trình

 

9 2 1 6 4 0. . .

x x x

m m m   

nghiệm đúng với mọi

 

01;x

06m

6m

6m

0m

Lời giải

Chọn B

Ta có

 

9 2 1 6 4 0. . .

x x x

m m m   

 

2 1 0

m m m

   

    

   

   

Đặt









. Vì

 

01;x

nên

t

Khi đó bất phương trình trở thành

 

2 1 0.m t m t m   

 





Đặt

 





 









 

01f t t



   

Dựa vào bảng biến thiên ta có

 

6lim

m f t





 



 

1







Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 55

 Ví dụ 7.5.3

Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình sau có tập

nghiệm là









 

   

2 2 1 1 5 3 5 0



     

m 

m 

m 

m 

Lời giải

Chọn D

Phương trình đã cho tương đương

   

1 5 3 5

2 2 1 0 1

   



   

   

   

Đặt











, ta được:

     

2 2 1 0 2 2 1 0 2 f m m t t t mt m

         

BPT nghiệm đúng

0x

nên BPT có nghiệm

01t



Phương trình

 

0ft

có 2 nghiệm

,tt

thỏa

01tt  

 

2 1 0 0 5

4 2 0 0 5







   



  

  

   









. Vậy

m 

thỏa Ycbt.

 Ví dụ 7.5.4

Tất cả các giá trị của

để bất phương trình

   

3 1 12 2 6 3 0

x x x

mm    

có

nghiệm đúng

0x

là:

 

2; 

2( ; ] 

;



 





;









Lời giải

Chọn D

Đặt

t

. Do

01xt  

Khi đó ta có:

   

3 1 2 1 0 1,m t m t t      

 

3 2 1 1 1

t t m t t t m t

  

           



Xét hàm số

   

trên ;

  

 



 

7 6 1

;

f t t





     



Do đó

2lim (t)





  

thỏa mãn yêu cầu bài toán

Ghi chú:

Sử dụng

   

maxf

minf

m f x x D m x x D

       

       

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 56

A. LÝ THUYẾT CHUNG.

Dạng 01.

 

01log ;

x b a a  

1a 

log

x b x a  

01a

log

x b x a  

Dạng 02.

 

01log ;

x b a a  

1a 

log

x b x a  

01a

log

x b x a  

B. CÁC DẠNG BÀI TẬP.

 Dạng 8.1. Bất phương trình logarit cơ bản

 Ta có hai chú ý sau:



khi

log

khi

u a a



  





  





. 

0 0 1

khi

log

khi

u a a









   





 Ví dụ 8.1.1

Tập nghiệm của bất phương trình

 

2 1 1log x   

là:

;







. B.

;









. C.

;







. D.

;









Lời giải

Chọn C

Ta có:

 

2 1 2

2 1 1

2 1 0 1

log .













       















 Ví dụ 8.1.2

Tập nghiệm của bất phương trình

 

2 1 2log x 

là:

1 25

2 32

x

. B.

x 

. C.

x 

. D.

x 

Lời giải

Chọn A

Điều kiện

x 

 

log logx 

9 25

16 32

xx    

. Kết hợp với điều kiện ta được

1 25

2 32

x

BẤT PHƯƠNG TRÌNH LOGARIT

LŨY THỪA – MŨ – LOGARIT

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 57

 Dạng 8.2. Đưa về cùng cơ số

 Dùng biến đổi logarit để đưa về cùng cơ số

khi > 1

log log

khi 0 < < 1

u v a













 Ví dụ 8.2.1

Bất phương trình

   

2 1 2log logxx  

có tập nghiệm

là











. B.

 

21;S 

. C.









. D.









Lời giải

Chọn A

Bất phương trình đã cho

0 2 1 2 1

x x x        

Tập nghiệm là :











 Ví dụ 8.2.2

Xác định tập nghiệm

của bất phương trình

 

44ln lnxx

   

12; \ .S  

 

2\.S 

 

2;.S  

 

1;.S  

Lời giải

Chọn A

Ta có

 

4 4 0

ln ln









   











 Ví dụ 8.2.3

Tập nghiệm của bất phương trình

 

2 3 1 2 1log logx x x   

là:

































Lời giải

Chọn C

Điều kiện:

2 3 1 0

2 1 0



    





  



   

















Ta có:

 

2 3 1 2 1log logx x x   

 

2 3 1 2 1log logx x x    

2 2 2

2 3 1 4 4 1 2 0 0

.x x x x x x x            

(thỏa mãn điều kiện)

Vậy tập nghiệm của bất phương trình đã cho là









Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 58

 Dạng 8.3. Đặt ẩn phụ

 Tìm một

 

log

chung, đặt làm ẩn phụ

để đưa bất phương trình về bất phương trình ẩn

giải bất phương trình tìm

sau đó tìm

★ Chú ý: Nếu đặt

 

log log ,log ,log log ,log

a a a x

t x x t x t x x t a

       

 Ví dụ 8.3.1

Bất phương trình

0 2 0 2

log logxx  

có tập nghiệm là:

125 25









 

23;S 

. C.









. D.

 

03;S 

Lời giải

Chọn A

Điều kiện:

0x 

0 2 0 2 0 2

5 6 2 3

125 25

, , ,

log log logx x x        

 Ví dụ 8.3.2

Nghiệm nguyên nhỏ nhất của bất phương trình

3 3 0log log



là:

3x 

1x 

. C.

2x 

. D.

4x 

Lời giải

Chọn D

Điều kiện:

013;;x x x  

 

3 3 0 0

log

log log

log

log . log











     









 Ví dụ 8.3.3

Nếu đặt

logtx

thì bất phương trình

 

4 2 2

2 1 2

log log log log





  





trở thành bất phương trình nào?

13 36 0tt  

5 9 0tt  

13 36 0tt  

. D.

13 36 0tt  

Lời giải

Chọn C

Điều kiện:

0x 

 

4 2 2

2 1 2

log log log log





  





   

4 2 4 2

2 2 2 2 2 2

3 3 9 5 2 4 0 13 36 0log log log log log logx x x x x x          

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 59

 Dạng 8.4. Mũ hóa

 Với điều kiện các biểu thức

 

và

 

xác định, ta thường đưa các bất phương trình

logarit về các dạng cơ bản sau:

   

log

f x g x

 

khi a

f x a

khi a

f x a



































 Ví dụ 8.4.1

Bất phương trình

 

9 72 1log log



có tập nghiệm là:

73 2log ;S







. B.



72 2log ;S









73 2log ;S







. D.



2;S



 



Lời giải

Chọn D

Điều kiện

73logx 

 

9 72 1 9 72 9 3 72 0 3 9 2log log log

x x x x x

xx            

 Ví dụ 8.4.2

Nghiệm nguyên lớn nhất của bất phương trình

 

4 3 2 1log .





là:

3x 

. B.

2x 

1x 

. D.

1x 

Lời giải

Chọn C

 

1 1 2 1 2

4 3 2 1 4 3 3 3 4 3 0 0 3 4 4log . . . log

x x x x x x

  

           

Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 60

 Dạng 8.5. Chứa tham số

 Sử dụng PP giải BPT logarit kết hợp công thức, tnh chất của mũ, lũy thừa, logarit.

 Khai thác điều kiện bài toán.

 Xử lý bài toán và chọn giá trị m thỏa ĐK bài toán (cách “mò”).

 Ví dụ 8.5.1

Tìm tất cả các giá trị thực của tham số

để bất phương trình

 

51log

m

có

nghiệm

1x 

2m 

. B.

2m 

. C.

2m 

. D.

2m 

Lời giải

Chọn A

 

1 5 1 4 5 1 2 2log

xm        

 Ví dụ 8.5.2

Tìm tất cả giá trị thực của tham số m để bất phương trình

 

41log x x m  

nghiệm đúng

x

7m 

. B.

7m

. C.

4m

. D.

47m

Lời giải

Chọn B

 

4 1 4 3 0 0 7log x x m x x x m x m               

 Ví dụ 8.5.3

Tìm tất cả giá trị thực của tham số m để

 

4log logmx x

vô nghiệm?

44m  

. B.











. C.

4m

. D.

44m  

Lời giải

Chọn A

 

2 2 2

4 4 4 0log logmx x mx x x mx        

40x mx  

vô nghiệm

4 0 0 4 4 x mx x R m           

 Ví dụ 8.5.4

Tìm tất cả các giá trị thực của tham số

sao cho khoảng

 

23;

thuộc tập nghiệm

của bất phương trình

   

1 4 1log log (1)x x x m    

12 13;m







. B.

12 13;m







. C.

13 12;m







. D.

13 12;m



  



Lời giải

Chọn A

 

4 4 5

()

x x m

m x x f x

m x x g x

x x m







   









   





  



Hệ trên thỏa mãn

 

23;x

 

12 2

12 13

13 2

max khi

min khi

m f x x





   



    



  





Tổng Hợp Lý Thuyết Năm học: 2023-2024

 Biên soạn: Gv

Lê Minh Tâm

- 093.337.6281 Trang 61

 Ví dụ 8.5.5

Tìm

để bất phương trình

   

1 1 4log logx mx x m    

thoã mãn

x

10m  

. B.

10m  

. C.

23m

. D.

23m

Lời giải

Chọn A

BPT thoã mãn

x

.

 

5 1 4

mx x m

x mx x m



  







   







 

16 4 0

5 4 5 0

16 4 5 0

mx x m

m x x m



























  







      

  





    













  















 Ví dụ 8.5.6

Tìm tất cả các giá trị thực của tham số

để bất phương trình

 

0 02 2 0 02

log log log

m

có nghiệm với mọi

 

0;x 

01.m

1.m 

2.m 

1.m 

Lời giải

Chọn D

Đk:

0;xm

Ta có:

 

0 02 2 0 02

3 1 0

log log log , ; .

mx    

 

3 1 0log , ; .

mx     

 

3 1 2 0, ; .

x     

Xét hàm

 

fx

trên

 

0;

. Ta có

   

3 3 0 0.ln , ; .

f x x



    

Để phương trình có nghiệm với mọi

 

0;x 

ta phải có



1m

∞

Bấm Tải xuống để xem toàn bộ.

| 1/125

| | Tải xuống

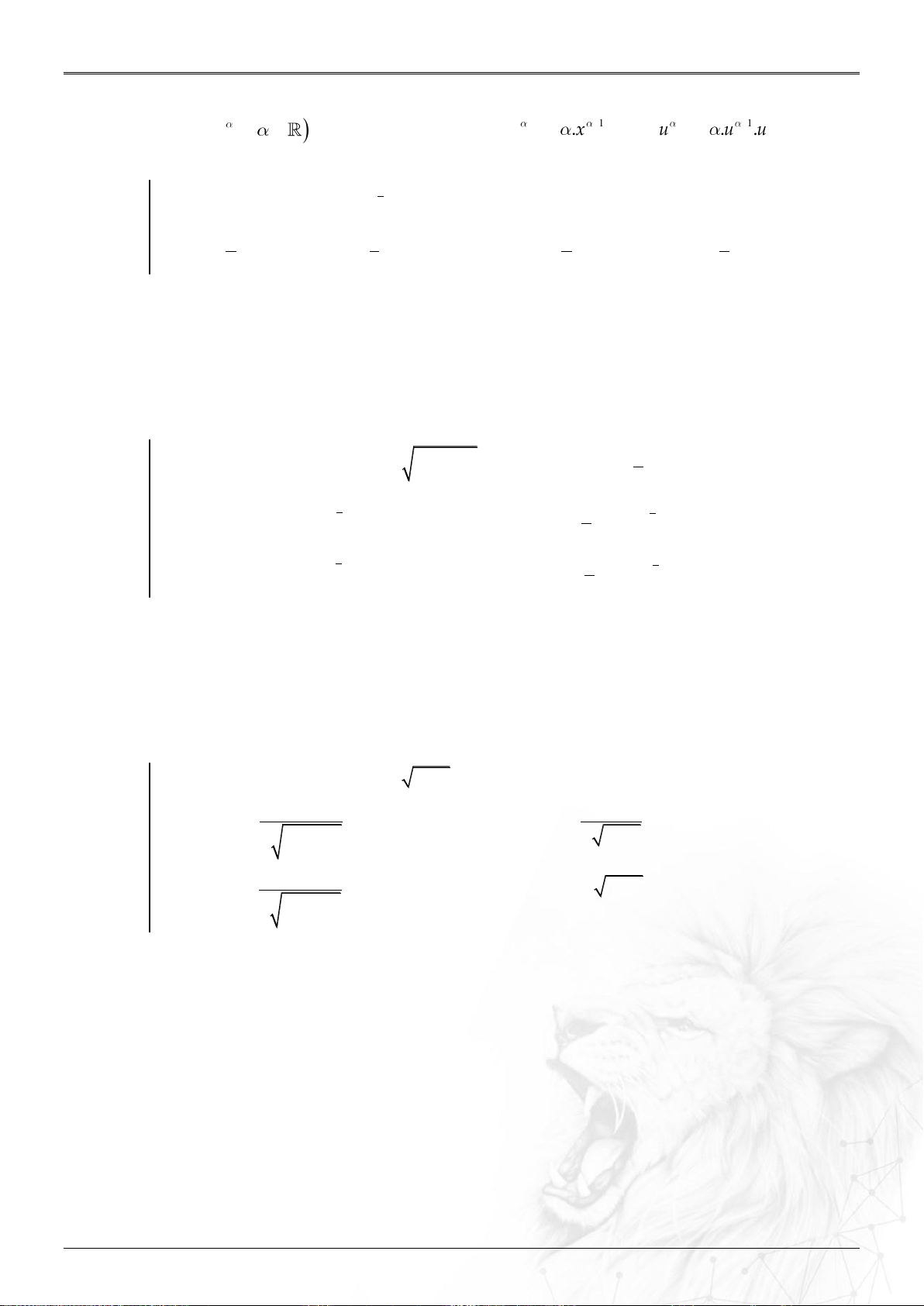
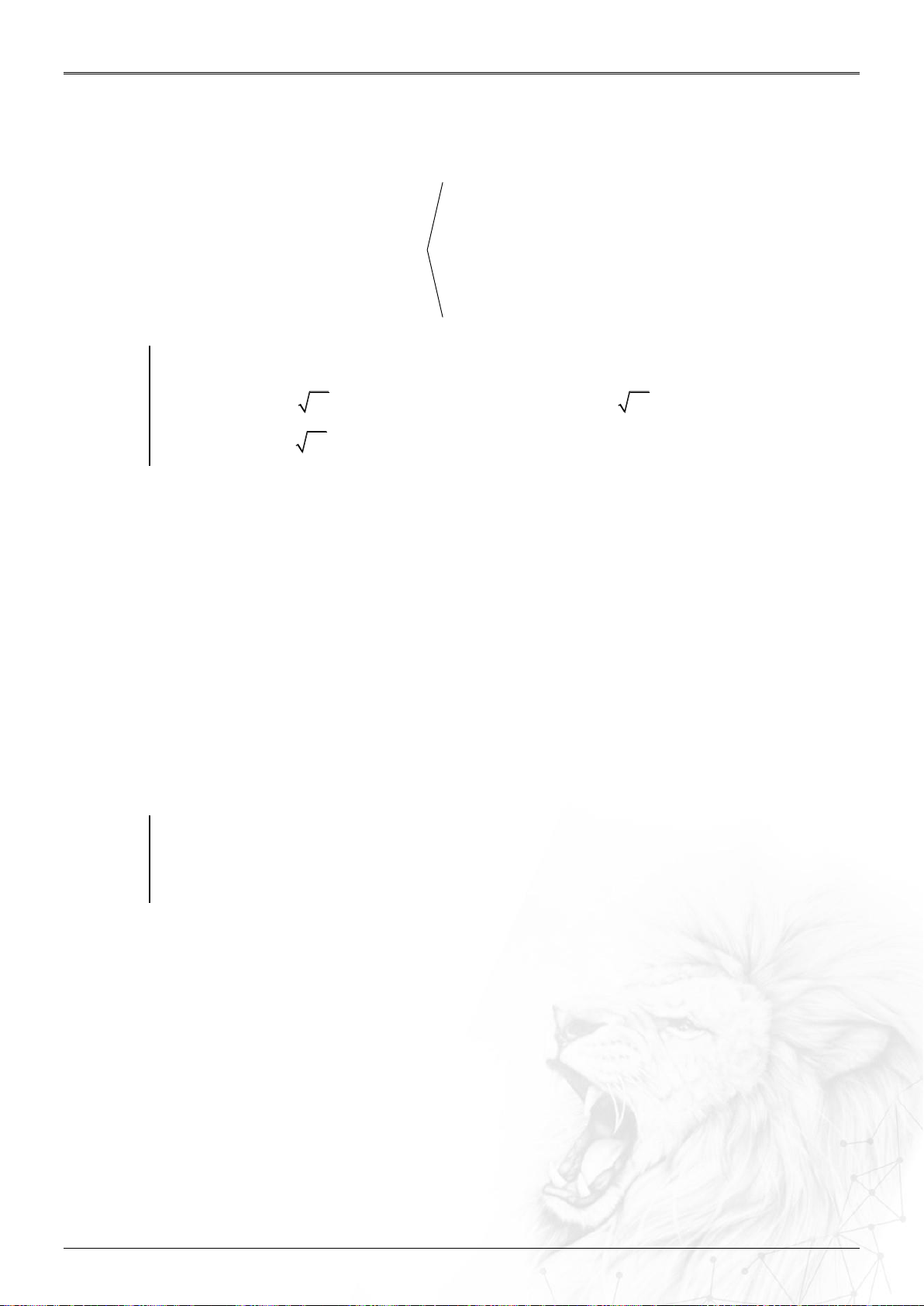
Preview text:

TÀ T I À I L I L Ệ I U Ệ U D À D N À H N H C H C O H O K H K ỐI Ố I12 1 Mục lục
 Chủ đề 01. LŨY THỪA – HÀM SỐ LŨY THỪA
 Dạng 1.1. Rút gọn và tính giá trị biểu thức ........................................................................... 6
 Dạng 1.2. So sánh các biểu thức chứa lũy thừa ................................................................... 7
 Dạng 1.3. Tập xác định hàm số lũy thừa ............................................................................... 8
 Dạng 1.4. Đạo hàm số lũy thừa ................................................................................................ 9
 Dạng 1.5. Đồ thị hàm số lũy thừa ........................................................................................... 10
 Chủ đề 02. LOGARIT
 Dạng 2.1. Tính giá trị biểu thức................................................................................................ 12
 Dạng 2.2. Biểu diễn logarit ....................................................................................................... 13
 Dạng 2.3. Mệnh đề đúng – sai ................................................................................................. 14
 Chủ đề 03. HÀM SỐ MŨ – HÀM SỐ LOGARIT
 Dạng 3.1. Tập xác định của hàm số logarit ........................................................................ 18
 Dạng 3.2. Đạo hàm hàm số mũ – logarit ............................................................................. 20
 Dạng 3.3. Khảo sát hàm số mũ – logarit .............................................................................. 21
 Chủ đề 04. BÀI TOÁN LÃI SUẤT
 Chủ đề 05. PHƯƠNG TRÌNH MŨ
 Dạng 5.1. Phương trình mũ cơ bản ......................................................................................... 31
 Dạng 5.2. Đưa về cùng cơ số ................................................................................................... 32
 Dạng 5.3. Logarit hóa ............................................................................................................... 33
 Dạng 5.4. Đặt ẩn phụ dễ thấy ................................................................................................ 34
 Dạng 5.5. Đặt ẩn phụ với phương trình đẳng cấp ............................................................. 35
 Dạng 5.6. Đặt ẩn phụ với tích hai cơ số bằng 1 .................................................................. 36
 Dạng 5.7. Phương pháp hàm số ............................................................................................. 37
 Dạng 5.8. Phương trình chứa tham số .................................................................................. 39
 Chủ đề 06. PHƯƠNG TRÌNH LOGARIT
 Dạng 6.1. Phương trình logarit cơ bản ................................................................................. 41
 Dạng 6.2. Đưa về cùng cơ số .................................................................................................. 42
 Dạng 6.3. Mũ hóa ....................................................................................................................... 43
 Dạng 6.4. Đặt ẩn phụ dễ thấy ................................................................................................44
 Dạng 6.5. Phương pháp hàm số ............................................................................................ 45
 Dạng 6.6. Phương trình chứa tham số ................................................................................. 47
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Chủ đề 07. BẤT PHƯƠNG TRÌNH MŨ
 Dạng 7.1. Bất phương trình mũ cơ bản ............................................................................... 50
 Dạng 7.2. Đưa về cùng cơ số ................................................................................................... 51
 Dạng 7.3. Đặt ẩn phụ ................................................................................................................. 52
 Dạng 7.4. Logarit hóa ............................................................................................................... 53
 Dạng 7.5. Chứa tham số .......................................................................................................... 54
 Chủ đề 08. BẤT PHƯƠNG TRÌNH LOGARIT
 Dạng 8.1. Bất phương trình logarit cơ bản ......................................................................... 56
 Dạng 8.2. Đưa về cùng cơ số ................................................................................................... 57
 Dạng 8.3. Đặt ẩn phụ.................................................................................................................58
 Dạng 8.4. Mũ hóa ........................................................................................................................ 59
 Dạng 8.5. Chứa tham số ........................................................................................................... 60
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 2
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
LŨY THỪA – MŨ – LOGARIT
LŨY THỪA – HÀM SỐ LŨY THỪA A. LÝ THUYẾT CHUNG. 1. Lũy thừa: 1.1. Định nghĩa.
 Cho số thực b và số nguyên dương nn  2 .
Số a được gọi là căn bậc n của số b nếu n a  b . Chú ý: n lẻ
b  Có duy nhất một căn bậc n của b, ký hiệu n b .
b  0  Không tồn tại căn bậc n của b
b  0  Có một căn bậc n của b là 0 n chẵn
 Có hai bậc n của a là hai số đối nhau,
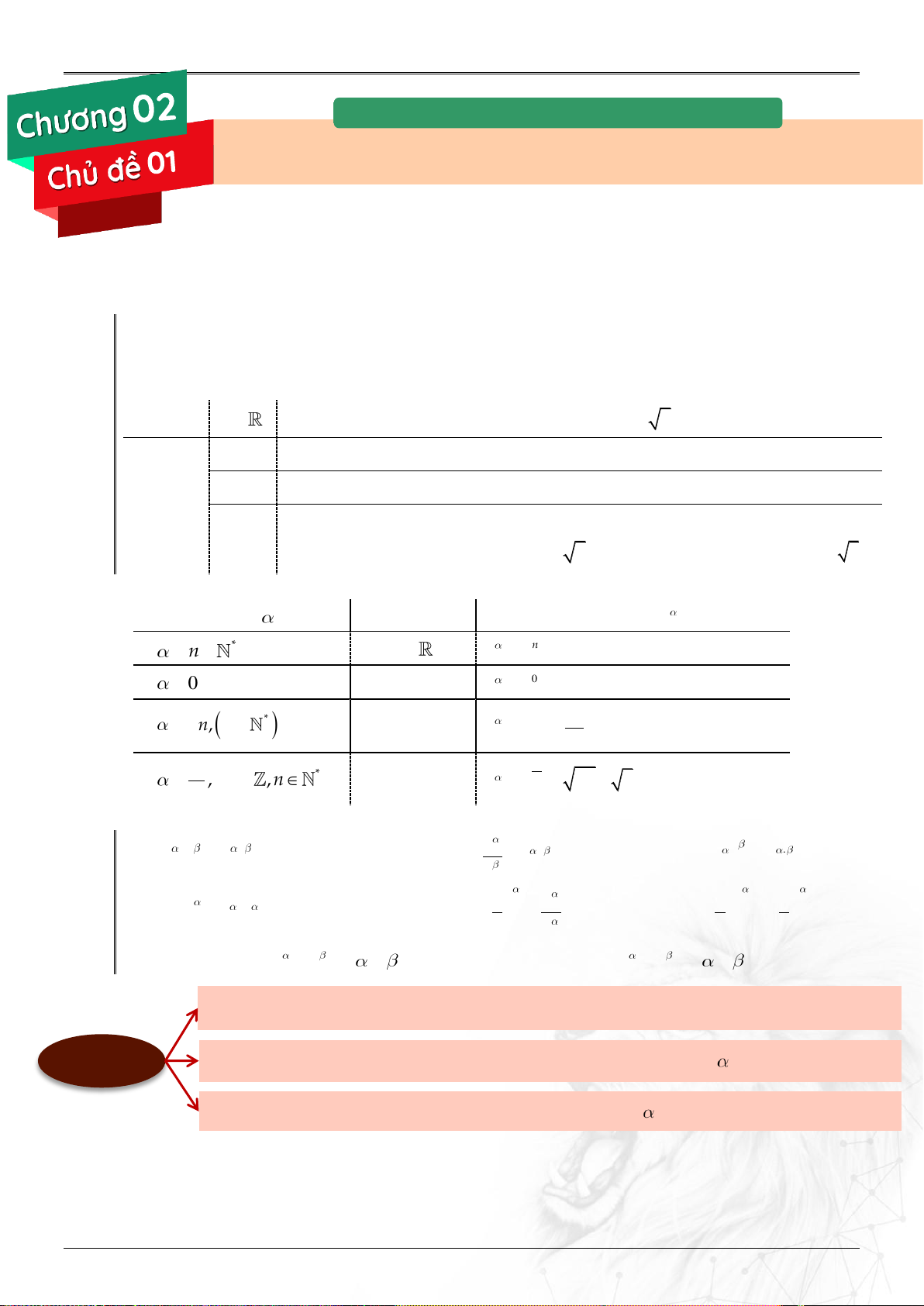
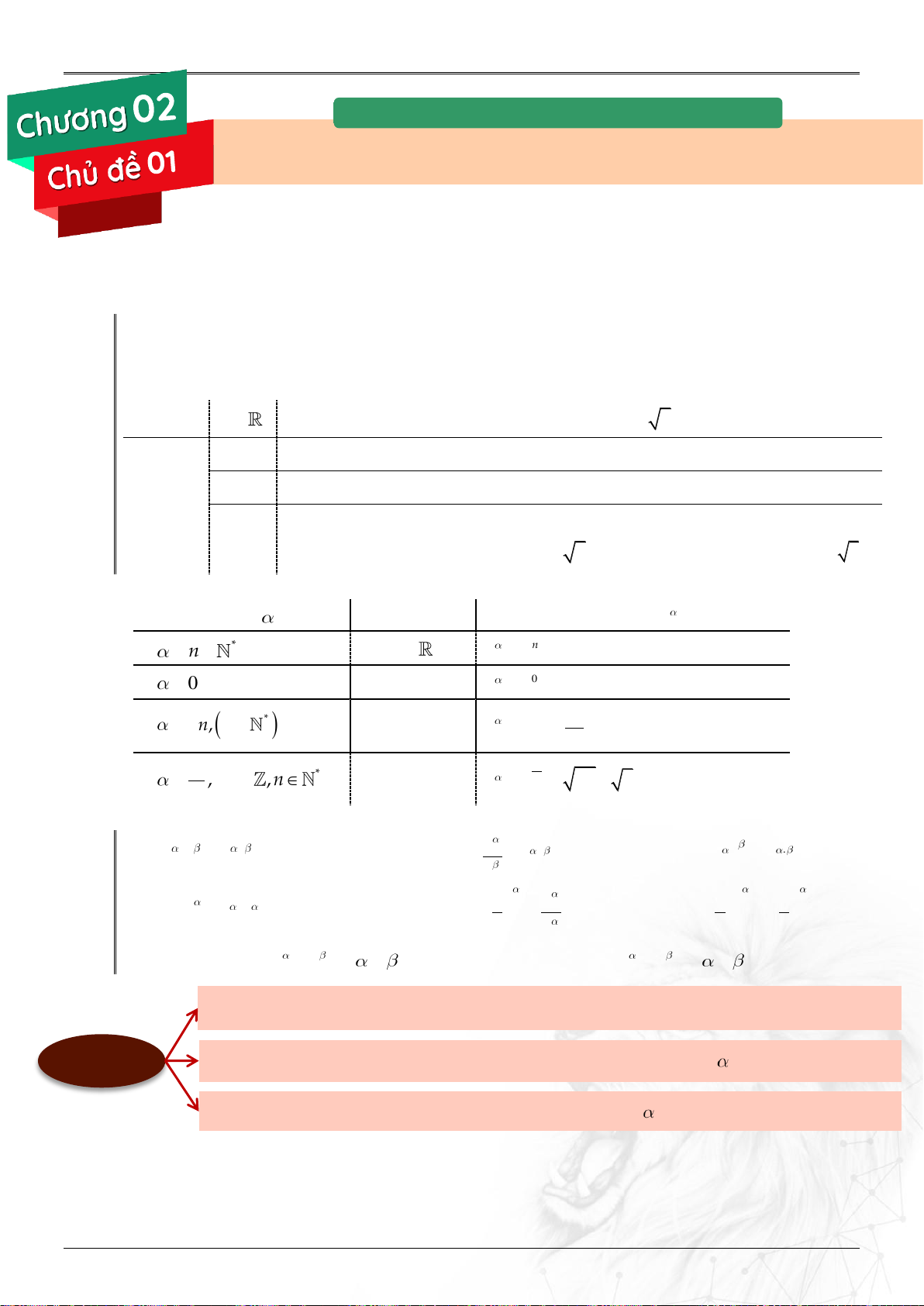
b  0  Căn có giá trị dương ký hiệu là n b , căn có giá trị âm ký hiệu là n  b . 1.2. Công thức. Số mũ Cơ số a Lũy thừa a *  n a n a  a  . a .
a ..a (n là thừa số a)  0 a  0 0 a  a 1    1 n  * , n   a  0 n a  a  n a m m   * , m ,n  a  0 n m n
a  a  a ,n n
a  b  a  b  n 1.3. Tính chất. ⓵ a .a a   ⓶ a a   ⓷   . a  a a       
⓸ ab  a .b ⓹ a a    ⓺ a b       b  b  b   a 
⓻ Nếu a 1 thì a  a   .
⓼ Nếu 0  a 1 thì a  a   .
Các tính chất trên đúng trong trường hợp số mũ nguyên hoặc không.nguyên CHÚ Ý
Khi xét lũy thừa với số mũ 0 và số mũ nguyên âm thì cơ số phải khác 0.
Khi xét lũy thừa với số mũ không nguyên thì cơ số phải dương.
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 3
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
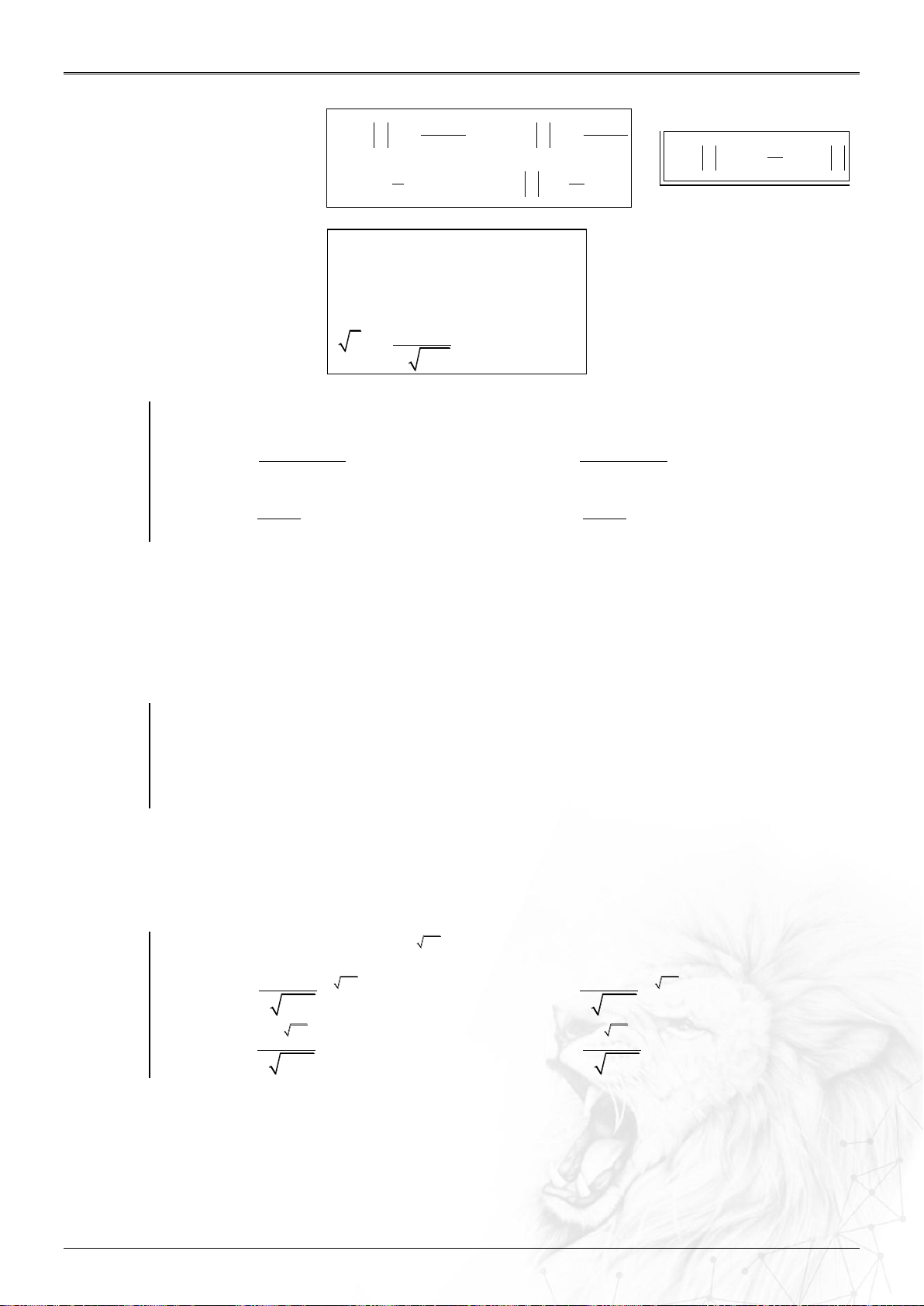
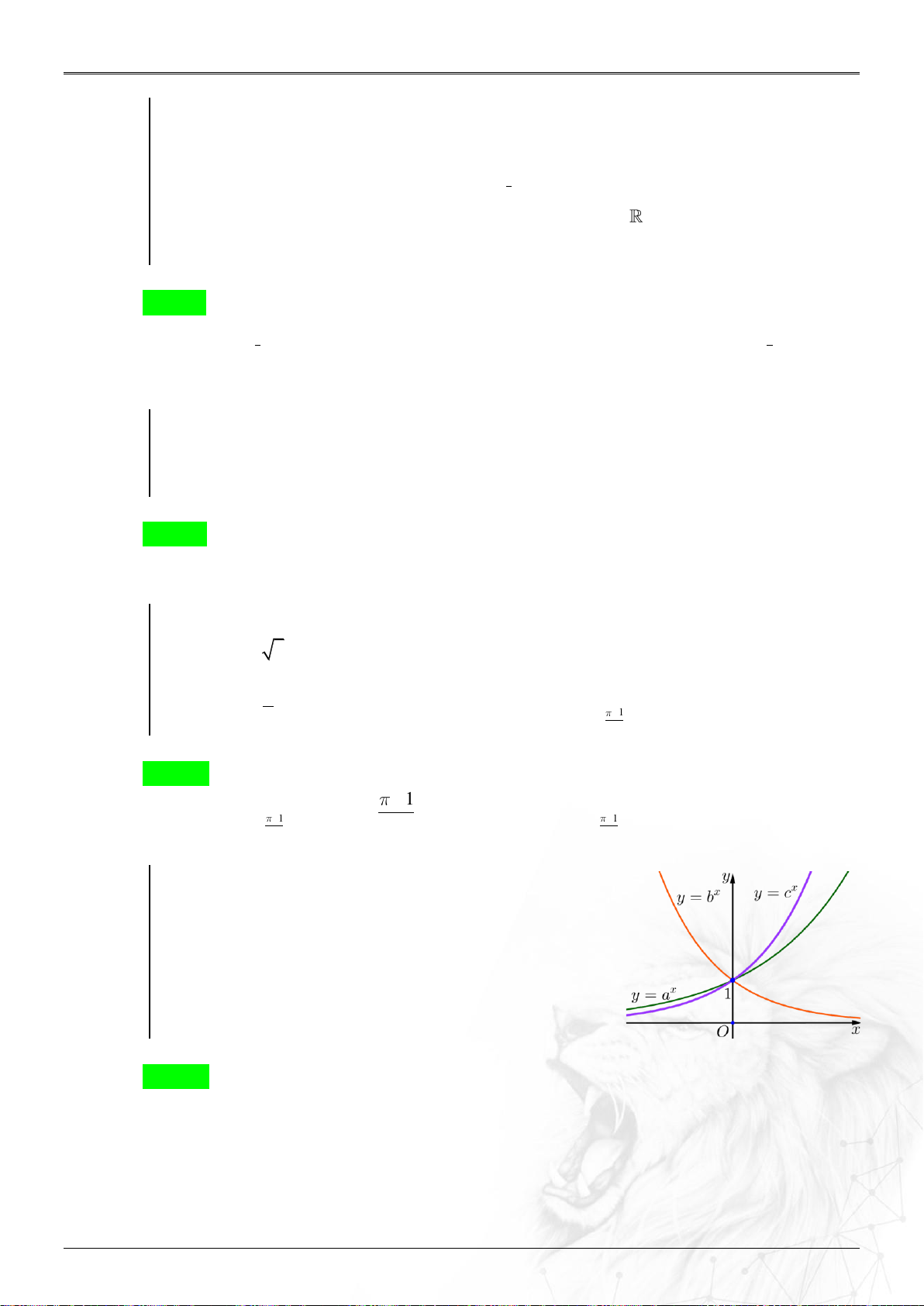
1.4. Tính chất căn bậc n. Với *
a,b  ,n ta có ⓵ n n
a  a, a  ⓶ n n  . n ab a b , a  ;b n ⓷ a a n  , a  , b   0 n b b m
⓸ n m  n a a  , a
  0,n nguyên dương, m nguyên. ⓹ n m nm a  a , a
  0,n,m nguyên dương. ⓺ p q Nếu  thì n p m q
a  a , a
  0,m,n nguyên dương, p,q nguyên. n m Đặc biệt: n m.n m a  a .
2. Hàm số lũy thừa: 2.1. Khái niệm.
 Hàm số y  x với  được gọi là hàm số lũy thừa.
2.2. Tập xác định.
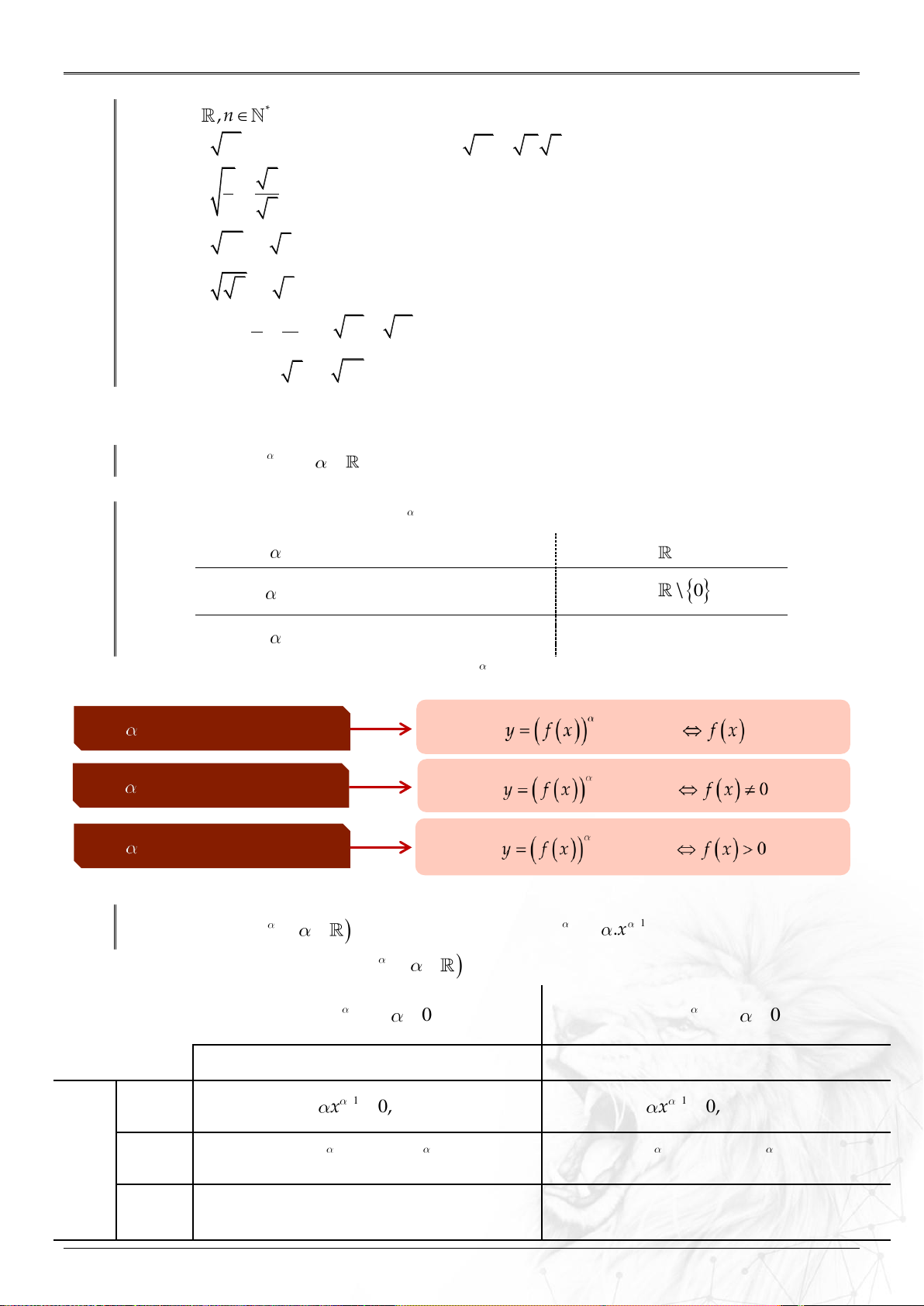
 Tập xác định của hàm số y  x là:
⓵ Nếu là số nguyên dương D 
⓶ Nếu nguyên âm hoặc bằng 0. D   \  0
⓷ Nếu không nguyên D  0; 
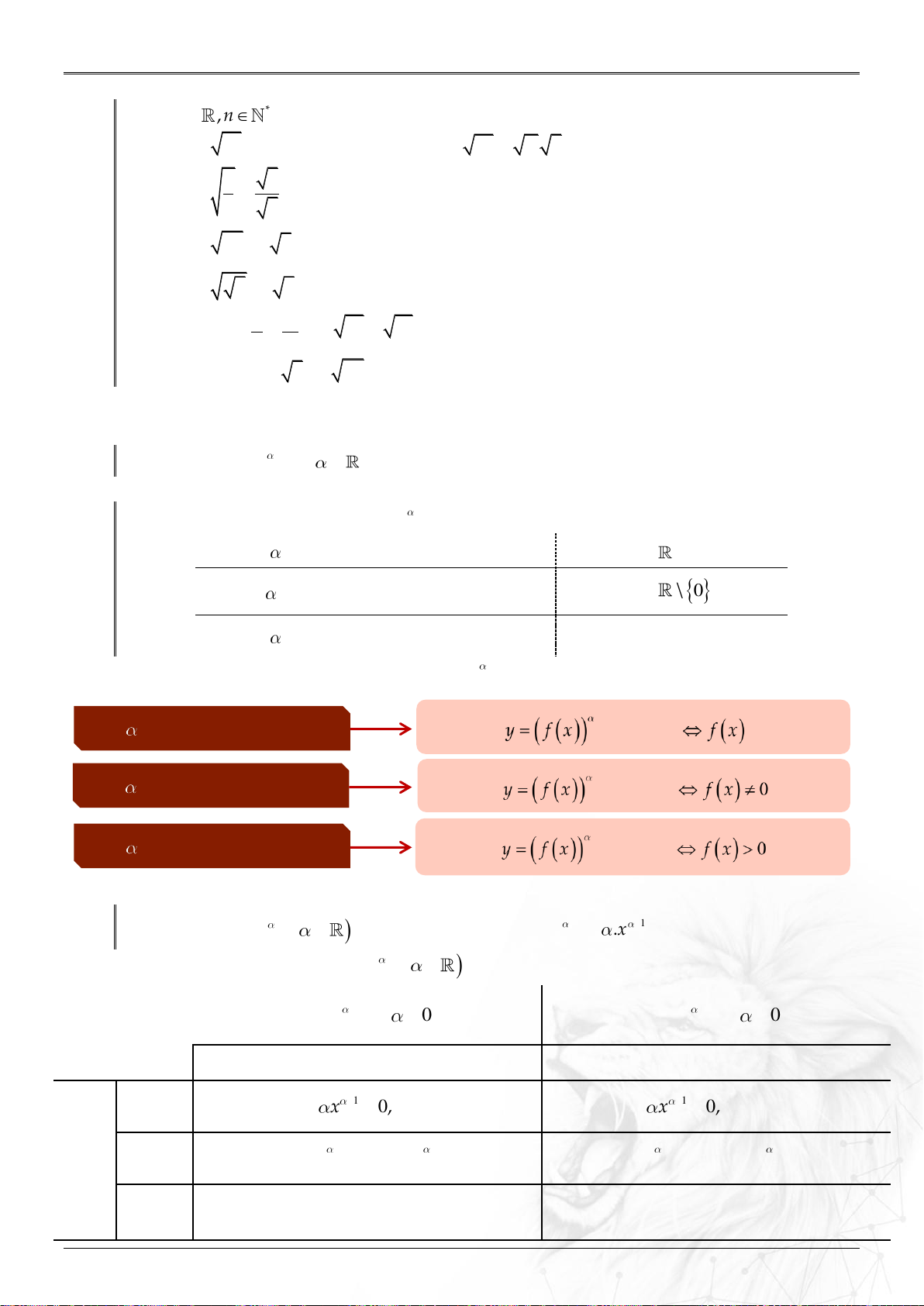
※ Tổng quát: Tập xác định của hàm số y   f x . Khi NGUYÊN DƯƠNG Hàm số xác định xác định. Khi NGUYÊN ÂM Hàm số xác định . Khi KHÔNG NGUYÊN Hàm số xác định 2.3. Đạo hàm.  
Hàm số y  x ,    có đạo hàm x   0 và x  1  .x  .
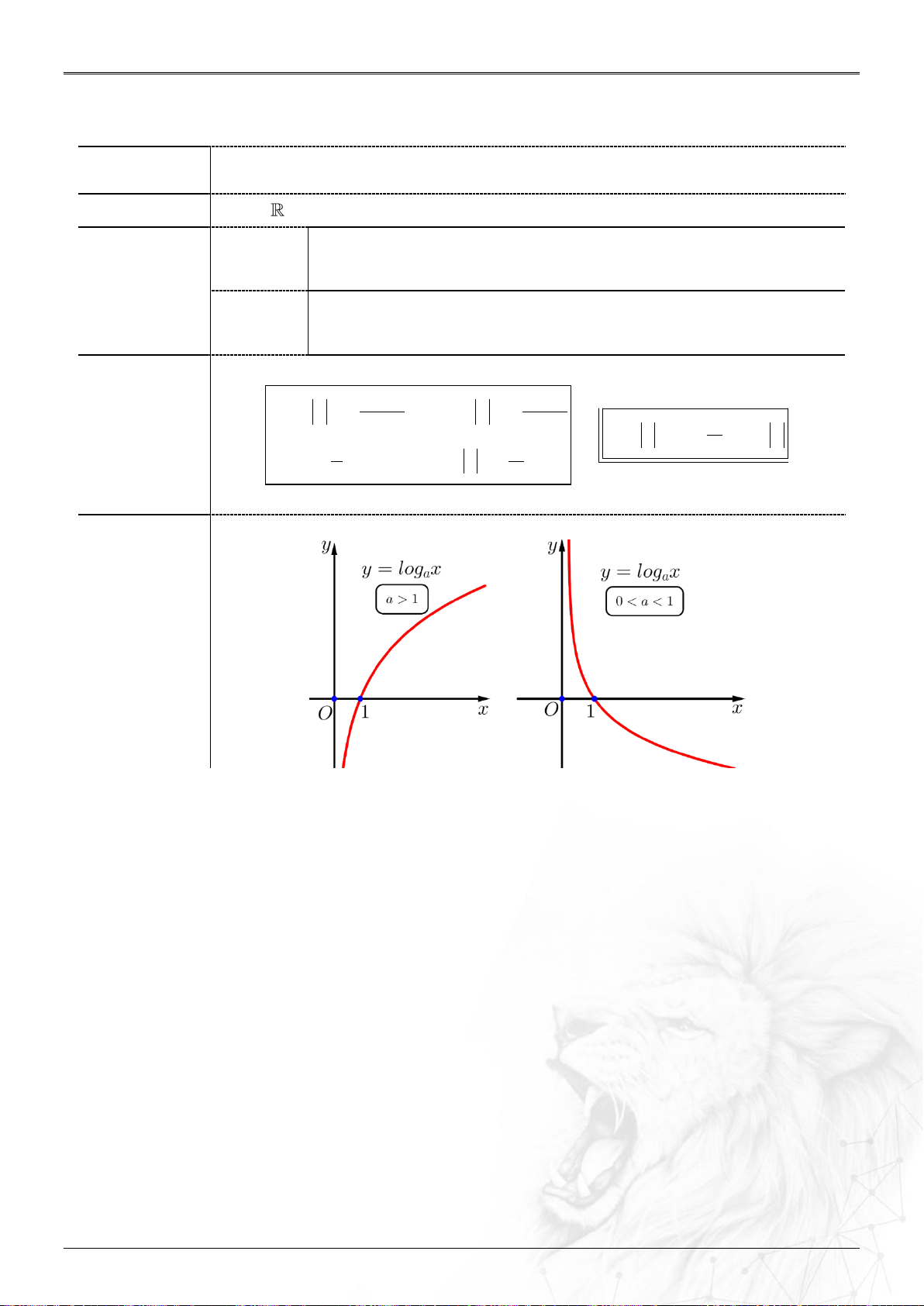
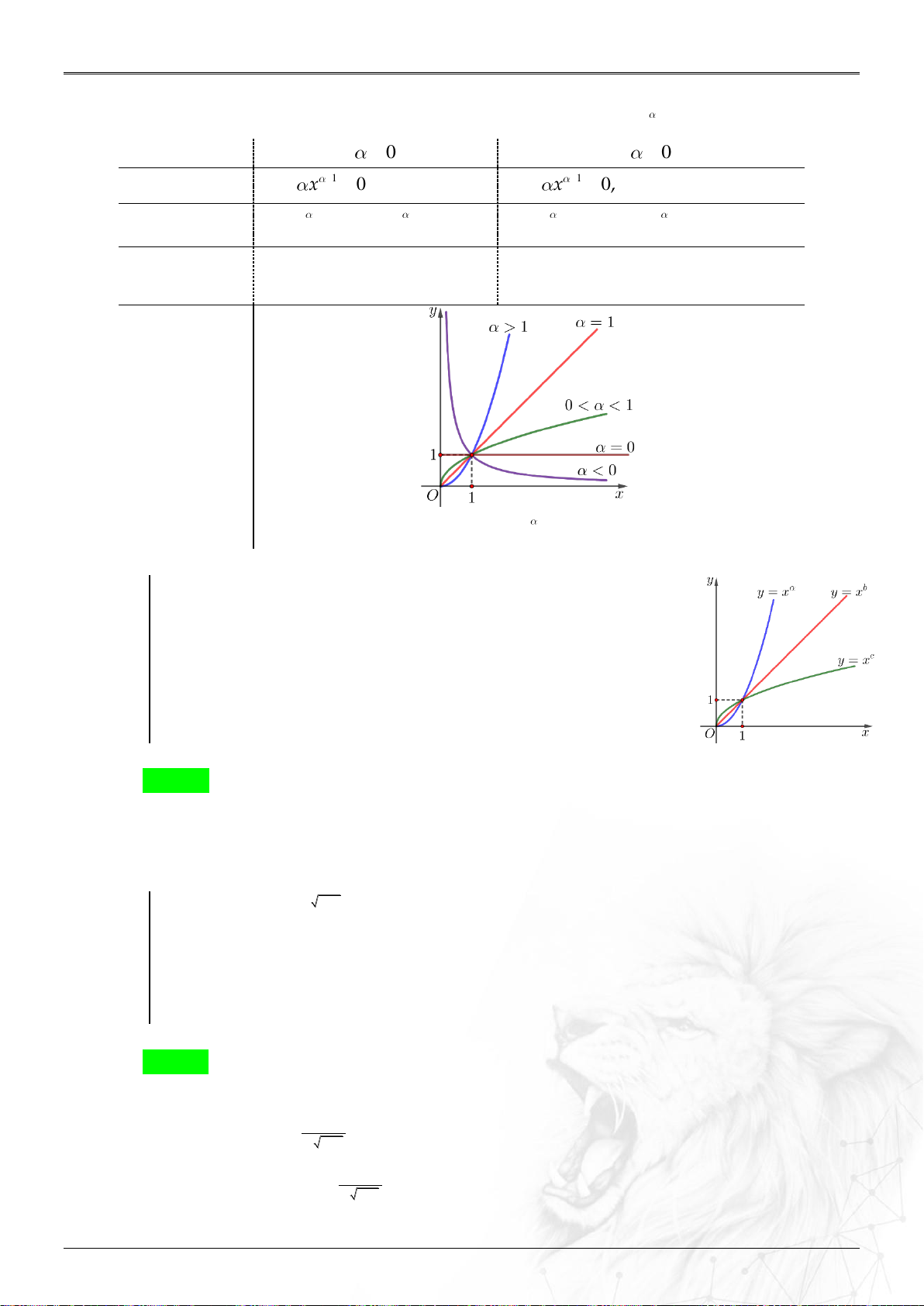
2.4. Khảo sát hàm số lũy thừa y  x ,   .
y  x với  0
y  x với  0 Tập khảo sát 0; 0; Đạo 1 y x     0, x   0. 1 y x     0, x   0. hàm Sự Giới       biến lim x 0, lim x . lim x , lim x 0. hạn   x 0  x x 0  x thiên Tiệm
Nhận Ox là tiệm cận ngang. Không có. cận
Nhận Oy là tiệm cận đứng.
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 4
Tổng Hợp Lý Thuyết
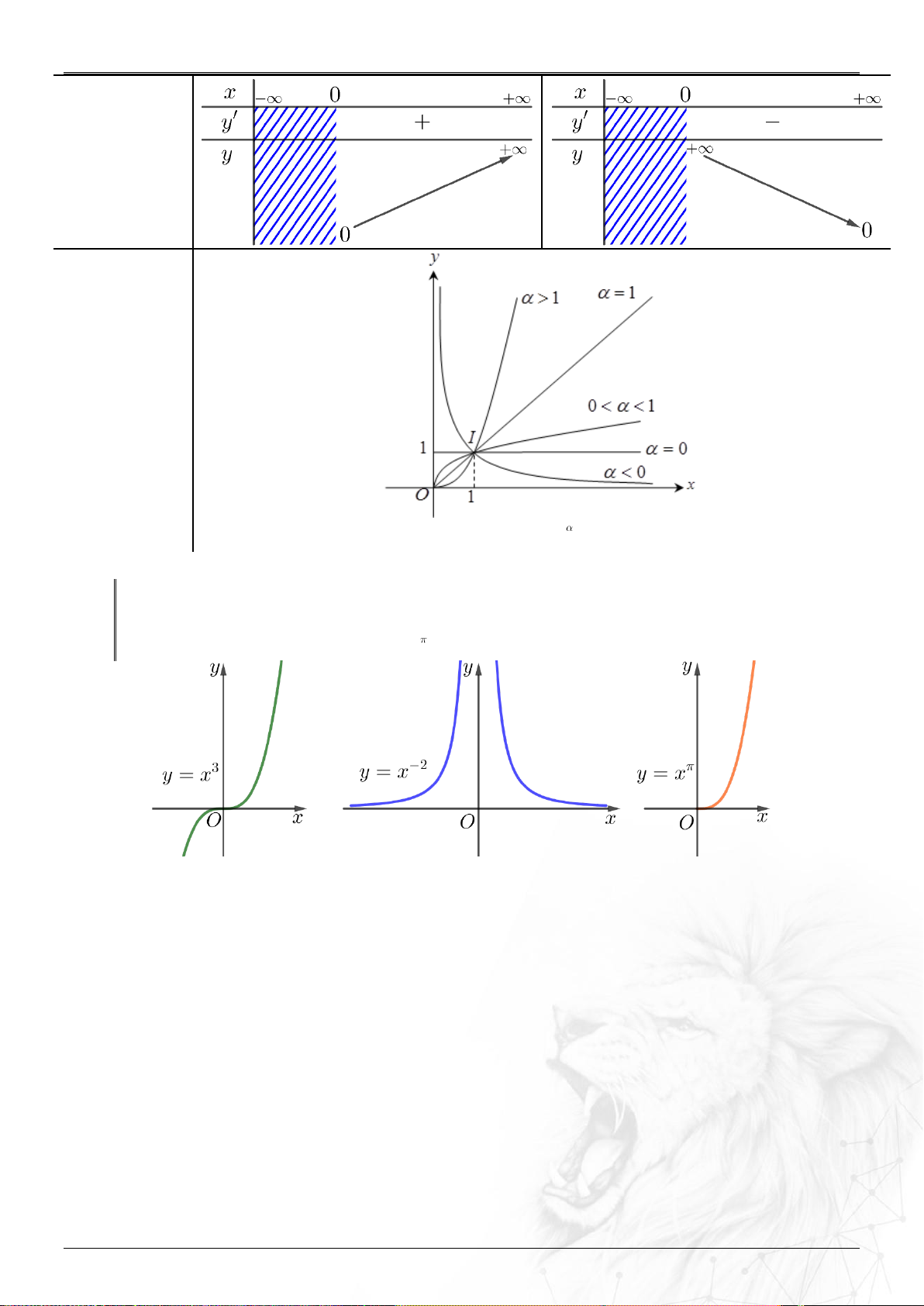
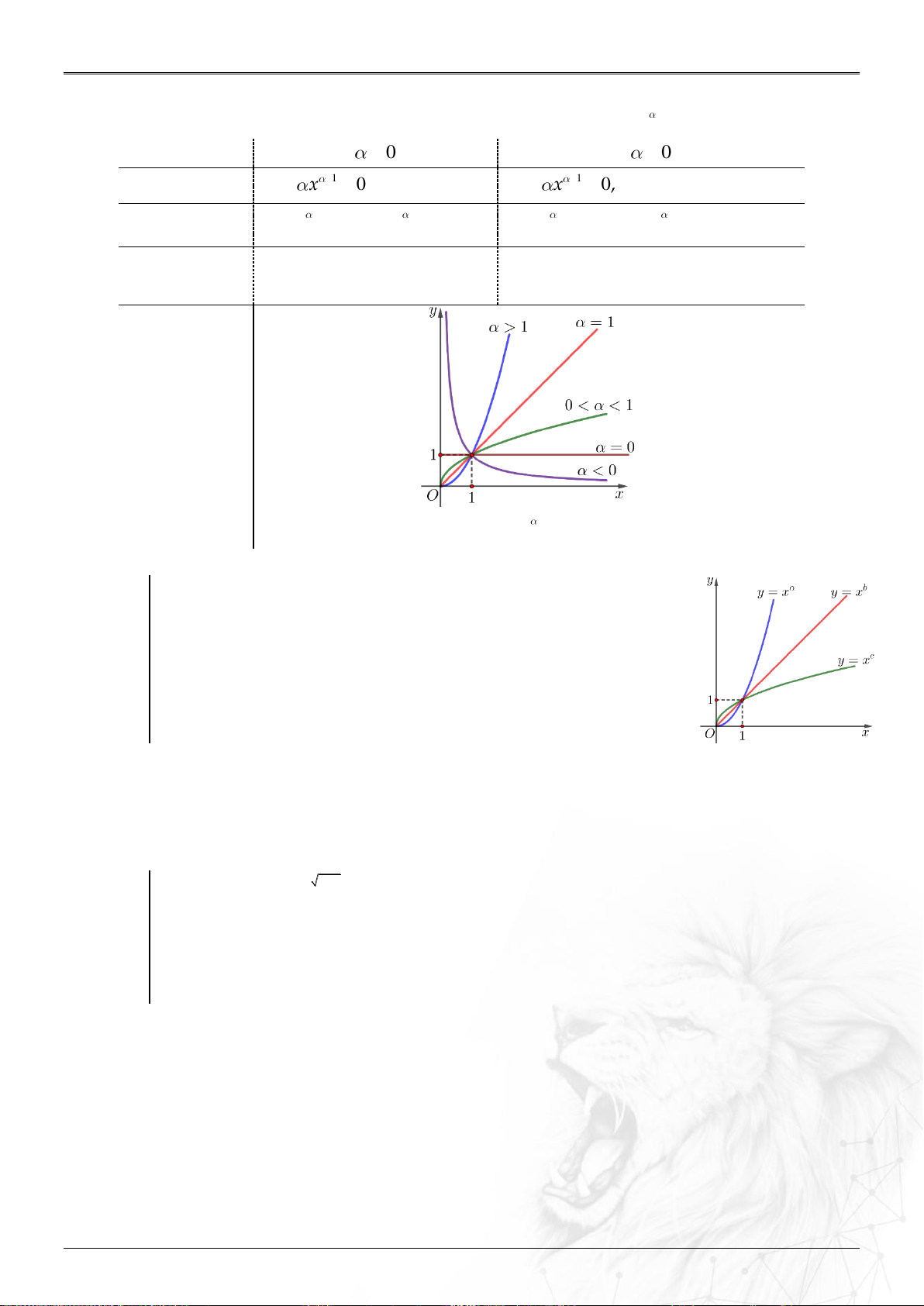
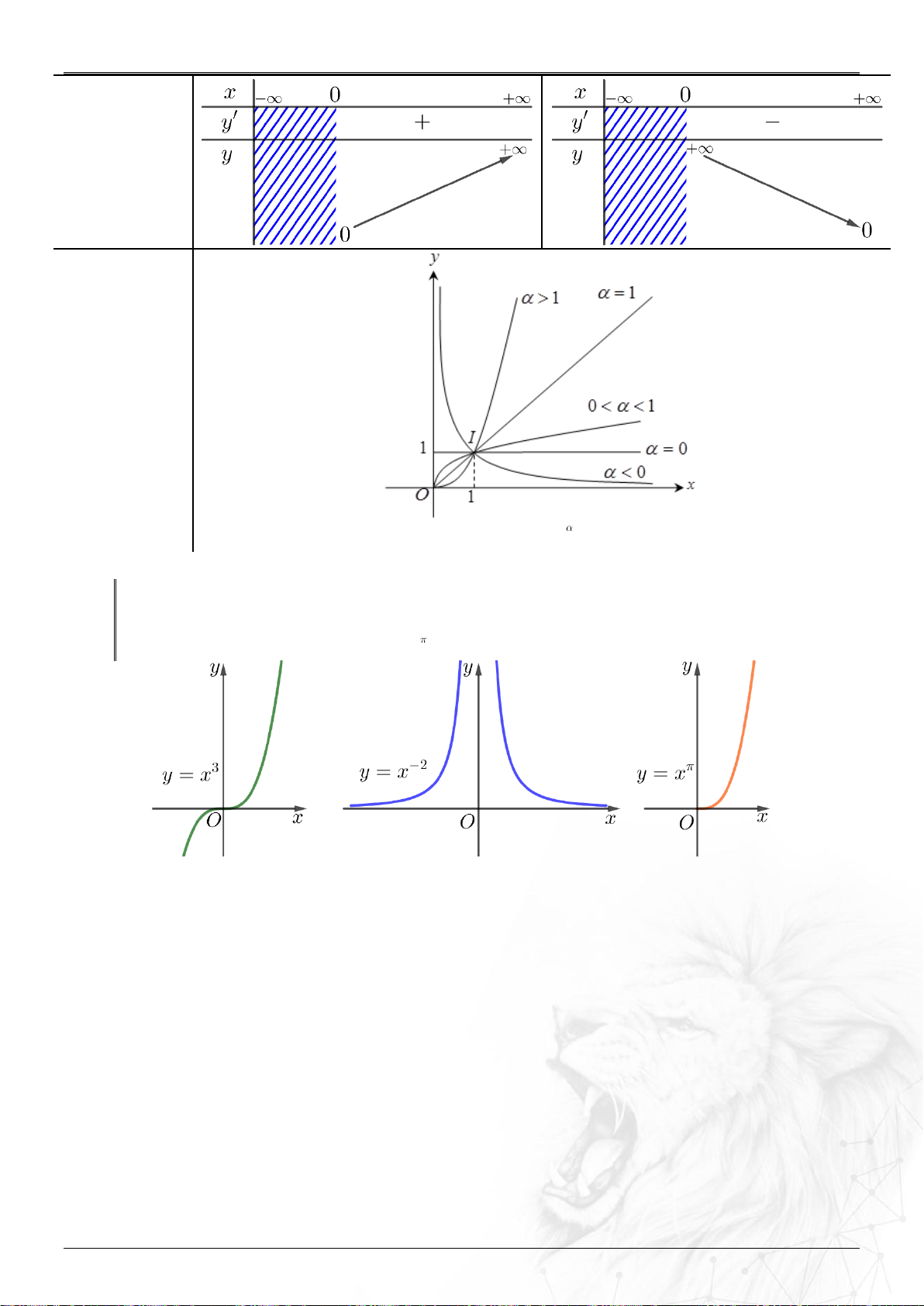
Năm học: 2023-2024 Bảng biến thiên Đồ thị
Đồ thị của hàm số lũy thừa y  x luôn đi qua điểm I 1;  1 . Lưu ý:
 Khi khảo sát hàm số lũy thừa với số mũ cụ thể, ta phải xét hàm số đó trên toàn bộ tập xác định của nó.  Chẳng hạn: 3 2 y x , y x   , y  x .
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 5
Tổng Hợp Lý Thuyết
Năm học: 2023-2024 B. CÁC DẠNG BÀI TẬP.
 Dạng 1.1. Rút gọn và tính giá trị biểu thức
 Sử dụng phối hợp linh hoạt các tính chất của lũy thừa.
 Chọn a;b là các số thực dương và x; y là các số thực tùy ý, ta có: ⓵ a .a a   ⓶ a a   ⓷   . a  a a       
⓸ ab  a .b ⓹ a a    ⓺ a b       b  b  b   a 
⓻ Nếu a 1 thì a  a   . ⓼ Nếu 0  a 1 thì a  a   .  Ví dụ 1.1.1
Đưa các biểu thức sau về dạng lũy thừa 3 ⓵ 2 4 b a
a a a  0 ⓶
⓷ 5 3 a,b  0. 0 75 16 , a b Lời giải
⓵ . .................................................................................................................................................
⓶ ..................................................................................................................................................
⓷ ..................................................................................................................................................  Ví dụ 1.1.2
Rút gọn các biểu thức sau đây: ⓵  4 a  4 5 ⓶ 4 2
81a b b  0 ⓷ 8 4 x x   1
x   1. Lời giải
⓵ . .................................................................................................................................................
⓶ ..................................................................................................................................................
⓷ ..................................................................................................................................................  Ví dụ 1.1.3 1  1  1  1 
Cho a  2  3 ,b  2  3 . Tính A  a   1  b   1 . Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 6
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 1.2. So sánh các biểu thức chứa lũy thừa
 Ta có hai cách làm như sau:
Đưa về cùng cơ số Cho a : , m n . Khi đó 01
⓵ Với a 1 m n 
a  a  m  n ;
⓶ Với 0  a 1 m n 
a  a  m  n .
Đưa về cùng số mũ 02
Với 0  a  b và m là số nguyên thì ⓵ m m
a  b  m  0 ⓶ m m
a  b  m  0 .  Ví dụ 1.2.1
So sánh các số sau: ⓵ 300 7 và 400 7 ⓶  5000 1 và  . 2 8000 1 2 Lời giải ⓵ 300 7 và 400 7 ⓶  và  2 8000 1 2 5000 1  Ví dụ 1.2.2
So sánh các số sau: ⓵ 20 20 và 30 15 . ⓶ 100 2 và 30 20 . ⓷   7  3 1 và   8 3 1 .
⓸ 34 và    34 1 . Lời giải ⓵ 20 20 và 30 15 . ⓶ 100 2 và 30 20 .  ⓷   7  3 1 và   8 3 1 .
⓸ 34 và    34 1 .  Ví dụ 1.2.3
So sánh 2 số p và q biết: p q ⓵ p q  .
⓶  5  1   5  1 . Lời giải ⓵ p q  p q .
⓶  5  1   5  1 .
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 7
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 1.3. Tập xác định hàm số lũy thừa
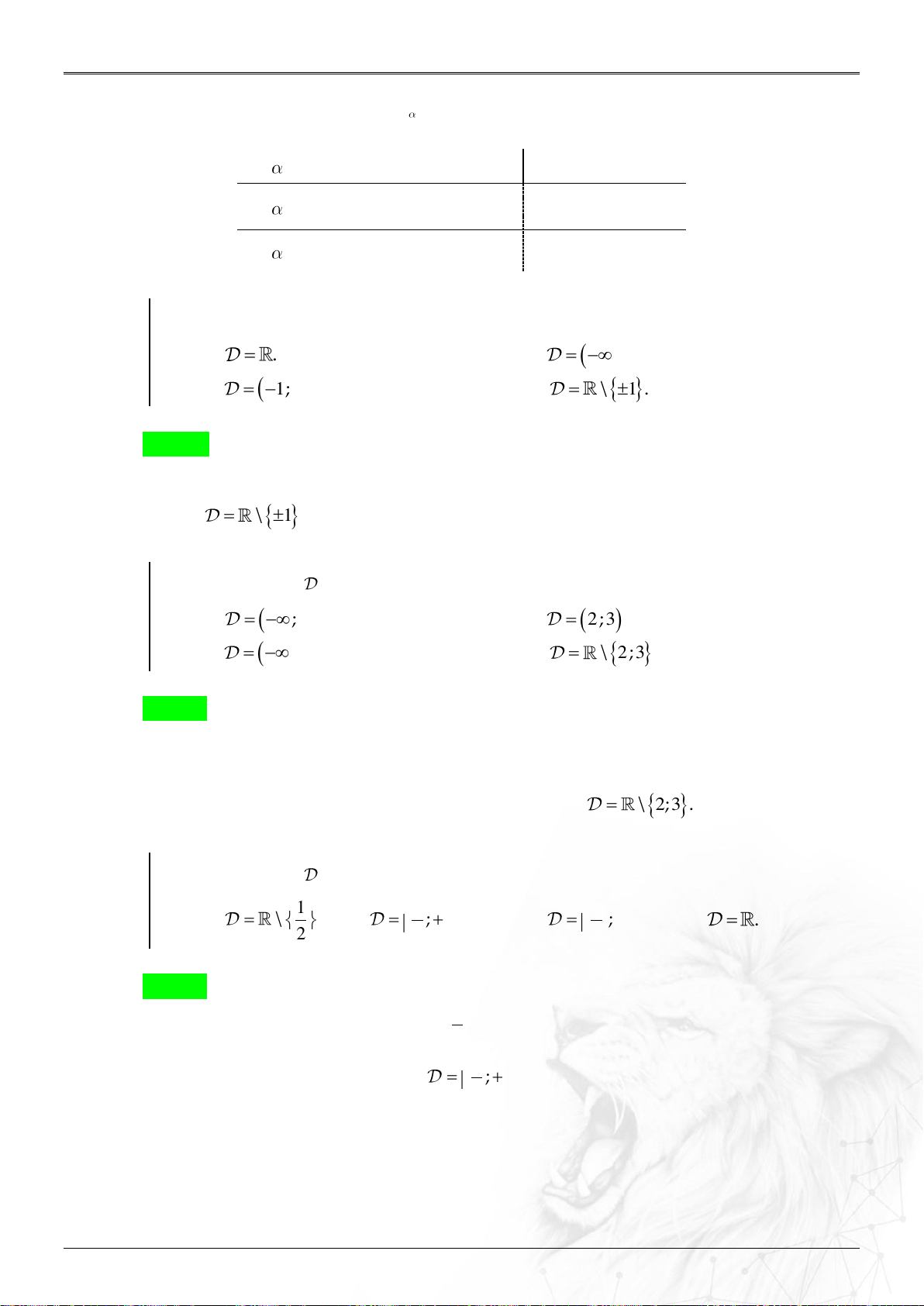
 Tập xác định của hàm số y   f x là:
⓵ là số nguyên dương
f x xác định.
⓶ nguyên âm hoặc bằng 0. f x  0 ⓷ không nguyên f x  0  Ví dụ 1.3.1 
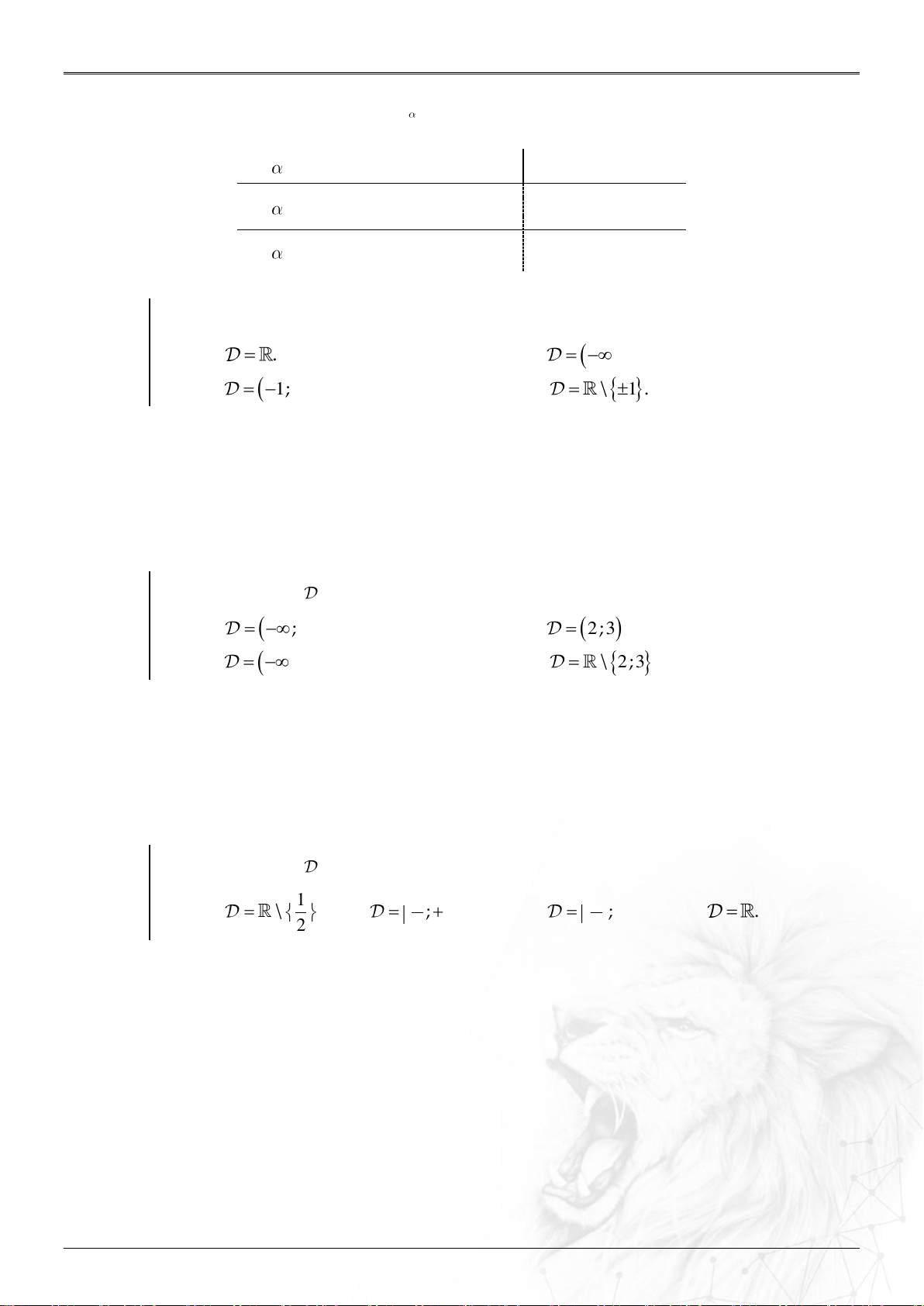
Tìm tập xác định của hàm số y  x   2 2 1 A.  . B.   ;  
1  1 ;  . C.   1  ;  1 . D.   \   1 . Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 1.3.2  Tìm tập xác định
của hàm số y  x  x   2019 2 5 6 A.
 ;23; . B.  2;3 . C.   ; 2  3  ;     . D.   \ 2;  3 . Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 1.3.3 e Tìm tập xác định
của hàm số y  2x   1 1  1   1  A.  \ . B.  ;    . C.  ;     . D.  . 2  2   2  Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 8
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 1.4. Đạo hàm số lũy thừa  
 Hàm số y  x ,    có đạo hàm x   0 và x  1  x   u  1 .
 .u  .u .  Ví dụ 1.4.1
Cho hàm số f x   x  56 2 3 .Tính f 2. 5 5 5 5 A. . B. . C.  . D.  6 3 6 3 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 1.4.2  1 
Tìm đạo hàm của hàm số y    x5 3 1 3 trên khoảng   ;  .  3  5
A. y '     x23 5 1 3 .
B. y '  1 3x43 . 3 5
C. y '     x43 5 1 3 .
D. y '  1 3x23 3 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 1.4.3
Tìm đạo hàm của hàm số 4
y  x  2 , x  2  1 1 A. y '  . B. y'  . 4  4 x  23 4 4 x 2 1 C. y '  . D. 3
y '  4 x  2 2 x  23 4 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 9
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 1.5. Đồ thị hàm số lũy thừa
 Ta lưu ý các yếu tố trong sự biến thiên của hàm số lũy thừa y  x với  0  0  Đạo hàm 1 y x     0 1 y  x  0, x   0. Giới hạn
lim x  0, lim x   . 
lim x  , lim x  0.   x 0  x x 0  x
Nhận Ox là tiệm cận ngang. Tiệm cận Không có.
Nhận Oy là tiệm cận đứng. Đồ thị
Đồ thị của hàm số lũy thừa y  x luôn đi qua điểm I 1;  1 .  Ví dụ 1.5.1
Hình vẽ bên là đồ thị các hàm số a y  x , b y  x , c
y  x trên miền
0;. Hỏi số a , b, c số nào nhận giá trị trong khoảng 0; 1? A. a .
B. a&c . C. b . D. c Lời giải
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 1.5.2 Cho hàm số 2023 y x 
. Mệnh đề nào đúng về đường tiệm cận của đồ thị hàm số?
A. Có một tiệm cận ngang và một tiệm cận đứng.
B. Không có tiệm cận ngang và có một tiệm cận đứng.
C. Có một tiệm cận ngang và không có tiệm cận đứng.
D. Không có tiệm cận. Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 10
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
LŨY THỪA – MŨ – LOGARIT LOGARIT A. LÝ THUYẾT CHUNG. 1. Định nghĩa.
Cho hai số dương a, b với a 1.
 Số thỏa mãn đẳng thức a  b được gọi là lôgarit cơ số a của b và kí hiệu là log b . a
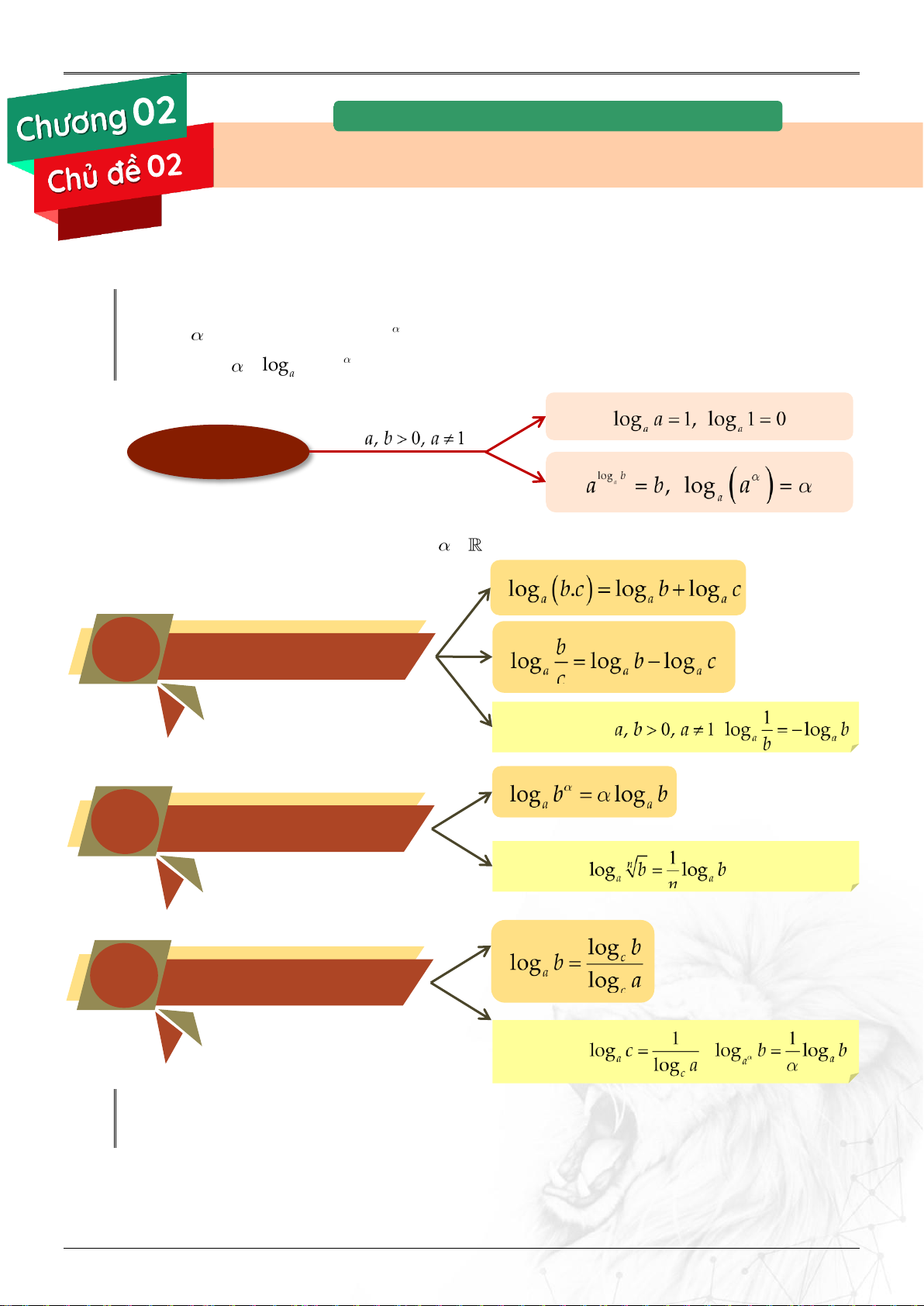
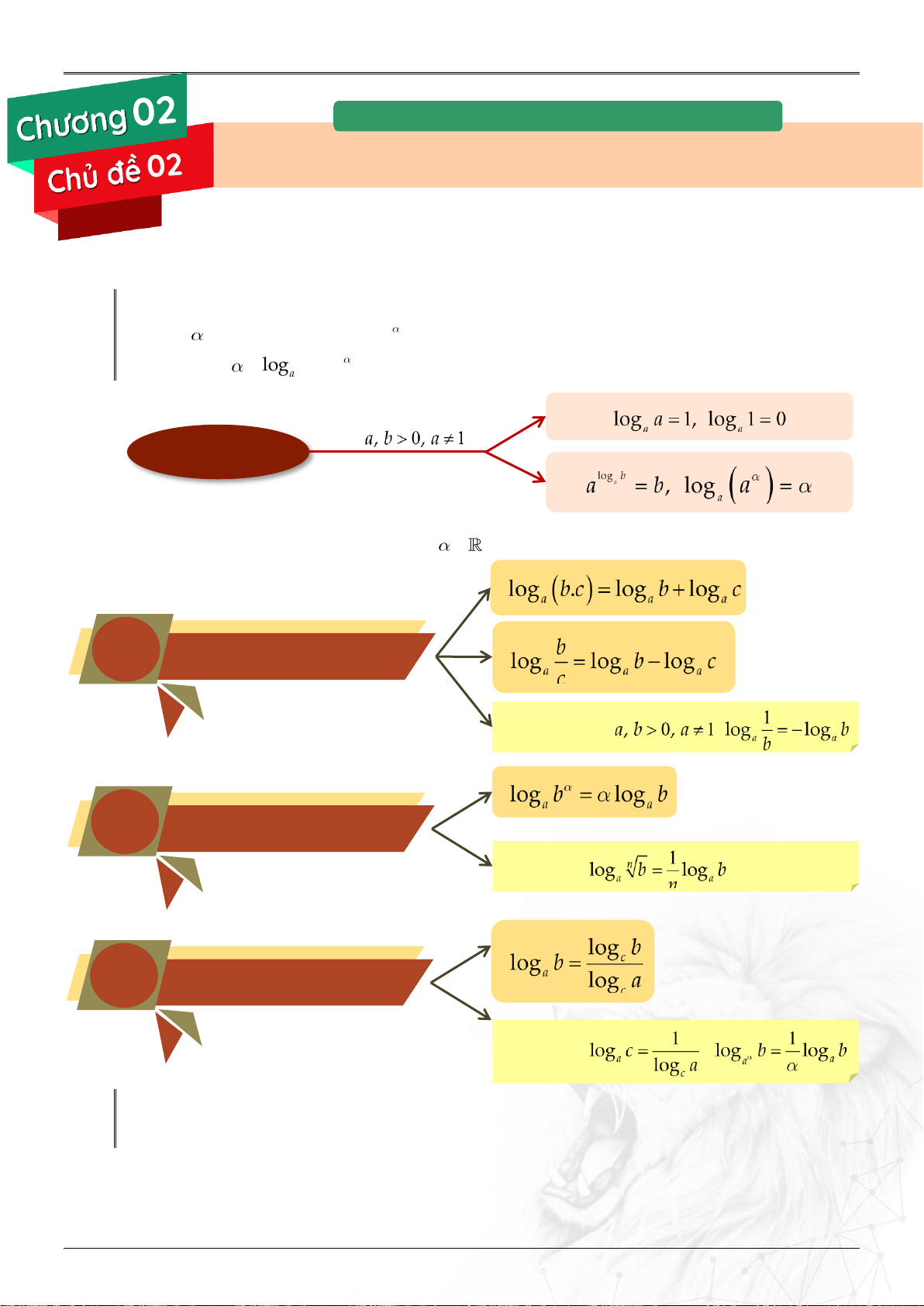
 Ta viết:  log b  a  . b a 2. Tính chất. Cho TÍNH CHẤT 3. Công thức.
 Cho 3 số dương a, b ,c với a 1;c 1 và   , ta có các công thức sau:
1 Tích tổng – Thương hiệu Đặc biệt: với 2 Lũy thừa Đặc biệt: 3 Đổi cơ số Đặc biệt: ;
 Logarit thập phân và Logarit tự nhiên
 Logarit thập phân là logarit cơ số 10. Viết : log b  logb  lgb 10
 Logarit tự nhiên là logarit cơ số e . Viết : log b  lnb e
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 11
Tổng Hợp Lý Thuyết
Năm học: 2023-2024 B. CÁC DẠNG BÀI TẬP.
 Dạng 2.1. Tính giá trị biểu thức
 Áp dụng các tính chất – công thức để biến đổi:
⓵ log a 1, log 1 0 a a ⓶ log ba a
 b, log a  a   ⓷ log b c  b  c (Tích – tổng) a  .  01 log log Tính chất a a ⓸ b log
 log b  log c (Thương – hiệu) a a a c 1
Đặc biệt : với a, b  0, a  1 log  log b a a b
⓵ log b  log b ⓶ 1 log b  log b a a a a 02
Công thức bay 1
Đặc biệt: log n b  log b a a n ⓵ log b log c b 
⓶ log b  log .clog b a log a a a c 03 Đổi cơ số c 1
Đặc biệt : log c  . a log a c  Ví dụ 2.1.1 log 4
Cho 0  a 1. Tính giá trị của biểu thức a a . A. 16. B. 2 . C. 4 . D. 12 Lời giải
.......................................................................................................................................................  Ví dụ 2.1.2
Tính giá trị của biểu thức A  2log 12  3log 5  log 15  log 150 . 2 2 2 2 A. 2  . B. 2 3 . C. 3 . D. 3 2 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 2.1.3 Rút gọn biểu thức 2 4 6 8
K  log b  2 log b  3log b  4log b ta được 2 3 4 a a a a 1
A. 4log b . B. log b .
C. 3log b .
D. log a a a a 2 b Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 12
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 2.2. Biểu diễn logarit
 Ta thực hiện theo các bước sau
 Bước 01. Biến đổi các biểu thức logarit phụ thuộc vào tham số a và b .
 Bước 02. Đặt các biểu thức logarit của các số nguyên tố là các ẩn x, y,z …. Từ đó ta
thu được phương trình hoặc hệ phương trình với các ẩn x, y, z …. Ta tìm
các ẩn này theo a,b
 Bước 03. Giải hệ tìm được tìm x, y,z … theo a,b . Từ đó tính được biểu thức theo các log b 1
tham số a,b Các công thức nền tảng là log c b  và  log a a log a log b b c a  Ví dụ 2.2.1
Cho a  log 14 . Biểu diễn log 16 theo a 2 49 2 2 A. .
C. a  3. D. 3a a  . B. 1 a Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 2.2.2
Cho a  log 18 và b  log 60. Tính log 2 theo a và b 5 5 3 b  2 2 3a  ab
a  2b  2 a  2 A. . B. . D. 2a  b 5a  . C. 4 2a  b 1 a 1 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 13
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 2.3. Mệnh đề đúng – sai
 Ta lưu ý các công thức sau
⓵ log a 1, log 1 0 a a ⓶ log ba a
 b, log a  a   ⓷ log b c  b  c (Tích – tổng) a  .  log log 01 Tính chất a a ⓸ b log
 log b  log c (Thương – hiệu) a a a c 1
Đặc biệt : với a, b  0, a  1 log  log b a a b
⓵ log b  log b ⓶ 1 log b  log b a a a a 02
Công thức bay 1
Đặc biệt: log n b  log b a a n ⓵ log b log c b 
⓶ log b  log .clog b a log a a a c 03 Đổi cơ số c 1
Đặc biệt : log c  . a log a c  Ví dụ 2.3.1
Cho a,b,c  0; a  1; b  1. , Trong các khẳng định sau, khẳng định nào sai? 1 A. log b  . B. log .
b log c  log c . a log a a b a b
C. log b  c b . D. log b c  b  c . a  .  log log c loga a a a Lời giải
.......................................................................................................................................................  Ví dụ 2.3.2
Cho a,b,c  0 và a,b  1, Trong các khẳng định sau, khẳng định nào sai? A. log b a a  b.
B. log b  log c  b  c . a a log c C. log a c  .
D. log b  log c  b  c . b log b a a a Lời giải
.......................................................................................................................................................  Ví dụ 2.3.3
Cho a,b,c  0 và a,b  1, Trong các khẳng định sau, khẳng định nào sai? 1 A.  log a . B. log .
b log c  log c . log b b a b a a b C. log  .
b c  log b  c .
D. log b  log c  log . a a   a a a c Lời giải
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 14
Tổng Hợp Lý Thuyết
Năm học: 2023-2024  Ví dụ 2.3.4
Cho a  0,b  0 thỏa mãn 2 2
a  b  7ab . Mệnh đề đúng trong các mệnh đề sau là: a  b 1
A. 2log a  logb  log7ab . B. log
 log a  logb. 3 2 1 3
C. 3log a  b  log a  log b .
D. log a  b  log a  log b. 2 2 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 2.3.5
Với mọi số a , b  0 thỏa mãn 2 2
9a  b 10ab thì đẳng thức đúng là.
log 3a  b log a  log b
A. 2log 3a  b  log a  log b . B.  . 4 2 3a  b 1
C. log a  log b   1  1. D. log
 log a  logb . 4 2 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 15
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
LŨY THỪA – MŨ – LOGARIT
HÀM SỐ MŨ – HÀM SỐ LOGARIT A. LÝ THUYẾT CHUNG. 1. Hàm số mũ. Hàm số mũ x
y  a , a  0,a   1
Tập xác định D  . f x
Tập giá trị
T  0;  , nghĩa là khi giải phương trình mà đặt t  a thì t  0. f x gx a 1 Hàm số x
y  a đồng biến, khi đó: a  a
 f x  gx . Đơn điệu f x gx 0  a 1 Hàm số x
y  a nghịch biến, khi đó: a  a
 f x  gx .    x a  x
 a .ln a   u
a   u . u  a .ln a    x e  x
 e   ue  u Đạo hàm  e .u   u
n u   n n 1 . n u 
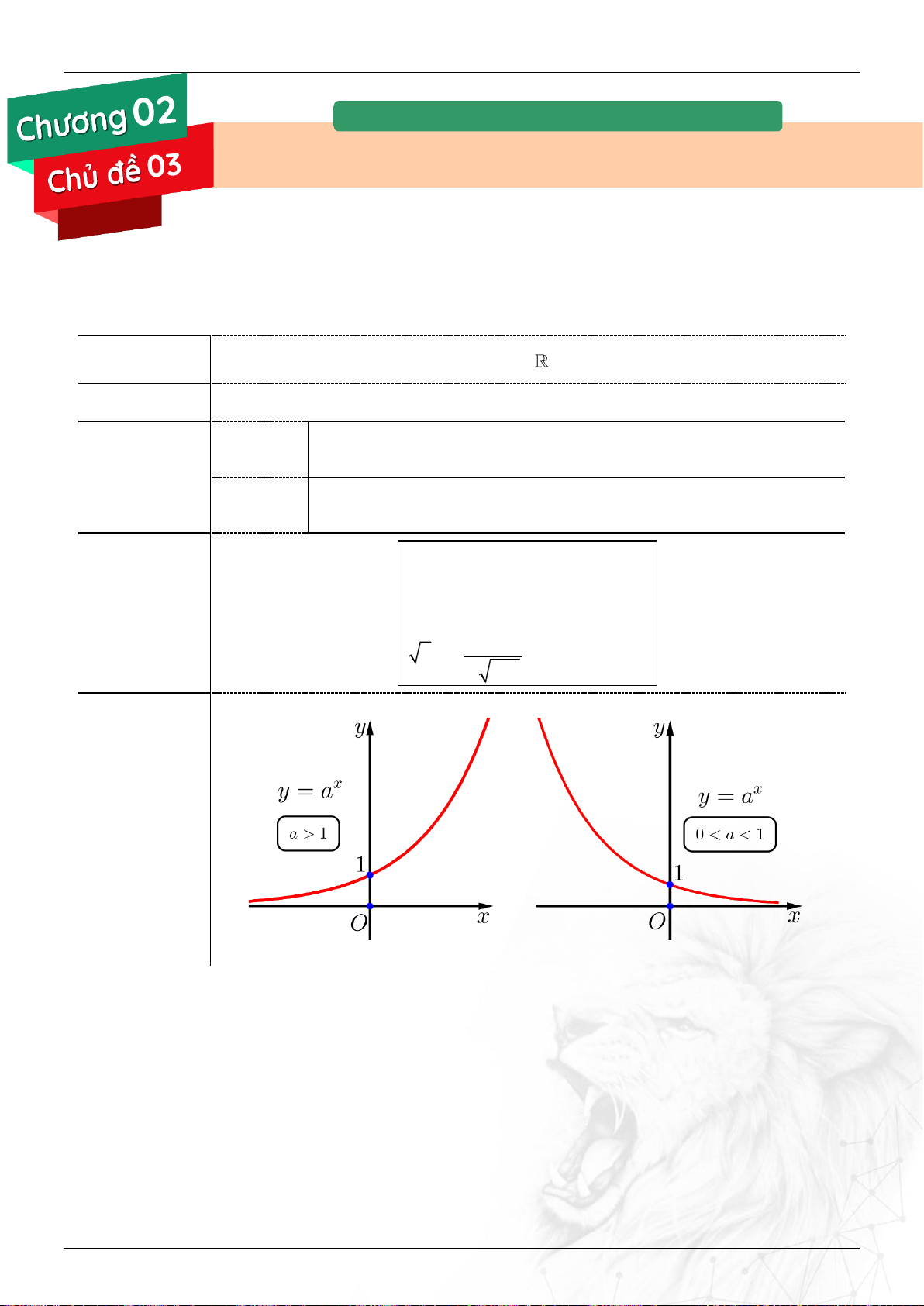
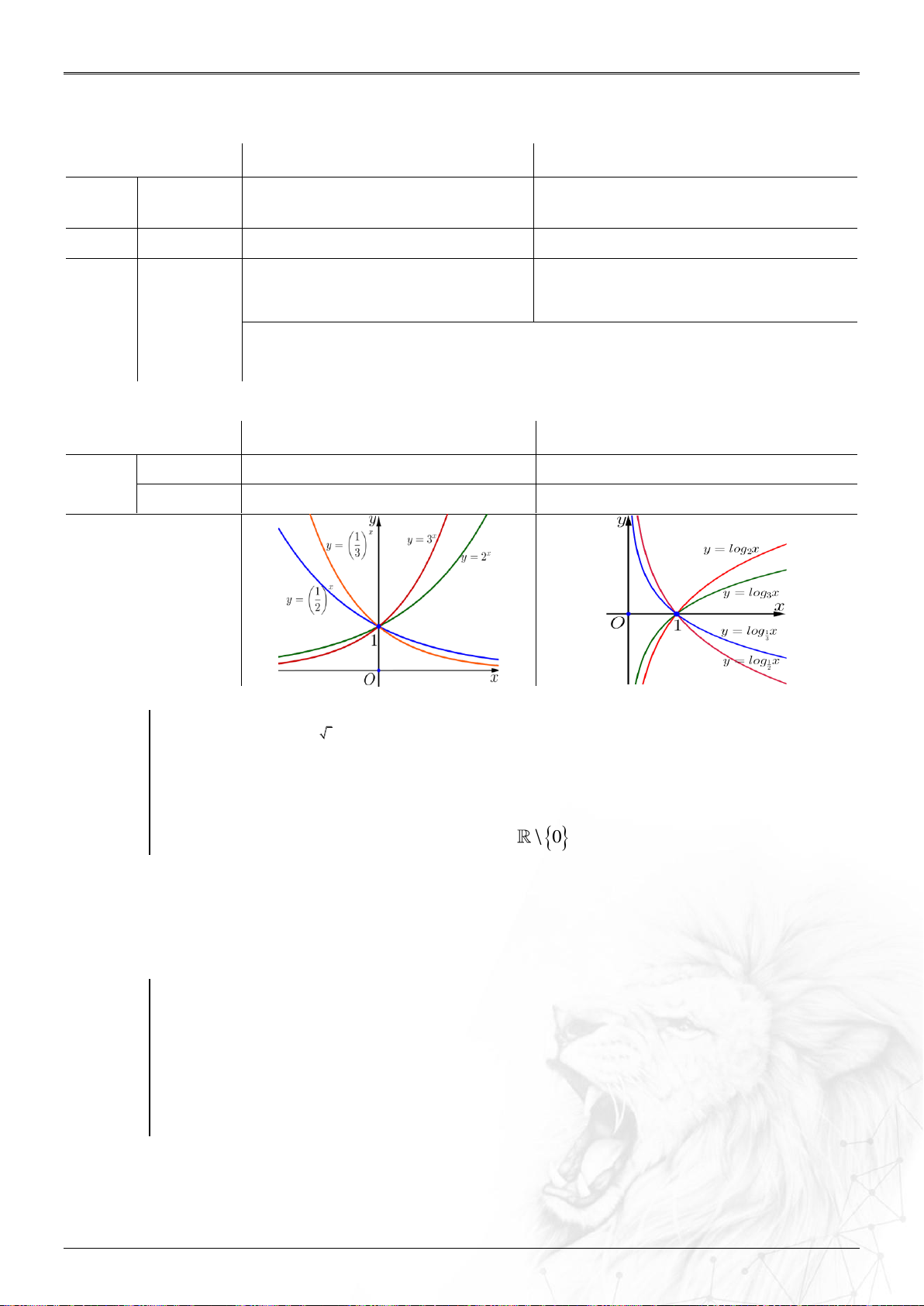
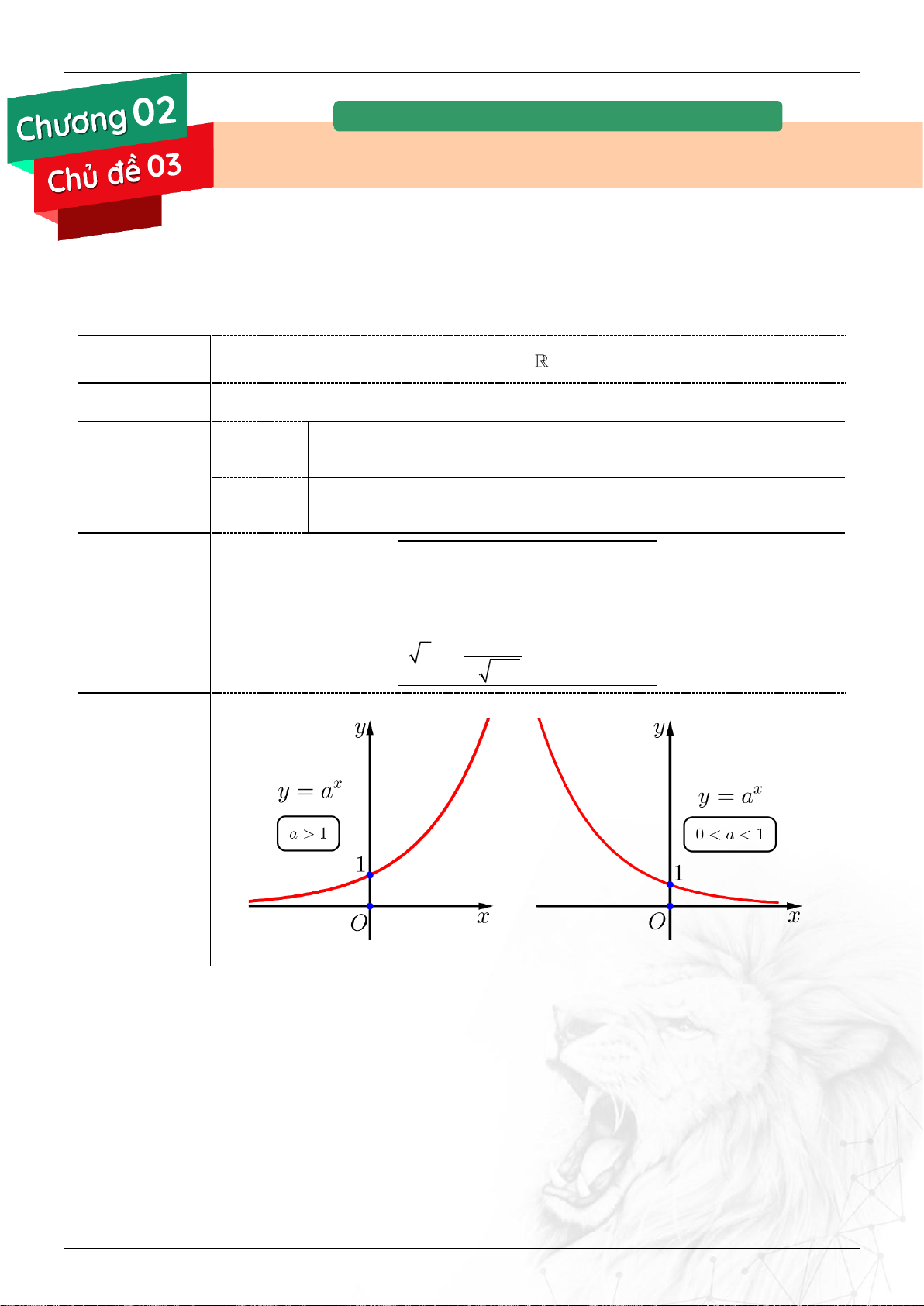
Nhận trục hoành làm đường tiệm cận ngang Đồ thị
 Nhận xét: Đồ thị hàm số x
y  a a  
1 đối xứng với đồ thị hàm số x
y  a 0  a   1 qua Oy.
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 16
Tổng Hợp Lý Thuyết
Năm học: 2023-2024 2. Hàm số logarit.
Hàm số logarit y  log x, a  a  x  a  0, 1; 0
Tập xác định
D  0;   .
Tập giá trị T 
, nghĩa là khi giải PT mà đặt t  log x thì t không có điều kiện. a
Hàm số y  log x đồng biến trên D , khi đó: a a 1
log f x  log g x  f x  g x . a a       Đơn điệu
Hàm số y  log x nghịch biến trên D , khi đó: a 0  a 1
log f x  log g x  f x  g x . a a          u log x   u  a  1 loga  . x ln a . u ln a  u  Đạo hàm  lnn u  n 1
 n ln u  u u ln x 1
 , x  0  (ln u)  x u
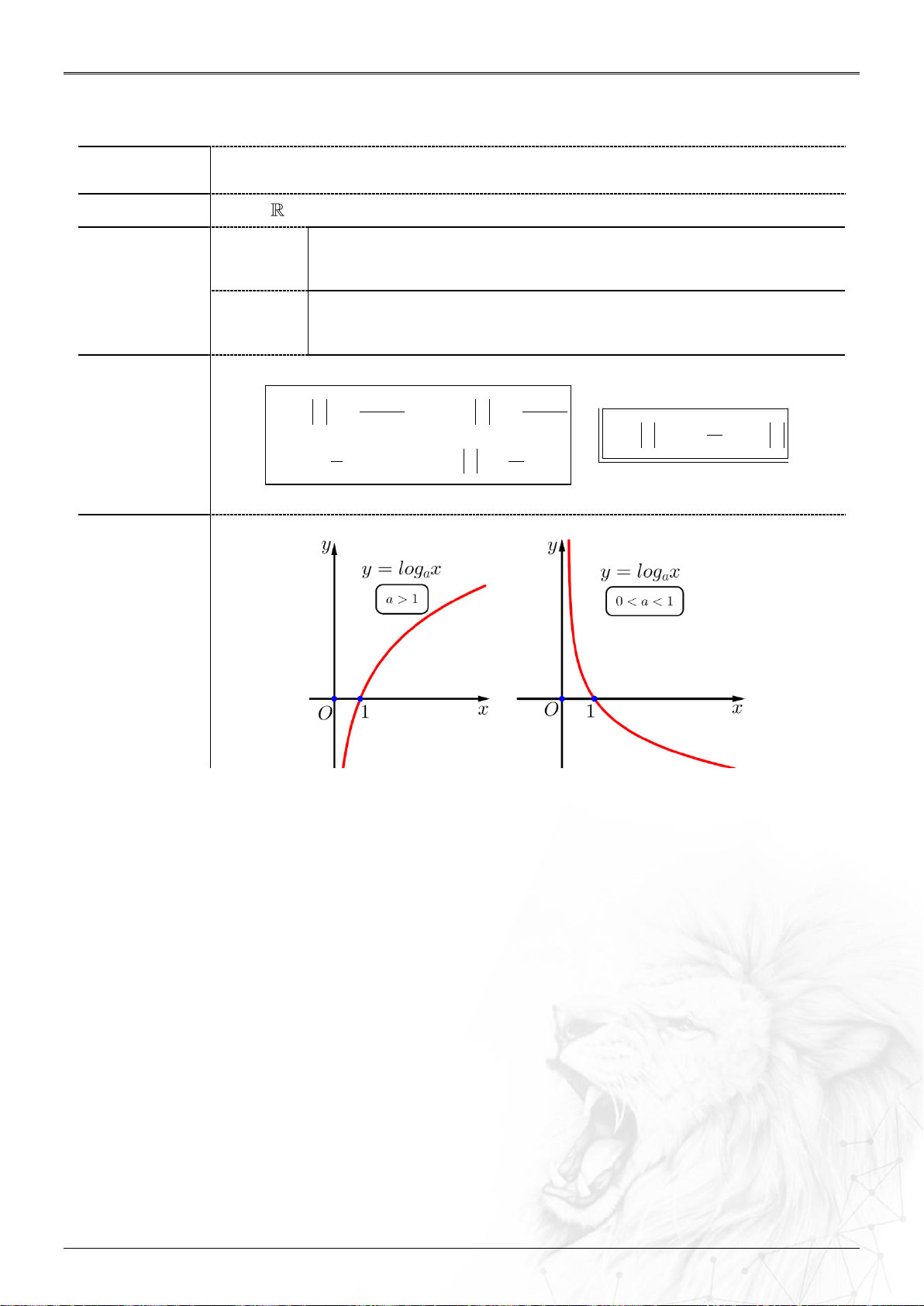
Nhận trục tung làm đường tiệm cận đứng Đồ thị
 Nhận xét:
Đồ thị hàm số y  log x a 
đối xứng với đồ thị hàm số y  log x
 a  qua Ox. a 0 1 a  1
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 17
Tổng Hợp Lý Thuyết
Năm học: 2023-2024 B. CÁC DẠNG BÀI TẬP.
 Dạng 3.1. Tập xác định của hàm số logarit a  0 
 Điều kiện xác định của hàm số y  log f x : a  1 . a
  fx0  n
Đặc biệt: với hàm số y  log  f x  f x : g x     
 ta lưu ý “mũ n” của  
gx  0   n Nếu n 2 
ĐKXĐ của hàm số y  log
 f x  gx 1 . g x     
 : fx0
gx  0   n Nếu n 2 
 ĐKXĐ của hàm số y  log
 f x  gx 1 . g x     
 : fx0
Tóm lại nếu f x hoặc gx có “mũ n” ta chú ý xem “n” chẵn hay lẻ.  Ví dụ 3.1.1
Tìm tập xác định D của hàm số y  log 2x 1 . 3    1   1   1 
A. D  ;    . B. D  ;     .
C. D  0;   . D. D   ;     .  2   2   2  Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 3.1.2
Tìm tập xác định D của hàm số y  log  2
x  3x  2 . A. D   2  , 1  .  
B. D  , 2   1  , . C. D   2  ,  1 .
D. D  , 2     1  ,   . Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 3.1.3
Tập xác định của hàm số: y  log x  2 2 là A. B.  \  2 .
C. 2;  . D. 2;    . Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 18
Tổng Hợp Lý Thuyết
Năm học: 2023-2024  Ví dụ 3.1.4 2  x
Tập xác định của hàm số: y  log là 1 x  2 2 A. 0; 2   B. 0; 2. C.  ;  2  0;2   . D.  2  ; 2 . Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 3.1.5 2021
Tập xác định của hàm số: 2 y  log
x  3x  2  ln 3  x là 2      x 1
A. D  ;   1   1  ;00; 
1  2;3 B. D  ;   1  2;3 .
C. D  ;   1   1  ;  1  2;3 .
D. D  ;   1 . Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 3.1.6
Tìm tất cả các giá trị thực của tham số m để hàm số 2
y  ln(x  2mx  4) có tập xác định D  ? m  2 A. 2   m  2 B.  . m  2   C. m  2  . D. 2
  m  2. Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 19
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 3.2. Đạo hàm hàm số mũ – logarit    u log x   u  a  1 loga     x a u a u
Đạo hàm hàm số logarit: .ln .ln  lnn u  n 1
 n ln  u  u u ln x 1
 , x  0  (ln u)  x u    x a  x
 a .ln a   u
a   u . u  a .ln a  
 Đạo hàm hàm số mũ:  xe x
 e   ue  u  e .u   u
n u   n n 1 . n u   Ví dụ 3.2.1
Đạo hàm của hàm số y  log 4x 1 là 3   1 4 A. y   . B. y  . . 4x   1 ln 3 4x 1ln3 ln 3 4 ln 3 C. y  . D. y  . . 4x 1 4x 1 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 3.2.2 2 Hàm số 2 2 x x y   có đạo hàm là 2 A.   22 4 1 2 x x y x     ln2 B. 2 2 x x y    ln2 . 2 C.      2x x y x ln  2 4 1 2
2x  x D.   2 2 2 2 2 x x y x x     ln2 . Lời giải
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 3.2.3
Tính đạo hàm của hàm số 1 2 x y   . ln 2 ln 2 A. 1   2 . x y B. 1   2 . x y . 2 1 x 2 1 x 1 2 x  1 2 x C. y  D. y  . 2 1 x 2 1 x Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 20
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 3.3. Khảo sát hàm số mũ – logarit
 Ta cần lưu ý các vấn đề sau: Hàm số Mũ x
y  a 1  a  0
Hàm số Logarit y  log x  a  a 1 0
 a 1HS đồng biến.
 a 1HS đồng biến. 01
Đơn điệu  0 a 1HS nghịch biến.
 0  a 1HS nghịch biến. 02
Tiệm cận Nhận Ox làm TCN. Nhận Oy làm TCĐ. Nằm bên trên Ox . Nằm bên phải Oy .
Luôn đi qua điểm 0;  1 .
Luôn đi qua điểm 1;0 . 03 Đồ thị ĐTHS x
y  a 1  a  0 đối xứng y  log x  a 
qua y  x (đường a 1 0
phân xác góc phần tư thứ nhất).
 Với bài toán xét thứ tự cơ số ta nhớ như sau: Hàm số Mũ x
y  a 1  a  0
Hàm số Logarit y  log x  a  a 1 0 1
Càng gần Oy cơ số càng lớn.
Càng gần Ox cơ số càng lớn. Cơ số
0  a 1 Càng gần Oy cơ số càng bé.
Càng gần Ox cơ số càng bé.
Hình minh họa  Ví dụ 3.3.1
Cho hàm số y  log x . Mệnh đề nào dưới đây là mệnh đề sai? 3
A. Hàm số đã cho đồng biến trên tập xác định.
B. Đồ thị hàm số đã cho không có tiệm cận ngang.
C. Đồ thị hàm số đã cho có một tiệm cận đứng là trục Oy .
D. Hàm số đã cho có tập xác định D   \  0 . Lời giải
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 3.3.2
Cho hàm số y  log x . Mệnh đề nào dưới đây sai? 2
A. Đạo hàm của hàm số là 2
y  x ln 2 .
B. Đồ thị hàm số nhận trục Oy làm tiệm cận đứng.
C. Tập xác định của hàm số là  ;  .
D. Hàm số đồng biến trên khoảng 0;  . Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 21
Tổng Hợp Lý Thuyết
Năm học: 2023-2024  Ví dụ 3.3.3
Tìm mệnh đề đúng trong các mệnh đề sau:
A. Hàm số y  log x với a 1 là một hàm số nghịch biến trên khoảng 0, . a
B. Đồ thị hàm số y  log x và y  log x với 0  a 1 đối xứng với nhau qua Ox. a 1 a
C. Hàm số y  log x với 0  a 1 có tập xác định là . a
D. Hàm số y  log x với 0  a 1 là một hàm số đồng biến trên khoảng 0, a Lời giải
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 3.3.4
Đồ thị hàm số y  logx  
1 nhận đường thẳng nào dưới đây làm tiệm cận đứng ? A. x 1 B. y  1  . C. x  1 
D. x  0 . Lời giải
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 3.3.5
Hàm số nào sau đây nghịch biến trên tập xác định của nó? x
A. y   5
B. y  log x . 2e x  5 
C. y    D. y  log x .   2  1 6 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 3.3.6 Cho các hàm số x  , x y a y  b và x
y  c lần lượt có đồ
thị như hình vẽ bên dưới. Hãy so sánh a,b,c .
A. a  b  c
B. a  b  c .
C. a  b  c
D. b  a  c . Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 22
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
LŨY THỪA – MŨ – LOGARIT BÀI TOÁN LÃI SUẤT A. LÝ THUYẾT CHUNG. 1. Lãi đơn.
 Số tiền lãi chỉ tính trên số tiền gốc mà không tính trên số tiền lãi do số tiền gốc sinh ra.
 Công thức tính lãi đơn:  Trong đó:
V : Số tiền cả vốn lẫn lãi sau n kỳ hạn; n  1 . n V V r n 0  
V : Số tiền gửi ban đầu; 0
n : Số kỳ hạn tính lãi;
r : Lãi suất định kỳ, tính theo %. 2. Lãi kép.
 Số tiền lãi không chỉ tính trên số tiền gốc mà còn tính trên số tiền lãi do tiền gốc đó sinh
ra thay đổi theo từng định kỳ.
 Ta có các loại lãi kép sau:
2.1. Lãi kép, gửi một lần:  Trong đó:
T : Số tiền cả vốn lẫn lãi sau n kỳ hạn; n n  1 n T T r
T : Số tiền gửi ban đầu; 0   0
n : Số kỳ hạn tính lãi;
r : Lãi suất định kỳ, tính theo %.
2.2. Lãi kép liên tục:  Trong đó:
T : Số tiền cả vốn lẫn lãi sau n kỳ hạn; n  . nr n T T e 0
T : Số tiền gửi ban đầu; 0
n : Số kỳ hạn tính lãi;
r : Lãi suất định kỳ, tính theo %.
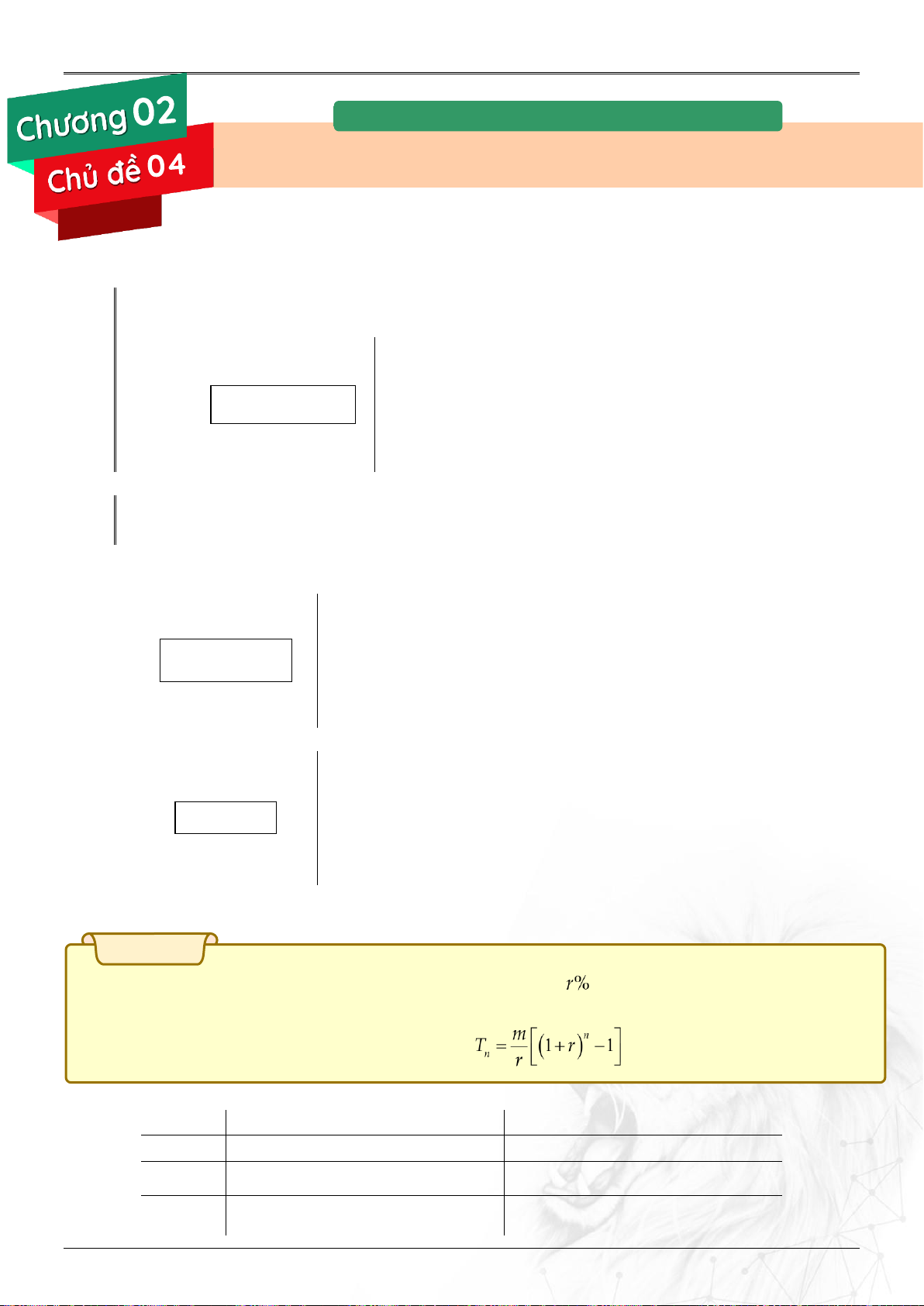
2.3. Lãi kép, gửi định kỳ.
2.3.1. Trường hợp gửi tiền định kì cuối tháng. Bài toán 1
Cứ cuối mỗi tháng gửi vào ngân hàng m triệu, lãi suất kép (tháng hoặc năm).
Hỏi sau n (tháng hoặc năm) số tiền thu được là bao nhiêu?
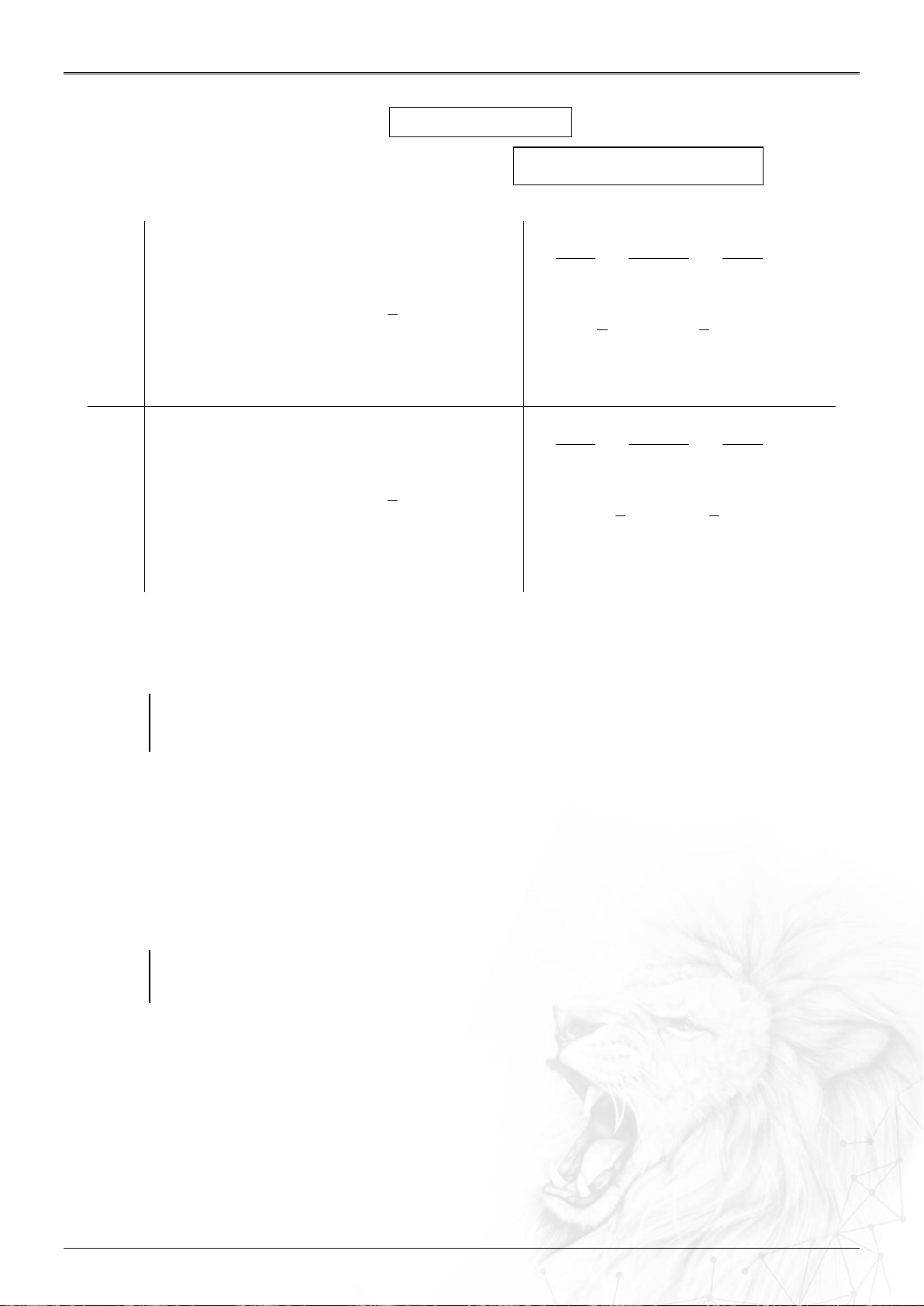
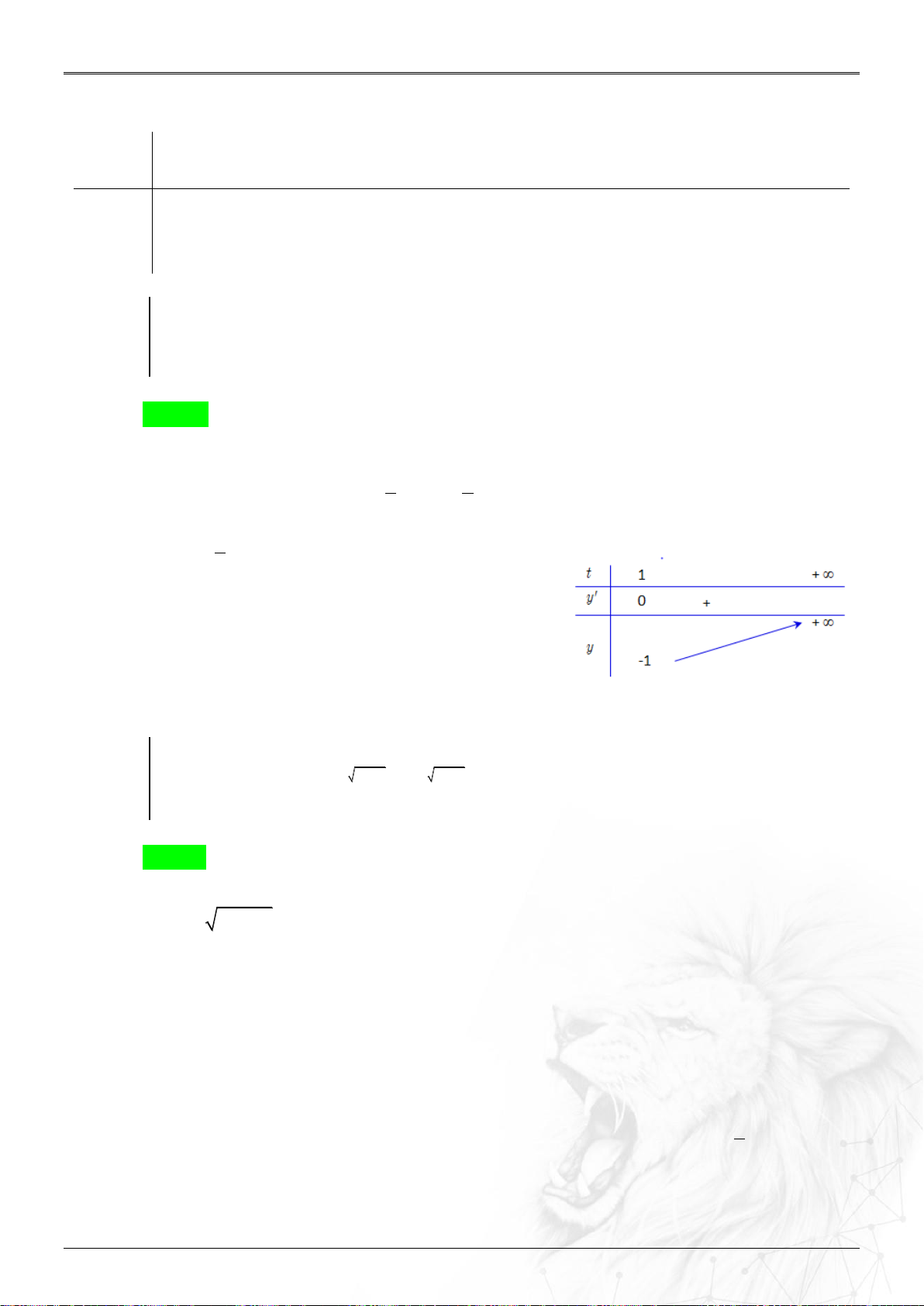
Người ta chứng minh được số tiền thu được là: .
 Chứng minh Tháng Đầu tháng Cuối tháng 1 Chưa gửi m 2 m
m1 r  m 2 3
m1 r  m
m1 r  m1 r  m
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 23
Tổng Hợp Lý Thuyết
Năm học: 2023-2024 … … … n 1  n
m1 r  ... m1 r  m   n 1 n 1 
Vậy sau tháng n ta được số tiền T  m  r
  m  r  m m   1 r
 ... 1 r 1 n 1  ... 1    ,   n
Ta thấy trong ngoặc là tổng n số hạng của cấp số nhân có u  1, u   r q   r n 1  1 , 1 1 n   q 1 m n Biết rằng:  
S  u  ...  u  u . nên T   r  n 1  1 n 1 n 1 q 1 r   Bài toán 2
Cứ cuối mỗi tháng gửi vào ngân hàng m triệu, lãi suất kép
(tháng hoặc năm). Sau n (tháng
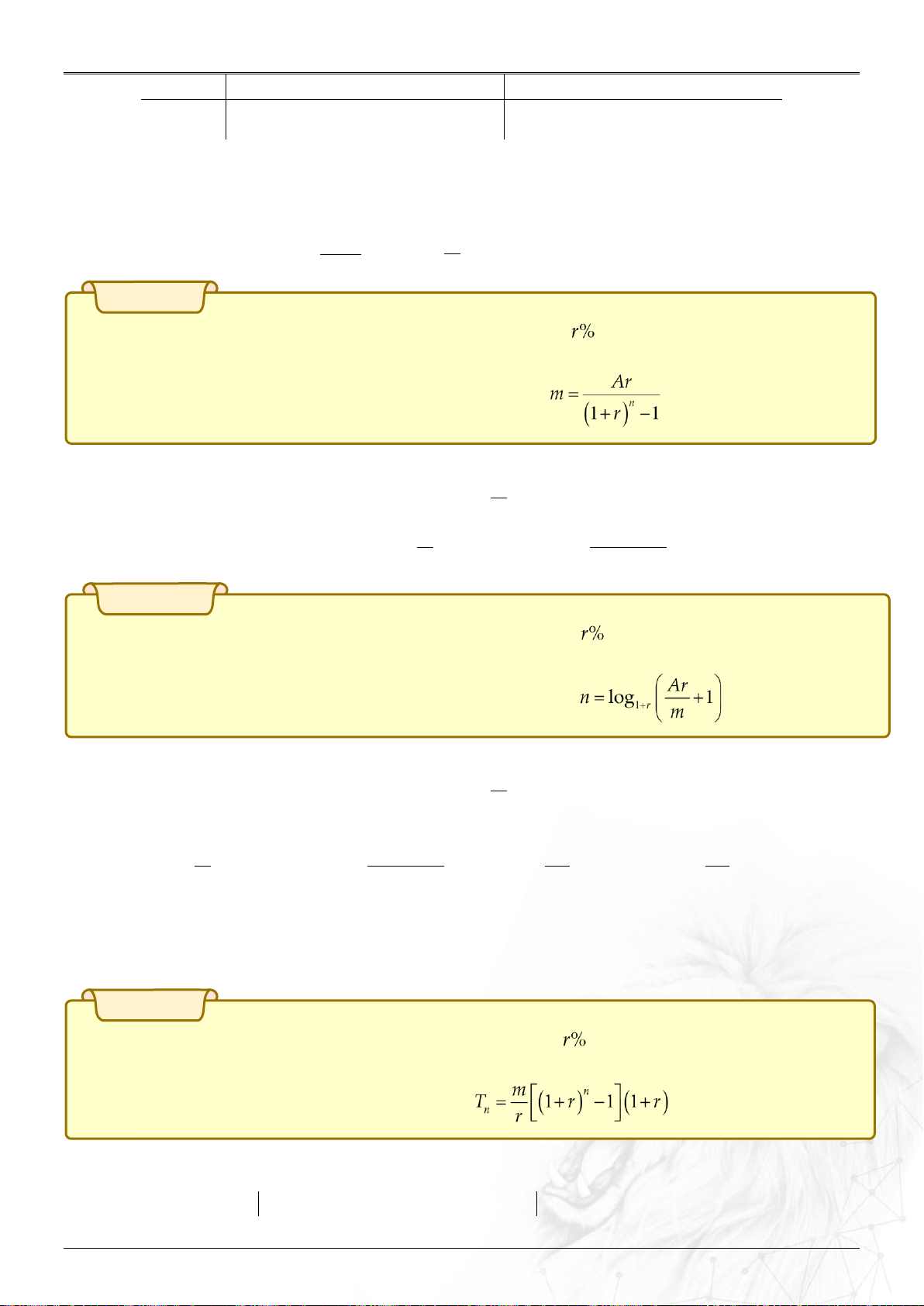
hoặc năm) số tiền thu được là A triệu. Hỏi số tiền gửi mỗi tháng m là bao nhiêu?
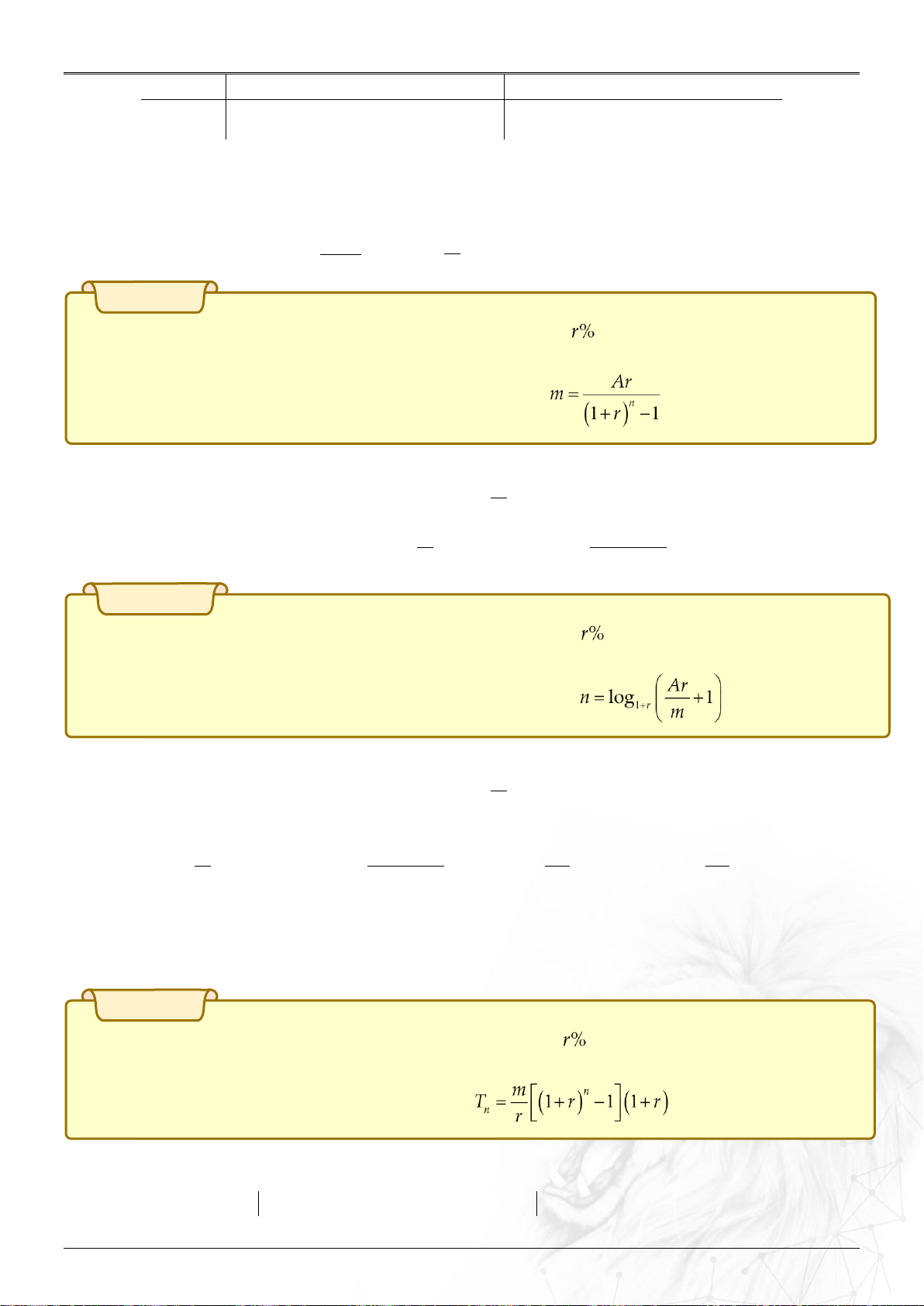
Người ta chứng minh được số tiền cần gửi mỗi tháng là: .
 Chứng minh  m n
Áp dụng bài toán 1 ta có số tiền thu được là T  r     n 1  1 r   ,  m n   Ar
Mà đề cho số tiền đó chính là A nên A 
1r 1  m  . r    n 1 r 1 Bài toán 3
Cứ cuối mỗi tháng gửi vào ngân hàng m triệu, lãi suất kép
(tháng hoặc năm). Sau n (tháng
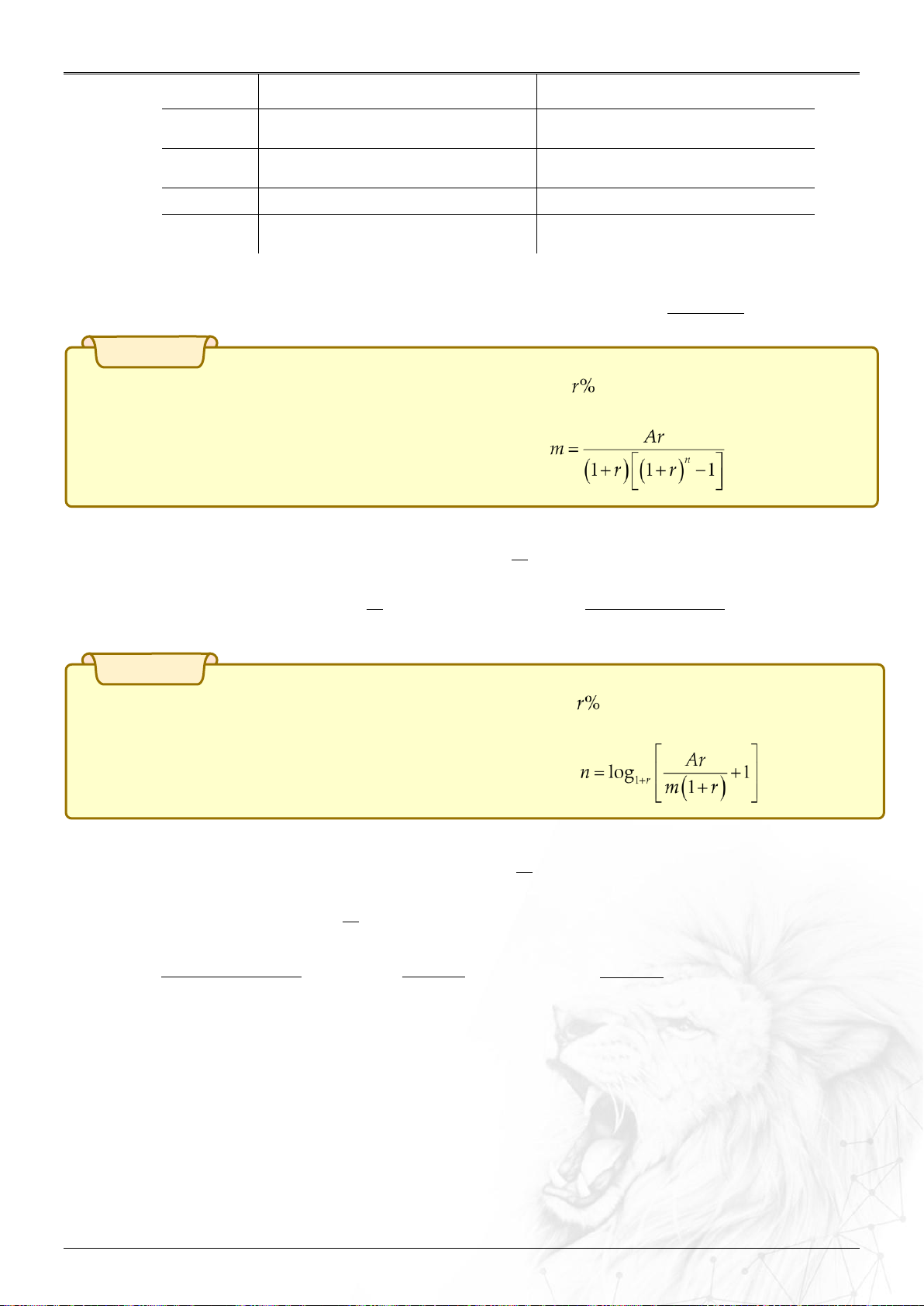
hoặc năm) số tiền thu được là A triệu. Hỏi số tháng hoặc năm n là bao nhiêu?
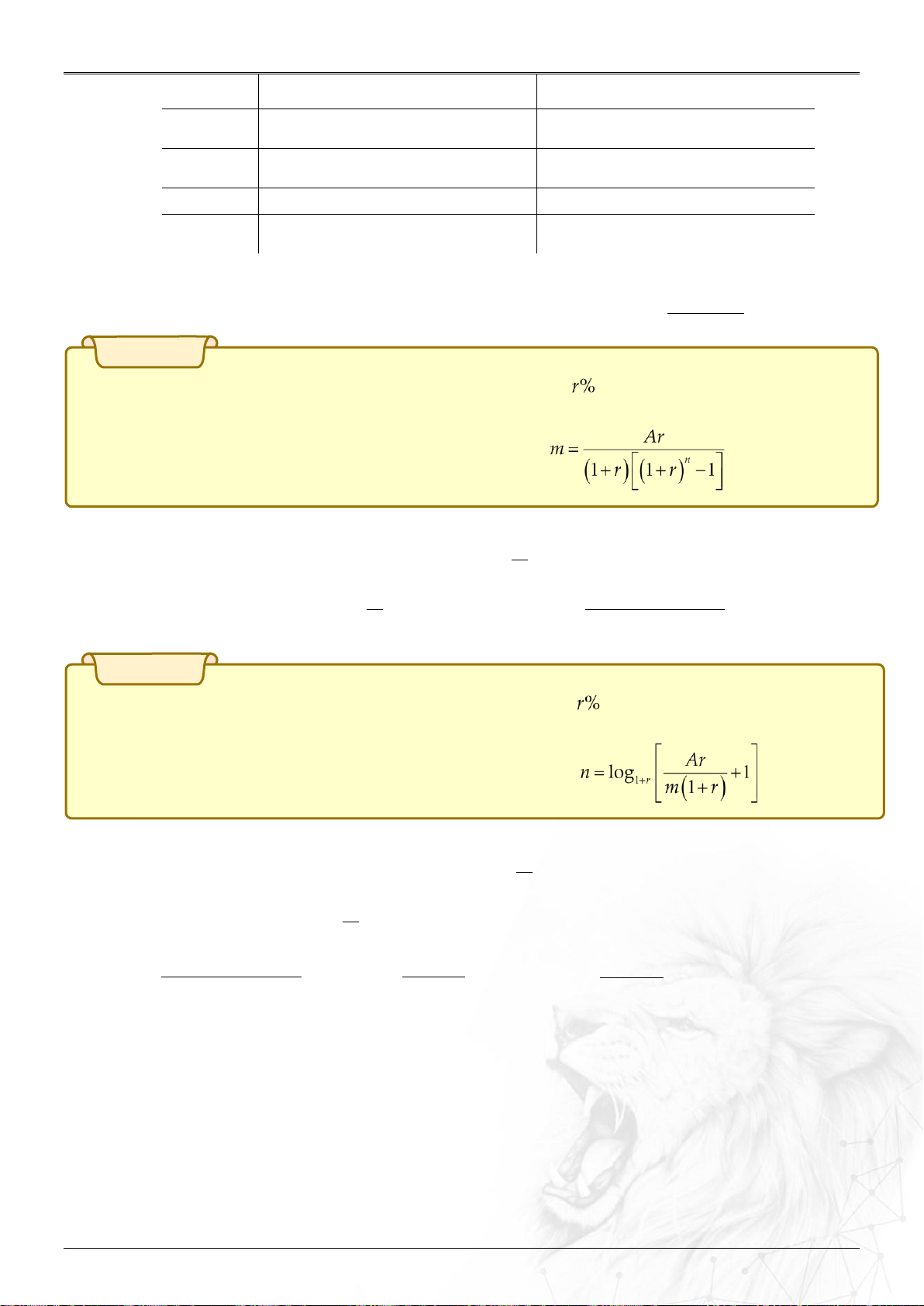
Người ta chứng minh được số tháng thu được đề bài cho là: .
 Chứng minh  m n
Áp dụng bài toán 1 ta có số tiền thu được là T  r     n 1  1 r   .
 Đề cho số tiền đó chính là A nên: m    n  Ar n Ar  Ar  A
1 r  1  m    r    n       n 1  r   log r 1  1 1 1 1 m  m r 
 Như vậy trong trường hợp 2.3.1 này ta cần nắm vững công thức bài toán 1 từ đó có thể dễ
dàng biến đổi ra các công thức ở bài toán 2, bài toán 3.
2.3.2. Trường hợp gửi tiền định kì đầu tháng. Bài toán 4
Cứ đầu mỗi tháng gửi vào ngân hàng m triệu, lãi suất kép (tháng hoặc năm).
Hỏi sau n (tháng hoặc năm) số tiền thu được là bao nhiêu?
Người ta chứng minh được số tiền thu được là: .
 Chứng minh
 Ta xây dựng bảng sau: Tháng Đầu tháng Cuối tháng
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 24
Tổng Hợp Lý Thuyết
Năm học: 2023-2024 1 m m1 r 2 2
m1 r  m
m1 r  m1 r 2 3 2 3
m1 r  m1 r  m
m1 r  m1 r  m1 r … … … n n …
m1 r  ... m1 r
 Vậy sau tháng n ta được số tiền: n  r  T m r m r m  r r             m  r n  n n ...     ...    1  1 1 1 1 1 1   r Bài toán 5
Cứ đầu mỗi tháng gửi vào ngân hàng m triệu, lãi suất kép
(tháng hoặc năm). Sau n (tháng
hoặc năm) số tiền thu được là A triệu. Hỏi số tiền gửi mỗi tháng m là bao nhiêu?
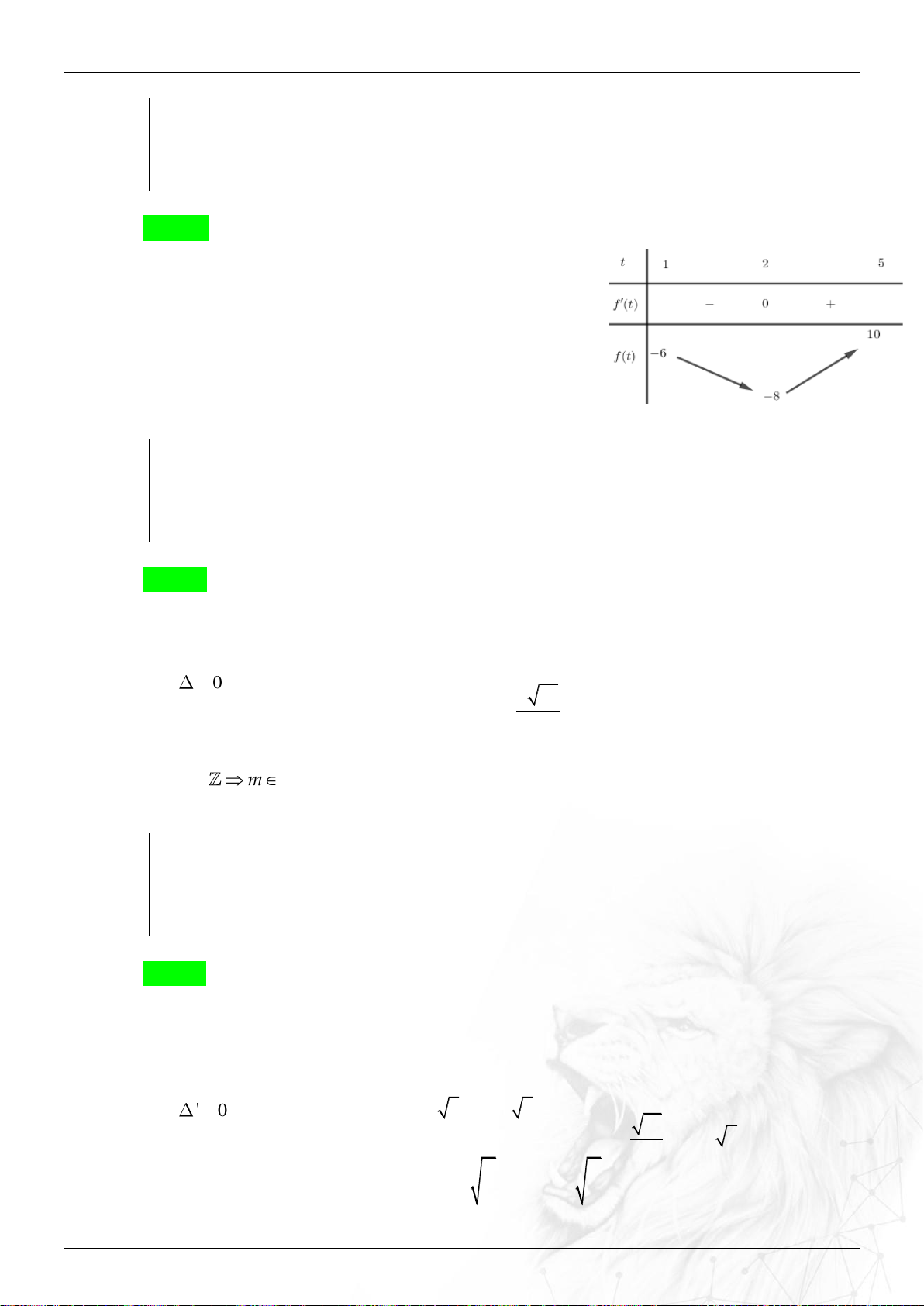
Người ta chứng minh được số tiền cần gửi mỗi tháng là: .
 Chứng minh  m n
Áp dụng bài toán 4. Ta có số tiền thu được là: T  r      r n 1  1 1  r   ,  m n   Ar
Mà đề cho số tiền đó là A nên A 
1r 1 1r  m  . r    n  
1 r 1 r 1   Bài toán 6
Cứ đầu mỗi tháng gửi vào ngân hàng m triệu, lãi suất kép
(tháng hoặc năm). Sau n (tháng
hoặc năm) số tiền thu được là A triệu. Hỏi số tháng hoặc năm n là bao nhiêu?
Người ta chứng minh được số tháng thu được đề bài cho là: .
 Chứng minh  m n
Áp dụng bài toán 4. Ta có: số tiền thu được là: T  r      r n 1  1 1  r   .  m n
Đề cho số tiền đó là A nên: A   
1 r 1 1 r r   Ar       n Ar Ar m 1 r         n log 1  .
   n  m   r 1 r m  1 r r r  1 1 1 1 1     
 Như vậy trong trường hợp 2.3.2 ta cần nắm vững công thức bài toán 4 từ đó có thể dễ dàng
biến đổi ra các công thức ở bài toán 5, bài toán 6.
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 25
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
2.3.3. Trường hợp vay nợ và trả tiền định kì đầu tháng. Bài toán 7
Vay ngân hàng A triệu đồng. Cứ đầu mỗi tháng (năm) trả ngân hàng m triệu, lãi suất kép
(tháng hoặc năm). Hỏi sau n (tháng hoặc năm) số tiền còn nợ là bao nhiêu?
Người ta chứng minh được số tiền còn nợ là: .
 Chứng minh
 Ta xây dựng bảng sau: Tháng Đầu tháng Cuối tháng 1 A  m
Am1r  A1rm1r 2 2 2
A1 r  m1 r  m
A1 r  m1 r  m1 r 2 2 3 3 2 3
A1 r  m1 r  m1 r  m A1 r  m1 r  m1 r  m1 r … … … n n 2 n …
A1 r  m1 r ... m1 r  m1 r
 Vậy sau tháng n ta còn nợ số tiền:
T  A  r  m  r   m  r  m  r n  n  n ...  2 1 1 1 1  n     n  n n r A r m r ...  r        
 A  r  m  r 1  1 1 1 1 1 1   . r
3. Bài toán tăng trưởng dân số.  Công thức tính:  Trong đó:    m X n X  m n 1 r
r : tỉ lệ tăng dân số từ năm n đến năm m. 
X : dân số năm m. m,n  
; m  n m
X : dân số năm n. n X 
Từ đó ra có công thức tính tỉ lệ tăng dân số là m
r  mn 1 . Xm  Ví dụ 4.1
Bà Hoa gửi 0,45% triệu vào tài khoản định kỳ tính lãi kép với lãi suất là 8% / năm.
Tính số tiền lãi thu được sau 10 năm. Lời giải
 Áp dụng công thức tính lãi kép, sau 10 năm số tiền cả gốc và lãi bà Hoa thu về là   n A r    , 10 1 100 1 0 08  215,892triệu đồng.
 Suy ra số tiền lãi bà Hoa thu về sau 10năm là 215,892 100 115,892 triệu đồng.  Ví dụ 4.2
Một người muốn gửi tiết kiệm ở ngân hàng và hi vọng sau 4 năm có được 850 triệu
đồng để mua nhà. Biết lãi suất ngân hàng mỗi tháng trong thời điểm hiện tại là
0,45% . Hỏi người đó mỗi tháng phải gửi vào ngân hàng tối thiểu bao nhiêu tiền
để đủ số tiền mua nhà ? (giả sử số tiền mỗi tháng là như nhau và lãi suất trong 4 năm là không thay đổi). Lời giải
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 26
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Giả sử người này gửi tiền ở thời điểm t nào đó , kể từ thời điểm này sau 4 năm (48
tháng) ông muốn có số tiền 850 triệu.
 Như vậy rõ ràng ta có thể coi đây là bài toán gửi tiền định kì đầu tháng. A r
 Áp dụng bài toán 5 ta có số tiền phải gửi mỗi tháng là : m    . n  
1 r  1 r 1  
 Theo bài ra n  48,r  0,45%,A  850 .  850 0 . , 45%
Thay vào  ta được m    , triệu đồng.  
1 0, 45% 1 0,45% 15 833 48 1    Ví dụ 4.3
Một bà mẹ Việt Nam anh hùng được hưởng số tiền là 4 triệu đồng trên một tháng
(chuyển vào tài khoản của mẹ ở ngân hàng vào đầu tháng). Từ tháng 1 năm 2016 mẹ
không đi rút tiền mà để lại ngân hàng và được tính lãi suất 1% trên một tháng.
Đến tháng 12 năm 2016 mẹ rút toàn bộ số tiền (gồm số tiền của 12 tháng và số tiền đã
gửi tháng 1). Hỏi khi đó mẹ lĩnh về bao nhiêu tiền ? (kết quả làm tròn theo đơn vị nghìn đồng). Lời giải
 Nếu ban đầu gửi vào a đồng, từ đầu tháng sau gửi thêm a đồng (không đổi) vào
đầu mỗi tháng với lãi suất r% trong n tháng thì tổng số tiền thu được là : a A a
 r  rn 4      1 1 1  4 
11% 11%11 1 4  50,73 r   1%   triệu đồng.
 n 11 là tính từ đầu tháng 2 đến cuối tháng 12.  Ví dụ 4.4
Đầu năm 2016, anh Hùng có xe công nông trị giá 100 triệu đồng. Biết mỗi tháng
thì xe công nông hao mòn mất 0, 4% giá trị, đồng thời làm ra được 6 triệu đồng
(số tiền làm ra mỗi tháng là không đổi). Hỏi sau một năm, tổng số tiền (bao gồm giá tiền
xe công nông và tổng số tiền anh Hùng làm ra) anh Hùng có là bao nhiêu? Lời giải
 Sau một năm số tiền anh Hùng làm ra là 6 1 . 2  72 triệu đồng
 Sau một năm giá trị xe công nông còn 12 100 1
(  0,4%)  95,3042 triệu đồng
 Vậy sau một năm số tiền anh Hùng có là 167,3042 triệu đồng  Ví dụ 4.5
Bác B gởi tiết kiệm số tiền ban đầu là 50 triệu đồng theo kỳ hạn 3 tháng với lãi suất
0,72% tháng. Sau một năm bác B rút cả vốn lẫn lãi và gởi theo kỳ hạn 6 tháng với lãi
suất 0,78% tháng. Sau khi gởi đúng một kỳ hạn 6 tháng do gia đình có việc bác gởi
thêm 3 tháng nữa thì phải rút tiền trước hạn cả gốc lẫn lãi được số tiền là 57 6 . 94 9 . 45,55
đồng (chưa làm tròn). Biết rằng khi rút tiền trước hạn lãi suất được tính theo lãi suất
không kỳ hạn, tức tính theo hàng tháng. Trong số 3 tháng bác gởi thêm lãi suất là Lời giải
 Số tiền bác B rút ra sau năm đầu:T  50 0 . 00 0 . 00 * 1 0,0072 * 34 1
 Số tiền bác B rút ra sau sáu tháng tiếp theo:T  T * 1 0,0078* 6 2 1  
 Số tiền bác B rút ra sau ba tháng tiếp theo: 57 6 . 94 9 . 45,55
T  T * 1 r3  57 6 . 94 9 . 45,55  r  3 1  0,004  0,4% . 3 2 T2
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 27
Tổng Hợp Lý Thuyết
Năm học: 2023-2024  Ví dụ 4.6
Bạn Nam là sinh viên của một trường Đại học, muốn vay tiền ngân hàng với lãi suất
ưu đãi trang trải kinh phí học tập hàng năm. Đầu mỗi năm học, bạn ấy vay ngân hàng
số tiến 10 triệu đồng với lãi suất là 4% . Tính số tiền mà Nam nợ ngân hàng sau 4 năm,
biết rằng trong 4 năm đó, ngân hàng không thay đổi lãi suất ( kết quả làm tròn đến nghìn đồng). Lời giải
 Tổng số tiền bạn Nam vay ( gốc và lãi) sau 4 năm là: A 
  , 4    , 3    , 2 6 6 6 6 10 1 0 04 10 1 0 04 10 1 0 04 10 10,04 4   ,  
10 1 0,04 1 1 0,04  1 0,042  1 0,043 1 1 0 04 6 6 10 1 0,04   .         ,  44163256 1 1 0 04
 Nên A  44163000 đồng  Ví dụ 4.7
Một giáo viên được nhận lương khởi điểm là 8 0 . 00 0
. 00 đồng/tháng. Cứ sau hai năm
lương mỗi tháng của giáo viên đó được tăng thêm 10% so với mức lương hiện tại.
Tính tổng số tiền T (đồng) giáo viên đó nhận được sau 6 năm làm việc. Lời giải
 Lương 2 năm đầu tiên của giáo viên đó nhận được là 6 6 T  8 1 . 0 2 . 4 192 1 . 0 (đồng) 1
 Theo công thức tính lãi kép, lương 2 năm tiếp theo giáo viên đó nhận được: T  24 8 . 1 . 0 .110%1 6 6  212,2 1 . 0 (đồng) 2
 Lương 2 năm cuối cùng giáo viên đó nhận được: T  24 8 . 1 . 0 .110%2 6 6  232,32 1 . 0 (đồng) 3
 Tổng số tiền T (đồng) giáo viên đó nhận được sau 6 năm làm việc:
T  T T T  635,520,000 (đồng). 1 2 3  Ví dụ 4.8
Anh Hưng đi làm được lĩnh lương khởi điểm 4 0 . 00 0
. 00 đồng/tháng. Cứ 3 năm, lương
của anh Hưng lại được tăng thêm 7% /1 tháng. Hỏi sau 36 năm làm việc anh Hưng
nhận được tất cả bao nhiêu tiền? (Kết quả làm tròn đến hàng nghìn đồng). Lời giải
 Gọi a là số tiền lương khởi điểm, r là lương được tăng thêm.
+ Số tiền lương trong ba năm đầu tiên: 36a
+ Số tiền lương trong ba năm kế tiếp: a  . a r  a    r1 36 36 1
+ Số tiền lương trong ba năm kế tiếp: a  r2 36 1 …
+ Số tiền lương trong ba năm cuối: a  r11 36 1 .
 Vậy sau 36 năm làm việc anh Hưng nhận được:
  r1  r2  r3 ... r11 1 1 1 1 1 .a 3 . 6  2 5 . 75 9 . 36983 2 5 . 75 9 . 37 0 . 00   đồng.
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 28
Tổng Hợp Lý Thuyết
Năm học: 2023-2024  Ví dụ 4.9
Một người đem gửi tiền tiết kiệm vào một ngân hàng với lãi suất 1% một tháng. Biết
rằng cứ sau mỗi quý ( 3 tháng) thì lãi sẽ được cộng dồn vào vốn gốc. Hỏi sau tối thiểu
bao nhiêu năm thì người đó nhận lại được số tiền bao gồm cả vốn lẫn lãi gấp ba lần số tiền ban đầu Lời giải
 Gọi a là số tiền người đó gửi ban đầu
 Số tiền nhận được cả gốc lẫn lãi sau N năm là   N T a  , 4 1 0 03 T    N
 , 4   N.ln ,  ln 3 3 1 0 03 3 4 1 03  ln 3  N   9,29 a 4 ln1, 03  Ví dụ 4.10
Một người vay ngân hàng một tỷ đồng theo phương thức trả góp để mua nhà. Nếu
cuối mỗi tháng, bắt đầu từ tháng thứ nhất người đó trả 40 triệu đồng và chịu lãi số
tiền chưa trả là 0,65% mỗi tháng (biết lãi suất không thay đổi) thì sau bao lâu người
đó trả hết số tiền trên? Lời giải
 Gọi A là số tiền vay, a là số tiền gửi hàng tháng r là lãi suất mỗi tháng.
 Đến cuối tháng thứ n thì số tiền còn nợ là: a        n 1 r      T  A n n n n
1 r   a 1 r 1
1  1 r 2 ...1  A1 r    r
 Hết nợ đồng nghĩa T  0 a  n  1 r       a Ar n a a A  r 1 n 1   0 
1r   n  log r 1r r r a  Ar
 Áp dụng với A  1 (tỷ), a  0,04 (tỷ), r  0,0065 ta được n  27,37 .
 Vậy cần trả 28 tháng.  Ví dụ 4.11
Năm 2014, một người đã tiết kiệm được x triệu đồng và dùng số tiền đó để mua nhà
nhưng trên thực tế người đó phải cần 1,55x triệu đồng. Người đó quyết định gửi tiết
kiệm vào ngân hàng với lãi suất là 6,9% / năm theo hình thức lãi kép và không rút
trước kỳ hạn. Hỏi năm nào người đó mua được căn nhà đó (giả sử rằng giá bán căn
nhà đó không thay đổi). Lời giải  n
Số tiền người gửi tiết kiệm sau n năm là x1 6,9%  n n
Ta cần tìm n để x1 6,9% 1,55x  1 6,9% 1,55  n  6,56...
 Do đó, người gửi tiết kiệm cần gửi trọn 7 kỳ hạn, tức là 7 năm.
 Vậy đến năm 2021 người đó sẽ có đủ tiền cần thiết.
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 29
Tổng Hợp Lý Thuyết
Năm học: 2023-2024  Ví dụ 4.12
Một người gửi ngân hàng 100 triệu đồng theo hình thức lãi kép, lãi suất 0,5% một
tháng (kể từ tháng thứ 2, tiền lãi được tính theo phần trăm tổng tiền có được của tháng
trước đó và tiền lãi của tháng sau đó). Hỏi sau ít nhất bao nhiêu tháng, người đó có
nhiều hơn 125 triệu đồng? Lời giải  n
Số tiền cả vốn lẫn lãi người gởi sau n tháng: 1001 0,005 100 1 . ,005n S    (triệu đồng) 1,005n S S   n  log . 1,005 100 100
 Để có số tiền S 125 (triệu đồng) thì phải sau thời gian S 125 n  log  log  44,74(tháng) 1,005 1,005 100 100
 Vậy: sau ít nhất 45 tháng người đó có nhiều hơn 125 triệu đồng.  Ví dụ 4.13
Ông Nam gởi 100 triệu đồng vào ngân hàng theo thể thức lãi kép kì hạn 1 năm với lãi
suất là 12% một năm. Sau n năm ông Nam rút toàn bộ số tiền (cả vốn lẫn lãi). Tìm số
nguyên dương n nhỏ nhất để số tiền lãi nhận được lớn hơn 40 triệu đồng (giả sử lãi
suất hàng năm không thay đổi) Lời giải
 Gọi T là tiền vốn lẫn lãi sau t tháng, a là số tiền ban đầu n
 Tháng 1 t  
1 : T  a 1 r 1  
 Tháng 2 t  2 : T  a1 r2 2 ……………….  t
Tháng nt  n :T  a  r n 1  T 140 n a
T  a  r  t    (tháng) n   ln ln t 100 1
ln   r ln  % 33,815 1 1 1  t
Để số tiền lãi nhận được lớn hơn 40 triệu thì n   2,818 12  Vậy n  3.  Ví dụ 4.14
Tỉ lệ tăng dân số ở Việt Nam được duy trì ở mức 1,05%. Theo số liệu của Tổng cục
thống kê, dân số Việt Nam năm 2014 có 90.728.900 người. Với tốc độ tăng dân số
như thế đến năm 2030 thì dân số của Việt Nam là bao nhiêu? Lời giải
 Từ năm 2014 đến năm 2030 cách nhau số năm là: 2030 2014 16 năm.
 Dân số Việt Nam năm 2030 : A  9072890011,05%16 107232574 (người). 16
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 30
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
LŨY THỪA – MŨ – LOGARIT PHƯƠNG TRÌNH MŨ A. LÝ THUYẾT CHUNG.
 Phương trình mũ cơ bản: x
a  b a  0, a   1 .
 Phương trình có một nghiệm duy nhất khi b  0.
 Phương trình vô nghiệm khi b  0 . B. CÁC DẠNG BÀI TẬP.
 Dạng 5.1. Phương trình mũ cơ bản
 Giải phương trình mũ cơ bản: x
a  b a  0, a   1 .  Khi đó x
a  b  x  log b a Lưu ý:
 Phương trình có một nghiệm duy nhất khi b  0.
 Phương trình vô nghiệm khi b  0 .  Ví dụ 5.1.1 1
Phương trình 3x  4 có nghiệm là
A. x  log 3 .
B. x  log 2 .
C. x  log 3 .
D. x  log 4 . 2 3 4 3 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 5.1.2
Nghiệm của phương trình 8x  4 là 2 1 1 A. x  .
B. x   . C. x  . D. x  2  . 3 2 2 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 5.1.3
Nghiệm của phương trình x x 1  x x 1 2 2 3 3     là 3 2 A. x  log .
B. x 1.
C. x  0 . D. x  log . 3 4 4 3 2 3 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 31
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 5.2. Đưa về cùng cơ số f x gx
Với a  0 , a 1: a  a
 f x  gx .  Ví dụ 5.2.1  1 Phương trình 2x 1 2   0 có nghiệm là 8 A. x  1  .
B. x  2 . C. x  2  .
D. x 1. Lời giải
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 5.2.2 x 2
Tìm tập nghiệm của phương trình 1 2  4x . A. 4  3,4   3 . B. 2  3,2   3 . C.  4   3, 4   3. D.  2   3, 2   3. Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 5.2.3 x 1   1 
Nghiệm của phương trình  125x   là  25  2 1 A.  . B. 4 . C.  . D. 1 5 8 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 5.2.4 2 x 1  x2  1 
Tìm tập hợp tất cả các nghiệm của phương trình    2 2 .  4  11  2   2   11 A.   . B.   . C.   . D.    2  11  11  2  Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 32
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 5.3. Logarit hóa 0    a  1, b  0  f x Phương trình a  b   . f  x   log b a  f x gx f x gx Phương trình a  b  log a  log b  f x  g x b a a    .loga f x gx hoặc log a  log b  f x a  g x b b  .logb  .  Ví dụ 5.3.1
Tìm tập nghiệm S của phương trình x 1 2   8 .
A. S    3 . B. S    2 .
C. S  0;  2 . D. S    12 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 5.3.2 x x
Tìm tập nghiệm S của phương trình 4 3 3  4 . log log 4    4  3 
A. S   . B. S    . 1  log 3   4   1log 3  log log 4    4  3  C. S   . D. S    log   4 log 4   log 3   4 3  4  Lời giải
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 5.3.3
Giải phương trình sau: x. x , . x  51 2 5 0 2 10 3 3 1 A. x  .
B. x  0 . C. x  1  . D. x   log 2 2 2 4 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 5.3.4 Cho phương trình x x 1 4 2   3  0. Khi đặt 2x t 
ta được phương trình nào sau đây A. 2
2t  3t  0 .
B. 4t 3  0 . C. 2
t  t  3  0 . D. 2
t  2t  3  0 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 33
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 5.4. Đặt ẩn phụ dễ thấy gx    g x t a 0   
Biến đổi quy về dạng: f a
  00  a  1     .  f  t  0 9x  t  3x
 Thông thường sẽ gặp các cơ số: 4x 
t  2x ;t  0 . 25x  t  5x  Ví dụ 5.4.1
Tập nghiệm của phương trình 9x 5 3 . x   6  0 là
A. S  1;log 2 . B. S   log 2 . C. S    1 . D. S     3  3  Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 5.4.2
Số nghiệm của phương trình x x 1 4 4 . 9 2 .   8  0 (*) là: A. 3 . B. 1. C. 2 . D. 0 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 5.4.3 Giải phương trình 12 2 x 15 2
. x 8  0 * . 3 A. x  .
B. x  0 . C. x  1  .
D. x  5 2 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 34
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 5.5. Đặt ẩn phụ với phương trình đẳng cấp
 Phương trình đẳng cấp có dạng: 2 2 . m X  . n XY  . p Y  0 .  2 f x f x
Khi đó với phương trình mũ đẳng cấp có dạng: . m a  . n  . a b   2 f x  . p b  0
 Phương pháp làm như sau: f x 2 f x a  .ab   2 f x b . m  . n  . p  0 2 f x 2 f x 2 f x b b b f x 01   2 f x a 2 Chia 2 vế cho b f x f x , đặt    t  0 .        a a b   . m      . n    p  0  b    b    2  . m t  .
n t  p  0 . f x 2 f x a  .ab   2 f x b . m  . n  . p  0 2 f x 2 f x 2 f x a a a f x 02   2 f x b Chia 2 vế cho a , đặt  f x f x 2   t  0 .        b b a   m  . n    . p    0    a   a     2  m  . n t  . p t  0 .  Lưu ý:
Đây là dạng sẽ có trong bài “Bất phương trình mũ”, lúc giải BPT mũ ta cần chú ý đến cơ
số lớn hay bé hơn 1. Để giảm sai sót chúng ta hãy “chia 2 vế” cho cơ số bé nhất !!!  Ví dụ 5.5.1
Giải phương trình sau: 8x 18x 2 2 . 7x   (*)
A. x 1.
B. x  log 2 . C. x  1  .
D. x  0 3 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 5.5.2
Số nghiệm của phương trình: 25x 15x 2 9 . x   (*) là: A. 0 . B. 3 . C. 1. D. 2 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 35
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 5.6. Đặt ẩn phụ với tích hai cơ số bằng 1
 Phương trình đẳng cấp có dạng: 2 2 . m X  . n XY  . p Y  0 .  f x f x
Phương trình mũ ta xét có dạng: . m a  . n b
 p  0  trong đó .ab 1.
 Phương pháp làm như sau: 1 f x f x 1 Vì .
a b  1 b  
 Đặt t  a ,t  0  b  . a t 1 Khi đó  2  . m t  .
n  p  0  . m t  n  . p t  0 . t  Ví dụ 5.6.1 x x
Tìm tích các nghiệm của phương trình  2   1
  2  1  2 2  0 . A. 2 . B. 1. C. 0 . D. 1 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 5.6.2 x x Phương trình 3 5  3 5  3 2 . x     có tổng các nghiệm là A. 0 . B. 1. C. 1. D. 2 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 36
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 5.7. Phương pháp hàm số
 Định lí. Nếu hàm số y  f x là hàm số liên tục và đồng biến trên  ;
a b , y  gx là hàm số
liên tục và nghịch biến trên  ;
a b thì phương trình f x  gx có tối đa một nghiệm trên  ; a b .
 Phương pháp làm như sau:
 Biến đổi phương trình đã cho về dạng f x  k , với k là hằng số
 Chứng minh f x là hàm đồng biến( nghịch biến) trên tập xác định.
01  Tìm x sao cho f x  k 0  0
 Kết luận x là nghiệm duy nhất của phương trình f x  k . 0
 Biến đổi phương trình đã cho về dạng f x  gx, với D ,D lần lượt là tập xác định 1 2
của hai hàm số f x , gx
02  Chứng minh f xlà hàm đồng biến và gx nghịch biến trên tập D  D (hay ngược lại) 1 2
 Tìm x sao cho f x  g x 0   0 0
 Kết luận x là nghiệm duy nhất của phương trình f x  gx. 0
 Biến đổi phương trình đã cho về dạng f u  f v, với hàm số f t là hàm đồng
03 biến(hay nghịch biến).
 Phương trình f u  f v  u  v .  Lưu ý:
⓵ Nếu f xvà gx là hàm đồng biến(nghịch biến) trên  ;ab thì f x gx cũng là
hàm đồng biến (nghịch biến) trên  ; a b . ⓶ Hàm số x
y  a đồng biến khi a 1và nghịch biến khi 0  a 1.  Ví dụ 5.7.1
Phương trình 2016x  2x  2018  0 có tất cả bao nhiêu nghiệm thực? A. 1. B. 2. C. 3 . D. 4 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 5.7.2 2
Tổng các nghiệm của phương trình x x x 1  5 2 3  3
15  2x  x là: A. 6  . B. 1. C. 5 . D. 2 . Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 37
Tổng Hợp Lý Thuyết
Năm học: 2023-2024  Ví dụ 5.7.3 Phương trình    1 2 . x x
 x 1 có bao nhiêu nghiệm thực A. 1. B. 0 . C. 3 . D. 2 . Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 5.7.3 x x x
Phương trình  3  2    3  2    10  có tất cả bao nhiêu nghiệm thực? A. 1. B. 0 . C. 3 . D. 2 . Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 38
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 5.8. Phương trình chứa tham số
 Để giải bài toán tìm tham số m trong phương trình mũ ta có hai cách phổ biến:
 Cô lập được tham số m.
01  Ta dùng đồ thị hàm số để biện luận số nghiệm (bài toán tương giao).
 Không cô lập được tham số m và có liên quan đến Vi-ét.
02  Đặt ẩn phụ đưa về phương trình bậc hai/bậc ba.
 Kết hợp định lý Vi-ét để giải quyết yêu cầu bài toán  Ví dụ 5.8.1
Có bao nhiêu giá trị nguyên dương của tham số m để phương trình 16x  2 1 . 2x  (  2) 9 . x m  0 có nghiệm dương? A. 2 . B. 4 . C. 3 . D. 1. Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 5.8.2
Có bao nhiêu giá trị nguyên của tham số m để phương trình 2 2 4xx 4 9  4 3 . xx
 2m1 0 có nghiệm? A. 27 . B. 25 . C. 23. D. 24 . Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 39
Tổng Hợp Lý Thuyết
Năm học: 2023-2024  Ví dụ 5.8.3 Gọi  ;
a b là tập các giá trị của tham số m để phương trình 2 2 x 8 x e
e  m  0 có
đúng hai nghiệm thuộc khoảng 0;ln5 . Tổng a  b là A. 2 . B. 4 . C. 6  . D. 14 . Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 5.8.4
Gọi S là tập hợp các giá trị nguyên của tham số m sao cho phương trình x x 1  2 25  m 5 .
 7m 7  0 có hai nghiệm phân biệt.
Hỏi S có bao nhiêu phần tử. A. 7 . B. 1. C. 2 . D. 3 . Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 5.8.5
Gọi S là tất cả các giá trị nguyên của tham số m sao cho phương trình x x 1  2 4  m 2 .
 2m 5  0 có hai nghiệm phân biệt.
Hỏi S có bao nhiêu phần tử. A. 2 . B. 1. C. 3 . D. 5 . Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 40
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
LŨY THỪA – MŨ – LOGARIT
PHƯƠNG TRÌNH LOGARIT A. LÝ THUYẾT CHUNG.
 Phương trình logarit cơ bản: log f x  b a  0, a  . a 1
 Lưu ý: khi giải phương trình logarit cần phải có điều kiện để logarit tồn tại. B. CÁC DẠNG BÀI TẬP.
 Dạng 6.1. Phương trình logarit cơ bản
 Giải phương trình logarit cơ bản: log x  b a  Khi đó log b
x  b  x  a a  a  a  0, 1  Ví dụ 6.1.1
Tìm tập nghiệm S của phương trình log x  2  2. 4   A. S    16 . B. S    18 . C. S    10 . D. S    14 . Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 6.1.2
Phương trình log x 1  3 có bao nhiêu nghiệm ? 2 A. 0 . B. 1. C. 2 . D. 3 . Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 6.1.3 2 Phương trình 2 log
x  2  8 có tất cả bao nhiêu nghiệm thực? 4 2   A. 2. B. 3. C. 4. D. 8. Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 41
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 6.2. Đưa về cùng cơ số
 Cho 1 a  0 . Với điều kiện các biểu thức f x và gx xác định, ta thường đưa các phương
trình logarit về các dạng cơ bản sau:  f x  0
 Loại 1: log f x  b   . a     f  x b   a  f x  0
 Loại 2: log f x  log g x   . a a     f  x   g x  Ví dụ 6.2.1
Phương trình lnx  
1  ln x  3  lnx  7 có bao nhiêu nghiệm ? A. 0 . B. 2 . C. 1. D. 4 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 6.2.2
Giải phương trình 2 log  2
x  x 1  log x 1 . 2    2
A. vô nghiệm.
B. x  2.
C. x  0, x  2. D. x  3. Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 6.2.3
Số nghiệm của phương trình log x 12 .log 2 1 là: 4   x A. 0. B. 2. C. 3. D. 1 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 6.2.4
Tập nghiệm của phương trình log x  4  2log 14  x  4 là 3   9   A. S    5 .
B. S    5 .
C. S    5 . D. S     . Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 42
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 6.3. Mũ hóa
 Với điều kiện các biểu thức f x và gx xác định, ta thường đưa các phương trình logarit về các dạng cơ bản sau:
 f x   log f x  g x  a    a       0 0 1  f  x gx  a  Ví dụ 6.3.1
Tập nghiệm của phương trình log  x 1
5   25x  2 là: 2  A. S    1 .
B. S  log 5 . 3   1   1  C. S  0;  . D. S     log 5  log 4   4  5  Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 6.3.2
Số nghiệm của phương trình log  x 2 x 1 25 2     x là A. 0 . B. 1. C. 2 . D. 3 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 43
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 6.4. Đặt ẩn phụ dễ thấy
 Giải phương trình f log g x  , 0  a   1 . a   0
 Bước 01. Đặt t  log g x * a  
 Bước 02. Tìm điều kiện của t (nếu có)
 Bước 03. Đưa về giải phương trình f t  0 đã biết cách giải.
 Bước 04. Thay vào * để tìm x .  Ví dụ 6.4.1 Giải phương trình 2
log x  4log x  3  0 . 3 3 A. S    1 . B. S    27 .
C. S  3; 2  7 . D. S    3 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 6.4.2
Số nghiệm của phương trình log x  log 64  1 là 2 x A. 0 . B. 3 . C. 2 . D. 1 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 6.4.3
Tích các nghiệm phương trình 2 2
log x  log x 1  5  0 là 3 3 A. 0 . B. 3 . C. 2 . D. 1 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 44
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 6.5. Phương pháp hàm số
 Định lí. Nếu hàm số y  f x là hàm số liên tục và đồng biến trên  ;
a b , y  gx là hàm số
liên tục và nghịch biến trên  ;
a b thì phương trình f x  gx có tối đa một nghiệm trên  ; a b .
 Phương pháp làm như sau:
 Biến đổi phương trình đã cho về dạng f x  k , với k là hằng số
 Chứng minh f x là hàm đồng biến( nghịch biến) trên tập xác định.
01  Tìm x sao cho f x  k 0  0
 Kết luận x là nghiệm duy nhất của phương trình f x  k . 0
 Biến đổi phương trình đã cho về dạng f x  gx, với D ,D lần lượt là tập xác định 1 2
của hai hàm số f x , gx
02  Chứng minh f xlà hàm đồng biến và gx nghịch biến trên tập D  D (hay ngược lại) 1 2
 Tìm x sao cho f x  g x 0   0 0
 Kết luận x là nghiệm duy nhất của phương trình f x  gx. 0
 Biến đổi phương trình đã cho về dạng f u  f v, với hàm số f t là hàm đồng
03 biến(hay nghịch biến).
 Phương trình f u  f v  u  v .  Lưu ý:
⓵ Nếu f xvà gx là hàm đồng biến(nghịch biến) trên  ;ab thì f x gx cũng là
hàm đồng biến (nghịch biến) trên  ; a b . ⓶ Hàm số x
y  a đồng biến khi a 1và nghịch biến khi 0  a 1.  Ví dụ 6.5.1
Phương trình log x  2  log x 1 có bao nhiêu nghiệm? 2   3   A. 1. B. 2. C. 3 . D. 4 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 45
Tổng Hợp Lý Thuyết
Năm học: 2023-2024  Ví dụ 6.5.2
Giải phương trình log x  2  log 3x  4  2 . 3   7  
A. x  5 .
B. x 1
C. x  3. D. x  1  Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 6.5.3
Giải phương trình log  2
x  x  6  x  log (x  2)  4 . 2  2 A. 5 x  . B. x  1 
C. x  4 .
D. x  3 2 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 46
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 6.6. Phương trình chứa tham số
 Để giải bài toán tìm tham số m trong phương trình logarit ta có hai cách phổ biến:
 Cô lập được tham số m.
01  Ta dùng đồ thị hàm số để biện luận số nghiệm (bài toán tương giao).
 Không cô lập được tham số m và có liên quan đến Vi-ét.
02  Đặt ẩn phụ đưa về phương trình bậc hai/bậc ba.
 Kết hợp định lý Vi-ét để giải quyết yêu cầu bài toán  Ví dụ 6.6.1
Tìm tất cả các giá trị thực của tham số m để phương trình 2
log x  mlog x 1  0 có nghiệm duy nhất nhỏ hơn 1. 3 3 A. m  2  . B. m  1  .
C. m  2 .
D. m 1. Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 6.6.2
Tìm tất cả các giá trị thực của tham số m để phương trình 2
log x  mlog x  2m  7  0 có hai nghiệm x , x thỏa mãn x .x  81. 3 3 1 2 1 2
A. m 12 .
B. m  0 .
C. m  2 .
D. m  4 . Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 47
Tổng Hợp Lý Thuyết
Năm học: 2023-2024  Ví dụ 6.6.3
Tìm tất cả các giá trị thực của tham số m để phương trình
log mx  2logx   1 có nghiệm duy nhất. m  4 m  4 A.  . B. m  1  .
C. m  2 . D.  . m  0 m  0 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 6.6.4
Tìm tất cả các giá trị thực của tham số m để phương trình 4x 1 log
 m  0 có nghiệm. 2 4x 1 m  4 m  4 A.  . B. m  1  .
C. m  2 . D.  . m  0 m  0 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 48
Tổng Hợp Lý Thuyết
Năm học: 2023-2024  Ví dụ 6.6.5
Tìm tất cả các giá trị thực của tham số m để phương trình m  2 1 log
x  2  m  5 log
x  2  m 1  0 có nghiệm thuộc 2; 4 . 1     1   2 2 m  1 7 m 1 A.  . B. 3   m  . C. 1
  m  7. D.  . m  3 3 m  0 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 6.6.6
Tìm tất cả các giá trị thực của tham số m để phương trình
log  m 1 x  log
x  2 có nghiệm duy nhất. 5      5 m 1 m  1 m  1 A.  .
B. 1 m  3 . C.  . D.  . m  3 m  7 m  1 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 49
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
LŨY THỪA – MŨ – LOGARIT
BẤT PHƯƠNG TRÌNH MŨ A. LÝ THUYẾT CHUNG. b  0
Tập nghiệm của bất phương trình là .
Dạng 01. x    x a 1 a b x b .
a  b a  0;a   1 . log a b  0 0  a 1 x
a  b  x  log b . a b  0
Tập nghiệm của bất phương trình là .
Dạng 02. x    x a 1 a b x b .
a  b a  0;a   1 log . a b  0 0  a 1 x
a  b  x  log b . a B. CÁC DẠNG BÀI TẬP.
 Dạng 7.1. Bất phương trình mũ cơ bản
 Xem lại mục “Lý thuyết chung”
 Bất phương trình mũ cơ bản: x
a  b a  0;a   1 . Chú ý đến cơ số.  Ví dụ 7.1.1
Tập nghiệm của bất phương trình 3x  9 là
A. S  2;  .
B. S  2;   .
C. S  2;  
 . D. S   1  ; 2. Lời giải
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 7.1.2 x  1 
Tập nghiệm của bất phương trình  4   là  2  A. S   2  ; 2.
B. S  2;   .
C. S  0;  . D. S  0;  1 . Lời giải
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 7.1.3
Tập nghiệm của bất phương trình x x 1 2 3   là   A.  ;  log 3  ;log 3 . C.  . D. 0;  1 . 2  . B. 2    3  Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 50
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 7.2. Đưa về cùng cơ số
 Ta có hai chú ý như sau: ⓵     Với  1, f x g x a a  a
 f x  gx ⓶ x x Với 0  a  1, f g a  a
 f x  gx  Ví dụ 7.2.1 2
Tìm tập nghiệm của bất phương trình: x x x 1 5 25  
A. S   ;   1 . B. S   1  ; 2   . C. S   1
 ;2. D. S  ;0 . Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 7.2.2 1    1 x
Tìm tập nghiệm của bất phương trình: x 1 2    16 
A. S  2;  .
B. S  ;0 .
C. S  0;   . D. S  ;   . Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 7.2.3 2 x 2 x  1  1
Tìm số nghiệm nguyên dương của bất phương trình  .    5  125 A. 3 . B. 4 . C. 5 . D. 6 . Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 7.2.4 2 3  x  1  Giải bất phương trình 2x 1  3    ta được tập nghiệm:  3   1   1  A. ;    .
B. 1;  . C.   ;1 . D.  ;   
1  1;  .  3   3  Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 51
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 7.3. Đặt ẩn phụ
 Phương pháp đặt ẩn phụ ta thường sử dụng một số phương pháp sau:
Ở đây ta xét bất phương trình dạng f x  0 , các trường hợp khác tiến hành tương tự. ⓵ nx n  Bất phương trình dạng 1 x A a  A a ... x
 A a  A  0. n n 1  1 0 Đặt x
t  a (t  0) , ta thu được bất phương trình dạng n n 1
A t  A t   ...  A t  A  0 . n n 1  1 0 ⓶ x Bất phương trình dạng 2x    2x Aa
B ab  Cb  0 . x  a 
Chia cả hai vế cho 2x
b rồi đặt t    , t  0 , ta được 2 . A t  .
B t  C  0.  b  ⓷ f x gx
f x gx
Bất phương trình dạng Aa
 Bb C  0, trong đó a b  k . f x gx Bk Đặt a
 t(t  0)  b
 k. , ta thu được bất phương trình mới At   C  0 . t  Ví dụ 7.3.1 5
Nghiệm của bất phương trình x x e e   là 2 1 1 A. x 
hoặc x  2 . B.  x  2 . 2 2
C. ln2  x  ln2.
D. x  ln2. Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 7.3.2
Bất phương trình 9x 3x 
 6  0 có tập nghiệm là A. ;  1 . B.  ;  2
 3; . C. 1; . D.  2  ;3. Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 7.3.3  1 2
Tập hợp nghiệm của bất phương trình 3x 2 3   là 27x 3 1 A. 0;  1 . . B. 1; 2. . C.  . . D. 2;3.. 3 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 52
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 7.4. Logarit hóa 0    a  1, b  0  f x Phương trình a  b   . f  x   log b a  f x gx f x gx Phương trình a  b  log a  log b  f x  g x b a a    .loga f x gx hoặc log a  log b  f x a  g x b b  .logb  .  Ví dụ 7.4.1 2
Tìm tập S của bất phương trình: 3x 5 . x  1 A. log 3;0 log 5;0
log 3;0 . D. log 5;0 . 3  5  . B.  . C.  5  3  Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 7.4.2 log . 3x  1 0 5 1
Tìm tập S của bất phương trình: 4  9  4 
A. 5;   . B. ;    .
C. ; 2 .
D. 1;  .  3  Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 7.4.3 x 1 
Giải bất phương trình: 27 2 . x x  72
A. log 3;0  3;  . B. 1  ; 2  . 2     1  C.  2  ; 2. D.   ; 2  .  2  Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 53
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 7.5. Chứa tham số
 Sử dụng PP giải BPT logarit kết hợp công thức, tính chất của mũ, lũy thừa, logarit.
 Khai thác điều kiện bài toán.
 Xử lý bài toán và chọn giá trị m thỏa ĐK bài toán (cách “mò”).  Ví dụ 7.5.1
Cho bất phương trình: 9x     1 3 . x m  m  0  
1 . Tìm tất cả các giá trị của tham số
m để bất phương trình   1 nghiệm đúng x  1. 3 3
A. m   . B. m   .
C. m  3  2 2. D. m  3  2 2. 2 2 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 7.5.2
Tìm m để bất phương trình 9 . x  2   1 6 . x  4 . x m m m
 0 nghiệm đúng với mọi x 0;  1 .
A. 0  m  6 B. m  6
C. m  6
D. m  0 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 54
Tổng Hợp Lý Thuyết
Năm học: 2023-2024  Ví dụ 7.5.3
Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình sau có tập x x nghiệm là  ;   0 : x 1 m2  2m  
1 1 5  3 5  0 . 1 1 1 1
A. m   B. m  C. m 
D. m   2 2 2 2 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 7.5.4
Tất cả các giá trị của m để bất phương trình 3  
1 12x  2  6x  3x m m  0 có nghiệm đúng x   0 là:  1   1  A.  2  ;  B. (; 2] C. ;    D. 2  ;     3   3  Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 55
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
LŨY THỪA – MŨ – LOGARIT
BẤT PHƯƠNG TRÌNH LOGARIT A. LÝ THUYẾT CHUNG.
Dạng 01. a 1 log b
x  b  x  a a
log x  b a  0; a  . a 1 0a1 log b
x  b  x  a . a
Dạng 02. a 1 log b
x  b  x  a a
log x  b a  0; a  a 1. 0a1 log b
x  b  x  a . a B. CÁC DẠNG BÀI TẬP.
 Dạng 8.1. Bất phương trình logarit cơ bản
 Ta có hai chú ý sau: b     b     0 u a khi a 0 u a khi a 1
log u  b   .
 log u  b   . a b u  a khi a 0  a  1 0 b  
u  a khi 0  a  1  Ví dụ 8.1.1
Tập nghiệm của bất phương trình log 2x 1  1  là: 1   2  3   3   1 3   3  A. 1  ;  . B. ;    . C.  ;  . D.   ;  .  2   2   2 2   2  Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 8.1.2
Tập nghiệm của bất phương trình log 2x 1  2 là: 3   4 1 25 25 1 1 A.  x  . B. x  . C. x  . D. x  . 2 32 32 2 2 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 56
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 8.2. Đưa về cùng cơ số
0  u  v khi a > 1
 Dùng biến đổi logarit để đưa về cùng cơ số log u  log v   . a a
u  v  0 khi 0 < a < 1  Ví dụ 8.2.1 Bất phương trình log 2x 1  log
x  2 có tập nghiệm S là 3   3   4 4  1   1   1  A. S   
;1 . B. S   2  ;  1 . C. S   ;1 
 . D. S    ;1 .  2   2   2  Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 8.2.2
Xác định tập nghiệm S của bất phương trình 2
ln x  ln4x  4 .
A. S  1;   \  2 . B. S   \  2 .
C. S  2; .
D. S  1; . Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 8.2.3
Tập nghiệm của bất phương trình log  2
2x  3x 1  log 2x 1 là: 4  2    1   1   1   1 
A. S   ;1 B. S  0  ;  C. S   
;1 D. S    ; 0   2   2   2   2  Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 57
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 8.3. Đặt ẩn phụ
 Tìm một log f x chung, đặt làm ẩn phụ t để đưa bất phương trình về bất phương trình ẩn a  
t giải bất phương trình tìm t sau đó tìm x . ★ 1 2 1
Chú ý: Nếu đặt 2 2
t  log x  log x  t
 ,log x  t,log x  log x  t ,log a  . 2 a 1 a  a  2 x a t a  Ví dụ 8.3.1 Bất phương trình 2 log x  5log x  6  có tập nghiệm là: 0,2 0,2  1 1   1  A. S   ;
 B. S  2;3 . C. S  0  ;
 . D. S  0;3 . 125 25   25  Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 8.3.2
Nghiệm nguyên nhỏ nhất của bất phương trình log 3  log 3  0 là: x x 3
A. x  3 B. x 1.
C. x  2 .
D. x  4 . Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 8.3.3
Nếu đặt t  log x thì bất phương trình 2 3  x   32  4 2 2 log x  log    9log  4  
log  x trở thành bất phương trình nào? 1 2 1 2 2   2 8    x  2 A. 4 2
t 13t  36  0 B. 4 2
t  5t  9  0 . C. 4 2
t 13t  36  0 . D. 4 2
t 13t  36  0 . Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 58
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 8.4. Mũ hóa
 Với điều kiện các biểu thức f x và gx xác định, ta thường đưa các bất phương trình
logarit về các dạng cơ bản sau:  f  x  0    f  x khi a gx 1  a
log f x  g x  . a      f  x  0     f  x khi a gx 0 1  a  Ví dụ 8.4.1 Bất phương trình log   có tập nghiệm là: x log 9x 72 1 3   A. S  log 73; 2 S  log 72; 2 3   . B.  3  .
C. S  log 73; 2 S   ;   3  . D.  2. Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 8.4.2
Nghiệm nguyên lớn nhất của bất phương trình log  x 1
4.3   2x 1 là: 3 
A. x  3 . B. x  2 .
C. x 1. D. x  1  . Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 59
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 8.5. Chứa tham số
 Sử dụng PP giải BPT logarit kết hợp công thức, tính chất của mũ, lũy thừa, logarit.
 Khai thác điều kiện bài toán.
 Xử lý bài toán và chọn giá trị m thỏa ĐK bài toán (cách “mò”).  Ví dụ 8.5.1
Tìm tất cả các giá trị thực của tham số m để bất phương trình log 5x 1  m có 2   nghiệm x 1?
A. m  2 . B. m  2 .
C. m  2 .
D. m  2 . Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 8.5.2
Tìm tất cả giá trị thực của tham số m để bất phương trình log  2
x  4x  m  1 3  nghiệm đúng x   ?
A. m  7 . B. m  7 .
C. m  4 .
D. 4  m  7 . Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 8.5.3
Tìm tất cả giá trị thực của tham số m để log  2 mx  x  log 4 vô nghiệm? 1  1 5 5 m  4 A. 4
  m  4 . B.  .
C. m  4 . D. 4
  m  4. m  4   Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 60
Tổng Hợp Lý Thuyết
Năm học: 2023-2024  Ví dụ 8.5.4
Tìm tất cả các giá trị thực của tham số m sao cho khoảng 2;3 thuộc tập nghiệm
của bất phương trình log  2 x   1  log  2
x  4x  m 1 (1) . 5 5  A. m  1  2;13   . B. m 1  2;13   . C. m  1  3;12 
 . D. m 1  3; 1  2   . Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 8.5.5
Tìm m để bất phương trình 1 log  2 x   1  log  2
mx  4x  m thoã mãn x   5 5  A. 1
  m  0 . B. 1   m  0.
C. 2  m  3.
D. 2  m  3. Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................  Ví dụ 8.5.6
Tìm tất cả các giá trị thực của tham số m để bất phương trình log log 3x 1  log
m có nghiệm với mọi x ;0 0,02  2   0 ,02
A. 0  m 1. B. m 1.
C. m  2.
D. m 1. Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 61 TÀ T I À I L I L Ệ I U Ệ U D À D N À H N H C H C O H O K H K ỐI Ố 1 2 1 Mục lục
 Chủ đề 01. LŨY THỪA – HÀM SỐ LŨY THỪA
 Dạng 1.1. Rút gọn và tính giá trị biểu thức ........................................................................... 6
 Dạng 1.2. So sánh các biểu thức chứa lũy thừa ................................................................... 7
 Dạng 1.3. Tập xác định hàm số lũy thừa ............................................................................... 8
 Dạng 1.4. Đạo hàm số lũy thừa ................................................................................................ 9
 Dạng 1.5. Đồ thị hàm số lũy thừa ........................................................................................... 10
 Chủ đề 02. LOGARIT
 Dạng 2.1. Tính giá trị biểu thức................................................................................................ 12
 Dạng 2.2. Biểu diễn logarit ....................................................................................................... 13
 Dạng 2.3. Mệnh đề đúng – sai ................................................................................................. 14
 Chủ đề 03. HÀM SỐ MŨ – HÀM SỐ LOGARIT
 Dạng 3.1. Tập xác định của hàm số logarit ........................................................................ 18
 Dạng 3.2. Đạo hàm hàm số mũ – logarit ............................................................................. 20
 Dạng 3.3. Khảo sát hàm số mũ – logarit .............................................................................. 21
 Chủ đề 04. BÀI TOÁN LÃI SUẤT
 Chủ đề 05. PHƯƠNG TRÌNH MŨ
 Dạng 5.1. Phương trình mũ cơ bản ......................................................................................... 31
 Dạng 5.2. Đưa về cùng cơ số ................................................................................................... 32
 Dạng 5.3. Logarit hóa ............................................................................................................... 33
 Dạng 5.4. Đặt ẩn phụ dễ thấy ................................................................................................ 34
 Dạng 5.5. Đặt ẩn phụ với phương trình đẳng cấp ............................................................. 35
 Dạng 5.6. Đặt ẩn phụ với tích hai cơ số bằng 1 .................................................................. 36
 Dạng 5.7. Phương pháp hàm số ............................................................................................. 37
 Dạng 5.8. Phương trình chứa tham số .................................................................................. 39
 Chủ đề 06. PHƯƠNG TRÌNH LOGARIT
 Dạng 6.1. Phương trình logarit cơ bản ................................................................................. 41
 Dạng 6.2. Đưa về cùng cơ số .................................................................................................. 42
 Dạng 6.3. Mũ hóa ....................................................................................................................... 43
 Dạng 6.4. Đặt ẩn phụ dễ thấy ................................................................................................44
 Dạng 6.5. Phương pháp hàm số ............................................................................................ 45
 Dạng 6.6. Phương trình chứa tham số ................................................................................. 47
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Chủ đề 07. BẤT PHƯƠNG TRÌNH MŨ
 Dạng 7.1. Bất phương trình mũ cơ bản ............................................................................... 50
 Dạng 7.2. Đưa về cùng cơ số ................................................................................................... 51
 Dạng 7.3. Đặt ẩn phụ ................................................................................................................. 52
 Dạng 7.4. Logarit hóa ............................................................................................................... 53
 Dạng 7.5. Chứa tham số .......................................................................................................... 54
 Chủ đề 08. BẤT PHƯƠNG TRÌNH LOGARIT
 Dạng 8.1. Bất phương trình logarit cơ bản ......................................................................... 56
 Dạng 8.2. Đưa về cùng cơ số ................................................................................................... 57
 Dạng 8.3. Đặt ẩn phụ.................................................................................................................58
 Dạng 8.4. Mũ hóa ........................................................................................................................ 59
 Dạng 8.5. Chứa tham số ........................................................................................................... 60
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 2
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
LŨY THỪA – MŨ – LOGARIT
LŨY THỪA – HÀM SỐ LŨY THỪA A. LÝ THUYẾT CHUNG. 1. Lũy thừa: 1.1. Định nghĩa.
 Cho số thực b và số nguyên dương nn  2 .
Số a được gọi là căn bậc n của số b nếu n a  b . Chú ý: n lẻ
b  Có duy nhất một căn bậc n của b, ký hiệu n b .
b  0  Không tồn tại căn bậc n của b
b  0  Có một căn bậc n của b là 0 n chẵn
 Có hai bậc n của a là hai số đối nhau,
b  0  Căn có giá trị dương ký hiệu là n b , căn có giá trị âm ký hiệu là n  b . 1.2. Công thức. Số mũ Cơ số a Lũy thừa a *  n a n a  a  . a .
a ..a (n là thừa số a)  0 a  0 0 a  a 1    1 n  * , n   a  0 n a  a  n a m m   * , m ,n  a  0 n m n
a  a  a ,n n
a  b  a  b  n 1.3. Tính chất. ⓵ a .a a   ⓶ a a   ⓷   . a  a a       
⓸ ab  a .b ⓹ a a    ⓺ a b       b  b  b   a 
⓻ Nếu a 1 thì a  a   .
⓼ Nếu 0  a 1 thì a  a   .
Các tính chất trên đúng trong trường hợp số mũ nguyên hoặc không.nguyên CHÚ Ý
Khi xét lũy thừa với số mũ 0 và số mũ nguyên âm thì cơ số phải khác 0.
Khi xét lũy thừa với số mũ không nguyên thì cơ số phải dương.
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 3
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
1.4. Tính chất căn bậc n. Với *
a,b  ,n ta có ⓵ n n
a  a, a  ⓶ n n  . n ab a b , a  ;b n ⓷ a a n  , a  , b   0 n b b m
⓸ n m  n a a  , a
  0,n nguyên dương, m nguyên. ⓹ n m nm a  a , a
  0,n,m nguyên dương. ⓺ p q Nếu  thì n p m q
a  a , a
  0,m,n nguyên dương, p,q nguyên. n m Đặc biệt: n m.n m a  a .
2. Hàm số lũy thừa: 2.1. Khái niệm.
 Hàm số y  x với  được gọi là hàm số lũy thừa.
2.2. Tập xác định.
 Tập xác định của hàm số y  x là:
⓵ Nếu là số nguyên dương D 
⓶ Nếu nguyên âm hoặc bằng 0. D   \  0
⓷ Nếu không nguyên D  0; 
※ Tổng quát: Tập xác định của hàm số y   f x . Khi NGUYÊN DƯƠNG Hàm số xác định xác định. Khi NGUYÊN ÂM Hàm số xác định . Khi KHÔNG NGUYÊN Hàm số xác định 2.3. Đạo hàm.  
Hàm số y  x ,    có đạo hàm x   0 và x  1  .x  .
2.4. Khảo sát hàm số lũy thừa y  x ,   .
y  x với  0
y  x với  0 Tập khảo sát 0; 0; Đạo 1 y x     0, x   0. 1 y x     0, x   0. hàm Sự Giới       biến lim x 0, lim x . lim x , lim x 0. hạn   x 0  x x 0  x thiên Tiệm
Nhận Ox là tiệm cận ngang. Không có. cận
Nhận Oy là tiệm cận đứng.
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 4
Tổng Hợp Lý Thuyết
Năm học: 2023-2024 Bảng biến thiên Đồ thị
Đồ thị của hàm số lũy thừa y  x luôn đi qua điểm I 1;  1 . Lưu ý:
 Khi khảo sát hàm số lũy thừa với số mũ cụ thể, ta phải xét hàm số đó trên toàn bộ tập xác định của nó.  Chẳng hạn: 3 2 y x , y x   , y  x .
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 5
Tổng Hợp Lý Thuyết
Năm học: 2023-2024 B. CÁC DẠNG BÀI TẬP.
 Dạng 1.1. Rút gọn và tính giá trị biểu thức
 Sử dụng phối hợp linh hoạt các tính chất của lũy thừa.
 Chọn a;b là các số thực dương và x; y là các số thực tùy ý, ta có: ⓵ a .a a   ⓶ a a   ⓷   . a  a a       
⓸ ab  a .b ⓹ a a    ⓺ a b       b  b  b   a 
⓻ Nếu a 1 thì a  a   . ⓼ Nếu 0  a 1 thì a  a   .  Ví dụ 1.1.1
Đưa các biểu thức sau về dạng lũy thừa 3 ⓵ 2 4 b a
a a a  0 ⓶
⓷ 5 3 a,b  0. 0 75 16 , a b Lời giải 1 1 2   2 1 1 2.2 3 5  1 3 3  2 2     3 13 6 ⓵ 2 4   2 2 2 4 a a   .
a a    a   a . ⓶ 6    2 .     0,75 16 2 3 3 2 4 4 1 1 2 2  2 ⓷ 5 15 15 b a b a  b  5 15 15 3  .
 a .b    1 1 a b  a  5 15 a b  Ví dụ 1.1.2
Rút gọn các biểu thức sau đây: ⓵  4 a  4 5 ⓶ 4 2
81a b b  0 ⓷ 8 4 x x   1
x   1. Lời giải
⓵ a  4  a  2 5 5 ⓶ 4 2 2 2
81a b  9a b  9a b (do b  0 ).
⓷ x x  4 8 2 2 4 1
 x . x 1  x x   1 (do x  1   x1 0).  Ví dụ 1.1.3 1  1  1  1 
Cho a  2  3 ,b  2  3 . Tính A  a   1  b   1 . Lời giải  a     1 1 2 3   2  3   2 3 Ta có: .  b     1 1 2 3   2  3 2  3   
 A  a   1 b   1 1 1
     1     1     1    1 1 1 6 2 3 1 2 3 1 3 3 3 3    1. 3  3 3  3 9  3
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 6
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 1.2. So sánh các biểu thức chứa lũy thừa
 Ta có hai cách làm như sau:
Đưa về cùng cơ số Cho a : , m n . Khi đó 01
⓵ Với a 1 m n 
a  a  m  n ;
⓶ Với 0  a 1 m n 
a  a  m  n .
Đưa về cùng số mũ 02
Với 0  a  b và m là số nguyên thì ⓵ m m
a  b  m  0 ⓶ m m
a  b  m  0 .  Ví dụ 1.2.1
So sánh các số sau: ⓵ 300 7 và 400 7 ⓶  5000 1 và  . 2 8000 1 2 Lời giải ⓵ 300 7 và 400 7 ⓶  5000 1 và  2 8000 1 2
Ta có 7 1 và 300  400 nên 300 400 7  7 . 5000 8000
Ta có 1  1 và 5000  8000 nên  1    1 2 2  2  Ví dụ 1.2.2
So sánh các số sau: ⓵ 20 20 và 30 15 . ⓶ 100 2 và 30 20 . ⓷   7  3 1 và   8 3 1 .
⓸ 34 và    34 1 . Lời giải ⓵ 20 20 và 30 15 . ⓶ 100 2 và 30 20 . 3 2 15  3375  400  20 . 10 3 2 1024  8000  20 . 10 10 10 10 Do đó 30   3    2  20 15 15 20  20 .
Do đó 100   10    3  30 2 2 20  2 .  ⓷   7  3 1 và   8 3 1 .
⓸ 34 và    34 1 .  7 8   và  3  4  0 nên     34 34 1 .
3 1  1 và 7  8 nên  3   1   3  1 . 1  Ví dụ 1.2.3
So sánh 2 số p và q biết: p q ⓵ p q  .
⓶  5  1   5  1 . Lời giải ⓵ p q  p q .
⓶  5  1   5  1 .
Ta có  1 nên p  q .
Ta có 5 1  1 nên p  q .
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 7
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 1.3. Tập xác định hàm số lũy thừa
 Tập xác định của hàm số y   f x là:
⓵ là số nguyên dương
f x xác định.
⓶ nguyên âm hoặc bằng 0. f x  0 ⓷ không nguyên f x  0  Ví dụ 1.3.1 
Tìm tập xác định của hàm số y  x   2 2 1 A.  . B.   ;  
1  1 ;  . C.   1  ;  1 . D.   \   1 . Lời giải Chọn D 
 Hàm số y  x   2 2 1 xác định khi 2
x 1 0  x  1  .  Vậy   \  
1 là tập xác định của hàm số đã cho.  Ví dụ 1.3.2  Tìm tập xác định
của hàm số y  x  x   2019 2 5 6 A.
 ;23; . B.  2;3 . C.   ; 2  3  ;     . D.   \ 2;  3 . Lời giải Chọn C  x  2
 Hàm số y  x  x   2019 2 5 6
xác định khi và chỉ khi 2
x  5x  6  0   . x  3 
 Vậy tập xác định của hàm số y  x  x   2019 2 5 6 là   \ 2;  3 .  Ví dụ 1.3.3 e Tìm tập xác định
của hàm số y  2x   1 1  1   1  A.  \ . B.  ;    . C.  ;     . D.  . 2  2   2  Lời giải Chọn C  1
Điều kiện xác định: 2x 1  0  x  . 2    1
Vậy tập xác định cúa hàm số là  ;     2 
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 8
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 1.4. Đạo hàm số lũy thừa  
 Hàm số y  x ,    có đạo hàm x   0 và x  1  x   u  1 .
 .u  .u .  Ví dụ 1.4.1
Cho hàm số f x   x  56 2 3 .Tính f 2. 5 5 5 5 A. . B. . C.  . D.  6 3 6 3 Lời giải Chọn B    2 Tập xác định ;     3   5 
Ta có f x   x  56 2 3
 f x  2x 3 16  f   5 2  . 3 3  Ví dụ 1.4.2  1 
Tìm đạo hàm của hàm số y    x5 3 1 3 trên khoảng   ;  .  3  5
A. y '     x23 5 1 3 .
B. y '  1 3x43 . 3 5
C. y '     x43 5 1 3 .
D. y '  1 3x23 3 Lời giải Chọn A  1
Với điều kiện x  , ta có y    x    x5 5 3 3 1 3 1 3 . 3 ' 5 2 2    5
Khi đó: y '  1 3x3  
.1 3x'.1 3x3  5  13x3 3    Ví dụ 1.4.3
Tìm đạo hàm của hàm số 4
y  x  2 , x  2  1 1 A. y '  . B. y'  . 4  4 x  23 4 4 x 2 1 C. y '  . D. 3
y '  4 x  2 2 x  23 4 Lời giải Chọn A x 2'  1 Có y'   . 4 x  23 4 x  23 4 4
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 9
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 1.5. Đồ thị hàm số lũy thừa
 Ta lưu ý các yếu tố trong sự biến thiên của hàm số lũy thừa y  x với  0  0  Đạo hàm 1 y x     0 1 y  x  0, x   0. Giới hạn
lim x  0, lim x   . 
lim x  , lim x  0.   x 0  x x 0  x
Nhận Ox là tiệm cận ngang. Tiệm cận Không có.
Nhận Oy là tiệm cận đứng. Đồ thị
Đồ thị của hàm số lũy thừa y  x luôn đi qua điểm I 1;  1 .  Ví dụ 1.5.1
Hình vẽ bên là đồ thị các hàm số a y  x , b y  x , c
y  x trên miền
0;. Hỏi số a , b, c số nào nhận giá trị trong khoảng 0; 1? A. a .
B. a&c . C. b . D. c Lời giải Chọn D
 Nhìn vào hình vẽ, ta thấy đồ thị hàm số b
x là đường thẳng nên ta có được b 1.  Khi x 1 thì b c
x  x  x . Do đó 0  c 1.  Ví dụ 1.5.2 Cho hàm số 2023 y x 
. Mệnh đề nào đúng về đường tiệm cận của đồ thị hàm số?
A. Có một tiệm cận ngang và một tiệm cận đứng.
B. Không có tiệm cận ngang và có một tiệm cận đứng.
C. Có một tiệm cận ngang và không có tiệm cận đứng.
D. Không có tiệm cận. Lời giải Chọn A
 Tập xác định: D  0;  .  1 Ta có lim y  lim
  nên đồ thị có một tiệm cận đứng x  0   2023 x0 x0 x  1
Mặt khác lim y  lim
 0 nên đồ thị có tiệm cận ngang y  0   2023 x x x
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 10
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
LŨY THỪA – MŨ – LOGARIT LOGARIT A. LÝ THUYẾT CHUNG. 1. Định nghĩa.
Cho hai số dương a, b với a 1.
 Số thỏa mãn đẳng thức a  b được gọi là lôgarit cơ số a của b và kí hiệu là log b . a
 Ta viết:  log b  a  . b a 2. Tính chất. Cho TÍNH CHẤT 3. Công thức.
 Cho 3 số dương a, b ,c với a 1;c 1 và   , ta có các công thức sau:
1 Tích tổng – Thương hiệu Đặc biệt: với 2 Lũy thừa Đặc biệt: 3 Đổi cơ số Đặc biệt: ;
 Logarit thập phân và Logarit tự nhiên
 Logarit thập phân là logarit cơ số 10. Viết : log b  logb  lgb 10
 Logarit tự nhiên là logarit cơ số e . Viết : log b  lnb e
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 11
Tổng Hợp Lý Thuyết
Năm học: 2023-2024 B. CÁC DẠNG BÀI TẬP.
 Dạng 2.1. Tính giá trị biểu thức
 Áp dụng các tính chất – công thức để biến đổi:
⓵ log a 1, log 1 0 a a ⓶ log ba a
 b, log a  a   ⓷ log b c  b  c (Tích – tổng) a  .  01 log log Tính chất a a ⓸ b log
 log b  log c (Thương – hiệu) a a a c 1
Đặc biệt : với a, b  0, a  1 log  log b a a b
⓵ log b  log b ⓶ 1 log b  log b a a a a 02
Công thức bay 1
Đặc biệt: log n b  log b a a n ⓵ log b log c b 
⓶ log b  log .clog b a log a a a c 03 Đổi cơ số c 1
Đặc biệt : log c  . a log a c  Ví dụ 2.1.1 log 4
Cho 0  a 1. Tính giá trị của biểu thức a a . A. 16. B. 2 . C. 4 . D. 12 Lời giải Chọn A 2 log 4 Ta có 2log 4 log 4 2 a a a a  a  a  4 16 .  Ví dụ 2.1.2
Tính giá trị của biểu thức A  2log 12  3log 5  log 15  log 150 . 2 2 2 2 A. 2  . B. 2 3 . C. 3 . D. 3 2 Lời giải Chọn C 18000 2 3
A  log 12  log 5  log 15 log 150 2 3  log 12 5 .  log 15 1 . 50  log  log 8  3 2 2 2 2 2 2 2 2 2250  Ví dụ 2.1.3 Rút gọn biểu thức 2 4 6 8
K  log b  2 log b  3log b  4log b ta được 2 3 4 a a a a 1
A. 4log b . B. log b .
C. 3log b .
D. log a a a a 2 b Lời giải Chọn A 2 4 6 8
K  log b  2 log b  3log b  4 log b  2 log b  4log b  6log b  8log b  4log b 2 3 4 a a a a a a a a a
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 12
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 2.2. Biểu diễn logarit
 Ta thực hiện theo các bước sau
 Bước 01. Biến đổi các biểu thức logarit phụ thuộc vào tham số a và b .
 Bước 02. Đặt các biểu thức logarit của các số nguyên tố là các ẩn x, y,z …. Từ đó ta
thu được phương trình hoặc hệ phương trình với các ẩn x, y, z …. Ta tìm
các ẩn này theo a,b
 Bước 03. Giải hệ tìm được tìm x, y,z … theo a,b . Từ đó tính được biểu thức theo các log b 1
tham số a,b Các công thức nền tảng là log c b  và  log a a log a log b b c a  Ví dụ 2.2.1
Cho a  log 14 . Biểu diễn log 16 theo a 2 49 2 2 A. .
C. a  3. D. 3a a  . B. 1 a Lời giải Chọn A 1 2 2 2 Ta có 4
log 16  log 2  2 log 2  2.    . 2 49 7 7 log 7 14 log 14  log 2 a 1 2 log  2 2 2 2  Ví dụ 2.2.2
Cho a  log 18 và b  log 60. Tính log 2 theo a và b 5 5 3 b  2 2 3a  ab
a  2b  2 a  2 A. . B. . D. 2a  b 5a  . C. 4 2a  b 1 a 1 Lời giải Chọn C
a  log 18  log 2  2log 3 Đầu tiên ta có hệ 5 5 5  .
b  log 60  2 log 2  log 3 1  5 5 5
Đặt x  log 2 và y  log 3 từ đó ta có hệ phương trình bậc nhất hai ẩn 5 5 
a  2b  2    x  x log 2 2y  a  5   3   . 2
 x  y  b 1 2a  b 1 y  log 3  5  3 log 2 a  b  Nên 5 log 2  2 2  . 3 log 3 2a  b 1 5
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 13
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 2.3. Mệnh đề đúng – sai
 Ta lưu ý các công thức sau
⓵ log a 1, log 1 0 a a ⓶ log ba a
 b, log a  a   ⓷ log b c  b  c (Tích – tổng) a  .  log log 01 Tính chất a a ⓸ b log
 log b  log c (Thương – hiệu) a a a c 1
Đặc biệt : với a, b  0, a  1 log  log b a a b
⓵ log b  log b ⓶ 1 log b  log b a a a a 02
Công thức bay 1
Đặc biệt: log n b  log b a a n ⓵ log b log c b 
⓶ log b  log .clog b a log a a a c 03 Đổi cơ số c 1
Đặc biệt : log c  . a log a c  Ví dụ 2.3.1
Cho a,b,c  0; a  1; b  1. , Trong các khẳng định sau, khẳng định nào sai? 1 A. log b  . B. log .
b log c  log c . a log a a b a b
C. log b  c b . D. log b c  b  c . a  .  log log c loga a a a Lời giải Chọn C 1
Câu C sai, vì log b  b c loga a c  Ví dụ 2.3.2
Cho a,b,c  0 và a,b  1, Trong các khẳng định sau, khẳng định nào sai? A. log b a a  b.
B. log b  log c  b  c . a a log c C. log a c  .
D. log b  log c  b  c . b log b a a a Lời giải Chọn D
Câu D sai, vì khẳng định đó chỉ đúng khi a 1, còn khi 0  a 1 log b  log c  b  c a a  Ví dụ 2.3.3
Cho a,b,c  0 và a,b  1, Trong các khẳng định sau, khẳng định nào sai? 1 A.  log a . B. log .
b log c  log c . log b b a b a a b C. log  .
b c  log b  c .
D. log b  log c  log . a a   a a a c Lời giải Chọn C
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 14
Tổng Hợp Lý Thuyết
Năm học: 2023-2024 Câu C sai, vì log  .
b c  log b  log c a a a  Ví dụ 2.3.4
Cho a  0,b  0 thỏa mãn 2 2
a  b  7ab . Mệnh đề đúng trong các mệnh đề sau là: a  b 1
A. 2log a  logb  log7ab . B. log
 log a  logb. 3 2 1 3
C. 3log a  b  log a  log b .
D. log a  b  log a  log b. 2 2 Lời giải Chọn B Ta có 2 2
a  b  7ab    a  b a b2 2  9ab   ab 9 2  a  b  a  b  log
 log ab  2log  log a    log b  3  3  Ví dụ 2.3.5
Với mọi số a , b  0 thỏa mãn 2 2
9a  b 10ab thì đẳng thức đúng là.
log 3a  b log a  log b
A. 2log 3a  b  log a  log b . B.  . 4 2 3a  b 1
C. log a  log b   1  1. D. log
 log a  logb . 4 2 Lời giải Chọn D Ta có 2 2
9a  b 10ab 2 2
 9a  6ab  b 16ab
  a  b2 3 16ab  ab2 3    a b 3a b 1 log  3 log ab  2log
 log a  log b  log
 log a  logb. 16 4 4 2
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 15
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
LŨY THỪA – MŨ – LOGARIT
HÀM SỐ MŨ – HÀM SỐ LOGARIT A. LÝ THUYẾT CHUNG. 1. Hàm số mũ. Hàm số mũ x
y  a , a  0,a   1
Tập xác định D  . f x
Tập giá trị
T  0;  , nghĩa là khi giải phương trình mà đặt t  a thì t  0. f x gx a 1 Hàm số x
y  a đồng biến, khi đó: a  a
 f x  gx . Đơn điệu f x gx 0  a 1 Hàm số x
y  a nghịch biến, khi đó: a  a
 f x  gx .    x a  x
 a .ln a   u
a   u . u  a .ln a    x e  x
 e   ue  u Đạo hàm  e .u   u
n u   n n 1 . n u 
Nhận trục hoành làm đường tiệm cận ngang Đồ thị
 Nhận xét: Đồ thị hàm số x
y  a a  
1 đối xứng với đồ thị hàm số x
y  a 0  a   1 qua Oy.
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 16
Tổng Hợp Lý Thuyết
Năm học: 2023-2024 2. Hàm số logarit.
Hàm số logarit y  log x, a  a  x  a  0, 1; 0
Tập xác định
D  0;   .
Tập giá trị T 
, nghĩa là khi giải PT mà đặt t  log x thì t không có điều kiện. a
Hàm số y  log x đồng biến trên D , khi đó: a a 1
log f x  log g x  f x  g x . a a       Đơn điệu
Hàm số y  log x nghịch biến trên D , khi đó: a 0  a 1
log f x  log g x  f x  g x . a a          u log x   u  a  1 loga  . x ln a . u ln a  u  Đạo hàm  lnn u  n 1
 n ln u  u u ln x 1
 , x  0  (ln u)  x u
Nhận trục tung làm đường tiệm cận đứng Đồ thị
 Nhận xét:
Đồ thị hàm số y  log x a 
đối xứng với đồ thị hàm số y  log x
 a  qua Ox. a 0 1 a  1
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 17
Tổng Hợp Lý Thuyết
Năm học: 2023-2024 B. CÁC DẠNG BÀI TẬP.
 Dạng 3.1. Tập xác định của hàm số logarit a  0 
 Điều kiện xác định của hàm số y  log f x : a  1 . a
  fx0  n
Đặc biệt: với hàm số y  log  f x  f x : g x     
 ta lưu ý “mũ n” của  
gx  0   n Nếu n 2 
ĐKXĐ của hàm số y  log
 f x  gx 1 . g x     
 : fx0
gx  0   n Nếu n 2 
 ĐKXĐ của hàm số y  log
 f x  gx 1 . g x     
 : fx0
Tóm lại nếu f x hoặc gx có “mũ n” ta chú ý xem “n” chẵn hay lẻ.  Ví dụ 3.1.1
Tìm tập xác định D của hàm số y  log 2x 1 . 3    1   1   1 
A. D  ;    . B. D  ;     .
C. D  0;   . D. D   ;     .  2   2   2  Lời giải Chọn D 1
Hàm số y  log 2x 1 có nghĩa khi 2x 1  0  x   3   2  1 
Vậy TXĐ là D   ;     2   Ví dụ 3.1.2
Tìm tập xác định D của hàm số y  log  2
x  3x  2 . A. D   2  , 1  .  
B. D  , 2   1  , . C. D   2  ,  1 .
D. D  , 2     1  ,   . Lời giải Chọn B x  2  Điều kiện 2
x  3x  2  0    D  , 2  1,. x  1    Ví dụ 3.1.3
Tập xác định của hàm số: y  log x  2 2 là A. B.  \  2 .
C. 2;  . D. 2;    . Lời giải Chọn B
Hàm số y  log x  2
2 xác định nếu x  2 2  0  x  2 .
Vậy tập xác định D   \  2 .
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 18
Tổng Hợp Lý Thuyết
Năm học: 2023-2024  Ví dụ 3.1.4 2  x
Tập xác định của hàm số: y  log là 1 x  2 2 A. 0; 2   B. 0; 2. C.  ;  2  0;2   . D.  2  ; 2 . Lời giải Chọn A  2  x  2  log x  0   1 1       x x ; 2    0 2  x 2 ;    ĐKXĐ: 2       x  ;  .  2  2 x  x   x      2  ; 2 0 2 0 0  x  2 x  2  Ví dụ 3.1.5 2021
Tập xác định của hàm số: 2 y  log
x  3x  2  ln 3  x là 2      x 1
A. D  ;   1   1  ;00; 
1  2;3 B. D  ;   1  2;3 .
C. D  ;   1   1  ;  1  2;3 .
D. D  ;   1 . Lời giải Chọn A x  1 x 1  0   x  0  x 1  1  ĐKXĐ: 
 x  2  D  ; 1  1;0  0;1  2;3 . 2        
x  3x  2  0 x 1 3    x  0  x  3  Ví dụ 3.1.6
Tìm tất cả các giá trị thực của tham số m để hàm số 2
y  ln(x  2mx  4) có tập xác định D  ? m  2 A. 2   m  2 B.  . m  2   C. m  2  . D. 2
  m  2. Lời giải Chọn D
Hàm số có tập xác định là 2
 x  2mx  4  0, x   2
 '  m  4  0  2   m  2
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 19
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 3.2. Đạo hàm hàm số mũ – logarit    u log x   u  a  1 loga     x a u a u
Đạo hàm hàm số logarit: .ln .ln  lnn u  n 1
 n ln  u  u u ln x 1
 , x  0  (ln u)  x u    x a  x
 a .ln a   u
a   u . u  a .ln a  
 Đạo hàm hàm số mũ:  xe x
 e   ue  u  e .u   u
n u   n n 1 . n u   Ví dụ 3.2.1
Đạo hàm của hàm số y  log 4x 1 là 3   1 4 A. y   . B. y  . . 4x   1 ln 3 4x 1ln3 ln 3 4 ln 3 C. y  . D. y  . . 4x 1 4x 1 Lời giải Chọn D 1 u  4
Với x   . Áp dụng công thức log u  ta có y  . a  4 uln a 4x 1ln3  Ví dụ 3.2.2 2 Hàm số 2 2 x x y   có đạo hàm là 2 A.   22 4 1 2 x x y x     ln2 B. 2 2 x x y    ln2 . 2 C.      2x x y x ln  2 4 1 2
2x  x D.   2 2 2 2 2 x x y x x     ln2 . Lời giải Chọn B  2 2 ' 2
Ta có:    2x x  2x x 
ln2 2       2 2 2 2 4 1 2 x x y x x x ln2.  Ví dụ 3.2.3
Tính đạo hàm của hàm số 1 2 x y   . ln 2 ln 2 A. 1   2 . x y B. 1   2 . x y . 2 1 x 2 1 x 1 2 x  1 2 x C. y  D. y  . 2 1 x 2 1 x Lời giải Chọn D  1  ln 2 1 y  
2 x.ln 2. 1 x  1x    2 . .ln 2. hay 1   2 . x y 2 1 x 2 1 x
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 20
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 3.3. Khảo sát hàm số mũ – logarit
 Ta cần lưu ý các vấn đề sau: Hàm số Mũ x
y  a 1  a  0
Hàm số Logarit y  log x  a  a 1 0
 a 1HS đồng biến.
 a 1HS đồng biến. 01
Đơn điệu  0 a 1HS nghịch biến.
 0  a 1HS nghịch biến. 02
Tiệm cận Nhận Ox làm TCN. Nhận Oy làm TCĐ. Nằm bên trên Ox . Nằm bên phải Oy .
Luôn đi qua điểm 0;  1 .
Luôn đi qua điểm 1;0 . 03 Đồ thị ĐTHS x
y  a 1  a  0 đối xứng y  log x  a 
qua y  x (đường a 1 0
phân xác góc phần tư thứ nhất).
 Với bài toán xét thứ tự cơ số ta nhớ như sau: Hàm số Mũ x
y  a 1  a  0
Hàm số Logarit y  log x  a  a 1 0 1
Càng gần Oy cơ số càng lớn.
Càng gần Ox cơ số càng lớn. Cơ số
0  a 1 Càng gần Oy cơ số càng bé.
Càng gần Ox cơ số càng bé.
Hình minh họa  Ví dụ 3.3.1
Cho hàm số y  log x . Mệnh đề nào dưới đây là mệnh đề sai? 3
A. Hàm số đã cho đồng biến trên tập xác định.
B. Đồ thị hàm số đã cho không có tiệm cận ngang.
C. Đồ thị hàm số đã cho có một tiệm cận đứng là trục Oy .
D. Hàm số đã cho có tập xác định D   \  0 . Lời giải Chọn D
Điều kiện: x  0 nên TXĐ D  0; .  Ví dụ 3.3.2
Cho hàm số y  log x . Mệnh đề nào dưới đây sai? 2
A. Đạo hàm của hàm số là 2
y  x ln 2 .
B. Đồ thị hàm số nhận trục Oy làm tiệm cận đứng.
C. Tập xác định của hàm số là  ;  .
D. Hàm số đồng biến trên khoảng 0;  . Lời giải Chọn C
Hàm số y  log x xác định trên khoảng 0;  . 2
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 21
Tổng Hợp Lý Thuyết
Năm học: 2023-2024  Ví dụ 3.3.3
Tìm mệnh đề đúng trong các mệnh đề sau:
A. Hàm số y  log x với a 1 là một hàm số nghịch biến trên khoảng 0, . a
B. Đồ thị hàm số y  log x và y  log x với 0  a 1 đối xứng với nhau qua Ox. a 1 a
C. Hàm số y  log x với 0  a 1 có tập xác định là . a
D. Hàm số y  log x với 0  a 1 là một hàm số đồng biến trên khoảng 0, a Lời giải Chọn B
Ta có: y  log x  log       x log x
Đồ thị các hàm số y log x và y log x với 1 1 a a a 1 a a
0  a 1đối xứng với nhau qua trục hoành.  Ví dụ 3.3.4
Đồ thị hàm số y  logx  
1 nhận đường thẳng nào dưới đây làm tiệm cận đứng ? A. x 1 B. y  1  . C. x  1 
D. x  0 . Lời giải Chọn C
Đồ thị hàm số y  logx  
1 có đường tiệm cận đứng là x  1  .  Ví dụ 3.3.5
Hàm số nào sau đây nghịch biến trên tập xác định của nó? x
A. y   5
B. y  log x . 2e x  5 
C. y    D. y  log x .   2  1 6 Lời giải Chọn D 1 Hàm số y  log x có cơ số
1 nên hàm số y  log
x nghịch biến trên TXĐ. 1   6 1 6 6  Ví dụ 3.3.6 Cho các hàm số x  , x y a y  b và x
y  c lần lượt có đồ
thị như hình vẽ bên dưới. Hãy so sánh a,b,c .
A. a  b  c
B. a  b  c .
C. a  b  c
D. b  a  c . Lời giải Chọn D Ta thấy x
y  b là hàm số mũ nghịch biến nên 0  b 1. x  , x y
a y  c là hàm số mũ đồng biến nên a,c  1. Và đồ thị x
y  c gần trục Oy hơn x
y  a nên a  c .
Từ đó c  a  b .
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 22
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
LŨY THỪA – MŨ – LOGARIT BÀI TOÁN LÃI SUẤT A. LÝ THUYẾT CHUNG. 1. Lãi đơn.
 Số tiền lãi chỉ tính trên số tiền gốc mà không tính trên số tiền lãi do số tiền gốc sinh ra.
 Công thức tính lãi đơn:  Trong đó:
V : Số tiền cả vốn lẫn lãi sau n kỳ hạn; n  1 . n V V r n 0  
V : Số tiền gửi ban đầu; 0
n : Số kỳ hạn tính lãi;
r : Lãi suất định kỳ, tính theo %. 2. Lãi kép.
 Số tiền lãi không chỉ tính trên số tiền gốc mà còn tính trên số tiền lãi do tiền gốc đó sinh
ra thay đổi theo từng định kỳ.
 Ta có các loại lãi kép sau:
2.1. Lãi kép, gửi một lần:  Trong đó:
T : Số tiền cả vốn lẫn lãi sau n kỳ hạn; n n  1 n T T r
T : Số tiền gửi ban đầu; 0   0
n : Số kỳ hạn tính lãi;
r : Lãi suất định kỳ, tính theo %.
2.2. Lãi kép liên tục:  Trong đó:
T : Số tiền cả vốn lẫn lãi sau n kỳ hạn; n  . nr n T T e 0
T : Số tiền gửi ban đầu; 0
n : Số kỳ hạn tính lãi;
r : Lãi suất định kỳ, tính theo %.
2.3. Lãi kép, gửi định kỳ.
2.3.1. Trường hợp gửi tiền định kì cuối tháng. Bài toán 1
Cứ cuối mỗi tháng gửi vào ngân hàng m triệu, lãi suất kép (tháng hoặc năm).
Hỏi sau n (tháng hoặc năm) số tiền thu được là bao nhiêu?
Người ta chứng minh được số tiền thu được là: .
 Chứng minh Tháng Đầu tháng Cuối tháng 1 Chưa gửi m 2 m
m1 r  m 2 3
m1 r  m
m1 r  m1 r  m
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 23
Tổng Hợp Lý Thuyết
Năm học: 2023-2024 … … … n 1  n
m1 r  ... m1 r  m   n 1 n 1 
Vậy sau tháng n ta được số tiền T  m  r
  m  r  m m   1 r
 ... 1 r 1 n 1  ... 1    ,   n
Ta thấy trong ngoặc là tổng n số hạng của cấp số nhân có u  1, u   r q   r n 1  1 , 1 1 n   q 1 m n Biết rằng:  
S  u  ...  u  u . nên T   r  n 1  1 n 1 n 1 q 1 r   Bài toán 2
Cứ cuối mỗi tháng gửi vào ngân hàng m triệu, lãi suất kép
(tháng hoặc năm). Sau n (tháng
hoặc năm) số tiền thu được là A triệu. Hỏi số tiền gửi mỗi tháng m là bao nhiêu?
Người ta chứng minh được số tiền cần gửi mỗi tháng là: .
 Chứng minh  m n
Áp dụng bài toán 1 ta có số tiền thu được là T  r     n 1  1 r   ,  m n   Ar
Mà đề cho số tiền đó chính là A nên A 
1r 1  m  . r    n 1 r 1 Bài toán 3
Cứ cuối mỗi tháng gửi vào ngân hàng m triệu, lãi suất kép
(tháng hoặc năm). Sau n (tháng
hoặc năm) số tiền thu được là A triệu. Hỏi số tháng hoặc năm n là bao nhiêu?
Người ta chứng minh được số tháng thu được đề bài cho là: .
 Chứng minh  m n
Áp dụng bài toán 1 ta có số tiền thu được là T  r     n 1  1 r   .
 Đề cho số tiền đó chính là A nên: m    n  Ar n Ar  Ar  A
1 r  1  m    r    n       n 1  r   log r 1  1 1 1 1 m  m r 
 Như vậy trong trường hợp 2.3.1 này ta cần nắm vững công thức bài toán 1 từ đó có thể dễ
dàng biến đổi ra các công thức ở bài toán 2, bài toán 3.
2.3.2. Trường hợp gửi tiền định kì đầu tháng. Bài toán 4
Cứ đầu mỗi tháng gửi vào ngân hàng m triệu, lãi suất kép (tháng hoặc năm).
Hỏi sau n (tháng hoặc năm) số tiền thu được là bao nhiêu?
Người ta chứng minh được số tiền thu được là: .
 Chứng minh
 Ta xây dựng bảng sau: Tháng Đầu tháng Cuối tháng
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 24
Tổng Hợp Lý Thuyết
Năm học: 2023-2024 1 m m1 r 2 2
m1 r  m
m1 r  m1 r 2 3 2 3
m1 r  m1 r  m
m1 r  m1 r  m1 r … … … n n …
m1 r  ... m1 r
 Vậy sau tháng n ta được số tiền: n  r  T m r m r m  r r             m  r n  n n ...     ...    1  1 1 1 1 1 1   r Bài toán 5
Cứ đầu mỗi tháng gửi vào ngân hàng m triệu, lãi suất kép
(tháng hoặc năm). Sau n (tháng
hoặc năm) số tiền thu được là A triệu. Hỏi số tiền gửi mỗi tháng m là bao nhiêu?
Người ta chứng minh được số tiền cần gửi mỗi tháng là: .
 Chứng minh  m n
Áp dụng bài toán 4. Ta có số tiền thu được là: T  r      r n 1  1 1  r   ,  m n   Ar
Mà đề cho số tiền đó là A nên A 
1r 1 1r  m  . r    n  
1 r 1 r 1   Bài toán 6
Cứ đầu mỗi tháng gửi vào ngân hàng m triệu, lãi suất kép
(tháng hoặc năm). Sau n (tháng
hoặc năm) số tiền thu được là A triệu. Hỏi số tháng hoặc năm n là bao nhiêu?
Người ta chứng minh được số tháng thu được đề bài cho là: .
 Chứng minh  m n
Áp dụng bài toán 4. Ta có: số tiền thu được là: T  r      r n 1  1 1  r   .  m n
Đề cho số tiền đó là A nên: A   
1 r 1 1 r r   Ar       n Ar Ar m 1 r         n log 1  .
   n  m   r 1 r m  1 r r r  1 1 1 1 1     
 Như vậy trong trường hợp 2.3.2 ta cần nắm vững công thức bài toán 4 từ đó có thể dễ dàng
biến đổi ra các công thức ở bài toán 5, bài toán 6.
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 25
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
2.3.3. Trường hợp vay nợ và trả tiền định kì đầu tháng. Bài toán 7
Vay ngân hàng A triệu đồng. Cứ đầu mỗi tháng (năm) trả ngân hàng m triệu, lãi suất kép
(tháng hoặc năm). Hỏi sau n (tháng hoặc năm) số tiền còn nợ là bao nhiêu?
Người ta chứng minh được số tiền còn nợ là: .
 Chứng minh
 Ta xây dựng bảng sau: Tháng Đầu tháng Cuối tháng 1 A  m
Am1r  A1rm1r 2 2 2
A1 r  m1 r  m
A1 r  m1 r  m1 r 2 2 3 3 2 3
A1 r  m1 r  m1 r  m A1 r  m1 r  m1 r  m1 r … … … n n 2 n …
A1 r  m1 r ... m1 r  m1 r
 Vậy sau tháng n ta còn nợ số tiền:
T  A  r  m  r   m  r  m  r n  n  n ...  2 1 1 1 1  n     n  n n r A r m r ...  r        
 A  r  m  r 1  1 1 1 1 1 1   . r
3. Bài toán tăng trưởng dân số.  Công thức tính:  Trong đó:    m X n X  m n 1 r
r : tỉ lệ tăng dân số từ năm n đến năm m. 
X : dân số năm m. m,n  
; m  n m
X : dân số năm n. n X 
Từ đó ra có công thức tính tỉ lệ tăng dân số là m
r  mn 1 . Xm  Ví dụ 4.1
Bà Hoa gửi 0,45% triệu vào tài khoản định kỳ tính lãi kép với lãi suất là 8% / năm.
Tính số tiền lãi thu được sau 10 năm. Lời giải
 Áp dụng công thức tính lãi kép, sau 10 năm số tiền cả gốc và lãi bà Hoa thu về là   n A r    , 10 1 100 1 0 08  215,892triệu đồng.
 Suy ra số tiền lãi bà Hoa thu về sau 10năm là 215,892 100 115,892 triệu đồng.  Ví dụ 4.2
Một người muốn gửi tiết kiệm ở ngân hàng và hi vọng sau 4 năm có được 850 triệu
đồng để mua nhà. Biết lãi suất ngân hàng mỗi tháng trong thời điểm hiện tại là
0,45% . Hỏi người đó mỗi tháng phải gửi vào ngân hàng tối thiểu bao nhiêu tiền
để đủ số tiền mua nhà ? (giả sử số tiền mỗi tháng là như nhau và lãi suất trong 4 năm là không thay đổi). Lời giải
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 26
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Giả sử người này gửi tiền ở thời điểm t nào đó , kể từ thời điểm này sau 4 năm (48
tháng) ông muốn có số tiền 850 triệu.
 Như vậy rõ ràng ta có thể coi đây là bài toán gửi tiền định kì đầu tháng. A r
 Áp dụng bài toán 5 ta có số tiền phải gửi mỗi tháng là : m    . n  
1 r  1 r 1  
 Theo bài ra n  48,r  0,45%,A  850 .  850 0 . , 45%
Thay vào  ta được m    , triệu đồng.  
1 0, 45% 1 0,45% 15 833 48 1    Ví dụ 4.3
Một bà mẹ Việt Nam anh hùng được hưởng số tiền là 4 triệu đồng trên một tháng
(chuyển vào tài khoản của mẹ ở ngân hàng vào đầu tháng). Từ tháng 1 năm 2016 mẹ
không đi rút tiền mà để lại ngân hàng và được tính lãi suất 1% trên một tháng.
Đến tháng 12 năm 2016 mẹ rút toàn bộ số tiền (gồm số tiền của 12 tháng và số tiền đã
gửi tháng 1). Hỏi khi đó mẹ lĩnh về bao nhiêu tiền ? (kết quả làm tròn theo đơn vị nghìn đồng). Lời giải
 Nếu ban đầu gửi vào a đồng, từ đầu tháng sau gửi thêm a đồng (không đổi) vào
đầu mỗi tháng với lãi suất r% trong n tháng thì tổng số tiền thu được là : a A a
 r  rn 4      1 1 1  4 
11% 11%11 1 4  50,73 r   1%   triệu đồng.
 n 11 là tính từ đầu tháng 2 đến cuối tháng 12.  Ví dụ 4.4
Đầu năm 2016, anh Hùng có xe công nông trị giá 100 triệu đồng. Biết mỗi tháng
thì xe công nông hao mòn mất 0, 4% giá trị, đồng thời làm ra được 6 triệu đồng
(số tiền làm ra mỗi tháng là không đổi). Hỏi sau một năm, tổng số tiền (bao gồm giá tiền
xe công nông và tổng số tiền anh Hùng làm ra) anh Hùng có là bao nhiêu? Lời giải
 Sau một năm số tiền anh Hùng làm ra là 6 1 . 2  72 triệu đồng
 Sau một năm giá trị xe công nông còn 12 100 1
(  0,4%)  95,3042 triệu đồng
 Vậy sau một năm số tiền anh Hùng có là 167,3042 triệu đồng  Ví dụ 4.5
Bác B gởi tiết kiệm số tiền ban đầu là 50 triệu đồng theo kỳ hạn 3 tháng với lãi suất
0,72% tháng. Sau một năm bác B rút cả vốn lẫn lãi và gởi theo kỳ hạn 6 tháng với lãi
suất 0,78% tháng. Sau khi gởi đúng một kỳ hạn 6 tháng do gia đình có việc bác gởi
thêm 3 tháng nữa thì phải rút tiền trước hạn cả gốc lẫn lãi được số tiền là 57 6 . 94 9 . 45,55
đồng (chưa làm tròn). Biết rằng khi rút tiền trước hạn lãi suất được tính theo lãi suất
không kỳ hạn, tức tính theo hàng tháng. Trong số 3 tháng bác gởi thêm lãi suất là Lời giải
 Số tiền bác B rút ra sau năm đầu:T  50 0 . 00 0 . 00 * 1 0,0072 * 34 1
 Số tiền bác B rút ra sau sáu tháng tiếp theo:T  T * 1 0,0078* 6 2 1  
 Số tiền bác B rút ra sau ba tháng tiếp theo: 57 6 . 94 9 . 45,55
T  T * 1 r3  57 6 . 94 9 . 45,55  r  3 1  0,004  0,4% . 3 2 T2
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 27
Tổng Hợp Lý Thuyết
Năm học: 2023-2024  Ví dụ 4.6
Bạn Nam là sinh viên của một trường Đại học, muốn vay tiền ngân hàng với lãi suất
ưu đãi trang trải kinh phí học tập hàng năm. Đầu mỗi năm học, bạn ấy vay ngân hàng
số tiến 10 triệu đồng với lãi suất là 4% . Tính số tiền mà Nam nợ ngân hàng sau 4 năm,
biết rằng trong 4 năm đó, ngân hàng không thay đổi lãi suất ( kết quả làm tròn đến nghìn đồng). Lời giải
 Tổng số tiền bạn Nam vay ( gốc và lãi) sau 4 năm là: A 
  , 4    , 3    , 2 6 6 6 6 10 1 0 04 10 1 0 04 10 1 0 04 10 10,04 4   ,  
10 1 0,04 1 1 0,04  1 0,042  1 0,043 1 1 0 04 6 6 10 1 0,04   .         ,  44163256 1 1 0 04
 Nên A  44163000 đồng  Ví dụ 4.7
Một giáo viên được nhận lương khởi điểm là 8 0 . 00 0
. 00 đồng/tháng. Cứ sau hai năm
lương mỗi tháng của giáo viên đó được tăng thêm 10% so với mức lương hiện tại.
Tính tổng số tiền T (đồng) giáo viên đó nhận được sau 6 năm làm việc. Lời giải
 Lương 2 năm đầu tiên của giáo viên đó nhận được là 6 6 T  8 1 . 0 2 . 4 192 1 . 0 (đồng) 1
 Theo công thức tính lãi kép, lương 2 năm tiếp theo giáo viên đó nhận được: T  24 8 . 1 . 0 .110%1 6 6  212,2 1 . 0 (đồng) 2
 Lương 2 năm cuối cùng giáo viên đó nhận được: T  24 8 . 1 . 0 .110%2 6 6  232,32 1 . 0 (đồng) 3
 Tổng số tiền T (đồng) giáo viên đó nhận được sau 6 năm làm việc:
T  T T T  635,520,000 (đồng). 1 2 3  Ví dụ 4.8
Anh Hưng đi làm được lĩnh lương khởi điểm 4 0 . 00 0
. 00 đồng/tháng. Cứ 3 năm, lương
của anh Hưng lại được tăng thêm 7% /1 tháng. Hỏi sau 36 năm làm việc anh Hưng
nhận được tất cả bao nhiêu tiền? (Kết quả làm tròn đến hàng nghìn đồng). Lời giải
 Gọi a là số tiền lương khởi điểm, r là lương được tăng thêm.
+ Số tiền lương trong ba năm đầu tiên: 36a
+ Số tiền lương trong ba năm kế tiếp: a  . a r  a    r1 36 36 1
+ Số tiền lương trong ba năm kế tiếp: a  r2 36 1 …
+ Số tiền lương trong ba năm cuối: a  r11 36 1 .
 Vậy sau 36 năm làm việc anh Hưng nhận được:
  r1  r2  r3 ... r11 1 1 1 1 1 .a 3 . 6  2 5 . 75 9 . 36983 2 5 . 75 9 . 37 0 . 00   đồng.
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 28
Tổng Hợp Lý Thuyết
Năm học: 2023-2024  Ví dụ 4.9
Một người đem gửi tiền tiết kiệm vào một ngân hàng với lãi suất 1% một tháng. Biết
rằng cứ sau mỗi quý ( 3 tháng) thì lãi sẽ được cộng dồn vào vốn gốc. Hỏi sau tối thiểu
bao nhiêu năm thì người đó nhận lại được số tiền bao gồm cả vốn lẫn lãi gấp ba lần số tiền ban đầu Lời giải
 Gọi a là số tiền người đó gửi ban đầu
 Số tiền nhận được cả gốc lẫn lãi sau N năm là   N T a  , 4 1 0 03 T    N
 , 4   N.ln ,  ln 3 3 1 0 03 3 4 1 03  ln 3  N   9,29 a 4 ln1, 03  Ví dụ 4.10
Một người vay ngân hàng một tỷ đồng theo phương thức trả góp để mua nhà. Nếu
cuối mỗi tháng, bắt đầu từ tháng thứ nhất người đó trả 40 triệu đồng và chịu lãi số
tiền chưa trả là 0,65% mỗi tháng (biết lãi suất không thay đổi) thì sau bao lâu người
đó trả hết số tiền trên? Lời giải
 Gọi A là số tiền vay, a là số tiền gửi hàng tháng r là lãi suất mỗi tháng.
 Đến cuối tháng thứ n thì số tiền còn nợ là: a        n 1 r      T  A n n n n
1 r   a 1 r 1
1  1 r 2 ...1  A1 r    r
 Hết nợ đồng nghĩa T  0 a  n  1 r       a Ar n a a A  r 1 n 1   0 
1r   n  log r 1r r r a  Ar
 Áp dụng với A  1 (tỷ), a  0,04 (tỷ), r  0,0065 ta được n  27,37 .
 Vậy cần trả 28 tháng.  Ví dụ 4.11
Năm 2014, một người đã tiết kiệm được x triệu đồng và dùng số tiền đó để mua nhà
nhưng trên thực tế người đó phải cần 1,55x triệu đồng. Người đó quyết định gửi tiết
kiệm vào ngân hàng với lãi suất là 6,9% / năm theo hình thức lãi kép và không rút
trước kỳ hạn. Hỏi năm nào người đó mua được căn nhà đó (giả sử rằng giá bán căn
nhà đó không thay đổi). Lời giải  n
Số tiền người gửi tiết kiệm sau n năm là x1 6,9%  n n
Ta cần tìm n để x1 6,9% 1,55x  1 6,9% 1,55  n  6,56...
 Do đó, người gửi tiết kiệm cần gửi trọn 7 kỳ hạn, tức là 7 năm.
 Vậy đến năm 2021 người đó sẽ có đủ tiền cần thiết.
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 29
Tổng Hợp Lý Thuyết
Năm học: 2023-2024  Ví dụ 4.12
Một người gửi ngân hàng 100 triệu đồng theo hình thức lãi kép, lãi suất 0,5% một
tháng (kể từ tháng thứ 2, tiền lãi được tính theo phần trăm tổng tiền có được của tháng
trước đó và tiền lãi của tháng sau đó). Hỏi sau ít nhất bao nhiêu tháng, người đó có
nhiều hơn 125 triệu đồng? Lời giải  n
Số tiền cả vốn lẫn lãi người gởi sau n tháng: 1001 0,005 100 1 . ,005n S    (triệu đồng) 1,005n S S   n  log . 1,005 100 100
 Để có số tiền S 125 (triệu đồng) thì phải sau thời gian S 125 n  log  log  44,74(tháng) 1,005 1,005 100 100
 Vậy: sau ít nhất 45 tháng người đó có nhiều hơn 125 triệu đồng.  Ví dụ 4.13
Ông Nam gởi 100 triệu đồng vào ngân hàng theo thể thức lãi kép kì hạn 1 năm với lãi
suất là 12% một năm. Sau n năm ông Nam rút toàn bộ số tiền (cả vốn lẫn lãi). Tìm số
nguyên dương n nhỏ nhất để số tiền lãi nhận được lớn hơn 40 triệu đồng (giả sử lãi
suất hàng năm không thay đổi) Lời giải
 Gọi T là tiền vốn lẫn lãi sau t tháng, a là số tiền ban đầu n
 Tháng 1 t  
1 : T  a 1 r 1  
 Tháng 2 t  2 : T  a1 r2 2 ……………….  t
Tháng nt  n :T  a  r n 1  T 140 n a
T  a  r  t    (tháng) n   ln ln t 100 1
ln   r ln  % 33,815 1 1 1  t
Để số tiền lãi nhận được lớn hơn 40 triệu thì n   2,818 12  Vậy n  3.  Ví dụ 4.14
Tỉ lệ tăng dân số ở Việt Nam được duy trì ở mức 1,05%. Theo số liệu của Tổng cục
thống kê, dân số Việt Nam năm 2014 có 90.728.900 người. Với tốc độ tăng dân số
như thế đến năm 2030 thì dân số của Việt Nam là bao nhiêu? Lời giải
 Từ năm 2014 đến năm 2030 cách nhau số năm là: 2030 2014 16 năm.
 Dân số Việt Nam năm 2030 : A  9072890011,05%16 107232574 (người). 16
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 30
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
LŨY THỪA – MŨ – LOGARIT PHƯƠNG TRÌNH MŨ A. LÝ THUYẾT CHUNG.
 Phương trình mũ cơ bản: x
a  b a  0, a   1 .
 Phương trình có một nghiệm duy nhất khi b  0.
 Phương trình vô nghiệm khi b  0 . B. CÁC DẠNG BÀI TẬP.
 Dạng 5.1. Phương trình mũ cơ bản
 Giải phương trình mũ cơ bản: x
a  b a  0, a   1 .  Khi đó x
a  b  x  log b a Lưu ý:
 Phương trình có một nghiệm duy nhất khi b  0.
 Phương trình vô nghiệm khi b  0 .  Ví dụ 5.1.1 1
Phương trình 3x  4 có nghiệm là
A. x  log 3 .
B. x  log 2 .
C. x  log 3 .
D. x  log 4 . 2 3 4 3 Lời giải Chọn C 1 1 Ta có 3x  4 
 log 4  x  log 3 . 3 4 x  Ví dụ 5.1.2
Nghiệm của phương trình 8x  4 là 2 1 1 A. x  .
B. x   . C. x  . D. x  2  . 3 2 2 Lời giải Chọn A 2
Ta có: 8x  4  x  log 4 2  x  log 2  8 3 2 3  Ví dụ 5.1.3
Nghiệm của phương trình x x 1  x x 1 2 2 3 3     là 3 2 A. x  log .
B. x 1.
C. x  0 . D. x  log . 3 4 4 3 2 3 Lời giải Chọn A x     3 3 3 x x 1 x x 1 2  2  3  3  3 2 . x  4 3 . x    x    log 3  2  4 4 2
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 31
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 5.2. Đưa về cùng cơ số f x gx
Với a  0 , a 1: a  a
 f x  gx .  Ví dụ 5.2.1  1 Phương trình 2x 1 2   0 có nghiệm là 8 A. x  1  .
B. x  2 . C. x  2  .
D. x 1. Lời giải Chọn A  1 Ta có 2x 1 2x 1  3 2 0 2 2      x  1  8  Ví dụ 5.2.2 x 2
Tìm tập nghiệm của phương trình 1 2  4x . A. 4  3,4   3 . B. 2  3,2   3 . C.  4   3, 4   3. D.  2   3, 2   3. Lời giải Chọn B     x 2  x 2 3 1 x x 2 2 Ta có 1 2 2  4  2
 2 x  x   2 1
 2x  x  4x 1  0   . x  2  3  Ví dụ 5.2.3 x 1   1 
Nghiệm của phương trình  125x   là  25  2 1 A.  . B. 4 . C.  . D. 1 5 8 Lời giải Chọn A x 1   1  2 x  x  2 Ta có 1 3  125  5  5 x  2  x  
1  3x  x     .  25  5  Ví dụ 5.2.4 2 x 1  x2  1 
Tìm tập hợp tất cả các nghiệm của phương trình    2 2 .  4  11  2   2   11 A.   . B.   . C.   . D.    2  11  11  2  Lời giải Chọn C 2 x 1  x2  1  Ta có    2 2  4  x2 3x2 3x  2       1 2x 1  2 2 2 2  2 2 .  4  x2 2  2  2  4  x  2   x     2 11
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 32
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 5.3. Logarit hóa 0    a  1, b  0  f x Phương trình a  b   . f  x   log b a  f x gx f x gx Phương trình a  b  log a  log b  f x  g x b a a    .loga f x gx hoặc log a  log b  f x a  g x b b  .logb  .  Ví dụ 5.3.1
Tìm tập nghiệm S của phương trình x 1 2   8 .
A. S    3 . B. S    2 .
C. S  0;  2 . D. S    12 Lời giải Chọn B x 1
2   8  x 1  log 8  x 1  3  x  2 . 2  Ví dụ 5.3.2 x x
Tìm tập nghiệm S của phương trình 4 3 3  4 . log log 4    4  3 
A. S   . B. S    . 1  log 3   4   1log 3  log log 4    4  3  C. S   . D. S    log   4 log 4   log 3   4 3  4  Lời giải Chọn B 4x 3x 3  4 4x 3x  .log 4 log log 4 4  3    log 3x x .log 4  x  .
x log 3  log log 4  x  . 4 4  3  4  3  1 log 3 4  Ví dụ 5.3.3
Giải phương trình sau: x. x , . x  51 2 5 0 2 10 3 3 1 A. x  .
B. x  0 . C. x  1  . D. x   log 2 2 2 4 Lời giải Chọn D x PT   .  5x5 2 5  0,2 1 . 0
 x  log0,25x 5  4x  6 3 1 log 2  x   .log 2 . 2 4  Ví dụ 5.3.4 Cho phương trình x x 1 4 2   3  0. Khi đặt 2x t 
ta được phương trình nào sau đây A. 2
2t  3t  0 .
B. 4t 3  0 . C. 2
t  t  3  0 . D. 2
t  2t  3  0 Lời giải Chọn D Phương trình 4x 2 2 . x   3  0
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 33
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 5.4. Đặt ẩn phụ dễ thấy gx    g x t a 0   
Biến đổi quy về dạng: f a
  00  a  1     .  f  t  0 9x  t  3x
 Thông thường sẽ gặp các cơ số: 4x 
t  2x ;t  0 . 25x  t  5x  Ví dụ 5.4.1
Tập nghiệm của phương trình 9x 5 3 . x   6  0 là
A. S  1;log 2 . B. S   log 2 . C. S    1 . D. S     3  3  Lời giải Chọn A x 9x 5 3 . x   6  0  23 5 3.x    6  0  x2 3 5 3 . x    6  0 (**) t  2 
t  3x  2 x  log 2 Đặt 3x t   0. Khi đó: (**) 2
 t 5t  6  0     3   t  3 
  t  3x  3 x 1
Vậy nghiệm của phương trình là x  1 x  log 2 . 3  Ví dụ 5.4.2
Số nghiệm của phương trình x x 1 4 4 . 9 2 .   8  0 (*) là: A. 3 . B. 1. C. 2 . D. 0 Lời giải Chọn C x   2  4   2x t  0 x  1  (*) 2 4 2 . x 18 2 . x   8  0    1   . 2   4
 t 18t  8  0 2x  x  2  2
Vậy phương trình có hai nghiệm x  1  và x  2 .  Ví dụ 5.4.3 Giải phương trình 12 2 x 15 2
. x 8  0 * . 3 A. x  .
B. x  0 . C. x  1  .
D. x  5 2 Lời giải Chọn C * 2 2 2 . x 15 2 . x   8  0 t   2x  0     2x t  0  1 1 . x 2 2 2 15 2 . x   8  0       2x t   x  1  2 2
 t 15t 8  0  2 2   t  8 
Vậy phương trình có nghiệm x  1  .
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 34
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 5.5. Đặt ẩn phụ với phương trình đẳng cấp
 Phương trình đẳng cấp có dạng: 2 2 . m X  . n XY  . p Y  0 .  2 f x f x
Khi đó với phương trình mũ đẳng cấp có dạng: . m a  . n  . a b   2 f x  . p b  0
 Phương pháp làm như sau: f x 2 f x a  .ab   2 f x b . m  . n  . p  0 2 f x 2 f x 2 f x b b b f x 01   2 f x a 2 Chia 2 vế cho b f x f x , đặt    t  0 .        a a b   . m      . n    p  0  b    b    2  . m t  .
n t  p  0 . f x 2 f x a  .ab   2 f x b . m  . n  . p  0 2 f x 2 f x 2 f x a a a f x 02   2 f x b Chia 2 vế cho a , đặt  f x f x 2   t  0 .        b b a   m  . n    . p    0    a   a     2  m  . n t  . p t  0 .  Lưu ý:
Đây là dạng sẽ có trong bài “Bất phương trình mũ”, lúc giải BPT mũ ta cần chú ý đến cơ
số lớn hay bé hơn 1. Để giảm sai sót chúng ta hãy “chia 2 vế” cho cơ số bé nhất !!!  Ví dụ 5.5.1
Giải phương trình sau: 8x 18x 2 2 . 7x   (*)
A. x 1.
B. x  log 2 . C. x  1  .
D. x  0 3 Lời giải Chọn D x  2 x 3x    3 x 3   3  t    0    3  (*)  1  2   .     2   t   1    x  0 .  2   2    2  3 2 2
 t  t 1  0
Vậy phương trình có nghiệm x  0 .  Ví dụ 5.5.2
Số nghiệm của phương trình: 25x 15x 2 9 . x   (*) là: A. 0 . B. 3 . C. 1. D. 2 Lời giải Chọn C x    x  5 t    0 2 x x    5   x 5   5  t    0     3   5  (*)    2  0        3     1    x  0 .  3   3     t 1  3  2 t   t  2  0   t  2  
Vậy phương trình có nghiệm x  0 .
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 35
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 5.6. Đặt ẩn phụ với tích hai cơ số bằng 1
 Phương trình đẳng cấp có dạng: 2 2 . m X  . n XY  . p Y  0 .  f x f x
Phương trình mũ ta xét có dạng: . m a  . n b
 p  0  trong đó .ab 1.
 Phương pháp làm như sau: 1 f x f x 1 Vì .
a b  1 b  
 Đặt t  a ,t  0  b  . a t 1 Khi đó  2  . m t  .
n  p  0  . m t  n  . p t  0 . t  Ví dụ 5.6.1 x x
Tìm tích các nghiệm của phương trình  2   1
  2  1  2 2  0 . A. 2 . B. 1. C. 0 . D. 1 Lời giải Chọn B Ta có:  2   1  2   1  1 x x
Đặt t   2  
1 , điều kiện t  0 . Suy ra    1 2 1  t 1
Phương trình trở thành:  t  2 2  0 t x
t  2 1 2 1  2 1 x 1  2  
 t  2 2t 1  0   . x x 
t  2 1  2  1  2 1  2  1   2   1 1  x  1  
Vậy tích của hai nghiệm x x  1. 1   1  1 2    Ví dụ 5.6.2 x x Phương trình 3 5  3 5  3 2 . x     có tổng các nghiệm là A. 0 . B. 1. C. 1. D. 2 Lời giải Chọn A       x x x x  3 5   3 5  3 5 3 5  3 2 . x        3   . 2   2      x x  3 5  3 5   3 5   3 5  Thấy    1       . 2  2   2   2         x  3 5   3 5  1 Đặt t     0      2      2 t   x  3 5  3 5  3  5    t     2 2 1   x 1 2 2
 t   3  t  3t 1 0       x 1 t           x  1 3 5  3 5 3 5 3 5 t         2  2  2  2     
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 36
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 5.7. Phương pháp hàm số
 Định lí. Nếu hàm số y  f x là hàm số liên tục và đồng biến trên  ;
a b , y  gx là hàm số
liên tục và nghịch biến trên  ;
a b thì phương trình f x  gx có tối đa một nghiệm trên  ; a b .
 Phương pháp làm như sau:
 Biến đổi phương trình đã cho về dạng f x  k , với k là hằng số
 Chứng minh f x là hàm đồng biến( nghịch biến) trên tập xác định.
01  Tìm x sao cho f x  k 0  0
 Kết luận x là nghiệm duy nhất của phương trình f x  k . 0
 Biến đổi phương trình đã cho về dạng f x  gx, với D ,D lần lượt là tập xác định 1 2
của hai hàm số f x , gx
02  Chứng minh f xlà hàm đồng biến và gx nghịch biến trên tập D  D (hay ngược lại) 1 2
 Tìm x sao cho f x  g x 0   0 0
 Kết luận x là nghiệm duy nhất của phương trình f x  gx. 0
 Biến đổi phương trình đã cho về dạng f u  f v, với hàm số f t là hàm đồng
03 biến(hay nghịch biến).
 Phương trình f u  f v  u  v .  Lưu ý:
⓵ Nếu f xvà gx là hàm đồng biến(nghịch biến) trên  ;ab thì f x gx cũng là
hàm đồng biến (nghịch biến) trên  ; a b . ⓶ Hàm số x
y  a đồng biến khi a 1và nghịch biến khi 0  a 1.  Ví dụ 5.7.1
Phương trình 2016x  2x  2018  0 có tất cả bao nhiêu nghiệm thực? A. 1. B. 2. C. 3 . D. 4 Lời giải Chọn A
Xét hàm số :    2016x f x
 2x  2018. Tập xác định:
Khi đó    2016x f x ln 2016  2  0, x
  . Do đó hàm số luôn đồng biến trên . Mà f  
1  0 nên x 1 là nghiệm duy nhất của phương trình.  Ví dụ 5.7.2 2
Tổng các nghiệm của phương trình x x x 1  5 2 3  3
15  2x  x là: A. 6  . B. 1. C. 5 . D. 2 . Lời giải Chọn D 2 Phương trình x x 2 x 1  5  3
 x  x  3  x 15 (1)
Xét hàm số :    3t f t  t, t   .
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 37
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
Khi đó    3t f t ln3 1  0, t
  . Do đó hàm số luôn đồng biến trên . x  
Do đó phương trình (1)  f  2
x  x  f x   2
15  x  x  x  3 15   . x  5 Vậy x  3
 , x  5 là của phương trình.  Ví dụ 5.7.3 Phương trình    1 2 . x x
 x 1 có bao nhiêu nghiệm thực A. 1. B. 0 . C. 3 . D. 2 . Lời giải Chọn D 
Vì x 1 không là nghiệm của phương trình nên ta có    1 1 2
. x  1  2x x x x  x 1 Hàm số 2x y  đồng biến trên R , x 1 Hàm số y  ; và 1; .
x  nghịch biến trên  1 1
Do đó phương trình đã cho có hai nghiệm.  Ví dụ 5.7.3 x x x
Phương trình  3  2    3  2    10  có tất cả bao nhiêu nghiệm thực? A. 1. B. 0 . C. 3 . D. 2 . Lời giải Chọn A  x x x x x
 3  2   3  2 
3  2    3  2    10        1     10 10     x x      
Xét hàm số f x 3 2 3 2           10 10     Ta có: f 2 1 3  2 3  2
Hàm số f x nghịch biến trên do các cơ số 1; 1 10 10
Vậy phương trình có nghiệm duy nhất là x  2 .
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 38
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 5.8. Phương trình chứa tham số
 Để giải bài toán tìm tham số m trong phương trình mũ ta có hai cách phổ biến:
 Cô lập được tham số m.
01  Ta dùng đồ thị hàm số để biện luận số nghiệm (bài toán tương giao).
 Không cô lập được tham số m và có liên quan đến Vi-ét.
02  Đặt ẩn phụ đưa về phương trình bậc hai/bậc ba.
 Kết hợp định lý Vi-ét để giải quyết yêu cầu bài toán  Ví dụ 5.8.1
Có bao nhiêu giá trị nguyên dương của tham số m để phương trình 16x  2 1 . 2x  (  2) 9 . x m  0 có nghiệm dương? A. 2 . B. 4 . C. 3 . D. 1. Lời giải Chọn A
Phương trình 16x  2 1 . 2x  (  2) 9 . x m  0 có nghiệm x  0; 2 x x  4   4 
Phương trình tương đương  2.
 (m  2)  0       có nghiệm x  0;  3   3  x  4  Đặt t  ,t  1;      3    2
  t  2.t (m 2)  0, t  1; 2
 t  2.t  2  , m t  1; Xét 2
y  t  2.t
Phương trình có nghiệm t
 1; khi 2m  1   m 3  Ví dụ 5.8.2
Có bao nhiêu giá trị nguyên của tham số m để phương trình 2 2 4xx 4 9  4 3 . xx
 2m1 0 có nghiệm? A. 27 . B. 25 . C. 23. D. 24 . Lời giải Chọn B
ĐKXĐ: x  0; 4   . Đặt 2
t  4x  x với x  0; 4 
 thì t  0; 2   Đặt 3t u  với t  0; 2   thì u 1  ;9  
Khi đó, tìm m đề phương trình 2
u  4u  2m 1  0 có nghiệm thuộc đoạn 1  ;9   . 2  2m  u
  4u1, với u 1  ;9  
Xét hàm số f u 2  u
  4u1  f u  2
 u 4  0  u  2 . Ta có, f  
1  4 , f 2  5, f 9  4  4 . 5
Do đó, phương trình có nghiệm khi và chỉ khi 4
 4  2m  5  2  2  m  . 2
Vậy có 25 số nguyên của tham số m .
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 39
Tổng Hợp Lý Thuyết
Năm học: 2023-2024  Ví dụ 5.8.3 Gọi  ;
a b là tập các giá trị của tham số m để phương trình 2 2 x 8 x e
e  m  0 có
đúng hai nghiệm thuộc khoảng 0;ln5 . Tổng a  b là A. 2 . B. 4 . C. 6  . D. 14 . Lời giải Chọn D Đặt x
t  e ; x 0; ln5 tương ứng t 1;5 . Phương trình thành 2
2t 8t  m . Xét f t 2
 2t 8t với t 1;5 có f t  4t 8
Phương trình đã cho có 2 nghiệm pb thuộc 0;ln5
Khi f t  m có hai nghiệm t 1;5  8   m  6   Ví dụ 5.8.4
Gọi S là tập hợp các giá trị nguyên của tham số m sao cho phương trình x x 1  2 25  m 5 .
 7m 7  0 có hai nghiệm phân biệt.
Hỏi S có bao nhiêu phần tử. A. 7 . B. 1. C. 2 . D. 3 . Lời giải Chọn C Xét x x 1  2 25  m 5 .
 7m 7  0   1 . Đặt  5x t
t  0 .   2 2
1  t  5mt  7m  7  0 2 . YCBT   
1 có hai nghiệm phân biệt  2 có hai nghiệm phân biệt t ,t  0 1 2 2    25m  4 2 7m  7  0 0     2 21 S   0  5  m  0  1 m  .   3 2 P  0 7  m  7  0 
Mà m  m2; 
3 . Vậy có 2 giá trị nguyên của tham số m .  Ví dụ 5.8.5
Gọi S là tất cả các giá trị nguyên của tham số m sao cho phương trình x x 1  2 4  m 2 .
 2m 5  0 có hai nghiệm phân biệt.
Hỏi S có bao nhiêu phần tử. A. 2 . B. 1. C. 3 . D. 5 . Lời giải Chọn B x x 1  2 x x 2 4  m 2 .
 2m 5  0  4  2m 2 .  2m 5  0 (1) Đặt  2x t
,t  0 . Phương trình (1) thành: 2 2 t  2 .
m t  2m  5  0 (2)
YCBT  (2) có 2 nghiệm dương phân biệt  2 2   '  0
m  2m  5  0  5  m  5     10  S
  0  2m  0  m  0   m  5. 2    2 P  0 2  m  5  0  5 5 m   hoac m   2 2
Do m nguyên nên m  2 . Vậy S chỉ có một phần tử
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 40
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
LŨY THỪA – MŨ – LOGARIT
PHƯƠNG TRÌNH LOGARIT A. LÝ THUYẾT CHUNG.
 Phương trình logarit cơ bản: log f x  b a  0, a  . a 1
 Lưu ý: khi giải phương trình logarit cần phải có điều kiện để logarit tồn tại. B. CÁC DẠNG BÀI TẬP.
 Dạng 6.1. Phương trình logarit cơ bản
 Giải phương trình logarit cơ bản: log x  b a  Khi đó log b
x  b  x  a a  a  a  0, 1  Ví dụ 6.1.1
Tìm tập nghiệm S của phương trình log x  2  2. 4   A. S    16 . B. S    18 . C. S    10 . D. S    14 . Lời giải Chọn B x  2  0 x  2 x  2
Ta có log x  2  2        x 18 . 4   log  x2 2   log 4 2 x  2  4 x 18 4 4  Ví dụ 6.1.2
Phương trình log x 1  3 có bao nhiêu nghiệm ? 2 A. 0 . B. 1. C. 2 . D. 3 . Lời giải Chọn C
Điều kiện: x 1 0  x 1. x 1  8 x  9
Phương trình tương đương với    x 1  8  x  7     Ví dụ 6.1.3 2 Phương trình 2 log
x  2  8 có tất cả bao nhiêu nghiệm thực? 4 2   A. 2. B. 3. C. 4. D. 8. Lời giải Chọn B 2 2 log x  2  8   1 4 2    ĐK: 2
x  2  0  x   2   2          x 4 x 2 x 2 x     8 2 2 4 1 2 2  x  2 2 2  4     2 x  0 x  0.
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 41
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 6.2. Đưa về cùng cơ số
 Cho 1 a  0 . Với điều kiện các biểu thức f x và gx xác định, ta thường đưa các phương
trình logarit về các dạng cơ bản sau:  f x  0
 Loại 1: log f x  b   . a     f  x b   a  f x  0
 Loại 2: log f x  log g x   . a a     f  x   g x  Ví dụ 6.2.1
Phương trình lnx  
1  ln x  3  lnx  7 có bao nhiêu nghiệm ? A. 0 . B. 2 . C. 1. D. 4 Lời giải Chọn C x  Điều kiện x  1
 , phương trình  x  x   1 1 3  x  7   . x  4  
Kết hợp điều kiện ta có nghiệm của phương trình là x 1.  Ví dụ 6.2.2
Giải phương trình 2 log  2
x  x 1  log x 1 . 2    2
A. vô nghiệm.
B. x  2.
C. x  0, x  2. D. x  3. Lời giải Chọn C x 1 0 Phương trình  log  2
x  x 1  log x 1    x  2 . 2  2   2
x  x 1 x 1  Ví dụ 6.2.3
Số nghiệm của phương trình log x 12 .log 2 1 là: 4   x A. 0. B. 2. C. 3. D. 1 Lời giải Chọn D
Điều kiện : 0  x 1 x  3  L
log x 12 .log 2  1  log x 12  log x  x  x 12  0   4   x 2   2 2   2 x  4  N  Ví dụ 6.2.4
Tập nghiệm của phương trình log x  4  2log 14  x  4 là 3   9   A. S    5 .
B. S    5 .
C. S    5 . D. S     . Lời giải Chọn A Điều kiện 4   x 14.
Ta có: log x  4  2log 14  x  4 3   9  
 log x  4  log 14  x  4  log x  4 14  x  4 2 4
 x 10x  56  3  x  5. 3    3   3  
So với điều kiện ta được S    5 .
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 42
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 6.3. Mũ hóa
 Với điều kiện các biểu thức f x và gx xác định, ta thường đưa các phương trình logarit về các dạng cơ bản sau:
 f x   log f x  g x  a    a       0 0 1  f  x gx  a  Ví dụ 6.3.1
Tập nghiệm của phương trình log  x 1
5   25x  2 là: 2  A. S    1 .
B. S  log 5 . 3   1   1  C. S  0;  . D. S     log 5  log 4   4  5  Lời giải Chọn C Điều kiện x 1 5   25x  0 . 5x 1  x  0 log  x 1 5   25x  2 x 1 5    25x  4 2 5 x 5 5 . x    4  0     . 2  5x  4  x  log 4  5
Kết hợp với điều kiện, ta được tập nghiệm của phương trình đã cho là S  0;log 4 . 5   Ví dụ 6.3.2
Số nghiệm của phương trình log  x 2 x 1 25 2     x là A. 0 . B. 1. C. 2 . D. 3 Lời giải Chọn B Điều kiện x 2x 1 25 2    0 . log  x 2 x 1 25 2     x x 2x 1 25 2    10x x x     2 x x  2   2  25x 2 4 . x 10x    4 10  1 2   0      2  1  0       25   25   5   5 
t  1 loai x  2   Đặt   
t t  0 . Khi đó  trở thành 2
2t  t 1  0  .   1 5  t  thoa  2 x 1  2  1 1 t       x  log  log 2 . 2  5  2 2 5 2 5 2  
Kết hợp với điều kiện, ta được tập nghiệm của phương trình đã cho là S  log 2 . 5   2 
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 43
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 6.4. Đặt ẩn phụ dễ thấy
 Giải phương trình f log g x  , 0  a   1 . a   0
 Bước 01. Đặt t  log g x * a  
 Bước 02. Tìm điều kiện của t (nếu có)
 Bước 03. Đưa về giải phương trình f t  0 đã biết cách giải.
 Bước 04. Thay vào * để tìm x .  Ví dụ 6.4.1 Giải phương trình 2
log x  4log x  3  0 . 3 3 A. S    1 . B. S    27 .
C. S  3; 2  7 . D. S    3 Lời giải Chọn C
Điều kiện: x  0 . Đặt log x  t . 3 t 1 log x 1 x  3 PT 2
 t  4t  3  0   3      S  3;2  7 . t  3 log x  3  x  27 3  Ví dụ 6.4.2
Số nghiệm của phương trình log x  log 64  1 là 2 x A. 0 . B. 3 . C. 2 . D. 1 Lời giải Chọn C
Điều kiện : 0  x 1.
Phương trình  log x  6log 2 1. Đặt t  log x , t  0 2 x 2   2 x 8 6 t  t 6  0 t  3 log x  3 PT  t  1     2     1 . t t   0  t  2  log x  2    x  2  4  1 
Kết hợp điều kiện, suy ra phương trình đã cho có tập nghiệm là S  8  ; .  4   Ví dụ 6.4.3
Tích các nghiệm phương trình 2 2
log x  log x 1  5  0 là 3 3 A. 0 . B. 3 . C. 2 . D. 1 Lời giải Chọn D
Điều kiện: x  0 . Đặt 2
log x 1  t , t   1 . 3 t  2 N 2  
PT  t  t  6  0  t  3   L 3 log x  3 x  3 2 2 3
 log x 1  2  log 1  4     3 3  3 log x   3   x  3 3
Kết hợp điều kiện, suy ra phương trình đã cho có tập nghiệm là S   3  3 3 ; 3 .
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 44
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 6.5. Phương pháp hàm số
 Định lí. Nếu hàm số y  f x là hàm số liên tục và đồng biến trên  ;
a b , y  gx là hàm số
liên tục và nghịch biến trên  ;
a b thì phương trình f x  gx có tối đa một nghiệm trên  ; a b .
 Phương pháp làm như sau:
 Biến đổi phương trình đã cho về dạng f x  k , với k là hằng số
 Chứng minh f x là hàm đồng biến( nghịch biến) trên tập xác định.
01  Tìm x sao cho f x  k 0  0
 Kết luận x là nghiệm duy nhất của phương trình f x  k . 0
 Biến đổi phương trình đã cho về dạng f x  gx, với D ,D lần lượt là tập xác định 1 2
của hai hàm số f x , gx
02  Chứng minh f xlà hàm đồng biến và gx nghịch biến trên tập D  D (hay ngược lại) 1 2
 Tìm x sao cho f x  g x 0   0 0
 Kết luận x là nghiệm duy nhất của phương trình f x  gx. 0
 Biến đổi phương trình đã cho về dạng f u  f v, với hàm số f t là hàm đồng
03 biến(hay nghịch biến).
 Phương trình f u  f v  u  v .  Lưu ý:
⓵ Nếu f xvà gx là hàm đồng biến(nghịch biến) trên  ;ab thì f x gx cũng là
hàm đồng biến (nghịch biến) trên  ; a b . ⓶ Hàm số x
y  a đồng biến khi a 1và nghịch biến khi 0  a 1.  Ví dụ 6.5.1
Phương trình log x  2  log x 1 có bao nhiêu nghiệm? 2   3   A. 1. B. 2. C. 3 . D. 4 Lời giải Chọn A  x 1  0 Điều kiện 
 x  2. Đặt log x  2  log x 1  t 2   3   x  2  0
x  2  2t t t       1 2
 3t  2t  1  3t  1 2t    1      .
 x 1 3t  3   3 
Dễ thấy t 1 là một nghiệm của  . t t     t t     Xét f t 1 2    
   f t 1 1 2 2
   ln    ln  0 , f t nghịch biến trên ,  3   3   3  3  3  3
g t 1 là hàm hằng   có một nghiệm duy nhất t 1  x  4.
Kết hợp với điều kiện, ta được nghiệm của phương trình đã cho là x  4 .
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 45
Tổng Hợp Lý Thuyết
Năm học: 2023-2024  Ví dụ 6.5.2
Giải phương trình log x  2  log 3x  4  2 . 3   7  
A. x  5 .
B. x 1
C. x  3. D. x  1  Lời giải Chọn B  x  2   4
Điều kiện của phương trình là  4  x   . x    3  3
Phương trình có một nghiệm x 1  4 
Xét f x  log x  2  log 3x  4 trên  ;    3   7    3  1 3
Ta có : f x     . x  ln  x  0 2 3 3 4 ln 7    4
f x đồng biến trên  ;  
 ; gx  2 là hàm hằng.  3 
Nên phương trình đã cho có một nghiệm duy nhất x 1.  Ví dụ 6.5.3
Giải phương trình log  2
x  x  6  x  log (x  2)  4 . 2  2 A. 5 x  . B. x  1 
C. x  4 .
D. x  3 2 Lời giải Chọn C 2
x  x  6  0 Điều kiện:   x  3. x  2  0 PT  log  2
x  x  6  log
x  2  4  x 2  2   2 x  x  6  log
 4  x  log x  3  x  4 (2) 2 2   x  . 2
Vì log 4  3  4  4 nên phương trình (2) có một nghiệm x  43;  . 2  
Xét hàm số f x  log x 3  x , 2   1
Ta có f x     , x
  ; nên f x đồng biến trên tập xác định. x  3 1 0 3  ln 2
Do đó phương trình đã cho có một nghiệm duy nhất x  4 .
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 46
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 6.6. Phương trình chứa tham số
 Để giải bài toán tìm tham số m trong phương trình logarit ta có hai cách phổ biến:
 Cô lập được tham số m.
01  Ta dùng đồ thị hàm số để biện luận số nghiệm (bài toán tương giao).
 Không cô lập được tham số m và có liên quan đến Vi-ét.
02  Đặt ẩn phụ đưa về phương trình bậc hai/bậc ba.
 Kết hợp định lý Vi-ét để giải quyết yêu cầu bài toán  Ví dụ 6.6.1
Tìm tất cả các giá trị thực của tham số m để phương trình 2
log x  mlog x 1  0 có nghiệm duy nhất nhỏ hơn 1. 3 3 A. m  2  . B. m  1  .
C. m  2 .
D. m 1. Lời giải Chọn A
Điều kiện: x  0 . Vì phương trình có nghiệm nhỏ hơn 1 nên suy ra 0  x 1. 1 Đặt log
x  t , với 0  x 1 t  0 . Phương trình 2
 t  mt 1 0  t   m (*) . 3 t
Phương trình đã cho có nghiệm duy nhất nhở hơn 1
 (*) có nghiệm duy nhất trên ;0 . 1 1 t 1(;0)
Xét f (t)  t  trên ; 0 , ta có: f (t) 1  0   . t 2 t t  1  (  ; 0)
Dựa vào bảng biến thiên ta được m  2
 thỏa mãn đề bài toán.  Ví dụ 6.6.2
Tìm tất cả các giá trị thực của tham số m để phương trình 2
log x  mlog x  2m  7  0 có hai nghiệm x , x thỏa mãn x .x  81. 3 3 1 2 1 2
A. m 12 .
B. m  0 .
C. m  2 .
D. m  4 . Lời giải Chọn D
Điều kiện: x  0 . Giả sử phương trình có hai nghiệm x , x . 1 2
Đặt t  log x , phương trình 2
 t  mt  2m 7  0 (*) . 3
Phương trình đã cho có 2 nghiệm x , x  (*) có hai nghiệm t , t 1 2 1 2 2
 m 8m  28  0 m   .
Theo Vi-et: t  t  log x  log x  m  log x x  m  log 81  m  4  m (thỏa). 1 2 3 1 3 2 3  1 2  3
Vậy với m  4 là giá trị cần tìm.
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 47
Tổng Hợp Lý Thuyết
Năm học: 2023-2024  Ví dụ 6.6.3
Tìm tất cả các giá trị thực của tham số m để phương trình
log mx  2logx   1 có nghiệm duy nhất. m  4 m  4 A.  . B. m  1  .
C. m  2 . D.  . m  0 m  0 Lời giải Chọn A
Điều kiện: x  1  . Ta có x 
log mx  log x    mz  x    2 2 1 2 1 1  m 
( vì x  0 không thỏa). x 2 (x 1) 2 x 1 x 1( 1  ; ) Xét f (x)  trên ( 1
 ; )\{0} . Ta có: f (x)   0   . x 2 x x  1  ( 1  ;   ) m  4
Dựa vào bảng biến thiên, ta thấy phương trình có nghiệm duy nhất   . m  0  Ví dụ 6.6.4
Tìm tất cả các giá trị thực của tham số m để phương trình 4x 1 log
 m  0 có nghiệm. 2 4x 1 m  4 m  4 A.  . B. m  1  .
C. m  2 . D.  . m  0 m  0 Lời giải Chọn A
Điều kiện: 4x 1  0  x  0. t 1 Đặt 4x t 
, với x  0  t 1. Phương trình trở thành m  log (*) . 2 t 1 t 1 2
Xét f (t)  log
trên 1;  . Ta có f (t)   0, t  1. 2 t 1  2t  1ln2
Suy ra hàm số f t đồng biến trên khoảng 1;  .
Dựa vào bảng biến thiên, ta thấy phương trình có nghiệm  m  0
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 48
Tổng Hợp Lý Thuyết
Năm học: 2023-2024  Ví dụ 6.6.5
Tìm tất cả các giá trị thực của tham số m để phương trình m  2 1 log
x  2  m  5 log
x  2  m 1  0 có nghiệm thuộc 2; 4 . 1     1   2 2 m  1 7 m 1 A.  . B. 3   m  . C. 1
  m  7. D.  . m  3 3 m  0 Lời giải Chọn B Đặt t  log
x  2 , do 2  x  4  0  x  2  2  t  1  . 1   2 2 t  5t 1
Phương trình  m   2
1 t  m  5t  m 1  0  m  * 2   t  t 1
Để phương trình đã cho có nghiệm thuộc 2; 4
 * có nghiệm thuộc khoảng  1  ;  . t  2   t  1 t  1 4 4  ;  5t 1 Xét f t 2  , với t  1
 . Ta có f 't   0   . 2 t  t 1
t t 2 2 t  1     1   1 ;  7
Dựa vào bảng biến thiên, ta suy ra 3   m  . 3  Ví dụ 6.6.6
Tìm tất cả các giá trị thực của tham số m để phương trình
log  m 1 x  log
x  2 có nghiệm duy nhất. 5      5 m 1 m  1 m  1 A.  .
B. 1 m  3 . C.  . D.  . m  3 m  7 m  1 Lời giải Chọn C
m x  x 2 1 2   1 x  PT  
. Do x  0 không thỏa (1)     2 2 1  m  1 . x  2 x x  4
Xét f x  2 2  1trên  2
 ;00; có: f 'x 1  0  x  2 . x 2 x m  1 
Từ vào bảng biến thiên, ta thấy f x  m có nghiệm duy nhất   . m  7
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 49
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
LŨY THỪA – MŨ – LOGARIT
BẤT PHƯƠNG TRÌNH MŨ A. LÝ THUYẾT CHUNG. b  0
Tập nghiệm của bất phương trình là .
Dạng 01. x    x a 1 a b x b .
a  b a  0;a   1 . log a b  0 0  a 1 x
a  b  x  log b . a b  0
Tập nghiệm của bất phương trình là .
Dạng 02. x    x a 1 a b x b .
a  b a  0;a   1 log . a b  0 0  a 1 x
a  b  x  log b . a B. CÁC DẠNG BÀI TẬP.
 Dạng 7.1. Bất phương trình mũ cơ bản
 Xem lại mục “Lý thuyết chung”
 Bất phương trình mũ cơ bản: x
a  b a  0;a   1 . Chú ý đến cơ số.  Ví dụ 7.1.1
Tập nghiệm của bất phương trình 3x  9 là
A. S  2;  .
B. S  2;   .
C. S  2;  
 . D. S   1  ; 2. Lời giải Chọn C
3x  9  x  log 9  x  2. Vậy tập nghiệm là S  2;    . 3  Ví dụ 7.1.2 x  1 
Tập nghiệm của bất phương trình  4   là  2  A. S   2  ; 2.
B. S  2;   .
C. S  0;  . D. S  0;  1 . Lời giải Chọn B x
 1   4  x  log 4  x  2   
. Vậy tập nghiệm là S  2;   . 1  2  2  Ví dụ 7.1.3
Tập nghiệm của bất phương trình x x 1 2 3   là   A.  ;  log 3  ;log 3 . C.  . D. 0;  1 . 2  . B. 2    3  Lời giải Chọn B x    2 Ta có: x x 1 2  3  2x  3 3 . x   3  x    log 3. 2  3  3
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 50
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 7.2. Đưa về cùng cơ số
 Ta có hai chú ý như sau: ⓵     Với  1, f x g x a a  a
 f x  gx ⓶ x x Với 0  a  1, f g a  a
 f x  gx  Ví dụ 7.2.1 2
Tìm tập nghiệm của bất phương trình: x x x 1 5 25  
A. S   ;   1 . B. S   1  ; 2   . C. S   1
 ;2. D. S  ;0 . Lời giải Chọn B 2 2 x x x 1  x x 2x2 2 2 5  25  5  5
 x  x  2x  2  x  x  2  0  1
  x  2  S   1  ; 2   .  Ví dụ 7.2.2 1    1 x
Tìm tập nghiệm của bất phương trình: x 1 2    16 
A. S  2;  .
B. S  ;0 .
C. S  0;   . D. S  ;   . Lời giải Chọn B 1 2 4     4 x  x  4 x   x 1        1  x x 1   x 0 1 2 2 2        x   x  x  0 . 16  x  0 x  0 x  0  Ví dụ 7.2.3 2 x 2 x  1  1
Tìm số nghiệm nguyên dương của bất phương trình  .    5  125 A. 3 . B. 4 . C. 5 . D. 6 . Lời giải Chọn B 2 x 2x  1  1 Ta có 2    
x  2x  3  x  
1 x  3  0  1   x  3  5  125
Vì phương trình tìm nghiệm nguyên dương nên các nghiệm là x  1; 2;  3 .  Ví dụ 7.2.4 2 3  x  1  Giải bất phương trình 2x 1  3    ta được tập nghiệm:  3   1   1  A. ;    .
B. 1;  . C.   ;1 . D.  ;   
1  1;  .  3   3  Lời giải Chọn C 2 3  x  1   1 Ta có 2x 1 2  3  3  
x  2x 1    x  1 .  3  3
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 51
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 7.3. Đặt ẩn phụ
 Phương pháp đặt ẩn phụ ta thường sử dụng một số phương pháp sau:
Ở đây ta xét bất phương trình dạng f x  0 , các trường hợp khác tiến hành tương tự. ⓵ nx n  Bất phương trình dạng 1 x A a  A a ... x
 A a  A  0. n n 1  1 0 Đặt x
t  a (t  0) , ta thu được bất phương trình dạng n n 1
A t  A t   ...  A t  A  0 . n n 1  1 0 ⓶ x Bất phương trình dạng 2x    2x Aa
B ab  Cb  0 . x  a 
Chia cả hai vế cho 2x
b rồi đặt t    , t  0 , ta được 2 . A t  .
B t  C  0.  b  ⓷ f x gx
f x gx
Bất phương trình dạng Aa
 Bb C  0, trong đó a b  k . f x gx Bk Đặt a
 t(t  0)  b
 k. , ta thu được bất phương trình mới At   C  0 . t  Ví dụ 7.3.1 5
Nghiệm của bất phương trình x x e e   là 2 1 1 A. x 
hoặc x  2 . B.  x  2 . 2 2
C. ln2  x  ln2.
D. x  ln2. Lời giải Chọn C Ta có x x x e  e   e    e
 e     e     x  . x  x2 5 1 5 1 2 5 x 2 0 x 2 ln 2 ln 2 2 e 2 2  Ví dụ 7.3.2
Bất phương trình 9x 3x 
 6  0 có tập nghiệm là A. ;  1 . B.  ;  2
 3; . C. 1; . D.  2  ;3. Lời giải Chọn D x x
     x 2 9 3 6 0 3 3x  6  0  2
  3x  3  x 1.  Ví dụ 7.3.3  1 2
Tập hợp nghiệm của bất phương trình 3x 2 3   là 27x 3 1 A. 0;  1 . . B. 1; 2. . C.  . . D. 2;3.. 3 Lời giải Chọn C 3  1 2 3 x 1 2 Ta có 3x 2 3      x 3 27 3 9 3 x 3  x2 3 3 1 3 6 3 . x  
 9  0  3 x 32 3 3
 0  3 x  3  0  x  . 3
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 52
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 7.4. Logarit hóa 0    a  1, b  0  f x Phương trình a  b   . f  x   log b a  f x gx f x gx Phương trình a  b  log a  log b  f x  g x b a a    .loga f x gx hoặc log a  log b  f x a  g x b b  .logb  .  Ví dụ 7.4.1 2
Tìm tập S của bất phương trình: 3x 5 . x  1 A. log 3;0 log 5;0
log 3;0 . D. log 5;0 . 3  5  . B.  . C.  5  3  Lời giải Chọn C 2 2 3x 5
. x  1  log 3x.5x  2
 0  x  xlog 3  0  log 3  x  0 nên S  log 3;0 . 5  5 5 5  Ví dụ 7.4.2 log . 3x  1 0 5 1
Tìm tập S của bất phương trình: 4  9  4 
A. 5;   . B. ;    .
C. ; 2 .
D. 1;  .  3  Lời giải Chọn B
Điều kiện: 3x 1 0 . log 3x 1  1 4 0 5 .   log 4  log  log
3x 1  log 3  3x 1  3  x  . 4 4 0 5 .   0 5 9 . 3  Ví dụ 7.4.3 x 1 
Giải bất phương trình: 27 2 . x x  72
A. log 3;0  3;  . B. 1  ; 2  . 2     1  C.  2  ; 2. D.   ; 2  .  2  Lời giải Chọn A
Điều kiện x  0 . 3x3  x 1    3  3 3x 3 x 2 3 2 Bất phương trình  x  x 2 3   3 2 .  3 2 . 3    3  2 x x 2 3 2x x3 x  3  1  3  log 3  log 2 x x 
 x 3log 2  x 3   log 2  0  . 3 3 3 x 3  x  x  3 
x  3N 1  Xét   x  3  log 2  0      . 3 1  x   log 2 
x   log 3 N  2   3  x
Vậy tập nghiệm của bất phương trình là log 3;0  3;  . 2   
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 53
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 7.5. Chứa tham số
 Sử dụng PP giải BPT logarit kết hợp công thức, tính chất của mũ, lũy thừa, logarit.
 Khai thác điều kiện bài toán.
 Xử lý bài toán và chọn giá trị m thỏa ĐK bài toán (cách “mò”).  Ví dụ 7.5.1
Cho bất phương trình: 9x     1 3 . x m  m  0  
1 . Tìm tất cả các giá trị của tham số
m để bất phương trình   1 nghiệm đúng x  1. 3 3
A. m   . B. m   .
C. m  3  2 2. D. m  3  2 2. 2 2 Lời giải Chọn A Đặt 3x t 
. Vì x 1 t  3 2 t  t Bất phương trình 2
t  m  
1 .t  m  0 t   3   m t   . t  nghiệm đúng 3 1 2 2
Xét g t  t  2  , t
  3, g't 1  , t
  . Hàm số đồng biến trên 3;    t 1 t   0 3 2 1 và g   3 3  . 2 3 3
Yêu cầu bài toán tương đương m   m   . 2 2  Ví dụ 7.5.2
Tìm m để bất phương trình 9 . x  2   1 6 . x  4 . x m m m
 0 nghiệm đúng với mọi x 0;  1 .
A. 0  m  6 B. m  6
C. m  6
D. m  0 Lời giải Chọn B x x  9   3  Ta có 9 . x  2   1 6 . x  4 . x m m m  0  . m    2m 1    m  0 .  4   2  x  3  3
Đặt t    . Vì x0;  1 nên 1  t   2  2 t
Khi đó bất phương trình trở thành 2 .
m t  2m  
1 t  m  0  m   . t  2 1 t t  1
Đặt f t 
 f t        , f t 0 t 1. t  2 1 t  3 1 3 t 1 1 2 f  t   0    f t  6
Dựa vào bảng biến thiên ta có m  lim f t  6. 3 t 2
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 54
Tổng Hợp Lý Thuyết
Năm học: 2023-2024  Ví dụ 7.5.3
Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình sau có tập x x nghiệm là  ;   0 : x 1 m2  2m  
1 1 5  3 5  0 . 1 1 1 1
A. m   B. m  C. m 
D. m   2 2 2 2 Lời giải Chọn D x 1 5   3 5 
Phương trình đã cho tương đương 2m  2m   1       0   1  . 2   2      x 1 5  Đặt t     0  , ta được: 2   
m   m  1 2 2 1
 t  0  f t 2
 t  2mt  2m 1 0 2 t BPT nghiệm đúng x
  0 nên BPT có nghiệm 0  t 1, 
Phương trình f t  0 có 2 nghiệm t ,t thỏa t  0 1 t 1 2 1 2
 f 0  0 2m 1 0 m  0  ,5  1     
. Vậy m   thỏa Ycbt.  f    1  0 4  m  2  0 m  0,5 2  Ví dụ 7.5.4
Tất cả các giá trị của m để bất phương trình 3  
1 12x  2  6x  3x m m  0 có nghiệm đúng x   0 là:  1   1  A.  2  ;  B. (; 2] C. ;    D. 2  ;     3   3  Lời giải Chọn D
Đặt 2x  t . Do x  0  t 1.
Khi đó ta có:  m   2 3
1 t  2  mt 1 0, t  1  t   t   3t t 2 2 1 2 2 m  t
  2t 1 t  1  m  t  1 2 3t  t 2 t   2t 1 2 7t  6t 1
Xét hàm số f t 
trên 1;   f t   0 t   1;  2   2   3t  t  2 3t  t
Do đó m  lim f (t)  2 thỏa mãn yêu cầu bài toán  t 1  Ghi chú:
 m  f x x
  D  m  maxf x x   D Sử dụng
 m  f x x
  D  m  minf x x   D
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 55
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
LŨY THỪA – MŨ – LOGARIT
BẤT PHƯƠNG TRÌNH LOGARIT A. LÝ THUYẾT CHUNG.
Dạng 01. a 1 log b
x  b  x  a a
log x  b a  0; a  . a 1 0a1 log b
x  b  x  a . a
Dạng 02. a 1 log b
x  b  x  a a
log x  b a  0; a  a 1. 0a1 log b
x  b  x  a . a B. CÁC DẠNG BÀI TẬP.
 Dạng 8.1. Bất phương trình logarit cơ bản
 Ta có hai chú ý sau: b     b     0 u a khi a 0 u a khi a 1
log u  b   .
 log u  b   . a b u  a khi a 0  a  1 0 b  
u  a khi 0  a  1  Ví dụ 8.1.1
Tập nghiệm của bất phương trình log 2x 1  1  là: 1   2  3   3   1 3   3  A. 1  ;  . B. ;    . C.  ;  . D.   ;  .  2   2   2 2   2  Lời giải Chọn C  3 x  2x 1 2  1 3 Ta có: 2 log 2x 1  1        x  . 1   2  x 1  0 1 2 2 2 x   2  Ví dụ 8.1.2
Tập nghiệm của bất phương trình log 2x 1  2 là: 3   4 1 25 25 1 1 A.  x  . B. x  . C. x  . D. x  . 2 32 32 2 2 Lời giải Chọn A 1 Điều kiện x  2 9 1 25 log 2x 1  9 25 log  2x 1  x 
. Kết hợp với điều kiện ta được  x  3   3 16 16 32 2 32 4 4
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 56
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 8.2. Đưa về cùng cơ số
0  u  v khi a > 1
 Dùng biến đổi logarit để đưa về cùng cơ số log u  log v   . a a
u  v  0 khi 0 < a < 1  Ví dụ 8.2.1 Bất phương trình log 2x 1  log
x  2 có tập nghiệm S là 3   3   4 4  1   1   1  A. S   
;1 . B. S   2  ;  1 . C. S   ;1 
 . D. S    ;1 .  2   2   2  Lời giải Chọn A 1
Bất phương trình đã cho  0  2x 1  x  2    x  1. 2  1 
Tập nghiệm là : S    ;1 .  2   Ví dụ 8.2.2
Xác định tập nghiệm S của bất phương trình 2
ln x  ln4x  4 .
A. S  1;   \  2 . B. S   \  2 .
C. S  2; .
D. S  1; . Lời giải Chọn A
x  4x  4 x  2
Ta có ln x  ln 4x  4 2 2     4  x  4  0 x 1  Ví dụ 8.2.3
Tập nghiệm của bất phương trình log  2
2x  3x 1  log 2x 1 là: 4  2    1   1   1   1 
A. S   ;1 B. S  0  ;  C. S   
;1 D. S    ; 0   2   2   2   2  Lời giải Chọn C  1      2 x 1 x
2x  3x 1 0  1 Điều kiện: 2     x   . 2  x 1  0 1 2 x    2 Ta có: log  2
2x  3x 1  log 2x 1 4  2  
 log 2x  3x  
1  log 2x  2 2 1 4 4 1 2 2 2
 2x  3x 1 4x  4x 1 2x  x  0    x  0. (thỏa mãn điều kiện) 2  1 
Vậy tập nghiệm của bất phương trình đã cho là S    ; 0  .  2 
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 57
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 8.3. Đặt ẩn phụ
 Tìm một log f x chung, đặt làm ẩn phụ t để đưa bất phương trình về bất phương trình ẩn a  
t giải bất phương trình tìm t sau đó tìm x . ★ 1 2 1
Chú ý: Nếu đặt 2 2
t  log x  log x  t
 ,log x  t,log x  log x  t ,log a  . 2 a 1 a  a  2 x a t a  Ví dụ 8.3.1 Bất phương trình 2 log x  5log x  6  có tập nghiệm là: 0,2 0,2  1 1   1  A. S   ;
 B. S  2;3 . C. S  0  ;
 . D. S  0;3 . 125 25   25  Lời giải Chọn A
Điều kiện: x  0 1 1 2 log  5log x  6
  2  log x  3   x  0,2 0,2 0,2 125 25  Ví dụ 8.3.2
Nghiệm nguyên nhỏ nhất của bất phương trình log 3  log 3  0 là: x x 3
A. x  3 B. x 1.
C. x  2 .
D. x  4 . Lời giải Chọn D
Điều kiện: x  0; x  1; x  3 1  log x  0 0  x 1 log 3  log 3  0   0     x x log . x log x 1 log x  1  x  3 3 3  3  3 3  Ví dụ 8.3.3
Nếu đặt t  log x thì bất phương trình 2 3  x   32  4 2 2 log x  log    9log  4  
log  x trở thành bất phương trình nào? 1 2 1 2 2   2 8    x  2 A. 4 2
t 13t  36  0 B. 4 2
t  5t  9  0 . C. 4 2
t 13t  36  0 . D. 4 2
t 13t  36  0 . Lời giải Chọn C
Điều kiện: x  0 3  x   32  4 2 2 log x  log    9log  4   log  x 1 2 1 2 2   2 8    x  2
 log x 3log x 32 4  95 2log x 2 4 2
 4log x  0  log x 13log x  36  0 2 2 2 2 2 2
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 58
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 8.4. Mũ hóa
 Với điều kiện các biểu thức f x và gx xác định, ta thường đưa các bất phương trình
logarit về các dạng cơ bản sau:  f  x  0    f  x khi a gx 1  a
log f x  g x  . a      f  x  0     f  x khi a gx 0 1  a  Ví dụ 8.4.1 Bất phương trình log   có tập nghiệm là: x log 9x 72 1 3   A. S  log 73; 2 S  log 72; 2 3   . B.  3  .
C. S  log 73; 2 S   ;   3  . D.  2. Lời giải Chọn D
Điều kiện x  log 73 3 log      x        x  x log 9x 72 1 log 9x 72 9x 3x 72 0 3x 9 2 3   3    Ví dụ 8.4.2
Nghiệm nguyên lớn nhất của bất phương trình log  x 1
4.3   2x 1 là: 3 
A. x  3 . B. x  2 .
C. x 1. D. x  1  . Lời giải Chọn C log  x 1 4.3   x 1  2x 1  2  2 1  4 3 .  3  3 x  4 3
. x  0  0  3x x  4  x  log 4 3 3
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 59
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
 Dạng 8.5. Chứa tham số
 Sử dụng PP giải BPT logarit kết hợp công thức, tính chất của mũ, lũy thừa, logarit.
 Khai thác điều kiện bài toán.
 Xử lý bài toán và chọn giá trị m thỏa ĐK bài toán (cách “mò”).  Ví dụ 8.5.1
Tìm tất cả các giá trị thực của tham số m để bất phương trình log 5x 1  m có 2   nghiệm x 1?
A. m  2 . B. m  2 .
C. m  2 .
D. m  2 . Lời giải Chọn A
 1  5x 1  4  log 5x x 1  2  m  2 2    Ví dụ 8.5.2
Tìm tất cả giá trị thực của tham số m để bất phương trình log  2
x  4x  m  1 3  nghiệm đúng x   ?
A. m  7 . B. m  7 .
C. m  4 .
D. 4  m  7 . Lời giải Chọn B log  2
x  4x  m 2  1 x
   x  4x  m  3  0 x   0  m  7 3  Ví dụ 8.5.3
Tìm tất cả giá trị thực của tham số m để log  2 mx  x  log 4 vô nghiệm? 1  1 5 5 m  4 A. 4
  m  4 . B.  .
C. m  4 . D. 4
  m  4. m  4   Lời giải Chọn A log  2 mx  x  2 2
 log 4  mx  x  4  x  mx  4  0 1 1 5 5 2
x  mx  4  0 vô nghiệm 2
 x  mx  4  0 x
 R   0  4   m  4  Ví dụ 8.5.4
Tìm tất cả các giá trị thực của tham số m sao cho khoảng 2;3 thuộc tập nghiệm
của bất phương trình log  2 x   1  log  2
x  4x  m 1 (1) . 5 5  A. m  1  2;13   . B. m 1  2;13   . C. m  1  3;12 
 . D. m 1  3; 1  2   . Lời giải Chọn A 2 
x  4x  m 2 2 x   
m  x  4 1
x  f x 1 ( )   5   2      2 m 4x 4x 5 g     x x 4x m 0 m  max f  x  1  2 khi x  2
Hệ trên thỏa mãn x     2; 3 2 x 3       m  f x 12 m 13. min 13 khi x  2  2x3
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 60
Tổng Hợp Lý Thuyết
Năm học: 2023-2024  Ví dụ 8.5.5
Tìm m để bất phương trình 1 log  2 x   1  log  2
mx  4x  m thoã mãn x   5 5  A. 1
  m  0 . B. 1   m  0.
C. 2  m  3.
D. 2  m  3. Lời giải Chọn A 2
mx  4x  m  0 BPT thoã mãn x   .  x   5   2 x   2
1  mx  4x  m m  0  m  0 m  2     2 2
mx  4x  m  0 16  4m  0   m  2   x         m  . 5   m   2 3 2     5  m  0 x 4x 5 m 0 m  5     16  4  5m2  0 m  3  m  7  Ví dụ 8.5.6
Tìm tất cả các giá trị thực của tham số m để bất phương trình log log 3x 1  log
m có nghiệm với mọi x ;0 0,02  2   0 ,02
A. 0  m 1. B. m 1.
C. m  2.
D. m 1. Lời giải Chọn D
Đk: x  ; m  0. Ta có: log log 3x 1  log m , x   ;0 . 0,02  2   0,02  
 log 3x 1  m , x    ; 0 . 2    
 3x 1 2m , x  ;0. Xét hàm   3x f x 
1 trên ;0 . Ta có    3x f x .ln3  0 , x  ;0. x ∞ 0 y' + 2 y 1
Để phương trình có nghiệm với mọi x ;0 ta phải có 2m  2  m 1.
 Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 61

Tổng hợp lý thuyết lũy thừa – mũ – logarit – Lê Minh Tâm

Thông tin :

Tài liệu liên quan:

Toán 11: Một vài mô hình toán học sử dụng hàm số mũ và hàm số lôgarit - Sách Kết Nối Tri Thức

Toán 11 Bài 18: Lũy thừa với số mũ thực sách Kết Nối Tri Thức

Toán 11 Bài 19: Lôgarit sách Kết Nối Tri Thức

Toán 11 Bài 21: Phương trình, bất phương trình mũ và lôgarit sách Kết Nối Tri Thức

Top 200 câu vận dụng cao đạo hàm ôn thi THPT môn Toán