Tổng hợp và Tìm hiểu về Robot MPL800II môn Robot công nghiệp | Trường Đại Học Thái Nguyên

lOMoAR cPSD| 45740413 5 / 1/2018 B ÀI TẬP LỚN K Ĩ T HIỂU THUẬT ÌM ROBOT MPL800II ROBOT Mã lớp: 103134 | Nhóm 1 lOMoAR cPSD| 45740413 LỜI NÓI ĐẦU
Ngày nay nước ta đang tiến hành công nghiệp hóa hiện đại hóa ngày một mạnh mẽ, dần
dần lao động chân tay sẽ được thay thế bằng tự động. Và robot là một lực lượng sinh ra để
giảm lao động cho con người, nó càng ngày càng đóng vai trò quan trọng trong công nghiệp.
Ở trong bài tập lớn này chúng em xin trình bày tìm hiểu của mình về Robot MPL800II
do hãng Yaskawa sản xuất. Tuy vậy, trong lúc tìm hiểu chúng em không tránh khỏi những
thiếu sót, mong cô bổ sung và sửa chữa để bài tập lớn của chúng em thêm hoàn thiện.
Cuối cùng, chúng em xin cảm ơn cô Nguyễn Phạm Thục Anh đã tận tình giảng dạy,
giúp đỡ bọn em khi thực hiện bài tập lớn này ạ.
Những người thực hiện Nhóm 1 MỤC LỤC
CHƯƠNG 1: GIỚI THIỆU ROBOT MPL800 II ................................................................ 2
1.1. Giới thiệu ............................................................................................................... 2
1.2. Ứng dụng của Robot MPL800 II trong công nghiệp ............................................. 4
1.3. Kết cấu cơ khí ........................................................................................................ 5
1.4. Thông số kỹ thuật ................................................................................................... 6
CHƯƠNG 2: ĐỘNG HỌC THUẬN CỦA ROBOT MPL800 II ........................................ 7
2.1. Tính toán công thức ............................................................................................... 7
2.2. Giao diện lập trình trên Matlab ............................................................................ 10
CHƯƠNG 3: MA TRẬN JACOBY .................................................................................. 10
3.1. Tính toán công thức ............................................................................................. 10
3.2. Giao diện lập trình Matlab ................................................................................... 12
CHƯƠNG 4: ĐỘNG HỌC NGƯỢC ROBOT .................................................................. 12
CHƯƠNG 5: THIẾT KẾ QUỸ ĐẠO CỦA CÁC KHỚP DẠNG BẬC 3 ........................ 15
CHƯƠNG 6: XÂY DỰNG MÔ HÌNH ĐỘNG LỰC HỌC TRÊN TOOLBOX ............. 21
SIMMECHANICS/MATLAB .......................................................................................... 21
6.1. Xây dựng phương trình động lực học cho Robot MPL800 II (3 góc đầu tiên): .. 21 lOMoAR cPSD| 45740413
6.2. Mô hình 3D của tay máy Robot ....................................................................... .. 23
6.3. Mô hình Robot trên Simmechanics/Matlab ......................................................... 26
PHỤ LỤC: ......................................................................................................................... 28
Danh mục hình ảnh ............................................................................................................ 28
Danh mục bảng: ................................................................................................................. 28
TÀI LIỆU THAM KHẢO ................................................................................................. 29 23
CHƯƠNG 1: GIỚI THIỆU ROBOT MPL800 II 1.1. Giới thiệu.
Robot MPL800 II được sản xuất bởi hãng Robot nổi tiếng Yaskawa. Yaskawa là tập đoàn
hàng đầu thế giới trong sản xuất và cung cấp các sản phẩm trong lĩnh vực robot công nghiệp,
biến tần, truyền động điện…Trong lĩnh vực robot công nghiệp, hãng đã sản xuất tất cả các loại
robot như: robot gắp (Handling), robot nâng bốc, đóng gói (Picking/packing, palletizing) Robot
hàn, hàn điểm (Arc handling, spot welding), Robot sơn (Painting), Robot lắp ráp ( Assembly/distributing)…
Hinh 1.1: Một số loại Robot của hãng Yaskawa.
Robot công nghiệp MPL800 II là loại robot có tốc độ cao, tính linh hoạt và hiệu suất làm
việc lớn, đảm bảo độ tin cậy chính xác. lOMoAR cPSD| 45740413 Hinh 1.2: Robot MPL800 II. lOMoAR cPSD| 45740413
Robot MPL800 II có các đặc điểm chính là: Số bậc tự do: 4 bậc.
Có cơ cấu, khung thiết kế vững chắc, có khả năng mang các tải từ 80kg đến 800kg ở tốc
độ cao. Những robot này cho phép đạt được cân bằng quán tính cao nhất cho ứng dụng bốc xếp hàng.
Chiều ngang 3.1 m và chiều dọc 3 m cùng khả năng xoay 360 độ, cho phép chúng có thể
tích hợp làm việc cùng lúc với nhiều băng tải và các vị trí xếp pallet khác nhau.
Ống dẫn khí nén và cáp điều khiển các trục cũng như cáp tín hiệu fieldbus được tích hợp
đi ngầm bên trong tay máy, thiết kế này giúp nâng cao sự an toàn và duy trì sự bền bỉ, giảm
thiểu tối đa khả năng va chạm với các thiết bị ngoại vi.
Robot MPL tương thích với bộ điều khiển DX200 hoặc nền tảng MLX200 tích hợp PLC.
1.2. Ứng dụng của Robot MPL800 II trong công nghiệp.
Đây là loại robot phù hợp với các ứng dụng về đóng gói (điều khiển dỡ và đóng gói vào
khay, hộp, thùng carton, túi, …).
Các hoạt chất bôi trơn ở trong hộp số robot dòng MPL được chứng nhận tiêu chuẩn an
toàn NSF-H1. Đây là tiêu chuẩn đặc biệt quan trọng trong ngành thực phẩm và đồ uống. Do
vậy Robot MPL có thể áp dụng rộng rãi trong nhiều ngành công nghiệp như: thực phẩm và
nước giải khát, nhà kho và các sản phẩm công nghiệp khác.
Hinh 1.3: Ứng dụng của Robot MPL800 II trong công nghiệp.
Tuy nhiên thì robot MPL là dòng robot chuyên dụng, thích hợp và được ưu tiên dùng cho
các ứng dụng nâng bốc, di chuyển hàng có khối lượng lớn lên đến 800kg, sử dụng trong rất lOMoAR cPSD| 45740413
nhiều ngành như: nước giải khát, thực phẩm, gạch, xi măng…do các đặc điểm chuyên dụng của robot MPL.
1.3. Kết cấu cơ khí.
Kết cấu cơ khí của robot thể hiện như trong hình vẽ:
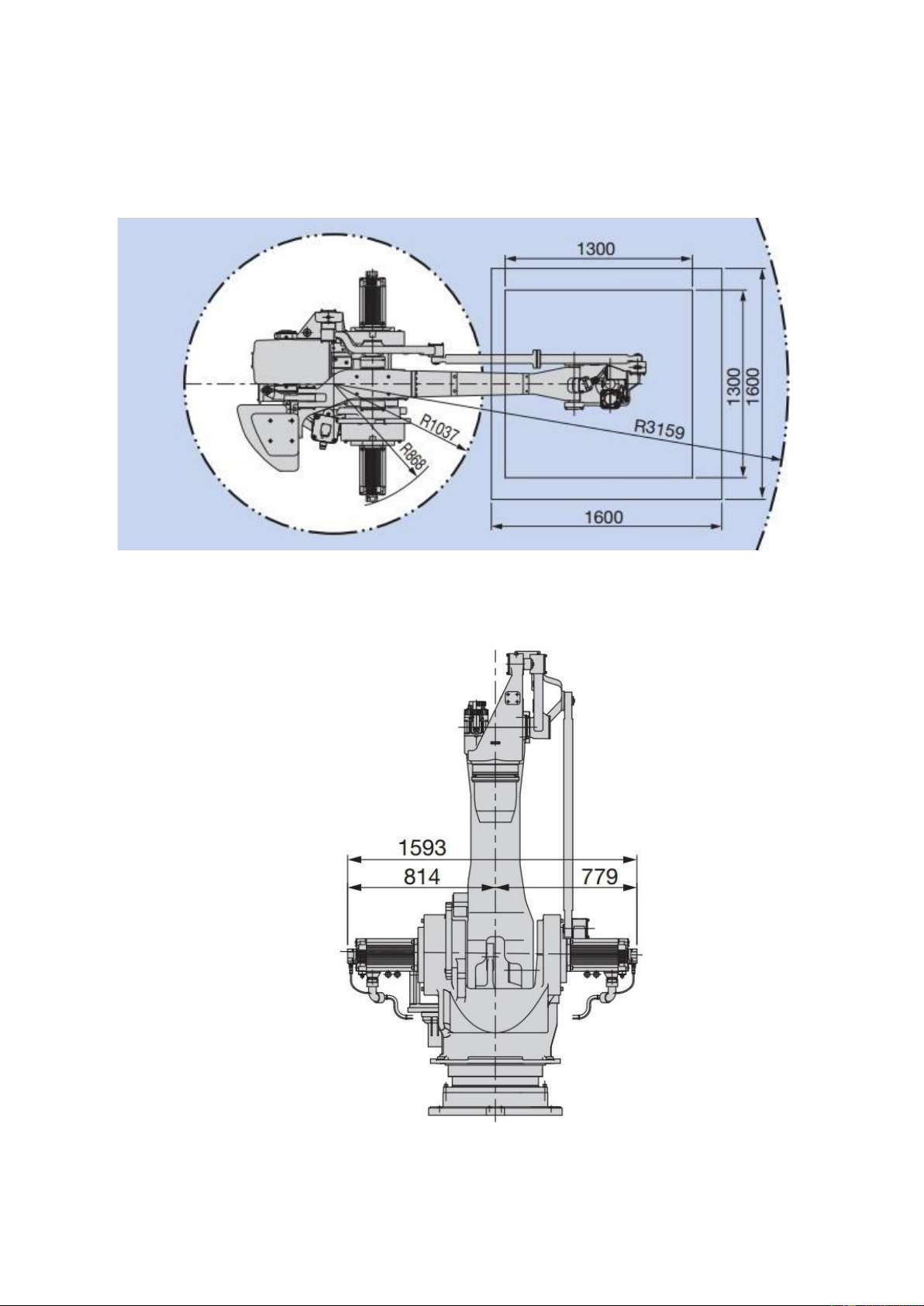
Hinh 1.4: Robot MPL800 II khi nhìn từ trên xuống.
Kết cấu cơ khí của Rotbot MPL800 II nhìn từ đằng sau:
Hinh 1.5: Robot MPL800 II khi nhìn từ đằng sau.
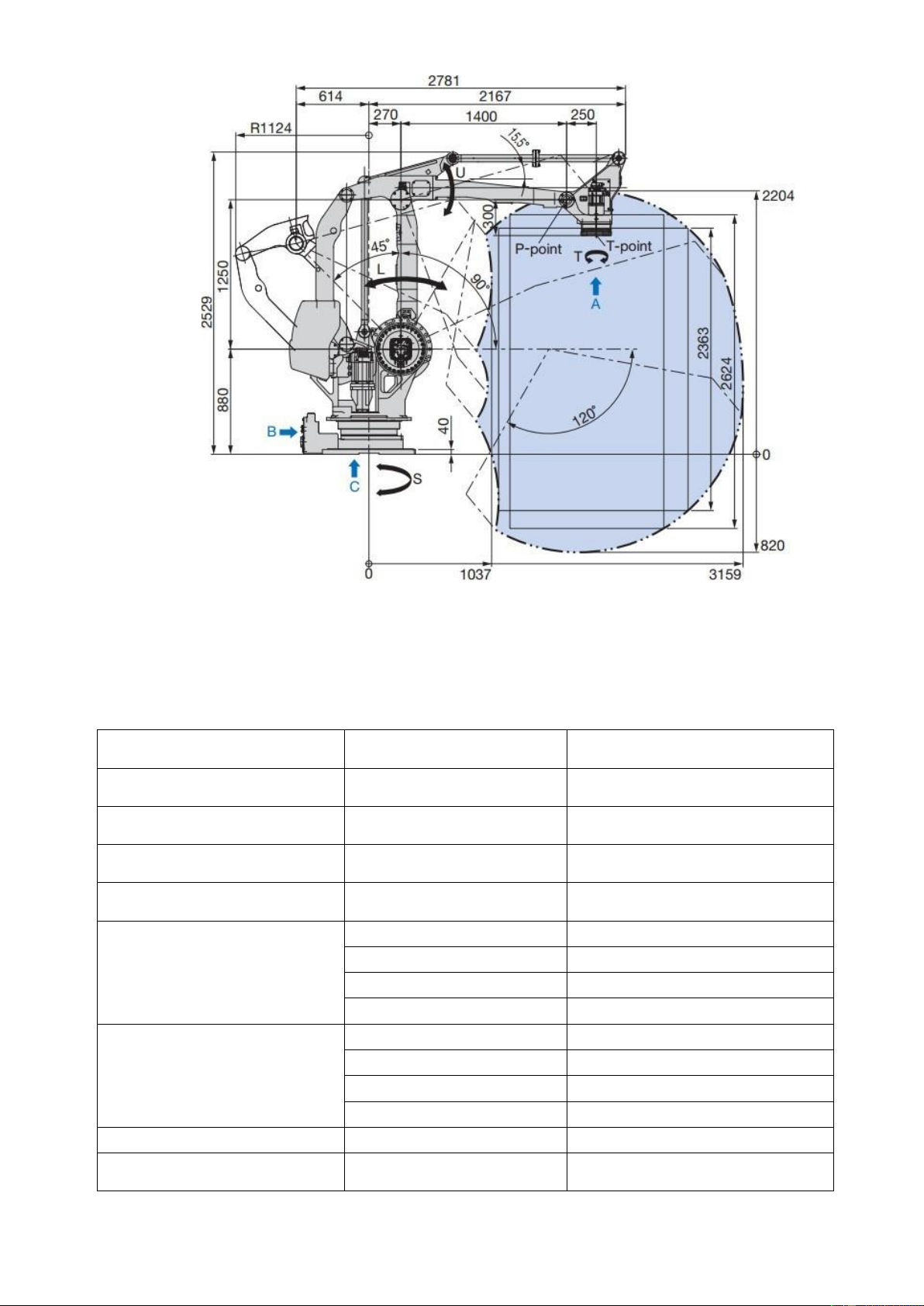
Kết cấu cơ khí của robot khi nhìn ngang: lOMoAR cPSD| 45740413
Hinh 1.6: Robot MPL800 II khi nhìn ngang.
1.4. Thông số kỹ thuật.
Các thông số kỹ thuật chính của Robot MPL800 II được trình bày trong bảng sau:
Bảng 1.1: Bảng thông số kỹ thuật chính của Robot MPL800 II. Mẫu MOTOMAN-MPL800 II Kiểu YR-MPL0800-J00 Trục điều khiển
4 khớp nối theo thiều dọc Tải trọng nâng 800kg Khả năng lặp lại ±0.5mm Trục S – quay -180˚ – +180˚ Trục L – Phạm vi chuyển động cánh tay dưới -45˚ – +90˚ Trục U – cánh tay trên -120˚ – +15˚ Trục T – cổ tay -360˚ – +360˚ Trục S – quay 1.13 rad/s, 65˚/s Trục L – Tốc độ tối đa cánh tay dưới 1.13 rad/s, 65˚/s Trục U – cánh tay trên 1.13 rad/s, 65˚/s Trục T – cổ tay 2.18 rad/s, 125˚/s Quán tính cho phép Trục T – cổ tay 500kg৹m2 Khối lượng 2550kg lOMoAR cPSD| 45740413 Nhiệt độ 0˚C đến +45˚C Độ ẩm
20 - 80% RH (không ngưng tụ) Độ rung 4.9m/𝑠2 hoặc ít hơn
Không có khí hoặc chất lỏng ăn Điều kiện môi trường
mòn, hoặc các khí gây nổ Khác
Không có nước, dầu hoặc bụi
Không có nhiễu điện quá mức (plasma) Yêu cầu nguồn 10kVA
CHƯƠNG 2: ĐỘNG HỌC THUẬN CỦA ROBOT MPL800 II
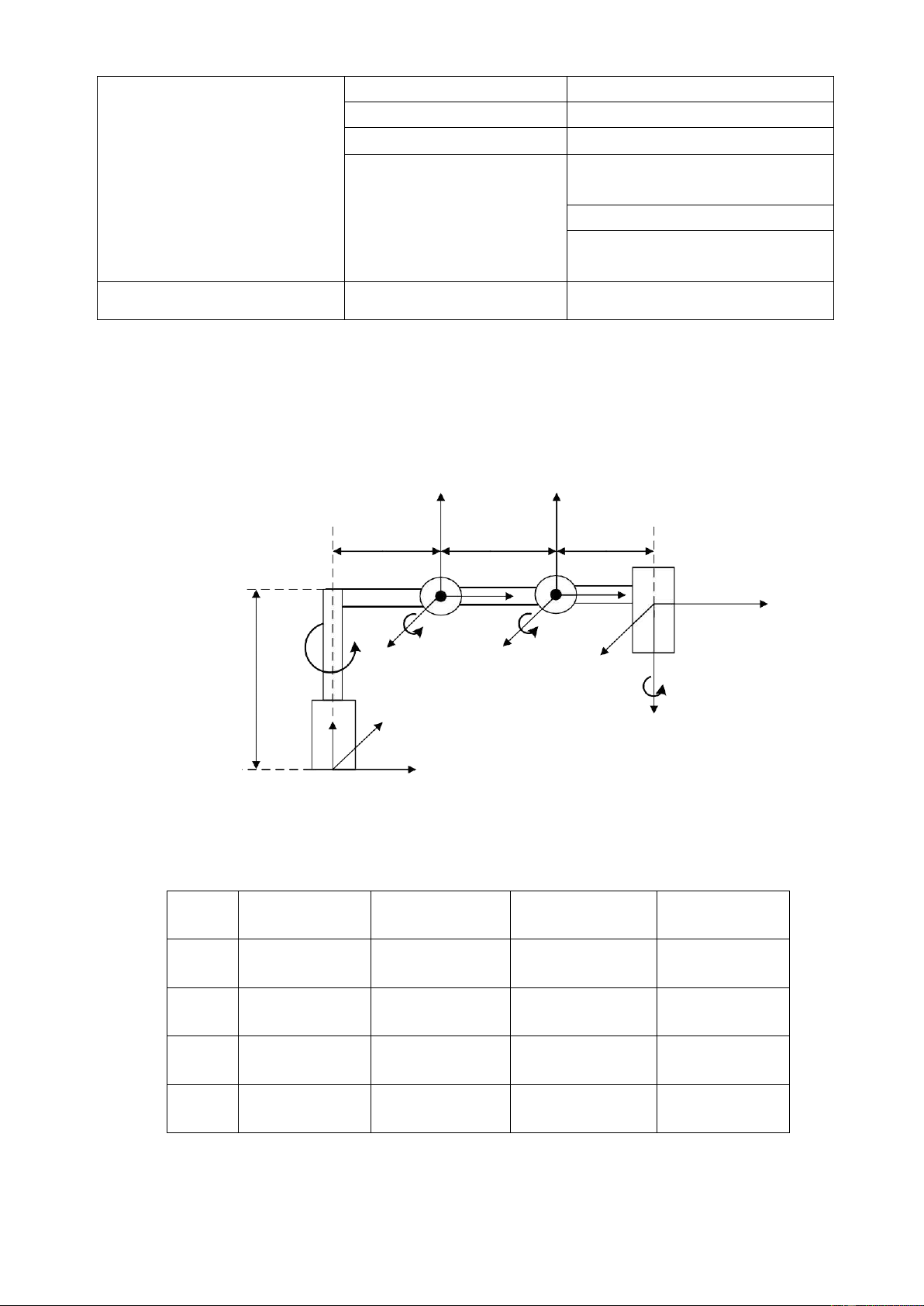
2.1. Tính toán công thức. Y1 Y2 a1=270 a2=1250 a3=1650 Z1 X1 X2 X3,4 Z2 d1= Y3,4 Z3,4 880 Z0 Y0 X0
Hinh 2.1: Mô hình Robot MPL800 II
Bảng 2.1: Bảng Denavit-Hartenberg. i 𝑎𝑖 𝛼𝑖 𝜃𝑖 𝑑𝑖 1 𝑎1 = 270 90° 𝜃1 𝑑1 = 880 2 𝑎2 = 1250 0 𝜃2 0 3 𝑎3 = 1650 90° 𝜃3 0 4 0 0 𝜃4 0 Ta xét:
𝑇10 = 𝑅𝑜𝑡𝑧(𝜃1).𝑡𝑟𝑎𝑛𝑧(𝑑1). 𝑡𝑟𝑎𝑛𝑥 (𝑎1).𝑅𝑜𝑡𝑥(𝛼1) lOMoAR cPSD| 45740413 cos(𝜃1) −sin(𝜃1) 0 0 1 0 0 0 1 0 0 𝑎1 =[sin(𝜃1) cos(𝜃1) 0 0]. [0 1 0 0 ]. [0 1 0 0 ]. 0 0 1 0 0 0 1 𝑑1 0 0 1 0 0 0 0 1 0 0 0 1 0 0 0 1 1 0 0 0 0 cos(90°) −sin(90°) 0 [ ] 0 sin(90°) cos(90°) 0 (2.1) 0 0 0 1
𝑇21 = 𝑅𝑜𝑡𝑧(𝜃2.𝑡𝑟𝑎𝑛𝑥 (𝑎2) cos(𝜃2) −sin(𝜃2) 0 0 1 0 0 𝑎2 = [sin(𝜃2) cos(𝜃2) 0 0]. [0 1 0 0 ] 0 0 1 0 0 0 1 0 0 0 0 1 0 0 0 1 cos(𝜃2) −sin(𝜃2) 0 𝑎2. cos(𝜃2) = [sin(𝜃02)
cos(𝜃0 2) 01 𝑎2 . sin(𝜃02)] 0 0 0 1 cos(𝜃2) −sin(𝜃2) 0 1250. cos(𝜃2) = [sin(𝜃02)
cos(𝜃0 2) 01 1250. sin(𝜃02)] (2.2) 0 0 0 1
𝑇32 = 𝑅𝑜𝑡𝑧(𝜃3). 𝑡𝑟𝑎𝑛𝑥(𝑎3). 𝑅𝑜𝑡𝑥(𝛼3) cos(𝜃3) −sin(𝜃3) 0 0 1 0 0 𝑎3 1 0 0 0 = [sin(𝜃03)
cos(𝜃0 3) 1 00 0] [00 0 11 000 ] . [0 cos(90°sin(90°))−cos(90°)sin(90°) 00] 0 0 0 0 1 0 0 0 1 0 0 0 1 (2.3) cos(𝜃3) 0 sin(𝜃3) 𝑎3. cos(𝜃3) = [sin(𝜃03)
10 −cos(𝜃0 3) 𝑎3. sin(𝜃0 3)] 0 0 0 1 cos(𝜃4) −sin(𝜃4) 0 0
𝑇43 = 𝑅𝑜𝑡𝑧(𝜃4) = [sin(𝜃40) cos(𝜃0 4) 01 00] (2.4) lOMoAR cPSD| 45740413 0 0 0 1 Vậy ta có ma trận:
𝑇0=𝑇0. 𝑇1. 𝑇2. 𝑇3 = 4 1 2 3 4 cos(𝜃1) 0 sin(𝜃1) 𝑎1. cos(𝜃1) cos(𝜃2) −sin(𝜃2) 0 𝑎2. cos(𝜃2) [sin(𝜃01)
0 −1cos(𝜃0 1) 𝑎1. sin(𝜃𝑑1)]. [sin(𝜃02)
cos(𝜃0 2) 10 𝑎2. sin(𝜃0 2)]. 1 0 0 0 1 0 0 0 1 cos(𝜃3) 0 sin(𝜃3) 𝑎3. cos(𝜃3) cos(𝜃4) −sin(𝜃4) 0 0 [sin(𝜃3) 0 −cos(𝜃3)
𝑎3. sin(𝜃3)]. [sin(𝜃4) cos(𝜃4) 0 0] = (2.5) 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 1 𝑎11 𝑎12 𝑎13 𝑎14 𝑎
[𝑎3121 𝑎𝑎3223𝑎𝑎3323𝑎𝑎2434] 𝑎41 𝑎42 𝑎43 𝑎44 Trong đó:
𝑎11 = cos(𝜃1). cos(𝜃4). cos(𝜃2 + 𝜃3) + sin(𝜃1). sin(𝜃4)
𝑎12 = - cos(𝜃1). cos(𝜃2 + 𝜃3). sin(𝜃4) + sin(𝜃1). cos(𝜃4)
𝑎13 = cos(𝜃1). sin(𝜃2 + 𝜃3)
𝑎14 = 𝑎3.cos(𝜃1). cos(𝜃2 + 𝜃3) + 𝑎2.cos(𝜃1). cos(𝜃2) + 𝑎1. cos(𝜃1)
= 1650 cos(𝜃1). cos(𝜃2 + 𝜃3) + 1250 cos(𝜃1). cos(𝜃2) + 270 cos(𝜃1)
𝑎21 = sin(𝜃1).cos(𝜃2 + 𝜃3) . cos(𝜃4) - cos(𝜃1). sin(𝜃4)
𝑎22 = - sin(𝜃1).cos(𝜃2 + 𝜃3) . sin(𝜃4) - cos(𝜃1). cos(𝜃4)
𝑎23 = sin(𝜃1). sin(𝜃2 + 𝜃3)
𝑎24 = 𝑎3. sin(𝜃1). cos(𝜃2 + 𝜃3) + 𝑎2. sin(𝜃1). cos(𝜃2) + 𝑎1. sin(𝜃1)
= 1650 sin(𝜃1). cos(𝜃2 + 𝜃3) + 1250 sin(𝜃1). cos(𝜃2) + 270 sin(𝜃1)
𝑎31 = sin(𝜃2 + 𝜃3) . cos(𝜃4)
𝑎32 = - sin(𝜃2 + 𝜃3) . sin(𝜃4) 𝑎33 = - cos(𝜃2 + 𝜃3)
𝑎34 = 𝑎3.sin(𝜃2 + 𝜃3) + 𝑑1 + 𝑎2. sin(𝜃2)
= 1650 sin(𝜃2 + 𝜃3) + 880 + 1250 sin(𝜃2) 𝑎41 = 0 lOMoAR cPSD| 45740413 𝑎42 = 0 𝑎43 = 0 𝑎44 = 1
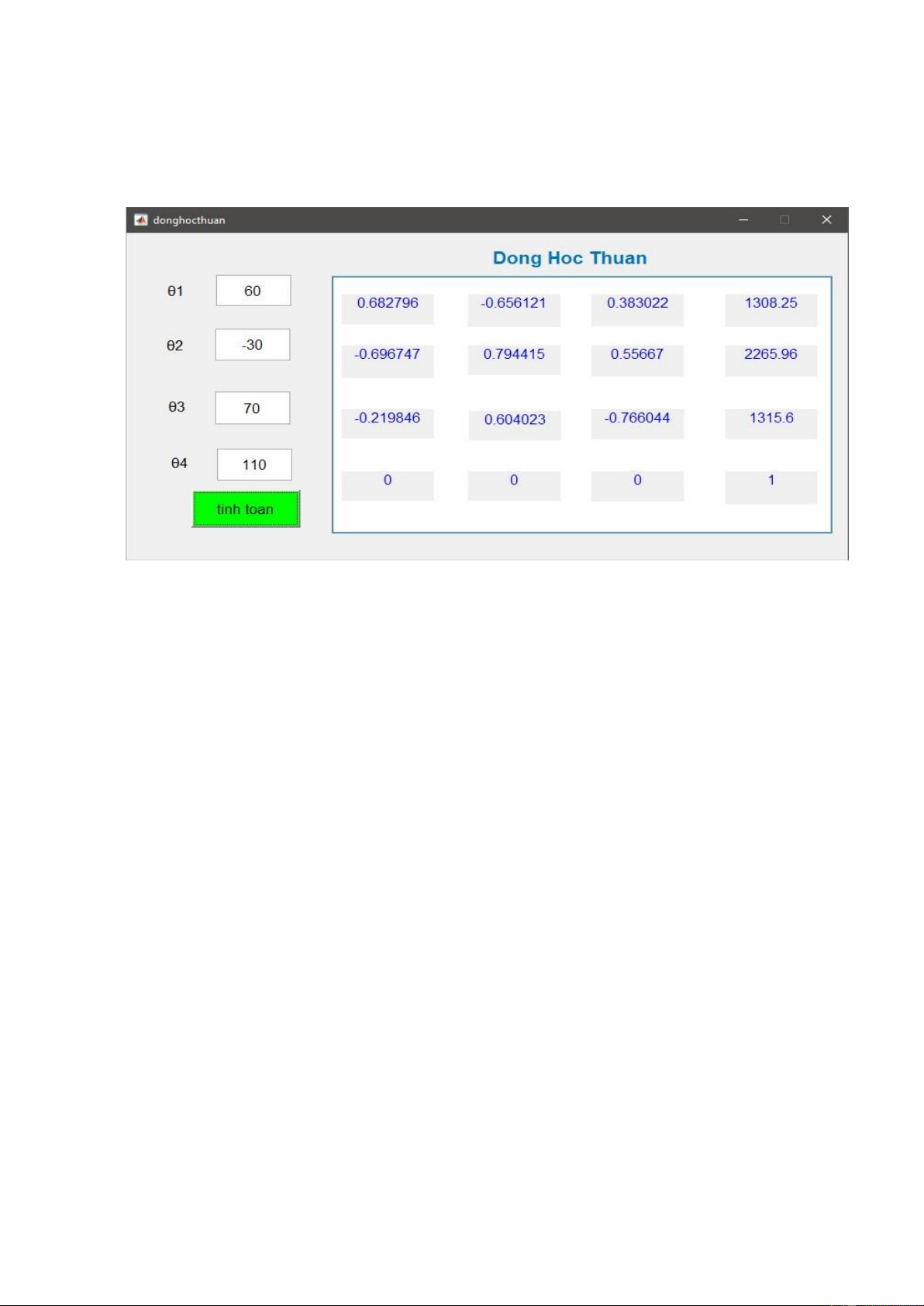
2.2. Giao diện lập trình trên Matlab
Hinh 2.2: Giao diện lập trình Matlab tính động học thuận.
CHƯƠNG 3: MA TRẬN JACOBY
3.1. Tính toán công thức.
Tìm các ma trận 𝑇0, 𝑇1, 𝑇2, 𝑇3. 4 4 4 4 𝑇0 = 4 𝐶1𝐶23𝐶4 + 𝑆1𝑆4
−𝐶1𝐶23𝑆4 + 𝑆1𝐶4 𝐶1𝑆23
𝐶1(𝑎3𝐶23 + 𝑎2𝐶2 + 𝑎1𝐶1)
[𝑆1𝐶23𝐶4 − 𝐶1𝑆4
−𝑆1𝐶23𝑆4 − 𝐶1𝐶4 𝑆1𝑆23
𝑆1(𝑎3𝐶23 + 𝑎2𝐶2 + 𝑎1𝐶1)] (3.1) 𝑆23𝐶4 −𝑆23𝑆4 −𝐶23
𝑎3𝑆23 + 𝑑1 + 𝑎2𝑆2 0 0 0 1
𝑪𝟐𝟑𝑪𝟒 −𝑪𝟐𝟑𝑺𝟒 𝑺𝟐𝟑
𝒂𝟑𝑪𝟐𝟑 + 𝒂𝟐𝑪𝟐 (3.2) 𝑪 𝑺 𝑪 +
𝑻𝟏 𝟒 = [𝑺𝟐𝟑𝑺 𝟒𝟒 − 𝑪𝟐𝟑𝟒𝑺𝟒 − 𝟎𝟐𝟑 𝒂𝟑𝑺𝟐𝟑 𝟎 𝒂𝟐𝑺𝟐 ] 𝟎 𝟎 𝟎 𝟏 𝐶3𝐶4 −𝐶3𝑆4 𝑆3 𝑎3𝐶3 lOMoAR cPSD| 45740413 𝐶 𝑆 𝑆 𝐶
𝑇42 = [𝑆3𝑆 44 − 𝐶3 44 − 03 𝑎30𝑆3 ] (3.3) 0 0 0 1 𝐶4 −𝑆4 0 0 𝑇3 = [𝑆4 𝐶4 0 0] (3.4) 4 0 0 1 0 0 0 0 1 Vậy ma trận 𝐽𝐻 là:
⎡−−𝑆𝐶44((𝑎𝑎33𝐶𝐶2323 ++ 𝑎 𝑎22𝐶𝐶22 ++ 𝑎 𝑎11𝐶𝐶11))
−𝑎𝑎22𝑆𝑆33𝑆𝐶44 00 00⎤ ⎢ ⎥ 𝐽𝐻 = ⎢⎢ 𝑆230𝐶4 −𝑎3 −𝑆 𝑎42𝐶3 −𝑎𝑆34 00⎥⎥ (3.5) ⎢ −𝑆23𝑆4 𝐶4 𝐶4 0⎥ [ −𝐶23 0 0 1] Vậy ma trận Jacoby là: 𝐽 = [ 𝑅40 0 ] . 𝐽𝐻 0 𝑅0 4
⎡ −𝑆1(𝑎3𝐶23 + 𝑎2𝐶2 + 𝑎1𝐶1)
𝐶1(−𝑎3𝑆23−𝑎2𝐶2) −𝐶1𝑎3𝑆23 0 ⎤ ⎥ ⎢ 𝑆 𝐶
1(−𝑎3𝑆23−𝑎2𝑆2) −𝑆1𝑎3𝑆23 0
1(𝑎3𝐶23 + 𝑎2𝐶2 + 𝑎1𝐶1) 𝑎 𝐶 +𝑎 𝐶 𝑎 𝐶 0 (3.3) 0 ⎥ 3 23 2 2 3 23 = ⎢ ⎢ 1 1 1 23⎥ 0 𝑆 𝑆 𝐶 𝑆 ⎢ 0 −𝐶1 −𝐶1 𝑆1𝑆23⎥ [ 1 0 0 −𝐶23 ]
Thay số a1 = 270, a2 =1250, a3 =1650 ta được: 𝐽
⎡ −𝑆1(1650𝐶23 + 1250𝐶2 + 270𝐶1)
𝐶1(−1650𝑆23 − 1250𝐶2) −𝐶11650𝑆23 0 (3.4) ⎢ 𝐶
𝑆1(−1650𝑆23 − 1250𝑆2) −𝑆11650𝑆23
1(1650𝐶23 + 1250𝐶2 + 270𝐶1) 1650𝐶 + 1250𝐶 0 1650𝐶 ⎤ 0 ⎥ 23 2 23 = ⎢ 0 0 𝑆1 𝑆1 ⎢ ⎥ 𝐶1𝑆23⎥ −𝐶1 −𝐶1 ⎢ 0 𝑆1𝑆23⎥ 0 0 [ 1 −𝐶23 ] lOMoAR cPSD| 45740413
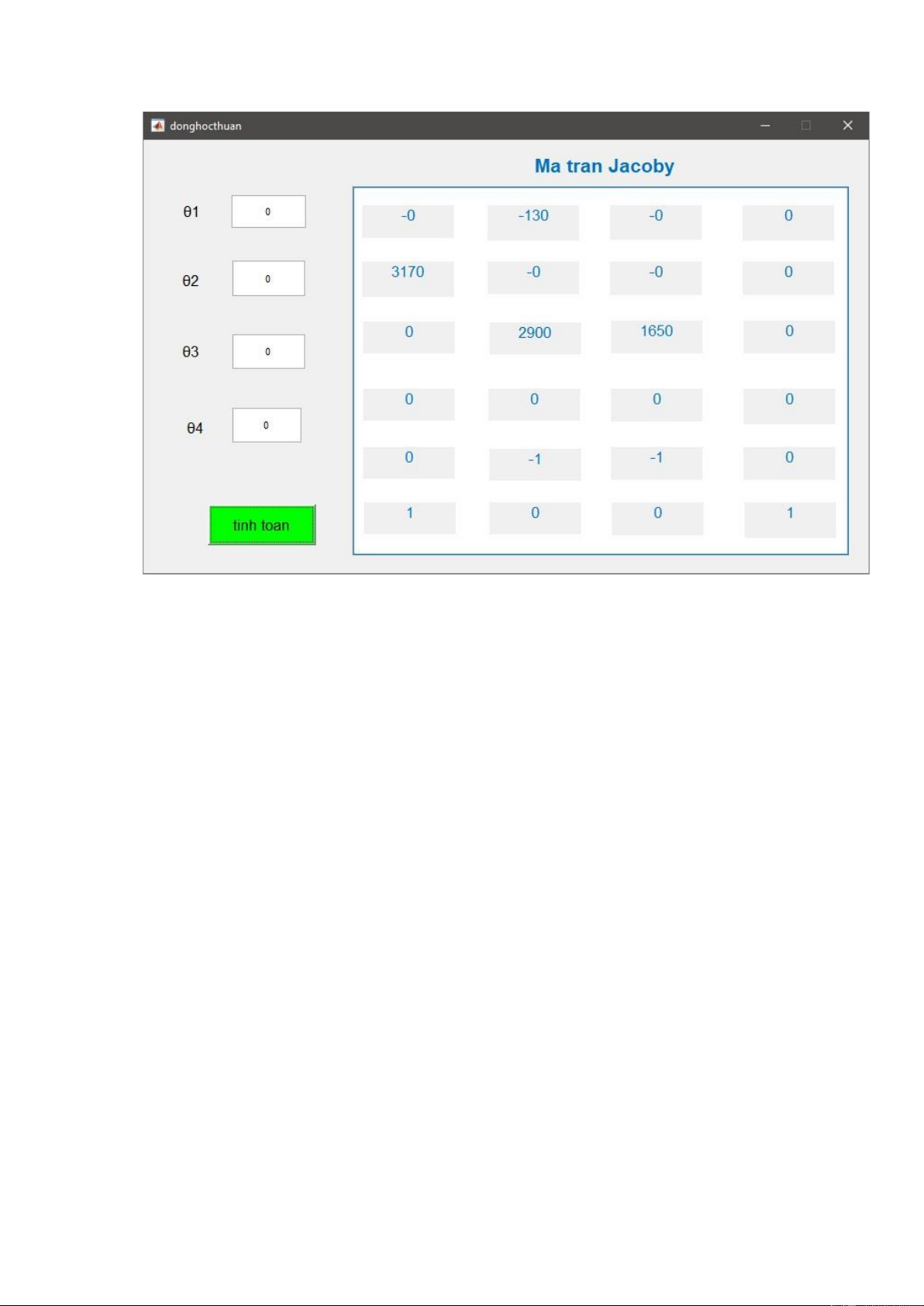
3.2. Giao diện lập trình Matlab.
Hinh 3.1: Giao diện lập trình Matlab tính ma trận Jacoby.
CHƯƠNG 4: ĐỘNG HỌC NGƯỢC ROBOT 𝑛𝑛𝑥 T0 = T0. T1. T2. T3 = 𝑦 𝑝𝑝
𝑜𝑜𝑦𝑥 𝑎𝑎𝑦𝑥 𝑦𝑥] (4.1) 𝑛 4 1 2 3 4 [ 𝑧 𝑜𝑧 𝑎𝑧 𝑝𝑧 0 0 0 0 Với:
𝑛𝑥 = cos(θ1). cos(θ4). cos(θ2 + θ3) + sin(θ1). sin(θ4)
𝑜𝑥 = - cos(θ1). cos(θ2 + θ3). sin(θ4) + sin(θ1). cos(θ4)
𝑎𝑥 = cos(θ1). sin(θ2 + θ3)
𝑝𝑥 = a3. cos(θ1). cos(θ2 + θ3) + a2. cos(θ1). cos(θ2) + a1. cos(θ1)
𝑛𝑦 = sin(θ1).cos(θ2 + θ3) . cos(θ4) - cos(θ1). sin(θ4)
𝑜𝑦 = - sin(θ1).cos(θ2 + θ3) . sin(θ4) - cos(θ1). cos(θ4)
𝑎𝑦 = sin(θ1). sin(θ2 + θ3)
𝑝𝑦 = a3. sin(θ1). cos(θ2 + θ3) + a2. sin(θ1). cos(θ2) + a1. sin(θ1)
𝑛𝑧 = sin(θ2 + θ3) . cos(θ4)
𝑜𝑧 = - sin(θ2 + θ3) . sin(θ4) 𝑎𝑧 = - cos(θ2 + θ3) VT1 cos(θ1). nx + sin(θ1). ny cos(θ1). ox + sin(θ1). oy cos(θ1). ax + sin(θ1). ay
cos(θ1). px + sin(θ1). py − a1 ⎡ nz oz az pz − d1 ⎤ lOMoAR cPSD| 45740413 = ⎢ ⎥
⎢sin(θ1). nx − cos(θ1). ny sin(θ1). ox − cos(θ1). oy sin(θ1). ax − cos(θ1). ay
sin(θ1). px − cos(θ1). py ⎥ (4.5) [ 0 0 0 1 ]
cos(θ2 + θ3). cos(θ4) −cos(θ2 + θ3). sin(θ4) sin(θ2 + θ3) a3cos(θ2 + θ3) + a2cos(θ2)
VP1 = [sin(θ2 + θ3). cos(θ4)
−sin(θ2 + θ3). sin(θ4) −cos(θ2 + θ3)
a3sin(θ2 + θ3) + a2sin(θ2) ] (4.6) sin(θ4) cos(θ4) 0 0 0 0 0 1
Cân bằng 2 vế ta có các phương trình sau:
sin(θ1). px − cos(θ1). py = 0 Suy (4.7) ra: θ1 = ATAN2(py , px) θ1 = ATAN2(−py , −px) (4.8)
{sin(θ4) = sin(θ1). nx − cos(θ1). ny cos(θ ) = sin(θ ). o − cos(θ ). o 4 1 x 1 y Suy ra:
θ4 = ATAN2(sin(θ1). nx − cos(θ1), sin(θ1). ox − cos(θ1). oy ) cos(θ {
1). px + sin(θ1). py − a1 = a3cos(θ2 + θ3) + a2cos(θ2) (4.9)
𝑝𝑧 = a3. sin(θ2 + θ3) + d1 + a2. sin(θ2) Áp
dụng phương pháp phân ly biến:
𝑉𝑇 = (𝑇0)−1𝑇0 = 𝑇0. 𝑇1. 𝑇2. 𝑇3 = 𝑉𝑃 (4.2) 1 4 1 2 3 4 Ta có: cos(θ1) 0 sin(θ1) 𝑎1. cos(θ1) 𝑎 (4.3) 𝑇 1. sin(θ1) 10 = [sin(θ01) 10 −cos0(θ1) 𝑑1 ] 0 0 0 1 Suy ra: cos(θ1) sin(θ1) 0 −𝑎1 0 0 1 −𝑑1] (4.4) (T0)−1 = [ 0 0 1 sin(θ1) −cos(θ1) 0 1 0 0
pz − d1 = a3sin(θ2 + θ3) + a2sin(θ2) Đặt: lOMoAR cPSD| 45740413
{m = 𝑎𝑎3sin(3θcos2 + θ(θ23 + θ) + 𝑎3) 2+sin(θ 𝑎2cos(θ2) 2) n =
Bình phương cả 2 vế ta được: { mn 2
2 = = ( (aa sin3cos((θθ + θ 2 + θ3))))2 + 2 + 22. a. a sin3cos((θθ + θ 2 + θ3). a). a 2cos(θ2) + (a2cos(θ2))2 sin(θ2) + 3 2 3 3 2 3 2(a2sin(θ2))2
Cộng hai phương trình ta được: m2 + n2 = a 2 2 3 + a2 + 2a3a2 cos(θ3) (4.10) Suy ra: m2 + n2 − a 2 2 3 − a2 cos(θ3) =
sin(θ3) = ±√1 − (cos(θ3))2
⇒ θ3 = ATAN2(sin(θ3), cos(θ3))
Sử dụng phép đảo vị trị Robot Planar ta có:
θ2 = 𝐴𝑇𝐴𝑁2(𝑝2, 𝑝1) − 𝐴𝑇𝐴𝑁2(𝑎3. sin(θ3) , 𝑎2 + 𝑎3 cos(θ3)) Trong đó:
𝑝1 = cos(θ1). px + sin(θ1). py − a1 𝑝2 = pz − d1
Điều kiện góc quay của từng khớp: 180 1 180 0 135 120 2 15.5 360 3 4 360
Kết luận giá trị góc 1,2,3,4 chỉ phụ thuộc vào px, py, pz, nx, ny, ox, oy, Điều
kiện các thông số nhập vào phải thỏa mãn các điều kiện sau:
−(𝑎1 + 𝑎2 + 𝑎3) ≤ 𝑝𝑥, 𝑝𝑦 ≤ 𝑎1 + 𝑎2 + 𝑎3
𝑑1 ≤ 𝑝𝑧 ≤ 𝑎1 + 𝑎2 + 𝑑1
−1 ≤ 𝑛𝑥, 𝑛𝑦, 𝑜𝑥, 𝑜𝑦 ≤ 1
Và các giá trị vecto n, o, a tương ứng tạo thành một tam diện thuận. lOMoAR cPSD| 45740413
CHƯƠNG 5: THIẾT KẾ QUỸ ĐẠO CỦA CÁC KHỚP DẠNG BẬC 3
Quỹ đạo của từng khớp có dạng:
𝜃𝑖(𝑡) = 𝑎𝑖0 + 𝑎𝑖1𝑡 + 𝑎𝑖2𝑡2 + 𝑎𝑖3𝑡3 (5.1)
Vận tốc tại mỗi khớp: 𝜃̇ (5.2)
𝑖 (𝑡) = 𝑎𝑖1 + 2𝑎𝑖2𝑡 + 3𝑎𝑖3𝑡2
Với 𝑖 = ̅1̅,̅4̅ tương ứng với 4 khớp.
Ta được hệ các phương trình sau:
𝜃1(𝑡) = 𝑎10 + 𝑎11𝑡 + 𝑎12𝑡2 + 𝑎13𝑡3
𝜃2(𝑡) = 𝑎20 + 𝑎21𝑡 + 𝑎22𝑡2 + 𝑎23𝑡3 (5.3)
𝜃3(𝑡) = 𝑎30 + 𝑎31𝑡 + 𝑎32𝑡2 + 𝑎33𝑡3
𝜃4(𝑡) = 𝑎40 + 𝑎41𝑡 + 𝑎42𝑡2 + 𝑎43𝑡3
Giả sử Robot đi từ điểm A tới điểm B trong thời gian là t(s) với điều kiện là vận tốc tại
2 thời điểm đầu và cuối bằng 0.
Từ đó ta có hệ phương trình sau:
𝜃𝑖(0) = 𝑎𝑖0 = 𝜃𝑖(𝐴)
𝜃𝑖(𝑡) = 𝑎𝑖0 + 𝑎𝑖1𝑡 + 𝑎𝑖2𝑡2 + 𝑎𝑖3𝑡3 = 𝜃𝑖(𝐵) (5.4)
𝜃̇𝑖 (0) = 𝑎𝑖1 = 0;
𝜃̇𝑖 (𝑡) = 𝑎𝑖1 + 2𝑎𝑖2𝑡 + 3𝑎𝑖3𝑡2 = 0
Từ đây ta sẽ xây dựng được quỹ đạo dạng bậc 3 cho từng khớp. Sử dụng động học đảo ta có:
Khi Robot di chuyển từ vị trí A(𝑝𝑥 , 𝑝𝑦, 𝑝𝑧, 𝑛𝑥 , 𝑛𝑦, 𝑜𝑥 , 𝑜𝑦 ) = (270, 0, 3780, 0, - , 0,
) suy ra các góc theta tương ứng là:
𝑞𝐴 = [𝜃1𝐴, 𝜃2𝐴, 𝜃3𝐴, 𝜃4𝐴]𝑇 = [ 0, 90, 0, 45]𝑇 (5.5)
Vị trí điểm B(𝑝𝑥, 𝑝𝑦, 𝑝𝑧, 𝑛𝑥, 𝑛𝑦, 𝑜𝑥, 𝑜𝑦 ) = (2009.7069, 1160.3048, 597.1573, 0.28033,
0.7392, 0.7392, -0.57322) suy ra các góc theta tương ứng là:
𝑞𝐵 = [𝜃1𝐵, 𝜃2𝐵, 𝜃3𝐵, 𝛳𝜃4𝐵 ]𝑇 = [30, 45, −90, −30]𝑇 (5.6) trong thời gian t = 5s. lOMoAR cPSD| 45740413 Từ đây ta có được:
Phương trình quỹ đạo của khớp 1 với các hệ số như sau: 𝑎10 = 𝜃1(𝐴) = 0 𝑎11 = 0 3 3 (5.7)
𝑎12 = 𝑡2 (𝜃1(𝐵) − 𝜃1(𝐴)) = 52 2(30 − 0) = 3.6 2
𝑎13 = − 𝑡3 (𝜃1(𝐵) − 𝜃1(𝐴)) = − 53 (30 − 0) = −0.48 Ta có
phương trình quỹ đạo khớp 1:
𝜃1(𝑡) = 3.6𝑡2 − 0.48𝑡3 Phương (5.8) trình vận tốc: (5.9)
𝜃̇1(𝑡) = 7.2𝑡 − 1.44𝑡2 Phương trình gia tốc: (5.10)
𝜃̈1(𝑡) = 7.2 − 2.88𝑡
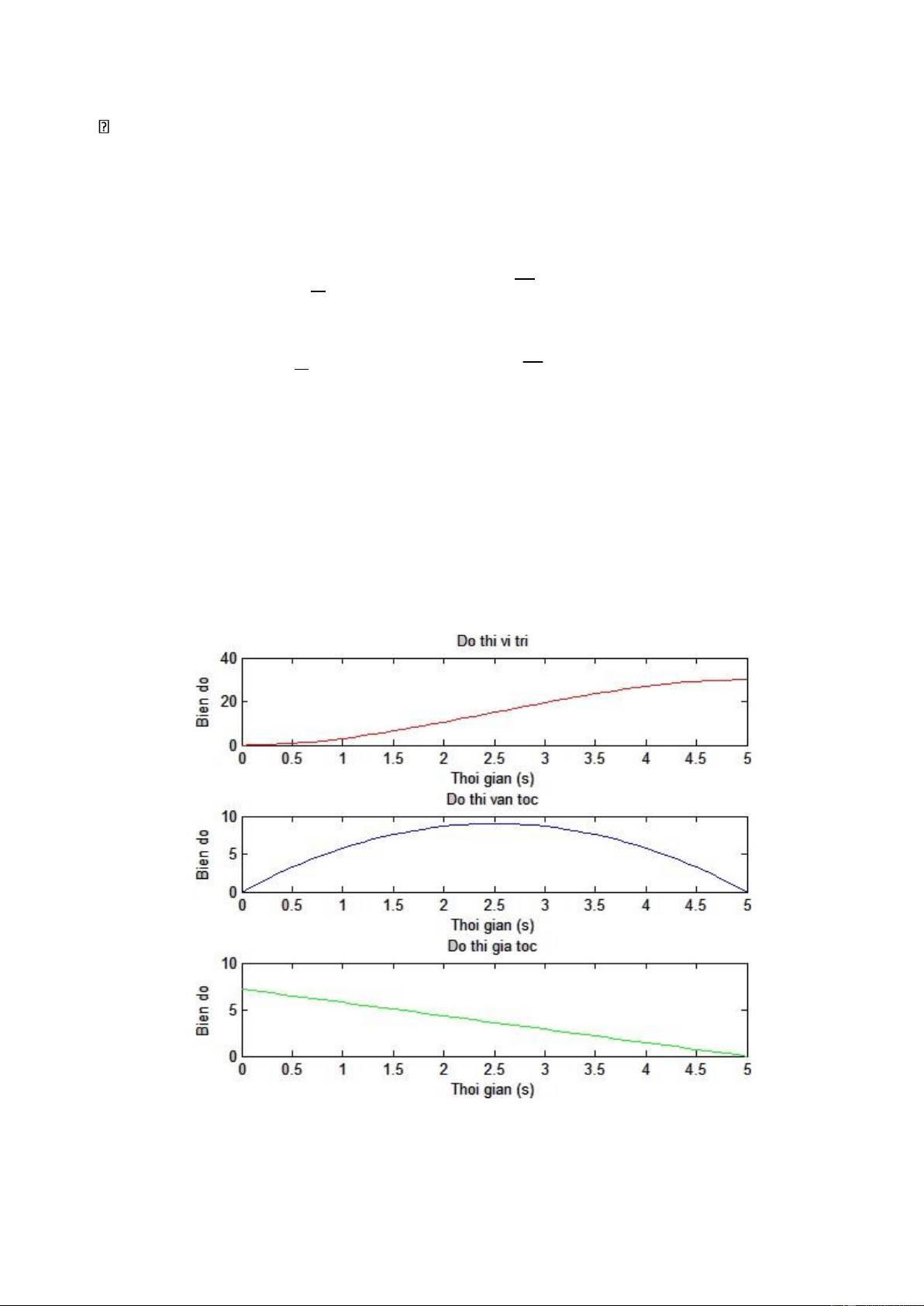
Kết quả mô phỏng trên Matlab:
Hinh 5.1: Đồ thị vị trí, vận tốc, gia tốc khớp thứ nhất. lOMoAR cPSD| 45740413
Phương trình quỹ đạo của khớp 2 với các hệ số như sau: 𝑎20 = 𝛳2(𝐴) = 90; 𝑎21 = 0; (5.11) 𝑎 = −5.4;
𝑎23 = − 𝑡3 (𝛳2(𝐵) − 𝛳2(𝐴)) = − 53 (45 − 90) = 0.72;
Ta có phương trình quỹ đạo khớp 2:
𝛳2(𝑡) = 90 − 5.4𝑡2 + 0.72𝑡3 Phương (5.12) trình vận tốc: (5.13
𝛳̇2(𝑡) = −10.8𝑡 + 2.16𝑡2 ) Phương trình gia tốc: (5.14)
𝛳̈2(𝑡) = −10.8 + 4.32𝑡
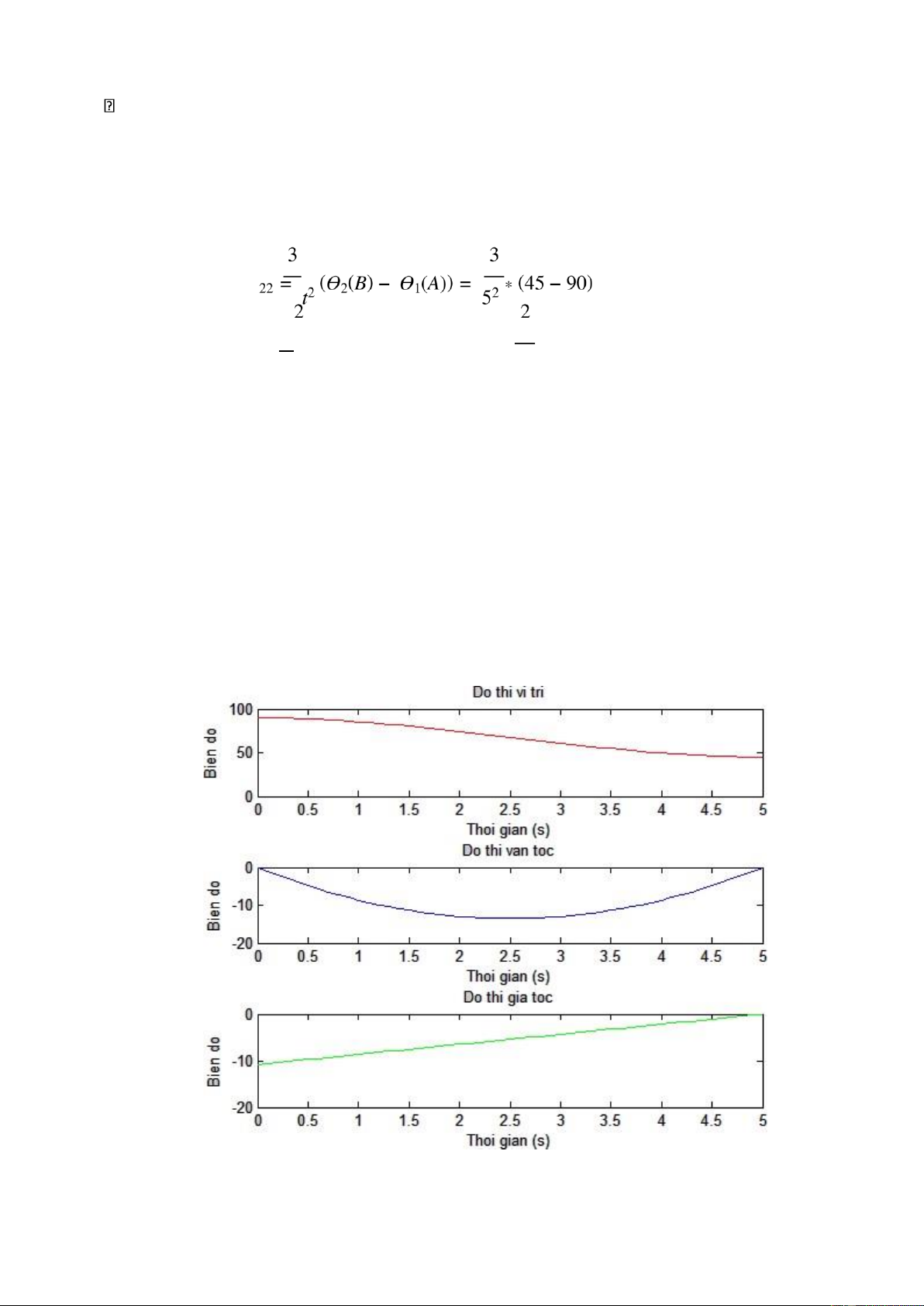
Kết quả mô phỏng trên Matlab: lOMoAR cPSD| 45740413
Hinh 5.2: Đồ thị vị trí, vận tốc, gia tốc khớp thứ hai.
Phương trình quỹ đạo của khớp 3 với các hệ số như sau: 𝑎30 = 𝜃3(𝐴) = 0 𝑎31 = 0 3 3 (5.15)
𝑎32 = 𝑡2 (𝜃3(𝐵) − 𝜃3(𝐴)) = 52 (−90 −2 0) = −10.8 2
𝑎33 = − 𝑡3 (𝜃3(𝐵) − 𝜃3(𝐴)) = − 53 (−90 − 0) = 1.44 Ta có
phương trình quỹ đạo khớp 3:
𝜃3(𝑡) = −10.8𝑡2 + 1.44𝑡3 Phương (5.16) trình vận tốc: (5.17)
𝜃̇3(𝑡) = −21.6𝑡 + 4.32𝑡2 Phương trình gia tốc: (5.1
𝜃̈3(𝑡) = −21.6 + 8.64𝑡 8)
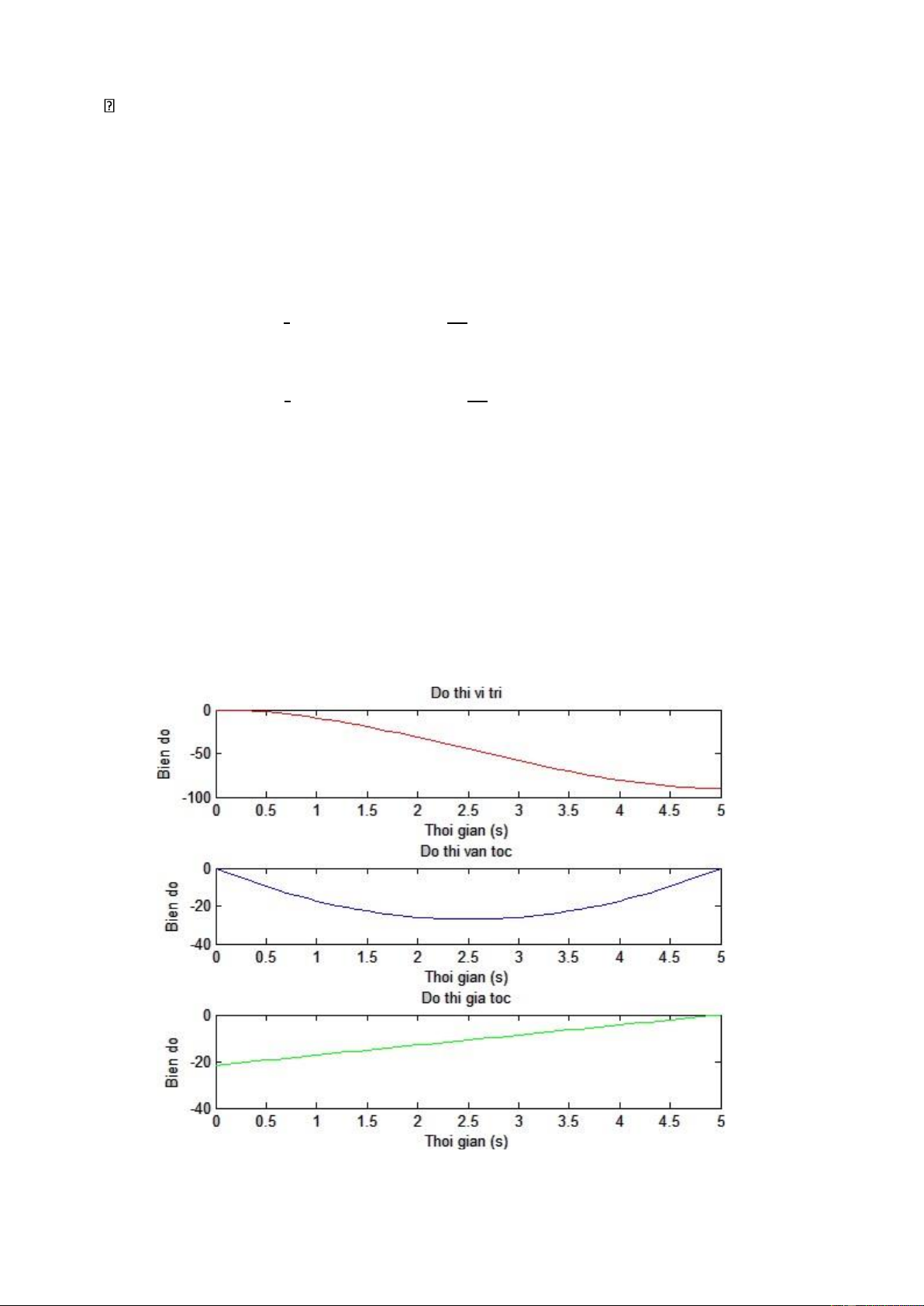
Kết quả mô phỏng trên Matlab: lOMoAR cPSD| 45740413
Hinh 5.3: Đồ thị vị trí, vận tốc, gia tốc khớp thứ ba.
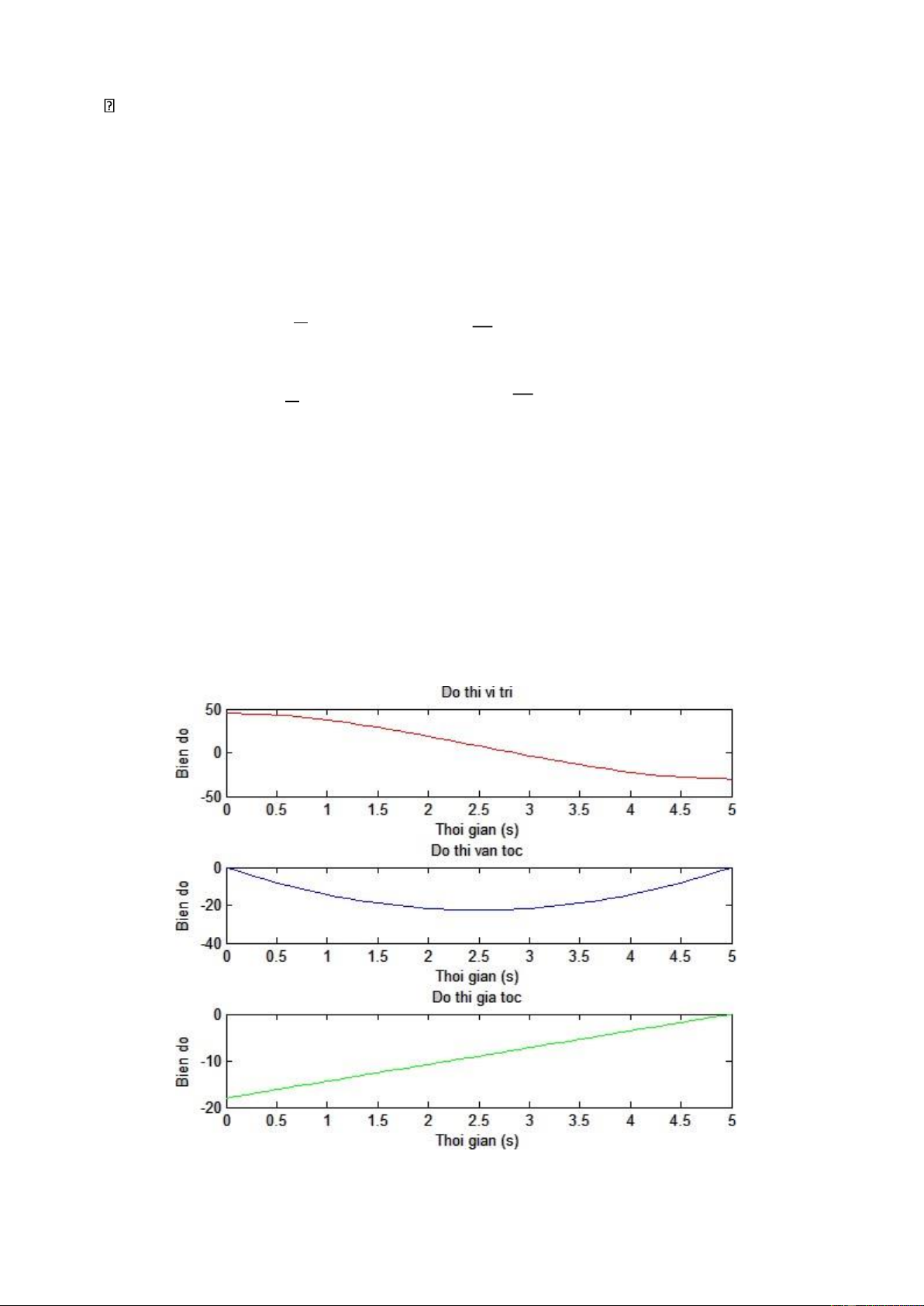
Phương trình quỹ đạo của khớp 4 với các hệ số như sau: 𝑎40 = 𝜃4(𝐴) = 45 𝑎41 = 0 3 3 (5.19)
𝑎42 = 𝑡2 (𝜃4(𝐵) − 𝜃4(𝐴)) = 5 2 (−30 −2 45) = −9 2
𝑎43 = − 𝑡3 (𝜃4(𝐵) − 𝜃4(𝐴)) = − 53 (−30 − 45) = 1.2 Ta có
phương trình quỹ đạo khớp 4:
𝜃4(𝑡) = 45 − 9𝑡2 + 1.2𝑡3 Phương (5.20) trình vận tốc: (5.21)
𝜃̇4(𝑡) = −18𝑡 + 3.6𝑡2 Phương trình gia tốc: (5.22
𝜃̈4(𝑡) = −18 + 7.2𝑡 )
Kết quả mô phỏng trên Matlab: