Tổng ôn tập TN THPT 2020 môn Toán: Hàm số lũy thừa – hàm số mũ – hàm số logarit

Tài liệu gồm 60 trang, được tổng hợp và biên soạn bởi thầy giáo Nguyễn Bảo Vương, tuyển chọn các câu hỏi và bài tập trắc nghiệm chuyên đề hàm số lũy thừa – hàm số mũ – hàm số logarit

112 56 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 6: Hàm số mũ và hàm số lôgarit (KNTT)

Môn: Toán 11

Thông tin:

60 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
A. BIẾN ĐỔI CÔNG THỨC
CÁC CÔNG THỨC MŨ – LOGARIT CẦN NHỚ
Cho a và b là các số thực dương, x và y là những số thực tùy ý.
n
a a.a.a...a
x
x
x
a a
b
b
x y x y
a a .a
x
y
x
y
a a
y 2; y
x
x y n
y n
a 1
a a
a a
.
0
u x
u x 1,
x 0
y x
x.y x y
a a a
n n n
a. b ab
nn 2;
x
x x
a .b a.b
m
m
n
n
m
n
a a a
Cho
0 a 1
và
b, c 0
.
x
a
log b x b a
a a a
b
log log b log c
c
a
a
1
log b log b
a
a
a
log b khi
log b
log b khi
c
a
c
log b
log b
log a
a
b
1
log b ,
log a
a
ln b
log b
ln a
a a
log 1 0, log a 1
b b a
log c log a log b
a c b a
a a a
log b.c log b log c
e
10
ln b log b
lg b log b log b
MỨC ĐỘ NHẬN BIẾT
Câu 1. Với
a
là số thực dương tùy ý,
2
2
log a
bằng:
A.
2
2 log a
. B.
2
1
log
2
a
. C.
2
2log a
. D.
2
1
log
2
a
.
Câu 2. Với
a
là hai số thực dương tùy ý,
3
2
log a
bằng
A.
2
3
log
2
a
. B.
2
1
log
3
a
. C.
2
3 log a
. D.
2
3log a
.
Câu 3. Cho
a
là số thực dương khác
1
. Tính
log
a
a
.
A.
2
. B.
2
. C.
1
2
. D.
1
.
Câu 4. Cho
a
là số thực dương khác
4
. Tính
3
4
I log
64
a
a
.
A.
3I
. B.
1
3
I
. C.
3I
. D.
1
3
I
.
Câu 5. Cho
0 1a
. Giá trị của biểu thức
3
2
log .
a
P a a
là
HÀM SỐ LŨY THỪA - MŨ - LOGARIT
Vấn đề 9
n số a
lẻ
chẵn
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
4
3
. B.
3
. C.
5
3
. D.
5
2
.
Câu 6. Giá trị của
2 3 4 63
log 3.log 4.log 5....log 64A
bằng
A.
5
. B.
4
. C.
6
. D.
3
.
Câu 7. Với các số thực
, 0a b
bất kì, rút gọn biểu thức
2
2 1
2
2log logP a b
ta được
A.
2
2
log 2P ab
. B.
2
2
logP ab
. C.
2
2
log
a
P
b
. D.
2
2
2
log
a
P
b
.
Câu 8. Với
a
,
b
là hai số thực dương,
2 5
5
log
25
a b
bằng
A.
5 5
2log 5log 25a b
. B.
5 5
2log 5log 2a b
.
C.
5 5
2log 5log 25a b
. D.
5 5
2log 5log 2a b
.
Câu 9. Cho
a
là số thực dương bất kì, giá trị nào dưới đây có cùng giá trị với
3
log(10 )?a
A.
3loga
B.
3
10loga
C.
1 3loga
D.
3log(10 )a
Câu 10. Với
a
,
b
là hai số dương tùy ý,
6 7
log a b
bằng
A.
6log 7log .a b
B.
6log 7log .a b
C.
1 1
log log .
6 7
a b
D.
42log ab
Câu 11. Cho
a
là số thực dương khác
1
. Tính
3
3log
a
I a
A.
1I
. B.
9I
. C.
1
9
I
. D.
1
3
I
.
Câu 12. Với
a
và
b
là các số thực dương. Biểu thức
5
log
a
a b
bằng
A.
5 log
a
b
. B.
5 log
a
b
. C.
1
log
5
a
b
. D.
5log
a
b
.
Câu 13. Cho các số thực dương
a
,
b
thỏa mãn
2log 5log 1a b
. Mệnh đề nào sau đây đúng.
A.
2 5
10a b
. B.
2 5 10a b
. C.
2 5 1a b
. D.
2 5
10a b
.
Câu 14. Cho
b
là số thực dương khác
1
. Tính
1
6
2
log .
b
P b b
.
A.
3P
. B.
7
2
P
. C.
13
2
P
. D.
6P
.
Câu 15. Với
a
,
b
là hai số dương tùy ý,
4
5
log
a
b
bằng
A.
4log 5loga b
. B.
4log 5loga b
. C.
4
log log
5
a b
. D.
4
log log
5
a b
.
Câu 16. Cho và là hai số thực dương thỏa mãn
2 1
2
log log
a
a
b
. Mệnh đề nào dưới đây đúng?
A.
1b
. B.
2
b a
. C.
a b
. D.
2
a b
.
Câu 17. Cho
0 1a
. Giá trị của biểu thức
3
log .
a
P a a
là
A.
1
3
. B.
3
. C.
4
3
. D.
5
3
.
Câu 18. Với
a
là số thực dương bất kỳ, mệnh đề nào dưới đây đúng?
a
b
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
A.
. B.
7
1
log log
7
a a
. C.
7
loga 7log a
. D.
1
log 7 log
7
a a
.
Câu 19. Cho
a
và
b
là các số thực dương bất kì. Chọn khẳng định sai.
A.
3
5
1
ln ln 3ln ln
5
a b a b
. B.
log log loga b ab
.
C.
2
log 10 10 log logab a b
. D.
ln ln ln
a
a b
b
.
Câu 20. Với
a
là số thực dương tùy ý,
2
3
log 9
a
bằng:
A.
3
2log a
. B.
3
3 2log a
. C.
3
2 2log a
. D.
3
4log a
.
Câu 21. Với
a
,
b
là hai số dương tùy ý,
3 4
log
a b
bằng
A.
3log 4log .a b
B.
4log 3log .a b
C.
1
log 3log .
4
a b
D.
1
2log log .
3
a b
Câu 22. Đặt
4
log 5
a
, khi đó
25
log 64
bằng
A.
3
2
a
. B.
3
2a
. C.
2
3a
. D.
2
3
a
.
Câu 23. Với
a
,
b
là hai số dương tùy ý,
5
3
2
3
log
a
b
bằng
A.
3 3
1 2log 5log .a b
B.
3 3
5 5log 2log .a b
C.
3 3
1 5log 2log .a b
D.
3 3
5 1 log 2log .a b
Câu 24. Đặt
12
log 3
a
, khi đó
9
log 16
bằng
A.
1
a
a
. B.
1
a
a
. C.
1
a
a
. D.
1
a
a
.
Câu 25. Với
a
,
b
là hai số dương tùy ý,
5
3
2
3
log
a
b
bằng
A.
3 3
1 2log 5log .a b
B.
3 3
5 5log 2log .a b
C.
3 3
1 5log 2log .a b
D.
3 3
5 1 log 2log .a b
Câu 26. Với
a
,
b
là hai số dương tùy ý,
5
3
log
10
b
a
bằng
A.
5log 1 3log .b a
B.
5log 3 1 log .b a
C.
5log 3 3log .b a
D.
5log 1 3log .b a
Câu 27. Đặt
2
log 9
a
, khi đó
3
log 18
bằng
A.
2 2a
a
. B.
2 2
a
a
. C.
1
a
a
. D.
2 2
a
a
.
Câu 28. Với
a
,
b
,
c
là ba số dương tùy ý,
3
2
log
b
ac
bằng
A.
3log log 2logb a c
. B.
3log log 2 logb a c
.
C.
3 log log 2logb a c
. D.
3 log log 2logb a c
.
Câu 29. Đặt
6
log 4
a
, khi đó
36
log 24
bằng
A.
1a
. B.
1
1
2
a
. C.
2
1a
. D.
2
a
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 30. Với
m
,
n
là hai số thực dương tuỳ ý,
3
2
100
log
m
n
bằng
A.
2 3log 2logm n
. B.
2 3log 2logm n
.
C.
2 3log 2logm n
. D.
1 1 1
log log
2 3 2
m n
.
Câu 31. Đặt
3
log 15
a
, khi đó
25
log 27
bằng
A.
3 1
2
a
. B.
3
2 1
a
. C.
2
3 1
a
. D.
2 1
3
a
.
Câu 32. Với
a
,
b
là hai số thực tuỳ ý,
2 4
log
a b
bằng
A.
2log 4loga b
. B.
2log 4loga b
. C.
2log 4loga b
. D.
2log 4loga b
.
Câu 33. Đặt
3
log 2
a
, khi đó
32
log 81
e
bằng
A.
5
4
e
a
. B.
4
5
e
a
. C.
5
4
e
a
. D.
4
5
e
a
.
Câu 34. Với
a
,
b
là hai số thực dương tuỳ ý,
3 5
ln e.
a b
bằng
A.
5ln 3lna b
. B.
3ln 5lna b
. C.
1 3ln 5lna b
. D.
1 5ln 3lna b
.
Câu 35. Đặt
5
log 2
a
, khi đó
125
16
log ln e
bằng
A.
3
4
a
. B.
3
4a
. C.
4
3a
. D.
4
3
a
.
Câu 36. Với
a
,
b
là hai số thực dương,
4 2
2
log
16
a b
bằng
A.
2log 4log 4
a b
. B.
4 log 1 2loga b
.
C.
2 2
2log 4log 4
a b
. D.
2 2
4 log 1 2loga b
.
Câu 37. Cho
5 7
a
. Tính
49
log 125
theo
a
.
A.
3
2
a
. B.
3
2a
. C.
2
3a
. D.
2
3
a
.
Câu 38. Rút gọn biểu thức
3
2log
2
5
3 log .log 25
a
a
P a
.
A.
2
2
a
. B.
2
2
a
. C.
2
4
a
. D.
2
4
a
.
Câu 39. Cho
a
là số thực dương khác
1
. Tính
log
a
a
.
A.
2
. B.
2
. C.
1
2
. D.
1
.
Câu 40. Giá trị của
3log 4
; 0, 1
a
a a a
bằng
A.
2
. B.
3
. C.
4
. D.
8
.
Câu 41. Rút gọn biểu thức
2
3
2 2
5
log log
a
a
R
b b
(với
;
1
0a a
và
0
b
).
A.
15
log
4
a
b
R
. B.
4log
a
b
. C.
11
log
4
a
b
. D.
15
log
8
a
b
.
Câu 42. Rút gọn biểu thức
2
3
2 2
5
log log
a
a
R
b b
(với
;
1
0a a
và
0
b
).
A.
15
log
4
a
b
R
. B.
4log
a
b
. C.
11
log
4
a
b
. D.
15
log
8
a
b
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Câu 43. Với
a
và
b
là hai số thực dương tùy ý,
3 4
2
log a b
bằng
A.
2 2
1 1
log log
3 4
a b
B.
2 2
3log 4loga b C.
2 4
2 log loga b
D.
2 2
4log 3loga b
MỨC ĐỘ THÔNG HIỂU
Câu 44. Xét tất cả các số dương
a
và
b
thỏa mãn
2 8
log log ( )a ab . Mệnh đề nào dưới đây đúng?
A.
2
a b
. B.
3
a b
. C.
a b
. D.
2
a b
.
Câu 45. Xét số thực
a
và
b
thỏa mãn
3 9
log 3 .9 log 3
a b
. Mệnh đề nào dưới đây đúng
A.
2 2a b
. B.
4 2 1a b
. C.
4 1ab
. D.
2 4 1a b
.
Câu 46. Cho
a
và
b
là hai số thực dương thỏa mãn
3
27ab . Giá trị của
3 3
log 6loga b bằng
A.
3
. B.
6
. C.
9
. D.
1
.
Câu 47. Cho
a
và
b
là hai số thực dương thỏa mãn
2 2
4
log log 2
3
a b
. Giá trị của
3 4
.a b
bằng
A.
8
. B.
6
. C.
64
. D.
32
.
Câu 48. Cho
a
và
b
là hai số thực dương thỏa mãn
5
2
1
9
a
b
. Giá trị của
3 3
5log 2loga b
A.
1
3
. B.
1
2
. C.
2
. D.
2
.
Câu 49. Cho
a
và
b
là hai số thực dương thỏa mãn
4 2
1
log log
2
a b
. Giá trị của
2 4
.a b
bằng
A.
1
2
. B.
1
4
. C.
1
4
. D.
4
.
Câu 50. Cho
a
và
b
là hai số thực dương thỏa mãn
2
3 1
3
log log 2a b
. Giá trị của
a
b
bằng
A.
9
. B.
3
. C.
1
9
. D.
1
3
.
Câu 51. Với các số thực
, 0a b
bất kì, rút gọn biểu thức
2 2
2 1
2
log logP a b
ta được
A.
2
2
log
a
P
b
. B.
2
2
logP ab
. C.
2
1
2
log
a
P
b
. D.
2 2
2
logP a b
.
Câu 52. Với mọi số thực dương
a
và
b
thoả mãn
2 2
8a b ab
, mệnh đề nào dưới đây đúng?
A.
1
log log log
2
a b a b
. B.
1
log 1 log log
2
a b a b
.
C.
log 1 log loga b a b
. D.
1
log log log
2
a b a b
.
Câu 53. Cho và là hai số thực dương thỏa mãn
2 4
log logb ab
. Mệnh đề nào dưới đây đúng?
A.
a b
. B.
1a
. C.
2
1a b
. D.
2
a b
.
Câu 54. Cho
0a
,
0b
thỏa mãn
2 2
4 5a b ab
. Khẳng định nào sau đây đúng?
A.
2 log log
log
3 2
a b a b
. B.
5log 2 log loga b a b
.
C.
2log 2 5 log loga b a b
. D.
log 1 log 1a b
.
a
b
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 55. Cho
,a b
là các số thực dương khác 1, thoả
3 3
2
log log
3
a b
b a
. Mệnh đề nào dưới đây là
đúng?
A.
3
a b
. B.
3
2
3 3
b a a
. C.
3
b a
. D.
a b
.
Câu 56. Cho
0, 0
a b
thỏa mãn
2 2
9 10a b ab
.Khẳng định nào sau đây đúng?
A.
log 1 log 1
a b
. B.
3 log log
log
4 2
a b a b
.
C.
3log 3 log loga b a b
. D.
2log 3 2log loga b a b
.
Câu 57. Cho các số dương
, a b
thõa mãn
2 2
4 9 13a b ab
. Chọn câu trả lời đúng.
A.
log 2 3 log 2log
a b a b
. B.
1
log 2 3 3log 2log
4
a b a b
.
C.
2 3 1
log log log
5 2
a b
a b
. D.
2 3 1
log log log
4 2
a b
a b
.
Câu 58. Cho các số thực
, , , ,x a b c d
dương thoả mãn
4
log 2log 2 3log 4log
x a b c
. Biểu diễn
x
theo
, ,a b c
được kết quả là:
A.
2
3
2a
x
b c
. B.
2
3
4a
x
b c
. C.
2
3
2
a c
x
b
. D.
2
2
2
a c
x
b
.
Câu 59. Cho
, 0
a b
, nếu
2
8 4
log log 5
a b
và
2
4 8
log log 7
a b
thì giá trị của
ab
bằng:
A.
9
2
. B.
72
. C.
9
. D.
18
2
.
Câu 60. Cho
a
,
b
,
c
là ba số thực dương thỏa mãn
3 2
8
a b c
. Giá trị của
2 1
2
2
3log log loga b c
bằng
A.
8
. B.
4
. C.
3
. D.
6
.
Câu 61. Cho
a
,
b
,
c
là ba số thực dương thỏa mãn
2 3
4a b c
. Giá trị của
2ln 3ln lna b c
bằng
A.
2ln2
. B.
ln2
. C.
4
. D.
2
.
Câu 62. Cho
x
và
y
là hai số thực dương khác
1
thỏa mãn
2
8 1
xy
. Giá trị của
1 2
log 2 log 2
x y
bằng
A.
3
. B.
3
. C.
4
. D.
4
.
Câu 63. Cho
log 2
a
b
với
a
,
0
b
,
a
khác 1. Khẳng định nào sau đây sai?
A.
log 3
a
ab
. B.
2
log 4
a
a b
. C.
2
log 4
a
b
. D.
2
log 3
a
ab
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
B. HÀM SỐ LŨY THỪA – MŨ - LOGARIT
HÀM LŨY THỪA HÀM SỐ MŨ HÀM SỐ LOGARIT
Dạng:
y x
y u
với
u
là đa
thức đại số.
Tập xác định:
Nếu
.
ÑK
u
Nếu
0.
0
ÑK
u

Nếu
0.
ÑK
u 
Đạo hàm:
1
1
.
y x y x
y u y u u


Dạng:
x
u
y a
y a
với
0
.
1
a
a
Tập xác định:
.D
Đạo hàm:
ln
ln .
x x
u u
y a y a a
y a y a a u


.
Đặc biệt:
( )
( ) .
x x
u u
e e
e e u
với
2,71828...e
Sự biến thiên:
x
y a
.
Nếu
1a
thì hàm đồng biến
trên
. Nếu
0 1a
thì hàm
nghịch biến trên
.
Dạng:
log
log
a
a
y x
y u
với
0
.
1
a
a
Đặc biệt:
ln ;a e y x
10 log lga y x x 
.
Điều kiện xác định:
0
u
.
Đạo hàm:
1
log
ln
log
ln
a
a
y x y
x a
u
y u y
u a


.
Đặc biệt:
1
(ln )
(ln )
x
x
u
u
u
.
Sự biến thiên:
log
a
y x
. Nếu
1a
: hàm đồng biến trên
(0; )
.
Nếu
0 1a
: hàm nghịch biến trên
(0; ).
ĐỒ THỊ HÀM SỐ MŨ ĐỒ THỊ HÀM SỐ LOGARIT
Ta thấy:
0 1; 0 1
x x
a a b b
.
Ta thấy:
1; 1.
x x
c c d d 
So sánh a với b: Đứng trên cao, bắn mũi tên từ trái
sang phải, trúng
x
a
trước nên
a b
.
So sánh c với d: Đứng trên cao, bắn mũi tên từ trái
sang phải, trúng
x
c
trước nên
.c d
Vậy
0 1 .b a d c
Ta thấy:
log 0 1; log 0 1
a b
x a x b 
.
Ta thấy:
log 1; log 1.
c d
x c x d 
So sánh a với b: Đứng trên cao, bắn mũi tên từ
phải sang trái, trúng
log
b
x
trước:
.b a
So sánh c với d: Đứng trên cao, bắn mũi tên từ
phải sang trái, trúng
log
d
x
trước:
.d c
Vậy
0 1a b c d
.
Câu 1. Tập xác định của hàm số
2
logy x
là
A.
0; .
B.
; . 
C.
0; .
D.
2; .
Câu 2.
Đạo hàm của hàm số
2
4
x
y
là
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
2
2.4 ln 4
x
y
. B.
2
4 .ln 2
x
y
. C.
2
4 ln 4
x
y
. D.
2
2.4 ln 2
x
y
Câu 3. Đạo hàm của hàm số
2018
x
y
là
A.
2018 ln 2018
x
y
. B.
2018 ln
x
y x
. C.
2018
x
y
. D.
2018
ln 2018
x
y
.
Câu 4. Đạo hàm của hàm số
2
2 3 2
e
x x
y
là
A.
2
2 3 2 2
e . 2 3 2
x x
y x x
. B.
2
2 3 2
e . 4 3
x x
y x
.
C.
2
2 3 2
e
x x
y
. D.
2
2 3 1
e . 4 3
x x
y x
.
Câu 5. Hàm số
2 1
2018
x
y
có đạo hàm tại điểm
1x
là
A.
4036.ln2018
. B.
1 2018.ln 2018
y
.
C.
1 2018
y
. D.
1 4036
y
.
Câu 6. Tính đạo hàm của hàm số
2 3
2
x
y
.
A.
2 2
2 ln 4
x
y
. B.
2
4 ln 4
x
y
. C.
2 2
2 ln16
x
y
. D.
2 3
2 ln 2
x
y
.
Câu 7. Tập xác định của hàm số
ln 2
y x
là
A.
;2
. B.
;2

. C.
;
. D.
0;
.
Câu 8. Tập xác định của hàm số
5
x
y
là
A.
\ 0
. B.
0;

. C.
;

. D.
0;

.
Câu 9. Tập xác định của hàm số
2
3
y x
là
A.
\ 3
. B.
3;

. C.
;

. D.
\ 0
.
Câu 10. Tìm đạo hàm của hàm số
2x
y e
.
A.
2x
y e
. B.
2 1
2
x
y xe
. C.
2
2
x
y e
. D.
2 1
2
x
y e
.
Câu 11. Tìm đạo hàm của hàm số
7
logy x
.
A.
ln7
y
x
. B.
1
y
x
. C.
7
y
x
. D.
1
ln 7
y
x
.
Câu 12. Tìm đạo hàm của hàm số
5
x
y
.
A.
5
x
y
. B.
5 ln5
x
y
. C.
5
ln5
x
y
. D.
1
5
x
y x
.
Câu 13. Hàm số
2
log 4
f x x
có đạo hàm
A.
2
ln10
4
f x
x
. B.
2
1
4 ln10
f x
x
.
C.
2
2
4 .ln10
x
f x
x
. D.
2
2
4
x
f x
x
.
Câu 14. Hàm số
2
ln
f x x x
có đạo hàm
A.
2
2 1
.ln10
x
f x
x x
. B.
2
2 1
x x
f x
x
.
C.
2
1
f x
x x
. D.
2
2 1x
f x
x x
.
Câu 15. Hàm số
2
lnf x x
có đạo hàm
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
A.
2.ln x
f x
x
. B.
2.lnf x x
. C.
2
.ln
f x
x x
. D.
ln x
f x
x
.
Câu 16. Hàm số
2
1
5
x
f x
có đạo hàm
A.
2
2
1 .5
x
f x x
. B.
2
1
2 .5 .ln 5
x
f x x
.
C.
2
2
2 . 1 .5
x
f x x x
. D.
2
1
5 .ln 5
x
f x
.
Câu 17. Hàm số
3
2
log
f x x x
có đạo hàm
A.
3
ln2
f x
x x
. B.
3
1
ln 2
f x
x x
.
C.
2
3
3 1 ln 2
x
f x
x x
. D.
2
3
3 1
ln 2
x
f x
x x
.
Câu 18. Hàm số
2
ln 3f x x x
có đạo hàm
A.
2
ln10
3
f x
x x
. B.
2
1
3
f x
x x
. C.
2
3x
2 3
x
f x
x
. D.
2
2 3
3
x
f x
x x
.
Câu 19. Hàm số
2
5x
2
x
f x
có đạo hàm
A.
2
5
2
ln 2
x x
f x
. B.
2
5
2 5 2
ln 2
x x
x
f x
.
C.
2
5
2 ln 2
x x
f x
. D.
2
5
2 2 5 ln 2
x x
f x x
.
Câu 20. Hàm số
2
3
e
x x
f x
có đạo hàm
A.
2
3
e
x x
f x
. B.
2
3 2
e 3
x x
f x x x
.
C.
2
3
e
2 3
x x
f x
x
. D.
2
3
e 2 3
x x
f x x
.
Câu 21. Hàm số
3
3
e
x
y
có đạo hàm là
A.
3
3
e
x
. B.
3
2 3
3 e
x
x
. C.
3
3 3
3 e
x
x
. D.
3
4
3
3 e
4
x
x
x
.
Câu 22.
Đạo hàm của hàm số
2
4
x
y là
A.
2
2.4 ln 4
x
y
. B.
2
4 .ln 2
x
y
. C.
2
4 ln 4
x
y
. D.
2
2.4 ln 2
x
y
Câu 23. Cho hàm số
1
3
x
y
. Đẳng thức nào sau đây đúng?
A.
1
3
x
y
. B.
1
3 .ln 3
x
y
. C.
1
.3
x
y x
. D.
1
1 .3 .ln 3
x
y x
.
Câu 24. Đạo hàm của hàm số
2
2 3 2
e
x x
y
là
A.
2
2 3 2 2
e . 2 3 2
x x
y x x
. B.
2
2 3 2
e . 4 3
x x
y x
.
C.
2
2 3 2
e
x x
y
. D.
2
2 3 1
e . 4 3
x x
y x
.
Câu 25. Tìm đạo hàm của hàm số
2 3
2
x
y
.
A.
2 2
2 ln 4
x
y
. B.
2
4 ln 4
x
y
. C.
2 2
2 ln16
x
y
. D.
2 3
2 ln 2
x
y
.
C. BÀI TOÁN THỰC TẾ
1. Lãi đơn:Khách hàng gửi vào ngân hàng
A
đồng với lãi đơn
r
/kì hạn thì số tiền khách hàng
nhận được cả vốn lẫn lãi sau
n
kì hạn (
n *
) là
n
S A nAr A nr
1
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2. Lãi kép: Khách hàng gửi vào ngân hàng
A
đồng với lãi kép
r
/kì hạn thì số tiền khách hàng
nhận được cả vốn lẫn lãi sau
n
kì hạn (
n *
) là
n
n
S A r
1
Từ đó ta có thể tìm các giá trị:
n
n
S
r
A
1
n
n
S
A
r
1
n
r
S
n
A
1
log
3. Bài toán tăng trưởng dân số: Công thức tính tăng trưởng dân số
m n
m n
X X r m n m n
1 , , ,
trong đó:
r
là tỉ lệ tăng dân số từ năm
n
đến năm
m
m
X
là dân số năm
m
n
X
là dân số năm
n
Từ đó ta có công thức tính tỉ lệ tăng dân số là:
m
m n
n
X
r
X
1
4. Vay vốn trả góp: Vay ngân hàng số tiền là
A
đồng với lãi suất
r
/tháng. Sau đúng một tháng
kể từ ngày vay, bắt đầu hoàn nợ, hai lần hoàn nợ cách nhau đúng một tháng, mỗi lần hoàn nợ số
tiền là
X
đồng. Ta có công thức tính số tiền còn lại sau
n
tháng:
n
n
n
r
S A r X
r
1 1
1
5. Tiền gửi hàng tháng: Đầu mỗi tháng khách hàng gửi vào ngân hàng số tiền
A
đồng với lãi
kép
r
/tháng thì số tiền khách hàng nhận được cả vốn lẫn lãi sau
n
tháng (
n *
) (nhận tiền
cuối tháng, khi ngân hàng đã tính lãi) là
n
S
1 1 1
n
n
A
S r r
r
Từ đó ta có
n
r
S r
n
A r
1
.
log 1
1
n
n
S r
A
r r
.
1 1 1
Câu 1. Để dự báo dân số của một quốc gia, người ta sử dụng công thức
;
nr
S Ae
trong đó
A
là dân số
của năm lấy làm mốc tính,
S
là dân số sau
n
năm,
r
là tỉ lệ tăng dân số hàng năm. Năm 2017,
dân số Việt nam là
93.671.600
người (Tổng cục Thống kê, Niên giám thống kê 2017, Nhà xuất
bản Thống kê, Tr 79). Giả sử tỉ lệ tăng dân số hàng năm không đổi là
0,81%,
dự báo dân số Việt
nam năm 2035 là bao nhiêu người (kết quả làm tròn đến chữ số hàng trăm)?
A.
109.256.100
. B.
108.374.700
. C.
107.500.500
. D.
108.311.100
.
Câu 2. Để quảng bá cho sản phẩm A, một công ty dự định tổ chức quảng cáo theo hình thức quảng cáo
trên truyền hình. Nghiên cứu của công ty cho thấy: nếu sau
n
lần quảng cáo được phát thì tỉ lệ
người xem quảng cáo đó mua sản phẩm A tuân theo công thức
0,015
1
1 49e
n
P n
. Hỏi cần phát
ít nhất bao nhiêu lần quảng cáo để tỉ lệ người xem mua sản phẩm đạt trên
30%?
A.
202
. B.
203
. C.
206
. D.
207
.
Câu 3. Sự tăng trưởng của một loài vi khuẩn tuân theo công thức
.e
rt
S A
, trong đó
A
là số lượng vi
khuẩn ban đầu,
r
là tỉ lệ tăng trưởng
0
r
,
t
là thời gian tăng trưởng. Biết rằng số lượng vi
khuẩn ban đầu là
100
con và sau
5
giờ có
300
con. Hỏi sau
20
giờ có bao nhiêu con?
A.
8100
con. B.
9000
con. C.
7000
con. D.
8500
con.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Câu 4. Dân số thế giới được ước tính theo công thức
0
ni
S S e
, trong đó
0
S
là dân số của năm lấy làm
mốc tính,
S
là dân số sau
n
năm,
i
là tỷ lệ tăng dân số hàng năm. Tỷ lệ tăng dân số hàng năm của
nước ta là
1,14%/
năm. Năm 2019 dân số nước ta là 97 575 490 người. Hỏi đến năm nào dân số
nước ta đạt ngưỡng 100 000 000 người
A. 2022. B. 2021. C. 2024. D. 2023.
Câu 5. Để dự báo dân số của một tỉnh X, người ta sử dụng công thức
.e
nr
S A
, trong đó
A
là dân số của
năm lấy làm mốc tính,
S
là dân số sau
n
năm,
r
là tỉ lệ tăng dân số hàng năm. Năm
2016
, dân số
tỉnh X là
8.326.550
người. Giả sử tỉ lệ tăng dân số hàng năm không đổi là
0,9%
, dự báo dân số
tỉnh X năm
2026
là bao nhiêu người (kết quả làm tròn đến chữ số hàng đơn vị)?
A.
9.029.068
. B.
9.110.697
. C.
9.139.063
. D.
10.311.124
.
Câu 6. Khi đèn flash của máy ảnh tắt, pin ngay lập tức bắt đầu sạc lại tụ điện của đèn flash, nơi lưu trữ
điện tich được cho bởi công thức
/
0
( ) 1 e
t a
Q t Q
(dung lượng sạc tối đa là
0
Q
và
t
được tính
bằng giây). Mất bao lâu đề sạc lại tụ điện thành 90% công suất nếu
2?
a
A.
4
giây. B.
5
giây. C.
4.6
giây. D.
4.5
giây.
Câu 7. Để dự báo dân số của một quốc gia, người ta sử dụng công thức
.e
nr
S A
, trong đó
A
là dân số
của năm lấy làm mốc tính,
S
là dân số sau
n
năm,
r
là tỉ lệ tăng dân số hàng năm. Năm
2018
,
dân số Việt Nam là
94.665.973
người (Tổng cục thống kê, Niên giám thống kê
2018
, Nhà xuất
bản Thống kê, Tr.
87
). Giả sử tỉ lệ tăng dân số hàng năm không đổi là
0,85%
, dự báo đến năm
nào dân số Việt Nam vượt mốc
100.000.000
người?
A.
2022
. B.
2023
. C.
2024
. D.
2025
.
Câu 8. Áp suất không khí
P
(đo bằng milimet thủy ngân, kí hiệu là
mmHg
) suy giảm mũ so với độ cao
x
(so với mực nước biển và đo bằng mét) theo công thức
0
.e
xi
P P
, trong đó
0
760
P mmHg
là
áp suất ở mực nước biển,
i
là hệ số suy giảm. Biết rằng ở độ cao
1000m
thì áp suất của không khí
là
672,71
mmHg
. Hỏi áp suất không khí ở độ cao
4125m
là bao nhiêu (làm tròn đến hàng phần
trăm)?
A.
495, 4598263
mmHg
. B.
459, 46
mmHg
. C.
495,459
mmHg
. D.
459,5
mmHg
Câu 9. Một mặt hàng kinh doanh theo hình thức đa cấp với số lượng nhân viên ban đầu
A
sau
t
(lần hội
thảo) được xấp xỉ bởi đẳng thức
0,2
0
.e
t
A t A
, trong đó
0
A
là số nhân viên ban đầu. Số lượng
nhân viên tham dự ban đầu tham gia kinh doanh là
100
thì sau ít nhất bao nhiêu lần hội thảo, số
lượng nhân viên đạt đến
700
người?
A.
9
. B.
9, 729
. C.
10
. D.
9, 7
.
Câu 10. Vận dụng thông tư số 14/2017/TT-NHNN của Ngân hàng Nhà nước quy định về phương pháp
tính lãi trong hoạt động nhận tiền gửi, có hiệu lực từ ngày 1/1/2018, ngân hàng A đã tính số tiền
lãi theo một kì bằng số ngày của kì gửi nhân với số tiền lãi của một năm chia cho 365. Một khách
hàng gửi 100 triệu đồng vào ngân hàng vào ngày 4/7/2018 với lãi suất 5%/năm, kì hạn 1 tháng,
ngày tính lãi hàng tháng là ngày 4/7, biết rằng trong khi gửi khác hàng không đến rút lãi về, ngân
hàng tính theo thể thức lãi kép. Đến ngày 4/9/2018, người đó đến ngân hàng rút cả vốn lẫn lãi về.
Hỏi số tiền (tính bằng nghìn đồng) khách hàng nhận được là số nào sau đây:
A. 100835. B. 100836. C. 100834. D. 100851.
Câu 11. Trong phòng thí nghiệm nghiên cứu về vi khuẩn tại bênh viện Trung ương Huế, loại vi khuẩn X
gây bệnh cho người có tốc độ tăng trưởng bình quân là
15%
/ ngày. Bệnh viện tiến hành nuôi cấy
mẫu bệnh phẩm do vi khuẩn X gây ra, với ước lượng số vi khuẩn ban đầu là 100 triệu (ước lượng
lúc 9 giờ của ngày đầu tiên nuôi cấy). Bệnh viện nhận thấy rằng có thể trị bệnh do vi khuẩn X gây
ra bằng thuốc kháng sinh Y. Cứ 500 mg thuốc kháng sinh Y có thể tiêu diệt được 10 triệu vi
khuẩn và thuốc có tác dụng hầu như ngay lập tức và không có tác dụng kéo dài thêm. Bác sĩ quyết
định lúc 9 giờ sáng hàng ngày (kể từ ngày thứ hai nuôi cấy mẫu bệnh phẩm) dùng
gx
thuốc
kháng sinh Y để tiến hành nghiên cứu trên mẫu bệnh phẩm thì thấy rằng sau khi tiến hành thí
nghiệm ở ngày thứ 15 ngày kể từ ngày nuôi cấy hoàn thành thì mẫu bệnh phẩm không còn vi
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
khuẩn X. Hỏi số thuốc kháng sinh Y mà bác sĩ dùng hàng ngày để tiến hành nghiên cứu trên là
bao nhiêu? (lấy kết quả gần đúng)
A.
0,855
g. B.
1
g. C.
8,5
g. D.
2
g.
Câu 12. Một em học sinh 15 tuổi được hưởng số tiền thừa kế là 300 000 000 đồng. Số tiền này được gửi
tại một ngân hàng với kỳ hạn thanh toán 1 năm và học sinh này chỉ nhận được số tiền ( cả gốc và
lãi) khi đủ 18 tuổi. Biết rằng khi đủ 18 tuổi em này nhận được số tiền là 368 544 273 đồng. Vậy
lãi suất của ngân hàng gần nhất với số nào sau đây?( Với giả thiết lãi suất không đổi trong suốt
quá trình gửi)
A.
5,5% /
năm. B.
7% /
năm. C.
7,5% /
năm. D.
5,7% /
năm.
Câu 13. Bố An để dành cho An 100 000 000 đồng để học đại học trong một ngân hàng theo hình thức lãi
kép với lãi suất
0,75%
một tháng. Mỗi tháng An đến rút 3 000 000 đồng để chi phí sinh hoạt. Hỏi
sau 1 năm số tiền còn lại là bao nhiêu?( Làm tròn kết quả đến hàng đơn vị)
A.
71857930
đồng. B.
71857931
đồng. C.
73380690
đồng. D.
73380689
đồng.
Câu 14. Một người gửi số tiền
100
triệu đồng vào một ngân hàng với lãi suất
0,65%
trên tháng. Biết rằng
nếu người đó không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được nhập vào
vốn ban đầu (người ta gọi đó là lãi kép). Hỏi số tiền lãi người đó có được sau
2
năm, nếu trong
khoảng thời gian này người đó không rút tiền ra và lãi suất không đổi là bao nhiêu?
A.
24
100.(1,0065)
triệu đồng. B.
2
100.(1,0065) 100
triệu đồng.
C.
24
100.(1,0065) 100
triệu đồng. D.
24
100.(2,0065) 100
triệu đồng.
Câu 15. Ông Nam gửi
100
triệu đồng vào ngân hàng theo thể thức lãi kép, kì hạn
1
năm với lãi suất
7, 56%
một năm. Hỏi sau bao nhiêu năm gửi ông Nam sẽ có ít nhất
150
triệu đồng từ số tiền gửi
ban đầu? (giả sử lãi suất không thay đổi).
A.
5
năm. B.
6
năm. C.
7
năm. D.
8
năm.
Câu 16. Vào ngày 3/8/2018, một người vay ngân hàng số tiền 50 triệu đồng, trả góp trong thời gian 10
tháng, lãi suất 5%/năm, với thỏa thuận là cứ đến ngày tính tiền lãi, người đó phải đến ngân hàng
trả phần tiền gốc bằng số tiền vay ban đầu chia đều cho các lần trả và số lãi phát sinh trong tháng
trước (hình thức dư nợ giảm dần). Hỏi số tiền anh phải trả cho ngân hàng vào ngày 3/12/2018 là
bao nhiêu?
A. 5,45 triệu đồng. B. 5,4 triệu đồng.
C. 10,85 triệu đồng. D. 5,5 triệu đồng.
Câu 17. Vào đầu mỗi năm anh Thắng gửi vào ngân hàng số tiền 30 triệu đồng với kì hạn 1 năm, lãi suất
7%/năm (mỗi lần gửi cách nhau 1 năm). Hỏi sau ít nhất bao nhiêu năm (sau khi ngân hàng đã tính
lãi cho lần gửi cuối cùng) thì anh Thắng được số tiền cả gốc lẫn lãi từ 500 triệu đồng trở lên? (biết
rằng trong suốt thời gian gửi tiền, anh Thắng không đến rút lãi về, ngân hàng tính theo thể thức lãi
kép và lãi suất hàng năm không đổi)
A. 7 năm. B. 8 năm. C.
11
năm. D. 10 năm.
Câu 18. Ông Q.BN mang 150 triệu đồng gửi vào ngân hàng với lãi suất 7% một năm. Ông KN cũng đem
300 triệu đồng gửi vào ngân hàng khác với lãi suất
1,72%
một quí. Sau 10 năm, hai ông cùng đến
ngân hàng rút tiền ra để mua xe. ( Lưu ý: tiền lãi được tính theo công thức lãi kép và được làm
tròn đến hàng triệu). Biết 2 ông cùng muốn mua 1 loại xe có giá là 456 triệu. Nếu số tiền mang
theo không đủ, hai ông có thể trả góp cho hãng xe phần còn thiếu theo hình thức sau: Đúng một
tháng kể từ ngày nhận được xe, người mua bắt đầu đóng tiền góp; hai lần trả liên tiếp cách nhau
đúng một tháng, số tiền trả mỗi tháng là như nhau và phải trả trong 1 năm. Biết rằng mỗi tháng
hang xe chỉ tính lãi trên số dư nợ thực tế của tháng đó. Hỏi mỗi tháng người mua phải trả bao
nhiêu tiền cho hãng xe, lãi suất của hãng là 1,8%/tháng.Khẳng định nào sau đây là đúng
A. Ông Q.BN mỗi tháng phải trả thêm 15 triệu.
B. Ông KN mỗi tháng phải trả thêm 5 triệu.
C. Ông Q.BN cần trả thêm hơn 180 triệu trong 12 tháng.
D. Ôn KN cần trả thêm 15 triệu mỗi tháng.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Câu 19. Ông A cần mua nhà ở nhưng số tiền của ông không đủ để mua nhà ở, ông đi vay ngân hàng
1
tỉ
đồng với lãi suất ưu đãi là
9%
/năm. Ông ta muốn hoàn nợ cho ngân hàng theo cách: Sau đúng
một năm kể từ ngày vay, ông bắt đầu hoàn nợ; hai lần hoàn nợ liên tiếp cách nhau đúng một năm,
số tiền hoàn nợ ở mỗi năm là như nhau và ông A trả hết nợ sau đúng
10
năm kể từ ngày vay. Biết
rằng mỗi năm ngân hàng chỉ tính lãi trên số dư nợ thực tế của năm đó. Hỏi số tiền mỗi tháng ông
ta cần trả cho ngân hàng gần nhất với số tiền nào dưới đây?
A.
155,820
triệu đồng. B.
146,947
triệu đồng.
C.
166,8
triệu đồng. D.
236,736
triệu đồng.
Câu 20. Ông A vay ngân hàng
500
triệu đồng với lãi suất 1%/tháng. Ông ta muốn hoàn nợ cho ngân hàng
theo cách: Sau đúng một tháng kể từ ngày vay, ông bắt đầu hoàn nợ; hai lần hoàn nợ liên tiếp cách
nhau đúng một tháng, số tiền hoàn nợ ở mỗi tháng là 12 triệu đồng. Biết rằng mỗi tháng ngân
hàng chỉ tính lãi trên số dư nợ thực tế của tháng đó. Hỏi số tháng mà ông A cần trả hết nợ ngân
hàng là bao nhiêu kể từ khi vay? (tháng cuối cùng có thể trả số nợ không quá 12 triệu đồng)
A.
55
tháng. B.
54
triệu đồng.
C.
56
triệu đồng. D. không bao giờ trả hết nợ.
Câu 21. Ông A là một người già không có khả năng lao động, trước khi không thể lao động kiếm sống ông
ấy có dành dụm được một khoản tiền để gửi tiết kiệm ngân hàng với lãi suất ưu đãi dành cho
người già là
0,9%
tháng. Sau khi gửi tiết kiệm ngân hàng, đủ mỗi tháng gửi, ông A đến ngân
hàng rút ra một khoản tiền là 5 triệu đồng để chi tiêu hàng ngày. Sau đúng 5 năm kể từ ngày gửi
tiết kiệm, số tiền tiết kiệm còn lại của ông ấy là 100 triệu đồng. Hỏi số tiền ban đầu mà ông A gửi
tiết kiệm là bao nhiêu? (lấy kết quả gần đúng)
A.
289,440
triệu đồng. B.
291,813
triệu đồng.
C.
287,044
triệu đồng. D.
233,663
triệu đồng.
D. PHƯƠNG TRÌNH – BẤT PHƯƠNG TRÌNH CƠ BẢN
1. Đạo hàm của hàm số mũ và lôgarit
( ) . .
u u
e u e
( ) . .ln .
u u
a u a a
(ln )
u
u
u
(log )
ln
a
u
u
u a
2. Phương trình mũ – lôgarit
Đặt điều kiện trước khi giải. Ta có một số kết quả cần nhớ sau:
0 log .
x
a
a b x b
log .
b
a
x b x a
( ) ( )
( ) ( ).
f x g x
a a f x g x
log ( ) log ( ) ( ) ( ).
a a
f x g x f x g x
3. Bất phương trình mũ và lôgarit
Đặt điều kiện trước khi giải. Giải xong được tập nghiệm nhớ giao (lấy phần chung) với điều kiện.
Nếu
( ) ( )
log
( ) ( )
1
log
log ( ) log ( ) ( ) ( )
x
a
f x g x
b
a
a a
a b x b
a a f x g x
a
x b x a
f x g x f x g x
(cùng chiều)
( ) ( )
log
( ) ( )
0 1
log
log ( ) log ( ) ( ) ( )
x
a
f x g x
b
a
a a
a b x b
a a f x g x
a
x b x a
f x g x f x g x
(ngược chiều)
4. Các phương pháp giải phương trình, bất phương trình mũ và lôgarit: Biến đổi tương đương, Đặt ẩn
phụ, Sử dụng tính đơn điệu hàm số, sử dụng đánh giá bằng bất đẳng thức,….
Câu 1. Nghiệm của phương trình
3
log 2 1 2
x
là:
A.
3
x
. B.
5
x
. C.
9
2
x
. D.
7
2
x
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 2. Tập nghiệm của bất phương trình
2
1 9
5 5
x x x
là
A.
2;4
. B.
4;2
. C.
; 2 4;
 
. D.
; 4 2;
 
.
Câu 3. Nghiệm của phương trình
1
3 27
x
là
A.
4
x
. B.
3
x
. C.
2
x
. D.
1x
.
Câu 4. Tập nghiệm của bất phương trình
9 2.3 3 0
x x
là
A.
0;

. B.
0;

. C.
1;

. D.
1;

.
Câu 5. Nghiệm của phương trình
3
log 2 1 3 0
x
là
A.
1
. B.
5
. C.
14
. D.
4
.
Câu 6. Tập nghiệm của phương trình
2
1
2 2
x x
là
A.
1;2
T
. B.
1
T
. C.
2
T
. D.
1; 2
T
.
Câu 7. Nghiệm của phương trình
7
log 3 2 1
x
là
A.
2
3
. B.
1
. C.
3
. D.
2
.
Câu 8. Nghiệm của phương trình
3
log ( 5) 2
x
là:
A.
4
x
. B.
14
x
. C.
2
x
. D.
9
x
.
Câu 9. Nghiệm của phương trình
4 2
7 49 0
x
là
A.
2
. B.
1
. C.
3
. D.
3
2
.
Câu 10. Số nghiệm của phương trình
2
log 2 9 1
x x
là:
A.
1
. B.
2
. C. Vô nghiệm. D.
3
.
Câu 11. Nghiệm của phương trình
3 1
1
5
25
x
là
A.
1
3
. B.
1
. C.
1
. D.
3
.
Câu 12. Nghiệm của phương trình
2 2 3
2 3 2 3
x x
là:
A.
5x
. B.
1
3
x
. C.
1x
. D.
1x
.
Câu 13. Nghiệm của phương trình
2
3
2 16
x x
là
A.
1
4
x
x
. B.
1
4
x
x
. C.
1
4
x
x
. D.
4
x
.
Câu 14. Nghiệm của phương trình
3
1
25
25
x
là:
A.
1x
. B.
1
x
. C.
2
x
. D.
2
x
.
Câu 15. Nghiệm của phương trình
2 1
1
2
4
x
là
A.
1
2
x
. B.
3
2
x
C.
1
.
2
x
D.
3
.
2
x
Câu 16. Tập nghiệm của bất phương trình
2
3
log 2 1
x x
là:
A.
; 3 1;
 
. B.
3;1
. C.
; 3 1;
 
. D.
1:
.
Câu 17. Tập nghiệm của bất phương trình
4 5.2 4 0
x x
là
A.
;0 2;
 
. B.
0;2
. C.
;1 4;
 
. D.
1;4
.
Câu 18. Nghiệm nhỏ nhất của phương trình
2
5
log 3 5 1
x x
là
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
A.
3
. B.
1
. C.
3
. D.
0
.
Câu 19. Tập nghiệm của bất phương trình
2
3 3
log 3 log 3 1x x
là
A.
;1 2;
. B.
1
;1 2;
3
. C.
1
;1
3
. D.
2;
.
Câu 20. Bất phương trình
2
2
log 2 1 1x x
có tập nghiệm là
A.
1 2; 1 2 . B.
; 1 2 1 2;  .
C.
1x
. D.
.
Câu 21. Tập nghiệm của bất phương trình
2
1 1
3 0
4 2
x x
là
A.
3;1
. B.
0;
. C.
; 3 1; 
. D.
;0
.
Câu 22. Tập nghiệm của phương trình
2
0,25
log 3 1x x
là:
A.
4
. B.
1; 4
. C.
3 2 2 3 2 2
;
2 2
. D.
1; 4
.
Câu 23. Tập nghiệm của bất phương trình
2
2 1 3 5
1 1
3 3
x x x
là
A.
1;6
. B.
6;1
. C.
; 6 1;
.D.
; 1 6;
.
Câu 24. Nghiệm của phương trình
1
1
4
16
x
là
A.
1
2
x
B.
2.x
C.
1
.
2
x
D.
2.x
Câu 25. Tập nghiệm của bất phương trình
2
4
1
log 2 3
2
x x
là
A.
3;1
. B.
; 3 1; 
.
C.
3;1
. D.
1 6; 3 1; 1 6 .
Câu 26. Tập nghiệm của bất phương trình
2
6 0
x x
e e
là
A.
3;2
. B.
;2
. C.
;ln 2
. D.
ln2;
.
Câu 27. Tổng bình phương các nghiệm của phương trình bằng
A.
6
. B.
5
. C.
13
. D.
25
.
Câu 28. Tập nghiệm của bất phương trình
2
5 4 8
2 2
x x x
là
A.
2;6
. B.
( ; 2] [6; ) 
. C.
6;2
. D.
( ; 6] [2; ) 
.
Câu 29. Tìm nghiệm của phương trình
2
log 5 3x
.
A.
14x
. B.
11x
. C.
8x
. D.
13x
.
Câu 30. Tìm tập nghiệm của bất phương trình sau:
log 2 1x
.
A.
2x
. B.
2 8x
. C.
8x
. D.
8x
.
Câu 31. Tập nghiệm của bất phương trình
2
2 2
log log 6 0x x
là
2
1
2
log 5 7 0
x x
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
1
0; 8;
4

. B.
1
0; 8;
4

. C.
1
;8
4
. D.
1
; 8;
4

.
Câu 32. Phương trình
2 1
5 125
x
có nghiệm là
A.
5
2
x
. B.
1x
. C.
3
x
. D.
3
2
x
.
Câu 33. Tập nghiệm của bất phương trình
0,5 0,5
log 1 log 2 1
x x
là
A.
;2

. B.
2;

. C.
2;2
. D.
1
;2
2
.
Câu 34. Phương trình
2
2
3 1
x x
có nghiệm là
A.
0
x
,
2
x
. B.
0
x
,
2
x
. C.
1
x
,
3
x
. D.
1x
,
3
x
.
Câu 35. Tìm tập nghiệm của bất phương trình
log 2 log 5 1
x x
.
A.
2
x
. B.
. C.
0
x
. D.
7 0
x
.
Câu 36. Tập nghiệm của bất phương trình
2 2
3 3
log 2log 3 0
x x
là
A.
3;27
. B.
;3 27;
 
. C.
3;27
. D.
0;3 27;
.
Câu 37. Tìm tập nghiệm
S
của phương trình
2
2
5 5
x x
.
A.
S
. B.
1
0;
2
S
. C.
0;2
S
. D.
1
;1
2
S
.
Câu 38. Tập nghiệm của bất phương trình
3
3
3
3log 1 log 2 1 3
x x
A.
1;2
. B.
1
;2
2
. C.
1
;2
2
. D.
2;

.
Câu 39. Phương trình
2
2 8
x
có nghiệm là
A.
6
x
. B.
10
x
. C.
14
x
. D.
5
x
.
Câu 40. Tìm số nghiệm nguyên của bất phương trình
2
3
log 2 1 1
x x
A. 2. B. 3. C. 1. D. 4.
Câu 41. Tập nghiệm của bất phương trình
2
1 1
5 5
log 2log 3 0
x x
là
A.
1
0; 5;
125

. B.
1
; 5;
125
 
.
C.
1
;5
125
. D.
1
0; 5;
125

.
Câu 42. Số nghiệm của phương trình
2
2
log 2 4 2
x x
là:
A.
2
. B.
1
. C.
0
. D.
3
.
Câu 43. Tập nghiệm của bất phương trình
2
2
2 8
x x
là
A.
( ; 1)
. B.
(3; )
.
C.
( 1;3)
. D.
( ; 1) (3; ) 
.
Câu 44. Tập nghiệm của phương trình
6
log 5 1
x x
là
A.
2;3
. B.
4;6
. C.
1; 6
. D.
1;6
.
Câu 45. Tập nghiệm của bất phương trình
2
4
1
27
3
x x
là
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
A.
( ; 1)
. B.
(3; )
. C.
( 1;3)
. D.
( ;1) (3; ) 
.
Câu 46. Phương trình
ln ln 2 1 0
x x
có bao nhiêu nghiệm?
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 47. Phương trình
2
log 72 2logx x
có nghiệm là:
A.
1
. B.
2
. C.
6
. D.
4
.
Câu 48. Số nghiệm nguyên dương của bất phương trình
2
1
5
25
x
x
là
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 49. Tập nghiệm của phương trình
2
ln(2 1) 0
x x
là
A.
0
. B.
1
0 ;
2
. C.
1
2
. D.
.
Câu 50. Tập nghiệm của bất phương trình:
0,4 0,4
log (5 2) log 3 6
x x
là:
A.
;2 .

B.
0;2 .
C.
2
;2 .
5
D.
2; .
Câu 51. Phương trình
2
2 1
4 0.125
x x
có bao nhiêu nghiệm?
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 52. Tập nghiệm của bất phương trình
1 2 2 1
3 6 3 6
x x x x
là:
A.
2
; log 5 .

B.
2
log 5;0 .
C.
2
log 5; . 
D.
1
; .
10

Câu 53. Tìm tập nghiệm của bất phương trình:
2 4 5 11
10 3 10 3
x x
?
A.
1; .
B.
;1 .
C.
5; .
D.
;5 .

Câu 54. Phương trình
2 1
2
5 log 32
x
có nghiệm là
A.
1x
. B.
2
3
x
. C.
3
2
x
. D.
1
2
x
.
Câu 55. Tìm số nghiệm nguyên của bất phương trình:
1
3
log (2 5) 2
x
?
A.
4.
B.
5.
C.
6.
D. Vô số.
Câu 56. Cho phương trình
2 10 4
3 6.3 2 0 1
x x
. Nếu đặt
5
3 0
x
t t
thì
1
trở thành phương trình
nào?
A.
2
9 6 2 0
t t
. B.
2
18 2 0
t t
. C.
2
2 2 0
t t
. D.
2
9 2 2 0
t t
.
Câu 57. Nghiệm của phương trình
3 6
2 1
x
là
A.
1
3
x
. B.
3
x
. C.
2
x
. D.
1
2
x
.
Câu 58. Nghiệm của phương trình
2
log 2 2 3
x
là
A.
3
x
. B.
2
x
. C.
4
x
. D.
5
x
.
Câu 59. Tích hai nghiệm của phương trình
2
3 3
log 6log 8 0
x x
bằng
A.
90
. B.
729
. C.
8
. D.
6
.
Câu 60. Tìm tập nghiệm của phương trình
2
log( 6 7) log( 3)
x x x
.
A.
4;5 .
B.
5 .
C.
3;4 .
D.
.
Câu 61. Tính tổng các nghiệm của phương trình
2
log 3 1 9
x x
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
3
. B.
9
. C
.
9
1
0
. D.
3
.
Câu
62. Phương trình
2
2
l
og 3 log 1 3
x
x
có nghiệ
m là một số
A. chẵn. B. chia hết cho
3
. C
. chia hết cho
7
. D. chia hế
t cho
5
.
Câu
63. Tổng tất cả các nghiệm của phương trình
5
l
og 9 5 1
x
x
bằng
A.
2
. B.
1
. C
.
9
. D
.
5
.
Câu
64. Tổng tất cả các nghiệm của phương trình
l
og(8.5 20 ) log25
x
x
x
bằng
A.
16
. B.
3
. C
.
2
5
. D
.
8
.
Câu
65. Tổng tất cả các nghiệm của phương trình
2
3
(2 9).3 9.2 0
x
x x x
bằng
A.
3
. B.
2
. C
.
0
. D
.
2
.
Câu
66. Phương trình
2
2
2
log 3 1 2log 3 1 3 0
x
x
có 2 nghiệm
1
x
;
2
x
1
2
( )x x
và
1 2 3
l
og
a
x
x
b
với
a,b
,
0
b
và
a
b
là phân
số tối giản. Tính
a
b
.
A.
5
a
b
. B.
5
a
b
. C
.
1
1
a
b
. D
.
1a
b
.
Câu
67. Tổng tất cả các nghiệm của phương trình
4
l
og 9 4 1
x
x
bằng:
A.
2
. B.
1
. C
.
4
. D
.
3
.
Câu
68. Số nghiệm của phương trình
7
l
og 6 7 1
x
x
bằng:
A.
2
. B.
3
. C
.
0
. D.
1
.
Câu
69. Tổng tất cả các nghiệm của phương trình
2
l
n( 5 4) log2.ln10
x
x
bằ
ng
A.
1
. B.
6
. C
.
7
. D.
5
.
Câu
70. Tổng tất cả các nghiệm của phương trình
1
3
l
og 4.3 1 2 1
x
x
bằ
ng:
A.
1
. B.
2
. C
.
7
. D
.
3
.
Câu
71. Số nghiệm của phương trình
5
l
og 3
2
l
og 9 2 5
x
x
bằ
ng:
A.
2
. B.
1
. C
.
7
. D
.
3
.
-------------------- HẾT --------------------
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
A. BIẾN ĐỔI CÔNG THỨC
CÁC CÔNG THỨC MŨ – LOGARIT CẦN NHỚ
Cho a và b là các số thực dương, x và y là những số thực tùy ý.
n
a a.a.a...a
x
x
x
a a
b
b
x y x y
a a .a
x
y
x
y
a a
y 2; y
x
x y n
y n
a 1
a a
a a
.
0
u x
u x 1,
x 0
y x
x.y x y
a a a
n n n
a. b ab
nn 2;
x
x x
a .b a.b
m
m
n
n
m
n
a a a
Cho
0 a 1
và
b, c 0
.
x
a
log b x b a
a a a
b
log log b log c
c
a
a
1
log b log b
a
a
a
log b khi
log b
log b khi
c
a
c
log b
log b
log a
a
b
1
log b ,
log a
a
ln b
log b
ln a
a a
log 1 0, log a 1
b b a
log c log a log b
a c b a
a a a
log b.c log b log c
e
10
ln b log b
lg b log b log b
MỨC ĐỘ NHẬN BIẾT
Câu 1. Với
a
là số thực dương tùy ý,
2
2
log a
bằng:
A.
2
2 log a
. B.
2
1
log
2
a
. C.
2
2log a
. D.
2
1
log
2
a
.
Lời giải
Chọn C
Với
0; 0; 1.a b a
Với mọi
. Ta có công thức:
log log .
a a
b b
Vậy:
2
2 2
log 2loga a
.
Câu 2. Với
a
là hai số thực dương tùy ý,
3
2
log a
bằng
A.
2
3
log
2
a
. B.
2
1
log
3
a
. C.
2
3 log a
. D.
2
3log a
.
Lời giải
Chọn D
Ta có:
3
2 2
log 3log .a a
Câu 3. Cho
a
là số thực dương khác
1
. Tính
log
a
a
.
HÀM SỐ LŨY THỪA - MŨ - LOGARIT
Vấn đề 9
n số a
lẻ
chẵn
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
2
. B.
2
. C.
1
2
. D.
1
.
Lời giải
Chọn A
Ta có:
1
2
log log 2log 2
a
a
a
a a a
.
Câu 4. Cho
a
là số thực dương khác
4
. Tính
3
4
I log
64
a
a
.
A.
3I
. B.
1
3
I
. C.
3I
. D.
1
3
I
.
Lời giải
Chọn A
Ta có
3
4
I log
64
a
a
3
4
log
4
a
a
3
.
Câu 5. Cho
0 1a
. Giá trị của biểu thức
3 2
log .
a
P a a
là
A.
4
3
. B.
3
. C.
5
3
. D.
5
2
.
Lời giải
Chọn C
Ta có:
3 2
log .
a
P a a
2
3
log .
a
a a
5
3
log
a
a
5
3
.
Câu 6. Giá trị của
2 3 4 63
log 3.log 4.log 5....log 64A
bằng
A.
5
. B.
4
. C.
6
. D.
3
.
Lời giải
Chọn C
Áp dụng công thức đổi cơ số, ta có
.
Câu 7. Với các số thực
, 0a b
bất kì, rút gọn biểu thức
2
2 1
2
2log logP a b
ta được
A.
2
2
log 2P ab
. B.
2
2
logP ab
. C.
2
2
log
a
P
b
. D.
2
2
2
log
a
P
b
.
Lời giải
Chọn B
Ta có
2
2 1
2
2log logP a b
2
2 2
2 2 2
log log loga b ab
.
Câu 8. Với
a
,
b
là hai số thực dương,
2 5
5
log
25
a b
bằng
A.
5 5
2log 5log 25a b
. B.
5 5
2log 5log 2a b
.
C.
5 5
2log 5log 25a b
. D.
5 5
2log 5log 2a b
.
Lời giải
Chọn D
Ta có
2 5
2 5 2 5
5 5 5 5 5 5 5 5
log log log 25 log log log 25 2log 5log 2
25
a b
a b a b a b
.
6
2 3 4 63 2 4 63 2 2
log 3.log 4.log 5...log 64 log 4.log 5...log 64 l
og 64 log 2 6
A
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Câu 9. Cho
a
là số thực dương bất kì, giá trị nào dưới đây có cùng giá trị với
3
log(10 )?a
A.
3loga
B.
3
10loga
C.
1 3loga
D.
3log(10 )a
Lời giải
Chọn C
Ta có
3 3
log(10 ) log10 log 1 3loga a a
Câu 10. Với
a
,
b
là hai số dương tùy ý,
6 7
log
a b
bằng
A.
6log 7log .a b
B.
6log 7log .a b
C.
1 1
log log .
6 7
a b
D.
42log
ab
Lời giải
Chọn A
Có
6 7 6 7
log log log 6 log 7loga b a b a b
.
Câu 11. Cho
a
là số thực dương khác
1
. Tính
3
3log
a
I a
A.
1I
. B.
9
I
. C.
1
9
I
. D.
1
3
I
.
Lời giải
Chọn A
Ta có
3
3log
a
I a
log 1
a
a
.
Câu 12. Với
a
và
b
là các số thực dương. Biểu thức
5
log
a
a b
bằng
A.
5 log
a
b
. B.
5 log
a
b
. C.
1
log
5
a
b
. D.
5log
a
b
.
Lời giải
Chọn B
Ta có:
5 5
log log log
a a a
a b a b
5 log
a
b
.
Câu 13. Cho các số thực dương
a
,
b
thỏa mãn
2log 5log 1
a b
. Mệnh đề nào sau đây đúng.
A.
2 5
10
a b
. B.
2 5 10
a b
. C.
2 5 1a b
. D.
2 5
10
a b
.
Lời giải
Chọn A
Ta có:
2log 5log 1
a b
2 5
log log 1
a b
2 5
log 1
a b
2 5
10
a b
.
Câu 14. Cho
b
là số thực dương khác
1
. Tính
1
6
2
log .
b
P b b
.
A.
3
P
. B.
7
2
P
. C.
13
2
P
. D.
6
P
.
Lời giải
Chọn C
Ta có
1
6
2
log .
b
P b b
13
2
log
b
b
13
2
.
Câu 15. Với
a
,
b
là hai số dương tùy ý,
4
5
log
a
b
bằng
A.
4log 5loga b
. B.
4log 5loga b
. C.
4
log log
5
a b
. D.
4
log log
5
a b
.
Lời giải
Chọn B
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Có
4
4 5
5
log log log 4log 5log
a
a b a b
b
.
Câu 16. Cho và là hai số thực dương thỏa mãn
2 1
2
log log
a
a
b
. Mệnh đề nào dưới đây đúng?
A.
1b
. B.
2
b a
. C.
a b
. D.
2
a b
.
Lời giải
Chọn D
Ta có:
2 1
2
log log
a
a
b
1 2
2 2 2 2
1
log log log log
a a a
a a a b
b b b a
.
Câu 17. Cho
0 1a
. Giá trị của biểu thức
3
log .
a
P a a
là
A.
1
3
. B.
3
. C.
4
3
. D.
5
3
.
Lời giải
Chọn C
Ta có:
3
log .
a
P a a
1
3
log .
a
a a
4
3
log
a
a
4
3
.
Câu 18. Với
a
là số thực dương bất kỳ, mệnh đề nào dưới đây đúng?
A.
log 7 7loga a
. B.
7
1
log log
7
a a
.
C.
7
loga 7log a
. D.
1
log 7 log
7
a a
.
Lời giải
Chọn C
Vì với
0a
thì
7
loga 7log a
Câu 19. Cho
a
và
b
là các số thực dương bất kì. Chọn khẳng định sai.
A.
3
5
1
ln ln 3ln ln
5
a b a b
. B.
log log loga b ab
.
C.
2
log 10 10 log logab a b
. D.
ln ln ln
a
a b
b
.
Lời giải
Chọn C
Ta có:
2
log 10 2log 10ab ab
2 2 log 2 loga b
.
Câu 20. Với
a
là số thực dương tùy ý,
2
3
log 9a
bằng:
A.
3
2log a
. B.
3
3 2log a
. C.
3
2 2log a
. D.
3
4log a
.
Lời giải
Chọn C
Ta có
2 2
3 3 3 3
log 9 log 9 log 2 2loga a a
Câu 21. Với
a
,
b
là hai số dương tùy ý,
3 4
log a b
bằng
A.
3log 4log .a b
B.
4log 3log .a b
C.
1
log 3log .
4
a b
D.
1
2log log .
3
a b
Lời giải
Chọn A
a
b
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Có
3 4 3 4
log log log 3log 4loga b a b a b
.
Câu 22. Đặt
4
log 5
a
, khi đó
25
log 64
bằng
A.
3
2
a
. B.
3
2a
. C.
2
3a
. D.
2
3
a
.
Lời giải
Chọn B
Ta có
2
3
25 5
5
3 3
log 64 log 4 log 4
2 2a
.
Câu 23. Với
a
,
b
là hai số dương tùy ý,
5
3
2
3
log
a
b
bằng
A.
3 3
1 2log 5log .a b
B.
3 3
5 5log 2log .a b
C.
3 3
1 5log 2log .a b
D.
3 3
5 1 log 2log .a b
Lời giải
Chọn C
Có
5
5 2 5
3 3 3 3 3 3 3 3
2
3
log log 3 log log 3 log 2log 1 5log 2log .
a
a b a b a b
b
Câu 24. Đặt
12
log 3
a
, khi đó
9
log 16
bằng
A.
1
a
a
. B.
1
a
a
. C.
1
a
a
. D.
1
a
a
.
Lời giải
Chọn A
Ta có
12
12
9 3
12
12
log
log 4 1
3
log 16 log 4
log 3
a
a a
.
Câu 25. Với
a
,
b
là hai số dương tùy ý,
5
3
2
3
log
a
b
bằng
A.
3 3
1 2log 5log .a b
B.
3 3
5 5log 2log .a b
C.
3 3
1 5log 2log .a b
D.
3 3
5 1 log 2log .a b
Lời giải
Chọn C
Có
5
5 2 5
3 3 3 3 3 3 3 3
2
3
log log 3 log log 3 log 2log 1 5log 2log .
a
a b a b a b
b
Câu 26. Với
a
,
b
là hai số dương tùy ý,
5
3
log
10
b
a
bằng
A.
5log 1 3log .b a
B.
5log 3 1 log .b a
C.
5log 3 3log .b a
D.
5log 1 3log .b a
Lời giải
Chọn D
Có
5
5 3 3
3
log log log 10 5log log10 log 5log 1 3log .
10
b
b a b a b a
a
Câu 27. Đặt
2
log 9
a
, khi đó
3
log 18
bằng
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
2 2a
a
. B.
2 2
a
a
. C.
1
a
a
. D.
2 2
a
a
.
Lời giải
Chọn D
Ta có
3 3
2 2
1 2 2 2 2
log 18 log 2 2 2 2 2
log 3 log 9
a
a a
.
Câu 28. Với
a
,
b
,
c
là ba số dương tùy ý,
3
2
log
b
ac
bằng
A.
3log log 2logb a c
. B.
3log log 2 logb a c
.
C.
3 log log 2logb a c
. D.
3 log log 2logb a c
.
Lời giải
Chọn A
Có
3
3 2
2
log log log log 3log log 2log
b
b a c b a b
ac
.
Câu 29. Đặt
6
log 4
a
, khi đó
36
log 24
bằng
A.
1a
. B.
1
1
2
a
. C.
2
1a
. D.
2
a
.
Lời giải
Chọn B
Ta có
2
36 6
6
1 1 1
log 24 log 6.4 log 4 1
2 2 2
a
.
Câu 30. Với
m
,
n
là hai số thực dương tuỳ ý,
3
2
100
log
m
n
bằng
A.
2 3log 2logm n
. B.
2 3log 2logm n
.
C.
2 3log 2logm n
. D.
1 1 1
log log
2 3 2
m n
.
Lời giải
Chọn A
Ta có
3
3 2
2
100
log log100 log log 2 3log 2log 2 3log 2log
m
m n m n m n
n
.
Câu 31. Đặt
3
log 15
a
, khi đó
25
log 27
bằng
A.
3 1
2
a
. B.
3
2 1
a
. C.
2
3 1
a
. D.
2 1
3
a
.
Lời giải
Chọn B
Ta có:
25 5
3
3 3 1 3
log 27 log 3 .
2 2 log 5 2 1
a
.
Vì
3 3 3 3
log 15 log 3.5 1 log 5 log 5 1a a
.
Câu 32. Với
a
,
b
là hai số thực tuỳ ý,
2 4
log
a b
bằng
A.
2log 4loga b
. B.
2log 4loga b
. C.
2log 4loga b
. D.
2log 4loga b
.
Lời giải
Chọn D
Ta có
2 4 2 4
log log log 2 log 4 loga b a b a b
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Câu 33. Đặt
3
log 2
a
, khi đó
32
log 81
e
bằng
A.
5
4
e
a
. B.
4
5
e
a
. C.
5
4
e
a
. D.
4
5
e
a
.
Lời giải
Chọn B
Ta có:
2
32 3
4 1
4 4
.
log 3
log 81 5 log 2
5 5
e e e e
a
.
Câu 34. Với
a
,
b
là hai số thực dương tuỳ ý,
3 5
ln e.
a b
bằng
A.
5ln 3lna b
. B.
3ln 5lna b
. C.
1 3ln 5lna b
. D.
1 5ln 3lna b
.
Lời giải
Chọn C
Ta có
3 5 3 5
ln e. ln e ln ln 1 3ln 5lna b a b a b
.
Câu 35. Đặt
5
log 2
a
, khi đó
125
16
log ln e
bằng
A.
3
4
a
. B.
3
4a
. C.
4
3a
. D.
4
3
a
.
Lời giải
Chọn B
Ta có:
125
16 16 2
5
3 3 1 3
log ln e log 125 log 5 .
4 4 log 2 4a
.
Câu 36. Với
a
,
b
là hai số thực dương,
4 2
2
log
16
a b
bằng
A.
2log 4log 4
a b
. B.
4 log 1 2loga b
.
C.
2 2
2log 4log 4
a b
. D.
2 2
4 log 1 2loga b
.
Lời giải
Chọn D
Ta có
4 2
4 2
2 2 2 2 2 2 2 2
log log log log 16 4log 2log 4 4 log 1 2log
16
a b
a b a b a b
.
Câu 37. Cho
5 7
a
. Tính
49
log 125
theo
a
.
A.
3
2
a
. B.
3
2a
. C.
2
3a
. D.
2
3
a
.
Lời giải
Chọn B
Ta có:
49 7
5 5
3 3 1 3 1 3
log 125 log 5 . .
2 2 log 7 2 log 5 2
a
a
.
Câu 38. Rút gọn biểu thức
3
2log
2
5
3 log .log 25
a
a
P a
.
A.
2
2
a
. B.
2
2
a
. C.
2
4
a
. D.
2
4
a
.
Lời giải
Chọn D
Điều kiện:
0
1
a
a
.
Ta có:
3 3
2
2log log
2
5 5
3 log .log 25 3 2 log . 2log 5
a a
a a
P a a
2
5
4 log .log 5
a
a a
2
4
a
.
Câu 39. Cho
a
là số thực dương khác
1
. Tính
log
a
a
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
2
. B.
2
. C.
1
2
. D.
1
.
Lời giải
Chọn A
Ta có:
1
2
log log 2log 2
a
a
a
a a a
.
Câu 40. Giá trị của
3log 4
; 0, 1
a
a a a
bằng
A.
2
. B.
3
. C.
4
. D.
8
.
Lời giải
Chọn D
Ta có
3
2
4
3 3
3log 4
log
log 4
2 2
4 8
a
a
a
a a a
.
Câu 41. Rút gọn biểu thức
2
3
2 2
5
log log
a
a
R
b b
(với
;
1
0a a
và
0
b
).
A.
15
log
4
a
b
R
. B.
4log
a
b
. C.
11
log
4
a
b
. D.
15
log
8
a
b
.
Lời giải
Chọn C
2
53
2 2
3 5 11
lolo
g log log .
2 4
g
4
log
a a a a
a
b b b b b
R
Câu 42. Rút gọn biểu thức
2
3
2 2
5
log log
a
a
R
b b
(với
;
1
0a a
và
0
b
).
A.
15
log
4
a
b
R
. B.
4log
a
b
. C.
11
log
4
a
b
. D.
15
log
8
a
b
.
Lời giải
Chọn C
2
53
2 2
3 5 11
lolo
g log log .
2 4
g
4
log
a a a a
a
b b b b b
R
Câu 43. Với
a
và
b
là hai số thực dương tùy ý,
3 4
2
log
a b
bằng
A.
2 2
1 1
log log
3 4
a b
B.
2 2
C.
2 4
2 log log
a b
D.
2 2
Lời giải
Chọn B
Ta có:
3 4 3 4
2 2 2 2 2
log log log 3log 4loga b a b a b
.
MỨC ĐỘ THÔNG HIỂU
Câu 44. Xét tất cả các số dương
a
và
b
thỏa mãn
2 8
log log ( )a ab
. Mệnh đề nào dưới đây đúng?
A.
2
a b
. B.
3
a b
. C.
a b
. D.
2
a b
.
Lời giải
Chọn D
Theo đề ta có:
2 8 2 2 2 2
3 3 2
2 2
1
log log ( ) log log ( ) 3log log ( )
3
log log ( )
a ab a ab a ab
a ab a ab a b
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Câu 45. Xét số thực
a
và
b
thỏa mãn
3 9
log 3 .9 log 3
a b
. Mệnh đề nào dưới đây đúng
A.
2 2
a b
. B.
4 2 1
a b
. C.
4 1
ab
. D.
2 4 1
a b
.
Lời giải
Chọn D
Ta có:
2
2
3 9 3
3
1
2
2
3 3
log 3 .9 log 3 log 3 .3 log 3
1
log 3 log 3 2 2 4 1.
2
a b a b
a b
a b a b
Câu 46. Cho
a
và
b
là hai số thực dương thỏa mãn
3
27
ab
. Giá trị của
3 3
log 6loga b
bằng
A.
3
. B.
6
. C.
9
. D.
1
.
Lời giải
Chọn B
Sử dụng quy tắc logarit một tích ta có:
3
3 3 3 3 3
1
log 3log log 3 log 6log 6
2
a b ab a b
.
Câu 47. Cho
a
và
b
là hai số thực dương thỏa mãn
2 2
4
log log 2
3
a b
. Giá trị của
3 4
.a b
bằng
A.
8
. B.
6
. C.
64
. D.
32
.
Lời giải
Chọn C
Sử dụng quy tắc logarit một tích cho hai số dương
a
và
b
ta có
3 4 3 4 6 3 4
2 2 2 2 2
4
log log 2 3log 4log 6 log . 6 2 64
3
a b a b a b a b a b
.
Câu 48. Cho
a
và
b
là hai số thực dương thỏa mãn
5
2
1
9
a
b
. Giá trị của
3 3
A.
1
3
. B.
1
2
. C.
2
. D.
2
.
Lời giải
Chọn D
Sử dụng quy tắc logarit một thương cho hai số dương
a
và
b
ta có
5
5 2
3 3 3 3 3 3
2
1
5log 2log log log log log 2
9
a
a b a b
b
.
Câu 49. Cho
a
và
b
là hai số thực dương thỏa mãn
4 2
1
log log
2
a b
. Giá trị của
2 4
.a b
bằng
A.
1
2
. B.
1
4
. C.
1
4
. D.
4
.
Lời giải
Chọn B
Sử dụng quy tắc logarit một tích cho hai số dương
a
và
b
ta có
4 2 2 2 2 2
1 1 1
log log log log log 2log 1
2 2 2
a b a b a b
2 2 2 4
2
1 1
log . 1
2 4
a b ab a b
.
Câu 50. Cho
a
và
b
là hai số thực dương thỏa mãn
2
3 1
3
log log 2
a b
. Giá trị của
a
b
bằng
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
9
. B.
3
. C.
1
9
. D.
1
3
.
Lời giải
Chọn B
Sử dụng quy tắc logarit một thương cho hai số dương
a
và
b
ta có
2 2
2 2
3 1 3 3 3
3
log log 2 log log 2 log 2 9 3
a a a
a b a b
b b
b
.
Câu 51. Với các số thực
, 0a b
bất kì, rút gọn biểu thức
2 2
2 1
2
log logP a b
ta được
A.
2
2
log
a
P
b
. B.
2
2
logP ab
. C.
2
1
2
log
a
P
b
. D.
2 2
2
logP a b
.
Lời giải
Chọn B
Ta có
2 2
2 1
2
log logP a b
2
2 2
2 2 2
log log loga b ab
.
Câu 52. Với mọi số thực dương
a
và
b
thoả mãn
2 2
8a b ab
, mệnh đề nào dưới đây đúng?
A.
1
log log log
2
a b a b
. B.
1
log 1 log log
2
a b a b
.
C.
log 1 log loga b a b
. D.
1
log log log
2
a b a b
.
Lời giải
Chọn B
Ta có
2
2 2 2 2
8 2 10 10a b ab a ab b ab a b ab
.
2
log log 10a b ab
.
2log 1 log loga b a b
.
1
log 1 log log
2
a b a b
.
Câu 53. Cho và là hai số thực dương thỏa mãn
2 4
log logb ab
. Mệnh đề nào dưới đây đúng?
A.
a b
. B.
1a
. C.
2
1a b
. D.
2
a b
.
Lời giải
Chọn A
Ta có:
2 2
2 4 2 2 2 2
1
log log log log log log
2
b ab b ab b ab b ab a b
Câu 54. Cho
0a
,
0b
thỏa mãn
2 2
4 5a b ab
. Khẳng định nào sau đây đúng?
A.
2 log log
log
3 2
a b a b
. B.
5log 2 log loga b a b
.
C.
2log 2 5 log loga b a b
. D.
log 1 log 1a b
.
Lời giải
Chọn A
Ta có:
2 2
2 2
4 5 2 9 log 2 log 9a b ab a b ab a b ab
2
2.log 2 2.log3 log log 2.log log log
3
a b
a b a b a b
2 log log
log
3 2
a b a b
a
b
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Câu 55. Cho
,a b
là các số thực dương khác 1, thoả
3 3
2
log log
3
a b
b a
. Mệnh đề nào dưới đây là đúng?
A.
3
a b
. B.
3
2
3 3
b a a
. C.
3
b a
. D.
a b
.
Lời giải
Chọn D
Ta có:
3 3
2
log log log log 2
3
a b
a b
b a b a
2
1
log 2 log 1 0 log 1.
log
a a a
a
b b b
b
Suy ra:
a b
.
Câu 56. Cho
0, 0
a b
thỏa mãn
2 2
9 10a b ab
.Khẳng định nào sau đây đúng?
A.
log 1 log 1
a b
. B.
3 log log
log
4 2
a b a b
.
C.
3log 3 log loga b a b
. D.
2log 3 2log loga b a b
.
Lời giải
Chọn B
Ta có
2 2
9 10a b ab
2
3
16
a b
ab
2
3
log log
16
a b
ab
( do
0, 0
a b
)
3
2log log log
4
a b
a b
3 log log
log
4 2
a b a b
.
Câu 57. Cho các số dương
, a b
thõa mãn
2 2
4 9 13a b ab
. Chọn câu trả lời đúng.
A.
log 2 3 log 2log
a b a b
. B.
1
log 2 3 3log 2log
4
a b a b
.
C.
2 3 1
log log log
5 2
a b
a b
. D.
2 3 1
log log log
4 2
a b
a b
.
Lời giải
Chọn C
Ta có
2
2 2 2 2
2 3
4 9 13 4 12 9 25 2 3 25
5
a b
a b ab a ab b ab a b ab ab
Suy ra
2 3 2 3 1
log log log log log
5 5 2
a b a b
ab a b
.
Câu 58. Cho các số thực
, , , ,x a b c d
dương thoả mãn
4
log 2log 2 3log 4log
x a b c
. Biểu diễn
x
theo
, ,a b c
được kết quả là:
A.
2
3
2a
x
b c
. B.
2
3
4a
x
b c
. C.
2
3
2
a c
x
b
. D.
2
2
2
a c
x
b
.
Lời giải
Chọn B
2 3
4
log 2log 2 3log 4log log log 4 log logx a b c x a b c
2 2
3 3
4 4
log log
a a
x x
b c b c
.
Câu 59. Cho
, 0
a b
, nếu
2
8 4
log log 5
a b
và
2
4 8
log log 7
a b
thì giá trị của
ab
bằng:
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
9
2
. B.
72
. C.
9
. D.
18
2
.
Lời giải
Chọn A
Ta có:
2
6
2 2
8 4
2
2 3
2
4 8
2 2
1
log log 5
log log 5
log 6
2
3
1 log 3
log log 7 2
log log 7
3
a b
a b
a
a
b
a b b
a b
.
Suy ra:
6 3 9
2 .2 2
ab
.
Câu 60. Cho
a
,
b
,
c
là ba số thực dương thỏa mãn
3 2
8
a b c
. Giá trị của
2 1
2
2
3log log loga b c
bằng
A.
8
. B.
4
. C.
3
. D.
6
.
Lời giải
Chọn C
Với các số thực dương
a
,
b
,
c
ta có:
2 1
2
2
3log log loga b c
3
2 2 2
log 2log loga b c
3 2
2 2 2
log log loga b c
3 2
2 2
log log 8 3
a b c
.
Câu 61. Cho
a
,
b
,
c
là ba số thực dương thỏa mãn
2 3
4a b c
. Giá trị của
2ln 3ln lna b c
bằng
A.
2ln 2
. B.
ln2
. C.
4
. D.
2
.
Lời giải
Chọn A
Với các số thực dương
a
,
b
,
c
ta có:
2 3
2 3
4 4
a b
a b c
c
Và
2 3
2 3
2ln 3ln ln ln 3ln ln ln ln4 2ln 2
a b
a b c a b c
c
.
Câu 62. Cho
x
và
y
là hai số thực dương khác
1
thỏa mãn
2
8 1
xy
. Giá trị của
1 2
log 2 log 2
x y
bằng
A.
3
. B.
3
. C.
4
. D.
4
.
Lời giải
Chọn A
Với
x
,
y
là các số thực dương khác
1
ta có:
2 2
1
8 1
8
xy xy
.
Và
2 2
2 2 2 2 2 2
1 2 1
log 2.log log log log log 3
log 2 log 2 8
x y
x y x y xy
.
Câu 63. Cho
log 2
a
b
với
a
,
0
b
,
a
khác 1. Khẳng định nào sau đây sai?
A.
log 3
a
ab
. B.
2
log 4
a
a b
. C.
2
log 4
a
b
. D.
2
log 3
a
ab
.
Lời giải
Chọn D
Ta có:
•
log log log 1 2 3
a a a
ab a b
. Suy ra phương án A đúng.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
•
2 2
log log log 2 2 4
a a a
a b a b
. Suy ra phương án B đúng.
•
2
log 2log 2.2 4
a a
b b
. Suy ra phương án C đúng.
•
2 2
log log log 1 2.2 5
a a a
ab a b
. Suy ra phương án D sai.
B. HÀM SỐ LŨY THỪA – MŨ - LOGARIT
HÀM LŨY THỪA HÀM SỐ MŨ HÀM SỐ LOGARIT
Dạng:
y x
y u
với
u
là đa
thức đại số.
Tập xác định:
Nếu
.
ÑK
u
Nếu
0.
0
ÑK
u

Nếu
0.
ÑK
u 
Đạo hàm:
1
1
.
y x y x
y u y u u


Dạng:
x
u
y a
y a
với
0
.
1
a
a
Tập xác định:
.D
Đạo hàm:
ln
ln .
x x
u u
y a y a a
y a y a a u


.
Đặc biệt:
( )
( ) .
x x
u u
e e
e e u
với
2,71828...e
Sự biến thiên:
x
y a
.
Nếu
1a
thì hàm đồng biến
trên
. Nếu
0 1a
thì hàm
nghịch biến trên
.
Dạng:
log
log
a
a
y x
y u
với
0
.
1
a
a
Đặc biệt:
ln ;a e y x 
10 log lga y x x 
.
Điều kiện xác định:
0u
.
Đạo hàm:
1
log
ln
log
ln
a
a
y x y
x a
u
y u y
u a


.
Đặc biệt:
1
(ln )
(ln )
x
x
u
u
u
.
Sự biến thiên:
log
a
y x
. Nếu
1a
: hàm đồng biến trên
(0; )
.
Nếu
0 1a
: hàm nghịch biến trên
(0; ).
ĐỒ THỊ HÀM SỐ MŨ ĐỒ THỊ HÀM SỐ LOGARIT
Ta thấy:
0 1; 0 1
x x
a a b b
.
Ta thấy:
1; 1.
x x
c c d d 
So sánh a với b: Đứng trên cao, bắn mũi tên từ trái
sang phải, trúng
x
a
trước nên
a b
.
So sánh c với d: Đứng trên cao, bắn mũi tên từ trái
sang phải, trúng
x
c
trước nên
.c d
Vậy
0 1 .b a d c
Ta thấy:
log 0 1; log 0 1
a b
x a x b 
.
Ta thấy:
log 1; log 1.
c d
x c x d 
So sánh a với b: Đứng trên cao, bắn mũi tên từ
phải sang trái, trúng
log
b
x
trước:
.b a
So sánh c với d: Đứng trên cao, bắn mũi tên từ
phải sang trái, trúng
log
d
x
trước:
.d c
Vậy
0 1a b c d
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 1. Tập xác định của hàm số
2
logy x
là
A.
0; .
B.
; . 
C.
0; .
D.
2; .
Lời giải
Chọn C
Điều kiện xác định của hàm số
2
logy x
là
0
x
.
Vậy tập xác định của hàm số
2
logy x
là
0; .
D

Câu 2.
Đạo hàm của hàm số
2
4
x
y
là
A.
2
2.4 ln 4
x
y
. B.
2
4 .ln 2
x
y
. C.
2
4 ln 4
x
y
. D.
2
2.4 ln 2
x
y
Lời giải
Chọn A
2
2.4 .ln 4
x
y
.
Câu 3. Đạo hàm của hàm số
2018
x
y
là
A.
2018 ln 2018
x
y
. B.
2018 ln
x
y x
. C.
2018
x
y
. D.
2018
ln 2018
x
y
.
Lời giải
Chọn A
Có
2018
x
y
2018 .ln 2018
x
y
.
Câu 4. Đạo hàm của hàm số
2
2 3 2
e
x x
y
là
A.
2
2 3 2 2
e . 2 3 2
x x
y x x
. B.
2
2 3 2
e . 4 3
x x
y x
.
C.
2
2 3 2
e
x x
y
. D.
2
2 3 1
e . 4 3
x x
y x
.
Lời giải
Chọn B
Có
2
2 3 2
e
x x
y
2
2 3 2
e . 4 3
x x
y x
.
Câu 5. Hàm số
2 1
2018
x
y
có đạo hàm tại điểm
1x
là
A.
4036.ln 2018
. B.
1 2018.ln 2018
y
.
C.
1 2018
y
. D.
1 4036
y
.
Lời giải
Chọn A
2 1
2018
x
y
2 1
2018 .ln 2018.2
x
y
1 2018.ln 2018.2 4036.ln 2018
y
.
Câu 6. Tính đạo hàm của hàm số
2 3
2
x
y
.
A.
2 2
2 ln 4
x
y
. B.
2
4 ln 4
x
y
. C.
2 2
2 ln16
x
y
. D.
2 3
2 ln 2
x
y
.
Lời giải
Chọn C
Áp dụng công thức đạo hàm
. .ln
u u
a u a a
Ta có
2 3
2 3 2 ln 2
x
y x
2 3
2 ln 4
x
2 2
2 ln16
x
.
Câu 7. Tập xác định của hàm số
ln 2
y x
là
A.
;2
. B.
;2

. C.
;
. D.
0;
.
Lời giải
Chọn B
Hàm số
ln 2
y x
xác định
2 0 2
x x
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Vậy tập xác định của hàm số đã cho là
;2

.
Câu 8. Tập xác định của hàm số
5
x
y
là
A.
\ 0
. B.
0;

. C.
;

. D.
0;

.
Lời giải
Chọn C
Hàm số
5
x
y
xác định với mọi
x
.
Vậy tập xác định của hàm số đã cho là
;

.
Câu 9. Tập xác định của hàm số
2
3
y x
là
A.
\ 3
. B.
3;

. C.
;

. D.
\ 0
.
Lời giải
Chọn A
Hàm số
2
3
y x
xác định
3 0 3
x x
.
Vậy tập xác định của hàm số đã cho là
\ 3
.
Câu 10. Tìm đạo hàm của hàm số
2x
y e
.
A.
2x
y e
. B.
2 1
2
x
y xe
. C.
2
2
x
y e
. D.
2 1
2
x
y e
.
Lời giải
Chọn C
Đạo hàm của hàm số
2x
y e
là:
2 2
2 . 2
x x
y x e e
.
Câu 11. Tìm đạo hàm của hàm số
7
logy x
.
A.
ln7
y
x
. B.
1
y
x
. C.
7
y
x
. D.
1
ln 7
y
x
.
Lời giải
Chọn D
Đạo hàm của hàm số
7
logy x
là:
1
ln 7
y
x
.
Câu 12. Tìm đạo hàm của hàm số
5
x
y
.
A.
5
x
y
. B.
5 ln5
x
y
. C.
5
ln5
x
y
. D.
1
5
x
y x
.
Lời giải
Chọn B
Đạo hàm của hàm số
5
x
y
là:
5 ln5
x
y
.
Câu 13. Hàm số
2
log 4
f x x
có đạo hàm
A.
2
ln10
4
f x
x
. B.
2
1
4 ln10
f x
x
.
C.
2
2
4 .ln10
x
f x
x
. D.
2
2
4
x
f x
x
.
Lời giải:
Chọn C
Ta có:
2
2 2
4
2
4 .ln10 4 .ln10
x
x
f x
x x
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 14. Hàm số
2
ln
f x x x
có đạo hàm
A.
2
2 1
.ln10
x
f x
x x
. B.
2
2 1
x x
f x
x
.
C.
2
1
f x
x x
. D.
2
2 1x
f x
x x
.
Lời giải
Chọn D
Ta có:
2
2 2
2 1
x x
x
f x
x x x x
.
Câu 15. Hàm số
2
lnf x x
có đạo hàm
A.
2.ln x
f x
x
. B.
2.lnf x x
. C.
2
.ln
f x
x x
. D.
ln x
f x
x
.
Lời giải
Chọn A
Ta có:
2.ln
2.ln . ln
x
f x x x
x
.
Câu 16. Hàm số
2
1
5
x
f x
có đạo hàm
A.
2
2
1 .5
x
f x x
. B.
2
1
2 .5 .ln 5
x
f x x
.
C.
2
2
2 . 1 .5
x
f x x x
. D.
2
1
5 .ln 5
x
f x
.
Lời giải
Chọn B
Ta có:
2 2
1 2 1
5 .ln5. 1 2 .5 .ln5
x x
f x x x
.
Câu 17. Hàm số
3
2
log
f x x x
có đạo hàm
A.
3
ln2
f x
x x
. B.
3
1
ln 2
f x
x x
.
C.
2
3
3 1 ln 2
x
f x
x x
. D.
2
3
3 1
ln 2
x
f x
x x
.
Lời giải
Chọn D
Áp dụng công thức
log
ln
a
u x
u x
u x a
.
Vậy
3
2
3 3
3 1
ln 2 ln 2
x x
x
f x
x x x x
.
Câu 18. Hàm số
2
ln 3f x x x
có đạo hàm
A.
2
ln10
3
f x
x x
. B.
2
1
3
f x
x x
.
C.
2
3x
2 3
x
f x
x
. D.
2
2 3
3
x
f x
x x
.
Lời giải
Chọn D
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
Áp dụng công thức
ln
u x
u x
u x
.
Vậy
2
2 2
3
2 3
3 3
x x
x
f x
x x x x
.
Câu 19. Hàm số
2
5x
2
x
f x
có đạo hàm
A.
2
5
2
ln 2
x x
f x
. B.
2
5
2 5 2
ln 2
x x
x
f x
.
C.
2
5
2 ln 2
x x
f x
. D.
2
5
2 2 5 ln 2
x x
f x x
.
Lời giải
Chọn D
Áp dụng công thức
ln
u x u x
a a u x a
.
Vậy
2 2
5 2 5
2 5 ln 2 2 2 5 ln 2
x x x x
f x x x x
.
Câu 20. Hàm số
2
3
e
x x
f x
có đạo hàm
A.
2
3
e
x x
f x
. B.
2
3 2
e 3
x x
f x x x
.
C.
2
3
e
2 3
x x
f x
x
. D.
2
3
e 2 3
x x
f x x
.
Lời giải
Chọn D
Áp dụng công thức
e e
u x u x
u x
.
Vậy
2 2
3 2 3
e 3 e 2 3
x x x x
f x x x x
.
Câu 21. Hàm số
3
3
e
x
y
có đạo hàm là
A.
3
3
e
x
. B.
3
2 3
3 e
x
x
. C.
3
3 3
3 e
x
x
. D.
3
4
3
3 e
4
x
x
x
.
Lời giải
Chọn B
Đạo hàm của hàm số
3
3
e
x
y
là
3 3
3 3 2 3
3 .e 3 .e
x x
y x x
.
Câu 22.
Đạo hàm của hàm số
2
4
x
y
là
A.
2
2.4 ln 4
x
y
. B.
2
4 .ln 2
x
y
. C.
2
4 ln 4
x
y
. D.
2
2.4 ln 2
x
y
Lời giải
Chọn A
2
2.4 .ln 4
x
y
.
Câu 23. Cho hàm số
1
3
x
y
. Đẳng thức nào sau đây đúng?
A.
1
3
x
y
. B.
1
3 .ln 3
x
y
. C.
1
.3
x
y x
. D.
1
1 .3 .ln3
x
y x
.
Lời giải
Chọn B
Đạo hàm của hàm số
1
3
x
y
là
1 1
1 .3 .ln 3 3 .ln 3
x x
y x
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 24. Đạo hàm của hàm số
2
2 3 2
e
x x
y
là
A.
2
2 3 2 2
e . 2 3 2
x x
y x x
. B.
2
2 3 2
e . 4 3
x x
y x
.
C.
2
2 3 2
e
x x
y
. D.
2
2 3 1
e . 4 3
x x
y x
.
Lời giải
Chọn B
Có
2
2 3 2
e
x x
y
2
2 3 2
e . 4 3
x x
y x
.
Câu 25. Tìm đạo hàm của hàm số
2 3
2
x
y
.
A.
2 2
2 ln 4
x
y
. B.
2
4 ln 4
x
y
. C.
2 2
2 ln16
x
y
. D.
2 3
2 ln 2
x
y
.
Lời giải
Chọn C
Áp dụng công thức đạo hàm
. .ln
u u
a u a a
Ta có
2 3
2 3 2 ln 2
x
y x
2 3
2 ln 4
x
2 2
2 ln16
x
.
C. BÀI TOÁN THỰC TẾ
1. Lãi đơn:Khách hàng gửi vào ngân hàng
A
đồng với lãi đơn
r
/kì hạn thì số tiền khách hàng nhận
được cả vốn lẫn lãi sau
n
kì hạn (
n *
) là
n
S A nAr A nr
1
2. Lãi kép: Khách hàng gửi vào ngân hàng
A
đồng với lãi kép
r
/kì hạn thì số tiền khách hàng nhận
được cả vốn lẫn lãi sau
n
kì hạn (
n *
) là
n
n
S A r
1
Từ đó ta có thể tìm các giá trị:
n
n
S
r
A
1
n
n
S
A
r
1
n
r
S
n
A
1
log
3. Bài toán tăng trưởng dân số: Công thức tính tăng trưởng dân số
m n
m n
X X r m n m n
1 , , ,
trong đó:
r
là tỉ lệ tăng dân số từ năm
n
đến năm
m
m
X
là dân số năm
m
n
X
là dân số năm
n
Từ đó ta có công thức tính tỉ lệ tăng dân số là:
m
m n
n
X
r
X
1
4. Vay vốn trả góp: Vay ngân hàng số tiền là
A
đồng với lãi suất
r
/tháng. Sau đúng một tháng kể
từ ngày vay, bắt đầu hoàn nợ, hai lần hoàn nợ cách nhau đúng một tháng, mỗi lần hoàn nợ số tiền là
X
đồng. Ta có công thức tính số tiền còn lại sau
n
tháng:
n
n
n
r
S A r X
r
1 1
1
5. Tiền gửi hàng tháng: Đầu mỗi tháng khách hàng gửi vào ngân hàng số tiền
A
đồng với lãi kép
r
/tháng thì số tiền khách hàng nhận được cả vốn lẫn lãi sau
n
tháng (
n *
) (nhận tiền cuối
tháng, khi ngân hàng đã tính lãi) là
n
S
1 1 1
n
n
A
S r r
r
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
Từ đó ta có
n
r
S r
n
A r
1
.
log 1
1
n
n
S r
A
r r
.
1 1 1
Câu 1. Để dự báo dân số của một quốc gia, người ta sử dụng công thức
;
nr
S Ae
trong đó
A
là dân số của
năm lấy làm mốc tính,
S
là dân số sau
n
năm,
r
là tỉ lệ tăng dân số hàng năm. Năm 2017, dân số
Việt nam là
93.671.600
người (Tổng cục Thống kê, Niên giám thống kê 2017, Nhà xuất bản Thống
kê, Tr 79). Giả sử tỉ lệ tăng dân số hàng năm không đổi là
0,81%,
dự báo dân số Việt nam năm 2035
là bao nhiêu người (kết quả làm tròn đến chữ số hàng trăm)?
A.
109.256.100
. B.
108.374.700
. C.
107.500.500
. D.
108.311.100
.
Lời giải
Chọn B
Lấy năm 2017 làm mốc, ta có
93.671.600; 2035 2017 18
A n
Dân số Việt Nam vào năm 2035 là
.
0,
1
81
100
8
93.671.600. 108.374.700
S e
Câu 2. Để quảng bá cho sản phẩm A, một công ty dự định tổ chức quảng cáo theo hình thức quảng cáo trên
truyền hình. Nghiên cứu của công ty cho thấy: nếu sau
n
lần quảng cáo được phát thì tỉ lệ người xem
quảng cáo đó mua sản phẩm A tuân theo công thức
0,015
1
1 49e
n
P n
. Hỏi cần phát ít nhất bao
nhiêu lần quảng cáo để tỉ lệ người xem mua sản phẩm đạt trên
30%?
A.
202
. B.
203
. C.
206
. D.
207
.
Lời giải
Chọn B
Theo bài ra ta có
0,015
1
0,3
1 49e
n
0,015
10
1 49e
3
n
0,015
7
e
147
n
7
0,015 ln
147
n
1 7
ln 202,97
0,015 147
n
.
Vậy ít nhất 203 lần quảng cáo.
Câu 3. Sự tăng trưởng của một loài vi khuẩn tuân theo công thức
.e
rt
S A
, trong đó
A
là số lượng vi khuẩn
ban đầu,
r
là tỉ lệ tăng trưởng
0
r
,
t
là thời gian tăng trưởng. Biết rằng số lượng vi khuẩn ban
đầu là
100
con và sau
5
giờ có
300
con. Hỏi sau
20
giờ có bao nhiêu con?
A.
8100
con. B.
9000
con. C.
7000
con. D.
8500
con.
Lời giải
Chọn A
Theo đề ra ta có
5 5
1
100. 300 3 ln3
5
r r
e e r
Sau
20
giờ từ
100
con vi khuẩn sẽ có:
1
ln3 .20
5
100. 8100
S e
con.
Câu 4. Dân số thế giới được ước tính theo công thức
0
ni
S S e
, trong đó
0
S
là dân số của năm lấy làm mốc
tính,
S
là dân số sau
n
năm,
i
là tỷ lệ tăng dân số hàng năm. Tỷ lệ tăng dân số hàng năm của nước ta
là
1,14%/
năm. Năm 2019 dân số nước ta là 97 575 490 người. Hỏi đến năm nào dân số nước ta đạt
ngưỡng 100 000 000 người
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A. 2022. B. 2021. C. 2024. D. 2023.
Lời giải
Chọn A
Áp dụng công thức:
0
ni
S S e
.Trong đó
0
S
là dân số nước ta năm 2019,
n
S
là dân số nước ta sau
n
năm,
i
là tỷ lệ tăng dân số hàng năm.
Vậy
0
1 1 100000000
ln ln 2,153
0,0114 97575490
n
S
n
i S
Sau 3 năm tức là đến năm 2022.
Câu 5. Để dự báo dân số của một tỉnh X, người ta sử dụng công thức
.e
nr
S A
, trong đó
A
là dân số của
năm lấy làm mốc tính,
S
là dân số sau
n
năm,
r
là tỉ lệ tăng dân số hàng năm. Năm
2016
, dân số
tỉnh X là
8.326.550
người. Giả sử tỉ lệ tăng dân số hàng năm không đổi là
0,9%
, dự báo dân số tỉnh
X năm
2026
là bao nhiêu người (kết quả làm tròn đến chữ số hàng đơn vị)?
A.
9.029.068
. B.
9.110.697
. C.
9.139.063
. D.
10.311.124
.
Lời giải
Chọn B
Lấy năm
2016
làm mốc, ta có:
2026 2016 10, 0,9, 8.326.550
n r A
Từ đây ta suy ra dân số tỉnh X năm
2026
là:
10.0,9%
8.326.550 9110697
nr
S Ae e
.
Câu 6. Khi đèn flash của máy ảnh tắt, pin ngay lập tức bắt đầu sạc lại tụ điện của đèn flash, nơi lưu trữ điện
tich được cho bởi công thức
/
0
( ) 1 e
t a
Q t Q
(dung lượng sạc tối đa là
0
Q
và
t
được tính bằng
giây). Mất bao lâu đề sạc lại tụ điện thành 90% công suất nếu
2?
a
A.
4
giây. B.
5
giây. C.
4.6
giây. D.
4.5
giây.
Lời giải
Chọn B
Theo đè bài ta cần tìm
t
thỏa
2 2
0 0
( ) 1 e 0,9 e 0,1 ln 0,1 2ln10 4.605
2
t t
t
Q t Q Q t
Vậy ít nhất 5 giây thì pin sẽ sạc tụ điện đèn flash thành 90% công suất.
Câu 7. Để dự báo dân số của một quốc gia, người ta sử dụng công thức
.e
nr
S A
, trong đó
A
là dân số của
năm lấy làm mốc tính,
S
là dân số sau
n
năm,
r
là tỉ lệ tăng dân số hàng năm. Năm
2018
, dân số
Việt Nam là
94.665.973
người (Tổng cục thống kê, Niên giám thống kê
2018
, Nhà xuất bản Thống
kê, Tr.
87
). Giả sử tỉ lệ tăng dân số hàng năm không đổi là
0,85%
, dự báo đến năm nào dân số Việt
Nam vượt mốc
100.000.000
người?
A.
2022
. B.
2023
. C.
2024
. D.
2025
.
Lời giải
Chọn D
Thay
100.000.000
S
,
94.665.973
A
,
0,85% 0,0085
r
vào
.e
nr
S A
ta được
0,0085
100.000.000
100.000.000 94.665.973 e ln : 0,0085 6, 45.
94.665.973
n
n
Vậy đến năm
2025
dân số Việt Nam sẽ vượt mốc
100.000.000
người.
Câu 8. Áp suất không khí
P
(đo bằng milimet thủy ngân, kí hiệu là
mmHg
) suy giảm mũ so với độ cao
x
(so với mực nước biển và đo bằng mét) theo công thức
0
.e
xi
P P
, trong đó
0
760
P mmHg
là áp suất
ở mực nước biển,
i
là hệ số suy giảm. Biết rằng ở độ cao
1000m
thì áp suất của không khí là
672,71
mmHg
. Hỏi áp suất không khí ở độ cao
4125m
là bao nhiêu (làm tròn đến hàng phần trăm)?
A.
495, 4598263
mmHg
. B.
459, 46
mmHg
. C.
495,459
mmHg
. D.
459,5
mmHg
Lời giải
Chọn A
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
Theo giả thiết ta có
1000
672,71 760.e
i
672,71
1000
e
760
i
1 672,71
ln
1000 760
i
.
Với
0
1 672,71
4125 ; ln ; 760
1000 760
x m i P mmHg
ta được:
1 672,71
4125. ln
1000 760
760.e 459, 4598263.
P
Câu 9. Một mặt hàng kinh doanh theo hình thức đa cấp với số lượng nhân viên ban đầu
A
sau
t
(lần hội
thảo) được xấp xỉ bởi đẳng thức
0,2
0
.e
t
A t A
, trong đó
0
A
là số nhân viên ban đầu. Số lượng nhân
viên tham dự ban đầu tham gia kinh doanh là
100
thì sau ít nhất bao nhiêu lần hội thảo, số lượng
nhân viên đạt đến
700
người?
A.
9
. B.
9, 729
. C.
10
. D.
9, 7
.
Lời giải
Chọn C
Từ giả thiết ta suy ra
0,2
100.e
t
A t
. Để số lượng là
700
người thì
0,2
100.e 700
t
A t
2
1
e 7 ln7 10
0.2
t
t
.
Câu 10. Vận dụng thông tư số 14/2017/TT-NHNN của Ngân hàng Nhà nước quy định về phương pháp tính
lãi trong hoạt động nhận tiền gửi, có hiệu lực từ ngày 1/1/2018, ngân hàng A đã tính số tiền lãi theo
một kì bằng số ngày của kì gửi nhân với số tiền lãi của một năm chia cho 365. Một khách hàng gửi
100 triệu đồng vào ngân hàng vào ngày 4/7/2018 với lãi suất 5%/năm, kì hạn 1 tháng, ngày tính lãi
hàng tháng là ngày 4/7, biết rằng trong khi gửi khác hàng không đến rút lãi về, ngân hàng tính theo
thể thức lãi kép. Đến ngày 4/9/2018, người đó đến ngân hàng rút cả vốn lẫn lãi về. Hỏi số tiền (tính
bằng nghìn đồng) khách hàng nhận được là số nào sau đây:
A. 100835. B. 100836. C. 100834. D. 100851.
Lời giải
Chọn D
Do tháng 7 và tháng 8 đều có 31 ngày nên số tiền khách hàng nhận được là:
6
5% 5%
100.10 . 1 .31 . 1 .31 100851000
365 365
đồng
Câu 11. Trong phòng thí nghiệm nghiên cứu về vi khuẩn tại bênh viện Trung ương Huế, loại vi khuẩn X gây
bệnh cho người có tốc độ tăng trưởng bình quân là
15%
/ ngày. Bệnh viện tiến hành nuôi cấy mẫu
bệnh phẩm do vi khuẩn X gây ra, với ước lượng số vi khuẩn ban đầu là 100 triệu (ước lượng lúc 9
giờ của ngày đầu tiên nuôi cấy). Bệnh viện nhận thấy rằng có thể trị bệnh do vi khuẩn X gây ra bằng
thuốc kháng sinh Y. Cứ 500 mg thuốc kháng sinh Y có thể tiêu diệt được 10 triệu vi khuẩn và thuốc
có tác dụng hầu như ngay lập tức và không có tác dụng kéo dài thêm. Bác sĩ quyết định lúc 9 giờ
sáng hàng ngày (kể từ ngày thứ hai nuôi cấy mẫu bệnh phẩm) dùng
gx
thuốc kháng sinh Y để tiến
hành nghiên cứu trên mẫu bệnh phẩm thì thấy rằng sau khi tiến hành thí nghiệm ở ngày thứ 15 ngày
kể từ ngày nuôi cấy hoàn thành thì mẫu bệnh phẩm không còn vi khuẩn X. Hỏi số thuốc kháng sinh
Y mà bác sĩ dùng hàng ngày để tiến hành nghiên cứu trên là bao nhiêu? (lấy kết quả gần đúng)
A.
0,855
g. B.
1
g. C.
8,5
g. D.
2
g.
Lời giải
Chọn A
Gọi số vi khuẩn ban đầu là
M
, số vi khuẩn bị tiêu diệt mỗi ngày là
m
, tốc độ tăng trưởng mỗi ngày
là
r
.
Hết ngày thứ nhất, số vi khuẩn có trong mẫu bệnh phẩm là
1
M Mr M r
.
Ngay sau đó, lúc 9 giờ bác sĩ tiến hành thí nghiệm bằng thuốc Y và số vi khuẩn bị tiêu diệt là
m
nên
số vi khuẩn còn lại ngay sau 9h ngày thứ hai là
1
M r m
.
Do đó hết ngày thứ hai, số vi khuẩn có trong bệnh phẩm là
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
1 1
M r m r
2
1 1
M r m r
.
Ngay sau đó, lúc 9 giờ ngày 3, bác sĩ lại tiến hành thí nghiệm băng thuốc Y và số vi khuẩn bị tiêu
diệt là
m
nên số vi khuẩn còn lại ngay sau 9h ngày thứ ba là
2
1 1
M r m r m
.
Do đó hết ngày thứ ba, số vi khuẩn còn lại là
2
1 1 1
M r m r m r
3 2
1 1 1
M r m r m r m
.
Cứ tiếp tục lập luận như vậy ta thấy ngay sau 9h ngày thứ
n
,
2
n
, số vi khuẩn còn lại là
1 2
1 1 1 ... 1
n n n
M r m r m r m r m
1 1
1
n
n
m r
M r
r
.
Ngay sau 9h ngày thứ n = 15 hết số vi khuẩn nên ta có:
1 1
1 0
n
n
m r
M r
r
6
1
17,102.10
1 1
n
n
M r r
m
r
.
1 g chất Y sẽ tiêu diệt được
20
triệu vi khuẩn. Do đó số thuốc mà bác sĩ tiến hành nghiên cứu hàng
ngày là
6
6
17,102.10
0,855 g
20.10
.
Câu 12. Một em học sinh 15 tuổi được hưởng số tiền thừa kế là 300 000 000 đồng. Số tiền này được gửi tại
một ngân hàng với kỳ hạn thanh toán 1 năm và học sinh này chỉ nhận được số tiền ( cả gốc và lãi) khi
đủ 18 tuổi. Biết rằng khi đủ 18 tuổi em này nhận được số tiền là 368 544 273 đồng. Vậy lãi suất của
ngân hàng gần nhất với số nào sau đây?( Với giả thiết lãi suất không đổi trong suốt quá trình gửi)
A.
5,5% /
năm. B.
7% /
năm. C.
7,5% /
năm. D.
5,7% /
năm.
Lời giải
Chọn B
Áp dụng công thức lãi kép
0
(1 )
n
n
A A r
, với
0 3
300000000; 368544273; 3
A A n
, ta tính
r
.
Ta có:
3
368544273
1 7,1%
300000000
r
Phân tích phương án nhiễu
Phương án A. Học sinh dễ nhầm theo kiểu
18 15 1 4
n
Khi đó
4
368544273
1 5,3%
300000000
r
Phương án C. Sử dụng sai công thức tính lãi đơn
0
(1 )
n
A A rn
Khi đó
0
1 1 368544273
1 1 7,6%
3 300000000
n
A
r
n A
Phương án D. Sử dụng sai công thức tính lãi đơn
0
(1 )
n
A A rn
và
18 15 1 4
n
Khi đó
0
1 1 368544273
1 1 5,7%
4 300000000
n
A
r
n A
Câu 13. Bố An để dành cho An 100 000 000 đồng để học đại học trong một ngân hàng theo hình thức lãi kép
với lãi suất
0,75%
một tháng. Mỗi tháng An đến rút 3 000 000 đồng để chi phí sinh hoạt. Hỏi sau 1
năm số tiền còn lại là bao nhiêu?( Làm tròn kết quả đến hàng đơn vị)
A.
71857930
đồng. B.
71857931
đồng. C.
73380690
đồng. D.
73380689
đồng.
Lời giải
Chọn B
Gọi
0
A
là số tiền ban đầu,
r
là tỷ lệ lãi suất hàng tháng,
x
là số tiền rút ra hàng tháng,
n
S
là số tiền
thực có sau
n
tháng.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
Nếu không rút tiền ra thì sau 1 tháng số tiền An có là
1 0
(1 )A A r
.
Số tiền thực có sau 1 tháng là:
1 0
(1 )S A r x
.
Số tiền thực có sau 2 tháng là:
2
2
2 0 0
1 1
(1 ) 1 (1 )
x r
S A r x r x A r
r
.
Số tiền thực có sau 3 tháng là:
3
3
3 2 0
1 1
1 (1 )
x r
S S r x A r
r
.
……………
Số tiền thực có sau
n
tháng là:
0
1 1
(1 )
n
n
n
x r
S A r
r
Vậy sau 1 năm tức là 12 tháng số tiền còn lại
là:
12
12
12
3000000 1 0,0075 1
100000000(1 0,0075) 71857930,7
0,0075
S
Câu 14. Một người gửi số tiền
100
triệu đồng vào một ngân hàng với lãi suất
0,65%
trên tháng. Biết rằng nếu
người đó không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được nhập vào vốn ban
đầu (người ta gọi đó là lãi kép). Hỏi số tiền lãi người đó có được sau
2
năm, nếu trong khoảng thời
gian này người đó không rút tiền ra và lãi suất không đổi là bao nhiêu?
A.
24
100.(1,0065)
triệu đồng. B.
2
100.(1,0065) 100
triệu đồng.
C.
24
100.(1,0065) 100
triệu đồng. D.
24
100.(2,0065) 100
triệu đồng.
Lời giải
Chọn C
Áp dụng công thức lãi kép
(1 )
n
n
S A r
với
100,
A
0,0065,
r
24
n
thì số tiền người đó có
được sau
2
năm (
24
tháng) là:
24 24
24
100.(1 0,0065) 100.(1,0065)
S
triệu đồng.
Vậy số tiền lãi người đó có được sau
2
năm là
24
100.(1,0065) 100
triệu đồng.
Câu 15. Ông Nam gửi
100
triệu đồng vào ngân hàng theo thể thức lãi kép, kì hạn
1
năm với lãi suất
7,56%
một năm. Hỏi sau bao nhiêu năm gửi ông Nam sẽ có ít nhất
150
triệu đồng từ số tiền gửi ban
đầu? (giả sử lãi suất không thay đổi).
A.
5
năm. B.
6
năm. C.
7
năm. D.
8
năm.
Lời giải
Chọn B
Áp dụng công thức lãi kép
(1 )
n
n
S A r
với
100,
A
7,56% 0,0756,
r
150
n
S
ta được
1,0756
150 100 1 0,0756 1,0756 1,5 log 1,5 5,56.
n
n
n
Vậy sau khoảng
6
năm gửi ông Nam sẽ có ít nhất
150
triệu đồng từ số tiền gửi ban đầu.
Câu 16. Vào ngày 3/8/2018, một người vay ngân hàng số tiền 50 triệu đồng, trả góp trong thời gian 10 tháng,
lãi suất 5%/năm, với thỏa thuận là cứ đến ngày tính tiền lãi, người đó phải đến ngân hàng trả phần
tiền gốc bằng số tiền vay ban đầu chia đều cho các lần trả và số lãi phát sinh trong tháng trước (hình
thức dư nợ giảm dần). Hỏi số tiền anh phải trả cho ngân hàng vào ngày 3/12/2018 là bao nhiêu?
A. 5,45 triệu đồng. B. 5,4 triệu đồng.
C. 10,85 triệu đồng. D. 5,5 triệu đồng.
Lời giải
Chọn A
Tính đến ngày 3/12, khách hàng đã có 3 lần trả tiền gốc vào các ngày 3/9, 3/10, 3/11 nên số tiền gốc
còn lại tính từ ngày 3/11/2018 là
50 3.5 35
triệu đồng
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 24 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Số tiền lãi cần trả cho ngân hàng từ ngày 3/11/2018 đến ngày 3/12/2018 là
6
10%
35.10 . .30 288000
365
đồng
Số tiền khách hàng phải trả trong ngày 3/12/2018 là
5000000 288000 5288000
đồng
Câu 17. Vào đầu mỗi năm anh Thắng gửi vào ngân hàng số tiền 30 triệu đồng với kì hạn 1 năm, lãi suất
7%/năm (mỗi lần gửi cách nhau 1 năm). Hỏi sau ít nhất bao nhiêu năm (sau khi ngân hàng đã tính lãi
cho lần gửi cuối cùng) thì anh Thắng được số tiền cả gốc lẫn lãi từ 500 triệu đồng trở lên? (biết rằng
trong suốt thời gian gửi tiền, anh Thắng không đến rút lãi về, ngân hàng tính theo thể thức lãi kép và
lãi suất hàng năm không đổi)
A. 7 năm. B. 8 năm. C.
11
năm. D. 10 năm.
Lời giải
Chọn C
Gọi
N
là số năm anh Thắng gửi ngân hàng
Lần gửi đầu tiên anh Thắng gửi 30 triệu đồng, đến hết năm thứ
N
anh được tính cả vốn và lãi cho số
tiền này là:
6
30.10 .(1 7%)
N
Lần gửi thứ 2 anh Thắng gửi 30 triệu đồng, đến hết năm thứ
N
anh được tính cả vốn và lãi cho số
tiền này là:
6 1
30.10 .(1 7%)
N
…
Lần gửi thứ
N
anh Thắng gửi 30 triệu đồng, đến hết năm thứ
N
anh được tính cả vốn và lãi cho số
tiền này là:
6 1
30.10 .(1 7%)
Tổng số tiền anh Thắng nhận được là
6 6 1 6 6
1 (1 7%)
30.10 .(1 7%) 30.10 .(1 7%) ... 30.10 .(1 7%) 30.10 .(1 7%)
1 (1 7%)
N
N N
Để số tiền từ 500 triệu đồng trở lên thì
6 6
1 (1 7%)
30.10 .(1 7%) 500.10
1 (1 7%)
N
Giải ra ta được
10,89
N
nên số năm cần gửi tối thiểu là
11
năm
Câu 18. Ông Q.BN mang 150 triệu đồng gửi vào ngân hàng với lãi suất 7% một năm. Ông KN cũng đem 300
triệu đồng gửi vào ngân hàng khác với lãi suất
1,72%
một quí. Sau 10 năm, hai ông cùng đến ngân
hàng rút tiền ra để mua xe. ( Lưu ý: tiền lãi được tính theo công thức lãi kép và được làm tròn đến
hàng triệu). Biết 2 ông cùng muốn mua 1 loại xe có giá là 456 triệu. Nếu số tiền mang theo không đủ,
hai ông có thể trả góp cho hãng xe phần còn thiếu theo hình thức sau: Đúng một tháng kể từ ngày
nhận được xe, người mua bắt đầu đóng tiền góp; hai lần trả liên tiếp cách nhau đúng một tháng, số
tiền trả mỗi tháng là như nhau và phải trả trong 1 năm. Biết rằng mỗi tháng hang xe chỉ tính lãi trên
số dư nợ thực tế của tháng đó. Hỏi mỗi tháng người mua phải trả bao nhiêu tiền cho hãng xe, lãi suất
của hãng là 1,8%/tháng.Khẳng định nào sau đây là đúng
A. Ông Q.BN mỗi tháng phải trả thêm 15 triệu.
B. Ông KN mỗi tháng phải trả thêm 5 triệu.
C. Ông Q.BN cần trả thêm hơn 180 triệu trong 12 tháng.
D. Ôn KN cần trả thêm 15 triệu mỗi tháng.
Lời giải
Chọn C
Số tiền mỗi ông nhận được là:
Ông Q.BN:
10
150. 1 7% 295,0727036 295
triệu
Ông KN:
40
300 1 1,72% 593.4379488 593
triệu
Vậy ông KN không cần trả góp
Số tiền ông Q.BN phải góp hàng tháng là:
12
12
1,8 1,8
456 295 1 .
100 100
15,03771828
1,8
1 1
100
X
triệu
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
Tổng số tiền ông Q.BN phải trả thêm sau 12 tháng là: 180.4526193 triệu.
Câu 19. Ông A cần mua nhà ở nhưng số tiền của ông không đủ để mua nhà ở, ông đi vay ngân hàng
1
tỉ đồng
với lãi suất ưu đãi là
9%
/năm. Ông ta muốn hoàn nợ cho ngân hàng theo cách: Sau đúng một năm kể
từ ngày vay, ông bắt đầu hoàn nợ; hai lần hoàn nợ liên tiếp cách nhau đúng một năm, số tiền hoàn nợ
ở mỗi năm là như nhau và ông A trả hết nợ sau đúng
10
năm kể từ ngày vay. Biết rằng mỗi năm
ngân hàng chỉ tính lãi trên số dư nợ thực tế của năm đó. Hỏi số tiền mỗi tháng ông ta cần trả cho
ngân hàng gần nhất với số tiền nào dưới đây?
A.
155,820
triệu đồng. B.
146,947
triệu đồng.
C.
166,8
triệu đồng. D.
236,736
triệu đồng.
Lời giải
Chọn A
Gọi số tiền vay ban đầu là
M
, số tiền hoàn nợ mỗi năm là
m
, lãi suất một năm là
r
.
Hết năm thứ nhất, số tiền cả vốn lẫn lãi ông A nợ ngân hàng là
1
M Mr M r
.
Ngay sau đó ông A hoàn nợ số tiền
m
nên số tiền để tính lãi cho năm thứ hai là
1
M r m
.
Do đó hết năm thứ hai, số tiền cả vốn lẫn lãi ông A nợ ngân hàng là
1 1
M r m r
2
1 1
M r m r
.
Ngay sau đó ông A lại hoàn nợ số tiền
m
nên số tiền để tính lãi cho năm thứ ba là
2
1 1
M r m r m
.
Do đó hết năm thứ ba, số tiền cả vốn lẫn lãi ông A nợ ngân hàng là
2
1 1 1
M r m r m r
3 2
1 1 1
M r m r m r m
.
Cứ tiếp tục lập luận như vậy ta thấy sau năm thứ
n
,
2
n
, số tiền cả vốn lẫn lãi ông A nợ ngân hàng
là
1 2
1 1 1 ... 1
n n n
M r m r m r m r m
1 1
1
n
n
m r
M r
r
.
Sau năm thứ
n
trả hết nợ thì ta có
1 1
1 0
n
n
m r
M r
r
1
1 1
n
n
M r r
m
r
.
Thay số với
1.000.000.000
M
,
9%
r
,
10
n
ta được
155,820
m
(triệu đồng).
Câu 20. Ông A vay ngân hàng
500
triệu đồng với lãi suất 1%/tháng. Ông ta muốn hoàn nợ cho ngân hàng
theo cách: Sau đúng một tháng kể từ ngày vay, ông bắt đầu hoàn nợ; hai lần hoàn nợ liên tiếp cách
nhau đúng một tháng, số tiền hoàn nợ ở mỗi tháng là 12 triệu đồng. Biết rằng mỗi tháng ngân hàng
chỉ tính lãi trên số dư nợ thực tế của tháng đó. Hỏi số tháng mà ông A cần trả hết nợ ngân hàng là bao
nhiêu kể từ khi vay? (tháng cuối cùng có thể trả số nợ không quá 12 triệu đồng)
A.
55
tháng. B.
54
triệu đồng.
C.
56
triệu đồng. D. không bao giờ trả hết nợ.
Lời giải
Chọn A
Gọi số tiền vay ban đầu là
M
, số tiền hoàn nợ mỗi tháng là
m
, lãi suất một tháng là
r
.
Hết tháng thứ nhất, số tiền cả vốn lẫn lãi ông A nợ ngân hàng là
1
M Mr M r
.
Ngay sau đó ông A hoàn nợ số tiền
m
nên số tiền để tính lãi cho tháng thứ hai là
1
M r m
.
Do đó hết tháng thứ hai, số tiền cả vốn lẫn lãi ông A nợ ngân hàng là
1 1
M r m r
2
1 1
M r m r
.
Ngay sau đó ông A lại hoàn nợ số tiền
m
nên số tiền để tính lãi cho tháng thứ ba là
2
1 1
M r m r m
.
Do đó hết tháng thứ ba, số tiền cả vốn lẫn lãi ông A nợ ngân hàng là
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 26 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
1 1 1
M r m r m r
3 2
1 1 1
M r m r m r m
.
Cứ tiếp tục lập luận như vậy ta thấy sau tháng thứ
n
,
2
n
, số tiền cả vốn lẫn lãi ông A nợ ngân
hàng là
1 2
1 1 1 ... 1
n n n
M r m r m r m r m
1 1
1
n
n
m r
M r
r
.
Sau tháng thứ
n
trả hết nợ thì ta có
1 1
1 0 (1)
n
n
m r
M r
r
1
1 log
n
r
m m
r n
m Mr m Mr
.
Thay số với
500.000.000
M
,
1%
r
,
12.000.000
m
ta được
1,01
12
log 54,168
7
n
, vì
n
là số
tự nhiên nên ta chọn
55
n
tháng.
Câu 21. Ông A là một người già không có khả năng lao động, trước khi không thể lao động kiếm sống ông ấy
có dành dụm được một khoản tiền để gửi tiết kiệm ngân hàng với lãi suất ưu đãi dành cho người già
là
0,9%
tháng. Sau khi gửi tiết kiệm ngân hàng, đủ mỗi tháng gửi, ông A đến ngân hàng rút ra một
khoản tiền là 5 triệu đồng để chi tiêu hàng ngày. Sau đúng 5 năm kể từ ngày gửi tiết kiệm, số tiền tiết
kiệm còn lại của ông ấy là 100 triệu đồng. Hỏi số tiền ban đầu mà ông A gửi tiết kiệm là bao nhiêu?
(lấy kết quả gần đúng)
A.
289,440
triệu đồng. B.
291,813
triệu đồng.
C.
287,044
triệu đồng. D.
233,663
triệu đồng.
Lời giải
Chọn A
Gọi số tiền ban đầu là
M
, lãi suất một tháng là
r
.
Hết tháng thứ nhất, số tiền cả vốn lẫn lãi ông A có trong ngân hàng là
1
M Mr M r
.
Ngay sau đó ông A rút 5 triệu đồng để chi tiêu nên số tiền để tính lãi cho tháng thứ hai là
1 5
M r
.
Do đó hết tháng thứ hai, số tiền cả vốn lẫn lãi ông A có trong ngân hàng là
1 5 1
M r r
2
1 5 1
M r r
.
Ngay sau đó ông A lại rút 5 triệu để chi tiêu nên số tiền để tính lãi cho tháng thứ ba là
2
1 5 1 5
M r r
.
Cứ tiếp tục lập luận như vậy ta thấy sau tháng thứ
n
,
2
n
, số tiền cả vốn lẫn lãi ông A có trong
ngân hàng là
1 2
1 5 1 5 1 ... 5 1 5
n n n
M r r r r
5 1 1
1
n
n
r
M r
r
.
Sau 5 năm tức là 60 tháng, số tiền còn lại trong ngân hàng là 100 triệu nên ta có
60
60
5 1 1
1 200
r
M r
r
60
60
5 1 1
100
289,440
1
r
r
M
r
triệu đồng.
D. PHƯƠNG TRÌNH – BẤT PHƯƠNG TRÌNH CƠ BẢN
1. Đạo hàm của hàm số mũ và lôgarit
( ) . .
u u
e u e
( ) . .ln .
u u
a u a a
(ln )
u
u
u
(log )
ln
a
u
u
u a
2. Phương trình mũ – lôgarit
Đặt điều kiện trước khi giải. Ta có một số kết quả cần nhớ sau:
0 log .
x
a
a b x b
log .
b
a
x b x a
( ) ( )
( ) ( ).
f x g x
a a f x g x
log ( ) log ( ) ( ) ( ).
a a
f x g x f x g x
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27
3. Bất phương trình mũ và lôgarit
Đặt điều kiện trước khi giải. Giải xong được tập nghiệm nhớ giao (lấy phần chung) với điều kiện.
Nếu
( ) ( )
log
( ) ( )
1
log
log ( ) log ( ) ( ) ( )
x
a
f x g x
b
a
a a
a b x b
a a f x g x
a
x b x a
f x g x f x g x
(cùng chiều)
( ) ( )
log
( ) ( )
0 1
log
log ( ) log ( ) ( ) ( )
x
a
f x g x
b
a
a a
a b x b
a a f x g x
a
x b x a
f x g x f x g x
(ngược chiều)
4. Các phương pháp giải phương trình, bất phương trình mũ và lôgarit: Biến đổi tương đương, Đặt ẩn phụ,
Sử dụng tính đơn điệu hàm số, sử dụng đánh giá bằng bất đẳng thức,….
Câu 1. Nghiệm của phương trình
3
log 2 1 2
x
là:
A.
3
x
. B.
5
x
. C.
9
2
x
. D.
7
2
x
.
Lời giải
Chọn B
Điều kiện:
1
2 1 0
2
x x
Ta có
3
2
1
log 2 1 2
2
2 1 3
x
x
x
1
2
5
x
x
5
x
.
Vậy phương trình có nghiệm
5
x
.
Câu 2. Tập nghiệm của bất phương trình
2
1 9
5 5
x x x
là
A.
2;4
. B.
4;2
.
C.
; 2 4;

. D.
; 4 2;
 
.
Lời giải
Chọn A
2
1 9 2 2
5 5 1 9 2 8 0 2 4
x x x
x x x x x x
.
Vậy Tập nghiệm của bất phương trình là
2;4
.
Câu 3. Nghiệm của phương trình
1
3 27
x
là
A.
4
x
. B.
3
x
. C.
2
x
. D.
1x
.
Lời giải
Chọn A
Ta có:
1
3 27
x
1 3
3 3
x
1 3
x
4
x
.
Vậy nghiệm của phương trình là
4
x
.
Câu 4. Tập nghiệm của bất phương trình
9 2.3 3 0
x x
là
A.
0;

. B.
0;

. C.
1;

. D.
1;

.
Lời giải
Chọn B
9 2.3 3 0 3 1 3 3 0 3 1
x x x x x
(vì
3 0,
x
x
)
0
x
.
Vậy tập nghiệm của bất phương trình đã cho là
0;

.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 28 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 5. Nghiệm của phương trình
3
log 2 1 3 0
x
là
A.
1
. B.
5
. C.
14
. D.
4
.
Lời giải
Chọn C
Điều kiện:
1
2 1 0
2
x x
.
Ta có:
3
log 2 1 3 0
x
3
log 2 1 3
x
.
1
2
2 1 27
x
x
14
x
.
Vậy phương trình có 1 nghiệm là
14
x
.
Câu 6. Tập nghiệm của phương trình
2
1
2 2
x x
là
A.
1;2
T
. B.
1
T
. C.
2
T
. D.
1; 2
T
.
Lời giải
Chọn D
Ta có:
2
1
2 2
x x
2
1 1
x x
2
1
2 0
2
x
x x
x
.
Vậy tập nghiệm của phương trình là
1; 2
T
.
Câu 7. Nghiệm của phương trình
7
log 3 2 1
x
là
A.
2
3
. B.
1
. C.
3
. D.
2
.
Lời giải
Chọn D
Điều kiện:
3
3 2 0
2
x x
7
log 3 2 1
x
3 2 7
x
2
x
. (Thỏa mãn)
Vậy phương trình có 1 nghiệm là
2
x
.
Câu 8. Nghiệm của phương trình
3
log ( 5) 2
x
là:
A.
4
x
. B.
14
x
. C.
2
x
. D.
9
x
.
Lời giải
Chọn B
3
log ( 5) 2
x
2
5 0
5 9 14
5 3
x
x x
x
Vậy nghiệm của phương trình là
14x
.
Câu 9. Nghiệm của phương trình
4 2
7 49 0
x
là
A.
2
. B.
1
. C.
3
. D.
3
2
.
Lời giải
Chọn B
4 2
7 49 0
x
4 2
7 49
x
4 2 2
7 7
x
4 2 2
x
1x
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29
Vậy phương trình có 1 nghiệm là
1x
.
Câu 10. Số nghiệm của phương trình
2
log 2 9 1
x x
là:
A.
1
. B.
2
. C. Vô nghiệm. D.
3
.
Lời giải
Chọn B
Ta có:
2
2 9 0
x x x R
. Suy ra:
2 2
log 2 9 1 2 9 10
x x x x
2
2 1 0
x x
1 2
1 2
x
x
.
Vậy số nghiệm của phương trình là
2.
Câu 11. Nghiệm của phương trình
3 1
1
5
25
x
là
A.
1
3
. B.
1
. C.
1
. D.
3
.
Lời giải
Chọn C
3 1
1
5
25
x
3 1 2
5 5
x
3 1 2
x
1
x
.
Vậy phương trình có 1 nghiệm là
1
x
.
Câu 12. Nghiệm của phương trình
2 2 3
2 3 2 3
x x
là:
A.
5x
. B.
1
3
x
. C.
1x
. D.
1x
.
Lời giải
Chọn A
Ta có:
2 2 3
2 3 2 3
x x
2 1 . 2 3
2 3 2 3
x x
2 2 3
2 3 2 3
x x
2 2 3x x
5
x
. Vậy nghiệm của phương trình là
5x
.
Câu 13. Nghiệm của phương trình
2
3
2 16
x x
là
A.
1
4
x
x
. B.
1
4
x
x
. C.
1
4
x
x
. D.
4
x
.
Lời giải
Chọn C
2 2
3 3 4
2 16 2 2
x x x x
2
3 4
x x
2
3 4 0
x x
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 30 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
1
4
x
x
Vậy phương trình có 2 nghiệm là
1x
và
4
x
.
Câu 14. Nghiệm của phương trình
3
1
25
25
x
là:
A.
1x
. B.
1
x
. C.
2
x
. D.
2
x
.
Lời giải
Chọn C
Ta có:
3 3 1
1
25 25 25 .
25
3 1.
2.
x x
x
x
Vậy nghiệm của phương trình là
2x
.
Câu 15. Nghiệm của phương trình
2 1
1
2
4
x
là
A.
1
2
x
. B.
3
2
x
C.
1
.
2
x
D.
3
.
2
x
Lời giải
Chọn A
Ta có
2 1 2 1 2
1 1
2 2 2 2 1 2 .
4 2
x x
x x
Câu 16. Tập nghiệm của bất phương trình
2
3
log 2 1
x x
là:
A.
; 3 1;
 
. B.
3;1
. C.
; 3 1;
 
. D.
1:

.
Lời giải
Chọn A
Ta có:
2
3
log 2 1
x x
2 2
3
2 3 2 3 0
1
x
x x x x
x
*
Vậy bất phương trình đã cho có tập nghiệm là
; 3 1;x
 
.
Câu 17. Tập nghiệm của bất phương trình
4 5.2 4 0
x x
là
A.
;0 2;

. B.
0;2
. C.
;1 4;
 
. D.
1;4
.
Lời giải
Chọn A
Đặt
2 0 .
x
t t
Phương trình đã cho trở thành:
2
1 2 1 0
5 4 0 .
4 2
2 4
x
x
t x
t t
t x
Vậy tập nghiệm của bất phương trình đã cho là
;0 2;
 
.
Câu 18. Nghiệm nhỏ nhất của phương trình
2
5
log 3 5 1
x x
là
A.
3
. B.
1
. C.
3
. D.
0
.
Lời giải
Chọn D
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 31
ĐK
x
vì
2
3 5 0,x x x
2 2 2
5
3
log 3 5 1 3 5 5 3 0
0
x
x x x x x x
x
.
Vậy nghiệm nhỏ nhất của phương trình
2
5
log 3 5 1
x x
là 0.
Câu 19. Tập nghiệm của bất phương trình
2
3 3
log 3 log 3 1
x x
là
A.
;1 2;
. B.
1
;1 2;
3
. C.
1
;1
3
. D.
2;
.
Lời giải
Chọn B
Điều kiện:
1
3 1 0 .
3
x x
Ta có
2
3 3
log 3 log 3 1
x x
2 2
3 3 1 3 2 0
x x x x
1
2
x
x
.
Kết hợp với điều kiện ta được
1
1
3
2
x
x
Vậy tập nghiệm của bất phương trình là
1
;1 2; .
3
S
Câu 20. Bất phương trình
2
2
log 2 1 1
x x
có tập nghiệm là
A.
1 2; 1 2
. B.
; 1 2 1 2;
 
.
C.
1
x
. D.
.
Lời giải
Chọn B
Ta có:
2
2
log 2 1 1
x x
2 2
2 2
1
2 1 0 2 1 0 1 2
1 2
2 1 2 2 1 0
1 2
1 2
x
x x x x x
x
x x x x
x
x
Câu 21. Tập nghiệm của bất phương trình
2
1 1
3 0
4 2
x x
là
A.
3;1
. B.
0;

. C.
; 3 1;
 
. D.
;0

.
Lời giải
Chọn B
Đặt
1
, 0 .
2
x
t t
Ta được phương trình:
2
2 3 0
t t
3 1 0 1t t t
1
1 0.
2
x
x
Vậy tập nghiệm của bất phương trình là
0;
.
Câu 22. Tập nghiệm của phương trình
2
0,25
log 3 1
x x
là:
A.
4
. B.
1; 4
. C.
3 2 2 3 2 2
;
2 2
. D.
1; 4
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 32 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Lời giải
Chọn D
Ta có:
2
2
0,25
1
2
2
0
0
3
3 0
3
log 3 1
4
3 0,25
3 4 0
1
x
x
x
x x
x
x x
x n
x x
x x
x n
Vậy tập nghiệm của phương trình là
1; 4
S
.
Câu 23. Tập nghiệm của bất phương trình
2
2 1 3 5
1 1
3 3
x x x
là
A.
1;6
. B.
6;1
. C.
; 6 1;

.D.
; 1 6;

.
Lời giải
Chọn A
Ta có
2
2 1 3 5
2 2
1 1
2 1 3 5 5 6 0 1 6.
3 3
x x x
x x x x x x
Vậy tập nghiệm của bất phương trình là
1;6
Câu 24. Nghiệm của phương trình
1
1
4
16
x
là
A.
1
2
x
B.
2.
x
C.
1
.
2
x
D.
2.
x
Lời giải
Chọn A
Ta có
1 1
2
1 1 1
4 4 4 2 .
16 2
x x
x
x
Câu 25. Tập nghiệm của bất phương trình
2
4
1
log 2 3
2
x x
là
A.
3;1
. B.
; 3 1;
 
.
C.
3;1
. D.
1 6; 3 1; 1 6
.
Lời giải
Chọn D
Ta có:
2
4
1
log 2 3
2
x x
2
1
2
2
3
2 3 0
*
1
1 6; 3 1; 1 6
2 3 4
1 6 1 6
x
x x
x
x
x x
x
Câu 26. Tập nghiệm của bất phương trình
2
6 0
x x
e e
là
A.
3;2
. B.
;2

. C.
;ln 2

. D.
ln2;

.
Lời giải
Chọn C
Đặt
, 0 .
x
t e t
Bất phương trình đã cho trở thành:
2
6 0 2 3 0 2 2 ln 2.
x
t t t t t e x
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 33
Vậy tập nghiệm của bất phương trình là
;ln 2
.
Câu 27. Tổng bình phương các nghiệm của phương trình bằng
A.
6
. B.
5
. C.
13
. D.
25
.
Lời giải
Chọn C
ĐK:
x
vì
2
5 7 0,x x x
2 2 2 2 2
1 1 2 1 2
2
log 5 7 0 5 7 1 5 6 0 2 3 13x x x x x x x x x x
Câu 28. Tập nghiệm của bất phương trình
2
5 4 8
2 2
x x x
là
A.
2;6
. B.
( ; 2] [6; ) 
. C.
6;2
. D.
( ; 6] [2; ) 
.
Lời giải
Chọn B
Ta có :
2
5 4 8
2 2
2
2 2 5 4 8 4 12 0 .
6
x x x
x
x x x x x
x
Vậy tập nghiệm của bất phương trình là
( ; 2] [6; ) 
Câu 29. Tìm nghiệm của phương trình
2
log 5 3x
.
A.
14x
. B.
11x
. C.
8x
. D.
13x
.
Lời giải
Chọn D
Ta có:
2
log 5 3 5 8 13
x x x
.
Câu 30. Tìm tập nghiệm của bất phương trình sau:
log 2 1x
.
A.
2x
. B.
2 8x
. C.
8x
. D.
8x
.
Lời giải
Chọn C
log 2 1x
2 0 2
8
2 10 8
x x
x
x x
(*)
Vậy tập nghiệm của bất phương trình là
8x
.
Câu 31. Tập nghiệm của bất phương trình
2
2 2
log log 6 0x x
là
A.
1
0; 8;
4
. B.
1
0; 8;
4

. C.
1
;8
4
. D.
1
; 8;
4
 
.
Lời giải
Chọn B
Điều kiện :
0.x
Đặt
2
log xt
.
Khi đó bất phương trình đã cho trở thành:
2
2
2
3
2
1
log 2
2
2
6 0 .
4
3 log 3
2 8
x
x
t
t t
t x
x
Kết hợp với điều kiện, nghiệm của bất phương trình là:
S
1
0; 8; .
4

Câu 32. Phương trình
2 1
5 125
x
có nghiệm là
2
1
2
log 5 7 0
x x
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 34 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
5
2
x
. B.
1x
. C.
3
x
. D.
3
2
x
.
Lời giải
Chọn B
Ta có:
2 1
5 125
x
2 1 3
5 5
x
2 1 3
x
1x
.
Câu 33. Tập nghiệm của bất phương trình
0,5 0,5
log 1 log 2 1
x x
là
A.
;2

. B.
2;

. C.
2;2
. D.
1
;2
2
.
Lời giải
Chọn D
Điều kiện:
1
1 0
1
1
2 1 0
2
2
x
x
x
x
x
Ta có
0,5 0,5
log 1 log 2 1 1 2 1 2
x x x x x
Kết hợp với điều kiện ta được tập nghiệm của bất phương trình là
1
;2
2
Câu 34. Phương trình
2
2
3 1
x x
có nghiệm là
A.
0
x
,
2
x
. B.
0
x
,
2
x
. C.
1
x
,
3
x
. D.
1x
,
3
x
.
Lời giải
Chọn A
Ta có
2
2
3 1
x x
2
2 0
3 3
x x
2
2 0
x x
0
2
x
x
.
Câu 35. Tìm tập nghiệm của bất phương trình
log 2 log 5 1
x x
.
A.
2
x
. B.
. C.
0
x
. D.
7 0
x
.
Lời giải
Chọn C
Để bất phương trình có nghĩa
2 0 2
5 0 5
x x
x x
2
x
(*)
log 2 log 5 1
x x
log ( 2)( 5) 1
x x
2 2
7
7 10 10 7 0
0
x
x x x x
x
(**)
Từ (*) và (**)
0
x
Vậy tập nghiệm của bất phương trình là
0
x
.
Câu 36. Tập nghiệm của bất phương trình
2 2
3 3
log 2log 3 0
x x
là
A.
3;27
. B.
;3 27;
 
. C.
3;27
. D.
0;3 27;
.
Lời giải
Chọn C
Điều kiện :
0.
x
Khi đó:
2 2 2
3 3 3 3
log 2log 3 0 log 4log 3 0
x x x x
Đặt
3
log x
t
.
Bất phương trình đã cho trở thành:
2 3
3
4 3 0 1 3 1 log x 3 3 x 3 27.
t t t
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 35
Kết hợp với điều kiện, nghiệm của bất phương trình là:
S
3;27 .
Câu 37. Tìm tập nghiệm
S
của phương trình
2
2
5 5
x x
.
A.
S
. B.
1
0;
2
S
. C.
0;2
S
. D.
1
;1
2
S
.
Lời giải
Chọn D
2
2 2 2
1
5 5 2 1 2 1 0
1
2
x x
x
x x x x
x
Câu 38. Tập nghiệm của bất phương trình
3
3
3
3log 1 log 2 1 3
x x
A.
1;2
. B.
1
;2
2
. C.
1
;2
2
. D.
2;

.
Lời giải
Chọn A
Điều kiện:
1
1 0
1
1
2 1 0
2
x
x
x
x
x
.
3 3 3 3 3
3log 1 3log 2 1 3 log 1 log 2 1 1 log 1 2 1 1
x x x x x x
2
1
1 2 1 3 2 3 2 0 2
2
x x x x x
.
Kết hợp điều kiện, bất phương trình có tập nghiệm là
1;2
S
.
Câu 39. Phương trình
2
2 8
x
có nghiệm là
A.
6
x
. B.
10
x
. C.
14
x
. D.
5
x
.
Lời giải
Chọn D
Ta có :
2
2 8 2 3 5
x
x x
.
Câu 40. Tìm số nghiệm nguyên của bất phương trình
2
3
log 2 1 1
x x
A. 2. B. 3. C. 1. D. 4.
Lời giải
Chọn A
Ta có:
2
3
log 2 1 1
x x
2
2
1
2 1 0
1 3 1 3
2 1 3
x
x x
x
x x
Tập nghiệm của bất phương trình là
1 3; 1 1; 1 3
Có 2 giá trị nguyên thuộc khoảng nghiệm của bất phương trình là
2; 0.
x x
.
Câu 41. Tập nghiệm của bất phương trình
2
1 1
5 5
log 2log 3 0
x x
là
A.
1
0; 5;
125

. B.
1
; 5;
125
 
. C.
1
;5
125
. D.
1
0; 5;
125

.
Lời giải
Chọn D
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 36 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Điều kiện :
0.
x
Đặt
1
5
log x
t
.
Khi đó bất phương trình đã cho trở thành:
1
1
5
2
3
1
5
1
log 1
5
1
5
2 3 0 .
3 log 3
1 1
5 125
x
x
t
t t
t x
x
Kết hợp với điều kiện, nghiệm của bất phương trình là:
S
1
0; 5; .
125

Câu 42. Số nghiệm của phương trình
2
2
log 2 4 2
x x
là:
A.
2
. B.
1
. C.
0
. D.
3
.
Lời giải
Chọn A
Ta có
2
2 4 0,x x x
.
Khi đó
2
2
log 2 4 2
x x
2
2 4 4
x x
0
2
x
x
.
Câu 43. Tập nghiệm của bất phương trình
2
2
2 8
x x
là
A.
( ; 1)
. B.
(3; )
.
C.
( 1;3)
. D.
( ; 1) (3; ) 
.
Lời giải
Chọn C
Ta có:
2 2
2 2 3 2 2
2 8 2 2 2 3 2 3 0 1 3.
x x x x
x x x x x
Câu 44. Tập nghiệm của phương trình
6
log 5 1
x x
là
A.
2;3
. B.
4;6
. C.
1; 6
. D.
1;6
.
Lời giải
Chọn A
Điều kiện
5 0
x x
5 0
x x
0 5
x
.
Phương trình tương đương với
5 6
x x
2
5 6 0
x x
2
3
x
x
(thỏa mãn điều kiện).
Vậy phương trình có tập nghiệm là
2;3
S
.
Câu 45. Tập nghiệm của bất phương trình
2
4
1
27
3
x x
là
A.
( ; 1)
. B.
(3; )
. C.
( 1;3)
. D.
( ;1) (3; ) 
.
Lời giải.
Chọn D
Ta có:
2 2
4 4 3
2 2
1
1 1 1
27 4 3 4 3 0
3
3 3 3
x x x x
x
x x x x
x
.
Câu 46. Phương trình
ln ln 2 1 0
x x
có bao nhiêu nghiệm?
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn B
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 37
Điều kiện
0
2 1 0
x
x
1
2
x
.
Khi đó, phương trình tương đương với:
ln 2 1 0
x x
2
2 1 0
x x
1
1
2
x
x
So sánh với điều kiện ta được
1x
là nghiệm.
Câu 47. Phương trình
2
log 72 2logx x
có nghiệm là:
A.
1
. B.
2
. C.
6
. D.
4
.
Lời giải
Chọn C
Điều kiện
2
72 0
0
x
x
0 72
x
.
Khi đó, phương trình tương đương với:
2 2
log 72 logx x
2
2 72
x
6
x
.
So sánh với điều kiện ta có
6
x
thỏa mãn.
Câu 48. Số nghiệm nguyên dương của bất phương trình
2
1
5
25
x
x
là
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn C
2 2 2
1
5 5 5 2 2 2
25
x
x x x
x x x
. Do
x
nguyên dương nên
1, 2
x
Câu 49. Tập nghiệm của phương trình
2
ln(2 1) 0
x x
là
A.
0
. B.
1
0 ;
2
. C.
1
2
. D.
.
Lời giải
Chọn B
Ta có:
2
ln(2 1) 0
x x
2 0
2 1 e
x x
2
2 0
x x
Vậy, phương trình có tập nghiệm:
1
0 ;
2
S
.
Câu 50. Tập nghiệm của bất phương trình:
0,4 0,4
log (5 2) log 3 6
x x
là:
A.
;2 .

B.
0;2 .
C.
2
;2 .
5
D.
2; .
Lời giải
Chọn C
Điều kiện:
2
.
5
x
0,4 0,4
log (5 2) log 3 6
x x
5 2 3 6.
x x
2 4 2.
x x
Kết hợp với điều kiện, ta có tập nghiệm của bất phương trình là:
2
;2
5
.
Câu 51. Phương trình
2
2 1
4 0.125
x x
có bao nhiêu nghiệm?
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 38 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn C
Ta có:
2
2 1
4 0.125
x x
2
2 4 2 3
2 2
x x
2
2 4 1 0
x x
2 2
2
2 2
2
x
x
Vậy, phương trình có hai nghiệm.
Câu 52. Tập nghiệm của bất phương trình
1 2 2 1
3 6 3 6
x x x x
là:
A.
2
; log 5 .

B.
2
log 5;0 .
C.
2
log 5; . 
D.
1
; .
10

Lời giải
Chọn A
1 2 2 1
3 6 3 6
x x x x
3.3 36.6 9.3 6.6
x x x x
30.6 6.3
x x
2
1 1
2 log
5 5
x
x
2
log 5.
x
Vậy tập nghiệm của bất phương trình là:
2
; log 5

.
Câu 53. Tìm tập nghiệm của bất phương trình:
2 4 5 11
10 3 10 3
x x
?
A.
1; .
B.
;1 .
C.
5; .
D.
;5 .

Lời giải
Chọn C
Ta có:
1
10 3 10 3 1 10 3 10 3
2 4 5 11 2 4 5 11
10 3 10 3 10 3 10 3
x x x x
2 4 5 11
x x
5.
x
Vậy tập nghiệm của bất phương trình là:
5;

.
Câu 54. Phương trình
2 1
2
5 log 32
x
có nghiệm là
A.
1x
. B.
2
3
x
. C.
3
2
x
. D.
1
2
x
.
Lời giải
Chọn C
Ta có:
2 1
2
5 log 32
x
2 1
1
2
x
3
2
x
Vậy, phương trình có nghiệm:
3
2
x
Câu 55. Tìm số nghiệm nguyên của bất phương trình:
1
3
log (2 5) 2
x
?
A.
4.
B.
5.
C.
6.
D. Vô số.
Lời giải
Chọn B
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 39
1
3
log (2 5) 2
x
2
2 5 0
1
2 5
3
x
x
5
2
2 5 9
x
x
5
2
2
x
Các nghiệm nguyên của bất phương trình là:
2; 1;0;1;2
. Vậy bất phương trình có
5
nghiệm
nguyên.
Câu 56. Cho phương trình
2 10 4
3 6.3 2 0 1
x x
. Nếu đặt
5
3 0
x
t t
thì
1
trở thành phương trình
nào?
A.
2
9 6 2 0
t t
. B.
2
18 2 0
t t
. C.
2
2 2 0
t t
. D.
2
9 2 2 0
t t
.
Lời giải
Chọn C
2 5
2 10 4 5
3 6.3 2 0 3 2.3 2 0
x
x x x
.
Vậy khi đặt
5
3 0
x
t t
thì
1
trở thành phương trình
2
2 2 0
t t
.
Câu 57. Nghiệm của phương trình
3 6
2 1
x
là
A.
1
3
x
. B.
3
x
. C.
2
x
. D.
1
2
x
.
Lời giải
Chọn D
Ta có
3 6
1
2 1 3 6 0 .
2
x
x x
Câu 58. Nghiệm của phương trình
2
log 2 2 3
x
là
A.
3
x
. B.
2
x
. C.
4
x
. D.
5
x
.
Lời giải
Chọn D
Điều kiện
1.
x
2
log 2 2 3 2 2 8 5.
x x x
Vậy tập nghiệm phương trình đã cho là
5 .
Câu 59. Tích hai nghiệm của phương trình
2
3 3
log 6log 8 0
x x
bằng
A.
90
. B.
729
. C.
8
. D.
6
.
Lời giải
Chọn B
Đk:
0
x
;
2
3 3
log 6log 8 0
x x
3
3
log 4
log 2
x
x
4
2
3
3
x
x
;
4 2
3 .3 729
.
Câu 60. Tìm tập nghiệm của phương trình
2
log( 6 7) log( 3)
x x x
.
A.
4;5 .
B.
5 .
C.
3;4 .
D.
.
Lời giải
Chọn B
Đk:
2
6 7 0
3 0
x x
x
3 2
x
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 40 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
log( 6 7) log( 3)
x x x
2
6 7 3x x x
5
2
x
x
.
Nhận nghiệm
5
x
, loại nghiệm
2
x
.
Câu 61. Tính tổng các nghiệm của phương trình
2
log 3 1 9
x x
.
A.
3
. B.
9
. C.
9
10
. D.
3
.
Lời giải
Chọn D
Phương trình tương đương với
2 9
3 1 10
x x
2 9
3 1 10 0
x x
.
9
5 4.10 0
nên phương trình có hai nghiệm
1
x
và
2
x
phân biệt.
Theo định lý Viét, ta có
1 2
3
x x
.
Câu 62. Phương trình
2 2
log 3 log 1 3
x x
có nghiệm là một số
A. chẵn. B. chia hết cho
3
. C. chia hết cho
7
. D. chia hết cho
5
.
Lời giải
Chọn D
Điều kiện:
3
x
.
2 2
log 3 log 1 3
x x
2
log 3 1 3
x x
2
4 3 8
x x
2
4 5 0
x x
1
5
x
x
.
So điều kiện phương trình có nghiệm
5
x
.
Câu 63. Tổng tất cả các nghiệm của phương trình
5
log 9 5 1
x
x
bằng
A.
2
. B.
1
. C.
9
. D.
5
.
Lời giải
Chọn B
Ta có:
1 2
5
9 61
5
2
log 9 5 1 9 5 5 5 9.5 5 0
9 61
5
2
x
x x x x x
x
x
5
5
9 61
log
2
9 61
log
2
x
x
Tổng tất cả các nghiệm :
5 5 5
9 61 9 61 81 61
log log log 1
2 2 4
.
Câu 64. Tổng tất cả các nghiệm của phương trình
log(8.5 20 ) log 25
x x
x bằng
A.
16
. B.
3
. C.
25
. D.
8
.
Lời giải
Chọn B
Ta có :
log(8.5 20 ) log 25.10 8.5 20 25.10 (1)
x x x x x x
Chia 2 vế phương trình (1) cho
5
x
ta được phương trình :
8 4 25.2 (2)
x x
Đặt
2
x
t
,
(t > 0)
Phương trình (2) trở thành
2
25 + 8 = 0 3
t t
, gọi
1 2
,t t
là hai nghiệm của
3
thì
1 2
. 8
t t
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 41
Hai nghiệm của
2
là
1 2 1 2 2 2
log , logx t x t
, ta có:
Ta có
1 2 2 1 2 1 2 1 2 2
log log log . log 8 3
x x t t t t
.
Câu 65. Tổng tất cả các nghiệm của phương trình
2
3 (2 9).3 9.2 0
x x x x
bằng
A.
3
. B.
2
. C.
0
. D.
2
.
Lời giải
Chọn B
Đặt
3
x
t
,
0t
Phương trình trở thành:
2
9
(2 9) 9.2 0
2
x x
x
t
t t
t
* Với
9 3 9 2
x
t x
* Với
3
2 3 2 1 0
2
x
x x x
t x
Vậy, phương trình có hai nghiệm
1
0
x
;
2
2
x
1 2
2
x x
.
Câu 66. Phương trình
2
2 2
log 3 1 2log 3 1 3 0
x x
có 2 nghiệm
1
x
;
2
x
1 2
( )x x
và
1 2 3
log
a
x x
b
với
a,b
,
0
b
và
a
b
là phân số tối giản. Tính
a b
.
A.
5
a b
. B.
5
a b
. C.
11
a b
. D.
1a b
.
Lời giải
Chọn A
Ta có:
2
2
2 2
2
log 3 1 3
log 3 1 2log 3 1 3 0
log 3 1 1
x
x x
x
.
*Với
2 3
1 9
log 3 1 3 3 1 log
8 8
x x
x
.
*Với
2
log 3 1 1 3 1 2 1
x x
x
.
Suy ra
1 2 3 3
9 3
log 1 log
8 8
x x
.
Vậy
3
a
,
8
b
5
a b
.
Câu 67. Tổng tất cả các nghiệm của phương trình
4
log 9 4 1
x
x
bằng:
A.
2
. B.
1
. C.
4
. D.
3
.
Lời giải
Chọn B
Điều kiện
9 4 0
x
4
log 9 4 1
x
x
2
4
9 4 4 9.4 4 0
4
x x x
x
9 65
4
2
9 65
4
2
x
x
4
4
9 65
log
2
9 65
log
2
x
x
Tổng tất cả các nghiệm
4 4
9 65 9 65
log log 1
2 2
.
Câu 68. Số nghiệm của phương trình
7
log 6 7 1
x
x
bằng:
A.
2
. B.
3
. C.
0
. D.
1
.
Lời giải
Chọn D
NGUY
ỄN BẢO VƯƠNG - 0946798489
Trang 42 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
7
log 6 7 1
x
x
2
1
6 7.
7 7.7 6.7 1 0
7
x x
x
x
7 1
1
7
7
x
x
0
x
Số nghiệm của
phương trình bằng
1
.
Câu 69. Tổng tất
cả các nghiệm của phương trình
2
ln
( 5 4) log2.ln10
x x
bằng
A.
1
. B.
6
. C.
7
. D.
5
.
Lời
giải
Chọn D
ĐK:
2
5 4 0
x x
5 4
1
2
x
hoặc
5 4
1
2
x
Ta có:
2
ln
( 5 4) log2.ln10
x x
2
ln
( 5 4) ln 2
x x
2
5 6
0
x x
6( )
1( )
x N
x N
Vậy, phương trình có hai nghiệm
1
1
x
,
2
6
x
1 2
5
x x
.
Câu 70. Tổng tất
cả các nghiệm của phương trình
1
3
log 4.3 1 2 1
x
x
bằng:
A.
1
. B.
2
. C.
7
. D.
3
.
Lời
giải
Chọn A
Điều
kiện
1
4.
3 1 0
x
1
3
lo
g 4.3 1 2 1
x
x
2
1 4
.3
.3 1 0
3 3
x x
3 3
3 1
x
x
1
0
x
x
Tổng tất cả các nghiệm
1 0 1
.
Câu 71. Số nghiệm của
phương trình
5
log
3
2
log 9 2 5
x
x
bằng:
A.
2
. B.
1
. C.
7
. D.
3
.
Lời
giải
Chọn
B
Điều
kiện
9 2
0
3 0
x
x
5
log
3
2
log
9 2 5
x
x
2
lo
g 9 2 3
x
x
2
8
9 2
2 9.2 8 0
2
x x
x
x
2 8
2
1
x
x
3
0
x l
x
0
x
Số nghiệm của phương trình bằng
1
.
-------------------- HẾT --------------------
| 1/60
| | Tải xuống

Có thể bạn quan tâm:

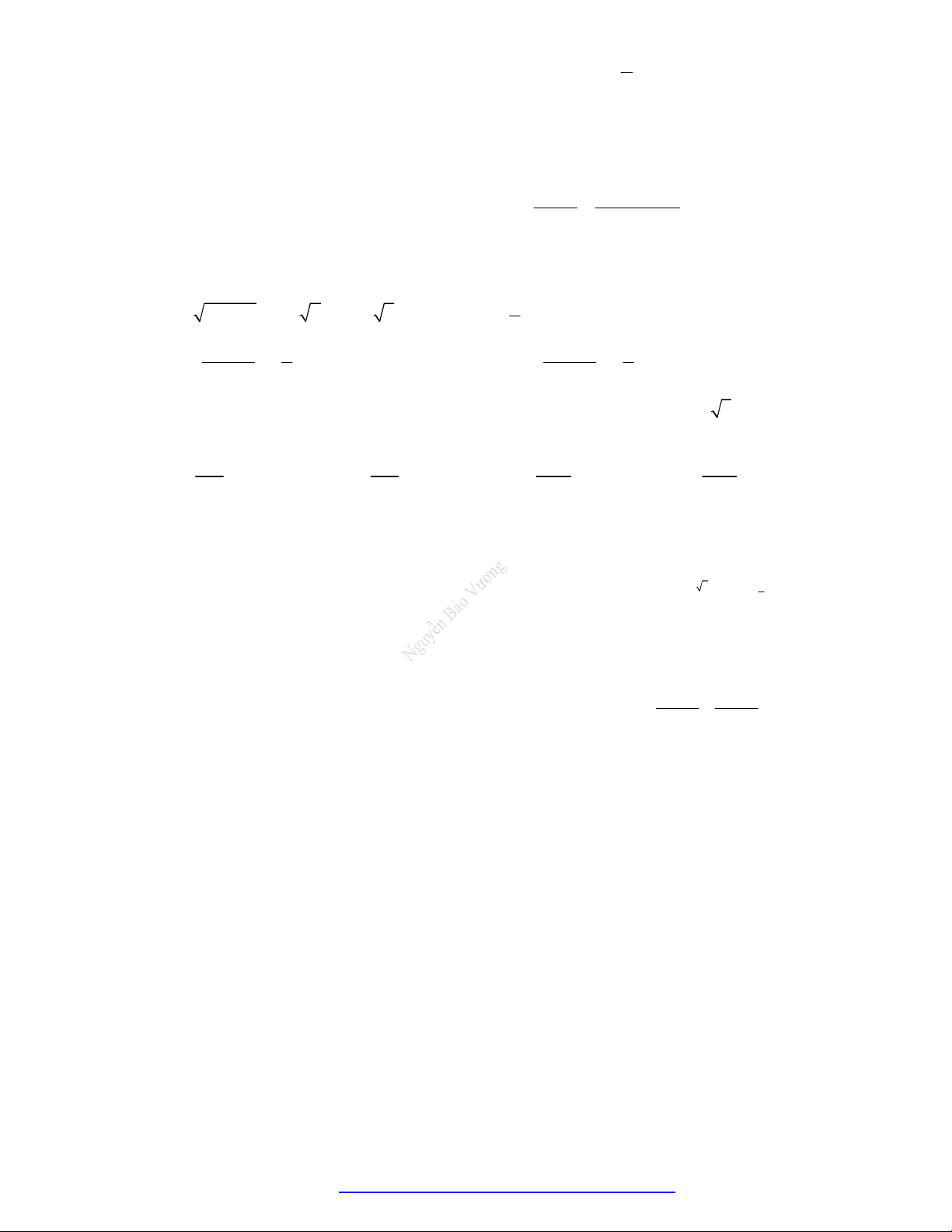
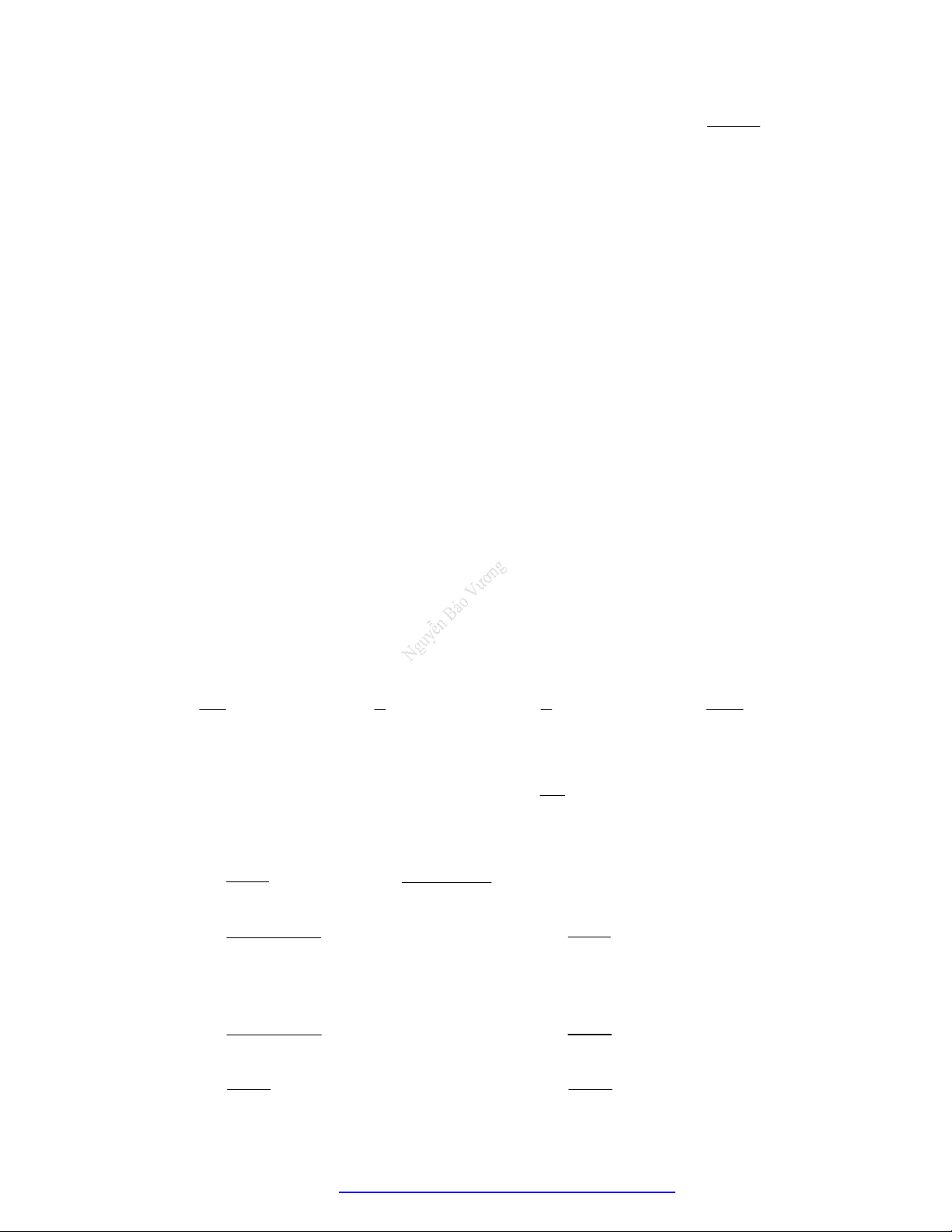
Preview text:


TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 Vấn đề 9
HÀM SỐ LŨY THỪA - MŨ - LOGARIT
A. BIẾN ĐỔI CÔNG THỨC
CÁC CÔNG THỨC MŨ – LOGARIT CẦN NHỚ
Cho a và b là các số thực dương, x và y là những số thực tùy ý.  n a  a.a.a...a  x x a a       x   n số a b b  xy x y a  a .a x  y x y a  a y 2; y      x   a  1   0 u x x y n a   a  .     y n  u x 1, a a        x   0  y x   x.y   x    y a a a   n n n
a. b  ab n  2; n       x x x a .b a.b  m    m m n n n a a  a
Cho 0  a  1 và b, c  0 .  x log b  x  b  a b a  log  log b  log c a a a c 1  log b khi   log    a lẻ  b log b  a a   log b  a  log b khi   chẵn a  log b 1 ln b  c log b   log b  , log b  a log a a log a a ln a c b  log 1  0, log a  1  log c log a log b a  c  b  a a a b b a
 log b.c  log b  log c ln  b  log b a   a a   e  lg  b  log b  log b  10 
MỨC ĐỘ NHẬN BIẾT Câu 1.
Với a là số thực dương tùy ý, 2 log a bằng: 2 1 1
A. 2  log a . B.  log a . C. 2 log a . D. log a . 2 2 2 2 2 2 Câu 2.
Với a là hai số thực dương tùy ý, log  3 a bằng 2  3 1 A. log a .
B. log a .
C. 3  log a .
D. 3 log a . 2 2 2 3 2 2 Câu 3.
Cho a là số thực dương khác 1. Tính log a . a 1 A. 2. B. 2  . C. . D. 1. 2 3  a Câu 4.
Cho a là số thực dương khác 4. Tính I  log . a   64 4   1 1 A. I  3 . B. I  . C. I  3 . D. I   . 3 3 Câu 5.
Cho 0  a  1 . Giá trị của biểu thức P   3 2 log . a a là a
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489 4 5 5 A. . B. 3 . C. . D. . 3 3 2 Câu 6.
Giá trị của A  log 3.log 4.log 5....log 64 bằng 2 3 4 63 A. 5 . B. 4 . C. 6 . D. 3 . Câu 7.
Với các số thực a,b  0 bất kì, rút gọn biểu thức 2
P  2log a  log b ta được 2 1 2 2  a   2a A. P  log  2 2ab . B. P  log ab . C. P  log . D. P  log . 2  2 2  2   2    b  2  b  2 5  a b Câu 8.
Với a , b là hai số thực dương, log bằng 5   25  
A. 2log a  5log b  25 .
B. 2log a  5log b  2 . 5 5 5 5
C. 2log a  5log b  25 .
D. 2log a  5log b  2 . 5 5 5 5 Câu 9.
Cho a là số thực dương bất kì, giá trị nào dưới đây có cùng giá trị với 3 log(10a )? A. 3log a B. 3 10 log a C. 1 3log a D. 3log(10a)
Câu 10. Với a , b là hai số dương tùy ý,  6 7
log a b  bằng 1 1
A. 6 log a  7 log . b
B. 6 log a  7 log . b C. log a  log . b
D. 42 log ab 6 7
Câu 11. Cho a là số thực dương khác 1. Tính 3 I  3log a a 1 1 A. I  1. B. I  9 . C. I  . D. I  . 9 3
Câu 12. Với a và b là các số thực dương. Biểu thức  5 log a b bằng a  1
A. 5  log b .
B. 5  log b .
C. log b . D. 5log b . a a 5 a a
Câu 13. Cho các số thực dương a , b thỏa mãn 2 log a  5log b  1 . Mệnh đề nào sau đây đúng. A. 2 5 a b  10 .
B. 2a  5b  10 .
C. 2a  5b  1. D. 2 5
a b  10 . 1  
Câu 14. Cho b là số thực dương khác 1. Tính 6 2 P  log b .b . b     7 13 A. P  3 . B. P  . C. P  . D. P  6 . 2 2 4  a
Câu 15. Với a , b là hai số dương tùy ý, log  bằng 5  b   4 4
A. 4 log a  5log b .
B. 4 log a  5log b . C.
log a  logb . D. log a  logb . 5 5  a
Câu 16. Cho a và b là hai số thực dương thỏa mãn log  log
a . Mệnh đề nào dưới đây đúng? 2   1    b  2
A. b  1. B. 2
b a .
C. a b . D. 2 a b .
Câu 17. Cho 0  a  1 . Giá trị của biểu thức P   3 log . a a là a  1 4 5 A. . B. 3 . C. . D. . 3 3 3
Câu 18. Với a là số thực dương bất kỳ, mệnh đề nào dưới đây đúng?
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 1 1
A. log 7a  7 log a . B. 7 log a  log a . C. 7
loga  7 log a .
D. log 7a  log a . 7 7
Câu 19. Cho a và b là các số thực dương bất kì. Chọn khẳng định sai. 1 A. 3 5
ln a  ln b  3ln a  ln b .
B. log a  log b  log ab . 5 a C. ab2 log 10
 10  log a  log b . D. ln
 ln a  ln b . b
Câu 20. Với a là số thực dương tùy ý, log  2 9a bằng: 3  A. 2log a .
B. 3 2log a .
C. 2  2log a . D. 4log a . 3 3 3 3
Câu 21. Với a , b là hai số dương tùy ý,  3 4
log a b  bằng 1 1
A. 3log a  4 log . b
B. 4 log a  3log . b C. log a  3log . b
D. 2 log a  log . b 4 3
Câu 22. Đặt log 5  a , khi đó log 64 bằng 4 25 3a 3 2 2a A. . B. . C. . D. . 2 2a 3a 3 5  3a
Câu 23. Với a , b là hai số dương tùy ý, log bằng 3  2  b  
A. 1 2 log a  5 log . b
B. 5  5log a  2 log . b 3 3 3 3
C. 1 5 log a  2 log . b
D. 51 log a  2log b . 3 3  3 3
Câu 24. Đặt log 3  a , khi đó log 16 bằng 12 9 1 a 1 a a a A. . B. . C. . D. . a a 1 a 1 a 5  3a
Câu 25. Với a , b là hai số dương tùy ý, log bằng 3  2  b  
A. 1 2 log a  5 log . b
B. 5  5log a  2 log . b 3 3 3 3
C. 1 5 log a  2 log . b
D. 51 log a  2log b . 3 3  3 3 5  b
Câu 26. Với a , b là hai số dương tùy ý, log  bằng 3  10a  
A. 5log b 1 3log . a
B. 5log b  31 log a. C. 5logb  3 3log .
a D. 5log b 1 3log . a
Câu 27. Đặt log 9  a , khi đó log 18 bằng 2 3 2  2a a a 2a  2 A. . B. . C. . D. . a 2  2a 1 a a 3  b   
Câu 28. Với a , b , c là ba số dương tùy ý, log  bằng 2   ac 
A. 3 log b  log a  2 log c .
B. 3 log b  log a  2 log c .
C. 3log b log a  2 log c .
D. 3log b log a 2 log c .
Câu 29. Đặt log 4  a , khi đó log 24 bằng 6 36 1 2 a
A. a 1 . B. a   1 . C. . D. . 2 a 1 2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489 3  100m
Câu 30. Với m , n là hai số thực dương tuỳ ý, log  bằng 2  n  
A. 2  3log m  2 log n . B. 2  3log m  2 log n . 1 1 1 C. 2
  3log m  2 log n . D.  log m  log n . 2 3 2
Câu 31. Đặt a  log 15 , khi đó log 27 bằng 3 25 3a   1 3 2 2 a   1 A. . B. . C. . D. . 2 2a   1 3a   1 3
Câu 32. Với a , b là hai số thực tuỳ ý,  2 4
log a b  bằng
A. 2 log a  4 log b .
B. 2 log a  4 log b .
C. 2 log a  4 log b .
D. 2 log a  4 log b .
Câu 33. Đặt a  log 2 , khi đó log32 81 e bằng 3 5a 4 5 4a A. 4 e . B. 5 e a . C. 4 e a . D. 5 e .
Câu 34. Với a , b là hai số thực dương tuỳ ý,  3 5
ln e.a b  bằng
A. 5ln a  3ln b .
B. 3ln a  5ln b .
C. 1 3ln a  5ln b .
D. 1 5ln a  3ln b .
Câu 35. Đặt a  log 2 , khi đó log  125 ln e bằng 16  5 3a 3 4 4a A. . B. . C. . D. . 4 4a 3a 3 4 2  a b
Câu 36. Với a , b là hai số thực dương, log bằng 2   16  
A. 2 log a  4log b  4 .
B. 4log a   1  2 log b .
C. 2 log a  4 log b  4 .
D. 4log a 1  2 log b . 2  2 2 2
Câu 37. Cho 5a  7 . Tính log 125 theo a . 49 3a 3 2 2a A. . B. . C. . D. . 2 2a 3a 3
Câu 38. Rút gọn biểu thức 2 log a 3 2 P  3  log a .log 25 . 5 a A. 2 a  2 . B. 2 a  2 . C. 2 a  4 . D. 2 a  4 .
Câu 39. Cho a là số thực dương khác 1. Tính log a . a 1 A. 2 . B. 2  . C. . D. 1. 2 a
Câu 40. Giá trị của  a 3log 4 ;a  0,a  1 bằng A. 2 . B. 3 . C. 4 . D. 8 . 3 5
Câu 41. Rút gọn biểu thức 2 2
R  log b  log b (với a  ;
0 a  1 và b  0 ). 2 a a 15 11 15 A. R  log b . B. 4 log b . C. log b . D. log b . 4 a a 4 a 8 a 3 5
Câu 42. Rút gọn biểu thức 2 2
R  log b  log b (với a  ;
0 a  1 và b  0 ). 2 a a 15 11 15 A. R  log b . B. 4 log b . C. log b . D. log b . 4 a a 4 a 8 a
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Câu 43. Với a và b là hai số thực dương tùy ý, log  3 4 a b bằng 2  1 1 A. log a  log b
B. 3log a  4 log b
C. 2log a  log b D. 4 log a  3log b 2 4  2 2 3 4 2 2 2 2
MỨC ĐỘ THÔNG HIỂU
Câu 44. Xét tất cả các số dương a và b thỏa mãn log a  log (ab) . Mệnh đề nào dưới đây đúng? 2 8 A. 2 a b . B. 3 a b .
C. a b . D. 2 a b .
Câu 45. Xét số thực a và b thỏa mãn log
3a.9b  log 3 . Mệnh đề nào dưới đây đúng 3   9
A. a  2b  2 .
B. 4a  2b  1 .
C. 4ab  1.
D. 2a  4b  1.
Câu 46. Cho a và b là hai số thực dương thỏa mãn 3
ab  27 . Giá trị của log a  6 log b bằng 3 3 A. 3 . B. 6 . C. 9 . D. 1. 4
Câu 47. Cho a và b là hai số thực dương thỏa mãn log a
log b  2 . Giá trị của 3 4 a .b bằng 2 2 3 A. 8 . B. 6 . C. 64 . D. 32 . 5 a 1
Câu 48. Cho a và b là hai số thực dương thỏa mãn 
. Giá trị của 5log a  2log b 2 b 9 3 3 1 1 A. . B. . C. 2 . D. 2  . 3 2 1
Câu 49. Cho a và b là hai số thực dương thỏa mãn log a  log b   . Giá trị của 2 4 a .b bằng 4 2 2 1 1 1 A. . B. . C.  . D. 4  . 2 4 4 a
Câu 50. Cho a và b là hai số thực dương thỏa mãn 2
log a  log b  2 . Giá trị của bằng 3 1 b 3 1 1 A. 9 . B. 3 . C. . D. . 9 3
Câu 51. Với các số thực a,b  0 bất kì, rút gọn biểu thức 2 2
P  log a  log b ta được 2 1 2 2 2  a   a A. P  log . B. P  log ab . C. P  log .
D. P  log  2 2 a b . 2  2  2 2   1    b   b  2
Câu 52. Với mọi số thực dương a và b thoả mãn 2 2
a b  8ab , mệnh đề nào dưới đây đúng? 1 1
A. log a b  log a  log b .
B. log a b  1 log a  log b . 2 2 1
C. log a b  1 log a  log b .
D. log a b 
 log a  log b . 2
Câu 53. Cho a và b là hai số thực dương thỏa mãn log b  log
ab . Mệnh đề nào dưới đây đúng? 2 4  
A. a b .
B. a  1 . C. 2 a b  1 . D. 2 a b .
Câu 54. Cho a  0 , b  0 thỏa mãn 2 2
a  4b  5ab . Khẳng định nào sau đây đúng? a  2b log a  log b A. log  .
B. 5log a  2b  log a  log b . 3 2
C. 2 log a  2b  5log a  log b .
D. log a   1  log b  1.
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489 2
Câu 55. Cho a, b là các số thực dương khác 1, thoả log b  log a
. Mệnh đề nào dưới đây là 3 3 a b 3 đúng? 3 3
A. a b .
B. b a3 2 3 3  a .
C. b a .
D. a b .
Câu 56. Cho a  0, b  0 thỏa mãn 2 2
a  9b  10ab .Khẳng định nào sau đây đúng? a  3b log a  log b
A. log a   1  log b  1. B. log  . 4 2
C. 3log a  3b  log a  log b .
D. 2 log a  3b  2log a  log b .
Câu 57. Cho các số dương a, b thõa mãn 2 2
4a  9b  13ab . Chọn câu trả lời đúng. 1
A. log 2a  3b  log a  2 log b . B.
log 2a  3b  3log a  2 log b . 4
 2a  3b  1
 2a  3b  1 C. log   
log a  log b. D. log   
log a  log b .  5  2  4  2
Câu 58. Cho các số thực x, a, b, c, d dương thoả mãn x   a 4 log 2 log 2
 3log b  4 log c . Biểu diễn x
theo a, b, c được kết quả là: 2 2a 2 4a 2 2a c 2 2a c A. x  . B. x  . C. x  . D. x  . 3 b c 3 b c 3 b 2 b
Câu 59. Cho a, b  0 , nếu 2
log a  log b  5 và 2
log a  log b  7 thì giá trị của ab bằng: 8 4 4 8 A. 9 2 . B. 72 . C. 9 . D. 18 2 . 3 2
Câu 60. Cho a, b , c là ba số thực dương thỏa mãn a b c  8 . Giá trị của 3log a  log
b  log c bằng 2 1 2 2 A. 8 . B. 4. C. 3 . D. 6 . 2 3
Câu 61. Cho a , b , c là ba số thực dương thỏa mãn a b  4c . Giá trị của 2 ln a  3 ln b  ln c bằng A. 2 ln 2 . B. ln 2 . C. 4 . D. 2 . 1 2
Câu 62. Cho x và y là hai số thực dương khác 1 thỏa mãn 2
8xy  1. Giá trị của  bằng log 2 log 2 x y A. 3  . B. 3 . C. 4 . D. 4 .
Câu 63. Cho log b  2 với a , b  0 , a khác 1. Khẳng định nào sau đây sai? a
A. log ab  3 . B. a b  . C. b  . D. ab  . a  2 log  3 a  2 log  4 a  2 log  4 a
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
B. HÀM SỐ LŨY THỪA – MŨ - LOGARIT HÀM LŨY THỪA HÀM SỐ MŨ HÀM SỐ LOGARIT y  log xa  0 a Dạng: với  . y  log u a  1 ax Đặc biệt: y aa  0 Dạng: với  . a e   y  ln x ; y xu y a a  1  Dạng: với u là đa a  10 
y  log x  lg x . y u
Tập xác định: D  . 
Điều kiện xác định: u  0 . thức đại số. Đạo hàm: Đạo hàm: x x Tập xác định: y a 
y  a ln a . 1     Nếu ÑK     u  .  y log x y u u y a 
y  a ln . a ua x ln a     . x x Nếu ÑK   u  0. (e )  e u   0
y  log u   y   Đặc biệt: với a ( u e ) u   e . uu ln a Nếu ÑK
   u   0. e  2,71828... 1 (ln x)  Đạo hàm: x Sự biến thiên: x y a . Đặc biệt: .   1 y x 
y   x u
Nếu a  1 thì hàm đồng biến (ln u )  u   1 y u 
y  u  . u
trên  . Nếu 0  a  1 thì hàm Sự biến thiên: y  log x . Nếu a nghịch biến trên  .
a  1 : hàm đồng biến trên (0; ) .
Nếu 0  a  1 : hàm nghịch biến trên (0; ).
ĐỒ THỊ HÀM SỐ MŨ
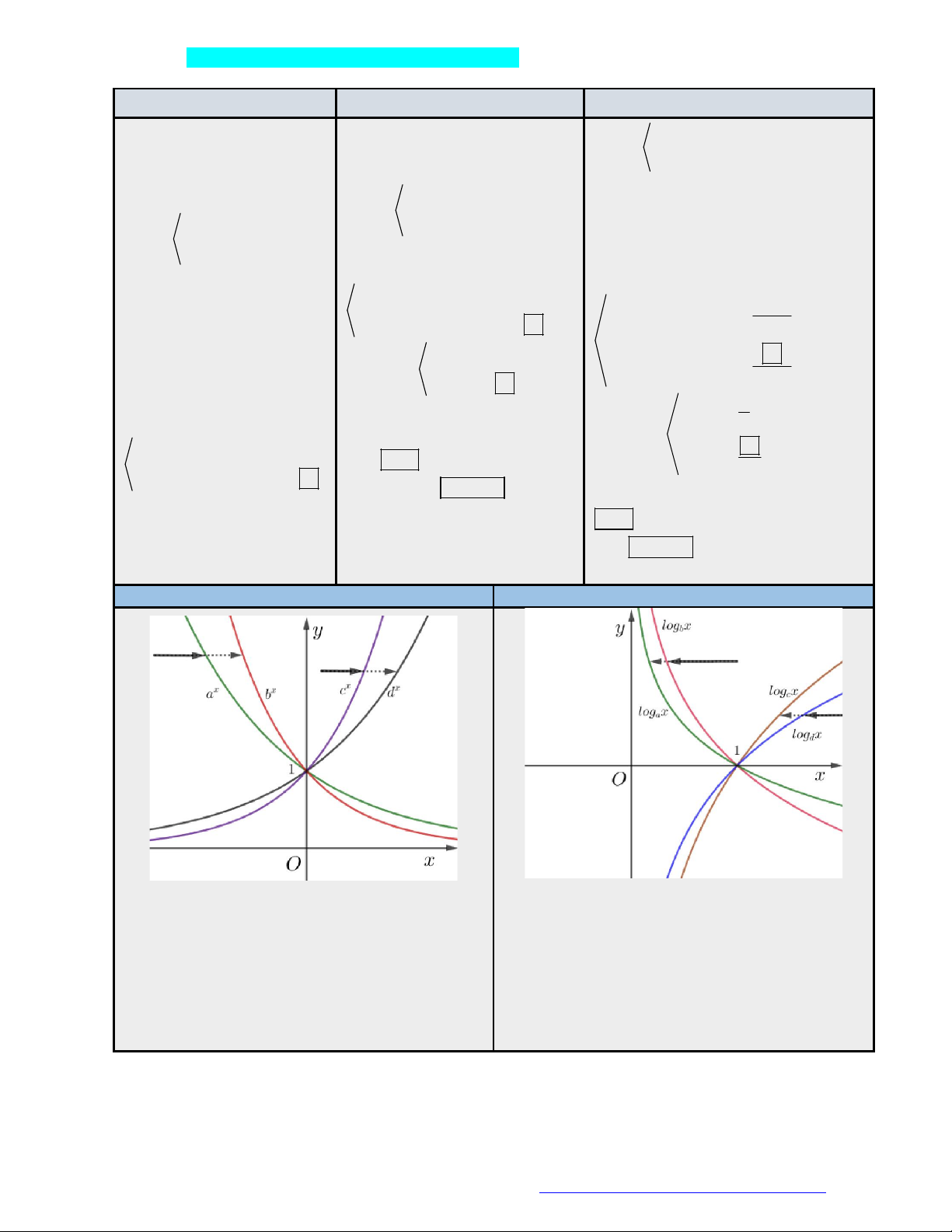
ĐỒ THỊ HÀM SỐ LOGARIT
Ta thấy: x  0   1; x a a
b  0  b  1.
Ta thấy: log x  0  a  1; log x  0  b  1. a b
Ta thấy: x   1; x c c
d  d  1.
Ta thấy: log x  c  1; log x  d  1. c d
So sánh a với b: Đứng trên cao, bắn mũi tên từ trái So sánh a với b: Đứng trên cao, bắn mũi tên từ
sang phải, trúng x
a trước nên a b .
phải sang trái, trúng log x trước: b  . a b
So sánh c với d: Đứng trên cao, bắn mũi tên từ trái So sánh c với d: Đứng trên cao, bắn mũi tên từ
sang phải, trúng x
c trước nên c d.
phải sang trái, trúng log x trước: d  . c d
Vậy 0  b a  1  d  . c
Vậy 0  a b  1  c d . Câu 1.
Tập xác định của hàm số y  log x là 2
A. 0; . B.  ;  .
C. 0;.
D. 2; . Câu 2. Đạo hàm của hàm số 2 4 x y  là
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
NGUYỄN BẢO VƯƠNG - 0946798489 A. 2 2.4 x y  ln 4 . B. 2 4 x y  .ln 2 . C. 2 4 x y  ln 4 . D. 2 2.4 x y  ln 2 Câu 3. Đạo hàm của hàm số 2018x y  là 2018x A. 2018x y 
ln 2018 . B.   2018x y ln x . C. 2018x y  . D. y  . ln 2018 2 Câu 4. Đạo hàm của hàm số 2 3 2 e x x y    là 2 2 A. 2 x 3x2 y   2 e
. 2x  3x  2 . B. 2 x 3 x2 y  e .4x  3 . 2 2 C. 2 3 2 e x x y     . D. 2 x 3x 1 y e    .4x  3 . Câu 5. Hàm số 2 1 2018 x y  
có đạo hàm tại điểm x  1 là A. 4036.ln 2018 . B. y  1  2018.ln 2018 . C. y  1  2018 . D. y  1  4036 . Câu 6.
Tính đạo hàm của hàm số 2 3 2 x y   . A. 2 x2 y  2 ln 4 . B. x2 y  4 ln 4 . C. 2 x2 y  2 ln16 . D. 2 x3 y  2 ln 2 . Câu 7.
Tập xác định của hàm số y  ln 2  x là A.  ;   2 . B.  ;  2 . C.  ;   . D. 0; . Câu 8.
Tập xác định của hàm số 5x y  là A.  \   0 . B. 0;  . C.  ;   . D. 0;  .  Câu 9.
Tập xác định của hàm số y   x   2 3 là A.  \  3  . B.  3  ;  . C.  ;   . D.  \   0 .
Câu 10. Tìm đạo hàm của hàm số 2x y e . A. 2 x y  e . B. 2 1 2 x y xe    . C. 2   2 x y e . D. 2 1 2 x y e    .
Câu 11. Tìm đạo hàm của hàm số y  log x . 7 ln 7 1 7 1 A. y  . B. y  . C. y  . D. y  . x x x x ln 7
Câu 12. Tìm đạo hàm của hàm số 5x y  . 5x A. 5x y  . B. 5x y  ln5 . C. y  . D. 1 5x y x    . ln 5
Câu 13. Hàm số f x   2
log 4  x  có đạo hàm ln10 1
A. f  x  .
B. f  x  . 2 4  x  2 4  x ln10 2  x 2  x
C. f  x  .
D. f  x  .  2 4  x .ln10 2 4  x
Câu 14. Hàm số f x   2
ln x x có đạo hàm 2x 1 2 x x
A. f  x  .
B. f  x  .  2 x x.ln10 2x 1 1 2x 1
C. f  x  .
D. f  x  . 2 x x 2 x x
Câu 15. Hàm số f x 2
 ln x có đạo hàm
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 2.ln x 2 ln x
A. f  x  .
B. f  x  2.ln x .
C. f  x  .
D. f  x  . x . x ln x x Câu 16. Hàm số   2 1 5x f x   có đạo hàm A.       2 2 1 .5x f x x .
B. f x 2 x 1 2 .5 x    .ln 5 . C.       2 2 2 . 1 .5x f x x x .
D. f x 2 x 1 5    .ln 5 .
Câu 17. Hàm số f x  log  3
x x có đạo hàm 2  ln 2 1
A. f  x  .
B. f  x  . 3 x x  3 x xln 2  2 3x   1 ln 2 2 3x 1
C. f  x  .
D. f  x  . 3 x x  3 x xln 2
Câu 18. Hàm số f x   2
ln x  3x có đạo hàm ln10 1 2 x  3x 2x  3
A. f  x  .
B. f  x  .
C. f  x  .
D. f  x  . 2 x  3x 2 x  3x 2x  3  2 x  3xCâu 19. Hàm số   2 5x 2x f x   có đạo hàm 2 x 5 x x 2 xx   2 5 2 5 2
A. f  x  .
B. f  x  . ln 2 ln 2 2 C.   2 x 5 2 x f x    ln 2 . D.   x 5  2 x f x
2x  5 ln 2 . Câu 20. Hàm số   2 3 ex x f x   có đạo hàm 2 A.   2 3 ex x f x    . B.   x 3x f x   2 e
x  3x. 2 x 3 e x 2
C. f  x  . D.   x 3  e x f x
2x  3 . 2x  3 3 3 Câu 21. Hàm số ex y   có đạo hàm là 4 3 3   3 x A. 3 ex  . B. 2 3 3 ex x  . C.   3 3 3 3 ex x   . D. x 3  3x e   . 4  
Câu 22. Đạo hàm của hàm số 2 4 x y  là A. 2 2.4 x y  ln 4 . B. 2 4 . x y  ln 2 . C. 2 4 x y  ln 4 . D. 2 2.4 x y  ln 2 Câu 23. Cho hàm số 1 3x y  
. Đẳng thức nào sau đây đúng? A. 1 3x y    . B. x 1 y 3    .ln 3 . C. 1 .3x y x    . D. yxx 1 1 .3     .ln 3 . 2
Câu 24. Đạo hàm của hàm số 2 3 2 e x x y    là 2 2 A. 2 x 3x2 y   2 e
. 2x  3x  2 . B. 2 x 3 x2 y  e .4x  3 . 2 2 C. 2 3 2 e x x y     . D. 2 x 3 x 1 y e    .4x  3 .
Câu 25. Tìm đạo hàm của hàm số 2 3 2   x y . A. 2 x2 y  2 ln 4 . B. x2 y  4 ln 4 . C. 2 x2 y  2 ln16 . D. 2 x3 y  2 ln 2 . C. BÀI TOÁN THỰC TẾ
1. Lãi đơn:Khách hàng gửi vào ngân hàng A đồng với lãi đơn r /kì hạn thì số tiền khách hàng
nhận được cả vốn lẫn lãi sau n kì hạn ( n   * ) là S A nAr A 1  nr n  
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
NGUYỄN BẢO VƯƠNG - 0946798489
2. Lãi kép: Khách hàng gửi vào ngân hàng A đồng với lãi kép r /kì hạn thì số tiền khách hàng
nhận được cả vốn lẫn lãi sau n kì hạn ( n   * ) là S A 1  r n n S SS
Từ đó ta có thể tìm các giá trị: r n n  1 n A n n  log   A  1 r     1 Ar n  
3. Bài toán tăng trưởng dân số: Công thức tính tăng trưởng dân số  X
X 1 r m n , m,n   
  ,m n trong đó: m n  
r là tỉ lệ tăng dân số từ năm n đến năm m
X là dân số năm m m
X là dân số năm n n X
Từ đó ta có công thức tính tỉ lệ tăng dân số là: r m m n  1 Xn
4. Vay vốn trả góp: Vay ngân hàng số tiền là A đồng với lãi suất r /tháng. Sau đúng một tháng
kể từ ngày vay, bắt đầu hoàn nợ, hai lần hoàn nợ cách nhau đúng một tháng, mỗi lần hoàn nợ số
tiền là X đồng. Ta có công thức tính số tiền còn lại sau n tháng: n
1  r n  1
S A 1  rX n   r
5. Tiền gửi hàng tháng: Đầu mỗi tháng khách hàng gửi vào ngân hàng số tiền A đồng với lãi
kép r /tháng thì số tiền khách hàng nhận được cả vốn lẫn lãi sau n tháng (n   * ) (nhận tiền A n
cuối tháng, khi ngân hàng đã tính lãi) là S Sr      r n 1  1 1  n r    S r .  S r . Từ đó ta có n n  log   1 n A 1 r
   A1  r   n    
1  r  1  r   1     Câu 1.
Để dự báo dân số của một quốc gia, người ta sử dụng công thức nr
S Ae ; trong đó A là dân số
của năm lấy làm mốc tính, S là dân số sau n năm, r là tỉ lệ tăng dân số hàng năm. Năm 2017,
dân số Việt nam là 93.671.600 người (Tổng cục Thống kê, Niên giám thống kê 2017, Nhà xuất
bản Thống kê, Tr 79). Giả sử tỉ lệ tăng dân số hàng năm không đổi là 0,81%, dự báo dân số Việt
nam năm 2035 là bao nhiêu người (kết quả làm tròn đến chữ số hàng trăm)? A. 109.256.100 . B. 108.374.700 . C. 107.500.500 . D. 108.311.100 . Câu 2.
Để quảng bá cho sản phẩm A, một công ty dự định tổ chức quảng cáo theo hình thức quảng cáo
trên truyền hình. Nghiên cứu của công ty cho thấy: nếu sau n lần quảng cáo được phát thì tỉ lệ 1
người xem quảng cáo đó mua sản phẩm A tuân theo công thức P n  . Hỏi cần phát 0  ,015 1 49e n
ít nhất bao nhiêu lần quảng cáo để tỉ lệ người xem mua sản phẩm đạt trên 30%? A. 202 . B. 203. C. 206 . D. 207 . Câu 3.
Sự tăng trưởng của một loài vi khuẩn tuân theo công thức  .ert S A
, trong đó A là số lượng vi
khuẩn ban đầu, r là tỉ lệ tăng trưởng r  0  , t là thời gian tăng trưởng. Biết rằng số lượng vi
khuẩn ban đầu là 100 con và sau 5 giờ có 300 con. Hỏi sau 20 giờ có bao nhiêu con? A. 8100 con. B. 9000 con. C. 7000 con. D. 8500 con.
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 Câu 4.
Dân số thế giới được ước tính theo công thức ni
S S e , trong đó S là dân số của năm lấy làm 0 0
mốc tính, S là dân số sau n năm, i là tỷ lệ tăng dân số hàng năm. Tỷ lệ tăng dân số hàng năm của
nước ta là 1,14% / năm. Năm 2019 dân số nước ta là 97 575 490 người. Hỏi đến năm nào dân số
nước ta đạt ngưỡng 100 000 000 người A. 2022. B. 2021. C. 2024. D. 2023. Câu 5.
Để dự báo dân số của một tỉnh X, người ta sử dụng công thức  .enr S A
, trong đó A là dân số của
năm lấy làm mốc tính, S là dân số sau n năm, r là tỉ lệ tăng dân số hàng năm. Năm 2016 , dân số
tỉnh X là 8.326.550 người. Giả sử tỉ lệ tăng dân số hàng năm không đổi là 0,9 % , dự báo dân số
tỉnh X năm 2026 là bao nhiêu người (kết quả làm tròn đến chữ số hàng đơn vị)? A. 9.029.068 . B. 9.110.697 . C. 9.139.063 . D. 10.311.124 . Câu 6.
Khi đèn flash của máy ảnh tắt, pin ngay lập tức bắt đầu sạc lại tụ điện của đèn flash, nơi lưu trữ
điện tich được cho bởi công thức ( )  / 1 e   t a Q t Q
(dung lượng sạc tối đa là Q và t được tính 0  0
bằng giây). Mất bao lâu đề sạc lại tụ điện thành 90% công suất nếu a  2? A. 4 giây. B. 5 giây. C. 4.6 giây. D. 4.5 giây. Câu 7.
Để dự báo dân số của một quốc gia, người ta sử dụng công thức  .enr S A
, trong đó A là dân số
của năm lấy làm mốc tính, S là dân số sau n năm, r là tỉ lệ tăng dân số hàng năm. Năm 2018 ,
dân số Việt Nam là 94.665.973 người (Tổng cục thống kê, Niên giám thống kê 2018 , Nhà xuất
bản Thống kê, Tr. 87 ). Giả sử tỉ lệ tăng dân số hàng năm không đổi là 0,85 % , dự báo đến năm
nào dân số Việt Nam vượt mốc 100.000.000 người? A. 2022 . B. 2023 . C. 2024 . D. 2025 . Câu 8.
Áp suất không khí P (đo bằng milimet thủy ngân, kí hiệu là mmHg ) suy giảm mũ so với độ cao
x (so với mực nước biển và đo bằng mét) theo công thức  .exi P P
, trong đó P  760mmHg là 0 0
áp suất ở mực nước biển, i là hệ số suy giảm. Biết rằng ở độ cao 1000m thì áp suất của không khí
là 672, 71mmHg . Hỏi áp suất không khí ở độ cao 4125m là bao nhiêu (làm tròn đến hàng phần trăm)?
A. 495, 4598263mmHg . B. 459, 46mmHg .
C. 495, 459mmHg . D. 459, 5mmHg Câu 9.
Một mặt hàng kinh doanh theo hình thức đa cấp với số lượng nhân viên ban đầu A sau t (lần hội
thảo) được xấp xỉ bởi đẳng thức   0,2  .e t A t A
, trong đó A là số nhân viên ban đầu. Số lượng 0 0
nhân viên tham dự ban đầu tham gia kinh doanh là 100 thì sau ít nhất bao nhiêu lần hội thảo, số
lượng nhân viên đạt đến 700 người? A. 9 . B. 9, 729 . C. 10 . D. 9, 7 .
Câu 10. Vận dụng thông tư số 14/2017/TT-NHNN của Ngân hàng Nhà nước quy định về phương pháp
tính lãi trong hoạt động nhận tiền gửi, có hiệu lực từ ngày 1/1/2018, ngân hàng A đã tính số tiền
lãi theo một kì bằng số ngày của kì gửi nhân với số tiền lãi của một năm chia cho 365. Một khách
hàng gửi 100 triệu đồng vào ngân hàng vào ngày 4/7/2018 với lãi suất 5%/năm, kì hạn 1 tháng,
ngày tính lãi hàng tháng là ngày 4/7, biết rằng trong khi gửi khác hàng không đến rút lãi về, ngân
hàng tính theo thể thức lãi kép. Đến ngày 4/9/2018, người đó đến ngân hàng rút cả vốn lẫn lãi về.
Hỏi số tiền (tính bằng nghìn đồng) khách hàng nhận được là số nào sau đây: A. 100835. B. 100836. C. 100834. D. 100851.
Câu 11. Trong phòng thí nghiệm nghiên cứu về vi khuẩn tại bênh viện Trung ương Huế, loại vi khuẩn X
gây bệnh cho người có tốc độ tăng trưởng bình quân là 15% / ngày. Bệnh viện tiến hành nuôi cấy
mẫu bệnh phẩm do vi khuẩn X gây ra, với ước lượng số vi khuẩn ban đầu là 100 triệu (ước lượng
lúc 9 giờ của ngày đầu tiên nuôi cấy). Bệnh viện nhận thấy rằng có thể trị bệnh do vi khuẩn X gây
ra bằng thuốc kháng sinh Y. Cứ 500 mg thuốc kháng sinh Y có thể tiêu diệt được 10 triệu vi
khuẩn và thuốc có tác dụng hầu như ngay lập tức và không có tác dụng kéo dài thêm. Bác sĩ quyết
định lúc 9 giờ sáng hàng ngày (kể từ ngày thứ hai nuôi cấy mẫu bệnh phẩm) dùng x g thuốc
kháng sinh Y để tiến hành nghiên cứu trên mẫu bệnh phẩm thì thấy rằng sau khi tiến hành thí
nghiệm ở ngày thứ 15 ngày kể từ ngày nuôi cấy hoàn thành thì mẫu bệnh phẩm không còn vi
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
NGUYỄN BẢO VƯƠNG - 0946798489
khuẩn X. Hỏi số thuốc kháng sinh Y mà bác sĩ dùng hàng ngày để tiến hành nghiên cứu trên là
bao nhiêu? (lấy kết quả gần đúng) A. 0,855 g. B. 1g. C. 8,5 g. D. 2 g.
Câu 12. Một em học sinh 15 tuổi được hưởng số tiền thừa kế là 300 000 000 đồng. Số tiền này được gửi
tại một ngân hàng với kỳ hạn thanh toán 1 năm và học sinh này chỉ nhận được số tiền ( cả gốc và
lãi) khi đủ 18 tuổi. Biết rằng khi đủ 18 tuổi em này nhận được số tiền là 368 544 273 đồng. Vậy
lãi suất của ngân hàng gần nhất với số nào sau đây?( Với giả thiết lãi suất không đổi trong suốt quá trình gửi) A. 5, 5% / năm. B. 7% / năm. C. 7,5% / năm. D. 5, 7% / năm.
Câu 13. Bố An để dành cho An 100 000 000 đồng để học đại học trong một ngân hàng theo hình thức lãi
kép với lãi suất 0, 75% một tháng. Mỗi tháng An đến rút 3 000 000 đồng để chi phí sinh hoạt. Hỏi
sau 1 năm số tiền còn lại là bao nhiêu?( Làm tròn kết quả đến hàng đơn vị) A. 71857930 đồng. B. 71857931 đồng. C. 73380690 đồng. D. 73380689 đồng.
Câu 14. Một người gửi số tiền 100 triệu đồng vào một ngân hàng với lãi suất 0, 65% trên tháng. Biết rằng
nếu người đó không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được nhập vào
vốn ban đầu (người ta gọi đó là lãi kép). Hỏi số tiền lãi người đó có được sau 2 năm, nếu trong
khoảng thời gian này người đó không rút tiền ra và lãi suất không đổi là bao nhiêu? A. 24
100.(1, 0065) triệu đồng. B. 2
100.(1,0065) 100 triệu đồng. C. 24
100.(1, 0065) 100 triệu đồng. D. 24
100.(2, 0065) 100 triệu đồng.
Câu 15. Ông Nam gửi 100 triệu đồng vào ngân hàng theo thể thức lãi kép, kì hạn 1 năm với lãi suất
7, 56% một năm. Hỏi sau bao nhiêu năm gửi ông Nam sẽ có ít nhất 150 triệu đồng từ số tiền gửi
ban đầu? (giả sử lãi suất không thay đổi). A. 5 năm. B. 6 năm. C. 7 năm. D. 8 năm.
Câu 16. Vào ngày 3/8/2018, một người vay ngân hàng số tiền 50 triệu đồng, trả góp trong thời gian 10
tháng, lãi suất 5%/năm, với thỏa thuận là cứ đến ngày tính tiền lãi, người đó phải đến ngân hàng
trả phần tiền gốc bằng số tiền vay ban đầu chia đều cho các lần trả và số lãi phát sinh trong tháng
trước (hình thức dư nợ giảm dần). Hỏi số tiền anh phải trả cho ngân hàng vào ngày 3/12/2018 là bao nhiêu?
A. 5,45 triệu đồng.
B. 5,4 triệu đồng.
C. 10,85 triệu đồng.
D. 5,5 triệu đồng.
Câu 17. Vào đầu mỗi năm anh Thắng gửi vào ngân hàng số tiền 30 triệu đồng với kì hạn 1 năm, lãi suất
7%/năm (mỗi lần gửi cách nhau 1 năm). Hỏi sau ít nhất bao nhiêu năm (sau khi ngân hàng đã tính
lãi cho lần gửi cuối cùng) thì anh Thắng được số tiền cả gốc lẫn lãi từ 500 triệu đồng trở lên? (biết
rằng trong suốt thời gian gửi tiền, anh Thắng không đến rút lãi về, ngân hàng tính theo thể thức lãi
kép và lãi suất hàng năm không đổi) A. 7 năm. B. 8 năm. C. 11 năm. D. 10 năm.
Câu 18. Ông Q.BN mang 150 triệu đồng gửi vào ngân hàng với lãi suất 7% một năm. Ông KN cũng đem
300 triệu đồng gửi vào ngân hàng khác với lãi suất 1,72% một quí. Sau 10 năm, hai ông cùng đến
ngân hàng rút tiền ra để mua xe. ( Lưu ý: tiền lãi được tính theo công thức lãi kép và được làm
tròn đến hàng triệu). Biết 2 ông cùng muốn mua 1 loại xe có giá là 456 triệu. Nếu số tiền mang
theo không đủ, hai ông có thể trả góp cho hãng xe phần còn thiếu theo hình thức sau: Đúng một
tháng kể từ ngày nhận được xe, người mua bắt đầu đóng tiền góp; hai lần trả liên tiếp cách nhau
đúng một tháng, số tiền trả mỗi tháng là như nhau và phải trả trong 1 năm. Biết rằng mỗi tháng
hang xe chỉ tính lãi trên số dư nợ thực tế của tháng đó. Hỏi mỗi tháng người mua phải trả bao
nhiêu tiền cho hãng xe, lãi suất của hãng là 1,8%/tháng.Khẳng định nào sau đây là đúng
A. Ông Q.BN mỗi tháng phải trả thêm 15 triệu.
B. Ông KN mỗi tháng phải trả thêm 5 triệu.
C. Ông Q.BN cần trả thêm hơn 180 triệu trong 12 tháng.
D. Ôn KN cần trả thêm 15 triệu mỗi tháng.
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Câu 19. Ông A cần mua nhà ở nhưng số tiền của ông không đủ để mua nhà ở, ông đi vay ngân hàng 1 tỉ
đồng với lãi suất ưu đãi là 9% /năm. Ông ta muốn hoàn nợ cho ngân hàng theo cách: Sau đúng
một năm kể từ ngày vay, ông bắt đầu hoàn nợ; hai lần hoàn nợ liên tiếp cách nhau đúng một năm,
số tiền hoàn nợ ở mỗi năm là như nhau và ông A trả hết nợ sau đúng 10 năm kể từ ngày vay. Biết
rằng mỗi năm ngân hàng chỉ tính lãi trên số dư nợ thực tế của năm đó. Hỏi số tiền mỗi tháng ông
ta cần trả cho ngân hàng gần nhất với số tiền nào dưới đây?
A. 155,820 triệu đồng. B. 146,947 triệu đồng.
C. 166,8 triệu đồng.
D. 236, 736 triệu đồng.
Câu 20. Ông A vay ngân hàng 500 triệu đồng với lãi suất 1%/tháng. Ông ta muốn hoàn nợ cho ngân hàng
theo cách: Sau đúng một tháng kể từ ngày vay, ông bắt đầu hoàn nợ; hai lần hoàn nợ liên tiếp cách
nhau đúng một tháng, số tiền hoàn nợ ở mỗi tháng là 12 triệu đồng. Biết rằng mỗi tháng ngân
hàng chỉ tính lãi trên số dư nợ thực tế của tháng đó. Hỏi số tháng mà ông A cần trả hết nợ ngân
hàng là bao nhiêu kể từ khi vay? (tháng cuối cùng có thể trả số nợ không quá 12 triệu đồng) A. 55 tháng.
B. 54 triệu đồng.
C. 56 triệu đồng.
D. không bao giờ trả hết nợ.
Câu 21. Ông A là một người già không có khả năng lao động, trước khi không thể lao động kiếm sống ông
ấy có dành dụm được một khoản tiền để gửi tiết kiệm ngân hàng với lãi suất ưu đãi dành cho
người già là 0,9% tháng. Sau khi gửi tiết kiệm ngân hàng, đủ mỗi tháng gửi, ông A đến ngân
hàng rút ra một khoản tiền là 5 triệu đồng để chi tiêu hàng ngày. Sau đúng 5 năm kể từ ngày gửi
tiết kiệm, số tiền tiết kiệm còn lại của ông ấy là 100 triệu đồng. Hỏi số tiền ban đầu mà ông A gửi
tiết kiệm là bao nhiêu? (lấy kết quả gần đúng)
A. 289, 440 triệu đồng. B. 291,813 triệu đồng.
C. 287, 044 triệu đồng. D. 233, 663 triệu đồng.
D. PHƯƠNG TRÌNH – BẤT PHƯƠNG TRÌNH CƠ BẢN
1. Đạo hàm của hàm số mũ và lôgarit uu  ( u )  . u e
ue .  ( u )  . u a
ua .lna.  (ln u)    (log u)   u a u lna
2. Phương trình mũ – lôgarit
Đặt điều kiện trước khi giải. Ta có một số kết quả cần nhớ sau: x
a b  0  x  log b.  log b
x b x a . a a f (x ) g(x )  aa
f (x)  g(x).  log f (x)  log g(x)  f (x)  g(x). a a
3. Bất phương trình mũ và lôgarit
Đặt điều kiện trước khi giải. Giải xong được tập nghiệm nhớ giao (lấy phần chung) với điều kiện. x
a b x  log b a f (x ) g(x )  aa
f (x)  g(x)
Nếu a  1 
(cùng chiều)  log b
x b x a a
 log f (x)  log g(x)  f (x)  g(x) a ax
a b x  log b a f (x ) g(x )  aa
f (x)  g(x)
0  a  1 
(ngược chiều)  log b
x b x a a
 log f (x)  log g(x)  f (x)  g(x) a a
4. Các phương pháp giải phương trình, bất phương trình mũ và lôgarit: Biến đổi tương đương, Đặt ẩn
phụ, Sử dụng tính đơn điệu hàm số, sử dụng đánh giá bằng bất đẳng thức,…. Câu 1.
Nghiệm của phương trình log 2x 1  2 là: 3   9 7 A. x  3 . B. x  5 . C. x  . D. x  . 2 2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
NGUYỄN BẢO VƯƠNG - 0946798489 2 Câu 2.
Tập nghiệm của bất phương trình x 1  x x9 5  5 là A. 2; 4 . B. 4; 2 . C.  ;
 2  4;  . D.  ;  4   2;  . Câu 3.
Nghiệm của phương trình x 1 3   27 là
A. x  4 .
B. x  3 .
C. x  2 .
D. x  1 . Câu 4.
Tập nghiệm của bất phương trình 9x 2.3x   3  0 là
A. 0;  .
B. 0;  .
C. 1; .
D. 1; . Câu 5.
Nghiệm của phương trình log
2x 1  3  0 là 3   A. 1. B. 5. C. 14. D. 4 . 2 Câu 6.
Tập nghiệm của phương trình x x 1 2   2 là
A. T  1;  2 .
B. T    1 .
C. T    2 .
D. T  1;  2 . Câu 7.
Nghiệm của phương trình log 3  2x  1 là 7   2 A. . B. 1. C. 3. D. 2  . 3 Câu 8.
Nghiệm của phương trình log (x  5)  2 là: 3
A. x  4 .
B. x 14 .
C. x  2 .
D. x  9 . Câu 9.
Nghiệm của phương trình 42 7 x  49  0 là 3 A. 2 . B. 1. C. 3. D. . 2
Câu 10. Số nghiệm của phương trình  2
log x  2x  9  1 là: A. 1. B. 2 .
C. Vô nghiệm. D. 3 . x 1
Câu 11. Nghiệm của phương trình 3 1 5  là 25 1 A. . B. 1. C. 1  . D. 3 . 3 x 2 2 x3
Câu 12. Nghiệm của phương trình 2  3  2  3 là: 1
A. x  5 . B. x  .
C. x  1 .
D. x  1. 3 2
Câu 13. Nghiệm của phương trình x 3 2 x  16 là x  1  x  1  x  1 A.  . B.  . C.  . D. x  4 . x  4  x  4  x  4  x 1
Câu 14. Nghiệm của phương trình 3 25  là: 25
A. x  1 . B. x  1  .
C. x  2 .
D. x  2 . x 1
Câu 15. Nghiệm của phương trình 2 1 2  là 4 1 3 1 3 A. x    .
B. x    C. x  . D. x  . 2 2 2 2
Câu 16. Tập nghiệm của bất phương trình log  2
x  2x  1 là: 3  A.  ;  3
   1;  . B.  3   ;1 . C.  ;   
3 1;  . D. 1:  .
Câu 17. Tập nghiệm của bất phương trình 4x 5.2x   4  0 là A.  ;
 0  2;  . B. 0; 2 . C.  
;1  4;  . D. 1;4 .
Câu 18. Nghiệm nhỏ nhất của phương trình log  2
x  3x  5  1 là 5 
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 A.  3 . B. 1. C. 3 . D. 0 .
Câu 19. Tập nghiệm của bất phương trình log  2 x  3  log 3x 1 là 3  3    1   1  A. ;  1 2;  .
B.  ;1 2;    . C.  ;1 . D. 2;   . 3       3 
Câu 20. Bất phương trình log  2
x  2x 1  1 có tập nghiệm là 2  A. 1 2; 1   2  . B.  ;  1   2   1   2;  . C. x  1  . D. . x x2  1   1 
Câu 21. Tập nghiệm của bất phương trình   3  0     là  4   2  A.  3   ;1 . B. 0;  . C. ;  
3 1;  . D. ;0 .
Câu 22. Tập nghiệm của phương trình log  2 x  3x  1  là: 0,25   3  2 2 3  2 2   A.   4 . B. 1;   4 . C.  ;  . D. 1;  4 .  2 2    2 2 x 1  x 3x5  1   1 
Câu 23. Tập nghiệm của bất phương trình      là  3   3  A.  1  ; 6 . B.  6  ;  1 .
C. ; 61;  .D. ;   1 6;   . 1 1
Câu 24. Nghiệm của phương trình 4 x  là 16 1 1 A. x    B. x  2.  C. x  . D. x  2. 2 2 1
Câu 25. Tập nghiệm của bất phương trình log  2
x  2x  3  là 4  2 A.  3  ;  1 . B.  ;  3    1;  . C.  3   ;1 . D. 1 6; 3   1; 1   6 .
Câu 26. Tập nghiệm của bất phương trình 2x x ee  6  0 là A. 3; 2 . B.  ; 2 . C. ;ln 2 . D. ln 2; .
Câu 27. Tổng bình phương các nghiệm của phương trình log  2
x  5x  7  0 1  bằng 2 A. 6 . B. 5 . C. 13 . D. 25 . 2 5 x4 x x8
Câu 28. Tập nghiệm của bất phương trình  2    2  là A.  2  ;  6 . B. ( ;  2
 ] [6; ) . C.  6  ; 2. D. ( ;  6  ] [2; ) .
Câu 29. Tìm nghiệm của phương trình log x  5  3 . 2  
A. x  14 . B. x  11 . C. x  8 . D. x  13 .
Câu 30. Tìm tập nghiệm của bất phương trình sau: log  x  2  1. A. x  2  . B. 2   x  8. C. x  8 . D. x  8  .
Câu 31. Tập nghiệm của bất phương trình 2
log x  log x  6  0 là 2 2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
NGUYỄN BẢO VƯƠNG - 0946798489  1   1   1   1  A. 0;  8;    . B. 0;  8;     . C. ;8   . D. ;  8;     . 4     4   4   4 
Câu 32. Phương trình 2x 1
5   125 có nghiệm là 5 3 A. x  . B. x  1 . C. x  3 . D. x  . 2 2
Câu 33. Tập nghiệm của bất phương trình log x 1  log 2x 1 là 0,5   0,5    1  A. ; 2 . B. 2;  . C.  2  ;  2 . D. ; 2  . 2    2
Câu 34. Phương trình x 2 3
x  1 có nghiệm là
A. x  0 , x  2 .
B. x  0 , x  2  . C. x  1  , x  3 .
D. x 1, x  3  .
Câu 35. Tìm tập nghiệm của bất phương trình log  x  2  log  x  5  1. A. x  2  . B.  . C. x  0 .
D. 7  x  0 .
Câu 36. Tập nghiệm của bất phương trình 2 2
log x  2 log x  3  0 là 3 3 A. 3;27 . B.  ;
 3  27;  . C. 3; 27 .
D. 0;3 27;  . 2
Câu 37. Tìm tập nghiệm S của phương trình 2
5 x x  5 .  1   1  A. S  . B. S  0  ;  .
C. S  0;  2 .
D. S   ;1 .  2  2 
Câu 38. Tập nghiệm của bất phương trình 3log  x   1  log 2x 1  3 3 3   3  1   1  A. 1; 2 . B. ; 2  . C. ; 2  . D. 2;  . 2      2 
Câu 39. Phương trình x2 2  8 có nghiệm là
A. x  6 . B. x  10 . C. x  14 . D. x  5 .
Câu 40. Tìm số nghiệm nguyên của bất phương trình log  2
x  2x  1  1 3  A. 2. B. 3. C. 1. D. 4.
Câu 41. Tập nghiệm của bất phương trình 2
log x  2 log x  3  0 là 1 1 5 5  1   1  A. 0;  5;    . B.  ;   5;     . 125     125   1   1  C. ;5   . D. 0;  5;     .  125   125 
Câu 42. Số nghiệm của phương trình log  2
x  2x  4  2 là: 2  A. 2 . B. 1. C. 0 . D. 3 . 2
Câu 43. Tập nghiệm của bất phương trình x 2 2 x  8 là A. ( ;  1  ) .
B. (3; ) . C. ( 1  ;3) . D. ( ;  1
 )  (3; ) .
Câu 44. Tập nghiệm của phương trình log  x 5  x   1 6     là A. 2;  3 . B. 4;  6 . C. 1;  6  . D.  1  ;  6 . 2 x 4 x  1 
Câu 45. Tập nghiệm của bất phương trình  27   là  3 
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 A. ( ;  1  ) .
B. (3; ) . C. ( 1  ;3) . D. ( ;
 1)  (3; ) .
Câu 46. Phương trình ln x  ln 2x  
1  0 có bao nhiêu nghiệm? A. 0 . B. 1. C. 2 . D. 3 .
Câu 47. Phương trình  2
log 72  x   2 log x có nghiệm là: A. 1. B. 2 . C. 6 . D. 4 . x x  1 
Câu 48. Số nghiệm nguyên dương của bất phương trình 2 5    là  25  A. 0 . B. 1. C. 2 . D. 3 .
Câu 49. Tập nghiệm của phương trình 2
ln(2x x 1)  0 là  1   1  A.   0 . B. 0 ;  . C.   . D.  .  2   2 
Câu 50. Tập nghiệm của bất phương trình: log (5x  2)  log 3x  6 là: 0,4 0,4    2  A.  ;  2. B. 0; 2. C.  ; 2 .  
D. 2; .  5  2
Câu 51. Phương trình x 2x 1 4
  0.125 có bao nhiêu nghiệm? A. 0 . B. 1. C. 2 . D. 3 .
Câu 52. Tập nghiệm của bất phương trình x 1  x2 x2 x 1 3 6 3 6     là:  1 
A. ;  log 5 .
B.  log 5; 0 .
C.  log 5;  . D. ;  . 2  2  2     10  2 x4 5 x 1  1
Câu 53. Tìm tập nghiệm của bất phương trình:  10  3   10  3 ?
A. 1;  . B. ;  1 .
C. 5; .
D. ;5. x
Câu 54. Phương trình  52 1  log 32 có nghiệm là 2 2 3 1
A. x  1 . B. x  . C. x  . D. x  . 3 2 2
Câu 55. Tìm số nghiệm nguyên của bất phương trình: log (2x  5)  2 ? 1 3 A. 4. B. 5. C. 6. D. Vô số.
Câu 56. Cho phương trình 2x 1  0 x4 3  6.3  2  0   1 . Nếu đặt x5 t  3
t  0 thì  
1 trở thành phương trình nào? A. 2
9t  6t  2  0 . B. 2
t 18t  2  0 . C. 2
t  2t  2  0 . D. 2
9t  2t  2  0 .
Câu 57. Nghiệm của phương trình 36 2 x  1 là 1 1 A. x  . B. x  3 . C. x  2 . D. x  . 3 2
Câu 58. Nghiệm của phương trình log 2x  2  3 là 2   A. x  3 . B. x  2 . C. x  4 . D. x  5 .
Câu 59. Tích hai nghiệm của phương trình 2
log x  6 log x  8  0 bằng 3 3 A. 90 . B. 729 . C. 8 . D. 6 .
Câu 60. Tìm tập nghiệm của phương trình 2
log(x  6x  7)  log(x  3) . A. 4;  5 . B.   5 . C. 3;  4 . D.  .
Câu 61. Tính tổng các nghiệm của phương trình  2
log x  3x   1  9 .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
NGUYỄN BẢO VƯƠNG - 0946798489 A. 3 . B. 9 . C. 9 10 . D. 3 .
Câu 62. Phương trình log x  3  log
x 1  3 có nghiệm là một số 2   2   A. chẵn. B. chia hết cho 3 . C. chia hết cho 7 . D. chia hết cho 5 .
Câu 63. Tổng tất cả các nghiệm của phương trình log
9  5x  1 x bằng 5   A. 2 . B. 1. C. 9 . D. 5 .
Câu 64. Tổng tất cả các nghiệm của phương trình log(8.5x  20x )  x  log 25 bằng A. 16 . B. 3 . C. 25 . D. 8 .
Câu 65. Tổng tất cả các nghiệm của phương trình 2 3 x (2x 9).3x 9.2x     0 bằng A. 3 . B. 2 . C. 0 . D. 2  .
Câu 66. Phương trình 2 log 3x 1 2 log 3x  
1  3  0 có 2 nghiệm x ;
x (x x ) và 2   2   1 2 1 2  a a x x  log
với a, b   , b  0 và
là phân số tối giản. Tính a b . 1 2 3    b b
A. a b  5  .
B. a b  5 .
C. a b  11.
D. a b  1.
Câu 67. Tổng tất cả các nghiệm của phương trình log
9  4x  1  x bằng: 4   A. 2 . B. 1. C. 4 . D. 3 .
Câu 68. Số nghiệm của phương trình log
6  7x x 1 bằng: 7   A. 2 . B. 3 . C. 0 . D. 1.
Câu 69. Tổng tất cả các nghiệm của phương trình 2
ln(x  5x  4)  log 2.ln10 bằng A. 1. B. 6 . C. 7 . D. 5 .
Câu 70. Tổng tất cả các nghiệm của phương trình log  x 1
4.3  1  2x 1 bằng: 3  A. 1. B. 2 . C. 7 . D. 3 .
Câu 71. Số nghiệm của phương trình log 9  2x  5  x bằng: 2   log5 3  A. 2 . B. 1. C. 7 . D. 3 .
-------------------- HẾT --------------------
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 Vấn đề 9
HÀM SỐ LŨY THỪA - MŨ - LOGARIT
A. BIẾN ĐỔI CÔNG THỨC
CÁC CÔNG THỨC MŨ – LOGARIT CẦN NHỚ
Cho a và b là các số thực dương, x và y là những số thực tùy ý.  n a  a.a.a...a  x x a a       x   n số a b b  xy x y a  a .a x  y x y a  a y 2; y      x   a  1   0 u x x y n a   a  .     y n  u x 1, a a        x   0  y x   x.y   x    y a a a   n n n
a. b  ab n  2; n       x x x a .b a.b  m    m m n n n a a  a
Cho 0  a  1 và b, c  0 .  x log b  x  b  a b a  log  log b  log c a a a c 1  log b khi   log    a lẻ  b log b  a a   log b  a  log b khi   chẵn a  log b 1 ln b  c log b   log b  , log b  a log a a log a a ln a c b  log 1  0, log a  1  log c log a log b a  c  b  a a a b b a
 log b.c  log b  log c ln  b  log b a   a a   e  lg  b  log b  log b  10 
MỨC ĐỘ NHẬN BIẾT Câu 1.
Với a là số thực dương tùy ý, 2 log a bằng: 2 1 1
A. 2  log a . B.  log a . C. 2 log a . D. log a . 2 2 2 2 2 2 Lời giải Chọn C
Với a  0; b  0; a  1. Với mọi  . Ta có công thức: log b   log . b a a Vậy: 2
log a  2 log a . 2 2 Câu 2.
Với a là hai số thực dương tùy ý, log  3 a bằng 2  3 1 A. log a .
B. log a .
C. 3  log a .
D. 3 log a . 2 2 2 3 2 2 Lời giải Chọn D Ta có: log  3 a  3 log a. 2  2 Câu 3.
Cho a là số thực dương khác 1. Tính log a . a
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489 1 A. 2. B. 2  . C. . D. 1. 2 Lời giải Chọn A Ta có: log a  log
a  2 log a  2 . 1 a a 2 a 3  a Câu 4.
Cho a là số thực dương khác 4. Tính I  log . a   64 4   1 1 A. I  3 . B. I  . C. I  3 . D. I   . 3 3 Lời giải Chọn A 3 3  a   a  Ta có I  log  log  3 . a     64 a  4  4   4 Câu 5.
Cho 0  a  1 . Giá trị của biểu thức P   3 2 log . a a là a  4 5 5 A. . B. 3 . C. . D. . 3 3 2 Lời giải Chọn C 2   5 5 Ta có: P   3 2 log . a a 3  log . a a 3  log a  . aa   a   3 Câu 6.
Giá trị của A  log 3.log 4.log 5....log 64 bằng 2 3 4 63 A. 5 . B. 4 . C. 6 . D. 3 . Lời giải Chọn C
Áp dụng công thức đổi cơ số, ta có 6
A  log 3.log 4.log 5...log 64  log 4.log 5...log 64  log 64  log 2  6 . 2 3 4 63 2 4 63 2 2 Câu 7.
Với các số thực a,b  0 bất kì, rút gọn biểu thức 2
P  2log a  log b ta được 2 1 2 2  a   2a A. P  log  2 2ab . B. P  log ab . C. P  log . D. P  log . 2  2 2  2   2    b  2  b Lời giải Chọn B Ta có 2
P  2log a  log b  log a  log b  log ab . 2 2 2  2 2 2 2 1 2 2 5  a b Câu 8.
Với a , b là hai số thực dương, log bằng 5   25  
A. 2 log a  5log b  25 .
B. 2 log a  5log b  2 . 5 5 5 5
C. 2 log a  5log b  25 .
D. 2 log a  5log b  2 . 5 5 5 5 Lời giải Chọn D 2 5  a b  Ta có log  log    2 5
a b   log 25  log  2 a   log  5 b
 log 25  2 log a  5log b  2 . 5 5 5 5 5  5 5 5 25  
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 Câu 9.
Cho a là số thực dương bất kì, giá trị nào dưới đây có cùng giá trị với 3 log(10a )? A. 3log a B. 3 10 log a C. 1 3log a D. 3log(10a) Lời giải Chọn C Ta có 3 3
log(10a )  log10  log a  1 3log a
Câu 10. Với a , b là hai số dương tùy ý,  6 7
log a b  bằng 1 1
A. 6 log a  7 log . b
B. 6 log a  7 log . b C. log a  log . b
D. 42 log ab 6 7 Lời giải Chọn A Có  6 7 a b  6 7 log
 log a  log b  6 log a  7 log b .
Câu 11. Cho a là số thực dương khác 1. Tính 3 I  3log a a 1 1 A. I  1. B. I  9 . C. I  . D. I  . 9 3 Lời giải Chọn A Ta có 3 I  3log
a  log a  1. a a
Câu 12. Với a và b là các số thực dương. Biểu thức  5 log a b bằng a  1
A. 5  log b .
B. 5  log b .
C. log b . D. 5log b . a a 5 a a Lời giải Chọn B Ta có:  5 a b 5 log
 log a  log b  5  log b . a a a a
Câu 13. Cho các số thực dương a , b thỏa mãn 2 log a  5log b  1 . Mệnh đề nào sau đây đúng. A. 2 5 a b  10 .
B. 2a  5b  10 .
C. 2a  5b  1. D. 2 5
a b  10 . Lời giải Chọn A
Ta có: 2 log a  5 log b  1 2 5
 log a  log b  1   2 5 log a b  1 2 5  a b  10 . 1  
Câu 14. Cho b là số thực dương khác 1. Tính 6 2 P  log b .b . b     7 13 A. P  3 . B. P  . C. P  . D. P  6 . 2 2 Lời giải Chọn C 1   13 13 Ta có 6 2 P  log b .b 2  log b  . b   b   2 4  a
Câu 15. Với a , b là hai số dương tùy ý, log  bằng 5  b   4 4
A. 4 log a  5log b .
B. 4 log a  5log b . C.
log a  logb . D. log a  log b . 5 5 Lời giải Chọn B
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489 4  a  Có 4 5 log
 log a  log b  4 log a  5log b  . 5  b    a
Câu 16. Cho a và b là hai số thực dương thỏa mãn log  log
a . Mệnh đề nào dưới đây đúng? 2   1    b  2
A. b  1. B. 2
b a .
C. a b . D. 2 a b . Lời giải Chọn D a   a   a   a 1 Ta có: log  log a  log   log a  log  log a    a b . 2   2   1 2 2   1   2   2  b   b   b b a 2
Câu 17. Cho 0  a  1. Giá trị của biểu thức P   3 log . a a là a  1 4 5 A. . B. 3 . C. . D. . 3 3 3 Lời giải Chọn C 1   4 4 Ta có: P   3 log . a a 3  log . a a 3  log a  . aa   a   3
Câu 18. Với a là số thực dương bất kỳ, mệnh đề nào dưới đây đúng? 1
A. log 7a  7 log a . B. 7 log a  log a . 7 1 C. 7
loga  7 log a .
D. log 7a  log a . 7 Lời giải Chọn C
Vì với a  0 thì 7 loga  7 log a
Câu 19. Cho a và b là các số thực dương bất kì. Chọn khẳng định sai. 1 A. 3 5
ln a  ln b  3ln a  ln b .
B. log a  log b  log ab . 5 a C. ab2 log 10
 10  log a  log b . D. ln
 ln a  ln b . b Lời giải Chọn C 2
Ta có: log 10ab  2 log 10ab  2  2 log a  2 log b .
Câu 20. Với a là số thực dương tùy ý, log  2 9a bằng: 3  A. 2log a .
B. 3 2log a .
C. 2  2log a . D. 4log a . 3 3 3 3 Lời giải Chọn C Ta có log  2 9a  2
 log 9  log a  2  2 log a 3 3 3 3
Câu 21. Với a , b là hai số dương tùy ý,  3 4
log a b  bằng 1 1
A. 3log a  4 log . b
B. 4 log a  3log . b C. log a  3log . b
D. 2 log a  log . b 4 3 Lời giải Chọn A
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 Có  3 4 a b  3 4 log
 log a  log b  3 log a  4 log b .
Câu 22. Đặt log 5  a , khi đó log 64 bằng 4 25 3a 3 2 2a A. . B. . C. . D. . 2 2a 3a 3 Lời giải Chọn B 3 3 Ta có 3 log 64  log 4  log 4  . 2 25 5 5 2 2a 5  3a
Câu 23. Với a , b là hai số dương tùy ý, log bằng 3  2  b  
A. 1 2 log a  5 log .
b B. 5  5log a  2 log . b 3 3 3 3
C. 1 5 log a  2 log .
b D. 51 log a  2log b . 3 3  3 3 Lời giải Chọn C 5  3a  Có log  log 3a
 log b  log 3  log a  2 log b  1 5log a  2 log . b 2   5  2 5 3 3 3 3 3 3 3 3 b  
Câu 24. Đặt log 3  a , khi đó log 16 bằng 12 9 1 a 1 a a a A. . B. . C. . D. . a a 1 a 1 a Lời giải Chọn A 12 log12 log 4 1 a Ta có 12 3 log 16  log 4    . 9 3 log 3 a a 12 5  3a
Câu 25. Với a , b là hai số dương tùy ý, log bằng 3  2  b  
A. 1 2 log a  5 log .
b B. 5  5log a  2 log . b 3 3 3 3
C. 1 5 log a  2 log .
b D. 51 log a  2log b . 3 3  3 3 Lời giải Chọn C 5  3a  Có log  log 3a
 log b  log 3  log a  2 log b  1 5log a  2 log . b 2   5  2 5 3 3 3 3 3 3 3 3 b   5  b
Câu 26. Với a , b là hai số dương tùy ý, log  bằng 3  10a  
A. 5log b 1 3log . a
B. 5log b  31 log a.
C. 5log b  3  3log .
a D. 5log b 1 3log . a Lời giải Chọn D 5  b  Có 5 log  log b  log    3 10a  3
 5log b  log10  log a   5log b 1 3log . a 3 10a    
Câu 27. Đặt log 9  a , khi đó log 18 bằng 2 3
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489 2  2a a a 2a  2 A. . B. . C. . D. . a 2  2a 1 a a Lời giải Chọn D 1 2 2 2a  2
Ta có log 18  log 2  2   2   2   2  . 3 3 log 3 log 9 a a 2 2 3  b   
Câu 28. Với a , b , c là ba số dương tùy ý, log  bằng 2   ac 
A. 3 log b  log a  2 log c .
B. 3 log b  log a  2 log c .
C. 3log b log a  2 log c .
D. 3log blog a 2log c . Lời giải Chọn A 3  b  Có 3 log  log b     2 log a  log c
 3log b  log a  2 log b . 2  ac  
Câu 29. Đặt log 4  a , khi đó log 24 bằng 6 36 1 2 a
A. a 1 . B. a   1 . C. . D. . 2 a 1 2 Lời giải Chọn B 1 1 1 Ta có log 24  log 6.4   log 4  a 1 . 2 36   6   6 2 2 2 3  100m
Câu 30. Với m , n là hai số thực dương tuỳ ý, log  bằng 2  n  
A. 2  3log m  2 log n . B. 2  3log m  2 log n . 1 1 1 C. 2
  3log m  2 log n . D.  log m  log n . 2 3 2 Lời giải Chọn A 3  100m  Ta có 3 2 log
 log100  log m  log n  2  3log m  2 log n  2  3log m  2 log n  . 2  n  
Câu 31. Đặt a  log 15 , khi đó log 27 bằng 3 25 3a   1 3 2 2 a   1 A. . B. . C. . D. . 2 2a   1 3a   1 3 Lời giải Chọn B 3 3 1 3 Ta có: log 27  log 3  .  . 25 5 2 2 log 5 2 a 1 3  
Vì a  log 15  log 3.5  1 log 5  log 5  a 1. 3 3   3 3
Câu 32. Với a , b là hai số thực tuỳ ý,  2 4
log a b  bằng
A. 2 log a  4 log b .
B. 2 log a  4 log b .
C. 2 log a  4 log b .
D. 2 log a  4 log b . Lời giải Chọn D Ta có  2 4 a b  2 4 log
 log a  log b  2 log a  4 log b .
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Câu 33. Đặt a  log 2 , khi đó log 81 32 e bằng 3 5a 4 5 4a A. 4 e . B. 5 e a . C. 4 e a . D. 5 e . Lời giải Chọn B 4 1 4 4 . log2 3 Ta có: log32 81 5 log3 2 5 5 e e e e a    .
Câu 34. Với a , b là hai số thực dương tuỳ ý,  3 5
ln e.a b  bằng
A. 5ln a  3ln b .
B. 3ln a  5ln b .
C. 1 3ln a  5ln b .
D. 1 5ln a  3ln b . Lời giải Chọn C Ta có  3 5 a b  3 5 ln e.
 ln e  ln a  ln b  1  3ln a  5 ln b .
Câu 35. Đặt a  log 2 , khi đó log  125 ln e bằng 16  5 3a 3 4 4a A. . B. . C. . D. . 4 4a 3a 3 Lời giải Chọn B 3 3 1 3 Ta có: log  125 ln e  log 125  log 5  .  . 16  16 2 4 4 log 2 4a 5 4 2  a b
Câu 36. Với a , b là hai số thực dương, log bằng 2   16  
A. 2 log a  4 log b  4 . B. 4 log a   1  2 log b .
C. 2 log a  4 log b  4 . D. 4log a 1  2log b . 2  2 2 2 Lời giải Chọn D 4 2  a b  Ta có 4 2 log
 log a  log b  log 16  4 log a  2 log b  4  4 log a 1  2 log b . 2   2 2 2 2 2  2  2 16  
Câu 37. Cho 5a  7 . Tính log 125 theo a . 49 3a 3 2 2a A. . B. . C. . D. . 2 2a 3a 3 Lời giải Chọn B 3 3 1 3 1 3 Ta có: log 125  log 5  .  .  . 49 7 2 2 log 7 2 log 5a 2a 5 5
Câu 38. Rút gọn biểu thức 2 log a 3 2 P  3  log a .log 25 . 5 a A. 2 a  2 . B. 2 a  2 . C. 2 a  4 . D. 2 a  4 . Lời giải Chọn D a  0 Điều kiện:  . a  1  2 Ta có: 2 log3 a 2 P  3  log a .log 25  3 a  2 log a . 2 log 5 2
a  4 log a.log 5 5 a  log3   5   a  5 a 2  a  4 .
Câu 39. Cho a là số thực dương khác 1. Tính log a . a
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
NGUYỄN BẢO VƯƠNG - 0946798489 1 A. 2 . B. 2  . C. . D. 1. 2 Lời giải Chọn A Ta có: log
a  log a  2log a  2 . 1 a a 2 a a
Câu 40. Giá trị của  a 3log 4 ;a  0, a  1 bằng A. 2 . B. 3 . C. 4 . D. 8 . Lời giải Chọn D 3 3 3 3log 4 a log 4 2 Ta có  a a log 4 2 a 2  aa  4  8 . 3 5
Câu 41. Rút gọn biểu thức 2 2
R  log b  log b (với a  ;
0 a  1 và b  0 ). 2 a a 15 11 15 A. R  log b . B. 4 log b . C. log b . D. log b . 4 a a 4 a 8 a Lời giải Chọn C 3 5 3 5 11 2 2
R  log b  log b  log b  log b  log . b 2 a 2 a 4 a 4 a a 3 5
Câu 42. Rút gọn biểu thức 2 2
R  log b  log b (với a  ;
0 a  1 và b  0 ). 2 a a 15 11 15 A. R  log b . B. 4 log b . C. log b . D. log b . 4 a a 4 a 8 a Lời giải Chọn C 3 5 3 5 11 2 2
R  log b  log b  log b  log b  log . b 2 a 2 a 4 a 4 a a
Câu 43. Với a và b là hai số thực dương tùy ý, log  3 4 a b bằng 2  1 1 A. log a  log b
B. 3log a  4 log b
C. 2log a  log b D. 4 log a  3log b 2 4  2 2 3 4 2 2 2 2 Lời giải Chọn B Ta có: log  3 4 a b  3 4
 log a  log b  3 log a  4 log b . 2 2 2 2 2
MỨC ĐỘ THÔNG HIỂU
Câu 44. Xét tất cả các số dương a và b thỏa mãn log a  log (ab) . Mệnh đề nào dưới đây đúng? 2 8 A. 2 a b . B. 3 a b .
C. a b . D. 2 a b . Lời giải Chọn D Theo đề ta có: 1
log a  log (ab)  log a
log (ab)  3log a  log (ab) 2 8 2 2 2 2 3 3 3 2
 log a  log (ab)  a ab a b 2 2
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Câu 45. Xét số thực a và b thỏa mãn log
3a.9b  log 3 . Mệnh đề nào dưới đây đúng 3   9
A. a  2b  2 .
B. 4a  2b  1 .
C. 4ab  1.
D. 2a  4b  1. Lời giải Chọn D Ta có:
log 3a.9b   log 3  log  a 2 3 .3 b  log 3 3 9 3  2 3 1 ab 1 2 2  log 3
 log 3  a  2b
 2a  4b  1. 3 3 2
Câu 46. Cho a và b là hai số thực dương thỏa mãn 3
ab  27 . Giá trị của log a  6 log b bằng 3 3 A. 3 . B. 6 . C. 9 . D. 1. Lời giải Chọn B
Sử dụng quy tắc logarit một tích ta có:
1 log a 3log b  log  3 ab
 3  log a  6 log b  6 . 3 3 3  3 3 2 4
Câu 47. Cho a và b là hai số thực dương thỏa mãn log a
log b  2 . Giá trị của 3 4 a .b bằng 2 2 3 A. 8 . B. 6 . C. 64 . D. 32 . Lời giải Chọn C
Sử dụng quy tắc logarit một tích cho hai số dương a và b ta có 4 log a
log b  2  3log a  4 log b  6  log  3 4 a .b  3 4 6 3 4
 6  a b  2  a b  64 . 2 2 2 2 2 3 5 a 1
Câu 48. Cho a và b là hai số thực dương thỏa mãn 
. Giá trị của 5log a  2log b 2 b 9 3 3 1 1 A. . B. . C. 2 . D. 2  . 3 2 Lời giải Chọn D
Sử dụng quy tắc logarit một thương cho hai số dương a và b ta có 5  a   1 5 2 
5 log a  2 log b  log a  log b  log  log  2  . 3 3 3 3 3  2  3    b   9  1
Câu 49. Cho a và b là hai số thực dương thỏa mãn log a  log b   . Giá trị của 2 4 a .b bằng 4 2 2 1 1 1 A. . B. . C.  . D. 4  . 2 4 4 Lời giải Chọn B
Sử dụng quy tắc logarit một tích cho hai số dương a và b ta có 1 1 1
log a  log b   
log a  log b  
 log a  2 log b  1 4 2 2 2 2 2 2 2 2  log  1 1 2 . a b  2 2 4  1   ab   a b  . 2 2 4 a
Câu 50. Cho a và b là hai số thực dương thỏa mãn 2
log a  log b  2 . Giá trị của bằng 3 1 b 3
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
NGUYỄN BẢO VƯƠNG - 0946798489 1 1 A. 9 . B. 3 . C. . D. . 9 3 Lời giải Chọn B
Sử dụng quy tắc logarit một thương cho hai số dương a và b ta có 2 2 a a a 2 2
log a  log b  2  log a  log b  2  log  2   9   3 . 3 1 3 3 3 b b b 3
Câu 51. Với các số thực a,b  0 bất kì, rút gọn biểu thức 2 2
P  log a  log b ta được 2 1 2 2 2  a   a A. P  log . B. P  log ab . C. P  log .
D. P  log  2 2 a b . 2  2  2 2   1    b   b  2 Lời giải Chọn B Ta có 2 2
P  log a  log b  log a  log b  log ab . 2 2 2  2 2 2 2 1 2
Câu 52. Với mọi số thực dương a và b thoả mãn 2 2
a b  8ab , mệnh đề nào dưới đây đúng? 1 1
A. log a b  log a  log b .
B. log a b  1 log a  log b . 2 2 1
C. log a b  1 log a  log b .
D. log a b 
 log a  log b . 2 Lời giải Chọn B
Ta có a b ab a ab b
ab  a b2 2 2 2 2 8 2 10  10ab .  a b2 log  log 10ab .
 2 log a b  1 log a  logb . 1
 log a b  1 log a  log b . 2
Câu 53. Cho a và b là hai số thực dương thỏa mãn log b  log
ab . Mệnh đề nào dưới đây đúng? 2 4  
A. a b .
B. a  1 . C. 2 a b  1 . D. 2 a b . Lời giải Chọn A 1
Ta có: log b  log ab  log b  log ab 2
 log b  log ab 2
b ab a b 2 4 2 2 2 2 2
Câu 54. Cho a  0 , b  0 thỏa mãn 2 2
a  4b  5ab . Khẳng định nào sau đây đúng? a  2b log a  log b A. log  .
B. 5log a  2b  log a  log b . 3 2
C. 2 log a  2b  5log a  log b .
D. log a   1  log b  1. Lời giải Chọn A 2 2 Ta có: 2 2 a 4b 5aba 2b 9ab
log a 2b          log 9ab   a  2b a  2b log a  log b
 2.log a  2b  2.log 3  log a  log b  2.log
 log a  log b  log  3 3 2
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 2
Câu 55. Cho a, b là các số thực dương khác 1, thoả log b  log a
. Mệnh đề nào dưới đây là đúng? 3 3 a b 3 3 3
A. a b .
B. b a3 2 3 3  a .
C. b a .
D. a b . Lời giải Chọn D 2
Ta có: log b  log a
 log b  log a  2 3 3 3 a b a b 1  log b   2  b    b
Suy ra: a b . a loga 2 1 0 log 1. log a b a
Câu 56. Cho a  0, b  0 thỏa mãn 2 2
a  9b  10ab .Khẳng định nào sau đây đúng? a  3b log a  log b
A. log a  
1  log b  1 . B. log  . 4 2
C. 3log a  3b  log a  log b .
D. 2 log a  3b  2log a  log b . Lời giải Chọn B a b2 3 Ta có 2 2
a  9b  10ab   ab 16 a b2 3  log
 log ab ( do a  0, b  0 ) 16 a  3b  2 log
 log a  log b 4 a  3b log a  log b  log  . 4 2
Câu 57. Cho các số dương a, b thõa mãn 2 2
4a  9b  13ab . Chọn câu trả lời đúng. 1
A. log 2a  3b  log a  2 log b . B.
log 2a  3b  3log a  2 log b . 4
 2a  3b  1
 2a  3b  1 C. log   
log a  log b. D. log   
log a  log b .  5  2  4  2 Lời giải Chọn C 2a  3b
Ta có 4a  9b  13ab  4a 12ab  9b  25ab  2a  3b2 2 2 2 2  25ab   ab 5
 2a  3b
 2a  3b  1 Suy ra log  log ab  log     
log a  log b .  5   5  2
Câu 58. Cho các số thực x, a, b, c, d dương thoả mãn x   a 4 log 2 log 2
 3log b  4 log c . Biểu diễn x theo
a, b, c được kết quả là: 2 2a 2 4a 2 2a c 2 2a c A. x  . B. x  . C. x  . D. x  . 3 b c 3 b c 3 b 2 b Lời giải Chọn B x   a 4 log 2 log 2
 3log b  4 log c  log x  log  2 4a   log  3
b   log c 2 2 4a 4a log x  log  x  . 3 3 b c b c
Câu 59. Cho a, b  0 , nếu 2
log a  log b  5 và 2
log a  log b  7 thì giá trị của ab bằng: 8 4 4 8
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
NGUYỄN BẢO VƯƠNG - 0946798489 A. 9 2 . B. 72 . C. 9 . D. 18 2 . Lời giải Chọn A 1 2
log a  log b  5 6 2 2
log a  log b  5    log a  6  a  2 3 Ta có: 8 4 2        . 2 3
log a  log b  7 1 log b  3    2 b   2 4 8
log a  log b  7  2 2   3 Suy ra: 6 3 9 ab  2 .2  2 . 3 2
Câu 60. Cho a, b , c là ba số thực dương thỏa mãn a b c  8 . Giá trị của 3log a  log
b  log c bằng 2 1 2 2 A. 8 . B. 4. C. 3 . D. 6 . Lời giải Chọn C
Với các số thực dương a, b , c ta có:
3log a  log b  log c 2 1 2 2 3
 log a  2log b  log c 2 2 2 3 2
 log a  log b  log c 2 2 2  log  3 2
a b c  log 8  3 . 2  2 2 3
Câu 61. Cho a , b , c là ba số thực dương thỏa mãn a b  4c . Giá trị của 2 ln a  3 ln b  ln c bằng A. 2 ln 2 . B. ln 2 . C. 4 . D. 2 . Lời giải Chọn A 2 3 a b
Với các số thực dương a , b , c ta có: 2 3 a b  4c   4 c 2 3 a b Và 2 3
2 ln a  3ln b  ln c  ln a  3ln b  ln c  ln  ln 4  2ln 2 . c 1 2
Câu 62. Cho x và y là hai số thực dương khác 1 thỏa mãn 2
8xy 1. Giá trị của  bằng log 2 log 2 x y A. 3  . B. 3 . C. 4 . D. 4 . Lời giải Chọn A 1
Với x , y là các số thực dương khác 1 ta có: 2 2
8xy  1  xy  . 8 1 2 1 Và 2 
 log x  2.log y  log x  log y  log  2 xy  log  3  . 2 2 2 2 2  2 log 2 log 2 8 x y
Câu 63. Cho log b  2 với a , b  0 , a khác 1. Khẳng định nào sau đây sai? a
A. log ab  3 . B. a b  . C. b  . D. ab  . a  2 log  3 a  2 log  4 a  2 log  4 a Lời giải Chọn D Ta có:
• log ab  log a  log b  1 2  3 . Suy ra phương án A đúng. a a a
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 •  2 a b 2 log
 log a  log b  2  2  4 . Suy ra phương án B đúng. a a a •  2
log b   2log b  2.2  4. Suy ra phương án C đúng. a a •  2 ab  2 log
 log a  log b  1 2.2  5 . Suy ra phương án D sai. a a a
B. HÀM SỐ LŨY THỪA – MŨ - LOGARIT HÀM LŨY THỪA HÀM SỐ MŨ HÀM SỐ LOGARIT y  log xa  0 Dạng: a với  . y  log u a  1 ax Đặc biệt: y aa  0 Dạng: với  . a e   y  ln x ; y xu y a a  1  Dạng: với u là đa a  10 
y  log x  lg x . y u
Tập xác định: D  . 
Điều kiện xác định: u  0 . thức đại số. Đạo hàm: Đạo hàm: x x Tập xác định: y a 
y  a ln a . 1     Nếu ÑK     u  .  y log x y u u y a 
y  a ln . a ua x ln a     . x x Nếu ÑK   u  0. (e )  e u   0
y  log u   y   Đặc biệt: với a ( u e ) u   e . uu ln a Nếu ÑK
   u   0. e  2,71828... 1 (ln x )  Đạo hàm: x Sự biến thiên: x y a . Đặc biệt: .   1 y x 
y   x u
Nếu a  1 thì hàm đồng biến (ln u )  u   1 y u 
y  u  . u
trên  . Nếu 0  a  1 thì hàm Sự biến thiên: y  log x . Nếu a nghịch biến trên  .
a  1 : hàm đồng biến trên (0; ) .
Nếu 0  a  1 : hàm nghịch biến trên (0; ).
ĐỒ THỊ HÀM SỐ MŨ
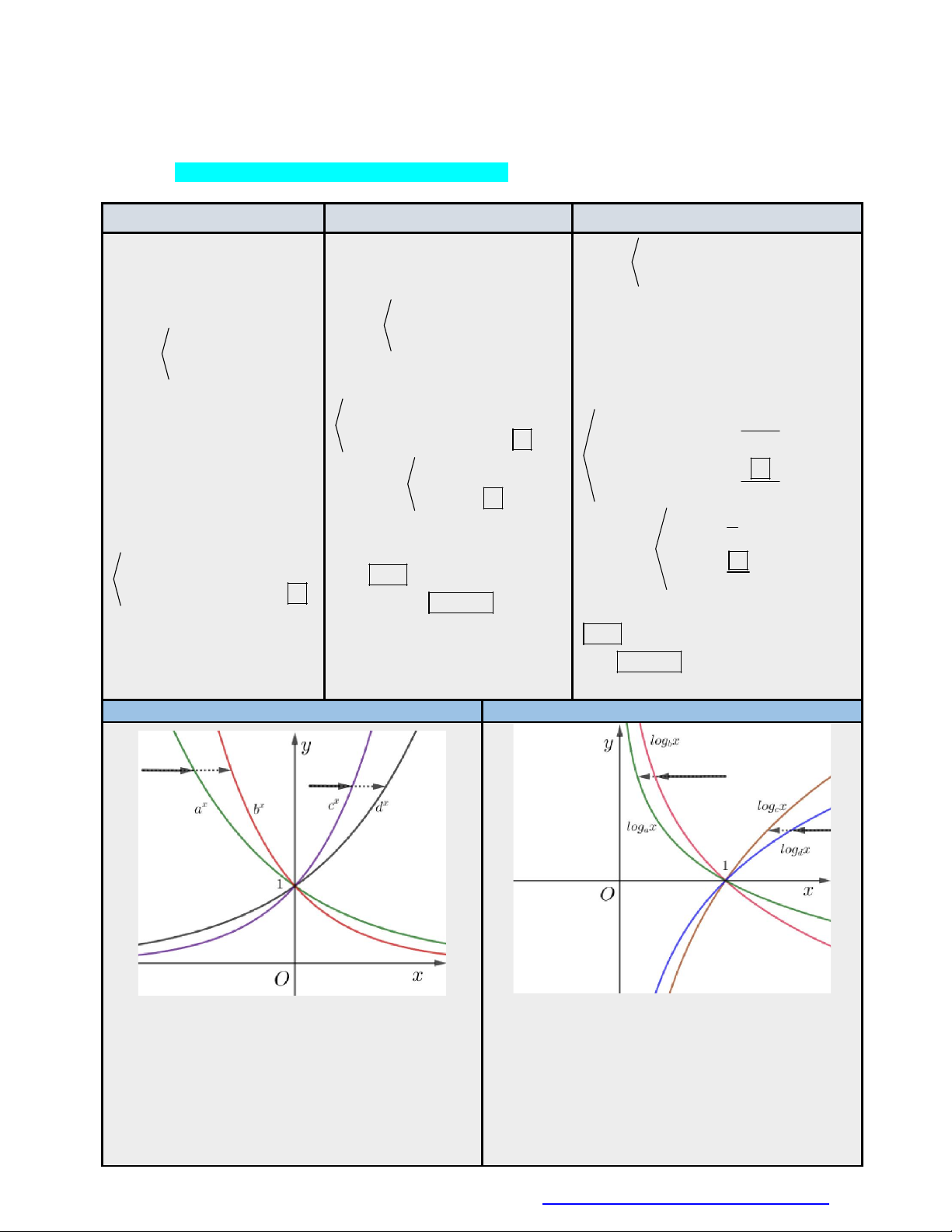
ĐỒ THỊ HÀM SỐ LOGARIT
Ta thấy: x  0   1; x a a
b  0  b  1.
Ta thấy: log x  0  a  1; log x  0  b  1. a b
Ta thấy: x   1; x c c
d  d  1.
Ta thấy: log x  c  1; log x  d  1. c d
So sánh a với b: Đứng trên cao, bắn mũi tên từ trái So sánh a với b: Đứng trên cao, bắn mũi tên từ
sang phải, trúng x
a trước nên a b .
phải sang trái, trúng log x trước: b  . a b
So sánh c với d: Đứng trên cao, bắn mũi tên từ trái So sánh c với d: Đứng trên cao, bắn mũi tên từ
sang phải, trúng x
c trước nên c d.
phải sang trái, trúng log x trước: d  . c d
Vậy 0  b a  1  d  . c
Vậy 0  a b  1  c d .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
NGUYỄN BẢO VƯƠNG - 0946798489 Câu 1.
Tập xác định của hàm số y  log x là 2
A. 0; . B.  ;  .
C. 0; .
D. 2; . Lời giải Chọn C
Điều kiện xác định của hàm số y  log x là x  0 . 2
Vậy tập xác định của hàm số y  log x là D  0;. 2 Câu 2. Đạo hàm của hàm số 2 4 x y  là A. 2 2.4 x y  ln 4 . B. 2 4 . x y  ln 2 . C. 2 4 x y  ln 4 . D. 2 2.4 x y  ln 2 Lời giải Chọn A 2 2.4 x y  .ln 4 . Câu 3. Đạo hàm của hàm số 2018x y  là 2018x A. 2018x y 
ln 2018 . B.   2018x y ln x . C. 2018x y  . D. y  . ln 2018 Lời giải Chọn A Có 2018x y   2018 . x y  ln 2018 . 2 Câu 4. Đạo hàm của hàm số 2 3 2 e x x y    là 2 2 A. 2 x 3 x2 y   2 e
. 2x  3x  2 . B. 2 x 3 x2 y  e .4x  3 . 2 2 C. 2 3 2 e x x y     . D. 2 x 3 x 1 y e    .4x  3 . Lời giải Chọn B 2 2 Có 2 3 2 e x x y     2 x 3 x2 y  e .4x  3 . Câu 5. Hàm số 2 1 2018 x y  
có đạo hàm tại điểm x  1 là A. 4036.ln 2018 . B. y  1  2018.ln 2018 . C. y  1  2018 . D. y  1  4036 . Lời giải Chọn A 2 1 2018 x y    2 x 1 y 2018   
.ln 2018.2  y 
1  2018.ln 2018.2  4036.ln 2018 . Câu 6.
Tính đạo hàm của hàm số 2 3 2 x y   . A. 2 x2 y  2 ln 4 . B. x2 y  4 ln 4 . C. 2 x2 y  2 ln16 . D. 2 x3 y  2 ln 2 . Lời giải Chọn C
Áp dụng công thức đạo hàm  u   . u a
ua .ln a Ta có yx  2x3 2 3     2 ln 2 2 x3  2 ln 4 2 x2  2 ln16 . Câu 7.
Tập xác định của hàm số y  ln 2  x là A.  ;   2 . B.  ;  2 . C.  ;   . D. 0; . Lời giải Chọn B
Hàm số y  ln 2  x xác định  2  x  0  x  2 .
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Vậy tập xác định của hàm số đã cho là  ;  2 . Câu 8.
Tập xác định của hàm số 5x y  là A.  \   0 . B. 0;  . C.  ;   . D. 0;  . Lời giải Chọn C Hàm số 5x y
xác định với mọi x   .
Vậy tập xác định của hàm số đã cho là  ;   .  Câu 9.
Tập xác định của hàm số y   x   2 3 là A.  \   3  . B.  3  ;  . C.  ;   . D.  \  0 . Lời giải Chọn A
Hàm số y   x   2 3
xác định  x  3  0  x  3  .
Vậy tập xác định của hàm số đã cho là  \   3  .
Câu 10. Tìm đạo hàm của hàm số 2x y e . A. 2x y  e . B. 2 1 2 x y xe    . C. 2   2 x y e . D. 2 1 2 x y e    . Lời giải Chọn C Đạo hàm của hàm số 2x y e là:   2x 2 2    .  2 x y x e e .
Câu 11. Tìm đạo hàm của hàm số y  log x . 7 ln 7 1 7 1 A. y  . B. y  . C. y  . D. y  . x x x x ln 7 Lời giải Chọn D 1
Đạo hàm của hàm số y  log x là: y  . 7 x ln 7
Câu 12. Tìm đạo hàm của hàm số 5x y  . 5x A. 5x y  . B. 5x y  ln5 . C. y  . D. 1 5x y x    . ln 5 Lời giải Chọn B Đạo hàm của hàm số 5x y  là: 5x y  ln5.
Câu 13. Hàm số f x   2
log 4  x  có đạo hàm ln10 1
A. f  x  .
B. f  x  . 2 4  x  2 4  x ln10 2  x 2  x
C. f  x  .
D. f  x  .  2 4  x .ln10 2 4  x Lời giải: Chọn C  2  4  x  2  x
Ta có: f  x   .  2 4  x .ln10  2 4  x .ln10
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 14. Hàm số f x   2
ln x x có đạo hàm 2x 1 2 x x
A. f  x  .
B. f  x  .  2 x x.ln10 2x 1 1 2x 1
C. f  x  .
D. f  x  . 2 x x 2 x x Lời giải Chọn D  2  x x 2x 1
Ta có: f  x   . 2 2 x x x x
Câu 15. Hàm số f x 2
 ln x có đạo hàm 2.ln x 2 ln x
A. f  x  .
B. f  x  2.ln x .
C. f  x  .
D. f  x  . x . x ln x x Lời giải Chọn A 2.ln x
Ta có: f x 2.ln . x ln x    . x Câu 16. Hàm số   2 1 5x f x   có đạo hàm A.       2 2 1 .5x f x x
. B. f x 2 x 1 2 .5 x    .ln 5 . C.       2 2 2 . 1 .5x f x x x .
D. f x 2 x 1 5    .ln 5 . Lời giải Chọn B 2 2 
Ta có: f  xx 1    2 x   x 1 5 .ln 5. 1  2 . x 5  .ln 5 .
Câu 17. Hàm số f x  log  3
x x có đạo hàm 2  ln 2 1
A. f  x  .
B. f  x  . 3 x x  3 x xln 2  2 3x   1 ln 2 2 3x 1
C. f  x  .
D. f  x  . 3 x x  3 x xln 2 Lời giải Chọn D u   x
Áp dụng công thức log u x  . a  
u x ln a  3  x x 2 3x 1
Vậy f  x   .  3
x xln 2  3 x xln 2
Câu 18. Hàm số f x   2
ln x  3x có đạo hàm ln10 1
A. f  x  .
B. f  x  . 2 x  3x 2 x  3x 2 x  3x 2x  3
C. f  x  .
D. f  x  . 2x  3  2 x  3xLời giải Chọn D
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 u   x
Áp dụng công thức ln u x  . u x  2  x  3x 2x  3
Vậy f  x   . 2 2 x  3x x  3x Câu 19. Hàm số   2 5x 2x f x   có đạo hàm 2 x 5 x x 2 xx   2 5 2 5 2
A. f  x  .
B. f  x  . ln 2 ln 2 2 C.   2 x 5 2 x f x    ln 2 . D.   x 5  2 x f x
2x  5 ln 2 . Lời giải Chọn D  Áp dụng công thức ux a uxa
u x  ln a . 2 2  Vậy   x 5 x   2   x 5 2 5 ln 2  2 x f x x x
2x  5 ln 2 . Câu 20. Hàm số   2 3 ex x f x   có đạo hàm 2 A.   2 3 ex x f x    . B.   x 3x f x   2 e
x  3x . 2 x 3 e x 2
C. f  x  . D.   x 3  e x f x
2x  3 . 2x  3 Lời giải Chọn D  Áp dụng công thức ux e  ux e
u x  . 2 2  Vậy   x 3x   2   x 3 e 3  e x f x x x
2x  3 . 3 3 Câu 21. Hàm số ex y   có đạo hàm là 4 3 3   3 x A. 3 ex  . B. 2 3 3 ex x  . C.   3 3 3 3 ex x   . D. x 3  3x e   . 4   Lời giải Chọn B 3  Đạo hàm của hàm số 3 ex y  
là y   x   3 3 3 x 3 2 x 3 3 .e  3x .e . 2
Câu 22. Đạo hàm của hàm số 4 x y  là A. 2 2.4 x y  ln 4 . B. 2 4 . x y  ln 2 . C. 2 4 x y  ln 4 . D. 2 2.4 x y  ln 2 Lời giải Chọn A 2 2.4 . x y  ln 4 . Câu 23. Cho hàm số 1 3x y  
. Đẳng thức nào sau đây đúng? A. 1 3x y    . B. x 1 y 3    .ln 3 . C. 1 .3x y x    . D. yxx 1 1 .3     .ln 3 . Lời giải Chọn B Đạo hàm của hàm số 1 3x y   là yxx 1 x 1 1 .3 .ln 3 3       .ln 3 .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
NGUYỄN BẢO VƯƠNG - 0946798489 2
Câu 24. Đạo hàm của hàm số 2 3 2 e x x y    là 2 2 A. 2 x 3x2 y   2 e
. 2x  3x  2 . B. 2 x 3 x2 y  e .4x  3 . 2 2 C. 2 3 2 e x x y     . D. 2 x 3 x 1 y e    .4x  3 . Lời giải Chọn B 2 2 Có 2 3 2 e x x y     2 x 3 x 2 y  e .4x  3 .
Câu 25. Tìm đạo hàm của hàm số 2 3 2   x y . A. 2 x2 y  2 ln 4 . B. x2 y  4 ln 4 . C. 2 x2 y  2 ln16 . D. 2 x3 y  2 ln 2 . Lời giải Chọn C u
Áp dụng công thức đạo hàm    . u a u a .ln a Ta có yx  2x3 2 3     2 ln 2 2 x3  2 ln 4 2 x 2  2 ln16 . C. BÀI TOÁN THỰC TẾ
1. Lãi đơn:Khách hàng gửi vào ngân hàng A đồng với lãi đơn r /kì hạn thì số tiền khách hàng nhận
được cả vốn lẫn lãi sau n kì hạn (n   * ) là S A nAr A 1  nr n  
2. Lãi kép: Khách hàng gửi vào ngân hàng A đồng với lãi kép r /kì hạn thì số tiền khách hàng nhận
được cả vốn lẫn lãi sau n kì hạn (n   * ) là S A 1  r n n S SS
Từ đó ta có thể tìm các giá trị: r n n  1 n A n n  log   A  1 r   1  A   r n  
3. Bài toán tăng trưởng dân số: Công thức tính tăng trưởng dân số  X
X 1 r m n , m,n   
  ,m n trong đó: m n  
r là tỉ lệ tăng dân số từ năm n đến năm m
X là dân số năm m m
X là dân số năm n n X
Từ đó ta có công thức tính tỉ lệ tăng dân số là: r m m n  1 Xn
4. Vay vốn trả góp: Vay ngân hàng số tiền là A đồng với lãi suất r /tháng. Sau đúng một tháng kể
từ ngày vay, bắt đầu hoàn nợ, hai lần hoàn nợ cách nhau đúng một tháng, mỗi lần hoàn nợ số tiền là 1  r n n  1
X đồng. Ta có công thức tính số tiền còn lại sau n tháng: S A 1  rX n   r
5. Tiền gửi hàng tháng: Đầu mỗi tháng khách hàng gửi vào ngân hàng số tiền A đồng với lãi kép
r /tháng thì số tiền khách hàng nhận được cả vốn lẫn lãi sau n tháng (n   * ) (nhận tiền cuối A n
tháng, khi ngân hàng đã tính lãi) là S Sr      r n 1  1 1  n r  
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020S r .  S r . Từ đó ta có n n  log   1 n A 1 r
   A1  r   n    
1  r  1  r   1     Câu 1.
Để dự báo dân số của một quốc gia, người ta sử dụng công thức nr
S Ae ; trong đó A là dân số của
năm lấy làm mốc tính, S là dân số sau n năm, r là tỉ lệ tăng dân số hàng năm. Năm 2017, dân số
Việt nam là 93.671.600 người (Tổng cục Thống kê, Niên giám thống kê 2017, Nhà xuất bản Thống
kê, Tr 79). Giả sử tỉ lệ tăng dân số hàng năm không đổi là 0,81%, dự báo dân số Việt nam năm 2035
là bao nhiêu người (kết quả làm tròn đến chữ số hàng trăm)? A. 109.256.100 . B. 108.374.700 . C. 107.500.500 . D. 108.311.100 . Lời giải Chọn B
Lấy năm 2017 làm mốc, ta có A  93.671.600;n  2035  2017  18 0,81 1 . 8
 Dân số Việt Nam vào năm 2035 là 100
S  93.671.600.e  108.374.700 Câu 2.
Để quảng bá cho sản phẩm A, một công ty dự định tổ chức quảng cáo theo hình thức quảng cáo trên
truyền hình. Nghiên cứu của công ty cho thấy: nếu sau n lần quảng cáo được phát thì tỉ lệ người xem 1
quảng cáo đó mua sản phẩm A tuân theo công thức P n 
. Hỏi cần phát ít nhất bao 0  ,015 1 49e n
nhiêu lần quảng cáo để tỉ lệ người xem mua sản phẩm đạt trên 30%? A. 202 . B. 203. C. 206 . D. 207 . Lời giải Chọn B 1 Theo bài ra ta có  0,3 0  ,015 1 49e nn 10 0,015  1 49e  3  n 7 0,015  e  147 7  0  , 015n  ln 147 1 7  n   ln  202, 97 . 0, 015 147
Vậy ít nhất 203 lần quảng cáo. Câu 3.
Sự tăng trưởng của một loài vi khuẩn tuân theo công thức  .ert S A
, trong đó A là số lượng vi khuẩn
ban đầu, r là tỉ lệ tăng trưởng r  0  , t là thời gian tăng trưởng. Biết rằng số lượng vi khuẩn ban
đầu là 100 con và sau 5 giờ có 300 con. Hỏi sau 20 giờ có bao nhiêu con? A. 8100 con. B. 9000 con. C. 7000 con. D. 8500 con. Lời giải Chọn A r r 1 Theo đề ra ta có 5 5 100.e  300  e  3  r  ln 3 5  1  ln 3 .20  
Sau 20 giờ từ 100 con vi khuẩn sẽ có:  5 S 100.   e  8100 con. Câu 4.
Dân số thế giới được ước tính theo công thức ni
S S e , trong đó S là dân số của năm lấy làm mốc 0 0
tính, S là dân số sau n năm, i là tỷ lệ tăng dân số hàng năm. Tỷ lệ tăng dân số hàng năm của nước ta
là 1,14% / năm. Năm 2019 dân số nước ta là 97 575 490 người. Hỏi đến năm nào dân số nước ta đạt
ngưỡng 100 000 000 người
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
NGUYỄN BẢO VƯƠNG - 0946798489 A. 2022. B. 2021. C. 2024. D. 2023. Lời giải Chọn A Áp dụng công thức: ni
S S e .Trong đó S là dân số nước ta năm 2019, S là dân số nước ta sau n 0 0 n
năm, i là tỷ lệ tăng dân số hàng năm. 1 S 1 100000000
Vậy n  ln n  ln  2,153 i S 0,0114 97575490 0
Sau 3 năm tức là đến năm 2022. Câu 5.
Để dự báo dân số của một tỉnh X, người ta sử dụng công thức  .enr S A
, trong đó A là dân số của
năm lấy làm mốc tính, S là dân số sau n năm, r là tỉ lệ tăng dân số hàng năm. Năm 2016 , dân số
tỉnh X là 8.326.550 người. Giả sử tỉ lệ tăng dân số hàng năm không đổi là 0,9 % , dự báo dân số tỉnh
X năm 2026 là bao nhiêu người (kết quả làm tròn đến chữ số hàng đơn vị)? A. 9.029.068 . B. 9.110.697 . C. 9.139.063 . D. 10.311.124 . Lời giải Chọn B
Lấy năm 2016 làm mốc, ta có: n  2026  2016  10, r  0, 9, A  8.326.550
Từ đây ta suy ra dân số tỉnh X năm 2026 là: nr 10.0,9%
S Ae  8.326.550e  9110697 . Câu 6.
Khi đèn flash của máy ảnh tắt, pin ngay lập tức bắt đầu sạc lại tụ điện của đèn flash, nơi lưu trữ điện
tich được cho bởi công thức ( )  / 1 e   t a Q t Q
(dung lượng sạc tối đa là Q và t được tính bằng 0  0
giây). Mất bao lâu đề sạc lại tụ điện thành 90% công suất nếu a  2? A. 4 giây. B. 5 giây. C. 4.6 giây. D. 4.5 giây. Lời giải Chọn B
Theo đè bài ta cần tìm t thỏa  t t    t 2 2
Q(t)  Q 1 e  0,9Q  e  0,1  
 ln 0,1  t  2 ln10  4.605 0   0 2  
Vậy ít nhất 5 giây thì pin sẽ sạc tụ điện đèn flash thành 90% công suất. Câu 7.
Để dự báo dân số của một quốc gia, người ta sử dụng công thức  .enr S A
, trong đó A là dân số của
năm lấy làm mốc tính, S là dân số sau n năm, r là tỉ lệ tăng dân số hàng năm. Năm 2018 , dân số
Việt Nam là 94.665.973 người (Tổng cục thống kê, Niên giám thống kê 2018 , Nhà xuất bản Thống
kê, Tr. 87 ). Giả sử tỉ lệ tăng dân số hàng năm không đổi là 0,85 % , dự báo đến năm nào dân số Việt
Nam vượt mốc 100.000.000 người? A. 2022 . B. 2023 . C. 2024 . D. 2025 . Lời giải Chọn D
Thay S  100.000.000 , A  94.665.973 , r  0,85 %  0, 0085 vào  .enr S A ta được n  100.000.000 0,0085 
100.000.000  94.665.973  e  n  ln : 0, 0085  6, 45.    94.665.973 
Vậy đến năm 2025 dân số Việt Nam sẽ vượt mốc 100.000.000 người. Câu 8.
Áp suất không khí P (đo bằng milimet thủy ngân, kí hiệu là mmHg ) suy giảm mũ so với độ cao x
(so với mực nước biển và đo bằng mét) theo công thức  .exi P P
, trong đó P  760mmHg là áp suất 0 0
ở mực nước biển, i là hệ số suy giảm. Biết rằng ở độ cao 1000m thì áp suất của không khí là
672, 71mmHg . Hỏi áp suất không khí ở độ cao 4125m là bao nhiêu (làm tròn đến hàng phần trăm)?
A. 495, 4598263mmHg . B. 459, 46mmHg .
C. 495, 459mmHg . D. 459, 5mmHg Lời giải Chọn A
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 672, 71 1 672, 71 Theo giả thiết ta có 1000 1000i 672, 71  760.e i  e   i  ln . 760 1000 760 1 672, 71 Với x  4125 ; m i  ln
; P  760mmHg ta được: 0 1000 760 1 672,71 4125. ln 1000 760 P  760.e  459, 4598263. Câu 9.
Một mặt hàng kinh doanh theo hình thức đa cấp với số lượng nhân viên ban đầu A sau t (lần hội
thảo) được xấp xỉ bởi đẳng thức   0,2  .e t A t A
, trong đó A là số nhân viên ban đầu. Số lượng nhân 0 0
viên tham dự ban đầu tham gia kinh doanh là 100 thì sau ít nhất bao nhiêu lần hội thảo, số lượng
nhân viên đạt đến 700 người? A. 9 . B. 9, 729 . C. 10 . D. 9, 7 . Lời giải Chọn C Từ giả thiết ta suy ra   0,2  100.e t A t
. Để số lượng là 700 người thì t 1   0,2  100.e t A t  700 2  e  7  t  ln 7  10 . 0.2
Câu 10. Vận dụng thông tư số 14/2017/TT-NHNN của Ngân hàng Nhà nước quy định về phương pháp tính
lãi trong hoạt động nhận tiền gửi, có hiệu lực từ ngày 1/1/2018, ngân hàng A đã tính số tiền lãi theo
một kì bằng số ngày của kì gửi nhân với số tiền lãi của một năm chia cho 365. Một khách hàng gửi
100 triệu đồng vào ngân hàng vào ngày 4/7/2018 với lãi suất 5%/năm, kì hạn 1 tháng, ngày tính lãi
hàng tháng là ngày 4/7, biết rằng trong khi gửi khác hàng không đến rút lãi về, ngân hàng tính theo
thể thức lãi kép. Đến ngày 4/9/2018, người đó đến ngân hàng rút cả vốn lẫn lãi về. Hỏi số tiền (tính
bằng nghìn đồng) khách hàng nhận được là số nào sau đây: A. 100835. B. 100836. C. 100834. D. 100851. Lời giải Chọn D
Do tháng 7 và tháng 8 đều có 31 ngày nên số tiền khách hàng nhận được là:  5%   5% 6  100.10 . 1  .31 . 1  .31  100851000     đồng  365   365 
Câu 11. Trong phòng thí nghiệm nghiên cứu về vi khuẩn tại bênh viện Trung ương Huế, loại vi khuẩn X gây
bệnh cho người có tốc độ tăng trưởng bình quân là 15% / ngày. Bệnh viện tiến hành nuôi cấy mẫu
bệnh phẩm do vi khuẩn X gây ra, với ước lượng số vi khuẩn ban đầu là 100 triệu (ước lượng lúc 9
giờ của ngày đầu tiên nuôi cấy). Bệnh viện nhận thấy rằng có thể trị bệnh do vi khuẩn X gây ra bằng
thuốc kháng sinh Y. Cứ 500 mg thuốc kháng sinh Y có thể tiêu diệt được 10 triệu vi khuẩn và thuốc
có tác dụng hầu như ngay lập tức và không có tác dụng kéo dài thêm. Bác sĩ quyết định lúc 9 giờ
sáng hàng ngày (kể từ ngày thứ hai nuôi cấy mẫu bệnh phẩm) dùng x g thuốc kháng sinh Y để tiến
hành nghiên cứu trên mẫu bệnh phẩm thì thấy rằng sau khi tiến hành thí nghiệm ở ngày thứ 15 ngày
kể từ ngày nuôi cấy hoàn thành thì mẫu bệnh phẩm không còn vi khuẩn X. Hỏi số thuốc kháng sinh
Y mà bác sĩ dùng hàng ngày để tiến hành nghiên cứu trên là bao nhiêu? (lấy kết quả gần đúng) A. 0,855 g. B. 1g. C. 8,5 g. D. 2 g. Lời giải Chọn A
Gọi số vi khuẩn ban đầu là M , số vi khuẩn bị tiêu diệt mỗi ngày là m , tốc độ tăng trưởng mỗi ngày là r .
Hết ngày thứ nhất, số vi khuẩn có trong mẫu bệnh phẩm là M Mr M 1 r .
Ngay sau đó, lúc 9 giờ bác sĩ tiến hành thí nghiệm bằng thuốc Y và số vi khuẩn bị tiêu diệt là m nên
số vi khuẩn còn lại ngay sau 9h ngày thứ hai là M 1 r  m .
Do đó hết ngày thứ hai, số vi khuẩn có trong bệnh phẩm là
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
NGUYỄN BẢO VƯƠNG - 0946798489 2
M 1 r   m 1 r   
M 1 r   m 1 r  .
Ngay sau đó, lúc 9 giờ ngày 3, bác sĩ lại tiến hành thí nghiệm băng thuốc Y và số vi khuẩn bị tiêu 2
diệt là m nên số vi khuẩn còn lại ngay sau 9h ngày thứ ba là M 1 r   m 1 r   m .
Do đó hết ngày thứ ba, số vi khuẩn còn lại là  3 2 M r 2 1
m 1 r m    
1 r   M 1 r   m1 r   m 1 r   m .  
Cứ tiếp tục lập luận như vậy ta thấy ngay sau 9h ngày thứ n , n  2 , số vi khuẩn còn lại là m  n 1 r  1     n  
M   r n m   r n 1  m   r n 2 1 1 1
 ...  m 1 r   m M 1 r   . r
Ngay sau 9h ngày thứ n = 15 hết số vi khuẩn nên ta có: m  n 1 r  1   M n 1 r r M n 1 r       0 6  m   17,102.10 . rn 1 r  1
1 g chất Y sẽ tiêu diệt được 20 triệu vi khuẩn. Do đó số thuốc mà bác sĩ tiến hành nghiên cứu hàng 6 17,102.10 ngày là  0,855 g . 6 20.10
Câu 12. Một em học sinh 15 tuổi được hưởng số tiền thừa kế là 300 000 000 đồng. Số tiền này được gửi tại
một ngân hàng với kỳ hạn thanh toán 1 năm và học sinh này chỉ nhận được số tiền ( cả gốc và lãi) khi
đủ 18 tuổi. Biết rằng khi đủ 18 tuổi em này nhận được số tiền là 368 544 273 đồng. Vậy lãi suất của
ngân hàng gần nhất với số nào sau đây?( Với giả thiết lãi suất không đổi trong suốt quá trình gửi) A. 5, 5% / năm. B. 7% / năm. C. 7,5% / năm. D. 5, 7% / năm. Lời giải Chọn B
Áp dụng công thức lãi kép A A (1 r)n , với A  300000000; A  368544273; n  3 , ta tính r . n 0 0 3 368544273 Ta có: 3 r  1  7,1% 300000000
Phân tích phương án nhiễu Phương án
A. Học sinh dễ nhầm theo kiểu n 18 1  51 4 368544273 Khi đó 4 r  1  5,3% 300000000 Phương án
C. Sử dụng sai công thức tính lãi đơn A A (1  rn) n 0 1  A  1 368544273  Khi đó n r  1  1  7,6%     n A 3    300000000 0  Phương án
D. Sử dụng sai công thức tính lãi đơn A A (1  rn) và n 18 1  51 4 n 0 1  A  1  368544273  n r  1  1  5,7% Khi đó     n A 4    300000000 0 
Câu 13. Bố An để dành cho An 100 000 000 đồng để học đại học trong một ngân hàng theo hình thức lãi kép
với lãi suất 0, 75% một tháng. Mỗi tháng An đến rút 3 000 000 đồng để chi phí sinh hoạt. Hỏi sau 1
năm số tiền còn lại là bao nhiêu?( Làm tròn kết quả đến hàng đơn vị) A. 71857930 đồng. B. 71857931 đồng. C. 73380690 đồng. D. 73380689 đồng. Lời giải Chọn B
Gọi A là số tiền ban đầu, r là tỷ lệ lãi suất hàng tháng, S là số tiền 0
x là số tiền rút ra hàng tháng, n
thực có sau n tháng.
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Nếu không rút tiền ra thì sau 1 tháng số tiền An có là A A (1 r) . 1 0
Số tiền thực có sau 1 tháng là: S A (1 r)  x . 1 0
x 1 r 2 1  
Số tiền thực có sau 2 tháng là: S
A (1 r) x1 r  2 x A (1 r)           . 2 0 0 r
x 1 r 3 1  
Số tiền thực có sau 3 tháng là:  
S S 1 r  3
x A (1 r)  . 3 2 0 r …………… x  n 1 r  1  
Số tiền thực có sau n tháng là: S A (1 r)n      n 0 r
Vậy sau 1 năm tức là 12 tháng số tiền còn lại
3000000 1 0,007512 1   là: 12 S 100000000(1 0, 0075)       71857930, 7 12 0, 0075
Câu 14. Một người gửi số tiền 100 triệu đồng vào một ngân hàng với lãi suất 0, 65% trên tháng. Biết rằng nếu
người đó không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được nhập vào vốn ban
đầu (người ta gọi đó là lãi kép). Hỏi số tiền lãi người đó có được sau 2 năm, nếu trong khoảng thời
gian này người đó không rút tiền ra và lãi suất không đổi là bao nhiêu? A. 24 100.(1,0065) triệu đồng. B. 2
100.(1,0065) 100 triệu đồng. C. 24
100.(1, 0065) 100 triệu đồng. D. 24
100.(2, 0065) 100 triệu đồng. Lời giải Chọn C
Áp dụng công thức lãi kép S A(1 r)n với A  100, r  0, 0065, n  24 thì số tiền người đó có n
được sau 2 năm ( 24 tháng) là: 24 24 S  100.(1  0, 0065)
 100.(1, 0065) triệu đồng. 24
Vậy số tiền lãi người đó có được sau 2 năm là 24
100.(1, 0065) 100 triệu đồng.
Câu 15. Ông Nam gửi 100 triệu đồng vào ngân hàng theo thể thức lãi kép, kì hạn 1 năm với lãi suất
7, 56% một năm. Hỏi sau bao nhiêu năm gửi ông Nam sẽ có ít nhất 150 triệu đồng từ số tiền gửi ban
đầu? (giả sử lãi suất không thay đổi). A. 5 năm. B. 6 năm. C. 7 năm. D. 8 năm. Lời giải Chọn B
Áp dụng công thức lãi kép S A(1 r)n với A  100, r  7, 56%  0, 0756, S  150 ta được n n n
150  100 1 0, 0756  1, 0756n  1,5  n  log 1, 5  5, 56. 1,0756
Vậy sau khoảng 6 năm gửi ông Nam sẽ có ít nhất 150 triệu đồng từ số tiền gửi ban đầu.
Câu 16. Vào ngày 3/8/2018, một người vay ngân hàng số tiền 50 triệu đồng, trả góp trong thời gian 10 tháng,
lãi suất 5%/năm, với thỏa thuận là cứ đến ngày tính tiền lãi, người đó phải đến ngân hàng trả phần
tiền gốc bằng số tiền vay ban đầu chia đều cho các lần trả và số lãi phát sinh trong tháng trước (hình
thức dư nợ giảm dần). Hỏi số tiền anh phải trả cho ngân hàng vào ngày 3/12/2018 là bao nhiêu?
A. 5,45 triệu đồng.
B. 5,4 triệu đồng.
C. 10,85 triệu đồng.
D. 5,5 triệu đồng. Lời giải Chọn A
Tính đến ngày 3/12, khách hàng đã có 3 lần trả tiền gốc vào các ngày 3/9, 3/10, 3/11 nên số tiền gốc
còn lại tính từ ngày 3/11/2018 là 50  3.5  35 triệu đồng
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
NGUYỄN BẢO VƯƠNG - 0946798489 10%
Số tiền lãi cần trả cho ngân hàng từ ngày 3/11/2018 đến ngày 3/12/2018 là 6 35.10 . .30  288000 365 đồng
Số tiền khách hàng phải trả trong ngày 3/12/2018 là 5000000  288000  5288000 đồng
Câu 17. Vào đầu mỗi năm anh Thắng gửi vào ngân hàng số tiền 30 triệu đồng với kì hạn 1 năm, lãi suất
7%/năm (mỗi lần gửi cách nhau 1 năm). Hỏi sau ít nhất bao nhiêu năm (sau khi ngân hàng đã tính lãi
cho lần gửi cuối cùng) thì anh Thắng được số tiền cả gốc lẫn lãi từ 500 triệu đồng trở lên? (biết rằng
trong suốt thời gian gửi tiền, anh Thắng không đến rút lãi về, ngân hàng tính theo thể thức lãi kép và
lãi suất hàng năm không đổi) A. 7 năm. B. 8 năm. C. 11 năm. D. 10 năm. Lời giải Chọn C
Gọi N là số năm anh Thắng gửi ngân hàng
Lần gửi đầu tiên anh Thắng gửi 30 triệu đồng, đến hết năm thứ N anh được tính cả vốn và lãi cho số tiền này là: 6 30.10 .(1 7%)N
Lần gửi thứ 2 anh Thắng gửi 30 triệu đồng, đến hết năm thứ N anh được tính cả vốn và lãi cho số tiền này là: 6 1 30.10 .(1 7%)N   …
Lần gửi thứ N anh Thắng gửi 30 triệu đồng, đến hết năm thứ N anh được tính cả vốn và lãi cho số tiền này là: 6 1 30.10 .(1  7%)
Tổng số tiền anh Thắng nhận được là   N N  1 (1 7%)N 6 6 1 6 6
30.10 .(1 7%)  30.10 .(1 7%)
 ...  30.10 .(1 7%)  30.10 .(1 7%) 1 (1 7%) 1 (1 7%)N  
Để số tiền từ 500 triệu đồng trở lên thì 6 6 30.10 .(1 7%)  500.10 1 (1 7%)
Giải ra ta được N  10,89 nên số năm cần gửi tối thiểu là 11 năm
Câu 18. Ông Q.BN mang 150 triệu đồng gửi vào ngân hàng với lãi suất 7% một năm. Ông KN cũng đem 300
triệu đồng gửi vào ngân hàng khác với lãi suất 1,72% một quí. Sau 10 năm, hai ông cùng đến ngân
hàng rút tiền ra để mua xe. ( Lưu ý: tiền lãi được tính theo công thức lãi kép và được làm tròn đến
hàng triệu). Biết 2 ông cùng muốn mua 1 loại xe có giá là 456 triệu. Nếu số tiền mang theo không đủ,
hai ông có thể trả góp cho hãng xe phần còn thiếu theo hình thức sau: Đúng một tháng kể từ ngày
nhận được xe, người mua bắt đầu đóng tiền góp; hai lần trả liên tiếp cách nhau đúng một tháng, số
tiền trả mỗi tháng là như nhau và phải trả trong 1 năm. Biết rằng mỗi tháng hang xe chỉ tính lãi trên
số dư nợ thực tế của tháng đó. Hỏi mỗi tháng người mua phải trả bao nhiêu tiền cho hãng xe, lãi suất
của hãng là 1,8%/tháng.Khẳng định nào sau đây là đúng
A. Ông Q.BN mỗi tháng phải trả thêm 15 triệu.
B. Ông KN mỗi tháng phải trả thêm 5 triệu.
C. Ông Q.BN cần trả thêm hơn 180 triệu trong 12 tháng.
D. Ôn KN cần trả thêm 15 triệu mỗi tháng. Lời giải Chọn C
Số tiền mỗi ông nhận được là: Ông Q.BN:   10 150. 1 7%
 295, 0727036  295 triệu Ông KN:   40 300 1 1,72%
 593.4379488  593 triệu
Vậy ông KN không cần trả góp 12  1,8  1,8 456  295 1 .    100  100
Số tiền ông Q.BN phải góp hàng tháng là: X   15, 03771828 triệu 12  1,8  1  1    100 
Trang 24 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Tổng số tiền ông Q.BN phải trả thêm sau 12 tháng là: 180.4526193 triệu.
Câu 19. Ông A cần mua nhà ở nhưng số tiền của ông không đủ để mua nhà ở, ông đi vay ngân hàng 1 tỉ đồng
với lãi suất ưu đãi là 9% /năm. Ông ta muốn hoàn nợ cho ngân hàng theo cách: Sau đúng một năm kể
từ ngày vay, ông bắt đầu hoàn nợ; hai lần hoàn nợ liên tiếp cách nhau đúng một năm, số tiền hoàn nợ
ở mỗi năm là như nhau và ông A trả hết nợ sau đúng 10 năm kể từ ngày vay. Biết rằng mỗi năm
ngân hàng chỉ tính lãi trên số dư nợ thực tế của năm đó. Hỏi số tiền mỗi tháng ông ta cần trả cho
ngân hàng gần nhất với số tiền nào dưới đây?
A. 155,820 triệu đồng. B. 146,947 triệu đồng.
C. 166,8 triệu đồng.
D. 236, 736 triệu đồng. Lời giải Chọn A
Gọi số tiền vay ban đầu là M , số tiền hoàn nợ mỗi năm là m , lãi suất một năm là r .
Hết năm thứ nhất, số tiền cả vốn lẫn lãi ông A nợ ngân hàng là M Mr M 1 r  .
Ngay sau đó ông A hoàn nợ số tiền m nên số tiền để tính lãi cho năm thứ hai là M 1 r   m .
Do đó hết năm thứ hai, số tiền cả vốn lẫn lãi ông A nợ ngân hàng là 2
M 1 r   m 1 r   
M 1 r   m 1 r  .
Ngay sau đó ông A lại hoàn nợ số tiền m nên số tiền để tính lãi cho năm thứ ba là M   r 2 1
m 1 r   m .
Do đó hết năm thứ ba, số tiền cả vốn lẫn lãi ông A nợ ngân hàng là M r 2 1
m 1 rm    
1 r  M   r3  m  r2 1 1
m 1 r   m .  
Cứ tiếp tục lập luận như vậy ta thấy sau năm thứ n , n  2 , số tiền cả vốn lẫn lãi ông A nợ ngân hàng là m  n 1 r  1     n  
M   r n m   r n 1  m   r n 2 1 1 1
 ...  m 1 r   m M 1 r   . r
Sau năm thứ n trả hết nợ thì ta có m  n 1 r  1   M n 1 r r M n 1 r       0  m  . rn 1 r  1
Thay số với M  1.000.000.000 , r  9% , n  10 ta được m  155,820 (triệu đồng).
Câu 20. Ông A vay ngân hàng 500 triệu đồng với lãi suất 1%/tháng. Ông ta muốn hoàn nợ cho ngân hàng
theo cách: Sau đúng một tháng kể từ ngày vay, ông bắt đầu hoàn nợ; hai lần hoàn nợ liên tiếp cách
nhau đúng một tháng, số tiền hoàn nợ ở mỗi tháng là 12 triệu đồng. Biết rằng mỗi tháng ngân hàng
chỉ tính lãi trên số dư nợ thực tế của tháng đó. Hỏi số tháng mà ông A cần trả hết nợ ngân hàng là bao
nhiêu kể từ khi vay? (tháng cuối cùng có thể trả số nợ không quá 12 triệu đồng) A. 55 tháng.
B. 54 triệu đồng.
C. 56 triệu đồng.
D. không bao giờ trả hết nợ. Lời giải Chọn A
Gọi số tiền vay ban đầu là M , số tiền hoàn nợ mỗi tháng là m , lãi suất một tháng là r .
Hết tháng thứ nhất, số tiền cả vốn lẫn lãi ông A nợ ngân hàng là M Mr M 1 r  .
Ngay sau đó ông A hoàn nợ số tiền m nên số tiền để tính lãi cho tháng thứ hai là M 1 r  m .
Do đó hết tháng thứ hai, số tiền cả vốn lẫn lãi ông A nợ ngân hàng là 2
M 1 r   m 1 r   
M 1 r   m 1 r  .
Ngay sau đó ông A lại hoàn nợ số tiền m nên số tiền để tính lãi cho tháng thứ ba là M   r 2 1
m 1 r   m .
Do đó hết tháng thứ ba, số tiền cả vốn lẫn lãi ông A nợ ngân hàng là
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
NGUYỄN BẢO VƯƠNG - 0946798489M r 2 1
m 1 r m    
1 r  M   r3  m   r2 1 1
m 1 r   m .  
Cứ tiếp tục lập luận như vậy ta thấy sau tháng thứ n , n  2 , số tiền cả vốn lẫn lãi ông A nợ ngân hàng là m  n 1 r  1     n  
M   r n m   r n 1  m   r n 2 1 1 1
 ...  m 1 r   m M 1 r   . r
Sau tháng thứ n trả hết nợ thì ta có m  n 1 r  1   n m m M n 1 r     
 0 (1)  1 r    n  log . r 1r m Mr m Mr 12
Thay số với M  500.000.000 , r  1% , m  12.000.000 ta được n  log
 54,168 , vì n là số 1,01 7
tự nhiên nên ta chọn n  55 tháng.
Câu 21. Ông A là một người già không có khả năng lao động, trước khi không thể lao động kiếm sống ông ấy
có dành dụm được một khoản tiền để gửi tiết kiệm ngân hàng với lãi suất ưu đãi dành cho người già
là 0,9% tháng. Sau khi gửi tiết kiệm ngân hàng, đủ mỗi tháng gửi, ông A đến ngân hàng rút ra một
khoản tiền là 5 triệu đồng để chi tiêu hàng ngày. Sau đúng 5 năm kể từ ngày gửi tiết kiệm, số tiền tiết
kiệm còn lại của ông ấy là 100 triệu đồng. Hỏi số tiền ban đầu mà ông A gửi tiết kiệm là bao nhiêu?
(lấy kết quả gần đúng)
A. 289, 440 triệu đồng. B. 291,813 triệu đồng.
C. 287, 044 triệu đồng. D. 233, 663 triệu đồng. Lời giải Chọn A
Gọi số tiền ban đầu là M , lãi suất một tháng là r .
Hết tháng thứ nhất, số tiền cả vốn lẫn lãi ông A có trong ngân hàng là M Mr M 1 r  .
Ngay sau đó ông A rút 5 triệu đồng để chi tiêu nên số tiền để tính lãi cho tháng thứ hai là
M 1 r   5 .
Do đó hết tháng thứ hai, số tiền cả vốn lẫn lãi ông A có trong ngân hàng là 2
M 1 r   5 1 r   
M 1 r   51 r  .
Ngay sau đó ông A lại rút 5 triệu để chi tiêu nên số tiền để tính lãi cho tháng thứ ba là M   r 2 1
 5 1 r   5 .
Cứ tiếp tục lập luận như vậy ta thấy sau tháng thứ n , n  2 , số tiền cả vốn lẫn lãi ông A có trong ngân hàng là n 5 1 r  1     n
M   r n    r n 1    r n 2 1 5 1 5 1
 ...  51 r   5 M 1 r       . r
Sau 5 năm tức là 60 tháng, số tiền còn lại trong ngân hàng là 100 triệu nên ta có 5 1 r 60 1     5 1 r 60 1   100  M 1 r 60      200 rM
 289, 440 triệu đồng. r 1 r 60
D. PHƯƠNG TRÌNH – BẤT PHƯƠNG TRÌNH CƠ BẢN
1. Đạo hàm của hàm số mũ và lôgarit uu  ( u )  . u e
ue .  ( u )  . u a
ua .lna.  (ln u)    (log u)   u a u lna
2. Phương trình mũ – lôgarit
Đặt điều kiện trước khi giải. Ta có một số kết quả cần nhớ sau: x
a b  0  x  log b.  log b
x b x a . a a f (x ) g(x )  aa
f (x)  g(x).  log f (x)  log g(x)  f (x)  g(x). a a
Trang 26 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
3. Bất phương trình mũ và lôgarit
Đặt điều kiện trước khi giải. Giải xong được tập nghiệm nhớ giao (lấy phần chung) với điều kiện. x
a b x  log b a f (x ) g(x )  aa
f (x)  g(x)
Nếu a  1 
(cùng chiều)  log b
x b x a a
 log f (x)  log g(x)  f (x)  g(x) a ax
a b x  log b a f (x ) g(x )  aa
f (x)  g(x)
0  a  1 
(ngược chiều)  log b
x b x a a
 log f (x)  log g(x)  f (x)  g(x) a a
4. Các phương pháp giải phương trình, bất phương trình mũ và lôgarit: Biến đổi tương đương, Đặt ẩn phụ,
Sử dụng tính đơn điệu hàm số, sử dụng đánh giá bằng bất đẳng thức,…. Câu 1.
Nghiệm của phương trình log 2x 1  2 là: 3   9 7 A. x  3 . B. x  5 . C. x  . D. x  . 2 2 Lời giải Chọn B 1
Điều kiện: 2x 1  0  x  2  1  1 x  x  Ta có log 2x 1  2   2   x  5 . 3    2 2 2x 1  3   x  5 
Vậy phương trình có nghiệm x  5 . 2 Câu 2.
Tập nghiệm của bất phương trình x 1  x x9 5  5 là A. 2; 4. B. 4; 2. C.  ;
 2 4;  . D.  ;  4   2;  . Lời giải Chọn A 2 x 1  x x9 2 2 5  5
x 1  x x  9  x  2x  8  0  2   x  4 .
Vậy Tập nghiệm của bất phương trình là 2; 4 . Câu 3.
Nghiệm của phương trình x 1 3   27 là
A. x  4 .
B. x  3 .
C. x  2 .
D. x  1 . Lời giải Chọn A Ta có: x 1 3   27 x 1  3  3
 3  x 1  3  x  4 .
Vậy nghiệm của phương trình là x  4 . Câu 4.
Tập nghiệm của bất phương trình 9x 2.3x   3  0 là
A. 0;  .
B. 0;  .
C. 1;  .
D. 1;  . Lời giải Chọn B 9x 2.3x 3 0 3x  1 3x 3 0 3x        
 1 (vì 3x  0, x   )  x  0 .
Vậy tập nghiệm của bất phương trình đã cho là 0;  .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27
NGUYỄN BẢO VƯƠNG - 0946798489 Câu 5.
Nghiệm của phương trình log
2x 1  3  0 là 3   A. 1. B. 5. C. 14. D. 4 . Lời giải Chọn C 1
Điều kiện: 2x 1  0  x  . 2 Ta có: log
2x 1  3  0  log 2x 1  3 . 3   3    1 x    2  x  14 . 2x 1  27 
Vậy phương trình có 1 nghiệm là x  14 . 2 Câu 6.
Tập nghiệm của phương trình x x 1 2   2 là
A. T  1;  2 .
B. T    1 .
C. T    2 .
D. T  1;   2 . Lời giải Chọn D x  1 2
Ta có: x x 1 2   2 2
x x 1  1 2
x x  2  0   . x  2 
Vậy tập nghiệm của phương trình là T  1;   2 . Câu 7.
Nghiệm của phương trình log 3  2x  1 là 7   2 A. . B. 1. C. 3. D. 2  . 3 Lời giải Chọn D 3
Điều kiện: 3  2x  0  x  2
log 3  2x  1  3  2x  7 7    x  2  . (Thỏa mãn)
Vậy phương trình có 1 nghiệm là x  2  . Câu 8.
Nghiệm của phương trình log (x  5)  2 là: 3
A. x  4 .
B. x 14 .
C. x  2 .
D. x  9 . Lời giải Chọn B log (x  5)  2 3 x  5  0  
x  5  9  x  14 2 x  5  3 
Vậy nghiệm của phương trình là x  14 . Câu 9.
Nghiệm của phương trình 42 7 x  49  0 là 3 A. 2 . B. 1. C. 3. D. . 2 Lời giải Chọn B 4 2 7 x  49  0 42 x  7  49 42 x 2  7  7  4  2x  2
x  1.
Trang 28 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Vậy phương trình có 1 nghiệm là x  1 .
Câu 10. Số nghiệm của phương trình  2
log x  2x  9 1 là: A. 1. B. 2 .
C. Vô nghiệm. D. 3 . Lời giải Chọn B Ta có: 2
x  2x  9  0 x
  R . Suy ra:  2 x x   2 log 2
9  1  x  2x  9  10 2
x  2x 1  0  x  1 2   .  x  1 2 
Vậy số nghiệm của phương trình là 2. x 1
Câu 11. Nghiệm của phương trình 3 1 5  là 25 1 A. . B. 1. C. 1  . D. 3 . 3 Lời giải Chọn C x 1 3 1 5  3x 1  2 5 5   25  3x 1  2  x  1  .
Vậy phương trình có 1 nghiệm là x  1  . x2 2 x3
Câu 12. Nghiệm của phương trình 2  3  2  3 là: 1
A. x  5 . B. x  .
C. x  1.
D. x  1. 3 Lời giải Chọn A Ta có:
  x2    2x3 2 3 2 3  x   x
 2  3  2  2  3 1 . 2 3   
x2    2x3 2 3 2 3
x  2  2x  3
x  5 . Vậy nghiệm của phương trình là x  5 . 2
Câu 13. Nghiệm của phương trình x 3 2 x  16 là  x  1  x  1  x  1 A.  . B.  . C.  . D. x  4 . x  4  x  4  x  4  Lời giải Chọn C 2 2 x 3x x 3x 4 2  16  2  2 2
x  3x  4 2
x  3x  4  0
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29
NGUYỄN BẢO VƯƠNG - 0946798489x  1  x  4 
Vậy phương trình có 2 nghiệm là x  1 và x  4 . x 1
Câu 14. Nghiệm của phương trình 3 25  là: 25
A. x  1 . B. x  1  .
C. x  2 .
D. x  2 . Lời giải Chọn C Ta có: x 1 3 x3 1 25   25  25 . 25  x  3  1  .  x  2.
Vậy nghiệm của phương trình là x  2 . x 1
Câu 15. Nghiệm của phương trình 2 1 2  là 4 1 3 1 3
A. x    .
B. x    C. x  . D. x  . 2 2 2 2 Lời giải Chọn A x 1 x  1 Ta có 2 1 2 1 2 2   2  2
 2x 1  2  x   . 4 2
Câu 16. Tập nghiệm của bất phương trình log  2
x  2x  1 là: 3  A.  ;  3
   1;  . B.  3   ;1 . C.  ;   
3 1;  . D. 1:  . Lời giải Chọn A x  3  Ta có: log  2
x  2x  1  2 2
x  2x  3  x  2x  3  0  * 3  x 1 
Vậy bất phương trình đã cho có tập nghiệm là x  ;  3    1;  .
Câu 17. Tập nghiệm của bất phương trình 4x 5.2x   4  0 là A.  ;
 0  2;  . B. 0; 2 . C.  
;1  4;  . D. 1;4 . Lời giải Chọn A Đặt  2x t
t  0. Phương trình đã cho trở thành: t  1 2x  1  x  0 2
t  5t  4  0      .  t  4  2x  4 x  2  
Vậy tập nghiệm của bất phương trình đã cho là ;0  2; .
Câu 18. Nghiệm nhỏ nhất của phương trình log  2
x  3x  5  1 là 5  A.  3 . B. 1. C. 3 . D. 0 . Lời giải Chọn D
Trang 30 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 ĐK x   vì 2
x  3x  5  0, x   x  3 log  2
x  3x  5 2 2
 1  x  3x  5  5  x  3x  0  . 5 x  0 
Vậy nghiệm nhỏ nhất của phương trình log  2
x  3x  5  1 là 0. 5 
Câu 19. Tập nghiệm của bất phương trình log  2 x  3  log 3x 1 là 3  3    1   1  A. ;  1 2;  .
B.  ;1 2;    . C.  ;1 . D. 2;   . 3       3  Lời giải Chọn B 1
Điều kiện: 3x 1  0  x   . 3 x  1 Ta có log  2 x  3  log 3x 1 2 2
x  3  3x  1  x  3x  2  0  . 3  3   x  2   1   x  1
Kết hợp với điều kiện ta được  3 x  2   1 
Vậy tập nghiệm của bất phương trình là S   ;1  2;    . 3   
Câu 20. Bất phương trình log  2
x  2x 1  1 có tập nghiệm là 2  A. 1 2; 1   2  . B.  ;  1
  2   1 2; . C. x  1  . D. . Lời giải Chọn Bx  1 2 2 
x  2x 1  0 
x  2x 1  0  x  1   2 Ta có: log  2
x  2x 1  1       x  1   2   2  2 2
x  2x 1  2 
x  2x 1  0    x  1   2   x  1 2  x x2  1   1 
Câu 21. Tập nghiệm của bất phương trình   3  0     là  4   2  A.  3   ;1 . B. 0;  . C. ;  
3 1;  . D. ;0 . Lời giải Chọn B x  1  Đặt t  ,
  t  0. Ta được phương trình:  2  x  1 2 
t  2t  3  0  t  3t   1  0  t  1   1  x  0.    2 
Vậy tập nghiệm của bất phương trình là 0;   .
Câu 22. Tập nghiệm của phương trình log  2 x  3x  1  là: 0,25   3  2 2 3  2 2   A.   4 . B. 1;   4 . C.  ;  . D. 1;  4 . 2 2    
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 31
NGUYỄN BẢO VƯƠNG - 0946798489 Lời giải Chọn D x  0 x  0  2 
x  3x  0 x  3    Ta có: log  2 x  3x  1     x  3   0,25     x  3x   0, 25 1 2  x  4 n   2 
x  3x  4  0   x  1  n 
Vậy tập nghiệm của phương trình là S  1;  4 . 2 2 x 1  x 3x5  1   1 
Câu 23. Tập nghiệm của bất phương trình      là  3   3  A.  1  ;6. B.  6  ;  1 .
C. ; 61;  .D. ;   1 6;   . Lời giải Chọn A 2 2 x 1  x 3 x5  1   1  Ta có 2 2 
 2x 1  x  3x  5  x  5x  6  0  1  x  6.      3   3 
Vậy tập nghiệm của bất phương trình là  1  ;6 1 1
Câu 24. Nghiệm của phương trình 4 x  là 16 1 1
A. x    B. x  2.  C. x  . D. x  2. 2 2 Lời giải Chọn A 1 1 1  1 1 Ta có 2 4 x   4x  4   2   x   . 16 x 2 1
Câu 25. Tập nghiệm của bất phương trình log  2
x  2x  3  là 4  2 A.  3   ;1 . B.  ;  3    1;  . C.  3  ;  1 . D.  1   6; 3    1; 1   6 . Lời giải Chọn D Ta có: log  1 2
x  2x  3  4  2 2 x  3
x  2x  3  0     *    x  1 1   x   1
  6; 3 1;1 6  2 2
x  2x  3  4   1 6  x  1   6 
Câu 26. Tập nghiệm của bất phương trình 2x x ee  6  0 là A. 3; 2 . B.  ; 2 . C. ;ln 2 . D. ln 2; . Lời giải Chọn C Đặt x
t e , t  0.Bất phương trình đã cho trở thành:
2   6  0    2  3  0   2 x t t t t t
e  2  x  ln 2.
Trang 32 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Vậy tập nghiệm của bất phương trình là ;ln 2 .
Câu 27. Tổng bình phương các nghiệm của phương trình log  2
x  5x  7  0 1  bằng 2 A. 6 . B. 5 . C. 13 . D. 25 . Lời giải Chọn C ĐK: x   vì 2
x  5x  7  0, x   log  2
x  5x  7 2 2 2 2
 0  x  5x  7  1  x  5x  6  0  x  2  x  3  x x  13 1 1 2 1 2 2 2 5 x4 x x8
Câu 28. Tập nghiệm của bất phương trình  2    2  là A.  2  ;  6 . B. ( ;  2
 ] [6; ) . C.  6  ; 2. D. ( ;  6  ] [2; ) . Lời giải Chọn B Ta có : 2  xx x x   2 5 4   2 8 2 2 2
 5x  4  x x  8  x  4x 12  0  . x  6 
Vậy tập nghiệm của bất phương trình là ( ;  2]  [6; )
Câu 29. Tìm nghiệm của phương trình log x  5  3 . 2  
A. x  14 . B. x  11 . C. x  8 . D. x  13 . Lời giải Chọn D Ta có: log
x  5  3  x  5  8  x  13 . 2  
Câu 30. Tìm tập nghiệm của bất phương trình sau: log  x  2  1. A. x  2  . B. 2   x  8. C. x  8 . D. x  8  . Lời giải Chọn C x  2  0  x  2
log  x  2 1      x  8 (*) x  2  10 x  8  
Vậy tập nghiệm của bất phương trình là x  8 .
Câu 31. Tập nghiệm của bất phương trình 2
log x  log x  6  0 là 2 2  1   1   1   1  A. 0;  8;    . B. 0;  8;     . C. ;8   . D. ;  8;     . 4     4   4   4  Lời giải Chọn B
Điều kiện : x  0. Đặt t  log x . 2   1 2 t  2 log x  2 x  2 
Khi đó bất phương trình đã cho trở thành: 2 2 t t 6 0        4 .   t  3 log x  3    2 3  x  2  8   1 
Kết hợp với điều kiện, nghiệm của bất phương trình là: S  0;  8;    .  4 
Câu 32. Phương trình 2x 1 5  125 có nghiệm là
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 33
NGUYỄN BẢO VƯƠNG - 0946798489 5 3 A. x  . B. x  1 . C. x  3 . D. x  . 2 2 Lời giải Chọn B Ta có: 2x1 5  125 2 x 1 3  5
 5  2x 1  3  x  1.
Câu 33. Tập nghiệm của bất phương trình log x 1  log 2x 1 là 0,5   0,5    1  A. ; 2 . B. 2;  . C.  2  ; 2 . D. ; 2  . 2    Lời giải Chọn D x  1  x 1  0  1 Điều kiện:    1  x  2x 1  0 x  2    2 Ta có log x 1  log
2x 1  x 1  2x 1  x  2 0,5   0,5    1 
Kết hợp với điều kiện ta được tập nghiệm của bất phương trình là ; 2  2    2
Câu 34. Phương trình x 2 3
x  1 có nghiệm là
A. x  0 , x  2 .
B. x  0 , x  2  . C. x  1  , x  3 .
D. x 1, x  3  . Lời giải Chọn A x  0 2 2 Ta có x 2 3 x  1 x 2 x 0  3  3 2
x  2x  0   . x  2 
Câu 35. Tìm tập nghiệm của bất phương trình log  x  2  log  x  5  1. A. x  2  . B.  . C. x  0 .
D. 7  x  0 . Lời giải Chọn C x  2  0 x  2 
Để bất phương trình có nghĩa      x  2  (*) x  5  0 x  5    x  7 
log  x  2  log  x  5  1  log(x  2)(x  5) 1 2 2
x  7x 10  10  x  7x  0   x  0  (**)
Từ (*) và (**)  x  0
Vậy tập nghiệm của bất phương trình là x  0 .
Câu 36. Tập nghiệm của bất phương trình 2 2
log x  2 log x  3  0 là 3 3 A. 3;27 . B.  ;
 3  27;  . C. 3; 27 .
D. 0;3 27; . Lời giải Chọn C
Điều kiện : x  0. Khi đó: 2 2 2
log x  2 log x  3  0  log x  4 log x  3  0 3 3 3 3 Đặt t  log x . 3
Bất phương trình đã cho trở thành: 2 3
t  4t  3  0  1  t  3  1  log x  3  3  x  3  27. 3
Trang 34 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Kết hợp với điều kiện, nghiệm của bất phương trình là: S  3;27. 2
Câu 37. Tìm tập nghiệm S của phương trình 2
5 x x  5 .  1   1  A. S   . B. S  0  ;  .
C. S  0;  2 .
D. S   ;1 .  2   2  Lời giải Chọn D x  1 2 2 x x 2 2 5 5 2x x 1 2x x 1 0           1  x    2
Câu 38. Tập nghiệm của bất phương trình 3log  x   1  log 2x 1  3 3 3   3  1   1  A. 1; 2. B. ; 2  . C. ; 2  . D. 2;  . 2      2  Lời giải Chọn A x  1 x 1  0  Điều kiện:    1  x  1. 2x 1  0 x     2 3 log x 1  3log 2x 1  3  log x 1  log
2x 1  1  log  x 1 2x 1   1 3   3   3   3   3      1    x   1 2x   2
1  3  2x  3x  2  0   x  2 . 2
Kết hợp điều kiện, bất phương trình có tập nghiệm là S  1; 2 .
Câu 39. Phương trình x2 2  8 có nghiệm là
A. x  6 . B. x  10 . C. x  14 . D. x  5 . Lời giải Chọn D Ta có : x2 2
 8  x  2  3  x  5 .
Câu 40. Tìm số nghiệm nguyên của bất phương trình log  2
x  2x  1  1 3  A. 2. B. 3. C. 1. D. 4. Lời giải Chọn A 2 
x  2x 1  0 x  1   Ta có: log  2
x  2x 1  1    3   2
x  2x 1  3   1   3  x  1   3 
Tập nghiệm của bất phương trình là 1 3;  1   1  ; 1 3 
Có 2 giá trị nguyên thuộc khoảng nghiệm của bất phương trình là x  2; x  0. .
Câu 41. Tập nghiệm của bất phương trình 2
log x  2 log x  3  0 là 1 1 5 5  1   1   1  A. 0;  5;    . B.  ;   5;     . C. ;5   . D. 125     125   125   1  0;  5;     .  125  Lời giải Chọn D
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 35
NGUYỄN BẢO VƯƠNG - 0946798489
Điều kiện : x  0. Đặt t  log x . 1 5
Khi đó bất phương trình đã cho trở thành: 1    1 log x 1    1  x   5   t  1   5 2 5  t 2t 3 0        .   3 t 3 log x 3     1  1  1    5 x       5  125  1 
Kết hợp với điều kiện, nghiệm của bất phương trình là: S  0;  5;    .  125 
Câu 42. Số nghiệm của phương trình log  2
x  2x  4  2 là: 2  A. 2 . B. 1. C. 0 . D. 3 . Lời giải Chọn A Ta có 2
x  2x  4  0, x    . x  0 Khi đó log  2
x  2x  4  2 2
x  2x  4  4  . 2  x  2  2
Câu 43. Tập nghiệm của bất phương trình x 2 2 x  8 là A. ( ;  1  ) .
B. (3; ) . C. ( 1  ;3) . D. ( ;  1
 )  (3; ) . Lời giải Chọn C 2 2 Ta có: x 2x x 2 x 3 2 2 2  8  2
 2  x  2x  3  x  2x  3  0  1
  x  3.
Câu 44. Tập nghiệm của phương trình log  x 5  x   1 6     là A. 2;  3 . B. 4;  6 . C. 1;  6  . D. 1;  6 . Lời giải Chọn A
Điều kiện x 5  x  0  xx  5  0  0  x  5 . x  2
Phương trình tương đương với x 5  x  6 2
x  5x  6  0  
(thỏa mãn điều kiện). x  3 
Vậy phương trình có tập nghiệm là S  2;  3 . 2 x 4 x  1 
Câu 45. Tập nghiệm của bất phương trình  27   là  3  A. ( ;  1  ) .
B. (3; ) . C. ( 1  ;3) . D. ( ;
 1)  (3; ) . Lời giải. Chọn D 2 2 x 4 x x 4 x 3  1   1   1   x  1 Ta có: 2 2  27  
x  4x  3
  x  4x  3  0         .  3   3   3  x  3 
Câu 46. Phương trình ln x  ln 2x  
1  0 có bao nhiêu nghiệm? A. 0 . B. 1. C. 2 . D. 3 . Lời giải Chọn B
Trang 36 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020x  0 1 Điều kiện   x  . 2x 1  0  2
Khi đó, phương trình tương đương với: x  1
ln  x 2x   1   0 2   
 2x x 1  0  1 x    2
So sánh với điều kiện ta được x  1 là nghiệm.
Câu 47. Phương trình  2
log 72  x   2 log x có nghiệm là: A. 1. B. 2 . C. 6 . D. 4 . Lời giải Chọn C 2 72  x  0 Điều kiện   0  x  72 . x  0 
Khi đó, phương trình tương đương với:  2  x  2 log 72  log x 2
 2x  72  x  6 .
So sánh với điều kiện ta có x  6 thỏa mãn. x x  1 
Câu 48. Số nghiệm nguyên dương của bất phương trình 2 5    là  25  A. 0 . B. 1. C. 2 . D. 3 . Lời giải Chọn C x x  1 2  x2 2 5   5
 5 x x  2  2x x  2  
. Do x nguyên dương nên x 1,  2  25 
Câu 49. Tập nghiệm của phương trình 2
ln(2x x 1)  0 là  1   1  A.   0 . B. 0 ;  . C.   . D.  .  2   2  Lời giải Chọn B Ta có: 2
ln(2x x 1)  0  2 0
2x x 1  e  2 2x x  0  1 
Vậy, phương trình có tập nghiệm: S  0 ;  .  2 
Câu 50. Tập nghiệm của bất phương trình: log (5x  2)  log 3x  6 là: 0,4 0,4    2  A.  ;  2. B. 0; 2. C.  ; 2 .  
D. 2; .  5  Lời giải Chọn C 2
Điều kiện: x   . 5 log (5x  2)  log 3x  6 0,4 0,4  
 5x  2  3x  6.
 2x  4  x  2 .  2 
Kết hợp với điều kiện, ta có tập nghiệm của bất phương trình là:  ; 2   .  5  2
Câu 51. Phương trình x 2x 1 4
  0.125 có bao nhiêu nghiệm?
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 37
NGUYỄN BẢO VƯƠNG - 0946798489 A. 0 . B. 1. C. 2 . D. 3 . Lời giải Chọn C  2  2 x  2 2 2
Ta có: x 2x 1 4
  0.125  2x 4x2 3 2 2   2
2x  4x 1  0    2  2 x   2
Vậy, phương trình có hai nghiệm.
Câu 52. Tập nghiệm của bất phương trình x 1  x2 x2 x 1 3 6 3 6     là:  1 
A. ;  log 5 .
B.  log 5; 0 .
C.  log 5;  . D. ;  . 2  2  2     10  Lời giải Chọn A x 1  x2 x2 x 1 3 6 3 6     3.3x 36.6x 9.3x 6.6x     30.6x 6.3x   x 1 1  2   x  log2 5 5  x   log 5. 2
Vậy tập nghiệm của bất phương trình là:  ;   log 5 . 2  2 x4 5 x 1  1
Câu 53. Tìm tập nghiệm của bất phương trình:  10  3   10  3 ?
A. 1;  . B. ;  1 .
C. 5; .
D. ;5. Lời giải Chọn C  Ta có:               1 10 3 10 3 1 10 3 10 3   2x4  
  5x 11  
 2x4    5x 11  10 3 10 3 10 3 10 3  2  x  4  5  x 11  x  5.
Vậy tập nghiệm của bất phương trình là: 5;  . x
Câu 54. Phương trình  52 1  log 32 có nghiệm là 2 2 3 1
A. x  1 . B. x  . C. x  . D. x  . 3 2 2 Lời giải Chọn C x 2x 1 3
Ta có:  52 1  log 32   1  x  2 2 2 3
Vậy, phương trình có nghiệm: x 2
Câu 55. Tìm số nghiệm nguyên của bất phương trình: log (2x  5)  2 ? 1 3 A. 4. B. 5. C. 6. D. Vô số. Lời giải Chọn B
Trang 38 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020  2x  5  0  log (2x  5)  2 2   1   1  2x  5  3      3   5  x   5   2    x  2  2 2x  5  9 
Các nghiệm nguyên của bất phương trình là: 2  ; 1
 ;0;1; 2 . Vậy bất phương trình có 5 nghiệm nguyên. 2 x 1  0 x4 3  6.3  2  0   1 x5 t  3 t  0   1
Câu 56. Cho phương trình . Nếu đặt thì trở thành phương trình nào? A. 2
9t  6t  2  0 . B. 2
t 18t  2  0 . C. 2
t  2t  2  0 . D. 2
9t  2t  2  0 . Lời giải Chọn C 2x 1  0 x4 2 x5 x5 3  6.3  2  0  3  2.3  2  0 . Vậy khi đặt x5 t  3
t  0 thì  
1 trở thành phương trình 2
t  2t  2  0 .
Câu 57. Nghiệm của phương trình 36 2 x  1 là 1 1 A. x  . B. x  3 . C. x  2 . D. x  . 3 2 Lời giải Chọn D x 1 Ta có 3 6 2
 1  3  6x  0  x  . 2
Câu 58. Nghiệm của phương trình log 2x  2  3 là 2   A. x  3 . B. x  2 . C. x  4 . D. x  5 . Lời giải Chọn D
Điều kiện x  1. log
2x  2  3  2x  2  8  x  5. 2  
Vậy tập nghiệm phương trình đã cho là   5 .
Câu 59. Tích hai nghiệm của phương trình 2
log x  6 log x  8  0 bằng 3 3 A. 90. B. 729 . C. 8 . D. 6 . Lời giải Chọn B log x  4 4 x  3 Đk: x  0 ; 2
log x  6 log x  8  0  3  ; 3 3   log x  2 2  3 x  3  4 2 3 .3  729 .
Câu 60. Tìm tập nghiệm của phương trình 2
log(x  6x  7)  log(x  3) . A. 4;  5 . B.   5 . C. 3;  4 . D.  . Lời giải Chọn B 2
x  6x  7  0 Đk:   x  3  2 . x  3  0 
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 39
NGUYỄN BẢO VƯƠNG - 0946798489x  5 2
log(x  6x  7)  log(x  3)  2
x  6x  7  x  3   . x  2 
Nhận nghiệm x  5 , loại nghiệm x  2 .
Câu 61. Tính tổng các nghiệm của phương trình  2
log x  3x   1  9 . A. 3 . B. 9 . C. 9 10 . D. 3 . Lời giải Chọn D
Phương trình tương đương với 2 9 x 3x 1 10    2 9 x 3x 1 10      0 . 9 5 4.10   
 0 nên phương trình có hai nghiệm x và x phân biệt. 1 2
Theo định lý Viét, ta có x x  3 . 1 2
Câu 62. Phương trình log x  3  log
x 1  3 có nghiệm là một số 2   2   A. chẵn. B. chia hết cho 3 . C. chia hết cho 7 . D. chia hết cho 5 . Lời giải Chọn D
Điều kiện: x  3 . log x  3  log
x 1  3  log  x  3 x 1   3 2    2   2     x  1 2
x  4x  3  8 2
x  4x  5  0   . x  5 
So điều kiện phương trình có nghiệm x  5 .
Câu 63. Tổng tất cả các nghiệm của phương trình log 9  5x  1 x bằng 5   A. 2 . B. 1. C. 9 . D. 5 . Lời giải Chọn B   x 9 61 5   x xx x x 2 Ta có: log 9  5  1 2
 1 x  9  5  5
 5  9.5  5  0   5   x 9 61 5   2  9  61 x  log  5 2    9  61  x  log5  2 9  61 9  61 81  61
Tổng tất cả các nghiệm : log  log  log  1 . 5 5 5 2 2 4
Câu 64. Tổng tất cả các nghiệm của phương trình log(8.5x  20x )  x  log 25 bằng A. 16 . B. 3 . C. 25 . D. 8 . Lời giải Chọn B Ta có : log(8.5x 20x ) log 25.10x 8.5x 20x 25.10x      (1)
Chia 2 vế phương trình (1) cho 5x ta được phương trình : 8 4x 25.2x   (2) Đặt 2x t , (t > 0)
Phương trình (2) trở thành 2
t  25t + 8 = 0 3 , gọi t ,t là hai nghiệm của 3 thì t .t  8 1 2 1 2
Trang 40 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Hai nghiệm của 2 là x  log t , x  log t , ta có: 1 2 1 2 2 2
Ta có x x  log t  log t  log t .t  log 8  3 . 1 2 2 1 2 1 2 1 2 2
Câu 65. Tổng tất cả các nghiệm của phương trình 2 3 x (2x 9).3x 9.2x     0 bằng A. 3 . B. 2 . C. 0 . D. 2  . Lời giải Chọn B Đặt 3x t  , t  0 t  9
Phương trình trở thành: 2
t  (2x  9)t  9.2x  0   t  2x  * Với  9  3x t  9  x  2 x x x x  3 
* Với t  2  3  2   1  x  0    2 
Vậy, phương trình có hai nghiệm x  0 ; x  2  x x  2 . 1 2 1 2  a
Câu 66. Phương trình 2 log 3x 1 2 log 3x  
1  3  0 có 2 nghiệm x ; x (x x ) và x x  log 2   2   1 2 1 2 1 2 3    b a
với a, b   , b  0 và
là phân số tối giản. Tính a b . b
A. a b  5  .
B. a b  5 .
C. a b  11.
D. a b  1. Lời giải Chọn A log 3x 1  3  2   Ta có: 2 log 3x 1  2 log
3x 1  3  0   . 2   2   log 3x 1  1 2    x x 1 9
*Với log 3 1  3  3 1   x  log . 2   3 8 8 *Với log
3x 1  1  3x 1  2  x  1. 2   9 3
Suy ra x x  log 1  log . 1 2 3 3 8 8
Vậy a  3, b  8  a b  5  .
Câu 67. Tổng tất cả các nghiệm của phương trình log
9  4x  1  x bằng: 4   A. 2 . B. 1. C. 4 . D. 3 . Lời giải Chọn B Điều kiện 9 4x   0    9  65 x 9 65 4   x  log  4 x 4 2 2 log
9  4x  1  x 2  9  4 
 4 x  9.4x  4  0     4   4x    9  65 x 9 65 4   x  log  2 4  2 9  65 9  65
Tổng tất cả các nghiệm log  log  1 . 4 4 2 2
Câu 68. Số nghiệm của phương trình log
6  7x x 1 bằng: 7   A. 2 . B. 3 . C. 0 . D. 1. Lời giải Chọn D
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 41
NGUYỄN BẢO VƯƠNG - 0946798489 7x  1 1 log
6  7x x  1 x 2  6 
 7.7  7.7 x  6.7x 1  0    x  0 7    x 1 7x 7   7
Số nghiệm của phương trình bằng 1.
Câu 69. Tổng tất cả các nghiệm của phương trình 2
ln(x  5x  4)  log 2.ln10 bằng A. 1. B. 6 . C. 7 . D. 5 . Lời giải Chọn D 5  41 5  41 ĐK: 2
x  5x  4  0  x  hoặc x  2 2 Ta có: 2
ln(x  5x  4)  log 2.ln10  2
ln(x  5x  4)  ln 2 x  6(N ) 2
x  5x  6  0  x  1  (N ) 
Vậy, phương trình có hai nghiệm x  1
 , x  6  x x  5 . 1 2 1 2
Câu 70. Tổng tất cả các nghiệm của phương trình log  x 1
4.3  1  2x 1 bằng: 3  A. 1. B. 2 . C. 7 . D. 3 . Lời giải Chọn A Điều kiện x 1 4.3  1  0 1 3x  3 x  1 x 4 log  x 1
4.3  1  2x 1 2
 .3  .3x 1  0   3    3 3 3x  1  x  0 
Tổng tất cả các nghiệm 1  0  1 .
Câu 71. Số nghiệm của phương trình log 9  2x  5  x bằng: 2   log5 3  A. 2 . B. 1. C. 7 . D. 3 . Lời giải Chọn B 9   2x  0
Điều kiện  3 x  0  2x  8 x 8 log 9  2x  5  x  log
9  2x  3  x 2  9  2 
 2 x  9.2x  8  0  2   2   log5 3   2x 2x  1 
x  3l     x  0 x  0 
Số nghiệm của phương trình bằng 1.
-------------------- HẾT --------------------
Trang 42 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Document Outline

  • 9. Hàm số lũy thừa - mũ - logarit - câu hỏi.pdf
  • 9. Hàm số lũy thừa - mũ - logarit- đáp án.pdf