Tổng ôn tập TN THPT 2020 môn Toán: Khối tròn xoay và thể tích khối tròn xoay Toán 12

Tài liệu gồm 73 trang, được tổng hợp và biên soạn bởi thầy giáo Nguyễn Bảo Vương, tuyển chọn các câu hỏi và bài tập trắc nghiệm các chuyên đề: Khối tròn xoay và thể tích khối tròn xoay; có đáp án và lời giải chi tiết.Mời các bạn đón xem.

65 33 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 2: Mặt nón, mặt trụ, mặt cầu

Môn: Toán 12

Thông tin:

72 trang 8 tháng trước

Tác giả:

Profile Lan Tường
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
MẶT TRỤ, MẶT NÓN – MẶT CẦU
MẶT NÓN Các yếu tố mặt nón: Một số công thức:
Hình thành: Quay
vuông
SOM
quanh trục
SO
, ta được
mặt nón như hình bên
với:
h SO
r OM
.
Đường cao:
h SO
. (
SO
cũng
được gọi là trục của hình nón).
Bán kính đáy:
.r OA OB OM
Đường sinh:
.l SA SB SM
Góc ở đỉnh:
.ASB
Thiết diện qua trục:
SAB
cân
tại
.S
Góc giữa đường sinh và mặt
đáy:
.SAO SBO SMO
Chu vi đáy:
2 .p r
Diện tích đáy:
2
đ
.S r
Thể tích:
đ
2
1 1
. . .
3 3
V h S h r
(liên tưởng đến thể tích khối chóp).
Diện tích xung quanh: .
xq
S rl
Diện tích toàn phần:
2
.
tp xq
S S S rl r
đ
MẶT TRỤ Các yếu tố mặt trụ: Một số công thức:
Hình thành: Quay hình chữ
nhật
ABCD
quanh đường
trung bình
OO
, ta có mặt trụ
như hình bên.
Đường cao:
.h OO
Đường sinh:
.l AD BC
Ta
có:
.l h
Bán kính đáy:
.r OA OB O C O D
Trục (∆) là đường thẳng đi qua
hai điểm
, .O O
Thiết diện qua trục: Là hình
chữ nhật
.ABCD
Chu vi đáy:
2 .p r
Diện tích đáy:
2
đ
.S r
Thể tích khối trụ:
2
. .V h S h r
đ
.
Diện tích xung quanh:
2 . .
xq
S r h
Diện tích toàn
phần:
đ
2
2 2 . 2 .
tp xq
S S S r h r
MẶT CẦU Một số công thức:
Mặt cầu ngoại tiếp đa diện
Mặt cầu nội tiếp đa diện
Hình thành: Quay đường
tròn tâm
I
, bán kính
2
AB
R
quanh trục
AB
, ta có mặt cầu
như hình vẽ.
Tâm
,I
bán kính
R IA IB IM
.
Đường kính
2AB R
.
Thiết diện qua tâm mặt cầu: Là
đường tròn tâm
I
, bán kính
R
.
Diện tích mặt cầu:
2
4S R
.
Thể tích khối cầu:
3
4
3
R
V
.
Mặt cầu ngoại
tiếp đa diện là mặt
cầu đi qua tất cả
đỉnh của đa diện
đó.
Mặt cầu nội tiếp
đa diện là mặt
cầu tiếp xúc với
tất cả các mặt của
đa diện đó.
KHỐI TRÒN XOAY - THỂ TÍCH KHỐI TRÒN XOAY
Vấn đề 11
h
l
l
l
r
O
A
B
S
M
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
CÂU HỎI MỨC ĐỘ NHẬN BIẾT
Câu 1. Diện tích xung quanh của hình nón có độ dài đường sinh
và bán kính đáy
r
bằng
A.
4
rl
. B.
2
rl
. C.
rl
. D.
1
3
rl
.
Câu 2. Cho khối nón có chiều cao
3
h
và bán kính đáy
4r
. Thể tích của khối nón đã cho bằng
A.
16
. B.
48
. C.
36
. D.
4
.
Câu 3. Cho mặt cầu có bán kính
2R
. Diện tích của mặt cầu đã cho bằng
A.
32
3
. B.
8
. C.
16
. D.
4
.
Câu 4. Diện tích xung quanh của hình trụ có độ dài đường sinh
và bán kính đáy
r
bằng
A.
4
rl
. B.
rl
. C.
1
3
rl
. D.
2
rl
.
Câu 5. Công thức tính diện tích mặt cầu bán kính
r
là
A.
2
S r
. B.
3
4
3
S r
. C.
2
3
4
S r
. D.
2
4
S r
.
Câu 6. Cho hình nón tròn xoay có bán kính đường tròn đáy
r
, chiều cao
h
và đường sinh
.
Kết luận nào sau đây sai?
A.
2
1
3
V r h
. B.
2
tp
S rl r
. C.
2 2 2
h r l
. D.
xq
S rl
.
Câu 7. Gọi
l
,
h
,
r
lần lượt là độ dài đường sinh, chiều cao và bán kính mặt đáy của hình nón. Diện tích
xung quanh
xq
S
của hình nón là
A.
xq
S rh
. B.
xq
S rl
. C.
2
xq
S rl
. D.
2
1
3
xq
S r h
.
Câu 8. Cho khối nón có bán kính đáy
3
R
và chiều cao
3h
. Thể tích của khối nón đã cho bằng
A.
3
. B.
9
. C.
3 3
. D.
3
.
Câu 9. Thể tích khối cầu bán kính
6 cm
bằng
A.
3
144 cm
B.
3
288 cm
C.
3
162 cm
D.
3
864 cm
Câu 10. Tìm độ dài đường cao của hình trụ biết hình trụ có diện tích xung quanh là
xq
S
và bán kính
r
?
A.
2
xq
S
r
. B.
xq
S
r
. C.
2
xq
r
S
. D.
xq
r
S
.
Câu 11. Diện tích xung quanh của hình trụ có độ dài đường sinh
và bán kính
r
bằng
A.
4
rl
. B.
2
rl
. C.
rl
. D.
1
3
rl
.
Câu 12. Cho hình trụ
( )T
có thiết diện qua trục của hình trụ là hình vuông có cạnh bằng
a
. Diện tích xung
quanh của hình trụ đã cho bằng
A.
2
2
a
. B.
2
2
a
. C.
2
a
. D.
2
3
2
a
.
Câu 13. Cho khối nón có chiều cao
6h
và bán kính đáy bằng
r
. Biết bán kính đáy
r
bằng một nửa
chiều cao
h
. Thể tích của khối nón đã cho bằng
A.
18
. B.
54
. C.
36
. D.
12
.
Câu 14. Diện tích của một mặt cầu bằng
2
16
cm
. Bán kính của mặt cầu đó là
A.
2cm
. B.
2cm
. C.
4cm
. D.
2 3
cm
.
Câu 15. Diện tích xung quanh của hình trụ có diện tích một đáy là
S
và độ dài đường sinh
l
bằng?
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
A.
2
l S
. B.
2Sl
. C.
2 l
S
. D.
l S
.
Câu 16. Cho khối nón có chiều cao
6h
và bán kính đáy bằng
r
. Biết thể tích của khối nón đã cho
8V
. Tính bán kính đáy.
A.
2r
. B.
1
3
. C.
4
3
. D.
4
.
Câu 17. Thể tích khối cầu có đường kính
2a
bằng
A.
3
4
3
a
. B.
3
4
a
. C.
3
32
3
a
. D.
2
4 .a
.
Câu 18. Cho hình trụ có độ dài đường sinh
và bán kính
r
. Nếu độ dài đường sinh khối trụ tăng lên 3 lần,
diện tích đáy không đổi thì thể tích của khối trụ sẽ tăng lên
A. 3 lần. B.
1
3
lần. C.
9
lần. D.
27
lần.
Câu 19. Diện tích toàn phần của hình nón có độ dài đường sinh
và đường kính đáy
2r
bằng
A.
rl
. B.
2
2 4
rl r
. C.
2
rl r
. D.
1
3
rl
.
Câu 20. Bán kính
r
của khối cầu có thể tích
3
36 cm
V
là
A.
3 cm
r
. B.
27 cm
r
. C.
3
48 cm
r
. D.
3
9 cm
r
.
Câu 21. Tìm bán kính
r
của hình nón biết hình nón có diện tích xung quanh là
xq
S
và độ dài đường sinh
l
?
A.
xq
S
l
. B.
2
xq
S
l
. C.
xq
l
S
. D.
2
xq
l
S
.
Câu 22. Trong không gian cho tam giác vuông tại
A
,
AB a
và
3AC a
. Tính độ dài đường sinh của
hình nón có được khi quay tam giác
ABC
xung quanh trục
AB
.
A.
2l a
. B.
2l a
. C.
l a
. D.
3l a
.
Câu 23. Diện tích xung quanh của hình trụ có bán kính đáy
2R
và đường sinh
6l
bằng
A.
24
. B.
12
. C.
4
. D.
8
.
Câu 24. Cho hình nón có bán kính đáy bằng
1
, góc giữa đường sinh và trục của hình nón bằng
0
30
. Diện
tích xung quanh của hình nón đã cho bằng
A.
4 3
3
. B.
3
. C.
2 3
3
. D.
2
.
Câu 25. Cho khối trụ có chiều cao bằng bán kính đáy và diện tích thiết diện qua trục của khối trụ bằng
16.
Thể tích khối trụ đã cho bằng
A.
64
. B.
64
3
. C.
16 2
. D.
16 2
3
.
Câu 26. Hình trụ có thiết diện qua trục là một hình vuông có cạnh bằng 20cm. Thể tích của khối trụ tương
ứng bằng:
A.
3
800
cm
. B.
3
8000
cm
. C.
3
400
cm
. D.
3
2000
cm
.
CÂU HỎI MỨC ĐỘ THÔNG HIỂU
Câu 27. Trong không gian cho hình chữ nhật
ABCD
,
, 2AB a AC a
. Khi quay hình chữ nhật
ABCD
quanh cạnh
AD
thì đường gấp khúc
ABCD
tạo thành một hình trụ. Diện tích xung quanh của
hình trụ đó bằng
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
2
4 a
. B.
2
2 a
3
. C.
2
a
3
. D.
2
2 3 a .
Câu 28. Trong không gian, cho tam giác
ABC
vuông tại
A
,
AB a
và
2AC a
. Khi quay tam giác
ABC
quanh cạnh góc vuông
AB
thì đường gấp khúc
ACB
tạo thành một hình nón. Diện tích
xung quanh hình nón đó bằng
A.
2
5 a
. B.
2
5 a
. C.
2
2 5 a
. D.
2
10 a
.
Câu 29. Cho hình trụ có bán kính đáy bằng
3
. Biết rằng khi cắt hình trụ đã cho bởi một mặt phẳng qua
trục, thiết diện thu được là một hình vuông. Diện tích xung quanh của hình trụ đã cho bằng
A.
18
. B.
36
. C.
54
. D.
27
.
Câu 30. Cho một chiếc cốc hình nón chứa đầy trà như hình vẽ. Người
X
uống một phần trà sao cho chiều
cao của nó giảm đi
1
3
so với chiều cao của trà trong cốc. Người
Y
uống phần trà còn lại trong
cốc. Khi đó khẳng định nào đúng.
A. Người
X
uống lượng trà bằng 5,75 lần lượng trà của người
Y
uống.
B. Hai người
X
và
Y
uống lượng trà bằng nhau.
C. Người
X
uống lượng trà bằng 2,375 lần lượng trà của người
Y
uống.
D. Người
X
uống lượng trà bằng một nửa lượng trà của người
Y
uống.
Câu 31. Cắt hình trụ
T
bằng một mặt phẳng song song với trục và cách trục một khoảng bằng
2cm
được thiết diện là một hình vuông có diện tích bằng
2
16cm
. Thể tích của
T
là
A.
3
32 cm
. B.
3
16 cm
. C.
3
64 cm
. D.
3
8 cm
.
Câu 32. Cho hai tấm tôn hình chữ nhật đều có kích thước
1,5 8m m
. Tấm tôn thứ nhất được chế tạo thành
một hình hộp chữ nhật không đáy, không nắp, có thiết diện ngang là một hình vuông (mặt phẳng
vuông góc với đường cao của hình hộp và cắt các mặt bên của hình hộp theo các đoạn giao tuyến
tạo thành một hình vuông) và có chiều cao
1,5m
; còn tấm tôn thứ hai được chế tạo thành một hình
trụ không đáy, không nắp và cũng có chiều cao
1,5m
. Gọi
1
V ,
2
V theo thứ tự là thể tích của khối
hộp chữ nhật và thể tích của khối trụ. Tính tỉ số
1
2
V
V
.
A.
1
2
V
V
. B.
1
2
4
V
V
. C.
1
2
2
V
V
. D.
1
2
3
V
V
.
Câu 33. Một hình trụ có bán kính đáy
5r a
và khoảng cách giữa hai đáy bằng
7a
. Cắt khối trụ bởi một
mặt phẳng song song với trục và cách trục một khoảng bằng
3a
. Diện tích của thiết diện được tạo
nên bằng
A.
2
56a
. B.
2
35a
. C.
2
21a
. D.
2
70a
.
Câu 34. Cho một cái bể nước hình hộp chữ nhật có ba kích thước
2 ,3 ,2m m m
lần lượt là chiều dài, chiều
rộng, chiều cao của lòng trong đựng nước của bể. Hàng ngày nước ở trong bể được lấy ra bởi một
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
cái gáo hình trụ có chiều cao là
5cm
và bán kính đường tròn đáy là
4cm
. Trung bình một ngày
được múc ra
170
gáo nước để sử dụng (Biết mỗi lần múc là múc đầy gáo). Hỏi sau bao nhiều
ngày thì bể hết nước biết rằng ban đầu bể đầy nước?
.
A.
280
ngày. B.
282
ngày. C.
281
ngày. D.
283
ngày.
Câu 35. Trong không gian, cho hình chữ nhật
ABCD
,
2AB a
và
3AC a
. Khi quay hình chữ nhật
ABCD
quanh cạnh
AB
thì đường gấp khúc
BCDA
tạo thành một hình trụ. Diện tích xung quanh
của hình trụ đó bằng
A.
2
6 5 a
. B.
2
12 a
. C.
2
4 5 a
. D.
2
20 a
.
Câu 36. Trong không gian, cho tam giác
ABC
vuông tại
A
,
2AB a
và
3AC a
. Khi quay tam giác
ABC
quanh cạnh góc vuông
AB
thì đường gấp khúc
ACB
tạo thành một hình nón. Diện tích
toàn phần của hình nón đó bằng
A.
2
3 13 a
. B.
2 2
3 13 4 .a a
C.
2 2
3 13 9 .a a
D.
2
42 .a
Câu 37. Cho hình trụ
( )T
có thiết diện qua trục của hình trụ là một hình chữ nhật có diện tích bằng
48
và
chu vi bằng
28
. Biết chiều dài của hình chữ nhật lớn hơn đường kính mặt đáy của hình trụ
T
.
Diện tích xung quanh của hình trụ đã cho bằng
A.
96
. B.
48
. C.
24
. D.
32
.
Câu 38. Cho hình trụ có thiết diện qua trục là một hình vuông. Thiết diện của hình trụ tạo bởi mặt phẳng
song song và cách trục một khoảng bằng
a
có diện tích bằng
2
8 3a
. Thể tích của khối trụ là
A.
2
16 a
. B.
3
16 a
. C.
3
32 a
. D.
3
16
3
a
.
Câu 39. Cho hình nón có bán kính đáy
3r
. Biết rằng khi cắt khối nón đó bằng một mặt phẳng qua trục
của nó, ta được thiết diện là một tam giác đều. Diện tích xung quanh của hình nón bằng
A.
6 3
. B.
36
. C.
18
. D.
9
.
Câu 40. Trong không gian, cho tam giác
ABC
vuông tại
A
,
3AB a
và
5BC a
. Khi quay tam giác
ABC
quanh cạnh góc vuông
AB
thì đường gấp khúc
ACB
tạo thành một hình nón. Diện tích
xung quanh hình nón đó bằng
A.
2
20a
. B.
2
15 a
. C.
2
20 a
. D.
2
80 a
.
Câu 41. Thiết diện qua trục của một hình nón là một tam giác vuông cân có cạnh góc vuông bằng
a
. Diện
tích xung quanh của hình nón bằng
A.
2
2a
. B.
2
2
2
a
. C.
2
a
. D. .
Câu 42. Cho khối nón có độ dài đường sinh bằng
5a
và đường cao bằng
4a
. Thể tích khối nón bằng
A.
3
80
3
a
. B.
3
15 a
. C.
3
12 a
. D.
3
36 a
.
Câu 43. Một chi tiết máy là phần còn lại của một khối trụ có bán kính đáy
r
sau khi đã đục bỏ phần bên
trong là một khối trụ có bán kính đáy
2
r
(tham khảo hình vẽ).
2
2
a
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Biết thể tích khối trụ nhỏ bị đục bỏ bằng
3
20 cm
. Thể tích của khối chi tiết máy đó là
A.
3
40 cm
. B.
3
60 cm
. C.
3
80 cm
. D.
3
70 cm
.
Câu 44. Cho khối nón có thiết diện qua trục là tam giác đều
SAB
cạnh
a
. Thể tích khối nón bằng
A.
3
3
8
a
. B.
3
24
a
. C.
3
12
a
. D.
3
3
24
a
.
Câu 45. Một khối đồ chơi gồm hai khối cầu
1 2
,H H
tiếp xúc với nhau, lần lượt có bán kính tương
ứng là
1 2
,r r thỏa mãn
2 1
1
2
r r
(tham khảo hình vẽ).
Biết rằng thể tích của toàn bộ khối đồ chơi bằng
3
180cm
. Thể tích của khối cầu
1
H
bằng
A.
3
90 cm B.
3
120 cm C.
3
160 cm D.
3
135 cm
Câu 46. Cho khối nón có thiết diện qua trục là tam giác
SAB
vuông tại
S
với cạnh
SA a
. Thể tích khối
nón bằng
A.
3
2
12
a
. B.
3
3
a
. C.
3
12
a
. D.
3
2
4
a
.
Câu 47. Một chi tiết máy gồm 3 khối trụ có cùng chiều cao
h
gắn với nhau (như hình vẽ).
Khối trụ lớn có bán kính đáy
r
lớn gấp đôi bán kính đáy của hai khối trụ nhỏ (hai khối trụ nhỏ
bằng nhau). Biết thể tích của cả khối chi tiết máy đó bằng
3
90cm . Tính thể tích của khối trụ lớn ở
giữa.
A.
3
30cm . B.
3
45cm . C.
3
70cm . D.
3
60cm .
Câu 48. Một chiếc bánh sinh nhật gồm ba khối trụ
1 2 3
, ,H H H
xếp chồng lên nhau, lần lượt có bán
kính đáy và chiều cao tương ứng là
1 1 2 2 3 3
, ; , ; ,r h r h r h thỏa mãn
1 2 3 1 2 3
2 3 , 2r r r h h h (tham
khảo hình vẽ).
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Biết rằng thể tích của khối
3
H
bằng
3
80cm
. Thể tích của toàn bộ chiếc bánh sinh nhật bằng
A.
3
890cm
. B.
3
980cm
. C.
3
900cm
. D.
3
800cm
.
Câu 49. Cho khối nón có thể tích bằng
3
3 a
và đường cao bằng
3a
. Độ dài đường sinh của khối nón
đã cho bằng
A.
6a
. B.
2a
. C.
2a
. D.
a
.
Câu 50. Một khối đồ chơi gồm một hình cầu
1
H
bán kính
R
và một hình nón
2
H
xếp chồng lên nhau,
lần lượt có bán kính đáy và đường sinh là
,r l
thỏa mãn
1
2
r l
và
3
.
2
l R
(hình vẽ).
Biết tổng diện tích mặt cầu
1
H
và diện tích toàn phần của hình nón
2
H
là
3
91cm .
Tính diện
tích của khối cầu
1
H
.
A.
3
16cm .
B.
3
104
cm .
5
C.
3
64cm .
D.
3
26
cm .
5
Câu 51. Cho hình trụ có bán kính đáy bằng
1 cm
. Một mặt phẳng qua trục của hình trụ và cắt hình trụ theo
thiết diện là hình vuông. Tính thể tích của khối trụ đã cho.
A.
3
8 cm
. B.
3
2 cm
. C.
3
16
cm
3
. D.
3
16 cm
.
Câu 52. Thể tích của khối cầu ngoại tiếp bát diện đều có cạnh bằng
2a
là:
A.
3
2
6
a
. B.
3
2
3
a
. C.
3
4 2
3
a
. D.
3
4
3
a
.
Câu 53. Cho hình nón có thiết diện qua trục là tam giác vuông có cạnh huyền
2a
. Tính diện tích xung
quanh
xq
S
của hình nón đó
A.
2
2
.
6
xq
a
s
B.
2
2
.
3
xq
a
s
C.
2
2
.
2
xq
a
s
D.
2
2
.
3
xq
a
s
Câu 54. Trong không gian cho tứ giác
ABCD
là một nửa lục giác đều nội tiếp đường tròn đường kính
2CD a
. Khi quay tứ giác
ABCD
quanh cạnh
AB
thì tạo thành một khối tròn xoay. Thể tích
khối tròn xoay đó bằng
A.
3
a
. B.
3
2 a
. C.
3
5
4
a
. D.
3
3
2
a
.
Câu 55. Cho một hình nón có góc ở đỉnh
60
, bán kính đáy bằng
a
. Diện tích toàn phần hình nón đó là
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
2
a
. B.
2
3
a
. C.
2
2
a
. D.
2
3
a
.
Câu 56. Cho hình lập phương
.
ABCD A B C D
cạnh bằng
a
. Thể tích khối cầu có tâm
A
và tiếp xúc với
đường thẳng
A C
bằng
A.
3
2
3
a
. B.
3
8 6
27
a
. C.
3
3
2
a
. D.
3
6
a
.
Câu 57. Cho hình chóp tứ giác đều
ABCD
S
có cạnh đáy bằng
a
, diện tích mỗi mặt bên bằng
2
a
. Thể
tích khối nón đỉnh S và đường tròn đáy nội tiếp hình vuông ABCD bằng:
A.
3
15
24
a
. B.
3
15
8
a
. C.
3
15
12
a
. D.
3
15
18
a
.
Câu 58. Cho hai khối cầu có bán kính lần lượt bằng
a
và
2a
. Tỉ số giữa thể tích của khối cầu nhỏ với
thể tích của khối cầu lớn bằng
A.
1
4
. B.
4
. C.
1
8
. D.
8
.
Câu 59. Cho hình trụ có chiều cao bằng bán kính đáy và bằng 5 cm. Mặt phẳng
song song với trục,
cắt hình trụ theo một thiết diện có chu vi bằng 26 cm. Khoảng cách từ
đến trục của hình trụ
bằng
A. 4 cm. B. 5 cm. C. 2 cm. D. 3 cm.
Câu 60. Cho tam giác vuông cân
ABC
có
2AB BC a
. Khi quay tam giác
ABC
quanh đường thẳng
đi qua
B
và song song với
AC
ta thu được một khối tròn xoay có thể tích bằng
A.
3
2
a
. B.
3
2
3
a
. C.
3
4
3
a
. D.
3
a
.
Câu 61. Một hình trụ có diện tích xung quanh bằng
64
và thiết diện qua trục của hình trụ này là một
hình vuông. Thể tích hình trụ đó bằng
A.
512
. B.
128
. C.
64
. D.
256
.
Câu 62. Cho hình chóp tứ giác đều
.
S ABCD
có cạnh đáy bằng
a
, cạnh bên hợp với đáy góc
60
. Hình
nón
N
có đỉnh
S
, đáy là đường tròn nội tiếp tứ giác
ABCD
. Diện tích xung quanh của hình
nón
N
bằng
A.
2
7
4
a
. B.
2
2
3
a
. C.
2
3
2
a
. D.
2
2
a
.
Câu 63. Trong không gian, cho hình chữ nhật
ABCD
,
, 2AB a AC a
. Khi quay hình chữ nhật
ABCD
quanh cạnh
AD
thì đường gấp khúc
ABCD
tạo thành một hình trụ. Diện tích xung quanh của
hình trụ đó bằng
A.
2
3
a
. B.
2
2
3
a
. C.
2
4
a
. D.
2
2 3
a
.
Câu 64. Cho hình nón có đường cao
a
. Biết rằng khi cắt hình nón đã cho một mặt phẳng đi qua đỉnh của
hình nón và cách tâm của đáy hình nón một khoảng
3
a
, thiết diện thu được tạo thành một tam giác
vuông. Thể tích khối nón được giới hạn bởi hình nón đã cho bằng
A.
3
5
12
a
. B.
3
3
a
. C.
3
4
9
a
. D.
3
5
9
a
.
Câu 65. Khối tròn xoay sinh bởi một tam giác đều cạnh
a
(kể cả điểm trong) khi quay quanh một đường
thẳng chứa một cạnh của tam giác đó có thể tích bằng
A.
3
8
a
. B.
3
3
6
a
. C.
3
4
a
. D.
3
3
12
a
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Câu 66. Cho hình chóp đều
.
S ABCD
có
AB a
, cạnh bên hợp với đáy góc
0
45
. Diện tích xung quanh
của hình nón đỉnh
S
với đáy là đường tròn nội tiếp hình vuông bằng
A.
2
2
a
. B.
2
3
4
a
. C.
2
4
a
. D.
2
2
a
.
Câu 67. Một hình nón có thiết diện qua trục là một tam giác vuông cân có cạnh góc vuông bằng
a
. Diện
tích xung quanh của hình nón bằng:
A.
2
2
4
a
. B.
2
2 2
3
a
. C.
2
2
2
a
. D.
2
2
a
.
Câu 68. Cho hình chữ nhật
ABCD
có
2 2AC a
và
45
ACB
. Quay hình chữ nhật
ABCD
quanh
cạnh
AB
thì đường gấp khúc
ADCB
tạo thành hình trụ. Diện tích toàn phần
tp
S
của hình trụ là
A.
2
16
tp
S a
. B.
2
10
tp
S a
. C.
2
12
tp
S a
. D.
2
8
tp
S a
.
Câu 69. Trong không gian, cho tam giác
ABC
vuông tại
A
,
AB a
,
60
ABC
. Tính độ dài đường sinh
l
của hình nón, nhận được khi quay tam giác
ABC
quanh trục
AC
.
A.
2l a
. B.
2l a
. C.
l a
. D.
3l a
.
Câu 70. Trong không gian, cho hình chữ nhật
ABCD
có
4, 5
AB AC
. Gọi
,M N
lần lượt là trung
điểm của
AD
và
BC
. Quay hình chữ nhật đó xung quanh trục
MN
, ta được một hình trụ. Tính
diện tích toàn phần
TP
S
của hình trụ đó.
A.
8
TP
S
. B.
33
2
TP
S
. C.
81
2
TP
S
. D.
24
TP
S
.
Câu 71. Cho tứ diện đều
ABCD
có cạnh bằng
4
. Tính diện tích xung quanh
xq
S
của hình trụ có một
đường tròn đáy là đường tròn nội tiếp tam giác
BCD
và chiều cao bằng chiều cao của tứ diện
ABCD
.
A.
16 2
3
xq
S
. B.
8 2
xq
S
. C.
16 3
3
xq
S
. D.
8 3
xq
S
.
Câu 72. Cho hình chóp tứ giác đều
.
S ABCD
có cạnh đáy bằng
a
, góc giữa cạnh bên
SA
và mặt phẳng
đáy bằng
30
. Tính diện tích xung quanh
xq
S
của hình trụ có một đường tròn đáy là đường tròn
nội tiếp hình vuông
ABCD
và chiều cao bằng chiều cao của hình chóp
.
S ABCD
.
A.
2
6
6
xq
a
S
. B.
2
3
6
xq
a
S
. C.
2
6
12
xq
a
S
. D.
2
3
12
xq
a
S
.
Câu 73. Cho hình lăng trụ tam giác đều
.
ABC A B C
có
AB a
, góc giữa
AC
và
ABC
bằng
30
.
Tính thể tích
V
của khối trụ nội tiếp hình lăng trụ
.
ABC A B C
.
A.
3
3
12
a
V
. B.
3
3
36
a
V
. C.
3
3
108
a
V
. D.
3
3
72
a
V
.
Câu 74. Cho tứ diện đều
ABCD
có cạnh bằng
5
. Tính thể tích
V
của khối nón nội tiếp tứ diện
ABCD
.
A.
25 6
108
V
. B.
125 3
108
V
. C.
125 6
108
V
. D.
25 6
36
V
.
Câu 75. Cho tứ diện đều
ABCD
cạnh bằng
3a
. Tính diện tích xung quanh
xq
S
của hình trụ có đáy là
đường tròn ngoại tiếp tam giác
BCD
và có chiều cao bằng chiều cao của tứ diện đều
ABCD
.
A.
2
2 3
xq
S a
. B.
2
2
xq
S a
. C.
2
3
xq
S a
. D.
2
2 2
xq
S a
.
Câu 76. Cho một lăng trụ tam giác đều
. ' ' 'ABC A B C
có cạnh đáy bằng
a
. Góc giữa
'A C
và mặt phẳng
đáy bằng
60
O
. Tính diện tích xung quanh
xq
S
của hình nón có đáy là đường tròn nội tiếp tam giác
ABC
và đỉnh là trong tâm của tam giác
' ' 'A B C
.
A.
2
333
36
xq
a
S
. B.
2
111
36
xq
a
S
. C.
2
333
6
xq
a
S
. D.
2
111
6
xq
a
S
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 77. Cho lăng trụ đứng
. ' ' 'ABC A B C
, đáy
ABC
là một tam giác vuông tại cân
A
,
AB a
, cạnh
'AA
hợp với
'B C
góc 60
o
. Tính thể tích của khối trụ ngoại tiếp lăng trụ
. ' ' 'ABC A B C
theo
a
.
A.
3
3
18
a
V
. B.
3
3
6
a
V
. C.
3
3
3
a
V
. D.
3
2
6
a
V
.
Câu 78. Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông tại
C
,
, 2AC a BC a
, mặt phẳng
SAB
vuông góc với mặt phẳng
ABC
và tam giác
SAB
vuông cân tại
S
. Tính thể tích của
khối nón có đỉnh là
S
và đáy là đường tròn ngoại tiếp tam giác
ABC
.
A.
3
5
24
a
V
. B.
3
5 5
12
a
V
. C.
3
5 5
24
a
V
. D.
3
3 3
24
a
V
.
Câu 79. Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông tại
A
,
SA
vuông góc với mặt phẳng
ABC
, tam giác
SBC
đều cạnh
a
, góc giữa mặt phẳng
SBC
và mặt phẳng đáy là
30
. Tính
thể tích
V
của khối trụ có một đường tròn đáy là đường tròn ngoại tiếp tam giác
ABC
và chiều
cao bằng khoảng cách từ
S
đến mặt phẳng
ABC
.
A.
3
2
4
a
V
. B.
3
2
16
a
V
. C.
3
3
4
a
V
. D.
3
3
16
a
V
.
Câu 80. Cho lăng trụ đứng
.
ABC A B C
có đáy là tam giác đều cạnh
a
. Mặt phẳng
AB C
tạo với mặt
phẳng đáy góc
60
. Tính diện tích xung quanh
xq
S
của hình trụ có một đường tròn đáy là đường
tròn nội tiếp tam giác
ABC
và chiều cao bằng chiều cao của hình lăng trụ
.
ABC A B C
.
A.
2
3
2
xq
a
S
. B.
2
3 3
12
xq
a
S
. C.
2
3
6
xq
a
S
. D.
2
3
xq
S a
.
Câu 81. Cho hình hộp chữ nhật
.
ABCD A B C D
,
2 ,
AB a AD a
,
AC
cắt
BD
tại
O
, góc
60
A BA
.
Tính thể tích của khối nón có đỉnh là
O
và đáy là đường tròn ngoại tiếp hình chữ nhật
A B C D
.
A.
3
5 3
6
a
V
. B.
3
3
6
a
V
. C.
3
5 5
6
a
V
. D.
3
5 3
2
a
V
.
CÂU HỎI MỨC ĐỘ VẬN DỤNG - VDC
Câu 82. Cho hình nón có tâm đáy là
I
. Một mặt phẳng đi qua đỉnh hình nón và cắt hình nón theo một
thiết diện là tam giác đều có diện tích bằng
3 3
, đồng thời cắt đường tròn đáy tại hai điểm.
,A B
thì
0
120
AIB
. Diện tích xung quanh của hình nón đã cho bằng
A.
8 3
. B.
8 2
3
. C.
4 1 3
. D.
4 3
.
Câu 83. Cho hình nón đỉnh
S
có chiều cao bằng
3 2
. Gọi
,B C
là 2 điểm thuộc đường tròn đáy sao cho
SBC
vuông tại
S
và có chu vi bằng
10 5 2
. Thể tích của khối nón được giới hạn bởi hình
nón đã cho bằng:
A.
7 2
. B.
21 2
. C.
43 2
. D.
14 2
.
Câu 84. Cho hình nón có chiều cao bằng
2 5
. Một mặt phẳng đi qua đỉnh hình nón và cắt hình nón theo
một thiết diện là tam giác đều có diện tích bằng
9 3
. Thể tích của khối nón được giới hạn bởi
hình nón đã cho bằng
A.
32 5
3
. B.
32
. C.
32 5
. D.
96
.
Câu 85. Cho hình trụ có chiều cao bằng 6a. Biết rằng khi cắt hình trụ đã cho bởi một mặt phẳng song song
với trục và cách trục một khoảng bằng 3a, thiết diện thu được là một hình vuông. Thể tích của
khối trụ được giới hạn bởi hình trụ đã cho bằng
A.
3
216
a
. B.
3
150
a
. C.
3
54
a
. D.
3
108
a
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Câu 86. Cho hình trụ có bán kính đáy là 4 cm, một mặt phẳng không vuông góc với đáy và cắt hai mặt đáy
theo hai dây cung song song
, ' 'AB A B
mà
' ' 6cm
AB A B
(hình vẽ). Biết diện tích tứ giác
' 'ABB A
bằng 60 cm
2
. Tính chiều cao của hình trụ đã cho.
A.
6 2
cm. B.
4 3
cm. C.
8 2
cm. D.
5 3
cm.
Câu 87. Khi cắt một hình trụ bởi hai mặt phẳng cùng song song với trục. Với mặt phẳng thứ nhất cách trục
một khoảng bằng
,a
thiết diện thu được là một hình vuông. Còn mặt phẳng thứ hai cách trục một
khoảng bằng
6
,
2
a
thiết diện thu được là một hình chữ nhật có diện tích bằng
2
2 2
a
. Thể tích
của khối trụ được giới hạn bởi hình trụ đã cho bằng
A.
3
4
.
3
a
B.
3
8 3 .
a
C.
3
4 .a
D.
3
4 .a
Câu 88. Cho hình nón đỉnh
S
, tâm đường tròn đáy là
O
và có đường kính bằng
4a
. Mặt phẳng
P
đi
qua
S
cắt đường tròn đáy tại hai điểm
A
và
B
sao cho
2 3AB a
. Gọi
D
là điểm đối xứng của
A
qua
O
. Biết khoảng cách từ
D
đến mặt phẳng
P
bằng
2 5
5
a
. Tính thể tích khối nón.
A.
3
2
a
. B.
3
2
3
a
. C.
3
2 13
3
a
. D.
3
4
3
a
.
Câu 89. Cho hình nón đỉnh
S
có đường tròn đáy tâm
O
bán kính
2R a
. Trên đường tròn đáy lấy hai
điểm
A
và
B
sao cho tam giác
OAB
đều. Biết diện tích tam giác
SAB
bằng
2 2a
. Thể tích
hình nón đã cho bằng:
A.
3
58
a
. B.
3
29
a
. C.
3
29
3
a
. D.
3
58
3
a
.
Câu 90. Cho hình trụ có hai đáy là hai đường tròn
O
và
O
, chiều cao bằng
3a
và bán kính đáy
a
.
Một mặt phẳng
đi qua trung điểm của
OO
và cắt đường tròn đáy theo một dây cung có độ
dài
2a
. Góc tạo bởi mặt phẳng
với mặt đáy gần với giá trị nào nhất.
A.
50
. B.
51
C.
39
. D.
41
.
Câu 91. Cho tam giác
ABC
đều có cạnh bằng
2a
. Từ tâm của đáy, dựng đường thẳng
vuông góc với
mặt phẳng
ABC
. Trên
lấy điểm
S
sao cho khoảng cách từ
A
đến mặt phẳng
SBC
bằng
12
7
a
. Khi đó thể tích khối nón có đỉnh là
S
và đường tròn đáy là đường tròn ngoại tiếp
ABC
bằng
A.
3
4
9
a
. B.
3
16
3
a
. C.
3
16
9
a
. D.
3
4
3
a
.
Câu 92. Cho mặt cầu
S
tâm
O
và các điểm
A
,
B
,
C
nằm trên mặt cầu
S
sao cho
3
AB
,
4
AC
,
5
BC
và khoảng cách từ
O
đến mặt phẳng
ABC
bằng
1
. Thể tích của khối cầu
S
bằng
A.
20 5
3
. B.
7 21
2
. C.
29 29
6
. D.
4 17
3
.
Câu 93. Cho hình nón có chiều cao bằng
a
. Biết rằng khi cắt hình nón đã cho bởi một mặt phẳng đi qua
đỉnh hình nón và cách tâm của đáy hình nón một khoảng bằng
3
a
, thiết diện thu được là một tam
giác vuông. Thể tích của khối nón được giới hạn bởi hình nón đã cho bằng
A.
3
4
9
a
. B.
3
5
9
a
. C.
3
3
a
. D.
3
5
12
a
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 94. Một khối trụ có bán kính đáy
2r a
.
,O O
lần lượt là tâm đường tròn đáy. Một mặt phẳng song
song với trục và cách trục
15
2
a
, cắt đường tròn
O
tại hai điểm
,A B
. Biết thể tích của khối tứ
diện
OO AB
bằng
3
15
4
a
. Độ dài đường cao của hình trụ bằng
A.
a
. B.
6a
. C.
3a
. D.
2a
.
Câu 95. Cho hình lăng trụ tam giác đều có . Gọi là trung điểm
. Bán kính mặt cầu ngoại tiếp khối chóp bằng
A. B. C. D.
Câu 96. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông cân tại
B
và
.AC a
Hình chiếu vuông
góc của đỉnh
S
lên mặt phẳng
ABC
là điểm
H
đối xứng với
B
qua
AC
. Góc giữa hai mặt
phẳng
SAC
và
0
45 .ABC
Diện tích mặt cầu ngoại tiếp hình chóp
.S ABC
bằng:
A.
2
2 a
. B.
2
2
3
a
. C.
2
5 a
. D.
2
5
4
a
.
Câu 97. Cho hai khối nón có chung trục
3SS r
. Khối nón thứ nhất có đỉnh
S
đáy là hình tròn tâm
S
bán kính
r
. Khối nón thứ hai có đỉnh
S
đáy là hình tròn tâm
S
bán kính
2r
. Thể tích phần
chung của hai khối nón bằng
A.
3
4
27
r
. B.
3
9
r
. C.
3
4
9
r
. D.
3
4
3
r
.
Câu 98. Cho hình chóp
.S ABC
có
( )SA ABC
,
3AB
,
2AC
và
30BAC
. Gọi
,M N
lần lượt là
hình chiếu của
A
lên
,SB SC
. Bán kính
R
của mặt cầu ngoại tiếp hình chóp
.A BCNM
là
A.
2R
. B.
13
R
. C.
1R
. D.
2R
.
Câu 99. Có một bể hình hộp chữ nhật chứa đầy nước. Người ta cho ba khối nón giống nhau có thiết diện
qua trục là một tam giác vuông cân vào bể sao cho ba đường tròn đáy của ba khối nón đôi một
tiếp xúc với nhau, một khối nón có đường tròn đáy tiếp xúc với một cạnh của đáy bể và hai khối
nón còn lại có đường tròn đáy tiếp xúc với hai cạnh của đáy bể. Sau đó người ta đặt lên đỉnh của
ba khối nón một khối cầu có bán kính bằng
4
3
lần bán kính đáy khối nón. Biết khối cầu vừa đủ
ngập trong nước và tổng lượng nước trào ra là
337
24
(lit). Thể tích nước ban đầu trong bể thuộc
khoảng nào dưới đây? (tính theo đơn vị lít).
A. (150;151) B. (151;152) C. (139;140) D. (138;139).
Câu 100. Cho hình trụ có chiều cao bằng
6a
. Biết rằng khi cắt hình trụ đã cho bởi một mặt phẳng song
song với trục và cách trục một khoảng bằng
3a
, thiết diện thu được là một hình vuông. Thể tích
của khối trụ được giới hạn bởi hình trụ đã cho bằng
A.
3
216 a
. B.
3
150 a
. C.
3
54 a
. D.
3
108 a
.
Câu 101. Cho hình trụ có chiều cao bằng
6a
. Biết rằng khi cắt hình trụ đã cho bởi một mặt phẳng song
song với trục và cách trục một khoảng bằng
3a
, thiết diện thu được là một hình chữ nhật có diện
tích
2
48a
. Thể tích của khối trụ được giới hạn bởi hình trụ đã cho bằng
A.
3
216
a
. B.
3
180 a
. C.
3
54
a
. D.
3
150 a
.
Câu 102. Cho hình chóp
.S ABC
có
SA
vuông góc với mặt phẳng đáy, góc giữa
SBC
và mặt phẳng đáy
bằng
60
. Nếu
ABC
là tam giác đều cạnh
3a
thì bán kính mặt cầu ngoại tiếp hình chóp
S.ABC
bằng
A.
43
4
a
. B.
43
8
a
. C.
43
12
a
. D.
43
6
a
. ' ' 'ABC A B C
' 2 ;
AA a BC a
M
'BB
. ' ' 'M A B C
3 3
.
8
a
13
.
2
a
21
.
6
a
2 3
.
3
a
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Câu 103. Cho hình chóp
ABCD
có đáy là hình thang vuông tại
A
và
D
. Biết
SA
vuông góc với
ABCD
,
, AB BC a
2 , 2
AD a SA a
. Gọi
E
là trung điểm của
AD
. Bán kính mặt cầu đi qua các
điểm
, , , ,S A B C E
bằng
A.
3
2
a
. B.
30
6
a
. C.
6
3
a
. D.
a
.
Câu 104. Một hình trụ có bán kính đáy bằng chiều cao và bằng
a
. Một hình vuông
ABCD
có
,AB CD
là
hai dây cung của hai đường tròn đáy và mặt phẳng
ABCD
không vuông góc với đáy. Diện tích
hình vuông đó bằng.
A.
2
5
4
a
. B.
2
5 2
4
a
. C.
2
5a
. D.
2
5
2
a
.
Câu 105. Cho ba hình cầu có bán kính lần lượt là
1 2 3
, ,R R R
đôi một tiếp xúc nhau và cùng tiếp xúc với mặt
phẳng
( )P
. Các tiếp điểm của ba hình cầu với mặt phẳng (P) lập thành một tam giác có độ dài các
cạnh lần lượt là
2;3;4
. Tính tổng
1 2 3
:R R R
A.
61
12
. B.
67
12
. C.
53
12
. D.
59
12
.
Câu 106. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình bình hành, các cạnh bên của hình chóp bằng
6
cm
,
4
AB cm
. Khi thể tích khối chóp
.
S ABCD
đạt giá trị lớn nhất, tính diện tích mặt cầu
ngoại tiếp
.
S ABCD
.
A.
2
12
cm
. B.
2
4
cm
. C.
2
9
cm
. D.
2
36
cm
.
Câu 107. Cho hình tứ diện
ABCD
có
AD ABC
,
ABC
là tam giác vuông tại
B
. Biết
2( )BC cm
, 2 3( ), 6( )AB cm AD cm
. Quay các tam giác
ABC
và
ABD
( bao gồm cả điểm bên trong
2
tam
giác) xung quanh đường thẳng
AB
ta được
2
khối tròn xoay. Thể tích phần chung của
2
khối
tròn xoay đó bằng
A.
3
3 ( )cm
B.
3
5 3
( )
2
cm
C.
3
3 3
( )
2
cm
. D.
3
64 3
( )
3
cm
.
Câu 108. Huyền có một tấm bìa như hình vẽ, Huyền muốn biến đường tròn đó thành một cái phễu hình nón.
Khi đó Huyền phải cắt bỏ hình quạt tròn
AOB
rồi dán
OA
,
OB
lại với nhau. Gọi
x
là góc ở tâm
hình quạt tròn dùng làm phễu. Tìm
x
để thể tích phểu lớn nhất?
A.
2 6
3
B.
3
C.
2
D.
4
Câu 109. Cho hình trụ có hai đáy là hai hình tròn
O
và
,O
thiết diện qua trục của hình trụ là hình
vuông. Gọi
,A B
là hai điểm lần lượt nằm trên hai đường tròn
O
và
.O
Biết
2AB a
và
khoẳng cách giữa hai đường thẳng
AB
và
OO
bằng
3
.
2
a
Bán kính đáy bằng
A.
14
.
3
a
B.
14
.
2
a
C.
14
.
4
a
D.
14
.
9
a
Câu 110. Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông cân tại
B
,
3 2
AB BC a
,
0
90
SAB SCB
. Biết khoảng cách từ
A
đến mặt phẳng
( )SBC
bằng
2 3a
. Tính thể tích mặt
cầu ngoại tiếp hình chóp
.
S ABC
.
A.
3
72 18
a
. B.
3
18 18
a
. C.
3
6 18
a
. D.
3
24 18
a
.
NGUYỄ
N BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 111
. Cho hình trụ có đáy là hai đường tròn tâm
O
và
O
,
bán kính đáy bằng chiều cao và bằng
2a
.
Trên đường tròn đáy có tâm
O
lấ
y điểm
A
,
D
tr
ên đường tròn tâm
O
lấy
điểm
B
,
C
sa
o cho
//AB
CD
và
A
B
khôn
g cắt
'OO
.
Tính
AD
để
thể tích khối chóp
'
.O ABCD
đạt
giá trị lớn nhất.
A.
2
2AD a
B.
4AD
a
C
.
4
3
3
AD a
D.
2AD
a
Câu 112
. Trong không gian với hệ tọa độ
Oxy
z
,
cho hai mặt phẳng song song
:
2 2 1 0,P x y z
:
2 2 5 0Q x y z
và điểm
1
;1;1A
nằm
trong khoảng giữa hai
mặt phẳng này. Gọi
S
là mặt cầu đi qua
A
và tiếp xúc với cả
P
và
.Q
Biết khi
S
thay
đổi thì tâm
I
của
nó luôn thuộc đường tròn
C
cố định. Diện tíc
h hình tròn giới hạn bởi
C
là
A
.
2
3
. B.
4
9
. C
.
16
9
. D.
8
9
.
Câu 113
. Cho hình chóp
.S ABCD
có
SA
vuông
góc với mặt phẳng
ABCD
,
tứ giác
ABCD
là hì
nh thang
vuông với cạnh đáy
,
AD BC
.
3
3 AD CB a
,
A
B a
, 3SA
a . Điểm
I
t
hỏa mãn
3
AD AI
,
M
là
trung điểm
S
D
,
H
là
giao điểm của
A
M
và
S
I
.
Gọi
,
E F
lầ
n lượt là hình
chiếu của
A
l
ên
,
SB SC
.
Tính thể tích
V
của
khối nón có đáy là đường tròn ngoại tiếp tam giác
E
FH
và đỉnh thuộc mặt phẳng
A
BCD
.
A.
3
5
5
a
V
. B.
3
2
5
a
V
. C
.
3
5
a
V
. D.
3
1
0 5
a
V
.
Câu 114
. Cho một miếng tôn hình tròn có bán kính
5
0 cm
.
Biết hình nón có thể tích lớn nhất khi diện tích
toàn phần của hình nón bằng diện tích miếng tôn ở trên. Khi đó hình nón có bán kính đáy là:
A.
10 2 cm . B.
50 2 cm . C.
20
cm
. D.
2
5 cm
.
Câu 115. Cho hình nón
N
có đường cao
SO h
và
bán kính đáy bằng
R
,
gọi
M
là
điểm trên đoạn
SO
,
đặ
t
O
M x
,
0 x
h
.
C
là
thiết diện của mặt phẳng
P
vuôn
g góc với trục
S
O
tạ
i
M
,
với
hình nón
N
.
Tìm
x
để thể
tích khối nón đỉnh
O
đá
y là
C
lớn
nhất.
A.
2
h
. B.
2
2
h
. C
.
3
2
h
. D.
3
h
.
Câu 116
. Bạn Hoàn có một tấm bìa hình tròn như hình vẽ, Hoàn muốn biến hình tròn đó thành một hình cái
phễu hình nón. Khi đó Hoàn phải cắt bỏ hình quạt tròn
A
OB
rồi
dán hai bán kính
O
A
và
O
B
lại
với nhau (diện tích chỗ dán nhỏ không đáng kể). Gọi
x
là
góc ở tâm hình quạt tròn dùng làm
phễu. Tìm
x
để t
hể tích phễu lớn nhất?
A.
4
. B.
3
. C.
2
6
3
. D.
2
.
-------------------- HẾT --------------------
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
MẶT TRỤ, MẶT NÓN – MẶT CẦU
MẶT NÓN Các yếu tố mặt nón: Một số công thức:
Hình thành: Quay
vuông
SOM
quanh trục
SO
, ta được
mặt nón như hình bên
với:
h SO
r OM
.
Đường cao:
h SO
. (
SO
cũng
được gọi là trục của hình nón).
Bán kính đáy:
.r OA OB OM
Đường sinh:
.l SA SB SM
Góc ở đỉnh:
.ASB
Thiết diện qua trục:
SAB
cân
tại
.S
Góc giữa đường sinh và mặt
đáy:
.SAO SBO SMO
Chu vi đáy:
2 .p r
Diện tích đáy:
2
đ
.S r
Thể tích:
đ
2
1 1
. . .
3 3
V h S h r
(liên tưởng đến thể tích khối chóp).
Diện tích xung quanh: .
xq
S rl
Diện tích toàn phần:
2
.
tp xq
S S S rl r
đ
MẶT TRỤ Các yếu tố mặt trụ: Một số công thức:
Hình thành: Quay hình chữ
nhật
ABCD
quanh đường
trung bình
OO
, ta có mặt trụ
như hình bên.
Đường cao:
.h OO
Đường sinh:
.l AD BC
Ta
có:
.l h
Bán kính đáy:
.r OA OB O C O D
Trục (∆) là đường thẳng đi qua
hai điểm
, .O O
Thiết diện qua trục: Là hình
chữ nhật
.ABCD
Chu vi đáy:
2 .p r
Diện tích đáy:
2
đ
.S r
Thể tích khối trụ:
2
. .V h S h r
đ
.
Diện tích xung quanh:
2 . .
xq
S r h
Diện tích toàn
phần:
đ
2
2 2 . 2 .
tp xq
S S S r h r
MẶT CẦU Một số công thức:
Mặt cầu ngoại tiếp đa diện
Mặt cầu nội tiếp đa diện
Hình thành: Quay đường
tròn tâm
I
, bán kính
2
AB
R
quanh trục
AB
, ta có mặt cầu
như hình vẽ.
Tâm
,I
bán kính
R IA IB IM
.
Đường kính
2AB R
.
Thiết diện qua tâm mặt cầu: Là
đường tròn tâm
I
, bán kính
R
.
Diện tích mặt cầu:
2
4
S R
.
Thể tích khối cầu:
3
4
3
R
V
.
Mặt cầu ngoại
tiếp đa diện là mặt
cầu đi qua tất cả
đỉnh của đa diện
đó.
Mặt cầu nội tiếp
đa diện là mặt
cầu tiếp xúc với
tất cả các mặt của
đa diện đó.
KHỐI TRÒN XOAY - THỂ TÍCH KHỐI TRÒN XOAY
Vấn đề 11
h
l
l
l
r
O
A
B
S
M
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
CÂU HỎI MỨC ĐỘ NHẬN BIẾT
Câu 1. Diện tích xung quanh của hình nón có độ dài đường sinh
l
và bán kính đáy
r
bằng
A.
4
rl
. B.
2
rl
. C.
rl
. D.
1
3
rl
.
Lời giải
Chọn C
Áp dụng công thức diện tích xung quanh hình nón.
Câu 2. Cho khối nón có chiều cao
3
h
và bán kính đáy
4r
. Thể tích của khối nón đã cho bằng
A.
16
. B.
48
. C.
36
. D.
4
.
Lời giải
Chọn A
Ta có công thức thể tích khối nón
2
1 1
. . . . .16.3 16
3 3
V r h
.
Câu 3. Cho mặt cầu có bán kính
2R
. Diện tích của mặt cầu đã cho bằng
A.
32
3
. B.
8
. C.
16
. D.
4
.
Lời giải
Chọn C
2
4 16
S R
Câu 4. Diện tích xung quanh của hình trụ có độ dài đường sinh
và bán kính đáy
r
bằng
A.
4
rl
. B.
rl
. C.
1
3
rl
. D.
2
rl
.
Lời giải
Chọn D
Diện tích xung quanh của hình trụ
2
S rl
.
Câu 5. Công thức tính diện tích mặt cầu bán kính
r
là
A.
2
S r
. B.
3
4
3
S r
. C.
2
3
4
S r
. D.
2
4
S r
.
Lời giải
Chọn D
Công thức tính diện tích mặt cầu bán kính
r
là
2
4
S r
.
Câu 6. Cho hình nón tròn xoay có bán kính đường tròn đáy
r
, chiều cao
h
và đường sinh
.
Kết luận nào sau đây sai?
A.
2
1
3
V r h
. B.
2
tp
S rl r
. C.
2 2 2
h r l
. D.
xq
S rl
.
Lời giải
Chọn C
Ta có tam giác
SOB
vuông tại
O
nên:
2 2 2 2 2 2
h r l h l r
.
h
r
O
l
S
A
B
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Câu 7. Gọi
l
,
h
,
r
lần lượt là độ dài đường sinh, chiều cao và bán kính mặt đáy của hình nón. Diện
tích xung quanh
xq
S
của hình nón là
A.
xq
S rh
. B.
xq
S rl
. C.
2
xq
S rl
. D.
2
1
3
xq
S r h
.
Lời giải
Chọn B
Diện tích xung quanh
xq
S
của hình nón là
xq
S rl
.
Câu 8. Cho khối nón có bán kính đáy
3
R
và chiều cao
3h
. Thể tích của khối nón đã cho bằng
A.
3
. B.
9
. C.
3 3
. D.
3
.
Lời giải
Chọn A
Ta có công thức thể tích khối nón
2
1 1
. . . . .3.3 3
3 3
V r h
.
Câu 9. Thể tích khối cầu bán kính
6 cm
bằng
A.
3
144 cm
B.
3
288 cm
C.
3
162 cm
D.
3
864 cm
Lời giải
Chọn B
Vì thể tích cần tìm là
3 3 3
4 4
. .6 288 cm
3 3
V R
.
Câu 10. Tìm độ dài đường cao của hình trụ biết hình trụ có diện tích xung quanh là
xq
S
và bán kính
r
?
A.
2
xq
S
r
. B.
xq
S
r
. C.
2
xq
r
S
. D.
xq
r
S
.
Lời giải
Chọn A
Bằng công thức tính diện tích xung quanh của hình trụ: (đường cao hình trụ
h
bằng đường
sinh
).
2
2
xq
xq
S
S rh h
r
.
Câu 11. Diện tích xung quanh của hình trụ có độ dài đường sinh
và bán kính
r
bằng
A.
4
rl
. B.
2
rl
. C.
rl
. D.
1
3
rl
.
Lời giải
Chọn A
Theo công thức tính diện tích xung quanh của hình trụ ta có
2
xq
S rl
Câu 12. Cho hình trụ
( )T
có thiết diện qua trục của hình trụ là hình vuông có cạnh bằng
a
. Diện tích
xung quanh của hình trụ đã cho bằng
A.
2
2
a
. B.
2
2
a
. C.
2
a
. D.
2
3
2
a
.
Lời giải
Chọn C
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Giả sử thiết diện qua trục của hình trụ là hình vuông
ABCD
có cạnh bằng
a
.
Ta có:
l AD a
;
2 2
AB a
r OA
.
Vậy diện tích xung quanh của hình trụ là
2
2 2 . .
2
xq
a
S rl a a
.
Câu 13. Cho khối nón có chiều cao
6h
và bán kính đáy bằng
r
. Biết bán kính đáy
r
bằng một nửa
chiều cao
h
. Thể tích của khối nón đã cho bằng
A.
18
. B.
54
. C.
36
. D.
12
.
Lời giải
Chọn A
Bán kính đáy:
6
3
2 2
h
r
Ta có công thức thể tích khối nón
2
1 1
. . . . .9.6 18
3 3
V r h
.
Câu 14. Diện tích của một mặt cầu bằng
2
16 cm
. Bán kính của mặt cầu đó là
A.
2cm
. B.
2cm
. C.
4cm
. D.
2 3 cm
.
Lời giải
Chọn B
Ta có:
2 2
4 16 4 2( ).R R R cm
Câu 15. Diện tích xung quanh của hình trụ có diện tích một đáy là
S
và độ dài đường sinh
l
bằng?
A.
2l S
. B.
2Sl
. C.
2 l
S
. D.
l S
.
Lời giải
Chọn A
Ta có diện tích 1 đáy là:
2
S
S r r
.
Công thức tính diện tích xung quanh của hình trụ:
2 2 . 2. .
xq
S
S rl l l S
.
Câu 16. Cho khối nón có chiều cao
6h
và bán kính đáy bằng
r
. Biết thể tích của khối nón đã cho
8V
. Tính bán kính đáy.
A.
2r
. B.
1
3
. C.
4
3
. D.
4
.
Lời giải
Chọn A
Ta có công thức thể tích khối nón
2
1 3 3.8
. . . 2
3 .6
V
V r h r
h
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Câu 17. Thể tích khối cầu có đường kính
2a
bằng
A.
3
4
3
a
. B.
3
4
a
. C.
3
32
3
a
. D.
2
4 .a
.
Lời giải
Chọn A
Theo công thức
3 3
4 4
3 3
V r V a
.
Câu 18. Cho hình trụ có độ dài đường sinh
và bán kính
r
. Nếu độ dài đường sinh khối trụ tăng lên 3
lần, diện tích đáy không đổi thì thể tích của khối trụ sẽ tăng lên
A. 3 lần. B.
1
3
lần. C.
9
lần. D.
27
lần.
Lời giải
Chọn A
Ta có: đường cao hình trụ
h
bằng đường sinh
.
Thể tích khối trụ ban đầu:
V B.h
(
B
là diện tích đáy;
h
là chiều cao).
Gọi
' '. 'V B h
, với
' , ' 3B B h h
là thể tích sau khi tăng chiều cao của khối trụ lên 3 lần.
' '. ' .3 3. . 3V B h B h B h V
.
Câu 19. Diện tích toàn phần của hình nón có độ dài đường sinh
và đường kính đáy
2r
bằng
A.
rl
. B.
2
2 4
rl r
. C.
2
rl r
. D.
1
3
rl
.
Lời giải
Chọn C
Vì đường kính đáy
2r
nên bán kính đáy là
r
. Theo công thức tính diện tích toàn phần của hình
nón ta có
2
TP
S rl r
Câu 20. Bán kính
r
của khối cầu có thể tích
3
36 cm
V
là
A.
3 cm
r
. B.
27 cm
r
. C.
3
48 cm
r
. D.
3
9 cm
r
.
Lời giải
Chọn A
Thể tích khối cầu được tính theo công thức:
3 3 3
4 3
27 3 cm
3 4
V
V r r r r
.
Câu 21. Tìm bán kính
r
của hình nón biết hình nón có diện tích xung quanh là
xq
S
và độ dài đường sinh
l
?
A.
xq
S
l
. B.
2
xq
S
l
. C.
xq
l
S
. D.
2
xq
l
S
.
Lời giải
Chọn A
Bằng công thức tính diện tích xung quanh của hình nón:
xq
xq
S
S rl r
l
.
Câu 22. Trong không gian cho tam giác vuông tại
A
,
AB a
và
3AC a
. Tính độ dài đường sinh
của hình nón có được khi quay tam giác
ABC
xung quanh trục
AB
.
A.
2l a
. B.
2l a
. C.
l a
. D.
3l a
.
Lời giải
Chọn B
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Khi quay tam giác
ABC
xung quanh trục
AB
, ta có:
Chiều cao
h AB a
; bán kính 3R AC a .
Đường sinh
2 2 2 2
3 2l h R a a a
.
Câu 23. Diện tích xung quanh của hình trụ có bán kính đáy
2R
và đường sinh
6l
bằng
A.
24
. B.
12
. C.
4
. D.
8
.
Lời giải
Chọn A
Diện tích xung quanh của hình trụ là
2 2 .2.6 24S rl
Câu 24. Cho hình nón có bán kính đáy bằng
1
, góc giữa đường sinh và trục của hình nón bằng
0
30
.
Diện tích xung quanh của hình nón đã cho bằng
A.
4 3
3
. B. 3
. C.
2 3
3
. D.
2
.
Lời giải
Chọn D
Ta có
0
sin30 2
r
l r
l
.
2
. . 2 2
xq
S r l r
.
Câu 25. Cho khối trụ có chiều cao bằng bán kính đáy và diện tích thiết diện qua trục của khối trụ bằng
16.
Thể tích khối trụ đã cho bằng
A.
64
. B.
64
3
. C.
16 2
. D.
16 2
3
.
Lời giải
Chọn A
Diện tích thiết diện qua trục của khối trụ là
2
1
.2 .
2
S R R R
Theo giả thiết, ta có
2
16 4 4.R R h
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Thể tích của khối trụ bằng
2
64 .V h R
Câu 26. Hình trụ có thiết diện qua trục là một hình vuông có cạnh bằng 20cm. Thể tích của khối trụ
tương ứng bằng:
A.
3
800 cm
. B.
3
8000 cm
. C.
3
400 cm
. D.
3
2000 cm
.
Lời giải
Chọn D
Ta có thiết diện qua trục của hình trụ là hình vuông có cạnh bằng 20cm, do đó bán kính của
hình trụ
20r
cm, chiều cao của hình trụ
20h
cm. Suy ra
2 2 3
.10 .20 2000V r h cm
.
CÂU HỎI MỨC ĐỘ THÔNG HIỂU
Câu 27. Trong không gian cho hình chữ nhật
ABCD
,
, 2AB a AC a
. Khi quay hình chữ nhật
ABCD
quanh cạnh
AD
thì đường gấp khúc
ABCD
tạo thành một hình trụ. Diện tích xung
quanh của hình trụ đó bằng
A.
2
4 a
. B.
2
2 a
3
. C.
2
a
3
. D.
2
2 3 a .
Lời giải
Chọn D
Hình trụ được tạo thành có
2 2
3,h AC AB a r a nên
2
2 2 3
xq
S rh a
.
Câu 28. Trong không gian, cho tam giác
ABC
vuông tại
A
,
AB a
và
2AC a
. Khi quay tam giác
ABC
quanh cạnh góc vuông
AB
thì đường gấp khúc
ACB
tạo thành một hình nón. Diện tích
xung quanh hình nón đó bằng
A.
2
5 a
. B.
2
5 a
. C.
2
2 5 a
. D.
2
10 a
.
Lời giải
Chọn C
2 2
5BC AB AC a
.
Diện tích xung quanh hình nón cần tìm là
2
. . .2 . 5 2 5S AC BC a a a
.
Câu 29. Cho hình trụ có bán kính đáy bằng
3
. Biết rằng khi cắt hình trụ đã cho bởi một mặt phẳng qua
trục, thiết diện thu được là một hình vuông. Diện tích xung quanh của hình trụ đã cho bằng
A.
18
. B.
36
. C.
54
. D.
27
.
Lời giải
Chọn B
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Giả sử thiết diện qua trục của hình trụ là hình vuông
ABCD
.
Theo giả thiết ta có bán kính đáy của hình trụ
3r 2 6h AD DC r l
.
Vậy diện tích xung quanh của hình trụ là:
2 2 .3.6 36
xq
S rl
.
Câu 30. Cho một chiếc cốc hình nón chứa đầy trà như hình vẽ. Người
X
uống một phần trà sao cho
chiều cao của nó giảm đi
1
3
so với chiều cao của trà trong cốc. Người
Y
uống phần trà còn lại
trong cốc. Khi đó khẳng định nào đúng.
A. Người
X
uống lượng trà bằng 5,75 lần lượng trà của người
Y
uống.
B. Hai người
X
và
Y
uống lượng trà bằng nhau.
C. Người
X
uống lượng trà bằng 2,375 lần lượng trà của người
Y
uống.
D. Người
X
uống lượng trà bằng một nửa lượng trà của người
Y
uống.
Lời giải
Chọn C
Gọi
2
1
3
V R h
là thể tích trà có trong chiếc cốc hình nón đó ( với
R
là bán kính đáy hình nón
và
h
là chiều cao hình nón).
Sau khi người
X
uống thì lượng trà còn lại người
Y
uống là
2
1 2 2
.
3 3 3
Y
R h
V
2
8
81
R h
.
Khi đó người
X
đã uống một lượng trà bằng
X Y
V V V
2
19
81
R h
.
Vậy
19
2,375
8
X
Y
V
V
.
Câu 31. Cắt hình trụ
T
bằng một mặt phẳng song song với trục và cách trục một khoảng bằng
2cm
được thiết diện là một hình vuông có diện tích bằng
2
16cm
. Thể tích của
T
là
A.
3
32 cm
. B.
3
16 cm
. C.
3
64 cm
. D.
3
8 cm
.
Lời giải
Chọn A
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Giả sử thiết diện là hình vuông
ABB A
như hình vẽ.
Với
2I O cm
và
2
16 4 .
ABB A
S AB AB cm
Ta có
2
2
2 2
2
AB
r OA OI cm
.
Mà
2
2 3
4 . . 2 2 .4 32
T d
h AA V S h r h cm .
Câu 32. Cho hai tấm tôn hình chữ nhật đều có kích thước
1,5 8m m
. Tấm tôn thứ nhất được chế tạo
thành một hình hộp chữ nhật không đáy, không nắp, có thiết diện ngang là một hình vuông
(mặt phẳng vuông góc với đường cao của hình hộp và cắt các mặt bên của hình hộp theo các
đoạn giao tuyến tạo thành một hình vuông) và có chiều cao
1,5m
; còn tấm tôn thứ hai được chế
tạo thành một hình trụ không đáy, không nắp và cũng có chiều cao
1,5m
. Gọi
1
V ,
2
V theo thứ
tự là thể tích của khối hộp chữ nhật và thể tích của khối trụ. Tính tỉ số
1
2
V
V
.
A.
1
2
V
V
. B.
1
2
4
V
V
. C.
1
2
2
V
V
. D.
1
2
3
V
V
.
Lời giải
Chọn B
Thiết diện ngang của hình hộp chữ nhật là hình vuông nên hình hộp có đáy là hình vuông cạnh
là
8
2 m
4
, chiều cao là
1,5 m
2 3
1
2 .1,5 6 mV
.
Hình trụ có đáy là hình tròn có chu vi là
8 m
.Suy ra bán kính hình tròn đáy là
4
.
Thể tích khối trụ là
2
2
4 24
. .1,5V
.
Vậy
1
2
V
V
6
24
4
.
Câu 33. Một hình trụ có bán kính đáy
5r a
và khoảng cách giữa hai đáy bằng
7a
. Cắt khối trụ bởi
một mặt phẳng song song với trục và cách trục một khoảng bằng
3a
. Diện tích của thiết diện
được tạo nên bằng
A.
2
56a
. B.
2
35a
. C.
2
21a
. D.
2
70a
.
Lời giải
Chọn A
Theo đề
7 ; 5 ; 3AA BB a OA r a OI a
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Áp dụng định lý Py-ta-go tính
2 2
4IA OA OI a
suy ra
8AB a
.
Diện tích hình chữ nhật
2
8 .7 56ABB A a a a
.
Câu 34. Cho một cái bể nước hình hộp chữ nhật có ba kích thước
2 ,3 ,2m m m
lần lượt là chiều dài,
chiều rộng, chiều cao của lòng trong đựng nước của bể. Hàng ngày nước ở trong bể được lấy ra
bởi một cái gáo hình trụ có chiều cao là
5cm
và bán kính đường tròn đáy là
4cm
. Trung bình
một ngày được múc ra
170
gáo nước để sử dụng (Biết mỗi lần múc là múc đầy gáo). Hỏi sau
bao nhiều ngày thì bể hết nước biết rằng ban đầu bể đầy nước?
.
A.
280
ngày. B.
282
ngày. C.
281
ngày. D.
283
ngày.
Lời giải
Chọn C
Thể tích nước được đựng đầy trong bể là
3
2.3.2 12V m
.
Thể tích nước đựng đầy trong gáo là
2 3 3
4 .5 80
12500
g
V cm m
.
Một ngày bể được múc ra
170
gáo nước tức là trong một ngày lượng nước được lấy ra bằng:
3
17
170.
1250
m g
V V m
.
Ta có
12
280,8616643
17
1250
m
V
V
sau
281
ngày bể sẽ hết nước.
Câu 35. Trong không gian, cho hình chữ nhật
ABCD
,
2AB a
và
3AC a
. Khi quay hình chữ nhật
ABCD
quanh cạnh
AB
thì đường gấp khúc
BCDA
tạo thành một hình trụ. Diện tích xung
quanh của hình trụ đó bằng
A.
2
6 5 a
. B.
2
12 a
. C.
2
4 5 a
. D.
2
20 a
.
Lời giải
Chọn C
Khi quay hình chữ nhật
ABCD
quanh cạnh
AB
thì đường gấp khúc
BCDA
tạo thành một
hình trụ có chiều cao
2h AB a
, đáy là hình tròn bán kính
2 2
5r BC AC AB a
,
Khi đó diện tích xung quanh của là
2
2 2 .2 . 5 4 5
xq
S rh a a a
.
Câu 36. Trong không gian, cho tam giác
ABC
vuông tại
A
,
2AB a
và
3AC a
. Khi quay tam giác
ABC
quanh cạnh góc vuông
AB
thì đường gấp khúc
ACB
tạo thành một hình nón. Diện tích
toàn phần của hình nón đó bằng
A.
2
3 13 a
. B.
2 2
3 13 4 .a a
C.
2 2
3 13 9 .a a
D.
2
42 .a
Lời giải
Chọn C
Khi quay tam giác
ABC
quanh cạnh góc vuông
AB
thì đường gấp khúc
ACB
tạo thành một
hình nón có bán kính đường tròn đáy là
3 ,r AC a
đường sinh
2 2
13.l BC AB AC a
Khi đó diện tích xung quanh của hình nón là
2
3 13 .
xq
S rl a
Khi đó diện tích toàn phần của hình nón là
2 2
3 13 9 .
tp
S a a
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Câu 37. Cho hình trụ
( )T
có thiết diện qua trục của hình trụ là một hình chữ nhật có diện tích bằng
48
và chu vi bằng
28
. Biết chiều dài của hình chữ nhật lớn hơn đường kính mặt đáy của hình
trụ
T
. Diện tích xung quanh của hình trụ đã cho bằng
A.
96
. B.
48
. C.
24
. D.
32
.
Lời giải
Chọn B
Giả sử thiết diện qua trục của hình trụ là hình chữ nhật
ABCD
.
Gọi
l
và
r
là độ dài đường sinh và bán kính đáy của hình trụ,
2 0 (*)l r
.
Ta có
2
2 48 2 (14 2 ) 48 3; 8( / (*))
7 12 0
2(2 ) 28 14 2 4; 6(lo¹i)
14 2
rl r r r l t m
r r
r l l r r l
l r
Vậy diện tích xung quanh của hình trụ là
2 2 .3.8 48
xq
S rl
.
Câu 38. Cho hình trụ có thiết diện qua trục là một hình vuông. Thiết diện của hình trụ tạo bởi mặt phẳng
song song và cách trục một khoảng bằng
a
có diện tích bằng
2
8 3a
. Thể tích của khối trụ là
A.
2
16 a
. B.
3
16 a
. C.
3
32 a
. D.
3
16
3
a
.
Lời giải
Chọn B
Gọi
R
là bán kính đáy hình trụ, do thiết diện qua trục là một hình vuông nên
2Rl
.
Thiết diện của hình trụ tạo bởi mặt phẳng song song và cách trục một khoảng bằng
a
là hình
chữ nhật
DABC
khi đó
OI a
với
I
là trung điểm
BC
ta có
2 2 2 2
2IC R a BC R a
.
Diện tích hình chữ nhật là
2 2 2
D
. 4 8 3
ABC
S AB BC R R a a
.
4 2 2 2
12 0R R a a
2 2 2 2
4 3 0R a R a
2R a
từ đó
2 4h l R a
.
Thể tích khối trụ là
2 3
16V R h a
.
Câu 39. Cho hình nón có bán kính đáy
3r
. Biết rằng khi cắt khối nón đó bằng một mặt phẳng qua
trục của nó, ta được thiết diện là một tam giác đều. Diện tích xung quanh của hình nón bằng
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
6 3
. B.
36
. C.
18
. D.
9
.
Lời giải
Chọn C
Giả sử thiết diện qua trục của hình nón là tam giác đều
SAB
.
Gọi
l
là độ dài đường sinh của hình nón.
Ta có:
3r OA
;
0
3
6
sin 30 1/ 2
OA
l SA
.
Vậy diện tích xung quanh của hình nón là:
.3.6 18
xq
S rl
.
Câu 40. Trong không gian, cho tam giác
ABC
vuông tại
A
,
3AB a
và
5BC a
. Khi quay tam giác
ABC
quanh cạnh góc vuông
AB
thì đường gấp khúc
ACB
tạo thành một hình nón. Diện tích
xung quanh hình nón đó bằng
A.
2
20a
. B.
2
15 a
. C.
2
20 a
. D.
2
80 a
.
Lời giải
Chọn C
Khi quay tam giác
ABC
quanh cạnh góc vuông
AB
thì đường gấp khúc
ACB
tạo thành một
hình nón có bán kính đường tròn đáy là
2 2
4r AC BC AB a
, đường sinh
5l BC a
Khi đó diện tích xung quanh của hình nón là
2
20 .
xq
S rl a
Câu 41. Thiết diện qua trục của một hình nón là một tam giác vuông cân có cạnh góc vuông bằng
a
.
Diện tích xung quanh của hình nón bằng
A.
2
2a
. B.
2
2
2
a
. C.
2
a
. D. .
Lời giải
Chọn B
Giả sử thiết diện qua trục của hình nón là tam giác
SAB
vuông cân đỉnh
S
.
Gọi
l
và
r
lần lượt là độ dài đường sinh và bán kính đáy của hình nón.
2
2
a
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Ta có:
l SA a
;
0
2
.sin 45 .
2
r OA SA a
.
Vậy diện tích xung quanh của hình nón là:
2
2 2
. .
2 2
xq
a a
S rl a
.
Câu 42. Cho khối nón có độ dài đường sinh bằng
5a
và đường cao bằng
4a
. Thể tích khối nón bằng
A.
3
80
3
a
. B.
3
15 a
. C.
3
12 a
. D.
3
36 a
.
Lời giải
Chọn C
Theo giả thiết:
2 2
5 , 4 3l a h a r l h a
Suy ra
2
2 3
1 1
3 4 12
3 3
V r h a a a
.
3
2
2
1 1 8
2 2
3 3 3
a
V r h a a
.
Câu 43. Một chi tiết máy là phần còn lại của một khối trụ có bán kính đáy
r
sau khi đã đục bỏ phần bên
trong là một khối trụ có bán kính đáy
2
r
(tham khảo hình vẽ).
Biết thể tích khối trụ nhỏ bị đục bỏ bằng
3
20 cm
. Thể tích của khối chi tiết máy đó là
A.
3
40 cm
. B.
3
60 cm
. C.
3
80 cm
. D.
3
70 cm
.
Lời giải
Chọn B
Gọi chiều cao khối trụ là
h
.
Thể tích khối chi tiết máy:
2
20V r h
Mà thể tích khối trụ nhỏ bên trong là
2
2 2
1
20 80
2 4
r
h r h r h
Vậy
3
80 20 60V cm
Câu 44. Cho khối nón có thiết diện qua trục là tam giác đều
SAB
cạnh
a
. Thể tích khối nón bằng
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
3
3
8
a
. B.
3
24
a
. C.
3
12
a
. D.
3
3
24
a
.
Lời giải
Chọn D
Tam giác
SAB
đều cạnh
a
nên:
2
3
2
3 1 1 3 3
,
2 2 3 3 2 2 24
a a a a a
OB SO V r h
.
Câu 45. Một khối đồ chơi gồm hai khối cầu
1 2
,H H
tiếp xúc với nhau, lần lượt có bán kính tương
ứng là
1 2
,r r thỏa mãn
2 1
1
2
r r
(tham khảo hình vẽ).
Biết rằng thể tích của toàn bộ khối đồ chơi bằng
3
180cm
. Thể tích của khối cầu
1
H
bằng
A.
3
90 cm
B.
3
120 cm
C.
3
160 cm
D.
3
135 cm
Lời giải
Chọn C
Thể tích khối
1
H
là
3
1 1
4
3
V r
Thể tích khối
2
H
là
3
2 2
4
3
V r
Tổng thể tích 2 khối là
3
3 3 3 3
1 2 1 2 1 1 1 1
4 4 4 4 1 9 4 9
3 3 3 3 2 8 3 8
V V V r r r r r V
Suy ra
1 1
9
180 160
8
V V
Câu 46. Cho khối nón có thiết diện qua trục là tam giác
SAB
vuông tại
S
với cạnh
SA a
. Thể tích
khối nón bằng
A.
3
2
12
a
. B.
3
3
a
. C.
3
12
a
. D.
3
2
4
a
.
Lời giải
Chọn A
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Theo tính chất của hình nón ta có
SA SB l
.
Vậy tam giác
SAB
vuông cân tại
S
suy ra
2
, 2
2
a
SA SB a AB a SO OB
Vậy
2
3
2
1 1 2 2 2
3 3 2 2 12
a a a
V r h
.
Câu 47. Một chi tiết máy gồm 3 khối trụ có cùng chiều cao
h
gắn với nhau (như hình vẽ).
Khối trụ lớn có bán kính đáy
r
lớn gấp đôi bán kính đáy của hai khối trụ nhỏ (hai khối trụ nhỏ
bằng nhau). Biết thể tích của cả khối chi tiết máy đó bằng
3
90cm . Tính thể tích của khối trụ lớn
ở giữa.
A.
3
30cm . B.
3
45cm . C.
3
70cm . D.
3
60cm .
Lời giải
Chọn D
Thể tích khối trụ lớn ở giữa:
2
1
V r h
Tổng thể tích chi tiết máy:
2
2 2
1
3 3
2
2 2 2
r
V r h h r h V
Suy ra:
1
3
90
2
V
. Do đó:
1
60V
Câu 48. Một chiếc bánh sinh nhật gồm ba khối trụ
1 2 3
, ,H H H
xếp chồng lên nhau, lần lượt có bán
kính đáy và chiều cao tương ứng là
1 1 2 2 3 3
, ; , ; ,r h r h r h
thỏa mãn
1 2 3 1 2 3
2 3 , 2r r r h h h
(tham
khảo hình vẽ).
Biết rằng thể tích của khối
3
H
bằng
3
80cm
. Thể tích của toàn bộ chiếc bánh sinh nhật bằng
A.
3
890cm
. B.
3
980cm
. C.
3
900cm
. D.
3
800cm
.
Lời giải
Chọn A
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Thể tích khối
3
H
là
2
3 3 3
80V r h
Thể tích khối
2
H
là
2
2
2 2 2 3 3 3
3 1 9
2 2 8
V r h r h V
Thể tích khối
1
H
là
2
2
1 1 1 3 3 3
3 9V r h r h V
Thể tích toàn bộ chiếc bánh sinh nhật bằng:
1 2 3 3 3 3 3
9 89
9 890
8 8
V V V V V V V
Câu 49. Cho khối nón có thể tích bằng
3
3 a
và đường cao bằng
3a
. Độ dài đường sinh của khối
nón đã cho bằng
A.
6a
. B.
2a
. C.
2a
. D.
a
.
Lời giải
Chọn A
Bán kính đáy của hình nón:
3
3 3 3
3
3
V a
r a
h
a
.
Độ dài đường sinh của khối nón là:
2 2
3 3 6l a a a .
Câu 50. Một khối đồ chơi gồm một hình cầu
1
H
bán kính
R
và một hình nón
2
H
xếp chồng lên
nhau, lần lượt có bán kính đáy và đường sinh là
,r l
thỏa mãn
1
2
r l
và
3
.
2
l R
(hình vẽ).
Biết tổng diện tích mặt cầu
1
H
và diện tích toàn phần của hình nón
2
H
là
3
91cm .
Tính
diện tích của khối cầu
1
H
.
A.
3
16cm .
B.
3
104
cm .
5
C.
3
64cm .
D.
3
26
cm .
5
Lời giải
Chọn C
Diện tích toàn bộ khối đồ chơi là
1 2
1
2 2
( ) tp ( )
2
2
( )
4 .R . . .
3 3 3 91
4 . . . . .S
4 2 4 64
H H
H
S S S r l r
R R R R
1
3
( )
64 cm .
H
S
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
Câu 51. Cho hình trụ có bán kính đáy bằng
1 cm
. Một mặt phẳng qua trục của hình trụ và cắt hình trụ
theo thiết diện là hình vuông. Tính thể tích của khối trụ đã cho.
A.
3
8 cm
. B.
3
2 cm
. C.
3
16
cm
3
. D.
3
16 cm
.
Lời giải
Chọn B
Thiết diện qua trục của hình trụ là hình vuông
ABCD
.
Khi đó ta có:
2 2.1 2cmAB r
,
2cmh l AD AB
.
Vậy thể tích của khối trụ đã cho là:
2 2 3
.1 .2 2 cmV r h
.
Câu 52. Thể tích của khối cầu ngoại tiếp bát diện đều có cạnh bằng
2a
là:
A.
3
2
6
a
. B.
3
2
3
a
. C.
3
4 2
3
a
. D.
3
4
3
a
.
Lời giải
Chọn D
Xét khối bát diện đều:
Khối cầu ngoại tiếp bát diện đều có tâm
O
, bán kính
3
2 4
3
2
a
R a V a
.
Câu 53. Cho hình nón có thiết diện qua trục là tam giác vuông có cạnh huyền
2a
. Tính diện tích xung
quanh
xq
S
của hình nón đó
A.
2
2
.
6
xq
a
s
B.
2
2
.
3
xq
a
s
C.
2
2
.
2
xq
a
s
D.
2
2
.
3
xq
a
s
Lời giải
Chọn C
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có:
2
2 2 2
. . . . .
2 2
2 2
xq
AB a a a
SA SB a S HB SB a
Câu 54. Trong không gian cho tứ giác
ABCD
là một nửa lục giác đều nội tiếp đường tròn đường kính
2CD a
. Khi quay tứ giác
ABCD
quanh cạnh
AB
thì tạo thành một khối tròn xoay. Thể
tích khối tròn xoay đó bằng
A.
3
a
. B.
3
2 a
. C.
3
5
4
a
. D.
3
3
2
a
.
Lời giải
Chọn C
Vẽ hình chữ nhật
DFEC
.
Gọi
1
V
là thể tích khối trụ tròn xoay sinh ra khi quay hình chữ nhật
DFEC
quanh cạnh
FE
.
2
V
là thể tích khối nón tròn xoay sinh ra khi quay hình tam giác vuông
DFA
quanh cạnh
FA
.
Khi đó, thể tích khối tròn xoay cần tìm là
1 2
2V V V
Ta có
3
2
a
DF OI
,
2
a
AF AI
.
2
3
2
1
3 3
2 2
2 2
a a
V r a a
,
2
3
2
2
1 1 3
3 3 2 2 8
a a a
V r h
.
3 3 3
1 2
3 5
2 2
2 8 4
a a a
V V V
.
Câu 55. Cho một hình nón có góc ở đỉnh
60
, bán kính đáy bằng
a
. Diện tích toàn phần hình nón đó là
A.
2
a
. B.
2
3 a
. C.
2
2 a
. D.
2
3 a
.
Lời giải
Chọn B
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
Gọi
,S O
lần lượt là đỉnh và tâm đáy của hình nón,
A
là điểm trên đường tròn đáy, theo giả
thiết ta có:
sin sin30 2
1
2
AO a
ASO SA a
SA
2 2 2
. . . .2 3
tp
S OA SA OA a a a a
.
Câu 56. Cho hình lập phương
.ABCD A B C D
cạnh bằng
a
. Thể tích khối cầu có tâm
A
và tiếp xúc
với đường thẳng
A C
bằng
A.
3
2
3
a
. B.
3
8 6
27
a
. C.
3
3
2
a
. D.
3
6 a
.
Lời giải
Chọn B.
Kẻ
AH A C
, khi đó
AH
là bán kính mặt cầu tâm
A
tiếp xúc với đường thẳng
A C
.
Trong tam giác vuông
A AC
, ta có
2 2 2 2 2 2
1 1 1 1 1 3
2 2AH A A AC a a a
2
2
2 6
3 3
a a
AH AH
.
Vậy
3
3
3
4 4 6 8 6
3 3 3 27
a a
V AH
.
Câu 57. Cho hình chóp tứ giác đều
ABCDS
có cạnh đáy bằng
a
, diện tích mỗi mặt bên bằng
2
a
. Thể
tích khối nón đỉnh S và đường tròn đáy nội tiếp hình vuông ABCD bằng:
A.
3
15
24
a
. B.
3
15
8
a
. C.
3
15
12
a
. D.
3
15
18
a
.
Lời giải
Chọn A
a
30°
O
A
S
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Gọi M là trung điểm CD.
h SO
2 2
2 2 2 2 2 2
1 1 1
. . . . . 4
2 2 2 4 4
SCD
a a
S SM CD SO OM CD h a a h a
15
2
h a
Đường tròn đáy nội tiếp hình vuông ABCD nên bán kính là
2
a
R
.
2
2 3
1 1 15 15
. .
3 3 2 2 24
a
V R h a a
Câu 58. Cho hai khối cầu có bán kính lần lượt bằng
a
và
2a
. Tỉ số giữa thể tích của khối cầu nhỏ với
thể tích của khối cầu lớn bằng
A.
1
4
. B.
4
. C.
1
8
. D.
8
.
Lời giải
Chọn C
Thể tích của khối cầu nhỏ có bán kính
a
là:
3
3 3
1 1
4 4 4
3 3 3
V R a a
.
Thể tích của khối cầu lớn có bán kính
2a
là:
3
3 3 3
2 2
4 4 4 32
2 .8
3 3 3 3
V R a a a
.
Tỉ số giữa thể tích của khối cầu nhỏ với thể tích của khối cầu lớn bằng:
3
1
3
2
4
1
3
32
8
3
a
V
V
a
.
Câu 59. Cho hình trụ có chiều cao bằng bán kính đáy và bằng 5 cm. Mặt phẳng
song song với trục,
cắt hình trụ theo một thiết diện có chu vi bằng 26 cm. Khoảng cách từ
đến trục của hình
trụ bằng
A. 4 cm. B. 5 cm. C. 2 cm. D. 3 cm.
Lời giải
Chọn D
Gọi
O
và
O
là tâm của hai đường tròn đáy của hình trụ.
M
O
C
S
D
A
B
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
Vì mặt phẳng
song song với trục
OO
nên
cắt hình trụ theo thiết diện là một hình chữ
nhật, gọi là
ABCD
với
AB
là dây cung của đường tròn
O
,
CD
là dây cung của đường tròn
O
.
Hình chữ nhật
ABCD
có chu vi bằng 26 cm và có
5 cmAD
nên
8 cmAB
.
Gọi
M
là trung điểm của
AB
. Khi đó
OM AB
và
OM AD
nên
OM
.
Do đó
2 2
, 3 cmd OO OM OA MA
.
Câu 60. Cho tam giác vuông cân
ABC
có
2AB BC a
. Khi quay tam giác
ABC
quanh đường
thẳng đi qua
B
và song song với
AC
ta thu được một khối tròn xoay có thể tích bằng
A.
3
2 a
. B.
3
2
3
a
. C.
3
4
3
a
. D.
3
a
.
Lời giải
Chọn A
Ta có
2AC a
và
OA a
.
Thể tích khối trụ khi quay
'OACO
quanh
'OO
là
2 3
1
. 2V OA AC a
.
Thể tích khối nón khi quay
OAB
quanh
OB
là
3
2
2
1
.
3 3
a
V OA OB
.
Thể tích khối tròn xoay khi quay tam giác
ABC
quanh
'OO
là
3
1 2
4
2
3
a
V V V
.
Câu 61. Một hình trụ có diện tích xung quanh bằng
64
và thiết diện qua trục của hình trụ này là một
hình vuông. Thể tích hình trụ đó bằng
A.
512
. B.
128
. C.
64
. D.
256
.
Lời giải
Chọn B
Gọi
, r h
lần lượt là bán kính đáy và chiều cao hình trụ.
Vì thiết diện qua trục của hình trụ là hình vuông nên ta có
2h r
.
r
r
h
O'
O
D
C
B
A
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có
64
xq
S
2 64rh
2 . .2 64r r
2
4 . 64r
2
16r
4r
.
Với
4r
suy ra
2 2.4 8h r
.
Vậy thể tích của hình trụ là
2
V r h
2
.4 .8 128
. Chọn B
Câu 62. Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
a
, cạnh bên hợp với đáy góc
60
. Hình
nón
N
có đỉnh
S
, đáy là đường tròn nội tiếp tứ giác
ABCD
. Diện tích xung quanh của hình
nón
N
bằng
A.
2
7
4
a
. B.
2
2
3
a
. C.
2
3
2
a
. D.
2
2
a
.
Lời giải
Chọn A
Ta có
ABCD
là hình vuông cạnh
a
nên
2 2
2
2
2 2
AC a
AC AB BC a AH
.
Mà
, 60SH ABCD SA ABCD SAH .
Suy ra
6
.tan 60
2
a
SH AH
.
Bán kính hình nón
N
là
2 2
AB a
R HM
Do đó đường sinh
2 2
7
2
a
l SM SH HM
.
Vậy diện tích xung quanh hình nón
N
là:
2
7
4
xq
a
S Rl
.
Câu 63. Trong không gian, cho hình chữ nhật
ABCD
,
, 2AB a AC a
. Khi quay hình chữ nhật
ABCD
quanh cạnh
AD
thì đường gấp khúc
ABCD
tạo thành một hình trụ. Diện tích xung
quanh của hình trụ đó bằng
A.
2
3
a
. B.
2
2
3
a
. C.
2
4 a
. D.
2
2 3 a
.
Lời giải
Chọn D
H
B
A
D
C
S
M
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
Khi quay hình chữ nhật
ABCD
quanh cạnh
AD
thì đường gấp
khúc
ABCD
tạo thành một hình trụ có:
Bán kính đáy:
R AB a
.
Chiều cao:
2 2 2 2
4 3 .h AD AC DC a a a
Diện tích xung quanh của hình trụ đã cho:
2
2 2 3
xq
S Rh a
.
Câu 64. Cho hình nón có đường cao
a
. Biết rằng khi cắt hình nón đã cho một mặt phẳng đi qua đỉnh
của hình nón và cách tâm của đáy hình nón một khoảng
3
a
, thiết diện thu được tạo thành một
tam giác vuông. Thể tích khối nón được giới hạn bởi hình nón đã cho bằng
A.
3
5
12
a
. B.
3
3
a
. C.
3
4
9
a
. D.
3
5
9
a
.
Bài giải
Chọn A
Gọi
,B C
là giao điểm của mặt phẳng và đường tròn đáy,
I
là trung điểm của
BC
và
OH
là
khoảng cách từ tâm
O
đến
SBC
.
Ta có:
2
2 2 2 2 2
1 1 1 1 1 1 2
4
3
a
OI
OH OI OS OI a
a
.
2 2 2 2
3 2 3 2 5
2
4 2 2
a a a
SI SO OI BC SI r OB OI IB
2
3
1 5 5
3 2 12
a a
V a
.
Câu 65. Khối tròn xoay sinh bởi một tam giác đều cạnh
a
(kể cả điểm trong) khi quay quanh một
đường thẳng chứa một cạnh của tam giác đó có thể tích bằng
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 24 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
3
8
a
. B.
3
3
6
a
. C.
3
4
a
. D.
3
3
12
a
.
Lời giải
Chọn C
Giả sử tam giác
ABC
đều cạnh
a
có
H
là trung điểm
AC
.
Khi quay tam giác
ABC
quanh cạnh
AC
ta được khối tròn xoay có thể tích bằng
2
lần thể
tích hình nón tạo thành khi quay tam giác
AHB
quanh trục
AH
, do đó thể tích cần tìm bằng
2
3
2
1 2 3
2 .
3 3 2 2 4
a a a
BH AH
.
Câu 66. Cho hình chóp đều
.S ABCD
có
AB a
, cạnh bên hợp với đáy góc
0
45
. Diện tích xung quanh
của hình nón đỉnh
S
với đáy là đường tròn nội tiếp hình vuông bằng
A.
2
2
a
. B.
2
3
4
a
. C.
2
4
a
. D.
2
2 a
.
Lời giải
Chọn B
Ta có
2 2
2 3
,
2 2 2
a a a
r HD SH h l r h
2
3
4
a
S
.
Câu 67. Một hình nón có thiết diện qua trục là một tam giác vuông cân có cạnh góc vuông bằng
a
.
Diện tích xung quanh của hình nón bằng:
A.
2
2
4
a
. B.
2
2 2
3
a
. C.
2
2
2
a
. D.
2
2a
.
Lời giải
Chọn C
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
Thiết diện qua trục hình nón là
ABC ABC
vuông cân tại
A
.
Do đó
2 2
;
2 2 2
BC AC a
l AC a r
.
Diện tích xung quanh hình nón là
2
2
2
a
S rl
.
Câu 68. Cho hình chữ nhật
ABCD
có
2 2AC a
và
45ACB
. Quay hình chữ nhật
ABCD
quanh
cạnh
AB
thì đường gấp khúc
ADCB
tạo thành hình trụ. Diện tích toàn phần
tp
S
của hình trụ là
A.
2
16
tp
S a
. B.
2
10
tp
S a
. C.
2
12
tp
S a
. D.
2
8
tp
S a
.
Lời giải
Chọn D
Hình chữ nhật
ABCD
có
2 2AC a
và
45ACB
nên nó là hình vuông.
2AB BC CD DA a
.
Khi quay hình chữ nhật quanh cạnh
AB
ta được hình trụ có chiều cao
2h AB a
và bán
kính đáy là
2r BC a
.
2
2 2 8
tp
S rl rh a
.
Câu 69. Trong không gian, cho tam giác
ABC
vuông tại
A
,
AB a
,
60ABC . Tính độ dài đường
sinh
l
của hình nón, nhận được khi quay tam giác
ABC
quanh trục
AC
.
A.
2l a
. B.
2l a
. C.
l a
. D. 3l a .
Lời giải
Chọn B
Khi quay tam giác
ABC
quanh trục
AC
thì cạnh huyền
BC
tạo thành đường sinh, có độ dài
2
cos cos60
AB a
l BC a
B
.
Câu 70. Trong không gian, cho hình chữ nhật
ABCD
có
4, 5AB AC
. Gọi
,M N
lần lượt là trung
điểm của
AD
và
BC
. Quay hình chữ nhật đó xung quanh trục
MN
, ta được một hình trụ.
Tính diện tích toàn phần
TP
S của hình trụ đó.
A. 8
TP
S
. B.
33
2
TP
S
. C.
81
2
TP
S
. D. 24
TP
S
.
Lời giải
Chọn B
Ta có:
4; 5 3AB AC BC
.
Khi quay hình chữ nhật
ABCD
quanh trục
MN
ta được hình trụ có:
3
2 2 2
AD BC
r
.
Chiều cao hình trụ
4h AB
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 26 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Vậy
3 3 33
2 ( ) 2 ( ) 2 4
2 2 2
tp
S r r l r r h
.
Câu 71. Cho tứ diện đều
ABCD
có cạnh bằng
4
. Tính diện tích xung quanh
xq
S
của hình trụ có một
đường tròn đáy là đường tròn nội tiếp tam giác
BCD
và chiều cao bằng chiều cao của tứ diện
ABCD
.
A.
16 2
3
xq
S
. B. 8 2
xq
S
. C.
16 3
3
xq
S
. D. 8 3
xq
S
.
Lời giải
Chọn A.
Tam giác
BCD
đều cạnh
4
có diện tích:
2
4 3
4 3
4
BCD
S
.
Áp dụng công thức tính nhanh thể tích khối tứ diện đều cạnh
a
là
3
2 16
2
12 3
ABCD
a
V V
.
Độ dài đường cao khối tứ diện:
3
4 2
3
ABCD
BCD
V
h
S
.
Bán kính đáy đường tròn nội tiếp tam giác
BCD
:
4 3 2 3
6 3
S
r
p
.
Vậy diện tích xung quanh của hình trụ là:
2 3 4 2 16 2
2 2 . .
3 3
3
xq
S rh
.
Câu 72. Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
a
, góc giữa cạnh bên
SA
và mặt phẳng
đáy bằng
30
. Tính diện tích xung quanh
xq
S
của hình trụ có một đường tròn đáy là đường
tròn nội tiếp hình vuông
ABCD
và chiều cao bằng chiều cao của hình chóp
.S ABCD
.
A.
2
6
6
xq
a
S
. B.
2
3
6
xq
a
S
. C.
2
6
12
xq
a
S
. D.
2
3
12
xq
a
S
.
Lời giải
Chọn A.
Gọi
O
là giao điểm của
AC
và
BD
. Khi đó
SO ABCD
,
2AC a
.
Góc giữa
SA
và mặt phẳng đáy bằng
30
30SAO
.
2 3 6
.tan 30 .
2 3 6
a a
SO AO
.
Vậy chiều cao của hình trụ là
6
6
a
h
.
O
A
D
C
B
S
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27
Bán kính của đường tròn nội tiếp hình vuông
ABCD
cạnh
a
là
2
a
r
.
Diện tích xung quanh của hình trụ là
2
6 6
2 2
2 6 6
xq
a a a
S rl
.
Câu 73. Cho hình lăng trụ tam giác đều
.ABC A B C
có
AB a
, góc giữa
AC
và
ABC
bằng
30
.
Tính thể tích
V
của khối trụ nội tiếp hình lăng trụ
.ABC A B C
.
A.
3
3
12
a
V
. B.
3
3
36
a
V
. C.
3
3
108
a
V
. D.
3
3
72
a
V
.
Lời giải
Chọn B.
Độ dài đường trung tuyến trong tam giác đều cạnh
a
là
3
2
a
.
Bán kính của đường tròn nội tiếp tam giác đều cạnh
a
là
1 3 3
.
3 2 6
a a
r
.
Góc giữa
AC
và
ABC
bằng
30
nên
30C AC
,
3
.tan30
3
a
C C AC
.
Chiều cao của khối trụ là
3
3
a
h
.
Thể tích khối trụ nội tiếp hình lăng trụ
.ABC A B C
là
2
3
2
3 3 3
6 3 36
a a a
V r h
.
Câu 74. Cho tứ diện đều
ABCD
có cạnh bằng
5
. Tính thể tích
V
của khối nón nội tiếp tứ diện
ABCD
.
A.
25 6
108
V
. B.
125 3
108
V
. C.
125 6
108
V
. D.
25 6
36
V
.
Lời giải
Chọn C.
Tam giác đều cạnh
5
có độ dài đường cao là
5 3
2
.
Bán kính đáy đường tròn nội tiếp tam giác cạnh
5
là
1 5 3 5 3
3 2 6
r
.
Độ dài đường cao khối tứ diện là
2
2
2 5 3 25 50 5 6
5 25
3 2 3 3 3
h
.
Thể tích của khối nón nội tiếp tứ diện đều cạnh
5
là:
2
2
1 1 5 3 5 6 125 6
3 3 6 3 108
V r h
.
B'
A'
C'
A
B
C
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 28 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 75. Cho tứ diện đều
ABCD
cạnh bằng
3a
. Tính diện tích xung quanh
xq
S
của hình trụ có đáy là
đường tròn ngoại tiếp tam giác
BCD
và có chiều cao bằng chiều cao của tứ diện đều
ABCD
.
A.
2
2 3
xq
S a
. B.
2
2
xq
S a
. C.
2
3
xq
S a
. D.
2
2 2
xq
S a
.
Lời giải
Chọn D.
Độ dài đường trung tuyến trong tam giác đều cạnh
3a
là
3 3 3
2 2
a a
.
Bán kính đáy đường tròn ngoại tiếp tam giác
BCD
là
2 3
3 2
a
R a
.
Độ dài đường cao khối tứ diện là
2
2
3 2h a a a .
Vậy diện tích xung quanh của hình trụ là:
2
2 2 . . 2 2 2
xq
S Rh a a a
.
Câu 76. Cho một lăng trụ tam giác đều
. ' ' 'ABC A B C
có cạnh đáy bằng
a
. Góc giữa
'A C
và mặt phẳng
đáy bằng
60
O
. Tính diện tích xung quanh
xq
S
của hình nón có đáy là đường tròn nội tiếp tam
giác
ABC
và đỉnh là trong tâm của tam giác
' ' 'A B C
.
A.
2
333
36
xq
a
S
. B.
2
111
36
xq
a
S
. C.
2
333
6
xq
a
S
. D.
2
111
6
xq
a
S
.
Lời giải
Chọn A.
Độ dài đường trung tuyến trong tam giác đều cạnh
a
là
3
2
a
.
Bán kính của đường tròn nội tiếp tam giác đều cạnh
a
là
1 3 3
.
3 2 6
a a
r
.
Góc giữa
'A C
và mặt phẳng đáy bằng
60
nên
60A CA
.
.tan 60 3AA AC a
. Chiều cao của hình nón là
3h a
,
B'
A'
C'
A
B
C
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29
2
2
2
2
3 3 111
3 3
6 36 6
a a a
l a a
Diện tích xung quanh của hình nón là
2
3 111 333
6 6 36
xq
a a a
S rl
.
Câu 77. Cho lăng trụ đứng
. ' ' 'ABC A B C
, đáy
ABC
là một tam giác vuông tại cân
A
,
AB a
, cạnh
'AA
hợp với
'B C
góc 60
o
. Tính thể tích của khối trụ ngoại tiếp lăng trụ
. ' ' 'ABC A B C
theo
a
.
A.
3
3
18
a
V
. B.
3
3
6
a
V
. C.
3
3
3
a
V
. D.
3
2
6
a
V
.
Lời giải
Chọn B.
Gọi
H
là trung điểm của
B C
H
là tâm của đường tròn ngoại tiếp
A B C
.
Bán kính của đường tròn ngoại tiếp
A B C
là
2
2 2
B C a
r A H
.
Cạnh
'AA
hợp với
'B C
góc
60
, vì
//BB AA
nên
60BB C
.
3
tan 60 3
BC a
BB
. Chiều cao của khối trụ là
3
3
a
h
.
Thể tích của khối trụ ngoại tiếp lăng trụ
. ' ' 'ABC A B C
là:
2
3
2
2 3 3
2 3 6
a a a
V r h
.
Câu 78. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông tại
C
,
, 2AC a BC a
, mặt phẳng
SAB
vuông góc với mặt phẳng
ABC
và tam giác
SAB
vuông cân tại
S
. Tính thể tích của
khối nón có đỉnh là
S
và đáy là đường tròn ngoại tiếp tam giác
ABC
.
A.
3
5
24
a
V
. B.
3
5 5
12
a
V
. C.
3
5 5
24
a
V
. D.
3
3 3
24
a
V
.
Lời giải
Chọn C.
A
B
C
C'
B'
A'
H
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 30 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ABC
là tam giác vuông tại
C
nên
2 2
5AB CA CB a
.
Gọi
H
là trung điểm của
AB
H
là tâm của đường tròn ngoại tiếp
ABC
và
SH ABC
.
Bán kính của đường tròn ngoại tiếp
ABC
là
5
2 2
AB a
r
.
Tam giác
SAB
vuông cân tại
S
nên
5
2 2
AB a
SH
.
Thể tích của khối nón có đỉnh là
S
và đáy là đường tròn ngoại tiếp tam giác
ABC
là:
2
3
2
1 1 5 5 5 5
3 3 2 2 24
a a a
V r h
.
Câu 79. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông tại
A
,
SA
vuông góc với mặt phẳng
ABC
, tam giác
SBC
đều cạnh
a
, góc giữa mặt phẳng
SBC
và mặt phẳng đáy là
30
. Tính
thể tích
V
của khối trụ có một đường tròn đáy là đường tròn ngoại tiếp tam giác
ABC
và chiều
cao bằng khoảng cách từ
S
đến mặt phẳng
ABC
.
A.
3
2
4
a
V
. B.
3
2
16
a
V
. C.
3
3
4
a
V
. D.
3
3
16
a
V
.
Lời giải
Chọn D.
Gọi
M
là trung điểm của
BC
.
Từ giả thiết
M
là tâm của đường tròn ngoại tiếp
ABC
và
30SMA
.
3 3
.sin 30
2 4
a a
SM SA SM
.
H
A
B
S
C
30°
S
B
A
C
M
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 31
Bán kính của khối trụ
2
a
r
, chiều cao của khối trụ
3
4
a
h
.
Thể tích của khối trụ có một đường tròn đáy là đường tròn ngoại tiếp tam giác
ABC
và chiều
cao bằng khoảng cách từ
S
đến mặt phẳng
ABC
là
2
3
2
3 3
2 4 16
a a a
V r h
.
Câu 80. Cho lăng trụ đứng
.ABC A B C
có đáy là tam giác đều cạnh
a
. Mặt phẳng
AB C
tạo với mặt
phẳng đáy góc
60
. Tính diện tích xung quanh
xq
S
của hình trụ có một đường tròn đáy là
đường tròn nội tiếp tam giác
ABC
và chiều cao bằng chiều cao của hình lăng trụ
.ABC A B C
.
A.
2
3
2
xq
a
S
. B.
2
3 3
12
xq
a
S
. C.
2
3
6
xq
a
S
. D.
2
3
xq
S a
.
Lời giải
Chọn A.
Gọi
M
là trung điểm của
B C
,
3
2
a
A M
.
Bán kính đường tròn nội tiếp tam giác
ABC
là
3
6
a
r
.
Từ giả thiết
3 3
60 .tan60 3
2 2
a a
AMA AA A M
.
Diện tích xung quanh
xq
S
của hình trụ có một đường tròn đáy là đường tròn nội tiếp tam giác
ABC
và chiều cao bằng chiều cao của hình lăng trụ
.ABC A B C
là:
2
3 3 3
2 2 . .
6 2 2
xq
a a a
S Rh
.
Câu 81. Cho hình hộp chữ nhật
.ABCD A B C D
,
2 ,AB a AD a
,
AC
cắt
BD
tại
O
, góc
60A BA
. Tính thể tích của khối nón có đỉnh là
O
và đáy là đường tròn ngoại tiếp hình chữ
nhật
A B C D
.
A.
3
5 3
6
a
V
. B.
3
3
6
a
V
. C.
3
5 5
6
a
V
. D.
3
5 3
2
a
V
.
Lời giải
Chọn A.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 32 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có
2 2
4 5A C a a a
.
Bán kính của đường tròn ngoại tiếp hình chữ nhật
A B C D
là
5
2
a
R
.
Từ giả thiết
60 .tan60 2 3A BA AA AB a
.
Thể tích của khối nón có đỉnh là
O
và đáy là đường tròn ngoại tiếp hình chữ nhật
A B C D
:
2
3
2
1 1 5 5 3
2 3
3 3 2 6
a a
V r h a
.
CÂU HỎI MỨC ĐỘ VẬN DỤNG - VDC
Câu 82. Cho hình nón có tâm đáy là
I
. Một mặt phẳng đi qua đỉnh hình nón và cắt hình nón theo một
thiết diện là tam giác đều có diện tích bằng
3 3
, đồng thời cắt đường tròn đáy tại hai điểm.
,A B
thì
0
120AIB
. Diện tích xung quanh của hình nón đã cho bằng
A.
8 3
. B.
8 2
3
. C.
4 1 3
. D.
4 3
.
Lời giải
Chọn D
Gọi
O
là đỉnh hình nón, thiết diện là tam giác đều
OAB
.
2
2
4
3 4.3 3
12 2 3
4
3 3
OAB
OAB
S
OA
S OA l OA AB
.
Tam giác
IAB
cân có góc
0
120AIB
nên
2 2 2 0 2
2 . . 120 3 12AB IA IB IA IBcos IA
Suy ra
2R IA
.
Diện tích xung quanh của hình nón là
. .2.2 3 4 3
xq
S Rl
.
Câu 83. Cho hình nón đỉnh
S
có chiều cao bằng
3 2
. Gọi
,B C
là 2 điểm thuộc đường tròn đáy sao
cho
SBC
vuông tại
S
và có chu vi bằng
10 5 2
. Thể tích của khối nón được giới hạn bởi
hình nón đã cho bằng:
O
D
C
C'
B'
A'
D'
B
A
I
A
O
B
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 33
O
C
B
S
A.
7 2
. B.
21 2
. C.
43 2
. D.
14 2
.
Lời giải
Chọn A
Gọi độ dài đường sinh
0SB SC x x
.
Xét
SBC
vuông cân tại
S
, suy ra:
2BC x
.
Có:
10 5 2 2 10 5 2SB SC BC x x x
2 2 10 5 2
5.
x
x
Xét
SOB
:
2
2 2 2
5 3 2 7R OC SB SO
.
Thể tích khối nón:
2
2
1 1
. 7 .3 2 7 2
3 3
V R h
(đvtt).
Câu 84. Cho hình nón có chiều cao bằng 2 5 . Một mặt phẳng đi qua đỉnh hình nón và cắt hình nón
theo một thiết diện là tam giác đều có diện tích bằng 9 3 . Thể tích của khối nón được giới hạn
bởi hình nón đã cho bằng
A.
32 5
3
. B.
32
. C. 32 5
. D.
96
.
Lời giải
Chọn A
Theo giả thiết tam giác
SAB
đều,
9 3
SAB
S
và
2 5SO
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 34 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
3
9 3 9 3 6
4
SAB
AB
S AB
.
SAB
đều
6SA AB
.
Xét
SOA
vuông tại
O
, theo định lý Pytago ta có:
2
2 2 2
6 2 5 4OA SA SO .
Thể tích hình nón bằng
2 2 2
1 1 1 32 5
. . 4 .2 5
3 3 3 3
V r h OA SO
.
Câu 85. Cho hình trụ có chiều cao bằng 6a. Biết rằng khi cắt hình trụ đã cho bởi một mặt phẳng song
song với trục và cách trục một khoảng bằng 3a, thiết diện thu được là một hình vuông. Thể tích
của khối trụ được giới hạn bởi hình trụ đã cho bằng
A.
3
216 a
. B.
3
150 a
. C.
3
54 a
. D.
3
108 a
.
Lời giải
Chọn D
Lấy 2 điểm
M
,
N
lần lượt nằm trên đường tron tâm
O
sao cho
6MN a
.
Từ
M
,
N
lần lượt kẻ các đường thẳng song song với trục
'OO
, cắt đường tròn tâm
'O
tại
Q
,
P
.
Thiết diện ta thu được là hình vuông
MNPQ
có cạnh bằng 6a.
Gọi
H
là trung điểm của
PQ
. Suy ra
OH PQ
.
Vì
'OO MNPQ
nên ta có
', ', 'd OO MNPQ d O MNPQ O H
.
Từ giả thiết, ta có
' 3O H a
. Do đó
'O HP
là tam giác vuông cân tại
H
.
Suy ra bán kính đường tròn đáy của hình trụ là
2 2
' ' 3 2O P O H HP a
.
Vậy thể tích của khối trụ cần tìm là:
2
3
6 . . 3 2 108V a a a
.
Câu 86. Cho hình trụ có bán kính đáy là 4 cm, một mặt phẳng không vuông góc với đáy và cắt hai mặt
đáy theo hai dây cung song song
, ' 'AB A B
mà
' ' 6cmAB A B
(hình vẽ). Biết diện tích tứ
giác
' 'ABB A
bằng 60 cm
2
. Tính chiều cao của hình trụ đã cho.
A.
6 2
cm. B.
4 3
cm. C.
8 2
cm. D.
5 3
cm.
Lời giải
Chọn A
H
P
Q
O
O'
C
B
D
A
M
N
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 35
Dựng đường sinh
'B C
và
'A D
, ta có tứ giác
' 'A B CD
là hình chữ nhật nên
// ' 'CD A B
và
' ' 6 cmCD A B
. Vậy
//CD AB
và
6 cmCD AB
. Do đó tứ giác
ABCD
là hình bình hành
và nội tiếp được nên là hình chữ nhật. Từ đó
AB BC
, mặt khác
'CAB B
nên
( ') 'AB BCB AB BB
Vậy
' 'ABB C
là hình bình hành có một góc vuông nên là hình chữ nhật. Ta có
' '
. '
ABB A
S AB BB nên
60
' 10 cm
6
BB
. Xét tam giác
'BB C
vuông tại
C
có
2 2 2
' 'B C BB BC
mà
2 2 2
64 36 28BC AC AB
nên
2
' 100 28 72 ' 6 2 cmB C B C
.
Vậy chiều cao hình trụ là
6 2 cm
.
Câu 87. Khi cắt một hình trụ bởi hai mặt phẳng cùng song song với trục. Với mặt phẳng thứ nhất cách
trục một khoảng bằng
,a
thiết diện thu được là một hình vuông. Còn mặt phẳng thứ hai cách
trục một khoảng bằng
6
,
2
a
thiết diện thu được là một hình chữ nhật có diện tích bằng
2
2 2a
. Thể tích của khối trụ được giới hạn bởi hình trụ đã cho bằng
A.
3
4
.
3
a
B.
3
8 3 .a
C.
3
4 .a
D.
3
4 .a
Lời giải
Chọn D
Gọi
R
là bán kính đáy hình trụ.
Giả sử cắt bởi mặt phẳng thứ nhất được hình vuông
DABC
; khi đó
OI a
với
I
là trung điểm
BC
ta có
2 2
2 2h l BC IB R a
.
6 2cm
6 cm
C
A
B
D
B'
A'
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 36 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Cắt bởi mặt phẳng thứ hai được hình chữ nhật
DA B C
; khi đó
6
2
a
OK
với
K
là trung
điểm
B C
ta có
2
2
6
2 2
4
a
B C KB R
.
Diện tích
2 2
2 2 2 2 2 2 2
6 6
2 .2 4 . 2 2
4 4
A B C D
a a
S R a R R a R a
.
2 2
2 2 2 2 2 2 2
6a 6
2 .2 4 . 2 2
4 4
A B C D
a
S R a R R a R a
4 2
2 5 2 0
R R
a a
2
2
R
a
hoặc
2
1
2
R
a
(loại do
R a
)
2R a
.
Thể tích khối trụ là
2 2
4V R h a
.
Câu 88. Cho hình nón đỉnh
S
, tâm đường tròn đáy là
O
và có đường kính bằng
4a
. Mặt phẳng
P
đi
qua
S
cắt đường tròn đáy tại hai điểm
A
và
B
sao cho
2 3AB a
. Gọi
D
là điểm đối xứng
của
A
qua
O
. Biết khoảng cách từ
D
đến mặt phẳng
P
bằng
2 5
5
a
. Tính thể tích khối
nón.
A.
3
2a
. B.
3
2
3
a
. C.
3
2 13
3
a
. D.
3
4
3
a
.
Lời giải
Chọn B
Theo đề bài, có
2R OA a
.
Vì
D
là điểm đối xứng với
A
qua
O
nên
O
là trung điểm của
AD
.
, ,
5
2 ,
2 5
,
d D SAB d D SAB
AD
d O SAB
AO
d O SAB
.
Gọi
I
là trung điểm
AB
, suy ra
OI AB
.
Mà
AB SO
nên
AB SOI
.
Kẻ
OH SI H SI OH AB OH SAB
.
Do đó:
5
,
5
d O SAB OH
.
Xét
2
2
2 2
: 2 3OAI OI OA IA a a a .
I
O
D
A
B
S
H
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 37
Xét
2 2 2
1 1 1 1
:
2
SOI SO a
OH SO OI
.
Thể tích khối nón:
3
2
2
1 1 1 2
. 2 .
3 3 2 3
a
V R h a a
(đvtt).
Câu 89. Cho hình nón đỉnh
S
có đường tròn đáy tâm
O
bán kính
2R a
. Trên đường tròn đáy lấy
hai điểm
A
và
B
sao cho tam giác
OAB
đều. Biết diện tích tam giác
SAB
bằng
2 2a
. Thể
tích hình nón đã cho bằng:
A.
3
58 a
. B.
3
29a
. C.
3
29
3
a
. D.
3
58
3
a
.
Lời giải
Chọn D
Theo đề có
2R OA a
.
OAB
đều nên
2
2
2 . 3
3
4 2
OAB
a
S a
và
6
2
a
OI
.
Ta có:
SO OAB
suy ra
O
là hình chiếu của
S
lên
OAB
.
Do đó:
OAB
là hình chiếu
SAB
lên mp
OAB
.
Áp dụng công thức: .cos
OAB SAB
S S
(
,SAB OAB
.
6
cos
8
OAB
SAB
S
S
.
Mặt khác:
,
OI AB
SAB OAB SIO
SI AB
.
Xét
SOI
:
6 8
cos 4
8
6
OI OI
SI a
SI
.
2 2
58
2
SO SI OI
.
Thể tích khối nón:
3
2
2
1 1 58 58
. 2 .
3 3 2 3
a
V R h a
(đvtt).
I
O
B
A
S
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 38 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 90. Cho hình trụ có hai đáy là hai đường tròn
O
và
O
, chiều cao bằng
3a
và bán kính đáy
a
. Một mặt phẳng
đi qua trung điểm của
OO
và cắt đường tròn đáy theo một dây cung có
độ dài
2a
. Góc tạo bởi mặt phẳng
với mặt đáy gần với giá trị nào nhất.
A.
50
. B.
51
C.
39
. D.
41
.
Lời giải
Chọn B
Gọi
I
là trung điểm của
OO
. Mặt phẳng thiết diện cắt đường tròn đáy theo dây cung
AB
.
Dựng
OH AB
AB OIH OIH IAB
.
Ta có
O
là hình chiếu của
I
lên mặt phẳng đáy. Do vậy góc giữa
và mặt phẳng đáy là góc
IHO
Xét tam giác
OHB
vuông tại
H
2 2
2
2
a
OH OB BH
Xét tam giác vuông
OIH
vuông tại
O
0
3 2 6
tan : 50 46'
2 2 2
IO a a
IHO IHO
OH
Câu 91. Cho tam giác
ABC
đều có cạnh bằng
2a
. Từ tâm của đáy, dựng đường thẳng
vuông góc với
mặt phẳng
ABC
. Trên
lấy điểm
S
sao cho khoảng cách từ
A
đến mặt phẳng
SBC
bằng
12
7
a
. Khi đó thể tích khối nón có đỉnh là
S
và đường tròn đáy là đường tròn ngoại tiếp
ABC
bằng
A.
3
4
9
a
. B.
3
16
3
a
. C.
3
16
9
a
. D.
3
4
3
a
.
Lời giải
Chọn C
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 39
Gọi
O
là tâm của đáy,
M
là trung điểm của
BC
.
Vì
ABC
đều nên:
2 3
3
a
R OA
và
2 3 3
6 3
a a
OM
(
R
bán kính đường tròn ngoại
tiếp
ABC
).
Mặt khác:
Dễ thấy
12 4
, 3 , ,
7 7
d A SBC d O SBC a d O SBC a
.
Ta có:
BC OM
BC SOM
BC SO
.
Trong
SOM
, kẻ
OH SM H SM
suy ra
OH BC
nên
OH SBC
.
4
,
7
OH d O SBC a
.
Xét
2 2 2
1 1 1
: 4SOM SO a
OH SO OM
.
Suy ra thể tích khối nón:
2
3
2
1 1 2 3 16
. .4
3 3 3 9
a a
V R h a
(đvtt).
Câu 92. Cho mặt cầu
S
tâm
O
và các điểm
A
,
B
,
C
nằm trên mặt cầu
S
sao cho
3AB
,
4AC
,
5BC
và khoảng cách từ
O
đến mặt phẳng
ABC
bằng
1
. Thể tích của khối cầu
S
bằng
A.
20 5
3
. B.
7 21
2
. C.
29 29
6
. D.
4 17
3
.
Lời giải
Chọn C
A
M
O
B
S
C
H
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 40 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Từ
3AB
,
4AC
,
5BC ABC
vuông tại
A
đường tròn
C
ngoại tiếp
ABC
có
bán kính
5
2 2
BC
r
.
Lại có
C
là đường tròn giao tuyến của mặt phẳng
ABC
và mặt cầu
S
.
Suy ra
2 2 2
29
;
4
R d O ABC r
29
2
R
là bán kính mặt cầu
S
.
Vậy
3
4 29 29
3 6
S
V R
.
Câu 93. Cho hình nón có chiều cao bằng
a
. Biết rằng khi cắt hình nón đã cho bởi một mặt phẳng đi qua
đỉnh hình nón và cách tâm của đáy hình nón một khoảng bằng
3
a
, thiết diện thu được là một
tam giác vuông. Thể tích của khối nón được giới hạn bởi hình nón đã cho bằng
A.
3
4
9
a
. B.
3
5
9
a
. C.
3
3
a
. D.
3
5
12
a
.
Lời giải
Chọn D
Mặt phẳng đi qua đỉnh hình nón và cách tâm của đáy hình nón một khoảng bằng
3
a
có thiết
diện là tam giác vuông
SAB
như hình vẽ.
Kẻ
;OK AB OH SK
.
Ta có:
AB OK
AB SO
suy ra
AB SOK AB OH
và
OH SK
nên
OH SAB
. Do đó
;
3
a
d O SAB OH
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 41
Xét tam giác vuông
SOK
có:
2 2 2
1 1 1
OH SO OK
2 2
a
OK ;
2 2
3
2 2
a
SK SO OK ;
Vì
OK AB
nên
K
là trung điểm của
AB
. Tam giác vuông
SAB
có
3
2 2
a
SK KB
.
Xét tam giác vuông
OKB
có:
2 2
5
2
a
OB OK KB
;
Vậy thể tích khối nón cần tìm là:
2
3
2
1 1 5 5
. . . . . .
3 3 2 12
a a
V OB SO a
.
Câu 94. Một khối trụ có bán kính đáy
2r a
.
,O O
lần lượt là tâm đường tròn đáy. Một mặt phẳng
song song với trục và cách trục
15
2
a
, cắt đường tròn
O
tại hai điểm
,A B
. Biết thể tích của
khối tứ diện
OO AB
bằng
3
15
4
a
. Độ dài đường cao của hình trụ bằng
A.
a
. B.
6a
. C.
3a
. D.
2a
.
Lời giải
Chọn C
Vẽ đường sinh
AC
, khi đó mặt phẳng
ABC
song song với
OO
và cách
OO
một khoảng
15
2
a
.
Gọi
I
là trung điểm
AB
, ta có
15
, ,
2
a
d OO ABC d O ABC O I
.
Bán kính
2O A a
suy ra
2
2 2 2
15
2 2 2 4
4
a
BA IA O A O I a a
.
Thể tích tứ diện
OO AB
bằng
3
15
4
a
nên ta
có :
3 3
1 15 1 15 15
. . . . . . 3
6 4 6 2 4
a a a
OO IO AB OO a OO a
.
Vậy hình trụ có chiều cao
3OO a
.
Câu 95. Cho hình lăng trụ tam giác đều có . Gọi là trung điểm
. Bán kính mặt cầu ngoại tiếp khối chóp bằng
A. B. C. D.
Lời giải
. ' ' 'ABC A B C
' 2 ;
AA a BC a
M
'BB
. ' ' 'M A B C
3 3
.
8
a
13
.
2
a
21
.
6
a
2 3
.
3
a
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 42 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Chọn C
Gọi lần lượt là trung điểm và lần lượt là tâm đường tròn ngoại tiếp các
tam giác và Khi đó mặt cầu ngoại
tiếp khối chóp cũng là mặt cầu ngoại tiếp
khối lăng trụ
Gọi là trung điểm . Suy ra I là tâm mặt cầu cần
tìm. Suy ra . Ta có:
Và: .
Nên: .
Chọn C
Câu 96. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác
vuông cân tại
B
và
.AC a
Hình chiếu vuông góc của đỉnh
S
lên mặt phẳng
ABC
là điểm
H
đối xứng với
B
qua
AC
. Góc giữa hai mặt phẳng
SAC
và
0
45 .ABC
Diện tích mặt
cầu ngoại tiếp hình chóp
.S ABC
bằng:
A.
2
2 a
. B.
2
2
3
a
. C.
2
5 a
. D.
2
5
4
a
.
Lời giải
Chọn D
Gọi O là trung điểm AC.
Ta có H là điểm đối xứng của B qua AC nên ABCH là hình vuông.
.
2 2
HB a
HB AC a HO
.
Theo đề bài ta có:
0
( );( ) , 45SAC ABC SO HO SOH
Suy ra:
SHO
vuông cân tại H
2
a
SH
.
Ta có:
SAB AB (SHA)
SBC BC (SHC)
vu«ng t¹i A
vu«ng t¹i C
Tâm mặc cầu ngoại tiếp hình chóp S.ABC là trung điểm I của SB
,N P
'; 'AA CC
, 'O O
MNP
' ' 'A B C
. ' ' 'M A B C
. ' ' 'MNP A B C
I
'OO
'IB R
2 . 3 3
' '
3.2 3
a a
O B
1 1
' ' '
2 4 2
a
IO OO AA
2 2
21
' ' ' '
6
a
IB R O I O B
I
O
B
A
C
H
S
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 43
Ta có:
2 2
5 SB 5
SB SH HB a R SI a
2 2 4
Vậy diện tích mặt cầu cần tìm là:
2
2
5 5
4 a a
4 4
Câu 97. Cho hai khối nón có chung trục
3SS r
. Khối nón thứ nhất có đỉnh
S
đáy là hình tròn tâm
S
bán kính
r
. Khối nón thứ hai có đỉnh
S
đáy là hình tròn tâm
S
bán kính
2r
. Thể tích phần
chung của hai khối nón bằng
A.
3
4
27
r
. B.
3
9
r
. C.
3
4
9
r
. D.
3
4
3
r
.
Lời giải
Chọn C
Ta có thể tích phần chung là tổng thể tích của khối chóp có đỉnh
S
, trục
SO
và đường tròn đáy
có bán kính
OM
và khối chóp có đỉnh
S
, trục
S O
và đường tròn đáy có bán kính
OM
.
Ta có:
1
tan
3 3
OM SA r
OS M
OS SS r
và
2 2
tan
3 3
OM S B r
OSM
OS SS r
Suy ra:
1
1
3
. 2
2
2
3
OM OS
OS OS
OS OM
2
2
3
OS r
OM r
OS r
Vậy
2 3
2 2 2
1 1 1 1 4 4
. . . . . . .3 .
3 3 3 3 9 9
r r
V SO OM S O OM SS OM r
Câu 98. Cho hình chóp
.S ABC
có
( )SA ABC
, 3AB ,
2AC
và
30BAC . Gọi
,M N
lần lượt
là hình chiếu của
A
lên
,SB SC
. Bán kính
R
của mặt cầu ngoại tiếp hình chóp
.A BCNM
là
A.
2R
. B.
13R
. C.
1R
. D.
2R
.
Lời giải
Chọn C
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 44 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
● Xét tam giác
AMB
vuông tại
M
nên tâm của tam giác
AMB
là trung điểm của cạnh
AB
.
Khi đó, trong
( )ABC
kẻ đường trung trực
d
của
AB
thì tâm mặt cầu cần tìm nằm trên
d
.
● Xét tam giác
ANC
vuông tại
N
nên tâm của tam giác
ANC
là trung điểm của
AC
. Khi đó,
trong
( )ABC
, kẻ đường trung trực
'd
của
AC
thì tâm mặt cầu cần tìm nằm trên
'd
.
Điểm
'I d d
là tâm của mặt cầu ngoại tiếp hình chóp
.A BCNM
.
Mà
d
và
'd
cùng nằm trong
( )ABC
nên
I
cũng chính là tâm đường tròn ngoại tiếp tam giác
ABC
.
Suy ra bán kính mặt cầu bằng bán kính đường tròn ngoại tiếp tam giác
ABC
.
● Áp dụng định lý
cosin
trong tam giác
ABC
có:
2 2 2
2. . . 1BC AB AC AB AC cosA
1BC
● Áp dụng công thức hàm
sin
:
1
2 1.
sin 2.sin 2.sin 30
BC BC
R R
A A
Câu 99. Có một bể hình hộp chữ nhật chứa đầy nước. Người ta cho ba khối nón giống nhau có thiết
diện qua trục là một tam giác vuông cân vào bể sao cho ba đường tròn đáy của ba khối nón đôi
một tiếp xúc với nhau, một khối nón có đường tròn đáy tiếp xúc với một cạnh của đáy bể và hai
khối nón còn lại có đường tròn đáy tiếp xúc với hai cạnh của đáy bể. Sau đó người ta đặt lên
đỉnh của ba khối nón một khối cầu có bán kính bằng
4
3
lần bán kính đáy khối nón. Biết khối
cầu vừa đủ ngập trong nước và tổng lượng nước trào ra là
337
24
(lit). Thể tích nước ban đầu
trong bể thuộc khoảng nào dưới đây? (tính theo đơn vị lít).
A. (150;151) B. (151;152) C. (139;140) D. (138;139).
Lời giải
Chọn B
- Đầu tiên, ta quan tâm tới mặt phẳng đáy của hình hộp:
Dễ thấy tam giác
IJE
nối tâm của ba mặt cầu là một tam giác đều cạnh
2R
.
Dễ thấy
4AB R
và
2 3AD MI KE EP R .
d
d'
I
N
M
A
C
B
S
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 45
- Tiếp theo, ta quan tâm tới chiều cao của hình hộp:
Ta coi hình cầu có tâm
S
, chạm với khối nón có tâm đáy
I
tại
U
và bán kính cầu
4
3
R
SU
.
Hạ
SO
vuông góc mặt phẳng đáy. Dễ thấy chân đường cao
O
là tâm tam giác đều
IJE
.
Dễ tính được
2 3
3
R
IO
, áp dụng định lý Pitago cho tam giác
SHU
, ta được
2
3
R
SH
.
Chiều cao của hình hộp là
2 4 5
3
3 3 3
R R R
h SH HO SL R R
.
- Ta chỉ cần tính bán kính của mỗi hình nón nữa là xong. Dễ thấy thể tích nước tràn ra bằng thể
tích các khối nón và cầu có trong hình hộp.
Như vậy,
3
2 3 3
337 1 4 4 337 81 3
3 3. . . .
24 3 3 3 81 24 2
n c
V V R R R R R R dm
- Vậy thể tích hình hộp bằng
3
81
. . 4 . 2 3 .3 12 2 3 2 3 151,14
2
V AB AD h R R R R
(dm).
Câu 100. Cho hình trụ có chiều cao bằng
6a
. Biết rằng khi cắt hình trụ đã cho bởi một mặt phẳng song
song với trục và cách trục một khoảng bằng
3a
, thiết diện thu được là một hình vuông. Thể
tích của khối trụ được giới hạn bởi hình trụ đã cho bằng
A.
3
216 a
. B.
3
150 a
. C.
3
54 a
. D.
3
108 a
.
Lời giải
Chọn D
Gọi
O
và
O
là tâm hai đáy của hình trụ.
Giả sử thiết diện thu được khi cắt hình trụ đã cho bởi một mặt phẳng song song với trục là hình
vuông
ABCD
.
Theo giả thiết ta có
6AB BC OO a
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 46 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Gọi
I
là trung điểm
AB
. Suy ra
OI AB
và
1
3
2
AI AB a
.
Mà
OI BC
nên
OI ABCD
.
Vì
//OO ABCD
nên
; ; 3d OO ABCD d O ABCD OI a
.
Xét tam giác
AOI
vuông tại
I
và có
3OI AI a
3 2OA a
.
Thể tích khối trụ là:
2
. .V R h
2
. .OA OO
2
. 3 2 . 6a a
3
108 a
.
Câu 101. Cho hình trụ có chiều cao bằng
6a
. Biết rằng khi cắt hình trụ đã cho bởi một mặt phẳng song
song với trục và cách trục một khoảng bằng
3a
, thiết diện thu được là một hình chữ nhật có
diện tích
2
48a
. Thể tích của khối trụ được giới hạn bởi hình trụ đã cho bằng
A.
3
216 a
. B.
3
180 a
. C.
3
54 a
. D.
3
150 a
.
Lời giải
Chọn D
Gọi
O
và
O
là tâm hai đáy của hình trụ.
Giả sử thiết diện thu được khi cắt hình trụ đã cho bởi một mặt phẳng song song với trục là hình
chữ nhật
ABCD
có
6AB BC OO a
,
2
48 8
ABCD
S a AB a
Gọi
I
là trung điểm
AB
. Suy ra
OI AB
và
1
4
2
AI AB a
.
Mà
OI BC
nên
OI ABCD
.
Vì
//OO ABCD
nên
; ; 3d OO ABCD d O ABCD OI a
.
Xét tam giác
AOI
vuông tại
I
và có
3 , 4OI a AI a
5OA a
.
Thể tích khối trụ là:
2
. .V R h
2
. .OA OO
2
3
. 5 . 6 150a a a
.
Câu 102. Cho hình chóp
.S ABC
có
SA
vuông góc với mặt phẳng đáy, góc giữa
SBC
và mặt phẳng
đáy bằng
60
. Nếu
ABC
là tam giác đều cạnh 3a thì bán kính mặt cầu ngoại tiếp hình chóp
S.ABC
bằng
A.
43
4
a
. B.
43
8
a
. C.
43
12
a
. D.
43
6
a
-----Lời giải
Chọn A
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 47
Gọi H là trung điểm AB
AH BC
tại
H
, 60SAB ABC SHA
3 3 3
2 2
a a
AH SA
Gọi
I
là tâm của
ABC
Dựng
đi qua
, / /I SA
Dựng
là trung trực của
SA
Gọi
J
Vì
AJ J JB JC
S AJ J J
A SJ JB JC J
J
là tâm mặt cầu ngoại tiếp
SABC
Bán kính mặt cầu
AR J
Gọi M là trung điểm SA
Khi đó:
2 2
AJ MA MJ
2
2
2 2
3 3
2
43
4 4 4
a
SA a
R AI a
.
Câu 103. Cho hình chóp
ABCD
có đáy là hình thang vuông tại
A
và
D
. Biết
SA
vuông góc với
ABCD
,
, AB BC a
2 , 2 AD a SA a
. Gọi
E
là trung điểm của
AD
. Bán kính mặt cầu đi
qua các điểm
, , , ,S A B C E
bằng
A.
3
2
a
. B.
30
6
a
. C.
6
3
a
. D.
a
.
Lời giải
Chọn D
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 48 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta thấy các tam giác
; ; SAC SBC SEC
vuông tại
, ,A C E
. Vậy các điểm
, , , ,S A B C E
nằm
trên mặt cầu đường kính
2 2
.
2 2
SC SA AC
SC R a
Câu 104. Một hình trụ có bán kính đáy bằng chiều cao và bằng
a
. Một hình vuông
ABCD
có
,AB CD
là
hai dây cung của hai đường tròn đáy và mặt phẳng
ABCD
không vuông góc với đáy. Diện
tích hình vuông đó bằng.
A.
2
5
4
a
. B.
2
5 2
4
a
. C.
2
5a
. D.
2
5
2
a
.
Lời giải
Chọn D
Kẻ đường sinh
A A
. Khi đó ta có
0
90
CD AD
CD A AD CD A O A DC
CD A A
.
Ta có
A DC
là góc nội tiếp chắn nửa đường tròn
2A C a
.
Đặt cạnh hình vuông
ABCD
là
x
.
Ta có
2 2 2 2 2
2
2 2 2 2
2 2 2
5
2 4
2
ABCD
A D AD A A x a
a
x a a x S
A D DC A C
.
Câu 105. Cho ba hình cầu có bán kính lần lượt là
1 2 3
, ,R R R đôi một tiếp xúc nhau và cùng tiếp xúc với
mặt phẳng
( )P
. Các tiếp điểm của ba hình cầu với mặt phẳng (P) lập thành một tam giác có độ
dài các cạnh lần lượt là
2;3;4
. Tính tổng
1 2 3
:R R R
A.
61
12
. B.
67
12
. C.
53
12
. D.
59
12
.
Lời giải
Chọn A
Gọi tâm của ba mặt cầu lần lượt là
1 2 3
O ;O ;O
và
A;B;C
lần lượt là hình chiếu vuông góc của
1 2 3
O ;O ;O
lên
( P )
. Không mất tổng quát, giả sử
1 2 3
R R R
và theo đó
AB AC BC
K
L
H
A
B
C
O
1
O
3
O
2
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 49
Gọi
L
là hình chiếu vuông góc của
2
O
lên
1
O A
và
,H K
lần lượt là hình chiếu của
2
O
lên
1 2
O A;O B
Ta có
1 2 1 2 1 1 2
O O R R ;O L R R và
2 2 2
2 1 2 1
O L (O O ) (O L )
2 2 2
1 2 1 2 1 2
4 4( R R ) ( R R ) R R
Tương tự, ta có
2 2 2
1 3 1 3 1 3
3 4( R R ) ( R R ) R R
;
2 2 2
2 3 2 3 2 3
2 4( R R ) ( R R ) R R
Ta có hệ
1 2
2 3
1 3
4
1
9
4
R R
R R
R R
1
3
1 3
1 2
4
9
4
4
R
R
R R
R R
3
1
2
3
4
3
4
3
R
R
R
. Suy ra
1 2 3
61
.
12
R R R
Câu 106. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành, các cạnh bên của hình chóp bằng
6 cm
,
4AB cm
. Khi thể tích khối chóp
.S ABCD
đạt giá trị lớn nhất, tính diện tích mặt cầu
ngoại tiếp
.S ABCD
.
A.
2
12 cm
. B.
2
4 cm
. C.
2
9 cm
. D.
2
36 cm
.
Lời giải
Chọn D
Gọi
O
là giao điểm của
AC
và
BD
.
Ta có
SAC
cân tại
S
nên
SO AC
và
SBD
cân tại S nên
SO BD
.
Khi đó
.SO ABCD
Ta có:
SAO SBO SCO SDO OA OB OC OD
Vậy hình bình hành
ABCD
là hình chữ nhật.
Đặt
2
2 2
16
4 .
2 2
AC x
BC x AC x AO
Xét
SAO
vuông tại
O
, ta có:
2 2
2 2
16 8
6
4 2
x x
SO SA AO
Thể tích khối chóp
.S ABCD
là:
2
2
.
1 1 8 2
. . .4 . 8 .
3 3 2 3
S ABCD ABCD
x
V SO S x x x
Áp dụng bất đẳng thức :
2 2
2
a b
ab ta có:
2 2
2
2 2 8 8
. 8 . . .
3 3 2 3
x x
V x x
Dấu
" "
xảy ra
2
8 2. x x x
Do đó:
2, 1. BC SO
Gọi
M
là trung điểm của
SA
, trong
SAO
kẻ đường trung trực của
SA
cắt
SO
tại
I
.
Khi đó mặt cầu ngoại tiếp khối chóp
.S ABCD
có tâm
I
và bán kính
.R IS
M
I
O
D
C
B
A
S
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 50 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Vì
( . )SMI SOA g g ∽
nên
2
6
3 3( ).
2. 2.1
SI SM SA
SI R cm
SA SO SO
Diện tích mặt cầu ngoại tiếp khối chóp
.S ABCD
là:
2 2 2
4 4 .3 36 ( )R cm
.
Câu 107. Cho hình tứ diện
ABCD
có
AD ABC
,
ABC
là tam giác vuông tại
B
. Biết
2( )BC cm
, 2 3( ), 6( )AB cm AD cm
. Quay các tam giác
ABC
và
ABD
( bao gồm cả điểm bên trong
2
tam
giác) xung quanh đường thẳng
AB
ta được
2
khối tròn xoay. Thể tích phần chung của
2
khối
tròn xoay đó bằng
A.
3
3 ( )cm
B.
3
5 3
( )
2
cm
C.
3
3 3
( )
2
cm
. D.
3
64 3
( )
3
cm
.
Lời giải
Chọn C
Dễ thấy
1
AD ABC AD R
Gọi
M BD AC
và N là hình chiếu của M trên AB. Dễ dàng chứng minh được tỉ lệ:
(1)
MN AN
BC AB
; và
(2)
MN BN
AD AB
(1) 3 1
3 ;
(2) 4 4
AD AN AN BN
BC BN AB AB
3 3 3 3
; ;
2 2 2
AN BN MN
Phần thể tích chung của 2 khối tròn xoay là phần thể tích khi quay tam giác
AMB
xung quanh
trục AB. Gọi
1
V
là thể tích khối tròn xoay khi quay tam giác
BMN
xung quanh AB
Và
2
V
là thể tích khối tròn xoay khi quay tam giác
AMN
xung quanh AB
Dễ tính được:
1
3 3
( )
8
V dvtt
và
2 1 2
9 3 3 3
( ) ( )
8 2
V dvtt V V dvtt
. Chọn C.
Câu 108. Huyền có một tấm bìa như hình vẽ, Huyền muốn biến đường tròn đó thành một cái phễu hình
nón. Khi đó Huyền phải cắt bỏ hình quạt tròn
AOB
rồi dán
OA
,
OB
lại với nhau. Gọi
x
là
góc ở tâm hình quạt tròn dùng làm phễu. Tìm
x
để thể tích phểu lớn nhất?
A.
2 6
3
B.
3
C.
2
D.
4
Lời giải
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 51
Chọn A
Ta có diện tích của hình phểu
2
2 2
xq
R x xR
S r
là bán kính của đáy phểu;
2 r
x
R
2 2 2 2 4 2 6
1 1 1
.
3 3 3
V r h r R r r R r
là thể tích của phểu
Xét hàm số phụ
4 2 6 3 2 5
. 4 . 6y r R r y r R r
2 2
6
0 2. 3 0
3
y R r r R
Vậy
y
max thì
V
và
V
max khi
6 2 2 6 2 6
3 3 3
R r R
r x x x
R R
Câu 109. Cho hình trụ có hai đáy là hai hình tròn
O
và
,O
thiết diện qua trục của hình trụ là hình
vuông. Gọi
,A B
là hai điểm lần lượt nằm trên hai đường tròn
O
và
.O
Biết
2AB a
và
khoẳng cách giữa hai đường thẳng
AB
và
OO
bằng
3
.
2
a
Bán kính đáy bằng
A.
14
.
3
a
B.
14
.
2
a
C.
14
.
4
a
D.
14
.
9
a
Lời giải
Chọn C
R
O
B
A
h
R
B;A
O
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 52 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Dựng đường sinh
BC
gọi
H
là trung điểm của đoạn
.AB
Ta có
3
,
2
a
d OO AB OH
Giả sử bán kính đáy của hình trụ là
,r
do thiết diện qua trục của hình trụ là hình vuông suy ra
2BC r
2 2 2 2
4 4 ,AC AB BC a r
mặt khác
2
2 2 2 2 2
3
2 2 4 3
4
a
AC OA OH r r a
Ta có phương trình
2 2 2 2
14
4 4 4 3 .
4
a
a r r a r
Câu 110. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông cân tại
B
,
3 2 AB BC a
,
0
90 SAB SCB
. Biết khoảng cách từ
A
đến mặt phẳng
( )SBC
bằng
2 3a
. Tính thể tích
mặt cầu ngoại tiếp hình chóp
.S ABC
.
A.
3
72 18
a
. B.
3
18 18
a
. C.
3
6 18
a
. D.
3
24 18
a
.
Lời giải
Chọn D
H
C
B
A
O'
O
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 53
Gọi ,I H lần lượt là trung điểm của cạnh
SB
và
AC
Mặt khác, theo giả thiết ta có Δ ,ΔSAB SCB lần lượt là các tam giác vuông tại
A
và
C
IA IB IC IS
I
là tâm mặt cầu ngoại tiếp hình chóp
.S ABC
Mặt khác:
ΔABC
vuông tại
B
H
là tâm đường tròn ngoại tiếp
ΔABC
IH ABC
Ta có:
;
2 ; 3
;
d A SBC
AC
d H SBC a
HC
d H SBC
Gọi
K
là trung điểm của cạnh
BC
/ / ,HK BC HK AB AB BC
Lại có:
BC IH IH ABC BC IHK
Mặt khác:
BC SBC SBC IHK
theo giao tuyến
IK
Trong
IHK
, gọi
HP IK HP SBC
tại
P
; 3HP d H SBC a
Xét
2 2 2 2 2
1 1 1 1 1
Δ : 3
4
IHK HI a
HP HI HK HI AB
Xét
2 2
Δ : 3 2IHB IB IH HB a R
. Vậy
3 3
4
24 18
3
V πR πa
Câu 111. Cho hình trụ có đáy là hai đường tròn tâm
O
và
O
, bán kính đáy bằng chiều cao và bằng
2a
.
Trên đường tròn đáy có tâm
O
lấy điểm
A
,
D
trên đường tròn tâm
O
lấy điểm
B
,
C
sao
cho
//AB CD
và
AB
không cắt
'OO
. Tính
AD
để thể tích khối chóp
'.O ABCD
đạt giá trị lớn
nhất.
A.
2 2AD a
B.
4AD a
C.
4 3
3
AD a
D.
2AD a
Lời giải
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 54 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Kẻ đường thẳng qua
'O
song song với
AB
cắt mặt phẳng chứa đường tròn
( )O
tại
1
O .
Lúc đó
1
. 'AO D BO C là một hình lăng trụ chiều cao bằng
2a
.
Vì
AD BC
nên
'BO C OAD
S S
Ta có thể tích của khối chóp
'.O ABCD
:
1
3
' . ' '
1 2 2 2 1 8
.2 . .2 . .2 . .2 .2 .sin
3 3 3 3 2 3
O ABCD AO D BO C BO C OAD
a
V V a S a S a a a AOD
.
0
'
max
90 2 2
O ABCD
V AOD AD a
.
Câu 112. Trong không gian với hệ tọa độ
Oxyz
, cho hai mặt phẳng song song
:2 2 1 0,P x y z
:2 2 5 0Q x y z
và điểm
1;1;1A
nằm trong khoảng giữa hai
mặt phẳng này. Gọi
S
là mặt cầu đi qua
A
và tiếp xúc với cả
P
và
.Q
Biết khi
S
thay
đổi thì tâm
I
của nó luôn thuộc đường tròn
C
cố định. Diện tích hình tròn giới hạn bởi
C
là
A.
2
3
. B.
4
9
. C.
16
9
. D.
8
9
.
Lời giải
Bán kính mặt cầu
S
:
2
2 2
5 1
1
, . 1
2
2 1 2
R d P Q
Tâm
I
của mặt cầu
S
nằm trên mặt phẳng
R
cách đều
P
và
.Q
Phương trình mặt phẳng
: 2 2 2 0R x y z
O
1
O
C
D
B
A
O'
A
K
I
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 55
Tâm
I
của mặt cầu
S
nằm trên mặt cầu
'
S
có tâm
A
bán kính
1R IA
Gọi
K
là hình chiếu của
A
trên
R
2
2 2
2. 1 1 2.1 2
1
,
3
2 1 2
AK d A R
Tâm
I
của mặt cầu
S
nằm trên đường tròn
C
là giao của mặt cầu
'
S
và mặt phẳng
R
có tâm
K
và bán kính
2
2 2 2
1 2 2
1
3 3
r KI AI AK
Diện tích hình tròn giới hạn bởi
C
là:
2
8
9
r
.
Câu 113. Cho hình chóp
.S ABCD
có
SA
vuông góc với mặt phẳng
ABCD
, tứ giác
ABCD
là hình
thang vuông với cạnh đáy
, AD BC
.
3 3 AD CB a
,
AB a
, 3SA a . Điểm
I
thỏa mãn
3
AD AI
,
M
là trung điểm
SD
,
H
là giao điểm của
AM
và
SI
. Gọi
, E F
lần lượt là hình
chiếu của
A
lên
, SB SC
. Tính thể tích
V
của khối nón có đáy là đường tròn ngoại tiếp tam
giác
EFH
và đỉnh thuộc mặt phẳng
ABCD
.
A.
3
5 5
a
V
. B.
3
2 5
a
V
. C.
3
5
a
V
. D.
3
10 5
a
V
.
Lời giải
Nhận xét: Tứ giác
ABCI
là hình vuông. Dễ chứng minh
BC SAB
và
BI SC
.
EA SB
EA SBC
EA BC
EA SC
.
EA SC
SC AEF
FA SC
.
Trong tam giác vuông
SAB
có
2
2
3
4
SE SA
SB SB
.
Trong tam giác
SAD
có
. . 1
HS AI MD
HI AD MS
3
HS
HI
3
4
SH
SI
.
Trong tam giác
SBI
có
3
4
SE SH
SB SI
// EH BI
. Do
BI SC
nên
EH SC
.
Suy ra các điểm
, , , A E F H
cùng thuộc mặt phẳng đi qua
A
và vuông góc với
SC
.
Gọi
K
là trung điểm
AF
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 56 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Vì
EA EF
AH FH
K
là tâm đường tròn ngoại tiếp tam giác
EFH
.
Ta có:
.
SA AC
AF
SC
3. 2
5
a a
a
6
5
a
.
Suy ra bán kính đáy của khối nón là
1 6
2
2 5
a
R AF .
Gọi
O
là tâm hình vuông
ABCI
.
Do
//
SC EFH
OK EFH O
OK SC
là đỉnh của khối nón.
Chiều cao của khối nón là
1
2
h FC
2 2
1
2
AC AF
2 2
1 6
2
2 5
a a
5
a
.
Vậy thể tích khối nón là
2
2
1 1 6
. . . . .
3 3
2 5 5
a a
V R h
3
10 5
a
.
Câu 114. Cho một miếng tôn hình tròn có bán kính
50 cm
. Biết hình nón có thể tích lớn nhất khi diện
tích toàn phần của hình nón bằng diện tích miếng tôn ở trên. Khi đó hình nón có bán kính đáy
là:
A.
10 2 cm
. B.
50 2 cm
. C.
20 cm
. D.
25 cm
.
Lời giải
Ta có diện tích miếng tôn là
2
.2500 cm
S
.
Diện tích toàn phần của hình nón là:
2
. .
tp
S R R l
.
Thỏa mãn yêu cầu bài toán ta có:
2
. . 2500
R R l
2
. 2500
R R l A
A
l R
R
.
Thể tích khối nón là:
2
1
.
3
V R h
2 2 2
1
.
3
V R l R
2
2 2
1
.
3
A
V R R R
R
2
2
2
1
. 2
3
A
V R A
R
2 2 4
1
. . 2 .
3
V A R A R
2
3
2
1
. 2
3 8 4
A A
V A R
1
.
3 2 2
A A
V
. Dấu bằng xảy ra khi
25
4
A
R
, vậy
V
đạt GTLN khi
25
R
.
Câu 115. Cho hình nón
N
có đường cao
SO h
và bán kính đáy bằng
R
, gọi
M
là điểm trên đoạn
SO
, đặt
OM x
,
0
x h
.
C
là thiết diện của mặt phẳng
P
vuông góc với trục
SO
tại
M
, với hình nón
N
. Tìm
x
để thể tích khối nón đỉnh
O
đáy là
C
lớn nhất.
A.
2
h
. B.
2
2
h
. C.
3
2
h
. D.
3
h
.
Lời giải
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 57
Ta có
BM
là bán kính đường tròn
C
.
Do tam giác
SBM SAO ∽
nên
BM SM
AO SO
.AO SM
BM
SO
R h x
BM
h
.
Thể tích của khối nón đỉnh
O
đáy là
C
là:
2
1
.
3
V BM OM
2
1
3
R h x
x
h
2
2
2
1
3
R
h x x
h
.
Xét hàm số
2
2
2
1
3
R
f x h x x
h
,
0 x h
ta có
Ta có
2
2
1
3
3
R
f x h x h x
h
;
2
2
1
0 3
3 3
R h
f x h x h x x
h
.
Lập bảng biến thiên ta có
Từ bảng biến ta có thể tích khối nón đỉnh
O
đáy là
C
lớn nhất khi
3
h
x
.
Câu 116. Bạn Hoàn có một tấm bìa hình tròn như hình vẽ, Hoàn muốn biến hình tròn đó thành một hình
cái phễu hình nón. Khi đó Hoàn phải cắt bỏ hình quạt tròn
AOB
rồi dán hai bán kính
OA
và
OB
lại với nhau (diện tích chỗ dán nhỏ không đáng kể). Gọi
x
là góc ở tâm hình quạt tròn
dùng làm phễu. Tìm
x
để thể tích phễu lớn nhất?
NG
UYỄN BẢO VƯƠNG - 0946798489
Trang 58 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
4
. B.
3
. C.
2 6
3
. D.
2
.
Lời giải
Dựa vào hình vẽ, độ dài cung
AB
lớn bằng
Rx
, bán kính hình nón
2
Rx
r
Đường c
ao của hình nón
2 2
h R
r
2 2
2
2
4
R x
R
2 2
4
2
R
x
Thể
tích khối nón (phễu)
2
1
3
V r h
2 2
2
2
2
1
. .
4
3 4 2
R x R
x
3
4 2
2
2
4
24
R
x x
The
o Cauchy ta có
3
2
2 2
2
2
4
. .
4
2 2 27
x x
x
3
2 3
27
R
V
.
Dấu bằ
ng xảy ra khi
2
2 2
4
2
x
x
2 6
3
x
. V
ậy thể tích phễu lớn nhất khi
2 6
3
x
.
-------------------- HẾT --------------------
| 1/72
| | Tải xuống

Có thể bạn quan tâm:

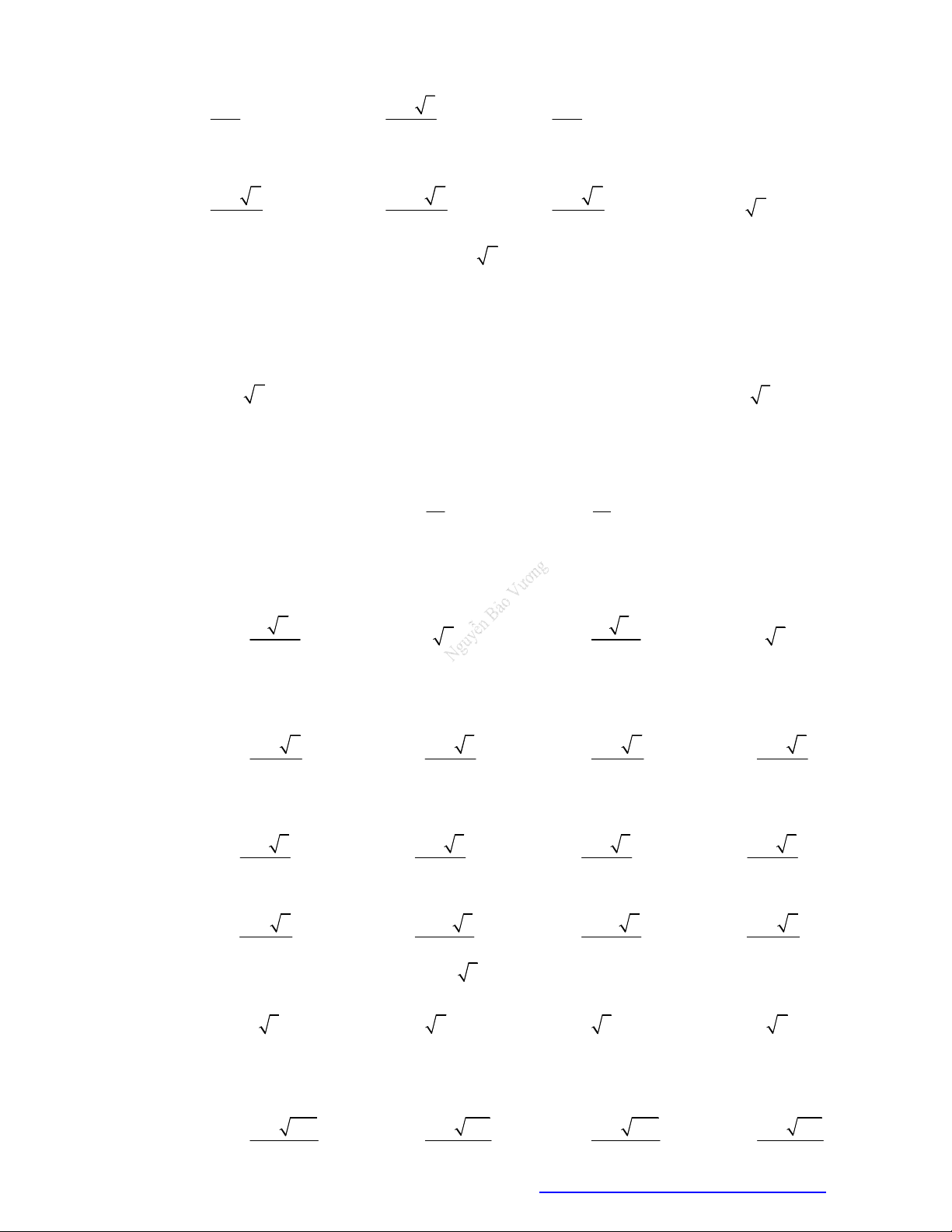
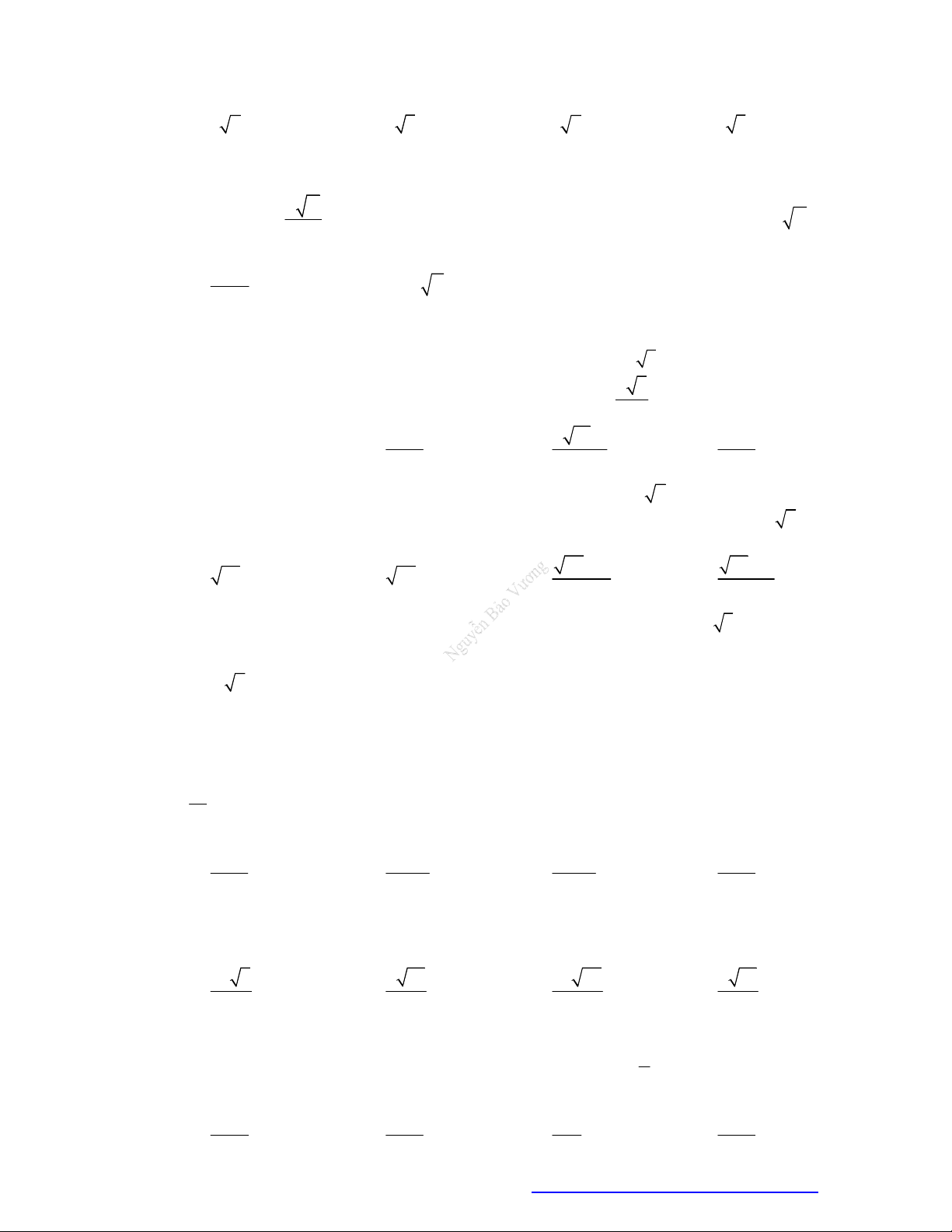
Preview text:


TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 Vấn đề 11
KHỐI TRÒN XOAY - THỂ TÍCH KHỐI TRÒN XOAY
MẶT TRỤ, MẶT NÓN – MẶT CẦU MẶT NÓN
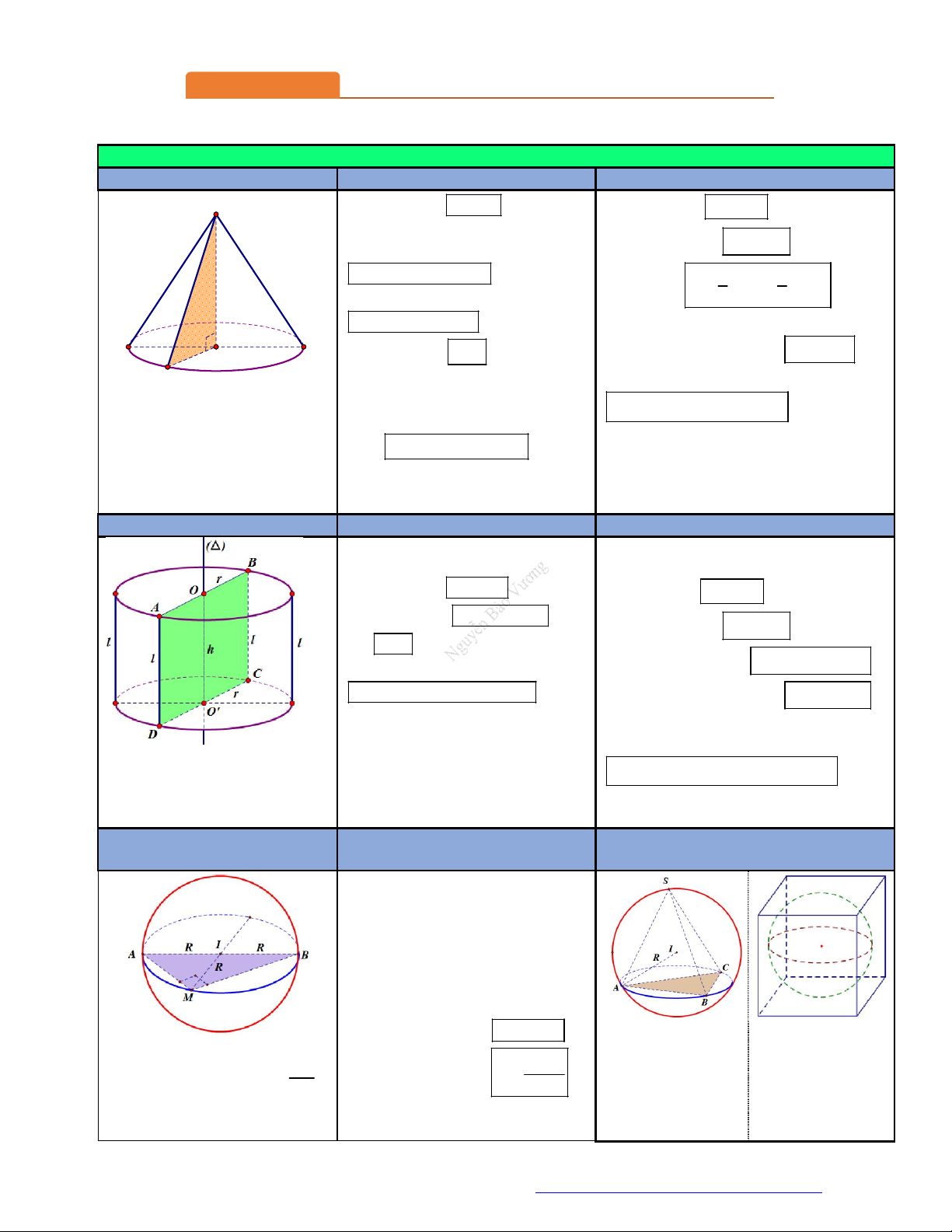
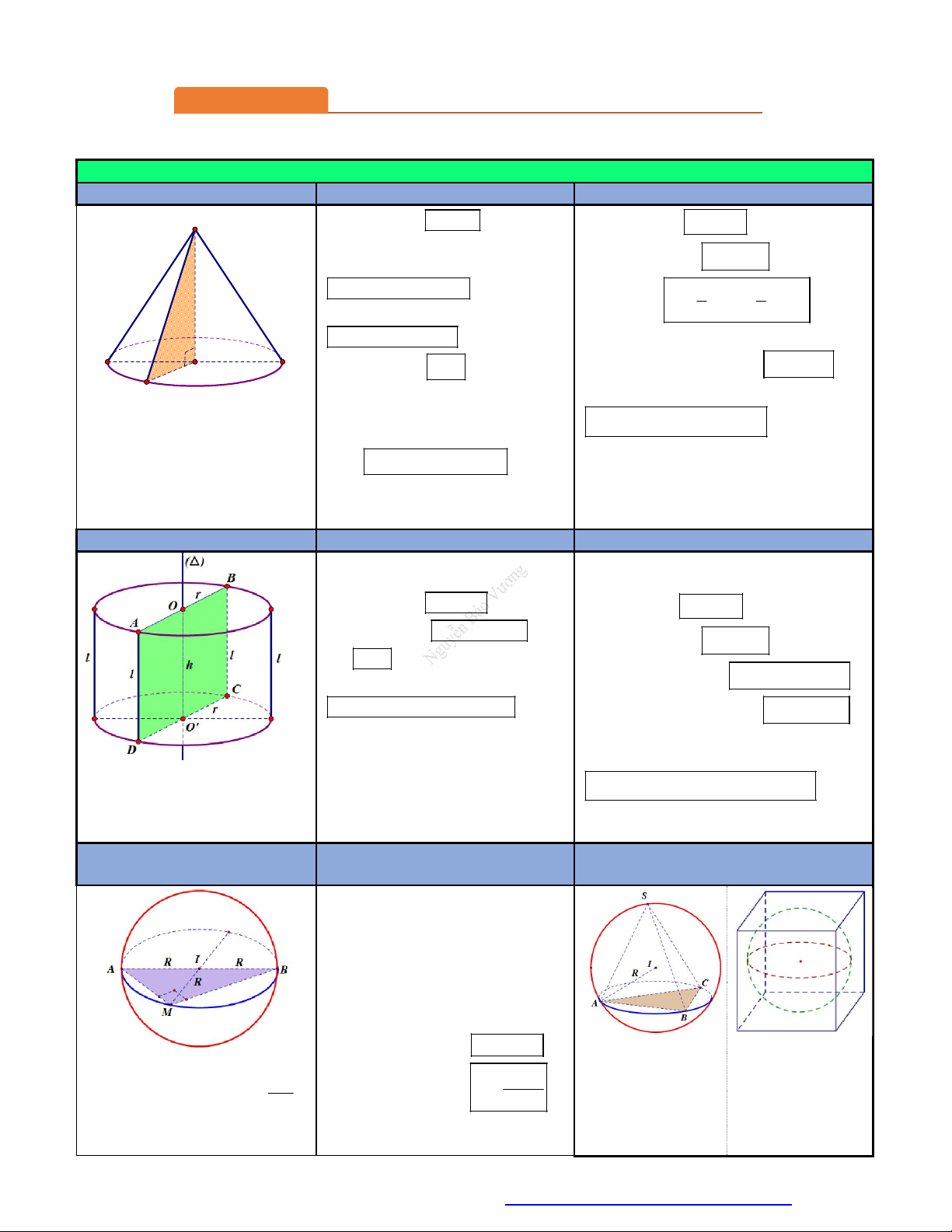
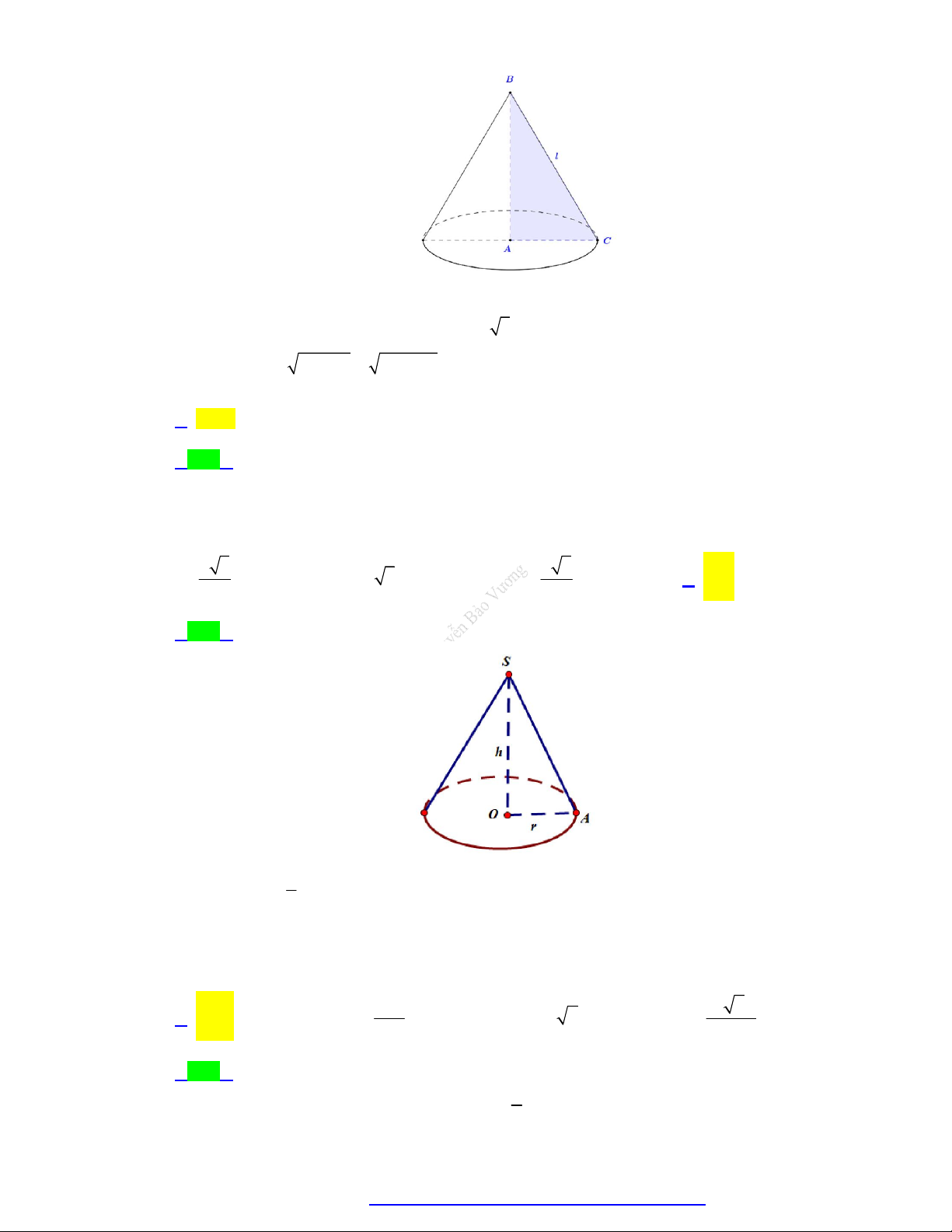
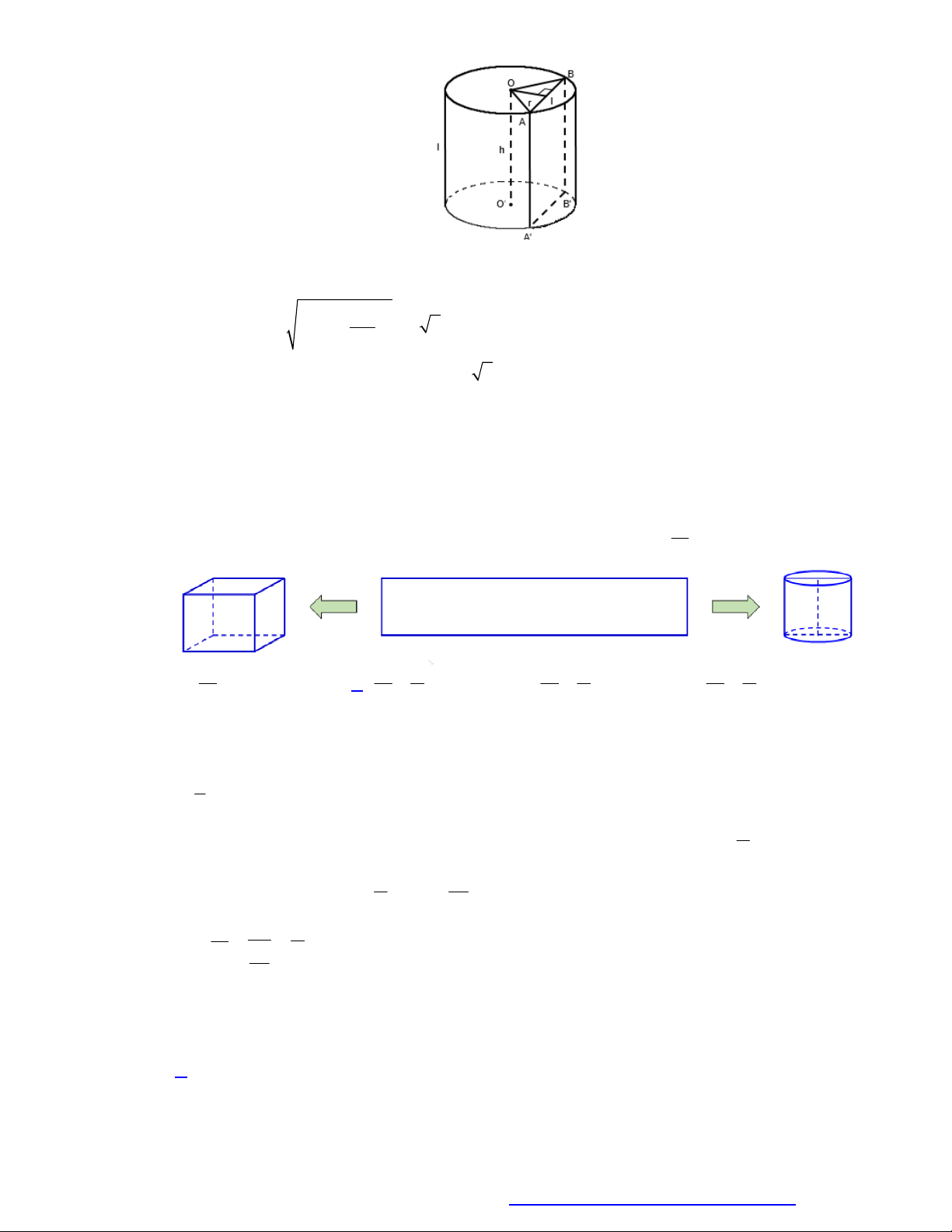
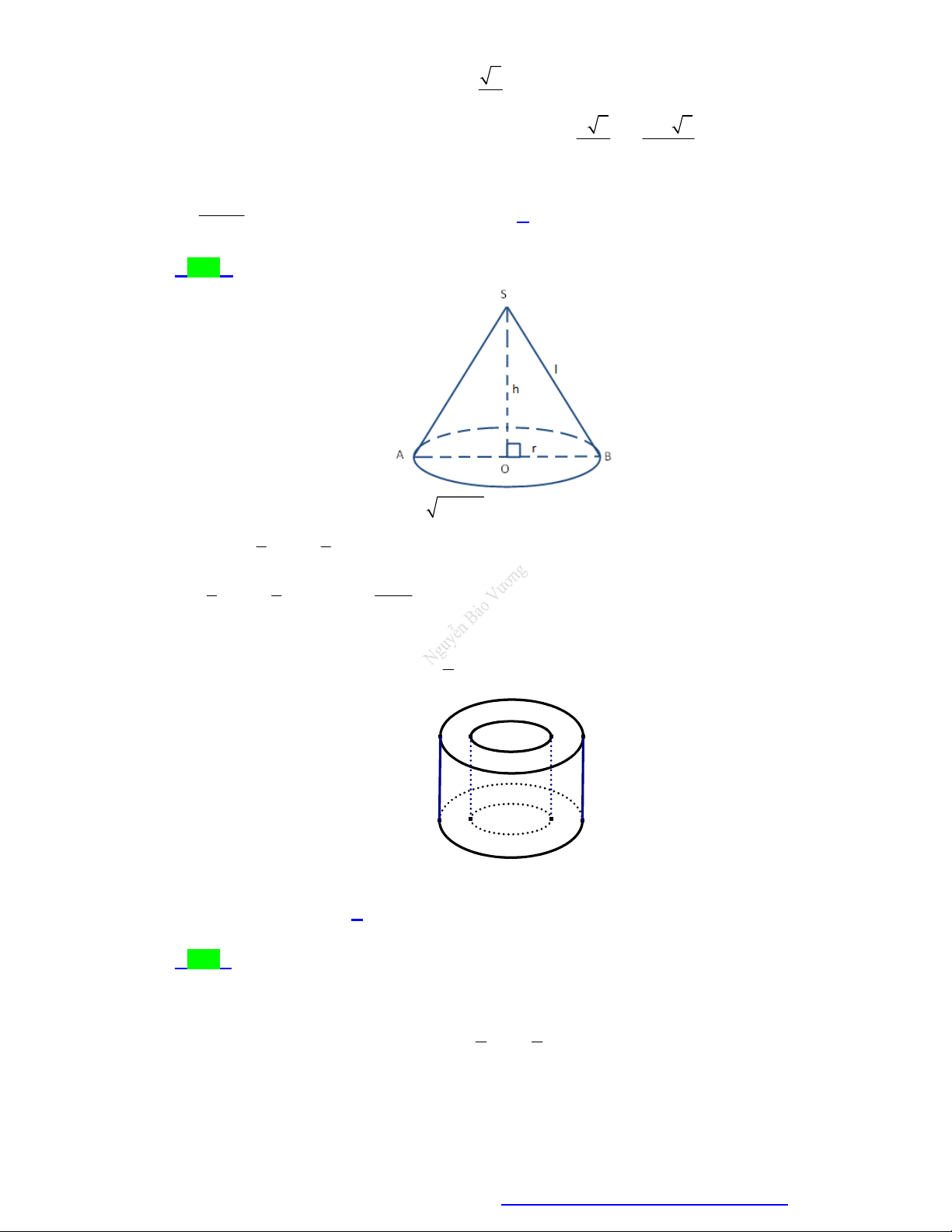
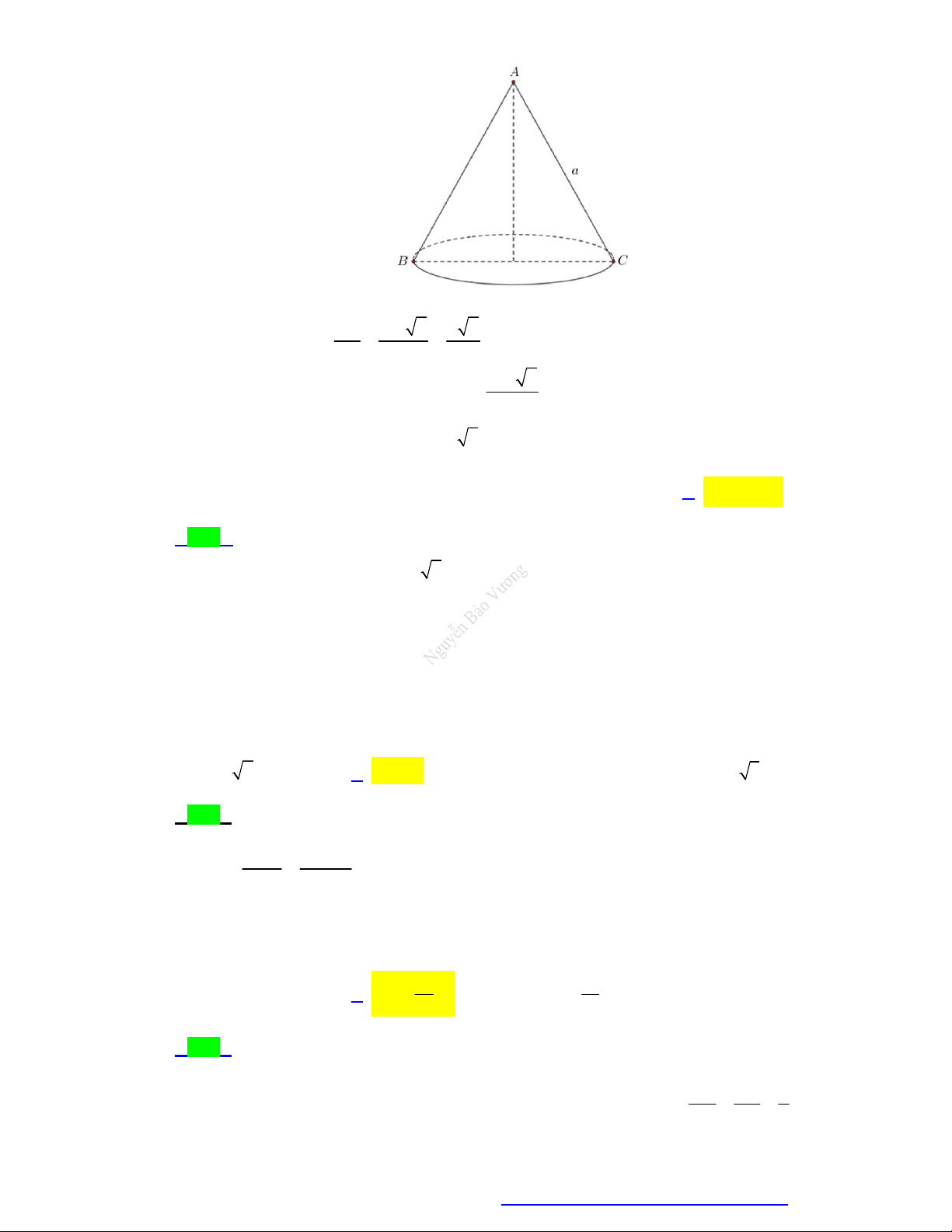
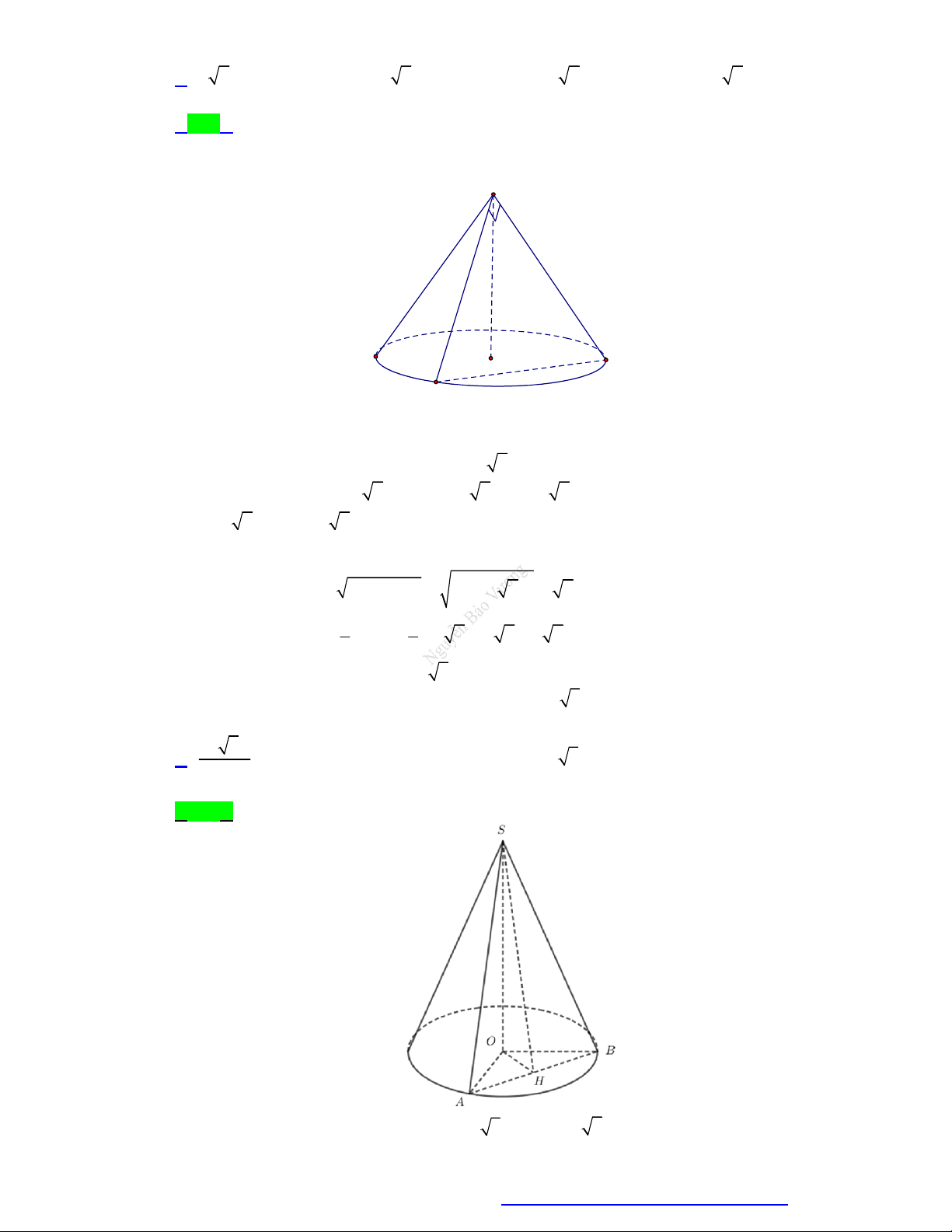
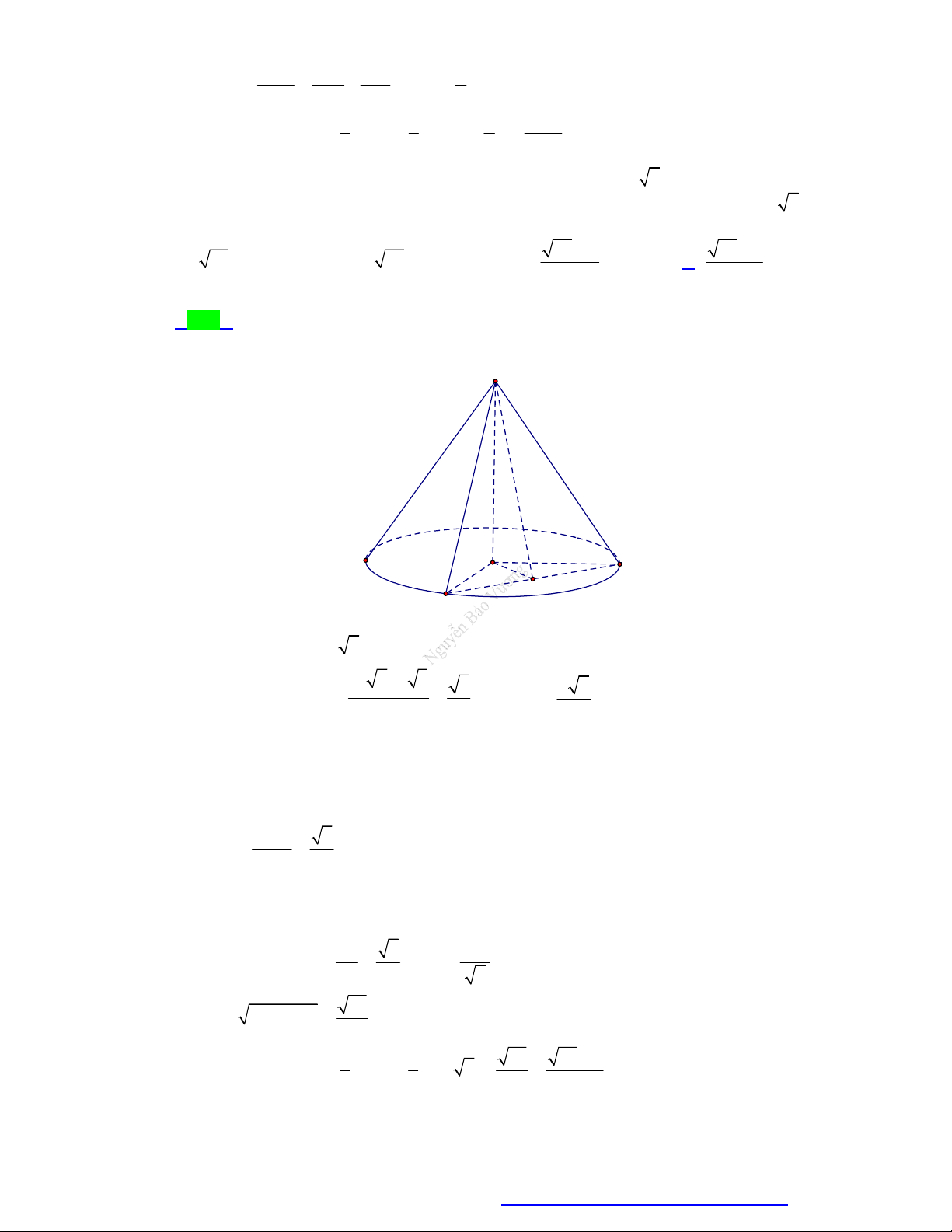
Các yếu tố mặt nón:
Một số công thức: S
Đường cao: h SO . ( SO cũng
Chu vi đáy: p  2 r .
được gọi là trục của hình nón). Diện tích đáy: 2 S   r . Bán kính đáy: đ
r OA OB OM . 1 1 l h Thể tích: 2 V  . h S  . h r . l l Đường sinh: đ 3 3
l SA SB SM .
(liên tưởng đến thể tích khối chóp). A B rS   rl O
Diện tích xung quanh: .
Góc ở đỉnh: ASB . xq M
Thiết diện qua trục: SAB cân
Diện tích toàn phần:
Hình thành: Quay  vuông tại S. 2
S S S   rl   r .
SOM quanh trục SO , ta được tp xq đ
Góc giữa đường sinh và mặt mặt nón như hình bên   
đáy: SAO SBO SMO . h SO với:  . r OMMẶT TRỤ
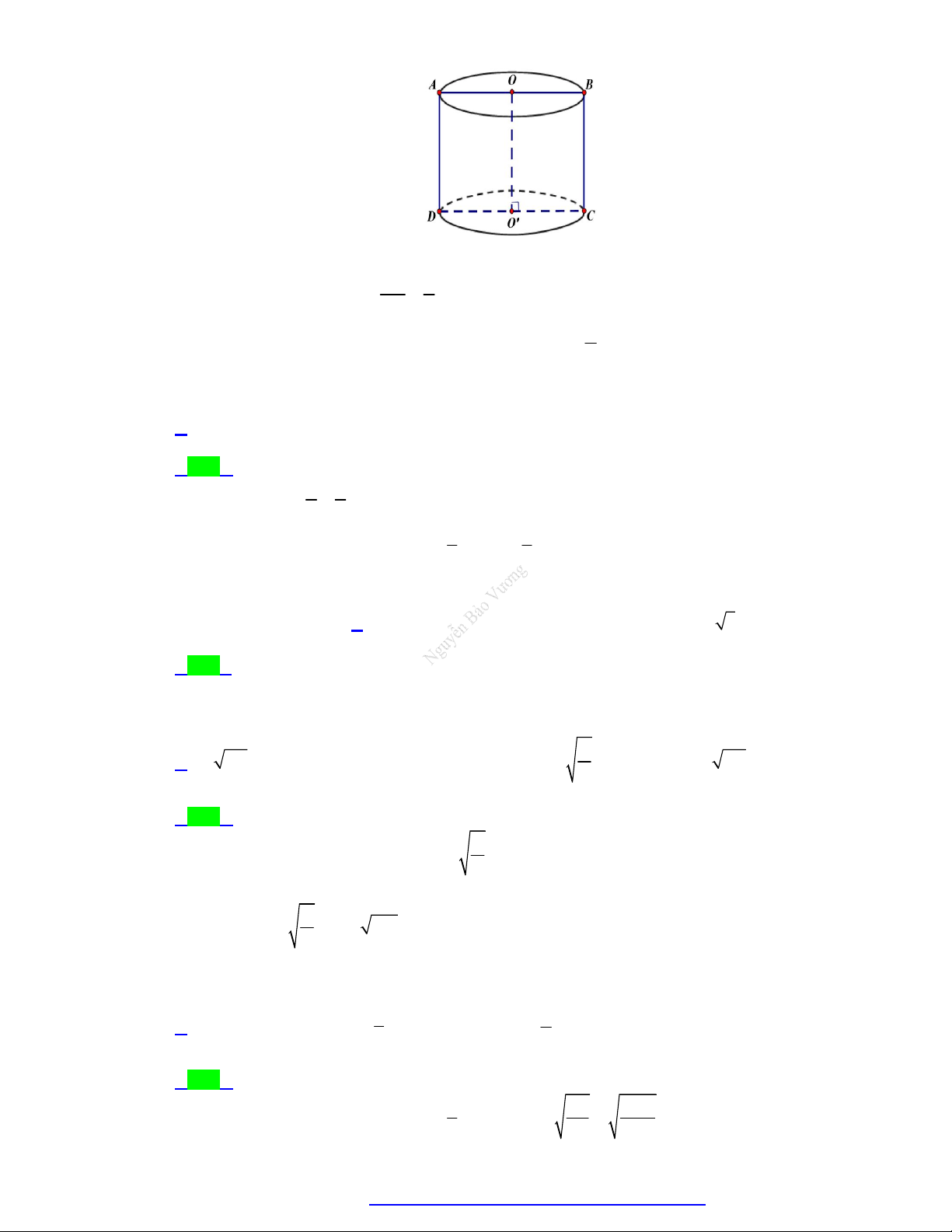
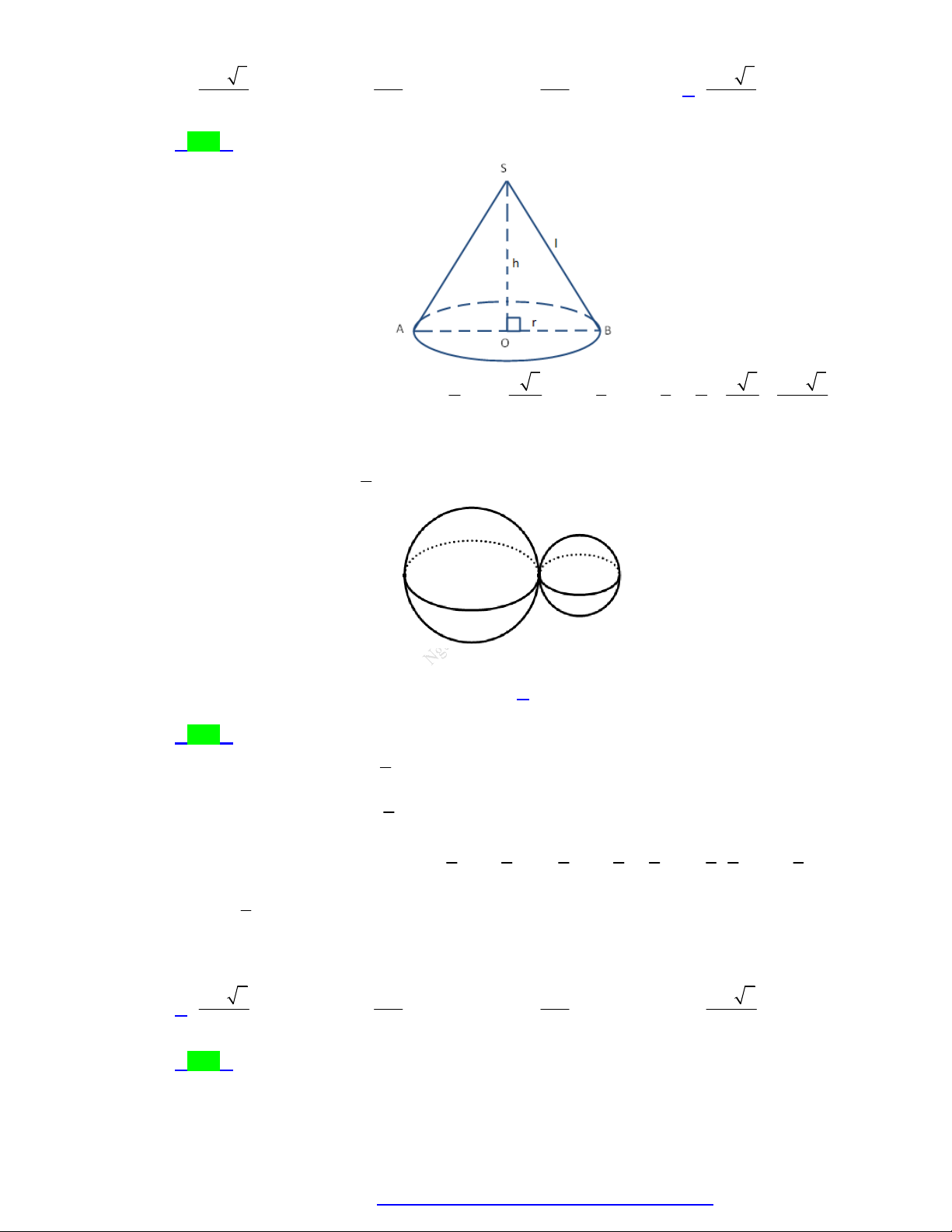
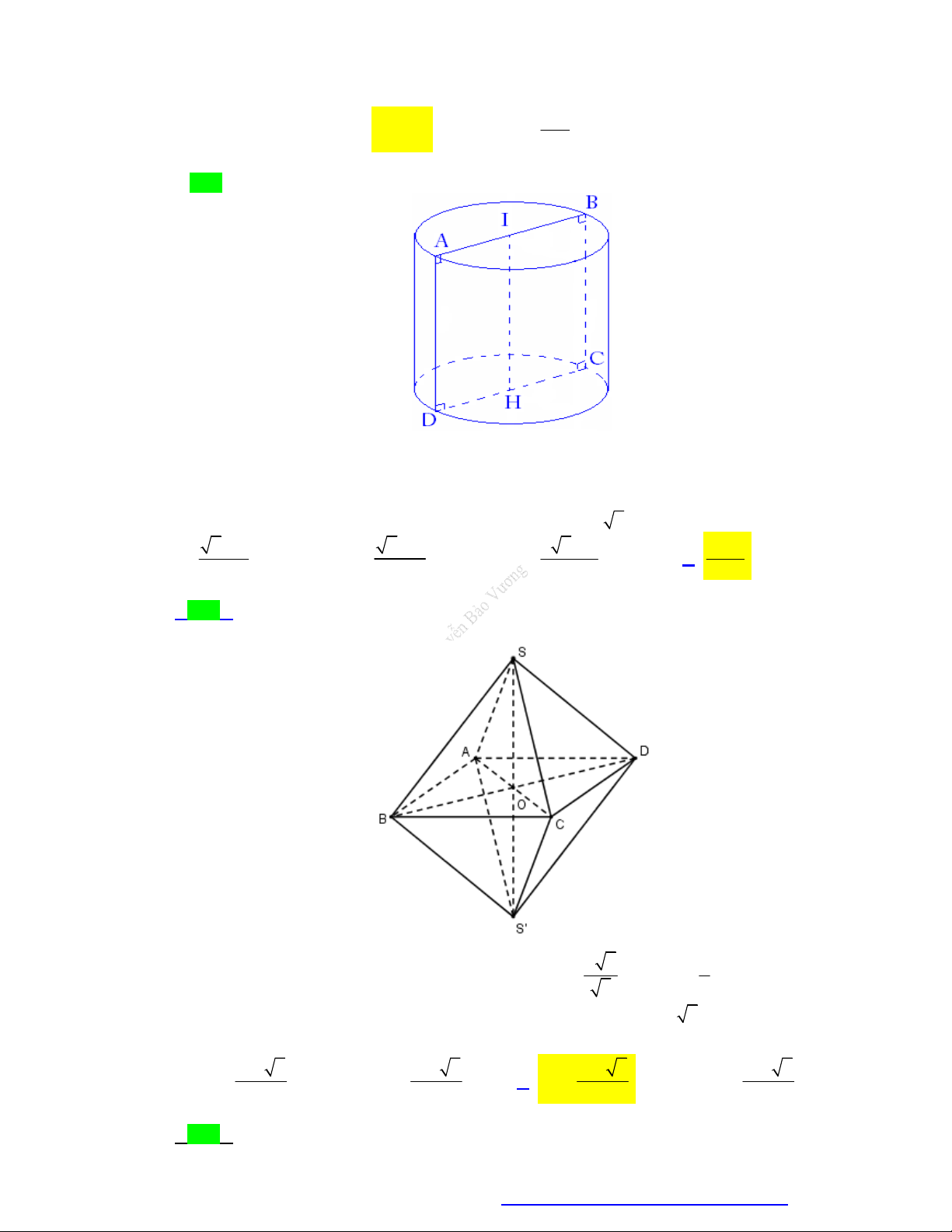
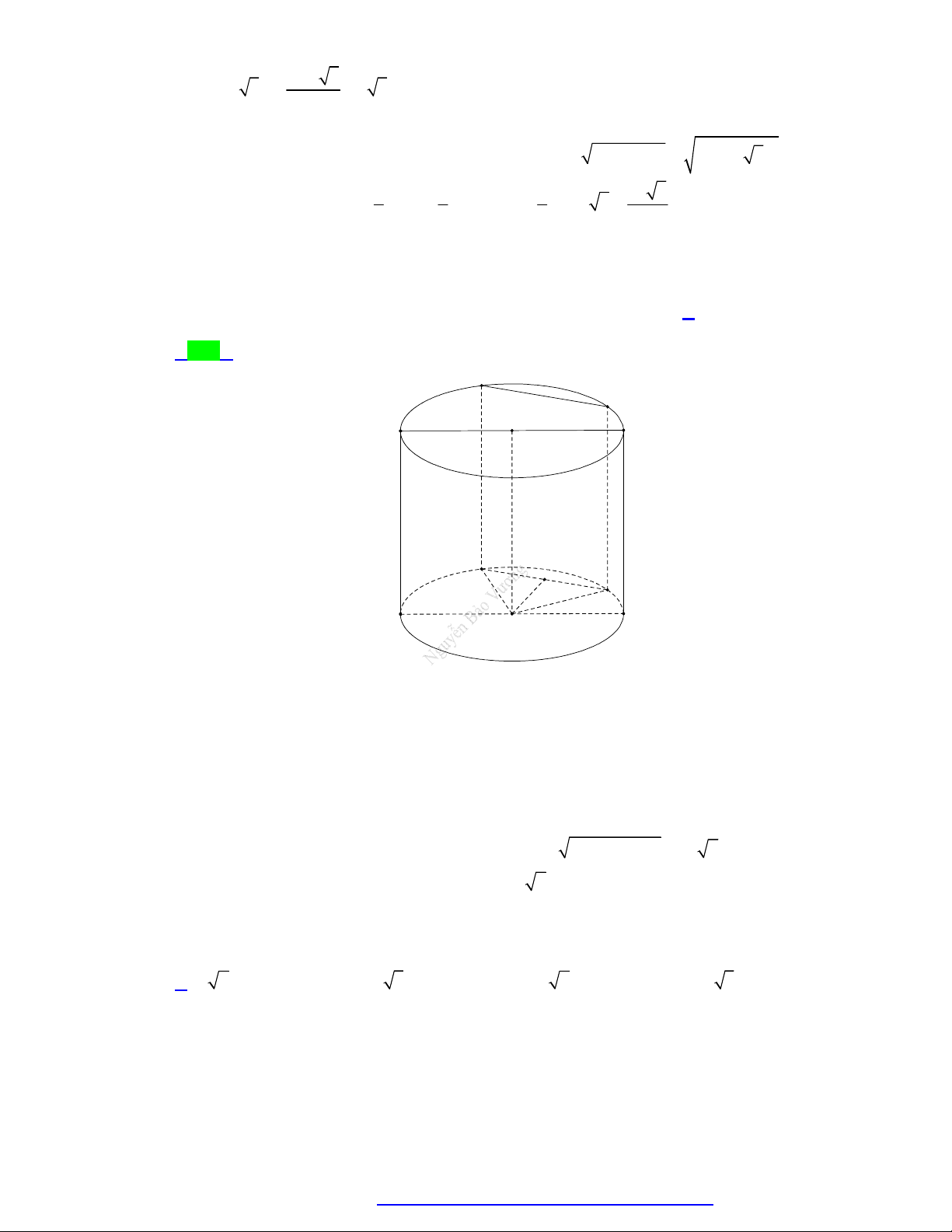
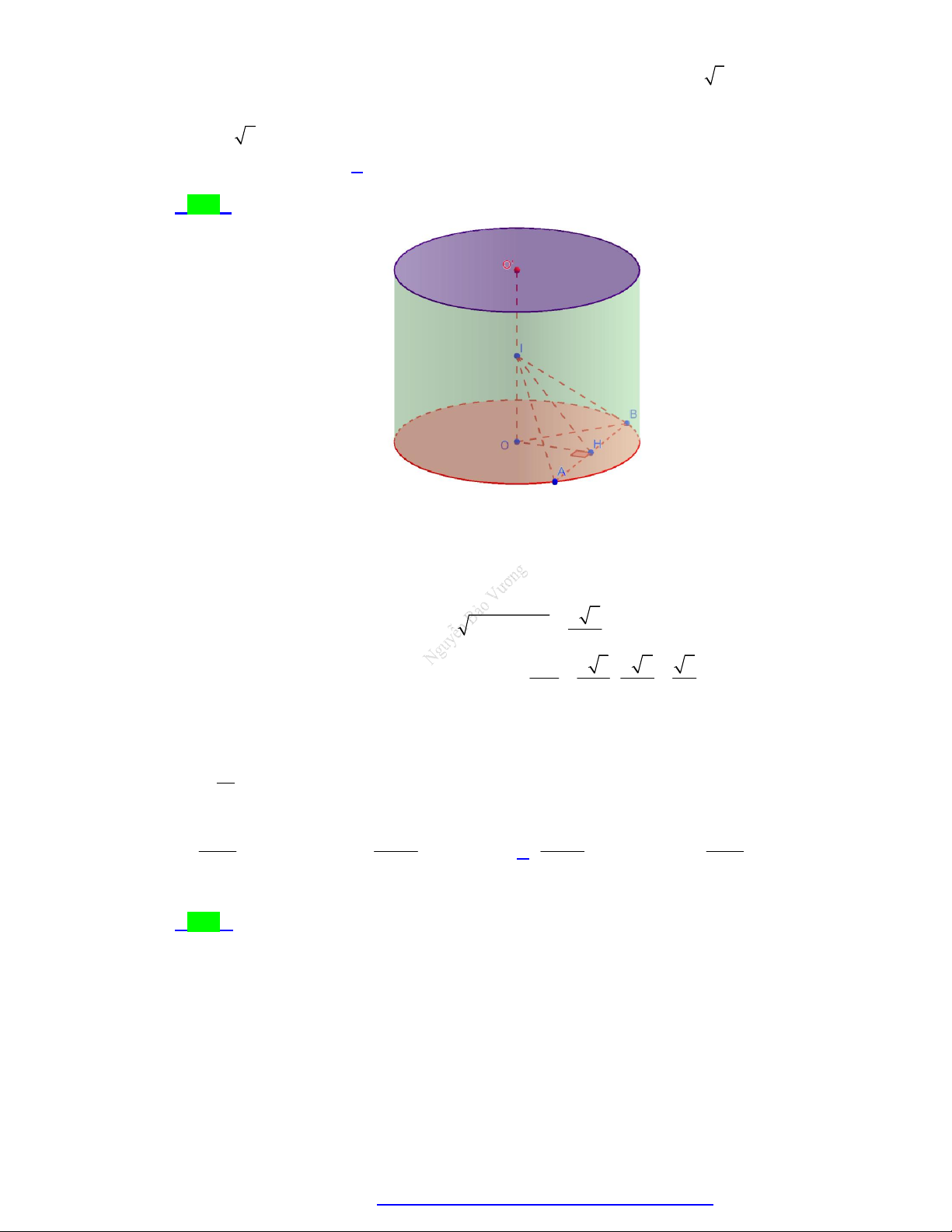
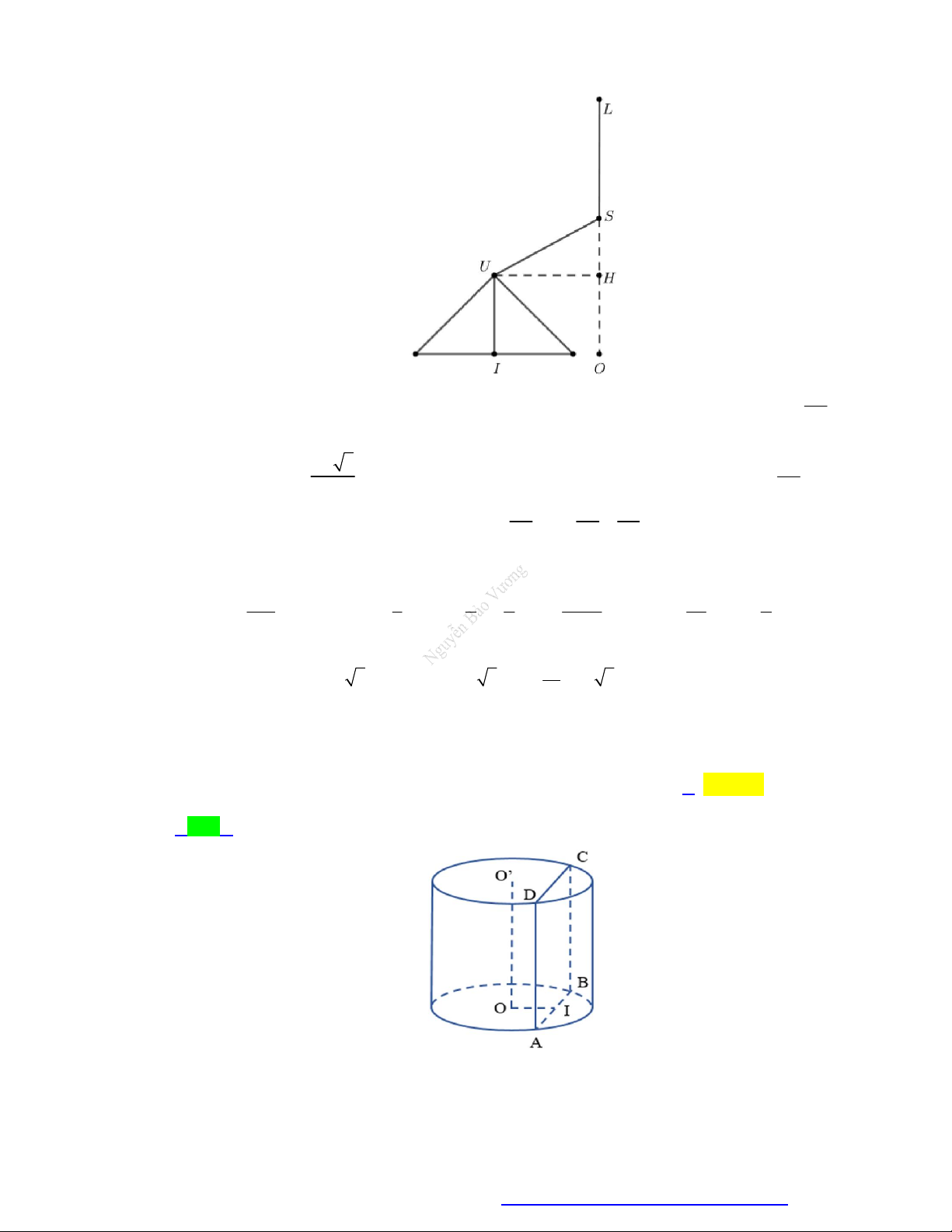
Các yếu tố mặt trụ:
Một số công thức:
Đường cao: h OO .
Chu vi đáy: p  2 r .
Đường sinh: l AD BC . Ta Diện tích đáy: 2 S   r . đ có: l h .   
Thể tích khối trụ: 2 V . h S . h r . Bán kính đáy: đ
r OA OB O C   O D  .
Diện tích xung quanh: S  2 r.h . xq
Trục (∆) là đường thẳng đi qua Diện tích toàn
hai điểm O, O . phần:
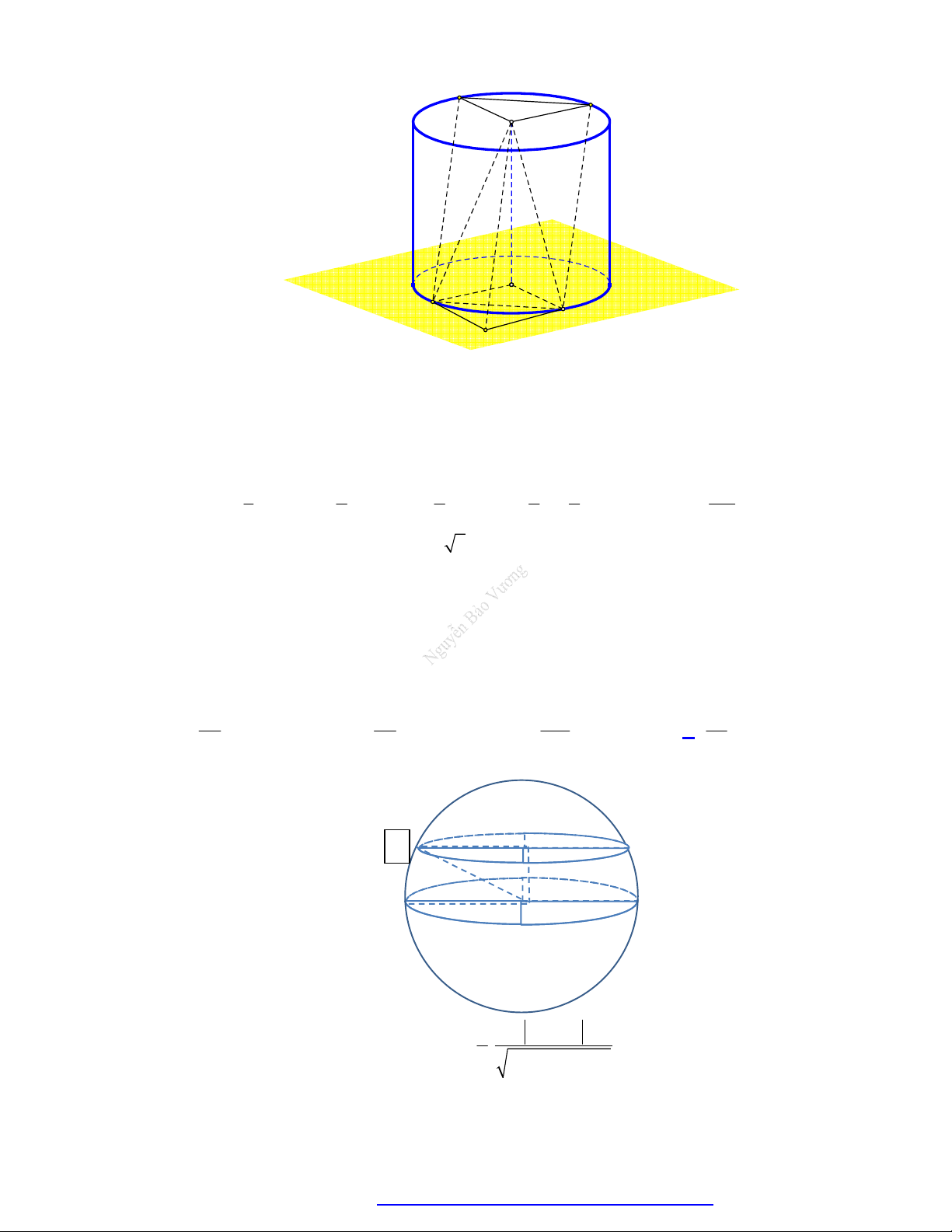
Hình thành: Quay hình chữ
Thiết diện qua trục: Là hình 2   
nhật ABCD quanh đường S S 2S 2 . r h 2 r . chữ nhật ABC . D tp xq đ
trung bình OO , ta có mặt trụ như hình bên.
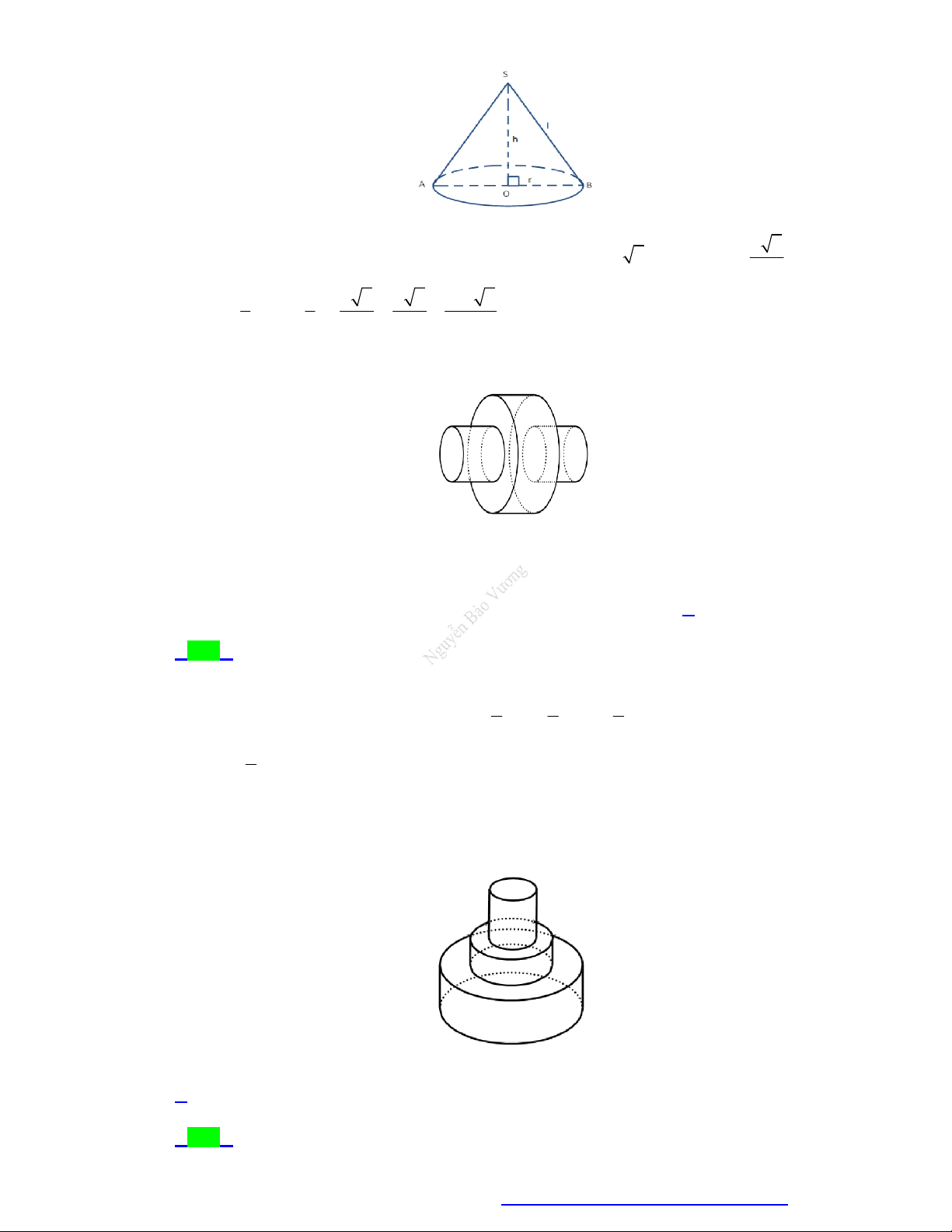
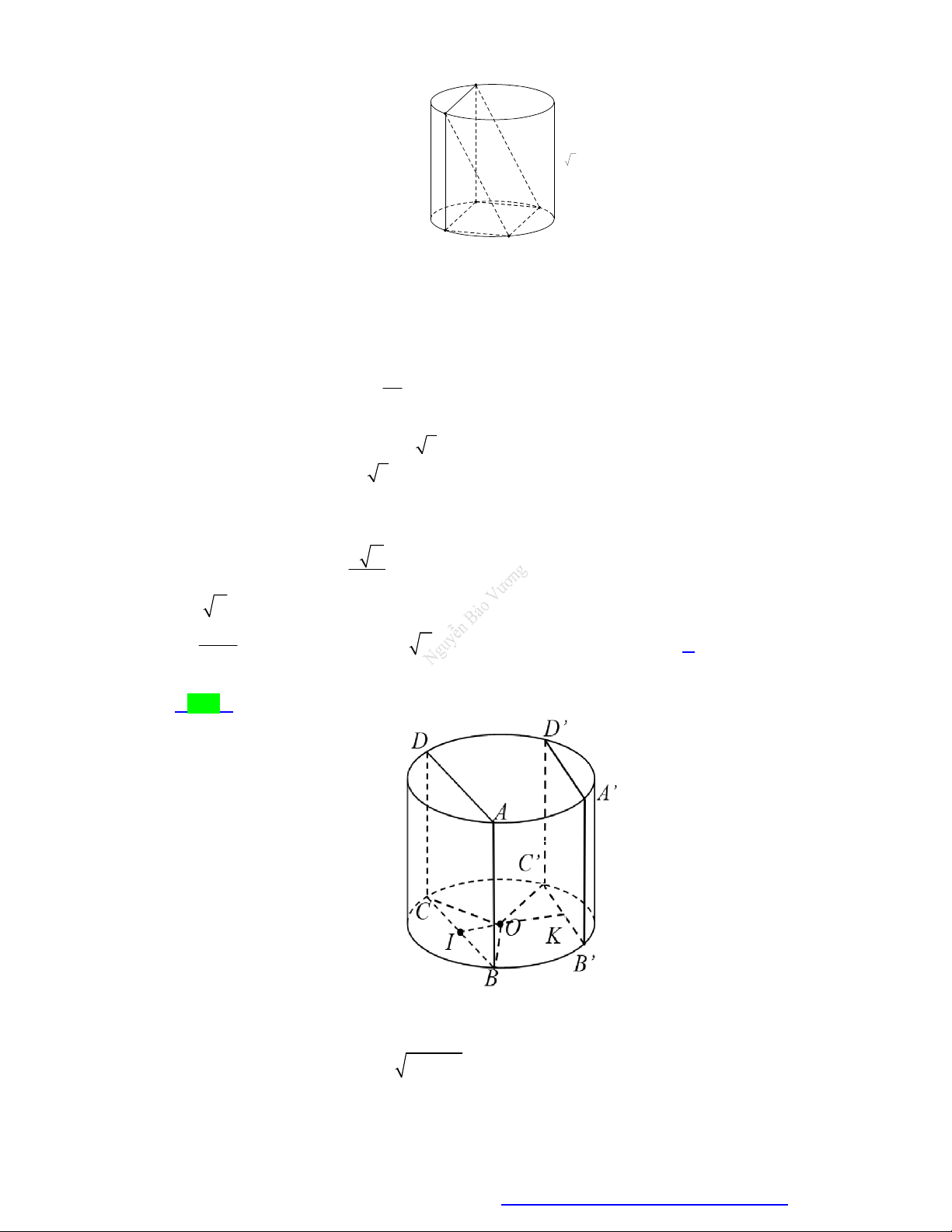
Mặt cầu ngoại tiếp đa diện MẶT CẦU
Một số công thức:
Mặt cầu nội tiếp đa diện
Tâm I , bán kính
R IA IB IM .
Đường kính AB  2R .
Thiết diện qua tâm mặt cầu: Là
đường tròn tâm I , bán kính R .
Diện tích mặt cầu: 2 S  4 R . Mặt cầu ngoại
Mặt cầu nội tiếp
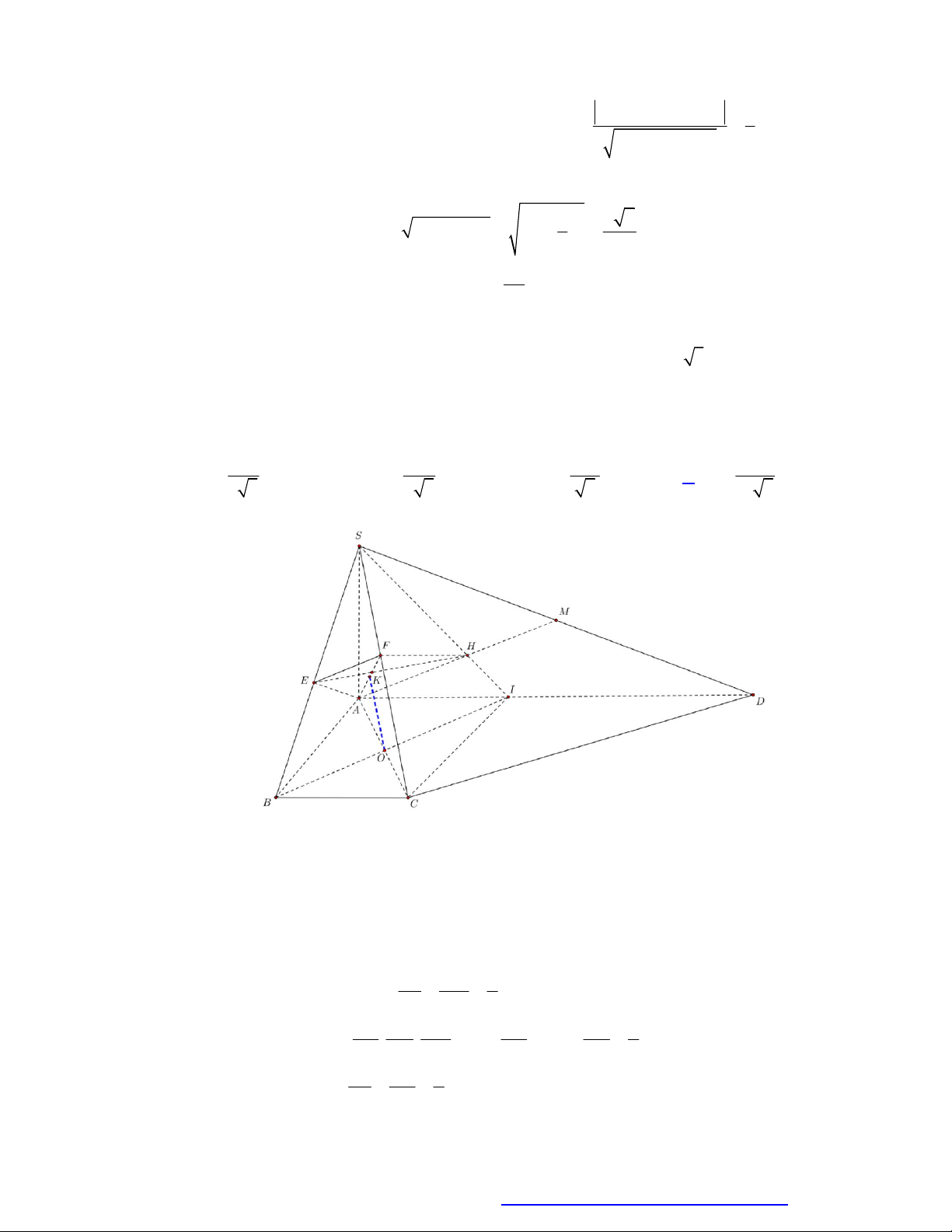
Hình thành: Quay đường 3
tiếp đa diện là mặt đa diện là mặt AB 4 R
tròn tâm I , bán kính R
Thể tích khối cầu: V  . cầu đi qua tất cả cầu tiếp xúc với 2 3 đỉnh của đa diện tất cả các mặt của
quanh trục AB , ta có mặt cầu đó. đa diện đó. như hình vẽ.
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489
CÂU HỎI MỨC ĐỘ NHẬN BIẾT Câu 1.
Diện tích xung quanh của hình nón có độ dài đường sinh l và bán kính đáy r bằng 1
A. 4 rl . B. 2 rl .
C. rl . D. rl . 3 Câu 2.
Cho khối nón có chiều cao h  3 và bán kính đáy r  4. Thể tích của khối nón đã cho bằng A. 16 . B. 48 . C. 36 . D. 4 . Câu 3.
Cho mặt cầu có bán kính R  2 . Diện tích của mặt cầu đã cho bằng 32 A. . B. 8 . C. 16 . D. 4 . 3 Câu 4.
Diện tích xung quanh của hình trụ có độ dài đường sinh l và bán kính đáy r bằng 1
A. 4 rl .
B. rl .
C. rl .
D. 2 rl . 3 Câu 5.
Công thức tính diện tích mặt cầu bán kính r là 4 3 A. 2 S  r . B. 3 S   r . C. 2 S   r . D. 2 S  4 r . 3 4 Câu 6.
Cho hình nón tròn xoay có bán kính đường tròn đáy r , chiều cao h và đường sinh l .
Kết luận nào sau đây sai? 1 A. 2 V   r h . B. 2
S   rl   r . C. 2 2 2
h r l . D. S   rl . 3 tp xq Câu 7.
Gọi l , h , r lần lượt là độ dài đường sinh, chiều cao và bán kính mặt đáy của hình nón. Diện tích xung quanh S của hình nón là xq 1 A. S   rh . B. S   rl . C. S  2 rl . D. 2 S   r h . xq xq xq xq 3 Câu 8.
Cho khối nón có bán kính đáy R  3 và chiều cao h  3 . Thể tích của khối nón đã cho bằng A. 3 . B. 9 . C. 3 3 . D.  3 . Câu 9.
Thể tích khối cầu bán kính 6 cm bằng A.   3 144 cm  B.   3 288 cm  C.   3 162 cm  D.   3 864 cm 
Câu 10. Tìm độ dài đường cao của hình trụ biết hình trụ có diện tích xung quanh là S và bán kính r ? xq S S xq xq 2 rr A. . B. . C. . D. . 2rr S S xq xq
Câu 11. Diện tích xung quanh của hình trụ có độ dài đường sinh l và bán kính r bằng 1 A. 4rl . B. 2rl . C. rl . D. rl . 3
Câu 12. Cho hình trụ (T ) có thiết diện qua trục của hình trụ là hình vuông có cạnh bằng a . Diện tích xung
quanh của hình trụ đã cho bằng 2  a 2 3 a A. 2 2 a . B. . C. 2  a . D. . 2 2
Câu 13. Cho khối nón có chiều cao h  6 và bán kính đáy bằng r . Biết bán kính đáy r bằng một nửa
chiều cao h . Thể tích của khối nón đã cho bằng A. 18 . B. 54 . C. 36 . D. 12 .
Câu 14. Diện tích của một mặt cầu bằng   2 16
cm  . Bán kính của mặt cầu đó là A. 2  cm . B. 2 cm . C. 4 cm . D. 2 3 cm .
Câu 15. Diện tích xung quanh của hình trụ có diện tích một đáy là S và độ dài đường sinh l bằng?
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
A. 2l S . B. 2Sl . C. 2l .
D. l S . S
Câu 16. Cho khối nón có chiều cao h  6 và bán kính đáy bằng r . Biết thể tích của khối nón đã cho
V  8 . Tính bán kính đáy. 1 4 A. r  2 . B. . C. . D. 4 . 3 3
Câu 17. Thể tích khối cầu có đường kính 2a bằng 3 4 a 3 32 a A. . B. 3 4 a . C. . D. 2 4.a . 3 3
Câu 18. Cho hình trụ có độ dài đường sinh l và bán kính r . Nếu độ dài đường sinh khối trụ tăng lên 3 lần,
diện tích đáy không đổi thì thể tích của khối trụ sẽ tăng lên 1 A. 3 lần. B. lần. C. 9 lần. D. 27 lần. 3
Câu 19. Diện tích toàn phần của hình nón có độ dài đường sinh l và đường kính đáy 2r bằng 1 A. rl . B. 2
2 rl  4 r . C. 2
rl   r . D. rl . 3
Câu 20. Bán kính r của khối cầu có thể tích V    3 36 cm  là
A. r  3cm . B. r  27 cm . C. 3 r  48 cm . D. 3 r  9 cm .
Câu 21. Tìm bán kính r của hình nón biết hình nón có diện tích xung quanh là S và độ dài đường sinh xq l ? S Sl 2l xq xq A. . B. . C. . D. . l 2l S S xq xq
Câu 22. Trong không gian cho tam giác vuông tại A , AB a và AC a 3 . Tính độ dài đường sinh của
hình nón có được khi quay tam giác ABC xung quanh trục AB .
A. l a 2 .
B. l  2a .
C. l a .
D. l a 3 .
Câu 23. Diện tích xung quanh của hình trụ có bán kính đáy R  2 và đường sinh l  6 bằng A. 24 . B. 12 . C. 4 . D. 8 .
Câu 24. Cho hình nón có bán kính đáy bằng 1, góc giữa đường sinh và trục của hình nón bằng 0 30 . Diện
tích xung quanh của hình nón đã cho bằng 4 3 2 3 A.  . B. 3 . C.  . D. 2 . 3 3
Câu 25. Cho khối trụ có chiều cao bằng bán kính đáy và diện tích thiết diện qua trục của khối trụ bằng 16.
Thể tích khối trụ đã cho bằng 64 16 2 A. 64 . B. . C. 16 2 . D. . 3 3
Câu 26. Hình trụ có thiết diện qua trục là một hình vuông có cạnh bằng 20cm. Thể tích của khối trụ tương ứng bằng: A. 3 800 cm . B. 3 8000 cm . C. 3 400 cm . D. 3 2000 cm .
CÂU HỎI MỨC ĐỘ THÔNG HIỂU
Câu 27. Trong không gian cho hình chữ nhật ABCD , AB a, AC  2a . Khi quay hình chữ nhật ABCD
quanh cạnh AD thì đường gấp khúc ABCD tạo thành một hình trụ. Diện tích xung quanh của hình trụ đó bằng
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489 2 2 a  2 a  A. 2 4 a  . B. . C. . D. 2 2 3 a  . 3 3
Câu 28. Trong không gian, cho tam giác ABC vuông tại A , AB a và AC  2a . Khi quay tam giác
ABC quanh cạnh góc vuông AB thì đường gấp khúc ACB tạo thành một hình nón. Diện tích
xung quanh hình nón đó bằng A. 2 5 a . B. 2 5 a . C. 2 2 5a . D. 2 10 a .
Câu 29. Cho hình trụ có bán kính đáy bằng 3 . Biết rằng khi cắt hình trụ đã cho bởi một mặt phẳng qua
trục, thiết diện thu được là một hình vuông. Diện tích xung quanh của hình trụ đã cho bằng A. 18 . B. 36 . C. 54 . D. 27 .
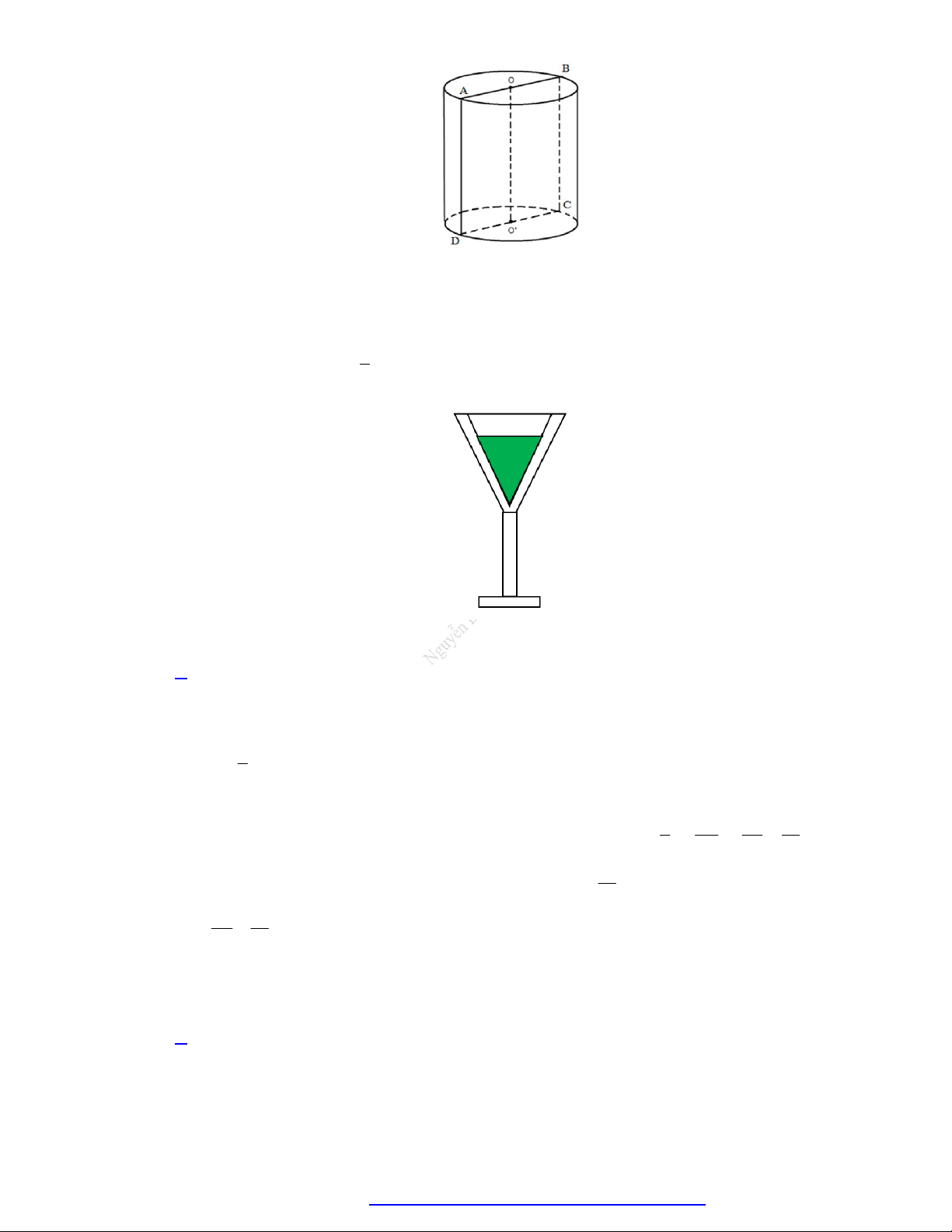
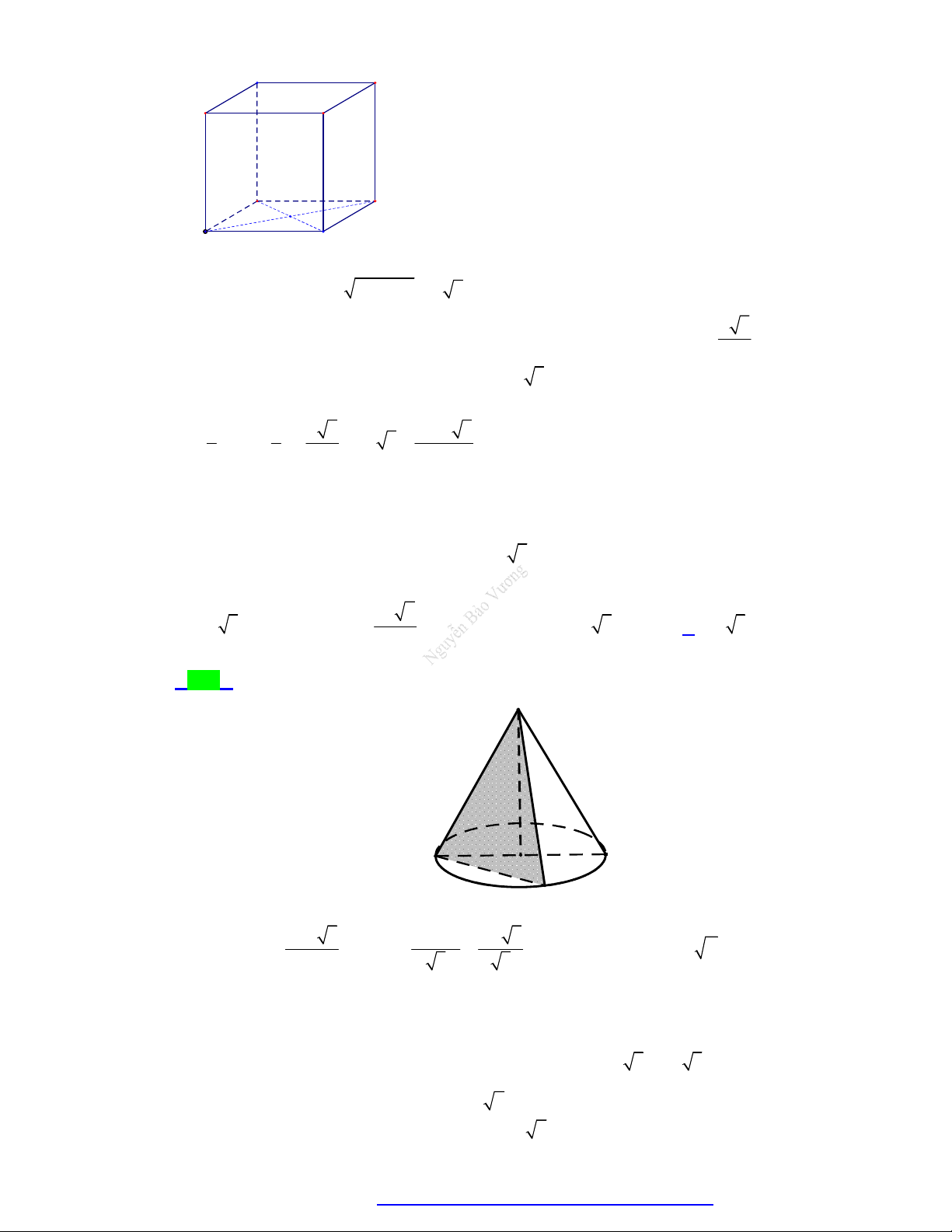
Câu 30. Cho một chiếc cốc hình nón chứa đầy trà như hình vẽ. Người X uống một phần trà sao cho chiều 1 cao của nó giảm đi
so với chiều cao của trà trong cốc. Người Y uống phần trà còn lại trong 3
cốc. Khi đó khẳng định nào đúng.
A. Người X uống lượng trà bằng 5,75 lần lượng trà của người Y uống.
B. Hai người X và Y uống lượng trà bằng nhau.
C. Người X uống lượng trà bằng 2,375 lần lượng trà của người Y uống.
D. Người X uống lượng trà bằng một nửa lượng trà của người Y uống.
Câu 31. Cắt hình trụ T  bằng một mặt phẳng song song với trục và cách trục một khoảng bằng 2cm
được thiết diện là một hình vuông có diện tích bằng 2
16cm . Thể tích của T  là A.   3 32 cm  . B.   3 16 cm  . C.   3 64 cm  . D.   3 8 cm  .
Câu 32. Cho hai tấm tôn hình chữ nhật đều có kích thước 1, 5m  8m . Tấm tôn thứ nhất được chế tạo thành
một hình hộp chữ nhật không đáy, không nắp, có thiết diện ngang là một hình vuông (mặt phẳng
vuông góc với đường cao của hình hộp và cắt các mặt bên của hình hộp theo các đoạn giao tuyến
tạo thành một hình vuông) và có chiều cao 1, 5m ; còn tấm tôn thứ hai được chế tạo thành một hình
trụ không đáy, không nắp và cũng có chiều cao 1, 5m . Gọi V , V theo thứ tự là thể tích của khối 1 2 V
hộp chữ nhật và thể tích của khối trụ. Tính tỉ số 1 . V2 V VVVA. 1   . B. 1  . C. 1  . D. 1  . V V 4 V 2 V 3 2 2 2 2
Câu 33. Một hình trụ có bán kính đáy r  5a và khoảng cách giữa hai đáy bằng 7a . Cắt khối trụ bởi một
mặt phẳng song song với trục và cách trục một khoảng bằng 3a . Diện tích của thiết diện được tạo nên bằng A. 2 56a . B. 2 35a . C. 2 21a . D. 2 70a .
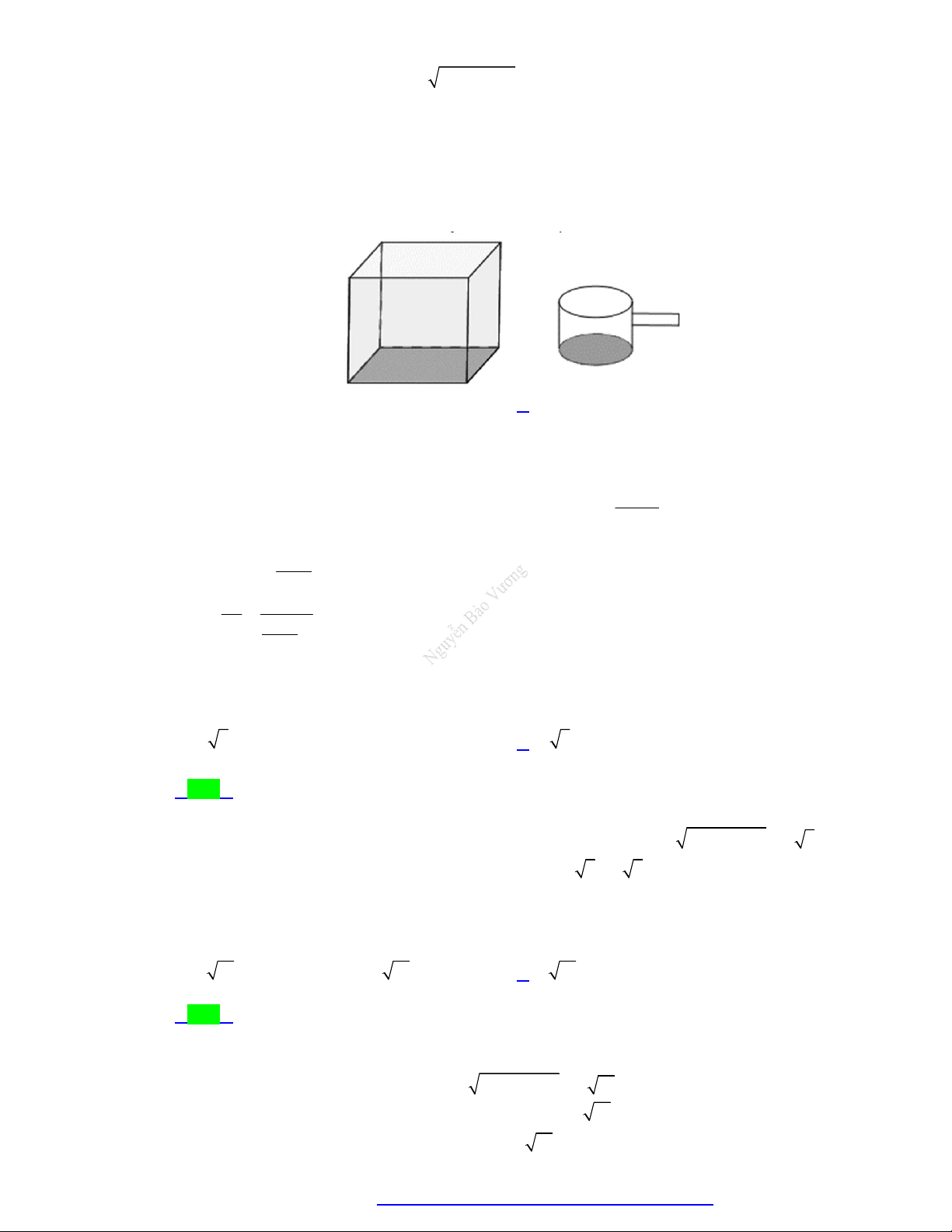
Câu 34. Cho một cái bể nước hình hộp chữ nhật có ba kích thước 2 m ,3m ,2 m lần lượt là chiều dài, chiều
rộng, chiều cao của lòng trong đựng nước của bể. Hàng ngày nước ở trong bể được lấy ra bởi một
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
cái gáo hình trụ có chiều cao là 5cm và bán kính đường tròn đáy là 4cm . Trung bình một ngày
được múc ra 170 gáo nước để sử dụng (Biết mỗi lần múc là múc đầy gáo). Hỏi sau bao nhiều
ngày thì bể hết nước biết rằng ban đầu bể đầy nước? . A. 280 ngày. B. 282 ngày. C. 281 ngày. D. 283 ngày.
Câu 35. Trong không gian, cho hình chữ nhật ABCD , AB  2a và AC  3a . Khi quay hình chữ nhật
ABCD quanh cạnh AB thì đường gấp khúc BCDA tạo thành một hình trụ. Diện tích xung quanh
của hình trụ đó bằng A. 2 6 5 a . B. 2 12 a . C. 2 4 5 a . D. 2 20 a .
Câu 36. Trong không gian, cho tam giác ABC vuông tại A , AB  2a và AC  3a . Khi quay tam giác
ABC quanh cạnh góc vuông AB thì đường gấp khúc ACB tạo thành một hình nón. Diện tích
toàn phần của hình nón đó bằng A. 2 3 13 a . B. 2 2
3 13 a  4 a . C. 2 2
3 13 a  9 a . D. 2 42 a .
Câu 37. Cho hình trụ (T ) có thiết diện qua trục của hình trụ là một hình chữ nhật có diện tích bằng 48 và
chu vi bằng 28 . Biết chiều dài của hình chữ nhật lớn hơn đường kính mặt đáy của hình trụ T  .
Diện tích xung quanh của hình trụ đã cho bằng A. 96 . B. 48 . C. 24 . D. 32 .
Câu 38. Cho hình trụ có thiết diện qua trục là một hình vuông. Thiết diện của hình trụ tạo bởi mặt phẳng
song song và cách trục một khoảng bằng a có diện tích bằng 2 8a
3 . Thể tích của khối trụ là 3 16 a A. 2 16 a . B. 3 16a . C. 3 32 a . D. . 3
Câu 39. Cho hình nón có bán kính đáy r  3 . Biết rằng khi cắt khối nón đó bằng một mặt phẳng qua trục
của nó, ta được thiết diện là một tam giác đều. Diện tích xung quanh của hình nón bằng A. 6 3 . B. 36 . C. 18 . D. 9 .
Câu 40. Trong không gian, cho tam giác ABC vuông tại A , AB  3a và BC  5a . Khi quay tam giác
ABC quanh cạnh góc vuông AB thì đường gấp khúc ACB tạo thành một hình nón. Diện tích
xung quanh hình nón đó bằng A. 2 20a . B. 2 15 a . C. 2 20 a . D. 2 80 a .
Câu 41. Thiết diện qua trục của một hình nón là một tam giác vuông cân có cạnh góc vuông bằng a . Diện
tích xung quanh của hình nón bằng 2  a 2 2  a A. 2  a 2 . B. . C. 2  a . D. . 2 2
Câu 42. Cho khối nón có độ dài đường sinh bằng 5a và đường cao bằng 4a . Thể tích khối nón bằng 3 80 a A. . B. 3 15 a . C. 3 12a . D. 3 36a . 3
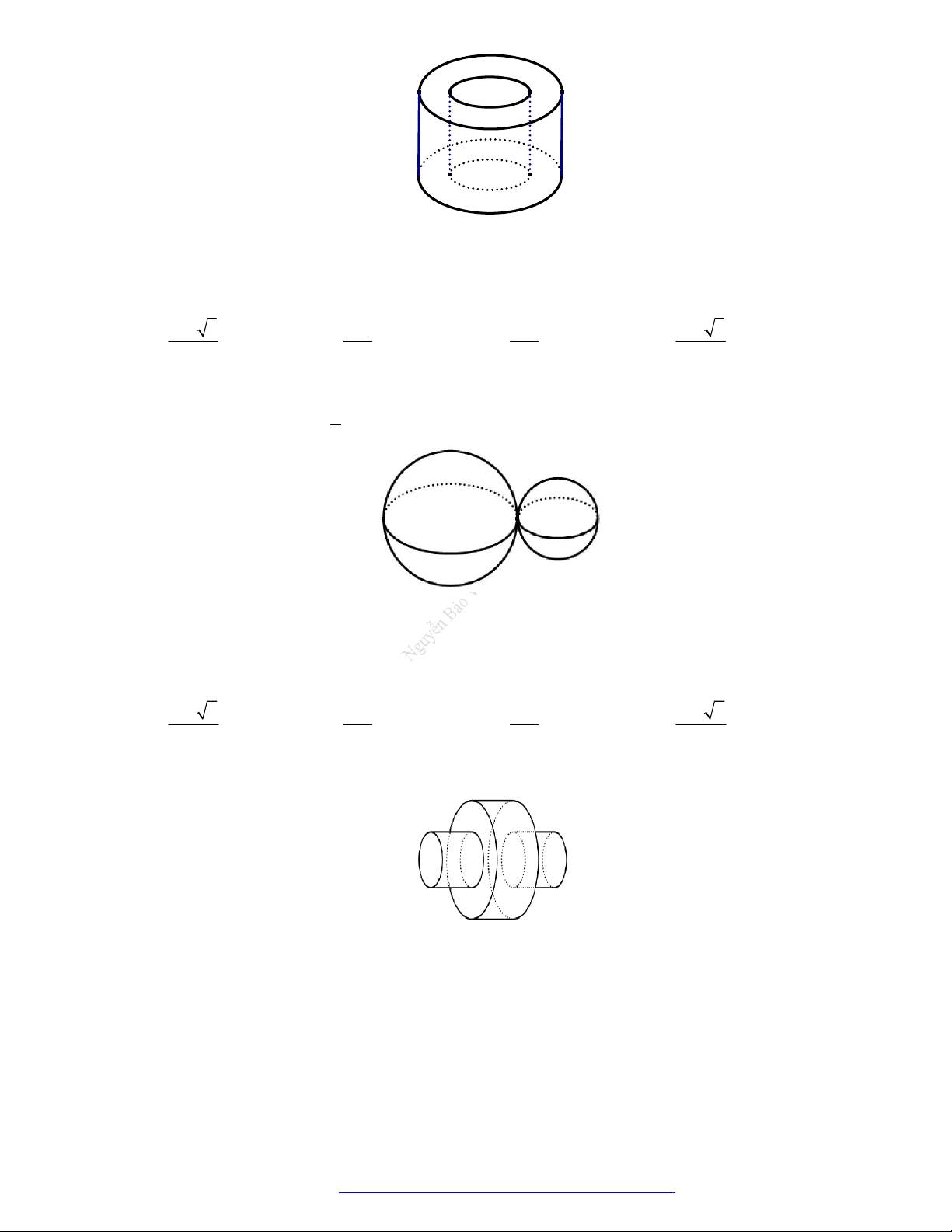
Câu 43. Một chi tiết máy là phần còn lại của một khối trụ có bán kính đáy r sau khi đã đục bỏ phần bên r
trong là một khối trụ có bán kính đáy (tham khảo hình vẽ). 2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489
Biết thể tích khối trụ nhỏ bị đục bỏ bằng  3
20 cm  . Thể tích của khối chi tiết máy đó là A.  3 40 cm  . B.  3 60 cm  . C.  3 80 cm  . D.  3 70 cm  .
Câu 44. Cho khối nón có thiết diện qua trục là tam giác đều SAB cạnh a . Thể tích khối nón bằng 3  a 3 3  a 3  a 3  a 3 A. . B. . C. . D. . 8 24 12 24
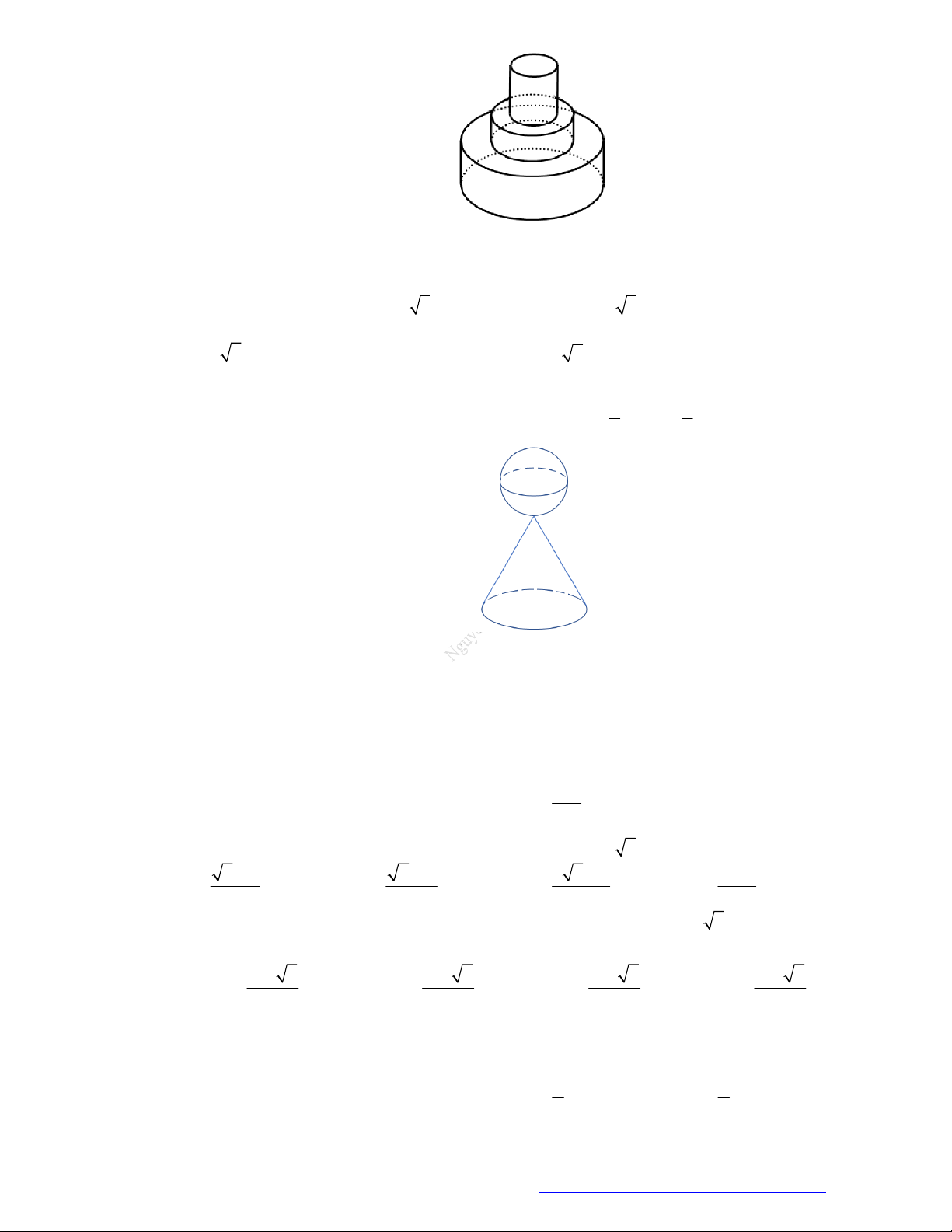
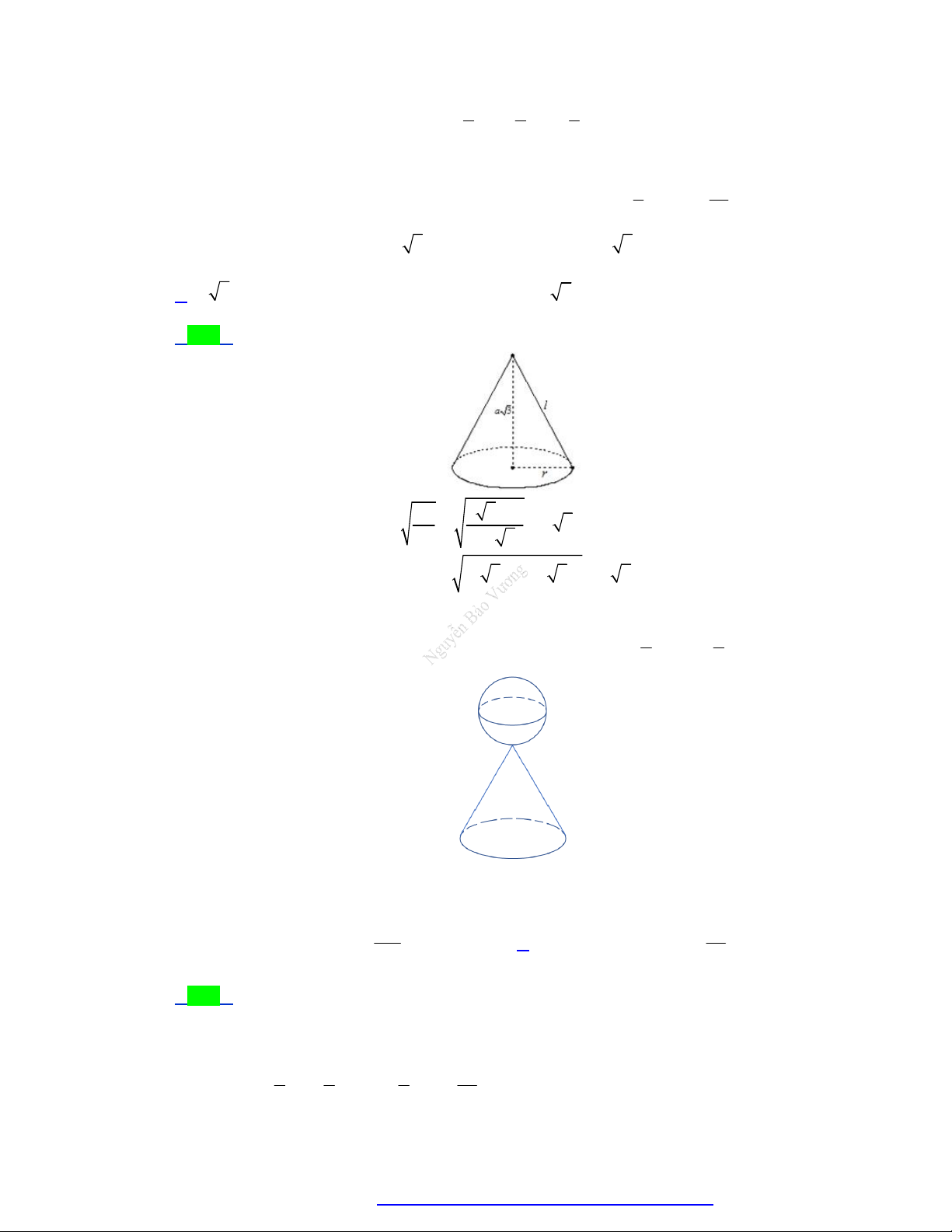
Câu 45. Một khối đồ chơi gồm hai khối cầu  H , H tiếp xúc với nhau, lần lượt có bán kính tương 1   2  1
ứng là r , r thỏa mãn r
r (tham khảo hình vẽ). 1 2 2 1 2
Biết rằng thể tích của toàn bộ khối đồ chơi bằng 3
180cm . Thể tích của khối cầu  H bằng 1  A. 3 90 cm B. 3 120 cm C. 3 160 cm D. 3 135 cm
Câu 46. Cho khối nón có thiết diện qua trục là tam giác SAB vuông tại S với cạnh SA a . Thể tích khối nón bằng 3  a 2 3  a 3  a 3  a 2 A. . B. . C. . D. . 12 3 12 4
Câu 47. Một chi tiết máy gồm 3 khối trụ có cùng chiều cao h gắn với nhau (như hình vẽ).
Khối trụ lớn có bán kính đáy r lớn gấp đôi bán kính đáy của hai khối trụ nhỏ (hai khối trụ nhỏ
bằng nhau). Biết thể tích của cả khối chi tiết máy đó bằng 3
90 cm . Tính thể tích của khối trụ lớn ở giữa. A. 3 30 cm . B. 3 45cm . C. 3 70 cm . D. 3 60 cm .
Câu 48. Một chiếc bánh sinh nhật gồm ba khối trụ  H , H , H xếp chồng lên nhau, lần lượt có bán 1   2   3 
kính đáy và chiều cao tương ứng là r , h ; r , h ; r , h thỏa mãn r  2r  3r , h  2h h (tham 1 1 2 2 3 3 1 2 3 1 2 3 khảo hình vẽ).
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Biết rằng thể tích của khối  H bằng 3
80cm . Thể tích của toàn bộ chiếc bánh sinh nhật bằng 3  A. 3 890 cm . B. 3 980 cm . C. 3 900 cm . D. 3 800 cm .
Câu 49. Cho khối nón có thể tích bằng 3
3 a và đường cao bằng a 3 . Độ dài đường sinh của khối nón đã cho bằng A. a 6 . B. 2a . C. a 2 . D. a .
Câu 50. Một khối đồ chơi gồm một hình cầu  H bán kính R và một hình nón  H xếp chồng lên nhau, 2  1  1 3
lần lượt có bán kính đáy và đường sinh là r, l thỏa mãn r l và l  . R (hình vẽ). 2 2
Biết tổng diện tích mặt cầu  H và diện tích toàn phần của hình nón  H là 3 91cm . Tính diện 2  1 
tích của khối cầu  H . 1  104 26 A. 3 16cm . B. 3 cm . C. 3 64cm . D. 3 cm . 5 5
Câu 51. Cho hình trụ có bán kính đáy bằng 1 cm . Một mặt phẳng qua trục của hình trụ và cắt hình trụ theo
thiết diện là hình vuông. Tính thể tích của khối trụ đã cho. 16 A. 3 8 cm . B. 3 2 cm . C. 3 cm . D. 3 16 cm . 3
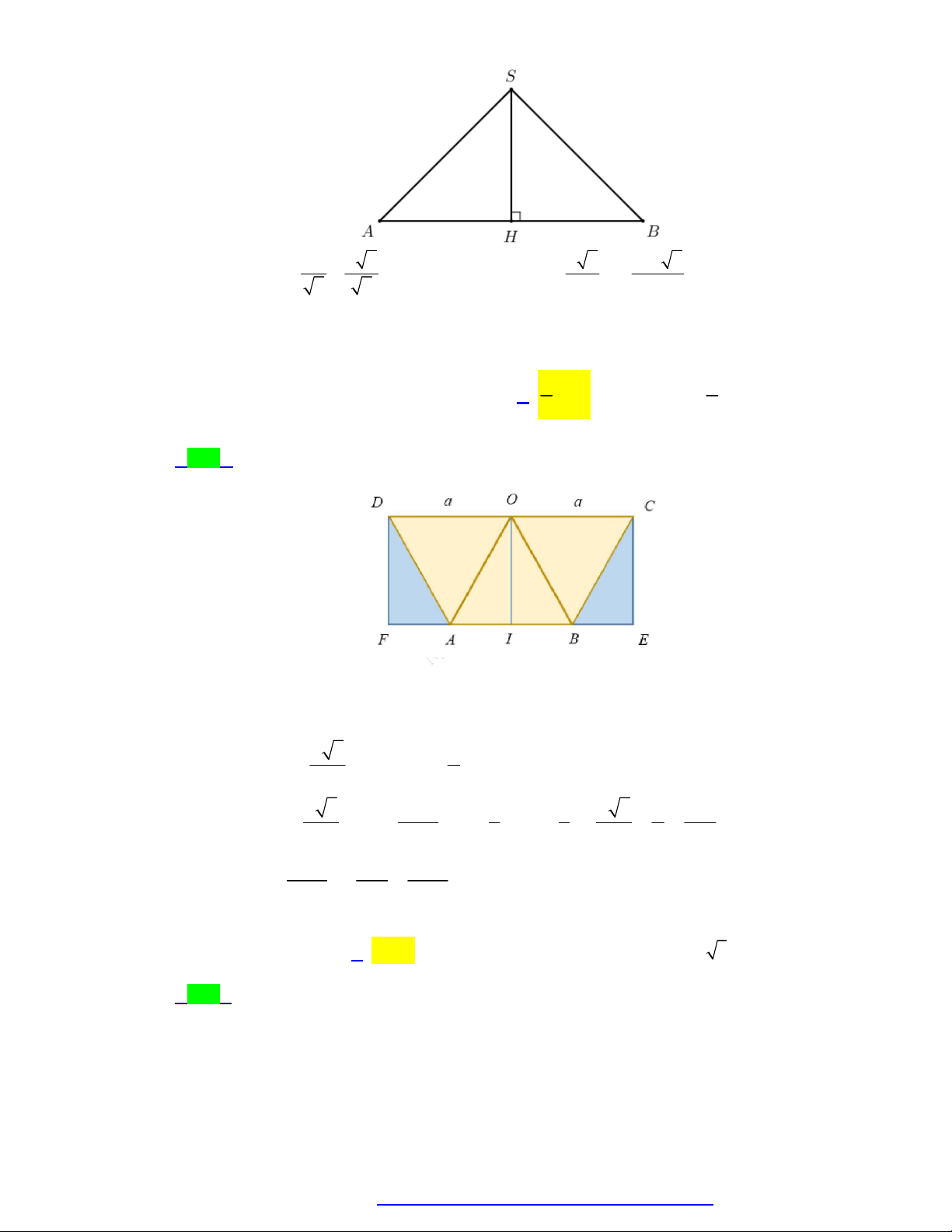
Câu 52. Thể tích của khối cầu ngoại tiếp bát diện đều có cạnh bằng a 2 là: 3 2 a 3 2 a 3 4 2 a 3 4 a A. . B. . C. . D. . 6 3 3 3
Câu 53. Cho hình nón có thiết diện qua trục là tam giác vuông có cạnh huyền a 2 . Tính diện tích xung
quanh S của hình nón đó xq 2  a 2 2  a 2 2  a 2 2  a 2 A. s  . B. s  . C. s  . D. s  . xq 6 xq 3 xq 2 xq 3
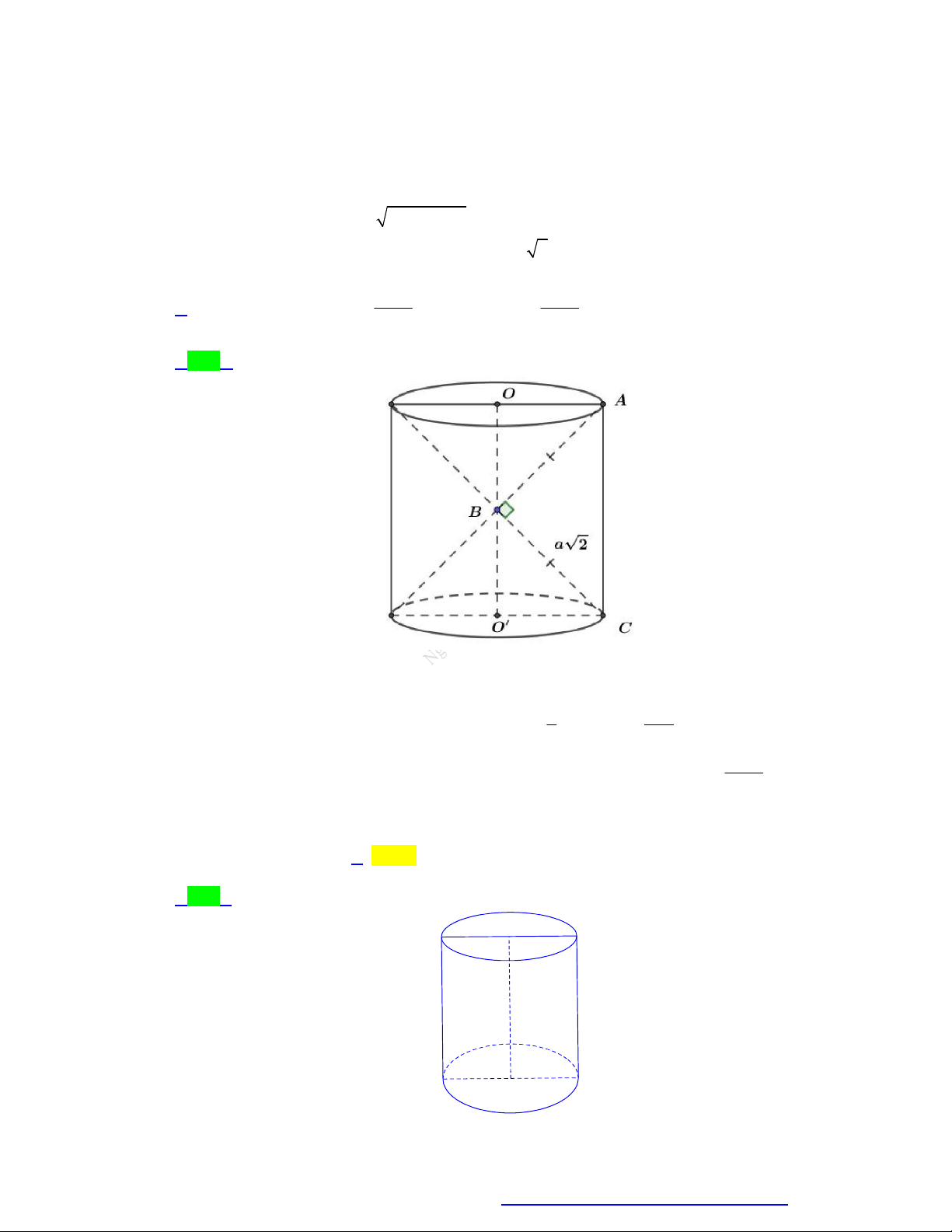
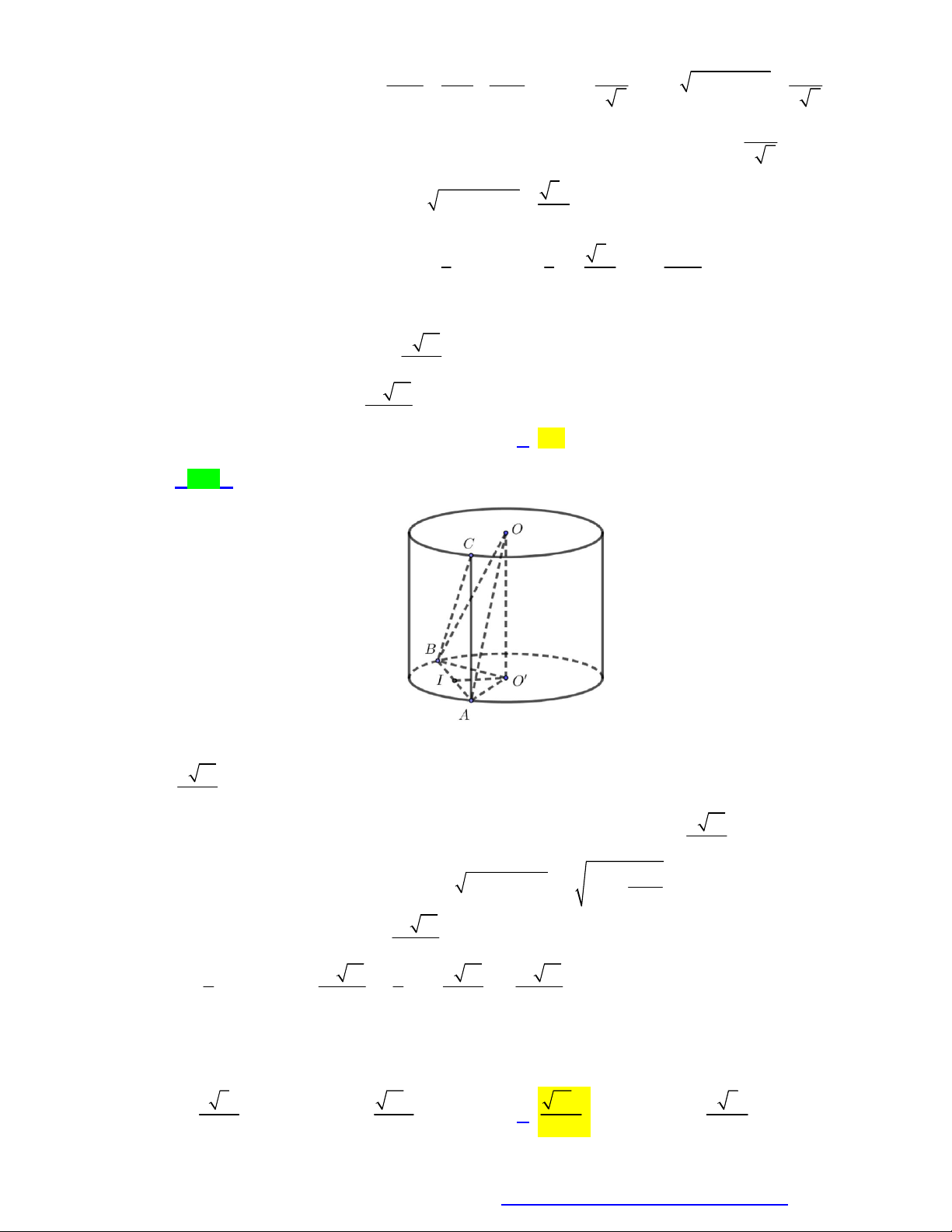
Câu 54. Trong không gian cho tứ giác ABCD là một nửa lục giác đều nội tiếp đường tròn đường kính
CD  2a . Khi quay tứ giác ABCD quanh cạnh AB thì tạo thành một khối tròn xoay. Thể tích khối tròn xoay đó bằng 5 3 A. 3  a . B. 3 2 a . C. 3  a . D. 3  a . 4 2
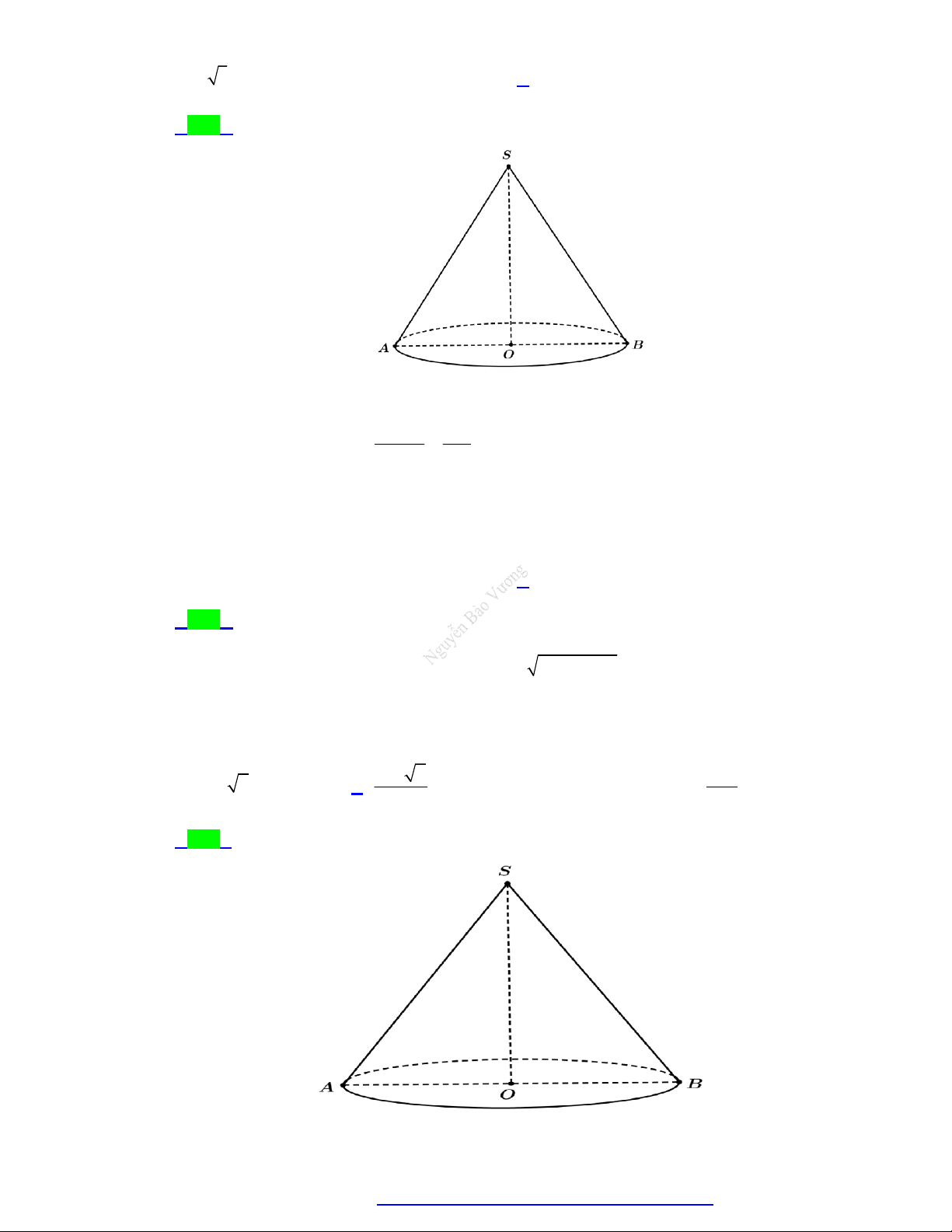
Câu 55. Cho một hình nón có góc ở đỉnh 60 , bán kính đáy bằng a . Diện tích toàn phần hình nón đó là
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
NGUYỄN BẢO VƯƠNG - 0946798489 A. 2  a . B. 2 3 a . C. 2 2 a . D. 2 3 a .
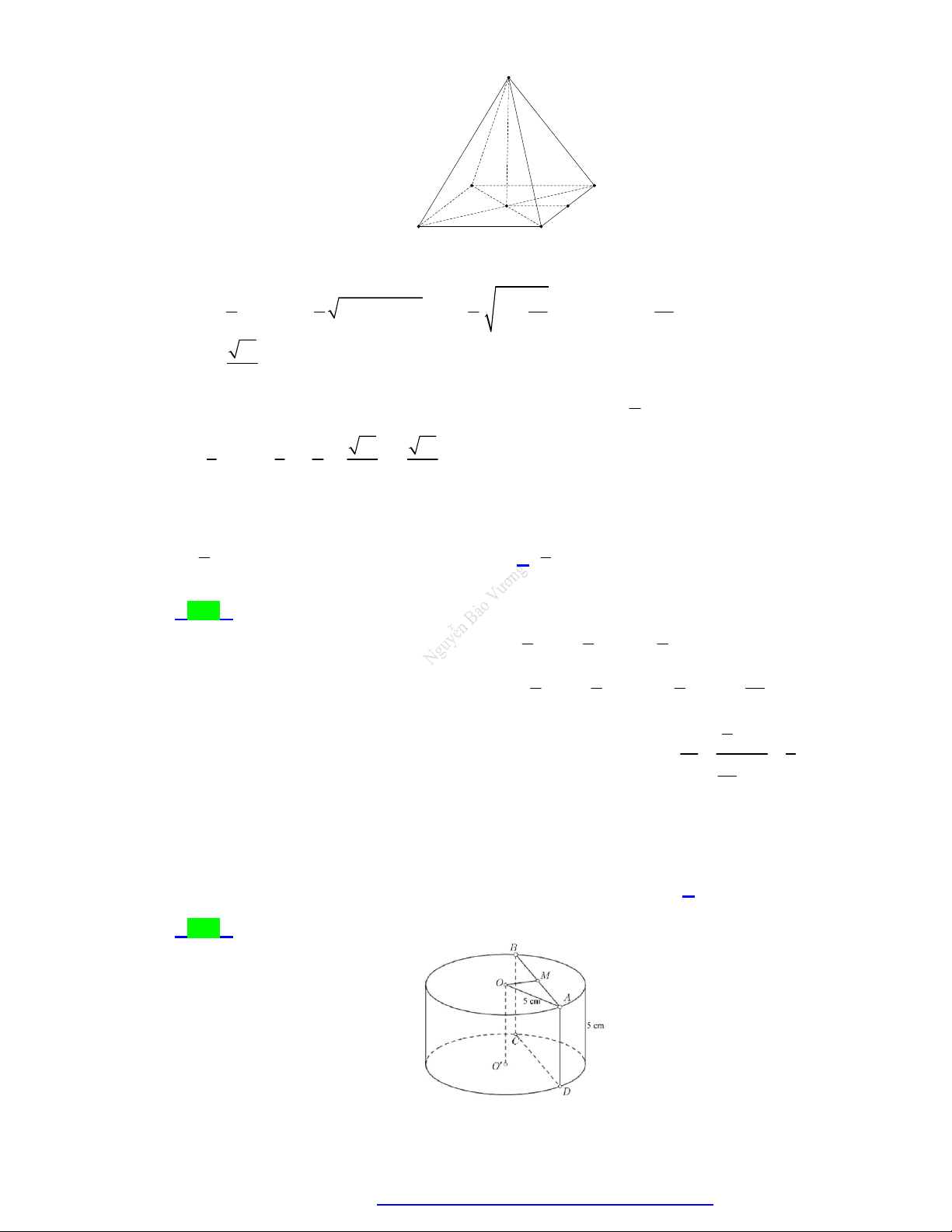
Câu 56. Cho hình lập phương ABC . D AB CD
  cạnh bằng a . Thể tích khối cầu có tâm A và tiếp xúc với
đường thẳng AC bằng 3 2 a 3 8 6 a 3 3 a A. . B. . C. . D. 3 6 a . 3 27 2
Câu 57. Cho hình chóp tứ giác đều S ABCD có cạnh đáy bằng a , diện tích mỗi mặt bên bằng 2 a . Thể
tích khối nón đỉnh S và đường tròn đáy nội tiếp hình vuông ABCD bằng: 15 15 15 15 A. 3  a . B. 3  a . C. 3  a . D. 3  a . 24 8 12 18
Câu 58. Cho hai khối cầu có bán kính lần lượt bằng a và 2a . Tỉ số giữa thể tích của khối cầu nhỏ với
thể tích của khối cầu lớn bằng 1 1 A. . B. 4 . C. . D. 8 . 4 8
Câu 59. Cho hình trụ có chiều cao bằng bán kính đáy và bằng 5 cm. Mặt phẳng   song song với trục,
cắt hình trụ theo một thiết diện có chu vi bằng 26 cm. Khoảng cách từ   đến trục của hình trụ bằng A. 4 cm. B. 5 cm. C. 2 cm. D. 3 cm.
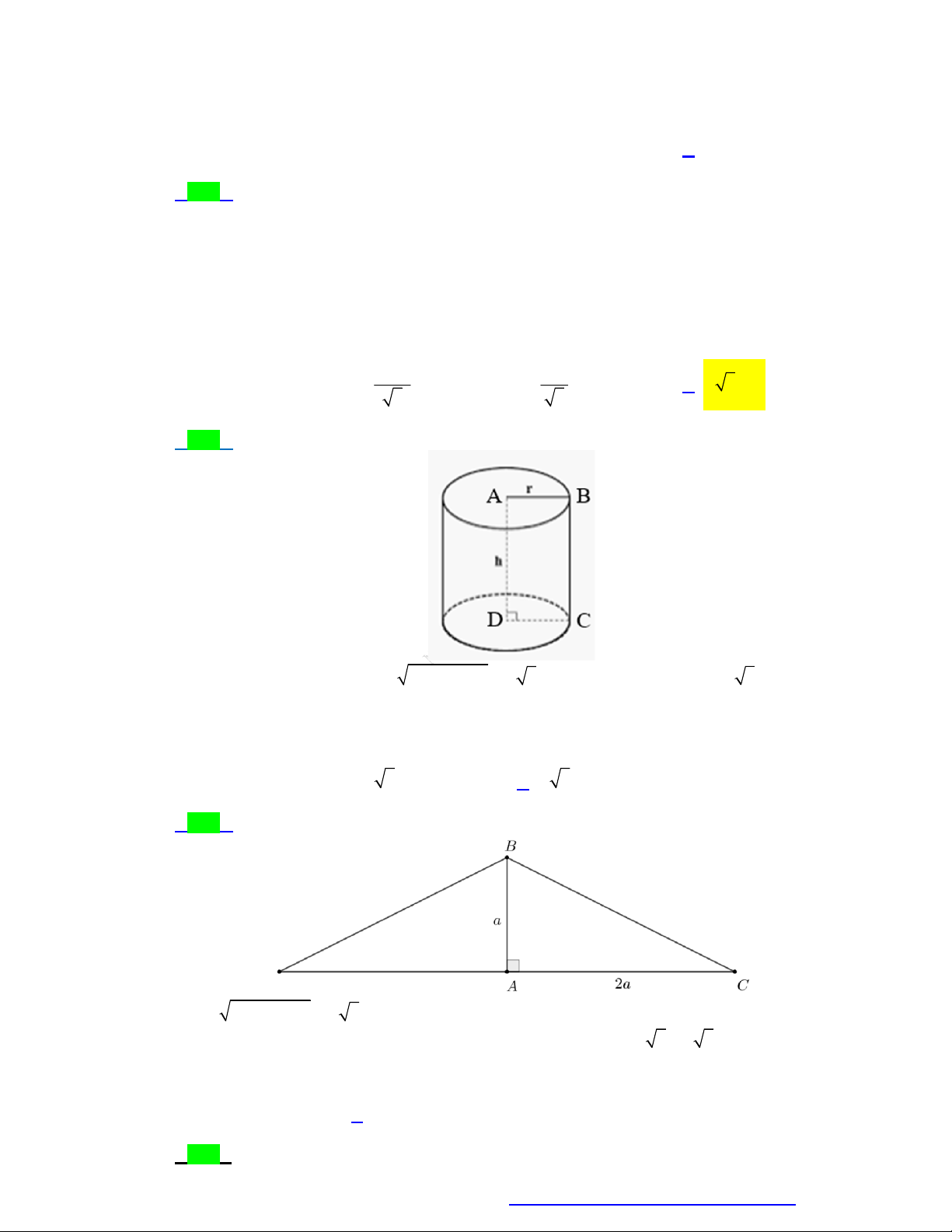
Câu 60. Cho tam giác vuông cân ABC có AB BC a 2 . Khi quay tam giác ABC quanh đường thẳng
đi qua B và song song với AC ta thu được một khối tròn xoay có thể tích bằng 3 2 a 3 4 a A. 3 2 a . B. . C. . D. 3  a . 3 3
Câu 61. Một hình trụ có diện tích xung quanh bằng 64 và thiết diện qua trục của hình trụ này là một
hình vuông. Thể tích hình trụ đó bằng A. 512 . B. 128 . C. 64 . D. 256 .
Câu 62. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a , cạnh bên hợp với đáy góc 60 . Hình
nón  N  có đỉnh S , đáy là đường tròn nội tiếp tứ giác ABCD . Diện tích xung quanh của hình
nón  N  bằng 2 7 a 2 2 a 2 3 a 2  a A. . B. . C. . D. . 4 3 2 2
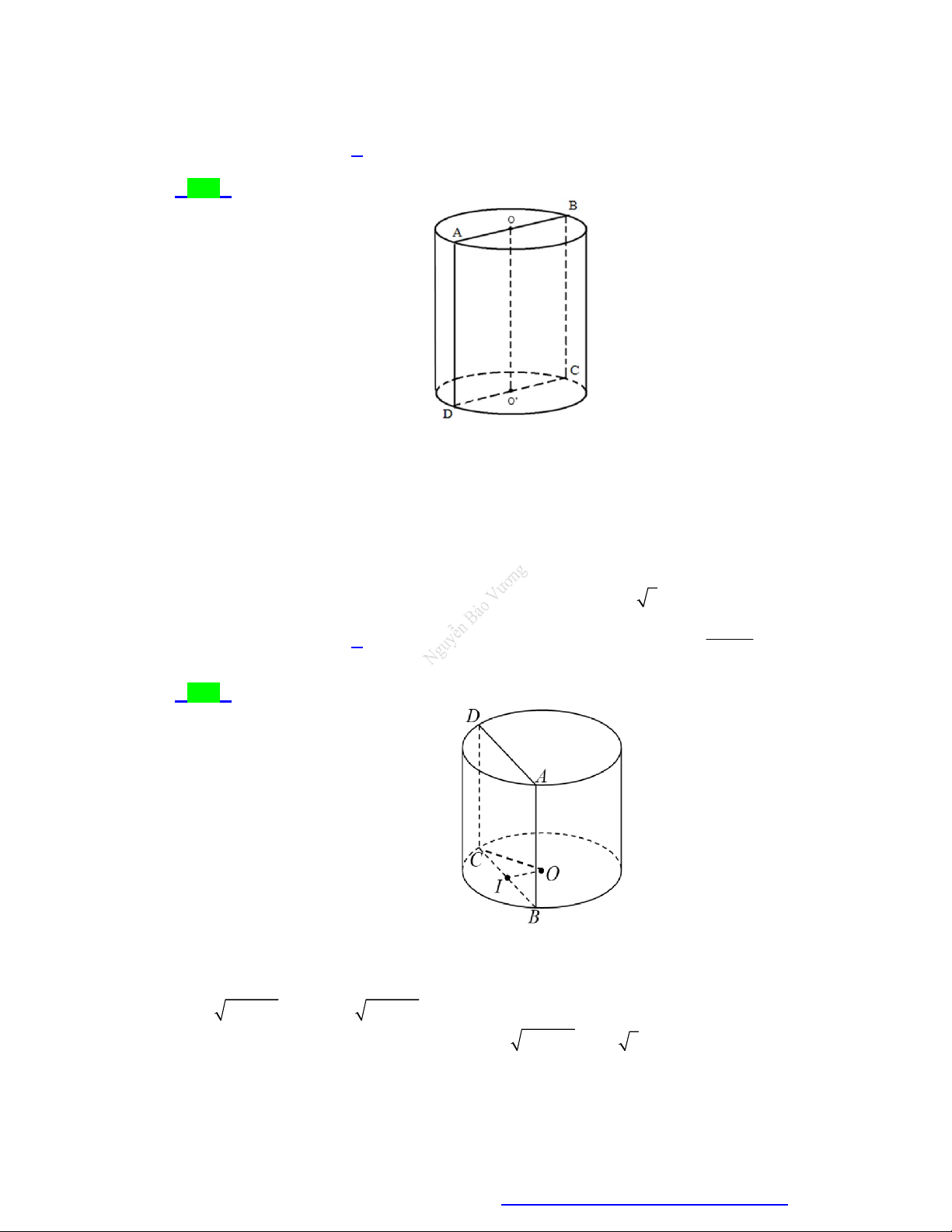
Câu 63. Trong không gian, cho hình chữ nhật ABCD , AB a, AC  2a . Khi quay hình chữ nhật ABCD
quanh cạnh AD thì đường gấp khúc ABCD tạo thành một hình trụ. Diện tích xung quanh của
hình trụ đó bằng 2  a 2 2 a A. . B. . C. 2 4 a . D. 2 2 3 a . 3 3
Câu 64. Cho hình nón có đường cao a . Biết rằng khi cắt hình nón đã cho một mặt phẳng đi qua đỉnh của a
hình nón và cách tâm của đáy hình nón một khoảng
, thiết diện thu được tạo thành một tam giác 3
vuông. Thể tích khối nón được giới hạn bởi hình nón đã cho bằng 3 5 a 3  a 3 4 a 3 5 a A. . B. . C. . D. . 12 3 9 9
Câu 65. Khối tròn xoay sinh bởi một tam giác đều cạnh a (kể cả điểm trong) khi quay quanh một đường
thẳng chứa một cạnh của tam giác đó có thể tích bằng 3  a 3  a 3 3  a 3  a 3 A. . B. . C. . D. . 8 6 4 12
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Câu 66. Cho hình chóp đều S.ABCD có AB a , cạnh bên hợp với đáy góc 0 45 . Diện tích xung quanh
của hình nón đỉnh S với đáy là đường tròn nội tiếp hình vuông bằng 2  a 2  a 3 2  a A. . B. . C. . D. 2 2 a . 2 4 4
Câu 67. Một hình nón có thiết diện qua trục là một tam giác vuông cân có cạnh góc vuông bằng a . Diện
tích xung quanh của hình nón bằng: 2  a 2 2 2 a 2 2  a 2 A. . B. . C. . D. 2  a 2 . 4 3 2
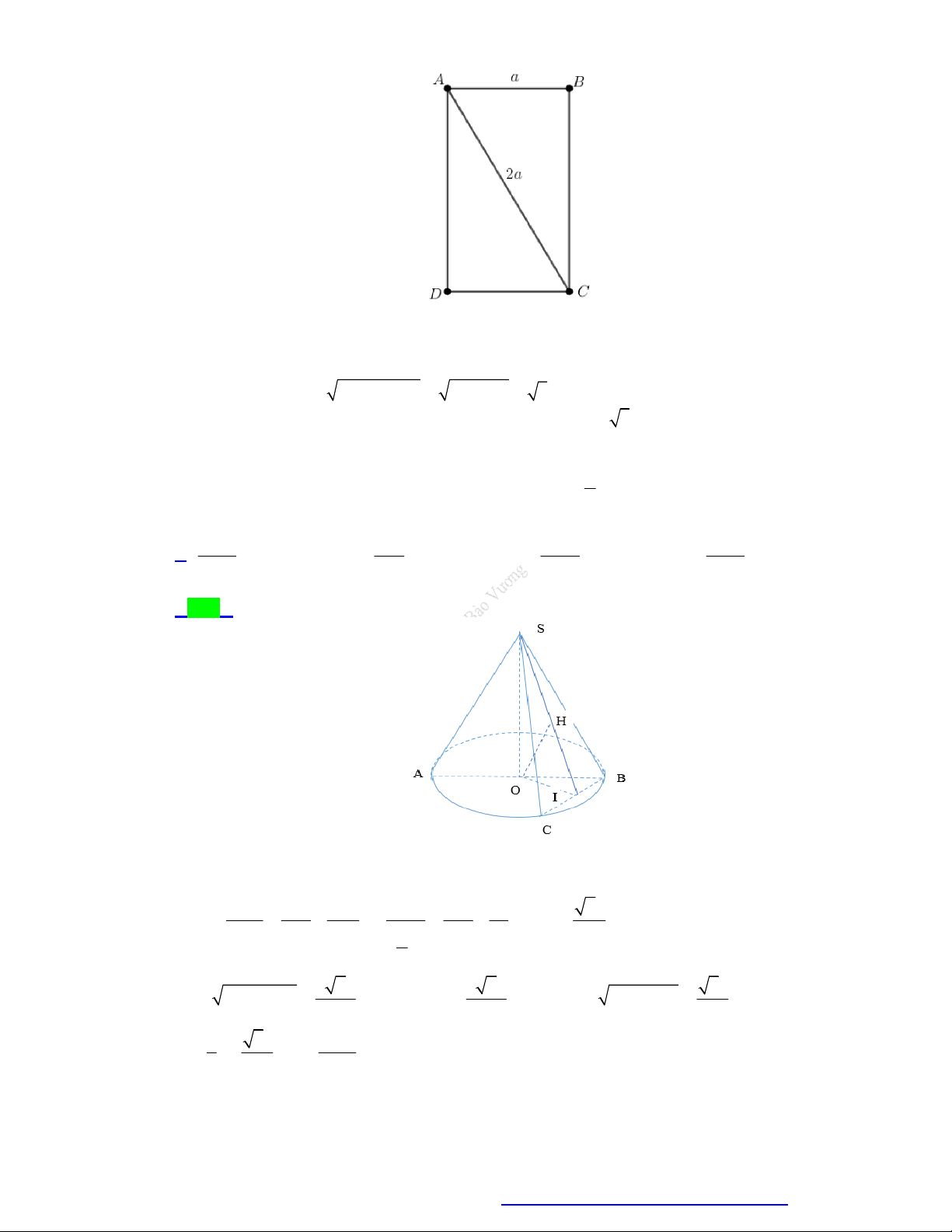
Câu 68. Cho hình chữ nhật ABCD có AC  2a 2 và 
ACB  45 . Quay hình chữ nhật ABCD quanh
cạnh AB thì đường gấp khúc ADCB tạo thành hình trụ. Diện tích toàn phần S của hình trụ là tp A. 2
S  16 a . B. 2
S  10 a . C. 2
S  12 a . D. 2
S  8 a . tp tp tp tp
Câu 69. Trong không gian, cho tam giác ABC vuông tại A , AB a , 
ABC  60 . Tính độ dài đường sinh
l của hình nón, nhận được khi quay tam giác ABC quanh trục AC .
A. l a 2 .
B. l  2a .
C. l a .
D. l a 3 .
Câu 70. Trong không gian, cho hình chữ nhật ABCD có AB  4, AC  5 . Gọi M , N lần lượt là trung
điểm của AD và BC . Quay hình chữ nhật đó xung quanh trục MN , ta được một hình trụ. Tính
diện tích toàn phần S của hình trụ đó. TP 33 81 A. S  8 . B. S   . C. S   . D. S  24 . TP TP 2 TP 2 TP
Câu 71. Cho tứ diện đều ABCD có cạnh bằng 4 . Tính diện tích xung quanh S của hình trụ có một xq
đường tròn đáy là đường tròn nội tiếp tam giác BCD và chiều cao bằng chiều cao của tứ diện ABCD . 16 2 16 3 A. S  . B. S  8 2 . C. S  . D. S  8 3 . xq 3 xq xq 3 xq
Câu 72. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a , góc giữa cạnh bên SA và mặt phẳng
đáy bằng 30 . Tính diện tích xung quanh S của hình trụ có một đường tròn đáy là đường tròn xq
nội tiếp hình vuông ABCD và chiều cao bằng chiều cao của hình chóp S.ABCD . 2  a 6 2  a 3 2  a 6 2  a 3 A. S  . B. S  . C. S  . D. S  . xq 6 xq 6 xq 12 xq 12
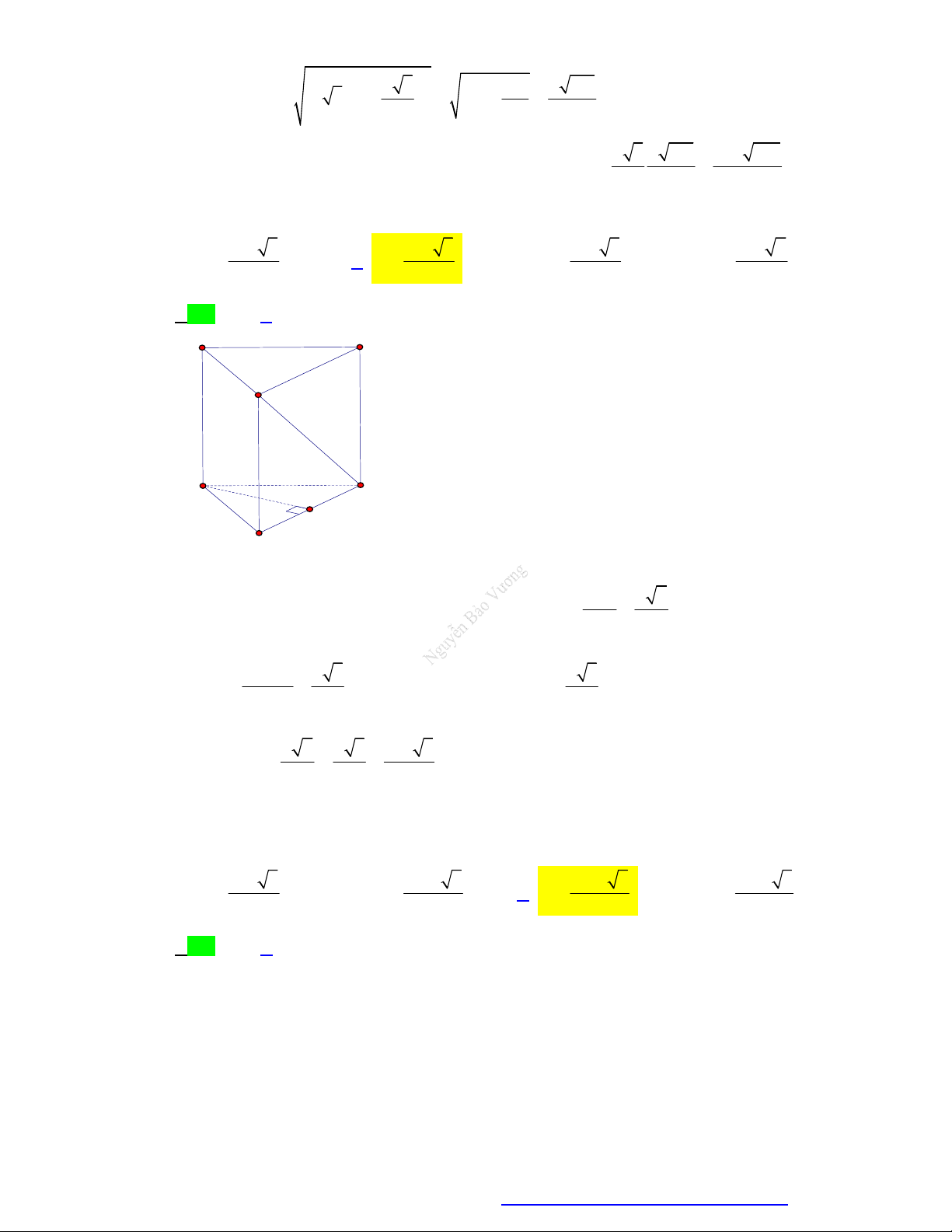
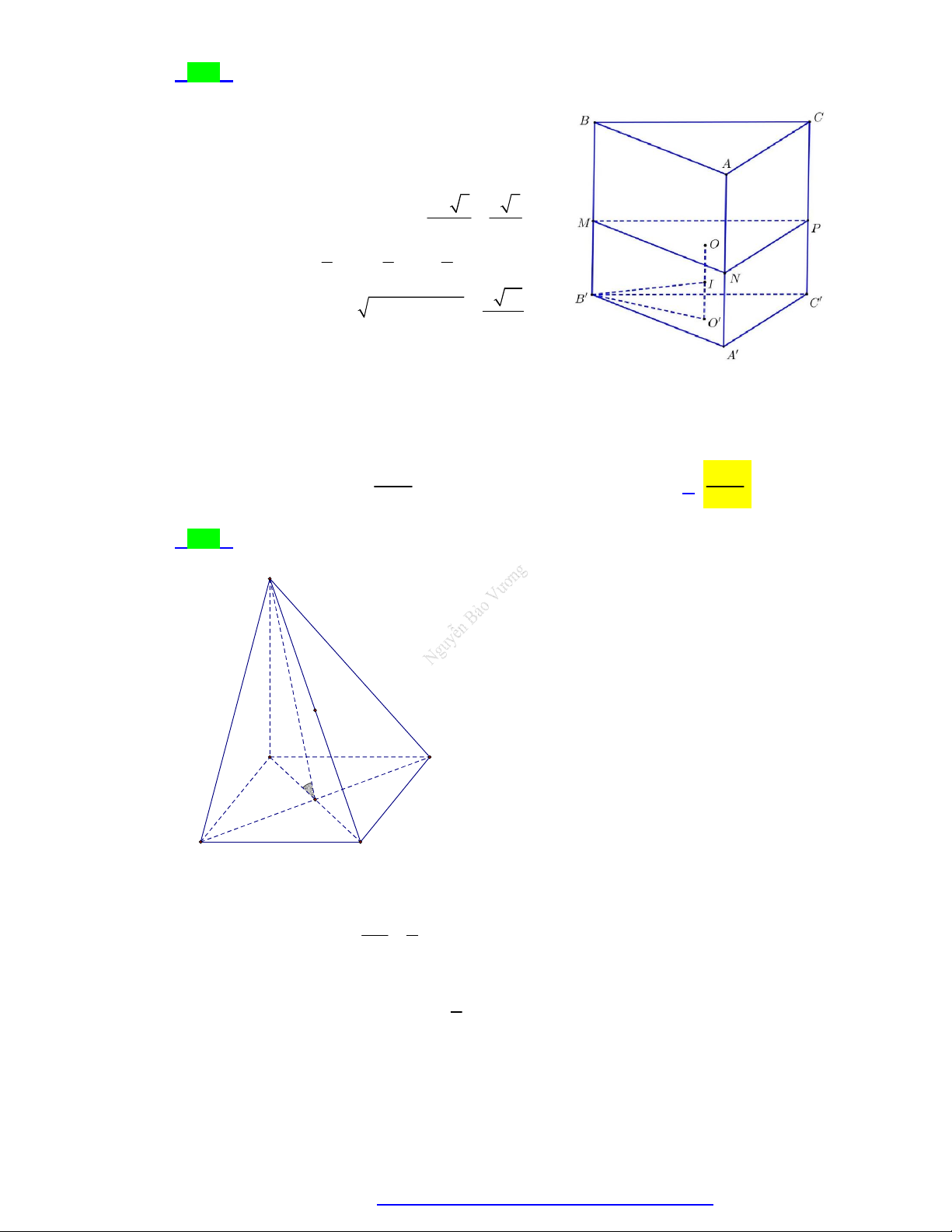
Câu 73. Cho hình lăng trụ tam giác đều ABC.A BC
  có AB a , góc giữa AC và  ABC  bằng 30 .
Tính thể tích V của khối trụ nội tiếp hình lăng trụ ABC.A BC   . 3  a 3 3  a 3 3  a 3 3  a 3 A. V  . B. V  . C. V  . D. V  . 12 36 108 72
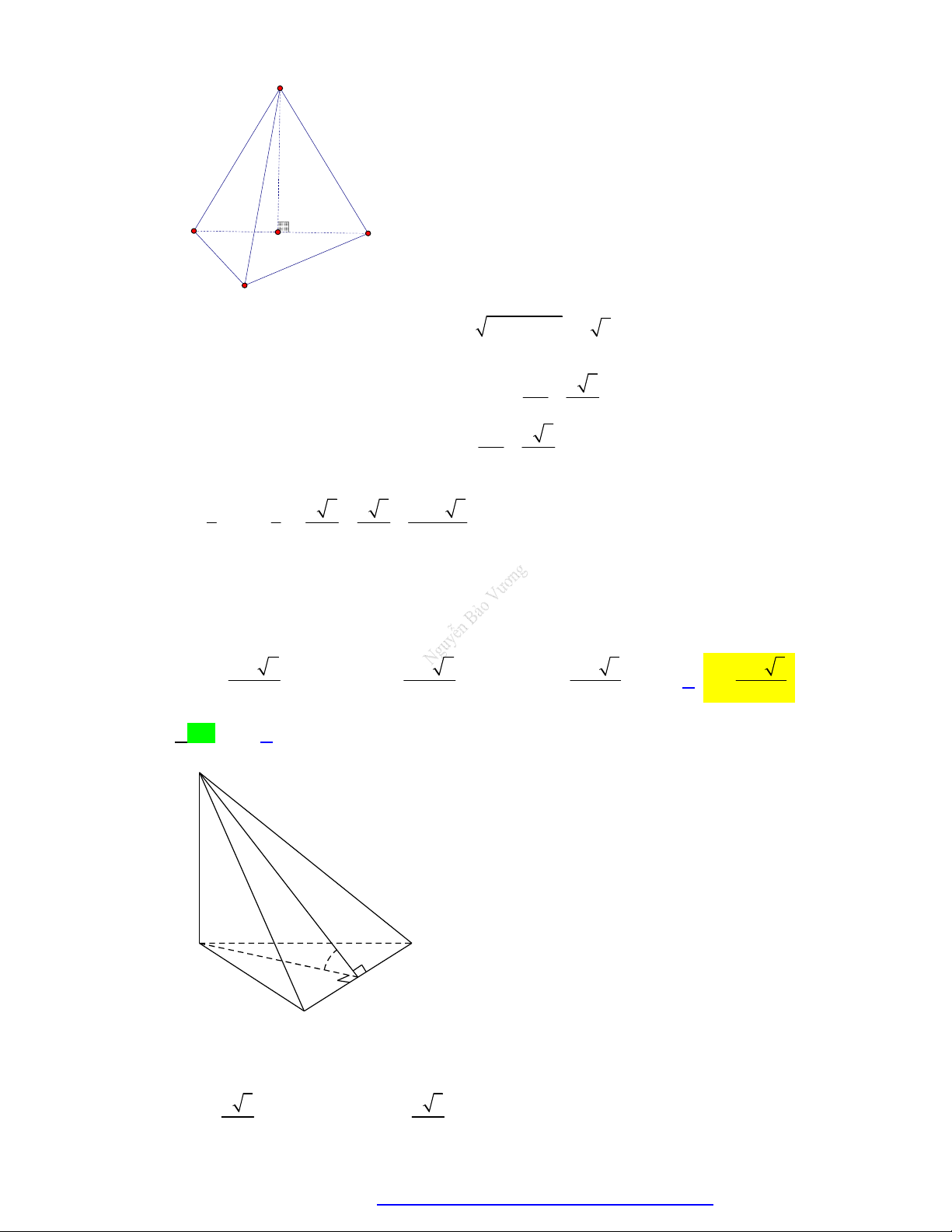
Câu 74. Cho tứ diện đều ABCD có cạnh bằng 5 . Tính thể tích V của khối nón nội tiếp tứ diện ABCD .  25 6 125 3 125 6  25 6 A. V  . B. V  . C. V  . D. V  . 108 108 108 36
Câu 75. Cho tứ diện đều ABCD cạnh bằng a 3 . Tính diện tích xung quanh S của hình trụ có đáy là xq
đường tròn ngoại tiếp tam giác BCD và có chiều cao bằng chiều cao của tứ diện đều ABCD . A. 2
S  2 3 a . B. 2 S  2 a . C. 2 S  3 a . D. 2
S  2 2 a . xq xq xq xq
Câu 76. Cho một lăng trụ tam giác đều ABC.A' B 'C ' có cạnh đáy bằng a . Góc giữa A'C và mặt phẳng
đáy bằng 60O . Tính diện tích xung quanh S của hình nón có đáy là đường tròn nội tiếp tam giác xq
ABC và đỉnh là trong tâm của tam giác A' B 'C ' . 2  a 333 2  a 111 2  a 333 2  a 111 A. S  . B. S  . C. S  . D. S  . xq 36 xq 36 xq 6 xq 6
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 77. Cho lăng trụ đứng ABC.A' B 'C ' , đáy ABC là một tam giác vuông tại cân A , AB a , cạnh AA'
hợp với B 'C góc 60o. Tính thể tích của khối trụ ngoại tiếp lăng trụ AB .
C A' B 'C ' theo a . 3  a 3 3  a 3 3  a 3 3  a 2 A. V  . B. V  . C. V  . D. V  . 18 6 3 6
Câu 78. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C , AC a, BC  2a , mặt phẳng
SAB vuông góc với mặt phẳng  ABC và tam giác SAB vuông cân tại S . Tính thể tích của
khối nón có đỉnh là S và đáy là đường tròn ngoại tiếp tam giác ABC . 3  a 5 3  a 5 5 3  a 5 5 3  a 3 3 A. V  . B. V  . C. V  . D. V  . 24 12 24 24
Câu 79. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A , SA vuông góc với mặt phẳng
ABC  , tam giác SBC đều cạnh a , góc giữa mặt phẳng SBC và mặt phẳng đáy là 30 . Tính
thể tích V của khối trụ có một đường tròn đáy là đường tròn ngoại tiếp tam giác ABC và chiều
cao bằng khoảng cách từ S đến mặt phẳng  ABC  . 3  a 2 3  a 2 3  a 3 3  a 3 A. V  . B. V  . C. V  . D. V  . 4 16 4 16
Câu 80. Cho lăng trụ đứng ABC.A BC
  có đáy là tam giác đều cạnh a . Mặt phẳng AB C   tạo với mặt
phẳng đáy góc 60 . Tính diện tích xung quanh S của hình trụ có một đường tròn đáy là đường xq
tròn nội tiếp tam giác ABC và chiều cao bằng chiều cao của hình lăng trụ ABC.A BC   . 2 3 a 2 3 3 a 2 3 a A. S  . B. S  . C. S  . D. 2 S  3 a . xq 2 xq 12 xq 6 xq
Câu 81. Cho hình hộp chữ nhật ABC . D A BCD
  , AB  2a, AD a , AC cắt BD tại O , góc A BA  60 .
Tính thể tích của khối nón có đỉnh là O và đáy là đường tròn ngoại tiếp hình chữ nhật A BCD   . 3  a 5 3 3  a 3 3  a 5 5 3  a 5 3 A. V  . B. V  . C. V  . D. V  . 6 6 6 2
CÂU HỎI MỨC ĐỘ VẬN DỤNG - VDC
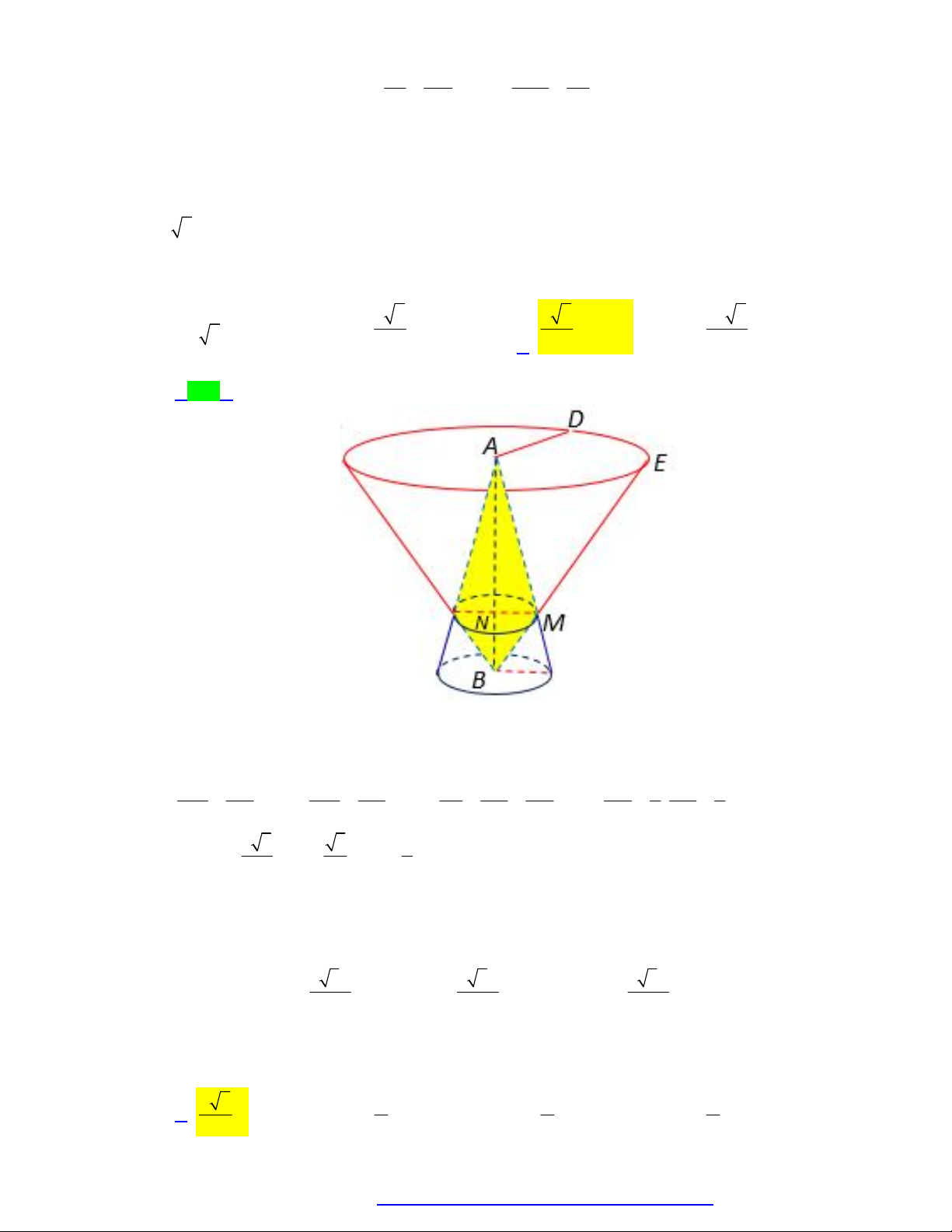
Câu 82. Cho hình nón có tâm đáy là I . Một mặt phẳng đi qua đỉnh hình nón và cắt hình nón theo một
thiết diện là tam giác đều có diện tích bằng 3 3 , đồng thời cắt đường tròn đáy tại hai điểm. , A B  thì 0
AIB  120 . Diện tích xung quanh của hình nón đã cho bằng 8 2 A. 8 3 . B. . C. 4 1 3 . D. 4 3 . 3
Câu 83. Cho hình nón đỉnh S có chiều cao bằng 3 2 . Gọi B, C là 2 điểm thuộc đường tròn đáy sao cho S
BC vuông tại S và có chu vi bằng 10  5 2 . Thể tích của khối nón được giới hạn bởi hình nón đã cho bằng: A. 7 2 . B. 21 2 . C. 43 2 . D. 14 2 .
Câu 84. Cho hình nón có chiều cao bằng 2 5 . Một mặt phẳng đi qua đỉnh hình nón và cắt hình nón theo
một thiết diện là tam giác đều có diện tích bằng 9 3 . Thể tích của khối nón được giới hạn bởi
hình nón đã cho bằng 32 5 A. . B. 32 . C. 32 5 . D. 96 . 3
Câu 85. Cho hình trụ có chiều cao bằng 6a. Biết rằng khi cắt hình trụ đã cho bởi một mặt phẳng song song
với trục và cách trục một khoảng bằng 3a, thiết diện thu được là một hình vuông. Thể tích của
khối trụ được giới hạn bởi hình trụ đã cho bằng A. 3 216 a . B. 3 150 a . C. 3 54 a . D. 3 108 a .
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Câu 86. Cho hình trụ có bán kính đáy là 4 cm, một mặt phẳng không vuông góc với đáy và cắt hai mặt đáy
theo hai dây cung song song AB, A ' B ' mà AB A' B '  6 cm (hình vẽ). Biết diện tích tứ giác
ABB ' A ' bằng 60 cm2. Tính chiều cao của hình trụ đã cho. A. 6 2 cm. B. 4 3 cm. C. 8 2 cm. D. 5 3 cm.
Câu 87. Khi cắt một hình trụ bởi hai mặt phẳng cùng song song với trục. Với mặt phẳng thứ nhất cách trục
một khoảng bằng a, thiết diện thu được là một hình vuông. Còn mặt phẳng thứ hai cách trục một a 6 khoảng bằng
, thiết diện thu được là một hình chữ nhật có diện tích bằng 2 2a 2 . Thể tích 2
của khối trụ được giới hạn bởi hình trụ đã cho bằng 3 4 a A. . B. 3 8 a 3 . C. 3 4a . D. 3 4 a . 3
Câu 88. Cho hình nón đỉnh S , tâm đường tròn đáy là O và có đường kính bằng 4a . Mặt phẳng  P đi
qua S cắt đường tròn đáy tại hai điểm A và B sao cho AB  2 3a . Gọi D là điểm đối xứng của 2 5
A qua O . Biết khoảng cách từ D đến mặt phẳng  P bằng
a . Tính thể tích khối nón. 5 3 2a  3 2 13a 3 4a A. 3 2a  . B. . C. . D. . 3 3 3
Câu 89. Cho hình nón đỉnh S có đường tròn đáy tâm O bán kính R a 2 . Trên đường tròn đáy lấy hai
điểm A và B sao cho tam giác OAB đều. Biết diện tích tam giác SAB bằng 2 2a . Thể tích hình nón đã cho bằng: 3 29a  3 58a A. 3 58 a . B. 3 29a  . C. . D. . 3 3
Câu 90. Cho hình trụ có hai đáy là hai đường tròn O và O , chiều cao bằng a 3 và bán kính đáy a.
Một mặt phẳng   đi qua trung điểm của OO và cắt đường tròn đáy theo một dây cung có độ
dài a 2 . Góc tạo bởi mặt phẳng   với mặt đáy gần với giá trị nào nhất. A. 50 . B. 51 C. 39 . D. 41 .
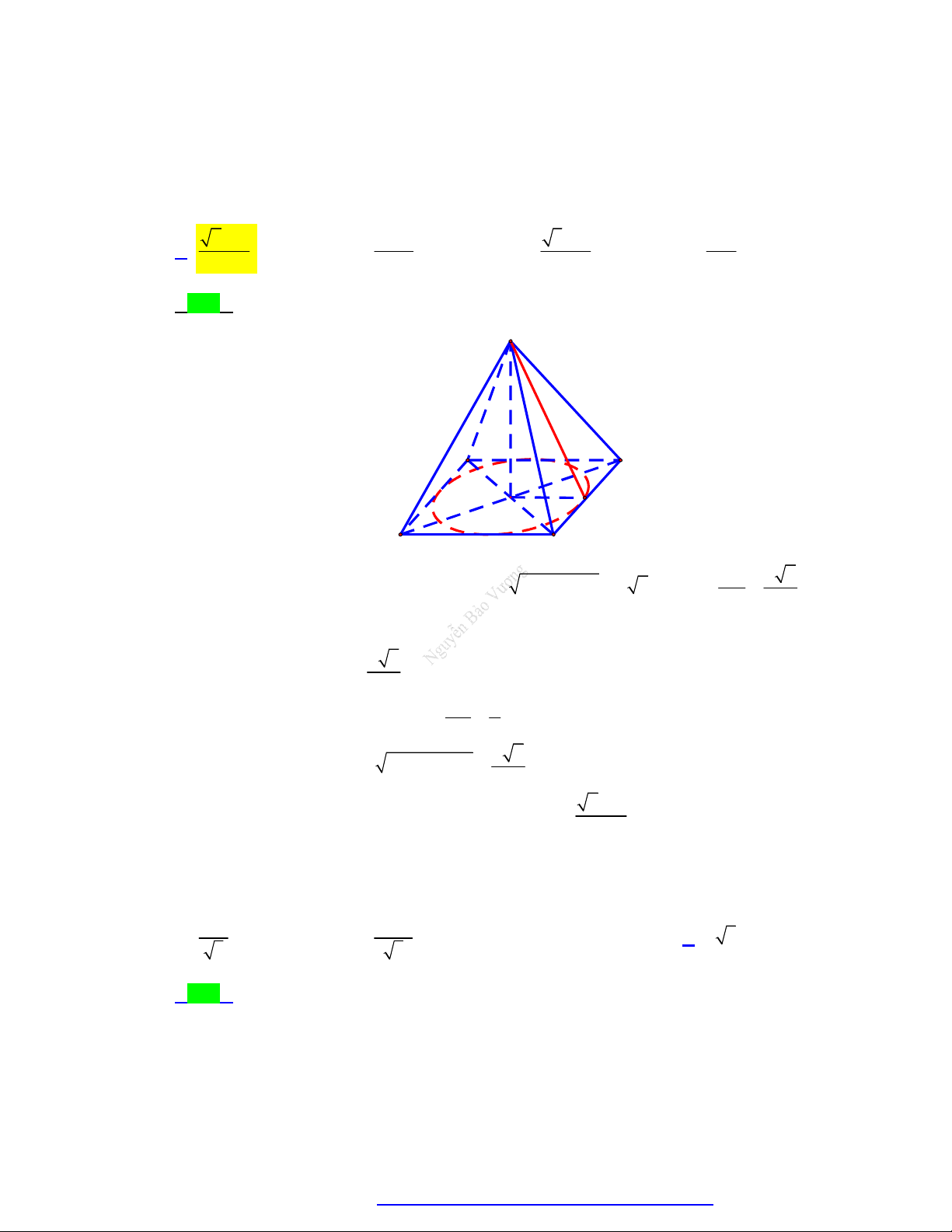
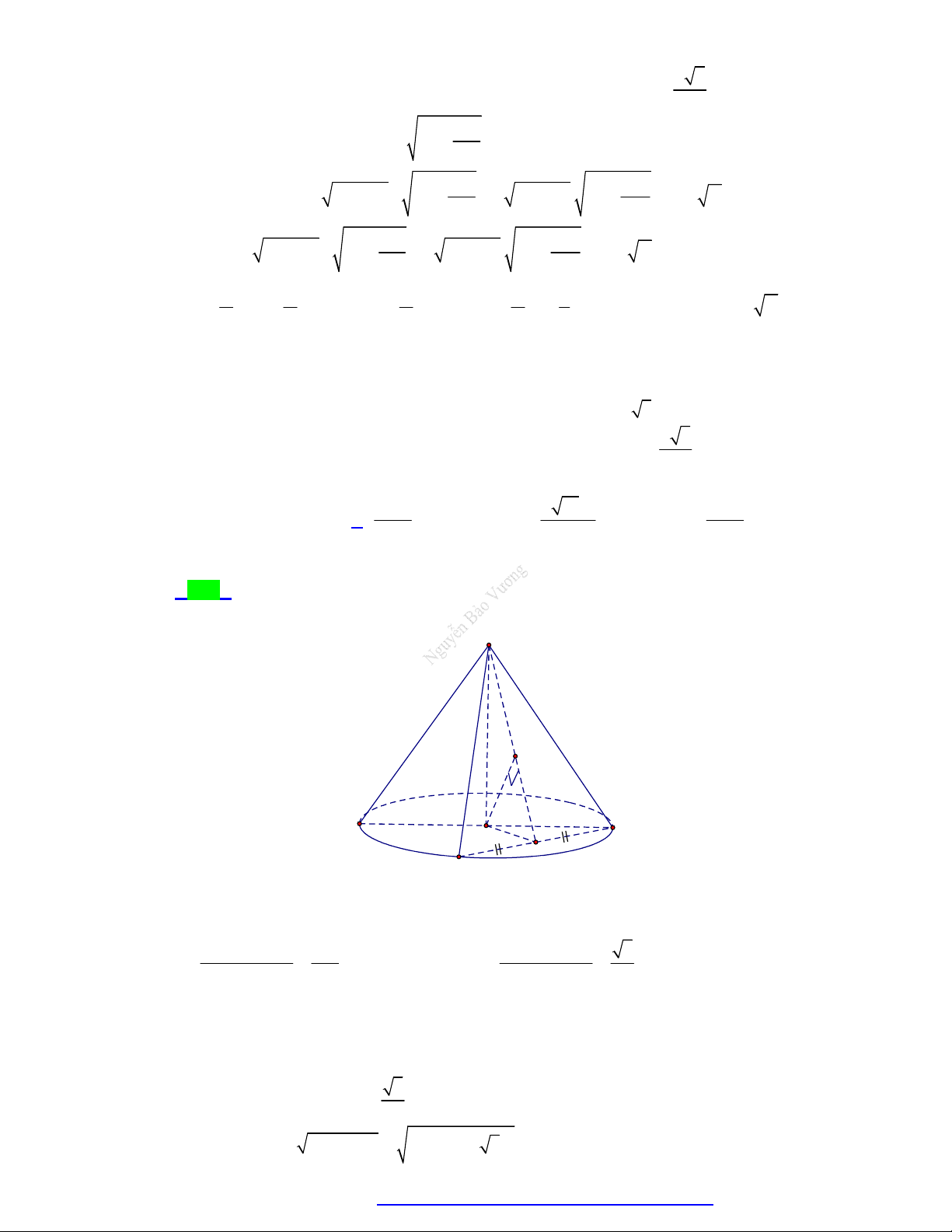
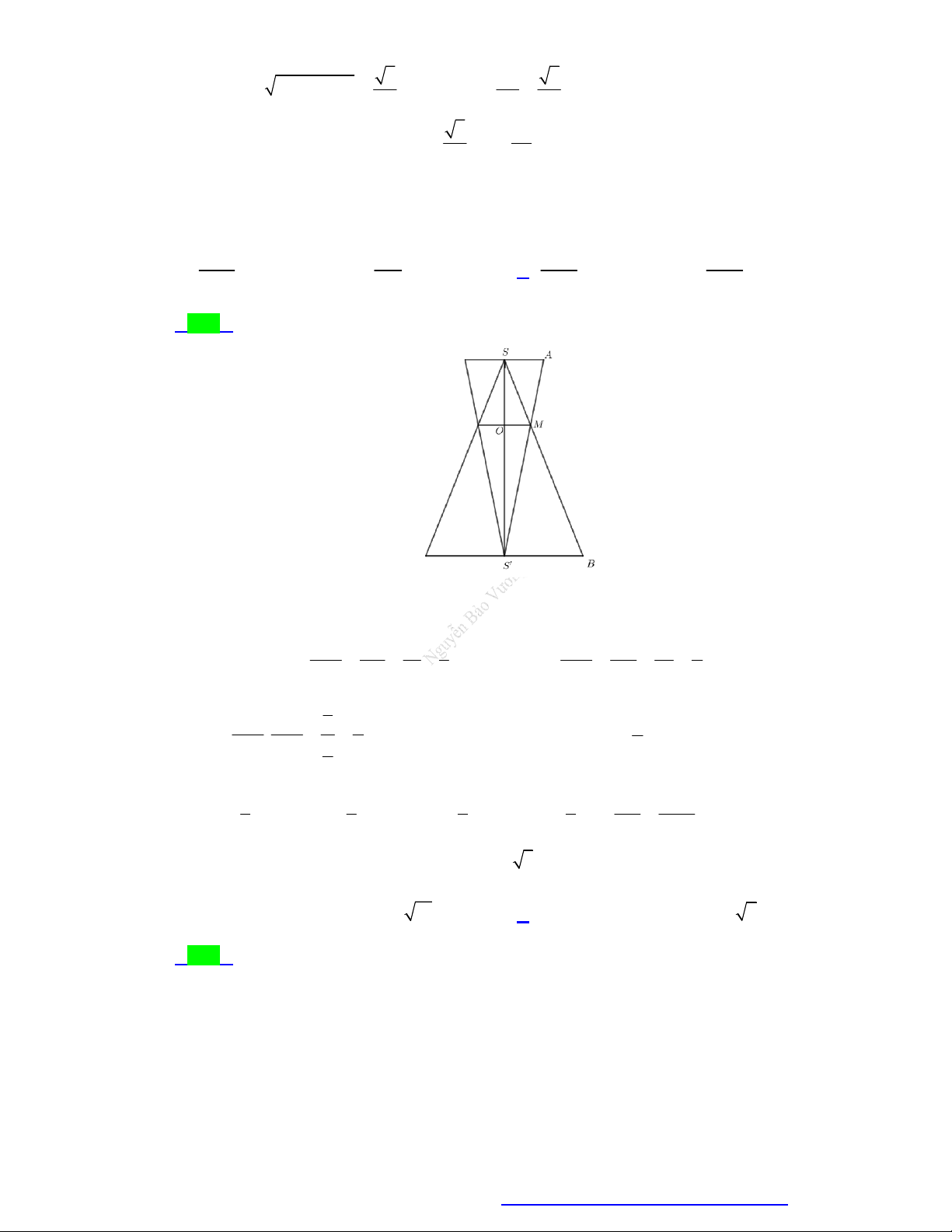
Câu 91. Cho tam giác ABC đều có cạnh bằng 2a . Từ tâm của đáy, dựng đường thẳng  vuông góc với
mặt phẳng  ABC  . Trên  lấy điểm S sao cho khoảng cách từ A đến mặt phẳng SBC  bằng
12 a . Khi đó thể tích khối nón có đỉnh là S và đường tròn đáy là đường tròn ngoại tiếp 7 ABC bằng 3 4a  3 16a  3 16a  3 4a A. . B. . C. . D. . 9 3 9 3
Câu 92. Cho mặt cầu S  tâm O và các điểm A , B , C nằm trên mặt cầu S  sao cho AB  3, AC  4 ,
BC  5 và khoảng cách từ O đến mặt phẳng  ABC bằng 1. Thể tích của khối cầu S  bằng 20 5 7 21 29 29 4 17 A.  . B.  . C.  . D.  . 3 2 6 3
Câu 93. Cho hình nón có chiều cao bằng a . Biết rằng khi cắt hình nón đã cho bởi một mặt phẳng đi qua a
đỉnh hình nón và cách tâm của đáy hình nón một khoảng bằng
, thiết diện thu được là một tam 3
giác vuông. Thể tích của khối nón được giới hạn bởi hình nón đã cho bằng 3 4 a 3 5 a 3  a 3 5 a A. . B. . C. . D. . 9 9 3 12
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
NGUYỄN BẢO VƯƠNG - 0946798489
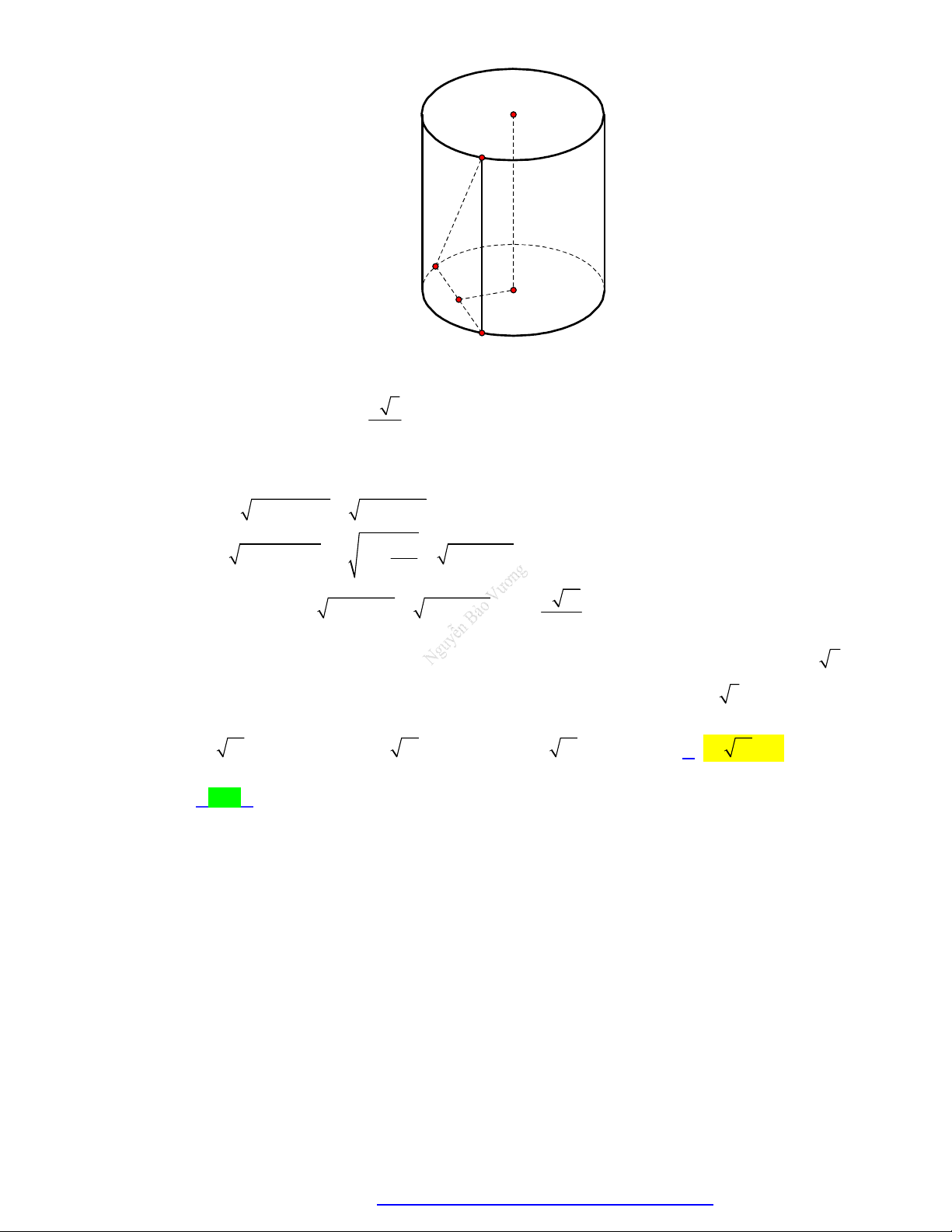
Câu 94. Một khối trụ có bán kính đáy r  2a . O, O lần lượt là tâm đường tròn đáy. Một mặt phẳng song a 15
song với trục và cách trục
, cắt đường tròn O tại hai điểm ,
A B . Biết thể tích của khối tứ 2 3 a 15 diện OO AB bằng
. Độ dài đường cao của hình trụ bằng 4 A. a . B. 6a . C. 3a . D. 2a .
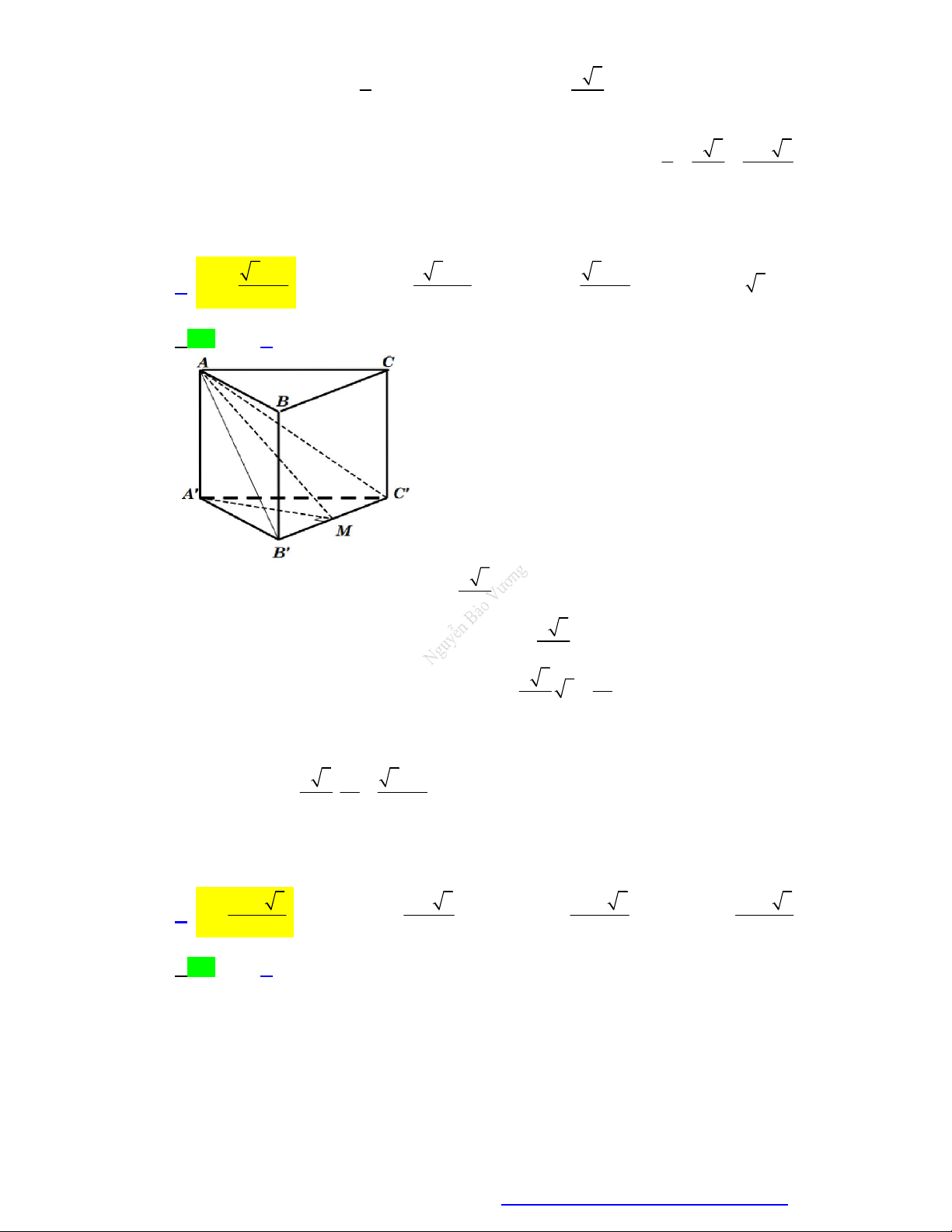
Câu 95. Cho hình lăng trụ tam giác đều ABC.A' B 'C ' có AA '  2a; BC a . Gọi M là trung điểm
BB ' . Bán kính mặt cầu ngoại tiếp khối chóp M.A' B 'C ' bằng 3 3a 13a 21a 2 3a A. . B. . C. . D. . 8 2 6 3
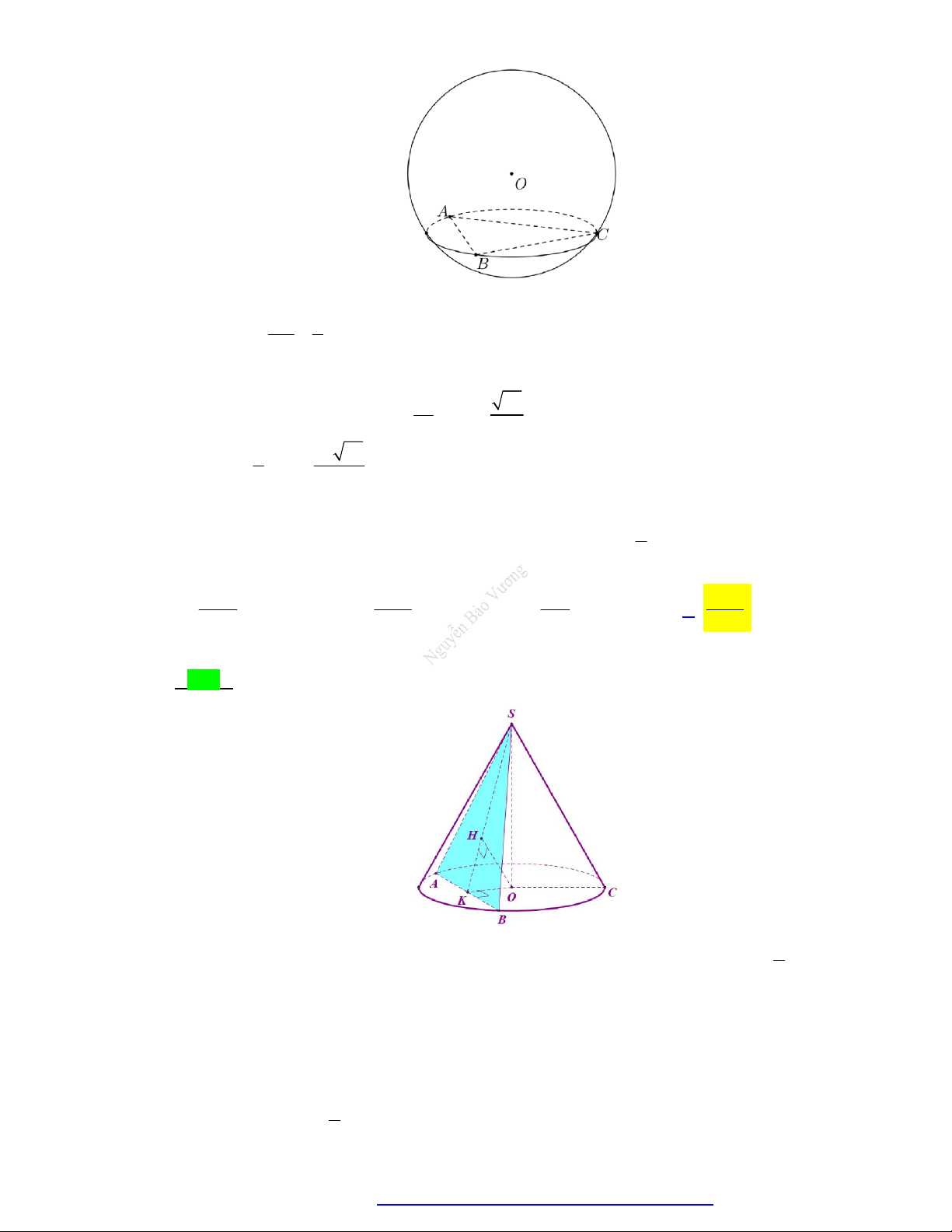
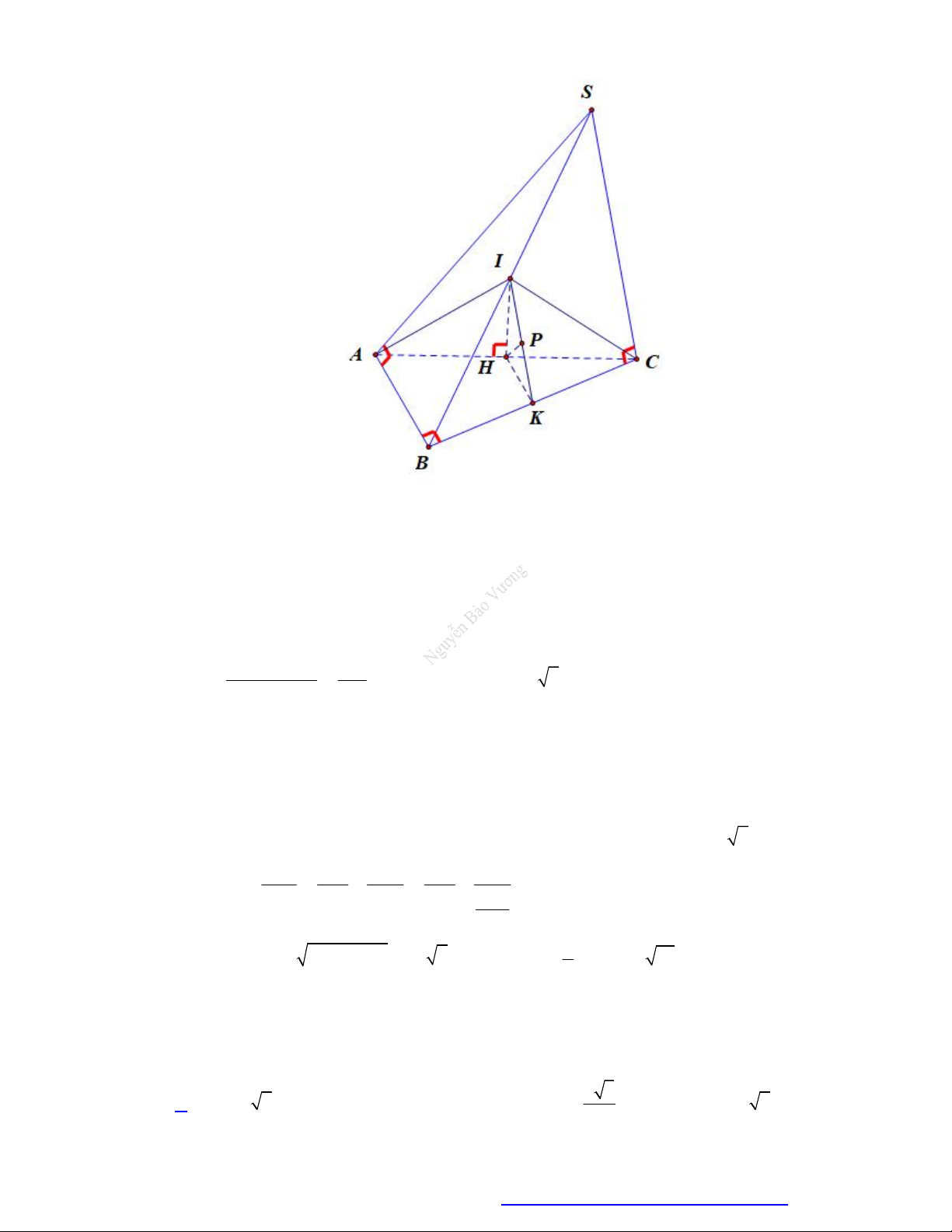
Câu 96. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B và AC  .
a Hình chiếu vuông
góc của đỉnh S lên mặt phẳng  ABC  là điểm H đối xứng với B qua AC . Góc giữa hai mặt
phẳng SAC  và  ABC  0
 45 . Diện tích mặt cầu ngoại tiếp hình chóp S.ABC bằng: 2 2 a 2 5 a A. 2 2 a . B. . C. 2 5 a . D. . 3 4
Câu 97. Cho hai khối nón có chung trục SS  3r . Khối nón thứ nhất có đỉnh S đáy là hình tròn tâm S
bán kính r . Khối nón thứ hai có đỉnh S đáy là hình tròn tâm S bán kính 2r . Thể tích phần
chung của hai khối nón bằng 3 4 r 3  r 3 4 r 3 4 r A. . B. . C. . D. . 27 9 9 3
Câu 98. Cho hình chóp S.ABC có SA  ( ABC) , AB  3 , AC  2 và 
BAC  30 . Gọi M , N lần lượt là
hình chiếu của A lên S ,
B SC . Bán kính R của mặt cầu ngoại tiếp hình chóp . A BCNM là A. R  2 . B. R  13 . C. R  1 . D. R  2 .
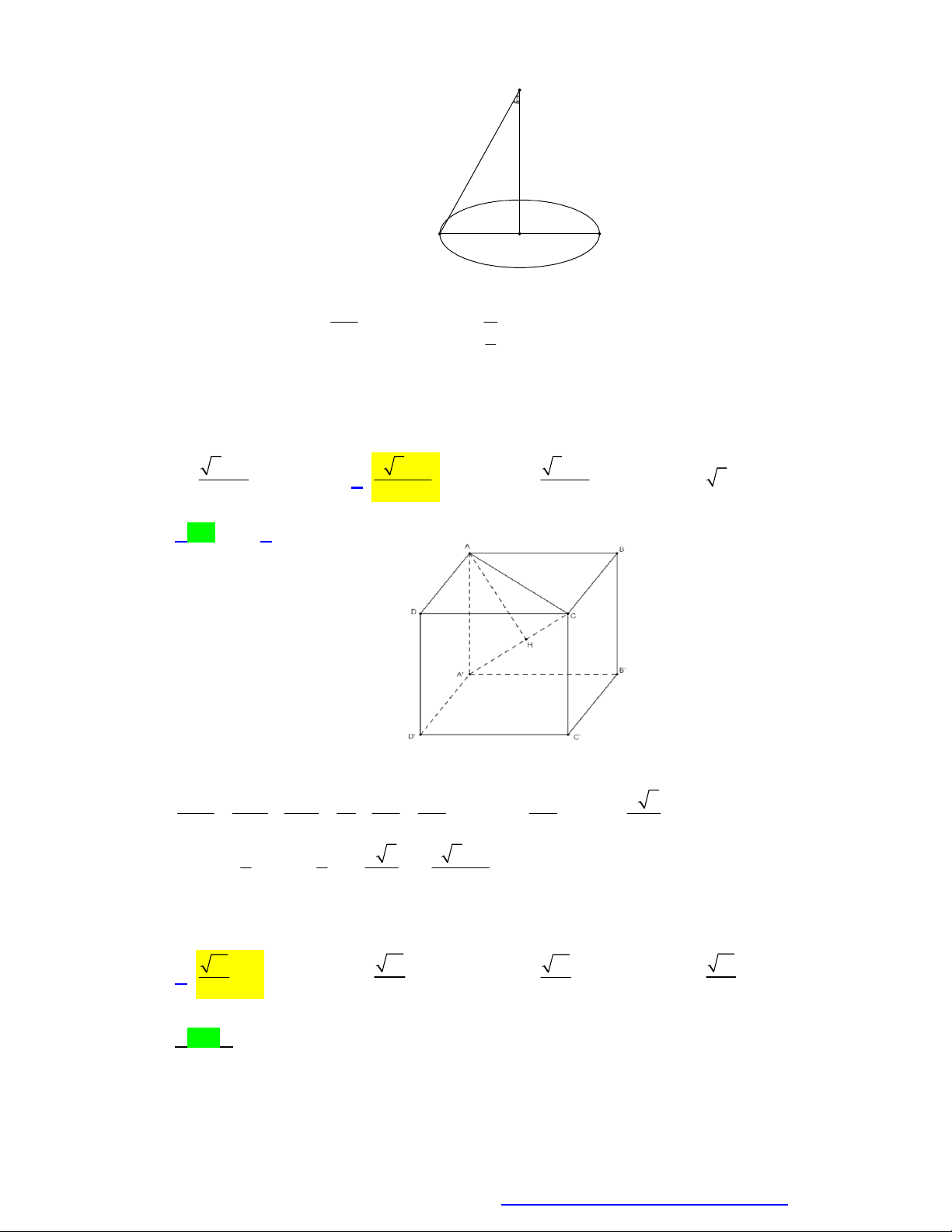
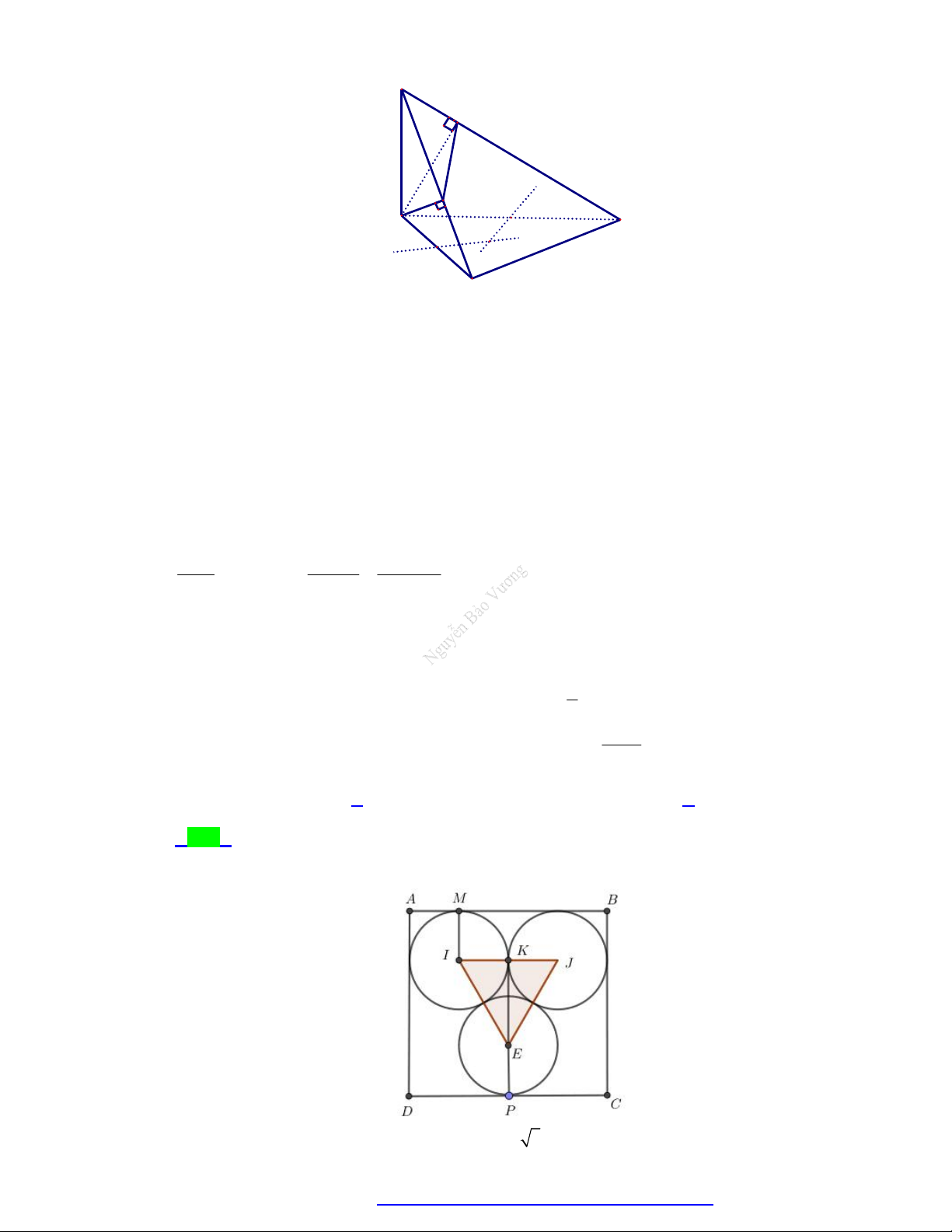
Câu 99. Có một bể hình hộp chữ nhật chứa đầy nước. Người ta cho ba khối nón giống nhau có thiết diện
qua trục là một tam giác vuông cân vào bể sao cho ba đường tròn đáy của ba khối nón đôi một
tiếp xúc với nhau, một khối nón có đường tròn đáy tiếp xúc với một cạnh của đáy bể và hai khối
nón còn lại có đường tròn đáy tiếp xúc với hai cạnh của đáy bể. Sau đó người ta đặt lên đỉnh của 4
ba khối nón một khối cầu có bán kính bằng
lần bán kính đáy khối nón. Biết khối cầu vừa đủ 3 337
ngập trong nước và tổng lượng nước trào ra là
(lit). Thể tích nước ban đầu trong bể thuộc 24
khoảng nào dưới đây? (tính theo đơn vị lít). A. (150;151) B. (151;152) C. (139;140) D. (138;139).
Câu 100. Cho hình trụ có chiều cao bằng 6a . Biết rằng khi cắt hình trụ đã cho bởi một mặt phẳng song
song với trục và cách trục một khoảng bằng 3a , thiết diện thu được là một hình vuông. Thể tích
của khối trụ được giới hạn bởi hình trụ đã cho bằng A. 3 216 a . B. 3 150 a . C. 3 54 a . D. 3 108 a .
Câu 101. Cho hình trụ có chiều cao bằng 6a . Biết rằng khi cắt hình trụ đã cho bởi một mặt phẳng song
song với trục và cách trục một khoảng bằng 3a , thiết diện thu được là một hình chữ nhật có diện tích 2
48a . Thể tích của khối trụ được giới hạn bởi hình trụ đã cho bằng A. 3 216 a . B. 3 180 a . C. 3 54 a . D. 3 150 a .
Câu 102. Cho hình chóp S.ABC có SA vuông góc với mặt phẳng đáy, góc giữa SBC  và mặt phẳng đáy
bằng 60 . Nếu ABC là tam giác đều cạnh a 3 thì bán kính mặt cầu ngoại tiếp hình chóp S.ABC bằng a 43 a 43 a 43 a 43 A. . B. . C. . D. 4 8 12 6
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Câu 103. Cho hình chóp ABCD có đáy là hình thang vuông tại A và D . Biết SA vuông góc với ABCD ,
AB BC a, AD  2a, SA a 2 . Gọi E là trung điểm của AD . Bán kính mặt cầu đi qua các điểm S, ,
A B, C, E bằng a 3 a 30 a 6 A. . B. . C. . D. a . 2 6 3
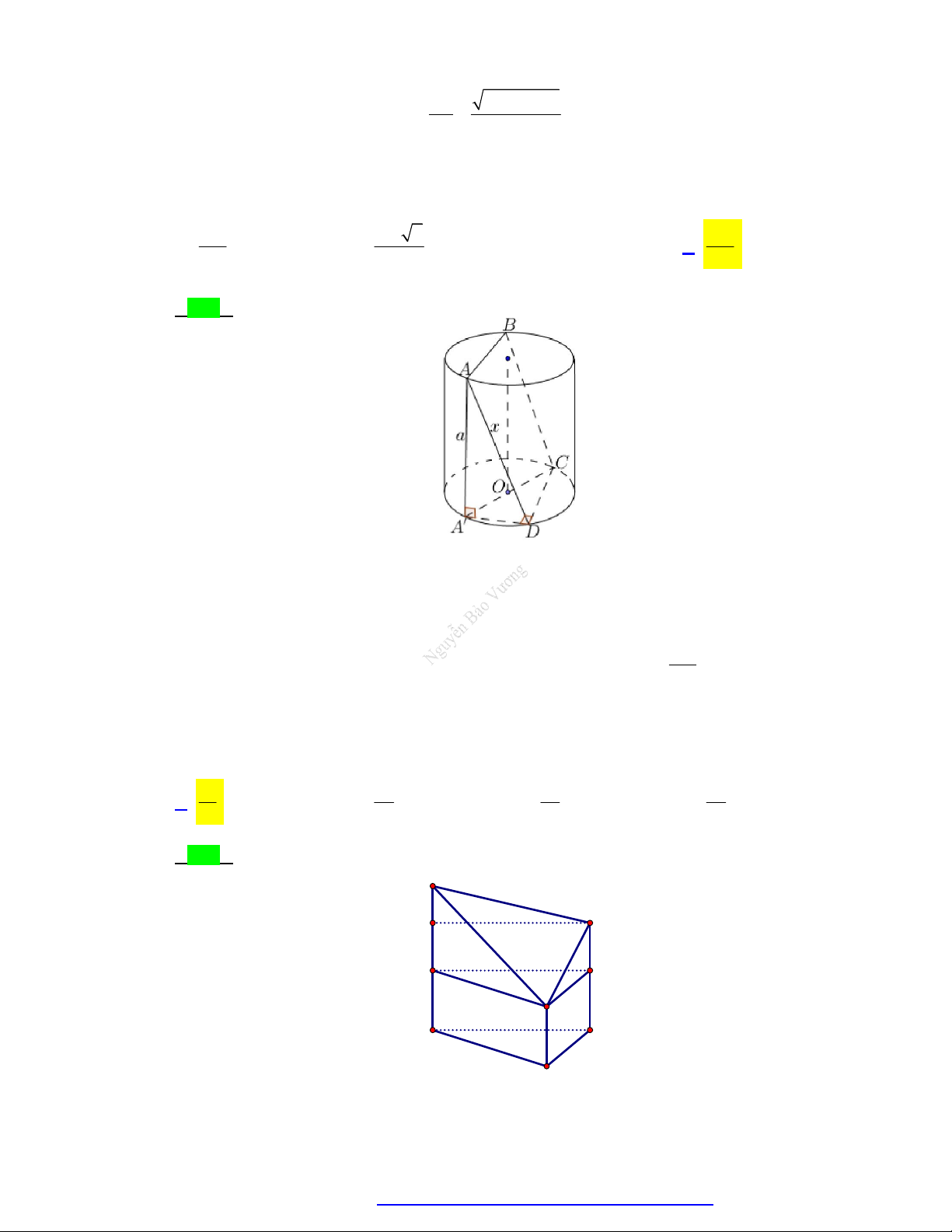
Câu 104. Một hình trụ có bán kính đáy bằng chiều cao và bằng a . Một hình vuông ABCD có AB, CD là
hai dây cung của hai đường tròn đáy và mặt phẳng  ABCD không vuông góc với đáy. Diện tích hình vuông đó bằng. 2 5a 2 5a 2 2 5a A. . B. . C. 2 5a . D. . 4 4 2
Câu 105. Cho ba hình cầu có bán kính lần lượt là R , R , R đôi một tiếp xúc nhau và cùng tiếp xúc với mặt 1 2 3
phẳng (P) . Các tiếp điểm của ba hình cầu với mặt phẳng (P) lập thành một tam giác có độ dài các
cạnh lần lượt là 2;3; 4 . Tính tổng R R R : 1 2 3 61 67 53 59 A. . B. . C. . D. . 12 12 12 12
Câu 106. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, các cạnh bên của hình chóp bằng
6 cm , AB  4 cm . Khi thể tích khối chóp S.ABCD đạt giá trị lớn nhất, tính diện tích mặt cầu
ngoại tiếp S.ABCD . A. 2 12 cm . B. 2 4 cm . C. 2 9 cm . D. 2 36 cm .
AD  ABC BC  2(cm)
Câu 107. Cho hình tứ diện ABCD có
, ABC là tam giác vuông tại B . Biết
,AB  2 3(cm),AD  6(cm). Quay các tam giác ABC và ABD ( bao gồm cả điểm bên trong 2 tam
giác) xung quanh đường thẳng AB ta được 2 khối tròn xoay. Thể tích phần chung của 2 khối tròn xoay đó bằng 5 3 3 3 64 3 3 3 3 3 (  cm ) (  cm ) (  cm ) 3 (  cm ) A. B. 2 C. 2 . D. 3 .
Câu 108. Huyền có một tấm bìa như hình vẽ, Huyền muốn biến đường tròn đó thành một cái phễu hình nón.
Khi đó Huyền phải cắt bỏ hình quạt tròn AOB rồi dán OA , OB lại với nhau. Gọi x là góc ở tâm
hình quạt tròn dùng làm phễu. Tìm x để thể tích phểu lớn nhất? 2 6    A. B. C. D. 3 3 2 4
Câu 109. Cho hình trụ có hai đáy là hai hình tròn O và O, thiết diện qua trục của hình trụ là hình vuông. Gọi ,
A B là hai điểm lần lượt nằm trên hai đường tròn O và O. Biết AB  2a và a 3
khoẳng cách giữa hai đường thẳng AB và OO bằng . Bán kính đáy bằng 2 a 14 a 14 a 14 a 14 A. . B. . C. . D. . 3 2 4 9
Câu 110. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B , AB BC  3a 2 ,   0
SAB SCB  90 . Biết khoảng cách từ A đến mặt phẳng (SBC) bằng 2a 3 . Tính thể tích mặt
cầu ngoại tiếp hình chóp S.ABC . A. 3 72 18 a . B. 3 18 18 a . C. 3 6 18 a . D. 3 24 18 a .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 111. Cho hình trụ có đáy là hai đường tròn tâm O và O , bán kính đáy bằng chiều cao và bằng 2a .
Trên đường tròn đáy có tâm O lấy điểm A , D trên đường tròn tâm O lấy điểm B , C sao cho
AB//CD và AB không cắt OO ' . Tính AD để thể tích khối chóp O '.ABCD đạt giá trị lớn nhất. 4 3
A. AD  2 2a
B. AD  4a C. AD a D. AD  2a 3 Câu 112. Trong không gian với hệ tọa độ Oxyz , cho hai mặt phẳng song song
P :2x y  2z 1  0, Q :2x y  2z  5  0 và điểm A 1  ;1 
;1 nằm trong khoảng giữa hai
mặt phẳng này. Gọi S  là mặt cầu đi qua A và tiếp xúc với cả  P và Q. Biết khi  S  thay
đổi thì tâm I của nó luôn thuộc đường tròn C cố định. Diện tích hình tròn giới hạn bởi C là 2 4 16 8 A. . B. . C. . D. . 3 9 9 9
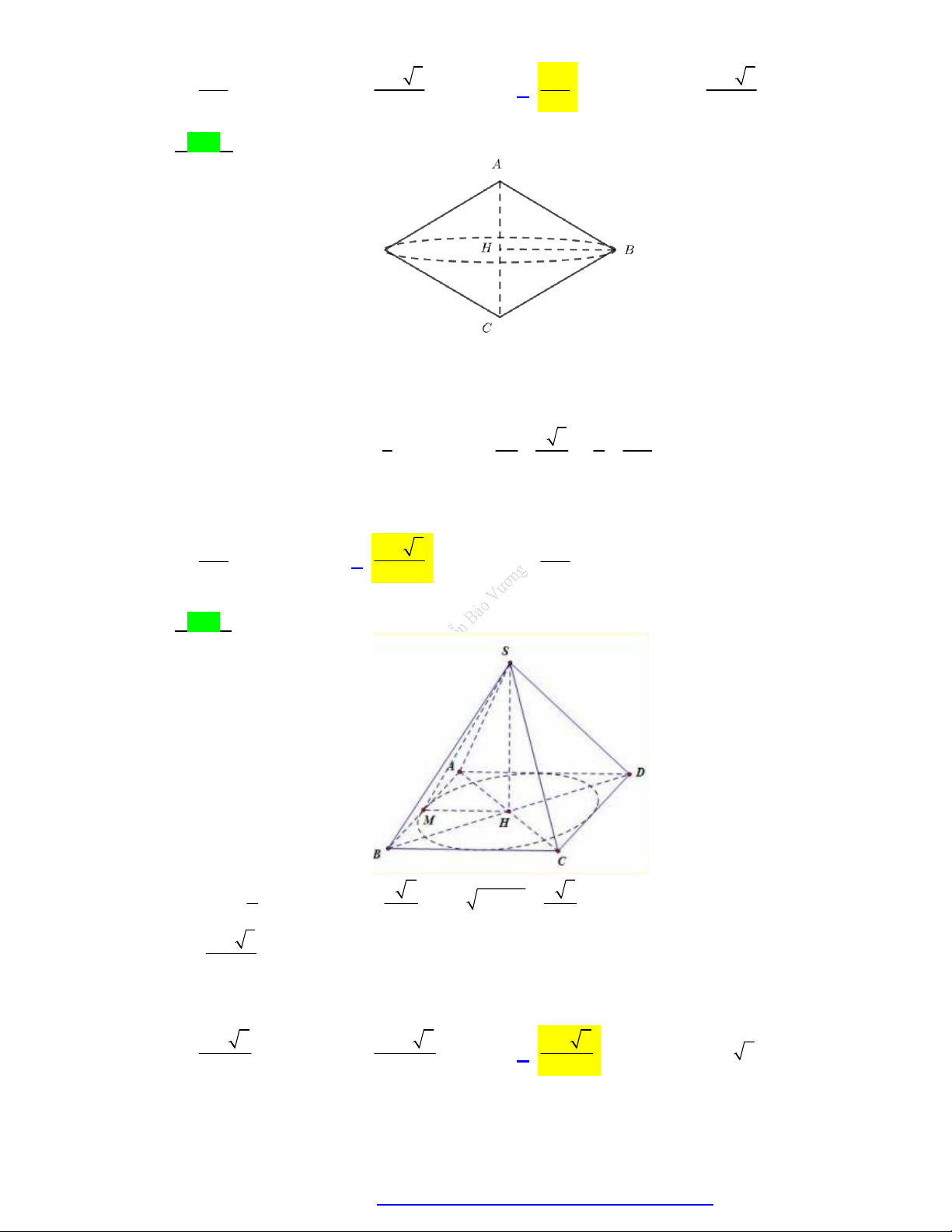
Câu 113. Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng  ABCD , tứ giác ABCD là hình thang
vuông với cạnh đáy AD, BC . AD  3CB  3a , AB a , SA a 3 . Điểm I thỏa mãn  
AD  3AI , M là trung điểm SD , H là giao điểm của AM và SI . Gọi E, F lần lượt là hình
chiếu của A lên SB, SC . Tính thể tích V của khối nón có đáy là đường tròn ngoại tiếp tam giác
EFH và đỉnh thuộc mặt phẳng  ABCD . 3  a 3  a 3  a 3  a A. V  . B. V  . C. V  . D. V  . 5 5 2 5 5 10 5
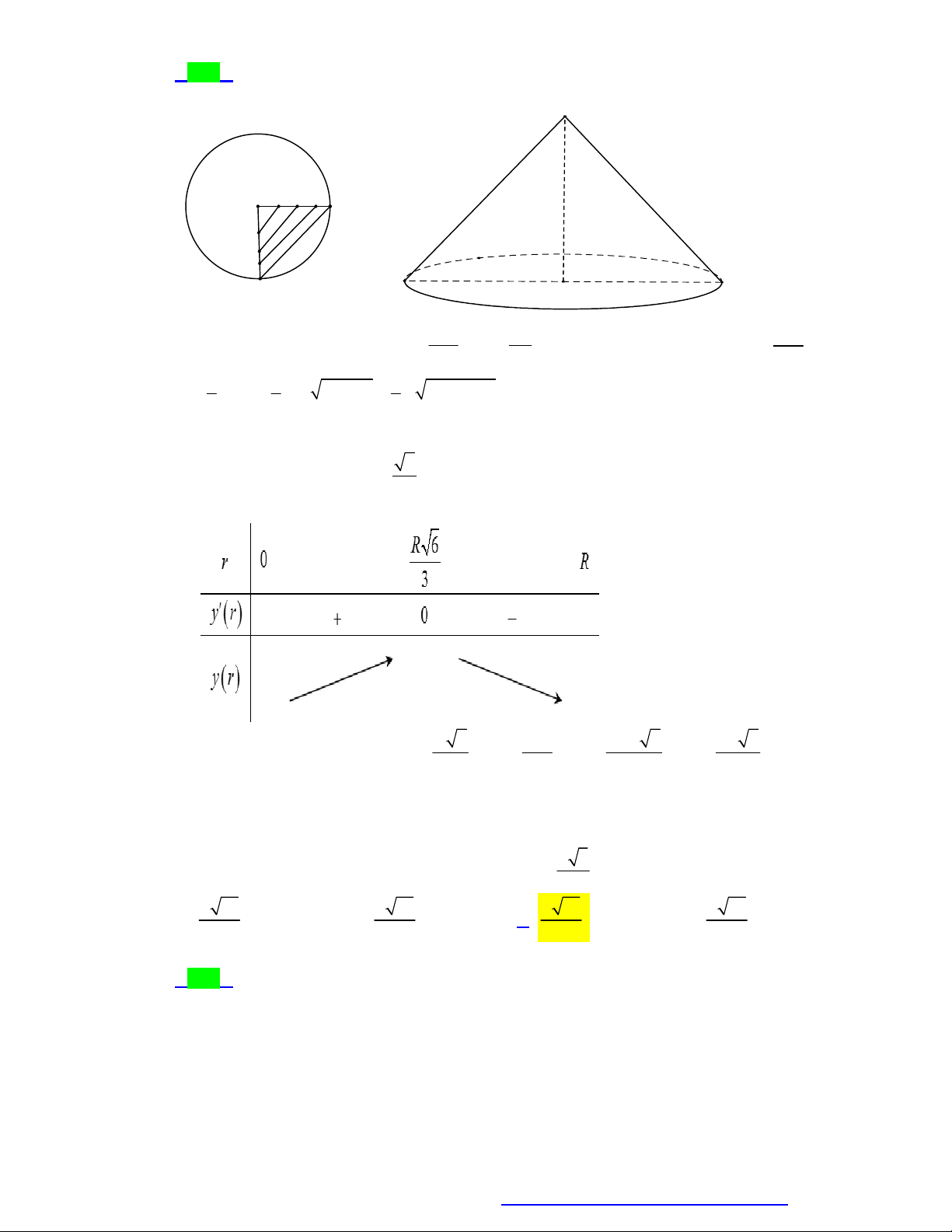
Câu 114. Cho một miếng tôn hình tròn có bán kính 50 cm . Biết hình nón có thể tích lớn nhất khi diện tích
toàn phần của hình nón bằng diện tích miếng tôn ở trên. Khi đó hình nón có bán kính đáy là: A. 10 2 cm . B. 50 2 cm . C. 20 cm . D. 25 cm .
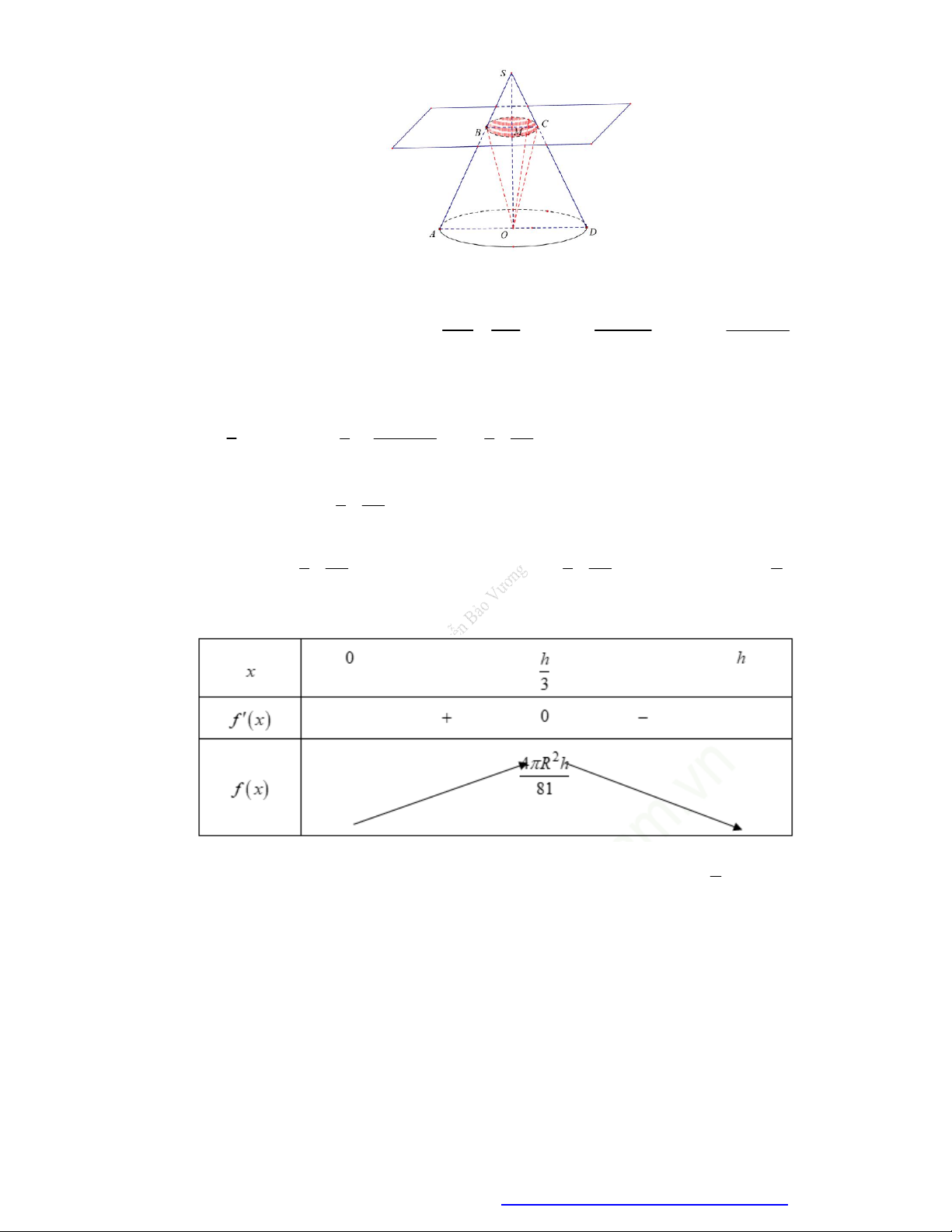
Câu 115. Cho hình nón  N  có đường cao SO h và bán kính đáy bằng R , gọi M là điểm trên đoạn SO ,
đặt OM x , 0  x h . C  là thiết diện của mặt phẳng  P vuông góc với trục SO tại M , với
hình nón  N  . Tìm x để thể tích khối nón đỉnh O đáy là C  lớn nhất. h h 2 h 3 h A. . B. . C. . D. . 2 2 2 3
Câu 116. Bạn Hoàn có một tấm bìa hình tròn như hình vẽ, Hoàn muốn biến hình tròn đó thành một hình cái
phễu hình nón. Khi đó Hoàn phải cắt bỏ hình quạt tròn AOB rồi dán hai bán kính OA và OB lại
với nhau (diện tích chỗ dán nhỏ không đáng kể). Gọi x là góc ở tâm hình quạt tròn dùng làm
phễu. Tìm x để thể tích phễu lớn nhất?   2 6  A. . B. . C.  . D. . 4 3 3 2
-------------------- HẾT --------------------
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 Vấn đề 11
KHỐI TRÒN XOAY - THỂ TÍCH KHỐI TRÒN XOAY
MẶT TRỤ, MẶT NÓN – MẶT CẦU MẶT NÓN
Các yếu tố mặt nón:
Một số công thức: S
Đường cao: h SO . ( SO cũng
Chu vi đáy: p  2 r .
được gọi là trục của hình nón). Diện tích đáy: 2 S   r . Bán kính đáy: đ
r OA OB OM . 1 1 l h Thể tích: 2 V  . h S  . h r . l l Đường sinh: đ 3 3
l SA SB SM .
(liên tưởng đến thể tích khối chóp). A B r
Diện tích xung quanh: S   rl . O
Góc ở đỉnh: ASB . xq M
Thiết diện qua trục: SAB cân
Diện tích toàn phần:
Hình thành: Quay  vuông tại S. 2
S S S   rl   r .
SOM quanh trục SO , ta được tp xq đ
Góc giữa đường sinh và mặt mặt nón như hình bên   
đáy: SAO SBO SMO . h SO với:  . r OMMẶT TRỤ
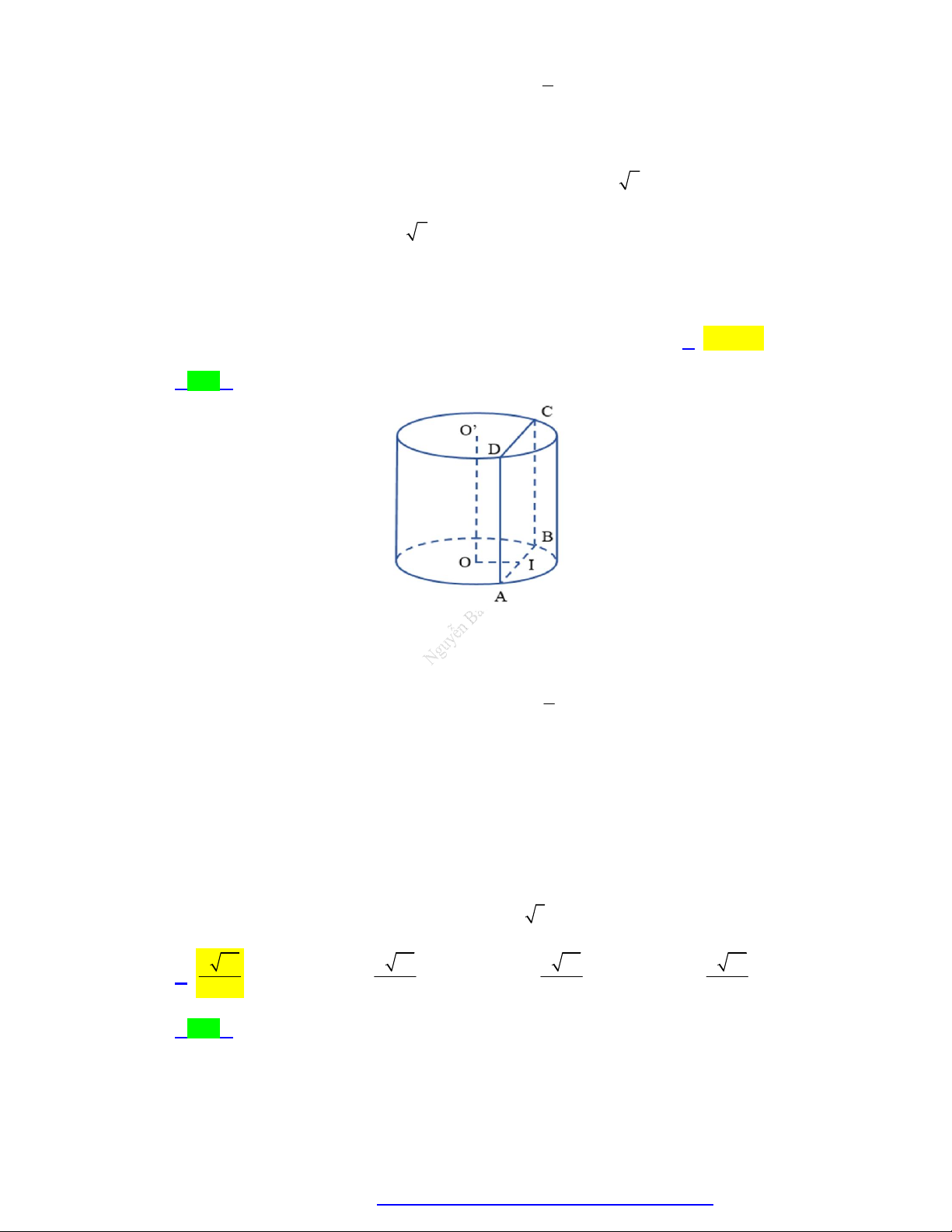
Các yếu tố mặt trụ:
Một số công thức:
Đường cao: h OO .
Chu vi đáy: p  2 r .
Đường sinh: l AD BC . Ta Diện tích đáy: 2 S   r . đ có: l h .    V h S h r . Bán kính đáy:
Thể tích khối trụ: 2 . . đ
r OA OB O C   O D  .
Diện tích xung quanh: S  2 r.h . xq
Trục (∆) là đường thẳng đi qua Diện tích toàn
hai điểm O, O . phần:
Hình thành: Quay hình chữ
Thiết diện qua trục: Là hình 2   
nhật ABCD quanh đường S S 2S 2 . r h 2 r . chữ nhật ABC . D tp xq đ
trung bình OO , ta có mặt trụ như hình bên.
Mặt cầu ngoại tiếp đa diện MẶT CẦU
Một số công thức:
Mặt cầu nội tiếp đa diện
Tâm I , bán kính
R IA IB IM .
Đường kính AB  2R .
Thiết diện qua tâm mặt cầu: Là
đường tròn tâm I , bán kính R .
Diện tích mặt cầu: 2 S  4 R . Mặt cầu ngoại
Mặt cầu nội tiếp
Hình thành: Quay đường 3
tiếp đa diện là mặt đa diện là mặt AB 4 R
tròn tâm I , bán kính R
Thể tích khối cầu: V  . cầu đi qua tất cả cầu tiếp xúc với 2 3 đỉnh của đa diện tất cả các mặt của
quanh trục AB , ta có mặt cầu đó. đa diện đó. như hình vẽ.
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489
CÂU HỎI MỨC ĐỘ NHẬN BIẾT Câu 1.
Diện tích xung quanh của hình nón có độ dài đường sinh l và bán kính đáy r bằng 1
A. 4 rl . B. 2 rl .
C. rl . D. rl . 3 Lời giải Chọn C
Áp dụng công thức diện tích xung quanh hình nón. Câu 2.
Cho khối nón có chiều cao h  3 và bán kính đáy r  4 . Thể tích của khối nón đã cho bằng A. 16 . B. 48 . C. 36 . D. 4 . Lời giải Chọn A 1 1
Ta có công thức thể tích khối nón 2
V  ..r .h  ..16.3  16 . 3 3 Câu 3.
Cho mặt cầu có bán kính R  2 . Diện tích của mặt cầu đã cho bằng 32 A. . B. 8 . C. 16 . D. 4 . 3 Lời giải Chọn C 2
S  4 R  16 Câu 4.
Diện tích xung quanh của hình trụ có độ dài đường sinh l và bán kính đáy r bằng 1
A. 4 rl .
B. rl .
C. rl .
D. 2 rl . 3 Lời giải Chọn D
Diện tích xung quanh của hình trụ S  2 rl . Câu 5.
Công thức tính diện tích mặt cầu bán kính r là 4 3 A. 2 S   r . B. 3 S   r . C. 2 S   r . D. 2 S  4 r . 3 4 Lời giải Chọn D
Công thức tính diện tích mặt cầu bán kính r là 2 S  4 r . Câu 6.
Cho hình nón tròn xoay có bán kính đường tròn đáy r , chiều cao h và đường sinh l .
Kết luận nào sau đây sai? 1 A. 2 V   r h . B. 2
S   rl   r . C. 2 2 2
h r l . D. S   rl . 3 tp xq Lời giải Chọn C S h l A O B r
Ta có tam giác SOB vuông tại O nên: 2 2 2 2 2 2
h r l h l r .
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 Câu 7.
Gọi l , h , r lần lượt là độ dài đường sinh, chiều cao và bán kính mặt đáy của hình nón. Diện tích xung quanh S của hình nón là xq 1 A. S   rh . B. S   rl . C. S  2 rl . D. 2 S   r h . xq xq xq xq 3 Lời giải Chọn B
Diện tích xung quanh S của hình nón là S   rl . xq xq Câu 8.
Cho khối nón có bán kính đáy R  3 và chiều cao h  3 . Thể tích của khối nón đã cho bằng A. 3 . B. 9 . C. 3 3 . D.  3 . Lời giải Chọn A 1 1
Ta có công thức thể tích khối nón 2
V  . .r .h  . .3.3  3 . 3 3 Câu 9.
Thể tích khối cầu bán kính 6 cm bằng A.   3 144 cm  B.   3 288 cm  C.   3 162 cm  D.   3 864 cm  Lời giải Chọn B 4 4
Vì thể tích cần tìm là 3 3 V
 .R   .6  288  3 cm  . 3 3
Câu 10. Tìm độ dài đường cao của hình trụ biết hình trụ có diện tích xung quanh là S và bán kính r ? xq S S xq xq 2 rr A. . B. . C. . D. . 2 rr S S xq xq Lời giải Chọn A
Bằng công thức tính diện tích xung quanh của hình trụ: (đường cao hình trụ h bằng đường sinh l ). S S  2 xqrh h  . xq 2 r
Câu 11. Diện tích xung quanh của hình trụ có độ dài đường sinh l và bán kính r bằng 1 A. 4rl . B. 2rl . C. rl . D. rl . 3 Lời giải Chọn A
Theo công thức tính diện tích xung quanh của hình trụ ta có S  2 rl xq
Câu 12. Cho hình trụ (T ) có thiết diện qua trục của hình trụ là hình vuông có cạnh bằng a . Diện tích
xung quanh của hình trụ đã cho bằng 2  a 2 3 a A. 2 2 a . B. . C. 2  a . D. . 2 2 Lời giải Chọn C
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489
Giả sử thiết diện qua trục của hình trụ là hình vuông ABCD có cạnh bằng a . AB a
Ta có: l AD a ; r OA   . 2 2 a
Vậy diện tích xung quanh của hình trụ là 2 S
 2 rl  2 . .a   a . xq 2
Câu 13. Cho khối nón có chiều cao h  6 và bán kính đáy bằng r . Biết bán kính đáy r bằng một nửa
chiều cao h . Thể tích của khối nón đã cho bằng A. 18 . B. 54 . C. 36 . D. 12 . Lời giải Chọn A h 6 Bán kính đáy: r    3 2 2 1 1
Ta có công thức thể tích khối nón 2
V  ..r .h  ..9.6  18 . 3 3
Câu 14. Diện tích của một mặt cầu bằng   2 16
cm  . Bán kính của mặt cầu đó là A. 2  cm . B. 2 cm . C. 4 cm . D. 2 3 cm . Lời giải Chọn B Ta có: 2 2
4 R  16  R  4  R  2(cm).
Câu 15. Diện tích xung quanh của hình trụ có diện tích một đáy là S và độ dài đường sinh l bằng? 
A. 2l S . B. 2Sl . C. 2l .
D. l S . S Lời giải Chọn A S
Ta có diện tích 1 đáy là: 2
S   r r  . 
Công thức tính diện tích xung quanh của hình trụ: S S  2 rl  2
.l  2.l .S . xq
Câu 16. Cho khối nón có chiều cao h  6 và bán kính đáy bằng r . Biết thể tích của khối nón đã cho
V  8 . Tính bán kính đáy. 1 4 A. r  2 . B. . C. . D. 4 . 3 3 Lời giải Chọn A 1 3V 3.8
Ta có công thức thể tích khối nón 2
V  ..r .h r    2 . 3  h .6
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Câu 17. Thể tích khối cầu có đường kính 2a bằng 3 4 a 3 32 a A. . B. 3 4 a . C. . D. 2 4.a . 3 3 Lời giải Chọn A 4 4 Theo công thức 3 3 V   r V   a . 3 3
Câu 18. Cho hình trụ có độ dài đường sinh l và bán kính r . Nếu độ dài đường sinh khối trụ tăng lên 3
lần, diện tích đáy không đổi thì thể tích của khối trụ sẽ tăng lên 1 A. 3 lần. B. lần. C. 9 lần. D. 27 lần. 3 Lời giải Chọn A
Ta có: đường cao hình trụ h bằng đường sinh l .
Thể tích khối trụ ban đầu: V B.h ( B là diện tích đáy; h là chiều cao).
Gọi V '  B '.h ' , với B '  B, h '  3h là thể tích sau khi tăng chiều cao của khối trụ lên 3 lần.
V '  B '.h '  . B 3h  3. . B h  3V .
Câu 19. Diện tích toàn phần của hình nón có độ dài đường sinh l và đường kính đáy 2r bằng 1 A. rl . B. 2
2 rl  4 r . C. 2
rl   r . D. rl . 3 Lời giải Chọn C
Vì đường kính đáy 2r nên bán kính đáy là r . Theo công thức tính diện tích toàn phần của hình nón ta có 2 S
  rl   r TP
Câu 20. Bán kính r của khối cầu có thể tích V    3 36 cm  là
A. r  3cm . B. r  27 cm . C. 3 r  48 cm . D. 3 r  9 cm . Lời giải Chọn A
Thể tích khối cầu được tính theo công thức: 4 3V 3 3 3 V   r r
r  27  r  3cm . 3 4
Câu 21. Tìm bán kính r của hình nón biết hình nón có diện tích xung quanh là S và độ dài đường sinh xq l ? S Sl 2l xq xq A. . B. . C. . D. . l 2l S S xq xq Lời giải Chọn A S
Bằng công thức tính diện tích xung quanh của hình nón: xq S
  rl r  . xql
Câu 22. Trong không gian cho tam giác vuông tại A , AB a và AC a 3 . Tính độ dài đường sinh
của hình nón có được khi quay tam giác ABC xung quanh trục AB .
A. l a 2 .
B. l  2a .
C. l a .
D. l a 3 . Lời giải Chọn B
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489
Khi quay tam giác ABC xung quanh trục AB , ta có:
Chiều cao h AB a ; bán kính R AC a 3 . Đường sinh 2 2 2 2
l h R a  3a  2a .
Câu 23. Diện tích xung quanh của hình trụ có bán kính đáy R  2 và đường sinh l  6 bằng A. 24 . B. 12 . C. 4 . D. 8 . Lời giải Chọn A
Diện tích xung quanh của hình trụ là S  2 rl  2 .2.6  24
Câu 24. Cho hình nón có bán kính đáy bằng 1, góc giữa đường sinh và trục của hình nón bằng 0 30 .
Diện tích xung quanh của hình nón đã cho bằng 4 3 2 3 A.  . B. 3 . C.  . D. 2 . 3 3 Lời giải Chọn D r Ta có 0 sin 30   l  2r . l 2 S
  .r.l  2 r  2 . xq
Câu 25. Cho khối trụ có chiều cao bằng bán kính đáy và diện tích thiết diện qua trục của khối trụ bằng
16. Thể tích khối trụ đã cho bằng 64 16 2 A. 64 . B. . C. 16 2 . D. . 3 3 Lời giải Chọn A 1
Diện tích thiết diện qua trục của khối trụ là 2 S  .
R 2R R . 2 Theo giả thiết, ta có 2
R  16  R  4  h  4.
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Thể tích của khối trụ bằng 2
V hR  64.
Câu 26. Hình trụ có thiết diện qua trục là một hình vuông có cạnh bằng 20cm. Thể tích của khối trụ tương ứng bằng: A. 3 800 cm . B. 3 8000 cm . C. 3 400 cm . D. 3 2000 cm . Lời giải Chọn D
Ta có thiết diện qua trục của hình trụ là hình vuông có cạnh bằng 20cm, do đó bán kính của
hình trụ r  20 cm, chiều cao của hình trụ h  20 cm. Suy ra 2 2 3
V   r h   .10 .20  2000 cm .
CÂU HỎI MỨC ĐỘ THÔNG HIỂU
Câu 27. Trong không gian cho hình chữ nhật ABCD , AB a, AC  2a . Khi quay hình chữ nhật
ABCD quanh cạnh AD thì đường gấp khúc ABCD tạo thành một hình trụ. Diện tích xung
quanh của hình trụ đó bằng 2 2 a  2 a  A. 2 4 a  . B. . C. . D. 2 2 3 a  . 3 3 Lời giải Chọn D
Hình trụ được tạo thành có 2 2 h
AC AB a 3, r a nên 2 S
 2 rh  2 3a . xq
Câu 28. Trong không gian, cho tam giác ABC vuông tại A , AB a và AC  2a . Khi quay tam giác
ABC quanh cạnh góc vuông AB thì đường gấp khúc ACB tạo thành một hình nón. Diện tích
xung quanh hình nón đó bằng A. 2 5 a . B. 2 5 a . C. 2 2 5 a . D. 2 10 a . Lời giải Chọn C 2 2 BC
AB AC a 5 .
Diện tích xung quanh hình nón cần tìm là 2
S   . AC . BC   .2a.a 5  2 5 a .
Câu 29. Cho hình trụ có bán kính đáy bằng 3 . Biết rằng khi cắt hình trụ đã cho bởi một mặt phẳng qua
trục, thiết diện thu được là một hình vuông. Diện tích xung quanh của hình trụ đã cho bằng A. 18 . B. 36 . C. 54 . D. 27 . Lời giải Chọn B
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
NGUYỄN BẢO VƯƠNG - 0946798489
Giả sử thiết diện qua trục của hình trụ là hình vuông ABCD .
Theo giả thiết ta có bán kính đáy của hình trụ r  3  h AD DC  2r  6  l .
Vậy diện tích xung quanh của hình trụ là: S
 2 rl  2 .3.6  36 . xq
Câu 30. Cho một chiếc cốc hình nón chứa đầy trà như hình vẽ. Người X uống một phần trà sao cho 1
chiều cao của nó giảm đi
so với chiều cao của trà trong cốc. Người Y uống phần trà còn lại 3
trong cốc. Khi đó khẳng định nào đúng.
A. Người X uống lượng trà bằng 5,75 lần lượng trà của người Y uống.
B. Hai người X và Y uống lượng trà bằng nhau.
C. Người X uống lượng trà bằng 2,375 lần lượng trà của người Y uống.
D. Người X uống lượng trà bằng một nửa lượng trà của người Y uống. Lời giải Chọn C 1 Gọi 2
V   R h là thể tích trà có trong chiếc cốc hình nón đó ( với R là bán kính đáy hình nón 3
và h là chiều cao hình nón). 2 1  2R  2h 8
Sau khi người X uống thì lượng trà còn lại người Y uống là V   . 2   R h . Y   3  3  3 81 19
Khi đó người X đã uống một lượng trà bằng V V V 2   R h . X Y 81 V 19 Vậy X   2, 375 . V 8 Y
Câu 31. Cắt hình trụ T  bằng một mặt phẳng song song với trục và cách trục một khoảng bằng 2cm
được thiết diện là một hình vuông có diện tích bằng 2
16cm . Thể tích của T  là A.   3 32 cm  . B.   3 16 cm  . C.   3 64 cm  . D.   3 8 cm  . Lời giải Chọn A
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Giả sử thiết diện là hình vuông ABBA như hình vẽ.
Với O I  2cm và 2 S
AB  16  AB  4 . cm ABBA 2  AB  Ta có 2
r OA OI   2 2   cm .  2  2 Mà 2 h A
A   V S h   r h   cm . T d      3 4 . . 2 2 .4 32 
Câu 32. Cho hai tấm tôn hình chữ nhật đều có kích thước 1, 5m  8m . Tấm tôn thứ nhất được chế tạo
thành một hình hộp chữ nhật không đáy, không nắp, có thiết diện ngang là một hình vuông
(mặt phẳng vuông góc với đường cao của hình hộp và cắt các mặt bên của hình hộp theo các
đoạn giao tuyến tạo thành một hình vuông) và có chiều cao 1, 5m ; còn tấm tôn thứ hai được chế
tạo thành một hình trụ không đáy, không nắp và cũng có chiều cao 1, 5m . Gọi V , V theo thứ 1 2 V
tự là thể tích của khối hộp chữ nhật và thể tích của khối trụ. Tính tỉ số 1 . V2 V VVVA. 1   . B. 1  . C. 1  . D. 1  . V V 4 V 2 V 3 2 2 2 2 Lời giải Chọn B
Thiết diện ngang của hình hộp chữ nhật là hình vuông nên hình hộp có đáy là hình vuông cạnh 8 là  
2 m , chiều cao là 1,  5 m 2
V  2 .1, 5  6 3 m . 1  4 4
Hình trụ có đáy là hình tròn có chu vi là 
8 m .Suy ra bán kính hình tròn đáy là .  2  4  24
Thể tích khối trụ là V   . .1, 5  . 2       V 6  Vậy 1   . V 24 4 2 
Câu 33. Một hình trụ có bán kính đáy r  5a và khoảng cách giữa hai đáy bằng 7a . Cắt khối trụ bởi
một mặt phẳng song song với trục và cách trục một khoảng bằng 3a . Diện tích của thiết diện được tạo nên bằng A. 2 56a . B. 2 35a . C. 2 21a . D. 2 70a . Lời giải Chọn A
Theo đề AA  BB  7a;OA r  5a;OI  3a .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
NGUYỄN BẢO VƯƠNG - 0946798489
Áp dụng định lý Py-ta-go tính 2 2
IA OA OI  4a suy ra AB  8a .
Diện tích hình chữ nhật 2 ABB A    8 .
a 7a  56a .
Câu 34. Cho một cái bể nước hình hộp chữ nhật có ba kích thước 2 m ,3m ,2m lần lượt là chiều dài,
chiều rộng, chiều cao của lòng trong đựng nước của bể. Hàng ngày nước ở trong bể được lấy ra
bởi một cái gáo hình trụ có chiều cao là 5cm và bán kính đường tròn đáy là 4cm . Trung bình
một ngày được múc ra 170 gáo nước để sử dụng (Biết mỗi lần múc là múc đầy gáo). Hỏi sau
bao nhiều ngày thì bể hết nước biết rằng ban đầu bể đầy nước? . A. 280 ngày. B. 282 ngày. C. 281 ngày. D. 283 ngày. Lời giải Chọn C
Thể tích nước được đựng đầy trong bể là V    3 2.3.2 12 m  . 
Thể tích nước đựng đầy trong gáo là 2 V     cmm . g  3   3 4 .5 80  12500
Một ngày bể được múc ra 170 gáo nước tức là trong một ngày lượng nước được lấy ra bằng: 17 V  170.V   m . m g  3  1250 Ta có V 12 
 280,8616643  sau 281 ngày bể sẽ hết nước. V 17 m  1250
Câu 35. Trong không gian, cho hình chữ nhật ABCD , AB  2a và AC  3a . Khi quay hình chữ nhật
ABCD quanh cạnh AB thì đường gấp khúc BCDA tạo thành một hình trụ. Diện tích xung
quanh của hình trụ đó bằng A. 2 6 5 a . B. 2 12 a . C. 2 4 5 a . D. 2 20 a . Lời giải Chọn C
Khi quay hình chữ nhật ABCD quanh cạnh AB thì đường gấp khúc BCDA tạo thành một
hình trụ có chiều cao h AB  2a , đáy là hình tròn bán kính 2 2 r BC
AC AB a 5 ,
Khi đó diện tích xung quanh của là 2 S
 2 rh  2 .2 .
a a 5  4 5 a . xq
Câu 36. Trong không gian, cho tam giác ABC vuông tại A , AB  2a và AC  3a . Khi quay tam giác
ABC quanh cạnh góc vuông AB thì đường gấp khúc ACB tạo thành một hình nón. Diện tích
toàn phần của hình nón đó bằng A. 2 3 13 a . B. 2 2
3 13 a  4 a . C. 2 2
3 13 a  9 a . D. 2 42 a . Lời giải Chọn C
Khi quay tam giác ABC quanh cạnh góc vuông AB thì đường gấp khúc ACB tạo thành một
hình nón có bán kính đường tròn đáy là r AC  3a, đường sinh 2 2 l BC
AB AC a 13.
Khi đó diện tích xung quanh của hình nón là 2 S
  rl  3 13 a . xq
Khi đó diện tích toàn phần của hình nón là 2 2
S  3 13 a  9 a . tp
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Câu 37. Cho hình trụ (T ) có thiết diện qua trục của hình trụ là một hình chữ nhật có diện tích bằng
48 và chu vi bằng 28 . Biết chiều dài của hình chữ nhật lớn hơn đường kính mặt đáy của hình
trụ T  . Diện tích xung quanh của hình trụ đã cho bằng A. 96 . B. 48 . C. 24 . D. 32 . Lời giải Chọn B
Giả sử thiết diện qua trục của hình trụ là hình chữ nhật ABCD .
Gọi l và r là độ dài đường sinh và bán kính đáy của hình trụ, l  2r  0 (*) .  rl   rr   2 2 48 2 (14 2 ) 48
r  7r  12  0
r  3;l  8(t / m(*)) Ta có       
2(2r l)  28 l  14    2r l  14  2r r  4;l    6 (lo¹i)
Vậy diện tích xung quanh của hình trụ là S
 2 rl  2.3.8  48 . xq
Câu 38. Cho hình trụ có thiết diện qua trục là một hình vuông. Thiết diện của hình trụ tạo bởi mặt phẳng
song song và cách trục một khoảng bằng a có diện tích bằng 2 8a
3 . Thể tích của khối trụ là 3 16 a A. 2 16 a . B. 3 16a . C. 3 32 a . D. . 3 Lời giải Chọn B
Gọi R là bán kính đáy hình trụ, do thiết diện qua trục là một hình vuông nên l  2R .
Thiết diện của hình trụ tạo bởi mặt phẳng song song và cách trục một khoảng bằng a là hình chữ nhật AB D
C khi đó OI a với I là trung điểm BC ta có 2 2 2 2 IC
R a BC  2 R a .
Diện tích hình chữ nhật là 2 2 2 SA .
B BC  4R R a  8a 3 . AB D C 4 2 2 2
R R a 12a  0   2 2 R a  2 2 4
R  3a   0  R  2a từ đó h l  2R  4a . Thể tích khối trụ là 2 3
V   R h 16 a .
Câu 39. Cho hình nón có bán kính đáy r  3 . Biết rằng khi cắt khối nón đó bằng một mặt phẳng qua
trục của nó, ta được thiết diện là một tam giác đều. Diện tích xung quanh của hình nón bằng
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
NGUYỄN BẢO VƯƠNG - 0946798489 A. 6 3 . B. 36 . C. 18 . D. 9 . Lời giải Chọn C
Giả sử thiết diện qua trục của hình nón là tam giác đều SAB .
Gọi l là độ dài đường sinh của hình nón. OA 3
Ta có: r OA  3 ; l SA    6 . 0 sin 30 1 / 2
Vậy diện tích xung quanh của hình nón là: S
  rl   .3.6  18 . xq
Câu 40. Trong không gian, cho tam giác ABC vuông tại A , AB  3a và BC  5a . Khi quay tam giác
ABC quanh cạnh góc vuông AB thì đường gấp khúc ACB tạo thành một hình nón. Diện tích
xung quanh hình nón đó bằng A. 2 20a . B. 2 15 a . C. 2 20 a . D. 2 80 a . Lời giải Chọn C
Khi quay tam giác ABC quanh cạnh góc vuông AB thì đường gấp khúc ACB tạo thành một
hình nón có bán kính đường tròn đáy là 2 2 r AC
BC AB  4a , đường sinh l BC  5a
Khi đó diện tích xung quanh của hình nón là 2 S
  rl  20 a . xq
Câu 41. Thiết diện qua trục của một hình nón là một tam giác vuông cân có cạnh góc vuông bằng a .
Diện tích xung quanh của hình nón bằng 2  a 2 2  a A. 2  a 2 . B. . C. 2  a . D. . 2 2 Lời giải Chọn B
Giả sử thiết diện qua trục của hình nón là tam giác SAB vuông cân đỉnh S .
Gọi l và r lần lượt là độ dài đường sinh và bán kính đáy của hình nón.
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 2
Ta có: l SA a ; 0 r OA  . SA sin 45  . a . 2 2 a 2  a 2
Vậy diện tích xung quanh của hình nón là: S   rl   . .a  . xq 2 2
Câu 42. Cho khối nón có độ dài đường sinh bằng 5a và đường cao bằng 4a . Thể tích khối nón bằng 3 80 a A. . B. 3 15a . C. 3 12a . D. 3 36a . 3 Lời giải Chọn C Theo giả thiết: 2 2
l  5a, h  4a r l h  3a 1 1
Suy ra V   r h   3a2 2 3
4a  12 a . 3 3 3 1 1 8 a
V   r h   2a2 2 2a  . 3 3 3
Câu 43. Một chi tiết máy là phần còn lại của một khối trụ có bán kính đáy r sau khi đã đục bỏ phần bên r
trong là một khối trụ có bán kính đáy (tham khảo hình vẽ). 2
Biết thể tích khối trụ nhỏ bị đục bỏ bằng  3
20 cm  . Thể tích của khối chi tiết máy đó là A.  3 40 cm  . B.  3 60 cm  . C.  3 80 cm  . D.  3 70 cm  . Lời giải Chọn B
Gọi chiều cao khối trụ là h .
Thể tích khối chi tiết máy: 2
V   r h  20 2  r  1
Mà thể tích khối trụ nhỏ bên trong là 2 2  h
r h  20   r h  80    2  4 Vậy V     3 80 20 60 cm
Câu 44. Cho khối nón có thiết diện qua trục là tam giác đều SAB cạnh a . Thể tích khối nón bằng
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
NGUYỄN BẢO VƯƠNG - 0946798489 3  a 3 3  a 3  a 3  a 3 A. . B. . C. . D. . 8 24 12 24 Lời giải Chọn D 2 3 a a 3 1 1  a a 3  a 3
Tam giác SAB đều cạnh a nên: 2 OB  , SO   V   r h      . 2 2 3 3  2  2 24
Câu 45. Một khối đồ chơi gồm hai khối cầu  H , H tiếp xúc với nhau, lần lượt có bán kính tương 1   2  1
ứng là r , r thỏa mãn r
r (tham khảo hình vẽ). 1 2 2 1 2
Biết rằng thể tích của toàn bộ khối đồ chơi bằng 3
180cm . Thể tích của khối cầu  H bằng 1  A. 3 90 cm B. 3 120 cm C. 3 160 cm D. 3 135 cm Lời giải Chọn C 4
Thể tích khối  H là 3 V   r 1  1 1 3 4
Thể tích khối  H là 3 V   r 2  2 2 3 3 4 4 4 4  1  9  4  9
Tổng thể tích 2 khối là 3 3 3 3
V V V
r   r   r   r   rV 1 2 1 2 1  1   1  1 3 3 3 3  2  8  3  8 9
Suy ra V  180  V  160 1 1 8
Câu 46. Cho khối nón có thiết diện qua trục là tam giác SAB vuông tại S với cạnh SA a . Thể tích khối nón bằng 3  a 2 3  a 3  a 3  a 2 A. . B. . C. . D. . 12 3 12 4 Lời giải Chọn A
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Theo tính chất của hình nón ta có SA SB l . a 2
Vậy tam giác SAB vuông cân tại S suy ra SA SB a, AB a 2  SO OB  2 2 3 1 1  a 2  a 2  a 2 Vậy 2
V   r h      . 3 3  2  2 12  
Câu 47. Một chi tiết máy gồm 3 khối trụ có cùng chiều cao h gắn với nhau (như hình vẽ).
Khối trụ lớn có bán kính đáy r lớn gấp đôi bán kính đáy của hai khối trụ nhỏ (hai khối trụ nhỏ
bằng nhau). Biết thể tích của cả khối chi tiết máy đó bằng 3
90 cm . Tính thể tích của khối trụ lớn ở giữa. A. 3 30 cm . B. 3 45cm . C. 3 70 cm . D. 3 60 cm . Lời giải Chọn D
Thể tích khối trụ lớn ở giữa: 2 V   r h 1 2  r  3 3
Tổng thể tích chi tiết máy: 2 2
V   r h  2 h   r h V   1  2  2 2 3
Suy ra: V  90 . Do đó: V  60 1 2 1
Câu 48. Một chiếc bánh sinh nhật gồm ba khối trụ  H , H , H xếp chồng lên nhau, lần lượt có bán 1   2   3 
kính đáy và chiều cao tương ứng là r , h ; r , h ; r , h thỏa mãn r  2r  3r , h  2h h (tham 1 1 2 2 3 3 1 2 3 1 2 3 khảo hình vẽ).
Biết rằng thể tích của khối  H bằng 3
80cm . Thể tích của toàn bộ chiếc bánh sinh nhật bằng 3  A. 3 890 cm . B. 3 980 cm . C. 3 900 cm . D. 3 800 cm . Lời giải Chọn A
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
NGUYỄN BẢO VƯƠNG - 0946798489
Thể tích khối  H là 2
V   r h  80 3  3 3 3 2  3   1  9
Thể tích khối  H là 2
V   r h   r hV 2  2 2 2  3   3  3  2   2  8
Thể tích khối  H là V   r h   3r h  9V 1 1 1  3 2 2 1  3 3 9 89
Thể tích toàn bộ chiếc bánh sinh nhật bằng: V V V  9V V V V  890 1 2 3 3 3 3 3 8 8
Câu 49. Cho khối nón có thể tích bằng 3
3 a và đường cao bằng a 3 . Độ dài đường sinh của khối nón đã cho bằng A. a 6 . B. 2a . C. a 2 . D. a . Lời giải Chọn A 3 3V 3 3 a
Bán kính đáy của hình nón: r    a 3 .  ha 3 2 2
Độ dài đường sinh của khối nón là: l  a 3  a 3  a 6 .
Câu 50. Một khối đồ chơi gồm một hình cầu  H bán kính R và một hình nón  H xếp chồng lên 2  1  1 3
nhau, lần lượt có bán kính đáy và đường sinh là r, l thỏa mãn r l và l  . R (hình vẽ). 2 2
Biết tổng diện tích mặt cầu  H và diện tích toàn phần của hình nón  H là 3 91cm . Tính 2  1 
diện tích của khối cầu  H . 1  104 26 A. 3 16cm . B. 3 cm . C. 3 64cm . D. 3 cm . 5 5 Lời giải Chọn C
Diện tích toàn bộ khối đồ chơi là 2 2 S SS
 4 .R   .r.l   .r ( 1 H ) tp ( H2 ) 2  3   3   3  91 2  4 .R   . R . R   . R  .S       ( 1 H )  4   2   4  64 3  S  64 cm . ( 1 H )  
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Câu 51. Cho hình trụ có bán kính đáy bằng 1 cm . Một mặt phẳng qua trục của hình trụ và cắt hình trụ
theo thiết diện là hình vuông. Tính thể tích của khối trụ đã cho. 16 A. 3 8 cm . B. 3 2 cm . C. 3 cm . D. 3 16 cm . 3 Lời giải Chọn B
Thiết diện qua trục của hình trụ là hình vuông ABCD .
Khi đó ta có: AB  2r  2.1  2cm , h l AD AB  2cm .
Vậy thể tích của khối trụ đã cho là: 2 2 3
V   r h   .1 .2  2 cm .
Câu 52. Thể tích của khối cầu ngoại tiếp bát diện đều có cạnh bằng a 2 là: 3 2 a 3 2 a 3 4 2 a 3 4 a A. . B. . C. . D. . 6 3 3 3 Lời giải Chọn D
Xét khối bát diện đều: a 2 4
Khối cầu ngoại tiếp bát diện đều có tâm O , bán kính 3 R   a V   a . 2 3
Câu 53. Cho hình nón có thiết diện qua trục là tam giác vuông có cạnh huyền a 2 . Tính diện tích xung
quanh S của hình nón đó xq 2  a 2 2  a 2 2  a 2 2  a 2 A. s  . B. s  . C. s  . D. s  . xq 6 xq 3 xq 2 xq 3 Lời giải Chọn C
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
NGUYỄN BẢO VƯƠNG - 0946798489 2 AB a 2 a 2  a 2
Ta có: SA SB    a S   .H . B SB   . .a  . xq 2 2 2 2
Câu 54. Trong không gian cho tứ giác ABCD là một nửa lục giác đều nội tiếp đường tròn đường kính
CD  2a . Khi quay tứ giác ABCD quanh cạnh AB thì tạo thành một khối tròn xoay. Thể
tích khối tròn xoay đó bằng 5 3 A. 3  a . B. 3 2 a . C. 3  a . D. 3  a . 4 2 Lời giải Chọn C
Vẽ hình chữ nhật DFEC .
Gọi V là thể tích khối trụ tròn xoay sinh ra khi quay hình chữ nhật DFEC quanh cạnh FE . 1
V là thể tích khối nón tròn xoay sinh ra khi quay hình tam giác vuông DFA quanh cạnh FA . 2
Khi đó, thể tích khối tròn xoay cần tìm là V V  2V 1 2 a 3 a
Ta có DF OI  , AF AI  . 2 2 2 2 3  a 3  3 a 3 1 1  a 3  aa 2
V   r 2a   2   2a  , V   r h      . 1 2 2 2   3 3 2 2 8   3 3 3 3 aa 5 a
V V  2V   2  . 1 2 2 8 4
Câu 55. Cho một hình nón có góc ở đỉnh 60 , bán kính đáy bằng a . Diện tích toàn phần hình nón đó là A. 2  a . B. 2 3 a . C. 2 2 a . D. 2 3 a . Lời giải Chọn B
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 S 30° a A O
Gọi S, O lần lượt là đỉnh và tâm đáy của hình nón, A là điểm trên đường tròn đáy, theo giả  AOa
thiết ta có: sin ASO   sin 30  SA   2a SA 1 2 2
S   OA SA   OA    2 a a a  2 . . . .2  3 a tp .
Câu 56. Cho hình lập phương ABC . D AB CD
  cạnh bằng a . Thể tích khối cầu có tâm A và tiếp xúc
với đường thẳng AC bằng 3 2 a 3 8 6 a 3 3 a A. . B. . C. . D. 3 6 a . 3 27 2 Lời giải Chọn B.
Kẻ AH AC , khi đó AH là bán kính mặt cầu tâm A tiếp xúc với đường thẳng AC .
Trong tam giác vuông AAC , ta có 1 1 1 1 1 3 2 2a a 6      2  AH   AH  . 2 2 2 2 2 2 AH AA AC a 2a 2a 3 3 3 3 4 4  a 6  8 6 a Vậy 3 V   AH      . 3 3  3  27  
Câu 57. Cho hình chóp tứ giác đều S ABCD có cạnh đáy bằng a , diện tích mỗi mặt bên bằng 2 a . Thể
tích khối nón đỉnh S và đường tròn đáy nội tiếp hình vuông ABCD bằng: 15 15 15 15 A. 3  a . B. 3  a . C. 3  a . D. 3  a . 24 8 12 18 Lời giải Chọn A
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
NGUYỄN BẢO VƯƠNG - 0946798489 S A D O M B C
Gọi M là trung điểm CD. h SO 2 2 1 1 1 a a 2 2 2 2 2 2 S  .SM .CD
SO OM .CD  . h
.a a h   4a SCD 2 2 2 4 4 15  h a 2 a
Đường tròn đáy nội tiếp hình vuông ABCD nên bán kính là R  . 2 2 1 1  a  15 15 2 3
V   R h   . . a   a   3 3  2  2 24
Câu 58. Cho hai khối cầu có bán kính lần lượt bằng a và 2a . Tỉ số giữa thể tích của khối cầu nhỏ với
thể tích của khối cầu lớn bằng 1 1 A. . B. 4 . C. . D. 8 . 4 8 Lời giải Chọn C 4 4 4
Thể tích của khối cầu nhỏ có bán kính a là: V   R   a3 3 3   a . 1 1 3 3 3 4 4 4 32
Thể tích của khối cầu lớn có bán kính 2a là: V   R   2a3 3 3 3   .8a   a . 2 2 3 3 3 3 4 3  a V 1
Tỉ số giữa thể tích của khối cầu nhỏ với thể tích của khối cầu lớn bằng: 1 3   . V 32 3 8 2  a 3
Câu 59. Cho hình trụ có chiều cao bằng bán kính đáy và bằng 5 cm. Mặt phẳng   song song với trục,
cắt hình trụ theo một thiết diện có chu vi bằng 26 cm. Khoảng cách từ   đến trục của hình trụ bằng A. 4 cm. B. 5 cm. C. 2 cm. D. 3 cm. Lời giải Chọn D
Gọi O và O là tâm của hai đường tròn đáy của hình trụ.
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Vì mặt phẳng   song song với trục OO nên   cắt hình trụ theo thiết diện là một hình chữ
nhật, gọi là ABCD với AB là dây cung của đường tròn O , CD là dây cung của đường tròn O .
Hình chữ nhật ABCD có chu vi bằng 26 cm và có AD  5 cm nên AB  8 cm .
Gọi M là trung điểm của AB . Khi đó OM AB và OM AD nên OM    .
Do đó d OO   2 2 ,
OM OA MA  3 cm .
Câu 60. Cho tam giác vuông cân ABC có AB BC a 2 . Khi quay tam giác ABC quanh đường
thẳng đi qua B và song song với AC ta thu được một khối tròn xoay có thể tích bằng 3 2 a 3 4 a A. 3 2 a . B. . C. . D. 3  a . 3 3 Lời giải Chọn A
Ta có AC  2a và OA a .
Thể tích khối trụ khi quay OACO ' quanh OO ' là 2 3
V   OA .AC  2 a . 1 3 1  a
Thể tích khối nón khi quay OAB quanh OB là 2
V   OA .OB  . 2 3 3 3 4 a
Thể tích khối tròn xoay khi quay tam giác ABC quanh OO ' là V V  2V  . 1 2 3
Câu 61. Một hình trụ có diện tích xung quanh bằng 64 và thiết diện qua trục của hình trụ này là một
hình vuông. Thể tích hình trụ đó bằng A. 512 . B. 128 . C. 64 . D. 256 . Lời giải Chọn B O' D C h r B A r O
Gọi r, h lần lượt là bán kính đáy và chiều cao hình trụ.
Vì thiết diện qua trục của hình trụ là hình vuông nên ta có h  2r .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
NGUYỄN BẢO VƯƠNG - 0946798489 Ta có S
 64  2 rh  64  2 .r.2r  64 2  4 .r  64 2
r  16  r  4 . xq
Với r  4 suy ra h  2r  2.4  8 .
Vậy thể tích của hình trụ là 2 V   r h 2
  .4 .8  128 . Chọn B
Câu 62. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a , cạnh bên hợp với đáy góc 60 . Hình
nón  N  có đỉnh S , đáy là đường tròn nội tiếp tứ giác ABCD . Diện tích xung quanh của hình
nón  N  bằng 2 7 a 2 2 a 2 3 a 2  a A. . B. . C. . D. . 4 3 2 2 Lời giải Chọn A S A D H M B C AC a 2
Ta có ABCD là hình vuông cạnh a nên 2 2 AC
AB BC a 2  AH   . 2 2
Mà SH   ABCD  SA ABCD   ,  SAH  60 . a 6
Suy ra SH AH . tan 60  . 2 AB a
Bán kính hình nón  N  là R HM   2 2 a 7 Do đó đường sinh 2 2 l SM SH HM  . 2 2 7 a
Vậy diện tích xung quanh hình nón  N  là: S   Rl  . xq 4
Câu 63. Trong không gian, cho hình chữ nhật ABCD , AB a, AC  2a . Khi quay hình chữ nhật
ABCD quanh cạnh AD thì đường gấp khúc ABCD tạo thành một hình trụ. Diện tích xung
quanh của hình trụ đó bằng 2  a 2 2 a A. . B. . C. 2 4 a . D. 2 2 3 a . 3 3 Lời giải Chọn D
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Khi quay hình chữ nhật ABCD quanh cạnh AD thì đường gấp
khúc ABCD tạo thành một hình trụ có:
Bán kính đáy: R AB a . Chiều cao: 2 2 2 2 h AD
AC DC  4a a  3 . a
 Diện tích xung quanh của hình trụ đã cho: 2 S
 2 Rh  2 3 a . xq
Câu 64. Cho hình nón có đường cao a . Biết rằng khi cắt hình nón đã cho một mặt phẳng đi qua đỉnh a
của hình nón và cách tâm của đáy hình nón một khoảng
, thiết diện thu được tạo thành một 3
tam giác vuông. Thể tích khối nón được giới hạn bởi hình nón đã cho bằng 3 5 a 3  a 3 4 a 3 5 a A. . B. . C. . D. . 12 3 9 9 Bài giải Chọn A
Gọi B, C là giao điểm của mặt phẳng và đường tròn đáy, I là trung điểm của BC và OH là
khoảng cách từ tâm O đến  SBC . 1 1 1 1 1 1 2a Ta có:       OI  . 2 2 2 2 2 2 OH OI OSa OI a 4     3  3 2a 3 2a 5a 2 2 2 2 SI SO OI
BC  2SI
r OB OI IB  4 2 2 2 3 1  5a  5 a V     a  . 3  2  12  
Câu 65. Khối tròn xoay sinh bởi một tam giác đều cạnh a (kể cả điểm trong) khi quay quanh một
đường thẳng chứa một cạnh của tam giác đó có thể tích bằng
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
NGUYỄN BẢO VƯƠNG - 0946798489 3  a 3  a 3 3  a 3  a 3 A. . B. . C. . D. . 8 6 4 12 Lời giải Chọn C
Giả sử tam giác ABC đều cạnh a có H là trung điểm AC .
Khi quay tam giác ABC quanh cạnh AC ta được khối tròn xoay có thể tích bằng 2 lần thể
tích hình nón tạo thành khi quay tam giác AHB quanh trục AH , do đó thể tích cần tìm bằng 2 3 1 2  a 3  aa 2
2   BH . AH      . 3 3  2  2 4  
Câu 66. Cho hình chóp đều S.ABCD có AB a , cạnh bên hợp với đáy góc 0 45 . Diện tích xung quanh
của hình nón đỉnh S với đáy là đường tròn nội tiếp hình vuông bằng 2  a 2  a 3 2  a A. . B. . C. . D. 2 2 a . 2 4 4 Lời giải Chọn B a a 2 a 3 Ta có 2 2 r
, HD SH h
l r h  2 2 2 2  a 3 S  . 4
Câu 67. Một hình nón có thiết diện qua trục là một tam giác vuông cân có cạnh góc vuông bằng a .
Diện tích xung quanh của hình nón bằng: 2  a 2 2 2 a 2 2  a 2 A. . B. . C. . D. 2  a 2 . 4 3 2 Lời giải Chọn C
Trang 24 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Thiết diện qua trục hình nón là ABC  ABC vuông cân tại A . BC AC 2 a 2
Do đó l AC a ; r    . 2 2 2 2  a 2
Diện tích xung quanh hình nón là S   rl  . 2
Câu 68. Cho hình chữ nhật ABCD có AC  2a 2 và 
ACB  45 . Quay hình chữ nhật ABCD quanh
cạnh AB thì đường gấp khúc ADCB tạo thành hình trụ. Diện tích toàn phần S của hình trụ là tp A. 2
S  16 a . B. 2
S  10 a . C. 2
S  12 a . D. 2
S  8 a . tp tp tp tp Lời giải Chọn D
Hình chữ nhật ABCD có AC  2a 2 và 
ACB  45 nên nó là hình vuông.
AB BC CD DA  2a .
Khi quay hình chữ nhật quanh cạnh AB ta được hình trụ có chiều cao h AB  2a và bán
kính đáy là r BC  2a . 2
S  2 rl  2 rh  8 a . tp
Câu 69. Trong không gian, cho tam giác ABC vuông tại A , AB a , 
ABC  60 . Tính độ dài đường
sinh l của hình nón, nhận được khi quay tam giác ABC quanh trục AC .
A. l a 2 .
B. l  2a .
C. l a .
D. l a 3 . Lời giải Chọn B
Khi quay tam giác ABC quanh trục AC thì cạnh huyền BC tạo thành đường sinh, có độ dài AB a l BC    2a . cos B cos 60
Câu 70. Trong không gian, cho hình chữ nhật ABCD có AB  4, AC  5 . Gọi M , N lần lượt là trung
điểm của AD và BC . Quay hình chữ nhật đó xung quanh trục MN , ta được một hình trụ.
Tính diện tích toàn phần S của hình trụ đó. TP 33 81 A. S  8 . B. S   . C. S   . D. S  24 . TP TP 2 TP 2 TP Lời giải Chọn B
Ta có: AB  4; AC  5  BC  3 . AD BC 3
Khi quay hình chữ nhật ABCD quanh trục MN ta được hình trụ có: r    . 2 2 2
Chiều cao hình trụ h AB  4 .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
NGUYỄN BẢO VƯƠNG - 0946798489 3  3  33
Vậy S  2 r(r l)  2 r(r h)  2   4  . tp   2  2  2
Câu 71. Cho tứ diện đều ABCD có cạnh bằng 4 . Tính diện tích xung quanh S của hình trụ có một xq
đường tròn đáy là đường tròn nội tiếp tam giác BCD và chiều cao bằng chiều cao của tứ diện ABCD . 16 2 16 3 A. S  . B. S  8 2 . C. S  . D. S  8 3 . xq 3 xq xq 3 xq Lời giải Chọn A. 2 4 3
Tam giác BCD đều cạnh 4 có diện tích: S   4 3 . BCD 4 3 a 2 16
Áp dụng công thức tính nhanh thể tích khối tứ diện đều cạnh a là V   V  2 . 12 ABCD 3 3V 4 2
 Độ dài đường cao khối tứ diện: ABCD h   . SBCD 3 S 4 3 2 3
Bán kính đáy đường tròn nội tiếp tam giác BCD : r    . p 6 3 2 3 4 2 16 2
Vậy diện tích xung quanh của hình trụ là: S  2 rh  2 . .  . xq 3 3 3
Câu 72. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a , góc giữa cạnh bên SA và mặt phẳng
đáy bằng 30 . Tính diện tích xung quanh S của hình trụ có một đường tròn đáy là đường xq
tròn nội tiếp hình vuông ABCD và chiều cao bằng chiều cao của hình chóp S.ABCD . 2  a 6 2  a 3 2  a 6 2  a 3 A. S  . B. S  . C. S  . D. S  . xq 6 xq 6 xq 12 xq 12 Lời giải Chọn A. S D C O A B
Gọi O là giao điểm của AC và BD . Khi đó SO   ABCD , AC a 2 . 
Góc giữa SA và mặt phẳng đáy bằng 30  SAO  30 . a 2 3 a 6 SO  . AO tan 30  .  . 2 3 6 a 6
Vậy chiều cao của hình trụ là h  . 6
Trang 26 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 a
Bán kính của đường tròn nội tiếp hình vuông ABCD cạnh a là r  . 2 2 a a 6  a 6
Diện tích xung quanh của hình trụ là S  2 rl  2  . xq 2 6 6
Câu 73. Cho hình lăng trụ tam giác đều ABC.A BC
  có AB a , góc giữa AC và  ABC bằng 30 .
Tính thể tích V của khối trụ nội tiếp hình lăng trụ ABC.A BC   . 3  a 3 3  a 3 3  a 3 3  a 3 A. V  . B. V  . C. V  . D. V  . 12 36 108 72 Lời giải Chọn B. B' A' C' B A C a 3
Độ dài đường trung tuyến trong tam giác đều cạnh a là . 2 1 a 3 a 3
Bán kính của đường tròn nội tiếp tam giác đều cạnh a là r  .  . 3 2 6 a 3
Góc giữa AC và  ABC  bằng 30 nên C A
C  30,  C C
  AC. tan 30  . 3 a 3
Chiều cao của khối trụ là h  . 3 2 3  a 3  a 3  a 3
Thể tích khối trụ nội tiếp hình lăng trụ ABC.A BC   là 2
V   r h      .  6  3 36  
Câu 74. Cho tứ diện đều ABCD có cạnh bằng 5 . Tính thể tích V của khối nón nội tiếp tứ diện ABCD .  25 6 125 3 125 6  25 6 A. V  . B. V  . C. V  . D. V  . 108 108 108 36 Lời giải Chọn C. 5 3
Tam giác đều cạnh 5 có độ dài đường cao là . 2 1 5 3 5 3
Bán kính đáy đường tròn nội tiếp tam giác cạnh 5 là r   . 3 2 6 2  2 5 3  25 50 5 6
Độ dài đường cao khối tứ diện là 2 h  5     25    .  3 2  3 3 3  
Thể tích của khối nón nội tiếp tứ diện đều cạnh 5 là: 2 1 1  5 3  5 6 125 6 2
V   r h      . 3 3  6  3 108  
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 75. Cho tứ diện đều ABCD cạnh bằng a 3 . Tính diện tích xung quanh S của hình trụ có đáy là xq
đường tròn ngoại tiếp tam giác BCD và có chiều cao bằng chiều cao của tứ diện đều ABCD . A. 2
S  2 3 a . B. 2 S  2 a . C. 2 S  3 a . D. 2
S  2 2 a . xq xq xq xq Lời giải Chọn D. a 3 3 3a
Độ dài đường trung tuyến trong tam giác đều cạnh a 3 là  . 2 2 2 3a
Bán kính đáy đường tròn ngoại tiếp tam giác BCD là R   a . 3 2
Độ dài đường cao khối tứ diện là h  a 2 2 3  a a 2 .
Vậy diện tích xung quanh của hình trụ là: 2
S  2 Rh  2. .
a a 2  2 2 a . xq
Câu 76. Cho một lăng trụ tam giác đều AB .
C A' B 'C ' có cạnh đáy bằng a . Góc giữa A'C và mặt phẳng
đáy bằng 60O . Tính diện tích xung quanh S của hình nón có đáy là đường tròn nội tiếp tam xq
giác ABC và đỉnh là trong tâm của tam giác A' B 'C ' . 2  a 333 2  a 111 2  a 333 2  a 111 A. S  . B. S  . C. S  . D. S  . xq 36 xq 36 xq 6 xq 6 Lời giải Chọn A. B' A' C' B A C a 3
Độ dài đường trung tuyến trong tam giác đều cạnh a là . 2 1 a 3 a 3
Bán kính của đường tròn nội tiếp tam giác đều cạnh a là r  .  . 3 2 6 
Góc giữa A'C và mặt phẳng đáy bằng 60 nên A CA  60 .
AA  A .
C tan 60  a 3 . Chiều cao của hình nón là h a 3 ,
Trang 28 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 2 2     aa a l a 3 2 3 3 111 2     3a    6  36 6   2 a 3 a 111  a 333
Diện tích xung quanh của hình nón là S   rl    . xq 6 6 36
Câu 77. Cho lăng trụ đứng AB .
C A' B 'C ' , đáy ABC là một tam giác vuông tại cân A , AB a , cạnh
AA' hợp với B'C góc 60o. Tính thể tích của khối trụ ngoại tiếp lăng trụ AB .
C A' B 'C ' theo a . 3  a 3 3  a 3 3  a 3 3  a 2 A. V  . B. V  . C. V  . D. V  . 18 6 3 6 Lời giải Chọn B. A B C A' B' H C'
Gọi H là trung điểm của B C
   H là tâm của đường tròn ngoại tiếp AB C   . B C   a 2
Bán kính của đường tròn ngoại tiếp AB C
  là r A H    . 2 2 
Cạnh AA' hợp với B'C góc 60, vì BB//AA nên BB C   60 . BC a 3 a 3  BB  
. Chiều cao của khối trụ là h  . tan 60 3 3
Thể tích của khối trụ ngoại tiếp lăng trụ AB .
C A' B 'C ' là: 2 3  a 2  a 3  a 3 2
V   r h      .  2  3 6  
Câu 78. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C , AC a, BC  2a , mặt phẳng
SAB vuông góc với mặt phẳng  ABC và tam giác SAB vuông cân tại S . Tính thể tích của
khối nón có đỉnh là S và đáy là đường tròn ngoại tiếp tam giác ABC . 3  a 5 3  a 5 5 3  a 5 5 3  a 3 3 A. V  . B. V  . C. V  . D. V  . 24 12 24 24 Lời giải Chọn C.
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29
NGUYỄN BẢO VƯƠNG - 0946798489 S A H B C
ABC là tam giác vuông tại C nên 2 2
AB CA CB a 5 .
Gọi H là trung điểm của AB H là tâm của đường tròn ngoại tiếp ABC và SH   ABC  . AB a 5
Bán kính của đường tròn ngoại tiếp ABC là r   . 2 2 AB a 5
Tam giác SAB vuông cân tại S nên SH   . 2 2
Thể tích của khối nón có đỉnh là S và đáy là đường tròn ngoại tiếp tam giác ABC là: 2 3 1 1  a 5  a 5  a 5 5 2
V   r h      . 3 3  2  2 24  
Câu 79. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A , SA vuông góc với mặt phẳng
ABC  , tam giác SBC đều cạnh a , góc giữa mặt phẳng SBC và mặt phẳng đáy là 30 . Tính
thể tích V của khối trụ có một đường tròn đáy là đường tròn ngoại tiếp tam giác ABC và chiều
cao bằng khoảng cách từ S đến mặt phẳng  ABC  . 3  a 2 3  a 2 3  a 3 3  a 3 A. V  . B. V  . C. V  . D. V  . 4 16 4 16 Lời giải Chọn D. S C A 30° M B
Gọi M là trung điểm của BC . 
Từ giả thiết  M là tâm của đường tròn ngoại tiếp ABC và SMA  30 . a 3 a 3 SM
SA SM .sin 30  . 2 4
Trang 30 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 a a 3
Bán kính của khối trụ r
, chiều cao của khối trụ h  . 2 4
Thể tích của khối trụ có một đường tròn đáy là đường tròn ngoại tiếp tam giác ABC và chiều 2 3  a a 3  a 3
cao bằng khoảng cách từ S đến mặt phẳng  ABC  là 2
V   r h      .  2  4 16
Câu 80. Cho lăng trụ đứng AB . C AB C
  có đáy là tam giác đều cạnh a . Mặt phẳng AB C   tạo với mặt
phẳng đáy góc 60 . Tính diện tích xung quanh S của hình trụ có một đường tròn đáy là xq
đường tròn nội tiếp tam giác ABC và chiều cao bằng chiều cao của hình lăng trụ AB . C A BC   . 2 3 a 2 3 3 a 2 3 a A. S  . B. S  . C. S  . D. 2 S  3 a . xq 2 xq 12 xq 6 xq Lời giải Chọn A. a 3
Gọi M là trung điểm của B C  , A M   . 2 a 3
Bán kính đường tròn nội tiếp tam giác ABC là r  . 6  a 3 3a
Từ giả thiết AMA  60  AA  A M  .tan 60  3  . 2 2
Diện tích xung quanh S của hình trụ có một đường tròn đáy là đường tròn nội tiếp tam giác xq
ABC và chiều cao bằng chiều cao của hình lăng trụ ABC.A BC   là: 2 a 3 3a 3 a
S  2 Rh  2. .  . xq 6 2 2
Câu 81. Cho hình hộp chữ nhật ABC . D A BCD
  , AB  2a, AD a , AC cắt BD tại O , góc  A B
A  60 . Tính thể tích của khối nón có đỉnh là O và đáy là đường tròn ngoại tiếp hình chữ nhật A BCD   . 3  a 5 3 3  a 3 3  a 5 5 3  a 5 3 A. V  . B. V  . C. V  . D. V  . 6 6 6 2 Lời giải Chọn A.
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 31
NGUYỄN BẢO VƯƠNG - 0946798489 D' C' A' B' D C O A B Ta có 2 2 AC 
a  4a a 5 . a 5
Bán kính của đường tròn ngoại tiếp hình chữ nhật A BCD   là R  . 2  Từ giả thiết A B
A  60  AA  A .
B tan 60  2a 3 .
Thể tích của khối nón có đỉnh là O và đáy là đường tròn ngoại tiếp hình chữ nhật AB CD   : 2 3 1 1  a 5   a 5 3 2
V   r h     2a 3  . 3 3  2  6  
CÂU HỎI MỨC ĐỘ VẬN DỤNG - VDC
Câu 82. Cho hình nón có tâm đáy là I . Một mặt phẳng đi qua đỉnh hình nón và cắt hình nón theo một
thiết diện là tam giác đều có diện tích bằng 3 3 , đồng thời cắt đường tròn đáy tại hai điểm. , A B  thì 0
AIB  120 . Diện tích xung quanh của hình nón đã cho bằng 8 2 A. 8 3 . B. . C. 4 1 3 . D. 4 3 . 3 Lời giải Chọn D O A I B
Gọi O là đỉnh hình nón, thiết diện là tam giác đều OAB . 2 OA 3 4S 4.3 3 2 OAB S   OA  
 12  l OA AB  2 3 . OAB 4 3 3 
Tam giác IAB cân có góc 0 AIB  120 nên 2 2 2 0 2
AB IA IB  2I . A I . B co 1
s 20  3IA 12
Suy ra R IA  2 .
Diện tích xung quanh của hình nón là S
  .Rl   .2.2 3  4 3 . xq
Câu 83. Cho hình nón đỉnh S có chiều cao bằng 3 2 . Gọi B, C là 2 điểm thuộc đường tròn đáy sao cho S
BC vuông tại S và có chu vi bằng 10  5 2 . Thể tích của khối nón được giới hạn bởi hình nón đã cho bằng:
Trang 32 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 A. 7 2 . B. 21 2 . C. 43 2 . D. 14 2 . Lời giải Chọn A S O C B
Gọi độ dài đường sinh SB SC x x  0 . Xét S
BC vuông cân tại S , suy ra: BC x 2 .
Có: SB SC BC  10  5 2  x x x 2  10  5 2
 2  2  x  10  5 2  x  5. Xét S
OB : R OC SB SO    2 2 2 2 5 3 2  7 . 1 1
Thể tích khối nón: V   R h   . 7 2 2 .3 2  7 2 (đvtt). 3 3
Câu 84. Cho hình nón có chiều cao bằng 2 5 . Một mặt phẳng đi qua đỉnh hình nón và cắt hình nón
theo một thiết diện là tam giác đều có diện tích bằng 9 3 . Thể tích của khối nón được giới hạn
bởi hình nón đã cho bằng 32 5 A. . B. 32 . C. 32 5 . D. 96 . 3 Lời giải Chọn A
Theo giả thiết tam giác SAB đều, S
 9 3 và SO  2 5 . SAB
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 33
NGUYỄN BẢO VƯƠNG - 0946798489 2 AB 3 S  9 3   9 3  AB  6 . SAB 4 SA
B đều SA AB  6 .
Xét SOA vuông tại O , theo định lý Pytago ta có: OA SA SO    2 2 2 2 6 2 5  4 . 1 1 1 32 5 Thể tích hình nón bằng 2 2 2
V   r h   .OA .SO   4 .2 5   . 3 3 3 3
Câu 85. Cho hình trụ có chiều cao bằng 6a. Biết rằng khi cắt hình trụ đã cho bởi một mặt phẳng song
song với trục và cách trục một khoảng bằng 3a, thiết diện thu được là một hình vuông. Thể tích
của khối trụ được giới hạn bởi hình trụ đã cho bằng A. 3 216 a . B. 3 150 a . C. 3 54 a . D. 3 108 a . Lời giải Chọn D M N A O B Q H P D O' C
Lấy 2 điểm M , N lần lượt nằm trên đường tron tâm O sao cho MN  6a .
Từ M , N lần lượt kẻ các đường thẳng song song với trục OO ' , cắt đường tròn tâm O ' tại Q , P .
Thiết diện ta thu được là hình vuông MNPQ có cạnh bằng 6a.
Gọi H là trung điểm của PQ . Suy ra OH PQ .
Vì OO '  MNPQ nên ta có d OO ',MNPQ  d O ',MNPQ  O ' H .
Từ giả thiết, ta có O ' H  3a . Do đó O ' HP là tam giác vuông cân tại H .
Suy ra bán kính đường tròn đáy của hình trụ là 2 2
O ' P O ' H HP  3a 2 .
Vậy thể tích của khối trụ cần tìm là: V a   a 2 3 6 . . 3 2  108 a .
Câu 86. Cho hình trụ có bán kính đáy là 4 cm, một mặt phẳng không vuông góc với đáy và cắt hai mặt
đáy theo hai dây cung song song AB, A ' B ' mà AB A' B '  6 cm (hình vẽ). Biết diện tích tứ
giác ABB ' A ' bằng 60 cm2. Tính chiều cao của hình trụ đã cho. A. 6 2 cm. B. 4 3 cm. C. 8 2 cm. D. 5 3 cm. Lời giải Chọn A
Trang 34 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 B' A' 6 2cm C B 6 cm D A
Dựng đường sinh B ' C và A ' D , ta có tứ giác A' B ' CD là hình chữ nhật nên CD//A' B ' và
CD A ' B '  6 cm . Vậy CD//AB và CD AB  6 cm . Do đó tứ giác ABCD là hình bình hành
và nội tiếp được nên là hình chữ nhật. Từ đó AB BC , mặt khác AB B 'C nên
AB  (BCB ')  AB BB '
Vậy ABB ' C ' là hình bình hành có một góc vuông nên là hình chữ nhật. Ta có 60 S  .
AB BB ' nên BB ' 
 10 cm . Xét tam giác BB ' C vuông tại C có ABB ' A' 6 2 2 2
B ' C BB '  BC mà 2 2 2
BC AC AB  64  36  28 nên 2
B ' C  100  28  72  B ' C  6 2 cm .
Vậy chiều cao hình trụ là 6 2 cm .
Câu 87. Khi cắt một hình trụ bởi hai mặt phẳng cùng song song với trục. Với mặt phẳng thứ nhất cách
trục một khoảng bằng a, thiết diện thu được là một hình vuông. Còn mặt phẳng thứ hai cách a 6 trục một khoảng bằng
, thiết diện thu được là một hình chữ nhật có diện tích bằng 2 2 2a
2 . Thể tích của khối trụ được giới hạn bởi hình trụ đã cho bằng 3 4 a A. . B. 3 8 a 3 . C. 3 4a . D. 3 4 a . 3 Lời giải Chọn D
Gọi R là bán kính đáy hình trụ.
Giả sử cắt bởi mặt phẳng thứ nhất được hình vuông ABCD ; khi đó OI a với I là trung điểm BC ta có 2 2
h l BC  2IB  2 R a .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 35
NGUYỄN BẢO VƯƠNG - 0946798489 a 6
Cắt bởi mặt phẳng thứ hai được hình chữ nhật AB C  D
  ; khi đó OK  với K là trung 2 2 6a điểm B C   ta có 2 B C
   2KB  2 R  . 4 2 2 6a 6 a Diện tích 2 2 2 2 2 2 2 S
 2 R a .2 R
 4 R a . R   2 a 2 . AB CD   4 4 2 2 6a 6 a 2 2 2 2 2 2 2 S
 2 R a .2 R
 4 R a . R   2 a 2 A BCD   4 4 4 2 2 2  R   R   R   R  1  2  5  2  0       2   hoặc   
(loại do R a )  R a 2 .  a   a   a   a  2 Thể tích khối trụ là 2 2
V   R h  4 a .
Câu 88. Cho hình nón đỉnh S , tâm đường tròn đáy là O và có đường kính bằng 4a . Mặt phẳng  P đi
qua S cắt đường tròn đáy tại hai điểm A và B sao cho AB  2 3a . Gọi D là điểm đối xứng 2 5
của A qua O . Biết khoảng cách từ D đến mặt phẳng  P bằng
a . Tính thể tích khối 5 nón. 3 2a  3 2 13a 3 4a A. 3 2a  . B. . C. . D. . 3 3 3 Lời giải Chọn B S H D O A I B
Theo đề bài, có R OA  2a .
Vì D là điểm đối xứng với A qua O nên O là trung điểm của AD .
d D,SAB AD
d D,SAB 5  
 2  d O,SAB   .
d O,SAB AO 2 5
Gọi I là trung điểm AB , suy ra OI AB .
Mà AB SO nên AB   SOI  .
Kẻ OH SI H SI   OH AB OH   SAB .
Do đó: d O SAB 5 ,  OH  . 5
Xét OAI OI OA IA   a  a 2 2 2 2 : 2 3  a .
Trang 36 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 1 1 1 1 Xét SOI :    SO a . 2 2 2 OH SO OI 2 3 1 1 2 1 2a  Thể tích khối nón: 2
V   R h   .2a . a  (đvtt). 3 3 2 3
Câu 89. Cho hình nón đỉnh S có đường tròn đáy tâm O bán kính R a 2 . Trên đường tròn đáy lấy
hai điểm A và B sao cho tam giác OAB đều. Biết diện tích tam giác SAB bằng 2 2a . Thể
tích hình nón đã cho bằng: 3 29a  3 58a A. 3 58 a . B. 3 29a  . C. . D. . 3 3 Lời giải Chọn D S O A I B
Theo đề có R OA a 2 . a 22 . 3 3 a 6 OAB đều nên 2 S   a và OI  . OAB 4 2 2
Ta có: SO  OAB suy ra O là hình chiếu của S lên OAB . Do đó: O
AB là hình chiếu S
AB lên mp OAB .
Áp dụng công thức: SS
.cos (  SAB,OAB . OAB SAB S 6  cos OAB     . S 8 SAB OI AB Mặt khác: 
 SAB OAB  ,  SIO   . SI ABOI 6 8OI Xét SOI :  cos    SI   4a . SI 8 6 58 2 2  SO SI OI  . 2 3 2 1 1 58 58a  Thể tích khối nón: 2
V   R h   .a 2  .  (đvtt). 3 3 2 3
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 37
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 90. Cho hình trụ có hai đáy là hai đường tròn O và O , chiều cao bằng a 3 và bán kính đáy
a . Một mặt phẳng   đi qua trung điểm của OO và cắt đường tròn đáy theo một dây cung có
độ dài a 2 . Góc tạo bởi mặt phẳng   với mặt đáy gần với giá trị nào nhất. A. 50 . B. 51 C. 39 . D. 41 . Lời giải Chọn B
Gọi I là trung điểm của OO . Mặt phẳng thiết diện cắt đường tròn đáy theo dây cung AB .
Dựng OH AB AB  OIH   OIH    IAB .
Ta có O là hình chiếu của I lên mặt phẳng đáy. Do vậy góc giữa   và mặt phẳng đáy là góc  IHO a 2
Xét tam giác OHB vuông tại H 2 2
OH OB BH  2 IO a 3 a 2 6
Xét tam giác vuông OIH vuông tại O   0  tan IHO   :   IHO  50 46 ' OH 2 2 2
Câu 91. Cho tam giác ABC đều có cạnh bằng 2a . Từ tâm của đáy, dựng đường thẳng  vuông góc với
mặt phẳng  ABC . Trên  lấy điểm S sao cho khoảng cách từ A đến mặt phẳng  SBC  12 bằng
a . Khi đó thể tích khối nón có đỉnh là S và đường tròn đáy là đường tròn ngoại tiếp 7 ABC bằng 3 4a  3 16a  3 16a  3 4a A. . B. . C. . D. . 9 3 9 3 Lời giải Chọn C
Trang 38 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 S H A O B M C
Gọi O là tâm của đáy, M là trung điểm của BC . 2a 3 2a 3 a 3 Vì A
BC đều nên: R OA  và OM  
( R bán kính đường tròn ngoại 3 6 3 tiếp ABC ). Mặt khác: 12 4 Dễ thấy d  ,
A SBC   3d O,SBC  
a d O,SBC   a . 7 7 BC OM Ta có: 
BC  SOM  . BC SO
Trong SOM  , kẻ OH SM H SM  suy ra OH BC nên OH  SBC .
OH d O SBC  4 ,  a . 7 1 1 1 Xét SOM :    SO  4a . 2 2 2 OH SO OM 2 3 1 1  2a 3  16a
Suy ra thể tích khối nón: 2
V   R h   .  .4a  (đvtt). 3 3  3  9  
Câu 92. Cho mặt cầu  S  tâm O và các điểm A , B , C nằm trên mặt cầu  S  sao cho AB  3 ,
AC  4 , BC  5 và khoảng cách từ O đến mặt phẳng  ABC bằng 1. Thể tích của khối cầu S  bằng 20 5 7 21 29 29 4 17 A.  . B.  . C.  . D.  . 3 2 6 3 Lời giải Chọn C
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 39
NGUYỄN BẢO VƯƠNG - 0946798489
Từ AB  3 , AC  4 , BC  5  ABC vuông tại A  đường tròn C ngoại tiếp ABC có BC 5 bán kính r   . 2 2
Lại có C  là đường tròn giao tuyến của mặt phẳng  ABC và mặt cầu S  . 29 29 Suy ra 2 2 R d  ; O ABC 2  r   R
là bán kính mặt cầu S  . 4 2 4 29 29 Vậy 3 V   R   . S  3 6
Câu 93. Cho hình nón có chiều cao bằng a . Biết rằng khi cắt hình nón đã cho bởi một mặt phẳng đi qua a
đỉnh hình nón và cách tâm của đáy hình nón một khoảng bằng
, thiết diện thu được là một 3
tam giác vuông. Thể tích của khối nón được giới hạn bởi hình nón đã cho bằng 3 4 a 3 5 a 3  a 3 5 a A. . B. . C. . D. . 9 9 3 12 Lời giải Chọn D a
Mặt phẳng đi qua đỉnh hình nón và cách tâm của đáy hình nón một khoảng bằng có thiết 3
diện là tam giác vuông SAB như hình vẽ. Kẻ OK A ; B OH SK .  AB OK Ta có: 
suy ra AB  SOK   AB OH và OH SK nên OH  SAB . Do đó AB SO   a d ;
O SAB  OH  . 3
Trang 40 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 1 1 1 a 3a
Xét tam giác vuông SOK có:    OK  ; 2 2 SK SO OK  ; 2 2 2 OH SO OK 2 2 2 2 3a
Vì OK AB nên K là trung điểm của AB . Tam giác vuông SAB có SK KB  . 2 2 5a
Xét tam giác vuông OKB có: 2 2
OB OK KB  ; 2 2 3 1 1  5a  5 a
Vậy thể tích khối nón cần tìm là: 2
V  . .OB .SO  . .  .a  . 3 3  2  12  
Câu 94. Một khối trụ có bán kính đáy r  2a . O, O lần lượt là tâm đường tròn đáy. Một mặt phẳng a 15
song song với trục và cách trục
, cắt đường tròn O tại hai điểm ,
A B . Biết thể tích của 2 3 a 15 khối tứ diện OO AB bằng
. Độ dài đường cao của hình trụ bằng 4 A. a . B. 6a . C. 3a . D. 2a . Lời giải Chọn C
Vẽ đường sinh AC , khi đó mặt phẳng  ABC song song với OO và cách OO một khoảng a 15 . 2 a
Gọi I là trung điểm AB , ta có d OO  ABC   d O  ABC  15 , ,  O I   . 2 2 15a Bán kính O A   2a suy ra 2 2 2
BA  2IA  2 O A   O I   2 4a   a . 4 3 a 15
Thể tích tứ diện OO AB bằng nên ta 4 3 3 1 a 15 1 a 15 a 15
có : .OO .IO .AB   .OO . .a
OO  3a . 6 4 6 2 4
Vậy hình trụ có chiều cao OO  3a .
Câu 95. Cho hình lăng trụ tam giác đều AB .
C A' B 'C ' có AA '  2a; BC a . Gọi M là trung điểm
BB ' . Bán kính mặt cầu ngoại tiếp khối chóp M.A' B 'C ' bằng 3 3a 13a 21a 2 3a A. . B. . C. . D. . 8 2 6 3 Lời giải
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 41
NGUYỄN BẢO VƯƠNG - 0946798489 Chọn C
Gọi N , P lần lượt là trung điểm AA ';CC ' và O, O ' lần lượt là tâm đường tròn ngoại tiếp các tam giác MNP và A
 ' B 'C ' Khi đó mặt cầu ngoại
tiếp khối chóp M.A' B 'C ' cũng là mặt cầu ngoại tiếp khối lăng trụ MN .
P A' B 'C '
Gọi I là trung điểm OO ' . Suy ra I là tâm mặt cầu cần 2 . a 3 a 3
tìm. Suy ra IB '  R . Ta có: O ' B '   3.2 3 1 1 a Và: IO '  OO '  AA '  . 2 4 2 a 21 Nên: 2 2
IB '  R O ' I O ' B '  . 6 Chọn C
Câu 96. Cho hình chóp S.ABC có đáy ABC là tam giác
vuông cân tại B và AC  .
a Hình chiếu vuông góc của đỉnh S lên mặt phẳng  ABC  là điểm
H đối xứng với B qua AC . Góc giữa hai mặt phẳng  SAC  và  ABC  0  45 . Diện tích mặt
cầu ngoại tiếp hình chóp S.ABC bằng: 2 2 a 2 5 a A. 2 2 a . B. . C. 2 5 a . D. . 3 4 Lời giải Chọn D S I H C O A B
Gọi O là trung điểm AC.
Ta có H là điểm đối xứng của B qua AC nên ABCH là hình vuông. HB a
HB AC a HO   . . 2 2
Theo đề bài ta có:  SAC
ABC    SO HO  0 ( );( ) ,  SOH  45 a
Suy ra: SHO vuông cân tại H  SH  . 2  S
 AB vu«ng t¹i A AB  (SHA)  Ta có: 
 SBC vu«ng t¹i C BC  (SHC) 
 Tâm mặc cầu ngoại tiếp hình chóp S.ABC là trung điểm I của SB
Trang 42 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 5 SB 5 Ta có: 2 2 SB  SH  HB  a  R  SI   a 2 2 4 2  5  5
Vậy diện tích mặt cầu cần tìm là: 2 4 a   a  4  4  
Câu 97. Cho hai khối nón có chung trục SS  3r . Khối nón thứ nhất có đỉnh S đáy là hình tròn tâm S
bán kính r . Khối nón thứ hai có đỉnh S đáy là hình tròn tâm S bán kính 2r . Thể tích phần
chung của hai khối nón bằng 3 4 r 3  r 3 4 r 3 4 r A. . B. . C. . D. . 27 9 9 3 Lời giải Chọn C
Ta có thể tích phần chung là tổng thể tích của khối chóp có đỉnh S , trục SO và đường tròn đáy
có bán kính OM và khối chóp có đỉnh S , trục S O
 và đường tròn đáy có bán kính OM . OM SA r OM S Br Ta có:  1 tanOS M      và  2 2 tan OSM     OSSS 3r 3 OS SS 3r 3 1 OM OS 1 OS   r 2 Suy ra: 3 .  
OS  2OS    OM r OSOM 2 2 OS  2r 3  3 2 3 1 1 1 1 4r 4 r Vậy 2 2 2
V   .SO.OM   .S O
 .OM   .SS .OM   .3r.  3 3 3 3 9 9
Câu 98. Cho hình chóp S.ABC có SA  ( ABC) , AB  3 , AC  2 và 
BAC  30 . Gọi M , N lần lượt
là hình chiếu của A lên S ,
B SC . Bán kính R của mặt cầu ngoại tiếp hình chóp . A BCNM là A. R  2 . B. R  13 . C. R  1 . D. R  2 . Lời giải Chọn C
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 43
NGUYỄN BẢO VƯƠNG - 0946798489 S N d' M A C d I B
● Xét tam giác AMB vuông tại M nên tâm của tam giác AMB là trung điểm của cạnh AB .
Khi đó, trong ( ABC) kẻ đường trung trực d của AB thì tâm mặt cầu cần tìm nằm trên d .
● Xét tam giác ANC vuông tại N nên tâm của tam giác ANC là trung điểm của AC . Khi đó,
trong ( ABC) , kẻ đường trung trực d ' của AC thì tâm mặt cầu cần tìm nằm trên d ' .
 Điểm I d d ' là tâm của mặt cầu ngoại tiếp hình chóp . A BCNM .
Mà d và d ' cùng nằm trong ( ABC) nên I cũng chính là tâm đường tròn ngoại tiếp tam giác ABC .
Suy ra bán kính mặt cầu bằng bán kính đường tròn ngoại tiếp tam giác ABC .
● Áp dụng định lý cosin trong tam giác ABC có: 2 2 2
BC AB AC  2.A .
B AC.cosA  1  BC  1
● Áp dụng công thức hàm sin : BC BC 1  2R R    1. sin A 2.sin A 2.sin 30
Câu 99. Có một bể hình hộp chữ nhật chứa đầy nước. Người ta cho ba khối nón giống nhau có thiết
diện qua trục là một tam giác vuông cân vào bể sao cho ba đường tròn đáy của ba khối nón đôi
một tiếp xúc với nhau, một khối nón có đường tròn đáy tiếp xúc với một cạnh của đáy bể và hai
khối nón còn lại có đường tròn đáy tiếp xúc với hai cạnh của đáy bể. Sau đó người ta đặt lên 4
đỉnh của ba khối nón một khối cầu có bán kính bằng
lần bán kính đáy khối nón. Biết khối 3 337
cầu vừa đủ ngập trong nước và tổng lượng nước trào ra là
(lit). Thể tích nước ban đầu 24
trong bể thuộc khoảng nào dưới đây? (tính theo đơn vị lít). A. (150;151) B. (151;152) C. (139;140) D. (138;139). Lời giải Chọn B
- Đầu tiên, ta quan tâm tới mặt phẳng đáy của hình hộp:
Dễ thấy tam giác IJE nối tâm của ba mặt cầu là một tam giác đều cạnh 2R .
Dễ thấy AB  4R và AD MI KE EP  2  3 R .
Trang 44 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
- Tiếp theo, ta quan tâm tới chiều cao của hình hộp: 4R
Ta coi hình cầu có tâm S , chạm với khối nón có tâm đáy I tại U và bán kính cầu SU  . 3
Hạ SO vuông góc mặt phẳng đáy. Dễ thấy chân đường cao O là tâm tam giác đều IJE . 2R 3 2R
Dễ tính được IO
, áp dụng định lý Pitago cho tam giác SHU , ta được SH  . 3 3 2R 4R 5R
Chiều cao của hình hộp là h SH HO SL   R    3R . 3 3 3
- Ta chỉ cần tính bán kính của mỗi hình nón nữa là xong. Dễ thấy thể tích nước tràn ra bằng thể
tích các khối nón và cầu có trong hình hộp. 3 337 1 4  4  337 81 3 Như vậy, 2 3 3
  3V V  3. . R R   . R  .R R   R dm n c     24 3 3  3  81 24 2
- Vậy thể tích hình hộp bằng V  . AB A . D h  4 . R 2  3 .
R 3R  12 2  3 81 3 R  2  3 151,14 (dm). 2
Câu 100. Cho hình trụ có chiều cao bằng 6a . Biết rằng khi cắt hình trụ đã cho bởi một mặt phẳng song
song với trục và cách trục một khoảng bằng 3a , thiết diện thu được là một hình vuông. Thể
tích của khối trụ được giới hạn bởi hình trụ đã cho bằng A. 3 216 a . B. 3 150 a . C. 3 54 a . D. 3 108 a . Lời giải Chọn D
Gọi O và O là tâm hai đáy của hình trụ.
Giả sử thiết diện thu được khi cắt hình trụ đã cho bởi một mặt phẳng song song với trục là hình vuông ABCD .
Theo giả thiết ta có AB BC OO  6a .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 45
NGUYỄN BẢO VƯƠNG - 0946798489 1
Gọi I là trung điểm AB . Suy ra OI AB và AI AB  3a . 2
Mà OI BC nên OI   ABCD .
Vì OO//  ABCD nên d OO; ABCD  d O; ABCD  OI  3a .
Xét tam giác AOI vuông tại I và có OI AI  3a OA  3a 2 . Thể tích khối trụ là: 2 2
V  .R .h 2
  .OA .OO   .3a 2  .6a 3  108 a .
Câu 101. Cho hình trụ có chiều cao bằng 6a . Biết rằng khi cắt hình trụ đã cho bởi một mặt phẳng song
song với trục và cách trục một khoảng bằng 3a , thiết diện thu được là một hình chữ nhật có diện tích 2
48a . Thể tích của khối trụ được giới hạn bởi hình trụ đã cho bằng A. 3 216 a . B. 3 180 a . C. 3 54 a . D. 3 150 a . Lời giải Chọn D
Gọi O và O là tâm hai đáy của hình trụ.
Giả sử thiết diện thu được khi cắt hình trụ đã cho bởi một mặt phẳng song song với trục là hình
chữ nhật ABCD có AB BC OO  6a , 2 S
 48a AB  8a ABCD 1
Gọi I là trung điểm AB . Suy ra OI AB và AI AB  4a . 2
Mà OI BC nên OI   ABCD .
Vì OO//  ABCD nên d OO; ABCD  d O; ABCD  OI  3a .
Xét tam giác AOI vuông tại I và có OI  3a, AI  4a OA  5a . Thể tích khối trụ là: 2
V  .R .h 2 2
  .OA .OO    a  a 3 . 5 . 6  150a .
Câu 102. Cho hình chóp S.ABC có SA vuông góc với mặt phẳng đáy, góc giữa  SBC  và mặt phẳng
đáy bằng 60 . Nếu ABC là tam giác đều cạnh a 3 thì bán kính mặt cầu ngoại tiếp hình chóp S.ABC bằng a 43 a 43 a 43 a 43 A. . B. . C. . D. 4 8 12 6 -----Lời giải Chọn A
Trang 46 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 Gọi H là trung điểm AB
AH BC tại H
 SAB  ABC   ,  SHA  60 3a 3a 3 AH   SA  2 2
Gọi I là tâm của ABC
Dựng  đi qua I ,  / /SA
Dựng  là trung trực của SA Gọi J      Vì J    A JJB JC J     S J  A J  A J
JB JC  S J
J là tâm mặt cầu ngoại tiếp SABC
Bán kính mặt cầu R  A J Gọi M là trung điểm SA Khi đó: 2 2 A JMA MJ 2  3a 3    2 SA 2 a 43 2   2  R   AI   a  . 4 4 4
Câu 103. Cho hình chóp ABCD có đáy là hình thang vuông tại A và D . Biết SA vuông góc với
ABCD , AB BC a, AD  2a, SA a 2 . Gọi E là trung điểm của AD . Bán kính mặt cầu đi qua các điểm S, ,
A B, C, E bằng a 3 a 30 a 6 A. . B. . C. . D. a . 2 6 3 Lời giải Chọn D
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 47
NGUYỄN BẢO VƯƠNG - 0946798489
Ta thấy các tam giác SAC; SBC; SEC vuông tại ,
A C, E . Vậy các điểm S, ,
A B, C, E nằm 2 2 SC SA AC
trên mặt cầu đường kính SC R    . a 2 2
Câu 104. Một hình trụ có bán kính đáy bằng chiều cao và bằng a . Một hình vuông ABCD có AB, CD là
hai dây cung của hai đường tròn đáy và mặt phẳng  ABCD không vuông góc với đáy. Diện
tích hình vuông đó bằng. 2 5a 2 5a 2 2 5a A. . B. . C. 2 5a . D. . 4 4 2 Lời giải Chọn D CD   AD
Kẻ đường sinh AA . Khi đó ta có 
CD   A AD 0
CD AO ADC   90 . CD A A   Ta có AD
C là góc nội tiếp chắn nửa đường tròn  A C   2a .
Đặt cạnh hình vuông ABCD là x . 2 2 2 2 2 2   A D   AD A A   x a 5a Ta có 2 2 2 2 
 2x a  4a x S  . 2 2 2 ABCDA D   DC A C  2 
Câu 105. Cho ba hình cầu có bán kính lần lượt là R , R , R đôi một tiếp xúc nhau và cùng tiếp xúc với 1 2 3
mặt phẳng (P) . Các tiếp điểm của ba hình cầu với mặt phẳng (P) lập thành một tam giác có độ
dài các cạnh lần lượt là 2;3; 4 . Tính tổng R R R : 1 2 3 61 67 53 59 A. . B. . C. . D. . 12 12 12 12 Lời giải Chọn A O1 L O2 H K O3 A B C
Gọi tâm của ba mặt cầu lần lượt là O ;O ;O và 1 2 3
A;B;C lần lượt là hình chiếu vuông góc của
O ;O ;O lên ( P ). Không mất tổng quát, giả sử R R R và theo đó AB AC BC 1 2 3 1 2 3
Trang 48 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Gọi L là hình chiếu vuông góc của O lên O A và H , K lần lượt là hình chiếu của O lên 2 1 2 O A;O B 1 2
Ta có O O R R ;O L R R và 2 2 2
O L ( O O ) ( O L ) 1 2 1 2 1 1 2 2 1 2 1 2 2 2
 4  ( R R ) ( R R )  4R R 1 2 1 2 1 2 Tương tự, ta có 2 2 2
3  ( R R ) ( R R )  4R R ; 2 2 2
2  ( R R ) ( R R )  4R R 1 3 1 3 1 3 2 3 2 3 2 3  R1   4   3 RR R R  4 3  3  1 2 4   9  61
Ta có hệ R R  1  R R
 R  3 . Suy ra R R R  . 2 3 1 3 1 1 2 3  4 12 9   4 R R  R R  4 R  1 3 1 2  4 2   3 
Câu 106. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, các cạnh bên của hình chóp bằng
6 cm , AB  4 cm . Khi thể tích khối chóp S.ABCD đạt giá trị lớn nhất, tính diện tích mặt cầu
ngoại tiếp S.ABCD . A. 2 12 cm . B. 2 4 cm . C. 2 9 cm . D. 2 36 cm . Lời giải Chọn D S M I A D O B C
Gọi O là giao điểm của AC và BD .
Ta có SAC cân tại S nên SO AC và SBD cân tại S nên SO BD .
Khi đó SO   ABCD.
Ta có: SAO  SBO  SCO  SDO OA OB OC OD
Vậy hình bình hành ABCD là hình chữ nhật. 2 AC 16  x Đặt 2 2
BC x AC  4  x AO   . 2 2 2 2 16  x 8  x
Xét SAO vuông tại O , ta có: 2 2 SO
SA AO  6   4 2 2 1 1 8  x 2
Thể tích khối chóp S.ABCD là: 2 VS . O S  . .4x  . 8  x .x S. ABCD 3 ABCD 3 2 3 2 2 a b 2 2 2 2 8  x x 8
Áp dụng bất đẳng thức : ab  ta có: 2 V  . 8  x .x  .  . 2 3 3 2 3 Dấu "  " xảy ra 2 
8  x x x  2. Do đó: BC  2, SO  1.
Gọi M là trung điểm của SA , trong SAO kẻ đường trung trực của SA cắt SO tại I .
Khi đó mặt cầu ngoại tiếp khối chóp S.ABCD có tâm I và bán kính R IS.
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 49
NGUYỄN BẢO VƯƠNG - 0946798489 2 SI SM SA 6 Vì SMI ∽ SO ( A g.g) nên   SI  
 3  R  3(cm). SA SO 2.SO 2.1
Diện tích mặt cầu ngoại tiếp khối chóp S.ABCD là: 2 2 2
4 R  4.3  36 (cm ) .
AD  ABC
Câu 107. Cho hình tứ diện ABCD có
, ABC là tam giác vuông tại B . Biết BC  2(cm)
,AB  2 3(cm),AD  6(cm). Quay các tam giác ABC và ABD ( bao gồm cả điểm bên trong 2 tam
giác) xung quanh đường thẳng AB ta được 2 khối tròn xoay. Thể tích phần chung của 2 khối tròn xoay đó bằng 5 3 3 3 64 3 3 3 3 3 (  cm ) (  cm ) (  cm ) 3 (  cm ) A. B. 2 C. 2 . D. 3 . Lời giải Chọn C
Dễ thấy AD  ABC   AD R1
Gọi M   BD AC và N là hình chiếu của M trên AB. Dễ dàng chứng minh được tỉ lệ: MN AN MN BN (1) AD AN AN 3 BN 1  (1) ; và  (2)     3   ;  BC AB AD AB (2) BC BN AB 4 AB 4 3 3 3 3  AN  ; BN  ; MN  2 2 2
Phần thể tích chung của 2 khối tròn xoay là phần thể tích khi quay tam giác  AMB xung quanh
trục AB. Gọi V là thể tích khối tròn xoay khi quay tam giác BMN xung quanh AB 1
Và V là thể tích khối tròn xoay khi quay tam giác AMN xung quanh AB 2 3 3 9 3 3 3
Dễ tính được: V  (dvtt) và V
(dvtt)  V V  (dvtt) . Chọn C. 1 8 2 1 2 8 2
Câu 108. Huyền có một tấm bìa như hình vẽ, Huyền muốn biến đường tròn đó thành một cái phễu hình
nón. Khi đó Huyền phải cắt bỏ hình quạt tròn AOB rồi dán OA, OB lại với nhau. Gọi x là
góc ở tâm hình quạt tròn dùng làm phễu. Tìm x để thể tích phểu lớn nhất? 2 6    A. B. C. D. 3 3 2 4 Lời giải
Trang 50 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 Chọn A O R O R B h B;A A 2 R x xR 2 r
Ta có diện tích của hình phểu S   r
là bán kính của đáy phểu;  x xq 2 2 R 1 1 1 2 2 2 2 4 2 6
V   r h   r
R r   r .R r là thể tích của phểu 3 3 3 Xét hàm số phụ 4 2 6 3 2 5
y r .R r y  4r .R  6r 6 2 2
y  0  2.R  3r  0  r R 3 R 6 2 r 2 R 6 2 6
Vậy y max thì V và V max khi r   x   x   x  3 R 3R 3
Câu 109. Cho hình trụ có hai đáy là hai hình tròn O và O , thiết diện qua trục của hình trụ là hình vuông. Gọi ,
A B là hai điểm lần lượt nằm trên hai đường tròn O và O. Biết AB  2a và a 3
khoẳng cách giữa hai đường thẳng AB và OO bằng . Bán kính đáy bằng 2 a 14 a 14 a 14 a 14 A. . B. . C. . D. . 3 2 4 9 Lời giải Chọn C
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 51
NGUYỄN BẢO VƯƠNG - 0946798489 O' B A O H C
Dựng đường sinh BC gọi H là trung điểm của đoạn A . B a 3
Ta có d OO , AB  OH  2
Giả sử bán kính đáy của hình trụ là r, do thiết diện qua trục của hình trụ là hình vuông suy ra BC  2r 2 2 2 2  AC
AB BC  4a  4r , mặt khác 2 3a 2 2 2 2 2
AC  2 OA OH  2 r   4r  3a 4 a 14 Ta có phương trình 2 2 2 2 4a  4r
4r  3a r  . 4
Câu 110. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B , AB BC  3a 2 ,   0
SAB SCB  90 . Biết khoảng cách từ A đến mặt phẳng (SBC) bằng 2a 3 . Tính thể tích
mặt cầu ngoại tiếp hình chóp S.ABC . A. 3 72 18 a . B. 3 18 18 a . C. 3 6 18 a . D. 3 24 18 a . Lời giải Chọn D
Trang 52 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Gọi I, H lần lượt là trung điểm của cạnh SB và AC
Mặt khác, theo giả thiết ta có ΔSAB, ΔSCB lần lượt là các tam giác vuông tại A và C
IA IB IC IS
I là tâm mặt cầu ngoại tiếp hình chóp . S ABC
Mặt khác: ΔABC vuông tại B H là tâm đường tròn ngoại tiếp ΔABC
IH  ABC
dA;SBC AC Ta có: 
 2  dH; SBC 
dH SBC   a 3 ; HC
Gọi K là trung điểm của cạnh BC HK BC HK / / AB, AB BC
Lại có: BC IH IH  ABC BC  IHK
Mặt khác: BC  SBC  SBC  IHK theo giao tuyến IK
Trong IHK , gọi HP IK HP  SBC tại P HP dH;SBC  a 3 1 1 1 1 1 Xét ΔIHK :      HI  3a 2 2 2 2 2 HP HI HK HI AB 4 4 Xét 2 2
ΔIHB : IB IH HB  3a 2  R . Vậy 3 3
V πR  24 18πa 3
Câu 111. Cho hình trụ có đáy là hai đường tròn tâm O và O , bán kính đáy bằng chiều cao và bằng 2a .
Trên đường tròn đáy có tâm O lấy điểm A , D trên đường tròn tâm O lấy điểm B , C sao
cho AB//CD và AB không cắt OO ' . Tính AD để thể tích khối chóp O '.ABCD đạt giá trị lớn nhất. 4 3
A. AD  2 2a
B. AD  4a C. AD a D. AD  2a 3 Lời giải
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 53
NGUYỄN BẢO VƯƠNG - 0946798489 B C O' O A D O1
Kẻ đường thẳng qua O ' song song với AB cắt mặt phẳng chứa đường tròn (O) tại O . 1 Lúc đó AO .
D BO 'C là một hình lăng trụ chiều cao bằng 2a . 1
Vì AD BC nên SS BO 'C OAD
Ta có thể tích của khối chóp O '.ABCD : 1 2 2 2 1  3 8a VV  .2 . a S  .2 . a S  .2 . a .2 . a 2 . a sin AOD  . O ' ABCD 1
AO D.BO 'C BO  ' 3 3 C 3 OAD 3 2 3 VAOD   AD a . ABCD   0 90 2 2 O ' max
Câu 112. Trong không gian với hệ tọa độ
Oxyz , cho hai mặt phẳng song song
P :2x y  2z 1  0, Q :2x y  2z  5  0 và điểm A 1  ;1 
;1 nằm trong khoảng giữa hai
mặt phẳng này. Gọi S  là mặt cầu đi qua A và tiếp xúc với cả  P và Q. Biết khi  S  thay
đổi thì tâm I của nó luôn thuộc đường tròn C cố định. Diện tích hình tròn giới hạn bởi C là 2 4 16 8 A. . B. . C. . D. . 3 9 9 9 Lời giải K I A 1 5    1
Bán kính mặt cầu S  : R d  P,Q  .  1 2 2   2 2 2 1  2
Tâm I của mặt cầu  S  nằm trên mặt phẳng  R cách đều  P và Q.
Phương trình mặt phẳng  R : 2x y  2z  2  0
Trang 54 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Tâm I của mặt cầu  S  nằm trên mặt cầu  '
S  có tâm A bán kính R IA  1 2.  1 1 2.1 2 1
Gọi K là hình chiếu của A trên  R  AK d  ,
A R     2 2 2 3 2 1  2
Tâm I của mặt cầu  S  nằm trên đường tròn C là giao của mặt cầu  '
S  và mặt phẳng  R 2  1  2 2
có tâm K và bán kính 2 2 2 r KI
AI AK  1      3  3 8
Diện tích hình tròn giới hạn bởi C là: 2  r  . 9
Câu 113. Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng  ABCD , tứ giác ABCD là hình
thang vuông với cạnh đáy AD, BC . AD  3CB  3a , AB a , SA a 3 . Điểm I thỏa mãn  
AD  3AI , M là trung điểm SD , H là giao điểm của AM và SI . Gọi E, F lần lượt là hình
chiếu của A lên SB, SC . Tính thể tích V của khối nón có đáy là đường tròn ngoại tiếp tam
giác EFH và đỉnh thuộc mặt phẳng  ABCD . 3  a 3  a 3  a 3  a A. V  . B. V  . C. V  . D. V  . 5 5 2 5 5 10 5 Lời giải
Nhận xét: Tứ giác ABCI là hình vuông. Dễ chứng minh BC  SAB và BI SC . EA SB
EA  SBC   EA SC . EA   BCEA SC
SC   AEF  . FA   SC 2 SE SA 3
Trong tam giác vuông SAB có   . 2 SB SB 4 HS AI MD HS SH 3
Trong tam giác SAD có . .  1   3   . HI AD MS HI SI 4 SE SH 3
Trong tam giác SBI có  
EH //BI . Do BI SC nên EH SC . SB SI 4 Suy ra các điểm ,
A E, F , H cùng thuộc mặt phẳng đi qua A và vuông góc với SC .
Gọi K là trung điểm AF .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 55
NGUYỄN BẢO VƯƠNG - 0946798489EA EF Vì 
K là tâm đường tròn ngoại tiếp tam giác EFH . AH   FH S . A AC a 3.a 2 a 6 Ta có: AF    . SC a 5 5 1 a 6
Suy ra bán kính đáy của khối nón là R AF  . 2 2 5
Gọi O là tâm hình vuông ABCI . 
SC   EFH  Do 
OK   EFH   O là đỉnh của khối nón. OK //  SC 1 1 1 6 a
Chiều cao của khối nón là h FC 2 2  AC AF 2 2  2a a  . 2 2 2 5 5 2 1 1  a 6  a 3  a
Vậy thể tích khối nón là 2
V  . R .h  . .  .  . 3 3  2 5  5   10 5
Câu 114. Cho một miếng tôn hình tròn có bán kính 50 cm . Biết hình nón có thể tích lớn nhất khi diện
tích toàn phần của hình nón bằng diện tích miếng tôn ở trên. Khi đó hình nón có bán kính đáy là: A. 10 2 cm . B. 50 2 cm . C. 20 cm . D. 25cm . Lời giải
Ta có diện tích miếng tôn là S    2 .2500 cm  .
Diện tích toàn phần của hình nón là: 2
S   R   . . R l . tp A
Thỏa mãn yêu cầu bài toán ta có: 2  R  . . R l  2500 2  R  .
R l  2500  A l   R . R Thể tích khối nón là: 2 1 1 1  A 2 
V   R .h 2 2 2
V   R . l R 2 2
V   R .  RR   3 3 3  R  2 2 1 A 1 3 1 AA 2 
V   R .  2 A 2 2 4
V   . A .R  2 . A R 2  V   .  2 A R  2   3 R 3 3 8  4  1 A A AV   .
. Dấu bằng xảy ra khi R
 25 , vậy V đạt GTLN khi R  25 . 3 2 2 4
Câu 115. Cho hình nón  N  có đường cao SO h và bán kính đáy bằng R , gọi M là điểm trên đoạn
SO , đặt OM x , 0  x h . C  là thiết diện của mặt phẳng  P vuông góc với trục SO tại
M , với hình nón  N  . Tìm x để thể tích khối nón đỉnh O đáy là C  lớn nhất. h h 2 h 3 h A. . B. . C. . D. . 2 2 2 3 Lời giải
Trang 56 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Ta có BM là bán kính đường tròn C  . BM SM A . O SM
R h x
Do tam giác SBM ∽ SAO nên   BM   BM  . AO SO SO h
Thể tích của khối nón đỉnh O đáy là C  là: 1 2 2
R h x 2 1  1 R 2
V   BM .OM   x    
h xx . 3 3 h 2   3 h 2 1 R 2
Xét hàm số f x  
h xx , 0  x h ta có 2 3 h 2 1 R 2 1 R h
Ta có f  x  
h xh  3x ; f  x  0  
h xh  3x  x  . 2 3 h 2 3 h 3
Lập bảng biến thiên ta có h
Từ bảng biến ta có thể tích khối nón đỉnh O đáy là C  lớn nhất khi x  . 3
Câu 116. Bạn Hoàn có một tấm bìa hình tròn như hình vẽ, Hoàn muốn biến hình tròn đó thành một hình
cái phễu hình nón. Khi đó Hoàn phải cắt bỏ hình quạt tròn AOB rồi dán hai bán kính OA và
OB lại với nhau (diện tích chỗ dán nhỏ không đáng kể). Gọi x là góc ở tâm hình quạt tròn
dùng làm phễu. Tìm x để thể tích phễu lớn nhất?
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 57
NGUYỄN BẢO VƯƠNG - 0946798489   2 6  A. . B. . C.  . D. . 4 3 3 2 Lời giải Rx
Dựa vào hình vẽ, độ dài cung AB lớn bằng Rx , bán kính hình nón r  2 2 2 R x R
Đường cao của hình nón 2 2 h R r 2  R  2 2  4  x 2 4 2 1 2 2 1 R x R 3 R
Thể tích khối nón (phễu) 2 V   r h 2 2   . . 4  x 4  x  2 2 4  x 2  3 2 3 4 2 24 4 x x  3  2 2  3 2 2 2 2 3 R Theo Cauchy ta có . .4  x    V  . 2 2 27 27 2 x 2 6 2 6 Dấu bằng xảy ra khi 2 2
 4  x x
 . Vậy thể tích phễu lớn nhất khi x   . 2 3 3
-------------------- HẾT --------------------
Trang 58 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/