Tổng ôn tập TN THPT 2020 môn Toán: Phương trình – bất phương trình – GTLN – GTNN mũ và logaritTổng ôn tập TN THPT 2020 môn Toán: Phương trình – bất phương trình – GTLN – GTNN mũ và logarit

Tài liệu gồm 96 trang, được tổng hợp và biên soạn bởi thầy giáo Nguyễn Bảo Vương, tuyển chọn các câu hỏi và bài tập trắc nghiệm các chuyên đề: phương trình và bất phương trình mũ và logarit, GTLN – GTNN

86 43 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 6: Hàm số mũ và hàm số lôgarit (KNTT)

Môn: Toán 11

Thông tin:

96 trang 7 tháng trước

Tác giả:

Profile Kim Oanh
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
A. PHƯƠNG PHÁP GIẢI PHƯƠNG TRÌNH – BPT MŨ -LOGARIT
Thường sử dụng các phương pháp sau:
1. Phương pháp đưa về cùng cơ số.
1/ Phương trình – Bất phương trình mũ cơ bản
 Phương trình mũ
+ Nếu
a 0, a 1
thì
f x g x
a a f x g x
+ Nếu a chứa ẩn thì
f x g x
a 1
a a a 1 f x g x 0
f x g x
.
+
f x g x
a b
f x g x
a a
log a log b
a
f x log b.g x
(logarit hóa).
 Bất phương trình mũ
+ Nếu
a 1
thì
f x g x
a a f x g x
. (cùng chiều)
+ Nếu
0 a 1
thì
f x g x
a a f x g x
. (ngược chiều)
+ Nếu a chứa ẩn thì
f x g x
a a a 1 f x g x 0
.
2/ Phương trình logarit – Bất phương trình logarit cơ bản
 Phương trình logarit
+ Nếu
b
a
a 0, a 1 : log x b x a
1
+ Nếu
a a
a 0, a 1 : log f x log g x f x g x
2
+ Nếu
g x
a
a 0, a 1 : log f x g x f x a
(mũ hóa)
3
 Bất phương trình logarit
+ Nếu
a 1
thì
a a
log f x log g x f x g x
(cùng chiều)
+ Nếu
0 a 1
thì
a a
log f x log g x f x g x
(ngược chiều)
+ Nếu a chứa ẩn thì
a
a
a
log B 0 a 1 B 1 0
log A
0 A 1 B 1 0
log B
.
Các bước giải phương trình & bất phương trình mũ – logarit
Bước 1. Đặt điều kiện (điều kiện đại số
điều kiện loga), ta cần chú ý:
ĐK
a
0 a 1
log b
b 0
và
Đ
Đ
K
a
K
a
log f x f x 0
log f x f x 0
.
Bước 2. Dùng các công thức và biến đổi đưa về các cơ bản trên, rồi giải.
Bước 3. So với điều kiện và kết luận nghiệm.
2. Phương pháp đặt ẩn phụ.
I/ Đặt ẩn phụ cho phương trình mũ
Loại 1.
f x
PP
P a 0
đặt
f x
t a , t 0
.
Loại 2.
λ
f x
2.f x 2.f x
.a . a.b .b 0
PP
Chia hai vế cho
2.f x
b ,
rồi đặt
f x
a
t 0
b
(chia
cho cơ số lớn nhất hoặc nhỏ nhất).
PHƯƠNG TRÌNH - BẤT PHƯƠNG TRÌNH - MIN MAX LOGARIT
Vấn đề 10
mũ lẻ
mũ chẵn
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Loại 3.
f x f x
a b c
với
a.b 1
PP
đặt
f x f x
1
t a b
t
.
Loại 4.
f x g x
f x g x
f x
g x
a .a
.a .a b 0
a
a
PP
đặt
f x
g x
u a
v a
.
II/ Đặt ẩn phụ cho phương trình logarit
Loại 1.
PP
a
P log f x 0
đặt
a
t log f x
.
Loại 2. Sử dụng công thức
b b
log c log a
a c
để đặt
b b
log x log a
t a t x
.
Lưu ý
Trên đây là một số dạng cơ bản thường gặp về phương trình mũ và loga, còn bất phương trình ta cũng
làm tương tự nhưng lưu ý về chiều biến thiên. Về phương diện tổng quát, ta đi tìm mối liên hệ
giữa biến để đặt ẩn phụ, đưa về phương trình (bất phương trình) đại số hoặc hệ phương trình đại
số mà đã biết cách giải. Từ đó, tìm ra được nghiệm. Ngoài ra, còn một số trường hợp đặt ẩn phụ
không hoàn toàn. Nghĩa là sau khi đặt ẩn phụ t vẫn còn x. Ta giải phương trình theo t với x được
xem như là hằng số bằng cách lập biệt thức ∆ hoặc đưa về tích số.
3. Phương pháp hàm số.
I/ Cơ sở lý thuyết và vận dụng cơ sở lý thuyết để tìm hướng giải
Thông thường ta sẽ vận dụng nội dung các định lý (và các kết quả) sau:
Nếu hàm số
y f x
đơn điệu một chiều trên D thì phương trình
f x 0
không quá một nghiệm
trên D.
Để vận dụng định lý này, ta cần nhẩm được
1
nghiệm
o
x x
của phương trình, rồi chỉ rõ hàm
đơn điệu một chiều trên D (luôn đồng biến hoặc luôn nghịch biến trên D) và kết luận
o
x x
là
nghiệm duy nhất.
Hàm số
f t
đơn điệu một chiều trên khoảng
a; b
và tồn tại
u; v a;b
thì
f u f v u v
".
Để áp dụng định lý này, ta cần xây dựng hàm đặc trưng
f t
.
Hàm số
y f t
xác định và liên tục trên D:
Nếu
f t
đồng biến trên D và
u, v D
thì
f u f v u v
.
Nếu
f t
nghịch biến trên D và
u, v D
thì
f u f v u v
.
Để vận dụng nội dung định lí này trong giải bất phương trình, người ra đề thường cho dưới hai
hình thức và có hai hướng xử lí thường gặp sau:
 Nếu đề yêu cầu giải
f x 0
:
Nhẩm nghiệm của
f x 0
trên miền xác định D, chẳng hạn
o
x x
.
Xét hàm số
y f x
trên D và chỉ rõ nó đơn điệu tăng một chiều (đơn điệu giảm một chiều). Khi đó:
o o
f x 0 f x f x x x
nếu hàm số đơn điệu tăng trên D và
o
x x
nếu hàm số đơn
điệu giảm trên D.
 Nếu đề bài yêu cầu giải
f x 0
mà không nhẩm được nghiệm
o
x x
của
f x 0
thì cần biến đổi
f x 0 f g x f h x
với việc xây dựng hàm đặc trưng
y f t ,
rồi chỉ ra hàm
f t
là
đồng biến (nghịch biến). Khi đó
f g x f h x g x f x
hay g x f x
.
Ta sẽ làm tương tự nếu đề cho
f x 0, f x 0
hoặc
f x 0
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Nếu hàm số
y f x
có đạo hàm
f ' x
liên tục và thỏa mãn
f ' x 0
có một nghiệm trên D thì
phương trình
f x 0
không quá
2
nghiệm trên D.
II/ Một số loại toán cơ bản thường gặp khi sử dụng đơn điệu hàm
Loại 1.
a
f x
log . g x f x
g x
1
 Tìm tập xác định D.
 Biến đổi
a a
1 log f x log g x .g x .f x
a a
log f x .f x log g x .g x
f f x f g x
.
Xét hàm số đặc trưng
a
f t .t log t
trên miền D và chỉ ra hàm số này luôn đơn điệu một chiều
trên D và
f f x f g x f x g x
.
Loại 2.
a b
log f x log g x
2
 Nếu
a b
thì
2 f x g x
: đây là dạng toán khá quen thuộc.
 Nếu
a 1 b 1 0
PP
Dùng phương pháp đoán nghiệm và chứng minh đó là nghiệm duy
nhất.
 Nếu
a 1 b 1 0
PP
Đặt ẩn phụ kết hợp mũ hóa phương trình.
Tìm tập xác định D và đặt
t
t
a b
f x a
log f x log g x t
g x b
và biến đổi phương trình về dạng:
t t
f t A B 1
và giải bằng phương pháp đoán nghiệm và chứng minh nghiệm này duy nhất
và tìm x khi biết t.
Dạng toán:
a b
. log f x . log g x
ta cũng làm tương tự bằng cách đặt
γ
a b
log f x log g x .t
với
γ
là bội số chung nhỏ nhất của
và
.
Loại 3.
a
f x
log g x log b
3
 Đặt điều kiện:
f x 0
và
0 g x 1
.
 Sử dụng công thức đổi cơ số thì
b
a
b
log f x
3 log b
log g x
b a b
log f x log b. log g x
b a
log f x log g x
(đây là loại 2).
Loại 4.
λ
x
a
a p log x qx r
4
PP
Đặt ẩn phụ
λ
a
log x y
để đưa về hệ phương trình đối xứng loại II hay gần đối xứng và
sử dụng phương pháp hàm để tìm được
x y
.
Phương trình dạng
log , log ,
a b
f x y g x y
.
Phương pháp: đặt
log , log ,
a b
t f x y g x y
và chuyển về hệ
,
,
t
t
f x y a
g x y b
và đánh giá chặn giá
trị
t
. Từ đó chọn giá trị nguyên của
x
thích hợp và thử lại xem với giá trị nguyên của
x
đã chọn
thì hệ phương trình có nghiệm
t
trong miền đã chặn hay không?
Kiến thức để đánh giá chặn giá trị
t
:
+ Điều kiện có nghiệm của phương trình bậc 2.
+ Bất đẳng thức Cauchy, BCS…
+ Tính chất biến thiên của hàm số.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 1. Cho
x
,
y
là các số thực dương thỏa mãn
9 6 4
log log log 2
x y x y
. Giá trị của
x
y
bằng
A.
2
. B.
1
2
. C.
2
3
log
2
. D.
3
2
log 2
.
Câu 2. Biết
1 2 1 2
;
x x x x
là hai nghiệm của phương trình
2
2
2
4 4 1
log 6 4
x x
x x
x
và
1 2
1
2
4
x x a b
với
,a b
là các số nguyên dương. Giá trị
P a b
là
A.
14P
. B.
13
P
. C.
15
P
. D.
16
P
.
Câu 3. Biết
30
log 10
a ,
30
log 150
b và
1 1 1
2000
2 2 2
log 15000
x a y b z
x a y b z
với
1 1 1 2 2 2
; y ;z ; ; y ;z
x x là các số
nguyên, tính
1
2
x
S
x
.
A.
1
2
S
. B.
2
S
. C.
2
3
S
. D.
1
S
.
Câu 4. Cho các số thực dương
,x y
khác 1 và thỏa mãn
log log
log log
x y
x y
y x
x y x y
.
Giá trị của
2 2
x xy y
bằng
A. 0. B. 3. C. 1. D. 2.
Câu 5. Cho các số thực dương
a
,
b
thỏa mãn
log log log log 100
a b a b
và
log a
,
logb
,
log
a
,
log
b
đều là các số nguyên dương. Tính
P ab
.
A.
164
10 .
B.
100
10 .
C.
200
10 .
D.
144
10 .
Câu 6. Cho
9 4 2
log 5 ; log 7 ; log 3
a b c
.Biết
24
log 175
mb nac
pc q
.Tính
2 3 4 A m n p q
A.
27
B.
25
C.
23
D.
29
Câu 7. Cho
x
,
y
là các số thực lớn hơn
1
thoả mãn
2 2
6
x y xy
. Tính
12 12
12
1 log log
2log 3
x y
M
x y
.
A.
1
4
M
. B.
1M
. C.
1
2
M
. D.
1
3
M
.
Câu 8. Cho
2
ln 1 sin 6
f x a x x b x
với
a
,
b
. Biết
log log e 2
f
. Tính
log ln10
f
.
A.
4
. B.
10
. C.
8
. D.
2
.
Câu 9. Cho
x -x
9 + 9 = 14
và
x -x
x+1 1-x
6+3(3 +3 ) a
=
2-3 -3 b
với
a
b
là phân số tối giản. Tính
. .P a b
A.
10.
P
B.
45.
P
C.
10.
P
D.
45.
P
Câu 10. Biết phương trình
1
3
27 27 16 3 6 0
3
x x x
x
có các nghiệm
3
, log x a x b
và
3
logx c
với
, 0.
a b c
Tỉ số
b
c
thuộc khoảng nào sau đây?
A.
(3; ).
B.
3 5
;
2 2
C.
3
1;
2
D.
5
;3
2
Câu 11. Cho hai số thực dương
,a b
thỏa
4 6 9
log log log
a b a b
. Tính
a
b
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
A.
1
2
. B.
1 5
2
. C.
1 5
2
. D.
1 5
2
.
Câu 12. Gọi a là một nghiệm của phương trình
2log log 2log
4.2 6 18.3 0
x x x
. Khẳng định nào sau đây
đúng khi đánh giá về
a
?
A.
2
10 1
a
. B.
2
10
a
. C.
2
1 2
a a
. D.
1
100
a
.
Câu 13. Tổng các nghiệm của phương trình sau
1
7
7 6log 6 5 1
x
x
bằng
A.
2
. B.
3
. C.
1
. D.
10
.
Câu 14. Bất phương trình
9 2 5 3 9 2 1 0
x x
x x
có tập nghiệm là
; ;S a b c
. Tính
tổng
a b c
?
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 15. Phương trình
2 2 2
sin cos sin
2 3 4.3
x x x
có bao nhiêu nghiệm thuộc
2017; 2017
.
A.
1284
. B.
4034
. C.
1285
. D.
4035
.
Câu 16. Cho các số thực dương
,x y
thỏa mãn
6 9 4
log log log 2 2x y x y
. Tính tỉ số
x
y
?
A.
2
3
x
y
. B.
2
3 1
x
y
. C.
2
3 1
x
y
. D.
3
2
x
y
.
Câu 17. Số nghiệm của phương trình
5
log 3
2
x
x
là:
A.
0
. B.
1
. C.
3
. D.
2
.
Câu 18. Phương trình
3 3 3 3 4 4 3
3 3 3 3 10
x x x x
có tổng các nghiệm là?
A.
0
. B.
2
. C.
3
. D.
4
.
Câu 19. Tìm tập nghiệm
S
của bất phương trình
2
2
3 1 3
3 1
x
x
x
.
A.
3
;0 log 2;
 
. B.
3
0;log 2
.
C.
1
0; 2;
2

. D.
0;

.
Câu 20. Cho
x
,
y
là các số thực dương thỏa mãn
25 15 9
log log log
2 4
x x y
y
và
2
x a b
y
, với
a
,
b
là các số nguyên dương, tính
a b
.
A.
14
a b
. B.
3
a b
. C.
21
a b
. D.
34
a b
.
Câu 21. Biết rằng phương trình
1009
2 3
log 1 2018logx x
có nghiệm duy nhất
0
x
. Khẳng định nào dưới
đây đúng?
A.
1 1
1008 1006
0
3 3
x
. B.
2
1009
0
3
x
. C.
1
1008
0
1 3
x
. D.
1
1007
0
3 1
x
.
Câu 22. Phương trình
3 2
2log cot log cosx x
có bao nhiêu nghiệm trong khoảng
0;2018
?
A.
2018
nghiệm. B.
1008
nghiệm. C.
2017
nghiệm. D.
1009
nghiệm.
Câu 23. Cho dãy số
n
u
thỏa mãn
3 5 4
log 2 63 2log 8 8
n
u u n
,
*
n
. Đặt
1 2
...
n n
S u u u
. Tìm số nguyên dương lớn nhất
n
thỏa mãn
2
2
.
148
. 75
n n
n n
u S
u S
.
A.
18
. B.
17
. C.
16
. D.
19
.
Câu 24. Số nghiệm của phương trình
2 2
3 5
log 2 log 2 2
x x x x
là
A.
3
. B.
2
. C.
1
. D.
4
.
Câu 25. Tìm giá trị gần đúng tổng các nghiệm của bất phương trình sau:
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2 6 5 4 3 2
2
22 22
3 3
22 22 2 4
2log 2log 5 13 4 24 2 27 2 1997 2016 0
3 3 log log
x x
x x x x x
x x
A.
12,3
. B.
12
. C.
12,1
. D.
12,2
.
Câu 26. Tìm tích tất cả các nghiệm của phương trình
2
log 100
log 10
1 log
4.3 9.4 13.6
x
x
x
.
A.
100
. B.
10
. C.
1
. D.
1
10
.
Câu 27. Tập nghiệm của bất phương trình
2 2
2.7 7.2 351. 14
x x x
có dạng là đoạn
;S a b
. Giá trị
2b a
thuộc khoảng nào dưới đây?
A.
3; 10
. B.
4;2
. C.
7;4 10
. D.
2 49
;
9 5
.
Câu 28. Tập nghiệm của bất phương trình
2
2
2 2 2 2 1 2 1
x x x
là
A.
;0
S 
. B.
1;S

. C.
0;1
S
. D.
3;S

.
Câu 29. Bất phương trình
2 2
1 1 1
2 2 2 2
x x x x
có tập nghiệm
;S a b
. Khi đó
a b
bằng
A.
2
. B.
3
. C.
1
. D.
10
.
Câu 30. Tập nghiệm của bất phương trình
2
log 5
5 21 5 21 2
x x
x
là
A.
2;1
S
. B.
1;1
S
. C.
1;5
S
. D.
1;S

.
Câu 31. Có bao nhiêu cặp số nguyên
;x y
thỏa mãn
0 2020
x
và
3
log 3 3 2 9
y
x x y
?
A.
2019
. B.
6
. C.
2020
. D.
4
.
Câu 32. Có bao nhiêu cặp số nguyên
,x y
thỏa mãn
2 2
9
log 3 9 1
x y
x y
?
A.
7
. B.
6
. C.
10
. D.
9
.
Câu 33. Có bao nhiêu giá trị nguyên của tham số
m
sao cho tồn tại duy nhất cặp số thực
,x y
thỏa mãn
2 2
18
x y
và
3 3
log 2 log
x y m y m x m
?
A.
3
. B.
2
. C.
4
. D.
5
.
Câu 34. Biết
1 2 1 2
, ( )x x x x
là hai nghiệm của phương trình
2
2
3
2 1
log 2 3
3
x x
x x
x
và
1 2
4 2
x x a b
, với
,a b
là hai số nguyên dương. Tính
a b
A.
9
a b
. B.
12
a b
. C.
7
a b
. D.
14
a b
.
Câu 35. Có bao nhiêu cặp số nguyên
;x y
thỏa mãn
0 2020
x
và
2
log 4 4 1 2
y
x x y
?
A.
10
. B.
11
. C.
2020
. D.
4
.
Câu 36. Có bao nhiêu số nguyên
x
sao cho tồn tại số thực
y
thỏa mãn
2 2
2 3
log 4 log 4
x y x y
.
A.
3
. B. Vô số. C.
2
. D.
4
.
Câu 37. Có bao nhiêu cặp số nguyên
;x y
thoả mãn
0 2020
x
và
2
2 ln 1 1
y
x x x y e
?
A.
0
. B.
7
. C.
1
. D.
8
.
Câu 38. Có bao nhiêu số nguyên
x
sao cho tồn tại số thực
y
thỏa mãn
2 2
3 4
log ( ) log 2
x y x y
?
A.
1
B.
3
C.
2
D. Vô số
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Câu 39. Có bao nhiêu cặp số nguyên dương
;x y
thỏa mãn đồng thời hai điều kiện:
6
1 10x
và
2
2 2 2
log 10 20 20 10 2 1
y
x x y x x
?
A.
4
. B.
2
. C.
3
. D.
1
.
Câu 40. Có bao nhiêu số nguyên
10y
sao cho tồn tại số nguyên
x
thỏa mãn
2
2
2 2 1
5 2 5 1
y
y
x x x
x
?
A.
10
B.
1
C.
5
D. Vô số
Câu 41. Có bao nhiêu cặp số nguyên dương
;x y
thoả mãn
1 2020 x
và
1
2
2 2 log 2
y y
y x x
A.
2021
. B.
10
. C.
2020
. D.
11
.
Câu 42. Có bao nhiêu số nguyên
x
sao cho tồn tại số thực
y
thỏa mãn
2 2
2 2
3
2log log 1 3 log 1x y x y
A.
1
B.
3
C.
2
D.
5
Câu 43. Có bao nhiêu cặp số nguyên
;x y
thỏa mãn
0 2020y
và
3
2 1
log 1 2 ?
x
x
y
y
A.
2019
. B.
11
. C.
2020
. D.
4
.
Câu 44. Biết
1
x
,
2
x
là hai nghiệm của phương trình
2
2
7
4 4 1
log 4 1 6
2
x x
x x
x
và
1 2
1
2
4
x x a b
với
a
,
b
là hai số nguyên dương. Tính
a b
.
A.
13 a b
. B.
11 a b
. C.
16 a b
. D.
14 a b
.
Câu 45. Biết phương trình
5 3
2 1 1
log 2log
2
2
x x
x
x
có một nghiệm dạng
2 x a b
trong đó
,a b
là các số nguyên. Tính
2 a b
.
A.
3
. B.
8
. C.
4
. D.
5
.
Câu 46. Số nghiệm thực của phương trình
6
6 3log 5 1 2 1
x
x x
là
A.
0
. B.
2
. C.
1
. D.
3
.
Câu 47. Tính tổng
S
tất cả các nghiệm của phương trình
1
5 3
ln 5 5.3 30 10 0
6 2
x x
x x
x
x
.
A.
1S
. B.
2S
. C.
1S
. D.
3S
.
Câu 48. Số nghiệm của phương trình
2
1 2
80
ln 2.3 2 80 ln3
3
x
x
x
x
là
A.
2
. B.
3
. C.
1
. D.
0
.
B. BÀI TOÁN CHỨA THAM SỐ
Dạng 1. Tìm m để có nghiệm (hoặc có k nghiệm) trên D?
— Bước 1. Tách m ra khỏi biến số và đưa về dạng .
— Bước 2. Khảo sát sự biến thiên của hàm số trên D.
— Bước 3. Dựa vào bảng biến thiên để xác định giá trị của tham số để đường thẳng nằm
ngang cắt đồ thị hàm số .
— Bước 4. Kết luận các giá trị cần tìm của để phương trình có nghiệm (hoặc có k
nghiệm) trên D.
Lưu ý
f t; m 0
f t A m
f t
A m
y A m
y f t
A m
f t A m
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
— Nếu hàm số có giá trị lớn nhất và giá trị nhỏ nhất trên D thì giá trị cần tìm là những m
thỏa mãn: .
— Nếu bài toán yêu cầu tìm tham số để phương trình có k nghiệm phân biệt, ta chỉ cần dựa vào bảng biến
thiên để xác định sao cho đường thẳng nằm ngang cắt đồ thị hàm số tại k điểm
phân biệt.
Dạng 2. Tìm m để bất phương trình hoặc có nghiệm trên miền D?
— Bước 1. Tách tham số m ra khỏi biến số t và đưa về dạng hoặc .
— Bước 2. Khảo sát sự biến thiên của hàm số trên D.
— Bước 3. Dựa vào bảng biến thiên xác định các giá trị của tham số m để bất phương trình có nghiệm:
+ có nghiệm trên .
+ có nghiệm trên .
Lưu ý
— Bất phương trình nghiệm đúng .
— Bất phương trình nghiệm đúng .
Câu 1. Cho phương trình
2
2 2
log 2 2 log 2 0x m x m
(
m
là tham số thực). Tập hợp tất cả các
giá trị của
m
để phương trình đã cho có hai nghiệm phân biệt thuộc đoạn
1;2
là
A.
1;2
. B.
1;2
. C.
1;2
. D.
2;
.
Câu 2. Cho phương trình
3 2
2 2 2
2log 7log 4log 3 0
2
x
x
x x m
(
m
là tham số thực). Có tất cả
bao nhiêu giá trị nguyên dương của
m
để phương trình đã cho có đúng hai nghiệm phân biệt?
A.
78
. B.
80
. C.
81
. D.
79
.
Câu 3. Cho phương trình
2
2 2
2log 3log 2 9 1 3 0
x x
x x m m
(
m
là tham số thực). Gọi
S
là
tập hợp tất cả các giá trị nguyên dương của
m
để phương trình đã cho có đúng hai nghiệm phân
biệt. Tính tổng tất cả các phần tử của
S
.
A.
3238
. B.
3236
. C.
3237
. D.
3239
.
Câu 4. Cho phương trình
2
3 3
2log 3log 2 3 .2 0
x x
x x m (
m
là tham số thực). Gọi
S
là tập hợp tất
cả các giá trị nguyên dương của
m
để phương trình đã cho có đúng hai nghiệm phân biệt. Tính
tổng tất cả các phần tử của
S
.
A.
741
. B.
742
. C.
740
. D.
703
.
Câu 5. Cho phương trình
2
2lg lg 1 lg
2 4 3 0
x x x x
m
(
m
là tham số thực). Gọi
S
là tập hợp tất cả các giá
trị nguyên dương của
m
để phương trình đã cho có đúng hai nghiệm phân biệt. Tổng của phần tử nhỏ
nhất và phần tử lớn nhất
S
bằng
A.
100
3 1
. B.
100
3 1
. C.
99
3
. D.
99
3 1
.
Câu 6. Cho phương trình
3.2 .log 12log 2 4 5 0
x x x
x x m
(
m
là tham số thực). Có tất cả bao
nhiêu giá trị nguyên dương của
m
để phương trình đã cho có đúng hai nghiệm phân biệt?
A.
24
. B.
25
. C.
23
. D.
22
.
Câu 7. Cho phương trình
2 2
2 2
log 3 log 3 2 2 1 0x m x m m
(
m
là tham số thực). Tìm tất cả các số
thực
m
để phương trình có hai nghiệm phân biệt thuộc đoạn
1;9
.
A.
1
3 .
2
m
B.
2m
. C.
. D.
1 1
2 2
m
.
y f t
A m
t D t D
min f t A m max f t
y A m
y f t
f t; m 0
f t; m 0
A m f t
A m f t
f t
A m f t
t D
D A m max f t
A m f t
t D
D A m min f t
A m f t
t D
t D A m min f t
A m f t
t D
t D A m max f t
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Câu 8. Cho phương trình
2 2
2 2
log ( 3)log 2 3 0
x m x m m
(
m
là tham số thực). Có bao nhiêu giá trị
nguyên của tham số
m
để phương trình đã cho có đúng một nghiệm thuộc đoạn
1
;32
4
?
A.
4
. B.
5
. C.
6
. D.
7
.
Câu 9. Cho phương trình
9 ( 5)3 3 6 0
x x
m m
(
m
là tham số thực ). Có bao nhiêu giá trị
nguyên của
m
để phương trình đã cho có 2 nghiệm phân biệt thuộc đoạn
1;2
.
A.
6
. B.
7
. C.
m R
. D.
1
.
Câu 10. Cho phương trình
2 2 2
2 2
log log 2 0
x x m m
(
m
là tham số thực). Có bao nhiêu giá trị nguyên
của tham số
m
để phương trình đã cho có đúng một nghiệm thuộc đoạn
1
;16
8
?
A.
3
. B.
2
. C.
1
. D.
4
.
Câu 11. Cho phương trình
2 2
2 2
log 2 2log 1 0
x x m
.Có bao nhiêu giá trị nguyên của tham số
m
để
phương trình có đúng một nghiệm thuộc đoạn
1
;16
2
?
A.
10
. B.
7
. C.
5
. D.
6
.
Câu 12. Cho phương trình
2 2 2
2 2 2
log log 2 3 log 0
x x m m x
(
m
là tham số thực). Có bao nhiêu
giá trị nguyên của tham số
m
để phương trình đã cho có 3 nghiệm phân biệt
1
8
x
?
A.
3
. B.
5
. C.
2
. D.
4
.
Câu 13. Cho phương trình
2
1 2020 2 2020 2 0
x x
m m
(
m
là tham số thực). Tập hợp tất cả
các giá trị của
m
để phương trình đã cho có 2 nghiệm phân biệt thuộc đoạn
0;2
là
A.
2;2021
. B.
m R
. C.
2;

. D.
2;2021
.
Câu 14. Cho phương trình
2 2
3 3 81
log ( 3)log 2 3 1 log 0
x m x m m x
(
m
là tham số thực). Có bao
nhiêu giá trị nguyên của tham số
m
để phương trình đã cho có 3 nghiệm phân biệt
1
27
x
?
A.
4
. B.
3
. C.
2
. D.
5
.
Câu 15.
Cho phương trình
2
2021 2021
log 2021 2 log 2
x m x m
(
m
là tham số thực).
Tổng tất cả các giá trị nguyên của
m
để phương trình đã cho có hai nghiệm phân biệt thuộc đoạn
3
1; 2021
là:
A.
10
. B.
8
. C. vô số. D.
13
.
Câu 16. Cho phương trình
2 2 2
2 2 2
log log 2 3 log 0
x x m m x
(
m
là tham số thực). Có bao nhiêu
giá trị nguyên của tham số
m
để phương trình đã cho có 2 nghiệm phân biệt
1
8
x
?
A.
7
. B.
6
. C.
5
. D.
8
.
Câu 17. Có bao nhiêu giá trị nguyên của
m
để phương trình
2 2
1 1 1 1
9 2 3 2 1 0
x x
m m
có
nghiệm thực?
A.
4
. B.
5
. C.
6
. D.
7
.
Câu 18. Cho phương trình
2
log 2log 2 1
a a
x x
. Số giá trị nguyên của
0;2020
a
để phương trình
trên có 1 nghiệm thực là
A.
0
. B.
2018
. C.
2019
. D.
2020
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 19. Cho phương trình
3 2
1
2
2
log 6 2log 14 29 2 0
mx x x x
, số giá trị nguyên của
m
để
phương trình có 3 nghiệm thực phân biệt là
A.
1
. B.
0
. C.
23
. D.
5
.
Câu 20. Phương trình
2 2
3 3
log log 1 2 1 0
x x m
có nghiệm trên đoạn
3
1;3
khi
;m a b
. Khi đó
giá trị biểu thức
.T a b
bằng
A.
0
. B.
1
. C.
1
4
. D.
4
.
Câu 21. Phương trình
2 2
3 3
log log 1 2 1 0
x x m
có nghiệm trên đoạn
3
1;3
khi
;m a b
. Khi đó
giá trị biểu thức
.T a b
bằng
A.
0.
B.
1.
C.
1
.
4
D.
4.
Câu 22. Cho phương trình
2
3 3
3log 2log 1 5 0
x
x x m
(
m
là tham số thực). Có tất cả bao nhiêu giá
trị nguyên dương của
m
để phương trình đã cho có đúng hai nghiệm phân biệt?
A. Vô số. B.
120
. C.
121
. D.
124
.
Câu 23. Cho phương trình
2
4 2 2
log 2 1 log 2 1 logx x x m
(
m
là tham số thực). Có tất cả bao
nhiêu giá trị nguyên của
m
để phương trình đã cho có nghiệm?
A.
0
. B.
1
. C.
2
. D. Vô số.
Câu 24. Tìm tập hợp tất cả giá trị của tham số thực
m
để phương trình
2
2 2
log 4log 0
x x m
có
nghiệm thuộc khoảng
0 ;1
.
A.
4 ;
. B.
4 ;
. C.
4 ;0
. D.
2 ;0
.
Câu 25. Cho phương trình
3 2
2 2 2
2020 2log 7log 4log 2 3 0
x
x x x m
(
m
là tham số thực). Có tất
cả bao nhiêu giá trị nguyên dương của
m
để phương trình đã cho có đúng hai nghiệm phân biệt?
A.
79
. B.
80
. C. Vô số. D.
78
.
Câu 26. Cho phương trình
2
3 3
2log 3log 2 5 .3 0
x x
x x m
(
m
là tham số thực). Gọi
S
là tập hợp
tất cả các giá trị nguyên dương của
m
để phương trình đã cho có đúng hai nghiệm phân biệt. Tính
tổng tất cả các phần tử của
S
.
A.
4950
. B.
2475
. C. Vô số. D.
4949
.
Câu 27.
Cho phương trình
2
2
1 1
2 2
1
1 log 2 4 5 log 4 4 0
2
m x m m
x
(
m
là tham số thực). Có
tất cả bao nhiêu giá trị nguyên của tham số
m
để phương trình có nghiệm thuộc
5
;4
2
.
A.
6
. B.
5
. C.
4
. D. Vô số.
Câu 28. Cho phương trình
2
2 2
2log 3log 2 16 1 4 0
x x
x x m m
(
m
là tham số thực). Gọi
S
là
tập hợp tất cả các giá trị nguyên dương của
m
để phương trình đã cho có đúng ba nghiệm phân
biệt. Tổng tất cả các phần tử của
S
là
A.
32637
. B.
32640
. C.
255
. D.
256
.
Câu 29. Giá trị lớn nhất của tham số
m
sao cho bất phương trình
2 2
5 5
1 log 1 log 4
x mx x m
nghiệm đúng với mọi
x
thuộc
là
A.
2
. B.
3
. C.
5
2
. D.
4
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Câu 30. Giá trị lớn nhất của tham số
m
sao cho bất phương trình
2 2
5 5
1 log 1 log 4
x mx x m
nghiệm đúng với mọi
x
thuộc
là:
A.
2
. B.
3
. C.
5
2
. D.
4
.
Câu 31. Cho phương trình
2
7 7
log 3log 2 5 0
x
x x m
(
m
là tham số thực). Gọi
S
là tập hợp tất
cả các giá trị nguyên dương của
m
để phương trình đã cho có đúng hai nghiệm phân biệt. Tổng
của phần tử nhỏ nhất và phần tử lớn nhất
S
bằng
A.
49
5
. B.
49
5 1
. C.
48
5
. D.
49
5 1
.
Câu 32. Cho phương trình
2
2 2
2log 5log 2 5 0
x
x x m
(
m
là tham số thực). Có tất cả bao nhiêu
giá trị nguyên dương của
m
để phương trình đã cho có đúng hai nghiệm phân biệt?
A. 616. B. 615. C. vô số. D. 617.
Câu 33. Có bao nhiêu giá trị nguyên của tham số
2019; 2019
m
để phương
trình
2 1 2 1
2019 0
1 2
x
x mx m
x x
có đúng 3 nghiệm thực phân biệt?
A.
4038
. B.
2019
. C.
2017
. D.
4039
.
Câu 34. Có bao nhiêu giá trị nguyên của tham số
m
để tồn tại cặp số
;x y
thỏa mãn
3 5 3 1
e e 1 2 2
x y x y
x y
, đồng thời thỏa mãn
2 2
3 3
log 3 2 1 6 log 9 0
x y m x m
?
A.
6
. B.
5
. C.
8
. D.
7
.
Câu 35. Có bao nhiêu số nguyên của
m
để phương trình
2
2 2
log 2 2log 4 2 1
x m x x x m
có hai
nghiệm thực phân biệt?
A.
2
. B.
3
. C.
1
. D.
4
Câu 36. Tìm tổng tất cả các giá trị nguyên của
m
để phương trình
3
3 3 3 2 3
3 9 24 .3 3 1
x m x x x
x x x m
có 3 nghiệm phân biệt.
A.
45
. B.
34
. C.
27
. D.
38
.
Câu 37. Tìm các giá trị
m
để phương trình
sin 5 cos 5
sin 5 cos 10
3 log 5
x x m
x x
m
có nghiệm.
A.
6 6
m
. B.
5 5
m
. C.
5 6 5 6
m
. D.
6 5
m
.
Câu 38. Cho phương trình
2
2 log
x
m x m
với
m
là tham số. Có bao nhiêu giá trị nguyên của
18;18
m
để phương trình đã cho có hai nghiệm?
A.
20
. B.
17
. C.
9
. D.
21
.
Câu 39. Cho phương trình
3 2 3 2
3 1 3 1 2
3 2
81 3
3 2
1
2 .log 3 1 2 2 .log 0
3 1 2
m m x x
x x
m m
Gọi
S
là tập hợp tất cả các giá trị
m
nguyên để phương trình đã cho có
6
nghiệm hoặc
7
nghiệm
hoặc
8
nghiệm phân biệt. Tính tổng bình phương tất cả các phần tử của tập
S
.
A.
20
. B.
19
. C.
14
. D.
28
.
Câu 40. Cho phương trình
2
2
2 2
2 log 2 4 log 2 2
x a
x
x x a
. Gọi
S
là tập hợp các giá trị
a
thuộc đoạn
0;2020
và chia hết cho 3 để phương trình có hai nghiệm. Hãy tính tổng các phần tử
của
S
.
A.
0
. B.
2041210
. C.
680403
. D.
680430
.
Câu 41. Có bao nhiêu giá trị thực của tham số
a
để phương trình
2
2 2
1
2
2
4 log 2 3 2 log 2 2 0
x a
x x
x x x a
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
có 3 nghiệm thực phân biệt ?
A.
0
. B.
2
. C.
1
. D.
3
.
Câu 42. Tìm tổng tất cả các giá trị của tham số
a
để phương trình
2
2
2 1 2
2 3
3 log 2 2
x x x a
x x
x a
có
đúng ba nghiệm phân biệt.
A.
2
. B.
3
. C.
1
. D.
0
.
Câu 43. Tìm số giá trị nguyên của
m
thuộc
20; 20
để phương trình
2 2 2
2
log ( 4) (2 9) 1 (1 2 ) 4
x m x x m x m x
có nghiệm.
A. 12. B. 23. C. 25. D. 10.
C. GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT
Câu 1. Xét các số thực dương
, , ,a b x y
thoả mãn
1, 1a b
và
x y
a b ab
. Giá trị nhỏ nhất của
biểu thức
2P x y
thuộc tập hợp nào dưới đây?
A.
1;2
. B.
5
2;
2
. C.
3;4
. D.
5
;3
2
.
Câu 2. Xét các số thực dương
a
,
b
,
x
,
y
thỏa mãn
1
a
,
1b
và
4
x y
a b ab
. Giá trị nhỏ nhất của
biểu thức
4 P x y
thuộc tập hợp nào dưới đây?
A.
1;2
. B.
5
2;
2
. C.
1;2
. D.
0;1
.
Câu 3. Xét các số thực
a
,
b
,
0
c
thỏa mãn
3 5 15
a b c
. Giá trị nhỏ nhất của biểu thức
2 2 2
4( ) P a b c a b c
thuộc tập hợp nào dưới đây?
A.
1;2
. B.
5; 1
. C.
2;4
. D.
4;6
.
Câu 4. Xét các số thực dương
a
,
b
,
c
,
x
,
y
,
z
thỏa mãn
1
a
,
1b
,
1c
và
x y z
a b c abc
.
Giá trị nhỏ nhất của biểu thức
1
2
P x y z
thuộc tập hợp nào dưới đây?
A.
10;13
. B.
7;10
. C.
3;5
. D.
5;7
.
Câu 5. Xét các số thực dương
, , ,a b x y
thỏa mãn
1, 1
a b
và
2 2
.
x y
a b a b
. Giá trị nhỏ nhất của
biểu thức
.P x y
là
A.
9
4
P
. B.
6
2
P
. C.
3
2
P
. D.
4
9
P
.
Câu 6. Xét các số thực dương
, , ,a b x y
thỏa mãn
1, 1
a b
và
2
2
x
y
y
x
a b ab
. Giá trị nhỏ nhất của biểu
thức
.P x y
là
A.
2P
. B.
4P
. C.
3
P
. D.
1P
.
Câu 7. Xét các số thực dương
, , , , ,a b c x y z
thỏa mãn
1, 1, 1, 2
a b c y
và
1 2 1x y z
a b c abc
.
Giá trị nhỏ nhất của biểu thức
P x y z
là
A.
13
P
. B.
3
P
. C.
9
P
. D.
1P
.
Câu 8. Xét các số thực dương
x
,
y
thỏa mãn
3
1
log 3 2 4
2
xy
xy x y
x y
. Tìm giá trị nhỏ nhất
min
P
của
P x y
.
A.
min
9 11 19
9
P
. B.
min
9 11 19
9
P
. C.
min
18 11 29
9
P
. D.
min
2 11 3
3
P
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Câu 9. Xét các số thực dương
x
,
y
thỏa mãn
1 2
ln 3 1
x
x y
x y
. Tìm giá trị nhỏ nhất
min
P
của biểu
thức
1 1
1
P
x
xy
.
A.
min
8
P
. B.
min
16
P
. C.
min
9
P
. D.
min
2
P
.
Câu 10. Xét các số thực dương
x
,
y
thỏa mãn
2 3
3 3 6
3
x y
x y
x y
. Tìm giá trị nhỏ nhất
min
P
của
9 3 3 1
4 4
2
P
x
xy
.
A.
min
2
P
. B.
min
22 15 3
2
P
. C.
min
20
P
. D.
min
35 36 2
4
P
.
Câu 11. Cho hai số thực
a
,
b
thỏa
4
3
a b
và
3
2
16log 3log
12 16
a a
b
a
P a
b
có giá trị nhỏ nhất. Tính
a b
.
A.
7
2
. B.
4
. C.
11
2
. D.
6
.
Câu 12. Cho hai số thực dương
x
,
y
thỏa mãn
2 1
2
3
1
xy x y
x y
xy
. Tìm giá trị nhỏ nhất
min
S
của biểu thức
4S x y
.
A.
min
4 3 9
S
. B.
min
6 4 3
S
. C.
min
2 3 2
S
. D.
min
4 3 6
S
.
Câu 13. Cho
,x y
là hai số thực dương thỏa mãn
2 2 2
2 2 2 2
4 9.3 4 9 .7 .
x y x y y x
Giá trị nhỏ nhất của
biểu thức
2 18
x y
P
x
là
A.
9.
B.
3 2
.
2
C.
1 9 2.
D.
17.
Câu 14. Cho các số dương
,x y
thỏa mãn
5
1
log 3 2 4
2 3
x y
x y
x y
. Giá trị nhỏ nhất của biểu thức
4 9
6 2
A x y
x y
bằng
A.
31 6
.
4
B.
11 3.
C.
27 2
.
2
D.
19.
Câu 15. Cho hai số thực
,x y
lớn hơn 1 và thỏa mãn
.( ) .( ) .
y x
x x e y y e
y e x e
Tìm giá trị nhỏ nhất của biểu
thức
log log .
x y
P xy x
A.
2
2
. B.
2 2
. C.
1 2 2
2
. D.
1 2
2
.
Câu 16. Cho hai số thực
,x y
thỏa mãn
0 , 1x y
trong đó
,x y
không đồng thời bằng 0 hoặc 1 và
3
log 1 . 1 2 0
1
x y
x y
xy
. Tìm giá trị nhỏ nhất của
P
với
2P x y
A.
2
. B.
1
. C.
1
2
. D.
0
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 17. Xét các số thực dương
x
,
y
thỏa mãn
1 2
ln 3 1
x
x y
x y
. Tìm giá trị nhỏ nhất
min
P
của
1 1
P
x
xy
.
A.
min
8
P
. B.
min
4
P
. C.
min
2
P
. D.
min
16
P
.
Câu 18. Cho hai số thực
,x y
không âm thỏa mãn
2
2
2 1
2 1 log
1
y
x x y
x
. Giá trị nhỏ nhất của biểu
thức
2 1 2
4 2 1
x
P e x y
là
A.
1
2
. B.
1
. C.
1
2
. D.
1
.
Câu 19. Cho hai số thực dương
x
,
y
thay đổi thỏa mãn đẳng thức
2
2 1 2
1 .2 .2 .
xy x y
xy x y
Tìm giá
trị nhỏ nhất
min
y
của
y
.
A.
min
3
y
. B.
min
2
y
. C.
min
1
y
. D.
min
3
y
.
Câu 20. Cho
,
, 1
x y
x y
sao cho
3 3
ln 2 ln3 19 6 ( 2 )
x
x y xy x y
y
. Tìm giá trị nhỏ nhất
m
của
biểu thức
1
3
T x
x y
.
A.
1 3
m
. B.
2
m
. C.
5
4
m
. D.
1
m
.
Câu 21. Cho
;x y
là các số thực dương thỏa mãn điều kiện
4 4
3 5
5 1 3 4
3 5
xy
x y x y
xy
x y x
.
Tìm giá trị nhỏ nhất của biểu thức
P x y
.
A.
3
. B.
5 2 5
. C.
3 2 5
. D.
1 5
.
Câu 22. Cho
x
,
y
là các số thực dương thỏa mãn
2 2
3 5
5 1 3 ( 2)
3 5
xy
x y x y
xy
x y x
. Tìm giá trị
nhỏ nhất của biểu thức
T x y
.
A.
min
2 3 2
T
. B.
min
3 2 3
T
. C.
min
1 5
T
. D.
min
5 3 2
T
.
Câu 23. Xét các số thực dương
,x y
thỏa mãn
3
3
log 3 1
1
x y
xy y x
xy
. Tìm giá trị nhỏ nhất của biểu
thức
1
A x
y
.
A.
min
14
3
A
. B.
min
14
3
A
. C.
min
6
A
. D.
min
6
A
.
Câu 24. Cho
, 0
x y
thỏa
2
2 2
2
4 2
2019 0
2
x y
x y
x
. Tìm giá trị nhỏ nhất
min
P
của
2 4P y x
.
A.
2018
. B.
2019
. C.
1
2
. D.
2
.
Câu 25. Cho
2
số thực dương
,x y
thỏa mãn
1
3
log 1 1 9 1 1
y
x y x y
. Giá trị nhỏ nhất
của biểu thức
2P x y
là
A.
min
11
2
P
. B.
min
27
5
P
. C.
min
5 6 3
P
. D.
min
3 6 2
P
.
Câu 26. Xét các số thực dương
,x y
thỏa mãn
3
1
log 3 3 4
3
y
xy x y
x xy
. Tìm giá trị nhỏ nhất
min
P
của
P x y
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
A.
min
4
3 4
3
P
. B.
min
4
3 4
3
P
. C.
min
4
3 4
9
P
. D.
min
4
3 4
9
P
.
Câu 27. Xé
t các số thực dương
,x y
t
hỏa mãn
2
2
3
l
og 3 3 .
2
x y
x
x y y xy
x
y xy
Tìm
giá trị
lớn nhất
m
ax
P
của
biểu thức
3
2 1
.
6
x y
P
x y
A.
3
. B.
2
. C.
1
. D.
4
.
Câu 28. Xét các số thực dương
x
,
y
thỏa
mãn
2
2
1
2
2
20
18
1
x
y
x
y
x
. Tìm
giá trị nhỏ nhất
m
in
P
của
2 3P y x
.
A.
m
in
1
2
P
. B.
m
in
7
8
P
. C.
m
in
3
4
P
. D.
mi
n
5
6
P
.
Câu 29. Cho
2
số thực dương
,x y
thỏa mãn
1
3
l
og 1 1 9 1 1
y
x
y x y
. Giá trị nhỏ nhất
của biểu thức
2P
x y
là
A.
m
in
11
2
P
. B.
min
27
5
P
. C.
mi
n
5
6 3
P
. D.
m
in
3
6 2
P
.
Câu 30. Cho hai số thực dương
,x
y
thỏa mãn
2
2
l
og log 6 6x x x y y x
. Giá trị nhỏ nhất của
biểu thức
6
8
3
2P x y
x y
bằng
A.
59
3
. B.
19
. C.
53
3
. D.
8
6 2
.
Câu 31. Cho
,x y
là
các số dương thỏa mãn
2
2
2 2
2
2 2
5
l
og 1 10 9 0
1
0
x y
x xy y
x xy y
.
Gọi
,
m
M
lần
lượt là giá trị lớn nhất, giá trị nhỏ nhất của
2
2
2
9x xy y
P
xy y
. Tính
10
T M m
.
A.
6
0
T
. B.
9
4
T
. C.
1
04
T
. D.
5
0
T
.
Câu 32. Vậy
min
6
A
.Cho
các số thực dương
x
và
y
thỏa
mãn
2
2 2
2
2 2 2
4
9.3 4 9 .7
x
y x y y x
.
Tìm giá
trị nhỏ nhất của biểu thức
2
18
x
y
P
x
.
A.
9
P
. B.
3
2
2
P
.
C.
1
9 2
P
. D. Hà
m số không có giá trị nhỏ nhất.
Câu 33. Cho
,x
y
l
à các số thực lớn hơn
1
sao
cho
y
x
e e
x
x y y
y
e x e
.
Tìm giá trị nhỏ nhất của biểu
thức:
l
og log
x y
P
xy x
.
A.
2
2
. B.
2
2
. C.
1
2 2
2
. D.
1
2
2
.
Câu 34. Tính giá trị của biểu thức
2
2
1P x y xy
biết
rằng
2
2
1
1
2
4
log 14 2 1
x
x
y
y
với
0
x
và
1
3
1
2
y
.
A.
4P
. B.
2P
. C.
1P
. D.
3
P
.
Câu 35. Cho ha
i số thực
x
,
y
thỏa mãn
1
0
2
x
,
1
0
2
y
và
l
og 11 2 2 4 1x y y x
. Xét biểu
thức
2
16
2 3 2 5P yx x y y
.
Gọi
m
,
M
lần
lượt là giá trị nhỏ nhất và giá trị lớn nhất của
P
. Khi đó giá trị của
4
T
m M
bằng bao nhiêu?
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
16
. B.
18
. C.
1
7
. D.
19
.
-------------------- HẾT --------------------
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
A. PHƯƠNG PHÁP GIẢI PHƯƠNG TRÌNH – BPT MŨ -LOGARIT
Thường sử dụng các phương pháp sau:
1. Phương pháp đưa về cùng cơ số.
1/ Phương trình – Bất phương trình mũ cơ bản
 Phương trình mũ
+ Nếu
a 0, a 1
thì
f x g x
a a f x g x
+ Nếu a chứa ẩn thì
f x g x
a 1
a a a 1 f x g x 0
f x g x
.
+
f x g x
a b
f x g x
a a
log a log b
a
f x log b.g x
(logarit hóa).
 Bất phương trình mũ
+ Nếu
a 1
thì
f x g x
a a f x g x
. (cùng chiều)
+ Nếu
0 a 1
thì
f x g x
a a f x g x
. (ngược chiều)
+ Nếu a chứa ẩn thì
f x g x
a a a 1 f x g x 0
.
2/ Phương trình logarit – Bất phương trình logarit cơ bản
 Phương trình logarit
+ Nếu
b
a
a 0, a 1 : log x b x a
1
+ Nếu
a a
a 0, a 1 : log f x log g x f x g x
2
+ Nếu
g x
a
a 0, a 1 : log f x g x f x a
(mũ hóa)
3
 Bất phương trình logarit
+ Nếu
a 1
thì
a a
log f x log g x f x g x
(cùng chiều)
+ Nếu
0 a 1
thì
a a
log f x log g x f x g x
(ngược chiều)
+ Nếu a chứa ẩn thì
a
a
a
log B 0 a 1 B 1 0
log A
0 A 1 B 1 0
log B
.
Các bước giải phương trình & bất phương trình mũ – logarit
Bước 1. Đặt điều kiện (điều kiện đại số
điều kiện loga), ta cần chú ý:
ĐK
a
0 a 1
log b
b 0
và
Đ
Đ
K
a
K
a
log f x f x 0
log f x f x 0
.
Bước 2. Dùng các công thức và biến đổi đưa về các cơ bản trên, rồi giải.
Bước 3. So với điều kiện và kết luận nghiệm.
2. Phương pháp đặt ẩn phụ.
I/ Đặt ẩn phụ cho phương trình mũ
PHƯƠNG TRÌNH - BẤT PHƯƠNG TRÌNH - MIN MAX LOGARIT
Vấn đề 10
mũ lẻ
mũ chẵn
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Loại 1.
f x
PP
P a 0
đặt
f x
t a , t 0
.
Loại 2.
λ
f x
2.f x 2.f x
.a . a.b .b 0
PP
Chia hai vế cho
2.f x
b ,
rồi đặt
f x
a
t 0
b
(chia cho
cơ số lớn nhất hoặc nhỏ nhất).
Loại 3.
f x f x
a b c
với
a.b 1
PP
đặt
f x f x
1
t a b
t
.
Loại 4.
f x g x
f x g x
f x
g x
a .a
.a .a b 0
a
a
PP
đặt
f x
g x
u a
v a
.
II/ Đặt ẩn phụ cho phương trình logarit
Loại 1.
PP
a
P log f x 0
đặt
a
t log f x
.
Loại 2. Sử dụng công thức
b b
log c log a
a c
để đặt
b b
log x log a
t a t x
.
Lưu ý
Trên đây là một số dạng cơ bản thường gặp về phương trình mũ và loga, còn bất phương trình ta cũng làm
tương tự nhưng lưu ý về chiều biến thiên. Về phương diện tổng quát, ta đi tìm mối liên hệ giữa biến
để đặt ẩn phụ, đưa về phương trình (bất phương trình) đại số hoặc hệ phương trình đại số mà đã biết
cách giải. Từ đó, tìm ra được nghiệm. Ngoài ra, còn một số trường hợp đặt ẩn phụ không hoàn toàn.
Nghĩa là sau khi đặt ẩn phụ t vẫn còn x. Ta giải phương trình theo t với x được xem như là hằng số
bằng cách lập biệt thức ∆ hoặc đưa về tích số.
3. Phương pháp hàm số.
I/ Cơ sở lý thuyết và vận dụng cơ sở lý thuyết để tìm hướng giải
Thông thường ta sẽ vận dụng nội dung các định lý (và các kết quả) sau:
Nếu hàm số
y f x
đơn điệu một chiều trên D thì phương trình
f x 0
không quá một nghiệm trên
D.
Để vận dụng định lý này, ta cần nhẩm được
1
nghiệm
o
x x
của phương trình, rồi chỉ rõ hàm
đơn điệu một chiều trên D (luôn đồng biến hoặc luôn nghịch biến trên D) và kết luận
o
x x
là
nghiệm duy nhất.
Hàm số
f t
đơn điệu một chiều trên khoảng
a; b
và tồn tại
u; v a; b
thì
f u f v u v
".
Để áp dụng định lý này, ta cần xây dựng hàm đặc trưng
f t
.
Hàm số
y f t
xác định và liên tục trên D:
Nếu
f t
đồng biến trên D và
u, v D
thì
f u f v u v
.
Nếu
f t
nghịch biến trên D và
u, v D
thì
f u f v u v
.
Để vận dụng nội dung định lí này trong giải bất phương trình, người ra đề thường cho dưới hai
hình thức và có hai hướng xử lí thường gặp sau:
 Nếu đề yêu cầu giải
f x 0
:
Nhẩm nghiệm của
f x 0
trên miền xác định D, chẳng hạn
o
x x
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Xét hàm số
y f x
trên D và chỉ rõ nó đơn điệu tăng một chiều (đơn điệu giảm một chiều). Khi đó:
o o
f x 0 f x f x x x
nếu hàm số đơn điệu tăng trên D và
o
x x
nếu hàm số đơn điệu
giảm trên D.
Nếu đề bài yêu cầu giải
f x 0
mà không nhẩm được nghiệm
o
x x
của
f x 0
thì cần biến đổi
f x 0 f g x f h x
với việc xây dựng hàm đặc trưng
y f t ,
rồi chỉ ra hàm
f t
là đồng
biến (nghịch biến). Khi đó
f g x f h x g x f x
hay g x f x
.
Ta sẽ làm tương tự nếu đề cho
f x 0, f x 0
hoặc
f x 0
.
Nếu hàm số
y f x
có đạo hàm
f ' x
liên tục và thỏa mãn
f ' x 0
có một nghiệm trên D thì
phương trình
f x 0
không quá
2
nghiệm trên D.
II/ Một số loại toán cơ bản thường gặp khi sử dụng đơn điệu hàm
Loại 1.
a
f x
log . g x f x
g x
1
 Tìm tập xác định D.
 Biến đổi
a a
1 log f x log g x .g x .f x
a a
log f x .f x log g x .g x
f f x f g x
.
 Xét hàm số đặc trưng
a
f t .t log t
trên miền D và chỉ ra hàm số này luôn đơn điệu một chiều trên
D và
f f x f g x f x g x
.
Loại 2.
a b
log f x log g x
2
 Nếu
a b
thì
2 f x g x
: đây là dạng toán khá quen thuộc.
 Nếu
a 1 b 1 0
PP
Dùng phương pháp đoán nghiệm và chứng minh đó là nghiệm duy nhất.
 Nếu
a 1 b 1 0
PP
Đặt ẩn phụ kết hợp mũ hóa phương trình.
Tìm tập xác định D và đặt
t
t
a b
f x a
log f x log g x t
g x b
và biến đổi phương trình về dạng:
t t
f t A B 1
và giải bằng phương pháp đoán nghiệm và chứng minh nghiệm này duy nhất và
tìm x khi biết t.
Dạng toán:
a b
. log f x . log g x
ta cũng làm tương tự bằng cách đặt
γ
a b
log f x log g x .t
với
γ
là bội số chung nhỏ nhất của
và
.
Loại 3.
a
f x
log g x log b
3
 Đặt điều kiện:
f x 0
và
0 g x 1
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
 Sử dụng công thức đổi cơ số thì
b
a
b
log f x
3 log b
log g x
b a b
log f x log b. log g x
b a
log f x log g x
(đây là loại 2).
Loại 4.
λ
x
a
a p log x qx r
4
PP
Đặt ẩn phụ
λ
a
log x y
để đưa về hệ phương trình đối xứng loại II hay gần đối xứng và sử
dụng phương pháp hàm để tìm được
x y
.
Phương trình dạng
log , log ,
a b
f x y g x y
.
Phương pháp: đặt
log , log ,
a b
t f x y g x y
và chuyển về hệ
,
,
t
t
f x y a
g x y b
và đánh giá chặn giá trị
t
. Từ đó chọn giá trị nguyên của
x
thích hợp và thử lại xem với giá trị nguyên của
x
đã chọn thì hệ
phương trình có nghiệm
t
trong miền đã chặn hay không?
Kiến thức để đánh giá chặn giá trị
t
:
+ Điều kiện có nghiệm của phương trình bậc 2.
+ Bất đẳng thức Cauchy, BCS…
+ Tính chất biến thiên của hàm số.
Câu 1. Cho
x
,
y
là các số thực dương thỏa mãn
9 6 4
log log log 2
x y x y
. Giá trị của
x
y
bằng
A.
2
. B.
1
2
. C.
2
3
log
2
. D.
3
2
log 2
.
Lời giải
Chọn B
Đặt
9 6 4
log log log 2
t x y x y
. Khi đó
9
6
2 4
t
t
t
x
y
x y
2.9 6 4
t t t
9 3
2. 1 0
4 2
t t
3
1
2
3 1
2 2
t
t
3 1
2 2
t
.
Do đó:
9 3 1
6 2 2
t t
x
y
.
Câu 2. Biết
1 2 1 2
;
x x x x
là hai nghiệm của phương trình
2
2
2
4 4 1
log 6 4
x x
x x
x
và
1 2
1
2
4
x x a b
với
,a b
là các số nguyên dương. Giá trị
P a b
là
A.
14P
. B.
13
P
. C.
15
P
. D.
16
P
.
Lời giải
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Chọn A
Điều kiện
2
2
2 1
4 4 1 1
0 0 0,
2
x
x x
x x
x x
.
2
2 2
2
2 2 2
4 4 1
log 6 4 log 2 1 log 2 1 2 1
x x
x x x x x x
x
2 2
2 2
log 2 1 2 1 log 2 2 1
x x x x
.
Xét hàm số
2
log
f t t t
với
0
t
.
Ta có
1
1 0
ln 2.
f t
t
với
0
t
suy ra
3
log
f t t t
đồng biến trên
0;
.
Xét
1
0;
2
x
, từ
1
ta có
2 2
2
3 5
4
2 1 2 2 1 2 4 6 1 0
3 5
4
x l
f x f x x x x x
x
.
Xét
1
;
2

x
, từ
1
ta có
2 2
2
3 5
4
2 1 2 2 1 2 4 6 1 0
3 5
4
x
f x f x x x x x
x l
.
Do đó, phương trình
2
2
2
4 4 1
log 6 4
x x
x x
x
có hai nghiệm phân biệt
1 2
3 5 3 5
;
4 4
x x
.
Suy ra
1 2
1
2 9 5
4
x x
. Suy ra
9, 5 14
a b P a b
.
Câu 3. Biết
30
log 10
a ,
30
log 150
b và
1 1 1
2000
2 2 2
log 15000
x a y b z
x a y b z
với
1 1 1 2 2 2
; y ;z ; ; y ;z
x x là các số
nguyên, tính
1
2
x
S
x
.
A.
1
2
S
. B.
2
S
. C.
2
3
S
. D.
1
S
.
Lời giải
Chọn A
Ta có
30 30 30
2000
30 30 30
log 15000 log 150 2log 10
log 15000
log 2000 log 2 3log 10
1
Ta có
30 30 30 30 30
log 10 log 5 log 2 log 2 log 5
a a
2
30 30 30
log 150 1 log 5 log 5 1 b b
thay vào
2
ta được
30
log 2 1
a b
Ta có
2000
2 2
log 1500
1 3 4 1
b a a b
a b a a b
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Suy ra
1
2
2 1
4 2
x
S
x
.
Câu 4. Cho các số thực dương
,x y
khác 1 và thỏa mãn
log log
log log
x y
x y
y x
x y x y
.
Giá trị của
2 2
x xy y
bằng
A. 0. B. 3. C. 1. D. 2.
Lời giải
Chọn D
ĐK:
x y
.
Ta có
1
1
1
log
log log
log
log log
log log
log log
x
x y
x
x y
x y
x
x
y
y
y x
x
y
x y
x y x y
x y x y
x y x y
2 2
2 2
2 2
1
1
1
2
1
log log 0 log 0
x x x
y
xy
y
x
x
x xy y
x y
x y x y x y
.
Câu 5. Cho các số thực dương
a
,
b
thỏa mãn
log log log log 100
a b a b
và
log a
,
logb
,
log
a
,
log
b
đều là các số nguyên dương. Tính
P ab
.
A.
164
10 .
B.
100
10 .
C.
200
10 .
D.
144
10 .
Lời giải
Chọn A
Ta có:
log log log log 100
a b a b
log log 2 log 2 log 200
a b a b
2 2
log 1 log 1 202 81 121
a b
*
Mà
log a
,
logb
,
log
a
,
log
b
đều là các số nguyên dương nên
64
100
100
64
log 1 9
log 64 10
log 1 11
log 100 10
*
log 100
10
log 1 11
log 64
10
log 1 9

a
a a
b
b b
a
a
a
b
b
b
Vậy:
64 100 164
10 .10 10 .
P ab
Câu 6. Cho
9 4 2
log 5 ; log 7 ; log 3
a b c
.Biết
24
log 175
mb nac
pc q
.Tính
2 3 4 A m n p q
A.
27
B.
25
C.
23
D.
29
Lời giải
Chọn B
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Ta có
2
24 24 24 24
7 5
1 2
log 175 log 7.5 log 7 2log 5
log 24 log 24
3 3
7 7 5 5
3 2 3 2
1 2 1 2
1 3 1 3
log 3 log 2 log 3 log 2
log 7 log 7 log 5 log 5
2 3 2 3 2 3
1 2 1 2
1 3 1 3 1 3 1 3
1
log 7.log 2 log 7 log 5 log 3.log 5 2 2a c.2a
2 .
b
b
c
1 2 2 4a 2 4a
3 3
3 3 3
2 2 2ac 2ac
b c b c
c c
c c c
b b
.
2 3 4 2 8 3 12 25.
A m n p q
Câu 7. Cho
x
,
y
là các số thực lớn hơn
1
thoả mãn
2 2
6
x y xy
. Tính
12 12
12
1 log log
2log 3
x y
M
x y
.
A.
1
4
M
. B.
1M
. C.
1
2
M
. D.
1
3
M
.
Lời giải
Chọn B
Ta có
2 2 2 2
6 6 0 *
x y xy x xy y
.
Do
x
,
y
là các số thực dương lớn hơn
1
nên ta chia cả 2 vế của
*
cho
2
y
ta
được
2
3
3
6 0
2
2
x
x y n
y
x x
x
y y
x y l
y
Vậy
3x y
(1).
Mặt khác
12 12
12
1 log log
2log 3
x y
M
x y
12
2
12
log 12
log 3
xy
x y
(2).
Thay (1) vào (2) ta có
2
12
2
12
log 36
1
log 36
y
M
y
.
Câu 8. Cho
2
ln 1 sin 6
f x a x x b x
với
a
,
b
. Biết
log loge 2
f
. Tính
log ln10
f
.
A.
4
. B.
10
. C.
8
. D.
2
.
Lời giải
Chọn B
Đặt
0
log loge
x
Có:
2
0 0 0 0
ln 1 sin 6 2
f x a x x b x
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có
0
1
log ln10 log log loge
loge
f f f f x
2
0 0 0 0
ln 1 sin 6
f x a x x b x
2
0 0 0
ln 1 sin 6
a x x b x
2
0 0 0 0
ln 1 sin 6 12 12 10
a x x b x f x .
Câu 9. Cho
x -x
9 + 9 = 14
và
x -x
x+1 1-x
6+3(3 +3 ) a
=
2-3 -3 b
với
a
b
là phân số tối giản. Tính
. .P a b
A.
10.
P
B.
45.
P
C.
10.
P
D.
45.
P
Lời giải
Chọn B
Ta có
2 2 2 2
2
9 9 14 3 2.3 .3 3 16
3 3 16 3 3 4.
x x x x x x
x x x x
1 1
6 3(3 3 ) 6 3(3 3 ) 6 3(3 3 )
2 3 3 2 3.3 3.3
2 3. 3 3
6 3.4 18 9
45.
2 3.4 10 5
x x x x x x
x x x x
x x
a
ab
b
Câu 10. Biết phương trình
1
3
27 27 16 3 6 0
3
x x x
x
có các nghiệm
3
, log x a x b
và
3
logx c
với
, 0.
a b c
Tỉ số
b
c
thuộc khoảng nào sau đây?
A.
(3; ).
B.
3 5
;
2 2
C.
3
1;
2
D.
5
;3
2
Lời giải
Chọn D
Ta có
1 3 3
3
27 27 16 3 6 0 3 27.3 16 3 3.3 6 0 1
3
x x x x x x x
x
Đặt
3 3 3 3 3 3 3
3 3.3 3 27.3 3 3 3.3 .3 .3.3
x x x x x x x x
t t
3 3 3 3
3 27.3 9 3 3.3
x x x x
Khi đó
2
3 2
2
3 3.3 1 3 3 3 0
1
1 7 6 0 3 3 3.3 3 3 3.3 3 0
2
3 3.3 2 3 2.3 3 0
x x x x
x x x x
x x x x
t
t t t
t
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
3
3
13 1 13 1
3 log
2 2
21 3 21 3 13 1
3 log 2.9.
2 2
21 3
1
3 3
x
x
x
x
b
x
c
x
Câu 11. Cho hai số thực dương
,a b
thỏa
4 6 9
log log log
a b a b
. Tính
a
b
.
A.
1
2
. B.
1 5
2
. C.
1 5
2
. D.
1 5
2
.
Lờigiải
Chọn D
Đặt
4 6 9
log log log
t a b a b
.
4
6 4 6 9
9
t
t t t t
t
a
b
a b
2
2 1 5
3 2
2 2
1 0
3 3
2 1 5
( )
3 2
t
t t
t
L
.
4 2 1 5
6 3 2
t
t
t
a
b
.
Câu 12. Gọi a là một nghiệm của phương trình
2log log 2log
4.2 6 18.3 0
x x x
. Khẳng định nào sau đây
đúng khi đánh giá về
a
?
A.
2
10 1
a
. B.
2
10
a
. C.
2
1 2
a a
. D.
1
100
a
.
Lờigiải
Chọn D
Điều kiện
0
x
.
Chia cả hai vế của phương trình cho
2log
3
x
ta được
2log log
2 2
4 18 0
3 3
x x
.
Đặt
log
2
3
x
t
,
0t
.
Ta có
2
4 18 0
t t
9
4
2
t
t L
.
Với
9
4
t
log
2 9
3 4
x
log 2
x
1
100
x
.
Vậy
1
100
a
.
Câu 13. Tổng các nghiệm của phương trình sau
1
7
7 6log 6 5 1
x
x
bằng
A.
2
. B.
3
. C.
1
. D.
10
.
Lờigiải
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Chọn B
Điều kiện:
5
.
6
x
Đặt
7
1 log 6 5
y x
thì ta có hệ phương trình
1
1
1 1
1
7
7 6 1 1
7 6 5
7 6 7 6
1 log 6 5
7 6 5
x
x
x y
y
y
y
x y
y x
x
(2)
Xét hàm số
1
7 6
t
f t t
với
5
6
t
thì
1
5
' 7 ln7 6 0,
6
t
f t t f t
đồng biến nên
2
f x f y x y
khi đó ta có phương trình
1
7 6 5 0.
x
x
(3)
Xét hàm số
1
7 6 5
x
g x x
với
5
6
x
thì
2
1 1
' 7 ln 7 6 " 7 ln 7 0
x x
g x g x
5
6
x
nên suy ra phương trình
0
g x
có không quá hai nghiệm.
Mặt khác
1 2 0
g g
nên
1x
và
2
x
là 2 nghiệm của phương trình (3).
Vậy phương trình đã cho có 2 nghiệm là
1x
và
2
x
.
Suy ra tổng các nghiệm của phương trình là
1 2 3
.
Câu 14. Bất phương trình
9 2 5 3 9 2 1 0
x x
x x
có tập nghiệm là
; ;S a b c

. Tính
tổng
a b c
?
A.
0
. B.
1
. C.
2
. D.
3
.
Lờigiải
Chọn D
Đặt
3
x
t
,
0t
.
Bất phương trình đã cho trở thành:
2
2 5 9 2 1 0
t x t x
9 2 1 0
t t x
TH1:
3 9 1
9 0 9
2 1 0 2 1 0
3 2 1 0 2
x
x
t t
t x t x
x
Xét bất phương trình
2
:
Đặt
3 2 1
x
g x x
trên
.
3 ln 3 2
x
g x
.
Gọi
0
x
là nghiệm duy nhất của phương trình
0
g x
,
0
0
x
Khi đó,
0
g x
có nhiều nhất hai nghiệm.
Xét thấy,
0
g x
có hai nghiệm là
0
x
và
1x
Ta có bảng biến thiên
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Từ bảng biến thiên ta có,
0
2
1
x
x
Ta lại có,
1 2 x
.
Kết hợp
1
và
2
suy ra,
2x
.
*
TH2:
3 9 3
9 0 9
2 1 0 2 1 0
3 2 1 0 4
x
x
t t
t x t x
x
Xét bất phương trình
4
:
Đặt
3 2 1
x
g x x
trên
.
3 ln 3 2
x
g x
.
Gọi
0
x
là nghiệm duy nhất của phương trình
0
g x
,
0
0x
Khi đó,
0g x
có nhiều nhất hai nghiệm.
Xét thấy,
0g x
có hai nghiệm là
0x
và
1x
Ta có bảng biến thiên
Từ bảng biến thiên ta có,
4 0 1 x
Ta lại có,
3 2 x
.
Kết hợp
3
và
4
suy ra,
0 1 x
.
**
Kết hợp
*
và
**
ta được tập nghiệm của BPT đã cho là
0;1 2; S
Câu 15. Phương trình
2 2 2
sin cos sin
2 3 4.3
x x x
có bao nhiêu nghiệm thuộc
2017; 2017
.
A.
1284
. B.
4034
. C.
1285
. D.
4035
.
Lờigiải
Chọn C
Ta có
2 2 2 2 2 2
sin os sin sin 1 sin sin
2 3 4.3 2 3 4.3
x c x x x x x
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Đặt
2
sin
x t
với
0;1
t
, ta có phương trình
3 2 1
2 4.3 3. 4
3 3 9
t t
t t
t
. Vì hàm số
2 1
3.
3 9
t t
f t
nghịch biến với
0;1
t
nên phương trình có nghiệm duy nhất
0t
. Do đó
sin 0
x x k
,
k
.
Vì
2017; 2017
x
nên ta có
2017 2017
2017 2017k k
nên có
1285
giá trị
nguyên của
k
thỏa mãn. Vậy có
1285
nghiệm.
Câu 16. Cho các số thực dương
,x y
thỏa mãn
6 9 4
log log log 2 2x y x y
. Tính tỉ số
x
y
?
A.
2
3
x
y
. B.
2
3 1
x
y
. C.
2
3 1
x
y
. D.
3
2
x
y
.
Lờigiải
Chọn B
Giả sử
6 9 4
log log log 2 2
x y x y t
. Ta có:
6 (1)
9 (2)
2 2 4 (3)
t
t
t
x
y
x y
.
Khi đó
6 2
0
9 3
t
t
t
x
y
.
Lấy (1), (2) thay vào (3) ta có
2.6 2.9 4
t t t
2
2 2
2. 2 0
3 3
t t
2 2
1 3
3
3 1
2
1 3
3
t
t
(thoûa)
(loaïi)
.
Câu 17. Số nghiệm của phương trình
5
log 3
2
x
x
là:
A.
0
. B.
1
. C.
3
. D.
2
.
Lờigiải
Chọn B
Đk:
3
x
Đặt
5
log 3
t x
5 3
t
x
, phương trình đã cho trở thành
2 5 3
t t
2 3 5
t t
2 1
3. 1
5 5
t t
(1)
Dễ thấy hàm số
2 1
3.
5 5
t t
f t
nghịch biến trên
và
1 1
f
nên phương trình (1) có
nghiệm duy nhất
1t
.
Với
1t
, ta có
5
log 3 1
x
2
x
Vậy phương trình có nghiệm duy nhất
2
x
.
Câu 18. Phương trình
3 3 3 3 4 4 3
3 3 3 3 10
x x x x
có tổng các nghiệm là?
A.
0
. B.
2
. C.
3
. D.
4
.
Lờigiải
Chọn A
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
3 3 3 3 4 4 3
3 3 3 3 10
x x x x
7
3 3 3 3
3 3
27 81 1 1
7 27.3 81.3 10 27. 3 81. 3 10 7'
3 3 3 3
x x x x
x x x x
Đặt
1 1
3 2 3 . 2
3 3
x x
x x
Côsi
t
3
3 3 2 3 3
2 3 3
1 1 1 1 1
3 3 3.3 . 3.3 . 3 3
3 3 3 3 3
x x x x x
x x x x x
t t t
Khi đó:
3
3 3 3
10 10
7 ' 27 3 81 10 2
27 3
t t t t t N
Với
10 1 10
3 7''
3 3 3
x
x
t
Đặt
3 0
x
y
. Khi đó:
2
3
1 10
7'' 3 10 3 0
1
3
3
y N
y y y
y
y N
Với
3 3 3 1
x
y x
.
Với
1 1
3 1
3 3
x
y x
.
Suy ra tổng các nghiệm của phương trình là:
1 1 0
.
Câu 19. Tìm tập nghiệm
S
của bất phương trình
2
2
3 1 3
3 1
x
x
x
.
A.
3
;0 log 2;
 
. B.
3
0;log 2
.
C.
1
0; 2;
2

. D.
0;

.
Lờigiải
Chọn A
Ta có bất phương trình:
2
3 (3 1) 2
2 2
3 1 3 3 1 3 3 1
3 1 3 1 3 1
x xx
x x x x
x x x
3 1 3 (3 1) 2
x x x
(*)
Đặt
3 1 1 3 1
x x
t t
Từ đó bất phương trình (*)
( 1)t 2 2 ( 1)t
t t t t
Trường hợp 1:
1 2
1 2
1
( 1) 0
0
t
t
t
t t
t
1 2 1 3 1 2 3 1 0
x x
t x
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Trường hợp 2:.
2 2 2
2 2
( 1) ( 2) 4 4
t t
t t t t t t t
3
2
2 3 2 log 2
4
3
x
t
t x
t
.
Kết luận nghiệm của bất phương trình là:
3
log 2
0
x
x
.
Câu 20. Cho
x
,
y
là các số thực dương thỏa mãn
25 15 9
log log log
2 4
x x y
y
và
2
x a b
y
, với
a
,
b
là
các số nguyên dương, tính
a b
.
A.
14
a b
. B.
3
a b
. C.
21
a b
. D.
34
a b
.
Lờigiải
Chọn D
Ta có
25
25
log
2
log
25 15 9
2
9 25
15
log log log
2 4
15
log log
4 2
x
x
y
x x y
y
x x
Đặt
25
log 2.25
2
t
x
t x
, ta được
2.25 15 4.9
t t t
2
5 5
2 4
3 3
t t
5
3
1 33
log
4
t
2.25 5 1 33
2.
15 3 2
t
t
t
x
y
.
Do đó
1
a
,
33
b
nên
34
a b
.
Câu 21. Biết rằng phương trình
1009
2 3
log 1 2018logx x
có nghiệm duy nhất
0
x
. Khẳng định nào dưới
đây đúng?
A.
1 1
1008 1006
0
3 3
x
. B.
2
1009
0
3
x
. C.
1
1008
0
1 3
x
. D.
1
1007
0
3 1
x
.
Lờigiải
Chọn C
Điều kiện:
0
x
.
Đặt
1009
2 3
log 1 2018logt x x
. Khi đó
0t
.
1009
2018
1 2
3
t
t
x
x
2
2 1 3
t t
2 1 3
t
t
3 1 2
t
t
3 1
1
2 2
t
t
(*).
Ta thấy hàm số
3 1
2 2
t
t
f t
luôn nghịch biến và liên tục trên
0;

và
2 1
f
nên
phương trình (*) có duy nhất một nghiệm
2t
.
1009
3
x
hay
1
1009
0
3
x
.
Mà
1 1
0
1009 1008
nên
1
1008
0
1 3
x
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Câu 22. Phương trình
3 2
2log cot log cosx x
có bao nhiêu nghiệm trong khoảng
0;2018
?
A.
2018
nghiệm. B.
1008
nghiệm. C.
2017
nghiệm. D.
1009
nghiệm.
Lờigiải
Chọn A
Đk:
sin 0
cos x>0
x
.
2
3 2 3 2
2log cot log cos log cot log cosx x x x
2 2
3 3 2
log cos log sin log cosx x x
2 2
3 3 2
log cos log 1 s log cosx co x x
Đặt
2
log cosx osx=2
t
t c
.
Phương trình trở thành
2
3
2
2
log 4 3 12
1 2
t
t t t
t
t
hay
4
4 1
3
t
t
Hàm số
4
4
3
t
t
f t
đồng biến trên
Mặt khác
1 1
f
nên
1
x
là nghiệm của phương trình.
Do đó phương trình có nghiệm duy nhất
1
t
.
2
1
log cosx=-1 cos .2
2 3
x x k
.
1 6053
6 6
0;2018
1 6055
6 6
k
x
k
.
Vậy trong khoảng
0;2018
có
1009.2 2018
nghiệm.
Câu 23. Cho dãy số
n
u
thỏa mãn
3 5 4
log 2 63 2log 8 8
n
u u n
,
*
n
. Đặt
1 2
...
n n
S u u u
. Tìm số nguyên dương lớn nhất
n
thỏa mãn
2
2
.
148
. 75
n n
n n
u S
u S
.
A.
18
. B.
17
. C.
16
. D.
19
.
Lờigiải
Chọn A
Ta có
*
n
,
3 5 4
log 2 63 2log 8 8
n
u u n
3 5 2
log 2 63 log 8 8
n
u u n
.
Đặt
3 5
log 2 63
t u
5
2 63 3
8 8 2
t
t
n
u
u n
5
5
2 63 3
32 2
t
t
u
u
( với
5
n
)
1 3 2.2
t t
2
t
8 4
n
u n
. Khi đó
5
36
u
Với
8 4
n
u n
và
5
36
u
, ta có:
3 5 4 3 4
log 2 63 2log 8 8 log 2.36 63 2log 8 4 8 8
n
u u n n n
3 4
log 9 2log 4 2 2
đúng
*
n
.
Ta có:
1
8 1 4 8 4 8
n n
u u n n
. Vậy
n
u
là cấp số cộng có số hạng đầu
1
4
u
, công sai
8
d
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
1
2
1 2
.
... 4
2
n
n n
u u n
S u u u n
.
Do đó
2
2
2
2
8 4 .16
.
148
. 16 4 .4 75
n n
n n
n n
u S
u S n n
19
n
.
Câu 24. Số nghiệm của phương trình
2 2
3 5
log 2 log 2 2
x x x x
là
A.
3
. B.
2
. C.
1
. D.
4
.
Lờigiải
Chọn B
ĐK:
0; 2
x x
.
Đặt
2
2t x x
2
2 2 2x x t
3 5
log log 2
t t
.
Đặt
3 5
log log 2
t t u
3
5
log
log 2
t u
t u
3
2 5
u
u
t
t
5 2 3
u u
5 2 3
5 2 3
u u
u u
5 3 2
3 2 5
u u
u u
5 3 2 (1)
.
3 1
2 1 (2)
5 5
u u
u u
 Xét
1 :5 3 2
u u
Ta thấy
0
u
là 1 nghiệm, dùng phương pháp hàm số hoặc dùng BĐT để chứng minh nghiệm
0
u
là
duy nhất.
Với
2
0 1 2 1 0
u t x x
, phương trình này vô nghiệm.
 Xét
3 1
2 : 2 1
5 5
u u
Ta thấy
1
u
là 1 nghiệm, dùng phương pháp hàm số hoặc dùng BĐT để chứng minh nghiệm
1
u
là duy nhất.
Với
2
1 3 2 3 0
u t x x
, phương trình có 2 nghiệm phân biệt thỏa
0; 2
x x
.
BÌNH LUẬN
Cho
1
f x g x
nếu
,
f x g x
đối nghịch nhau nghiêm ngặt hoặc
g x const
và
f x
tăng, giảm nghiêm ngặt thì (1) có nghiệm duy nhất.
Câu 25. Tìm giá trị gần đúng tổng các nghiệm của bất phương trình sau:
2 6 5 4 3 2
2
22 22
3 3
22 22 2 4
2log 2log 5 13 4 24 2 27 2 1997 2016 0
3 3 log log
x x
x x x x x
x x
A.
12,3
. B.
12
. C.
12,1
. D.
12,2
.
Lờigiải
Chọn C
Điều kiện:
0 1x
.
Ta có
6 5 4 3 2
24 2 27 2 1997 2016
x x x x x
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
2 2
3 2 3 6 4 2
1 22 26 1997 2015 0
x x x x x x
,
x
.
Do đó bất phương trình đã cho tương đương với
2
2
22 22
3 3
22 22 2 4
2log 2log 5 13 4 0
3 3 log log
x x
x x
.
Đặt
22
log
3
x
t
, ta có bất phương trình
2 2
2 2 5 2 4 4 13
t t t t
2 2
2
2
1 3 13
1 1
2 2 2
t t
.
Đặt
1 3
;
2 2
u t
và
1 ;1v t
. Ta có
13
2
u v u v
.
Dấu bằng xảy ra khi
1
3 4
2
2 1 3 3
1 2 5
t
t t t
t
5
4
22
12,06 12,1
3
x
.
Nghiệm trên thỏa điều kiện.
Câu 26. Tìm tích tất cả các nghiệm của phương trình
2
log 100
log 10
1 log
4.3 9.4 13.6
x
x
x
.
A.
100
. B.
10
. C.
1
. D.
1
10
.
Lờigiải
Chọn C
ĐK:
0x
.
PT
2.log 10 2.log 10 log 10
4.3 9.2 13.6
x x x
2log 10 log 10
3 3
4. 13. 9 0
2 2
x x
Đặt
log 10
3
0
2
x
t
thì phương trình trở thành:
log 10
2
log 10
3
1
1
2
4 13 9 0
9
3 9
4
2 4
x
x
t
t t
t
1
log 10 0
10
log 10 2
10
x
x
x
x
.
Suy ra tích các nghiệm bằng
1
.
Câu 27. Tập nghiệm của bất phương trình
2 2
2.7 7.2 351. 14
x x x
có dạng là đoạn
;S a b
. Giá trị
2b a
thuộc khoảng nào dưới đây?
A.
3; 10
. B.
4;2
. C.
7;4 10
. D.
2 49
;
9 5
.
Lờigiải
Chọn C
2 2
2.7 7.2 351. 14
x x x
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
49.7 28.2 351. 14
x x x
2 2
7 2
49. 28. 351
14 14
x x
x x
7 2
49. 28. 351
2 7
x x
x x
.
Đặt
7
, 0
2
x
x
t t
thì bpt trở thành:
28
49 351
t
t
4 7
49 2
t
4 7 7
49 2 2
x
x
4 2
x
.
Khi đó
4;2
S
.
Giá trị
2 10
b a
7;4 10
.
Câu 28. Tập nghiệm của bất phương trình
2
2
2 2 2 2 1 2 1
x x x
là
A.
;0
S 
. B.
1;S

. C.
0;1
S
. D.
3;S

.
Lờigiải
Chọn C
Điều kiện xác định:
2 1 0 2 1 0
x x
x
Đặt
2 2
2 1 , 0 2 1 2 1
x x x
t t t t
Bất phương trình trở thành:
2 2
2 2
2 2 2 2
2
2
2 2 2
2
2 2
1 2 1 2 1 1 3 1
1 3
1 1 3 1
1
1
2 1 3
1.
1
1
t t t t t t
t t
t t t t
t
t
t t t
t
t
t
Do đó
2 1 1 2 1 1 2 2 1
x x x
x
.
Kết hợp điều kiện:
0 1x
.
Vậy bất phương trình có tập nghiệm là:
0;1
S
.
Câu 29. Bất phương trình
2 2
1 1 1
2 2 2 2
x x x x
có tập nghiệm
;S a b
. Khi đó
a b
bằng
A.
2
. B.
3
. C.
1
. D.
10
.
Lờigiải
Chọn B
ĐK:
1x
.
Bất phương trình đã cho tương đương với
2 2
1 1
1
.2 .2 2 2 2
2
x x x x
2 2
1 1
2 .2 4 2.2 2.2
x x x x
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
Đặt
2
1
2
2
x
x
u
v
, điều kiện
0
0
u
v
.
Bất phương trình trở thành
4 2 2 2 4 2 0 2 2 2 0 2 2 0
uv u v uv u v u v v u v
.
2 0 2
2 0 2
2 0 2
2 0 2
u u
v v
u u
v v
.
Kết hợp với điều kiện
0
0
u
v
ta được
2
2
2
1
2
1
2 2
1
2 1 1 1 1
0 2 0 2 2 1 1 1 1 2
0 2 1 1 1 1
1
0 2 2
2 1 1 2
1 1
2 2
x
x
x
x
x
u x x x x
v x x x
u x x
x
v x x
x
; 1 1;2
 x
Kết hợp điều kiện
1x
, ta suy ra tập nghiệm của bất phương trình đã cho là
1;2
S
.
Câu 30. Tập nghiệm của bất phương trình
2
log 5
5 21 5 21 2
x x
x
là
A.
2;1
S
. B.
1;1
S
. C.
1;5
S
. D.
1;S

.
Lờigiải
Chọn B
Ta có:
2
log 5
5 21 5 21 2
x x
x
5 21 5 21 2 .5
x x
x
5 21 5 21
5
2 2
x x
Đặt
5 21 5 21 1
, 0
2 2
x x
t t
t
, bất phương trình trở thành:
2
1 5 21 5 21
5 5 1 0
2 2
t t t t
t
.
Do đó ta có:
5 21 5 21 5 21
1 1.
2 2 2
x
x
Vậy bất phương trình có tập nghiệm là:
1;1
S
.
Câu 31. Có bao nhiêu cặp số nguyên
;x y
thỏa mãn
0 2020
x
và
3
log 3 3 2 9
y
x x y
?
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
2019
. B.
6
. C.
2020
. D.
4
.
Lời giải
Chọn D
Cách 1:
Ta có:
2
3 3
log 3 3 2 9 log 1 1 2 3
y y
x x y x x y
.
1
Đặt
3
log 1 1 3
t
x t x
.
Phương trình
1
trở thành:
2
3 2 3
t y
t y
2
Xét hàm số
3
u
f u u
trên
.
1 3 ln 3 0,
u
f u u
nên hàm số
f u
đồng biến trên
.
Do đó
2 2 2f t f y t y
3
log 1 2 1 9 9 1
y y
x y x x
Vì
9
0 2020 0 9 1 2020 1 9 2021 0 log 2021
y y
x y
3
log 2021 3,464
Do
0;1;2;3
y y
, có 4 giá trị của y nên cũng có 4 giá trị của
x
Vậy có 4 cặp số nguyên
;x y
.
Cách 2:
Ta có:
2
3 3
log 3 3 2 9 log 1 1 2 3
y y
x x y x x y
Xét hàm số
3
log 1 1
f x x x
với
0;2020
x
.
Ta có
1
1 0, 0;2020
1 ln3
f x x x
x
Hàm số
f x
đồng biến trên đoạn
0;2020
.
Suy ra
3 2
0 log 1 1 2020 1 log 2021 2021
f f x x x f f x
3
1 2 9 log 2021 2021 2028
y
y
Nếu
0
0 2 9 9 9 1
y y
y y
0
y
Khi đó
2 9 2 9 2027 9 2027 2 2027
y y y
y y y y
9
log 2027 3,465
y
3
y
0 3
y
0;1;2;3
y
. Do
f x
là hàm số luôn đồng biến nên với mỗi giá trị của
y
chỉ cho 1 giá trị của
x
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
+)
3
0 log 1 1 1 0
y x x x
+)
3 3
1 log 1 1 11 log 1 10 8
y x x x x x
+)
3 3
2 log 1 1 85 log 1 84 80
y x x x x x
+)
3 3
3 log 1 1 735 log 1 734 729
y x x x x x
Vậy có 4 cặp số nguyên
;x y
.
Câu 32. Có bao nhiêu cặp số nguyên
,x y
thỏa mãn
2 2
9
log 3 9 1
x y
x y
?
A.
7
. B.
6
. C.
10
. D.
9
.
Lời giải
Chọn B
Điều kiện:
2 2
,
0 9 1
3 9 0
x y
x y
x y
,
, 0,0 ; 0,1 ; 0, 1
3 9 0
x y
x y
x y
Khi đó
2 2
9 1
x y
nên ta có:
2 2
9
log 3 9 1
x y
x y
2 2
3 9 9
x y x y
2 2
9 3 9 0
x x y y
2 2
1 1 19
3
2 2 2
x y
Suy ra:
2
2
1 19
1 38 1 38
3
2 2
6 6
1 38 1 38
1 19
2 2
2 2

x
x
y
y
Do
,
x y
nên
0;1
2; 1; 0;1; 2
x
y
Kết hợp điều kiện, ta được
, 0, 2 ; 0,2 ; 1; 2 ; 1, 1 , 1,0 ; 1,1 ; 1,2
x y
Thử lại ta thấy cặp
, 1, 2
x y
không thỏa yêu cầu đề bài.
Vậy có
6
cặp số nguyên
,x y
thỏa yêu cầu bài toán.
Câu 33. Có bao nhiêu giá trị nguyên của tham số
m
sao cho tồn tại duy nhất cặp số thực
,x y
thỏa mãn
2 2
18
x y
và
3 3
log 2 log
x y m y m x m
?
A.
3
. B.
2
. C.
4
. D.
5
.
Lời giải
Chọn C
Điều kiện:
2
x m
y m
.
Ta có:
3 3
log 2 log
x y m y m x m
3 3
log log 2 2
x m x m y m y m
1
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Xét hàm số
3
log
f t t t
với
0t
.
Ta có:
1
1 0, 0
ln3
f t t
t
nên hàm số
f
đồng biến trên khoảng
0;

.
Do đó:
1 2
x m y m y x m
.
Theo giả thiết:
2
2 2 2 2 2
18 18 2 2 18 0
x y x x m g x x mx m
2
Để tồn tại duy nhất cặp số thực
,x y
thỏa yêu cầu bài toán thì phương trình
2
phải có duy nhất
một nghiệm
x m
(khi đó
2y m
do
y x m
).
Trường hợp 1:
2
có nghiệm kép
x m
2
36 0
6
6
0
2
2
m
m
m
m
m
y m
.
Trường hợp 2:
2
có hai nghiệm phân biệt
1 2
x m x
Nếu
1
x m
thì thay vào
2
ta được
2
3 10
5 18 0
5
m m
(loại do
m
)
Nếu
2
1 2
3 10 3 10
. 0 5 18 0
5 5
x m x a g m m m
Từ các trường hợp trên và
6; 1; 0;1
m m
.
Câu 34. Biết
1 2 1 2
, ( )x x x x
là hai nghiệm của phương trình
2
2
3
2 1
log 2 3
3
x x
x x
x
và
1 2
4 2
x x a b
, với
,a b
là hai số nguyên dương. Tính
a b
A.
9
a b
. B.
12
a b
. C.
7
a b
. D.
14
a b
.
Lời giải
Chọn D
Điều kiện:
0
1
x
x
Ta có:
2
2
3
2 1
log 2 3
3
x x
x x
x
2
2
3 3
log 1 2 1 log
x x x x x
2 2
3 3
log 1 1 log
x x x x
(1)
Xét hàm số
3
1
log 1 0, 0
.ln3
f t t t f t t
t
Phương trình (1) trở thành
1
2 2
2
2
3 5
2
1 1 3 1 0
3 5
2
x
f x f x x x x x
x
Vậy
1 2
4 2 9 5
x x
. Khi đó
9, 5 14
a b a b
Câu 35. Có bao nhiêu cặp số nguyên
;x y
thỏa mãn
0 2020
x
và
2
log 4 4 1 2
y
x x y
?
A.
10
. B.
11
. C.
2020
. D.
4
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
Lời giải
Chọn B
Đặt
2
2
log 4 4 4 4 2 2 1
t t
x t x x
.
Từ điều kiện
2
2
0 2020 0 2 1 2020 1 1 1 log 2021
t
x t
.
Theo giả thiết ta có:
2
1 2 1 2 *
t y
t y
.
Xét hàm số
1
2
u
f u u
với
2
1 1 log 2021
u
.
Có
1
2
' 1 2 .ln 2 0, 1;1 log 2021
u
f u u
nên hàm
f u
đồng biến trên đoạn
2
1;1 log 2021
.
Dựa vào
* 1 1 1 1
f t f y t y
.
Mặt khác
2 2 2
1 1 1 log 2021 1 1 1 log 2021 0 log 2021 10,98
t y y
.
Vì
0;1;2;3;4;5;6;7;8;9;10
y y
.
Vậy có 11 cặp số nguyên thỏa mãn ycbt.
Câu 36. Có bao nhiêu số nguyên
x
sao cho tồn tại số thực
y
thỏa mãn
2 2
2 3
log 4 log 4
x y x y
.
A.
3
. B. Vô số. C.
2
. D.
4
.
Lời giải
Chọn C
Điều kiện:
2 2
4 0
4 0
x y
x y
Đặt
2 2
2 3
log 4 log 4
t x y x y
2 2
4 2
4 3
t
t
x y
x y
Áp dụng bất đẳng thức B. C. S, ta có:
2 2 2
2 2 2 2 2
4 1. 2.2 1 2 . 2 5 4
x y x y x y x y
9 5.2
t t
9
2
log 5
t
Từ
2 2
4 2
t
x y
suy ra
9
2
log 5
2
2 2 2,1
t
x
Do
x
nên
1;0;1
x
Với
1
x
2
2
1
2 1 1
4 2 1
4
1
4 3 1
. 3 1 2
4
t
t
t
t
y
y
y
y
Thay
2
vào
1
ta được
9 2.3 4.2 5 0
t t t
Do
1
nên
2 1 0
t
0
t
.
Khi đó:
2
9 2.3 4.2 5 4 4.2 4 2.3 1 2 2 3.2 1 0
t t t t t t t t
nên không tồn tại giá trị
của
t
. Vậy loại
1
x
.
Với
0
x
9
2
9
2
2
log 4
log 4
4 2
1
4 3
.3
4
t
t
t
y
y
y
nhận
0
x
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 24 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Với
1x
2
2
1
2 1
4 2 1
4
1
4 3 1
. 3 1
4
t
t
t
t
y
y
y
y
.
Dễ thấy
0
0
t
y
là một nghiệm của hệ
nhận
1x
.
Vậy
0;1
x
.
Câu 37. Có bao nhiêu cặp số nguyên
;x y
thoả mãn
0 2020
x
và
2
2 ln 1 1
y
x x x y e
?
A.
0
. B.
7
. C.
1
. D.
8
.
Lời giải
Chọn C
Ta có:
2ln 1
2
2 ln 1 1 2ln 1
x
y y
x x x y e x e y e
1
.
Xét hàm số:
t
f t t e
, ta có:
1 0
t
f t e
nên hàm số
f t
đồng biến trên
.
Do đó:
1 2ln 1 2ln 1
f x f y y x
.
+ Do
0 2020
x
nên
1 1 2021 0 2ln 2021 15, 22
x y
.
Do
y
nên
0;1;2;...;14;15
y
.
Có
2
2ln 1 e 1
y
y x x
.
Với
0;1;2;...;14;15
y
thì chỉ có
0
y
thì
x
.
Vậy có duy nhất
1
cặp số nguyên
;x y
thoả mãn đề bài.
Câu 38. Có bao nhiêu số nguyên
x
sao cho tồn tại số thực
y
thỏa mãn
2 2
3 4
log ( ) log 2
x y x y
?
A.
1
B.
3
C.
2
D. Vô số
Phân tích
Lời giải
Chọn C
Điều kiện:
0
x y
.
Đặt
2 2
3 4
log ( ) log 2
x y x y t
, suy ra
2 2
3
2 4
t
t
x y
x y
2
2
3
3 2 4 1
t
t t
x y
y y
Phương trình
1
2
3 2.3 9 4 0
t t t
y y
. Phương trình phải có nghiệm nên:
2
3 3 1
9 3 9 4 0
2 2 2
t
t t t
t
.
Do đó:
2
2 2
0 3
2
2 2
x y
x
x y
0; 1
x
( vì
x
)
Thử lại:
Với
4
9
4
9
2
log 2
log 2
3
0
2 4
3
t
t
t
y
x
y
y
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
Với
2
1 3 0
1
0
1 2 4
t
t
y t
x
y
y
Với
2
3 1
1 2.9 4.3 3 4 0 2
2 1 4
t
t t t
t
y
x
y
Khi
0 9 4
t t
t
nên
2
vô nghiệm, khi
0 4 1
t
t
1 4 0
t
nên
2
cũng vô nghiệm.
Vậy
0;1
x
.
Câu 39. Có bao nhiêu cặp số nguyên dương
;x y
thỏa mãn đồng thời hai điều kiện:
6
1 10
x
và
2
2 2 2
log 10 20 20 10 2 1
y
x x y x x
?
A.
4
. B.
2
. C.
3
. D.
1
.
Lời giải
Chọn D
Điều kiện:
2
10 20 20 0
x x
, đúng
x
.
Ta có
2
2 2 2
log 10 20 20 10 2 1
y
x x y x x
2
2 2 2
2 1 log 10 2 2 10
y
x x x x y
2
2 2 2
2 1 log10 log 2 2 10
y
x x x x y
2
2 2 2
2 2 log 2 2 10
y
x x x x y
2
2
log 2 2
2 2
10 log 2 2 10
x x
y
x x y
(*).
Xét hàm
10
t
f t t
trên
.
Ta có
10 .ln10 1 0
t
f t
,
t
. Do đó
f t
đồng biến trên
.
Khi đó
(*)
2 2
log 2 2
f x x f y
2 2
log 2 2
x x y
2
2
2 2 10
y
x x
2
2
1 1 10
y
x
.
Vì
6
1 10
x
nên
2
2
2
6
1 1 1 10 10 1 1
y
x
2
2 6
0 log 10 1 1
y
.
Vì
y
nên
1;2;3
y
.
+ Với
1y
2
2 2 10
x x
2
2 8 0
x x
2 (ktm)
4 (tm)
x
x
.
+ Với
2
y
2 4
2 2 10
x x
2
2 9998 0
x x
(không có giá trị
x
nguyên nào thỏa mãn).
+ Với
3
y
2 9
2 2 10
x x
2
2 999999998 0
x x
(không có giá trị
x
nguyên nào thỏa
mãn).
Vậy có một cặp nguyên dương
; 4;1
x y
thỏa mãn yêu cầu bài toán.
Câu 40. Có bao nhiêu số nguyên
10
y
sao cho tồn tại số nguyên
x
thỏa mãn
2
2
2 2 1
5 2 5 1
y
y
x x x
x
?
A.
10
B.
1
C.
5
D. Vô số
Phân tích
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 26 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Phương trình dạng
f u f v
.
Phương pháp: Chứng minh
y f t
đơn điệu trên
;a b
. Từ phương trình suy ra
u v
. Từ đó tìm
sự liên hệ giữa 2 biến
,x y
và chọn
,x y
thích hợp.
Lời giải
Chọn C
Ta có:
2 2
2
2 2 1 2 2 1 2
5 2 5 1 5 2 1 5
y y
y y
x x x x x x
x x x x
Xét:
1
5
t
f t t
đồng biến trên
. Do đó từ phương trình trên suy ra:
2
2
2 2
2 1 1 2 2 1 2
y y
y y
x x x x x
.
Do
x
nguyên nên ta có
2
2
y
và
10
y
nên
0; 2; 4; 6;8
y
.
Câu 41. Có bao nhiêu cặp số nguyên dương
;x y
thoả mãn
1 2020
x
và
1
2
2 2 log 2
y y
y x x
A.
2021
. B.
10
. C.
2020
. D.
11
.
Lời giải
Chọn D
Theo đề bài,
1
2
2 2 log 2
y y
y x x
2 2
2
2 log 2 2 log
2
y
y y
x x
2 2
2 2
2 2 log 2 2 2 log
2
y
y y y y
x
x
2 2
2 2 2 2
2. 2 log 2 2 log
2 2
y y
y y
x x
1
.
Xét hàm số
2
2 logf t t t
,
0t
.
Vì
1
2 0
ln 2
f t
t
0
t
f t
đồng biến trên
0;
nên
1
2 2 2 2
1 2 2 2.2 2 2 2 2 2
2 2
y y
y y y y y y
x x
f f x x x
.
Do
1 2020
x
nên
2
0 1 log 2020 1 11,98
y y
.
Do
*
y
nên
1;2;3;...;11
y
, với mỗi giá trị
y
cho ta 1 giá trị
x
thoả đề.
Vậy có
11
cặp số nguyên
;x y
thoả mãn đề bài.
Câu 42. Có bao nhiêu số nguyên
x
sao cho tồn tại số thực
y
thỏa mãn
2 2
2 2
3
2log log 1 3 log 1
x y x y
A.
1
B.
3
C.
2
D.
5
Lời giải
Chọn C
Đặt:
2 2
2 2
3
2log log 1 3 log 1
t x y x y
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27
Suy ra:
2
2
log 1 3
2
2 2
2 2
1 3 .2
2
1 3
1 3
t
t
t
t
x y
x y
x y
x y
Ta có:
2
2 2
2
1 3 .2 2 1 3
1 3 2
1 3
2
1 3 1 3
2 2 2
t
t
t
t
t
t
x y x y
.
Xét
1 3
2 2
t
t
f t
nghịch biến trên
nên
1 3 1 3
1 1
2 2 2
t
t
f t f t
.
Do đó
2
log 1 3
2
2
2 2
0 2 2log 1 3
1 3 1 3
t
t
x y
x y
0; 1
x
( vì
x
)
Thử lại:
Với
1x
:
2
2
1 3 2 1
3
1 3 2 1 3 0
1 3 2 2 1 3 .2 3 1 0
t
t
t
t
t
t t
y
y
Ta có:
1 3 2 2 1 3 .2 3 1
t
t t
g x
liên tục trên
0;1
thỏa mãn
0 1 0
g g
nên
phương trình có nghiệm
0;1
t
.
Do đó với
1x
thì tồn tại số thực
y
thỏa mãn
2 2
2 2
3
2log log 1 3 log 1
x y x y
Với
1
x
:
2
2
1 3 2 1
3
1 3 2 1 3 0
1 3 2 2 1 3 .2 3 1 0
t
t
t
t
t
t t
y
y
Ta có:
1 3 2 2 1 3 .2 3 1 0, 1
t
t t
t
nên phương trình vô nghiệm.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 28 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Do đó với
1
x
thì không tồn tại số thực
y
thỏa mãn
2 2
2 2
3
2log log 1 3 log 1
x y x y
Với
0
x
:
2
2
1 3 2
1 3
1 3 2 3 1
1 3 2 3 1 0
t
t
t
t
t
t
y
y
Ta có:
1 3 2 3 1
t
t
h x
liên tục trên
1;0
thỏa mãn
1 0 0
h h
nên phương trình có
nghiệm
1;0
t
.
Do đó với
0
x
thì tồn tại số thực
y
thỏa mãn
2 2
2 2
3
2log log 1 3 log 1
x y x y
.
Vậy
0;1
x
.
Câu 43. Có bao nhiêu cặp số nguyên
;x y
thỏa mãn
0 2020
y
và
3
2 1
log 1 2 ?
x
x
y
y
A.
2019
. B.
11
. C.
2020
. D.
4
.
Lời giải
Chọn B
Từ giả thiết ta có:
0
2 1
0 2 1 0
0
x
x
y
x
y
y
Ta có: PT
3 3
log 2 1 2 1 log (*)
x x
y y
Xét hàm số
3
log
f t t t
trên
0;

Khi đó
1
1 0
ln 3
f t
t
do đó hàm số
3
log
f t t t
đồng biến trên
0;
(*) có dạng
2 1 2 1
x x
f f y y
Vì
2
0 2020 0 2 1 2020 1 2 2021 0 log 2021
x x
y x
2
0 log 2021
0;1;2;3;4;5;6;7;8;9;10
x
x
x
. Vậy có
11
cặp
;x y
thỏa mãn.
Câu 44. Biết
1
x
,
2
x
là hai nghiệm của phương trình
2
2
7
4 4 1
log 4 1 6
2
x x
x x
x
và
1 2
1
2
4
x x a b
với
a
,
b
là hai số nguyên dương. Tính
a b
.
A.
13
a b
. B.
11
a b
. C.
16
a b
. D.
14
a b
.
Lời giải
Chọn D
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29
Điều kiện:
1
0,
2
x x
.
Ta có:
2
2 2 2
7 7 7
4 4 1
log 4 1 6 log 4 4 1 4 4 1 log 2 2
2
x x
x x x x x x x x
x
.
Xét hàm số
7
log
f t t t
có
1
1 0
ln7
f t
t
0
t
nên là hàm số đồng biến trên
0;

.
Do đó ta có
2 2
3 5
4 4 1 2 4 6 1 0
4
x x x x x x
.
Khi đó
1 2
3 5 3 5 1
2 2 9 5
4 4 4
x x
hoặc
1 2
3 5 3 5 1
2 2 9 5
4 4 4
x x
.
Vậy
1 2
3 5 3 5
;
4 4
x x
. Do đó
9; 5
a b
và
9 5 14
a b
.
Câu 45. Biết phương trình
5 3
2 1 1
log 2log
2
2
x x
x
x
có một nghiệm dạng
2
x a b
trong đó
,a b
là các số nguyên. Tính
2
a b
.
A.
3
. B.
8
. C.
4
. D.
5
.
Lời giải
Chọn B
Ta có
5 3 5 3
2 1 1 2 1 1
log 2log log 2log 1 .
2
2 2
x x x x
x x
x x
ĐKXĐ:
1x
.
5 3 5 3
1 log 2 1 2log 2 log 2log 1 (*)
x x x x
Xét hàm số
5 3
log 2log 1
f t t t
, với
1t
.
1 2
0
.ln 5 1 ln 3
f t
t t
với mọi
1t
, suy ra
f t
đồng biến trên khoảng
1;
.
Từ (*) ta có
2 1
f x f x
nên suy ra
2
2 1 2 1 0 1 2
x x x x x
(do
1x
).
Suy ra
3 2 2 3; 2 2 8
x a b a b
.
Câu 46. Số nghiệm thực của phương trình
6
6 3log 5 1 2 1
x
x x
là
A.
0
. B.
2
. C.
1
. D.
3
.
Lời giải
Chọn B
Điều kiện:
1
5
x
.
PT:
6
log 5 1
6 6
6 3 3log 5 1 5 1 6 3 6 3log 5 1 (1)
x
x x
x x x x x
.
Xét hàm số
6 3
t
f t t
, vì
6 .ln 6 3 0,
t
f t t
nên
f t
đồng biến trên
.
Khi đó
1
6 6 6
log 5 1 log 5 1 log 5 1 0
f x f x x x x x
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 30 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Xét hàm số
6
log 5 1h x x x
trên
1
;
5

, ta có
5
1
5 1 ln6
h x
x
2
25 1
0,
5
5 1 ln 6
h x x
x
và
1
5
lim ; lim 1
x
x
h x h x


Bảng biến thiên:
Từ BBT suy ra phương trình
0h x
có nhiều nhất 2 nghiệm thuộc khoảng
1
;
5

Mà
0 0, 1 0h h
.
Vậy phương trình đã cho có đúng hai nghiệm
0, 1x x
.
Câu 47. Tính tổng
S
tất cả các nghiệm của phương trình
1
5 3
ln 5 5.3 30 10 0
6 2
x x
x x
x
x
.
A.
1S
. B.
2S
. C.
1S
. D.
3S
.
Lời giải
Chọn A
Điều kiện
1
.
3
x
Phương trình tương đương
ln 5 3 ln 6 2 5 5 3 5 6 2 0
x x x x
x x
ln 5 3 5 5 3 ln 6 2 5 6 2
x x x x
x x
(1).
Xét hàm số
ln 5 , 0f t t t t
. Có
1
' 5 0f t
t
,
0t
nên
f t
đồng biến trên
0;
.
Từ
1
suy ra
5 3 6 2
x x
f f x
5 3 6 2
x x
x 5 3 6 2 0
x x
x
Xét
5 3 6 2
x x
g x x
,
' 5 ln5 3 ln3 6
x x
g x
2 2
'' 5 ln 5 3 ln3 0
x x
g x
,
1
3
x
.
Nên
' 0g x
có không quá
1
nghiệm suy ra
0g x
có không quá
2
nghiệm trên
1
;
3

. Mà
0 1 0g g
. Vậy phương trình có tập nghiệm là
0,1
. Do đó
1.S
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 31
Câu 48. Số nghiệm của phương trình
2
1 2
80
ln 2.3 2 80 ln3
3
x
x
x
x
là
A.
2
. B.
3
. C.
1
. D.
0
.
Lời giải
Chọn C
PT
2 2 1 1
ln 80 2 80 ln 3 2.3 (1)
x x
x x
Xét hàm số
ln 2 , 0f t t t t
; Ta có:
1
2 0, 0f t t
t
Hàm số
f t
đồng biến trên
0;
.
Từ (1) suy ra
2 1 2 1 2 1 1 2
80 3 80 3 80 9 9 80 0
x x x x
f x f x x x
Xét hàm số
1 2
9 80
x
g x x
trên
. Ta có:
1
2
1
2.9 ln3 2
4.9 ln3 2
x
x
g x x
g x
2 2
0 9 0 9
0 log 2ln 3 1 ( ) log 2ln 3 1 3,7 0g x x x g x g
lim ; lim ( )
x x
g x g x
 

Bảng biến thiên:
Dựa vào bảng biến thiên ta có
' 0,g x x
hàm số
g x
đồng biến trên
phương trình
0g x
có nhiều nhất một nghiệm.
Mà
1 0g
Do đó phương trình đã cho có duy nhất 1 nghiệm.
B. BÀI TOÁN CHỨA THAM SỐ
Dạng 1. Tìm m để có nghiệm (hoặc có k nghiệm) trên D?
— Bước 1. Tách m ra khỏi biến số và đưa về dạng .
— Bước 2. Khảo sát sự biến thiên của hàm số trên D.
— Bước 3. Dựa vào bảng biến thiên để xác định giá trị của tham số để đường thẳng nằm
ngang cắt đồ thị hàm số .
— Bước 4. Kết luận các giá trị cần tìm của để phương trình có nghiệm (hoặc có k nghiệm)
trên D.
Lưu ý
f t; m 0
f t A m
f t
A m
y A m
y f t
A m
f t A m
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 32 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
— Nếu hàm số có giá trị lớn nhất và giá trị nhỏ nhất trên D thì giá trị cần tìm là những m thỏa
mãn: .
— Nếu bài toán yêu cầu tìm tham số để phương trình có k nghiệm phân biệt, ta chỉ cần dựa vào bảng biến thiên
để xác định sao cho đường thẳng nằm ngang cắt đồ thị hàm số tại k điểm phân biệt.
Dạng 2. Tìm m để bất phương trình hoặc có nghiệm trên miền D?
— Bước 1. Tách tham số m ra khỏi biến số t và đưa về dạng hoặc .
— Bước 2. Khảo sát sự biến thiên của hàm số trên D.
— Bước 3. Dựa vào bảng biến thiên xác định các giá trị của tham số m để bất phương trình có nghiệm:
+ có nghiệm trên .
+ có nghiệm trên .
Lưu ý
— Bất phương trình nghiệm đúng .
— Bất phương trình nghiệm đúng .
Câu 1. Cho phương trình
2
2 2
log 2 2 log 2 0x m x m
(
m
là tham số thực). Tập hợp tất cả các giá
trị của
m
để phương trình đã cho có hai nghiệm phân biệt thuộc đoạn
1;2
là
A.
1; 2
. B.
1;2
. C.
1;2
. D.
2;
.
Lời giải
Chọn C
2
2 2
log 2 2 log 2 0x m x m
2
2
1 log 2 log 2 0x m x m
*
Đặt
2
logt x g x
0 1t
và mỗi giá trị của
x
sẽ cho một giá trị của t
*
trở thành
2
1 2 2 0t m t m
2
2 1 2 2 0t t mt t m
2
1 1t m t
1 1 0t t m
1 1
1 2
t m
t
Với
1t
thì phương trình có một nghiệm
2x
Vậy để phương trình ban đầu có hai nghiệm phân biệt thì phương trình
1
phải có một nghiệm
1t
0 1 1m 1 2m
y f t
A m
t D t D
min f t A m max f t
y A m
y f t
f t; m 0
f t; m 0
A m f t
A m f t
f t
A m f t
t D
D A m max f t
A m f t
t D
D A m min f t
A m f t
t D
t D A m min f t
A m f t
t D
t D A m max f t
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 33
Vậy
1;2
m
để thoả mãn yêu cầu bài toán.
Câu 2. Cho phương trình
3 2
2 2 2
2log 7log 4log 3 0
2
x
x
x x m
(
m
là tham số thực). Có tất cả
bao nhiêu giá trị nguyên dương của
m
để phương trình đã cho có đúng hai nghiệm phân biệt?
A.
78
. B.
80
. C.
81
. D.
79
.
Lời giải
Chọn D.
Đk:
0
3
x
x
m
.
3 2
2 2 2
2log 7log 4log 3 0
2
x
x
x x m
2
2 2
log 2 . 2log 1 3 0
x
x x m
2
2
3
log 2
4
1 1
log
2
2
3
log
x
x
x
x x
m
x m
.
Với
1
m
thì
3
log 0
x m
(loại). Do đó phương trình có 2 nghiệm phân biệt
1
4,
2
x x
Với
1
m
thì
3
log 0
x m
nên luôn nhận nghiệm
3
logx m
.
Mà
1
4
2
nên phương trình có hai nghiệm phân biệt khi
1
2
3
1
log 4 3 81
2
m m
.
m
nguyên dương nên
3; 4; .., 80
m
.
Vậy có
79
giá trị
m
nguyên dương.
Câu 3. Cho phương trình
2
2 2
2log 3log 2 9 1 3 0
x x
x x m m
(
m
là tham số thực). Gọi
S
là tập
hợp tất cả các giá trị nguyên dương của
m
để phương trình đã cho có đúng hai nghiệm phân biệt.
Tính tổng tất cả các phần tử của
S
.
A.
3238
. B.
3236
. C.
3237
. D.
3239
.
Lời giải
Chọn A
Viết lại phương trình
2
2 2
2log 3log 2 3 1 3 0
x x
x x m
Đk:
0
3
x
x
m
.
2
2 2
2log 3log 2 9 1 3 0
x x
x x m m
2
2 2
2log 3log 2 3 1 3 0
x x
x x m
2
2
3
log 2
4
1 1
log
2
2
3
log
x
x
x
x x
m
x m
.
Với
1
m
thì
3
log 0
x m
(loại). Do đó phương trình có 2 nghiệm phân biệt
1
4,
2
x x
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 34 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Với
1
m
thì
3
log 0
x m
nên luôn nhận nghiệm
3
logx m
.
Mà
1
4
2
nên phương trình có hai nghiệm phân biệt khi
1
2
3
1
log 4 3 81
2
m m
.
m
nguyên dương nên
3; 4; .., 80
m
.
Tổng
1 2 3 ... 80 2 3238
.
Câu 4. Cho phương trình
2
3 3
2log 3log 2 3 .2 0
x x
x x m
(
m
là tham số thực). Gọi
S
là tập hợp tất cả
các giá trị nguyên dương của
m
để phương trình đã cho có đúng hai nghiệm phân biệt. Tính tổng tất
cả các phần tử của
S
.
A.
741
. B.
742
. C.
740
. D.
703
.
Lời giải
Chọn A.
Viết lại phương trình
2
3 3
3
2log 3log 2 0
2
x
x x m
Đk:
3
2
0
0
3
log
2
x
x
x
x m
m
(Do
m
nguyên dương nên tồn tại
3
2
log
m
).
2
3 3
3
2log 3log 2 0
2
x
x x m
3
3
3
2
log 2
9 0
1 1
log 0
2
3
log
3
2
x
x
x
x x
x m
m
.
Với
1
m
thì
3
2
log 0
x m
(loại). Do đó phương trình có 2 nghiệm phân biệt
1
9,
3
x x
Với
1
m
thì
3
2
log 0
x m
nên luôn nhận nghiệm
3
2
log
x m
.
Mà
1
9
3
nên phương trình có hai nghiệm phân biệt khi
1
9
3
3
2
1 3 3
log 9 1,26 38,44
2 2
3
m m
.
m
nguyên dương nên
2;3; 4; .., 38
m
.
Như vậy có tất cả các giá trị
m
là
1; 2; 3;; 4;...; 38
.
Tổng
1 2 3 ... 38 741
.
Câu 5. Cho phương trình
2
2lg lg 1 lg
2 4 3 0
x x x x
m
(
m
là tham số thực). Gọi
S
là tập hợp tất cả các giá trị
nguyên dương của
m
để phương trình đã cho có đúng hai nghiệm phân biệt. Tổng của phần tử nhỏ nhất và
phần tử lớn nhất
S
bằng
A.
100
3 1
. B.
100
3 1
. C.
99
3
. D.
99
3 1
.
Lời giải
Chọn A
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 35
Đk:
0
3
x
x
m
.
2
2lg lg 1 lg
2 4 3 0
x x x x
m
2
3
2
2lg lg 1 lg
log
3
2lg lg 2 2lg
2 4
x
x x x
x m
m
x x x
3
lg 2 100
1 1
lg
2
10
3
log
x
x x
x x
m
x m
.
Với
1
m
thì
3
log 0
x m
(loại). Do đó phương trình có 2 nghiệm phân biệt
1
100,
10
x x
.
Với
1
m
thì
3
log 0
x m
nên luôn nhận nghiệm
3
logx m
.
Mà
1
100
10
nên phương trình có hai nghiệm phân biệt khi
1
100
10
3
1
log 100 3 3
10
m m
.
m
nguyên dương nên
100
2;3; 4; .., 3 1
m
.
Do đó tổng của phần tử nhỏ nhất và phần tử lớn nhất bằng
100
3 1
.
Câu 6. Cho phương trình
3.2 .log 12log 2 4 5 0
x x x
x x m
(
m
là tham số thực). Có tất cả bao nhiêu
giá trị nguyên dương của
m
để phương trình đã cho có đúng hai nghiệm phân biệt?
A.
24
. B.
25
. C.
23
. D.
22
.
Lời giải
Chọn D
Đk:
0
5 ; 0
x
x
m m
.
3.2 .lg 12lg 2 4 5 0
x x x
x x m
3lg 1 2 4 5 0
x x
x m
3
5
2 4 2
1 1
lg
3
10
5
log ; 0
x
x
x
x x
m
x m m
.
Với
1
m
thì
5
log 0
x m
(loại). Do đó phương trình có 2 nghiệm phân biệt
3
1
2,
10
x x
.
Với
1
m
thì
5
log 0
x m
nên luôn nhận nghiệm
5
logx m
.
Mà
3
1
2
10
và vì
5
logx m
nên phương trình có hai nghiệm phân biệt khi
3
1
10
5
3
1
log 2 5 25
10
m m
,
m
nguyên nên
3; 4; .., 24
m
.
Vậy có
22
giá trị
m
nguyên dương.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 36 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 7. Cho phương trình
2 2
2 2
log 3 log 3 2 2 1 0
x m x m m
(
m
là tham số thực). Tìm tất cả các số thực
m
để phương trình có hai nghiệm phân biệt thuộc đoạn
1;9
.
A.
1
3 .
2
m
B.
2
m
. C.
. D.
1 1
2 2
m
.
Lời giải
Chọn C
Điều kiện:
0
x
.
PT:
2 2
3 3
log 3 log 3 2 2 1 0
x m x m m
2 2
3 3
log 3 log 2 1 0
x m x m m
.
3
3
log 1
log 2 1
x m
x m
Ta có
3
1;9 log 0;2
x x
Vậy để phương trình đã cho có hai nghiệm phân biệt thuộc đoạn
0;9
khi và chỉ khi
3 1
0 1 2
1 1
0 2 1 2
2 2
1 2 1
2
m
m
m m
m m
m
(Hệ vô nghiệm).
Câu 8. Cho phương trình
2 2
2 2
log ( 3)log 2 3 0
x m x m m
(
m
là tham số thực). Có bao nhiêu giá trị
nguyên của tham số
m
để phương trình đã cho có đúng một nghiệm thuộc đoạn
1
;32
4
?
A.
4
. B.
5
. C.
6
. D.
7
.
Lời giải
Chọn B
Đặt
2
logt x
. Do
1
;32
4
x
nên
2;5
t
và ứng với mỗi
2;5
t
cho ta một giá trị
1
;32
4
x
. Khi đó phương trình trở thành:
2 2 2 2
( 3) 2 3 0 2 3 3 0
t m t m m t mt m t m
( )( 2 ) 3( ) 0
3 2
t m
t m t m t m
t m
.
Với
m
nguyên, để phương trình có nghiệm duy nhất
2;5
t
, ta có các trường hợp sau:
TH1:
3 2
1
2;5
m m
m
m
.
TH2:
3 2 2 5 / 2
3 2 2;5
3 2 5 1
2;3;4;5
2;5
2;5 2;5
m m
m
m m
m
m
m m
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 37
TH3:
2
2
2;5
5
5
3 2 2;5
5
2 3 2 5
1
2
m
m
m
m
m
m
m
m
vô nghiệm
Vậy tổng cộng có 5 số nguyên của
m
thỏa đề.
Câu 9. Cho phương trình
9 ( 5)3 3 6 0
x x
m m
(
m
là tham số thực ). Có bao nhiêu giá trị
nguyên của
m
để phương trình đã cho có 2 nghiệm phân biệt thuộc đoạn
1;2
.
A.
6
. B.
7
. C.
m R
. D.
1
.
Lời giải
Chọn A
9 ( 5)3 3 6 0
3 3
3 3 3 2 3 3 0 3 3 3 2 0 .
3 2
x x
x
x x x x x
x
m m
m m
m
3 3 1
x
x
thỏa mãn
1;2
x
.
Mặt khác:
1;2 3 3;9
x
x
. Vậy để phương trình đã cho có 2 nghiệm phân biệt thuộc đoạn
1;2
khi và chỉ khi
3 2 9 1 7
1 7
2 3 1
m m
m
m m
mà
m
nguyên suy ra
2;3;4;5;6;7
m
nên có
6
giá trị nguyên của
.m
Câu 10. Cho phương trình
2 2 2
2 2
log log 2 0
x x m m
(
m
là tham số thực). Có bao nhiêu giá trị nguyên
của tham số
m
để phương trình đã cho có đúng một nghiệm thuộc đoạn
1
;16
8
?
A.
3
. B.
2
. C.
1
. D.
4
.
Lời giải
Chọn A
Đặt
2
logt x
. Do
1
;16
8
x
nên
3;4
t
và ứng với mỗi
3;4
t
cho ta một giá trị
1
;16
8
x
. Khi đó phương trình trở thành:
2 2
2 2 0 ( )( ) 2( ) 0
2
t m
t t m m t m t m t m
t m
.
Với
m
nguyên, để phương trình có nghiệm duy nhất
3;4
t
, ta có các trường hợp sau:
TH1:
2
1
3;4
m m
m
m
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 38 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TH2:
2 3 5
2 3;4
2 4 2
3
3;4
4;3 4;3
m m
m
m m
m
m
m m
.
TH3:
3 3
3;4
4 4
5
2 3;4
5;2 5;2
m m
m
m m
m
m
m m
.
Vậy tổng cộng có 5 số nguyên của
m
thỏa đề.
Câu 11. Cho phương trình
2 2
2 2
log 2 2log 1 0 x x m
.Có bao nhiêu giá trị nguyên của tham số
m
để
phương trình có đúng một nghiệm thuộc đoạn
1
;16
2
?
A.
10
. B.
7
. C.
5
. D.
6
.
Lời giải
Chọn D
Điều kiện:
0x
.
Biến đổi phương trình về dạng
2
2 2
1 log 4log 1 0x x m
2
2 2
log 2log x x m
.
Đặt
2
logt x
, với mỗi
1
;16
2
x
thì cho một giá trị
1;4t
.
Khi đó ta được phương trình
2
2t t m
.
Xét hàm số
2
2f t t t
trên đoạn
1;4
.
Ta có
2 2
f t t
,
0 1f t t
.
Bảng biến thiên của
f t
Từ bảng biến thiên suy ra
1 3;8 1;4;5;6;7;8 m m
có
6
giá trị của
m
thỏa mãn yêu
cầu bài toán.
Câu 12. Cho phương trình
2 2 2
2 2 2
log log 2 3 log 0x x m m x
(
m
là tham số thực). Có bao nhiêu giá
trị nguyên của tham số
m
để phương trình đã cho có 3 nghiệm phân biệt
1
8
x
?
A.
3
. B.
5
. C.
2
. D.
4
.
Lời giải
Chọn C
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 39
Ta cần tìm các giá trị nguyên của tham số
m
để phương trình đã cho có 3 nghiệm phân biệt
1
;8
8
x
.
Đặt
2
logt x
. Do
1
;8
8
x
nên
3;3
t
và ứng với mỗi
3;3
t
cho ta một giá trị
1
;8
8
x
.
Với điều kiện
3;3
t
phương trình trở thành:
2 2
3
2 2 3 0 (*)
2
t
t t m m t t m
t m
.
Với
m
nguyên, để phương trình đầu có 3 nghiệm
1
;8
8
x
(*)
có 3 nghiệm phân biệt
3;3
t
3 2 3 1 3
0;2
3 2 3 1 1
m m m
m
m m m
.
Câu 13. Cho phương trình
2
1 2020 2 2020 2 0
x x
m m
(
m
là tham số thực). Tập hợp tất cả
các giá trị của
m
để phương trình đã cho có 2 nghiệm phân biệt thuộc đoạn
0;2
là
A.
2;2021
. B.
m R
. C.
2;

. D.
2;2021
.
Lời giải
Chọn D
2
1 2020 2 2020 2 0
1 2 2020 2020 2020 2 2020 2 0
2020 1
2020 2020 1 0 .
2020 1
x x
x x x x
x
x x
x
m m
m m
m m
m
Theo bài ra ta có:
0; 2 2020 1;2020
x
x
.
Vậy để phương trình đã cho có 2 nghiệm phân biệt thuộc đoạn
0;2
khi và chỉ
khi
1 1 2020 2 2021
2 2021
1 1 2
m m
m
m m
.
Câu 14. Cho phương trình
2 2
3 3 81
log ( 3)log 2 3 1 log 0
x m x m m x
(
m
là tham số thực). Có bao
nhiêu giá trị nguyên của tham số
m
để phương trình đã cho có 3 nghiệm phân biệt
1
27
x
?
A.
4
. B.
3
. C.
2
. D.
5
.
Lời giải
Chọn B
Ta cần tìm các giá trị nguyên của tham số
m
để phương trình đã cho có 3 nghiệm phân biệt
1
;81
27
x
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 40 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Đặt
3
logt x
. Do
1
;81
27
x
nên
3;4
t
và ứng với mỗi
3;4
t
cho ta một giá trị
1
;81
27
x
. Với điều kiện
3;4
t
phương trình trở thành:
2 2
4
( 3) 2 3 4 0 (*)
3 2
t
t m t m m t t m
t m
.
Với
m
nguyên, phương trình đầu có 3 nghiệm phân biệt
1
;81
27
x
(*)
có 3 nghiệm phân biệt
3;4
t
1
3 3 2 4
1
0;2;3
2
3 3 2 4
1 4
m m
m
m
m m
m
.
Vậy tổng cộng có 3 số nguyên của
m
thỏa đề.
Câu 15.
Cho phương trình
2
2021 2021
log 2021 2 log 2
x m x m
(
m
là tham số thực).
Tổng tất cả các giá trị nguyên của
m
để phương trình đã cho có hai nghiệm phân biệt thuộc đoạn
3
1;2021
là:
A.
10
. B.
8
. C. vô số. D.
13
.
Lời giải
Chọn B
Xét phương trình
2
2021 2021
log 2021 2 log 2
x m x m
2
2021 2021
log 2021 2 log 2 0 1
x m x m
Điệu kiện
0
x
Phương trình
1
2
2021 2021
1 log 2 log 2 0
x m x m
2
2021 2021
log log 1 0
x m x m
2021
1
2021
2021
log 1
log 1
2021
m
x
x
x m
x
Để phương trình đã cho có 2 nghiệm phân biệt trên đoạn
3
1; 2021
thì:
1
1 3
2021 2021 2 2
1;3;4
0 1 3 1 4
1 2021 2020
m
m
m m
m
m m
Vậy tổng các giá trị
m
nguyên là:
1 3 4 8.
Câu 16. Cho phương trình
2 2 2
2 2 2
log log 2 3 log 0
x x m m x
(
m
là tham số thực). Có bao nhiêu giá
trị nguyên của tham số
m
để phương trình đã cho có 2 nghiệm phân biệt
1
8
x
?
A.
7
. B.
6
. C.
5
. D.
8
.
Lời giải
Chọn D
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 41
Ta cần tìm các giá trị nguyên của tham số
m
để phương trình đã cho có đúng hai nghiệm
1
;8
8
x
.
Đặt
2
logt x
. Do
1
;8
8
x
nên
3;3
t
và ứng với mỗi
3;3
t
cho ta một giá trị
1
;8
8
x
.
Với điều kiện
3;3
t
phương trình trở thành:
2 2
3
2 2 3 0
2
t
t t m m t t m
t m
.
Với
m
nguyên, phương trình đầu có 2 nghiệm
1
;8
8
x
(*)
có 2 nghiệm phân biệt
3;3
t
, ta
có các trường hợp sau:
TH1:
2
1
3;3
m m
m
m
.
TH2: Nếu
3
m
thì phương trình có 2 nghiệm
1, 3t t
. Nhận
3
m
.
TH3: Nếu
2 3 1
m m
thì phương trình có 2 nghiệm
1, 3t t
. Nhận
1
m
.
TH4:
2 3 1
2 3;3
2 3 1
3; 2;2
3;3
3;3 3;3
m m
m
m m
m
m
m m
.
TH5:
3 3
3;3
3 3
4;5
2 3;3
5;1 1;5
m m
m
m m
m
m
m m
.
Vậy
3;2; 1;1;2;3;4;5
m
tổng cộng có 5 số nguyên của
m
thỏa đề.
Câu 17. Có bao nhiêu giá trị nguyên của
m
để phương trình
2 2
1 1 1 1
9 2 3 2 1 0
x x
m m
có nghiệm
thực?
A.
4
. B.
5
. C.
6
. D.
7
.
Lời giải
Chọn C
Điều kiện
1 1x
. Đặt
2
1 1
3
x
t
, với
1 1 3 9x t
.
Khi đó phương trình đã cho trở thành:
2
2 2 1 0 1
t m t m
.
Ta có
2
2 1
1 2
2
t t
m
t
. Khi đó yêu cầu bài toán trở thành tìm
m
để phương trình:
2
có
nghiệm
3;9
t
.
Xét hàm số
2
2 1
2
t t
f t
t
trên
3;9
, có
2
2
4 3
0, 3;9
2
t t
f t t
t
. Do đó,
f t
đồng
biến trên
3;9
. Suy ra, phương trình
2
có nghiệm trên
3;9
khi và chỉ khi
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 42 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
64
3 9 4
7
f m f m
.
Vậy có
6
giá trị nguyên của
m
thỏa mãn đề bài.
Câu 18. Cho phương trình
2
log 2log 2 1
a a
x x
. Số giá trị nguyên của
0;2020a
để phương trình
trên có 1 nghiệm thực là
A.
0
. B.
2018
. C.
2019
. D.
2020
.
Lời giải
Chọn B
Điều kiện:
2
0
0 1
x
x
a
.
Phương trình
2
log 2 1
a
x x
2
2
2
2 1
2
2 2
x x a
x x a
x x a
.
Phương trình đã cho có 1 nghiệm thực khi và chỉ khi một trong hai phương trình
1
và
2
chỉ có 1
nghiệm
2; \ 0x
.
Xét hàm số
2
2f x x x
trên
2; \ 0D
, có bảng biến thiên như sau:
Từ bảng biến thiên, ta thấy yêu cầu bài toán thỏa mãn khi
1 1a a
.
Do đó, có
2018
giá trị nguyên của
a
trên
0;2020
thỏa mãn đề bài.
Câu 19. Cho phương trình
3 2
1
2
2
log 6 2log 14 29 2 0mx x x x
, số giá trị nguyên của
m
để
phương trình có 3 nghiệm thực phân biệt là
A.
1
. B.
0
. C.
23
. D.
5
.
Lời giải
Chọn B
Phương trình
2
3 2
2 2
14 29 2 0
log 6 log 14 29 2
x x
mx x x x
3 2
1
2
14
6 14 29 2 1
x
mx x x x
Nhận thấy
0x
không là nghiệm của
1
, nên
2
2
1 6 14 29x x m
x
2
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 43
Yêu cầu bài toán trở thành: tìm
m
để phương trình
2
có 3 nghiệm phân biệt trên
1
;2
14
.
Xét hàm số
2
2
2
6 14 29f x x x
x
trên
1
;2
14
, có
2
2
12 14 .f x x
x
. Suy ra bảng biến
thiên:
Từ bảng biến thiên ta thấy, phương trình
2
có 3 nghiệm phân biệt trên
1
;2
14
39
19
2
m
.
Do vậy, không có giá trị nguyên nào của
m
thỏa mãn đề bài.
Câu 20. Phương trình
2 2
3 3
log log 1 2 1 0x x m
có nghiệm trên đoạn
3
1;3
khi
;m a b
. Khi đó giá
trị biểu thức
.T a b
bằng
A.
0
. B.
1
. C.
1
4
. D.
4
.
Lời giải
Chọn A
Đặt
2 2 2
3 3
log 1 1 logt x t x
. Khi đó
3
1;3 1; 2x t
và phương trình đã cho trở thành:
2 2
1 2 1 0 2 2t t m t t m
2
.
Yêu cầu bài toán trở thành: tìm
m
để phương trình
2
có nghiệm
1;2t
.
Xét hàm số:
2
f t t t
có
2 1 0, 1;2f t t t
, suy ra hàm số đồng biến trên
1;2
.
Do đó, phương trình
2
có nghiệm trên
1;2
1 2 2 2 2 2 2 6 0 2f m f m m
.
Suy ra
0; 2 . 0a b T a b
.
Câu 21. Phương trình
2 2
3 3
log log 1 2 1 0x x m
có nghiệm trên đoạn
3
1;3
khi
;m a b
. Khi đó giá
trị biểu thức
.T a b
bằng
A.
0.
B.
1.
C.
1
.
4
D.
4.
Lời giải
Chọn A
Đặt
2 2 2
3 3
log 1 1 logt x t x
. Khi đó
3
1;3 1;2x t
và phương trình đã cho trở
thành:
2 2
1 2 1 0 2 2t t m t t m
2
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 44 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Yêu cầu bài toán trở thành: tìm
m
để phương trình
2
có nghiệm
1;2
t
.
Xét hàm số:
2
f t t t
có
2 1 0, 1;2
f t t t
, suy ra hàm số đồng biến trên
1;2
.
Do đó, phương trình
2
có nghiệm trên
1;2
1 2 2 2 0 2
f m f m
.
Suy ra
0; 2 . 0
a b T a b
.
Câu 22. Cho phương trình
2
3 3
3log 2log 1 5 0
x
x x m
(
m
là tham số thực). Có tất cả bao nhiêu giá trị
nguyên dương của
m
để phương trình đã cho có đúng hai nghiệm phân biệt?
A. Vô số. B.
120
. C.
121
. D.
124
.
Lời giải
Chọn C
Đk:
0
5
x
x
m
(*)
Phương trình
2
3 3
3log 2log 1 5 0
x
x x m
3
3
3
5
log 1
3
1 1
log
3
3
5
log
x
x
x
x x
m
x m
.
+Với
1
m
thì
5
log 0
x m
(loại nghiệm này do không thỏa (*)). Do đó phương trình có 2 nghiệm
phân biệt
3
1
3,
3
x x
. Suy ra nhận
1
m
.
+ Với
1
m
thì
5
log 0
x m
nên luôn nhận nghiệm
5
logx m
.
Mà
3
1
3
3
nên phương trình có hai nghiệm phân biệt khi
3
1
3
5
3
1
log 3 3.052 5 125
3
m m
.
Do
m
nguyên dương nên
4; .., 124
m
.
Vậy cả hai trường hợp có
121
giá trị
m
nguyên dương.
Câu 23. Cho phương trình
2
4 2 2
log 2 1 log 2 1 logx x x m
(
m
là tham số thực). Có tất cả bao
nhiêu giá trị nguyên của
m
để phương trình đã cho có nghiệm?
A.
0
. B.
1
. C.
2
. D. Vô số.
Lời giải
Chọn B
Điều kiện:
2
x
.
Có
2
4 2 2
log 2 1 log 2 1 logx x x m
2 2
2
log log
1 2
x m
x
2
2 1
m x
x
.
Xét hàm số
2
1
x
f x
x
trên
2;

.
Ta có
2
1
' 0
1
f x
x
,
2
x
.
Bảng biến thiên
f x
:
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 45
Từ bảng biến thiên ta suy ra phương trình có nghiệm khi
0 1 0 2
2
m
m
.
Có một giá trị nguyên của tham số
m
để phương trình có nghiệm là
1m
.
Câu 24. Tìm tập hợp tất cả giá trị của tham số thực
m
để phương trình
2
2 2
log 4 log 0x x m
có nghiệm
thuộc khoảng
0 ;1
.
A.
4 ;
. B.
4 ;
. C.
4 ;0
. D.
2 ;0
.
Lời giải
Chọn B
Đặt
2
logt x , với
0 ;1 0x t
.
Để phương trình đã cho có nghiệm thuộc khoảng
0 ;1
thì phương trình
2
4 0t t m
có nghiệm
0t
.
Xét hàm số
2
4 0 ; 2 4 0 2f t t t t f t t t
.
Ta có bảng biến thiên:
Vậy giá trị cần tìm là
4 ;m
.
Câu 25. Cho phương trình
3 2
2 2 2
2020 2log 7 log 4log 2 3 0
x
x x x m (
m
là tham số thực). Có tất cả
bao nhiêu giá trị nguyên dương của
m
để phương trình đã cho có đúng hai nghiệm phân biệt?
A.
79
. B.
80
. C. Vô số. D.
78
.
Lời giải
Chọn A
Đk:
0
3
x
x
m
(*)
3 2
2 2 2
2020 2log 7 log 4log 2 3 0
x
x x x m
2
2 2
log 2 . 2log 1 3 0
x
x x m
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 46 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
2
3
log 2
4
1 1
log
2
2
3
log
x
x
x
x x
m
x m
.
+ Với
1
m
thì
3
log 0
x m
(loại nghiệm này do không thỏa (*)). Do đó phương trình đã cho có
hai nghiệm phân biệt
1
4,
2
x x
. Suy ra nhận
1
m
.
+ Với
1
m
thì
3
log 0
x m
nên luôn nhận nghiệm
3
logx m
.
Mà
1
4
2
nên phương trình có hai nghiệm phân biệt khi
1
2
3
1
log 4 3 81
2
m m
.
Do
m
nguyên dương nên
3; 4; .., 80
m
.
Vậy cả hai trường hợp có
79
giá trị
m
nguyên dương.
Câu 26. Cho phương trình
2
3 3
2log 3log 2 5 .3 0
x x
x x m
(
m
là tham số thực). Gọi
S
là tập hợp tất
cả các giá trị nguyên dương của
m
để phương trình đã cho có đúng hai nghiệm phân biệt. Tính tổng
tất cả các phần tử của
S
.
A.
4950
. B.
2475
. C. Vô số. D.
4949
.
Lời giải
Chọn A
Phương trình tương đương:
2
3 3
5
2log 3log 2 0
3
x
x x m
.
Điều kiện
0
5
3
x
x
m
(*)
2
3 3
5
2log 3log 2 0
3
x
x x m
3
3
5
3
log 2
9
1 1
log
2
3
log
5
3
x
x
x
x x
x m
m
.
+ Với
1
m
thì
5
3
log 0
x m
(loại nghiệm này do không thỏa mãn (*)). Do đó phương trình có 2
nghiệm phân biệt
9
x
,
1
3
x
. Suy ra nhận
1
m
.
+ Với
1
m
thì
5
3
log 0
x m
nên luôn nhận nghiệm
5
3
log
x m
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 47
Mà
1
9
3
nên phương trình có hai nghiệm phân biệt khi
5
3
1
log 9
3
m
1
9
3
5 5
1,343 99,229
3 3
m
.
Do
m
nguyên dương nên
2;3;4;...,99m
.
Vậy cả hai trường hợp suy ra
1 2 3 ... 99 4950S
.
Câu 27.
Cho phương trình
2
2
1 1
2 2
1
1 log 2 4 5 log 4 4 0
2
m x m m
x
(
m
là tham số thực). Có tất
cả bao nhiêu giá trị nguyên của tham số
m
để phương trình có nghiệm thuộc
5
;4
2
.
A.
6
. B.
5
. C.
4
. D. Vô số.
Lời giải
Chọn A
Điều kiện:
2 0 2x x
.
Ta có:
2
2
1 1
2 2
1
1 log 2 4 5 log 4 4 0
2
m x m m
x
2
1 1
2 2
4 1 log 2 4 5 log 2 4 4 0 *m x m x m
.
Đặt
1
2
log 2t x
. Vì
5
;4
2
x
1;1t
.
Khi đó phương trình (*) trở thành
2
4 1 4 5 4 4 0m t m t m
2
2
2
5 1
1 5 1 0
1
t t
m t m t m m
t t
**
.
Xét hàm số
2
2
5 1
1
t t
f t
t t
,
1;1t
.
Ta có
2
2
2
4 4
1
t
f t
t t
.
0f t
1t
.
Ta có bảng biến thiên:
Dựa vào bảng biến thiên suy ra phương trình
**
có nghiệm khi
7
3
3
m
.
Suy ra có
6
giá trị nguyên của tham số
m
để phương trình đã cho có nghiệm thuộc
5
;4
2
.
t
2
1
1
2
'f t
f t
7
3
3
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 48 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 28. Cho phương trình
2
2 2
2log 3log 2 16 1 4 0
x x
x x m m
(
m
là tham số thực). Gọi
S
là tập
hợp tất cả các giá trị nguyên dương của
m
để phương trình đã cho có đúng ba nghiệm phân biệt.
Tổng tất cả các phần tử của
S
là
A.
32637
. B.
32640
. C.
255
. D.
256
.
Lời giải
Chọn A
Viết lại phương trình
2
2 2
2log 3log 2 4 1 4 0
x x
x x m
Đk:
0
4
x
x
m
(*)
Với điều kiện trên phương trình đã cho tương đương:
2
2
4
log 2
4
1 1
log
2
2
4
log
x
x
x
x x
m
x m
.
Với
1
m
thì
4
log 0
x m
(loại nghiệm này do không thỏa (*)). Do đó phương trình có 2 nghiệm
phân biệt
1
4,
2
x x
. Suy ra loại
1
m
.
Với
1
m
thì
4
log 0
x m
nên luôn nhận nghiệm
4
logx m
.
Mà
1
4
2
nên phương trình có hai nghiệm phân biệt khi
1
2
4
1
log 4 2,665 4 256
2
m m .
Do
m
nguyên dương nên
3; 4; .., 255
m
.
Ta có
1 2 3 ... 255 32640
suy ra
32640 3 32637
S
.
Câu 29. Giá trị lớn nhất của tham số
m
sao cho bất phương trình
2 2
5 5
1 log 1 log 4
x mx x m
nghiệm đúng với mọi
x
thuộc
là
A.
2
. B.
3
. C.
5
2
. D.
4
.
Lời giải
Chọn B
Điều kiện
2
4 0,mx x m x
2
0
2
' 4 0
m
m
m
Ta có
2 2
5 5
1 log 1 log 4
x mx x m
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 49
2 2
5 5
log 5 1 log 4x mx x m
2 2
5 1 4x mx x m
2 2
2
2
1 5 4 5
5 4 5
1
m x x x
x x
m
x
Xét hàm số
2
2
5 4 5
1
x x
f x
x
Ta có
2
2
2
4 4
'
1
x
f x
x
Bảng biến thiên
Từ bảng biến thiên ta suy ra
2
2
5 4 5
1
x x
m
x
,
x
3m
Kết hợp với điều kiện
2m
ta được
2 3m
.
Vậy giá trị lớn nhất của tham số
m
cần tìm là
3.
Câu 30. Giá trị lớn nhất của tham số
m
sao cho bất phương trình
2 2
5 5
1 log 1 log 4x mx x m
nghiệm đúng với mọi
x
thuộc
là:
A.
2
. B.
3
. C.
5
2
. D.
4
.
Lời giải
Chọn B
Điều kiện
2
4 0,mx x m x
2
0
2
' 4 0
m
m
m
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 50 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2 2
5 5
2 2
5 5
2 2
2 2
2
2
1 log 1 log 4
log 5 1 log 4
5 1 4
1 5 4 5
5 4 5
.
1
x mx x m
x mx x m
x mx x m
m x x x
x x
m
x
Xét hàm số
2
2
5 4 5
1
x x
f x
x
Ta có
2
2
2
4 4
'
1
x
f x
x
Bảng biến thiên
Từ bảng biến thiên ta suy ra
2
2
5 4 5
1
x x
m
x
,
x
3m
.
Kết hợp với điều kiện
2m
ta được
2 3m
.
Vậy giá trị lớn nhất của tham số
m
cần tìm là
3.
Câu 31. Cho phương trình
2
7 7
log 3log 2 5 0
x
x x m
(
m
là tham số thực). Gọi
S
là tập hợp tất cả
các giá trị nguyên dương của
m
để phương trình đã cho có đúng hai nghiệm phân biệt. Tổng của
phần tử nhỏ nhất và phần tử lớn nhất
S
bằng
A.
49
5
. B.
49
5 1
. C.
48
5
. D.
49
5 1
.
Lời giải
Chọn A
Đk:
0
5
x
x
m
(*)
2
7 7
log 3log 2 5 0
x
x x m
7
7
5
log 1
7
log 2 49
log
5
x
x
x
x x
x m
m
.
+ Với
1m
thì
5
log 0x m
(loại nghiệm này do không thỏa (*)). Do đó phương trình có 2 nghiệm
phân biệt
7, 49x x
. Suy ra nhận
1m
.
+ Với
1m
thì
5
log 0x m
nên luôn nhận nghiệm
5
logx m
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 51
Mà
49 7
nên phương trình có hai nghiệm phân biệt khi
7 49
5
7 log 49 5 5
m m
,
m
nguyên
nên
49
78125; 78126; ..., 5 1
m
.
Phần tử nhỏ nhất là
1
m
Phần tử lớn nhất là
49
5 1
m
Vậy có
49
5
S
.
Câu 32. Cho phương trình
2
2 2
2log 5log 2 5 0
x
x x m
(
m
là tham số thực). Có tất cả bao nhiêu giá
trị nguyên dương của
m
để phương trình đã cho có đúng hai nghiệm phân biệt?
A. 616. B. 615. C. vô số. D. 617.
Lời giải
Chọn A
Điều kiện
0 0
5 0 5
x x
x x
m m
(*).
Ta có
2
2 2
2log 5log 2 5 0
x
x x m
2
2 2
2log 5log 2 0 2
1
5 0 3
x
x x
m
.
Trong đó
2
2
log 2
4
2
1
log
2
2
x
x
x
x
(4).
Với
0
m
thì
5
5 log
x
m m x
.
Do đó, phương trình (1) có đúng hai nghiệm phân biệt khi và chỉ khi xảy ra các trường hợp sau:
TH1: (3) có nghiệm
5
log 0 0 1
x m m
. Kết hợp điều kiện (*) và (4) ta được
1
m
thì (1) có
hai nghiệm phân biệt
2
x
và
4
x
.
TH2:
1
m
, khi đó (*)
5
log 0
x m
.
Và do
4 2
nên (1) có hai nghiệm phân biệt khi và chỉ khi
5
2 log 4
m
2 4
5 5
m
Mà
m
nguyên dương nên ta có
10,11,...,624
m
, có 615 giá trị của
m
.
Vậy có 616 giá trị nguyên dương của
m
để phương trình có đúng hai nghiệm phân biệt.
Câu 33. Có bao nhiêu giá trị nguyên của tham số
2019; 2019
m
để phương
trình
2 1 2 1
2019 0
1 2
x
x mx m
x x
có đúng 3 nghiệm thực phân biệt?
A.
4038
. B.
2019
. C.
2017
. D.
4039
.
Lời giải
Chọn C
TXĐ:
\ 1;2 .
D
Ta có
2 1 2 1
2019 0
1 2
2 1 ( 2) 1
2019 0
1 2
2 1 1
2019 . (*)
1 2
x
x
x
x mx m
x x
x m x
x x
x
m
x x
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 52 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Đặt
2 1 1
( ) 2019 .
1 2
x
x
f x
x x
Khi đó
2 2
3 1
'( ) 2019 ln 2019 0 .
( 1) ( 2)
x
f x x D
x x
Ta có bảng biến thiên
Dựa vào bảng biến thiên, để phương trình
(*)
có 3 nghiệm thực phân biệt thì
2 2. m m
Mà
2019; 2019 m
và
m
nên có
2017
giá trị
m
thỏa mãn.
Câu 34. Có bao nhiêu giá trị nguyên của tham số
m
để tồn tại cặp số
;x y
thỏa mãn
3 5 3 1
e e 1 2 2
x y x y
x y
, đồng thời thỏa mãn
2 2
3 3
log 3 2 1 6 log 9 0x y m x m
?
A.
6
. B.
5
. C.
8
. D.
7
.
Lời giải
Chọn B
Ta có
3 5 3 1
e e 1 2 2
x y x y
x y
3 5 3 1
e 3 5 e 3 1
x y x y
x y x y
(1)
Xét hàm số
e
t
f t t
trên
. Ta có
e 1 0
t
f t
nên hàm số đồng biến trên
.
Khi đó (1)
3 5 3 1f x y f x y
3 5 3 1x y x y 2 1 2y x
.
Thế vào phương trình còn lại ta được
2 2
3 3
log 6 log 9 0x m x m
(2)
Đặt
3
logt x
. Số nghiệm của phương trình (2) chính là số nghiệm của phương trình
2 2
6 9 0t m t m
(3)
Phương trình (3) có nghiệm khi
0
2
3 12 0m m
0 4m
.
Do đó có
5
số nguyên
m
thỏa mãn.
Câu 35. Có bao nhiêu số nguyên của
m
để phương trình
2
2 2
log 2 2log 4 2 1 x m x x x m
có hai
nghiệm thực phân biệt?
A.
2
. B.
3
. C.
1
. D.
4
Lời giải
Chọn C
Điều kiện
0
2
x
m
x
2
2 2
log 2 2log 4 2 1 x m x x x m
2
2 2
2 2
2 2
log 2 2log 2 2 1
log 2 2 2 1 log
x m x x x m
x m x m x x
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 53
2 2
2 2
log 2 2 2 2 logx m x m x x
(1)
Xét
2
log , 0 f u u u u
1
' 1 0
ln 2
f u
u
, do đó hàm số đồng biến trên
(0; )
.
Khi đó (1)
2 2 2
2 2 2 2 4 2f x m f x x m x x x m
Xét hàm số
2
4 , 0g x x x x
Phương trình có 2 nghiệm dương khi
4 2 0 2 0 m m
suy ra có 1 giá trị nguyên.
Câu 36. Tìm tổng tất cả các giá trị nguyên của
m
để phương trình
3
3 3 3 2 3
3 9 24 .3 3 1
x m x x x
x x x m
có 3 nghiệm phân biệt.
A.
45
. B.
34
. C.
27
. D.
38
.
Lời giải
Chọn C
3
3
3
3 3 3 2 3
3
3 3 3
3
3 3 3
3 9 24 .3 3 1
3 3 27 3 .3 3 1
3 3 3 27 3 3 1
x m x x x
x m x x x
m x x
x x x m
x m x
x m x
3 3 3 3
1 3 27 27. 3 3 3
b a b a
b a b a
Đặt
3
3 ; 3a x b m x
, phương trình (1) trở thành
3 3 3 3
3 27 27. 3 3 3
b a b a
b a b a
.
Xét hàm số
3 2
3 ' 3 .ln 3 3 0,
t t
f t t f t t t
3
3
3 2
(1) 3 3
3 3 9 24 27
f a f b a b x m x
m x x x x x
3 2 2
9 24 27 ' 3 18 x 24
' 0 2 4
g x x x x g x x
g x x x
Đồ thị:
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 54 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Dựa vào đồ thị ta thấy điều kiện để phương trình có 3 nghiệm phân biệt là
7 11m
hay
8;9;10m
.
Câu 37. Tìm các giá trị
m
để phương trình
sin 5 cos 5
sin 5 cos 10
3 log 5
x x m
x x
m
có nghiệm.
A.
6 6 m
. B.
5 5 m
. C. 5 6 5 6 m . D.
6 5 m
.
Lời giải
Chọn C
Ta có
sin 5 cos 5
sin 5 cos 10
sin 5 cos 10
5
3 log 5
ln 5
3
3
ln sin 5 cos 10
x x m
x x
x x
m
m
m
x x
5
sin 5 cos 10
3 .ln sin 5 cos 10 3 .ln 5
m
x x
x x m
(1)
Xét
ln .3 , 5
t
f t t t
, vì
1
3 ln 3 ln 3 0, 5
t t
f t t t
t
nên hàm số
f t
đồng biến trên
(5; )
.
Khi đó
(1) sin 5 cos 10 5f x x f m
sin 5 cos 10 5
sin 5 cos 5
x x m
x x m
Mà
6 sin 5 cos 6 x x
nên để phương trình có nghiệm ta phải có
5 6 5 6.m
Câu 38. Cho phương trình
2
2 log
x
m x m
với
m
là tham số. Có bao nhiêu giá trị nguyên của
18;18m
để phương trình đã cho có hai nghiệm?
A.
20
. B.
17
. C.
9
. D.
21
.
Lời giải
Chọn B
Điều kiện
x m
PT
5
log ( )
2 2
2 log 2 2 log ( ) (1)
x m
x x
x x m x m x x m
Xét hàm số
2 ,
t
f t t t
; Ta có:
2 ln 2 1 0,
t
f t t
Hàm số
f t
đồng biến
trên
.
Từ (1) suy ra
2 2
log ( ) log ( )f x f x m x x m
2 2
x x
x m m x
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 55
Xét hàm số
2
x
g x x
trên
;m 
. Ta có:
' 1 2 ln 2
x
g x
;
2 2
' 0 2 ln 2 1 log log
x
g x x e
2 2 2 2 2
log log log log logg e e e
lim 2 ; lim ( )
m
x
x m
g x m g x


Bảng biến thiên:
Do đó. Phương trình đã cho có 2 nghiệm
2 2 2 2 2 2
2 log log log log log log 0,91
m
m m e e m e e
Vì
18;18
m
m
nên
17; 16; 15;....; 1 m
Vậy có 17 giá trị của
m
.
Câu 39. Cho phương trình
3 2 3 2
3 1 3 1 2
3 2
81 3
3 2
1
2 .log 3 1 2 2 .log 0
3 1 2
m m x x
x x
m m
Gọi
S
là tập hợp tất cả các giá trị
m
nguyên để phương trình đã cho có
6
nghiệm hoặc
7
nghiệm
hoặc
8
nghiệm phân biệt. Tính tổng bình phương tất cả các phần tử của tập
S
.
A.
20
. B.
19
. C.
14
. D.
28
.
Lời giải
Chọn A
Ta có
3 2 3 2
3 1 3 1 2
3 2
81 3
3 2
1
2 .log 3 1 2 2 .log 0
3 1 2
m m x x
x x
m m
3 2 3 2
3 1 2 3 1 2
3 2 3 2
3 3
2 .log 3 1 2 2 .log 3 1 2
x x m m
x x m m
.
Xét hàm số
3
2 .log
t
f t t
với
2t
; Ta có
3
1
2 ln 2.log 2 . 0 2
ln 3
t t
f t t t
t
.
Suy ra hàm số
f t
đồng biến trên
2;
.
Do đó phương trình tương đương với
3 2 3 2
3 1 3 1 1m m x x
.
Vẽ đồ thị hàm số
3 2
3 1g x x x
từ đó suy ra đồ thị
g x
và đồ thị của
g x
như hình vẽ.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 56 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Từ đồ thị suy ra
1
có
6,7,8
nghiệm
0 3g m
.
Từ đồ thị suy ra các giá trị nguyên của
m
là
3, 1,0,1,3
.
Vậy
20S
.
Câu 40. Cho phương trình
2
2
2 2
2 log 2 4 log 2 2
x a
x
x x a
. Gọi
S
là tập hợp các giá trị
a
thuộc
đoạn
0;2020
và chia hết cho 3 để phương trình có hai nghiệm. Hãy tính tổng các phần tử của
S
.
A.
0
. B.
2041210
. C.
680403
. D.
680430
.
Lời giải
Chọn C
Phương trình tương đương
2
2
2
2 2
2 log 2 2 log 2 2
x a
x
x x a
2
2
2
2 2
4.2 log 2 4.2 log 2 2
x a
x
x x a
2
2 2
2 2
2 2
2 log 2 2 log 2 2
x a
x
x x a
(*)
Xét hàm số
2 log , 2
t
f t t t
. Có
2
2
' 2 ln 2.log 0, 2
ln 2
t
t
f t t t
t
, nên
f t
đồng biến
2;
.
Khi đó (*)
2
2
2 2 2
2 2; 2 | | 2 2
f x f x a
x x a
2
2x x a
(1)
2
2
2 2
2
2 2 0 (2)
2 2 2 0 (3)
x x a
x x a
x x a x x a
Phương trình (2)
2
1 2a
, phương trình (3) có
(3)
1 2a
.
Vì
(3)
2
2 0
nên ít nhất một trong hai phương trình (2), (3) luôn có hai nghiệm phân biệt. Để
phương trình (1) có hai nghiệm phân biệt, ta xét các trường hợp sau:
* TH1: (2) có hai nghiệm phân biệt:
2
1
0 1 2 0
2
a a
. Khi đó
(3)
0
nên (3) vô
nghiệm. Trường hợp này thỏa mãn điều kiện bài toán.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 57
* TH1: (3) có hai nghiệm phân biệt:
(3)
1
0 1 2 0
2
a a
. Khi đó
(2)
0
nên (2) vô
nghiệm. Trường hợp này cũng thỏa mãn điều kiện bài toán.
Do đó phương trình đã cho có 2 nghiệm khi và chỉ khi
1 1
; ;
2 2
a
 
Vì
0;2020
a
và chia hết cho 3 nên
3;6;9;12;...,2019
a S
Tổng các phần tử của
S
là:
3 6 9 ... 2019 3.1 3.2 3.3 ... 3.673
673.674
3 1 2 3 ... 673 3. 680403
2
Câu 41. Có bao nhiêu giá trị thực của tham số
a
để phương trình
2
2 2
1
2
2
4 log 2 3 2 log 2 2 0
x a
x x
x x x a
có 3 nghiệm thực phân biệt ?
A.
0
. B.
2
. C.
1
. D.
3
.
Lời giải
Chọn D
PT đã cho tương đương với
1 1
2
2
2
2
2
2
2
1 1
log 2 3 log 2 2 0
2
2
x a
x x
x x x a
.
2
2
2
2
2 2
2
2
2
2 1 2
2 2
2 2
2 3 2
2 2
2 1
log 2 3 log 2 2
2
2
2 log 2 3 2 log 2 2
2 log 2 3 2 log 2 2 (1)
x a
x x
x a
x x
x a
x x
x x x a
x x x a
x x x a
Xét hàm số
2
2 .log , 2
t
f t t t
; Ta có:
2
2 ln 0, 2
ln 2
t
t
f t t t
t
Hàm số
f t
đồng
biến trên
2;

.
Từ (1) suy ra
2 2
2 3 2 2 2 3 2 2
f x x f x a x x x a
2
2 1 2
x x x a
(*)
2
2
2 2
2 1 2
4 2 1 0 (2)
2 1 2 2 1 (3)
x x x a
x x a
x x x a x a
Phương trình (*) có 3 nghiệm phân biệt nếu xảy ra một trong các trường hợp sau:
* TH1: (2) có hai nghiệm phân biệt và (3) có nghiệm kép khác hai nghiệm của (2):
2
(3)
3
0
3 2 0
1
2
2 1 0 1
2
0
2
a
a
a
a
a
* TH2: (3) có hai nghiệm phân biệt và (2) có nghiệm kép khác hai nghiệm của (3):
2
(3)
3
0
3 2 0
3
2
2 1 0 1
2
0
2
a
a
a
a
a
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 58 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
* TH3: (2) và (3) đều có hai nghiệm phân biệt, trong đó có một nghiệm chung:
Điều này xảy ra khi hệ
2
2
4 2 1 0
2 1
x x a
x a
có nghiệm
2
2
4 2 1 0 1
1 1
2 1
x x a x a x
a a
x a
 Khi
1
a
ta có:
2
trở thành
2
1
4 3 0
3
x
x x
x
3
trở thành
2
1
1
1
x
x
x
Khi đó: PT đã cho có 3 nghiệm.
Vậy
1 3
;1;
2 2
a
.
Câu 42. Tìm tổng tất cả các giá trị của tham số
a
để phương trình
2
2
2 1 2
2 3
3 log 2 2
x x x a
x x
x a
có
đúng ba nghiệm phân biệt.
A.
2
. B.
3
. C.
1
. D.
0
.
Lời giải
Chọn B
PT đã cho tương đương với
2
2 3 2 2
2
ln 2 2
3
ln 2 3
x x x a
x a
x x
2
2 2
2 3 2
3 .ln 2 3 3 .ln 2 2 (1)
x a
x x
x x x a
.
Xét hàm số
3 .ln , 2
t
f t t t
; Ta có:
3
3 ln3.ln 0, 2
t
t
f t t t
t
Hàm số
f t
đồng
biến trên
2;

.
Từ (1) suy ra
2 2
2 3 2 2 2 3 2 2
f x x f x a x x x a
2
2 1 2
x x x a
(*)
2
2
2 2
2 1 2
4 2 1 0 (2)
2 1 2 2 1 (3)
x x x a
x x a
x x x a x a
Phương trình (*) có 3 nghiệm phân biệt nếu xảy ra một trong các trường hợp sau:
* TH1: (2) có hai nghiệm phân biệt và (3) có nghiệm kép khác hai nghiệm của (2):
2
(3)
3
0
3 2 0
1
2
2 1 0 1
2
0
2
a
a
a
a
a
* TH2: (3) có hai nghiệm phân biệt và (2) có nghiệm kép khác hai nghiệm của (3):
2
(3)
3
0
3 2 0
3
2
2 1 0 1
2
0
2
a
a
a
a
a
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 59
* TH3: (2) và (3) đều có hai nghiệm phân biệt, trong đó có một nghiệm chung:
Điều này xảy ra khi hệ
2
2
4 2 1 0
2 1
x x a
x a
có nghiệm
2
2
4 2 1 0 1
1 1
2 1
x x a x a x
a a
x a
 Khi
1
a
ta có:
2
trở thành
2
1
4 3 0
3
x
x x
x
3
trở thành
2
1
1
1
x
x
x
Khi đó: PT đã cho có 3 nghiệm.
Vậy
1 3
;1;
2 2
a
.
Câu 43. Tìm số giá trị nguyên của
m
thuộc
20;20
để phương trình
2 2 2
2
log ( 4) (2 9) 1 (1 2 ) 4
x m x x m x m x
có nghiệm.
A. 12. B. 23. C. 25. D. 10.
Lời giải
Chọn B
Điều kiện xác định:
2 2
4 0
x m x x
.
2 2 2
2
log 4 2 9 1 1 2 4
x m x x m x m x
2 2 2
2
log 4 2 9 1 4 2 4
x x x m mx x x m x
2 2
2
2
4
log 2 9 1 4 2 4
4
x
m mx x x m x
x x
2
2 2
2
2
4 4
log 2 9 1 4 2 4
4
x m x mx
mx x x m x
x x
2 2 2 2
2 2
log 4 4 8 2 4 2 1 log 4 4
x m x mx x m x mx x x x x
2 2 2 2
2 2
log 8 2 4 2 8 2 4 2 log 4 4 1
x m x mx x m x mx x x x x
Xé
t hàm số
2
log
f t t t
,
0;
t
.
1
1 0, 0;
ln 2
f t t
t
nên hàm số đồng biến trên
0;

.
Khi đó
1
2 2
8 2 4 2 4
x m x mx x x
2 2
2 4 4 8 m x x x x x
2
8
2 1
4
x
m
x x
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 60 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
8 4
2 1
4
x x x
m
2
2 1 2 4 m x x x
2 2
1 2
4
2
m
x x x
.
Xét hàm số
2 2
( ) 4 g x x x x
với
;  x
.
Ta có
2
2
2
4
( ) 0,
4
x x
g x x
x
.
2
lim lim 4
 
x x
g x x x x
2
4
lim
4

x
x
x x
2
4
lim 2
4
1 1

x
x
;
2
2
4
lim lim 1 1
 

x x
g x x
x
.
Ta có bảng biến thiên của
( )g x
Để phương trình có nghiệm thì
1 2 5
2
2 2
m
m
.
Do
m
nguyên thuộc
20;20
nên số giá trị
m
là 23.
C. GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT
Câu 1. Xét các số thực dương
, , ,a b x y
thoả mãn
1, 1a b
và
x y
a b ab
. Giá trị nhỏ nhất của biểu
thức
2P x y
thuộc tập hợp nào dưới đây?
A.
1;2
. B.
5
2;
2
. C.
3;4
. D.
5
;3
2
.
Lời giải
Chọn D
Đặt
log
a
t b
. Vì
, 1a b
nên
0t
.
Ta có:
1 1
log 1 log 1
2 2
x
a a
a ab x ab b t
.
1 1 1
log 1 log 1
2 2
y
b b
b ab y ab a
t
.
Vậy
1 1
2 1 1
2
P x y t
t
3 1 3
2
2 2 2
t
t
.
Dấu đẳng thức xảy ra khi và chỉ khi
2
1
2
t
b a
t
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 61
Giá trị nhỏ nhất của biểu thức
2P x y
bằng
3
2
2
thuộc nửa khoảng
5
;3
2
.
Câu 2. Xét các số thực dương
a
,
b
,
x
,
y
thỏa mãn
1
a
,
1b
và
4
x y
a b ab
. Giá trị nhỏ nhất của
biểu thức
4 P x y
thuộc tập hợp nào dưới đây?
A.
1;2
. B.
5
2;
2
. C.
1;2
. D.
0;1
.
Lời giải
Chọn B
Theo bài ra ta có:
4
x y
a b ab
1 1
4 4
1 1
4 4
.
.
x
y
a a b
b a b
1 1
4 4
1 1
4 4
x
y
a b
b a
1 1
log
4 4
1 1
.log
4 4
a
b
x b
y a
Do đó:
4 P x y
1 1
log 1 log
4 4
a b
b a
5 1
log log
4 4
a b
b a
Đặt
log 0
a
t b t
. Vì
a
,
1b
nên
log log 1 0
a a
b
.
Khi đó
5 1 1
4 4
P t
t
5 1 1 9
2 .
4 4 4
t
t
. (Áp dụng BĐT Cô Si)
Vậy
P
đạt giá trị nhỏ nhất là
9
4
khi
2t
hay
2
b a
.
Câu 3. Xét các số thực
a
,
b
,
0
c
thỏa mãn
3 5 15
a b c
. Giá trị nhỏ nhất của biểu thức
2 2 2
4( ) P a b c a b c
thuộc tập hợp nào dưới đây?
A.
1;2
. B.
5; 1
. C.
2;4
. D.
4;6
.
Lời giải
Chọn B
Đặt
3
5
15
log
3 5 15 0 log
log
a b c
a t
t b t
c t
. Khi đó
2 2 2
3 5 15 3 5 15
log log log 4(log log log )
P t t t t t t
2 2 2
3 5 15 3 5 15
log 1 log 3 log 3 4log 1 log 3 log 3
t t
2 2 2
5 15 5 15
1 log 3 log 3 4 1 log 3 log 3
X X , (với
3
logX t
)
5 15
min
2 2
5 15
2 1 log 3 log 3
4
1 log 3 log 3
P P
,
khi
2 1 log 3 log 3
5 15
2 2
1 log 3 log 3
5 15
5
15
3
2 2
5 15
2 1 log 3 log 3
log 3
1 log 3 log 3
t t
Suy ra
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 62 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
5 15
2 2
5 15
2 1 log 3 log 3
5 15
2 2
1 log 3 log 3
5
15
5
2 1 log 3 log 3
5 15
2 2
1 log 3 log 3
5
15
15
2 1 log 3 log 3
1 log 3 log 3
log 3
log 3
a
b
c
.
Câu 4. Xét các số thực dương
a
,
b
,
c
,
x
,
y
,
z
thỏa mãn
1
a
,
1b
,
1c
và
x y z
a b c abc
. Giá
trị nhỏ nhất của biểu thức
1
2
P x y z
thuộc tập hợp nào dưới đây?
A.
10;13
. B.
7;10
. C.
3;5
. D.
5;7
.
Lời giải
Chọn D
Từ giả thiết ta có
1
1 log log
2
a a
x b c
,
1
1 log log
2
b b
y a c
,
1
1 log log
2
c c
z b a
. Khi đó ta có
2 4 log log log log log log
a b a c b c
P b a c a c b
.
Vì
1
a
,
1b
,
1c
nên
log 0
a
b
,
log 0
b
c
,
log 0
c
a
,
log 0
b
a
,
log 0
c
b
,
log 0
a
c
.
Áp dụng bất đẳng thức Cô Si ta được
log log 2 log .log
a b a b
b a b a
hay
log log 2
a b
b a
.
Tương tự
log log 2
a c
c a
và
log log 2
b c
c b
.
Do đó
2 10P
hay
5P
. Dấu
" "
xảy ra khi và chỉ khi
a b c
.
Vậy giá trị nhỏ nhất
min
5
P
.
Câu 5. Xét các số thực dương
, , ,a b x y
thỏa mãn
1, 1
a b
và
2 2
.
x y
a b a b
. Giá trị nhỏ nhất của biểu
thức
.P x y
là
A.
9
4
P
. B.
6
2
P
. C.
3
2
P
. D.
4
9
P
.
Lời giải
Chọn B
2 2
2
2
1 1
log
2 2
.
1 1
log
2 2
a
x y
b
x b
a b a b
y a
+)
2
1 1 1 1
log log
2 2 2 2
a b
xy b a
1 1 1
log log
4 2 4
a b
b a
3
2
(
, 1 log 0,log 0
a b
a b b a
).
Vì
6
0, 0
2
x y xy
. Dấu bằng xảy ra khi và chỉ khi
a b
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 63
Câu 6. Xét các số thực dương
, , ,a b x y
thỏa mãn
1, 1
a b
và
2
2
x
y
y
x
a b ab
. Giá trị nhỏ nhất của biểu
thức
.P x y
là
A.
2P
. B.
4P
. C.
3
P
. D.
1P
.
Lời giải
Chọn B
2
2
2
2
1 log
1 log
x
a
y
y
x
b
x
b
y
a b ab
y
a
x
.
Ta có
2 2
. 1 log 1 log
a a
x y
xy b b
y x
1 1 log log
a b
b a
4
(
, 1 log 0,log 0
a b
a b b a
).
Dấu bằng xảy ra khi và chỉ khi
a b
.
Câu 7. Xét các số thực dương
, , , , ,a b c x y z
thỏa mãn
1, 1, 1, 2
a b c y
và
1 2 1x y z
a b c abc
. Giá
trị nhỏ nhất của biểu thức
P x y z
là
A.
13
P
. B.
3
P
. C.
9
P
. D.
1P
.
Lời giải
Chọn C
1 2 1
1 1 log log
2 1 log log
1 1 log log
a
b
c
a
x y z
b
c
x b c
a b c abc y a c
z b a
.
Ta có:
1 2 1 3 log log log log log log
a c
a b b c
x y z b c c a b a
3 6
x y z
9
P
(
, , 1 log 0,log 0,log 0,log 0,log 0,log 0
a a b b c c
a b c b c a c a b
).
Dấu bằng xảy ra khi và chỉ khi
a b c
.
Câu 8. Xét các số thực dương
x
,
y
thỏa mãn
3
1
log 3 2 4
2
xy
xy x y
x y
. Tìm giá trị nhỏ nhất
min
P
của
P x y
.
A.
min
9 11 19
9
P
. B.
min
9 11 19
9
P
. C.
min
18 11 29
9
P
. D.
min
2 11 3
3
P
.
Lời giải
Chọn D
Theo đề bài suy ra:
1 0
xy
,
2 0
x y
.
Ta có:
3
1
log 3 2 4
2
xy
xy x y
x y
3 3
log 3 3 3 3 log 2 2xy xy x y x y
1
.
Xét hàm số:
3
log , 0
f t t t t
:
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 64 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
1
1 0, 0
ln3
f t t
t
.
Hàm số
f t
đồng biến trên khoảng
0;
.
Do đó:
1 3 3 2f xy f x y
3 2
3 3 2
1 3
y
xy x y x
y
.
Theo đề bài ta có:
, 0
x y
3
0
2
y
.
Ta có:
3 2
1 3
y
P x y y
y
3
0
2
y
.
Đạo hàm:
2
11
1
1 3
P
y
;
11 1 3
0 0;
3 2
P y
.
Ta có:
11 1 2 11 3 3 3
0 3; ;
3 3 2 2
P P P
. Vậy
min
2 11 3
3
P
.
Câu 9. Xét các số thực dương
x
,
y
thỏa mãn
1 2
ln 3 1
x
x y
x y
. Tìm giá trị nhỏ nhất
min
P
của biểu thức
1 1
1
P
x
xy
.
A.
min
8
P
. B.
min
16
P
. C.
min
9
P
. D.
min
2
P
.
Lời giải
Chọn C
Theo đề bài suy ra:
1
2
x
.
Ta có:
1 2
ln 3 1 ln 1 2 1 2 ln
x
x y x x x y x y
x y
1
.
Xét hàm số:
1
ln , 0 1 0, 0f t t t t f t t
t
Hàm số
f t
đồng biến trên khoảng
0;
.
Do đó:
1 1 2 1 2 3 1f x f x y x x y x y
Ta có:
2
1 1
1 1 1 1
1 1 1 9
3
2 2
P
x y x y
x x
xy
Vậy
min
2 11 3
3
P
khi
1
4
x y
.
Câu 10. Xét các số thực dương
x
,
y
thỏa mãn
2 3
3 3 6
3
x y
x y
x y
. Tìm giá trị nhỏ nhất
min
P
của
9 3 3 1
4 4
2
P
x
xy
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 65
A.
min
2
P
. B.
min
22 15 3
2
P
. C.
min
20
P
. D.
min
35 36 2
4
P
.
Lời giải
Chọn C
Từ giả thiết bài toán suy ra
0
2 1
x y
x y
.
Ta có:
2 3 1 2
1 2
3 3 6 3 1 2
3 .3 1 2 .3
3
x y
x y x y x y
x y
x y x y
x y x y
x y x y
1
.
Xét hàm số:
.3 , 0 3 .3 .ln3 0, 0
t t t
f t t t f t t t
.
Suy ra: hàm số
f t
đồng biến trên
0;
.
Do đó:
1 1 2 2 3 1f x y f x y x y
.
Ta có:
2
3
3
9 3 3 1 9 9 1 9 9 1 1
2
20
4 4 4 4 4 3 4 2 3 4
2 2 .3
P
x x x x y x y
xy x y
.
Vậy
min
20
P
khi
1 1
;
3 9
x y
.
Câu 11. Cho hai số thực
a
,
b
thỏa
4
3
a b
và
3
2
16log 3log
12 16
a a
b
a
P a
b
có giá trị nhỏ nhất. Tính
a b
.
A.
7
2
. B.
4
. C.
11
2
. D.
6
.
Lời giải
Chọn D
Ta có:
2
3 3
3
12 16 2 4 0, 12 16
4
b b b b b b b
.
Suy ra:
3
3 3 3
3
4 4
log log ,
12 16 3 12 16 3
a a
a a a a
a b a
b b b b
.
Do đó:
3
3
2 2
2
3
16log 3log 16log 3log 48 1 log
12 16
1 log
a a a a a
b b
a
a a
P a a b
b b
b
.
2
3
24 1 log 24 1 log 36
1 log
a a
a
P b b
b
.
Vậy
min
36
P
khi
4, 2
a b
.
Câu 12. Cho hai số thực dương
x
,
y
thỏa mãn
2 1
2
3
1
xy x y
x y
xy
. Tìm giá trị nhỏ nhất
min
S
của biểu thức
4S x y
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 66 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
min
4 3 9
S
. B.
min
6 4 3
S
. C.
min
2 3 2
S
. D.
min
4 3 6
S
.
Lời giải
Chọn D
Theo đề bài suy ra:
1 0
xy
.
Ta có:
2 1 1 2
2
3 1 .3 2 .3
1
xy x y xy x y
x y
xy x y
xy
1
.
Xét hàm số:
.3 , 0 3 .3 .ln3 0, 0
t t t
f t t t f t t t
Hàm số
f t
đồng biến trên khoảng
0;
.
Do đó:
1 2
1 1 2 1 2
1
x
f xy f x y xy x y y
x
Theo đề bài ta có:
, 0 1x y x
.
Ta có:
8 4
4
1
x
S x y x
x
,
1x
.
Đạo hàm:
2
12
1 0 12 1
1
S S x
x
.
Từ đó ta được
min
9 4 3
P
.
Câu 13. Cho
,x y
là hai số thực dương thỏa mãn
2 2 2
2 2 2 2
4 9.3 4 9 .7 .
x y x y y x
Giá trị nhỏ nhất của biểu
thức
2 18
x y
P
x
là
A.
9.
B.
3 2
.
2
C.
1 9 2.
D.
17.
Lời giải
Chọn A
Ta có
2 2 2 2 2 2
2 2 2 2 2 2 2( 2 ) 2 2
4 9.3 4 9 .7 4 3 4 3 .7
x y x y y x x y x y y x
2 2
2 2
2 2 2( 2 )
2 2 2( 2 )
4 3 4 3
(*).
7 7
x y x y
x y x y
Xét hàm số
4 3
( )
7
t
t
f t
trên
.
Ta có
1 3
( ) 4.
7 7
t t
f t
nghịch biến trên
.
2 2 2 2 2 2
(*) 2 2 2( 2 ) 2 2 2( 2 ) 2 2 2 2.
f x y f x y x y x y x y y x
Từ
đó
2
16 16 16
1 2 . 1 9.
x x
P x x P
x x x
Dấu
" "
xảy ra khi và chỉ khi
4.
x
Câu 14. Cho các số dương
,x y
thỏa mãn
5
1
log 3 2 4
2 3
x y
x y
x y
. Giá trị nhỏ nhất của biểu thức
4 9
6 2
A x y
x y
bằng
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 67
A.
31 6
.
4
B.
11 3.
C.
27 2
.
2
D.
19.
Lời giải
Chọn D
ĐK:
1
0
2 3
1
, 0
x y
x y
x y
x y
Ta có:
5
5 5
5 5
1
log 3 2 4
2 3
log 1 1 5 1 log 2 3 2 3
log 5 1 5 1 log 2 3 2 3 *
x y
x y
x y
x y x y x y x y
x y x y x y x y
Xét hàm số
5
( ) log
f t t t
trên
0;
, vì
1
( ) 1 0, 0;
ln5
f t t
t
nên hàm số
( )f t
đồng biến trên
0; .
* 5 1 2 3 3 2 5
x y x y x y
Mặt khác, ta có
4 9 4 9
6 2 9 4 3 2 2.6 2.6 5 19
A x y x y x y
x y x y
.
Dấu “ = ” xảy ra
4
9
2
9
3
4
3
2
3 2 5
x
x
x
y
y
y
x y
(thỏa mãn điều kiện).
Vậy GTNN của
A
là 19.
Câu 15. Cho hai số thực
,x y
lớn hơn 1 và thỏa mãn
.( ) .( ) .
y x
x x e y y e
y e x e
Tìm giá trị nhỏ nhất của biểu thức
log log .
x y
P xy x
A.
2
2
. B.
2 2
. C.
1 2 2
2
. D.
1 2
2
.
Lời giải
Chọn C
Với
, 1x y
, ta có
.( ) .( )
ln .( ) ln .( )
ln ln
ln ln
(1).
y x
y x
x x e y y e
x x e y y e
y x
y x
y e x e
y e x e
x y xe y x ye
y e x e
y y x x
Xét hàm số
( ) 1 ln
t t
g t te e t
trên
1; ,
có
1
( ) 0, 1.
t
g t te t
t
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 68 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Hàm số
( )g t
đồng biến trên
1;
nên
( ) (1) 1 0, 1.
g t g t
Xét hàm số
ln
( )
t
t e
f t
t t
trên
1;
, có
2
( )
'( ) 0, 1,
g t
f t t
t
nên
( )f t
đồng biến trên
(1; ).
Với
, 1x y
thì
(1) ( ) ( ) . f y f x y x
Đặt
log .
x
u y
Do
1 y x
nên
1.
u
Ta có
1 1
( ) .
2
u
P h u
u
Nhận thấy
2
2
2
'( )
2
u
h u
u
, nên
'( ) 0
h u
khi
2,
u
'( ) 0
h u
khi
1 2,
u
'( ) 0
h u
khi
2.
u
Dẫn tới
1 2 2
( ) 2 , 1,
2
P h u h u
đẳng thức xảy ra khi
2.
u
Vậy
1 2 2
min ,
2
P
đạt được khi
2
y x
và
1.
x
Câu 16. Cho hai số thực
,x y
thỏa mãn
0 , 1x y
trong đó
,x y
không đồng thời bằng 0 hoặc 1 và
3
log 1 . 1 2 0
1
x y
x y
xy
. Tìm giá trị nhỏ nhất của
P
với
2P x y
A.
2
. B.
1
. C.
1
2
. D.
0
.
Lời giải
Chọn B
Từ điều kiện đề bài và
0;1 0
1
x y
xy
xy
0;1 0x y xy
khi đó
3 3 3
log 1 . 1 2 0 log log 1 1 1
1
x y
x y x y x y xy xy
xy
Xét hàm số
3
log 0
f t t t t
có
1
1 0 0
.ln 3
f t t
t
f t
là hàm số đồng biến trên khoảng

0;
.
Vậy phương trình
1 1
1 1 2
1 1
x x
x y xy y P x
x x
Xét hàm số
1
( ) 2
1
x
f x x
x
với
0;1
x
có
2
2
( ) 2
1
f x
x
cho
0
( ) 0
2
x
f x
x
0;1
0 1; 1 2 min ( ) 1
f f f x
chọn B
Câu 17. Xét các số thực dương
x
,
y
thỏa mãn
1 2
ln 3 1
x
x y
x y
. Tìm giá trị nhỏ nhất
min
P
của
1 1
P
x
xy
.
A.
min
8
P
. B.
min
4
P
. C.
min
2
P
. D.
min
16
P
.
Lời giải
Chọn A
Điều kiện
1
0
2
x
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 69
Từ giả thiết
1 2
ln 3 1
x
x y
x y
ln 1 2 1 2 lnx x x y x y
1
Xét hàm số
lnf t t t
trên
0;
có
1
1 0f t
t
,
0t
do đó hàm
f t
đơn điệu.
Vậy
1 1 2 3 1x x y x y
2
Có
1 1 1 2 1 2
1 2
P
x x x y x x
xy
Đặt
1 2
1 2
g x
x x
, ta có
2 2
1 4
1 2
g x
x
x
suy ra
1
0
4
g x x
.
Do đó
1
0;
2
min 8g x
. Vậy
min
8P
.
Bổ sung: có thể đánh giá
1 1 1 2 1 2 4 1
1
1 2 8
2
P
x x x y x x
xy
x x
Câu 18. Cho hai số thực
,x y
không âm thỏa mãn
2
2
2 1
2 1 log
1
y
x x y
x
. Giá trị nhỏ nhất của biểu
thức
2 1 2
4 2 1
x
P e x y
là
A.
1
2
. B.
1
. C.
1
2
. D.
1
.
Lời giải
Chọn A
2
2
2 1
2 1 log
1
y
x x y
x
2 2
2 2
2 1 log 2 1 log 2 1 2 1x x y y
.
Xét hàm số
2
log , 0f t t t t
;
1
1 0, 0
.ln 2
f t t
t
Suy ra
2
2 1 2 1x y
2
2 2 1 1y x
.
2 1 2
4 2 1
x
P e x y
2
2 1 2
4 2 1 1 1
x
e x x
2 1 2
2 4
x
e x x g x
.
2 1
2 4 4
x
g x e x
là hàm số đồng biến trên nửa khoảng
0;
nên
0g x
có tối đa
1
nghiệm, nhẩm được nghiệm
1
2
x
nên nghiệm đó là duy nhất.
Vậy
1
min
2
P
tại
1
2
x
.
Câu 19. Cho hai số thực dương
x
,
y
thay đổi thỏa mãn đẳng thức
2
2 1 2
1 .2 .2 .
xy x y
xy x y
Tìm giá trị
nhỏ nhất
min
y
của
y
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 70 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
min
3
y
. B.
min
2
y
. C.
min
1
y
. D.
min
3
y
.
Lời giải
Chọn B
Ta có
2
2 1 2
1 2 2
xy x y
xy x y
2
2 1 2 1
2 1 1 2 2 1
xy x y
xy x y
Xét hàm
1 .2
t
f t t
với
1t
.
Khi đó
2 1 .2 .ln 2 0
t t
f t t
với
1t
.
Từ
2
1 2 1 1xy x y
2
2
2 1
x
y
x
2
2
2 2 4
0
2 1
x x
y
x
2
2 2 4 0
x x
2
1
x
x
Loại
1
x
vì điều kiện của
t
nên
2 2
f
.
Câu 20. Cho
,
, 1
x y
x y
sao cho
3 3
ln 2 ln3 19 6 ( 2 )
x
x y xy x y
y
. Tìm giá trị nhỏ nhất
m
của biểu
thức
1
3
T x
x y
.
A.
1 3
m
. B.
2
m
. C.
5
4
m
. D.
1
m
.
Lời giải
Chọn C
Ta có
3 3
3 3
ln 2 ln 3 19 6 ( 2 ) ln 2 2 ln 3 3 1
x
x y xy x y y x y x y y
y
Xét hàm số
3
ln
f t t t
với
0
t
có
2
1
3 0 0
f t t t f t
t
đồng biến
Vậy
1
1 2 3
4
y x y x y T x
x
Áp dụng bất đẳng thức AM-GM
1 3 1 3 1 3 1 3 1 5
2 .
4 4 4 4 4 4 4 4 2 4 2 4
x x x x x
T x
x x x
Dấu bằng xảy ra khi
1
x y
Câu 21. Cho
;x y
là các số thực dương thỏa mãn điều kiện
4 4
3 5
5 1 3 4
3 5
xy
x y x y
xy
x y x
. Tìm
giá trị nhỏ nhất của biểu thức
P x y
.
A.
3
. B.
5 2 5
. C.
3 2 5
. D.
1 5
.
Lời giải
Chọn B
Ta có
4 4
3 5
5 1 3 4
3 5
xy
x y x y
xy
x y x
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 71
4 4 1 1
5 3 4 5 3 1 1
x y x y xy xy
x y xy
.
Xét hàm số
5 3
t t
f t t
trên
.
Vì
5 .ln5 3 .ln 3 1 0;
t t
f t x
nên hàm số
f t
đồng biến trên
2
.
Từ
1
và
2
ta có
4 1 3
x y xy
. Dễ thấy
4
x
không thỏa mãn
3
.
Với
4
x
,
1
3
4
x
y
x
kết hợp điều kiện
0
y
suy ra
4
x
.
Do đó
1
4
x
P x y x
x
.
Xét hàm số
1
4
x
g x x
x
trên
4;
.
Ta có
2
5
1 0
4
g x
x
4 5
4 5
x
x
.
x
4
4 5

g x
–
0
g x

5 2 5

Dựa vào bảng biến thiên ta có
min
4;
min 5 2 5
P g x

.
Câu 22. Cho
x
,
y
là các số thực dương thỏa mãn
2 2
3 5
5 1 3 ( 2)
3 5
xy
x y x y
xy
x y x
. Tìm giá trị nhỏ
nhất của biểu thức
T x y
.
A.
min
2 3 2
T
. B.
min
3 2 3
T
. C.
min
1 5
T
. D.
min
5 3 2
T
.
Lời giải
Chọn B
Theo đề ra ta có
2 2
2 1
2 1
3 5
5 1 3 ( 2)
3 5
1 1
5 2 5 1
3 3
xy
x y x y
xy
x y xy
x y xy
x y x
x y xy
Xét
1
5
3
t
t
f t t
.
5 ln5 3 ln 3 1 0
t t
f t
1
2 1
2
x
x y xy y
x
.Do
1
0, 0 0 2
2
x
y x x
x
Ta có:
2
1 1
2 2
x x x
T x y x
x x
2
2
2 3 2;
4 1
0
2
2 3 2;
x
x x
T
x
x


Bảng biến thiên
Chỉnh lại bbt cho em,chỉ xét với
2
x
nhé,kết quả không thay đổi.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 72 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Từ bảng biến thiên ta thấy
min
3 2 3 T
tại
2 3 x
.
Câu 23. Xét các số thực dương
,x y
thỏa mãn
3
3
log 3 1
1
x y
xy y x
xy
. Tìm giá trị nhỏ nhất của biểu thức
1
A x
y
.
A.
min
14
3
A
. B.
min
14
3
A
. C.
min
6A
. D.
min
6A
.
Lời giải
Chọn D
Điều kiện:
3 0x y
.
3 3 3
3
log 3 1 log 3 log 1 3 1
1
x y
xy y x x y xy xy y x
xy
3 3
log 3 3 log 1 1 1x y x y xy xy
.
Xét hàm
3
log , 0f t t t t
.
1
1 0, 0
.ln3
f t t
t
.
Suy ra hàm số
f t
đồng biến trên
0;
nên
1
1 3 1
3
x
x y xy y
x
.
1 3
1
x
A x x
y x
.
Đặt
3
1
x
A A x x
x
2
4
1 0 3
1
A x x
x
do
, 0x y
.
Câu 24. Cho
, 0x y
thỏa
2
2 2
2
4 2
2019 0
2
x y
x y
x
. Tìm giá trị nhỏ nhất
min
P
của
2 4P y x
.
A.
2018
. B.
2019
. C.
1
2
. D.
2
.
Lời giải
Chọn D
Ta có:
2 2
2 2 2 4 4 2 4 2
2 2
4 2 4 2
2019 0 2019
2 2
x y x x x y
x y x y
x x

2
2
2 2 2 4 2
2019 . 2 2019 . 4 2 *
x x y
x x y
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 73
Đặt
2
2
, 0
4 2
u x
u v
v x y
Khi đó:
2 2
* 2019 . 2019 .
u v
u v
f u f v
với
2
2019 . ,( 0)
t
f t t t
2 2
' 2019 .2 ln 2019. 2019 0, 0
t t
f t t t
Do đó:
f u f v u v
2
2
2 4 2 2.
x x y y x
2
2
2 4 2 4 4 2 1 2 2
P y x x x x
.
Vậy
min
2 1
P x
.
Câu 25. Cho
2
số thực dương
,x y
thỏa mãn
1
3
log 1 1 9 1 1
y
x y x y
. Giá trị nhỏ nhất
của biểu thức
2P x y
là
A.
min
11
2
P
. B.
min
27
5
P
. C.
min
5 6 3
P
. D.
min
3 6 2
P
.
Lời giải
Chọn D
Ta có
1
3
log 1 1 9 1 1
y
x y x y
3 3
1 log 1 log 1 1 1 9
y x y x y
.
3 3
1 log 1 log 1 1 9
y x y x
3 3
9
log 1 1 log 1
1
x x y
y
3 3
9 9
log 1 1 2 2 log
1 1
x x
y y
.
Xét hàm số
3
log 2f t t t
với
0t
có
1
1 0
ln 3
f t
t
với mọi
0t
nên hàm số
f t
luôn đồng biến và liên tục trên

0;
.
Từ đó suy ra
9
1
1
x
y
8
9
1
1 1
y
x
y y
, do
0x
nên
0; 8
y
.
Vậy
8
9 9
2 2 2 1 2 1 3 3 6 2
1 1 1
y
P x y y y y
y y y
.
Vậy
min
3 6 2
P
khi
9 3
2 1 1
1
2
y y
y
.
Câu 26. Xét các số thực dương
,x y
thỏa mãn
3
1
log 3 3 4
3
y
xy x y
x xy
. Tìm giá trị nhỏ nhất
min
P
của
P x y
.
A.
min
4 3 4
3
P
. B.
min
4 3 4
3
P
. C.
min
4 3 4
9
P
. D.
min
4 3 4
9
P
.
Lời giải
Chọn B
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 74 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
3 3 3
1
log 3 3 4 log 1 log 3 3 3 4
3
y
xy x y y x xy xy x y
x xy
3 3
log 3 1 3 1 log 3 3y y x xy x xy
Xét hàm
3
log , 0f t t t t
có
1
' 1 0, 0
ln 3
f t t
t
. Suy ra hàm số đồng biến trên
0;

. Suy ra
3 3
log 3 1 3 1 log 3 3y y x xy x xy
3 1 3y x xy
3 1 3 1
1 3 1 3
y y
x x y y
y y
4 3 4
3
. Vậy
min
4 3 4
3
P
.
Câu 27. Xét các số thực dương
,x y
thỏa mãn
2 2
3
log 3 3 .
2
x y
x x y y xy
x y xy
Tìm giá trị
lớn nhất
max
P
của biểu thức
3 2 1
.
6
x y
P
x y
A.
3
. B.
2
. C.
1
. D.
4
.
Lời giải
Chọn C
Ta có:
2 2
3
log 3 3
2
x y
x x y y xy
x y xy
2 2 2 2
3 3
log 3 3 log 2 2
x y x y x y xy x y xy
.
Xét hàm số
3
log
f t t t
,
0t
có
1
1 0, 0
ln 3
f t t
t
. Vậy hàm số
f t
luôn đồng
biến và liên tục trên khoảng
0;

.
Do đó:
2 2 2 2
3 2 3 2
f x y f x y xy x y x y xy
1
Từ
1
2
3 2
xy x y x y
.
Ta có
2
1
1
2
x y
x x xy xy x y xy xy
Đẳng thức xảy ra khi và chỉ khi
1 x y
.
Do đó từ
1
, suy ra:
2
2
1
3 2
4
x y
x x y x y .
Đặt
t x y
,
0t
.
Suy ra:
2
2
2
1
2 1 3 2
2 1
3 22 3
4
6 6 4 6
t
t t t
x y x
t t
P f t
x y t t
.
Ta có:
2
2
3 36 135
0 3
4 6
t t
f t t
t
(nhận)
Bảng biến thiên
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 75
Dựa vào BBT, ta có
0;
max max 3 1

P f t f
khi và chỉ khi
1 2
3 1
x y x
x y y
.
Câu 28. Xét các số thực dương
x
,
y
thỏa mãn
2
2 1
2
2
2018
1
x y
x y
x
. Tìm giá trị nhỏ nhất
min
P
của
2 3P y x
.
A.
min
1
2
P
. B.
min
7
8
P
. C.
min
3
4
P
. D.
min
5
6
P
.
Lời giải
Chọn B
Cách 1: Ta có
2
2 1
2
2
2018
1
x y
x y
x
2
2018
2
2
2 1 log
1
x y
x y
x
2 2
2018 2018
2 1 2 2 log 2 log 1
x x y x y x
2 2
2018 2018
2 1 log 1 2 2 log 2
x x x y x y
Có dạng
2
1 2
với
2018
2 log
f t t t
,
0
t
.
Xét hàm số
2018
2 log
f t t t
,
0
t
, ta có
1
2 0
.ln 2018
f t
t
0
t
nên hàm số
f t
đồng biến trên khoảng
0;
. Khi đó
2
1 2
2
1 2
x x y
2
1
y x
.
Ta có
2 2
2 3 2 1 3 2 3 2
P y x x x x x
.
Bảng biến thiên
x
3
4
P

7
8

Vậy
min
7
8
P
khi
3
4
x
.
Câu 29. Cho
2
số thực dương
,x y
thỏa mãn
1
3
log 1 1 9 1 1
y
x y x y
. Giá trị nhỏ nhất của
biểu thức
2P x y
là
A.
min
11
2
P
. B.
min
27
5
P
. C.
min
5 6 3
P
. D.
min
3 6 2
P
.
Lời giải
Chọn D
Ta có
1
3
log 1 1 9 1 1
y
x y x y

3
0
t
f t
f t
0
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 76 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
3 3
1 log 1 log 1 1 1 9
y x y x y
.
3 3
1 log 1 log 1 1 9
y x y x
3 3
9
log 1 1 log 1
1
x x y
y
3 3
9 9
log 1 1 2 2 log
1 1
x x
y y
(*).
Xét hàm số
3
log 2f t t t
với
0t
có
1
1 0
ln 3
f t
t
với mọi
0t
nên hàm số
f t
luôn đồng biến và liên tục trên
0;

.
Từ (*) suy ra
9
1
1
x
y
9 8
1
1 1
y
x
y y
, do
0
x
nên
0;8
y
.
Vậy
8 9 9
2 2 2 1 2 1 3 3 6 2
1 1 1
y
P x y y y y
y y y
.
Vậy
min
3 6 2
P
khi
9 3
2 1 1
1
2
y y
y
.
Câu 30. Cho hai số thực dương
,x y
thỏa mãn
2 2
log log 6 6x x x y y x
. Giá trị nhỏ nhất của biểu
thức
6 8
3 2P x y
x y
bằng
A.
59
3
. B.
19
. C.
53
3
. D.
8 6 2
.
Lời giải
Chọn B
Điều kiện:
0
0 6
x
y
.
Từ giả thiết ta có:
2 2
2 2 2 2
log log 6 6 log log 6 6
x x x y y x x x x y x y
(*)
Xét hàm số
2
log
f t t t
với
0t
, Ta có
1
' 1 0, 0
ln 2
f t t
t
nên hàm
số
2
log
f t t t
đồng biến trên khoảng
0;

.
Do đó
2 2
* 6 6 6 6 **
f x f x y x x y x y x y
( do
0
x
)
Áp dụng Bất đẳng thức Cô si cho các cặp số dương và bất đẳng thức
**
, ta có:
6 8 3 3 6 8 3 3 6 8
3 2 .6 2 . 2 . 19
2 2 2 2 2 2
x y x y
P x y x y
x y x y x y
.
Đẳng thức xảy ra khi và chỉ khi
6
2
3 6
4
2
8
2
x y
x
x
y
x
y
y
. Vậy giá trị nhỏ nhất của
P
bằng 19.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 77
Câu 31. Cho
,x y
là các số dương thỏa mãn
2 2
2 2
2
2 2
5
log 1 10 9 0
10
x y
x xy y
x xy y
. Gọi
,m
M
lần lượt
là giá trị lớn nhất, giá trị nhỏ nhất của
2 2
2
9x xy y
P
xy y
. Tính
10
T M m
.
A.
60
T
. B.
94
T
. C.
104
T
. D.
50
T
.
Lời giải
Chọn B
2 2
2 2
2
2 2
5
log 1 10 9 0
10
x y
x xy y
x xy y
2 2 2 2 2 2 2 2
2 2 2
log 5 log 10 log 2 2 5 10 0
x y x xy y x y x xy y
2 2 2 2 2 2 2 2
2 2
log 2 10 2 5 log 10 10
x y x y x xy y x xy y
2 2 2 2
2 10 10
x y x xy y
vi)
2 2
10 9 0
x xy y
2
10 9 0
x x
y y
1 9
x
y
2 2
2
9x xy y
P
xy y
2
9
1
x x
y y
x
y
Đặt
x
t
y
, điều kiện:
1 9t
2
9
1
t t
f t
t
;
2
2
2 8
1
t t
f t
t
;
4
0
2
t
f t
t
11
1
2
f
;
2 5
f
;
99
9
10
f
Nên
99
10
M
,
5
m
. Vậy
10 94
T M m
.
Câu 32. Vậy
min
6
A
.Cho các số thực dương
x
và
y
thỏa mãn
2 2 2
2 2 2 2
4 9.3 4 9 .7
x y x y y x
. Tìm giá trị
nhỏ nhất của biểu thức
2 18
x y
P
x
.
A.
9
P
. B.
3 2
2
P
.
C.
1 9 2
P
. D. Hàm số không có giá trị nhỏ nhất.
Lời giải
Chọn A
Từ giả thiết ta đặt
2
2t x y
,
t
.
Phương trình
2 2 2
2 2 2 2
4 9.3 4 9 .7
x y x y y x
trở thành
49 7
4 9.3 4 9 . 4 7 49 9 9. 49 0
7 3
t
t t t t
t
.
Nhận thấy
2t
là nghiệm phương trình.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 78 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta chứng minh
2t
là nghiệm duy nhất của phương trình.
Xét
2t
:
7 49
t
và
7
9. 49
3
t
nên vế trái phương trình luôn dương, nên phương trình vô
nghiệm.
Xét
2t
:
7 49
t
và
7
9. 49
3
t
nên vế trái phương trình luôn âm, nên phương trình vô nghiệm.
Vậy
2
2 2
t x y
2
2
2
x
y
thay vào
2
2 18 16
x y x x
P
x x
16 16
1 2 . 1 9
x x
x x
. Dấu bằng đạt được khi
16
4
x x
x
.
Câu 33. Cho
,x y
là các số thực lớn hơn
1
sao cho
y x
e e
x x y y
y e x e
. Tìm giá trị nhỏ nhất của biểu thức:
log log
x y
P xy x
.
A.
2
2
. B.
2 2
. C.
1 2 2
2
. D.
1 2
2
.
Lời giải
Chọn C
Cách 1.
Ta có:
ln ln
y x y x
e e e e
x x y y x x y y
y e x e y e x e
ln ln
ln ln
y x
x y
x y
x y xe y x ye
x e y e
(*) (vì
ln
x
y e x
có
1
' 0; 1
x
y e x
x
nên
1 0
y y e
)
Xét hàm số:
ln
t
t
f t
t e
trên
1;

ta có
2
ln 1
'
ln
t t
t
t e te
f t
t e
. Với hàm số
ln 1
t t
g t t e te
có
1
' ln 1 ' 0, 1
t t t
g t t e te te t
t
Nên
1 1 ' 0; 1g t g f t t
y f t
là hàm nghịch biến trên
1;

nên với (*)
1f x f y y x
Khi đó
1 1 1 1 1 1 1 2 2
log log log 2 log .
2 2 log 2 2 log 2
x y x x
x x
P xy x y y
y y
Dấu “=” xảy ra khi:
2
2
1 1
log log 2
2 log
x x
x
y y y x
y
Vậy:
min
1 2 2
2
P
.
Câu 34. Tính giá trị của biểu thức
2 2
1P x y xy
biết rằng
2
2
1
1
2
4 log 14 2 1
x
x
y y
với
0
x
và
13
1
2
y
.
A.
4P
. B.
2P
. C.
1P
. D.
3
P
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 79
Lời giải
Chọn B
Xét
2
2
1
1
2
4 log 14 2 1
x
x
y y
.
Ta có
2
2
2
2
1
1
2 . 1
1
4 4 4
x
x
x
x
, dấu bằng xảy ra khi và chỉ khi
1
x
,.
Mặt khác
3
14 2 1 14 3 1 1
y y y y
.
Đặt
1t y
ta có
30
0
2
t
. Xét hàm số
3
3 14
f t t t
. Ta tìm GTLN – GTNN của hàm
số trên đoạn
30
0;
2
được
30
0;
2
30
min
2
f t f
56 9 30
4
;
30
0;
2
max 1 16
f t f
.
Suy ra
2 2
log 14 2 1 log 16 4
y y
,.
Từ và suy ra ta có
1
1 1
x
t y
1
0
x
y
. Thay vào
2P
.
Câu 35. Cho hai số thực
x
,
y
thỏa mãn
1
0
2
x
,
1
0
2
y
và
log 11 2 2 4 1x y y x
. Xét biểu thức
2
16 2 3 2 5P yx x y y
. Gọi
m
,
M
lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của
P
. Khi
đó giá trị của
4
T m M
bằng bao nhiêu?
A.
16
. B.
18
. C.
17
. D.
19
.
Lời giải
Chọn A
Ta có
log 11 2 2 4 1x y y x
2 2 log 11 2 1 0
x y x y
Đặt
2
t x y
,
0 11
t
. Phương trình trở thành:
2 log 11 1 0
t t
.
1
Xét hàm số
2 log 11 1
f t t t
trên khoảng
0;11
.
Có
1
2 0
11
y
t
,
0;11
t
. Do đó hàm số
f t
luôn đồng biến.
Dễ thấy
1
có nghiệm
1t
. Do đó
1t
là nghiệm duy nhất của
1
.
Suy ra
2 1
x y
. Khi đó
2
1
16 1 3 2 5
4
y
P y y y y
3 2
4 5 2 3y y y
.
Xét hàm số
3 2
4 5 2 3
g y y y y
trên
1
0;
2
, có
2
12 10 2 0
g y y y
,
1
0;
2
y
.
NGUY
ỄN BẢO VƯƠNG - 0946798489
Trang 80 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Do đó,
1
0;
2
min
0 3
g y
g
,
1
0;
2
ma
x 1 4
g y
g
.
Suy ra
m 3
,
m 4
.
Vậy T 4.3 4 16 .
-------------------- HẾT --------------------
| 1/96
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 Vấn đề 10
PHƯƠNG TRÌNH - BẤT PHƯƠNG TRÌNH - MIN MAX LOGARIT
A. PHƯƠNG PHÁP GIẢI PHƯƠNG TRÌNH – BPT MŨ -LOGARIT
Thường sử dụng các phương pháp sau:
1. Phương pháp đưa về cùng cơ số.
1/ Phương trình – Bất phương trình mũ cơ bản Phương trình mũ fx gx
+ Nếu a  0, a  1 thì a  a  f x  gx a  1 fx g  x    + Nếu a chứa ẩn thì a  a  a   1 f   x  gx  0      . f   x  gx  fx gx fx gx + a  b  log a  log b
 f x  log b.g x (logarit hóa). a   a a Bất phương trình mũ fx  g x + Nếu a  1 thì a  a
 f x  gx . (cùng chiều) fx gx + Nếu 0  a  1 thì a  a
 f x  gx . (ngược chiều) fx  g x + Nếu a chứa ẩn thì a a
a 1f x gx      0   .
2/ Phương trình logarit – Bất phương trình logarit cơ bản Phương trình logarit + Nếu a  0, a  1 : b
log x  b  x  a   1 a
+ Nếu a  0, a  1 : log f x  log g x  f x  g x 2 a   a       g x + Nếu a  0, a  1 : log f x  g x  f x  a (mũ hóa) 3 a        
Bất phương trình logarit
+ Nếu a  1 thì log f x  log g x  f x  g x (cùng chiều) a   a      
+ Nếu 0  a  1 thì log f x  log g x  f x  g x (ngược chiều) a   a      
log B  0  a 1 B 1  0  a   
+ Nếu a chứa ẩn thì  log A  . a  0   A   1 B   1  0  log B  a
Các bước giải phương trình & bất phương trình mũ – logarit
Bước 1. Đặt điều kiện (điều kiện đại số  điều kiện loga), ta cần chú ý:  0   a  1 log   f mũ lẻ   x Đ K   f x  0 a     ĐK log b    và   . a b   0   mũ chẵn  log   f   x Đ K   f x  0 a      
Bước 2. Dùng các công thức và biến đổi đưa về các cơ bản trên, rồi giải.
Bước 3. So với điều kiện và kết luận nghiệm.
2. Phương pháp đặt ẩn phụ.
I/ Đặt ẩn phụ cho phương trình mũ fx  fx Loại 1.   PP P a  0 
 đặt t  a , t  0 . fx   f x a  2.fx 2.f x 2.fx   Loại 2. .  a  .  a.      b  λ.b  0 PP   Chia hai vế cho b , t     0 rồi đặt  (chia b
cho cơ số lớn nhất hoặc nhỏ nhất).
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489 fx fx 1  fx fx Loại 3. a  b  c với a.b  1 PP   đặt t  a  b  . t  fx gx a .a  fx u   a  fx   g x Loại 4.  f .  a  x   .  a  b  0 PP a   đặt  .  gx v  a  gx  a
II/ Đặt ẩn phụ cho phương trình logarit
 Loại 1. Plog f x PP  0   đặt t  log f x . a   a
 Loại 2. Sử dụng công thức log c log a log x log a b b a  c để đặt b b t  a  t  x .  Lưu ý
Trên đây là một số dạng cơ bản thường gặp về phương trình mũ và loga, còn bất phương trình ta cũng
làm tương tự nhưng lưu ý về chiều biến thiên. Về phương diện tổng quát, ta đi tìm mối liên hệ
giữa biến để đặt ẩn phụ, đưa về phương trình (bất phương trình) đại số hoặc hệ phương trình đại
số mà đã biết cách giải. Từ đó, tìm ra được nghiệm. Ngoài ra, còn một số trường hợp đặt ẩn phụ
không hoàn toàn. Nghĩa là sau khi đặt ẩn phụ t vẫn còn x. Ta giải phương trình theo t với x được
xem như là hằng số bằng cách lập biệt thức ∆ hoặc đưa về tích số.
3. Phương pháp hàm số.
I/ Cơ sở lý thuyết và vận dụng cơ sở lý thuyết để tìm hướng giải
Thông thường ta sẽ vận dụng nội dung các định lý (và các kết quả) sau:
 Nếu hàm số y  f  
x đơn điệu một chiều trên D thì phương trình f  
x  0 không quá một nghiệm trên D.
 Để vận dụng định lý này, ta cần nhẩm được 1 nghiệm x  x của phương trình, rồi chỉ rõ hàm o
đơn điệu một chiều trên D (luôn đồng biến hoặc luôn nghịch biến trên D) và kết luận x  x là o nghiệm duy nhất.  Hàm số f  
t đơn điệu một chiều trên khoảng a; 
b và tồn tại u; v  a;b thì
f u  f v  u  v ".
 Để áp dụng định lý này, ta cần xây dựng hàm đặc trưng f   t .  Hàm số y  f  
t xác định và liên tục trên D: Nếu f  
t đồng biến trên D và u, v  D thì f u  f v  u  v . Nếu f  
t nghịch biến trên D và u
 , v  D thì f u  f v  u  v .
 Để vận dụng nội dung định lí này trong giải bất phương trình, người ra đề thường cho dưới hai
hình thức và có hai hướng xử lí thường gặp sau:
Nếu đề yêu cầu giải f x  0 :
Nhẩm nghiệm của f x  0 trên miền xác định D, chẳng hạn x  x . o
Xét hàm số y  f x trên D và chỉ rõ nó đơn điệu tăng một chiều (đơn điệu giảm một chiều). Khi đó:
f x  0  f x  f x  x  x nếu hàm số đơn điệu tăng trên D và x  x nếu hàm số đơn o  o o
điệu giảm trên D.
Nếu đề bài yêu cầu giải f x  0 mà không nhẩm được nghiệm x  x của f x  0 thì cần biến đổi o f x 0 f g x f h x     y  f t , f t   
 với việc xây dựng hàm đặc trưng
  rồi chỉ ra hàm   là
đồng biến (nghịch biến). Khi đó f g    x f h    x   g   x  f x  hay g  x  f x   .
Ta sẽ làm tương tự nếu đề cho f x  0, f x  0 hoặc f x  0 .
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
 Nếu hàm số y  f x có đạo hàm f 'x liên tục và thỏa mãn f 'x  0 có một nghiệm trên D thì
phương trình f x  0 không quá 2 nghiệm trên D.
II/ Một số loại toán cơ bản thường gặp khi sử dụng đơn điệu hàm f x  Loại 1. log . g x f x     a      g x     1
Tìm tập xác định D. Biến đổi  
1  log f x  log g x  .  g x  .  f x a   a        log f x  .  f x  log g x  .  g x f f x f g    x   a     a       .
Xét hàm số đặc trưng f   t  .
 t  log t trên miền D và chỉ ra hàm số này luôn đơn điệu một chiều a trên D và f f  x f g    x   f   x  gx  .
Loại 2. log f x  log g x 2 a   b   Nếu a  b thì  
2  f x  gx: đây là dạng toán khá quen thuộc. Nếu a   1 b   1  0 PP 
 Dùng phương pháp đoán nghiệm và chứng minh đó là nghiệm duy nhất. Nếu a   1 b   1  0 PP 
 Đặt ẩn phụ kết hợp mũ hóa phương trình.  t f  x  a 
Tìm tập xác định D và đặt log f x  log g x  t  
và biến đổi phương trình về dạng: a   b     g  x t  b    t t
f t  A  B  1 và giải bằng phương pháp đoán nghiệm và chứng minh nghiệm này duy nhất và tìm x khi biết t.  Dạng toán: .  log f x  .
 log g x ta cũng làm tương tự bằng cách đặt a   b  
 log f x   log gx  γ.t với γ là bội số chung nhỏ nhất của  và  . a b  Loại 3. log g x  log b   3 f x     a
Đặt điều kiện: f x  0 và 0  gx  1. log f x b  
Sử dụng công thức đổi cơ số thì   3   log gx log b a b
 log f x  log b.log g x  log f x  log g x (đây là loại 2). b   a   b   a b    Loại 4. x a   p log x    qx  r   4 a λ  PP 
 Đặt ẩn phụ log λx    y để đưa về hệ phương trình đối xứng loại II hay gần đối xứng và a 
sử dụng phương pháp hàm để tìm được x  y .
Phương trình dạng log f x, y  log g x, y . a b   f   x, yta
Phương pháp: đặt t  log f x, y  log g x, y và chuyển về hệ và đánh giá chặn giá a b  g   x, y tb
trị t . Từ đó chọn giá trị nguyên của x thích hợp và thử lại xem với giá trị nguyên của x đã chọn
thì hệ phương trình có nghiệm t trong miền đã chặn hay không?
Kiến thức để đánh giá chặn giá trị t :
+ Điều kiện có nghiệm của phương trình bậc 2.
+ Bất đẳng thức Cauchy, BCS…
+ Tính chất biến thiên của hàm số.
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489 x Câu 1.
Cho x , y là các số thực dương thỏa mãn log x  log y  log
2x y . Giá trị của bằng 9 6 4   y 1  3  A. 2 . B. . C. log   . D. log 2 . 3 2 2  2  2 2
4x 4x 1   Câu 2.
Biết x ; x x x
là hai nghiệm của phương trình 2 log 
  6x4x và 1 2  1 2  2      x  1 x  2x
a b với a, b là các số nguyên dương. Giá trị P a b là 1 2   4 A. P 14 . B. P 13 . C. P 15 . D. P 16 .
x a y b z Câu 3.
Biết a  log 10 , b  log 150 và 1 1 1 log 15000 
với x ; y ; z ; x ; y ; z là các số 30 30 2000
x a y b z 1 1 1 2 2 2 2 2 2 nguyên, tính 1  x S . x2 1 2 A. S  . B. S  2 . C. S  . D. S  1 . 2 3 l  og y  log  x x y Câu 4.
Cho các số thực dương x, y khác 1 và thỏa mãn  . l  og x y x y x    logy      Giá trị của 2 2
x xy y bằng A. 0. B. 3. C. 1. D. 2. Câu 5.
Cho các số thực dương a , b thỏa mãn
log a  log b  log a  log b 100 và log a ,
log b , log a , log b đều là các số nguyên dương. Tính P ab . A. 164 10 . B. 100 10 . C. 200 10 . D. 144 10 . mb nac Câu 6. Cho log 5  ; a log 7  ;
b log 3  c .Biết log 175 
.Tính A m  2n  3 p  4q 9 4 2 24 pc q A. 27 B. 25 C. 23 D. 29
1 log x  log y Câu 7.
Cho x , y là các số thực lớn hơn 1 thoả mãn 2 2
x  6 y xy . Tính 12 12 M  . 2 log x  3y 12   1 1 1 A. M  . B. M 1 . C. M  . D. M  . 4 2 3 Câu 8. Cho
f x  a  2
ln x x 1bsin x  6 với a , b   . Biết f loglog e  2 . Tính f logln10. A. 4 . B. 10 . C. 8 . D. 2 . x -x 6+3(3 +3 ) a a Câu 9. Cho x -x 9 + 9 = 14 và = với
là phân số tối giản. Tính P  . a . b x+1 1-x 2-3 -3 b b A. P 10. B. P  4  5. C. P  1  0. D. P  45.   xx x 3
Câu 10. Biết phương trình 1 27  27 16 3      6  0 
có các nghiệm x a, x  log b và  3x  3 b
x  log c với a  , b c  0. Tỉ số
thuộc khoảng nào sau đây? 3 c 3 5  3 5  A. (3;). B.  ;       C. 1  ;  D.  ;3 2 2  2 2  a
Câu 11. Cho hai số thực dương a,b thỏa log a  log b  log a b . Tính . 4 6 9   b
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 1 1 5 1   5 1   5 A. . B. . C. . D. . 2 2 2 2
Câu 12. Gọi a là một nghiệm của phương trình 2 log x log x 2 log 4.2 6 18.3 x  
 0 . Khẳng định nào sau đây
đúng khi đánh giá về a ? 1 A. a  2 10  1. B. 2 a 10 . C. 2
a a  1  2 . D. a  . 100
Câu 13. Tổng các nghiệm của phương trình sau x 1 7   6 log 6x  5 1 bằng 7   A. 2 . B. 3 . C. 1. D. 10 .
Câu 14. Bất phương trình 9x  2   53x x  9 2x  
1  0 có tập nghiệm là S   ; a b ; c  . Tính
tổng a b c ? A. 0 . B. 1. C. 2 . D. 3 . 2 2 2
Câu 15. Phương trình sin x cos x sin 2 3 4.3 x  
có bao nhiêu nghiệm thuộc  2  017; 2017 . A. 1284 . B. 4034 . C. 1285 . D. 4035 . x
Câu 16. Cho các số thực dương ,
x y thỏa mãn log x  log y  log
2x  2 y . Tính tỉ số ? 6 9 4   y x 2 x 2 x 2 x 3 A.  . B.  . C.  . D.  . y 3 y 3 1 y 3  1 y 2
Câu 17. Số nghiệm của phương trình log5 3 2 xx là: A. 0 . B. 1. C. 3. D. 2 .
Câu 18. Phương trình 33x 33x 4 x 4 x 3 3  3  3  3
 10 có tổng các nghiệm là? A. 0 . B. 2 . C. 3. D. 4 . x x 2
Câu 19. Tìm tập nghiệm S của bất phương trình 2 3 1  3  . 3x 1 A.  ;
 0 log 2;  . B. 0;log 2 . 3  3   1  C. 0;   2;    . D. 0;  .    2  x x y xa b
Câu 20. Cho x , y là các số thực dương thỏa mãn log  log y  log và  , với a , 25 15 9 2 4 y 2
b là các số nguyên dương, tính a b .
A. a b  14 .
B. a b  3 .
C. a b  21 .
D. a b  34 .
Câu 21. Biết rằng phương trình log  1009 1 x
 2018 log x có nghiệm duy nhất x . Khẳng định nào dưới 2  3 0 đây đúng? 1 1 2 1 1 A. 1008 1006 3  x  3 . B. 1009 x  3 . C. 1008 1  x  3 . D. 1007 3  x  1. 0 0 0 0
Câu 22. Phương trình 2 log cot x  log
cos x có bao nhiêu nghiệm trong khoảng 0; 2018  ? 3   2   A. 2018 nghiệm. B. 1008 nghiệm. C. 2017 nghiệm. D. 1009 nghiệm.
Câu 23. Cho dãy số u thỏa mãn log 2u  63  2log u  8n  8 , * n   . Đặt 3  5  4  nn u .S 148
S u u  ...  u . Tìm số nguyên dương lớn nhất n thỏa mãn n 2n  . n 1 2 n u .S 75 2n n A. 18 . B. 17 . C. 16 . D. 19 .
Câu 24. Số nghiệm của phương trình 2
log x  2x  log  2
x  2x  2 là 3 5  A. 3. B. 2 . C. 1. D. 4 .
Câu 25. Tìm giá trị gần đúng tổng các nghiệm của bất phương trình sau:
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489    22 22 2 4  2 2 log  2 log  5  13    4 x x x x x    x x   6 5 4 3 2 24 2 27 2 1997 2016 0 2  3 3 log x log x 22 22    3 3  A. 12,3 . B. 12 . C. 12,1. D. 12, 2 .  2 log 100 x  log10 x
Câu 26. Tìm tích tất cả các nghiệm của phương trình 1log 4.3  9.4  13.6 x . 1 A. 100 . B. 10 . C. 1. D. . 10
Câu 27. Tập nghiệm của bất phương trình x2 x2 2.7  7.2
 351. 14x có dạng là đoạn S   ; a b. Giá trị
b  2a thuộc khoảng nào dưới đây?  2 49  A. 3; 10  . B. 4; 2 . C.  7;4 10  . D. ;   .  9 5 
Câu 28. Tập nghiệm của bất phương trình  x   x  x      2 2 2 2 2 2 1 2 1 là
A. S   ;  0 .
B. S  1;  .
C. S  0  ;1 . D. S   3  ;  . 2 2
Câu 29. Bất phương trình x x 1  1  x x 1 2 2 2 2    
có tập nghiệm S   ;
a b . Khi đó a b bằng A. 2 . B. 3 . C. 1. D. 10 . x x
Câu 30. Tập nghiệm của bất phương trình       xlog2 5 5 21 5 21  2 là A. S   2   ;1 . B. S   1   ;1 .
C. S  1;  5 .
D. S  1;  .
Câu 31. Có bao nhiêu cặp số nguyên x; y thỏa mãn 0  x  2020 và log 3  3   2  9y x x y ? 3   A. 2019 . B. 6 . C. 2020 . D. 4 .
Câu 32. Có bao nhiêu cặp số nguyên  , x y  thỏa mãn log
3x y  9  1? 2 2   9 x y A. 7 . B. 6 . C. 10 . D. 9 .
Câu 33. Có bao nhiêu giá trị nguyên của tham số m sao cho tồn tại duy nhất cặp số thực  , x y thỏa mãn 2 2
x y  18 và x y m  log y  2m  log x m ? 3   3   A. 3 . B. 2 . C. 4 . D. 5 . 2
x  2x 1 
Câu 34. Biết x , x (x x ) là hai nghiệm của phương trình 2 log
x  2  3x và 1 2 1 2 3   3x  
4x  2x a b , với ,
a b là hai số nguyên dương. Tính a b 1 2
A. a b  9 .
B. a b  12 .
C. a b  7 .
D. a b  14 .
Câu 35. Có bao nhiêu cặp số nguyên x; y thỏa mãn 0  x  2020 và log 4  4   1 2y x x y ? 2   A. 10 . B. 11. C. 2020 . D. 4 .
Câu 36. Có bao nhiêu số nguyên x sao cho tồn tại số thực y thỏa mãn log  2 2 x  4 y  log x  4 y . 2  3   A. 3 . B. Vô số. C. 2 . D. 4 .
Câu 37. Có bao nhiêu cặp số nguyên  x; y thoả mãn 0  x  2020 và      2 2 ln 1  1 y x x xy e ? A. 0 . B. 7 . C. 1. D. 8 .
Câu 38. Có bao nhiêu số nguyên x sao cho tồn tại số thực y thỏa mãn log (x y)  log  2 2 x  2y ? 3 4  A. 1 B. 3 C. 2 D. Vô số
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Câu 39. Có bao nhiêu cặp số nguyên dương  ;
x y thỏa mãn đồng thời hai điều kiện: 6 1  x  10 và
x x   2 2 y 2 2 log 10 20
20  10  y x  2x 1? A. 4 . B. 2 . C. 3 . D. 1.
Câu 40. Có bao nhiêu số nguyên
y  10 sao cho tồn tại số nguyên x thỏa mãn y y 2  xx x     x  2 2 2 1 5 2 5 1 ? A. 10 B. 1 C. 5 D. Vô số
Câu 41. Có bao nhiêu cặp số nguyên dương  x; y thoả mãn 1  x  2020 và 2y y 2x log  y 1 x 2      2  A. 2021 . B. 10 . C. 2020 . D. 11. Câu 42. Có bao nhiêu số nguyên x sao cho tồn tại số thực y thỏa mãn
2log  x y  log 1 3  log  2 2
x y 1 2 2 3  A. 1 B. 3 C. 2 D. 5  2x 1 
Câu 43. Có bao nhiêu cặp số nguyên  ;
x y thỏa mãn 0  y  2020 và log  1 2x y ? 3   y   A. 2019 . B. 11. C. 2020 . D. 4 . 2
 4x  4x 1  Câu 44. Biết
x , x là hai nghiệm của phương trình 2 log
 4x 1  6x và 1 2 7   2  x  1 x  2x
a b với a , b là hai số nguyên dương. Tính a b . 1 2   4
A. a b  13 .
B. a b  11.
C. a b  16 .
D. a b  14 . 2 x 1  x 1 
Câu 45. Biết phương trình log  2 log  
có một nghiệm dạng x a b 2 trong đó 5 3   x 2 2   x  ,
a b là các số nguyên. Tính 2a b . A. 3 . B. 8 . C. 4 . D. 5 .
Câu 46. Số nghiệm thực của phương trình 6x  3log
5x 1  2x 1 là 6   A. 0 . B. 2 . C. 1. D. 3 .
 5x  3x
Câu 47. Tính tổng S tất cả các nghiệm của phương trình x 1 ln
 5   5.3x  30x 10  0   . 6x  2   A. S  1. B. S  2 . C. S  1  . D. S  3. 2 x  80
Câu 48. Số nghiệm của phương trình x 1  2 ln  2.3
 2 x  80  ln 3 là 3x A. 2 . B. 3 . C. 1. D. 0 .
B. BÀI TOÁN CHỨA THAM SỐ
Dạng 1. Tìm m để f t; m  0 có nghiệm (hoặc có k nghiệm) trên D?
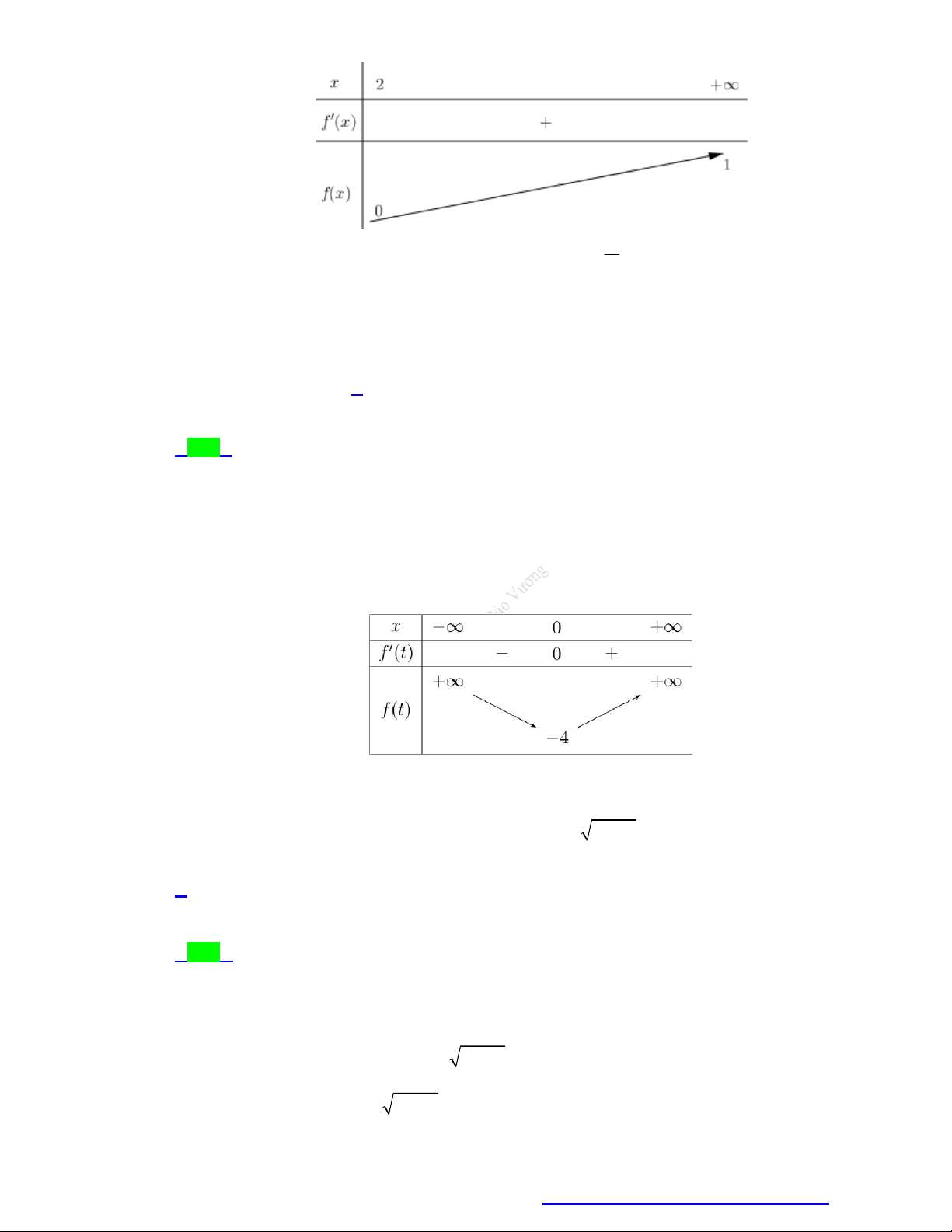
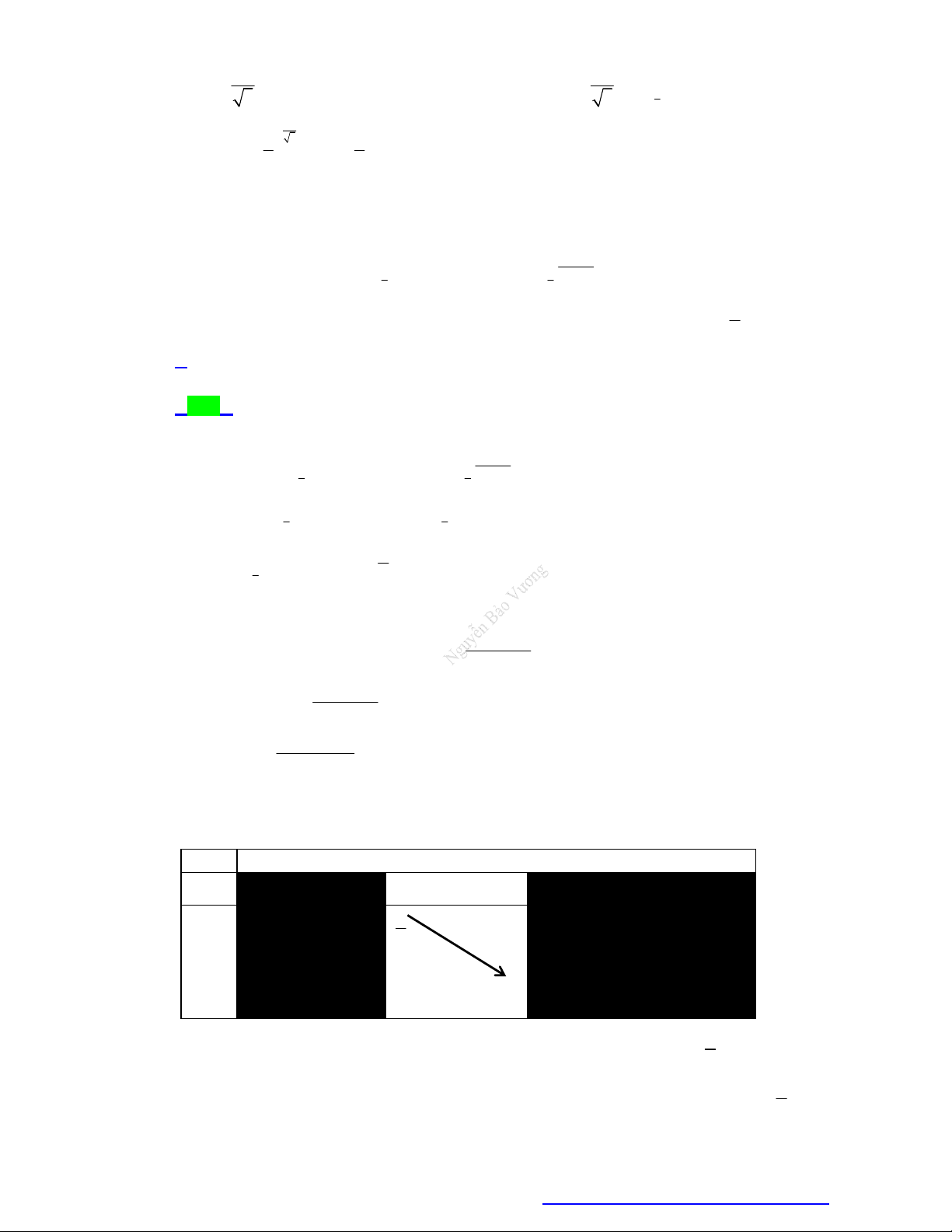
— Bước 1. Tách m ra khỏi biến số và đưa về dạng f   t  Am.
— Bước 2. Khảo sát sự biến thiên của hàm số f   t trên D.
— Bước 3. Dựa vào bảng biến thiên để xác định giá trị của tham số Am để đường thẳng y  Am nằm
ngang cắt đồ thị hàm số y  f   t .
— Bước 4. Kết luận các giá trị cần tìm của  A 
m để phương trình f  
t  Am có nghiệm (hoặc có k nghiệm) trên D. Lưu ý
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
NGUYỄN BẢO VƯƠNG - 0946798489
— Nếu hàm số y  f  
t có giá trị lớn nhất và giá trị nhỏ nhất trên D thì giá trị Am cần tìm là những m thỏa mãn: min f  
t  Am  max f   t . t D  t D 
— Nếu bài toán yêu cầu tìm tham số để phương trình có k nghiệm phân biệt, ta chỉ cần dựa vào bảng biến
thiên để xác định sao cho đường thẳng y  Am nằm ngang cắt đồ thị hàm số y  f   t tại k điểm phân biệt.
Dạng 2. Tìm m để bất phương trình f t; m  0 hoặc f t; m  0 có nghiệm trên miền D?
— Bước 1. Tách tham số m ra khỏi biến số t và đưa về dạng Am  f  
t hoặc Am  f   t .
— Bước 2. Khảo sát sự biến thiên của hàm số f   t trên D.
— Bước 3. Dựa vào bảng biến thiên xác định các giá trị của tham số m để bất phương trình có nghiệm: + Am  f  
t có nghiệm trên D  Am  max f   t . t D  + Am  f  
t có nghiệm trên D  Am  min f   t . t D   Lưu ý
— Bất phương trình Am  f   t nghiệm đúng t
  D  Am  min f   t . t D 
— Bất phương trình Am  f   t nghiệm đúng t
  D  Am  max f   t . t D  Câu 1. Cho phương trình 2 log
2x m  2 log x m  2  0 ( m là tham số thực). Tập hợp tất cả các 2     2
giá trị của m để phương trình đã cho có hai nghiệm phân biệt thuộc đoạn 1; 2 là A. 1; 2 . B. 1; 2. C. 1; 2 . D. 2;  .   x   Câu 2. Cho phương trình 3 2
2 log x  7 log x  4 log 3x m  0 
( m là tham số thực). Có tất cả 2 2 2      2  
bao nhiêu giá trị nguyên dương của m để phương trình đã cho có đúng hai nghiệm phân biệt? A. 78 . B. 80 . C. 81. D. 79 . Câu 3. Cho phương trình  2 2 log  3log  2 9x  1 3x x x m
m  0 ( m là tham số thực). Gọi S là 2 2   
tập hợp tất cả các giá trị nguyên dương của m để phương trình đã cho có đúng hai nghiệm phân
biệt. Tính tổng tất cả các phần tử của S . A. 3238 . B. 3236 . C. 3237 . D. 3239 . Câu 4. Cho phương trình  2 2 log  3log  2 3x  .2x x x m
 0 ( m là tham số thực). Gọi S là tập hợp tất 3 3 
cả các giá trị nguyên dương của m để phương trình đã cho có đúng hai nghiệm phân biệt. Tính
tổng tất cả các phần tử của S . A. 741. B. 742 . C. 740 . D. 703 . 2 Câu 5.
Cho phương trình  2lg xlgx 1lg 2  4
x  3x m  0 (m là tham số thực). Gọi S là tập hợp tất cả các giá
trị nguyên dương của m để phương trình đã cho có đúng hai nghiệm phân biệt. Tổng của phần tử nhỏ
nhất và phần tử lớn nhất S bằng A. 100 3 1. B. 100 3 1 . C. 99 3 . D. 99 3 1 . Câu 6.
Cho phương trình 3.2x.log 12log  2x  4 5x x x
m  0 ( m là tham số thực). Có tất cả bao
nhiêu giá trị nguyên dương của m để phương trình đã cho có đúng hai nghiệm phân biệt? A. 24 . B. 25 . C. 23 . D. 22 . Câu 7. Cho phương trình 2
log x  3m log 3x 2
 2m  2m 1  0 ( m là tham số thực). Tìm tất cả các số 2 2
thực m để phương trình có hai nghiệm phân biệt thuộc đoạn 1;  9 . 1 1 1 A. 3   m  . B. m   2 . C.  . D.   m  . 2 2 2
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 Câu 8. Cho phương trình 2 2
log x  (m  3)log x  2m  3m  0 ( m là tham số thực). Có bao nhiêu giá trị 2 2  1 
nguyên của tham số m để phương trình đã cho có đúng một nghiệm thuộc đoạn ;32  ? 4    A. 4 . B. 5 . C. 6 . D. 7 . Câu 9.
Cho phương trình 9x  (  5)3x m
 3m  6  0 ( m là tham số thực ). Có bao nhiêu giá trị
nguyên của m để phương trình đã cho có 2 nghiệm phân biệt thuộc đoạn 1;2 . A. 6 . B. 7 .
C. m R . D. 1.
Câu 10. Cho phương trình 2 2 2
log x  log x m  2m  0 ( m là tham số thực). Có bao nhiêu giá trị nguyên 2 2 1 
của tham số m để phương trình đã cho có đúng một nghiệm thuộc đoạn ;16  ? 8    A. 3 . B. 2 . C. 1. D. 4 .
Câu 11. Cho phương trình 2 log 2x 2
 2 log x m 1  0 .Có bao nhiêu giá trị nguyên của tham số m để 2 2  1 
phương trình có đúng một nghiệm thuộc đoạn ;16  ? 2    A. 10 . B. 7 . C. 5 . D. 6 .
Câu 12. Cho phương trình  2 2 2
log x  log x m  2m
3  log x  0 ( m là tham số thực). Có bao nhiêu 2 2  2 1
giá trị nguyên của tham số m để phương trình đã cho có 3 nghiệm phân biệt x  ? 8 A. 3 . B. 5 . C. 2 . D. 4 . 2
Câu 13. Cho phương trình 1 2020x     2 2020x m
m  2  0 ( m là tham số thực). Tập hợp tất cả
các giá trị của m để phương trình đã cho có 2 nghiệm phân biệt thuộc đoạn 0;  2 là A. 2;202  1 . B. m   R . C. 2;  . D. 2;  2021 .
Câu 14. Cho phương trình  2 2
log x  (m  3)log x  2m  3m
1 log x  0 ( m là tham số thực). Có bao 3 3  81 1
nhiêu giá trị nguyên của tham số m để phương trình đã cho có 3 nghiệm phân biệt x  ? 27 A. 4 . B. 3 . C. 2 . D. 5 .
Câu 15. Cho phương trình 2 log
2021x m  2 log
x  2  m ( m là tham số thực). 2021     2021
Tổng tất cả các giá trị nguyên của m để phương trình đã cho có hai nghiệm phân biệt thuộc đoạn 3 1  ; 2021    là: A. 10 . B. 8 . C. vô số. D. 13 .
Câu 16. Cho phương trình  2 2 2
log x  log x m  2m
3  log x  0 ( m là tham số thực). Có bao nhiêu 2 2  2 1
giá trị nguyên của tham số m để phương trình đã cho có 2 nghiệm phân biệt x  ? 8 A. 7 . B. 6 . C. 5 . D. 8 . 2 2
Câu 17. Có bao nhiêu giá trị nguyên của m để phương trình 1 1x     1 1 9 2 3  x m  2m 1  0 có nghiệm thực? A. 4 . B. 5 . C. 6 . D. 7 .
Câu 18. Cho phương trình 2
log x  2 log  x  2  1. Số giá trị nguyên của a  0; 2020 để phương trình a a
trên có 1 nghiệm thực là A. 0 . B. 2018 . C. 2019 . D. 2020 .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 19. Cho phương trình log  3
mx  6x   2log  2 14 
x  29x  2  0 , số giá trị nguyên của m để 1 2  2
phương trình có 3 nghiệm thực phân biệt là A. 1. B. 0 . C. 23. D. 5 .
Câu 20. Phương trình 2 2
log x  log x 1  2m 1  0 có nghiệm trên đoạn 3 1;
 3  khi m a ;b. Khi đó 3 3  
giá trị biểu thức T a.b bằng 1 A. 0 . B. 1. C.  . D. 4 . 4
Câu 21. Phương trình 2 2
log x  log x 1  2m 1  0 có nghiệm trên đoạn 3 1
 ;3  khi m a;b. Khi đó 3 3  
giá trị biểu thức T  . a b bằng 1 A. 0. B. 1. C.  . D. 4. 4 2 x
Câu 22. Cho phương trình 3log x  2log x 1 5  m  0 ( m là tham số thực). Có tất cả bao nhiêu giá 3 3 
trị nguyên dương của m để phương trình đã cho có đúng hai nghiệm phân biệt? A. Vô số. B. 120 . C. 121. D. 124 .
Câu 23. Cho phương trình log  2
x  2x 1  log
x  2  1 log m ( m là tham số thực). Có tất cả bao 4  2   2
nhiêu giá trị nguyên của m để phương trình đã cho có nghiệm? A. 0 . B. 1. C. 2 . D. Vô số.
Câu 24. Tìm tập hợp tất cả giá trị của tham số thực m để phương trình 2
log x  4 log x m  0 có 2 2
nghiệm thuộc khoảng 0 ;  1 .
A. 4 ;   . B.  4  ;    . C.  4  ;0 . D. 2 ; 0.
Câu 25. Cho phương trình 2020  3 2 2 log  7 log  4 log 2 3x x x x
m  0 ( m là tham số thực). Có tất 2 2 2  
cả bao nhiêu giá trị nguyên dương của m để phương trình đã cho có đúng hai nghiệm phân biệt? A. 79 . B. 80 . C. Vô số. D. 78 .
Câu 26. Cho phương trình  2 2 log  3log  2 5x  .3x x x m
 0 ( m là tham số thực). Gọi S là tập hợp 3 3 
tất cả các giá trị nguyên dương của m để phương trình đã cho có đúng hai nghiệm phân biệt. Tính
tổng tất cả các phần tử của S . A. 4950 . B. 2475 . C. Vô số. D. 4949 . 2 1 2
Câu 27. Cho phương trình m   1 log x  2  4 m  5 log
 4m  4  0 ( m là tham số thực). Có 1     1 x  2 2 2  5 
tất cả bao nhiêu giá trị nguyên của tham số m để phương trình có nghiệm thuộc ; 4  . 2    A. 6 . B. 5 . C. 4 . D. Vô số.
Câu 28. Cho phương trình  2 2 log  3log  2 16x  1 4x x x m
m  0 ( m là tham số thực). Gọi S là 2 2   
tập hợp tất cả các giá trị nguyên dương của m để phương trình đã cho có đúng ba nghiệm phân
biệt. Tổng tất cả các phần tử của S là A. 32637 . B. 32640 . C. 255 . D. 256 .
Câu 29. Giá trị lớn nhất của tham số m sao cho bất phương trình 1 log  2 x   1  log  2
mx  4x m 5 5 
nghiệm đúng với mọi x thuộc  là 5 A. 2 . B. 3 . C. . D. 4 . 2
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Câu 30. Giá trị lớn nhất của tham số m sao cho bất phương trình 1 log  2 x   1  log  2
mx  4x m 5 5 
nghiệm đúng với mọi x thuộc  là: 5 A. 2. B. 3 . C. . D. 4. 2
Câu 31. Cho phương trình  2  log  3log  2 5x x x
m  0 ( m là tham số thực). Gọi S là tập hợp tất 7 7 
cả các giá trị nguyên dương của m để phương trình đã cho có đúng hai nghiệm phân biệt. Tổng
của phần tử nhỏ nhất và phần tử lớn nhất S bằng A. 49 5 . B. 49 5 1. C. 48 5 . D. 49 5 1.
Câu 32. Cho phương trình  2 2 log  5log  2 5x x x
m  0 ( m là tham số thực). Có tất cả bao nhiêu 2 2 
giá trị nguyên dương của m để phương trình đã cho có đúng hai nghiệm phân biệt? A. 616. B. 615. C. vô số. D. 617. Câu 33. Có bao nhiêu giá trị nguyên của tham số
m  2019; 2019 để phương x mx m x 2 1  2 1 trình 2019  
 0 có đúng 3 nghiệm thực phân biệt? x 1 x  2 A. 4038 . B. 2019 . C. 2017 . D. 4039 .
Câu 34. Có bao nhiêu giá trị nguyên của tham số m để tồn tại cặp số  ; x y thỏa mãn 3x5 y x3 y 1 e e  
 1 2x  2 y , đồng thời thỏa mãn 2
log 3x  2y   1  m  6 2
log x m  9  0 ? 3 3 A. 6 . B. 5 . C. 8 . D. 7 .
Câu 35. Có bao nhiêu số nguyên của m để phương trình log 2x m 2
 2 log x x  4x  2m 1 có hai 2 2 nghiệm thực phân biệt? A. 2 . B. 3 . C. 1. D. 4 Câu 36. Tìm tổng tất cả các giá trị nguyên của m để phương trình 3
x3 m3 x   3 2     x3 3 9 24 .3  3x x x x m
 1 có 3 nghiệm phân biệt. A. 45 . B. 34 . C. 27 . D. 38 .
Câu 37. Tìm các giá trị m để phương trình sin x 5 cos xm 5 3  log m  5 có nghiệm.
sin x 5 cos x 10   
A. 6  m  6 .
B. 5  m  5 .
C. 5  6  m  5  6 .
D.  6  m  5 .
Câu 38. Cho phương trình 2x m  log
x m với m là tham số. Có bao nhiêu giá trị nguyên của 2   m  1
 8;18 để phương trình đã cho có hai nghiệm? A. 20 . B. 17 . C. 9 . D. 21.
Câu 39. Cho phương trình   3 2  m m
x x   2 .log  x 3x 1 2 3 2 3 1 3 1 2 1 3 2 2 .log        0 81 3 3 2
m  3m 1  2   
Gọi S là tập hợp tất cả các giá trị m nguyên để phương trình đã cho có 6 nghiệm hoặc 7 nghiệm
hoặc 8 nghiệm phân biệt. Tính tổng bình phương tất cả các phần tử của tập S . A. 20 . B. 19. C. 14 . D. 28 . 2
Câu 40. Cho phương trình 2x log  2
x  2  4 xa log
2 x a  2 2  2   
 . Gọi S là tập hợp các giá trị a
thuộc đoạn 0; 2020 và chia hết cho 3 để phương trình có hai nghiệm. Hãy tính tổng các phần tử của S . A. 0 . B. 2041210 . C. 680403. D. 680430 .
Câu 41. Có bao nhiêu giá trị thực của tham số a để phương trình 4 xa log   2  3 2 2  x 2  2 x x x log
2 x a  2  0 1 2   2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
NGUYỄN BẢO VƯƠNG - 0946798489
có 3 nghiệm thực phân biệt ? A. 0 . B. 2 . C. 1. D. 3 . 2
Câu 42. Tìm tổng tất cả các giá trị của tham số a để phương trình x 2x 1  2 3 xa  log
2 x a  2 có 2 x 2 x3  
đúng ba nghiệm phân biệt. A. 2 . B. 3 . C. 1. D. 0 .
Câu 43. Tìm số giá trị nguyên của m thuộc 20; 20 để phương trình 2 2 2
log (x m x x  4)  (2m  9)x 1 (1 2m) x  4 có nghiệm. 2 A. 12. B. 23. C. 25. D. 10.
C. GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT Câu 1.
Xét các số thực dương , a , b ,
x y thoả mãn a 1, b  1 và x y a b
ab . Giá trị nhỏ nhất của
biểu thức P x  2 y thuộc tập hợp nào dưới đây?  5   5  A. 1; 2 . B. 2;   . C. 3; 4 . D. ;3   .  2   2  Câu 2.
Xét các số thực dương a , b , x , y thỏa mãn a  1 , b  1 và x y 4
a b ab . Giá trị nhỏ nhất của
biểu thức P x  4 y thuộc tập hợp nào dưới đây?  5  A. 1; 2 . B. 2;   . C. 1; 2 . D. 0  ;1 .  2  Câu 3.
Xét các số thực a , b , c  0 thỏa mãn 3a 5b 15  
c . Giá trị nhỏ nhất của biểu thức 2 2 2
P a b c  4(a b c) thuộc tập hợp nào dưới đây? A.  1  ; 2 . B.  5  ;   1 . C. 2; 4 . D. 4;6 . Câu 4.
Xét các số thực dương a , b , c , x , y , z thỏa mãn a  1 , b  1, c  1 và x y z a b c abc . 1
Giá trị nhỏ nhất của biểu thức P x y z
thuộc tập hợp nào dưới đây? 2 A. 10;13 . B. 7;10 . C. 3;5 . D. 5;7 . 2 2 Câu 5.
Xét các số thực dương a, , b ,
x y thỏa mãn a  1,b  1 và x y ab  .
a b . Giá trị nhỏ nhất của biểu thức P  . x y là 9 6 3 4 A. P  . B. P  . C. P  . D. P  . 4 2 2 9 2 2 x y Câu 6.
Xét các số thực dương a, b, x, y thỏa mãn a  1, b  1 và y x ab
ab . Giá trị nhỏ nhất của biểu
thức P x.y là
A. P  2 .
B. P  4 .
C. P  3. D. P 1. Câu 7.
Xét các số thực dương a, b, c, x, y, z thỏa mãn a  1, b  1, c  1, y  2 và x 1  y 2 z 1 a b c     abc .
Giá trị nhỏ nhất của biểu thức P x y z là
A. P  13.
B. P  3 .
C. P  9 . D. P  1 . 1 xy Câu 8.
Xét các số thực dương x , y thỏa mãn log
 3xy x  2 y  4 . Tìm giá trị nhỏ nhất P 3 x  2y min
của P x y . 9 11 19 9 11 19 18 11  29 2 11  3 A. P. B. P. C. P. D. P  . min 9 min 9 min 9 min 3
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 1 2x Câu 9.
Xét các số thực dương x , y thỏa mãn ln
 3x y 1 . Tìm giá trị nhỏ nhất P của biểu x y min 1 1 thức P   1 . x xy A. P  8 . B. P  16 . C. P  9 . D. P  2 . min min min min    3 3x 6 y
Câu 10. Xét các số thực dương x , y thỏa mãn 2 3 3 x y
. Tìm giá trị nhỏ nhất P của x y min 9 3 3 1 P    . 4x 2 xy 4 22 15 3 35  36 2 A. P  2 . B. P. C. P  20 . D. P. min min 2 min min 4 4 3  a
Câu 11. Cho hai số thực a , b thỏa a b  và 2 P  16 log  3log a  
có giá trị nhỏ nhất. Tính 3 a 12b 16 a   b a b . 7 11 A. . B. 4 . C. . D. 6 . 2 2     x y xy x y 2
Câu 12. Cho hai số thực dương x , y thỏa mãn 2 1 3 
. Tìm giá trị nhỏ nhất S của biểu thức xy 1 min
S x  4 y . A. S  4 3  9 . B. S  6  4 3 . C. S  2 3  2 . D. S  4 3  6 . min min min min 2 2 2 Câu 13. Cho ,
x y là hai số thực dương thỏa mãn x 2  y   x 2 
y  2yx 2 4 9.3 4 9 .7
. Giá trị nhỏ nhất của x  2 y 18 biểu thức P  là x 3  2 A. 9. B. . C. 1 9 2. D. 17. 2
x y 1 
Câu 14. Cho các số dương , x y thỏa mãn log
 3x  2 y  4 . Giá trị nhỏ nhất của biểu thức 5   2x  3  y  4 9
A  6x  2 y   bằng x y 31 6 27 2 A. . B. 11 3. C. . D. 19. 4 2 y x
Câu 15. Cho hai số thực ,
x y lớn hơn 1 và thỏa mãn x.( x )e y .( y )e y e x e
. Tìm giá trị nhỏ nhất của biểu thức P  log xy  log . x x y 2 1 2 2 1 2 A. . B. 2 2 . C. . D. . 2 2 2
Câu 16. Cho hai số thực x, y thỏa mãn 0  x, y  1 trong đó x, y không đồng thời bằng 0 hoặc 1 và  x y  log  x 1 . y 1
2 0 . Tìm giá trị nhỏ nhất của P với P  2x y 3
          1   xy  1 A. 2 . B. 1 . C. . D. 0 . 2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
NGUYỄN BẢO VƯƠNG - 0946798489  1 2x
Câu 17. Xét các số thực dương x , y thỏa mãn ln  3x y   
1. Tìm giá trị nhỏ nhất P của x  min  y  1 1 P   . x xy A. P  8 . B. P  4 . C. P  2 . D. P  16 . min min min min 2 y 1
Câu 18. Cho hai số thực x, y không âm thỏa mãn 2
x  2x y 1  log
. Giá trị nhỏ nhất của biểu 2 x 1 thức 2 x 1  2 P e
 4x  2 y 1 là 1 1 A.  . B. 1. C. . D. 1. 2 2
Câu 19. Cho hai số thực dương x , y thay đổi thỏa mãn đẳng thức    xy     2 2 1 2 1 .2 .2x y xy x y . Tìm giá trị nhỏ nhất y của y . min A. y  3 . B. y  2 . C. y  1. D. y  3 . min min min min x, y     x    Câu 20. Cho          sao cho 3 3 ln 2 x ln 3 19 y 6xy(x 2 y)  
. Tìm giá trị nhỏ nhất m của x, y 1   y  1
biểu thức T x  . x  3y 5
A. m 1 3 .
B. m  2 . C. m  .
D. m 1. 4 xy 3 5xy Câu 21. Cho  
x; y là các số thực dương thỏa mãn điều kiện 4 x 4 5   x 1 3
y yx  4 . 3xy 5
Tìm giá trị nhỏ nhất của biểu thức P x y . A. 3 . B. 5  2 5 . C. 3 2 5 . D. 1 5 . xy xy 3 5
Câu 22. Cho x , y là các số thực dương thỏa mãn 2  x2 5   x 1   3
y y(x  2) . Tìm giá trị 3xy 5
nhỏ nhất của biểu thức T x y . A. T  2  3 2 . B. T  3  2 3 . C. T  1 5 . D. T  5  3 2 . min min min min x  3 y
Câu 23. Xét các số thực dương , x y thỏa mãn log
xy  3 y x 1. Tìm giá trị nhỏ nhất của biểu 3 xy 1 1
thức A x  . y 14 14 A. A  . B. A   . C. A  6  . D. A  6 . min 3 min 3 min min  2 2 x y  2 4x y  2 Câu 24. Cho , x y  0 thỏa 2019 
 0 . Tìm giá trị nhỏ nhất P
của P  2y 4x .  min x  22 1 A. 2018 . B. 2019 . C. . D. 2 . 2 y1
Câu 25. Cho 2 số thực dương x, y thỏa mãn log  x 1 y 1 9
x 1 y 1 . Giá trị nhỏ nhất 3              
của biểu thức P x  2y là 11 27 A. P  . B. P  . C. P  5  6 3 . D. P  3  6 2 . min 2 min 5 min min 1 y
Câu 26. Xét các số thực dương x, y thỏa mãn log
 3xy x  3y  4 . Tìm giá trị nhỏ nhất P 3 x  3xy min
của P x y .
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 4 3  4 4 3  4 4 3  4 4 3  4 A. P  . B. P  . C. P  . D. P  . min 3 min 3 min 9 min 9 x y
Câu 27. Xét các số thực dương x, y thỏa mãn log
x x  3  y y  3  xy. Tìm giá trị 3 2 2
x y xy  2 3x  2 y 1 lớn nhất P
của biểu thức P  . max x y  6 A. 3 . B. 2 . C. 1. D. 4 .  2 2 x y  1 2x y
Câu 28. Xét các số thực dương x , y thỏa mãn 2018 
. Tìm giá trị nhỏ nhất P của  min x  2 1
P  2 y  3x . 1 7 3 5 A. P  . B. P  . C. P  . D. P  . min 2 min 8 min 4 min 6 y 1 
Câu 29. Cho 2 số thực dương x, y thỏa mãn log  x 1 y 1   9  x 1 y 1 3         . Giá trị nhỏ nhất
của biểu thức P x  2 y là 11 27 A. P. B. P. C. P  5  6 3 . D. P  3   6 2 . min 2 min 5 min min
Câu 30. Cho hai số thực dương x, y thỏa mãn log x x x y  log
6  y  6x . Giá trị nhỏ nhất của 2   2   6 8
biểu thức P  3x  2 y   bằng x y 59 53 A. . B. 19 . C. . D. 8  6 2 . 3 3 2 2 x  5 y
Câu 31. Cho x, y là các số dương thỏa mãn 2 2 log
 1  x  10xy  9 y  0 . Gọi M ,m lần 2 2 2
x  10xy y 2 2
x xy  9 y
lượt là giá trị lớn nhất, giá trị nhỏ nhất của P
. Tính T  10 M m . 2 xy y A. T  60 . B. T  94 . C. T  104 . D. T  50 . 2 2 2 Câu 32. Vậy A
 6 .Cho các số thực dương x và y thỏa mãn x 2 y    x 2 y   2yx 2 4 9.3 4 9 .7 . Tìm giá min x  2 y 18
trị nhỏ nhất của biểu thức P  . x 3  2 A. P  9 . B. P  . 2
C. P  1 9 2 .
D. Hàm số không có giá trị nhỏ nhất. y x e e
Câu 33. Cho x, y là các số thực lớn hơn 1 sao cho x x y   y y e x
e  . Tìm giá trị nhỏ nhất của biểu thức: P  log xy  log x . x y 2 1  2 2 1  2 A. . B. 2 2 . C. . D. . 2 2 2 2 1 x  1 
Câu 34. Tính giá trị của biểu thức 2 2
P x y xy 1 biết rằng 2 4 x  log 1  4  y  2 y 1 với 2     13
x  0 và 1  y  . 2 A. P  4 . B. P  2 . C. P  1 . D. P  3 . 1 1
Câu 35. Cho hai số thực x , y thỏa mãn 0  x  , 0  y
và log 11 2x y  2 y  4x 1. Xét biểu 2 2 thức 2
P  16 yx  2x 3y  2  y  5 . Gọi m , M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của
P . Khi đó giá trị của T  4m M  bằng bao nhiêu?
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
NGUYỄN BẢO VƯƠNG - 0946798489 A. 16 . B. 18 . C. 17 . D. 19 .
-------------------- HẾT --------------------
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 Vấn đề 10
PHƯƠNG TRÌNH - BẤT PHƯƠNG TRÌNH - MIN MAX LOGARIT
A. PHƯƠNG PHÁP GIẢI PHƯƠNG TRÌNH – BPT MŨ -LOGARIT
Thường sử dụng các phương pháp sau:
1. Phương pháp đưa về cùng cơ số.
1/ Phương trình – Bất phương trình mũ cơ bản Phương trình mũ fx gx
+ Nếu a  0, a  1 thì a  a  f x  gx a  1 fx g  x    + Nếu a chứa ẩn thì a  a  a  
1 f xgx  0      . f   x  gx  fx gx fx gx + a  b  log a  log b
 f x  log b.g x (logarit hóa). a   a a Bất phương trình mũ fx  g x + Nếu a  1 thì a  a
 f x  gx . (cùng chiều) fx gx + Nếu 0  a  1 thì a  a
 f x  gx . (ngược chiều) fx  g x + Nếu a chứa ẩn thì a a
a 1f x gx      0   .
2/ Phương trình logarit – Bất phương trình logarit cơ bản Phương trình logarit + Nếu a  0, a  1 : b
log x  b  x  a   1 a
+ Nếu a  0, a  1 : log f x  log g x  f x  g x 2 a   a       g x + Nếu a  0, a  1 : log f x  g x  f x  a (mũ hóa) 3 a        
Bất phương trình logarit
+ Nếu a  1 thì log f x  log g x  f x  g x (cùng chiều) a   a      
+ Nếu 0  a  1 thì log f x  log g x  f x  g x (ngược chiều) a   a      
log B  0  a 1 B 1  0  a   
+ Nếu a chứa ẩn thì  log A  . a  0   A   1 B   1  0  log B  a
Các bước giải phương trình & bất phương trình mũ – logarit
Bước 1. Đặt điều kiện (điều kiện đại số  điều kiện loga), ta cần chú ý:  mũ lẻ 0   a  1 log  f   x Đ K   f x  0 a     ĐK log b    và   mũ chẵn . a b   0    log   f   x Đ K   f x  0 a      
Bước 2. Dùng các công thức và biến đổi đưa về các cơ bản trên, rồi giải.
Bước 3. So với điều kiện và kết luận nghiệm.
2. Phương pháp đặt ẩn phụ.
I/ Đặt ẩn phụ cho phương trình mũ
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489  fx fx Loại 1.   PP P a  0 
 đặt t  a , t  0 . fx   f x a  2.fx 2.fx   Loại 2. .  a  .  a.b   2.fx  λ.b  0 PP   Chia hai vế cho b , t     0 rồi đặt  (chia cho b
cơ số lớn nhất hoặc nhỏ nhất). fx fx 1  fx fx Loại 3. a  b  c với a.b  1 PP   đặt t  a  b  . t  fx gx a .a  f  x u   a fx  gx  Loại 4.  f .  a  x  .  a  b  0  PP a   đặt  .  gx v  a  gx  a
II/ Đặt ẩn phụ cho phương trình logarit
 Loại 1. Plog f x PP  0   đặt t  log f x . a   a
 Loại 2. Sử dụng công thức log c log a log x log a b b a  c để đặt b b t  a  t  x .  Lưu ý
Trên đây là một số dạng cơ bản thường gặp về phương trình mũ và loga, còn bất phương trình ta cũng làm
tương tự nhưng lưu ý về chiều biến thiên. Về phương diện tổng quát, ta đi tìm mối liên hệ giữa biến
để đặt ẩn phụ, đưa về phương trình (bất phương trình) đại số hoặc hệ phương trình đại số mà đã biết
cách giải. Từ đó, tìm ra được nghiệm. Ngoài ra, còn một số trường hợp đặt ẩn phụ không hoàn toàn.
Nghĩa là sau khi đặt ẩn phụ t vẫn còn x. Ta giải phương trình theo t với x được xem như là hằng số
bằng cách lập biệt thức ∆ hoặc đưa về tích số.
3. Phương pháp hàm số.
I/ Cơ sở lý thuyết và vận dụng cơ sở lý thuyết để tìm hướng giải
Thông thường ta sẽ vận dụng nội dung các định lý (và các kết quả) sau:
 Nếu hàm số y  f  
x đơn điệu một chiều trên D thì phương trình f  
x  0 không quá một nghiệm trên D.
 Để vận dụng định lý này, ta cần nhẩm được 1 nghiệm x  x của phương trình, rồi chỉ rõ hàm o
đơn điệu một chiều trên D (luôn đồng biến hoặc luôn nghịch biến trên D) và kết luận x  x là o nghiệm duy nhất.  Hàm số f  
t đơn điệu một chiều trên khoảng a; 
b và tồn tại u; v  a; 
b thì f u  f v  u  v ".
 Để áp dụng định lý này, ta cần xây dựng hàm đặc trưng f   t .  Hàm số y  f  
t xác định và liên tục trên D: Nếu f  
t đồng biến trên D và u, v  D thì f u  f v  u  v . Nếu f  
t nghịch biến trên D và u
 , v  D thì f u  f v  u  v .
 Để vận dụng nội dung định lí này trong giải bất phương trình, người ra đề thường cho dưới hai
hình thức và có hai hướng xử lí thường gặp sau:
Nếu đề yêu cầu giải f x  0 :
Nhẩm nghiệm của f x  0 trên miền xác định D, chẳng hạn x  x . o
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Xét hàm số y  f x trên D và chỉ rõ nó đơn điệu tăng một chiều (đơn điệu giảm một chiều). Khi đó:
f x  0  f x  f x  x  x nếu hàm số đơn điệu tăng trên D và x  x nếu hàm số đơn điệu o  o o giảm trên D.
Nếu đề bài yêu cầu giải f x  0 mà không nhẩm được nghiệm x  x của f x  0 thì cần biến đổi o f x 0 f g x f h x        
 với việc xây dựng hàm đặc trưng y f  
t , rồi chỉ ra hàm f   t là đồng
biến (nghịch biến). Khi đó f g    x f h    x   g   x  f x  hay g  x  f x   .
Ta sẽ làm tương tự nếu đề cho f x  0, f x  0 hoặc f x  0 .
 Nếu hàm số y  f x có đạo hàm f 'x liên tục và thỏa mãn f 'x  0 có một nghiệm trên D thì
phương trình f x  0 không quá 2 nghiệm trên D.
II/ Một số loại toán cơ bản thường gặp khi sử dụng đơn điệu hàm f x  Loại 1. log . g x f x     a      g x     1
Tìm tập xác định D. Biến đổi  
1  log f x  log g x  .  g x  .  f x a   a        log f x  .  f x  log g x  .  g x f f x f g    x   a     a       .
Xét hàm số đặc trưng f   t  .
 t  log t trên miền D và chỉ ra hàm số này luôn đơn điệu một chiều trên a D và f f  x f g    x   f   x  gx  .
Loại 2. log f x  log g x 2 a   b   Nếu a  b thì  
2  f x  gx: đây là dạng toán khá quen thuộc. Nếu a   1 b   1  0 PP 
 Dùng phương pháp đoán nghiệm và chứng minh đó là nghiệm duy nhất. Nếu a   1 b   1  0 PP 
 Đặt ẩn phụ kết hợp mũ hóa phương trình.  t f  x  a 
Tìm tập xác định D và đặt log f x  log g x  t  
và biến đổi phương trình về dạng: a   b     g  x t  b    t t
f t  A  B  1 và giải bằng phương pháp đoán nghiệm và chứng minh nghiệm này duy nhất và tìm x khi biết t.  Dạng toán: .  log f x  .  log g x ta cũng làm tương tự bằng cách đặt a   b  
 log f x   log gx  γ.t với γ là bội số chung nhỏ nhất của  và  . a b  Loại 3. log g x  log b   3 f x     a
Đặt điều kiện: f x  0 và 0  gx  1.
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489 log f x b  
Sử dụng công thức đổi cơ số thì   3   log gx log b a b
 log f x  log b.log g x  log f x  log g x (đây là loại 2). b   a   b   a b    Loại 4. x a   p log x    qx  r   4 a λ  PP 
 Đặt ẩn phụ log λx    y để đưa về hệ phương trình đối xứng loại II hay gần đối xứng và sử a 
dụng phương pháp hàm để tìm được x  y .
Phương trình dạng log f x, y  log g x, y . a b   f   x, yta
Phương pháp: đặt t  log f x, y  log g x, y và chuyển về hệ
và đánh giá chặn giá trị a b  g   x, y tb
t . Từ đó chọn giá trị nguyên của x thích hợp và thử lại xem với giá trị nguyên của x đã chọn thì hệ
phương trình có nghiệm t trong miền đã chặn hay không?
Kiến thức để đánh giá chặn giá trị t :
+ Điều kiện có nghiệm của phương trình bậc 2.
+ Bất đẳng thức Cauchy, BCS…
+ Tính chất biến thiên của hàm số. x Câu 1.
Cho x , y là các số thực dương thỏa mãn log x  log y  log
2x y . Giá trị của bằng 9 6 4   y 1  3  A. 2 . B. . C. log   . D. log 2 . 3 2 2  2  2 Lời giải Chọn B x  9t
Đặt t  log x  log y  log
2x y . Khi đó t t ty  6t  2.9  6  4 9 6 4  
2x y  4tt  3    1 t t   t  9   3   2   3  1  2.  1  0           .  4   2  t  3  1  2  2      2  2 t t x  9   3  1 Do đó:        . y  6   2  2 2
4x 4x 1   Câu 2.
Biết x ; x x x
là hai nghiệm của phương trình 2 log 
  6x4x và 1 2  1 2  2      x  1 x  2x
a b với a, b là các số nguyên dương. Giá trị P a b là 1 2   4 A. P 14 . B. P 13 . C. P 15 . D. P 16 . Lời giải
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 Chọn A 4x  4x 1  x 2 2 2 1 1 Điều kiện  0 
 0  x  0, x  . x x 2 2 4x  4x 1 log
 6x 4x  log 2x 2 1  log x    2x  2 2 1  2x 1 2 2 2 x  log 2x 2 1 2x  2
1  log 2x  2x 1 . 2 2    
Xét hàm số f t  log t t với t  0 . 2
Ta có f t 1 
1 0 với t  0 suy ra f t log t t đồng biến trên 0;   . ln 2.t 3  1
Xét x  0;    , từ   1 ta có  2  3  5 x  l  f
x 2 f x x 2 2 4 2 1 2 2
1  2x  4x  6x 1  0   . 3 5  x   4 1  Xét x  ;    , từ   1 ta có 2   3  5  x   f
x 2 f x x 2 2 4 2 1 2 2
1  2x  4x  6x 1  0   . 3 5 x  l  4 2
4x 4x 1   Do đó, phương trình 2 log 
  6x4x có hai nghiệm phân biệt 2      x  3 5 3  5 x  ; x  . 1 2 4 4 1
Suy ra x  2x
9  5 . Suy ra a  9, b  5  P a b  14 . 1 2   4
x a y b z Câu 3.
Biết a  log 10 , b  log 150 và 1 1 1 log 15000 
với x ; y ; z ; x ; y ; z là các số 30 30 2000
x a y b z 1 1 1 2 2 2 2 2 2 nguyên, tính 1  x S . x2 1 2 A. S  . B. S  2 . C. S  . D. S  1 . 2 3 Lời giải Chọn A log 15000 log 150  2 log 10 Ta có 30 30 30 log 15000     1 2000 log 2000 log 2  3log 10 30 30 30
Ta có a  log 10  log 5  log 2  log 2  a  log 5   2 30 30 30 30 30
b  log 150  1 log 5  log 5  b 1  thay vào  
2 ta được log 2  a b 1 30 30 30 30 b  2a 2a b Ta có log 1500   2000
a b 1 3a 4a b 1
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489 x 2 1 Suy ra 1 S    . x 4 2 2 l  og y  log  x x y Câu 4. Cho các số thực dương ,
x y khác 1 và thỏa mãn  . l  og x y x y x    logy      Giá trị của 2 2
x xy y bằng A. 0. B. 3. C. 1. D. 2. Lời giải Chọn D ĐK: x y .  1  1  y   l
 og y  log x l  og y    x y  xx Ta có   log  y x    l  og x y x y x y x
  logy           l  og x y x y x
  logy      l  og x y x y x    log  1     x  1  1   y y     xy 1    2 2   x   x  
x xy y  2 . 2 2  x y x y x y x y x    x         x     2 2   1 log log 0 log  0   Câu 5.
Cho các số thực dương a , b thỏa mãn log a  log b  log a  log b 100 và log a , log b ,
log a , log b đều là các số nguyên dương. Tính P ab . A. 164 10 . B. 100 10 . C. 200 10 . D. 144 10 . Lời giải Chọn A
Ta có: log a  log b  log a  log b 100  2 2
log a  log b  2 log a  2 log b  200   log a   1  log b   1  202  81121   *
Mà log a , log b , log a , log b đều là các số nguyên dương nên  a        64 log 1 9 l  og a  64 a 10         b     100 log 1 11  b  b    log 100 10       *      100  a    l  og a 100 log 1 11  a    10        64     log b  64    b    b  10 log 1 9      Vậy: 64 100 164
P ab  10 .10 10 . mb nac Câu 6. Cho log 5  ; a log 7  ;
b log 3  c .Biết log 175 
.Tính A m  2n  3 p  4q 9 4 2 24 pc q A. 27 B. 25 C. 23 D. 29 Lời giải Chọn B
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 1 2 Ta có 2
log 175  log 7.5  log 7  2 log 5    24 24 24 24 log 24 log 24 7 5 1 2 1 2     3 3 log 3  log 2 log 3 log 2 1 3 1 3 7 7 5 5   log 7 log 7 log 5 log 5 3 2 3 2 1 2 1 2     1 3 1 3 1 3 1 3     log 7.log 2 log 7 log 5 log 3.log 5 1 2b 2a c.2a 2 3 2 3 2 3 2 . b c 1 2 2b 4ac 2b  4a     c . c 3 c 3 c  3 c  3 c  3   2b 2b 2ac 2ac
A m  2n  3 p  4q  2  8  3 12  25.
1 log x  log y Câu 7.
Cho x , y là các số thực lớn hơn 1 thoả mãn 2 2
x  6 y xy . Tính 12 12 M  . 2 log x  3y 12   1 1 1 A. M  . B. M 1 . C. M  . D. M  . 4 2 3 Lời giải Chọn B Ta có 2 2 2 2
x 6 y xy x xy 6 y  0  * .
Do x , y là các số thực dương lớn hơn 1 nên ta chia cả 2 vế của   * cho 2 y ta   x  2 3     x x y
x  3y n  
được    6  0         y   y x x  2   yl  2   y
Vậy x  3 y (1).
1 log x  log y log 12xy Mặt khác 12 12 M  12  (2). 2 log x  3y log x  3 y 12  2 12   2 log 36 y Thay (1) vào (2) ta có 12 M  1. 2 log 36 y 12 Câu 8. Cho
f x  a  2
ln x x 1bsin x  6 với a , b   . Biết f loglog e 2 . Tính f logln  10 . A. 4 . B. 10 . C. 8 . D. 2 . Lời giải Chọn B Đặt x  log log e 0  
Có: f x   a ln  2
x x 1  b sin x  6  2 0 0 0  0
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
NGUYỄN BẢO VƯƠNG - 0946798489   1      
Ta có f logln10  f log        
f loglog e  f x 0    log e 
f x   a ln  2
x 1  x b sin x  6  a ln  2
x x 1  b sin x  6 0 0  0 0 0   0 0    a ln 2
x x 1  b sin x  6 12   f x 12 10 . 0 0  0  0   x -x 6+3(3 +3 ) a a Câu 9. Cho x -x 9 + 9 = 14 và = với
là phân số tối giản. Tính P  . a . b x+1 1-x 2-3 -3 b b A. P 10. B. P  45  . C. P  10  . D. P  45. Lời giải Chọn B Ta có xx 2 x 2 x 2  x 2 9  9 14  3  2.3 .3 3 x 16
 3x 3x2 16  3x 3x  4.
6  3(3x  3x )
6  3(3x  3x )
6  3(3x  3x )   x 1  1 2 3 3 x
2 3.3x 3.3x 2 
3. 3x  3x  6  3.4 18 a 9        ab  45.  23.4 10 b 5   xx x 3
Câu 10. Biết phương trình 1 27  27 16  3      6  0 
có các nghiệm x a, x  log b và x  log c  3x  3 3 b
với a  , b c  0. Tỉ số
thuộc khoảng nào sau đây? c 3 5  3 5  A. (3;). B.  ;       1  ;   ;3  C. D. 2 2  2 2  Lời giải Chọn D Ta có   xx x 3 1 3x 3 27  27 16  3  
   6  0  3 27.3 x 16
 3x 3.3x x 6  0  1  3  Đặt xx 3 3x 3  x  3x 3  x  3x 3 3 3.3 3 27.3 3 3 3.3 .3 .3.3        x t t 3x 3  x  3x 3 3 27.3 9 3 3.3     x xx 2  t     x x 1 3 3.3 1 3 3 3  0     x x  Khi đó   3  2
1  t  7t  6  0  t  3  3 3.3
 3  3 x  3.3x 3  0       xx 2 t  2  3 3.3  2
3 x  2.3x 3  0  
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020   x 13 1 13 1 3   x  log3  2  2     b x 21 3 213 13 1 3     x  log    2.9.   3 2 2 c 21 3    x  3  3 x  1       a
Câu 11. Cho hai số thực dương a, b thỏa log a  log b  log a b . Tính . 4 6 9   b 1 1 5 1   5 1   5 A. . B. . C. . D. . 2 2 2 2 Lờigiải Chọn D
Đặt t  log a  log b  log a b . 4 6 9   t    2  1 5 a  4t      2t t  2   2   3  2   b  6t
 4t  6t  9t   1  0      . t    3   3   2  1 5
a b  9t    (L)    3  2 t a 4t  2  1  5      . b 6t  3  2
Câu 12. Gọi a là một nghiệm của phương trình 2 log x log x 2 log 4.2 6 18.3 x  
 0 . Khẳng định nào sau đây
đúng khi đánh giá về a ? 1 A. a  2 10  1. B. 2 a 10 . C. 2
a a 1  2 . D. a  . 100 Lờigiải Chọn D
Điều kiện x  0 . 2 log x log x  2   2 
Chia cả hai vế của phương trình cho 2log 3 x ta được 4  18  0     .  3   3  log x  2  Đặt t    , t  0 .  3   9 t  Ta có 2
4t t 18  0   4 .  t  2   L  9 log x  2  9 1 Với t     
 log x  2  x  . 4  3  4 100 1 Vậy a  . 100
Câu 13. Tổng các nghiệm của phương trình sau x 1 7   6 log 6x  5 1 bằng 7   A. 2 . B. 3 . C. 1. D. 10 . Lờigiải
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
NGUYỄN BẢO VƯƠNG - 0946798489 Chọn B 5
Điều kiện: x  . 6 Đặt y 1  log
6x  5 thì ta có hệ phương trình 7   x 1 7   6   y   x 1 1 1  7   6 y  5 x 1  y 1     7
 6x  7   6 y (2) y 1  log  6x  5 y 1 7   6x  5  7  5 t  5
Xét hàm số f t t 1 7  
 6t với t
thì f 't  1  7 ln 7  6  0, t  
f t  đồng biến nên 6 6
2  f x  f y  x y khi đó ta có phương trình x 1
7   6x  5  0. (3) 5 5
Xét hàm số g xx 1 7  
 6x  5 với x  thì   x   x g x g x       2 1 1 ' 7 ln 7 6 " 7 ln 7  0 x   6 6
nên suy ra phương trình g x  0 có không quá hai nghiệm. Mặt khác g  
1  g 2  0 nên x  1 và x  2 là 2 nghiệm của phương trình (3).
Vậy phương trình đã cho có 2 nghiệm là x  1 và x  2 .
Suy ra tổng các nghiệm của phương trình là 1 2  3.
Câu 14. Bất phương trình 9x  2   53x x  9 2x  
1  0 có tập nghiệm là S  a;b c;  . Tính
tổng a b c ? A. 0 . B. 1. C. 2 . D. 3 . Lờigiải Chọn D Đặt  3x t , t  0 .
Bất phương trình đã cho trở thành: 2
t  2x  
5 t  92x  
1  0  t  9t  2x   1  0 xt  9  0 t  9 3  9    1 TH1:     
t  2x 1  0
t  2x  1  0 x   3  2x 1  0  2 
Xét bất phương trình 2 : Đặt    3x g x
 2x 1 trên  .    3x g x ln 3  2 .
Gọi x là nghiệm duy nhất của phương trình g   x   0 , x  0 0 0
Khi đó, g x  0 có nhiều nhất hai nghiệm.
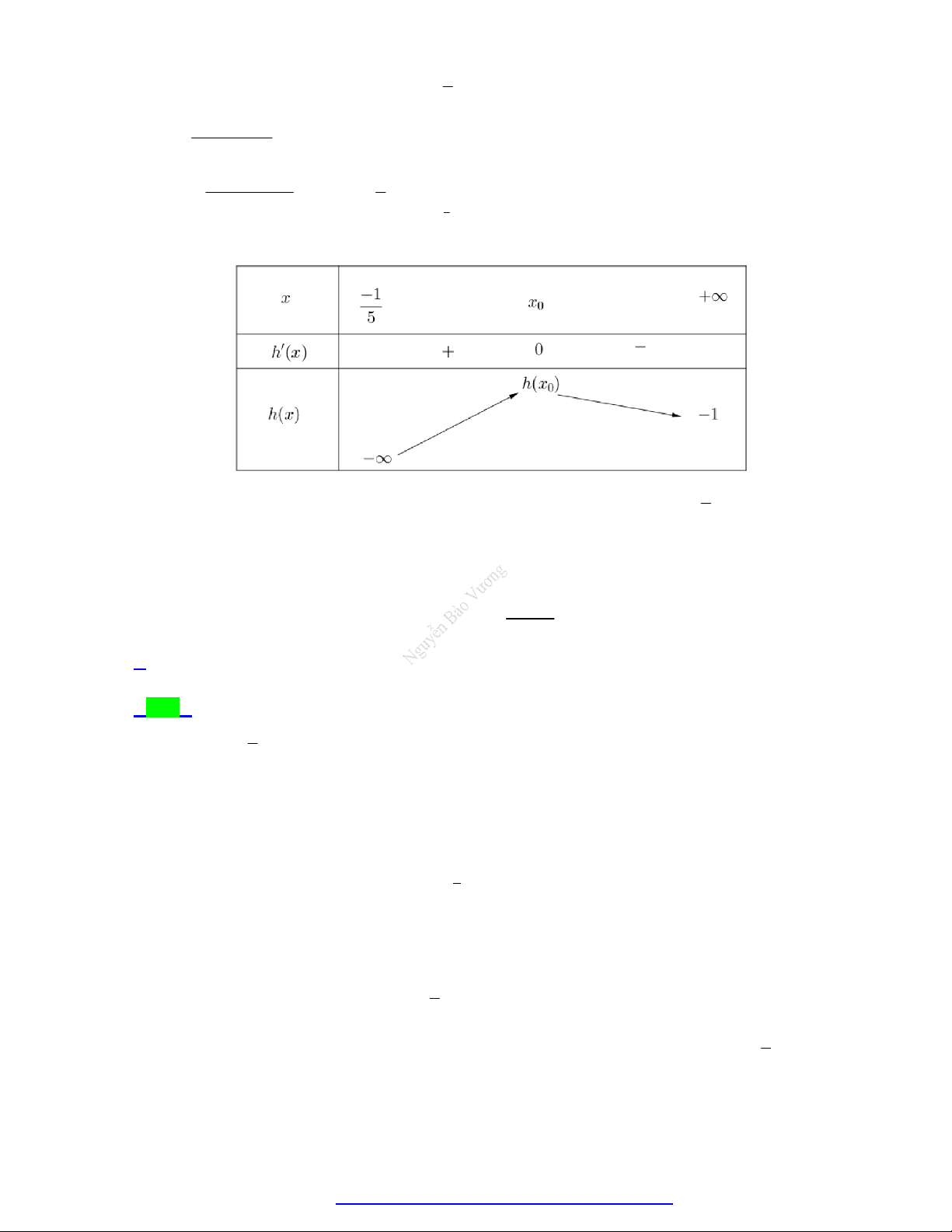
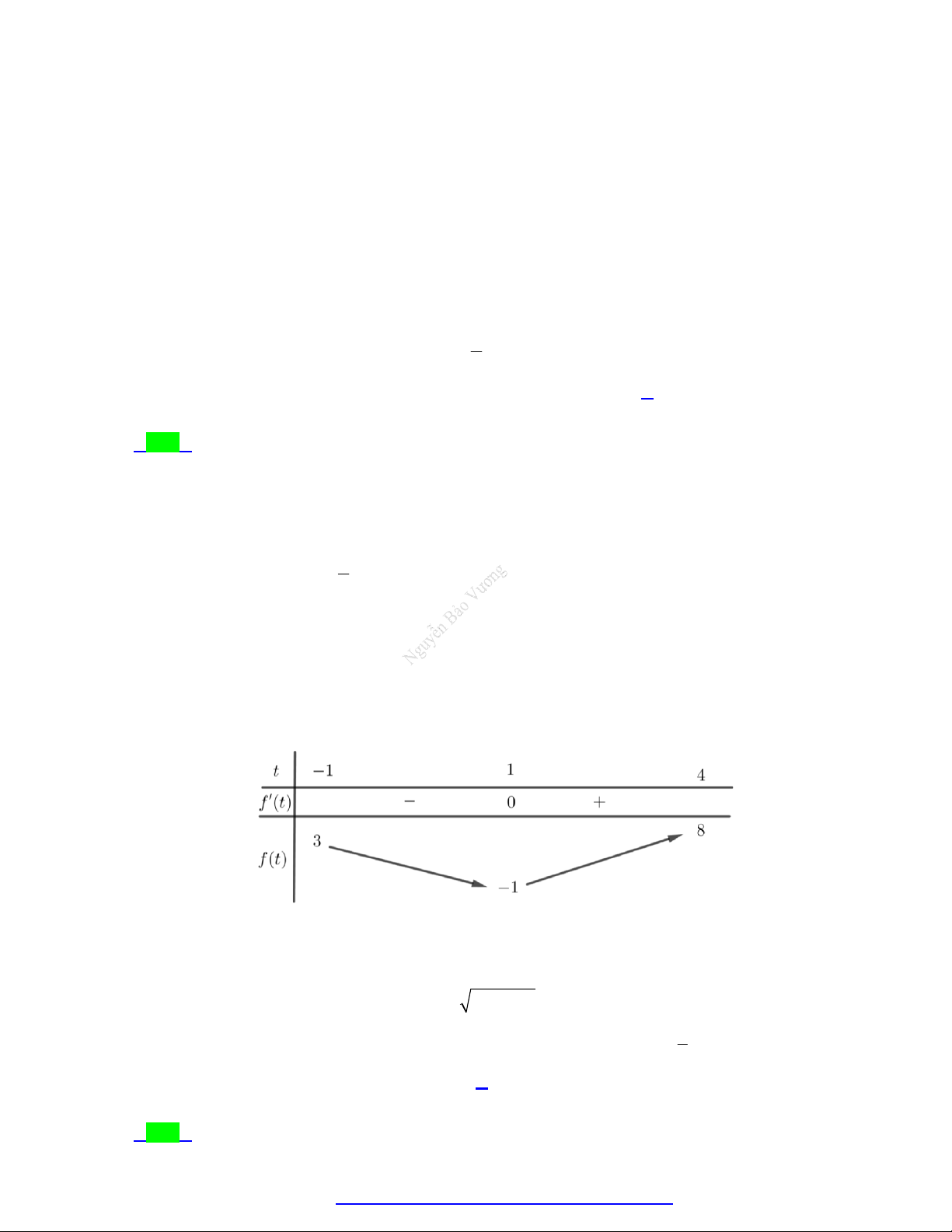
Xét thấy, g x  0 có hai nghiệm là x  0 và x  1 Ta có bảng biến thiên
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020x  0
Từ bảng biến thiên ta có, 2   x  1  Ta lại có,   1  x  2 .
Kết hợp 1 và 2 suy ra, x  2 .   * xt  9  0 t  9 3  9  3 TH2:     
t  2x 1  0
t  2x 1  0 x   3  2x 1  0  4 
Xét bất phương trình 4 : Đặt    3x g x
 2x 1 trên  .     3x g x ln 3  2 .
Gọi x là nghiệm duy nhất của phương trình g  x  0 , x  0 0 0
Khi đó, g x  0 có nhiều nhất hai nghiệm.
Xét thấy, g x  0 có hai nghiệm là x  0 và x  1 Ta có bảng biến thiên
Từ bảng biến thiên ta có, 4  0  x  1
Ta lại có, 3  x  2 .
Kết hợp 3 và 4 suy ra, 0  x  1. ** Kết hợp  
* và ** ta được tập nghiệm của BPT đã cho là S  0;  1 2;  2 2 2
Câu 15. Phương trình sin x cos x sin 2 3 4.3 x  
có bao nhiêu nghiệm thuộc  2  017; 2017 . A. 1284 . B. 4034 . C. 1285 . D. 4035 . Lờigiải Chọn C 2 2 2 2 2 2 Ta có sin x os c x sin x sin x 1sin x sin 2  3  4.3  2  3  4.3 x
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
NGUYỄN BẢO VƯƠNG - 0946798489 Đặt 2
sin x t với t 0;  1 , ta có phương trình t t t t  2   1 t 3 t  2   1   2   4.3   3.  4    
. Vì hàm số f t    3.  
  nghịch biến với t 0;  1 3t  3   9   3   9 
nên phương trình có nghiệm duy nhất t  0 . Do đó sin x  0  x k , k   . 20  17 2017 Vì x  2  017; 2017 nên ta có 2
 017  k  2017   k  nên có 1285 giá trị  
nguyên của k thỏa mãn. Vậy có 1285 nghiệm. x
Câu 16. Cho các số thực dương ,
x y thỏa mãn log x  log y  log
2x  2 y . Tính tỉ số ? 6 9 4   y x 2 x 2 x 2 x 3 A.  . B.  . C.  . D.  . y 3 y 3 1 y 3 1 y 2 Lờigiải Chọn B x  6t (1) 
Giả sử log x  log y  log
2x  2 y t . Ta có:  y  9t (2) . 6 9 4  
2x  2y  4t (3)  t x 6t  2  Khi đó    0   . y 9t  3 
Lấy (1), (2) thay vào (3) ta có t  2  2   1 3  (thoûa) 2t t    2   2   3  3 1 2.6t 2.9t 4t      2.  2  0      .  3   3  t  2    1 3   (loaïi)  3 
Câu 17. Số nghiệm của phương trình log 3 5   2 xx là: A. 0 . B. 1. C. 3. D. 2 . Lờigiải Chọn B Đk: x  3  Đặt t  log x  3   5t x
 3 , phương trình đã cho trở thành 5   t t  2   1  2t 5t   3 2t 3 5t   
    3.   1 (1)  5   5  t t  2   1 
Dễ thấy hàm số f t      3.  nghịch biến trên  và f  
1  1 nên phương trình (1) có  5   5 
nghiệm duy nhất t 1.
Với t 1, ta có log
x  3  1  x  2 5  
Vậy phương trình có nghiệm duy nhất x  2 .
Câu 18. Phương trình 33x 33 x 4 x 4 x 3 3  3  3  3
 10 có tổng các nghiệm là? A. 0 . B. 2 . C. 3. D. 4 . Lờigiải Chọn A
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 33x 33 x 4 x 4 x 3 3  3  3  3  10 7 x 27 x 81  x 1   x 1   7 3 3 3 3  27.3   81.3   10  27. 3   81. 3   10 7 ' 3x x  3x   x    3 3  3   3  Côsi x 1 x 1 Đặt t  3   2 3 .  2 3x 3x 3  x 1  x x 1 x 1 1 x 1 3 3 2 3 3  t  3   3  3.3 .  3.3 .   3   t  3tx x 2 x 3 x 3  3  3 3 3 3 x 3 10 10
Khi đó: 7 '  27  3 t  3t  3 3
 81t  10  t   t   2  N  27 3 10 x 1 10 Với t   3   7'  3 3x 3
y  3  N  1 10 Đặt 3x y   0 . Khi đó: 7 '  2 y 3y 10 y 3 0          1 y 3
y  N   3 Với  3  3x y  3  x  1 . 1 x 1 Với y   3   x  1  . 3 3
Suy ra tổng các nghiệm của phương trình là: 1   1  0 . x x 2
Câu 19. Tìm tập nghiệm S của bất phương trình 2 3 1  3  . 3x 1 A.  ;
 0 log 2;  . B. 0;log 2 . 3  3   1  C. 0;   2;    . D. 0;  .    2  Lờigiải Chọn A x   x 2 x x 2 3x (3x 1) 2 Ta có bất phương trình: 2 3 1  3   3 1  3   3x 1  3x 1 3x 1 3x 1 3x 1 3x (3x    1)  2 (*)
Đặt  3x  1  1  3x tt 1
Từ đó bất phương trình (*)  t  (t 1) t  2  t  2  (t 1) t Trường hợp 1: 1   t  2 1   t  2  x x   t  1
 1  t  2  1  3  1  2  3  1  x  0 . (t 1)t  0  t  0 
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
NGUYỄN BẢO VƯƠNG - 0946798489 Trường hợp 2:. t   2 t   2 t   2  x     
4  t  2  3  2  x  log 2 . 2 2 2 3
(t 1)t  (t  2)
t t t  4t  4   t    3  x  log 2
Kết luận nghiệm của bất phương trình là: 3  . x  0  x x y xa b
Câu 20. Cho x , y là các số thực dương thỏa mãn log  log y  log và 
, với a , b là 25 15 9 2 4 y 2
các số nguyên dương, tính a b .
A. a b  14 .
B. a b  3 .
C. a b  21 .
D. a b  34 . Lờigiải Chọn D x  log25 2 y  15 x x y    Ta có log  log y  log x  25 15 9  log25 2 2 4  x 15 x log  log 9 25   4 2 x 2t t  5   5  Đặt t  log
x  2.25t , ta được 2.25t 15t 4.9t    2   4 25     2  3   3  t 1   33 x 2.25t  5  1 33  t  log    2.  . 5   4 y 15t  3  2 3
Do đó a  1, b  33 nên a b  34 .
Câu 21. Biết rằng phương trình log  1009 1 x
 2018log x có nghiệm duy nhất x . Khẳng định nào dưới 2  3 0 đây đúng? 1 1 2 1 1 A. 1008 1006 3  x  3 . B. 1009 x  3 . C. 1008 1  x  3 . D. 1007 3  x  1 . 0 0 0 0 Lờigiải Chọn C
Điều kiện: x  0 . Đặt t  log  1009 1 x
 2018log x . Khi đó t  0 . 2  3 1009 t 1  t   x  2t t t  3   1   t t t t     2 2 1
 3  2 1   3   3 1  2      1   (*). 2018   x  3t  2  2    t t  3   1 
Ta thấy hàm số f t   
    luôn nghịch biến và liên tục trên 0;  và f 2  1 nên  2   2   
phương trình (*) có duy nhất một nghiệm t  2 . 1 1009  x  3 hay 1009 x  3 . 0 1 1 1 Mà 0   nên 1008 1  x  3 . 1009 1008 0
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Câu 22. Phương trình 2 log cot x  log
cos x có bao nhiêu nghiệm trong khoảng 0; 2018  ? 3   2   A. 2018 nghiệm. B. 1008 nghiệm. C. 2017 nghiệm. D. 1009 nghiệm. Lờigiải Chọn A si  n x  0 Đk:  . cos x>0 
2 log cot x  log cos x  log cot x2  log cos x 3 2 3 2   2 2
 log cos x  log sin x  log cos x 3 3 2   2
 log cos x  log  2
1 co s x  log cos x 3 3  2  
Đặt  log cosx  osx=2t t c . 2 2 t 2 t  4 
Phương trình trở thành  log
t  4t  3t 12t hay  4t  1 3 2   1 2 t  3  t  4  Hàm số     4t f t   đồng biến trên   3 
Mặt khác f   1  1 nên x  1
 là nghiệm của phương trình.
Do đó phương trình có nghiệm duy nhất t  1  . 1 
log cosx=-1  cos x   x    k.2 . 2 2 3  1 6053   k   x     6 6 0; 2018   . 1 6055   k  6 6
Vậy trong khoảng 0; 2018  có 1009.2  2018 nghiệm.
Câu 23. Cho dãy số u thỏa mãn log 2u  63  2log u  8n  8 , * n   . Đặt 3  5  4  nn u .S 148
S u u  ...  u . Tìm số nguyên dương lớn nhất n thỏa mãn n 2n  . n 1 2 n u .S 75 2n n A. 18 . B. 17 . C. 16 . D. 19 . Lờigiải Chọn A Ta có * n   , log
2u  63  2 log u  8n  8  log 2u  63  log
u  8n  8 . 3  5  2  n  3  5  4  n
2u  63  3t t  2u  63  3  Đặt t  log 2u  63 5  5  ( với n  5 ) 3  5    t
u  8n  8  2tu   32  2 n  5 1 3t 2.2t   
t  2  u  8n  4 . Khi đó u  36 n 5
Với u  8n  4 và u  36 , ta có: n 5 log 2u  63  2 log
u  8n  8  log 2.36  63  2 log
8n  4  8n  8 3  5  4  n  3   4  
 log 9  2 log 4  2  2 đúng * n   . 3 4 Ta có: u
u  8 n 1  4  8n  4  8 . Vậy u là cấp số cộng có số hạng đầu u  4 , công sai n n 1  n     1 d  8.
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
NGUYỄN BẢO VƯƠNG - 0946798489
u u .n 1 n  2
S u u  ...  u   4n . n 1 2 n 2 u .S 8n  4 2 .16n 148 Do đó n 2n    n  19 . u .S n n n n 16 4 2 .4 75 2
Câu 24. Số nghiệm của phương trình 2
log x  2x  log  2
x  2x  2 là 3 5  A. 3. B. 2 . C. 1. D. 4 . Lờigiải Chọn B
ĐK: x  0; x  2 . Đặt 2
t x  2x 2
x  2x  2  t  2
 log t  log t  2 . 3 5  
Đặt log t  log t  2  u 3 5   log t u u   t  3 3    
log t  2  uu  t 5    2  5  5u 2 3u   
5u  3u  2 (1)
5u  2  3u
5u  3u  2      u u  .  3   1 
5u  2  3u u u  3  2  5   2  1 (2)      5   5  Xét   1 : 5u 3u   2
Ta thấy u  0 là 1 nghiệm, dùng phương pháp hàm số hoặc dùng BĐT để chứng minh nghiệm u  0 là duy nhất. Với 2
u  0  t  1
  x  2x 1 0, phương trình này vô nghiệm. u u  3   1  Xét 2 :  2  1      5   5 
Ta thấy u  1 là 1 nghiệm, dùng phương pháp hàm số hoặc dùng BĐT để chứng minh nghiệm u  1 là duy nhất. Với 2
u  1  t  3  x  2x  3  0 , phương trình có 2 nghiệm phân biệt thỏa x  0; x  2 . BÌNH LUẬN
Cho f x  g x 
1 nếu f x, g x đối nghịch nhau nghiêm ngặt hoặc g x  const và f x
tăng, giảm nghiêm ngặt thì (1) có nghiệm duy nhất.
Câu 25. Tìm giá trị gần đúng tổng các nghiệm của bất phương trình sau:    22 22 2 4  2 2 log  2 log  5  13    4 x x x x x    x x   6 5 4 3 2 24 2 27 2 1997 2016 0 2  3 3 log x log x 22 22    3 3  A. 12,3 . B. 12 . C. 12,1. D. 12, 2 . Lờigiải Chọn C
Điều kiện: 0  x  1. Ta có 6 5 4 3 2
24x  2x  27 x  2x  1997 x  2016
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
  x x 2   x  2 3 2 3 6 4 2
1  22x  26x 1997x  2015  0 , x  .
Do đó bất phương trình đã cho tương đương với    22 22 2 4  2 2 log  2 log  5  13    4  0  . x x 2  3 3 log x log x 22 22    3 3  22 Đặt t  log
, ta có bất phương trình x 3 2 2
2t  2t  5  2t  4t  4  13 2 2  1   3  13  t    1 t 2 2 1      .  2   2  2       1 3   13
Đặt u t  ; 
 và v  1 t; 
1 . Ta có u v u v  .  2 2  2 1 t  5 3 4 4  22  Dấu bằng xảy ra khi
2   2t 1  3  3t t   x   12, 06  12,1   . 1 t 2 5  3 
Nghiệm trên thỏa điều kiện.  2 log 100 x  log10 x
Câu 26. Tìm tích tất cả các nghiệm của phương trình 1log 4.3  9.4  13.6 x . 1 A. 100. B. 10 . C. 1. D. . 10 Lờigiải Chọn C ĐK: x  0 . 2 log10 x log10 x  3   3  PT 2.log10 x 2.log10 x log10 x  4.3  9.2  13.6  4. 13.  9  0      2   2  log10 x  3  Đặt t   0  
thì phương trình trở thành:  2  log10 x  3  t  1   1     x  1 log 10  0   2 x  2 
4t 13t  9  0   9     10 .   log10 xt      3  9 log 10x 2  4    x  10     2  4
Suy ra tích các nghiệm bằng 1.
Câu 27. Tập nghiệm của bất phương trình x2 x2 2.7  7.2
 351. 14x có dạng là đoạn S   ; a b . Giá trị
b  2a thuộc khoảng nào dưới đây?  2 49  A. 3; 10  . B. 4; 2 . C.  7; 4 10  . D. ;   .  9 5  Lờigiải Chọn C x2 x2 2.7  7.2  351. 14x
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
NGUYỄN BẢO VƯƠNG - 0946798489 49.7x 28.2x 351. 14x    2 x 2 7 2 x  49.  28.  351 14x 14x 7x 2x  49.  28.  351. 2x 7x 7x 28 Đặt t
, t  0 thì bpt trở thành: 49t   351 2x t 4 7 4 7x 7   t      4  x  2 . 49 2 49 2x 2 Khi đó S   4  ; 2 .
Giá trị b  2a  10   7;4 10  .
Câu 28. Tập nghiệm của bất phương trình  x   x  x      2 2 2 2 2 2 1 2 1 là A. S   ;  0 .
B. S  1;  .
C. S  0  ;1 . D. S   3  ;  . Lờigiải Chọn C
Điều kiện xác định: 2x 1  0  2x  1  x  0 Đặt
x   t t   x 2 x 2 2 1 ,
0  2 1  t  2  t  1
Bất phương trình trở thành:
t 1 22  t 1 2 2
1 t2  t   1
 t  31 t2 2 2 2 2  2 2 2  t 1  t  3 2  2 2  t   1 t   1
 t  3t   1   t   1  2 2 t
 2t 1  t  3 t   1      t  1. t  1 t  1  
Do đó 2x 1  1  2x 1  1  2x  2  x  1.
Kết hợp điều kiện: 0  x  1.
Vậy bất phương trình có tập nghiệm là: S  0  ;1 . 2 2
Câu 29. Bất phương trình x x 1  1  x x 1 2 2 2 2    
có tập nghiệm S  a;b . Khi đó a b bằng A. 2 . B. 3 . C. 1. D. 10 . Lờigiải Chọn B ĐK: x  1. 2 2 1  
Bất phương trình đã cho tương đương với x x 1 x x 1 .2 .2 2  2 2 2 2 2 x x 1  x x 1 2 .2 4 2.2 2.2     
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 2  xu  2 u  0 Đặt  , điều kiện  . x 1 v  2  v  0  
Bất phương trình trở thành
uv  4  2u  2v  uv  2u  4  2v  0  u v  2  2v  2  0  u  2v  2  0 . u  2  0 u  2   v  2  0 v  2       . u 2 0    u  2      v  2  0   v  2  u  0
Kết hợp với điều kiện  ta được v  0  2 x 2  u  2  2 x  1 2  x  1   x  1
x  1 x  1     x 1   0  v  2   0  2   2   x 1  1 x 1  1 x  2             2  2 0 u 2 x      0  2  2 x  1  1   x  1 1  x  1           v 2   x 1    x 1  1 x    x      2 2 2 1 1     x  ;    1 1; 2
Kết hợp điều kiện x  1, ta suy ra tập nghiệm của bất phương trình đã cho là S  1;2 . x x
Câu 30. Tập nghiệm của bất phương trình       xlog2 5 5 21 5 21  2 là A. S   2   ;1 . B. S   1   ;1 .
C. S  1;5 .
D. S  1;  . Lờigiải Chọn B Ta có: x xx x  5  21   5  21   x   x xlog2 5 5 21 5 21  2
 5  21  5  21  2 .x5        5  2   2      x x  5  21   5  21  1 Đặt    t  
  , t  0 , bất phương trình trở thành:  2   2  t     1 5  21 5  21 2
t   5  t  5t 1  0   t  . t 2 2 Do đó ta có: x 5  21  5  21  5  21      1   x  1. 2  2  2  
Vậy bất phương trình có tập nghiệm là: S   1   ;1 .
Câu 31. Có bao nhiêu cặp số nguyên x; y thỏa mãn 0  x  2020 và log 3  3   2  9y x x y ? 3  
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
NGUYỄN BẢO VƯƠNG - 0946798489 A. 2019 . B. 6 . C. 2020 . D. 4 . Lời giải Chọn D Cách 1: Ta có: log 3   3 
 2  9y  log    2
1  1  2  3 y x x y x x y .   1 3 3 Đặt log
1   1  3t x t x . 3   Phương trình   1 trở thành: t 2  3  2  3 y t y 2 Xét hàm số     3u f u u trên  .    1 3u f u
ln 3  0 , u   nên hàm số f u đồng biến trên  .
Do đó 2  f t  f 2 y  t  2 y  log
1  2  1  9y   9y x y x x 1 3   Vì 0 
 2020  0  9y 1  2020  1  9y x
 2021  0  y  log 2021 9 log 2021  3,464 3 
Do y    y  0;1; 2; 
3 , có 4 giá trị của y nên cũng có 4 giá trị của x
Vậy có 4 cặp số nguyên x; y . Cách 2: Ta có: log 3   3 
 2  9y  log    2
1  1  2  3 y x x y x x y 3 3
Xét hàm số f x  log x 1  x 1 với x  0; 2020. 3   1
Ta có f x 
1 0, x x 0;2020  
Hàm số f x đồng biến trên đoạn x   1 ln 3 0;2020.
Suy ra f 0  f x  log x 1  x 1  f 2020  1  f x  log 2021 2021 3       2  1  2  9y y  log 2021 2021  2028 3 Nếu y y 0
y  0  2 y  9  9  9  1  y  0 Khi đó
   2  9y    2  9y  2027  9y y y y
 2027  2y  2027
y  log 2027  3, 465  y  3  0  y  3 9  y  0;1;2; 
3 . Do f x là hàm số luôn đồng biến nên với mỗi giá trị của y chỉ cho 1 giá trị của x .
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 +) y  0  log
x 1  x 1  1  x  0 3   +) y  1  log
x 1  x 1  11  log
x 1  x  10  x  8 3   3   +) y  2  log
x 1  x 1  85  log
x 1  x  84  x  80 3   3   +) y  3  log
x 1  x 1  735  log
x 1  x  734  x  729 3   3  
Vậy có 4 cặp số nguyên x; y .
Câu 32. Có bao nhiêu cặp số nguyên  , x y thỏa mãn log
3x y  9  1? 2 2   9 x y A. 7 . B. 6 . C. 10 . D. 9 . Lời giải Chọn B
x  , y  
x  , y     Điều kiện: 2 2
0  9x y  1  
x, y     0,0; 0,  1 ; 0,   1  3
x y  9  0  
3x y  9  0  Khi đó 2 2
9x y  1 nên ta có: log
3x y  9  1 2 2
 3x y  9  9x y 2 2
 9x  3x y y  9  0 2 2   9 x y 2 2  1   1  19  3x   y        2   2  2 2  1  19 1   38 1 38  3x      x  2 2     6 6 Suy ra:    2   1  19 1   38 1 38 y    y      2   2   2 2 x   0;  1
Do x  , y   nên  y   2; 1; 0;1;  2 
Kết hợp điều kiện, ta được  , x y   0, 2  ; 0, 2; 1; 2  ; 1,   1 , 1,0; 1,  1 ; 1, 2
Thử lại ta thấy cặp  , x y  1, 2
  không thỏa yêu cầu đề bài.
Vậy có 6 cặp số nguyên  ,
x y thỏa yêu cầu bài toán.
Câu 33. Có bao nhiêu giá trị nguyên của tham số m sao cho tồn tại duy nhất cặp số thực  , x y  thỏa mãn 2 2
x y  18 và x y m  log y  2m  log x m ? 3   3   A. 3 . B. 2 . C. 4 . D. 5 . Lời giải Chọn C x m Điều kiện:  . y  2  m
Ta có: x y m  log y  2m  log x m 3   3    log
x m x m  log
y  2m y  2m   1 3   3  
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
NGUYỄN BẢO VƯƠNG - 0946798489
Xét hàm số f t   log t t với t  0 . 3 1
Ta có: f t  
1  0, t  0 nên hàm số f đồng biến trên khoảng 0; . t ln 3 Do đó:  
1  x m y  2m y x m . 2 Theo giả thiết: 2 2 2 x y
x   x m   g x 2 2 18 18
 2x  2mx m 18  0 2
Để tồn tại duy nhất cặp số thực  ,
x y thỏa yêu cầu bài toán thì phương trình 2 phải có duy nhất
một nghiệm x m (khi đó y  2m do y x m ). 2
  m  36  0  m  6 
Trường hợp 1: 2 có nghiệm kép x m    m   m  6 . y    2m m  0    2
Trường hợp 2: 2 có hai nghiệm phân biệt x m x 1 2 3 10
 Nếu x m thì thay vào 2 ta được 2
5m 18  0  m  
(loại do m   ) 1 5 3 10 3 10
 Nếu x m x  . a g m 2
 0  5m 18  0    m  1 2 5 5
Từ các trường hợp trên và m    m  6  ; 1; 0;  1 . 2
x  2x 1  Câu 34. Biết
x , x (x x ) là hai nghiệm của phương trình 2 log
x  2  3x và 1 2 1 2 3   3x  
4x  2x a b , với ,
a b là hai số nguyên dương. Tính a b 1 2
A. a b  9 .
B. a b  12 .
C. a b  7 .
D. a b  14 . Lời giải Chọn D x  0 Điều kiện:  x  1  Ta có: 2
x  2x 1  2 log
x  2  3x  log x 1
x  2x 1  log x x 3  2 2 3   3x 3    log  x  2 1   x  2 1
 log x x (1) 3 3 1
Xét hàm số f t   log t t f t  1  0, t   0 3   t.ln3  3  5 x   1 2 2 2
Phương trình (1) trở thành f x  
1   f x   x   2 1
x x  3x 1  0    3  5 x  2  2
Vậy 4x  2x  9  5 . Khi đó a  9,b  5  a b  14 1 2
Câu 35. Có bao nhiêu cặp số nguyên  ;
x y thỏa mãn 0  x  2020 và log 4  4   1  2y x x y ? 2   A. 10 . B. 11. C. 2020 . D. 4 .
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 Lời giải Chọn B
Đặt log 4x  4 t t2
t  4x  4  2  x  2 1 . 2 Từ điều kiện t2
0  x  2020  0  2
1 2020  1 t 11 log 2021. 2 Theo giả thiết ta có: t2 1 2  1 2y t y   * . Xét hàm số   1 2u f u u   
với 1 u 1 log 2021 . 2 Có f 'uu 1 1 2   
.ln 2  0, u  1;1 log 2021 nên hàm
f u đồng biến trên đoạn 2  1;1log 2021 . 2  Dựa vào  
*  f t  
1  f y  
1  t 1  y 1. Mặt khác 1 t 1
 1 log 20211 y 11 log 2021 0  y  log 202110,98 . 2 2 2
Vì y    y  0;1; 2;3; 4;5;6;7;8;9;1  0 .
Vậy có 11 cặp số nguyên thỏa mãn ycbt.
Câu 36. Có bao nhiêu số nguyên x sao cho tồn tại số thực y thỏa mãn log  2 2 x  4 y  log x  4 y . 2  3   A. 3 . B. Vô số. C. 2 . D. 4 . Lời giải Chọn C 2 2
x  4 y  0 Điều kiện:  x  4 y  0  2 2  t
x  4 y  2 Đặt t  log  2 2 x  4 y  log x  4 y  2  3   
x  4 y  3t
Áp dụng bất đẳng thức B. C. S, ta có:
x y2   x y 2   
 x   y2 2 2 2    2 2 4 1. 2.2 1 2 . 2 5 x  4 y
 9t  5.2t t  log 5 9 2 log 9 5 Từ 2 2  4  2t x y suy ra 2 t 2 x  2  2  2,1
Do x   nên x  1  ;0;  1  1 2 t 2 t y  2    y     1   1 4 2 1  4  Với x  1     
4 y  3t 1 1 
y  .3t   1 2   4 Thay 2 vào  
1 ta được 9t  2.3t  4.2t  5  0 Do  
1 nên 2t 1  0  t  0 . Khi đó: t t t   t t  
t    t  2 9 2.3 4.2 5 4 4.2 4 2.3 1 2 2
 3.2t 1  0 nên không tồn tại giá trị
của t . Vậy loại x  1  . t  log 4 9 2  t 4 y  2  2
 Với x  0      nhận x  0 . log t 9 4 1 4 y  3 2   y  .3  4
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
NGUYỄN BẢO VƯƠNG - 0946798489  1 2 t 2 t y  2    y     1 4 2 1  4
 Với x  1     .
4 y  3t 1 1 
y  .3t   1   4 t  0 Dễ thấy 
là một nghiệm của hệ  nhận x  1 . y  0  Vậy x 0;  1 .
Câu 37. Có bao nhiêu cặp số nguyên  x; y thoả mãn 0  x  2020 và      2 2 ln 1  1 y x x xy e ? A. 0 . B. 7 . C. 1. D. 8 . Lời giải Chọn C Ta có:      2 2 ln 1  1 y    2 ln    2ln   1 1 x y x x x y e xe
y e   1 . Xét hàm số:   t
f t t e , ta có:    1 t f t
e  0 nên hàm số f t  đồng biến trên  . Do đó:  
1  f 2ln  x  
1   f y  y  2ln  x   1 .
+ Do 0  x  2020 nên 1  x  1  2021  0  y  2 ln 2021  15, 22 .
Do y   nên y 0;1; 2;...;14;1  5 . y Có y   x   2 2ln 1  x  e 1.
Với y 0;1; 2;...;14;1 
5 thì chỉ có y  0 thì x   .
Vậy có duy nhất 1 cặp số nguyên  x; y thoả mãn đề bài.
Câu 38. Có bao nhiêu số nguyên x sao cho tồn tại số thực y thỏa mãn log (x y)  log  2 2 x  2 y ? 3 4  A. 1 B. 3 C. 2 D. Vô số Phân tích Lời giải Chọn C
Điều kiện: x y  0 . t
x y  3tx  3  y
Đặt log (x y)  log  2 2 x  2 yt , suy ra  3 4    2 2 2
x  2 y  4t t 2 t  3  y    2y  4   1  Phương trình   1  2 3
 2.3t  9t  4t y y
 0 . Phương trình phải có nghiệm nên: 2t t     t t    3  3 1 9 3 9 4  0    t    .  2  2 2 
0  x y  3 Do đó: 2 
x  2  x 0;   1 ( vì x   ) 2 2
x  2 y  2  Thử lại: t  log 2 t 4   y  3  Với 9 x  0     2 t log 4 2 2 y  4   9 y  3 
Trang 24 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 1    y  3tt  0 Với x  1     2 1
  2 y  4t y  0   
y  3t 1
Với x  1  
 2.9t  4.3t  3  4t  0 2 2
2 y 1  4t  Khi 0 9t 4t t   
nên 2 vô nghiệm, khi 0 4t t   1 1 4t  
 0 nên 2 cũng vô nghiệm. Vậy x 0;  1 .
Câu 39. Có bao nhiêu cặp số nguyên dương  ;
x y thỏa mãn đồng thời hai điều kiện: 6 1  x  10 và
x x   2 2 y 2 2 log 10 20
20  10  y x  2x 1? A. 4 . B. 2 . C. 3 . D. 1. Lời giải Chọn D Điều kiện: 2
10x  20x  20  0, đúng x    . Ta có
x x   2 2 y 2 2 log 10 20 20  10
y x  2x 1            2 2 2 2 2 1 log 10 2 2   10y x x x xy              2 2 2 2 2 1 log10 log 2 2  10y x x x xy           2 2 2 2 2 2 log 2 2  10y x x x xy  2 x x   
x x   2 log 2 2 2 y 2 10 log 2 2  10  y (*). Xét hàm   10t f tt trên  .
Ta có    10t f t
.ln10 1  0 , t   . Do đó f t  đồng biến trên  . Khi đó 2 (*)  f   2
x x    f  2 log 2 2 y    2 x x   2 log 2 2  y 2   2  2  10y x x       2 2 1 1  10y x . 2 2 Vì 6 2
1  x  10 nên     y x     6 1 1 1 10 10   1  1 y  2 2 6 0 log 10 1 1      .   Vì y
  nên y 1;2;  3 . x  2  (ktm) + Với y  1 2
x  2x  2 10 2
x  2x 8  0   . x  4 (tm)  + Với y  2 2 4
x  2x  2 10 2
x  2x 9998  0 (không có giá trị x nguyên nào thỏa mãn). + Với y  3 2 9
x  2x  2 10 2
x  2x 999999998  0 (không có giá trị x nguyên nào thỏa mãn).
Vậy có một cặp nguyên dương  ; x y  4; 
1 thỏa mãn yêu cầu bài toán.
Câu 40. Có bao nhiêu số nguyên
y  10 sao cho tồn tại số nguyên x thỏa mãn y y 2  xx x     x  2 2 2 1 5 2 5 1 ? A. 10 B. 1 C. 5 D. Vô số Phân tích
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
NGUYỄN BẢO VƯƠNG - 0946798489
Phương trình dạng f u  f v .
Phương pháp: Chứng minh y f t  đơn điệu trên  ;
a b . Từ phương trình suy ra u v . Từ đó tìm
sự liên hệ giữa 2 biến , x y và chọn , x y thích hợp. Lời giải Chọn C y 2 y y y 2 2 Ta có: 2  x2 x x 1      x   2  x2 x x 1  2 5 2 5 1  5  2  x 1  5  x x Xét:   1 5t f t  
t đồng biến trên  . Do đó từ phương trình trên suy ra: y y y y
x   x x   x  2 2 2 2 2 1 1
 2  2  x  1 2 . y
Do x nguyên nên ta có 2
2   và y  10 nên y  0; 2; 4; 6;  8 .
Câu 41. Có bao nhiêu cặp số nguyên dương  x; y thoả mãn 1  x  2020 và 2y y 2x log  y 1 x 2      2  A. 2021. B. 10 . C. 2020 . D. 11. Lời giải Chọn D Theo đề bài, 2 y y 2x log  y 1 x 2      2    y y 2y  2  log 2  2x  log x  2   2   2    x   y y y y 2 2y  2  2  log 2  2x  2  log 2   2   2   y y    x    x   y y 2 2 2 2 2. 2  log 2  2   log   1 . 2     2   2 2    
Xét hàm số f t   2t  log t , t  0 . 2 1
Vì f t   2   0 t
  0  f t  đồng biến trên 0;   t ln 2  x   x y 2 2 y y 2 2 y nên   1  f 2  y y y y 1  f  2 
 2.2  2x  2  2x  2  x  2    . 2 2  
Do 1  x  2020 nên 0  y 1  log 2020  1  y  11,98 . 2 Do *
y  nên y 1; 2;3;...;1 
1 , với mỗi giá trị y cho ta 1 giá trị x thoả đề.
Vậy có 11 cặp số nguyên  x; y thoả mãn đề bài. Câu 42. Có bao nhiêu số nguyên x sao cho tồn tại số thực y thỏa mãn
2 log  x y  log 1 3  log  2 2
x y 1 2 2 3  A. 1 B. 3 C. 2 D. 5 Lời giải Chọn C
Đặt: t  2 log  x y  log 1 3  log  2 2 x y 1 . 2 2 3 
Trang 26 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 2     2 t log 1 3 t 2      x y x y    1 3.2 2 Suy ra:    t t 2 2 2 2
x y 1  3
x y  1 3   Ta có:
x y2   2 2 2 x y    t
1 3 .2t  21 3  1 32t t .   1 3 2 t t  1   3  1 3        2  2    2   t t 1  3   
Xét f t      
 nghịch biến trên  nên 2  2      t t  1   3  1 3      
f t   f   1  t  1. 2  2    2   t log2  1 3 2
0  x y  2  2 log 1 3 2   Do đó   x 0;   1 ( vì x   ) t  2 2
x y  1 3  1 3  Thử lại: Với x  1:  y   1 32t 1  t 2  y  3  2    t 1 3  2t 1      3  0     t
1 3  2t  2 1 3.2t  3 1  0 t Ta có:   1 32t 2 1 3.2t g x    
 3 1 liên tục trên 0 
;1 thỏa mãn g 0 g   1  0 nên
phương trình có nghiệm t 0;  1 .
Do đó với x  1 thì tồn tại số thực y thỏa mãn 2 log  x y  log 1 3  log  2 2 x y 1 2 2 3  Với x  1 :  y   1 32t 1  t 2  y  3  2    t 1 3  2t 1      3  0     t
1 3  2t  2 1 3.2t  3 1  0 t
Ta có: 1 3 2t  2 1 3.2t  3 1  0, t
  1nên phương trình vô nghiệm.
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27
NGUYỄN BẢO VƯƠNG - 0946798489
Do đó với x  1 thì không tồn tại số thực y thỏa mãn
2 log  x y  log 1 3  log  2 2 x y 1 2 2 3  Với x  0 : 2  y   1 32tt 2  y  1 3    t 1 3 2t  3 1   t
1 3 2t  3 1  0 t Ta có:   1 3 2t h x  
 3 1 liên tục trên  1
 ;0 thỏa mãn h 
1 h 0  0 nên phương trình có nghiệm t  1  ;0 .
Do đó với x  0 thì tồn tại số thực y thỏa mãn 2 log  x y  log 1 3  log  2 2 x y 1 . 2 2 3  Vậy x 0;  1 .  2x 1 
Câu 43. Có bao nhiêu cặp số nguyên  ;
x y thỏa mãn 0  y  2020 và log  1 2x y ? 3   y   A. 2019 . B. 11. C. 2020 . D. 4 . Lời giải Chọn B y  0   2x 1 Từ giả thiết ta có: x
 0  2  1  x  0  yy  0  Ta có: PT  log
2x 1  2x 1  log y y (*) 3   3
Xét hàm số f t   log t t trên 0;   3 1
Khi đó f  t  
 1  0 do đó hàm số f t   log t t đồng biến trên 0;   t ln 3 3 (*) có dạng 2x   1      2x f f y y 1 Vì 0 
 2020  0  2x 1  2020  1  2x y
 2021  0  x  log 2021 2    0  x  log 2021 2   
x 0;1; 2;3; 4;5;6;7;8;9;1 
0 . Vậy có 11 cặp  x; y  thỏa mãn. x    2
 4x  4x 1  Câu 44. Biết x , x là hai nghiệm của phương trình 2 log
 4x 1  6x và 1 2 7   2  x  1 x  2x
a b với a , b là hai số nguyên dương. Tính a b . 1 2   4
A. a b  13 .
B. a b  11.
C. a b  16 .
D. a b  14 . Lời giải Chọn D
Trang 28 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 1
Điều kiện: x  0, x  . 2 2
 4x  4x 1  Ta có: 2 log
 4x 1  6x  log    2
4x  4x   2
1  4x  4x 1  log 2x  2x . 7 7 7   2  x  1
Xét hàm số f t   log t t có f t  
1  0 t  0 nên là hàm số đồng biến trên 0;  . 7 t ln 7 3  5 Do đó ta có 2 2
4x  4x 1  2x  4x  6x 1  0  x  . 4 Khi đó 3  5 3  5 1 3  5 3  5 1 x  2x   2 
9  5 hoặc x  2x   2  9  5 . 1 2   1 2   4 4 4 4 4 4 3  5 3  5 Vậy x  ; x
. Do đó a  9;b  5 và a b  9  5  14 . 1 2 4 4 2 x 1  x 1 
Câu 45. Biết phương trình log  2 log  
có một nghiệm dạng x a b 2 trong đó , a b 5 3   x 2 2   x
là các số nguyên. Tính 2a b . A. 3 . B. 8 . C. 4 . D. 5 . Lời giải Chọn B 2 x 1  x 1  2 x 1  x 1  Ta có log  2 log     log  2 log 1 . 5 3 5 3      x 2 2   x x  2 x  ĐKXĐ: x  1 .  
1  log 2 x 1  2log 2 x  log x  2log x 1 (*) 5   3 5 3  
Xét hàm số f t   log t  2 log t 1 , với t  1. 5 3   1 2
f t   
 0 với mọi t  1, suy ra f t  đồng biến trên khoảng 1;   . t.ln 5 t   1 ln 3
Từ (*) ta có f 2 x  
1  f x nên suy ra
x   x   x 2 2 1  2 x 1  0  x  1 2 (do x  1 ).
Suy ra x  3  2 2  a  3;b  2  2a b  8 .
Câu 46. Số nghiệm thực của phương trình 6x  3log
5x 1  2x 1 là 6   A. 0 . B. 2 . C. 1. D. 3 . Lời giải Chọn B 1
Điều kiện: x   . 5
PT:  6x  3x  3log 5x   x log6 5x  1
1  5x 1  6  3x  6  3log 5x 1 (1) . 6 6   Xét hàm số    6t f t
 3t , vì    6t f t .ln 6  3  0, t
   nên f t  đồng biến trên  . Khi đó  
1  f x  f log 5x 1  x  log 5x 1  log 5x 1  x  0 6   6   6  
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29
NGUYỄN BẢO VƯƠNG - 0946798489  1 
Xét hàm số h x  log 5x 1  x trên  ;  , ta có 6      5  5 h x  1 5x   1 ln 6 25 1
h  x    0, x   
và lim h x   ;
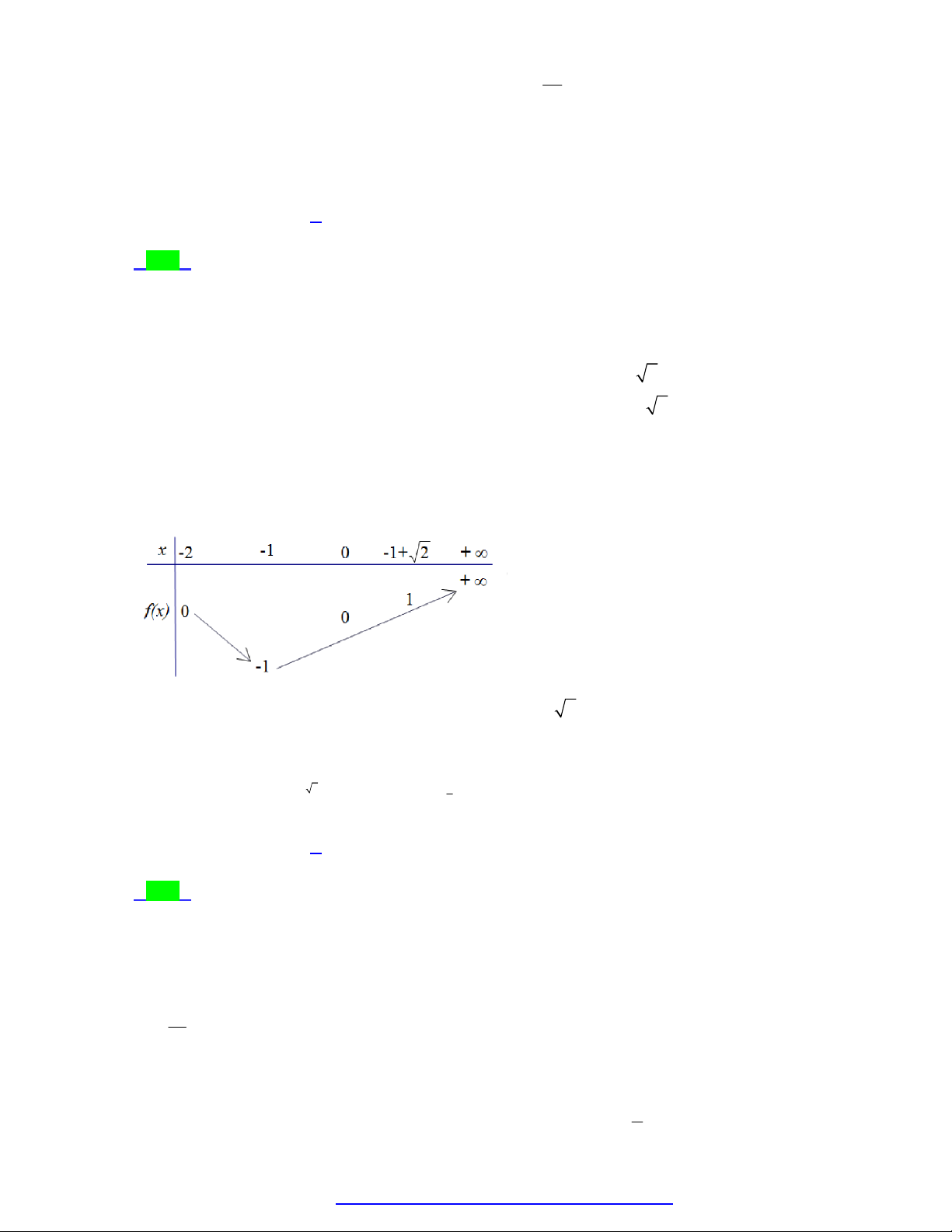
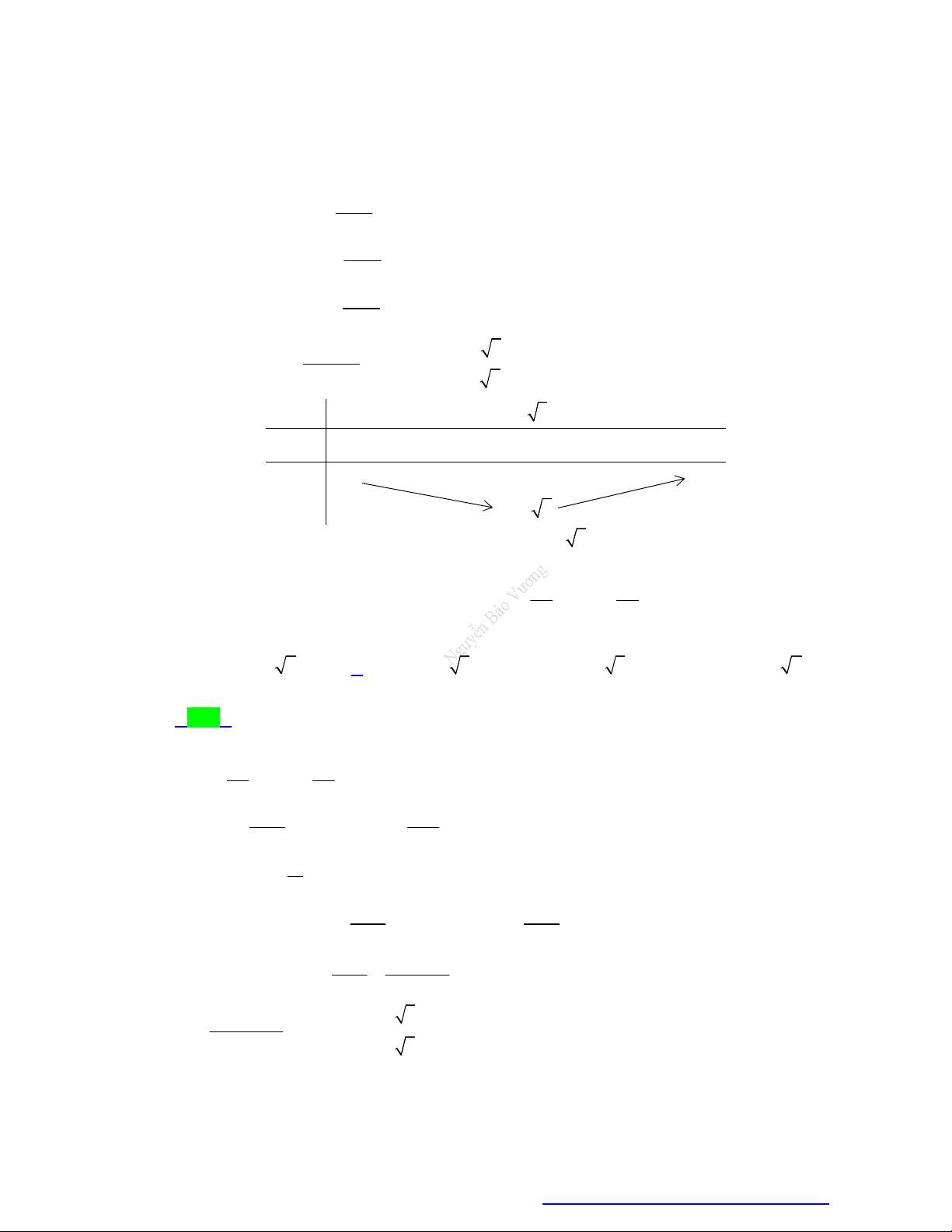
 lim h x  1  5x  2 1 ln 6 5  1 x   x     5  Bảng biến thiên:  1 
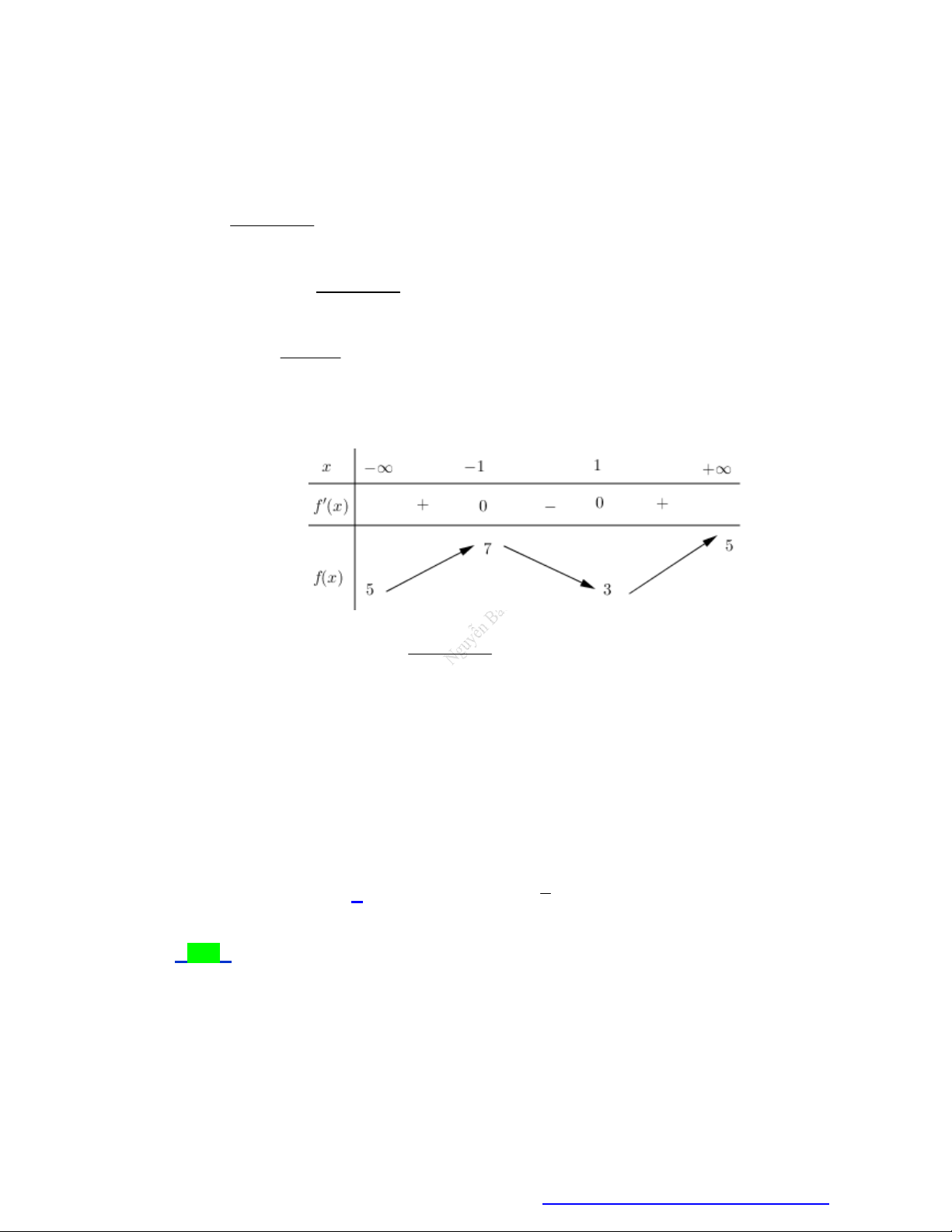
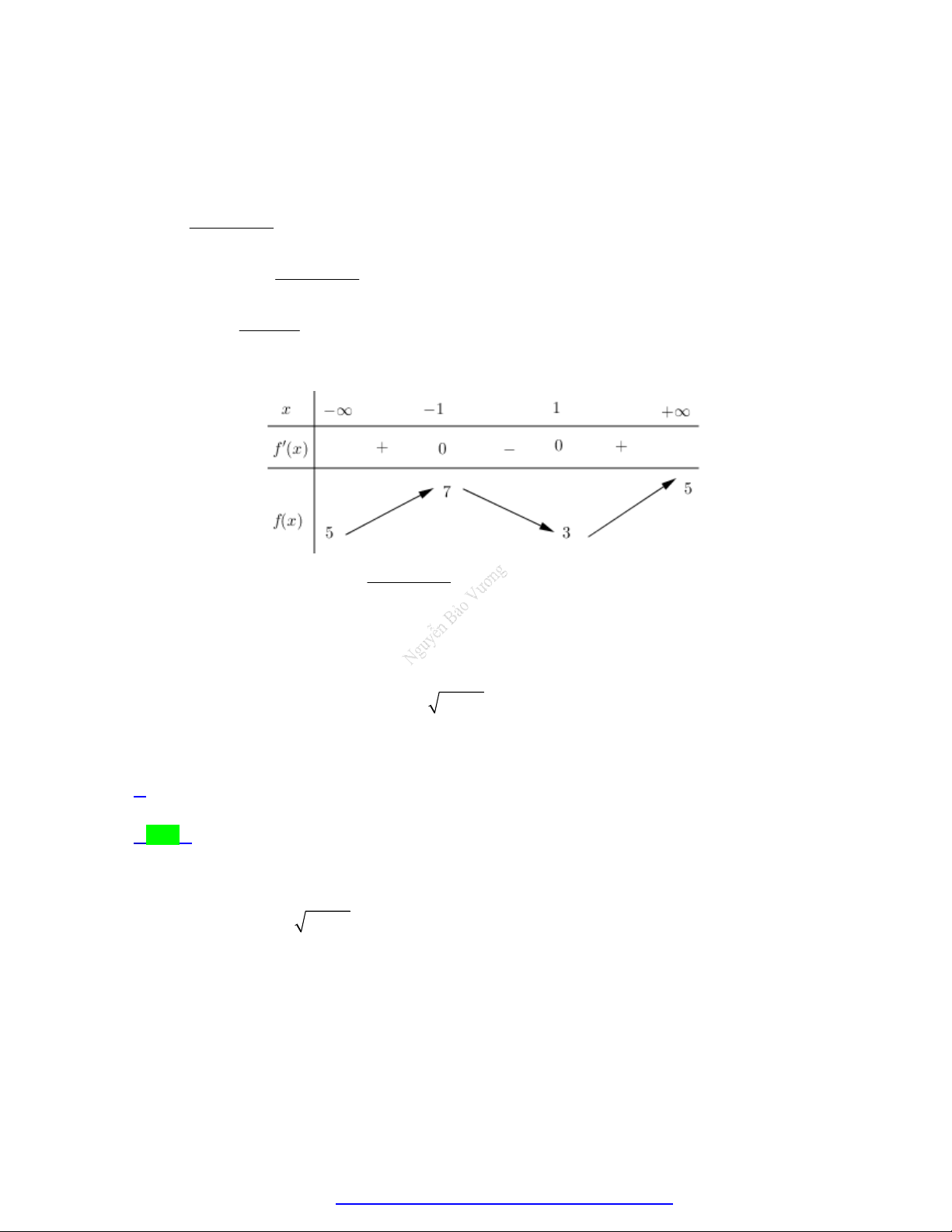
Từ BBT suy ra phương trình h x  0 có nhiều nhất 2 nghiệm thuộc khoảng  ;     5 
Mà h 0  0, h  1  0 .
Vậy phương trình đã cho có đúng hai nghiệm x  0, x  1 .
 5x  3x
Câu 47. Tính tổng S tất cả các nghiệm của phương trình x 1 ln
 5   5.3x  30x 10  0   . 6x  2   A. S  1. B. S  2 . C. S  1  . D. S  3. Lời giải Chọn A 1
Điều kiện x   . 3
Phương trình tương đương
ln 5x  3x   ln 6  2  55x  3x x
  56x  2  0
 ln 5x  3x   55x  3x   ln 6x  2  56x  2 (1). 1
Xét hàm số f t   ln t  5t,t  0 . Có f 't    5  0 ,  t  0 nên f t  đồng biến trên 0;   . t Từ   1 suy ra 5x  3x f
  f 6x  2  5x  3x  6x  2  5x  3x  6x  2  0
Xét    5x  3x g x
 6x  2 , '  5x ln 5 3x g x   ln 3  6 1   x  2 x g x    2 ' 5 ln 5 3 ln 3  0 , x    . 3  1 
Nên g ' x  0 có không quá 1 nghiệm suy ra g x  0 có không quá 2 nghiệm trên  ;    . Mà  3 
g 0  g  
1  0 . Vậy phương trình có tập nghiệm là 0,  1 . Do đó S  1.
Trang 30 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 2 x  80
Câu 48. Số nghiệm của phương trình x 1  2 ln  2.3
 2 x  80  ln 3 là 3x A. 2 . B. 3 . C. 1. D. 0 . Lời giải Chọn C PT 2 2 x 1  x 1 ln x 80 2 x 80 ln 3 2.3        (1) 1
Xét hàm số f t   ln t  2t, t
  0 ; Ta có: f t    2  0, t
  0  Hàm số f t  đồng biến trên t 0; . Từ (1) suy ra f  2 x
  f x 1 2 x 1  2 x 1  x 1  2 80 3  x  80  3  x  80  9  9  x  80  0
Xét hàm số g xx 1  2  9
x  80 trên  . Ta có: g xx 1  2.9  ln 3  2x
g  x  4.9x ln 32 1  2
g  x  0  x x  log  2
2 ln 3 1 g (x )  glog  2 2 ln 3 1  3, 7  0 0 9 0 9  
lim g x   ;  lim g (  x)   x x Bảng biến thiên:
Dựa vào bảng biến thiên ta có g ' x  0, x
    hàm số g x đồng biến trên   phương trình
g x  0 có nhiều nhất một nghiệm. Mà g   1  0
Do đó phương trình đã cho có duy nhất 1 nghiệm.
B. BÀI TOÁN CHỨA THAM SỐ
Dạng 1. Tìm m để f t; m  0 có nghiệm (hoặc có k nghiệm) trên D?
— Bước 1. Tách m ra khỏi biến số và đưa về dạng f   t  Am.
— Bước 2. Khảo sát sự biến thiên của hàm số f   t trên D.
— Bước 3. Dựa vào bảng biến thiên để xác định giá trị của tham số Am để đường thẳng y  Am nằm
ngang cắt đồ thị hàm số y  f   t .
— Bước 4. Kết luận các giá trị cần tìm của  A 
m để phương trình f  
t  Am có nghiệm (hoặc có k nghiệm) trên D. Lưu ý
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 31
NGUYỄN BẢO VƯƠNG - 0946798489
— Nếu hàm số y  f  
t có giá trị lớn nhất và giá trị nhỏ nhất trên D thì giá trị A 
m cần tìm là những m thỏa mãn: min f  
t  Am  max f   t . t D  t D 
— Nếu bài toán yêu cầu tìm tham số để phương trình có k nghiệm phân biệt, ta chỉ cần dựa vào bảng biến thiên
để xác định sao cho đường thẳng y  Am nằm ngang cắt đồ thị hàm số y  f  
t tại k điểm phân biệt.
Dạng 2. Tìm m để bất phương trình f t; 
m  0 hoặc f t; 
m  0 có nghiệm trên miền D?
— Bước 1. Tách tham số m ra khỏi biến số t và đưa về dạng A m  f  
t hoặc Am  f   t .
— Bước 2. Khảo sát sự biến thiên của hàm số f   t trên D.
— Bước 3. Dựa vào bảng biến thiên xác định các giá trị của tham số m để bất phương trình có nghiệm: + A m  f  
t có nghiệm trên D  Am  max f   t . t D  + A m  f  
t có nghiệm trên D  Am  min f   t . t D   Lưu ý
— Bất phương trình Am  f   t nghiệm đúng t
  D  Am  min f   t . t D 
— Bất phương trình Am  f   t nghiệm đúng t
  D  Am  max f   t . t D  Câu 1. Cho phương trình 2 log
2x m  2 log x m  2  0 ( m là tham số thực). Tập hợp tất cả các giá 2     2
trị của m để phương trình đã cho có hai nghiệm phân biệt thuộc đoạn 1; 2 là A. 1; 2 . B. 1; 2. C. 1; 2 . D. 2;  . Lời giải Chọn C 2 2 log
2x m  2 log x m  2  0  1
  log  x  m  2 log x m  2  0 * 2     2     2
Đặt t  log x g x  0  t  1 và mỗi giá trị của x sẽ cho một giá trị của t 2    2
* trở thành 1 t   m  2t m  2  0 2
t  2t 1 mt  2t m  2  0 2
t 1  m t   1  t  
1 t 1 m  0
t m 1   1   t  1 2 
Với t  1 thì phương trình có một nghiệm x  2
Vậy để phương trình ban đầu có hai nghiệm phân biệt thì phương trình  
1 phải có một nghiệm t  1
0  m 1  1  1  m  2
Trang 32 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Vậy m 1; 2 để thoả mãn yêu cầu bài toán.   x   Câu 2. Cho phương trình 3 2
2 log x  7 log x  4 log 3x m  0 
( m là tham số thực). Có tất cả 2 2 2      2  
bao nhiêu giá trị nguyên dương của m để phương trình đã cho có đúng hai nghiệm phân biệt? A. 78 . B. 80 . C. 81. D. 79 . Lời giải Chọn D. x  0 Đk:  . 3x m    x   3 2 2
2 log x  7 log x  4 log 3x m  0 x
 log x  2 . 2log x 1 3  m  0 2   2  2 2 2      2   log x  2 x  4 2   1 1  log x     x  . 2  2  2   3x m x  log m   3 1
Với m  1 thì x  log m  0 (loại). Do đó phương trình có 2 nghiệm phân biệt x  4, x  3 2
Với m  1 thì x  log m  0 nên luôn nhận nghiệm x  log m . 3 3 1 1 1 Mà 4 
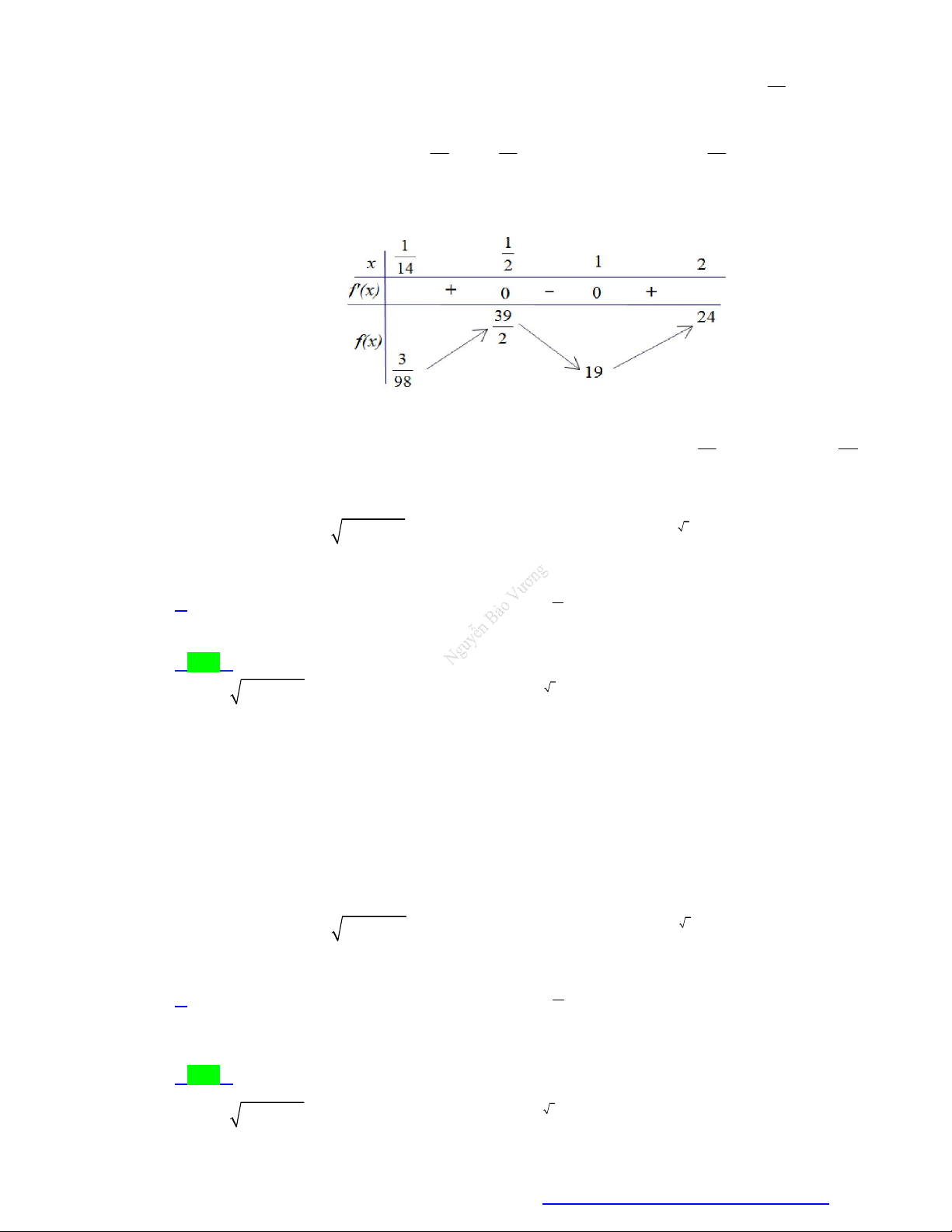
nên phương trình có hai nghiệm phân biệt khi 2  log m  4  3  m  81. 3 2 2
m nguyên dương nên m 3; 4; ..,  80 .
Vậy có 79 giá trị m nguyên dương. Câu 3. Cho phương trình  2 2 log  3log  2 9x  1 3x x x m
m  0 ( m là tham số thực). Gọi S là tập 2 2   
hợp tất cả các giá trị nguyên dương của m để phương trình đã cho có đúng hai nghiệm phân biệt.
Tính tổng tất cả các phần tử của S . A. 3238 . B. 3236 . C. 3237 . D. 3239 . Lời giải Chọn A
Viết lại phương trình  2 2 log  3log  2 3x 1 3x x xm  0 2 2     x  0 Đk:  . 3x m   2 2 log  3log  2 9x  1 3x x x mm  0   2 2 log  3log  2 3x 1 3x x xm  0 2 2     2 2    log x  2 x  4 2   1 1  log x     x  . 2  2  2   3x m x  log m   3 1
Với m  1 thì x  log m  0 (loại). Do đó phương trình có 2 nghiệm phân biệt x  4, x  . 3 2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 33
NGUYỄN BẢO VƯƠNG - 0946798489
Với m  1 thì x  log m  0 nên luôn nhận nghiệm x  log m . 3 3 1 1 1 Mà 4 
nên phương trình có hai nghiệm phân biệt khi 2  log m  4  3  m  81 . 3 2 2
m nguyên dương nên m 3; 4; ..,  80 .
Tổng 1 2  3  ...  80  2  3238 . Câu 4. Cho phương trình  2 2 log  3log  2 3x  .2x x x m
 0 ( m là tham số thực). Gọi S là tập hợp tất cả 3 3 
các giá trị nguyên dương của m để phương trình đã cho có đúng hai nghiệm phân biệt. Tính tổng tất
cả các phần tử của S . A. 741. B. 742 . C. 740 . D. 703 . Lời giải Chọn A. x  3 
Viết lại phương trình  2
2 log x  3log x  2  m  0 3 3     2  x  0 x  0  x  Đk:  3  
x  log m (Do m nguyên dương nên tồn tại log m ). 3 3     m   2 2  2     log x  2  x  9  0 3  x     3 1 1 2 
2 log x  3log x  2
m  0  log x     x   0 . 3 3     3  2  2  3  x   3  x  log m 3   m     2  2  1
Với m  1 thì x  log m  0 (loại). Do đó phương trình có 2 nghiệm phân biệt x  9, x  3 3 2
Với m  1 thì x  log m  0 nên luôn nhận nghiệm x  log m . 3 3 2 2 1 Mà 9 
nên phương trình có hai nghiệm phân biệt khi 3 1 9 3 1  3   3 
 log m  9  1, 26   m   38, 44 . 3     3  2   2  2
m nguyên dương nên m 2;3; 4; .., 3  8 .
Như vậy có tất cả các giá trị m là 1; 2; 3; ; 4;...;  38 .
Tổng 1 2  3  ...  38  741. 2 Câu 5.
Cho phương trình  2lg xlgx 1lg 2  4
x  3x m  0(m là tham số thực). Gọi S là tập hợp tất cả các giá trị
nguyên dương của m để phương trình đã cho có đúng hai nghiệm phân biệt. Tổng của phần tử nhỏ nhất và
phần tử lớn nhất S bằng A. 100 3 1. B. 100 3 1 . C. 99 3 . D. 99 3 1 . Lời giải Chọn A
Trang 34 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020x  0 Đk:  . 3x mx   3  mx  log m 2 2lg xlg x 1lg 3 2  4
x  3x m  0    2  2 2lg xlg x 1lg 2  4 x
2 lg x  lg x  2  2 lg x   lg x  2  x  100   1 1  lg x     x  .  2  10   3x mx  log m  3 1
Với m  1 thì x  log m  0 (loại). Do đó phương trình có 2 nghiệm phân biệt x  100, x  . 3 10
Với m  1 thì x  log m  0 nên luôn nhận nghiệm x  log m . 3 3 1 1 1 Mà 100 
nên phương trình có hai nghiệm phân biệt khi 10 100  log m  100  3  m  3 . 3 10 10
m nguyên dương nên m 100 2;3; 4; .., 3   1 .
Do đó tổng của phần tử nhỏ nhất và phần tử lớn nhất bằng 100 3 1 . Câu 6.
Cho phương trình 3.2x.log 12 log  2x  4 5x x x
m  0 ( m là tham số thực). Có tất cả bao nhiêu
giá trị nguyên dương của m để phương trình đã cho có đúng hai nghiệm phân biệt? A. 24 . B. 25 . C. 23 . D. 22 . Lời giải Chọn D x  0  Đk:  . 5x  ; m  m  0 
3.2x.lg 12lg  2x  4 5x x x
m  0  3lg  
1 2x  4 5x xm  0 2x  4 x  2   1 1   lg x     x  .   3 3 10   5x m  x  log ; m m  0 5    1
Với m  1 thì x  log m  0 (loại). Do đó phương trình có 2 nghiệm phân biệt x  2, x  . 5 3 10
Với m  1 thì x  log m  0 nên luôn nhận nghiệm x  log m . 5 5 1 Mà 2 
và vì x  log m nên phương trình có hai nghiệm phân biệt khi 3 5 10 1 1 3 10  log m  2  5
m  25 , m nguyên nên m 3; 4; .., 2  4 . 5 3 10
Vậy có 22 giá trị m nguyên dương.
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 35
NGUYỄN BẢO VƯƠNG - 0946798489 Câu 7. Cho phương trình 2
log x  3m log 3x 2
 2m  2m 1  0 ( m là tham số thực). Tìm tất cả các số thực 2 2
m để phương trình có hai nghiệm phân biệt thuộc đoạn 1;9 . 1 1 1
A. 3  m  . B. m   2 . C.  . D.   m  . 2 2 2 Lời giải Chọn C
Điều kiện: x  0 . PT: 2
log x  3m log 3x 2
 2m  2m 1  0 2 2
 log x  3m log x  2m m 1  0 . 3 3 3 3
log x  m 1 3   log x  2  m 1  3
Ta có x 1;9  log x  0; 2 3  
Vậy để phương trình đã cho có hai nghiệm phân biệt thuộc đoạn 0;9 khi và chỉ khi 3  m  1 
0  m 1  2    1 1 0  2
m 1  2    m  (Hệ vô nghiệm). 2 2  m 1 2m 1        m  2  Câu 8. Cho phương trình 2 2
log x  (m  3) log x  2m  3m  0 ( m là tham số thực). Có bao nhiêu giá trị 2 2  1 
nguyên của tham số m để phương trình đã cho có đúng một nghiệm thuộc đoạn ;32  ? 4    A. 4 . B. 5 . C. 6 . D. 7 . Lời giải Chọn B  1 
Đặt t  log x . Do x
;32 nên t 2;5 và ứng với mỗi t  2
 ;5 cho ta một giá trị 2  4     1  x  ;32 
. Khi đó phương trình trở thành: 4    2 2 2 2
t  (m  3)t  2m  3m  0  t mt  2m  3t  3m  0 t m  (t  ) m (t  2 ) m  3(t  ) m  0   . t  3  2m
Với m nguyên, để phương trình có nghiệm duy nhất t 2;5 , ta có các trường hợp sau:
m  3  2m  TH1:   m  1 . m   2;5  3  2m  2 m  5 / 2 3  2m   2;5   TH2:   3  2m  5   m  1   m  2  ;3; 4;  5 . m   2;5  m2;  5 m2;5  
Trang 36 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 m  2 m  2 m  2;5        m  5 TH3:   m  5      vô nghiệm 3  2m    2  ;5    5 2   3  2m  5 1  m     2
Vậy tổng cộng có 5 số nguyên của m thỏa đề. Câu 9.
Cho phương trình 9x  (  5)3x m
 3m  6  0 ( m là tham số thực ). Có bao nhiêu giá trị
nguyên của m để phương trình đã cho có 2 nghiệm phân biệt thuộc đoạn 1;  2 . A. 6 . B. 7 .
C. m R . D. 1. Lời giải Chọn A
9x  (m  5)3x  3m  6  0 xx   x   3  3 3 3
3  m  23x  3  0  3x  33x m  2  0   .
3x m  2 
3x  3  x  1 thỏa mãn x 1; 2 . Mặt khác: 1; 2 3x x  
3;9 . Vậy để phương trình đã cho có 2 nghiệm phân biệt thuộc đoạn 3   m  2  9 1   m  7
1;2 khi và chỉ khi     1  m  7 m  2  3 m  1  
mà m nguyên suy ra m  2;3;4;5;6; 
7 nên có 6 giá trị nguyên của m .
Câu 10. Cho phương trình 2 2 2
log x  log x m  2m  0 ( m là tham số thực). Có bao nhiêu giá trị nguyên 2 2 1 
của tham số m để phương trình đã cho có đúng một nghiệm thuộc đoạn ;16  ? 8    A. 3 . B. 2 . C. 1. D. 4 . Lời giải Chọn A 1 
Đặt t  log x . Do x
;16 nên t 3; 4 và ứng với mỗi t 3; 4 cho ta một giá trị 2 8    1  x  ;16 
. Khi đó phương trình trở thành: 8    t  m 2 2
t  2t m  2m  0  (t m)(t m)  2(t m)  0   . t m  2 
Với m nguyên, để phương trình có nghiệm duy nhất t 3; 4 , ta có các trường hợp sau:
m m  2  TH1:   m  1. m    3;4
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 37
NGUYỄN BẢO VƯƠNG - 0946798489 m  2  3 m  5 m  2   3;4   TH2:   m  2  4   m  2   m  3 . m    3  ; 4    m 4;  3 m  4  ;  3   m  3 m  3 m    3  ; 4   TH3:   m  4   m  4   m  5  . m  2    3  ; 4    m 5;2 m 5;2  
Vậy tổng cộng có 5 số nguyên của m thỏa đề.
Câu 11. Cho phương trình 2 log 2x 2
 2 log x m 1  0 .Có bao nhiêu giá trị nguyên của tham số m để 2 2  1 
phương trình có đúng một nghiệm thuộc đoạn ;16  ? 2    A. 10 . B. 7 . C. 5 . D. 6 . Lời giải Chọn D
Điều kiện: x  0 .
Biến đổi phương trình về dạng
1 log x2  4log x m 1  0 2
 log x  2log x m . 2 2 2 2 1
Đặt t  log x , với mỗi x   
;16 thì cho một giá trị t  1  ; 4 . 2  2   
Khi đó ta được phương trình 2
t  2t m .
Xét hàm số f t 2
t  2t trên đoạn  1  ; 4 .
Ta có f t   2t  2 , f t  0  t  1.
Bảng biến thiên của f t
Từ bảng biến thiên suy ra m   1  3; 
8  m  1; 4;5;6;7; 
8 có 6 giá trị của m thỏa mãn yêu cầu bài toán.
Câu 12. Cho phương trình  2 2 2
log x  log x m  2m
3  log x  0 ( m là tham số thực). Có bao nhiêu giá 2 2  2 1
trị nguyên của tham số m để phương trình đã cho có 3 nghiệm phân biệt x  ? 8 A. 3 . B. 5 . C. 2 . D. 4 . Lời giải Chọn C
Trang 38 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Ta cần tìm các giá trị nguyên của tham số m để phương trình đã cho có 3 nghiệm phân biệt 1  x  ;8  . 8    1  1 
Đặt t  log x . Do x
;8 nên t 3; 
3 và ứng với mỗi t 3; 
3 cho ta một giá trị x  ;8 . 2 8      8 
Với điều kiện t 3; 
3 phương trình trở thành: t  3  2 2 
t  2t m  2m 3  t  0  t m (*) .  t  2  m  1 
Với m nguyên, để phương trình đầu có 3 nghiệm x  ;8 
 (*) có 3 nghiệm phân biệt 8     3
  2  m m  3 1   m  3 t 3;  3    m    0;  2 . 3
  m  2  m  3 1   m  1   2
Câu 13. Cho phương trình 1 2020x     2 2020x m
m  2  0 ( m là tham số thực). Tập hợp tất cả
các giá trị của m để phương trình đã cho có 2 nghiệm phân biệt thuộc đoạn 0;  2 là A. 2;202  1 . B. m   R . C. 2;  . D. 2;  2021 . Lời giải Chọn D x  2 1 2020
 m  2 2020x m  2  0
 1 2 2020x  2020x m 2020x  2 2020x m  2  0  2020x 1
 2020x m 2020x m 1  0   .
 2020x m 1  Theo bài ra ta có: 0; 2 2020 x x    1; 2020 .
Vậy để phương trình đã cho có 2 nghiệm phân biệt thuộc đoạn 0;  2 khi và chỉ 1   m 1  2020 2  m  2021 khi     2  m  2021. m 1  1 m  2  
Câu 14. Cho phương trình  2 2
log x  (m  3)log x  2m  3m
1 log x  0 ( m là tham số thực). Có bao 3 3  81 1
nhiêu giá trị nguyên của tham số m để phương trình đã cho có 3 nghiệm phân biệt x  ? 27 A. 4 . B. 3 . C. 2 . D. 5 . Lời giải Chọn B
Ta cần tìm các giá trị nguyên của tham số m để phương trình đã cho có 3 nghiệm phân biệt  1  x  ;81  . 27   
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 39
NGUYỄN BẢO VƯƠNG - 0946798489  1 
Đặt t  log x . Do x  ;81 nên t  3
 ; 4 và ứng với mỗi t 3; 4 cho ta một giá trị 3  27     1  x  ;81 
. Với điều kiện t  3
 ; 4 phương trình trở thành: 27    t   4  2 2 
t  (m  3)t  2m  3m 4 t  0  t m (*)  . t   3 2m   1 
Với m nguyên, phương trình đầu có 3 nghiệm phân biệt x  ;81 
 (*) có 3 nghiệm phân biệt 27     1  3
  m  3  2m  4   m  1 t 3; 4    2  m   0;2;  3 . 3
  3  2m m  4   1  m  4 
Vậy tổng cộng có 3 số nguyên của m thỏa đề.
Câu 15. Cho phương trình 2 log
2021x m  2 log
x  2  m ( m là tham số thực). 2021     2021
Tổng tất cả các giá trị nguyên của m để phương trình đã cho có hai nghiệm phân biệt thuộc đoạn 3 1  ; 2021    là: A. 10 . B. 8 . C. vô số. D. 13 . Lời giải Chọn B Xét phương trình 2 log
2021x m  2 log x  2  m 2021     2021 2  log
2021x m  2 log
x m  2  0 1 2021     2021   Điệu kiện x  0 2
Phương trình 1  1 log xm  2 log
x m  2  0 2021    2021 2  log x m log
x m 1  0 2021 2021 log x  1 x  2021 2021     1 log x m 1 x  2021m  2021 
Để phương trình đã cho có 2 nghiệm phân biệt trên đoạn 3 1  ; 2021    thì: m 1  2021   2021 m  2 m  2       m 1;3;  4 m 1  3 1   2021  2020 0  m 1  3 1  m  4   
Vậy tổng các giá trị m nguyên là: 1  3  4  8.
Câu 16. Cho phương trình  2 2 2
log x  log x m  2m
3  log x  0 ( m là tham số thực). Có bao nhiêu giá 2 2  2 1
trị nguyên của tham số m để phương trình đã cho có 2 nghiệm phân biệt x  ? 8 A. 7 . B. 6 . C. 5 . D. 8 . Lời giải Chọn D
Trang 40 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 1 
Ta cần tìm các giá trị nguyên của tham số m để phương trình đã cho có đúng hai nghiệm x  ;8  . 8    1  1 
Đặt t  log x . Do x
;8 nên t 3; 
3 và ứng với mỗi t 3; 
3 cho ta một giá trị x  ;8 . 2 8      8 
Với điều kiện t 3; 
3 phương trình trở thành: t  3  2 2 
t  2t m  2m 3  t  0  t m .  t  2  m  1 
Với m nguyên, phương trình đầu có 2 nghiệm x  ;8 
 (*) có 2 nghiệm phân biệt t 3;  3 , ta 8    có các trường hợp sau: m  2  m  TH1:   m  1 . m    3  ;3 
TH2: Nếu m  3 thì phương trình có 2 nghiệm t  1
 ,t  3. Nhận m  3 .
TH3: Nếu 2  m  3  m  1 thì phương trình có 2 nghiệm t  1
 ,t  3. Nhận m  1. 2  m  3  m  1 2  m    3  ;3   TH4:   2  m  3   m  1 
m 3;2;  2 . m    3  ;3  m3;3 m3;3   m  3  m  3 m   3;  3   TH5:   m  3   m  3   m 4;  5 . 2  m    3  ;3  m 5  ;  1 m1;5   Vậy m 3;2; 1  ;1; 2;3; 4; 
5 tổng cộng có 5 số nguyên của m thỏa đề. 2 2
Câu 17. Có bao nhiêu giá trị nguyên của m để phương trình 1 1x     1 1 9 2 3  x m
 2m 1  0 có nghiệm thực? A. 4 . B. 5 . C. 6 . D. 7 . Lời giải Chọn C 2 Điều kiện 1
  x  1. Đặt 1 1 3 x t    , với 1
  x  1  3  t  9 .
Khi đó phương trình đã cho trở thành: 2
t  m  2t  2m 1  0   1 . 2 t  2t 1 Ta có   1 
m 2 . Khi đó yêu cầu bài toán trở thành tìm m để phương trình: 2 có t  2
nghiệm t 3;9 . 2 t  2t 1 2 t  4t  3
Xét hàm số f t  
trên 3;9 , có f t    0 , t
  3;9 . Do đó, f t  đồng 2   t  2 t  2
biến trên 3;9 . Suy ra, phương trình 2 có nghiệm trên 3;9 khi và chỉ khi
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 41
NGUYỄN BẢO VƯƠNG - 0946798489 64
f 3  m f 9  4  m  . 7
Vậy có 6 giá trị nguyên của m thỏa mãn đề bài.
Câu 18. Cho phương trình 2
log x  2 log  x  2  1. Số giá trị nguyên của a  0; 2020 để phương trình a a
trên có 1 nghiệm thực là A. 0 . B. 2018 . C. 2019 . D. 2020 . Lời giải Chọn B x  2  
Điều kiện: x  0 . 0  a  1  2  2
x  2x a   1 Phương trình 
x x   2 log
2   1  x x  2   a   . a       2
x  2x   a 2 
Phương trình đã cho có 1 nghiệm thực khi và chỉ khi một trong hai phương trình   1 và 2 chỉ có 1 nghiệm x   2  ;   \   0 .
Xét hàm số f x 2
x  2x trên D   2  ;   \  
0 , có bảng biến thiên như sau:
Từ bảng biến thiên, ta thấy yêu cầu bài toán thỏa mãn khi  a  1   a  1 .
Do đó, có 2018 giá trị nguyên của a trên 0; 2020 thỏa mãn đề bài.
Câu 19. Cho phương trình log  3
mx  6x   2 log  2 14 
x  29x  2  0 , số giá trị nguyên của m để 1 2  2
phương trình có 3 nghiệm thực phân biệt là A. 1. B. 0 . C. 23. D. 5 . Lời giải Chọn B 2  1
 4x  29x  2  0  Phương trình   log   3
mx  6x   log  2 1
 4x  29x  2 2 2    1  x  2   14  3 2
mx  6x  1
 4x  29x  2   1  2
Nhận thấy x  0 không là nghiệm của   1 , nên   2
1  6x 14x  29   m 2 . x
Trang 42 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020  1 
Yêu cầu bài toán trở thành: tìm m để phương trình 2 có 3 nghiệm phân biệt trên ; 2   .  14  2  1  2
Xét hàm số f x 2
 6x 14x  29  trên
; 2 , có f  x  12x 14  . . Suy ra bảng biến 2   x 2  14  x thiên:  1  39
Từ bảng biến thiên ta thấy, phương trình 2 có 3 nghiệm phân biệt trên ; 2    19  m  .  14  2
Do vậy, không có giá trị nguyên nào của m thỏa mãn đề bài.
Câu 20. Phương trình 2 2
log x  log x 1  2m 1  0 có nghiệm trên đoạn 3 1;
 3  khi m a;b. Khi đó giá 3 3  
trị biểu thức T a.b bằng 1 A. 0 . B. 1. C.  . D. 4 . 4 Lời giải Chọn A Đặt 2 2 2
t  log x 1  t 1  log x . Khi đó 3 x  1
 ;3   t 1; 2 và phương trình đã cho trở thành: 3 3   2 2
t 1  t  2m 1  0  t t  2m  2 2 .
Yêu cầu bài toán trở thành: tìm m để phương trình 2 có nghiệm t 1; 2 . Xét hàm số:   2
f t t t có f t   2t 1  0, t
 1; 2 , suy ra hàm số đồng biến trên 1; 2 .
Do đó, phương trình 2 có nghiệm trên 1; 2  f  
1  2m  2  f 2  2  2m  2  6  0  m  2 .
Suy ra a  0;b  2  T a.b  0 .
Câu 21. Phương trình 2 2
log x  log x 1  2m 1  0 có nghiệm trên đoạn 3 1
 ;3  khi m a;b. Khi đó giá 3 3  
trị biểu thức T  . a b bằng 1 A. 0. B. 1. C.  . D. 4. 4 Lời giải Chọn A Đặt 2 2 2
t  log x 1  t 1  log x . Khi đó 3 x  1
 ;3   t 1;2 và phương trình đã cho trở 3 3   thành: 2 2
t 1 t  2m 1  0  t t  2m  2 2 .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 43
NGUYỄN BẢO VƯƠNG - 0946798489
Yêu cầu bài toán trở thành: tìm m để phương trình 2 có nghiệm t 1; 2 . Xét hàm số:   2
f t t t có f t   2t 1  0, t
 1; 2 , suy ra hàm số đồng biến trên 1; 2 .
Do đó, phương trình 2 có nghiệm trên 1; 2  f  
1  2m  2  f 2  0  m  2 .
Suy ra a  0 ;b  2  T a.b  0 . 2 x
Câu 22. Cho phương trình 3log x  2log x 1 5  m  0 ( m là tham số thực). Có tất cả bao nhiêu giá trị 3 3 
nguyên dương của m để phương trình đã cho có đúng hai nghiệm phân biệt? A. Vô số. B. 120 . C. 121. D. 124 . Lời giải Chọn C x  0 Đk:  (*) 5x m  Phương trình  2 3log  2log 1 5x x xm  0 3 3  log x  1 x  3 3   1 1  log x     x  . 3 3  3  3   5x m x  log m   5
+Với m  1 thì x  log m  0 (loại nghiệm này do không thỏa (*)). Do đó phương trình có 2 nghiệm 5 1
phân biệt x  3, x
. Suy ra nhận m  1. 3 3
+ Với m  1 thì x  log m  0 nên luôn nhận nghiệm x  log m . 5 5 1 1 1 Mà 3 
nên phương trình có hai nghiệm phân biệt khi 3 3
 log m  3  3.052  5  m  125 . 3 5 3 3 3
Do m nguyên dương nên m 4; .., 1  24 .
Vậy cả hai trường hợp có 121 giá trị m nguyên dương.
Câu 23. Cho phương trình log  2
x  2x 1  log
x  2 1 log m ( m là tham số thực). Có tất cả bao 4  2   2
nhiêu giá trị nguyên của m để phương trình đã cho có nghiệm? A. 0 . B. 1. C. 2 . D. Vô số. Lời giải Chọn B
Điều kiện: x  2 .  x  2  m m x  2 Có log  2
x  2x 1  log
x  2  1 log m  log  log   . 4  2   2 2   2  x 1  2 2 x  1 x  2
Xét hàm số f x  trên 2;  . x 1 1
Ta có f ' x   0 , x   2 .  x  2 1
Bảng biến thiên f x :
Trang 44 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 m
Từ bảng biến thiên ta suy ra phương trình có nghiệm khi 0 
 1  0  m  2 . 2
Có một giá trị nguyên của tham số m để phương trình có nghiệm là m  1.
Câu 24. Tìm tập hợp tất cả giá trị của tham số thực m để phương trình 2
log x  4 log x m  0 có nghiệm 2 2 thuộc khoảng 0  ;1 .
A. 4 ;   . B.  4  ;    . C.  4  ;  0 . D. 2 ; 0. Lời giải Chọn B
Đặt t  log x , với x 0 ;  1  t  0 . 2
Để phương trình đã cho có nghiệm thuộc khoảng 0  ;1 thì phương trình 2
t  4t m  0 có nghiệm t  0 .
Xét hàm số f t 2
t  4tt   0 ;
f t  2t  4  0  t  2  . Ta có bảng biến thiên:
Vậy giá trị cần tìm là m  4  ;    .
Câu 25. Cho phương trình 2020  3 2 2  log  7 log  4 log 2 3x x x x
m  0 ( m là tham số thực). Có tất cả 2 2 2  
bao nhiêu giá trị nguyên dương của m để phương trình đã cho có đúng hai nghiệm phân biệt? A. 79 . B. 80 . C. Vô số. D. 78 . Lời giải Chọn A x  0 Đk:  (*) 3x m  2020 3 2 2 log  7 log  4 log 2 3x x x xm  0 2 2 2    log  22 . 2log 1 3x x xm  0 2  2 
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 45
NGUYỄN BẢO VƯƠNG - 0946798489 log x  2  x  4 2   1 1  log x     x  . 2  2  2   3x m x  log m   3
+ Với m  1 thì x  log m  0 (loại nghiệm này do không thỏa (*)). Do đó phương trình đã cho có 3 1
hai nghiệm phân biệt x  4, x
. Suy ra nhận m  1. 2
+ Với m  1 thì x  log m  0 nên luôn nhận nghiệm x  log m . 3 3 1 Mà 4 
nên phương trình có hai nghiệm phân biệt khi 2 1 1 2  log m  4  3  m  81 . 3 2
Do m nguyên dương nên m 3; 4; .., 8  0 .
Vậy cả hai trường hợp có 79 giá trị m nguyên dương.
Câu 26. Cho phương trình  2 2 log  3log  2 5x  .3x x x m
 0 ( m là tham số thực). Gọi S là tập hợp tất 3 3 
cả các giá trị nguyên dương của m để phương trình đã cho có đúng hai nghiệm phân biệt. Tính tổng
tất cả các phần tử của S . A. 4950 . B. 2475 . C. Vô số. D. 4949 . Lời giải Chọn A x  5 
Phương trình tương đương:  2 2
 log x  3log x  2  m  0 . 3 3     3  x  0  Điều kiện x  5  (*)  m    3    log x  2 x  9 3  x    5  2  1 1 2
 log x  3log x  2
m  0  log x    x  . 3 3     3  3  2  3  x   5  x  log m 5   m     3  3 
+ Với m  1 thì x  log m  0 (loại nghiệm này do không thỏa mãn (*)). Do đó phương trình có 2 5 3 1
nghiệm phân biệt x  9 , x
. Suy ra nhận m  1. 3
+ Với m  1 thì x  log m  0 nên luôn nhận nghiệm x  log m . 5 5 3 3
Trang 46 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 1 1 Mà 9 
nên phương trình có hai nghiệm phân biệt khi  log m  9 5 3 3 3 1 9 3  5   5   1, 343   m   99, 229     .  3   3 
Do m nguyên dương nên m 2;3; 4;...,9  9 .
Vậy cả hai trường hợp suy ra S  1 2  3  ...  99  4950 . 2 1 2
Câu 27. Cho phương trình m   1 log x  2  4 m  5 log
 4m  4  0 ( m là tham số thực). Có tất 1     1 x  2 2 2  5 
cả bao nhiêu giá trị nguyên của tham số m để phương trình có nghiệm thuộc ; 4  . 2    A. 6 . B. 5 . C. 4 . D. Vô số. Lời giải Chọn A
Điều kiện: x  2  0  x  2 . 2 1 Ta có: m   2 1 log x  2  4 m  5 log  4m  4  0 1     1 x  2 2 2  4 m   2 1 log
x  2  4 m  5 log
x  2  4m  4  0 * . 1     1     2 2  5  Đặt t  log
x  2 . Vì x  ; 4  t  1  ;  1 1    . 2    2
Khi đó phương trình (*) trở thành m   2 4
1 t  4m  5t  4m  4  0 2 t  5t 1  m   2
1 t  m  5t m 1  0  m  *  * . 2 t t 1 2 t  5t 1
Xét hàm số f t   , t  1  ;  1 . 2 t t 1 2 4t  4
Ta có f t   .
t t  2 2 1
f t   0  t  1 . Ta có bảng biến thiên: t  2  1  1 2  f 't  7 f t 3 3  7
Dựa vào bảng biến thiên suy ra phương trình *  * có nghiệm khi 3   m  . 3  5 
Suy ra có 6 giá trị nguyên của tham số m để phương trình đã cho có nghiệm thuộc ; 4  . 2   
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 47
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 28. Cho phương trình  2 2 log  3log  2 16x  1 4x x x m
m  0 ( m là tham số thực). Gọi S là tập 2 2   
hợp tất cả các giá trị nguyên dương của m để phương trình đã cho có đúng ba nghiệm phân biệt.
Tổng tất cả các phần tử của S là A. 32637 . B. 32640 . C. 255 . D. 256 . Lời giải Chọn A
Viết lại phương trình  2 2 log  3log  2 4x 1 4x x xm  0 2 2     x  0 Đk:  (*) 4x m
Với điều kiện trên phương trình đã cho tương đương: log x  2 x  4 2   1 1  log x     x  . 2  2  2   4x m x  log m   4
Với m  1 thì x  log m  0 (loại nghiệm này do không thỏa (*)). Do đó phương trình có 2 nghiệm 4 1
phân biệt x  4, x
. Suy ra loại m  1. 2
Với m  1 thì x  log m  0 nên luôn nhận nghiệm x  log m . 4 4 1 Mà 4 
nên phương trình có hai nghiệm phân biệt khi 2 1 1 2
 log m  4  2, 665  4  m  256 . 4 2
Do m nguyên dương nên m 3; 4; .., 25  5 .
Ta có 1 2  3  ...  255  32640 suy ra S  32640  3  32637 .
Câu 29. Giá trị lớn nhất của tham số m sao cho bất phương trình 1 log  2 x   1  log  2
mx  4x m 5 5 
nghiệm đúng với mọi x thuộc  là 5 A. 2 . B. 3 . C. . D. 4 . 2 Lời giải Chọn B m  0 Điều kiện 2
mx  4x m  0, x       m  2 2  '  4  m  0  Ta có 1 log  2 x   1  log  2
mx  4x m 5 5 
Trang 48 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020  log 5 2 x   1   log  2
mx  4x m 5 5      2 x   2 5
1  mx  4x m m  2 x   2
1  5x  4x  5 2 5x  4x  5  m  2 x 1 2 5x  4x  5
Xét hàm số f x  2 x 1 2 4x  4
Ta có f ' x  x  2 2 1 Bảng biến thiên 2 5x  4x  5
Từ bảng biến thiên ta suy ra m  , x   2 x 1  m  3
Kết hợp với điều kiện m  2 ta được 2  m  3.
Vậy giá trị lớn nhất của tham số m cần tìm là 3.
Câu 30. Giá trị lớn nhất của tham số m sao cho bất phương trình 1 log  2 x   1  log  2
mx  4x m 5 5 
nghiệm đúng với mọi x thuộc  là: 5 A. 2. B. 3 . C. . D. 4. 2 Lời giải Chọn B m  0 Điều kiện 2
mx  4x m  0, x       m  2 . 2  '  4  m  0 
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 49
NGUYỄN BẢO VƯƠNG - 0946798489 1 log  2 x   1  log  2
mx  4x m 5 5   log 5 2 x   1   log  2
mx  4x m 5 5     5 2 x   2
1  mx  4x mm  2 x   2
1  5x  4x  5 2 5x  4x  5  m  . 2 x 1 2 5x  4x  5
Xét hàm số f x  2 x 1 2 4x  4
Ta có f ' x  x  2 2 1 Bảng biến thiên 2 5x  4x  5
Từ bảng biến thiên ta suy ra m  , x    2 x 1  m  3 .
Kết hợp với điều kiện m  2 ta được 2  m  3.
Vậy giá trị lớn nhất của tham số m cần tìm là 3.
Câu 31. Cho phương trình  2  log  3log  2 5x x x
m  0 ( m là tham số thực). Gọi S là tập hợp tất cả 7 7 
các giá trị nguyên dương của m để phương trình đã cho có đúng hai nghiệm phân biệt. Tổng của
phần tử nhỏ nhất và phần tử lớn nhất S bằng A. 49 5 . B. 49 5 1. C. 48 5 . D. 49 5 1. Lời giải Chọn A x  0 Đk:  (*) 5x m   2  log  3log  2 5x x xm  0 7 7  log x  1 x  7 7  
 log x  2  x  49 . 7   5x mx  log m   5
+ Với m  1 thì x  log m  0 (loại nghiệm này do không thỏa (*)). Do đó phương trình có 2 nghiệm 5
phân biệt x  7, x  49 . Suy ra nhận m  1.
+ Với m  1 thì x  log m  0 nên luôn nhận nghiệm x  log m . 5 5
Trang 50 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Mà 49  7 nên phương trình có hai nghiệm phân biệt khi 7 49
7  log m  49  5  m  5 , m nguyên 5 nên m  49 78125; 78126; ..., 5   1 .
Phần tử nhỏ nhất là m  1 Phần tử lớn nhất là 49 m  5 1  Vậy có 49 S  5 .
Câu 32. Cho phương trình  2 2 log  5log  2 5x x x
m  0 ( m là tham số thực). Có tất cả bao nhiêu giá 2 2 
trị nguyên dương của m để phương trình đã cho có đúng hai nghiệm phân biệt? A. 616. B. 615. C. vô số. D. 617. Lời giải Chọn A x  0 x  0   Điều kiện    (*). x x 5  m  0  m  5  2
2 log x  5log x  2  0 2 2 2   Ta có  2 2 log  5log  2 5x x xm  0   . 2 2    1
 5x m  0 3  log x  2 2  x  4 Trong đó 2   1   (4). log x  2 x  2   2
Với m  0 thì 5x m  log m x . 5
Do đó, phương trình (1) có đúng hai nghiệm phân biệt khi và chỉ khi xảy ra các trường hợp sau:
TH1: (3) có nghiệm x  log m  0  0  m  1 . Kết hợp điều kiện (*) và (4) ta được m  1 thì (1) có 5
hai nghiệm phân biệt x  2 và x  4 .
TH2: m  1, khi đó (*)  x  log m  0 . 5 Và do 4 
2 nên (1) có hai nghiệm phân biệt khi và chỉ khi 2  log m  4 2 4  5  m  5 5
Mà m nguyên dương nên ta có m 10,11,..., 62 
4 , có 615 giá trị của m .
Vậy có 616 giá trị nguyên dương của m để phương trình có đúng hai nghiệm phân biệt. Câu 33. Có bao nhiêu giá trị nguyên của tham số
m  2019 ; 2019 để phương x mx m x 2 1  2 1 trình 2019  
 0 có đúng 3 nghiệm thực phân biệt? x 1 x  2 A. 4038 . B. 2019 . C. 2017 . D. 4039 . Lời giải Chọn C
TXĐ: D   \ 1;  2 . Ta có x mx m x 2 1  2 1 2019    0 x 1 x  2 x m x x 2 1 (  2) 1  2019    0 x 1 x  2 x x 2 1 1  2019     . m (*) x 1 x  2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 51
NGUYỄN BẢO VƯƠNG - 0946798489 x x 2 1 1
Đặt f (x)  2019   . Khi đó x 1 x  2 x 3 1
f '(x)  2019 ln 2019    0 x  . D 2 2 (x 1) (x  2) Ta có bảng biến thiên
Dựa vào bảng biến thiên, để phương trình (*) có 3 nghiệm thực phân biệt thì
m  2  m  2.
Mà m 2019; 2019 và m   nên có 2017 giá trị m thỏa mãn.
Câu 34. Có bao nhiêu giá trị nguyên của tham số m để tồn tại cặp số  ; x y thỏa mãn 3x5 y x3 y 1 e e  
 1 2x  2 y , đồng thời thỏa mãn 2
log 3x  2y   1  m  6 2
log x m  9  0 ? 3 3 A. 6 . B. 5 . C. 8 . D. 7 . Lời giải Chọn B Ta có 3x5y x3 y 1 e e  
 1 2x  2 y 3x5 yx yx3 y 1 e 3 5 e     
  x  3y   1 (1) Xét hàm số    et f t
t trên  . Ta có    et f t
1  0 nên hàm số đồng biến trên  .
Khi đó (1)  f 3x  5y  f x  3y  
1  3x  5 y x  3y 1  2 y  1  2x .
Thế vào phương trình còn lại ta được 2
log x  m  6 2
log x m  9  0 (2) 3 3
Đặt t  log x . Số nghiệm của phương trình (2) chính là số nghiệm của phương trình 3 2
t  m   2
6 t m  9  0 (3)
Phương trình (3) có nghiệm khi   0  2
3m 12m  0  0  m  4 .
Do đó có 5 số nguyên m thỏa mãn.
Câu 35. Có bao nhiêu số nguyên của m để phương trình log 2x m 2
 2 log x x  4x  2m  1 có hai 2 2 nghiệm thực phân biệt? A. 2 . B. 3 . C. 1. D. 4 Lời giải Chọn C x  0  Điều kiện  m x     2
log 2x m 2
 2 log x x  4x  2m  1 2 2
 log 2x m 2
 2 log x x  2 x  2m 1 2 2  
 log 2x m  2 x  2m 2 2
1  log x x 2 2
Trang 52 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
 log 2 2x m  2 x  2m 2 2
 log x x (1) 2 2
Xét f u   log u u, u  0 2   1 f 'u 
1  0 , do đó hàm số đồng biến trên (0; ) . u ln 2
Khi đó (1)  f   x m  f  2
x    x m 2 2 2 2 2 2
x x  4x  2m
Xét hàm số g x 2
x  4x,  x  0
Phương trình có 2 nghiệm dương khi 4  2m  0  2  m  0 suy ra có 1 giá trị nguyên. Câu 36. Tìm tổng tất cả các giá trị nguyên của m để phương trình 3
x3 m3 x   3 2     x3 3 9 24 .3  3x x x x m
 1 có 3 nghiệm phân biệt. A. 45 . B. 34 . C. 27 . D. 38 . Lời giải Chọn C 3 x3 m3 3 x   3 2
x  9x  24x mx3 .3  3x 1 3
3x  mx x 33 3 3 x3 27 m 3x       .3  3x 1   3
 3 mx   x  33 3 3 3
m  3x  27  3  3 x   1   b 3 3 a b 3 a 3
1  3  27  b a  27.  3  3  b  3  a Đặt 3 a  3  ;
x b m  3x , phương trình (1) trở thành b 3 3 a b 3 a 3
3  27  b a  27.  3  3  b  3  a .
Xét hàm số f t t 3 
t f t t 2 3 '
 3 .ln 3  3t  0, t  
(1)  f a  f b 3
a b  3  x m  3x
m  3  x3 3 2
 3x  x  9x  24x  27 g x 3 2
 x x x   g x 2 9 24 27 '  3  x 18 x 24
g ' x  0  x  2  x  4 Đồ thị:
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 53
NGUYỄN BẢO VƯƠNG - 0946798489
Dựa vào đồ thị ta thấy điều kiện để phương trình có 3 nghiệm phân biệt là 7  m  11 hay m 8;9;1  0 .
Câu 37. Tìm các giá trị m để phương trình sin x 5 cos xm 5 3  log m  5 có nghiệm.
sin x 5 cos x 1  0  
A. 6  m  6 .
B. 5  m  5 .
C. 5  6  m  5  6 .
D.  6  m  5. Lời giải Chọn C Ta có
sin x 5 cos xm 5 3  log m  5
sin x 5 cos x 1  0  
sin x 5 cos x 10 3  ln  m  5   m 5 3
ln sin x  5 cos x 10
sin x 5 cos x 1  0  3
.ln sin x  5 cos x 10 m 5  3 .ln  m  5 (1) 1 Xét
   ln  .3t f t t
, t  5 , vì    3t  ln  3t f t t
ln 3  0,t  5 nên hàm số f t  đồng biến trên t (5; ) . Khi đó
(1)  f sin x  5 cos x 10  f m 5
 sin x  5 cos x 10  m  5
 sin x  5 cos x  5  m
Mà  6  sin x  5 cos x  6 nên để phương trình có nghiệm ta phải có 5  6  m  5  6.
Câu 38. Cho phương trình 2x m  log
x m với m là tham số. Có bao nhiêu giá trị nguyên của 2   m  1
 8;18 để phương trình đã cho có hai nghiệm? A. 20 . B. 17 . C. 9 . D. 21. Lời giải Chọn B
Điều kiện x m
PT  2x x x m  log  x mx log5 (xm)  2  x  2  log (x  ) m (1) 2 2 Xét hàm số    2t f tt, t
   ; Ta có:    2t f t ln 2 1  0, t
    Hàm số f t  đồng biến trên  .
Từ (1) suy ra f x  f log (x m)  x  log (x m)    2x    2x x m m x 2  2
Trang 54 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Xét hàm số     2x g x x trên  ;
m  . Ta có: '  1 2x g x   ln 2 ; '   0  2x g x
ln 2  1  x  log
log e g log log e  log log e  log e 2  2  2  2  2  2  2
lim g x  m  2m; lim g(x)   xmx Bảng biến thiên:
Do đó. Phương trình đã cho có 2 nghiệm  2m m
m  log log e  log e m  log
log e  log e  0  , 91 2  2  2 2  2  2 m    Vì  nên m  1  7; 1  6; 1  5;....;   1 m   18;18 
Vậy có 17 giá trị của m .
Câu 39. Cho phương trình   3 2  m m
x x   2 .log  x 3x 1 2 3 2 3 1 3 1 2 1 3 2 2 .log        0 81 3 3 2
m  3m 1  2   
Gọi S là tập hợp tất cả các giá trị m nguyên để phương trình đã cho có 6 nghiệm hoặc 7 nghiệm
hoặc 8 nghiệm phân biệt. Tính tổng bình phương tất cả các phần tử của tập S . A. 20 . B. 19 . C. 14 . D. 28 . Lời giải Chọn A   3 2 3 2  m 3m 1   x 3x 1  2 1 Ta có 2 .log  3 2 x 3x 1 2 2 .log        0 81  3 3 2
m  3m 1  2    3 2 x x   m m    2
.log  x  3x 1  2 3 2 3 1 2 3 1 2 3 2  2 .log  3 2
m  3m 1  2 . 3 3  t t 1 Xét hàm số    2t f t
.log t với t  2 ; Ta có f t   2 ln 2.log t  2 .  0t  2 . 3 3 t ln 3
Suy ra hàm số f t  đồng biến trên 2; .
Do đó phương trình tương đương với 3 2 3 2
m  3m 1  x  3x 1   1 .
Vẽ đồ thị hàm số g x 3 2
x  3x 1 từ đó suy ra đồ thị g x và đồ thị của g x  như hình vẽ.
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 55
NGUYỄN BẢO VƯƠNG - 0946798489
Từ đồ thị suy ra  
1 có 6, 7,8 nghiệm  0  g m   3 .
Từ đồ thị suy ra các giá trị nguyên của m là 3, 1, 0,1, 3 . Vậy S  20 . 2
Câu 40. Cho phương trình 2x log  2
x  2  4 xa log
2 x a  2 2  2   
 . Gọi S là tập hợp các giá trị a thuộc
đoạn 0; 2020 và chia hết cho 3 để phương trình có hai nghiệm. Hãy tính tổng các phần tử của S . A. 0 . B. 2041210 . C. 680403. D. 680430 . Lời giải Chọn C
Phương trình tương đương 2 2x log  2
x  2  2 xa log
2 x a  2 2  2 2     2  4.2x log  2
x  2  4.2 xa log
2 x a  2 2  2 2     2 x 2  2 log  2
x  2  2 xa  log
2 x a  2 2  2 2 2     (*) t 2t Xét hàm số    2t f t
log t, t  2 . Có f 't   2 ln 2.log t   0, t
  2 , nên f t  đồng biến 2 t ln 2 2;   .  f   2
x  2  f 2 x a  2 Khi đó (*)    2
x  2 x a (1) 2
x  2  2; 2 | x a | 2  2  2
x  2 x a 2
x  2x  2a  0 (2)     2 x  2
  x a 2
x  2x  2a  0 (3)  
Phương trình (2)   1 2a , phương trình (3) có   1 2a . 2 (3)
Vì     2  0 nên ít nhất một trong hai phương trình (2), (3) luôn có hai nghiệm phân biệt. Để 2 (3)
phương trình (1) có hai nghiệm phân biệt, ta xét các trường hợp sau: 1
* TH1: (2) có hai nghiệm phân biệt:   0  1 2a  0  a  
. Khi đó   0 nên (3) vô 2 2 (3)
nghiệm. Trường hợp này thỏa mãn điều kiện bài toán.
Trang 56 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 1
* TH1: (3) có hai nghiệm phân biệt:   0  1 2a  0  a  . Khi đó    0 nên (2) vô (3) 2 (2)
nghiệm. Trường hợp này cũng thỏa mãn điều kiện bài toán.  1   1 
Do đó phương trình đã cho có 2 nghiệm khi và chỉ khi a   ;    ;       2   2 
Vì a 0; 2020 và chia hết cho 3 nên a S  3;6;9;12;..., 201  9
Tổng các phần tử của S là: 3  6  9  ...  2019  3.1 3.2  3.3  ...  3.673 673.674
 31 2  3  ...  673  3.  680403 2
Câu 41. Có bao nhiêu giá trị thực của tham số a để phương trình 4 xa log   2  3 2 2  x 2  2 x x x log
2 x a  2  0 1 2   2
có 3 nghiệm thực phân biệt ? A. 0 . B. 2 . C. 1. D. 3 . Lời giải Chọn D 1 1
PT đã cho tương đương với 2 log
x  2x  3  log    .  2 x a 2 0 1 2 xa   2 1 x 2 x 2   2 2 2 2 2  log x x   x a xa  1 2 2 3 log 2 2 2  2 2 2   x 2 2 2 x 2 x 2 x 1  2  log  2
x  2x  3  2 xa log 2 x a  2 2  2 2   2 x 2 x3  2 log  2
x  2x  3  2 xa  log 2 x a  2 (1) 2  2 2 2   t 2t Xét hàm số    2t f t .log t, t
  2 ; Ta có: f t   2 ln t   0, t
  2  Hàm số f t  đồng 2 t ln 2
biến trên 2;  . Từ (1) suy ra f  2
x x    f x a   2 2 3 2
2  x  2x  3  2 x a  2 2
x  2x 1  2 x a (*) 2
x  2x 1  2 x a 2
x  4x  2a 1  0 (2)     2
x  2x 1  2
  x a 2 x  2a 1 (3)  
Phương trình (*) có 3 nghiệm phân biệt nếu xảy ra một trong các trường hợp sau:
* TH1: (2) có hai nghiệm phân biệt và (3) có nghiệm kép khác hai nghiệm của (2):  3   0 a         2 3 2a 0  2 1       a    0 2a 1  0 1 2  (3)   a    2
* TH2: (3) có hai nghiệm phân biệt và (2) có nghiệm kép khác hai nghiệm của (3):  3   0 a         2 3 2a 0  2 3       a    0 2a 1  0 1 2  (3)   a    2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 57
NGUYỄN BẢO VƯƠNG - 0946798489
* TH3: (2) và (3) đều có hai nghiệm phân biệt, trong đó có một nghiệm chung: 2 
x  4x  2a 1  0
Điều này xảy ra khi hệ  có nghiệm 2 x  2a 1  2 
x  4x  2a 1  0 x ax  1      2 x  2a 1 a  1 a  1     x  1
Khi a  1 ta có: 2 trở thành 2
x  4x  3  0   x  3  x  1 3 trở thành 2 x  1   x  1  
Khi đó: PT đã cho có 3 nghiệm. 1 3 
Vậy a   ;1;  .  2 2  2
Câu 42. Tìm tổng tất cả các giá trị của tham số a để phương trình x 2x 1  2 3 xa  log
2 x a  2 có 2 x 2 x3  
đúng ba nghiệm phân biệt. A. 2 . B. 3 . C. 1. D. 0 . Lời giải Chọn B 2
ln 2 x a  2
x 2 x32 xa 2  
PT đã cho tương đương với 3  ln  2
x  2x  3 2 x 2 x3   2 3
.ln x  2x  3 2 xa 2  3
.ln 2 x a  2 (1) . t 3t Xét hàm số    3t f t .ln t, t
  2 ; Ta có: f t   3 ln 3.ln t   0, t
  2  Hàm số f t  đồng t
biến trên 2;  . Từ (1) suy ra f  2
x x    f x a   2 2 3 2
2  x  2x  3  2 x a  2 2
x  2x 1  2 x a (*) 2
x  2x 1  2 x a 2
x  4x  2a 1  0 (2)     2
x  2x 1  2
  x a 2 x  2a 1 (3)  
Phương trình (*) có 3 nghiệm phân biệt nếu xảy ra một trong các trường hợp sau:
* TH1: (2) có hai nghiệm phân biệt và (3) có nghiệm kép khác hai nghiệm của (2):  3   0 a         2 3 2a 0  2 1       a    0 2a 1  0 1 2  (3)   a    2
* TH2: (3) có hai nghiệm phân biệt và (2) có nghiệm kép khác hai nghiệm của (3):  3   0 a         2 3 2a 0  2 3       a    0 2a 1  0 1 2  (3)   a    2
Trang 58 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
* TH3: (2) và (3) đều có hai nghiệm phân biệt, trong đó có một nghiệm chung: 2 
x  4x  2a 1  0
Điều này xảy ra khi hệ  có nghiệm 2 x  2a 1  2 
x  4x  2a 1  0 x ax  1      2 x  2a 1 a  1 a  1     x  1
Khi a  1 ta có: 2 trở thành 2
x  4x  3  0   x  3  x  1 3 trở thành 2 x  1   x  1  
Khi đó: PT đã cho có 3 nghiệm. 1 3 
Vậy a   ;1;  .  2 2 
Câu 43. Tìm số giá trị nguyên của m thuộc 20; 20 để phương trình 2 2 2
log (x m x x  4)  (2m  9)x 1 (1 2m) x  4 có nghiệm. 2 A. 12. B. 23. C. 25. D. 10. Lời giải Chọn B Điều kiện xác định: 2 2
x m x x  4  0 . log  2 2
x m x x  4   2m 9 x 1 1 2m 2 x  4 2  log x 2
x  4  x  m 2 2
 2mx  9x 1
x  4  2m x  4 2  4x  2 2  log 
m   2mx  9x 1 x  4  2m x  4 2 2  x  4  x  2  4x m x 4     mx 2 2  log 
  2mx  9x 1
x  4  2m x  4 2  2 x 4     x   log  2
4x m x  4  mx   2
8x  2m x  4  2mx 1 log  2
x  4  x   2 x  4  x 2 2   log  2
8x  2m x  4  2mx   2
8x  2m x  4  2mx  log  2
x  4  x   2
x  4  x 1 Xé 2 2   
t hàm số f t   log t t , t  0;  . 2 1
f t  
1  0, t 0;   nên hàm số đồng biến trên 0;  . t ln 2 Khi đó   1 2 2
 8x  2m x  4  2mx x  4  x m  2 x   x   2 2 4
x  4  x 8x 8x  2m  1 2 x  4  x
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 59
NGUYỄN BẢO VƯƠNG - 0946798489 x  2 8 x  4  x  2m  1 4
m   x  2 2 1 2
x  4  x 1 2m 2 2
x x  4  x  . 2 Xét hàm số 2 2
g(x)  x x  4  x với x  ;   .
x  4  x2 2 Ta có g (  x)   0, x   . 2 x  4  4  4 g x x x x  lim x   lim  2 ; x x   2 lim lim 4          x 2 
x  4  x x 4  1 1 2 x   4  lim g x 2  lim x  1 1   . 2 x x     x 
Ta có bảng biến thiên của g( ) x 1 2m 5
Để phương trình có nghiệm thì  2   m  . 2 2
Do m nguyên thuộc 20; 20 nên số giá trị m là 23.
C. GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT Câu 1.
Xét các số thực dương , a , b ,
x y thoả mãn a  1, b  1 và x y a b
ab . Giá trị nhỏ nhất của biểu
thức P x  2 y thuộc tập hợp nào dưới đây?  5   5  A. 1;2 . B. 2;   . C. 3; 4 . D. ;3   .  2   2  Lời giải Chọn D
Đặt t  log b . Vì ,
a b 1 nên t  0 . a x 1 1
Ta có: a ab x  log ab   b   t . a 1 loga  1  2 2 y 1 1  1 
b ab y  log ab   a   . b 1 logb  1   2 2  t  1 1 3 t 1 3
Vậy P x  2 y
1 t 1      2 . 2 t 2 2 t 2 t 1
Dấu đẳng thức xảy ra khi và chỉ khi 2   b a . 2 t
Trang 60 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 3  5 
Giá trị nhỏ nhất của biểu thức P x  2 y bằng  2 thuộc nửa khoảng ;3   . 2  2  Câu 2.
Xét các số thực dương a , b , x , y thỏa mãn a  1 , b  1 và x y 4
a b ab . Giá trị nhỏ nhất của
biểu thức P x  4 y thuộc tập hợp nào dưới đây?  5  A. 1; 2 . B. 2;   . C. 1; 2 . D. 0  ;1 .  2  Lời giải Chọn B 1 1  1 1   1 1 xx x   log b 4 4
a a .b 4 4 ab   4 4 a Theo bài ra ta có: x y 4
a b ab       1 1 1 1  y 1 1 y   4 4 b a . y   .log ab 4 4 b   a   4 4 b 1 1 5 1
Do đó: P x  4 y  
log b 1 log a  
log b  log a 4 4 a b 4 4 a b
Đặt t  log b t  0 . Vì a , b  1 nên log b  log 1  0. a a a 5 1 1 5 1 1 9 Khi đó P   t    2 t.  . (Áp dụng BĐT Cô Si) 4 4 t 4 4 t 4 9
Vậy P đạt giá trị nhỏ nhất là khi t  2 hay 2 b a . 4 Câu 3.
Xét các số thực a , b , c  0 thỏa mãn 3a 5b 15  
c . Giá trị nhỏ nhất của biểu thức 2 2 2
P a b c  4(a b c) thuộc tập hợp nào dưới đây? A.  1  ; 2 . B.  5  ;   1 . C. 2; 4 . D. 4;6 . Lời giải Chọn B a  log t 3 a b c
Đặt 3  5  15  t  0  b  log t . Khi đó 5 c   log  t 15 2 2 2
P  log t  log t  log t  4(log t  log t  log t) 3 5 15 3 5 15 2  log t  2 2
1 log 3  log 3  4 log t 1 log 3  log 3 3 5 15  3  5 15  2  X  2 2
1 log 3  log 3  4 X 1 log 3  log 3 , (với X  log t ) 5 15   5 15  3
 21 log 3 log 3  5 15  PP    4  min , 2 2 1 log 3  log 3  5 15   2 1log 3log 3 5 15  21 log 3  log 3 2 2 1log 3log 3 5 15 khi 5 15 log t   t  3 3 2 2 1 log 3  log 3 5 15 Suy ra
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 61
NGUYỄN BẢO VƯƠNG - 0946798489 21 log 3  log 3 5 15  a  2 2 1 log 3  log 3 5 15  2 1log 3log  3 5 15 2 2 1log 3log 3 5 15 b  log 3 5  2 1log 3log  3 5 15 2 2 1log 3log 3 5 15 c   log 3 15 . Câu 4.
Xét các số thực dương a , b , c , x , y , z thỏa mãn a  1 , b  1, c  1 và x y z a b c abc . Giá 1
trị nhỏ nhất của biểu thức P x y z
thuộc tập hợp nào dưới đây? 2 A. 10;13 . B. 7;10 . C. 3;5 . D. 5;7 . Lời giải Chọn D Từ giả thiết ta có 1 1 1
x  1 log b  log c , y  1 log a  log c, z  1 log b  log a . Khi đó ta có 2 a a 2 b b 2 c c
2P  4  log b  log a  log c  log a  log c  log b . a b a c b c
Vì a  1 , b  1, c  1 nên log b  0 , log c  0 , log a  0 , log a  0 , log b  0 , log c  0 . a b c b c a
Áp dụng bất đẳng thức Cô Si ta được
log b  log a  2 log .
b log a hay log b  log a  2 . a b a b a b
Tương tự log c  log a  2 và log c  log b  2 . a c b c
Do đó 2P  10 hay P  5 . Dấu "  " xảy ra khi và chỉ khi a b c .
Vậy giá trị nhỏ nhất P  5 . min 2 2 Câu 5.
Xét các số thực dương a, , b ,
x y thỏa mãn a  1,b  1 và x y ab  .
a b . Giá trị nhỏ nhất của biểu thức P  . x y là 9 6 3 4 A. P  . B. P  . C. P  . D. P  . 4 2 2 9 Lời giải Chọn B  1 1 2 x  log b a  2 2 x y  2 2 ab  . a b   1 1 2
y  log a    2 b 2      1 1 1  +)  xy2 1 1 1 1  log b  log a       
log b  log a   a b    2 a 2   2 b 2   4 2 4  3 
( a,b  1 log b  0, log a  0 ). 2 a b 6
Vì x  0, y  0  xy
. Dấu bằng xảy ra khi và chỉ khi a b . 2
Trang 62 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 2 2 x y Câu 6.
Xét các số thực dương a, b, x, y thỏa mãn a  1, b  1 và y x ab
ab . Giá trị nhỏ nhất của biểu thức P  . x y là
A. P  2 .
B. P  4 .
C. P  3. D. P 1 . Lời giải Chọn B 2  x 2 2 x  1 log b yay y x abab   . 2
y 1 log a b   x 2 2 x y Ta có xy  .
 1 log b1 log b a ay x
 11 log b  log a a b
 4 ( a,b  1  log b  0, log a  0 ). a b
Dấu bằng xảy ra khi và chỉ khi a b . Câu 7.
Xét các số thực dương a, b, c, x, y, z thỏa mãn a  1, b  1, c  1, y  2 và x 1  y 2 z 1 a b c     abc . Giá
trị nhỏ nhất của biểu thức P x y z là
A. P  13 .
B. P  3 .
C. P  9 . D. P  1 . Lời giải Chọn C
x 1  1 log b  log c a ax 1  y 2 z 1  ab
c   abc   y  2  1 log a  log c . b b
z 11 log b  log a   c c
Ta có: x 1 y  2  z 1  3  log b  log c  log c  log a  log b  log a a b b c a c
x y z  3  6
P  9 ( a, ,
b c  1 log b  0, log c  0, log a  0, log c  0, log a  0, log b  0 ). a a b b c c
Dấu bằng xảy ra khi và chỉ khi a b c . 1 xy Câu 8.
Xét các số thực dương x , y thỏa mãn log
 3xy x  2 y  4 . Tìm giá trị nhỏ nhất P của 3 x  2y min
P x y . 9 11 19 9 11 19 18 11  29 2 11  3 A. P. B. P. C. P. D. P  . min 9 min 9 min 9 min 3 Lời giải Chọn D
Theo đề bài suy ra: 1 xy  0 , x  2 y  0 . 1 xy Ta có: log
 3xy x  2 y  4  log 3  3xy  3  3xy  log
x  2 y x  2 y   1 . 3   3   3 x  2y
Xét hàm số: f t   log t t, t  0 : 3  
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 63
NGUYỄN BẢO VƯƠNG - 0946798489 1
f t   1  0, t   0 . t ln 3
Hàm số f t  đồng biến trên khoảng 0;  . 3  2 y Do đó:  
1  f 3  3xy  f x  2y  3  3xy x  2 y x  . 1 3y 3 Theo đề bài ta có: ,
x y  0  0  y  . 2 3  2 y  3 
Ta có: P x y
y 0  y    . 1 3y  2  1  1 11 1  3  Đạo hàm: P 
1; P  0  y   0;   . 1 3y2 3  2   11 1  2 11  3  3  3 2 11  3
Ta có: P 0  3; P    ; P    . Vậy P  .  3  3 min  2  2   3 1 2x Câu 9.
Xét các số thực dương x , y thỏa mãn ln
 3x y 1. Tìm giá trị nhỏ nhất P của biểu thức x y min 1 1 P   1 . x xy A. P  8 . B. P  16 . C. P  9 . D. P  2 . min min min min Lời giải Chọn C 1
Theo đề bài suy ra: x  . 2 1 2x Ta có: ln
 3x y 1  ln 1 2x 1 2x  ln  x y  x y   1 . x y 1
Xét hàm số: f t   ln t t,t  0  f t   1  0,t  0 t
Hàm số f t  đồng biến trên khoảng 0;   . Do đó:  
1  f 1 2x  f x y  1 2x x y  3x y  1 1 1 1 1   2 1 1 Ta có: P   1   1  1  9 x xy x x y 3x y 2 2 2 11  3 1 Vậy P  khi x y  . min 3 4    3 3x 6 y
Câu 10. Xét các số thực dương x , y thỏa mãn 2 3 3 x y
. Tìm giá trị nhỏ nhất P của x y min 9 3 3 1 P    . 4x 2 xy 4
Trang 64 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 22 15 3 35  36 2 A. P  2 . B. P. C. P  20 . D. P. min min 2 min min 4 Lời giải Chọn C x y  0
Từ giả thiết bài toán suy ra  . x  2 y  1       3 3x 6y 3xy x y x y 1 2 Ta có: 2 3 3     x y    x y     1 . xy  .3x y 1 2  1 x 2 .3 y 1 2 x y 3 x y Xét hàm số:
   .3t ,  0     3t  .3t f t t t f t t .ln 3  0, t   0 .
Suy ra: hàm số f t  đồng biến trên 0;   . Do đó:  
1  f x y  f 1 x  2y  2x  3y  1. 2  3   3 9 3 3 1 9 9 1 9 9 1    2  1 Ta có: P             20 . 4x 2 xy 4 4x 2 .3 x y 4 4x x  3y 4 2x  3y 4 1 1 Vậy P
 20 khi x  ; y  . min 3 9 4 3  a
Câu 11. Cho hai số thực a , b thỏa a b  và 2 P  16 log  3log a  
có giá trị nhỏ nhất. Tính 3 a 12b 16 a   b a b . 7 11 A. . B. 4 . C. . D. 6 . 2 2 Lời giải Chọn D 2 3 Ta có: 3
b 12b 16  b  2 b  4 3  0, b  
b  12b 16 . 4 3 3 3 3 a a  4   a   a   4  Suy ra:  a b   log  log , a  . 3         12b 16 b  3 a  12b 16 a    b   3  3 3  a   a  3 Do đó: 2 2 P  16 log  3log a  16 log  3log a  48  b  . a   a a   a 1 loga  12b 16    b b b 1 log b a 2 3
P  24 1 log b   b   . a  241 loga  36 1 log b a 2 Vậy P
 36 khi a  4, b  2 . min     x y xy x y 2
Câu 12. Cho hai số thực dương x , y thỏa mãn 2 1 3 
. Tìm giá trị nhỏ nhất S của biểu thức xy 1 min
S x  4 y .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 65
NGUYỄN BẢO VƯƠNG - 0946798489 A. S  4 3  9 . B. S  6  4 3 . C. S  2 3  2 . D. S  4 3  6 . min min min min Lời giải Chọn D
Theo đề bài suy ra: xy 1  0 .     x y xy x y 2 Ta có: 2 1 3 
  xy   xy 1
1 .3   2x y  2
.3 xy   1 . xy 1 Xét hàm số:
   .3t ,  0     3t  .3t f t t t f t t .ln 3  0, t   0
Hàm số f t  đồng biến trên khoảng 0;  . 1 2x Do đó:  
1  f xy  
1  f 2x y  xy 1  2x y y x 1
Theo đề bài ta có: x, y  0  x  1 . 8x  4
Ta có: S x  4 y x  , x  1 . x 1 12 Đạo hàm: S 1 S   
 0  x  12 1 .  x  2 1 Từ đó ta được P  9  4 3 . min 2 2 2 Câu 13. Cho ,
x y là hai số thực dương thỏa mãn x 2  y   x 2 
y  2yx 2 4 9.3 4 9 .7
. Giá trị nhỏ nhất của biểu x  2 y 18 thức P  là x 3  2 A. 9. B. . C. 1 9 2. D. 17. 2 Lời giải Chọn A 2 2 2 2 2 2 Ta có x 2 y
x 2 y  2yx 2 x 2 y  2 2( x  2 y ) 2 y x  2 4 9.3 4 9 .7 4 3 4 3         .7   2 2 x 2 y 2 2( x 2 y ) 4  3 4  3   (*). 2 2 x 2 y  2 2( x 2 y ) 7 7 t t 4  3t  1   3 
Xét hàm số f (t) 
trên . Ta có f (t)  4.   
  nghịch biến trên . 7t  7   7   f  2 x y   2 2 2 2 2 (*) 2
2  f 2(x  2 y)  x  2 y  2  2(x  2 y)  x  2 y  2  2 y x  2.   Từ 2 x x  16 16 16 đó P   x   1  2 . x  1  P  9. x x x
Dấu "  " xảy ra khi và chỉ khi x  4.
x y 1 
Câu 14. Cho các số dương , x y thỏa mãn log
 3x  2 y  4 . Giá trị nhỏ nhất của biểu thức 5   2x  3  y  4 9
A  6x  2 y   bằng x y
Trang 66 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 31 6 27 2 A. . B. 11 3. C. . D. 19. 4 2 Lời giải Chọn D
x y 1  0  ĐK: 2x  3  y
x y  1  x, y  0  Ta có:
x y 1  log
 3x  2 y  4 5   2x  3  y
 log x y 1 1  5 x y 1  log 2x  3y  2x  3y 5      5  
 log 5 x y 1   5 x y 1  log
2x  3y  2x  3y * 5     5       1
Xét hàm số f (t)  log
t t trên 0;    , vì f (  t)  1  0, t
 0;  nên hàm số f (t) 5   t ln 5
đồng biến trên 0;  .
*  5 x y  
1  2x  3y  3x  2 y  5 Mặt khác, ta có 4 9  4   9 
A  6x  2 y    9x   4 y     
 3x  2 y   2.6  2.6  5  19 . x yx y    4 9x   x  2  x  9    3
Dấu “ = ” xảy ra  4y   
(thỏa mãn điều kiện). y 3   y
3x  2y  5   2  
Vậy GTNN của A là 19. y x
Câu 15. Cho hai số thực ,
x y lớn hơn 1 và thỏa mãn x.( x )e y.( y )e y e x e
. Tìm giá trị nhỏ nhất của biểu thức P  log xy  log . x x y 2 1 2 2 1 2 A. . B. 2 2 . C. . D. . 2 2 2 Lời giải Chọn C Với , x y  1, ta có y x x y .( x
e )e y x .( y e )e y x  ln  x y .( x
e )e   ln  y x .( y e )e   x ln y y
xe y ln x x ye ln y y e ln x x e     (1). y y x x t 1 Xét hàm số ( )  t t g t te
e 1 ln t trên 1; , có g (
t)  te   0, t   1. t
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 67
NGUYỄN BẢO VƯƠNG - 0946798489
Hàm số g(t) đồng biến trên 1;  nên g(t)  g(1) 1  0,t 1. ln t t e g(t)
Xét hàm số f (t)  
trên 1;  , có f '(t) 
 0,t  1, nên f (t) đồng biến trên (1; )  . t t 2 t
Với x, y  1 thì (1)  f ( y)  f (x)  y  . x 1 u 1 2 u  2 Đặt u  log .
y Do y x 1 nên u  1. Ta có P  ( h u) 
 . Nhận thấy h '(u)  , nên x 2 u 2 2u
h '(u)  0 khi u  2, h '(u)  0 khi 1  u  2, h '(u)  0 khi u  2. Dẫn tới
P h u h   1 2 2 ( ) 2 
,u  1, đẳng thức xảy ra khi u  2. 2 1 2 2 Vậy min P  , đạt được khi 2 y x và x  1. 2
Câu 16. Cho hai số thực x, y thỏa mãn 0  x, y  1 trong đó x, y không đồng thời bằng 0 hoặc 1 và  x y  log  x 1 . y 1
2 0 . Tìm giá trị nhỏ nhất của P với P  2x y 3
          1  xy  1 A. 2 . B. 1 . C. . D. 0 . 2 Lời giải Chọn B x y
Từ điều kiện đề bài và
 0; 1  xy  0  x y  0;1  xy  0 khi đó 1  xyx y  log  x 1 . y 1 2 0 log x y x y log 1 xy 1 xy 1 3
         3         3            1   xy  1
Xét hàm số f t  log t t t  0 có f t   1  0 t  0 3  t.ln 3
f t là hàm số đồng biến trên khoảng 0;  . 1 x 1 x Vậy phương trình 1  
x y  1  xy y   P  2x  1  x 1  x 1  x 2 x  0
Xét hàm số f (x)  2x
với x  0; 1 có f ( ) x  2 
cho f (x)  0   x  1    2 x   1 x    2
f 0  1; f  
1  2 min f (x)  1  chọn B 0;    1  1 2x
Câu 17. Xét các số thực dương x , y thỏa mãn ln  3x y   
1. Tìm giá trị nhỏ nhất P của x  min  y  1 1 P   . x xy A. P  8 . B. P  4 . C. P  2 . D. P  16 . min min min min Lời giải Chọn A 1
Điều kiện 0  x  . 2
Trang 68 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020  1 2x  Từ giả thiết ln  3x y   
1  ln 1 2x  1 2x  ln x y  x y 1 x   y  1
Xét hàm số f t  ln t t trên 0;  có f t   1  0 , t  0 do đó hàm f t đơn điệu. t
Vậy 1  1  2x x y  3x y  1 2 1 1 1 2 1 2 Có P       x xy x x y x 1  2x 1 2 1 4 1
Đặt g x   , ta có 
g x   
suy ra gx  0  x  . x 1  2x 2 x  2 1  2x 4
Do đó min g x  8 . Vậy P  8 . min  1   0 ;   2  1 1 1 2 1 2 4 1
Bổ sung: có thể đánh giá P         x xy x x y x 1  2x 1 8 x   x 2 2 y 1
Câu 18. Cho hai số thực x, y không âm thỏa mãn 2
x  2x y 1  log
. Giá trị nhỏ nhất của biểu 2 x 1 thức 2x 1  2 P e
 4x  2y 1 là 1 1 A.  . B. 1. C. . D. 1. 2 2 Lời giải Chọn A 2 y 1 2 2 2
x  2x y 1  log  2  x   1  log 2 x 1  log
2 y 1  2 y 1 . 2     2     2 x 1 1
Xét hàm số f t   t  log t , t  0 ; f t   1  0, t  0 2   t.ln 2 Suy ra  x  2 2
1  2y 1  y   x  2 2 2 1 1. 2x 1  2 P e
 4x  2y 1 x e  
x   x  2 2 1 2 4 2 1 11 2 x 1  2  e
 2x  4x g x . g x 2 x 1 2e   
 4x  4 là hàm số đồng biến trên nửa khoảng 0; nên g x  0 có tối đa 1 1
nghiệm, nhẩm được nghiệm x
nên nghiệm đó là duy nhất. 2 1 1 Vậy min P   tại x  . 2 2
Câu 19. Cho hai số thực dương x , y thay đổi thỏa mãn đẳng thức    xy      2 2 1 2 1 .2 .2x y xy x y . Tìm giá trị nhỏ nhất y của y . min
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 69
NGUYỄN BẢO VƯƠNG - 0946798489 A. y  3 . B. y  2 . C. y  1. D. y  3 . min min min min Lời giải Chọn B 2 Ta có    xy     2 2 1 2 1 2 2x y xy x yxy  2xy 1  2 x
y x y 1 2 1 1 2 2         1 Xét hàm       1 .2t f t t với t  1.
Khi đó    2t     1 .2t f t t .ln 2  0 với t   1. 2 x  2 Từ   2
1  2xy 1  x y 1  y  2x 1 2 2x  2x  4 x  2 y   0 2
 2x  2x  4  0   2x  2 1 x  1  
Loại x  1 vì điều kiện của t nên f 2  2 . x, y     x    Câu 20. Cho          sao cho 3 3 ln 2 x ln 3 19 y 6xy(x 2 y)  
. Tìm giá trị nhỏ nhất m của biểu x, y 1   y  1
thức T x  . x  3y 5
A. m 1 3 .
B. m  2 . C. m  .
D. m 1. 4 Lời giải Chọn C Ta có  x       x  
y xy x y
y x y x3   y y3 3 3 ln 2 ln 3 19 6 ( 2 ) ln 2 2 ln 3 3   1     y  1
Xét hàm số f t  t 3 ln
t với t  0 có f t 2
 3t  0 t  0  f tđồng biến t Vậy   1
1  2 y x  3y x y T x  4x
Áp dụng bất đẳng thức AM-GM 1 3x x 1 3x x 1 3x 1 3 1 5 T x       2 . 
    Dấu bằng xảy ra khi x y 1 4x 4 4 4x 4 4 4x 4 2 4 2 4 xy 3 5xy Câu 21. Cho   ;
x y là các số thực dương thỏa mãn điều kiện 4 x 4 5   x 1 3
y yx  4 . Tìm 3xy 5
giá trị nhỏ nhất của biểu thức P x y . A. 3 . B. 5  2 5 . C. 3 2 5 . D. 1 5 . Lời giải Chọn B xy 3 5xy Ta có 4 x 4 5   x 1
3  y yx  4 3xy 5
Trang 70 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020x4yx4 y xy 1  1 5 3   4  5 3 xy x yxy   1  1 . Xét hàm số
  5t 3t f tt trên  .
Vì    5t.ln 5  3t f t
.ln 3 1 0; x   nên hàm số f t đồng biến trên  2 . Từ  
1 và 2 ta có x  4 y xy   1 
3 . Dễ thấy x  4 không thỏa mãn   3 . x  Với x  4 ,   1 3  y
kết hợp điều kiện y  0 suy ra x  4 . x  4 x 1
Do đó P x y x  . x  4 x
Xét hàm số g x 1  x  trên 4; . x  4  5 x  4  5 
Ta có gx 1  0  .   x  2 4 x  4 5  x 4 4  5 
g x – 0   
g x 5  2 5
Dựa vào bảng biến thiên ta có P
 min g x  5 2 5 . min   4; xy xy 3 5
Câu 22. Cho x , y là các số thực dương thỏa mãn 2  x2 5   x 1   3
y y(x  2) . Tìm giá trị nhỏ 3xy 5
nhất của biểu thức T x y . A. T  2  3 2 . B. T  3  2 3 . C. T  1 5 . D. T  5  3 2 . min min min min Lời giải Chọn B Theo đề ra ta có xy xy 3 5 2  x2 5   x 1   3
y y(x  2) 3xy 5 xy 1 xy 1 2 1  5 
x  2 y  5   xy 1 x2 y xy 1 3 3  t 1
Xét f t   5   t . 
   5t ln 5  3  t f t ln 3 1  0 3t x 1 x 1
x  2 y xy 1  y
.Do y  0, x  0   0  x  2 x  2 x  2 2 x 1 x x 1
Ta có: T x y x   x  2 x  2 2 x  2  3 x x  2; 4 1     T    0    x  22
x  2  3  2;   Bảng biến thiên
Chỉnh lại bbt cho em,chỉ xét với x  2 nhé,kết quả không thay đổi.
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 71
NGUYỄN BẢO VƯƠNG - 0946798489
Từ bảng biến thiên ta thấy T
 3  2 3 tại x  2  3 . min x  3 y
Câu 23. Xét các số thực dương , x y thỏa mãn log
xy  3 y x  1 . Tìm giá trị nhỏ nhất của biểu thức 3 xy 1 1 A x  . y 14 14 A. A  . B. A   . C. A  6  . D. A  6 . min 3 min 3 min min Lời giải Chọn D
Điều kiện: x  3 y  0 . x  3 y log
xy  3 y x 1  log
x  3 y  log
xy  1  xy  3 y x  1 3 3   3   xy  1  log
x  3y x  3y  log
xy 1  xy 1 1 . 3     3    
Xét hàm f t   log t t, t  0 . 3 1
f t   1  0, t   0 . t.ln 3 x 1
Suy ra hàm số f t  đồng biến trên 0;   nên  
1  x  3 y xy 1  y  . x  3 1 x  3 A x   x  . y x 1 x  3 4
Đặt A Ax  x
A x  1
 0  x  3 do x, y  0 . x 1  x  2 1  2 2 x y  2 4x y  2 Câu 24. Cho , x y  0 thỏa 2019 
 0 . Tìm giá trị nhỏ nhất P
của P  2y 4x .  min x  22 1 A. 2018 . B. 2019 . C. . D. 2 . 2 Lời giải Chọn D
 2xy  4x y  2  2 2 2
2 x 4 x  4  
2 4 xy2 4x y  2 Ta có: 2019   0  2019  x  22 x  22  2 x22     x  2  2 4 x y  2 2019 . 2  2019
.4x y  2  * .
Trang 72 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020u  x   2 2 Đặt  u,v  0 v
  4xy 2  Khi đó:   2u 2 *  2019 .  2019 v u
.v f u  f v với   2  2019 t f t .t, (t  0)    2t 2 '
 2019 .2 ln 2019.  2019 t f t t  0, t  0
Do đó: f u  f v  u v  x  2 2 2
 4x y  2  y x  2.
P y x x x   x  2 2 2 4 2 4 4 2 1  2  2 . Vậy P  2  x 1. min y1
Câu 25. Cho 2 số thực dương x, y thỏa mãn log  x 1 y 1 9
x 1 y 1 . Giá trị nhỏ nhất 3              
của biểu thức P x  2y là 11 27 A. P  . B. P  . C. P  5  6 3 . D. P  3  6 2 . min 2 min 5 min min Lời giải Chọn D y1
Ta có log  x 1 y 1 9 x 1 y 1 3              
  y  1 log x 1 log y 1 x 1 y 1 9 . 3     3 
          
  y  1 log x 1 log y 1 x 1 9 3     3          9  log x 1 x 1 log y 1 3        3    y  1 9 9  log x 1 x 1 2 2 log . 3          y  3 1 y  1 1
Xét hàm số f t  log t t  2 với t  0 có f t 
 1  0 với mọi t  0 nên hàm số f t 3 t ln 3
luôn đồng biến và liên tục trên 0;  . 9 9 8  y
Từ đó suy ra x  1   x   1 
, do x  0 nên y  0; 8 . y  1 y  1 y  1 8  y 9 9
Vậy P x  2y
 2y  2y  1 
 2  y  1   3  3  6 2 . y  1 y  1 y  1 9 3 Vậy P
 3  6 2 khi 2  y  1   y   1 . min y  1 2 1 y
Câu 26. Xét các số thực dương , x y thỏa mãn log
 3xy x  3y  4 . Tìm giá trị nhỏ nhất P của 3 x  3xy min
P x y . 4 3  4 4 3  4 4 3  4 4 3  4 A. P  . B. P  . C. P  . D. P  . min 3 min 3 min 9 min 9 Lời giải Chọn B
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 73
NGUYỄN BẢO VƯƠNG - 0946798489 1 y log
 3xy x  3y  4  log 1 y  log
x  3xy  3xy x  3y  4 3 3   3   x  3xy
 log 3 1 y  3 1 y  log
x  3xy x  3xy 3     3     1
Xét hàm f t   log t t, t  0 có f 't  
1  0, t  0 . Suy ra hàm số đồng biến trên 3 t ln 3
0;  . Suy ra  log 3 1 y  3 1 y  log x  3xy x  3xy  31 y  x  3xy 3     3     31 y 31 y 4 3  4 4 3  4  x
x y y   . Vậy P  . 1 3y 1 3y 3 min 3 x y
Câu 27. Xét các số thực dương , x y thỏa mãn log
x x  3  y y  3  xy. Tìm giá trị 3 2 2
x y xy  2 3x  2 y 1 lớn nhất P
của biểu thức P  . max x y  6 A. 3 . B. 2 . C. 1. D. 4 . Lời giải Chọn C Ta có: x y log
x x  3  y y  3  xy 3 2 2
x y xy  2  log
3 x y   3 x y  log  2 2
x y xy  2 2 2
x y xy  2 . 3 3 1
Xét hàm số f t   log t t , t  0 có f t  
1  0, t  0 . Vậy hàm số f t  luôn đồng 3 t ln 3
biến và liên tục trên khoảng 0;  .
Do đó: f   x y  f  2 2
x y xy     x y 2 2 3 2 3
x y xy  2   1 2 Từ  
1  xy   x y  3 x y   2 . 2
x y 1 
Ta có x x xy xy x y   1  xy     xy  2 
Đẳng thức xảy ra khi và chỉ khi x y 1.
x y  2 1 2 Do đó từ   1 , suy ra: x
  x y  3 x y  2 . 4
Đặt t x y , t  0 . t  2 1 2 2 x y 2t 1
t  3t  2 2 1 x
3t  22t  3 Suy ra: 4 P   
f t  . x y  6 t  6 4t  6 2
3t  36t 135
Ta có: f t  
 0  t  3 (nhận) 4 t  62 Bảng biến thiên
Trang 74 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 t 0 3  f t   0  f t  x y 1 x  2
Dựa vào BBT, ta có max P  max f t   f 3  1 khi và chỉ khi    . 0; x y  3 y  1    2
2 x y   1 2x y
Câu 28. Xét các số thực dương x , y thỏa mãn 2018 
. Tìm giá trị nhỏ nhất P của  min x  2 1
P  2 y  3x . 1 7 3 5 A. P  . B. P  . C. P  . D. P  . min 2 min 8 min 4 min 6 Lời giải Chọn B  2
2 x y   1 2x y 2x y Cách 1: Ta có 2018   2  2 x y   1  log  2018 2 x  2 1  x   1  2 x  2
1  22x y  log
2x y  log  x  2 1 2018 2018  2 x  2 1  log  x  2 1
 2 2x y  log 2x y 2018   2018   2
Có dạng f  x  1  
f 2x y với f t   2t  log
t , t  0 .   2018 1
Xét hàm số f t   2t  log
t , t  0 , ta có f t   2 
 0 t  0 nên hàm số f t  2018 t.ln 2018 2
đồng biến trên khoảng 0;   . Khi đó f  x  1  
f 2x y   x  2 1  2x y 2
y x 1.  
Ta có P y x   2 x   2 2 3 2
1  3x  2x  3x  2 . Bảng biến thiên 3 x   4   P 7 8 7 3 Vậy P  khi x  . min 8 4 y 1 
Câu 29. Cho 2 số thực dương ,
x y thỏa mãn log  x 1 y 1   9  x 1 y  1 3        
. Giá trị nhỏ nhất của
biểu thức P x  2 y là 11 27 A. P. B. P. C. P  5  6 3 . D. P  3   6 2 . min 2 min 5 min min Lời giải Chọn D y 1 
Ta có log  x 1 y 1   9  x 1 y  1 3        
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 75
NGUYỄN BẢO VƯƠNG - 0946798489   y   1 log x 1  log
y 1   x 1 y 1  9  3   3       .   y   1 log x 1  log
y 1  x 1  9  3   3    9  log
x 1  x 1   log y 1 3   3   y 1 9 9  log
x 1  x 1 2   2  log (*). 3   3 y 1 y 1 1
Xét hàm số f t   log t t  2 với t  0 có f t  
1  0 với mọi t  0 nên hàm số f t  3 t ln 3
luôn đồng biến và liên tục trên 0;  . 9 9 8  y
Từ (*) suy ra x 1   x  1 
, do x  0 nên y  0;8 . y 1 y 1 y 1 8  y 9 9
Vậy P x  2 y
 2 y  2 y 1  2  y   1   3  3  6 2 . y 1 y 1 y 1 9 3 Vậy P  3
  6 2 khi 2  y   1   y  1. min y 1 2
Câu 30. Cho hai số thực dương x, y thỏa mãn log x x x y  log
6  y  6x . Giá trị nhỏ nhất của biểu 2   2   6 8
thức P  3x  2 y   bằng x y 59 53 A. . B. 19 . C. . D. 8  6 2 . 3 3 Lời giải Chọn Bx  0 Điều kiện:  . 0  y  6 
Từ giả thiết ta có: log x x x y  log 6  y 2 2
 6x  log x x  log x 6  y   x 6  y 2 2 2 2       (*) 1
Xét hàm số f t   log t t với t  0, Ta có f 't   1  0 , t   0 nên hàm 2 t ln 2
số f t   log t t đồng biến trên khoảng 0;  . 2
Do đó    f  2
x   f x  y 2 * 6
  x x 6  y  x  6  y x y  6*  *   ( do x  0 )
Áp dụng Bất đẳng thức Cô si cho các cặp số dương và bất đẳng thức *  * , ta có: 6 8 3  3x 6   y 8  3 3x 6 y 8
P  3x  2 y   
x y      .6  2 .  2 .  19     . x y 2  2 x  2 y 2 2 x 2 y    x y  6  3x 6 x  2
Đẳng thức xảy ra khi và chỉ khi    
. Vậy giá trị nhỏ nhất của P bằng 19. 2 x y  4    y 8   2 y
Trang 76 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 2 2 x  5 y
Câu 31. Cho x, y là các số dương thỏa mãn 2 2 log
 1  x  10xy  9 y  0 . Gọi M ,m lần lượt 2 2 2
x  10xy y 2 2
x xy  9 y
là giá trị lớn nhất, giá trị nhỏ nhất của P
. Tính T  10 M m . 2 xy y A. T  60 .
B. T  94 .
C. T  104 . D. T  50 . Lời giải Chọn B 2 2 x  5 y 2 2 log
 1  x  10xy  9 y  0 2 2 2
x  10xy y  log  2 2
x  5 y   log  2 2
x 10xy y   log 2  2 2 2
x  5 y    2 2
x 10xy y  0 2 2 2   log  2 2
2x 10 y   2 2 2
x  5 y   log  2 2
x 10xy y    2 2
x 10xy y 2 2  2 2 2 2
 2x 10 y x  10xy y vi) 2  x   x  2 2 x
x  10xy  9 y  0   10  9  0      1   9 y y     y 2  x x   9 2 2  
x xy  9 y y y P     2 xy y x 1 y x Đặt t
, điều kiện: 1  t  9 y 2 t t  9 2 t  2t  8 t  4 f t  
; f t  
; f t   0   t  1 t  12 t  2  11 99 f 1 
; f 2  5 ; f 9  2 10 99 Nên M
, m  5 . Vậy T  10 M m  94 . 10 2 2 2 Câu 32. Vậy A
 6 .Cho các số thực dương x và y thỏa mãn x 2 y    x 2 y   2yx 2 4 9.3 4 9 .7 . Tìm giá trị min x  2 y 18
nhỏ nhất của biểu thức P  . x 3  2 A. P  9 . B. P  . 2
C. P  1 9 2 .
D. Hàm số không có giá trị nhỏ nhất. Lời giải Chọn A Từ giả thiết ta đặt 2
t x  2 y , t   . 2 2 2 Phương trình x 2 y    x 2 y   2yx 2 4 9.3 4 9 .7 trở thành t   tt  49               . ttt 7 4 9.3 4 9 . 4 7 49 9 9. 49 0 7   3   
Nhận thấy t  2 là nghiệm phương trình.
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 77
NGUYỄN BẢO VƯƠNG - 0946798489
Ta chứng minh t  2 là nghiệm duy nhất của phương trình. t  7  
Xét t  2 : 7t  49 và 9.  49  
nên vế trái phương trình luôn dương, nên phương trình vô  3  nghiệm. t  7  
Xét t  2 : 7t  49 và 9.  49  
nên vế trái phương trình luôn âm, nên phương trình vô nghiệm.  3  2 x  2 2 x  2 y 18 x x 16 Vậy 2
t x  2y  2  y  thay vào P   2 x x 16 16 16  x  1  2 . x
1  9 . Dấu bằng đạt được khi x   x  4 . x x x y x e e Câu 33. Cho ,
x y là các số thực lớn hơn 1 sao cho x x y   y y e x
e  . Tìm giá trị nhỏ nhất của biểu thức: P  log xy  log x . x y 2 1  2 2 1  2 A. . B. 2 2 . C. . D. . 2 2 2 Lời giải Chọn C Cách 1. Ta có: y x y x  e  e e e x x y y       ln x
x    ln y   y y e x e y e x e       x y x 1  x ln y
y xe y ln x x ye   (*) (vì x
y e  ln x có y '  e   0; x   1 ln x x e ln y y e x
nên y y   1  e  0 ) t ln t t e 1 tte
Xét hàm số: f t  
trên 1; ta có f 't   . Với hàm số ln t t e ln t t e 2    ln t  1 t g t t ete có     t t     1 ' ln 1 ' t g t t e te   te  0, t   1 t
Nên g t   g  
1  1  f 't   0;t  1
y f t  là hàm nghịch biến trên 1; nên với (*) f x  f y  y x  1 1 1 1 1 1 1 1 2 2 Khi đó P  log xy  log x   log y    2 log . yx y 2 2 x log y 2 2 x log y 2 x x 1 1 Dấu “=” xảy ra khi: log y   y   y x x logx 2 2 2 2 log y x 1  2 2 Vậy: P  . min 2 2 1 x  1 
Câu 34. Tính giá trị của biểu thức 2 2
P x y xy 1 biết rằng 2 4 x  log 14   y  2
y 1 với x  0 2     13 và 1  y  . 2 A. P  4 . B. P  2 . C. P  1 . D. P  3 .
Trang 78 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 Lời giải Chọn B 2 1 x  1  Xét 2 4 x  log 1  4  y  2 y 1 . 2     2 1 2 1 x  1  2 x . 1  2 2 Ta có 4 x  4 x
 4 , dấu bằng xảy ra khi và chỉ khi x  1  ,. Mặt khác
  y   y   
y    y  3 14 2 1 14 3 1 1 . 30 Đặt t
y 1 ta có 0  t
. Xét hàm số f t  3  t
  3t 14 . Ta tìm GTLN – GTNN của hàm 2  30   30  56  9 30 số trên đoạn 0; 
 được min f t   f   
; max f t   f   1  16 . 2      30  2 4  30  0;     0;   2    2   Suy ra log 1  4  y  2
y  1  log 16  4 ,. 2   2   x  1   x  1 Từ và suy ra ta có    . Thay vào P  2 . t   y 1  1  y  0  1 1
Câu 35. Cho hai số thực x , y thỏa mãn 0  x  , 0  y
và log 11 2x y  2 y  4x 1. Xét biểu thức 2 2 2
P  16 yx  2x 3y  2  y  5 . Gọi m , M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của P . Khi
đó giá trị của T  4m M  bằng bao nhiêu? A. 16 . B. 18 . C. 17 . D. 19 . Lời giải Chọn A Ta có
log 11 2x y  2 y  4x 1  22x y  log 11 2x y 1  0
Đặt t  2x y , 0  t  11 . Phương trình trở thành: 2t  log 11 t  1  0 .   1
Xét hàm số f t   2t  log 11 t  1 trên khoảng 0;1  1 . 1 Có y  2   0 , t   0 
;11 . Do đó hàm số f t  luôn đồng biến. 11 t Dễ thấy  
1 có nghiệm t  1. Do đó t  1 là nghiệm duy nhất của   1 .   y2 1
Suy ra 2x  1 y . Khi đó P  16 y
 1 y3y  2  y  5 3 2
 4y  5y  2y  3 . 4  1 
Xét hàm số g y 3 2
 4 y  5 y  2 y  3 trên 0;  , có 2     1  g y 2
 12 y 10 y  2  0 , y  0;  . 2   
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 79
NGUYỄN BẢO VƯƠNG - 0946798489
Do đó, min g y  g 0  3 , max g y  g   1  4 .  1   1  0;  0; 2       2 
Suy ra m 3 , m 4 .
Vậy T 4.3 4 16 .
-------------------- HẾT --------------------
Trang 80 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Document Outline

  • 10. Phương trình - bất phương trình - minmax logarit câu hỏi
  • 10. Phương trình - bất phương trình - minmax logarit - đáp án