Tổng ôn tập TN THPT 2021 môn Toán: Khối tròn xoay Toán 12

Tài liệu gồm 87 trang, được tổng hợp bởi thầy giáo Nguyễn Bảo Vương, tuyển tập câu hỏi và bài tập trắc nghiệm chuyên đề khối tròn xoay, có đáp án và lời giải chi tiết.Mời các bạn đón xem.

58 29 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 2: Mặt nón, mặt trụ, mặt cầu

Môn: Toán 12

Thông tin:

87 trang 8 tháng trước

Tác giả:

Profile Lan Tường
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
MỨC ĐỘ NHẬN BIẾT
Câu 1. (Sở Vĩnh Phúc - 2021) Cho hình nón có độ dài đường sinh bằng
4
, diện tích xung quanh bằng
8
. Tính bán kính hình trong đáy
R
của hình nón đó.
A.
8R
. B.
4R
. C.
2R
. D.
1R
.
Câu 2. (Sở Vĩnh Phúc - 2021) Cho khối trụ có bán kính đáy
4r
và chiều cao
2h
. Tính thể tích khối
trụ đó.
A.
8
. B.
32
. C.
16
. D.
32
3
.
Câu 3. (Sở Lào Cai - 2021) Viết công thức tính diện tích xung quanh của hình trụ có đường cao
h
, bán
kính đường tròn đáy
R
.
A.
2
xq
S h
. B.
2
xq
S Rh
. C.
2
xq
S Rh
. D.
2
xq
S Rh
.
Câu 4. (Sở Lào Cai - 2021) Cho hình nón có diện tích xung quanh bằng
2
5 a
và bán kính đáy bằng
a
.
Độ dài đường sinh
của hình nón đã cho bằng:
A.
3 2a
. B.
5a
. C.
3a
. D.
5a
.
Câu 5. (Sở Hà Tĩnh - 2021) Cho khối cầu có bán kính
2r
. Thể tích của khối cầu đã cho bằng
A.
256
3
. B.
256
C.
64
. D.
32
3
.
Câu 6. (Sở Hà Tĩnh - 2021) Cho khối nón có bán kính đáy
4r
và chiều cao
2h
. Thể tích của khối
nón đó bằng
A.
32
3
. B.
32
. C.
8
3
. D.
8
.
Câu 7. (Sở Yên Bái - 2021) Mặt cầu có đường kính là 10. Diện tích S của mặt cầu bằng
A.
25S
. B.
5S
. C.
50S
. D.
100S
.
Câu 8. (Sở Tuyên Quang - 2021) Độ dài đường sinh hình nón có diện tích xung quanh bằng
2
6 a
và
đường kính đáy bằng
2a
là:
A.
2a
. B.
6a
. C.
3a
. D.
9a
.
Câu 9. (Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Cho hình nón có bán kính đáy bằng
4a
và chiều cao bằng
3a
. Diện tích xung quanh của hình nón bằng
A.
2
20 a
. B.
2
40 a
. C.
2
12 a
. D.
2
24 a
.
Câu 10. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Cắt khối trụ bởi một mặt phẳng qua trục được
thiết diện là một hình vuông. Tính thể tích của khối trụ biết bán kính đáy của khối trụ bằng
a
A.
3
4 a
B.
3
a
C.
3
2
3
a
D.
3
2 a
Câu 11. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Cho khối nón có bán kính 5r và chiều cao
3h
. Tính thể tích
V
của khối nón
A.
5V
. B. 5V
. C. 5V
. D. 5V
.
Câu 12. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Một hình trụ có bán kính đáy
5r cm
,
chiều cao
7h cm
. Diện tích xung quanh của hình trụ này là
A.
3
35
3
cm
. B.
3
70 cm
. C.
3
70
3
cm
. D.
3
35 cm
.
KHỐI TRÒN XOAY
Chủ đề 6
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 13. (Chuyên Lê Hồng Phong - TPHCM - 2021) Cho hình lăng trụ có đường kính đáy bằng
6cm
, độ
dài đường cao bằng
4cm
. Tính diện tích xung quanh của hình trụ này
.
A.
2
22
cm
. B.
2
24
cm
. C.
2
18
cm
. D.
2
20
cm
.
Câu 14. (Chuyên Lam Sơn - Thanh Hóa - 2021) Thể tích khối trụ có bán kính
r
và chiều cao
h
bằng:
A.
2
4
3
r h
. B.
2
1
3
r h
. C.
. D.
2
rh
.
Câu 15. (Chuyên Lam Sơn - Thanh Hóa - 2021) Thể tích của khối nón tròn xoay có đường kính đáy
bằng 6 và chiều cao bằng 5 là
A.
45
B.
15
C.
60
D.
180
Câu 16. (Chuyên Lam Sơn - Thanh Hóa - 2021) Diện tích của mặt cầu có bán kính
R
bằng.
A.
2 R
. B.
2
R
. C.
2
4
R
. D.
3
4
3
R
.
Câu 17. (Chuyên KHTN - 2021) Cho khối nón có bán kính đáy
r a
và chiều cao
2h a
. Thể tích của
khối nón đã cho bằng
A.
3
4
3
a
. B.
3
4
a
. C.
3
2
a
. D.
3
2
3
a
.
Câu 18. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Diện tích xung quanh của hình trụ có độ dài
đường sinh bằng
l
và bán kính
r
bằng
A.
2 .rl
B.
2
.r
C.
1
.
3
rl
D.
.rl
Câu 19. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Thể tích của hình nón có bán kính đáy
2r
và
đường cao
3
h
là
A.
6
. B.
2
. C.
4
. D.
12
.
Câu 20. (Chuyên Quốc Học Huế - 2021) Cho khối trụ có bán kính đáy bằng
r
và chiều cao
3
h
.
Thể tích của khối trụ đã cho bằng
A.
75
. B.
30
. C.
25
. D.
5
.
Câu 21. (Chuyên Quốc Học Huế - 2021) Cho khối nón có chiều cao bằng
2a
và bán kính đáy bằng
a
.
Thể tích của khối nón đã cho bằng
A.
3
4
3
a
. B.
3
2
3
a
. C.
3
3
a
. D.
3
2
a
.
Câu 22. (Chuyên Quốc Học Huế - 2021) Cắt hình trụ
T
bởi một mặt phẳng qua trục của nó, ta được thiết
diện là một hình vuông cạnh bằng 10. Diện tích xung quanh của
T
là
A.
100
. B.
150
. C.
50
. D.
200
.
Câu 23. (Chuyên Quang Trung - Bình Phước - 2021) Khối trụ có bán kính đáy, đường cao lần lượt là
,2a a
thì có thể tích bằng:
A.
3
2
a
. B.
3
2
3
a
. C.
3
a
. D.
3
3
a
.
Câu 24. (Chuyên Quang Trung - Bình Phước - 2021) Hình nón có bán kính đáy, đường cao lần lượt là
3, 4
thì diện tích xung quanh hình nón bằng:
A.
15
. B.
15
2
. C.
12
. D.
6
.
Câu 25. (Chuyên Ngoại Ngữ Hà Nội- 2021) Thể tích của khối trụ có chiều cao
2
h
và bán kính đáy
3
r
bằng?
A.
4
. B.
12
. C.
18
. D.
6
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Câu 26. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Tính diện tích xung quanh của một hình trụ có chiều
cao
20m
, chu vi đáy bằng
5m
.
A.
2
100m
. B.
2
50
m
. C.
2
100
m
. D.
2
50m
.
Câu 27. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Cho khối cầu bán kính
3
r
. Thể tích khối cầu đã cho
bằng
A.
36
. B.
32
3
. C.
8
3
. D.
16
.
Câu 28. (Chuyên Hạ Long - Quảng Ninh - 2021) Cho hình nón có bán kính đáy
6
r
và chiều cao
h
. Diện tích xung quanh của hình
nón đã cho bằng
A.
120
B.
64
C.
60
D.
80
Câu 29. (Chuyên Hạ Long - Quảng Ninh - 2021) Cho khối trụ có bán kính
3
r
và độ dài đường sinh
5l
. Thể tích của khối trụ đã cho bằng
A.
15 .
V
B.
12 .
V
C.
45 .
V
D.
36 .
V
Câu 30. (Chuyên ĐHSP Hà Nội - 2021) Cho mặt cầu có bán kính
3
2
r
. Diện tích của mặt cầu đã cho
bằng
A.
3
. B.
3
. C.
3 3
. D.
3
2
.
Câu 31. (Chuyên ĐHSP Hà Nội - 2021) Cho hình nón có thiết diện qua trục là một tam giác vuông cân có
cạnh huyền bằng
2a
. Diện tích xung quanh của hình nón bằng
A.
2
2a
. B.
2
2 2a
. C.
2
2
a
. D.
2
a
.
Câu 32. (Chuyên ĐHSP Hà Nội - 2021) Cho hình nón có đường kính đáy bằng
2
, đường cao bằng
3
.
Diện tích xung quanh của hình nón đã cho bằng
A.
3
. B.
10 1
. C.
10
. D.
6
.
Câu 33. (Chuyên ĐHSP Hà Nội - 2021) Cho hình trụ có bán kính đáy
3
r
và độ dài đường sinh
5l
.
Thể tích khối trụ đã cho bằng
A.
45
. B.
30
. C.
15
. D.
90
.
Câu 34. (Chuyên ĐH Vinh - Nghệ An - 2021) Cho góc ở đỉnh của một hình nón bằng
o
60
. Gọi
, ,r h l
lần
lượt là bán kính, đường cao, đường sinh của hình nón đó. Khẳng định nào sau đây đúng?
A.
2l r
. B.
. C.
2h r
. D.
l r
.
Câu 35. (Chuyên ĐH Vinh - Nghệ An - 2021) Chu vi của đường tròn lớn của mặt cầu
;S O R
là
A.
2
R
. B.
2
4
R
. C.
R
. D.
2 R
.
Câu 36. (Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Cho
ABH
vuông tại
H
,
3AH a
,
2BH a
. Quay
ABH
quanh trục
AH
ta được một khối nón có thể tích là
A.
4
. B.
3
18
a
. C.
3
4
3
a
. D.
3
12
a
.
Câu 37. (THPT Thanh Chương 1- Nghệ An - 2021) Cho hình cầu có đường kính bằng . Diện tích của
hình cầu đã cho bằng
A. B. C. D.
Câu 38. (THPT Nguyễn Huệ - Phú Yên - 2021) Thể tích khối cầu có bán kính
2a
bằng
A.
3
16
3
a
. B.
3
4
3
a
. C.
4
. D.
3
32
3
a
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 39. (THPT Nguyễn Huệ - Phú Yên - 2021) Cho hình chữ nhật
ABCD
(kể cả miền trong), quay hình
chữ nhật đó quanh một cạnh thì thể tích vật thể tròn xoay được tạo thành là:
A. Hình trụ. B. Khối nón. C. Khối trụ. D. Hình nón.
Câu 40. (THPT Nguyễn Huệ - Phú Yên - 2021) Hình nón có đường sinh bằng
6
, diện tích xung quanh
bằng
12
. Bán kính đường tròn đáy của
hình nón đó bằng
A.
4
. B.
2
. C.
1
2
. D.
1
.
Câu 41. (THPT Lương Thế Vinh - 2021) Cho hình trụ có độ dài đường sinh
5l
và bán kính đáy
3
r
.
Diện tích xung quanh của hình trụ đã cho bằng
A.
30
B.
15
. C.
5
. D.
24
.
Câu 42. (THPT Lương Thế Vinh - 2021) Cho khối nón có bán kính đáy là
2r
và chiều cao
3
h .
Tính thể tích của khối nón đã cho là?
A.
4 3
. B.
2 3
3
. C.
4 3
3
. D.
4
3
.
Câu 43. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho hình trụ có bán kính đáy
3
r và chiều cao
4
h
. Diện tích xung quanh của hình trụ bằng.
A.
8 3
. B.
2 3
. C.
4 3
. D.
16 3
.
Câu 44. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho hình nón có diện tích xung quanh bằng
2
3
a
và bán kính đáy bằng
a
. Độ dài đường sinh
l
của hình nón đã cho bằng
A.
5
2
a
l
. B.
3l a
. C.
3
2
a
l
. D.
2 2l a
.
Câu 45. (THPT Đào Duy Từ - Hà Nội - 2021) Cho khối nón có chu vi đáy
8
và chiều cao
3
h
. Thể
tích khối nón đã cho bằng
A.
12
. B.
4
. C.
16
. D.
24
.
Câu 46. (THPT Đào Duy Từ - Hà Nội - 2021) Cho hình nón có bán kính đáy
2r
và độ dài đường sinh
4l
. Diện tích xung quanh của hình nón đã cho bằng
A.
32
. B.
8
. C.
16
. D.
48
.
Câu 47. (THPT Đào Duy Từ - Hà Nội - 2021) Thể tích của khối cầu có bán kính
3
r
là
A.
64
. B.
48
. C.
8
. D.
36
.
Câu 48. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Diện tích của mặt cầu có đường kính bằng
4a
là
A.
2
16
S a
. B.
2
12
S a
. C.
2
8
S a
. D.
2
64
S a
.
Câu 49. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Thể tích của khối trụ tròn xoay có bán kính
r
, chiều
cao
h
bằng?
A.
2
3
r h
. B.
2
3
r h
. C.
. D.
2
2
r h
.
Câu 50. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho hình nón có bán kính đáy bằng
3
, độ dài đường
cao bằng
4
. Diện tích xung quanh của hình nón bằng:
A.
24
. B.
12
. C.
30
. D.
15
.
Câu 51. (THPT Chu Văn An - Thái Nguyên - 2021) Cho hình nón có độ dài đường sinh
4l
và bán
kính đáy
1
4
r
. Diện tích xung quanh của hình nón bằng
A.
2
. B.
. C.
2
. D.
4
.
Câu 52. (THPT Chu Văn An - Thái Nguyên - 2021) Cho khối cầu có thể tích là
36
. Diện tích mặt cầu
đã cho bằng
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
A.
36
. B.
16
. C.
18
. D.
12
.
Câu 53. (THPT Ba Đình - Thanh Hóa - 2021) Cho hình nón có bán kính đáy là
2
r
và độ dài đường
sinh
4.
l
Tính diện tích xung quanh
S
của hình nón đã cho.
A.
16 2
S
. B.
16
S
. C.
4 2
S
. D.
8 2
S
.
Câu 54. (THPT Ba Đình - Thanh Hóa - 2021) Cho khối cầu có thể tích
3
4 0
V a a
. Tính theo
a
bán kính của khối cầu.
A.
3
2R a
. B.
R a
. C.
3
4R a
. D.
3
3R a
.
Câu 55. (THPT Quế Võ 1 - Bắc Ninh - 2021) Diện tích xung quanh của hình trụ có độ dài đường sinh
l
và bán kính đáy
r
bằng
A.
4
rl
. B.
2
rl
. C.
rl
. D.
1
3
rl
.
Câu 56. (THPT Quốc Oai - Hà Nội - 2021) Một hình trụ có bán kính đáy
r a
, độ dài đường sinh
2l a
. Diện tích toàn phần của hình trụ là
A.
2
6
a
B.
2
2
a
C.
2
4
a
D.
2
5
a
Câu 57. (THPT Quốc Oai - Hà Nội - 2021) Cho khối nón có bán kính
và chiều cao
2
h
. Thể tích
của khối nón đã cho bằng:
A.
8
. B.
32
3
. C.
32
. D.
8
3
.
Câu 58. (THPT Quảng Xương 1-Thanh Hóa - 2021) Một khối trụ có thể tích
8
, độ dài đường cao
bằng 2. Khi đó bán kính đường tròn đáy bằng:
A.
4
. B.
2
. C.
2
. D.
4
.
Câu 59. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho mặt cầu có diện tích hình tròn lớn là
4
. Thể
tích khối cầu đã cho bằng
A.
B.
16 .
C.
64 .
D.
256
.
3
Câu 60. (THPT Quảng Xương 1-Thanh Hóa - 2021) Diện tích mặt cầu có bán kính
2R
là:
A.
2
4
R
. B.
2
4
3
R
. C.
2
16
R
. D.
2
16
3
R
.
Câu 61. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Một hình trụ có diện tích xung quanh bằng
2
4
a
và
bán kính đáy bằng
a
. Độ dài dường cao của hình trụ đó bằng
A.
a
. B.
4a
. C.
3a
. D.
2a
.
Câu 62. (THPT Phan Đình Phùng - Quảng Bình - 2021) Cho khối trụ có chiều cao
3
h
và bán kính
đáy
2.
r
Thể tích của khối trụ đã cho bằng
A.
18
B.
6
C.
4
D.
12
Câu 63. (THPT Phan Đình Phùng - Quảng Bình - 2021) Cho mặt cầu có bán kính
6.
R
Diện tích
S
của mặt cầu đã cho bằng
A.
144
S
B.
38
S
C.
36
S
D.
288
S
Câu 64. (THPT Phan Đình Phùng - Quảng Bình - 2021) Cho hình nón có bán kính đáy là
r
, đường cao
h
và đường sinh
l
. Diện tích xung quang
xq
S
hình nón đó là
A.
2
1
3
xq
S
πr h
. B.
xq
S
πrl
. C.
2
xq
S
πrl
. D.
xq
S
πrh
.
Câu 65. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Cho hình nón có bán kính đáy
3
r
và độ dài
đường cao
4
h
. Tính diện tích xung quanh hình nón đó.
A.
20
. B.
6
. C.
12
. D.
15
.
Câu 66. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Diện tích mặt cầu đường kính
4a
bằng
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
2
64
a
B.
2
16
a
C.
2
4a
D.
2
4 a
Câu 67. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho khối nón có chiều cao
2
h
và bán kính
đáy
3
r
. Thể tích của khối nón đã cho là
A.
6
. B.
18
. C.
6
. D.
36
.
Câu 68. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Diện tích toàn phần của hình trụ có thiết diện qua
trục là hình vuông cạnh
a
bằng
A.
2
2
a
. B.
2
3
2
a
. C.
2
2
a
. D.
2
a
.
Câu 69. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Một khối nón có diện tích xung quanh bằng
2
2 ( )cm
và bán kính đáy
1
( )
2
cm
. Khi đó độ dài đường sinh là
A.
3( )cm
. B.
4( )cm
. C.
2( )cm
. D.
1( )cm
.
Câu 70. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho khối nón có bán kính đáy
4r
và chiều cao
2
h
. Thể tích của khối nón đã cho bằng
A.
8
3
B.
8 .
C.
32
.
3
D.
32 .
Câu 71. ( THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho khối trụ có bán kính đáy
5
r
và chiều cao
3
h
.
Thể tích của khối trụ đã cho bằng
A.
5
. B.
30
. C.
25
. D.
75
.
Câu 72. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho khối cầu có bán kính
3
R
. Thể tích của khối cầu
đã cho bằng
A.
3
. B.
9
. C.
4
. D.
36
.
Câu 73. (THPT Đồng Quan - Hà Nội - 2021) Thể tích khối nón có chiều cao bằng
2,
bán kính hình tròn
đáy bằng
5
là:
A.
25
. B.
200
3
. C.
50
. D.
50
3
.
Câu 74. (THPT Lê Lợi - Thanh Hóa - 2021) Cho hình nón
N
có bán kính bằng
3
và đường sinh
bằng
5
. Tính thể tích
V
của khối nón
N
là
A.
36
. B.
12
. C.
20
. D.
60
.
Câu 75. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Cho một mặt cầu có diện tích là
S
, thể tích khối
cầu đó là
V
.Tính bán kính
R
của mặt cầu.
A.
3V
R
S
. B.
3
S
R
V
. C.
4V
R
S
. D.
3
V
R
S
.
Câu 76. (Trung Tâm Thanh Tường - 2021) Diện tích mặt cầu bán kính
a2
bằng:
A.
2
8 .a
B.
2
16 .a
C.
2
4 .a
D.
2
4
.
3
a
Câu 77. (Trung Tâm Thanh Tường - 2021) Diện tích xung quanh của hình trụ tròn xoay có bán kính đáy
bằng
4
và chiều cao bằng
3
là:
A.
12 .
B.
42 .
C.
24 .
D.
36 .
Câu 78. (Trung Tâm Thanh Tường - 2021) Cho khối nón có chiều cao
3
h
, bán kính đáy
4r
. Diện
tích xung quanh của khối nón đã cho bằng
A.
12
. B.
20
. C.
25
3
. D.
15
.
Câu 79. (Trung Tâm Thanh Tường -2021) Tính thể tích
V
của khối nón có bán kính và chiều cao cùng
bằng
6a
?
A.
3
12
V a
. B.
3
216
V a
. C.
3
18
V a
. D.
3
72
V a
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Câu 80. (THPT
Triệu Sơn - Thanh Hóa - 2021) Một hình nón có bán kính đáy bằng
4r
cm
và
độ dài
đường sinh
5l
cm
.Diệ
n tích xung quanh của khối nón đó bằng
A.
10
2
c
m
. B.
2
2
0
c
m
. C.
2
1
2
c
m
. D.
2
1
5
c
m
.
Câu 81. (THPT
Triệu Sơn - Thanh Hóa - 2021) Thể tích của khối cầu có bán kính
R
bằng
A.
2
4
R
. B.
2
R
. C.
3
1
3
R
. D.
3
4
3
R
.
Câu 82. (THPT
Trần Phú - Đà Nẵng - 2021) Cho hình trụ có bán kính đáy
2R
và
độ dài đường sinh
8l
.Diện tích toà
n phần của hình trụ đã cho bằng
A.
4
0
. B.
3
6
. C.
9
6
. D.
2
4
.
Câu 83. (THPT
Trần Phú - Đà Nẵng - 2021) Cho khối cầu có bán kính
2
R
. Thể tích của khối cầu
đã cho bằng
A.
4
. B.
8
. C.
8
2
3
. D.
4
2
3
.
BẢNG ĐÁP
ÁN
1.C
2.
B
3.
B
4.
B
5.D
6.
A
7.
D
8.C
9.C
10.D
11.A
12.B
13.B
14.C
15.
B
16.C
17.
D
18.
A
19.
C
20.A
21.B
22.A
23.A
24.A
25.
C
26.
A
27.
A
28.C
29.
C
30.
B
31.A
32.C
33.A
34
35.D
36.
A
37.B
38.
D
39.
C
40.
B
41.A
42.C
43.A
44.B
45.C
46.B
47.B
48.A
49.C
50.D
51.B
52.A
53.C
54.D
55.
B
56.
A
57.B
58.C
59.
A
60.
C
61.D
62.D
63.A
64.B
65.D
66
67.C
68.B
69.
B
70.
C
71.D
72.D
73.D
74.B
75.A
76.B
77.C
78.B
79.D
80.B
81.D
82.A
83.C
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
MỨC ĐỘ NHẬN BIẾT
Câu 1. (Sở Vĩnh Phúc - 2021) Cho hình nón có độ dài đường sinh bằng
4
, diện tích xung quanh bằng
8
. Tính bán kính hình trong đáy
R
của hình nón đó.
A.
8R
. B.
4R
. C.
2R
. D.
1R
.
Lời giải
Chọn C
Diện tích xung quanh của hình nón:
8 .4 2
xq
S Rl R R
.
Câu 2. (Sở Vĩnh Phúc - 2021) Cho khối trụ có bán kính đáy
4r
và chiều cao
2h
. Tính thể tích khối
trụ đó.
A.
8
. B.
32
. C.
16
. D.
32
3
.
Lời giải
Chọn B
Thể tích khối trụ là
2
32V r h
.
Câu 3. (Sở Lào Cai - 2021) Viết công thức tính diện tích xung quanh của hình trụ có đường cao
h
, bán
kính đường tròn đáy
R
.
A.
2
xq
S h
. B.
2
xq
S Rh
. C.
2
xq
S Rh
. D.
2
xq
S Rh
.
Lời giải
Chọn B
Câu 4. (Sở Lào Cai - 2021) Cho hình nón có diện tích xung quanh bằng
2
5 a
và bán kính đáy bằng
a
.
Độ dài đường sinh
của hình nón đã cho bằng:
A.
3 2a
. B.
5a
. C.
3a
. D.
5a
.
Lời giải
Chọn B
Ta có
2 2 2
5 5 5 5
xq
S a rl a al a l a
.
Câu 5. (Sở Hà Tĩnh - 2021) Cho khối cầu có bán kính
2r
. Thể tích của khối cầu đã cho bằng
A.
256
3
. B.
256
C.
64
. D.
32
3
.
Lời giải
Chọn D
Thể tích của khối cầu là:
3 3
4 4 32
.2
3 3 3
V r
.
Câu 6. (Sở Hà Tĩnh - 2021) Cho khối nón có bán kính đáy
4r
và chiều cao
2h
. Thể tích của khối
nón đó bằng
A.
32
3
. B.
32
. C.
8
3
. D.
8
.
Lời giải
Chọn A
Thể tích khối nón là
2
1 32
3 3
N
V r h
.
Câu 7. (Sở Yên Bái - 2021) Mặt cầu có đường kính là 10. Diện tích S của mặt cầu bằng
A.
25S
. B.
5S
. C.
50S
. D.
100S
.
KHỐI TRÒN XOAY
Chủ đề 6
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Lời giải
Chọn D
Vì mặt cầu có đường kính là 10
2 2
5 4 4 5 100
mc
R S R
.
Câu 8. (Sở Tuyên Quang - 2021) Độ dài đường sinh hình nón có diện tích xung quanh bằng
2
6
a
và
đường kính đáy bằng
2a
là:
A.
2a
. B.
6a
. C.
3a
. D.
9a
.
Lời giải
Chọn C
Ta có
2
6
3
2
xq
xq
S
a
S rl l a
r a
Câu 9. (Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Cho hình nón có bán kính đáy bằng
4a
và chiều cao bằng
3a
. Diện tích xung quanh của hình nón bằng
A.
2
20
a
. B.
2
40
a
. C.
2
12
a
. D.
2
24
a
.
Lời giải
Chọn C
Độ dài đường sinh của hình nón là:
2 2
2 2
3 4 5l r h a a a
.
Diện tích xung quanh của hình nón bằng:
2
3 .4 12
xq
S rl a a a
.
Câu 10. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Cắt khối trụ bởi một mặt phẳng qua trục được
thiết diện là một hình vuông. Tính thể tích của khối trụ biết bán kính đáy của khối trụ bằng
a
A.
3
4
a
B.
3
a
C.
3
2
3
a
D.
3
2
a
Lời giải
Chọn D
Vì thiết diện là hình vuông có cạnh bằng
a
nên ta có
2 2 3
2 2 .2 2
h r a V r h a a a
.
Câu 11. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Cho khối nón có bán kính
5
r và chiều cao
3
h
. Tính thể tích
V
của khối nón
A.
5
V
. B.
5
V
. C.
5
V
. D.
5
V
.
Lời giải
Chọn A
Ta có thể tích của khối nón
2
2
1 1
5 .3 5
3 3
V r h
Câu 12. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Một hình trụ có bán kính đáy
5r cm
,
chiều cao
7h cm
. Diện tích xung quanh của hình trụ này là
A.
3
35
3
cm
. B.
3
70
cm
. C.
3
70
3
cm
. D.
3
35
cm
.
Lời giải
Chọn B
Áp dụng công thức
3
2 70
S rl cm
r
h
O
S
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Câu 13. (Chuyên Lê Hồng Phong - TPHCM - 2021) Cho hình lăng trụ có đường kính đáy bằng
6cm
, độ
dài đường cao bằng
4cm
. Tính diện tích xung quanh của hình trụ này
.
A.
2
22
cm
. B.
2
24
cm
. C.
2
18
cm
. D.
2
20
cm
.
Lời giải
Chọn B
Bán kính đáy
6
2
3
r
; chiều cao
4
h
.
Có
2 2
2 . . 2 .3.4 24
xq
S r h cm cm
Câu 14. (Chuyên Lam Sơn - Thanh Hóa - 2021) Thể tích khối trụ có bán kính
r
và chiều cao
h
bằng:
A.
2
4
3
r h
. B.
2
1
3
r h
. C.
. D.
2
rh
.
Lời giải
Chọn C
Ta có:
2
V r h
.
Câu 15. (Chuyên Lam Sơn - Thanh Hóa - 2021) Thể tích của khối nón tròn xoay có đường kính đáy
bằng 6 và chiều cao bằng 5 là
A.
45
B.
15
C.
60
D.
180
Lời giải
Chọn B
Thể tích khối nón tròn xoay là
2 2
1 1
5 .3 .5 15
3 3
x V r h
.
Câu 16. (Chuyên Lam Sơn - Thanh Hóa - 2021) Diện tích của mặt cầu có bán kính
R
bằng.
A.
2 R
. B.
2
R
. C.
2
4
R
. D.
3
4
3
R
.
Lời giải
Chọn C
Diện tích của mặt cầu có bán kính
R
là
2
4
S R
.
Câu 17. (Chuyên KHTN - 2021) Cho khối nón có bán kính đáy
r a
và chiều cao
2h a
. Thể tích của
khối nón đã cho bằng
A.
3
4
3
a
. B.
3
4
a
. C.
3
2
a
. D.
3
2
3
a
.
Lời giải
Chọn D
Thể tích của khối nón đã cho là:
2
1
3
V r h
2
1
.2
3
a a
3
2
3
a
.
Câu 18. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Diện tích xung quanh của hình trụ có độ dài
đường sinh bằng
l
và bán kính
r
bằng
A.
2 .rl
B.
2
.r
C.
1
.
3
rl
D.
.rl
Lời giải
Chọn A
Diện tích xung quanh của hình trụ là
2
xq
S rl
.
Câu 19. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Thể tích của hình nón có bán kính đáy
2r
và
đường cao
3
h
là
A.
6
. B.
2
. C.
4
. D.
12
.
Lời giải
Chọn C
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Áp dụng công thức:
2
1
3
V r h
Thể tích hình nón là:
2
1
.2 .3 4
3
V
.
Câu 20. (Chuyên Quốc Học Huế - 2021) Cho khối trụ có bán kính đáy bằng
5r
và chiều cao
3h
.
Thể tích của khối trụ đã cho bằng
A.
75
. B.
30
. C.
25
. D.
5
.
Lời giải
Chọn A
Thể tích của khối trụ đã cho là
2 2
.5 .3 75V Bh r h
.
Câu 21. (Chuyên Quốc Học Huế - 2021) Cho khối nón có chiều cao bằng
2a
và bán kính đáy bằng
a
.
Thể tích của khối nón đã cho bằng
A.
3
4
3
a
. B.
3
2
3
a
. C.
3
3
a
. D.
3
2 a
.
Lời giải
Chọn B
Thể tích của khối nón
3
2 2
1 1 2
.2
3 3 3
a
V r h a a
.
Câu 22. (Chuyên Quốc Học Huế - 2021) Cắt hình trụ
T
bởi một mặt phẳng qua trục của nó, ta được thiết
diện là một hình vuông cạnh bằng 10. Diện tích xung quanh của
T
là
A.
100
. B.
150
. C.
50
. D.
200
.
Lời giải
Chọn A
Do thiết diện qua trục là một hình vuông cạnh bằng 10 nên ta có
10, 5l h r
.
Diện tích xung quanh của
T
là
2 2 .5.10 100
xq
S rl
.
Câu 23. (Chuyên Quang Trung - Bình Phước - 2021) Khối trụ có bán kính đáy, đường cao lần lượt là
,2a a
thì có thể tích bằng:
A.
3
2 a
. B.
3
2
3
a
. C.
3
a
. D.
3
3
a
.
Lời giải
Chọn A
Thể tích của khối trụ:
2 2 3
2 2V r h a a a
Câu 24. (Chuyên Quang Trung - Bình Phước - 2021) Hình nón có bán kính đáy, đường cao lần lượt là
3, 4
thì diện tích xung quanh hình nón bằng:
A.
15
. B.
15
2
. C.
12
. D.
6
.
Lời giải
Chọn A
Đường sinh:
2 2 2 2
4 3 5l h r
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Diện tích xung quanh hình nón:
.3.5 15
xq
S rl
.
Câu 25. (Chuyên Ngoại Ngữ Hà Nội- 2021) Thể tích của khối trụ có chiều cao
2h
và bán kính đáy
3
r
bằng?
A.
4
. B.
12
. C.
18
. D.
6
.
Lời giải
Chọn C
Thể tích khối trụ là:
2
18V r h
Câu 26. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Tính diện tích xung quanh của một hình trụ có chiều
cao
20m
, chu vi đáy bằng
5m
.
A.
2
100m
. B.
2
50 m
. C.
2
100 m
. D.
2
50m
.
Lời giải
Chọn A
Diện tích xung quanh của hình trụ:
2
2 5.20 100S rl m
.
Câu 27. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Cho khối cầu bán kính
3r
. Thể tích khối cầu đã cho
bằng
A.
36
. B.
32
3
. C.
8
3
. D.
16
.
Lời giải
Chọn A
Thể tích khối cầu là
3 3
4 4 .3
36
3 3
r
V
.
Câu 28. (Chuyên Hạ Long - Quảng Ninh - 2021) Cho hình nón có bán kính đáy
6r
và chiều cao
8h
. Diện tích xung quanh của hình
nón đã cho bằng
A.
120
B.
64
C.
60
D.
80
Lời giải.
CHỌN C
Ta có:
2 2
= 10l h r
.
Vây:
60
xq
S rl
Câu 29. (Chuyên Hạ Long - Quảng Ninh - 2021) Cho khối trụ có bán kính
3r
và độ dài đường sinh
5l
. Thể tích của khối trụ đã cho bằng
A.
15 .
V
B.
12 .
V
C.
45 .
V
D.
36 .
V
Lời giải
Chọn C
Thể tích của khối trụ là:
2 2 2
.3 .5 45 .
V r h r l
Câu 30. (Chuyên ĐHSP Hà Nội - 2021) Cho mặt cầu có bán kính
3
2
r
. Diện tích của mặt cầu đã cho
bằng
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
3
. B.
3
. C.
3 3
. D.
3
2
.
Lời giải
Chọn B
Ta có:
2
2
3
4 4 . 3
2
S r
.
Câu 31. (Chuyên ĐHSP Hà Nội - 2021) Cho hình nón có thiết diện qua trục là một tam giác vuông cân có
cạnh huyền bằng
2a
. Diện tích xung quanh của hình nón bằng
A.
2
2a
. B.
2
2 2a
. C.
2
2 a
. D.
2
a
.
Lời giải
Chọn A
Xét tam giác
SAB
vuông cân tại S có cạnh huyền
2AB a
nên
2SA SB a
.
Hình nón có
2
AB
r OB a
,
2l SB a
.
Nên
2
. . 2 2
xq
S rl a a a
.
Câu 32. (Chuyên ĐHSP Hà Nội - 2021) Cho hình nón có đường kính đáy bằng
2
, đường cao bằng
3
.
Diện tích xung quanh của hình nón đã cho bằng
A.
3
. B.
10 1
. C.
10
. D.
6
.
Lời giải
Chọn C
Ta có diện tích xung quanh của hình nón là
xq
S rl
.
Mà
2
1
2 2
d
r
suy ra
2 2 2 2
3 1 10l h r
. Vậy .1. 10 10
xq
S rl
.
Câu 33. (Chuyên ĐHSP Hà Nội - 2021) Cho hình trụ có bán kính đáy
3r
và độ dài đường sinh
5l
.
Thể tích khối trụ đã cho bằng
A.
45
. B.
30
. C.
15
. D.
90
.
Lời giải
Chọn A
Thể tích khối trụ đã cho là
2 2 2
.3 .5 45V r h r l
.
Câu 34. (Chuyên ĐH Vinh - Nghệ An - 2021) Cho góc ở đỉnh của một hình nón bằng
o
60
. Gọi
, ,r h l
lần
lượt là bán kính, đường cao, đường sinh của hình nón đó. Khẳng định nào sau đây đúng?
A.
2l r
. B.
h r
. C.
2h r
. D.
l r
.
Lời giải
Chọn A
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Tam giác
SAB
có
o
60ASB tam giác
SAB
đều và
O
là trung điểm
AB
nên
2l r
.
Câu 35. (Chuyên ĐH Vinh - Nghệ An - 2021) Chu vi của đường tròn lớn của mặt cầu
;S O R
là
A.
2
R
. B.
2
4 R
. C.
R
. D.
2 R
.
Lời giải
Chọn D
Đường tròn lớn của mặt cầu
;S O R
là đường tròn tâm
O
, bán kính
R
nên có chu vi là
2 R
.
Câu 36. (Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Cho
ABH
vuông tại
H
,
3AH a
,
2BH a
. Quay
ABH
quanh trục
AH
ta được một khối nón có thể tích là
A.
3
4 a
. B.
3
18 a
. C.
3
4
3
a
. D.
3
12 a
.
Lời giải
Chọn A
Khối nón có
3h AH a
,
2r BH a
.
Áp dụng công thức
2
2 3
1 1
. . 2 .3 4
3 3
V r h a a a
.
Câu 37. (THPT Thanh Chương 1- Nghệ An - 2021) Cho hình cầu có đường kính bằng . Diện tích của
hình cầu đã cho bằng
A. B. C. D.
Lời giải
Chọn B
Diện tích của mặt cầu là .
Câu 38. (THPT Nguyễn Huệ - Phú Yên - 2021) Thể tích khối cầu có bán kính
2a
bằng
A.
3
16
3
a
. B.
3
4
3
a
. C.
3
4 a
. D.
3
32
3
a
.
Lời giải
Chọn D
Thể tích khối cầu:
3
3 3
4 4 32
2
3 3 3
V R a a
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 39. (THPT Nguyễn Huệ - Phú Yên - 2021) Cho hình chữ nhật
ABCD
(kể cả miền trong), quay hình
chữ nhật đó quanh một cạnh thì thể tích vật thể tròn xoay được tạo thành là:
A. Hình trụ. B. Khối nón. C. Khối trụ. D. Hình nón.
Lời giải
Chọn C
Cho hình chữ nhật
ABCD
(kể cả miền trong), quay hình chữ nhật đó quanh một cạnh thì thể tích
vật thể tròn xoay được tạo thành là một khối trụ.
Câu 40. (THPT Nguyễn Huệ - Phú Yên - 2021) Hình nón có đường sinh bằng
6
, diện tích xung quanh
bằng
12
. Bán kính đường tròn đáy của
hình nón đó bằng
A.
4
. B.
2
. C.
1
2
. D.
1
.
Lời giải
Chọn B
Bán kính đường tròn đáy của hình nón đó là:
12
2
.6
r
.
Câu 41. (THPT Lương Thế Vinh - 2021) Cho hình trụ có độ dài đường sinh
5l
và bán kính đáy
3
r
.
Diện tích xung quanh của hình trụ đã cho bằng
A.
30
B.
15
. C.
5
. D.
24
.
Lời giải
Chọn A
Diện tích xung quanh của hình trụ là
xq
2 2 .5.3 30
S rl
.
Câu 42. (THPT Lương Thế Vinh - 2021) Cho khối nón có bán kính đáy là
2r
và chiều cao
3
h
.
Tính thể tích của khối nón đã cho là?
A.
4 3
. B.
2 3
3
. C.
4 3
3
. D.
4
3
.
Lời giải
Chọn C
Thể tích khối nón đã cho là
2 2
1 1 4 3
. . 3. 2
3 3 3
V h r
.
Câu 43. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho hình trụ có bán kính đáy
3
r và chiều cao
4
h
. Diện tích xung quanh của hình trụ bằng.
A.
8 3
. B.
2 3
. C.
4 3
. D.
16 3
.
Lời giải
Chọn A
2 2 2 . 3.4 8 3
xq
S rl rh
.
Câu 44. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho hình nón có diện tích xung quanh bằng
2
3
a
và bán kính đáy bằng
a
. Độ dài đường sinh
l
của hình nón đã cho bằng
A.
5
2
a
l
. B.
3l a
. C.
3
2
a
l
. D.
2 2l a
.
Lời giải
Chọn B
Hình nón có diện tích xung quanh là:
2
3
3
xq
xq
S
a
S rl l a
r a
.
Câu 45. (THPT Đào Duy Từ - Hà Nội - 2021) Cho khối nón có chu vi đáy
8
và chiều cao
3
h
. Thể
tích khối nón đã cho bằng
A.
12
. B.
4
. C.
16
. D.
24
.
Lời giải
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Chọn C
Chu vi đáy bằng
8 4
r
.
Thể tích khối nón đã cho là
2
1
16
3
V r h
.
Câu 46. (THPT Đào Duy Từ - Hà Nội - 2021) Cho hình nón có bán kính đáy
2r
và độ dài đường sinh
4l
. Diện tích xung quanh của hình nón đã cho bằng
A.
32
. B.
8
. C.
16
. D.
48
.
Lời giải
Chọn B
Ta có:
.2.4 8
xq
S rl
.
Câu 47. (THPT Đào Duy Từ - Hà Nội - 2021) Thể tích của khối cầu có bán kính
3r
là
A.
64
. B.
48
. C.
8
. D.
36
.
Lời giải
Chọn B
Thể tích của khối cầu có bán kính
3r
là
3 3
4 4
.3 48
3 3
V r
.
Câu 48. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Diện tích của mặt cầu có đường kính bằng
4a
là
A.
2
16S a
. B.
2
12S a
. C.
2
8S a
. D.
2
64S a
.
Lời giải
Chọn A
Bán kính mặt cầu là
4
2
2
a
R a
.
Diện tích của mặt cầu là
2
2 2
4 4 . 2 16S R a a
.
Câu 49. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Thể tích của khối trụ tròn xoay có bán kính
r
, chiều
cao
h
bằng?
A.
2
3
r h
. B.
2
3 r h
. C.
2
r h
. D.
2
2 r h
.
Lời giải
Chọn C
Thể tích khối trụ là:
2
V r h
Câu 50. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho hình nón có bán kính đáy bằng
3
, độ dài đường
cao bằng
4
. Diện tích xung quanh của hình nón bằng:
A.
24
. B.
12
. C.
30
. D.
15
.
Lời giải
Chọn D
Đường sinh
2 2
3 4 5l SA
.
Diện tích xung quanh hình nón:
.3.5 15
xq
S rl
.
Câu 51. (THPT Chu Văn An - Thái Nguyên - 2021) Cho hình nón có độ dài đường sinh
4l
và bán
kính đáy
1
4
r
. Diện tích xung quanh của hình nón bằng
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
2
. B.
. C.
2
. D.
4
.
Lời giải
Chọn B
Diện tích xung quanh của hình nón bằng
1
4
4
xq
S rl
.
Câu 52. (THPT Chu Văn An - Thái Nguyên - 2021) Cho khối cầu có thể tích là
36
. Diện tích mặt cầu
đã cho bằng
A.
36
. B.
16
. C.
18
. D.
12
.
Lời giải
Chọn D
3 3 2
4 4
36 3 4 36
3 3
xq
V R R R S R
.
Câu 53. (THPT Ba Đình - Thanh Hóa - 2021) Cho hình nón có bán kính đáy là
2
r
và độ dài đường
sinh
4.
l
Tính diện tích xung quanh
S
của hình nón đã cho.
A.
16 2
S
. B.
16
S
. C.
4 2
S
. D.
8 2
S
.
Lời giải
Chọn C
Ta có:
4 2
xq
S rl
.
Câu 54. (THPT Ba Đình - Thanh Hóa - 2021) Cho khối cầu có thể tích
3
4 0
V a a
. Tính theo
a
bán kính của khối cầu.
A.
3
2R a
. B.
R a
. C.
3
4R a
. D.
3
3R a
.
Lời giải
Chọn D
3 3
3
4
4 3
3
V R a R a
.
Câu 55. (THPT Quế Võ 1 - Bắc Ninh - 2021) Diện tích xung quanh của hình trụ có độ dài đường sinh
l
và bán kính đáy
r
bằng
A.
4
rl
. B.
2
rl
. C.
rl
. D.
1
3
rl
.
Lời giải
Chọn B
Diện tích xung quanh hình trụ bằng
2
xq
S rl
.
Câu 56. (THPT Quốc Oai - Hà Nội - 2021) Một hình trụ có bán kính đáy
r a
, độ dài đường sinh
2l a
. Diện tích toàn phần của hình trụ là
A.
2
6
a
B.
2
2
a
C.
2
4
a
D.
2
5
a
Lời giải
Chọn A
Hình trụ đã cho có
2 2 2
2 2 2 . .2 2 6
tp
S rl r a a a a
.
Câu 57. (THPT Quốc Oai - Hà Nội - 2021) Cho khối nón có bán kính
4r
và chiều cao
2
h
. Thể tích
của khối nón đã cho bằng:
A.
8
. B.
32
3
. C.
32
. D.
8
3
.
Lời giải
Chọn B
Thể tích của khối nón đã cho là:
2 2
1 1 32
4 .2
3 3 3
V r h
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Câu 58. (THPT Quảng Xương 1-Thanh Hóa - 2021) Một khối trụ có thể tích
8
, độ dài đường cao
bằng 2. Khi đó bán kính đường tròn đáy bằng:
A.
4
. B.
2
. C.
2
. D.
4
.
Lời giải
Chọn C
Diện tích hình tròn đáy là:
8
4
2
.
Bán kính đường tròn đáy là:
4
2
.
Câu 59. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho mặt cầu có diện tích hình tròn lớn là
4
. Thể
tích khối cầu đã cho bằng
A.
B.
16 .
C.
64 .
D.
256
.
3
Lời giải
Chọn A
Bán kính của hình tròn lớn của mặt cầu là bán kính của mặt cầu giả sử
R
.
Diện tích hình tròn lớn là
2
4 2.
R R
Thể tích khối cầu là
3
4 32
.
3 3
V R
Câu 60. (THPT Quảng Xương 1-Thanh Hóa - 2021) Diện tích mặt cầu có bán kính
2R
là:
A.
2
4
R
. B.
2
4
3
R
. C.
2
16
R
. D.
2
16
3
R
.
Lời giải
Chọn C
2
2
4 2 16
S R R
.
Câu 61. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Một hình trụ có diện tích xung quanh bằng
2
4
a
và
bán kính đáy bằng
a
. Độ dài dường cao của hình trụ đó bằng
A.
a
. B.
4a
. C.
3a
. D.
2a
.
Lời giải
Chọn D
Ta có
2
4
2 2
2 2
xq
xq
S
a
S rl l a
r a
.
Câu 62. (THPT Phan Đình Phùng - Quảng Bình - 2021) Cho khối trụ có chiều cao
3
h
và bán kính
đáy
2.
r
Thể tích của khối trụ đã cho bằng
A.
18
B.
6
C.
4
D.
12
Lời giải
Chọn D
Thể tích của khối trụ đã cho là:
2 2
. . .2 .3 12
V r h
Câu 63. (THPT Phan Đình Phùng - Quảng Bình - 2021) Cho mặt cầu có bán kính
6.
R
Diện tích
S
của mặt cầu đã cho bằng
A.
144
S
B.
38
S
C.
36
S
D.
288
S
Lời giải
Chọn A
Diện tích
S
của mặt cầu đã cho là:
2 2
4 4 .6 144
S R
Câu 64. (THPT Phan Đình Phùng - Quảng Bình - 2021) Cho hình nón có bán kính đáy là
r
, đường cao
h
và đường sinh
l
. Diện tích xung quang
xq
S
hình nón đó là
A.
2
1
3
xq
S
πr h
. B.
xq
S
πrl
. C.
2
xq
S
πrl
. D.
xq
S
πrh
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Lời giải
Chọn B
Có
xq
S πrl
nên chọn đáp án B
Câu 65. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Cho hình nón có bán kính đáy
3r
và độ dài
đường cao
4h
. Tính diện tích xung quanh hình nón đó.
A.
20
. B.
6
. C.
12
. D.
15
.
Lời giải
Chọn D.
Độ dài đường sinh hình nón là
2 2 2 2
3 4 5l r h
.
Diện tích xung quanh của hình nón là
.3.5 15
xq
S rl
.
Câu 66. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Diện tích mặt cầu đường kính
4a
bằng
A.
2
64 a
B.
2
16 a
C.
2
4a
D.
2
4 a
Lời giải
Chọn D
Đường kính
2 2
4 2 4 16
C
a R a S R a
.
Câu 67. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho khối nón có chiều cao
2h
và bán kính
đáy
3r
. Thể tích của khối nón đã cho là
A.
6
. B.
18
. C.
6
. D.
36
.
Lời giải
Chọn C
Ta có thể tích của khối nón đã cho là
2 2
1 1
.3 .2 6
3 3
V R h
.
Câu 68. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Diện tích toàn phần của hình trụ có thiết diện qua
trục là hình vuông cạnh
a
bằng
A.
2
2 a
. B.
2
3
2
a
. C.
2
2
a
. D.
2
a
.
Lời giải
Chọn B
Ta có hình trụ có thiết diện qua trục là hình vuông cạnh
a
nên
,
2
a
l h a r
.
Do đó
2
2
2
2
3
2 2 2 . . 2
2 2 2
tp xq d
a a a
S S S rl r a
.
Câu 69. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Một khối nón có diện tích xung quanh bằng
2
2 ( )cm
và bán kính đáy
1
( )
2
cm
. Khi đó độ dài đường sinh là
A.
3( )cm
. B.
4( )cm
. C.
2( )cm
. D.
1( )cm
.
Lời giải
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Chọn B
Ta có
2
4( )
1
.
2
xq
xq
S
S Rl l cm
R
.
Câu 70. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho khối nón có bán kính đáy
4r
và chiều cao
2
h
. Thể tích của khối nón đã cho bằng
A.
8
3
B.
8 .
C.
32
.
3
D.
32 .
Lời giải
Chọn C
Ta có thể tích khối nón là
2 2
1 1 32
.4 .2
3 3 3
V r h
:
Vậy ta chọn phương án C.
Câu 71. ( THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho khối trụ có bán kính đáy
r
và chiều cao
h
.
Thể tích của khối trụ đã cho bằng
A.
5
. B.
30
. C.
25
. D.
75
.
Lời giải
Chọn D
Ta có thể tích khối trụ:
2 2
3. .5 75
V hS h r
.
Câu 72. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho khối cầu có bán kính
3
R
. Thể tích của khối cầu
đã cho bằng
A.
3
. B.
9
. C.
4
. D.
36
.
Lời giải
Chọn D
Ta có thể tích khối cầu:
3 3
4 4
. .3 36
3 3
V R
.
Câu 73. (THPT Đồng Quan - Hà Nội - 2021) Thể tích khối nón có chiều cao bằng
2,
bán kính hình tròn
đáy bằng
5
là:
A.
25
. B.
200
3
. C.
50
. D.
50
3
.
Lời giải
Chọn D
2 2
1 1 50
.5 .2
3 3 3
V R h
.
Câu 74. (THPT Lê Lợi - Thanh Hóa - 2021) Cho hình nón
N
có bán kính bằng
3
và đường sinh
bằng
5
. Tính thể tích
V
của khối nón
N
là
A.
36
. B.
12
. C.
20
. D.
60
.
Lời giải
Chọn B
Ta có:
2 2 2 2
5 3 4
h l r
.
2 2
1 1
.3 .4 12
3 3
N
V r h
.
Câu 75. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Cho một mặt cầu có diện tích là
S
, thể tích khối
cầu đó là
V
.Tính bán kính
R
của mặt cầu.
A.
3V
R
S
. B.
3
S
R
V
. C.
4V
R
S
. D.
3
V
R
S
.
Lời giải
Chọn A
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
3
2
4
1 3
3
4 3
R
V V
R R
S R S
.
Câu 76. (Trung Tâm Thanh Tường - 2021) Diện tích mặt cầu bán kính
a2
bằng:
A.
2
8 .a
B.
2
16 .a
C.
2
4 .a
D.
2
4
.
3
a
Lời giải:
Chọn B.
Ta có:
2
2 2
4 4 . 2 16 S R a a
.
Câu 77. (Trung Tâm Thanh Tường - 2021) Diện tích xung quanh của hình trụ tròn xoay có bán kính đáy
bằng
4
và chiều cao bằng
3
là:
A.
12 .
B.
42 .
C.
24 .
D.
36 .
Lời giải:
Chọn C.
Ta có: Hình trụ tròn xoay có
3 l h
.
2 2 .4.3 24
xq
S Rl
.
Câu 78. (Trung Tâm Thanh Tường - 2021) Cho khối nón có chiều cao
3h
, bán kính đáy
4r
. Diện
tích xung quanh của khối nón đã cho bằng
A.
12
. B.
20
. C.
25
3
. D.
15
.
Lời giải
Chọn B
Đường sinh của khối nón là:
2 2
5l h r
.
Diện tích xung quanh của khối nón đã cho là:
.4.5 20
xq
S rl
.
Câu 79. (Trung Tâm Thanh Tường -2021) Tính thể tích
V
của khối nón có bán kính và chiều cao cùng
bằng
6a
?
A.
3
12V a
. B.
3
216V a
. C.
3
18V a
. D.
3
72V a
.
Lời giải
Chọn D
Khối nón có bán kính và chiều cao cùng bằng
6a
có thể tích là
2
3
1
6 .6 72
3
V a a a
.
Câu 80. (THPT Triệu Sơn - Thanh Hóa - 2021) Một hình nón có bán kính đáy bằng
4r cm
và độ dài
đường sinh
5l cm
.Diện tích xung quanh của khối nón đó bằng
A.
10
2
cm
. B.
2
20 cm
. C.
2
12 cm
. D.
2
15 cm
.
Lời giải
Chọn B
Ta có diện tích xung quanh của khối nón đó bằng
2
20
xq
S rl cm
Câu 81. (THPT Triệu Sơn - Thanh Hóa - 2021) Thể tích của khối cầu có bán kính
R
bằng
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
A.
2
4
R
. B.
2
R
. C.
3
1
3
R
. D.
3
4
3
R
.
Lời giải
Chọn
D
Thể t
ích của khối cầu có bán kính
R
bằ
ng
3
4
3
R
.
Câu 82. (THPT
Trần Phú - Đà Nẵng - 2021) Cho hình trụ có bán kính đáy
2R
và
độ dài đường sinh
8l
.Diện tích toà
n phần của hình trụ đã cho bằng
A
.
4
0
. B.
3
6
. C.
9
6
. D.
2
4
.
Lờ
i giải
Chọn
A
Diệ
n tích toàn phần của hình trụ đã cho bằng
2
2
2 40
tp
S
Rl R
.
Câu 83. (THPT
Trần Phú - Đà Nẵng - 2021) Cho khối cầu có bán kính
2
R
. Thể tích của khối cầu
đã cho bằng
A.
4
. B.
8
. C.
8
2
3
. D.
4
2
3
.
Lờ
i giải
Ta có
3
3
4
4 8 2
2
3 3 3
V
R
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
MỨC ĐỘ THÔNG HIỂU
Câu 1. (Sở Vĩnh Phúc - 2021) Cho mặt cầu
S
và mặt phẳng
P
, biết khoảng cách từ tâm của mặt cầu
S
đến mặt phẳng
P
bằng
a
. Mặt phẳng
P
cắt mặt cầu
S
theo giao tuyến là đường tròn
có chu vi 2 3 a
. Diện tích mặt cầu
S
bằng bao nhiêu?
A.
2
12 a
. B.
2
16 a
. C.
2
4 a
. D.
2
8 a
.
Câu 2. (Sở Vĩnh Phúc - 2021) Tính diện tích toàn phần
S
của mặt nón
N
biết thiết diện qua trục của
nó là một tam giác vuông có cạnh huyền bằng
2 2a
A.
2
2 2 2S a
. B.
2
4 4 2S a
. C.
2
2 4 2S a
. D.
2
4 2 2S a
.
Câu 3. (Sở Yên Bái - 2021) Cho khối nón có thể tích là
V
. Biết rằng khi cắt khối nón đã cho bởi một mặt
phẳng qua trục, thiết diện thu được là một tam giác đều có diện tích bằng
3
. Giá trị của
V
bằng
A.
4 .
B.
2 .
C.
3.
D.
3
.
3
Câu 4. (Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Cho hình chóp
.S ABCD
có đáy là
hình chữ nhật,
3AB
,
4AD
, cạnh bên
SA
vuông góc với mặt phẳng đáy, góc giữa
SC
và mặt
phẳng đáy là
45
. Tính bán kính mặt cầu ngoại tiếp hình chóp
.S ABCD
.
A.
5R
. B.
5 2R
. C.
5 2
2
R
. D.
5
2
R
.
Câu 5. (Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Cho hình lập phương có cạnh bằng
a
.
Thể tích khối cầu ngoại tiếp hình lập phương đó bằng
A.
3
3
3
a
. B.
3
4 3
3
a
. C.
3
4 3 a
. D.
3
3
2
a
.
Câu 6. (Chuyên Lê Hồng Phong - TPHCM - 2021) Cho hình lập phương
.ABCD A B C D
có cạnh
bằng
3a
. Quay đường tròn ngoại tiếp tam giác
A BD
quanh một đường kính của nó ta được một
mặt cầu. Tính diện tích mặt cầu này.
A.
2
27 a
. B.
2
21 a
. C.
2
24 a
. D.
2
25 a
.
Câu 7. (Chuyên Lê Hồng Phong - TPHCM - 2021) Cho khối nón có chiều cao
4 cm
, độ dài đường sinh
là
5 cm
. Tính thể tích khối nón.
A.
3
15 cm
. B.
3
12 cm
. C.
3
36 cm
. D.
3
45 cm
.
Câu 8. (Chuyên KHTN - 2021) Trong không gian cho tam giác
ABC
vuông cân tại đỉnh
A
và
2aBC
. Quay tam giác
ABC
quanh cạnh
BC
ta được khối tròn xoay. Thể tích của khối tròn
xoay đó bằng
A.
3
3
a
. B.
3
2 a
. C.
3
2
3
a
. D.
3
a
.
Câu 9. (Chuyên KHTN - 2021) Cho hình chóp
.S ABC
có đáy là tam giác
ABC
đều cạnh
a
,
SA
vuông
góc với mặt phẳng đáy,
2SA a
. Diện tích mặt cầu ngoại tiếp hình chóp bằng
A.
2
8
3
a
. B.
2
16
3
a
. C.
2
16
9
a
. D.
2
16 a
.
Câu 10. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Tam giác
ABC
vuông cân tại đỉnh
A
có cạnh
huyền là
2
. Quay tam giác
ABC
quanh trục
AB
thì được khối nón có thể tích là.
KHỐI TRÒN XOAY
Chủ đề 6
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
2
3
. B.
3
. C.
2
3
. D.
.
Câu 11. (Chuyên Quang Trung - Bình Phước - 2021) Từ một tấm tôn hình chữ nhật kích thước
h
và
a
,
người ta làm các thùng đựng nước hình trụ có chiều cao bằng
h
, theo hai cách sau (xem hình
minh họa dưới đây):
+ Cách 1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng.
+ Cách 2: Cắt tấm tôn ban đầu thành hai tấm bằng nhau, rồi gò mỗi tấm đó thành mặt xung quanh
của một thùng.
Kí hiệu
1
V là thể tích của thùng gò được theo cách 1 và
2
V là tổng thể tích của hai thùng gò được
theo cách 2. Tính tỉ số
1
2
V
V
A.
1
2
4
V
V
. B.
1
2
1
2
V
V
. C.
1
2
1
V
V
. D.
1
2
2
V
V
.
Câu 12. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho hình nón có diện tích xung quanh bằng
2
3 a
và bán
kính đáy bằng
a
. Độ dài đường sinh của hình nón đã cho bằng
A.
3a
. B.
2a
. C.
3
2
a
. D.
2 2a
.
Câu 13. (Chuyên Ngoại Ngữ Hà Nội- 2021) Trong không gian
Oxyz
, cho hình chữ nhật
ABCD
có
1, 2AB AD
. Gọi
,M N
lần lượt là trung điểm của
AD
và
BC
. Quay hình chữ nhật
ABCD
xung quanh trục
MN
ta được một hình trụ. Diện tích toàn phần của hình trụ đó là
A.
2
. B.
6
. C.
10
. D.
4
.
Câu 14. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho hình chóp tam giác đều
.S ABC
, có cạnh đáy bằng
3a
,
góc giữa cạnh bên và mặt đáy bằng
45
. Thể tích khối cầu ngoại tiếp hình chóp
.S ABC
bằng
A.
3
4 3a
. B.
3
4 3
3
a
. C.
3
4 2
3
a
. D.
3
4 2a
.
Câu 15. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Cho hình nón có chiều cao bằng
a
. Biết rằng khi cắt
hình nón đã cho bởi một mặt phẳng đi qua đỉnh hình nón và cách tâm của đáy hình nón một
khoảng bằng
3
a
, thiết diện thu được là một tam giác vuông. Thể tích của khối nón được giới hạn
bởi hình nón đã cho bằng
A.
3
5
9
a
. B.
3
3
a
. C.
3
4
9
a
. D.
3
5
12
a
.
Câu 16. (Chuyên Hạ Long - Quảng Ninh - 2021) Cho mặt cầu có diện tích là
36
. Thể tích của khổi cầu
được giới hạn bởi mặt cầu đã cho là
A.
27
. B.
108
. C.
81
. D.
36
.
Câu 17. (Chuyên Hạ Long - Quảng Ninh - 2021) Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều
cạnh
3a
, tam giác
SBC
vuông tại
S
và mặt phẳng
SBC
vuông góc với mặt phẳng
ABC
.
Diện tích mặt cầu ngoại tiếp hình chóp
.S ABC
bằng
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
A.
2
12 .a
B.
2
36 .a
C.
2
18 .a
D.
3
12 .a
Câu 18. (Chuyên ĐHSP Hà Nội - 2021) Cho hình chóp
.
S ABC
có đáy là tam giác vuông,
2 .SA SB SC AB BC a
Diện tích của mặt cầu ngoại tiếp hình chóp
.
S ABC
bằng
A.
2
8 2
3
a
. B.
2
8
3
a
. C.
2
32 3
3
a
. D.
8
.
Câu 19. (Chuyên ĐH Vinh - Nghệ An - 2021) Một khối trụ có đường cao bằng
2
, chu vi của thiết diện
qua trục gấp
3
lần đường kính đáy. Thể tích của khối trụ bằng
A.
2
. B.
32
. C.
8
3
. D.
8
.
Câu 20. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho khối lăng trụ đứng
.
ABC A B C
có đáy là tam giác đều
cạnh
a
,
2AB a
. Thể tích
V
của khối lăng trụ đã cho
A.
3
3
2
a
V
. B.
3
4
a
V
. C.
3
3
4
a
V
. D.
3
2V a
.
Câu 21. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho hình chóp
.
S ABC
có cạnh bên
SA
vuông góc với mặt
phẳng đáy
ABC
. Biết
SA a
, tam giác
ABC
là tam giác vuông cân tại
A
,
2AB a
. Tính theo
a
thể tích
V
của khối chóp
.
S ABC
.
A.
3
6
a
V
. B.
3
2
a
V
. C.
3
2
3
a
V
. D.
3
2V a
.
Câu 22. (THPT Thanh Chương 1- Nghệ An - 2021) Cắt hình nón bởi một mặt phẳng đi qua trục ta được
thiết diện là một tam giác vuông cân có cạnh huyền bằng . Thể tích V của khối nón đã cho
bằng
A. . B. . C. . D. .
Câu 23. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Trong không gian, cho tam giác
ABC
vuông tại
A
,
AB a
và
3BC a
. Thể tích của khối nón được tạo thành khi quay tam giác
ABC
xung
quanh trục
AB
bằng
A.
3
2
3
a
. B.
3
2
3
a
. C.
3
2
a
. D.
3
3
3
a
.
Câu 24. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho hình nón
N
có chiều cao bằng
a
. Một mặt
phẳng qua đỉnh
N
cắt
N
theo thiết diện là một tam giác đều có diện tích bằng
2
3a
. Thể tích
V
của khối nón giới hạn bởi
N
bằng
A.
3
3
V a
. B.
3
V a
. C.
3
5
3
V a
. D.
3
1
3
a
.
Câu 25. (THPT Đào Duy Từ - Hà Nội - 2021) Mặt phẳng đi qua trục hình trụ, cắt hình trụ theo thiết diện
là hình vuông cạnh
2a
. Thể tích khối trụ bằng:
A.
3
.a
B.
3
2
.
3
a
C.
3
3
a
. D.
3
2 .a
Câu 26. (THPT Chu Văn An - Thái Nguyên - 2021) Diện tích vải tối thiểu để may được một chiếc mũ
có hình dạng và kích thước(cùng đơn vị đo)
được cho bởi hình vẽ bên đó (không kể viền, mép) là bao nhiêu? Biết phía trên có dạng một
hình nón và phía dưới (vành mũ) có dạng hình vành khăn tròn.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
500
. B.
350
. C.
450
. D.
400
.
Câu 27. (THPT Ba Đình - Thanh Hóa - 2021) Cắt khối trụ bởi mặt phẳng qua trục ta được thiết diện là
hình chữ nhật
ABCD
có cạnh
,AB CD
thuộc hai đáy của hình trụ,
4 ; 5AB a AC a
. Tính thể
tích khối trụ.
A.
3
4V a
. B.
3
8V a
. C.
3
16V a
. D.
3
12V a
.
Câu 28. (THPT Quế Võ 1 - Bắc Ninh - 2021) Cho hình nón có bán kính bằng
5
và góc ở đỉnh bằng
60 .
Diện tích xung quanh của hình nón đã cho bằng
A.
50
. B.
100
. C.
50 3
3
. D.
100 3
3
.
Câu 29. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Đương kính của mặt cầu ngoại tiếp hình lập phương
có cạnh
3a
bằng
A.
3a
. B. 3a . C.
6a
. D.
3
2
a
.
Câu 30. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Hình trụ có bán kính đáy bằng
a
, chu vi thiết diện
qua trục bằng
10 .a
Thể tích khối trụ đã cho bằng
A.
3
3 a
. B.
3
4 a
. C.
3
a
. D.
3
5 a
.
Câu 31. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Thể tích khối cầu ngoại tiếp hình lập phương cạnh
a
là
A.
3
2
a
V
. B.
3
3
2
a
V
. C.
3
3
2
a
V
. D.
3
2
V a
.
Câu 32. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho hình nón đỉnh
S
có bán kính đáy
2R
. Biết diện
tích xung quanh của hình nón là
2 5
. Tính thể tích của khối nón.
A.
B.
5
.
3
C.
4
.
3
D.
2
.
3
Câu 33. (THPT Đồng Quan - Hà Nội - 2021) Một chiếc cốc hình trụ cao
15
cm dựng được nhiều nhất là
0,5
lít nước (bỏ qua độ dày của đáy cốc). Hỏi bán kính đường tròn đáy của chiếc cốc gần nhất với
giá trị nào trong các giá trị sau đây?
A.
3,26
cm. B.
3,90
cm. C.
3,23
cm. D.
3,28
cm.
Câu 34. (THPT Lê Lợi - Thanh Hóa - 2021) Thể tích của khối trụ có đường kính bằng
2a
, đường cao là
2a
là:
A.
3
4 a
. B.
3
a
. C.
3
2 a
. D.
3
3 a
.
Câu 35. (Trung Tâm Thanh Tường -2021) Thể tích của khối cầu ngoại tiếp hình lập phương cạnh bằng
2
.
A.
12
. B.
4
. C. 3
. D. 4 3
.
Câu 36. (THPT Triệu Sơn - Thanh Hóa - 2021) Thiết diện qua trục của một hình trụ là một hình vuông
có cạnh là
2a
.
TÀ
I LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Thể t
ích khối trụ được tạo nên bởi hình trụ này là
A.
3
2 a
. B.
3
2
3
a
. C.
3
8 a
. D.
3
8
3
a
.
Câu
37. (THPT Triệu Sơn - Thanh Hóa - 2021) Trong không gian, cho tam giác
A
BC
vuôn
g tại
A
c
ó
4AB a
và
3AC a
. Khi quay tam giác
ABC
quanh quanh cạnh góc vuông
AB
thì đường gấp
khúc
A
CB
tạo thành
một hình nón. Diện tích toàn phần của hình nón đó bằng
A.
2
1
5 a
. B.
2
2
4 a
. C.
2
3
6 a
. D.
2
2
0 a
.
Câu
38. (THPT Trần Phú - Đà Nẵng - 2021) Cho khối nón có thiết diện qua trục là một tam giác đều có
cạnh
3a
. T
hể tích của khối nón đã cho bằng
A.
3
3
8
a
. B.
3
8
a
. C.
3
9
8
a
. D.
3
3
8
a
.
BẢNG Đ
ÁP ÁN
1.
B
2.
A
3.D
4.
C
5.D
6.
C
7.B
8.
C
9.B
10.
B
11.D
12.A
13.
D
14.A
15.
D
16.D
17.
A
18.
D
19.D
20.
C
21.C
22.D
23.
A
24.B
25.
D
26.D
27.
D
28.
A
29.A
30.
A
31.B
32.D
33.
A
34.C
35.
D
36.A
37.
B
38.
D
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
MỨC ĐỘ THÔNG HIỂU
Câu 1. (Sở Vĩnh Phúc - 2021) Cho mặt cầu
S
và mặt phẳng
P
, biết khoảng cách từ tâm của mặt cầu
S
đến mặt phẳng
P
bằng
a
. Mặt phẳng
P
cắt mặt cầu
S
theo giao tuyến là đường tròn
có chu vi 2 3 a
. Diện tích mặt cầu
S
bằng bao nhiêu?
A.
2
12 a
. B.
2
16 a
. C.
2
4 a
. D.
2
8 a
.
Lời giải
Chọn B
Ta có:
Bán kính đường tròn giao tuyến của mặt phẳng
P
mặt cầu
S
là:
2 3
3
2 2
C a
r a
.
Suy ra bán kính mặt cầu
S
là:
2
2 2 2
3 2r r h a a a
.
Vậy diện tích mặt cầu
S
là:
2
2 2
4 4 2 16S r a a
.
Câu 2. (Sở Vĩnh Phúc - 2021) Tính diện tích toàn phần
S
của mặt nón
N
biết thiết diện qua trục của
nó là một tam giác vuông có cạnh huyền bằng
2 2a
A.
2
2 2 2S a
. B.
2
4 4 2S a
. C.
2
2 4 2S a
. D.
2
4 2 2S a
.
Lời giải
Chọn A.
Thiết diện qua trục là tam giác
SAB
vuông cân tại
S
nên
45A B
2
2
l
SO OA h r a
2
. 2.2 2 2
xq
S Rl a a a
KHỐI TRÒN XOAY
Chủ đề 6
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2 2 2
2 2 2 2 2 2
tp xq day
S S S a a a
Câu 3. (Sở Yên Bái - 2021) Cho khối nón có thể tích là
V
. Biết rằng khi cắt khối nón đã cho bởi một mặt
phẳng qua trục, thiết diện thu được là một tam giác đều có diện tích bằng
3
. Giá trị của
V
bằng
A.
4 .
B.
2 .
C.
3.
D.
3
.
3
Lời giải
Chọn D.
Gọi thiết diện qua trục là tam giác đều
2
2
3
3
4
3
SAB
SA SB AB
AB
SAB S
SO
2
1 1
. . 3.
3 2 3
AB
V SO
Câu 4. (Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Cho hình chóp
.S ABCD
có đáy là
hình chữ nhật,
3AB
,
4AD
, cạnh bên
SA
vuông góc với mặt phẳng đáy, góc giữa
SC
và mặt
phẳng đáy là
45
. Tính bán kính mặt cầu ngoại tiếp hình chóp
.S ABCD
.
A.
5R
. B.
5 2R
. C.
5 2
2
R
. D.
5
2
R
.
Lời giải
Chọn C
, , 45SC ABCD SC SA SCA
.
Khi đó,
SAC
vuông cân tại
A
5
SA AC
.
Gọi
AC BD O
, khi đó
O
là tâm của hình chữ nhật đáy. Suy ra: Tâm của mặt cầu ngoại tiếp
hình chóp
.S ABCD
thuộc đường thẳng
d
vuông góc với mặt phẳng đáy
d SC I
.
Mặt khác, do
SAC
vuông cân tại
A
nên
I
cách đều các điểm
, ,S A C
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Suy ra:
I
là tâm mặt cầu ngoại tiếp hình chóp
.S ABCD
có bán kính
5 2
2 2
SC
R SI
.
Câu 5. (Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Cho hình lập phương có cạnh bằng
a
.
Thể tích khối cầu ngoại tiếp hình lập phương đó bằng
A.
3
3
3
a
. B.
3
4 3
3
a
. C.
3
4 3 a
. D.
3
3
2
a
.
Lời giải
Chọn D
Ta có đường chéo của hình lập phương cạnh
a
bằng 3a .
Bán kính khối cầu ngoại tiếp của hình lập phương đó bằng:
3
2
a
R
.
Thể tích khối cầu ngoại tiếp hình lập phương đó bằng:
3
3
3
4 4 3 3
.
3 3 2 2
a a
V R
.
Câu 6. (Chuyên Lê Hồng Phong - TPHCM - 2021) Cho hình lập phương
.ABCD A B C D
có cạnh
bằng
3a
. Quay đường tròn ngoại tiếp tam giác
A BD
quanh một đường kính của nó ta được một
mặt cầu. Tính diện tích mặt cầu này.
A.
2
27 a
. B.
2
21 a
. C.
2
24 a
. D.
2
25 a
.
Lời giải
Chọn C
3 cạnh
, ,A B A D BD
là các đường chéo của hình vuông cạnh
3a
.
A BD
là tam giác đều cạnh
3 2a
.
Bán kính đường tròn ngoại tiếp tam giác
A BD
là:
3 3 6
6
3 3
BD a
R a
.
Suy ra mặt cầu được tạo ra có diện tích bằng:
2
2 2
4 4 6 24
mc
S R a a
.
Câu 7. (Chuyên Lê Hồng Phong - TPHCM - 2021) Cho khối nón có chiều cao
4 cm
, độ dài đường sinh
là
5 cm
. Tính thể tích khối nón.
A.
3
15 cm
. B.
3
12 cm
. C.
3
36 cm
. D.
3
45 cm
.
Lời giải
Chọn B
Theo giả thuyết có
2 2
4 , 5 3h cm l cm R l h cm
Vậy thể tích khối nón là
2 3
1
. . 12
3
nón
V R h cm
.
Câu 8. (Chuyên KHTN - 2021) Trong không gian cho tam giác
ABC
vuông cân tại đỉnh
A
và
2aBC
. Quay tam giác
ABC
quanh cạnh
BC
ta được khối tròn xoay. Thể tích của khối tròn
xoay đó bằng
A.
3
3
a
. B.
3
2 a
. C.
3
2
3
a
. D.
3
a
.
Lời giải
Chọn C
D
A
C
B
B'
C'
D'
A'
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Gọi
I
là trung điểm của
BC
. Khi quay tam giác
ABC
quanh cạnh
BC
ta được khối tròn xoay
gồm hai hình nón bằng nhau có chung mặt đáy ( như hình vẽ).
Ở mỗi hình nón ta có:
h BI a
;
r AI BI a
Khi đó
3
2 2
X
1 2 2
2. 2. . .
3 3 3
KT N
a
V V r h a a
Câu 9. (Chuyên KHTN - 2021) Cho hình chóp
.S ABC
có đáy là tam giác
ABC
đều cạnh
a
,
SA
vuông
góc với mặt phẳng đáy,
2SA a
. Diện tích mặt cầu ngoại tiếp hình chóp bằng
A.
2
8
3
a
. B.
2
16
3
a
. C.
2
16
9
a
. D.
2
16 a
.
Lời giải
Chọn B
Gọi
,I H
là trung điểm cạnh
,BC SA
,
G
là trọng tâm tam giác
ABC
.
Gọi
d
là đường thẳng vuông góc với mặt phẳng
ABC
tại trọng tâm
G
của tam giác
ABC
, kẻ
mặt phẳng trung trực của
SA
cắt
d
tại
O
.
O
là tâm mặt cầu ngoại tiếp hình chóp
.S ABC
, bán
kính mặt cầu đó là
2
2 2 2
3 2 3
3 3
a a
OA HA AG a
,
do đó diện tích mặt cầu đó là:
2
2
2
2 3 16
4 . 4 .
3 3
a a
S IA
.
Câu 10. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Tam giác
ABC
vuông cân tại đỉnh
A
có cạnh
huyền là
2
. Quay tam giác
ABC
quanh trục
AB
thì được khối nón có thể tích là.
A.
2
3
. B.
3
. C.
2
3
. D.
.
Lời giải
Chọn B
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Tam giác
ABC
vuông cân tại đỉnh
A
có cạnh huyền là
2
nên
1AB AC
.
Suy ra khối nón có bán kính đáy là
1r
và chiều cao là
1h
. Nên thể tích khối nón là
2
1
.
3 3
V r h
.
Câu 11. (Chuyên Quang Trung - Bình Phước - 2021) Từ một tấm tôn hình chữ nhật kích thước
h
và
a
,
người ta làm các thùng đựng nước hình trụ có chiều cao bằng
h
, theo hai cách sau (xem hình
minh họa dưới đây):
+ Cách 1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng.
+ Cách 2: Cắt tấm tôn ban đầu thành hai tấm bằng nhau, rồi gò mỗi tấm đó thành mặt xung quanh
của một thùng.
Kí hiệu
1
V là thể tích của thùng gò được theo cách 1 và
2
V là tổng thể tích của hai thùng gò được
theo cách 2. Tính tỉ số
1
2
V
V
A.
1
2
4
V
V
. B.
1
2
1
2
V
V
. C.
1
2
1
V
V
. D.
1
2
2
V
V
.
Lời giải
Chọn D
Gọi
1 2
,r r lần lượt là bán kính đáy của hai thùng gò được theo cách 1, cách 2.
Vì
1
1
2
2
2
2
2
2
4
a
r a
r
a
a
r
r
.
Ta có
2 2
1
1 2
2
, 2 2
2 4
V
a a
V h V h
V
.
Câu 12. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho hình nón có diện tích xung quanh bằng
2
3 a
và bán
kính đáy bằng
a
. Độ dài đường sinh của hình nón đã cho bằng
A.
3a
. B.
2a
. C.
3
2
a
. D.
2 2a
.
Lời giải
Chọn A
Diện tích xung quanh hình nón là
xp
S rl
.
B
A
C
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Suy ra đường sinh của hình nón là
2
3
3
xp
S
a
l a
r a
Câu 13. (Chuyên Ngoại Ngữ Hà Nội- 2021) Trong không gian
Oxyz
, cho hình chữ nhật
ABCD
có
1, 2AB AD
. Gọi
,M N
lần lượt là trung điểm của
AD
và
BC
. Quay hình chữ nhật
ABCD
xung quanh trục
MN
ta được một hình trụ. Diện tích toàn phần của hình trụ đó là
A.
2
. B.
6
. C.
10
. D.
4
.
Lời giải
Chọn D
Ta có :
1 ; 1
2
AD
r l AB
.
Vậy diện tích toàn phần của hình trụ :
2 2
2 2 2 .1.1 2. .1 4S rl r
.
Câu 14. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho hình chóp tam giác đều
.S ABC
, có cạnh đáy bằng
3a
,
góc giữa cạnh bên và mặt đáy bằng
45
. Thể tích khối cầu ngoại tiếp hình chóp
.S ABC
bằng
A.
3
4 3a
. B.
3
4 3
3
a
. C.
3
4 2
3
a
. D.
3
4 2a
.
Lời giải
Chọn A
Gọi
M
là trung điểm của
BC
,
H
là hình chiếu vuông góc của
S
lên
ABC
.
2
2
3 3 3 2
3 ; 3
2 2 3
a a
AM a AH AM a BH CH
Ta có góc giữa cạnh bên
SA
và mặt đáy
ABC
là
SAH .
tan 45 3.1 3.SH AH a a
Từ đó suy ra
SH HA HB HC
.
H
chính là tâm khối cầu ngoại tiếp hình chóp.
3
3 3
4 4
. 3 4 3
3 3
V R a a
.
Câu 15. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Cho hình nón có chiều cao bằng
a
. Biết rằng khi cắt
hình nón đã cho bởi một mặt phẳng đi qua đỉnh hình nón và cách tâm của đáy hình nón một
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
khoảng bằng
3
a
, thiết diện thu được là một tam giác vuông. Thể tích của khối nón được giới hạn
bởi hình nón đã cho bằng
A.
3
5
9
a
. B.
3
3
a
. C.
3
4
9
a
. D.
3
5
12
a
.
Lời giải
Chọn D
Gọi thiết diện qua đỉnh là tam giác vuông cân
SAB
và gọi
H
là trung điểm AB.
Kẻ
,
3
a
OK SH d O SAB OK
và ta có
2 2 2
1 1 1 2
.
4
a
OH
OK SO OH
Do tam giác
SAB
vuông cân tại
2 2
3 2
.
4
a
S AH SH SH SO OH
2
3
2 2 2
5 1 1 5 5
. . . .
2 3 3 2 12
a a a
OA OH AH V OA SO a
Vậy thể tích của khối nón được giới hạn bởi hình nón đã cho bằng
3
5
.
12
a
Câu 16. (Chuyên Hạ Long - Quảng Ninh - 2021) Cho mặt cầu có diện tích là
36
. Thể tích của khổi cầu
được giới hạn bởi mặt cầu đã cho là
A.
27
. B.
108
. C.
81
. D.
36
.
Lời giải
Chọn D
Gọi
r
là bán kính mặt cầu.
Ta có
2
4 36 3S r r
.
Thể tích của khổi cầu là
3 3
4 4
.3 36
3 3
V r
.
Câu 17. (Chuyên Hạ Long - Quảng Ninh - 2021) Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều
cạnh
3a
, tam giác
SBC
vuông tại
S
và mặt phẳng
SBC
vuông góc với mặt phẳng
ABC
.
Diện tích mặt cầu ngoại tiếp hình chóp
.S ABC
bằng
A.
2
12 .a
B.
2
36 .a
C.
2
18 .a
D.
3
12 .a
Lời giải
Chọn A
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Gọi
M
là trung điểm
BC
nên
M
là tâm đường tròn ngoại tiếp
SBC
.
Trong
ABC
thì
AM BC
và
SBC ABC
nên
AM SBC
. Gọi
O
là tâm mặt cầu ngoại tiếp
hình chóp
.
S ABC
thì
O AM
hay
O
là tâm đường tròn ngoại tiếp
ABC
. Do đó bán kính mặt
cầu ngoại tiếp hình chóp
.S ABC
bằng bán kính đường tròn ngoại tiếp
ABC
.
Trong
ABC
có
3
3
2sin 60
3
2.
2
o
AB a
R a
.
Vậy diện tích mặt cầu ngoại tiếp hình chóp
.S ABC
là
2 2
4 12S R a
.
Câu 18. (Chuyên ĐHSP Hà Nội - 2021) Cho hình chóp
.S ABC
có đáy là tam giác vuông,
2 .SA SB SC AB BC a
Diện tích của mặt cầu ngoại tiếp hình chóp
.S ABC
bằng
A.
2
8 2
3
a
. B.
2
8
3
a
. C.
2
32 3
3
a
. D.
2
8 a
.
Lời giải
Chọn D
Gọi
M
là trung điểm của
.AC
ABC
vuông có
AB BC
nên
ABC
vuông cân tại
.B
Khi đó
2 2 2AC AB a
và
MA MB MC
(1).
Mặt khác,
SAC
cân tại
S
có
2 , 2 2SA SC a AC a
nên tam giác
SAC
vuông cân tại
.S
Suy ra
MA MS MC
(2).
Từ (1), (2) suy ra
M
là tâm mặt cầu ngoại tiếp hình chóp
. .S ABC
Suy ra
2 2
2.
2 2
AC a
R SM a
Vậy diện tích mặt cầu ngoại tiếp hình chóp
.S ABC
là
2 2
4 8S R a
(đvdt).
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Câu 19. (Chuyên ĐH Vinh - Nghệ An - 2021) Một khối trụ có đường cao bằng
2
, chu vi của thiết diện
qua trục gấp
3
lần đường kính đáy. Thể tích của khối trụ bằng
A.
2
. B.
32
. C.
8
3
. D.
8
.
Lời giải
Chọn D
Gọi bán kính đáy của khối trụ là
r
, chiều cao là
h
, suy ra
2h
Giả sử thiết diện qua trục là hình chữ nhật
ABCD
( như hình vẽ)
Từ giả thiết suy ra
2 2 2 3.2 2r r r
Thể tích của khối trụ là
2
. 8V r h
.
Câu 20. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho khối lăng trụ đứng
.ABC A B C
có đáy là tam giác đều
cạnh
a
,
2AB a
. Thể tích
V
của khối lăng trụ đã cho
A.
3
3
2
a
V
. B.
3
4
a
V . C.
3
3
4
a
V . D.
3
2V a
.
Lời giải
Chọn C
Xét tam giác
ABB
vuông tạ
B
ta có:
2 2
3BB AB AB a
.
Tam giác ABC là tam giác đều cạnh
a
nên
2
0
1 3
. .sin 60 .
2 4
ABC
a
S AB AC
Thể tích
V
của khối lăng trụ đã cho là:
2 3
3 3
. 3
4 4
ABC
a a
V S BB a
.
Câu 21. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho hình chóp
.S ABC
có cạnh bên
SA
vuông góc với mặt
phẳng đáy
ABC
. Biết
SA a
, tam giác
ABC
là tam giác vuông cân tại
A
,
2AB a
. Tính theo
a
thể tích
V
của khối chóp
.S ABC
.
A.
3
6
a
V
. B.
3
2
a
V
. C.
3
2
3
a
V
. D.
3
2V a
.
a
2a
C'
B'
A
B
C
A'
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Lời giải
Chọn C
Tam giác
ABC
là tam giác vuông cân tại
A
nên
2AC AB a
.
Thể tích
V
của khối chóp
.S ABC
là
3
1 1 1 1 1 2
. . . . . .2 .2
3 3 2 3 2 3
ABC
a
V SA S SA AB AC a a a
.
Câu 22. (THPT Thanh Chương 1- Nghệ An - 2021) Cắt hình nón bởi một mặt phẳng đi qua trục ta được
thiết diện là một tam giác vuông cân có cạnh huyền bằng . Thể tích V của khối nón đã cho
bằng
A. . B. . C. . D. .
Lời giải
Chọn D
Gọi S, O lần lượt là đỉnh và tâm đường tròn đáy của hình nón. Một mặt phẳng đi qua trục cắt
hình nón theo thiết diện là tam giác vuông cân (như hình vẽ).
Ta có: .
Thể tích V của khối nón đã cho bằng: .
Câu 23. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Trong không gian, cho tam giác
ABC
vuông tại
A
,
AB a
và
3BC a
. Thể tích của khối nón được tạo thành khi quay tam giác
ABC
xung
quanh trục
AB
bằng
A.
3
2
3
a
. B.
3
2
3
a
. C.
3
2 a
. D.
3
3
3
a
.
Lời giải
Chọn A
Khối nón được tạo thành khi quay tam giác
ABC
vuông tại
A
xung quanh trục
AB
có đường cao
h AB a
và bán kính đáy
2 2
2r AC BC AB a
. Do đó thể tích khối nón :
3
2
1 2
3 3
a
V r h
.
Câu 24. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho hình nón
N
có chiều cao bằng
a
. Một mặt
phẳng qua đỉnh
N
cắt
N
theo thiết diện là một tam giác đều có diện tích bằng
2
3a . Thể tích
V
của khối nón giới hạn bởi
N
bằng
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
A.
3
3V a
. B.
3
V a
. C.
3
5
3
V a
. D.
3
1
3
a
.
Lời giải
Chọn B
Gọi thiết diện của hình nón
N
là tam giác đều
SAB
, chiều cao của hình nón là
SH a
.
Ta có
2 2 2
3
3 . 3 2
4
SAB
S a AB a AB a
và
3
. 3
2
SE AB a
.
Trong tam giác vuông
SHE
:
2 2 2 2
2HE SE SH a
.
Trong tam giác vuông
HEA
:
2 2 2 2 2 2
2 3 3HA HE EA a a a HA a .
Thể tích khối nón cần tìm:
2
2 3
1 1
. 3 .
3 3
V HA SH a a a
.
Câu 25. (THPT Đào Duy Từ - Hà Nội - 2021) Mặt phẳng đi qua trục hình trụ, cắt hình trụ theo thiết diện
là hình vuông cạnh
2a
. Thể tích khối trụ bằng:
A.
3
.a
B.
3
2
.
3
a
C.
3
3
a
. D.
3
2 .a
Lời giải
Chọn D
Mặt phẳng đi qua trục hình trụ, cắt hình trụ theo thiết diện là hình vuông cạnh
2 2 ;a h a R a
Thể tích hình trụ là:
2 2 3
. .2 2V R h a a a
(đvtt)
Câu 26. (THPT Chu Văn An - Thái Nguyên - 2021) Diện tích vải tối thiểu để may được một chiếc mũ
có hình dạng và kích thước(cùng đơn vị đo)
được cho bởi hình vẽ bên đó (không kể viền, mép) là bao nhiêu? Biết phía trên có dạng một
hình nón và phía dưới (vành mũ) có dạng hình vành khăn tròn.
A.
500
. B.
350
. C.
450
. D.
400
.
Lời giải
Chọn D
Ta thấy tổng
S
của diện tích vải để may được một chiếc mũ như trên được tính bằng tổng
diện tích xung quanh của hình nón với diện tích của hình vành khăn.
Ta có
2 2
.5.40 . 15 5 400S
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 27. (THPT Ba Đình - Thanh Hóa - 2021) Cắt khối trụ bởi mặt phẳng qua trục ta được thiết diện là
hình chữ nhật
ABCD
có cạnh
,AB CD
thuộc hai đáy của hình trụ,
4 ; 5AB a AC a
. Tính thể
tích khối trụ.
A.
3
4V a
. B.
3
8V a
. C.
3
16V a
. D.
3
12V a
.
Lời giải
Chọn D
Trong tam giác vuông
ABC
ta có :
2 2
3BC AC AB a
.
2 ; 3R a h a
.
Vậy
2
2 3
. 2 .3 12V R h a a a
.
Câu 28. (THPT Quế Võ 1 - Bắc Ninh - 2021) Cho hình nón có bán kính bằng
5
và góc ở đỉnh bằng
60 .
Diện tích xung quanh của hình nón đã cho bằng
A.
50
. B.
100
. C.
50 3
3
. D.
100 3
3
.
Lời giải
Chọn A
Gọi
60
là góc ở đỉnh của hình nón.
Ta có
1
sin 10.
2 2
r
l
l
Diện tích xung quanh của hình nón là
.5.10 50
xq
S rl
(đvdt).
Câu 29. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Đương kính của mặt cầu ngoại tiếp hình lập phương
có cạnh
3a
bằng
A.
3a
. B. 3a . C.
6a
. D.
3
2
a
.
Lời giải
Chọn A
Ta có mặt cầu ngoại tiếp hình lập
.ABCD A B C D
có đường kính bằng
2 2 2 2 2
3AC A A A C A A A B B C a
.
Câu 30. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Hình trụ có bán kính đáy bằng
a
, chu vi thiết diện
qua trục bằng
10 .a
Thể tích khối trụ đã cho bằng
A.
3
3 a
. B.
3
4 a
. C.
3
a
. D.
3
5 a
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Lời giải
Chọn A
Chu vi thiết diện qua trục bằng
10a
nên chiều cao của khối trụ bằng
3a
.
Thể tích khối trụ bằng
2 2 3
. . .3 3 .V r h a a a
Câu 31. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Thể tích khối cầu ngoại tiếp hình lập phương cạnh
a
là
A.
3
2
a
V
. B.
3
3
2
a
V
. C.
3
3
2
a
V
. D.
3
2
V a
.
Lời giải
Chọn B
Đường chéo hình lập phương cạnh
a
có độ dài là
3a
là đường kính của khối cầu ngoại tiếp hình
lập phương. Do đó khối cầu có bán kính
3
2
a
R
. Thể tích khối cầu là:
3
3
4 3 3
3 2 2
a
V a
.
Câu 32. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho hình nón đỉnh
S
có bán kính đáy
2R
. Biết diện
tích xung quanh của hình nón là
2 5
. Tính thể tích của khối nón.
A.
B.
5
.
3
C.
4
.
3
D.
2
.
3
Lời giải
Chọn D
Ta có
.2. 2 5 5.
xq
S Rl l l
Khi đó
2
2 2 2
5 2 1.
h l R
Do đó thể tích khối nón là
2 2
1 1 2
.2 .1 .
3 3 3
V R h
Vậy ta chọn phương án D.
Câu 33. (THPT Đồng Quan - Hà Nội - 2021) Một chiếc cốc hình trụ cao
15
cm dựng được nhiều nhất là
0,5
lít nước (bỏ qua độ dày của đáy cốc). Hỏi bán kính đường tròn đáy của chiếc cốc gần nhất với
giá trị nào trong các giá trị sau đây?
A.
3,26
cm. B.
3,90
cm. C.
3,23
cm. D.
3,28
cm.
Lời giải
Chọn A.
Ta có
2 2
500 .15 3.26
15
V
V r h r r
cm.
Câu 34. (THPT Lê Lợi - Thanh Hóa - 2021) Thể tích của khối trụ có đường kính bằng
2a
, đường cao là
2a
là:
A.
3
4
a
. B.
3
a
. C.
3
2
a
. D.
3
3 a
.
Lời giải
Chọn C
Ta có:
2
d
r a
2 3
2
V r h a
Câu 35. (Trung Tâm Thanh Tường -2021) Thể tích của khối cầu ngoại tiếp hình lập phương cạnh bằng
2
.
A.
12
. B.
4
. C.
3
. D.
4 3
.
Lời giải
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Chọn D
Bán kính mặt cầu ngoại tiếp hình lập phương cạnh bằng
2
là:
1
.2 3 3
2
R
.
Thể tích của khối cầu ngoại tiếp hình lập phương cạnh bằng
2
là:
3
4 4
3 3 4 3
3 3
V R
.
Câu 36. (THPT Triệu Sơn - Thanh Hóa - 2021) Thiết diện qua trục của một hình trụ là một hình vuông
có cạnh là
2a
.
Thể tích khối trụ được tạo nên bởi hình trụ này là
A.
3
2 a
. B.
3
2
3
a
. C.
3
8 a
. D.
3
8
3
a
.
Lời giải
Chọn A
Thiết diện qua trục là hình vuông
ABCD
có cạnh bằng
2a
.
Do đó:
2h a
;
r a
.
Thể tích của khối trụ bằng:
2 2 3
. .2 2V r h a a a
.
Câu 37. (THPT Triệu Sơn - Thanh Hóa - 2021) Trong không gian, cho tam giác
ABC
vuông tại
A
có
4AB a
và
3AC a
. Khi quay tam giác
ABC
quanh quanh cạnh góc vuông
AB
thì đường gấp
khúc
ACB
tạo thành một hình nón. Diện tích toàn phần của hình nón đó bằng
A.
2
15 a
. B.
2
24 a
. C.
2
36 a
. D.
2
20 a
.
Lời giải
Chọn B
Ta có:
2 2
2 2
4 3 5BC AB AC a a a
.
Do đó, hình nón đã cho có bán kính đường tròn đáy
3r a
, độ dài đường sinh
5l a
.
Vậy diện tích toàn phần của hình nón đã cho là:
2
2 2
.3 .5 . 3 24
tp xq d
S S S rl r a a a a
.
Câu 38. (THPT Trần Phú - Đà Nẵng - 2021) Cho khối nón có thiết diện qua trục là một tam giác đều có
cạnh
3a
. Thể tích của khối nón đã cho bằng
TÀ
I LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
A.
3
3
8
a
. B.
3
8
a
. C.
3
9
8
a
. D.
3
3
8
a
.
Lờ
i giải
Chọn D
Giả sử thiết diện qua trục là tam giác đều
SAB
.
Bán kính đáy
1
3
2 2
a
R AB
Đường
cao của khối nón là
2
2
2 2
3
3
3
4 2
a a
h SO SA OA a
.
Vậy thể tích của khối nón đã cho là
2
3
2
1 1 3 3 3
.
3 3 2 2 8
a a a
V R h
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
MỨC ĐỘ VẬN DỤNG
Câu 1. (Sở Lào Cai - 2021) Lon nước ngọt có hình trụ còn cốc uống nước có hình nón cụt (như hình vẽ
minh họa dưới đây). Khi rót nước ngọt từ lon ra cốc thì chiều cao
h
của phần nước ngọt còn lại
trong lon và chiều cao của phần nước ngọt có trong cốc là như nhau. Hỏi khi đó chiều cao
h
trong
lon nước gần nhất số nào sau đây?
A.
9,18cm
. B.
14,2cm
. C.
8,58cm
. D.
7,5cm
.
Câu 2. (Sở Hà Tĩnh - 2021) Cắt hình trụ bởi một mặt phẳng song song với trục và cách trục một khoảng
bằng
2
, thiết diện thu được là hình vuông có diện tích bằng
16
. Thể tích khối trụ bằng
A.
10 6
. B.
24
. C.
32
. D.
12 6
.
Câu 3. (Sở Yên Bái - 2021) Cho hình trụ có thiết diện qua trục là hình vuông
ABCD
cạnh
2 3cm
với
AB
là đường kính của đường tròn đáy tâm
O
. Gọi
M
là điểm thuộc cung
AB
của đường tròn
đáy sao cho
60ABM
. Thể tích của khối tứ diện
ACDM
là
A.
3
3V cm
. B.
3
7V cm
. C.
3
4V cm
. D.
3
6V cm
.
Câu 4. (Chuyên Lê Hồng Phong - TPHCM - 2021) Cho hình chóp tam giác đều có cạnh đáy bằng
6 và chiều cao
1h
.
Tính
diện tích mặt cầu ngoại tiếp hình chóp đã cho.
A.
27S
. B.
6S
. C.
5S
. D.
9S
.
Câu 5. (Chuyên Lê Hồng Phong - TPHCM - 2021) Cho hình nón có bán kính đáy bằng
5
và chiều cao
bằng
12
. Tính bán kính mặt cầu ngoại tiếp
hình nón.
A.
169
24
R
. B.
125
24
R
. C.
81
24
R
. D.
121
24
R
.
Câu 6. (Chuyên Lam Sơn - Thanh Hóa - 2021) Cho hình trụ có chiều cao bằng 5 3 . Cắt hình trụ đã
cho bởi mặt phẳng song song với trục và cách trục một khoảng bằng
1
, thiết diện thu được có diện
tích bằng
30
. Diện tích xung quanh của hình trụ đã cho bằng
A. 5 39
. B. 10 3
. C. 10 39
. D. 20 3
.
Câu 7. (Chuyên KHTN - 2021) Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông cân tại
B
,
3AB BC a
, góc
0
90SAB SCB và khoảng cách từ
A
đến mặt phẳng
SBC
bằng 6a .
Tính diện tích mặt cầu ngoại tiếp hình chóp
.S ABC
theo
a
.
A.
2
36 a
. B.
2
6 a
. C.
2
18 a
. D.
2
48 a
.
Câu 8. (Chuyên Hạ Long - Quảng Ninh - 2021) Cho khối nón có bán kính bằng 3 và khoảng cách từ
tâm của đáy đến một đường sinh bất kì bằng
12
.
5
Thể tích của khối nón đã cho bằng
A.
12 .
V
B.
18 .
V
C.
36 .
V
D.
24 .
V
KHỐI TRÒN XOAY
Chủ đề 6
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 9. (Chuyên ĐH Vinh - Nghệ An - 2021) Cho hình lăng trụ đứng
.
ABC A B C
có
2AB AA a
,
AC a
,
120
BAC
. Bán kính mặt cầu ngoại tiếp hình chóp
.
A BCC B
bằng
A.
30
3
a
. B.
10
3
a
. C.
30
10
a
. D.
33
3
a
.
Câu 10. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho hình chóp tứ giác
ABCD
có đáy
ABCD
là hình chữ
nhật,
, 3,AB a AD a SA
vuông góc với mặt phẳng đáy. Mặt phẳng
SBC
tạo với đáy một
góc
60
. Tính thể tích khối chóp
.
S ABCD
.
A.
3
3V a
. B.
3
V a
. C.
3
3
3
V a
. D.
3
3
a
V
.
Câu 11. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho khối lăng trụ tam giác
.
ABC A B C
mà mặt bên
ABB A
có diện tích bằng
2
2a
. Khoảng cách giữa
CC
và mặt
ABB A
bằng
a
. Thể tích khối
lăng trụ là
A.
3
.V a
B.
3
2
.
3
V a
C.
3
3 .V a
D.
3
1
.
3
V a
Câu 12. (THPT Thanh Chương 1- Nghệ An - 2021) Cắt hình trụ bởi mặt phẳng qua trục, thiết diện thu
được là hình chữ nhật có chu vi bằng Giá trị lớn nhất của thể tích khối trụ bằng
A. . B. . C. . D. .
Câu 13. (THPT Thanh Chương 1- Nghệ An - 2021) Trong không gian cho hình bình hành có
. Thể tích khối tròn xoay tạo thành khi quay hình bình hành
quanh cạnh bằng
A. . B. . C. . D. .
Câu 14. (THPT Nguyễn Huệ - Phú Yên - 2021) Cho hình thang vuông
ABCD
vuông tại
,A B
. Cạnh
2
AB BC
,
2 2
AD
. Thể tích khối tròn xoay tạo ra khi quay hình thang
ABCD
quanh
CD
là
A.
7
3
. B.
7 2
12
. C.
7
6
. D.
14
3
.
Câu 15. (THPT Nguyễn Huệ - Phú Yên - 2021) Một hình trụ
T
có chiều cao bằng đường kính đáy và
một hình nón
N
có đáy là đáy của hình trụ
T
, còn đỉnh là tâm của đáy còn lại của hình trụ
T
. Gọi
1 2
,S S
lần lượt là diện tích xung quanh của hình trụ
T
và hình nón
N
. Tỉ số
1
2
S
S
bằng
A.
3
5
. B.
4 5
5
. C.
7
9
. D.
1
2
.
Câu 16. (THPT Lương Thế Vinh - 2021) Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình thang vuông tại
A
và
B
với
1
AB BC
,
2AD
. Cạnh bên
1
SA
và
SA
vuông góc với đáy. Gọi E là trung điểm AD. Diện tích
mc
S
của mặt cầu ngoại tiếp hình chóp
.
S CDE
là
A.
5
mc
S
. B.
3
mc
S
. C.
11
mc
S
. D.
2
mc
S
.
Câu 17. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho hình lăng trụ tam giác đều có cạnh đáy bằng
a
, cạnh bên bằng
2a
. Thể tích của khối cầu ngoại tiếp hình lăng trụ đã cho bằng
A.
3
32 3
27
a
. B.
3
256
81
a
. C.
3
4
3
a
. D.
3
8 6
27
a
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Câu 18. (THPT Đào Duy Từ - Hà Nội - 2021) Cho hình nón
N
có đỉnh
S
, bán kính đáy bằng
1r
và
độ dài đường sinh bằng
2 2l
. Mặt cầu đi qua
S
và đường tròn đáy của
N
có bán kính bằng
A.
4 7
7
. B.
8 7
7
. C.
7
. D.
4
3
.
Câu 19. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Chohình nón có bán kính đáy bằng
3
và chiều cao
bằng
6
, một khối trụ có bán kính đáy thay đổi nội tiếp khối nón( như hình vẽ). Thể tích lớn nhất
của khối trụ bằng
A.
10
. B.
6
. C.
8
. D.
4
.
Câu 20. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho hình trụ có bán kính đáy bằng
4
. Biết rằng khi
cắt hình trụ đã cho bởi một mặt phẳng qua
trục, thiết diện thu được là một hình vuông. Diện tích toàn phần của hình trụ đã cho bằng
A.
106
. B.
64
. C.
80
. D.
96
.
Câu 21. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho hình chóp
.S ABC
có
SA ABC
, tam giác
ABC
vuông tại
B
,
3, 7SA BC AB
.
Tính bán kính
R
của mặt cầu ngoại tiếp hình chóp đã cho.
A.
5
2
R
. B.
5R
. C.
5R
. D.
5
2
R
.
Câu 22. (THPT Ba Đình - Thanh Hóa - 2021) Cho hình lăng trụ tam giác đều
.ABC A B C
có độ dài
cạnh đáy bằng
a
và chiều cao
2a
. Tính thể tích
V
của khối cầu ngoại tiếp hình lằng trụ
.ABC A B C
:
A.
3
32 3
.
27
a
V
B.
3
32 3
.
9
a
V
C.
3
8 3
.
27
a
V
D.
3
32 3
.
81
a
V
Câu 23. (THPT Quế Võ 1 - Bắc Ninh - 2021) Cho điểm
A
nằm trên mặt cầu
S
tâm
,O
bán kính
6R
cm.
,I K
là hai điểm trên đoạn
OA
sao cho
OI IK KA
. Các mặt phẳng
,P Q
lần
lượt đi qua
,I K
cùng vuông góc với
OA
và cắt mặt cầu
S
theo đường tròn có bán kính
1 2
; .r r
Tính tỉ số
1
2
.
r
r
A.
1
2
5
3 10
r
r
. B.
1
2
3 10
4
r
r
. C.
1
2
4
10
r
r
. D.
1
2
3 10
5
r
r
.
Câu 24. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho hình nón đỉnh
S
có đáy là đường tròn tâm
O
bán kính
1.
Trên đường tròn
O
lấy hai điểm
,A B
sao cho tam giác
OAB
vuông. Biết diện tích
tam giác
SAB
bằng
2,
thể tích khối nón đã cho bằng :
A.
14
2
V
. B.
14
3
V
. C.
14
6
V
. D.
14
12
V
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 25. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cắt một hình trụ bởi mặt phẳng song song với trục
ta được thiết diện là hình vuông có diện tích bằng
36
, biết khoảng cách từ tâm đáy đến thiết diện
bằng
1
. Tính thể tích của khối trụ giới hạn bởi hình trụ đã cho.
A.
20 .
B.
10 .
C.
30 .
D.
60 .
Câu 26. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Cho hình chóp S.ABCD có đáy ABCD là hình thang
vuông tại A và B. Biết
, 2 ,AB BC a AD a SA
vuông góc với đáy và
2 .SA a
Tính bán
kính mặt cầu ngoại tiếp hình chóp S.HCD với H là trung điểm của AD.
A.
11
2
a
. B.
10
2
a
. C.
a
. D.
3
2
a
.
Câu 27. (THPT Phan Đình Phùng - Quảng Bình - 2021) Cho hình nón có chiều cao
20h cm
, bán kính
đáy
25r cm
. Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm đáy đến mặt phẳng
chứa thiết diện là
12cm
. Tính diện tích
S
của thiết diện đó.
A.
2
500 cm
S
. B.
2
300 cm
S
. C.
2
406 cm
S
. D.
2
400 cm
S
.
Câu 28. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho hình trụ có thiết diện qua trục là hình vuông
cạnh
2a
. Mặt phẳng
P
song song với trục và cách trục một khoảng
2
a
. Tính diện tích thiết diện
của hình trụ cắt bởi mặt phẳng
P
.
A.
2
15a
. B.
2
2 3a
. C.
2
15
2
a
. D.
2
2 15a
.
Câu 29. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho hình lập phương
.
ABCD A B C D
cạnh
bằng
2a
. Một mặt cầu
S
đi qua các đỉnh của hình vuông
ABCD
đồng thời tiếp xúc với các
cạnh của hình vuông
A B C D
. Tính bán kính
R
của mặt cầu
S
?
A.
3
4
a
R
. B.
41
4
a
R
. C.
43
9
a
R
. D.
41
8
a
R
.
Câu 30. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho hình trụ có chiều cao
2a
và hình chữ nhật
ABCD
nằm trên mặt phẳng không vuông góc với đáy của hình trụ. Biết
AB
nằm trên đường tròn
đáy thứ nhất,
CD
nằm trên đường tròn đáy thứ hai của hình trụ và
AB CD a
, diện tích hình
chữ nhật
ABCD
bằng
2
2a
. Thể tích khối trụ đã cho bằng
A.
3
2
4
a
. B.
3
3 2
4
a
. C.
3
4
a
. D.
3
3
4
a
.
Câu 31. (THPT Đồng Quan - Hà Nội - 2021) Cho hình nón đỉnh
S
, đáy là đường tròn tâm
O
, bán kính
5
R
. Một thiết diện qua đỉnh
S
là tam giác đều
SAB
cạnh bằng
8
, khoảng cách từ
O
đến mặt
phẳng
SAB
bằng
A.
13
3
. B.
13
. C.
4 13
3
. D.
3 13
4
.
Câu 32. (THPT Lê Lợi - Thanh Hóa - 2021) Cho hình chóp
.
S ABC
với
SA
vuông góc với mặt phẳng
ABC
, tam giác
ABC
vuông tại
B
và
3BC a
,
60
BAC
. Gọi
H
,
K
lần lượt là hình
chiếu của
A
lên
SB
và
SC
. Mặt cầu đi qua các điểm
, , , ,A B C H K
có bán kính bằng
A.
a
. B.
2a
. C.
3a
. D.
2
a
.
Câu 33. (Trung Tâm Thanh Tường -2021) Cho hình vuông
ABCD
có cạnh bằng
6
, gọi
M
,
N
lần lượt
là trung điểm của
AB
,
AD
. Tính thể tích của vật tròn xoay sinh bởi tam giác
CM N
khi quay
quanh trục
AB
.
TÀ
I LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
A.
8
1
. B.
60
. C.
1
17
. D.
9
0
.
Câu
34. (THPT Trần Phú - Đà Nẵng - 2021) Một cái chao đèn là một phần của mặt xung quanh của một
mặt cầu có bán kính bằng
3
dm
như
hình vẽ. Vật liệu làm chao đèn là thủy tinh có giá
3
50.000
(đồng/dm
2
). Hỏi số tiền (làm tròn đến hàng nghìn) để làm chao đèn trên là bao nhiêu?
A.
15.401.000
đồng. B.
7.910.000
đồng. C.
6.322.000
đồng. D.
10.788.000
đồng.
Câu
35. (THPT Đoàn Thượng - Hải Dương - 2021) Cho hình chóp
S
ABCD
c
ó đáy là hình chữ nhật với
3
; 2AB AD
. Mặt bên
SAB
là tam giác đều và nằm trong mặt phẳng vuông góc với mặt
phẳng đáy. Tính thể tích khối cầu ngoại tiếp hình chóp
SABCD
.
A.
10
3
. B.
20
3
. C.
16
3
. D.
32
3
.
BẢNG ĐÁP ÁN
1.
C
2.B
3.A
4.
D
5.A
6.
D
7.A
8.A
9.
A
10.
B
11.A
12.A
13.B
14.D
15.B
16.C
17.A
18.A
19.C
20.D
21.D
22.A
23.C
24.C
25.
D
26.A
27.
A
28.B
29.D
30.
B
31.D
32.A
33.
A
34.B
35.
D
23
4
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
MỨC ĐỘ VẬN DỤNG
Câu 1. (Sở Lào Cai - 2021) Lon nước ngọt có hình trụ còn cốc uống nước có hình nón cụt (như hình vẽ
minh họa dưới đây). Khi rót nước ngọt từ lon ra cốc thì chiều cao
h
của phần nước ngọt còn lại
trong lon và chiều cao của phần nước ngọt có trong cốc là như nhau. Hỏi khi đó chiều cao
h
trong
lon nước gần nhất số nào sau đây?
A.
9,18cm
. B.
14,2cm
. C.
8,58cm
. D.
7,5cm
.
Lời giải
Chọn C
Gọi
r cm
là bán kính của hình tròn chia hình chóp cụt thành hai hình chóp cụt CC1 và CC2
(minh họa như hình vẽ), điều kiện:
2 4r
Ta có thể tích của khối chóp cụt ( cái cốc):
1 2CC CC CC
V V V
2 2 2 2 2 2
1 1 1
4 2 4.2 15 4 4. 15 2 2.
3 3 3
r r h r r h
2
28.15 16.15 15 60 6 2r r r h
2
2 6 15 60 180r h r r
2 6 15 6 2r h r r
15 2
2
r
h cm
(1).
Thể tích khối trụ (lon nước):
2 2T CC T
V V V
2 2
1
135 2 2. 9
3
r r h h
2
2. 31 405r r h
(2).
Từ (1) và (2) suy ra:
3
27 116 0 3,1 8,58r r r h cm
.
Câu 2. (Sở Hà Tĩnh - 2021) Cắt hình trụ bởi một mặt phẳng song song với trục và cách trục một khoảng
bằng
2
, thiết diện thu được là hình vuông có diện tích bằng
16
. Thể tích khối trụ bằng
A. 10 6
. B.
24
. C.
32
. D. 12 6
.
Lời giải
Chọn B
KHỐI TRÒN XOAY
Chủ đề 6
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Thiết diện cắt bởi mặt phẳng song song với trục là hình vuông
ABCD
có diện tích bằng
16
nên
ta có:
2
16 16 4
ABCD
S AB AB CD h
.
Gọi
H
là trung điểm cạnh
AB
.
Do mặt phẳng
ABCD
cách trục
OO
một khoảng bằng
2
nên ta có
2OH
.
Trong
OHB
vuông tại
H
, ta có
2
2
AB
HB
;
2OH
.
Khi đó
2 2
2 4 6r OB OH HB
.
Vậy thể tích khối trụ là
2
2
. 6 .4 24V r h
(đvtt).
Câu 3. (Sở Yên Bái - 2021) Cho hình trụ có thiết diện qua trục là hình vuông
ABCD
cạnh
2 3cm
với
AB
là đường kính của đường tròn đáy tâm
O
. Gọi
M
là điểm thuộc cung
AB
của đường tròn
đáy sao cho
60ABM
. Thể tích của khối tứ diện
ACDM
là
A.
3
3V cm
. B.
3
7V cm
. C.
3
4V cm
. D.
3
6V cm
.
Lời giải
Chọn A
Ta có:
2
1 1
. 2 3 6
2 2
ACD ABCD
S S
Kẻ
,MH AB MH ABCD d M ACD MH
MAB
vuông tại M có
cos60 3MB AB
3
sin 60
2
MH MB
.
1 1 3
. .6. 3
3 3 2
ACDM M ACD ACD
V V S MH
.
O'
O
A
B
C
D
M
H
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Câu 4. (Chuyên Lê Hồng Phong - TPHCM - 2021) Cho hình chóp tam giác đều có cạnh đáy bằng
6
và chiều cao
1h
.
Tính
diện tích mặt cầu ngoại tiếp hình chóp đã cho.
A.
27
S
. B.
6
S
. C.
5
S
. D.
9
S
.
Lời giải
Chọn D
Cho hình chóp tam giác đều
.S ABC
có cạnh đáy bằng 6AB và chiều cao
1h SH
.
Ta có:
I
là trung điểm
BC
và
3 2
2
AI
.
Khi đó
2
2.
3
AH AI
M
là trung điểm
SA
. Trong
SAH
đường trung trực của
SA
cắt
SH
tại
O
. Suy ra
O
là tâm mặt
cầu ngoại tiếp hình chóp.
Xét hai tam giác đồng dạng
SAH
và
SOM
ta có
2
2
SA SH SA
SO
SO SM h
.
2 2
3SA SH AH
.
2
3 9
; 4 4 . 9
2 4
R SO S R
.
Câu 5. (Chuyên Lê Hồng Phong - TPHCM - 2021) Cho hình nón có bán kính đáy bằng
5
và chiều cao
bằng
12
. Tính bán kính mặt cầu ngoại tiếp
hình nón.
A.
169
24
R
. B.
125
24
R
. C.
81
24
R
. D.
121
24
R
.
Lời giải
Chọn A
Gọi
,h r
lần lượt là chiều cao và bán kính đường tròn đáy của hình nón.
Theo bài ra thì
12, 5h r
.
Gọi
S
là
đỉnh của hình nón,
H
là tâm đường tròn đáy của hình nón,
M
là một điểm bất kì
I
M
H
O
C
B
A
S
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
thuộc đường tròn đáy của hình nón. Khi đó mặt cầu ngoại tiếp hình nón phải có tâm
O
thuộc
đoạn
SH
.
Ta có bán kính mặt cầu ngoại tiếp hình nón là:
R SO OM
.
Xét tam giác
OHM
vuông tại
H
có
2 2 2
OM OH HM
2
2 2
OM SH SO HM
2
2 2
12 5R R
169
169 24 0
24
R R
.
Câu 6. (Chuyên Lam Sơn - Thanh Hóa - 2021) Cho hình trụ có chiều cao bằng 5 3 . Cắt hình trụ đã
cho bởi mặt phẳng song song với trục và cách trục một khoảng bằng
1
, thiết diện thu được có diện
tích bằng
30
. Diện tích xung quanh của hình trụ đã cho bằng
A. 5 39
. B. 10 3
. C. 10 39
. D. 20 3
.
Lời giải
Chọn D
Thiết diện thu được là hình chữ nhật
ABB A
:
.
ABB A
S AB AA
⇔
30
2 3
5 3
ABB A
S
AB
AA
⇒
3
2
AB
AH
Xét
OAH
vuông tại
H
:
2 2
1 3 2R OA OH AH
Diện tích xung quanh của hình trụ là:
2 . . 2 .2.5 3 20 3
xq
S R h
.
Câu 7. (Chuyên KHTN - 2021) Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông cân tại
B
,
3AB BC a
, góc
0
90SAB SCB và khoảng cách từ
A
đến mặt phẳng
SBC
bằng
6a
.
Tính diện tích mặt cầu ngoại tiếp hình chóp
.S ABC
theo
a
.
A.
2
36 a
. B.
2
6 a
. C.
2
18 a
. D.
2
48 a
.
Lời giải
Chọn A
1
5
√
3
O'
O
H
A
B
A'
B'
R
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Gọi
SD
là đường cao của hình chóp
.S ABC SD AB
mà
AB SA gt
nên
AB AD
.
Tương tự:
SD BC
, mà
BC SC gt BC CD
.
Tứ giác
ABCD
có 4 góc vuông và
AB BC
nên tứ giác
ABCD
là hình vuông.
Khi đó mặt cầu ngoại tiếp hình chóp S.ABC chính là mặt cầu ngoại tiếp hình chóp S.ABCD.
Kẻ
DH SC H SC
, mà
BC SCD BC DH
.
,DH SBC d D SBC DH
.
Mặt khác
2 2
.
/ / , , 6
SD CD
AD SBC d A SBC d D SBC DH a
SD CD
.
2
2
.3
6 3 2
3
SD a
a SD a
SD a
.
Do các đỉnh
, ,A C D
cùng nhìn đoạn thẳng
SB
dưới một góc
0
90
nên tâm của mặt cầu ngoại tiếp
hình chóp
.S ABCD
chính là trung điểm
I
của
SB
.
2 2
2 2
3 2 3 2
2 2 2
a a
SB SD BD
R
3a
.
Vậy diện tích mặt cầu ngoại tiếp hình chóp
.S ABC
là
2
2 2
4 4 3 36S R a a
.
Câu 8. (Chuyên Hạ Long - Quảng Ninh - 2021) Cho khối nón có bán kính bằng 3 và khoảng cách từ
tâm của đáy đến một đường sinh bất kì bằng
12
.
5
Thể tích của khối nón đã cho bằng
A.
12 .
V
B.
18 .
V
C.
36 .
V
D.
24 .
V
Lời giải
Chọn A
Gọi I là tâm đáy, OA là một đường sinh bất kì của khối nón. Gọi H là chân đường vuông góc hạ từ
I tới OA, suy ra OI là đường cao h của khối chóp và
3
12
5
IA
IH
Xét
OIA
vuông tại I, đường cao IH nên ta có:
2 2 2 2 2 2
1 1 1 1 1 1
IH OI IA OI IH IA
2
2
2 2
1 1 1
16 4 4.
3
12
5
OI OI h
OI
Vậy thể tích của khối chóp là:
2 2
1 1
.3 .4 12 .
3 3
V r h
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 9. (Chuyên ĐH Vinh - Nghệ An - 2021) Cho hình lăng trụ đứng
.ABC A B C
có
2AB AA a
,
AC a
,
120
BAC
. Bán kính mặt cầu ngoại tiếp hình chóp
.A BCC B
bằng
A.
30
3
a
. B.
10
3
a
. C.
30
10
a
. D.
33
3
a
.
Lời giải
Chọn A
Gọi
O
là tâm đường tròn ngoại tiếp tam giác
ABC
,
M
là trung điểm của
BB
.
Dựng đường thẳng
đi qua
O
và vuông góc với mặt phẳng
ABC
. Mặt phẳng trung trực của
đoạn
BB
cắt
tại
I
. Khi đó
I
là tâm mặt cầu ngoại tiếp hình chóp
.
A BCC B
.
Trong tam giác
ABC
, ta có:
2 2 2 2 2 2
2. . .cos 4 2.2 . .cos120 7BC AB AC AB AC BAC a a a a a .
7BC a .
Gọi
R
là bán kính đường tròn ngoại tiếp tam giác
ABC
, áp dụng định lí sin ta được:
21
2
sin 2sin 3
BC BC a
R R OB
A A
.
Bán kính mặt cầu cần tìm là
2
2 2 2 2 2
0
21 30
9 3
a a
R IB OB OI OB BM a
.
Câu 10. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho hình chóp tứ giác
ABCD
có đáy
ABCD
là hình chữ
nhật,
, 3,AB a AD a SA
vuông góc với mặt phẳng đáy. Mặt phẳng
SBC
tạo với đáy một
góc
60
. Tính thể tích khối chóp
.S ABCD
.
A.
3
3V a
. B.
3
V a
. C.
3
3
3
V a
. D.
3
3
a
V .
Lời giải
Chọn B
S
A
B
C
D
60
a
3a
Ta có:
BC AB
BC SAB BC SB
BC SA
.
I
M
O
C'
A'
B
C
A
B'
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Do
,
, , 60
,
BC SBC ABCD
AB ABCD AB BC
SBC ABCD SB AB SBA
SB SBC SB BC
.
Xét tam giác vuông
SBA
: .tan60 3SA AB a .
Vậy
2 3
.
1 1
. . . 3. 3
3 3
S ABCD ABCD
V SA S a a a
.
Câu 11. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho khối lăng trụ tam giác
.ABC A B C
mà mặt bên
ABB A
có diện tích bằng
2
2a
. Khoảng cách giữa
CC
và mặt
ABB A
bằng
a
. Thể tích khối
lăng trụ là
A.
3
.V a
B.
3
2
.
3
V a
C.
3
3 .V a
D.
3
1
.
3
V a
Lời giải
Chọn
A
Xét khối chóp
. ' ' ' 'ABCD A B C D
ta có:
. .
1
2
ABC A B C ABCD A B C D
V V
.
Mà
.
,
.
ABCD A B C D ABB A
C ABB A
V S d
2 3
,
. 2 . 2
ABB A
CC ABB A
S d a a a
.
Khi đó
3
. .
1
2
ABC A B C ABCD A B C D
V V a
.
Câu 12. (THPT Thanh Chương 1- Nghệ An - 2021) Cắt hình trụ bởi mặt phẳng qua trục, thiết diện thu
được là hình chữ nhật có chu vi bằng Giá trị lớn nhất của thể tích khối trụ bằng
A. . B. . C. . D. .
Lời giải
Chọn A
B
A
D
C
A'
D'
C'
B'
B'
B
A'
O
O'
A
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Gọi
lần lượt là bán kính đáy và chiều cao của hình trụ.
Theo đề có
Có
Câu 13. (THPT Thanh Chương 1- Nghệ An - 2021) Trong không gian cho hình bình hành có
. Thể tích khối tròn xoay tạo thành khi quay hình bình hành
quanh cạnh bằng
A. . B. . C. . D. .
Lời giải
Chọn B
Kẻ
Khối tròn xoay được tạo ra khi hình bình hành ABCD quay quanh trục AB gồm khối tròn xoay do
hình thang vuông quay quanh cạnh và khối nón tròn xoay do tam giác vuông
quay quanh cạnh
Do nên khối tròn xoay do hình bình hành quay quanh trục có thể
tích bằng thể tích khối trụ do hình chữ nhật quay quanh cạnh
Ta có
Vậy thể tích khối tròn xoay cần tìm bằng: .
Câu 14. (THPT Nguyễn Huệ - Phú Yên - 2021) Cho hình thang vuông
ABCD
vuông tại
,A B
. Cạnh
2AB BC
,
2 2AD
. Thể tích khối tròn xoay tạo ra khi quay hình thang
ABCD
quanh
CD
là
A.
7
3
. B.
7 2
12
. C.
7
6
. D.
14
3
.
Lời giải
Chọn D
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Gọi
E
là giao điểm của hai đường thẳng
AB
và
CD
.
Gọi
A
và
B
lần lượt là các điểm đối xứng với
,A B
qua đường thẳng
CD
.
Gọi
I
là trung điểm của đoạn
BB
.
Ta có
1
2
BC EB EC
EC ED
AD EA ED
và
AB BE
.
Khi đó, các khối nón đỉnh
E
, đỉnh
C
có đáy là đường tròn
;I IB
bằng nhau; các khối nón đỉnh
E
và đỉnh
D
có đáy là đường tròn
,C CA
bằng nhau.
Gọi
1
V là thể tích của khối nón đỉnh
D
, đáy là đường tròn
,C CA
Gọi
2
V
là thể tích của khối nón đỉnh
C
, đáy là đường tròn
,I IB
Gọi
V
là thể tích của khối tròn xoay khi quay hình thang
ABCD
quanh trục
CD
.
Ta có
2 2
1
2 1
2
AC AB BC IB AC
.
ACD
vuông cân tại
1 1
2 1
2 2
C CD AC IC EC AC
Do đó
2 2
1
1 1 8
. . .2 .2
3 3 3
V AC CD
2 2
2
1 1 1
. . .1 .1
3 3 3
V BI IC
Vậy
1 2
14
2 2
3
V V V
.
Câu 15. (THPT Nguyễn Huệ - Phú Yên - 2021) Một hình trụ
T
có chiều cao bằng đường kính đáy và
một hình nón
N
có đáy là đáy của hình trụ
T
, còn đỉnh là tâm của đáy còn lại của hình trụ
T
. Gọi
1 2
,S S lần lượt là diện tích xung quanh của hình trụ
T
và hình nón
N
. Tỉ số
1
2
S
S
bằng
A.
3
5
. B.
4 5
5
. C.
7
9
. D.
1
2
.
Lời giải
Chọn B
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Gọi
R
là bán kính đường tròn đáy của hình trụ
T
chiều cao của hình trụ
T
là
2h R
Ta có
2
1
2 2 .2 4S Rh R R R
Hình nón
N
có đường sinh
2 2 2 2
4 5l R h R R R
Khi đó,
2
2
5S Rl R
Vậy
2
1
2
2
4 4 5
5
5
S R
S
R
.
Câu 16. (THPT Lương Thế Vinh - 2021) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thang vuông tại
A
và
B
với
1AB BC
,
2AD
. Cạnh bên
1SA
và
SA
vuông góc với đáy. Gọi E là trung điểm AD. Diện tích
mc
S
của mặt cầu ngoại tiếp hình chóp
.S CDE
là
A. 5
mc
S
. B. 3
mc
S
. C. 11
mc
S
. D. 2
mc
S
.
Lời giải
Chọn C
Đặt
, 2 ,AB BC a AD a SA a
với
1a
.
Gọi
H
là trung điểm của
CD
và
d
là đường thẳng đi qua
H
và vuông góc với đáy. Gọi
I
và
R
là tâm và bán kính mặt cầu ngoại tiếp hình chóp
. .S CDE
Suy ra
I
thuộc
d
. Đặt
.IH x
Trong
mp
ASIH
kẻ đường thẳng đi qua
I
và song song với
AH
cắt
AS
tại
K
.
Ta thấy tứ giác
ABCE
là hình vuông vì
// , 90,AE BC AE BC AB a ABC
2 2
90 , 2CED CE a CD CE DE a
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Ta có
2
2 2 2 2
.
2
a
ID IH HD x
Mặt khác vì
AE CE ED a ACD
vuông tại
C CD AC
.
Khi đó
2
2
2 2 2 2 2 2 2 2 2
2
2
a
IS IK KS AH KS AC CH KS a a x .
Suy ra:
2 2
2
2 2
3
2
2 2 2
a a a
x a a x x .
Vậy bán kính mặt cầu ngoại tiếp hình chóp
.S CDE
là
2 2
9 11
4 2 2
a a a
R ID .
2 2
4 11 11
mc
S R a
.
Câu 17. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho hình lăng trụ tam giác đều có cạnh đáy bằng
a
, cạnh bên bằng
2a
. Thể tích của khối cầu ngoại tiếp hình lăng trụ đã cho bằng
A.
3
32 3
27
a
. B.
3
256
81
a
. C.
3
4
3
a
. D.
3
8 6
27
a
.
Lời giải
Chọn A
Gọi
';G G
lần lượt là trọng tâm của các tam giác
ABC
và
A B C
Gọi
I
là trung điểm của
'GG
. Khi đó
I
là tâm của mặt cầu ngoại tiếp lăng trụ.
Ta có
2 3 3
.
3 2 3
a a
AG
Bán kính mặt cầu ngoại tiếp hình lăng trụ:
2
2 2 2
3 2 3
3 3
a a
IA G I G A a
.
Thể tích khối cầu ngoại tiếp lăng trụ đã cho:
3
3 3
4 4 2 3 32 3
.
3 3 3 27
V R a a
Câu 18. (THPT Đào Duy Từ - Hà Nội - 2021) Cho hình nón
N
có đỉnh
S
, bán kính đáy bằng
1r
và
độ dài đường sinh bằng
2 2l
. Mặt cầu đi qua
S
và đường tròn đáy của
N
có bán kính bằng
A.
4 7
7
. B.
8 7
7
. C.
7
. D.
4
3
.
Lời giải
Chọn A
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
+) Hình nón
N
có đường cao
SM
, đường sinh
2 2SA SB
, bán kính đường tròn đáy của
N
là
1AM
.
Ta có
2 2
7SM SA AM
.
+) Gọi
I
là tâm của mặt cầu
T
thì
I SM
, bán kính mặt cầu
T
là
IS IA R
.
Tam giác
IMA
vuông tại
M
có
2
2 2
1 7R R
4 7
8 2 7 0
7
a R R
.
Câu 19. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Chohình nón có bán kính đáy bằng
3
và chiều cao
bằng
6
, một khối trụ có bán kính đáy thay đổi nội tiếp khối nón( như hình vẽ). Thể tích lớn nhất
của khối trụ bằng
A.
10
. B.
6
. C.
8
. D.
4
.
Lời giải
Chọn C
Đặt
O , , 6,O l B O x SO h SO y
.
Áp dụng định lý Talet vào tam giác
SOB
ta được
2x
3 6
O B SO x y
y
OB SO
.
Ta có
6 6 2xl y
. Suy ra
2
6 2x . . 6 2xV x x x
.
Áp dụng bất đẳng thức Cô si cho ba số
,x x
và
6 2x
ta được
3
6 2x
. . 6 2x 8
3
x x
V x x
.
Thể tích lớn nhất của khối trụ bằng
8
.
4
a
R
M
A
S
I
B
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Câu 20. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho hình trụ có bán kính đáy bằng
4
. Biết rằng khi
cắt hình trụ đã cho bởi một mặt phẳng qua
trục, thiết diện thu được là một hình vuông. Diện tích toàn phần của hình trụ đã cho bằng
A.
106
. B.
64
. C.
80
. D.
96
.
Lời giải
Chọn D
Giả sử thiết diện qua trục của hình trụ là hình vuông
ABCD
.
Theo giả thiết ta có bán kính đáy của hình trụ
4r
2 8h l AD DC r
.
Vậy diện tích toàn phần của hình trụ là:
2
2 2 2 .4.8 2.16. 96
tp
S rl r
.
Câu 21. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho hình chóp
.S ABC
có
SA ABC
, tam giác
ABC
vuông tại
B
,
3, 7SA BC AB
.
Tính bán kính
R
của mặt cầu ngoại tiếp hình chóp đã cho.
A.
5
2
R
. B.
5R
. C.
5R
. D.
5
2
R
.
Lời giải
Chọn D
Đặt
, ,SA a AB b BC c
.
Ta có:
SA ABC SA AC
.
BC SA
BC SAB BC SB
BC AB
.
Gọi
O
là trung điểm
SC
, ta có các tam giác
,SAC SBC
vuông lần lượt tại
A
và
B
nên:
2
SC
OA OB OC OS
. Do đó mặt cầu đi qua bốn điểm
, , ,S A B C
có tâm
O
và bán kính
2
SC
R
.
Ta có:
2 2 2 2 2 2 2 2 2
.SC SB BC SA AB BC a b c
Suy ra
2 2 2
1 1 5
9 7 9
2 2 2
R a b c
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 22. (THPT Ba Đình - Thanh Hóa - 2021) Cho hình lăng trụ tam giác đều
.ABC A B C
có độ dài
cạnh đáy bằng
a
và chiều cao
2a
. Tính thể tích
V
của khối cầu ngoại tiếp hình lằng trụ
.ABC A B C
:
A.
3
32 3
.
27
a
V
B.
3
32 3
.
9
a
V
C.
3
8 3
.
27
a
V
D.
3
32 3
.
81
a
V
Lời giải
Chọn
A
Gọi
,I I
là tâm đường tròn ngoại tiếp
2
đáy của khối lăng trụ.
Khi đó
II
là trụ mặt cầu ngoại tiếp 2 đa giác đáy.
Gọi
O
là trung điểm
II
cũng là tâm mặt cầu ngoại tiếp khối lăng trụ đều
.ABC A B C
.
Ta có
2
2 2 2
2 3 2 3
.
3 2 3
a a
R AO AI OI a
Thể tích mặt cầu ngoại tiếp
3
3
3
4 4 2 3 32 3
.
3 3 3 27
a
V R a
Câu 23. (THPT Quế Võ 1 - Bắc Ninh - 2021) Cho điểm
A
nằm trên mặt cầu
S
tâm
,O
bán kính
6R
cm.
,I K
là hai điểm trên đoạn
OA
sao cho
OI IK KA
. Các mặt phẳng
,P Q
lần
lượt đi qua
,I K
cùng vuông góc với
OA
và cắt mặt cầu
S
theo đường tròn có bán kính
1 2
; .r r
Tính tỉ số
1
2
.
r
r
A.
1
2
5
3 10
r
r
. B.
1
2
3 10
4
r
r
. C.
1
2
4
10
r
r
. D.
1
2
3 10
5
r
r
.
Lời giải
Chọn C
F
I
B
E
C
A
O
I'
B'
C'A'
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Bán kính mặt cầu
S
là
6R
cm nên
6OA
cm
2OI IK KA
cm nên
4OK
cm.
Gọi một giao điểm của các mặt phẳng
,P Q
với mặt cầu
S
là
1 2
,
,
6
IM r IN r
M N
OM ON
.
Do đó, ta có
2 2 2 2
1
1
2 2 2 2
2
2
6 2 4 2
4 2 4
.
2 5 10
6 4 2 5
r OM OI
r
r
r ON OK
Câu 24. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho hình nón đỉnh
S
có đáy là đường tròn tâm
O
bán kính
1.
Trên đường tròn
O
lấy hai điểm
,A B
sao cho tam giác
OAB
vuông. Biết diện tích
tam giác
SAB
bằng
2,
thể tích khối nón đã cho bằng :
A.
14
2
V
. B.
14
3
V
. C.
14
6
V
. D.
14
12
V
.
Lời giải
Chọn C
Gọi
C
là trung điểm của
AB
. Ta có :
OAB
là hinh chiếu vuông góc của
SAB
lên mặt phẳng
đáy.
Khi đó :
2
.cos , cos ,
4
OAB
OAB SAB
SAB
S
S S OAB SAB OAB SAB
S
2
2 2
4
CO
SC CO
SC
và
2 2
7 SO SC CO CO
2
1 1 2
. .2 2 .2 1 2
2 2 2
SAB
S SC AB CO CO OC
14
2
SO
* Thể tích khối nón là :
2
1 1 14 14
. .
3 3 2 6
V r SO
Câu 25. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cắt một hình trụ bởi mặt phẳng song song với trục
ta được thiết diện là hình vuông có diện tích bằng
36
, biết khoảng cách từ tâm đáy đến thiết diện
bằng
1
. Tính thể tích của khối trụ giới hạn bởi hình trụ đã cho.
A.
20 .
B.
10 .
C.
30 .
D.
60 .
Lời giải
Chọn D
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Gọi thiết diện song song với trục là hình vuông
2
' ' 36 ' 6.ABB A AB AB AA
Gọi
H
là trung điểm của
.AB
Ta có
' ' , ' ' 1
'
OH AB
OH ABB A d O ABB A OH
OH AA
2 2 2 2 2
3 1 10 . . ' 60 .OA AH OH V OA AA
Vậy thể tích của khối trụ giới hạn bởi hình trụ đã cho là
60 .
Câu 26. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Cho hình chóp S.ABCD có đáy ABCD là hình thang
vuông tại A và B. Biết
, 2 ,AB BC a AD a SA
vuông góc với đáy và
2 .SA a
Tính bán
kính mặt cầu ngoại tiếp hình chóp S.HCD với H là trung điểm của AD.
A.
11
2
a
. B.
10
2
a
. C.
2
2
a
. D.
3
2
a
.
Lời giải
Chọn A
Ta có ABCH là hình vuông nên
.CH AD CH SAD
Lại có
2SA AD a
nên tam giác
SAD
vuông cân nên
0
45 .SDA
Mà
2 2
0
10
5 .
2
2sin 45
SHD
SH a
SH SA AH SH a R
Hình chóp
.C SHD
có cạnh bên vuông góc với mặt đáy nên
2
2
11
.
2 2
SHD
CH a
R R
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
Câu 27. (THPT Phan Đình Phùng - Quảng Bình - 2021) Cho hình nón có chiều cao
20h cm
, bán kính
đáy
25r cm
. Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm đáy đến mặt phẳng
chứa thiết diện là
12cm
. Tính diện tích
S
của thiết diện đó.
A.
2
500 cmS
. B.
2
300 cmS
. C.
2
406 cmS
. D.
2
400 cmS
.
Lời giải
Chọn A
Thiết diện đi qua đỉnh của hình nón tạo thành hình tam giác như hình vẽ.
Gọi tâm của đáy hình nón là
O
.
Gọi
M
là trung điểm
AB
SOM SAB
.
Hạ
OH SM
OH SAB
.
Đặt
0OM x x
. Trong tam giác
SOM
ta có :
2 2 2
1 1 1
OH OM SO
2 2 2
1 1 1
15
12 20
x cm
x
.
2 2
2 40AB R x
.
2 2
25SM SO OM
.
Vậy
2
1
. 500
2
SAB
S AB SM cm
.
Câu 28. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho hình trụ có thiết diện qua trục là hình vuông
cạnh
2a
. Mặt phẳng
P
song song với trục và cách trục một khoảng
2
a
. Tính diện tích thiết diện
của hình trụ cắt bởi mặt phẳng
P
.
A.
2
15a
. B.
2
2 3a
. C.
2
15
2
a
. D.
2
2 15a
.
Lời giải
Chọn B
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Gọi thiết diện qua trục là hình vuông
ABFE
2AB a
.
Mặt phẳng
P
là mặt phẳng
ABCD
song song với trục OO
.
Kẻ
OH AD
; ;
2
a
d OO P d O P OH
.
Xét tam giác
OAH
vuông tại
H
ta có:
2 2
AH AO OH
2
2
3
4 2
a a
a
3AD a
Vậy diện tích thiết diện cắt bởi mặt phẳng
P
bằng
2
2 . 3 2 3a a a
.
Câu 29. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho hình lập phương
.ABCD A B C D
cạnh
bằng
2a
. Một mặt cầu
S
đi qua các đỉnh của hình vuông
ABCD
đồng thời tiếp xúc với các
cạnh của hình vuông
A B C D
. Tính bán kính
R
của mặt cầu
S
?
A.
3
4
a
R
. B.
41
4
a
R
. C.
43
9
a
R
. D.
41
8
a
R
.
Lời giải
Chọn D
Gọi
, ,O O I
lần lượt là tâm của
ABCD
,
A B C D
,
S
.
Gọi
M
là trung điểm của
A B
.
Suy ra
IB IM R
,
OO a
,
2
a
O M
,
2
2
a
OB
.
Do
,OO ABCD OB ABCD OO OB
2
2 2 2
2
a
IO IB OB R
.
Do
,OO A B C D O M ABCD OO O M
2
2 2 2
4
a
IO IM O M R
.
M
O
O'
D'
C'
B'
A'
D
A
B
C
I
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
Ta có
IO IO OO
2 2
2 2
4 2
a a
R R a
2 2
2 2
4 2
a a
R a R
2 2 2
2 2 2 2
2
4 2 2
a a a
R a a R R
2
2
3
2 8
a a
R
41
8
a
R
(thỏa mãn).
Vậy
41
8
a
R
.
Câu 30. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho hình trụ có chiều cao
2a
và hình chữ nhật
ABCD
nằm trên mặt phẳng không vuông góc với đáy của hình trụ. Biết
AB
nằm trên đường tròn
đáy thứ nhất,
CD
nằm trên đường tròn đáy thứ hai của hình trụ và
AB CD a
, diện tích hình
chữ nhật
ABCD
bằng
2
2a
. Thể tích khối trụ đã cho bằng
A.
3
2
4
a
. B.
3
3 2
4
a
. C.
3
4
a
. D.
3
3
4
a
.
Lời giải
Chọn B
Gọi
EF
là hình chiếu vuông góc của dây cung
AB
xuống mặt phẳng chứa đường tròn đáy dưới.
Dễ thấy tứ giác
CDEF
là hình chữ nhật và
FD
là đường kính,
EF AB CD a
.
Ta có
2
2 , 2
ABCD
S a AB CD a AD BC a
. Sử dụng định lý Pi-ta-go
2ED a
;
3
3 2
2
a
FD a R R
. Do đó,
2
3
2
3 3 2
. . 2
2 4
a a
V R h a
.
Câu 31. (THPT Đồng Quan - Hà Nội - 2021) Cho hình nón đỉnh
S
, đáy là đường tròn tâm
O
, bán kính
5R
. Một thiết diện qua đỉnh
S
là tam giác đều
SAB
cạnh bằng
8
, khoảng cách từ
O
đến mặt
phẳng
SAB
bằng
A.
13
3
. B. 13 . C.
4 13
3
. D.
3 13
4
.
Lời giải
Chọn D
Gọi
I
là trung điểm của
.AB OI AB
Tam giác
SAB
đều cạnh bằng 8 4 3SI .
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Tam giác
OIA
vuông tại
I
có
2 2
1
4, 5 3
2
IA AB OA R OI OA IA
.
Tam giác
SOI
vuông tại
2 2
39
O SO SI OI
.
Ta có
, ,AB OI AB SO AB SOI
mà
AB SAB SOI SAB
Trong mặt phẳng
,SOI
dựng
OH SI
Ta có
,
SOI SAB
SOI SAB SI
OH SOI OH SI
OH SAB
,d O SAB OH
.
Tam giác
SOI
vuông tại
. 3 13
4
OI SO
O OH
SI
.
Vậy
3 13
,
4
d O SAB
.
Câu 32. (THPT Lê Lợi - Thanh Hóa - 2021) Cho hình chóp
.S ABC
với
SA
vuông góc với mặt phẳng
ABC
, tam giác
ABC
vuông tại
B
và 3BC a ,
60BAC . Gọi
H
,
K
lần lượt là hình
chiếu của
A
lên
SB
và
SC
. Mặt cầu đi qua các điểm
, , , ,A B C H K
có bán kính bằng
A.
a
. B.
2a
. C.
3a
. D.
2
a
.
Lời giải
Chọn A
Ta có
AK KC
,
AB BC
nên
,B K
nhìn
AC
dưới một góc vuông.
Lại có
BC SA
BC AH
BC AB
Mặt khác
AH SB
nên
AH SBC AH HC
, do đó
H
nhìn
AC
dưới một góc vuông.
Vậy
, , , ,A B C H K
đều thuộc mặt cầu đường kính
AC
.
Tam giác
ABC
vuông tại
B
nên
3
2
sin 60
sin
BC a
AC a
BAC
.
Bán kính mặt cầu ngoại tiếp là
2
AC
R a
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
Câu 33. (Trung Tâm Thanh Tường -2021) Cho hình vuông
ABCD
có cạnh bằng
6
, gọi
M
,
N
lần lượt
là trung điểm của
AB
,
AD
. Tính thể tích của vật tròn xoay sinh bởi tam giác
CM N
khi quay
quanh trục
AB
.
A.
81
. B.
60
. C.
117
. D.
90
.
Lời giải
Chọn A
Kéo dài
CN
cắt
AB
tại
E
. Khi đó:
1
2
EA AN
EB BC
6 12EA AB EB
.
Quay tam giác
EBC
quanh trục
AB
ta được hình nón. Khi đó thể tích khối nón đó là:
2 2
1
1 1
. . .6 .12 144
3 3
V BC EB
.
Thể tích khối nón đỉnh
E
, bán kính đáy
3AN
là:
2 2
2
1 1
. . .3 .6 18
3 3
V AN EA
.
Thể tích khối nón đỉnh
M
, bán kính đáy
3AN
là:
2 2
3
1 1
. . .3 .3 9
3 3
V AN AM
.
Thể tích khối nón đỉnh
M
, bán kính đáy
6BC
là:
2 2
4
1 1
. . .6 .3 36
3 3
V BC MB
.
Vậy thể tích của vật tròn xoay sinh bởi tam giác
CM N
khi quay quanh trục
AB
là:
1 2 3 4
144 18 9 36 81V V V V V
.
Câu 34. (THPT Trần Phú - Đà Nẵng - 2021) Một cái chao đèn là một phần của mặt xung quanh của một
mặt cầu có bán kính bằng
3dm
như hình vẽ. Vật liệu làm chao đèn là thủy tinh có giá
350.000
(đồng/dm
2
). Hỏi số tiền (làm tròn đến hàng nghìn) để làm chao đèn trên là bao nhiêu?
NGUYỄ
N BẢO VƯƠNG - 0946798489
A.
1
5.401.000
đồng. B.
7
.910.000
đồng. C
.
6
.322.000
đồng. D.
1
0.788.000
đồng.
Lời giải
Chọn B
+ Á
p dụng công thức diện tích chỏm cầu
2S
hR
.
T
a có diện tích chao đèn là :
2
23
3 23
2 2 . .3 (dm )
4 2
S hR
+ Số tiền làm chao đèn là :
3
23
.350000 7.910.000
2
đồng.
Câu 35. (THPT Đoàn Thượng - Hải Dương - 2021) Cho hình chóp
S
ABCD
c
ó đáy là hình chữ nhật với
3
; 2AB AD
.
Mặt bên
S
AB
là
tam giác đều và nằm trong mặt phẳng vuông góc với mặt
phẳng đáy. Tính thể tích khối cầu ngoại tiếp hình chóp
S
ABCD
.
A
.
10
3
. B.
2
0
3
. C.
16
3
. D.
3
2
3
.
Lời giải
Chọn
D
S
AB ABCD
,
kẻ
S
M AB SM ABCD
.
Gọi
I
là
giao điểm của hai đường chéo.
J
là
trọng tâm tam giác
SA
B
.
Dựng đường thẳng
qua
I
và
song song
S
M
, suy ra
l
à trục đường tròn ngoại tiếp hình chữ
nhật
A
BCD
.
Dựng đường thẳng
d
qua
J
và
song song với
MI
, suy
ra
d
l
à trục đường tròn ngoại tiếp của
tam giác
S
AB
.
Gọi
O d O
là tâm mặt cầu.
1
1 3 3
.
3
3 2
JM
SM
;
1
13
2 2
IA
AC
2
2 2 2 3
3
13 4 32
2
4 4 3 3
R OA OI IA JM IA V R
.
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
3
4
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
MỨC ĐỘ VẬN DỤNG CAO
Câu 1. (Sở Vĩnh Phúc - 2021) Cho mặt cầu
S
có bán kính không đổi là
R
. Một hình chóp lục giác đều
.S ABCDEF
nội tiếp mặt cầu
S
. Tìm giá trị lớn nhất
max
V
của thể tích khối chóp
. .S ABCDEF
A.
3
max
3 3
8
R
V
. B.
3
max
8 3
9
R
V
. C.
3
max
16 3
27
R
V
. D.
3
max
8 3
27
R
V
Câu 2. (Sở Tuyên Quang - 2021) Cho hình nón có chiều cao bằng
3
. Một mặt phẳng
đi qua đỉnh
hình nón và cắt hình nón
theo một thiết diện là tam giác đều, góc giữa trục của hình nón và mặt phẳng
là
45
. Thể
tích của hình nón đã cho bằng
A.
5 24
. B.
15
. C.
45
. D.
15 25
.
Câu 3. (Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Người ta chế tạo một món đồ chơi cho
trẻ em theo các công đoạn như sau: Trước tiên chế tạo ra hình nón tròn xoay có góc ở đỉnh là
2 60
bằng thủy tinh trong suốt. Sau đó đặt hai quả cầu nhỏ bằng thủy tinh có bán kính lớn,
nhỏ khác nhau sao cho hai mặt cầu tiếp xúc với nhau và đều tiếp xúc với mặt nón, quả cầu lớn tiếp
xúc với mặt đáy của hình nón, như hình vẽ bên dưới.
Biết rằng chiều cao của hình nón bằng
9cm
. Bỏ qua bề dày các lớp vỏ thủy tinh, tổng thể tích của
hai khối cầu bằng
A.
100
3
. B.
112
3
. C.
40
3
. D.
38
3
.
Câu 4. (Chuyên Quốc Học Huế - 2021) Tính thể tích lớn nhất của hình trụ nội tiếp trong mặt cầu có bán
kính
1
(hình trụ nội tiếp trong mặt cầu là hình trụ có hai đường tròn đáy thuộc mặt cầu).
A.
3
9
. B.
4 3
9
. C.
2 3
9
. D.
2 3
3
.
Câu 5. (Chuyên Ngoại Ngữ Hà Nội- 2021) Một hình trụ có thiết diện qua trục là hình chữ nhật có chu vi
bằng 12cm. Thể tích lớn nhất mà hình trụ có thể nhận được là
A.
3
16 cm
. B.
3
64 cm
. C.
3
32 cm
. D.
3
8 cm
.
Câu 6. (Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh bằng 1, mặt bên
SAB
là tam giác cân tại
S
và nằm trong mặt phẳng vuông
góc với mặt phẳng đáy. Tính thể tích
V
của khối cầu ngoại tiếp hình chóp đã cho biết
o
120ASB ?
KHỐI TRÒN XOAY
Chủ đề 6
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
13 78
27
. B.
5 15
54
. C.
5
3
. D.
4 3
27
.
Câu 7. (THPT Quế Võ 1 - Bắc Ninh - 2021) Cho hình trụ
T
có bán kính đáy và chiều cao đều bằng
,R
hai đáy là hai hình tròn
O
và
.O
Gọi
AA
và
BB
là hai đường sinh bất kì của
T
và
M
là một điểm di động trên đường tròn
.O
Thể tích lớn nhất của khối chóp
.M AA B B
bằng
bao nhiêu?
A.
3
3 3
4
R
. B.
3
3
4
R
. C.
3
3
3
R
. D.
3
3
2
R
.
Câu 8. (THPT Phan Đình Phùng - Quảng Bình - 2021) Một nhà máy sản xuất các hộp hình trụ kín cả
hai đầu có thể tích
V
cho trước. Mối quan hệ giữa bán kính đáy
R
và chiều cao
h
của hình trụ để
diện tích toàn phần của hình trụ nhỏ nhất là
A.
h R
. B.
3h R
. C.
2h R
. D.
2R h
.
Câu 9. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Cho hình lăng trụ đều
. ' ' 'ABC A B C
, biết góc giữa
hai mặt phẳng
'A BC
và
ABC
bằng
0
45
, diện tích tam giác
'A BC
bằng
2
6a
. Tính diện
tích xung quanh của hình trụ ngoại tiếp hình lăng trụ
. ' ' 'ABC A B C
.
A.
2
2 a
. B.
2
8 3
3
a
. C.
2
4 a
. D.
2
4 3
3
a
.
Câu 10. Một chậu nước hình bán cầu bằng nhôm có bán kính
10R dm
. Trong chậu có chứa sẵn một khối
nước hình chỏm cầu có chiều cao
4h dm
. Người ta bỏ vào chậu một viên bi hình cầu bằng kim
loại thì mặt nước dâng lên vừa phủ kín viên bi. Bán kính viên bi gần với số nào sau đây nhất?
A.
2,09 dm
. B.
9,63dm
. C.
3,07 dm
. D.
4,53dm
.
Câu 11. Sử dụng mảnh inox hình chữ nhật
ABCD
có diện tích bằng
2
1m
và cạnh
mBC x
để làm một
thùng đựng nước có đáy, không có nắp theo quy trình như sau: Chia hình chữ nhật
ABCD
thành
2
hình chữ nhật
ADNM
và
BCNM
, trong đó phần hình chữ nhật
ADNM
được gò thành phần
xung quanh hình trụ có chiều cao bằng
AM
; phần hình chữ nhật
BCNM
được cắt ra một hình
tròn để làm đáy của hình trụ trên (phần inox thừa được bỏ đi) Tính gần đúng giá trị
x
để thùng
nước trên có thể tích lớn nhất (coi như các mép nối không đáng kể).
A.
0,97m
. B.
1,37m
. C.
1,12m
. D.
1,02m
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Câu 12. Từ một tấm thép phẳng hình chữ nhật, người ta muốn làm một chiếc thùng đựng dầu hình trụ bằng
cách cắt ra hai hình tròn bằng nhau và một hình chữ nhật (phần tô đậm) sau đó hàn kín lại, như
trong hình vẽ dưới đây. Hai hình tròn làm hai mặt đáy, hình chữ nhật làm thành mặt xung quanh
của thùng đựng dầu (vừa đủ). Biết rằng đường tròn đáy ngoại tiếp một tam giác có kích thước là
50 ,70 ,80cm cm cm
(các mối ghép nối khi gò hàn chiếm diện tích không đáng kể. Lấy
3,14
).
Diện tích của tấm thép hình chữ nhật ban đầu gần nhất với số liệu nào sau đây?
A.
6,8
2
m
. B.
24,6
2
m
. C.
6,15
2
m
. D.
3,08
2
m
.
Câu 13.
Ông An cần làm một đồ trang trí như hình vẽ. Phần dưới là một phần của khối cầu bán kính
20 cm
làm bằng gỗ đặc, bán kính của đường tròn phần chỏm cầu bằng
10 cm
. Phần phía trên làm
bằng lớp vỏ kính trong suốt. Biết giá tiền của
2
1 m kính như trên là 1.500.000 đồng, giá triền của
3
1m gỗ là 100.000.000 đồng. Hỏi số tiền (làm tròn đến hàng nghìn) mà ông An mua vật liệu để
làm đồ trang trí là bao nhiêu.
A.
1.000.000
.
B.
1.100.000
.
C.
1.010.000
.
D.
1.005.000
Câu 14. Ông Bảo làm mái vòm ở phía trước ngôi nhà của mình bằng vật liệu tôn. Mái vòm đó là một phần
của mặt xung quanh của một hình trụ như hình bên dưới. Biết giá tiền của 1
2
m
tôn là
300.000
đồng. Hỏi số tiền (làm tròn đến hàng nghìn) mà ông Bảo mua tôn là bao nhiêu?
A.
18.850.000
đồng. B.
5.441.000
đồng. C.
9.425.000
đồng. D.
10.883.000
đồng.
Câu 15. Cổ động viên bóng đá của đội tuyển Indonesia muốn làm một chiếc mũ có dạng hình nón sơn hai
màu Trắng và Đỏ như trên quốc kỳ. Biết thiết diện qua trục của hình nón là tam giác vuông cân.
5 m
6 m
120
0
NGUYỄ
N BẢO VƯƠNG - 0946798489
Cổ động
viên muốn sơn màu Đỏ ở bề mặt phần hình nón có đáy là cung nhỏ
MBN
,
phần còn là
của hình nón sơn màu Trắng. Tính tỉ số phần diện tích hình nón được sơn màu Đỏ với phần diện
tích sơn màu Trắng.
A.
2
7
. B.
2
5
. C.
1
4
. D.
1
3
.
Câu 16. Một công ty sản xuất bồn đựng nước hình trụ có thể tích thực
3
1m
với chiều cao bằng
1m
. Biết bề
mặt xung quanh bồn được sơn bởi loại sơn màu xanh tô như hình vẽ và màu trắng là phần còn lại
của mặt xung quanh; với mỗi mét vuông bề mặt lượng sơn tiêu hao
0
.5
l
ít sơn. Công ty cần sơn
10000 bồn thì dư kiến cần bao nhiêu lít sơn màu xanh gần với số nào nhất, biết khi đo được dây
cung
1
mBF
A
.
6150
. B.
6250
. C.
1230
. D.
1250
.
BẢN
G ĐÁP ÁN
1.C
2.
B
3.B
4.
B
5.
D
6.B
7.
D
8.C
9.
C
10.A
11.
D
12.C
13.D
14.
D
15.D
16.
A
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
B
O
A
S
M
N
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
MỨC ĐỘ VẬN DỤNG CAO
Câu 1. (Sở Vĩnh Phúc - 2021) Cho mặt cầu
S
có bán kính không đổi là
R
. Một hình chóp lục giác đều
.S ABCDEF
nội tiếp mặt cầu
S
. Tìm giá trị lớn nhất
max
V
của thể tích khối chóp
. .S ABCDEF
A.
3
max
3 3
8
R
V
. B.
3
max
8 3
9
R
V
. C.
3
max
16 3
27
R
V
. D.
3
max
8 3
27
R
V
Lời giải
Chọn C
Ta có
.
1
; .
3
S ABCDEF ABCDEF
V d S ABCDEF S
và mặt cầu có tính đối xứng nên để tìm
max
V
ta
xét hình chóp
.S ABCDEF
như hình vẽ sau:
Đáy
ABCDEF
nội tiếp trong đường tròn tâm
H
bán kính
r
và tam giác
HAB
đều cạnh
2 2
r R x
. Đặt
0OH x x R
Ta có:
2 2
2
3 3
3
6 6.
4 2
ABCDEF HAB
R x
r
S S
.
Khi đó :
2 2 3 2 2 3
.
1 3 3
; . .
3 2 2
S ABCDEF ABCDEF
V d S ABCDEF S R x R x x Rx R x R
Xét hàm số
3 2 2 3
f x x Rx R x R
với
0; .x R
2 2
' 3 2 ; ' 0
3
(l)
R
x
f x x Rx R f x
x R
Ta có bẳng biến thiên:
KHỐI TRÒN XOAY
Chủ đề 6
H
S
O
F
E
A
D
C
B
r
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Vậy
3
max
3 16 3
.
2 3 27
R R
V f
Câu 2. (Sở Tuyên Quang - 2021) Cho hình nón có chiều cao bằng
3
. Một mặt phẳng
đi qua đỉnh
hình nón và cắt hình nón
theo một thiết diện là tam giác đều, góc giữa trục của hình nón và mặt phẳng
là
45
. Thể
tích của hình nón đã cho bằng
A.
5 24
. B.
15
. C.
45
. D.
15 25
.
Lời giải
Chọn B
Giả sử mặt phẳng
cắt hình nón theo thiết diện là tam giác
SAB
. Theo giả thiết thì
tam
giác
SAB
đều. Gọi
O
là tâm của đường tròn đáy;
,h r
lần lượt là đường cao và bán
kính của
hình nón.
Gọi
M
là trung điểm của
AB
, tam giác
OAB
cân đỉnh
O
nên
OM AB
và
SO AB
suy ra
AB SOM
.
Dựng
OK SM
(
K SM
).
Theo trên ta có
AB SOM
AB OK
OK SAB
.
Vậy góc tạo bởi giữa trục
SO
và mặt phẳng
SAB
là
45OSM .
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Xét tam giác vuông
SOM
có
3
cos 3 2, tan cos 3
2
2
SO
OSM SM OM SO OSM
SM
.
Do tam giác
SAB
đều nên
3 2 2.3 2
2 6 6
2
3 3
AB SM
SM AB AM .
Xét tam giác vuông
OAM
có
2 2
15r OA OM AM
. Suy ra thể tích của hình nón đã
cho là:
2
1 1
.15.3 15
3 3
V r h
.
Câu 3. (Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Người ta chế tạo một món đồ chơi cho
trẻ em theo các công đoạn như sau: Trước tiên chế tạo ra hình nón tròn xoay có góc ở đỉnh là
2 60
bằng thủy tinh trong suốt. Sau đó đặt hai quả cầu nhỏ bằng thủy tinh có bán kính lớn,
nhỏ khác nhau sao cho hai mặt cầu tiếp xúc với nhau và đều tiếp xúc với mặt nón, quả cầu lớn tiếp
xúc với mặt đáy của hình nón, như hình vẽ bên dưới.
Biết rằng chiều cao của hình nón bằng
9cm
. Bỏ qua bề dày các lớp vỏ thủy tinh, tổng thể tích của
hai khối cầu bằng
A.
100
3
. B.
112
3
. C.
40
3
. D.
38
3
.
Lời giải
Chọn B
Gọi
h
là chiều cao khối nón với
9h
.
Gọi
AB
là một đường kính của mặt đáy khối nón,
S
là đỉnh của khối nón và
,M N
lần lượt là
giao điểm của tiếp tuyến chung của hai mặt cầu với
,SA SB
như hình vẽ.
Ta có tam giác
SAB
đều nên bán kính của đường tròn nội tiếp
SAB
bằng
1
3
3
h
r
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Tương tự, tam giác
SMN
đều nên bán kính của đường tròn nội tiếp
OMN
bằng
1
2
1
3
r
r
.
Vậy tổng thể tích của hai khối cầu cần tìm là
3 3 3 3
1 2
4 4 112
( ) (3 1 )
3 3 3
V r r
.
Câu 4. (Chuyên Quốc Học Huế - 2021) Tính thể tích lớn nhất của hình trụ nội tiếp trong mặt cầu có bán
kính
1
(hình trụ nội tiếp trong mặt cầu là hình trụ có hai đường tròn đáy thuộc mặt cầu).
A.
3
9
. B.
4 3
9
. C.
2 3
9
. D.
2 3
3
.
Lời giải
Chọn B
Gọi
I
,
O
,
O
lần lượt là tâm mặt cầu, tâm đường tròn đáy trên và đáy dưới của hình trụ.
Gọi
h
,
R
,
r
lần lượt là chiều cao hình trụ, bán kính mặt cầu và bán kính đường tròn đáy của
hình trụ. Suy ra
2
h
h OO OI
;
1R
.
Khi đó
2
2
2 2 2
1
2 4
h h
R r r
.
Vậy thể tích của hình trụ là
2 3
2
. 1 .
4 4
h h
V r h h h
.
Xét hàm số
3
4
h
f h h
với
0h
.
Khi đó:
2
3
1
4
h
f h
. Suy ra
2
2
3 4 2 3
0 1 0
4 3 3
h
f h h h
.
Bảng biến thiên
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Vậy thể tích lớn nhất của hình trụ là
2
4 3
4 9
h
V h
(đvtt) khi
2 3
3
h
.
Câu 5. (Chuyên Ngoại Ngữ Hà Nội- 2021) Một hình trụ có thiết diện qua trục là hình chữ nhật có chu vi
bằng 12cm. Thể tích lớn nhất mà hình trụ có thể nhận được là
A.
3
16 cm
. B.
3
64 cm
. C.
3
32 cm
. D.
3
8 cm
.
Lời giải
Chọn D
Giả sử hình trụ có bán kính đáy là
a
và chiều cao
, 0h a h
.
Thiết diện qua trục là hình chữ nhật
ABCD
(như hình vẽ).
Theo giả thiết ta có:
2 2 12 6 2 0 3a h h a a
(vì
0h
).
Thể tích khối trụ là:
2 2 2
6 2 2 3V a h a a a a
Xét hàm số:
2 3 2
3 3 , 0;3f a a a f a a a a
.
Có
2
3 6f a a a
;
0
0
2
a
f a
a
.
Bảng biến thiên
Suy ra
0;3
max 2 4f a f
.
Vậy,
3
max
V 2 .4 8 cm
.
Câu 6. (Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh bằng 1, mặt bên
SAB
là tam giác cân tại
S
và nằm trong mặt phẳng vuông
góc với mặt phẳng đáy. Tính thể tích
V
của khối cầu ngoại tiếp hình chóp đã cho biết
o
120ASB ?
A.
13 78
27
. B.
5 15
54
. C.
5
3
. D.
4 3
27
.
Lời giải
Chọn B
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Gọi
H
là trung điểm của
AB
:
SH AB
(vì
SAB
cân tại
S
) ⇒
SH ABC
SH CH
và
CH AB
(vì
ABC
đều) ⇒
CH SAB
Gọi
I
và
J
lần lượt là tâm đường tròn ngoại tiếp
ABC
và
SAB
.
Qua
I
và
J
lần lượt kẻ đường thẳng
d
song song với
SH
và
d
song song với
CH
⇒
d
là trục của
ABC
và
d
là trục của
SAB
⇒ Giao điểm của
d
và
d
là tâm
O
và
OS
là
bán kính của khối cầu ngoại tiếp hình chóp
.S ABC
.
Áp dụng đính lí sin trong
SAB
:
2 2
sin
SAB
AB
R JS
ASB
⇔
o
1 3
2sin120 3
JS
Xét
ABC
đều:
3
2
CH
;
1 3
3 6
IH CH
Xét
OJS
vuông tại
J
:
2 2
2 2 2 2
3 3 15
6 3 6
OS OJ JS IH JS
3
3
4 4 15 5 15
. .
3 3 6 54
V OS
.
Câu 7. (THPT Quế Võ 1 - Bắc Ninh - 2021) Cho hình trụ
T
có bán kính đáy và chiều cao đều bằng
,R
hai đáy là hai hình tròn
O
và
.O
Gọi
AA
và
BB
là hai đường sinh bất kì của
T
và
M
là một điểm di động trên đường tròn
.O
Thể tích lớn nhất của khối chóp
.M AA B B
bằng
bao nhiêu?
A.
3
3 3
4
R
. B.
3
3
4
R
. C.
3
3
3
R
. D.
3
3
2
R
.
Lời giải
Chọn D
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Để tìm giá trị lớn nhất của thể tích của các khối chóp
.M AA B B
ta chỉ cần xét các loại hình chóp
.M AA B B
trong đó
M
là giao điểm của đường tròn
O
và đường trung trực của đoạn
.AB
Khi
đó
O
thuộc đoạn
MI
(với
I
là trung điểm của
AB
).
Đặt
0 .OI x x R
Khi đó
MI R x
và
.
MI AB
MI AA B B
MI AA
Ta có
2 2 2 2
2 2 2 .AB AI OA OI R x
Suy ra thể tích của khối chóp
.M AA B B
là
2 2
.
1 1 2
. . . . . .
3 3 3
M AA B B AA B B
V S MI AA AB MI R R x R x
2
2 2 2 2
.
4
.
9
M AA B B
V R R x R x
Áp dụng bất đẳng thức AM-GM, ta có
2
2 2
1
3 3
3
R x R x R x R x R x R x
4
4
1 3 3 27
.
3 4 16
R x R x R x R x R
Dấu “
” xảy ra khi và chỉ khi
3 3
.
0;
2
R x R x
R
x
x R
Vậy
2
3
2
2 3
max .
3 2 2 2
R R R
V R R R
Câu 8. (THPT Phan Đình Phùng - Quảng Bình - 2021) Một nhà máy sản xuất các hộp hình trụ kín cả
hai đầu có thể tích
V
cho trước. Mối quan hệ giữa bán kính đáy
R
và chiều cao
h
của hình trụ để
diện tích toàn phần của hình trụ nhỏ nhất là
A.
h R
. B.
3h R
. C.
2h R
. D.
2R h
.
Lời giải
Chọn C
Đặt
R x
, điều kiện
0x
.
2
2
V
V x h h
x
3
h V
R x
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
2
2
2 2 2
TP
V V
S R h R x x x
x x
.
Xét hàm số:
2
2
2
V
f x x
x
với
0x
.
Ta có:
3
2 2
2 4 2
4
V x V
f x x
x x
.
Khi đó:
3
0
2
V
f x x
.
Ta có BBT:
Từ BBT trên ta thấy
TP
S nhỏ nhất khi
3
2
V
x
Khi đó:
2 2
2
h V
h R
V
R
.
Câu 9. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Cho hình lăng trụ đều
. ' ' 'ABC A B C
, biết góc giữa
hai mặt phẳng
'A BC
và
ABC
bằng
0
45
, diện tích tam giác
'A BC
bằng
2
6a
. Tính diện
tích xung quanh của hình trụ ngoại tiếp hình lăng trụ
. ' ' 'ABC A B C
.
A.
2
2 a
. B.
2
8 3
3
a
. C.
2
4 a
. D.
2
4 3
3
a
.
Lời giải
Chọn C
Gọi
I
là trung điểm của
, ' .BC AI BC A I BC
Ta có
0
'
' ' , ' ' , ' , ' 45 .
,
A BC ABC BC
A I A BC A I BC A BC ABC A I AI A IA
AI ABC AI BC
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Do
'A A ABC
tại
A
, suy ra tam giác
'A BC
có hình chiếu vuông góc lên mặt đáy
ABC
là
tam giác
ABC
.
Áp dụng công thức tính diện tích hình chiếu của một đa giác, ta được
2 0 2
'
.cos ' , 6.cos45 3.
ABC A BC
S S A BC ABC a a
Tam giác
ABC
đều
2 2
2 2 2
3 3
3 4 2 .
4 4
ABC
AB AB
S a AB a AB a
Suy ra bán kính đường tròn ngoại tiếp tam giác
ABC
là
2 2 3 2 2 3 2 3
.
3 3 2 3 2 3
AB a a
r AI
Xét tam giác vuông cân
' ' 3.A IA A A AI a
Vậy diện tích xung quanh của hình trụ ngoại tiếp hình lăng trụ
. ' ' 'ABC A B C
bằng
2
2 3
2 2 . . 3 4 .
3
xq
a
S rl a a
Câu 10. Một chậu nước hình bán cầu bằng nhôm có bán kính
10R dm
. Trong chậu có chứa sẵn một khối
nước hình chỏm cầu có chiều cao
4h dm
. Người ta bỏ vào chậu một viên bi hình cầu bằng kim
loại thì mặt nước dâng lên vừa phủ kín viên bi. Bán kính viên bi gần với số nào sau đây nhất?
A.
2,09dm
. B.
9,63dm
. C.
3,07 dm
. D.
4,53dm
.
Lời giải
Chọn A
Gọi
x dm
là bán kính của viên bi,
0 5x
.
Thể tích viên bi là
3 3
1
4
( )
3
V x dm
Thể tích nước ban đầu:
2 3
0
416
.
3 3
h
V h R dm
Thể tích sau khi thả viên bi:
2
2
3
2
4 30 2
2
2 10 .
3 3
x x
x
V x dm
Ta có:
3 2
0 2 1
3 30 104 0 2,09 .V V V x x x dm
Câu 11. Sử dụng mảnh inox hình chữ nhật
ABCD
có diện tích bằng
2
1m và cạnh
mBC x
để làm một
thùng đựng nước có đáy, không có nắp theo quy trình như sau: Chia hình chữ nhật
ABCD
thành
2
hình chữ nhật
ADNM
và
BCNM
, trong đó phần hình chữ nhật
ADNM
được gò thành phần
xung quanh hình trụ có chiều cao bằng
AM
; phần hình chữ nhật
BCNM
được cắt ra một hình
tròn để làm đáy của hình trụ trên (phần inox thừa được bỏ đi) Tính gần đúng giá trị
x
để thùng
nước trên có thể tích lớn nhất (coi như các mép nối không đáng kể).
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
0,97m
. B.
1,37m
. C.
1,12m
. D.
1,02m
.
Lời giải
Chọn D
Ta có
1 1
. 1 m
AB BC AB
BC x
.
Gọi
m
r
là bán kính đáy hình trụ inox gò được, ta có chu vi hình tròn đáy bằng
m .
BC x
Do
đó
2 m
2
x
r x r
.
Như vậy
1
2 m
x x
BM r AM AB BM
x
.
Thể tích khối trụ inox gò được là
2
2 2
2
1 1
. .
2 4
x x
V r h x x
x
.
Xét hàm số
2
f x x x
với
0
x
.
2
3
f x x
;
0
3
f x x
;
0 0;
3
f x x
và
0 ;
3

f x x
.
Bởi vậy
f x
đồng biến trên khoảng
0;
3
và nghịch biến trên khoảng
;
3

.
Suy ra
0;
2 3
max
3 9

f x f
max
max
V f x
1,02 m
3
x
.
Câu 12. Từ một tấm thép phẳng hình chữ nhật, người ta muốn làm một chiếc thùng đựng dầu hình trụ bằng
cách cắt ra hai hình tròn bằng nhau và một hình chữ nhật (phần tô đậm) sau đó hàn kín lại, như
trong hình vẽ dưới đây. Hai hình tròn làm hai mặt đáy, hình chữ nhật làm thành mặt xung quanh
của thùng đựng dầu (vừa đủ). Biết rằng đường tròn đáy ngoại tiếp một tam giác có kích thước là
50 ,70 ,80cm cm cm
(các mối ghép nối khi gò hàn chiếm diện tích không đáng kể. Lấy
3,14
).
Diện tích của tấm thép hình chữ nhật ban đầu gần nhất với số liệu nào sau đây?
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
A.
6,8
2
m
. B.
24,6
2
m
. C.
6,15
2
m
. D.
3,08
2
m
.
Lời giải
Chọn C
Đổi:
50 0,5 ;70 0,7 ;80 0,8cm m cm m cm m
.
Xét tam giác nội tiếp đường tròn đáy có kích thước lần lượt là
0,5 ;0,7 ;0,8m m m
nên bán kính
đường tròn đáy của thùng đựng dầu là
4 1 1 0,5 1
0,5.0,
0
7.
,7
0,8 7 3
8
0
1
3
0,
R
.
Ta có
2h R
Diện tích hình chữ nhật ban đầu gấp
3
lần diện tích xung quanh của hình trụ.
Vậy
2
2
7 3
3
7693
3.2
0
6.3,14.2.R 6.3,14.2 6,1544
1250
S Rh
2
m
.
Câu 13.
Ông An cần làm một đồ trang trí như hình vẽ. Phần dưới là một phần của khối cầu bán kính
20 cm
làm bằng gỗ đặc, bán kính của đường tròn phần chỏm cầu bằng
10 cm
. Phần phía trên làm
bằng lớp vỏ kính trong suốt. Biết giá tiền của
2
1 m kính như trên là 1.500.000 đồng, giá triền của
3
1m gỗ là 100.000.000 đồng. Hỏi số tiền (làm tròn đến hàng nghìn) mà ông An mua vật liệu để
làm đồ trang trí là bao nhiêu.
A.
1.000.000
.
B.
1.100.000
.
C.
1.010.000
.
D.
1.005.000
Lời giải
Chọn D
Bán kính mặt cầu là
20R cm
; bán kính đường tròn phần chỏm cầu là
10r cm
.
Theo hình vẽ ta có
0
10 1
sin 30
20 2
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Diện tích phần làm kính là:
2 2
360 2.30 4000
.4 .20
360 3
S cm
.
Xét hình nón đỉnh là tâm mặt cầu, hình tròn đáy có bán kính bằng
2 2
10 ; 20 20 10 10 3r cm l R cm h cm
Thể tích phần chỏm cầu bằng
3 2
hom
2.30 4 1
. .
360 3 3
c cau
V R r h
=
3
16000 1000 3
9 3
cm
Vậy số tiền ông An cần mua vật liệu là:
4000 16000 1000 3
.150 .100 1.005.000
3 9 3
Câu 14. Ông Bảo làm mái vòm ở phía trước ngôi nhà của mình bằng vật liệu tôn. Mái vòm đó là một phần
của mặt xung quanh của một hình trụ như hình bên dưới. Biết giá tiền của 1
2
m
tôn là
300.000
đồng. Hỏi số tiền (làm tròn đến hàng nghìn) mà ông Bảo mua tôn là bao nhiêu?
A.
18.850.000
đồng. B.
5.441.000
đồng. C.
9.425.000
đồng. D.
10.883.000
đồng.
Lời giải
Chọn D
Gọi
r
là bán kính đáy của hình trụ. Khi đó:
0
6
2 2 3.
sin120
r r
Sử dụng hệ thức lượng trong tam giác, ta có góc ở tâm của cung này bằng
0
120
.
Và độ dài cung này bằng
1
3
chu vi đường tròn đáy.
Suy ra diện tích của mái vòm bằng
1
3
xq
S
,
(với
xq
S
là diện tích xung quanh của hình trụ).
Do đó, giá tiền của mái vòm là
1 1 1
.300.000 . 2 .300.000 . 2 .2 3.5 .300.000 10882796,19.
3 3 3
xq
S rl
Câu 15. Cổ động viên bóng đá của đội tuyển Indonesia muốn làm một chiếc mũ có dạng hình nón sơn hai
màu Trắng và Đỏ như trên quốc kỳ. Biết thiết diện qua trục của hình nón là tam giác vuông cân.
Cổ động viên muốn sơn màu Đỏ ở bề mặt phần hình nón có đáy là cung nhỏ
MBN
, phần còn là
của hình nón sơn màu Trắng. Tính tỉ số phần diện tích hình nón được sơn màu Đỏ với phần diện
tích sơn màu Trắng.
5 m
6 m
120
0
2 3 m 2 3 m
120
0
6 m
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
A.
2
7
. B.
2
5
. C.
1
4
. D.
1
3
.
Lời giải
Chọn D
Ta có
2SO OA OB r SM r MN
Do dó tam giác
OMN
vuông cân tại
O
.
Gọi
S
là diện tích xung quanh của hình nón,
d
S
là diện tích xung quanh của phần hình nón được
sơn màu đỏ, ứng với góc
0
90MON
nên
0
1
0
90 1 1
.
4 3
360
d
t
S
S
S S
Câu 16. Một công ty sản xuất bồn đựng nước hình trụ có thể tích thực
3
1m
với chiều cao bằng
1m
. Biết bề
mặt xung quanh bồn được sơn bởi loại sơn màu xanh tô như hình vẽ và màu trắng là phần còn lại
của mặt xung quanh; với mỗi mét vuông bề mặt lượng sơn tiêu hao
0.5
lít sơn. Công ty cần sơn
10000 bồn thì dư kiến cần bao nhiêu lít sơn màu xanh gần với số nào nhất, biết khi đo được dây
cung
1 mBF
A.
6150
. B.
6250
. C.
1230
. D.
1250
.
Lời giải
Chọn A
Gọi
r
là bán kính đường tròn đáy,
Ta có:
2
1
.V r h r
Xét tam giác
O BF
ta có
2 2
2
2
Cos( ) 1 2,178271695
2 2
r BF
BO F BO F
r
(rad)
B
O
A
S
M
N
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Vậy độ dà
i cung
B
F
:
.
1,2289582
l
r
(m
)
Tổng số lít sơn màu xanh cho mỗi bồn nước là:
.
.0.5 0.6144791001
T
l h
(lí
t)
Vậy tổng số sơn cần cho
10
000
bồn
61
45
S
(lí
t)
| 1/87
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


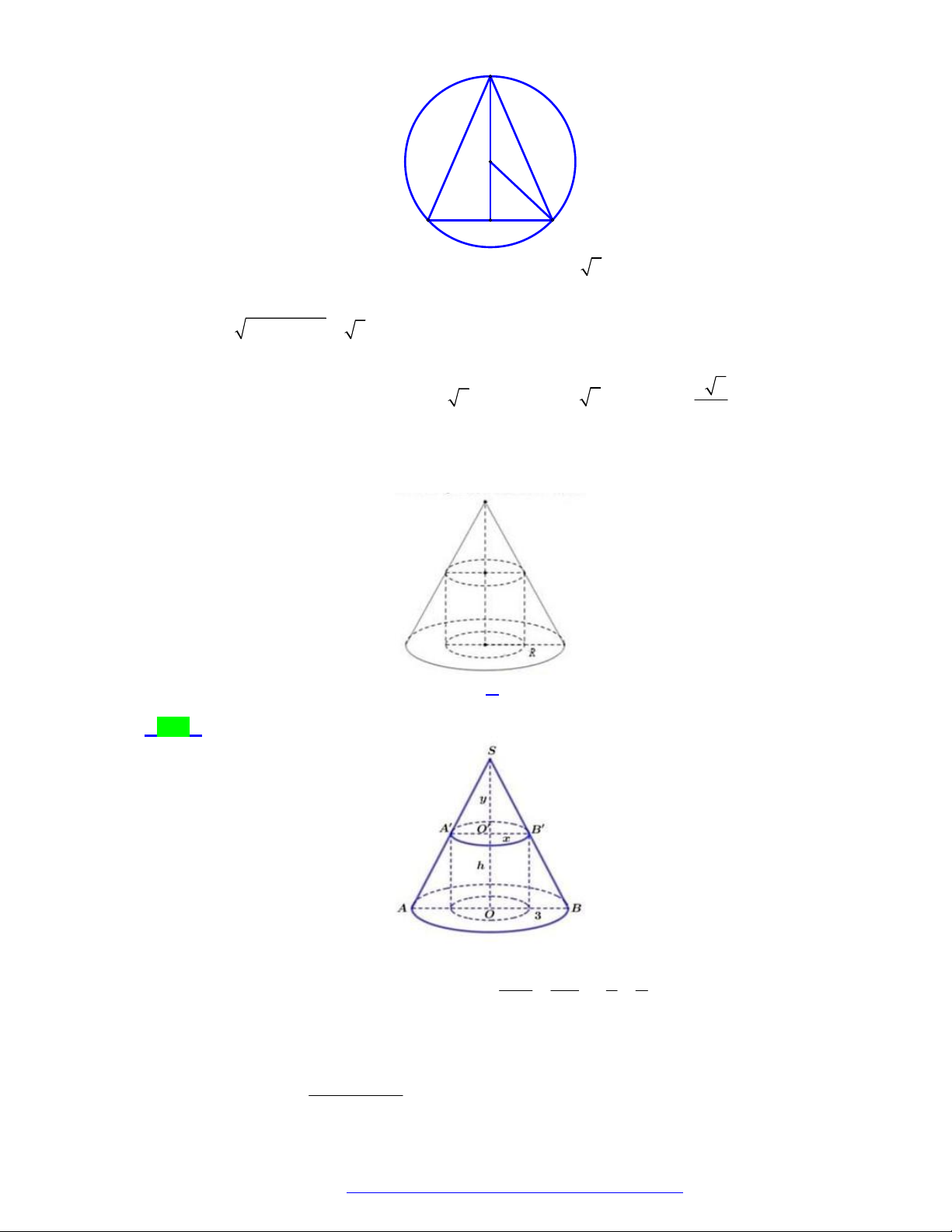
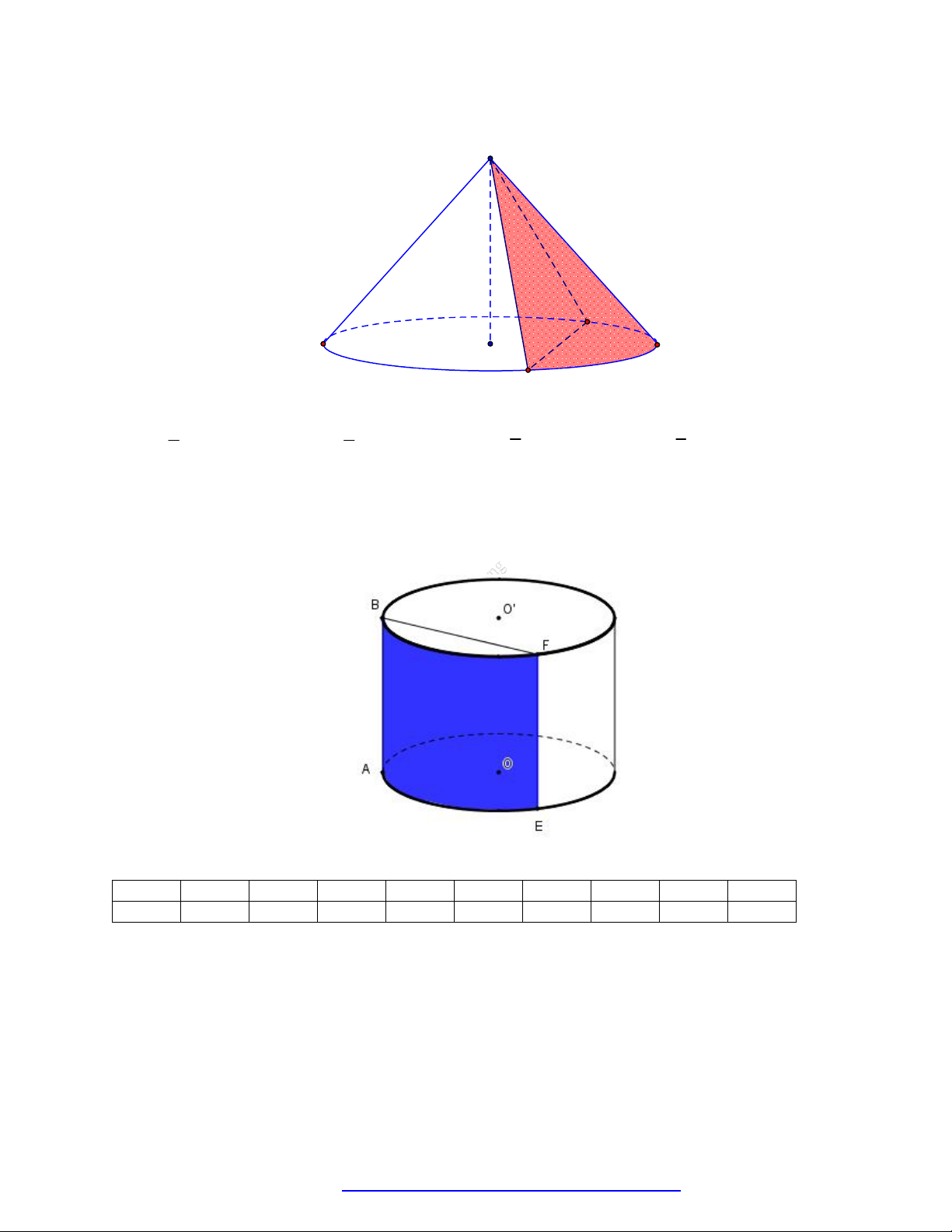
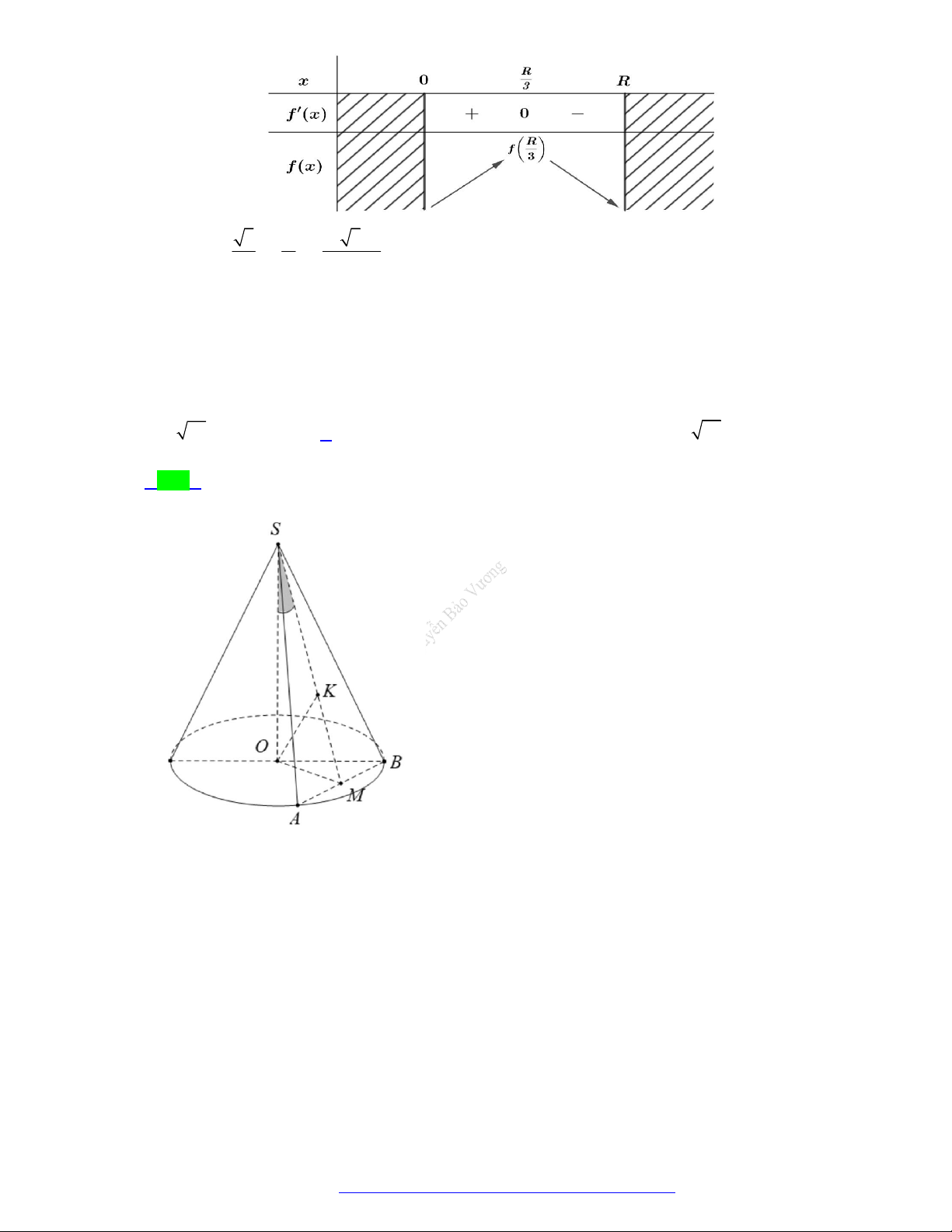
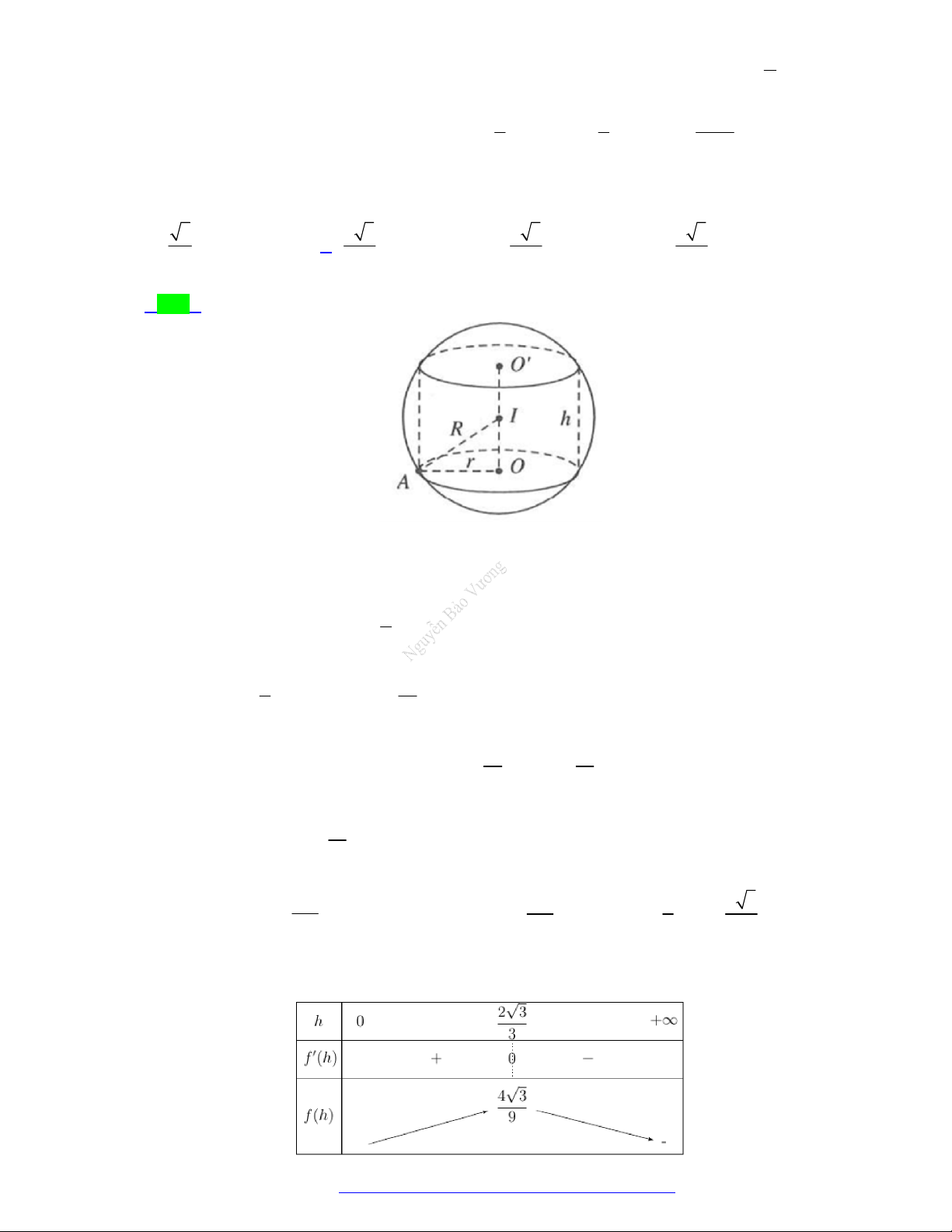
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Chủ đề 6 KHỐI TRÒN XOAY
MỨC ĐỘ NHẬN BIẾT Câu 1.
(Sở Vĩnh Phúc - 2021) Cho hình nón có độ dài đường sinh bằng 4 , diện tích xung quanh bằng
8 . Tính bán kính hình trong đáy R của hình nón đó.
A. R  8 .
B. R  4 .
C. R  2 . D. R  1 . Câu 2.
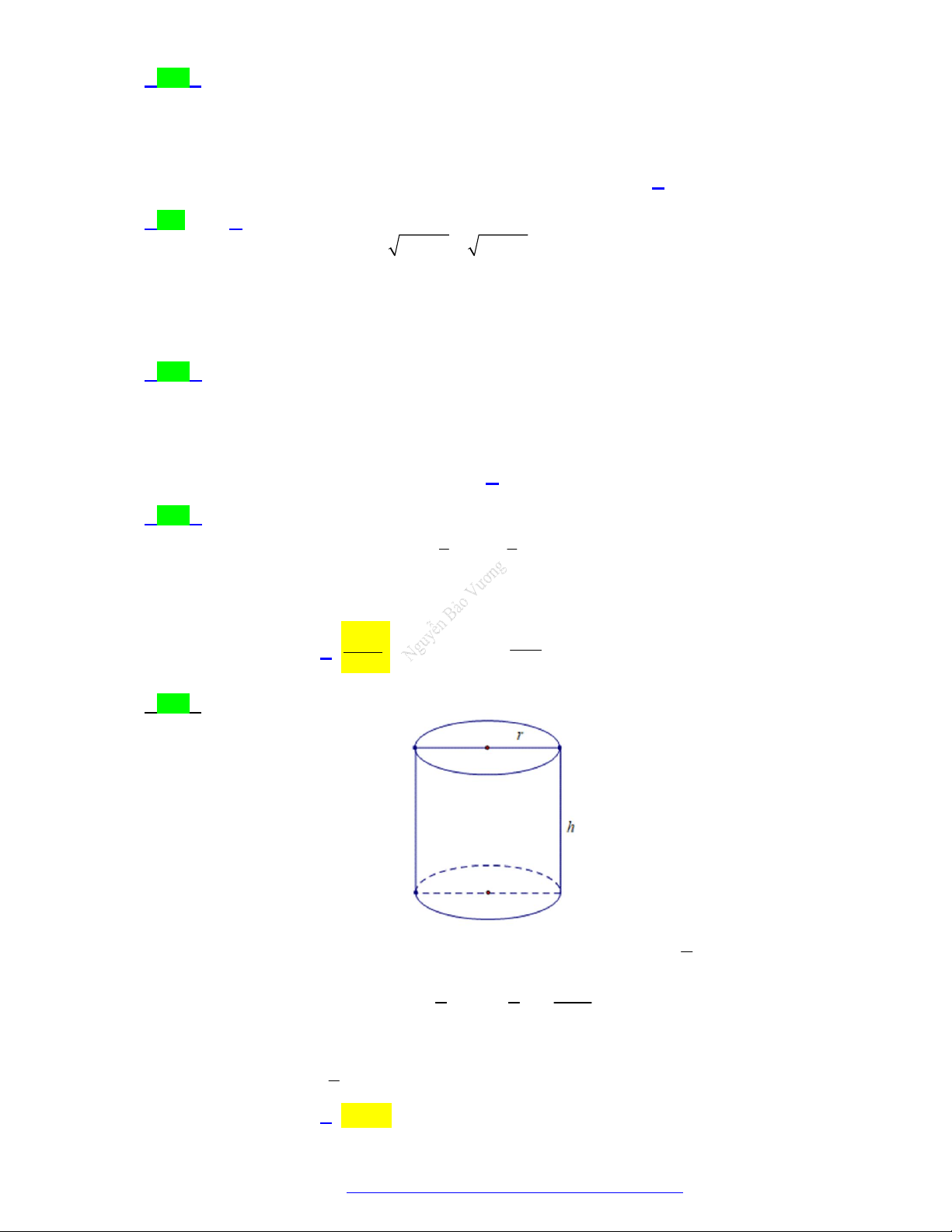
(Sở Vĩnh Phúc - 2021) Cho khối trụ có bán kính đáy r  4 và chiều cao h  2 . Tính thể tích khối trụ đó. 32 A. 8 . B. 32 . C. 16 . D. . 3 Câu 3.
(Sở Lào Cai - 2021) Viết công thức tính diện tích xung quanh của hình trụ có đường cao h , bán
kính đường tròn đáy R . 2 A. S  2 SRh S   Rh xqh . B. S  2 xqRh . C. 2 xq . D. xq . Câu 4.
(Sở Lào Cai - 2021) Cho hình nón có diện tích xung quanh bằng 2
5 a và bán kính đáy bằng a . Độ dài đường sinh
của hình nón đã cho bằng:
A. 3 2a . B. 5a . C. 3a . D. a 5 . Câu 5.
(Sở Hà Tĩnh - 2021) Cho khối cầu có bán kính r  2 . Thể tích của khối cầu đã cho bằng 256 32 A. . B. 256 C. 64 . D. . 3 3 Câu 6.
(Sở Hà Tĩnh - 2021) Cho khối nón có bán kính đáy r  4 và chiều cao h  2 . Thể tích của khối nón đó bằng 32 8 A. . B. 32 . C. . D. 8 . 3 3 Câu 7.
(Sở Yên Bái - 2021) Mặt cầu có đường kính là 10. Diện tích S của mặt cầu bằng
A. S  25 . B. S  5 .
C. S  50 .
D. S  100 . Câu 8.
(Sở Tuyên Quang - 2021) Độ dài đường sinh hình nón có diện tích xung quanh bằng 2 6a và
đường kính đáy bằng 2a là: A. 2a . B. 6a . C. 3a . D. 9a . Câu 9.
(Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Cho hình nón có bán kính đáy bằng
4a và chiều cao bằng 3a . Diện tích xung quanh của hình nón bằng A. 2 20 a . B. 2 40 a . C. 2 12 a . D. 2 24 a .
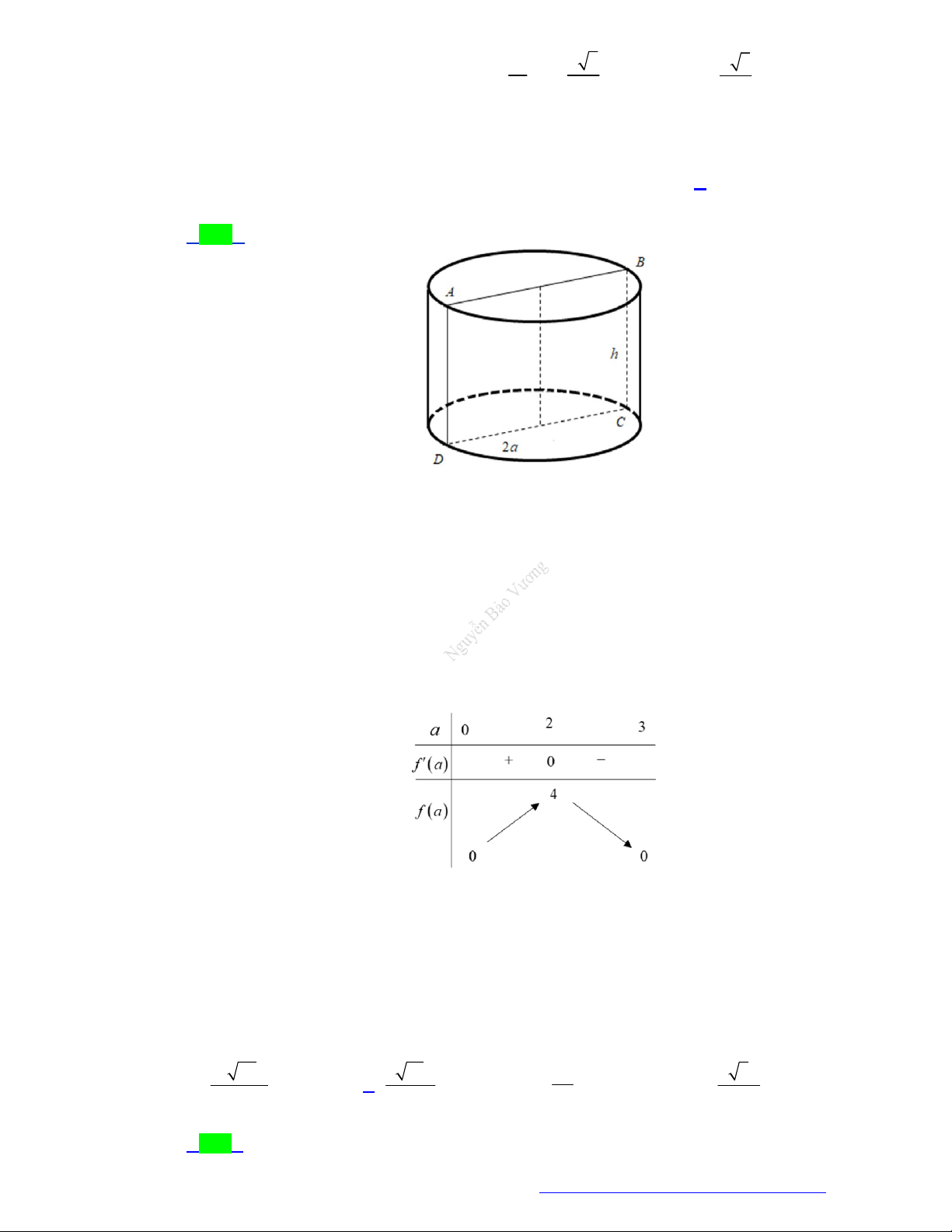
Câu 10. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Cắt khối trụ bởi một mặt phẳng qua trục được
thiết diện là một hình vuông. Tính thể tích của khối trụ biết bán kính đáy của khối trụ bằng a 2 A. 3 4 a B. 3  a C. 3  a D. 3 2 a 3
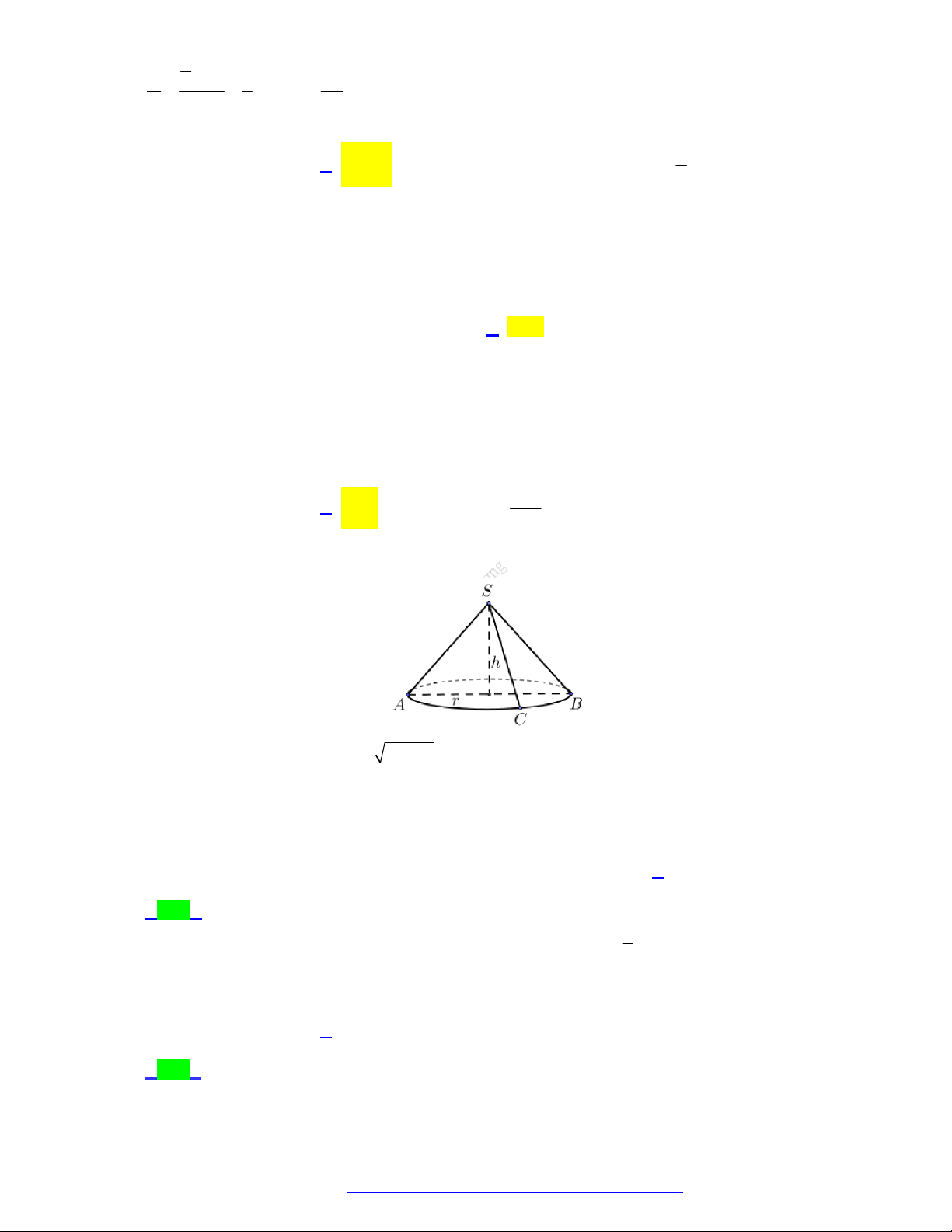
Câu 11. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Cho khối nón có bán kính r  5 và chiều cao
h  3 . Tính thể tích V của khối nón A. V  5 .
B. V   5 .
C. V   5 .
D. V   5 .
Câu 12. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Một hình trụ có bán kính đáy r  5cm , chiều cao
h  7cm . Diện tích xung quanh của hình trụ này là 35 70 A.   3 cm  . B.   3 70 cm  . C.   3 cm  . D.   3 35 cm  . 3 3
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489
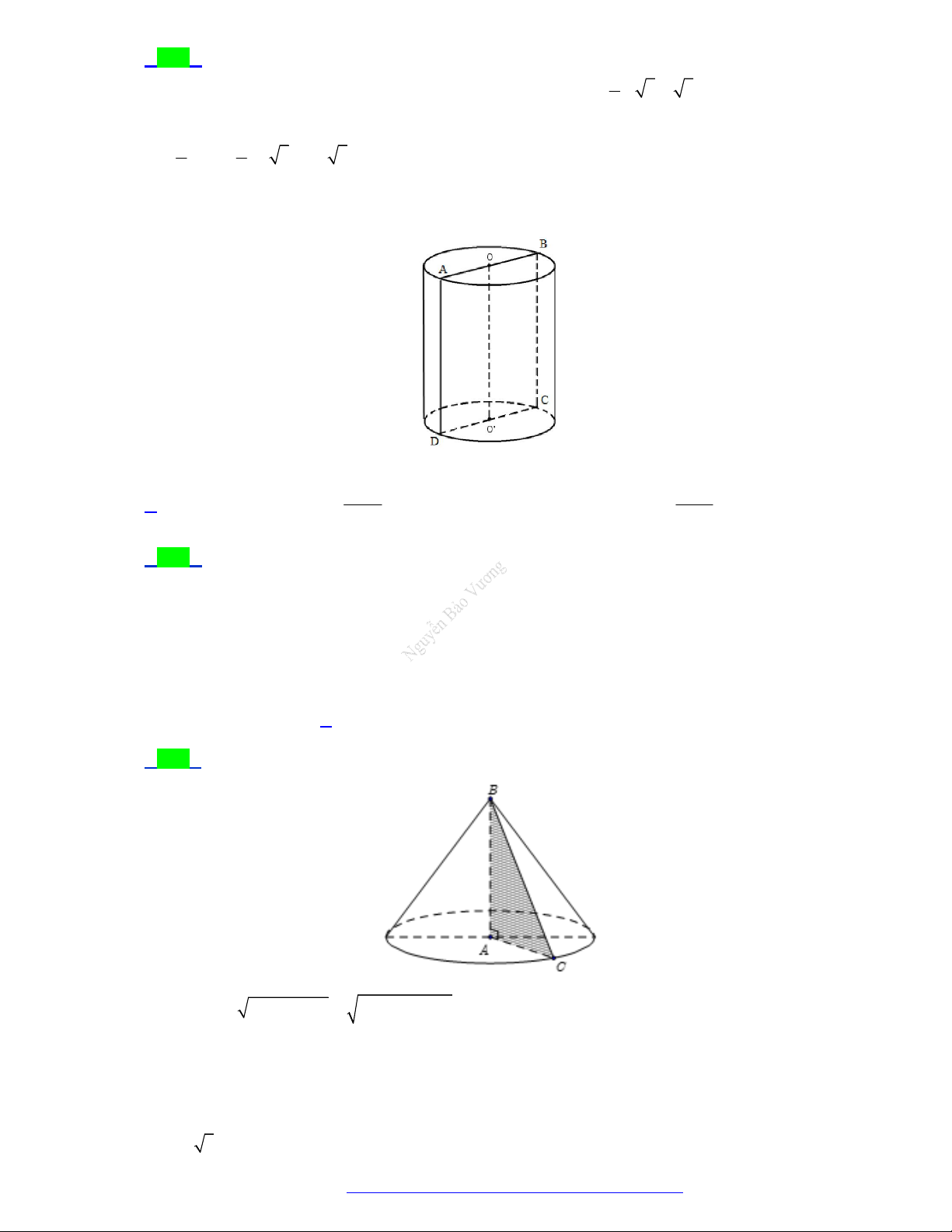
Câu 13. (Chuyên Lê Hồng Phong - TPHCM - 2021) Cho hình lăng trụ có đường kính đáy bằng 6cm , độ
dài đường cao bằng 4cm . Tính diện tích xung quanh của hình trụ này. A. 2 22 cm . B. 2 24 cm . C. 2 18 cm . D. 2 20 cm .
Câu 14. (Chuyên Lam Sơn - Thanh Hóa - 2021) Thể tích khối trụ có bán kính r và chiều cao h bằng: 4 1 A. 2  r h . B. 2  r h . C. 2  r h . D. 2 rh . 3 3
Câu 15. (Chuyên Lam Sơn - Thanh Hóa - 2021) Thể tích của khối nón tròn xoay có đường kính đáy
bằng 6 và chiều cao bằng 5 là A. 45 B. 15 C. 60 D. 180
Câu 16. (Chuyên Lam Sơn - Thanh Hóa - 2021) Diện tích của mặt cầu có bán kính R bằng. 4 A. 2 R . B. 2  R . C. 2 4 R . D. 3  R . 3
Câu 17. (Chuyên KHTN - 2021) Cho khối nón có bán kính đáy r a và chiều cao h  2a . Thể tích của khối nón đã cho bằng 3 4 a 3 2 a A. . B. 3 4 a . C. 3 2 a . D. . 3 3
Câu 18. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Diện tích xung quanh của hình trụ có độ dài
đường sinh bằng l và bán kính r bằng 1 A. 2 rl. B. 2  r . C. rl. D. rl. 3
Câu 19. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Thể tích của hình nón có bán kính đáy r  2 và
đường cao h  3 là A. 6 . B. 2 . C. 4 . D. 12 .
Câu 20. (Chuyên Quốc Học Huế - 2021) Cho khối trụ có bán kính đáy bằng r  5 và chiều cao h  3 .
Thể tích của khối trụ đã cho bằng A. 75 . B. 30 . C. 25 . D. 5 .
Câu 21. (Chuyên Quốc Học Huế - 2021) Cho khối nón có chiều cao bằng 2a và bán kính đáy bằng a .
Thể tích của khối nón đã cho bằng 3 4 a 3 2 a 3  a A. . B. . C. . D. 3 2 a . 3 3 3
Câu 22. (Chuyên Quốc Học Huế - 2021) Cắt hình trụ T  bởi một mặt phẳng qua trục của nó, ta được thiết
diện là một hình vuông cạnh bằng 10. Diện tích xung quanh của T  là A. 100 . B. 150 . C. 50 . D. 200 .
Câu 23. (Chuyên Quang Trung - Bình Phước - 2021) Khối trụ có bán kính đáy, đường cao lần lượt là
a, 2a thì có thể tích bằng: 3 2 a 3  a A. 3 2 a . B. . C. 3  a . D. . 3 3
Câu 24. (Chuyên Quang Trung - Bình Phước - 2021) Hình nón có bán kính đáy, đường cao lần lượt là
3, 4 thì diện tích xung quanh hình nón bằng: 15 A. 15 . B. . C. 12 . D. 6 . 2
Câu 25. (Chuyên Ngoại Ngữ Hà Nội- 2021) Thể tích của khối trụ có chiều cao h  2 và bán kính đáy r  3 bằng? A. 4 . B. 12 . C. 18 . D. 6 .
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Câu 26. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Tính diện tích xung quanh của một hình trụ có chiều
cao 20m , chu vi đáy bằng 5m . A. 2 100m . B. 2 50 m . C. 2 100 m . D. 2 50m .
Câu 27. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Cho khối cầu bán kính r  3. Thể tích khối cầu đã cho bằng 32 8 A. 36 . B. . C. . D. 16 . 3 3
Câu 28. (Chuyên Hạ Long - Quảng Ninh - 2021) Cho hình nón có bán kính đáy r  6 và chiều cao
h  8 . Diện tích xung quanh của hình nón đã cho bằng A. 120 B. 64 C. 60 D. 80
Câu 29. (Chuyên Hạ Long - Quảng Ninh - 2021) Cho khối trụ có bán kính r  3 và độ dài đường sinh
l  5 . Thể tích của khối trụ đã cho bằng
A. V  15 .
B. V  12 .
C. V  45 .
D. V  36 . 3
Câu 30. (Chuyên ĐHSP Hà Nội - 2021) Cho mặt cầu có bán kính r
. Diện tích của mặt cầu đã cho 2 bằng 3 A. 3 . B. 3 . C. 3 3 . D.  . 2
Câu 31. (Chuyên ĐHSP Hà Nội - 2021) Cho hình nón có thiết diện qua trục là một tam giác vuông cân có
cạnh huyền bằng 2a . Diện tích xung quanh của hình nón bằng A. 2  2a . B. 2 2 2a . C. 2 2 a . D. 2  a .
Câu 32. (Chuyên ĐHSP Hà Nội - 2021) Cho hình nón có đường kính đáy bằng 2 , đường cao bằng 3 .
Diện tích xung quanh của hình nón đã cho bằng A. 3 . B.  10   1  . C. 10 . D. 6 .
Câu 33. (Chuyên ĐHSP Hà Nội - 2021) Cho hình trụ có bán kính đáy r  3 và độ dài đường sinh l  5 .
Thể tích khối trụ đã cho bằng A. 45 . B. 30 . C. 15 . D. 90 .
Câu 34. (Chuyên ĐH Vinh - Nghệ An - 2021) Cho góc ở đỉnh của một hình nón bằng o
60 . Gọi r, h,l lần
lượt là bán kính, đường cao, đường sinh của hình nón đó. Khẳng định nào sau đây đúng?
A. l  2r .
B. h r .
C. h  2r .
D. l r .
Câu 35. (Chuyên ĐH Vinh - Nghệ An - 2021) Chu vi của đường tròn lớn của mặt cầu S  ; O R là A. 2  R . B. 2 4 R . C. R . D. 2 R .
Câu 36. (Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Cho A
BH vuông tại H , AH  3a ,
BH  2a . Quay A
BH quanh trục AH ta được một khối nón có thể tích là 4 A. 3 4 a . B. 3 18 a . C. 3  a . D. 3 12 a . 3
Câu 37. (THPT Thanh Chương 1- Nghệ An - 2021) Cho hình cầu có đường kính bằng . Diện tích của hình cầu đã cho bằng A. B. C. D.
Câu 38. (THPT Nguyễn Huệ - Phú Yên - 2021) Thể tích khối cầu có bán kính 2a bằng 16 4 32 A. 3  a . B. 3  a . C. 3 4 a . D. 3  a . 3 3 3
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489
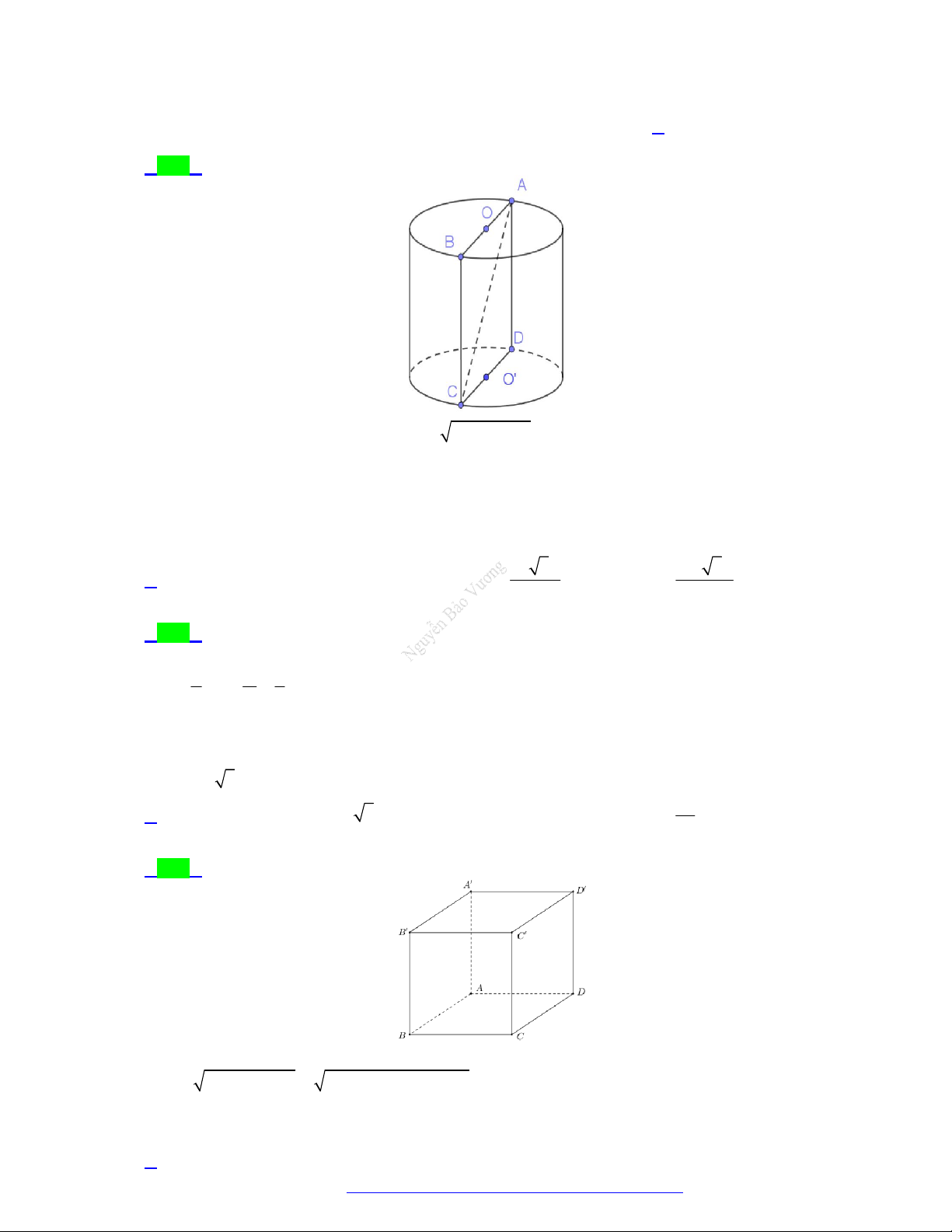
Câu 39. (THPT Nguyễn Huệ - Phú Yên - 2021) Cho hình chữ nhật ABCD (kể cả miền trong), quay hình
chữ nhật đó quanh một cạnh thì thể tích vật thể tròn xoay được tạo thành là: A. Hình trụ. B. Khối nón. C. Khối trụ. D. Hình nón.
Câu 40. (THPT Nguyễn Huệ - Phú Yên - 2021) Hình nón có đường sinh bằng 6 , diện tích xung quanh
bằng 12 . Bán kính đường tròn đáy của hình nón đó bằng 1 A. 4 . B. 2 . C. . D. 1. 2
Câu 41. (THPT Lương Thế Vinh - 2021) Cho hình trụ có độ dài đường sinh l  5 và bán kính đáy r  3.
Diện tích xung quanh của hình trụ đã cho bằng A. 30 B. 15 . C. 5 . D. 24 .
Câu 42. (THPT Lương Thế Vinh - 2021) Cho khối nón có bán kính đáy là r  2 và chiều cao h  3 .
Tính thể tích của khối nón đã cho là? 2 3 4 3 4 A. 4 3 . B. . C. . D. . 3 3 3
Câu 43. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho hình trụ có bán kính đáy r  3 và chiều cao
h  4 . Diện tích xung quanh của hình trụ bằng. A. 8 3 . B. 2 3 . C. 4 3 . D. 16 3 .
Câu 44. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho hình nón có diện tích xung quanh bằng 2 3 a
và bán kính đáy bằng a . Độ dài đường sinh l của hình nón đã cho bằng 5a 3a A. l  .
B. l  3a . C. l  .
D. l  2 2a . 2 2
Câu 45. (THPT Đào Duy Từ - Hà Nội - 2021) Cho khối nón có chu vi đáy 8 và chiều cao h  3 . Thể
tích khối nón đã cho bằng A. 12 . B. 4 . C. 16 . D. 24 .
Câu 46. (THPT Đào Duy Từ - Hà Nội - 2021) Cho hình nón có bán kính đáy r  2 và độ dài đường sinh
l  4. Diện tích xung quanh của hình nón đã cho bằng A. 32 . B. 8 . C. 16 . D. 48 .
Câu 47. (THPT Đào Duy Từ - Hà Nội - 2021) Thể tích của khối cầu có bán kính r  3 là A. 64 . B. 48 . C. 8 . D. 36 .
Câu 48. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Diện tích của mặt cầu có đường kính bằng 4a là A. 2 S  16 a . B. 2 S  12 a . C. 2 S  8 a . D. 2 S  64 a .
Câu 49. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Thể tích của khối trụ tròn xoay có bán kính r , chiều cao h bằng? 2  r h A. . B. 2 3 r h . C. 2  r h . D. 2 2 r h . 3
Câu 50. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho hình nón có bán kính đáy bằng 3 , độ dài đường
cao bằng 4 . Diện tích xung quanh của hình nón bằng: A. 24 . B. 12 . C. 30 . D. 15 .
Câu 51. (THPT Chu Văn An - Thái Nguyên - 2021) Cho hình nón có độ dài đường sinh l  4 và bán 1 kính đáy r
. Diện tích xung quanh của hình nón bằng 4  A. 2 . B.  . C. . D. 4 . 2
Câu 52. (THPT Chu Văn An - Thái Nguyên - 2021) Cho khối cầu có thể tích là 36 . Diện tích mặt cầu đã cho bằng
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 A. 36 . B. 16 . C. 18 . D. 12 .
Câu 53. (THPT Ba Đình - Thanh Hóa - 2021) Cho hình nón có bán kính đáy là r  2 và độ dài đường
sinh l  4. Tính diện tích xung quanh S của hình nón đã cho.
A. S  16 2 .
B. S  16 .
C. S  4 2 .
D. S  8 2 .
Câu 54. (THPT Ba Đình - Thanh Hóa - 2021) Cho khối cầu có thể tích 3
V  4 a a  0 . Tính theo a
bán kính của khối cầu. A. 3 R a 2 .
B. R a . C. 3 R a 4 . D. 3 R a 3 .
Câu 55. (THPT Quế Võ 1 - Bắc Ninh - 2021) Diện tích xung quanh của hình trụ có độ dài đường sinh l
và bán kính đáy r bằng 1 A. 4rl . B. 2rl . C. rl . D. rl . 3
Câu 56. (THPT Quốc Oai - Hà Nội - 2021) Một hình trụ có bán kính đáy r a , độ dài đường sinh
l  2a . Diện tích toàn phần của hình trụ là A. 2 6 a B. 2 2 a C. 2 4 a D. 2 5 a
Câu 57. (THPT Quốc Oai - Hà Nội - 2021) Cho khối nón có bán kính r  4 và chiều cao h  2 . Thể tích
của khối nón đã cho bằng: 32 8 A. 8 . B. . C. 32 . D. . 3 3
Câu 58. (THPT Quảng Xương 1-Thanh Hóa - 2021) Một khối trụ có thể tích 8 , độ dài đường cao
bằng 2. Khi đó bán kính đường tròn đáy bằng: A. 4 . B. 2 . C. 2 . D. 4 .
Câu 59. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho mặt cầu có diện tích hình tròn lớn là 4 . Thể
tích khối cầu đã cho bằng 32 256 A. . B. 16 .  C. 64 .  D. . 3 3
Câu 60. (THPT Quảng Xương 1-Thanh Hóa - 2021) Diện tích mặt cầu có bán kính 2R là: 4 16 A. 2 4 R . B. 2 R . C. 2 16 R . D. 2  R . 3 3
Câu 61. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Một hình trụ có diện tích xung quanh bằng 2 4 a và
bán kính đáy bằng a . Độ dài dường cao của hình trụ đó bằng A. a . B. 4a . C. 3a . D. 2a .
Câu 62. (THPT Phan Đình Phùng - Quảng Bình - 2021) Cho khối trụ có chiều cao h  3 và bán kính
đáy r  2. Thể tích của khối trụ đã cho bằng A. 18 B. 6 C. 4 D. 12
Câu 63. (THPT Phan Đình Phùng - Quảng Bình - 2021) Cho mặt cầu có bán kính R  6. Diện tích
S của mặt cầu đã cho bằng A. S  144 B. S  38 C. S  36 D. S  288
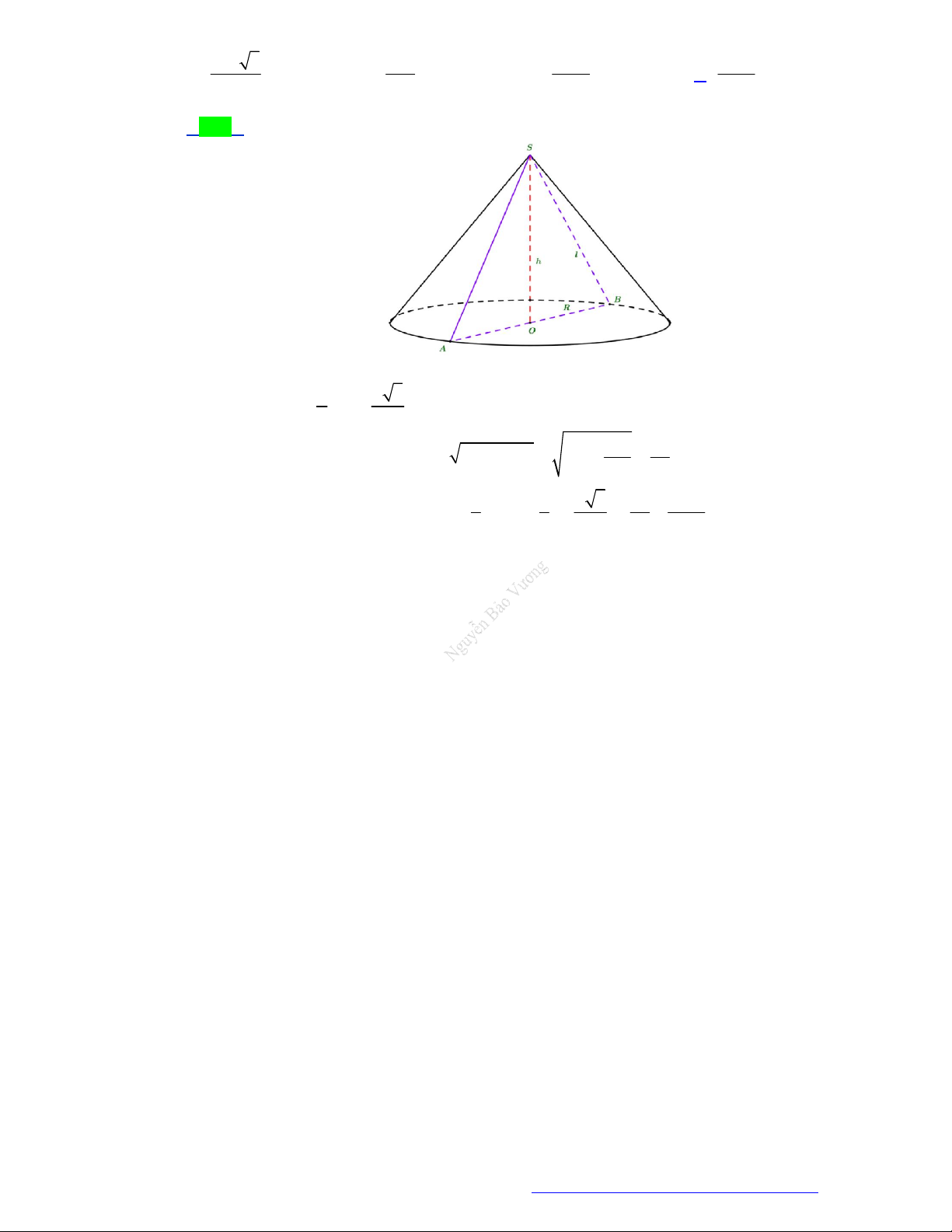
Câu 64. (THPT Phan Đình Phùng - Quảng Bình - 2021) Cho hình nón có bán kính đáy là r , đường cao
h và đường sinh l . Diện tích xung quang S hình nón đó là xq 1 A. 2 Sπr h . B. Sπrl . C. S  2πrl . D. Sπrh . xq 3 xq xq xq
Câu 65. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Cho hình nón có bán kính đáy r  3 và độ dài
đường cao h  4 . Tính diện tích xung quanh hình nón đó. A. 20 . B. 6 . C. 12 . D. 15 .
Câu 66. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Diện tích mặt cầu đường kính 4a bằng
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489 A. 2 64 a B. 2 16 a C. 2 4a D. 2 4 a
Câu 67. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho khối nón có chiều cao h  2 và bán kính
đáy r  3. Thể tích của khối nón đã cho là A. 6 . B. 18 . C. 6 . D. 36 .
Câu 68. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Diện tích toàn phần của hình trụ có thiết diện qua
trục là hình vuông cạnh a bằng 2 2 3 aa 2 A. 2 2 a . B. . C. . D. a . 2 2
Câu 69. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Một khối nón có diện tích xung quanh bằng 1 2
2 (cm ) và bán kính đáy (c )
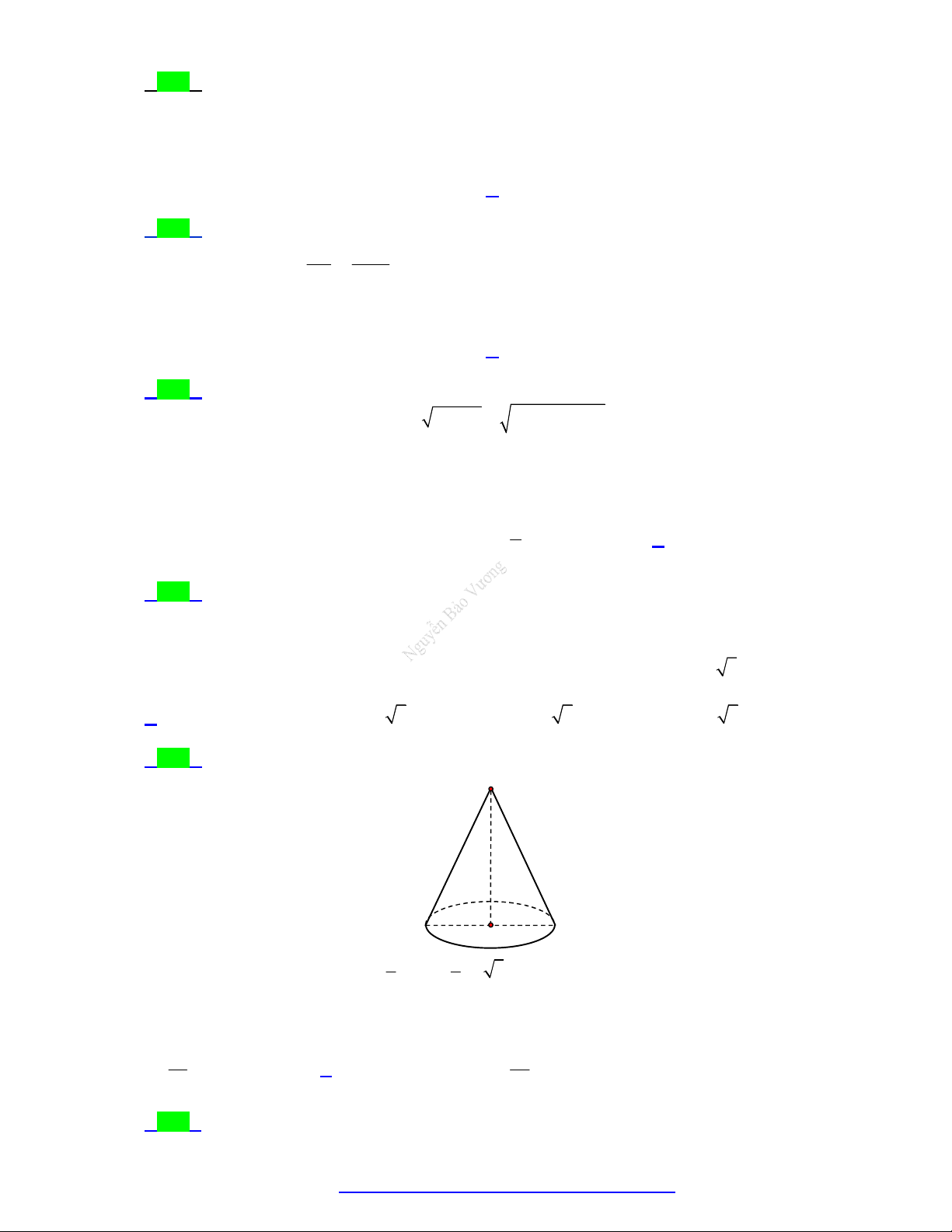
m . Khi đó độ dài đường sinh là 2 A. 3(cm) . B. 4(c ) m . C. 2(c ) m . D. 1(c ) m .
Câu 70. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho khối nón có bán kính đáy r  4 và chiều cao
h  2 . Thể tích của khối nón đã cho bằng 8 32 A. B. 8. C. . D. 32. 3 3
Câu 71. ( THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho khối trụ có bán kính đáy r  5 và chiều cao h  3 .
Thể tích của khối trụ đã cho bằng A. 5 . B. 30 . C. 25 . D. 75 .
Câu 72. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho khối cầu có bán kính R  3 . Thể tích của khối cầu đã cho bằng A. 3 . B. 9 . C. 4 . D. 36 .
Câu 73. (THPT Đồng Quan - Hà Nội - 2021) Thể tích khối nón có chiều cao bằng 2, bán kính hình tròn đáy bằng 5 là: 200 50 A. 25 . B. . C. 50 . D. . 3 3
Câu 74. (THPT Lê Lợi - Thanh Hóa - 2021) Cho hình nón  N  có bán kính bằng 3 và đường sinh
bằng 5 . Tính thể tích V của khối nón  N  là A. 36 . B. 12 . C. 20 . D. 60 .
Câu 75. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Cho một mặt cầu có diện tích là S , thể tích khối
cầu đó là V .Tính bán kính R của mặt cầu. 3V S 4V V A. R  . B. R  . C. R  . D. R  . S 3V S 3S
Câu 76. (Trung Tâm Thanh Tường - 2021) Diện tích mặt cầu bán kính 2a bằng: 4 A. 2 8 a . B. 2 16 a . C. 2 4 a . D. 2  a . 3
Câu 77. (Trung Tâm Thanh Tường - 2021) Diện tích xung quanh của hình trụ tròn xoay có bán kính đáy
bằng 4 và chiều cao bằng 3 là: A. 12 . B. 42 . C. 24 . D. 36 .
Câu 78. (Trung Tâm Thanh Tường - 2021) Cho khối nón có chiều cao h  3 , bán kính đáy r  4. Diện
tích xung quanh của khối nón đã cho bằng 25 A. 12 . B. 20 . C. . D. 15 . 3
Câu 79. (Trung Tâm Thanh Tường -2021) Tính thể tích V của khối nón có bán kính và chiều cao cùng bằng 6a ? A. 3 V  12 a . B. 3
V  216 a . C. 3 V  18 a . D. 3 V  72 a .
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Câu 80. (THPT Triệu Sơn - Thanh Hóa - 2021) Một hình nón có bán kính đáy bằng r  4cm và độ dài
đường sinh l  5cm .Diện tích xung quanh của khối nón đó bằng A. 10 2 cm . B. 2 20 cm . C. 2 12 cm . D. 2 15 cm .
Câu 81. (THPT Triệu Sơn - Thanh Hóa - 2021) Thể tích của khối cầu có bán kính R bằng 1 4 A. 2 4 R . B. 2  R . C. 3  R . D. 3  R . 3 3
Câu 82. (THPT Trần Phú - Đà Nẵng - 2021) Cho hình trụ có bán kính đáy R  2 và độ dài đường sinh
l  8 .Diện tích toàn phần của hình trụ đã cho bằng A. 40 . B. 36 . C. 96 . D. 24 .
Câu 83. (THPT Trần Phú - Đà Nẵng - 2021) Cho khối cầu có bán kính R
2 . Thể tích của khối cầu đã cho bằng 8 2 4 2 A. 4 . B. 8 . C. . D. . 3 3 BẢNG ĐÁP ÁN 1.C 2.B 3.B 4.B 5.D 6.A 7.D 8.C 9.C 10.D 11.A 12.B 13.B 14.C 15.B 16.C 17.D 18.A 19.C 20.A 21.B 22.A 23.A 24.A 25.C 26.A 27.A 28.C 29.C 30.B 31.A 32.C 33.A 34 35.D 36.A 37.B 38.D 39.C 40.B 41.A 42.C 43.A 44.B 45.C 46.B 47.B 48.A 49.C 50.D 51.B 52.A 53.C 54.D 55.B 56.A 57.B 58.C 59.A 60.C 61.D 62.D 63.A 64.B 65.D 66 67.C 68.B 69.B 70.C 71.D 72.D 73.D 74.B 75.A 76.B 77.C 78.B 79.D 80.B 81.D 82.A 83.C
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Chủ đề 6 KHỐI TRÒN XOAY
MỨC ĐỘ NHẬN BIẾT Câu 1.
(Sở Vĩnh Phúc - 2021) Cho hình nón có độ dài đường sinh bằng 4 , diện tích xung quanh bằng
8 . Tính bán kính hình trong đáy R của hình nón đó.
A. R  8 .
B. R  4 .
C. R  2 . D. R  1 . Lời giải Chọn C
Diện tích xung quanh của hình nón: S
  Rl  8   R.4  R  2 . xq Câu 2.
(Sở Vĩnh Phúc - 2021) Cho khối trụ có bán kính đáy r  4 và chiều cao h  2 . Tính thể tích khối trụ đó. 32 A. 8 . B. 32 . C. 16 . D. . 3 Lời giải Chọn B
Thể tích khối trụ là 2
V   r h  32 . Câu 3.
(Sở Lào Cai - 2021) Viết công thức tính diện tích xung quanh của hình trụ có đường cao h , bán
kính đường tròn đáy R . 2 A. S  2   SRh S   Rh xq h . B. S 2 xq Rh . C. 2 xq . D. xq . Lời giải Chọn B Câu 4.
(Sở Lào Cai - 2021) Cho hình nón có diện tích xung quanh bằng 2
5 a và bán kính đáy bằng a . Độ dài đường sinh
của hình nón đã cho bằng:
A. 3 2a . B. 5a . C. 3a . D. a 5 . Lời giải Chọn B Ta có 2 2 2 S
 5 a   rl  5 a   al  5 a l  5a . xq Câu 5.
(Sở Hà Tĩnh - 2021) Cho khối cầu có bán kính r  2 . Thể tích của khối cầu đã cho bằng 256 32 A. . B. 256 C. 64 . D. . 3 3 Lời giải Chọn D 4 4 32
Thể tích của khối cầu là: 3 3 V   r  .2  . 3 3 3 Câu 6.
(Sở Hà Tĩnh - 2021) Cho khối nón có bán kính đáy r  4 và chiều cao h  2 . Thể tích của khối nón đó bằng 32 8 A. . B. 32 . C. . D. 8 . 3 3 Lời giải Chọn A 1 32 Thể tích khối nón là 2
V   r h  . N 3 3 Câu 7.
(Sở Yên Bái - 2021) Mặt cầu có đường kính là 10. Diện tích S của mặt cầu bằng
A. S  25 . B. S  5 .
C. S  50 .
D. S  100 .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489 Lời giải Chọn D
Vì mặt cầu có đường kính là 10 2 2
R  5  S
 4 R  4 5  100 . mc Câu 8.
(Sở Tuyên Quang - 2021) Độ dài đường sinh hình nón có diện tích xung quanh bằng 2 6a và
đường kính đáy bằng 2a là: A. 2a . B. 6a . C. 3a . D. 9a . Lời giải Chọn C 2 Sxq 6 a Ta có S
 rl l    3a xqr 2a Câu 9.
(Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Cho hình nón có bán kính đáy bằng
4a và chiều cao bằng 3a . Diện tích xung quanh của hình nón bằng A. 2 20 a . B. 2 40 a . C. 2 12 a . D. 2 24 a . Lời giải Chọn C 2 2
Độ dài đường sinh của hình nón là: 2 2 l
r h  3a  4a  5a .
Diện tích xung quanh của hình nón bằng: 2 S   rl   3 .
a 4a  12 a . xq
Câu 10. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Cắt khối trụ bởi một mặt phẳng qua trục được
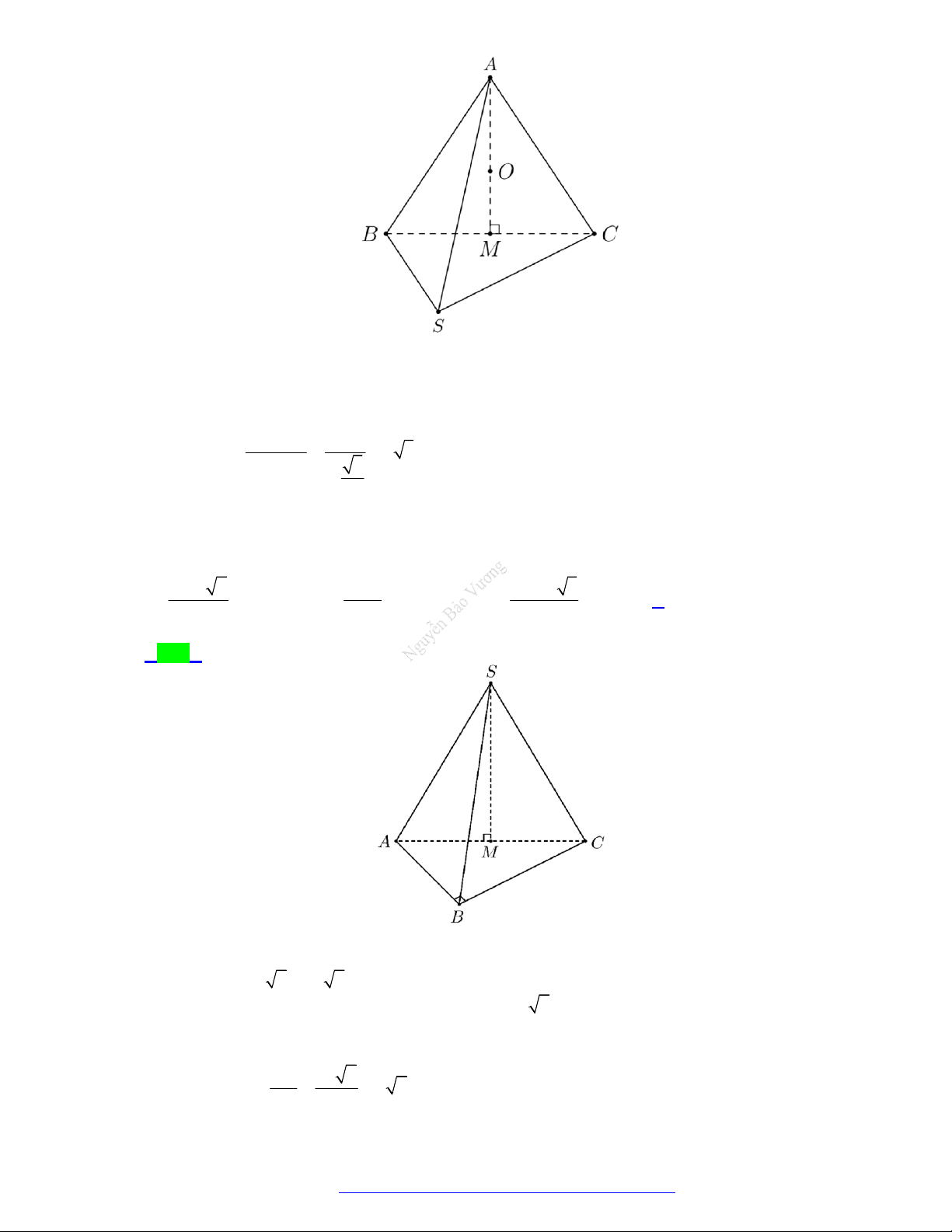
thiết diện là một hình vuông. Tính thể tích của khối trụ biết bán kính đáy của khối trụ bằng a 2 A. 3 4 a B. 3  a C. 3  a D. 3 2 a 3 Lời giải Chọn D
Vì thiết diện là hình vuông có cạnh bằng a nên ta có 2 2 3
h  2r  2a V   r h   a .2a  2 a .
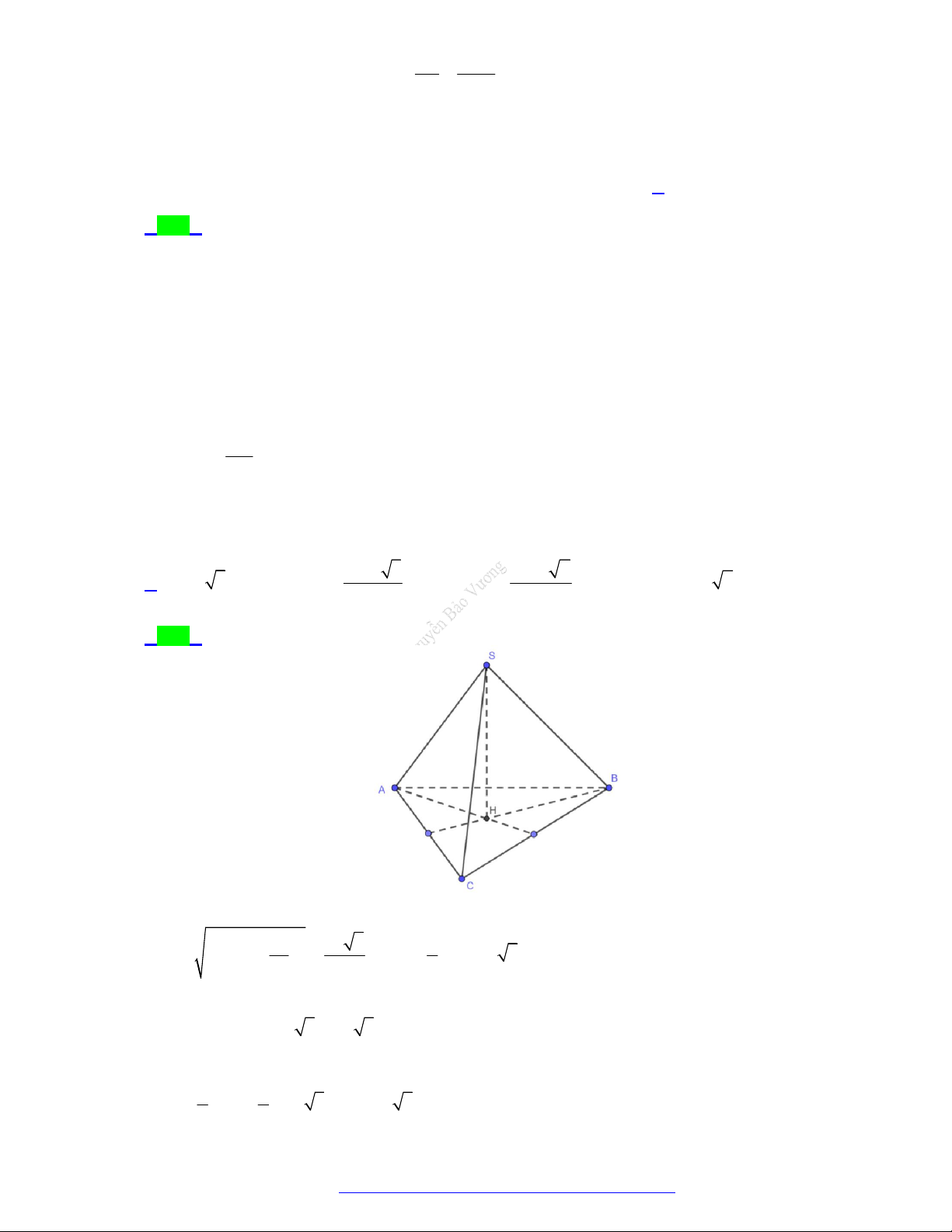
Câu 11. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Cho khối nón có bán kính r  5 và chiều cao
h  3 . Tính thể tích V của khối nón A. V  5 .
B. V   5 .
C. V   5 .
D. V   5 . Lời giải Chọn A S h r O 1 1
 Ta có thể tích của khối nón V   r h    52 2 .3  5 3 3
Câu 12. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Một hình trụ có bán kính đáy r  5cm , chiều cao
h  7cm . Diện tích xung quanh của hình trụ này là 35 70 A.   3 cm  . B.   3 70 cm  . C.   3 cm  . D.   3 35 cm  . 3 3 Lời giải Chọn B
Áp dụng công thức S   rl    3 2 70 cm
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Câu 13. (Chuyên Lê Hồng Phong - TPHCM - 2021) Cho hình lăng trụ có đường kính đáy bằng 6cm , độ
dài đường cao bằng 4cm . Tính diện tích xung quanh của hình trụ này. A. 2 22 cm . B. 2 24 cm . C. 2 18 cm . D. 2 20 cm . Lời giải Chọn B 6 Bán kính đáy r
 2 ; chiều cao h  4 . 3 Có 2 2 S
 2.r.h  2 .3.4 cm  24 cm xq
Câu 14. (Chuyên Lam Sơn - Thanh Hóa - 2021) Thể tích khối trụ có bán kính r và chiều cao h bằng: 4 1 A. 2  r h . B. 2  r h . C. 2  r h . D. 2 rh . 3 3 Lời giải Chọn C Ta có: 2 V   r h .
Câu 15. (Chuyên Lam Sơn - Thanh Hóa - 2021) Thể tích của khối nón tròn xoay có đường kính đáy
bằng 6 và chiều cao bằng 5 là A. 45 B. 15 C. 60 D. 180 Lời giải Chọn B 1 1
 Thể tích khối nón tròn xoay là 2 2
x  5  V   r h   .3 .5  15 . 3 3
Câu 16. (Chuyên Lam Sơn - Thanh Hóa - 2021) Diện tích của mặt cầu có bán kính R bằng. 4 A. 2 R . B. 2  R . C. 2 4 R . D. 3  R . 3 Lời giải Chọn C
 Diện tích của mặt cầu có bán kính R là 2 S  4 R .
Câu 17. (Chuyên KHTN - 2021) Cho khối nón có bán kính đáy r a và chiều cao h  2a . Thể tích của khối nón đã cho bằng 3 4 a 3 2 a A. . B. 3 4 a . C. 3 2 a . D. . 3 3 Lời giải Chọn D 1 1 3 2 a
Thể tích của khối nón đã cho là: 2 V   r h 2
  a .2a  . 3 3 3
Câu 18. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Diện tích xung quanh của hình trụ có độ dài
đường sinh bằng l và bán kính r bằng 1 A. 2 rl. B. 2  r . C. rl. D. rl. 3 Lời giải Chọn A
Diện tích xung quanh của hình trụ là S  2 rl . xq
Câu 19. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Thể tích của hình nón có bán kính đáy r  2 và
đường cao h  3 là A. 6 . B. 2 . C. 4 . D. 12 . Lời giải Chọn C
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489 1  Áp dụng công thức: 2 V   r h 3 1
 Thể tích hình nón là: 2
V  .2 .3  4 . 3
Câu 20. (Chuyên Quốc Học Huế - 2021) Cho khối trụ có bán kính đáy bằng r  5 và chiều cao h  3 .
Thể tích của khối trụ đã cho bằng A. 75 . B. 30 . C. 25 . D. 5 . Lời giải Chọn A
Thể tích của khối trụ đã cho là 2 2
V Bh   r h   .5 .3  75 .
Câu 21. (Chuyên Quốc Học Huế - 2021) Cho khối nón có chiều cao bằng 2a và bán kính đáy bằng a .
Thể tích của khối nón đã cho bằng 3 4 a 3 2 a 3  a A. . B. . C. . D. 3 2 a . 3 3 3 Lời giải Chọn B 3 1 1 2 a Thể tích của khối nón 2 2
V   r h   a .2a  . 3 3 3
Câu 22. (Chuyên Quốc Học Huế - 2021) Cắt hình trụ T  bởi một mặt phẳng qua trục của nó, ta được thiết
diện là một hình vuông cạnh bằng 10. Diện tích xung quanh của T  là A. 100 . B. 150 . C. 50 . D. 200 . Lời giải Chọn A
Do thiết diện qua trục là một hình vuông cạnh bằng 10 nên ta có l h  10, r  5 .
Diện tích xung quanh của T  là S  2 rl  2 .5.10  100 . xq
Câu 23. (Chuyên Quang Trung - Bình Phước - 2021) Khối trụ có bán kính đáy, đường cao lần lượt là
a, 2a thì có thể tích bằng: 3 2 a 3  a A. 3 2 a . B. . C. 3  a . D. . 3 3 Lời giải Chọn A
Thể tích của khối trụ: 2 2 3
V   r h   a 2a  2 a
Câu 24. (Chuyên Quang Trung - Bình Phước - 2021) Hình nón có bán kính đáy, đường cao lần lượt là
3, 4 thì diện tích xung quanh hình nón bằng: 15 A. 15 . B. . C. 12 . D. 6 . 2 Lời giải Chọn A Đường sinh: 2 2 2 2
l h r  4  3  5
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Diện tích xung quanh hình nón: S
  rl   .3.5  15 . xq
Câu 25. (Chuyên Ngoại Ngữ Hà Nội- 2021) Thể tích của khối trụ có chiều cao h  2 và bán kính đáy r  3 bằng? A. 4 . B. 12 . C. 18 . D. 6 . Lời giải Chọn C
Thể tích khối trụ là: 2
V   r h  18
Câu 26. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Tính diện tích xung quanh của một hình trụ có chiều
cao 20m , chu vi đáy bằng 5m . A. 2 100m . B. 2 50 m . C. 2 100 m . D. 2 50m . Lời giải Chọn A
Diện tích xung quanh của hình trụ: 2
S  2 rl  5.20  100m .
Câu 27. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Cho khối cầu bán kính r  3. Thể tích khối cầu đã cho bằng 32 8 A. 36 . B. . C. . D. 16 . 3 3 Lời giải Chọn A 3 3 4 r 4 .3
Thể tích khối cầu là V    36 . 3 3
Câu 28. (Chuyên Hạ Long - Quảng Ninh - 2021) Cho hình nón có bán kính đáy r  6 và chiều cao
h  8 . Diện tích xung quanh của hình nón đã cho bằng A. 120 B. 64 C. 60 D. 80 Lời giải. CHỌN C Ta có: 2 2
l= h r  10 . Vây: S   rl  60 xq
Câu 29. (Chuyên Hạ Long - Quảng Ninh - 2021) Cho khối trụ có bán kính r  3 và độ dài đường sinh
l  5 . Thể tích của khối trụ đã cho bằng
A. V  15 .
B. V  12 .
C. V  45 .
D. V  36 . Lời giải Chọn C
Thể tích của khối trụ là: 2 2 2
V   r h   r l   .3 .5  45 . 3
Câu 30. (Chuyên ĐHSP Hà Nội - 2021) Cho mặt cầu có bán kính r
. Diện tích của mặt cầu đã cho 2 bằng
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489 3 A. 3 . B. 3 . C. 3 3 . D.  . 2 Lời giải Chọn B 2  3  Ta có: 2
S  4 r  4 .   3 . 2  
Câu 31. (Chuyên ĐHSP Hà Nội - 2021) Cho hình nón có thiết diện qua trục là một tam giác vuông cân có
cạnh huyền bằng 2a . Diện tích xung quanh của hình nón bằng A. 2  2a . B. 2 2 2a . C. 2 2 a . D. 2  a . Lời giải Chọn A
Xét tam giác SAB vuông cân tại S có cạnh huyền AB  2a nên SA SB a 2 . AB
Hình nón có r OB
a , l SB a 2 . 2 Nên 2 S   rl   . .
a a 2   2a . xq
Câu 32. (Chuyên ĐHSP Hà Nội - 2021) Cho hình nón có đường kính đáy bằng 2 , đường cao bằng 3 .
Diện tích xung quanh của hình nón đã cho bằng A. 3 . B.  10   1  . C. 10 . D. 6 . Lời giải Chọn C
Ta có diện tích xung quanh của hình nón là S   rl . xq d 2 Mà r    1 suy ra 2 2 2 2
l h r  3 1  10 . Vậy S
  rl   .1. 10  10 . 2 2 xq
Câu 33. (Chuyên ĐHSP Hà Nội - 2021) Cho hình trụ có bán kính đáy r  3 và độ dài đường sinh l  5 .
Thể tích khối trụ đã cho bằng A. 45 . B. 30 . C. 15 . D. 90 . Lời giải Chọn A
Thể tích khối trụ đã cho là 2 2 2
V   r h   r l   .3 .5  45 .
Câu 34. (Chuyên ĐH Vinh - Nghệ An - 2021) Cho góc ở đỉnh của một hình nón bằng o
60 . Gọi r, h, l lần
lượt là bán kính, đường cao, đường sinh của hình nón đó. Khẳng định nào sau đây đúng?
A. l  2r .
B. h r .
C. h  2r .
D. l r . Lời giải Chọn A
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Tam giác SAB có  o
ASB  60  tam giác SAB đều và O là trung điểm AB nên l  2r .
Câu 35. (Chuyên ĐH Vinh - Nghệ An - 2021) Chu vi của đường tròn lớn của mặt cầu S  ; O R là A. 2  R . B. 2 4 R . C. R . D. 2 R . Lời giải Chọn D
Đường tròn lớn của mặt cầu S  ;
O R là đường tròn tâm O , bán kính R nên có chu vi là 2 R .
Câu 36. (Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Cho AB
H vuông tại H , AH  3a ,
BH  2a . Quay A
BH quanh trục AH ta được một khối nón có thể tích là 4 A. 3 4 a . B. 3 18 a . C. 3  a . D. 3 12 a . 3 Lời giải Chọn A
Khối nón có h AH  3a , r BH  2a . 1 1
Áp dụng công thức V   r h  . .2a2 2 3
.3a  4 a . 3 3
Câu 37. (THPT Thanh Chương 1- Nghệ An - 2021) Cho hình cầu có đường kính bằng . Diện tích của hình cầu đã cho bằng A. B. C. D. Lời giải Chọn B
Diện tích của mặt cầu là .
Câu 38. (THPT Nguyễn Huệ - Phú Yên - 2021) Thể tích khối cầu có bán kính 2a bằng 16 4 32 A. 3  a . B. 3  a . C. 3 4 a . D. 3  a . 3 3 3 Lời giải Chọn D 4 4 32
Thể tích khối cầu: V
R   2a3 3 3   a . 3 3 3
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 39. (THPT Nguyễn Huệ - Phú Yên - 2021) Cho hình chữ nhật ABCD (kể cả miền trong), quay hình
chữ nhật đó quanh một cạnh thì thể tích vật thể tròn xoay được tạo thành là: A. Hình trụ. B. Khối nón. C. Khối trụ. D. Hình nón. Lời giải Chọn C
Cho hình chữ nhật ABCD (kể cả miền trong), quay hình chữ nhật đó quanh một cạnh thì thể tích
vật thể tròn xoay được tạo thành là một khối trụ.
Câu 40. (THPT Nguyễn Huệ - Phú Yên - 2021) Hình nón có đường sinh bằng 6 , diện tích xung quanh
bằng 12 . Bán kính đường tròn đáy của hình nón đó bằng 1 A. 4 . B. 2 . C. . D. 1. 2 Lời giải Chọn B 12
 Bán kính đường tròn đáy của hình nón đó là: r   2 .  .6
Câu 41. (THPT Lương Thế Vinh - 2021) Cho hình trụ có độ dài đường sinh l  5 và bán kính đáy r  3.
Diện tích xung quanh của hình trụ đã cho bằng A. 30 B. 15 . C. 5 . D. 24 . Lời giải Chọn A
Diện tích xung quanh của hình trụ là S
 2 rl  2 .5.3  30 . xq
Câu 42. (THPT Lương Thế Vinh - 2021) Cho khối nón có bán kính đáy là r  2 và chiều cao h  3 .
Tính thể tích của khối nón đã cho là? 2 3 4 3 4 A. 4 3 . B. . C. . D. . 3 3 3 Lời giải Chọn C 1 1 4 3
Thể tích khối nón đã cho là 2 2 V  .
h r  . 3. 2  . 3 3 3
Câu 43. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho hình trụ có bán kính đáy r  3 và chiều cao
h  4 . Diện tích xung quanh của hình trụ bằng. A. 8 3 . B. 2 3 . C. 4 3 . D. 16 3 . Lời giải Chọn A S  2 rl  2 rh  2 .  3.4  8 3 . xq
Câu 44. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho hình nón có diện tích xung quanh bằng 2 3 a
và bán kính đáy bằng a . Độ dài đường sinh l của hình nón đã cho bằng 5a 3a A. l  .
B. l  3a . C. l  .
D. l  2 2a . 2 2 Lời giải Chọn B 2 Sxq 3 a
 Hình nón có diện tích xung quanh là: S   rl l    3a . xqra
Câu 45. (THPT Đào Duy Từ - Hà Nội - 2021) Cho khối nón có chu vi đáy 8 và chiều cao h  3 . Thể
tích khối nón đã cho bằng A. 12 . B. 4 . C. 16 . D. 24 . Lời giải
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Chọn C
 Chu vi đáy bằng 8  r  4 . 1
 Thể tích khối nón đã cho là 2
V   r h  16 . 3
Câu 46. (THPT Đào Duy Từ - Hà Nội - 2021) Cho hình nón có bán kính đáy r  2 và độ dài đường sinh
l  4. Diện tích xung quanh của hình nón đã cho bằng A. 32 . B. 8 . C. 16 . D. 48 . Lời giải Chọn B
 Ta có: S   rl   .2.4  8 . xq
Câu 47. (THPT Đào Duy Từ - Hà Nội - 2021) Thể tích của khối cầu có bán kính r  3 là A. 64 . B. 48 . C. 8 . D. 36 . Lời giải Chọn B 4 4
 Thể tích của khối cầu có bán kính r  3 là 3 3 V
r   .3  48 . 3 3
Câu 48. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Diện tích của mặt cầu có đường kính bằng 4a là A. 2 S  16 a . B. 2 S  12 a . C. 2 S  8 a . D. 2 S  64 a . Lời giải Chọn A 4a
Bán kính mặt cầu là R   2a . 2
Diện tích của mặt cầu là S   R    a2 2 2 4 4 . 2  16 a .
Câu 49. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Thể tích của khối trụ tròn xoay có bán kính r , chiều cao h bằng? 2  r h A. . B. 2 3 r h . C. 2  r h . D. 2 2 r h . 3 Lời giải Chọn C
Thể tích khối trụ là: 2 V   r h
Câu 50. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho hình nón có bán kính đáy bằng 3 , độ dài đường
cao bằng 4 . Diện tích xung quanh của hình nón bằng: A. 24 . B. 12 . C. 30 . D. 15 . Lời giải Chọn D  Đường sinh 2 2
l SA  3  4  5 .
 Diện tích xung quanh hình nón: S   rl   .3.5  15 . xq
Câu 51. (THPT Chu Văn An - Thái Nguyên - 2021) Cho hình nón có độ dài đường sinh l  4 và bán 1 kính đáy r
. Diện tích xung quanh của hình nón bằng 4
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
NGUYỄN BẢO VƯƠNG - 0946798489A. 2 . B.  . C. . D. 4 . 2 Lời giải Chọn B 1
Diện tích xung quanh của hình nón bằng S
  rl  4    . xq 4
Câu 52. (THPT Chu Văn An - Thái Nguyên - 2021) Cho khối cầu có thể tích là 36 . Diện tích mặt cầu đã cho bằng A. 36 . B. 16 . C. 18 . D. 12 . Lời giải Chọn D 4 4 3 3 2 V   R
R  36  R  3  S  4 R  36 . 3 3 xq
Câu 53. (THPT Ba Đình - Thanh Hóa - 2021) Cho hình nón có bán kính đáy là r  2 và độ dài đường
sinh l  4. Tính diện tích xung quanh S của hình nón đã cho.
A. S  16 2 .
B. S  16 .
C. S  4 2 .
D. S  8 2 . Lời giải Chọn C Ta có: S
  rl  4 2 . xq
Câu 54. (THPT Ba Đình - Thanh Hóa - 2021) Cho khối cầu có thể tích 3
V  4 a a  0 . Tính theo a
bán kính của khối cầu. A. 3 R a 2 .
B. R a . C. 3 R a 4 . D. 3 R a 3 . Lời giải Chọn D 4 3 3 3 V
R  4 a R a 3 . 3
Câu 55. (THPT Quế Võ 1 - Bắc Ninh - 2021) Diện tích xung quanh của hình trụ có độ dài đường sinh l
và bán kính đáy r bằng 1 A. 4rl . B. 2rl . C. rl . D. rl . 3 Lời giải Chọn B
Diện tích xung quanh hình trụ bằng S  2rl . xq
Câu 56. (THPT Quốc Oai - Hà Nội - 2021) Một hình trụ có bán kính đáy r a , độ dài đường sinh
l  2a . Diện tích toàn phần của hình trụ là A. 2 6 a B. 2 2 a C. 2 4 a D. 2 5 a Lời giải Chọn A Hình trụ đã cho có 2 2 2
S  2 rl  2 r  2 . .2
a a  2 a  6 a . tp
Câu 57. (THPT Quốc Oai - Hà Nội - 2021) Cho khối nón có bán kính r  4 và chiều cao h  2 . Thể tích
của khối nón đã cho bằng: 32 8 A. 8 . B. . C. 32 . D. . 3 3 Lời giải Chọn B 1 1 32
Thể tích của khối nón đã cho là: 2 2
V   r h   4 .2  3 3 3
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Câu 58. (THPT Quảng Xương 1-Thanh Hóa - 2021) Một khối trụ có thể tích 8 , độ dài đường cao
bằng 2. Khi đó bán kính đường tròn đáy bằng: A. 4 . B. 2 . C. 2 . D. 4 . Lời giải Chọn C 8
Diện tích hình tròn đáy là:  4 . 2 4
Bán kính đường tròn đáy là:  2 . 
Câu 59. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho mặt cầu có diện tích hình tròn lớn là 4 . Thể
tích khối cầu đã cho bằng 32 256 A. . B. 16 .  C. 64 .  D. . 3 3 Lời giải Chọn A
Bán kính của hình tròn lớn của mặt cầu là bán kính của mặt cầu giả sử R .
Diện tích hình tròn lớn là 2 R   4  R  2. 4 32 Thể tích khối cầu là 3 V  R  . 3 3
Câu 60. (THPT Quảng Xương 1-Thanh Hóa - 2021) Diện tích mặt cầu có bán kính 2R là: 4 16 A. 2 4 R . B. 2 R . C. 2 16 R . D. 2  R . 3 3 Lời giải Chọn C
S    R2 2 4 2  16 R .
Câu 61. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Một hình trụ có diện tích xung quanh bằng 2 4 a và
bán kính đáy bằng a . Độ dài dường cao của hình trụ đó bằng A. a . B. 4a . C. 3a . D. 2a . Lời giải Chọn D 2 Sxq 4 a Ta có S
 2 rl l    2a . xq 2 r 2 a
Câu 62. (THPT Phan Đình Phùng - Quảng Bình - 2021) Cho khối trụ có chiều cao h  3 và bán kính
đáy r  2. Thể tích của khối trụ đã cho bằng A. 18 B. 6 C. 4 D. 12 Lời giải Chọn D
Thể tích của khối trụ đã cho là: 2 2
V   .r .h   .2 .3  12
Câu 63. (THPT Phan Đình Phùng - Quảng Bình - 2021) Cho mặt cầu có bán kính R  6. Diện tích
S của mặt cầu đã cho bằng A. S  144 B. S  38 C. S  36 D. S  288 Lời giải Chọn A
Diện tích S của mặt cầu đã cho là: 2 2
S  4 R  4 .6  144
Câu 64. (THPT Phan Đình Phùng - Quảng Bình - 2021) Cho hình nón có bán kính đáy là r , đường cao
h và đường sinh l . Diện tích xung quang S hình nón đó là xq 1 A. 2 Sπr h . B. Sπrl . C. S  2πrl . D. Sπrh . xq 3 xq xq xq
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
NGUYỄN BẢO VƯƠNG - 0946798489 Lời giải Chọn B Có S
πrl nên chọn đáp án B xq
Câu 65. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Cho hình nón có bán kính đáy r  3 và độ dài
đường cao h  4 . Tính diện tích xung quanh hình nón đó. A. 20 . B. 6 . C. 12 . D. 15 . Lời giải Chọn D.
Độ dài đường sinh hình nón là 2 2 2 2
l r h  3  4  5 .
Diện tích xung quanh của hình nón là S
  rl   .3.5  15 . xq
Câu 66. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Diện tích mặt cầu đường kính 4a bằng A. 2 64 a B. 2 16 a C. 2 4a D. 2 4 a Lời giải Chọn D Đường kính 2 2
4a R  2a S  4 R  16 a . C
Câu 67. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho khối nón có chiều cao h  2 và bán kính
đáy r  3. Thể tích của khối nón đã cho là A. 6 . B. 18 . C. 6 . D. 36 . Lời giải Chọn C 1 1
Ta có thể tích của khối nón đã cho là 2 2
V   R h   .3 .2  6 . 3 3
Câu 68. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Diện tích toàn phần của hình trụ có thiết diện qua
trục là hình vuông cạnh a bằng 2 2 3 aa 2 A. 2 2 a . B. . C. . D. a . 2 2 Lời giải Chọn B a
Ta có hình trụ có thiết diện qua trục là hình vuông cạnh a nên l h a, r  . 2 2 2 aa  3 a Do đó 2
S S S
 2 rl  2 r  2. .a  2  . tp xq 2d   2  2  2
Câu 69. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Một khối nón có diện tích xung quanh bằng 1 2
2 (cm ) và bán kính đáy (c )
m . Khi đó độ dài đường sinh là 2 A. 3(c ) m . B. 4(c ) m . C. 2(c ) m . D. 1(c ) m . Lời giải
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Chọn B Sxq 2 Ta có S
  Rl l    4(cm) . xqR 1  . 2
Câu 70. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho khối nón có bán kính đáy r  4 và chiều cao
h  2 . Thể tích của khối nón đã cho bằng 8 32 A. B. 8. C. . D. 32. 3 3 Lời giải Chọn C 1 1 32
Ta có thể tích khối nón là 2 2
V   r h   .4 .2  : 3 3 3 Vậy ta chọn phương án C.
Câu 71. ( THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho khối trụ có bán kính đáy r  5 và chiều cao h  3 .
Thể tích của khối trụ đã cho bằng A. 5 . B. 30 . C. 25 . D. 75 . Lời giải Chọn D
Ta có thể tích khối trụ: 2 2
V hS hr  3. .5  75 .
Câu 72. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho khối cầu có bán kính R  3 . Thể tích của khối cầu đã cho bằng A. 3 . B. 9 . C. 4 . D. 36 . Lời giải Chọn D 4 4
Ta có thể tích khối cầu: 3 3 V   R  . .3  36 . 3 3
Câu 73. (THPT Đồng Quan - Hà Nội - 2021) Thể tích khối nón có chiều cao bằng 2, bán kính hình tròn đáy bằng 5 là: 200 50 A. 25 . B. . C. 50 . D. . 3 3 Lời giải Chọn D 1 2 1 2 50 V
R h   .5 .2  . 3 3 3
Câu 74. (THPT Lê Lợi - Thanh Hóa - 2021) Cho hình nón  N  có bán kính bằng 3 và đường sinh
bằng 5 . Tính thể tích V của khối nón  N  là A. 36 . B. 12 . C. 20 . D. 60 . Lời giải Chọn B Ta có: 2 2 2 2
h l r  5  3  4 . 1 1 2 2 V
  r h   .3 .4  12 . N  3 3
Câu 75. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Cho một mặt cầu có diện tích là S , thể tích khối
cầu đó là V .Tính bán kính R của mặt cầu. 3V S 4V V A. R  . B. R  . C. R  . D. R  . S 3V S 3S Lời giải Chọn A
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
NGUYỄN BẢO VƯƠNG - 0946798489 4 3  R V 1 3 3 V   R R  . 2 S 4 R 3 S
Câu 76. (Trung Tâm Thanh Tường - 2021) Diện tích mặt cầu bán kính 2a bằng: 4 A. 2 8 a . B. 2 16 a . C. 2 4 a . D. 2  a . 3 Lời giải: Chọn B.
Ta có: S   R    a2 2 2 4 4 . 2  16 a .
Câu 77. (Trung Tâm Thanh Tường - 2021) Diện tích xung quanh của hình trụ tròn xoay có bán kính đáy
bằng 4 và chiều cao bằng 3 là: A. 12 . B. 42 . C. 24 . D. 36 . Lời giải: Chọn C.
Ta có: Hình trụ tròn xoay có l h  3 . S
 2 Rl  2 .4.3  24 . xq
Câu 78. (Trung Tâm Thanh Tường - 2021) Cho khối nón có chiều cao h  3 , bán kính đáy r  4 . Diện
tích xung quanh của khối nón đã cho bằng 25 A. 12 . B. 20 . C. . D. 15 . 3 Lời giải Chọn B
Đường sinh của khối nón là: 2 2
l h r  5 .
Diện tích xung quanh của khối nón đã cho là: S
  rl   .4.5  20 xq  .
Câu 79. (Trung Tâm Thanh Tường -2021) Tính thể tích V của khối nón có bán kính và chiều cao cùng bằng 6a ? A. 3 V  12 a . B. 3
V  216 a . C. 3 V  18 a . D. 3 V  72 a . Lời giải Chọn D 1
Khối nón có bán kính và chiều cao cùng bằng 6a có thể tích là V   6a2 3
.6a  72 a . 3
Câu 80. (THPT Triệu Sơn - Thanh Hóa - 2021) Một hình nón có bán kính đáy bằng r  4cm và độ dài
đường sinh l  5cm .Diện tích xung quanh của khối nón đó bằng A. 10 2 cm . B. 2 20 cm . C. 2 12 cm . D. 2 15 cm . Lời giải Chọn B
Ta có diện tích xung quanh của khối nón đó bằng 2 S
  rl  20 cm xq
Câu 81. (THPT Triệu Sơn - Thanh Hóa - 2021) Thể tích của khối cầu có bán kính R bằng
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 1 4 A. 2 4 R . B. 2  R . C. 3  R . D. 3  R . 3 3 Lời giải Chọn D 4
Thể tích của khối cầu có bán kính R bằng 3  R . 3
Câu 82. (THPT Trần Phú - Đà Nẵng - 2021) Cho hình trụ có bán kính đáy R  2 và độ dài đường sinh
l  8 .Diện tích toàn phần của hình trụ đã cho bằng A. 40 . B. 36 . C. 96 . D. 24 . Lời giải Chọn A
Diện tích toàn phần của hình trụ đã cho bằng 2
S  2 Rl  2 R  40 . tp
Câu 83. (THPT Trần Phú - Đà Nẵng - 2021) Cho khối cầu có bán kính R
2 . Thể tích của khối cầu đã cho bằng 8 2 4 2 A. 4 . B. 8 . C. . D. . 3 3 Lời giải 4 4 8 2 Ta có V   R    2 3 3  . 3 3 3
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Chủ đề 6 KHỐI TRÒN XOAY
MỨC ĐỘ THÔNG HIỂU Câu 1.
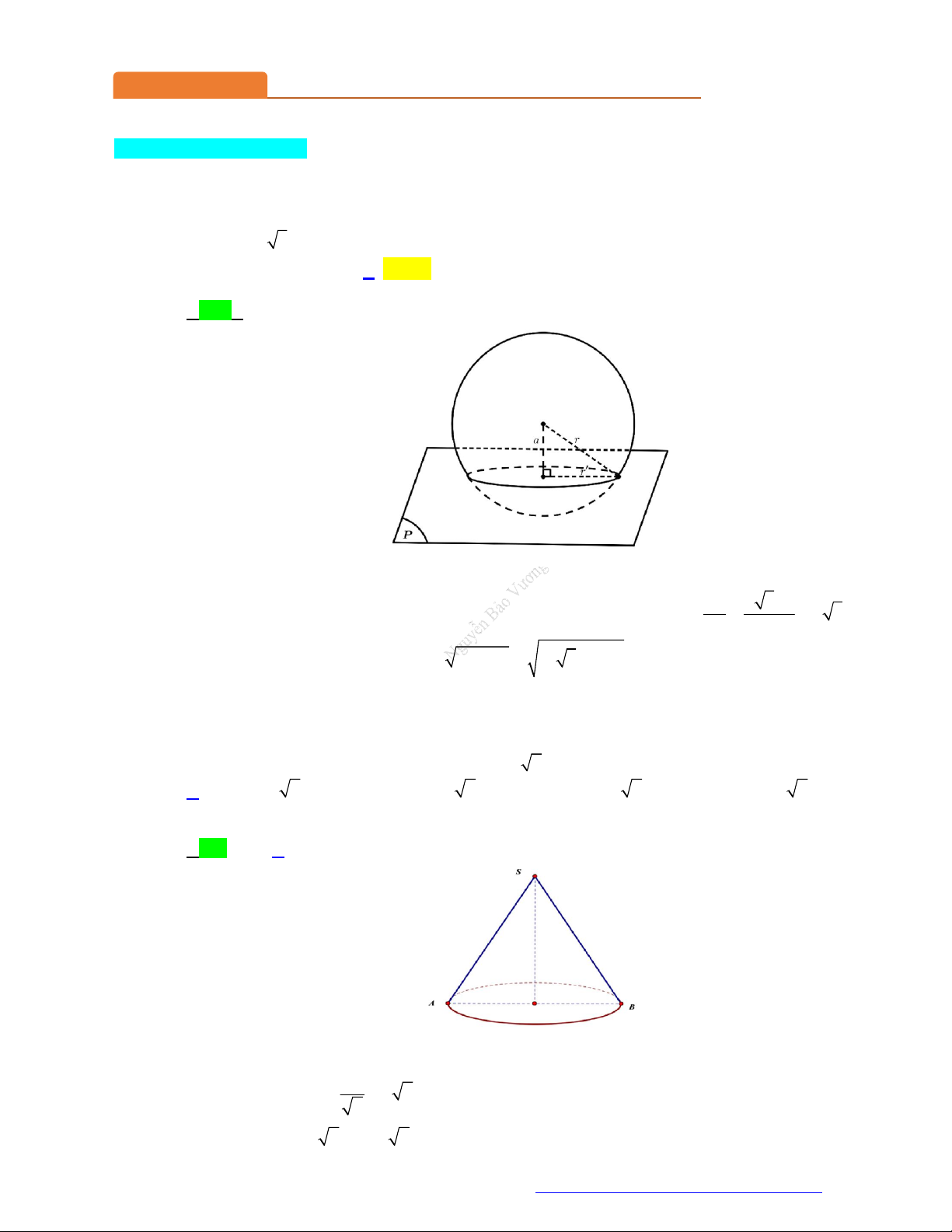
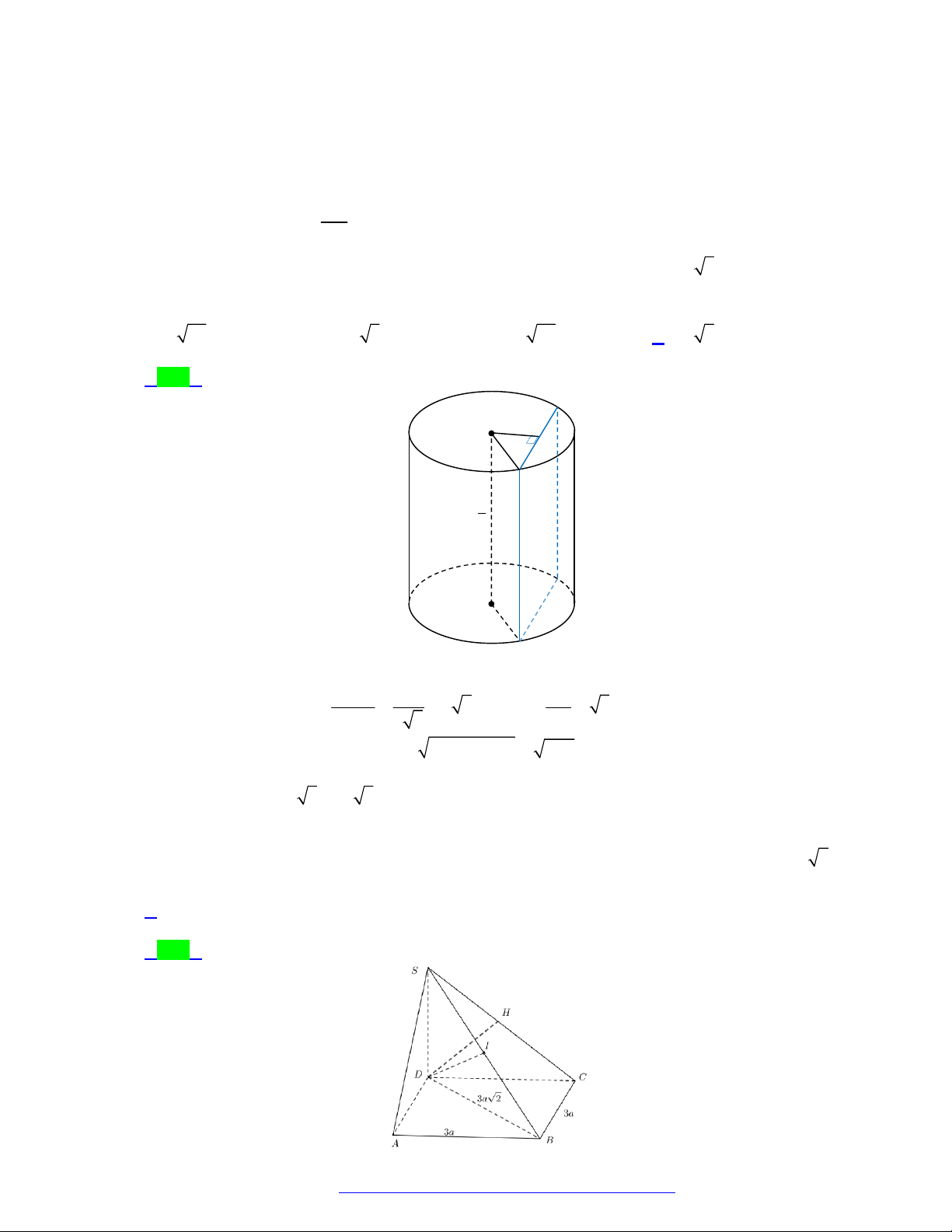
(Sở Vĩnh Phúc - 2021) Cho mặt cầu  S  và mặt phẳng  P , biết khoảng cách từ tâm của mặt cầu
S  đến mặt phẳng P bằng a . Mặt phẳng P cắt mặt cầu S  theo giao tuyến là đường tròn
có chu vi 2 3 a . Diện tích mặt cầu S  bằng bao nhiêu? A. 2 12 a . B. 2 16 a . C. 2 4 a . D. 2 8 a . Câu 2.
(Sở Vĩnh Phúc - 2021) Tính diện tích toàn phần S của mặt nón  N  biết thiết diện qua trục của
nó là một tam giác vuông có cạnh huyền bằng 2 2a A. S     2 2
2 2  a . B. S     2 4
4 2  a . C. S     2 2
4 2  a . D. S     2 4 2 2  a . Câu 3.
(Sở Yên Bái - 2021) Cho khối nón có thể tích là V . Biết rằng khi cắt khối nón đã cho bởi một mặt
phẳng qua trục, thiết diện thu được là một tam giác đều có diện tích bằng 3 . Giá trị của V bằng  3 A. 4 . B. 2 . C.  3. D. . 3 Câu 4.
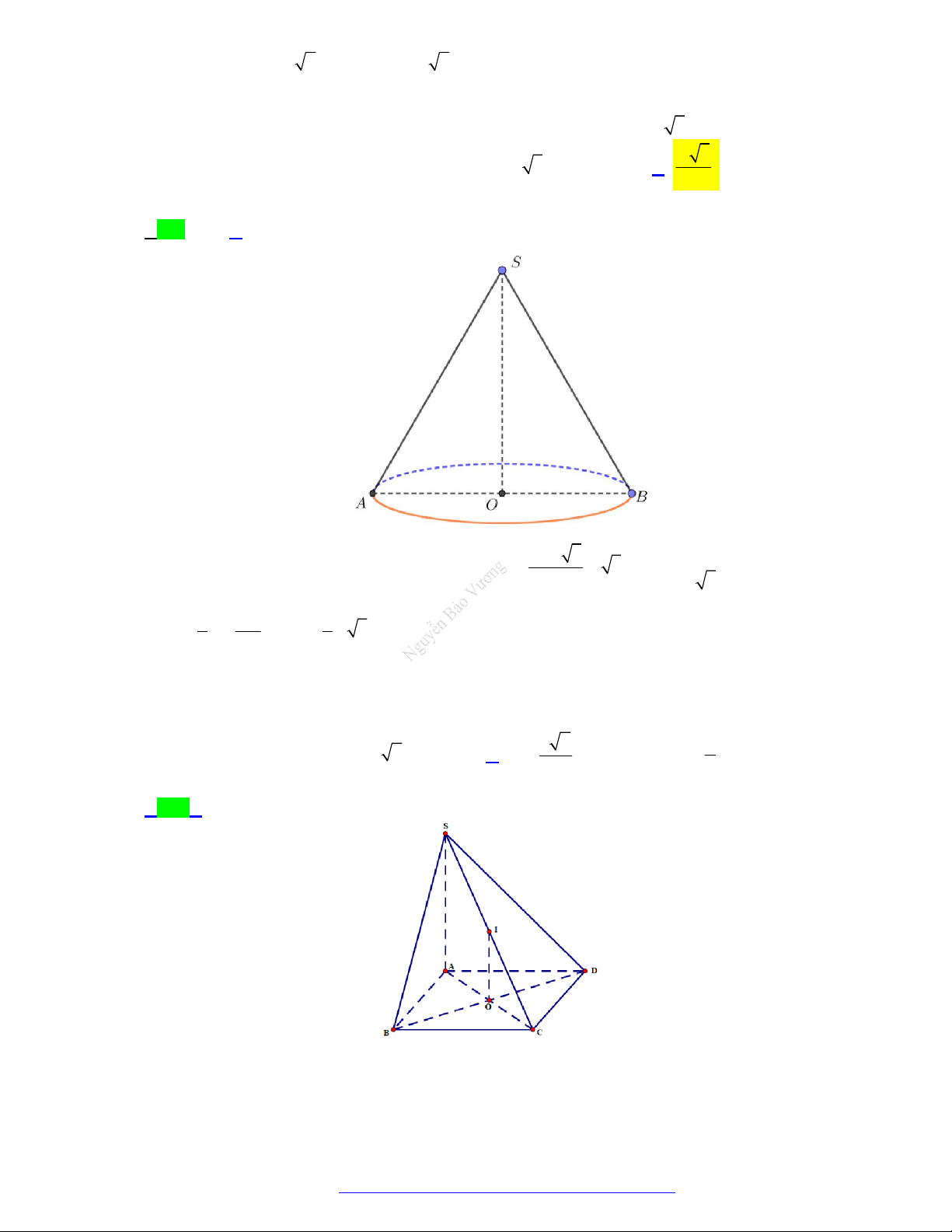
(Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Cho hình chóp S.ABCD có đáy là
hình chữ nhật, AB  3 , AD  4 , cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa SC và mặt
phẳng đáy là 45 . Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD . 5 2 5 A. R  5 . B. R  5 2 . C. R  . D. R  . 2 2 Câu 5.
(Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Cho hình lập phương có cạnh bằng a .
Thể tích khối cầu ngoại tiếp hình lập phương đó bằng 3  a 3 4 3 3  a 3 A. . B. 3  a . C. 3 4 3 a . D. . 3 3 2 Câu 6.
(Chuyên Lê Hồng Phong - TPHCM - 2021) Cho hình lập phương ABC . D A BCD   có cạnh
bằng 3a . Quay đường tròn ngoại tiếp tam giác A BD
quanh một đường kính của nó ta được một
mặt cầu. Tính diện tích mặt cầu này. A. 2 27 a . B. 2 21 a . C. 2 24 a . D. 2 25 a . Câu 7.
(Chuyên Lê Hồng Phong - TPHCM - 2021) Cho khối nón có chiều cao 4 cm , độ dài đường sinh
là 5 cm . Tính thể tích khối nón. A. 3 15 cm . B. 3 12 cm . C. 3 36 cm . D. 3 45 cm . Câu 8.
(Chuyên KHTN - 2021) Trong không gian cho tam giác ABC vuông cân tại đỉnh A và
BC  2a . Quay tam giác ABC quanh cạnh BC ta được khối tròn xoay. Thể tích của khối tròn xoay đó bằng 3  a 3 2 a A. . B. 3 2 a . C. . D. 3  a . 3 3 Câu 9.
(Chuyên KHTN - 2021) Cho hình chóp S.ABC có đáy là tam giác ABC đều cạnh a , SA vuông
góc với mặt phẳng đáy, SA  2a . Diện tích mặt cầu ngoại tiếp hình chóp bằng 2 8 a 2 16 a 2 16 a A. . B. . C. . D. 2 16 a . 3 3 9
Câu 10. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Tam giác ABC vuông cân tại đỉnh A có cạnh
huyền là 2 . Quay tam giác ABC quanh trục AB thì được khối nón có thể tích là.
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489  2  2 A. . B. . C. . D.  . 3 3 3
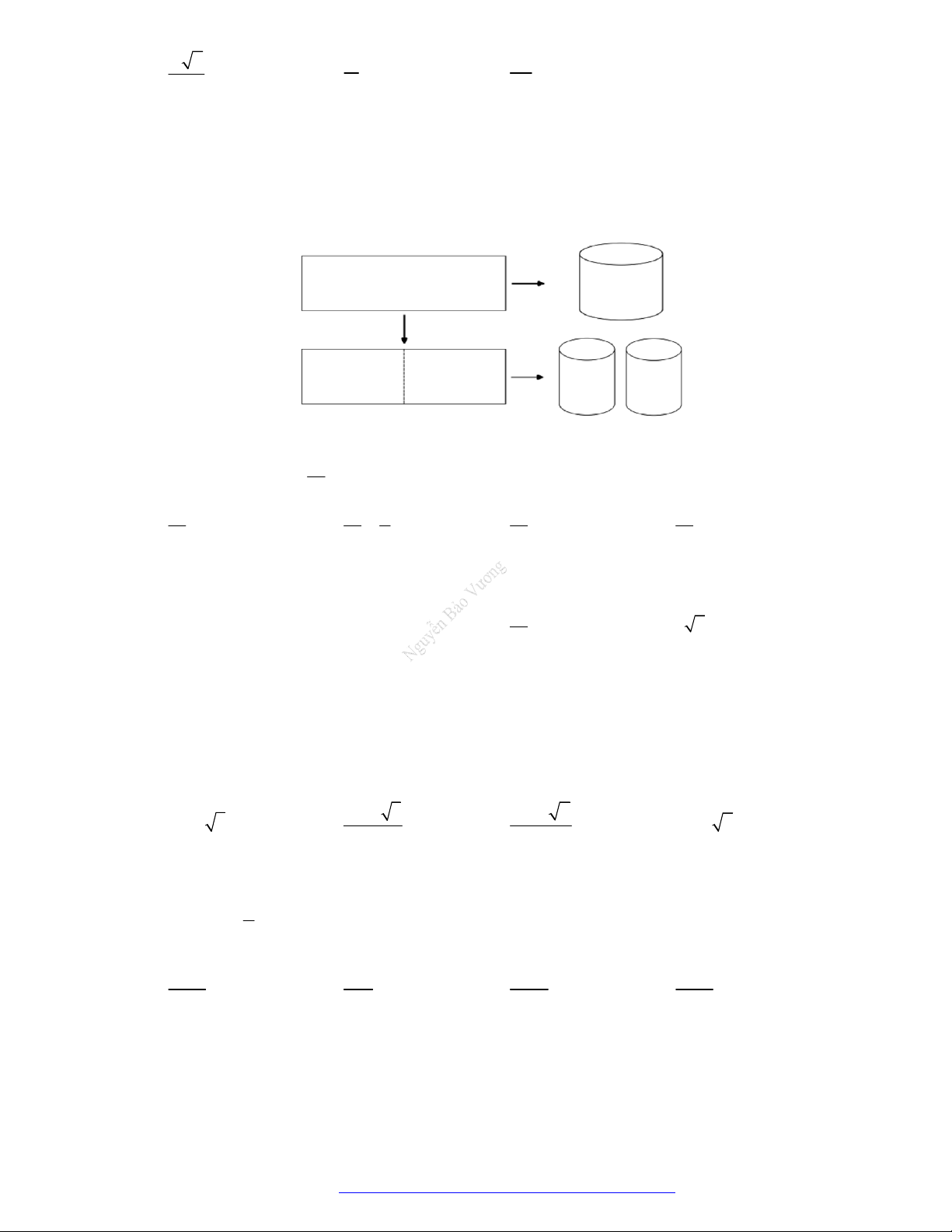
Câu 11. (Chuyên Quang Trung - Bình Phước - 2021) Từ một tấm tôn hình chữ nhật kích thước h và a ,
người ta làm các thùng đựng nước hình trụ có chiều cao bằng h , theo hai cách sau (xem hình minh họa dưới đây):
+ Cách 1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng.
+ Cách 2: Cắt tấm tôn ban đầu thành hai tấm bằng nhau, rồi gò mỗi tấm đó thành mặt xung quanh của một thùng.
Kí hiệu V là thể tích của thùng gò được theo cách 1 và V là tổng thể tích của hai thùng gò được 1 2 V
theo cách 2. Tính tỉ số 1 V2 V V 1 V V A. 1  4 . B. 1  . C. 1  1. D. 1  2 . V V 2 V V 2 2 2 2
Câu 12. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho hình nón có diện tích xung quanh bằng 2 3 a và bán
kính đáy bằng a . Độ dài đường sinh của hình nón đã cho bằng 3a A. 3a . B. 2a . C. . D. 2 2a . 2
Câu 13. (Chuyên Ngoại Ngữ Hà Nội- 2021) Trong không gian Oxyz , cho hình chữ nhật ABCD có
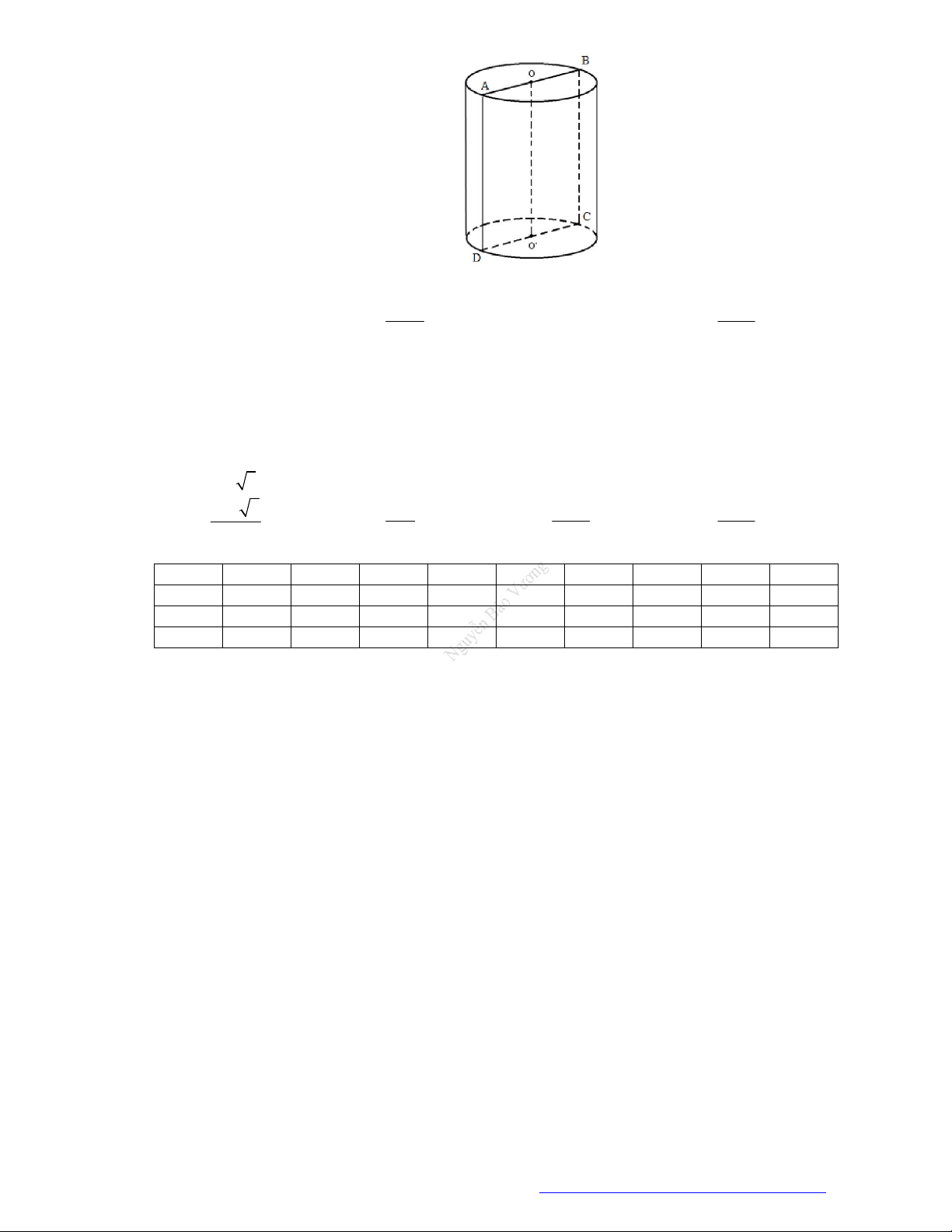
AB  1, AD  2 . Gọi M , N lần lượt là trung điểm của AD và BC . Quay hình chữ nhật ABCD
xung quanh trục MN ta được một hình trụ. Diện tích toàn phần của hình trụ đó là A. 2 . B. 6 . C. 10 . D. 4 .
Câu 14. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho hình chóp tam giác đều S.ABC , có cạnh đáy bằng 3a ,
góc giữa cạnh bên và mặt đáy bằng 45 . Thể tích khối cầu ngoại tiếp hình chóp S.ABC bằng 3 4 a 3 3 4 a 2 A. 3 4 a 3 . B. . C. . D. 3 4 a 2 . 3 3
Câu 15. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Cho hình nón có chiều cao bằng a . Biết rằng khi cắt
hình nón đã cho bởi một mặt phẳng đi qua đỉnh hình nón và cách tâm của đáy hình nón một a khoảng bằng
, thiết diện thu được là một tam giác vuông. Thể tích của khối nón được giới hạn 3
bởi hình nón đã cho bằng 3 5 a 3  a 3 4 a 3 5 a A. . B. . C. . D. . 9 3 9 12
Câu 16. (Chuyên Hạ Long - Quảng Ninh - 2021) Cho mặt cầu có diện tích là 36 . Thể tích của khổi cầu
được giới hạn bởi mặt cầu đã cho là A. 27 . B. 108 . C. 81 . D. 36 .
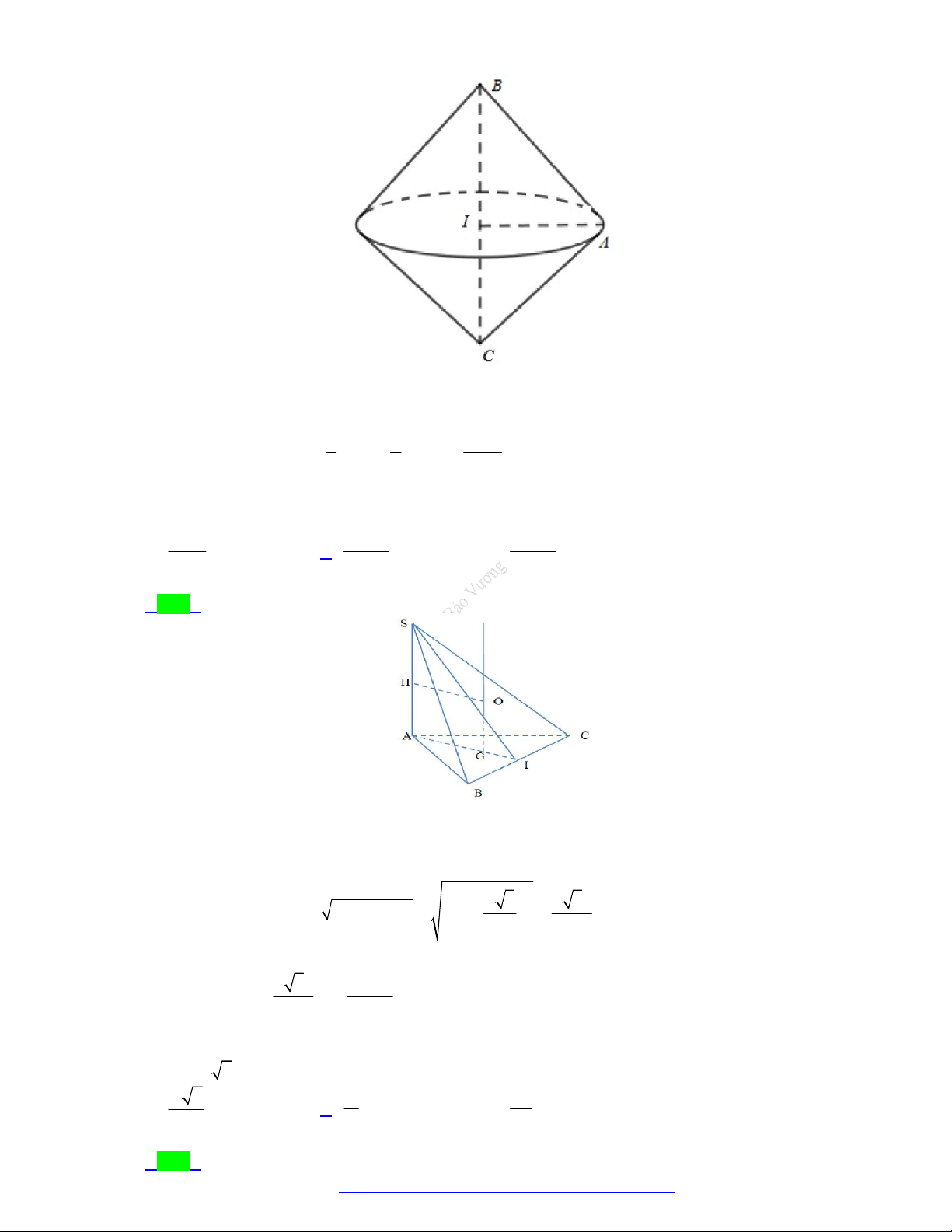
Câu 17. (Chuyên Hạ Long - Quảng Ninh - 2021) Cho hình chóp S.ABC có đáy ABC là tam giác đều
cạnh 3a , tam giác SBC vuông tại S và mặt phẳng  SBC vuông góc với mặt phẳng  ABC .
Diện tích mặt cầu ngoại tiếp hình chóp S.ABC bằng
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 A. 2 12 a . B. 2 36 a . C. 2 18 a . D. 3 12 a .
Câu 18. (Chuyên ĐHSP Hà Nội - 2021) Cho hình chóp S.ABC có đáy là tam giác vuông,
SA SB SC AB BC  2 .
a Diện tích của mặt cầu ngoại tiếp hình chóp S.ABC bằng 2 8 a 2 2 8 a 2 32 a 3 A. . B. . C. . D. 2 8 a . 3 3 3
Câu 19. (Chuyên ĐH Vinh - Nghệ An - 2021) Một khối trụ có đường cao bằng 2 , chu vi của thiết diện
qua trục gấp 3 lần đường kính đáy. Thể tích của khối trụ bằng 8 A. 2 . B. 32 . C. . D. 8 . 3
Câu 20. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho khối lăng trụ đứng ABC.AB C
  có đáy là tam giác đều
cạnh a , AB  2a . Thể tích V của khối lăng trụ đã cho 3 3a 3 a 3 3a A. V  . B. V  . C. V  . D. 3 V  2a . 2 4 4
Câu 21. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho hình chóp S.ABC có cạnh bên SA vuông góc với mặt
phẳng đáy  ABC  . Biết SA a , tam giác ABC là tam giác vuông cân tại A , AB  2a . Tính theo
a thể tích V của khối chóp S.ABC . 3 a 3 a 3 2a A. V  . B. V  . C. V  . D. 3 V  2a . 6 2 3
Câu 22. (THPT Thanh Chương 1- Nghệ An - 2021) Cắt hình nón bởi một mặt phẳng đi qua trục ta được
thiết diện là một tam giác vuông cân có cạnh huyền bằng
. Thể tích V của khối nón đã cho bằng A. . B. . C. . D. .
Câu 23. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Trong không gian, cho tam giác ABC vuông tại
A , AB a và BC a 3 . Thể tích của khối nón được tạo thành khi quay tam giác ABC xung
quanh trục AB bằng 3 3 2 aa 2 3  a 3 A. . B. . C. 3 2a . D. . 3 3 3
Câu 24. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho hình nón  N  có chiều cao bằng a . Một mặt
phẳng qua đỉnh  N  cắt  N  theo thiết diện là một tam giác đều có diện tích bằng 2 3a . Thể tích
V của khối nón giới hạn bởi  N  bằng 5 1 A. 3 V  3 a . B. 3
V   a . C. 3 V   a . D. 3  a . 3 3
Câu 25. (THPT Đào Duy Từ - Hà Nội - 2021) Mặt phẳng đi qua trục hình trụ, cắt hình trụ theo thiết diện
là hình vuông cạnh 2a . Thể tích khối trụ bằng: 3 2 a 3  a A. 3  a . B. . C. . D. 3 2 a . 3 3
Câu 26. (THPT Chu Văn An - Thái Nguyên - 2021) Diện tích vải tối thiểu để may được một chiếc mũ
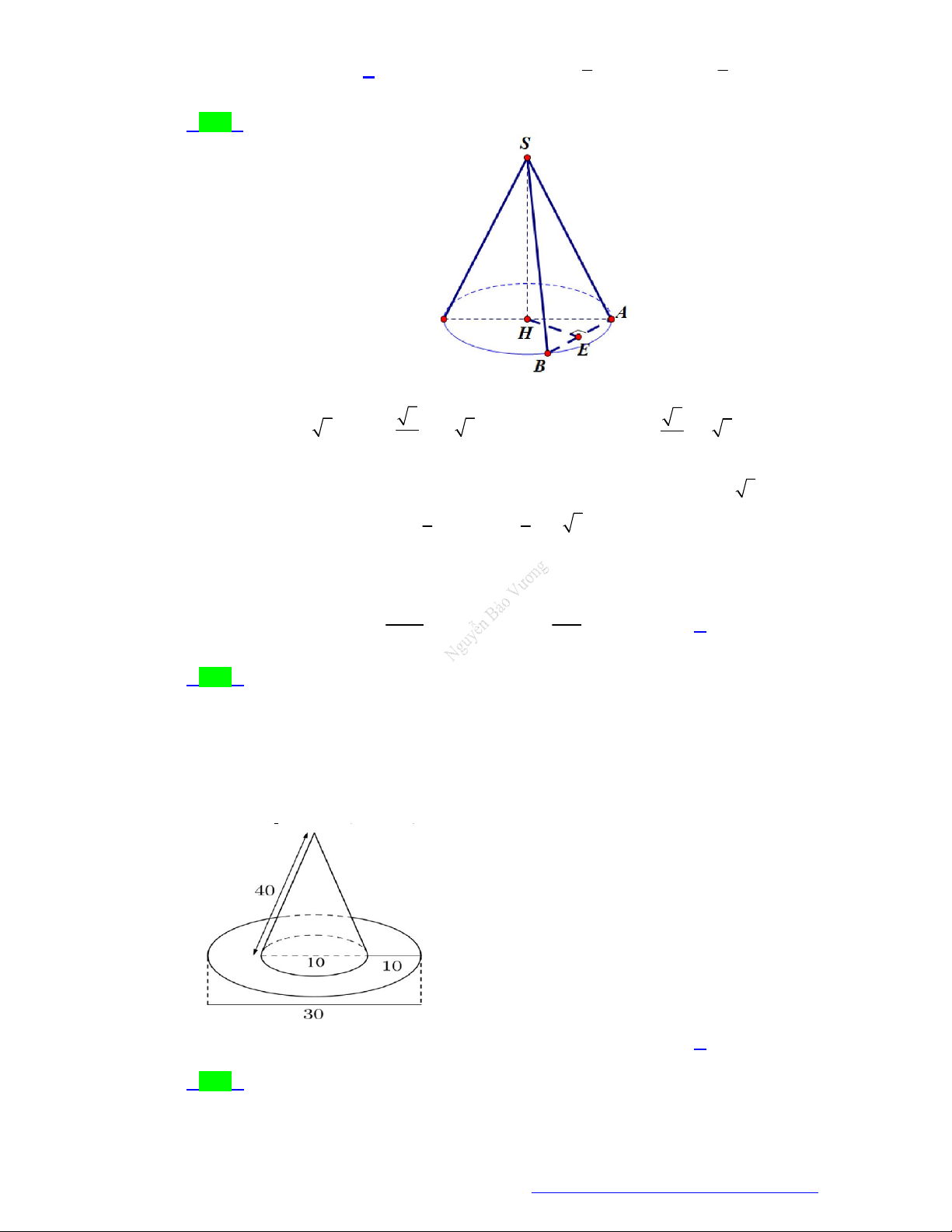
có hình dạng và kích thước(cùng đơn vị đo)
được cho bởi hình vẽ bên đó (không kể viền, mép) là bao nhiêu? Biết phía trên có dạng một
hình nón và phía dưới (vành mũ) có dạng hình vành khăn tròn.
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489 A. 500 . B. 350 . C. 450 . D. 400 .
Câu 27. (THPT Ba Đình - Thanh Hóa - 2021) Cắt khối trụ bởi mặt phẳng qua trục ta được thiết diện là
hình chữ nhật ABCD có cạnh AB,CD thuộc hai đáy của hình trụ, AB  4 ;
a AC  5a . Tính thể tích khối trụ. A. 3 V  4 a . B. 3 V  8 a . C. 3 V  16 a . D. 3 V  12 a .
Câu 28. (THPT Quế Võ 1 - Bắc Ninh - 2021) Cho hình nón có bán kính bằng 5 và góc ở đỉnh bằng 60 . 
Diện tích xung quanh của hình nón đã cho bằng 50 3 100 3 A. 50 . B. 100 . C. . D. . 3 3
Câu 29. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Đương kính của mặt cầu ngoại tiếp hình lập phương có cạnh a 3 bằng 3a A. 3a . B. a 3 . C. 6a . D. . 2
Câu 30. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Hình trụ có bán kính đáy bằng a , chu vi thiết diện qua trục bằng 10 .
a Thể tích khối trụ đã cho bằng A. 3 3 a . B. 3 4 a . C. 3  a . D. 3 5 a .
Câu 31. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Thể tích khối cầu ngoại tiếp hình lập phương cạnh a là 3 a 3 3a 3 3aA. V  . B. V  . C. V  . D. 3 V a . 2 2 2 2
Câu 32. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho hình nón đỉnh S có bán kính đáy R  2 . Biết diện
tích xung quanh của hình nón là 2 5 . Tính thể tích của khối nón. 5 4 2 A. B. . C. . D. . 3 3 3
Câu 33. (THPT Đồng Quan - Hà Nội - 2021) Một chiếc cốc hình trụ cao 15 cm dựng được nhiều nhất là
0,5 lít nước (bỏ qua độ dày của đáy cốc). Hỏi bán kính đường tròn đáy của chiếc cốc gần nhất với
giá trị nào trong các giá trị sau đây? A. 3, 26 cm. B. 3, 90 cm. C. 3, 23 cm. D. 3, 28 cm.
Câu 34. (THPT Lê Lợi - Thanh Hóa - 2021) Thể tích của khối trụ có đường kính bằng 2a , đường cao là 2a là: A. 3 4a . B. 3 a . C. 3 2a . D. 3 3 a  .
Câu 35. (Trung Tâm Thanh Tường -2021) Thể tích của khối cầu ngoại tiếp hình lập phương cạnh bằng 2 . A. 12 . B. 4 . C. 3 . D. 4 3 .
Câu 36. (THPT Triệu Sơn - Thanh Hóa - 2021) Thiết diện qua trục của một hình trụ là một hình vuông có cạnh là 2a .
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Thể tích khối trụ được tạo nên bởi hình trụ này là 3 2 a 3 8 a A. 3 2 a . B. . C. 3 8 a . D. . 3 3
Câu 37. (THPT Triệu Sơn - Thanh Hóa - 2021) Trong không gian, cho tam giác ABC vuông tại A có
AB  4a và AC  3a . Khi quay tam giác ABC quanh quanh cạnh góc vuông AB thì đường gấp
khúc ACB tạo thành một hình nón. Diện tích toàn phần của hình nón đó bằng A. 2 15 a . B. 2 24 a . C. 2 36 a . D. 2 20 a .
Câu 38. (THPT Trần Phú - Đà Nẵng - 2021) Cho khối nón có thiết diện qua trục là một tam giác đều có
cạnh a 3 . Thể tích của khối nón đã cho bằng 3  a 3 3  a 3 9 a 3 3 a A. . B. . C. . D. . 8 8 8 8 BẢNG ĐÁP ÁN 1.B 2.A 3.D 4.C 5.D 6.C 7.B 8.C 9.B 10.B 11.D 12.A 13.D 14.A 15.D 16.D 17.A 18.D 19.D 20.C 21.C 22.D 23.A 24.B 25.D 26.D 27.D 28.A 29.A 30.A 31.B 32.D 33.A 34.C 35.D 36.A 37.B 38.D
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Chủ đề 6 KHỐI TRÒN XOAY
MỨC ĐỘ THÔNG HIỂU Câu 1.
(Sở Vĩnh Phúc - 2021) Cho mặt cầu  S  và mặt phẳng  P , biết khoảng cách từ tâm của mặt cầu
S  đến mặt phẳng P bằng a . Mặt phẳng P cắt mặt cầu S  theo giao tuyến là đường tròn
có chu vi 2 3 a . Diện tích mặt cầu S  bằng bao nhiêu? A. 2 12 a . B. 2 16 a . C. 2 4 a . D. 2 8 a . Lời giải Chọn B Ta có: C 2 3 a
Bán kính đường tròn giao tuyến của mặt phẳng  P mặt cầu  S  là: r    a 3 . 2 2
Suy ra bán kính mặt cầu  S  là: r r  h  a 2 2 2 2 3  a  2a .
Vậy diện tích mặt cầu S  là: S   r    a2 2 2 4 4 2  16 a . Câu 2.
(Sở Vĩnh Phúc - 2021) Tính diện tích toàn phần S của mặt nón  N  biết thiết diện qua trục của
nó là một tam giác vuông có cạnh huyền bằng 2 2a A. S     2 2
2 2  a . B. S     2 4
4 2  a . C. S     2 2
4 2  a . D. S     2 4 2 2  a . Lời giải Chọn A.  
Thiết diện qua trục là tam giác SAB vuông cân tại S nên A B  45 l
SO OA h r   a 2 2 2  S
  Rl   .a 2.2a  2 2 a xq
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489 2 2
S S S
a   a     2 2 2 2 2 2 2  a tp xq day Câu 3.
(Sở Yên Bái - 2021) Cho khối nón có thể tích là V . Biết rằng khi cắt khối nón đã cho bởi một mặt
phẳng qua trục, thiết diện thu được là một tam giác đều có diện tích bằng 3 . Giá trị của V bằng  3 A. 4 . B. 2 . C.  3. D. . 3 Lời giải Chọn D. 2
SA SB AB  2 AB 3 
Gọi thiết diện qua trục là tam giác đều SAB S   3  SAB  4 SO  3  2 1  AB  1  V   . .SO   3.   3  2  3 Câu 4.
(Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Cho hình chóp S.ABCD có đáy là
hình chữ nhật, AB  3 , AD  4 , cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa SC và mặt
phẳng đáy là 45 . Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD . 5 2 5 A. R  5 . B. R  5 2 . C. R  . D. R  . 2 2 Lời giải Chọn C
SC ABCD  SC SA  , ,  SCA  45 . Khi đó, S
AC vuông cân tại A SA AC  5 .
Gọi AC BD O , khi đó O là tâm của hình chữ nhật đáy. Suy ra: Tâm của mặt cầu ngoại tiếp
hình chóp S.ABCD thuộc đường thẳng d vuông góc với mặt phẳng đáy  d SC I . Mặt khác, do S
AC vuông cân tại A nên I cách đều các điểm S, , A C .
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 SC 5 2
Suy ra: I là tâm mặt cầu ngoại tiếp hình chóp S.ABCD có bán kính R SI   . 2 2 Câu 5.
(Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Cho hình lập phương có cạnh bằng a .
Thể tích khối cầu ngoại tiếp hình lập phương đó bằng 3  a 3 4 3 3  a 3 A. . B. 3  a . C. 3 4 3 a . D. . 3 3 2 Lời giải Chọn D
 Ta có đường chéo của hình lập phương cạnh a bằng a 3 . a 3
Bán kính khối cầu ngoại tiếp của hình lập phương đó bằng: R  . 2 3 3 4 4  a 3   a 3
 Thể tích khối cầu ngoại tiếp hình lập phương đó bằng: 3 V   R   .   . 3 3  2  2   Câu 6.
(Chuyên Lê Hồng Phong - TPHCM - 2021) Cho hình lập phương ABC . D A BCD   có cạnh
bằng 3a . Quay đường tròn ngoại tiếp tam giác A BD
quanh một đường kính của nó ta được một
mặt cầu. Tính diện tích mặt cầu này. A. 2 27 a . B. 2 21 a . C. 2 24 a . D. 2 25 a . Lời giải Chọn C A' D' B' C' A D B C
3 cạnh AB , AD , BD là các đường chéo của hình vuông cạnh 3a .  A B
D là tam giác đều cạnh 3a 2 . BD 3 3a 6
 Bán kính đường tròn ngoại tiếp tam giác A BD  là: R    a 6 . 3 3
Suy ra mặt cầu được tạo ra có diện tích bằng: S
  R   a 2 2 2 4 4 6  24 a . mc Câu 7.
(Chuyên Lê Hồng Phong - TPHCM - 2021) Cho khối nón có chiều cao 4 cm , độ dài đường sinh
là 5 cm . Tính thể tích khối nón. A. 3 15 cm . B. 3 12 cm . C. 3 36 cm . D. 3 45 cm . Lời giải Chọn B Theo giả thuyết có 2 2 h  4 c ,
m l  5 cm R l h  3 cm 1
Vậy thể tích khối nón là 2 3 V
  .R .h  12 cm . nón 3 Câu 8.
(Chuyên KHTN - 2021) Trong không gian cho tam giác ABC vuông cân tại đỉnh A và
BC  2a . Quay tam giác ABC quanh cạnh BC ta được khối tròn xoay. Thể tích của khối tròn xoay đó bằng 3  a 3 2 a A. . B. 3 2 a . C. . D. 3  a . 3 3 Lời giải Chọn C
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489
 Gọi I là trung điểm của BC . Khi quay tam giác ABC quanh cạnh BC ta được khối tròn xoay
gồm hai hình nón bằng nhau có chung mặt đáy ( như hình vẽ).
 Ở mỗi hình nón ta có: h BI a ; r AI BI a 3 1 2 2 a  Khi đó 2 2 V
 2.V  2.  r h  . .a a KTX N 3 3 3 Câu 9.
(Chuyên KHTN - 2021) Cho hình chóp S.ABC có đáy là tam giác ABC đều cạnh a , SA vuông
góc với mặt phẳng đáy, SA  2a . Diện tích mặt cầu ngoại tiếp hình chóp bằng 2 8 a 2 16 a 2 16 a A. . B. . C. . D. 2 16 a . 3 3 9 Lời giải Chọn B
Gọi I, H là trung điểm cạnh BC, SA , G là trọng tâm tam giác ABC .
Gọi d là đường thẳng vuông góc với mặt phẳng  ABC tại trọng tâm G của tam giác ABC , kẻ
mặt phẳng trung trực của SA cắt d tại O. O là tâm mặt cầu ngoại tiếp hình chóp S.ABC , bán 2  a 3  2 3a kính mặt cầu đó là 2 2 2 OA
HA AG a     ,  3  3  
do đó diện tích mặt cầu đó là: 2 2  2 3a  16 a 2
S  4 .IA  4 .   .  3  3  
Câu 10. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Tam giác ABC vuông cân tại đỉnh A có cạnh
huyền là 2 . Quay tam giác ABC quanh trục AB thì được khối nón có thể tích là.  2  2 A. . B. . C. . D.  . 3 3 3 Lời giải Chọn B
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 B A C
 Tam giác ABC vuông cân tại đỉnh A có cạnh huyền là 2 nên AB AC  1.
 Suy ra khối nón có bán kính đáy là r  1 và chiều cao là h 1. Nên thể tích khối nón là 1  2 V r  .h  . 3 3
Câu 11. (Chuyên Quang Trung - Bình Phước - 2021) Từ một tấm tôn hình chữ nhật kích thước h và a ,
người ta làm các thùng đựng nước hình trụ có chiều cao bằng h , theo hai cách sau (xem hình minh họa dưới đây):
+ Cách 1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng.
+ Cách 2: Cắt tấm tôn ban đầu thành hai tấm bằng nhau, rồi gò mỗi tấm đó thành mặt xung quanh của một thùng.
Kí hiệu V là thể tích của thùng gò được theo cách 1 và V là tổng thể tích của hai thùng gò được 1 2 V
theo cách 2. Tính tỉ số 1 V2 V V 1 V V A. 1  4 . B. 1  . C. 1  1. D. 1  2 . V V 2 V V 2 2 2 2 Lời giải Chọn D
 Gọi r , r lần lượt là bán kính đáy của hai thùng gò được theo cách 1, cách 2. 1 2  a 2 r a r  1 1     2 Vì  a   . 2 r a  2  2 r   2   4 2 2  a   a V  Ta có 1 V   , h V  2 h   2 . 1   2    2   4  V2
Câu 12. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho hình nón có diện tích xung quanh bằng 2 3 a và bán
kính đáy bằng a . Độ dài đường sinh của hình nón đã cho bằng 3a A. 3a . B. 2a . C. . D. 2 2a . 2 Lời giải Chọn A
Diện tích xung quanh hình nón là S   rl . xp
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489 2 Sxp 3 a
Suy ra đường sinh của hình nón là l    3a ra
Câu 13. (Chuyên Ngoại Ngữ Hà Nội- 2021) Trong không gian Oxyz , cho hình chữ nhật ABCD có
AB  1, AD  2 . Gọi M , N lần lượt là trung điểm của AD và BC . Quay hình chữ nhật ABCD
xung quanh trục MN ta được một hình trụ. Diện tích toàn phần của hình trụ đó là A. 2 . B. 6 . C. 10 . D. 4 . Lời giải Chọn D AD Ta có : r
 1 ; l AB  1 . 2
Vậy diện tích toàn phần của hình trụ : 2 2
S  2 rl  2 r  2 .1.1  2. .1  4 .
Câu 14. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho hình chóp tam giác đều S.ABC , có cạnh đáy bằng 3a ,
góc giữa cạnh bên và mặt đáy bằng 45 . Thể tích khối cầu ngoại tiếp hình chóp S.ABC bằng 3 4 a 3 3 4 a 2 A. 3 4 a 3 . B. . C. . D. 3 4 a 2 . 3 3 Lời giải Chọn A
Gọi M là trung điểm của BC , H là hình chiếu vuông góc của S lên  ABC . 2  a a AM   a2 3 3 3 2 3   ; AH
AM a 3  BH CH    2  2 3
Ta có góc giữa cạnh bên SA và mặt đáy  ABC  là  SAH .
SH AH tan 45  a 3.1  a 3.
Từ đó suy ra SH HA HB HC .
H chính là tâm khối cầu ngoại tiếp hình chóp. 4 4  V   R   .a 33 3 3  4 a 3 . 3 3
Câu 15. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Cho hình nón có chiều cao bằng a . Biết rằng khi cắt
hình nón đã cho bởi một mặt phẳng đi qua đỉnh hình nón và cách tâm của đáy hình nón một
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 a khoảng bằng
, thiết diện thu được là một tam giác vuông. Thể tích của khối nón được giới hạn 3
bởi hình nón đã cho bằng 3 5 a 3  a 3 4 a 3 5 a A. . B. . C. . D. . 9 3 9 12 Lời giải Chọn D
Gọi thiết diện qua đỉnh là tam giác vuông cân SAB và gọi H là trung điểm AB. a 1 1 1 a 2
Kẻ OK SH d O,SAB  OK  và ta có    OH  . 3 2 2 2 OK SO OH 4 3a 2
Do tam giác SAB vuông cân tại 2 2
S AH SH SH SO OH  . 4 2 3 a 5 1 1  a 5  5 a 2 2 2
OA OH AH
V   .OA .SO     .a  . 2 3 3  2  12   3 5 a
Vậy thể tích của khối nón được giới hạn bởi hình nón đã cho bằng . 12
Câu 16. (Chuyên Hạ Long - Quảng Ninh - 2021) Cho mặt cầu có diện tích là 36 . Thể tích của khổi cầu
được giới hạn bởi mặt cầu đã cho là A. 27 . B. 108 . C. 81 . D. 36 . Lời giải Chọn D
Gọi r là bán kính mặt cầu. Ta có 2
S  4 r  36  r  3 . 4 4
Thể tích của khổi cầu là 3 3 V   r   .3  36 . 3 3
Câu 17. (Chuyên Hạ Long - Quảng Ninh - 2021) Cho hình chóp S.ABC có đáy ABC là tam giác đều
cạnh 3a , tam giác SBC vuông tại S và mặt phẳng  SBC  vuông góc với mặt phẳng  ABC .
Diện tích mặt cầu ngoại tiếp hình chóp S.ABC bằng A. 2 12 a . B. 2 36 a . C. 2 18 a . D. 3 12 a . Lời giải Chọn A
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
NGUYỄN BẢO VƯƠNG - 0946798489
Gọi M là trung điểm BC nên M là tâm đường tròn ngoại tiếp SBC . Trong A
BC thì AM BC và SBC   ABC nên AM   SBC . Gọi O là tâm mặt cầu ngoại tiếp
hình chóp S.ABC thì O AM hay O là tâm đường tròn ngoại tiếp A
BC . Do đó bán kính mặt
cầu ngoại tiếp hình chóp S.ABC bằng bán kính đường tròn ngoại tiếp ABC . AB 3a Trong A
BC có R    a 3 . 2 sin 60o 3 2. 2
Vậy diện tích mặt cầu ngoại tiếp hình chóp S.ABC là 2 2
S  4 R  12 a .
Câu 18. (Chuyên ĐHSP Hà Nội - 2021) Cho hình chóp S.ABC có đáy là tam giác vuông,
SA SB SC AB BC  2 .
a Diện tích của mặt cầu ngoại tiếp hình chóp S.ABC bằng 2 8 a 2 2 8 a 2 32 a 3 A. . B. . C. . D. 2 8 a . 3 3 3 Lời giải Chọn D
Gọi M là trung điểm của AC.
ABC vuông có AB BC nên ABC vuông cân tại . B
Khi đó AC AB 2  2a 2 và MA MB MC (1).
Mặt khác, SAC cân tại S có SA SC  2a, AC  2a 2 nên tam giác SAC vuông cân tại S.
Suy ra MA MS MC (2).
Từ (1), (2) suy ra M là tâm mặt cầu ngoại tiếp hình chóp S.ABC. AC 2a 2
Suy ra R SM    a 2. 2 2
Vậy diện tích mặt cầu ngoại tiếp hình chóp S.ABC là 2 2
S  4 R  8 a (đvdt).
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Câu 19. (Chuyên ĐH Vinh - Nghệ An - 2021) Một khối trụ có đường cao bằng 2 , chu vi của thiết diện
qua trục gấp 3 lần đường kính đáy. Thể tích của khối trụ bằng 8 A. 2 . B. 32 . C. . D. 8 . 3 Lời giải Chọn D
Gọi bán kính đáy của khối trụ là r , chiều cao là h , suy ra h  2
Giả sử thiết diện qua trục là hình chữ nhật ABCD ( như hình vẽ)
Từ giả thiết suy ra 2 2r  2  3.2r r  2
 Thể tích của khối trụ là 2
V   r .h  8 .
Câu 20. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho khối lăng trụ đứng ABC.A BC
  có đáy là tam giác đều
cạnh a , AB  2a . Thể tích V của khối lăng trụ đã cho 3 3a 3 a 3 3a A. V  . B. V  . C. V  . D. 3 V  2a . 2 4 4 Lời giải Chọn C A' C' B' 2a A C a B
Xét tam giác ABB vuông tạ B ta có: 2 2 BB 
AB  AB a 3 . 2 1 a 3
Tam giác ABC là tam giác đều cạnh a nên 0 SA . B AC.sin 60  . ABC 2 4 2 3 a 3 3a
Thể tích V của khối lăng trụ đã cho là: V S .BB  a 3  . ABC 4 4
Câu 21. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho hình chóp S.ABC có cạnh bên SA vuông góc với mặt
phẳng đáy  ABC  . Biết SA a , tam giác ABC là tam giác vuông cân tại A , AB  2a . Tính theo
a thể tích V của khối chóp S.ABC . 3 a 3 a 3 2a A. V  . B. V  . C. V  . D. 3 V  2a . 6 2 3
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
NGUYỄN BẢO VƯƠNG - 0946798489 Lời giải Chọn C
Tam giác ABC là tam giác vuông cân tại A nên AC AB  2a .
Thể tích V của khối chóp S.ABC là 3 1 1 1 1 1 2a V S . A SS . A A . B AC  . . a .2 . a 2a  . 3 ABC 3 2 3 2 3
Câu 22. (THPT Thanh Chương 1- Nghệ An - 2021) Cắt hình nón bởi một mặt phẳng đi qua trục ta được
thiết diện là một tam giác vuông cân có cạnh huyền bằng
. Thể tích V của khối nón đã cho bằng A. . B. . C. . D. . Lời giải Chọn D
 Gọi S, O lần lượt là đỉnh và tâm đường tròn đáy của hình nón. Một mặt phẳng đi qua trục cắt
hình nón theo thiết diện là tam giác vuông cân (như hình vẽ).  Ta có: .
 Thể tích V của khối nón đã cho bằng: .
Câu 23. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Trong không gian, cho tam giác ABC vuông tại
A , AB a và BC a 3 . Thể tích của khối nón được tạo thành khi quay tam giác ABC xung
quanh trục AB bằng 3 3 2 aa 2 3  a 3 A. . B. . C. 3 2a . D. . 3 3 3 Lời giải Chọn A
Khối nón được tạo thành khi quay tam giác ABC vuông tại A xung quanh trục AB có đường cao
h AB a và bán kính đáy 2 2 r AC
BC AB a 2 . Do đó thể tích khối nón : 3 1 2 a 2 V   r h  . 3 3
Câu 24. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho hình nón  N  có chiều cao bằng a . Một mặt
phẳng qua đỉnh  N  cắt  N  theo thiết diện là một tam giác đều có diện tích bằng 2 3a . Thể tích
V của khối nón giới hạn bởi  N  bằng
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 5 1 A. 3 V  3 a . B. 3
V   a . C. 3 V   a . D. 3  a . 3 3 Lời giải Chọn B
 Gọi thiết diện của hình nón  N  là tam giác đều SAB , chiều cao của hình nón là SH a . 3 3  Ta có 2 2 2 Sa 3  AB .  a
3  AB  2a và SE  . ABa 3 . SAB 4 2
 Trong tam giác vuông SHE : 2 2 2 2
HE SE SH  2a .
 Trong tam giác vuông HEA : 2 2 2 2 2 2
HA HE EA  2a a  3a HA a 3 . 1 1
 Thể tích khối nón cần tìm: V   HA .SH   a 32 2 3 .a   a . 3 3
Câu 25. (THPT Đào Duy Từ - Hà Nội - 2021) Mặt phẳng đi qua trục hình trụ, cắt hình trụ theo thiết diện
là hình vuông cạnh 2a . Thể tích khối trụ bằng: 3 2 a 3  a A. 3  a . B. . C. . D. 3 2 a . 3 3 Lời giải Chọn D
Mặt phẳng đi qua trục hình trụ, cắt hình trụ theo thiết diện là hình vuông cạnh 2a h  2 ;
a R a Thể tích hình trụ là: 2 2 3
V   R h   .a .2a  2 a (đvtt)
Câu 26. (THPT Chu Văn An - Thái Nguyên - 2021) Diện tích vải tối thiểu để may được một chiếc mũ
có hình dạng và kích thước(cùng đơn vị đo)
được cho bởi hình vẽ bên đó (không kể viền, mép) là bao nhiêu? Biết phía trên có dạng một
hình nón và phía dưới (vành mũ) có dạng hình vành khăn tròn. A. 500 . B. 350 . C. 450 . D. 400 . Lời giải Chọn D
 Ta thấy tổng S của diện tích vải để may được một chiếc mũ như trên được tính bằng tổng
diện tích xung quanh của hình nón với diện tích của hình vành khăn. Ta có S      2 2 .5.40 . 15  5   400 .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 27. (THPT Ba Đình - Thanh Hóa - 2021) Cắt khối trụ bởi mặt phẳng qua trục ta được thiết diện là
hình chữ nhật ABCD có cạnh AB,CD thuộc hai đáy của hình trụ, AB  4 ;
a AC  5a . Tính thể tích khối trụ. A. 3 V  4 a . B. 3 V  8 a . C. 3 V  16 a . D. 3 V  12 a . Lời giải Chọn D
Trong tam giác vuông ABC ta có : 2 2 BC
AC AB  3a .  R  2 ; a h  3a .
Vậy V   R h    a2 2 3 . 2
.3a  12 a .
Câu 28. (THPT Quế Võ 1 - Bắc Ninh - 2021) Cho hình nón có bán kính bằng 5 và góc ở đỉnh bằng 60 . 
Diện tích xung quanh của hình nón đã cho bằng 50 3 100 3 A. 50 . B. 100 . C. . D. . 3 3 Lời giải Chọn A
Gọi   60 là góc ở đỉnh của hình nón. 1  r Ta có  sin   l  10. 2 2 l
Diện tích xung quanh của hình nón là S
  rl  .5.10  50 (đvdt). xq
Câu 29. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Đương kính của mặt cầu ngoại tiếp hình lập phương có cạnh a 3 bằng 3a A. 3a . B. a 3 . C. 6a . D. . 2 Lời giải Chọn A
Ta có mặt cầu ngoại tiếp hình lập ABC . D A BCD
  có đường kính bằng 2 2 2 2 2 AC 
AA AC 
AA A B    B C    3a .
Câu 30. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Hình trụ có bán kính đáy bằng a , chu vi thiết diện qua trục bằng 10 .
a Thể tích khối trụ đã cho bằng A. 3 3 a . B. 3 4 a . C. 3  a . D. 3 5 a .
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Lời giải Chọn A
Chu vi thiết diện qua trục bằng 10a nên chiều cao của khối trụ bằng 3a .
Thể tích khối trụ bằng 2 2 3
V   .r h   .a .3a  3 a .
Câu 31. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Thể tích khối cầu ngoại tiếp hình lập phương cạnh a là 3 a 3 3a 3 3aA. V  . B. V  . C. V  . D. 3 V a . 2 2 2 2 Lời giải Chọn B
Đường chéo hình lập phương cạnh a có độ dài là a 3 là đường kính của khối cầu ngoại tiếp hình a 3
lập phương. Do đó khối cầu có bán kính R
. Thể tích khối cầu là: 2 3 3 4  3   3a V    a   . 3  2  2  
Câu 32. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho hình nón đỉnh S có bán kính đáy R  2 . Biết diện
tích xung quanh của hình nón là 2 5 . Tính thể tích của khối nón. 5 4 2 A. B.  . C.  . D.  . 3 3 3 Lời giải Chọn D Ta có S
  Rl   .2.l  2 5  l  5. xq 2 Khi đó 2 2 2
h l R  5  2  1. 1 1 2
Do đó thể tích khối nón là 2 2 V
R h   .2 .1   . 3 3 3 Vậy ta chọn phương án D.
Câu 33. (THPT Đồng Quan - Hà Nội - 2021) Một chiếc cốc hình trụ cao 15 cm dựng được nhiều nhất là
0, 5 lít nước (bỏ qua độ dày của đáy cốc). Hỏi bán kính đường tròn đáy của chiếc cốc gần nhất với
giá trị nào trong các giá trị sau đây? A. 3, 26 cm. B. 3, 90 cm. C. 3, 23 cm. D. 3, 28 cm. Lời giải Chọn A. V Ta có 2 2
V r h  500  r .15  r   3.26 cm. 15
Câu 34. (THPT Lê Lợi - Thanh Hóa - 2021) Thể tích của khối trụ có đường kính bằng 2a , đường cao là 2a là: A. 3 4 a  . B. 3 a . C. 3 2 a  . D. 3 3 a  . Lời giải Chọn C d Ta có: r   a 2 2 3
V   r h  2 a
Câu 35. (Trung Tâm Thanh Tường -2021) Thể tích của khối cầu ngoại tiếp hình lập phương cạnh bằng 2 . A. 12 . B. 4 . C. 3 . D. 4 3 . Lời giải
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
NGUYỄN BẢO VƯƠNG - 0946798489 Chọn D 1
Bán kính mặt cầu ngoại tiếp hình lập phương cạnh bằng 2 là: R  .2 3  3 . 2
Thể tích của khối cầu ngoại tiếp hình lập phương cạnh bằng 2 là: 4 4 3
V   R   3 3  4 3 . 3 3
Câu 36. (THPT Triệu Sơn - Thanh Hóa - 2021) Thiết diện qua trục của một hình trụ là một hình vuông có cạnh là 2a .
Thể tích khối trụ được tạo nên bởi hình trụ này là 3 2 a 3 8 a A. 3 2 a . B. . C. 3 8 a . D. . 3 3 Lời giải Chọn A
Thiết diện qua trục là hình vuông ABCD có cạnh bằng 2a .
Do đó: h  2a ; r a .
Thể tích của khối trụ bằng: 2 2 3
V   r h   .a .2a  2 a .
Câu 37. (THPT Triệu Sơn - Thanh Hóa - 2021) Trong không gian, cho tam giác ABC vuông tại A có
AB  4a và AC  3a . Khi quay tam giác ABC quanh quanh cạnh góc vuông AB thì đường gấp
khúc ACB tạo thành một hình nón. Diện tích toàn phần của hình nón đó bằng A. 2 15 a . B. 2 24 a . C. 2 36 a . D. 2 20 a . Lời giải Chọn B 2 2 Ta có: 2 2 BC
AB AC  4a  3a  5a .
Do đó, hình nón đã cho có bán kính đường tròn đáy r  3a , độ dài đường sinh l  5a .
Vậy diện tích toàn phần của hình nón đã cho là:
S S S   rl   r   a a    a2 2 2 .3 .5 . 3  24 a . tp xq d
Câu 38. (THPT Trần Phú - Đà Nẵng - 2021) Cho khối nón có thiết diện qua trục là một tam giác đều có
cạnh a 3 . Thể tích của khối nón đã cho bằng
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 3  a 3 3  a 3 9 a 3 3 a A. . B. . C. . D. . 8 8 8 8 Lời giải Chọn D
Giả sử thiết diện qua trục là tam giác đều SAB . 1 a 3 Bán kính đáy R AB  2 2 2 3a 3a
Đường cao của khối nón là 2 2 2 h SO
SA OA  3a   . 4 2 2 3 1 1  a 3  3a 3 a
Vậy thể tích của khối nón đã cho là 2
V   R h     .  . 3 3  2  2 8  
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Chủ đề 6 KHỐI TRÒN XOAY
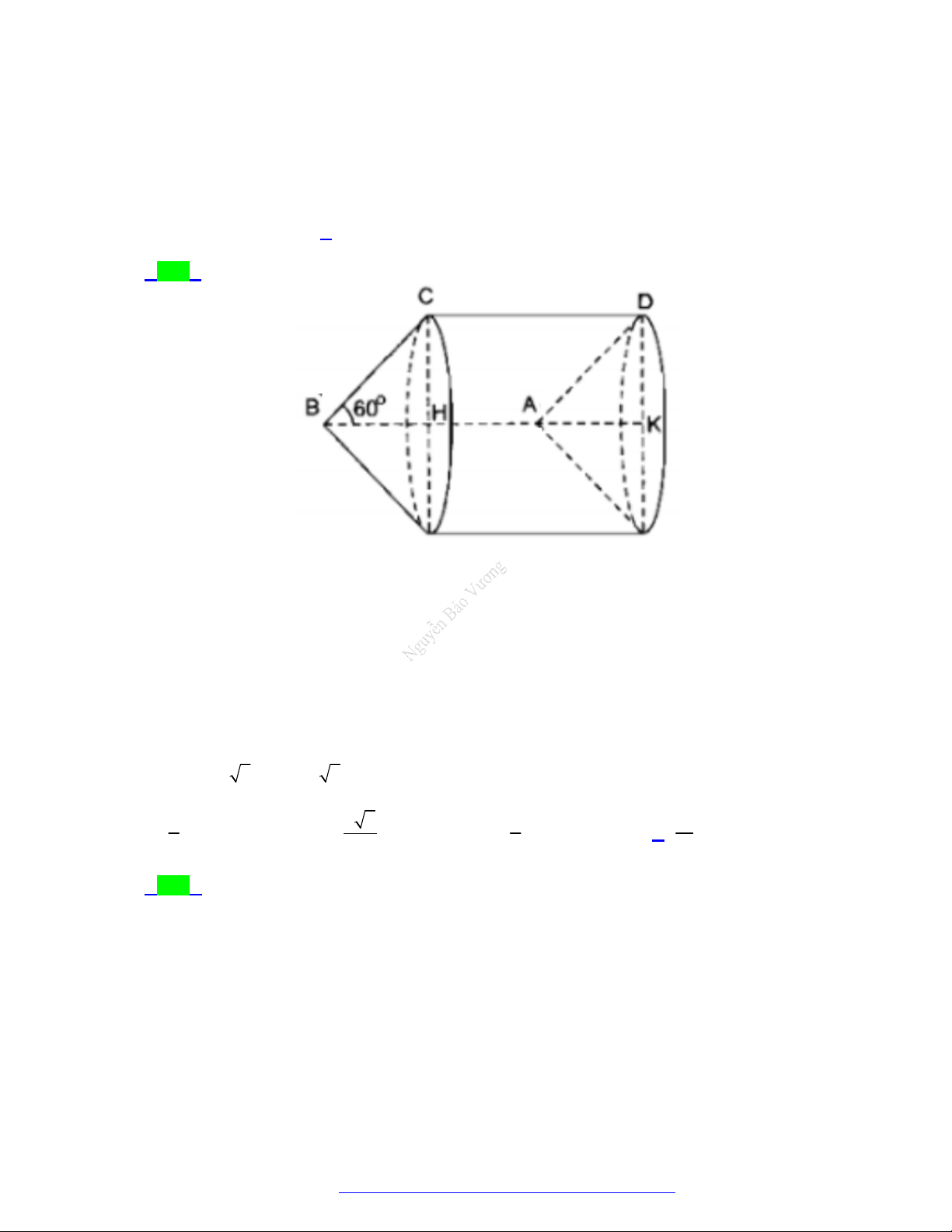
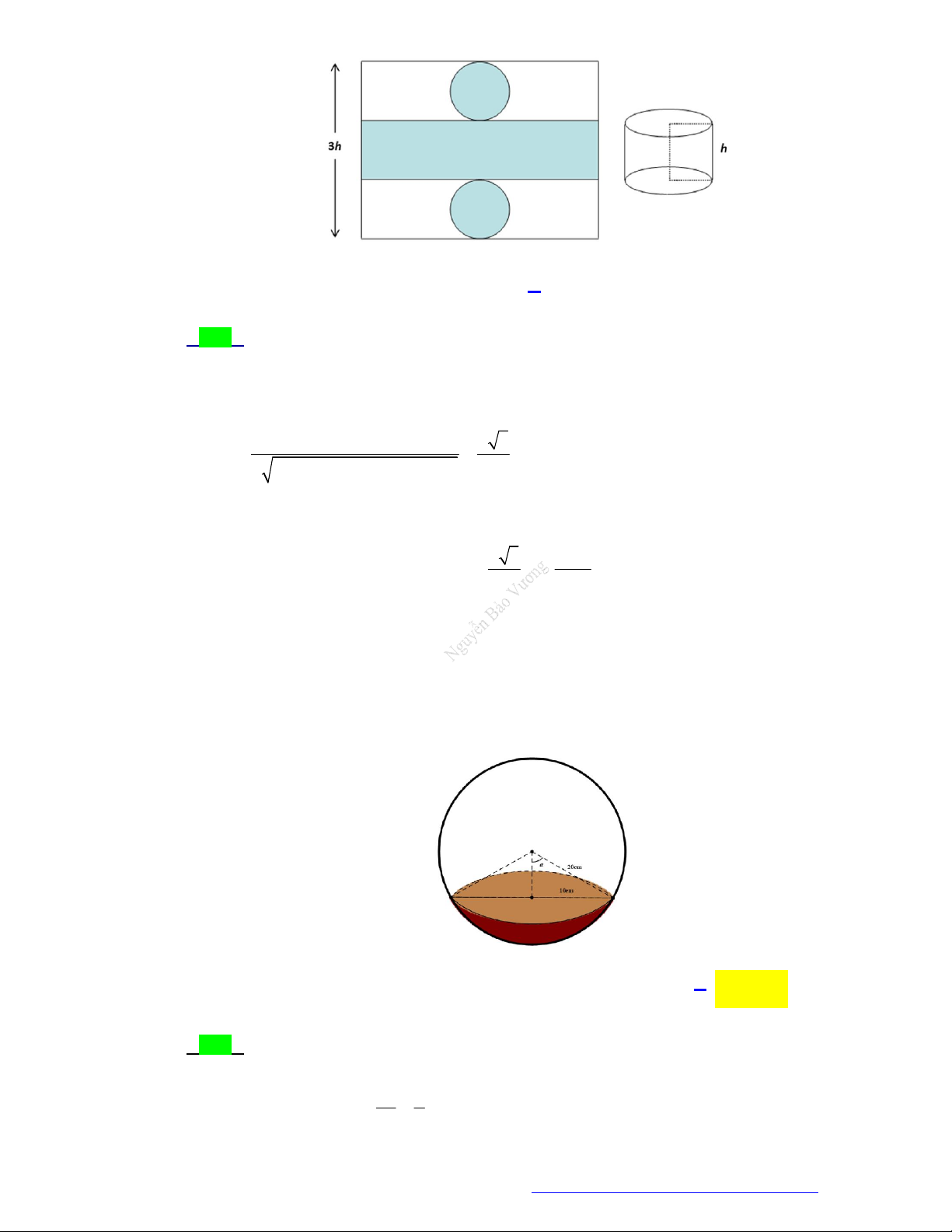
MỨC ĐỘ VẬN DỤNG Câu 1.
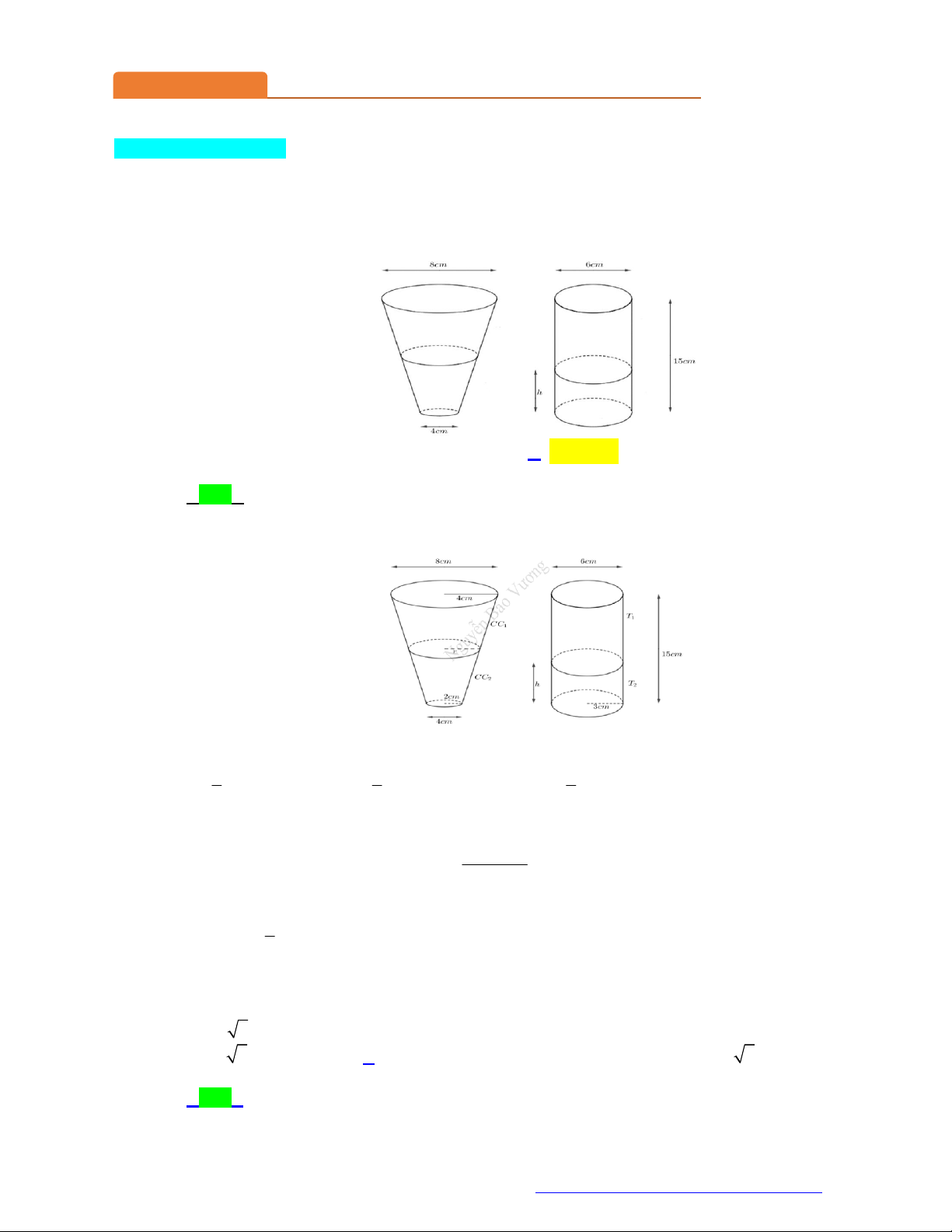
(Sở Lào Cai - 2021) Lon nước ngọt có hình trụ còn cốc uống nước có hình nón cụt (như hình vẽ
minh họa dưới đây). Khi rót nước ngọt từ lon ra cốc thì chiều cao h của phần nước ngọt còn lại
trong lon và chiều cao của phần nước ngọt có trong cốc là như nhau. Hỏi khi đó chiều cao h trong
lon nước gần nhất số nào sau đây?
A. 9,18 cm .
B. 14, 2 cm .
C. 8, 58 cm . D. 7, 5cm . Câu 2.
(Sở Hà Tĩnh - 2021) Cắt hình trụ bởi một mặt phẳng song song với trục và cách trục một khoảng
bằng 2 , thiết diện thu được là hình vuông có diện tích bằng 16 . Thể tích khối trụ bằng A. 10 6 . B. 24 . C. 32 . D. 12 6 . Câu 3.
(Sở Yên Bái - 2021) Cho hình trụ có thiết diện qua trục là hình vuông ABCD cạnh 2 3cm với
AB là đường kính của đường tròn đáy tâm O. Gọi M là điểm thuộc cung 
AB của đường tròn 
đáy sao cho ABM  60 . Thể tích của khối tứ diện ACDM là A. V   3 3 cm  . B. V   3 7 cm  . C. V   3 4 cm  . D. V   3 6 cm  . Câu 4.
(Chuyên Lê Hồng Phong - TPHCM - 2021) Cho hình chóp tam giác đều có cạnh đáy bằng
6 và chiều cao h  1. Tính diện tích mặt cầu ngoại tiếp hình chóp đã cho.
A. S  27 . B. S  6 . C. S  5 . D. S  9 . Câu 5.
(Chuyên Lê Hồng Phong - TPHCM - 2021) Cho hình nón có bán kính đáy bằng 5 và chiều cao
bằng 12 . Tính bán kính mặt cầu ngoại tiếp hình nón. 169 125 81 121 A. R  . B. R  . C. R  . D. R  . 24 24 24 24 Câu 6.
(Chuyên Lam Sơn - Thanh Hóa - 2021) Cho hình trụ có chiều cao bằng 5 3 . Cắt hình trụ đã
cho bởi mặt phẳng song song với trục và cách trục một khoảng bằng 1, thiết diện thu được có diện
tích bằng 30 . Diện tích xung quanh của hình trụ đã cho bằng A. 5 39 . B. 10 3 . C. 10 39 . D. 20 3 . Câu 7.
(Chuyên KHTN - 2021) Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B ,
AB BC  3a , góc   0
SAB SCB  90 và khoảng cách từ A đến mặt phẳng  SBC  bằng a 6 .
Tính diện tích mặt cầu ngoại tiếp hình chóp S.ABC theo a . A. 2 36 a . B. 2 6 a . C. 2 18 a . D. 2 48 a . Câu 8.
(Chuyên Hạ Long - Quảng Ninh - 2021) Cho khối nón có bán kính bằng 3 và khoảng cách từ 12
tâm của đáy đến một đường sinh bất kì bằng
. Thể tích của khối nón đã cho bằng 5
A. V  12 .
B. V  18 .
C. V  36 .
D. V  24 .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489 Câu 9.
(Chuyên ĐH Vinh - Nghệ An - 2021) Cho hình lăng trụ đứng ABC.AB C
  có AB AA  2a , 
AC a , BAC 120 . Bán kính mặt cầu ngoại tiếp hình chóp . A BCC B   bằng 30a 10a 30a 33a A. . B. . C. . D. . 3 3 10 3
Câu 10. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho hình chóp tứ giác ABCD có đáy ABCD là hình chữ
nhật, AB a, AD a 3, SA vuông góc với mặt phẳng đáy. Mặt phẳng SBC tạo với đáy một
góc 60 . Tính thể tích khối chóp S.ABCD . 3 3 a A. 3 V  3a . B. 3 V a . C. 3 V a . D. V  . 3 3
Câu 11. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho khối lăng trụ tam giác ABC.AB C   mà mặt bên ABB A
  có diện tích bằng 2
2a . Khoảng cách giữa CC và mặt  ABB A
  bằng a . Thể tích khối lăng trụ là 2 1 A. 3 V a . B. 3 V a . C. 3 V  3a . D. 3 V a . 3 3
Câu 12. (THPT Thanh Chương 1- Nghệ An - 2021) Cắt hình trụ bởi mặt phẳng qua trục, thiết diện thu
được là hình chữ nhật có chu vi bằng
Giá trị lớn nhất của thể tích khối trụ bằng A. . B. . C. . D. .
Câu 13. (THPT Thanh Chương 1- Nghệ An - 2021) Trong không gian cho hình bình hành có
. Thể tích khối tròn xoay tạo thành khi quay hình bình hành quanh cạnh bằng A. . B. . C. . D. .
Câu 14. (THPT Nguyễn Huệ - Phú Yên - 2021) Cho hình thang vuông ABCD vuông tại , A B . Cạnh AB BC
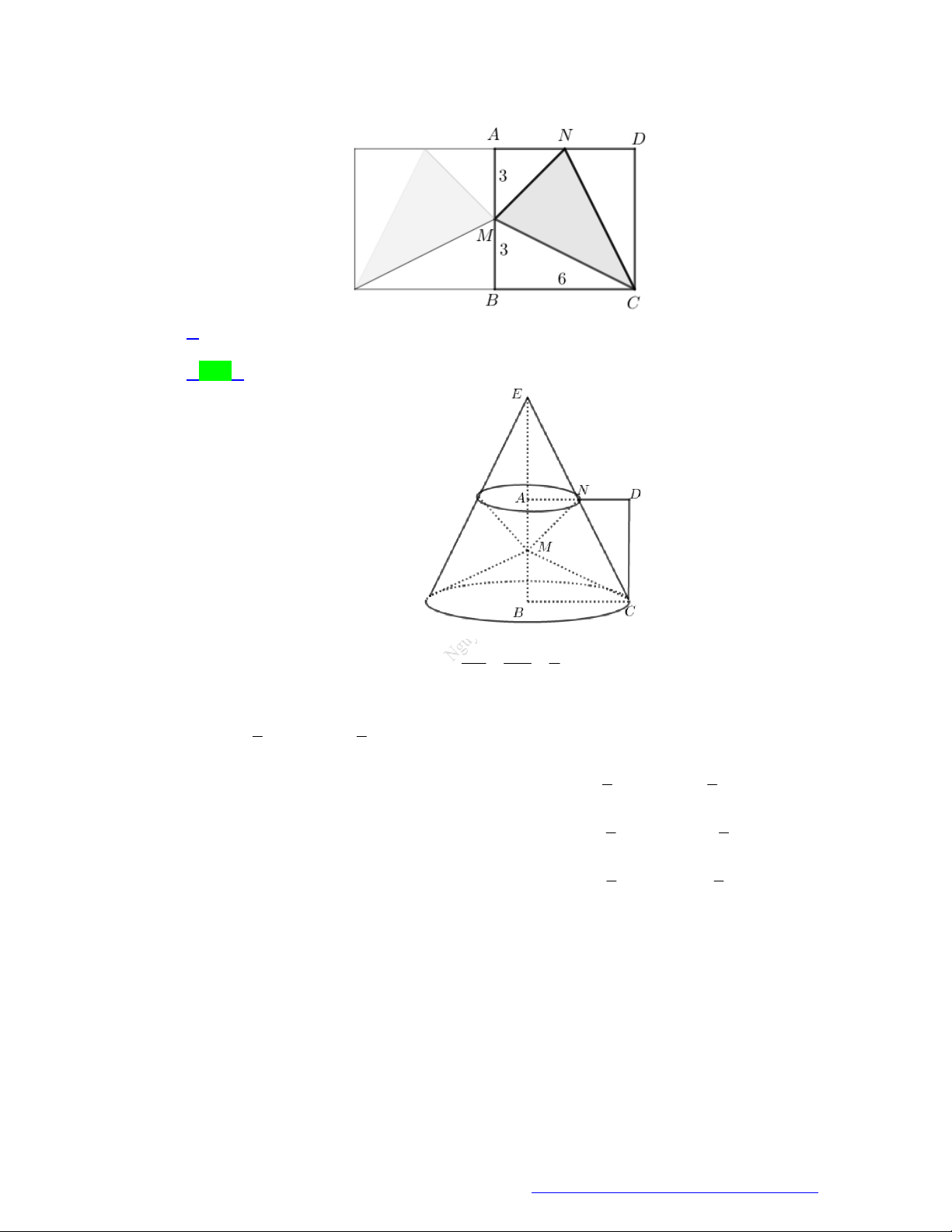
2 , AD  2 2 . Thể tích khối tròn xoay tạo ra khi quay hình thang ABCD quanh CD là 7 7 2 7 14 A.  . B.  . C.  . D.  . 3 12 6 3
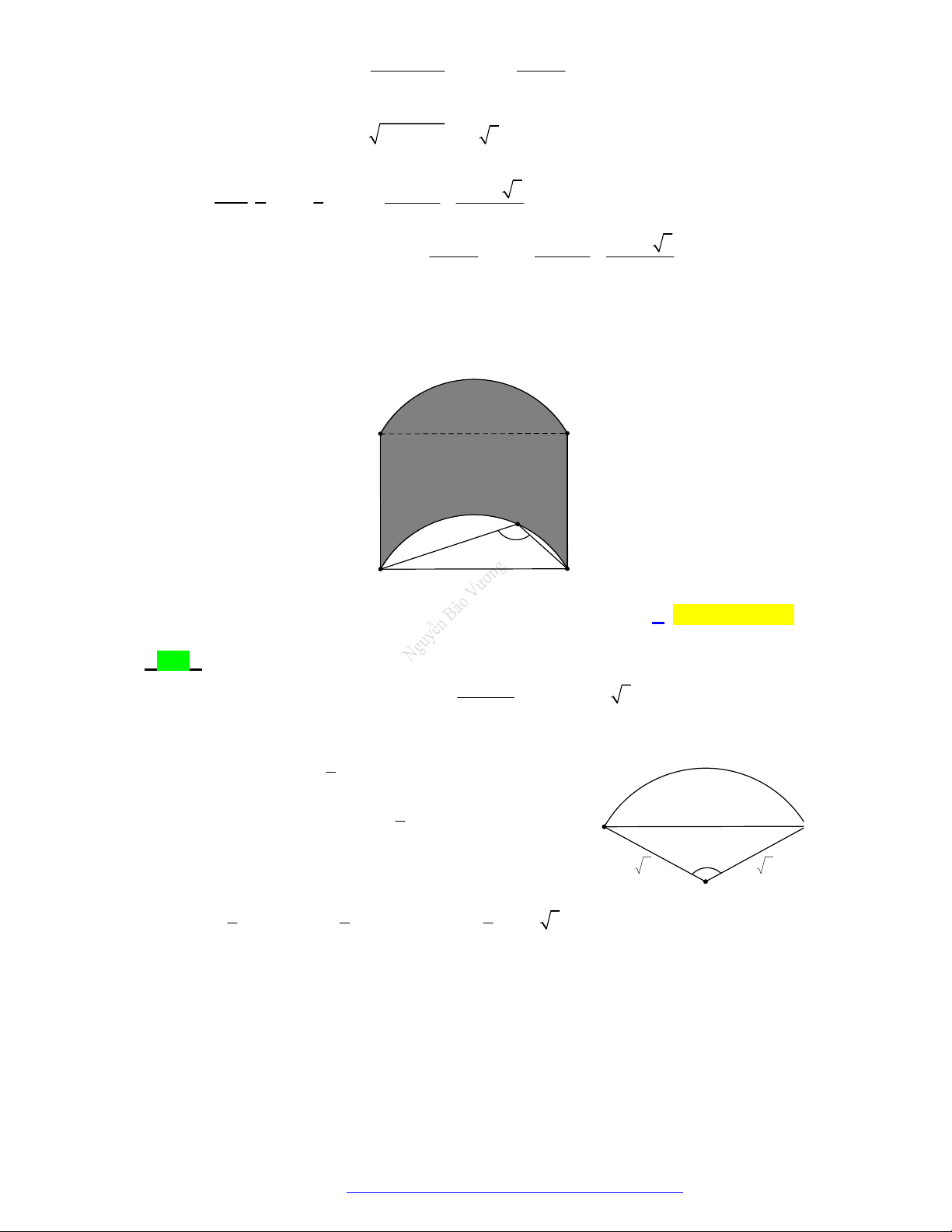
Câu 15. (THPT Nguyễn Huệ - Phú Yên - 2021) Một hình trụ T  có chiều cao bằng đường kính đáy và
một hình nón  N  có đáy là đáy của hình trụ T  , còn đỉnh là tâm của đáy còn lại của hình trụ  S
T  . Gọi S , S lần lượt là diện tích xung quanh của hình trụ T  và hình nón  N  . Tỉ số 1 1 2 S2 bằng 3 4 5 7 1 A. . B. . C. . D. . 5 5 9 2
Câu 16. (THPT Lương Thế Vinh - 2021) Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại
A và B với AB BC  1,
AD  2 . Cạnh bên SA  1 và SA vuông góc với đáy. Gọi E là trung điểm AD. Diện tích Smc
của mặt cầu ngoại tiếp hình chóp S.CDE là A. S  5 . B. S  3 . C. S  11 . D. S  2 . mc mc mc mc
Câu 17. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho hình lăng trụ tam giác đều có cạnh đáy bằng
a , cạnh bên bằng 2a . Thể tích của khối cầu ngoại tiếp hình lăng trụ đã cho bằng 3 32 3 a 3 256 a 3 4 a 3 8 6 a A. . B. . C. . D. . 27 81 3 27
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Câu 18. (THPT Đào Duy Từ - Hà Nội - 2021) Cho hình nón  N  có đỉnh S , bán kính đáy bằng r  1 và
độ dài đường sinh bằng l  2 2 . Mặt cầu đi qua S và đường tròn đáy của  N  có bán kính bằng 4 7 8 7 4 A. . B. . C. 7 . D. . 7 7 3
Câu 19. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Chohình nón có bán kính đáy bằng 3 và chiều cao
bằng 6 , một khối trụ có bán kính đáy thay đổi nội tiếp khối nón( như hình vẽ). Thể tích lớn nhất của khối trụ bằng A. 10 . B. 6 . C. 8 . D. 4 .
Câu 20. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho hình trụ có bán kính đáy bằng 4 . Biết rằng khi
cắt hình trụ đã cho bởi một mặt phẳng qua
trục, thiết diện thu được là một hình vuông. Diện tích toàn phần của hình trụ đã cho bằng A. 106 . B. 64 . C. 80 . D. 96 .
Câu 21. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho hình chóp S.ABC có SA   ABC  , tam giác
ABC vuông tại B , SA BC  3, AB  7 .
Tính bán kính R của mặt cầu ngoại tiếp hình chóp đã cho. 5 5 A. R  . B. R  5 . C. R  5 . D. R  . 2 2
Câu 22. (THPT Ba Đình - Thanh Hóa - 2021) Cho hình lăng trụ tam giác đều ABC.A BC   có độ dài
cạnh đáy bằng a và chiều cao 2a . Tính thể tích V của khối cầu ngoại tiếp hình lằng trụ
ABC.AB C   : 3 32 3 a 3 32 3 a 3 8 3 a 3 32 3 a A. V  . B. V  . C. V  . D. V  . 27 9 27 81
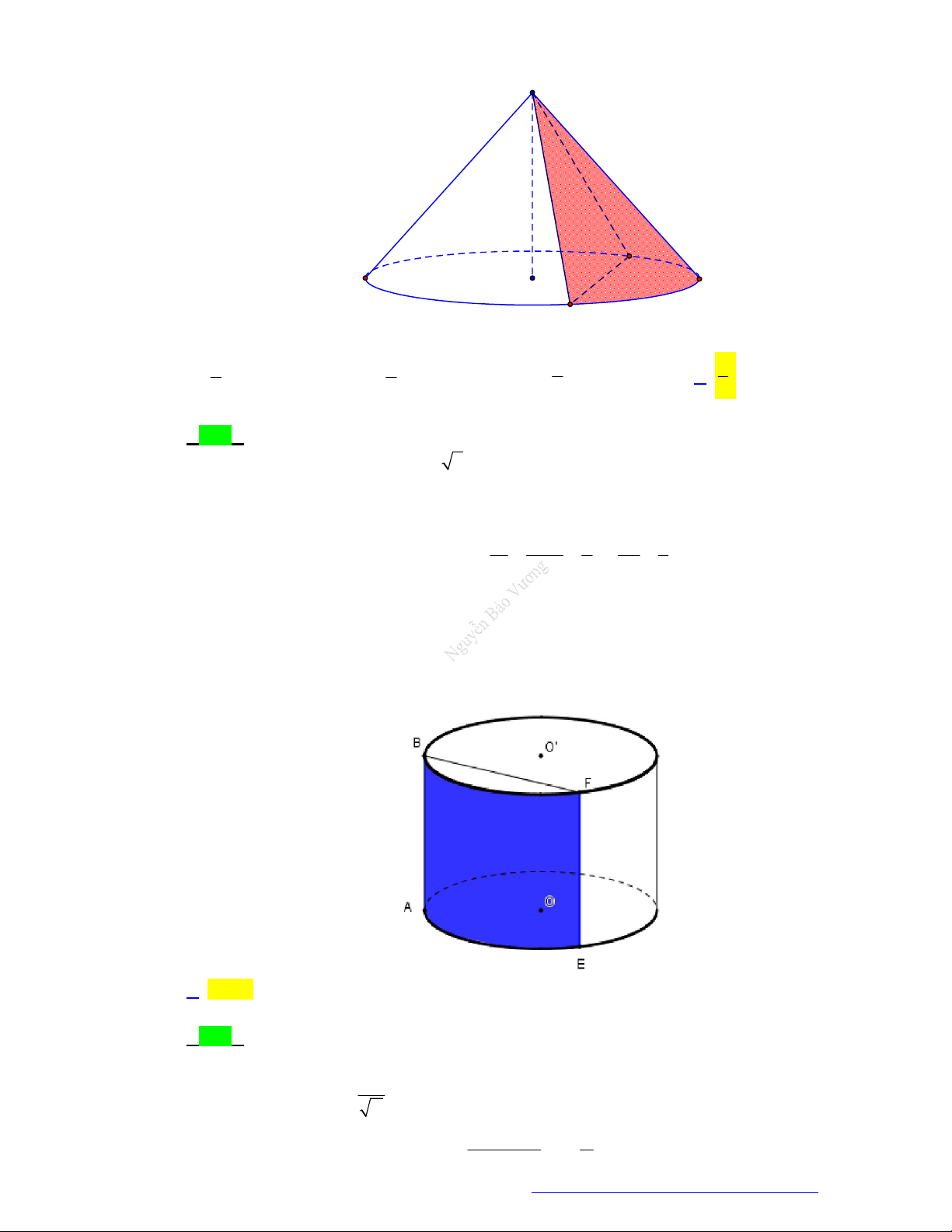
Câu 23. (THPT Quế Võ 1 - Bắc Ninh - 2021) Cho điểm A nằm trên mặt cầu  S  tâm O, bán kính
R  6 cm. I , K là hai điểm trên đoạn OA sao cho OI IK KA . Các mặt phẳng P,Q lần
lượt đi qua I , K cùng vuông góc với OA và cắt mặt cầu S  theo đường tròn có bán kính r ;r . 1 2 r Tính tỉ số 1 . r2 r 5 r 3 10 r 4 r 3 10 A. 1  . B. 1  . C. 1  . D. 1  . r 3 10 r 4 r 10 r 5 2 2 2 2
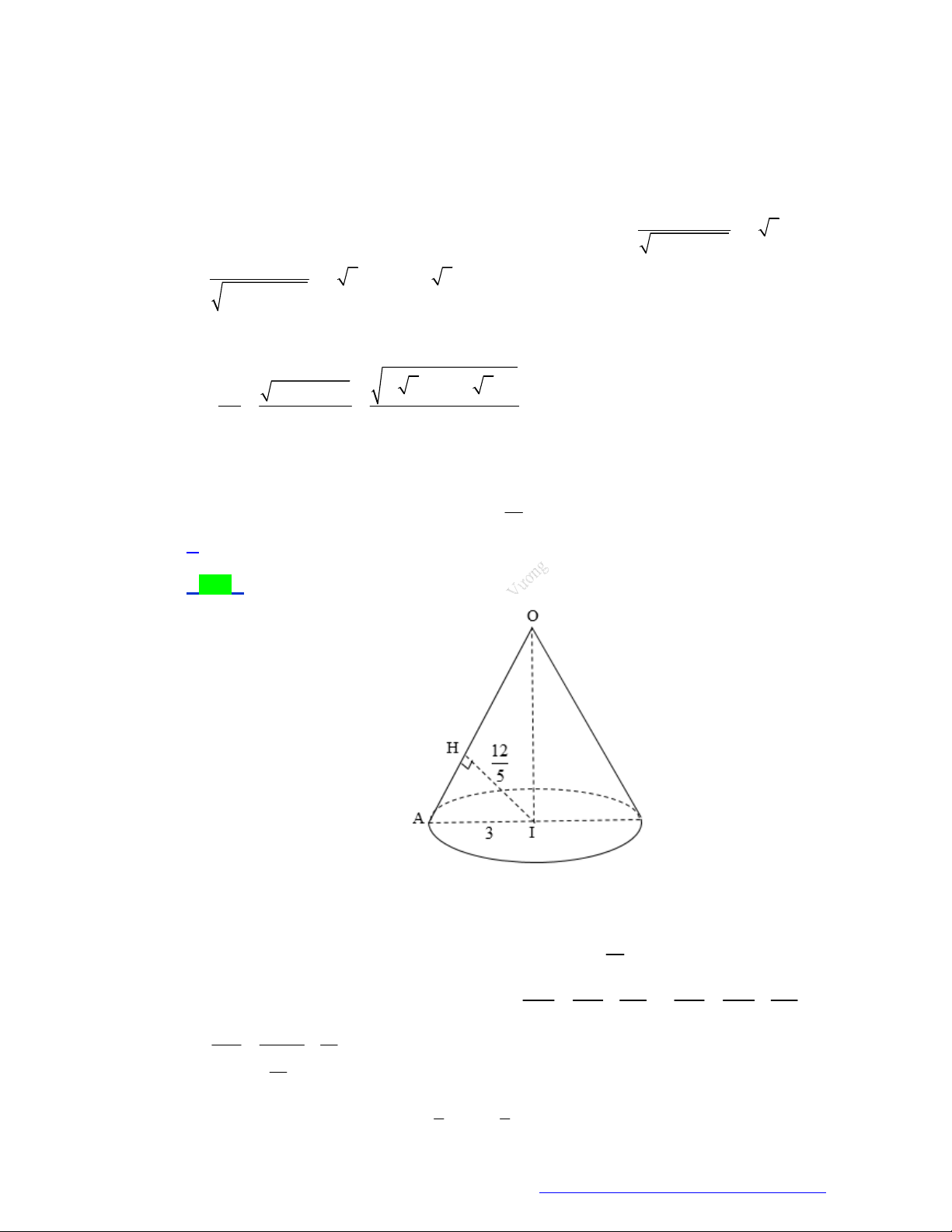
Câu 24. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho hình nón đỉnh S có đáy là đường tròn tâm O
bán kính 1. Trên đường tròn O lấy hai điểm ,
A B sao cho tam giác OAB vuông. Biết diện tích
tam giác SAB bằng 2, thể tích khối nón đã cho bằng :  14  14  14  14 A. V  . B. V  . C. V  . D. V  . 2 3 6 12
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489
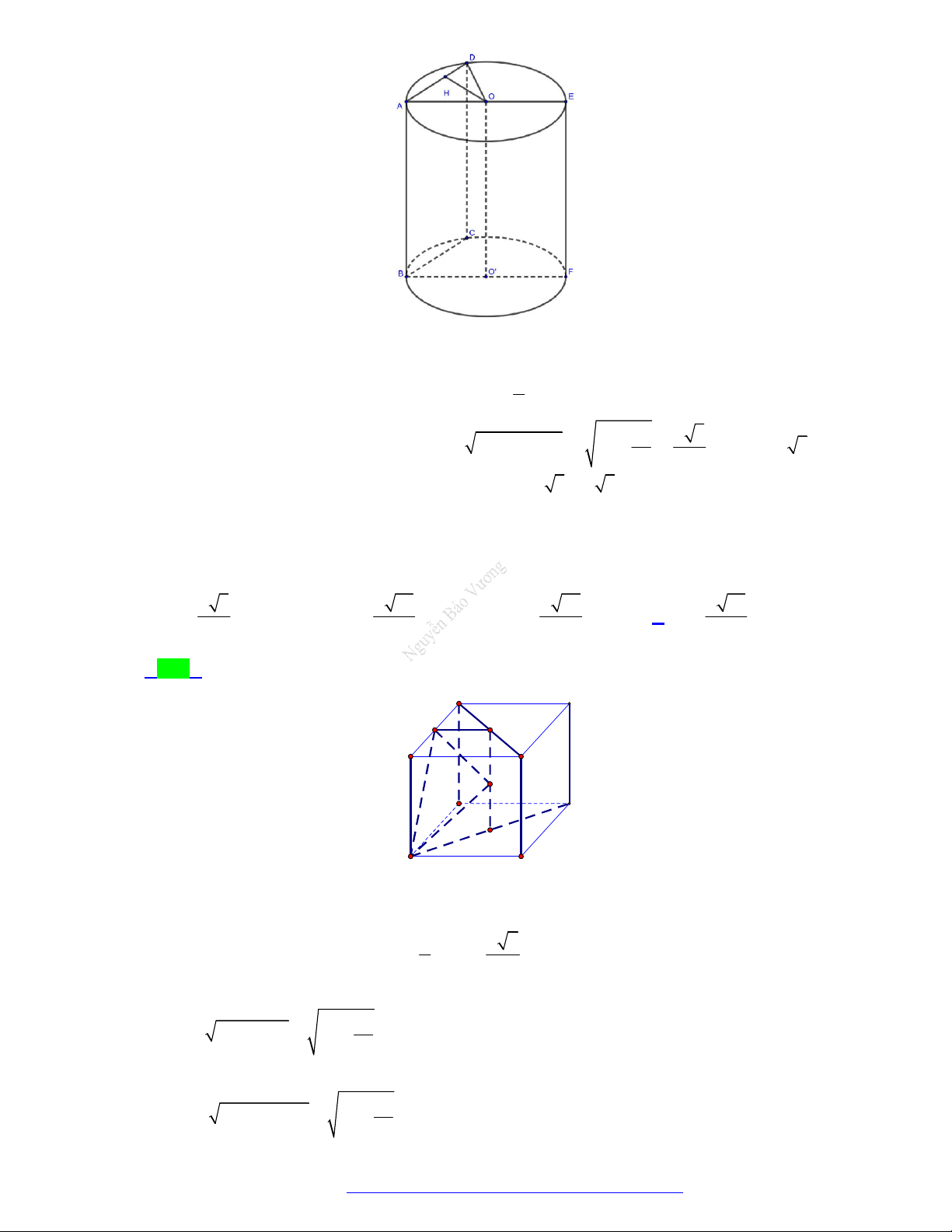
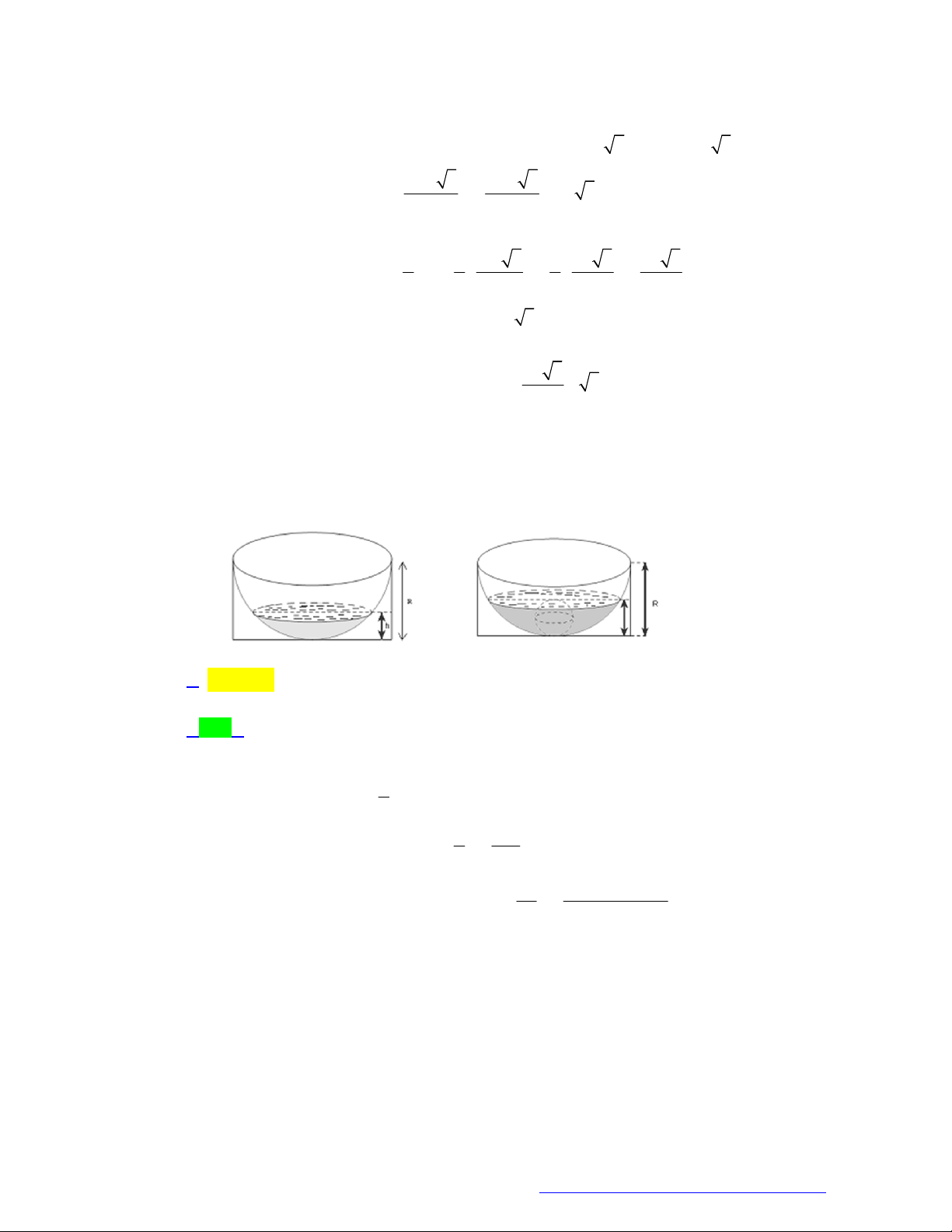
Câu 25. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cắt một hình trụ bởi mặt phẳng song song với trục
ta được thiết diện là hình vuông có diện tích bằng 36 , biết khoảng cách từ tâm đáy đến thiết diện
bằng 1. Tính thể tích của khối trụ giới hạn bởi hình trụ đã cho. A. 20 . B. 10 . C. 30 . D. 60 .
Câu 26. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và
B. Biết AB BC a, AD  2a, SA vuông góc với đáy và SA  2 . a Tính bán
kính mặt cầu ngoại tiếp hình chóp S.HCD với H là trung điểm của AD. a 11 a 10 a 2 a 3 A. . B. . C. . D. . 2 2 2 2
Câu 27. (THPT Phan Đình Phùng - Quảng Bình - 2021) Cho hình nón có chiều cao h  20cm , bán kính
đáy r  25cm . Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm đáy đến mặt phẳng
chứa thiết diện là 12cm . Tính diện tích S của thiết diện đó. A. 2 S  500 cm . B. 2 S  300 cm . C. 2 S  406 cm . D. 2 S  400 cm .
Câu 28. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho hình trụ có thiết diện qua trục là hình vuông a
cạnh 2a . Mặt phẳng P song song với trục và cách trục một khoảng
. Tính diện tích thiết diện 2
của hình trụ cắt bởi mặt phẳng P . 2 15a A. 2 15a . B. 2 2 3a . C. . D. 2 2 15a . 2
Câu 29. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho hình lập phương ABC . D A BCD   cạnh
bằng 2a. Một mặt cầu S  đi qua các đỉnh của hình vuông ABCD đồng thời tiếp xúc với các
cạnh của hình vuông A BCD
  . Tính bán kính R của mặt cầu S  ? a 3 a 41 a 43 a 41 A. R  . B. R  . C. R  . D. R  . 4 4 9 8
Câu 30. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho hình trụ có chiều cao a 2 và hình chữ nhật
ABCD nằm trên mặt phẳng không vuông góc với đáy của hình trụ. Biết AB nằm trên đường tròn
đáy thứ nhất, CD nằm trên đường tròn đáy thứ hai của hình trụ và AB CD a , diện tích hình
chữ nhật ABCD bằng 2
2a . Thể tích khối trụ đã cho bằng 3 a 2 3 3 a 2 3  a 3 3 a A. . B. . C. . D. . 4 4 4 4
Câu 31. (THPT Đồng Quan - Hà Nội - 2021) Cho hình nón đỉnh S , đáy là đường tròn tâm O , bán kính
R  5 . Một thiết diện qua đỉnh S là tam giác đều SAB cạnh bằng 8 , khoảng cách từ O đến mặt
phẳng SAB bằng 13 4 13 3 13 A. . B. 13 . C. . D. . 3 3 4
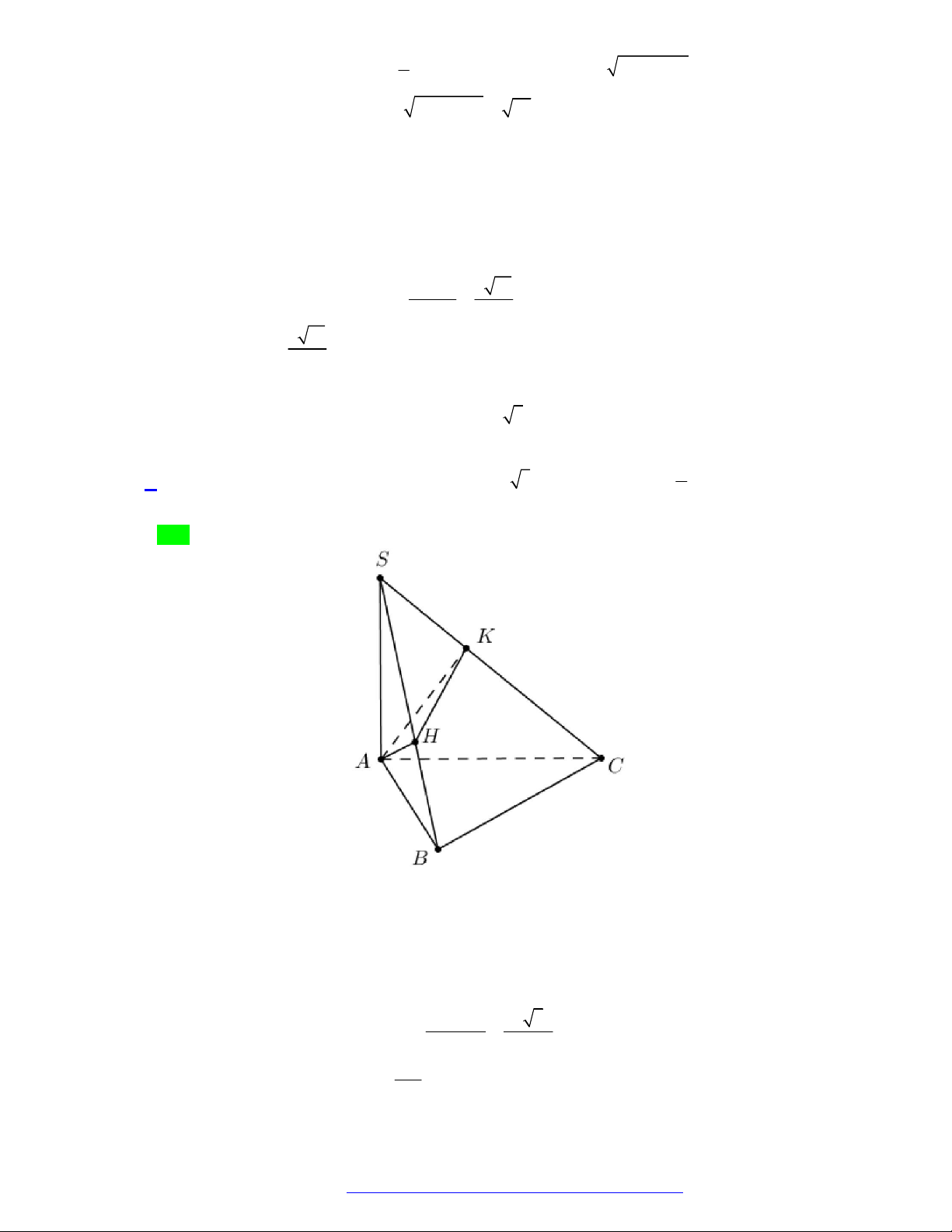
Câu 32. (THPT Lê Lợi - Thanh Hóa - 2021) Cho hình chóp S.ABC với SA vuông góc với mặt phẳng
ABC , tam giác ABC vuông tại B và BC a 3 , 
BAC  60 . Gọi H , K lần lượt là hình
chiếu của A lên SB và SC . Mặt cầu đi qua các điểm ,
A B, C, H , K có bán kính bằng a A. a . B. 2a . C. 3a . D. . 2
Câu 33. (Trung Tâm Thanh Tường -2021) Cho hình vuông ABCD có cạnh bằng 6 , gọi M , N lần lượt
là trung điểm của AB , AD . Tính thể tích của vật tròn xoay sinh bởi tam giác CM N khi quay quanh trục AB .
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 A. 81 . B. 60 . C. 117 . D. 90 .
Câu 34. (THPT Trần Phú - Đà Nẵng - 2021) Một cái chao đèn là một phần của mặt xung quanh của một
mặt cầu có bán kính bằng 3dm như hình vẽ. Vật liệu làm chao đèn là thủy tinh có giá
350.000 (đồng/dm2). Hỏi số tiền (làm tròn đến hàng nghìn) để làm chao đèn trên là bao nhiêu? 23 4 A. 15.401.000 đồng. B. 7.910.000 đồng. C. 6.322.000 đồng. D. 10.788.000 đồng.
Câu 35. (THPT Đoàn Thượng - Hải Dương - 2021) Cho hình chóp SABCD có đáy là hình chữ nhật với
AB  3; AD  2 . Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt
phẳng đáy. Tính thể tích khối cầu ngoại tiếp hình chóp SABCD . 10 20 16 32 A. . B. . C. . D. . 3 3 3 3 BẢNG ĐÁP ÁN 1.C 2.B 3.A 4.D 5.A 6.D 7.A 8.A 9.A 10.B 11.A 12.A 13.B 14.D 15.B 16.C 17.A 18.A 19.C 20.D 21.D 22.A 23.C 24.C 25.D 26.A 27.A 28.B 29.D 30.B 31.D 32.A 33.A 34.B 35.D
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Chủ đề 6 KHỐI TRÒN XOAY
MỨC ĐỘ VẬN DỤNG Câu 1.
(Sở Lào Cai - 2021) Lon nước ngọt có hình trụ còn cốc uống nước có hình nón cụt (như hình vẽ
minh họa dưới đây). Khi rót nước ngọt từ lon ra cốc thì chiều cao h của phần nước ngọt còn lại
trong lon và chiều cao của phần nước ngọt có trong cốc là như nhau. Hỏi khi đó chiều cao h trong
lon nước gần nhất số nào sau đây?
A. 9,18 cm .
B. 14, 2 cm .
C. 8, 58 cm . D. 7, 5cm . Lời giải Chọn C
Gọi r cm là bán kính của hình tròn chia hình chóp cụt thành hai hình chóp cụt CC1 và CC2
(minh họa như hình vẽ), điều kiện: 2  r  4
Ta có thể tích của khối chóp cụt ( cái cốc): VVV CC CC1 CC 2 1    1 1 2 2
4  2  4.215    2 2
4  r  4.r 15  h    2 2
r  2  2.r h 3 3 3    2 28.15
16.15 15r  60r   r  6 2h  r   2 2
6 h  15r  60r 180 15r  2
 2r  6 h  15r  6r  2  h  cm (1). 2
Thể tích khối trụ (lon nước): V VV T CC 2 T 2 1  135    2 2
r  2  2.r h  9 h   2
r  2.r  3  1 h  405 (2). 3 Từ (1) và (2) suy ra: 3
r  27r 116  0  r  3,1  h  8,58cm . Câu 2.
(Sở Hà Tĩnh - 2021) Cắt hình trụ bởi một mặt phẳng song song với trục và cách trục một khoảng
bằng 2 , thiết diện thu được là hình vuông có diện tích bằng 16 . Thể tích khối trụ bằng A. 10 6 . B. 24 . C. 32 . D. 12 6 . Lời giải Chọn B
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489
 Thiết diện cắt bởi mặt phẳng song song với trục là hình vuông ABCD có diện tích bằng 16 nên ta có: 2 S
 16  AB  16  AB  4  CD h . ABCD
 Gọi H là trung điểm cạnh AB .
 Do mặt phẳng  ABCD cách trục OO một khoảng bằng 2 nên ta có OH  2 . AB Trong O
HB vuông tại H , ta có HB   2 ; OH  2 . 2 Khi đó 2 2
r OB OH HB  2  4  6 .
 Vậy thể tích khối trụ là V   r h    2 2 . 6 .4  24 (đvtt). Câu 3.
(Sở Yên Bái - 2021) Cho hình trụ có thiết diện qua trục là hình vuông ABCD cạnh 2 3cm với
AB là đường kính của đường tròn đáy tâm O. Gọi M là điểm thuộc cung 
AB của đường tròn 
đáy sao cho ABM  60 . Thể tích của khối tứ diện ACDM là A. V   3 3 cm  . B. V   3 7 cm  . C. V   3 4 cm  . D. V   3 6 cm  . Lời giải D O' C O H A B M Chọn A Ta có: SS   ACD ABCD  2 1 1 . 2 3 6 2 2
Kẻ MH AB MH   ABCD  d M , ACD  MH
MAB vuông tại M có MB AB cos 60  3 3
MH MB sin 60  2 1 1 3 VVS .MH  .6.  3 . ACDM M . ACD 3 ACD 3 2
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Câu 4.
(Chuyên Lê Hồng Phong - TPHCM - 2021) Cho hình chóp tam giác đều có cạnh đáy bằng
6 và chiều cao h  1. Tính diện tích mặt cầu ngoại tiếp hình chóp đã cho.
A. S  27 . B. S  6 . C. S  5 . D. S  9 . Lời giải Chọn D S M B H I A C O
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng AB  6 và chiều cao h SH  1. 3 2
Ta có: I là trung điểm BC và AI  . 2 2 Khi đó AH AI  2. 3
M là trung điểm SA . Trong SAH  đường trung trực của SA cắt SH tại O . Suy ra O là tâm mặt
cầu ngoại tiếp hình chóp. 2 SA SH SA
Xét hai tam giác đồng dạng SAH và SOM ta có   SO  . SO SM 2h 2 2
SA SH AH  3 . 3 9 2  R SO
; S  4 R  4 .  9 . 2 4 Câu 5.
(Chuyên Lê Hồng Phong - TPHCM - 2021) Cho hình nón có bán kính đáy bằng 5 và chiều cao
bằng 12 . Tính bán kính mặt cầu ngoại tiếp hình nón. 169 125 81 121 A. R  . B. R  . C. R  . D. R  . 24 24 24 24 Lời giải Chọn A
 Gọi h, r lần lượt là chiều cao và bán kính đường tròn đáy của hình nón.
Theo bài ra thì h  12, r  5 .
Gọi S là đỉnh của hình nón, H là tâm đường tròn đáy của hình nón, M là một điểm bất kì
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489
thuộc đường tròn đáy của hình nón. Khi đó mặt cầu ngoại tiếp hình nón phải có tâm O thuộc đoạn SH .
 Ta có bán kính mặt cầu ngoại tiếp hình nón là: R SO OM .
Xét tam giác OHM vuông tại H có 2 2 2
OM OH HM     2 2 2 OM SH SOHM R    R2 2 2 12  5 169
 169  24R  0  R  . 24 Câu 6.
(Chuyên Lam Sơn - Thanh Hóa - 2021) Cho hình trụ có chiều cao bằng 5 3 . Cắt hình trụ đã
cho bởi mặt phẳng song song với trục và cách trục một khoảng bằng 1, thiết diện thu được có diện
tích bằng 30 . Diện tích xung quanh của hình trụ đã cho bằng A. 5 39 . B. 10 3 . C. 10 39 . D. 20 3 . Lời giải Chọn D B O 1 H R A 5√3 B' O' A'
 Thiết diện thu được là hình chữ nhật ABB A   : S 30 AB SA . B AA ⇔ ABB A AB      2 3 ⇒ AH   3 ABB A   AA 5 3 2  Xét O
AH vuông tại H : 2 2
R OA OH AH  1 3  2
 Diện tích xung quanh của hình trụ là: S  2 . .
R h  2 .2.5 3  20 3 . xq Câu 7.
(Chuyên KHTN - 2021) Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B ,
AB BC  3a   , góc 0
SAB SCB  90 và khoảng cách từ A đến mặt phẳng SBC bằng a 6 .
Tính diện tích mặt cầu ngoại tiếp hình chóp S.ABC theo a . A. 2 36 a . B. 2 6 a . C. 2 18 a . D. 2 48 a . Lời giải Chọn A
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Gọi SD là đường cao của hình chóp S.ABC SD AB mà AB SAgt nên AB AD .
Tương tự: SD BC , mà BC SC gt   BC CD .
Tứ giác ABCD có 4 góc vuông và AB BC nên tứ giác ABCD là hình vuông.
Khi đó mặt cầu ngoại tiếp hình chóp S.ABC chính là mặt cầu ngoại tiếp hình chóp S.ABCD.
Kẻ DH SC H SC , mà BC   SCD  BC DH .
DH  SBC  d  ,
D SBC  DH . . SD CD
Mặt khác AD / /  SBC   d  ,
A SBC   d D,SBC   DH   a 6 . 2 2 SD CD .3 SD a
a 6  SD  3 2a . SD  3a2 2 Do các đỉnh ,
A C, D cùng nhìn đoạn thẳng SB dưới một góc 0
90 nên tâm của mặt cầu ngoại tiếp
hình chóp S.ABCD chính là trung điểm I của SB .  a2    a SB SD BD 2 2 2 3 2 3 2 R     3a . 2 2 2
Vậy diện tích mặt cầu ngoại tiếp hình chóp S.ABC là S   R    a2 2 2 4 4 3  36 a . Câu 8.
(Chuyên Hạ Long - Quảng Ninh - 2021) Cho khối nón có bán kính bằng 3 và khoảng cách từ 12
tâm của đáy đến một đường sinh bất kì bằng
. Thể tích của khối nón đã cho bằng 5
A. V  12 .
B. V  18 .
C. V  36 .
D. V  24 . Lời giải Chọn A
Gọi I là tâm đáy, OA là một đường sinh bất kì của khối nón. Gọi H là chân đường vuông góc hạ từ IA  3 
I tới OA, suy ra OI là đường cao h của khối chóp và  12 IH    5 1 1 1 1 1 1
Xét OIA vuông tại I, đường cao IH nên ta có:      2 2 2 2 2 2 IH OI IA OI IH IA 1 1 1 2   
OI  16  OI  4  h  4. 2 2 2 OI  12 3     5  1 1
Vậy thể tích của khối chóp là: 2 2 V   r h   .3 .4  12 . 3 3
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489 Câu 9.
(Chuyên ĐH Vinh - Nghệ An - 2021) Cho hình lăng trụ đứng ABC.AB C
  có AB AA  2a , AC a
, BAC  120 . Bán kính mặt cầu ngoại tiếp hình chóp . A BCC B   bằng 30a 10a 30a 33a A. . B. . C. . D. . 3 3 10 3 Lời giải Chọn A B' C' I M A' O B C A
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC , M là trung điểm của BB .
Dựng đường thẳng  đi qua O và vuông góc với mặt phẳng  ABC . Mặt phẳng trung trực của
đoạn BB cắt  tại I . Khi đó I là tâm mặt cầu ngoại tiếp hình chóp . A BCC B   .
Trong tam giác ABC , ta có: 2 2 2  2 2 2
BC AB AC  2.A .
B AC.cos BAC  4a a  2.2 . a .
a cos120  7a .
BC a 7 .
Gọi R là bán kính đường tròn ngoại tiếp tam giác ABC , áp dụng định lí sin ta được: BC BC a 21  2R R    OB . sin A 2sin A 3 2 21a 30a
Bán kính mặt cầu cần tìm là 2 2 2 2 2
R IB OB OI OB BM   a  . 0 9 3
Câu 10. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho hình chóp tứ giác ABCD có đáy ABCD là hình chữ
nhật, AB a, AD a 3, SA vuông góc với mặt phẳng đáy. Mặt phẳng SBC  tạo với đáy một
góc 60 . Tính thể tích khối chóp S.ABCD . 3 3 a A. 3 V  3a . B. 3 V a . C. 3 V a . D. V  . 3 3 Lời giải Chọn B S A a 3 D a 60 B CBC AB Ta có: 
BC  SAB  BC SB . BC SA
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
BC  SBC    ABCD   Do AB  
ABCDAB BC  SBC  ABCD  SB AB   , , ,  SBA  60   .
SB  SBC, SB BC
Xét tam giác vuông SBA : SA  .
AB tan 60  a 3 . 1 1 Vậy 2 3 V  . . SA S  .a 3.a 3  a . S . ABCD 3 ABCD 3
Câu 11. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho khối lăng trụ tam giác ABC.AB C   mà mặt bên ABB A
  có diện tích bằng 2
2a . Khoảng cách giữa CC và mặt  ABB A
  bằng a . Thể tích khối lăng trụ là 2 1 A. 3 V a . B. 3 V a . C. 3 V  3a . D. 3 V a . 3 3 Lời giải Chọn A A' D' B' C' A D B C Xét khối chóp ABC .
D A' B 'C ' D ' ta có: 1 VV .
ABC. AB C   ABCD. 2 AB CD   Mà VS .d 2 3  S .d
 2a .a  2a .
ABCD. AB CD   ABB A   C,ABB A   ABB A   CC,ABB A   1 Khi đó 3 VVa .
ABC. AB C   ABCD.     2 A B C D
Câu 12. (THPT Thanh Chương 1- Nghệ An - 2021) Cắt hình trụ bởi mặt phẳng qua trục, thiết diện thu
được là hình chữ nhật có chu vi bằng
Giá trị lớn nhất của thể tích khối trụ bằng A. . B. . C. . D. . Lời giải Chọn A B' O' A' B O A
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
NGUYỄN BẢO VƯƠNG - 0946798489  Gọi
lần lượt là bán kính đáy và chiều cao của hình trụ. Theo đề có  Có
Câu 13. (THPT Thanh Chương 1- Nghệ An - 2021) Trong không gian cho hình bình hành có
. Thể tích khối tròn xoay tạo thành khi quay hình bình hành quanh cạnh bằng A. . B. . C. . D. . Lời giải Chọn B  Kẻ
Khối tròn xoay được tạo ra khi hình bình hành ABCD quay quanh trục AB gồm khối tròn xoay do hình thang vuông quay quanh cạnh
và khối nón tròn xoay do tam giác vuông quay quanh cạnh  Do
nên khối tròn xoay do hình bình hành quay quanh trục có thể
tích bằng thể tích khối trụ do hình chữ nhật quay quanh cạnh Ta có
Vậy thể tích khối tròn xoay cần tìm bằng: .
Câu 14. (THPT Nguyễn Huệ - Phú Yên - 2021) Cho hình thang vuông ABCD vuông tại , A B . Cạnh AB BC
2 , AD  2 2 . Thể tích khối tròn xoay tạo ra khi quay hình thang ABCD quanh CD là 7 7 2 7 14 A.  . B.  . C.  . D.  . 3 12 6 3 Lời giải Chọn D
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Gọi E là giao điểm của hai đường thẳng AB và CD .
Gọi A và B lần lượt là các điểm đối xứng với ,
A B qua đường thẳng CD .
Gọi I là trung điểm của đoạn BB . BC EB EC 1 Ta có   
EC ED và AB BE . AD EA ED 2
Khi đó, các khối nón đỉnh E , đỉnh C có đáy là đường tròn  I; IB bằng nhau; các khối nón đỉnh
E và đỉnh D có đáy là đường tròn C,CA bằng nhau.
Gọi V là thể tích của khối nón đỉnh D , đáy là đường tròn C,CA 1
Gọi V là thể tích của khối nón đỉnh C , đáy là đường tròn  I, IB 2
Gọi V là thể tích của khối tròn xoay khi quay hình thang ABCD quanh trục CD . 1 Ta có 2 2 AC
AB BC  2  IB AC  1. 2 1 1
ACD vuông cân tại C CD AC  2  IC EC AC  1 2 2 Do đó 1 1 8 2 2
V   .AC .CD   .2 .2   1 3 3 3 1 1 1 2 2
V   .BI .IC   .1 .1   2 3 3 3 14
Vậy V  2V  2V   . 1 2 3
Câu 15. (THPT Nguyễn Huệ - Phú Yên - 2021) Một hình trụ T  có chiều cao bằng đường kính đáy và
một hình nón  N  có đáy là đáy của hình trụ T  , còn đỉnh là tâm của đáy còn lại của hình trụ  S
T  . Gọi S , S lần lượt là diện tích xung quanh của hình trụ T  và hình nón  N  . Tỉ số 1 1 2 S2 bằng 3 4 5 7 1 A. . B. . C. . D. . 5 5 9 2 Lời giải Chọn B
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
NGUYỄN BẢO VƯƠNG - 0946798489
Gọi R là bán kính đường tròn đáy của hình trụ T
 chiều cao của hình trụ T  là h  2R Ta có 2
S  2 Rh  2 .2 R R  4 R 1
Hình nón  N  có đường sinh 2 2 2 2 l
R h R  4R R 5 Khi đó, 2
S   Rl  5 R 2 2 S 4 R 4 5 Vậy 1   . 2 S 5 R 5 2
Câu 16. (THPT Lương Thế Vinh - 2021) Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại
A và B với AB BC  1,
AD  2 . Cạnh bên SA  1 và SA vuông góc với đáy. Gọi E là trung điểm AD. Diện tích Smc
của mặt cầu ngoại tiếp hình chóp S.CDE là A. S  5 . B. S  3 . C. S  11 . D. S  2 . mc mc mc mc Lời giải Chọn C
 Đặt AB BC a, AD  2a, SA a với a  1.
Gọi H là trung điểm của CD và d là đường thẳng đi qua H và vuông góc với đáy. Gọi I và R
là tâm và bán kính mặt cầu ngoại tiếp hình chóp S.CD .
E Suy ra I thuộc d . Đặt IH  . x Trong
mp  ASIH  kẻ đường thẳng đi qua I và song song với AH cắt AS tại K .  
Ta thấy tứ giác ABCE là hình vuông vì AE // BC, AE BC AB  , a ABC  90  2 2  CED  90 ,
CE a CD CE DE a 2 .
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 2 a Ta có 2 2 2 2
ID IH HD x  . 2
Mặt khác vì AE CE ED a A
CD vuông tại C CD AC . 2 a 2 Khi đó 2 2 2 2 2 2 2 2 2
IS IK KS AH KS AC CH KS  2a
 a x . 2 2 2 a a 2 3a Suy ra: 2 2 x   2a
 a x  x  . 2 2 2 2 2 9a a a 11
 Vậy bán kính mặt cầu ngoại tiếp hình chóp S.CDE là R ID    . 4 2 2 2 2  S
 4 R  11 a  11 . mc
Câu 17. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho hình lăng trụ tam giác đều có cạnh đáy bằng
a , cạnh bên bằng 2a . Thể tích của khối cầu ngoại tiếp hình lăng trụ đã cho bằng 3 32 3 a 3 256 a 3 4 a 3 8 6 a A. . B. . C. . D. . 27 81 3 27 Lời giải Chọn A
Gọi G ';G lần lượt là trọng tâm của các tam giác ABC và A BC  
Gọi I là trung điểm của GG ' . Khi đó I là tâm của mặt cầu ngoại tiếp lăng trụ. 2 a 3 a 3 Ta có AG  .  3 2 3 2  a 3  2 3a
Bán kính mặt cầu ngoại tiếp hình lăng trụ: 2 2 2 IA G I   G A   a     .  3  3   3 4 4  2 3  32 3
Thể tích khối cầu ngoại tiếp lăng trụ đã cho: 3 3 V   R    a   a . 3 3  3  27  
Câu 18. (THPT Đào Duy Từ - Hà Nội - 2021) Cho hình nón  N  có đỉnh S , bán kính đáy bằng r  1 và
độ dài đường sinh bằng l  2 2 . Mặt cầu đi qua S và đường tròn đáy của  N  có bán kính bằng 4 7 8 7 4 A. . B. . C. 7 . D. . 7 7 3 Lời giải Chọn A
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
NGUYỄN BẢO VƯƠNG - 0946798489 S 4a I R B M A
+) Hình nón  N  có đường cao SM , đường sinh SA SB  2 2 , bán kính đường tròn đáy của
N  là AM  1 . Ta có 2 2
SM SA AM  7 .
+) Gọi I là tâm của mặt cầu T  thì I SM , bán kính mặt cầu T  là IS IA R . 4 7
Tam giác IMA vuông tại M có R     R 2 2 2 1 7
 8  2a 7R  0  R  . 7
Câu 19. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Chohình nón có bán kính đáy bằng 3 và chiều cao
bằng 6 , một khối trụ có bán kính đáy thay đổi nội tiếp khối nón( như hình vẽ). Thể tích lớn nhất của khối trụ bằng A. 10 . B. 6 . C. 8 . D. 4 . Lời giải Chọn C
Đặt OO  l, B O
   x, SO h  6, SO  y . O B   SOx y
Áp dụng định lý Talet vào tam giác SOB ta được     y  2x . OB SO 3 6
Ta có l  6  y  6  2x . Suy ra 2
V   x 6  2x   . x . x 6  2x .
Áp dụng bất đẳng thức Cô si cho ba số x, x và 6  2x ta được 3
x x  6  2x  V   . x .
x 6  2x    8   .  3 
Thể tích lớn nhất của khối trụ bằng 8 .
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Câu 20. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho hình trụ có bán kính đáy bằng 4 . Biết rằng khi
cắt hình trụ đã cho bởi một mặt phẳng qua
trục, thiết diện thu được là một hình vuông. Diện tích toàn phần của hình trụ đã cho bằng A. 106 . B. 64 . C. 80 . D. 96 . Lời giải Chọn D
 Giả sử thiết diện qua trục của hình trụ là hình vuông ABCD .
 Theo giả thiết ta có bán kính đáy của hình trụ r  4  h l AD DC  2r  8 .
 Vậy diện tích toàn phần của hình trụ là: 2
S  2 rl  2 r  2.4.8  2.16.  96 . tp
Câu 21. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho hình chóp S.ABC có SA   ABC  , tam giác
ABC vuông tại B , SA BC  3, AB  7 .
Tính bán kính R của mặt cầu ngoại tiếp hình chóp đã cho. 5 5 A. R  . B. R  5 . C. R  5 . D. R  . 2 2 Lời giải Chọn D
 Đặt SA a, AB  ,
b BC c .
 Ta có: SA   ABC  SA AC . BC SA
BC   SAB  BC SB . BC AB
 Gọi O là trung điểm SC , ta có các tam giác SAC, SBC vuông lần lượt tại A và B nên: SC
OA OB OC OS
. Do đó mặt cầu đi qua bốn điểm S, ,
A B, C có tâm O và bán kính 2 SC R  . 2 Ta có: 2 2 2 2 2 2 2 2 2
SC SB BC SA AB BC a b c . 1 1 5 Suy ra 2 2 2 R
a b c  9  7  9  . 2 2 2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 22. (THPT Ba Đình - Thanh Hóa - 2021) Cho hình lăng trụ tam giác đều ABC.AB C   có độ dài
cạnh đáy bằng a và chiều cao 2a . Tính thể tích V của khối cầu ngoại tiếp hình lằng trụ ABC.A BC   : 3 32 3 a 3 32 3 a 3 8 3 a 3 32 3 a A. V  . B. V  . C. V  . D. V  . 27 9 27 81 Lời giải Chọn A F A' C' I' B' O C A I E B
Gọi I , I là tâm đường tròn ngoại tiếp 2 đáy của khối lăng trụ.
Khi đó II  là trụ mặt cầu ngoại tiếp 2 đa giác đáy.
Gọi O là trung điểm II  cũng là tâm mặt cầu ngoại tiếp khối lăng trụ đều ABC.A BC  . 2  2 a 3  2 3a Ta có 2 2 2 R AO
AI OI     a  .  3 2  3   3 3 4 4  2 3  32 3 a
Thể tích mặt cầu ngoại tiếp 3 V   R    a   . 3 3  3  27  
Câu 23. (THPT Quế Võ 1 - Bắc Ninh - 2021) Cho điểm A nằm trên mặt cầu  S  tâm O, bán kính
R  6 cm. I , K là hai điểm trên đoạn OA sao cho OI IK KA . Các mặt phẳng P,Q lần
lượt đi qua I , K cùng vuông góc với OA và cắt mặt cầu S  theo đường tròn có bán kính r ; r . 1 2 r Tính tỉ số 1 . r2 r 5 r 3 10 r 4 r 3 10 A. 1  . B. 1  . C. 1  . D. 1  . r 3 10 r 4 r 10 r 5 2 2 2 2 Lời giải Chọn C
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Bán kính mặt cầu S  là R  6 cm nên OA  6 cm  OI IK KA  2 cm nên OK  4 cm.
IM r , IN r
Gọi một giao điểm của các mặt phẳng  P,Q với mặt cầu  S  là 1 2 M , N   . OM ON  6  2 2 2 2
r OM OI  6  2  4 2  r 4 2 4 Do đó, ta có 1 1     . 2 2 2 2 r 2 5 10
r ON OK  6  4  2 5 2  2
Câu 24. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho hình nón đỉnh S có đáy là đường tròn tâm O
bán kính 1. Trên đường tròn O lấy hai điểm ,
A B sao cho tam giác OAB vuông. Biết diện tích
tam giác SAB bằng 2, thể tích khối nón đã cho bằng :  14  14  14  14 A. V  . B. V  . C. V  . D. V  . 2 3 6 12 Lời giải Chọn C
Gọi C là trung điểm của AB . Ta có : OAB là hinh chiếu vuông góc của SAB lên mặt phẳng đáy. S Khi đó : SS OAB SAB OAB SAB OAB SAB          2 .cos , cos ,   OAB    S 4 SAB CO 2  
SC  2 2CO và 2 2 SO
SC CO CO 7 SC 4 1 1 2 2 SSC.AB  .2 2 .2 CO
1 CO  2  OC  SAB 2 2 2 14  SO  2 1 1 14 14
* Thể tích khối nón là : 2 V  r .SO  .    3 3 2 6
Câu 25. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cắt một hình trụ bởi mặt phẳng song song với trục
ta được thiết diện là hình vuông có diện tích bằng 36 , biết khoảng cách từ tâm đáy đến thiết diện
bằng 1 . Tính thể tích của khối trụ giới hạn bởi hình trụ đã cho. A. 20 . B. 10 . C. 30 . D. 60 . Lời giải Chọn D
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
NGUYỄN BẢO VƯƠNG - 0946798489
Gọi thiết diện song song với trục là hình vuông 2
ABB ' A '  AB  36  AB AA '  6.
Gọi H là trung điểm của A . B OH AB Ta có 
OH   ABB ' A'  d O, ABB ' A'  OH  1 OH AA'  2 2 2 2 2  OA
AH OH  3 1  10  V   .OA .AA '  60 .
Vậy thể tích của khối trụ giới hạn bởi hình trụ đã cho là 60 .
Câu 26. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và
B. Biết AB BC a, AD  2a, SA vuông góc với đáy và SA  2 . a Tính bán
kính mặt cầu ngoại tiếp hình chóp S.HCD với H là trung điểm của AD. a 11 a 10 a 2 a 3 A. . B. . C. . D. . 2 2 2 2 Lời giải Chọn A
Ta có ABCH là hình vuông nên CH AD CH  SAD.
Lại có SA AD  2a nên tam giác SAD vuông cân nên  0 SDA  45 . SH a 10 Mà 2 2
SH SA AH SH a 5  R   . SHD 2sin  0 45  2 2  CH a 11
Hình chóp C.SHD có cạnh bên vuông góc với mặt đáy nên 2 R R   . SHD    2  2
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Câu 27. (THPT Phan Đình Phùng - Quảng Bình - 2021) Cho hình nón có chiều cao h  20cm , bán kính
đáy r  25cm . Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm đáy đến mặt phẳng
chứa thiết diện là 12cm . Tính diện tích S của thiết diện đó. A. 2 S  500 cm . B. 2 S  300 cm . C. 2 S  406 cm . D. 2 S  400 cm . Lời giải Chọn A
Thiết diện đi qua đỉnh của hình nón tạo thành hình tam giác như hình vẽ.
Gọi tâm của đáy hình nón là O .
Gọi M là trung điểm AB
 SOM   SAB .
Hạ OH SM OH  SAB . 1 1 1
Đặt OM x x  0 . Trong tam giác SOM ta có :   2 2 2 OH OM SO 1 1 1   
x  15cm . 2 2 2 x 12 20 2 2
AB  2 R x  40 . 2 2 SM SO OM  25 . 1 Vậy 2 SA .
B SM  500cm . SAB 2
Câu 28. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho hình trụ có thiết diện qua trục là hình vuông a
cạnh 2a . Mặt phẳng P song song với trục và cách trục một khoảng
. Tính diện tích thiết diện 2
của hình trụ cắt bởi mặt phẳng P . 2 15a A. 2 15a . B. 2 2 3a . C. . D. 2 2 15a . 2 Lời giải Chọn B
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
NGUYỄN BẢO VƯƠNG - 0946798489
Gọi thiết diện qua trục là hình vuông ABFE AB  2a .
Mặt phẳng P là mặt phẳng ABCD song song với trục OO . a
Kẻ OH AD d O O ;P  d  ;
O P  OH  . 2 2 a a
Xét tam giác OAH vuông tại H ta có: 2 2 AH AO OH 2 3  a    AD a 3 4 2
Vậy diện tích thiết diện cắt bởi mặt phẳng P bằng 2 2 .
a a 3  2 3a .
Câu 29. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho hình lập phương ABC . D A BCD   cạnh
bằng 2a. Một mặt cầu S  đi qua các đỉnh của hình vuông ABCD đồng thời tiếp xúc với các
cạnh của hình vuông A BCD
  . Tính bán kính R của mặt cầu S  ? a 3 a 41 a 43 a 41 A. R  . B. R  . C. R  . D. R  . 4 4 9 8 Lời giải Chọn D A' D' M O' B' C' I A D O B C Gọi O, O ,
I lần lượt là tâm của ABCD , A BCD   , S  .
Gọi M là trung điểm của AB . a a 2
Suy ra IB IM R , OO  a , O M   , OB  . 2 2
Do OO   ABCD,OB   ABCD  OO  OB 2 a 2 2 2  IO IB OB R  . 2
Do OO   AB CD  ,O M
  ABCD  OO  O M  2 a 2 2 2  IO  IM O M   R  . 4
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 2 2 a a 2 2 a a
Ta có IO IO  OO 2 2  R   R   a 2 2  R   a R  4 2 4 2 2 2 2 a a a 2 a 3a 2 2 2 2 a 41  R
a  2a R  R  2  R    R  (thỏa mãn). 4 2 2 2 8 8 a 41 Vậy R  . 8
Câu 30. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho hình trụ có chiều cao a 2 và hình chữ nhật
ABCD nằm trên mặt phẳng không vuông góc với đáy của hình trụ. Biết AB nằm trên đường tròn
đáy thứ nhất, CD nằm trên đường tròn đáy thứ hai của hình trụ và AB CD a , diện tích hình
chữ nhật ABCD bằng 2
2a . Thể tích khối trụ đã cho bằng 3 a 2 3 3 a 2 3  a 3 3 a A. . B. . C. . D. . 4 4 4 4 Lời giải Chọn B
Gọi EF là hình chiếu vuông góc của dây cung AB xuống mặt phẳng chứa đường tròn đáy dưới.
Dễ thấy tứ giác CDEF là hình chữ nhật và FD là đường kính, EF AB CD a . Ta có 2 S
 2a , AB CD a AD BC  2a . Sử dụng định lý Pi-ta-go  ED a 2 ; ABCD 2 a 3 3  a 3  3 a 2
FD a 3  2R R  . Do đó, 2
V   R h   .  .a 2  . 2  2  4  
Câu 31. (THPT Đồng Quan - Hà Nội - 2021) Cho hình nón đỉnh S , đáy là đường tròn tâm O , bán kính
R  5 . Một thiết diện qua đỉnh S là tam giác đều SAB cạnh bằng 8 , khoảng cách từ O đến mặt
phẳng SAB bằng 13 4 13 3 13 A. . B. 13 . C. . D. . 3 3 4 Lời giải Chọn D
Gọi I là trung điểm của AB OI A . B
Tam giác SAB đều cạnh bằng 8  SI  4 3 .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
NGUYỄN BẢO VƯƠNG - 0946798489 1
Tam giác OIA vuông tại I có 2 2 IA
AB  4, OA R  5  OI OA IA  3 . 2
Tam giác SOI vuông tại 2 2
O SO SI OI  39 .
Ta có AB OI , AB SO AB  SOI , mà AB  SAB  SOI   SAB
Trong mặt phẳng SOI , dựng OH SI
SOI    SAB  Ta có 
SOI    SAB  SI
OH  SAB  d  ,
O SAB  OH .
OH  SOI ,OH SIOI.SO 3 13
Tam giác SOI vuông tại O OH   . SI 4
Vậy d O SAB 3 13 ,  . 4
Câu 32. (THPT Lê Lợi - Thanh Hóa - 2021) Cho hình chóp S.ABC với SA vuông góc với mặt phẳng
ABC , tam giác ABC vuông tại B và BC a 3 , 
BAC  60 . Gọi H , K lần lượt là hình
chiếu của A lên SB và SC . Mặt cầu đi qua các điểm ,
A B, C, H , K có bán kính bằng a A. a . B. 2a . C. 3a . D. . 2 Lời giải Chọn A
Ta có AK KC , AB BC nên B, K nhìn AC dưới một góc vuông. BC SA Lại có   BC AH BC AB
Mặt khác AH SB nên AH   SBC   AH HC , do đó H nhìn AC dưới một góc vuông. Vậy ,
A B, C, H , K đều thuộc mặt cầu đường kính AC . BC a 3
Tam giác ABC vuông tại B nên AC     2a . sin BAC sin 60 AC
Bán kính mặt cầu ngoại tiếp là R   a . 2
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Câu 33. (Trung Tâm Thanh Tường -2021) Cho hình vuông ABCD có cạnh bằng 6 , gọi M , N lần lượt
là trung điểm của AB , AD . Tính thể tích của vật tròn xoay sinh bởi tam giác CM N khi quay quanh trục AB . A. 81 . B. 60 . C. 117 . D. 90 . Lời giải Chọn A EA AN 1
 Kéo dài CN cắt AB tại E . Khi đó:  
EA AB  6  EB  12 . EB BC 2
 Quay tam giác EBC quanh trục AB ta được hình nón. Khi đó thể tích khối nón đó là: 1 1 2 2
V  .BC .EB  .6 .12 144 . 1 3 3 1 1
 Thể tích khối nón đỉnh E , bán kính đáy AN  3 là: 2 2
V  . AN .EA  .3 .6 18 . 2 3 3 1 1
 Thể tích khối nón đỉnh M , bán kính đáy AN  3 là: 2 2
V  . AN . AM  .3 .3  9 . 3 3 3 1 1
 Thể tích khối nón đỉnh M , bán kính đáy BC  6 là: 2 2
V  .BC .MB  .6 .3  36 . 4 3 3
 Vậy thể tích của vật tròn xoay sinh bởi tam giác CM N khi quay quanh trục AB là:
V V V V V  144 18  9  36  81 . 1 2 3 4
Câu 34. (THPT Trần Phú - Đà Nẵng - 2021) Một cái chao đèn là một phần của mặt xung quanh của một
mặt cầu có bán kính bằng 3dm như hình vẽ. Vật liệu làm chao đèn là thủy tinh có giá
350.000 (đồng/dm2). Hỏi số tiền (làm tròn đến hàng nghìn) để làm chao đèn trên là bao nhiêu?
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
NGUYỄN BẢO VƯƠNG - 0946798489 23 4 A. 15.401.000 đồng. B. 7.910.000 đồng. C. 6.322.000 đồng. D. 10.788.000 đồng. Lời giải Chọn B
+ Áp dụng công thức diện tích chỏm cầu S  2 hR . 23 3 23
Ta có diện tích chao đèn là : 2
S  2 hR  2 . .3   (dm ) 4 2 3 23
+ Số tiền làm chao đèn là :
 .350000  7.910.000 đồng. 2
Câu 35. (THPT Đoàn Thượng - Hải Dương - 2021) Cho hình chóp SABCD có đáy là hình chữ nhật với
AB  3; AD  2 . Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt
phẳng đáy. Tính thể tích khối cầu ngoại tiếp hình chóp SABCD . 10 20 16 32 A. . B. . C. . D. . 3 3 3 3 Lời giải Chọn D
SAB   ABCD , kẻ SM AB SM   ABCD .
Gọi I là giao điểm của hai đường chéo. J là trọng tâm tam giác SAB .
Dựng đường thẳng  qua I và song song SM , suy ra  là trục đường tròn ngoại tiếp hình chữ nhật ABCD .
Dựng đường thẳng d  qua J và song song với MI , suy ra d  là trục đường tròn ngoại tiếp của tam giác SAB .
Gọi O  d     O là tâm mặt cầu. 1 1 3 3 1 13 JM SM  . ; IA AC  3 3 2 2 2 3 13 4 32 2 2 2 2 3
R OA OI IA JM IA    2  V   R  . 4 4 3 3
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Chủ đề 6 KHỐI TRÒN XOAY
MỨC ĐỘ VẬN DỤNG CAO Câu 1.
(Sở Vĩnh Phúc - 2021) Cho mặt cầu S  có bán kính không đổi là R . Một hình chóp lục giác đều
S.ABCDEF nội tiếp mặt cầu S  . Tìm giá trị lớn nhất S ABCDEF m
V ax của thể tích khối chóp . . 3 3 3R 3 8 3R 3 16 3R 3 8 3R A. m V ax  . B. m V ax  . C. m V ax  . D. m V ax  8 9 27 27 Câu 2.
(Sở Tuyên Quang - 2021) Cho hình nón có chiều cao bằng 3 . Một mặt phẳng   đi qua đỉnh
hình nón và cắt hình nón
theo một thiết diện là tam giác đều, góc giữa trục của hình nón và mặt phẳng   là 45. Thể
tích của hình nón đã cho bằng A. 5 24 . B. 15 . C. 45 . D. 15 25 . Câu 3.
(Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Người ta chế tạo một món đồ chơi cho
trẻ em theo các công đoạn như sau: Trước tiên chế tạo ra hình nón tròn xoay có góc ở đỉnh là
2  60 bằng thủy tinh trong suốt. Sau đó đặt hai quả cầu nhỏ bằng thủy tinh có bán kính lớn,
nhỏ khác nhau sao cho hai mặt cầu tiếp xúc với nhau và đều tiếp xúc với mặt nón, quả cầu lớn tiếp
xúc với mặt đáy của hình nón, như hình vẽ bên dưới.
Biết rằng chiều cao của hình nón bằng 9cm . Bỏ qua bề dày các lớp vỏ thủy tinh, tổng thể tích của hai khối cầu bằng 100 112 40 38 A. . B. . C. . D. . 3 3 3 3 Câu 4.
(Chuyên Quốc Học Huế - 2021) Tính thể tích lớn nhất của hình trụ nội tiếp trong mặt cầu có bán
kính 1 (hình trụ nội tiếp trong mặt cầu là hình trụ có hai đường tròn đáy thuộc mặt cầu). 3 4 3 2 3 2 3 A.  . B.  . C.  . D.  . 9 9 9 3 Câu 5.
(Chuyên Ngoại Ngữ Hà Nội- 2021) Một hình trụ có thiết diện qua trục là hình chữ nhật có chu vi
bằng 12cm. Thể tích lớn nhất mà hình trụ có thể nhận được là A.   3 16 cm  . B.   3 64 cm  . C.   3 32 cm  . D.   3 8 cm  . Câu 6.
(Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Cho hình chóp S.ABC có đáy ABC
là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông
góc với mặt phẳng đáy. Tính thể tích V của khối cầu ngoại tiếp hình chóp đã cho biết  o ASB  120 ?
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489 13 78 5 15 5 4 3 A. . B. . C. . D. . 27 54 3 27 Câu 7.
(THPT Quế Võ 1 - Bắc Ninh - 2021) Cho hình trụ T  có bán kính đáy và chiều cao đều bằng
R, hai đáy là hai hình tròn O và O. Gọi AA và BB là hai đường sinh bất kì của T  và
M là một điểm di động trên đường tròn O. Thể tích lớn nhất của khối chóp M .AAB B  bằng bao nhiêu? 3 3R 3 3 R 3 3 R 3 3 R 3 A. . B. . C. . D. . 4 4 3 2 Câu 8.
(THPT Phan Đình Phùng - Quảng Bình - 2021) Một nhà máy sản xuất các hộp hình trụ kín cả
hai đầu có thể tích V cho trước. Mối quan hệ giữa bán kính đáy R và chiều cao h của hình trụ để
diện tích toàn phần của hình trụ nhỏ nhất là
A. h R .
B. h  3R .
C. h  2R .
D. R  2h . Câu 9.
(THPT Mai Anh Tuấn - Thanh Hóa - 2021) Cho hình lăng trụ đều AB .
C A' B 'C ' , biết góc giữa
hai mặt phẳng  A' BC  và  ABC bằng 0
45 , diện tích tam giác A' BC bằng 2 a 6 . Tính diện
tích xung quanh của hình trụ ngoại tiếp hình lăng trụ AB .
C A' B 'C ' . 2 8 a 3 2 4 a 3 A. 2 2 a . B. . C. 2 4 a . D. . 3 3
Câu 10. Một chậu nước hình bán cầu bằng nhôm có bán kính R  10 dm . Trong chậu có chứa sẵn một khối
nước hình chỏm cầu có chiều cao h  4 dm . Người ta bỏ vào chậu một viên bi hình cầu bằng kim
loại thì mặt nước dâng lên vừa phủ kín viên bi. Bán kính viên bi gần với số nào sau đây nhất?
A. 2, 09 dm .
B. 9, 63 dm .
C. 3, 07 dm . D. 4, 53 dm .
Câu 11. Sử dụng mảnh inox hình chữ nhật ABCD có diện tích bằng 2
1m và cạnh BC x m để làm một
thùng đựng nước có đáy, không có nắp theo quy trình như sau: Chia hình chữ nhật ABCD thành
2 hình chữ nhật ADNM và BCNM , trong đó phần hình chữ nhật ADNM được gò thành phần
xung quanh hình trụ có chiều cao bằng AM ; phần hình chữ nhật BCNM được cắt ra một hình
tròn để làm đáy của hình trụ trên (phần inox thừa được bỏ đi) Tính gần đúng giá trị x để thùng
nước trên có thể tích lớn nhất (coi như các mép nối không đáng kể).
A. 0,97m .
B. 1, 37m .
C. 1,12m .
D. 1, 02m .
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Câu 12. Từ một tấm thép phẳng hình chữ nhật, người ta muốn làm một chiếc thùng đựng dầu hình trụ bằng
cách cắt ra hai hình tròn bằng nhau và một hình chữ nhật (phần tô đậm) sau đó hàn kín lại, như
trong hình vẽ dưới đây. Hai hình tròn làm hai mặt đáy, hình chữ nhật làm thành mặt xung quanh
của thùng đựng dầu (vừa đủ). Biết rằng đường tròn đáy ngoại tiếp một tam giác có kích thước là 50c , m 70c ,
m 80cm (các mối ghép nối khi gò hàn chiếm diện tích không đáng kể. Lấy   3,14 ).
Diện tích của tấm thép hình chữ nhật ban đầu gần nhất với số liệu nào sau đây? A. 6,8  2 m  . B. 24, 6  2 m  . C. 6,15  2 m  . D. 3, 08  2 m  .
Ông An cần làm một đồ trang trí như hình vẽ. Phần dưới là một phần của khối cầu bán kính
Câu 13. 20 cm làm bằng gỗ đặc, bán kính của đường tròn phần chỏm cầu bằng 10 cm . Phần phía trên làm
bằng lớp vỏ kính trong suốt. Biết giá tiền của 2
1 m kính như trên là 1.500.000 đồng, giá triền của 3
1 m gỗ là 100.000.000 đồng. Hỏi số tiền (làm tròn đến hàng nghìn) mà ông An mua vật liệu để
làm đồ trang trí là bao nhiêu. A. 1.000.000 B. 1.100.000 C. 1.010.000 D. 1.005.000 . . .
Câu 14. Ông Bảo làm mái vòm ở phía trước ngôi nhà của mình bằng vật liệu tôn. Mái vòm đó là một phần
của mặt xung quanh của một hình trụ như hình bên dưới. Biết giá tiền của 1 2 m tôn là 300.000
đồng. Hỏi số tiền (làm tròn đến hàng nghìn) mà ông Bảo mua tôn là bao nhiêu? 5 m 1200 6 m
A. 18.850.000 đồng.
B. 5.441.000 đồng.
C. 9.425.000 đồng.
D. 10.883.000 đồng.
Câu 15. Cổ động viên bóng đá của đội tuyển Indonesia muốn làm một chiếc mũ có dạng hình nón sơn hai
màu Trắng và Đỏ như trên quốc kỳ. Biết thiết diện qua trục của hình nón là tam giác vuông cân.
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489
Cổ động viên muốn sơn màu Đỏ ở bề mặt phần hình nón có đáy là cung nhỏ  MBN , phần còn là
của hình nón sơn màu Trắng. Tính tỉ số phần diện tích hình nón được sơn màu Đỏ với phần diện tích sơn màu Trắng. S M B A O N 2 2 1 1 A. . B. . C. . D. . 7 5 4 3
Câu 16. Một công ty sản xuất bồn đựng nước hình trụ có thể tích thực 3
1m với chiều cao bằng 1m. Biết bề
mặt xung quanh bồn được sơn bởi loại sơn màu xanh tô như hình vẽ và màu trắng là phần còn lại
của mặt xung quanh; với mỗi mét vuông bề mặt lượng sơn tiêu hao 0.5 lít sơn. Công ty cần sơn
10000 bồn thì dư kiến cần bao nhiêu lít sơn màu xanh gần với số nào nhất, biết khi đo được dây cung BF  1 m A. 6150 . B. 6250 . C. 1230 . D. 1250 . BẢNG ĐÁP ÁN 1.C 2.B 3.B 4.B 5.D 6.B 7.D 8.C 9.C 10.A 11.D 12.C 13.D 14.D 15.D 16.A
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Chủ đề 6 KHỐI TRÒN XOAY
MỨC ĐỘ VẬN DỤNG CAO Câu 1.
(Sở Vĩnh Phúc - 2021) Cho mặt cầu S  có bán kính không đổi là R . Một hình chóp lục giác đều
S.ABCDEF nội tiếp mặt cầu S  . Tìm giá trị lớn nhất S ABCDEF m
V ax của thể tích khối chóp . . 3 3 3R 3 8 3R 3 16 3R 3 8 3R A. m V ax  . B. m V ax  . C. m V ax  . D. m V ax  8 9 27 27 Lời giải Chọn C 1 Ta có V
và mặt cầu có tính đối xứng nên để tìm V ta S. ABCDEF
d S; ABCDEF .S ABCDEF max 3
xét hình chóp S.ABCDEF như hình vẽ sau: S O B C r A D H F E
Đáy ABCDEF nội tiếp trong đường tròn tâm H bán kính r và tam giác HAB đều cạnh 2 2
r R x . Đặt OH x 0  x R   2 2 2 3 3 3 R x r  Ta có: S  6S  6. ABCDEF HAB  . 4 2 Khi đó : 1
VS ABCDEF d  3 3
S;  ABCDEF .S  . ABCDEF
R x 2 2 R x    3 2 2 3 .
x Rx R x R  3 2 2 Xét hàm số   3 2 2 3
f x  x Rx R x R với x  0; R  .  R x f x 2 2 ' 3x 2Rx
R ; f ' x 0        3  x  R(l)  Ta có bẳng biến thiên:
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489 3 3  R  16 3R Vậy m V ax  f  .   2  3  27 Câu 2.
(Sở Tuyên Quang - 2021) Cho hình nón có chiều cao bằng 3 . Một mặt phẳng   đi qua đỉnh
hình nón và cắt hình nón
theo một thiết diện là tam giác đều, góc giữa trục của hình nón và mặt phẳng   là 45. Thể
tích của hình nón đã cho bằng A. 5 24 . B. 15 . C. 45 . D. 15 25 . Lời giải Chọn B
Giả sử mặt phẳng   cắt hình nón theo thiết diện là tam giác SAB . Theo giả thiết thì tam
giác SAB đều. Gọi O là tâm của đường tròn đáy; h, r lần lượt là đường cao và bán kính của hình nón.
Gọi M là trung điểm của AB , tam giác OAB cân đỉnh O nên OM AB và SO AB suy ra
AB   SOM  .
Dựng OK SM ( K SM ).
Theo trên ta có AB   SOM   AB OK OK   SAB . 
Vậy góc tạo bởi giữa trục SO và mặt phẳng  SAB là OSM  45 .
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 SO 3
Xét tam giác vuông SOM có   cos OSM   SM
 3 2,OM SO tan cos OSM  3 . SM 2 2 AB 3 2SM 2.3 2
Do tam giác SAB đều nên SM   AB    2 6  AM  6 . 2 3 3
Xét tam giác vuông OAM có 2 2
r OA OM AM  15 . Suy ra thể tích của hình nón đã 1 1 cho là: 2
V   r h   .15.3  15 . 3 3 Câu 3.
(Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Người ta chế tạo một món đồ chơi cho
trẻ em theo các công đoạn như sau: Trước tiên chế tạo ra hình nón tròn xoay có góc ở đỉnh là
2  60 bằng thủy tinh trong suốt. Sau đó đặt hai quả cầu nhỏ bằng thủy tinh có bán kính lớn,
nhỏ khác nhau sao cho hai mặt cầu tiếp xúc với nhau và đều tiếp xúc với mặt nón, quả cầu lớn tiếp
xúc với mặt đáy của hình nón, như hình vẽ bên dưới.
Biết rằng chiều cao của hình nón bằng 9cm . Bỏ qua bề dày các lớp vỏ thủy tinh, tổng thể tích của hai khối cầu bằng 100 112 40 38 A. . B. . C. . D. . 3 3 3 3 Lời giải Chọn B
Gọi h là chiều cao khối nón với h  9 .
Gọi AB là một đường kính của mặt đáy khối nón, S là đỉnh của khối nón và M , N lần lượt là
giao điểm của tiếp tuyến chung của hai mặt cầu với S , A SB như hình vẽ. h
Ta có tam giác SAB đều nên bán kính của đường tròn nội tiếp SAB  bằng r   3 . 1 3
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489 r
Tương tự, tam giác SMN đều nên bán kính của đường tròn nội tiếp OMN bằng 1 r   1 . 2 3 4 4 112
Vậy tổng thể tích của hai khối cầu cần tìm là 3 3 3 3 V
 (r r )   (3 1 )  . 1 2 3 3 3 Câu 4.
(Chuyên Quốc Học Huế - 2021) Tính thể tích lớn nhất của hình trụ nội tiếp trong mặt cầu có bán
kính 1 (hình trụ nội tiếp trong mặt cầu là hình trụ có hai đường tròn đáy thuộc mặt cầu). 3 4 3 2 3 2 3 A.  . B.  . C.  . D.  . 9 9 9 3 Lời giải Chọn B
 Gọi I , O , O lần lượt là tâm mặt cầu, tâm đường tròn đáy trên và đáy dưới của hình trụ.
 Gọi h , R , r lần lượt là chiều cao hình trụ, bán kính mặt cầu và bán kính đường tròn đáy của h
hình trụ. Suy ra h OO  OI  ; R  1 . 2 2 2  h h  Khi đó 2 2 2 R
r r  1   .  2  4 2 3  h   h
 Vậy thể tích của hình trụ là 2
V   r h  . 1 .h h       . 4 4     3  h
Xét hàm số f h  h     với h  0 . 4   2  3h  2  3h  4 2 3
Khi đó: f h  1  2 
 . Suy ra f h  0  1   0  h   h    . 4   4 3 3   Bảng biến thiên
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 2  h  4 3 2 3
Vậy thể tích lớn nhất của hình trụ là V h       (đvtt) khi h  . 4 9   3 Câu 5.
(Chuyên Ngoại Ngữ Hà Nội- 2021) Một hình trụ có thiết diện qua trục là hình chữ nhật có chu vi
bằng 12cm. Thể tích lớn nhất mà hình trụ có thể nhận được là A.   3 16 cm  . B.   3 64 cm  . C.   3 32 cm  . D.   3 8 cm  . Lời giải Chọn D
Giả sử hình trụ có bán kính đáy là a và chiều cao h  , a h  0 .
Thiết diện qua trục là hình chữ nhật ABCD (như hình vẽ).
Theo giả thiết ta có: 22a h  12  h  6  2a  0  a  3 (vì h  0 ). Thể tích khối trụ là: 2 2 V ah a    a 2 6 2  2 a  3 a
Xét hàm số: f a 2
a   a  f a 3 2 3
 a  3a , a 0;3 . a  0 Có f a 2  3
a  6a ; f a  0   . a  2  Bảng biến thiên
Suy ra max f a  f 2  4 . 0;3 Vậy, V  2 .  4  8  3 cm . max  Câu 6.
(Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Cho hình chóp S.ABC có đáy ABC
là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông
góc với mặt phẳng đáy. Tính thể tích V của khối cầu ngoại tiếp hình chóp đã cho biết  o ASB  120 ? 13 78 5 15 5 4 3 A. . B. . C. . D. . 27 54 3 27 Lời giải Chọn B
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489
 Gọi H là trung điểm của AB : SH AB (vì SAB cân tại S ) ⇒ SH   ABC
SH CH và CH AB (vì ABC đều) ⇒ CH  SAB
 Gọi I và J lần lượt là tâm đường tròn ngoại tiếp ABC và SAB .
Qua I và J lần lượt kẻ đường thẳng d song song với SH và d song song với CH
⇒ d là trục của ABC và d là trục của SAB ⇒ Giao điểm của d và d là tâm O và OS là
bán kính của khối cầu ngoại tiếp hình chóp S.ABC . AB 1 3
 Áp dụng đính lí sin trong SAB :   2R  2JS  ⇔ JS   SAB o sin ASB 2 sin120 3 3 1 3
Xét ABC đều: CH  ; IH CH  2 3 6 2 2  3   3  15 Xét O
JS vuông tại J : 2 2 2 2
OS OJ JS
IH JS         6   3  6     3 4 4  15  5 15  3 V   .OS   .   . 3 3  6  54   Câu 7.
(THPT Quế Võ 1 - Bắc Ninh - 2021) Cho hình trụ T  có bán kính đáy và chiều cao đều bằng
R, hai đáy là hai hình tròn O và O. Gọi AA và BB là hai đường sinh bất kì của T  và
M là một điểm di động trên đường tròn O. Thể tích lớn nhất của khối chóp M .AAB B  bằng bao nhiêu? 3 3R 3 3 R 3 3 R 3 3 R 3 A. . B. . C. . D. . 4 4 3 2 Lời giải Chọn D
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Để tìm giá trị lớn nhất của thể tích của các khối chóp M .AAB B
 ta chỉ cần xét các loại hình chóp
M .AAB B
 trong đó M là giao điểm của đường tròn O và đường trung trực của đoạn A . B Khi
đó O thuộc đoạn MI (với I là trung điểm của AB ).
Đặt OI x 0  x R. MI AB
Khi đó MI R x và 
MI   AA BB  . MI AA  Ta có 2 2 2 2
AB  2AI  2 OA OI  2 R x .
Suy ra thể tích của khối chóp M .AAB B  là 1 1 2 V  .S
.MI  .AA .A . B MI R R x R x M AA BBAAB B    2 2 . . 3 3 3 4  VR R x R x M AAB B   2 2 2  2 2 . .  9
Áp dụng bất đẳng thức AM-GM, ta có 1
R x2  2 2
R x    R x R x R x3R  3x 3 4 4
1  R x R x R x  3R  3x  27R   .   3  4  16
R x  3R  3xR
Dấu “  ” xảy ra khi và chỉ khi   x  . x   0; R 2  2 3 2  R   R R 3 Vậy 2 maxV R R R   .     3  2   2  2 Câu 8.
(THPT Phan Đình Phùng - Quảng Bình - 2021) Một nhà máy sản xuất các hộp hình trụ kín cả
hai đầu có thể tích V cho trước. Mối quan hệ giữa bán kính đáy R và chiều cao h của hình trụ để
diện tích toàn phần của hình trụ nhỏ nhất là
A. h R .
B. h  3R .
C. h  2R .
D. R  2h . Lời giải Chọn C
Đặt R x , điều kiện x  0 . V h V 2
V   x h h    . 2  x 3 Rx
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
NGUYỄN BẢO VƯƠNG - 0946798489V  2V S
 2 R h R 2  2 xx   2 x . TP  2    xx 2V
Xét hàm số: f x 2 
 2 x với x  0 . x 3 2V 4 x  2V
Ta có: f  x    4 x  . 2 2 x x V
Khi đó: f  x 3  0  x  . 2 Ta có BBT: V
Từ BBT trên ta thấy S nhỏ nhất khi 3 x TP 2 h V Khi đó: 
 2  h  2R . R V  2 Câu 9.
(THPT Mai Anh Tuấn - Thanh Hóa - 2021) Cho hình lăng trụ đều AB .
C A' B 'C ' , biết góc giữa
hai mặt phẳng  A' BC  và  ABC bằng 0
45 , diện tích tam giác A' BC bằng 2 a 6 . Tính diện
tích xung quanh của hình trụ ngoại tiếp hình lăng trụ AB .
C A' B 'C ' . 2 8 a 3 2 4 a 3 A. 2 2 a . B. . C. 2 4 a . D. . 3 3 Lời giải Chọn C
Gọi I là trung điểm của BC AI BC, A ' I BC.
  A' BC    ABC   BC
Ta có A' I   A' BC , A' I BC   A' BC , ABC 
  A'I, AI   0
A ' IA  45 .
AI   ABC, AI BC
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Do A' A   ABC  tại A , suy ra tam giác A' BC có hình chiếu vuông góc lên mặt đáy  ABC là tam giác ABC .
Áp dụng công thức tính diện tích hình chiếu của một đa giác, ta được SS .cos A BC ABCaa BC  ' ,   2 0 2 6.cos45 3. ABC A' 2 2 AB 3 AB 3 Tam giác ABC đều 2 2 2  S    a
3  AB  4a AB  2 . a ABC 4 4
Suy ra bán kính đường tròn ngoại tiếp tam giác ABC là 2 2  AB 3  2  2a 3  2a 3 r AI        . 3 3  2  3  2  3    
Xét tam giác vuông cân A ' IA A ' A AI a 3.
Vậy diện tích xung quanh của hình trụ ngoại tiếp hình lăng trụ ABC.A' B 'C ' bằng 2a 3 2 S  2 rl  2 .
.a 3  4 a . xq 3
Câu 10. Một chậu nước hình bán cầu bằng nhôm có bán kính R  10 dm . Trong chậu có chứa sẵn một khối
nước hình chỏm cầu có chiều cao h  4 dm . Người ta bỏ vào chậu một viên bi hình cầu bằng kim
loại thì mặt nước dâng lên vừa phủ kín viên bi. Bán kính viên bi gần với số nào sau đây nhất?
A. 2, 09 dm .
B. 9, 63 dm .
C. 3, 07 dm . D. 4,53 dm . Lời giải Chọn A
Gọi x dm là bán kính của viên bi, 0  x  5 . 4  Thể tích viên bi là 3 3 V   x (dm ) 1 3  h  416
Thể tích nước ban đầu: 2 V   h R       3 dm . 0   3  3 2 2  2x
4 x 30  2x
Thể tích sau khi thả viên bi: V   2x 10      3 dm . 2   3  3 Ta có: 3 2
V V V  3x  30x 104  0  x  2, 09 d . m 0 2 1
Câu 11. Sử dụng mảnh inox hình chữ nhật ABCD có diện tích bằng 2
1m và cạnh BC x m để làm một
thùng đựng nước có đáy, không có nắp theo quy trình như sau: Chia hình chữ nhật ABCD thành
2 hình chữ nhật ADNM và BCNM , trong đó phần hình chữ nhật ADNM được gò thành phần
xung quanh hình trụ có chiều cao bằng AM ; phần hình chữ nhật BCNM được cắt ra một hình
tròn để làm đáy của hình trụ trên (phần inox thừa được bỏ đi) Tính gần đúng giá trị x để thùng
nước trên có thể tích lớn nhất (coi như các mép nối không đáng kể).
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
NGUYỄN BẢO VƯƠNG - 0946798489
A. 0,97m .
B. 1, 37m .
C. 1,12m .
D. 1, 02m . Lời giải Chọn D 1 1 Ta có .
AB BC  1  AB   m. BC x
Gọi r m là bán kính đáy hình trụ inox gò được, ta có chu vi hình tròn đáy bằng BC x m. Do x
đó 2 r x r  m . 2 x 1 x
Như vậy BM  2r
AM AB BM   m .  x  2  x   1 x  1
Thể tích khối trụ inox gò được là 2
V   r h   . .   x  2       x . 2   2   x   4
Xét hàm số f xx  2 
  x  với x  0 .  f  x 2
   3x ; f  x  0  x  ; 3      
f  x  0  x  0;
 và f  x  0  x   ;  .   3      3        
Bởi vậy f x đồng biến trên khoảng  0;
 và nghịch biến trên khoảng  ;  .   3      3      2 3 
Suy ra max f x  f     Vf xx   1, 02 m . max   0;  3  9 max   3
Câu 12. Từ một tấm thép phẳng hình chữ nhật, người ta muốn làm một chiếc thùng đựng dầu hình trụ bằng
cách cắt ra hai hình tròn bằng nhau và một hình chữ nhật (phần tô đậm) sau đó hàn kín lại, như
trong hình vẽ dưới đây. Hai hình tròn làm hai mặt đáy, hình chữ nhật làm thành mặt xung quanh
của thùng đựng dầu (vừa đủ). Biết rằng đường tròn đáy ngoại tiếp một tam giác có kích thước là 50c , m 70c ,
m 80cm (các mối ghép nối khi gò hàn chiếm diện tích không đáng kể. Lấy   3,14 ).
Diện tích của tấm thép hình chữ nhật ban đầu gần nhất với số liệu nào sau đây?
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 A. 6,8  2 m  . B. 24, 6  2 m  . C. 6,15  2 m  . D. 3, 08  2 m  . Lời giải Chọn C
Đổi: 50cm  0,5 ;
m 70cm  0, 7 ;
m 80cm  0,8m .
Xét tam giác nội tiếp đường tròn đáy có kích thước lần lượt là 0,5 ; m 0, 7 ;
m 0,8m nên bán kính
đường tròn đáy của thùng đựng dầu là 0, 5.0, 7.0,8 7 3 R   .
4 11 0,51 0,71 0,8 30
Ta có h  2R
Diện tích hình chữ nhật ban đầu gấp 3 lần diện tích xung quanh của hình trụ. 2  7 3  7693 Vậy 2
S  3.2 Rh  6.3,14.2.R  6.3,14.2 2     6,1544 m  .  30  1250  
Ông An cần làm một đồ trang trí như hình vẽ. Phần dưới là một phần của khối cầu bán kính
Câu 13. 20 cm làm bằng gỗ đặc, bán kính của đường tròn phần chỏm cầu bằng 10 cm . Phần phía trên làm
bằng lớp vỏ kính trong suốt. Biết giá tiền của 2
1 m kính như trên là 1.500.000 đồng, giá triền của 3
1 m gỗ là 100.000.000 đồng. Hỏi số tiền (làm tròn đến hàng nghìn) mà ông An mua vật liệu để
làm đồ trang trí là bao nhiêu. A. 1.000.000 B. 1.100.000 C. 1.010.000 D. 1.005.000 . . . Lời giải Chọn D
Bán kính mặt cầu là R  20 cm ; bán kính đường tròn phần chỏm cầu là r  10cm . 10 1 Theo hình vẽ ta có 0 sin      30 . 20 2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
NGUYỄN BẢO VƯƠNG - 0946798489 360  2.30 4000
Diện tích phần làm kính là: 2 S  .4 .20   2 cm  . 360 3
Xét hình nón đỉnh là tâm mặt cầu, hình tròn đáy có bán kính bằng 2 2
r  10 cm ; l R  20 cm h  20 10  10 3cm
Thể tích phần chỏm cầu bằng 2.30 4 1   3 2 16000 1000 3 V
.  R   r .h =   3 cm c hom cau 360 3 3 9 3 4000  16000 1000 3 
Vậy số tiền ông An cần mua vật liệu là: .150    .100  1.005.000 3  9 3   
Câu 14. Ông Bảo làm mái vòm ở phía trước ngôi nhà của mình bằng vật liệu tôn. Mái vòm đó là một phần
của mặt xung quanh của một hình trụ như hình bên dưới. Biết giá tiền của 1 2 m tôn là 300.000
đồng. Hỏi số tiền (làm tròn đến hàng nghìn) mà ông Bảo mua tôn là bao nhiêu? 5 m 1200 6 m
A. 18.850.000 đồng.
B. 5.441.000 đồng.
C. 9.425.000 đồng.
D. 10.883.000 đồng. Lời giải Chọn D 6
Gọi r là bán kính đáy của hình trụ. Khi đó:
 2r r  2 3. 0 sin120
Sử dụng hệ thức lượng trong tam giác, ta có góc ở tâm của cung này bằng 0 120 . 1
Và độ dài cung này bằng chu vi đường tròn đáy. 3 1
Suy ra diện tích của mái vòm bằng S , 6 m 3 xq
(với S là diện tích xung quanh của hình trụ). 1200 xq 2 3 m 2 3 m
Do đó, giá tiền của mái vòm là 1 1 1
S .300.000  .  rl    xq 2 .300.000
.2 .2 3.5.300.000 10882796,19. 3 3 3
Câu 15. Cổ động viên bóng đá của đội tuyển Indonesia muốn làm một chiếc mũ có dạng hình nón sơn hai
màu Trắng và Đỏ như trên quốc kỳ. Biết thiết diện qua trục của hình nón là tam giác vuông cân.
Cổ động viên muốn sơn màu Đỏ ở bề mặt phần hình nón có đáy là cung nhỏ  MBN , phần còn là
của hình nón sơn màu Trắng. Tính tỉ số phần diện tích hình nón được sơn màu Đỏ với phần diện tích sơn màu Trắng.
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 S M B A O N 2 2 1 1 A. . B. . C. . D. . 7 5 4 3 Lời giải Chọn D
Ta có SO OA OB r SM r 2  MN
Do dó tam giác OMN vuông cân tại O .
Gọi S là diện tích xung quanh của hình nón, Sd là diện tích xung quanh của phần hình nón được 0 S 90 1 S 1
sơn màu đỏ, ứng với góc  0 MON  90 nên 1 d     . 0 S 360 4 S 3 t
Câu 16. Một công ty sản xuất bồn đựng nước hình trụ có thể tích thực 3
1m với chiều cao bằng 1m . Biết bề
mặt xung quanh bồn được sơn bởi loại sơn màu xanh tô như hình vẽ và màu trắng là phần còn lại
của mặt xung quanh; với mỗi mét vuông bề mặt lượng sơn tiêu hao 0.5 lít sơn. Công ty cần sơn
10000 bồn thì dư kiến cần bao nhiêu lít sơn màu xanh gần với số nào nhất, biết khi đo được dây cung BF  1 m A. 6150 . B. 6250 . C. 1230 . D. 1250 . Lời giải Chọn A
Gọi r là bán kính đường tròn đáy, 1 Ta có: 2
V   r .h r   2 2 2r BF  Xét tam giác O BF ta có  Cos(BO F  )   1  BO F   2,178271695 (rad) 2 2r 2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
NGUYỄN BẢO VƯƠNG - 0946798489
Vậy độ dài cung BF : l r.  1, 2289582 (m)
Tổng số lít sơn màu xanh cho mỗi bồn nước là: T l. .
h 0.5  0.6144791001 (lít)
Vậy tổng số sơn cần cho 10000 bồn S  6145 (lít)
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Document Outline

  • [NBV]-Chủ đề 6. Khối tròn xoay-Mức độ nhận biết-câu hỏi
  • [NBV]-Chủ đề 6. Khối tròn xoay-Mức độ nhận biết-đáp án
  • [NBV]-Chủ đề 6. Khối tròn xoay-Mức độ thông hiểu-câu hỏi
  • [NBV]-Chủ đề 6. Khối tròn xoay-Mức độ thông hiểu-đáp án
  • [NBV]-Chủ đề 6. Khối tròn xoay-Mức độ vận dụng-câu hỏi
  • [NBV]-Chủ đề 6. Khối tròn xoay-Mức độ vận dụng-đáp án
  • [NBV]-Chủ đề 6. Khối tròn xoay-Mức độ VDC-câu hỏi
  • [NBV]-Chủ đề 6. Khối tròn xoay-Mức độ VDC-đáp án