Top 10 bài tập xác suất thống kê hay nhất | Đại học kiến trúc Hà Nội

lOMoARcPSD| 45467961 lOMoAR cPSD| 45467961 Bài 1 1: Lấy 3 viên cùng màu •
Gọi A là biến cố: “Lấy được 3 viên cùng màu.”
Để lấy được 3 viên cùng màu, chúng ta có 2 trường hợp: 1. Lấy 3 viên xanh. 2. Lấy 3 viên đỏ. •
Xác suất lấy 3 viên xanh:
o Số cách lấy 3 viên xanh từ 5 viên xanh là 5C3 (số tổ hợp chập 3 của 5).
o Số cách lấy 3 viên đỏ từ 9 viên đỏ là 9C3. o Tổng số cách lấy 3 viên từ tất cả
bi là 14C3 (tổng số tổ hợp chập 3 của 14). o Xác suất lấy 3 viên xanh:
P(A - 3 vieˆn xanh)= 5C3/14C3 •
Xác suất lấy 3 viên đỏ cũng tương tự. •
Suy ra xác suất lấy 3 viên cùng màu là 2*5C3/14C3 2 Lấy cả 2 loại bi •
Gọi B là biến cố: “Lấy được cả 2 loại bi.” Để lấy cả 2 loại bi,
chúng ta có 2 trường hợp:
1. Lấy 2 viên xanh và 1 viên đỏ.
2. Lấy 2 viên đỏ và 1 viên xanh. •
Xác suất lấy 2 viên xanh và 1 viên đỏ:
o Số cách lấy 2 viên xanh từ 5 viên xanh là 5C2.
o Số cách lấy 1 viên đỏ từ 9 viên đỏ là 9C1. o Tổng số cách lấy 3
viên từ tất cả bi là 14C3. o Xác suất lấy 2 viên xanh và 1 viên đỏ:
(5C2*9C1)/14C3 o Xác suất 2 viên đỏ và 1 viên xanh cũng tương tự.
Suy ra xác suất lấy cả hai loại bi là 2(5C2*9C1)/14C3 Bài 2 1: Lấy 4 viên cùng màu lOMoARcPSD| 45467961 •
Gọi A là biến cố: “Lấy được 4 viên cùng màu.” Để lấy được 4 viên
cùng màu, chúng ta có 2 trường hợp:
1. Lấy 4 viên xanh từ hộp 1.
2. Lấy 4 viên đỏ từ hộp 2. •
Xác suất lấy 4 viên xanh từ hộp 1:
o Số cách lấy 4 viên xanh từ 6 viên xanh là 6C4 (số tổ hợp chập 4 của 6). o Số
cách lấy 0 viên đỏ từ 4 viên đỏ là 4C0. o Tổng số cách lấy 4 viên từ hộp 1 là
10C4 (tổng số tổ hợp chập 4 của 10).
o Xác suất lấy 4 viên xanh từ hộp 1: o 6C4/10C4
o Xác suất lấy 4 viên đỏ từ hộp 2 là 6C4/10C4 o Vậy xác suất lấy 4 viên bi cùng màu là 2(6C4)/10C4 2
Lấy được 3 viên xanh và 1 viên đỏ (hoặc 3 viên đỏ và 1 viên xanh) từ cả hai hộp: •
Gọi B là biến cố: “Lấy được 3 viên xanh và 1 viên đỏ.” Để lấy 3 viên xanh và 1 viên
đỏ, chúng ta có 2 trường hợp:
1. Lấy 3 viên xanh từ hộp 1 và 1 viên đỏ từ hộp 2.
2. Lấy 2 viên xanh từ hộp 1 và 2 viên đỏ từ hộp 2. •
Xác suất lấy 3 viên xanh và 1 viên đỏ:(6C3*4C1)/10C4 •
Xác suất lấy 2 viên xanh và 2 viên đỏ (6C2*4C2)/10C4 •
Tổng xác suất lầy 3x 1đ là ((6C3*4C1)+ (6C2*4C2)/10C4 Lấy 2 xanh và 2 đỏ •
Gọi C là biến cố: “Lấy được 2 viên xanh và 2 viên đỏ.” Để lấy 2 viên xanh và 2 viên
đỏ, chúng ta có 2 trường hợp:
1. Lấy 2 viên xanh từ hộp 1 và 2 viên đỏ từ hộp 2. 2. Lấy 2 viên đỏ từ hộp
1 và 2 viên xanh từ hộp 2.
Xác suất lấy 2 viên xanh và 2 viên đỏ:
o Số cách lấy 2 viên xanh từ 6 viên xanh là C26. o Số cách
lấy 2 viên đỏ từ 4 viên đỏ là C24. o Tổng số cách lấy 4 viên
từ hộp 1 là C410. o Xác suất lấy 2x 2đ hôp 1 là
(6C2*4C2)/10C4 o Xác suất 2x 2đ hộp 2 là
(5C2*7C2)/12C4 o Xác suất lấy 2x 2đ là (6C2*4C2)/10C4+(5C2*7C2)/12C4 Bài 3
Xác suất lấy dc chính phẩm lần 1 là 8/12
Xác suất để lấy dc chính phẩm laanf 2 là 7/11 lOMoARcPSD| 45467961
Xác suất lấy dc chính phẩm 2 lần là (8/12)*(7/11)
Bài 4: Xác suất để mục tiêu bị trunhs bom là 0,6.0,7 Bài 5
1. Có hai trường hợp: 1x 1đ, 1đ và 1v, 1x 1v 1x 1đ: 5C1*7C1/21C2 1đ 1v 7*9/21C2 1x 1v 5*9/21C2
Xs lấy 2 bi khác màu là 5C1*7C1/21C2+7*9/21C2+5*9/21C2
2. Xác suất lấy 3 bi cùng màu
Xác suất lấy dc 3x+3đ+3v (5C3+7C3+9C3)/21C3 Bài 6
1Xác suất lấy dc ít nhất 1 mặt 6 là 2/12
2Tổng số chấm lớn hơn 9: các cặp giá trị có thể xảy ra là 4,6 (5,5) 5,6 (6,4) 6,5 và 6,6 Do đó xác suất là 6/36
3 Có 36 cặp giá trị có thể xảy ra. Có 8 cặp thỏa mãn hiệu bằng 2 (3,1), (4,2), (5,3), (6,4), (1,3),
(2,4), (3,5), và (4,6). Do đó, xác suất là 8/36
4Mỗi xx có 6 mặt, Tỉ lệ xx2 ra mặt lẻ là ½.Mà xx1 mặt 4. Suy ra xác suất này là 1/6*1/2
5Xúc xắc 2lẻ, 1chawxn có xác suất là 3/6*3/6
Bài 7 Không gian mẫu 12C2
Xs để cả hai lần lấy dc chính phẩm là 8C2/12C2
Xác suất lần 2 lấy được phế phẩm, lần 1 được chính phẩm: Khi lấy ngẫu nhiên 2 sản phẩm mà
không hoàn lại, xác suất lần 1 lấy được chính phẩm và lần 2 lấy được phế phẩm là 8/12*4/11 Bài 8
Đây là bài toán phân phối nhị thức. Xác suất có 5 sp cần bảo hành là P(5)=C(25,5)×(0.25)׿.
Tương tự với 6 và 7: P(6)=C(25,6)×(0.26)׿
P(7)=C(25,7)×(0.27)׿ P(A)=P(5)+P(6)+P(7). lOMoARcPSD| 45467961
Tương tự với không quá 4 sản phẩm phải mang đi bảo hành: P(A)=P(0)+P(1)+P(2)+P(3)+P(4)=
C(25,0)×(0.20)׿
Bài 9 1. là Xác suất lấy hộp 1 là 1/3, và xác suất lấy được chính phẩm từ hộp 1 là 6/10. Vậy,
xác suất lấy hộp 1 và lấy được chính phẩm là 1/3×6/10=1/5.
Xác suất lấy hộp 2 là 1/3, và xác suất lấy được chính phẩm từ hộp 2 là 10/15=2/3. Vậy,
xác suất lấy hộp 2 và lấy được chính phẩm là 1/3×2/3=2/9.
Xác suất lấy hộp 3 là 1/3, và xác suất lấy được chính phẩm từ hộp 3 là 15/20=3/4. Vậy,
xác suất lấy hộp 3 và lấy được chính phẩm là 1/3×3/4=1/4.
Vậy, xác suất lấy được chính phẩm khi lấy ngẫu nhiên 1 hộp và lấy từ hộp đó 1 sản phẩm là tổng của ba xác suất trên
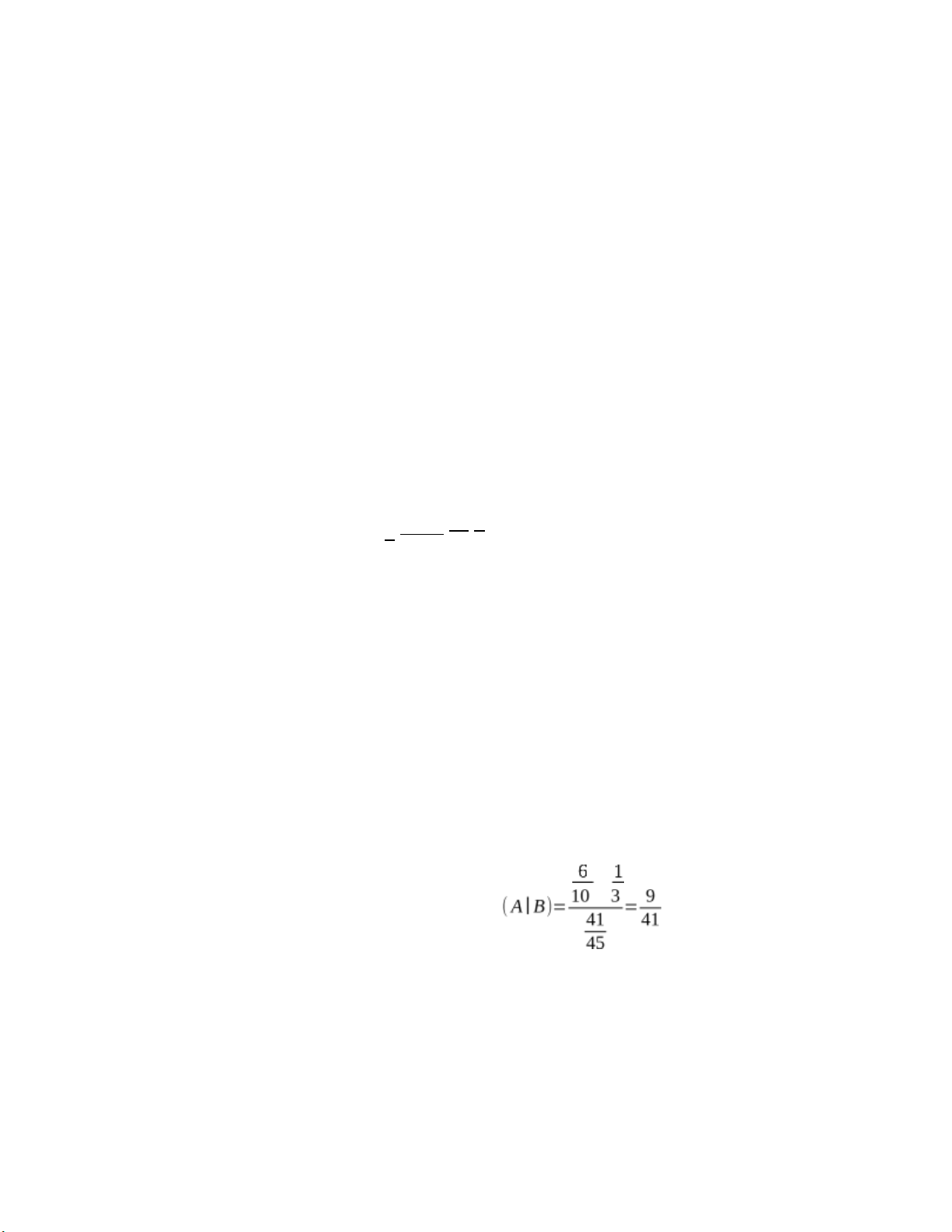
2.Áp dụng công thức BayesP(A∣ B)= P(B∣ A)×P(A) P(B) Trong đó: •
A là sự kiện chính phẩm được lấy ra từ hộp thứ nhất. •
B là sự kiện lấy được chính phẩm. •
P(A∣ B) là xác suất chính phẩm được lấy ra từ hộp thứ nhất khi biết đã lấy được chính phẩm. •
P(B∣ A) là xác suất lấy được chính phẩm khi biết chính phẩm được lấy ra từ hộp thứ nhất. •
P(A) là xác suất chính phẩm được lấy ra từ hộp thứ nhất. •
P(B) là xác suất lấy được chính phẩm. •
P(B∣ A)=6/10 (xác suất lấy được chính phẩm từ hộp thứ nhất). •
P(A)=1/3 (xác suất chọn hộp thứ nhất). •
P(B)=41/45 (xác suất lấy được chính phẩm từ bất kỳ hộp nào, như đã tính ở trên). ×
Thay các giá trị này vào công thức Bayes, ta được: P Bài 10
1. Lấy 1 xanh hộp 1 và bỏ vào hộp 2: 10/13*6/15=4/13
Lấy 1 đỏ hộp 1 và bỏ vào hộp 2: 3/13*7/16
Vậy xác suất lấy ngẫu nhiên 1 bi từ hộp 2 dc bi đỏ là 4/13+21/208 lOMoARcPSD| 45467961
2. Trường hợp bi bỏ vào từ hộp 1sang hộp 2 là bi xanh Xác suất lấy một bi xanh từ
hộp 1 và bỏ vào hộp 2 là 10/13
Sau khi bỏ bi xanh vào hộp 2, hộp 2 sẽ có 9 bi xanh và 6 bi đỏ. Vậy xác suất lấy 2
bi đỏ từ hộp 2 là: 6/15*5/14=1/7
Do đó, xác suất của trường hợp này là × =
Trường hợp bi bỏ vào từ hộp 1 sang hộp 2 là bi đỏ:
Xác suất lấy một bi đỏ từ hộp 1 và bỏ vào hộp 2 là 3/13
Sau khi bỏ bi đỏ vào hộp 2, hộp 2 sẽ có 8 bi xanh và 7 bi đỏ. Vậy xác suất lấy 2 bi đỏ từ hộp 2 là
7/16*6/15=7/40 Do đó, xác suất của trường hợp này là × =
Cuối cùng, xác suất để bi bỏ vào từ hộp 1 sang hộp 2 là bi xanh sau khi đã lấy được 2 bi đỏ từ
hộp 2 là tỷ lệ của trường hợp 1 trên tổng cả hai trường hợp, tức là = 91 520
3. Trường hợp bi bỏ vào từ hộp 1 sang hộp 2 là bi xanh:
Xác suất lấy một bi xanh từ hộp 1 và bỏ vào hộp 2 là
Sau khi bỏ bi xanh vào hộp 2, hộp 2 sẽ có 9 bi xanh và 6 bi đỏ. Vậy xác suất lấy
một bi xanh từ hộp 2 là 9/15
Do đó xác suất th này là 10/13*9/15
Trường hợp bi bỏ vào từ hộp 1 sang hộp 2 là bi đỏ:
Xác suất lấy một bi đỏ từ hộp 1 và bỏ vào hộp 2 là3/13
Sau khi bỏ bi đỏ vào hộp 2, hộp 2 sẽ có 8 bi xanh và 7 bi đỏ. Vậy xác suất lấy một bi xanh từ hộp 2 là 8/16
Do đó, xác suất của trường hợp này là 3/13*8/16
Cuối cùng, xác suất để bi bỏ vào từ hộp 1 sang hộp 2 là bi đỏ sau khi đã lấy được
một bi xanh từ hộp 2 là tỷ lệ của trường hợp 2 trên tổng cả hai trường hợp, tức là = = lOMoARcPSD| 45467961 +