TOP 120 câu trắc nghiệm hai mặt phẳng vuông góc (có đáp án)

TOP 120 câu trắc nghiệm hai mặt phẳng vuông góc có đáp án và lời giải chi tiết rất hay được soạn dưới dạng file PDF gồm 44 trang. Bài tập được phân thành các dạng: Lý thuyết hai mặt phẳng vuông góc; góc giữa hai mặt phẳng; chứng minh hai mặt phẳng vuông góc; chứng minh đường thẳng vuông góc với mặt phẳng và các bài toán liên quan; tính độ dài đoạn thẳng, diện tích hình chiếu, chu vi và diện tích đa giác; xác định thiết diện chứa một đường thẳng và vuông góc với một mặt phẳng. Các bạn xem và tải về ở dưới.

143 72 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 7: Quan hệ vuông góc trong không gian (KNTT)

Môn: Toán 11

Thông tin:

44 trang 9 tháng trước

Tác giả:

Profile Thùy Dương (H)
Trang 1
BÀI TẬP TRẮC NGHIỆM HAI MẶT PHẲNG VUÔNG GÓC
A – LÝ THUYẾT TÓM TẮT
1. Góc giữa hai mặt phẳng
•
• Giả sử (P) Ç (Q) = c. Từ I Î c, dựng Þ
Chú ý:
2. Diện tích hình chiếu của một đa giác
Gọi S là diện tích của đa giác (H) trong (P), S¢ là diện tích của hình chiếu (H¢) của (H) trên (Q), j =
. Khi đó: S¢ = S.cosj
3. Hai mặt phẳng vuông góc
• (P) ^ (Q) Û
• Điều kiện để hai mặt phẳng vuông góc với nhau:
4. Tính chất
• •
•
B – BÀI TẬP
Câu 1: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai mặt phẳng cùng vuông góc với một mặt phẳng thứ ba thì vuông góc với nhau.
B. Qua một đường thẳng cho trước có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
C. Các mặt phẳng cùng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước thì
luôn đi qua một đường thẳng cố định.
D. Hai mặt phẳng cùng song song với một mặt phẳng thứ ba thì song song với nhau.
Hướng dẫn giải:
Chọn C
Câu 2: Chọn mệnh đề đúng trong các mệnh đề sau đây:
A. Cho hai đường thẳng và vuông góc với nhau, mặt phẳng nào vuông góc với đường này thì
song song với đường kia.
B. Cho đường thẳng , mọi mặt phẳng chứa thì .
C. Cho hai đường thẳng chéo nhau và , luôn luôn có mặt phẳng chứa đường này và vuông góc
với đường thẳng kia.
D. Cho hai đường thẳng và vuông góc với nhau, nếu mặt phẳng chứa và mặt phẳng
chứa thì .
Hướng dẫn giải:
Chọn B
Câu 3: Cho hình chóp tứ giác có đáy là hình vuông và có một cạnh bên vuông góc với đáy.
Xét bốn mặt phẳng chứa bốn mặt bên và mặt phẳng chứa mặt đáy. Trong các mệnh đề sau mệnh đề
nào đúng?
∑
( )
∂
( )
()
(),() ,
()
aP
PQ ab
bQ
ì
^
Þ=
í
^
î
(),
(),
aPac
bQbc
ì
Ì^
í
Ì^
î
∑
( )
∂
( )
(),() ,PQ ab=
∑
( )
00
0(),()90PQ££
∑
( )
(),()PQ
∑
( )
0
(),() 90PQ=
()
() ()
()
Pa
PQ
aQ
ì
É
Þ^
í
^
î
() ()
() ()
,()
PQ
AP a P
aAa Q
ì
^
ï
ÎÞÌ
í
ï
'^
î
() ()
() () ()
() ()
PQa
PR aR
QR
ì
Ç=
ï
^Þ^
í
ï
^
î
a
b
( )
a
a
^
( )
b
a
( )
( )
ba
^
a
b
a
b
( )
a
a
( )
b
b
( )
( )
ab
^
.S ABCD
Trang 2
A. Có ba cặp mặt phẳng vuông góc với nhau. B. Có hai cặp mặt phẳng vuông góc với nhau.
C. Có năm cặp mặt phẳng vuông góc với nhau. D. Có bốn cặp mặt phẳng vuông góc với nhau.
Hướng dẫn giải:
Chọn C
Câu 4: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì vuông góc với nhau.
B. Hai đường thẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau.
C. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì cắt nhau.
D. Một mặt phẳng và một đường thẳng không thuộc cùng vuông góc với đường thẳng
thì .
Hướng dẫn giải:
Chọn D
Câu 5: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Nếu hình hộp có bốn mặt bên là hình chữ nhật thì nó là hình hộp chữ nhật.
B. Nếu hình hộp có ba mặt bên là hình chữ nhật thì nó là hình hộp chữ nhật.
C. Nếu hình hộp có hai mặt bên là hình chữ nhật thì nó là hình hộp chữ nhật.
D. Nếu hình hộp có năm mặt bên là hình chữ nhật thì nó là hình hộp chữ nhật.
Hướng dẫn giải:
Chọn D
Câu 6: Trong các mệnh đề sau đây, hãy tìm mệnh đề đúng.
A. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thứ ba thì song song với nhau.
B. Nếu hai mặt vuông góc với nhau thì mọi đường thẳng thuộc mặt phẳng này sẽ vuông góc với mặt
phẳng kia.
C. Hai mặt phẳng và vuông góc với nhau và cắt nhau theo giao tuyến . Với mỗi điểm
thuộc và mỗi điểm thuộc thì ta có đường thẳng vuông góc với .
D. Nếu hai mặt phẳng và đều vuông góc với mặt phẳng thì giao tuyến của và
nếu có sẽ vuông góc với .
Hướng dẫn giải:
Theo Định lí . Chọn D
Câu 7: Cho hai mặt phẳng và vuông góc với nhau và gọi .
I. Nếu và thì . II. Nếu thì .
III. Nếu b ^ d thì b Ì (a) hoặc b Ì (b). IV. Nếu (g) ^ d thì (g) ^ (a) và (g) ^ (b).
Các mệnh đề đúng là :
A. I, II và III. B. III và IV. C. II và III. D. I, II và IV.
Hướng dẫn giải:
Chọn D.
Câu 8: Cho hai mặt phẳng và cắt nhau và một điểm không thuộc và . Qua
có bao nhiêu mặt phẳng vuông góc với và ?
A. 1. B. 2. C. 3. D. Vô số.
Hướng dẫn giải:
Chọn A.
Câu 9: Cho hai mặt phẳng và , là một đường thẳng nằm trên . Mệnh đề nào sau đây sai
?
A. Nếu với thì . B. Nếu thì
C. Nếu cắt thì cắt . D. Nếu thì .
Hướng dẫn giải:
Gọi nếu thì . Chọn B.
Câu 10: Chọn mệnh đề đúng trong các mệnh đề sau đây:
( )
P
a
( )
P
b
( )
//Pa
( )
a
( )
b
d
A
( )
a
B
( )
b
AB
d
( )
a
( )
b
( )
g
d
( )
a
( )
b
( )
g
( )
2109 11tr SGK HH CB-- -
( )
a
( )
b
( ) ( )
d
ab
=Ç
( )
a
a
Ì
ad^
( )
a
b
^
( )
d
a
¢
^
dd
¢
^
( )
P
( )
Q
M
( )
P
( )
Q
M
( )
P
( )
Q
( )
P
( )
Q
a
( )
P
//a b
( ) ( )
bP Q= Ç
( )
a// Q
( ) ( )
PQ^
( )
.aQ^
a
( )
Q
( )
P
( )
Q
( ) ( )
//PQ
( )
//aQ
( ) ( )
=bP QÇ
//a b
( )
//aQ
Trang 3
A. Qua một điểm có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
B. Cho hai đường thẳng chéo nhau và đồng thời . Luôn có mặt phẳng chứa và
.
C. Cho hai đường thẳng và vuông góc với nhau. Nếu mặt phẳng chứa và mặt phẳng
chứa thì .
D. Qua một đường thẳng có duy nhất một mặt phẳng vuông góc với một đường thẳng khác.
Hướng dẫn giải:
Chọn B.
Câu 11: Cho hai mặt phẳng và song song với nhau và một điểm không thuộc và
. Qua có bao nhiêu mặt phẳng vuông góc với và ?
A. . B. . C. . D. Vô số.
Hướng dẫn giải:
Qua dựng đường thẳng vuông cóc với và . Khi đó có vô số mặt phẳng xoay quanh
thỏa yêu cầu bài toán.
Chọn D.
Câu 12: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai mặt phẳng cùng vuông góc với một mặt phẳng thứ ba thì vuông góc với nhau.
B. Hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này sẽ vuông góc
với mặt phẳng kia.
C. Hai mặt phẳng cùng vuông góc với một mặt phẳng thì song song với nhau.
D. Cả ba mệnh đề trên đều sai.
Hướng dẫn giải:
Chọn D.
Câu 13: Trong các mệnh đề sau đây, mệnh đề nào là đúng?
A. Một mặt phẳng và một đường thẳng không thuộc cùng vuông góc với đường thẳng
thì (a) song song với
B. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì vuông góc với nhau.
C. Hai mặt phẳng cùng vuông góc với một mặt phẳng thì cắt nhau.
D. Hai đường thẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau
Hướng dẫn giải:
Đáp án đúng.
Đáp án sai.
Đáp án sai.
Đáp án sai.
Chọn A.
Câu 14: Trong các mệnh đề sau, mệnh đề nào sai?
A. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
B. Qua một đường thẳng có duy nhất một mặt phẳng vuông góc với một đường thẳng cho trước.
C. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
a
b
ab^
( )
a
a
( )
b
a
^
a
b
( )
a
a
( )
b
b
( )
( )
ab
^
( )
P
( )
Q
M
( )
P
( )
Q
M
( )
P
( )
Q
2
3
1
M
d
( )
P
( )
Q
d
()
a
a
()
a
b
.a
A
B
C
D
Trang 4
D. Qua một điểm có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
Hướng dẫn giải:
Đáp án đúng
Qua một đường thẳng có vô số mặt phẳng
vuông góc với một mặt phẳng đúng
Đáp án đúng.
Qua một điểm có vô số mặt phẳng vuông
góc với một mặt phẳng cho trước. Đáp án
sai.
Câu 15: Trong các mệnh đề sau, mệnh đề nào sai?
A. Cho đường thẳng vuông góc với đường thẳng và nằm trong mặt phẳng Mọi mặt
phẳng chứa và vuông góc với thì vuông góc với
B. Nếu đường thẳng vuông góc với đường thẳng và mặt phẳng chứa mặt phẳng
chứa thì vuông góc với
C. Cho đường thẳng vuông góc với mặt phẳng
mọi mặt phẳng chứa thì vuông
góc với
D. Qua một điểm có duy nhất một mặt phẳng vuông góc với một đường thẳng cho trước.
Hướng dẫn giải:
Đáp án đúng.
Đáp án sai.
Đáp án đúng.
Đáp án đúng.
Câu 16: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai mặt phẳng cùng song song với một mặt phẳng thứ ba thì song song với nhau.
B. Qua một đường thẳng cho trước có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho
trước.
C. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với hai mặt phẳng cắt nhau
cho trước.
A
B
C
D
a
b
b
( )
.P
( )
Q
a
b
( )
P
( )
.Q
a
b
( )
P
,a
( )
Q
b
( )
P
( )
.Q
a
( )
,P
( )
Q
a
( )
P
( )
.Q
A
B
C
D
Trang 5
D. Hai mặt phẳng cùng vuông góc với một mặt phẳng thứ ba thì vuông góc với nhau.
Hướng dẫn giải:
Qua một điểm có duy nhất một mặt phẳng vuông góc với một đường thẳng cho trước, đường thẳng đó
là giao tuyến của hai mặt phẳng cắt nhau đã cho. Chọn C.
Câu 17: Cho là các đường thẳng. Mệnh đề nào sau đây là đúng?
A. Cho . Mọi mặt phẳng chứa đều vuông góc với .
B. Nếu và mặt phẳng chứa ; mặt phẳng chứa b thì .
C. Cho nằm trong mặt phẳng . Mọi mặt phẳng chứa và vuông góc với thì
.
D. Cho , mọi mặt phẳng chứa trong đó và thì đều vuông góc với mặt phẳng
.
Hướng dẫn giải:
Chọn C
Câu 18: Cho hai đường thẳng chéo nhau và đồng thời . Chỉ ra mệnh đề đúng trong các
mệnh đề sau:
A. mặt phẳng chứa và đường vuông góc chung của và thì .
B. mặt phẳng chứa và chứa đường thẳng thì .
C. mặt phẳng chứa , chứa thì .
D. mặt phẳng chứa b thì mặt phẳng .
Hướng dẫn giải:
Chọn A
Giả sử là đoạn vuông góc chung của và thì mà
Câu 19: Cho các mệnh đề sau với và là hai mặt phẳng vuông góc với nhau với giao tuyến
và là các đường thẳng. Các mệnh đề sau, mệnh đề nào đúng?
A. Nếu thì hoặc . B. Nếu thì .
C. Nếu và thì . D. Nếu thì hoặc .
Hướng dẫn giải:
Chọn C
Do , , nên
Câu 20: Chỉ ra mệnh đề đúng trong các mệnh đề sau:
A. Cho hai đường thẳng song song và và đường thẳng sao cho . Mọi mặt phẳng
chứa thì đều vuông góc với mặt phẳng .
B. Cho , mọi mặt phẳng chứa thì .
C. Cho , mọi mặt phẳng chứa đều vuông góc với .
D. Cho , nếu và thì .
Hướng dẫn giải:
Câu A sai vì có thể trùng nhau.
Câu C sai vì khi cắt nhau, mặt phẳng không vuông góc với .
Câu D sai vì khi chéo nhau và vuông góc với nhau, ta gọi là mặt phẳng chứa , song song
với và là mặt phẳng chứa và song song với thì
Chọn B.
Câu 21: Mệnh đề nào sau đây là đúng?
,,abc
ab^
b
a
ab^
( )
a
a
( )
b
( ) ( )
ba
^
ab^
( )
a
( )
b
a
b
( ) ( )
ba
^
//ab
( )
a
c
ca^
cb^
( )
,ab
a
b
ab^
(
)
Q
b
a
b
mp(Q) a^
(
)
R
b
'ba^
( )
mp R a^
(
)
a
a
mp( )b
b
() ()a^b
(
)
P
(
)
Pa^
AB
a
b
( ) ( )
,mp Q AB bº
( )
, , ,aABaba ABb^^^
( )
ampQÞ^
( )
a
( )
b
( ) ( )
m
ab
=Ç
a, b, c, d
bm^
( )
b
a
Ì
( )
b
b
Ì
bm^
( )
d
a
^
( )
a
a
Ì
am^
( )
a
b
^
//cm
( )
//c
a
( )
//c
b
( )
a
a
Ì
am^
() ()a^b
( )
a
b
^
a
b
c
,cacb^^
()
a
c
( )
,ab
()a
a
^
( )
b
a
( ) ( )
ba
^
ab^
b
a
ab^
()a
a
Ì
( )
b
b
Ì
( ) ( )
ab
^
,ab
,ab
( )
,ab
a
,ab
( )
a
a
b
( )
b
b
a
( ) ( )
//
ab
Trang 6
A. Hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này sẽ vuông góc
với mặt phẳng kia.
B. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì vuông góc với nhau.
C. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
D. Hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này và vuông góc
với giao tuyến của hai mặt phẳng sẽ vuông góc với mặt phẳng kia.
Hướng dẫn giải:
Mệnh đề A sai vì có thể xảy ra trường hợp hai mặt phẳng vuông góc với nhau nhưng đường thẳng
thuộc mặt phẳng này song song với mặt phẳng kia.
Mệnh đề B sai vì xảy ra trường hợp hai mặt phẳng song song.
Mệnh đề C sai vì xảy ra trường hợp hai mặt phẳng vuông góc.
Chọn đáp án D
Câu 22: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai đường thẳng không cắt nhau, không song song thì chéo nhau.
B. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song.
C. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song.
D. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song.
Hướng dẫn giải:
Mệnh đề sai vì còn trường hợp chéo nhau hoặc trùng nhau.
Mênh đề C sai vì còn trường hợp hai đường thẳng chéo nhau.
Mênh đề D sai vì còn trường hợp hai mặt phẳng vuông góc với nhau.
Chọn B.
Câu 23: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho
trước.
B. Có duy nhất một mặt phẳng đi qua một đường thẳng cho trước và vuông góc với một mặt phẳng
cho trước.
C. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho
trước.
D. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho
trước.
Hướng dẫn giải:
* Có vô số đường thẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước,
chúng nằm trong mặt phẳng đi qua điểm đó và vuông góc với một đường thẳng cho trước Þ “Có duy
nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước”: SAI
* Có vô số mặt phẳng đi qua một đường thẳng cho trước và vuông góc với một mặt phẳng cho trước,
trong trường hợp: đường thẳng cho trước vuông góc với mặt phẳng cho trước Þ:Có duy nhất một mặt
phẳng đi qua một đường thẳng cho trước và vuông góc với một mặt phẳng cho trước”: SAI
* Có vố số mặt phẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước Þ”Có
duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước”: SAI
Chọn D
Câu 24: Cho hình chóp có đường cao . Xét các mệnh đề sau:
(I) .
(II) trùng với tâm đường tròn ngoại tiếp tam giác .
(III) Tam giác là tam giác đều.
(IV) là trực tâm tam giác .
.S ABC
SH
SA SB SC==
H
ABC
ABC
H
ABC
Trang 7
Các yếu tố nào chưa đủ để kết luận là hình chóp đều?
A. (III) và (IV). B. (II) và (III). C. (I) và (II). D. (IV) và (I).
Hướng dẫn giải:
Chọn C
Câu 25: Cho hình chóp có đáy là tam giác đều. Trong các mệnh đề sau, mệnh đề nào
đúng?
A. là hình chóp đều nếu các mặt bên của nó là tam giác cân đỉnh
B. là hình chóp đều nếu góc giữa các mặt phẳng chứa các mặt bên và mặt phẳng đáy bằng
nhau.
C. là hình chóp đều nếu các mặt bên của nó là tam giác cân.
D. là hình chóp đều nếu các mặt bên có diện tích bằng nhau.
Hướng dẫn giải:
Chọn A
Câu 26: Trong lăng trụ đều, khẳng định nào sau đây sai?
A. Đáy là đa giác đều.
B. Các mặt bên là những hình chữ nhật nằm trong mặt phẳng vuông góc với đáy.
C. Các cạnh bên là những đường cao.
D. Các mặt bên là những hình bình hành.
Hướng dẫn giải:
Vì lăng trụ đều nên các cạnh bằng nhau. Do đó đáy là đa giác đều.
Vì lăng trụ đều là lăng trụ đứng nên các mặt bên vuông góc với đáy.
Vì lăng trụ đều là lăng trụ đứng nên các cạnh bên vuông góc với đáy.
Vì lăng trụ đều là lăng trụ đứng nên các cạnh bên bằng nhau và cùng vuông góc với đáy. Do đó các
mặt bên là những hình vuông.
Chọn D.
Câu 27: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Nếu hình hộp có hai mặt là hình vuông thì nó là hình lập phương.
B. Nếu hình hộp có ba mặt chung một đỉnh là hình vuông thì nó là hình lập phương.
C. Nếu hình hộp có bốn đường chéo bằng nhau thì nó là hình lập phương.
D. Nếu hình hộp có sau mặt bằng nhau thì nó là hình lập phương.
Hướng dẫn giải:
Đây là câu hỏi lý thuyết.
Chọn đáp án B
Câu 28: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Nếu hình hộp có hai mặt là hình chữ nhật thì nó là hình hộp chữ nhật.
B. Nếu hình hộp có năm mặt là hình chữ nhật thì nó là hình hộp chữ nhật.
C. Nếu hình hộp có bốn mặt là hình chữ nhật thì nó là hình hộp chữ nhật.
D. Nếu hình hộp có ba mặt là hình chữ nhật thì nó là hình hộp chữ nhật.
Hướng dẫn giải:
Chọn đáp án B
A sai vì đáy có thể là hình bình hành.
B đúng
C sai vì đáy có thể là hình bình hành
D sai vì đáy có thể là hình bình hành.
Câu 29: Hình hộp là hình hộp gì nếu tứ diện đều.
A. Hình lập phương. B. Hình hộp chữ nhật.
C. Hình hộp thoi. D. Đáp số khác.
Hướng dẫn giải:
Chọn đáp án A
.S ABC
.S ABC
ABC
.S ABC
.S
.S ABC
.S ABC
.S ABC
.A
.B
.C
.D
.ABCD A B C D
¢¢¢¢
AB C D
¢¢¢
Trang 8
Câu 30: Hình hộp trở thành hình lăng trụ tứ giác đều khi phải thêm các điều kiện nào
sau đây?
A. Tất cả các cạnh đáy bằng nhau và cạnh bên vuông góc với mặt đáy.
B. Có một mặt bên vuông góc với mặt đáy và đáy là hình vuông.
C. Các mặt bên là hình chữ nhật và mặt đáy là hình vuông.
D. Cạnh bên bằng cạnh đáy và cạnh bên vuông góc với mặt đáy.
Hướng dẫn giải:
Chọn đáp án C
Câu 31: Hình hộp là hình hộp gì nếu tứ diện có các cạnh đối vuông góc.
A. Hình lập phương. B. Hình hộp tam giác.
C. Hình hộp thoi. D. Hình hộp tứ giác.
Hướng dẫn giải:
Ta có suy ra Hình hộp là hình lập phương.
Câu 32: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Góc giữa mặt phẳng và mặt phẳng bằng góc nhọn giữa mặt phẳng và mặt phẳng
(R) khi mặt phẳng song song với mặt phẳng .
B. Góc giữa mặt phẳng và mặt phẳng bằng góc nhọn giữa mặt phẳng và mặt phẳng
khi mặt phẳng song song với mặt phẳng (hoặc ).
C. Góc giữa hai mặt phẳng luôn là góc nhọn.
D. Cả ba mệnh đề trên đều đúng.
Hướng dẫn giải:
Chọn đáp án D
Câu 33: Cho hình chóp tam giác với đường cao . Trong các mệnh đề sau mệnh đề nào
đúng
A. trùng với tâm đường tròn ngoại tiếp tam giác khi và chỉ khi các cạnh bên bằng nhau
B. là trung điểm của một cạnh đáy khi hình hộp đó có một mặt bên vuông góc với mặt đáy.
C. trùng với tâm đường tròn nội tiếp tam giác khi các góc giữa các mặt phẳng chứa các
mặt bên và mặt phẳng đáy bằng nhau.
D. thuộc cạnh đáy thì hình chóp đó có một mặt bên vuông góc với đáy
Hướng dẫn giải:
Chọn đáp án A
Câu 34: Trong các mệnh đề sau, mệnh đề nào sai?
A. Hình lăng trụ tam giác có hai mặt bên là hình chữ nhật là hình lăng trụ đứng.
B. Hình chóp có đáy là đa giác đều và có các cạnh bên bằng nhau là hình chóp đều.
C. Hình lăng trụ đứng có đáy là đa giác đều là hình lăng trụ đều.
D. Hình lăng trụ có đáy là đa giác đều là hình lăng trụ đều.
Hướng dẫn giải:
Giả sử lăng trụ có các mặt bên là hình chữ nhật, khi
đó ta có . Vậy là
lăng trụ đứng.
Theo định nghĩa hình chóp đều và hình lăng trụ đều ta có đáp án B, C đúng.
Đáp án D sai.
Câu 35: Cho và là hai mặt phẳng vuông góc với nhau và giao tuyến của chúng là đường thẳng
Gọi
là các đường thẳng. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Nếu và thì . B. Nếu thì .
C. Nếu thì hoặc . D. Nếu thì .
.ABCD A B C D
¢¢¢¢
.’’’ ’ABCD A B C D
’’ ’AA B D
AA' B'D', A'D' AB', A'B' AD'^^^
.’’’ ’ABCD A B C D
( )
P
( )
Q
( )
P
( )
Q
( )
R
( )
P
( )
Q
( )
P
( )
R
( )
Q
( )
R
( ) ( )
QRº
.S ABC
SH
H
ABC
H
H
ABC
H
.' ' 'ABC A B C
( ) ( )
'' , ''AA B B AA C C
( )
'
'
'
AA AB
AA ABC
AA AC
^
ì
Þ^
í
^
î
.' ' 'ABC A B C
( )
P
( )
Q
.m
,,,abcd
( )
aPÌ
am^
( )
aQ^
cm^
( )
cQ^
bm^
( )
bPÌ
( )
bQÌ
dm^
( )
dP^
Trang 9
Hướng dẫn giải:
Áp dụng hệ quả 1: Nếu hai mặt phẳng vuông góc với nhau thì bất cứ đường thẳng nào nằm
trong mặt phẳng này và vuông góc với giao tuyến thì vuông góc với mặt phẳng kia.
Chọn đáp án A.
Trang 10
DẠNG 1: GÓC GIỮA HAI MẶT PHẲNG.
Phương pháp:
Để tính góc giữa hai mặt phẳng và ta có thể thực hiện theo một trong các cách sau:
Cách 1. Tìm hai đường thẳng lần lượt vuông góc với hai mặt phẳng và . Khi đó
góc giữa hai đường thẳng chính là góc giữa hai mặt phẳng và .
.
Cách 2. Tìm hai vec tơ có giá lần lượt vuông góc với và
khi đó góc giữa hai mặt phẳng và xác định bởi .
Cách 3. Sử dụng công thức hình chiếu , từ đó để tính thì ta cần tính và .
Cách 4. Xác định cụ thể góc giữa hai mặt phẳng rồi sử dụng hệ thức lượng trong tam giác để tính. Ta
thường xác định góc giữa hai mặt phẳng theo một trong hai cách sau:
a)
Tìm giao tuyến
Chọn mặt phẳng
Tìm các giao tuyến
b)
Tìm giao tuyến
Lấy .Dựng hình chiếu của trên
Dựng .
Phương pháp này có nghĩa là tìm hai đường thẳng nằm trong hai mặt phẳng và vuông góc với
giao tuyến tại một điểm trên giao tuyến.
Câu 1: Cho tứ diện có và . Gọi là trung điểm của . Khẳng định nào
sau đây sai?
A. Góc giữa hai mặt phẳng và là .
B. Góc giữa hai mặt phẳng và là .
C. .
H
( )
b
a, b
( )
α
,,Ox Oy Oz
,,ABC
1=+ =OA OB OC
OABC
∑
∑
∑
++OBA ABC OCB
.' ' 'ABC A B C
,' 2== =AB AC a AA a
M
AB
( )
a
M
'BC
cos
j
a
b
a
b
p
q
γ
β
α
,MN
,AB BC
( )
a
( ) ( )
( )
∑
( )
∑
,,= ab
ab
φ
β
α
M
N
H
SB
,,MNP
,,''AB BC C D
.' ' ' 'ABCD A B C D
MN
BD
'AD
MN
ABCD
AC AD=
BC BD=
I
CD
( )
ABC
( )
ABD
∑
CBD
( )
ACD
( )
BCD
∑
AIB
( )
( )
BCD AIB^
Trang 11
D. .
Hướng dẫn giải:
Tam giác cân tại có trung điểm đáy Þ
(1)
Tam giác cân tại có trung điểm đáy Þ
(2)
(1) và (2) Þ . Vậy A: sai
Chọn A
Câu 2: Cho hình chóp tứ giác , có đáy là hình thoi tâm cạnh bằng và góc
, cạnh và vuông góc với mặt phẳng . Trong tam giác kẻ
tại . Tính số đo góc .
A. . B. . C. . D. .
Hướng dẫn giải:
Ta có ;
.
với là hình chiếu của lên , là hình chiếu của lên .
Vậy chọn đáp án .
Câu 3: Cho tứ diện đều . Góc giữa và bằng
. Chọn khẳng định đúng trong các khẳng định sau?
A. . B. . C. . D. .
Hướng dẫn giải:
Đặt . Gọi là trung điểm của .
Tam giác đều cạnh nên và .
Tam giác đều nên và .
Do đó, .
Tam giác có . Chọn A.
Câu 4: Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng . Tính của góc giữa một mặt bên
và một mặt đáy.
A. . B. . C. . D. .
Hướng dẫn giải:.
Chọn C.
( )
( )
ACD AIB^
BCD
B
I
CD
CD BI^
ACD
A
I
CD
CD AI^
( )
CD ABI^
.S ABCD
ABCD
I
A
!
0
60A =
6
2
a
SC =
SC
( )
ABCD
SAC
IK SA^
K
∑
BKD
0
60
0
45
0
90
0
30
22
.
;( 2 3)
CS CA
CH a CA AI a
CS CA
====
+
11
22
IK CH a IB ID====
H
C
SA
K
I
SA
C
ABCD
( )
ABC
( )
ABD
a
1
cos
3
a
=
1
cos
4
a
=
0
60
a
=
1
cos
5
a
=
AB a=
I
AB
ABC
a
CI AB^
3
2
a
CI =
ABD
DI AB^
3
2
a
DI =
( ) ( )
( )
( )
∑
,,ABC ABD CI DI CID
a
===
CID
22 2
2
22 2
2
33
1
44 2
cos
3
2. . 3
33
2. .
2
22
aa a
a
IC ID CD
a
IC ID
aa
a
+-
+-
====
a
cosin
2
1
3
1
3
1
2
1
Trang 12
Giả sử gọi hình chóp tứ giác đều có tất cả các cạnh đều bằng
là có đường cao .
Ta có: . Gọi là trung điểm .
Dễ chứng minh được và
.
Từ giả thiết suy ra là tam giác đều cạnh có là
đường trung tuyến .
.
Câu 5: Cho hình chóp có hai mặt bên và vuông góc với mặt phẳng ,
tam giác vuông cân ở và có đường cao . Gọi là hình chiếu vuông góc của
lên . Khẳng định nào sau đây sai ?
A. . B. .
C. . D. .
Hướng dẫn giải:
Ta có .
.
Mặt khác, nên .
Chọn D.
Câu 6: Cho hình chóp có đáy là hình thoi tâm cạnh và có góc . Đường
thẳng vuông góc với mặt phẳng đáy và . Gọi là trung điểm và là
trung điểm . Góc giữa hai mặt phẳng và là
A. B. C. D.
Hướng dẫn giải:
! đều nên . Mặt khác (1).
! Do (2).
! Từ (1) và (2), suy ra
Vậy, góc giữa và bằng
Câu 7: Cho hình chóp có đáy là hình thoi cạnh và có . Góc giữa
hai mặt phẳng và bằng
A. . B. . C. . D. .
a
.S ABCD
SH
( ) ( )
SCD ABCD CDÇ=
M
CD
SM CD^
HM CD^
( ) ( )
( )
( )
∑
,,SCD A BCD SM HM SM H
a
Þ===
SCDD
a
SM
3
2
a
SMÞ=
1
2
cos
33
2
a
HM
SM
a
a
Þ===
.S ABC
( )
SAB
( )
SAC
( )
ABC
ABC
A
AH
( )
HBCÎ
O
A
( )
SBC
( )
SC AB C^
O SHÎ
( ) ( )
SAH SBC^
( ) ( )
∑
(
)
∑
,SBC ABC SBA=
( ) ( )
( ) ( )
( ) ( )
( )
SAB ABC
SAC ABC SA ABC SA BC
SAB SAC SA
^
ü
ï
^Þ^Þ^
ý
ï
Ç=
þ
( )
BC AH
BC SAH BC SH
BC SA
^
ü
Þ^ Þ^
ý
^
þ
AH BC^
( ) ( )
( )
( )
∑
,,SBC ABC SH AH SHA==
.S ABCD
O
a
∑
0
60BAD =
SO
( )
ABCD
3
4
a
SO =
E
BC
F
BE
( )
SOF
( )
SBC
o
90 .
o
60 .
o
30 .
o
45 .
BCDD
DE BC^
//OF DE BC OFÞ^
( )
SO ABCD BC SO^Þ^
( ) ( ) ( )
.BC SOF SBC SOF^Þ^
( )
SOF
( )
SBC
o
90 .
.S ABCD
ABCD
a
SA SB SC a== =
( )
SBD
( )
ABCD
30
o
90
o
60
o
45
o
Trang 13
Hướng dẫn giải:
Gọi là chân đường vuông góc của xuống mặt phẳng đáy ( )
Þ các hình chiếu: Þ là tâm đường tròn
Mà tam giác cân tại (vì ) Þ tâm phải nằm trên Þ
Vậy có nên góc
.
Chọn B
Câu 8: Cho hình chóp tứ giác đều , có đáy là hình vuông tâm . Các cạnh bên và các
cạnh đáy đều bằng . Gọi là trung điểm . Góc giữa hai mặt phẳng và bằng:
A. . B. . C. . D. .
Hướng dẫn giải:
Gọi là trung điểm . Có
;
. Do đó
Vậy chọn đáp án .
Câu 9: Cho tam giác vuông tại . Cạnh nằm trong mặt phẳng , cạnh ,
tạo với một góc . Chọn khẳng định đúng trong các khẳng định sau?
A. tạo với góc . B. tạo với góc .
C. tạo với góc . D. tạo với góc .
Hướng dẫn giải:
Gọi là hình chiếu vuông góc của lên mặt phẳng .
Khi đó, và
.
Tam giác vuông tại nên
.
Tam giác vuông tại nên
.
Chọn C.
H
S
( )
ABCD
( )
SH ABCD^
SA SB SC a== =
HA HB HC==
H
( )
ABC
ABC
B
BA BC a==
H
BD
( )
SH SBDÌ
( )
( )
( ) ( )
SH ABCD
SBD ABCD
SH SBD
^ü
Þ^
ý
Ì
þ
( ) ( )
[ ]
,90
o
SBD ABC D =
.S ABCD
ABCD
O
a
M
SC
( )
MBD
( )
ABCD
0
90
0
60
0
45
0
30
'M
OC
2
11 2
...2
2224
MBD
aa
SMOBDa
D
===
2
111
...2.2
224 4
BM D
a
SMOBDaa
¢
D
¢
== =
0
2
cos 45
2
BM D
BMD
S
S
aa
¢
D
D
==Þ=
C
ABC
A
AB a=
( )
P
2AC a=
AC
( )
P
0
60
( )
ABC
( )
P
0
45
BC
( )
P
0
30
BC
( )
P
0
45
BC
( )
P
0
60
H
C
( )
P
( )
( )
( )
∑
0
,, 60AC P AC AH CAH===
( )
( )
( )
∑
,,BC P BC AH CBH
a
===
AHC
H
∑ ∑
0
6
sin .sin 2.sin 60
2
CH a
CAH CH AC CAH a
AC
=Þ= = =
CHB
H
( )
0
2
2
6
2
2
sin 45
2
2
a
CH a
BC
aa
aa
== = Þ=
+
Trang 14
Câu 10: Cho hình chóp có và đáy vuông ở . Khẳng định nào sau đây sai
?
A. .
B. .
C. Vẽ góc là góc giữa hai mặt phẳng và .
D. Góc giữa hai mặt phẳng và là góc .
Hướng dẫn giải:
Chọn D.
Ta có: nên đáp án A đúng.
. Nên đáp
án B đúng
.
Nên đáp án C đúng.
Ta có: nên đáp án D sai.
Câu 11: Cho tứ diện có và . Gọi là trung điểm của . Khẳng định
nào sau đây sai ?
A. Góc giữa hai mặt phẳng và là góc .
B. .
C. Góc giữa hai mặt phẳng và là góc .
D. .
Hướng dẫn giải:
Chọn C.
Ta có: .
Nên đáp án C sai
Câu 12: Cho hình chóp có và , gọi là trung điểm . Góc giữa hai
mặt phẳng và là góc nào sau đây?
A. Góc . B. Góc . C. Góc . D. Góc .
Hướng dẫn giải:
Chọn A.
Ta có:
.
.S ABC
( )
SA ABC^
ABC
A
( ) ( )
SAB ABC^
( ) ( )
SAB SAC^
, AH BC H BC^ÎÞ
AHS
( )
SBC
( )
ABC
( )
SBC
( )
SAC
∑
SCB
( ) ( ) ( )
SA ABC SAB ABCÞ^^
( ) ( )
SAB SACÞ^
( )
;AH BC BC SA BC SAH^^Þ^
( ) ( )
∑
(
)
∑
,SH BC SBC ABC SHAÞ^Þ =
( ) ( )
SBC SAC SCÇ=
ABCD
AC AD=
BC BD=
I
CD
( )
ACD
( )
BCD
∑
AIB
( ) ( )
BCD AIB^
( )
ABC
( )
ABD
∑
CBD
( ) ( )
ACD AIB^
( ) ( )
ABC ABD AB
BC AB
BD AB
Ç=
ì
ï
^
í
ï
^
î
( ) ( )
( )
∑
∑
,ABD ABC CBDÞ¹
.S ABC
( )
SA ABC^
AB BC^
I
BC
( )
SBC
( )
ABC
SBA
SCA
SCB
SIA
,BC SA BC AB BC SB^^Þ^
( ) ( )
( )
( )
,
,
SBC ABC BC
AB BC AB ABC
SB BC SB SBC
Ç=
ì
ï
Þ^ Ì
í
ï
^Ì
î
( ) ( )
( )
∑
∑
,SBC ABC SBAÞ=
Trang 15
Câu 13: Cho hình chóp có đáy là hình vuông và , gọi là tâm hình
vuông . Khẳng định nào sau đây sai?
A. Góc giữa hai mặt phẳng và là góc .
B. Góc giữa hai mặt phẳng và là góc .
C. Góc giữa hai mặt phẳng và là góc
.
D. .
Hướng dẫn giải:
Chọn C.
Ta có:
.
Nên đáp án C sai.
Câu 14: Cho hình chóp có đáy là hình vuông tâm . Biết ,
và đường tròn ngoại tiếp có bán kính bằng . Gọi là góc hợp bởi mặt bên
với đáy. Khi đó
A. . B. . C. . D. .
Hướng dẫn giải:
Chọn D.
Gọi là trung điểm của .
Khi đó
.
Ta có: .
.
Câu 15: Cho hình chóp tam giác đều với . Góc giữa và bằng .
Chọn khẳng định đúng trong các khẳng định sau?
A. . B. .
C. . D. .
Hướng dẫn giải: C
.S ABCD
ABCD
( )
SA ABCD^
O
ABCD
( )
SBC
( )
ABCD
∑
ABS
( )
SBD
( )
ABCD
∑
SOA
( )
SAD
( )
ABCD
∑
SDA
( ) ( )
SAC SBD^
( ) ( )
( )
( )
,
D,
SAD ABCD AD
AB AD AB ABCD
SA A SA SAD
Ç=
ì
ï
^Ì
í
ï
^Ì
î
( ) ( )
( )
∑
∑
,SAD ABCD SABÞ=
.S ABCD
ABCD
O
( )
SO ABCD^
3SO a=
ABCD
a
a
( )
SCD
tan ?
a
=
3
2
3
2
6
6
6
M
CD
CD OM
CD SO
^
ì
í
^
î
( ) ( )
( )
∑
∑
,CD SM SCD ABCD SMO
a
Þ^ Þ = =
22ROAa AC a AB ADa==Þ=Þ= =
2
tan 6
2
aSO
OM
OM
a
Þ= Þ = =
S.ABC
SA = 2AB
( )
SAB
( )
ABC
a
0
60
a
=
1
cos
35
a
=
1
cos
45
a
=
1
cos
25
a
=
Trang 16
Gọi O là tâm của tam giác đều ABC
Gọi suy ra H là trung điểm AB( vì đều)
và
Tìm góc giữa và
(1)
Ta có
Từ (1) suy ra
Từ đó ta có :
Chọn B
Câu 16: Cho tam giác cân có đường cao , chứa trong mặt phẳng .
Gọi là hình chiếu vuông góc của lên mặt phẳng . Biết tam giác vuông tại . Gọi
là góc giữa và . Chọn khẳng định đúng trong các khẳng định sau?
A. . B. . C. . D. .
Hướng dẫn giải:
Ta có .
Do đó:
.
Mặt khác, tam giác vuông tại nên .
Ta có .
Chọn D.
Câu 17: Trong không gian cho tam giác đều và hình vuông cạnh nằm trên hai mặt
phẳng vuông góc. Gọi , lần lượt là trung điểm của , . Ta có của góc tạo bởi hai mặt
phẳng và bằng :
CO AB HÇ=
ABCD
OH ABÞ^
113 3
.
332 6
AB AB
OH CH== =
( )
SAB
( )
ABC
( ) ( )
( )
( )
SAB ABC AB
OH AB
SO AB SO ABC
Ç=
ì
ï
^
í
ï
^^
î
SH ABÞ^
( ) ( )
, ( )
,()
SAB ABC AB
OH AB OH ABC
SH AB SH SAB
Ç=
ì
ï
^Ì
í
ï
^Ì
î
∑
( )
∑
( )
∑
();( ) ;SAB ABC SH OH SHO
a
Þ===
( )
2
2
22
15
2
22
AB
SH SA AH AB AB
æö
=-= - =
ç÷
èø
3
6
1
cos
15 3 5
2
A
OH
SH
A
B
B
a
== =
ABC
3AH a=
3,BC a=
BC
( )
P
'A
A
( )
P
'A BC
'A
j
( )
P
( )
ABC
0
60
j
=
0
45
j
=
2
cos
3
j
=
0
30
j
=
( )
'
''
BC AA
BC A AH BC A H
BC AH
^
ì
Þ^ Þ^
í
^
î
( ) ( )
( ) ( )
( )
( )
∑
'
,' ,' '
,'
ABC A BC BC
ABC A BC AH A H AHA
BC AH BC A H
Ç=
ì
ï
Þ==
í
^^
ï
î
'A BC
'A
13
'
22
a
AH BC==
3
'1
2
cos
2
3
a
AH
AH
a
j
===
SAB
ABCD
a
H
K
AB
CD
tan
( )
SAB
( )
SCD
Trang 17
A. . B. . C. . D. .
Hướng dẫn giải:
Ta có:
Gọi với
Do đó:
Mặt khác: ; mà
Vì là trung điểm của (vì
)
(theo định lí ba đường vuông góc)
Do đó: là góc giữa và
Mà là đường cao trong đều cạnh
Xét vuông tại có: .
Vậy chọn đáp án .
Câu 18: Cho hình chóp có đáy là hình chữ nhật tâm và khoảng cách từ đến
bằng . Biết và . Gọi là góc giữa hai mặt phẳng và
. Khẳng định nào sau đây sai?
A. . B. . C. . D. .
Hướng dẫn giải:
Chọn D.
Gọi là khoảng cách từ đến
Khi đó và ,
Vậy đáp án D sai.
Câu 19: Cho hình lăng trụ có đáy là hình thoi, . Các cạnh bên vuông
góc với đáy và . Khẳng định nào sau đây sai ?
A. Các mặt bên của hình lăng trụ là các hình chữ nhật.
B. Góc giữa hai mặt phẳng và
có số đo bằng .
C. Hai mặt bên và vuông góc với
hai đáy.
D. Hai hai mặt bên và bằng
nhau.
Hướng dẫn giải:
2
3
23
3
3
3
3
2
( ) ( )
SSAB SCDÎÇ
( ) ( )
dSAB SCD=Ç
;Î !!dSdABCD
( ) ( )
dSAB SCD=Ç
( ) ( )
SAB ABCD^
( ) ( )
HK AB hv HK SAB^Þ^
H
AB
SH AB SH dÞ^Þ^
!dAB
d SKÞ^
∑
KSH
a
=
( )
SAB
( )
SCD
SH
SABD
3
2
a
aSHÞ=
SHKD
H
23
tan
3
3
2
HK a
SH
a
a
== =
B
.S ABCD
ABCD
O
A
BD
2
5
a
( )
SA ABCD^
2SA a=
a
( )
ABCD
( )
SBD
( ) ( )
SAB SAD^
( ) ( )
SAC ABCD^
tan 5
a
=
∑
SOA
a
=
AK
A
BD
2
5
a
AK =
BD AK^
BD SA^
( ) ( )
( )
∑
∑
, A tan 5.
SA
SBD ABCD SK
AK
aa
==Þ ==
.ABCD A B C D
¢¢¢¢
ABCD
2AC a=
AA a
¢
=
( )
AA C C
¢¢
( )
BB D D
¢¢
60°
( )
AA C
¢
( )
BB D
¢
( )
AA B B
¢¢
( )
AA D D
¢¢
Trang 18
Chọn B.
Ta có: các cạnh bên vuông góc với đáy, đáy là hình thoi nên
Các mặt bên của hình lăng trụ là các hình chữ nhật.
Hai mặt bên và vuông góc với hai đáy.
Hai hai mặt bên và bằng nhau.
suy ra đáp án A,C,D đúng.
Mặt khác hai đáy và là các hình thoi nên . Suy ra đáp án B
sai.
Câu 20: Cho hình lập phương . Gọi là góc giữa hai mặt phẳng và
. Chọn khẳng định đúng trong các khẳng định sau?
A. . B. . C. . D. .
Hướng dẫn giải:
là góc giữa hai mặt phẳng và là
Ta có
Chọn đáp án A.
Câu 21: Cho hình chóp có đáy là hình vuông
có tâm O và . Khẳng định nào sau đây sai ?
A. Góc giữa hai mặt phẳng và là góc .
B. .
C. Góc giữa hai mặt phẳng và là góc .
D. Góc giữa hai mặt phẳng và là góc .
Hướng dẫn giải:
Ta có:
. Vậy A đúng
Ta có:
Mà . Vậy B đúng
Ta có:
. Vậy C đúng
Ta có:
( )
AA C
¢
( )
BB D
¢
( )
AA B B
¢¢
( )
AA D D
¢¢
ABCD
ABCD
¢¢¢¢
( ) ( )
AA C C BB D D
¢¢ ¢¢
^
111 1
.ABCD A B C D
a
( )
11
ADCB
()ABCD
0
45a =
0
30a =
0
60a =
0
90a =
a
( )
11
ADCB
()ABCD
∑
MNPa =
0
tan 1 45
MP
NP
aa==fi=
.S ABCD
ABCD
( )
SA ABCD^
( )
SBC
( )
ABCD
∑
ABS
( ) ( )
SAC SBD^
( )
SBD
( )
ABCD
∑
SOA
( )
SAD
( )
ABCD
∑
SDA
( ) ( )
SBC ABCD CDÇ=
( )
( )
,
,
AB BC AB ABCD
SB BC SB SBC
^Ì
ì
ï
í
^Ì
ï
î
( )
∑
(
)
∑
();SBC ABCD ABSÞ=
( )
BD AC
BD SAC
BD SA
^
ì
Þ^
í
^
î
( ) ( ) ( )
BD SBD SAC SBDÌÞ^
( ) ( )
SBD ABCD BDÇ=
( )
( )
,
,
AO BD AB ABCD
SO BD SO SBD
^Ì
ì
ï
í
^Ì
ï
î
( )
∑
(
)
∑
();SBD ABCD SOAÞ=
( ) ( )
SAD ABCD BDÇ=
( )
( )
,
,
AB AD AB ABCD
SA AD SA SAD
^Ì
ì
ï
í
^Ì
ï
î
Trang 19
. Vậy D sai.
Câu 22: Tính của góc giữa hai mặt của một tứ diện đều.
A. B. C. D.
Hướng dẫn giải:
Gọi là trung điểm của khi đó
Góc giữa hai mặt của tứ diện bằng
Ta có
Trong tam giác có :
Câu 23: Cho hình chóp tứ giác đều có . Góc giữa và bằng . Chọn
khẳng định đúng trong các khẳng định sau?
A. . B. . C. . D. .
Hướng dẫn giải:
Gọi độ dài cạnh của hình chóp đều là . Gọi là
trung điểm của ta có (vì tam giác đều) và
(vì tam giác đều). Vậy, góc giữa hai mặt phẳng
và chính là góc .
Ta có : (đường chéo hình vuông),
(đường cao tam giác đều)
Áp dụng định lý cosin cho góc trong tam giác ta có :
Vậy
Câu 24: Cho hình chóp có đáy là hình thoi cạnh và góc . Các cạnh
đều bằng . Gọi là góc của hai mặt phẳng và . Giá trị
bằng bao nhiêu?
A. B. C. D.
Hướng dẫn giải:
( )
∑
(
)
∑
0
(); 90SAD AB CD SABÞ==
cosin
1
.
3
1
.
2
2
.
3
3
.
2
H
AC
;BH AC DH AC^^
∑
BHD
3
2
a
BH DH==
BHD
∑
222
2..cosBD BH HD BH HD BHD=+-
∑
∑
22 2
2
33 3
2.cos
44 4
1
cos
3
aa a
aBHD
BHD
Þ= + -
Þ=
.S ABCD
SA SB=
( )
SAB
( )
SAD
a
1
cos
3
a
=-
2
cos
5
a
=
0
60
a
=
2
cos
3
a
=
.S ABCD
a
I
SB
DI SB^
SBD
AI SB^
SAB
()SAB
()SAD
∑
AID
2AD a=
3
2
a
AI DI==
I
AID
∑
( )
22
2
22 2
33
2
22
1
cos( )
2. 3
33
2. .
22
aa
a
AI DI AD
AID
AD DI
aa
æöæö
+-
ç÷ç÷
+-
èøèø
== =-
æöæö
ç÷ç÷
èøèø
1
cos
3
a
=-
.S ABCD
ABCD
a
∑
0
60ABC =
,,SA SB SC
3
2
a
j
( )
SAC
( )
ABCD
tan
j
25
35
53
3
Trang 20
Do và nên tam giác đều.
Gọi là hình chiếu của lên .
Do nên là tâm đường tròn ngoại tiế tam
giác .
Ta có : .
Mặt khác, ,
Câu 25: Cho hình chóp có đáy là hình thang vuông tại và .
Cạnh bên SA vuông góc với đáy và . Chọn khẳng định sai
trong các khẳng định sau?
A. .
B. Giao tuyến của và song song với .
C. tạo với một góc .
D. tạo với đáy một góc .
Hướng dẫn giải:
+Ta có:
Mà (A đúng)
+
B đúng
+
Ta có:
Suy ra góc giữa và là .
(C sai)
Vậy chọn C.
Câu 26: Cho hình hộp chữ nhật có , . Gọi là góc giữa
đường chéo và đáy . Tính .
A. . B. . C. . D. .
Hướng dẫn giải:.
Chọn B.
AB BC=
∑
0
60ABC =
ABC
H
A
( )
ABCD
SA SB SC==
H
ABC
( ) ( )
( ) ( )
( )
( )
∑
,
,,
ì
Ç=
ï
í
^^
ï
î
Þ==
SAC ABCD AC
SO AC HO AC
SAC ABCD SO HO SOH
1133
.
3326
aa
HO BO== =
22
22
35
43
23
aa a
SH SB BH=-=-=
.S ABCD
ABCD
A
D
2,AB a=
AD DC a==
2SA a=
( ) ( )
SBC SAC^
( )
SAB
( )
SCD
AB
( )
SDC
( )
BCD
0
60
( )
SBC
0
45
( )
BC SA
BC SAB
BC AB
^
ì
Þ^
í
^
î
( ) ( ) ( )
BC SBC SBC SACÌÞ^
( ) ( )
( )
( )
( ) ( )
//
//
SAD SAB S
AB CD
SAD SAB Sx AB
AB SAB
CD SCD
Ç=
ì
ï
ï
ÞÇ=
í
Ì
ï
ï
Ì
î
( ) ( )
SCD BCD CDÇ=
( )
( )
,
,
AD CD AD BCD
SD CD SD SCD
^Ì
ì
ï
í
^Ì
ï
î
( )
SDC
( )
BCD
∑
SDA
∑ ∑
0
tan 2 54 44 '
SA
SDA SDA
AD
==Þ =
.ABCD A B C D
¢¢¢¢
AB AA a
¢
==
2AD a=
a
AC
¢
ABCD
a
20 45
a
¢
»°
24 5
a
¢
»°
30 18
a
¢
»°
25 48
a
¢
»°
Trang 21
Từ giả thiết ta suy ra: là hình chiếu
vuông góc của lên mặt phẳng
.
Áp dụng định lý Pytago trong tam giác vuông tại ta
có:
.
Áp dụng hệ thức lượng trong tam giác vuông tại ta
có:
.
Câu 27: Cho hình lập phương . Xét mặt phẳng . Trong các mệnh đề sau
mệnh đề nào đúng?
A. Góc giữa mặt phẳng và các mặt phẳng chứa các cạnh của hình lập phương bằng mà
.
B. Góc giữa mặt phẳng và các mặt phẳng chứa các cạnh của hình lập phương bằng mà
.
C. Góc giữa mặt phẳng và các mặt phẳng chứa các cạnh của hình lập phương phụ thuộc
vào kích thước của hình lập phương.
D. Góc giữa mặt phẳng và các mặt phẳng chứa các cạnh của hình lập phương bằng nhau.
Hướng dẫn giải:
là hình lặp phương nên hình chiếu của tam giác
lên các mặt chứa các cạnh của hình lặp phương là các tam
giác bằng nhau. Gọi là diện tích các tam giác này
Lại có .
Vậy chọn đáp án .
Câu 28: Cho hình chóp tam giác đều có cạnh đáy bằng và đường cao bằng cạnh đáy.
Tính số đo góc hợp bởi cạnh bên và mặt đáy.
A. . B. . C. . D. .
Hướng dẫn giải:.
Chọn C.
+ Vì và hay
là hình chiếu vuông góc của lên
.
+ Gọi , lần lượt là trung điểm của , .
Vì là tam giác đều cạnh nên dễ tính được : .
Từ giả thiết suy ra là trọng tậm
.
+ Áp dụng hệ thức lượng trong tam giác vuông tại ta có:
( )
AA ABCD
¢
^
ACÞ
AC
¢
( )
ABCD
( )
( )
( )
∑
,,AC ABCD AC AC ACA
a
¢¢¢
Þ===
ABC
B
222222
45AC AB BC a a a=+=+=
5AC aÞ=
AA C
¢
A
1
tan
55
AA a
AC
a
a
¢
== =
24 5
a
¢
Þ» °
.' ' ' 'ABCD A B C D
( )
'ABD
( )
'ABD
a
1
tan
2
a
=
( )
'ABD
a
1
sin
3
a
=
( )
'ABD
( )
'ABD
.' ' ' 'ABCD A B C D
'A BD
1
S
1'
.
AB D
SS cos
a
=
D
.S ABC
a
SH
30°
45°
60°
75°
( )
SH ABC^
( )
AN ABCÌ
SH ANÞ^
SH AHÞ^
Þ
AH
SA
( )
ABC
Þ
( )
( )
( )
∑
,,SA AB C SA AH SAH==
M
N
AC
BC
ABCD
a
3
2
a
AN =
H
ABCD
2233
.
3323
aa
AH ANÞ= = =
SHA
H
Trang 22
.
Câu 29: Cho hình chóp tứ giác đều có cạnh đáy bằng và chiều cao bằng . Tính số đo của
góc giữa mặt bên và mặt đáy.
A. . B. . C. . D. .
Hướng dẫn giải:.
Chọn B.
Giả sử hình chóp đã cho là có đường cao .
Ta có: .
Gọi là trung điểm của dễ chứng minh được
và .
.
Mặt khác:
Áp dụng hệ thức lượng trong tam giác vuông tại , ta có :
.
Câu 30: Tính của góc giữa hai mặt của một tứ diện đều.
A. . B. . C. . D. .
Hướng dẫn giải:.
Chọn D.
Giả sử tứ diện đều đã cho là có cạnh .
Ta có: .
Gọi là trung điểm . Khi đó dễ dàng chứng minh được và .
.
Ta dễ tính được: .
Áp dụng hệ quả của định lý cô sin trong tam giác ta có:
.
Câu 31: Cho hình chóp có đáy là hình vuông cạnh . Cạnh bên vuông góc với
đáy và . Gọi là góc giữa hai mặt phẳng và . Chọn khẳng định đúng trong
các khẳng định sau?
A. . B. . C. . D. .
Hướng dẫn giải:
∑
tan 3
3
3
SH a
SAH
AH
a
== =
∑
60SAHÞ=°
2a
2
2a
30°
45°
60°
75°
.S ABCD
SH
( ) ( )
ABCD SCD CDÇ=
M
CD
Þ
SM CD^
HM CD^
Þ
( ) ( )
( )
( )
∑
,,ABCD SCD HM SM SMH==
12
22
a
HM AD==
SHM
H
∑
22
tan . 1
2
2
SH a
SMH
HM
a
== =
∑
45SMHÞ=°
cosin
2
3
3
2
2
1
3
1
ABCD
a
( ) ( )
ABC BCD BCÇ=
E
BC
AE BC^
DE BC^
( ) ( )
( )
( )
∑
,,ABC BCD AE DE AEDÞ==
3
2
a
AE DE==
AED
∑
22 2
2
222
2
33
1
44 2
cos
3
2. . 3
33
2. .
2
22
aa a
a
AE DE AD
AED
a
AE DE
aa
+-
+-
====
.S ABCD
ABCD
a
SA
3SA a=
j
()SB C
()SCD
10
cos
24
j
=
1
cos
24
j
=
10
sin
24
j
=
1
sin
24
j
=
Trang 23
Ta có
Vì nên chân đường cao hạ từ và đến của hai tam giác đó trùng nhau
và độ dài đường cao bằng nhau
Do đó
Ta có
Lại có và là trung điểm nên hay
vuông tại
Ta có
Chọn đáp án C.
Câu 32: Cho hình chóp có đáy là hình vuông cạnh . Cạnh bên vuông góc với
đáy và . Góc giữa hai mặt phẳng và bằng bao nhiêu?
A. B. C. D.
Hướng dẫn giải:
Ta có: (vì )
Trong mặt phẳng , kẻ thì ta có
Khi đó
Trong tam giác , kẻ đường cao thì
Mà là trung điểm và nên
Tam giác vuông tại có
Vậy hai mặt phẳng và hợp với nhau một góc .
Câu 33: Lăng trụ tam giác đều có cạnh đáy bằng . Gọi là điểm trên cạnh sao
cho . Tang của góc hợp bởi hai mặt phẳng và là:
A. . B. . C. . D. .
Hướng dẫn giải:
Gọi là tâm đường tròn ngoại tiếp tam giác . Khi đó,
.
2SB SD a==
(c.c.c)SCD SCBD=D
B
D
SC
BH DHfi=
(
)
∑
∑
(),()SBC SCD D H B j==
22 2222
2
22
111115 25
44 5
BD a
OB OD
BH DH a
BH SB BC a a a
== =
=+ =+=fi ==
BH DH=
O
BD
HO BD^
HOBD
O
22
22
25 2 30
5210
aa
OH BH OB a
ʈʈ
Á˜Á˜
=-= - =
Á˜Á˜
˯˯
30
2
610
10
2
sin ;sin
242 4
25 25
55
OH OB
BH BH
jj
== = == =
.S ABCD
ABCD
a
SA
SA a=
()SB C
()SCD
0
30
0
45
0
90
0
60
SC BD^
,BD AC BD SA^^
()SA C
OI SC^
()SC BID^
∑
( )
∑
(),()SBC SCD BID=
SAC
AH
2
3
a
AH =
O
AC
OI AH!
6
a
OI =
IOD
O
∑ ∑
0
tan 3 60OID OID=Þ =
()SB C
()SCD
0
60
.ABC A B C
¢¢¢
a
M
AA
¢
3
4
a
AM =
( )
MBC
( )
ABC
2
2
2
1
2
O
ABC
( )
AO ABC
¢
^
Trang 24
Trong mặt phẳng , dựng . Vì tam giác đều nên .
Ta có .
Do đó, .
Tam giác vuông tại nên . Chọn D.
Câu 34: Cho hình chóp có đáy là hình vuông cạnh . , . Xác
định để hai mặt phẳng và tạo với nhau góc .
A. B. C. D.
Hướng dẫn giải:
* Trong dựng ta chứng minh được (1)
Trong dựng ta chứng minh được (2)
Từ (1) và (2) Þgóc
* Ta chứng minh được . Do đó, nếu góc thì đều Þ
vuông tại có là đường cao Þ Þ
(3)
Và có Þ (4)
Ta chứng minh được Þ Þ
(5)
Thế (3)&(5) vào Þ Û
Û Û Û
Chọn C
Câu 35: Cho hình chóp có đáy là hình thoi tâm Biết và
đường tròn nội tiếp có bán kính bằng Tính góc hợp bởi mỗi mặt bên với đáy.
A. B. C. D.
Hướng dẫn giải:
Chọn C
Ta có và lần lượt vuông góc với
Theo định lí ba đường vuông góc ta có
Từ đó suy ra
Xét tam giác vuông tại ta có
Vậy mỗi mặt bên hợp với đáy các góc bằng nhau và bằng
Câu 36: Cho hình chóp có đáy là tam giác vuông tại
( )
ABC
AH BC^
ABC
3
2
a
AH =
( )
BC AH
BC A HA BC MH
BC A O
^
ü
¢
Þ^ Þ^
ý
¢
^
þ
( ) ( )
( )
( )
∑
,,MBC ABC MH AH MHA
a
===
MAH
A
3
3
4
tan
2
3
2
a
AM
AH
a
a
== =
.S ABCD
ABCD
a
( )
SA ABCD^
SA x=
x
( )
SBC
( )
SCD
60
o
3
2
a
x =
2
a
x =
xa=
2xa=
( )
SAB
AI SB^
( )
AI SBC^
( )
SAD
AJ SD^
( )
AJ SCD^
( )
( )
∑
(),() ,SBC SCD AI AJ IAJ==
AI AJ=
∑
60
o
IAJ =
AIJD
AI AJ IJ==
SABD
A
AI
..AI SB SA AB=
.SA AB
AI
SB
=
2
.SA SI SB=
2
SA
SI
SB
=
//IJ BD
IJ SI
BD SB
=
.SI BD
IJ
SB
=
(4)
=
2
2
.SA BD
SB
AI IJ=
.SA BD
AB
SB
=
..AB SB SA BD=
22
..2ax a xa+=
22 2
2xa x+=
xa=
.S ABCD
ABCD
.O
( )
,3SO ABCD SO a^=
ABCD
.a
0
30 .
0
45 .
0
60 .
0
75 .
()SO ABCD^
,,,OM ON OP OQ
,,,AB BC CD DA
,,,SM AB SN BC SP CD SQ DA^^^^
∑
∑
∑
∑
SM O SNO SPO SQO===
SMO
O
∑ ∑
0
tan 3 60SMO SMO=Þ =
0
60
.S ABC
ABC
Trang 25
Gọi lần lượt
là trung điểm của các cạnh và . Góc giữa hai mặt phẳng và là :
A. . B. . C. . D. .
Hướng dẫn giải:
Ta có:
Góc giữa hai mặt phẳng và là :
Chọn C.
Câu 37: Cho tam giác đều có cạnh bằng và nằm trong mặt
phẳng . Trên các đường thẳng vuông góc với tại lần lượt lấy nằm trên cùng một
phía đối với sao cho . Góc giữa và bằng bao nhiêu?
A. B. C. D.
Hướng dẫn giải:
Gọi .
Ta có: .
Mặt khác, ta có: ,
.
Gọi là trung điểm , ta có .
Do đó .
Suy ra tam giác cân tại .
Gọi là trung điểm , ta có .
Suy ra
Vậy .
Chọn B.
Câu 38: Cho góc tam diện Sxyz với , , . Trên các tia , , lần
lượt lấy các điểm sao cho . Góc giữa hai mặt phẳng và bằng
:
A. B. C. D.
Hướng dẫn giải:
Chọn B
Áp dụng định lí Côsin trong tam giác , ta có
( )
,.BSA ABC^
,EF
AB
AC
( )
SEF
( )
SBC
∑
CSF
∑
BSF
∑
BSE
∑
CSE
( )
SEF
( )
// //SBC Sx EF BCÇ=
( )
BC AB
BC SAB
BC SA
^
ì
Þ^
í
^
î
,BC SE BC SBÞ^ ^
,SB Sx SE SxÞ^ ^
Þ
( )
SEF
( )
SBC
∑
BSE
ABC
a
( )
P
( )
P
,BC
,DE
( )
P
3
,3
2
BD a CE a==
( )
P
( )
ADE
0
30
0
60
0
90
0
45
( ) ( )
( )
,ABC ADE
j
=
2
3
4
ABC
a
S =
2
222
37
42
aa
AD AB BD a=+=+=
22 22
32AE AC CE a a a=+=+=
F
EC
DF BC a==
2
22 2
37
42
aa
DE DF FE a=+=+=
ADE
D
H
AE
2
22 2
73
42
aa
DH AD AH a=-=-=
2
1133
...2
2222
ADE
aa
SDHAE a== =
2
2
3
1
4
cos 60
2
3
2
o
ABC
ADE
a
S
S
a
jj
== =Þ=
∂
0
120xSy =
∂
0
60ySz =
∂
0
90zSx =
Sx
Sy
Sz
,,ABC
SA SB SC a== =
()SAB
()ABC
0
15
0
90
0
45
0
60
SAB
3AB a=
Trang 26
Tam giác vuông cân tại nên ; tam
giác đều nên .
Vì nên tam giác vuông tại
Gọi là trung điểm thì ta có
Mà nên
Vậy
Câu 39: Cho tam giác đều cạnh . Gọi lần lượt là đường thẳng đi qua và vuông
góc với . là mặt phẳng qua và hợp với góc . cắt lần lượt tại
và . biết đặt . Chọn khẳng định đúng trong các khẳng định sau?
A. . B. . C. . D. .
Hướng dẫn giải:
Ta có: với .
Do đó .
Mặt khác,
.
Chọn A.
SAC
S
2AC a=
SBC
BC a=
22 2
AC BC AB+=
ABC
C
H
AB
()
HA HB HC
SH ABC
SA SB SC
==
ì
Þ^
í
==
î
()SH SABÌ
()( )SAB ABC^
∑
( )
0
(),( )90SAB ABC =
ABC
a
,
BC
dd
,BC
( )
ABC
( )
P
A
( )
ABC
0
60
( )
P
,
BC
dd
D
E
6
,3.
2
AD a AE a==
∑
DAE
j
=
2
sin
6
j
=
0
60
j
=
3
sin
6
j
=
0
30
j
=
.cos
ABC ADE
SS
a
=
( ) ( )
( )
0
,60ABC ADE
a
==
2
2
0
3
3
4
cos cos 60 2
ABC
ADE
a
S
a
S
a
== =
2
1316 2
. .sin . . 3.sin sin
2222
6
ADE
aa
SADAE a
jjj
=Û= Þ=
I
K
H
z
y
x
S
C
B
A
60
0
Trang 27
DẠNG 2: CHỨNG MINH HAI MẶT PHẲNG VUÔNG GÓC, CHỨNG MINH
ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG VÀ CÁC BÀI TOÁN LIÊN
QUAN
Phương pháp:
* Chứng minh hai mặt phẳng vuông góc
Để chứng minh (P) ^ (Q), ta có thể chứng minh bởi một trong các cách sau:
• Chứng minh trong (P) có một đường thẳng a mà a ^ (Q).
• Chứng minh
* Chứng minh đường thẳng vuông góc với mặt phẳng
Để chứng minh d ^ (P), ta có thể chứng minh bởi một trong các cách sau:
• Chứng minh d Ì (Q) với (Q) ^ (P) và d vuông góc với giao tuyến c của (P) và (Q).
• Chứng minh d = (Q) Ç (R) với (Q) ^ (P) và (R) ^ (P).
• Sử dụng các cách chứng minh đã biết ở phần trước.
Câu 1: Cho tứ diện ABCD có . Trong vẽ các đường cao và cắt nhau ở
. Trong vẽ tại . Khẳng định nào sau đây sai ?
A. . B. . C. . D. .
Hướng dẫn giải:
* Ta có .
Vậy “ ”: ĐÚNG.
*
.
Vậy “ ”: ĐÚNG.
* Ta có .
Vậy “ ”: ĐÚNG.
* “ ”: SAI
Chọn C
Câu 2: Cho tứ diện có hai mặt phẳng và cùng vuông góc với . Gọi
và là hai đường cao của tam giác , là đường cao của tam giác . Chọn khẳng định
sai trong các khẳng định sau?
A. . B. .
C. . D. .
Hướng dẫn giải:
∑
( )
0
(),() 90PQ=
( )
AB BCD^
BCDD
BE
DF
O
( )
ADC
DK AC^
K
( )
( )
ADC ABE^
( )
( )
ADC DFK^
( ) ( )
ADC ABC^
( )
( )
BDC ABE^
( )
( )
( )
( )
CD BE
CD ABE
ADC ABE
CD AB
CD ADC
^
ü
Þ
^ü
ý
Þ^
^
ý
þ
Ì
þ
( )
( )
ADC ABE^
( )
( )
( )
( )
( )
( )
^
ü
Þ
^ü
ý
Þ
^^
ü
ý
þ
Þ
^ü
Ì
ý
þ
Þ^
^
ý
þ
Ì
þ
DF BC
DF ABC
DF AB DF AC
AC DFK
SC ABC
ADC DFK
DK AC
AC ADC
( )
( )
ADC DFK^
( )
( )
( )
( )
CD BE
CD ABE
BDC ABE
CD AB
CD BDC
^
ü
Þ
^ü
ý
Þ^
^
ý
þ
Ì
þ
( )
( )
BDC ABE^
( ) ( )
ADC ABC^
ABCD
( )
ABC
( )
ABD
( )
DBC
BE
DF
BCD
DK
ACD
()( )ABE ADC^
()()ABD ADC^
()()ABC DFK^
()()DFK ADC^
Trang 28
Ta có: .
Mặt khác: nên câu A
đúng.
nên câu C
đúng.
Theo trên ta có nên .
Vậy ta có . Do đó câu D đúng.
Chọn B.
Câu 3: Cho hình hộp chữ nhật . Khẳng định nào sau đây không đúng?
A. Tồn tại điểm cách đều tám đỉnh của hình hộp.
B. Hình hộp có 6 mặt là 6 hình chữ nhật.
C. Hai mặt và vuông góc nhau.
D. Hình hộp có 4 đường chéo bằng nhau và đồng qui tại trung điểm của mỗi đường.
Hướng dẫn giải:
Chọn C
Câu 4: Cho hình chóp có hai mặt bên và vuông góc với đáy . Khẳng
định nào sau đây sai ?
A. Đáy là đa giác đều.
B. Các mặt bên là những hình chữ nhật nằm trong mặt phẳng vuông góc với đáy.
C. Các cạnh bên là những đường cao.
D. Các mặt bên là những hình bình hành.
Hướng dẫn giải:
Ta có: . Do
đó câu và đúng
Sai. vì nếu thì hai mặt phẳng
và phải vuông góc với nhau theo giao tuyến
( ) ( )
( ) ( )
( ) ( )
( )
ABC BCD
ABD BCD AB BCD
ABC ABD AB
^
ì
ï
^Þ^
í
ï
Ç=
î
( )
CD BE
CD ABE
CD AB
^
ì
Þ^
í
^
î
( ) ( )
( ) ( ) ( )
ABC BCD
ABC BCD BC DF ABC
DF BC
^
ì
ï
Ç=Þ^
í
ï
^
î
( )
DF ABC^
DF AC^
( ) ( ) ( )
AC DF
AC DKF ACD DKF
AC DK
^
ì
Þ^ Þ ^
í
^
î
.ABCD A B C D
¢¢¢¢
O
ACC A
¢¢
BDD B
¢¢
.S ABC
( )
SBC
( )
SAC
( )
ABC
( ) ( )
( ) ( )
( ) ( )
( )
SBC ABC
SAC ABC SC ABC
SC SBC SAC
ì
^
ï
^Þ^
í
ï
=Ç
î
A
B
.C
'A SBÎ
( )
SAB
( )
SBC
SB
Trang 29
Ta có: theo giao tuyến
Mà là đường cao của . Vậy đúng
Vậy chọn đáp án .
Câu 5: Cho hình lăng trụ . Hình chiếu vuông góc của lên trùng với trực
tâm của tam giác . Khẳng định nào sau đây không đúng?
A. là hình chữ nhật. B. .
C. . D. .
Hướng dẫn giải:
Ta có nên ,nếu
thì vô lý vì trùng .
Chọn D.
Câu 6: Cho hình chóp có và đáy là
tam giác cân ở . Gọi là hình chiếu vuông góc của lên . Khẳng định nào sau đây đúng?
A. . B. trùng với trọng tâm tam giác .
C. . D. ( là trung điểm của ).
Hướng dẫn giải:
Chọn D.
Gọi là trung điểm của mà
.
Khi đó là hình chiếu vuông góc của lên . Suy ra
.
Câu 7: Cho hình chóp có hai mặt bên và
vuông góc với đáy . Khẳng định nào sau đây sai?
A. .
B. Nếu là hình chiếu vuông góc của lên thì .
C. .
D. là đường cao của tam giác thì .
Hướng dẫn giải:
Chọn B.
Ta có: .
Gọi là hình chiếu vuông góc của lên ,
.D
( )
( )
( ) ( )
SC ABC
SAC ABC
SC SAC
ì
^
ï
Þ^
í
Ì
ï
î
AC
BK
ABCD
( )
BK AC BK SACÞ^Þ^
.D
D
.’’’ ’ABCD A B C D
’A
( )
ABC
H
ABC
’’BB C C
( ) ( )
’ ’’’AA H A B C^
( ) ( )
’’ ’BB C C AA H^
( ) ( )
’’ ’’AA B B BB C C^
( )
’BC A AH^
’BC BB^
( ) ( )
’’ ’’AA B B BB C C^
BC AB^
H
A
.S ABC
( )
SA ABC^
ABC
A
H
A
( )
SBC
H SBÎ
H
SBC
H SCÎ
H SIÎ
I
BC
I
BC
AI BCÞ^
BC SA^
( )
BC SAIÞ^
H
A
( )
SBC
H SIÎ
.S ABC
( )
SBC
( )
SAC
( )
ABC
( )
SC AB C^
A
¢
A
( )
SBC
A SB
¢
Î
( ) ( )
SAC ABC^
BK
ABC
( )
BK SAC^
( ) ( )
( ) ( )
( ) ( )
( )
SAC SBC SC
SAC ABC SC ABC
SBC ABC
Ç=
ì
ï
^Þ^
í
ï
^
î
A
¢
A
( )
SBC
B
A'
S
A
C
Trang 30
khi đó .
Suy ra đáp án B sai
Câu 8: Cho hình chóp có hai mặt bên và vuông góc với đáy , tam giác
vuông cân ở và có đường cao . Gọi là hình chiếu vuông góc của lên
. Khẳng định nào sau đây đúng?
A. . B. .
C. . D. Góc giữa và là góc .
Hướng dẫn giải:
Chọn B.
Ta có: .
Gọi là trung điểm của
mà .
Khi đó là hình chiếu vuông góc
của lên
Thì suy ra và .
Vậy đáp án B đúng.
Câu 9: Cho hình lăng trụ đứng có đáy là tam giác vuông cân ở . là trung điểm
. Khẳng định nào sau đây sai ?
A. Các mặt bên của là các hình chữ nhật bằng nhau.
B. là mặt phẳng trung trực của .
C. Nếu là hình chiếu vuông góc của lên thì .
D. Hai mặt phẳng và vuông góc nhau.
Hướng dẫn giải:
Chọn A.
Vì là tam giác vuông cân ở
nên các mặt bên của lăng trụ không bằng nhau.
Vậy đáp án A sai.
Câu 10: Cho hình hộp chữ nhật . Khẳng định nào sau đây không đúng?
A. Hình hộp có mặt là hình chữ nhật.
B. Hai mặt và vuông góc nhau.
C. Tồn tại điểm cách đều tám đỉnh của hình hộp.
D. Hình hộp có đường chéo bằng nhau và đồng qui tại trung điểm của mỗi đường.
Hướng dẫn giải:
( )
AA SBC AA BC A BC
¢¢¢
^Þ^ÞÎ
.S ABC
( )
SAB
( )
SAC
( )
ABC
ABC
A
(), AH H BCÎ
O
A
( )
SBC
( )
SC AB C^
( ) ( )
SAH SBC^
O SCÎ
( )
SBC
( )
ABC
∑
SBA
( ) ( )
( ) ( )
( ) ( )
( )
SAB SAC SA
SAC ABC SA ABC
SAB ABC
Ç=
ì
ï
^Þ^
í
ï
^
î
H
BC
AH BCÞ^
BC SA^
O
A
( )
SBC
O SIÎ
( ) ( )
( )
∑
∑
,SBC ABC SHA=
.ABC A B C
¢¢¢
ABC
A
H
BC
.ABC A B C
¢¢¢
( )
AA H
¢
BC
O
A
( )
ABC
¢
OAH
¢
Î
( )
AA B B
¢¢
( )
AA C C
¢¢
ABC
A
AB AC BCÞ= ¹
.ABCD A B C D
¢¢¢¢
6
6
( )
ACC A
¢¢
( )
BDD B
¢¢
O
4
A
B
C
B'
C'
A'
H
Trang 31
Chọn B.
Ta có: là hình chữ nhật nên không vuông
góc với
Suy ra hai mặt và không vuông
góc với nhau.
Vậy đáp án B sai.
Câu 11: Cho hình lập phương . Mặt phẳng không vuông góc với mặt phẳng
nào dưới đây?
A. . B. . C. . D. .
Hướng dẫn giải:
* Gọi .
Tam giác đều có là đường trung tuyến nên
.
.
nên A đúng.
* Ta có
nên
B đúng.
* Gọi .
Tam giác đều có là đường trung tuyến nên .
.
nên C đúng. Chọn D.
Câu 12: Cho hình lập phương có cạnh bằng . Khẳng định nào sau đây sai?
A. Tam giác là tam giác đều.
B. Nếu là góc giữa và thì .
C. là hình chữ nhật có diện tích bằng .
D. Hai mặt và ở trong hai mặt phẳng vuông góc với nhau.
Hướng dẫn giải:.
Chọn C.
+ Cách 1: Chứng minh trực tiếp chỉ ra là đáp án sai.
Từ giả thiết dễ dàng tính được .
Mặt khác vì là hình lập phương nên suy ra
.
Xét tứ giác có là hình chữ
nhật có các cạnh và .
ABCD
AC
BD
( )
ACC A
¢¢
( )
BDD B
¢¢
111 1
.ABCD A B C D
( )
1
ABD
( )
1
AB D
( )
11
ACC A
( )
1
ABD
( )
11
ABC
11
IAB AB=Ç
1
ABD
DI
1
DI A B^
( )
11 1
DA AA B B DA A B^Þ^
( )
1
11
1
AB DI
AB ABD
AB AD
^
ü
Þ^
ý
^
þ
( ) ( ) ( )
11 1 11
1
BD AC
BD ACC A A BD ACC A
BD AA
^
ü
Þ^ Þ ^
ý
^
þ
11
JAD AD=Ç
1
ABD
BJ
1
BJ A D^
( )
11 1
BA AA D D BA A D^Þ^
( )
1
11
1
AD BJ
AB ABD
AD BA
^
ü
Þ^
ý
^
þ
.ABCD A B C D
¢¢¢¢
a
AB C
¢
a
AC
¢
( )
ABCD
2
cos
3
a
=
ACC A
¢¢
2
2a
( )
AA C C
¢¢
( )
BB D D
¢¢
C
2AC a=
.ABCD A B C D
¢¢¢¢
∑
90AA C
¢¢
=°
ACC A
¢¢
∑
//
90
AA CC
AA CC a
AA C
ì
¢¢
ï
¢¢
==
í
ï
¢¢
=°
î
Þ
ACC A
¢¢
a
2a
Trang 32
Diện tích hình chữ nhật là : (đvdt)
đáp án sai.
+ Cách 2: Chứng minh 3 đáp án , , đều đúng và suy ra đáp án sai.
Câu 13: Cho hình chóp có đường cao . Xét các mệnh đề sau:
I) .
II) trùng với tâm đường tròn ngoại tiếp tam giác .
III) Tam giác là tam giác đều.
IV) là trực tâm tam giác .
Các yếu tố nào chưa đủ để kết luận là hình chóp đều?
A. và . B. và . C. và . D. và .
Hướng dẫn giải:.
Chọn A.
Câu 14: Cho hình lập phương cạnh bằng . Khẳng định nào sau đây sai?
A. Hai mặt và vuông góc nhau.
B. Bốn đường chéo , , , bằng nhau và bằng .
C. Hai mặt và là hai hình vuông bằng nhau.
D. .
Hướng dẫn giải:.
Chọn C.
Vì theo giả thiết ta dễ dàng chỉ ra được:
+ và cắt cùng nằm trong
. Mà đáp án
đúng.
+ đáp án đúng.
+ Áp dụng đình lý Pytago trong tam giác vuông tại ta có:
.
Áp dụng định lý Pytago trong tam giác vuông tại ta có:
. Hoàn toàn tương tự ta tính được độ dài các
đường chéo còn lại của hình lập phương đều bằng nhau và bằng đáp án đúng.
+ Xét tứ giác có là hình chữ nhật. hoàn toàn tương tự ta cũng
chỉ ra cũng là hình chữ nhật có các cạnh là và .
Hai mặt và là hai hình vuông bằng nhau đáp án sai.
Câu 15: Cho hình lăng trụ . Hình chiếu vuông góc của lên trùng với trực
tâm của tam giác . Khẳng định nào sau đây không đúng?
A. . B.
.
C. là hình chữ nhật. D.
.
Hướng dẫn giải:
Chọn A.
ACC A
¢¢
2
.2 2Saa a==
Þ
C
A
B
D
C
.S ABC
SH
SA SB SC==
H
ABC
ABC
H
ABC
.S ABC
( )
I
( )
II
( )
II
( )
III
( )
III
( )
IV
( )
IV
( )
I
.ABCD A B C D
¢¢¢¢
a
ACC A
¢¢
BDD B
¢¢
AC
¢
AC
¢
BD
¢
BD
¢
3a
ACC A
¢¢
BDD B
¢¢
AC BD
¢
^
.ABCD A B C D
¢¢¢¢
AC BD
AC BB
^
ì
í
¢
^
î
BD
BB
¢
( )
BB D D
¢¢
( )
AC BB D D
¢¢
Þ^
( )
BD BB D D
¢¢¢
Ì
AC BD
¢
Þ^
Þ
D
( )
( )
( ) ( )
AC ACC A
ACC A BB D D
AC BB D D
¢¢
Ì
ì
ï
¢¢ ¢ ¢
Þ^
í
¢¢
^
ï
î
Þ
A
BAD
¢¢ ¢
A
¢
22 2222
2BD BA AD a a a
¢¢ ¢¢ ¢¢
=+ =+=
BB D
¢¢
B
¢
22 2222
23BD BB B D a a a
¢¢¢¢
=+ =+=
3BD a
¢
Þ=
3a
Þ
B
ACC A
¢¢
∑
//
3
90
AC A C
AC A C a
ACC A
AA CC a
ACC
¢¢
ì
ï
¢¢
==
ï
¢¢
Þ
í
¢¢
==
ï
ï
¢
=°
î
BDD B
¢¢
a
3a
Þ
ACC A
¢¢
BDD B
¢¢
Þ
C
.ABCD A B C D
¢¢¢¢
A
¢
( )
ABC
H
ABC
( ) ( )
AA B B BB C C^
¢¢ ¢¢
( ) ( )
AA H A B C
¢¢¢¢
^
BB C C
¢¢
( ) ( )
BB C C AA H
¢¢
^
¢
Trang 33
Gọi là hình chiếu vuông góc của lên
nên đáp án B,C,D đúng.
Câu 16: Hình hộp trở thành hình lăng trụ tứ giác đều khi phải thêm các điều kiện nào
sau đây?
A. Tất cả các cạnh đáy bằng nhau và cạnh bên vuông góc với mặt đáy.
B. Cạnh bên bằng cạnh đáy và cạnh bên vuông góc với mặt đáy.
C. Có một mặt bên vuông góc với mặt đáy và đáy là hình vuông.
D. Các mặt bên là hình chữ nhật và mặt đáy là hình vuông.
Hướng dẫn giải:
Chọn D.
Theo lí thuyết lăng trụ tứ giác đều là lăng trụ đứng có đáy là hình vuông.
Câu 17: Cho hình lăng trụ tứ giác đều có cạnh đáy bằng , góc giữa hai mặt phẳng
và có số đo bằng . Cạnh bên của hình lăng trụ bằng:
A. . B. . C. . D. .
Hướng dẫn giải:.
Chọn B.
Ta có: .
Từ giả thiết ta dễ dàng chứng minh được: mà
. Mặt khác: .
.
Áp dụng hệ thức lượng trong tam giác vuông tại ta có:
.
Câu 18: Cho hai mặt phẳng vuông góc và có giao tuyến . Lấy , cùng thuộc D và lấy
trên (P), trên (Q) sao cho , và . Thiết diện của tứ diện
khi cắt bởi mặt phẳng đi qua và vuông góc với là hình gì?
A. Tam giác cân. B. Hình vuông. C. Tam giác đều. D. Tam giác vuông.
Hướng dẫn giải:
Gọi là trung điểm của . Vì tam giác vuông cân
tại nên .
Ta có .
.
K
A
BC
( )
,,HAKBCAKBCAH BC AAH
¢¢
ÞÎ ^ ^ Þ ^
( ) ( )
( ) ( )
AA H A B C
BB C C AA H
BC BB
¢¢¢¢
^
ì
ï
¢¢ ¢
Þ^
í
ï
¢
^
î
.ABCD A B C D
¢¢¢¢
.ABCD A B C D
¢¢¢¢
a
( )
ABCD
( )
ABC
¢
60°
3a
3a
2a
2a
( ) ( )
ABCD ABC AB
¢
Ç=
( )
AB BB C C
¢¢
^
( )
CB BBCC
¢¢¢
Ì
AB C B
¢
Þ^
CB AB^
( ) ( )
( )
( )
∑
,,60ABCD ABC CB C B CBC
¢¢¢
Þ===°
BCC
¢
C
∑ ∑
tan .tan .tan 60 3
CC
CBC CC CB CBC a a
CB
¢
¢¢ ¢
=Þ= = °=
( )
P
( )
Q
D
A
B
C
D
AC AB^
BD AB^
AB AC BD==
ABCD
( )
a
A
CD
I
BC
ABC
A
AI BC^
( ) ( )
( ) ( )
( )
( )
PQ
PQd BDPBDAI
QBDd
^
ü
ï
Ç=Þ^Þ^
ý
ï
É^
þ
( )
AI BC
AI BCD AI CD
AI BD
^
ü
Þ^ Þ^
ý
^
þ
Trang 34
Trong , dựng đường thẳng đi qua và vuông góc với cắt tại .
Thiết diện của tứ diện khi cắt bởi mặt phẳng là tam giác .
Vì nên tam giác là tam giác vuông tại .
Chọn D.
Câu 19: Cho hai tam giác và nằm trên hai mặt phẳng vuông góc với nhau và
. với giá trị nào của thì hai mặt phẳng và vuông
góc.
A. . B. . C. . D. .
Hướng dẫn giải:
vuông cân tại
( Với là trung điểm ; là trung điểm )
Vậy chọn đáp án .
( )
ACD
A
CD
CD
H
ABCD
( )
a
AHI
( )
AI BCD AI HI^Þ^
AHI
I
ACD
BCD
;2AC AD BC BD a CD x==== =
x
( )
ABC
( )
ABD
3
3
a
2
a
2
2
a
3
a
YCBT CJDÛD
J
22
22 2
3
42 2( )
223
AB a a a
IJ IC ID x AI x x
+
Û= = = Û = = - Û=
I
CD
J
AB
A
Trang 35
DẠNG 3: TÍNH ĐỘ DÀI ĐOẠN THẲNG, DIỆN TÍCH HÌNH CHIẾU, CHU VI
VÀ DIỆN TÍCH ĐA GIÁC
Câu 1: Cho hình hộp chữ nhật có , , . Độ dài đường chéo
là
A. . B. .
C. . D. .
Hướng dẫn giải:
Từ sách giáo khoa, đường chéo hình hộp chữ nhật
Chọn A
Câu 2: Cho hình hộp có , , . Nếu
thì hình hộp là
A. Hình lập phương. B. Hình hộp chữ nhật C. Hình hộp thoi. D. Hình hộp đứng.
Hướng dẫn giải:
Þhình bình hành là hình chữ nhật
Þhình bình hành là hình chữ nhật
Þhình bình hành là hình chữ nhật
Chọn B
Câu 3: Cho hai mặt phẳng và vuông góc với nhau. Người ta lấy trên giao tuyến của hai
mặt phẳng đó hai điểm và sao cho . Gọi là một điểm trên , là một điểm trên
sao cho , cùng vuông góc với giao tuyến và , . Độ dài là:
A. . B. . C. . D. .
Hướng dẫn giải:
Tam giác vuông tại nên .
Ta có .
.ABCD A B C D
¢¢¢¢
AB a=
BC b=
CC c
¢
=
AC
¢
222
'AC a b c=++
222
'AC a b c=- + +
222
'AC a b c=+-
222
'AC a b c=-+
222
'AC a b c=++
.ABCD A B C D
¢¢¢¢
AB a=
BC b=
CC c
¢
=
222
AC BD B D a b c
¢¢¢
===++
AC BD
¢¢
=
ABC D
¢¢
BD B D
¢¢
=
BDD B
¢¢
AC B D
¢¢
=
ADC B
¢¢
( )
P
( )
Q
d
A
B
8AB =
C
( )
P
D
( )
Q
AC
BD
d
6AC =
24BD =
CD
20
22
30
26
ABC
A
2222
86 10BC AB AC=+=+=
( ) ( )
( ) ( )
( )
( )
PQ
P Q d BD P BD BC
Q BD d
^
ü
ï
Ç=Þ^Þ^
ý
ï
É^
þ
Trang 36
Tam giác vuông tại nên .
Chọn D.
Câu 4: Cho ba tia , , vuông góc nhau từng đôi một. Trên , , lần lượt lấy các điểm
, , sao cho . Khẳng định nào sau đây sai?
A. là hình chóp đều.
B. Tam giác có diện tích .
C. Tam giác có chu vi .
D. Ba mặt phẳng , , vuông góc với nhau từng đôi một.
Hướng dẫn giải:.
Chọn C.
+ Áp dụng định lý Pytago trong tam giác vuông tại ta có:
.
Hoàn toàn tương tự ta tính được .
là tam giác đều. Mặt khác theo giả thiết
các mặt bên của hình chóp là
các tam giác cân tại là hình chóp đều đáp án
đúng.
+ Chu vi là:
đáp án
sai.
+ Nửa chu vi Diện tích là: . Diện tích
là:
(đvdt).
đáp án đúng.
+ Dễ chứng minh được , .
đáp án đúng.
Câu 5: Cho hình thoi có cạnh bằng và . Trên đường thẳng vuông góc với mặt phẳng
tại ( là tâm của ), lấy điểm sao cho tam giác là tam giác đều. Khẳng
định nào sau đây đúng?
A. là hình chóp đều.
B. Hình chóp có các mặt bên là các tam giác cân.
C. .
D. và hợp với mặt phẳng những góc bằng
nhau.
Hướng dẫn giải:.
Chọn C.
Xét có , là tam giác đều
cạnh . Vì là tâm của nên suy ra là đường trung
BCD
B
22 22
24 10 26CD BD BC=+=+=
Ox
Oy
Oz
Ox
Oy
Oz
A
B
C
OA OB OC a== =
.O ABC
ABC
2
3
2
a
S =
ABC
32
2
2
a
p =
( )
OAB
( )
OBC
( )
OCA
OAB
O
222222
2AB OA OB a a a=+=+=
2AB aÞ=
2BC AC a==
ABCÞD
OA OB OC a== =
Þ
.O ABC
O
.O ABCÞ
Þ
A
ABCD
222232pABACBCa a a a=++= + + =
Þ
C
ABCD
32
2
a
p =
ABCD
33
342
3232 32 2 322 2 3 3
2.
22 22 28 42
aa aa aa aa
Sa
æöæö
=-= = ==
ç÷ç÷
ç÷ç÷
èøèø
Þ
B
( )
( )
( )
( ) ( )
( ) ( )
OA OBC
OAB OBC
OA OAB
OAC OBC
OA OAC
^
ì
^
ì
ï
ï
ÌÞ
íí
^
ï
ï
î
Ì
î
( )
( )
( ) ( )
OB OAC
OAB OAC
OB OAB
^
ì
ï
Þ^
í
Ì
ï
î
Þ
D
ABCD
a
!
60A =°
( )
ABCD
O
O
ABCD
S
SAC
.S ABCD
.S ABCD
3
2
a
SO =
SA
SB
( )
ABCD
ABDD
!
60A =°
AB AD a==
Þ
ABDD
a
O
ABCD
AO
Trang 37
tuyến trong đều cạnh nên dễ tính được .
Mặt khác theo giả thiết là tam giác đều .
Câu 6: Cho hình chóp cụt đều với đáy lớn có cạnh bằng . Đáy nhỏ có
cạnh bằng , chiều cao . Khẳng định nào sau đây sai?
A. Ba đường cao , , đồng qui tại .
B. .
C. Góc giữa mặt bên mặt đáy là góc ( là trung điểm ).
D. Đáy lớn có diện tích gấp lần diện tích đáy nhỏ .
Hướng dẫn giải:.
Chọn B.
+ Đáp án đúng.
+ Gọi là trung điểm của .
Từ giả thiết dễ dàng chỉ ra được .
Mặt khác là tam giác đều cạnh , có là đường trung
tuyến .
Áp dụng định lý Pytago trong vuông tại ta có:
. Vì là hình chóp cụt đều nên
đáp án sai.
+ Ta có: . Vì cân tại và là trung điểm của nên suy ra
. Mặt khác là tam giác đều có là trung điểm của .
đáp án đúng.
+ Ta có: đáp án đúng.
Câu 7: Cho hình chóp cụt tứ giác đều cạnh của đáy nhỏ bằng và cạnh của
đáy lớn bằng . Góc giữa cạnh bên và mặt đáy bằng . Tính chiều cao của hình
chóp cụt đã cho.
A. . B. . C.
. D. .
Hướng dẫn giải:.
Chọn A.
ABDD
a
3
2
a
AO =
23AC AO aÞ= =
SAC
3SA SC AC aÞ= = =
33
3.
22
a
SO aÞ= =
.ABC A B C
¢¢¢
ABC
a
ABC
¢¢¢
2
a
2
a
OO
¢
=
AA
¢
BB
¢
CC
¢
S
2
a
AA BB CC
¢¢ ¢
== =
SIO
I
BC
ABC
4
ABC
¢¢¢
A
I
BC
1
2
AA OO
SA SO
¢¢
==
2SO OO a
¢
Þ= =
ABCD
a
AI
3
2
a
AIÞ=
23 3
.
32 3
aa
AOÞ= =
SOAD
O
2
2
22 22
3 12
39
aa
SA SO AO a
æö
=+ =+ =
ç÷
ç÷
èø
23
3
a
SAÞ=
3
3
a
AA
¢
Þ=
.ABC A B C
¢¢¢
3
3
a
AA BB CC
¢¢ ¢
== =
Þ
B
( ) ( )
SBC AB C BCÇ=
SBCD
S
I
BC
SI BC^
ABCD
I
BC
AI BCÞ^
( ) ( )
( )
( ) ( )
∑
,,,SBC ABC SI AI SI OI SIOÞ===
Þ
C
1
. . .sin
. 2 .2
2
4
1
..
. . .sin
2
ABC
ABC
AB AC A
S
AB AC A B A C
SABACABAC
AB AC A
D
¢¢¢
D
¢¢ ¢ ¢
====
¢¢ ¢ ¢ ¢¢ ¢ ¢
¢¢ ¢ ¢ ¢
Þ
D
.ABCD A B C D
¢¢¢¢
ABCD
3
a
ABCD
¢¢¢¢
a
60°
OO
¢
6
6
a
OO
¢
=
3
2
a
OO
¢
=
26
3
a
OO
¢
=
32
4
a
OO
¢
=
Trang 38
Ta có là hình chiếu vuông góc của lên
.
Từ giả thiết dễ dàng chỉ ra được .
Vì là tam giác vuông cân tại có là đường cao nên ta có:
.
Áp dụng hệ thức lượng trong vuông tại ta có:
.
Câu 8: Cho hình lăng trụ lục giác đều có cạnh bên bằng và là hình
vuông. Cạnh đáy của lăng trụ bằng:
A. . B. . C. . D. .
Hướng dẫn giải:.
Chọn B.
Tổng số đo các góc của hình lục giác là . Vì
là hình lục giác đều nên mỗi góc của hình lục giác đều là
. Vì là hình lục giác đều nên ta suy
ra:
+ là tia phân giác của góc và .
+ Tam giác vuông tại .
Xét tam giác vuông tại có và ta suy ra:
Câu 9: Cho hình lăng trụ tứ giác đều có là hình vuông, cạnh bằng . Cạnh
đáy của hình lăng trụ bằng:
A. . B. . C. . D. .
Hướng dẫn giải:.
Chọn A.
Từ giả thiết ta sauy ra vuông cân tại
.
Áp dụng hệ thức lượng trong vuông cân tại có
và cạnh , ta có:
.
( )
SO A B C D B D SO B D
¢¢¢¢¢¢¢ ¢¢¢
^ÉÞ^
OD
¢¢
Þ
SD
¢
( )
ABCD
¢¢¢¢
( )
( )
( )
∑
,,60SD ABCD SD O D SD O
¢¢¢¢¢¢
Þ===°
1
3
AA OO
SA SO
¢¢
==
¢¢
ADC
¢¢¢
D
D
¢
DO
¢¢
222222
111112
DO AD DC a a a
=+=+=
¢¢ ¢¢ ¢¢
2
2
2
a
DO
¢¢
Þ=
2
2
a
DO
¢¢
Þ=
SD O
¢¢
D
O
¢
tan 60
SO
OD
¢
°=
¢¢
26
. tan 60 . 3
22
aa
SO O D
¢¢¢
Þ= °= =
1166
.
3326
aa
OO SO
¢¢
Þ= = =
.ABCDEF A B C D E F
¢¢¢¢¢¢
a
ADD A
¢¢
a
2
a
3
3a
2
2a
4.180 720°= °
ABCDEF
ABCDEF
120°
∑
120FABÞ=°
ABCDEF
AD
∑
FAB
∑
EDC
∑
∑
60
2
FAB
FADÞ==°
AFD
F
AFD
F
∑
60FAD =°
AD a=
∑
∑
cos
1
.cos .cos 60 . .
22
AF
FAD
AD
a
AF AD FAD a a
=
Þ= = °==
.ABCD A B C D
¢¢¢¢
ACC A
¢¢
a
2
2a
2a
3
3a
3a
ABCD
B
∑
∑
45BAC BCAÞ==°
ABCD
B
∑
45BAC =°
AC a=
∑
cos
AB
BAC
AC
=
∑
22
.cos .cos 45 .
22
a
AB AC BAC a aÞ= = °= =
Trang 39
Câu 10: Cho hình lăng trụ tam giác đều có cạnh đáy bằng và cạnh bên bằng .
Gọi và lần lượt là trọng tâm của hai đáy và . Khẳng định nào sau đây đúng khi nói
về ?
A. là hình chữ nhật có hai kích thước là và .
B. là hình vuông có cạnh bằng .
C. là hình chữ nhật có diện tích bằng .
D. là hình vuông có diện tích bằng .
Hướng dẫn giải:.
Chọn B.
Gọi là trung điểm . Khi đó ta dễ dàng tính được :
.
Vì là trọng tâm tam giác nên:
.
là hình vuông có cạnh bằng .
Câu 11: Cho hai tam giác và nằm trên hai mặt phẳng vuông góc với nhau và
, . Tính theo và ?
A. . B. .
C. . D. .
Hướng dẫn giải:
Gọi là trung điểm của . Vì tam giác cân tại và tam giác cân tại nên
, .
Ta có
.
.
Tam giác vuông tại nên
. Chọn C.
Câu 12: Cho hai tam giác và nằm trên hai mặt phẳng vuông góc với nhau và
, . Gọi lần lượt là trung điểm của và . Tính theo
và ?
A. . B. . C. . D. .
.ABC A B C
¢¢¢
23a
2a
G
G
¢
ABC
ABC
¢¢¢
AA G G
¢¢
AA G G
¢¢
2a
3a
AA G G
¢¢
2a
AA G G
¢¢
2
6a
AA G G
¢¢
2
8a
M
BC
3
23. 3
2
AM a a==
G
ABC
22
.3 2
33
AG AM a a AA
¢
====
AA G G
¢¢
Þ
2a
ACD
BCD
AC AD BC BD a====
2CD x=
AB
a
x
( )
22
2AB a x=+
22
AB a x=-
( )
22
2AB a x=-
22
AB a x=+
H
CD
ACD
A
BCD
B
AH CD^
BH CD^
( ) ( )
( ) ( )
( )
( )
ACD BCD
ACD BCD CD AH BCD AH BH
ACD AH CD
^
ü
ï
Ç=Þ^Þ^
ý
ï
É^
þ
( )
2222
..ACD BCD c c c AH BH BC CH a xD=D Þ== - =-
AHB
H
( )
22 22
2AB AH BH a x=+=-
ACD
BCD
AC AD BC BD a====
2CD x=
,IJ
AB
CD
IJ
a
x
22
2
ax
IJ
-
=
( )
22
2
2
ax
IJ
+
=
( )
22
2
2
ax
IJ
-
=
22
2
ax
IJ
+
=
Trang 40
Hướng dẫn giải:
Ta có: . Vậy
tam giác vuông tại
Ta có: .
Do đó tam giác vuông cân tại . Suy ra
Chọn C.
Câu 13: Cho hình chóp đều có cạnh đáy bằng , góc giữa một mặt bên và mặt đáy bằng .
Tính độ dài đường cao .
A. . B. . C. . D. .
Hướng dẫn giải:.
Chọn A.
Ta có: . Gọi , lần lượt là trung điểm của
các cạnh và .
Dễ chứng minh được và .
.
Ta dễ tính được: . Vì là chân đường cao của hình chóp
đều nên trùng với trọng tâm của tam giác
.
Áp dụng hệ thức lượng trong tam giác vuông tại ta có :
.
Câu 14: Cho hình lăng trụ đứng có , , . Khẳng định nào
sau đây sai?
A. Đáy là tam giác vuông.
B. Hai mặt và vuông góc nhau.
C. Góc giữa hai mặt phẳng và có số đo bằng .
D. .
Hướng dẫn giải:.
Chọn D.
+ Cách 1: Chứng minh trực tiếp chỉ ra là đáp án sai.
Từ giả thiết dễ dàng suy ra .
Áp dụng định lý Pytago trong tam giác vuông tại ta có:
đáp án
sai.
+ Cách 2: Chứng minh 3 đáp án , , đều đúng
suy ra đáp án sai.
( ) ( )
( ) ( )
( )
CD AJ
ACD BCD AJ BCD AJ BJ
ACD BCD CD
ì
^
ï
^Þ^Þ^
í
ï
Ç=
î
ABJ
J
22
AJ BJ a x== -
ABJ
J
( )
22
2
2
22
ax
AJ
IJ
-
==
.S ABC
a
60°
SH
2
a
SH =
3
2
a
SH =
2
3
a
SH =
3
3
a
SH =
( ) ( )
SBC AB C BCÇ=
M
N
BC
AC
SM BC^
AM BC^
( ) ( )
( )
( )
∑
∑
,, 60SBC ABC SM AM SM A SMHÞ====°
3
2
a
AM =
H
.S ABC
H
ABC
1133
.
3326
aa
MH AMÞ= = =
SHM
H
∑
tan
SH
SMH
MH
=
∑
333
. tan . tan 60 . 3
6662
aaaa
SH MH SMHÞ= = °= ==
.ABC A B C
¢¢¢
AB AA a
¢
==
2BC a=
5CA a=
ABC
( )
AA B B
¢¢
( )
BB C
¢¢
( )
ABC
( )
ABC
¢
45°
22AC a
¢
=
D
CC AA a
¢¢
==
ACC
¢
C
22 2222
56AC AC CC a a a
¢¢
=+ =+=
6AC a
¢
Þ=
Þ
D
A
B
C
D
Trang 41
Câu 15: Cho hình chóp tứ giác , có đáy là hình thoi tâm cạnh bằng và góc
, cạnh và vuông góc với mặt phẳng . Trong tam giác kẻ
tại . Tính độ dài được
A. B. C. D.
Hướng dẫn giải:
Tam giác đồng dạng tam giác Þ Þ
và đều cạnh Þ Þ
vuông tại Þ =
=
Vậy
Chọn A
Câu 16: Cho tam giác và mặt phẳng Biết góc giữa mặt phẳng và mặt phẳng là
. Hình chiếu của tam giác trên mặt phẳng là tam giác Tìm hệ thức liên hệ giữa
diện tích tam giác và diện tích tam giác
A. B.
C. D.
Hướng dẫn giải:
Qua B kẻ mặt phẳng cắt lần lượt tại
khi đó
Góc giữa mặt phẳng và mặt phẳng bằng góc giữa
mặt phẳng và và bằng
Kẻ
Vậy
.S ABCD
ABCD
I
a
!
0
60A =
6
2
a
SC =
SC
( )
ABCD
SCA
IK SA^
K
IK
2
a
3
3
a
3
a
2
2
a
AKI
ACS
IK AI
SC SA
=
.SC AI
IK
SA
=
BCDD
ABDD
a
3
2
a
IA IC==
3AC a=
SACD
C
22
SA SC AC=+
( )
2
2
6
3
2
a
a
æö
+
ç÷
èø
32
2
a
2
a
IK =
ABC
( )
.P
( )
P
( )
ABC
j
ABC
( )
P
.ABC
¢¢¢
ABC
.ABC
¢¢¢
'''
.cot .
ABC ABC
SS
j
DD
=
'''
.sin .
ABC ABC
SS
j
DD
=
'''
.tan .
ABC ABC
SS
j
DD
=
'''
.cos .
ABC ABC
SS
j
DD
=
( ) ( )
//QP
;AA CC
¢¢
11
;AC
11
A B C A BC
SS
¢¢¢
=
( )
P
( )
ABC
( )
ABC
( )
11
BA C
j
1
AH BF A H BF^Þ ^
11
1
1
.
2
1
.cos .
2
.cos
ABC
ABC
SAHBF
AH BF
S
j
j
=
=
=
'''
.cos .
ABC ABC
SS
j
DD
=
Trang 42
DẠNG 4: XÁC ĐỊNH THIẾT DIỆN CHỨA MỘT ĐƯỜNG THẲNG VÀ VUÔNG
GÓC VỚI MỘT MẶT PHẲNG.
Phương pháp:
Cho mặt phẳng và đường thẳng không vuông góc với .Xác định mặt phẳng chứa và
vuông góc với
.
Để giải bài toán này ta làm theo các bước sau:
• Chọn một điểm
• Dựng đường thẳng đi qua và vuông góc với . Khi đó chính là mặt phẳng .
Câu 1: Cho hình chóp , đáy là hình vuông, . Gọi là mặt phẳng
chứa và vuông góc với , cắt chóp theo thiết diện là hình gì?
A. hình bình hành. B. hình thang vuông.
C. hình thang không vuông. D. hình chữ nhật.
Hướng dẫn giải:
Dựng
Ta có .
Suy ra
mà suy ra
Do đó
Vì nên .
Từ đó thiết diện là hình thang .
Mặt khác nên
Vậy thiết diện là hình thang vuông tại và .
Chọn đáp án B.
Ta có , mà . Chon A
Câu 2: Cho hình chóp với là hình chữ nhật tâm có vuông
góc với đáy và . Gọi là mặt phẳng qua và vuông góc với Diện tích thiết diện
của và hình chóp bằng bao nhiêu?
A. . B. . C. . D. .
Hướng dẫn giải:
Gọi là đoạn thẳng qua vuông góc ( thuộc ) ta có nên
là thiết diện cần tìm.
vuông tại nên .
Chọn B.
( )
a
a
( )
a
( )
b
a
( )
a
a
b
d
β
α
A
H
ÎAa
b
A
( )
a
( )
,mp a b
( )
b
.S ABCD
ABCD
()SA ABCD^
()a
AB
()SCD
()a
.S ABCD
AH CD^
()
CD SA
CD SAD
CD AD
¸
^
Ô
fi^
˝
^
Ô
˛
CD AH^
()AH SCDÃ
()AH aÃ
(
)
()AHBa ∫
(
)
//CDa
(
)
() //( )SAD HK CD K SCa «= Œ
ABKH
()AB SAD^
AB AH^
A
H
22
2, ,
22
aa
AC a OC SO SC OC===-=
1
22
a
SO OC OM SC^Þ = =
.S ABCD
ABCD
O
, 2 . AB a AD a SA==
SA a=
( )
P
SO
( )
.SAD
( )
P
.S ABCD
2
3
2
a
2
2
2
a
2
2
a
2
a
MN
O
AD
, MN
, AD BC
( )
MN SAD^
SMN
D
SMN
M
2
.2
22
SMN
SM MN
Sa==
Trang 43
Câu 3: Cho hai mặt phẳng vuông góc và có giao tuyến . Lấy , cùng thuộc và lấy
trên , trên sao cho , và . Diện tích thiết diện
của tứ diện khi cắt bởi mặt phẳng đi qua và vuông góc với là?
A. B. C. D.
Hướng dẫn giải:
Chọn C.
Ta có:
Gọi là trung điểm , ta có
Trong mặt phẳng , kẻ thì ta có
Khi đó mặt phẳng cắt tứ diện theo thiết diện là tam
giác
Mặt khác tam giác vuông cân tại nên .
Trong tam giác vuông , kẻ đường cao thì
và
Vậy: thiết diện cần tìm là tam giác vuông tại và có diện tích
Câu 4: Cho hình lăng trụ đứng có đáy là tam giác vuông tại , với ,
, cạnh bên . Mặt phẳng đi qua và vuông góc với .Thiết diện của lăng trụ cắt bởi
mặt phẳng có hình:
A. . B. . C. . D. .
Hướng dẫn giải:
Gọi là mặt phẳng đi qua và vuông góc với . Từ ta dựng , Vì
nên .
Mặt khác trong mặt phẳng dựng và cắt tại 1 điểm (điểm gì đề
chưa có cho nên cho tạm điểm ).
Từ và ta có :
Chọn đáp án
()P
()Q
D
A
B
D
C
()P
D
()Q
AC AB^
BD AB^
AB AC BD a===
ABCD
()
a
A
CD
2
2
12
a
2
2
8
a
2
3
12
a
2
3
8
a
() ()
() () ()
(),
PQ
PQ BDP
BD Q BD
^
ì
ï
Ç=D Þ^
í
ï
Ì^D
î
H
BC
AH BC
AH CD
AH BD
^
ì
Þ^
í
^
î
()BCD
HI CD^
()CD AHI^
()
a
ABCD
AHI
ABC
A
2BC a=
BCD
BK
2
3
a
BK =
6
a
HI =
AHI
H
2
3
12
a
S =
.’’’ABC A B C
ABC
A
AB c=
AC b=
’AA h=
( )
P
’A
’BC
( )
P
.1 .2hvàh
.2 .3hvàh
.2h
.1h
()P
'A
BC
'A
'' ''AK BC^
()( '')ABC BCC B^
'' '' ''( '') '' 'AK BC AK BCC B AK BC^Þ ^ Þ ^
(1)
('')BCC B
''Kx BC^
'BB
N
(2)
N
(1)
(2)
'''
'('')
''
BC A K
BC A K N
BC K N
^
ì
Þ^
í
^
î
A
Trang 44
Câu 5: Cho hình lập phương có cạnh bằng . Cắt hình lập phương bởi mặt phẳng
trung trực của . Thiết diện là hình gì?
A. Hình vuông. B. Lục giác đều.
C. Ngũ giác đều. D. Tam giác đều.
Hướng dẫn giải:
Ta có là hình chiếu của lên .
mà nên
Ta có
Lại có suy ra
Từ và suy ra
Mặt phẳng trung trực là mặt phẳng đi qua
trung điểm của và
Từ và suy ra
Do đó
Qua dựng
Dựng
Mà
Suy ra thiết diện là lục giác đều.
Chọn đáp án B.
Câu 6: Cho hình lập phương có cạnh bằng Cắt hình lập phương bởi mặt phẳng
trung trực của Diện tích thiết diện là
A. B. C. D.
Hướng dẫn giải:
Ta có mặt phẳng trung trực của cắt hình lập phương
theo thiết diện là lục giác đều cạnh
Khi đó
.' ' ' 'ABCD A B C D
a
'AC
AC
'AC
()ABCD
AC BD^
', (1)AC BD^
('')
'
'(''
AD AA B B
AB AD
AB AABB
¸
^
Ô
fi^
˝
Ã
Ô
˛
''A B AB^
'('')
' ' , (2)
'( '')
AB ABCD
AC A B
AC AB C D
¸
^
Ô
fi^
˝
Ã
Ô
˛
(1)
(2)
'(' ), (3)AC A BD^
'AC
()a
I
'AC
() ', (4)ACa ^
(3)
(4)
( ) qua
( )//( ' )
mp I
A BD
a
a
Ï
Ô
Ì
Ô
Ó
I
//MQ BD
//A'D
NP// ' ' //
//B'C//A'D
//
MN
BD BD
QK
KH BD
2
2
a
MN NP PQ QK KM=== = =
.ABCD A B C D
¢¢¢¢
.a
.AC
¢
2
3
.
2
a
S =
2
.Sa=
2
3
.
4
a
S =
2
33
.
4
a
S =
AC
¢
.ABCD A B C D
¢¢¢¢
MNPQRDS
12
22
a
BC
¢
=
2
1223 33
6. .
22 2 2 4
aa
Sa==
| 1/44
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

BÀI TẬP TRẮC NGHIỆM HAI MẶT PHẲNG VUÔNG GÓC
A – LÝ THUYẾT TÓM TẮT
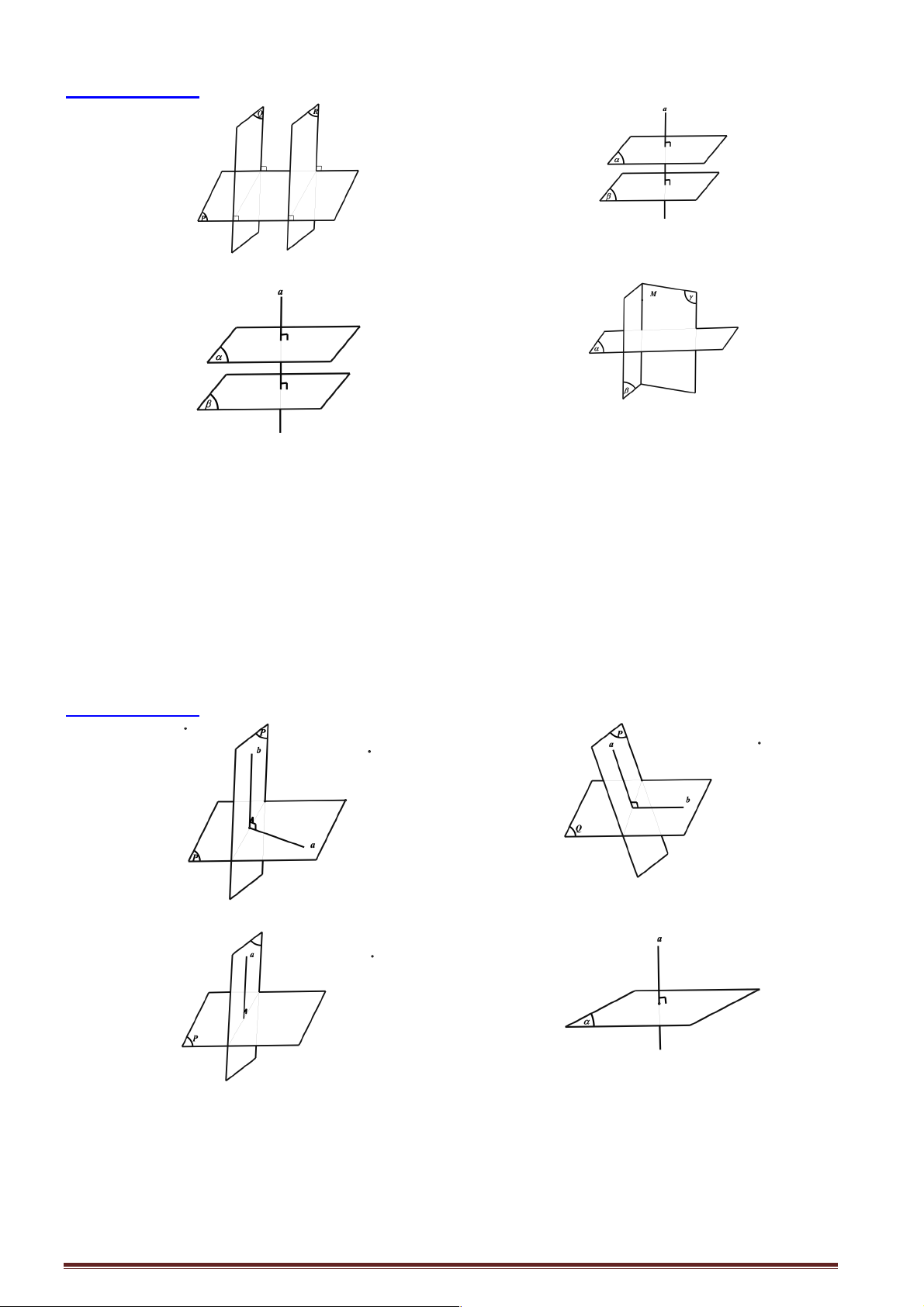
1. Góc giữa hai mặt phẳng ì ^ • a (P) ∑ í Þ ((P),(Q)) ∂ = ( , a b) îb ^ (Q) ì Ì ^
• Giả sử (P) Ç (Q) = c. Từ I Î c, dựng a (P), a c í Þ ∑ ((P),(Q)) ∂ = ( , a b)
îb Ì (Q),b ^ c Chú ý: 0 ∑ £ ( P Q ) 0 0 ( ),( ) £ 90
2. Diện tích hình chiếu của một đa giác
Gọi S là diện tích của đa giác (H) trong (P), S¢ là diện tích của hình chiếu (H¢) của (H) trên (Q), j = ∑
((P),(Q)). Khi đó: S¢ = S.cosj
3. Hai mặt phẳng vuông góc • (P) ^ (Q) Û ∑ ( P Q ) 0 ( ),( ) = 90 ì É
• Điều kiện để hai mặt phẳng vuông góc với nhau: (P) a í Þ (P) ^ (Q) îa ^ (Q) 4. Tính chất ì ^ Ç =
• (P) (Q),(P) (Q) c í Þ a ^ (Q) •
îa Ì (P),a ^ c ( ì P) ^ (Q) ï íAÎ(P) Þ a Ì (P) ïîa ' , A a ^ (Q) (
ì P) Ç(Q) = a ï • ( í P) ^ (R)
Þ a ^ (R) ( ïî Q) ^ (R) B – BÀI TẬP
Câu 1: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai mặt phẳng cùng vuông góc với một mặt phẳng thứ ba thì vuông góc với nhau.
B. Qua một đường thẳng cho trước có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
C. Các mặt phẳng cùng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước thì
luôn đi qua một đường thẳng cố định.
D. Hai mặt phẳng cùng song song với một mặt phẳng thứ ba thì song song với nhau.
Hướng dẫn giải: Chọn C
Câu 2: Chọn mệnh đề đúng trong các mệnh đề sau đây:
A. Cho hai đường thẳng a và b vuông góc với nhau, mặt phẳng nào vuông góc với đường này thì
song song với đường kia.
B. Cho đường thẳng a ^ (a ), mọi mặt phẳng (b ) chứa a thì (b ) ^ (a ).
C. Cho hai đường thẳng chéo nhau a và b , luôn luôn có mặt phẳng chứa đường này và vuông góc với đường thẳng kia.
D. Cho hai đường thẳng a và b vuông góc với nhau, nếu mặt phẳng (a ) chứa a và mặt phẳng
(b ) chứa b thì (a ) ^ (b ).
Hướng dẫn giải: Chọn B
Câu 3: Cho hình chóp tứ giác S.ABCD có đáy là hình vuông và có một cạnh bên vuông góc với đáy.
Xét bốn mặt phẳng chứa bốn mặt bên và mặt phẳng chứa mặt đáy. Trong các mệnh đề sau mệnh đề nào đúng? Trang 1
A. Có ba cặp mặt phẳng vuông góc với nhau.
B. Có hai cặp mặt phẳng vuông góc với nhau.
C. Có năm cặp mặt phẳng vuông góc với nhau. D. Có bốn cặp mặt phẳng vuông góc với nhau.
Hướng dẫn giải: Chọn C
Câu 4: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì vuông góc với nhau.
B. Hai đường thẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau.
C. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì cắt nhau.
D. Một mặt phẳng ( P) và một đường thẳng a không thuộc ( P) cùng vuông góc với đường thẳng
b thì ( P) //a .
Hướng dẫn giải: Chọn D
Câu 5: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Nếu hình hộp có bốn mặt bên là hình chữ nhật thì nó là hình hộp chữ nhật.
B. Nếu hình hộp có ba mặt bên là hình chữ nhật thì nó là hình hộp chữ nhật.
C. Nếu hình hộp có hai mặt bên là hình chữ nhật thì nó là hình hộp chữ nhật.
D. Nếu hình hộp có năm mặt bên là hình chữ nhật thì nó là hình hộp chữ nhật.
Hướng dẫn giải: Chọn D
Câu 6: Trong các mệnh đề sau đây, hãy tìm mệnh đề đúng.
A. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thứ ba thì song song với nhau.
B. Nếu hai mặt vuông góc với nhau thì mọi đường thẳng thuộc mặt phẳng này sẽ vuông góc với mặt phẳng kia.
C. Hai mặt phẳng (a ) và (b ) vuông góc với nhau và cắt nhau theo giao tuyến d . Với mỗi điểm
A thuộc (a )và mỗi điểm B thuộc (b ) thì ta có đường thẳng AB vuông góc với d .
D. Nếu hai mặt phẳng (a ) và (b ) đều vuông góc với mặt phẳng (g )thì giao tuyến d của (a ) và
(b )nếu có sẽ vuông góc với (g ).
Hướng dẫn giải: Theo Định lí 2( 1
tr 09 - SGK - HH11-CB). Chọn D
Câu 7: Cho hai mặt phẳng (a ) và (b ) vuông góc với nhau và gọi d = (a ) Ç(b ).
I. Nếu a Ì (a ) và a ^ d thì a ^ (b ).
II. Nếu d¢ ^ (a ) thì d¢ ^ d .
III. Nếu b ^ d thì b Ì (a) hoặc b Ì (b).
IV. Nếu (g) ^ d thì (g) ^ (a) và (g) ^ (b).
Các mệnh đề đúng là : A. I, II và III. B. III và IV. C. II và III. D. I, II và IV.
Hướng dẫn giải: Chọn D.
Câu 8: Cho hai mặt phẳng (P) và(Q) cắt nhau và một điểm M không thuộc (P) và (Q). Qua M
có bao nhiêu mặt phẳng vuông góc với (P) và (Q)? A. 1. B. 2. C. 3. D. Vô số.
Hướng dẫn giải: Chọn A.
Câu 9: Cho hai mặt phẳng (P) và (Q), a là một đường thẳng nằm trên (P). Mệnh đề nào sau đây sai ?
A. Nếu a//b với b = (P)Ç(Q) thì a// (Q .)
B. Nếu ( P) ^ (Q) thì a ^ (Q).
C. Nếu a cắt (Q) thì (P) cắt (Q).
D. Nếu (P) / / (Q) thì a / / (Q).
Hướng dẫn giải:
Gọi b=(P) Ç(Q) nếu a//b thì a / / (Q). Chọn B.
Câu 10: Chọn mệnh đề đúng trong các mệnh đề sau đây: Trang 2
A. Qua một điểm có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
B. Cho hai đường thẳng chéo nhau a và b đồng thời a ^ b. Luôn có mặt phẳng (a ) chứa a và (a) ^ b.
C. Cho hai đường thẳng a và b vuông góc với nhau. Nếu mặt phẳng (a ) chứa a và mặt phẳng
(b ) chứa b thì (a ) ^ (b ).
D. Qua một đường thẳng có duy nhất một mặt phẳng vuông góc với một đường thẳng khác.
Hướng dẫn giải: Chọn B.
Câu 11: Cho hai mặt phẳng (P) và (Q) song song với nhau và một điểm M không thuộc (P) và
(Q). Qua M có bao nhiêu mặt phẳng vuông góc với (P) và (Q)? A. 2 . B. 3 . C. 1. D. Vô số.
Hướng dẫn giải:
Qua M dựng đường thẳng d vuông cóc với (P) và (Q). Khi đó có vô số mặt phẳng xoay quanh d thỏa yêu cầu bài toán. Chọn D.
Câu 12: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai mặt phẳng cùng vuông góc với một mặt phẳng thứ ba thì vuông góc với nhau.
B. Hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này sẽ vuông góc với mặt phẳng kia.
C. Hai mặt phẳng cùng vuông góc với một mặt phẳng thì song song với nhau.
D. Cả ba mệnh đề trên đều sai.
Hướng dẫn giải: Chọn D.
Câu 13: Trong các mệnh đề sau đây, mệnh đề nào là đúng?
A. Một mặt phẳng (a ) và một đường thẳng a không thuộc (a ) cùng vuông góc với đường thẳng
b thì (a) song song với . a
B. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì vuông góc với nhau.
C. Hai mặt phẳng cùng vuông góc với một mặt phẳng thì cắt nhau.
D. Hai đường thẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau
Hướng dẫn giải: Đáp án A đúng. Đáp án B sai. Đáp án D sai. Đáp án C sai. Chọn A.
Câu 14: Trong các mệnh đề sau, mệnh đề nào sai?
A. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
B. Qua một đường thẳng có duy nhất một mặt phẳng vuông góc với một đường thẳng cho trước.
C. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau. Trang 3
D. Qua một điểm có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
Hướng dẫn giải:
Qua một đường thẳng có vô số mặt phẳng
vuông góc với một mặt phẳng B đúng Đáp án A đúng
Qua một điểm có vô số mặt phẳng vuông
góc với một mặt phẳng cho trước. Đáp án Đáp án C đúng. D sai.
Câu 15: Trong các mệnh đề sau, mệnh đề nào sai?
A. Cho đường thẳng a vuông góc với đường thẳng b và b nằm trong mặt phẳng (P). Mọi mặt
phẳng (Q) chứa a và vuông góc với b thì (P) vuông góc với (Q) .
B. Nếu đường thẳng a vuông góc với đường thẳng b và mặt phẳng (P)chứa a, mặt phẳng (Q)
chứa b thì (P) vuông góc với (Q).
C. Cho đường thẳng a vuông góc với mặt phẳng (P), mọi mặt phẳng (Q) chứa a thì (P) vuông góc với (Q).
D. Qua một điểm có duy nhất một mặt phẳng vuông góc với một đường thẳng cho trước.
Hướng dẫn giải: Đáp án B sai. Đáp án A đúng. Đáp án C đúng. Đáp án D đúng.
Câu 16: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai mặt phẳng cùng song song với một mặt phẳng thứ ba thì song song với nhau.
B. Qua một đường thẳng cho trước có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
C. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với hai mặt phẳng cắt nhau cho trước. Trang 4
D. Hai mặt phẳng cùng vuông góc với một mặt phẳng thứ ba thì vuông góc với nhau.
Hướng dẫn giải:
Qua một điểm có duy nhất một mặt phẳng vuông góc với một đường thẳng cho trước, đường thẳng đó
là giao tuyến của hai mặt phẳng cắt nhau đã cho. Chọn C.
Câu 17: Cho a,b, c là các đường thẳng. Mệnh đề nào sau đây là đúng?
A. Cho a ^ b . Mọi mặt phẳng chứa b đều vuông góc với a .
B. Nếu a ^ b và mặt phẳng (a )chứa a ; mặt phẳng (b ) chứa b thì (b ) ^ (a ).
C. Cho a ^ b nằm trong mặt phẳng (a ). Mọi mặt phẳng (b ) chứa a và vuông góc với b thì (b) ^ (a).
D. Cho a//b , mọi mặt phẳng (a ) chứa ctrong đó c ^ a và c ^ b thì đều vuông góc với mặt phẳng ( ,ab).
Hướng dẫn giải: Chọn C
Câu 18: Cho hai đường thẳng chéo nhau a và b đồng thời a ^ b . Chỉ ra mệnh đề đúng trong các mệnh đề sau: A. mặt phẳng
chứa và đường vuông góc chung của và thì ^ . ( ) Q b a b mp(Q) a
B. mặt phẳng R chứa b và chứa đường thẳng b ' ^ a thì mp(R) ^ a. ( )
C. mặt phẳng a chứa a , mp( )
b chứa b thì (a) ^ ( ) b . ( )
D. mặt phẳng P chứa b thì mặt phẳng ^ . ( ) ( ) P a
Hướng dẫn giải: Chọn A
Giả sử AB là đoạn vuông góc chung của a và b thì mp(Q) º ( A , B b) mà a ^ A , B a ^ ,
b a ^ ( A ,
B b) Þ a ^ mp(Q)
Câu 19: Cho các mệnh đề sau với (a ) và (b ) là hai mặt phẳng vuông góc với nhau với giao tuyến
m = (a ) Ç(b ) và a, b, c, d là các đường thẳng. Các mệnh đề sau, mệnh đề nào đúng?
A. Nếu b ^ m thì b Ì (a ) hoặc b Ì (b ).
B. Nếu b ^ m thì d ^ (a ).
C. Nếu a Ì (a ) và a ^ m thì a ^ (b ).
D. Nếu c//m thì c// (a ) hoặc c// (b ).
Hướng dẫn giải: Chọn C
Do a Ì (a ), a ^ m, (a) ^ ( ) b nên a ^ (b )
Câu 20: Chỉ ra mệnh đề đúng trong các mệnh đề sau:
A. Cho hai đường thẳng song song a và b và đường thẳng c sao cho c ^ a,c ^ b. Mọi mặt phẳng
(a ) chứa c thì đều vuông góc với mặt phẳng ( , a b).
B. Cho a ^ (a ), mọi mặt phẳng (b ) chứa a thì (b ) ^ (a ).
C. Cho a ^ b , mọi mặt phẳng chứa b đều vuông góc với a .
D. Cho a ^ b , nếu a Ì (a ) và b Ì (b ) thì (a ) ^ (b ).
Hướng dẫn giải:
Câu A sai vì a,b có thể trùng nhau.
Câu C sai vì khi a,b cắt nhau, mặt phẳng ( ,
a b) không vuông góc với a .
Câu D sai vì khi a,b chéo nhau và vuông góc với nhau, ta gọi (a ) là mặt phẳng chứa a , song song
với b và (b ) là mặt phẳng chứa b và song song với a thì (a ) // (b ) Chọn B.
Câu 21: Mệnh đề nào sau đây là đúng? Trang 5
A. Hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này sẽ vuông góc với mặt phẳng kia.
B. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì vuông góc với nhau.
C. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
D. Hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này và vuông góc
với giao tuyến của hai mặt phẳng sẽ vuông góc với mặt phẳng kia.
Hướng dẫn giải:
Mệnh đề A sai vì có thể xảy ra trường hợp hai mặt phẳng vuông góc với nhau nhưng đường thẳng
thuộc mặt phẳng này song song với mặt phẳng kia.
Mệnh đề B sai vì xảy ra trường hợp hai mặt phẳng song song.
Mệnh đề C sai vì xảy ra trường hợp hai mặt phẳng vuông góc. Chọn đáp án D
Câu 22: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai đường thẳng không cắt nhau, không song song thì chéo nhau.
B. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song.
C. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song.
D. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song.
Hướng dẫn giải:
Mệnh đề sai vì còn trường hợp chéo nhau hoặc trùng nhau.
Mênh đề C sai vì còn trường hợp hai đường thẳng chéo nhau.
Mênh đề D sai vì còn trường hợp hai mặt phẳng vuông góc với nhau. Chọn B.
Câu 23: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.
B. Có duy nhất một mặt phẳng đi qua một đường thẳng cho trước và vuông góc với một mặt phẳng cho trước.
C. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
D. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.
Hướng dẫn giải:
* Có vô số đường thẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước,
chúng nằm trong mặt phẳng đi qua điểm đó và vuông góc với một đường thẳng cho trước Þ “Có duy
nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước”: SAI
* Có vô số mặt phẳng đi qua một đường thẳng cho trước và vuông góc với một mặt phẳng cho trước,
trong trường hợp: đường thẳng cho trước vuông góc với mặt phẳng cho trước Þ:Có duy nhất một mặt
phẳng đi qua một đường thẳng cho trước và vuông góc với một mặt phẳng cho trước”: SAI
* Có vố số mặt phẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước Þ”Có
duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước”: SAI Chọn D
Câu 24: Cho hình chóp S.ABC có đường cao SH . Xét các mệnh đề sau:
(I) SA = SB = SC .
(II) H trùng với tâm đường tròn ngoại tiếp tam giác ABC .
(III) Tam giác ABC là tam giác đều.
(IV) H là trực tâm tam giác ABC . Trang 6
Các yếu tố nào chưa đủ để kết luận S.ABC là hình chóp đều? A. (III) và (IV). B. (II) và (III). C. (I) và (II). D. (IV) và (I).
Hướng dẫn giải: Chọn C
Câu 25: Cho hình chóp S.ABC có đáy ABC là tam giác đều. Trong các mệnh đề sau, mệnh đề nào đúng?
A. S.ABC là hình chóp đều nếu các mặt bên của nó là tam giác cân đỉnh S.
B. S.ABC là hình chóp đều nếu góc giữa các mặt phẳng chứa các mặt bên và mặt phẳng đáy bằng nhau.
C. S.ABC là hình chóp đều nếu các mặt bên của nó là tam giác cân.
D. S.ABC là hình chóp đều nếu các mặt bên có diện tích bằng nhau.
Hướng dẫn giải: Chọn A
Câu 26: Trong lăng trụ đều, khẳng định nào sau đây sai?
A. Đáy là đa giác đều.
B. Các mặt bên là những hình chữ nhật nằm trong mặt phẳng vuông góc với đáy.
C. Các cạnh bên là những đường cao.
D. Các mặt bên là những hình bình hành.
Hướng dẫn giải: .
A Vì lăng trụ đều nên các cạnh bằng nhau. Do đó đáy là đa giác đều. .
B Vì lăng trụ đều là lăng trụ đứng nên các mặt bên vuông góc với đáy.
C. Vì lăng trụ đều là lăng trụ đứng nên các cạnh bên vuông góc với đáy. .
D Vì lăng trụ đều là lăng trụ đứng nên các cạnh bên bằng nhau và cùng vuông góc với đáy. Do đó các
mặt bên là những hình vuông. Chọn D.
Câu 27: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Nếu hình hộp có hai mặt là hình vuông thì nó là hình lập phương.
B. Nếu hình hộp có ba mặt chung một đỉnh là hình vuông thì nó là hình lập phương.
C. Nếu hình hộp có bốn đường chéo bằng nhau thì nó là hình lập phương.
D. Nếu hình hộp có sau mặt bằng nhau thì nó là hình lập phương.
Hướng dẫn giải:
Đây là câu hỏi lý thuyết. Chọn đáp án B
Câu 28: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Nếu hình hộp có hai mặt là hình chữ nhật thì nó là hình hộp chữ nhật.
B. Nếu hình hộp có năm mặt là hình chữ nhật thì nó là hình hộp chữ nhật.
C. Nếu hình hộp có bốn mặt là hình chữ nhật thì nó là hình hộp chữ nhật.
D. Nếu hình hộp có ba mặt là hình chữ nhật thì nó là hình hộp chữ nhật.
Hướng dẫn giải: Chọn đáp án B
A sai vì đáy có thể là hình bình hành. B đúng
C sai vì đáy có thể là hình bình hành
D sai vì đáy có thể là hình bình hành.
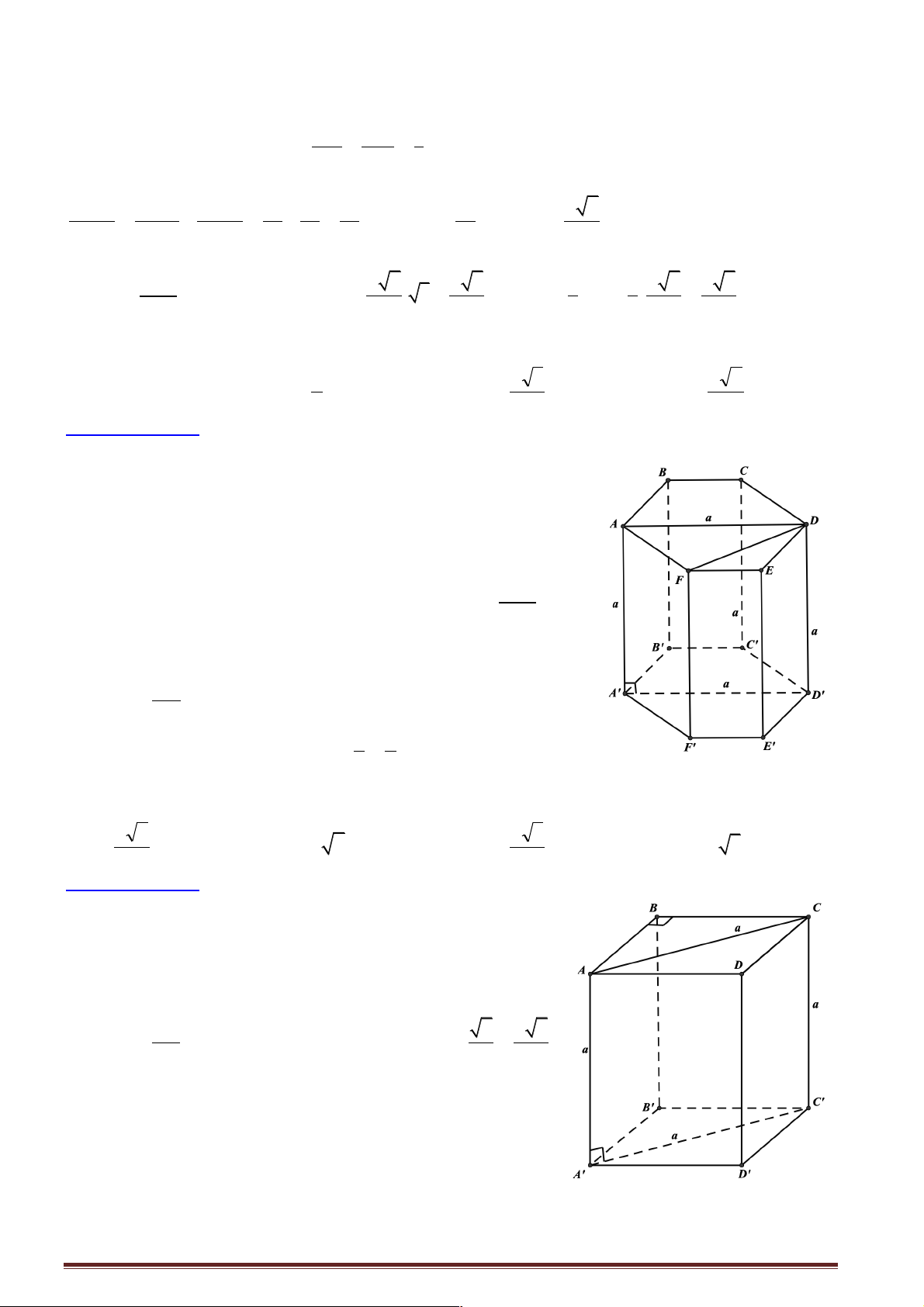
Câu 29: Hình hộp ABC . D A¢B C ¢ D
¢ ¢ là hình hộp gì nếu tứ diện AB C ¢ D ¢ ¢ đều.
A. Hình lập phương.
B. Hình hộp chữ nhật. C. Hình hộp thoi. D. Đáp số khác.
Hướng dẫn giải: Chọn đáp án A Trang 7
Câu 30: Hình hộp ABC . D A¢B C ¢ D
¢ ¢ trở thành hình lăng trụ tứ giác đều khi phải thêm các điều kiện nào sau đây?
A. Tất cả các cạnh đáy bằng nhau và cạnh bên vuông góc với mặt đáy.
B. Có một mặt bên vuông góc với mặt đáy và đáy là hình vuông.
C. Các mặt bên là hình chữ nhật và mặt đáy là hình vuông.
D. Cạnh bên bằng cạnh đáy và cạnh bên vuông góc với mặt đáy.
Hướng dẫn giải: Chọn đáp án C
Câu 31: Hình hộp ABC . D ’ A ’ B C’ ’
D là hình hộp gì nếu tứ diện ’ AA ’ B ’
D có các cạnh đối vuông góc.
A. Hình lập phương.
B. Hình hộp tam giác. C. Hình hộp thoi.
D. Hình hộp tứ giác.
Hướng dẫn giải:
Ta có AA' ^ B'D', A'D' ^ AB', A'B' ^ AD' suy ra Hình hộp ABC . D ’ A ’ B C’ ’
D là hình lập phương.
Câu 32: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Góc giữa mặt phẳng (P) và mặt phẳng (Q) bằng góc nhọn giữa mặt phẳng (P) và mặt phẳng
(R) khi mặt phẳng (Q) song song với mặt phẳng (R).
B. Góc giữa mặt phẳng (P) và mặt phẳng (Q) bằng góc nhọn giữa mặt phẳng (P) và mặt phẳng
(R) khi mặt phẳng (Q) song song với mặt phẳng (R) (hoặc (Q) º (R)).
C. Góc giữa hai mặt phẳng luôn là góc nhọn.
D. Cả ba mệnh đề trên đều đúng.
Hướng dẫn giải: Chọn đáp án D
Câu 33: Cho hình chóp tam giác S.ABC với đường cao SH . Trong các mệnh đề sau mệnh đề nào đúng
A. H trùng với tâm đường tròn ngoại tiếp tam giác ABC khi và chỉ khi các cạnh bên bằng nhau
B. H là trung điểm của một cạnh đáy khi hình hộp đó có một mặt bên vuông góc với mặt đáy.
C. H trùng với tâm đường tròn nội tiếp tam giác ABC khi các góc giữa các mặt phẳng chứa các
mặt bên và mặt phẳng đáy bằng nhau.
D. H thuộc cạnh đáy thì hình chóp đó có một mặt bên vuông góc với đáy
Hướng dẫn giải: Chọn đáp án A
Câu 34: Trong các mệnh đề sau, mệnh đề nào sai?
A. Hình lăng trụ tam giác có hai mặt bên là hình chữ nhật là hình lăng trụ đứng.
B. Hình chóp có đáy là đa giác đều và có các cạnh bên bằng nhau là hình chóp đều.
C. Hình lăng trụ đứng có đáy là đa giác đều là hình lăng trụ đều.
D. Hình lăng trụ có đáy là đa giác đều là hình lăng trụ đều.
Hướng dẫn giải: Giả sử lăng trụ
có các mặt bên ( AA'B'B),( AA'C 'C) là hình chữ nhật, khi
ABC.A' B 'C ' ìAA' ^ AB í Þ AA' ^ ( ABC)
đó ta có îAA' ^ AC . Vậy là lăng trụ đứng.
ABC.A' B 'C '
Theo định nghĩa hình chóp đều và hình lăng trụ đều ta có đáp án B, C đúng. Đáp án D sai.
Câu 35: Cho (P)và (Q)là hai mặt phẳng vuông góc với nhau và giao tuyến của chúng là đường thẳng . m Gọi a, , b ,
c d là các đường thẳng. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Nếu a Ì (P)và a ^ m thì a ^ (Q).
B. Nếu c ^ m thì c ^ (Q).
C. Nếu b ^ m thì b Ì (P)hoặc b Ì (Q).
D. Nếu d ^ m thì d ^ (P). Trang 8
Hướng dẫn giải:
Áp dụng hệ quả 1: Nếu hai mặt phẳng vuông góc với nhau thì bất cứ đường thẳng nào nằm
trong mặt phẳng này và vuông góc với giao tuyến thì vuông góc với mặt phẳng kia. Chọn đáp án A. Trang 9
DẠNG 1: GÓC GIỮA HAI MẶT PHẲNG. Phương pháp:
Để tính góc giữa hai mặt phẳng H và (b ) ta có thể thực hiện theo một trong các cách sau:
Cách 1. Tìm hai đường thẳng a,b lần lượt vuông góc với hai mặt phẳng (α) và Ox,Oy,Oz . Khi đó
góc giữa hai đường thẳng ,
A B,C chính là góc giữa hai mặt phẳng OA = OB + OC = 1 và OABC . ∑ ∑ ∑
OBA + ABC + OCB.
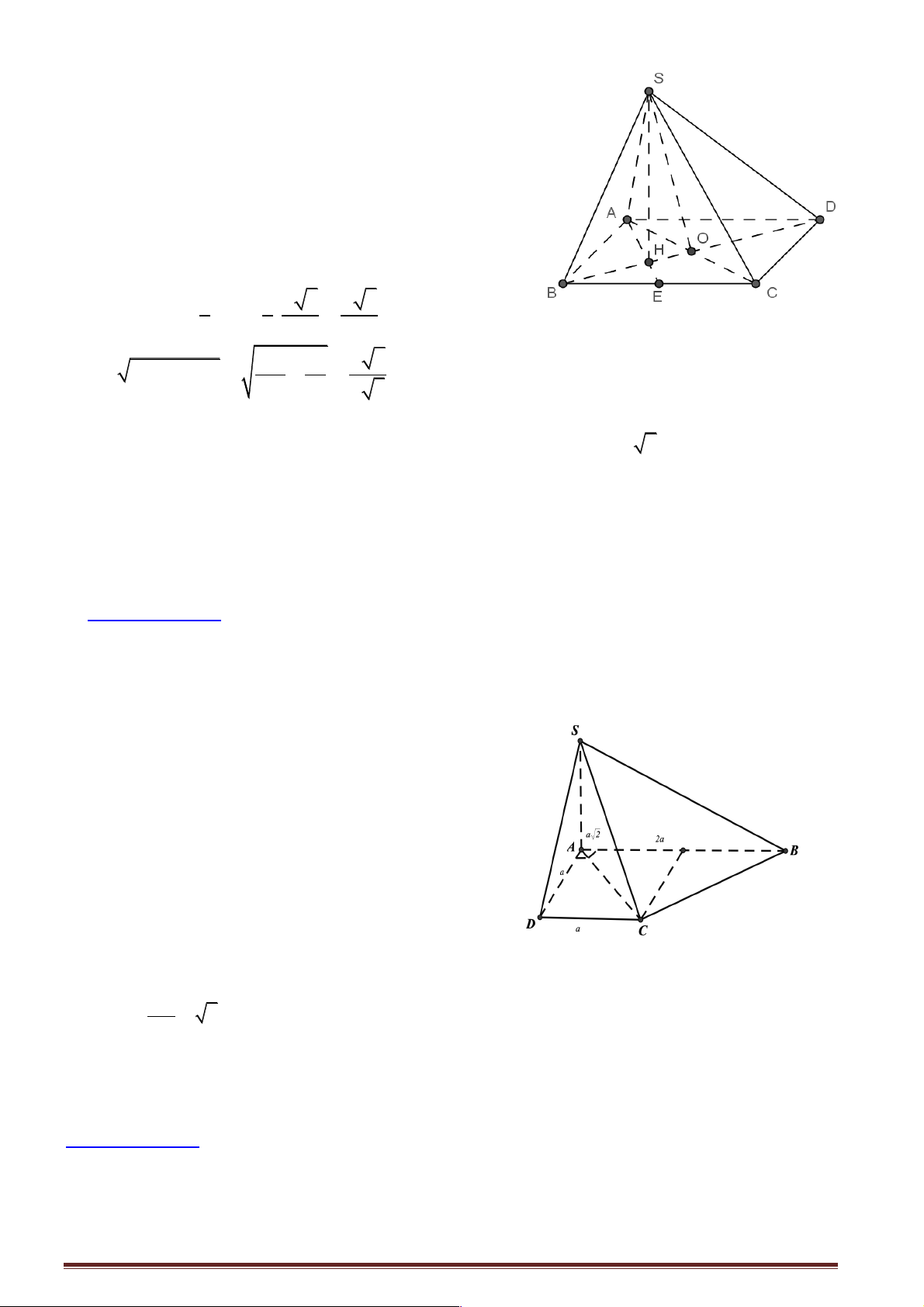
Cách 2. Tìm hai vec tơ ABC.A' B 'C ' có giá lần lượt vuông góc với AB = AC = a, AA' = a 2 và M
khi đó góc giữa hai mặt phẳng AB và (a ) xác định bởi M .
Cách 3. Sử dụng công thức hình chiếu B 'C , từ đó để tính cosj thì ta cần tính a và b .
Cách 4. Xác định cụ thể góc giữa hai mặt phẳng rồi sử dụng hệ thức lượng trong tam giác để tính. Ta
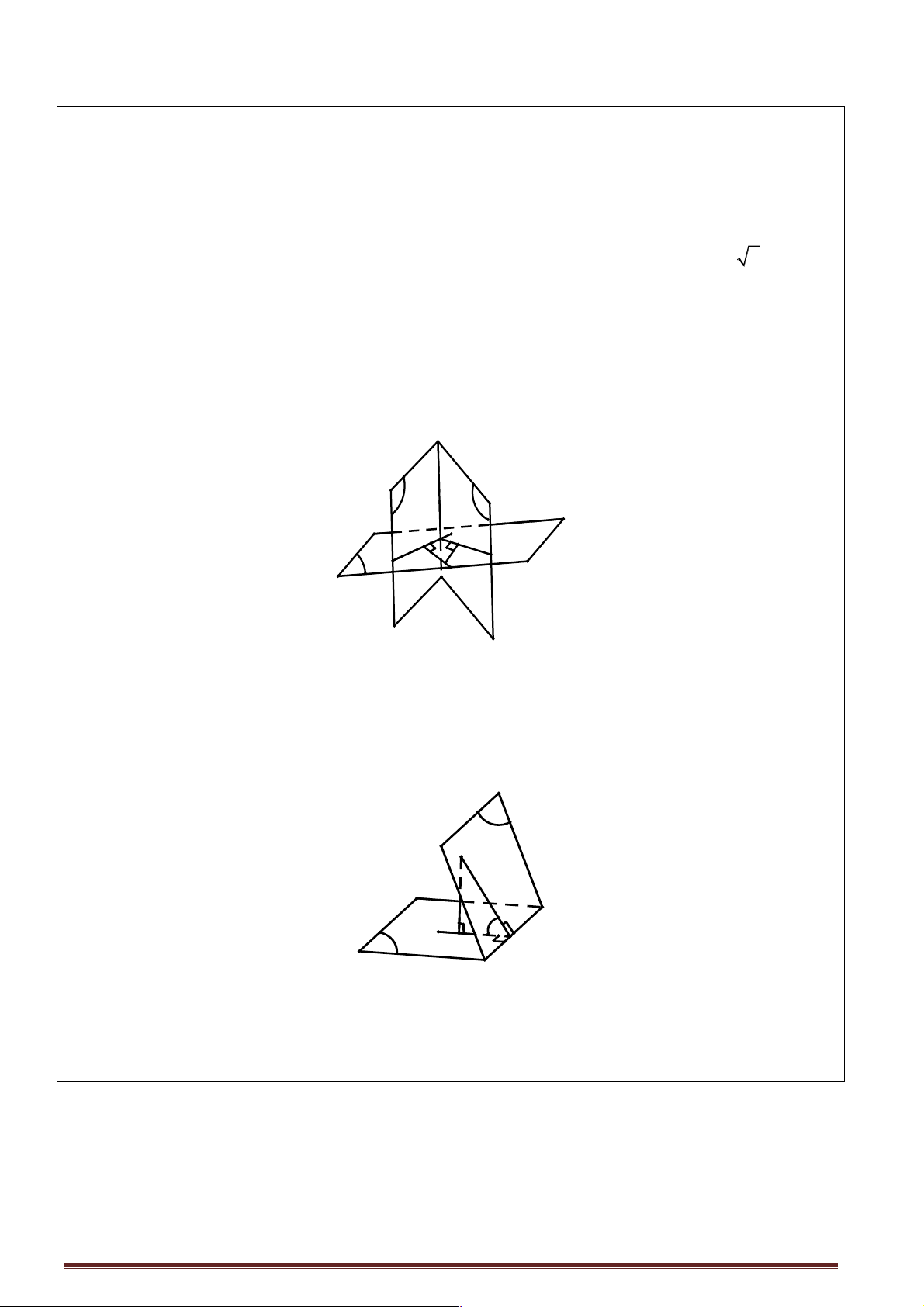
thường xác định góc giữa hai mặt phẳng theo một trong hai cách sau: a) α β a b p q γ
Tìm giao tuyến M , N
Chọn mặt phẳng AB, BC Tìm các giao tuyến (a ) ((a ) ∑ (b )) = (∑ , a,b) b) β M φ α H N Tìm giao tuyến SB
Lấy M , N, P .Dựng hình chiếu AB, BC,C ' D ' của ABC .
D A' B 'C ' D ' trên MN Dựng BD .
Phương pháp này có nghĩa là tìm hai đường thẳng nằm trong hai mặt phẳng AD ' và vuông góc với
giao tuyến MN tại một điểm trên giao tuyến.
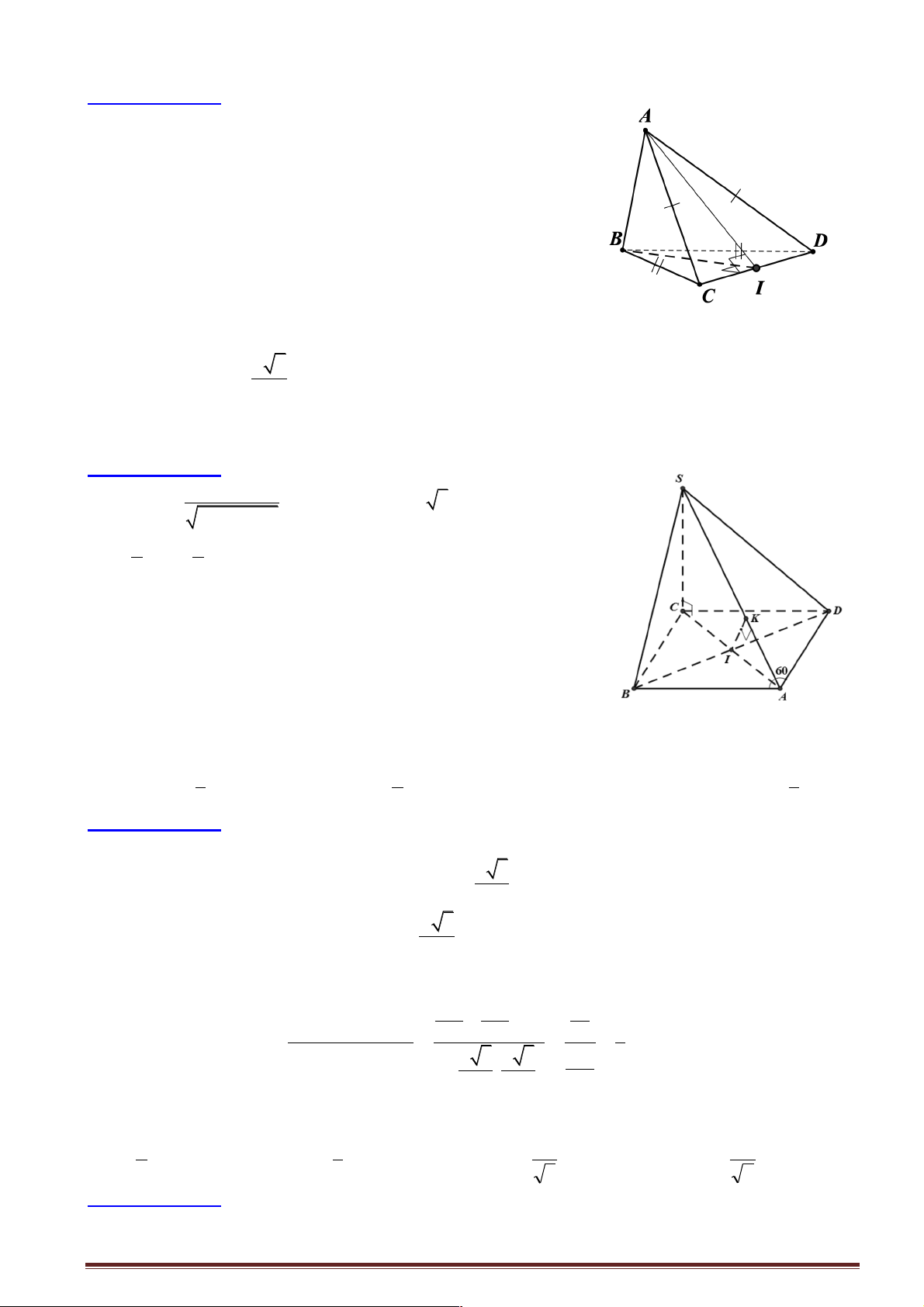
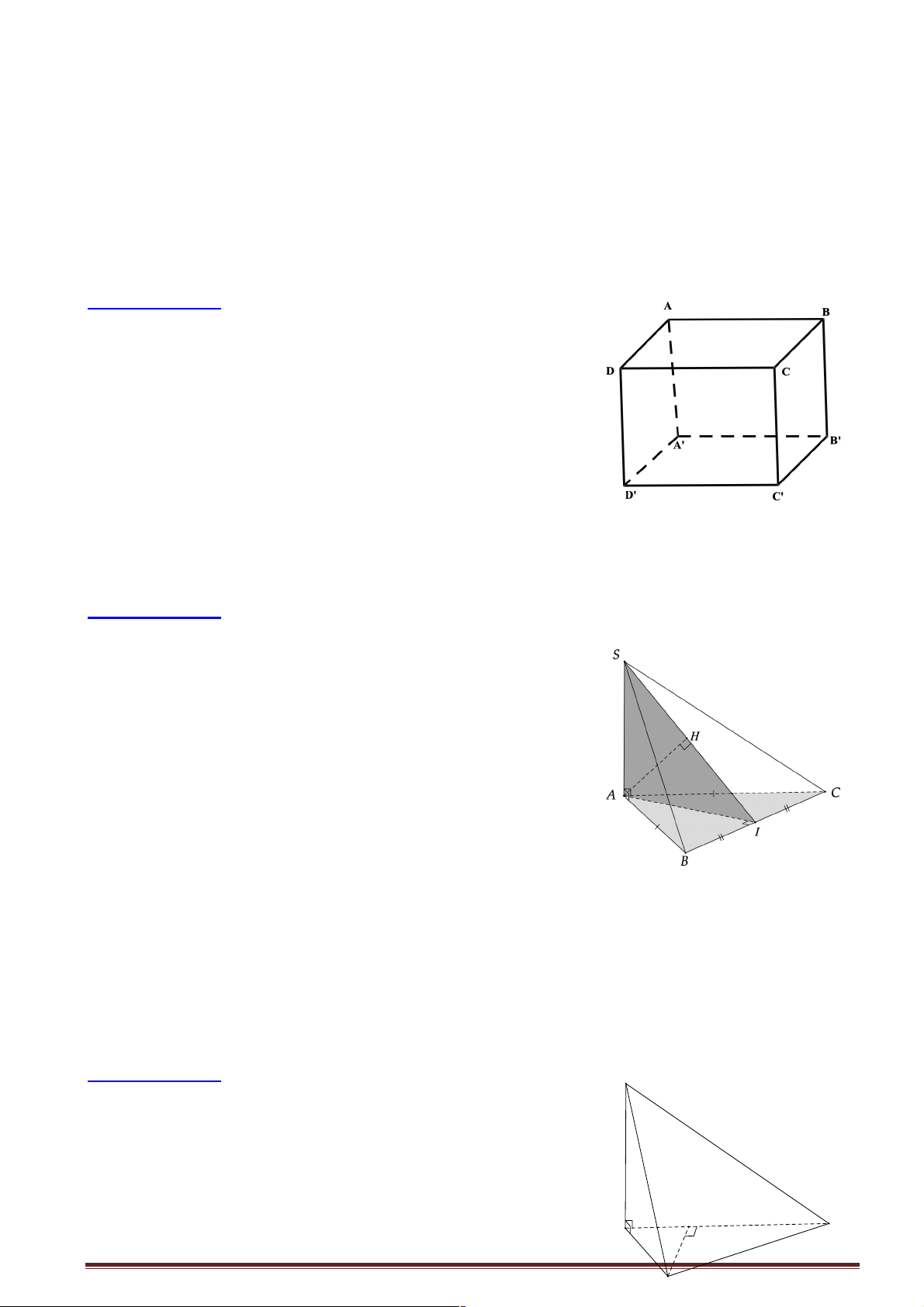
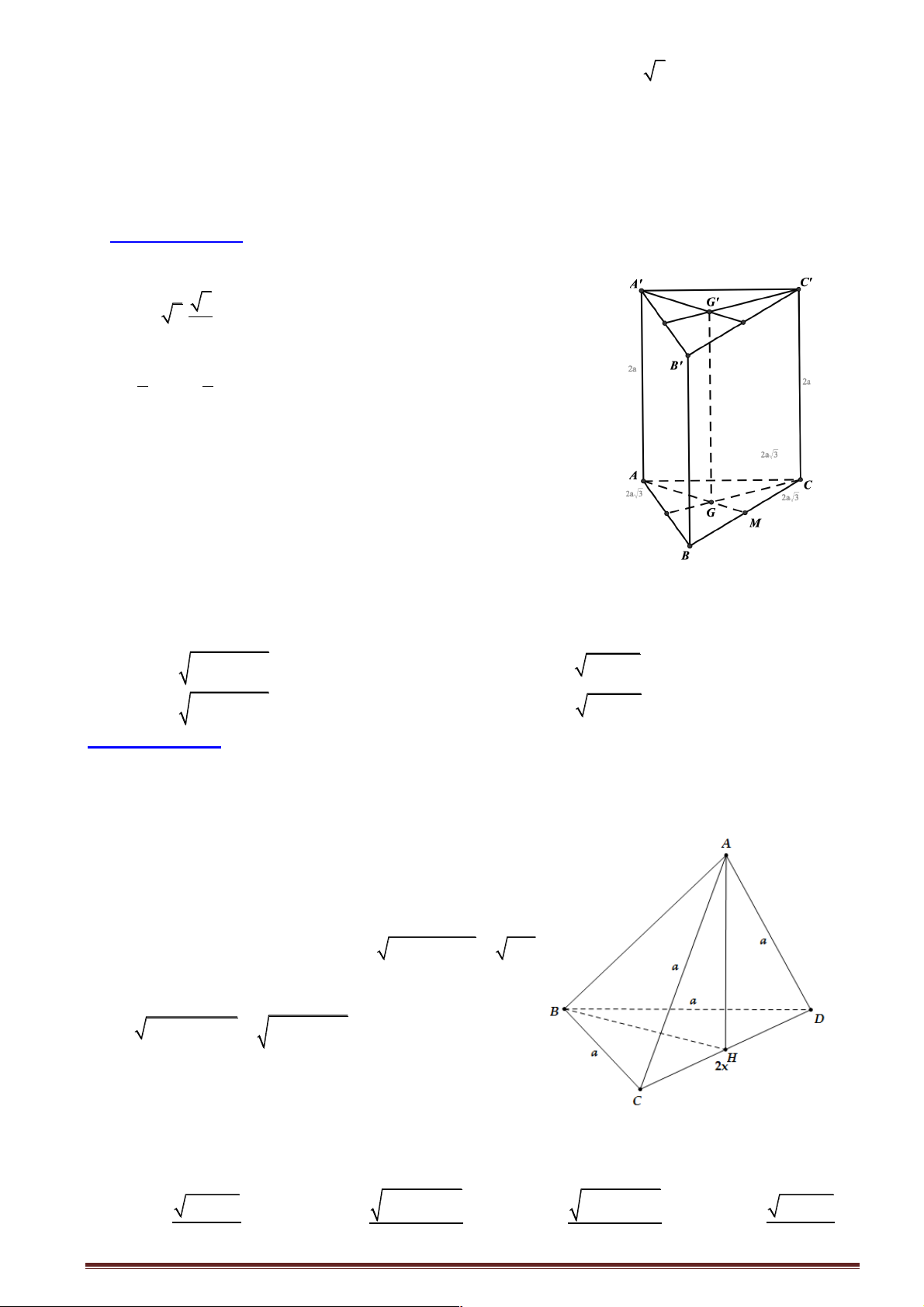
Câu 1: Cho tứ diện ABCD có AC = AD và BC = BD . Gọi I là trung điểm của CD . Khẳng định nào sau đây sai?
A. Góc giữa hai mặt phẳng ( ABC) và ( ABD) là ∑ CBD.
B. Góc giữa hai mặt phẳng ( ACD) và (BCD) là ∑ AIB.
C. (BCD) ^ ( AIB). Trang 10
D. ( ACD) ^ ( AIB).
Hướng dẫn giải:
Tam giác BCD cân tại B có I trung điểm đáy CD ÞCD ^ BI (1)
Tam giác ACD cân tại A có I trung điểm đáy CD ÞCD ^ AI (2)
(1) và (2) Þ CD ^ ( ABI ). Vậy A: sai Chọn A
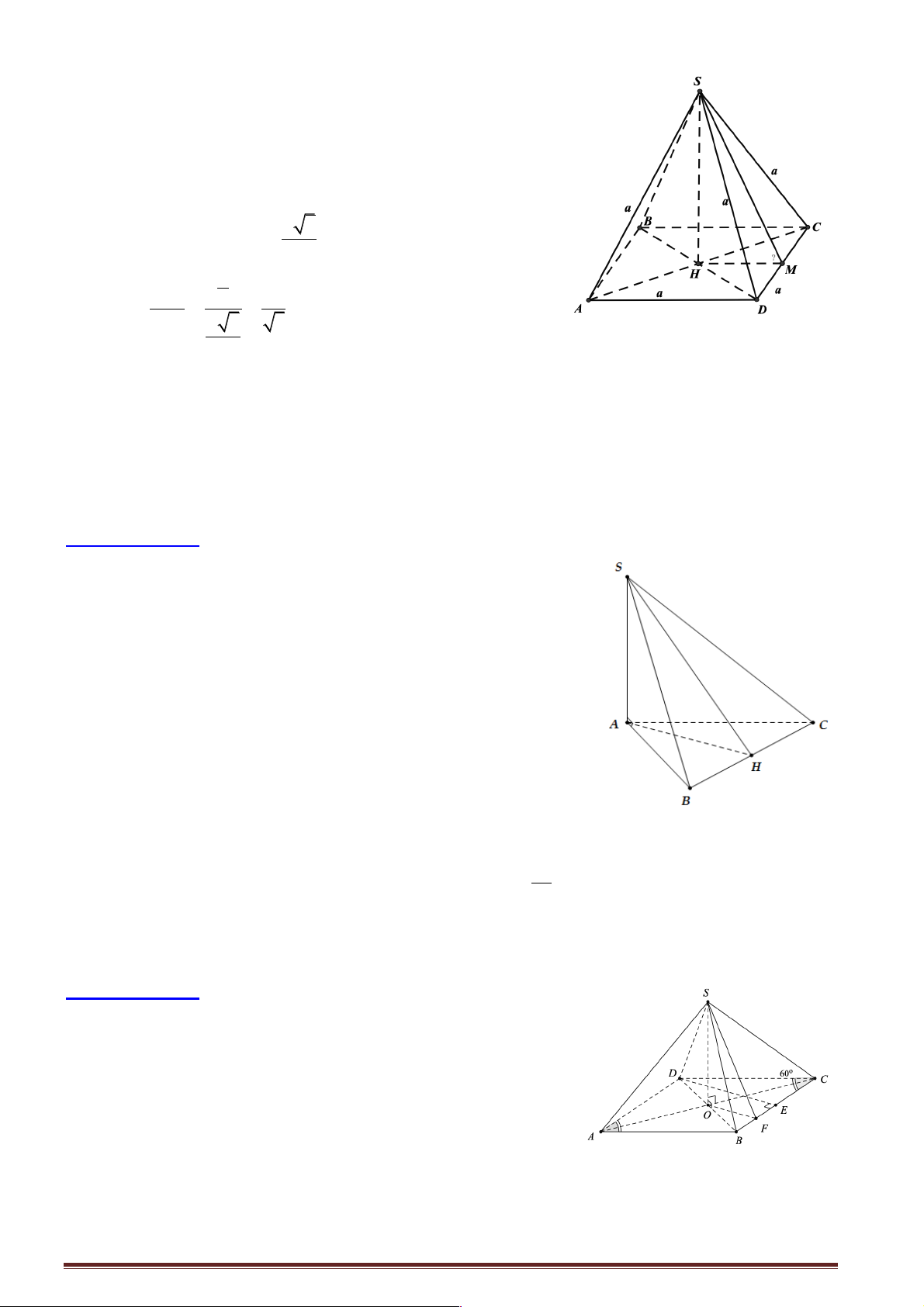
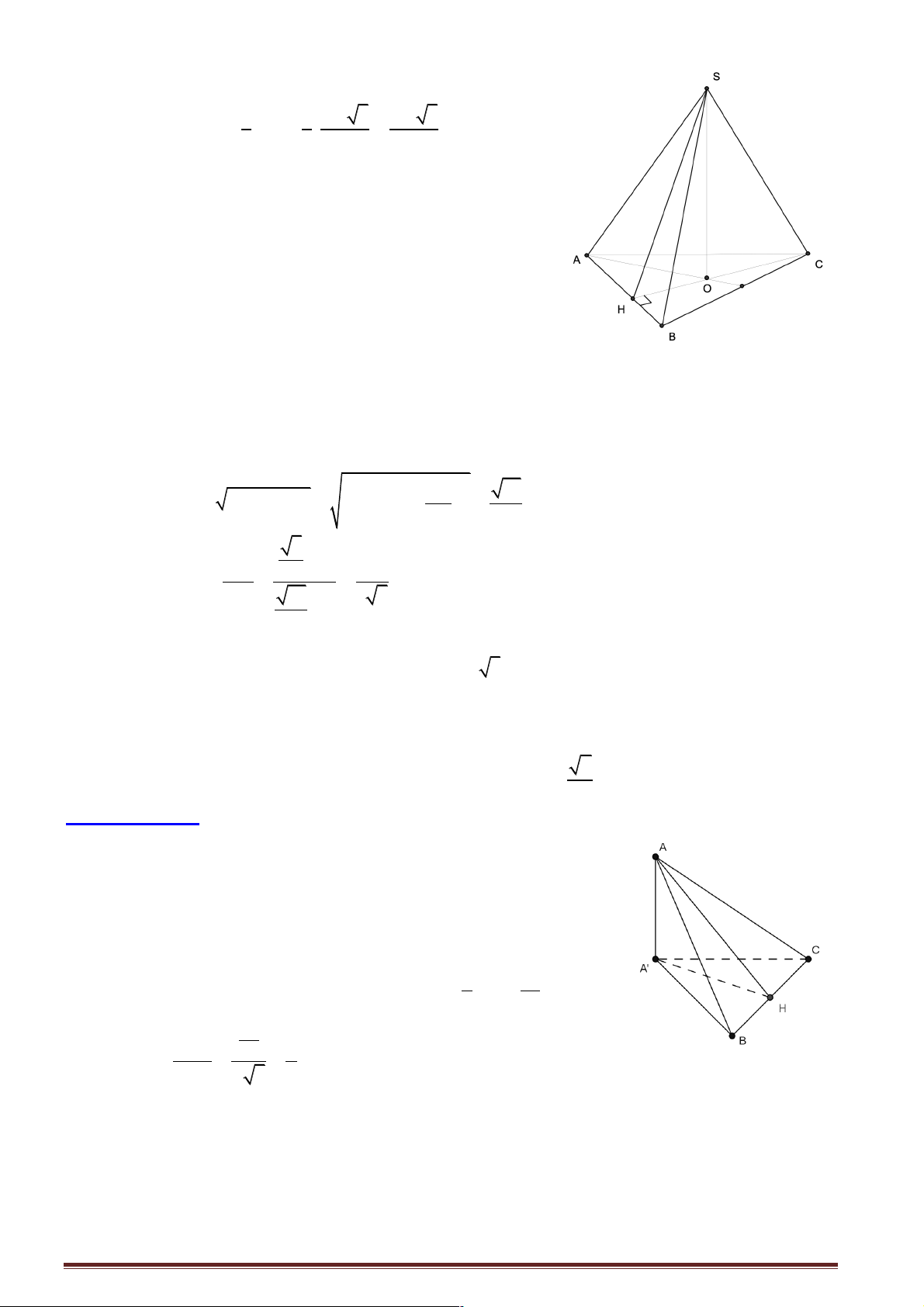
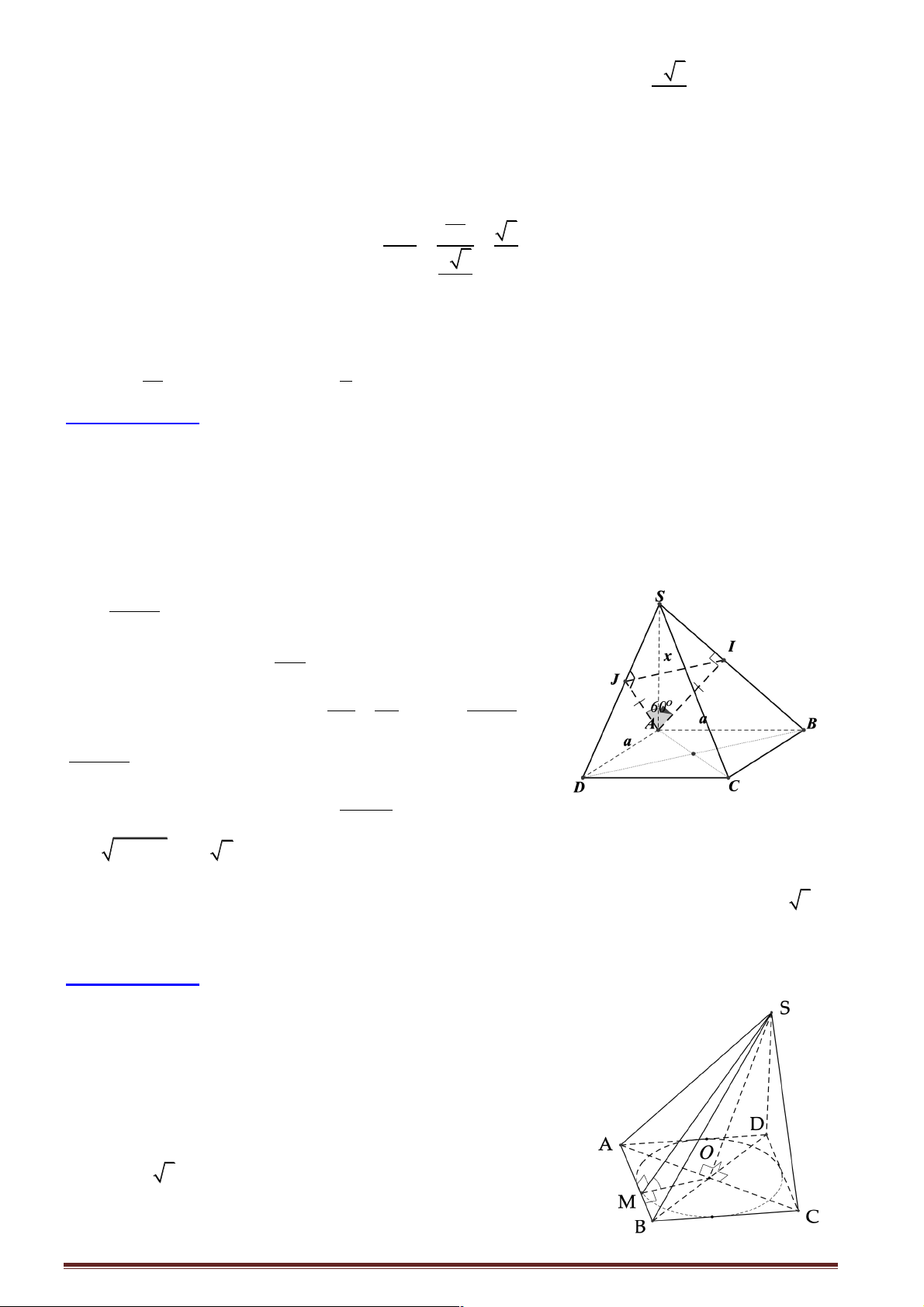
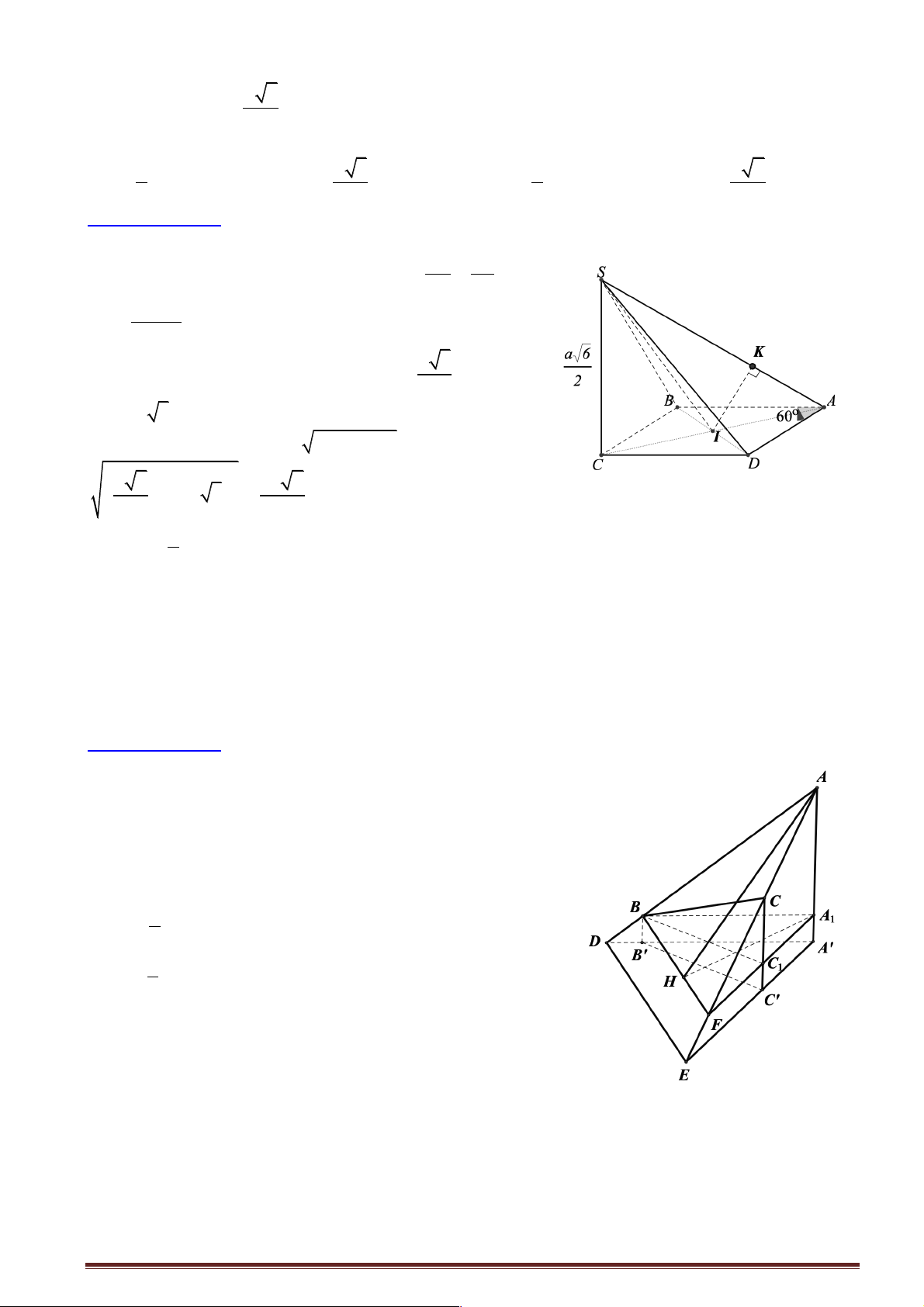
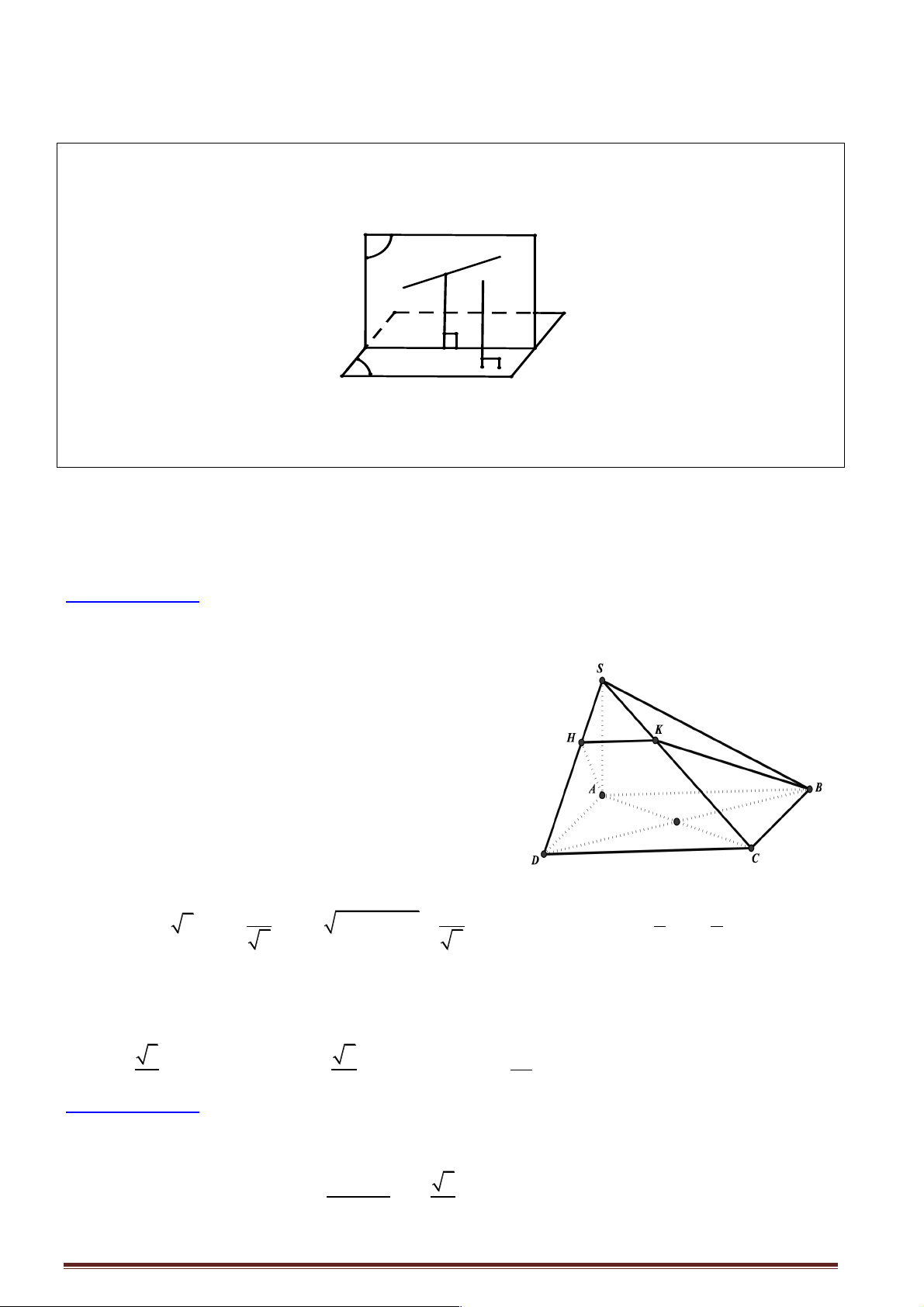
Câu 2: Cho hình chóp tứ giác S.ABCD , có đáy ABCD là hình thoi tâm I cạnh bằng A và góc ! 0 a A = 6 60 , cạnh SC =
và SC vuông góc với mặt phẳng ( ABCD). Trong tam giác SAC kẻ 2
IK ^ SA tại K . Tính số đo góc ∑ BKD. A. 0 60 . B. 0 45 . C. 0 90 . D. 0 30 .
Hướng dẫn giải: CS.CA Ta có CH = = ;(
a CA = 2AI = a 3) ; 2 2 CS + CA 1 1
IK = CH = a = IB = ID. 2 2
với H là hình chiếu của C lên SA , K là hình chiếu của I lên SA .
Vậy chọn đáp án C .
Câu 3: Cho tứ diện đều ABCD . Góc giữa ( ABC) và ( ABD) bằng
a . Chọn khẳng định đúng trong các khẳng định sau? 1 A. cosa = 1 . B. cosa = . C. 0 a = 1 60 . D. cosa = . 3 4 5
Hướng dẫn giải:
Đặt AB = a . Gọi I là trung điểm của AB . a
Tam giác ABC đều cạnh a nên CI ^ 3 AB và CI = . 2 a
Tam giác ABD đều nên DI ^ 3 AB và DI = . 2
Do đó, (( ABC) ( ABD)) = (CI DI ) ∑ , , = CID =a . 2 2 2 3a 3a 2 a 2 2 2 + - a
IC + ID - CD 1 Tam giác CID có 4 4 2 cosa = = = = . Chọn A. 2 2.IC.ID a 3 a 3 3a 3 2. . 2 2 2
Câu 4: Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a . Tính cosin của góc giữa một mặt bên và một mặt đáy. 1 1 1 1 A. . B. . C. . D. . 2 3 3 2
Hướng dẫn giải:. Chọn C. Trang 11
Giả sử gọi hình chóp tứ giác đều có tất cả các cạnh đều bằng a
là S.ABCD có đường cao SH .
Ta có: (SCD)Ç( ABCD) = CD. Gọi M là trung điểm CD.
Dễ chứng minh được SM ^ CD và HM ^ CD
Þ ((SCD) (ABCD)) = (SM HM ) ∑ , , = SMH =a .
Từ giả thiết suy ra SC
D D là tam giác đều cạnh a có SM là a 3
đường trung tuyến Þ SM = . 2 a HM 1 2 Þ cosa = = = . SM a 3 3 2
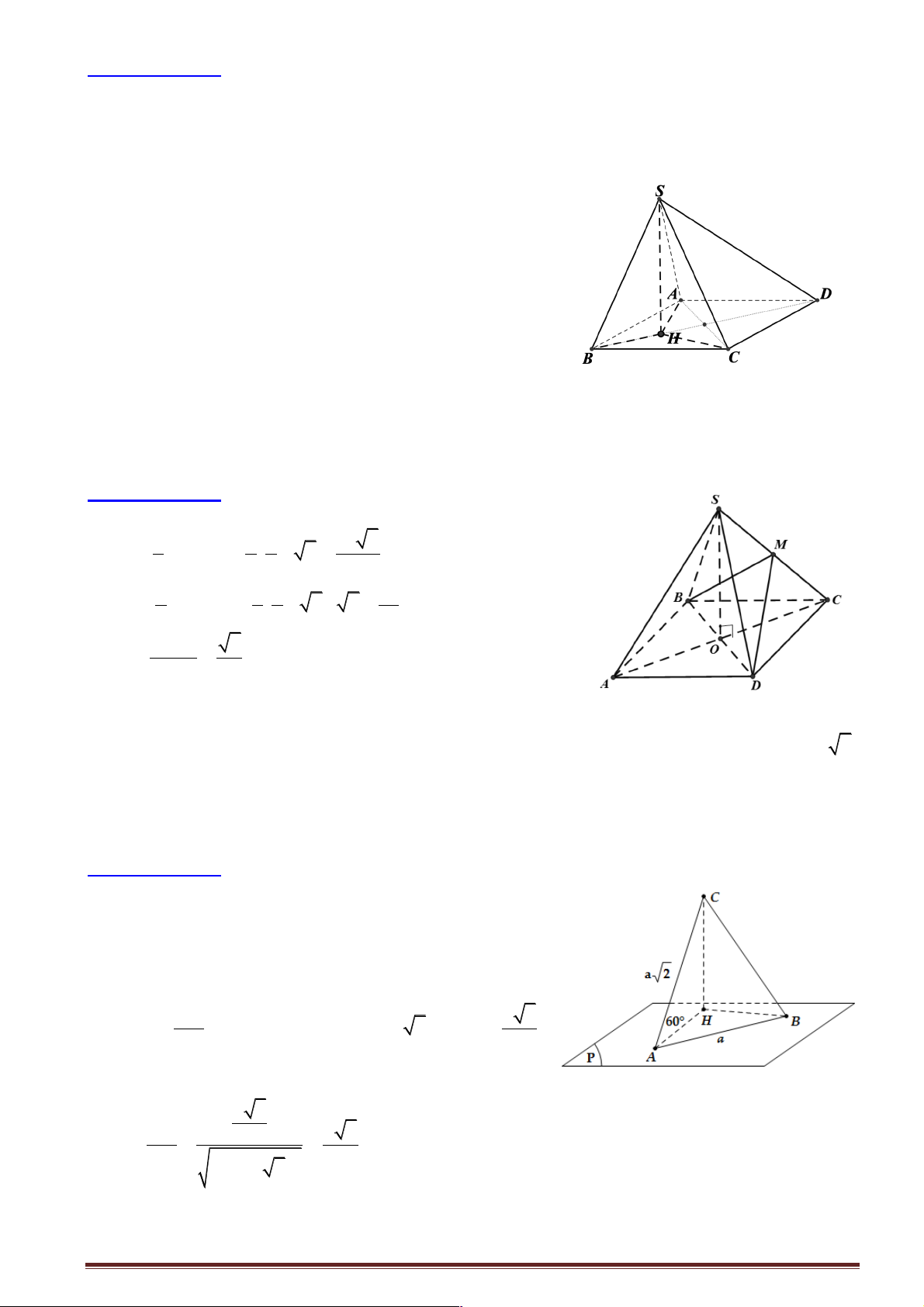
Câu 5: Cho hình chóp S.ABC có hai mặt bên (SAB) và (SAC) vuông góc với mặt phẳng ( ABC),
tam giác ABC vuông cân ở A và có đường cao AH (H ÎBC). Gọi O là hình chiếu vuông góc của
A lên (SBC). Khẳng định nào sau đây sai ?
A. SC ^ ( ABC).
B. O Î SH .
C. (SAH ) ^ (SBC). D. (SBC) ∑ ( (ABC) = SBA. ) ∑ ,
Hướng dẫn giải: (SAB) ^ (ABC) ü ï
Ta có (SAC) ^ ( ABC)
ý Þ SA ^ ( ABC) Þ SA ^ BC . ( ï
SAB) Ç(SAC) = SAþ
BC ^ AH üýÞ BC ^(SAH)Þ BC ^ SH . BC ^ SA þ
Mặt khác, AH ^ BC nên ((SBC) ( ABC)) = (SH AH ) ∑ , , = SHA. Chọn D.
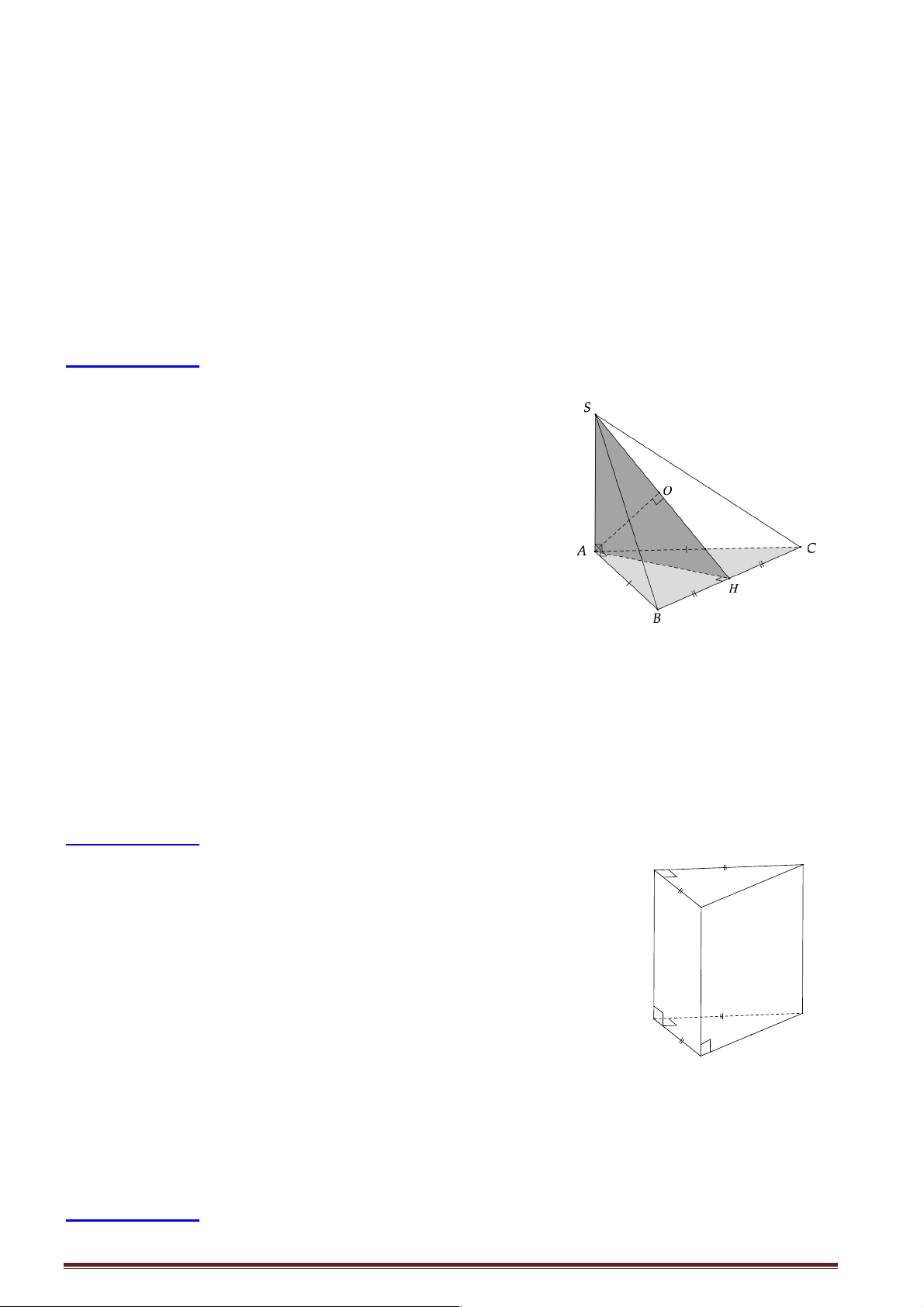
Câu 6: Cho hình chóp S.ABCD có đáy là hình thoi tâm O cạnh a và có góc ∑ 0 BAD = 60 . Đường 3a
thẳng SO vuông góc với mặt phẳng đáy ( ABCD) và SO =
. Gọi E là trung điểm BC và F là 4
trung điểm BE . Góc giữa hai mặt phẳng (SOF ) và (SBC) là A. o 90 . B. o 60 . C. o 30 . D. o 45 .
Hướng dẫn giải: BCD D
đều nên DE ^ BC . Mặt khác OF //DE Þ BC ^ OF (1).
Do SO ^ ( ABCD) Þ BC ^ SO (2).
Từ (1) và (2), suy ra BC ^ (SOF) Þ (SBC) ^ (SOF ).
Vậy, góc giữa (SOF ) và (SBC) bằng o 90 .
Câu 7: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và có SA = SB = SC = a . Góc giữa
hai mặt phẳng (SBD) và ( ABCD) bằng A. 30o. B. 90o. C. 60o . D. 45o . Trang 12
Hướng dẫn giải:
Gọi H là chân đường vuông góc của S xuống mặt phẳng đáy ( ABCD) ( SH ^ ( ABCD))
SA = SB = SC = a Þ các hình chiếu: HA = HB = HC Þ H là tâm đường tròn ( ABC)
Mà tam giác ABC cân tại B (vì BA = BC = a ) Þ tâm H phải nằm trên BD Þ SH Ì (SBD) SH ^ ( ABCD)ü Vậy có
ý Þ (SBD) ^ ( ABCD) nên góc SH Ì (SBD) þ [( ),( )] 90o SBD ABCD = . Chọn B
Câu 8: Cho hình chóp tứ giác đều S.ABCD , có đáy ABCD là hình vuông tâm O . Các cạnh bên và các
cạnh đáy đều bằng a . Gọi M là trung điểm SC . Góc giữa hai mặt phẳng (MBD) và ( ABCD) bằng: A. 0 90 . B. 0 60 . C. 0 45 . D. 0 30 .
Hướng dẫn giải:
Gọi M ' là trung điểm OC . Có 2 1 1 a a 2 S = M . O BD = . .a 2 = ; MBD D 2 2 2 4 2 1 1 1 a S = ¢ = = D ¢ M . O BD . .a 2.a 2 . Do đó BM D 2 2 4 4 SD ¢ 2 BM D 0 cosa = = Þ a = 45 S 2 BM D D
Vậy chọn đáp án C .
Câu 9: Cho tam giác ABC vuông tại A . Cạnh AB = a nằm trong mặt phẳng (P), cạnh AC = a 2,
AC tạo với (P) một góc 0
60 . Chọn khẳng định đúng trong các khẳng định sau?
A. ( ABC) tạo với (P) góc 0 45 .
B. BC tạo với (P) góc 0 30 .
C. BC tạo với (P) góc 0 45 .
D. BC tạo với (P) góc 0 60 .
Hướng dẫn giải:
Gọi H là hình chiếu vuông góc của C lên mặt phẳng (P).
Khi đó, ( AC (P)) = ( AC AH ) ∑ 0 , , = CAH = 60 và
(BC (P)) =(BC AH) ∑ , , = CBH =a .
Tam giác AHC vuông tại H nên ∑ CH ∑ a 6 0 sin CAH =
Þ CH = AC.sin CAH = a 2.sin 60 = AC 2 .
Tam giác CHB vuông tại H nên a 6 CH a 2 2 0 sina = = = Þ a = 45 . BC a + (a )2 2 2 2 Chọn C. Trang 13
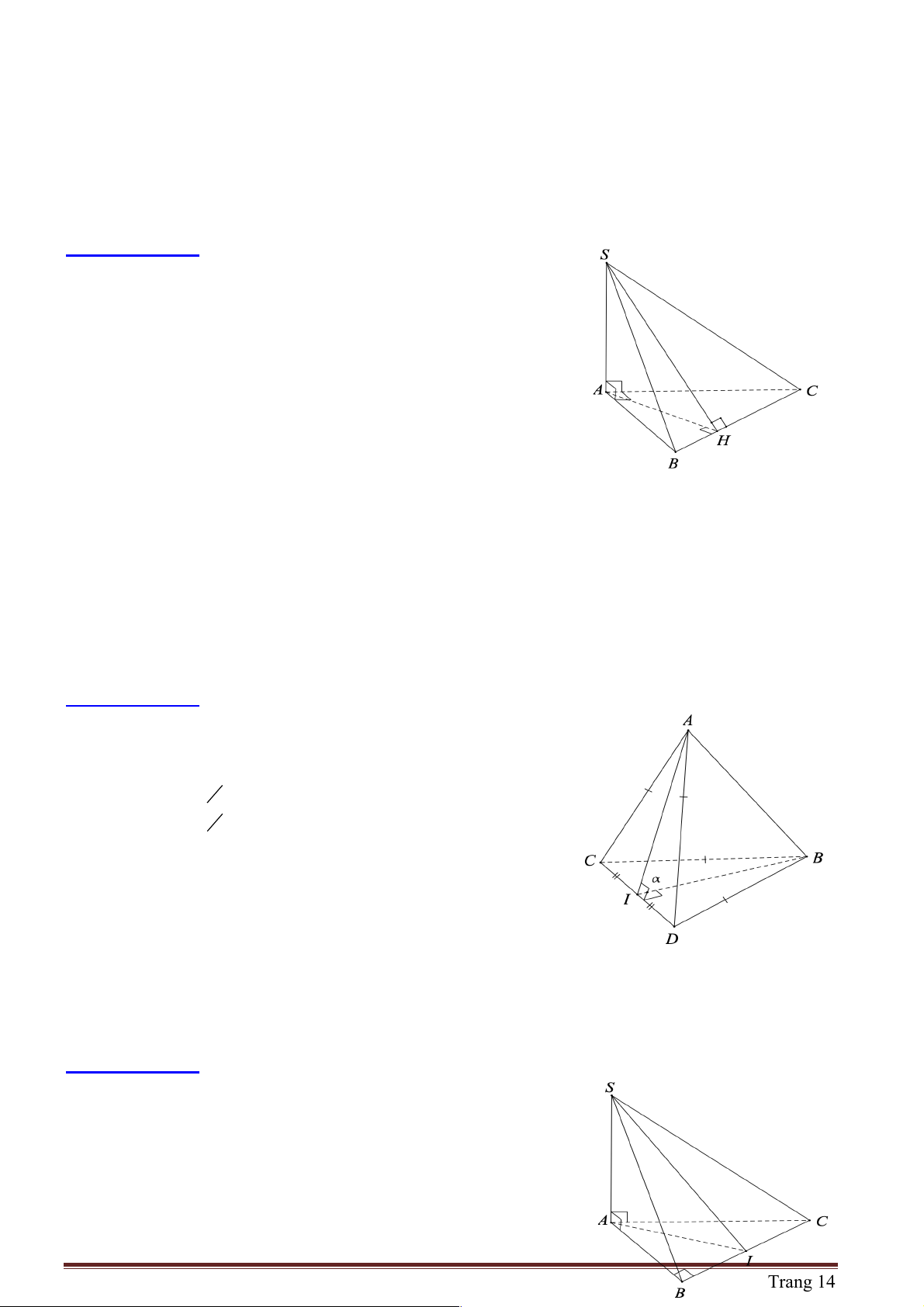
Câu 10: Cho hình chóp S.ABC có SA ^ ( ABC) và đáy ABC vuông ở A. Khẳng định nào sau đây sai ?
A. (SAB) ^ ( ABC).
B. (SAB) ^ (SAC).
C. Vẽ AH ^ BC, H Î BC Þ góc AHS là góc giữa hai mặt phẳng (SBC) và ( ABC).
D. Góc giữa hai mặt phẳng (SBC) và (SAC) là góc ∑ SCB.
Hướng dẫn giải: Chọn D.
Ta có: SA ^ ( ABC) Þ (SAB) ^ ( ABC) nên đáp án A đúng.
AB ^ AC, AB ^ SA Þ AB ^ (SAC) Þ (SAB) ^ (SAC). Nên đáp án B đúng
AH ^ BC; BC ^ SA Þ BC ^ (SAH )
Þ SH ^ BC Þ (SBC) ∑ ( (ABC) = SHA. ) ∑ , Nên đáp án C đúng.
Ta có: (SBC)Ç(SAC) = SC nên đáp án D sai.
Câu 11: Cho tứ diện ABCD có AC = AD và BC = BD . Gọi I là trung điểm của CD . Khẳng định nào sau đây sai ?
A. Góc giữa hai mặt phẳng ( ACD) và (BCD) là góc ∑ AIB.
B. (BCD) ^ ( AIB).
C. Góc giữa hai mặt phẳng ( ABC) và ( ABD) là góc ∑ CBD.
D. ( ACD) ^ ( AIB).
Hướng dẫn giải: Chọn C. (
ì ABC) Ç( ABD) = AB ï Ta có: ∑ í BC ^ AB
Þ (( ABD) ( ABC)) ∑ , ¹ CBD. ï BD ^ AB î Nên đáp án C sai
Câu 12: Cho hình chóp S.ABC có SA ^ ( ABC) và AB ^ BC , gọi I là trung điểm BC . Góc giữa hai
mặt phẳng (SBC) và ( ABC) là góc nào sau đây? A. Góc SBA. B. Góc SCA . C. Góc SCB . D. Góc SIA .
Hướng dẫn giải: Chọn A. Ta có: BC ^ S ,
A BC ^ AB Þ BC ^ SB
ì (SBC)Ç( ABC) = BC ï Þ ∑
íAB ^ BC, AB Ì ( ABC) Þ ((SBC) ( ABC)) ∑ , = SBA.
ï SB ^ BC,SB Ì î (SBC) Trang 14
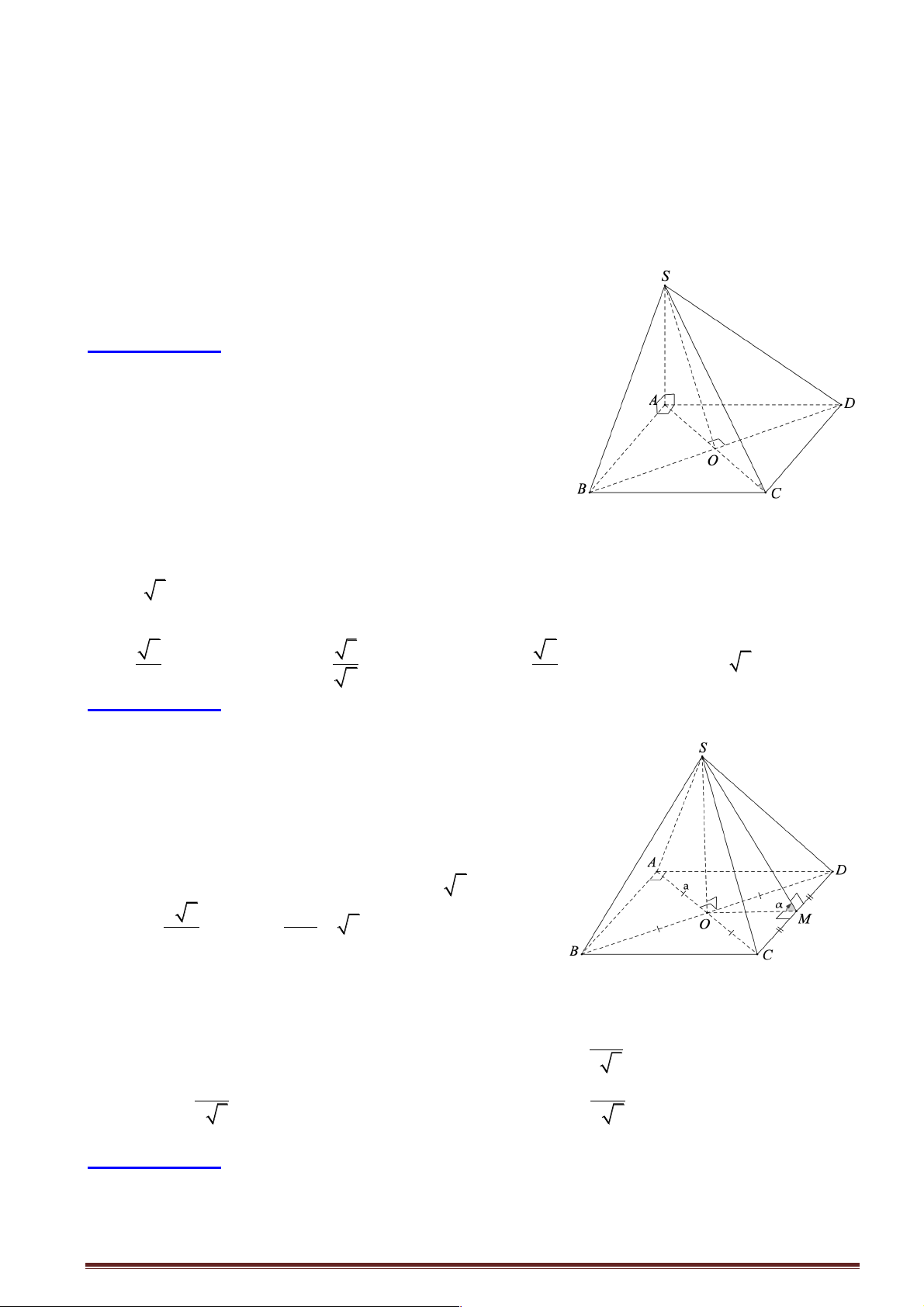
Câu 13: Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA ^ ( ABCD), gọi O là tâm hình
vuông ABCD . Khẳng định nào sau đây sai?
A. Góc giữa hai mặt phẳng (SBC) và ( ABCD) là góc ∑ ABS .
B. Góc giữa hai mặt phẳng (SBD) và ( ABCD) là góc ∑ SOA.
C. Góc giữa hai mặt phẳng (SAD) và ( ABCD) là góc ∑ SDA.
D. (SAC) ^ (SBD).
Hướng dẫn giải: Chọn C.
ì (SAD)Ç( ABCD) = AD ï Ta có: íAB ^ ,
AD AB Ì ( ABCD) ï SA ^ D, A SA Ì î (SAD) Þ ((SAD) ∑ (ABCD)) ∑ , = SAB. Nên đáp án C sai.
Câu 14: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O . Biết SO ^ ( ABCD),
SO = a 3 và đường tròn ngoại tiếp ABCD có bán kính bằng a . Gọi a là góc hợp bởi mặt bên
(SCD) với đáy. Khi đó tana = ? 3 3 6 A. . B. . C. . D. 6 . 2 2 6
Hướng dẫn giải: Chọn D.
Gọi M là trung điểm của CD . CD ì ^ OM Khi đó í î CD ^ SO
Þ CD ^ SM Þ ((SCD) ∑ (ABCD)) ∑ , = SMO = a .
Ta có: R = OA = a Þ AC = 2a Þ AB = AD = a 2 . a 2 SO Þ OM = Þ tana = = 6 . 2 OM
Câu 15: Cho hình chóp tam giác đều S.ABC với SA = 2AB . Góc giữa (SAB) và ( ABC) bằng a .
Chọn khẳng định đúng trong các khẳng định sau? A. 0 a = 1 60 . B. cosa = . 3 5 1 C. cosa = 1 . D. cosa = . 4 5 2 5
Hướng dẫn giải: C Trang 15
Gọi O là tâm của tam giác đều ABC
Gọi CO Ç AB = H suy ra H là trung điểm AB( vì ABC D đều) Þ AB AB OH ^ 1 1 3 3
AB và OH = CH = . = 3 3 2 6
Tìm góc giữa (SAB) và ( ABC) ì
(SAB)Ç(ABC) = AB ï í OH ^ AB ïSO ^ AB î (SO ^ (ABC)) Þ SH ^ AB (1) Ta có
ì (SAB) Ç( ABC) = AB ï
íOH ^ AB, OH Ì (ABC)
ïSH ^ AB,SH Ì (SAB) î ∑ Þ ( SAB ABC ) ∑ = (SH OH ) ∑ ( );( ) ; = SHO = a 2 æ AB ö 15
Từ (1) suy ra SH = SA - AH = (2AB)2 2 2 - = AB ç ÷ è 2 ø 2 3 A OH B Từ đó ta có : 6 1 cosa = = = SH 15 3 5 AB 2 Chọn B
Câu 16: Cho tam giác cân ABC có đường cao AH = a 3 , BC = 3a, BC chứa trong mặt phẳng (P).
Gọi A' là hình chiếu vuông góc của A lên mặt phẳng (P). Biết tam giác A' BC vuông tại A'. Gọi j
là góc giữa (P) và ( ABC) . Chọn khẳng định đúng trong các khẳng định sau? 2 A. 0 j = 60 . B. 0 j = 45 . C. cosj = . D. 0 j = 30 . 3
Hướng dẫn giải: ìBC ^ AA' Ta có í
Þ BC ^ ( A' AH ) Þ BC ^ A'H . îBC ^ AH Do đó: (
ìï ABC)Ç( A'BC) = BC í
Þ (( ABC),( A'BC)) = ( AH, A'H ) ∑ = AHA' .
ïîBC ^ AH, BC ^ A'H 1 3a
Mặt khác, tam giác A' BC vuông tại A' nên A' H = BC = . 2 2 3a A' H 1 Ta có 2 cosj = = = . AH a 3 2 Chọn D.
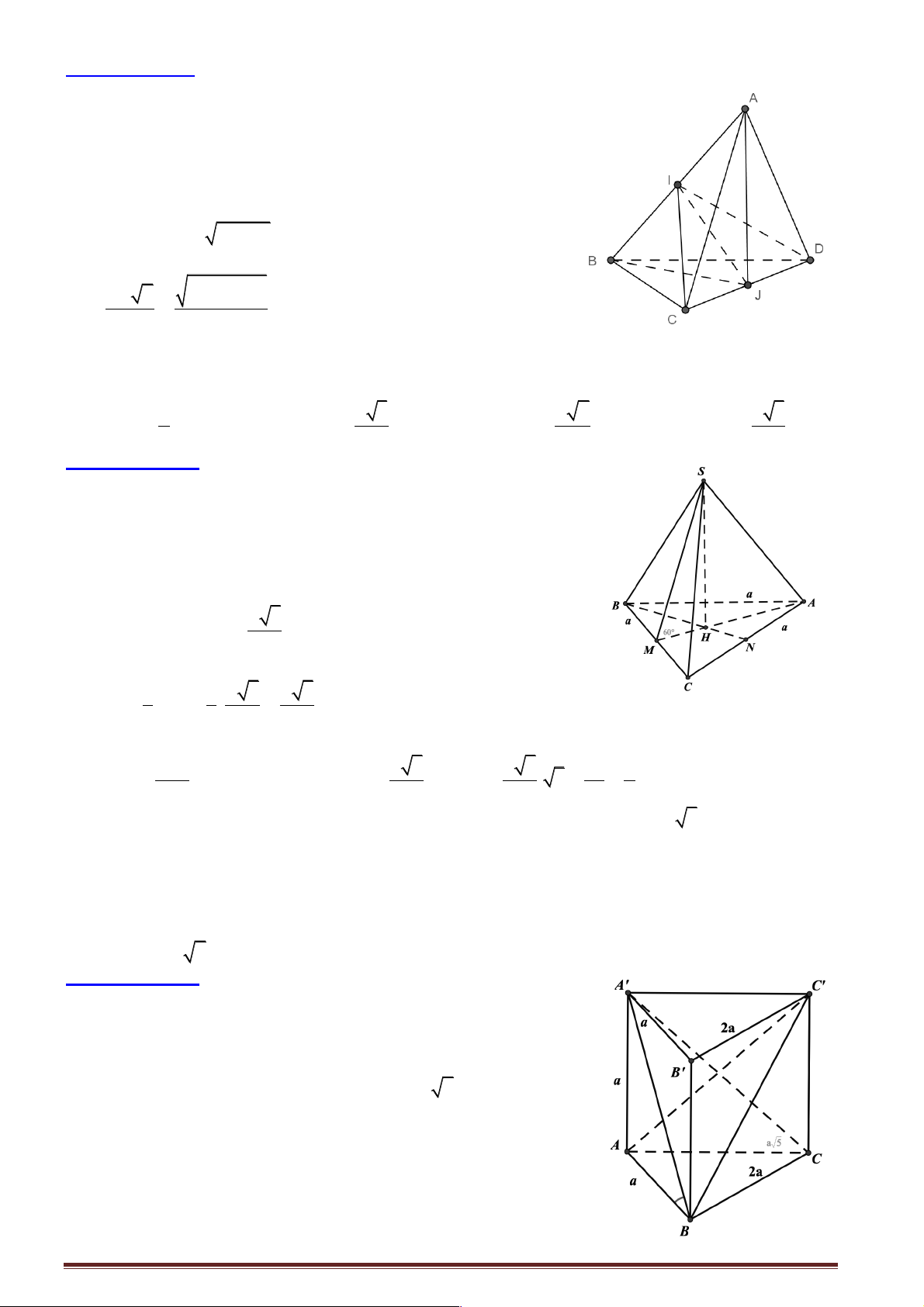
Câu 17: Trong không gian cho tam giác đều SAB và hình vuông ABCD cạnh a nằm trên hai mặt
phẳng vuông góc. Gọi H , K lần lượt là trung điểm của AB , CD . Ta có tan của góc tạo bởi hai mặt
phẳng (SAB) và (SCD) bằng : Trang 16 2 2 3 3 3 A. . B. . C. . D. . 3 3 3 2
Hướng dẫn giải:
Ta có: S Î(SAB)Ç(SCD)
Gọi d = (SAB)Ç(SCD) với d ÎS;d ! AB ! CD
Do đó: d = (SAB)Ç(SCD)
Mặt khác: (SAB) ^ ( ABCD); mà HK ^ AB(hv) Þ HK ^ (SAB)
Vì H là trung điểm của AB Þ SH ^ AB Þ SH ^ d (vì d ! AB)
Þ d ^ SK (theo định lí ba đường vuông góc) Do đó: ∑
KSH = a là góc giữa (SAB) và (SCD) Mà
SH là đường cao trong SA D B đều cạnh a 3 a Þ SH = 2 HK a 2 3 Xét SH
D K vuông tại H có: tana = = = . SH a 3 3 2
Vậy chọn đáp án B .
Câu 18: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O và khoảng cách từ A đến 2a BD bằng
. Biết SA ^ ( ABCD) và SA = 2a . Gọi a là góc giữa hai mặt phẳng ( ABCD) và 5
(SBD). Khẳng định nào sau đây sai?
A. (SAB) ^ (SAD).
B. (SAC) ^ ( ABCD). C. tana = 5 . D. ∑ a = SOA.
Hướng dẫn giải: Chọn D.
Gọi AK là khoảng cách từ A đến BD 2a Khi đó AK =
và BD ^ AK , BD ^ SA 5 (( ) ∑(ABCD)) ∑ SA SBD , = A SK = a Þ tana = = 5. AK Vậy đáp án D sai.
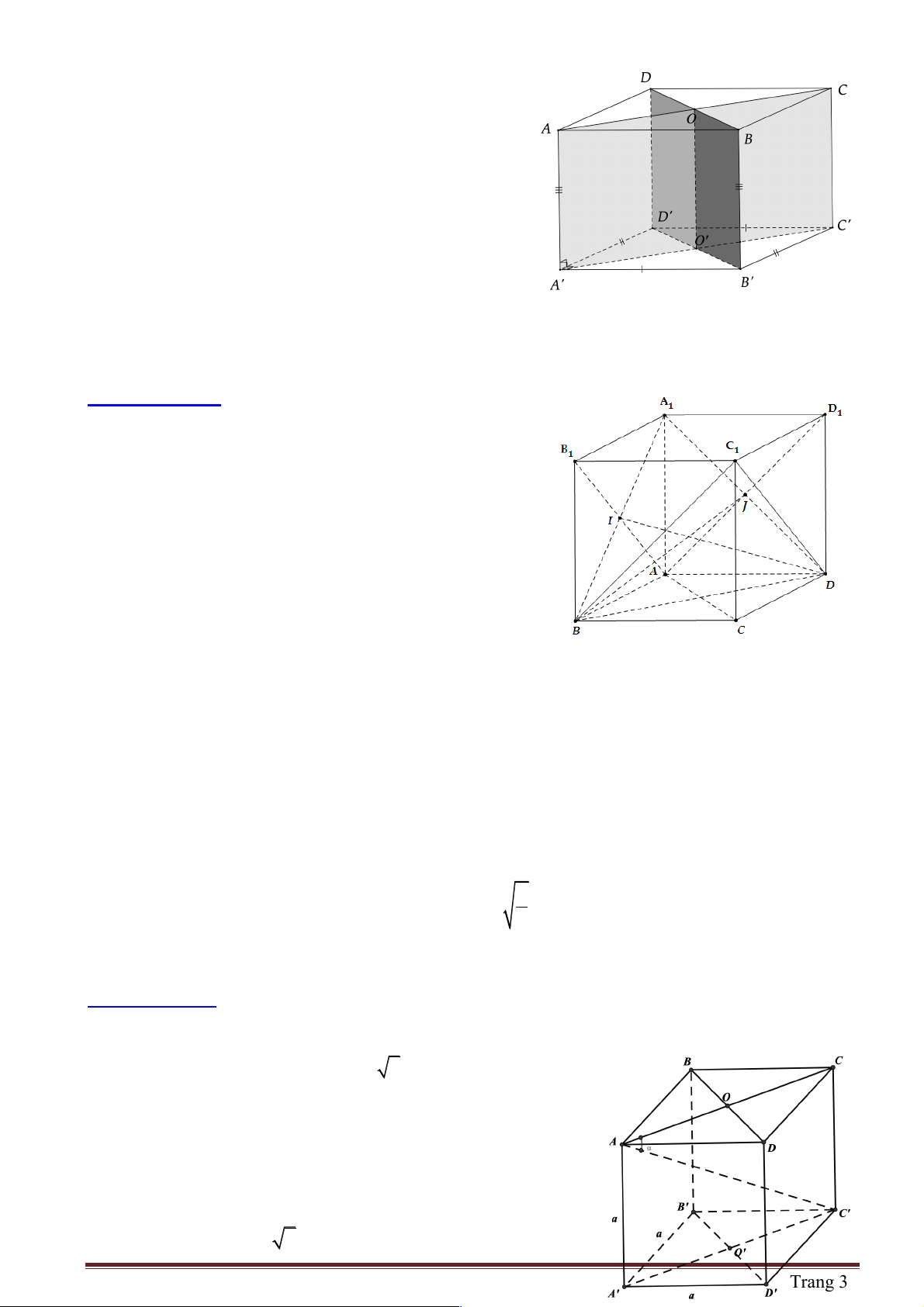
Câu 19: Cho hình lăng trụ ABC . D A¢B C ¢ D
¢ ¢ có đáy ABCD là hình thoi, AC = 2a . Các cạnh bên vuông
góc với đáy và AA¢ = a . Khẳng định nào sau đây sai ?
A. Các mặt bên của hình lăng trụ là các hình chữ nhật.
B. Góc giữa hai mặt phẳng ( AA C ¢ C ¢ ) và (BB D ¢ D
¢ ) có số đo bằng 60°.
C. Hai mặt bên ( AA C ¢ ) và (BB D ¢ ) vuông góc với hai đáy.
D. Hai hai mặt bên ( AA B ¢ B ¢ ) và ( AA D ¢ D ¢ ) bằng nhau.
Hướng dẫn giải: Trang 17 Chọn B.
Ta có: các cạnh bên vuông góc với đáy, đáy là hình thoi nên
Các mặt bên của hình lăng trụ là các hình chữ nhật. Hai mặt bên ( AA C ¢ ) và (BB D
¢ ) vuông góc với hai đáy.
Hai hai mặt bên ( AA B ¢ B ¢ ) và ( AA D ¢ D ¢ ) bằng nhau.
suy ra đáp án A,C,D đúng.
Mặt khác hai đáy ABCD và A¢B C ¢ D
¢ ¢ là các hình thoi nên ( AA C ¢ C ¢ ) ^ (BB D ¢ D
¢ ). Suy ra đáp án B sai.
Câu 20: Cho hình lập phương ABC .
D A B C D . Gọi a là góc giữa hai mặt phẳng ( A DCB 1 1 ) và 1 1 1 1
(ABCD) . Chọn khẳng định đúng trong các khẳng định sau? A. 0 a = 45 . B. 0 a = 30 . C. 0 a = 60 . D. 0 a = 90 .
Hướng dẫn giải:
a là góc giữa hai mặt phẳng ( A DCB (ABCD) 1 1 ) và là ∑ a = MNP MP Ta có 0 tana = =1fi a = 45 NP Chọn đáp án A.
Câu 21: Cho hình chóp S.ABCD có đáy ABCD là hình vuông
có tâm O và SA ^ ( ABCD). Khẳng định nào sau đây sai ?
A. Góc giữa hai mặt phẳng (SBC) và ( ABCD) là góc ∑ ABS .
B. (SAC) ^ (SBD).
C. Góc giữa hai mặt phẳng (SBD) và ( ABCD) là góc ∑ SOA.
D. Góc giữa hai mặt phẳng (SAD) và ( ABCD) là góc ∑ SDA.
Hướng dẫn giải:
Ta có: (SBC) Ç( ABCD) = CD
ìAB ^ BC, AB Ì ï (ABCD) í
ïSB ^ BC, SB Ì î (SBC) Þ SBC ( ∑ ( ABCD)) ∑ ( );
= ABS . Vậy A đúng ìBD ^ AC í Þ BD ^ (SAC)
Ta có: îBD ^ SA
Mà BD Ì (SBD) Þ (SAC) ^ (SBD). Vậy B đúng
Ta có: (SBD) Ç( ABCD) = BD
ìAO ^ BD, AB Ì ï ( ABCD) í
ïSO ^ BD, SO Ì î (SBD) Þ SBD ( ∑ ( ABCD)) ∑ ( );
= SOA. Vậy C đúng
Ta có: (SAD) Ç( ABCD) = BD
ìAB ^ AD, AB Ì ï (ABCD) í
ïSA ^ AD, SA Ì î (SAD) Trang 18 Þ SAD ( ∑ ( ABCD)) ∑ 0 ( );
= SAB = 90 . Vậy D sai.
Câu 22: Tính cosin của góc giữa hai mặt của một tứ diện đều. 1 1 2 3 A. . B. . C. . D. . 3 2 3 2
Hướng dẫn giải:
Gọi H là trung điểm của AC khi đó BH ^ AC; DH ^ AC
Góc giữa hai mặt của tứ diện bằng ∑ BHD a 3 Ta có BH = DH = 2
Trong tam giác BHD có : 2 2 2 ∑
BD = BH + HD - 2BH.H . D cos BHD 2 2 2 3a 3a 3a 2 ∑ Þ a = + - 2 .cos BHD 4 4 4 ∑ 1 Þ cos BHD = 3
Câu 23: Cho hình chóp tứ giác đều S.ABCD có SA = SB . Góc giữa (SAB) và (SAD) bằng a . Chọn
khẳng định đúng trong các khẳng định sau? 1 A. cosa = - 2 . B. cosa = . C. 0 a = 2 60 . D. cosa = . 3 5 3
Hướng dẫn giải:
Gọi độ dài cạnh của hình chóp đều S.ABCD là a . Gọi I là
trung điểm của SB ta có DI ^ SB (vì tam giác SBD đều) và
AI ^ SB (vì tam giác SAB đều). Vậy, góc giữa hai mặt phẳng
(SAB) và (SAD) chính là góc ∑ AID. a Ta có : AD = 3
a 2 (đường chéo hình vuông), AI = DI = 2
(đường cao tam giác đều)
Áp dụng định lý cosin cho góc I trong tam giác AID ta có : 2 2
æ a 3 ö æ a 3 ö ç ÷ + ç ÷ - a 2 2 2 2 ( )2 ∑
AI + DI - AD 2 2 è ø è ø 1 cos(AID) = = = - 2 . AD DI
æ a 3 ö æ a 3 ö 3 2.ç ÷.ç ÷ 2 2 è ø è ø 1 Vậy cosa = - 3
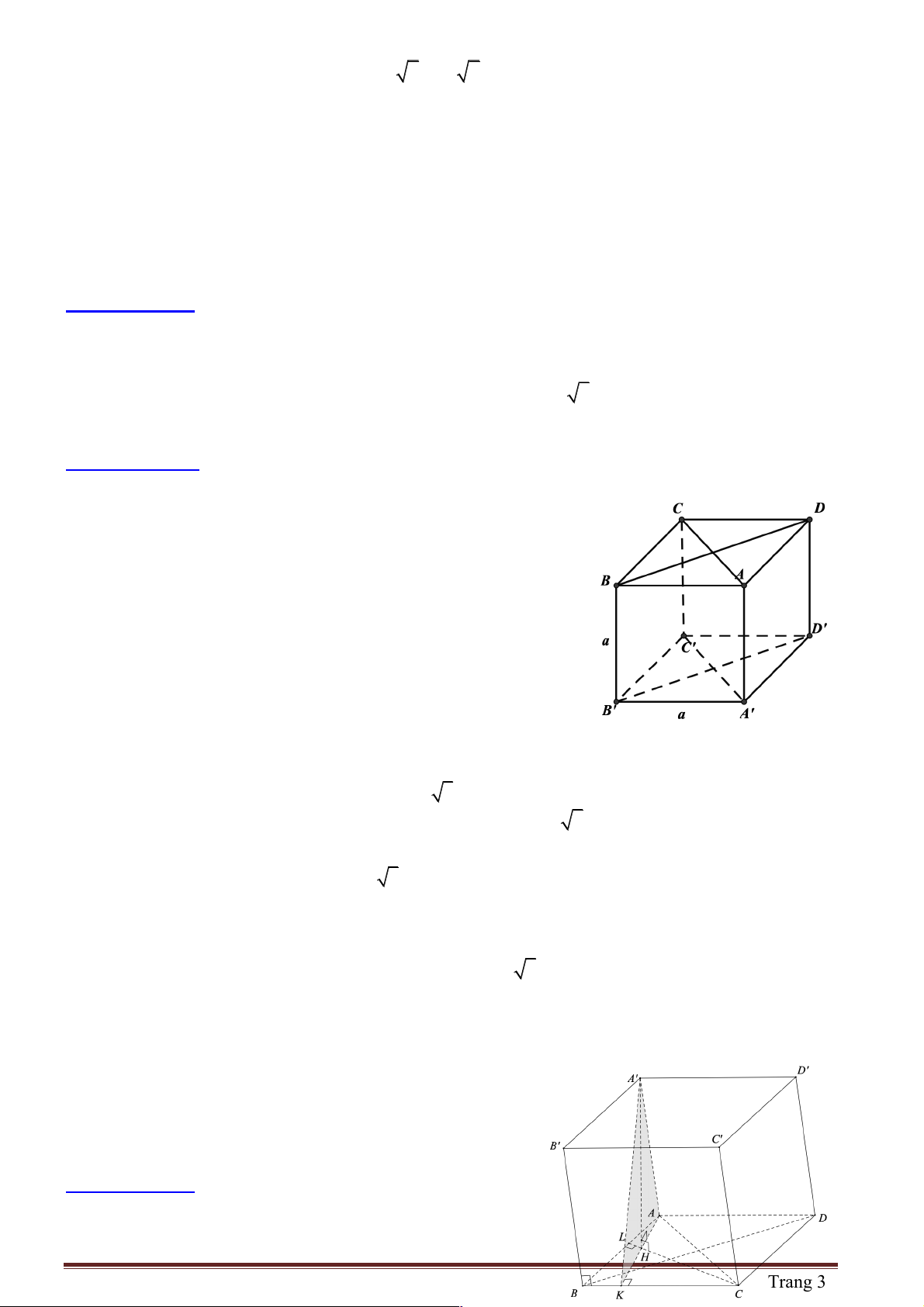
Câu 24: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và góc ∑ 0 ABC = 60 . Các cạnh , SA SB, SC 3 đều bằng a
. Gọi j là góc của hai mặt phẳng (SAC) và ( ABCD). Giá trị tanj 2 bằng bao nhiêu? A. 2 5 B. 3 5 C. 5 3 D. 3
Hướng dẫn giải: Trang 19
Do AB = BC và ∑ 0
ABC = 60 nên tam giác ABC đều.
Gọi H là hình chiếu của A lên ( ABCD).
Do SA = SB = SC nên H là tâm đường tròn ngoại tiế tam giác ABC . (
ìï SAC) Ç( ABCD) = AC í
Ta có : ïîSO ^ AC, HO ^ AC .
Þ ((SAC),( ABCD)) = (SO,HO) ∑ = SOH 1 1 a 3 a 3
Mặt khác, HO = BO = . = , 3 3 2 6 2 2 3a a a 5 2 2
SH = SB - BH = - = 4 3 2 3
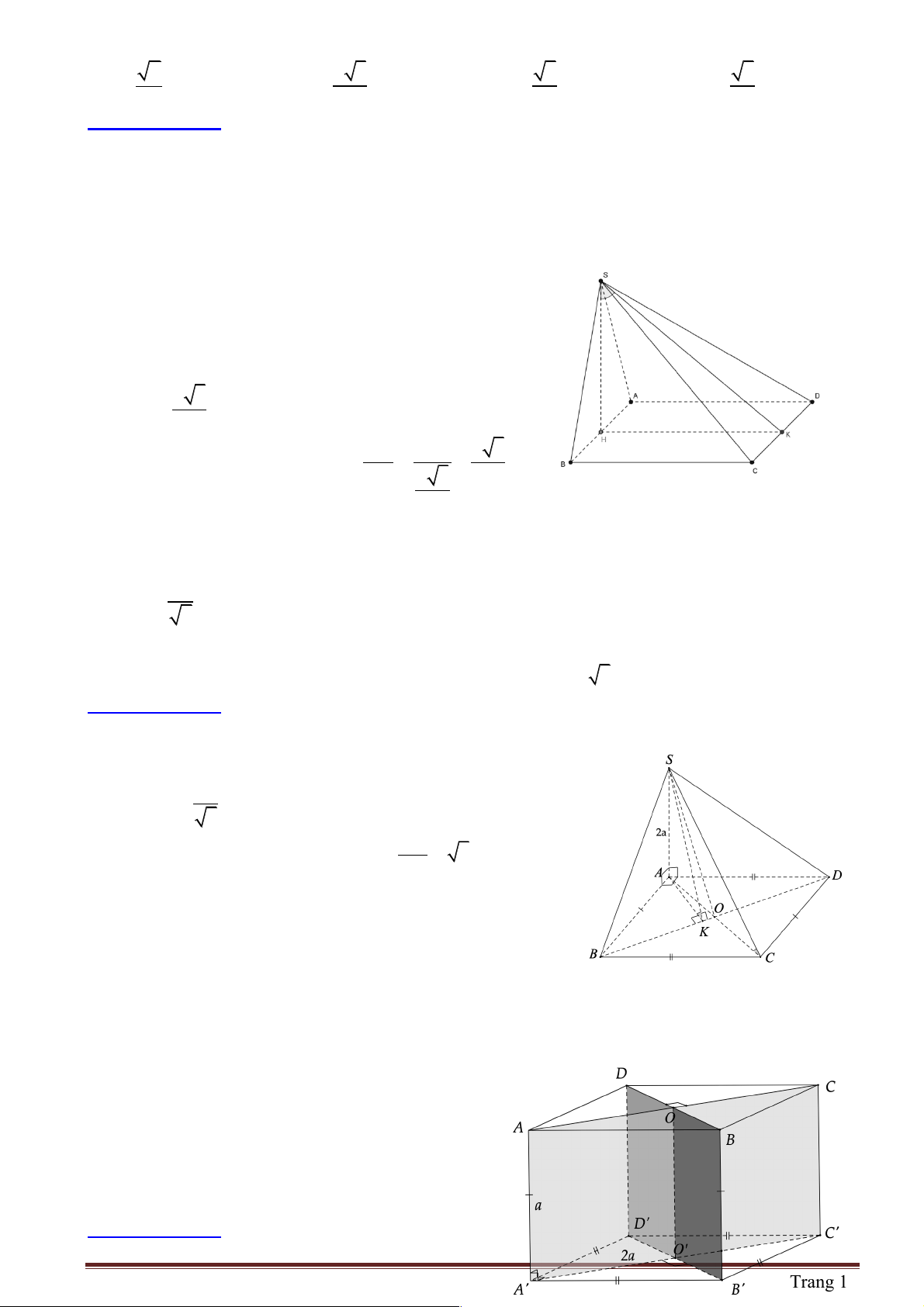
Câu 25: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D . AB = 2a,
AD = DC = a
Cạnh bên SA vuông góc với đáy và SA = a 2 . Chọn khẳng định sai
trong các khẳng định sau?
A. (SBC) ^ (SAC).
B. Giao tuyến của (SAB) và (SCD) song song với AB .
C. (SDC) tạo với (BCD)một góc 0 60 .
D. (SBC) tạo với đáy một góc 0 45 .
Hướng dẫn giải: ìBC ^ SA í Þ BC ^ (SAB)
+Ta có: îBC ^ AB
Mà BC Ì (SBC) Þ (SBC) ^ (SAC) (A đúng)
(ìSAD)Ç(SAB) = S ïAB/ /CD ï í Ì ï ( )
Þ (SAD)Ç(SAB) = Sx / /AB AB SAB CD ï Ì î (SCD) + B đúng
+ (SCD)Ç(BCD) = CD
ìAD ^ CD, AD Ì ï (BCD) Ta có: í
ïSD ^ CD, SD Ì î (SCD)
Suy ra góc giữa (SDC) và (BCD) là ∑ . SDA ∑ SA ∑ 0 tan SDA =
= 2 Þ SDA = 54 44' (C sai) AD Vậy chọn C.
Câu 26: Cho hình hộp chữ nhật ABC . D A¢B C ¢ D
¢ ¢ có AB = AA¢ = a , AD = 2a . Gọi a là góc giữa
đường chéo A¢C và đáy ABCD . Tính a . A. a » 20 45 ° ¢ . B. a » 24 5 ° ¢ . C. a » 30 18 ° ¢ . D. a » 25 48 ° ¢ .
Hướng dẫn giải:. Chọn B. Trang 20
Từ giả thiết ta suy ra: AA¢ ^ ( ABCD) Þ AC là hình chiếu
vuông góc của A¢C lên mặt phẳng ( ABCD) Þ (A C
¢ (ABCD)) = (A C ¢ AC) ∑ , , = A C ¢ A =a.
Áp dụng định lý Pytago trong tam giác ABC vuông tại B ta có: 2 2 2 2 2 2
AC = AB + BC = a + 4a = 5a Þ AC = a 5 .
Áp dụng hệ thức lượng trong tam giác AA¢C vuông tại A ta có: AA¢ a 1 tana = = = Þ a » 24 5 ° ¢. AC a 5 5
Câu 27: Cho hình lập phương ABC .
D A' B 'C ' D ' . Xét mặt phẳng ( A'BD). Trong các mệnh đề sau
mệnh đề nào đúng?
A. Góc giữa mặt phẳng ( A'BD) và các mặt phẳng chứa các cạnh của hình lập phương bằng a mà 1 tana = . 2
B. Góc giữa mặt phẳng ( A'BD) và các mặt phẳng chứa các cạnh của hình lập phương bằng a mà 1 sina = . 3
C. Góc giữa mặt phẳng ( A'BD) và các mặt phẳng chứa các cạnh của hình lập phương phụ thuộc
vào kích thước của hình lập phương.
D. Góc giữa mặt phẳng ( A'BD) và các mặt phẳng chứa các cạnh của hình lập phương bằng nhau.
Hướng dẫn giải: ABC .
D A' B 'C ' D ' là hình lặp phương nên hình chiếu của tam giác
A' BD lên các mặt chứa các cạnh của hình lặp phương là các tam
giác bằng nhau. Gọi S là diện tích các tam giác này 1 Lại có S = S .cosa . 1 AB'D
Vậy chọn đáp án D .
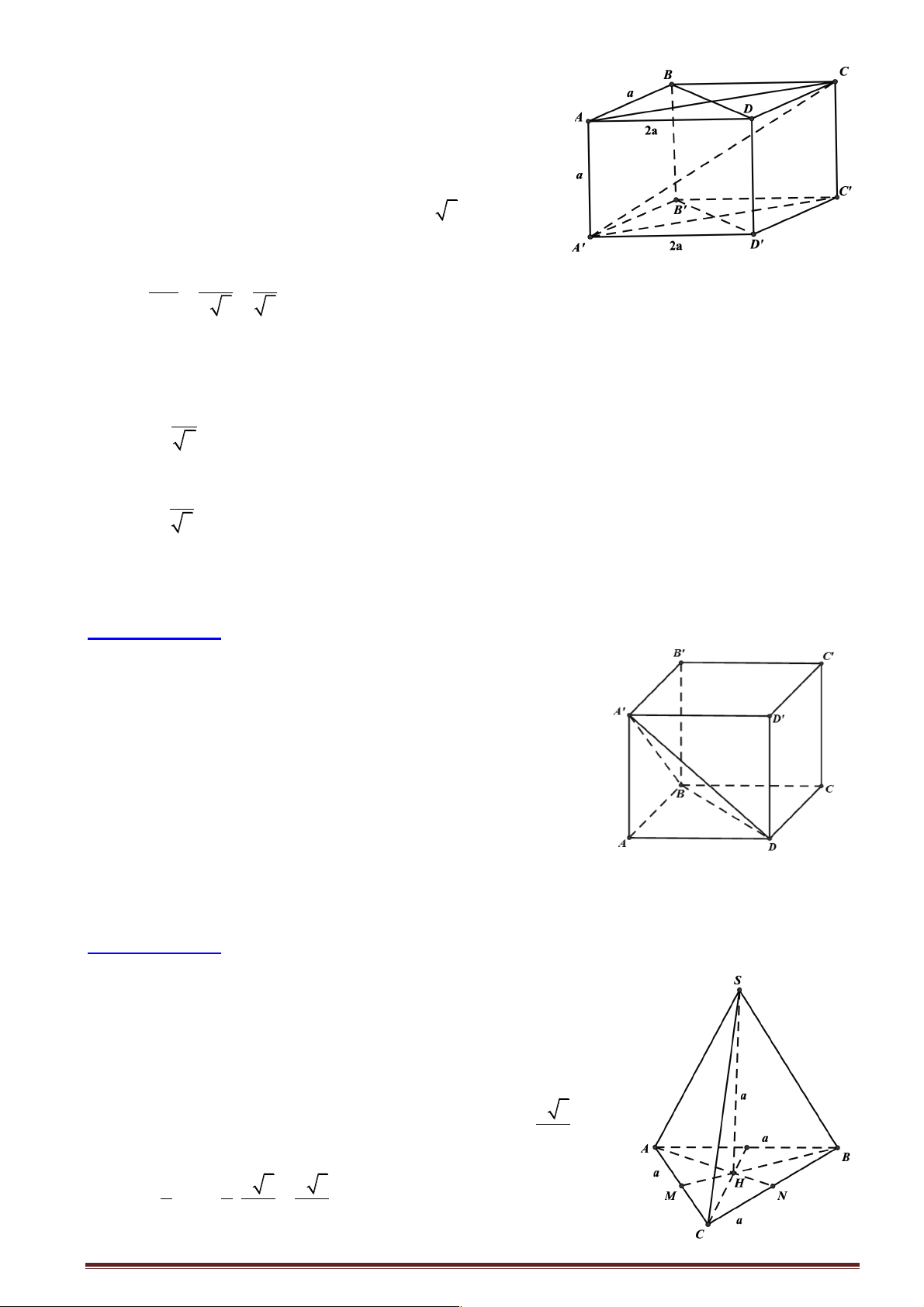
Câu 28: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và đường cao SH bằng cạnh đáy.
Tính số đo góc hợp bởi cạnh bên và mặt đáy. A. 30° . B. 45°. C. 60° . D. 75° .
Hướng dẫn giải:. Chọn C.
+ Vì SH ^ ( ABC) và AN Ì ( ABC) Þ SH ^ AN hay Þ SH ^ AH
Þ AH là hình chiếu vuông góc của SA lên ( ABC) Þ
(SA (ABC)) =(SA AH) ∑ , , = SAH .
+ Gọi M , N lần lượt là trung điểm của AC , BC . a 3 Vì ABC D
là tam giác đều cạnh a nên dễ tính được : AN = . 2
Từ giả thiết suy ra H là trọng tậm ABC D 2 2 a 3 a 3 Þ AH = AN = . = . 3 3 2 3
+ Áp dụng hệ thức lượng trong tam giác SHA vuông tại H ta có: Trang 21 ∑ SH a tan SAH = = = 3 ∑ Þ SAH = 60°. AH a 3 3 a 2
Câu 29: Cho hình chóp tứ giác đều có cạnh đáy bằng a 2 và chiều cao bằng . Tính số đo của 2
góc giữa mặt bên và mặt đáy. A. 30° . B. 45°. C. 60° . D. 75° .
Hướng dẫn giải:. Chọn B.
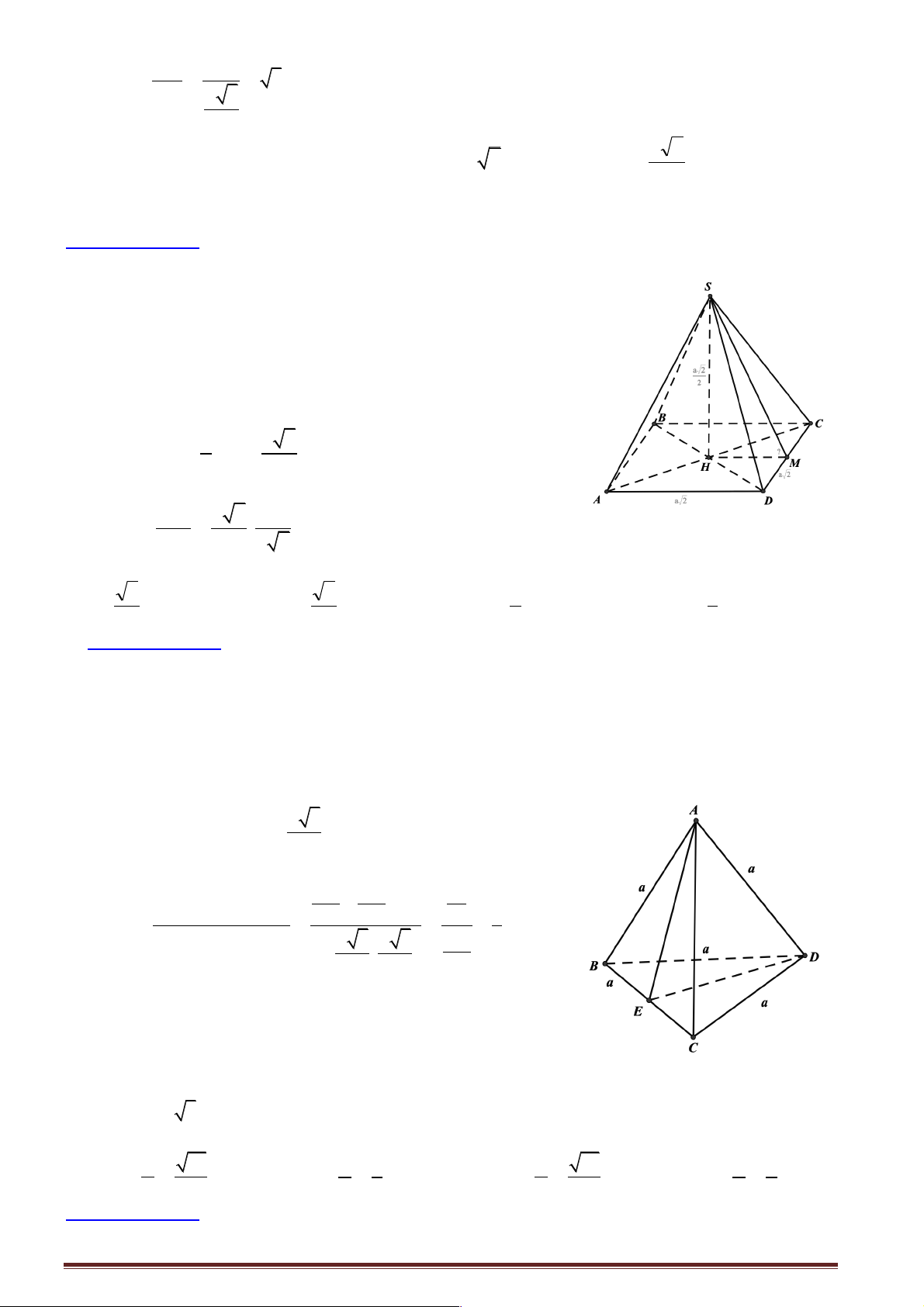
Giả sử hình chóp đã cho là S.ABCD có đường cao SH .
Ta có: ( ABCD)Ç(SCD) = CD.
Gọi M là trung điểm của CD Þ dễ chứng minh được SM ^ CD và HM ^ CD .
Þ ((ABCD) (SCD)) = (HM SM ) ∑ , , = SMH . 1 a 2
Mặt khác: HM = AD = 2 2
Áp dụng hệ thức lượng trong tam giác SHM vuông tại H , ta có : ∑ SH a 2 2 tan SMH = = . =1 ∑ Þ SMH = 45°. HM 2 a 2
Câu 30: Tính cosin của góc giữa hai mặt của một tứ diện đều. 3 2 1 1 A. . B. . C. . D. . 2 3 2 3
Hướng dẫn giải:. Chọn D.
Giả sử tứ diện đều đã cho là ABCD có cạnh a .
Ta có: ( ABC)Ç(BCD) = BC.
Gọi E là trung điểm BC . Khi đó dễ dàng chứng minh được AE ^ BC và DE ^ BC .
Þ ((ABC) (BCD)) = (AE DE) ∑ , , = AED. a 3
Ta dễ tính được: AE = DE = . 2
Áp dụng hệ quả của định lý cô sin trong tam giác AED ta có: 2 2 2 3a 3a 2 a + - a ∑ 2 2 2
AE + DE - AD 1 4 4 2 cos AED = = = = . 2 2.AE.DE a 3 a 3 3a 3 2. . 2 2 2
Câu 31: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Cạnh bên SA vuông góc với
đáy và SA = a 3 . Gọi j là góc giữa hai mặt phẳng (SBC) và (SCD). Chọn khẳng định đúng trong các khẳng định sau? j 10 j j j A. cos = 1 . B. cos = 10 . C. sin = 1 . D. sin = . 2 4 2 4 2 4 2 4
Hướng dẫn giải: Trang 22
Ta có SB = SD = 2a Vì SC D D = SC
D B (c.c.c) nên chân đường cao hạ từ B và D đến SC của hai tam giác đó trùng nhau
và độ dài đường cao bằng nhau fi BH = DH Do đó ∑ ∑
(SBC),(SCD) = DHB =j ( ) Ta có BD a 2 OB = OD = = 2 2 1 1 1 1 1 5 2 5 = + = + = fi BH = DH = a 2 2 2 2 2 2 BH SB BC 4a a 4a 5
Lại có BH = DH và O là trung điểm BD nên HO ^ BD hay HOB D vuông tại O 2 2
Ê2 5a ˆ Êa 2 ˆ 30 2 2
OH = BH - OB = Á ˜ - Á ˜ = a Á 5 ˜ Á 2 ˜ 10 Ë ¯ Ë ¯ 30 2 j OH 6 j OB 10 Ta có 10 2 sin = = = ;sin = = = 2 BH 2 5 4 2 BH 2 5 4 5 5 Chọn đáp án C.
Câu 32: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Cạnh bên SA vuông góc với
đáy và SA = a . Góc giữa hai mặt phẳng (SBC) và (SCD) bằng bao nhiêu? A. 0 30 B. 0 45 C. 0 90 D. 0 60
Hướng dẫn giải:
Ta có: SC ^ BD (vì BD ^ AC, BD ^ SA)
Trong mặt phẳng (SAC), kẻ OI ^ SC thì ta có SC ^ (BID) Khi đó ∑ ( SBC SCD ) ∑ ( ),( ) = BID a 2
Trong tam giác SAC , kẻ đường cao AH thì AH = 3 a
Mà O là trung điểm AC và OI ! AH nên OI = 6
Tam giác IOD vuông tại O có ∑ ∑ 0
tan OID = 3 Þ OID = 60
Vậy hai mặt phẳng (SBC) và (SCD) hợp với nhau một góc 0 60 .
Câu 33: Lăng trụ tam giác đều ABC.A¢B C
¢ ¢ có cạnh đáy bằng a . Gọi M là điểm trên cạnh AA¢ sao 3a cho AM =
. Tang của góc hợp bởi hai mặt phẳng (MBC) và ( ABC) là: 4 2 1 A. . B. 2 . C. . D. . 2 2
Hướng dẫn giải:
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC . Khi đó, A O ¢ ^ (ABC). Trang 23 a 3
Trong mặt phẳng ( ABC), dựng AH ^ BC . Vì tam giác ABC đều nên AH = . 2 BC ^ AH ü Ta có ý Þ BC ^ ( A H
¢ A) Þ BC ^ MH . BC ^ A O ¢ þ
Do đó, ((MBC) ( ABC)) = (MH AH ) ∑ , , = MHA =a . 3a AM 3
Tam giác MAH vuông tại A nên 4 tana = = = . Chọn D. AH a 3 2 2
Câu 34: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . SA ^ ( ABCD), SA = x . Xác
định x để hai mặt phẳng (SBC) và (SCD) tạo với nhau góc 60o. 3a a A. x = B. x =
C. x = a
D. x = 2a 2 2
Hướng dẫn giải:
* Trong (SAB) dựng AI ^ SB ta chứng minh được AI ^ (SBC) (1)
Trong (SAD) dựng AJ ^ SD ta chứng minh được AJ ^ (SCD) (2)
Từ (1) và (2) Þgóc ( SBC SCD ) = ( AI AJ ) ∑ ( ),( ) , = IAJ
* Ta chứng minh được AI = AJ . Do đó, nếu góc ∑ 60o IAJ = thì AI
D J đều Þ AI = AJ = IJ SA
D B vuông tại A có AI là đường cao Þ AI.SB = . SA AB Þ . SA AB AI = (3) SB 2 SA Và có 2
SA = SI.SB Þ SI = (4) SB IJ SI SI BD (4)
Ta chứng minh được IJ //BD Þ = . Þ IJ = = BD SB SB 2 SA .BD (5) 2 SB
Thế (3)&(5) vào AI = . SA BD IJ Þ AB = Û . AB SB = . SA BD SB Û 2 2 . a x + a = . x a 2 Û 2 2 2
x + a = 2x Û x = a Chọn C
Câu 35: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm .
O Biết SO ^ ( ABCD), SO = a 3 và
đường tròn nội tiếp ABCD có bán kính bằng .
a Tính góc hợp bởi mỗi mặt bên với đáy. A. 0 30 . B. 0 45 . C. 0 60 . D. 0 75 .
Hướng dẫn giải: Chọn C
Ta có SO ^ (ABCD) và OM ,ON,OP,OQ lần lượt vuông góc với
AB, BC,CD, DA
Theo định lí ba đường vuông góc ta có SM ^ A ,
B SN ^ BC, SP ^ , CD SQ ^ DA Từ đó suy ra ∑ ∑ ∑ ∑
SMO = SNO = SPO = SQO
Xét tam giác SMO vuông tại O ta có ∑ ∑ 0
tan SMO = 3 Þ SMO = 60
Vậy mỗi mặt bên hợp với đáy các góc bằng nhau và bằng 0 60
Câu 36: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại Trang 24 ,
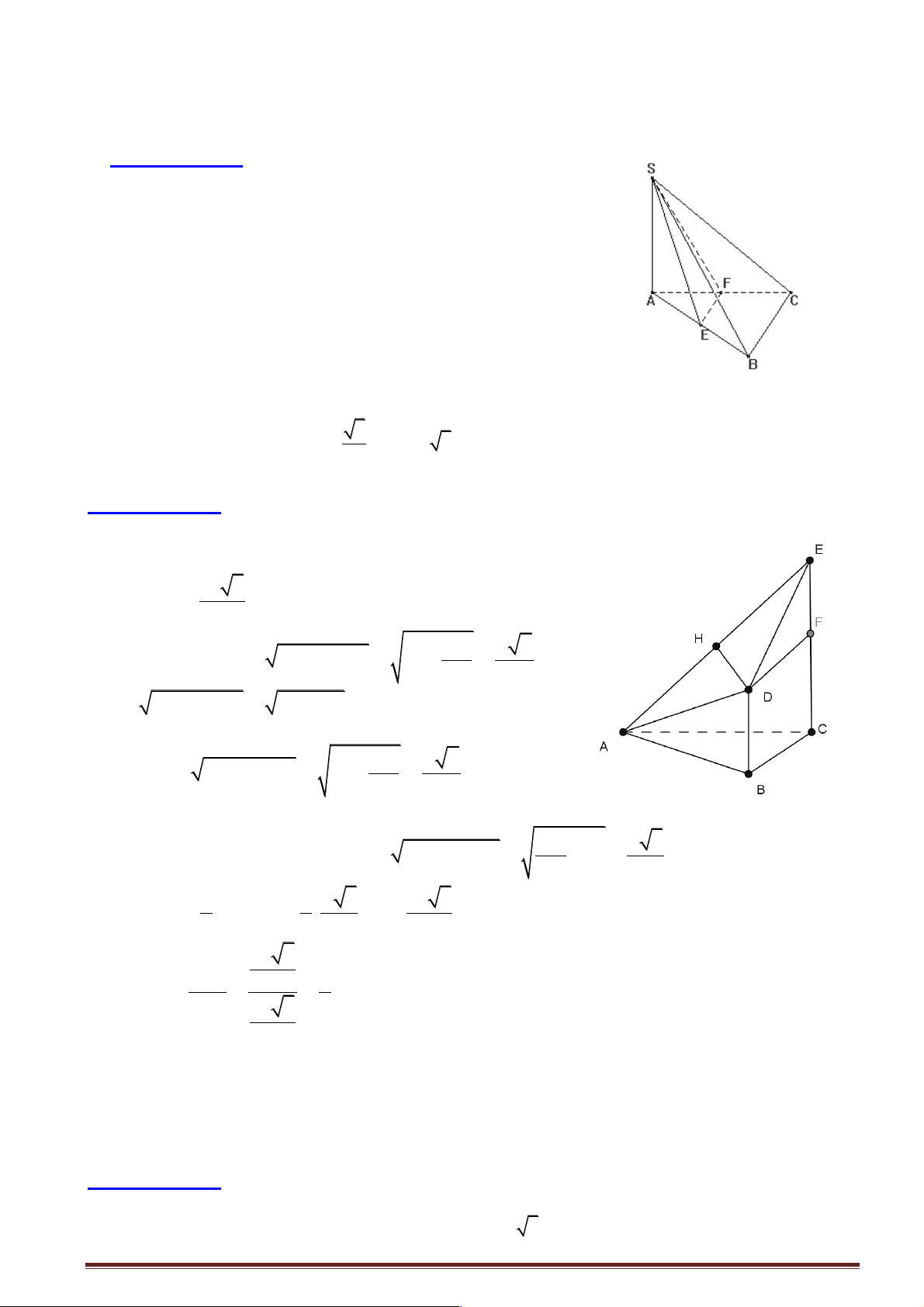
B SA ^ ( ABC).Gọi E, F lần lượt
là trung điểm của các cạnh AB và AC . Góc giữa hai mặt phẳng (SEF ) và (SBC) là : A. ∑ CSF. B. ∑ BSF. C. ∑ BSE. D. ∑ CSE.
Hướng dẫn giải:
Ta có: (SEF ) Ç(SBC) = Sx / /EF / /BC ìBC ^ AB í Þ BC ^ (SAB) î ^ BC SA
Þ BC ^ SE, BC ^ SB
Þ SB ^ Sx, SE ^ Sx
Þ Góc giữa hai mặt phẳng (SEF ) và (SBC) là : ∑ BSE Chọn C.
Câu 37: Cho tam giác đều ABC có cạnh bằng a và nằm trong mặt
phẳng (P). Trên các đường thẳng vuông góc với (P)tại B,C lần lượt lấy D, E nằm trên cùng một 3
phía đối với (P) sao cho BD = a
,CE = a 3 . Góc giữa ( P) và ( ADE) bằng bao nhiêu? 2 A. 0 30 B. 0 60 C. 0 90 D. 0 45
Hướng dẫn giải:
Gọi j = (( ABC),( ADE)). 2 a 3 Ta có: S = . ABC 4 2 3a a 7 Mặt khác, ta có: 2 2 2
AD = AB + BD = a + = , 4 2 2 2 2 2
AE = AC + CE = a + 3a = 2a.
Gọi F là trung điểm EC , ta có DF = BC = a . 2 3a a 7 Do đó 2 2 2
DE = DF + FE = a + = . 4 2
Suy ra tam giác ADE cân tại D . 2 7a a 3
Gọi H là trung điểm AE , ta có 2 2 2
DH = AD - AH = - a = . 4 2 2 1 1 a 3 a 3 Suy ra S = DH.AE = . .2a = ADE 2 2 2 2 2 a 3 S 1 Vậy ABC 4 cosj = = = Þ j = 60o. 2 S a ADE 3 2 2 Chọn B.
Câu 38: Cho góc tam diện Sxyz với ∂ 0 xSy =120 , ∂ 0 ySz = 60 , ∂ 0
zSx = 90 . Trên các tia Sx , Sy , Sz lần lượt lấy các điểm ,
A B,C sao cho SA = SB = SC = a . Góc giữa hai mặt phẳng (SAB) và (ABC) bằng : A. 0 15 B. 0 90 C. 0 45 D. 0 60
Hướng dẫn giải: Chọn B
Áp dụng định lí Côsin trong tam giác SAB , ta có AB = a 3 Trang 25
Tam giác SAC vuông cân tại S nên AC = a 2 ; tam S
giác SBC đều nên BC = a . I Vì 2 2 2
AC + BC = AB nên tam giác ABC vuông tại C 600
Gọi H là trung điểm AB thì ta có H K B A
ìHA = HB = HC x y í Þ SH ^ (ABC)
îSA = SB = SC
Mà SH Ì (SAB) nên (SAB) ^ (ABC) C z Vậy ∑ ( SAB ABC ) 0 ( ),( ) = 90
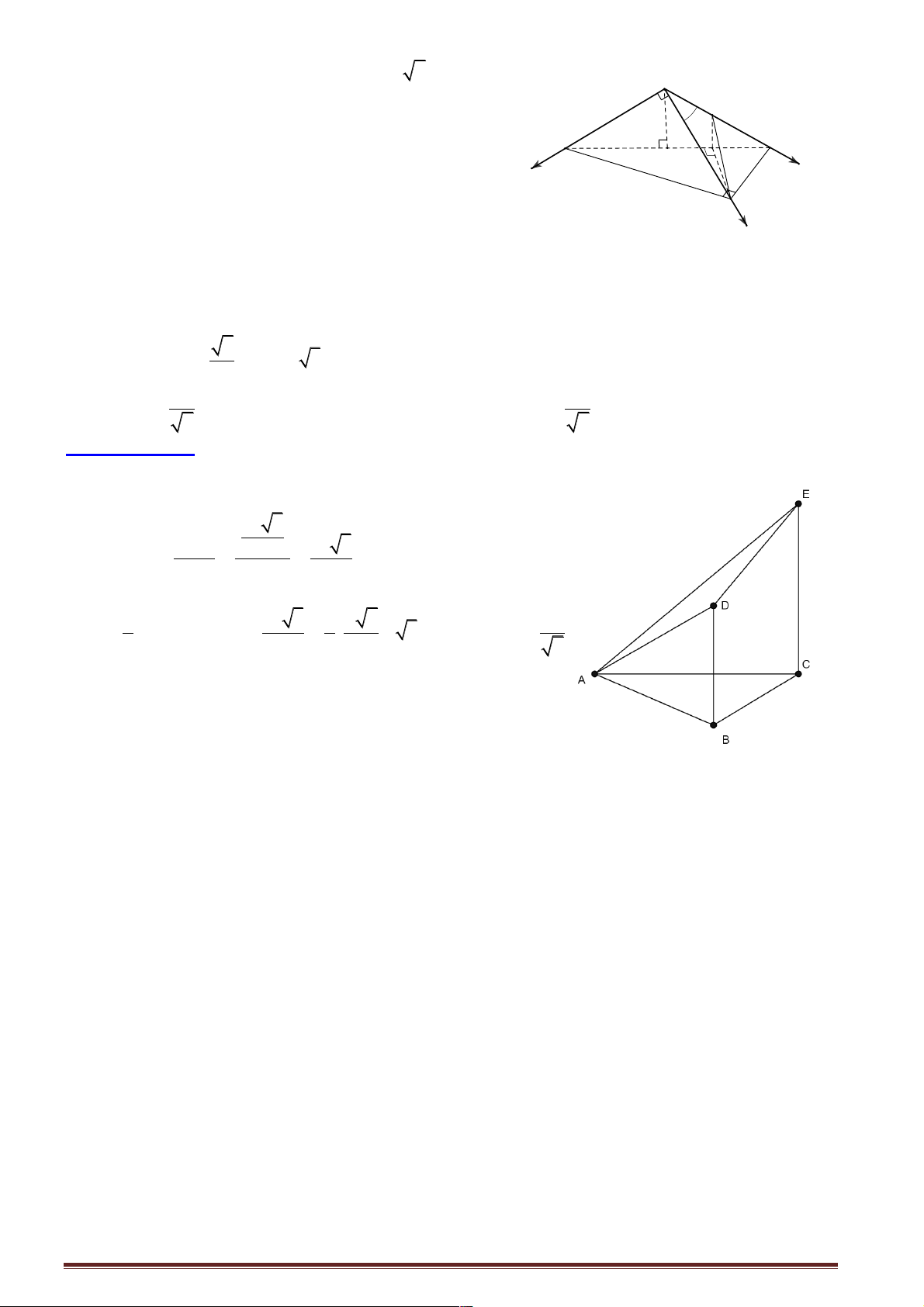
Câu 39: Cho tam giác đều ABC cạnh a . Gọi d , d lần lượt là đường thẳng đi qua B,C và vuông B C
góc với ( ABC). (P) là mặt phẳng qua A và hợp với ( ABC) góc 0
60 . (P) cắt d ,d lần lượt tại D B C 6
và E . biết AD = a
, AE = a 3. đặt ∑
DAE = j. Chọn khẳng định đúng trong các khẳng định sau? 2 2 A. sinj = . B. 0 j = 3 60 . C. sinj = . D. 0 j = 30 . 6 6
Hướng dẫn giải: Ta có: S = S
.cosa với a = (( ABC) ( ADE)) 0 , = 60 . ABC ADE 2 a 3 2 S a 3 Do đó ABC 4 S = = = . ADE 0 cosa cos 60 2 Mặt khác, 2 1 a 3 1 a 6 2 S = A . D AE.sinj Û = . .a 3.sinj Þ sinj = ADE 2 2 2 2 6 . Chọn A. Trang 26
DẠNG 2: CHỨNG MINH HAI MẶT PHẲNG VUÔNG GÓC, CHỨNG MINH
ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG VÀ CÁC BÀI TOÁN LIÊN QUAN Phương pháp:
* Chứng minh hai mặt phẳng vuông góc
Để chứng minh (P) ^ (Q), ta có thể chứng minh bởi một trong các cách sau:
• Chứng minh trong (P) có một đường thẳng a mà a ^ (Q). • Chứng minh ∑ ( P Q ) 0 ( ),( ) = 90
* Chứng minh đường thẳng vuông góc với mặt phẳng
Để chứng minh d ^ (P), ta có thể chứng minh bởi một trong các cách sau:
• Chứng minh d Ì (Q) với (Q) ^ (P) và d vuông góc với giao tuyến c của (P) và (Q).
• Chứng minh d = (Q) Ç (R) với (Q) ^ (P) và (R) ^ (P).
• Sử dụng các cách chứng minh đã biết ở phần trước.
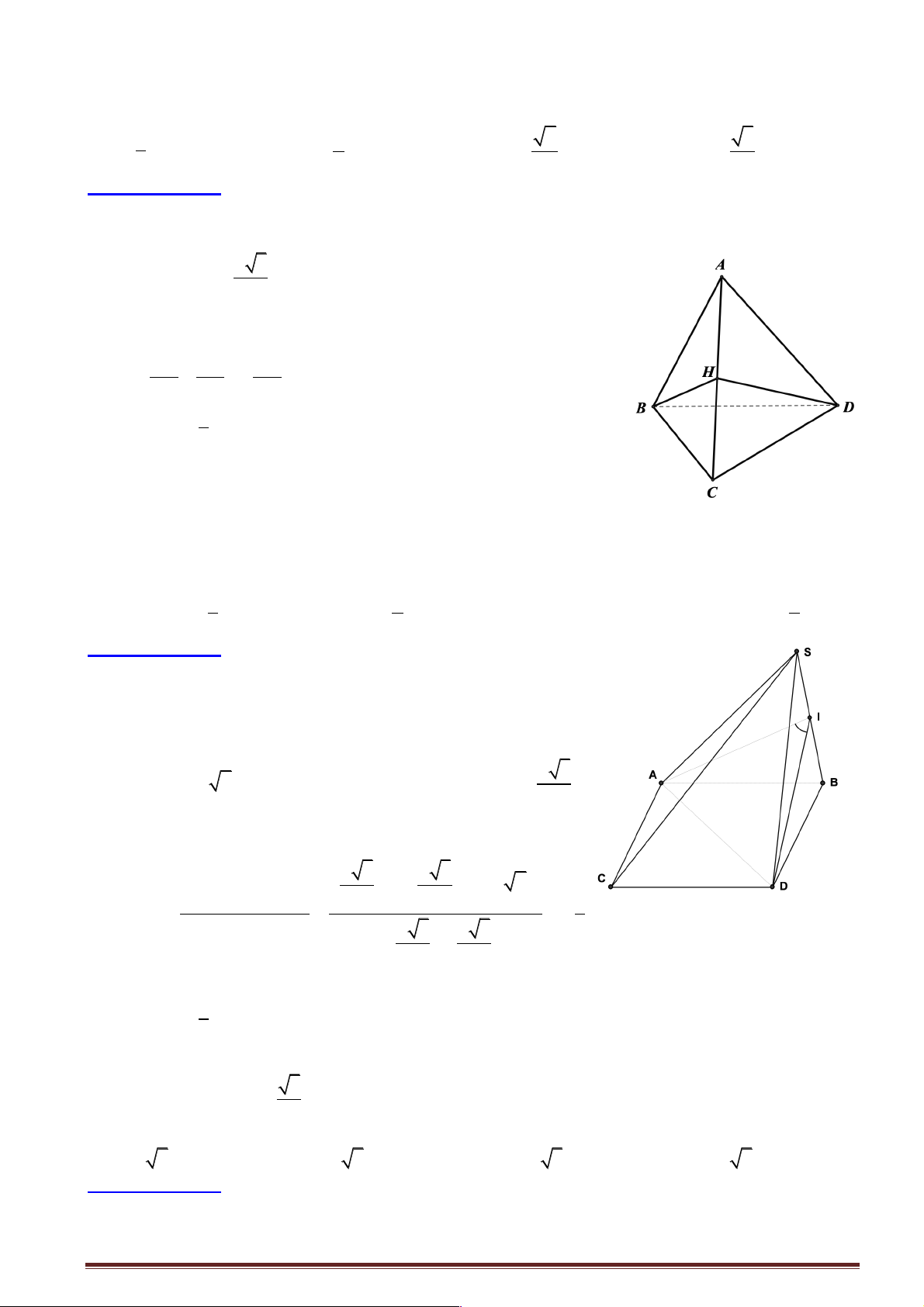
Câu 1: Cho tứ diện ABCD có AB ^ (BCD). Trong BCD D
vẽ các đường cao BE và DF cắt nhau ở
O . Trong ( ADC) vẽ DK ^ AC tại K . Khẳng định nào sau đây sai ?
A. ( ADC) ^ ( ABE).
B. ( ADC) ^ (DFK ).
C. ( ADC) ^ ( ABC).
D. (BDC) ^ ( ABE).
Hướng dẫn giải: CD ^ BEü * Ta có
ý Þ CD ^ ( ABE) ü . CD ^ ABþ
ý Þ ( ADC) ^ ( ABE) CD Ì ( ADC)þ
Vậy “ ( ADC) ^ ( ABE)”: ĐÚNG. *
DF ^ BCüýÞ DF ^(ABC)ü . DF ^ ABþ ý Þ DF ^ AC SC Ì ( ABC ) ü þ
ý Þ AC ^ (DFK )ü DK ^ ACþ
ý Þ ( ADC) ^ (DFK ) AC Ì ( ADC )þ
Vậy “ ( ADC) ^ (DFK )”: ĐÚNG. CD ^ BEü * Ta có
ý Þ CD ^ ( ABE) ü . CD ^ ABþ
ý Þ (BDC) ^ ( ABE) CD Ì (BDC)þ
Vậy “ (BDC) ^ ( ABE)”: ĐÚNG.
* “ ( ADC) ^ ( ABC)”: SAI Chọn C
Câu 2: Cho tứ diện ABCD có hai mặt phẳng ( ABC) và ( ABD) cùng vuông góc với (DBC). Gọi BE
và DF là hai đường cao của tam giác BCD , DK là đường cao của tam giác ACD . Chọn khẳng định
sai trong các khẳng định sau?
A. (ABE) ^ (ADC) .
B. (ABD) ^ (ADC).
C. (ABC) ^ (DFK) .
D. (DFK) ^ (ADC).
Hướng dẫn giải: Trang 27 ( ì ABC) ^ (BCD) ï Ta có: ( í ABD) ^ (BCD) Þ AB ^ (BCD). ( ï ABC î )Ç( ABD) = AB CD ì ^ BE Mặt khác: í
Þ CD ^ ( ABE) nên câu A CD î ^ AB đúng. ( ì ABC) ^ (BCD) ï (
í ABC) Ç(BCD) = BC Þ DF ^ ( ABC) nên câu C ïDF ^ BC î đúng.
Theo trên ta có DF ^ ( ABC) nên DF ^ AC . ìAC ^ DF Vậy ta có í
Þ AC ^ (DKF ) Þ ( ACD) ^ (DKF ). Do đó câu D đúng. îAC ^ DK Chọn B.
Câu 3: Cho hình hộp chữ nhật ABC . D A¢B C ¢ D
¢ ¢ . Khẳng định nào sau đây không đúng?
A. Tồn tại điểm O cách đều tám đỉnh của hình hộp.
B. Hình hộp có 6 mặt là 6 hình chữ nhật.
C. Hai mặt ACC A ¢ ¢ và BDD B ¢ ¢ vuông góc nhau.
D. Hình hộp có 4 đường chéo bằng nhau và đồng qui tại trung điểm của mỗi đường.
Hướng dẫn giải: Chọn C
Câu 4: Cho hình chóp S.ABC có hai mặt bên (SBC) và (SAC) vuông góc với đáy ( ABC). Khẳng
định nào sau đây sai ?
A. Đáy là đa giác đều.
B. Các mặt bên là những hình chữ nhật nằm trong mặt phẳng vuông góc với đáy.
C. Các cạnh bên là những đường cao.
D. Các mặt bên là những hình bình hành.
Hướng dẫn giải: ( ì SBC) ^ ( ABC) ï Ta có: ( í SAC) ^ ( ABC)
Þ SC ^ ( ABC). Do ïSC = (SBC)Ç î (SAC)
đó câu A và B đúng
C. Sai. vì nếu A'Î SB thì hai mặt phẳng (SAB)
và (SBC)phải vuông góc với nhau theo giao tuyến SB Trang 28 ìSC ^ ï (ABC) . D Ta có: í
Þ (SAC) ^ ( ABC) theo giao tuyến AC ïSC Ì î (SAC)
Mà BK là đường cao của ABC D
Þ BK ^ AC Þ BK ^ (SAC). Vậy . D đúng
Vậy chọn đáp án D .
Câu 5: Cho hình lăng trụ ABC . D ’ A ’ B C’ ’
D . Hình chiếu vuông góc của ’
A lên ( ABC) trùng với trực tâm H c
ủa tam giác ABC . Khẳng định nào sau đây không đúng? A. ’
BB C’C là hình chữ nhật. B. ( ’ AA H ) ^ ( ’ A ’ B ’ C ). C. ( ’ BB ’ C C) ^( ’ AA H ). D. ( ’ AA ’ B B) ^ ( ’ BB ’ C C).
Hướng dẫn giải: Ta có BC ^ ( ’ A AH ) nên BC ^ ’ BB ,nếu ( ’ AA ’ B B) ^ ( ’ BB ’ C C)
thì BC ^ AB vô lý vì H trùng A . Chọn D.
Câu 6: Cho hình chóp S.ABC có SA ^ ( ABC) và đáy ABC là
tam giác cân ở A . Gọi H là hình chiếu vuông góc của A lên (SBC). Khẳng định nào sau đây đúng?
A. H Î SB .
B. H trùng với trọng tâm tam giác SBC .
C. H Î SC .
D. H Î SI ( I là trung điểm của BC ).
Hướng dẫn giải: Chọn D.
Gọi I là trung điểm của BC Þ AI ^ BC mà BC ^ SA Þ BC ^ (SAI ).
Khi đó H là hình chiếu vuông góc của A lên (SBC). Suy ra H Î SI .
Câu 7: Cho hình chóp S.ABC có hai mặt bên (SBC) và (SAC)
vuông góc với đáy ( ABC). Khẳng định nào sau đây sai?
A. SC ^ ( ABC).
B. Nếu A¢ là hình chiếu vuông góc của A lên (SBC) thì A¢Î SB .
C. (SAC) ^ ( ABC).
D. BK là đường cao của tam giác ABC thì BK ^ (SAC).
Hướng dẫn giải: S Chọn B. (
ì SAC)Ç(SBC) = SC ï
Ta có: í (SAC) ^ ( ABC) Þ SC ^ ( ABC). ï (SBC) ^ î (ABC) A'
Gọi A¢ là hình chiếu vuông góc của A lên (SBC), B C Trang 29 A
khi đó AA¢ ^ (SBC) Þ AA¢ ^ BC Þ A¢ÎBC . Suy ra đáp án B sai
Câu 8: Cho hình chóp S.ABC có hai mặt bên (SAB) và (SAC) vuông góc với đáy ( ABC), tam giác
ABC vuông cân ở A và có đường cao AH, (H Î BC). Gọi O là hình chiếu vuông góc của A lên
(SBC). Khẳng định nào sau đây đúng?
A. SC ^ ( ABC).
B. (SAH ) ^ (SBC).
C. O Î SC .
D. Góc giữa (SBC) và ( ABC) là góc ∑ SBA.
Hướng dẫn giải: Chọn B. (
ì SAB) Ç(SAC) = SA ï
Ta có: í (SAC) ^ ( ABC) Þ SA ^ ( ABC). ï (SAB) ^ î (ABC)
Gọi H là trung điểm của BC Þ AH ^ BC
mà BC ^ SA Þ BC ^ (SAH ) Þ (SBC) ^ (SAH ).
Khi đó O là hình chiếu vuông góc
của A lên (SBC)
Thì suy ra O Î SI và ((SBC) ∑ (ABC)) ∑ , = SHA.
Vậy đáp án B đúng.
Câu 9: Cho hình lăng trụ đứng ABC.A¢B C
¢ ¢ có đáy ABC là tam giác vuông cân ở A . H là trung điểm
BC . Khẳng định nào sau đây sai ?
A. Các mặt bên của ABC.A¢B C
¢ ¢ là các hình chữ nhật bằng nhau. B. ( AA H
¢ ) là mặt phẳng trung trực của BC .
C. Nếu O là hình chiếu vuông góc của A lên ( A B
¢ C) thì OÎ A¢H .
D. Hai mặt phẳng ( AA B ¢ B ¢ ) và ( AA C ¢ C ¢ ) vuông góc nhau.
Hướng dẫn giải: Chọn A. A' C'
Vì ABC là tam giác vuông cân ở A Þ AB = AC ¹ BC B'
nên các mặt bên của lăng trụ không bằng nhau. Vậy đáp án A sai. A C H B
Câu 10: Cho hình hộp chữ nhật ABC . D A¢B C ¢ D
¢ ¢ . Khẳng định nào sau đây không đúng?
A. Hình hộp có 6 mặt là 6 hình chữ nhật.
B. Hai mặt ( ACC A ¢ ¢) và (BDD B ¢ ¢) vuông góc nhau.
C. Tồn tại điểm O cách đều tám đỉnh của hình hộp.
D. Hình hộp có 4 đường chéo bằng nhau và đồng qui tại trung điểm của mỗi đường.
Hướng dẫn giải: Trang 30 Chọn B.
Ta có: ABCD là hình chữ nhật nên AC không vuông góc với BD
Suy ra hai mặt ( ACC A ¢ ¢) và (BDD B ¢ ¢) không vuông góc với nhau. Vậy đáp án B sai.
Câu 11: Cho hình lập phương ABC .
D A B C D . Mặt phẳng ( A BD 1
) không vuông góc với mặt phẳng 1 1 1 1 nào dưới đây? A. ( AB D (ACC A (ABD (ABC 1 1 ) 1 ) 1 1 ) 1 ). B. . C. . D. .
Hướng dẫn giải:
* Gọi I = AB Ç A B. 1 1
Tam giác A BD đều có DI là đường trung tuyến nên 1 DI ^ A B . 1
DA ^ ( AA B B Þ DA ^ A B 1 1 ) . 1 A B ^ DI ü 1 ý Þ A B ^ AB D 1 ( 1 ) nên A đúng. A B ^ AD 1 þ * Ta có
BD ^ AC üýÞ BD ^(ACC A Þ ABD ^ ACC A 1 1 ) ( 1 ) ( 1 1 ) nên BD ^ AA1þ B đúng.
* Gọi J = AD Ç A D. 1 1
Tam giác A BD đều có BJ là đường trung tuyến nên BJ ^ A D. 1 1
BA ^ ( AA D D Þ BA ^ A D 1 1 ) . 1 A D ^ BJ ü 1 ý Þ A B ^ ABD 1 (
1 ) nên C đúng. Chọn D. A D ^ BA 1 þ
Câu 12: Cho hình lập phương ABC . D A¢B C ¢ D
¢ ¢ có cạnh bằng a . Khẳng định nào sau đây sai?
A. Tam giác AB C ¢ là tam giác đều. 2
B. Nếu a là góc giữa AC¢ và ( ABCD) thì cosa = . 3 C. ACC A
¢ ¢ là hình chữ nhật có diện tích bằng 2 2a .
D. Hai mặt ( AA C ¢ C ¢ ) và (BB D ¢ D
¢ ) ở trong hai mặt phẳng vuông góc với nhau.
Hướng dẫn giải:. Chọn C.
+ Cách 1: Chứng minh trực tiếp chỉ ra C là đáp án sai.
Từ giả thiết dễ dàng tính được AC = a 2. Mặt khác vì ABC . D A¢B C ¢ D
¢ ¢ là hình lập phương nên suy ra ∑ AA C ¢ ¢ = 90°. ìAA¢ / /CC¢ ï Xét tứ giác ACC A
¢ ¢ có íAA¢ = CC¢ = a Þ ACC A ¢ ¢ là hình chữ ï∑ îAA¢C¢ = 90°
nhật có các cạnh a và a 2. Trang 31
Diện tích hình chữ nhật ACC A ¢ ¢ là : 2 S = .
a a 2 = a 2 (đvdt)
Þ đáp án C sai.
+ Cách 2: Chứng minh 3 đáp án A , B , D đều đúng và suy ra đáp án C sai.
Câu 13: Cho hình chóp S.ABC có đường cao SH . Xét các mệnh đề sau:
I) SA = SB = SC .
II) H trùng với tâm đường tròn ngoại tiếp tam giác ABC .
III) Tam giác ABC là tam giác đều.
IV) H là trực tâm tam giác ABC .
Các yếu tố nào chưa đủ để kết luận S.ABC là hình chóp đều?
A. (I ) và (II ).
B. (II ) và (III ).
C. (III ) và (IV ).
D. (IV ) và (I ).
Hướng dẫn giải:. Chọn A.
Câu 14: Cho hình lập phương ABC . D A¢B C ¢ D
¢ ¢ cạnh bằng a . Khẳng định nào sau đây sai?
A. Hai mặt ACC A ¢ ¢ và BDD B ¢ ¢ vuông góc nhau.
B. Bốn đường chéo AC¢, A¢C , BD¢, B D
¢ bằng nhau và bằng a 3.
C. Hai mặt ACC A ¢ ¢ và BDD B
¢ ¢ là hai hình vuông bằng nhau.
D. AC ^ BD¢.
Hướng dẫn giải:. Chọn C.
Vì theo giả thiết ABC . D A¢B C ¢ D
¢ ¢ ta dễ dàng chỉ ra được: ìAC ^ BD + í
và BD cắt BB¢ cùng nằm trong (BB D ¢ D ¢ ) îAC ^ BB¢ Þ AC ^ (BB D ¢ D
¢ ). Mà BD¢ Ì (BB D ¢ D
¢ ) Þ AC ^ BD¢ Þ đáp án D đúng. ìAC Ì ï ( ACC A¢¢) + í Þ ( ACC A ¢ ¢) ^ (BB D ¢ D
¢ ) Þ đáp án A đúng. ïAC ^ î (BB D ¢ D ¢ )
+ Áp dụng đình lý Pytago trong tam giác B A
¢ ¢D¢ vuông tại A¢ ta có: 2 2 2 2 2 2 B D ¢ ¢ = B A ¢ ¢ + A D
¢ ¢ = a + a = 2a .
Áp dụng định lý Pytago trong tam giác BB D
¢ ¢ vuông tại B¢ ta có: 2 2 2 2 2 2
BD¢ = BB¢ + B D
¢ ¢ = a + 2a = 3a Þ BD¢ = a 3. Hoàn toàn tương tự ta tính được độ dài các
đường chéo còn lại của hình lập phương đều bằng nhau và bằng a 3 Þ đáp án B đúng.
ìAC / / A¢C¢ ï
ïAC = A¢C¢ = a 3 + Xét tứ giác ACC A ¢ ¢ có í Þ ACC A
¢ ¢ là hình chữ nhật. hoàn toàn tương tự ta cũng
AA¢ = CC¢ = a ï ï∑ îACC¢ = 90° chỉ ra BDD B
¢ ¢ cũng là hình chữ nhật có các cạnh là a và a 3 . Þ Hai mặt ACC A ¢ ¢ và BDD B
¢ ¢ là hai hình vuông bằng nhau Þ đáp án C sai.
Câu 15: Cho hình lăng trụ ABC . D A¢B C ¢ D
¢ ¢ . Hình chiếu vuông góc của A¢ lên ( ABC)t rùng với trực
tâm H của tam giác ABC . Khẳng định nào sau đây không đúng? A. ( AA B ¢ B ¢ ) ^ (BB C ¢ C ¢ ). B. (AA H ¢ ) ^ (A B ¢ C ¢ ¢). C. BB C ¢ C ¢ là hình chữ nhật. D. (BB C ¢ C ¢ ) ^ (AA H ¢ ).
Hướng dẫn giải: Chọn A. Trang 32
Gọi K là hình chiếu vuông góc của A lên BC
Þ H Î AK, BC ^ AK, BC ^ A H ¢ Þ BC ^ (AA H ¢ ) ì ( AA H ¢ ) ^ ( A B ¢ C ¢ ¢) Þ ( ï í BB C ¢ C ¢ ) ^ ( AA H
¢ ) nên đáp án B,C,D đúng. ï BC ^ BB¢ î
Câu 16: Hình hộp ABC . D A¢B C ¢ D
¢ ¢ trở thành hình lăng trụ tứ giác đều khi phải thêm các điều kiện nào sau đây?
A. Tất cả các cạnh đáy bằng nhau và cạnh bên vuông góc với mặt đáy.
B. Cạnh bên bằng cạnh đáy và cạnh bên vuông góc với mặt đáy.
C. Có một mặt bên vuông góc với mặt đáy và đáy là hình vuông.
D. Các mặt bên là hình chữ nhật và mặt đáy là hình vuông.
Hướng dẫn giải: Chọn D.
Theo lí thuyết lăng trụ tứ giác đều là lăng trụ đứng có đáy là hình vuông.
Câu 17: Cho hình lăng trụ tứ giác đều ABC . D A¢B C ¢ D
¢ ¢ có cạnh đáy bằng a , góc giữa hai mặt phẳng
(ABCD)và (ABC¢) có số đo bằng60°. Cạnh bên của hình lăng trụ bằng: A. 3a . B. a 3 . C. 2a . D. a 2.
Hướng dẫn giải:. Chọn B.
Ta có: ( ABCD)Ç( ABC¢) = AB.
Từ giả thiết ta dễ dàng chứng minh được: AB ^ (BB C ¢ C ¢ ) mà C B ¢ Ì (BB C ¢ C ¢ ) Þ AB ^ C B
¢ . Mặt khác: CB ^ AB .
Þ ((ABCD) (ABC¢)) = (CB C B ¢ ) ∑ , , = CBC¢ = 60°.
Áp dụng hệ thức lượng trong tam giác BCC¢ vuông tại C ta có: ∑ CC¢ ¢ = Þ ¢ ∑ tan CBC CC = . CB tan CBC¢ = .
a tan 60° = a 3 . CB
Câu 18: Cho hai mặt phẳng vuông góc (P) và (Q) có giao tuyến D . Lấy A , B cùng thuộc D và lấy
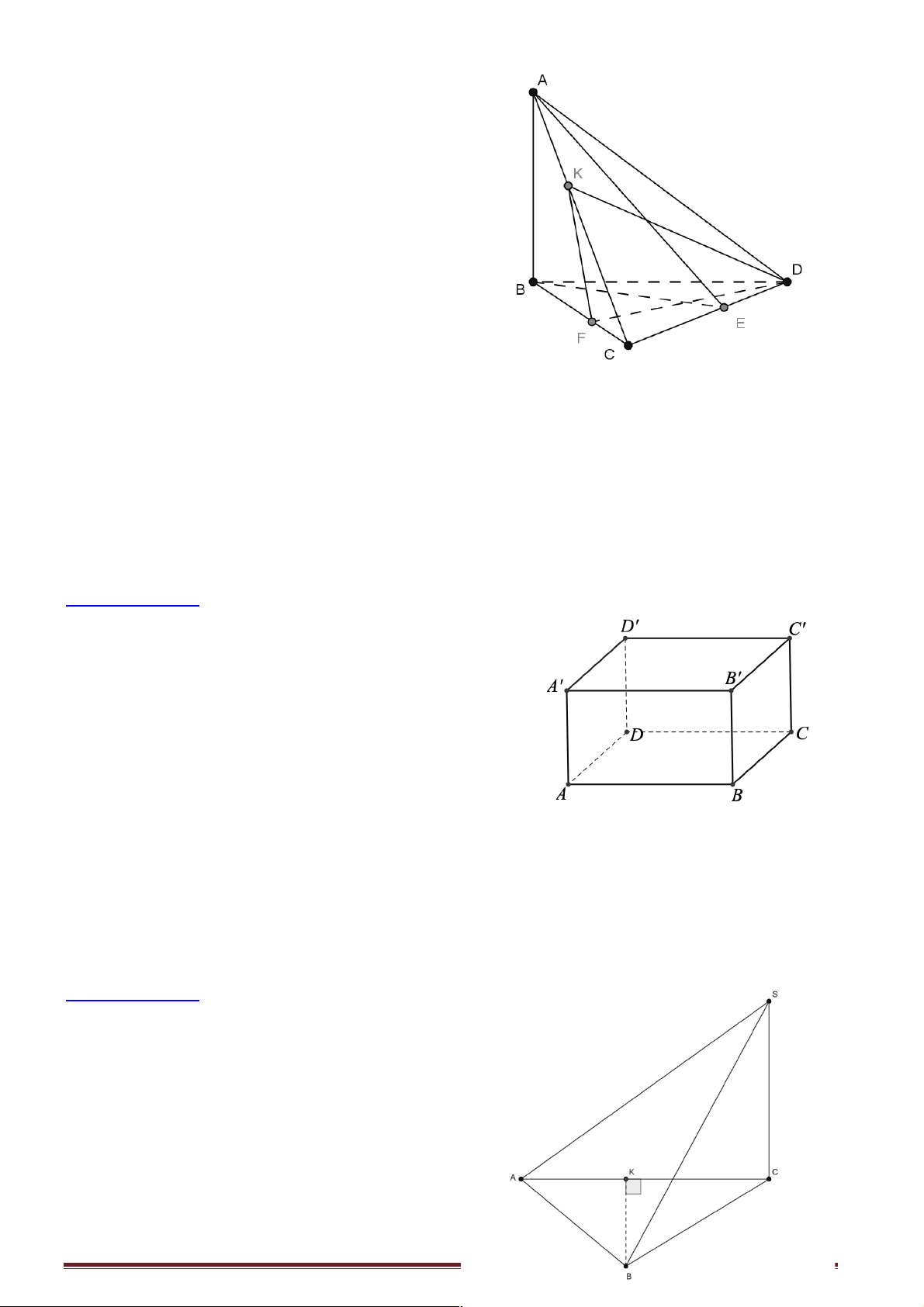
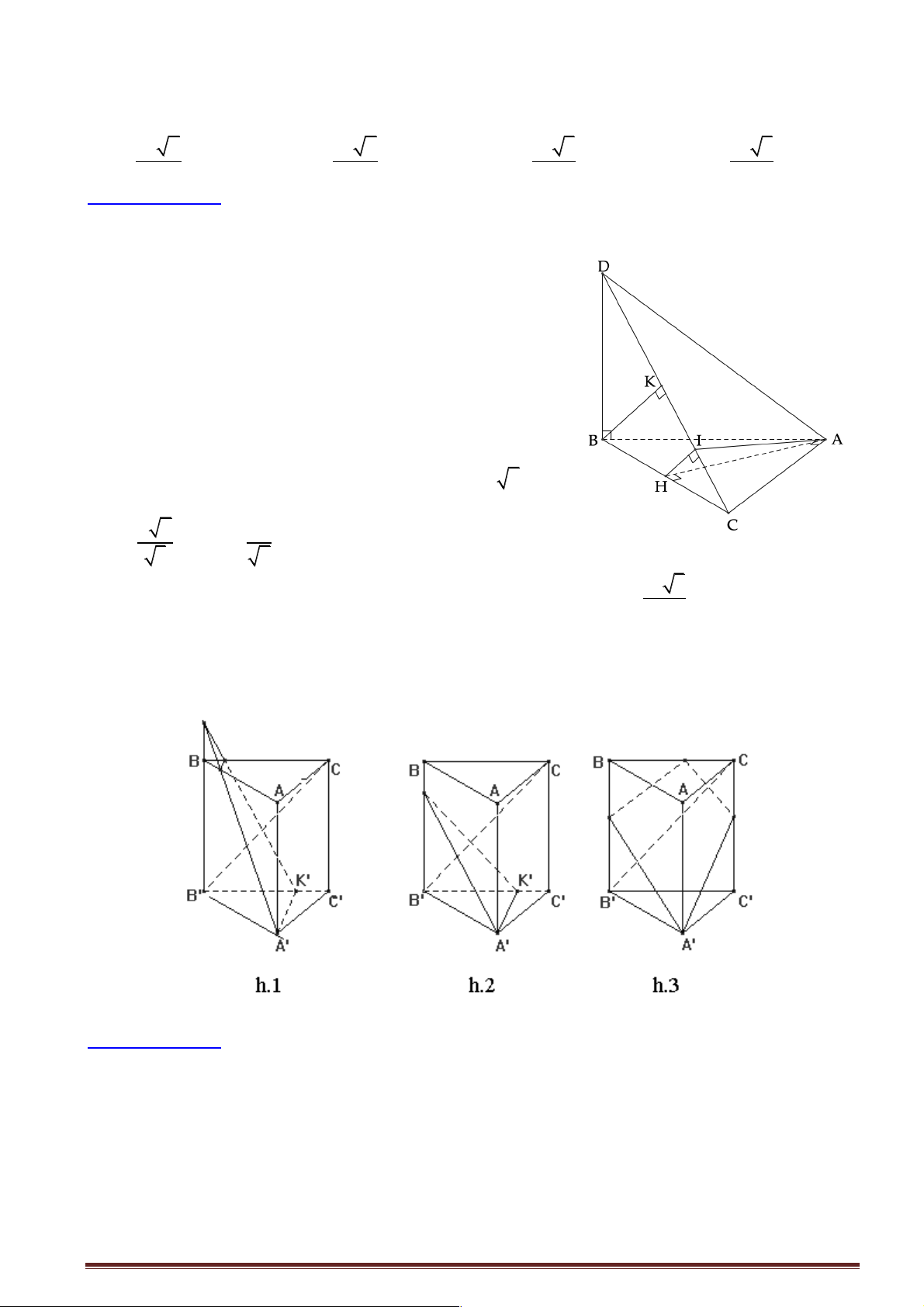
C trên (P), D trên (Q) sao cho AC ^ AB , BD ^ AB và AB = AC = BD . Thiết diện của tứ diện
ABCD khi cắt bởi mặt phẳng (a ) đi qua A và vuông góc với CD là hình gì? A. Tam giác cân. B. Hình vuông. C. Tam giác đều. D. Tam giác vuông.
Hướng dẫn giải:
Gọi I là trung điểm của BC . Vì tam giác ABC vuông cân
tại A nên AI ^ BC . (P) ^ (Q) ü ï
Ta có (P) Ç(Q) = d ý Þ BD ^ (P) Þ BD ^ AI . ( ï
Q) É BD ^ d þ
AI ^ BC üýÞ AI ^(BCD)Þ AI ^CD. AI ^ BDþ Trang 33
Trong ( ACD), dựng đường thẳng đi qua A và vuông góc với CD cắt CD tại H .
Thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (a ) là tam giác AHI .
Vì AI ^ (BCD) Þ AI ^ HI nên tam giác AHI là tam giác vuông tại I . Chọn D.
Câu 19: Cho hai tam giác ACD và BCD nằm trên hai mặt phẳng vuông góc với nhau và
AC = AD = BC = BD = ;
a CD = 2x. với giá trị nào của x thì hai mặt phẳng ( ABC) và ( ABD) vuông góc. a 3 a a 2 a A. . B. . C. . D. . 3 2 2 3
Hướng dẫn giải: YCBT Û C
D JD vuông cân tại J 2 2 AB a + a a 3 2 2 2
Û IJ = IC = ID = Û 4x = 2AI = 2( - x ) Û x = 2 2 3
( Với I là trung điểm CD ; J là trung điểm AB )
Vậy chọn đáp án A. Trang 34
DẠNG 3: TÍNH ĐỘ DÀI ĐOẠN THẲNG, DIỆN TÍCH HÌNH CHIẾU, CHU VI VÀ DIỆN TÍCH ĐA GIÁC
Câu 1: Cho hình hộp chữ nhật ABC . D A¢B C ¢ D
¢ ¢ có AB = a , BC = b , CC¢ = c . Độ dài đường chéo AC¢ là A. 2 2 2
AC ' = a + b + c . B. 2 2 2
AC ' = -a + b + c . C. 2 2 2
AC ' = a + b - c . D. 2 2 2
AC ' = a -b + c .
Hướng dẫn giải:
Từ sách giáo khoa, đường chéo hình hộp chữ nhật 2 2 2
AC ' = a + b + c Chọn A
Câu 2: Cho hình hộp ABC . D A¢B C ¢ D
¢ ¢ có AB = a , BC = b , CC¢ = c. Nếu 2 2 2
AC¢ = BD¢ = B D
¢ = a +b + c thì hình hộp là
A. Hình lập phương.
B. Hình hộp chữ nhật C. Hình hộp thoi.
D. Hình hộp đứng.
Hướng dẫn giải:
AC¢ = BD¢ Þhình bình hành ABC D ¢ ¢ là hình chữ nhật BD¢ = B D
¢ Þhình bình hành BDD B ¢ ¢ là hình chữ nhật AC¢ = B D
¢ Þhình bình hành ADC B ¢ ¢ là hình chữ nhật Chọn B
Câu 3: Cho hai mặt phẳng (P) và (Q) vuông góc với nhau. Người ta lấy trên giao tuyến d của hai
mặt phẳng đó hai điểm A và B sao cho AB = 8 . Gọi C là một điểm trên (P), D là một điểm trên
(Q) sao cho AC , BD cùng vuông góc với giao tuyến d và AC = 6, BD = 24. Độ dài CD là: A. 20 . B. 22 . C. 30 . D. 26 .
Hướng dẫn giải:
Tam giác ABC vuông tại A nên 2 2 2 2
BC = AB + AC = 8 + 6 =10. (P) ^ (Q) ü ï
Ta có (P) Ç(Q) = d ý Þ BD ^ (P) Þ BD ^ BC . ( ï
Q) É BD ^ d þ Trang 35
Tam giác BCD vuông tại B nên 2 2 2 2
CD = BD + BC = 24 +10 = 26. Chọn D.
Câu 4: Cho ba tia Ox , Oy , Oz vuông góc nhau từng đôi một. Trên Ox , Oy , Oz lần lượt lấy các điểm
A , B , C sao cho OA = OB = OC = a . Khẳng định nào sau đây sai? A. .
O ABC là hình chóp đều. 2 a 3
B. Tam giác ABC có diện tích S = . 2 3a 2
C. Tam giác ABC có chu vi 2 p = . 2
D. Ba mặt phẳng (OAB), (OBC), (OCA) vuông góc với nhau từng đôi một.
Hướng dẫn giải:. Chọn C.
+ Áp dụng định lý Pytago trong tam giác OAB vuông tại O ta có: 2 2 2 2 2 2
AB = OA + OB = a + a = 2a Þ AB = a 2 .
Hoàn toàn tương tự ta tính được BC = AC = a 2 . Þ ABC D
là tam giác đều. Mặt khác theo giả thiết
OA = OB = OC = a Þ các mặt bên của hình chóp . O ABC là
các tam giác cân tại O Þ .
O ABC là hình chóp đều Þ đáp án A đúng. + Chu vi ABC D là:
2 p = AB + AC + BC = a 2 + a 2 + a 2 = 3a 2 Þ đáp án C sai. a
+ Nửa chu vi Diện tích ABC D 3 2 là: p = . Diện tích ABC D 2 là: 3 3 3 4 2 3a 2 æ 3a 2 ö 3a 2 æ a 2 ö 3a 2 2a 2 3a a 3 S = ç - a 2 ÷ = ç ÷ = . = = (đvdt). 2 ç 2 ÷ 2 ç 2 ÷ 2 8 4 2 è ø è ø
Þ đáp án B đúng. OA ì ^ (OBC) ï ( ì OAB ï ) ^ (OBC) OB ì ^ ï (OAC)
+ Dễ chứng minh được OA í Ì (OAB) Þ í , í
Þ (OAB) ^ (OAC). ï ( ï OAC î ) ^ (OBC) OB ï Ì î (OAB) OA Ì î (OAC)
Þ đáp án D đúng.
Câu 5: Cho hình thoi ABCD có cạnh bằng a và !A = 60°. Trên đường thẳng vuông góc với mặt phẳng
(ABCD) tại O (O là tâm của ABCD), lấy điểm S sao cho tam giác SAC là tam giác đều. Khẳng
định nào sau đây đúng?
A. S.ABCD là hình chóp đều.
B. Hình chóp S.ABCD có các mặt bên là các tam giác cân. 3a C. SO = . 2
D. SA và SB hợp với mặt phẳng ( ABCD) những góc bằng nhau.
Hướng dẫn giải:. Chọn C. Xét ABD D
có !A = 60°, AB = AD = a Þ ABD D là tam giác đều
cạnh a . Vì O là tâm của ABCD nên suy ra AO là đường trung Trang 36 a 3 tuyến trong ABD D
đều cạnh a nên dễ tính được AO =
Þ AC = 2AO = a 3. 2 a
Mặt khác theo giả thiết SAC là tam giác đều Þ SA = SC = AC = 3 3
a 3 Þ SO = a 3. = . 2 2
Câu 6: Cho hình chóp cụt đều ABC.A¢B C
¢ ¢ với đáy lớn ABC có cạnh bằng a . Đáy nhỏ A¢B C ¢ ¢ có a a
cạnh bằng , chiều cao OO¢ = . Khẳng định nào sau đây sai? 2 2
A. Ba đường cao AA¢ , BB¢ , CC¢ đồng qui tại S . a
B. AA¢ = BB¢ = CC¢ = . 2
C. Góc giữa mặt bên mặt đáy là góc SIO ( I là trung điểm BC ).
D. Đáy lớn ABC có diện tích gấp 4 lần diện tích đáy nhỏ A¢B C ¢ ¢.
Hướng dẫn giải:. Chọn B.
+ Đáp án A đúng.
+ Gọi I là trung điểm của BC . AA¢ OO¢ 1
Từ giả thiết dễ dàng chỉ ra được =
= Þ SO = 2OO¢ = a . SA SO 2 Mặt khác ABC D
là tam giác đều cạnh a , có AI là đường trung a 3 a a tuyến Þ AI = 2 3 3 Þ AO = . = . 2 3 2 3
Áp dụng định lý Pytago trong SO
D A vuông tại O ta có: 2 2 æ a 3 ö 12a 2 2 2 2 2a 3
SA = SO + AO = a + ç ÷ = Þ SA = ç 3 ÷ 9 è ø 3 a 3 Þ AA¢ =
. Vì ABC.A¢B C
¢ ¢ là hình chóp cụt đều nên 3 a 3
AA¢ = BB¢ = CC¢ =
Þ đáp án B sai. 3
+ Ta có: (SBC)Ç( ABC) = BC. Vì SB
D C cân tại S và I là trung điểm của BC nên suy ra SI ^ BC . Mặt khác ABC D
là tam giác đều có I là trung điểm của BC Þ AI ^ BC .
Þ ((SBC) (ABC)) = (SI AI ) = (SI OI ) ∑ , , ,
= SIO Þ đáp án C đúng. 1 . . AB AC.sin A S . AB AC 2A¢B .2 ¢ A¢C¢ + Ta có: ABC D 2 = = =
= 4 Þ đáp án D đúng. S 1 ¢ ¢ ¢ ¢ ¢ ¢ ¢ ¢ D ¢ ¢ ¢ A B .A C A B .A C A B C
.A¢B .¢A¢C .¢sin A¢ 2 a
Câu 7: Cho hình chóp cụt tứ giác đều ABC . D A¢B C ¢ D
¢ ¢ cạnh của đáy nhỏ ABCD bằng và cạnh của 3
đáy lớn A¢B C ¢ D
¢ ¢ bằng a . Góc giữa cạnh bên và mặt đáy bằng 60°. Tính chiều cao OO¢ của hình chóp cụt đã cho. a 6 a A. OO¢ = 3 . B. OO¢ = . C. 6 2 2a 6 a OO¢ = 3 2 . D. OO¢ = . 3 4
Hướng dẫn giải:. Chọn A. Trang 37
Ta có SO¢ ^ ( A B ¢ C ¢ D ¢ ¢) É B D
¢ ¢ Þ SO¢ ^ B D ¢ ¢ Þ O D
¢ ¢ là hình chiếu vuông góc của SD¢ lên (A B ¢ C ¢ D
¢ ¢) Þ(SD¢ (ABCD)) = (SD¢ O D ¢ ¢) ∑ , , = SD O ¢ ¢ = 60°. AA¢ OO¢ 1
Từ giả thiết dễ dàng chỉ ra được = = . SA¢ SO¢ 3 Vì A D ¢D C
¢ ¢ là tam giác vuông cân tại D¢ có D O
¢ ¢ là đường cao nên ta có: 1 1 1 1 1 2 2 = + = + = a a 2 Þ D O ¢ ¢ = 2 Þ D O ¢ ¢ = . 2 2 2 2 2 2 D O ¢ ¢ A D ¢ ¢ D C ¢ ¢ a a a 2 2
Áp dụng hệ thức lượng trong SD D O
¢ ¢ vuông tại O¢ ta có: SO¢ a 2 a 6 a a tan 60° = Þ SO¢ = O D ¢ .¢tan 60° = . 3 = 1 1 6 6
Þ OO¢ = SO¢ = . = . O D ¢ ¢ 2 2 3 3 2 6
Câu 8: Cho hình lăng trụ lục giác đều ABCDEF.A B ¢ C ¢ D ¢ E ¢ F
¢ ¢ có cạnh bên bằng a và ADD A ¢ ¢ là hình
vuông. Cạnh đáy của lăng trụ bằng: a a 3 a 2 A. a . B. . C. . D. . 2 3 2
Hướng dẫn giải:. Chọn B.
Tổng số đo các góc của hình lục giác là 4.180° = 720° . Vì ABCDEF
là hình lục giác đều nên mỗi góc của hình lục giác đều ABCDEF là 120° ∑
Þ FAB =120°. Vì ABCDEF là hình lục giác đều nên ta suy ra: ∑ FAB
+ AD là tia phân giác của góc ∑ FAB và ∑ EDC ∑ Þ FAD = = 60°. 2
+ Tam giác AFD vuông tại F .
Xét tam giác AFD vuông tại F có ∑
FAD = 60° và AD = a ta suy ra: ∑ AF cos FAD = AD ∑ 1 a Þ AF = .c AD os FAD = .c a os 60° = . a = . 2 2
Câu 9: Cho hình lăng trụ tứ giác đều ABC . D A¢B C ¢ D ¢ ¢ có ACC A
¢ ¢ là hình vuông, cạnh bằng a . Cạnh
đáy của hình lăng trụ bằng: a 2 a 3 A. . B. a 2. C. . D. a 3 . 2 3
Hướng dẫn giải:. Chọn A.
Từ giả thiết ta sauy ra ABC D vuông cân tại B ∑ ∑
Þ BAC = BCA = 45°.
Áp dụng hệ thức lượng trong ABC D
vuông cân tại B có ∑
BAC = 45° và cạnh AC = a , ta có: ∑ AB a cos BAC = ∑ 2 2
Þ AB = AC.cos BAC = .c a os 45° = . a = AC 2 2 . Trang 38
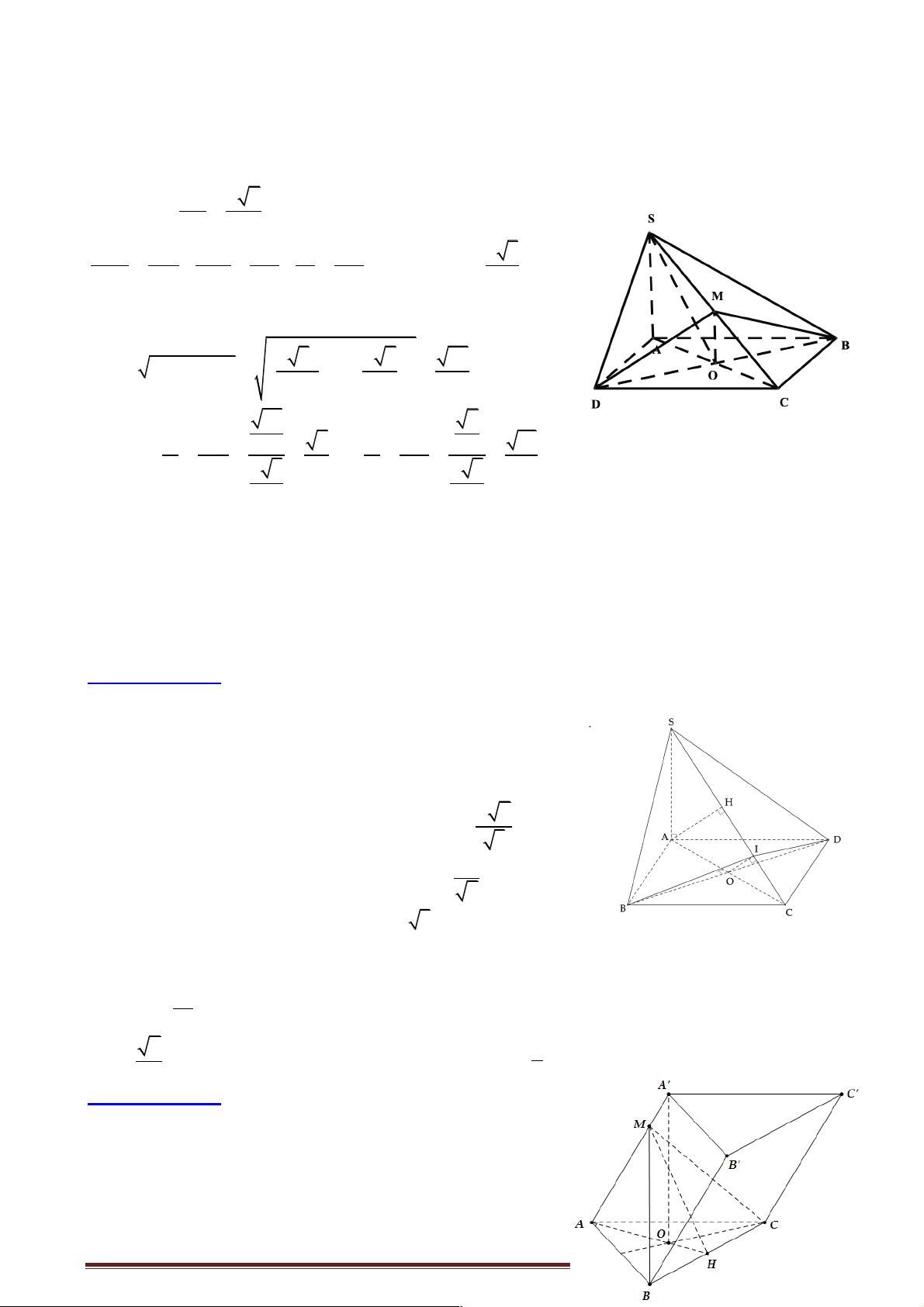
Câu 10: Cho hình lăng trụ tam giác đều ABC.A¢B C
¢ ¢ có cạnh đáy bằng 2a 3 và cạnh bên bằng 2a .
Gọi G và G¢ lần lượt là trọng tâm của hai đáy ABC và A¢B C
¢ ¢. Khẳng định nào sau đây đúng khi nói về AA¢G G ¢ ?
A. AA¢G G
¢ là hình chữ nhật có hai kích thước là 2a và 3a .
B. AA¢G G
¢ là hình vuông có cạnh bằng 2a .
C. AA¢G G
¢ là hình chữ nhật có diện tích bằng 2 6a .
D. AA¢G G
¢ là hình vuông có diện tích bằng 2 8a .
Hướng dẫn giải:. Chọn B.
Gọi M là trung điểm BC . Khi đó ta dễ dàng tính được : 3 AM = 2a 3. = 3a. 2
Vì G là trọng tâm tam giác ABC nên: 2 2
AG = AM = .3a = 2a = AA¢. 3 3 Þ AA¢G G
¢ là hình vuông có cạnh bằng 2a .
Câu 11: Cho hai tam giác ACD và BCD nằm trên hai mặt phẳng vuông góc với nhau và
AC = AD = BC = BD = a , CD = 2x . Tính AB theo a và x ? A. AB = ( 2 2 2 a + x ) . B. 2 2
AB = a - x . C. AB = ( 2 2 2 a - x ) . D. 2 2
AB = a + x .
Hướng dẫn giải:
Gọi H là trung điểm của CD . Vì tam giác ACD cân tại A và tam giác BCD cân tại B nên
AH ^ CD , BH ^ CD . Ta có ( ACD) ^ (BCD) ü ( ï
ACD) Ç(BCD) = CDý Þ AH ^ (BCD) Þ AH ^ BH . ( ï
ACD) É AH ^ CD þ AC D D = BC D D(c c c) 2 2 2 2
. . Þ AH = BH = BC - CH = a - x .
Tam giác AHB vuông tại H nên 2 2
AB = AH + BH = ( 2 2
2 a - x ) . Chọn C.
Câu 12: Cho hai tam giác ACD và BCD nằm trên hai mặt phẳng vuông góc với nhau và
AC = AD = BC = BD = a , CD = 2x . Gọi I, J lần lượt là trung điểm của AB và CD . Tính IJ theo a và x ? 2 2 a - x ( 2 2 2 a + x ) ( 2 2 2 a - x ) 2 2 a + x A. IJ = . B. IJ = . C. IJ = . D. IJ = . 2 2 2 2 Trang 39
Hướng dẫn giải: CD ì ^ AJ ï Ta có: ( í ACD) ^ (BCD)
Þ AJ ^ (BCD) Þ AJ ^ BJ . Vậy ( ï ACD î )Ç(BCD) = CD
tam giác ABJ vuông tại J Ta có: 2 2
AJ = BJ = a - x .
Do đó tam giác ABJ vuông cân tại J . Suy ra ( 2 2 2 2 a - x AJ ) IJ = = 2 2 Chọn C.
Câu 13: Cho hình chóp đều S.ABC có cạnh đáy bằng a , góc giữa một mặt bên và mặt đáy bằng 60°.
Tính độ dài đường cao SH . a a a a A. SH = 3 . B. SH = 2 . C. SH = 3 . D. SH = . 2 2 3 3
Hướng dẫn giải:. Chọn A.
Ta có: (SBC)Ç( ABC) = BC. Gọi M , N lần lượt là trung điểm của
các cạnh BC và AC .
Dễ chứng minh được SM ^ BC và AM ^ BC .
Þ ((SBC) (ABC)) = (SM AM ) ∑ ∑ , ,
= SMA = SMH = 60°. a 3
Ta dễ tính được: AM =
. Vì H là chân đường cao của hình chóp 2
đều S.ABC nên H trùng với trọng tâm của tam giác ABC 1 1 a 3 a 3 Þ MH = AM = . = . 3 3 2 6
Áp dụng hệ thức lượng trong tam giác SHM vuông tại H ta có : ∑ SH a a a a tan SMH = ∑ 3 3 3
Þ SH = MH.tan SMH = .tan 60° = . 3 = = . MH 6 6 6 2
Câu 14: Cho hình lăng trụ đứng ABC.A¢B C
¢ ¢ có AB = AA¢ = a , BC = 2a , CA = a 5 . Khẳng định nào sau đây sai?
A. Đáy ABC là tam giác vuông.
B. Hai mặt ( AA B ¢ B ¢ ) và (BB C ¢ ¢) vuông góc nhau.
C. Góc giữa hai mặt phẳng ( ABC) và ( A B
¢ C) có số đo bằng 45°.
D. AC¢ = 2a 2 .
Hướng dẫn giải:. Chọn D.
+ Cách 1: Chứng minh trực tiếp chỉ ra D là đáp án sai.
Từ giả thiết dễ dàng suy ra CC¢ = AA¢ = a .
Áp dụng định lý Pytago trong tam giác ACC¢ vuông tại C ta có: 2 2 2 2 2 2
AC¢ = AC + CC¢ = 5a + a = 6a Þ AC¢ = a 6 Þ đáp án D sai.
+ Cách 2: Chứng minh 3 đáp án A , B , C đều đúng
suy ra đáp án D sai. Trang 40
Câu 15: Cho hình chóp tứ giác S.ABCD , có đáy ABCD là hình thoi tâm I cạnh bằng a và góc ! a 0 A = 6 60 , cạnh SC =
và SC vuông góc với mặt phẳng ( ABCD). Trong tam giác SCA kẻ 2
IK ^ SA tại K . Tính độ dài IK được a a 3 a a 2 A. B. C. D. 2 3 3 2
Hướng dẫn giải: IK AI
Tam giác AKI đồng dạng tam giác ACS Þ = Þ SC SA SC.AI IK = SA a 3 BCD D và ABD D
đều cạnh a Þ IA = IC = Þ 2 AC = a 3 SA
D C vuông tại C Þ 2 2
SA = SC + AC = 2 æ a ö 3a 2 ç ÷ + (a )2 6 3 = è 2 ø 2 a Vậy IK = 2 Chọn A
Câu 16: Cho tam giác ABC và mặt phẳng (P). Biết góc giữa mặt phẳng (P) và mặt phẳng ( ABC) là
j . Hình chiếu của tam giác ABC trên mặt phẳng (P) là tam giác A¢B C
¢ .¢ Tìm hệ thức liên hệ giữa
diện tích tam giác ABC và diện tích tam giác A¢B C ¢ .¢ A. S = S .cotj. B. S = S .sinj. A D 'B'C ' A D BC A D 'B'C ' A D BC C. S = S .tanj. D. S = S .cosj. A D 'B'C ' A D BC A D 'B'C' A D BC
Hướng dẫn giải:
Qua B kẻ mặt phẳng (Q) // (P) cắt AA ;¢CC¢ lần lượt tại A ;C 1 1 khi đó S = ¢ ¢ ¢ S A B C 1 A 1 BC
Góc giữa mặt phẳng (P) và mặt phẳng ( ABC) bằng góc giữa
mặt phẳng ( ABC)và (BAC j 1 1 ) và bằng
Kẻ AH ^ BF Þ A H ^ BF 1 1 S = A H.BF 1 A B 1 C 1 2 1 = AH.cosj.BF 2 = S .cosj ABC Vậy S = S .cosj. A D 'B'C' A D BC Trang 41
DẠNG 4: XÁC ĐỊNH THIẾT DIỆN CHỨA MỘT ĐƯỜNG THẲNG VÀ VUÔNG
GÓC VỚI MỘT MẶT PHẲNG. Phương pháp:
Cho mặt phẳng (a ) và đường thẳng a không vuông góc với (a ).Xác định mặt phẳng (b ) chứa a và vuông góc với (a ) β a A b d α H .
Để giải bài toán này ta làm theo các bước sau:
• Chọn một điểm AÎ a
• Dựng đường thẳng b đi qua A và vuông góc với (a ). Khi đó mp(a,b) chính là mặt phẳng (b ).
Câu 1: Cho hình chóp S.ABCD , đáy ABCD là hình vuông, SA ^ (ABCD). Gọi (a) là mặt phẳng
chứa AB và vuông góc với (SCD), (a) cắt chóp S.ABCD theo thiết diện là hình gì? A. hình bình hành. B. hình thang vuông.
C. hình thang không vuông. D. hình chữ nhật.
Hướng dẫn giải: Dựng AH ^ CD CD ^ SA ¸Ô Ta có
˝ fi CD ^ (SAD). CD ^ ADÔ ˛ Suy ra CD ^ AH
mà AH Ã (SCD) suy ra AH Ã (a)
Do đó a ∫ AHB ( ) ( ) Vì a
nên a « SAD = HK CD K SC Œ . ( ) //CD ( ) ( ) // ( )
Từ đó thiết diện là hình thang ABKH .
Mặt khác AB ^ (SAD) nên AB ^ AH
Vậy thiết diện là hình thang vuông tại A và H . Chọn đáp án B. a a a Ta có 2 2
AC = a 2,OC =
, SO = SC - OC = 1
, mà SO ^ OC Þ OM = SC = . Chon A 2 2 2 2
Câu 2: Cho hình chóp S.ABCD với ABCD là hình chữ nhật tâm O có AB = a, AD = 2 . a SA vuông
góc với đáy và SA = a . Gọi (P)là mặt phẳng qua SO và vuông góc với (SAD). Diện tích thiết diện
của (P) và hình chóp S.ABCD bằng bao nhiêu? 3 2 2 a A. 2 a . B. 2 a . C. . D. 2 a . 2 2 2
Hướng dẫn giải:
Gọi MN là đoạn thẳng qua O vuông góc AD ( M , N thuộc ,
AD BC ) ta có MN ^( SAD) nên
SMN là thiết diện cần tìm. D SM.MN 2
SMN vuông tại M nên 2 S = = a . SMN 2 2 Chọn B. Trang 42
Câu 3: Cho hai mặt phẳng vuông góc (P) và (Q) có giao tuyến D . Lấy A , B cùng thuộc D và lấy
C trên (P), D trên (Q) sao cho AC ^ AB , BD ^ AB và AB = AC = BD = a . Diện tích thiết diện
của tứ diện ABCD khi cắt bởi mặt phẳng (a ) đi qua A và vuông góc với CD là? 2 a 2 2 a 2 2 a 3 2 a 3 A. B. C. D. 12 8 12 8
Hướng dẫn giải: Chọn C. Ta có: ì(P) ^ (Q) ï í(P) Ç(Q) = D Þ BD ^ (P)
ïBD Ì (Q),BD ^ D î ìAH ^ BC
Gọi H là trung điểm BC , ta có í Þ AH ^ CD îAH ^ BD
Trong mặt phẳng (BCD) , kẻ HI ^ CD thì ta có CD ^ (AHI )
Khi đó mặt phẳng (a ) cắt tứ diện ABCD theo thiết diện là tam giác AHI
Mặt khác tam giác ABC vuông cân tại A nên BC = a 2 .
Trong tam giác vuông BCD , kẻ đường cao BK thì a 2 a BK = và HI = 3 6 2 a 3
Vậy: thiết diện cần tìm là tam giác AHI vuông tại H và có diện tích S = 12
Câu 4: Cho hình lăng trụ đứng ABC. ’ A ’
B C’ có đáy ABC là tam giác vuông tại A , với AB = c , AC = b , cạnh bên ’
AA = h . Mặt phẳng (P) đi qua ’
A và vuông góc với ’
B C .Thiết diện của lăng trụ cắt bởi
mặt phẳng (P) có hình: A. .1 h và .2 h . B. .2 h và .3 h . C. .2 h . D. .1 h .
Hướng dẫn giải:
Gọi (P) là mặt phẳng đi qua A' và vuông góc với BC . Từ A' ta dựng A' K ' ^ B 'C ' , Vì
(ABC) ^ (BCC ' B ') nên A' K ' ^ B 'C ' Þ A' K ' ^ (BCC ' B ') Þ A' K ' ^ BC ' (1) .
Mặt khác trong mặt phẳng (BCC ' B ') dựng K ' x ^ B 'C và cắt B ' B tại 1 điểm N (2) (điểm gì đề
chưa có cho nên cho tạm điểm N ).
ìBC ' ^ A' K ' Từ (1) và (2)ta có : í
Þ BC ' ^ (A' K ' N)
îBC ' ^ K ' N
Chọn đáp án A Trang 43
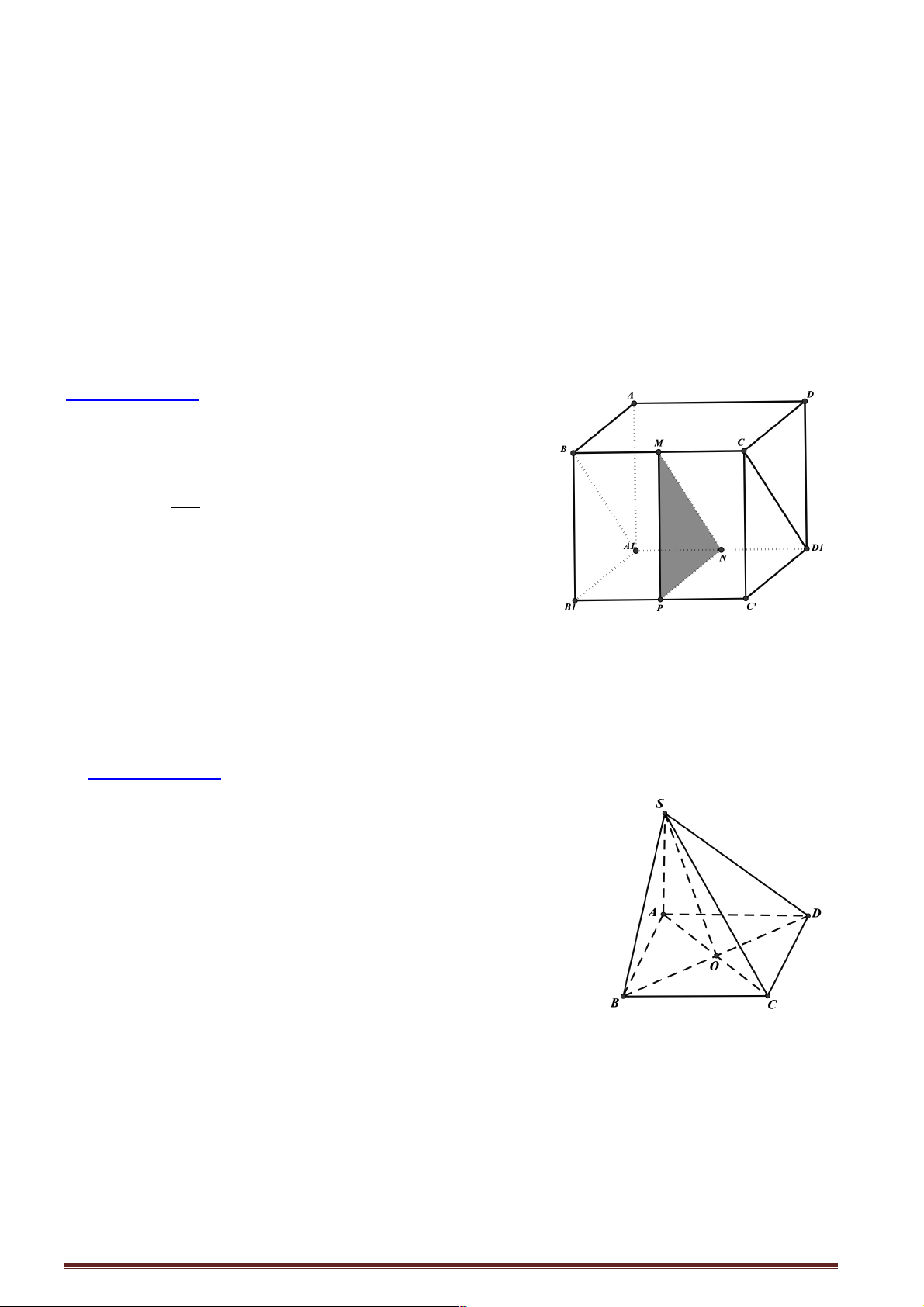
Câu 5: Cho hình lập phương ABC .
D A' B 'C ' D ' có cạnh bằng a . Cắt hình lập phương bởi mặt phẳng
trung trực của AC ' . Thiết diện là hình gì? A. Hình vuông. B. Lục giác đều. C. Ngũ giác đều. D. Tam giác đều.
Hướng dẫn giải:
Ta có AC là hình chiếu của AC ' lên (ABCD) .
mà AC ^ BD nên AC ' ^ , BD (1)
AD ^ (AA' B ' B)¸Ô Ta có
˝ fi A' B ^ AD
A' B Ã (AA' B ' B Ô ˛
Lại có A' B ^ AB ' suy ra
A' B ^ (AB 'C ' D)¸Ô
˝ fi AC ' ^ A' B, (2)
AC ' Ã (AB 'C ' D) Ô ˛
Từ (1) và (2) suy ra AC ' ^ (A' BD), (3)
Mặt phẳng trung trực AC ' là mặt phẳng (a) đi qua
trung điểm I của AC ' và (a) ^ AC ', (4) Ï mp Ô (a) qua I Từ (3) và (4) suy ra Ì (
Ô a)//(A' BD) Ó Do đó
Qua I dựng MQ//BD Dựng MN //A'D
NP//B ' D ' //BD QK //B'C//A'D KH //BD a 2
Mà MN = NP = PQ = QK = KM = 2
Suy ra thiết diện là lục giác đều. Chọn đáp án B.
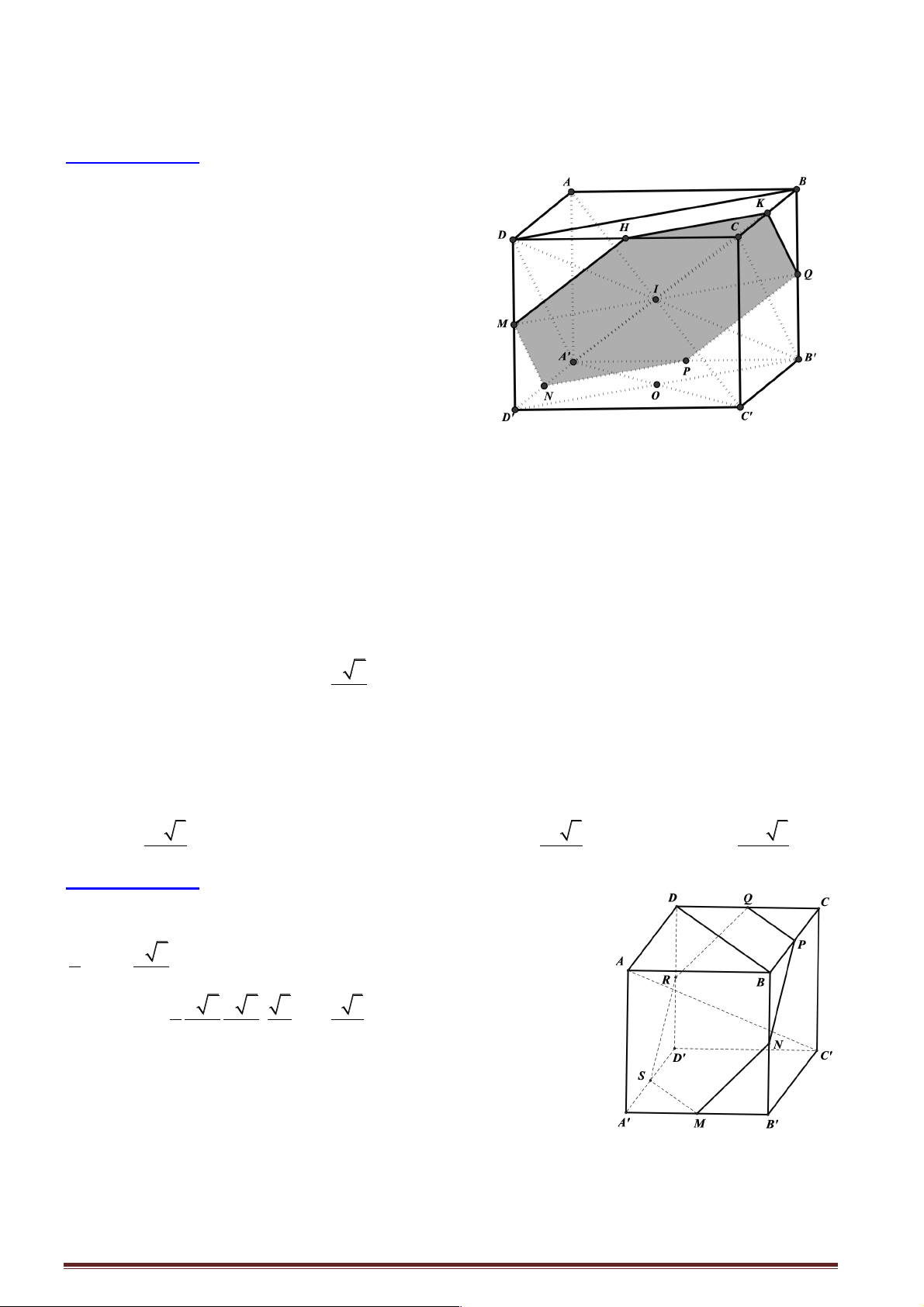
Câu 6: Cho hình lập phương ABC . D A¢B C ¢ D ¢ ¢ có cạnh bằng .
a Cắt hình lập phương bởi mặt phẳng
trung trực của AC .¢ Diện tích thiết diện là 2 a 3 2 a 3 2 3a 3 A. S = . B. 2 S = a . C. S = . D. S = . 2 4 4
Hướng dẫn giải:
Ta có mặt phẳng trung trực của AC¢cắt hình lập phương ABC . D A¢B C ¢ D
¢ ¢ theo thiết diện là lục giác đều MNPQRDS cạnh 1 a 2 B C ¢ = 2 2 1 a 2 a 2 3 3 3 Khi đó 2 S = 6. . = a 2 2 2 2 4 Trang 44