TOP 130 câu trắc nghiệm đường thẳng vuông góc với mặt phẳng (có đáp án)

TOP 130 câu trắc nghiệm đường thẳng vuông góc với mặt phẳng có đáp án và lời giải rất hay được viết dưới dạng file word gồm 46 trang. Bài tập được phân thành các dạng:chứng minh đường thẳng vuông góc với mặt phẳng và đường thẳng vuông góc đường thẳng; tính góc giữa đường thẳng và mặt phẳng; thiết diện và các bài toán liên quan. Các bạn xem và tải về ở dưới.

24 12 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung Toán 11

Môn: Toán 11

Thông tin:

45 trang 9 tháng trước

Tác giả:

Profile Thùy Dương (H)
Trang 1
BÀI TẬP TRẮC NGHIỆM
ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG
A – LÝ THUYẾT TÓM TẮT
1. Định nghĩa
d ^ (P) Û d ^ a, "a Ì (P)
2. Điều kiện để đường thẳng vuông góc với mặt phẳng
3. Tính chất
• Mặt phẳng trung trực của một đoạn thẳng là mặt phẳng vuông góc với đoạn thẳng tại trung
điểm của nó.
Mặt phẳng trung trực của đoạn thẳng là tập hợp các điểm cách đều hai đầu mút của đoạn thẳng
đó.
• •
• •
• •
4. Định lí ba đường vuông góc
Cho , a¢ là hình chiếu của a trên (P). Khi đó b ^ a Û b ^ a¢
5. Góc giữa đường thẳng và mặt phẳng
• Nếu d ^ (P) thì = 90
0
.
• Nếu thì = với d¢ là hình chiếu của d trên (P).
Chú ý: 0
0
£ £ 90
0
.
B – BÀI TẬP
Câu 1: Cho hai đường thẳng phân biệt và mặt phẳng , trong đó . Mệnh đề nào sau
đây là sai?
A. Nếu thì . B. Nếu thì .
C. Nếu thì . D. Nếu thì .
Hướng dẫn giải:
Chọn D.
Câu 2: Trong không gian cho đường thẳng và điểm . Qua có mấy đường thẳng vuông góc với
D cho trước?
A. . B. . C. . D. Vô số.
Hướng dẫn giải:
Chọn D.
Qua điểm có thể dựng vô số đường thẳng vuông góc với , các đường thẳng đó cùng nằm trong
một mặt phẳng vuông góc với .
Câu 3: Mệnh đề nào sau đây có thể sai?
A. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song.
B. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song.
C. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì song song.
D. Một đường thẳng và một mặt phẳng (không chứa đường thẳng đã cho) cùng vuông góc với một
đường thẳng thì song song nhau.
Hướng dẫn giải:
Chọn C.
,(),
()
,
ab P a b O
dP
dadb
ì
ÌÇ=
Þ^
í
^^
î
()
()
ab
Pb
Pa
ì
⁄⁄
Þ^
í
^
î
(), ()
ab
ab
aPbP
ì
¹
Þ ⁄⁄
í
^^
î
()()
()
()
PQ
aQ
aP
ì
⁄⁄
Þ^
í
^
î
() ()
() )
() ,()
PQ
PQ
PaQa
ì
¹
Þ ⁄⁄(
í
^^
î
()
()
aP
ba
bP
ì
⁄⁄
Þ^
í
^
î
()
)
,( )
aP
aP
abP b
ì
Ë
Þ⁄⁄(
í
^^
î
∑
( )
,( )dP
()dP^
∑
( )
,( )dP
∑
( )
,'dd
∑
( )
,( )dP
,ab
( )
P
( )
aP^
( )
bP^
//ba
( )
//bP
ba^
//ba
( )
bP^
ba^
( )
//bP
D
O
O
1
2
3
O
D
D
Trang 2
Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì song song chỉ đúng khi ba
đường thẳng đó đồng phẳng.
Câu 4: Khẳng định nào sau đây sai?
A. Nếu đường thẳng thì vuông góc với hai đường thẳng trong .
B. Nếu đường thẳng vuông góc với hai đường thẳng nằm trong thì .
C. Nếu đường thẳng vuông góc với hai đường thẳng cắt nhau nằm trong thì vuông góc
với bất kì đường thẳng nào nằm trong .
D. Nếu và đường thẳng thì .
Hướng dẫn giải:
Chọn B.
Đường thẳng vuông góc với hai đường thẳng nằm trong thì chỉ đúng khi hai đường
thẳng đó cắt nhau.
Câu 5: Trong không gian tập hợp các điểm cách đều hai điểm cố định và là
A. Mặt phẳng trung trực của đoạn thẳng . B. Đường trung trực của đoạn thẳng .
C. Mặt phẳng vuông góc với tại . D. Đường thẳng qua và vuông góc với .
Hướng dẫn giải:
Chọn A.
Theo định nghĩa mặt phẳng trung trực.
Câu 6: Trong không gian cho đường thẳng và điểm . Qua có bao nhiêu đường thẳng vuông góc
với cho trước?
A. Vô số. B. 2. C. 3. D. 1.
Hướng dẫn giải:
Chọn A.
Câu 7: Qua điểm cho trước, có bao nhiêu mặt phẳng vuông góc với đường thẳng cho trước?
A. B. Vô số C. D.
Hướng dẫn giải:
Theo tiên đề qua điểm cho trước có duy nhất một mặt phẳng vuông góc với đường thẳng D
Chọn đáp án A.
Câu 8: Trong không gian cho đường thẳng không nằm trong mp , đường thẳng được gọi là
vuông góc với mp nếu:
A. vuông góc với hai đường thẳng phân biệt nằm trong mp
B. vuông góc với đường thẳng mà song song với mp
C. vuông góc với đường thẳng nằm trong mp
D. vuông góc với mọi đường thẳng nằm trong mp
Hướng dẫn giải:
Đường thẳng được gọi là vuông góc với mặt phẳng nếu vuông góc với mọi đường thẳng
trong mặt phẳng .(ĐN đường thẳng vuông góc với mặt phẳng). Vậy đáp án D đúng.
Câu 9: Cho là các đường thẳng trong không gian. Tìm mệnh đề sai trong các mệnh đề sau.
A. Nếu và thì
B. Nếu vuông góc với mặt phẳng và thì
C. Nếu và thì
D. Nếu , và cắt thì vuông góc với mặt phẳng
Hướng dẫn giải:
Nếu thì và có thể trùng nhau nên đáp án A sai.
Câu 10: Trong các mệnh đề sau, mệnh đề nào sai?
( )
d
a
^
d
( )
a
d
( )
a
( )
d
a
^
d
( )
a
d
( )
a
( )
d
a
^
( )
//a
a
da^
d
( )
a
( )
d
a
^
M
A
B
AB
AB
AB
A
A
AB
D
O
O
D
O
D
1
3
2
O
D
( )
P
D
( )
P
( )
.P
a
a
( )
P
a
( )
.P
( )
.P
D
( )
P
D
( )
P
,,abc
ab^
bc^
// .ac
a
( )
a
( )
//b
a
.ab^
//ab
bc^
.ca^
ab^
bc^
a
c
b
( )
,.ac
ab
bc
^
ì
í
^
î
a
c
Trang 3
A. Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho
trước.
B. Có duy nhất một mặt phẳng đi qua một đường thẳng cho trước và vuông góc với một mặt phẳng
cho trước.
C. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho
trước.
D. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho
trước.
Hướng dẫn giải:
Qua một điểm cho trước có thể kẻ được vô số mặt phẳng vuông góc với mặt phẳng cho trước.
Vậy chọn đáp án .
Câu 11: Chọn mệnh đề đúng trong các mệnh đề sau?
A. Nếu và thì B. Nếu và thì .
C. Nếu và thì . D. Nếu và thì .
Câu 12: Cho hai đường thẳng và . Chỉ ra mệnh đề đúng trong các mệnh đề sau:
A. Nếu và thì . B. Nếu và thì .
C. Nếu và thì . D. Nếu và thì .
Hướng dẫn giải:
Câu A sai vì có thể vuông góc với .
Câu B đúng bởi sao cho , . Khi đó .
Câu C sai vì có thể nằm trong .
Câu D sai vì có thể nằm trong .
Vậy chọn B.
Câu 13: Chỉ ra mệnh đề sai trong các mệnh đề sau:
A. Hai đường thẳng chéo nhau và vuông góc với nhau. Khi đó có một và chỉ một mp chứa đường
thẳng này và vuông góc với đường thẳng kia.
B. Qua một điểm cho trước có một mặt phẳng duy nhất vuông góc với một đường thẳng D cho
trước.
C. Qua một điểm cho trước có một và chỉ một đường thẳng vuông góc với một đường thẳng cho
trước.
D. Qua một điểm cho trước có một và chỉ một đường thẳng vuông góc với một mặt phẳng cho
trước.
Câu 14: Tập hợp các điểm cách đều các đỉnh của một tam giác là đường thẳng vuông góc với mặt
phẳng chứa tam giác đó và đi qua:
A. Tâm đường tròn ngoại tiếp tam giác đó. B. Trọng tâm tam giác đó.
C. Tâm đường tròn nội tiếp tam giác đó. D. Trực tâm tam giác đó.
Câu 15: mệnh đề đúng trong các mặt phẳng sau:
A. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song.
B. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song.
C. Hai đường thẳng cùng vuông góc với một mặt phẳng thì song song.
D. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song.
Hướng dẫn giải::
Đáp án A sai vì hai đường thẳng đó có thể chéo nhau.
Đáp án B sai vì hai mặt phẳng đó có thể cắt nhau.
Đáp án C sai vì hai đường thẳng đó có thể trùng nhau.
Chọn đáp án D.
Câu 16: Chỉ ra mệnh đề sai trong các mệnh đề sau:
A. Cho hai đường thẳng vuông góc với nhau, mặt phẳng nào vuông góc với đường thẳng này thì
cũng vuông góc với đường thẳng kia.
B. Hai đường thẳng phân biệt cùng vuông góc với một mp thì song song với nhau.
D
( )
aP^
ba^
( )
.!bP
( )
!aP
!ab
( )
!bP
( )
!aP
ba^
( )
bP^
( )
!aP
( )
bP^
ba^
,ab
( )
mp P
( )
//aP
ba^
( )
//bP
( )
//aP
( )
bP^
ab^
( )
//aP
ba^
( )
bP^
( )
aP^
ba^
( )
//bP
b
a
( ) ( )
//aP a P
¢
Þ$ Ì
//aa
¢
( )
bP ba
¢
^Þ^
abÞ^
b
( )
P
b
( )
P
O
O
O
Trang 4
C. Cho hai mp song song, đường thẳng nào vuông góc với mặt mp này thì cũng vuông góc với mp
kia.
D. Cho hai đường thẳng song song, mặt phẳng nào vuông góc với đường thẳng này thì cũng vuông
góc với đường thẳng kia.
Hướng dẫn giải:
Vì qua một đường thẳng dựng được vô số mặt phẳng
Câu 17: Trong các mệnh đề sau, mệnh đề nào sai?
A. Nếu đường thẳng song song với mặt phẳng và đường thẳng vuông góc với thì
vuông góc với mặt phẳng
B. Nếu đường thẳng song song với đường thẳng và song song với mặt phẳng thì
song song hoặc nằm trên mặt phẳng
C. Nếu đường thẳng song song với mặt phẳng và đường thẳng vuông góc với mặt phẳng
thì vuông góc với
D. Một đường thẳng vuông góc với hai đường thẳng cắt nhau trong một mặt phẳng thì nó vuông
góc với mặt phẳng đó.
Hướng dẫn giải:
Giả sử xét hình lập phương như hình vẽ có
nhưng
Chọn đáp án A.
Câu 18: Cho hình chóp có và tam giác vuông tại . Vẽ ,
. Khẳng định nào sau đây đúng?
A. trùng với trọng tâm tam giác . B. trùng với trực tâm tam giác .
C. trùng với trung điểm của . D. trùng với trung điểm của .
Hướng dẫn giải:
Chọn C.
Do nên . Suy ra là tâm đường tròn
ngoại tiếp .
Mà vuông tại nên là trung điểm của .
Câu 19: Cho hình chóp thỏa mãn . Tam giác vuông tại . Gọi là
hình chiếu vuông góc của lên . Chọn khẳng định sai trong các khẳng định sau?
A. . B. .
C. . D.
.
Hướng dẫn giải:.
Chọn A.
a
( )
P
b
a
b
( )
.P
a
b
b
( )
P
a
( )
.P
a
( )
P
b
( )
P
a
.b
.' ' ' 'ABCD A B C D
( )
''//
'' ''
AB ABCD
BC AB
Ï
Ô
Ô
Ì
Ô
^
Ô
Ó
( )
''// .BC ABCD
.S ABC
SA SB SC==
ABC
B
( )
SH ABC^
( )
HABCÎ
H
ABC
H
ABC
H
AC
H
BC
SA SB SC==
HA HB HC==
H
ABCD
ABCD
B
H
AC
.S ABC
SA SB SC==
ABC
A
H
S
( )
mp ABC
( ) ( )
SBH SCH SHÇ=
( ) ( )
SAH SBH SHÇ=
AB SH^
( ) ( )
SAH SCH SHÇ=
( ) ( ) ( )
SBH SCH SBCÇ=
Trang 5
Câu 20: Cho hình chóp có các cạnh bên bằng nhau . Gọi là hình
chiếu của lên mặt đáy . Khẳng định nào sau đây sai?
A. .
B. Tứ giác là hình bình hành.
C. Tứ giác nội tiếp được trong đường tròn.
D. Các cạnh , , , hợp với đáy những góc bằng nhau.
Hướng dẫn giải:
Chọn B.
Vì hình chóp có các cạnh bên bằng nhau
và là hình chiếu của lên mặt đáy
Nên tâm đường tròn ngoại tiếp tứ giác
Suy ra . Nên đáp án B sai.
Câu 21: Cho hình chóp có và tam giác không vuông, gọi lần lượt là
trực tâm các tam giác và . Các đường thẳng thỏa mãn:
A. Đồng quy. B. Đôi một song song.
C. Đôi một chéo nhau. D. Đáp án
khác.
Hướng dẫn giải:
Gọi là đường cao của tam giác mà
nên
Câu 22: Cho hình chóp có các mặt bên tạo với đáy một góc
bằng nhau. Hình chiếu của trên là:
A. Tâm đường tròn nội tiếp tam giác B. Tâm đường tròn ngoại tiếp tam giác
C. Trọng tâm tam giác D. Giao điểm hai đường thẳng và
Hướng dẫn giải:
Gọi lần lượt là hình chiếu của lên các cạnh
Theo định lý ba đường vuông góc ta có lần lượt là hình chiếu của lên các cạnh
là tâm dường tròn nội tiếp của
Câu 23: Cho hình chóp đều, chọn mệnh đề sai trong các mệnh đề sau:
A. Chân đường cao của hình chóp đều trùng với tâm của đa giác đáy đó.
B. Tất cả những cạnh của hình chóp đều bằng nhau.
C. Đáy của hình chóp đều là miền đa giác đều.
D. Các mặt bên của hình chóp đều là những tam giác cân.
Hướng dẫn giải:
Hình chóp đều có thể có cạnh bên và cạnh đáy KHÔNG bằng nhau nên đáp án B sai.
Câu 24: Tính chất nào sau đây không phải là tính chất của hình lăng trụ đứng?
A. Các mặt bên của hình lăng trụ đứng là những hình bình hành.
B. Các mặt bên của hình lăng trụ đứng là những hình chữ nhật.
C. Các cạnh bên của hình lăng trụ đứng bằng nhau và song song với nhau.
D. Hai đáy của hình lăng trụ đứng có các cạnh đôi một song song và bằng nhau.
.S ABCD
SA SB SC SD== =
H
S
ABCD
HA HB HC HD== =
ABCD
ABCD
SA
SB
SC
SD
ABCD
.S ABCD
SA SB SC SD== =
H
S
ABCD
H
ABCD
HA HB HC HD== =
.S ABC
()SA ABC^
ABC
, HK
ABC
SBC
, , AH SK BC
AA
¢
ABC
'AA BCÞ^
BC SA^
'BC SA^
.S ABC
H
S
().ABC
.ABC
.ABC
.ABC
AC
.BD
,,MNP
S
,,.AB AC BC
,,MNP
H
,,.AB AC BC
∑
∑
∑
.SMH SNH SPH SMH SNH SPHÞ==ÞD=D=D
HM HN NPÞ==Þ
H
.ABCD
Trang 6
Hướng dẫn giải:
Chọn A.
Trang 7
DẠNG 1: CHỨNG MINH ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG
VÀ ĐƯỜNG THẲNG VUÔNG GÓC ĐƯỜNG THẲNG
Phương pháp:
* Chứng minh đường thẳng vuông góc với mặt phẳng
Muốn chứng minh đương thẳng ta có thể dùng môt trong hai cách sau.
Cách 1. Chứng minh vuông góc với hai đường thẳng cắt nhau trong .
Cách 2. Chứng minh vuông góc với đường thẳng mà vuông góc với .
Cách 3. Chứng minh d vuông góc với (Q) và (Q) // (P).
* Chứng minh hai đường thẳng vuông góc
Để chứng minh d ^ a, ta có thể chứng minh bởi một trong các cách sau:
• Chứng minh d vuông góc với (P) và (P) chứa a.
• Sử dụng định lí ba đường vuông góc.
• Sử dụng các cách chứng minh đã biết ở phần trước.
Câu : Cho hình chóp có và vuông ở , là đường cao của
. Khẳng định nào sau đây sai?
A. . B. . C. . D. .
Hướng dẫn giải:
Chọn C.
Do nên câu A đúng.
Do nên câu B và D đúng.
Vậy câu C sai.
Câu 1: Cho tứ diện có là tam giác vuông tại và
a) Khẳng định nào sau đây là đúng nhất. Chứng minh .
A. B.
C. D.
b) Gọi là đường cao của tam giác , thì khẳng định nào sau đây đúng nhất. Chứng minh
.
A. B.
C. D.
Hướng dẫn giải:.
a) Ta có nên .
Do đó Chọn A
( )
^d
a
d
,ab
( )
a
( ) ( )
( )
,
^
ì
ï
^
ï
Þ^
í
ÌÌ
ï
ï
Ç=
î
da
db
a
ab
abI
a
aa
d
a
a
( )
a
( )
( )
ì
ï
Þ^
í
^
ï
î
!da
d
a
a
a
.S ABCD
( )
SA ABCD^
ABCD
B
AH
SABD
SA BC^
AH BC^
AH AC^
AH SC^
( )
SA ABC^
( )
BC SAB^
SABC
ABC
B
( )
^SA ABC
( )
^BC SAB
( )
^BC SAB
( )
^BC SAC
∑
( )
0
,45=AD BC
∑
( )
0
,80=AD BC
AH
SAB
^AH SC
^AH AD
^AH SC
( )
^AH SAC
^AH AC
( )
^SA ABC
^SA BC
( )
^
ü
Þ^
ý
^
þ
BC SA
BC SAB
BC AB
A
B
C
D
H
Trang 8
b) Ta có
Vậy .Chọn B
Câu 2: Cho tứ diện có và . Khẳng định nào sau đây đúng?
A. . B. . C. . D. .
Hướng dẫn giải:
Chọn D.
Gọi là trung điểm của . Khi đó ta có
.
Câu 3: Cho hình chóp có và Số các mặt của tứ diện là tam
giác vuông là:
A. B. C. D.
Hướng dẫn giải:
Có là tam giác vuông tại
Ta có là các tam giác vuông tại
Mặt khác là tam giác vuông tại
Vậy bốn mặt của tứ diện đều là tam giác vuông. Nên đáp án D đúng.
Câu 4: Cho hình chóp có đáy là hình thoi tâm . Biết và . Khẳng
định nào sau đây sai?
A. . B. . C. . D. .
Hướng dẫn giải:
Chọn B.
Tam giác cân tại có là trung tuyến cũng là đường cao .
Tam giác cân tại có là trung tuyến cũng là đường cao .
Từ đó suy ra .
Do là hình thoi nên không vuông góc với . Do đó không vuông góc với .
Câu 5: Cho hình chóp có đáy là hình chữ nhật,
Gọi lần lượt là các đường cao của tam
giác và tam giác Chọn khẳng định đúng trong các
khẳng định sau ?
( )
^Þ^BC SAB BC AH
^
ü
Þ^
ý
^
þ
AH BC
AH SC
AH SB
ABCD
AB AC=
DB DC=
( )
AB ABC^
AC BD^
( )
CD ABD^
BC AD^
E
BC
( )
AE BC
BC ADE BC AD
DE BC
^
ì
Þ^ Þ^
í
^
î
.S ABC
()SA ABC^
.AB BC^
.S ABC
1.
3.
2.
4.
AB BC ABC^ÞD
.B
() ,
SA AB
SA ABC SAB SAC
SA AC
^
ì
^Þ ÞDD
í
^
î
.A
AB BC
BC SB SBC
SA BC
^
ì
Þ^ÞD
í
^
î
.B
.S ABCD
ABCD
O
SA SC=
SB SD=
( )
SO ABCD^
( )
CD SBD^
( )
AB SAC^
CD AC^
SAC
S
SO
SOÞ
SO ACÞ^
SBD
S
SO
SOÞ
SO BDÞ^
( )
SO ABCD^
ABCD
CD
BD
CD
( )
SBD
.S ABCD
ABCD
().SA ABCD^
;AE AF
SAB
.SAD
Trang 9
A. B. C. D.
Hướng dẫn giải:
Ta có:
Vậy:
Tương tự :
Từ vậy đáp án D đúng.
Câu 6: Cho hình chóp có cạnh và đáy là tam giác cân ở . Gọi và
lần lượt là trung điểm của và . Khẳng định nào sau đây sai?
A. . B. . C. . D. .
Hướng dẫn giải:
Chọn D.
Do cân tại nên . Suy ra . Vậy các câu A, B, C đúng nên D sai.
Câu 7: Cho tứ diện . Vẽ . Biết là trực tâm tam giác . Khẳng định nào
sau đây đúng?
A. . B. . C. . D. .
Hướng dẫn giải::
Chọn đáp án D.
Câu 8: Cho hình chóp có cạnh và đáy là tam giác cân ở . Gọi và
lần lượt là trung điểm của và . Khẳng định nào sau đây có thể sai ?
A. . B. . C. . D. .
Hướng dẫn giải::
Ta có .
Từ đó suy ra nên A, B, C đúng.
Đáp án D sai trong trường hợp và không bằng nhau Chọn đáp án D.
Câu 9: Cho tứ diện thoả mãn Gọi là hình chiếu của lên mp Đối
với ta có điểm là:
A. Trực tâm. B. Tâm đường tròn nội tiếp.
C. Trọng tâm. D. Tâm đường tròn ngoại tiếp.
Hướng dẫn giải:
( )
.SC AFB^
( )
.SC AEC^
( )
.SC AE D^
( )
.SC AEF^
( )
.
AB BC
BC SAB BC AE
SA BC
^
ì
Þ^ Þ^
í
^
î
( )
1
AE SB
AE SC
AE BC
^
ì
Þ^
í
^
î
( )
2AF SC^
( ) ( ) ( )
1; 2 .SC AEFÞ^
.S ABC
( )
SA ABC^
ABC
C
H
K
AB
SB
CH SA^
CH SB^
CH AK^
AK SB^
ABCD
C
CH AB^
( )
CH SAB^
ABCD
()AH BCD^
H
BCD
CD BD^
AC BD=
AB CD=
AB CD^
()
CD AH
CD ABH CD AB
CD BH
^
ì
Þ^ Þ^
í
^
î
®
.S ABC
()SA ABC^
ABC
C
H
K
AB
SB
CH AK^
CH SB^
CH SA^
AK SB^
()
CH AB
CH SAB
CH SA
^
ì
Þ^
í
^
î
,,CH AK CH SB CH SA^^^
SA
AB
®
SABC
.SA SB SC==
H
S
( )
.ABC
ABCD
H
Trang 10
Xét ba tam giác vuông có
chính là tâm đường tròn ngoại tiếp
Chọn đáp án D.
Câu 10: Cho tứ diện có đôi một vuông góc với nhau. Gọi là hình chiếu của
trên . Mệnh đề nào sai trong các mệnh đề sau:
A. là trực tâm .
B. là tâm đường tròn ngoại tiếp tam giác .
C. .
D. là đường cao của .
Hướng dẫn giải::
Ta có và .
Tương tự, ta có , suy ra đáp án A, D đúng.
Ta có , với , suy ra đáp án C đúng.
Chọn đáp án B.
Câu 11: Cho tứ diện có và . Gọi là hình chiếu vuông góc của lên
. Các khẳng định sau, khẳng định nào sai?
A. là trực tâm tam giác . B. .
C. . D. Các khẳng định trên đều sai.
Hướng dẫn giải::
Ta có . Tương tự
Suy ra là trực tâm . Suy ra đáp án A, B đúng.
Ta có , suy ra C đúng.
Chọn đáp án D.
Câu 12: Cho tứ diện có và Khẳng định nào sau đây đúng?
A. B. C. D.
Hướng dẫn giải:
Gọi là trung điểm của .
Chọn đáp án B.
( )
SH AH
SH ABC SH BH
SH CH
Ï
^
Ô
Ô
Ô
Ô
^fi^
Ì
Ô
Ô
^
Ô
Ô
Ó
,,SHA SHB SHCDDD
( )
chung
mà H A
SA SB SC
SHA SHB
B
SHC
SH
HA H CBHC H
Ï
==
Ô
Ô
fiD =
Œ
D=D
Ì
Ô
Ô
Ó
fi== fi
.ABCD
OABC
,,OA OB OC
H
O
()mp ABC
H
ABCD
H
ABC
2222
1111
OH OA OB OC
=++
CH
ABCD
()OA OBC OA BC^Þ^
OH BC^
()BC OAH BC AHÞ^ Þ^
AB CH^
222222
111111
OH OA OI OA OB OC
=+=++
I AH BC=Ç
®
ABCD
AB CD^
AC BD^
H
A
()mp BCD
H
BCD
()CD ABH^
AD BC^
()
CD AB
CD ABH CD BH
CD AH
^
ì
Þ^ Þ^
í
^
î
BD CH^
H
BCDD
BC AH
BC AD
BC DH
^
ì
Þ^
í
^
î
®
ABCD
AB AC=
.DB DC=
( )
. AB ABC^
.BC AD^
( )
. CD ABD^
.AC BD^
M
BC
( )
.
AB AC BC AM
BC ADM BC AD
DB DC BC DM
ÏÏ
=^
ÔÔ
ÔÔ
fifi^fi^
ÌÌ
ÔÔ
=^
ÔÔ
ÓÓ
Trang 11
Câu 13: Cho hình chóp có Gọi lần lượt là trực tâm các tam giác và
. Mệnh đề nào sai trong các mệnh đề sau?
A. B. C. D.
đồng quy.
Hướng dẫn giải:
Ta có
Ta có
Mặt khác có hay ,
tương tự nên
Gọi là giao điểm của và . Do
hay đường thẳng
trùng với đường thẳng . Hay đồng quy.
Do đó sai
Chọn đáp án C.
Câu 14: Cho hai hình chữ nhật và nằm trong hai mặt phẳng khác nhau sao cho hai
đường thẳng và vuông góc với nhau. Gọi và lần lượt là đường cao của hai tam giác
và . Chứng minh rằng :
a) Khẳng định nào sau đây là đúng về 2 tam giác và ?
A. và là các tam giác vuông B. và là các tam giác tù
C. và là các tam giác nhọn D. và là các tam giác cân
b) Khẳng định nào sau đây là sai?
A. B. C. D.
Hướng dẫn giải:.
a) Ta có
..
Vậy
,hay vuông tại .
Tương tự
vuông tại .
b) Ta có , mặt khác
.
Tương tự .
Câu 15: Cho hình chóp có đáy là hình thoi tâm . Biết .
a)Khẳng định nào sau đây là sai?.
A. B.
C. D. Cả A, B,
C đều sai
b) Khẳng định nào sau đây là sai?.
A. B. C.
D. Cả A, B, C đều sai
Hướng dẫn giải:.
SABC
( )
.SA ABC^
, HK
SBC
ABC
( )
.BC SAH^
( )
.HK SBC^
( )
.BC SAB^
, SH AK và BC
,()BC SA BC SH BC SAH^^Þ^
,()CK AB CK SA CK SAB hay CK SB^^Þ^ ^
()CH SB nên suy ra SB CHK^^
SB HK^
SC HK^
()HK SBC^
M
SH
BC
()BC SAH BC AM^Þ^
AM
AK
, SH AK và BC
( )
.BC SAB^
ABCD
ABEF
AC
BF
CH
FK
BCE
ADF
DACH
DBFK
DACH
DBFK
DACH
DBFK
DACH
DBFK
DACH
DBFK
^BF AH
∑
( )
0
,45=BF AH
^AC BK
( )
^AC BKF
( )
^
ü
Þ^
ý
^
þ
AB BC
AB BCE
AB BE
( )
^
ì
Þ^
í
^
î
CH AB
CH ABEF
CH BE
Þ^CH AH
DACH
H
( )
^
ü
Þ^
ý
^
þ
FK AD
FK ABCD
FK AB
ÞDBFK
K
( )
^Þ^CH ABEF CH BF
( )
^Þ^ Þ^AC BF BF ACH BF AH
( )
^
ü
Þ^ Þ^
ý
^
þ
AC KF
AC BKF AC BK
AC BF
.S ABCD
ABCD
O
,==SA SC SB SD
( )
^SO ABCD
^SO AC
^SO BD
( )
^AC SBD
^AC SO
^AC SB
E
C
A
B
D
F
H
K
O
A
B
C
D
S
Trang 12
a) Ta có là trung điểm của và
.
Tương tự .
Vậy .Chọn D
b) Ta có ( do là hình thoi).
Lại có ( do )
Suy ra .Chọn D
Câu 16: Cho hình chóp có đáy là hình thoi tâm Các khẳng định
sau, khẳng định nào sai?
A. B. C. D.
Hướng dẫn giải:
Ta có
Do tứ giác là hình thoi nên mà nên
không vuông góc
Chọn đáp án D.
Câu 17: Cho hình chóp có đáy là hình vuông và
. Gọi , , lần lượt là trung điểm của , và . Khẳng định nào sau đây
sai?
A. . B. .
C. Góc giữa và có số đo . D. .
Hướng dẫn giải:
Chọn C.
Do và nên . Vậy A
đúng.
Do và nên nên D đúng.
Do và nên nên
B đúng.
Vậy C sai.
Câu 18: Cho hình chóp có đáy là hình
vuông, Gọi là trung điểm của và .
Gọi là trung điểm của cạnh .
a) Khẳng định nào sau đây là sai?
A. B. C. D. Cả A, B, C đều
sai
b) Khẳng định nào sau đây là sai?.
A. B.
C. D. Cả A, B, C đều sai
Hướng dẫn giải:.
O
AC
=Þ^SA SC SO AC
^SO BD
( )
^
ü
Þ^
ý
^
þ
SO AC
SO ABCD
SO BD
^AC BD
ABCD
^AC SO
( )
^SO ABCD
( )
^Þ^AC SBD AC SD
.S ABCD
ABCD
,( ).OSA ABCD^
SA BD^
SC BD^
SO BD^
AD SC^
()SA ABCD SA BD^Þ^
ABCD
,BD AC^
SA BD^
() ,BD SAC hay BD SC BD SO^^^
AD
SC
.S ABCD
ABCD
( )
SA ABCD^
I
J
K
AB
BC
SB
( ) ( )
//IJK SAC
( )
BD IJK^
SC
BD
60°
( )
BD SAC^
//IJ A C
//IK SA
( ) ( )
//IJK SAC
BD AC^
BD SA^
( )
BD SAC^
( )
BD SAC^
( ) ( )
//IJK SAC
( )
BD IJK^
.S ABCD
ABCD
H
AB
( )
^SH ABC D
K
AD
^AC SH
^AC KH
( )
^AC SHK
^CK SD
^DH CK
∑
∑
0
90+=DKC ADH
Trang 13
a) Ta có
lại có
.
b) Dễ thấy
mà
hay , mặt khác ta có
.
Câu 19: Cho tứ diện có ba cạnh đôi một
vuông góC. Gọi là hình chiếu của lên Khẳng
định nào sau đây sai?
A. B.
C. là trực tâm D.
Hướng dẫn giải:
đáp án A
đúng.
Tương tự chứng minh được
Hạ
Ta có:
Đáp án B đúng.
Ta có: Tương tự
Từ và là trực tâm Đáp án C đúng.
Chọn đáp án D.
Câu 20: Cho hình chóp có . Gọi lần lượt là trực tâm các tam giác và
. Khẳng định nào sau đây là đúng
a) và đồng qui.
A. AH và BC chéo nhau B. AH và SK chéo nhau
C. và đồng qui. D. và không đồng qui.
b) Khẳng định nào sau đây là sai?.
A. B. C.
D. Cả A, B, C đều sai
c) .Khẳng định nào sau đây là sai?
A. B. C. D. Cả A, B, C đều sai
Hướng dẫn giải:.
a) Gọi , để chứng minh và đồng qui.
Ta cần chứng minh là đường cao của tam giác , nhưng điều
này đúng do và .
( )
^Þ^SH ABCD SH AC
ì
Þ^
í
^
î
!HK BD
AC HK
AC BD
∑ ∑
D=DÞ =AHD DKC AHD DKC
∑
∑
0
90+=AHD ADH
∑
∑
0
90Þ+ =DKC ADH
^DH CK
( )
^Þ^SH CK CK SDH
Þ^CK SD
OABC
, , OA OB OC
H
O
( )
.ABC
.OA BC^
2222
1111
.
OH OA OB OC
=++
H
.ABCD
2222
3.OH AB AC BC=++
( )
OA OB
OA OBC OA BC
OA OC
Ï
^
Ô
Ô
fi^ fi^fi
Ì
Ô
^
Ô
Ó
.OC AB^
.
OI BC
OH AI
Ï
^
Ô
Ô
Ì
Ô
^
Ô
Ó
( ) ( )
.
OI BC
BC OAI BC OH OH ABC
BC OA
Ï
^
Ô
Ô
fi^ fi^fi ^
Ì
Ô
^
Ô
Ó
222222
111111
OH OA OI OA OB OC
=+=++ fi
( ) ( )
1.
AB OC
AB OCH AB HC
AB OH
Ï
^
Ô
Ô
fi^ fi^
Ì
Ô
^
Ô
Ó
( )
2.BC OH^
( )
1
( )
2 Hfi
ABCDfi
.S ABC
( )
^SA ABC
,HK
ABC
SBC
,AH SK
BC
,AH SK
BC
,AH SK
BC
( )
^SB CHK
SB HK^
( )
^CH SAB
( )
^HK SBC
( )
^HK SBC
( )
^BC SAI
^BC HK
=ÇI AH BC
,AH SK
BC
SI
SBC
^BC SA
^BC AI
S
A
B
C
I
H
K
J
K
H
A
D
C
B
S
Trang 14
b) Ta có
thêm nữa ta có
Vậy .
b) Theo các chứng minh trên ta có
và do đó .
Câu 21: Cho hình tứ diện có , , đôi một vuông góc nhau. Hãy chỉ ra điểm cách
đều bốn điểm , , , .
A. là tâm đường tròn ngoại tiếp tam giác .
B. là trọng tâm tam giác .
C. là trung điểm cạnh .
D. là trung điểm cạnh .
Hướng dẫn giải:
Chọn D.
Gọi là trung điểm của .
Từ giả thiết ta có .
Vậy vuông tại .
Do đó (1)
Mặt khác
vuông tại .
Do đó (2)
Từ (1) và (2) ta có .
Câu 22: Cho tứ diện có và . Khẳng định nào sau đây đúng?
A. . B. . C. . D. .
Hướng dẫn giải:
Chọn D.
Gọi là trung điểm của . Khi đó ta có
.
Câu 23: Cho tứ diện . Vẽ . Biết là trực
tâm tam giác . Khẳng định nào sau đây không sai?
A. . B. . C.
. D. .
Hướng dẫn giải:
Chọn C.
Do .
Mặt khác, là trực tâm nên .
Suy ra nên .
^SB CK
( )
^
ì
Þ^ Þ^
í
^
î
CH AB
CH SAB CH SB
CH SA
( )
^SB CHK
( )
^Þ^SB CHK SB HK
( )
^Þ^BC SAI BC HK
( )
^HK SBC
ABCD
AB
BC
CD
O
A
B
C
D
O
ABC
O
ACD
O
BD
O
AD
O
AD
( )
AB CD
CD ABC CD AC
BC CD
^
ì
Þ^ Þ^
í
^
î
ACDD
C
OA OC OA==
( )
AB CD
AB BCD AB BD ABD
AB BC
^
ì
Þ^ Þ^ÞD
í
^
î
B
OA OB OD==
OA OB OC OD== =
ABCD
AB AC=
DB DC=
( )
AB ABC^
AC BD^
( )
CD ABD^
BC AD^
E
BC
( )
AE BC
BC ADE BC AD
DE BC
^
ì
Þ^ Þ^
í
^
î
ABCD
( )
AH BCD^
H
BCD
AB CD=
AC BD=
AB CD^
CD BD^
( )
AH BCD AH CD^Þ^
H
ABCD
BH CD^
( )
CD ABH^
CD AB^
Trang 15
Câu 24: Cho hình chóp có đáy là hình vuông cạnh , mặt bên là tam giác đều
và . Gọi lần lượt là trung điểm của các cạnh và .
a) Khẳng định nào sau đây là sai?.
A. B. C. A, B đều đúng D. A, B là sai
b) Khẳng định nào sau đây là sai?
A. B.
C. D. Cả A, B, C đều sai
Hướng dẫn giải:.
a) Vì là trung điểm của và tam giác đều nên
Lại có
Do đó
vuông tại
Vậy .
b) Ta có và
.
Tương tự ( như bài 32) và .
Câu 25: Cho hình lập phương . Đường thẳng vuông góc với mặt phẳng nào sau
đây?
A. . B. . C. . D. .
Hướng dẫn giải:
Ta có:
Từ
Vậy chọn đáp án .
Câu 26: Cho hình chóp có đáy là
hình thoi, là giao điểm của 2 đường chéo và .
Các khẳng định sau, khẳng định nào đúng?
A. . B. . C. . D. .
Hướng dẫn giải:
Ta có: là tam giác cân
Mặt khác: là trung điểm của (tính chất hình thoi)
Khi đó ta có:
Vậy chọn đáp án .
.S ABCD
ABCD
a
SAB
2=SC a
,HK
AB
AD
( )
^SH ABC D
^SH HC
^CK HD
^CK SD
^AC SK
H
AB
SAB
^SH AB
3
,2,
2
==
a
SH SC a
22
5
HC =
2
+=
a
DH DC
22
22 22
35
2
44
+=+==
aa
HC HS a SC
ÞDHSC
Þ^H SH HC
( )
^
ì
Þ^
í
^
î
SH HC
SH ABCD
SH AB
^AC HK
( )
AC SH AC SHK^Þ ^
Þ^AC SK
^CK HD
( )
^Þ^ Þ^CK SH CK SDH CK SD
.' ' ' 'ABCD A B C D
'AC
( )
'ABD
( )
''ADC
( )
''ACD
( )
''ABCD
( )
( )
( )
'' /
''' ''''
AD AD t cHV
AD CD CD ADDA
ì
^
ï
í
^^
ï
î
( ) ( )
''''' 1AD AC D AD ACÞ^ Þ^
( )
( )
( )
'' /
''' ''''
AB AB t cHV
AB BC BC ADDA
ì
^
ï
í
^^
ï
î
( ) ( )
''''' 2AB ABC AB ACÞ^ Þ^
( ) ( ) ( )
1, 2 ' 'AC A BDÞ^
A
.S ABCD
ABCD
O
SA SC=
( )
SA ABCD^
( )
BD SAC^
( )
AC SBD^
( )
AB SAC^
SA SC SAC=Þ
O
AC
AC SO^
( )
( )
/
AC BD t c hinh thoi
AC SBD
AC SO
ì^
ÞÞ^
í
^
î
C
K
H
D
B
C
A
S
Trang 16
Câu 27: Cho hình chóp có đáy là hình vuông, . Mặt phẳng qua và
vuông góc với cắt theo thứ tự tại . Chọn khẳng định sai trong các khẳng định
sau?
A. . B. . C. . D. .
Hướng dẫn giải:
Ta có:
Gọi
là mặt phẳng và vuông góc với
Qua kẻ
Khi đó:
Ta có: , mà không vuông góc với .
Vậy chọn đáp án .
Câu 28: Cho hình chóp trong đó là hình chữ nhật, . Trong các tam
giác sau tam giác nào không phải là tam giác vuông.
A. . B. . C. . D. .
Hướng dẫn giải:
Ta có :
Giả sử (vô lý)
Hay không thể là tam giác vuông
Vậy chọn đáp án .
Câu 29: Cho hình chóp có Gọi là hình
chiếu vuông góc của lên Chọn khẳng định đúng trong các khẳng định sau
A. là trung điểm . B. là trọng tâm tam giác .
C. là trung điểm . D. là trung điểm .
Hướng dẫn giải:
Gọi
Ta có : đều
vuông cân tại
vuông tại
Gọi là trung điểm của thì là tâm đường tròn
ngoại tiếp tam giác Gọi là trục của tam giác thi đi
qua và
.S ABCD
ABCD
( )
SA ABCD^
A
SC
,,SB SC SD
,,HMK
AK HK^
HK AM^
^BD HK
AH SB^
( )
( )
( )
HV
BD AC t c
BD SAC BD AM
BD SA gt
^
ì
ï
Þ^ Þ^
í
^
ï
î
/
,OACBDISOHK=Ç =Ç
( )
P
A
SC
I
( )
DÞD^ÞDÌ! BD AM P
,KSDHSB=DÇ =DÇ
( )
AK SDC^
( )
HK SDC K AKÇ=Þ
HK
A
.S ABCD
ABCD
( )
SA ABCD^
SBCD
SCDD
SABD
SBDD
( )
( )
( )
( )
HV
AB AD tc
AB SAD AB SD
AB SA SA ABCD
ì^
ï
Þ^ Þ^
í
^^
ï
î
( )
SB SD SD SAB^Þ^
SBDD
D
.S ABC
∑
∑
∑
00 0
120 , 60 , 90 , .BSC CSA ASB SA SB SC=====
I
S
( )
.mp ABC
I
AB
I
ABC
I
AC
I
BC
SA SB SC a== =
SAC!
AC SA aÞ==
SAB!
S
2AB aÞ=
∑
22
2..cos 3BC SB SC SB SC BSC a=+- =
22 2
AC AB BC ABCÞ+=Þ!
A
I
AC
I
.ABC
d
ABC
d
I
( )
dABC^
Trang 17
Mặt khác : nên . Vậy nên là hình chiếu vuông góc của lên
mặt phẳng
Vì lần lượt là trực tâm của tam giác và nên lần lượt thuộc và
Vậy đồng quy tại
Câu 30: Cho tứ diện có đôi một vuông góc với nhau. Gọi là hình chiếu của
trên mặt phẳng . Xét các mệnh đề sau :
I. Vì nên .
II. Do nên
III. Có và nên
IV. Từ và
A. . B. . C. . D. .
Hướng dẫn giải:
Ta có:
. Vậy đúng.
. Vậy đúng.
. Vậy đúng.
. Vậy đúng.
Vậy chọn đáp án .
Câu 31: Cho hình hộp Có đáy là hình thoi và Gọi
Hình chiếu của trên là :
A. trung điểm của B. trọng tâm
C. giao của hai đoạn và D. trọng tâm
Hướng dẫn giải:
Vì hình chiếu của trên trùng với
là tâm đường tròn ngoại tiếp
Mà tứ giác là hình thoi và nên là tam
giác đều
Từ & là trọng tâm
Chọn đáp án B.
SA SB SC==
SdÎ
( )
SI ABC^
I
S
( )
ABC
và HK
ABC
SBC
và HK
AA
¢
SA
¢
, , AH SK BC
A
¢
OABC
,,OA OB OC
H
O
( )
ABC
,OC OA OC OB^^
( )
OC OAB^
( )
AB OABÌ
( )
. 1AB OC^
( )
OH ABC^
( )
AB ABCÌ
( )
. 2AB OH^
( )
1
( )
2
( )
.AB OCH^
,, ,IIIIIIIV
,,IIIIII
,,II III IV
,IIV
( )
( )
,
OC OA
OC OB
OC OAB
OA OB O
OA OB OAB
^
ì
ï
^
ï
Þ^
í
Ç=
ï
ï
Ì
î
I
( )
( )
OC OAB
AB OC
AB OAB
^
ì
ï
Þ^
í
Ì
ï
î
II
( )
( )
OH ABC
AB OH
AB ABC
^
ì
ï
Þ^
í
Ì
ï
î
III
( )
( )
,
AB OC
AB OH AB OCH
OC OH O
OC OH OCH
ì
ï
^
ï
ï
^Þ^
í
ï
Ç=
ï
ï
Ì
î
IV
A
.' ' ' '.ABCD A B C D
∑
0
60=BAD
'''.AA AB AD==
.=«O AC BD
'A
( )
ABCD
.AO
.D ABD
AC
.BD
.D BCD
'''AA AB AD== fi
'A
( )
ABCD
H
( )
1.DABD
ABCD
∑
0
60=BAD
D BAD
( )
2.
( )
1
( )
2 fi H
.D ABD
Trang 18
DẠNG 2: TÍNH GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG
Phương pháp:
Để xác định góc giữa đường thẳng và mặt phẳng ta thực hiện theo các bước sau:
- Tìm giao điểm
- Dựng hình chiếu của một điểm xuống
- Góc chính là góc giữa đường thẳng và .
Lưu ý:
- Để dựng hình chiếu của điểm trên ta chọn một đường thẳng khi đó .
- Để tính góc ta sử dung hệ thức lượng trong tam giác vuông . Ngoài ra nếu không xác
định góc thì ta có thể tính góc giữa đường thẳng và mặt phẳng theo công thức
trong đó là VTCP của còn là vec tơ có giá vuông góc với .
-
Câu 1: Cho tứ diện có cạnh , , bằng nhau và vuông góc với nhau từng đôi một.
Khẳng định nào sau đây đúng?
A. Góc giữa và là góc . B. Góc giữa và là góc .
C. Góc giữa và là góc . D. Góc giữa và là góc .
Hướng dẫn giải:
Chọn A.
Từ giả thiết ta có .
Do đó .
Câu 2: Cho tam giác vuông cân tại và . Trên đường
thẳng qua vuông góc với lấy điểm sao cho .
Tính số đo góc giữa đường thẳng và .
A. . B. . C. . D. .
Hướng dẫn giải:
a
( )
a
a
a'
φ
α
O
A
A'
( )
Oa=Ça
'A
AaÎ
( )
a
∑
'AOA =j
a
( )
a
'A
A
( )
a
( )
b ^a
'AA b!
j
'OAAD
j
a
( )
a
.
sin
un
un
j=
!!
!!
u
!
a
n
!
( )
a
ABCD
AB
BC
BD
AC
( )
BCD
ACB
AD
( )
ABC
ADB
AC
( )
ABD
CAB
CD
( )
ABD
CBD
( )
AB BC
AB BCD
AB CD
^
ì
Þ^
í
^
î
( )
( )
∑
,AC BCD ACB=
ABC
A
BC a=
A
( )
ABC
S
6
2
a
SA =
SA
( )
ABC
30°
45°
60°
Trang 19
Chọn D.
.
Câu 3: Cho tứ diện có cạnh vuông góc với nhau từng đôi một. Khẳng định nào
sau đây đúng ?
A. Góc giữa và là góc . B. Góc giữa và là góc .
C. Góc giữa và là góc . D. Góc giữa và là góc .
Hướng dẫn giải:
Do vuông góc với nhau từng đôi một nên , suy ra là hình chiếu của
lên .
Chọn B.
Câu 4: Cho hình chóp có đáy là tam giác vuông cạnh huyền . Hình chiếu vuông
góc của lên trùng với trung điểm . Biết . Tính số đo của góc giữa và .
A. . B. . C. . D. .
Hướng dẫn giải:
Chọn C.
Gọi là trung điểm của suy ra
.
Ta có: .
.
Câu 5: Cho hình chóp , đáy là hình vuông cạnh bằng và . Biết
. Tính góc giữa và .
A. . B. . C. . D. .
Hướng dẫn giải:
Chọn A.
Ta có:
là hình vuông cạnh
.
( ) ( )
( )
,90SA ABC SA ABC^Þ =°
ABCD
, , AB BC BD
CD
( )
ABD
∑
CBD
AC
( )
BCD
∑
ACB
AD
( )
ABC
∑
ADB
AC
( )
ABD
∑
CBA
, , AB BC BD
( )
AB BCD^
BC
AC
( )
BCD
.S ABC
ABC
BC a=
S
( )
ABC
BC
SB a=
SA
( )
ABC
30°
45°
60°
75°
H
BC
1
22
a
AH BH CH BC=== =
( )
22
3
2
a
SH ABC SH SB BH^Þ=-=
( )
( )
∑
∑
,SA ABC SAH
a
==
tan 3 60
SH
AH
aa
Þ==Þ=°
.S ABCD
ABCD
a
( )
SA ABCD^
6
3
a
SA =
SC
( )
ABCD
30°
45°
60°
75°
( )
SA ABCD SA AC^Þ^
( )
( )
∑
∑
;SC ABCD SCA
a
Þ==
ABCD
a
6
2,
3
a
AC a SAÞ= =
3
tan 30
3
SA
AC
aa
Þ==Þ=°
Trang 20
Câu 6: Cho hình chóp có đáy là tam giác đều cạnh . Hình chiếu vuông góc của lên
trùng với trung điểm của cạnh . Biết tam giác là tam giác đều. Tính số đo của
góc giữa và
A. B. C. D.
Hướng dẫn giải:
Do là hình chiếu của lên mặt phẳng nên
Vậy là hình chiếu của lên mp
Ta có:
Mà: . Vậy tam giác vuông cân
tại
Câu 7: Cho hình thoi có tâm , . Lấy điểm không thuộc sao
cho . Biết . Tính số đo của góc giữa và .
A. . B. . C. . D. .
Hướng dẫn giải:
Chọn B.
Ta có:
.
Mặt khác
Suy ra số đo của góc giữa và bằng .
Câu 8: Cho hình chóp có đáy là tam giác đều cạnh . Hình chiếu vuông góc của lên
trùng với trung điểm của cạnh . Biết tam giác là tam giác đều.Tính số đo của góc
giữa và .
A. . B. . C. . D. .
Hướng dẫn giải:
Chọn B.
Ta có:
.
và là hai tam giác đều cạnh
vuông cân tại .
.S ABC
ABC
a
S
( )
ABC
H
BC
SBC
SA
( )
.ABC
0
60
0
75
0
45
0
30
H
S
( )
ABC
( )
SH ABC^
AH
SH
( )
ABC
( )
( )
( )
∑
;;SA ABC SA AH SAHÞ==
( )
SH ABC SH AH^Þ^
ABC SBC SH AH=Þ=!!
SAH
H
∑
0
45SAHÞ=
ABCD
O
;2A2AC a B CD==
S
( )
ABCD
( )
SO ABCD^
∑
1
tan
2
SBO =
SC
( )
ABCD
30°
45°
60°
75°
A2 22 4; CaAC a BD OB a== Þ==
∑
11
tan
22
SO
SBO SO OB a
OB
Þ==Û==
( )
( )
∑
∑
,;1
SO a
SC ABCD SCO
OC a
===
SC
( )
ABCD
45°
.S ABC
ABC
a
S
( )
ABC
H
BC
SBC
SA
( )
ABC
30°
45°
60°
75°
( ) ( )
( )
∑
∑
;SH ABC SH AH SA ABC SAH
a
^Þ^Þ ==
ABCD
SBCD
a
3
2
a
AH SHÞ==
3
2
a
AH SH SHAÞ== ÞD
H
45
a
Þ= °
Trang 21
Câu 9: Cho hình chóp có đáy là hình vuông cạnh ,
Gọi là góc giữa và mp Chọn khẳng định đúng trong các khẳng định sau ?
A. B. C. D.
Hướng dẫn giải:
Vì nên là hình chiếu vuông góc của lên
Góc giữa giữa và mp bằng góc
Xét tam giác vuông tại có:
Câu 10: Cho hình chóp đáy là hình vuông cạnh bằng và Biết
. Tính góc giữa và
A. B. C. D.
Hướng dẫn giải:
Tứ giác là hình vuông cạnh nên
là hình chiếu vuông góc của lên
là góc giữa và
Tam giác vuông tại nên
Chọn đáp án A.
Câu 11: Cho hình lập phương . Gọi là góc giữa và mp Chọn
khẳng định đúng trong các khẳng định sau?
A. B. C. D.
Hướng dẫn giải:
Gọi
mà là hình chiếu vuông
góc của lên là góc giữa và
Mà
Chọn đáp án D.
Câu 12: Cho hình chóp có và tam giác không vuông, gọi lần lượt là
trực tâm các và . Số đo góc tạo bởi và là?
.S ABCD
ABCD
a
(), 6.SA ABCD SA a^=
a
SC
().ABCD
0
30 .
a
=
3
cos .
3
a
=
0
45 .
a
=
0
60 .
a
=
()SA ABCD^
AC
SC
().ABCD
Þ
SC
()ABCD
&.SC AC
∑
.SCA
a
Þ=
SAC
A
0
6
tan 3 60 .
2
SA a
AC
a
aa
== =Þ=
.,SABCD
ABCD
a
( )
.SA ABCD^
6
3
SA
a
=
SC
( )
.ABCD
0
30 .
0
60 .
0
75 .
0
45 .
ABCD
a
2.AC a=
( )
SA ABCD AC^fi
SC
SC
( )
.ABCD
SAC
A
∑ ∑
0
61 1
tan . 30 .
3
23
SA a
SCA SCA
AC
a
== =fi =
.' ' ' 'ABCD A B C D
a
'AC
( )
''.ABCD
0
. 30
a
=
2
tan .
3
a
=
0
. 45
a
=
tan 2.
a
=
''
''
AC AC I
C D CD H
Ï
«=
Ô
Ô
Ì
Ô
«=
Ô
Ó
( )
''
'''
'''
CD CD
CD ABCD IH
CD AD
Ï
^
Ô
Ô
fi^ fi
Ì
Ô
^
Ô
Ó
'AC
( )
∑
'' 'ABCD C IHfi
'AC
( )
''.ABCD
∑
'1
tan ' .2 2.
2
CH
CIH
IH
===
.S ABC
()SA ABC^
ABC
,HK
ABCD
SBCD
HK
()mp SBC
Trang 22
S
C
B
A
A. . B. . C. . D. .
Hướng dẫn giải::
Gọi . Ta có và .
Ta lại có .
Mà , suy ra
Chọn đáp án B.
Câu 13: Cho hình chóp thỏa mãn . Gọi là hình chiếu vuông góc của lên
. Chọn khẳng định đúng trong các khẳng định sau?
A. là trực tâm tam giác .
B. là trọng tâm tam giác .
C. là tâm đường tròn ngoại tiếp tam giác .
D. là tâm đường tròn nội tiếp tam giác .
Hướng dẫn giải:
Do hình chóp có và nên là
trục của hình chóp . . Nên là tâm đường
tròn ngoại tiếp tam giác .
Vậy chọn C.
Câu 14: Cho hình chóp có đáy là tam giác vuông cạnh huyền . Hình chiếu
vuông góc của lên trùng với trung điểm . Biết . Tính số đo của góc giữa và
.
A. B. C. D.
Hướng dẫn giải:
Có nên là hình chiếu của lên
.
Áp dụng định lý Pytago
Xét tam giác có
.
Vậy chọn C.
Câu 15: Cho hình chóp có và vuông ở
. là đường cao của . Khẳng định nào sau đây sai ?
A. B. C.
D.
Hướng dẫn giải:
Do nên . Nên Phương án A đúng.
65°
90°
45°
120°
I AH BC=Ç
()( )()
BC SA
BC SAI SBC SAI
BC AI
^
ì
Þ^ Þ ^
í
^
î
K SIÎ
()()()
SB CK
SB CHK SBC CHK
SB CH
^
ì
Þ^ Þ ^
í
^
î
()( )HK SAI SHK=Ç
()HK SBC^
®
.S ABC
SA SB SC==
H
S
( )
mp ABC
H
ABC
H
ABC
H
ABC
H
ABC
.S ABC
SA SB SC==
( )
SH ABC^
SH
.S ABC
HA HB HCÞ==
H
ABC
.S ABC
ABC
BC a=
S
( )
ABC
BC
SB a=
SA
( )
ABC
0
30 .
0
45 .
0
60 .
0
75 .
,
2
a
AM BM SB a== =
( )
SM ABC^
AM
SA
( )
mp ABC
( )
( )
( )
∑
,,SA A BC SA AM SAMÞ==
22
3
2
a
SM SB AM=-=
SAM
∑
tan 3
SM
SAM
AM
==
∑
0
60SAMÞ=
.S ABC
( )
SA ABC^
ABCD
B
AH
SABD
.SA BC^
.AH BC^
.AH AC^
.AH SC^
( )
SA ABC^
SA BC^
Trang 23
Có . Phương án D đúng.
Suy ra , . Phương án B, D đúng.
Phương án C sai. Thật vậy với , ta có (vô lý).
Vậy chọn C.
Câu 16: Trong các mệnh đề sau mệnh đề nào đúng?
A. Góc giữa đường thẳng và mặt phẳng bằng góc giữa đường thẳng đó và hình chiếu của nó trên
mặt phẳng đã cho.
B. Góc giữa đường thẳng a và mặt phẳng bằng góc giữa đường thẳng và mặt phẳng khi
và song song (hoặc trùng với ).
C. Góc giữa đường thẳng a và mặt phẳng bằng góc giữa đường thẳng và mặt phẳng thì
mặt phẳng song song với mặt phẳng .
D. Góc giữa đường thẳng a và mặt phẳng bằng góc giữa đường thẳng và mặt phẳng thì
song song với .
Hướng dẫn giải:
Chọn B.
Câu 17: Cho góc tam diện với Trên các tia lần lượt
lấy các điểm sao cho . Tam giác có đặc điểm nào trong các số các đặc
điểm sau :
A. Vuông cân. B. Đều.
C. Cân nhưng không vuông. D. Vuông nhưng không cân.
Hướng dẫn giải:
Xét có .
đều
có .
Từ đó vuông tại
Vậy chọn D.
Câu 18: Cho hình chóp có và đáy là hình chữ nhật. Gọi là tâm của
và là trung điểm của . Khẳng định nào sau đây sai ?
A.
B.
C. là mặt phẳng trung trực của đoạn
D. Tam giác vuông ở
Hướng dẫn giải:
Có là đường trung bình tam giác nên nên
. Phương án A đúng.
Có . Phương án B đúng
Và nên phương án D đúng.
Phương án C sai. Thật vậy nếu là mặt phẳng trung trực
của (vô lý).
Vậy chọn C.
Câu 19: Trong các mệnh đề sau đây, mệnh đề nào là đúng?
( )
( )
( )
AH SB
AH SBC
AH BC BC SAB
^
ì
ï
Þ^
í
^^
ï
î
AH BC^
AH SC^
AH AC^
AH AC
AC AB
SA AC
^
ì
Þ^
í
^
î
( )
P
b
( )
P
a
b
a
b
( )
P
a
( )
Q
( )
P
( )
Q
( )
P
b
( )
P
a
b
Sxyz
∂
0
120 ,xSy =
∂
0
60 ,ySz =
∂
0
90 .zSx =
,,Sx Sy Sz
,,ABC
SA SB SC a== =
ABC
SABD
∑
222 2
2..cos 3 3AB SA SB SA SB ASB a AB a=+- =Þ=
SBCD
.BC aÞ=
SACD
22
2AB SA SC a=+=
ABCD
.C
.S ABCD
( )
SA ABCD^
ABCD
O
ABCD
I
SC
( )
.IO ABCD^
.BC SB^
( )
SAC
.BD
SCD
.D
IO
SAC
//IO SA
( )
IO A BCD^
BC AB
BC SB
BC SA
^
ì
Þ^
í
^
î
CD AD
CD SD
CD SA
^
ì
Þ^
í
^
î
( )
SAC
BD
BD ACÞ^
Trang 24
A. Nếu hai mặt phẳng vuông góc với nhau thì mọi đường thẳng thuộc mặt phẳng này sẽ vuông góc
với mặt phẳng kia.
B. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thứ ba thì song song với nhau.
C. Với mỗi điểm và mỗi điểm thì ta có đường thẳng vuông góc với giao
tuyến của và
D. Nếu hai mặt phẳng và đều vuông góc với mặt phẳng thì giao tuyến của và
nếu có sẽ vuông góc với
Hướng dẫn giải:
Phương án A sai vì nếu hai mặt phẳng vuông góc với nhau thì mọi đường thẳng thuộc mặt phẳng này
vuông góc với giao tuyến sẽ vuông góc với mặt phẳng kia.
Phương án B sai vì còn trường hợp hai mặt phẳng cắt nhau.
Phương án C sai.
Vậy chọn D.
Câu 20: Cho hình chóp có đáy là hình vuông cạnh , , .
Gọi là góc giữa và . Chọn khẳng định đúng trong các khẳng định sau?
A. B. C. D.
Hướng dẫn giải:
Do nên là hình chiếu của lên
Xét tam giác có
Vậy chọn B.
Câu 21: Cho hình chóp , với đáy là hình bình hành tâm đôi một
vuông góc . là mặt phẳng qua trung điểm của và vuông góc với . Thiết
diện của và hình chóp có diện tích bằng?
A. 20. B. 16. C. 17. D. 36.
Hướng dẫn giải:
Thiết diện là hình thang vuông đi qua trung điểm các cạnh , nên diện tích thiết diện là
Câu 22: Cho hình chóp có đáy là tam giác đều cạnh và . Gọi là
trọng tâm . Độ dài là:
A. . B. . C. . D. .
Hướng dẫn giải:
Theo bài ra hình chóp là hình chóp tam giác đều. Gọi là trung điểm của , ta có
.
Mặt khác ta có:
( )
A
a
Î
( )
B
b
Î
AB
d
( )
a
( )
.
b
( )
a
( )
b
( )
g
d
( )
a
( )
b
( )
.
g
.S ABCD
ABCD
a
( )
SA ABCD^
6SA a=
a
SC
( )
mp SAB
1
tan .
8
a
=
1
tan .
7
a
=
0
30 .
a
=
1
tan .
6
a
=
( )
BC SAB^
SB
SC
( )
SAB
( )
( )
( )
∑
,,SC SAB SC SB BSCÞ==
SBC
∑
1
tan .
77
BC a
BSC
SB
a
== =
.S ABDC
ABDC
;,,OADSAAB
8, 6AD SA==
()P
AB
AB
()P
;;;AB CD CS SB
11
().
(8 4)6
22
36
22
BC BC SA
dt
+
+
===
.S ABC
ABC
a
SA SB SC b== =
G
ABCD
SG
22
93
3
ba+
22
3
3
ba-
22
93
3
ba-
22
3
3
ba+
.S ABC
H
BC
(),SG ABC G AH^Î
2
2
3
,
24
aa
AH SH b==-
!
2
22
2
2
3
3
.sin . 1 ( ) 1
3
a
AG b a
SG SA SAG b b
SA b
-
®= = - = -=
Trang 25
Câu 23: Cho hình chóp có đáy là tam giác đều cạnh và . Gọi G là
trọng tâm . Xét mặt phẳng đi qua và vuông góc với . Tìm hệ thức liên hệ giữa và
để cắt tại điểm nằm giữa và .
A. . B. . C. . D. .
Hướng dẫn giải:
Để nằm giữa và thì
Chọn đáp án C
Câu 24: Cho tứ diện có đôi một vuông góc. Điểm cách đều là:
A. Trung điểm . B. Trung điểm . C. Trung điểm . D. Trung điểm .
Hướng dẫn giải:
Sử dụng tính chất trung điểm của tam giác vuông
Câu 25: Cho hình chóp có đáy là hình thoi tâm . Biết . Khẳng
định nào sau đây đúng ?
A. . B. . C. . D. .
Hướng dẫn giải:
Do hình chóp có đáy là hình thoi tâm , nên
Câu 26: Cho hình chóp có đáy là hình vuông. Mặt bên là tam giác đều có đường
cao vuông góc với . Gọi là góc giữa và . Chọn khẳng định đúng
trong các khẳng định sau?
A. . B. . C. . D. .
Hướng dẫn giải:
Gọi là trung điểm , suy ra . Ta có: . Suy ra
Câu 27: Cho tứ diện đều. Gọi là góc giữa và . Chọn khẳng định đúng trong
các khẳng định sau?
A. . B. . C. . D. .
Hướng dẫn giải::
Gọi là hình chiếu của lên , là độ dài cạnh của tứ diện .
Ta có , . Chọn đáp án A.
Câu 28: Cho tam giác vuông cân tại và . Trên đường thẳng qua vuông góc với
lấy điểm sao cho . Tính số đo góc giữa đường thẳng và
A. B. C. D.
Hướng dẫn giải:
Câu 29: Cho hình lập phương . Gọi là góc giữa
.S ABC
ABC
a
SA SB SC b== =
ABCD
()P
A
SC
a
b
()P
SC
1
C
S
C
2ba>
2ba<
2ab<
2ab>
1
C
S
C
! !
22
0
2
2
90 cos 0 0 2
2
ba
ASC ASC b a
b
-
<® >« >« >
ABCD
,,AB BC CD
,,,ABCD
BC
AD
AC
AB
.S ABCD
ABCD
O
,SA SC SB SD==
()AB SAC^
CD AC^
()SO ABCD^
()CD SBD^
.S ABCD
ABCD
O
,SA SC SB SD==
()SO ABCD^
.S ABCD
ABCD
SAB
AH
()mp ABCD
a
BD
()mp SAD
0
60
a
=
0
30
a
=
3
cos
22
a
=
3
sin
22
a
=
I
AS
!
()BI SAD IDB
a
^®=
3
,2
2
AB
BI BD AB==
3
sin
22
BI
BD
a
==
ABCD
a
AB
()mp BCD
3
cos
3
a
=
3
cos
4
a
=
cos 0
a
=
3
cos
2
a
=
H
A
()mp BCD
a
ABCD
∑
ABH
a
=
3
3
a
BH =
3
cos
3
BH
AB
a
==
®
ABC
A
BC a=
A
( )
ABC
S
6
2
a
SA =
SB
( )
.ABC
0
75
0
30
0
45
0
60
∑
∑
,( )SB ABC SBA
a
==
Þ
6
2
tan 3 60
2
a
SA
a
AB
o
aa
== =Þ=
111 1
.ABCD A B C D
a
Trang 26
và mp . Chọn khẳng định đúng trong các khẳng định sau?
A. B. C. D.
Hướng dẫn giải:
Ta có
Câu 30: Cho hình chóp có đáy là hình vuông cạnh . Đường thẳng vuông góc với mặt
phẳng đáy, . Góc giữa đường thẳng và mặt phẳng là , khi đó nhận giá trị
nào trong các giá trị sau?
A. . B. . C. . D. .
Hướng dẫn giải:
Ta có:
là hình chiếu của trên
là hình chiếu của trên
Từ
Xét tam giác vuông tại ta có:
Xét tam giác vuông tại ta có:
Vậy chọn đáp án .
Câu 31: Cho hình thoi có tâm , . Lấy điểm không thuộc sao cho
. Biết . Tính số đo của góc giữa và .
A. . B. . C. . D. .
Hướng dẫn giải:
Câu 32: Cho hình chóp có và tam giác
không vuông. Gọi lần lượt là trực tâm và . Số đo
góc tạo bởi và là:
A. . B. .
C. . D. .
Hướng dẫn giải:
Ta có:
Mà
Vậy chọn đáp án .
1
AC
( )
ABCD
0
45
a
=
1
tan
2
a
=
2
tan
3
a
=
0
30
a
=
( )
∑
∑
11
,AC ABCD CAC
a
==
1
1
tan
22
CC
a
AC
a
a
Þ===
.S ABCD
a
SA
SA a=
SC
( )
SAB
a
tan
a
tan 2
a
=
tan 3
a
=
1
tan
2
a
=
tan 1
a
=
( )
SSAB SÎÞ
S
( )
SAB
( )
1
( )
( )
( )
( )
/
BC AB t c HV
BC SAB
BC SA SA ABCD
ì
^
ï
Þ^
í
^^
ï
î
Þ
B
C
( )
SAB
( )
2
( ) ( ) ( )
∑
( )
∑
∑
1, 2 , ,SC SAB SC SB BSC
a
éù
Þ===
ëû
SAB
A
22
2SB SA AB a=+=
SBC
B
1
tan
22
BC a
SB
a
a
== =
C
ABCD
O
2AC a=
S
( )
ABCD
( )
SO ABCD^
∑
1
tan
2
SOB =
SC
( )
ABCD
0
75
0
45
0
30
0
60
.S ABC
( )
SA ABC^
ABC
,HK
ABCD
SBCD
SC
( )
BHK
0
45
0
120
0
90
0
65
( )
( )
( )
( )
BH AC gt
BH SAC BH SC
BH SA SA ABCD
ì^
ï
Þ^ Þ^
í
^^
ï
î
( )
BK SC SC BHK^Þ^
C
Trang 27
Trang 28
DẠNG 3: THIẾT DIỆN VÀ CÁC BÀI TOÁN LIÊN QUAN.
Phương pháp:
Để xác định thiết diện của mặt phẳng đi qua điểm và vuông góc với đường thẳng với một
hình chóp ta thực hiện theo một trong hai cách sau:
Cách 1. Tìm tất cả các đường thẳng vuông góc với , khi đó sẽ song song hoặc chứa các đường
thẳng này và ta chuyển về dạng thiết diện song song như đã biết ở ( dạng 2, §2 chương II).
Cách 2. Ta dựng mặt phẳng như sau:
Dựng hai đường thẳng cắt nhau cùng vuông góc với trong đó có một đường thẳng đi qua , khi
đó chính là mặt phẳng .
Câu 130: Cho hình chóp có đáy là tam giác đều, . Gọi là mặt phẳng
qua và vuông góc với . Thiết diện của và hình chóp là:
A. Hình thang vuông. B. Tam giác đều. C. Tam giác cân. D. Tam giác vuông.
Hướng dẫn giải:
Gọi là trung điểm của , kẻ .
Ta có .
Do đó hay thiết diện là tam giác .
Mà nên hay thiết diện là tam giác
vuông.
Chọn D.
Câu 1: Cho tứ diện đều cạnh , gọi là mặt phẳng qua và vuông góc với
Thiết diện của và hình chóp có diện tích bằng
A. . B. . C. D. .
Hướng dẫn giải:
Thiết diện là tam giác , với là trung điểm của . Gọi là trung điểm của .
( )
a
O
d
a
b
d
α
I
O
d
( )
a
( )
a
,ab
d
O
( )
a
( )
,mp a b
.S ABC
ABC
( )
SA ABC^
( )
P
B
SC
( )
P
.S ABC
I
AC
IH SC^
,BI AC BI SA BI SC^^Þ^
( )
SC BIH^
BIH
( )
BI SAC^
BI IH^
ABCD
12a =
( )
P
B
.AD
( )
P
36 2
40
36 3
36
BCE
E
AD
F
BC
Trang 29
Ta có ;
.
Diện tích thiết diện là:
.
Câu 2: Cho hình chóp có đáy là tam giác vuông tại , cạnh bên Mặt
phẳng đi qua trung điểm của và vuông góc với cắt lần lượt tại
Tứ giác là hình gì ?
A. Hình thang vuông. B. Hình thang cân. C. Hình bình hành. D. Hình chữ nhật.
Hướng dẫn giải:
Ta có:
Vậy
Mà
Từ
Tương tự ta có
Mà
Vậy thiết diện là hình thang vuông tại
Câu 3: Cho hình chóp có đáy là tam giác đều, là trung điểm của đường cao của
tam giác vuông góc với đáy. Gọi là điểm tùy ý trên (không trùng với và ). mặt
phẳng qua và vuông góc với . Thiết diện của và hình chóp là hình gì?
A. Hình thang cân B. Hình thang vuông C. Hình bình hành D. Tam giác vuông
Hướng dẫn giải:
Mặt phẳng vuông góc với nên song song với
Suy ra cắt theo giao tuyến là đường thẳng
qua và song song với cắt tại K
Từ giả thiết suy ra song song , do đó sẽ cắt
lần lượt là các đường thẳng qua và
song song với cắt lần lượt tại
. Do đó thiết diện là tứ giác
Ta có và cùng song song suy ra là
trung điểm của và là trung điểm của , lại có các
tam giác đều và tam giác cân tại suy ra
vuông góc với và dó đó là hình thang cân.
Chọn đáp án A.
Câu 4: Cho hình chóp có đáy là tam giác đều cạnh và ( ).
Gọi là trọng tâm . Xét mặt phẳng đi qua và vuông góc với tại điểm nằm giữa
và . Diện tích thiết diện của hình chóp khi cắt bởi mặt phẳng là
12 3
63
2
BE CE== =
22
62EF B E B F=-=
1
.362
2
SEFBC==
.S ABC
ABC
B
( )
.SA ABC^
( )
P
M
AB
SB
,,AC SC SB
,,.NPQ
MNPQ
.
AB BC
BC SB
SA BC
^
ì
Þ^
í
^
î
( )
( ) ( )
// 1 .
BC SB
PBC
PSB
^
ì
ï
Þ
í
^
ï
î
( ) ( ) ( )
2.PABCMNÇ=
( ) ( )
1; 2 //MN BCÞ
// ; //PQ BC PN SA
.SA BC PN NM^Þ^
MNPQ
.N
.S ABC
ABC
O
AH
, ABC SO
I
OH
O
H
( )
P
I
OH
( )
P
.S ABC
()P
OH
()P
SO
()P
()SAH
I
SO
SH
()P
BC
()P
(),()ABC SBC
I
K
BC
, , ,AB AC SB SC
,,, MNQP
MNPQ
MN
PQ
BC
I
MN
K
PQ
ABC
SBC
S
IK
MN
PQ
MNPQ
.S ABC
ABC
a
SA SB SC b== =
2ab>
G
ABCD
( )
P
A
SC
1
C
S
C
( )
P
Trang 30
A. . B. . C. . D.
.
Hướng dẫn giải:
Kẻ . Thiết diện là tam giác .
Ta có
Gọi là trung điểm của . Dễ thất tam giác cân tại ,
suy ra .
.
Do đó:
.
Chọn A.
Câu 5: Tam giác có , đường cao . Trên đường thẳng vuông góc với
tại , lấy điểm sao cho . Gọi lần lượt là trung điểm của và . Diện tích tam
giác bằng?
A. B. C. D.
Hướng dẫn giải:
Do
Mà . Do là trung điểm
Câu 6: Cho hình chóp có đáy là tam giác đều cạnh Gọi
là mặt phẳng đi qua và vuông góc với Thiết diện của hình chóp được cắt bởi có
diện tích bằng?
A. B.
C. D.
Hướng dẫn giải:
222
3
4
aba
S
b
-
=
222
3
2
aba
S
b
-
=
222
3
2
aba
S
b
+
=
222
3
4
aba
S
b
+
=
( )
AI SC AIB SC^Þ ^
AIB
∑ ∑
222
222
sin 1 cos 1 4
22
abb a
AI AC ACS a ACS a b a
ab b
æö
+-
==-=- =-
ç÷
èø
J
AB
AIB
I
IJ AB^
22 22
3
2
a
IJ AI AJ b a
b
=-= -
222
13
.
24
aba
SABIJ
b
-
==
ABC
2BC a=
2AD a=
( )
ABC
A
S
2SA a=
,EF
SB
SC
AEF
2
3
4
a
2
3
6
a
2
1
2
a
2
3
2
a
( )
,AD BC SA BC BC SAD^^Þ^
BC AH EF AHÞ^ Þ^
1
.
2
AEF
SEFAH
D
Þ=
1
2
EF BC a==
H
SD AH aÞ=
2
1
2
AEF
Sa
D
Þ=
.S ABC
ABC
( )
2, , .
3
2
aSA ABC SA a=^
( )
P
A
.BC
.S ABC
( )
P
2
3
.
8
a
2
3
.
2
a
2
3
.
4
a
2
2
.
3
a
Trang 31
Gọi là trung điểm của thì
Hiển nhiên
Mà
Từ và suy ra
Khi đó thiết diện của hình chóp được cắt bởi chính
là
vuông tại nên
Chọn đáp án C.
Câu 7: Cho hình chóp có đáy là tam giác đều cạnh , , . Gọi là
mặt phẳng đi qua và vuông góc với . Thiết diện của và hình chóp có diện tích bằng
?
A. B. C. D.
Hướng dẫn giải:
Kẻ
Thiết diện của mặt phẳng và hình chóp là tam giác có
diện tích :
Câu 8: Cho tứ diện có hai mặt và là hai tam giác đều cạnh là
điểm trên sao cho là mặt phẳng qua và vuông góc với Thiết
diện của và tứ diện có diện tích bằng?
A. B. C. D.
Hướng dẫn giải:
Gọi là trung điểm của .
Theo bài ra .
Kẻ Thiết diện của và tứ diện
là
M
BC
( )
1.BC AM^
3.AM a=
( ) ( )
2.SA ABC BC SA^fi^
( )
1
( )
2
( ) ( ) ( )
BC SAM P SAM^fi∫
.S ABC
( )
P
.SAMD
SAMD
A
2
1133
..3.
2224
SAM
aa
SSAAM a
D
== =
.S ABC
ABC
a
( )
SA ABC^
SA a=
( )
P
S
BC
( )
P
.S ABC
2
3
4
a
2
6
a
2
2
a
2
a
( ) ( )
,AE BC SA BC BC SAE P^^Þ^º
( )
P
.S ABC
SAE
2
1133
..
2224
SAE
a
SSAAEaa
D
===
SABC
( )
ABC
( )
SBC
.,
3
2
SAa a=
M
AB
( )
0 .AM b b a=<<
( )
P
M
.BC
( )
P
SABC
2
33
..
4
ab
a
-
æö
ç÷
èø
2
3
..
4
ab
a
-
æö
ç÷
èø
2
33
.
16
ab
a
-
æö
ç÷
èø
2
33
.
8
ab
a
-
æö
ç÷
èø
N
BC
( )
.
SB SC BC SN
BC SAN
AB AC BC AN
ÏÏ
=^
ÔÔ
ÔÔ
fifi^
ÌÌ
ÔÔ
=^
ÔÔ
ÓÓ
( )
( )
( ) ( )
//
MP
BC P
P SAN
Ï
Œ
Ô
Ô
^fi
Ì
Ô
Ô
Ó
// , //MI AN MK SA fi
( )
P
SABC
.KMID
Trang 32
là hai tam giác đều cạnh là tam giác đều cạnh
là tam giác đều cạnh
Chọn đáp án C.
Câu 9: Cho tứ diện đều cạnh , là đường cao của tam giác . Mặt phẳng
qua vuông góc với cắt mp theo đoạn giao tuyến có độ dài bằng ?
A. B. C. D.
Hướng dẫn giải:
Ta có :
Tương tự :
Suy ra :
Kẻ đi qua trọng tâm của và song song với
chính là mặt phẳng
Có thể nói nhanh theo tính chất tứ diện đều:
Gọi là trọng tâm thì là tâm và
Trong kẻ qua đường thẳng song song với cắt
lần lượt tại
Ta có . Vậy
.
Câu 10: Cho hình chóp , với đáy là hình thang vuông tại , đáy lớn ,
, vuông góc với mặt phẳng , . Gọi là trung điểm . là mặt phẳng qua
và vuông góc với . Thiết diện của và hình chóp có diện tích bằng?
A. . B. . C. . D. .
Hướng dẫn giải:
Do
Gọi là trung điểm của
Gọi là trung điểm của
Gọi là trung điểm của , mà
Vậy thiết diện của và hình chóp là hình thang vuông
tại
Ta có:
là đường trung bình của tam giác
là đường trung bình của tam giác
là đường trung bình của hình thang
Khi đó
ABC
SBC
Ï
D
Ô
Ô
Ì
Ô
D
Ô
Ó
3
2
a
aANSM SA SANfi== =fiD
3
2
a
KMIfiD
2
333
...
2 16
KMI
ab ab
S
aa
D
ʈ
--
˜
Á
fi=
˜
Á
˜
Á
˯
ABCD
12a =
AP
ACD
( )
P
B
AP
( )
ACD
9
6
8
7
( )
,CD AP CD BP CD APB BG CD^^Þ^Þ^
( )
,AD CM AD BM AD BCM AD BG^^Þ^Þ^
( )
BG ABC BG AP^Þ^
KL
G
ACDD
CD
AP KLÞ^
( )
PÞ
( )
BKL
( ) ( )
2
8
3
ACD BKL KL CDÞÇ===
G
ACDD
G
ACDD
()BG ACD^
()mp ACD
G
CD
,AC AD
,KL
()( ), ()BKL ACD AP KL AP BKL^^Þ^
() ( )PBKLº
( ) ( )
2
8
3
ACD BKL KL CDÞÇ===
.S ABCD
ABCD
A
8AD =
6BC =
SA
( )
ABCD
6SA =
M
AB
( )
P
M
AB
( )
P
10
20
15
16
( ) ( )
^Þ!PAB PSA
I
( )
ÞÞÌ!SB MI SA MI P
N
( )
CD MN AB MN PÞ^ÞÌ
K
Þ !SC IK BC
Þ!!MN BC MN IK
( )
IK PÞÌ
( )
P
MNKI
M
MI
SAB
1
3
2
MI SAÞ= =
IK
SBC
1
3
2
IK BCÞ= =
MN
ABCD
( )
1
7
2
MN AD BCÞ= +=
37
..315
22
MNKI
IK MN
SMI
++
===
Trang 33
Vậy chọn đáp án .
Câu 11: Cho tứ diện có đôi một vuông góc. Kẻ .
a) Khẳng định nào đúng nhất? là trực tâm của .
A. là trực tâm của . B. là tâm đường tròn nội tiếp của .
C. là trọng tâm của . D. là tâm đường tròn ngoại tiếp của
.
b) là tam giác gì?
A. là tam giác nhọn. B. là tam giác tù
C. là tam giác vuông D. là tam giác cân
c) Khẳng định nào sau đây là đúng nhất?
A. B.
C. D.
d) Tìm tập hợp các điểm trong không gian sao cho .
A. thuộc mặt phẳng đi qua và vuông góc với , trong đó là điểm cách đều 4 điểm
và là trọng tâm của tam giác
B. thuộc mặt phẳng đi qua và song song với ,trong đó là điểm cách đều 4 điểm
và. là trọng tâm của tam giác
C. thuộc mặt phẳng đi qua O và vuông góc với , trong đó là trọng tâm của tam giác
D. thuộc mặt phẳng đi qua O và song song với , trong đó là trọng tâm của tam giác
Hướng dẫn giải:.
a) Ta có
Lại có
Vậy
.
Tương tự .
Từ suy ra là trực tâm của tam giác .
b) Đặt
Ta có
Tương tự
Áp dụng định lí côsin cho tam giác ta có
suy ra nhọn.
Tương tự các góc nhọn.
C
OABC
,,OA OB OC
( )
^OH ABC
H
DABC
H
DABC
H
DABC
H
DABC
H
DABC
DABC
DABC
DABC
DABC
DABC
2222
DDDD
=++
ABC OAB OBC OCA
SSSS
2222
111
222
DDDD
=++
ABC OAB OBC OCA
SSSS
2222
1
2
DDDD
=++
ABC OAB OBC OCA
SSSS
2222
1
3
DDDD
=++
ABC OAB OBC OCA
SSSS
2222
DDDD
=++
ABC OAB OBC OCA
SSSS
M
22 2 2
3++ =MA MB MC MO
M
I
OG
I
,,,OABC
G
ABC
M
I
OG
I
,,,OABC
ABC
M
OG
G
ABC
M
OG
G
ABC
( )
^
ü
Þ^ Þ^
ý
^
þ
OA OB
OA OBC OA BC
OA OC
( )
^Þ^OH ABC OH BC
( )
^
ü
Þ^
ý
^
þ
BC OA
BC OAH
BC OH
( )
1Þ^BC AH
( )
^
ü
Þ^
ý
^
þ
AC OB
AC OBH
AC OH
( )
2Þ^BH AC
( ) ( )
1, 2
H
ABC
,,===OA a OB b OC c
2222
=+=+BC OB OC b c
22 22
,=+ =+AC a c AB a b
ABC
( ) ( )
( )
22 22 22
222
2222
()
cos
2.
2()
+++-+
+-
==
++
ab ac bc
AB AC BC
A
AB AC
abab
( )
2
2222
0
()
=>
++
a
abab
!
A
,BC
A
O
B
C
I
H
Trang 34
c) Ta có
d) Gọi là điểm cách đều 4 điểm và là trọng tâm của tam giác thì ta có :
( do
)
Vậy thuộc mặt phẳng đi qua và vuông góc với .
Câu 12: Cho hình chóp có đáy là hình vuông cạnh , và .
Gọi lần lượt là trung điểm các cạnh và . Tính .
A. B. C.
D.
Hướng dẫn giải:.
Ta có Tương tự
suy ra
nên thuộc trục đường tròn ngoại tiếp tam giác .
Mặt khác
vuông tại , lại có là trung điểm của nên là tâm đường tròn ngoại
tiếp tam giác , do đó .
Ta có
.
Câu 13: Cho hình vuông có tâm và cạnh bằng . Trên đường thẳng qua vuông góc với
lấy điểm . Biết góc giữa và có số đo bằng . Tính độ dài .
A. . B. . C. . D. .
Hướng dẫn giải:
Chọn B.
Do .
Do đó vuông cân tại nên .
Câu 14: Cho tứ diện có đôi một vuông góc. Gọi lần lượt là góc giữa các
đường thẳng với mặt phẳng .
( )( )
2222222
11
44
==+ +
ABC
SAIBCOIOAOBOC
22 22 2 2
11 1
44 4
=++OI BC OA OB OA OC
22 2
DD D
=++
OAB OBC OCA
SSS
I
,,,OABC
G
ABC
22 2 2
3++ =MA MB MC MO
( ) ( ) ( )
22 2
2
3( )Û+++++ = +
!!!" !!" !!!" !!" !!!" !!" !!!" !!"
MI IA MI IB MI IC MI IO
( )
3.Û++ =
!!" !!" !!" !!!" !!" !!!"
IA IB IC IM IO MI
3. 3. 0Û=Û=Û^
!! " !!!" !! " !!!" !!! "!!!"
IG M I IO IM OGM I M I OG
3++ =
!!" !!" !! " !! "
IA IB IC IG
M
I
OG
.S ABCD
ABCD
a
( )
^SA ABCD
=SA a
,IK
AB
SC
IK
2
2
=
a
IK
3
2
=
a
IK
2
3
=
a
IK
32
2
=
a
IK
2
22 2
5
22
æö
=+= +=
ç÷
èø
aa
IS AI AS a
5
2
==
a
ID IC
==IS ID IC
I
SCD
( )
^
ì
Þ^
í
^
î
CD AD
CD SAD
CD SA
Þ^ÞDCD SD SCD
D
K
SC
K
SCD
( )
^KI SCD
( )
22 22 22 2 2
11
44
=- =- =- +IK ID DK ID SC ID SA AC
( )
22
22
51 2
2
44 2 2
-+=Þ=
aaa
aa IK
ABCD
O
2a
O
( )
ABCD
S
SA
( )
ABCD
45°
SO
3SO a=
2SO a=
3
2
a
SO =
2
2
a
SO =
( ) ( )
( )
∑
,45SO ABC D SA A BCD SAO^Þ ==°
SAOD
O
2SO AO a==
ABCD
,,DA DB DC
,,
abg
,,DA DB DC
( )
ABC
K
I
A
D
C
B
S
Trang 35
Tìm Giá trị nhỏ nhất của .
A. B. 8 C. 1 D.
Hướng dẫn giải:.
Gọi là hình chiếu của trên
Khi đó là trực tâm của tam giác .
Và
Đặt
Gọi thì là đường cao của tam giác nên
Vậy
Tương tự và
Nhân theo vế các BĐT ta được ( đpcm)
Câu 15: Trong mặt phẳng cho đường tròn đường kính cố định và là điểm di động trên
đường tròn này. Trên đường thẳng vuông góc với tại lấy một điểm .
a) Khẳng định nào sau đây là đúng?
A. các mặt của tứ diện là tam giác vuông
B. các mặt của tứ diện là tam giác vuông cân
C. tam giác vuông tại A.
D. tam giác vuông cân tại .
b) Gọi lần lượt là hình chiếu của trên và . Khẳng định nào sau đây là sai?
A. . B. C. A, B đều đúng D. A, B đều sai
c) Tìm tập hợp điểm khi di động.
A. thuộc đường tròn đường kính .
B. thuộc đường tròn đường kính AC.
C. thuộc đường tròn đường kính BM.
D. thuộc đường tròn đường kính AB.
d) Tìm vị trí của để đoạn lớn nhất.
A. B.
C. D.
e) Tìm vị trí của để diện tích tam giác lớn nhất.
A. là các giao điểm của đường tròn đường kính với đường tròn tâm bán kính
B. là các giao điểm của đường tròn đường kính với đường tròn tâm bán kính
( )( )( )
222
2cot 2cot 2cot=+ + +M
abg
64
64 2
H
D
( )
ABC
H
ABC
( )
( )
∑
( )
∑
∑
,,===DA ABC DA AH DAH
a
,,===DA a DB b DC c
=ÇI AH BC
DI
DBC
22
.
==
+
DB DC bc
DI
BC
bc
( )
22 2
2
22
cot
+
==
ab c
DA
DI b c
a
( )
22 2
2
2
22
24
2cot 2 2
+
Þ+ =+ ³+ ³
ab c
aa
bc bc
bc
a
( )
2
4
2cot 1+³
a
bc
a
( )
2
4
2cot 2+³
b
ac
b
( )
2
4
2cot 3+³
c
ab
g
( ) ( ) ( )
1, 2,3
( )( )( )
222
2cot 2cot 2cot 64+++³
abg
( )
a
BC
M
d
( )
a
B
A
ABMC
ABMC
ACM
ACM
M
,HK
B
AM
AC
( )
^AC BHK
^BH AC
H
M
H
BK
H
H
H
M
AM
ºMC
ºMB
ºMH
ºMK
M
BHK
M
BC
B
22
.
2
2 +
BA BC
BA BC
M
BC
B
22
1.
2
2 +
BA BC
BA BC
A
D
C
B
I
H
Trang 36
C. là các giao điểm của đường tròn đường kính với đường tròn tâm bán kính
D. là các giao điểm của đường tròn đường kính với đường tròn tâm bán kính
Hướng dẫn giải:.
a) Ta có suy ra các tam giác và
vuông tại .
Tiếp theo ta có
hay tam giác vuông tại .
b) Ta có
.
Vậy .
c) Dễ thấy cố định và nên điểm thuộc đường tròn đường kính .Từ đó ta có tập
hợp các điểm là đường tròn đường kính .
d) mà không đỏi nên lớn nhất khi lớn nhất
.
e) Ta có không đổi nên
, lúc này vuông cân tại nên .
Ta có
nên
Vậy là các giao điểm của đường tròn đường kính
với đường tròn tâm bán kính
Câu 16: Cho hình chóp có đáy là hình chữ nhật với , mặt bên
là tam giác vuông tại , mặt bên vuông tại và .
a) Tính .
A. B. C. D.
b) Đường thẳng qua vuông góc với cắt lần lượt tại . Gọi là hình chiếu của
trên .Gọi là các giao điểm của với .
Khẳng định nào sau đây là đúng nhất?
A. B. C. D. Cả A, B, C đều
đúng
M
BC
B
22
.
3
2 +
BA BC
BA BC
M
BC
B
22
.
2 +
BA BC
BA BC
( )
^
ì
^Þ
í
^
î
AB BM
AB
AB BC
a
ABM
ABC
B
( )
^
ì
Þ^
í
^
î
MC MB
MC ABM
MC AB
Þ^MC AM
ACM
M
( )
^
ì
Þ^
í
^
î
BH AM
BH ACM
BH MC
BH ACÞ^
( )
^
ü
Þ^
ý
^
þ
AC BH
AC BHK
AC BK
BK
∑
0
90=BHK
H
BK
M
BK
22 2
=+MA AB BM
AB
AM
MB
Û=ÛºBM BC M C
22 2
1
.
244
+
=£ =
BHK
BH HK BK
SBHHK
2
max
4
=Û=
BHK
BK
SBHHK
DHBK
H
2
=
BK
BH
22 22 22
111111
;=+ = +
BH BA BM BK AB BC
22 22 222
11 1 1 1 12
2
æö
+=+Û=+
ç÷
èø
BA BC BM BA BM BA BC
22
.
2
Û=
+
BA BC
MB
BA BC
2
max
4
=Û
BHK
BK
S
22
.
2
Û=
+
BA BC
MB
BA BC
Û
M
BC
B
22
.
2 +
BA BC
BA BC
.S ABCD
ABCD
,3==AB a BC a
SBC
B
SCD
D
5=SD a
SA
=SA a
2=SA a
3=SA a
4=SA a
A
AC
,CB CD
,IJ
H
A
SC
,KL
,KL
,SB SD
( )
HIJ
( )
,^AK SBC
( )
^AL SCD
^AK SC
A
B
M
C
K
H
Trang 37
Hướng dẫn giải:.
a) vuông tại mà
.
Tương tự ta có nên .
Ta có
.
Vậy .
b) Do
Lại có
Dế thấy
Từ suy ra .
Lập luận tương tự ta có .
Câu 17: Cho hình chóp có đáy là tam giác vuông cân tại , và
. Gọi là điểm trên cạnh và , mặt phẳng đi qua và
vuông góc với
Giả sử thiết diện của hình chóp với là tứ giác .
a) Hỏi tứ giác là hình gì
A. Hình chữ nhật B. hình vuông C. hình thang D. hình bình hành
b) Tìm để diện tích thiết diện lớn nhất.
A. B. C. D.
Hướng dẫn giải:.
. Ta có
Do đó Tương tự
.
Thiết diện là tứ giác .
DSBC
Þ^B BC SB
( )
^Þ^BC AD BC SAB
Þ^BC SA
^SA CD
( )
^SA ABCD
22
22
6
2
=+=
Þ= - =
SC DS DC a
SB SC BC a
22
Þ= - =SA SB AB a
=SA a
( )
^
ì
Þ^ Þ^
í
^
î
IJ AC
IJ SAC IJ SC
IJ SA
( ) ( )
1^Þ ^Þ ^AH SC HIJ SC AK SC
( ) ( )
2^Þ^BC SAB BC AK
( ) ( )
1, 2
( )
^AK SBC
( )
^AL SCD
.S ABC
ABC
B
,3==AB a SA a
( )
^SA ABC
M
AB
( )
0=<<AM x x a
( )
a
M
AB
.S ABC
( )
a
MNPQ
MNPQ
x
MNPQ
2
a
x =
2
=
a
x
3
2
=
a
x
=xa
( )
( )
^
ì
ï
Þ
í
^
ï
î
!
AB
SA
SA AB
a
a
( ) ( )
( )
( )
( ) ( )
ÎÇ
ì
ï
ÌÞÇ=
í
ï
î
!
!
M SAB
SA SAB SAB MN SA
SA
a
a
a
( )
( )
^
ì
ï
Þ
í
^
ï
î
!
AB
BC
BC AB
a
a
( ) ( )
( )
( )
( ) ( )
,
ÎÇ
ì
ï
Ì
í
ï
î
ÞÇ = Î
!
!
MABC
BC ABC
BC
ABC MQ BC Q AC
a
a
a
( ) ( )
( )
( )
( ) ( )
,
ÎÇ
ì
ï
ÌÞÇ=Î
í
ï
î
!
!
N SBC
BC SBC SBC NP BC P SC
BC
a
a
a
MNPQ
L
K
I
J
D
B
C
A
S
H
Q
P
N
M
S
A
B
C
Trang 38
b) Ta có và nên là hình bình
hành.
Mặt khác . Vậy là hình chữ nhật.
b) Ta có ,
khi .
Câu 18: Cho hình vuông có tâm và cạnh bằng . Trên đường thẳng qua vuông góc với
lấy điểm . Biết góc giữa và có số đo bằng . Tính độ dài .
A. . B. . C. . D. .
Hướng dẫn giải:
Chọn B.
Do .
Do đó vuông cân tại nên .
Câu 19: Cho tứ diện có đôi một vuông góc và . Độ dài
:
A. . B. . C. . D. .
Hướng dẫn giải::
Ta có:
Mặt khác:
Vậy chọn đáp án .
Câu 20: Cho hình chóp có đáy là hình vuông cạnh , và .
Giả sử tồn tại tiết diện của hình chóp với mặt phẳng đi qua vuông góc với . Tính diện tích
thiết diện.
A. B. C. D.
, Þ!! !MN SA PQ SA MN PQ
, Þ!! !MQ BC NP BC MQ NP
MNPQ
ì
ï
Þ^
í
ï
^
î
!
!
MN SA
NP BC MN NP
SA BC
MNPQ
==MQ AM x
( )
( )
3
.
3
-
=Þ= = = -
axa
MN MB MB SA
MN a x
SA AB AB a
( )
2
22
3
.3 3[ ]
42 4
æö
==-=--£
ç÷
èø
MNPQ
aaa
SMNMQaxx x
2
3
max
4
=
MNPQ
a
S
2
=
a
x
ABCD
O
2a
O
( )
ABCD
S
SA
( )
ABCD
45°
SO
3SO a=
2SO a=
3
2
a
SO =
2
2
a
SO =
( ) ( )
( )
∑
,45SO ABC D SA A BCD SAO^Þ ==°
SAOD
O
2SO AO a==
ABCD
,,AB BC CD
,,AB a BC b CD c===
AD
222
abc++
222
abc+-
222
abc-+
222
abc-+ +
2222
BC CD BD BC CD b c^Þ= + = +
( )
AB BC
AB BCD AB BD
AB CD
^
ì
Þ^ Þ^
í
^
î
22222
AD AB BD a b c=+=++
A
.S ABCD
ABCD
a
( )
^SA ABCD
2=SA a
( )
a
A
SC
2
2
3
=
a
S
2
2
2
=
a
S
2
3
3
=
a
S
2
42
3
=
a
S
Trang 39
Hướng dẫn giải:.
Gọi là hình chiếu của trên thì .Trong gọi .
Ta có
, mặt khác nên .
Vậy
Thiết diện là tứ giác .
b) Do
Ta có cân tại., mà nên là
trung điểm của .
Vậy .
Câu 21: Cho hình chóp tam giác đều có cạnh đáy bằng , đường cao . Gọi là
điểm thuộc đường cao của tam giác . Xét mặt phẳng đi qua và vuông góc với .
Đặt . Giả sử tồn tại thiết diện của hình chóp khi cắt bởi .
Giả sử tính được diện tích thiết diện theo và . Xác định vị trí của để diện tích thiết diện lớn
nhất.
A. B. C. D.
Hướng dẫn giải:.
Vì là hình chóp đều nên
( là tâm tam giác ).Do đó mà
.
Tương tự ta cũng có
Trường hợp 1. thì thiết diện là điểm .
Trường hợp 2. thì thuộc đoạn .
Ta có :
Tương tự .
Thiết diện là tam giác .
K
A
SC
( )
ÎK
a
( )
SAC
=ÇI SO AK
( )
^
ü
Þ^
ý
^
þ
BD SA
BD SAC
BD AC
Þ^BD SC
( )
^ SC
a
( )
!BD
a
( ) ( )
( )
( )
ÎÇ
ì
ï
Ì
í
ï
î
!
I SBD
BD SBD
BD
a
a
( ) ( )
,,ÞÇ = Î Î!SBD HL BD H SD L SB
a
AHKL
1
.
2
ì
Þ^Þ =
í
^
î
!
AHKL
HL BD
HL AK S AH KL
BD AK
2== ÞDSA AC a SAC
^AK SC
K
SC
2
22
Þ===
SC a
AK a
2222
333
Þ===Þ= =!
HL SH SI a
HL BD HL BD
BD SD SO
2
12 2 2
.
23 3
==
AHKL
aa
Sa
.S ABC
a
2=SO a
M
'AA
ABC
( )
a
M
'AA
=AM x
( )
a
a
x
M
3
8
=
a
x
33
2
=
a
x
3
8
=
a
x
33
8
=
a
x
.S ABC
( )
^SO ABC
O
ABC
1
SO AA^
( ) ( )
1
Þ!!AA SO
aa
( )
!BC
a
0=x
A
3
0
3
<£
a
x
M
( )
¹AO M A
( ) ( )
( )
( )
( ) ( )
,,
ÎÇ
ì
ï
ÌÞÇ=ÎÎ
í
ï
î
!
!
MABC
BC ABC ABC IJ BC I AB J AC
BC
a
a
a
( ) ( )
( )
( )
( ) ( )
1
11
,
ÎÇ
ì
ï
ÌÞÇ=Î
í
ï
î
!
!
MSAA
SO SAA SAA MK SO K SA
SO
a
a
a
KIJ
O
I
A
D
C
B
S
H
L
K
K
J
I
A
1
S
A
C
B
O
M
Trang 40
Trường hợp 3. khi đó thuộc đoạn
Tương tự như trường hợp trên ta có:
.
.
Thiết diện là tứ giác .
Trường hợp 4. thì thiết diện là đoạn .
b) Xét các trường hợp:
,
, thì .
Ta có
Tương tự .
Vậy .
, dễ thây là hình thang nên
,
Vậy .
33
32
<<
aa
x
M
( )
0;¹¹OA M M A
( ) ( )
( )
( )
ÎÇ
ì
ï
Ì
í
ï
î
!
M ABC
BC ABC
BC
a
a
( ) ( )
,
,
ÞÇ =
ÎÎ
!ABC IJ BC
IABJAC
a
( ) ( )
( )
( )
1
1
ÎÇ
ì
ï
Ì
í
ï
î
!
MSAA
SO SAA
SO
a
a
( ) ( )
11
,ÞÇ = Î!SAA MN SO N SA
a
( ) ( )
( )
( )
( ) ( )
,
ÎÇ
ì
ï
ÌÞÇ=Î
í
ï
î
!
!
NSBC
BC SBC SBC EF IJ N EF
BC
a
a
a
IJEF
3
2
=
a
x
BC
00=Þ =
td
xS
3
2
=
a
x
0Þ=
td
S
3
0
3
<£
a
x
1
.
2
=
IJK
SIJMK
1
23
3
3
2
Þ= = Þ=!
IJ AM x x
IJ BC IJ
BC AA
a
23
3
3
== Þ=
MK AM x
MK x
SO AO
a
2
12 3
.2 3 2
23
==
IJK
x
Sxx
32
33
<<
aa
x
IJEF
( )
1
2
=+
IJEF
SIJEFMN
23
3
=
x
IJ
( )
11
3
3
23
3
6
-
== = Þ= -
a
x
EF SN OM
EF x a
BC SA OA
a
( )
1
1
3
2
23 2 3
3
6
-
== Þ=-
a
x
MA
MN
MN a x
SO OA
a
( )( )
2
433 3 23
3
=--
IJEF
Sxaax
E
F
N
J
I
A
1
S
A
C
B
O
M
Trang 41
Xét các trường hợp ta thấy lớn nhất trong trường hợp và khi
.
Câu 22: Cho tam giác tại có cạnh huyền nằm trên mặt phẳng và các cạnh góc vuông tạo
với các góc . Giả sử là độ lớn góc giữa đường cao với .Khẳng định nào sau đây
là đúng nhất?
A. B.
C. D.
Hướng dẫn giải:.
Kẻ thì là góc giữa và và dễ thấy
Đặt , ta có
.
Xét tam giác có
.
Ta có .
Câu 23: Cho hình chóp có đáy là hình vuông cạnh , tâm .
, đường thẳng tạo với hai mặt phẳng và các góc bằng nhau. Gọi
là hình chiếu của trên .
a)Tính khi
A. B. C. D.
b) Tính góc giữa đường thẳng với .
A. B.
C. D.
td
S
33
32
<<
aa
x
2
3
max
4
=
IJEF
a
S
33
8
=
a
x
ABC
C
( )
P
( )
P
,
ab
CK
( )
P
22
sin 2sin 2 sin= +
ab
22
sin sin sin= +
ab
22
1
sin sin sin
3
= +
ab
22
sin 2 sin sin= +
ab
( )
^CH P
∑
CKH
CK
( )
P
( )
( )
∑
∑
( )
( )
∑
∑
,,,== ==CA P CAH CB P CBH
ab
=CH h
,
sin sin
==
hh
CA CB
ab
22
222
22
sin sin
=+= +
hh
AB CA CB
ab
2
22
11
sin sin
æö
=+
ç÷
èø
h
ab
ABC
..=CK AB CA C B
22
222
.
.
sin sin
1 sin sin
sin sin
Þ= =
æö
+
ç÷
èø
hh
CA CB
CK
AB
h
ab
ab
ab
22
sin sin
=
+
h
ab
∑
22
sin sin sin== +
CH
CKH
CK
ab
.S ABCD
ABCD
a
O
( )
^SO ABCD
SA
( )
ABCD
( )
SBC
H
A
( )
SBC
SA
2
=
a
HB
5
2
a
5
3
a
5
4
a
3
2
a
SA
( )
ABCD
3
arctan
5
=
j
3
arctan
7
=
j
3
arctan
8
=
j
3
arctan
2
=
j
P
C
H
A
B
K
Trang 42
Hướng dẫn giải:.
a) Dễ thấy nên .
Gọi là trung điểm của thì ta có
Kẻ thì nên .
Kẻ cắt tại , khi đó ta có
nên do
đó .
Từ ta có .
Khi thì trong tam giác vuông có
.
.
b) .
Câu 24: Cho hình chóp có đáy là hình chữ nhật, , . Góc giữa
đường thẳng với các mặt phẳng và lần lượt là và .
a) Tính
A. B.
C. D.
b) Tính
A. B.
C. D.
Hướng dẫn giải:.
a) Do
Tương tự
.
b)
.
( )
( )
∑
∑
, ==SA ABCD SAO
j
( )
cos 1=SO SA
j
I
BC
( )
^
ì
Þ^
í
^
î
OI BC
BC SIO
SO BC
^OK SI
^OK BC
( )
^OK SBC
!At OK
CK
H
( )
( )
ì
ï
Þ^
í
^
ï
î
!AH CK
AH SBC
CK SBC
( )
( )
∑
∑
, ==SA SBC SAH
j
( )
cos 2=AH SA
j
( ) ( )
1, 2
=AH SO
2
=
a
BH
HAB
2
222
3
22
æö
=-=-=
ç÷
èø
aa
AH AB HB a
22
22
3325
2222
æöæö
Þ= = Þ= + = + =
ç÷ç÷
ç÷ç÷
èøèø
aaaa
SO AH SA SO OA
3
33
2
tan arctan
22
2
2
== =Þ=
a
SO
OA
a
jj
.S ABCD
ABCD
( )
^SA ABCD
=SC a
SC
( )
ABCD
( )
SAB
a
b
SA
sin=SA a
a
cos==SA a
a
tan=SA a
a
2 sin=SA a
a
AB
( ) ( )
1
cos cos
2
+-a
ab ab
( ) ( )
2cos cos+-a
ab ab
( ) ( )
3cos cos+-a
ab ab
( ) ( )
cos cos+-a
ab ab
( ) ( )
( )
∑
,^ÞSA ABCD SA ABCD
∑
.==SAC
a
( )
^
ì
Þ^
í
^
î
BC AB
BC SAB
BC SA
( )
( )
∑
∑
,Þ==SC SAB SBC
b
sin sin==SA SC a
aa
sin sin==SB SC a
bb
22 22 22
sin sin=-= -AB SB SA a a
ba
( ) ( )
1cos2 1cos2
22
cos cos
--
=-
=+-
a
a
ba
ab ab
H
I
O
D
A
B
C
S
K
β
α
A
D
C
B
S
Trang 43
Câu 25: Cho tứ diện có đôi một vuông góc. Gọi là trực tâm của tứ diện. Gọi
là ba góc tương ứng của tam giác .
Đặt . Khẳng định nào sau đây là đúng nhất?
A. B.
C. D.
Hướng dẫn giải:.
( HS tự giải)
Câu 26: Cho tứ diện có . Hình chiếu của trên mặt phẳng là trực tâm
tam giác .
a) Tính .
A. B. C. D.
b)Khẳng định nào sau đây là đúng nhất.
A. B.
C. D.
Hướng dẫn giải:.
a) Vì
Tương tự ta có , vì vậy
.
Từ suy ra ha .
b) Từ câu a) ta thấy tứ diện có các cạnh đôi một vuông góc.
Theo BĐT Cauchy-Schwraz ta có
Mà nên .
Đẳng thức xảy ra khi đều, kết hợp với chân đường cao của trùng với tâm
đáy ta được là hình chóp đều đỉnh .
Câu 27: Cho tứ diện có các cạnh đôi một vuông góc. là một điểm bất kì thuộc
miền trong tam giác .
a) Tìm giá trị nhỏ nhất của .
A. B. C. D.
OABC
,,OA OB OC
H
,,ABC
ABC
∑
∑ ∑
,,===AOH BOH COH
abg
222
sin sin sin
sin sin sin
==
ABC
abg
222
sin 2 sin 2 sin 2
sin 2 sin 2 sin 2
==
ABC
abg
222
sin 2 sin 2 sin 2
sin sin sin
==
ABC
abg
22 2
sin sin sin
sin 2 sin 2 sin 2
==
ABC
abg
ABCD
∑
0
90=BDC
H
D
ABC
ABC
∑
CDA
∑
0
60=CDA
∑
0
90=CDA
∑
0
45=CD A
∑
0
30=CDA
( )
( )
2
22 2
6 ++ ³++DA DB DC AB BC CA
( )
( )
2
22 2
65++ ³ ++DA DB DC AB BC CA
( )
( )
2
22 2
3 ++ ³++DA DB DC AB BC CA
( )
( )
2
22 2
23++ ³ ++DA DB DC AB BC CA
( )
^
ì
Þ^
í
^
î
BC DH
BC ADH
BC AH
( )
1Þ^BC DA
( )
^Þ^BDH AC DB AC
( )
^
ì
Þ^
í
^
î
DB DC
DB ACD
DB AC
( )
2Þ^DB DA
( ) ( )
1, 2
( )
^Þ^DA BCD DA DC
∑
0
90=CDA
ABCD
,,DA DB DC
( )
( )
2
222
3++ £ + +AB BC CA AB BC CA
222
222
222
ì
=+
ï
=+
í
ï
=+
î
AB DA DB
BC DB DC
CA DA DC
( )
( )
2
22 2
6++ £ + +AB BC CA DA DB DC
==ÞDAB BC CA ABC
D
.D ABC
D
OABC
,,OA OB OC
M
ABC
22 2
22 2
=++
MA MB MC
T
OA OB OC
min 3=T
min 2=T
min 4=T
min 6=T
H
D
B
A
C
M
N
Trang 44
b) Gọi là trực tâm tam giác và lần lượt là góc gữa đường thẳng với các đường
thẳng . Tìm giá trị lớn nhất của
A. B. C. D.
c) Tìm GTNN của
A. B. C. D.
Hướng dẫn giải:.
a) Gọi , kẻ thì ta có
kẻ . Khi đó
Suy ra .
Tương tự gọi là các điểm tương tự như thì ta có
Từ ta có
Gọi là trực tâm của tam giác thì ta đã biết kết quả quen thuộc
nên
Mặt khác
Tương tự nên
Do đó do .
Vậy khi .
Cách 2. Đặt . Do đồng phẳng nên tồn tại sao cho
.
Ta có , bình phương vô hướng ta được
.
Tương tự
H
ABC
,,
abg
OH
,,OA OB OC
Acotcotcot=
abg
2
max
4
=A
2
max
3
=A
1
max
2
=A
max 2=A
222
cos cos cos cos cos cos
cos cos cos
+++
=++S
ab bg ga
gab
min 6 3=S
min 3=S
min 6=S
min 4=S
=ÇN AM BC
1
!MM OA
( )
( )
1
1
ì^
ï
Þ^
í
ï
î
!
OA OBC
MM OBC
MM OA
11
,^ÎMA OA A OA
2222 22
111 1
=+ =+ -AM AA MA AA MO OA
( )( )
2
1111
=+- +OM AA OA AA OA
( )
2
1
2=+ -OM OA OA OA
22
1
2.=+-OM OA OA OA
( )
22
1
22
2
1 1=+-
OA
AM OM
OA OA OA
11
,BC
1
A
( )
22
1
22
2
1 2=+-
OB
MB OM
OB OB OB
( )
22
1
22
2
1 3=+-
OC
MC OM
OC OC OC
( ) ( ) ( )
1, 2,3
2
11 1
22 2
111
23
æö
æö
=++-+++
ç÷
ç÷
èø
èø
OA OB OC
TOM
OA OB OC OA OB OC
H
ABC
22 2 2
111 1
++ =
OA OB OC OH
2
11 1
2
23
æö
=- +++
ç÷
èø
OA OB OC
OM
T
OH OA OB OC
1
==
MBC
ABC
S
OA
NM
OA NA S
11
,==
MAC
MAB
ABC ABC
S
OB OC S
OB S OC S
11 1
1++ =
OA OB OC
OA OB OC
2
2
12=+³
OM
T
OH
³OM OH
min 2=T
ºMH
,,===
!!!" " !!!" " !!!" "
OA a OB b OC c
,,,ABCM
,,xyz
( )
1=++ ++=
!!!!" !!!" !!!" !!!"
OM xOA yOB zOC x y z
( )
1AM OM OA x a b c=-=-++
!!!!" !!!!" !!!" " " "
( ) ( )
22222
22
222222
222
11=- + + Þ =- + +
MA y b z c
AM x a y b z c x
OA a a
( ) ( )
222 22 22222
22
22 2 22 2
1, 1=+-+ =++-
MB x a z c MC x a y b
yz
OB b b OC c c
A
1
M
1
N
O
B
A
C
M
Trang 45
Vì vậy
( Theo Cauchy-Schwarz)
Vậy .
b) Dễ thấy .
Ta có
.
Lại có
Áp dụng CT (*) cho nhận các giá trị và kết hợp với thu được
.
Đặt thì bài toán trỏ thành
Cho thỏa . Chứng minh .
Ta có
.
Tương tự ta có :
và
Nhân theo từng vế các BĐT ta được .
c) Tương tự như câu b) ta có .
( )
22 2 2 22
222
111
1
æö
=++ + + +
ç÷
èø
Taxbycz
abc
2
111
...12
æö
³++ +=
ç÷
èø
ax by cz
abc
min 2=T
∑
∑ ∑
,,===AOH BOH COH
abg
222
22 2 2
111 1
1
æöæöæö
++ = Û + + =
ç÷ç÷ç÷
èøèøèø
OH OH OH
OA OB OC OH OA OB OC
( )
222
cos cos cos 1 1Û++=
abg
( )
2
22
222
11cot
1tan cos *
cos 1 tan 1 cot
+= Û = =
++
x
xx
xxx
x
,,
abg
( )
1
222
222
cot cot cot
1
1cot 1cot 1cot
++=
+++
abg
abg
( )
222
cot , cot , cot , , 0=== >xyz xyz
abg
,, 0>xyz
1
111
++=
+++
xyz
xyz
1
8
£xyz
( )( )
11 2
111 1 11 11
++=Û-=+³
+++ + ++ ++
xyz x yz yz
xyz x yz yz
( )( )
( )
1
2 2
111
Û³
+++
yz
xyz
( )( )
( )
1
23
111
³
+++
xz
yxz
( )( )
( )
1
2 4
111
³
+++
xy
zxy
( ) ( )( )
2,3 4
( )
1
8
£xyz dpcm
min 6 3=S
| 1/45
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

BÀI TẬP TRẮC NGHIỆM
ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG
A – LÝ THUYẾT TÓM TẮT 1. Định nghĩa d ^ (P) Û d ^ a, "a Ì (P)
2. Điều kiện để đường thẳng vuông góc với mặt phẳng ì Ì Ç = , a b (P),a b O í Þ d ^ (P) îd ^ , a d ^ b 3. Tính chất
• Mặt phẳng trung trực của một đoạn thẳng là mặt phẳng vuông góc với đoạn thẳng tại trung điểm của nó.
Mặt phẳng trung trực của đoạn thẳng là tập hợp các điểm cách đều hai đầu mút của đoạn thẳng đó. ì ⁄⁄ ì ¹ • a b a b í Þ (P) ^ b • í Þ a⁄⁄b ( î P) ^ a
îa ^ (P),b ^ (P) ì ⁄⁄ ì ¹ • (P) (Q) (P) (Q) í Þ a ^ (Q) • í Þ (P)⁄⁄(Q) îa ^ (P) ( î P) ^ , a (Q) ^ a ì ⁄⁄ ì Ë • a (P) a (P) í Þ b ^ a • í Þ a⁄ (P) îb ^ (P) îa ^ ,( b P) ^ b
4. Định lí ba đường vuông góc
Cho a ^ (P),b Ì (P), a¢ là hình chiếu của a trên (P). Khi đó b ^ a Û b ^ a¢
5. Góc giữa đường thẳng và mặt phẳng • Nếu d ^ (P) thì ∑ (d,(P)) = 900.
• Nếu d ^ (P) thì ∑ (d,(P)) = ∑
(d,d') với d¢ là hình chiếu của d trên (P). Chú ý: 00 £ ∑ (d,(P)) £ 900. B – BÀI TẬP
Câu 1: Cho hai đường thẳng phân biệt a, b và mặt phẳng(P ,
) trong đóa ^ (P . ) Mệnh đề nào sau đây là sai?
A. Nếu b ^ (P ) thì b//a .
B. Nếu b// (P ) thìb ^ a .
C. Nếu b//a thìb ^ (P . )
D. Nếu b ^ a thì b// (P . )
Hướng dẫn giải: Chọn D.
Câu 2: Trong không gian cho đường thẳng D và điểm O . Qua O có mấy đường thẳng vuông góc với D cho trước? A. 1. B. 2 . C. 3 . D. Vô số.
Hướng dẫn giải: Chọn D.
Qua điểm O có thể dựng vô số đường thẳng vuông góc với D , các đường thẳng đó cùng nằm trong
một mặt phẳng vuông góc với D .
Câu 3: Mệnh đề nào sau đây có thể sai?
A. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song.
B. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song.
C. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì song song.
D. Một đường thẳng và một mặt phẳng (không chứa đường thẳng đã cho) cùng vuông góc với một
đường thẳng thì song song nhau.
Hướng dẫn giải: Chọn C. Trang 1
Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì song song chỉ đúng khi ba
đường thẳng đó đồng phẳng.
Câu 4: Khẳng định nào sau đây sai?
A. Nếu đường thẳng d ^ (a ) thì d vuông góc với hai đường thẳng trong (a ).
B. Nếu đường thẳng d vuông góc với hai đường thẳng nằm trong (a ) thì d ^ (a ).
C. Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau nằm trong (a ) thì d vuông góc
với bất kì đường thẳng nào nằm trong (a ).
D. Nếu d ^ (a ) và đường thẳng a // (a ) thì d ^ a .
Hướng dẫn giải: Chọn B.
Đường thẳng d vuông góc với hai đường thẳng nằm trong (a ) thì d ^ (a ) chỉ đúng khi hai đường thẳng đó cắt nhau.
Câu 5: Trong không gian tập hợp các điểm M cách đều hai điểm cố định A và B là
A. Mặt phẳng trung trực của đoạn thẳng AB .
B. Đường trung trực của đoạn thẳng AB .
C. Mặt phẳng vuông góc với AB tại A .
D. Đường thẳng qua A và vuông góc với AB .
Hướng dẫn giải: Chọn A.
Theo định nghĩa mặt phẳng trung trực.
Câu 6: Trong không gian cho đường thẳng D và điểmO . Qua O có bao nhiêu đường thẳng vuông góc với D cho trước? A. Vô số. B. 2. C. 3. D. 1.
Hướng dẫn giải: Chọn A.
Câu 7: Qua điểm O cho trước, có bao nhiêu mặt phẳng vuông góc với đường thẳng D cho trước? A. 1 B. Vô số C. 3 D. 2
Hướng dẫn giải:
Theo tiên đề qua điểm O cho trước có duy nhất một mặt phẳng vuông góc với đường thẳng D Chọn đáp án A.
Câu 8: Trong không gian cho đường thẳng D không nằm trong mp (P), đường thẳng D được gọi là
vuông góc với mp (P) nếu:
A. vuông góc với hai đường thẳng phân biệt nằm trong mp (P).
B. vuông góc với đường thẳng a mà a song song với mp (P)
C. vuông góc với đường thẳng a nằm trong mp (P).
D. vuông góc với mọi đường thẳng nằm trong mp (P).
Hướng dẫn giải:
Đường thẳng D được gọi là vuông góc với mặt phẳng (P) nếu D vuông góc với mọi đường thẳng
trong mặt phẳng (P).(ĐN đường thẳng vuông góc với mặt phẳng). Vậy đáp án D đúng.
Câu 9: Cho a,b, c là các đường thẳng trong không gian. Tìm mệnh đề sai trong các mệnh đề sau.
A. Nếu a ^ b và b ^ c thì a / / . c
B. Nếu a vuông góc với mặt phẳng (a ) và b / / (a ) thì a ^ . b
C. Nếu a / /b và b ^ c thì c ^ . a
D. Nếu a ^ b , b ^ c và a cắt c thì b vuông góc với mặt phẳng ( , a c) .
Hướng dẫn giải: ìa ^ b Nếu í
thì a và c có thể trùng nhau nên đáp án A sai. îb ^ c
Câu 10: Trong các mệnh đề sau, mệnh đề nào sai? Trang 2
A. Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.
B. Có duy nhất một mặt phẳng đi qua một đường thẳng cho trước và vuông góc với một mặt phẳng cho trước.
C. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.
D. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
Hướng dẫn giải:
Qua một điểm cho trước có thể kẻ được vô số mặt phẳng vuông góc với mặt phẳng cho trước.
Vậy chọn đáp án D .
Câu 11: Chọn mệnh đề đúng trong các mệnh đề sau?
A. Nếu a ^ (P) và b ^ a thì b ! (P) .
B. Nếu a ! (P) và a ! b thì b ! (P).
C. Nếu a ! (P) và b ^ athì b ^ (P).
D. Nếu a ! (P) và b ^ (P) thì b ^ a.
Câu 12: Cho hai đường thẳng a,b và mp(P). Chỉ ra mệnh đề đúng trong các mệnh đề sau:
A. Nếu a// (P) và b ^ a thì b// (P).
B. Nếu a// (P) và b ^ (P) thì a ^ b.
C. Nếu a// (P) và b ^ a thì b ^ (P).
D. Nếu a ^ (P) và b ^ a thì b// (P).
Hướng dẫn giải:
Câu A sai vì b có thể vuông góc với a .
Câu B đúng bởi a// (P) Þ a
$ ¢ Ì (P) sao cho a//a¢, b ^ (P) Þ b ^ a¢. Khi đó Þ a ^ b.
Câu C sai vì b có thể nằm trong (P).
Câu D sai vì b có thể nằm trong (P). Vậy chọn B.
Câu 13: Chỉ ra mệnh đề sai trong các mệnh đề sau:
A. Hai đường thẳng chéo nhau và vuông góc với nhau. Khi đó có một và chỉ một mp chứa đường
thẳng này và vuông góc với đường thẳng kia.
B. Qua một điểm O cho trước có một mặt phẳng duy nhất vuông góc với một đường thẳng D cho trước.
C. Qua một điểm O cho trước có một và chỉ một đường thẳng vuông góc với một đường thẳng cho trước.
D. Qua một điểm O cho trước có một và chỉ một đường thẳng vuông góc với một mặt phẳng cho trước.
Câu 14: Tập hợp các điểm cách đều các đỉnh của một tam giác là đường thẳng vuông góc với mặt
phẳng chứa tam giác đó và đi qua:
A. Tâm đường tròn ngoại tiếp tam giác đó.
B. Trọng tâm tam giác đó.
C. Tâm đường tròn nội tiếp tam giác đó.
D. Trực tâm tam giác đó.
Câu 15: mệnh đề đúng trong các mặt phẳng sau:
A. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song.
B. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song.
C. Hai đường thẳng cùng vuông góc với một mặt phẳng thì song song.
D. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song.
Hướng dẫn giải::
Đáp án A sai vì hai đường thẳng đó có thể chéo nhau.
Đáp án B sai vì hai mặt phẳng đó có thể cắt nhau.
Đáp án C sai vì hai đường thẳng đó có thể trùng nhau. Chọn đáp án D.
Câu 16: Chỉ ra mệnh đề sai trong các mệnh đề sau:
A. Cho hai đường thẳng vuông góc với nhau, mặt phẳng nào vuông góc với đường thẳng này thì
cũng vuông góc với đường thẳng kia.
B. Hai đường thẳng phân biệt cùng vuông góc với một mp thì song song với nhau. Trang 3
C. Cho hai mp song song, đường thẳng nào vuông góc với mặt mp này thì cũng vuông góc với mp kia.
D. Cho hai đường thẳng song song, mặt phẳng nào vuông góc với đường thẳng này thì cũng vuông
góc với đường thẳng kia.
Hướng dẫn giải:
Vì qua một đường thẳng dựng được vô số mặt phẳng
Câu 17: Trong các mệnh đề sau, mệnh đề nào sai?
A. Nếu đường thẳng a song song với mặt phẳng (P
) và đường thẳng b vuông góc với a thì b
vuông góc với mặt phẳng (P).
B. Nếu đường thẳng a song song với đường thẳng b và b song song với mặt phẳng (P ) thì a
song song hoặc nằm trên mặt phẳng (P).
C. Nếu đường thẳng a song song với mặt phẳng (P
) và đường thẳng b vuông góc với mặt phẳng (P
) thì a vuông góc với . b
D. Một đường thẳng vuông góc với hai đường thẳng cắt nhau trong một mặt phẳng thì nó vuông
góc với mặt phẳng đó.
Hướng dẫn giải:
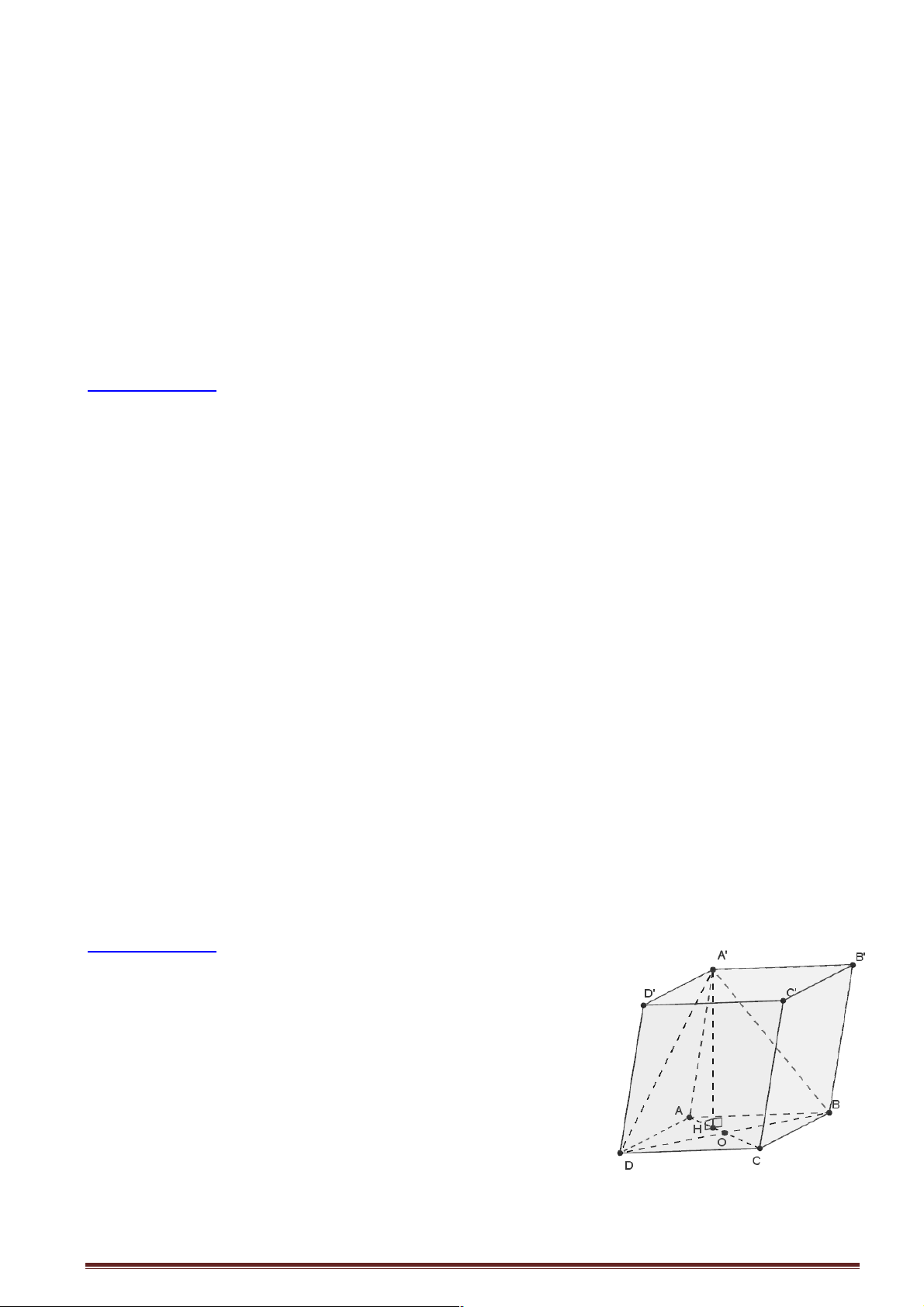
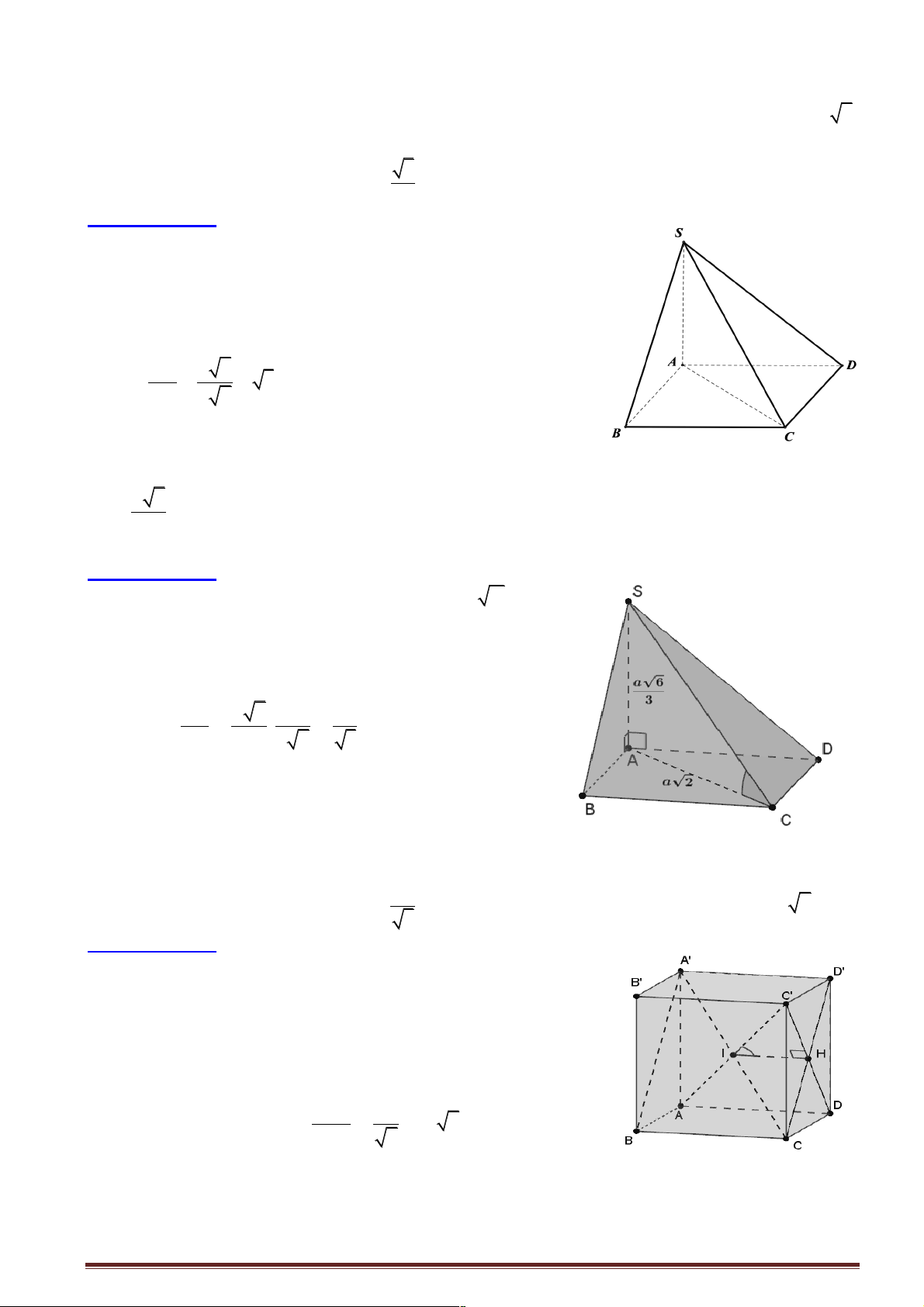
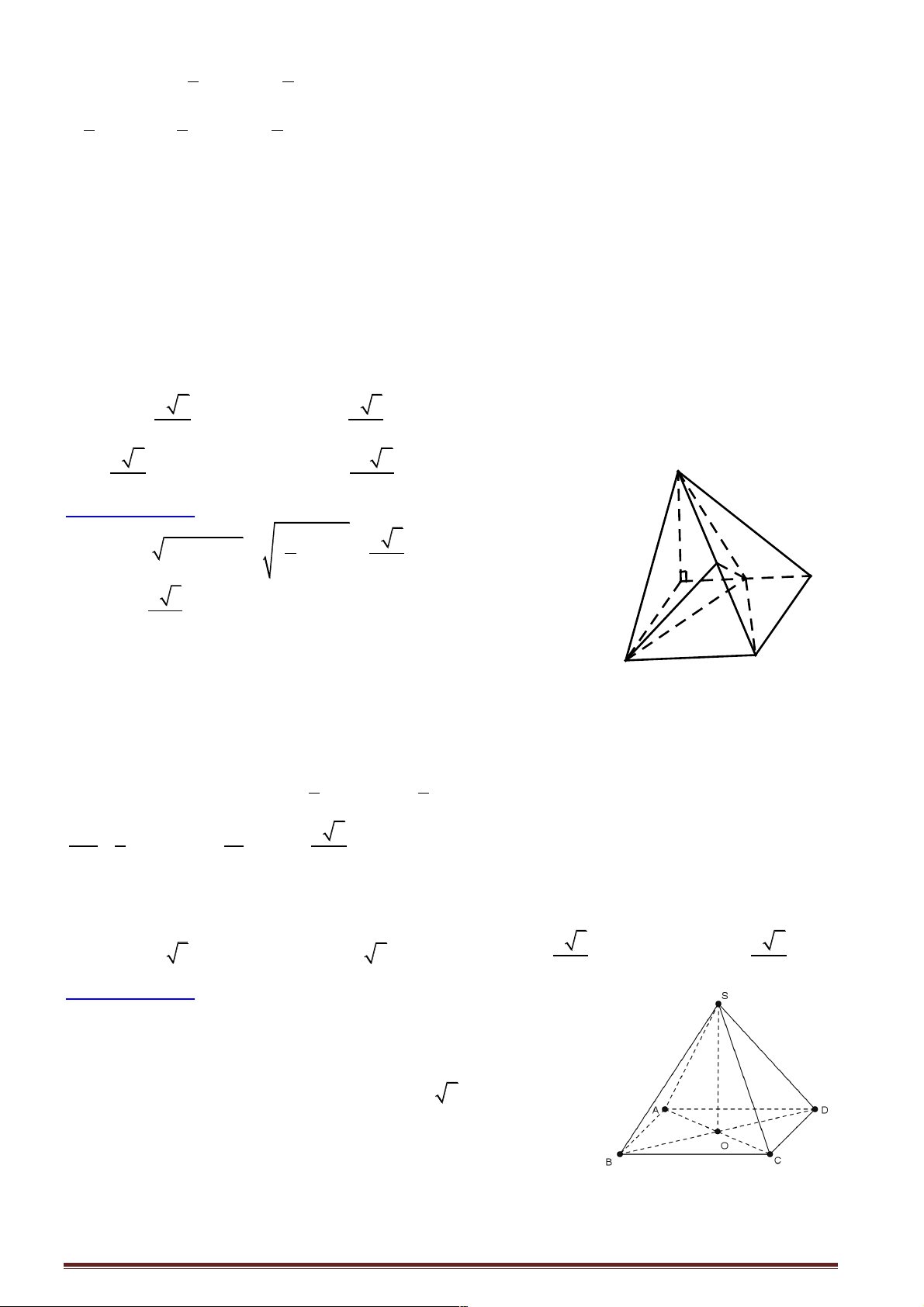
Giả sử xét hình lập phương ABC .
D A' B 'C ' D ' như hình vẽ có Ï A
Ô ' B '/ /(ABCD) Ô Ì
nhưng B'C '/ /(ABC ) D . B
Ô 'C ' ^ A'B' Ô Ó Chọn đáp án A.
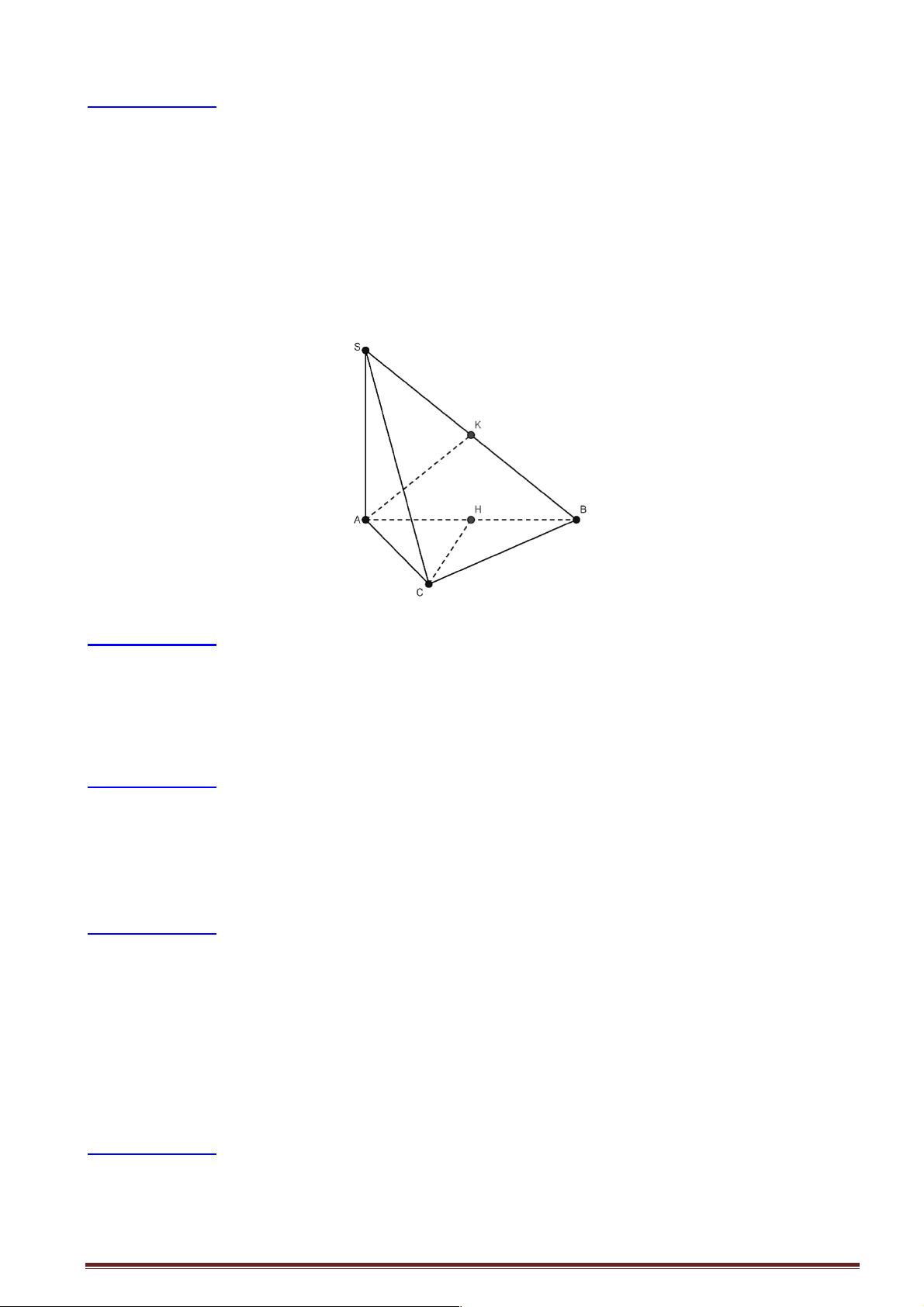
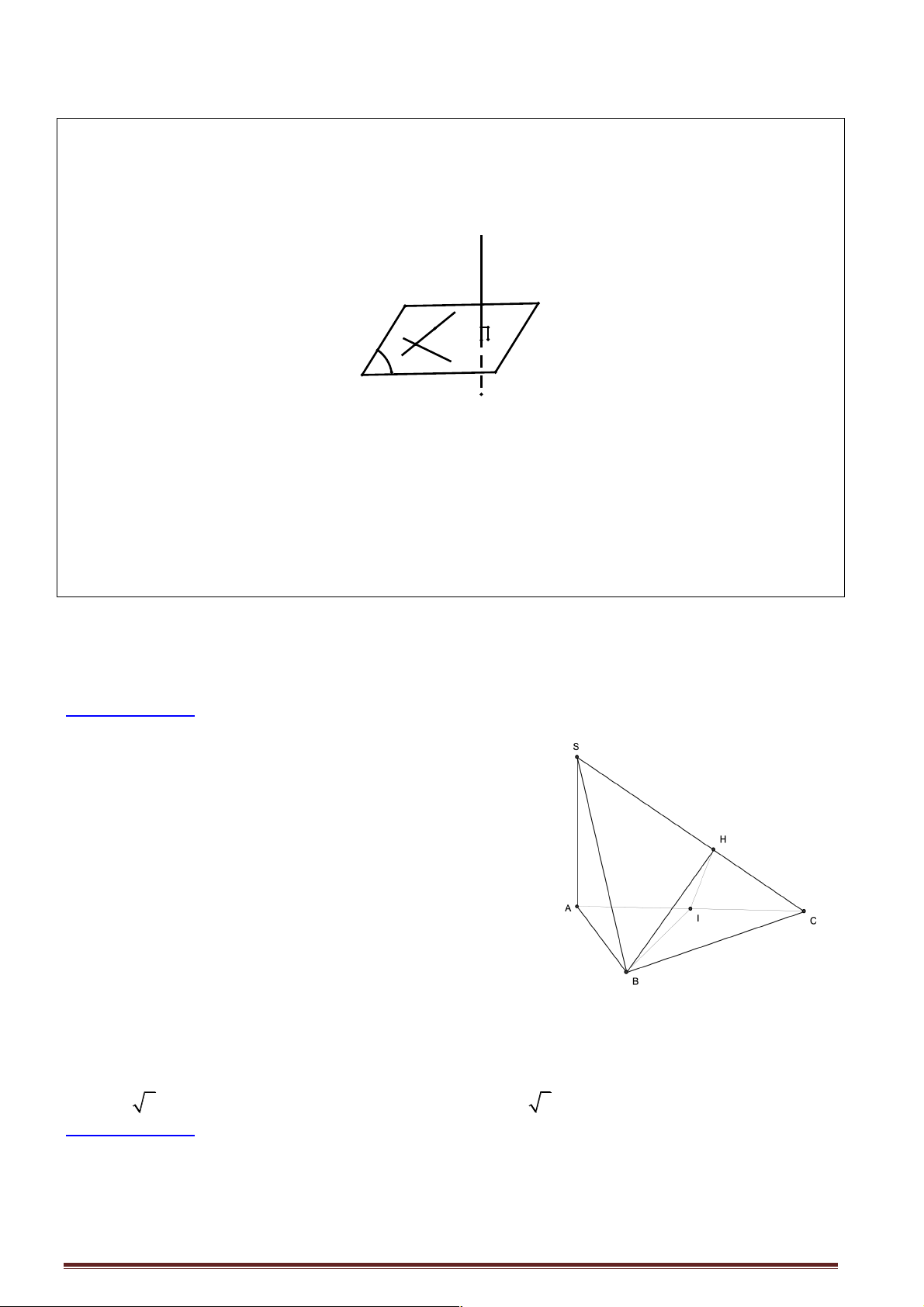
Câu 18: Cho hình chóp S.ABC có SA = SB = SC và tam giác ABC vuông tại B . Vẽ SH ^ ( ABC),
H Î( ABC). Khẳng định nào sau đây đúng?
A. H trùng với trọng tâm tam giác ABC .
B. H trùng với trực tâm tam giác ABC .
C. H trùng với trung điểm của AC .
D. H trùng với trung điểm của BC .
Hướng dẫn giải: Chọn C.
Do SA = SB = SC nên HA = HB = HC . Suy ra H là tâm đường tròn ngoại tiếp ABC D . Mà ABC D
vuông tại B nên H là trung điểm của AC .
Câu 19: Cho hình chóp S.ABC thỏa mãn SA = SB = SC . Tam giác ABC vuông tại A . Gọi H là
hình chiếu vuông góc của S lên mp( ABC). Chọn khẳng định sai trong các khẳng định sau?
A. (SBH )Ç( SCH ) = SH .
B. (SAH )Ç( SBH ) = SH .
C. AB ^ SH . D.
(SAH)Ç(SCH) = SH .
Hướng dẫn giải:.
(SBH )Ç( SCH ) = (SBC) Chọn A. Trang 4
Câu 20: Cho hình chóp S.ABCD có các cạnh bên bằng nhau SA = SB = SC = SD . Gọi H là hình
chiếu của S lên mặt đáy ABCD . Khẳng định nào sau đây sai?
A. HA = HB = HC = HD .
B. Tứ giác ABCD là hình bình hành.
C. Tứ giác ABCD nội tiếp được trong đường tròn.
D. Các cạnh SA , SB , SC , SD hợp với đáy ABCD những góc bằng nhau.
Hướng dẫn giải: Chọn B.
Vì hình chóp S.ABCD có các cạnh bên bằng nhau
SA = SB = SC = SD và H là hình chiếu của S lên mặt đáy ABCD
Nên H tâm đường tròn ngoại tiếp tứ giác ABCD
Suy ra HA = HB = HC = HD . Nên đáp án B sai.
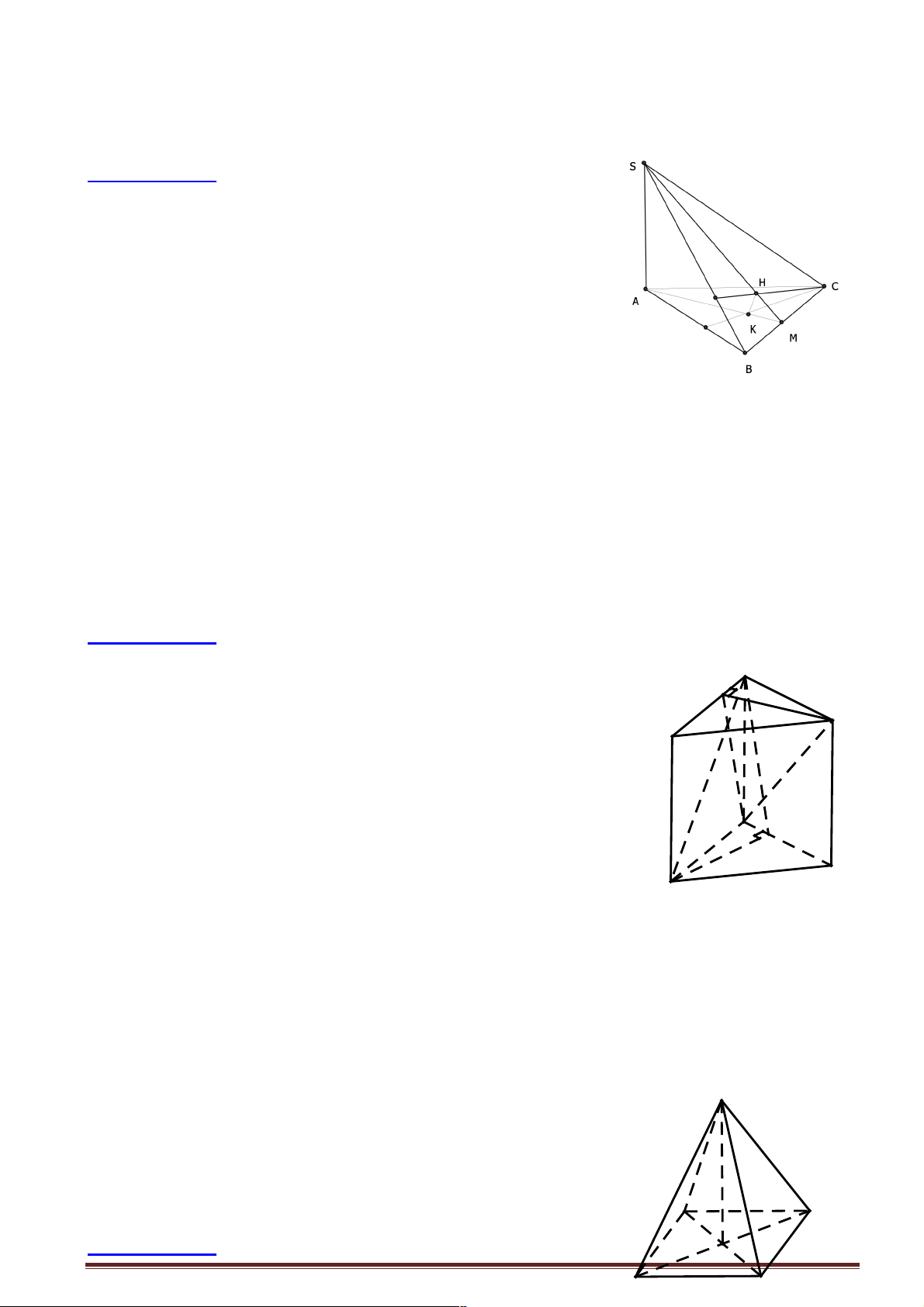
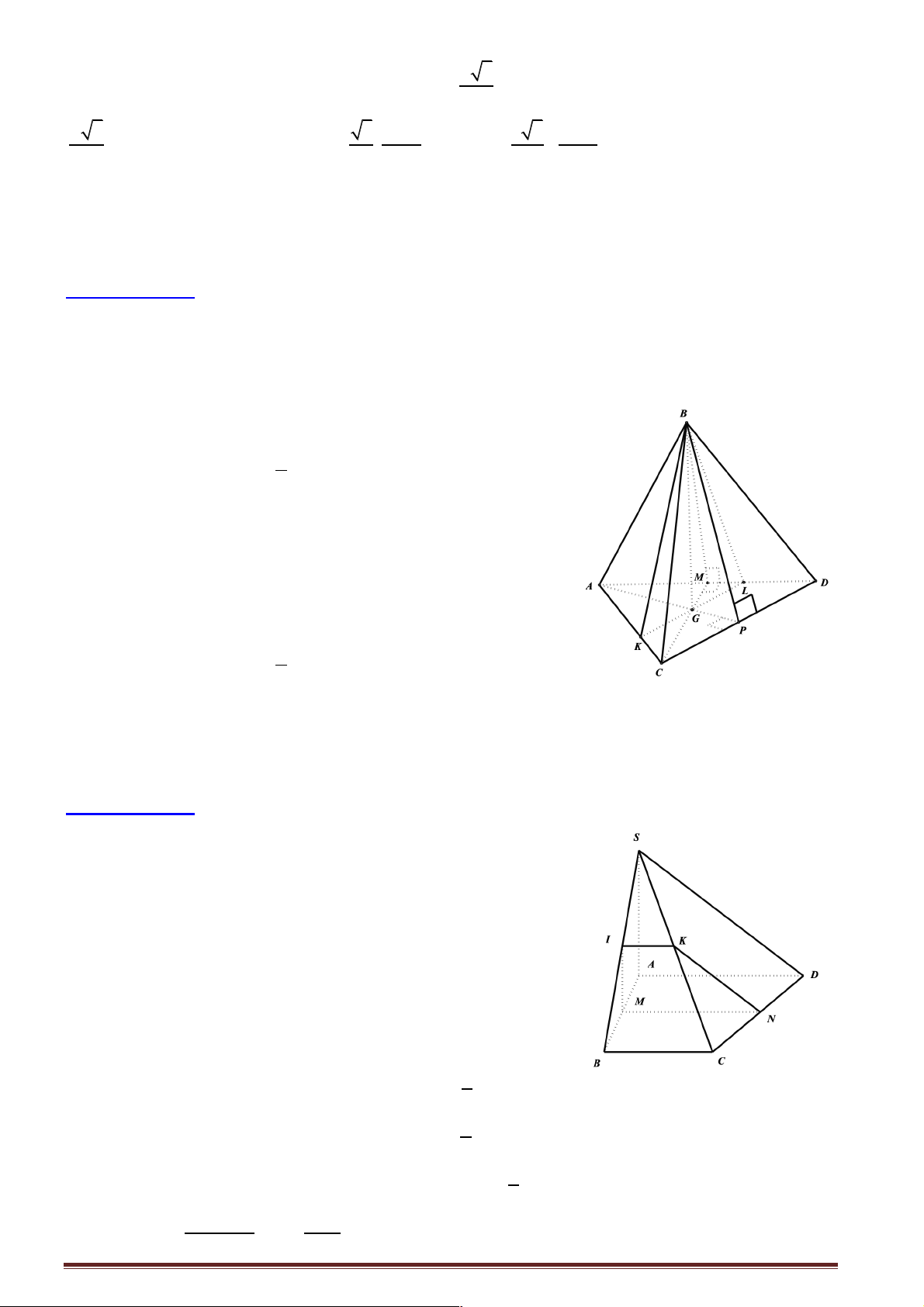
Câu 21: Cho hình chóp S.ABC có SA ^ (ABC) và tam giác ABC không vuông, gọi H , K lần lượt là
trực tâm các tam giác ABC và SBC . Các đường thẳng AH, SK, BC thỏa mãn: A. Đồng quy.
B. Đôi một song song.
C. Đôi một chéo nhau. D. Đáp án khác.
Hướng dẫn giải:
Gọi AA¢ là đường cao của tam giác ABC Þ AA' ^ BC mà
BC ^ SA nên BC ^ SA'
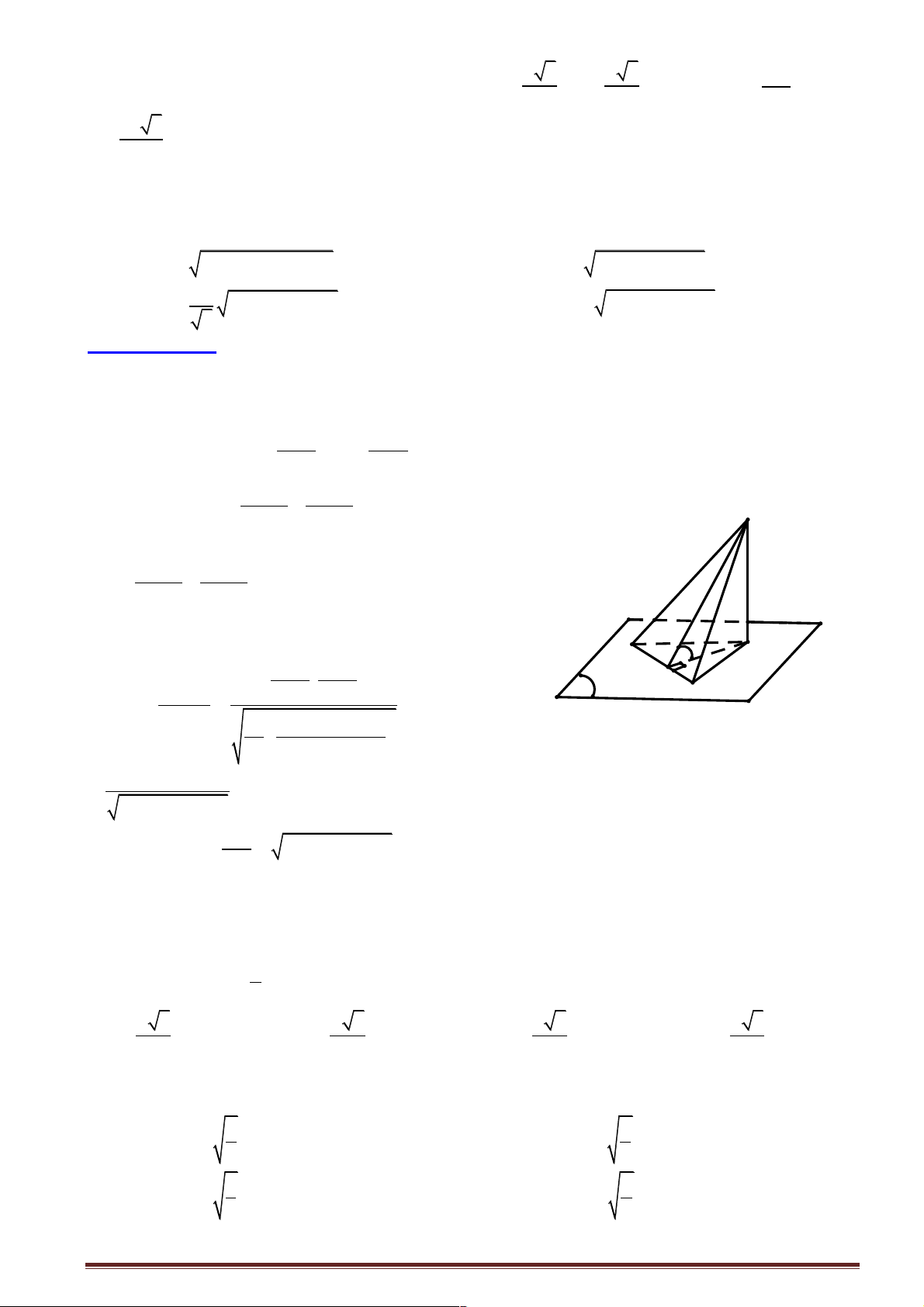
Câu 22: Cho hình chóp S.ABC có các mặt bên tạo với đáy một góc
bằng nhau. Hình chiếu H của S trên (ABC).là:
A. Tâm đường tròn nội tiếp tam giác ABC.
B. Tâm đường tròn ngoại tiếp tam giác ABC.
C. Trọng tâm tam giác ABC.
D. Giao điểm hai đường thẳng AC và . BD
Hướng dẫn giải:
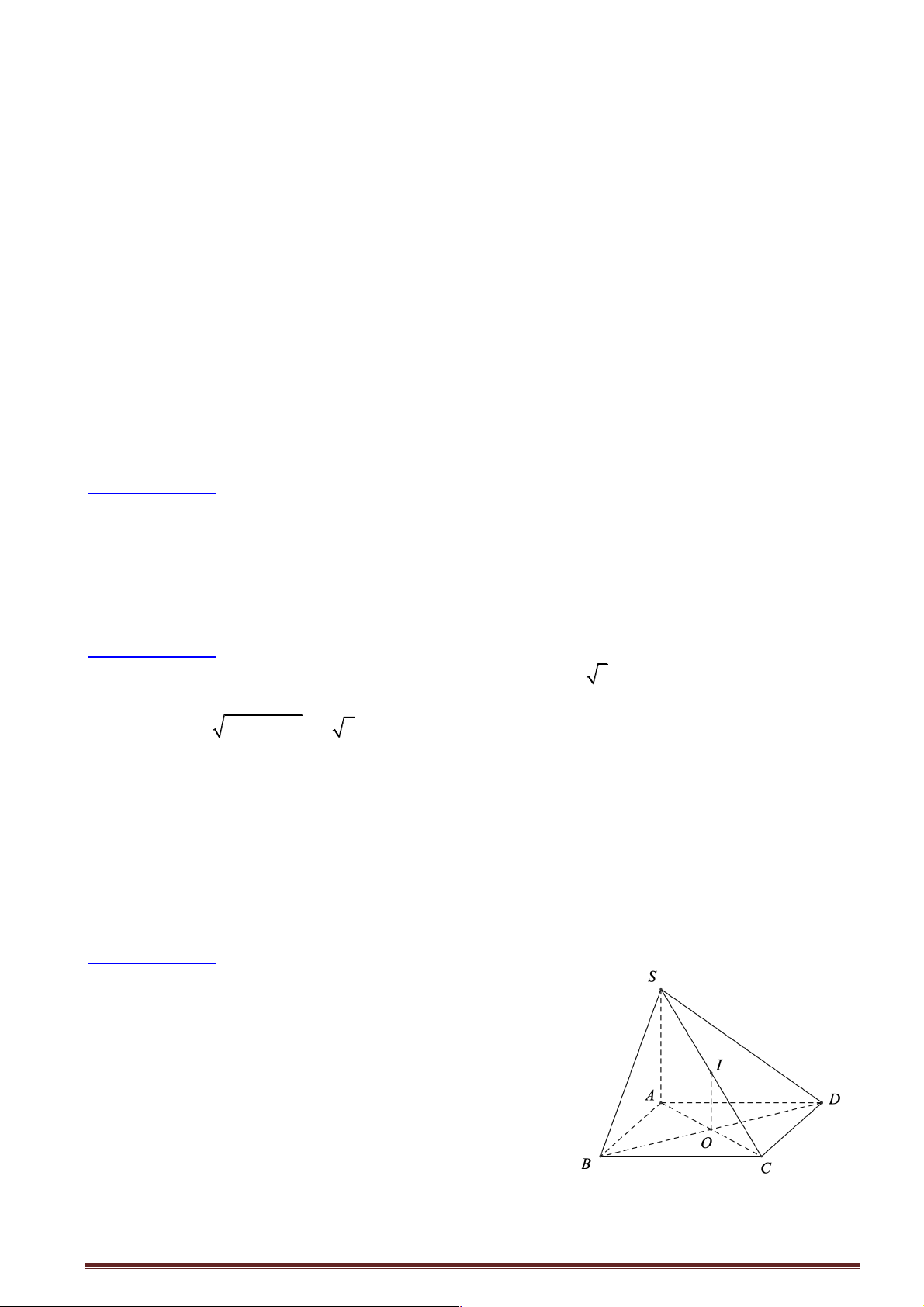
Gọi M , N, P lần lượt là hình chiếu của S lên các cạnh AB, AC, BC.
Theo định lý ba đường vuông góc ta có M , N, P lần lượt là hình chiếu của H lên các cạnh
AB, AC, BC. ∑ ∑ ∑
Þ SMH = SNH = SPH Þ SM D H = SN D H = SP D H.
Þ HM = HN = NP Þ H là tâm dường tròn nội tiếp của ABC D .
Câu 23: Cho hình chóp đều, chọn mệnh đề sai trong các mệnh đề sau:
A. Chân đường cao của hình chóp đều trùng với tâm của đa giác đáy đó.
B. Tất cả những cạnh của hình chóp đều bằng nhau.
C. Đáy của hình chóp đều là miền đa giác đều.
D. Các mặt bên của hình chóp đều là những tam giác cân.
Hướng dẫn giải:
Hình chóp đều có thể có cạnh bên và cạnh đáy KHÔNG bằng nhau nên đáp án B sai.
Câu 24: Tính chất nào sau đây không phải là tính chất của hình lăng trụ đứng?
A. Các mặt bên của hình lăng trụ đứng là những hình bình hành.
B. Các mặt bên của hình lăng trụ đứng là những hình chữ nhật.
C. Các cạnh bên của hình lăng trụ đứng bằng nhau và song song với nhau.
D. Hai đáy của hình lăng trụ đứng có các cạnh đôi một song song và bằng nhau. Trang 5
Hướng dẫn giải: Chọn A. Trang 6
DẠNG 1: CHỨNG MINH ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG
VÀ ĐƯỜNG THẲNG VUÔNG GÓC ĐƯỜNG THẲNG Phương pháp:
* Chứng minh đường thẳng vuông góc với mặt phẳng
Muốn chứng minh đương thẳng d ^ (a ) ta có thể dùng môt trong hai cách sau.
Cách 1. Chứng minh d vuông góc với hai đường thẳng a,b cắt nhau trong (a ). ìd ^ a ïd ^ ï b í Þ a ^ a a Ì (a ) b Ì ï (a) ( ) ,
ïîaÇb = I
Cách 2. Chứng minh d vuông góc với đường thẳng a mà a vuông góc với (a ). ìïd ! a ( í d a ïî a ) Þ ^ ( ) ^ a
Cách 3. Chứng minh d vuông góc với (Q) và (Q) // (P).
* Chứng minh hai đường thẳng vuông góc
Để chứng minh d ^ a, ta có thể chứng minh bởi một trong các cách sau:
• Chứng minh d vuông góc với (P) và (P) chứa a.
• Sử dụng định lí ba đường vuông góc.
• Sử dụng các cách chứng minh đã biết ở phần trước.
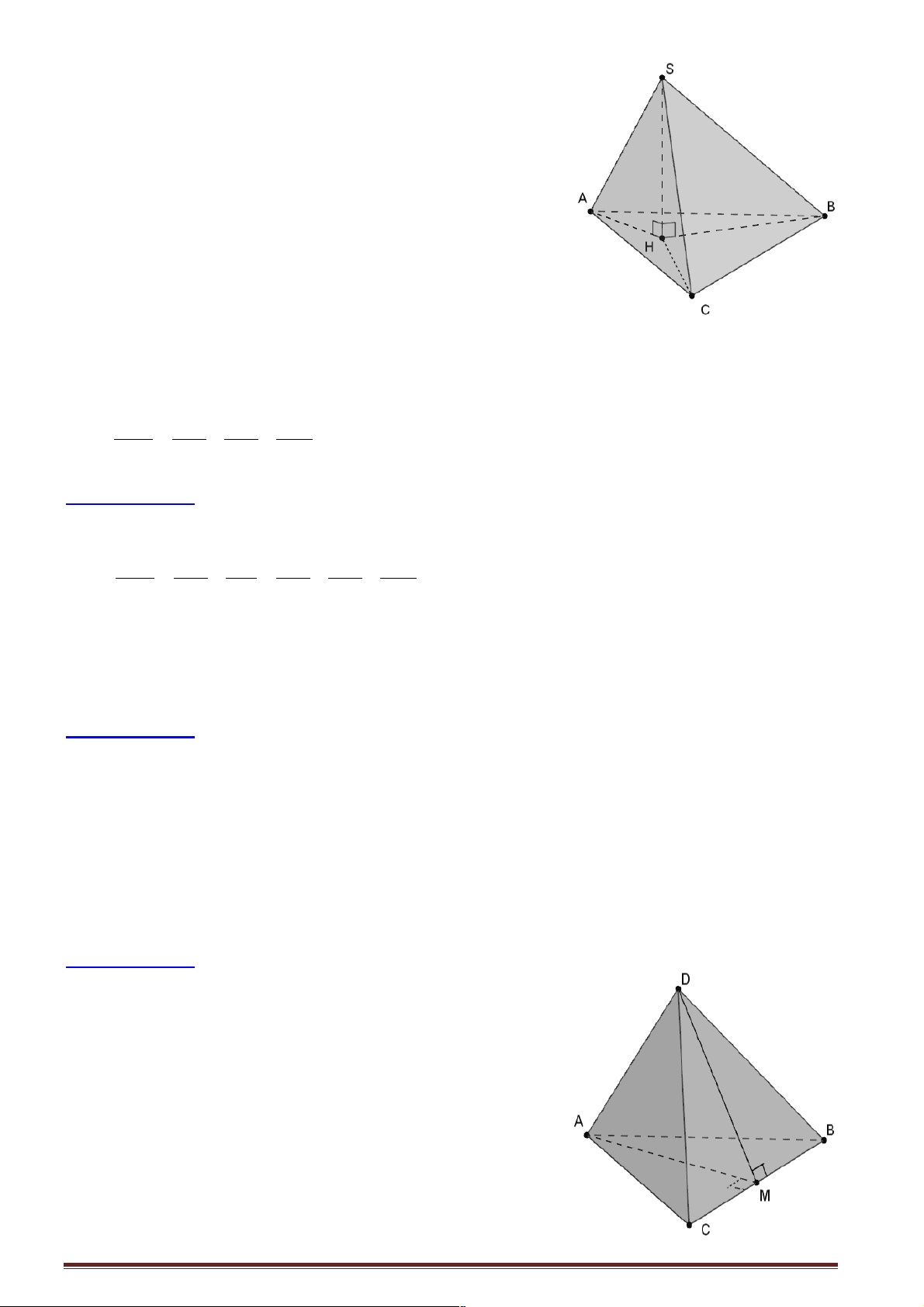
Câu : Cho hình chóp S.ABCD có SA ^ ( ABCD) và ABC D
vuông ở B , AH là đường cao của SA
D B . Khẳng định nào sau đây sai?
A. SA ^ BC .
B. AH ^ BC .
C. AH ^ AC .
D. AH ^ SC .
Hướng dẫn giải: Chọn C.
Do SA ^ ( ABC) nên câu A đúng.
Do BC ^ (SAB) nên câu B và D đúng. Vậy câu C sai.
Câu 1: Cho tứ diện SABC có ABC là tam giác vuông tại B và SA ^ ( ABC)
a) Khẳng định nào sau đây là đúng nhất. Chứng minh BC ^ (SAB).
A. BC ^ (SAB)
B. BC ^ (SAC) C. ∑ (AD BC) 0 , = 45 D. ∑ (AD BC) 0 , = 80
b) Gọi AH là đường cao của tam giác SAB , thì khẳng định nào sau đây đúng nhất. Chứng minh AH ^ SC .
A. AH ^ AD
B. AH ^ SC D
C. AH ^ (SAC)
D. AH ^ AC Hướng dẫn giải:.
a) Ta có SA ^ ( ABC) nên SA ^ BC . BC ^ SA ü Do đó
ý Þ BC ^ (SAB)Chọn A H BC ^ ABþ C A Trang 7 B
b) Ta có BC ^ (SAB) Þ BC ^ AH AH ^ BCü Vậy
ý Þ AH ^ SC .Chọn B AH ^ SB þ
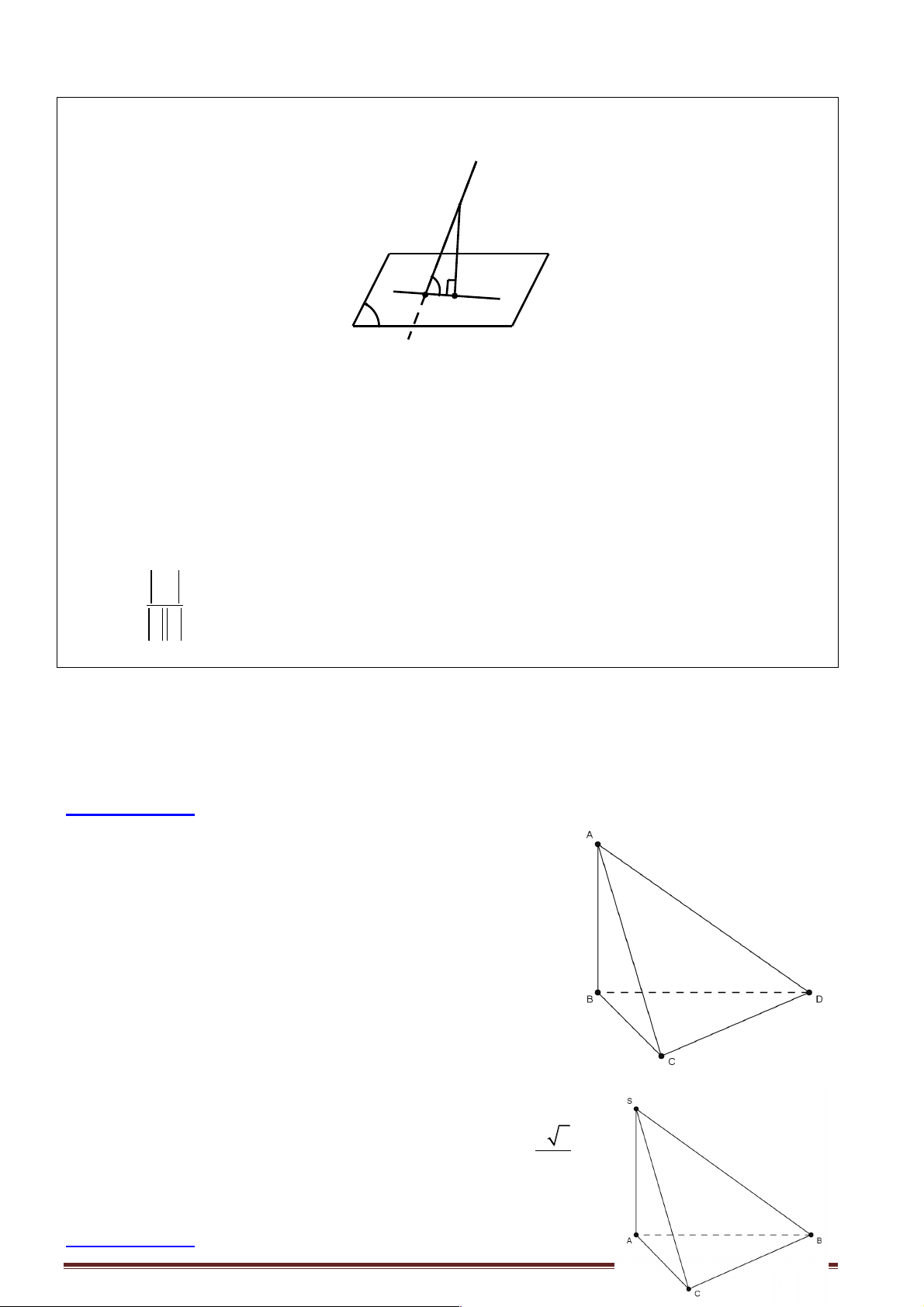
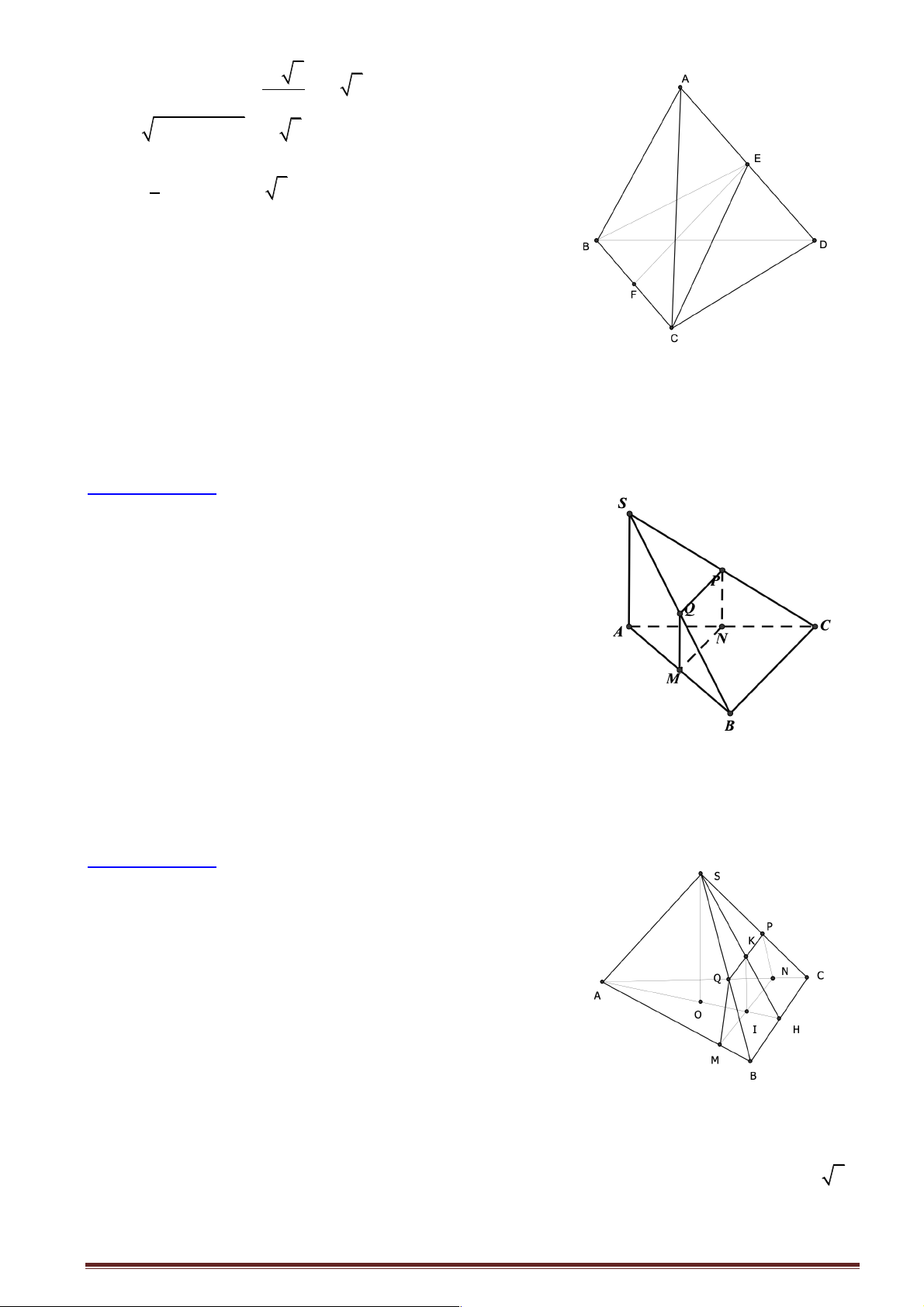
Câu 2: Cho tứ diện ABCD có AB = AC và DB = DC . Khẳng định nào sau đây đúng?
A. AB ^ ( ABC).
B. AC ^ BD .
C. CD ^ ( ABD).
D. BC ^ AD .
Hướng dẫn giải: Chọn D.
Gọi E là trung điểm của BC . Khi đó ta có ìAE ^ BC í
Þ BC ^ ( ADE) Þ BC ^ AD. îDE ^ BC
Câu 3: Cho hình chóp S.ABC có SA ^ (ABC) và AB ^ BC. Số các mặt của tứ diện S.ABC là tam giác vuông là: A. 1. B. 3. C. 2. D. 4.
Hướng dẫn giải:
Có AB ^ BC Þ AB
D C là tam giác vuông tại . B ìSA ^ AB
Ta có SA ^ (ABC) Þ í Þ SA D B, SA
D C là các tam giác vuông tại . A îSA ^ AC ìAB ^ BC Mặt khác í
Þ BC ^ SB Þ S
D BC là tam giác vuông tại . B îSA ^ BC
Vậy bốn mặt của tứ diện đều là tam giác vuông. Nên đáp án D đúng.
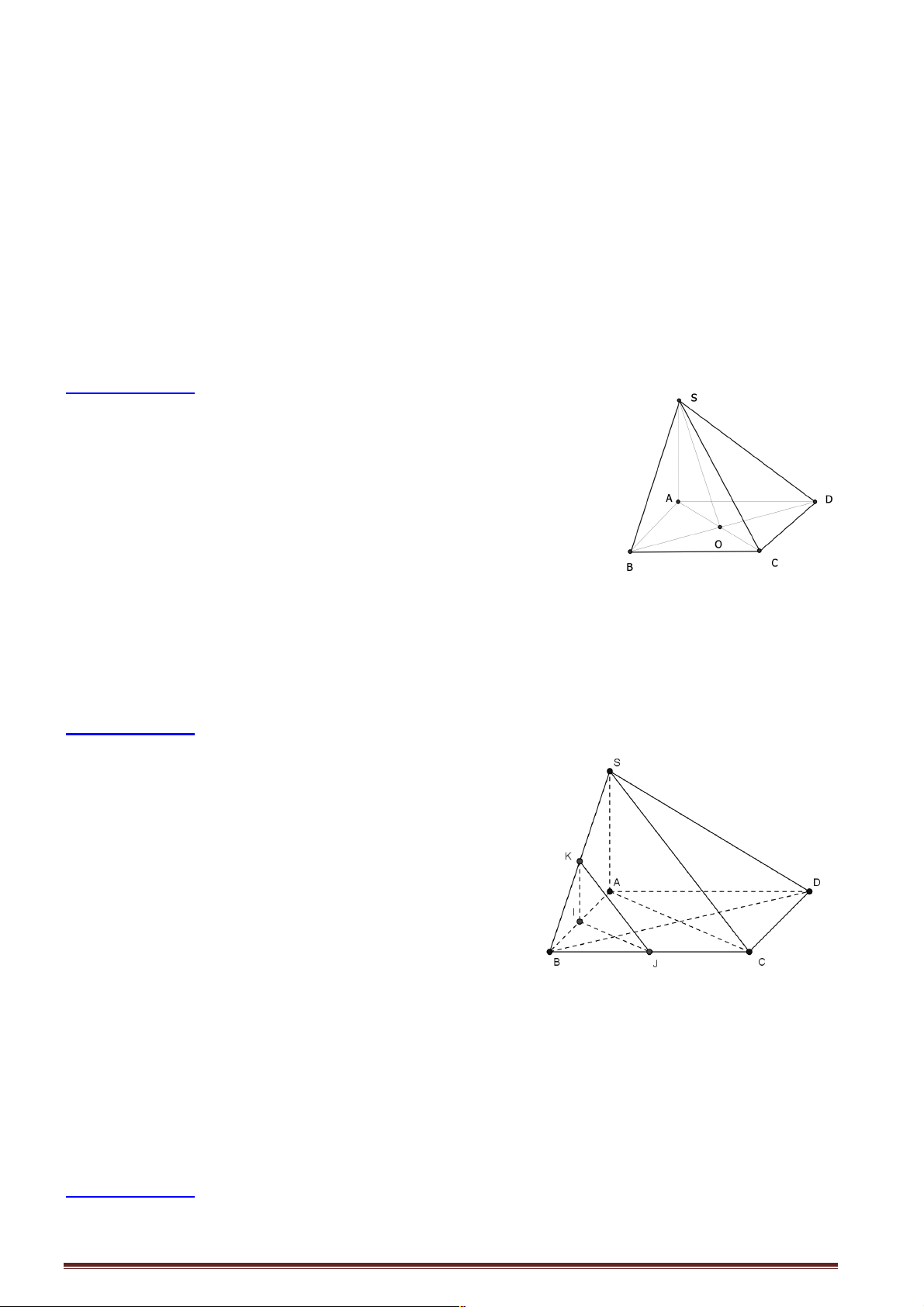
Câu 4: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O . Biết SA = SC và SB = SD . Khẳng
định nào sau đây sai?
A. SO ^ ( ABCD).
B. CD ^ (SBD).
C. AB ^ (SAC).
D. CD ^ AC .
Hướng dẫn giải: Chọn B.
Tam giác SAC cân tại S có SO là trung tuyến Þ SO cũng là đường cao Þ SO ^ AC .
Tam giác SBD cân tại S có SO là trung tuyến Þ SO cũng là đường cao Þ SO ^ BD .
Từ đó suy ra SO ^ ( ABCD).
Do ABCD là hình thoi nên CD không vuông góc với BD . Do đó CD không vuông góc với (SBD .)
Câu 5: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật,
SA ^ (ABCD).Gọi AE; AF lần lượt là các đường cao của tam
giác SAB và tam giác .
SAD Chọn khẳng định đúng trong các khẳng định sau ? Trang 8
A. SC ^ ( AFB).
B. SC ^ ( AEC).
C. SC ^ ( AED).
D. SC ^ ( AEF ).
Hướng dẫn giải: ìAB ^ BC Ta có: í
Þ BC ^ (SAB) Þ BC ^ AE. îSA ^ BC ìAE ^ SB Vậy: í Þ AE ^ SC ( ) 1 îAE ^ BC
Tương tự : AF ^ SC (2) Từ ( )
1 ;(2) Þ SC ^ ( AEF ).vậy đáp án D đúng.
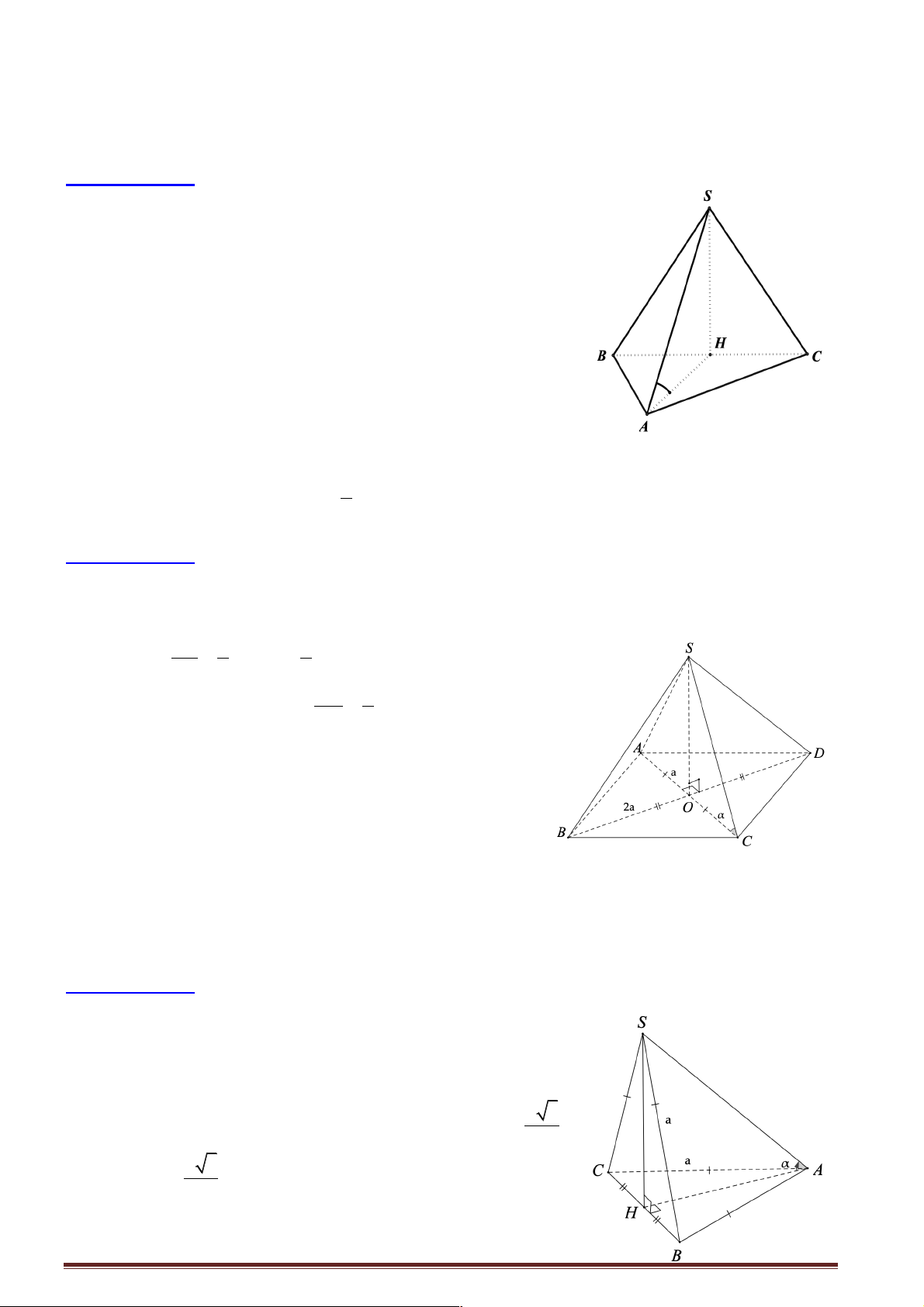
Câu 6: Cho hình chóp S.ABC có cạnh SA ^ ( ABC) và đáy ABC là tam giác cân ở C . Gọi H và K
lần lượt là trung điểm của AB và SB . Khẳng định nào sau đây sai?
A. CH ^ SA.
B. CH ^ SB .
C. CH ^ AK .
D. AK ^ SB .
Hướng dẫn giải: Chọn D. Do ABC D
cân tại C nên CH ^ AB . Suy ra CH ^ (SAB). Vậy các câu A, B, C đúng nên D sai.
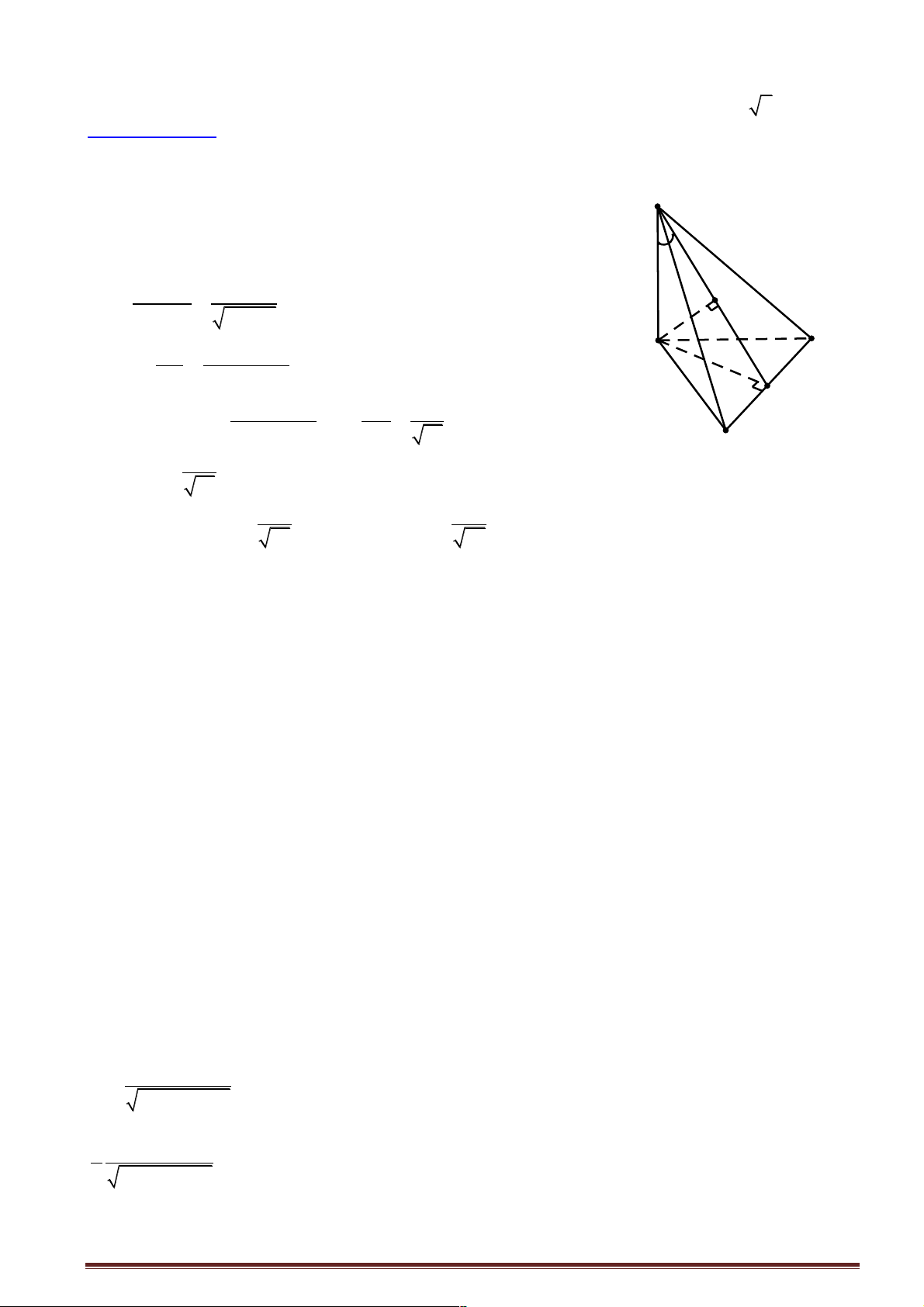
Câu 7: Cho tứ diện ABCD . Vẽ AH ^ (BCD) . Biết H là trực tâm tam giác BCD . Khẳng định nào sau đây đúng?
A. CD ^ BD .
B. AC = BD .
C. AB = CD .
D. AB ^ CD .
Hướng dẫn giải:: CD ì ^ AH í
Þ CD ^ (ABH ) Þ CD ^ AB ® Chọn đáp án D. CD î ^ BH
Câu 8: Cho hình chóp S.ABC có cạnh SA ^ (ABC) và đáy ABC là tam giác cân ở C . Gọi H và K
lần lượt là trung điểm của AB và SB . Khẳng định nào sau đây có thể sai ?
A. CH ^ AK .
B. CH ^ SB .
C. CH ^ SA.
D. AK ^ SB .
Hướng dẫn giải:: CH ì ^ AB Ta có í Þ CH ^ (SAB). CH î ^ SA
Từ đó suy ra CH ^ AK,CH ^ SB,CH ^ SA nên A, B, C đúng.
Đáp án D sai trong trường hợp SA và AB không bằng nhau ® Chọn đáp án D.
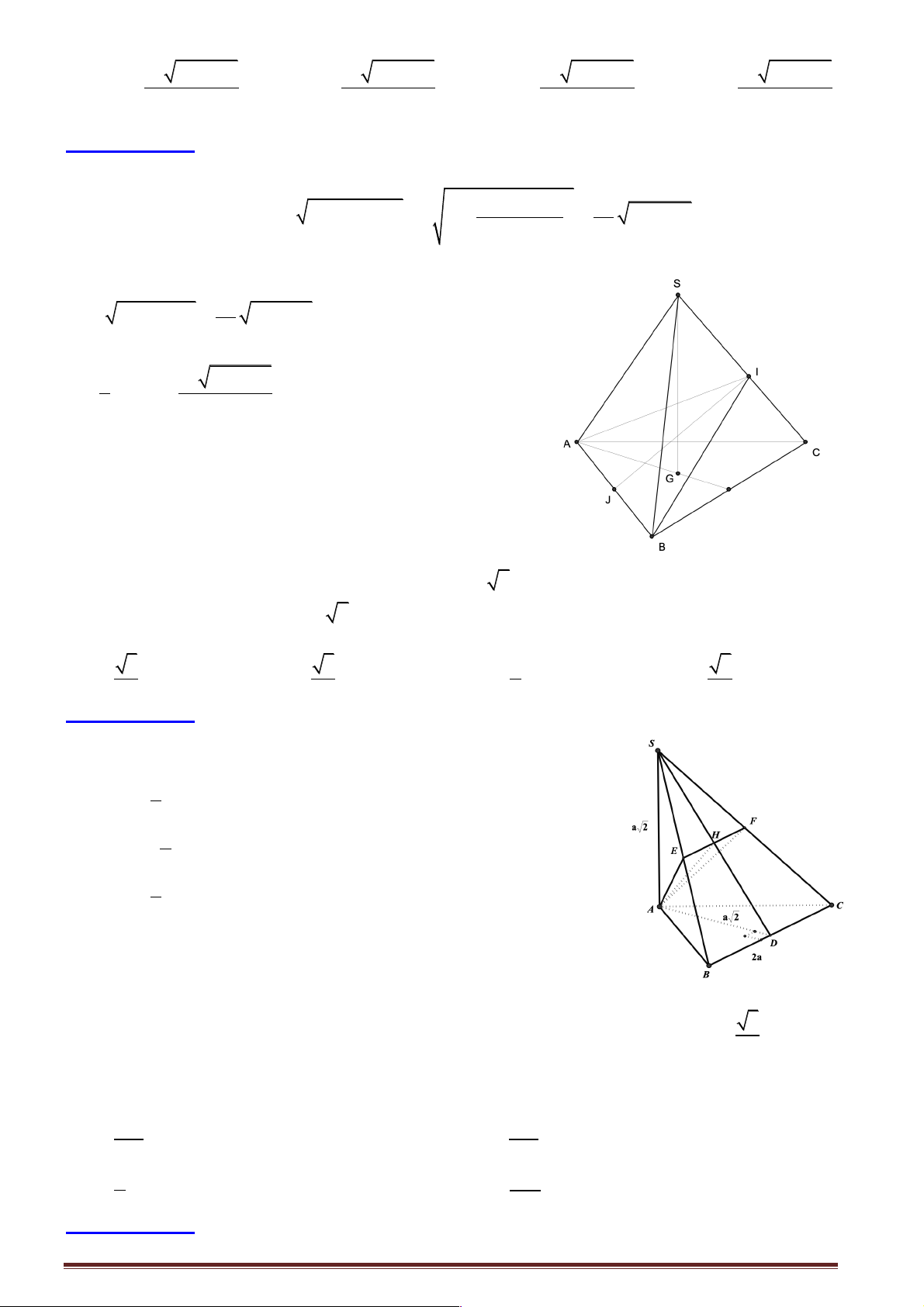
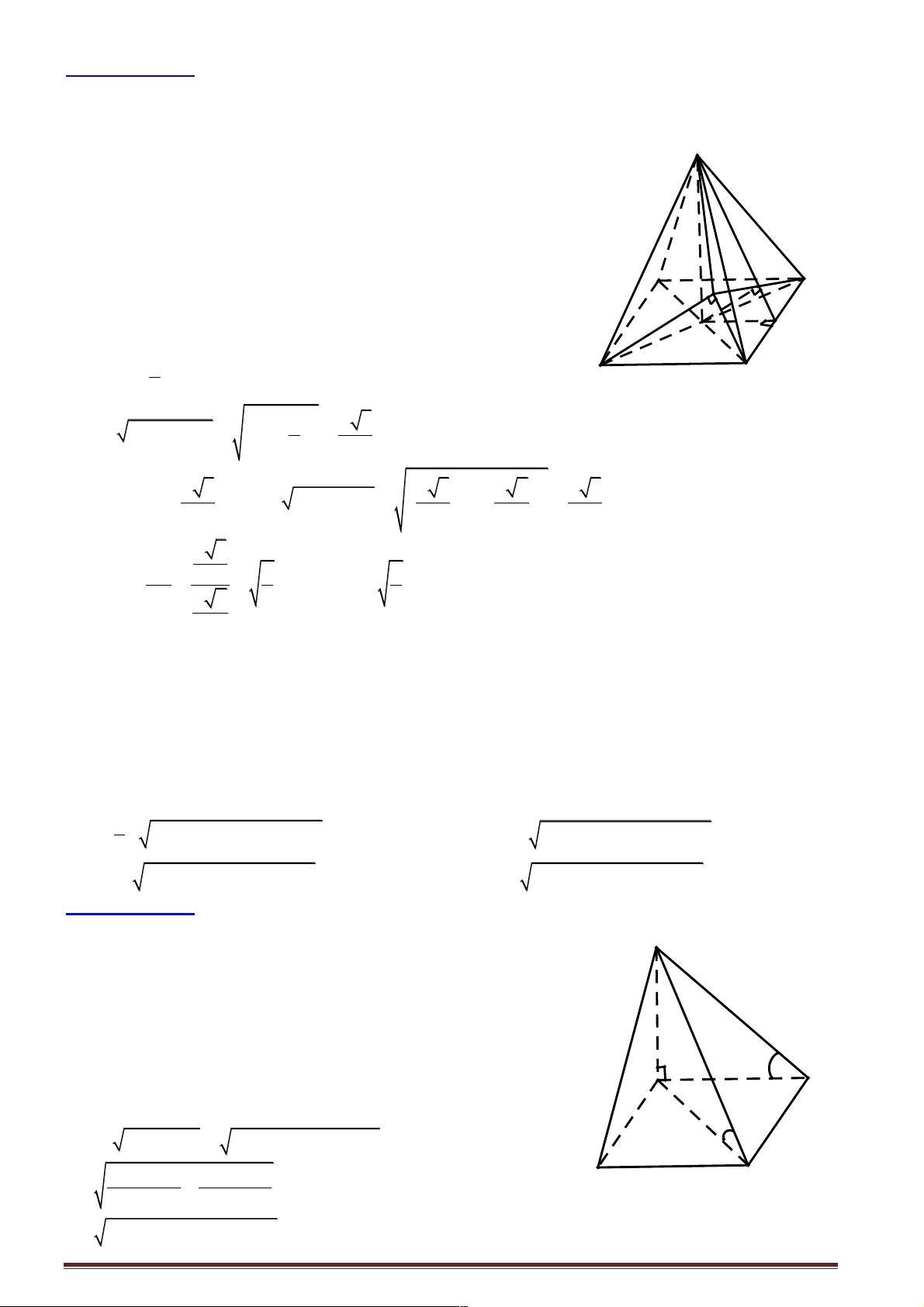
Câu 9: Cho tứ diện SABC thoả mãn SA = SB = SC. Gọi H là hình chiếu của S lên mp (ABC). Đối
với DABC ta có điểm H là: A. Trực tâm.
B. Tâm đường tròn nội tiếp. C. Trọng tâm.
D. Tâm đường tròn ngoại tiếp.
Hướng dẫn giải: Trang 9 Ï SH Ô ^ AH Ô Ô SH (ABC) Ì SH Ô ^ fi ^ BH ÔS Ô Ô H ^ CH Ô Ó
Xét ba tam giác vuông DSH , A DSH , B DSHC có Ï SA Ô = SB = SC Ô Ì
fi DSHA = DSHB = DSHC SH Ô chung Ô Ó
fi HA = HB = HC mà H ( Œ ABC)fi H
chính là tâm đường tròn ngoại tiếp DABC. Chọn đáp án D.
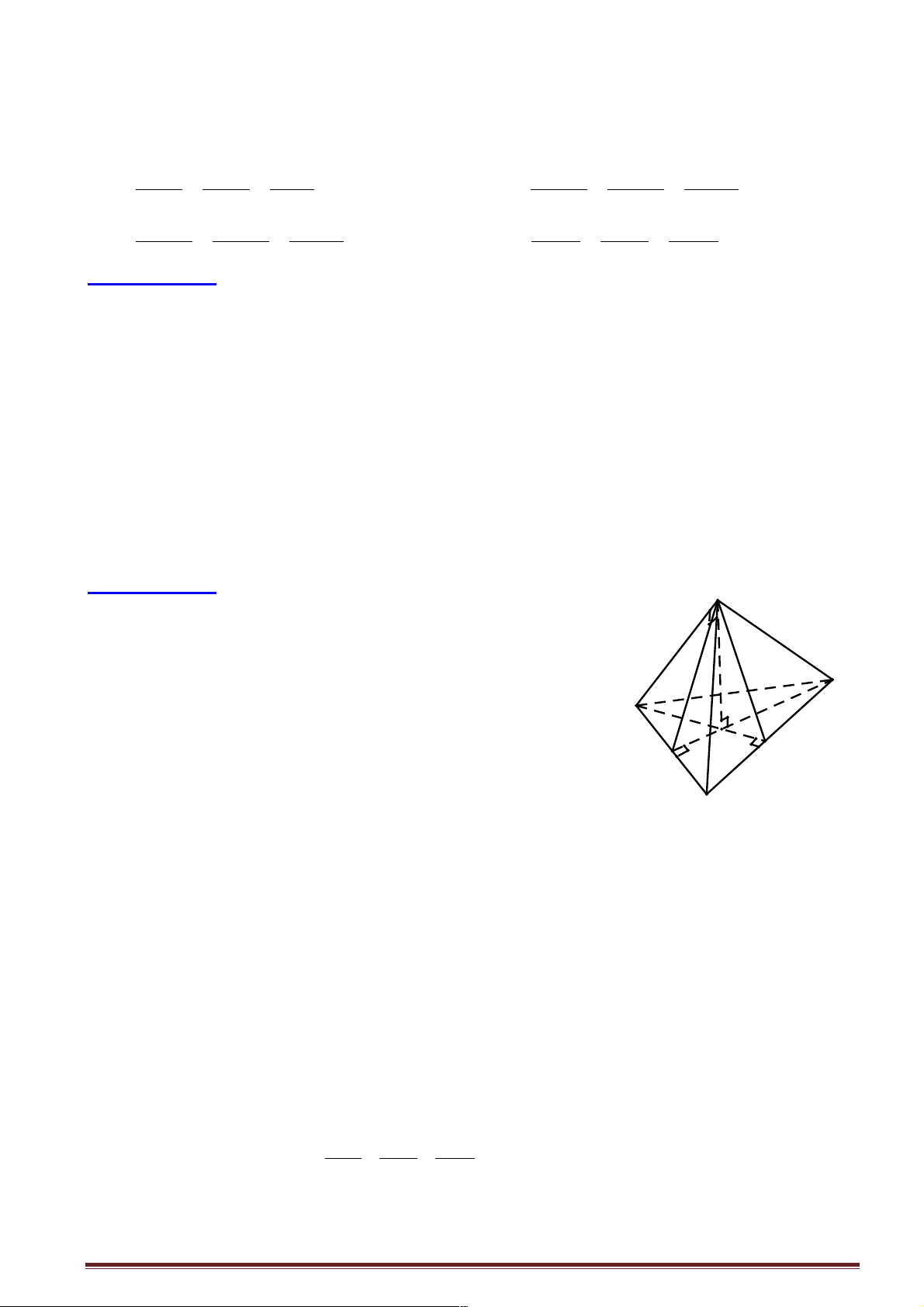
Câu 10: Cho tứ diện OABC có ,
OA OB,OC đôi một vuông góc với nhau. Gọi H là hình chiếu của O
trên mp(ABC) . Mệnh đề nào sai trong các mệnh đề sau:
A. H là trực tâm ABC D .
B. H là tâm đường tròn ngoại tiếp tam giác ABC . 1 1 1 1 C. = + + . 2 2 2 2 OH OA OB OC
D. CH là đường cao của ABC D .
Hướng dẫn giải::
Ta có OA ^ (OBC) Þ OA ^ BC và OH ^ BC Þ BC ^ (OAH ) Þ BC ^ AH .
Tương tự, ta có AB ^ CH , suy ra đáp án A, D đúng. 1 1 1 1 1 1 Ta có = + = + +
, với I = AH Ç BC , suy ra đáp án C đúng. 2 2 2 2 2 2 OH OA OI OA OB OC
® Chọn đáp án B.
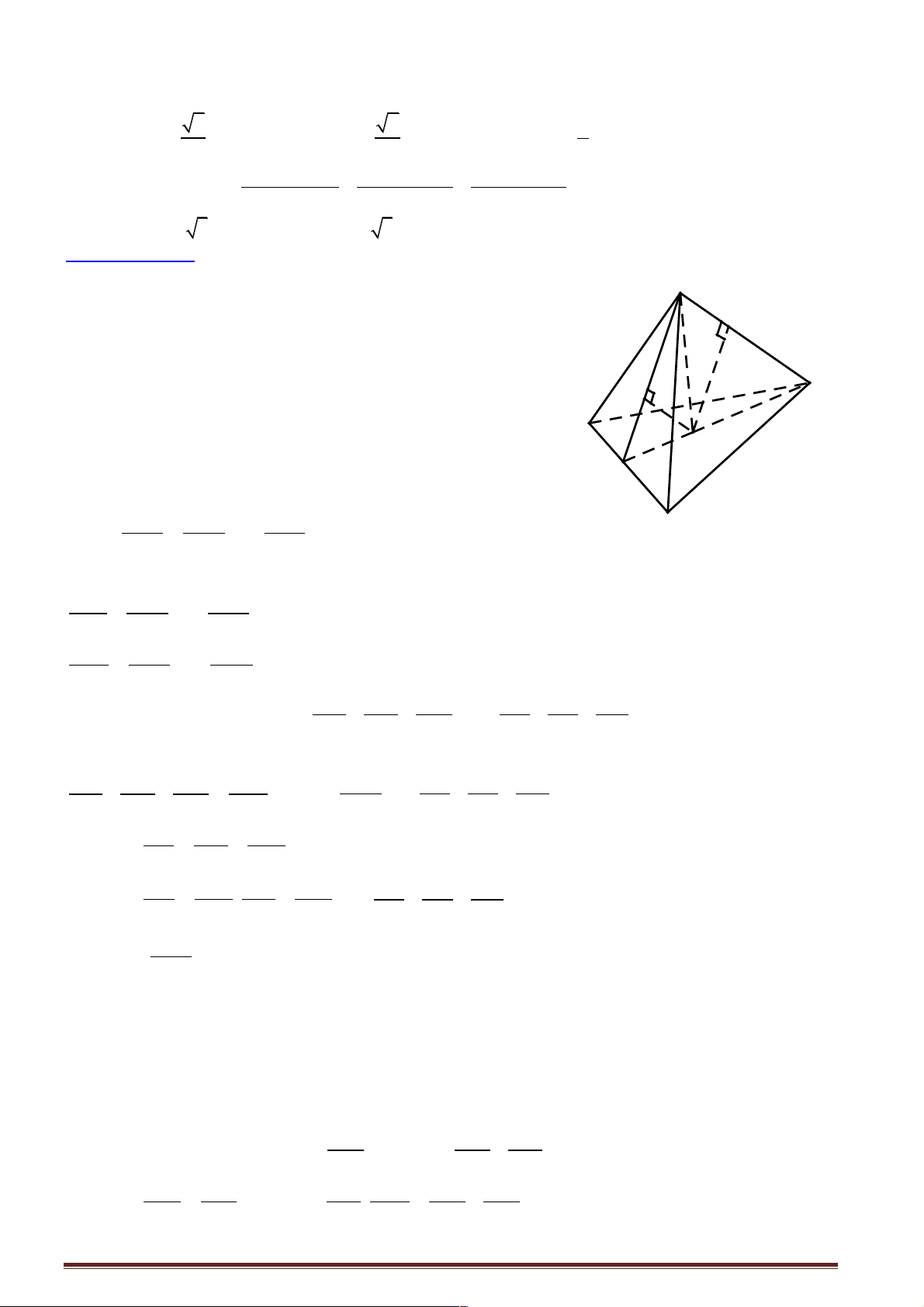
Câu 11: Cho tứ diện ABCD có AB ^ CD và AC ^ BD . Gọi H là hình chiếu vuông góc của A lên
mp(BCD). Các khẳng định sau, khẳng định nào sai?
A. H là trực tâm tam giác BCD .
B. CD ^ (ABH ) .
C. AD ^ BC .
D. Các khẳng định trên đều sai.
Hướng dẫn giải:: CD ì ^ AB Ta có í
Þ CD ^ (ABH ) Þ CD ^ BH . Tương tự BD ^ CH CD î ^ AH
Suy ra H là trực tâm BCD D
. Suy ra đáp án A, B đúng. ìBC ^ AH Ta có í
Þ BC ^ AD, suy ra C đúng. îBC ^ DH
® Chọn đáp án D.
Câu 12: Cho tứ diện ABCD có AB = AC và DB = DC. Khẳng định nào sau đây đúng?
A. AB ^ ( ABC). B. BC ^ . AD
C. CD ^ ( ABD). D. AC ^ . BD
Hướng dẫn giải:
Gọi M là trung điểm của BC . Ï AB Ô = AC Ï BC Ô ^ AM Ô Ô Ì fi Ì
fi BC ^ (ADM )fi BC ^ . AD DB Ô = DC B Ô C ^ DM Ô Ó Ô Ó Chọn đáp án B. Trang 10
Câu 13: Cho hình chóp SABC có SA ^ ( ABC). Gọi H, K lần lượt là trực tâm các tam giác SBC và
ABC . Mệnh đề nào sai trong các mệnh đề sau?
A. BC ^ (SAH ).
B. HK ^ (SBC).
C. BC ^ (SAB).
D. SH, AK và BC đồng quy.
Hướng dẫn giải:
Ta có BC ^ S ,
A BC ^ SH Þ BC ^ (SAH )
Ta có CK ^ AB,CK ^ SA ÞCK ^ (SAB) hay CK ^ SB
Mặt khác có CH ^ SB nên suy ra SB ^ (CHK) hay SB ^ HK ,
tương tự SC ^ HK nên HK ^ (SBC)
Gọi M là giao điểm của SH và BC . Do
BC ^ (SAH ) Þ BC ^ AM hay đường thẳng
AM trùng với đường thẳng AK . Hay SH , AK và BC đồng quy.
Do đó BC ^ (SAB). sai Chọn đáp án C.
Câu 14: Cho hai hình chữ nhật ABCD và ABEF nằm trong hai mặt phẳng khác nhau sao cho hai
đường thẳng AC và BF vuông góc với nhau. Gọi CH và FK lần lượt là đường cao của hai tam giác
BCE và ADF . Chứng minh rằng :
a) Khẳng định nào sau đây là đúng về 2 tam giác DACH và DBFK ?
A. DACH và DBFK là các tam giác vuông
B. DACH và DBFK là các tam giác tù
C. DACH và DBFK là các tam giác nhọn
D. DACH và DBFK là các tam giác cân
b) Khẳng định nào sau đây là sai?
A. BF ^ AH B. ∑ (BF AH) 0 , = 45
C. AC ^ BK
D. AC ^ (BKF)
Hướng dẫn giải:. AB ^ BCü a) Ta có A
ý Þ AB ^ (BCE) AB ^ BE þ K .. F ìCH ^ AB D Vậy í
Þ CH ^ ( ABEF ) îCH ^ BE
Þ CH ^ AH ,hay DACH vuông tại H . FK ^ ADü Tương tự B
ý Þ FK ^ ( ABCD) FK ^ AB þ H
Þ DBFK vuông tại K . E C
b) Ta có CH ^ ( ABEF) Þ CH ^ BF , mặt khác
AC ^ BF Þ BF ^ ( ACH ) Þ BF ^ AH . AC ^ KF ü Tương tự
ý Þ AC ^ (BKF ) Þ AC ^ BK . AC ^ BF þ
Câu 15: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O . Biết SA = SC, SB = SD.
a)Khẳng định nào sau đây là sai?.
A. SO ^ ( ABCD) B. S SO ^ AC
C. SO ^ BD D. Cả A, B, C đều sai
b) Khẳng định nào sau đây là sai?.
A. AC ^ (SBD)
B. AC ^ SO C. D AC ^ SB
D. Cả A, B, C đều sai A
Hướng dẫn giải:. O B Trang 11 C
a) Ta có O là trung điểm của AC và
SA = SC Þ SO ^ AC .
Tương tự SO ^ BD . SO ^ ACü Vậy
ý Þ SO ^ ( ABCD).Chọn D SO ^ BDþ
b) Ta có AC ^ BD ( do ABCD là hình thoi).
Lại có AC ^ SO ( do SO ^ ( ABCD))
Suy ra AC ^ (SBD) Þ AC ^ SD.Chọn D
Câu 16: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm ,
O SA^ (ABCD). Các khẳng định
sau, khẳng định nào sai?
A. SA ^ BD
B. SC ^ BD
C. SO ^ BD
D. AD ^ SC
Hướng dẫn giải:
Ta có SA ^ (ABCD) Þ SA^ BD
Do tứ giác ABCD là hình thoi nên BD ^ AC, mà SA ^ BD nên
BD ^ (SAC) hay BD ^ SC, BD ^ SO
AD không vuông góc SC Chọn đáp án D.
Câu 17: Cho hình chóp S.ABCD có đáy ABCD là hình vuông và
SA ^ ( ABCD). Gọi I , J , K lần lượt là trung điểm của AB , BC và SB . Khẳng định nào sau đây sai?
A. (IJK ) // (SAC).
B. BD ^ (IJK ).
C. Góc giữa SC và BD có số đo 60°.
D. BD ^ (SAC).
Hướng dẫn giải: Chọn C.
Do IJ // AC và IK // SA nên (IJK ) // (SAC). Vậy A đúng.
Do BD ^ AC và BD ^ SA nên BD ^ (SAC) nên D đúng.
Do BD ^ (SAC) và (IJK )// (SAC) nên BD ^ (IJK ) nên B đúng. Vậy C sai.
Câu 18: Cho hình chóp S.ABCD có đáy ABCD là hình
vuông, Gọi H là trung điểm của AB và SH ^ ( ABCD).
Gọi K là trung điểm của cạnh AD .
a) Khẳng định nào sau đây là sai?
A. AC ^ SH
B. AC ^ KH
C. AC ^ (SHK ) D. Cả A, B, C đều sai
b) Khẳng định nào sau đây là sai?.
A. CK ^ SD
B. DH ^ CK C. ∑ ∑ 0
DKC + ADH = 90
D. Cả A, B, C đều sai
Hướng dẫn giải:. Trang 12
a) Ta có SH ^ ( ABCD) Þ SH ^ AC S ìHK ! BD lại có í Þ AC ^ HK îAC ^ BD Þ AC ^ (SHK ). b) Dễ thấy ∑ ∑
DAHD = DDKC Þ AHD = DKC mà ∑ ∑ 0 AHD + ADH = 90 A H ∑ ∑ 0
Þ DKC + ADH = 90 hay DH ^ CK , mặt khác ta có B K
SH ^ CK Þ CK ^ (SDH ) Þ CK ^ SD . J
Câu 19: Cho tứ diện OABC có ba cạnh , OA ,
OB OC đôi một D C
vuông góC. Gọi H là hình chiếu của O lên (ABC). Khẳng
định nào sau đây sai? 1 1 1 1
A. OA ^ BC. B. = + + . 2 2 2 2 OH OA OB OC
C. H là trực tâm DABC. D. 2 2 2 2
3OH = AB + AC + BC .
Hướng dẫn giải: Ï OA Ô ^ OB Ô Ì
fi OA ^ (OBC)fi OA ^ BC fi đáp án A OA Ô ^ OC Ô Ó đúng.
Tương tự chứng minh được OC ^ . AB Ï OI Ô ^ BC Hạ Ô Ì . OH Ô ^ AI Ô Ó Ta có: Ï OI Ô ^ BC Ô Ì
fi BC ^ (OAI)fi BC ^ OH fi OH ^ (ABC). BC Ô ^ OA Ô Ó 1 1 1 1 1 1 = + = + +
fi Đáp án B đúng. 2 2 2 2 2 2 OH OA OI OA OB OC Ï AB Ô ^ OC Ta có: Ô Ì
fi AB ^ (OCH )fi AB ^ HC( )
1 . Tương tự BC ^ OH ( ) 2 . AB Ô ^ OH Ô Ó Từ ( ) 1 và ( )
2 fi H là trực tâm DABC fi Đáp án C đúng. Chọn đáp án D.
Câu 20: Cho hình chóp S.ABC có SA ^ ( ABC). Gọi H , K lần lượt là trực tâm các tam giác ABC và
SBC . Khẳng định nào sau đây là đúng
a) AH, SK và BC đồng qui.
A. AH và BC chéo nhau
B. AH và SK chéo nhau
C. AH, SK và BC đồng qui.
D. AH, SK và BC không đồng qui.
b) Khẳng định nào sau đây là sai?.
A. SB ^ (CHK )
B. SB ^ HK C. S
CH ^ (SAB)
D. Cả A, B, C đều sai
c) HK ^ (SBC).Khẳng định nào sau đây là sai?
A. HK ^ (SBC)
B. BC ^ (SAI )
C. BC ^ HK
D. Cả A, B, C đều sai
Hướng dẫn giải:.
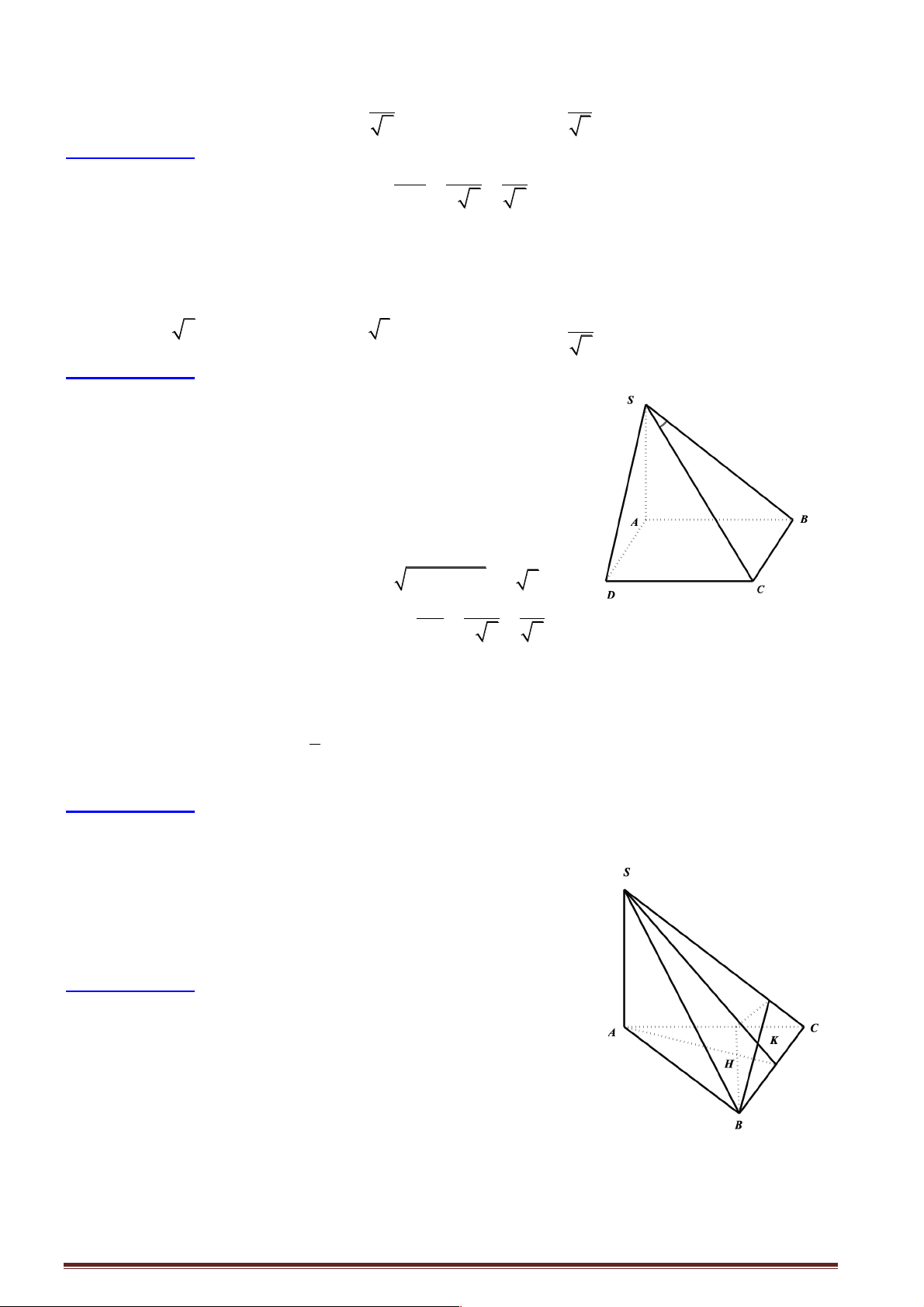
a) Gọi I = AH Ç BC , để chứng minh AH, SK và BC đồng qui. K A C
Ta cần chứng minh SI là đường cao của tam giác SBC , nhưng điều H
này đúng do BC ^ SA và BC ^ AI . I Trang 13 B
b) Ta có SB ^ CK ìCH ^ AB thêm nữa ta có í
Þ CH ^ (SAB) Þ CH ^ SB îCH ^ SA
Vậy SB ^ (CHK ).
b) Theo các chứng minh trên ta có
SB ^ (CHK ) Þ SB ^ HK và BC ^ (SAI ) Þ BC ^ HK do đó HK ^ (SBC).
Câu 21: Cho hình tứ diện ABCD có AB , BC , CD đôi một vuông góc nhau. Hãy chỉ ra điểm O cách
đều bốn điểm A , B , C , D .
A. O là tâm đường tròn ngoại tiếp tam giác ABC .
B. O là trọng tâm tam giác ACD .
C. O là trung điểm cạnh BD .
D. O là trung điểm cạnh AD .
Hướng dẫn giải: Chọn D.
Gọi O là trung điểm của AD . ìAB ^ CD Từ giả thiết ta có í
Þ CD ^ ( ABC) Þ CD ^ AC . îBC ^ CD Vậy ACD D vuông tại C .
Do đó OA = OC = OA (1) ìAB ^ CD Mặt khác í
Þ AB ^ (BCD) Þ AB ^ BD Þ ABD D îAB ^ BC vuông tại B .
Do đó OA = OB = OD (2)
Từ (1) và (2) ta có OA = OB = OC = OD .
Câu 22: Cho tứ diện ABCD có AB = AC và DB = DC . Khẳng định nào sau đây đúng?
A. AB ^ ( ABC).
B. AC ^ BD .
C. CD ^ ( ABD).
D. BC ^ AD .
Hướng dẫn giải: Chọn D.
Gọi E là trung điểm của BC . Khi đó ta có ìAE ^ BC í
Þ BC ^ ( ADE) Þ BC ^ AD. îDE ^ BC
Câu 23: Cho tứ diện ABCD . Vẽ AH ^ (BCD). Biết H là trực
tâm tam giác BCD . Khẳng định nào sau đây không sai?
A. AB = CD .
B. AC = BD . C.
AB ^ CD .
D. CD ^ BD .
Hướng dẫn giải: Chọn C.
Do AH ^ (BCD) Þ AH ^ CD.
Mặt khác, H là trực tâm ABC D nên BH ^ CD .
Suy ra CD ^ ( ABH ) nên CD ^ AB . Trang 14
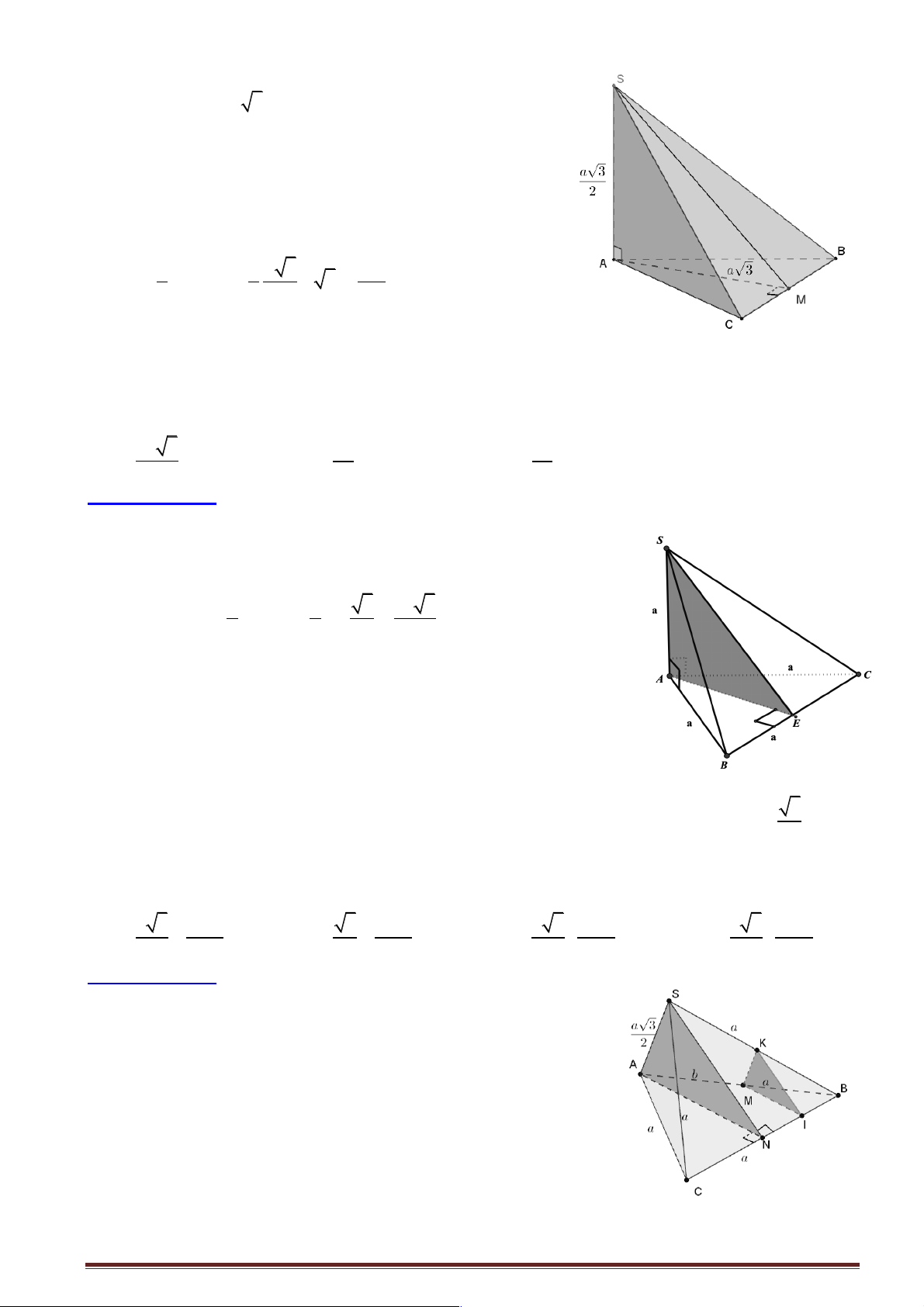
Câu 24: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , mặt bên SAB là tam giác đều
và SC = a 2. Gọi H , K lần lượt là trung điểm của các cạnh AB và AD.
a) Khẳng định nào sau đây là sai?.
A. SH ^ ( ABCD)
B. SH ^ HC
C. A, B đều đúng D. A, B là sai
b) Khẳng định nào sau đây là sai?
A. CK ^ HD
B. CK ^ SD
C. AC ^ SK
D. Cả A, B, C đều sai Hướng dẫn giải:.
a) Vì H là trung điểm của AB và tam giác SAB đều nên S SH ^ AB a 3 5 Lại có SH = , SC = a 2, 2 2 HC = + = a DH DC 2 2 2 2 3a 5a Do đó 2 2 2 2 HC + HS = + = 2a = SC 4 4
Þ DHSC vuông tại H Þ SH ^ HC K A D ìSH ^ HC Vậy í
Þ SH ^ ( ABCD). îSH ^ AB H
b) Ta có AC ^ HK và AC ^ SH Þ AC ^ (SHK) B Þ AC ^ SK . C
Tương tự CK ^ HD ( như bài 32) và CK ^ SH Þ CK ^ (SDH ) Þ CK ^ SD.
Câu 25: Cho hình lập phương ABC .
D A' B 'C ' D ' . Đường thẳng AC ' vuông góc với mặt phẳng nào sau đây?
A. ( A'BD).
B. ( A'DC ').
C. ( A'CD').
D. ( A'B'CD).
Hướng dẫn giải: Ta có:
ìï A'D ^ AD' (t / c HV ) í
A' D ^ C ' D ' î (C'D' ^ ï (A'D'DA))
Þ A'D ^ ( AC 'D') Þ A'D ^ AC' ( ) 1
ìï A'B ^ AB' (t / c HV ) í
A' B ^ B 'C ' î (B'C' ^ ï (A'D'DA))
Þ A'B ^ (AB'C ') Þ A'B ^ AC ' (2) Từ ( )
1 ,(2) Þ AC ' ^ ( A'BD)
Vậy chọn đáp án A.
Câu 26: Cho hình chóp S.ABCD có đáy ABCD là
hình thoi, O là giao điểm của 2 đường chéo và SA = SC .
Các khẳng định sau, khẳng định nào đúng?
A. SA ^ ( ABCD).
B. BD ^ (SAC).
C. AC ^ (SBD).
D. AB ^ (SAC).
Hướng dẫn giải:
Ta có: SA = SC Þ SAC là tam giác cân
Mặt khác: O là trung điểm của AC (tính chất hình thoi)
Khi đó ta có: AC ^ SO
ìAC ^ BD (t / c hinh thoi) Þ í Þ AC ^ (SBD) î AC ^ SO
Vậy chọn đáp án C . Trang 15
Câu 27: Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA ^ ( ABCD). Mặt phẳng qua A và
vuông góc với SC cắt SB, SC, SD theo thứ tự tại H, M , K . Chọn khẳng định sai trong các khẳng định sau?
A. AK ^ HK .
B. HK ^ AM .
C. BD ^ HK .
D. AH ^ SB .
Hướng dẫn giải: Ta có:
ìïBD ^ AC (t / c HV) í
Þ BD ^ SAC Þ BD ^ AM ïBD ^ S A î (gt) ( )
Gọi O = AC Ç B ,
D I = SO Ç HK
(P) là mặt phẳng A và vuông góc với SC
Qua I kẻ D ! BD Þ D ^ AM Þ D Ì (P)
Khi đó: K = D Ç S , D H = D Ç SB
Ta có: AK ^ (SDC), mà HK Ç(SDC) = K Þ AK không vuông góc với HK .
Vậy chọn đáp án A.
Câu 28: Cho hình chóp S.ABCD trong đó ABCD là hình chữ nhật, SA ^ ( ABCD). Trong các tam
giác sau tam giác nào không phải là tam giác vuông. A. SB D C . B. SC D D . C. SA D B . D. SB D D .
Hướng dẫn giải: Ta có :
ìïAB ^ AD (tc HV) í
Þ AB ^ SAD Þ AB ^ SD AB ^ S A î (SA^ ï (ABCD)) ( )
Giả sử SB ^ SD Þ SD ^ (SAB) (vô lý) Hay SB
D D không thể là tam giác vuông
Vậy chọn đáp án D .
Câu 29: Cho hình chóp S.ABC có ∑ 0 ∑ 0 ∑ 0
BSC =120 ,CSA = 60 , ASB = 90 , SA = SB = S .
C Gọi I là hình
chiếu vuông góc của S lên mp( ABC). Chọn khẳng định đúng trong các khẳng định sau
A. I là trung điểm AB .
B. I là trọng tâm tam giác ABC .
C. I là trung điểm AC .
D. I là trung điểm BC .
Hướng dẫn giải:
Gọi SA = SB = SC = a
Ta có : !SAC đều Þ AC = SA = a
!SAB vuông cân tại S Þ AB = a 2 2 2 ∑
BC = SB + SC - 2S .
B SC.cos BSC = a 3 2 2 2
Þ AC + AB = BC Þ!ABC vuông tại A
Gọi I là trung điểm của AC thì I là tâm đường tròn
ngoại tiếp tam giác ABC. Gọi d là trục của tam giác ABC thi d đi
qua I và d ^ ( ABC) Trang 16
Mặt khác : SA = SB = SC nên S Îd . Vậy SI ^ ( ABC) nên I là hình chiếu vuông góc của S lên mặt phẳng ( ABC)
Vì H và K lần lượt là trực tâm của tam giác ABC và SBC nên H và K lần lượt thuộc AA¢ và SA¢
Vậy AH, SK, BC đồng quy tại A¢
Câu 30: Cho tứ diện OABC có ,
OA OB,OC đôi một vuông góc với nhau. Gọi H là hình chiếu của O
trên mặt phẳng ( ABC). Xét các mệnh đề sau : I. Vì OC ^ ,
OA OC ^ OB nên OC ^ (OAB).
II. Do AB Ì (OAB)nên AB ^ O . C ( ) 1
III. Có OH ^ ( ABC) và AB Ì ( ABC)nên AB ^ OH. (2) IV. Từ ( )
1 và (2) AB ^ (OCH ).
A. I, II, III, IV .
B. I, II, III .
C. II, III, IV .
D. I, IV .
Hướng dẫn giải: Ta có: OC ì ^ OA OC ï ^ OB ï í
Þ OC ^ (OAB). Vậy I đúng.
OA ÇOB = O ï ï , OA OB Ì î (OAB) OC ì ^ ï (OAB) í
Þ AB ^ OC . Vậy II đúng. ïAB Ì î (OAB) OH ì ^ ï (ABC) í
Þ AB ^ OH . Vậy III đúng. ïAB Ì î (ABC) ì ï AB ^ OC
ïïí AB^OH Þ AB^(OCH). Vậy IV đúng. OC ï ÇOH = O ïO ï C,OH Ì î (OCH )
Vậy chọn đáp án A.
Câu 31: Cho hình hộp ABC .
D A' B 'C ' D '. Có đáy là hình thoi ∑ 0
BAD = 60 và A' A = A' B = A' . D Gọi O = AC « .
BD Hình chiếu của A' trên (ABCD )là : A. trung điểm của . AO B. trọng tâm D . ABD
C. giao của hai đoạn AC và . BD D. trọng tâm D . BCD
Hướng dẫn giải:
Vì A' A = A' B = A' D fi hình chiếu của A' trên (ABCD )trùng với
H là tâm đường tròn ngoại tiếp DABD ( ) 1 .
Mà tứ giác ABCD là hình thoi và ∑ 0
BAD = 60 nên DBAD là tam giác đều ( ) 2 . Từ ( ) 1 & ( )
2 fi H là trọng tâm DABD . Chọn đáp án B. Trang 17
DẠNG 2: TÍNH GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG Phương pháp:
Để xác định góc giữa đường thẳng a và mặt phẳng (a)ta thực hiện theo các bước sau: A a φ a' O α A'
- Tìm giao điểm O = aÇ(a)
- Dựng hình chiếu A' của một điểm A Î a xuống (a) - Góc ∑
AOA' = j chính là góc giữa đường thẳng a và (a). Lưu ý:
- Để dựng hình chiếu A' của điểm A trên (a) ta chọn một đường thẳng b ^ (a) khi đó AA' ! b.
- Để tính góc j ta sử dung hệ thức lượng trong tam giác vuông OAA D
'. Ngoài ra nếu không xác
định góc j thì ta có thể tính góc giữa đường thẳng a và mặt phẳng (a) theo công thức ! ! . u n ! !
sin j = ! ! trong đó u là VTCP của a còn n là vec tơ có giá vuông góc với (a). u n -
Câu 1: Cho tứ diện ABCD có cạnh AB , BC , BD bằng nhau và vuông góc với nhau từng đôi một.
Khẳng định nào sau đây đúng?
A. Góc giữa AC và (BCD) là góc ACB .
B. Góc giữa AD và ( ABC) là góc ADB.
C. Góc giữa AC và ( ABD) là góc CAB.
D. Góc giữa CD và ( ABD) là góc CBD .
Hướng dẫn giải: Chọn A. ìAB ^ BC Từ giả thiết ta có í Þ AB ^ (BCD). îAB ^ CD
Do đó ( AC (BCD)) ∑ , = ACB.
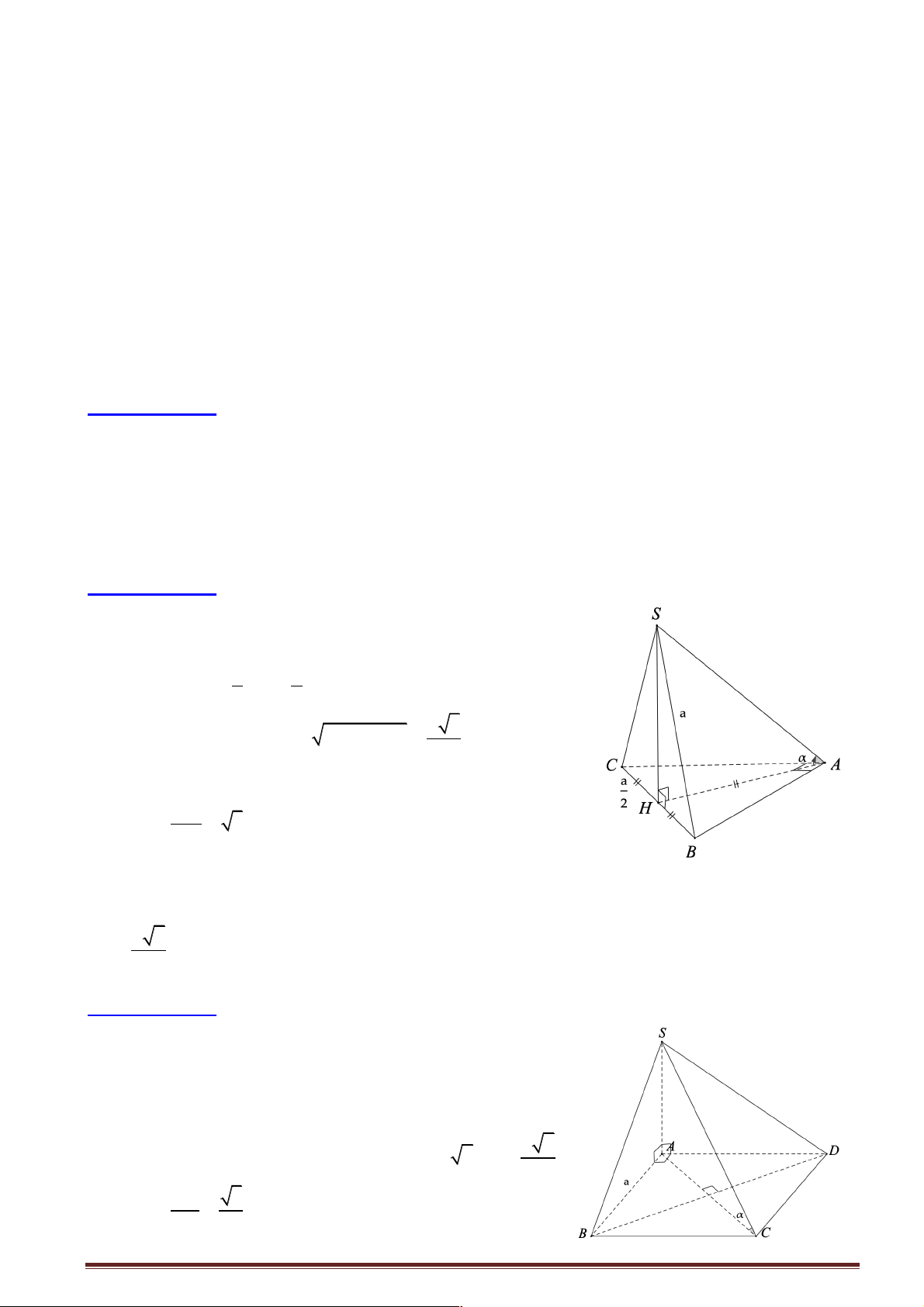
Câu 2: Cho tam giác ABC vuông cân tại A và BC = a . Trên đường a 6
thẳng qua A vuông góc với ( ABC) lấy điểm S sao cho SA = . 2
Tính số đo góc giữa đường thẳng SA và ( ABC). A. 30° . B. 45°. C. 60° . D. .
Hướng dẫn giải: Trang 18 Chọn D.
SA ^ ( ABC) Þ ( ,
SA ( ABC)) = 90°.
Câu 3: Cho tứ diện ABCD có cạnh AB, BC, BD vuông góc với nhau từng đôi một. Khẳng định nào sau đây đúng ?
A. Góc giữa CD và ( ABD) là góc ∑ CBD.
B. Góc giữa AC và (BCD) là góc ∑ ACB.
C. Góc giữa AD và ( ABC) là góc ∑ ADB.
D. Góc giữa AC và ( ABD) là góc ∑ CBA.
Hướng dẫn giải:
Do AB, BC, BD vuông góc với nhau từng đôi một nên AB ^ (BCD), suy ra BC là hình chiếu của AC lên (BCD). Chọn B.
Câu 4: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cạnh huyền BC = a . Hình chiếu vuông
góc của S lên ( ABC) trùng với trung điểm BC . Biết SB = a . Tính số đo của góc giữa SA và ( ABC). A. 30° . B. 45°. C. 60° . D. 75° .
Hướng dẫn giải: Chọn C.
Gọi H là trung điểm của BC suy ra 1 a
AH = BH = CH = BC = . 2 2 a 3
Ta có: SH ^ ( ABC) 2 2
Þ SH = SB - BH = . 2 ( ( ∑ )) ∑ ,
SA ABC = SAH = a SH Þ tana = = 3 Þ a = 60°. AH
Câu 5: Cho hình chóp S.ABCD , đáy ABCD là hình vuông cạnh bằng a và SA ^ ( ABCD). Biết a 6 SA =
. Tính góc giữa SC và ( ABCD). 3 A. 30° . B. 45°. C. 60° . D. 75° .
Hướng dẫn giải: Chọn A.
Ta có: SA ^ ( ABCD) Þ SA ^ AC Þ (SC ( ∑ABCD)) ∑ ; = SCA = a a 6
ABCD là hình vuông cạnh a Þ AC = a 2, SA = 3 SA 3 Þ tana = = Þ a = 30°. AC 3 Trang 19
Câu 6: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a . Hình chiếu vuông góc của S lên
(ABC) trùng với trung điểm H của cạnh BC . Biết tam giác SBC là tam giác đều. Tính số đo của
góc giữa SA và ( ABC) . A. 0 60 B. 0 75 C. 0 45 D. 0 30
Hướng dẫn giải:
Do H là hình chiếu của S lên mặt phẳng ( ABC) nên SH ^ ( ABC)
Vậy AH là hình chiếu của SH lên mp ( ABC)
Þ (SA ( ABC)) = (SA AH ) ∑ ; ; = SAH
Ta có: SH ^ ( ABC) Þ SH ^ AH
Mà: !ABC =!SBC Þ SH = AH . Vậy tam giác SAH vuông cân tại H ∑ 0 Þ SAH = 45
Câu 7: Cho hình thoi ABCD có tâm O , AC = 2 ;
a BD = 2AC . Lấy điểm S không thuộc ( ABCD) sao
cho SO ^ ( ABCD). Biết ∑ 1
tan SBO = . Tính số đo của góc giữa SC và ( ABCD). 2 A. 30° . B. 45°. C. 60° . D. 75° .
Hướng dẫn giải: Chọn B. Ta có: AC = 2 ;
a BD = 2AC = 4a Þ OB = 2a ∑ SO 1 1 Þ tan SBO =
= Û SO = OB = a. OB 2 2 SO a Mặt khác (SC ( ∑ABCD)) ∑ , = SC ; O = = 1 OC a
Suy ra số đo của góc giữa SC và ( ABCD) bằng 45°.
Câu 8: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a . Hình chiếu vuông góc của S lên
(ABC) trùng với trung điểm H của cạnh BC . Biết tam giác SBC là tam giác đều.Tính số đo của góc
giữa SA và ( ABC). A. 30° . B. 45°. C. 60° . D. 75° .
Hướng dẫn giải: Chọn B. Ta có:
SH ^ ( ABC) Þ SH ^ AH Þ (SA ( ∑ABC)) ∑ ; = SAH = a . a 3 ABC D và SB
D C là hai tam giác đều cạnh a Þ AH = SH = 2 a 3 Þ AH = SH = Þ S
D HA vuông cân tại H Þ a = 45° . 2 Trang 20
Câu 9: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA ^ (ABCD), SA = a 6.
Gọi a là góc giữa SC và mp (ABCD). Chọn khẳng định đúng trong các khẳng định sau ? A. 0 a = 3 30 . B. cosa = . C. 0 a = 45 . D. 0 a = 60 . 3
Hướng dẫn giải:
Vì SA ^ (ABCD) nên AC là hình chiếu vuông góc của SC lên (ABCD).
Þ Góc giữa giữa SC và mp (ABCD) bằng góc SC & AC. ∑ Þ a = SC . A Xét tam giác SAC vuông tại A có: SA a 6 0 tana = = = 3 Þ a = 60 . AC a 2
Câu 10: Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh bằng a và SA ^ (ABCD). Biết a 6 SA =
. Tính góc giữa SC và (ABCD). 3 A. 0 30 . B. 0 60 . C. 0 75 . D. 0 45 .
Hướng dẫn giải:
Tứ giác ABCD là hình vuông cạnh a nên AC = a 2.
SA ^ (ABCD)fi AC là hình chiếu vuông góc của SC lên ( ) ∑
ABCD fi SCA là góc giữa SC và (ABCD).
Tam giác SAC vuông tại A nên ∑ SA a 6 1 1 ∑ 0 tan SCA = = . = fi SCA = 30 . AC 3 a 2 3 Chọn đáp án A.
Câu 11: Cho hình lập phương ABC .
D A' B 'C ' D ' . Gọi a là góc giữa AC ' và mp (A'BCD ) ' . Chọn
khẳng định đúng trong các khẳng định sau? A. 0 a = 2 30 . B. tana = . C. 0 a = 45 . D. tana = 2. 3
Hướng dẫn giải: Ï A
Ô 'C « AC ' = I Gọi Ô Ì C
Ô ' D « CD ' = H Ô Ó Ï C Ô ' D ^ CD ' mà Ô Ì
fi C ' D ^ (A' BCD )
' fi IH là hình chiếu vuông C
Ô ' D ^ A' D ' Ô Ó
góc của AC ' lên (A BCD ) ∑ '
' fi C ' IH là góc giữa AC ' và ( C H A' BCD ) ' . Mà ∑ ' 1 tan C ' IH = = .2 = 2. IH 2 Chọn đáp án D.
Câu 12: Cho hình chóp S.ABC có SA ^ (ABC) và tam giác ABC không vuông, gọi H , K lần lượt là trực tâm các ABC D và SB
D C . Số đo góc tạo bởi HK và mp(SBC) là? Trang 21 A. 65° . B. 90° . C. 45°. D. 120° .
Hướng dẫn giải:: ìBC ^ SA
Gọi I = AH Ç BC . Ta có í
Þ BC ^ (SAI) Þ (SBC) ^ (SAI) và K Î SI . îBC ^ AI ìSB ^ CK Ta lại có í
Þ SB ^ (CHK) Þ (SBC) ^ (CHK). îSB ^ CH
Mà HK = (SAI) Ç (SHK), suy ra HK ^ (SBC)
® Chọn đáp án B.
Câu 13: Cho hình chóp S.ABC thỏa mãn SA = SB = SC . Gọi H là hình chiếu vuông góc của S lên
mp( ABC). Chọn khẳng định đúng trong các khẳng định sau?
A. H là trực tâm tam giác ABC .
B. H là trọng tâm tam giác ABC .
C. H là tâm đường tròn ngoại tiếp tam giác ABC .
D. H là tâm đường tròn nội tiếp tam giác ABC .
Hướng dẫn giải:
Do hình chóp S.ABC có SA = SB = SC và SH ^ ( ABC) nên SH là S
trục của hình chóp S.ABC . Þ HA = HB = HC . Nên H là tâm đường
tròn ngoại tiếp tam giác ABC . Vậy chọn C. A C B
Câu 14: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cạnh huyền BC = a . Hình chiếu
vuông góc của S lên ( ABC) trùng với trung điểm BC . Biết SB = a . Tính số đo của góc giữa SA và (ABC). A. 0 30 . B. 0 45 . C. 0 60 . D. 0 75 .
Hướng dẫn giải: a
AM = BM = , SB = a 2
Có SM ^ ( ABC) nên AM là hình chiếu của SA lên mp( ABC)
Þ (SA (ABC)) = (SA AM ) ∑ , , = SAM . Áp dụng định lý Pytago a 3 2 2
SM = SB - AM = 2
Xét tam giác SAM có ∑ SM tan SAM = = 3 ∑ 0 Þ SAM = 60 . AM Vậy chọn C.
Câu 15: Cho hình chóp S.ABC có SA ^ ( ABC) và ABC D vuông ở
B . AH là đường cao của SA
D B . Khẳng định nào sau đây sai ?
A. SA ^ BC.
B. AH ^ BC. C. AH ^ AC.
D. AH ^ SC.
Hướng dẫn giải:
Do SA ^ ( ABC) nên SA ^ BC . Nên Phương án A đúng. Trang 22 ìAH ^ SB ï Có í
Þ AH ^ SBC . Phương án D đúng. AH ^ BC î (BC ^ ï (SAB)) ( )
Suy ra AH ^ BC , AH ^ SC . Phương án B, D đúng. ì ^
Phương án C sai. Thật vậy với AH ^ AH AC AC , ta có í
Þ AC ^ AB (vô lý). îSA ^ AC Vậy chọn C.
Câu 16: Trong các mệnh đề sau mệnh đề nào đúng?
A. Góc giữa đường thẳng và mặt phẳng bằng góc giữa đường thẳng đó và hình chiếu của nó trên mặt phẳng đã cho.
B. Góc giữa đường thẳng a và mặt phẳng (P) bằng góc giữa đường thẳng b và mặt phẳng (P) khi
a và b song song (hoặc a trùng với b ).
C. Góc giữa đường thẳng a và mặt phẳng (P) bằng góc giữa đường thẳng a và mặt phẳng (Q) thì
mặt phẳng (P) song song với mặt phẳng (Q).
D. Góc giữa đường thẳng a và mặt phẳng (P) bằng góc giữa đường thẳng b và mặt phẳng (P) thì
a song song với b .
Hướng dẫn giải: Chọn B.
Câu 17: Cho góc tam diện Sxyz với ∂ 0 xSy =120 , ∂ 0 ySz = 60 , ∂ 0
zSx = 90 . Trên các tia Sx, Sy, Sz lần lượt lấy các điểm ,
A B,C sao cho SA = SB = SC = a . Tam giác ABC có đặc điểm nào trong các số các đặc điểm sau : A. Vuông cân. B. Đều.
C. Cân nhưng không vuông.
D. Vuông nhưng không cân.
Hướng dẫn giải: Xét SA D B có 2 2 2 ∑ 2
AB = SA + SB - 2S . A S .
B cos ASB = 3a Þ AB = a 3 . SB
D C đều Þ BC = . a SA D C có 2 2
AB = SA + SC = a 2 . Từ đó ABC D vuông tại C. Vậy chọn D.
Câu 18: Cho hình chóp S.ABCD có SA ^ ( ABCD) và đáy ABCD là hình chữ nhật. Gọi O là tâm của
ABCD và I là trung điểm của SC . Khẳng định nào sau đây sai ?
A. IO ^ ( ABCD). B. BC ^ . SB
C. (SAC) là mặt phẳng trung trực của đoạn . BD
D. Tam giác SCD vuông ở . D
Hướng dẫn giải:
Có IO là đường trung bình tam giác SAC nên IO//SA nên
IO ^ ( ABCD). Phương án A đúng. ìBC ^ AB Có í
Þ BC ^ SB. Phương án B đúng îBC ^ SA CD ì ^ AD Và í
Þ CD ^ SD nên phương án D đúng. CD î ^ SA
Phương án C sai. Thật vậy nếu (SAC) là mặt phẳng trung trực
của BD Þ BD ^ AC (vô lý). Vậy chọn C.
Câu 19: Trong các mệnh đề sau đây, mệnh đề nào là đúng? Trang 23
A. Nếu hai mặt phẳng vuông góc với nhau thì mọi đường thẳng thuộc mặt phẳng này sẽ vuông góc với mặt phẳng kia.
B. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thứ ba thì song song với nhau.
C. Với mỗi điểm AÎ(a ) và mỗi điểm BÎ(b ) thì ta có đường thẳng AB vuông góc với giao
tuyến d của (a ) và (b ).
D. Nếu hai mặt phẳng (a ) và (b ) đều vuông góc với mặt phẳng (g ) thì giao tuyến d của (a ) và
(b ) nếu có sẽ vuông góc với (g ).
Hướng dẫn giải:
Phương án A sai vì nếu hai mặt phẳng vuông góc với nhau thì mọi đường thẳng thuộc mặt phẳng này
vuông góc với giao tuyến sẽ vuông góc với mặt phẳng kia.
Phương án B sai vì còn trường hợp hai mặt phẳng cắt nhau. Phương án C sai. Vậy chọn D.
Câu 20: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA ^ ( ABCD), SA = a 6 .
Gọi a là góc giữa SC và mp(SAB). Chọn khẳng định đúng trong các khẳng định sau? 1 A. tana = 1 . B. tana = . C. 0 a = 1 30 . D. tana = . 8 7 6
Hướng dẫn giải:
Do BC ^ (SAB) nên SB là hình chiếu của SC lên (SAB)
Þ (SC (SAB)) = (SC SB) ∑ , , = BSC
Xét tam giác SBC có ∑ BC a 1 tan BSC = = = . SB a 7 7 Vậy chọn B.
Câu 21: Cho hình chóp S.ABDC , với đáy ABDC là hình bình hành tâm ; O AD, S , A AB đôi một
vuông góc AD = 8, SA = 6. (P)là mặt phẳng qua trung điểm của AB và vuông góc với AB . Thiết
diện của (P) và hình chóp có diện tích bằng? A. 20. B. 16. C. 17. D. 36.
Hướng dẫn giải:
Thiết diện là hình thang vuông đi qua trung điểm các cạnh ; AB C ;
D CS; SB , nên diện tích thiết diện là 1 1
(BC + BC). SA (8+ 4)6 2 2 dt = = = 36 2 2
Câu 22: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a và SA = SB = SC = b . Gọi G là trọng tâm ABC D . Độ dài SG là: 2 2 9b + 3a 2 2 b - 3a 2 2 9b - 3a 2 2 b + 3a A. . B. . C. . D. . 3 3 3 3
Hướng dẫn giải:
Theo bài ra hình chóp S.ABC là hình chóp tam giác đều. Gọi H là trung điểm của BC , ta có
SG ^ (ABC),G Î AH . 2 a 3 a Mặt khác ta có: 2 AH = , SH = b - 2 4 2 a 2 2 ! AG 3b - a 2 3 ® SG = . SA sin SAG = . b 1- ( ) = b 1- = 2 SA b 3 Trang 24
Câu 23: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a và SA = SB = SC = b . Gọi G là trọng tâm ABC D
. Xét mặt phẳng (P) đi qua A và vuông góc với SC . Tìm hệ thức liên hệ giữa a và
b để (P)cắt SC tại điểm C nằm giữa S và C . 1
A. b > a 2.
B. b < a 2 .
C. a < b 2 .
D. a > b 2.
Hướng dẫn giải: 2 2 2b - a
Để C nằm giữa S và C thì ! 0 !
ASC < 90 ® cos ASC > 0 «
> 0 « b 2 > a 1 2 2b Chọn đáp án C
Câu 24: Cho tứ diện ABCD có AB, BC,CD đôi một vuông góc. Điểm cách đều ,
A B,C, D là:
A. Trung điểm BC . B. Trung điểm AD .
C. Trung điểm AC .
D. Trung điểm AB .
Hướng dẫn giải:
Sử dụng tính chất trung điểm của tam giác vuông
Câu 25: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O . Biết SA = SC, SB = SD. Khẳng
định nào sau đây đúng ?
A. AB ^ (SAC) .
B. CD ^ AC .
C. SO ^ (ABCD).
D. CD ^ (SBD).
Hướng dẫn giải:
Do hình chóp S.ABCD có đáy ABCD là hình thoi tâm O , SA = SC, SB = SDnên SO ^ (ABCD)
Câu 26: Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Mặt bên SAB là tam giác đều có đường
cao AH vuông góc với mp(ABCD) . Gọi a là góc giữa BD và mp(SAD) . Chọn khẳng định đúng
trong các khẳng định sau? A. 0 a = 60 . B. 0 a = 3 30 . C. cosa = 3 . D. sina = . 2 2 2 2
Hướng dẫn giải: AB
Gọi I là trung điểm AS , suy ra ! BI ^ (S ) AD ®a = 3
IDB. Ta có: BI =
, BD = AB 2 . Suy ra 2 BI 3 sina = = BD 2 2
Câu 27: Cho tứ diện ABCD đều. Gọi a là góc giữa AB và mp(BCD) . Chọn khẳng định đúng trong các khẳng định sau? 3 A. cosa = 3 . B. cosa = . C. cosa = 3 0 . D. cosa = . 3 4 2
Hướng dẫn giải::
Gọi H là hình chiếu của A lên mp(BCD), a là độ dài cạnh của tứ diện ABCD . a BH Ta có ∑ a = 3 ABH , BH = 3 . cosa = =
® Chọn đáp án A. 3 AB 3
Câu 28: Cho tam giác ABC vuông cân tại A và BC = a . Trên đường thẳng qua A vuông góc với ( a 6
ABC) lấy điểm S sao cho SA =
. Tính số đo góc giữa đường thẳng SB và ( ABC) . 2 A. 0 75 B. 0 30 C. 0 45 D. 0 60
Hướng dẫn giải: a 6 ∑ ∑ SA ,(
SB ABC) = SBA = a Þ 2 tan = = = 3 Þ = 60o a a AB a 2
Câu 29: Cho hình lập phương ABC .
D A B C D . Gọi a là góc giữa 1 1 1 1 Trang 25
AC và mp ( ABCD). Chọn khẳng định đúng trong các khẳng định sau? 1 A. 0 a = 1 45 B. tana = 2 C. tana = D. 0 a = 30 2 3
Hướng dẫn giải: CC a 1
Ta có AC , ABCD = CAC = a 1 Þ tana = = = 1 ( ∑ ) ∑ 1 AC a 2 2
Câu 30: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a . Đường thẳng SA vuông góc với mặt
phẳng đáy, SA = a . Góc giữa đường thẳng SC và mặt phẳng (SAB) là a , khi đó tana nhận giá trị
nào trong các giá trị sau? A. tana = 2 . B. tana = 1 3 . C. tana = . D. tana = 1. 2
Hướng dẫn giải: Ta có:
S Î(SAB) Þ S là hình chiếu của S trên (SAB) ( ) 1
ìïBC ^ AB (t / c HV ) í Þ BC ^ SAB BC ^ S A î (SA^ ï (ABCD)) ( )
Þ B là hình chiếu của C trên (SAB) (2) Từ ( ) ( ) Þ éSC ë ( ∑SAB)ù = û (∑ SC SB) ∑ 1 , 2 , , = BSC = a
Xét tam giác SAB vuông tại A ta có: 2 2
SB = SA + AB = a 2 BC a 1
Xét tam giác SBC vuông tại B ta có: tana = = = SB a 2 2
Vậy chọn đáp án C .
Câu 31: Cho hình thoi ABCD có tâm O , AC = 2a . Lấy điểm S không thuộc ( ABCD) sao cho
SO ^ ( ABCD). Biết ∑ 1
tan SOB = . Tính số đo của góc giữa SC và ( ABCD). 2 A. 0 75 . B. 0 45 . C. 0 30 . D. 0 60 .
Hướng dẫn giải:
Câu 32: Cho hình chóp S.ABC có SA ^ ( ABC) và tam giác ABC
không vuông. Gọi H , K lần lượt là trực tâm ABC D và SB D C . Số đo
góc tạo bởi SC và (BHK ) là: A. 0 45 . B. 0 120 . C. 0 90 . D. 0 65 .
Hướng dẫn giải: Ta có:
ìïBH ^ AC (gt) í
Þ BH ^ SAC Þ BH ^ SC BH ^ S A î (SA ^ ï (ABCD)) ( )
Mà BK ^ SC Þ SC ^ (BHK )
Vậy chọn đáp án C . Trang 26 Trang 27
DẠNG 3: THIẾT DIỆN VÀ CÁC BÀI TOÁN LIÊN QUAN. Phương pháp:
Để xác định thiết diện của mặt phẳng (a) đi qua điểm O và vuông góc với đường thẳng d với một
hình chóp ta thực hiện theo một trong hai cách sau: d b O I α a
Cách 1. Tìm tất cả các đường thẳng vuông góc với d , khi đó (a) sẽ song song hoặc chứa các đường
thẳng này và ta chuyển về dạng thiết diện song song như đã biết ở ( dạng 2, §2 chương II).
Cách 2. Ta dựng mặt phẳng (a) như sau:
Dựng hai đường thẳng a,bcắt nhau cùng vuông góc với d trong đó có một đường thẳng đi qua O , khi
đó (a) chính là mặt phẳng mp(a,b).
Câu 130: Cho hình chóp S.ABC có đáy ABC là tam giác đều, SA ^ ( ABC). Gọi (P) là mặt phẳng
qua B và vuông góc với SC . Thiết diện của (P) và hình chóp S.ABC là:
A. Hình thang vuông. B. Tam giác đều. C. Tam giác cân. D. Tam giác vuông.
Hướng dẫn giải:
Gọi I là trung điểm của AC , kẻ IH ^ SC .
Ta có BI ^ AC, BI ^ SA Þ BI ^ SC .
Do đó SC ^ (BIH ) hay thiết diện là tam giác BIH .
Mà BI ^ (SAC) nên BI ^ IH hay thiết diện là tam giác vuông. Chọn D.
Câu 1: Cho tứ diện đều A BCD cạnha = 12 , gọi (P
) là mặt phẳng qua B và vuông góc với AD.
Thiết diện của (P
) và hình chóp có diện tích bằng A. 36 2 . B. 40 . C. 36 3 D. 36 .
Hướng dẫn giải:
Thiết diện là tam giác BCE , với E là trung điểm của A D . Gọi F là trung điểm của BC . Trang 28 12 3
Ta có BE = CE = = 6 3 ; 2 2 2
EF = BE - BF = 6 2 .
Diện tích thiết diện là: 1 S = EF.BC = 36 2 . 2
Câu 2: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , cạnh bên SA ^ ( ABC). Mặt
phẳng (P) đi qua trung điểm M của AB và vuông góc với SB cắt AC, SC, SB lần lượt tại N, P, . Q
Tứ giác MNPQ là hình gì ?
A. Hình thang vuông. B. Hình thang cân. C. Hình bình hành. D. Hình chữ nhật.
Hướng dẫn giải: ìAB ^ BC Ta có: í Þ BC ^ S . B îSA ^ BC ìBC ^ SB ï Vậy í Þ P / /BC 1 . ( ï P î ) ( ) ( ) ^ SB
Mà (P)Ç( ABC) = MN (2) . Từ ( )
1 ;(2) Þ MN / /BC
Tương tự ta có PQ / /BC; PN / /SA
Mà SA ^ BC Þ PN ^ NM .
Vậy thiết diện là hình thang MNPQ vuông tại N.
Câu 3: Cho hình chóp S.ABC có đáy ABC là tam giác đều, O là trung điểm của đường cao AH của
tam giác ABC, SO vuông góc với đáy. Gọi I là điểm tùy ý trên OH (không trùng với O và H ). mặt
phẳng (P) qua I và vuông góc với OH . Thiết diện của (P) và hình chóp S.ABC là hình gì? A. Hình thang cân B. Hình thang vuông C. Hình bình hành D. Tam giác vuông
Hướng dẫn giải:
Mặt phẳng (P) vuông góc với OH nên (P) song song với SO
Suy ra (P) cắt (SAH ) theo giao tuyến là đường thẳng
qua I và song song với SO cắt SH tại K
Từ giả thiết suy ra (P) song song BC , do đó (P) sẽ cắt
(ABC),(SBC) lần lượt là các đường thẳng qua I và K
song song với BC cắt ,
AB AC, S ,
B SC lần lượt tại
M , N,Q, P. Do đó thiết diện là tứ giác MNPQ
Ta có MN và PQ cùng song song BC suy ra I là
trung điểm của MN và K là trung điểm của PQ, lại có các
tam giác ABC đều và tam giác SBC cân tại S suy ra IK
vuông góc với MN và PQ dó đó MNPQ là hình thang cân. Chọn đáp án A.
Câu 4: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a và SA = SB = SC = b ( a > b 2 ).
Gọi G là trọng tâm ABC D
. Xét mặt phẳng (P) đi qua A và vuông góc với SC tại điểm C nằm giữa 1
S và C . Diện tích thiết diện của hình chóp khi cắt bởi mặt phẳng (P) là Trang 29 2 2 2 a 3b - a 2 2 2 a 3b - a 2 2 2 a 3b + a 2 2 2 a 3b + a A. S = . B. S = . C. S = . D. S = 4b 2b 2b 4b .
Hướng dẫn giải:
Kẻ AI ^ SC Þ ( AIB) ^ SC. Thiết diện là tam giác AIB .
æ a + b - b ö a Ta có ∑ ∑ 2 2 2 2 2 2
AI = AC sin ACS = a 1- cos ACS = a 1- ç ÷ = 4b - a è 2ab ø 2b
Gọi J là trung điểm của AB . Dễ thất tam giác AIB cân tại I ,
suy ra IJ ^ AB . a 2 2 2 2
IJ = AI - AJ = 3b - a . 2b Do đó: 2 2 2 1 a 3b - a S = A . B IJ = . 2 4b Chọn A.
Câu 5: Tam giác ABC có BC = 2a , đường cao AD = a 2 . Trên đường thẳng vuông góc với ( ABC)
tại A , lấy điểm S sao cho SA = a 2 . Gọi E, F lần lượt là trung điểm của SB và SC . Diện tích tam giác AEF bằng? 3 3 1 3 A. 2 a B. 2 a C. 2 a D. 2 a 4 6 2 2
Hướng dẫn giải:
Do AD ^ BC, SA ^ BC Þ BC ^ (SAD) Þ BC ^ AH Þ EF ^ AH 1 Þ S = EF.AH AEF D 2 1
Mà EF = BC = a. Do H là trung điểm SD Þ AH = a 2 1 2 Þ S = a AEF D 2 3
Câu 6: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a, SA ^ (ABC), SA = a . Gọi (P ) 2
là mặt phẳng đi qua A và vuông góc với BC. Thiết diện của hình chóp S.ABC được cắt bởi (P c ) ó diện tích bằng? 2 3a 2 3a A. . B. . 8 2 3 2 2a C. 2 a . D. . 4 3
Hướng dẫn giải: Trang 30
Gọi M là trung điểm của BC thì BC ^ AM ( ) 1 .
Hiển nhiên AM = a 3.
Mà SA ^ (ABC)fi BC ^ SA( ) 2 . Từ ( ) 1 và (2
) suy ra BC ^ (SAM )fi (P)∫ (SAM )
Khi đó thiết diện của hình chóp S.ABC được cắt bởi (P ) chính là DSAM .
DSAM vuông tại A nên 2 1 1 a 3 3a S = S . A AM = .a 3 = . DSAM 2 2 2 4 Chọn đáp án C.
Câu 7: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , SA ^ ( ABC), SA = a . Gọi (P) là
mặt phẳng đi qua S và vuông góc với BC . Thiết diện của (P) và hình chóp S.ABC có diện tích bằng ? 2 a 3 2 a 2 a A. B. C. D. 2 a 4 6 2
Hướng dẫn giải:
Kẻ AE ^ BC, SA ^ BC Þ BC ^ (SAE) º (P)
Thiết diện của mặt phẳng (P) và hình chóp S.ABC là tam giác SAE có 2 1 1 3 a 3 diện tích : S = S . A AE = . a a = SA D E 2 2 2 4 3
Câu 8: Cho tứ diện SABC có hai mặt (ABC ) và (SBC
) là hai tam giác đều cạnh a, SA = a . M là 2
điểm trên AB sao cho AM = b (0 < b < a). (P
) là mặt phẳng qua M và vuông góc với BC. Thiết diện của (P
) và tứ diện SABC có diện tích bằng? 2 3 3 æ a - b ö 2 3 æ a - b ö 2 3 3 æ a - b ö 2 3 3 æ a - b ö A. . . B. . . C. . D. ç ÷ ç ÷ ç ÷ . ç ÷ 4 è a ø 4 è a ø 16 è a ø 8 è a ø
Hướng dẫn giải:
Gọi N là trung điểm của BC . Ï SB Ô = SC Ï B Ô C ^ SN Ô Ô Ì fi Ì fi BC ^ (SAN). AB Ô = AC BC Ô ^ AN Ô Ó Ô Ó Ï M Ô ( Œ P) Theo bài ra BC (P) Ô ^ fi Ì . ( Ô P Ô )/ /(SAN ) Ó
Kẻ MI / / AN, MK / /SA fi Thiết diện của (P
) và tứ diện SABC là DKMI. Trang 31 Ï D Ô ABC Ô a 3 Ì
là hai tam giác đều cạnh a fi AN = SM =
= SA fi DSAN là tam giác đều cạnh ÔDSBC Ô Ó 2 a 3 2 3 a - b 3 3 a Ê - bˆ
fi DKMI là tam giác đều cạnh . fi S = .Á ˜ Á ˜ . 2 2 DKMI a 16 Á Ë a ˜¯ Chọn đáp án C.
Câu 9: Cho tứ diện đều ABCD cạnh a = 12 , AP là đường cao của tam giác ACD . Mặt phẳng (P)
qua B vuông góc với AP cắt mp ( ACD) theo đoạn giao tuyến có độ dài bằng ? A. 9 B. 6 C. 8 D. 7
Hướng dẫn giải:
Ta có : CD ^ A ,
P CD ^ BP Þ CD ^ ( APB) Þ BG ^ CD
Tương tự : AD ^ CM, AD ^ BM Þ AD ^ (BCM ) Þ AD ^ BG
Suy ra : BG ^ ( ABC) Þ BG ^ AP
Kẻ KL đi qua trọng tâm G của ACD D
và song song với CD Þ AP ^ KL
Þ (P) chính là mặt phẳng (BKL) Þ ( ACD)Ç(BKL) 2 = KL = CD = 8 3
Có thể nói nhanh theo tính chất tứ diện đều:
Gọi G là trọng tâm ACD D
thì G là tâm ACD D và BG ^ (ACD)
Trong mp(ACD) kẻ qua G đường thẳng song song với CD cắt
AC, AD lần lượt tại K, L Ta có
(BKL) ^ (ACD), AP ^ KL Þ AP ^ (BKL) . Vậy (P) º (BKL) Þ ( ACD)Ç(BKL) 2 = KL = CD = 8. 3
Câu 10: Cho hình chóp S.ABCD , với đáy ABCD là hình thang vuông tại A , đáy lớn AD = 8 , BC = 6
, SA vuông góc với mặt phẳng ( ABCD), SA = 6 . Gọi M là trung điểm AB . (P) là mặt phẳng qua
M và vuông góc với AB . Thiết diện của (P) và hình chóp có diện tích bằng? A. 10. B. 20 . C. 15. D. 16.
Hướng dẫn giải:
Do (P) ^ AB Þ (P) ! SA
Gọi I là trung điểm của SB Þ MI ! SA Þ MI Ì (P)
Gọi N là trung điểm của CD Þ MN ^ AB Þ MN Ì (P)
Gọi K là trung điểm của SC Þ IK ! BC , mà
MN ! BC Þ MN ! IK Þ IK Ì (P)
Vậy thiết diện của (P) và hình chóp là hình thang MNKI vuông tại M Ta có: 1
MI là đường trung bình của tam giác SAB Þ MI = SA = 3 2 1
IK là đường trung bình của tam giác SBC Þ IK = BC = 3 2 1
MN là đường trung bình của hình thang ABCD Þ MN = ( AD + BC) = 7 2 IK + MN 3 + 7 Khi đó S = .MI = .3 = 15 MNKI 2 2 Trang 32
Vậy chọn đáp án C .
Câu 11: Cho tứ diện OABC có ,
OA OB,OC đôi một vuông góc. Kẻ OH ^ ( ABC).
a) Khẳng định nào đúng nhất? H là trực tâm của DABC .
A. H là trực tâm của DABC .
B. H là tâm đường tròn nội tiếp của DABC .
C. H là trọng tâm của DABC .
D. H là tâm đường tròn ngoại tiếp của DABC .
b) DABC là tam giác gì?
A. DABC là tam giác nhọn.
B. DABC là tam giác tù
C. DABC là tam giác vuông
D. DABC là tam giác cân
c) Khẳng định nào sau đây là đúng nhất? 2 2 2 2 S = S + S + S DABC DOAB DOBC DOCA 1 1 1 1 A. 2 2 2 2 S = S + S + S B. 2 2 2 2 S = S + S + S DABC
2 DOAB 2 DOBC 2 DOCA 2 DABC DOAB DOBC DOCA 1 C. 2 2 2 2 S = S + S + S D. 2 2 2 2 S = S + S + S 3 DABC DOAB DOBC DOCA DABC DOAB DOBC DOCA
d) Tìm tập hợp các điểm M trong không gian sao cho 2 2 2 2
MA + MB + MC = 3MO .
A. M thuộc mặt phẳng đi qua I và vuông góc với OG , trong đó I là điểm cách đều 4 điểm , O , A ,
B C và G là trọng tâm của tam giác ABC
B. M thuộc mặt phẳng đi qua I và song song với OG ,trong đó I là điểm cách đều 4 điểm , O , A ,
B C và. là trọng tâm của tam giác ABC
C. M thuộc mặt phẳng đi qua O và vuông góc với OG , trong đó G là trọng tâm của tam giác ABC
D. M thuộc mặt phẳng đi qua O và song song với OG , trong đó G là trọng tâm của tam giác ABC
Hướng dẫn giải:. OA ^ OB ü a) Ta có
ý Þ OA ^ (OBC) Þ OA ^ BC OA ^ OCþ
Lại có OH ^ ( ABC) Þ OH ^ BC A BC ^ OA ü Vậy
ý Þ BC ^ (OAH ) BC ^ OH þ Þ BC ^ AH ( ) 1 . AC ^ OB ü H Tương tự
ý Þ AC ^ (OBH ) Þ BH ^ AC (2). AC ^ OH þ Từ ( )
1 ,(2) suy ra H là trực tâm của tam giác ABC . O C
b) Đặt OA = a,OB = , b OC = c I Ta có 2 2 2 2
BC = OB + OC = b + c B Tương tự 2 2 2 2
AC = a + c , AB = a + b
Áp dụng định lí côsin cho tam giác ABC ta có
AB + AC - BC ( 2 2 a + b ) 2 2
+ (a + c ) - ( 2 2 2 2 2 b + c ) cos A = = 2 . AB AC 2 ( 2 2 a + b ) 2 2 (a + b ) 2 = a > 0 suy ra ! A nhọn. ( 2 2 a + b ) 2 2 (a + b )
Tương tự các góc B,C nhọn. Trang 33 1 1 c) Ta có 2 2 2 S = AI BC = ( 2 2 OI + OA )( 2 2 OB + OC ABC ) 4 4 1 1 1 2 2 2 2 2 2
= OI BC + OA OB + OA OC 2 2 2 = S + S + S 4 4 4 DOAB DOBC DOCA
d) Gọi I là điểm cách đều 4 điểm , O , A ,
B C và G là trọng tâm của tam giác ABC thì ta có : 2 2 2 2
MA + MB + MC = 3MO !!!" !!" !!!" !!" !!!" !!" !!!" !!"
Û (MI + IA)2 +(MI + IB)2 +(MI + IC)2 2 = 3(MI + IO) !!" !!" !!" !!!" !!" !!!" !!" !!!" !!" !!!" !!!"!!!"
Û (IA+ IB + IC)IM = 3 . IO MI Û 3 . IG MI = 3 .
IO IM Û OGMI = 0 Û MI ^ OG ( do !!" !!" !!" !!"
IA+ IB + IC = 3IG)
Vậy M thuộc mặt phẳng đi qua I và vuông góc với OG .
Câu 12: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA ^ ( ABCD) và SA = a .
Gọi I, K lần lượt là trung điểm các cạnh AB và SC . Tính IK . 2 3 A. = a IK B. = a IK C. 2 2 2 S = a 3 2 IK D. = a IK 3 2
Hướng dẫn giải:. 2 æ a ö a 5 Ta có 2 2 2
IS = AI + AS = + a = Tương tự ç ÷ è 2 ø 2 K A B 5 I = = a ID IC suy ra 2
IS = ID = IC nên I thuộc trục đường tròn ngoại tiếp tam giác SCD . ìCD ^ AD D C Mặt khác í Þ CD ^ (SAD) îCD ^ SA
Þ CD ^ SD Þ DSCD vuông tại D , lại có K là trung điểm của SC nên K là tâm đường tròn ngoại
tiếp tam giác SCD , do đó KI ^ (SCD). 1 1 Ta có 2 2 2 2 2 2
IK = ID - DK = ID - SC = ID - ( 2 2 SA + AC ) 4 4 2 5a 1 - ( + a a a 2a ) 2 2 2 2 = Þ IK = . 4 4 2 2
Câu 13: Cho hình vuông ABCD có tâm O và cạnh bằng 2a . Trên đường thẳng qua O vuông góc với
(ABCD) lấy điểm S . Biết góc giữa SA và (ABCD) có số đo bằng 45°. Tính độ dài SO. a 3 a
A. SO = a 3 .
B. SO = a 2 . C. SO = 2 . D. SO = . 2 2
Hướng dẫn giải: Chọn B.
Do SO ^ ( ABCD) Þ (SA ( ABCD)) ∑ , = SAO = 45°. Do đó SA
D O vuông cân tại O nên SO = AO = a 2 .
Câu 14: Cho tứ diện ABCD có , DA ,
DB DC đôi một vuông góc. Gọi a, b ,g lần lượt là góc giữa các đường thẳng , DA ,
DB DC với mặt phẳng ( ABC). Trang 34
Tìm Giá trị nhỏ nhất của M = ( 2 + a)( 2 + b )( 2 2 cot 2 cot 2 + cot g ). A. 64 B. 8 C. 1 D. 64 2 Hướng dẫn giải:.
Gọi H là hình chiếu của D trên ( ABC)
Khi đó H là trực tâm của tam giác ABC . A Và (DA ( ∑ ABC)) = (∑ DA AH ) ∑ , , = DAH = a
Đặt DA = a, DB = , b DC = c
Gọi I = AH Ç BC thì DI là đường cao của tam giác DBC nên . = DB DC = bc DI H 2 2 BC b + c 2 DA a ( 2 2 b + c D C 2 ) cot a = = 2 2 DI b c 2 a ( 2 2 b + c ) I 2 2a 4a 2 Þ 2 + cot a = 2 + ³ 2 + ³ Vậy 2 2 b c bc bc B 4 2 2 + cot a ³ a ( ) 1 bc 4 4 Tương tự 2
2 + cot b ³ b (2) và 2 2 + cot g ³ c (3) ac ab Nhân theo vế các BĐT ( ) 1 ,(2),(3) ta được ( 2 + a)( 2 + b )( 2 2 cot 2 cot 2 + cot g ) ³ 64 ( đpcm)
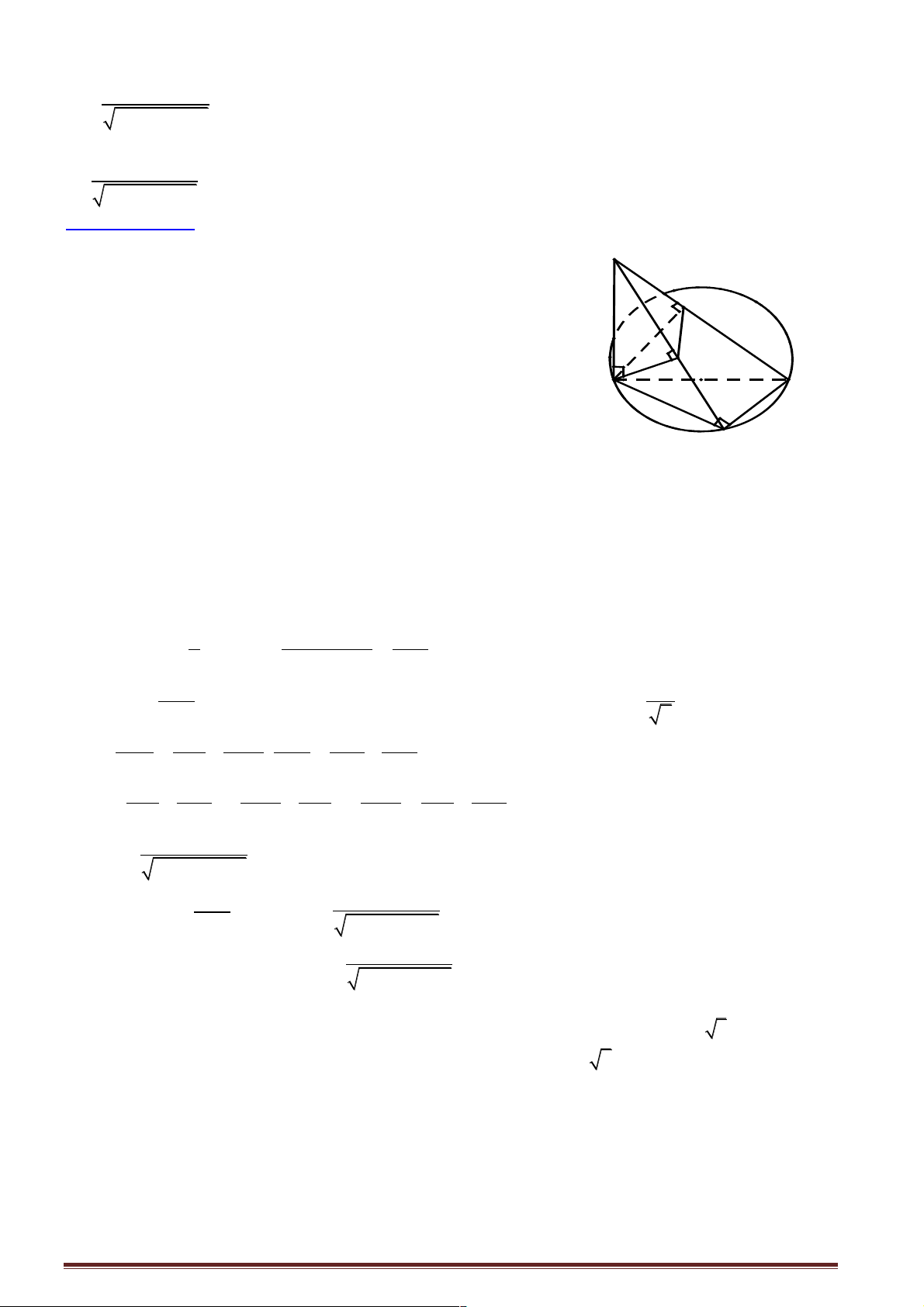
Câu 15: Trong mặt phẳng (a ) cho đường tròn đường kính cố định BC và M là điểm di động trên
đường tròn này. Trên đường thẳng d vuông góc với (a ) tại B lấy một điểm A .
a) Khẳng định nào sau đây là đúng?
A. các mặt của tứ diện ABMC là tam giác vuông
B. các mặt của tứ diện ABMC là tam giác vuông cân
C. tam giác ACM vuông tại A.
D. tam giác ACM vuông cân tại M .
b) Gọi H , K lần lượt là hình chiếu của B trên AM và AC . Khẳng định nào sau đây là sai?
A. AC ^ (BHK ).
B. BH ^ AC
C. A, B đều đúng
D. A, B đều sai
c) Tìm tập hợp điểm H khi M di động.
A. H thuộc đường tròn đường kính BK .
B. H thuộc đường tròn đường kính AC.
C. H thuộc đường tròn đường kính BM.
D. H thuộc đường tròn đường kính AB.
d) Tìm vị trí của M để đoạn AM lớn nhất.
A. M º C
B. M º B
C. M º H
D. M º K
e) Tìm vị trí của M để diện tích tam giác BHK lớn nhất.
A. M là các giao điểm của đường tròn đường kính BC với đường tròn tâm B bán kính . BA BC 2 2 2 2BA + BC
B. M là các giao điểm của đường tròn đường kính BC với đường tròn tâm B bán kính 1 . BA BC 2 2 2 2BA + BC Trang 35
C. M là các giao điểm của đường tròn đường kính BC với đường tròn tâm B bán kính . BA BC 3 2 2 2BA + BC
D. M là các giao điểm của đường tròn đường kính BC với đường tròn tâm B bán kính . BA BC 2 2 2BA + BC
Hướng dẫn giải:. ìAB BM a) Ta có AB ^ (a ) ^ Þ í
suy ra các tam giác ABM và A îAB ^ BC
ABC vuông tại B . K ìMC ^ MB Tiếp theo ta có í Þ MC ^ ( ABM ) îMC ^ AB H
Þ MC ^ AM hay tam giác ACM vuông tại M . B C ìBH ^ AM b) Ta có í Þ BH ^ ( ACM ) îBH ^ MC M
Þ BH ^ AC . AC ^ BH ü Vậy
ý Þ AC ^ (BHK ). AC ^ BK þ
c) Dễ thấy BK cố định và ∑ 0
BHK = 90 nên điểm H thuộc đường tròn đường kính BK .Từ đó ta có tập
hợp các điểm M là đường tròn đường kính BK . d) 2 2 2
MA = AB + BM mà AB không đỏi nên AM lớn nhất khi MB lớn nhất Û BM = BC Û M º C . 2 2 2 1 BH + HK BK e) Ta có S = BH.HK £ = không đổi nên BHK 2 4 4 2 BK max S =
Û BH = HK , lúc này DHBK vuông cân tại H nên = BK BH . BHK 4 2 1 1 1 1 1 1 Ta có = + ; = + 2 2 2 2 2 2 BH BA BM BK AB BC æ 1 1 ö 1 1 1 1 2 nên 2 + = + Û = + ç ÷ 2 2 2 2 2 2 2 è BA BC ø BM BA BM BA BC . Û = BA BC MB 2 2 2BA + BC 2 BK . BA BC Vậy max S = Û Û MB =
Û M là các giao điểm của đường tròn đường kính BHK 4 2 2 2BA + BC . BA BC
BC với đường tròn tâm B bán kính 2 2 2BA + BC
Câu 16: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a, BC = a 3 , mặt bên
SBC là tam giác vuông tại B , mặt bên SCD vuông tại D và SD = a 5 . a) Tính SA .
A. SA = a
B. SA = 2a
C. SA = 3a
D. SA = 4a
b) Đường thẳng qua A vuông góc với AC cắt CB,CD lần lượt tại I, J . Gọi H là hình chiếu của A
trên SC .Gọi K , L là các giao điểm K , L của SB,SD với (HIJ ).
Khẳng định nào sau đây là đúng nhất?
A. AK ^ (SBC),
B. AL ^ (SCD)
C. AK ^ SC D. Cả A, B, C đều đúng Trang 36 Hướng dẫn giải:.
a) DSBC vuông tại B Þ BC ^ SB mà BC ^ AD Þ BC ^ (SAB) Þ BC ^ SA .
Tương tự ta có SA ^ CD nên SA ^ ( ABCD). S Ta có 2 2
SC = DS + DC = a 6 L I H 2 2
Þ SB = SC - BC = a 2 K 2 2
Þ SA = SB - AB = a . A D Vậy SA = a . ìIJ ^ AC b) Do í
Þ IJ ^ (SAC) Þ IJ ^ SC J B C îIJ ^ SA
Lại có AH ^ SC Þ (HIJ ) ^ SC Þ AK ^ SC ( ) 1
Dế thấy BC ^ (SAB) Þ BC ^ AK (2) Từ ( )
1 ,(2) suy ra AK ^ (SBC).
Lập luận tương tự ta có AL ^ (SCD).
Câu 17: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B , AB = a, SA = a 3 và
SA ^ ( ABC). Gọi M là điểm trên cạnh AB và AM = x (0 < x < a), mặt phẳng (a ) đi qua M và vuông góc với AB
Giả sử thiết diện của hình chóp S.ABC với (a ) là tứ giác MNPQ.
a) Hỏi tứ giác MNPQ là hình gì
A. Hình chữ nhật B. hình vuông C. hình thang
D. hình bình hành
b) Tìm x để diện tích thiết diện MNPQ lớn nhất. a 3 A. x = B. = a x C. = a x
D. x = a 2 2 2
Hướng dẫn giải:. ( ìï a ) ^ AB . Ta có í Þ SA ! (a ) ïîSA ^ AB
ìM Î(SAB) Ç(a ) ï
Do đó íSA Ì (SAB)
Þ (a ) Ç(SAB) = MN ! SATương tự S ï îSA ! (a ) ( ìï a ) ^ AB í Þ BC ! (a ) P ïîBC ^ AB
ìM Î(a ) Ç( ABC) N ï íBC Ì ( ABC) C A ï Q îBC ! (a ) M
Þ (a ) Ç( ABC) = MQ ! BC,QÎ AC B
ìN Î(SBC) Ç(a ) ï íBC Ì (SBC)
Þ (a ) Ç(SBC) = NP ! BC, PÎ SC. ï îBC ! (a )
Thiết diện là tứ giác MNPQ. Trang 37
b) Ta có MN ! S ,
A PQ ! SA Þ MN ! PQ và MQ ! BC, NP ! BC Þ MQ ! NP nên MNPQ là hình bình hành. ìMN ! SA ï
Mặt khác íNP ! BC Þ MN ^ NP. Vậy MNPQ là hình chữ nhật. ïSA ^ î BC MN MB .
MB SA (a - x)a 3
b) Ta có MQ = AM = x, = Þ MN = = = 3(a - x) SA AB AB a 2 2 2 = = a a a S MN MQ a x x x MNPQ ( - ) æ ö 3 . 3 = 3[ - - ] £ ç ÷ 4 è 2 ø 4 2 a 3 max S = khi = a x . MNPQ 4 2
Câu 18: Cho hình vuông ABCD có tâm O và cạnh bằng 2a . Trên đường thẳng qua O vuông góc với
(ABCD) lấy điểm S . Biết góc giữa SA và (ABCD) có số đo bằng 45°. Tính độ dài SO. a 3 a
A. SO = a 3 .
B. SO = a 2 . C. SO = 2 . D. SO = . 2 2
Hướng dẫn giải: Chọn B.
Do SO ^ ( ABCD) Þ (SA ( ABCD)) ∑ , = SAO = 45°. Do đó SA
D O vuông cân tại O nên SO = AO = a 2 .
Câu 19: Cho tứ diện ABCD có AB, BC,CD đôi một vuông góc và AB = a, BC = ,
b CD = c . Độ dài AD : A. 2 2 2
a + b + c . B. 2 2 2
a + b - c . C. 2 2 2
a -b + c . D. 2 2 2
-a + b + c .
Hướng dẫn giải:: Ta có: 2 2 2 2
BC ^ CD Þ BD = BC + CD = b + c ìAB ^ BC Mặt khác: í
Þ AB ^ (BCD) Þ AB ^ BD îAB ^ CD 2 2 2 2 2
AD = AB + BD = a + b + c
Vậy chọn đáp án A.
Câu 20: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA ^ ( ABCD) và SA = a 2 .
Giả sử tồn tại tiết diện của hình chóp với mặt phẳng (a ) đi qua A vuông góc với SC . Tính diện tích thiết diện. 2 2 2 2 2 3 2 4 2 A. = a S B. = a S C. = a S D. = a S 3 2 3 3 Trang 38
Hướng dẫn giải:.
Gọi K là hình chiếu của A trên SC thì K Î(a ).Trong (SAC) gọi I = SO Ç AK . BD ^ SA ü Ta có
ý Þ BD ^ (SAC) BD ^ ACþ
Þ BD ^ SC , mặt khác (a) ^ SC nên BD ! (a).
ìI Î(a ) Ç(SBD) S ï
Vậy íBD Ì (SBD) ï îBD ! (a ) Þ (a)Ç( K L
SBD) = HL ! B , D H Î , SD LÎSB
Thiết diện là tứ giác AHKL . I H ìHL ! BD 1 B b) Do í
Þ HL ^ AK Þ S = AH.KL A îBD ^ AHKL AK 2
Ta có SA = AC = a 2 Þ DSAC cân tại., mà AK ^ SC nên K là O SC 2a
trung điểm của SC Þ AK = = = a. D C 2 2 HL SH SI 2 2 2a 2 HL ! BD Þ = = = Þ HL = BD = BD SD SO 3 3 3 2 1 2a 2 a 2 Vậy S = . a = . AHKL 2 3 3
Câu 21: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a , đường cao SO = 2a . Gọi M là
điểm thuộc đường cao AA' của tam giác ABC . Xét mặt phẳng (a ) đi qua M và vuông góc với AA'.
Đặt AM = x . Giả sử tồn tại thiết diện của hình chóp khi cắt bởi (a ).
Giả sử tính được diện tích thiết diện theo a và x . Xác định vị trí của M để diện tích thiết diện lớn nhất. 3 3 3 3 3 3 A. = a x B. = a x C. = a x D. = a x 8 2 8 8
Hướng dẫn giải:. S
Vì S.ABC là hình chóp đều nên
SO ^ ( ABC)( O là tâm tam giác ABC ).Do đó SO ^ AA mà 1 (a) K ! AA Þ SO ! a 1 ( ).
Tương tự ta cũng có BC ! (a )
Trường hợp 1. x = 0 thì thiết diện là điểm A . A 3 J C
Trường hợp 2. 0 < £ a x
thì M thuộc đoạn AO(M ¹ A). M 3 I O Ta có : A1
ìM Î( ABC) Ç(a ) ï B íBC Ì ( ABC)
Þ (a ) Ç( ABC) = IJ ! BC, I Î AB, J Î AC ï îBC ! (a )
ìM Î(a ) Ç(SAA1) ï
Tương tự íSO Ì (SAA
Þ a Ç SAA = MK ! SO, K Î SA 1 ) ( ) ( 1 ) . ï îSO ! (a )
Thiết diện là tam giác KIJ . Trang 39 a 3 a 3
Trường hợp 3. < x <
khi đó M thuộc đoạn S 3 2
OA(M ¹ 0;M ¹ A)
Tương tự như trường hợp trên ta có: F
ìM Î( ABC) Ç(a ) ï N íBC Ì ( ABC) E ï A îBC ! (a ) J C
Þ (a )Ç( ABC) = IJ ! BC,. O M
I Î AB, J Î AC A1 I
ìM Î(a ) Ç(SAA1) ï B íSO Ì (SAA
Þ (a )Ç(SAA = MN ! , SO N ÎSA 1 ) 1 ) . 1 ï îSO ! (a )
ìN Î(a ) Ç(SBC) ï íBC Ì (SBC)
Þ (a ) Ç(SBC) = EF ! IJ, N Î EF ï îBC ! (a )
Thiết diện là tứ giác IJEF . 3
Trường hợp 4. = a x
thì thiết diện là đoạn BC . 2 b) Xét các trường hợp: 3
x = 0 Þ S = 0, = a x Þ S = 0 td 2 td 3 1 0 < £ a x , thì S = IJ.MK . 3 IJK 2 IJ AM x 2x 3
Ta có IJ ! BC Þ = = Þ IJ = BC AA a 3 3 1 2 MK AM x Tương tự = = Þ MK = 2x 3. SO AO a 3 3 1 2x 3 Vậy 2 S = .2x 3 = 2x . IJK 2 3 a 3 a 2 < 1 x <
, dễ thây IJEF là hình thang nên S = (IJ + EF MN IJEF ) 3 3 2 a 3 2 3 x - = x EF SN OM IJ , 3 = = =
Þ EF = 2(x 3 - a) 3 BC SA OA a 3 1 1 6 a 3 - x MN MA1 2 = =
Þ MN = 2(3a - 2x 3) SO OA a 3 1 6 2 Vậy S = x a a x IJEF (4 3-3 )(3 -2 3). 3 Trang 40 a 3 a 3 2 3a
Xét các trường hợp ta thấy S lớn nhất trong trường hợp < x < và max S = khi td 3 2 IJEF 4 3 3 = a x . 8
Câu 22: Cho tam giác ABC tại C có cạnh huyền nằm trên mặt phẳng (P) và các cạnh góc vuông tạo
với (P) các góc a, b . Giả sử ¶ là độ lớn góc giữa đường cao CK với (P).Khẳng định nào sau đây là đúng nhất? A. 2 2
sin ¶ = 2sin a + 2sin b B. 2 2 sin ¶ = sin a + sin b 1 C. 2 2 sin ¶ = sin a + sin b D. 2 2
sin ¶ = 2 sin a + sin b 3 Hướng dẫn giải:.
Kẻ CH ^ (P) thì ∑
CKH là góc giữa CK và (P) và dễ thấy (CA ( ∑ P)) ∑ =CAH = a (CB ( ∑ P)) ∑ , , , =CBH = b h h
Đặt CH = h , ta có CA = ,CB = sina sin b 2 2 h h 2 2 2
AB = CA + CB = + C 2 2 sin a sin b æ 1 1 ö 2 = h + . ç 2 2 ÷ è sin a sin b ø
Xét tam giác ABC có CK.AB = C . A CB A H h h . K . CA CB sina sin P B Þ b CK = = 2 2 AB 1 æ sin a + sin b ö 2 ç 2 2 ÷ h è sin a sin b ø = h . 2 2 sin a + sin b CH Ta có ∑ 2 2 sin CKH = = sin a + sin b . CK
Câu 23: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , tâm O .
SO ^ ( ABCD), đường thẳng SA tạo với hai mặt phẳng ( ABCD) và (SBC) các góc bằng nhau. Gọi
H là hình chiếu của A trên (SBC). a)Tính SA khi = a HB 2 a 5 a 5 a 5 a 3 A. B. C. D. 2 3 4 2
b) Tính góc giữa đường thẳng SA với ( ABCD). 3 3 A. j = arctan B. j = arctan 5 7 3 3 C. j = arctan D. j = arctan 8 2 Trang 41 Hướng dẫn giải:.
a) Dễ thấy (SA ( ∑ABCD)) ∑ ,
= SAO = j nên SO = SAcosj ( ) 1 . ìOI ^ BC
Gọi I là trung điểm của BC thì ta có í Þ BC ^ (SIO) S îSO ^ BC
Kẻ OK ^ SI thì OK ^ BC nên OK ^ (SBC).
Kẻ At ! OK cắt CK tại H , khi đó ta có ìïAH ! CK í
Þ AH ^ SBC nên (SA ( ∑SBC)) ∑ , = SAH = j do ïCK ^ î (SBC) ( ) D K C H
đó AH = SAcosj (2). Từ ( )
1 ,(2) ta có AH = SO . O I Khi = a BH
thì trong tam giác vuông HAB có A B 2 2 æ a ö a 3 2 2 2
AH = AB - HB = a - = . ç ÷ è 2 ø 2 2 2 a 3
æ a 3 ö æ a 2 ö a 5 2 2 Þ SO = AH =
Þ SA = SO + OA = ç ÷ + ç ÷ = . 2 ç 2 ÷ ç 2 ÷ 2 è ø è ø a 3 SO 3 3 b) 2 tanj = = = Þ j = arctan . OA a 2 2 2 2
Câu 24: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA ^ ( ABCD), SC = a . Góc giữa
đường thẳng SC với các mặt phẳng ( ABCD) và (SAB) lần lượt là a và b . a) Tính SA
A. SA = a sina
B. SA == a cosa
C. SA = a tana
D. SA = 2a sina b) Tính AB 1
A. a cos(a + b )cos(a - b )
B. 2a cos(a + b )cos(a - b ) 2
C. 3a cos(a + b )cos(a - b )
D. a cos(a + b )cos(a - b ) Hướng dẫn giải:.
a) Do SA ^ ( ABCD) Þ (SA ( ∑ , ABCD)) S ∑ = SAC = a. ìBC ^ AB Tương tự í Þ BC ^ (SAB) îBC ^ SA Þ (SC ( ∑ SAB)) ∑ , = SBC = b . β
SA = SC sina = a sina A B
b) SB = SC sin b = asin b 2 2 2 2 2 2
AB = SB - SA = a sin b - a sin a α 1- cos 2b 1- cos 2a = a - D C 2 2 .
= a cos(a + b )cos(a - b ) Trang 42
Câu 25: Cho tứ diện OABC có ,
OA OB,OC đôi một vuông góc. Gọi H là trực tâm của tứ diện. Gọi ,
A B,C là ba góc tương ứng của tam giác ABC . Đặt ∑ ∑ ∑
a = AOH,b = BOH,g = COH . Khẳng định nào sau đây là đúng nhất? 2 2 2 sin a sin b sin g 2 2 2 sin 2a sin 2b sin 2g A. = = B. = = sin A sin B sin C sin 2A sin 2B sin 2C 2 2 2 sin 2a sin 2b sin 2g 2 2 2 sin a sin b sin g C. = = D. = = sin A sin B sin C
sin 2A sin 2B sin 2C Hướng dẫn giải:.
( HS tự giải)
Câu 26: Cho tứ diện ABCD có ∑ 0
BDC = 90 . Hình chiếu H của D trên mặt phẳng ABC là trực tâm tam giác ABC . a) Tính ∑ CDA. A. ∑ 0 CDA = 60 B. ∑ 0 CDA = 90 C. ∑ 0 CDA = 45 D. ∑ 0 CDA = 30
b)Khẳng định nào sau đây là đúng nhất.
A. (DA DB DC ) ( AB BC CA)2 2 2 2 6 + + ³ + +
B. (DA + DB + DC ) ³ ( AB + BC +CA)2 2 2 2 6 5
C. (DA DB DC ) ( AB BC CA)2 2 2 2 3 + + ³ + +
D. (DA + DB + DC ) ³ ( AB + BC +CA)2 2 2 2 2 3
Hướng dẫn giải:. D ìBC ^ DH a) Vì í Þ BC ^ ( ADH ) îBC ^ AH Þ BC ^ D A ( ) 1 A
Tương tự ta có (BDH ) ^ AC Þ DB ^ AC , vì vậy B ìDB ^ DC í
Þ DB ^ ( ACD) H îDB ^ AC M N Þ DB ^ DA (2). Từ ( )
1 ,(2) suy ra DA ^ (BCD) Þ DA ^ DC ha ∑ 0 CDA = 90 . C
b) Từ câu a) ta thấy tứ diện ABCD có các cạnh , DA ,
DB DC đôi một vuông góc.
Theo BĐT Cauchy-Schwraz ta có
(AB+ BC +CA)2 £ ( 2 2 2
3 AB + BC + CA ) 2 2 2
ìAB = DA + DB ï Mà 2 2 2
íBC = DB + DC nên ( AB + BC + CA)2 £ ( 2 2 2
6 DA + DB + DC ). ï 2 2 2 CA = DA + î DC
Đẳng thức xảy ra khi AB = BC = CA Þ DABC đều, kết hợp với chân đường cao của D trùng với tâm đáy ta được .
D ABC là hình chóp đều đỉnh D .
Câu 27: Cho tứ diện OABC có các cạnh ,
OA OB,OC đôi một vuông góc. M là một điểm bất kì thuộc
miền trong tam giác ABC . 2 2 2 MA MB MC
a) Tìm giá trị nhỏ nhất của T = + + . 2 2 2 OA OB OC
A. min T = 3
B. min T = 2
C. min T = 4
D. min T = 6 Trang 43
b) Gọi H là trực tâm tam giác ABC và a, b ,g lần lượt là góc gữa đường thẳng OH với các đường thẳng ,
OA OB,OC . Tìm giá trị lớn nhất của A = cota cot b cot g 2 2 1 A. max A = B. max A =
C. max A =
D. max A = 2 4 3 2 cosa + cos b cos b + cosg cosg + cosa c) Tìm GTNN của S = + + 2 2 2 cos g cos a cos b
A. min S = 6 3
B. min S = 3
C. min S = 6
D. min S = 4 Hướng dẫn giải:.
a) Gọi N = AM Ç BC , kẻ MM ! O A thì ta có 1 O ìïOA ^ (OBC) í Þ MM ^ OBC A1 1 ( ) ïîMM ! OA 1 kẻ MA ^ O ,
A A ÎOA. Khi đó 1 1 A 2 2 2 2 2 2
AM = AA + MA = AA + MO - OA M1 1 1 1 1 2
= OM + ( AA -OA AA +OA B 1 1 ) ( 1 1 ) M 2
= OM + OA(OA- 2OA1) N 2 2 = OM + OA - 2 . OA OA 1 2 2 AM OM 2 Suy ra 1 = +1- OA 1 C 2 2 ( ). OA OA OA
Tương tự gọi B ,C là các điểm tương tự như A thì ta có 1 1 1 2 2 MB OM 2 1 = +1- OB 2 2 2 ( ) OB OB OB 2 2 MC OM 2 1 = +1- OC 3 2 2 ( ) OC OC OC æ 1 1 1 ö æ OA OB OC ö Từ ( ) 1 ,(2),(3) ta có 2 1 1 1 T = OM + + - 2 + + + 3 ç 2 2 2 ÷ ç ÷ è OA OB OC ø è OA OB OC ø
Gọi H là trực tâm của tam giác ABC thì ta đã biết kết quả quen thuộc 1 1 1 1 2 + + = OM æ OA OB OC ö nên 1 1 1 T = - 2 + + + 3 2 2 2 2 ç ÷ OA OB OC OH 2 OH è OA OB OC ø OA NM S Mặt khác 1 = = MBC OA NA SABC OB S OC S OA OB OC Tương tự 1 MAC 1 = , = MAB nên 1 1 1 + + = 1 OB S OC S OA OB OC ABC ABC 2 OM Do đó T =
+1³ 2 do OM ³ OH . 2 OH
Vậy min T = 2 khi M º H . !!!" " !!!" " !!!" "
Cách 2. Đặt OA = a,OB = b,OC = c. Do , A ,
B C,M đồng phẳng nên tồn tại x, y, z sao cho !!!!" !!!" !!!" !!!"
OM = xOA + yOB + zOC (x + y + z = ) 1 . !!!!" !!!!" !!!" " " "
Ta có AM = OM -OA = (x - )
1 a + b + c , bình phương vô hướng ta được 2 2 2 2 2 = ( - )2 MA y b z c AM
x 1 a + y b + z c Þ = x -1 + + 2 ( )2 2 2 2 2 2 2 . 2 2 OA a a 2 2 2 2 2 2 2 2 2 2 MB x a z c MC x a y b Tương tự = + y -1 + , = + + z -1 2 2 ( )2 2 2 2 2 ( )2 OB b b OC c c Trang 44 æ 1 1 1 ö Vì vậy T = + + ç ÷( 2 2 2 2 2 2
a x + b y + c z +1 2 2 2 ) è a b c ø 2 æ 1 1 1 ö ³
.ax + .by + .cz +1 = 2 ( Theo Cauchy-Schwarz) ç ÷ è a b c ø Vậy min T = 2 . b) Dễ thấy ∑ ∑ ∑
a = AOH,b = BOH,g = COH . 2 2 2 1 1 1 1 æ OH ö æ OH ö æ OH ö Ta có + + = Û + + = 1 2 2 2 2 ç ÷ ç ÷ ç ÷ OA OB OC OH è OA ø è OB ø è OC ø 2 2 2
Û cos a + cos b + cos g =1 ( ) 1 . 2 1 1 cot x Lại có 2 2 1+ tan x = Û cos x = = * 2 2 2 ( ) cos x
1+ tan x 1+ cot x
Áp dụng CT (*) cho x nhận các giá trị a, b ,g và kết hợp với ( ) 1 thu được 2 2 2 cot a cot b cot g + + =1. 2 2 2 1+ cot a 1+ cot b 1+ cot g Đặt 2 2 2
x = cot a, y = cot b, z = cot g ( ,
x y, z > 0) thì bài toán trỏ thành x y z 1
Cho x, y, z > 0 thỏa + +
=1. Chứng minh xyz £ .
1+ x 1+ y 1+ z 8 x y z x y z yz Ta có + + =1 Û 1- = + ³ 2
1+ x 1+ y 1+ z
1+ x 1+ y 1+ z (1+ y)(1+ z) 1 Û ³ yz 2 2 . 1+ x (1+ y)(1+ z) ( ) Tương tự ta có : 1 ³ xz 1 xy 2 3 và ³ 2 4 1+ y (1+ x)(1+ z) ( ) 1+ z (1+ x)(1+ y) ( ) 1
Nhân theo từng vế các BĐT (2),(3)(4) ta được xyz £ (dpcm). 8
c) Tương tự như câu b) ta có min S = 6 3 . Trang 45