



Preview text:
BÀI TẬP TRẮC NGHIỆM KHOẢNG CÁCH
A – LÝ THUYẾT TÓM TẮT
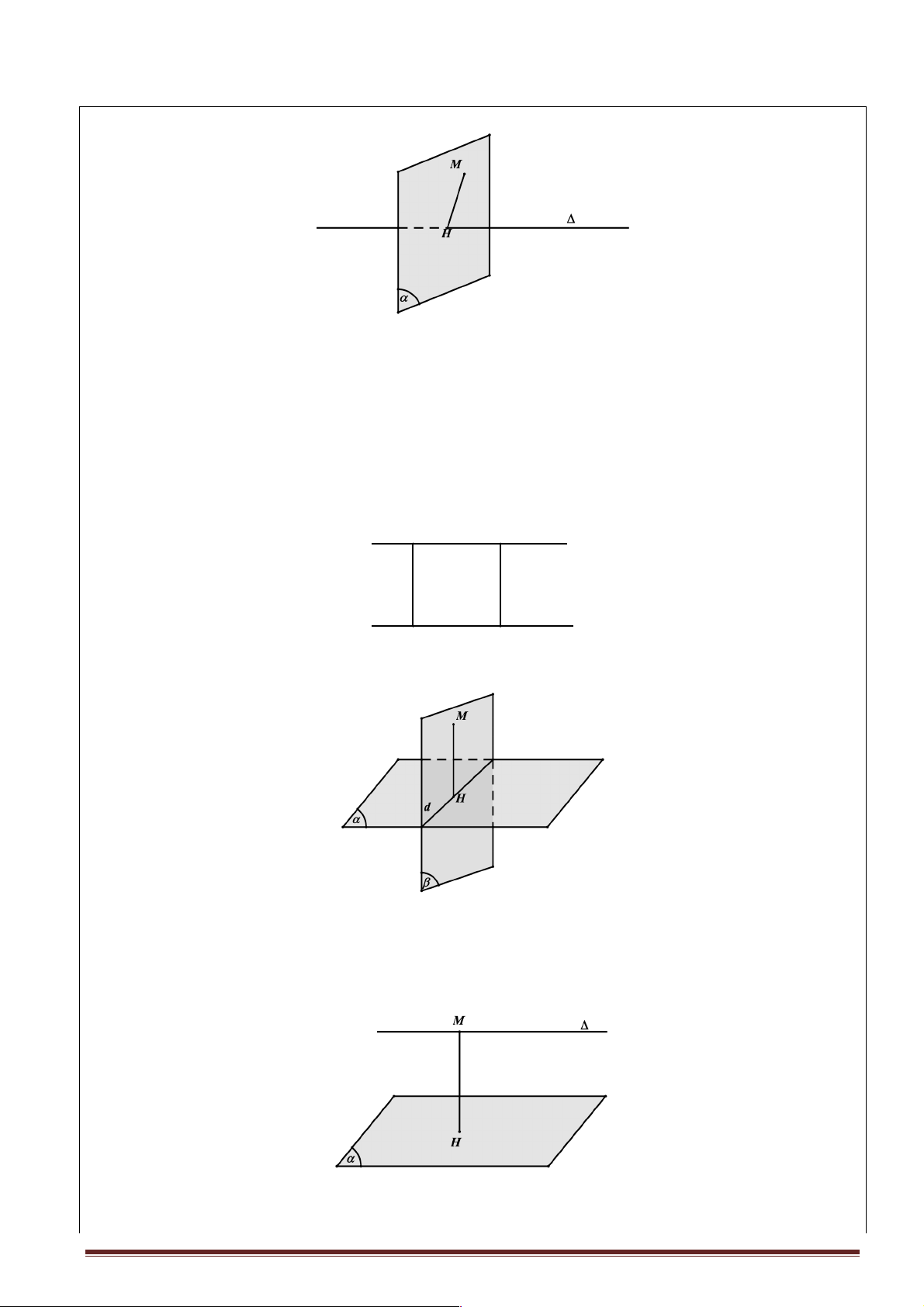
1. Khoảng cách từ một điểm tới một đường thẳng.
Cho điểm M và một đường thẳng D . Trong mp(M,D) gọi H là hình chiếu vuông góc của M trên
D . Khi đó khoảng cách MH được gọi là khoảng cách từ điểm M đến D.
d (M,D) = MH
Nhận xét: OH £ OM ,"M Î D
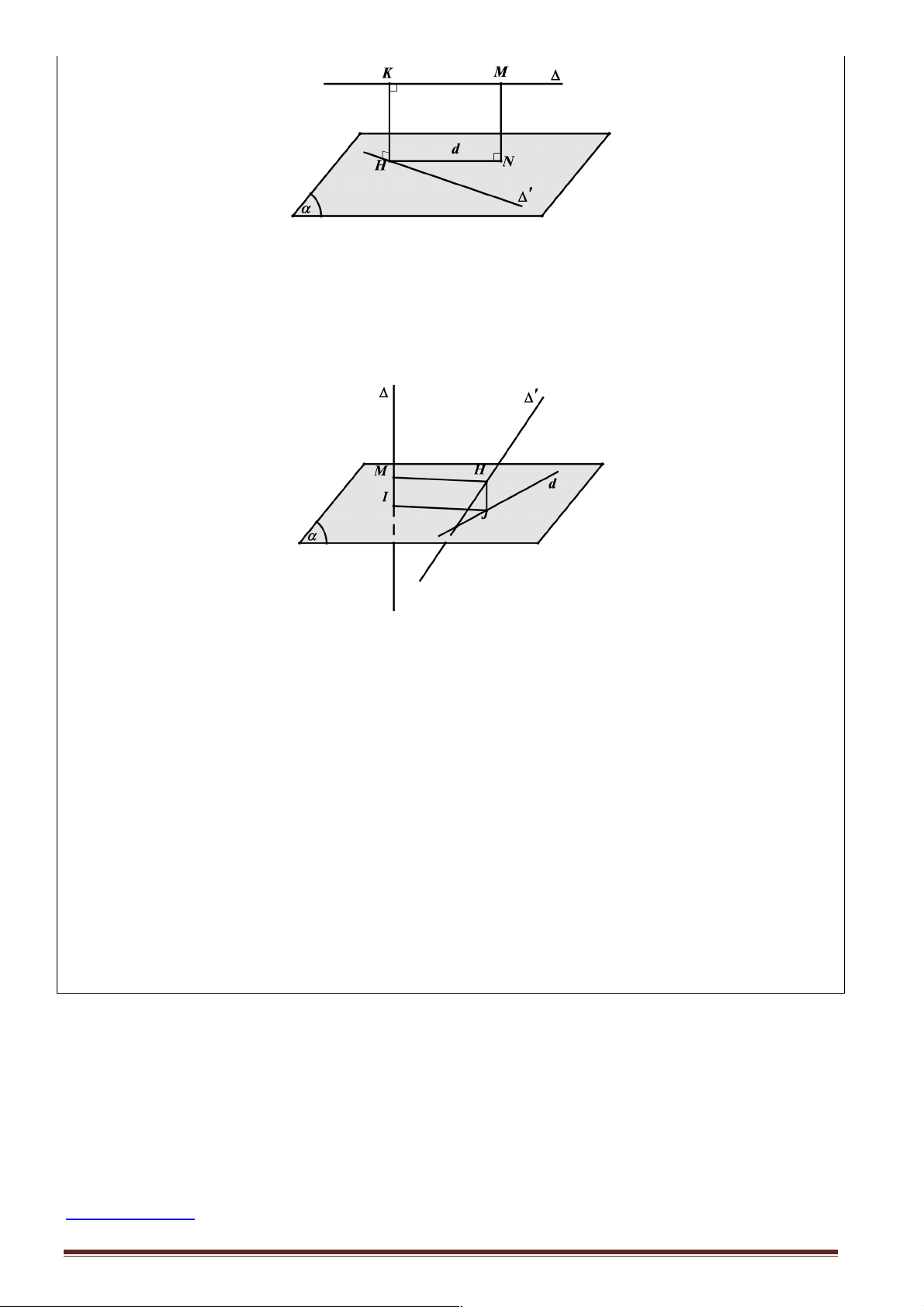
2. Khoảng cách giữa hai đường thẳng
Khoảng cách giữa hai đường thẳng D và D ' :
- Nếu D và D ' cắt nhau hoặc trùng nhau thì d(D, D ') = 0.
- Nếu D và D ' song song với nhau thì d(D, D ') = d(M, D ') = d(N , D) M K D D' H N
3. Khoảng cách từ một điểm tới một mặt phẳng.
Cho mặt phẳng (a )và một điểm M , gọi H là hình chiếu của điểm M trên mặt phẳng (a ). Khi đó
khoảng cách MH được gọi là khoảng cách từ điểm M đến mặt phẳng (a ).
d (M,(a )) = MH
4. Khoảng cách từ một đường thẳng tới một mặt phẳng.
Cho đường thẳng D và mặt phẳng (a ) song song với nhau. Khi đó khoảng cách từ một điểm bất kì
trên D đến mặt phẳng (a ) được gọi là khoảng cách giữa đường thẳng D và mặt phẳng (a ). Trang 1 d ( ,
D (a )) = d (M,(a)),M ÎD.
- Nếu D cắt (a ) hoặc D nằm trong (a ) thì d(D,(a )) = 0.
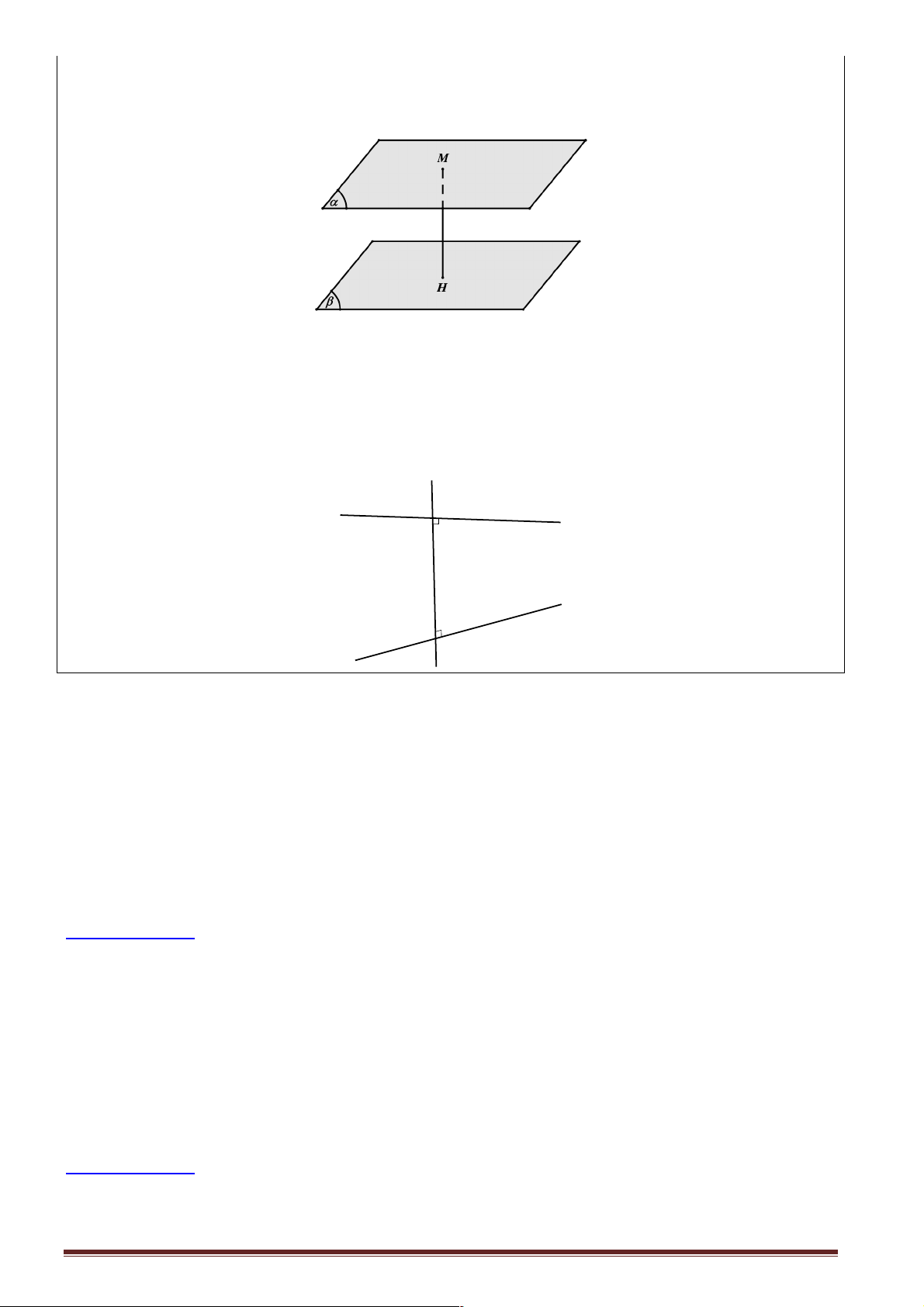
5. Khoảng cách giữa hai mặt phẳng.
Cho hai mặt phẳng (a ) và (b ) song song với nhau, khoảng cách từ một điểm bất kì trên mặt phẳng
này đến mặt phẳn kia được gọi là khoảng cách giữa hai mặt phẳng (a ) và (b ).
d ((a ),(b )) = d (M,(b )) = d (N,(a )) ,M Î(a ), N Î(b ).
6. Khoảng cách giữa hai đường thẳng.
Cho hai đường thẳng chéo nhau a,b. Độ dài đoạn vuông góc chung MN của a và b được gọi là
khoảng cách giữa hai đường thẳng a và b . M D D' N B – BÀI TẬP
Câu 1: Tìm mệnh đề sai trong các mệnh đề sau đây?
A. Khoảng cách giữa hai mặt phẳng song song là khoảng cách từ một điểm M bất kỳ trên mặt
phẳng này đến mặt phẳng kia.
B. Nếu hai đường thẳng a và b chéo nhau và vuông góc với nhau thì đường vuông góc chung của
chúng nằm trong mặt phẳng (a) chứa đường này và (a) vuông góc với đường kia.
C. Khoảng cách giữa hai đường thẳng chéo nhau a và b là khoảng cách từ một điểm M thuộc (a)
chứa a và song song với b đến một điểm N bất kì trên b.
D. Khoảng cách giữa đường thẳng a và mặt phẳng (a) song song với a là khoảng cách từ một điểm
A bất kì thuộc a tới mặt phẳng (a)
Hướng dẫn giải: Chọn đáp án A.
Câu 2: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Đường vuông góc chung của hai đường thẳng chéo nhau thì vuông góc với mặt phẳng chứa
đường thẳng này và song song với đường thẳng kia
B. Một đường thẳng là đường vuông góc chung của hai đường thẳng chéo nhau nếu nó vuông góc
với cả hai đường thẳng đó
C. Đường vuông góc chung của hai đường thẳng chéo nhau thì nằm trong mặt phẳng chứa đường
thẳng này và vuông góc với đường thẳng kia
D. Một đường thẳng là đường vuông góc chung của hai đường thẳng chéo nhau nếu nó cắt cả hai
đường thẳng đó.
Hướng dẫn giải: Đáp án A: Đúng
Đáp án B: Sai, do phát biểu này thiếu yếu tố cắt nhau.
Đáp án C: Sai, vì mặt phẳng đó chưa chắc đã tồn tại. Trang 2
Đáp án D: Sai, do phát biểu này thiếu yếu tố vuông góc. Chọn đáp án D.
Câu 3: Trong các mệnh đề sau, mệnh đề nào sai?
A. Nếu hai đường thẳng a và b chéo nhau và vuông góc với nhau thì đường thẳng vuông góc chung
của chúng nằm trong mặt phẳng (P) chứa đường thẳng này và vuông góc với đường thẳng kia.
B. Khoảng cách giữa đường thẳng a và mặt phẳng (P) song song với a là khoảng cách từ một điểm
A bất kỳ thuộc a tới mp(P).
C. Khoảng cách giữa hai đường thẳng chéo nhau a và b là khoảng cách từ một điểm M thuộc mặt
phẳng (P) chứa a và song song với b đến một điểm N bất kỳ trên b.
D. Khoảng cách giữa hai mặt phẳng song song là khoảng cách từ một điểm M bất kỳ trên mặt
phẳng này đến mặt phẳng kia.
Hướng dẫn giải: Chọn đáp án C.
DẠNG 1: TÍNH KHOẢNG CÁCH TỪ ĐIỂM M ĐẾN ĐƯỜNG THẲNG Δ . Phương pháp:
Để tính khoảng cách từ điểm M đến đường thẳng Δ ta cần xác định được hình chiếu H của điểm M
trên đường thẳng Δ , rồi xem MH là đường cao của một tam giác nào đó để tính. Điểm H thường
được dựng theo hai cách sau:
Trong mp(M,Δ) vẽ MH ^ Δ Þ d(M,Δ) = MH
Dựng mặt phẳng (α) qua M và vuông góc với Δ tại H Þ d(M,Δ) = MH.
Hai công thức sau thường được dùng để tính MH 1 1 1
ΔMAB vuông tại M và có đường cao AH thì = + . 2 2 2 MH MA MB 2S
MH là đường cao của ΔMABthì MAB MH = . AB
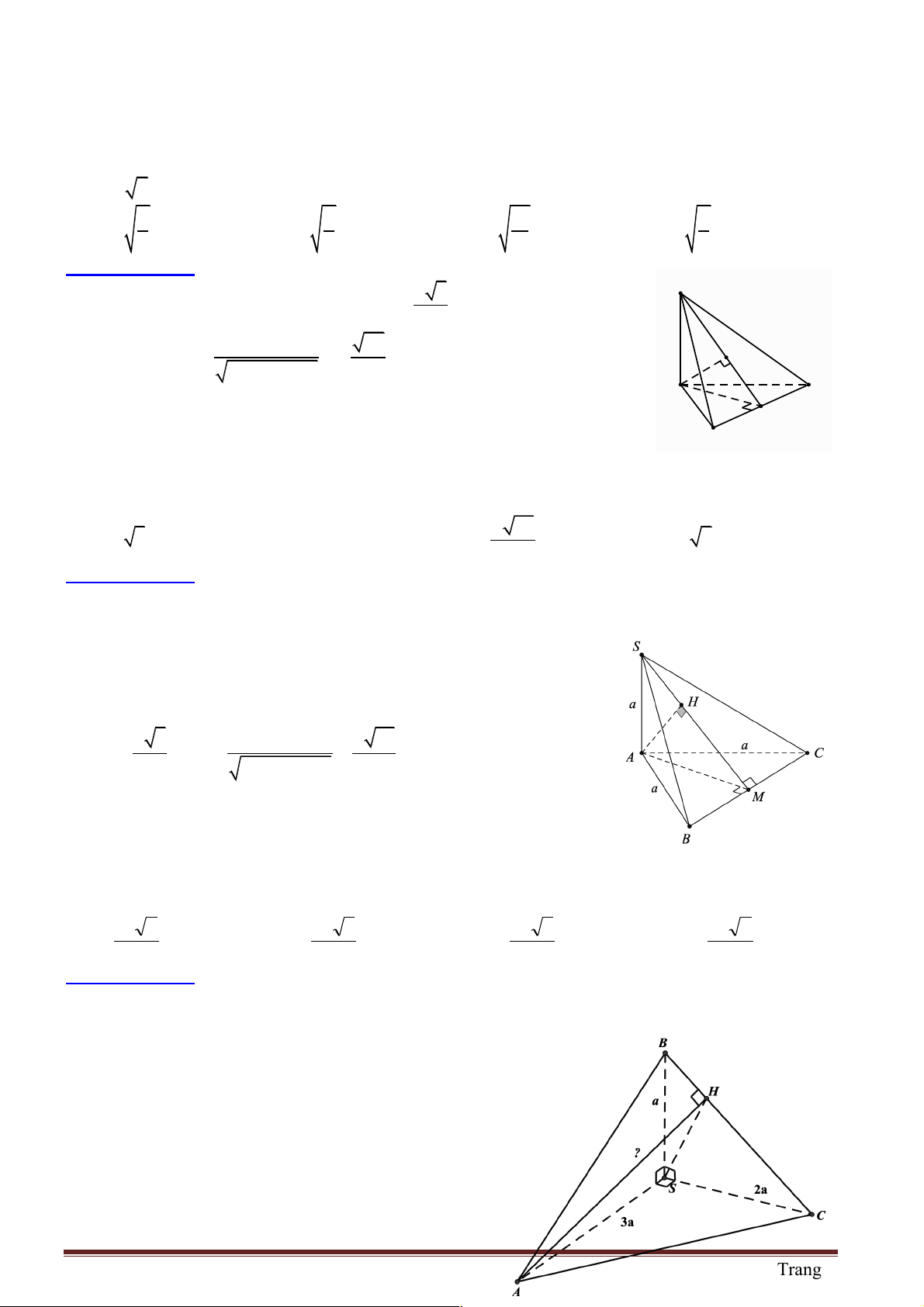
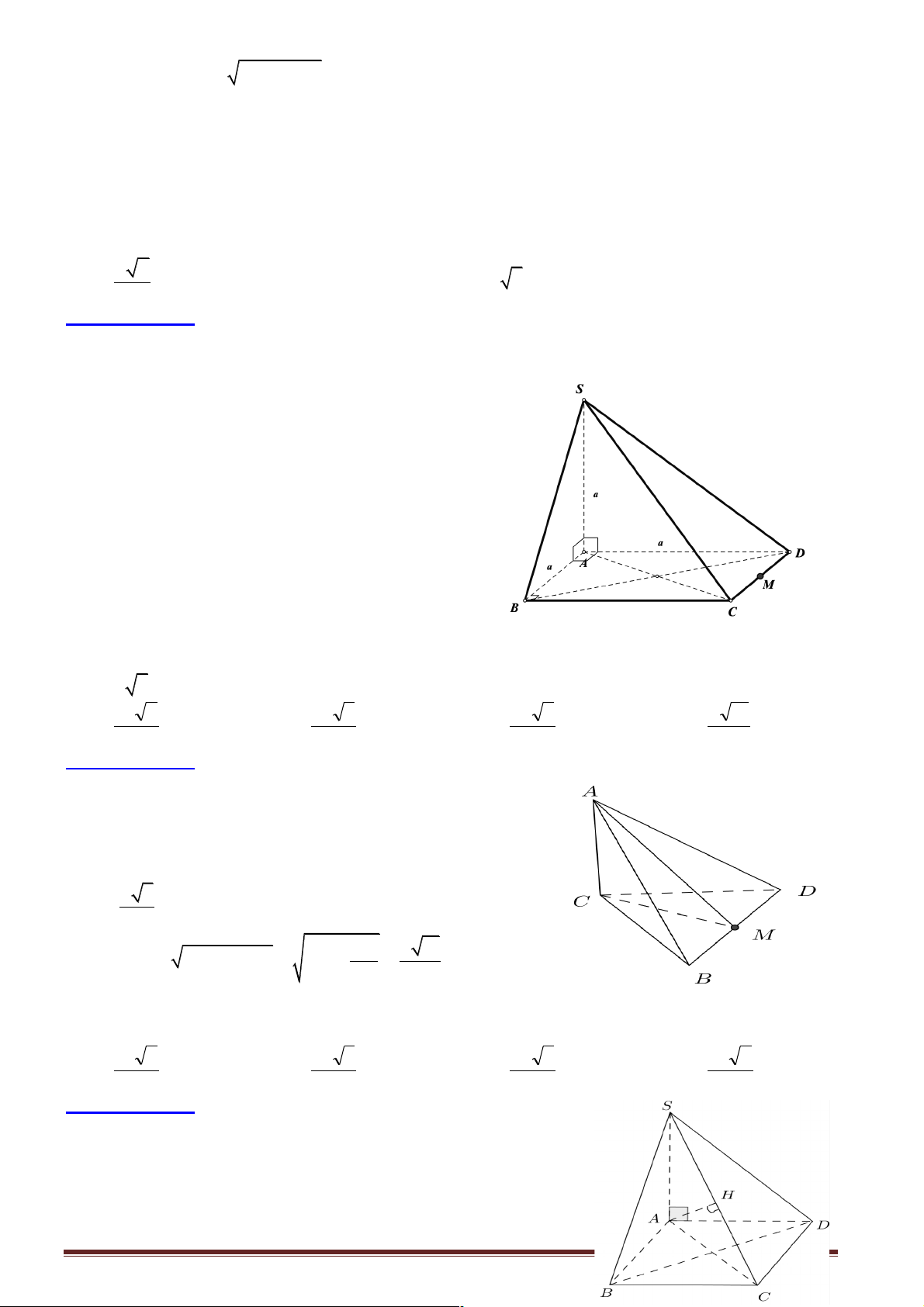
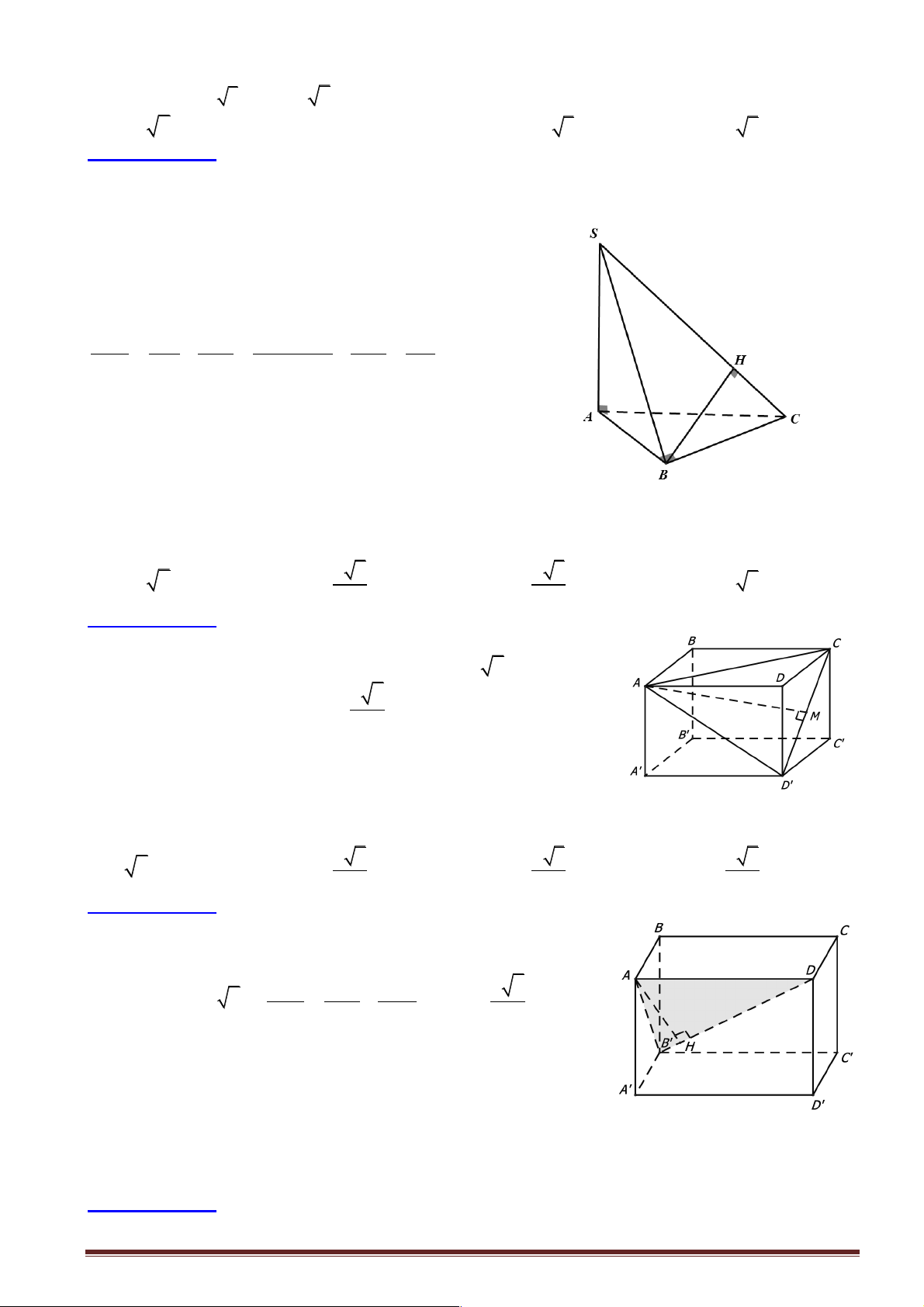
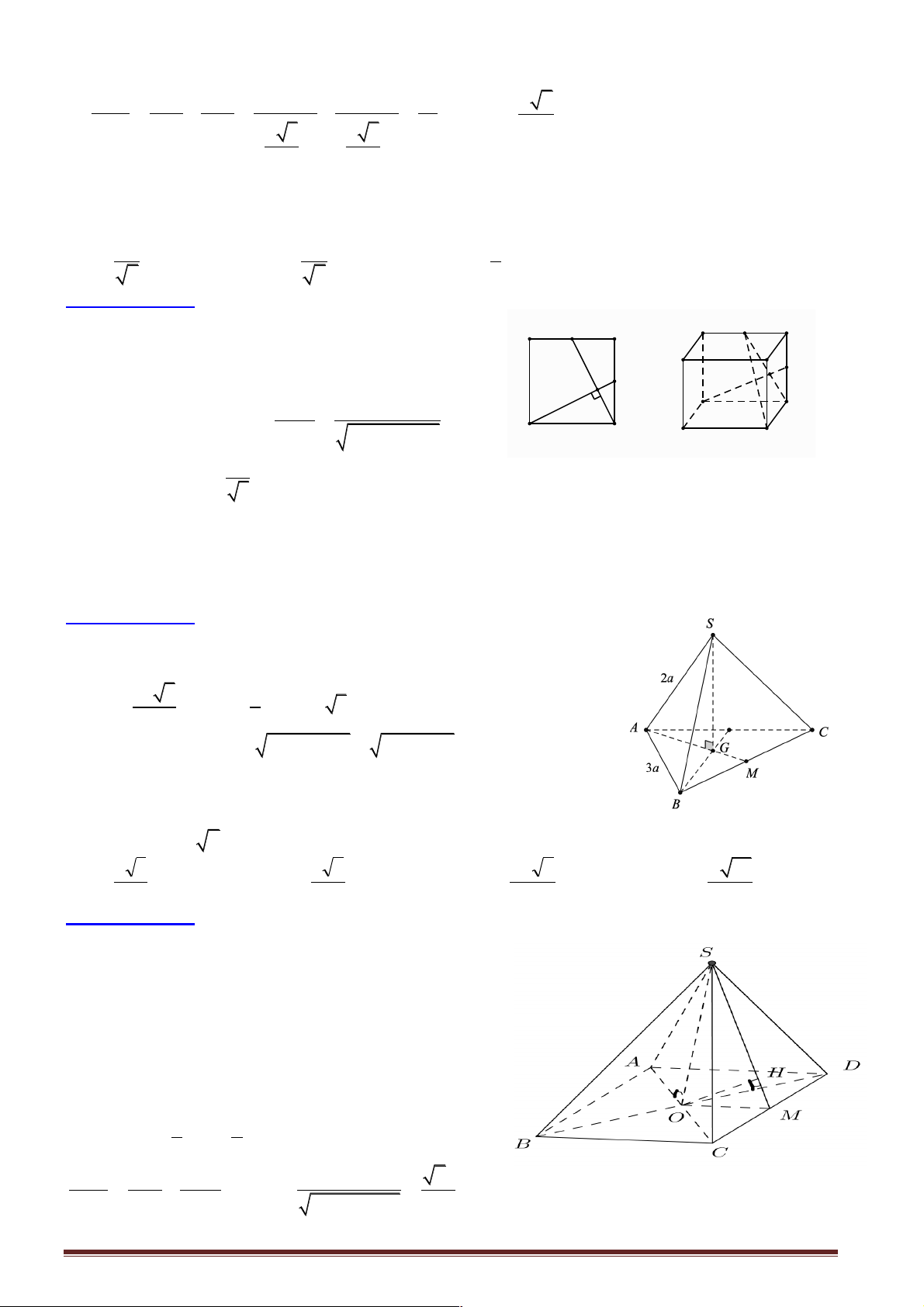
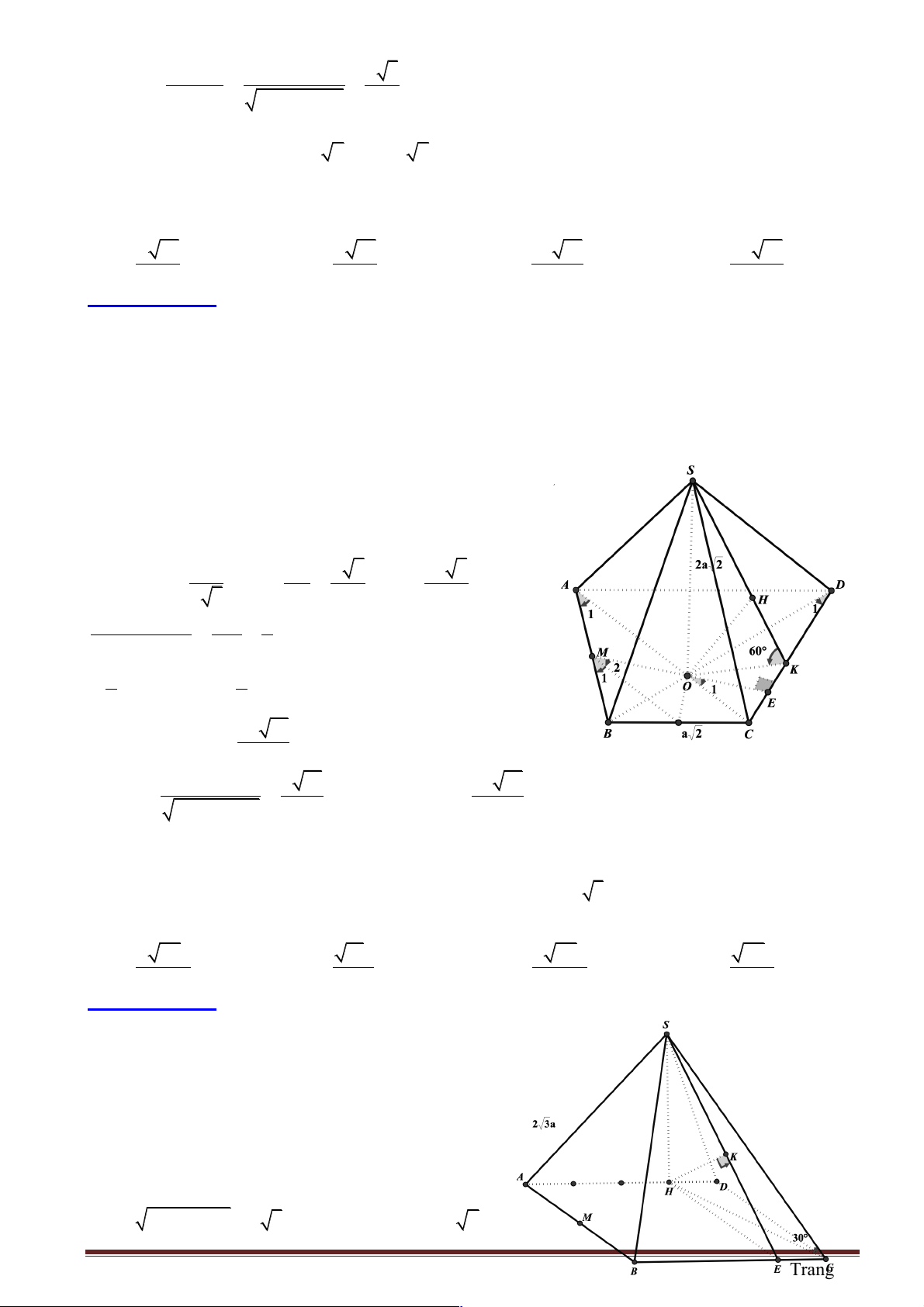
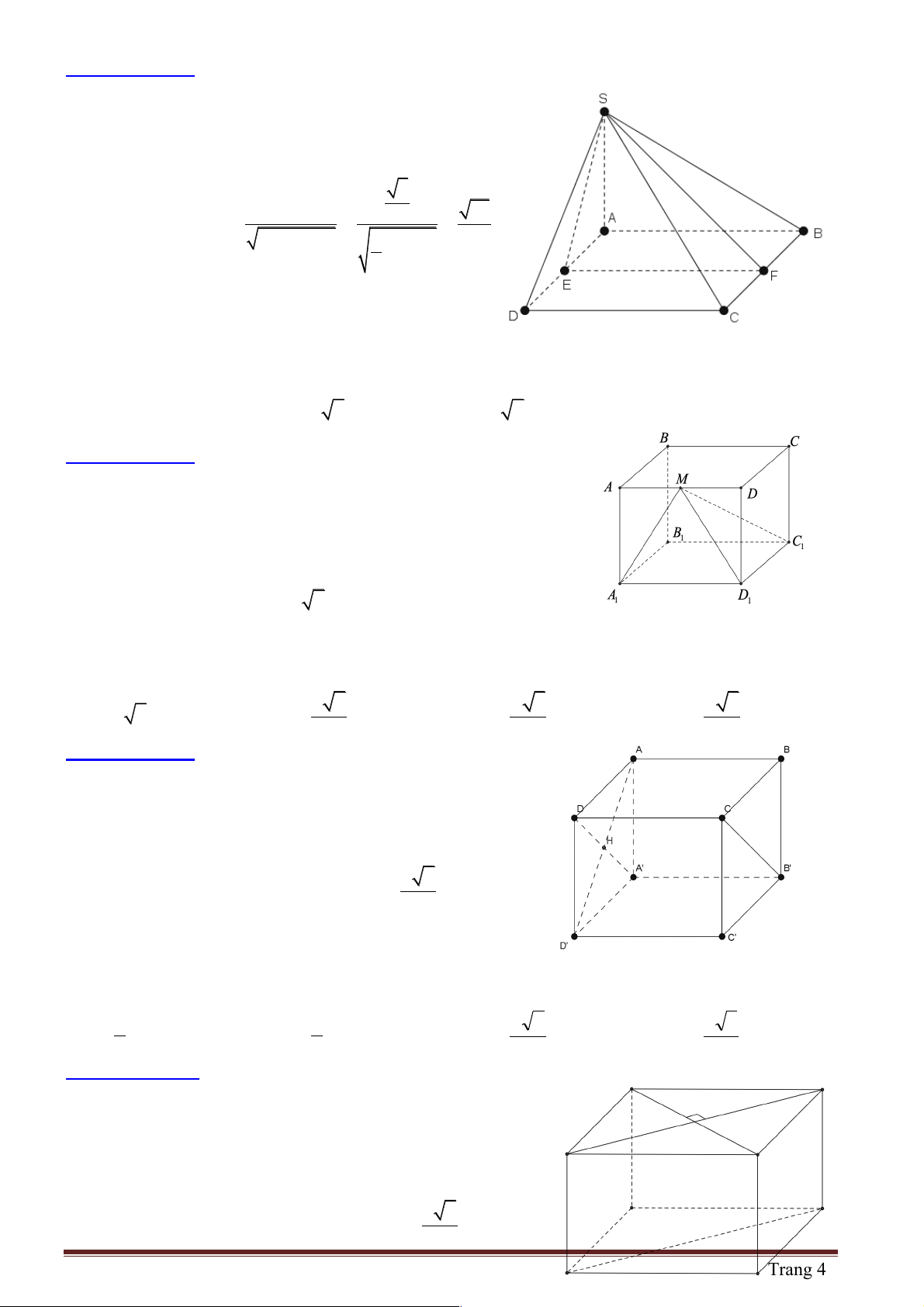
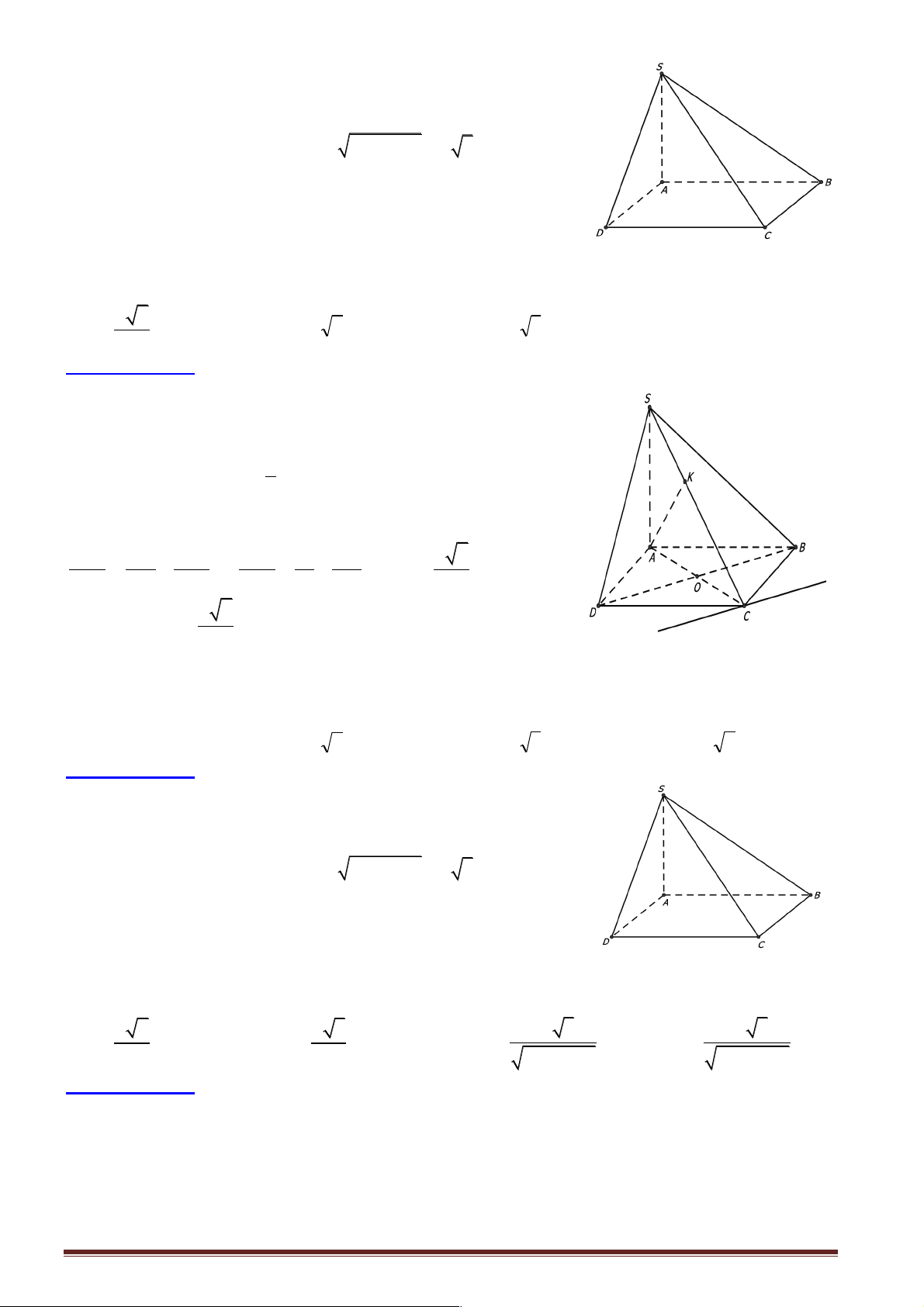
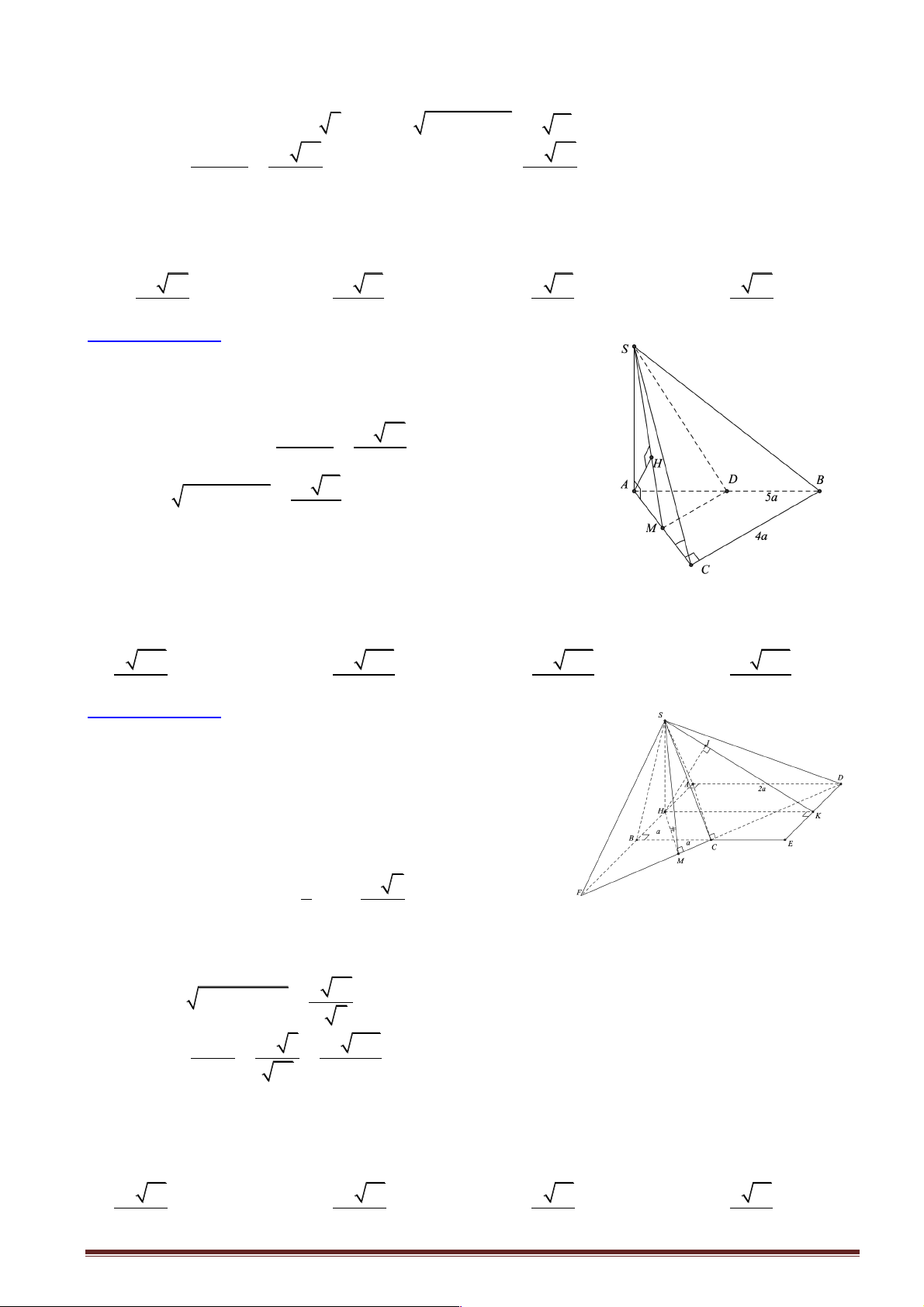
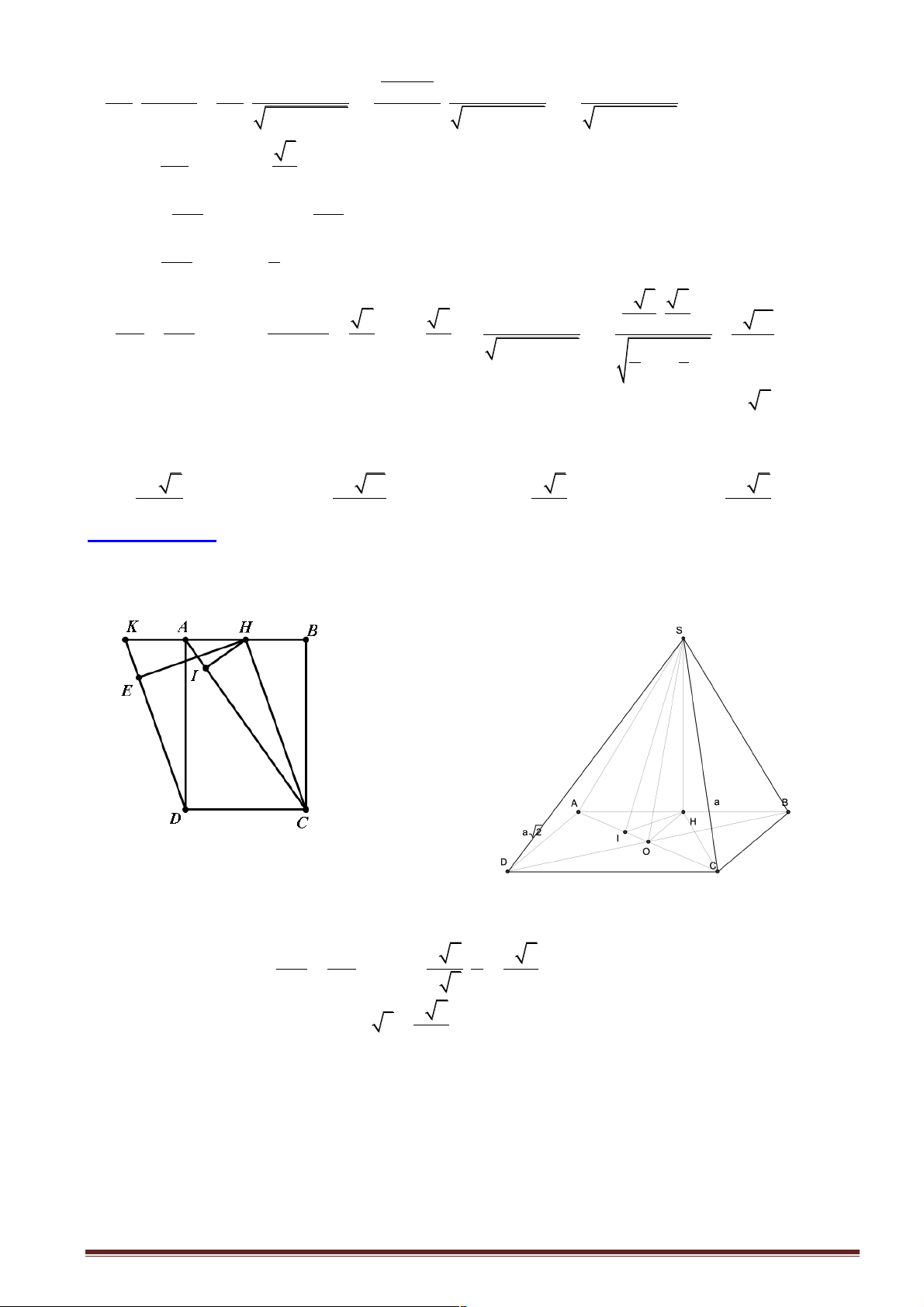
Câu 1: Cho hình chóp tam giác S.ABC với SA vuông góc với ( ABC) và SA = 3 . a Diện tích tam giác ABC bằng 2
2a , BC = a . Khoảng cách từ S đến BC bằng bao nhiêu? A. 2 . a B. 4 . a C. 3 . a D. 5 . a
Hướng dẫn giải:
Kẻ AH vuông góc với BC : 2 1 2.S 4a S = AH. ABC BC ® AH D = = = 4a ABC D 2 BC a
Khoảng cách từ S đến BC chính là SH
Dựa vào tam giác vuông SA D H ta có 2 2 2 2
SH = SA + AH = (3a) + (4a) = 5a
Câu 2: Cho hình chóp S.ABCD trong đó , SA A ,
B BC đôi một
vuông góc và SA = AB = BC = 1. Khoảng cách giữa hai điểm
S và C nhận giá trị nào trong các giá trị sau ? 3 A. 2. B. 3. C. 2. D. . 2
Hướng dẫn giải: ìSA ^ AB Do í
nên SA ^ (ABC) Þ SA ^ AC S îSA ^ BC Như vậy 2 2 2 2 2
SC = SA + AC = SA + (AB + BC ) = 3 Chọn đáp án B. A C Trang 3 B Câu 3: Cho hình chóp .
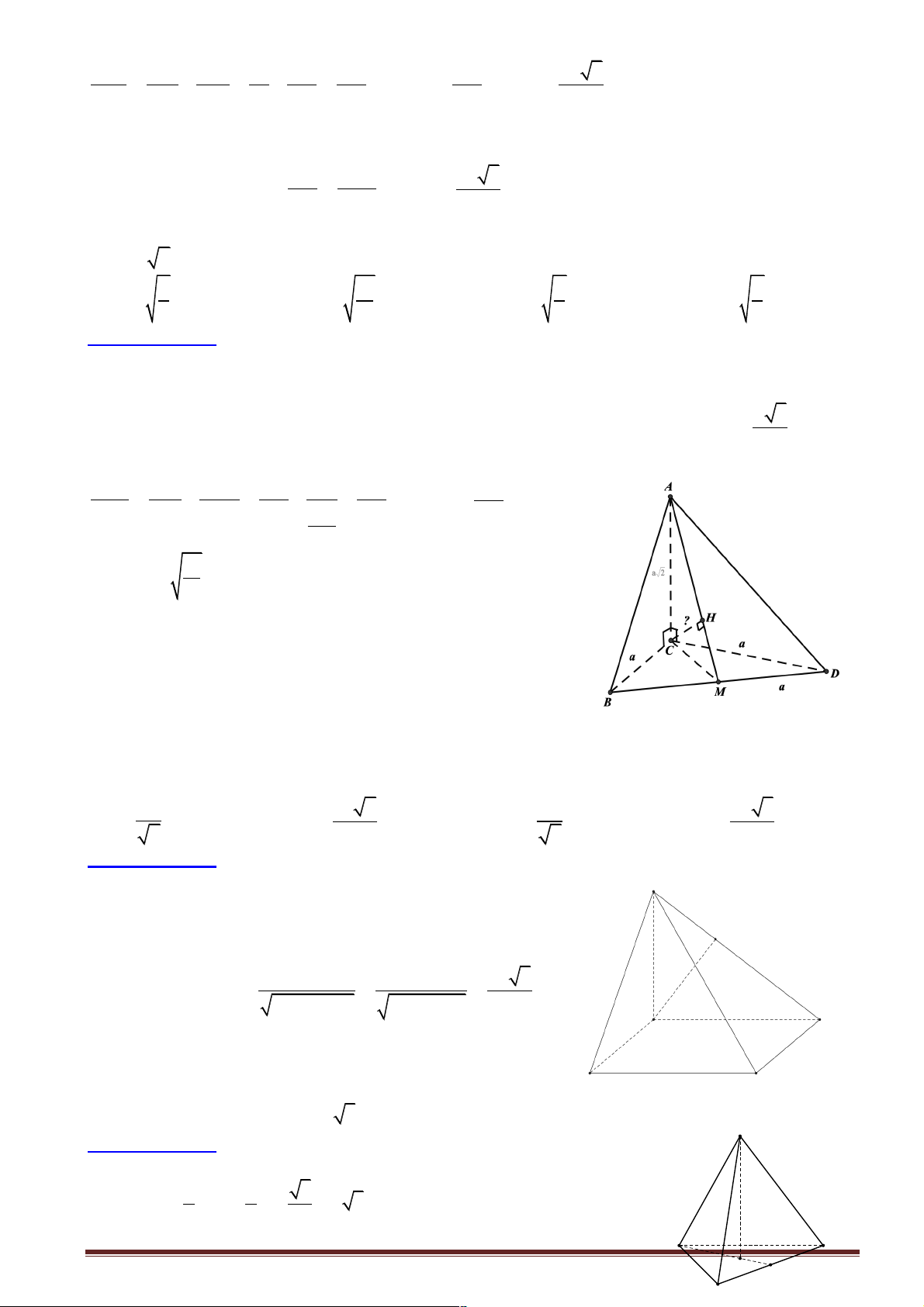
A BCD có cạnh AC ^ (BCD) và BCD là tam giác đều cạnh bằng . a Biết
AC = a 2 và M là trung điểm của .
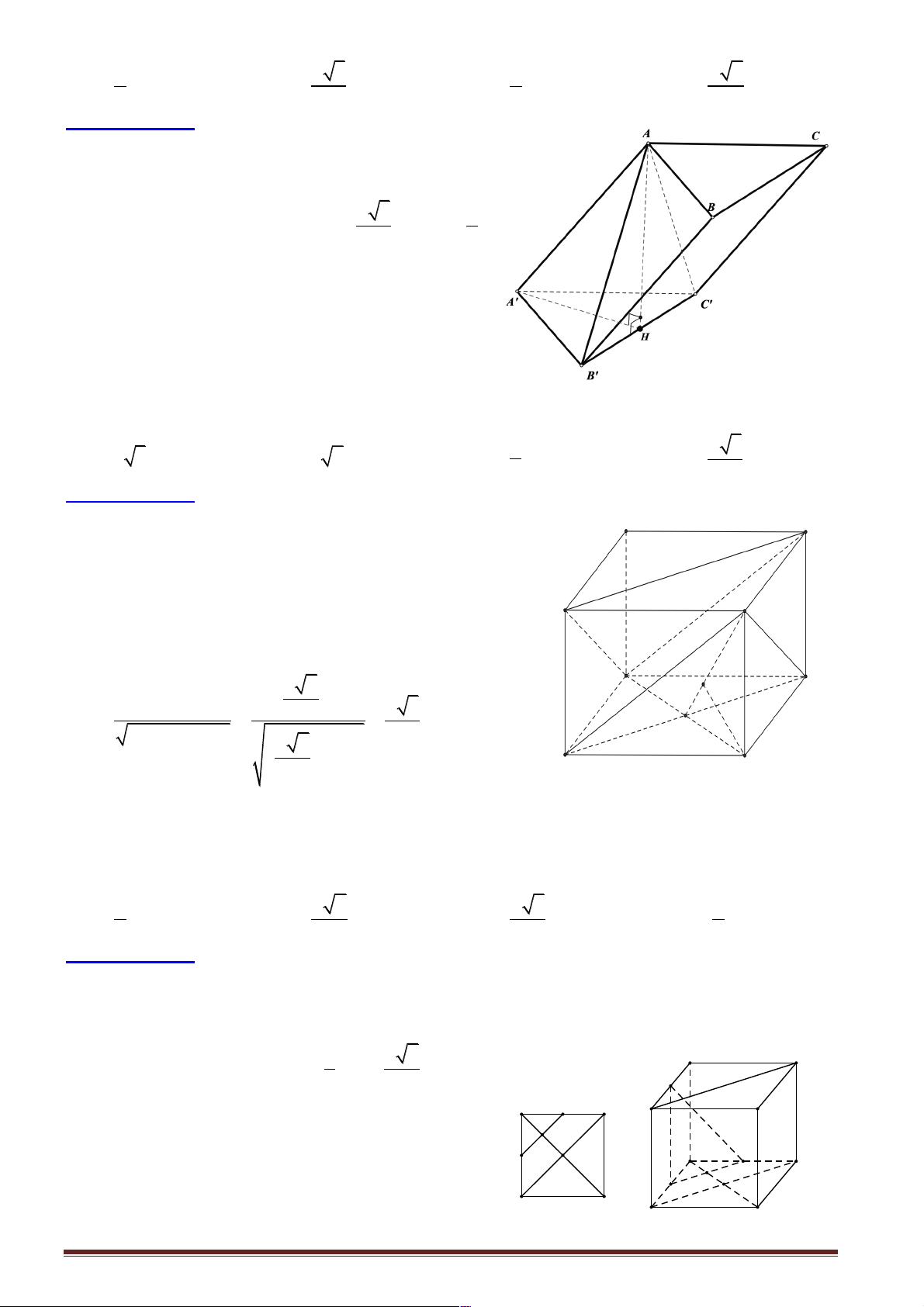
BD Khoảng cách từ C đến đường thẳng AM bằng 7 4 6 2 A. a . B. a . C. a . D. a . 5 7 11 3
Hướng dẫn giải: A a 3
Do D ABC đều cạnh a nên đường cao MC = 2 AC.MC 66 H
d (C, AM ) = CH = = a 2 2 AC + MC 11 C D Chọn đáp án C. M B
Câu 4: Trong mặt phẳng (P) cho tam giác đều ABC cạnh a . Trên tia Ax
vuông góc với mặt phẳng (P) lấy điểm S sao cho SA = a. Khoảng cách từ A đến (SBC )bằng a 21 A. a 5. B. 2 . a C. . D. a 3. 7
Hướng dẫn giải:
Gọi M là trung điểm của BC ; H là hình chiếu vuông góc của A trên SM .
Ta có BC ^ AM và BC ^ SA nên
BC ^ (SAM ) Þ BC ^ AH .
Mà AH ^ SM , do đó AH ^ (SBC). Vậy AH = d ( , A (SBC)). a 3 AS.AM a 21 AM = ; AH = = . 2 2 2 7 AS + AM Chọn đáp án C.
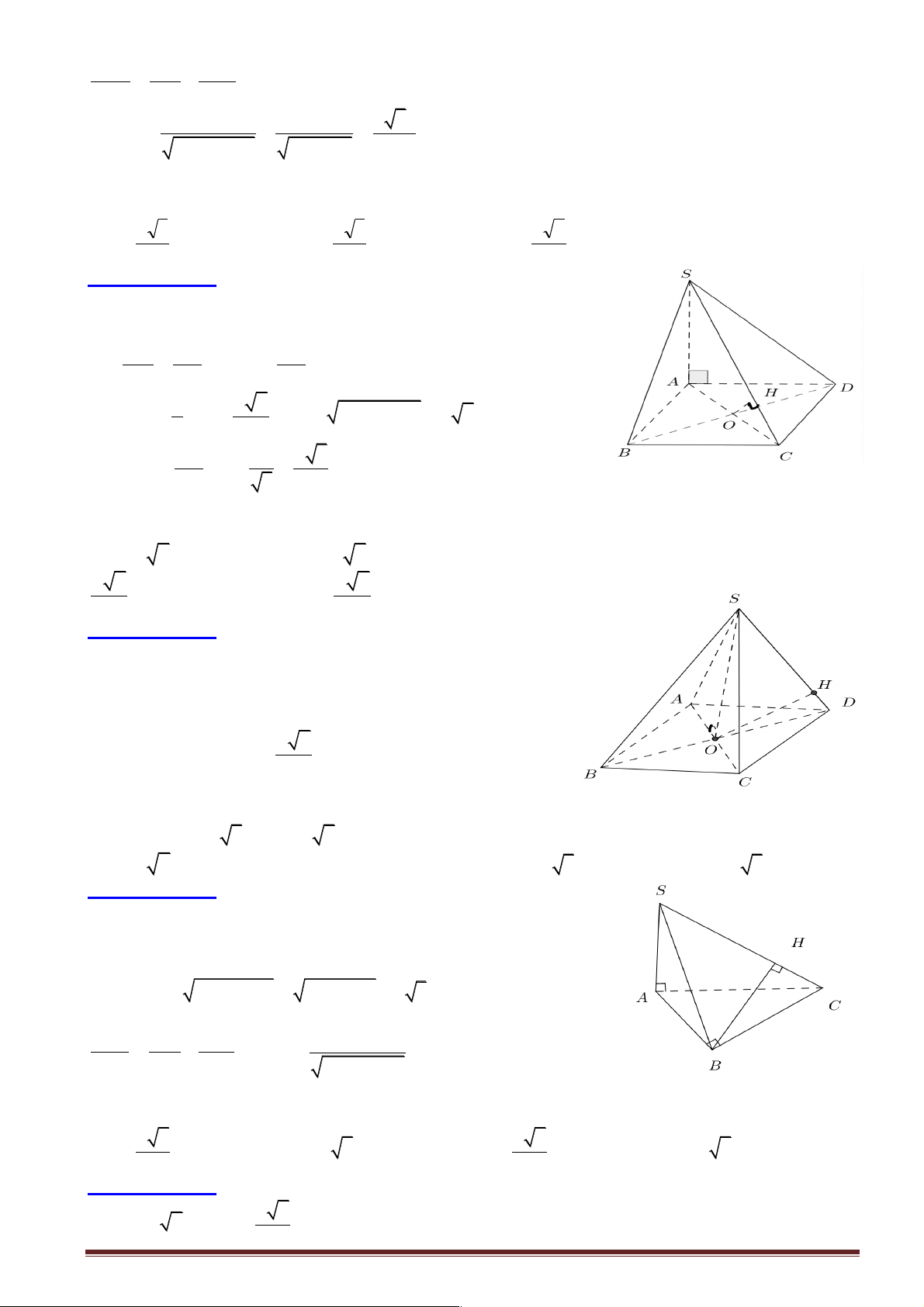
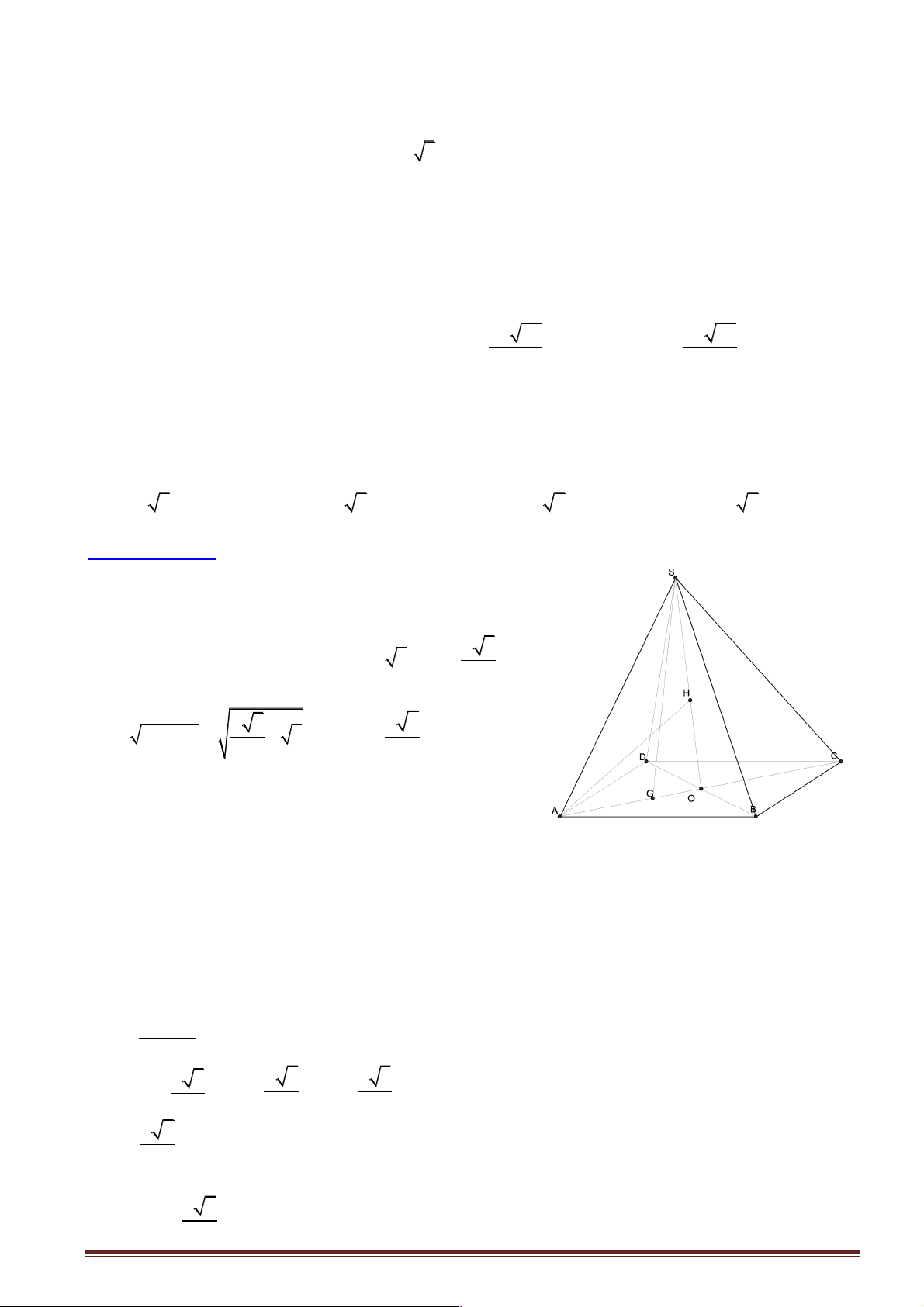
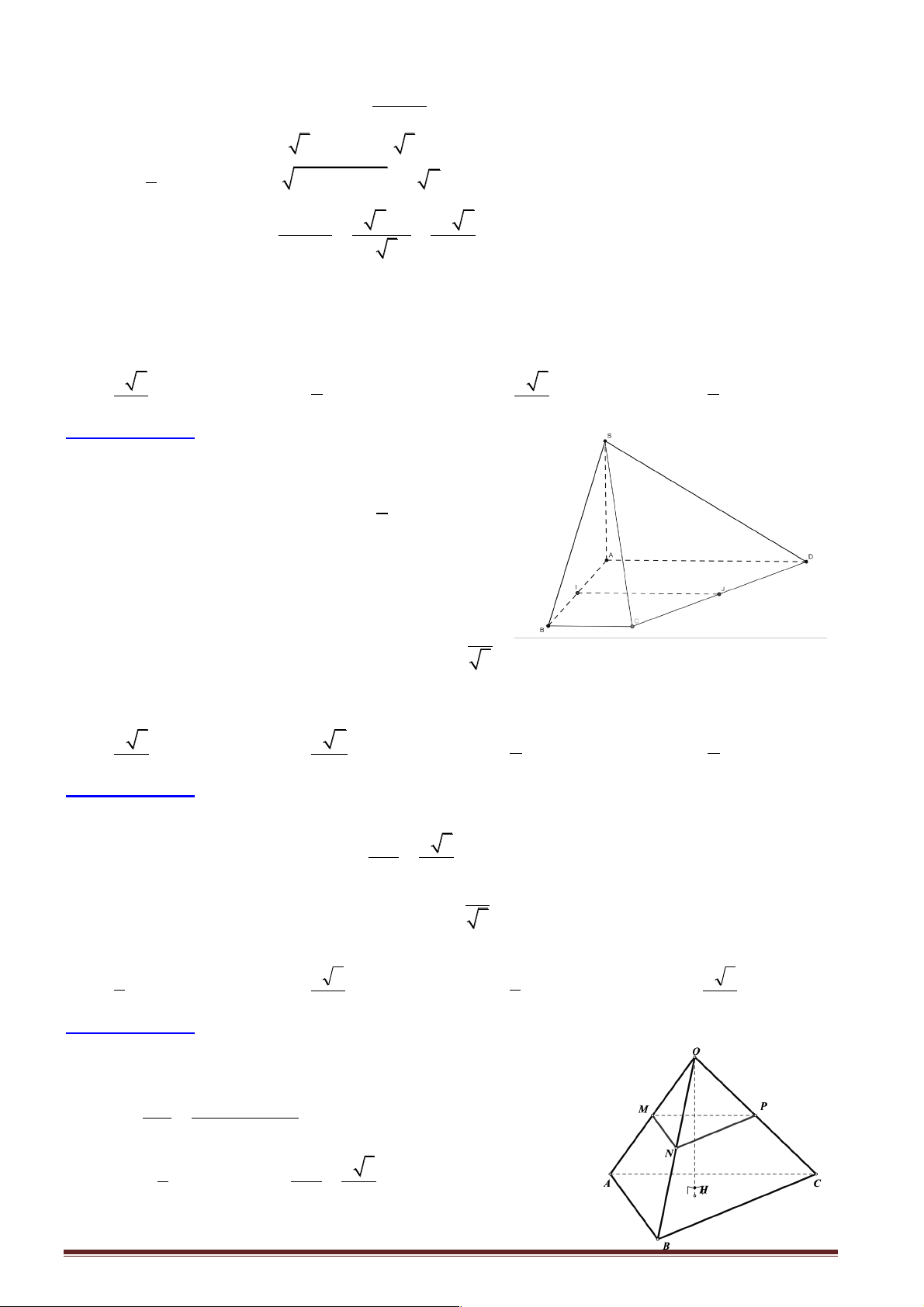
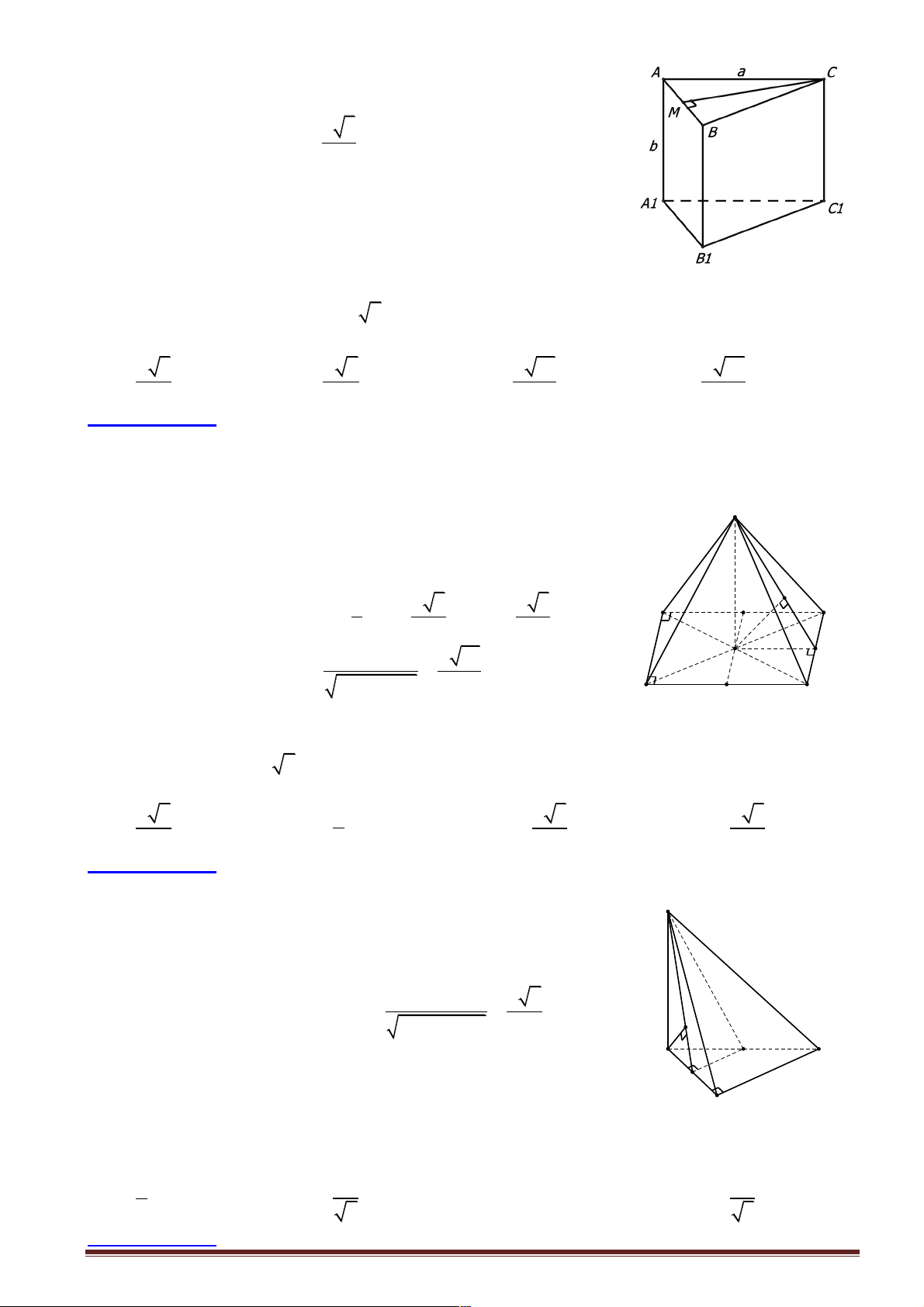
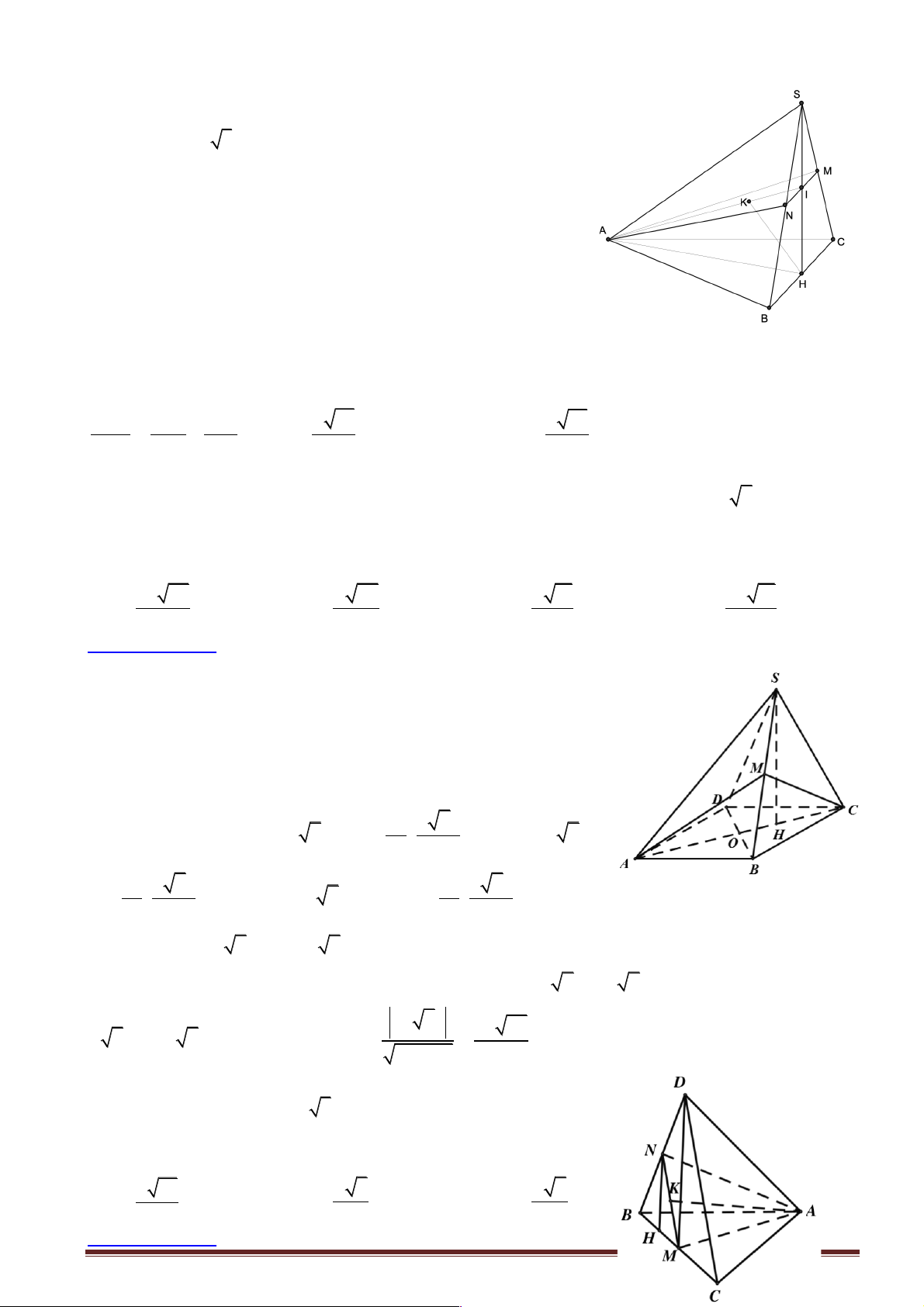
Câu 5: Cho tứ diện SABC trong đó SA , SB , SC vuông góc với nhau từng đôi một và SA = 3a ,
SB = a , SC = 2a . Khoảng cách từ A đến đường thẳng BC bằng: A. 3a 2 . B. 7a 5 . C. 8a 3 . D. 5a 6 . 2 5 3 6
Hướng dẫn giải: Chọn đáp án B.
+ Dựng AH ^ BC Þ d ( , A BC) = AH .
ìïAS ^ (SBC) É BC Þ AS ^ BC +
, AH cắt AS cùng í ïîAH ^ BC nằm trong (SAH ).
Þ BC ^ (SAH ) É SH Þ BC ^ SH . Xét trong SB
D C vuông tại S có SH là đường cao ta có: Trang 4 1 1 1 1 1 5 2 = + = + = a 2 4 Þ 2a 5 SH = Þ SH = . 2 2 2 2 2 2 SH SB SC a 4a 4a 5 5
+ Ta dễ chứng minh được AS ^ (SBC) É SH Þ AS ^ SH Þ AS
D H vuông tại S .
Áp dụng hệ thức lượng trong AS
D H vuông tại S ta có: 2 2 4a 49a 2 2 2 2 7a 5
AH = SA + SH = 9a + = Þ AH = . 5 5 5
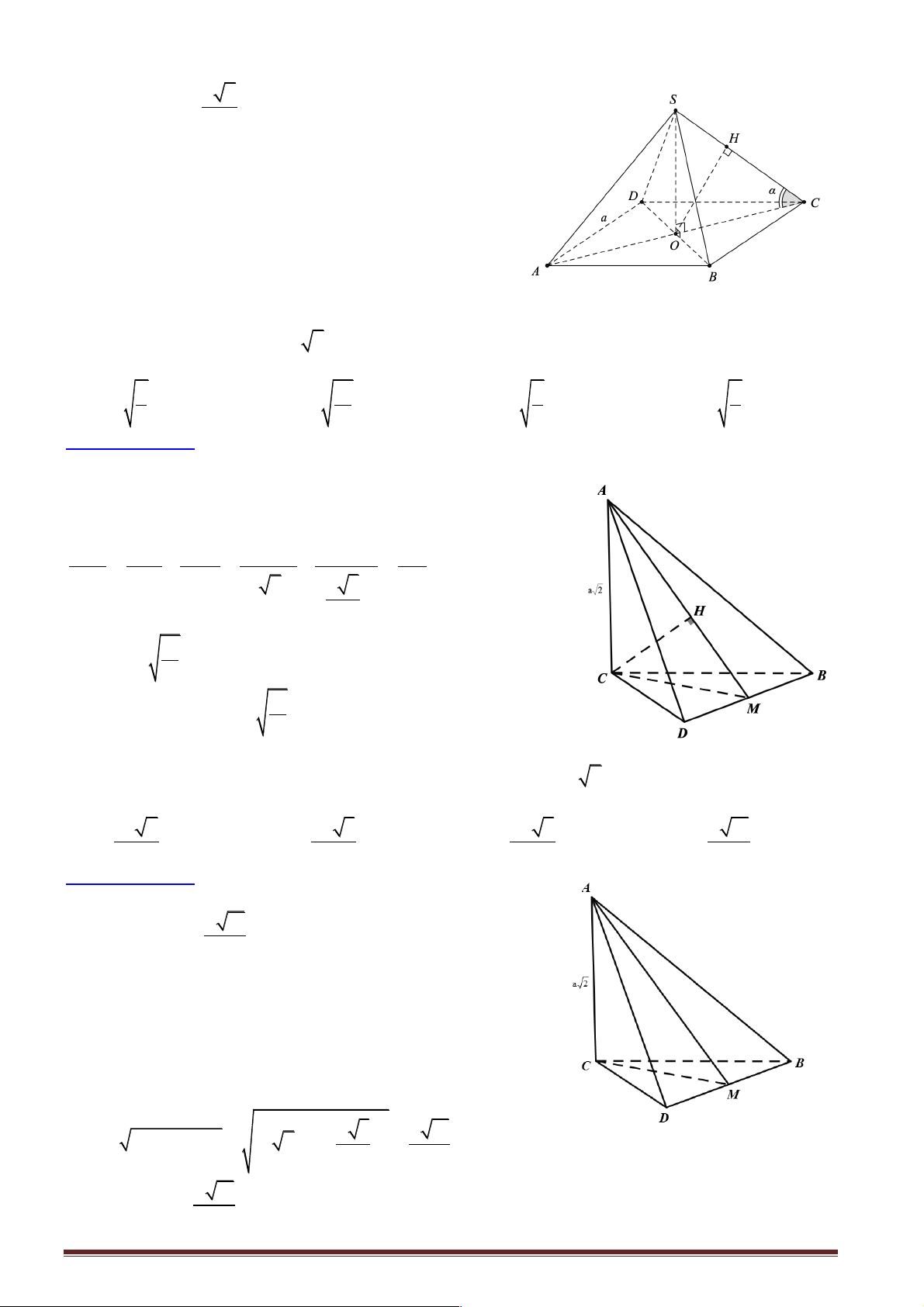
Câu 6: Cho hình chóp .
A BCD có cạnh AC ^ (BCD) và BCD là tam giác đều cạnh bằng a. Biết
AC = a 2 và M là trung điểm của BD . Khoảng cách từ C đến đường thẳng AM bằng 2 6 7 4 A. a . B. a . C. a . D. a . 3 11 5 7
Hướng dẫn giải: Chọn đáp án B.
Dựng CH ^ AM Þ d (C, AM ) = CH . Vì a 3 BCD D
là tam giác đều cạnh a và M là trung điểm của BD nên dễ tính được CM = . 2 Xét ACM D
vuông tại C có CH là đường cao, ta có: 1 1 1 1 1 11 2 = + = + = 6a 2 Þ CH = 2 2 2 2 2 2 CH CA CM 2a 3a 6a 11 4 6 Þ CH = a . 11
Câu 7: Cho hình chóp S.ABCD có SA ^ ( ABCD), đáy ABCD là hình chữ nhật. Biết AD = 2a, SA = .
a Khoảng cách từ A đến (SCD) bằng: 3a 3a 2 2a 2a 3 A. . B. . C. . D. . 7 2 5 3
Hướng dẫn giải:
SA ^ ( ABCD) nên SA ^ C ;
D AD ^ CD . S
Suy ra (SAD) ^ CD Trong (SAD) kẻ AH vuông góc SD tại H
H . Khi đó AH ^ (SCD) . SA AD . a 2a 2a 5 d ( ,
A (SCD)) = AH = = = .. 2 2 2 2 SA + AD a + (2a) 5 A D Chọn đáp án C.
Câu 8: Hình chóp đều S.ABC có cạnh đáy bằng 3a, cạnh bên B C bằng 2 .
a Khoảng cách từ S đến ( ABC) bằng : A. 2 . a B. a 3. C. . a D. S
Hướng dẫn giải:
Gọi O là chân đường cao của hình chóp. Ta có 2 2 3 AO = AH = .3 . a = a 3 3 3 2 A C O Trang 5 H B (O ABC ) 2 2 d ,(
) = SO = SA - AO = a Chọn đáp án C.
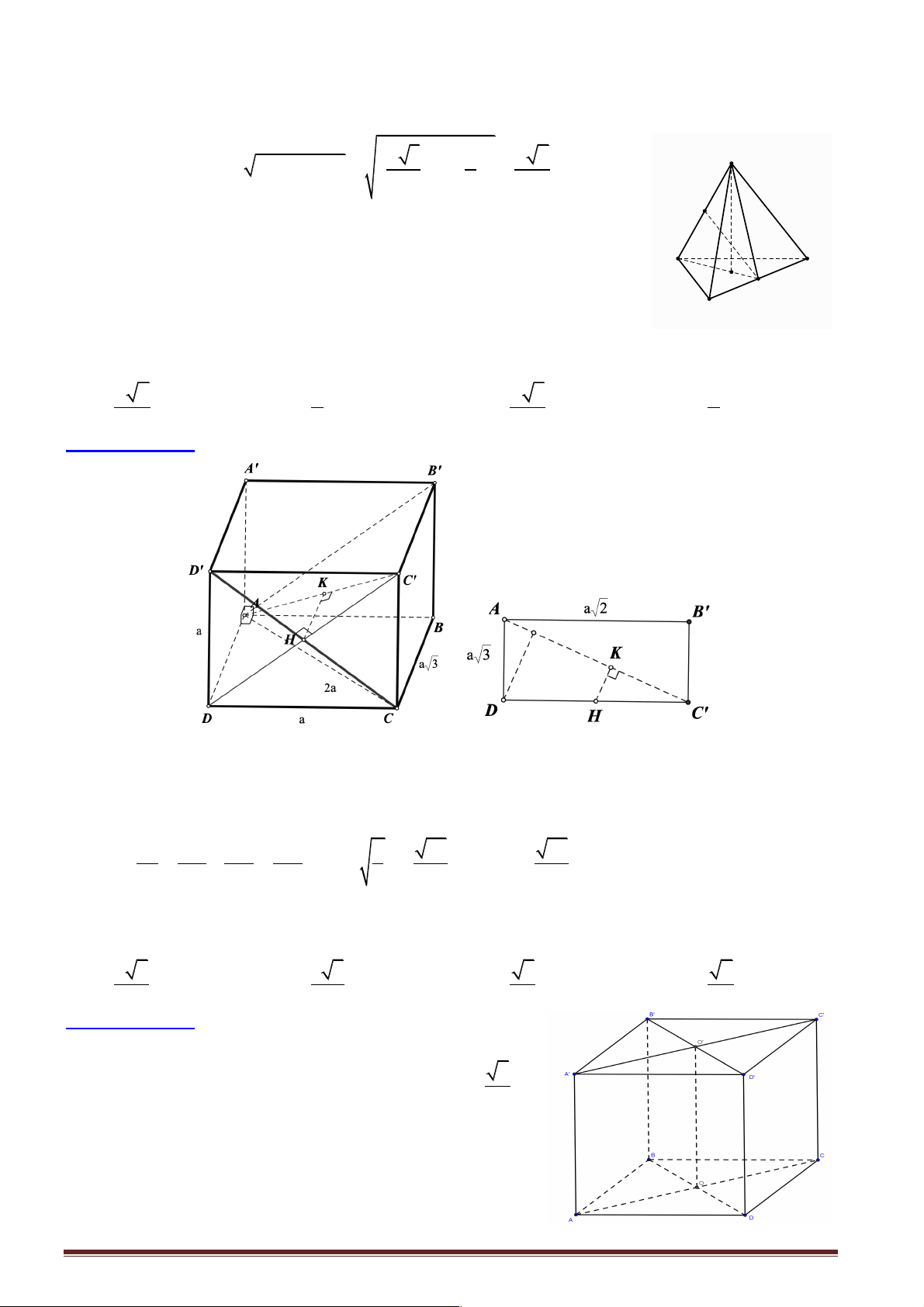
Câu 9: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a . Đường thẳng SA vuông góc với mặt
phẳng đáy, SA = a . Gọi M là trung điểm của CD . Khoảng cách từ M đến (SAB) nhận giá trị nào trong các giá trị sau? A. a 2 . B. 2 . a C. a 2. D. . a 2
Hướng dẫn giải:
þ Khoảng cách từ M đến (SAB): d (M,(SAB)) = d ( , D (SAB)) = . a Chọn đáp án D. Câu 10: Cho hình chóp .
A BCD có cạnh AC ^ (BCD)và BCD là tam giác đều cạnh bằng a. Biết
AC = a 2 và M là trung điểm của BD. Khoảng cách từ A đến đường thẳng BD bằng: 3a 2 2a 3 4a 5 a 11 A. . B. . C. . D. . 2 3 3 2
Hướng dẫn giải: Chọn D. ìAC ^ BD Ta có: í
Þ BD ^ AM (Định lý 3 đường vuông CM î ^ BD góc) Þ d ( ; A BD) = AM . a 3 CM = (vì tam giác BCD đều). 2 2 3a a 11 Ta có: 2 2 2
AM = AC + MC = 2a + = . 4 2
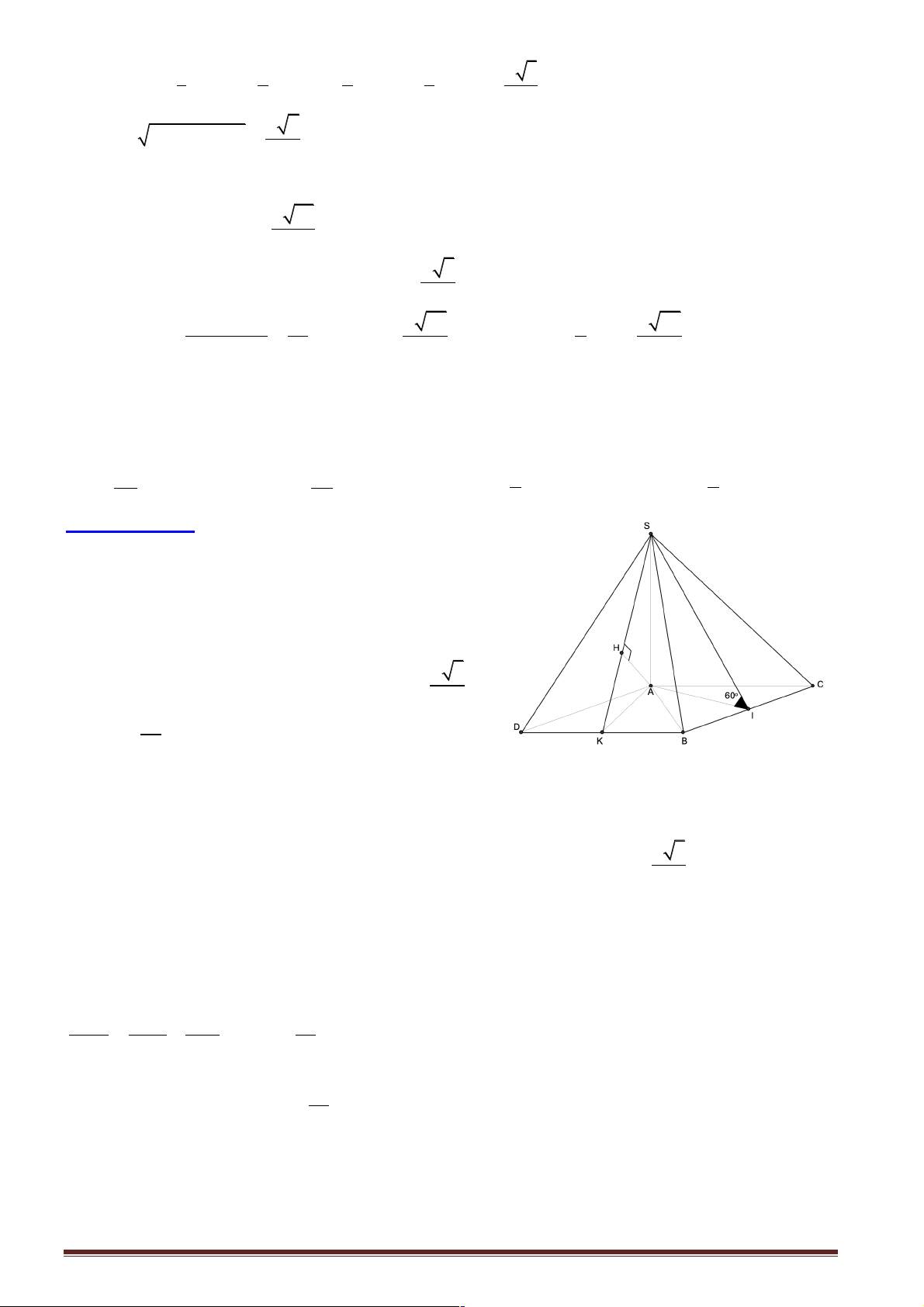
Câu 11: Cho hình chóp S.ABCD có SA ^ ( ABCD), đáy ABCD là hình thoi cạnh bằng a và ˆB = 60 . °
Biết SA = 2a . Tính khoảng cách từ A đến SC . 3a 2 4a 3 2a 5 5a 6 A. . B. . C. . D. . 2 3 5 2
Hướng dẫn giải: Chọn C.
Kẻ AH ^ SC , khi đó d ( ; A SC) = AH .
ABCD là hình thoi cạnh bằng a và ˆ
B = 60° Þ!ABC đều nên AC = a .
Trong tam giác vuông SAC ta có: Trang 6 1 1 1 = + 2 2 2 AH SA AC . SA AC 2 . a a 2 5a Þ AH = = = . 2 2 2 2 SA + AC 4a + a 5
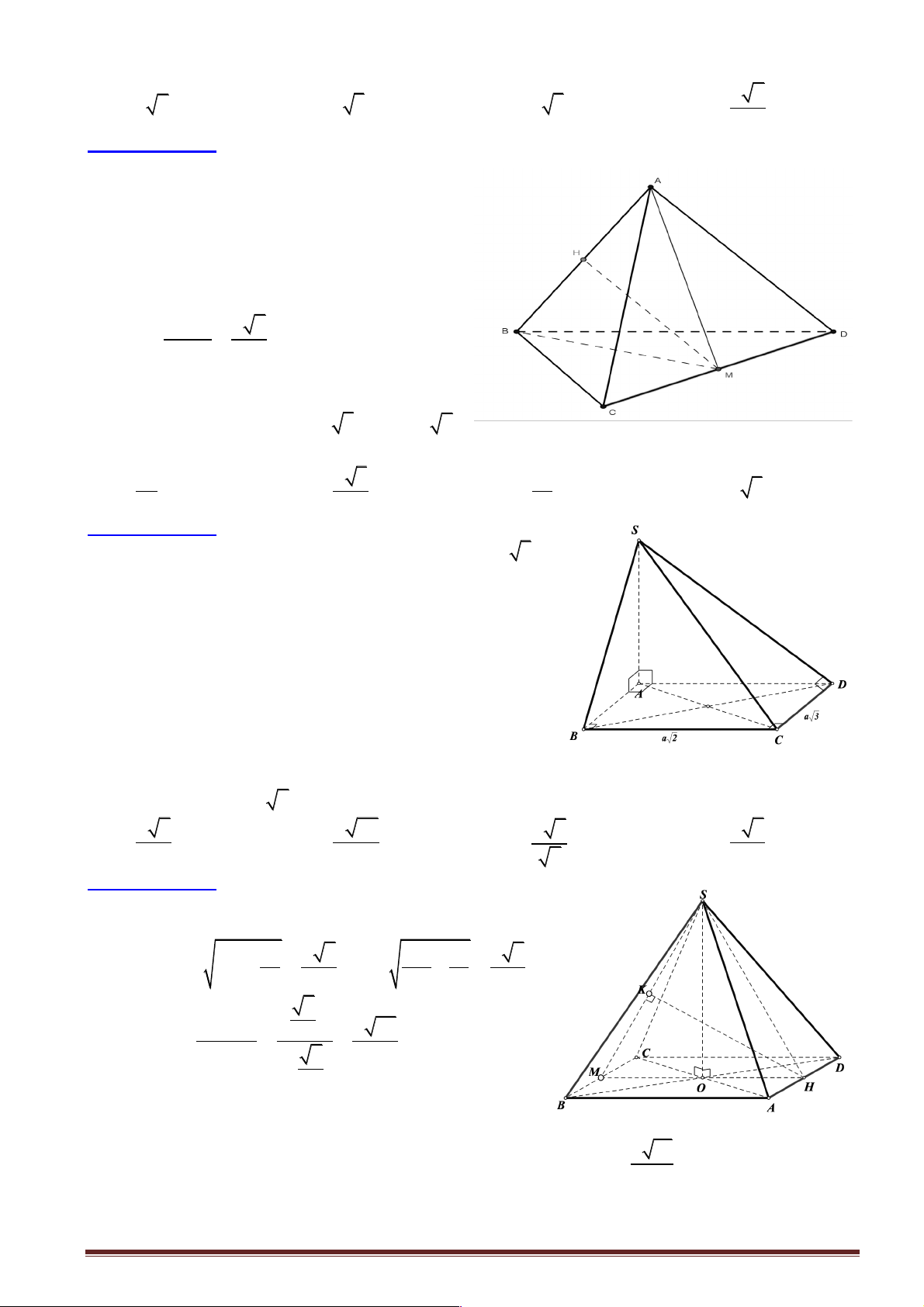
Câu 12: Cho hình chóp S.ABCD có SA ^ ( ABCD), SA = 2a , ABCD là hình vuông cạnh bằng a .
Gọi O là tâm của ABCD , tính khoảng cách từ O đến SC . a 3 a 3 a 2 A. . B. . C. . D. . 3 4 3
Hướng dẫn giải: Chọn A.
Kẻ OH ^ SC , khi đó d (O;SC) = OH . Ta có: !SAC " O ! CH (g-g) OH OC OC nên = Þ OH = .SA. SA SC SC 1 a 2 Mà: OC = AC = , 2 2
SC = SA + AC = a 6 . 2 2 OC a a 3 Vậy OH = .SA = = . SC 3 3
Câu 13: Cho hình chóp tứ giác đều có cạnh đáy bằng a và góc hợp bởi một cạnh bên và mặt đáy bằng
a . Khoảng cách từ tâm của đáy đến một cạnh bên bằng A. a 2 cota. B. a 2 tana . C. a 2 a cosa 2 . D. sina . 2 2
Hướng dẫn giải: Chọn D.
SO ^ ( ABCD), O là tâm của hình vuông ABCD .
Kẻ OH ^ SD , khi đó d (O;SD) = OH , ∑ a = SDO. a 2
Ta có: OH = OD sina = sina . 2
Câu 14: Cho hình chóp S.ABC trong đó SA , AB , BC vuông góc với nhau từng đôi một. Biết
SA = 3a , AB = a 3 , BC = a 6 . Khoảng cách từ B đến SC bằng A. a 2. B. 2a . C. 2a 3 . D. a 3 .
Hướng dẫn giải: Chọn B.
Vì SA , AB , BC vuông góc với nhau từng đôi một nên CB ^ SB .
Kẻ BH ^ SC , khi đó d ( ; B SC) = BH . Ta có: 2 2 2 2
SB = SA + AB = 9a + 3a = 2 3a.
Trong tam giác vuông SBC ta có: 1 1 1 = + . SB BC Þ BH = = 2a. 2 2 2 BH SB BC 2 2 SB + BC
Câu 15: Cho hình chóp tứ giác đều có cạnh đáy bằng a và góc hợp bởi một cạnh bên và mặt đáy bằng .
a Khoảng cách từ tâm của đáy đến một cạnh bên bằng: A. a 2 cosα B. a 2 tan C. a 2 sinα D. a 2 cotα 2 2
Hướng dẫn giải: a 2
AC = a 2 Þ OC = 2 Trang 7
Khoảng cách cần tìm là đoạn OH . a 2 OH = OC sina = sina. 2 Chọn đáp án C.
Câu 16: Cho tứ diện ABCD có cạnh bên AC vuông góc với mặt phẳng (BCD) và BCD là tam giác đều cạnh bằng .
a Biết AC = a 2 và M là trung điểm của .
BD Khoảng cách từ điểm C đến đường thẳng AM bằng 2 6 7 4 A. a . B. a . C. a . D. a . 3 11 5 7
Hướng dẫn giải: Chọn đáp án B.
Nối CM . Kẻ CH ^ AM
Suy ra d(C; AM ) = CH Xét ACM D có 1 1 1 1 1 11 = + = + = 2 2 2 CH AC CM (a 2)2 2 2 æ ö 6 3 a a ç ÷ 2 è ø 6 Þ CH = a 11 6
Vậy d(C; AM ) = CH = a . 11
Câu 17: Cho tứ diện ABCD có cạnh bên AC vuông góc với mặt
phẳng (BCD) và BCD là tam giác đều cạnh bằng .
a Biết AC = a 2 và M là trung điểm của . BD
Khoảng cách từ điểm A đến đường thẳng BD bằng 3a 2 2a 3 4a 5 a 11 A. . B. . C. . D. . 2 3 3 2
Hướng dẫn giải: Chọn đáp án D. Ta có a 11 d( ; A BD) =
AC ^ (BCD) Þ AC ^ BD 2
Lại có với M là trung điểm BD mà BCD D đều nên CM ^ BD ì AC ^ BD Từ đó ta có í Þ AM ^ BD CM î ^ BD Suy ra d(A;BD) = AM
Xét tam giác vuông ACM , ta có 2 = + = ( æ a ö a AM AC CM a 2 )2 3 11 2 2 + ç ÷ = ç 2 ÷ 2 è ø a 11 Vậy d( ; A BD) = . 2 Trang 8
Câu 18: Cho hình chóp S.ABC trong đó , SA A ,
B BC vuông góc với nhau từng đôi một. Biết
SA = 3a, AB = a 3, BC = a 6. Khoảng cách từ B đến SC bằng A. a 2. B. 2a . C. 2a 3 . D. a 3 .
Hướng dẫn giải: Chọn đáp án B. Ta có ì SA ^ AB í Þ SB ^ BC îAB ^ BC Suy ra SB
D C vuông tại B
Kẻ BH ^ SC . Ta có d( ; B SC) = BH Lại có 1 1 1 1 1 1 = + = + = 2 2 2 2 2 2 2 BH SB BC SA + AB BC 4a Þ d( ;
B SC) = BH = 2a .
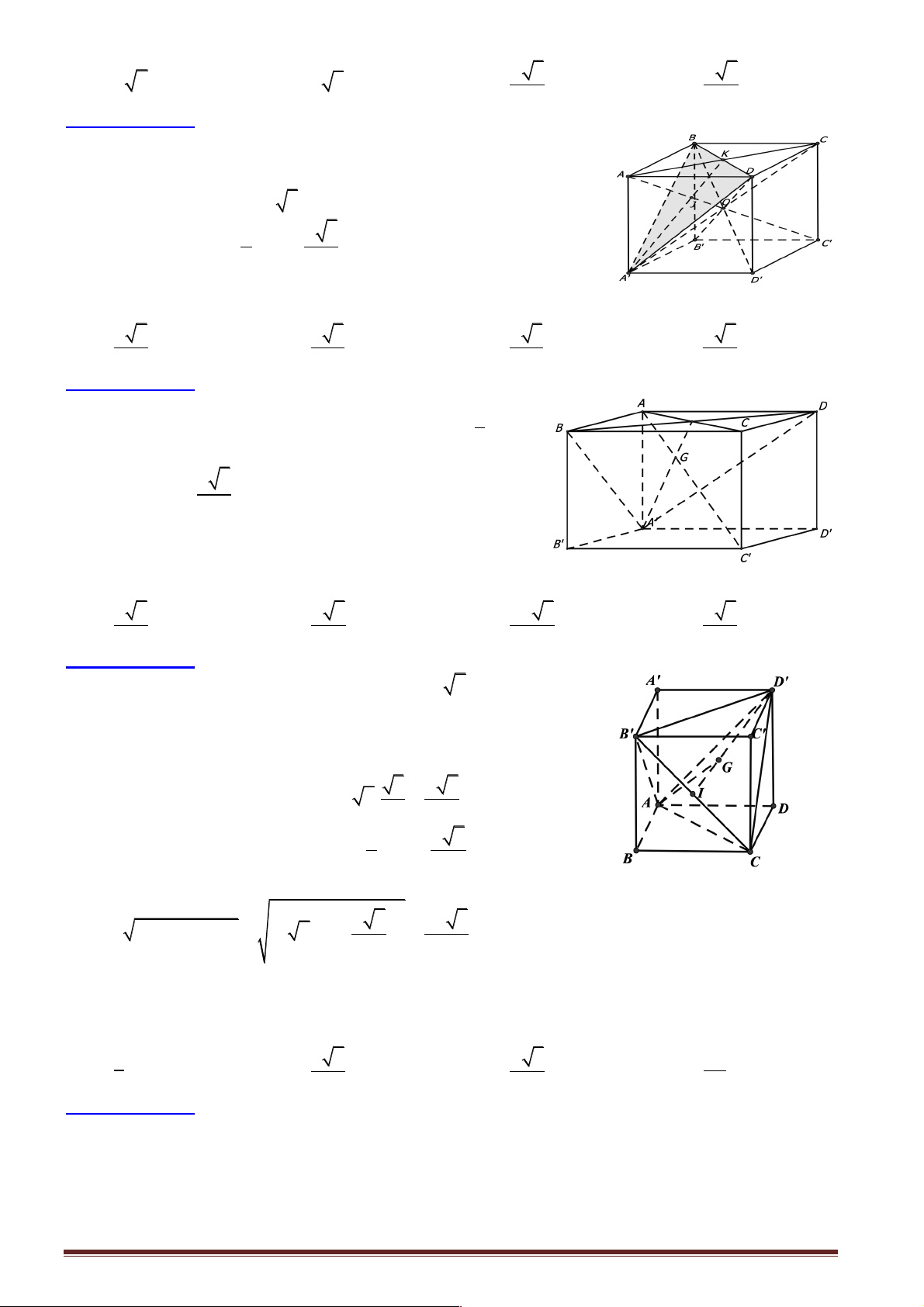
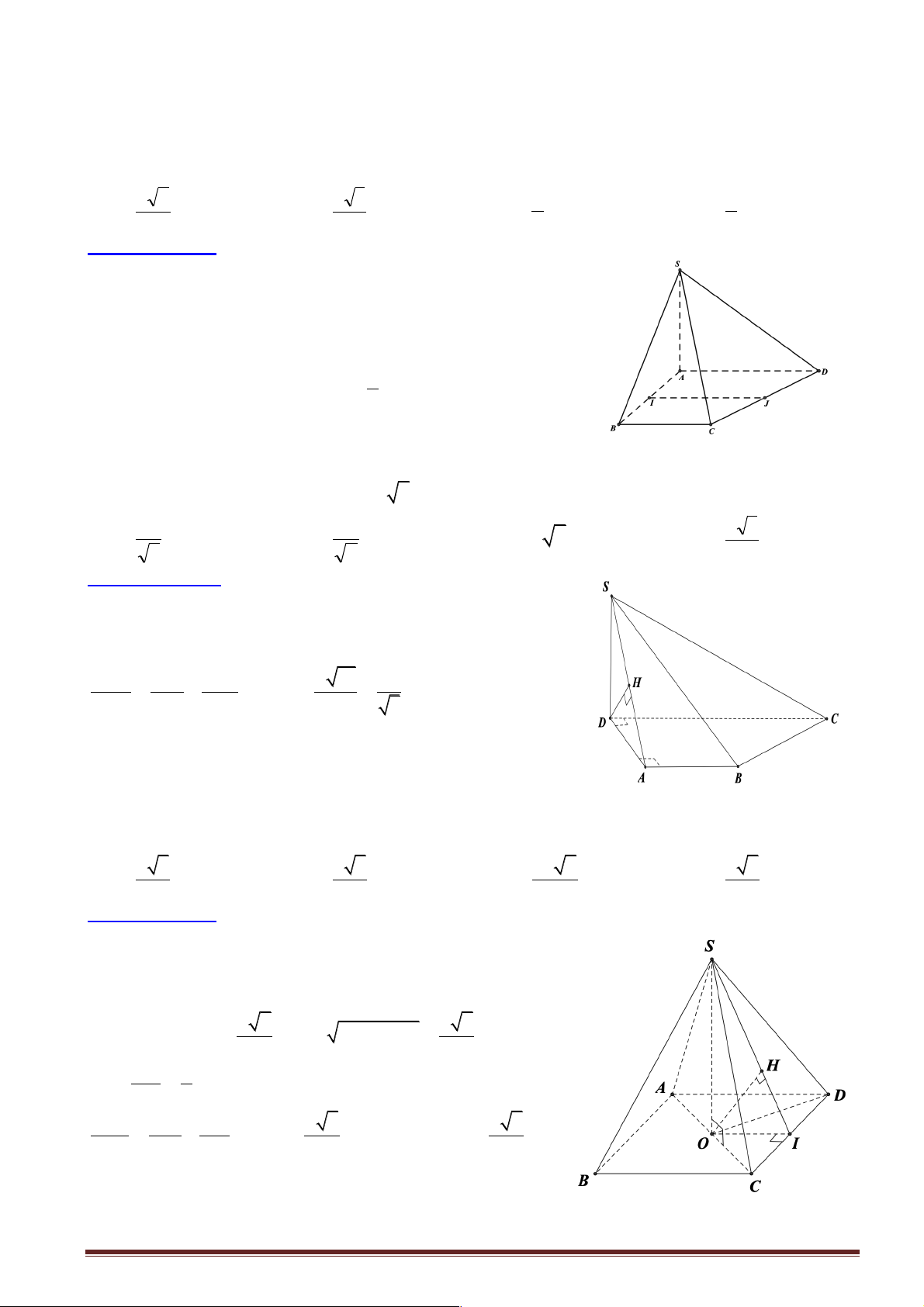
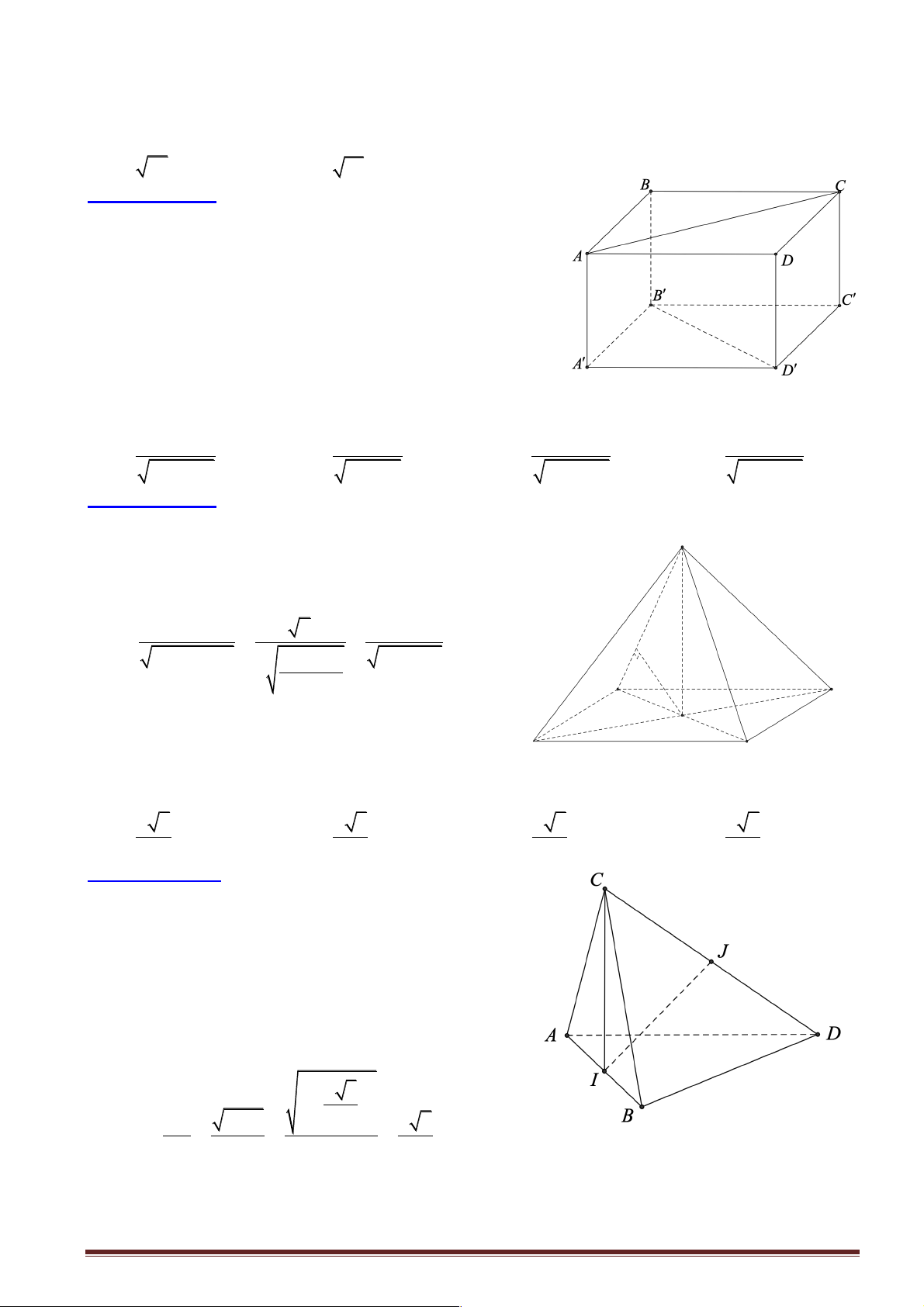
Câu 19: Cho hình lập phương ABC . D A¢B C ¢ D ¢ ¢ có cạnh bằng .
a Khoảng cách từ đỉnh A của hình lập
phương đó đến đường thẳng CD¢ bằng a 6 a 3 A. a 2. B. . C. . D. a 3 . 2 2
Hướng dẫn giải:
Gọi M là trung điểm của CD¢ . Do ABC . D A¢B C ¢ D ¢ ¢ là hình lập
phương nên tam giác ACD ' là tam giác đều cạnh a 2.
AM ^ CD¢ Þ d (A CD¢) a 6 , = AM = 2 Đáp án: B.
Câu 20: Cho hình lập phương ABC . D A¢B C ¢ D ¢ ¢ có cạnh bằng .
a Khoảng cách từ đỉnh A của hình lập
phương đó đến đường thẳng DB¢ bằng A. a 2. B. a 6 . C. a 3 . D. a 6 . 2 2 3
Hướng dẫn giải:
Gọi H là chân đường vuông góc hạ từ A xuống DB¢ . Dễ thấy
AD ^ (ABB' A¢) Þ AD D B'vuông đỉnh A . 1 1 1 a 6 AD = ; a AB¢ = a 2 Þ = + Þ AH = 2 2 2 AH AD AB' 3 Đáp án D.
Câu 21: Cho hình lập phương ABC . D A¢B C ¢ D ¢ ¢ có cạnh bằng .
a Khoảng cách từ ba điểm nào sau đây
đến đường chéo AC¢ bằng nhau ? A. A ,¢ , B C¢ .
B. B,C, D.
C. B ,¢C ,¢ D¢. D. , A A ,¢ D¢ .
Hướng dẫn giải: Trang 9
Dễ thấy các tam giác ABC ',C C ¢ ,
A ADC¢là các tam giác vuông
bằng nhau nên các đường cao hạ từ đỉnh góc vuông xuống canh huyền cũng bằng nhau. Vậy: d ( ,
B AC¢) = d (C, AC¢) = d ( , D AC¢) Đáp án B. Trang 10
DẠNG 2: TÍNH KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN ĐƯỜNG THẲNG, MẶT PHẲNG.
Để tính được khoảng từ điểm M đến mặt phẳng (α)thì điều quan trọng nhất là ta phải xác định được
hình chiếu của điểm M trên (a ).
Phương pháp này, chúng tôi chia ra làm 3 trường hợp sau (minh hoạ bằng hình vẽ):
TH 1: A là chân đường cao, tức là A ∫ H . S P a A K P D
Bước 1: Dựng AK ^ D Þ D ^ (SAK ) Þ (a ) ^ (SAK )
và (a )Ç(SAK ) = SK .
Bước 2: Dựng AP ^ SK Þ AP ^ (a ) Þ d ( , A (a )) = . AP
TH 2: Dựng đường thẳng AH, AH ! (a ). A H A' H' a Lúc đó: d ( ,
A (a )) = d (H,(a )) .
TH 2: Dựng đường thẳng AH, A H « (a )= {I . } A H A' I H' a d ( , A (a )) Lúc đó:
= IA Þ ( ,(a )) = IA d A .d (H,(a ))
d (H,(a )) IH IH
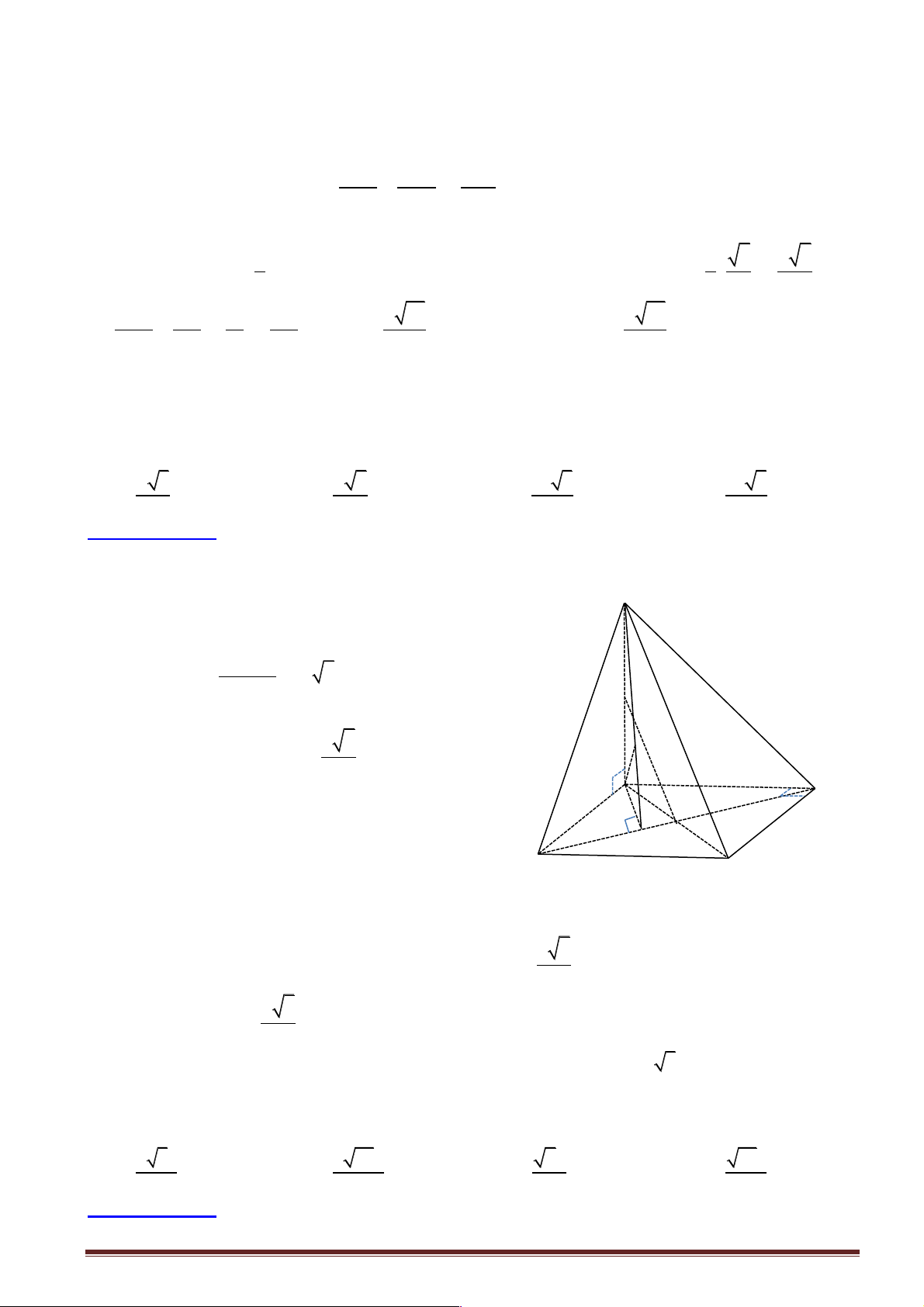
Một kết quả có nhiều ứng dụng để tính khoảng cách từ một điểm đến mặt phẳng đối với tứ diện
vuông (tương tư như hệ thức lượng trong tam giác vuông) là:
Nếu tứ diện OABC có ,
OA OB,OC đôi một vuông góc và có đường cao OH thì 1 1 1 1 = + + . 2 2 2 2 OH OA OB OC
Câu 1: Cho hình chóp S.ABC trong đó SA , AB , BC vuông góc với nhau từng đôi một. Biết
SA = a 3 , AB = a 3 . Khoảng cách từ A đến (SBC) bằng: a 3 a 2 2a 5 a 6 A. . B. . C. . D. . 2 3 5 2
Hướng dẫn giải: Trang 11 Chọn D.
Kẻ AH ^ SB . ìBC ^ SA Ta có: í
Þ BC ^ (SAB) Þ BC ^ AH . îBC ^ AB
Suy ra AH ^ (SBC) Þ d ( ;
A (SBC)) = AH .
Trong tam giác vuông SAB ta có: 1 1 1 = + . SA AB 6a Þ AH = = . 2 2 2 AH SA AB 2 2 SA + AB 2
Câu 2: Cho hình chóp S.ABCD có SA ^ ( ABCD), đáy ABCD là hình chữ nhật. Biết AD = 2a ,
SA = a . Khoảng cách từ A đến (SCD) bằng: 3a 2 2a 3 2a 3a A. . B. . C. . D. . 2 3 5 7
Hướng dẫn giải: Chọn C. Kẻ AH ^ SD , mà vì
CD ^ (SAD) Þ CD ^ AH nên d ( ; A SCD) = AH .
Trong tam giác vuông SAD ta có: 1 1 1 = + 2 2 2 AH SA AD . SA AD .2 a a 2a Þ AH = = = . 2 2 2 2 SA + AD 4a + a 5
Câu 3: Cho hình chóp tam giác đều S.ABC cạnh đáy bằng 2a và
chiều cao bằng a 3 . Tính khoảng cách từ tâm O của đáy ABC đến một mặt bên: a 5 2a 3 3 2 A. . B. . C. a . D. a . 2 3 10 5
Hướng dẫn giải: Chọn C.
SO ^ ( ABC), với O là trọng tâm của tam giác ABC . M là
trung điểm của BC . Kẻ OH ^ SM , ta có ìBC ^ SO í
Þ BC ^ (SOM ) Þ BC ^ OH îBC ^ MO
nên suy ra d (O;(SBC)) = OH . Ta có: 1 a 3 OM = AM = 3 3 1 1 1 = + 2 2 2 OH SO OM a 3 a 3. .O SO M 3a 3 3 Þ OH = = = = a. 2 2 SO + OM 3 30 10 2 2 3a + a 9
Câu 4: Cho tứ diện đều ABCD có cạnh bằng a . Khoảng cách từ A đến (BCD)bằng: a 6 a 6 a 3 a 3 A. . B. . C. . D. . 2 3 6 3
Hướng dẫn giải: Trang 12 Chọn B.
Ta có: AO ^ (BCD) Þ Olà trọng tâm tam giác BCD. ( a a d ; A (BCD)) 2 3 6 2 2 2
= AO = AB - BO = a - = . 9 3
Câu 5: Cho hình chóp S.ABCD có đáy là hình thoi tâm O cạnh a và có góc ∑ o
BAD = 60 .Đường thẳng 3
SO vuông góc với mặt phẳng đáy (ABCD) và = a SO
. Khoảng cách từ O đến mặt phẳng (SBC) 4 là: a 3a 3a A. a 3 . B. . C. . D. . 3 4 8 4
Hướng dẫn giải: Trong mặt phẳng ( D
ABC ): kẻ OK ^ BC (K ÎBC).
Mà BC ^ SO nên suy ra hai mặt phẳng (SOK ) và (SBC) vuông góc nhau theo giao tuyến SK.
Trong mặt phẳng (SOK ) :kẻ OH ^ SK (H ÎSK ).
Suy ra: OH ^ (SBC) Þ d ( ,
O (SBC)) = OH.
Câu 6: Cho hai tam giác ABC và ABD nằm trong hai
mặt phẳng hợp với nhau một góc 60o, ABC D cân ở C, ABD D cân ở .
D Đường cao DK của ABD D bằng12 . cm
Khoảng cách từ D đến ( ABC) bằng A. 3 3 cm B. 6 3 cm C. 6 cm D. 6 2 cm
Hướng dẫn giải:
Gọi M là trung điểm AB suy ra:
Gọi H là hình chiếu vuông góc của D lên CM
Þ DH = d(D,(ABC)) 0
DH = sin 60 .DM = 6 3 Chọn đáp án B.
Câu 7: Cho hình lập phương ABC . D A¢B C ¢ D ¢ ¢ có cạnh bằng .
a Khi đó khoảng cách từ tâm của hình
lập phương đến mặt phẳng (BDA¢) bằng Trang 13 A. a 2. B. a 3 a 3 a 3 . C. . D. . 3 6
Hướng dẫn giải:
Bài toán chứng minh AC¢ ^ (A B ¢ D)trong sách giáo
khoa đã có. Không chứng minh lại.
Dễ dàng tìm được AC¢ = a 3 d (O (A B ¢ D) 1 a 3 , = OJ = AC¢ = 6 6 Đáp án: D
Câu 8: Cho hình lập phương ABC . D A¢B C ¢ D ¢ ¢ cạnh .
a Khoảng cách từ A đến (BDA¢) bằng a 2 a 3 a 3 a 6 A. . B. . C. . D. . 2 3 2 3
Hướng dẫn giải: AC ' ^ (BDA¢) üï 1 Ta có ý Þ d ( ,
A BDA¢ ) = AG = AC¢
AC 'Ç(BDA¢) = { } ( ) G 3 ïþ
d (A (BCA¢) a 3 , = 3 Đáp án B.
Câu 9: Cho hình lập phương ABC . D A¢B C ¢ D ¢ ¢ cạnh .
a Khoảng cách từ A đến (B C ¢ D¢ )bằng a 2 a 3 2a 3 a 6 A. . B. . C. . D. . 2 3 3 3
Hướng dẫn giải:
Ta có: AB' = AC = AD' = B'D' = B'C = CD' = a 2
Nên tứ diện AB 'CD ' là tứ diện đều.
Gọi I là trung điểm B 'C , G là trọng tâm tam giác B 'CD '. Khi đó ta có: d ( ;
A (B'CD')) = AG 3 a 6
Vì tam giác B 'CD ' đều nên D ' I = a 2. = . 2 2 2 a 6
Theo tính chất trọng tâm ta có: D 'G = D ' I = . 3 3
Trong tam giác vuông AGD ' có: 2 æ a ö a
AG = D ' A - D 'G = (a 2)2 6 2 3 2 2 - ç ÷ = . Chọn C ç 3 ÷ 3 è ø
Câu 10: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A với AB = . a Mặt bên chứa
BC của hình chóp vuông góc với mặt đáy, hai mặt bên còn lại đều tạo với mặt đáy một góc 45 .! Tính
khoảng cách từ điểm S đến mặt phẳng đáy (ABC). a a 2 a 3 3a A. . B. . C. . D. . 2 2 2 2
Hướng dẫn giải: Trang 14
Gọi H là hình chiếu của S lên ( ABC), vì mặt bên (SBC) vuông
góc với (ABC) nên H Î BC.
Dựng HI ^ AB, HJ ^ AC , theo đề bài ta có ∑ ∑ 0
SIH = SJH = 45 .
Do đó tam giác SHI = SHJ (cạnh góc vuông - góc nhọn)
Suy ra HI = HJ . Lại có ! ! 0
B = C = 45 Þ B D IH = C
D JH Þ HB = HC
Vậy H trùng với trung điểm của BC . Từ đó ta có HI là đường AC a
trung bình của tam giác ABC nên HI = = . 2 2
Tam giác SHI vuông tại H và có ∑ 0 SIH = 45 Þ SH D I vuông cân. a
Do đó: SH = HI = .Chọn đáp án A. 2
Câu 11: Cho hình chóp tam giác đều S.ABC có cạnh bên bằng b, cạnh đáy bằng d , với d < b 3.
Hãy chọn khẳng định đúng trong các khẳng định bên dưới. 1
A. d (S,(ABC)) 2 2 = b - d .
B. d (S ABC ) 2 2 ,( ) = b - d . 2 1
C. d (S,(ABC)) 2 2 = b - d .
D. d (S ABC ) 2 2 ,( ) = b + d . 3
Hướng dẫn giải:
Gọi I là trung điểm của BC , H là trọng tâm tam giác ABC .
Do S.ABC là hình chóp đều nên SH ^ ( ABC) Þ d (S,( ABC)) = SH . 2 d d 3 Ta có 2 2 2
AI = AB - BI = d - = . 4 2 2 3 2 = = d AH AI 2 2 2 Þ = - = - d SH SA AH b . Chọn C . 3 3 3 3
Câu 12: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và đường cao = a SO . Khoảng 3
cách từ điểm O đến cạnh bên SA bằng A. a 6 a 3 a 6 . B. . C. a 3 . D. . 6 3
Hướng dẫn giải:
Vì hình chóp S.ABC đều có SO là đường cao Þ O là tâm của DABC
Gọi I là trung điểm cạnh BC . 3 2 3
Tam giác ABC đều nên = a AI Þ = = a AO AI . 2 3 3 Trang 15
Kẻ OH ^ SA . Þ d ( ,
O SA) = OH . Xét tam giác SOA vuông tại O : 1 1 1 1 1 6 6 = + = + = Þ = a OH . 2 2 2 2 2 2 OH SO OA æ 3 ö æ 3 ö a a a 6 ç ÷ ç ÷ 3 3 è ø è ø
Câu 13: Cho hình lập phương ABC .
D A B C D cạnh bằng .
a Gọi M là trung điểm của . AD Khoảng 1 1 1 1
cách từ A đến mặt phẳng (C D M 1 1 ) bằng bao nhiêu? 1 2a 2a 1 A. B. C. a D. a 5 6 2
Hướng dẫn giải:
Gọi N là trung điểm cạnh DD và H = A N ÇMD 1 1 1 A M D A M D
Khi đó ta chứng minh được A N ^ MD B C 1 1 N
suy ra A N ^ (C D M ) 1 1 1 H N 2 2 D A D A D A 1 1 1 1 1 1
Þ d ( A ,(C D M ) = AH = = 1 1 1 ) 2 2 A D A N 1 1 1 A D + ND B C 1 1 1 1 1 Þ ( 2a d A ,(C D M ) = 1 1 1 ) 5 Chọn đáp án A.
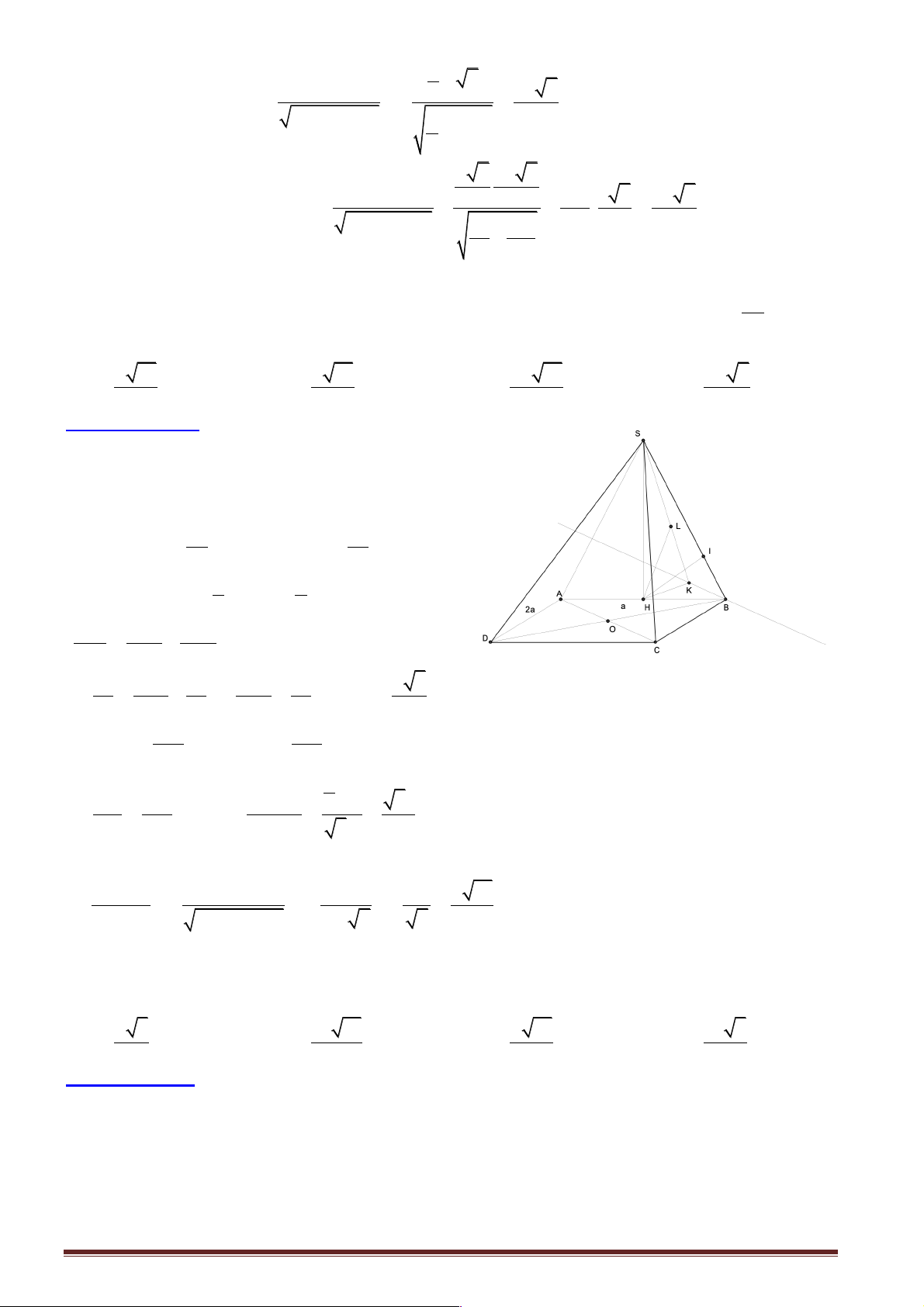
Câu 14: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 3a, cạnh bên bằng 2a . Khoảng cách
từ S đến mặt phẳng ( ABC) bằng: A. 4 . a B. 3 . a C. . a D. 2 . a
Hướng dẫn giải:
Gọi G là trọng tâm tam giác ABC . Do S.ABC là chóp đều nên SG ^ ( ABC). 3a 3 2 AM =
Þ AG = AM = a 3. 2 3 SA D G vuông tại 2 2 2 2
SG = SA - AG = 4a -3a = a . Chọn đáp án C.
Câu 15: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và
chiều cao bằng a 2. Tính khoảng cách từ tâm O của đáy ABCD đến một mặt bên: a 3 a 2 2a 5 a 10 A. . B. . C. . D. . 2 3 3 5
Hướng dẫn giải: Chọn B.
SO ^ ( ABCD), với O là tâm của hình vuông ABCD .
M là trung điểm của CD .
Kẻ OH ^ SM , ta có: ìDC ^ SO í
Þ DC ^ (SOM ) Þ DC ^ OH . îDC ^ MO nên suy ra d ( ;
O (SCD)) = OH . 1 a
Ta có: OM = AD = 2 2 1 1 1 = + . SO OM 2a Þ OH = = . 2 2 2 OH SO OM 2 2 SO + OM 3 Trang 16
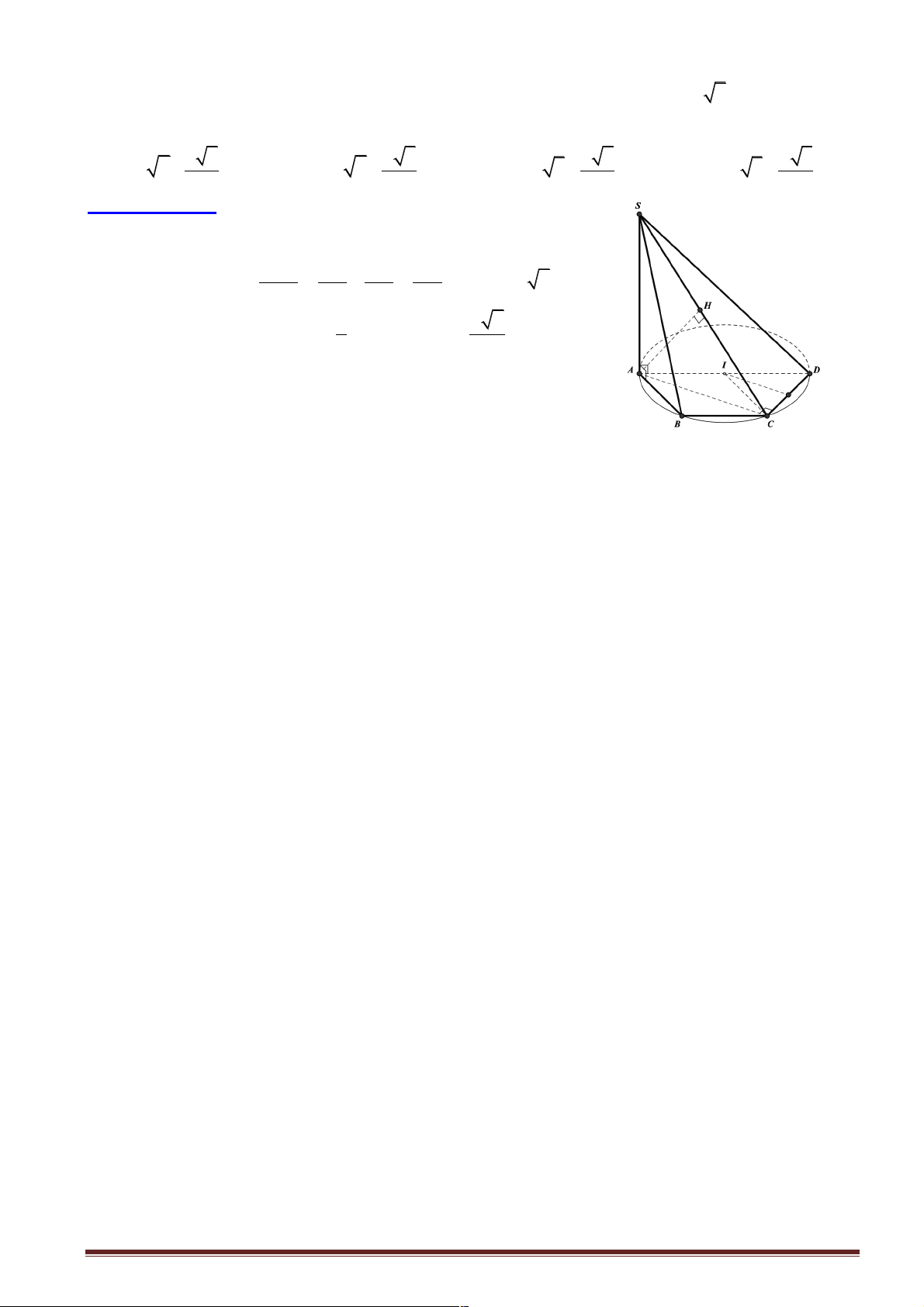
Câu 16: Cho hình chóp S.ABCD có đáy là nửa lục giác đều ABCD nội tiếp trong đường tròn đường
kính AD = 2a và có cạnh SA vuông góc với mặt phẳng đáy ( ABCD)với SA = a 6 . Khoảng cách từ
A và B đến mặt phẳng (SCD) lần lượt là:
A. a 2; a 2
B. a 2; a 3 C. a 2 a 3 a 3 ; D. a 3 ; 2 2 2 2
Hướng dẫn giải: 1 1 1 1 þ d ( ,
A (SCD)) = AH; = + = Þ AH = a 2 . 2 2 2 2 AH 6a 3a 2a 1 a 2
þ d (B,(SCD)) = d (I,(SCD)) = .d ( , A (SCD)) = . 2 2 Chọn đáp án A. Trang 17
Câu 17: Cho hình hộp chữ nhật ABC .
D A B C D có ba kích thước AB = a, AD = b, AA 1= c. Trong 1 1 1 1
các kết quả sau, kết quả nào sai?
A. khoảng cách giữa hai đường thẳng AB và CC1 bằng b.
B. khoảng cách từ A đến mặt phẳng (B ab 1BD) bằng . 2 2 a + b
C. khoảng cách từ A đến mặt phẳng (B abc 1BD) bằng . 2 2 2 a + b + c D. 2 2 2
BD = a + b + c 1
Hướng dẫn giải: þ d ( A ,
B CC = BC = b Þ 1 ) Câu A đúng. þ ( 2 2 + A ( 1 1 1 a b ab d , B BD = AH; = + = Þ AH = 1 )) . 2 2 2 AH a b (ab)2 2 2 a + b Câu B đúng. þ Suy ra câu C sai.
þ Suy ra câu D đúng, đường chéo hình chữ nhật bằng 2 2 2
BD = a + b + c . 1 Chọn đáp án C.
Câu 18: Cho hình chóp S.ABCD có mặt đáy là hình thoi tâm O, cạnh a và góc ∑ BAD =120!, đường cao SO = .
a Tính khoảng cách từ điểm O đến mặt phẳng (SBC). a 67 a 47 a 37 a 57 A. . B. . C. . D. . 19 19 19 19
Hướng dẫn giải:
Vì hình thoi ABCD có ∑ BAD bằng 120°
Suy ra tam giác ABC đều cạnh a .
Kẻ đường cao AM của tam giác ABC a 3 Þ AM = . 2 AM a 3
Kẻ OI ^ BC tại I Þ OI = = . 2 4
Kẻ OH ^ SI Þ OH ^ (SBC) Þ d ( ,
O (SBC)) = OH
Xét tam giác vuông SOI ta có: 1 1 1 a 57 = + Þ OH = . 2 2 2 OH SO OI 19 Chọn D .
Câu 19: Cho hình chóp S.ABCD có mặt đáy ABCD là hình chữ nhật với AB = 3 ; a AD = 2 . a Hình
chiếu vuông góc của đỉnh S lên mặt phẳng ( ABCD)
là điểm H thuộc cạnh AB sao cho AH = 2H . B Góc
giữa mặt phẳng (SCD) và mặt phẳng ( ABCD) bằng
60 .! Khoảng từ điểm A đến mặt phẳng (SBC) tính theo a bằng a 39 3a 39 A. . B. . C. . D. . 13 13
Hướng dẫn giải: Trang 18 Kẻ HK ^ CD
Þ góc giữa hai mặt phẳng (SCD) và ( ABCD) là ∑ SKH = 60°
Có HK = AD = 2a , SH = HK.tan 60° = 2a 3 Có BC ^ (SAB),
Kẻ HJ ^ SB , mà HJ ^ BC HJ ^ (SBC ) d ( , A (SBC)) BA = = 3
d (H,(SBC)) BH d ( ,
A (SBC)) = 3.d (H,(SBC)) = 3HJ 1 1 1 1 1 13 Mà = + = + = 2a 39 Þ HJ =
Þ d ( A (SBC)) 6a 39 , = . 2 2 2 2 2 2 HJ HB SH a 12a 12a 13 13 Chọn C .
Câu 20: Cho hình chóp S.ABCD có mặt đáy ABCD là hình thoi cạnh a; ∑
ABC = 120! . Hình chiếu
vuông góc của đỉnh S lên mặt phẳng ( ABCD) là trọng tâm G của tam giác ABD, ∑ ASC = 90 .!
Khoảng cách từ điểm A đến mặt phẳng (SBD) tính theo a bằng A. a 3 . B. a 3 . C. a 2 . D. a 6 . 6 3 3 3
Hướng dẫn giải: Xác định khoảng cách:
- Đặc điểm của hình: Có đáy là hình thoi, góc ∑ ABC = 120! nên tam giác a 3
ABD đều cạnh a; AC = a 3; AG = 3
Tam giác SAC vuông ở S , có đường cao SG nên a 3 a 6
SA = AG.AC =
.a 3 = a; SG = 3 3
Xét hình chóp S.ABD có chân đường cao trùng với tâm
của đáy nên SA = SB = SD = a .
- Dựng hình chiếu của A lên mặt phẳng (SBD): Kẻ đường cao AH của tam giác SAO với O là tâm của hình thoi. ìBD ^ AC í
Þ BD ^ (SAO) Þ BD ^ AH îBD ^ SG ìAH ^ BD í
Þ AH ^ (SBD) . Vậy d ( ,
A (SBD)) = AH îAH ^ SO - Tính độ dài AH . SG AO AH = SO a 3 a 6 a Với AO = ; SG = 3 ; SO = 2 3 2 a 6 AH = . 3
Cách khác: Nhận xét tứ diện S.ABD có tất cả các cạnh bằng a; Do đó S.ABD là tứ diện đều, vậy a 6 AH = SG = . 3 Trang 19 Chọn đáp án D .
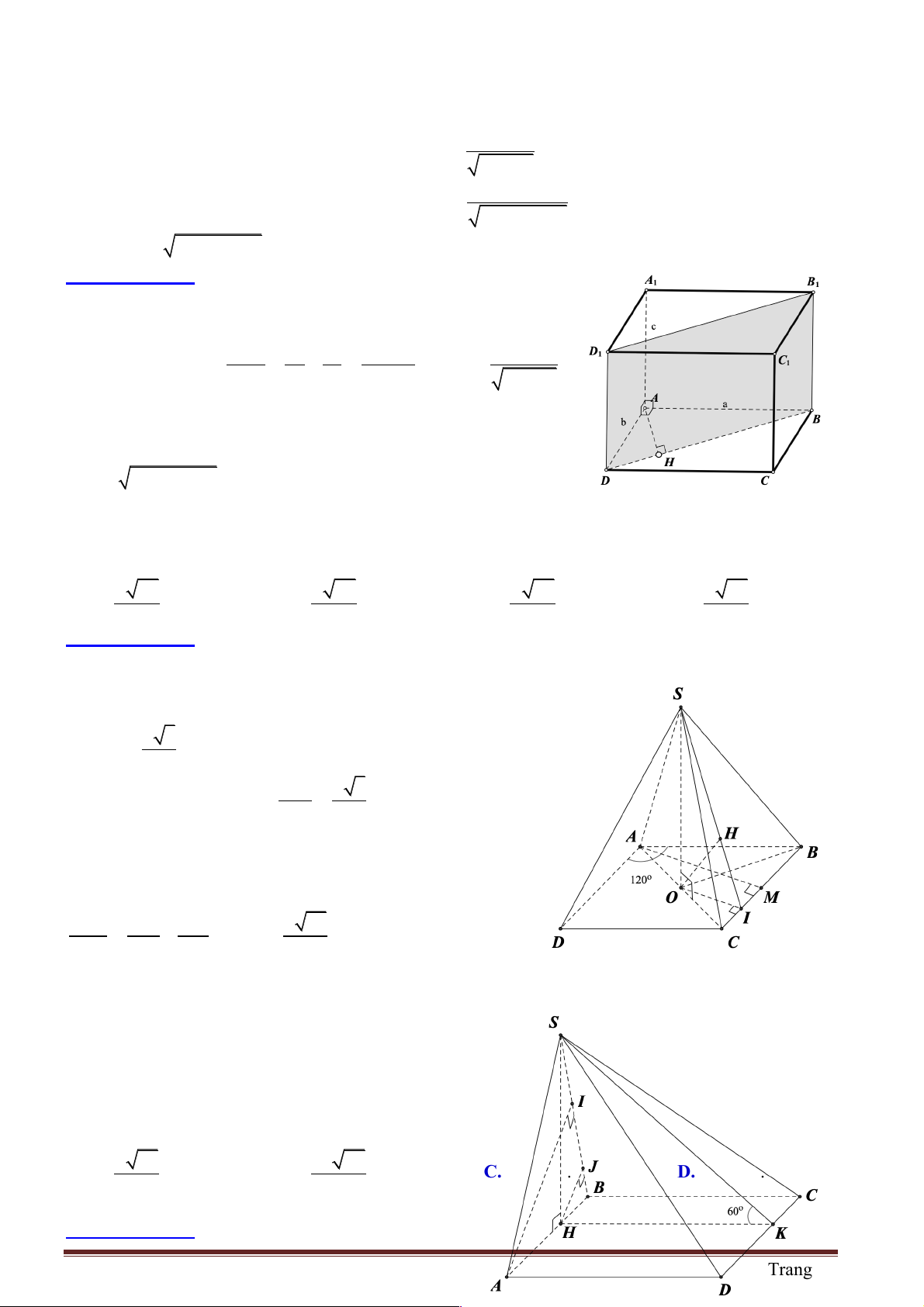
Câu 21: Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA = a và SA vuông góc với mặt
phẳng đáy. Gọi M , N lần lượt là trung điểm các cạnh AD, DC. Góc giữa mặt phẳng (SBM ) và mặt
phẳng ( ABCD) bằng 45 .! Khoảng cách từ điểm D đến mặt phẳng (SBM ) bằng a 3 a 2 a 3 a 2 A. . B. . C. . D. . 3 3 2 2
Hướng dẫn giải:
+ Đặc điểm của hình: Đáy là hình vuông
ABCD nên AN ^ BM .
Góc giữa mặt phẳng (SBM ) và mặt phẳng
(ABCD)là góc ∑AIS = 45!.Vậy tam giác ASI
vuông cân tại A . AI = a - Xác định khoảng cách: d ( ,
D (SBM )) = d ( ,
A (SBM )) = AH . Với H là
chân đường cao của tam giác ASI . 1 1 1 2 - Tính AH : = + = 2 2 2 2 AH AS AI a a 2 Þ AH = . Chọn đáp án D 2
Câu 22: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh .
a Hình chiếu vuông góc
của đỉnh S trên mặt phẳng ( ABCD) là trung điểm H của cạnh ,
AD góc giữa hai mặt phẳng
(SAC) và (ABCD) bằng 60 .! Khoảng cách từ H đến mặt phẳng (SBC) tính theo a bằng a 11 a 11 a 33 2a 33 A. . B. . C. . D. . 33 11 11 11
Hướng dẫn giải:
- Đặc điểm của hình: Góc giữa hai mặt phẳng
(SAC) và (ABCD) là ∑SIH = 60!. a 2 0 a 6 IH =
Þ SH = IH.tan 60 = 4 4
- Xác định khoảng cách: d (H,(SAC)) = HK . Với
HK là đường cao của tam giác SHM với M là trung điểm BC . - Tính HK . Xét tam giác vuông SHM có 1 1 1 1 1 11 = + = + = 2 2 2 2 HK HS HM æ a ö (a)2 2 3 6 a ç ÷ 4 è ø 33a HK = . Chọn đáp án C 11
Câu 23: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh .
a Hình chiếu vuông góc của S
lên mặt phẳng ( ABCD) trùng với trọng tâm của tam giác .
ABD Cạnh bên SD tạo với mặt phẳng
(ABCD) một góc bằng 60 .! Khoảng cách từ A tới mặt phẳng (SBC )tính theo a bằng Trang 20 A. 3a 285 . B. a 285 . C. a 285 . D. 5a 285 . 19 19 18 18
Hướng dẫn giải: a
Đặc điểm hình: Góc giữa SD tạo với mặt phẳng ( ABCD)là ∑ SDE = 60 .! 2 2 2 5
DE = OD + OE = ; 6 0 2 15 SE = DE.tan 60 = a 6 Xác định khoảng cách
d ( A (SBC)) 3
= d (E (SBC)) 3 , , = EH 2 2 Tính EH : 1 1 1 1 1 57 = + = + = 2 2 2 2 2 2 EH EK ES æ 2a ö æ ö 20 2 15 a a ç ÷ 3 ç ÷ è ø 6 è ø 2 5a EH = . Vậy 57
d ( A (SBC)) 3
= d (E (SBC)) 3 a 285 , , = EH = . 2 2 19
Chọn đáp án B .
Câu 24: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm I với AB = 2a 3; BC = 2a .
Biết chân đường cao H hạ từ đỉnh S xuống đáy ABCD trùng với trung điểm đoạn DI và SB hợp với
mặt phẳng đáy ( ABCD) một góc 60 .! Khoảng cách từ D đến (SBC) tính theo a bằng a 15 2a 15 4a 15 3a 15 A. . B. . C. . D. . 5 5 5 5
Hướng dẫn giải:
Đặc điểm của hình: Góc giữa SB tạo với mặt phẳng ( 3 ABCD)là ∑
SBM = 60 .! BM = BD = 3a; 4 0
SM = BM.tan 60 = 3 3a Xác định khoảng cách:
d (D (SBC)) 4
= d (M (SBC)) 4 , , = MH 3 3
Tính khoảng cách MH : 1 1 1 1 1 5 = + = + = 2 2 2 2 MH MK MS æ 3 ö (3 3 a .2 3 a a )2 2 27 ç ÷ è 4 ø 27 MH = a , vậy 5
d (D (SBC)) 4
= d (M (SBC)) 4 4 15 , , = MH = a 3 3 5
Chọn đáp án C .
Câu 25: Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB = a, AC = 2a, SA vuông góc với mặt
phẳng ( ABCD), SC tạo với mặt phẳng (SAB) một góc 30 .! Gọi M là một điểm trên cạnh AB sao cho BM = 3M .
A Khoảng cách từ điểm A đến mặt phẳng (SCM ) là Trang 21 A. 34a . B. 2 34a . C. 3 34a . D. 4 34a . 51 51 51 51
Đặc điểm của hình: SC tạo với mặt phẳng (SAB)góc ∑
CSB = 30 .! BC = 3a; 0
SB = BC.tan 30 = a; 2 æ 3a ö 57 a 2 MC = + 3a = a; MA = ; ç ÷ è 4 ø 4 4
AC = 2a ; AS = 2 2a 2S 19 AMC AK = = a MC 19
Xác định khoảng cách: d ( ,
A (SBC)) = AH Tính AH 1 1 1 1 1 153 = + = + = 2 2 2 2 AH AK AS æ ö ( )2 2 8 19 2 2 a a ç a ÷ 19 è ø
Vậy d ( A (SBC)) 2 34 , = AH = 51 Chọn đáp án B .
Câu 26: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh .
a Gọi M , N và P lần lượt là
trung điểm của các cạnh , AB AD và D .
C Gọi H là giao điểm của CN và DM , biết SH vuông góc
(ABCD), SH = a 3 . Khoảng cách từ điểm C đến mặt phẳng (SBP) tính theo a bằng a 2 a 3 a 3 a 2 A. . B. . C. . D. . 4 2 4 2
Hướng dẫn giải:
Ta chứng minh : NC ^ MD Thật vậy : AD D M = D D CM vì ! ! 0
A = D = 90 ; AD = DC; AM = DN ∑ ∑
Þ ADM = DCN; mà ∑ ∑ 0 ∑ ∑ 0
ADM + MDC = 90 Þ MDC + DCN = 90 Þ NC ^ MD
Ta có : BP ^ NC (MD / /BP);BP ^ SH Þ BP ^ (SNC) Þ (SBP) ^ (SNC)
Kẻ HE ^ SF Þ HE ^ (SBP) Þ d (H,(SBP)) = d(C,(SB ) P ) = HE 2 DC 2a 5 a 5 Do 2
DC = HC.NC Þ HC = = Þ HF = NC 5 5 Trang 22 SH.HF SH.HF a 3 Mà HE = = = 2 2 SF SH + HF 4
Câu 27: Cho hình chóp S.ABCD có đáy ABCD là hình thang cân có hai đường chéo AC, BD
vuông góc với nhau, AD = 2a 2; BC = a 2 . Hai mặt phẳng (SAC) và (SBD) cùng vuông góc với
mặt đáy ( ABCD). Góc giữa hai mặt phẳng (SCD) và ( ABCD) bằng 60 .! Khoảng cách từ M là
trung điểm đoạn AB đến mặt phẳng (SCD) là A. a 15 . B. a 15 . C. 3a 15 . D. 9a 15 . 2 20 20 20
Hướng dẫn giải:
Do (SAC) ^ ( ABCD),(SBD) ^ ( ABCD),(SAC)Ç(SBD) = SO Þ SO ^ ( ABCD)
Dựng góc giữa (SCD),(ABC ) D :
(SCD)Ç(ABCD) = DC. Kẻ OK ^ DC Þ SK ^ DC Þ (SCD) ∑ ( (ABCD) = SKO ) ∑ ,
Kéo dài MO cắt DC tại E Ta có : ! ∂ ! ∂ ∂ ∂ ! ∂ ! ! ∑ 0 ! 0
A = D ; A = M ; M = M = O Þ D = O ;O + EOD = 90 Þ E = 90 1 1 1 1 1 2 1 1 1 1 Þ E º K 2 . a a AB a 5 9a 5 Ta có: OK = ;OM = = ; MK = a 5 2 2 10
d(O,(SCD)) OE 9 =
= Þ d (M ,(SCD))
d(M ,(SCD)) ME 4 9 = d (O SCD ) 9 ,( ) = OH 4 4 2a 15 0 OS = OK.tan 60 = 5 OK.OS a 15 Þ OH = =
Þ d (M SCD ) 9a 15 ,( ) = 2 2 OK + OS 5 20
Câu 28: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, mặt bên SAD là tam giác vuông tại
S, hình chiếu vuông góc của S lên mặt phẳng ( ABCD) là điểm H thuộc cạnh AD sao cho HA = 3 .
HD Gọi M là trung điểm của cạnh .
AB Biết rằng SA = 2 3a và đường thẳng SC tạo với mặt
đáy một góc 30 .! Khoảng cách từ M đến mặt phẳng (SBC) tính theo a bằng A. 2 66a . B. 11a . C. 2 66a . D. 66a . 11 66 11 11
Hướng dẫn giải:
SC có hình chiếu vuông góc lên mp ( ABCD) là HC Þ SC ( ∑ABCD) ∑ 0 , = SCH = 30
Đặt AD = 4x (x > 0) Ta có : 2 2 2
SA = AH.AD Þ12a =12x Þ x = a Þ AD = 4a, AH = 3a, HD = a Mà : 2 2
SH = SA - AH = a 3 Þ HC = 3a Þ DC = 2 2a Trang 23
Kẻ HE ^ BC, SH ^ BC Þ (SHE) ^ (SBC) HK
Kẻ HK ^ SE Þ HK ^ (SBC) Þ d (H, SBC) = HK Þ d (M ,(SBC)) = 2 SH.EH 2a 66 HK = =
Þ d (M SBC ) a 66 ,( ) = 2 2 SH + EH 11 11
Câu 29: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm I, AB = a; BC = a 3 , tam giác
SAC vuông tại S. Hình chiếu vuông góc của S xuống mặt phẳng đáy trùng với trung điểm H của
đoạn AI. Khoảng cách từ điểm C đến mặt phẳng (SAB) tính theo a bằng a 3 a 3 3a 3 a 3 A. . B. . C. . D. . 2 4 4 2
Hướng dẫn giải: Ta có : 2 2
AC = AB + BC = 2a, mà SA D C vuông AB
tại S Þ SI = = a 2 2 a a 3 2 2 2
Þ SH = SI - HI = a - = 4 2 Kẻ HK ^ A ;
B AB ^ SH Þ AB ^ (KHS) Þ (SAB) ^ (KHS)
Mà (SAB)Ç(KHS) = SK . Kẻ
HE ^ SK Þ HE ^ (SAB) Þ d(H,(SC )
D ) = HE
d (C, SAB ) = Ç( ) ( ) CA A HC SAB Þ ( = = Þ = = SAB ) 4
d (C,(SAB)) 4d(H,(SAB)) 4HE d H ,( ) HA a 3 a 3 . HK.SH a 15 4 2 a HE = = =
Þ d (C SAB ) 2 15 ,( ) = 2 2 2 2 HK + SH 3a 3a 10 5 + 16 4
Câu 30: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a tâm O, hình chiếu vuông góc của S
trên ( ABCD) là trung điểm của ,
AO góc giữa (SCD) và ( ABCD) là 60 .! Khoảng cách từ trọng tâm
của tam giác SAB đến mặt phẳng (SCD) tính theo a bằng 2a 3 a 2 2a 2 a 3 A. . B. . C. . D. . 3 3 3 3
Hướng dẫn giải: Chọn D. Ta có: HI CH 3 3a = = Þ HI = AD CA 4 4 SH 3 3 0 tan 60 = Þ SH = a HI 4 2 2
æ 3 3a ö æ 3a ö 3 2 2
SI = SH + HI = ç ÷ + = a ç ÷ ç ÷ 4 è ø è 4 ø 2
d (G (SCD)) 3
= d (J (SCD)) 2
= d (K (SCD)) 2 4 , , ,
= . .d (H,(SCD)) 2 3 3 3 Trang 24 3 3 3a . 8 a
= d (H (SCD)) 8 8 SH.HI 8 3 4 4 , = HL = . = = a 9 9 9 SI 9 3a 3 2
Câu 31: Cho hình chóp S.ABC có đáy là tam giác ABC cân tại ,
A AB = AC = a, ∑ BAC =120!. Hình
chiếu vuông góc của đỉnh S trên mặt phẳng ( ABC) trùng với trọng tâm G của tam giác ABC. Cạnh
bên SC tạo với mặt phẳng đáy một góc a 3 sao cho tana =
. Khoảng cách từ điểm C đến mặt 7
phẳng (SAB) tính theo a bằng a 13 3a 13 5a 13 3a A. . B. . C. . D. . 13 13 13 13
Hướng dẫn giải: Chọn B. Ta có:
Gọi H là hình chiếu của J lên AB
Gọi G là hình chiếu của G lên AB
Gọi I là hình chiếu của G lên SZ 7 2 2 0
BJ = BA + AJ - 2 . BA AJ.co 1 s 20 = a 2 1 1 3a 0 S .A .
B AJ.sin120 = JH.AB Û JH = BAJ D = 2 2 4 GZ BG 2 3 = = Þ GZ = a JH BJ 3 6 SG 3 SG 3 SG tana = Û = Û = GC 7 BG 7 2 BJ 3 2 7 Û SG = . a = a 7 2
( (SAB)) = d (G (SAB)) . SG GZ d C, 3 , = 3GI = 3. SZ 3 . a a . SG GZ 3 13 6 = 3 = 3. = a 2 2 2 SG + GZ 13 æ ö 2 3 a + ç a ÷ 6 è ø
Câu 32: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng
60 .! Gọi M , N lần lượt là trung điểm của các cạnh ,
AB BC. Khoảng cách từ điểm C đến mặt phẳng
(SMN) tính theo a bằng a 7a 3a a A. . B. . C. . D. . 7 3 7 3
Hướng dẫn giải: Chọn A. Ta có: 2 3a Trong SG
D C vuông tại G suy ra SG = GC 3 = = a . 3 2
Gọi E, F lần lượt là hình chiếu của G trên MN và SE .
Khi đó d (C,(SMN)) = 3d (G,(SMN)) = 3GF Trang 25 1 GE = d (G ) 1 2
, AC = . .d (M ,AC) Ta có : 2 2 3 1 = d (M ) 1 = d (B ) a 3 , AC , AC = . 3 6 12 Trong SG
D E vuông tại H suy ra a 3 . . a GE SG 12 a GF = = = 2 2 2 GE + SG 7 æ a 3 ö 2 ç ÷ + a 12 è ø
Câu 33: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh .
a Gọi I là trung điểm của cạnh .
AB Hình chiếu vuông góc của đỉnh S lên mặt phẳng đáy là trung điểm H của CI , góc giữa đường
thẳng SA và mặt đáy bằng 60 .! Khoảng cách từ điểm H đến mặt phẳng (SBC) là a 21 a 21 4a 21 a 21 A. . B. . C. . D. . 4 29 29 29 2 29
Hướng dẫn giải: Chọn A. Ta có: Trong ACI D
có trung tuyến AH suy ra ( 2 2 AI + AC ) 2 2 2 -CI 7a a 7 AH = = = . 4 16 4 a 21 Trong SH
D A vuông tại H suy ra SH = AH 3 = 4
Gọi E, F lần lượt là hình chiếu của H trên BC và SE . Khi
đó d (H,(SBC)) = HF 1 1 a 3
Ta có : HE = d (I, BC) = d (A, BC) = . 2 4 8 Trong SH
D E vuông tại H suy ra a 3 a 21 . HE.SH a 21 8 4 HF = = = . 2 2 2 2 HE + SH 4 29
æ a 3 ö æ a 21 ö ç ÷ + ç ÷ 8 4 è ø è ø Trang 26
DẠNG 3: KHOẢNG CÁCH GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG SONG SONG.
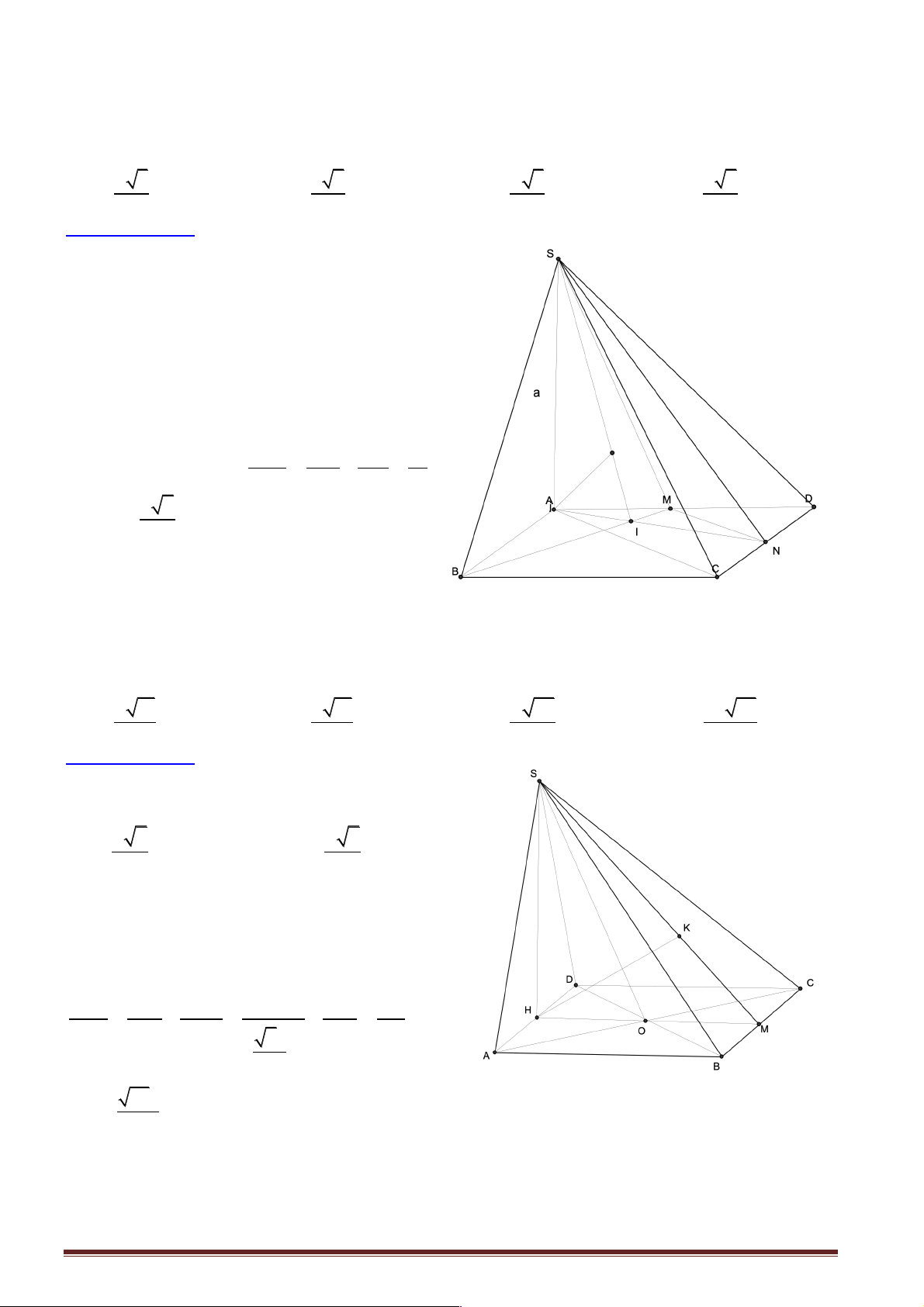
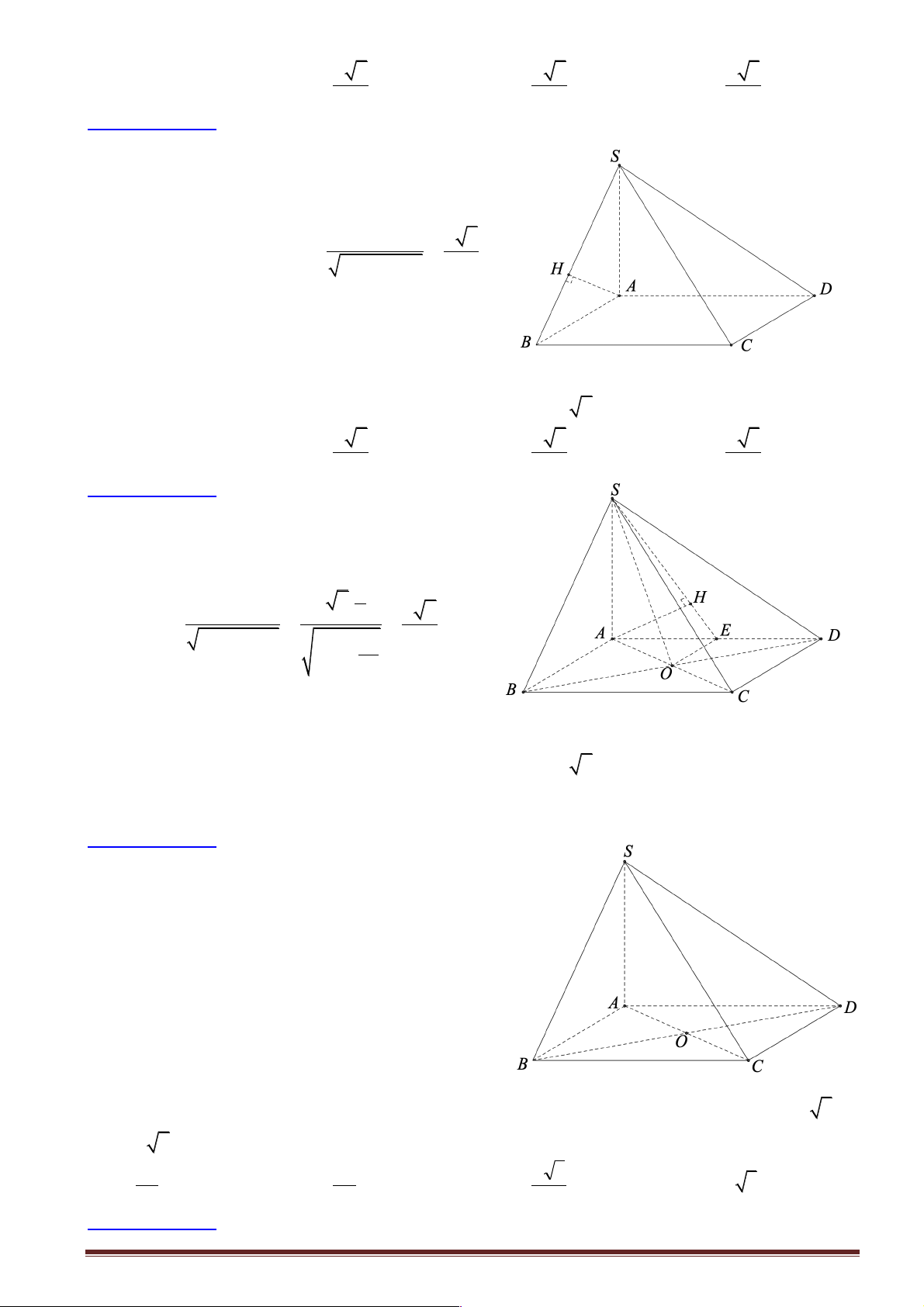
Câu 1: Cho hình chóp S.ABCD có SA ^ ( ABCD), đáy ABCD là hình thang vuông cạnh a . Gọi I
và J lần lượt là trung điểm của AB và CD . Tính khoảng cách giữa đường thẳng IJ và (SAD . ) a 2 a 3 a a A. . B. . C. . D. . 2 3 2 3
Hướng dẫn giải: Chọn C.
Ta có: Vì IJ // AD nên IJ // (SAD) Þ ( a
d IJ;(SAD)) = d (I;(SAD)) = IA = . 2
Câu 2: Cho hình thang vuông ABCD vuông ở A và D ,
AD = 2a . Trên đường thẳng vuông góc tại D với ( ABCD)
lấy điểm S với SD = a 2 . Tính khỏang cách giữa đường
thẳng DC và (SAB). 2a a a 3 A. . B. . C. a 2. D. . 3 2 3
Hướng dẫn giải: Chọn A.
Vì DC // AB nên DC // (SAB) Þ d (D ;
C (SAB)) = d ( ; D (SAB)). Kẻ DH ^ SA , do AB ^ AD , AB ^ SAnên
AB ^ (SAD) Þ DH ^ AB suy ra d ( ; D SC) = DH .
Trong tam giác vuông SAD ta có: 1 1 1 = + . SA AD 2a Þ DH = = . 2 2 2 DH SA AD 2 2 SA + AD 3 2a
Câu 3: Cho hình chóp .
O ABC có đường cao OH = . Gọi M 3
và N lần lượt là trung điểm của OA và OB . Khoảng cách giữa đường thẳng MN và ( ABC) bằng: a a 2 a a 3 A. . B. . C. . D. . 2 2 3 3
Hướng dẫn giải: Chọn D.
Vì M và N lần lượt là trung điểm của OA và OB nên MN //
AB MN // ( ABC). a
Ta có: d (MN ( ABC)) = d (M ( ABC)) 1 3 ; ; = OH = (vì M 2 3 là trung điểm của OA).
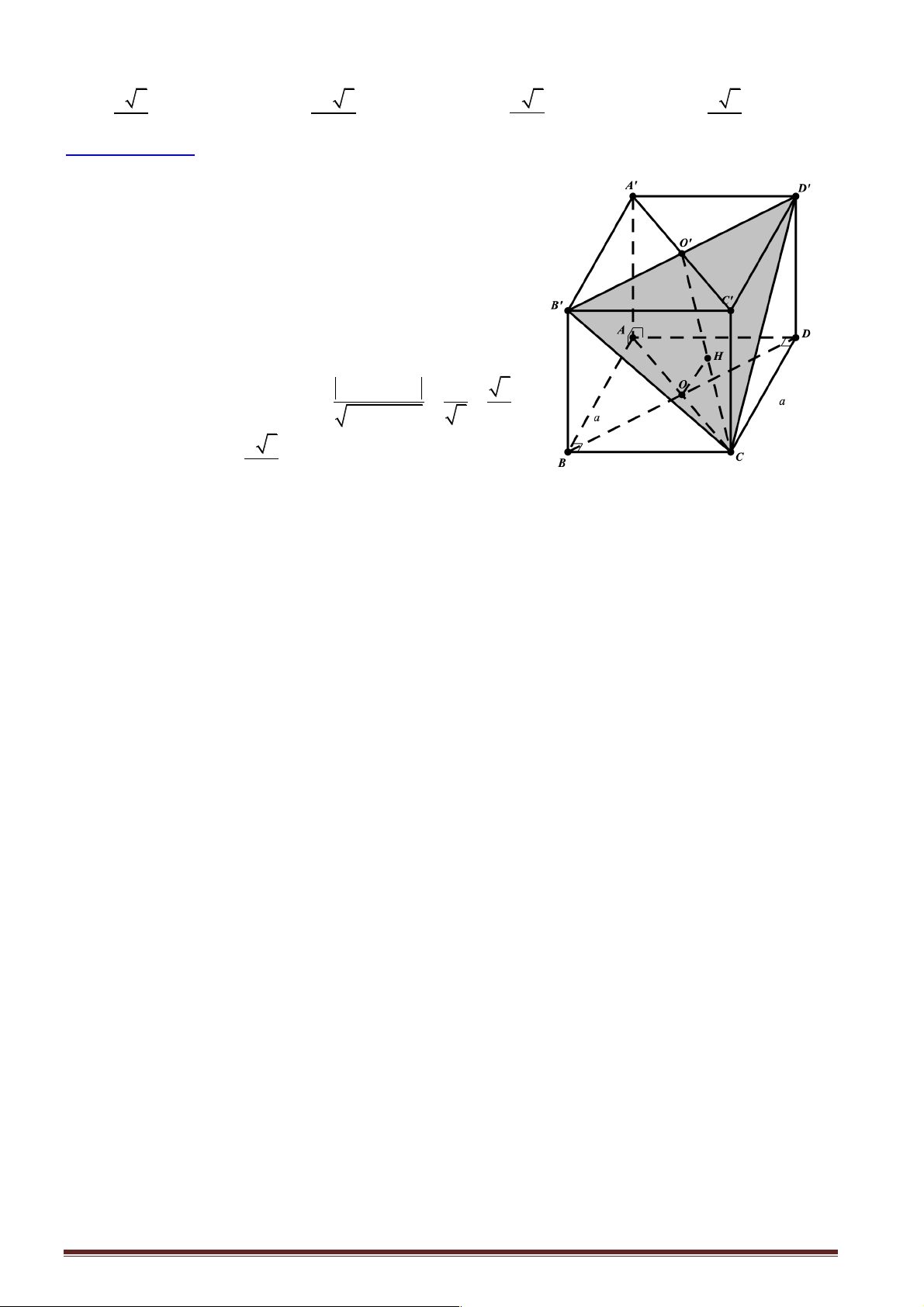
Câu 4: Cho hình chóp tứ giác đều S.ABCD có AB = SA = 2 . a
Khoảng cách từ đường thẳng AB đến (SCD) bằng bao nhiêu? S a 6 a 6 a A. . B. . C. . D. 2 3 2
Hướng dẫn giải: H A
Gọi I, M lần lượt là trung điểm cạnh AB và CD thì CD ^ (SIM ) D I Trang M O 27 B C
Vẽ IH ^ SM tại H Î SM thì IH ^ (SCD) Þ (
SCD ) = d (I SCD ) . SO IM d AB,( ) ,( ) = IH = SM
D SAB đều cạnh 2a Þ SI = a 3 Þ SM = a 3 1 Và 2 2
OM = IM = a Þ SO = SM - OM = a 2 2 SO IM a a a
Cuối cùng d ( AB SCD ) . 2.2 2 6 ,( ) = = = SM a 3 3 Chọn đáp án B.
Câu 5: Cho hình chóp S.ABCD có SA ^ ( ABCD), đáy ABCD là hình thang vuông có chiều cao
AB = a . Gọi I và J lần lượt là trung điểm của AB và CB . Tính khỏang cách giữa đường thẳng IJ và ( SAD). a 2 a a 3 a A. B. C. D. 2 2 3 3
Hướng dẫn giải:
IJ / / AD Þ IJ / /(SAD) a Þ d (IJ (S
, AD)) = d (I,(SAD)) = IA = . 2 Chọn đáp án B. 2a
Câu 6: Cho hình chóp .
O ABC có đường cao OH = . 3
Gọi M và N lần lượt là trung điểm của OA và OB . Tính khoảng cách giữa đường thẳng MN và (ABC). a 3 a 2 a a A. . B. . C. . D. . 3 2 2 3
Hướng dẫn giải:
Khoảng cách giữa đường thẳng MN và ( ABC):
d (MN ( ABC)) = d ((MNP) ( ABC)) OH a 3 , , = = . 2 3 2a
Câu 7: Cho hình chóp .
O ABC có đường cao OH =
. Gọi M và N lần lượt là trung điểm của OA 3 và .
OB Khoảng cách giữa đường thẳng MN và ( ABC) bằng a a 2 a a 3 A. . B. . C. . D. . 2 2 3 3
Hướng dẫn giải:
Do MN// ( ABC) Þ d (MN,( ABC)) = d (M,( ABC)) OA
d (O,( ABC)) = MA d (
= 2 Þ d (M, ABC ) M ,( ABC)) ( ) Lại có 1
= d (O ( ABC)) OH a 3 , = = 2 2 3 Chọn D . Trang 28 Chọn đáp án A.
Câu 8: Cho hình chóp S.ABCD có SA ^ ( ABCD), mặt đáy ABCD là hình thang vuông có chiều cao AB = .
a Gọi I và J lần lượt là trung điểm của AB và .
CD Tính khoảng cách giữa đường thẳng IJ và (SAD). a 2 a 3 a a A. . B. . C. . D. . 2 3 2 3
Hướng dẫn giải: .
SA ^ ( ABCD) Þ SA ^ AI
Lại có AI ^ AD ( hình thang vuông) suy ra IA ^ (SAD)
theo tính chất hình thang, nên IJ ! AD ( a
d IJ,(SAD)) = d (I,(SAD)) = IA = 2
Câu 9: Cho hình thang vuông ABCD vuông ở A và , D AD = 2 .
a Trên đường thẳng vuông góc với
(ABCD) tại D lấy điểm S với SD = a
2. Tính khoảng cách giữa DC và (SAB) . 2a a a 3 A. . B. . C. a 2. D. . 3 2 3
Hướng dẫn giải:
*Trong tam giác DHA, dựng DH ^ SA ;
*Vì DC / / AB Þ d (DC;(SAB)) = d ( ;
D (SAB)) = DH
Xét tam giác vuông SDA có : 1 1 1 a 12 2a = + Þ DH = = 2 2 2 DH SD AD 3 3 Chọn A.
Câu 10: Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng .
a Khi đó khoảng cách giữa
đường thẳng AB và mặt phẳng (SCD) bằng A. a 6 . B. a 6 . C. 2a 6 . D. a 6 . 2 4 9 3
Hướng dẫn giải:
Gọi O là tâm hình vuông ABCD
Khi đó SO ^ ( ABCD). Kẻ OI ^ C ,
D OH ^ SI Þ OH ^ (SCD) a 2 a 2 Ta tính được 2 2 AO =
, SO = SA - AO = 2 2 AD a OI = = 2 2 1 1 1 a 6 = + Þ a OH =
Þ d ( A (SCD)) 6 , = . 2 2 2 OH SO OI 6 3 Chọn D .
Câu 11: Cho hình lập phương ABC . D A¢B C ¢ D ¢ ¢ có cạnh bằng Trang 29 .
a Khi đó, khoảng cách giữa đường thẳng BD và mặt phẳng (CB D ¢ ¢) bằng A. a 2 . B. 2a 3 . C. a 3 . D. a 6 . 2 3 3 3
Hướng dẫn giải:
Gắn hệ trục tọa độ như hình vẽ
A(0;0;0); B(1;0;0); D(0;1;0); A¢(0;0; ) 1
C (1;1;0); B¢(1;0; ) 1 ; D¢(0;1; ) 1 ;C¢(1;1; ) 1 !!!" !!!!" CB¢ = (0; 1 - ) ;1 ;CD¢ = ( 1 - ;0 ) ;1
Viết phương trình mặt phẳng (CB D ¢ ¢) ! """! """"!
Có VTPT n = éCB ;¢CD¢ù = ( 1 - ; 1 - ;- ) 1 ë û (CB D ¢ ¢) ( :1 x - ) 1 + ( 1 y - ) 1 + (
1 z - 0) = 0 Û x + y + z - 2 = 0 + + -
d (BD (CB D
¢ ¢)) = d (B (CB D ¢ ¢)) 1 0 0 2 1 3 ; ; = = = 2 2 2 1 +1 +1 3 3 a
Vậy d (BD (CB D ¢ ¢)) 3 ; = . 3 Trang 30
DẠNG 4: KHOẢNG CÁCH GIỮA HAI MẶT PHẲNG SONG SONG
Câu 1: Cho hình lăng trụ tứ giác đều ABC . D A¢B C ¢ D
¢ ¢ có cạnh đáy bằng a . Gọi M , N , P lần lượt là
trung điểm của AD , DC , A' D '. Tính khoảng cách giữa hai mặt phẳng (MNP) và ( ACC ' .) a 3 a a A. . B. . C. . D. . 3 4 3
Hướng dẫn giải: Chọn D.
Ta có: (MNP)// ( ACA¢)
Þ d ((MNP) ( ACA¢)) = d ( ( ACA¢)) 1 a 2 ; P; = OD¢ = . 2 4
Câu 2: Cho hình lăng trụ tam giác ABC.A¢B C
¢ ¢ có các cạnh bên hợp với đáy những góc bằng 60°,
đáy ABC là tam giác đều và A¢ cách đều A , B , C . Tính khoảng cách giữa hai đáy của hình lăng trụ. a 3 2a A. a . B. a 2. C. . D. . 2 3
Hướng dẫn giải: Chọn A.
Vì !ABC đều và AA¢ = A¢B = A C ¢ Þ A AB
¢ C là hình chóp đều.
Gọi A¢H là chiều cao của lăng trụ, suy ra H là trọng tâm !ABC , ! A A ¢ H = 60°. a 3
A¢H = AH.tan 60° = 3 = a. 3
Câu 3: Cho hình lăng trụ tam giác .
ABC A B C có cạnh bên bằng .
a Các cạnh bên của lăng trụ tạo với 1 1 1 mặt đáy góc o
60 . Hình chiếu vuông góc của A lên mặt phẳng (A BC B C .
1 1 1 ) là trung điểm của 1 1
Khoảng cách giữa hai mặt đáy của lăng trụ bằng bao nhiêu? 3 a 2 a A. a . B. . C. a . D. . 2 3 2 2
Hướng dẫn giải: Ta có: ^ ( ) ∑ o A'H ABC ® A'AH = 60 .
d ( A'B'C'),(ABC) 3 o
= A'H = A' . A cos60 = a . 2 Chọn đáp án A.
Câu 4: Cho hình lăng trụ ABC.A¢B C
¢ ¢ có tất cả các cạnh đều
bằng a . Góc tạo bởi cạnh bên và mặt phẳng đáy bằng 30° . Hình chiếu H của A trên mặt phẳng (A B ¢ C
¢ ¢) thuộc đường thẳng B C
¢ ¢. Khoảng cách giữa hai mặt phẳng đáy là: Trang 31 a a 3 a a 2 A. . B. . C. . D. . 3 2 2 2
Hướng dẫn giải:
þ Do hình lăng trụ ABC.A¢B C
¢ ¢ có tất cả các cạnh đều bằng a suy ra a 3 a
AB¢ = AC¢ Þ B H ¢ = HC¢ Þ A H ¢ = Þ AH = . 2 2 Chọn đáp án C.
Câu 5: Cho hình lập phương ABC . D A¢B C ¢ D ¢ ¢ cạnh .
a Khoảng cách giữa ( AB C ¢ ) và (A D ¢ C¢) bằng : a a 3 A. a 3 . B. a 2. C. . D. . 3 3 Hướng dẫn giải: Ta có B C d ( AB C ¢ ),(A D
¢ C¢)) = d (B ,¢(A D
¢ C¢)) = d (D ,¢(A D ¢ C¢))
Gọi O¢ là tâm của hình vuông A¢B C ¢ D
¢ ¢ . Gọi I là hình
Chiếu của D¢ trên O D
¢ , suy ra I là hình chiếu của D¢ A D trên ( A D ¢ C¢). d é( AB C
¢ ),( A¢DC¢)ù = d éD ,¢( A D ¢ C¢)ù = ë û ë û B¢ C¢ a 2 I . ¢ . a D O¢ D D ¢ a 3 2 D I¢ = = = . 2 2 2 O¢ D O ¢ ¢ + D D ¢ 3 æ a 2 ö 2 ç ÷ + a A¢ D¢ 2 è ø Chọn đáp án D.
Câu 6: Cho hình lăng trụ tứ giác đều ABC . D A¢B C ¢ D
¢ ¢ có cạnh đáy bằng .
a Gọi M , N, P lần lượt là trung điểm của ,
AD DC, A D
¢ .¢ Tính khoảng cách giữa hai mặt phẳng (MNP) và ( ACC¢). a a 2 a 3 a A. . B. . C. . D. . 3 4 3 4
Hướng dẫn giải:
Nhận xét (ACC )¢ º (ACC A ¢ )¢
Gọi O = AC Ç B ,
D I = MN Ç BD
Khi đó, OI ^ AC, OI ^ AA¢ Þ OI ^ (ACC A ¢ )¢ a D' C'
Suy ra d ( MNP ACC¢ ) 1 2 ( ),( ) = OI = AC = 4 4 P Chọn đáp án B. N D C A ' B' I M O N D C M A B A B Trang 32
Câu 7: Cho hình lập phương ABC . D A¢B C ¢ D ¢ ¢ có cạnh bằng .
a Khoảng cách giữa hai mặt phẳng
(ACD¢) và (BA¢C¢) bằng
A. khoảng cách từ điểm D¢ đến đường thẳng A¢C¢.
B. khoảng cách giữa hai điểm B và D¢ .
C. khoảng cách giữa hai đường thẳng AC và A¢C¢.
D. khoảng cách giữa trọng tâm của hai tam giác ACD¢ và BA¢C¢
Hướng dẫn giải: Ta có (ACD ) ¢ / /(B ¢ A C )¢. DB¢ ^ (ACD )
¢ (đã chứng minh trong SGK) DB¢ ^ ( ¢ BA C ) ¢ Đáp án D.
Câu 8: Cho hình lập phương ABC . D A¢B C ¢ D ¢ ¢ có cạnh bằng .
a Khi đó, khoảng cách giữa hai mặt phẳng (CB D
¢ ¢) và (BDA¢) bằng a 2 a 3 2a 3 a 6 A. . B. . C. . D. . 2 3 3 3
Hướng dẫn giải:
Vì ( A'BD) / /(B'CD') nên ta có:
d (( A'BD),(B'CD')) = d (C;( A'BD)) = d ( ;
A ( A'BD)).
Vì AB = AD = AA' = a và A'B = A'D = BD = a 2 nên .
A A' BD là hình chóp tam giác đều.
Gọi I là trung điểm A' B, Glà trọng tâm tam giác A' BD . Khi đó ta có: d ( ;
A ( A'BD)) = AG 3 a 6
Vì tam giác A' BD đều nên DI = a 2. = . 2 2 2 a 6
Theo tính chất trọng tâm ta có: DG = DI = . 3 3
Trong tam giác vuông AGD có: 2 6a a 3 2 2 2
AG = AD - DG = a - = . Chọn B 9 3
Câu 9: Cho hình lập phương ABC . D A¢B C ¢ D ¢ ¢ cạnh .
a Khoảng cách giữa(ACB¢) và (DA¢C¢) bằng a 3 a A. a 3 . B. a 2. C. . D. . 3 3
Hướng dẫn giải:
Vì ( ACB') / /(DA'C ') nên ta có:
d (( ACB'),(DA'C ')) = d ( ;
D ( ACB')) = d ( ; B ( ACB')).
Vì BA = BB ' = BC = a và AB' = AC = CB' = a 2 nên .
B ACB ' là hình chóp tam giác đều.
Gọi I là trung điểm AC, Glà trọng tâm tam giác ACB ' . Khi đó ta có: d ( ;
B ( ACB')) = BG 3 a 6
Vì tam giác ACB ' đều nên B ' I = a 2. = . 2 2 Trang 33 2 a 6
Theo tính chất trọng tâm ta có: B 'G = B ' I = . 3 3
Trong tam giác vuông BGB ' có: 2 6a a 3 2 2 2
BG = BB ' - B 'G = a - = . Chọn C. 9 3
Câu 10: Cho hình hộp chữ nhật ABC .
D A' B 'C ' D ' có AB = 4, AD = 3. Mặt phẳng (ACD ') tạo với
mặt đáy một góc 60 .! Tính khoảng cách giữa hai mặt đáy của hình hộp. 6 3 12 3 4 3 5 3 A. . B. . C. . D. . 5 5 5 3
Hướng dẫn giải:
Gọi O là hình chiếu của D lên AC .
(ìACD')Ç(ABCD) = AC ï Ta có íAC ^ DO
ïAC ^ D'O î
(AC ^(ODD') ÉOD') Þ (D AC) ∑ ( (ABCD) = D OD = ) ∑ 0 ' , ' 60 AD DC 2 2 AC = 3 + 4 = . 12 5 ; DO = = AC 5 12 3
Khoảng cách giữa hai mặt đáy là 0 DD ' = . DO tan 60 = 5 Chọn đáp án B. Trang 34
DẠNG 5: KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG CHÉO NHAU. Phương pháp:
Để tính khoảng cách giữa hai đường thẳng chéo nhau ta có thể dùng một trong các cách sau:
Dựng đoạn vuông góc chung MN của a và b . Khi đó d ( ,
a b) = MN . Sau đây là một số cách dựng đoạn vuông góc chung thường dùng : Phương pháp 1
Chọn mặt phẳng (a ) chứa đường thẳng D và song song với D ' . Khi đó d(D, D ') = d(D ',(a )) Phương pháp 2
Dựng hai mặt phẳng song song và lần lượt chứa hai đường thẳng. Khoảng cách giữa hai mặt phẳng đó
là khoảng cách cần tìm.
Phương pháp 3 Dựng đoạn vuông góc chung và tính độ dài đoạn đó.
Trường hợp 1: D và D ' vừa chéo nhau vừa vuông góc với nhau
Bước 1: Chọn mặt phẳng (a ) chứa D ' và vuông góc với D tại I .
Bước 2: Trong mặt phẳng (a ) kẻ IJ ^ D '.
Khi đó IJ là đoạn vuông góc chung và d( , D D') = IJ .
Trường hợp 2: D và D ' chéo nhau mà không vuông góc với nhau
Bước 1: Chọn mặt phẳng (a ) chứa D ' và song song với D.
Bước 2: Dựng d là hình chiếu vuông góc của D xuống (a ) bằng cách lấy điểm M Î D dựng đoạn
MN ^ (a ), lúc đó d là đường thẳng đi qua N và song song với D.
Bước 3: Gọi H = d Ç D ', dựng HK ! MN
Khi đó HK là đoạn vuông góc chung và d( ,
D D') = HK = MN . Trang 35 Hoặc
Bước 1: Chọn mặt phẳng (a ) ^ D tại I .
Bước 2: Tìm hình chiếu d của D ' xuống mặt phẳng (a ).
Bước 3: Trong mặt phẳng (a ), dựng IJ ^ d , từ J dựng đường thẳng song song với D cắt D ' tại H ,
từ H dựng HM ! IJ .
Khi đó HM là đoạn vuông góc chung và d(D, D ') = HM = IJ .
Sử dụng phương pháp vec tơ !!!!" !!!" ìAM = xAB ï!!!" !!!" ïCN = yCD
a) MN là đoạn vuông góc chung của AB và CD khi và chỉ khi í!!!!" !!!" ïMN.AB = 0 ï!!!!" !!!" îMN.CD = 0 !!!" !" ìOH ^ u !" !!" 1 ïï!!!" !!"
b) Nếu trong (a ) có hai vec tơ không cùng phương u ,u thì OH = d (O,(a )) Û íOH ^ u 1 2 2 ïH Î(a) ïî !!!" !" ìOH.u = 0 1 ïï!!!" !!" Û íOH.u = 0. 2 ïH Î(a) ïî
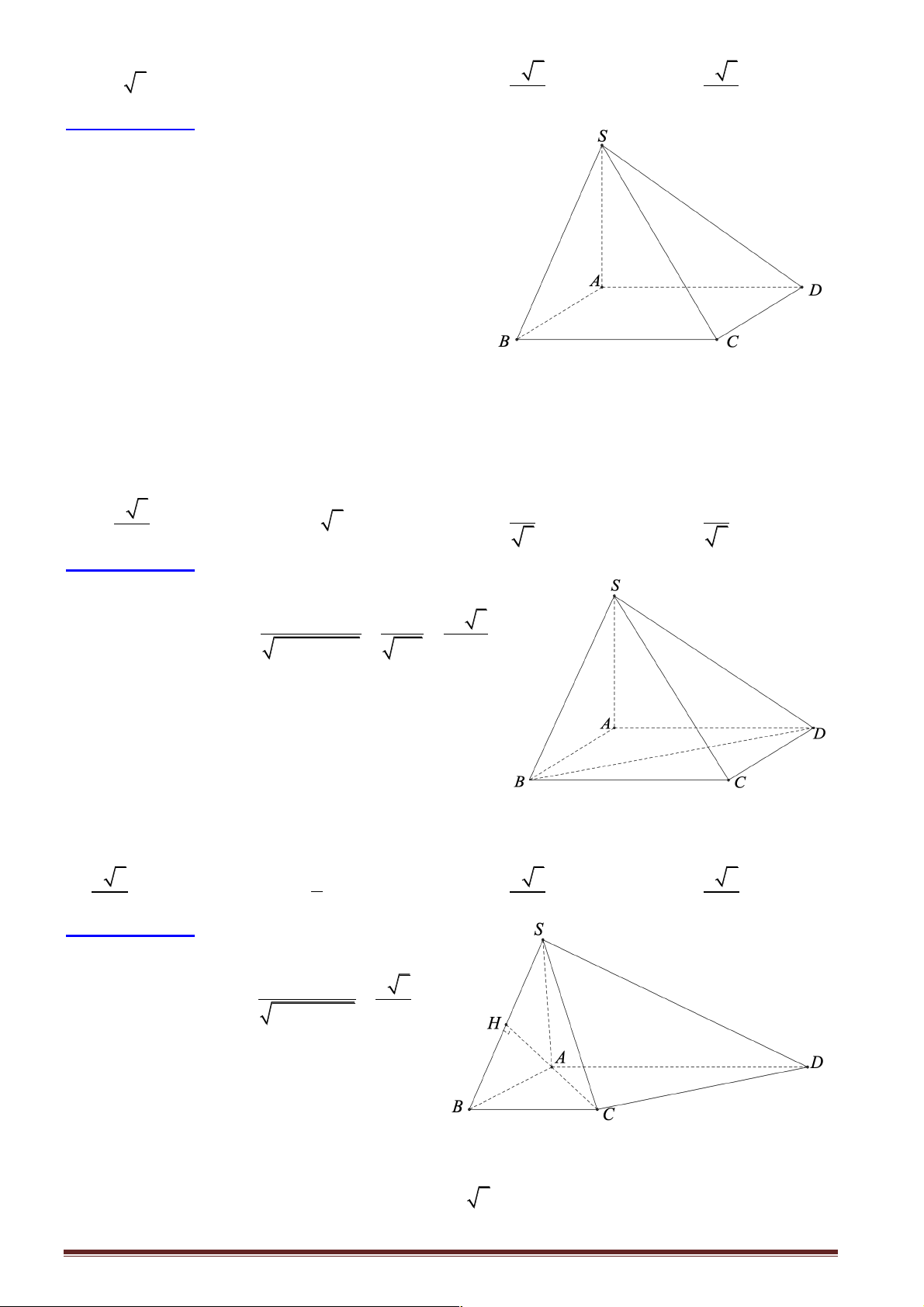
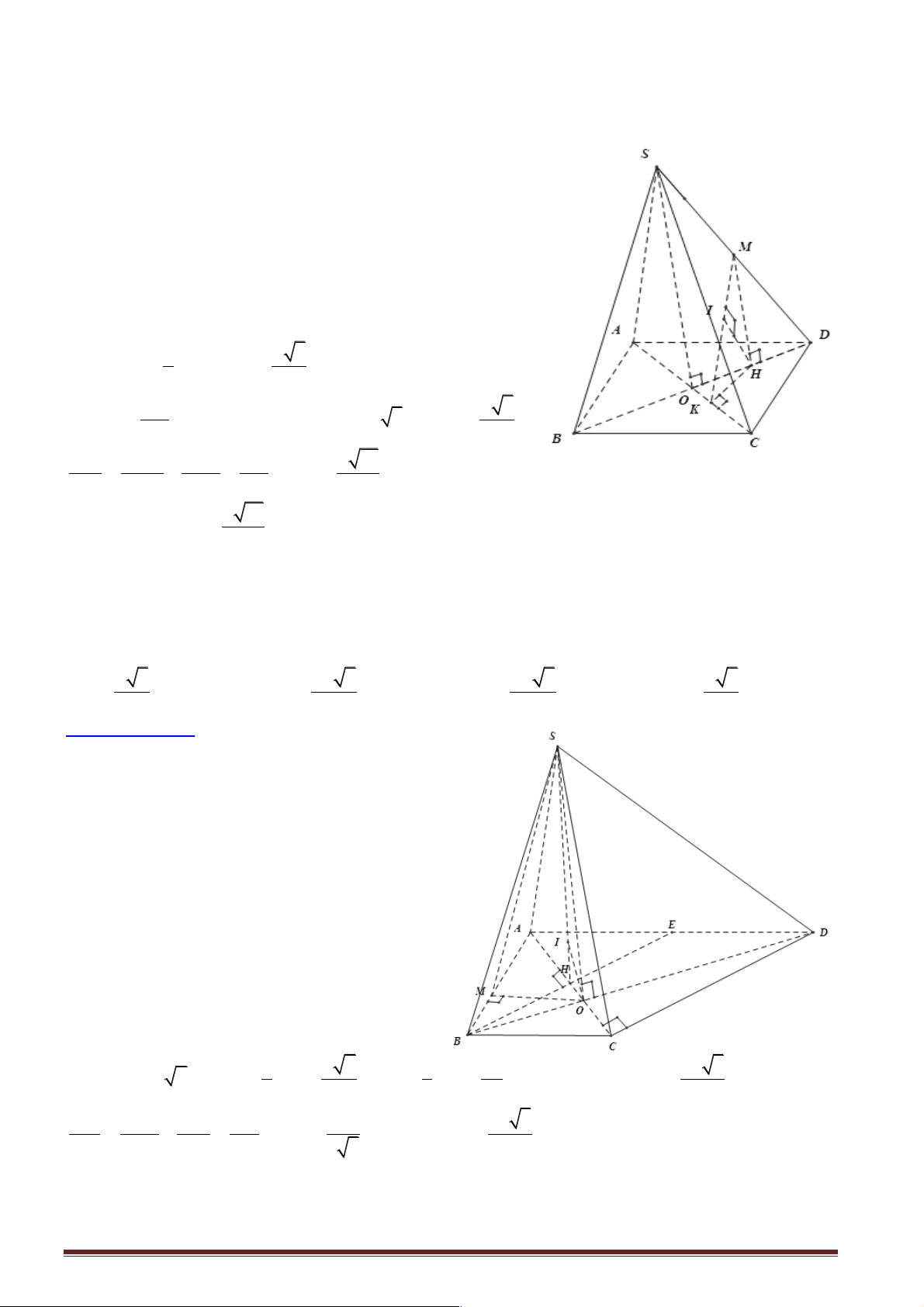
Câu 1: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, SA vuông góc với đáy
(ABCD). Gọi K, H theo thứ tự là hình chiếu vuông góc của A và O lên .
SD Chọn khẳng định đúng
trong các khẳng định sau?
A. Đoạn vuông góc chung của AC và SD là AK. B. Đoạn vuông góc chung của AC và SD là CD.
C. Đoạn vuông góc chung của AC và SD là OH. D. Các khẳng định trên đều sai.
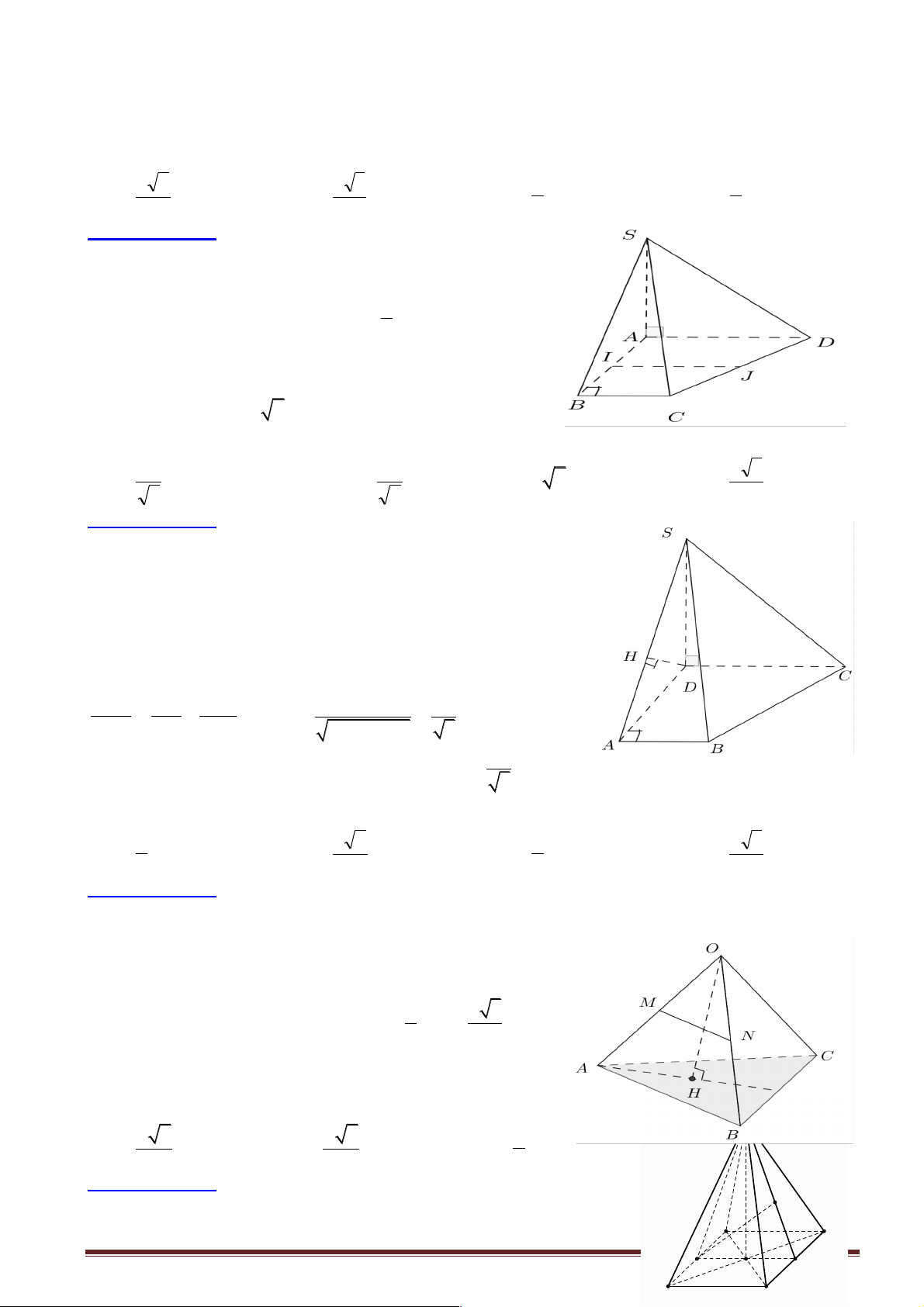
Hướng dẫn giải: Trang 36
Nếu AK ^ AC, do AK ^ AB Þ AK ^ (ABC) S
Þ AK º SA (vì SA ^ (ABC) Þ SA ^ SD Þ SA
D D có 2 góc vuông (vô K lý). H
Theo tính chất của hình vuông CD ^/ AC .
Nếu AC ^ OH, do AC ^ BD Þ AC ^ (SBD) Þ AC ^ SO Þ S D OA có 2 A D góc vuông (vô lý) O
Như vậy AC ^/ AK, AC ^/ CD, AC ^/ OH B C Chọn đáp án D.
Câu 2: Cho tứ diện đều ABCD có cạnh bằng a . Tính khoảng cách giữa AB và CD . a 3 a 2 a 2 a 3 A. B. . C. . D. . 2 3 2 3
Hướng dẫn giải: Chọn C.
Gọi M , N lần lượt là trung điểm của AB và CD . a 3
Khi đó NA = NB =
nên tam giác ANB cân, suy ra 2
NM ^ AB . Chứng minh tương tự ta có NM ^ DC , nên d ( A ; B CD) = MN . Ta có: S
= p p - AB p - BN p - AN ABN ( )( )( ) (p là nửa chu vi).
a + a 3 a + a 3 a a 2a = . . . = . 2 2 2 2 4 1 1 a Mặt khác: S = A . B MN = 2 . a MN Þ MN = . ABN 2 2 2 2 2 a a a
Cách khác. Tính 2 2 3 2
MN = AN - AM = - = . 4 4 2
Câu 3: Cho hình chóp S.ABCD có SA ^ ( ABCD), đáy ABCD là hình chữ nhật với AC = a 5 và
BC = a 2 . Tính khoảng cách giữa SD và BC . 3a 2a a 3 A. . B. . C. . D. a 3 . 4 3 2
Hướng dẫn giải: Chọn D.
Ta có: BC // (SAD) Þ d (B ;
C SD) = d (B ;
C (SAD)) = d ( ; B (SAD)). ìAB ^ AD Mà í
Þ AB ^ (SAD) Þ d ( ;
B (SAD)) = AB. îAB ^ SA Ta có: 2 2 2 2
AB = AC - BC = 5a - 2a = 3a.
Câu 4: Cho hình lập phương ABC . D A¢B C ¢ D
¢ ¢ có cạnh bằng a . Khoảng cách giữa BB ' và AC bằng: a a a 2 a 3 A. . B. . C. . D. . 2 3 2 3
Hướng dẫn giải: Chọn C. a
Ta có: d (BB¢ AC) = d (BB¢ ( ACC A¢)) 1 2 ; ; ' = DB = . 2 2 Trang 37
Câu 5: Cho hình lập phương ABC . D A¢B C ¢ D
¢ ¢ có cạnh bằng 1 (đvdt). Khoảng cách giữa AA' và BD ' bằng: 3 2 2 2 3 5 A. . B. . C. . D. . 3 2 5 7
Hướng dẫn giải: Chọn B.
Ta có: d ( AA¢ BD¢) = d (BB¢ (DBB D ¢ ¢)) 1 2 ; ; = AC = . 2 2
Câu 6: Cho tứ diện đều ABCD có cạnh bằng a . Khoảng cách giữa hai cạnh đối AB và CD bằng a 2 a 3 a a A. . B. . C. . D. . 2 2 2 3
Hướng dẫn giải: Chọn A.
Gọi M , N lần lượt là trung điểm của AB và CD . a 3
Khi đó NA = NB =
nên tam giác ANB cân, suy ra 2
NM ^ AB . Chứng minh tương tự ta có NM ^ DC , nên d ( A ; B CD) = MN . Ta có: S
= p p - AB p - BN p - AN ABN ( )( )( ) (p là nửa chu vi).
a + a 3 a + a 3 a a 2a = . . . = . 2 2 2 2 4 1 1 a Mặt khác: S = A . B MN = 2 . a MN Þ MN = . ABN 2 2 2
Câu 7: Cho khối lập phương ABCD.A' B 'C ' D '. Đoạn vuông góc chung của hai đường thẳng chéo
nhau AD và A'C ' là :
A. AA'.
B. BB '.
C. DA'. D. DD '.
Hướng dẫn giải: ìAA' ^ ï
( A'B'C 'D') í AA A C ïA C Ì î (A B C D ) ® ' ^ ' ' ' ' ' ' ' '
ìïAA' ^ ( ABCD) í ® AA' ^ AD ïîAD Ì (ABCD Chọn đáp án A.
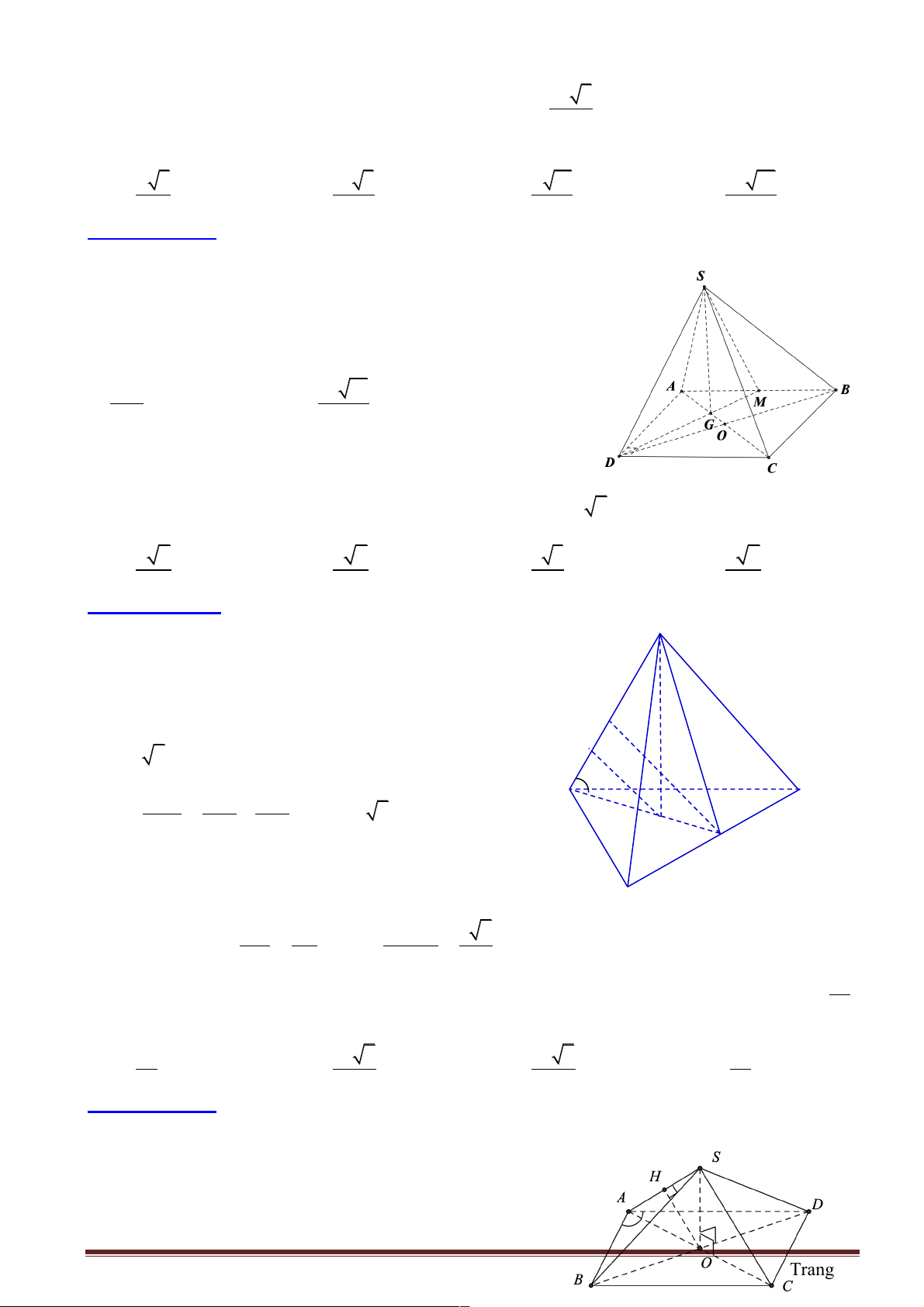
Câu 8: Cho hình chóp S.ABCD có đáy là hình vuông cạnh .
a Đường thẳng SA vuông góc với mặt phẳng đáy, SA = .
a Khoảng cách giữa hai đường thẳng SB và CD nhận giá trị nào trong các giá trị sau? A. . a B. a 2. C. a 3. D. 2 . a Trang 38
Hướng dẫn giải:
Ta có: d (C ,
D SB) = d (C ,
D (SAB)) = AD = a . Chọn phương án A.
Câu 9: Cho tứ diện OABC trong đó , OA , OB OC đôi
một vuông góc với nhau, OA = OB = OC = .
a Gọi I là trung điểm BC. Khoảng cách giữa AI và OC bằng bao nhiêu? a a 3 a A. a B. C. D. 5 2 2
Hướng dẫn giải:
Gọi J là trung điểm OB . Kẻ OH vuông góc AJ tại H .
Tam giác AOJ vuông tại O , có OH là đường cao A a . . a OA OJ 2 a OH = = = 2 2 2 OA + OJ 5 2 æ a ö a + ç ÷ è 2 ø
Ta có: OC//IJ nên OC// ( AIJ ) H Do đó: O C
d ( AI OC) = d (OC ( AIJ )) = d (O ( AIJ )) a 5 , , , = OH = . J I 5 Chọn đáp án B. B
Câu 10: Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và ,
B AB = BC = a, AD = 2 ,
a SA vuông góc với mặt đáy và SA = .
a Tính khoảng cách giữa SB và . CD a 2 a a 3 a 2 A. . B. . C. . D. . 4 2 3 2 Hướng dẫ giải: Gọi H là trung điểm AD ta có:
d(CD;SB) = d(D;(SBH)) = d(A;(SBH)) Mà 1 1 1 1 3 a 3 = + + = ® d(CD;SB) = 2 2 2 2 2 d (A;(SBH)) AS AB AH a 3 Chọn đáp án C
Câu 11: Cho hình vuông ABCD và tam giác đều SAD nằm trong hai mặt phẳng vuông góc với nhau và AD = .
a Tính khoảng cách giữa AD và . SB a 21 a 21 a 15 a 15 A. . B. . C. . D. . 3 7 5 3 Trang 39
Hướng dẫn giải:
Gọi E, F lần lượt là trung điểm AD, BC. Ta có:
AD, BC ^ (SFE), suy ra SF là hình chiếu của SB lên mặt phẳng (SEF) Nên 3 a a SE.FE 21 2 d(AD;SB) = d(E;SF) = = = a 2 2 SE + FE 3 7 2 2 a + a 4 Chọn đáp án B
Câu 12: Cho hình hộp chữ nhật ABC .
D A B C D có AA = 2 ,
a AD = 4a . Gọi M là trung điểm . AD 1 1 1 1 1
Khoảng cách giữa hai đường thẳng A B và C M bằng bao nhiêu? 1 1 1 A. 3 . a B. 2a 2 . C. a 2. D. 2 . a
Hướng dẫn giải:
Ta có A B //C D suy ra 1 1 1 1
d ( A B ,C M = d A B , C D M = d A , C D M 1 1 1 ) ( 1 1 ( 1 1 )) ( 1 ( 1 1 )) Vì AA = 2 ,
a AD = 4a và M là trung điểm AD nên A M ^ D M , 1 1 1
suy ra A M ^ C D M 1 ( 1 1 )
Þ d (A , C D M = AM = 2a 2 1 ( 1 1 )) . 1 Chọn đáp án B.
Câu 13: Cho hình lập phương ABC . D A¢B C ¢ D ¢ ¢ cạnh bằng .
a Khoảng cách giữa hai đường thẳng
AD¢ và A¢B¢ bằng bao nhiêu ? a 2 a 3 a 3 A. a 2. B. . C. . D. . 2 3 2
Hướng dẫn giải:
ìA'B ' ^ A' A Ta có í
Þ A'B ' ^ ( ADD' A').
îA'B ' ^ A'D'
Gọi H là giao điểm của AD ' với A' D .
Þ A' H ^ AD '
ìA' H ^ AD ' a 2 í
Þ d ( A'B '; AD ') = A'H = .
îA' H ^ A' B ' 2 Chọn B.
Câu 14: Cho hình lập phương ABC . D A¢B C ¢ D ¢ ¢ có cạnh bằng .
a Khoảng cách giữa BB¢ và AC bằng a a a 2 a 3 A. . B. . C. . D. . 2 3 2 3
Hướng dẫn giải: ( B ì C ï AA C ¢ C ¢ ) É AC Vì í
nên d (BB ;¢ AC) = d (BB ;¢( AA C ¢ C ¢ )). (AA C ¢ C ¢ )//BB¢ ïî I
Gọi I = AC Ç BD . Vì ABC . D A¢B C ¢ D ¢ ¢ là hình A D lập phương nên I B ^ ( AA C ¢ C ¢ ). B¢ a C¢
Suy ra d (BB¢ AC) = d (BB¢ ( AA C ¢ C ¢ )) 2 ; ; = IB = . 2 A¢ Trang 40 D¢ Chọn đáp án C.
Câu 15: Hình hộp chữ nhật ABC . D A¢B C ¢ D
¢ ¢ có AB = 3, AD = 4, AA¢ = 5. Khoảng cách giữa hai
đường thẳng AC và B D ¢ ¢ bằng bao nhiêu ? A. 34 . B. 41. C. 5 . D. 8 .
Hướng dẫn giải: ìï (ABCD)//(A B ¢ C ¢ D ¢ ¢) Ta có í ïAC Ì î (ABCD);B D ¢ ¢ Ì ( A B ¢ C ¢ D ¢ ¢)
Þ d ( AC;B D
¢ ¢) = d ( ABCD);(A B ¢ C ¢ D ¢ ¢)) = AA¢ = 5 Chọn đáp án C.
Câu 16: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng . h Tính khoảng
cách giữa hai đường thẳng chéo nhau SA và . BD ah ah ah ah A. . B. . C. . D. . 2 2 3a + h 2 2 a + h 2 2 2a + h 2 2 a + 2h
Hướng dẫn giải:
Gọi O = AC Ç BD . Gọi H là hình chiếu của O lên
SA . Vì S.ABCD là hình chóp đều nên S
BD ^ (SAC) Þ BD ^ OH . Suy ra OH
là đoạn vuông góc chung của BD, . SA OS.OA a 2.h ah OH = = = . H 2 2 2 2 2 2 OS + OA 2h + a 2h + a 2 2 A D Chọn đáp án D. O B C
Câu 17: Cho hai tam giác đều ABC và ABD cạnh x nằm trong hai mặt phẳng vuông góc với nhau.
Khi đó khoảng cách giữa hai đường thẳng AB và CD bằng x 6 x 3 x 3 x 6 A. . B. . C. . D. . 4 4 3 2
Hướng dẫn giải:
Gọi I, J lần lượt là trung điểm của AB, CD .
(ABC) ^ (ABD) và hai tam giác ABC và ABD đều nên
AB ^ (CDI ) và CI = DI suy ra IJ là đoạn vuông góc chung
Của hai đường thẳng AB, CD .
Vì tam giác CDI vuông tại I và J là trung điểm của CD 2 æ x 3 ö 2.ç ÷ 2 2 CD 2CI è ø x 6 Nên IJ = = = = . 2 2 2 4 Chọn đáp án A.
Câu 18: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt đáy (ABCD) và SA = .
a Tính theo a khoảng cách giữa SB và . CD Trang 41 a 2 a 3 A. a 2. B. a . C. . D. . 2 2
Hướng dẫn giải: Ta có d (S ;
B CD) = d (C ;
D (SAB)) = d ( ;
D (SAB)) = DA = a. Chọn đáp án B.
Câu 19: Cho hình chóp S.ABCD có mặt đáy ABCD là hình chữ nhật với AB = a, AD = 2a, SA
vuông góc với mặt đáy và SA = .
a Tính khoảng cách giữa SA và BD theo . a a 3 2a 2a A. . B. a 2. C. . D. . 2 3 5
Hướng dẫn giải:
Vì SA ^ ( ABCD) tại A và BD Ì ( ABCD) nên 2
d (SA BD) = d ( A BD) . AB AD 2a 2a 5 ; ; = = = . 2 2 2 AB + AD 5a 5 Chọn đáp án D.
Câu 20: Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và ,
B AB = BC = a, AD = 2 , a
SA vuông góc với mặt đáy và SA = .
a Tính khoảng cách giữa AD và . SB a 2 a a 3 a 2 A. . B. . C. . D. . 4 2 3 2
Hướng dẫn giải:
Vì AD ^ (SAB) tại A và SB Ì (SAB) nên
d ( AD SB) = d ( A SB) AS.AB a 2 ; ; = = . 2 2 AS + AB 2 Chọn đáp án D.
Câu 21: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh .
a Biết hai mặt bên (SAB) và
(SAD) cùng vuông góc với mặt phẳng đáy và SA = a 2. Khoảng cách giữa AD và SB là Trang 42 a 2 a 6 a 3 A. a . B. . C. . D. . 2 3 4
Hướng dẫn giải:
Vì hai mặt bên (SAB) và (SAD) cùng vuông góc
với mặt phẳng đáy nên SA ^ ( ABCD).
Vì AD ^ (SAB) tại A và SB Ì (SAB) nên
d ( AD SB) = d ( A SB) AS.AB a 6 ; ; = AH = = . 2 2 AS + AB 3 Chọn đáp án C.
Câu 22: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh .
a Biết hai mặt bên
(SAB) và (SAD) cùng vuông góc với mặt phẳng đáy và SA = a 2. Khoảng cách giữa SO và AB là a 2 a 6 a 3 A. a . B. . C. . D. . 3 3 4
Hướng dẫn giải:
Gọi E là trung điểm của AD khi đó d (S ;
O AB) = d (A ;
B (SOE)) = AH , với H là hình
chiếu của A lên SE . a a 2. . EA ES a 2 Ta có 2 AH = = = . 2 2 2 EA + ES a 3 2 2a + 4 Chọn đáp án B.
Câu 23: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh .
a Biết hai mặt bên
(SAB) và (SAD) cùng vuông góc với mặt phẳng đáy và SA = a 2. Khoảng cách giữa BD và SC là
A. độ dài của đoạn thẳng OA .
B. độ dài của đoạn thẳng BC .
C. khoảng cách từ điểm O đến cạnh SC .
D. khoảng cách từ điểm S đến đoạn BD .
Hướng dẫn giải:
Vì hai mặt bên (SAB) và (SAD) cùng vuông
góc với mặt phẳng đáy nên SA ^ ( ABCD).
Suy ra BD ^ (SAC) tại O , mà SC Ì (SAC) nên
Khoảng cách giữa BD và SC bằng
khoảng cách từ điểm O đến cạnh SC . Chọn đáp án C.
Câu 24: Cho hình chóp S.ABCD có SA ^ ( ABCD), đáy ABCD là hình chữ nhật với AC = a 5 và
BC = a 2. Tính khoảng cách giữa SD và BC. 3a 2a a 3 A. . B. . C. . D. a 3 . 4 3 2
Hướng dẫn giải: Trang 43
Dễ thấy BA ^ (SAD)
BC / / AD Þ BC / / (SAD) Þ d (BC,SD) = d (BC,(SAD)) = BA
Xét tam giác vuông ABC có 2 2
AB = 5a - 2a = a 3 Đáp án D
Câu 25: Cho hình chóp S.ABCD có ABCD là hình vuông cạnh ,
a SA ^ ( ABCD) và SA = . a Khoảng
cách giữa hai đường thẳng chéo nhau SC và BD bằng a 6 A. . B. a 6 . C. a 3 . D. a . 6
Hướng dẫn giải:
Dựng Cx / /BD , (a) = (SC,Cx)
Þ BD / / (a) Þ d (BD,SC) = d (BD,(a))
d (BD (a) = d (O (a) 1 , , = d ( , A (a) 2
Dựng AK ^ SC . Dễ thấy AK ^ (a) Þ d ( , A (a)) = AK 1 1 1 1 1 1 a 6 = + Û = + Þ AK = 2 2 2 2 2 2 AK SA AC AK a 2a 3 a
Vậy d (O (a) 6 , = 6 Đáp án A.
Câu 26: Cho hình chóp S.ABCD có ABCD là hình vuông cạnh ,
a SA ^ ( ABCD) và SA = . a Khoảng
cách giữa hai đường thẳng chéo nhau SB và CD bằng A. a . B. a 2. C. a 3 . D. a 6 .
Hướng dẫn giải:
Dễ thấy AD ^ (SAD)
CD / / AB Þ CD / / (SAB) Þ d (SB,DC) = d (CD,(SAB)) = AD = a
Xét tam giác vuông ABC có 2 2
AB = 5a - 2a = a 3 Đáp án A
Câu 27: Cho lăng trụ tam giác đều ABC.A B C có cạnh đáy bằng a, cạnh bên bằng . b Tính khoảng 1 1 1
cách giữa AB và CC . 1 a 2 a 3 ab 3 ab 3 A. . B. . C. . D. . 2 2 2 2 4a + 3b 2 2 3a + 2b
Hướng dẫn giải: Trang 44
Gọi M là trung điểm của AB
CC / AA Þ CC / ABB A Þ d AB,CC 1 1 1 ( 1 1 ) ( 1 ) . = d ( a 3 CC , ABB A = CM = 1 ( 1 1 ) 2 Đáp án B.
Câu 28: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và AB = 2a, BC = . a Các cạnh bên
của hình chóp bằng nhau và bằng a 2. Gọi E và F lần lượt là trung điểm của AB và CD; K là điểm bất kỳ trên .
AD Khoảng cách giữa hai đường thẳng EF và SK là: a 3 a 6 a 15 a 21 A. . B. . C. . D. . 3 3 5 7
Hướng dẫn giải:
Gọi O = AC Ç BD, I là trung điểm cạnh đáy BC.
Do SA = SB = SC = SD nên SO ^ (ABCD)
Từ đó ta chứng minh được BC ^ (SOI ) S
Þ OH ^ (SBC) (với OH ^ BC tại SI ) ìEF //(SBC) Do í
nên d (EF, SK ) = d (EF,(SBC)) = OH îSK Ì (SBC) E H 1 a 5 a 3 A B
Thực hiện tính toán để được OC = AC = Þ SO = 2 2 2 O I . SO OI a 21
Cuối cùng d (EF, SK ) = OH = = 2 2 7 SO + OI D F C Chọn đáp án D.
Câu 29: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại , B AB = ,
a cạnh bên SA vuông góc với đáy và
SA = a 2. Gọi M là trung điểm của .
AB Khoảng cách giữa SM và BC bằng bao nhiêu? a 2 a a 3 a 3 A. B. C. D. 3 2 3 2
Hướng dẫn giải:
Gọi N là trung điểm của cạnh đáy AC. Khi đó BC//(SMN) S
Nên d (SM, BC) = d ( ,
B (SMN)) = d ( , A (SMN))
Gọi H là hình chiếu vuông góc của A trên đoạn SM .
Ta có thể chứng minh được MN ^ (SAM ), từ đó
AH ^ SMN Þ d ( A SMN ) . SA AM a 2 ( ) ,( ) = AH = = H 2 2 3 SA + AM N A Chọn đáp án A. C M B
Câu 30: Cho tứ diện đều ABCD cạnh .
a Khoảng cách giữa hai đường thẳng AB và CD bằng bao nhiêu? a a a A. B. C. a D. 2 2 3
Hướng dẫn giải: Trang 45
Gọi M , N lần lượt là trung điểm các cạnh CD, AB
Tam giác MAB cân tại M và D NCD cân tại N
do đó MN ^ A ,
B MN ^ CD 2 2 A Þ ( æ a ö æ a ö a d AB,CD) 3 2 2 2
= MN = BM - NB = ç ÷ - = ç ÷ ç ÷ 2 è ø è 2 ø 2 N Chọn đáp án B. B D O M C
Câu 31: Cho hình hộp chữ nhật ABC . D A¢B C ¢ D
¢ ¢ có AB = AA¢ = a , AC = 2a . Tính khoảng cách giữa AC¢ và CD¢ : a 2 a a 3 a A. . B. . C. . D. . 2 3 2 2
Hướng dẫn giải:
þ Ta có hình chiếu của AC¢ trên mặt phẳng (DCC D
¢ ¢) là DC¢ ^ D C ¢ nên
AC¢ ^ D'C Þ ( ADC B
¢ ') ^ D'C tại điểm H là trung điểm CD¢ . Từ H ta kẻ
HK ^ AC¢ Þ d ( AC ,¢ D C ¢ ) = HK . 2 1 1 1 5a 6 30 30 þ Ta có = + = Þ d = a = a Þ HK = a 2 2 2 4 d 3a 2a 6a 5 5 10 Chọn đáp án D.
Câu 32: Cho hình lập phương ABC . D A¢B C ¢ D
¢ ¢ có cạnh bằng 1 (đvd). Khoảng cách giữa AA¢ và BD¢ bằng: 2 2 3 5 3 2 A. B. C. D. 5 7 3 2
Hướng dẫn giải:
AA'/ /BB ' Þ AA'/ /(DBB'D') Ta có : 2
Þ d(AA') = d ( ,
A (DBB ' D ')) = AO = . 2
Câu 33: Khoảng cách giữa hai cạnh đối trong một tứ diện đều Trang 46 cạnh a là : a 2 A. a 2. B. a 3 . C. a 5 . D. . 2
Hướng dẫn giải:
Gọi M là trung điểm DC , H là hình chiếu
vuông góc của M lên AB . ìBM ^ CD Ta có: í Þ CD ^ (ABM) îAM ^ CD CD ì ^ MH í
Þ MH = d(AB,CD) îAB ^ MH 2S a 2 ABM MH = = AB 2 Chọn đáp án D.
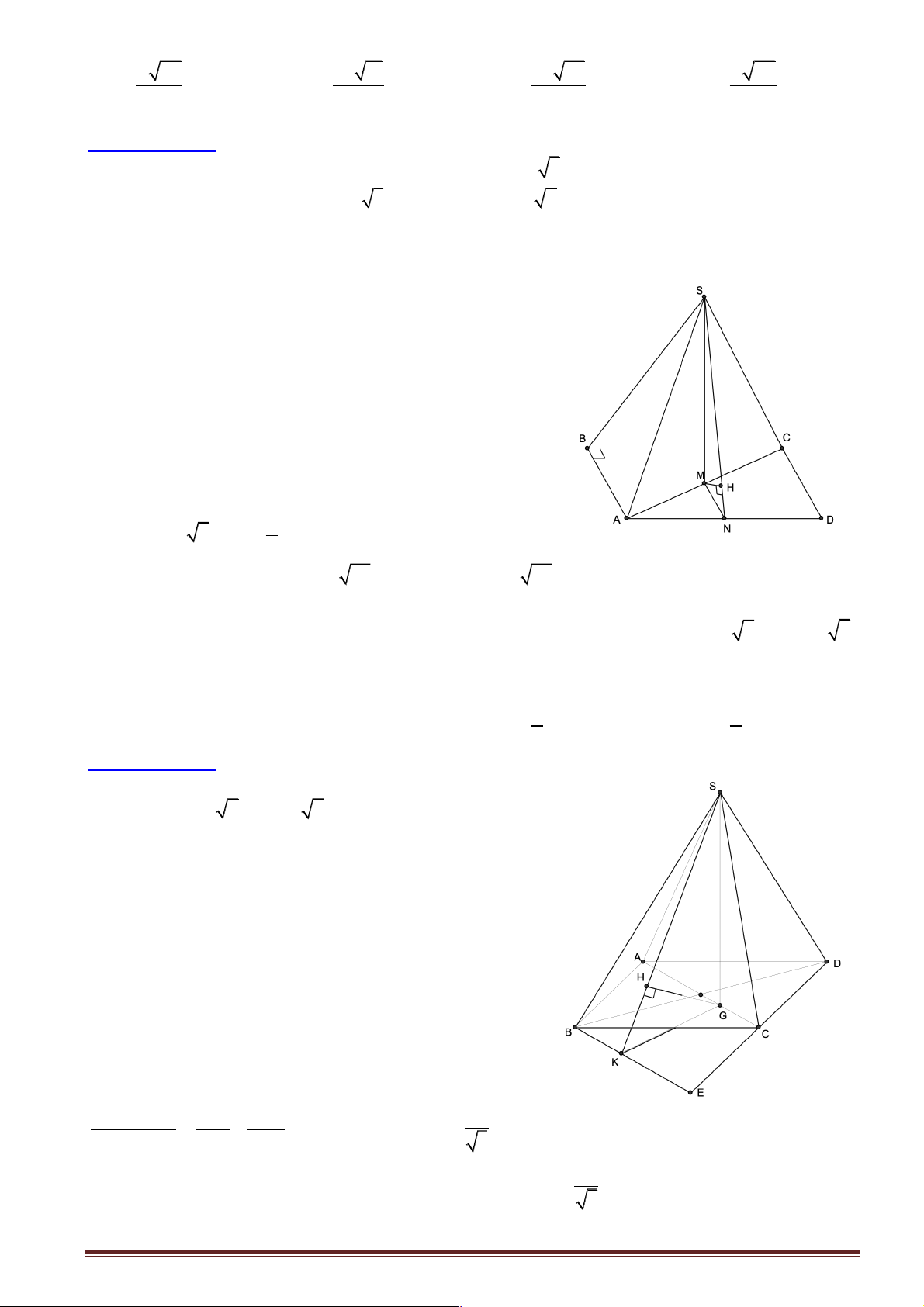
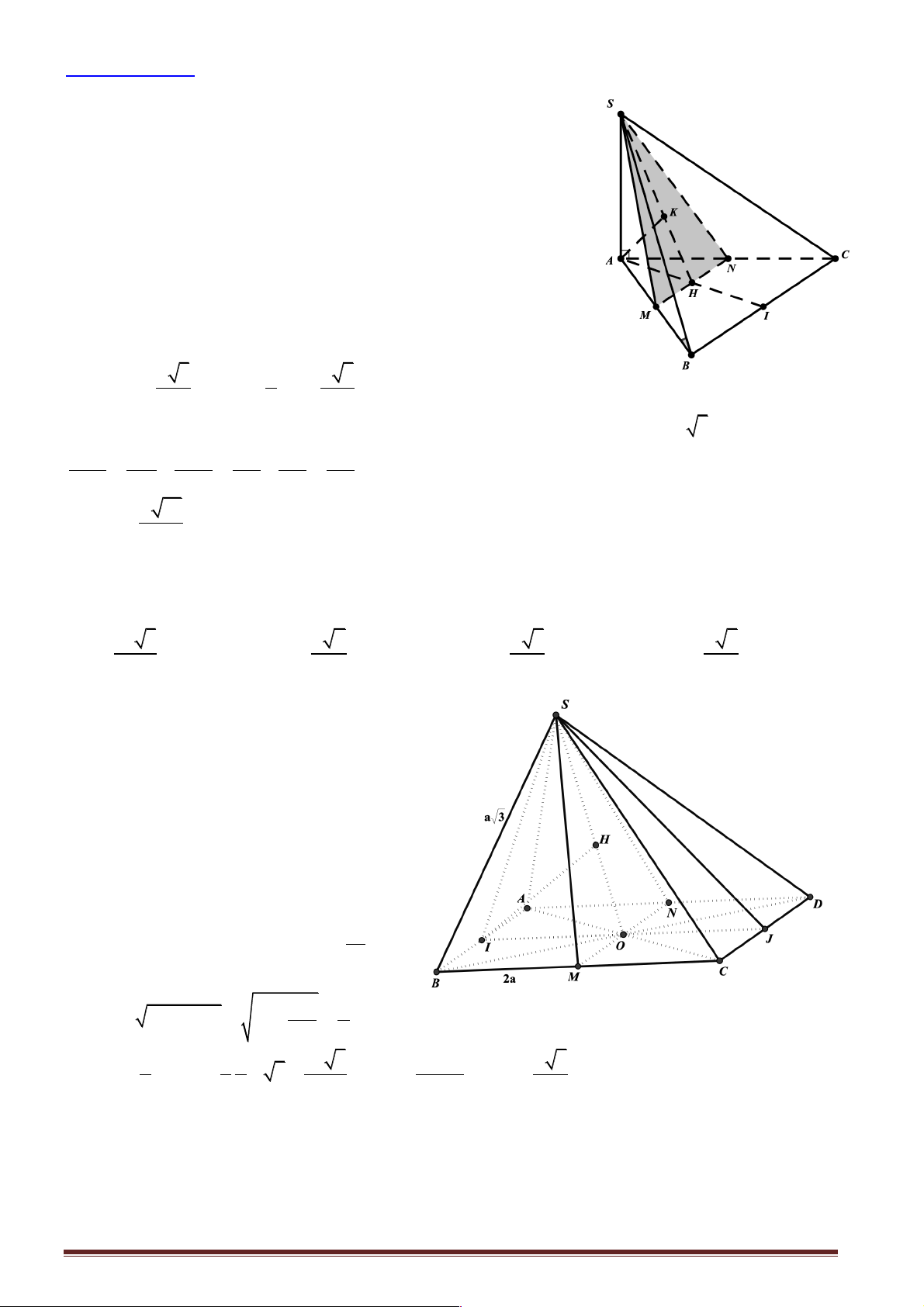
Câu 34: Cho hình chóp S.ABCD có đáy ABCD
là hình chữ nhật với AC = a 5 , BC = a 2 .
Đường thẳng SA vuông góc với mặt phẳng đáy. Tính khoảng cách giữa SD và BC. 2a a 3 3a A. . B. . C. . D. a 3. 3 2 4
Hướng dẫn giải:
þ Khoảng cách giữa SD và BC : d (BC, SD) = CD = a 3. Chọn đáp án D.
Câu 35: Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a . Các cạnh bên
SA = SB = SC = SD = a 2 . Khoảng cách giữa hai đường thẳng AD và SB là: a 7 a 42 a 6 a 6 A. B. C. D. 2 6 7 2
Hướng dẫn giải:
þ Khoảng cách giữa hai đường thẳng AD và SB là: HK . 2 2 2 a a a a a þ 2 7 7 6
SH = SM = 2a - = ; SO = - = . 4 2 4 4 2 6 a . . a SO MH a 42 þ Có : 2 HK = = = . SM 7 7 a 2 Chọn đáp án C. a 17
Câu 36: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SD = . Hình chiếu vuông góc 2
H của đỉnh S lên mặt phẳng ( ABCD) là trung điểm của cạnh .
AB Gọi K là trung điểm của . AD
Tính khoảng cách giữa hai đường SD và HK theo . a Trang 47 3a a 3 a 21 a 7 A. . B. . C. . D. . 7 5 7 5
Hướng dẫn giải: S
Ta có: HK / /BD Þ HK / / (SBD)
Þ d (HK,SD) = d (HK,(SBD)) = d (H,(SBD))
Kẻ HI ^ BD , HJ ^ SI J A K D
Khi đó: BD ^ HI , BD ^ SH Þ BD ^ (SHI ) Þ BD ^ HJ H O
Nên HJ ^ (SBD) Þ d (H,(SBD)) = HJ I 1 a 2 B
Ta có: HI = AO = và C 2 2 5 2 2 2 2 2 2 2 2
HD = HA + AD = a Þ SH = SD - HD = 3a 4 2 2 SH .HI 3 a 21 a Do đó: 2 2 HJ = = a Þ HJ =
. Vậy d (SD HK ) 21 , = 2 2 SH + HI 7 7 7 Chọn đáp án C.
Câu 37: Cho hình lăng trụ đứng . ABC A¢B C
¢ ¢ có đáy là tam giác vuông tại ,
A AB = AC = b và có cạnh bên bằng .
b Khoảng cách giữa hai đường thẳng AB¢ và BC bằng b 2 b 3 A. b . B. . C. b 3 . D. . 2 3
Hướng dẫn giải: A¢ C¢
Kẻ Ax / /BC Þ BC / / ( AB x ¢ )
Þ d (BC, AB¢) = d (BC,(AB x¢)) = d ( , B ( AB x ¢ )) B¢
Kẻ BD ^ Ax, BK ^ DB¢ Ta có: AD ^ ,
BD AD ^ BB¢ Þ AD ^ (BDB¢) K Þ AD ^ BK . Dó đó: A
BK ^ ( ADB¢) Þ d ( ,
B ( ADB¢)) = BK C b 2 D
Khi đó: BD = AH = H 2 x 2 2 BD .BB¢ b 3 Nên 2 BK = = B 2 2 BD + BB¢ 3 Chọn đáp án D.
Câu 38: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và ∑
ABC = 60 .! Hai mặt phẳng
(SAC) và (SBD) cùng vuông góc với đáy, góc giữa hai mặt phẳng (SAB) và (ABCD) bằng 30 .!
Khoảng cách giữa hai đường thẳng ,
SA CD theo a bằng: a 3 a 3 a 3 A. . B. . C. . D. a 3 . 2 4 3
Hướng dẫn giải:
Gọi O = AC Ç BD . Kẻ OI ^ AB , OH ^ SI Ta có: S
(SAC) ^ (ABCD),(SBD) ^(ABCD) Þ SO ^ (ABCD) (
ì SAB) Ç( ABCD) = AB ï Ta lại có: ∑ 0 íAB ^ OI Þ SAO = 30 ï H AB ^ SI î C B O Trang 48 I D A
Khi đó: CD / / AB Þ CD / / (SAB) Þ d (C ,
D SA) = d (C ,
D (SAB)) = d (C,(SAB)) = 2d ( , O (SAB)) Ta có: AB ^ S ,
O AB ^ OI Þ AB ^ (SOI ) Þ AB ^ OH
Nên OH ^ (SAB) Þ d ( ,
O (SAB)) = OH 1 1 a 3
Mà OC = AB = a nên ∑ ∑ 0 0
ABC = OCD = 60 Þ OI = OC.sin 60 = . 2 2 4 a 3 a 3 Do đó: 0 OH = OI.sin 30 =
Þ d (CD, SA) = 2OH = 8 4 Chọn đáp án B.
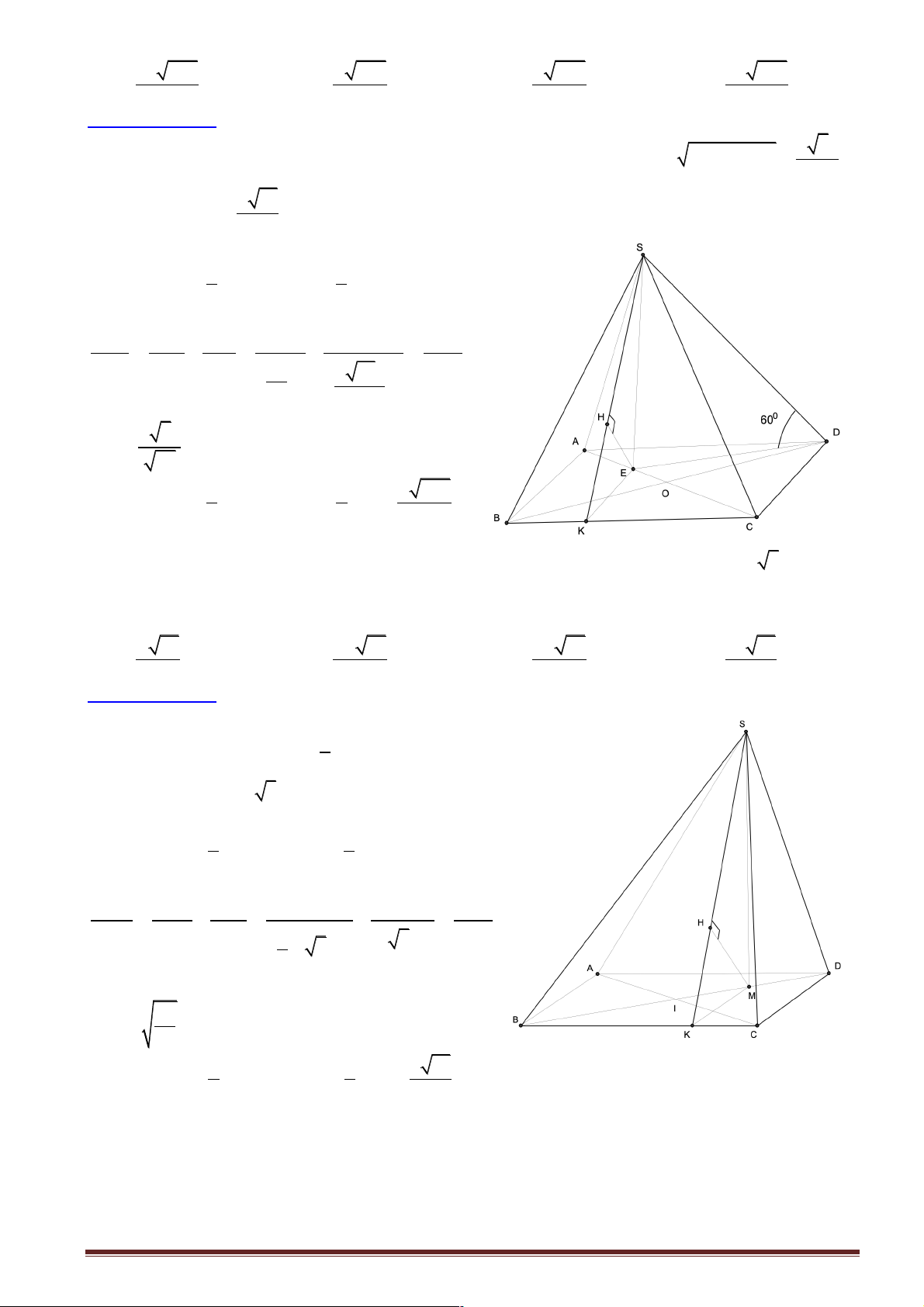
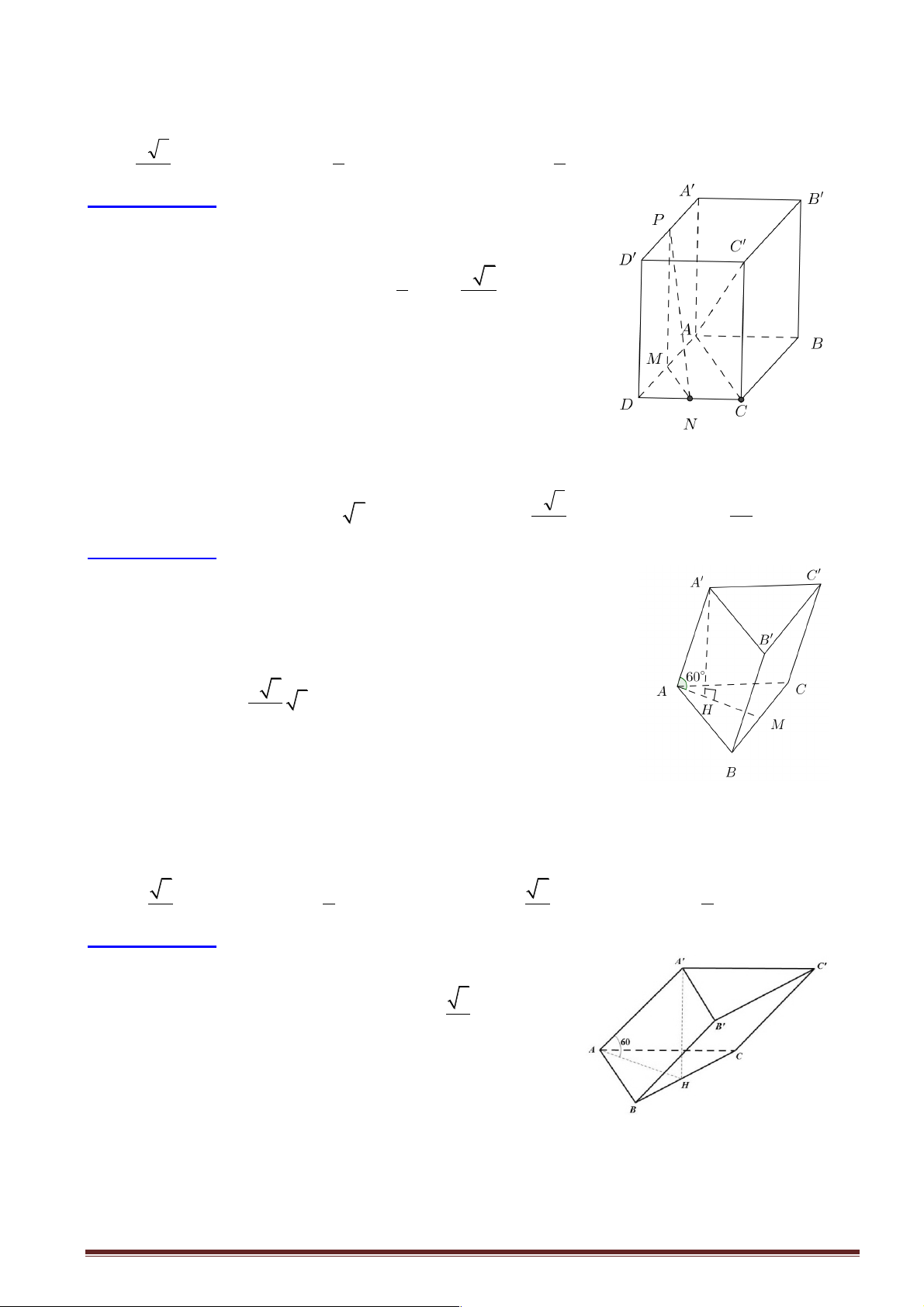
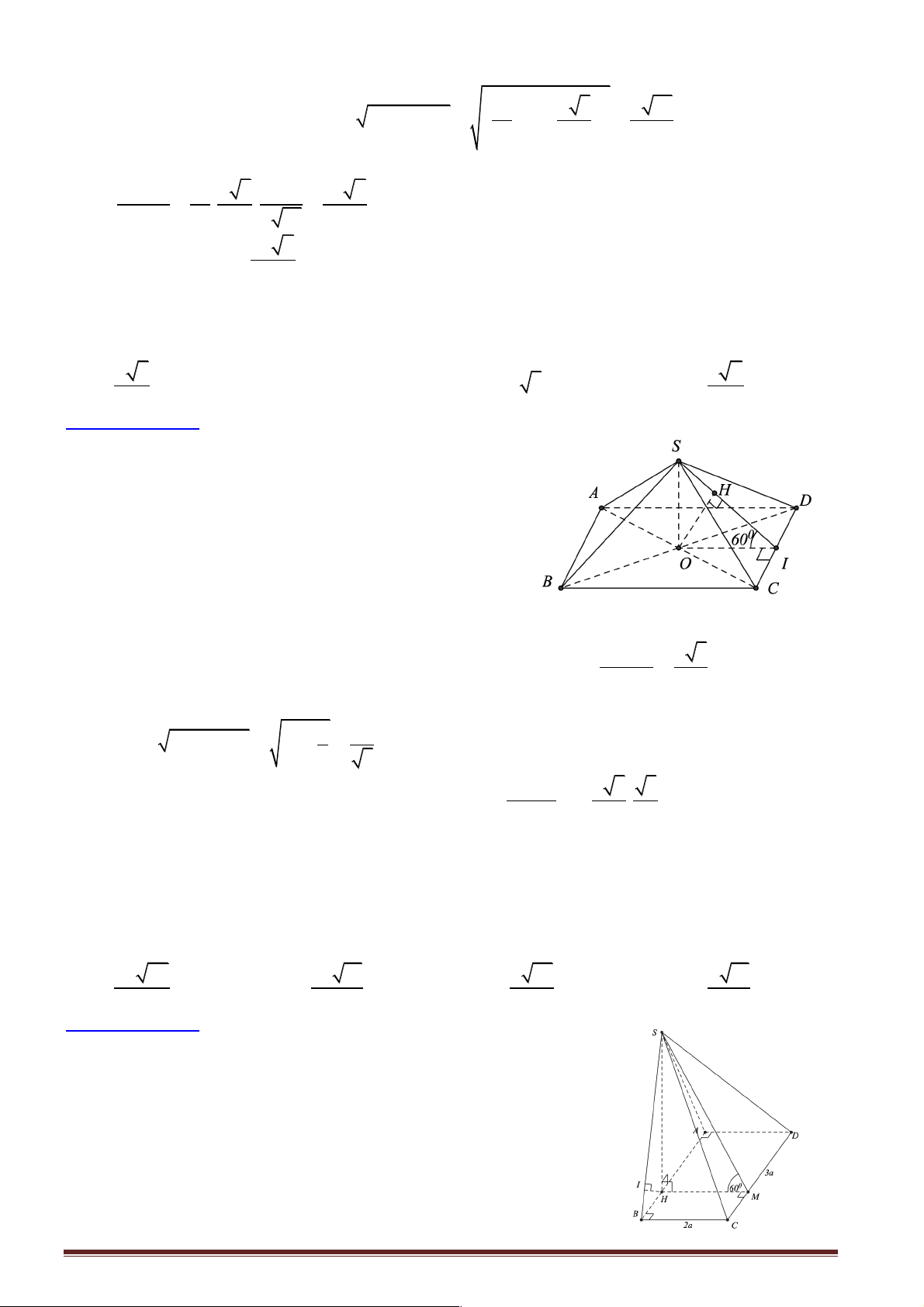
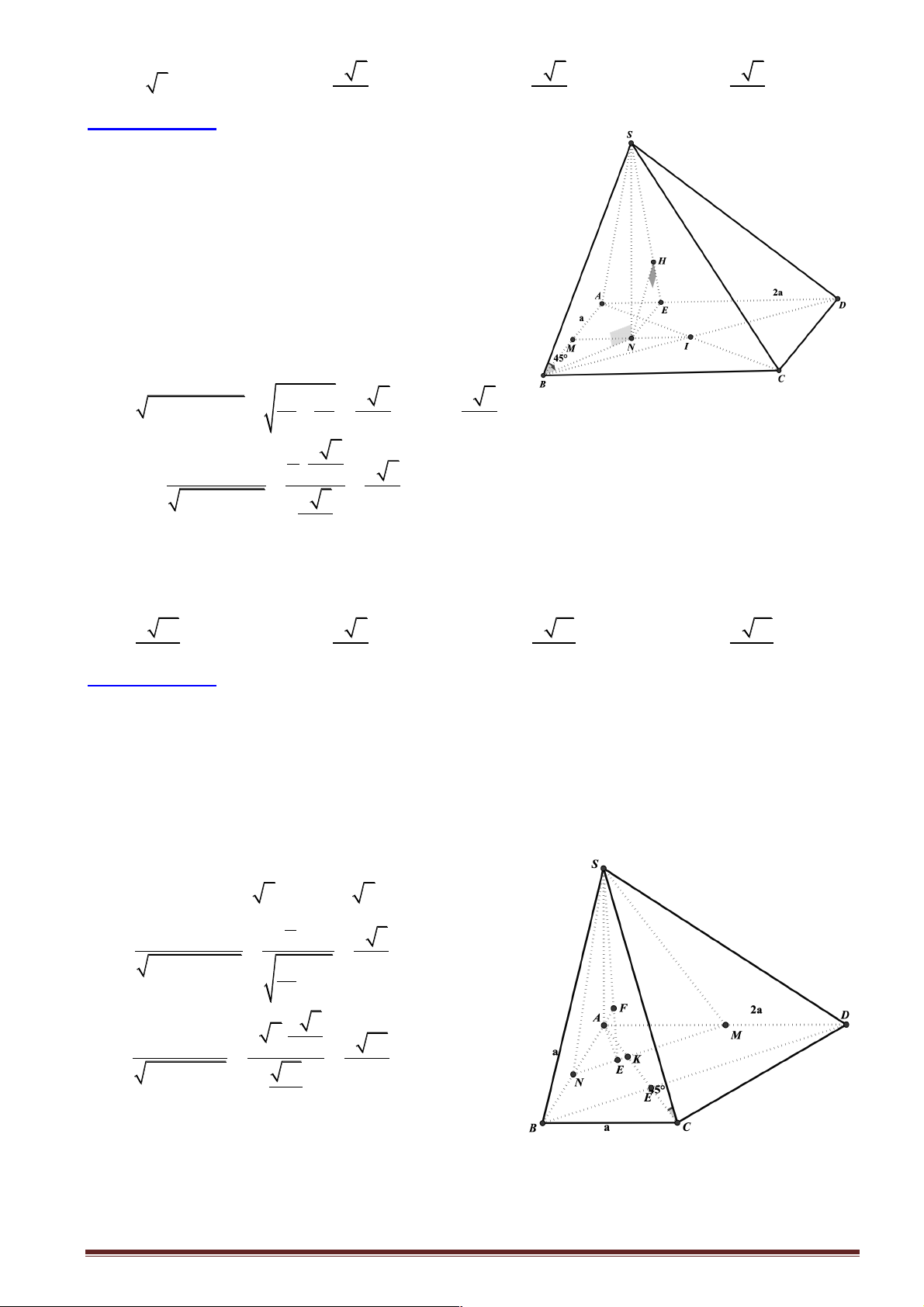
Câu 39: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm I, AB = 2 ;
a BD = 3AC , mặt bên
SAB là tam giác cân đỉnh ,
A hình chiếu vuông góc của đỉnh S trên mặt phẳng đáy trùng với trung
điểm H của AI. Khoảng cách giữa hai đường thẳng SB và CD bằng: a 35 2a 35 2a 7 2a 35 A. . B. . C. . D. . 7 7 7 35
Hướng dẫn giải: S
Ta có: CD / / AB Þ CD / / (SAB) Þ d (C ,
D SB) = d (C ,
D (SAB)) = d (C,(SAB)) = 4d (H,(SAB))
Kẻ MH ^ AB, HK ^ SM
Ta có: AB ^ HM , AB ^ SH Þ AB ^ (SHM ) Þ HK ^ AB K
Khi đó: HK ^ (SAB) Þ d (H,(SAB)) = HK A BI D Ta có: ∑ ∑ 0 tan BAC =
= 3 Þ BAC = 60 Þ ABC D đều M IA H 1 1 I
Þ AC = 2a Þ AH = AC = a 4 2 B C a 3 2 15a Mà 0 HM = AI.sin 60 = và 2 2 2
SH = SA - AH = 4 4 2 2 2 HM .SH 5a a 35 2a 35 Do đó: 2 HK = = Þ HK =
Þ d CD, SB = 4HK = 2 2 ( ) HM + SH 28 14 7 Chọn đáp án B.
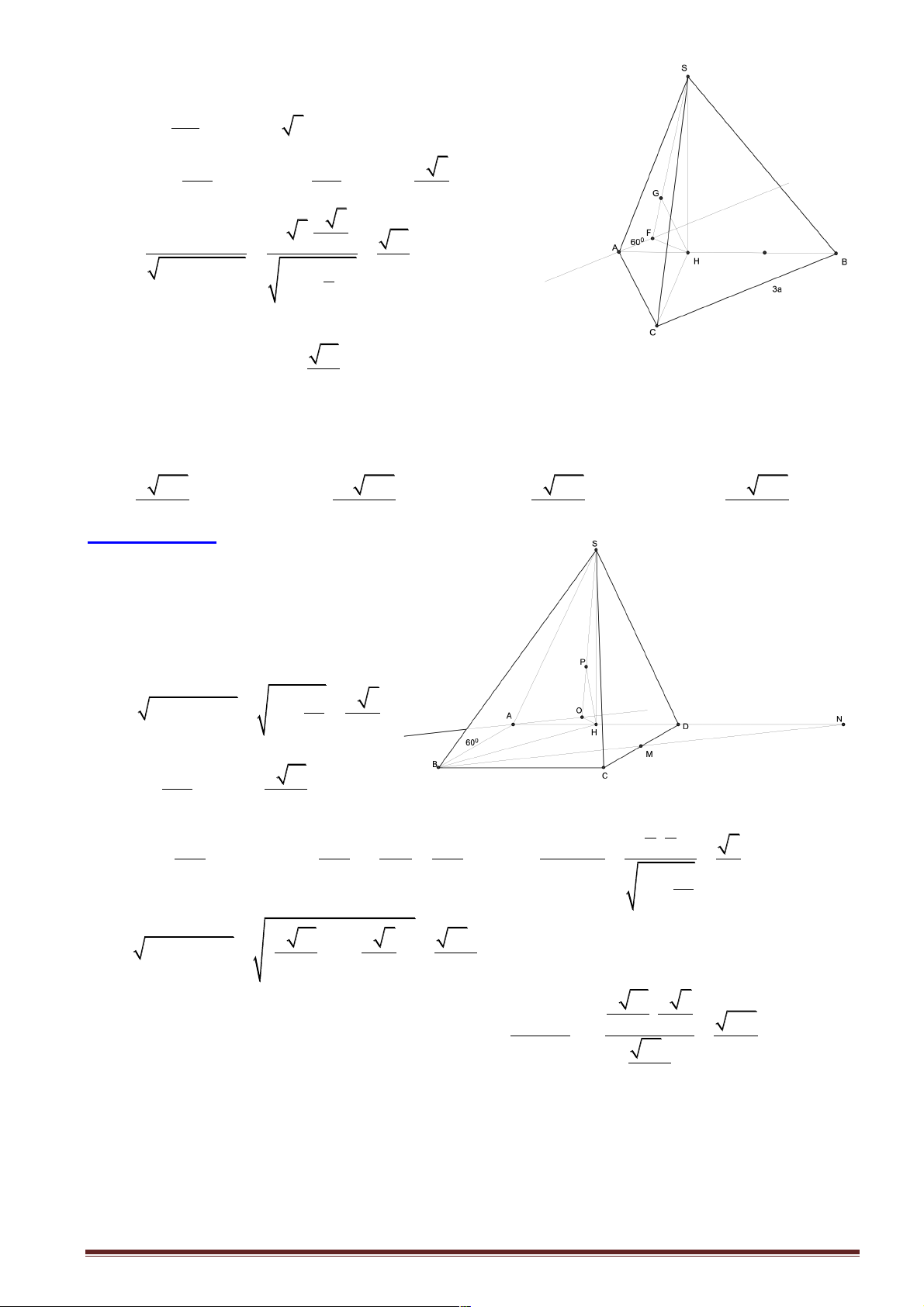
Câu 40: Cho hình chóp S.ABC có đáy là tam giác đều cạnh .
a Hình chiếu vuông góc của S trên mặt
phẳng ( ABC) là điểm H thuộc cạnh AB sao cho HA = 2 .
HB Góc giữa đường thẳng SC và mặt
phẳng ( ABC) bằng 60 .! Khoảng cách giữa hai đường thẳng SA và BC theo a là: a 42 a 42 3a 42 3a 42 A. . B. . C. . D. . 8 4 8 4
Hướng dẫn giải:
Kẻ Ax / /BC, HI ^ , Ax HK ^ SI .
Ta có: BC / / Ax Þ BC / / (SAx)
Þ d (BC SA) = d (BC (SAx)) = d (B (SAx)) 3 , , ,
= d (H,(SAx)) S 2
Ta lại có: AI ^ HI, AI ^ SH Þ AI ^ (SHI ) Þ AI ^ HK
Nên HK ^ (SAI ) Þ d (H,(SAI )) = HK
Gọi M là trung điểm của AB K B C H Trang 49 x I A 1 2 1 1 a 3
Khi đó: BH = a, AH = a, AM = a, HM = a,CM = 3 3 2 6 2 a 7 và 2 2
HC = CM - MH = 3
Mà SH ^ ( ABC) Þ CH là hình chiếu của SC lên ( ABC) nên ∑ 0 SCH = 60 a 21 Suy ra 0 SH = HC.tan 60 = 3 a 3 Do ∑ ∑ 0
ABC = HAI = 60 nên 0 HI = AH.sin 60 = 3 2 2 HI .SH 7 a 42 3 a 42 Khi đó: 2 2 HK = = a Þ HK =
Þ d BC, SA = HK = 2 2 ( ) HI + SH 24 12 2 8 Chọn đáp án
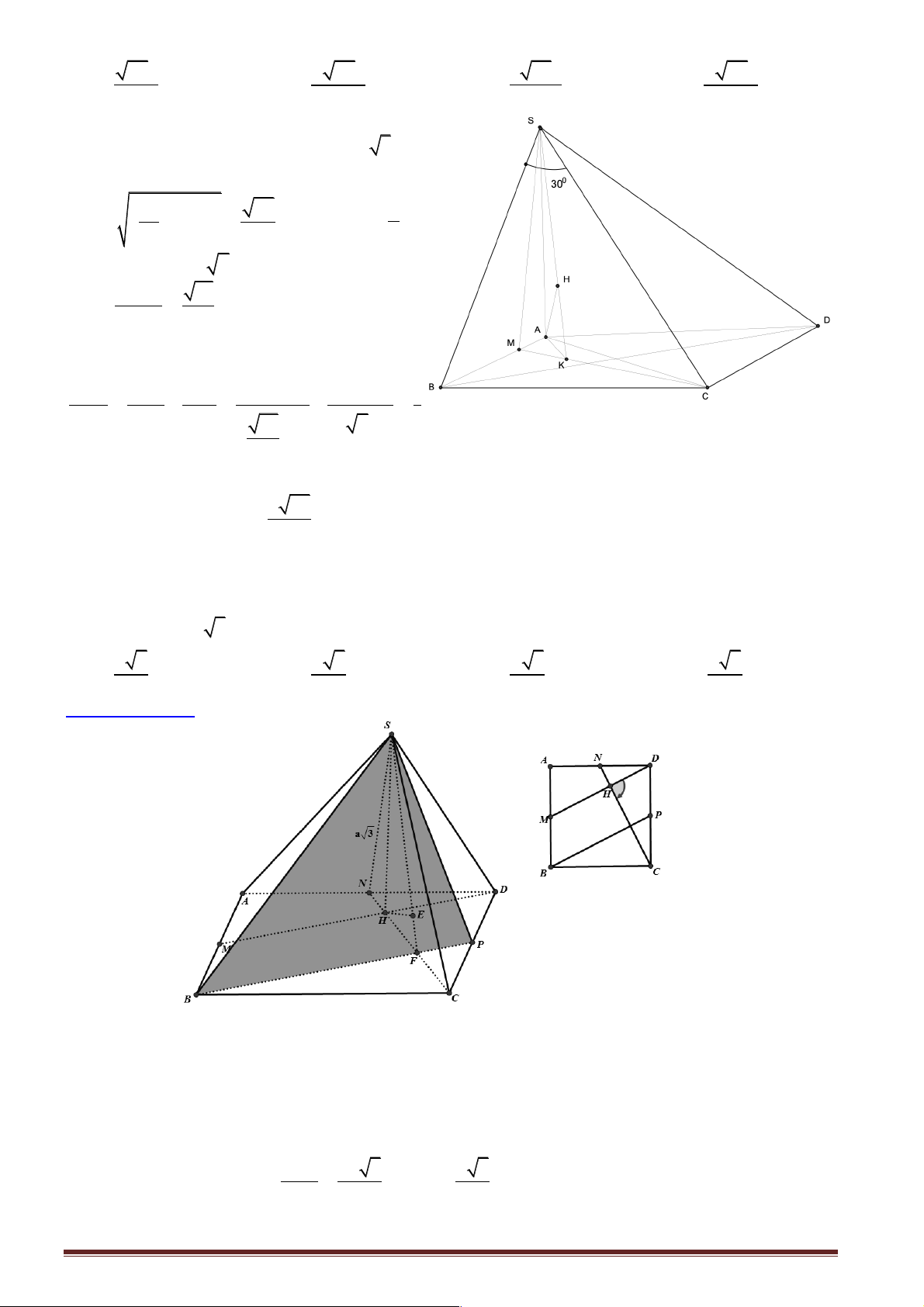
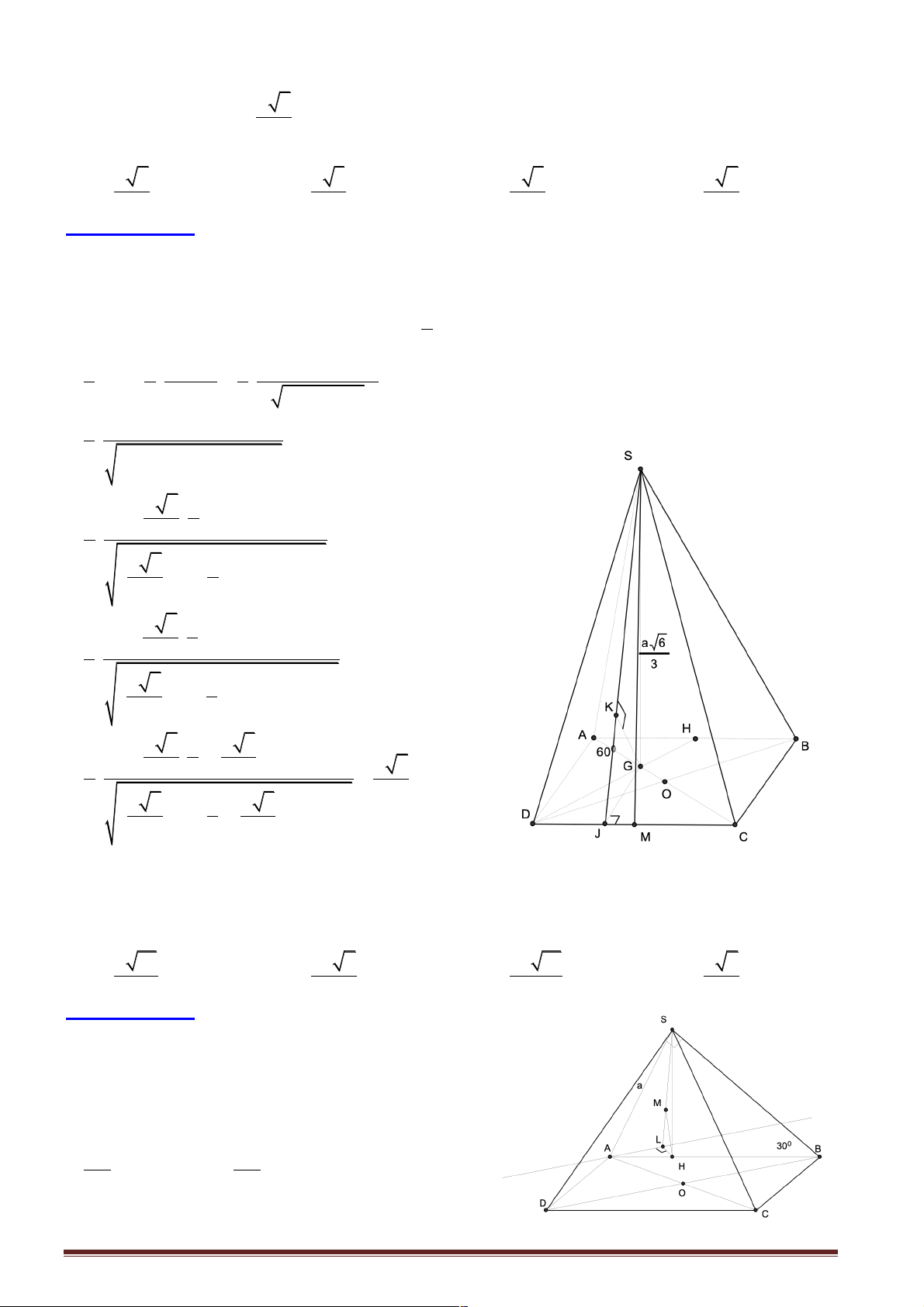
Câu 41: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , SA vuông góc với mặt phẳng
(ABC), gọi I là trung điểm cạnh BC . Biết góc giữa đường thẳng SI và mặt phẳng (ABC) bằng 0
60 . Khoảng cách giữa hai đường thẳng SB và AC. 4a 3a a a A. . B. . C. . D. . 3 4 4 3
Hướng dẫn giải:
Hình chiếu vuông góc của SI trên mặt phẳng ( ABC) là
AI nên góc giữa SI và
mặt phẳng ( ABC) là ∂
SIA(vì tam giác SIAvuông tại A nên ∂ SIAnhọn). Suy ra ∂ 0 SIA = 60 . a
Xét tam giác SIA vuông tại A , ∂ 0 SIA = 3 60 , AI = 2 3a nên SA = . 2
Dựng hình bình hành ACBD , tam giác ABC đều nên tam giác ABD đều. Ta có AC / / ,
BD AC Ë (SBD) Þ AC / / (SBD) mà (SBD) É SB Þ d ( AC,SB) = d ( , A (SBD)) . a
Gọi K là trung điểm đoạn BD, tam giác ABD đều suy ra AK ^ 3 BD và AK = mà BD ^ SAnên 2 BD ^ (SAK ).
Dựng AH ^ SK, H Î SK lại có AH ^ BD suy ra AH ^ (SBD) Vậy d ( ,
A (SBD)) = AH.
Xét tam giác SAK vuông tại vuông tại A , đường cao AH ta có 1 1 1 3a = + Þ AH = 2 2 2 AH AK AS 4 Þ (
SB) = d ( A (SBD)) 3a d AC, , = . 4 Đáp án B.
Câu 42: Cho hình chóp S.ABC tam giác ABC vuông tại B, BC = a, AC = 2a, tam giác SAB đều.
Hình chiếu của S lên mặt phẳng ( ABC) trùng với trung điểm M của AC. Khoảng cách giữa hai
đường thẳng SA và BC là: Trang 50 a 66 2a 11 2a 66 a 66 A. . B. . C. . D. . 11 11 11 11
Hướng dẫn giải:
Tam giác ABC vuông tại B, BC = a, AC = 2asuy ra AB = a 3 .
Tam giác SAM vuông tại M , SA = a 3, AM = a Þ SM = a 2 .
Dựng hình bình hành ABCD , gọi N là trung điểm của AD . Do ∑ 0
ABC = 90 suy ra ABCD là hình chữ nhật suy ra MN ^ .
AD Lại có SM ^ AD nên AD ^ (SMN ). Dựng MH ^ S , D H Î SN .
Theo trên có AD ^ (SMN ) Þ MH ^ AD Þ MH ^ (SAD).
Vậy d (M,(SAD)) = MH . Ta có BC / / ,
AD BC Ë (SAD) Þ BC / / (SAD) Þ d ( ,
SA BC ) = d (BC,(SAD)) Mà SA Ì (SAD) .
= d (C,(SAD)) = 2d (H,(SAD)) = 2MH.
Xét tam giác SMN vuông tại M , đường cao a
MH, SM = a 2, MN = có 2 1 1 1 a 66 = + Þ MH =
Þ d (SA BC) 2a 66 , = 2 2 2 MH MN MS 11 11
Câu 43: Cho hình chóp S.ABCD có đáy là hình bình hành với AB = 2a ; BC = a 2 ; BD = a 6 .
Hình chiếu vuông góc của S lên mặt phẳng ( ABCD) là trọng tâm G của tam giác BCD, biết SG = 2 .
a Khoảng cách giữa hai đường thẳng AC và SB theo a là: a a A. a . B. 2a . C. . D. . 2 3
Hướng dẫn giải:
Ta có ABCD là hình bình hành,
AB = 2a, BC = a 2, BD = a 6 nên ABCD là hình chữ nhật.
Dựng hình bình hành ACEB . Ta có
AC / /BE, AC Ë (SBE) Þ AC / / (SBE) mà (SBE) É SB vậy d (S ,
B AC) = d ( AC,(SBE)) = d ( , G (SBE)).
Dựng GK ^ BE, K Î BE lại có SG ^ BE nên BE ^ (SGK ) .
Dựng GH ^ SK, H Î SK lại có GH ^ BE nên
GH ^ (SBE) Þ d ( ,
G (SBE)) = GH .
Ta có GK = d ( ,
B AC). Tam giác ABC vuông tại B suy ra 1 1 1 a = +
vậy GK = d (B AC) 2 , = . 2 d (B, AC) 2 2 BA BC 3 2a
Xét tam giác SGK vuông tại G , đường cao GH, SG = 2a,GK = có 3 Trang 51 1 1 1 = +
Þ GH = a Þ d (SB, AC) = a. 2 2 2 GH GK GS Đáp án A.
Câu 44: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại , B AB = 4 ; a BC = 3 , a gọi I là
trung điểm của AB, hai mặt phẳng (SIC) và (SIB) cùng vuông góc với ( ABC), góc giữa hai mặt
phẳng (SAC) và ( ABC) bằng 60 .! Khoảng cách giữa hai đường thẳng SB và AC theo a là: 12a 3 3a 3 2a 3 5a 3 A. . B. . C. . D. . 5 5 5 3
Hướng dẫn giải:
Ta có (SIC),(SIB)cùng vuông góc với mặt phẳng ( ABC) nên SI ^ ( ABC).
Dựng hình bình hành ACBE . Ta có AC / /BE, AC Ë (SBE) Þ AC / / (SBE) mà (SBE) É SB vậy
d (SB, AC) = d ( AC,(SBE)) = d ( , A (SBE)) .
= 2d (I,(SBE))
Dựng IK ^ BE, K Î BE lại có SI ^ BE nên BE ^ (SGK ).
Dựng IH ^ SK, H Î SK lại có IH ^ BE nên IH ^ (SBE) Þ d (I,(SBE)) = IH.
Kéo dài IK cắt AC tại D mà
SI ^ AC Þ (SID) ^ AC .
Lại có (SAC) Ç( ABC) = AC .
(SAD)Ç(ABC) = AD
(SAD)Ç(ASC) = SD
Góc giữa (SAC)và( ABC) bằng ∑ SDI suy ra ∑ 0 SDI = 60 . 1
Ta có ID = IK = d (B, AC) 2
Mà tam giác ABC vuông tại B suy ra 1 1 1 = + vậy 2 d (B, AC) 2 2 BA BC = = ( AC) 12a ID IK d B, = . 5 12a a
Xét tam giác SID vuông tại I , ∑ 0 ID = , SDI = 12 3 60 suy ra SI = . 5 5
Xét tam giác SIK vuông tại I , đường cao IH có 1 1 1 6a 3 = + Þ IH =
Þ d (SB AC) 12a 3 , = . 2 2 2 IH IK IS 5 5
Đã sửa đáp án A.
Câu 45: Cho hình chóp S.ABC có đáy ABC là tam giác cân tại .
A Gọi H, M lần lượt là trung điểm
các cạnh BC và SC, SH vuông góc với ( ABC), SA = 2a và tạo với mặt đáy góc 60 .! Khoảng cách
giữa hai đường thẳng AM và BC là: a 3 a 7 a 21 a 7 A. . B. . C. . D. . 7 7 7 21 Trang 52
Hình chiếu vuông góc của SA trên mặt phẳng ( ABC) là HA .
Vậy góc giữa SA và ( ABC) là ∑ SAH . Ta có ∑ 0 SAH = 60 suy ra
AH = a, SH = a 3 .
Gọi N, I lần lượt là trung điểm của SB, SI .
Ta có mặt phẳng ( AMN )song song với BC và chứa AM . Vậy
d ( AM, BC) = d (BC,(SAM )) = d (H,(SAM )).
Dựng HK ^ AI, K Î AI .
Ta có BC ^ SH, BC ^ MH Þ BC ^ (SMH ) .
Þ BC ^ HK mà MN / /BC Þ HK ^ MN
Do HK ^ AI (cách dựng). Suy ra
HK ^ ( AMN ) Þ d (H,( AMN)) = HK.
Xét tam giác IAH vuông tại H , đường cao HK 1 1 1 a 21 = + Þ a HK =
, d (H ( AMN )) 21 , = HK = 2 2 2 HK HA HI 7 7 Đáp án C.
Câu 46: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, AD = 2 2a . Hình chiếu
vuông góc của điểm S trên mặt phẳng ( ABCD) trùng với trọng tâm tam giác .
BCD Đường thẳng SA
tạo với mặt phẳng ( ABCD) một góc 45 .! Khoảng cách giữa hai đường thẳng AC và SD theo a là: 2a 22 a 22 a 11 2a 11 A. . B. . C. . D. . 11 11 11 11
Hướng dẫn giải: Chọn A.
Gọi M là trung điểm của SB .
Mặt phẳng ( ACM ) chứa AC và song song SD . Do đó d(S ,
D AC) = d(S ,
D (ACM )) = d( , D (ACM )) .
Chọn hệ tọa độ Oxyz như hình vẽ. Khi đó ( ) æ ö B(a ) D( a ) 2a 4 2a A 0;0;0 , ;0;0 , 0;2 2 ;0 , S ç ; ;2a ÷,C ç ÷ ( ; a 2 2 ; a 0) 3 3 è ø
æ 5a 2 2a ö !!!" !!!!" æ a a ö M ç ; ;a ÷. AC = ( ;2 a 2 ; a 0) 5 2 2 ç ÷ , AM = ç ; ;a ÷ ç ÷ 6 3 è ø 6 3 è ø !!!" !!!!" Þ AC Ù AM = ( 2 2 2
2 2a ; -a ; - 2a ) !
Mặt phẳng ( ACM ) đi qua điểm A và có vtpt n = (2 2; 1
- ;- 2 ) nên có phương trình là 2 - 2a 2a 22
2 2x - y - 2z = 0 Þ d( ; D (ACM )) = = . 8 +1+ 2 11
Câu 47: Cho tứ diện ABCD có DA = DB = DC, tam giác ABC vuông tại ,
A AB = a, AC = a 3 . Ngoài ra DBC là tam giác vuông.
Tính khoảng cách giữa hai đường thẳng AM và CD, với M là
trung điểm của BC . a 21 a 3 a 7 A. . B. . C. . D. . 7 7 7
Hướng dẫn giải: Trang 53 Chọn A.
Gọi N là trung điểm .
BD Ta chứng minh được CD / / ( AMN ). Do đó d (C ,
D AM ) = d (C ,
D ( AMN )) = d (C,(AMN )).
Xét tứ diện ACMN . Thể tích tứ diện này là : 1 V = d C AMN S = d N ACM S ACMN ( ( )) 1 , . AM D N ( ,( )). 3 3 AC D M
d (N, ACM ).S
Suy ra d (C,( AMN )) ( ) AC D M = (*) S AM D N
Gọi H là trung điểm BM . Khi đó, NH / /DM suy ra NH ^ ( ACM ) nên
NH = d (N ( ACM )) 1 1 , = DM = . a (1) 2 2 2 1 a 3 S = S = . (2) AC D M 2 ABC D 4 1 æ 1 ö
Áp dụng công thức trung tuyến 2 2 2 2 2 AN =
AB + AD - DB = a Þ AN = . a ç ÷ 2 è 2 ø 1
Ta có AM = BC = a nên AM D N cân tại .
A Gọi K là trung điểm MN thì AK ^ MN. 2 CD a 2 a MN = =
. Trong tam giác vuông AKM D 14 , ta có AK = . 2 2 4 2 1 a 7 Suy ra S = AK.MN = . D (3) AMN 2 8 a a
Thay (1), (2), (3) vào (*) ta được d (C ( AMN )) 21 , =
. Vậy d (CD AM ) 21 , = . 7 7
Câu 48: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng a , hình chiếu của S mặt
phẳng ( ABC) là trung điểm H của cạnh AB . Góc tạo bởi SA và mặt phẳng ( ABC) bằng 60! .
Khoảng cách giữa hai đường thẳng SA và BC . 2 15 3 5 15 A. a . B. a . C. a . D. a . 5 5 5 5
Hướng dẫn giải: Chọn D.
Ta có: Từ A Kẻ Ax song song với BC .Từ H
kẻ HI ^ Ax .Từ H Kẻ KH ^ SI với SI thì: d (S , A BC) = d ( ,
B (SAx)) = 2d (H,(SAx)) = 2HK a 3 0 IH = AH.sin 60 = và 4 a a 3 0
SH = AH.ta n 60 = . 3 = 2 2 1 1 1 a 15 = + Þ HK = 2 2 2 HK SH IH 10
d (SA BC) = d (H (SAx)) a 15 , 2 , = 2HK = 5 Trang 54 3a
Câu 49: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SD =
. Hình chiếu vuông góc H 2
của đỉnh S lên mặt phẳng ( ABCD) là trung điểm của đoạn AB . Gọi K là trung điểm của đoạn AD .
Khoảng cách giữa hai đường thẳng HK và SD . a 2a a 3a A. . B. . C. . D. . 3 3 2 2
Hướng dẫn giải: Chọn A.
Ta có: SD cắt ( ABCD) tại D . Từ H kẻ HI ^ BD , HM ^ SI .Ta thấy HK song song BD :
d (HK,SD) = d (H,(SBD)) = HM SH D D : 2 9a æ ö
SH = SD - HD = - ( AD + AH ) 2 2 9a a 2 2 2 2 2 = - ça + ÷ = a 4 4 4 è ø AC a 2 IH = = 4 4 1 1 1 a = + Þ HM = 2 2 2 HM SH IH 3 ( a d S ,
A BC) = d (H,(SBD)) = HM = 3
Câu 50: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB = BC = a , SA vuông
góc với mặt phẳng (ABC), góc giữa đường thẳng SC và mặt phẳng (ABC) bằng 60 .! Khoảng cách
giữa hai đường thẳng SB và AC . 13 78 13 78 A. 2 . a . B. 2 . a . C. . a . D. . a . 13 13 13 13
Hướng dẫn giải: Chọn D.
Gọi I là trung điểm của AC . Qua B kẻ đường thẳng d song
song với AC , trong mặt phẳng ( ABC)kẻ AE vuông góc với d
tại E . Khi đó AE ^ BE và AE ^ AC .
Ta có: AC//BE Þ AC// (SBE) Þ d ( AC,SB) = d ( , A (SBE)).
Gọi AH là đường cao của (SAE), ta có ìBE ^ SA í
Þ BE ^ (SAE) Þ BE ^ AH îBE ^ AE
Mặt khác AH ^ SE nên AH ^ (SBE)
Do đó d ( AC, SB) = d ( ,
A (SBE)) = AH
Vì SA ^ ( ABC) nên hình chiếu của SC trên mặt phẳng (ABC) là AC suy ra gó giữa SC và mặt phẳng (ABC) là ∑ o SCA = 60 Trang 55 a Xét o SA
D E vuông tại A có: AH là đường cao, SA = tan 60 .AC = 3.a 2 = 2
a 6 , AE = BI = 2 1 1 1 2 1 13 nên = + = + = 2 2 2 2 2 2 AH AE SA a 6a 6a 2 6a a 78 2 Þ AH = Þ AH = 13 13 a Vậy d ( AC SB) 78 , = . 13
Câu 51: Cho hình chóp S.ABC có cạnh bên SA vuông góc với mặt phẳng đáy ( ABC), SA = a 6 ,
AB = AC = a 3 , góc ∑
BAC =120!, lấy điểm M trên cạnh BC sao cho MC = 2 . MB Khoảng cách
giữa hai đường thẳng SM và AC . 2a 42 a 42 a 3a A. . B. . C. . D. . 7 7 7 7
Hướng dẫn giải: Chọn B.
Dựa vào định lý Côsin trong tam giác ta có: 2 2 2 ∑
BC = AB + AC - 2 . AB AC.cos BAC 2 2 2
BC = 3a + 3a - 2.a 3.a 3.cos 2 1 0! 2 2
BC = 9a Þ BC = 3a 2
CM = BC = 2a . 3 2 2 2 ∑
AM = CM + CA - 2CM . . CA c s o MCA 2 2 2
AM = 4a + 3a - 2.2 . a a 3. os c 30! 2 2
AM = a Þ AM = a
Xét tam giác ACM có 2 2 2 2
CM = AM + AC = 4a nên tam giác ACM vuông tại A suy ra AC ^ AM
mà AC ^ SAnên AC ^ (SAM )
Gọi H là hình chiếu của A trên SM , ta có ìAH ^ AC í
Þ d ( AC,SM ) = AH îAH ^ SM
Xét tam giác SAM có SA = a 6 , AM = a , AH là đường cao nên 1 1 1 1 1 7 = + = + = 2 2 2 2 2 2 AH AM SA a 6a 6a 2 6a a 42 2 AH = Þ AH = 7 7
d ( AC SM ) a 42 , = 7
Câu 52: Trong không gian cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, mặt phẳng
(SAB) vuông góc với đáy, tam giác SAB vuông cân tại S. Khoảng cách giữa hai đường thẳng
SB và AC . 21 21 7 7 A. a . B. 3a . C. a . D. 2a . 7 7 7 7
Hướng dẫn giải: Chọn A. Trang 56
Kẻ SH ^ AB fi SH ^ (A BC ).
Kẻ BM / / A C fi A C / / (SBM ) fi d(A C ,SB ) = d(A C ,(SBM )) = d(A,(SBM )) = 2d(H,(SBM )).
Kẻ HK ^ BM, ta có: SH ^ BM (
ΠABC) fi BM ^ (SHK).
Kẻ HQ ^ SK , ta có:BM ^ HQ (S
ΠHK) fi HQ ^ (SBM) fi d(H,(SBM )) = HQ. 1 1 1
Xét tam giác vuông SHK ta có: = + . 2 2 2 HQ HK SH a o a 3 a 3 Trong đó: SH= AH=
(do tam giác SA B vuông cân tại S ), HK= HB.sin 0 6 = . = . 2 2 2 4 1 16 4 28 a 21 a 21 fi = + = fi HQ =
fi d(A C ,SB ) = 2HQ = . 2 2 2 2 HQ 3a a 3a 14 7
Câu 53: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, SD vuông góc với mặt
phẳng ( ABCD), AD = , a góc ∑
AOB =120!, góc giữa hai mặt phẳng (SBC) và ( ABCD) bằng 45 .!
Khoảng cách giữa hai đường thẳng AC và SB . a 3 a 6 3a 3 5a 6 A. . B. . C. . D. . 4 4 4 4
Hướng dẫn giải: Chọn B. Vì: BC ^ DC ¸Ô Ô ∑
˝ fi BC ^ (SDC ) fi SCD = 45o BC ^ SD Ô Ô ˛ A D fi SD = DC = = a 3. o tan 0 6 Kẻ a 3 OI / / SB(I S Œ D) fi ID= SI= , SB/ / (IA C ) fi 2
d(A C ,SB ) = d(SB,(IA C )) = d(B,(IA C ))
= d(D,(IA C )).
Kẻ IH ^ A C fi A C ^ (IDH ) fi DH ^ A C .
Kẻ DK ^ IH, ta có: DK ^ AC(AC ^ (DIH))
fi DK ^ (IAC) fi d(D,(IAC))= DK. o a 3
Xét tam giác vuông DHA : ta cóDH = a.sin 60 =
fi tam giác DHI vuông cân tại 2 o a 6
DK = DH . sin 45 = . 4
Câu 54: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, BC = a 3, AB = a; hai mặt phẳng
(SAC) và (SBD) cùng vuông góc với mặt đáy (ABCD) và đường thẳng SC tạo với mặt đáy
(ABCD) một góc 60 .! Khoảng cách giữa hai đường thẳng SB và AC . 2 5a 3 15a 5a 15a A. . B. . C. . D. . 5 5 5 5
Hướng dẫn giải: Chọn D. Trang 57
Gọi O là giao điểm của AC và BD .
Ta có (SAC)Ç(SBD) = ,
SO (SAC) ^ ( ABCD),(SBD) ^ ( ABCD) Þ SO ^ ( ABCD).
OC là hình chiếu vuông góc của SC trên mặt phẳng (ABCD) Þ (SC ( ∑ABCD)) ∑ 0 , = SCO = 60
Gọi M là trung điểm của SD Þ OM ! SB Þ SB ! ( ACM )
Trong mặt phẳng (SBD) kẻ MH ! SO Þ MH ^ ( ABCD) Khi đó d (S ,
B AC) = d (S ,
B ( ACM )) = d ( ,
B ( ACM )) = 2d (H,(ACM )) = 2HI . 1 a 3
Ta có HK = d (D, AC) = 2 4 AC a 3 Có 0 OC =
= a Þ SO = OC.tan 60 = a 3 Þ MH = 2 2 1 1 1 20 a 15 = + = Þ HI = . Vậy 2 2 2 2 HI HM HK 3a 10 d (SB AC) a 15 , = 2HI = . 5
Câu 55: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B với
AB = BC = a, AD = 2 .
a Các mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt đáy ( ABCD).
Biết góc giữa hai mặt phẳng (SAB) và ( ABCD) bằng 60 .! Khoảng cách giữa hai đường thẳng
CD và SB . a 3 2a 3 2a 3 a 3 A. . B. . C. . D. . 5 5 3 3
Hướng dẫn giải: Chọn B.
Gọi O là giao điểm của AC và BD . (SAC)Ç(SBD) = ,
SO (SAC) ^ ( ABCD), Ta có .
(SBD) ^ (ABCD) Þ SO ^ (ABCD)
Gọi E là trung điểm của AD , H = AC Ç BE
Þ BE ! CD Þ CD ! (SBE)
Þ d (CD,SB) = d (C,(SBE)).
= 3d (O,(SBE)) = 3OI OM ^ A ,
B SO ^ AB Þ SM ^ AB Kẻ
Þ ( SAB),(ABCD)) ∑ 0 = SMO = 60 1 a 2 1 2a 2a 3
Tính AC = a 2 Þ OH = AC = , 0 OM = AD =
Þ SO = OM.tan 60 = 6 6 3 3 3 1 1 1 75 2a 2a 3 = + = Þ OI = Þ d C , D SB = 2 2 2 2 ( ) . OI OH SO 4a 5 3 5 Trang 58
Câu 56: Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Đường thẳng SD tạo với đáy 3a 5
ABCD một góc 60 .! Gọi M là trung điểm . AB Biết MD =
, mặt phẳng (SDM ) và mặt phẳng 2
(SAC) cùng vuông góc với đáy. Khoảng cách giữa hai đường thẳng CD và SM theo a là: a 5 3a 5 a 15 3a 15 A. . B. . C. . D. . 4 4 4 4
Hướng dẫn giải: Chọn D.
Ta có (SMD) Ç(SAC) = SG suy ra SG ^ ( ABCD)
Kẻ GH ^ AB , GK ^ SH Khi đó,
d (DC,SM ) = d (DC,(SAB)) = d (D,(SAB)) GD =
d (G (SAB)) 3a 15 . , = 3GK = GM 4
Câu 57: Một hình chóp tam giác đều S.ABC có cạnh bên bằng 2 2 và tạo với mặt đáy một góc 45 .!
Tính khoảng cách giữa SA và BC . 3 2 3 2 3 3 3 2 A. . B. . C. . D. . 2 4 2 4
Hướng dẫn giải: Chọn A . S
+ Vì SABC là hình chóp tam giác đều nên SO ^ ( ABC)
( Với O là trọng tâm của ABC D ). + Xét SO
D A Vuông tại O có: J - ∑ 0 SAO = 45 mà H
SA = 2 2 nên OA = SO = 2. Þ AI = 3.
- Với H là chân đường cao hạ từ O 1 1 1 A C Ta có: = + Þ OH = 2. 2 2 2 OH OA SO O + Trong SI
D A Gọi J là chân đường cao hạ từ I xuống I .
SA Lại có BC ^ (SAI ) nên BC ^ IJ . Từ đó IJ là
đương vuông góc chung của SA & BC. B OH OA OH.AI 3 2 + Xét trong AI D J : = Þ IJ = = . IJ AI OA 2 a
Câu 58: Cho hình chóp S.ABCD có mặt đáy là hình thoi tâm O, cạnh ∑ a, BAD = 60! 3 và SO = . 4
Biết SA = SC và SB = .
SD Hỏi khoảng cách giữa SA và BD bằng bao nhiêu ? 3a 3a 7 3a 7 3a A. . B. . C. . D. . 7 14 7 14
Hướng dẫn giải: SO ^ ACü Ta có:
ý Þ SO ^ (ABCD) Þ DB ^ SO SO ^ DBþ DB ^ SO ü Ta có:
ý Þ BD ^ (SAC) BD ^ ACþ Trang 59
Trong mp (SAC), kẻ OH ^ SA (H Î S )
A , ta có: OH ^ S , A OH ^ BD 2 2 æ 3a ö æ a 3 ö a 21 Do đó: d(S ,
A DB) = OH . Ta có: 2 2
SA = SO + OA = + ç ÷ ç ÷ = 4 ç 2 ÷ è ø 4 è ø
Tam giác SOA vuông tại O, có OH là đường cao, ta có: . SO OA 3a a 3 4 3a 7 OH = = . . = SA 4 2 a 21 14 3a 7 Vậy d(S , A DB) = OH = . 14 Chọn B.
Câu 59: Cho hình chóp tứ giác đều S.ABCD có đường cao SO = 2, mặt bên hợp với mặt đáy một góc
60 .! Khi đó khoảng cách giữa hai đường thẳng AB và SD bằng 4 3 3 2 A. . B. 2 . C. 2 3 . D. . 3 2
Hướng dẫn giải:
Gọi I là trung điểm của CD . Ta có:
(SCD) ! (ABCD) = CD ü ï (SOI ) ^ CD ý
(SOI ) ! (ABCD) OI,(SOI) ! (SCD) SI ï = = þ ∑ Þ ( SCD ABCD ) ∑ 0 ( ),(
) = (OI,SI) = 60
Ta có: AB / /CD Þ AB / /(SCD) Þ d(A ,
B SD) = d(AB,(SCD)) = d( ,
A (SCD)) = 2d( , O (SCD)) SO 2 3
Trong mp (SOI ), kẻ OH ^ SI (H Î SI), ta có: OH ^ (SCD) và OI = = 0 tan 60 3
Do đó: d(O,(SCD)) = OH . 4 4 Ta có: 2 2 2
SI = SO + OI = 2 + = 3 3 . SO OI 2 3 3
Tam giác SOI vuông tại O, có đường cao OH nên OH = = 2. . = 1 SI 3 4 Do đó: d(A , B SD) = 2d( ,
O (SCD)) = 2OH = 2.1 = 2. Chọn B.
Câu 60: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = 3 ; a AD = 2 . a Hình chiếu
vuông góc của S lên mặt phẳng ( ABCD) là điểm H thuộc cạnh AB sao cho AH = 2H . B Góc giữa
mặt phẳng (SCD) và mặt phẳng ( ABCD) bằng 60 .! Khoảng cách giữa hai đường thẳng SC và AD theo a là 6a 39 6a 13 a 39 a 13 A. . B. . C. . D. . 13 13 13 13
Hướng dẫn giải:
Hình chiếu vuông góc của S lên mặt phẳng ( ABCD) là điểm H nên SH ^ (ABCD) .
Kẻ HM ^ CD(M ÎCD), ta có:
(ABCD) ! (SCD) = CD ü (SHM ) CD ï ^ ï ∑
ý Þ ((ABCD),(SCD)) ∑ 0 = SMH = 60 Ta có:
(SHM ) ! (ABCD) = HM ï
(SHM ) ! (SCD) = SM ïþ Trang 60
AD / /BC Þ AD / /(SBC) và d(A , D SC) = d( ,
A (SBC)) = 3d(H,(SBC))
Kẻ HI ^ SB (I Î SB), ta có: HI ^ (SBC) và d(H,(SBC)) = HI Ta có: 0
SH = HM.tan60 = 2 . a 3 và 2 2
SB = SH + HB = a 13 SH.HB 2a 39 a Suy ra: IH = = 6 39
. Vậy d(AD, SC) = 3HI = . Chọn A. SB 13 13
Câu 61: Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại C, AB = 5 ; a BC = 4 . a Cạnh SA
vuông góc với đáy và góc giữa mặt phẳng (SBC) với mặt đáy ( ABC) bằng 60 .! Gọi D là trung điểm của cạnh .
AB Khoảng cách giữa hai đường thẳng SD và BC là: 3a 39 3a 13 a 13 a 39 A. . B. . C. . D. . 13 13 13 13
Hướng dẫn giải:
Gọi M là trung điểm AC , ta có: BC / /(SMD)
Þ d(BC,SD) = d(C,(SMD)) = d( , A (SMD))
Kẻ AH ^ SM (H Î SM ), ta có: AH ^ (SMD) . SA AM 3a 39 Þ d( ,
A (SMD)) = AH = = SM 13 3a 13 Với 2 2
SM = SA + AM = . 2 Chọn A.
Câu 62: hình chóp S.ABCD có đáy ABCD là hình thang vuông ở
A và B, AB = BC = a, AD = 2a, tam giác SAB cân tại đỉnh S nằm
trong mặt phẳng vuông góc với đáy, mặt phẳng (SCD) tạo với đáy một góc 60 .!Khoảng cách
AB và SD là: a 177 6a 177 2a 177 3a 177 A. . B. . C. . D. . 59 59 59 59
Hướng dẫn giải:
Dựng hình chữ nhật ABED , ta có tam giác ACD vuông cân tại C .
Gọi H, K lần lượt là trung điểm AB, ED, ta có: SH ^ (ABCD) .
Gọi F là đối xứng của A qua B, kẻ HM ^ DF (M Î DF)
Suy ra: (SHM ) ^ DF và ∑ ∑ 0 (SC ) D ,(ABC ) D = SMH = 60 3 3a 2
Ta có: HM / / AC Þ HM = AC = 4 4
Ta có: AB / /ED Þ AB / /(SED) và d(AB,SD) = d(H,(SED))
Kẻ HI ^ SK , ta có: HI ^ (SED) và d(H,(SED)) = HI a 59 Ta có: 2 2
SK = SH + HK = 2 2 SI.IK 6a 3 6a 177 Suy ra: HI = = = . SK 59 59 Chọn B.
Câu 63: Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, SA vuông góc với mặt phẳng (ABC),
góc giữa SB và mặt phẳng (ABC) bằng 60° , M là trung điểm của .
AB Khoảng cách giữa hai đường
thẳng SM và BC là: 4a 51 2a 51 a 51 a 51 A. . B. . C. . D. . 51 3 51 17 Trang 61
Hướng dẫn giải:
Gọi N, I lần lượt là trung điểm của AC, BC .
MN là đường trung bình của ABC D Þ MNÄ BC Þ BCÄ (SMN )
Ta có: d (BC;SM ) = d (BC;(SMN)) = d (I;(SMN)) = d ( ; A (SMN )). Dễ thấy
BC ^ (SAI ) Þ MN ^ (SAI ) Þ (SMN ) ^ (SAI ) theo giao tuyến SH .
Trong mặt phẳng (SAI ) kẻ AK ^ SH Þ AK ^ (SMN )
Vậy d (BC;SM ) = d ( ;
A (SMN )) = AK a 3 1 a 3 Ta có: AI = Þ AH = AI = 2 2 4
Vì SA ^ ( ABC) nên (SB ( ABC)) = (SB AB) ∑ ; ;
= SBA = 60° Þ SA = A .t
B an 60° = a 3. 1 1 1 1 16 17 = + = + = 2 2 2 2 2 2 AK SA AH 3a 3a 3a a 51 Þ AK = . 17
Câu 64: Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông tâm O, cạnh bằng 2 . a Mặt
bên SAB là tam giác đều, SI vuông góc với (SCD) và I là trung điểm .
AB Khoảng cách giữa hai
đường thẳng SO và AB là: 3a 3 a 2 a 3 a 3 A. . B. . C. . D. . 2 2 2 3 Kẻ MN / / AB Þ d (S ,
O AB) = d (A ,
B (SMN)) = d (I,(SMN)) Ta có
AB ^ SI Þ MN ^ SI, AB ^ OI Þ MN ^ OI
Þ MN ^ (SOI) Þ (SMN) ^ (SOI ).Kẻ
IH ^ SO Þ IH ^ (SMN )
Þ IH = d (I;(SMN))
Gọi J là trung điểm của CD JI
Do SI ^ (SCD) Þ SI ^ SJ Þ SO = = a 2 + Do SI
D O cân tại O . kẻ OE ^ SI 2 3a a 2 2 2
Þ OE = OI - IE = a - = 4 2 2 1 1 a a 3 2S a 3 + S = OE.SI = .a 3 OS D I = Þ IH = Þ IH = OS D I 2 2 2 4 SO 2
Câu 65: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm I, AB = a, AD = 2 . a Gọi M là
trung điểm của cạnh AB và N là trung điểm đoạn MI. Hình chiếu vuông góc của điểm S lên mặt
phẳng ( ABCD) trùng với điểm N. Biết góc tạo bởi đường thẳng SB với mặt phẳng ( ABCD) bằng
45 .! Khoảng cách giữa hai đường thẳng MN và SD theo a là: Trang 62 a 6 a 6 a 6 A. a 6 . B. . C. . D. . 2 3 6
Hướng dẫn giải:
MN / / AD Þ MN / / (SAD) Þ d (MN, SD) Do
= d(MN,(SAD)) = d(N,(SAD)) Kẻ NE ^ A ,
D SN ^ AD Þ AD ^ (SNE) Þ (SAD) ^ (SNE)
NH ^ SE Þ NH ^ (SAD) Kẻ
Þ d (N,(SAD)) = d (MN,(SAD)) = NH Ta có : SB ( ∑ABCD) ∑ 0 ; = SBN = 45 Xét BM D N Þ 2 2 a a a 2 a 2 2 2
BN = BM + NM = + = Þ SN = 4 4 2 2 a a 2 . NE.NS a 6 Do 2 2 NH = = = 2 2 NE + NS a 3 6 2
Câu 66: hình chóp S.ABCD có đáy là hình thang vuông tại A và B ; AB = BC = ;
a AD = 2a ; SA
vuông góc với mặt phẳng ( ABCD), góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng 45 .! Gọi
M là trung điểm của cạnh AD . Khoảng cách giữa hai đường thẳng SM và BDlà: a 22 a 2 a 11 a 11 A. . B. . C. . D. . 11 11 22 2
Hướng dẫn giải: Ta có : SC ( ∑ABCD) ∑ 0 , = SCA = 45
Gọi E, K lần lượt là giao điểm của AC với , BD NM
Kẻ MN / /BD Þ BD / / (SMN) Þ d (SM, BD) = d (B ,
D (SMN)) = d (E,(SMN))
Do MN / /BD Þ K trung điểm AE Þ d ( ;
E (SMN)) = d ( , A (SMN))
Kẻ AE ^ MN, SA ^ MN Þ MN ^ (SAE) Þ (SAE) ^ (SMN )
Kẻ AF ^ SE Þ FA ^ (SMN ) Þ d ( ,( A SMN)) = FA Xét ABC D
Þ AC = a 2 Þ SA = a 2 a . . a AN AM a 5 2 AE = = = 2 2 2 AN + AM a 5 2 + a 4 a 5 a 2. . SA AE a 22 5 FA = = = 2 2 SA + AE 55 11 5 Trang 63
Câu 67: Cho hình thoi ABCD cạnh a, góc ∑
BAD = 60! . Gọi G là trọng tâm tam giác ABD, a SG ^ 6 (ABCD) và SG =
. Gọi M là trung điểm .
CD Tính khoảng cách giữa các đường thẳng 3
AB và SM theo a . a 2 a 3 a 5 a 7 A. . B. . C. . D. . 2 2 2 2
Hướng dẫn giải: Chọn A. Ta có:
Gọi J , K lần lượt là hình chiếu của H lên DC, SJ
d ( AB SM ) = d ( AB (SDC)) = d ( A (SDC)) 3 , , ,
= d (G,(SDC)) 2 ∑ 3 3 . SG GJ 3 . SG G . C sin GCJ = GK = . = . 2 2 2 2 SJ 2 SG + GJ ∑ 3 . SG GC.sin GCJ = . 2 ∑
SG + (GC.sinGCJ )2 2 a 6 2 0 . .AC.sin 30 3 3 3 = . 2 2 2 æ a 6 ö æ 2 0 ö ç ÷ + .AC.sin 30 ç ÷ 3 è ø è 3 ø a 6 2 0 . .2 AO.sin 30 3 3 3 = . 2 2 2 æ a 6 ö æ 2 0 ö ç ÷ + .2 AO.sin 30 ç ÷ 3 è ø è 3 ø a 6 2 a 3 0 . .2. .sin 30 3 a 2 3 3 2 = . = 2 2 2 2
æ a 6 ö æ 2 a 3 ö 0 ç ÷ + ç .2. .sin 30 ÷ 3 3 2 è ø è ø
Câu 68: Cho hình chóp S.ABCD , có đáy ABCD là hình vuông, tam giác SAB vuông tại S và nằm
trên mặt phẳng vuông góc với mặt đáy. Biết SA = a và cạnh bên SB tạo với mặt đáy ( ABCD) một góc 30 .
! Khoảng cách giữa hai đường thẳng SA và BD là: a 21 2a 7 2a 21 a 7 A. . B. . C. . D. . 7 7 7 7
Hướng dẫn giải: Chọn C. Ta có:
Vẽ đường thẳng d qua A và song song với AC
Gọi L, M lần lượt là hình chiếu của H lên d, SL d (S ,
A BD) = d (B ,
D (SAL)) = d ( , B (SAL)) BA BA =
.d (H,(SAL)) = .HM HA HA Trang 64 a BA SH.HL BA SH.HL 0 = SH.HL SH.HL . = . sin 30 = . = 4. 2 2 HA SL HA SH + HL 0 2 2 2 2 . . a cos60 SH + HL SH + HL SH 3 0 sin 60 = Þ SH = a SA 2 ∑ HL ∑ HL sin LAH = Û sin ABO = AH AH AH a 0 cos60 = Þ AH = SA 2 a 3 2 AO HL .A AO H 2 2 . .a Û = Û SH.HL 2 21 HL = = AH = a 2 4 4. = 4. = a AB AH AB 2 4 2 2 SH + HL 3 1 7 2 2 a + a 4 8
Câu 69: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a, AD = a 2 . Gọi H là
trung điểm của cạnh AB ; tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy ; góc
giữa hai mặt phẳng (SAC) và ( ABCD) bằng 60 .! Khoảng cách giữa hai đường thẳng CH và SD là : 2a 5 2a 10 a 5 2a 2 A. . B. . C. . D. . 5 5 5 5
Hướng dẫn giải: Chọn D.
Vì H là trung điểm của cạnh AB ; tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với
đáy nên SH ^ ( ABCD).
Gọi I là hình chiếu của H trên AC suy ra góc giữa hai mặt phẳng (SAC) và ( ABCD)là góc ∑ 0 SIH = 60 . IH BC a 2 a a 6 Ta có ABC D ! AI D H Þ = Û IH = . = . AH AC a 3 2 6 a Trong SH D 2
I vuông tại H có SH = IH 3 = . 2
Gọi K là điểm đối xứng của H qua A ta có tứ giác CDKH là hình bình hành suy ra CH song song với
mặt phẳng (SDK ) É SD.
Nên ta có: d (CH,SD) = d (CH,(SDK)) = d (H,(SDK))
Gọi E, F lần lượt là hình chiếu của H trên DK và SE. Khi đó ta có d (H,(SDK )) = HF . Trang 65 a .a 2
Ta có HE = d (B C) BH.BC 2a 2 2 2 , H = 2 = 2 = 2 2 2 BH + BC 3 a 2 + 2a 4 a 2 2a 2 2 SH.HE 2a 3 2 2a 2 Trong SH D E vuông tại H có 2 3 HF = = = . = .Chọn D. 2 2 2 2 SH + HE a 8a 3 5a 5 + 2 9
Câu 70: hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a, AD = 2a, tam giác SAB cân 2a
tại S và nằm trong mặt phẳng vuông góc với đáy. Khoảng cách từ D đến (SBC) bằng . Khoảng 3
cách giữa hai đường thẳng SB và AC là : a 10 a 10 2a 10 2a 5 A. . B. . C. . D. . 10 5 5 5
Hướng dẫn giải: Chọn B. Ta có:
Vẽ đường thẳng d qua A và song song với AC
Gọi K, I lần lượt là hình chiếu của H lên d, SK ( (SBC)) 2a =
Û d ( A (SBc)) 2a d D, , = 3 3 Û ( a a
d H,(SBC)) = Û HI = 3 3 1 1 1 = + 2 2 2 HI SH HB 9 1 4 1 5 Û = + Û = a 5 Û SH = 2 2 2 2 2 a SH a SH a 5 ∑ HK ∑ HK sin KBH = Û sin CAB = HB HB a .2 . a CB HK HB CB 5 2 a Û = Þ HK = = = AC HB AC 5.a 5
d ( AC,SB) = d ( ,
A (SBK)) = 2d (H,(SBK)) = 2HL 2 SH.HK SH.HK SH SH a 10 = 2 = 2 = 2. = 2 = 2 2 SK SH + HK SH 2 2 5
Câu 71: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 3a, có SH ^ (ABC) với H thuộc
cạnh AB sao cho AB = 3AH. Góc tạo bởi SA và mặt phẳng ( ABC) bằng 60 .! Khoảng cách giữa
hai đường thẳng SA và BC là: a 5 3a 15 a 15 3a 5 A. . B. . C. . D. . 5 5 5 5
Hướng dẫn giải: Chọn B. Ta có: Trang 66
Vẽ đường thẳng d qua A và song song với BC
Gọi F,G lần lượt là hình chiếu của H lên d, SF SH 0 tan 60 = Þ SH = a 3 a ∑ HF HF a 3 0 sin FAH = Û sin 60 = Þ HF = AH a 2 a 3 a 3. SH.HF 15 2 HG = = = a 2 2 SH + HF 3 5 2 2 3a + a 4 d (BC,S ) A = d ( , B (SAF))
= d (H (SAF )) 15 3 , = 3HG = 3 a 5
Câu 72: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, hình chiếu vuông góc của S
lên mặt phẳng ( ABCD) là trung điểm của ,
AD góc giữa đường thẳng SB và mặt đáy bằng 60 .! Gọi
M là trung điểm của DC. Khoảng cách giữa hai đường thẳng SA và BM là : a 285 3a 285 a 285 2a 285 A. . B. . C. . D. . 9 19 19 9
Hướng dẫn giải: Chọn C.
Vẽ đường thẳng d qua A và song song với BM
Gọi O, P lần lượt là hình chiếu của H lên d, SO Ta có: 2 2 2 2 a a 5
BH = AB + AH = a + = 4 2 SH a 15 0 tan 60 = Þ SH = BH 2 a a . ∑ OH ∑ OH CM OH CM .AH 5 2 2 sin OAH = Û sin MBC = Û = Û OH = = = a 2 AH AH BM AH BM a 10 2 a + 4 2 2
æ a 15 ö æ a 5 ö 95a 2 2
SO = SH + OH = ç ÷ + ç ÷ = ç 2 ÷ ç 10 ÷ 5 è ø è ø a 15 a 5 .
d (SA BM ) = d (N (SAO)) = d (H (SAO)) SH.OH 285 2 10 , , 4 , = 4HP = 4. = 4. = a SO 95a 19 5 Trang 67




