TOP 2 đề kiểm tra giữa học kỳ I Toán 9 năm 2023-2014 (có đáp án và lời giải chi tiết)

PHÒNG GD&ĐT KRÔNG ANA
ĐỀ KIỂM TRA, ĐÁNH GIÁ GIỮA KỲ 1
TRƯỜNG ………………. NĂM HỌC 2023 - 2024
MÔN TOÁN 9 – Khối lớp 9
Thời gian làm bài : 90 phút
(Đề thi có 02 trang)
(không kể thời gian phát đề)
Họ và tên học sinh :.................................................................... Lớp: ................... Mã đề 190
PHẦN CÂU HỎI TRẮC NGHIỆM
Câu 1. Cho số thực a  0 . Số nào sau đây là căn bậc hai số học của a?
A. 3 a . B. a .
C.  a .
D. a và  a .
Câu 2. Cho số thực a  0 . Số nào sau đây là căn bậc hai của a?
A.  a . B. 3 a . C. a .
D. a và  a .
Câu 3. Khẳng định nào đúng? A. 9  81. B. 9  3. C. 9  3  . D. 9  3  .
Câu 4. Điều kiện xác định của biểu thức 2x  8 là A. x  4  . B. x  4  .
C. x  4 . D. x  4.
Câu 5. Điều kiện xác định của biểu thức 2023  x là
A. x  2023 .
B. x  2023 . C. x  2023  . D. x  2023 . Câu 6.   2 3 2 bằng A. 2  3 . B. 2  3 . C. 1 . D. 3  2 .
Câu 7. Biết a  0 , b  0 . Khẳng định nào sau đây là đúng? A. a 
b  a  b (a  ) b .
B. a  b  a b . C. a 
b  a  b .
D. a  b  ab .
Câu 8. Chọn khẳng định đúng.
A. 3 27  3 . B. 3 27  9 . C. 3 27  9  . D. 3 2  7  3  .
Câu 9. Tam giác ABC vuông tại A, đường cao AH. Hệ thức nào sai? A. 2
AB  HB HC. B. 2
AB  HB BC.
C. AB AC  AH  BC. D. 2 2 2
AB  BC  AC .
Câu 10. “Trong tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng…”. Cụm từ
thích hợp điền vào chỗ trống là:
A. tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền.
B. tích hai cạnh góc vuông.
C. tích cạnh huyền và 1 cạnh góc vuông.
D. tổng nghịch đảo các bình phương của hai cạnh góc vuông.
Câu 11. Tam giác ABC vuông tại A, tan B bằng AB AB AC AC A. . B. . C. . D. . AC BC AB BC
Câu 12. Cho góc nhọn  . Khẳng định nào sai? Trang 1  A. 2 2
sin   cos   1. B.   sin tan . co  s  C.   cos tan . D. ta  n  cot 1. si  n
PHẦN CÂU HỎI TỰ LUẬN
Câu 13. (2,0 điểm) Thực hiện các phép tính sau: a) 2  8 . 4 3 27a b b)
(với a  0, b  0 ). 2 3a b 22 c) 18  5 8  . 11 1 15  3 d)  . 2  3 5 1
Câu 14. (1,0 điểm) Tìm x, biết: 4x  4  9x  9  x 1  8  1 3  x  3
Câu 15. (1,0 điểm) Cho biểu thức P   :   (Với
 x  2 x  2 x  x  4 x  4
x  0; x  4; x  9) a) Rút gọn P. b) So sánh P với 1.
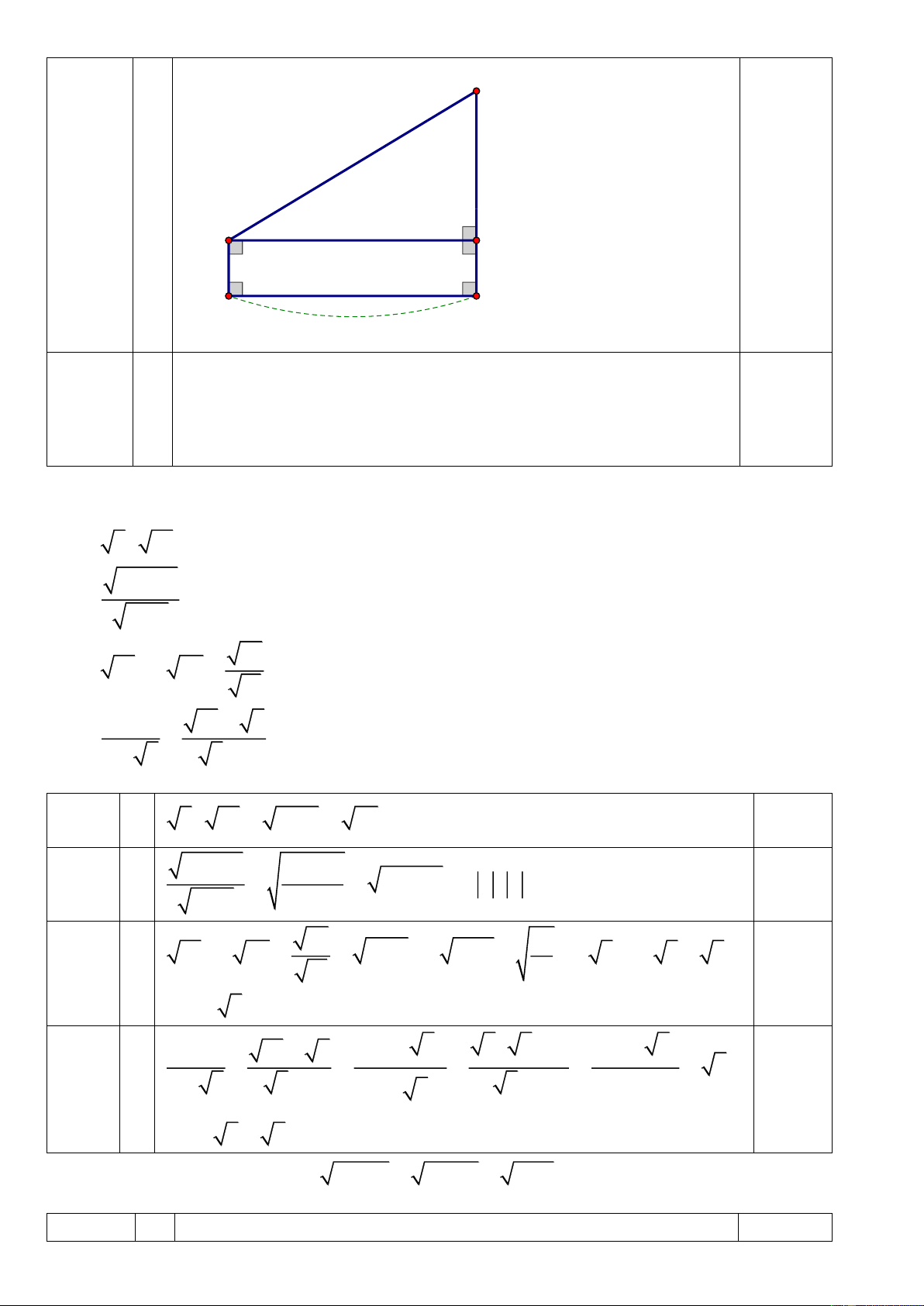
Câu 16. (2,0 điểm) Cho tam giác ABC vuông tại A có đường cao AH. Biết BH = 4cm và HC = 6 cm.
a) Tính độ dài các đoạn AH, AB.
b) Biết D, E lần lượt là hình chiếu của H trên AB và AC. Chứng minh: ∆AED ∆ABC. Câu 17. (1,0 điểm)
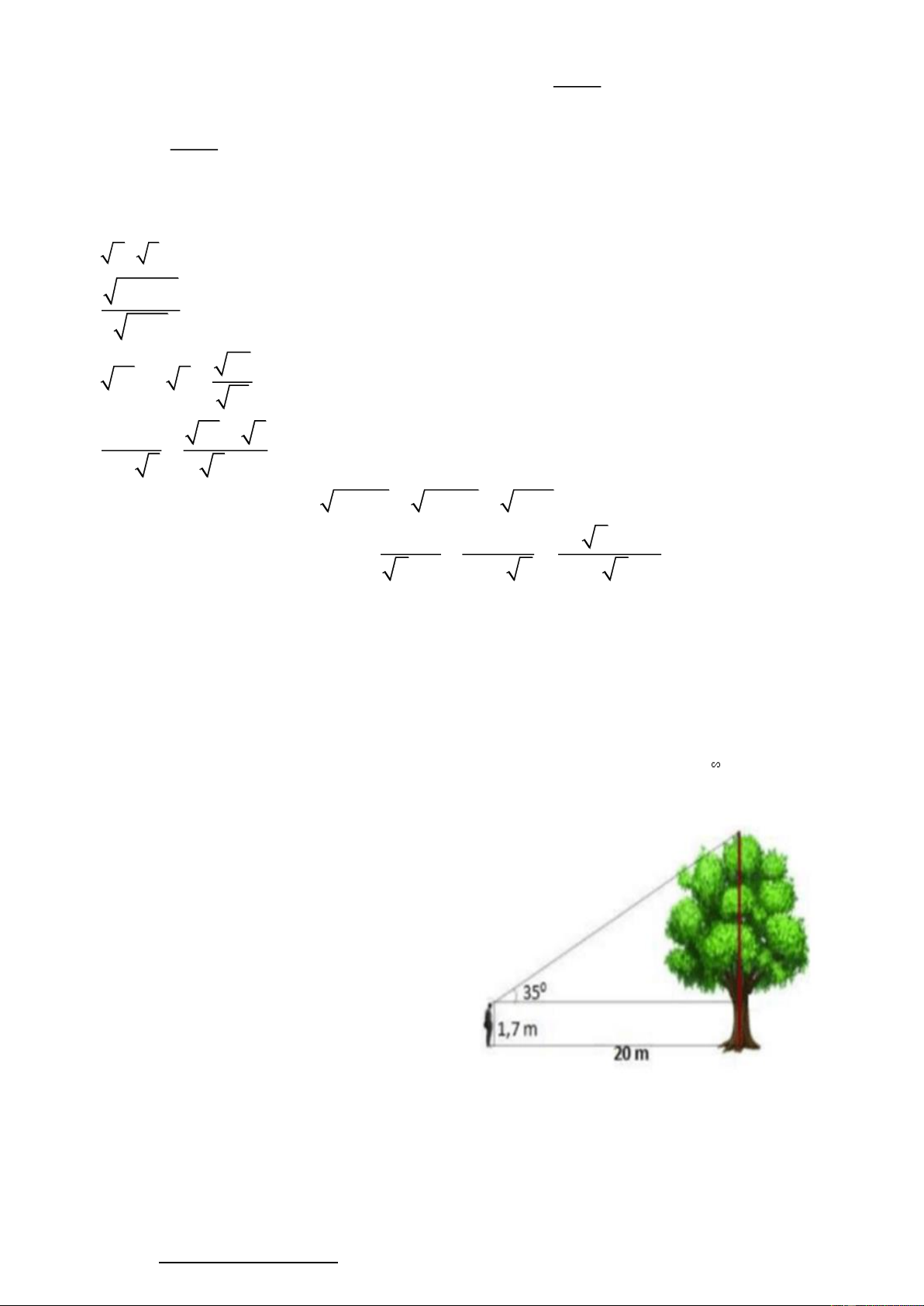
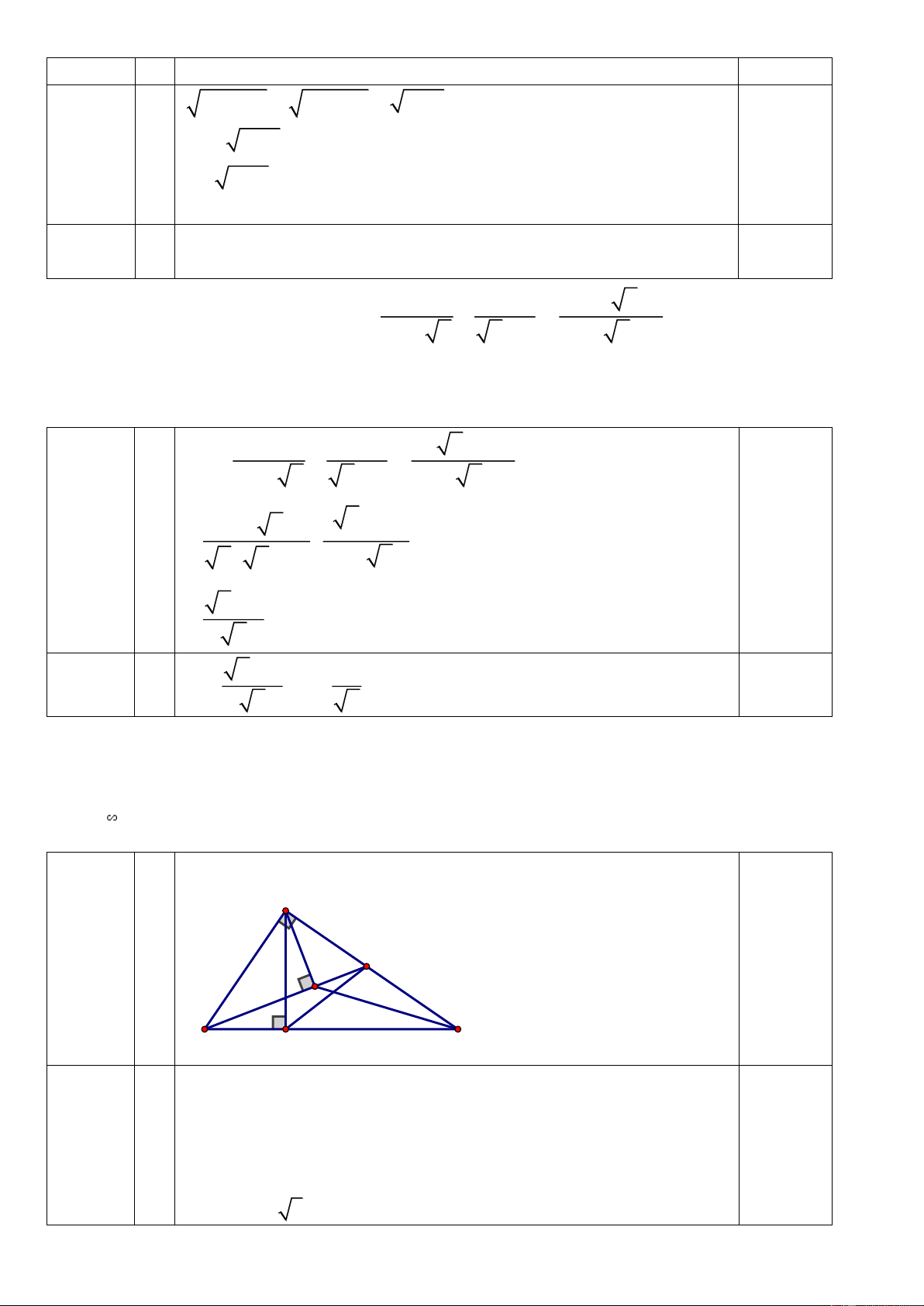
Một người đứng thẳng và dùng thước ngắm để đo
chiều cao của một cái cây. Biết khoảng cách từ
chân người đứng tới gốc cây là 20m, người đó
cao 1,7m, góc ngắm tạo bởi tia đi từ mắt tới ngọn
cây và tia đi từ mắt đến thân cây theo phương
nằm ngang là 350 (hình vẽ). Tính chiều cao của
cây (làm tròn đến số thập phân thứ hai).
------ HẾT ------ PHÒNG GD&ĐT KRÔNG ANA
ĐỀ KIỂM TRA, ĐÁNH GIÁ GIỮA KỲ 1
TRƯỜNG ………….. NĂM HỌC 2023 - 2024 Trang 2
MÔN TOÁN 9 – Khối lớp 9
Thời gian làm bài : 90 phút
(Đề thi có 02 trang)
(không kể thời gian phát đề)
Họ và tên học sinh :.................................................................... Lớp: ................... Mã đề 191
PHẦN CÂU HỎI TRẮC NGHIỆM
Câu 1. Cho số thực b  0 . Số nào sau đây là căn bậc hai số học của b?
A. b và  b .
B.  b . C. b . D. 3 b .
Câu 2. Cho số thực b  0 . Số nào sau đây là căn bậc hai của b? A. b .
B.  b .
C. b và  b . D. 3 b .
Câu 3. Khẳng định nào đúng? A. 4  2 . B. 4  2  . C. 4  16 . D. 4  2 
Câu 4. Điều kiện xác định của biểu thức 3x  6 là
A. x  2.
B. x  2 . C. x  2  . D. x  2  .
Câu 5. Điều kiện xác định của biểu thức 1975  x là
A. x  1975. B. x  1975  . C. x  1975  . D. x  1975. Câu 6.   2 5 2 bằng A. 1 . B. 2  5 . C. 5  2 . D. 5  2 .
Câu 7. Biết a  0 , b  0 . Khẳng định nào sau đây là đúng? a a A.  . B. a 
b  a  b . b b a a C. a 
b  a  b, (a  ) b . D.  . b b
Câu 8. Chọn khẳng định đúng. A. 3 27  3  . B. 3 27  9  . C. 3 27  3 . D. 3 27  9 .
Câu 9. Tam giác ABC vuông tại A, đường cao AH. Hệ thức nào sai? 1 1 1 A. 2
AH  HB BC B.   . 2 2 2 AH AB AC C. 2 2 2
BC  AB  AC . D. 2
AH  HB HC .
Câu 10. “Trong tam giác vuông, bình phương mỗi cạnh góc vuông bằng…”. Cụm từ thích hợp điền vào chỗ trống là:
A. tổng nghịch đảo các bình phương của hai cạnh góc vuông.
B. tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền.
C. tích hai cạnh góc vuông.
D. tích của cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền.
Câu 11. Tam giác ABC vuông tại A, sin B bằng Trang 3 AB AC AC AB A. . B. . C. . D. . AC BC AB BC
Câu 12. Cho góc nhọn  . Khẳng định nào sai?  A.   cos cot . B. ta  n  cot 1. si  n  C. 2 2
sin   cos   1. D.   sin cot . co  s
PHẦN CÂU HỎI TỰ LUẬN
Câu 13. (2,0 điểm) Thực hiện các phép tính sau: a) 3  12 . 4 3 50a b b)
(với a  0, b  0 ). 2 2a b 33 c) 12  5 27  . 11 4 15  5 d)  . 3  5 3 1
Câu 14. (1,0 điểm) Tìm x, biết: 4x  4  9x  9  x  1  12  1 1  1 x
Câu 15. (1,0 điểm) Cho biểu thức A   :  
(Với x  0; x  1).  x  2 x
x  2  x  4 x  4 a) Rút gọn A. b) So sánh A với 1.
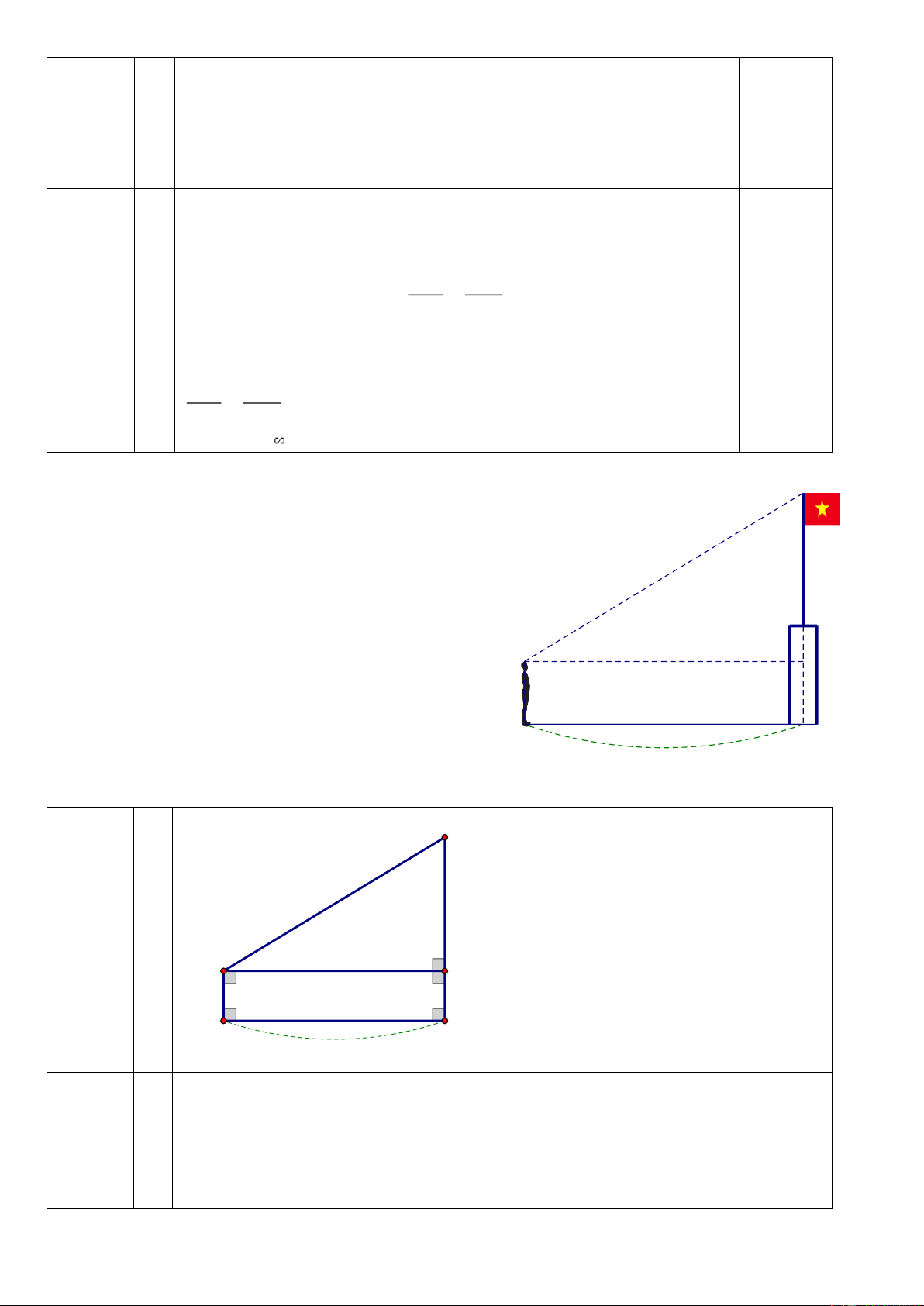
Câu 16. (2 điểm) Cho ∆ABC vuông tại A, AH là đường cao. Biết BH = 2cm, HC = 6 cm. a) Tính độ dài AH, AB.
b) Gọi M là điểm bất kỳ trên cạnh AC (M khác A, C). Kẻ AI  BM (I  BM ) . Chứng minh ∆BIC ∆BHM. Câu 17. (1,0 điểm)
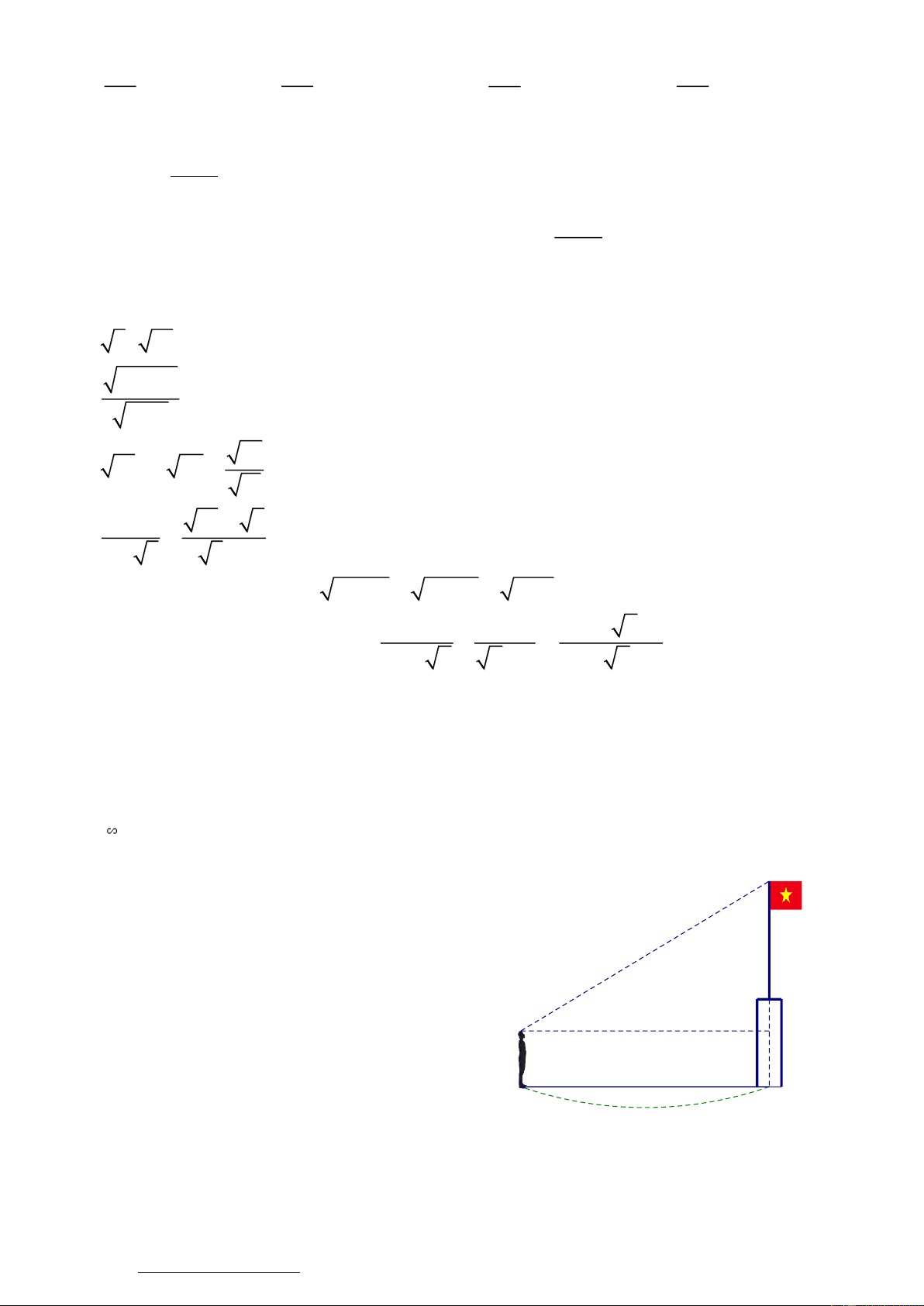
Một học sinh dùng giác kế, đứng cách chân cột
cờ 30m rồi chỉnh mặt thước ngắm cao bằng mắt
của mình để xác định góc tạo bởi tia sáng đi
thẳng từ đỉnh cột cờ với mắt tạo với phương nằm
ngang là 310. Biết khoảng cách từ mặt sân đến
mắt học sinh đó bằng 1,5m (hình vẽ). Tính chiều
cao cột cờ (làm tròn đến số thập phân thứ hai). 310 1,5m 30m
------ HẾT ------ PHÒNG GD&ĐT KRÔNG ANA ĐÁP ÁN TRƯỜNG THCS …
MÔN TOÁN 9 – Khối lớp 9 Trang 4
Thời gian làm bài : 90 phút
(Không kể thời gian phát đề)
Phần đáp án câu trắc nghiệm:
Tổng câu trắc nghiệm: 12. 190 191 1 B C 2 D C 3 B A 4 C B 5 B D 6 A D 7 D A 8 D C 9 A A 10 A D 11 C B 12 C D
Phần đáp án câu tự luận: Tổng câu tự luận: 5. Mã đề 190
Câu 13. (2,0 điểm) Thực hiện các phép tính sau: a) 2  8 . 4 3 27a b b)
(với a  0, b  0 ). 2 3a b 22 c) 18  5 8  . 11 1 15  3 d)  . 2  3 5 1 Gợi ý làm bài: Câu 0,5 a
2  8  2  8  16  4 13 điểm 4 3 4 3 27a b 27a b 0,5 b 2 2 
 9a b  3 a  b  3ab (vì a  0, b  0 ) 2 2 3 điể 3 a b a b m 22 22 2 2 18  5 8   3  2  5 2  2   3 2 10 2  2 0,5 c 11 11 điểm  6  2 Trang 5 3  5    1 1 15 3 2 3 2  3      3 2 0,5 d 2 2  3 5 1  2   3 5 1 1 điểm  2  3  3  2
Câu 14. (1,0 điểm) Tìm x, biết: 4x  4  9x  9  x 1  8 Gợi ý làm bài: Câu 14 Điều kiện: x 1 0,25 điểm
4(x 1  9(x 1)  x 1  8 0,5 điểm  4 x 1  8  x 1  2  x  5 (Nhận) 0,25 Vậy x  5 điểm  1 3  x  3
Câu 15. (1,0 điểm) Cho biểu thức P   :   (Với
 x  2 x  2 x  x  4 x  4
x  0; x  4; x  9). a) Rút gọn P. b) So sánh P với 1. Gợi ý làm bài: Câu 15 a  1 3  x  3 0,75 P   :    điểm x  2
x  2 x  x  4 x  4  x   x 2 3 2   x  x  2 x  3 x  2  x b x  2 2 0,25 P  1
1 (Với x  0; x  4; x  9). điểm x x
Câu 16. (2,0 điểm) Cho tam giác ABC vuông tại A có đường cao AH. Biết BH = 4cm và HC = 6 cm.
a) Tính độ dài các đoạn AH, AB.
b) Biết D, E lần lượt là hình chiếu của H trên AB và AC. Chứng minh: ∆AED ∆ABC. Gợi ý làm bài: Câu 16 Vẽ hình; Viết GT, KL. 0,5 điểm Trang 6 A E D B C H a ABC 
vuông tại A, có đường cao AH. Áp dụng hệ thức, ta có: 1,0 điểm 2
AH  HB  HC 2 AH  4  6 2 AH  24  AH  2 6cm 2
AB  HB  BC 2
AB  4  4  6 2 AB  40
 AB  2 10cm b A
 HB vuông tại H, có đường cao HD. Áp dụng hệ thức, ta có: 0,5 điểm 2
AH  AD  AB .
Chứng minh tương tự, ta có: 2
AH  AE  AC . AD AE
 AD  AB  AE  AC   AC AB Xét ∆AED và ∆ABC có: A chung AD AE  AC AB Vậy ∆AED ∆ABC. Câu 17. (1,0 điểm)
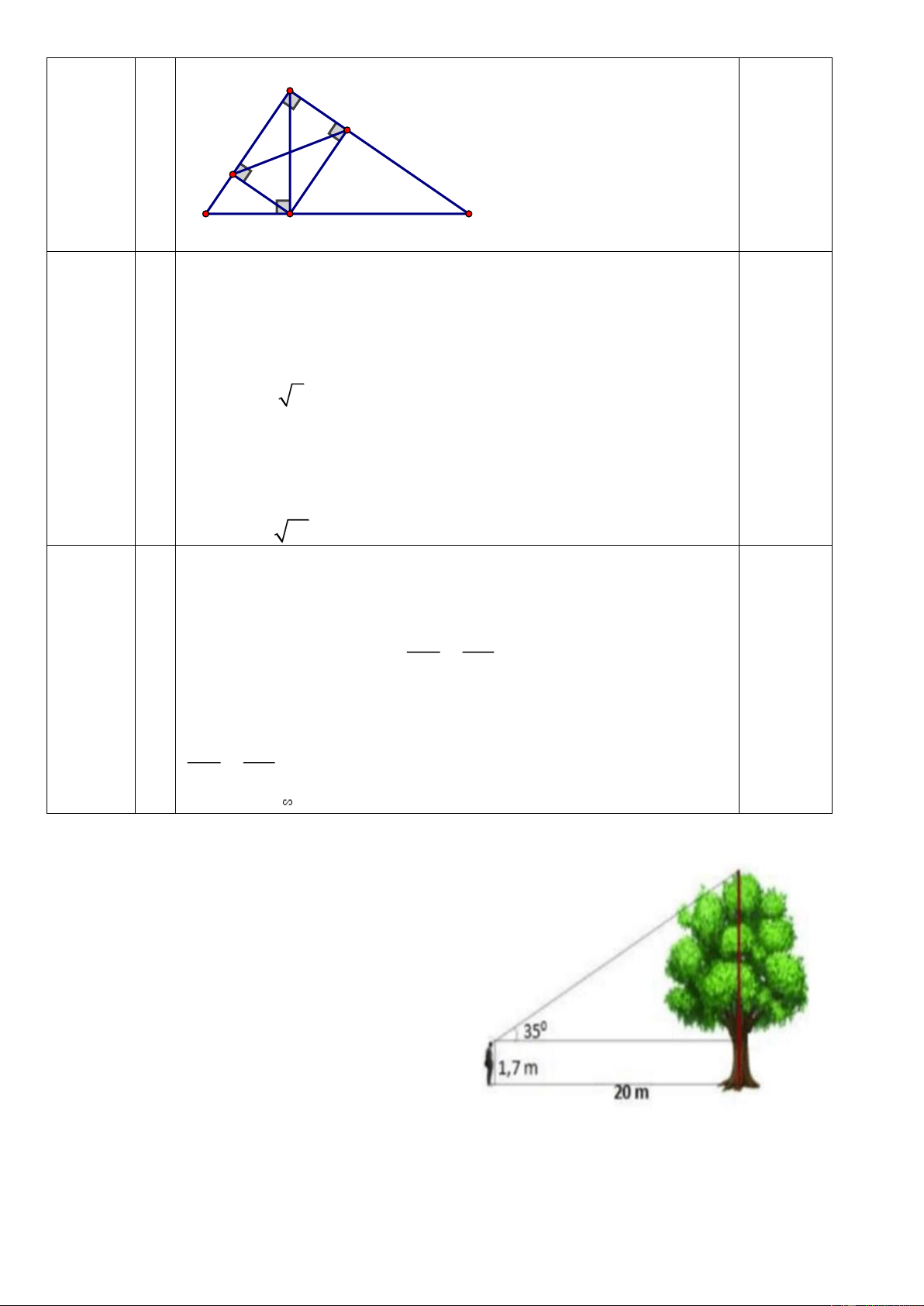
Một người đứng thẳng và dùng thước ngắm để đo
chiều cao của một cái cây. Biết khoảng cách từ
chân người đứng tới gốc cây là 20m, người đó
cao 1,7m, góc ngắm tạo bởi tia đi từ mắt tới ngọn
cây và tia đi từ mắt đến thân cây theo phương
nằm ngang là 350 (hình vẽ). Tính chiều cao của
cây (làm tròn đến số thập phân thứ hai). Gợi ý làm bài: Trang 7 C 0,25 Câu 17 điểm B 350 A 1,7m D E 20m
Vì ABDE là hình chữ nhật nên:
AE  BD 1,7 ;
m AB  DE  20m. 0,75 ABC  vuông tại A, ta có: 0
AC  AB  tan BAC  20  tan 35 . điểm Chiều của cây là: 0
EC  EA  AC  1,7  20  tan 35  15,70m Mã đề 191
Câu 13. (2,0 điểm) Thực hiện các phép tính sau: a) 3  12 . 4 3 50a b b)
(với a  0, b  0 ). 2 2a b 33 c) 12  5 27  . 11 4 15  5 d)  . 3  5 3 1 Gợi ý làm bài: Câu 0,5 a
3  12  3 12  36  6 13 điểm 4 3 4 3 50a b 50a b 0,5 b 2 2 
 25a b  5 a  b  5
 ab (vì a  0, b  0 ) 2 2 2 điể 2 a b a b m 33 33 2 2 12  5 27   2 3  5 3 3   2 3 15 3  3 0,5 c 11 11 điểm  1  2 3 4 
3 5 5 3  1 43 5 4 15 5       5 2 0,5 d 2 3  5 3 1  3   5 3 1 4 điểm  3  5  5  3
Câu 14. (1,0 điểm) Tìm x, biết: 4x  4  9x  9  x  1  12 Gợi ý làm bài: Câu 14 Điều kiện: x  1  0,25 Trang 8 điểm
4(x  1)  9(x  1)  x  1  12 0,5 điểm  4 x 1 12  x 1  3  x  8 (Nhận) 0,25 Vậy x  8 điểm  1 1  1 x
Câu 15. (1,0 điểm) Cho biểu thức A   :  
(Với x  0; x 1)  x  2 x
x  2  x  4 x  4 a) Rút gọn A. b) So sánh A với 1. Gợi ý làm bài: Câu 15 a  1 1  x 1 0,75 A   :    điểm x  2 x
x  2  x  4 x  4   x  x 2 1 2   x  x  2 1  x x  2  x b x  2 2 0,25 A  1
1 (Với x  0; x 1). điểm x x
Câu 16. (2 điểm) Cho ∆ABC vuông tại A, AH là đường cao. Biết BH = 2cm, HC = 6 cm. a) Tính độ dài AH, AB.
b) Gọi M là điểm bất kỳ trên cạnh AC (M khác A, C). Kẻ AI  BM (I  BM ) . Chứng minh ∆BIC ∆BHM. Gợi ý làm bài: Câu 16 Vẽ hình; Viết GT, KL. 0,5 điểm A M I B C H a ABC 
vuông tại A, có đường cao AH. Áp dụng hệ thức, ta có: 1,0 điểm 2
AH  HB  HC 2 AH  2  6 2 AH  12  AH  2 3cm Trang 9 2
AB  HB  BC 2
AB  2  2  6 2 AB  16  AB  4cm b ABM 
vuông tại A, có đường cao AI. Áp dụng hệ thức, ta có: 0,5 điểm 2
AB  BI  BM . Ta có: 2
AB  HB  BC (câu a). BI BC
 BI  BM  BH  BC   . BH BM Xét ∆BIC và ∆BHM có: B chung BI BC  BH BM Vậy ∆BIC ∆BHM. Câu 17. (1,0 điểm)
Một học sinh dùng giác kế, đứng cách chân cột
cờ 30m rồi chỉnh mặt thước ngắm cao bằng mắt
của mình để xác định góc tạo bởi tia sáng đi
thẳng từ đỉnh cột cờ với mắt tạo với phương nằm
ngang là 310. Biết khoảng cách từ mặt sân đến
mắt học sinh đó bằng 1,5m (hình vẽ). Tính chiều
cao cột cờ (làm tròn đến số thập phân thứ hai). 310 1,5m 30m Gợi ý làm bài: C 0,25 Câu 17 điểm 0 B 31 A 1,5m D E 30m
Vì ABDE là hình chữ nhật nên:
AE  BD 1,5 ;
m AB  DE  30m . 0,75 ABC  vuông tại A, ta có: 0
AC  AB  tan BAC  30  tan 31 . điểm
Chiều cao của cột cờ là: 0
EC  EA  AC  1,5  30  tan 31  19,53m Trang 10
KHUNG MA TRẬN VÀ BẢN ĐẶC TẢ MA TRẬN ĐỀ KIỂM TRA GIỮA KÌ I, MÔN TOÁN - LỚP 9
NĂM HỌC: 2023 – 2024 Chươn
Số câu hỏi theo mức độ nhận thức Nội dung/ Đơn TT g/
Mức độ đánh giá vị kiến thức Chủ đề Nhận biết Thông hiểu Vận dụng Vận dụng cao 3TN Nhận biết: Câu 1 Căn bậc hai
Nhận biết khái niệm về căn bậc hai số học. Căn Câu 2 bậc hai. Câu 3
Nhận biết giá trị của căn bậc hai. Điểm: 0,75 Căn thức bậc 3TN hai và hằng Thông hiểu: Câu 4 đẳng
Biết tìm điều kiện xác định của căn thức. Biết rút Câu 5 Căn thức 2 A  A
gọn căn thức đơn giản. Câu 6 bậc Điểm: 0,75 hai, Nhận biết: 1 căn Liên hệ giữa
- Nhận biết công thức khai phương 1 tích (1 1TN, 1TL 1TL
bậc ba phép nhân, phép thương) Câu 7 Câu 13b (16 tiết) chia và phép Thông hiểu: Câu 13a khai phương Điể m: 0,5
Biết tìm khai phương phương một tích, một Điểm: 0,75 thương. Biến đổi đơn Thông hiểu: 2TL giản biểu thức
- Hiểu phương pháp trục căn thức ở mẫu, đưa Câu 13c chứa căn thức
thừa số ra ngoài dấu căn, khai phương một Câu 13d bậc hai
thương để thu gọn. Điểm : 1,0 Rút gọn biểu 3TL Vận dụng: thức chứa căn Câu 14
- Biết vận dụng rút gọn căn thức để giải thức bậc hai Trang 11 phương trình. Câu 15a
- Biết vận dụng rút gọn căn thức để giải toán Câu 15b
tổng hợp về căn thức. Điểm: 2,0 Nhận biết : 1TN Căn bậc ba
- Biết giá trị căn bậc ba của số đơn giản. Câu 8 Điểm: 0,25 Nhận biết 2TN
- Nhận biết hệ thức lượng trong tam giác Câu 9 vuông. Câu 10
Một số hệ thức - Biết vẽ hình cơ bản liên quan hệ thức lượng. Điểm: 0,5 1TL về cạnh và 1TL Hệ Câu 16a đườ Thông hiểu ng cao Câu 16b thức
- Hiểu công thức hệ thức lượng để tìm độ dài Điểm: 1,5 lượ trong tam giác ng Điểm: 0,5 vuông
đường cao, cạnh của tam giác. giác Vận dụng cao: trong 2 tam
- Vận hệ thức để chứng minh tam giác đồng giác dạng. vuông Nhận biết 2TN (14
- Nhận biết được tỉ số lượng giác của góc Câu 11 tiết) Tỉ số lượng
nhọn trong tam giác vuông. Nhận biết công Câu 12 1TL giác của góc
thức tỉ số lượng giác đơn giản. Điểm: 0,5 Câu 17 nhọn Vận dụng Điểm: 1,0
- Vận dụng được công thức tỉ số lượng giác để
giải bài toán thực tế đơn giản. Tổng câu 10 7 4 1 Tỉ lệ % 27,5% 37,5% 30% 5% Tỉ lệ chung 65% 35% Trang 12