
Preview text:
CÂU 40: TÌM THAM SỐ ĐỂ HÀM SỐ ĐƠN ĐIỆU TRÊN MỘT KHOẢNG CHO TRƯỚC
MỨC VẬN DỤNG-VẬN DỤNG CAO
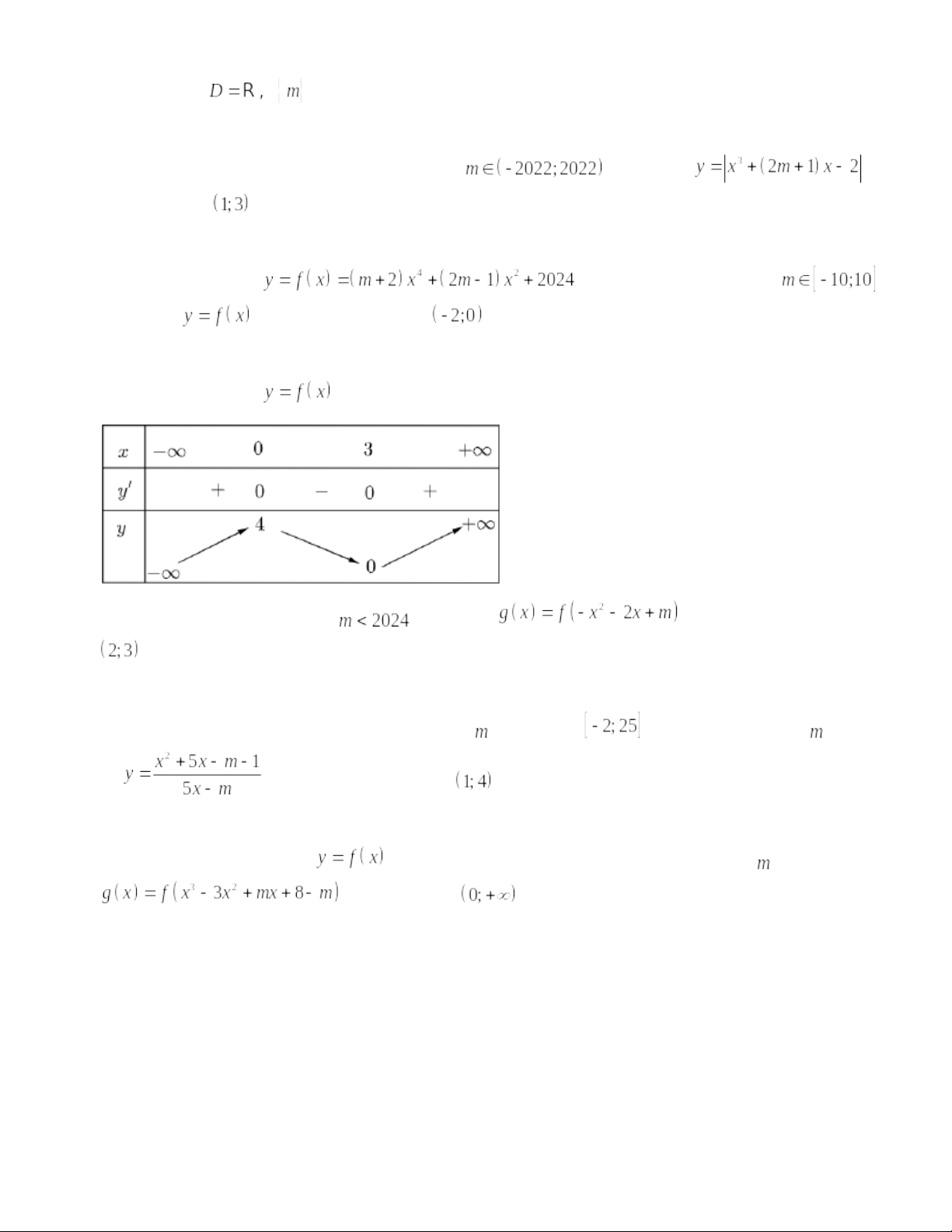
Câu 1: Tập hợp tất cả các giá trị của tham số để hàm số
đồng biến trên khoảng
là:
A. . B.
. C.
. D.
.
Câu 2: Có bao nhiêu giá trị nguyên của tham số thuộc khoảng
để hàm số
nghịch biến trên khoảng
.
A. . B.
. C.
. D.
.
Câu 3: Có bao nhiêu giá trị nguyên của tham số thuộc đoạn
sao cho ứng với mỗi
, hàm số
đồng biến trên khoảng
.
A. 24 . B. 2 . C. 20 . D. 6 .
Câu 4: Có bao nhiêu giá trị nguyên của tham số để hàm số
nghịch biến trên khoảng
và đồng biến trên khoảng
.
A. . B.
. C.
. D.
.
Câu 5: Tìm tập hợp tất cả các giá trị của tham số sao cho hàm số
nghịch biến trên khoảng
.
A. . B.
. C.
. D.
.
Câu 6: Có bao nhiêu giá trị nguyên của tham số thuộc đoạn
sao cho ứng với mỗi
, hàm số
nghịch biến trên khoảng
.
A. 8 . B. 15 . C. 14 . D. 6 .
Câu 7: Có bao nhiêu giá trị nguyên của tham số thuộc đoạn
sao cho ứng với mỗi
, hàm số
đồng biến trên khoảng
.
A. 17 . B. 15 . C. 14 . D. 16 .
Câu 8: Có bao nhiêu giá trị nguyên của tham số thuộc đoạn
sao cho ứng với mỗi
, hàm số
nghịch biến trên khoảng
.
Tập xác định: .
A. 1027 . B. 4045 . C. 4043 . D. 2025 .
Câu 9: Có bao nhiêu giá trị nguyên của tham số để hàm số
đồng biến trên
?
A. 4034 . B. 2022 . C. 4030 . D. 4032 .
Câu 10: Cho hàm số . Số các giá trị nguyên của
để hàm số
đồng biến trên khoảng
là
A. 10 . B. 9 . C. 11 . D. 8 .
Câu 11: Cho hàm số có bảng biến thiên như sau
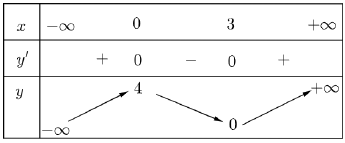
Có bao nhiêu số nguyên dương để hàm số
nghịch biến trên khoảng
?
A. 2014 . B. 2015 . C. 2013 . D. 2016 .
Câu 12: Có bao nhiêu giá trị nguyên của tham số thuộc đoạn
sao cho ứng với mỗi
, hàm số
nghịch biến trên khoảng
.
A. 8 . B. 15 . C. 14 . D. 6 .
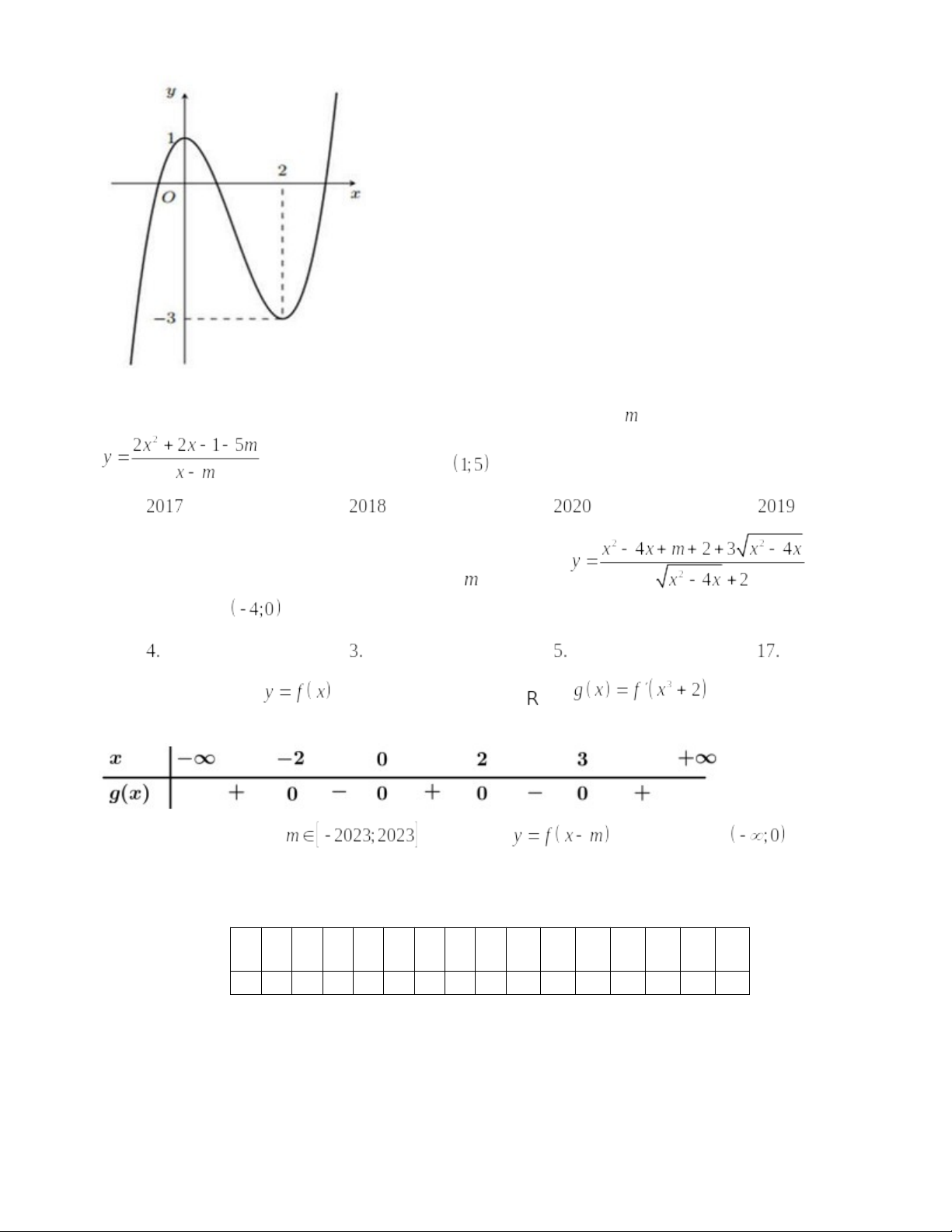
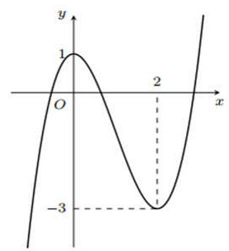
Câu 13: Cho hàm số bậc ba có đồ thị như hình bên. Có bao nhiêu số nguyên
để hàm số
đồng biến trên
?
A. 5 . B. 6 . C. 4 . D. 3 .
Câu 14: Có bao nhiêu giá trị nguyên dương bé hơn 2024 của tham số sao cho hàm số
nghịch biến trên khoảng
?
A. . B.
. C.
. D.
.
Câu 15: Có bao nhiêu giá trị nguyên dương của để hàm số
nghịch biến trên khoảng
?
A. B.
C.
D.
Câu 16: Cho hàm số có đạo hàm liên tục trên
và
có bảng xét dấu như sau:
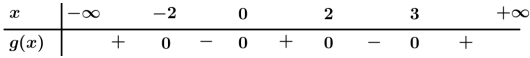
Có bao nhiêu số nguyên để hàm số
đồng biến trên
?
A. 2020 B. 2017 . C. 2018 . D. 2019 .
ĐÁP ÁN
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
C | B | C | D | A | D | D | C | C | B | A | D | C | D | A | C |




