





























Preview text:
SÔÛ GD&ÑT TP HOÀ CHÍ MINH
ÑEÀ THAM KHAÛO TUYEÅN SINH 10
PHOØNG GÑ&ÑT QUAÄN 3
NAÊM HOÏC: 2022 - 2023 MÔN: TOÁN 9 ĐỀ TH AM KHẢO
Đê thi gồm 8 câu hỏi tự luận. MÃ ĐỀ: Quận 3 - 2
Thời gian: 120 phút (không kể thời gian phát đề)
Câu 1. (1,5 điểm ) Cho P 2
: y 2x và D : y 3x 1.
a) Vẽ P và D trên cùng một hệ trục tọa độ.
b) Tìm tọa độ giao điểm của P và D bằng phép tính.
Câu 2. (1 điểm) Cho phương trình 2
x 10x 8 0 có hai nghiệm x ,x . Không giải phương trình 1 2
hãy tính giá trị của biểu thức A x x 2 2 x x . 1 2 1 2
Câu 3. (1 điểm) Các nhà khoa học về thống kê đã thiết lập được hàm số sau: At 0,08t 19,7 .
Trong đó At là độ tuổi trung bình các phụ nữ kết hôn lần đầu của thế giới; t là số năm kết
hôn, với gốc thời gian là 1950 . Hãy tính độ tuổi trung bình các phụ nữ kết hôn lần đầu lần
lượt vào các năm 1950 , 2000 , 2018 ¸ 2020 (làm tròn đến chữ số thập phân thứ hai).
Câu 4. (1 điểm) Một trường học có tổng số giáo viên là 80 80 người, hiện tại tuổi trung bình của giáo
viên là 35 tuổi .Trong đó, tuổi tuổi trung bình của giáo viên nữ là 32 tuổi và tuổi trung bình
của giáo viên nam là 38 tuổi. Hỏi 3 trường đó có bao nhiêu giáo viên nam, bao nhiêu giáo viên nữ?
Câu 5. (1 điểm) Bé An sống trong gia đình ba thế hệ gồm ông bà nội, ba mẹ, bé An và em trai. Chủ
nhật vừa rồi cả gia đình đi xem phim. Biết giá vé cho trẻ em (vé của bé An và em trai) được
giảm giá 50% ; vé người cao tuổi được giảm giá 25% (vé của ông bà nội ). Vé của ba mẹ
không được giảm giá. Ông nội bé An, người phải trả giá vé là 60 60 nghìn đồng, đang trả
tiền cho mọi người. Hỏi ông nội phải trả bao nhiêu tiền?
Câu 6. (1 điểm) Theo năm Dương lịch, chu kỳ Trái Đất quay quanh Mạt Trời là 365 ngày và ngày 1
(tức là 365,25 ngày). Khi đó, ngày này sẽ được tích lũy trong vòng 4 năm nên theo năm 4
Dương lịch thì cứ 4 năm lại có 1 năm là năm nhuận vào các năm chia hết cho 4 (tháng 2
của năm này sẽ có 29 ngày thay vì có 28 ngày như các năm không nhuận Dương lịch).
Tuy nhiên, vẫn có một số ngoại lệ đối với nguyên tắc trên vì có khi một năm Dương lịch lại
ngắn hơn 365,25 ngày nên với những năm có hai chữ số 0 ở cuối thì năm đó phải chia hết
cho 400 mới là năm nhuận Dương lịch.
a) Từ năm 1900 đến năm 2000 có bao nhiêu năm nhuận Dương lịch? Vì sao? Trang 1
b) Một nhà hộ sinh trong tháng 2 năm 2021 có 29 em bé chào đời là con của 29 gia đình
khác nhau. Có thể chắc chắn rằng có ít nhất 2 em bé chào đời cùng ngày hay không? Vì sao?
Câu 7. (1,0 điểm) Thớt là một dụng cụ sử dụng trong bếp của mỗi gia đình để thái, chặt, .... Một cái
thớt hình trụ có đường kính đáy 22 cm , cao 4 cm .
a) Tính tổng diện tích hai mặt thớt (làm tròn đến 2 cm ).
b) Cho biết loại gỗ làm thớt có khối lượng 3
500 kg / m . Hỏi thớt nặng bao nhiêu gam? Công
thức tính thể tích hình trụ là V .
S h ( S là diện tích đáy và h là chiều cao hình trụ).
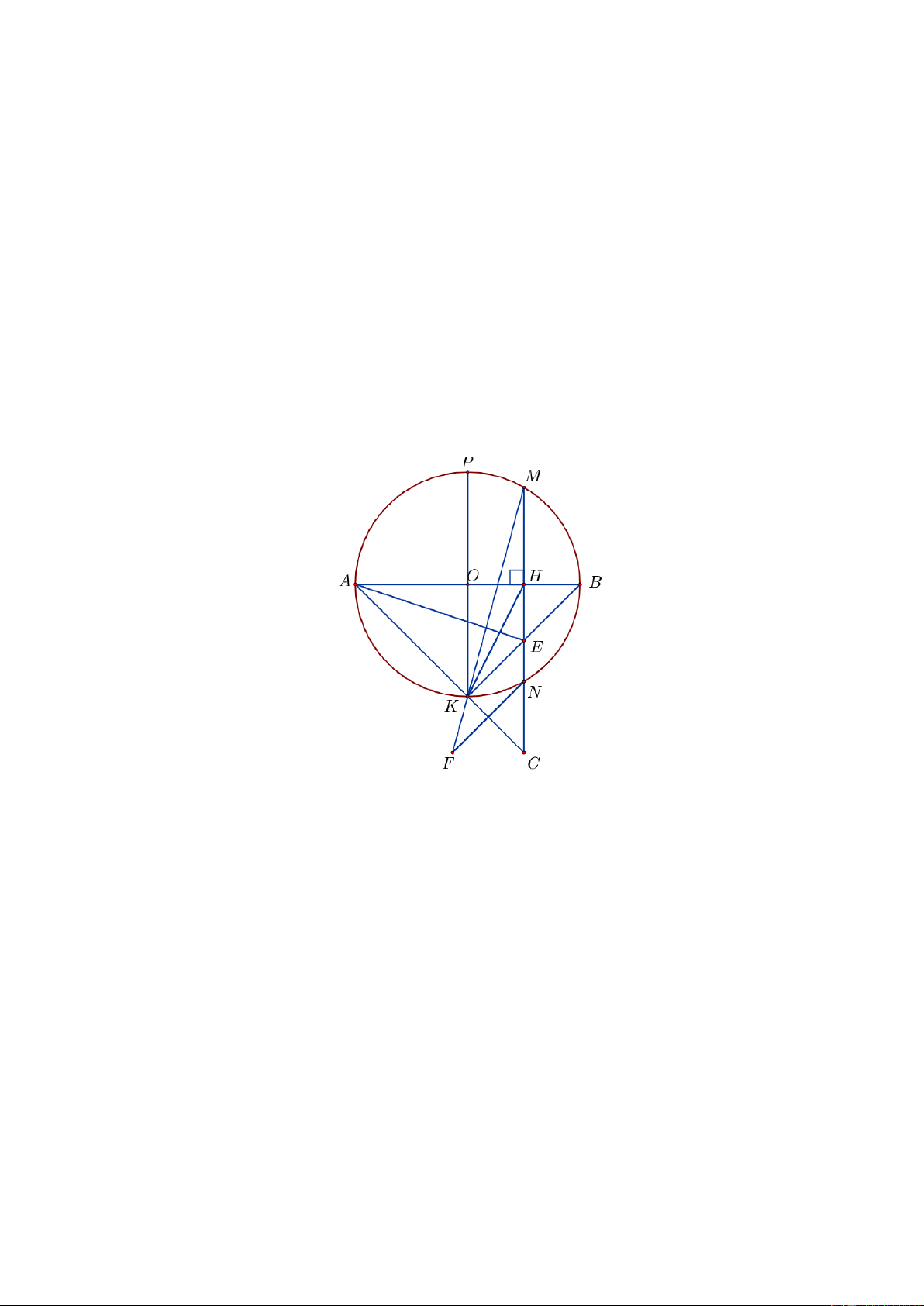
Câu 8. (2,5 điểm) Cho A
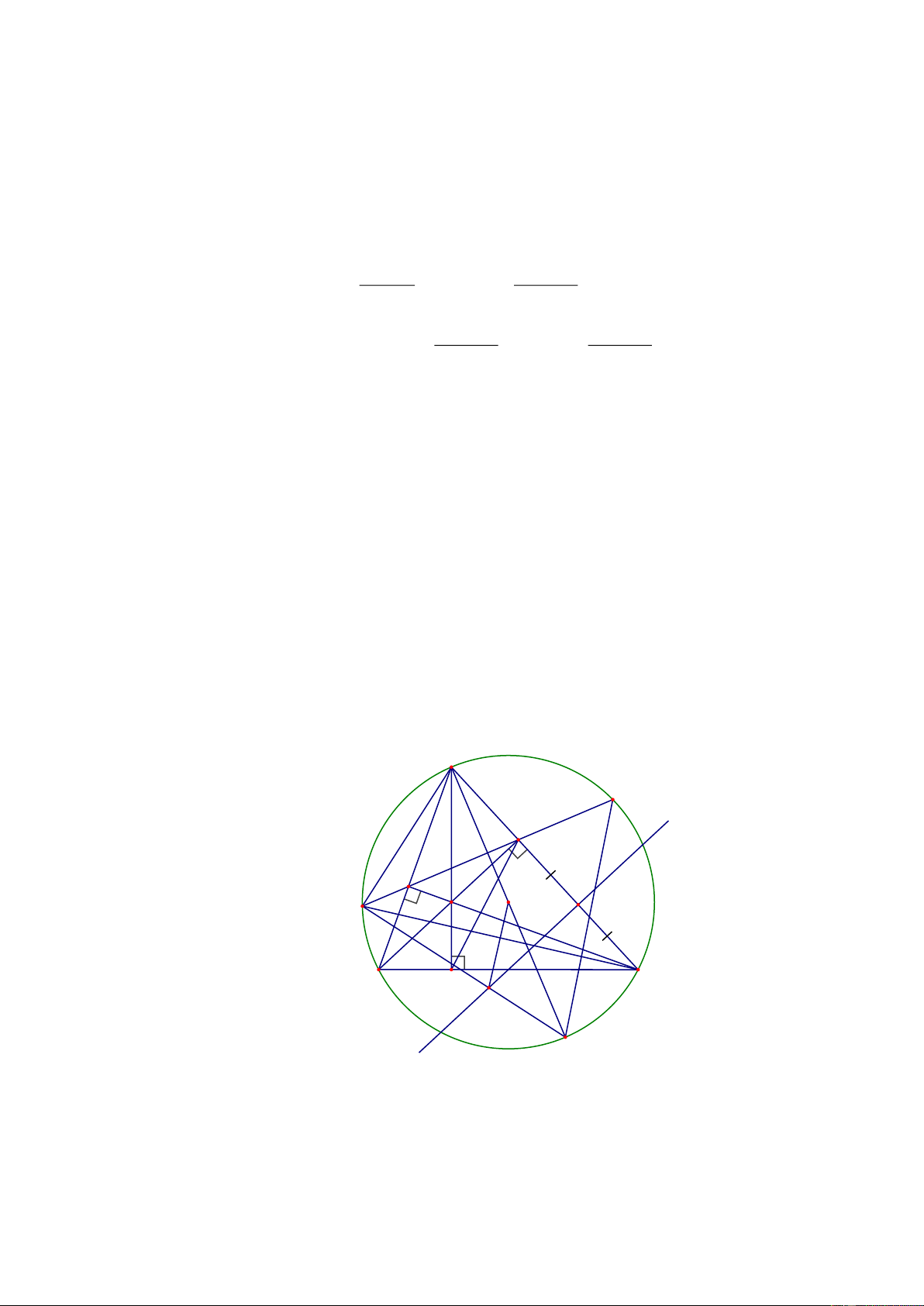
BC có 3 góc nhọn nội tiếp đường tròn O;R . Gọi M,P,Q lần lượt là
điểm chính giữa các cung BC , CA và AB . Gọi T là giao điểm của BP và CQ . Đường thẳng
vuông góc với BP tại B và đường thẳng vuông góc với CQ tại C cắt nhau ở I . Vẽ đường
kính MN của O . Gọi K là hình chiếu của I trên AB . a) Chứng minh: A KI” N
CM và tứ giác BICT nội tiếp.
b) PQ cắt AC tại H , MQ cắt BC tại V . Chứng minh 3 điểm H,T,V thẳng hàng.
c) Gọi OI d,IK r . Chứng minh: 2 2
d R 2Rr . ----HẾT--- Trang 2 HƯỚNG DẪN GIẢI
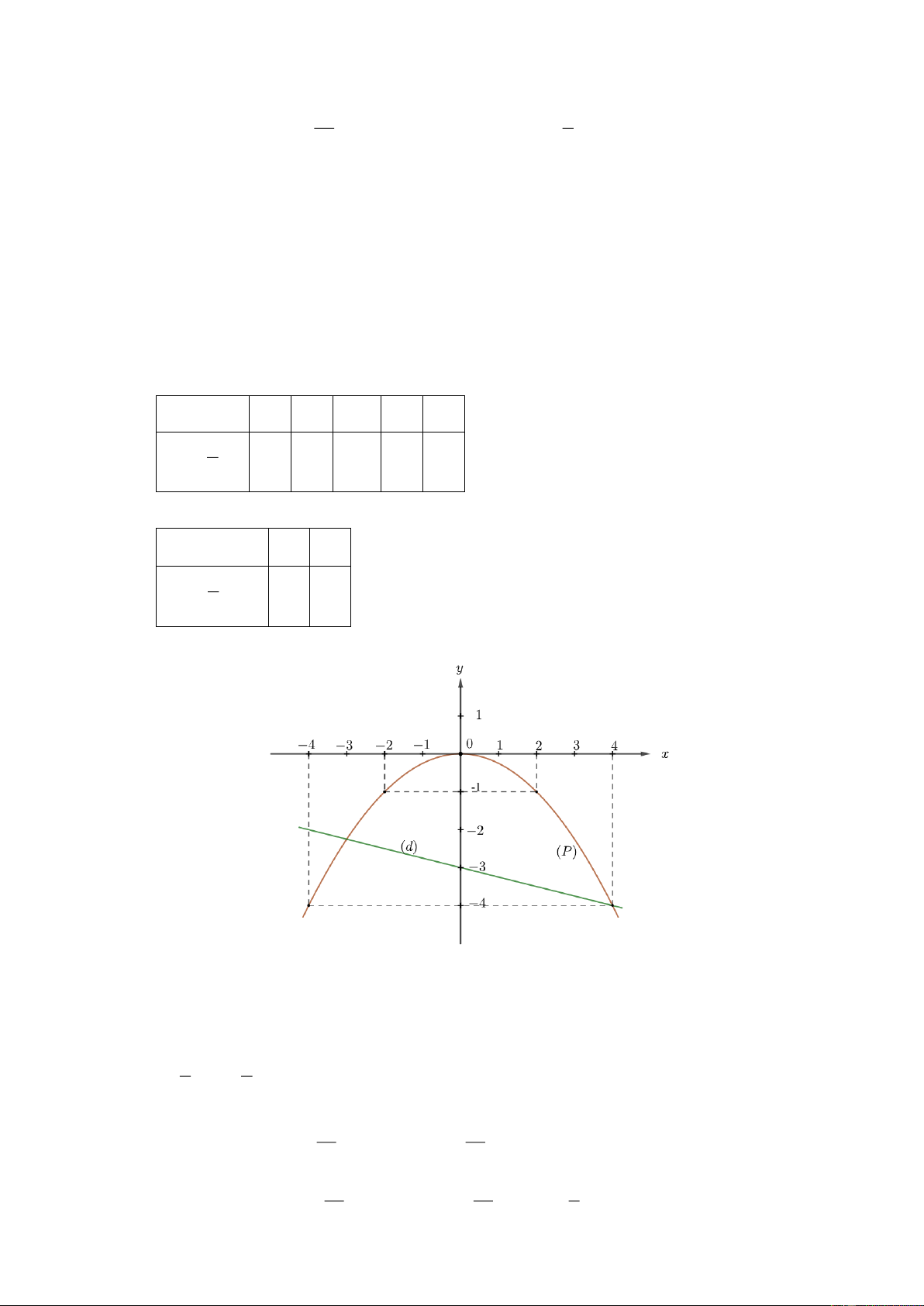
Câu 1. (1,5 điểm ) Cho P 2
: y 2x và D : y 3x 1.
a) Vẽ P và D trên cùng một hệ trục tọa độ.
b) Tìm tọa độ giao điểm của P và D bằng phép tính. Lời giải
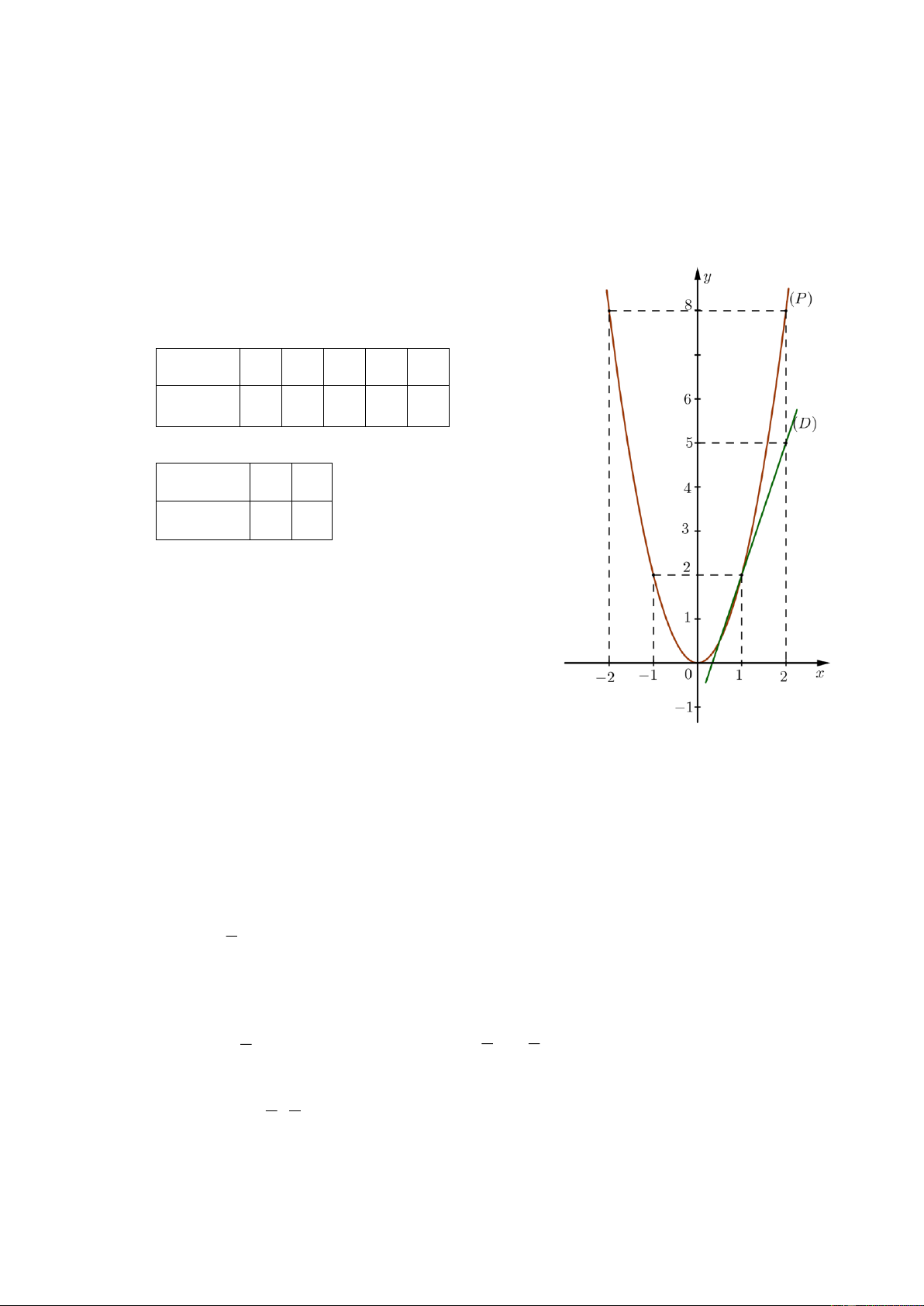
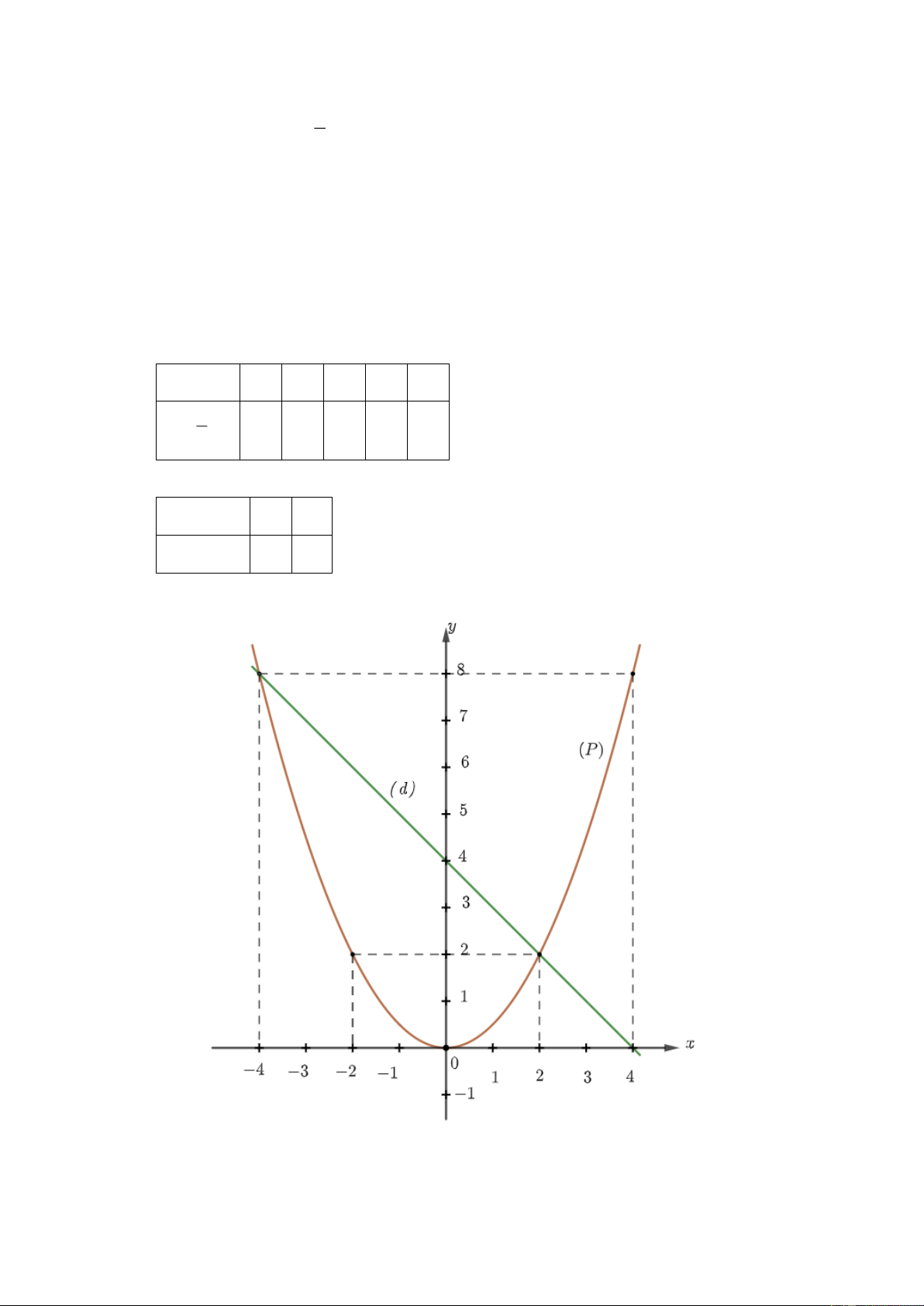
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ. BGT: x 2 1 0 1 2 2 y 2x 8 2 0 2 8 x 1 2 y 3x 1 2 5
b) Tìm tọa độ giao điểm của P và d bằng phép tính.
Phương trình hoành độ giao điểm của P và d : 2 2x 3x 1 2
2x 3x 1 0 x 1 1 x 2 Thay x 1 vào 2
y 2x , ta được: 2 y 2.1 2 . 2 1 1 1 Thay x vào 2
y 2x , ta được: y 2 . 2 2 2 1 1
Vậy 1; 2 , ; là hai giao điểm cần tìm. 2 2 Trang 3
Câu 2. (1 điểm) Cho phương trình 2
x 10x 8 0 có hai nghiệm x ,x . Không giải phương trình 1 2
hãy tính giá trị của biểu thức A x x 2 2 x x . 1 2 1 2 Lời giải 2 Vì 2
b 4ac 1 0 4.1. 8 132 0
Nên phương trình có hai nghiệm phân biệt x ,x . 1 2 b
S x x 10 1 2
Theo định lí Vi-et, ta có: a c
P x .x 8 1 2 a
Ta có: A x x 2 2 x x 1 2 1 2
A x x x x x x 1 2 1 2 1 2
A x x 2 x x 1 2 1 2
A x x 2 4x x x x 1 2 1 2 1 2 2 A 10 4. 8.10 1320.
Câu 3. (1 điểm) Các nhà khoa học về thống kê đã thiết lập được hàm số sau: At 0,08t 19,7 .
Trong đó At là độ tuổi trung bình các phụ nữ kết hôn lần đầu của thế giới; t là số năm kết
hôn, với gốc thời gian là 1950 . Hãy tính độ tuổi trung bình các phụ nữ kết hôn lần đầu lần
lượt vào các năm 1950 , 2000 , 2018 ¸ 2020 (làm tròn đến chữ số thập phân thứ hai). Lời giải
Độ tuổi trung bình kết hôn của phụ nữ năm 1950 :
At 0,081950 1950 19,7 19,7 tuổi.
Độ tuổi trung bình kết hôn của phụ nữ năm 2000 :
At 0,082000 1950 19,7 23,7 tuổi.
Độ tuổi trung bình kết hôn của phụ nữ năm 2018 :
At 0,082018 1950 19,7 25,14 tuổi.
Độ tuổi trung bình kết hôn của phụ nữ năm 2020 :
At 0,082020 1950 19,7 25,3 tuổi.
Câu 4. (1 điểm) Một trường học có tổng số giáo viên là 80 người, hiện tại tuổi trung bình của giáo
viên là 35 tuổi .Trong đó, tuổi tuổi trung bình của giáo viên nữ là 32 tuổi và tuổi trung bình Trang 4
của giáo viên nam là 38 tuổi. Hỏi trường đó có bao nhiêu giáo viên nam, bao nhiêu giáo viên nữ? Lời giải
Gọi x,y lần lượt là số giáo viên nam và số giáo viên nữ của trường học x,y *
Vì trường có tổng số giáo viên là 80 người, nên ta có phương trình: x y 80 1
Với độ tuổi trung bình của giáo viên, ta có phương trình: 38x 32y 35.80 2800 2
x y 80
x 40n
Từ 1 và 2 ta có hệ phương trình: .
38x 32y 2800 y 40 n
Vậy trường có 40 giáo viên nam và 40 giáo viên nữ.
Câu 5. (1 điểm) Bé An sống trong gia đình ba thế hệ gồm ông bà nội, ba mẹ, bé An và em trai. Chủ
nhật vừa rồi cả gia đình đi xem phim. Biết giá vé cho trẻ em (vé của bé An và em trai) được
giảm giá 50% ; vé người cao tuổi được giảm giá 25% (vé của ông bà nội ). Vé của ba mẹ
không được giảm giá. Ông nội bé An, người phải trả giá vé là 60 nghìn đồng, đang trả tiền
cho mọi người. Hỏi ông nội phải trả tất cả bao nhiêu tiền? (câu hỏi phải thêm chữ tất cả) Lời giải
Giá tiền vé khi chưa được giảm giá: 60000 : 1 25% 80000 đồng.
Tổng số tiền ông nội bé An phải trả cho tất cả mọi người:
2.80000 2.60000 2.800001 50% 360000đồng.
Câu 6. (1 điểm) Theo năm Dương lịch, chu kỳ Trái Đất quay quanh Mạt Trời là 365 ngày và ngày 1
(tức là 365,25 ngày). Khi đó, ngày này sẽ được tích lũy trong vòng 4 năm nên theo năm 4
Dương lịch thì cứ 4 năm lại có 1 năm là năm nhuận vào các năm chia hết cho 4 (tháng 2
của năm này sẽ có 29 ngày thay vì có 28 ngày như các năm không nhuận Dương lịch).
Tuy nhiên, vẫn có một số ngoại lệ đối với nguyên tắc trên vì có khi một năm Dương lịch lại
ngắn hơn 365,25 ngày nên với những năm có hai chữ số 0 ở cuối thì năm đó phải chia hết
cho 400 mới là năm nhuận Dương lịch.
a) Từ năm 1900 đến năm 2000 có bao nhiêu năm nhuận Dương lịch? Vì sao?
b) Một nhà hộ sinh trong tháng 2 năm 2021 có 29 em bé chào đời là con của 29 gia đình
khác nhau. Có thể chắc chắn rằng có ít nhất 2 em bé chào đời cùng ngày hay không? Vì sao? Trang 5 Lời giải
a) Từ năm 1900 đến năm 2000 có bao nhiêu năm nhuận Dương lịch? Vì sao?
Từ năm 1900 đến năm 2000 có những năm thỏa điều kiện là năm dương lịch là:
1904 ; 1908 ; 1912 ;…. 1996 ; 2000 . 2000 1904 Vậy có tất cả
1 25 năm là năm dương lịch. 4
b) Một nhà hộ sinh trong tháng 2 năm 2021 có 29 em bé chào đời là con của 29 gia đình
khác nhau. Có thể chắc chắn rằng có ít nhất 2 em bé chào đời cùng ngày hay không? Vì sao?
Vì năm 2021 không chia hết cho 4 nên năm 2021 không phải là năm nhuận dương lịch
Nên trong tháng 2 năm 2021 chỉ có 28 ngày.
Theo đề bài, có tất cả 29 em bé của 29 gia đình khác nhau chào đời trong tháng 02 / 2021
Do vậy, có ít nhất 2 em bé chào đời cùng một ngày.
Câu 7. (1,0 điểm) Thớt là một dụng cụ sử dụng trong bếp của mỗi gia đình để thái, chặt, .... Một cái
thớt hình trụ có đường kính đáy 22 cm , cao 4 cm .
a) Tính tổng diện tích hai mặt thớt (làm tròn đến 2 cm ).
b) Cho biết loại gỗ làm thớt có khối lượng 3
500 kg / m . Hỏi thớt
nặng bao nhiêu gam? Công thức tính thể tích hình trụ là V .
S h ( S là diện tích đáy và h là chiều cao hình trụ). Lời giải
a) Tính tổng diện tích hai mặt thớt (làm tròn đến 2 cm ).
Diện tích hai mặt của thớt hình trụ: 2 2 2
S 2. R 2..11 760cm .
b) Cho biết loại gỗ làm thớt có khối lượng 3
500 kg / m . Hỏi thớt nặng bao nhiêu gam? Công
thức tính thể tích hình trụ là V .
S h ( S là diện tích đáy và h là chiều cao hình trụ).
Thể tích của tấm gỗ hình trụ: 2 2 3 6 3 V .
S h .R .h .11 .4 484 cm 484.10 m . m
Áp dụng công thức: D m . D V V
Suy ra khối lượng của tấm gỗ hình trụ: 6 m 500.484.10
242 gram 760gram. Trang 6
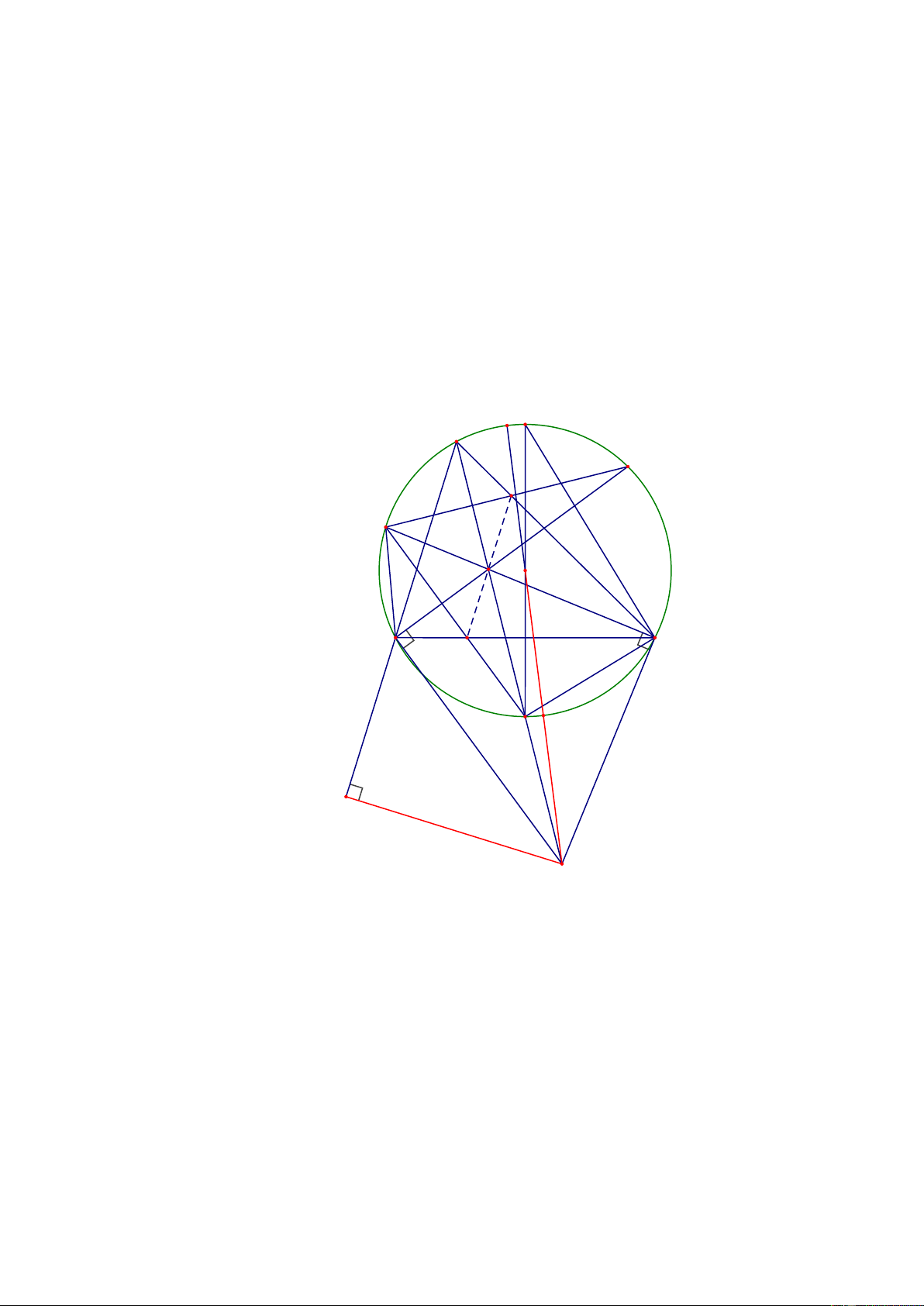
Câu 8. (2,5 điểm) Cho A
BC có 3 góc nhọn nội tiếp đường tròn O;R . Gọi M,P,Q lần lượt là
điểm chính giữa các cung BC , CA và AB . Gọi T là giao điểm của BP và CQ . Đường thẳng
vuông góc với BP tại B và đường thẳng vuông góc với CQ tại C cắt nhau ở I . Vẽ đường
kính MN của O . Gọi K là hình chiếu của I trên AB . a) Chứng minh: A KI” N
CM và tứ giác BICT nội tiếp.
b) PQ cắt AC tại H , MQ cắt BC tại V . Chứng minh 3 điểm H,T,V thẳng hàng.
c) Gọi OI d,IK r . Chứng minh: 2 2
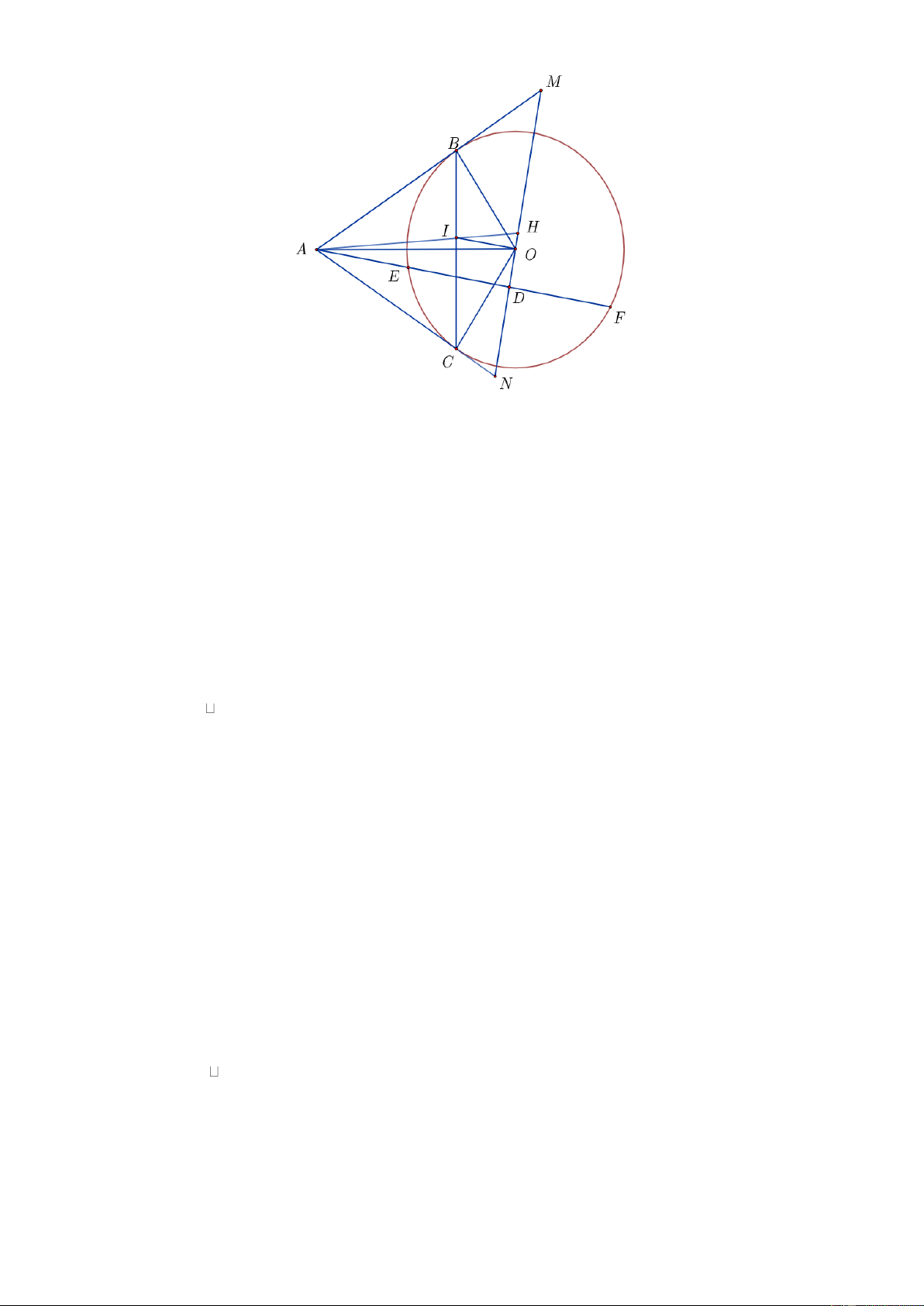
d R 2Rr . Lời giải S N A P H Q T O B V C M K K I a) Chứng minh: A KI” N
CM và tứ giác BICT nội tiếp.
Ta có: NCM 90 (gnt chắn nửa đường tròn O đường kính MN ) MN NC . Xét A KI và N CI , ta có:
AKI NCM 90
KAI CNM ( 2 gnt O cùng chắn hai cung BM CN ) A KI” N CM (g – g) Trang 7
Xét tứ giác BICT , có: T
BI 90BI BT T CI 90 CI CT
TBI TCI 180
Tứ giác BICT nội tiếp vì có hai góc đối bù nhau.
b) PQ cắt AC tại H , MQ cắt BC tại V . Chứng minh 3 điểm H,T,V thẳng hàng.
Xét tứ giác MCTV , ta có: VCT VMT ( 2 gnt cùng chắn AQ BQ )
Tứ giác MCTV nội tiếp vì có 2 đỉnh cùng nhìn một cạnh dưới 2 góc bằng nhau.
VTC VMC 180 .
Chứng minh tương tự: Tứ giác CPHT nội tiếp
HTC HOC 180
Mà: VTC VMC 180 (cmt)
Và HPC VMC 180 (tứ giác MCQP nội tiếp)
Nên: VTC HTC 180 Hay: HYV 180 .
Vậy 3 điểm H,T,V thẳng hàng.
c) Gọi OI d,IK r . Chứng minh: 2 2
d R 2Rr .
Ta có: MTC MAC ACT (góc ngoài A
TC tại đỉnh T )
MTC MCB BCQ CMT M
CT cân tại M . MC MT .
Dễ dàng Cm được MC MI
Nên: MC MI MT . Ta có: A KI” N CM (cmt) IK IA (tsđd) I . K MN I . A MC I . A MC 2Rr . MC MN Hay: I .
A IM 2Rr 1
Gọi K , S lần lượt là giao điểm của tia IO và O . Trang 8 Xét I MK và I SA, ta có: AIS chung
IKM IAS (tứ giác MKSA nội tiếp) I MK” I SA (g – g) IM IK
(tsđd) IM IA IK IS IO OKIO OS 2 2 . .
d R 2 IS IA
Từ 1 và 2 suy ra 2 2
d R 2Rr . ----HẾT---
SỞ GD&ĐT TP HỒ CHÍ MINH
ĐỀ THAM KHẢO TUYỂN SINH 10
PHÒNG GD&ĐT QUẬN 3
NĂM HỌC: 2021 - 2022 MÔN: TOÁN 9 ĐỀ TH AM KHẢO
Đê thi gồm 8 câu hỏi tự luận. MÃ ĐỀ: Quận 3 - 3
Thời gian: 120 phút (không kể thời gian phát đề)
Câu 1. (1,5 điểm). Cho P 2
: y x và đường thẳng d : y 3x 4 .
a) Vẽ đồ thị P và d trên cùng mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của P và d bằng phép tính.
Câu 2. (1 điểm). Cho phương trình 2 2x 5x 3
có 2 nghiệm là x ,x . Không giải phương trình, 1 2
hãy tính giá trị của biểu thức A x 3x x 3x . 1 2 2 1
Câu 3. (1 điểm). Tổng điều tra dân số và nhà ở năm 2019 được tiến hành vào thời điểm 0 giờ
ngày 1 / 4 / 2019 theo Quyết định số 772/QĐ-TTg ngày 26 / 6 / 2018 của Thủ tướng Chính
phủ. Đây là cuộc Tổng điều tra dân số và nhà ở lần thứ năm ở Việt Nam kể từ khi đất nước
thống nhất vào năm 1975 . Theo kết quả của cuộc tổng điều tra nói trên, tổng dân số của
Việt Nam là 96.208.984 người, trong đó nam ít hơn nữ 446.862 người và dân tộc Kinh
chiếm 85,3% dân số cả nước.
a) Dân tộc Kinh có bao nhiêu người (làm tròn đến hàng đơn vị)?
b) Tính số nam và số nữ của Việt Nam.
Câu 4. (1 điểm).
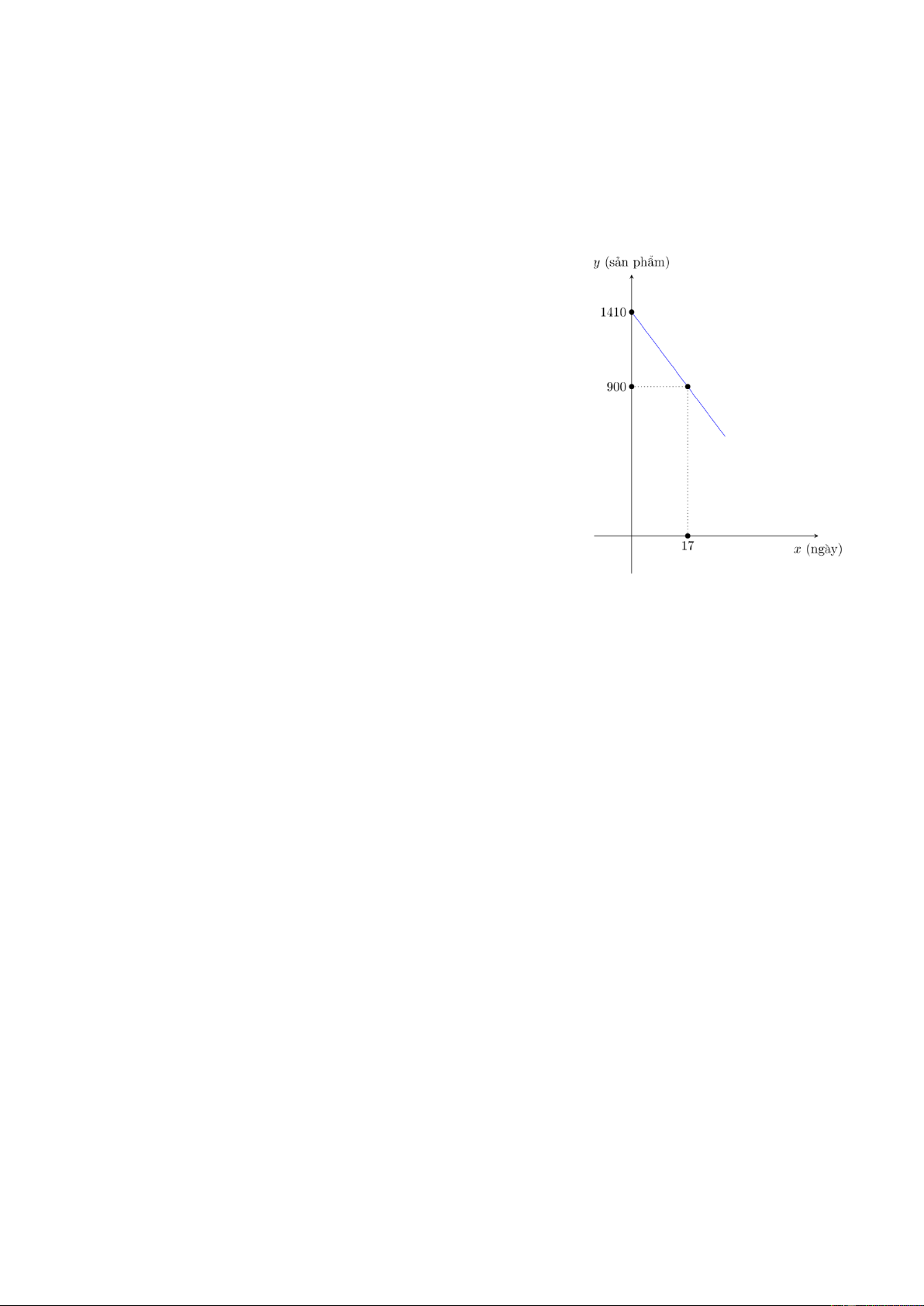
Một xí nghiệp cần bán thanh lý b sản phẩm. Số sản
phẩm y còn lại sau x ngày bán được xác định bởi hàm
số: y ax b có đồ thị như bên. Trang 9
a) Hãy dựa vào đồ thị xác định a,b và hàm số y .
b) Xí nghiệp cần bao nhiêu ngày để bán hết số sản phẩm cần thanh lý?
Câu 5. (1 điểm). Các bạn học sinh của lớp 9A dự định đóng góp một số tiền để mua tặng cho mỗi
em ở Mái ấm tình thương ba món quà (giá tiền các món quà đều như nhau). Khi các bạn
đóng đủ số tiền dự trù thì Mái ấm đã nhận chăm sóc thêm 9 em và giá tiền mỗi món quà
lại tăng thêm 5% nên số tiền có được vừa đủ để tặng mỗi em hai món quà. Hỏi có bao
nhiêu em ở Mái ấm lúc tặng quà?
Câu 6. (1 điểm).
Coi cả Trái Đất và Mặt Trăng đều có dạng
hình cầu và biết bán kính của Trái Đất là
khoảng 6371 km, bán kính của mặt trăng là khoảng 1737 km.
a) Hãy tính diện tích bề mặt của Trái Đất
và diện tích bề mặt của Mặt Trăng.
b) Biết 70,8% diện tích bề mặt Trái Đất là
nước. Hãy tính phần diện tích này?
(Làm tròn kết quả đến hàng triệu)
Câu 7. (1 điểm). Giá của một mặt hàng là 800.000 đồng. Nếu bán mặt hàng này với giá bằng một
nửa giá niêm yết thì lợi nhuận là 20% . Hỏi phải bán với giá bao nhiêu thì được lợi nhuận 60% ?
Câu 8. (2,5 điểm) Cho tam giác ABC nhọn AB AC nội tiếp đường tròn O có ba đường cao
AD,BE,CF cắt nhau tại H .
a) Chứng minh AEHF và ABDE là các tứ giác nội tiếp.
b) Đường thẳng EF cắt đường tròn O tại các điểm M,N ( M thuộc cung nhỏ AB ). Kẻ
đường kính AK của đường tròn O . Chứng minh tia EB là tia phân giác của góc DEF và KM N cân.
c) Đường trung trực của CE cắt MK tại Q . Chứng minh MA là tiếp tuyến của MEC và
OQ vuông góc MC . Trang 10 ----HẾT--- Trang 11 HƯỚNG DẪN GIẢI
Câu 1. (1,5 điểm). Cho P 2
: y x và đường thẳng d : y 3x 4 .
a) Vẽ đồ thị P và d trên cùng mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của P và d bằng phép tính. Lời giải
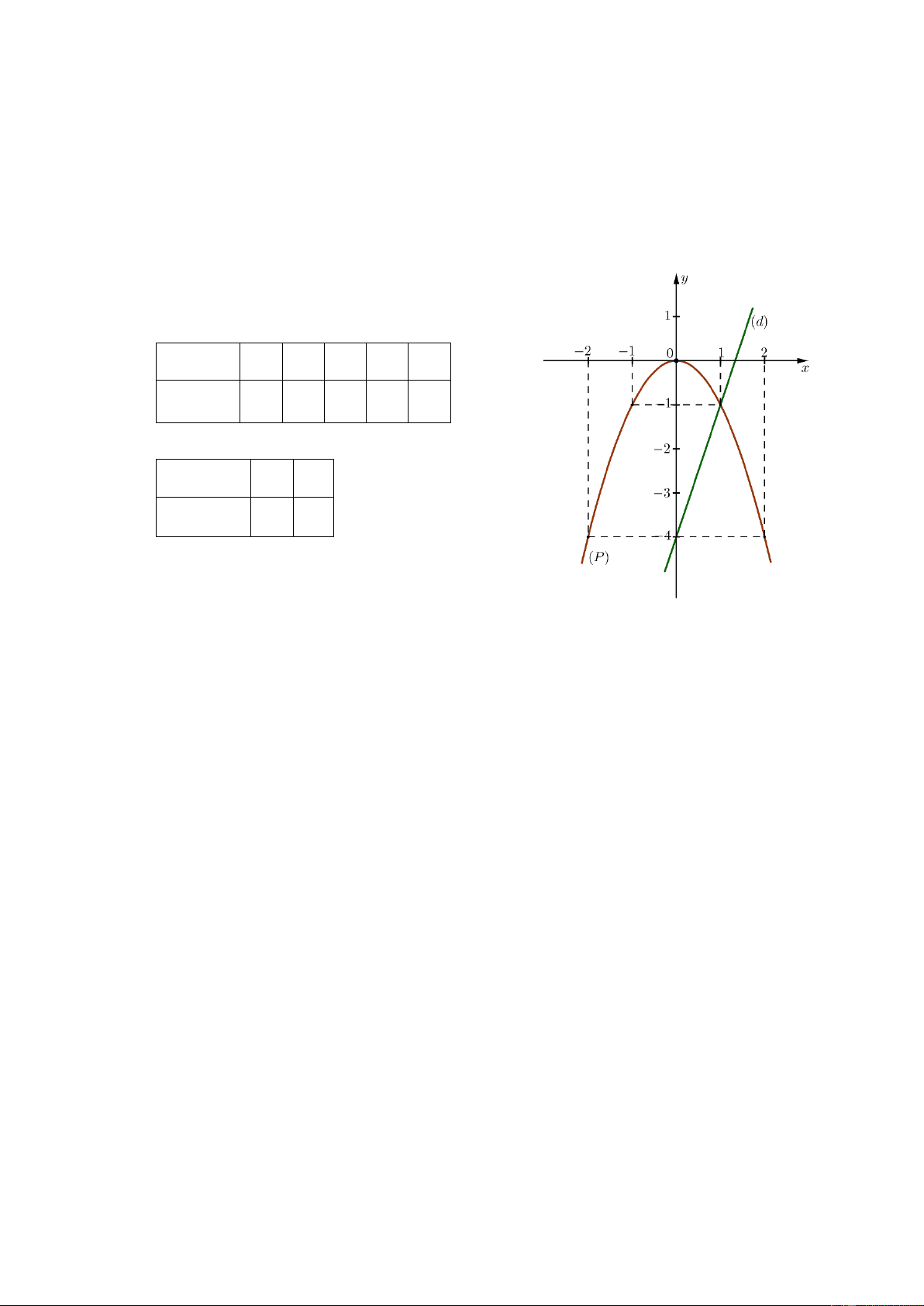
c) Vẽ đồ thị P và d trên cùng hệ trục tọa độ. BGT: x 2 1 0 1 2 2 y x 4 1 0 1 4 x 0 1 y 3x 4 4 1
d) Tìm tọa độ giao điểm của P và d bằng phép tính.
Phương trình hoành độ giao điểm của P và d : 2
x 3x 4 2
x 3x 4 0 x 1 x 4 Thay x 1 vào 2
y x , ta được: 2 y 1 1 . Thay x 4 vào 2
y x , ta được: y 2 4 1 6 . Vậy 1; 1 , 4
; 16 là hai giao điểm cần tìm.
Câu 2. (1 điểm). Cho phương trình 2 2x 5x 3
có 2 nghiệm là x ,x . Không giải phương trình, 1 2
hãy tính giá trị của biểu thức A x 3x x 3x . 1 2 2 1 Lời giải Trang 12 2 2x 5x 3 2
2x 5x 3 0 2
b 4ac 5 2 4.2.3 1 0. b 5
S x x 1 2
Theo định lí Vi-et, ta có: a 2 c 3
P x .x 1 2 a 2
Ta có: A x 3x x 3x 1 2 2 1 2 2
A x x 3x 3x 9x x 1 2 1
A 10x x 3 2 x x 1 2 2 2 1 2 1 2
A 10x x 3 x x 2 2x x 1 2 1 2 1 2 2 3 5 3 99 A 10. 3 2. . 2 2 2 4
Câu 3. (1 điểm). Tổng điều tra dân số và nhà ở năm 2019 được tiến hành vào thời điểm 0 giờ
ngày 1 / 4 / 2019 theo Quyết định số 772/QĐ-TTg ngày 26 / 6 / 2018 của Thủ tướng Chính
phủ. Đây là cuộc Tổng điều tra dân số và nhà ở lần thứ năm ở Việt Nam kể từ khi đất nước
thống nhất vào năm 1975 . Theo kết quả của cuộc tổng điều tra nói trên, tổng dân số của
Việt Nam là 96.208.984 người, trong đó nam ít hơn nữ 446.862 người và dân tộc Kinh
chiếm 85,3% dân số cả nước.
a) Dân tộc Kinh có bao nhiêu người (làm tròn đến hàng đơn vị)?
b) Tính số nam và số nữ của Việt Nam. Lời giải
a) Dân tộc Kinh có bao nhiêu người (làm tròn đến hàng đơn vị)?
Số người dân tộc Kinh: 85,3%.96208984 82066263 (người).
b) Tính số nam và số nữ của Việt Nam.
Gọi x (người), y (người) lần lượt là số nam và số nữ của Việt Nam x,y N * .
Tổng dân số của Việt Nam là 96208948 người nên ta có phương trình:
x y 96208984 1 .
Nam ít hơn nữ 446862 người nên ta có phương trình: x y 4 46862 2. Trang 13
x y 96208984 x 47881061
Từ 1 và 2 ta có hệ phương trình: . x y 4 46862 y 48327923
Vậy số nam của Việt Nam là 47881061 người và số nữ của Việt Nam là 48327923 người.
Câu 4. (1 điểm).
Một xí nghiệp cần bán thanh lý b sản phẩm. Số sản
phẩm y còn lại sau x ngày bán được xác định bởi hàm
số: y ax b có đồ thị như bên.
a) Hãy dựa vào đồ thị xác định a,b và hàm số y .
b) Xí nghiệp cần bao nhiêu ngày để bán hết số sản phẩm cần thanh lý? Lời giải
a) Hãy dựa vào đồ thị xác định a,b và hàm số y . Theo đề bài, ta có: x 0 Với
1410 0.a b 1 . y 1410 x 17 Với
900 17.a b 2. y 900
0a b 1410 a 30
Từ 1 và 2 ta có hệ phương trình: .
17a b 900 b 1410 Vậy: a 30
, b 1410 và y 30x 1410 .
b) Xí nghiệp cần bao nhiêu ngày để bán hết số sản phẩm cần thanh lý?
Thay y 0 vào y 30x 1410 , ta có: 0 3 0x 1410 30x 1410 x 47
Vậy cần 47 ngày để bán hết số sản phẩm cần thanh lý.
Câu 5. (1 điểm). Các bạn học sinh của lớp 9A dự định đóng góp một số tiền để mua tặng cho mỗi
em ở Mái ấm tình thương ba món quà (giá tiền các món quà đều như nhau). Khi các bạn Trang 14
đóng đủ số tiền dự trù thì Mái ấm đã nhận chăm sóc thêm 9 em và giá tiền mỗi món quà
lại tăng thêm 5% nên số tiền có được vừa đủ để tặng mỗi em hai món quà. Hỏi có bao
nhiêu em ở Mái ấm lúc tặng quà? Lời giải
Gọi x,y lần lượt là số em ở mái ấm và giá tiền mỗi món quà lúc dự định xN*,y 0 .
Số tiền mua quà lúc dự định là 3xy .
Số em ở mái ấm lúc tặng quà là x 9 .
Số tiền mỗi món quà lúc tặng quà là y1 5% 1,05y .
Số tiền mua quà lúc tặng quà là 2.1,05.yx 9 2,1yx 9.
Vì số tiền mua quà không không thay đổi nên ta có phương trình:
3xy 2,1yx 9
3x 2,1x 9
3x 2,1x 18,9
3x 2,1x 18,9 0,9x 18,9 x 21
Vậy số em ở mái ấm lúc tặng quà là 21 9 30 (em).
Câu 6. (1 điểm).
Coi cả Trái Đất và Mặt Trăng đều có dạng
hình cầu và biết bán kính của Trái Đất là
khoảng 6371 km, bán kính của mặt trăng là khoảng 1737 km.
a) Hãy tính diện tích bề mặt của Trái Đất
và diện tích bề mặt của Mặt Trăng.
b) Biết 70,8% diện tích bề mặt Trái Đất là
nước. Hãy tính phần diện tích này?
(Làm tròn kết quả đến hàng triệu) Lời giải
a) Hãy tính diện tích bề mặt của Trái Đất và diện tích bề mặt của Mặt Trăng.
Diện tích bề mặt của Trái Đất: 2 2
S 4 R 4 .6371 510000000 2 km . 1 1
Diện tích bề mặt của Mặt Trăng: 2 2
S 4 R 4 .1737 38000000 2 km . 2 2
b) Biết 70,8% diện tích bề mặt Trái Đất là nước. Hãy tính phần diện tích này? Trang 15
Diện tích nước bao phủ bề mặt Trái Đất: 2 70,8%.510000000 361000000 km .
Câu 7. (1 điểm). Giá của một mặt hàng là 800.000 đồng. Nếu bán mặt hàng này với giá bằng một
nửa giá niêm yết thì lợi nhuận là 20% . Hỏi phải bán với giá bao nhiêu thì được lợi nhuận 60% ? Lời giải 800000 1000000
Giá vốn của món hàng là: : 1 20% (đồng) . 2 3 1000000 1600000
Giá bán để được lợi nhuận 60% là: 160% (đồng) . 3 3
Câu 8. (2,5 điểm) Cho tam giác ABC nhọn AB AC nội tiếp đường tròn O có ba đường cao
AD,BE,CF cắt nhau tại H .
a) Chứng minh AEHF và ABDE là các tứ giác nội tiếp.
b) Đường thẳng EF cắt đường tròn O tại các điểm M,N ( M thuộc cung nhỏ AB ). Kẻ
đường kính AK của đường tròn O . Chứng minh tia EB là tia phân giác của góc DEF và KM N cân.
c) Đường trung trực của CE cắt MK tại Q . Chứng minh MA là tiếp tuyến của MEC và
OQ vuông góc MC . Lời giải A N E F M O H B D C Q K
a) Chứng minh AEHF và ABDE là các tứ giác nội tiếp.
AEH 90 ( BE là đường cao của A BC)
AFH 90 ( CF là đường cao của A BC) , A ,
E H,F cùng thuộc đường tròn đường kính AH Trang 16
Tứ giác AEHF nội tiếp.
ADB 90 ( AD là đường cao của A BC)
AEB 90 ( BE là đường cao của A BC) , A , B ,
D E cùng thuộc đường tròn đường kính AB
Tứ giác ABDE nội tiếp.
b) Chứng minh tia EB là tia phân giác của góc DEF và KM N cân.
AEHF nội tiếp (cmt) FAH FEH (cùng chắn cung FH ) 1
AEDB nội tiếp (cmt) FAH BED (cùng chắn cung BD ) 2
1,2 FEB BED
EB là tia phân giác của góc DEF .
BFC 90 ( CF là đường cao của A BC)
BEC 90 ( BE là đường cao của A BC)
B,F,E,C cùng thuộc đường tròn đường kính BC
Tứ giác BFEC nội tiếp
AFE ACB 1 ¼ Mà AFE =
(sđ AN + sđMB ) (góc có đỉnh ở bên trong đường tròn) 2 1 1 ACB = sđ AB =
(sđ AM + sđ MB ) (góc nội tiếp, M AB ) 2 2
sđ AN = sđ AM AN = AM
AK MN tại trung điểm của MN (liên hệ đường kính và dây)
AK là đường trung trực của MN KM KN KM
N cân tại K .
c) Chứng minh MA là tiếp tuyến của MEC và OQ vuông góc MC . AN = AM (cmt)
AMN ACM (hai góc nội tiếp chắn hai cung bằng nhau) 3 . Trang 17
Xét đường tròn MEC 1 MCE =
sđ ME (góc nội tiếp) 4 . 2 1
3,4 AME = sđ ME 2
MA là tiếp tuyến của đường tròn MEC (định lý đảo của định lý góc tạo bởi tia tiếp
tuyến và dây cung) 5
AMK 90 (góc nội tiếp chắn nửa đường tròn)
MK AM 6.
5,6 Tâm đường tròn MEC thuộc MK
Mà Q là giao điểm đường trung trực của CE và MK
Q là tâm đường tròn MEC .
Đường tròn O và đường tròn Q có CM là dây chung
OQ là đường trung trực của CM
OQ CM (tính chất đường nối tâm). ----HẾT---
SỞ GD&ĐT HỒ CHÍ MINH
ĐỀ THAM KHẢO TUYỂN SINH 10
PHÒNG GD&ĐT QUẬN 4
NĂM HỌC: 2021 - 2022 MÔN: TOÁN 9 ĐỀ TH AM KHẢO
Đêthigồm 8 câuhỏitựluận. MÃ ĐỀ: Quận 4 - 1
Thờigian: 120 phút (khôngkể thờigianphátđề)
Câu 1. ( 1,5 điểm ). Cho Parabol
và đường thẳng (d ) : y x 4 P 1 2 : y x 2
a) Vẽ đồ thị hàm số (P) và (d ) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d ) bằng phép tính.
Câu 2. ( 1,0 điểm ). Cho phương trình 2
x 5x 2 0 có hai nghiệm là x , x . Không giải phương trình, 1 2
hãy tính giá trị của biểu thức: 2 2
A x x x x . 1 2 1 2
Câu 3. ( 0,75 điểm ).Một năm bình thường sẽ có 12 tháng và 365 ngày. Khi một năm có số ngày
hoặc số trong tăng lên (theo Dương lịch hoặc theo Âm lịch) thì sẽ được gọi là năm nhuận,
trong đó có những ngày nhuận vào tháng nhuận. Năm nhuận là năm có 29 ngày tháng 2 Trang 18
Dương Lịch (không nhuận là 28 ngày). Cách tính năm nhuận theo Dương lịch là những năm
dương lịch nào chia hết cho 4 thì đó là năm nhuận.
Ví dụ: 2016 chia hết cho 4 nên năm 2016 là năm nhuận.
Ngoài ra, đối với thế kỷ (những năm có 2 số cuối là số 0) thì ta sẽ lấy số năm đó chia cho 400,
nếu như chia hết thì đó sẽ là năm nhuận (hoặc hai số đầu trong năm chia hết cho 4).
Vídụ: 1600 và 2000 là các năm nhuận nhưng 1700, 1800 và 1900 không phải năm nhuận.
a) Em hãy dùng quy tắc trên để xác định Năm 2022 có phải là năm nhuận dương lịch không?
b) Bạn Hòa nhớ rằng sinh nhật lần thứ 15 của bạn vào ngày 2/6/2022 là ngày thứ năm. Bạn
thắc mắc ngày mình sinh ra là ngày thứ mấy? Em hãy giúp bạn giải đáp thắc mắc đó.
Câu 4. (0,75 điểm).Một xe ôtô chuyển động theo hàm số 2
S 30t 4t , trong đó S (km) là quãng
đường xe đi được trong thời gian t (giờ); t là thời gian chuyển động của tính từ lúc 7h00
sáng. Xem như xe chuyển động đều trên một đoạn đường thẳng và không nghỉ.
a) Hỏi từ lúc 7h30 phút đến lúc 8h15 phút đã đi được quãng đường dài bao nhiêu km?
b) Đến lúc mấy giờ thì xe đi được quãng đường dài 34km (tính từ lúc 7h00)?
Câu 5. (1,0 điểm).Mộtngườimua 3 đôigiàyvớihìnhthứckhuyếnmãinhưsau: Nếu bạn một đôi giày và
mức giá thông thường, bạn sẽ được giá giảm 30% khi mua đôi thứ hai, và một đôi thứ ba về
một nửa giá ban đầu. Bạn Anh đã trả 1.320.000 cho 3 đôi giày.
a) Giá ban đầu của một đôi giày là bao nhiêu?
b) Nếu cửa hàng đưa ra hình thức khuyến mãi thứ là giảm 20% mỗi đôi giày. Bạn Anh nên
chọn hình thức khuyến mãi nào nếu mua ba đôi giày.
Câu 6. (1,0 điểm).Đổ nước vào một chiếc thùng hình trụ có bán kính đáy là 20 cm. Nghiêng thùng
cho mặt nước chạm vào miệng cốc và đáy cốc (như
hình vẽ) thì mặt nước tạo với đáy cốc một góc 30 .
a) Tính chiều cao của chiếc thùng hình trụ.
b) Tính thể tích của chiếc thùng?
(Kết quả làm tròn hai chữ số thập phân)
Câu 7. (1,0 điểm).Một đoàn y tế của Bệnh viện Chợ Rẫy, TP HCM gồm các bác sĩvà y tá tăng cường
về tỉnh Cà Mau để khám chữa bệnh cho người dân trong tỉnh. Đoàn gồm 135 người và có
tuổi trung bình là 40 tuổi. Tính số bác sĩ và y tá biết tuổi trung bình của các bác sĩ là 50 tuổi
và tuổi trung bình của các y tá là 35 tuổi. Trang 19
Câu 8. (3,0 điểm).Từ điểm A ở ngoài đường tròn tâm O, vẽ tiếp tuyến AB, AC với (O) (B, C là hai
tiếp điểm). Vẽ cát tuyến AEF với (O) sao cho AE < AF và tia AF nằm giữa tia OA và tia OC.
Gọi D là trung điểm của EF.
a) Chứng minh tứ giác AODC nội tiếp.
b) Gọi K là giao điểm của AF và BC. Chứng minh A . D AK A . E AF.
c) Đường thẳng OD cắt các tia AB, AC lần lượt tại hai điểm M và N. Đường thẳng vuông góc
với MN tại O cắt BC tại I, AI cắt MN tại H. Chứng minh H là trung điểm của MN. HƯỚNG DẪN GIẢI
Câu 1. ( 1,5 điểm ).Cho Parabol 1 d y x 2 và đường thẳng ( ) : 4 (P) : y x 2
a) Vẽ đồ thị hàm số (P) và (d ) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d ) bằng phép tính. Lời giải a) Bảng Giá Trị: x 1 2 y x 2 Trang 20 x 4 y x 4 4 8
b) Tìm tọa độ giao điểm của P và d bằng phép tính. P d
Phương trình hoành độ giao điểm của và : 1 x 4 2 2
x x 4 x 2x 8 0 2 x 2 1 2 1 y x 2 y .4 8 Thay x 4 vào 2 , ta được: 2 . 1 2 1 y x 2 y .( 2 ) 2 Thay x 2 vào 2 , ta được: 2 . 4;8 2 ;2 Vậy ,
là hai giao điểm cần tìm.
Câu 2. ( 1,0 điểm ). Cho phương trình 2
x 5x 2 0 có hai nghiệm là x , x . Không giải phương trình, 1 2
hãy tính giá trị của biểu thức: 2 2
A x x x x . 1 2 1 2 Lời giải 2
Phương trình x 5x 2 0 2 2
b ac Ta có 4 ( 5) 4.1.( 2) 33 0
Theo định lý Vi-et, ta có: b S x x 5 1 2 a c P x .x 2 1 2 a 2 2 2
A x x x x (x x ) 2x .x x x 1 2 1 2 1 2 1 2 1 2 2 2
A S 2P S 5 2.( 2 ) 5 34
Câu 3. ( 0,75 điểm ).Một năm bình thường sẽ có 12 tháng và 365 ngày. Khi một năm có số ngày hoặc
số trong tăng lên (theo Dương lịch hoặc theo Âm lịch) thì sẽ được gọi là năm nhuận, trong
đó có những ngày nhuận vào tháng nhuận. Năm nhuận là năm có 29 ngày tháng 2 Dương
Lịch (không nhuận là 28 ngày). Cách tính năm nhuận theo Dương lịch là những năm dương
lịch nào chia hết cho 4 thì đó là năm nhuận. Trang 21
Ví dụ: 2016 chia hết cho 4 nên năm 2016 là năm nhuận.
Ngoài ra, đối với thế kỷ (những năm có 2 số cuối là số 0) thì ta sẽ lấy số năm đó chia cho 400,
nếu như chia hết thì đó sẽ là năm nhuận (hoặc hai số đầu trong năm chia hết cho 4).
Vídụ: 1600 và 2000 là các năm nhuận nhưng 1700, 1800 và 1900 không phải năm nhuận.
a) Em hãy dùng quy tắc trên để xác định Năm 2022 có phải là năm nhuận dương lịch không?
b) Bạn Hòa nhớ rằng sinh nhật lần thứ 15 của bạn vào ngày 2/6/2022 là ngày thứ năm. Bạn
thắc mắc ngày mình sinh ra là ngày thứ mấy? Em hãy giúp bạn giải đáp thắc mắc đó. Lời giải
a) Năm 2022 không phải năm nhuận vì: 2022 chia 4 dư 2
b) Thứ bảy. Vì một tuần có 7 ngày =>Thứ 5 vào ngày thứ 2 của tháng 6 và ta có 7 – 5 = 2
ngày với 7 là 7 ngày trong tuần và 5 là ngày thứ 5. Vậy nếu quay về 15 năm trước đó,
ngày 2/6/2006 sẽ là ngày thứ 6, do được cộng thêm 1 đơn vị ngày sau này 1/6 và bắt đầu từ ngày 31/5
Câu 4. (0,75 điểm).Một xe ôtô chuyển động theo hàm số
, trong đó S (km) là quãng
đường xe đi được trong thời gian t (giờ); t là thời gian chuyển động của tính từ lúc 7h00
sáng. Xem như chuyển động trên một đoạn đường thẳng và không nghỉ.
a) Hỏi từ lúc 7h30 phút đến lúc 8h15 phút đã đi được quãng đường dài bao nhiêu km?
b) Đến lúc mấy giờ thì xe đi được quãng đường dài 34km (tính từ lúc 7h00)? Lời giải
a) Từ lúc 7h30 phút đến 8h15 phút ứng với t = 8h 15 phút – 7h 30 phút = 3 h, xe đi được 4 quãng đường là: 2 3 3 2
S 30t 4t 30. 4 29,75 km 4 4
b) Thời gian đi được quãng đường 34 km là: 2
S 30t 4t 34 2
4t 30t 34 0 t 1 4t 34 0
t 1 N 17 t L 2
Vậy vào lúc 7 + 1 = 8h x đi được quãng đường dài 34km Trang 22
Câu 5. (1,0 điểm).Mộtngườimua 3 đôigiàyvớihìnhthứckhuyếnmãinhưsau: Nếu bạn một đôi giày và
mức giá thông thường, bạn sẽ được giá giảm 30% khi mua đôi thứ hai, và một đôi thứ ba về
một nửa giá ban đầu. Bạn Anh đã trả 1.320.000 cho 3 đôi giày.
a) Giá ban đầu của một đôi giày là bao nhiêu?
b) Nếu cửa hàng đưa ra hình thức khuyến mãi thứ là giảm 20% mỗi đôi giày. Bạn Anh nên
chọn hình thức khuyến mãi nào nếu mua ba đôi giày. Lời giải
a) Gọi x là giá của mỗi đôi giày( xđồng )
Mua đôi giày thứ nhất với giá: x đồng
Mua đôi giày thứ hai với giá: (100% 30%) 70% 0, 7 x đồng
Mua đôi giày thứ ba với giá: (100% 50%) 50% 0, 5 x đồng
Giá ban đầu của một đôi giày là:
x 0, 7x 0,5x 1320000 x 600000
Vậy giá một đôi giày Là 600.000 đồng
b) Nếucửahàngđưarahìnhthứckhuyếnmãithứhailàgiảm 20%
mỗiđôigiàythìgiátiềncầntrảđểmua 3 đôigiàylà:
3.(600000 600000.20%) 1440000 đồng
Vậy bạn Anh nên theo khuyến mãi 1 để được giảm nhiều tiền nhất.
Câu 6. (1,0 điểm).Đổ nước vào một chiếc thùng hình trụ có bán kính đáy là 20 cm. Nghiêng thùng
cho mặt nước chạm vào miệng cốc và đáy cốc (như hình vẽ) thì mặt nước tạo với đáy cốc một góc .
a) Tính chiều cao của chiếc thùng hình trụ.
b) Tính thể tích của chiếc thùng?
(Kết quả làm tròn hai chữ số thập phân) Lời giải
a) Xét ABC vuông tại B ta có: AB 40 3 tan( ACB)
AB tan(ACB).BC tan(30 ).40 BC 3 40 3 h AB
Vậy chiều cao thùng hình trụ là: 3
b) Thể tích của chiếc thùng là: Trang 23 40 3 2 2
V r h .(20) . 9237.60 3 3 cm
Câu 7. (1,0 điểm).Một đoàn y tế của Bệnh viện Chợ Rẫy, TP HCM gồm các bác sĩvà y tá tăng cường
về tỉnh Cà Mau để khám chữa bệnh cho người dân trong tỉnh. Đoàn gồm 135 người và có
tuổi trung bình là 40 tuổi. Tính số bác sĩ và y tá biết tuổi trung bình của các bác sĩ là 50 tuổi
và tuổi trung bình của các y tá là 35 tuổi. Lời giải
Gọi số bác sĩ là a, số y tá là b (a,b : người)
Số người trong đoàn y tế là: a+b( người )
Tổng số tuổi của bác sĩ là y tá là: 50a 35b 135.40 Ta có hệ phương trình 50
a 35b 135.40 a 45 a b 135 b 90
Vậy có 45 bác sĩ và 90 y tá
Câu 8. (3,0 điểm).Từ điểm A ở ngoài đường tròn tâm O, vẽ tiếp tuyến AB, AC với (O) (B, C là hai
tiếp điểm). Vẽ cát tuyến AEF với (O) sao cho AE < AF và tia AF nằm giữa tia OA và tia OC.
Gọi D là trung điểm của EF.
a) Chứng minh tứ giác AODC nội tiếp.
b) Gọi K là giao điểm của AF và BC. Chứng minh
c) Đường thẳng OD cắt các tia AB, AC lần lượt tại hai điểm M và N. Đường thẳng vuông góc
với MN tại O cắt BC tại I, AI cắt MN tại H. Chứng minh H là trung điểm của MN. Lời giải Trang 24
a) Chứng minh tứ giác AODC nội tiếp.
Ta có AC tiếp tuyến của đường tròn tâm O => AC CO ACO 90
D là trung điểm EF => OD EF ODE 90 ( đường thẳng đi qua trung điểm dây cung )
⇨ Tứ giác AODC nội tiếp đường tròn( hai góc đối phụ nhau ) b) Chứng minh A . D AK A . E AF.
Xét ABF và AEB có BAF chung
ABE AFB ( góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung chắn bởi cung BE ) ⇨ ABF AEB (g,g) ⇨ 2
AB AE.AF (1)
Ta có tứ giác OBAC nội tiếp đường tròn bán kính OA
⇨ CBA COA BOA
Ta lại có tứ giác AODC nội tiếp đường tròn
⇨ CDA COA BCA
Xét ACK và ADC có: DAC chung
CDA BCA (cmt) ⇨ ACK ADC ( g.g) ⇨ 2
AC AK.AD (2)
Từ (1) , (2) và AB =AC ( tính chất 2 tiếp tuyến của 1 đường tròn ) => A . D AK A . E AF.
c) Chứng minh H là trung điểm của MN. Trang 25 M Q B H I A O E K D F P C N
Qua I kẻ đường thẳng vuông góc với OI , đường thẳng này lần lượt cắt AB , AC tại Q và P .
Xét tứ giác IOQB , ta có: OIQ OBQ 90
tứ giác IOQB nội tiếp vì có hai đỉnh cùng nhìn một cạnh dưới 2 góc bằng nhau.
OQI OBI .
Xét tứ giác IOCP , ta có: OIP OCP 90
tứ giác IOCP nội tiếp vì có hai đỉnh cùng nhìn một cạnh dưới 2 góc bằng nhau.
OQI OBI .
Mà: OQI OBI (cmt)
Và: OCI OBI ( O
BI cân tại O)
Nên: OQI OPI
OI là phân giác của POQ
Suy ra: OI là trung trực của PQ
I là trung điểm của PQ . Xét A
MH , ta có IQ//OM IQ AI OI (HQ Talet) 3 . MH AH Xét A
NH , ta có IP//ON IP AI OI (HQ Talet) 4 . NH AH Trang 26 IQ IP AI
Từ 3 và 4 suy ra: MH NH AH
Lại có: IP IQ (cmt)
Suy ra: HM HN ---HẾT---
SỞ GD&ĐT HỒ CHÍ MINH
ĐỀ THAM KHẢO TUYỂN SINH 10
PHÒNG GD&ĐT QUẬN 4
NĂM HỌC: 2021 - 2022 MÔN: TOÁN 9 ĐỀ TH AM KHẢO
Đê thi gồm 8 câu hỏi tự luận. MÃ ĐỀ: Quận 4 - 2
Thời gian: 120 phút (không kể thời gian phát đề) 1
Câu 9. (1,5 điểm). Cho P 2 : y
x và đường thẳng ( )
d : y 4 x . 2
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của P và d bằng phép tính.
Câu 10. (1 điểm). Cho phương trình 2 2
x 5x 1 0 có 2 nghiệm là x ,x . Không giải phương 1 2
trình, hãy tính giá trị của biểu thức P x 3 x x 3 x 2 2
3x 3x 10 . 1 2 2 1 1 2
Câu 11. (0,75 điểm). Một quán bán thức ăn mang đi có chương trình khuyến mãi như sau:
• Giảm 20% giá niêm yết cho sản phẩm là cà phê.
• Giảm 10% giá niêm yết cho sản phẩm là bánh mì.
• Đặc biệt: Nếu mua đủ một combo gồm 1 ly cà phê và 1 ổ bánh mì thì được giảm thêm
10% combo đó trên giá đã giảm.
Bạn Bình đến quán bán thức ăn đó và chọn mua được 7 ly cà phê có giá niêm yết 30 000
đồng mỗi ly và 5 ổ bánh mì có giá niêm yết 20 000 đồng mỗi ổ. Hỏi bạn Bình phải trả bao nhiêu tiền?
Câu 12. (0,75 điểm). Bạn Nam đi nhà sách mua một số tập để trang bị cho việc học của mình. Bạn
mua tập có giá là mỗi quyển 7 000 đồng. Phí gửi xe cho mỗi lượt là 5000 đồng.
a) Gọi x là số quyển tập bạn Nam mua và y là tổng số tiền bạn phải chi trả cho một lần đi
mua tập ở nhà sách đó (bao gồm tiền mua tập và phí gửi xe). Hãy biểu diễn y theo x .
b) Bạn Nam mang theo 90 000 đồng. Hỏi bạn Nam mua được nhiều nhất là bao nhiêu quyển tập? Trang 27
Câu 13. (1 điểm). Để phục vụ công tác phòng chống dịch COVID-19, ngoài việc thực hiện thông
điệp 5K thì giáo viên chủ nhiệm còn tổ chức cho các bạn học sinh lớp 9A cùng làm các
tấm chắn bảo hộ để tặng các chốt chống dịch.
Lớp 9A có tất cả 45 bạn, trong đó, mỗi bạn nam làm được 2 tấm chắn bảo hộ; mỗi bạn nữ
làm được 3 tấm chắn bảo hộ; riêng giáo viên của nhiệm làm được 5 tấm chắn bảo hộ. Vì
vậy, cả lớp 9A đã làm được 120 tấm chắn bảo hộ. Hỏi lớp 9A có bao nhiêu bạn nam? bao nhiêu bạn nữ?
Câu 14. (1 điểm). Một bình hình trụ có đường kính đáy 1dm , chiều cao 0,8dm bên trong có chứa
viên bi hình cầu có bán kính 3 cm . Hỏi phải đổ vào bình bao nhiêu lít nước để nước đầy
bình (làm tròn đến chữ số thập phân thứ nhất). Cho biết: • 2 V
r h với r là bán kính đáy; h là chiều cao hình trụ. tru 4 • 3 V
R với R là bán kính hình cầu. câu 3
Câu 15. (1 điểm). Một kho hàng nhập gạo (trong kho chưa có gạo) trong 4 ngày liên tiếp và mỗi
ngày (kể từ ngày thứ hai) đều nhập một lượng gạo bằng 120% lượng gạo đã nhập vào
kho trong một ngày trước đó. Sau đó, từ ngày thứ năm kho ngừng nhập và mỗi ngày kho
xuất một lượng gạo bằng lượng gạo ở trong một ngày trước đó.
a) Ngày thứ ba, sau khi nhập xong thì gạo trong kho có 910 tấn gạo. Hỏi ngày thứ nhất
kho đã nhập vào bao nhiêu tấn gạo?
b) Tính lượng gạo trong kho sau ngày thứ sáu từ khi bắt đầu nhập gạo? Câu 16.
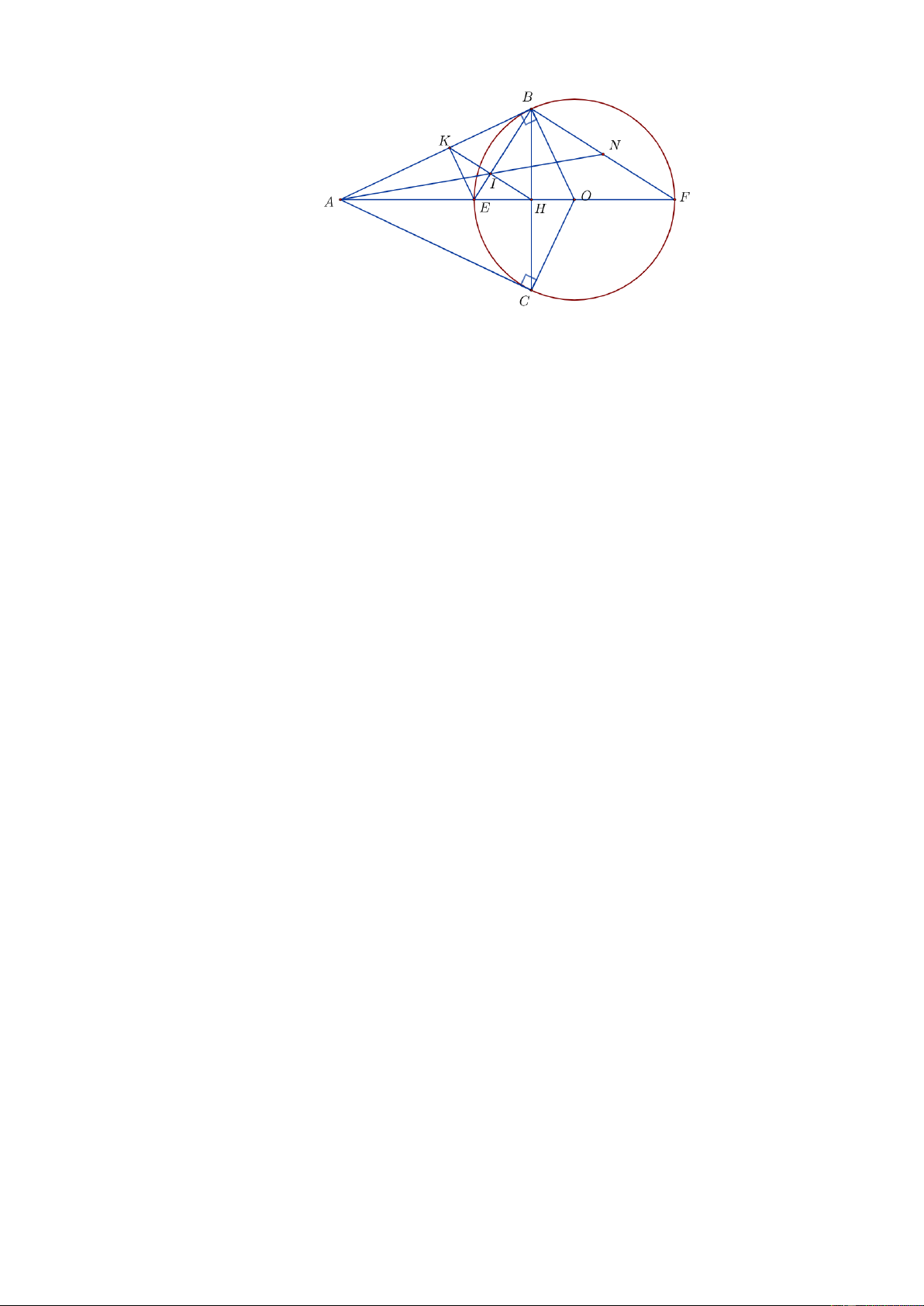
(3 điểm) Cho đường tròn ;
O R có đường kính AB vuông góc với dây MN tại H ( H
nằm giữa O và B . Trên tia MN lấy điểm C nằm ngoài ;
O R sao cho đoạn thẳng AC
cắt đường tròn O tại điểm K khác A , hai dây MN và BK cắt nhau ở E .
a) Chứng minh tứ giác AHEK nội tiếp và CAE đồng dạng với CHK .
b) Qua N kẻ đường thẳng vuông góc với AC và cắt tia MK tại F . Chứng minh tam giác NFK cân.
c) Giả sử KE KC . Chứng minh: OK / /MN và 2 2 2
KM BN 4R ----HẾT--- Trang 28 HƯỚNG DẪN GIẢI 1
Câu 1. (1,5 điểm) Cho P : y 2
x và đường thẳng (d ) : y 4 x . 2
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của P và d bằng phép tính. Lời giải
e) Vẽ đồ thị P và d trên cùng hệ trục tọa độ. Bảng giá trị: x 4 2 0 2 4 y 1 2 x 8 2 0 2 8 2 x 0 2 y 4 x 4 2
f) Tìm tọa độ giao điểm của P và d bằng phép tính.
Phương trình hoành độ giao điểm của P và d : Trang 29 1 x 2 2
x 4 x 2
x 2x 8 0 2 x 4 1 1
Thay x 2 vào y 2
x , ta được: y 2 .2 2 . 2 2 1 1
Thay x 4 vào y 2
x , ta được: y .( 2 4) 8 . 2 2
Vậy 2; 2 , 4;8 là hai giao điểm cần tìm.
Câu 2. (1 điểm) Cho phương trình 2 2
x 5x 1 0 có 2 nghiệm là x ,x . Không giải phương 1 2
trình, hãy tính giá trị của biểu thức 2 2
P x (3 x ) x (3 x ) 3x 3x 10 . 1 2 2 1 1 2 Lời giải Phương trình 2 2
x 5x 1 0 Ta có 2 2
b 4ac (5) 4.1.( 2 ) 33 0
Theo định lý Vi-et, ta có: b 5
S x x 1 2 a 2 c 1
P x .x 1 2 a 2 2 2
P x (3 x ) x (3 x ) 3x 3x 10 1 2 2 1 1 2 2
3x x x 3x x x 3[(x x ) 2x x ] 10 1 1 2 2 1 2 1 2 1 2 57 2
3S 2P 3(S 2P) 4
Câu 3. (1 điểm) Một quán bán thức ăn mang đi có chương trình khuyến mãi như sau:
• Giảm 20% giá niêm yết cho sản phẩm là cà phê.
• Giảm 10% giá niêm yết cho sản phẩm là bánh mì.
• Đặc biệt: Nếu mua đủ một combo gồm 1 ly cà phê và 1 ổ bánh mì thì được giảm thêm 10%
combo đó trên giá đã giảm.
Bạn Bình đến quán bán thức ăn đó và chọn mua được 7 ly cà phê có giá niêm yết 30.000
đồng mỗi ly và 5 ổ bánh mì có giá niêm yết 20.000 đồng mỗi ổ. Hỏi bạn Bình phải trả bao nhiêu tiền? Lời giải
Số tiền bánh mì sau khi giảm 10% là: 20000 20000.10% 18000 ( đồng ) Trang 30
Số tiền cà phê sau khi giảm 20% là: 30000 30000.20% 24000 ( đồng )
Số tiền bạn Bình phải trả là:
5.[(18000 24000) (18000 24000).10%] 2.24000 237000 ( đồng )
Câu 4. (1 điểm). Bạn Nam đi nhà sách mua một số tập để trang bị cho việc học của mình. Bạn mua
tập có giá là mỗi quyển 7.000 đồng. Phí gửi xe cho mỗi lượt là 5.000 đồng.
a) Gọi x là số quyển tập bạn Nam mua và y là tổng số tiền bạn phải chi trả cho một lần đi
mua tập ở nhà sách đó (bao gồm tiền mua tập và phí gửi xe). Hãy biểu diễn y theo x.
b) Bạn Nam mang theo 90.000 đồng. Hỏi bạn Nam mua được nhiều nhất là bao nhiêu quyển tập? Lời giải
a) y 7000x 5000 b) Ta có:
y 90000 7000x 5000 7000x 85000 x 12,14
Vậy bạn Nam mua được nhiều nhất là 12 sản phẩm
Câu 5. (1 điểm)Để phục vụ công tác phòng chống dịch COVID-19, ngoài việc thực hiện thông điệp
5K thì giáo viên chủ nhiệm còn tổ chức cho các bạn học sinh lớp 9A cùng làm các tấm chắn
bảo hộ để tặng các chốt chống dịch.
Lớp 9A có tất cả 45 bạn, trong đó, mỗi bạn nam làm được 2 tấm chắn bảo hộ; mỗi bạn nữ
làm được 3 tấm chắn bảo hộ; riêng giáo viên của nhiệm làm được 5 tấm chắn bảo hộ. Vì vậy,
cả lớp 9A đã làm được 120 tấm chắn bảo hộ. Hỏi lớp 9A có bao nhiêu bạn nam? bao nhiêu bạn nữ? trò ? Lời giải
Gọi x là số bạn nam trong lớp 9A
y là số bạn nữ trong lớp 9A
Theo đề bài ta có hệ phương trình:
2x 3y 120 5 x 20 x y 45 y 25
Vậy lớp 9A có 20 bạn nam và 25 bạn nữ Trang 31
Câu 6. (1 điểm) Một bình hình trụ có đường kính đáy 1 dm, chiều cao 0, 8 dm bên trong có chứa
viên bi hình cầu có bán kính 3cm. Hỏi phải đổ vào bình bao nhiêu lít nước để nước đầy bình
(làm tròn đến chữ số thập phân thứ nhất). Cho biết: • 2 V
r h với r là bán kính đáy; h là chiều cao hình trụ. tru 4 • 3 V
R với R là bán kính hình cầu. câu 3 Lời giải 1
Thể tích bình hình trụ là: 2 V r h 3 dm tru 5 4 9 Thể tích viên bi là: 3 V r 3 dm câu 3 250 1 9 41
Thể tích cần tìm là: V - V = - = 3 dm tru câu 5 250 250
Câu 7. (1 điểm)Một kho hàng nhập gạo (trong kho chưa có gạo) trong 4 ngày liên tiếp và mỗi ngày
(kể từ ngày thứ hai) đều nhập một lượng gạo bằng 120% lượng gạo đã nhập vào kho trong
một ngày trước đó. Sau đó, từ ngày thứ năm kho ngừng nhập và mỗi ngày kho xuất một 1 lượng gạo bằng
lượng gạo ở trong một ngày trước đó. 10
a) Ngày thứ ba, sau khi nhập xong thì gạo trong kho có 910 tấn gạo. Hỏi ngày thứ nhất
kho đã nhập vào bao nhiêu tấn gạo?
b) Tính lượng gạo trong kho sau ngày thứ sáu từ khi bắt đầu nhập gạo? Lời giải
a) Gọi số gạo nhập vào ngày 1 là: x ( tấn gạo )
số gạo nhập vào ngày 2 là: 1,2x ( tấn gạo )
số gạo nhập vào ngày 3 là: 2
1, 2.1, 2x (1, 2) x ( tấn gạo )
Số gạo ngày thứ nhất nhập sao cho ngày thứ 3 có 910 tấn gạo là:
x 1, 2x 1, 44x 910 x 250 ( tấn gạo)
b) Số gạo nhập vào ngày thứ 4 là: 3
1, 2.1, 2.1, 2x (1, 2) x
Lượng gạo trong kho sau 4 ngày là: 3
x 1, 2x 1, 44x (1, 2) x 5,368x
Lượng gạo xuất ra ngày thứ 5 là: 5, 368 .0
x ,1 0, 5368x Trang 32
Lượng gạo xuất ra ngày thứ 6 là:
(5, 368x 0, 5368x).0.1 0, 43812x
Câu 8. (3 điểm) Cho đường tròn (O; R) có đường kính AB vuông góc với dây MN tại H (H nằm giữa
O và B. Trên tia MN lấy điểm C nằm ngoài (O; R) sao cho đoạn thẳng AC cắt đường tròn (O;
R) tại điểm K khác A, hai dây MN và BK cắt nhau ở E.
a) Chứng minh tứ giác AHEK nội tiếp và CAE đồng dạng với CHK.
b) Qua N kẻ đường thẳng vuông góc với AC và cắt tia MK tại F. Chứng minh tam giác NFK cân.
c) Giả sử KE = KC. Chứng minh: OK / /MN và 2 2 2
KM BN 4R . Lời giải
a) Chứng minh tứ giác AHEK nội tiếp và CAE đồng dạng với CHK. Ta có: 90o AKB
(do AKB là góc nội tiếp chắn đường kính AB ) Ta có: 90o AHE (AH ) HE 180o AHE AKB
AHEK là tứ giác nội tiếp do có tổng hai góc đối bù nhau
KAE KHE Xét C AEvà C HK , ta có:
ACE : góc chung
KAE KHE C AE C ∽ HK Trang 33
b) Qua N kẻ đường thẳng vuông góc với AC và cắt tia MK tại F. Chứng minh tam giác NFK cân.
Do đường kính AB MN nên B là điểm chính giữa cung MN
NKB MKB (1)
Ta lại có: BK / /NF (cùng vuông góc với AC )
NKB KNF (2)
MKB MFN (3)
Từ (1), (2) và (3) MFN KNF hay KFN KNF K
NF cân tại K
c) Giả sử KE = KC. Chứng minh: OK / /MN và 2 2 2
KM BN 4R . 90o 90o AKB AK KB BKC KEC vuông tại K Mà KE KC Nên K
EC vuông cân tại K 45o KEC BEH Ta có: O
KB vuông cân tại O OK AB Mà MN AB Nên OK / /MN
Gọi P là giao điểm của OK với đường tròn do đó KP là đường kính và KP / /MN
Ta có tứ giác KPMN là hình thang cân nên KN HP Xét KM
P vuông tại M , ta có: 2 2 2
MP MK KP 2 2 2
KN MK (2R) 2 2 2
KN KM 4R ----HẾT--- Trang 34
SỞ GD&ĐT HỒ CHÍ MINH
ĐỀ THAM KHẢO TUYỂN SINH 10
PHÒNG GD&ĐT QUẬN 4
NĂM HỌC: 2021 - 2022 MÔN: TOÁN 9 ĐỀ TH AM KHẢO
Đêthigồm 8 câuhỏitựluận. MÃ ĐỀ: Quận 4 - 3
Thờigian: 120 phút (khôngkể thờigianphátđề) 1
Câu 1. (1,5 điểm). Cho P 2 : y
x và đường thẳng d 1
: y x 3 . 4 4
a) Vẽ đồ thị P và(d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của P và d bằng phép tính.
Câu 2. (1 điểm). Cho phương trình 2
3x 2x 6 0 có 2 nghiệm là x ,x . Không giải phương trình, 1 2 x x
hãy tính giá trị của biểu thức 1 2 M 1 1 . 2x 2x 2 1
Câu 3. (0 ,75điểm).Khi càng lên cao thì áp suất khí quyển càng giảm do không khí loãng dần. Để
tính áp suất khí quyển ở độ cao không quá cao so với mặt nước biển thường sử dụng công 2h thức: P 760
. Trong đó, P là áp suất khí quyển ( mmHg ); h là độ cao so với mực nước 25
biển m . Hỏi thành phố Bảo Lộc ở độ cao 1200m so mực nước biển thì áp suất của khí
quyển là bao nhiêu mmHg ?
Câu 4. (0,75 điểm). Một công ty chuyên cung cấp dịch vụ Internet với mức phí ban đầu khi lắp đặt
là 300 000 đồng. Cước phí y (đồng) là số tiền mà người sử dụng Internet cần trả hàng
tháng, và phụ thuộc vào thời gian sử dụng x tháng. Công thức biểu thị mối liên hệ giữa đại
lượng này là một hàm số bậc nhất. Xác định hệ số a và b . Biết rằng sau 2 tháng sử dụng thì
cước phí phải trả là 440 000 đồng.
Câu 5. (1 điểm). Chuẩn bị cho một buổi liên hoan chung vui cuối tuần của lớp 9A có 38 học sinh.
Giáo viên chủ nhiệm xuất quỹ 410 000 đồng và giao cho mỗi nam sinh một hộp bánh Tôm
có giá 15000 đồng/ 1 hộp. Mỗi nữ sinh mua một lốc có vài chai nước nhỏ có giá 6000 đồng/
1 lố. Tính số nam sinh và số nữ sinh của lớp 9A , biết sau khi đã mua xong tiền Căn tin thối lại là 2000 đồng. nữ?
Câu 6. (1 điểm). Một hồ bơi hình hộp chữ nhật có chiều dài 52m chiều rộng 10,2 m và đường chéo
của hồ này là 53,1m . (Làm tròn kết quả đến một chữ số thập phân).
a) Tính thể tích của hồ bơi này. Trang 35
b) Để bơm nước đầy hồ cần một số máy bơm mỗi giờ bơm lượng nước. Hỏi sau bao lâu
bơm nước đầy hồ bơi?
Câu 7. (1 điểm). Trong dịp tổ chức sinh nhật cho một bạn trong lớp. Nhóm học sinh cần mua số
lượng bánh ở một tiệm bánh có khuyến mãi, cứ mua kể từ cái bánh thứ 17 thì được giảm
800 đồng theo giá mỗi cái bánh. Nhóm học sinh mua 25 cái bánh với số tiền 192 800 đồng.
Hỏi giá tiền mỗi cái bánh ban đầu là bao nhiêu?
Câu 8. (3 điểm) Cho Cho ( O; R) đường kính EF . Trên tia FE lấy điểm A sao cho OA 2R, từ A
vẽ AB , AC lần lượt là hai tiếp tuyến của (O) .
a) Chứng minh tứ giác ABOC nội tiếp và AO BC tại H .
b) Vẽ đường thẳng qua H và song song với BF lần lượt cắt BE , BA tại I và K Chứng
minh: BH BK và EK AB .
c) Chứng minh đường thẳng AI đi qua trung điểm của BF . ----HẾT--- Trang 36 HƯỚNG DẪN GIẢI 1
Câu 1. (1,5 điểm) Cho P 2 : y
x và đường thẳng d 1
: y x 3 . 4 4
a) Vẽ đồ thị P và(d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của P và d bằng phép tính. Lời giải
a) Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ. Bảng giá trị: x 4 2 0 2 4 1 2 y x 4 1 0 1 4 4 x 0 4 1 4
y x 3 3 4
b) Tìm tọa độ giao điểm của P và d bằng phép tính.
Phương trình hoành độ giao điểm của P và d : 1 1 x 4 2 2
x x 3 x x 12 0 4 4 x 3 1 1 Thay x 4 vào 2 y x , ta được: 2 y .4 4 . 4 4 1 1 9 Thay x 3 vào 2 y x , ta được: 2 y .( 3 ) . 4 4 4 Trang 37 9 Vậy 4; 4 , 3,
là hai giao điểm cần tìm. 4
Câu 2. (1 điểm). Cho phương trình 2
3x 2x 6 0 có 2 nghiệm là x ,x . Không giải phương trình, 1 2 x x
hãy tính giá trị của biểu thức 1 2 M 1 1 . 2x 2x 2 1 Lời giải 2 Ta có 2
b 4ac 2 4.3. 6 76 0 b 2
S x x 1 2 a 3
Theo định lý Vi-et, ta có: c P x .x 2 1 2 a x x x x x x 1 2 1 2 1 2 M 1 1 1 2x 2x 2x 2x 4 x x 2 1 2 1 1 2 x x x x 2 2 2 2 5 5 x x 1 2 1 2 1 2 M 4 2x x 4 2x x 1 2 1 2 2 5 S 2P 5 M 4 2P 36
Câu 3. (0 ,75điểm).Khi càng lên cao thì áp suất khí quyển càng giảm do không khí loãng dần. Để
tính áp suất khí quyển ở độ cao không quá cao so với mặt nước biển thường sử dụng công 2h thức: P 760
. Trong đó, P là áp suất khí quyển ( mmHg ); h là độ cao so với mực nước 25
biển m . Hỏi thành phố Bảo Lộc ở độ cao 1200m so mực nước biển thì áp suất của khí
quyển là bao nhiêu mmHg ? Lời giải
Thành phố Bảo Lộc ở độ cao 1200 m so mực nước biển thì áp suất của khí quyển là: 2h 2.1200 P 760 760 664 mmHg . 25 25
Câu 4. (0,75 điểm). Một công ty chuyên cung cấp dịch vụ Internet với mức phí ban đầu khi lắp đặt
là 300 000 đồng. Cước phí y (đồng) là số tiền mà người sử dụng Internet cần trả hàng
tháng, và phụ thuộc vào thời gian sử dụng x tháng. Công thức biểu thị mối liên hệ giữa đại Trang 38
lượng này là một hàm số bậc nhất. Xác định hệ số a và b . Biết rằng sau 2 tháng sử dụng thì
cước phí phải trả là 440 000 đồng. Lời giải
Gọi y ax b là hàm số bậc nhất biểu thị cước phí khách hàng phải trả sau x tháng sử dụng x 0 Tại
0a b 300000 1 y 300000 x 2 Tại
2a b 440000 2 y 440000
0a b 300000 a 70000
Từ 1 và 2 , ta có hệ phương trình: .
2a b 440000 b 300000
Vậy a 70 000 và b 300000 .
Câu 5. (1 điểm). Chuẩn bị cho một buổi liên hoan chung vui cuối tuần của lớp 9A có 38 học sinh.
Giáo viên chủ nhiệm xuất quỹ 410 000 đồng và giao cho mỗi nam sinh một hộp bánh Tôm
có giá 15000 đồng/ 1 hộp. Mỗi nữ sinh mua một lốc có vài chai nước nhỏ có giá 6000 đồng/
1 lốc. Tính số nam sinh và số nữ sinh của lớp 9A , biết sau khi đã mua xong tiền Căn tin thối lại là 2000 đồng nữ? Lời giải
Gọi x,y lần lượt là số bạn nam và nữ trong lớp 9A x,y *
Vì cả lớp có 38 học sinh, nên ta có phương trình: x y 38 1
Tổng số tiền mua bánh tôm và nước: 15000x 6000y 410000 2000 4080002
x y 38
x 20n
Từ 1 và 2 ta có hệ phương trình: 1
5000x 6000y 408000 x 18 n
Vậy lớp 9A có 20 bạn nam và 18 bạn nữ
Câu 6. (1 điểm). Một hồ bơi hình hộp chữ nhật có chiều dài 52m chiều rộng 10,2 m và đường chéo
của hồ này là 53,1m . (Làm tròn kết quả đến một chữ số thập phân).
a) Tính thể tích của hồ bơi này. Trang 39
b) Để bơm nước đầy hồ cần một số máy bơm mỗi giờ bơm lượng nước. Hỏi sau bao lâu
bơm nước đầy hồ bơi? Lời giải
a) Chiều dài đường chéo mặt đáy hồ bơi là: 2 2 52 10,2 Chiều cao hồ bơi là: 2 2 2 2 53,1 52 10,2
Thể tích hồ bơi là: V 2 2 2 2 3 52.10,2. 53,1 52 10,2 1804,14m 1804,14
b) Thời gian bơm đầy hồ bơi là: 24,7h 72,9
Câu 7. (1 điểm). Trong dịp tổ chức sinh nhật cho một bạn trong lớp. Nhóm học sinh cần mua số
lượng bánh ở một tiệm bánh có khuyến mãi, cứ mua kể từ cái bánh thứ 17 thì được giảm
800 đồng theo giá mỗi cái bánh. Nhóm học sinh mua 25 cái bánh với số tiền 192 800 đồng.
Hỏi giá tiền mỗi cái bánh ban đầu là bao nhiêu? Lời giải
Gọi giá 1 cái bánh ban đầu là x ( đồng ) Theo đề bài ta có:
16x 25 16x 800 192800
25x 200000 x 8000
Vậy giá tiền một cái bánh ban đầu là 8 000 đồng. Câu 8.
(3 điểm) Cho Cho O; R đường kính EF . Trên tia FE lấy điểm A sao cho OA 2R, từ
A vẽ AB , AC lần lượt là hai tiếp tuyến của (O) .
a) Chứng minh tứ giác ABOC nội tiếp và AO BC tại H .
b) Vẽ đường thẳng qua H và song song với BF lần lượt cắt BE , BA tại I và K Chứng
minh: BH BK và EK AB .
c) Chứng minh đường thẳng AI đi qua trung điểm của BF . Lời giải Trang 40
a) Chứng minh tứ giác ABOC nội tiếp và AO BC tại H .
ABO 90(AB BO) Ta có:
ABO ACO 180
ACO 90(AC CO)
ABOC là tứ giác nội tiếp vì có tổng hai góc đối bù nhau. O
B OC R Ta có: AB AC
AO là đường trung trực của BC . AO BC
b) Vẽ đường thẳng qua H và song song với BF lần lượt cắt BE , BA tại I và K . Chứng
minh BH BK và EK AB .
Ta có: EBF là góc nội tiếp chắn nửa đường tròn nên EBF 90 EB BF
Ta có: HK / /BF KHE BFE Ta có: HI / /BF BE BF HI BE Xét B
HEvuông tại H , HI là đường cao nên ta có: KHE EBH
Mà BFE KBE KHE KBE
mà KHE EBH KBE EBH Xét B
HEvuông tại H , HI là đường cao nên ta có: BEH BHE
Mà tứ giác KBHE nội tiếp nên KHB KEB
KEB BEH Trang 41 Xét K BE và H BE, ta có: KBE EBH BE : chung KEB BEH K BE H BE KH HB
BKE BHE90 KE AC
c) Chứng minh đường thẳng AI đi qua trung điểm của BF .
Gọi N là giao điểm của AI và BF KI AI Xét A
BN có IK / /CN , theo định lý Thales: 1 BN AN IH AI Xét A
FN có IH / /FN , theo định lý Thales: 2 FN AN KI HI Từ (1) và (2), ta có: BN FN K BE H BE
KBI IBH Xét K IB và H IB , ta có: KBI IBH HI :chung
HIK BIH 90o K IB H IB
KI HI KI HI BN FN BN FN
Vậy N là trung điểm của BF ----HẾT--- Trang 42



